SOROK, FÜGGVÉNYSOROK SIMON ANDRÁS. m n=0 ca n = lim c m
|
|
|
- András Kis
- 5 évvel ezelőtt
- Látták:
Átírás
1 SOROK, FÜGGVÉNYSOROK SIMON ANDRÁS TARTALOMJEGYZÉK. Numrikus sorok.. limsup és limif 3.. Gyök- és háyadoskritérium 4.3. További kovrgciakritériumok 5.4. Példák 6.5. Zárójl, átrdzés 8. Függvéysorozatok, sorok 9.. Kritériumok gylts kovrgciára 3. Hatváysor 3 4. Fourir 7 5. Mgoldások. NUMERIKUS SOROK Sor: spciális sorozat (a részltösszgk sorozata)... Dfiíció. = a kovrgs, ha a részltösszgk s m = m = a sorozata az. Ilykor a sor összg = a = lim m s m. Vigyázat: a -l jlöljük a sort és a sorösszgt is... Állítás. liáris, azaz = a + b = = a + = b és = ca = c = a Biz. = a m + b = lim m = a m + b = lim m = a m + lim m = b = = a + = b és = ca m = lim m = ca = lim c m m = a m = c lim m = a = c = a vagyis azért liáris, mrt lim az. A dfiícióból látszik, hogy kovrgcia szmpotjából az lső éháy tag m számít (sorösszg szmpotjából prsz ig). Ezért az összs kovrgciakritériumba lég, hogy valamily idtől kzdv..3. Példák. () = ( ) divrgs, mrt s = vagy attól függő, hogy páros vagy páratla; thát lim s.
2 () Mértai sor: q k= qk = ( q + )/( q) (és prsz + ha q = ). Kövtkzésképp k= qk = { q ha q < divrgs ha q (3) = (+). Ez kovrgs, és a sorösszg, mrt (+) = + miatt s = ) k=( k k+ = ( ) + ( 3 ) ( + ) = Tétl (Cauchy). a kovrgs ( ɛ > )( N N)( m > > N) m k= a k < ɛ. Biz. Triviális a sorozatok kovrgciájára voatkozó Cauchy-ból: a kovrgs s kovrgs ( ɛ > )( N N)( m > > N) s m s < ɛ és s m s = m k=+ a k..5. Kövtkzméy. Ha a kovrgs, akkor a (= s s ). D a korátsm légségs fltétl a kovrgciájáak. Nmsokára láti fogjuk, hogy pl. m kovrgs..6. Állítás. Ha a, akkor a kovrgs s korlátos. Biz. a miatt s mooto ő, thát potosa akkor kovrgs, ha korlátos..7. Tétl (Kodzációs kritérium). Ha a, akkor = a kovrgs k= k a k kovrgs. Biz. Előző állítás miatt lég, hogy a részltszögk gyszrr korlátosak. Jlölj s ill. t a két sor. részltösszgét. ( ) Ida: a + a + a }{{ 3 } + a 4 + a 5 + a 6 + a }{{ 7 } + a +a +4a 4 + t korlátos, thát lég bláti, hogy s k+ t k. Idukció: k = : s = s = a = t. Thf. k és k -r igaz. s k+ = s k + (a k + a k a k + k ) s k + k a k t k + k a k = t k mrt a és id. flt. ( ) Ida: s 8 = a +a +a 3 + a }{{ 4 } +a 5 + a 6 + a 7 + a }{{ 8 } t 3 = a +a + a 4 + 4a 8 s korlátos, thát lég, hogy t k / s k. Idukció: k = : t / = a / a = s = s. Thf. k-ra igaz. t k+ / = t k / + / k+ a k+ s k + k a k+ s k+; az utolsó lépésb azt haszáltuk, hogy s k+ = s k + a k + + a k a k + k s k + k a k+..8. Kövtkzméy. = / ( harmoikus sor ) divrgs. Biz. /, thát az lőző tétl miatt potosa akkor divrgs, ha k= k / k = k= az.
3 Sőt:.9. Kövtkzméy. = / p kovrgs p >. Biz. Ha p, akkor trv. divrgs, mrt / p = p, z mg = (ha p = ), vagy (ha p < ), azaz smmikép sm. Thát ám. p >. D akkor p, thát / p, a tétl szrit thát kovrgs k= k / kp = k= ( p)k kovrgs p < (mért. sor) p <... Dfiíció. A a sor abszolút kovrgs, ha a kovrgs. Fltétls kovrgs, ha kovrgs, d m abszolút kovrgs... Állítás. Ha a abszolút kovrgs, akkor kovrgs. Biz. Cauchy: m k= a k háromszöggylőtlség m k= a k < ɛ... Tétl (Majorás/miorás kritérium). Ha a b (végülis) és b kov, akkor a abszolút kovrgs. Biz. Trv.: Cauchy vagy részltösszgk korlátossága... limsup és limif.3. Dfiíció. Az a valós sorozatra limsup a = ha a m korlátos flülről, és limsup a = sup E, ahol E = {lim a k : a k kovrgs részsorozata a -k} máskor. (Vagyis limsup a a sűrűsödési értékik suprmuma abba a kicsit kitrjszttt értlmb, hogy végtl, ha a végtl is sűrűsödési érték a -k.) Hasolóa: limif a = ha a m korlátos alulról, és limif a = if E máskor..4. Házi fladat. limif a = limsup a és limsup a = limif a.5. Állítás. limif a limsup a, és ha a kovrgs, akkor limif a = lim a = limsup a. Biz. Az lső állítás azért igaz, mrt if H sup H mid H halmazra, második mg mrt ha a kovrgs, akkor gytl sűrűsödési érték va..6. Állítás. limsup a < a potosa akkor, ha va olya q < a, amir valamily idtől kzdv a q. Biz. Ha a m korlátos flülről, akkor midkét oldal hamis. Ha korlátos flülről, akkor E = {lim a k : a k kovrgs részsorozata a -k}-vl: ( ) q = (a + limsup a ) < a jó lsz, mrt ha fölött végtl sok lm vola a -k, akkor (a flülről korlátosság miatt) az zk által alkotott részsorozatak Bolzao Wirstrass miatt vola kovrgs részsorozata, és aak határérték q > limsup a, ami lltmod aak, hogy limsup a = sup E. ( ) Mivl q fölött a -k csak végs sok tagja va, q-ál agyobb számhoz m tarthat a gytl részsorozata sm, azaz q flső korlátja E-k, és így limsup a q < a..7. Állítás. () Ha a < limsup a, akkor a < a végtl sok -r. () Ha a < limif a, akkor valamily idtől kzdv a a. 3
4 Biz. () Ha a m korlátos flülről, akkor igaz a koklúzió. Ha korlátos flülről, és csak végs sok -r igaz, hogy a < a, azaz valamily idtől kzdv a a, akkor a -k ics a-ál agyobb számhoz tartó kovrgs részsorozata; d akkor a flső korlátja E = {lim a k : a k kovrgs részsorozata a -k}-k, és zért limsup a = sup E a. () A fltvésből kövtkzik, hogy a alulról korlátos. Ha m igaz, hogy a a valamily idtől kzdv, akkor a < a végtl sokszor; d akkor az alulról korlátosság miatt az ilyk közül kiválasztható gy kovrgs részsorozat, és k a határérték a, kövtkzésképp a limif a, lltmodva a fltvésk..8. Házi fladat. Ezk az állítások m fordíthatók mg. Vigyázat: limsup m csrélhtő fl a szorzással: ha a =,,,,... és b =,,,,..., akkor limsup a limsup b = = limsup a b. Akkor sm fltétlül, ha az gyik sorozat kovrgs: a = /, b =..9. Állítás. Ha lim a R +, akkor limsup a b = lim a limsup b... Gyök- és háyadoskritérium.. Tétl (Gyökkritérium). () Ha va olya q <, amir valamily idtől kzdv a q, azaz (ld..6) ha limsup a < (spciálisa: ha lim a < ), akkor a abszolút kov, () ha a végtl sok -r (spciálisa (ld..7()): ha limsup a > ), akkor a divrgs. Biz. (): q kovrgs és majorálja a -t. () A fltvés miatt a végtl sok -r; thát a. limsup a = -ből smmi m kövtkzik a kovrgciájára voatkozóa: / divrgs, / kovrgs, oha midkttőr igaz z a fltétl... Példa. kovrgs, mrt = <... Tétl (Háyadoskritérium). () Ha va olya q <, amir valamily idtől kzdv a + /a q, azaz (ld..6) ha limsup a + /a < (spciálisa: ha lim a + /a < ), akkor a abszolút kovrgs. () Ha a + /a valamily idtől kzdv (spciálisa (ld..7()): ha limif a + /a > ), akkor a divrgs. Egyébkét bármi lht. Itt m lég a divrgciához, mit a gyökkritériumba, hogy a + /a végtl sokszor, mrt lgy a ttszőlgs kovrgs sor, és duplázzuk mg : a + a + a + a +... Az így kapott sor kovrgs, oha a + /a = mid páratla -r. D mutatja zt az alábbi összfésülős példa is, ami kovrgs, oha a + /a > végtl sokszor. Biz. Kovrgcia: ha mid > N-r a + /a q <, akkor ( > N) a + q a, amiből (idukcióval) a N+k q k a N, azaz ( > N) a q N a N = a N q. D a N q kovrgs mértai sor, thát majorás-kritérium miatt a is kovrgs. q N q N Divrgcia: Ha a + /a, azaz a + a mid > N-r, akkor a N utá mooto ő, thát a m tarthat -hoz. 4
5 .3. Példa.! ()! kovrgs, mrt a + a a háyadoskritérium gyakra célravztő.) = (+)! (+)! ()!! = + (+)(+) <. (Faktoriálisál Háyadoskritériumál is: / és / -r lim a + /a =, oha az gyik divrgs, a másik kovrgs. És: ha a az /, /3 összfésülés, akkor a kovrgs (mrt külökülö az; d gyökkritériummal is kijö), d a háyadoskritérium m működik: limif a + /a = lim(/3) =, limsup a + /a = lim(3/) =, limif a = lim /3 = / 3, limsup a = lim / = /. Ez mutatja, hogy háyadoskritériumba divrgciához m lég, hogy limsup > (mrt most, mégis kovrgs). (Ez a példa gy kicsit részltsbb: a = 3 + ha ps ha ptla a + a = = 3 + = ( 3 ) ha ps = ( 3 ) + ha ptla Thát limsup a + a lim a + a = lim ( 3 ) = és limif a + a lim a + a + = lim( 3 )(+) =.).3. További kovrgciakritériumok.4. Tétl (Itgrálkritérium). Ha f [, ]-, akkor = f () kovrgs f kovrgs. Nm muszáj -ál kzdi. y y ábra. Itgrálkritérium Biz. Mid N-r : N = f () N f N = f () (zk a {,,..., N} flosztáshoz tartozó alsó és flső összgk). F() = f mooto ő, thát potosa akkor kovrgs, ha korlátos. 5
6 ( ) kovrgs (=s), akkor mid -r (N = ) f N f N = f () s. ( ) kovrgs (=s), akkor mid N-r N = f () N f s, azaz a részltösszgk korlátosak,.6 miatt thát a sor kovrgs (mrt mgatív tagú). Alkalmazás: / p kovrgs p >. { p+ / p = p = p+ = p ha p p l ha p = { / p lim k p = [ ] k p = p ( ) = p ha p > p ( ) = ha p < lim k l k l = ha p =.5. Tétl (Itlligs összhasolító kritérium). Ha a < b és lim a b >, akkor a és b gyszrr kovrgsk vagy divrgsk. Biz. Ha lim = L, akkor valamily N-től kzdv L/ a /b L, azaz b a /L és a Lb. Ebből már a majorás-kritérium miatt kövtkzik az állítás..6. Tétl (Libiz). Ha sg a = ( ), a, akkor a kovrgs. És a hiba kisbb, mit az lső lhagyott tag abszolútérték, azaz = a m = a a m+. Biz. Lgy b = a. Thát b, és az ké, hogy a b + b b 3 + = = ( ) b sor kovrgál. Lgy s az. részltösszg. s mrt s (+) = s b + + b + s (mrt b + + b + ). s alulról korlátos mrt s = b + (b b 3 ) +(b }{{} 4 b 5 ) b }{{} b. Thát s kovrgs, modjuk s. Nod s + = s b + s = s. Thát s és s + összfésülés is s. Hibabcslés: mivl s s és (ugyaígy) s + s, () s + s s mid -r, thát azt kll bláti, hogy s s b + és s s + b +. D az lsőt átrdzv azt kapjuk, hogy s + = s b + s, ami igaz () miatt, a másodikat átrdzv pdig azt, hogy s s + + b + = s +, ami szité. Alkalmazás: altráló harmoikus sor ( ( ) /) kovrgs..4. Példák () = + () + (3) 3 kovrgs kojugálással + = ( ++, thát kovrgs ) 3/ + a divrgs (4).5 majorással gusztustala ( (.5) majorálja) vagy gyökkritérium, kovrgs (5) ( + ) gyökkritérium a = ( + ) < <, thát kovrgs. (6) + a divrgs (7) - vagy k -s kritérium (zk midig ugyaakkor alkalmazhatók): k a l k = = kovrgs l k (k l) k 6
7 (8) si (+) majorálja abszolút kovrgs (9) ( cos π ) Ld. lábjgyzt : cos π = si π és si π π / Thát. () ily már volt ( (+ ) élkül)! gyökkritérium, kovrgs. () majorálható ( ) -l. mrt si π / = si π π π π. () yilvá olya lsz, mit (l ) k l, ami divrgs, mrt miorálható -l. Azaz: bikább, mit l k, mrt lim l k = L H lim k l k = L H = L H lim k! = (3) k -kritériummal: l > / miatt k = k k = 4k/ ( 4/5) k (l ) l (l k ) lk (k l) k l (k/) k/ (k/) k/ kovrgs mértai sor. (4) 4 zt még lht majoráli -l, d ha l akkor már m lht. (+3) (Modjuk akkor is lht -l.) Hlytt midkét stb. () (5) +3 uz a duma, csak + hlytt -al; d. (6) divrgs mrt +3 (7) 3 kovrgs mrt /3 (8) l(3+) divrgs, mrt l(3+) 3+ (v.ö. ()) és 3+ (9) gyökkritérium, vagy (+ ) (+ ) kovrgs mértai sor () divrgs, mrt +si () kovrgs, mrt + () arctg divrgs mrt mrt arctg π/ (3) arctg ugyazért (4) arctg divrgs mrt mrt: arctg arctg y ta mrt lim = lim y ta y = ycos y lim y si y =. Mllslg ugyaígy arcsi arcsi y si : lim = lim y si y =. (5) arctg kovrgs mrt (az lőző (lim arctg = ) miatt lim f () a arctg f () = ha lim a f () = ). (6) arctg divrgs mrt = (7) divrgs, mrt + (ami érdks, mrt már kovrgs ttsz. p > -ra). +p (8) l gyökkritérium kovrgs (9) l, divrgs k -s kritériummal: k = k l k k l divrgs. (3) l(!) divrgs mrt l(!) = l+l+ +l() l és l az lőző szrit divrgs. liarizáló képltkt tudi kll: si = cos és cos = +cos 7
8 (3)! háyadoskritérium: a + = + ( + )! a ( + ) +! = ( + ) = ( + ) < thát kovrgs. (3) ( + ) trv. divrgs mrt a. (33) si π kovrgs mrt (34) l ( si π = si π π π π) m majorálható -l, d l / l (mrt lim = / L H lim ) l, kövtkzésképp kovrgs. k -s haszálatához tudi ké, hogy mooto. 3/ (35) l miorálja, thát divrgs (36) cos divrgs mrt (37) si kovrgs mrt (38) cos kovrgs mrt (39) cos abszolút kovrgs mrt majorálja (4) l( ± ) divrgs mrt mrt lim l(+) = (4) l( ± ) kovrgs mrt ugyazért. (4) ( ) = l érték / potossággal: Libiz, thát kovrgs, és ( ) = N l N ; thát olya N ké, amir Thát l l N = ( ) l N l N, azaz l(n N ), azaz N N, azaz N 3. /-él potosabb közlítés..5. Zárójl, átrdzés Kovrgs sorozatot bzárójlzük kovrgs marad (részltösszgk sorozata az rdti sor részltösszgik részsorozata). Divrgs sorozatot bzárójlzük m biztos, hogy divrgs marad (azaz kovrgsből m hagyhatuk l zárójlkt): ( ) + ( ) + ( ) +... a gy átrdzés: a π, ahol π : N N bijkció..7. Tétl (Rima). Abszolút kovrgs sor átrdzés m változtat a kovrgciá és az összg. Fltétls kovrgs sort viszot bárhogy át lht rdzi (úgy, hogy akárkihz tartso, mg úgy is, hogy divrgs lgy)..8. Példa. Egy példa, ami mutatja, hogy az átrdzés mgváltoztathatja a sorösszgt: az altráló harmoikus sorról tudjuk, hogy kovrgs, lgy modjuk S az összg (majd láti fogjuk később, hogy S = l, d z most léygtl). thát a kttő összg S = S = S = miközb az utolsó sor az lső gy átrdzés. 8
9 . FÜGGVÉNYSOROZATOK, SOROK.. Dfiíció (Potokéti kovrgcia). f f H R- ha H f () f (). = f = f H-, ha F k = k = f f H- (azaz ha ( H) = f () = f ()). Folytoos függvéyk lims m fltétlül folytoos (. ábra (a)): { ha [,) H = [,], f () = f () =. ha = Máshogy fogalmazva az a probléma, hogy a külöfél határértékképzésk m flcsrélhtők: lim lim f () = = lim (lim f )(). Más példa ugyarr (. ábra (b)): ha / H = R, f () = ha ( /,/) sg. ha / Zárt itrvallumo folytoos függvéyk lims m fltétlül korlátos (. ábra (c)): { { ha [,/] ha = H = [,], f () = f () = / ha (/,] / ha (,]. Példa arra, hogy f f, f itgrálható mid -r, d lim f f (. ábra (d)): ha [,/) H = [,], f () = ha [/,/). ha [/,] Ez jó mrt f = (/ )/ = =. 4 y 4 y y y 3 3. ábra. Kovrgs, d m gylts kovrgs függvéysorozatok.. Dfiíció. f gylts tart f -hz (f f ) H- ha ( ɛ > )( N N)( > N)( H) f () f () < ɛ. A = f függvéysor gylts kovrgs ha F k = k = f az (jl.: = f = f ). 9
10 A külöbség a potokéti kovrgciához képst az, hogy az utóbbiba ( ɛ > )( H)( N N)( > N) f () f () < ɛ-t kövtlük mg, azaz ott N függht -től, az gylts kovrgciáál m..3. Állítás. Ha f és f korlátosak a H halmazo, akkor f f H- f f, ahol ttszőlgs H- korlátos g függvéyr g = sup{ g() : H }. V.ö. potsorozatokak zzl a tulajdoságával: lim a = a lim d(a, a ) =. Biz. ( ) Mid ɛ > -ra va olya N, hogy mid > N-r és H-ra f () f () < ɛ/; d akkor mid > N-r f f = sup{ f () f () : H} < ɛ. ( ) Mid ɛ > -ra va olya N, hogy mid > N-r és H-ra f () f () sup{ f () f () : H} = f f < ɛ..4. Mgjgyzés. A H R halmazo korlátos függvéyk f g távolság, ahogya zt a fogalmat a többváltozós függvéyk ljé dfiiáltuk. Az lső két tulajdoság (két pot (vagyis most két függvéy!) távolsága potosa akkor, ha azoosak; és a távolság szimmtrikus) triviálisa igaz rá. D a háromszöggylőtlség is, mrt mid H-ra f () g() f () h() + h() g() f h + h g miatt f g = sup{ f () g() : H } f h + h g. y ɛ f lim f ɛ f 3. ábra. Egylts kovrgcia A fti példák gyik sm gylts kovrgs. Pl. az lső: ɛ = /4-hz ics jó N, mrt mid -r f (/ ) f (/ ) = f (/ ) = / > ɛ..5. Tétl (gylts kovrgcia & határérték). Ha f f H-, a torlódási potja H-ak, mid -r b = lim a f (), és L = lim b, akkor lim a f () = L. Vagyis lim ( lim f )() = lim lim f () a a ha a jobboldalo szrplő határértékk létzk és baloldalo a blső határérték gylts.
11 Valójába lég l flti, hogy a jobboldali blső lim létzik (és így az alábbi kövtkzméyb sm kll külö flti, hogy a kovrgs), mrt bből már kövtkzik a külső határérték létzés. Biz. Lgy ɛ > ; olya δ > kll, amir igaz, hogy ( Sδ(a)) f () L < ɛ. f f miatt va olya N, amir f f < ɛ 3 H- ha > N. L = lim b miatt va olya N, amir b L < ɛ 3, ha > N. Rögzítsük gy > ma(n, N )-t! lim a f () = b miatt va olya δ >, amir igaz, hogy ( Sδ(a)) f () b < ɛ 3. D akkor mid ily -r f () L = f () f () + f () b + b L f () f () + f () b + b L < 3 ɛ 3 = ɛ..6. Kövtkzméy. Ha = f = f H-, és a torlódási potja H-ak, akkor lim f () = a = (lim f ()) a ha a jobboldalo szrplő határértékk és összg létzk. Biz. Jlölj F = m f m. részltösszgét! Akkor a jobb oldal = (lim f m ()) = lim a m = (lim f ()) = lim (lim m a m a = f ()) = lim (lim F m()) m a (ahol a második gylőségb a függvéyhatárérték és a (végs) összg flcsrélhtőségét haszáltuk) és z F m f és a tétl miatt = lim a f ()..7. Tétl (gylts kovrgcia & folytoosság). Ha f f H- és mid -r f folytoos a H-ba, akkor f folytoos a-ba. Biz. Ha a izolált potja H-ak, akkor ics mit bizoyítai; külöb pdig f a-bli folytoossága miatt lim a f () = f (a) mid -r, és f f miatt lim f (a) = f (a). Thát létzik lim lim a f () = lim f (a) = f (a) és így.5 miatt lim a f () = f (a)..8. Kövtkzméy. Ha mid -r f folytoos a H-ba, = f = f, akkor f folytoos a-ba. Biz. A fltvés (és mrt folytoos függvéyk (végs) összg folytoos) miatt = f részltösszgi folytoosak a-ba, és mivl zk gylts tartaak f -hz, a tétl miatt f is az..9. Tétl (gylts kovrgcia & itgrálhatóság). Ha f R([a, b]), f f, akkor f R([a, b]) és b a f = lim b a f... Mgjgyzés. V.ö. a (c) példával, ahol a lim m is itgrálható, és a (d)-vl. Biz. (Csak azé, hogy ha f R([a, b]), akkor b a f = lim b a f.) Lgy ɛ >, N pdig olya, hogy f f < ɛ b a [a, b]- ha > N. Akkor b a f b a f = b a f f b a f f b ɛ a b a = ɛ... Kövtkzméy. Ha mid -r f R([a, b]), = f = f, akkor f R([a, b]) és b a f = = b a f.
12 Biz. A fltvés (és mrt R([a, b]) zárt összadásra) miatt = f részltösszgi itgrálhatók [a, b]-; és mivl a részltösszgi gylts tartaak f -hz, a tétl miatt f R([a, b]) és = b a f = lim m b m = a f b = lim m m a = f = b a f ahol a második gylőségb b a és (végs) összg flcsrélhtőségét haszáltuk, a harmadikba pdig a tétlt. Driválhatóság és gylts kovrgcia m ily szép: Példa arra, hogy f f, f driválható mid -r, d f f (shogy): f () = /si f (mrt r () = f () ld..5()-t alább) d f () = /cos = cos f (például mrt = -ba m). Példa olyara, hogy az gylts lim m is driválható: f = + (mrt, ismét.5()-t haszálva, r () = f () f () = + / = = / )... Tétl (gylts kovrgcia & driválhatóság). Ha mid -r f driválható (a, b)-, (a, b) f ( ) kovrgs és f g (a, b)-, akkor va olya f, hogy f f és f = g (a, b)-..3. Mgjgyzés. A (a, b) f ( ) kovrgs fltétl m hagyható l, pl. f. + + / f f f g = f.4. Kövtkzméy. Ha mid -r f driválható (a, b)-, (a, b) = f ( ) kovrgs és (a, b)- = f = g, akkor = f = f és f = g (a, b)-. Biz. A tétlt az F m = m = f és F m = m állítást. = f függvéysorozatokra alkalmazva kapjuk az.. Kritériumok gylts kovrgciára Végig: r () = f () f ()..5. Tétl. () Ha ( a )( H) r () a, akkor f f H-. () Ha H-bli sorozat, hogy r ( ), akkor f f H-. Biz. Az lső áll triviális az gylts kovrgcia dfiíciójából. A második is, mrt ha f f, akkor ( ɛ > ) N ( > N)( H) r () < ɛ, spciálisa r ( ) < ɛ, thát r ( ) (és így r ( )). (Avagy: r ( ) sup H f () f () = f f thát az utóbbi m tarthat -ba.) (Mgj.: ttől prsz f még lht kovrgs: a fti (b) példába lgy = /(); akkor r ( ) = f () f ( ) = / = /.).6. Házi fladat. A tétl () potjáak sgítségévl mutassuk mg, hogy a szakasz ljé, a potokéti kovrgcia dfiíciója utái égy függvéysorozat gyik sm gylts kovrgs..7. Példa. [,] mly részhalmazai (gylts) kovrgs f () =? { ha = f f = ha (,] A kovrgcia m lht gylts, mrt a határfüggvéy m folytoos. (, ]- már folytoos, d ott sm gylts a kovrgcia, mrt = (,], r ( ) = f ( ) =. D δ > -ra [δ,]- már gylts, mrt r () = δ.
13 .8. Tétl (Cauchy kritérium függvéysorozat gylts kovrgciájára). f f H- valamily f -r ( ɛ > )( N N)(, m > N)( H) f () f m () < ɛ. Azaz ( ɛ > )( N N)(, m > N) f f m < ɛ..9. Kövtkzméy (Wirstrass kritérium függvéysor gylts kovrgciájára). Ha ( H) f () a és a kovrgs, akkor f gylts kovrgs H-. Biz. Lgy F () = f k(). ɛ > -ra.4 miatt va olya N, hogy mid H-ra és > m > N-r F () F m () = m+ f k() m+ f k() m+ a k < ɛ, vagyis.8 szrit a részltösszgk sorozata gylts kovrgs... Példák (Wirstrass kritérium alkalmazására).. Hol (gylts) kovrgs 4 + 4? Wirstrass kritérium miatt midhol gylts kovrgs, mrt majorálja a kovrgs umrikus sor..! gylts kovrgs [ K, K]-:! K! és K! kovrgs (háyadoskritérium). Spcil kovrgs R-. D m gylts, mrt a f () =!, d m gylts, mrt = -r r ( ) = f ( ) =! függvéysorozat ugya. Márpdig.. Állítás. Ha f = f a H halmazo, akkor f H- (ahol a kostas függvéy). Biz. f + = F + F = F + f + f F F + f + f F.. 3. HATVÁNYSOR 3.. Dfiíció. c körüli hatváysor: a ( c) (d az gyszrűség kdvéért c = végig). 3.. Példák. () = mértai sor, thát tudjuk, hogy potosa akkor kovrgs, ha < (és azt is, hogy ilykor abszolút, és az összg /( )); hol gylts kovrgs? Ha δ <, akkor [ δ,δ]- gylts kovrgs a Wirstrass kritérium miatt ( δ és δ kov). D (,)- m gylts kovrgs: r () = /( ) k= k = /( ) ( + )/( ) = + /( ); thát = + -r r ( ) = ( )+. Az, hogy (,)- m gylts a kovrgcia, kijö.-ből is: f () = m tart gylts a kostas függvéyhz, mrt = -r f ( ) = ( ) (ld..5()!). () = / hol kov? Ha <, akkor ig, sőt, abszolút kovrgs mrt kovrgs és majorálja = / -t; ha >, akkor m, mrt /. Ha =, akkor divrgs (harmoikus sor), ha =, akkor kovrgs (altráló harmoikus sor). Thát a kovrgciaitrvallum [, ). (3) = / kovrgciaitrvalluma [,]; itt W-kritérium miatt gylts is kovrgs, mrt / / ; amúgy azért m kovrgs, mrt a ha a >. (4)! - kívül shol sm kovrgs (háyadoskritérium: a + a = (+)!+! = ( + ) ) Tétl. Lgy α = limsup a, R = /α (értlmszrű, ha α v. ). Ekkor a abszolút kovrgs ha < R, divrgs ha > R. (R a kovrgciasugár.) 3
14 A szélk bármi lht, a fti példák közül az lső három midhárom lhtőségt illusztrálja. Mllslg a tétlből látszik, hogy az lső három példába miért, a gydikb miért a kovrgciasugár. Biz. Ha < R, akkor limsup a = limsup a = {, ha R =, azaz ha limsup a = R < R R =, ha R < thát a gyökkritérium miatt a a umrikus sor abszolút kovrgs. És ugyaígy, ha > R, akkor limsup a >, thát divrgs Kövtkzméy. Ha a kovrgciasugara R, akkor mid δ > -ra a gylts kovrgs [ R + δ, R δ]-. Biz. a a (R δ) és a (R δ) kovrgs (mrt a kovrgciaitrvallum blsjéb abszolút a kovrgcia), thát a Wirstrass kritérium (.9) miatt kész Kövtkzméy. Hatváysor a kovrgciaitrvallum blsjéb lvő zárt itrvallumoko tagokét itgrálható Tétl. Ha = a kovrgciasugara R, f () = = a < R-r, akkor f driválható, és f () = = a ( R, R)-. Vagyis hatváysor a kovrgciaitrvalluma blsjéb tagokét driválható. Biz. Flthtjük, hogy R >, mrt R = -ra a tétl koklúziója ürs tljsül. Azt fogjuk bláti, hogy mid < q < R-r = a gylts kovrgs ( q, q)-..4 miatt bből, és abból, hogy = a kovrgál = -ra, kövtkzik, hogy f () = = a ( q, q)-, és, mivl z mid < q < R-r igaz, ( R, R)- is az, hisz mid ( R, R)-r va olya < q < R, hogy ( q, q). Lgy thát < q < R, és lgy r (q, R); mivl = a r kovrgs, lim a r =, thát valamily N idtől kzdv a r <, azaz a < r. D akkor mid ( q, q) és > N-r a < r q = q (q/r), és így, mivl = (q/r) a gyökkritérium miatt kovrgs umrikus sor, a Wirstrass kritériumból (.9) kövtkzik, hogy = a gylts kovrgs ( q, q) Kövtkzméy. A tétl fltétli mlltt f akárháyszor driválható és () f (k) () = =k ( ) ( k + )a k, spciálisa () f (k) () = k! a k Dfiíció (Taylor-sor). Az akárháyszor driválható f függvéy c körüli (formális) Taylorsora: f () (c) =! ( c), thát amit a fti kövtkzméy ad. (Ld. alább, hogy z miért formális!) f aalitikus c-b, ha f -t lőállítja a Taylor-sora c gy köryztéb Tétl (Taylor). Hatváysor határfüggvéyék Taylor-sora maga a hatváysor. Azaz hatváysor határfüggvéyék Taylor-sora a kovrgciaitrvallumba kovrgs és lőállítja a függvéyt. 4
15 A formális Taylor-sor lht, hogy csak -ba kovrgs, az is lht, hogy kovrgs d a f (pl.: f () = { / ha ha =, mrt f (k) () = mid k-ra (z m triviális!) ) és prsz az is lht, hogy kovrgs és = f. Példák utóbbira: = = /!, si = 3 /3!+ 5 /5! 7 /7!+ = = ( ) + /(+)!, cos = /!+ 4 /4! 6 /6!+ = = ( ) /(!). 3.3 sgítségévl héz kiszámoli a kovrgciasugarat (mrt kll hozzá, hogy lim! =, ami m triviális), d háyados-kritériummal köyű bláti, hogy midhol kovrgsk. Pl. : a + a = + (+)!! = +. Vagy si : a + a = +3 (+3)! (+)! = + (+)(+3). Amit még m tuduk, az az, hogy zk téylg lő is állítják- -t és társait. 3.. Tétl (Taylor formula Lagrag-fél maradéktaggal). Lgy f akárháyszor driválható ( R, R)-, N N, ( R, R). Akkor ξ [, ], hogy f () = N f (k) () k= k! k + f (N+) (ξ) (N+)! N+. (ξ -től és N-től is függ.) N = -ra z épp a Lagrag középérték tétl. 3.. Kövtkzméy. A tétl fltétli mlltt, ha I ( R, R) és K >, hogy ( I) f () () < K, akkor a Taylor-sora I- lőállítja f -t. Biz. Mid I-r f () N f (k) () k= k! k = f (N+) (ξ) (N+)! N+ K N+ (N+)! ha N. Pl. [ R, R]- p () () R. Vagy si () (). Ezért állítja lő a Taylor-sora -t és si -t. 3.. Példa. l(+ ) = +t gy kovrgs gomtriai sor összg: dt (z volt a logaritmus dfiíciója); t (,)-r az itgradus +t = ( t) = t + t t 3 ±... (bár, ahogy a szakasz ljé láttuk, (, )- m gylts). Thát z gy (, )- kovrgs hatváysor, kövtkzésképp (, ) zárt részitrvallumai, és így (, )-r [, ]- tagokét itgrálható. Vagyis l(+ ) = t+ t t 3 ±... dt = ±... = ( ) + + (,)-. A hatváysor kovrgciája gylts [, ]- (a Wirstrass-kritériumból z m jö ki, mrt ( ) + + -t m lht gy kovrgs umrikus sorral majoráli [,]-) mrt mid ily -r Libiz miatt a hiba kisbb, mit az lső lhagyott tag abszolútérték: r () ( ) Ebből.5() miatt kövtkzik az gylts kovrgcia. Ez utóbbi miatt, és mrt g() = ( ) + + és l( + ) mggyzk (,)-, + l = lim l( + ) = lim g() = lim ( ) +.6 = lim + ( ) + = ( ) + = ( ) = ( ) vagyis az altráló harmoikus sor összg l. Azt m thttük vola mg, hogy -t gyszrű bhlyttsítjük a ftib, mrt csak (,)- tudjuk, hogy a sor lőállítja l( + )-t Példa. arctg = kovrgs gomtriai sor összg: dt (z volt az arctg dfiíciója); t (,)-r az itgradus gy +t = +t ( t ) = t + t 4 t 6 ±... Thát z gy (,)- kovrgs hatváysor, kövtkzésképp (, ) zárt részitrvallumai, és így (, )-r 5
16 [, ]- tagokét itgrálható. Vagyis arctg = t + t 4 t 6 ±... dt = ±... = ( ) + + (,)-. Mit az lőző példába: a kovrgcia gylts [, ]- (z sm jö ki a Wirstrasskritériumból) mrt mid ily -r Libiz miatt a hiba kisbb, mit az lső lhagyott tag abszolútérték: r () ( ) Ebből.5() miatt kövtkzik az gylts kovrgcia. Az lőző példához hasolóa, mivl arctg = ( ) + + (,)-, -bli baloldali határértékük is mggyzik, és zért π = arctg = lim arctg = lim ( ) = + lim + ( ) + = ( ) +. És prsz itt sm thttük vola mg, hogy -t gyszrű bhlyttsítjük a ftib, mrt csak (, )- tudjuk, hogy a sor lőállítja arctg -t Mgjgyzés. f () = hatváysora ( ) prsz csak < -r kovrgs, hisz f -k szigularitása va -b. D g() = hatváysora ( + ( ) ) is, pdig aak ics szigularitása. Valójába dhogym: ±i-b, d z csak jövőr, kompl függvéytaba fog kidrüli Példák.. Lgy f () = =! ; f () () =? MO., mrt a sor midütt, így az origóba is az -t állítja lő, amik mid driváltja ömaga, thát f () () = =.. Lgy f () = =! ; f () () =? MO. Taylor sorából z a sor midütt az -t állítja lő, így midütt kovrgs hatváysor, thát határfüggvéyék, f () = -k Taylor sorába 5! = a = f () ()!, azaz f () () =! 5!. 3. Lgy f () = = ; f () () =? MO. A sor hatváysor, kovrgciaitrvallumáak blsj (limsup = lim( ) = miatt) a (, ) itrvallum. Ezért ott a sor saját f összgfüggvéyék körüli Taylor sora, azaz = a = f () ()!, kövtkzésképp f () () =!. 4. Lgy f () = ; f () () =? MO. Ld. a. példát! 5. Lgy f () = az origó kívül és f () =. Adja mg az f () értékét, ha létzik! MO. Taylor sora alapjá f () = =! = = (+)! = midütt kovrgs hatváysor határfüggvéy, így midütt akárháyszor driválható és Taylor sora az őt lőállító hatváysor. Kövtkzésképp f () = 6, amiből f () = Lgy mid valós -r F() = t dt. Számítsa ki az F( ), F() és F() értékkt század potossággal! 6
17 MO. körüli Taylor-sora alapjá = = ( )! midütt kovrgs hatváysor, thát tagokét itgrálható. Így F() = = ( t )! dt = = ( )! t dt = = ( ) +!( + ) Kövtkzésképp F() = = ( ) (+)!, ami Libiz típusú, így a hiba m agyobb, mit az lső lhagyott tag abszolút érték: r (+)! ( + )! 4 F() = Nyilvá F() = és, mivl páros, F( ) = F() körüli Taylor-sora. MO. f () =, f () = 4 3 6, f () =, f () () =, f () () =, f (3) () = 4, f (3) () =, f (4) () = 4, kövtkzésképp f () = f () ()! ( ) = ( )+( ) 3 +( ) FOURIER 4.. Állítás. () p priódusú függvéyt midgy mlyik p hosszúságú itrvallumo itgráljuk. () Ha f páratla, akkor a a f () d =. (3) si = (4) si mcos d = Biz.. Hlyttsítéss itgrál: b a f () d = u (b) u (a) f (u(t))u (t) dt = b+p a+p f (t p) dt = b+p a+p f (t) dt, ahol u(t) = t p. Kövtkzésképp b+p f = a b b f + a+p a f + b+p a+p f = b a f + a+p a f + b a f = a+p a f.. a a f () d = u (a) u ( a) f (u(t))u (t) dt = a a f ( t) dt = a a f (t) dt = a a f (t) dt, ahol u(t) = t. 3. si = π π si = az lőző kttő miatt, mrt si páratla, és mivl π/ szrit, zért π szrit is priodikus. 4. Mit az lőző. 4.. Állítás. Lgy, m N. Akkor () { π ha > cos = π ha = () ha m π cos mcos d = π ha = m > π ha = m = (3) { π ha m vagy m = = si msi d = π ha = m > Biz.. cos = = π és cos = [ si 7 ] π = = ha >.
18 , 3. Ha m = =, akkor midkét állítás triviális. Thát a továbbiakba flthtjük, hogy m +. Tudjuk: A kttőt összadva kapjuk, hogy ( ) cosαcosβ = kivova mg azt, hogy ( ) siαsiβ = ( ) miatt cos(α + β) = cosαcosβ siαsiβ cos(α β) = cosαcosβ + siαsiβ [ cos(α + β) + cos(α β) ] [ cos(α β) cos(α + β) ] cos mcos d = cos(m + ) + cos(m ) d () = cos(m ) d { () = ha m = π ha = m >, és ( )-ból ugyaígy kijö a Tétl. Ha f () = = (a cos +b si ) gylts, akkor a = π f ()cos d = π π f () d, a = π f ()cos d ha >, és b = π f ()si d. Biz. = -ra: > -ra: f () d = m= (a m f ()cos d = m= (a m b -k hasolóa. cos m d + b m si m d) = 4.(),4.(3) = a cos mcos d + b m si mcos d) 4.(),4.(4) = a Ha l a félpriódus, akkor a fti képltkb π l, π l. Pl. a = l És a sorflírásba is: f () = (a cos π l + b si π l ) Dfiíció. f (formális) Fourir-sora (a cos + b si ), ahol a = a = π f ()cos d ha >, és b = π f ()si d. 8 cos d 4.() = a π cos d 4.() = a π l f ()cos π l d. π f () d,
19 4.5. Mgjgyzés. Páros, π szrit priodikus függvéy Fourir-sora tiszta cosiuszos (b = ), páratlaé mg tiszta siuszos (a = ). Ez 4.(),()-ből kövtkzik, mrt mrt f ()si páratla ha f páros, és mrt f ()cos páratla ha f páratla. π f ()si d = f ()si d = π π f ()cos d = f ()cos d = π 4.6. Dfiíció. Az f valós függvéy szakaszokét folytoos az [a, b] itrvallumo, ha [a, b]- k csak végs sok potjába szakad, d mid szakadása lsőfajú (azaz a szakadási hlyk is vaak féloldali határértéki). f szakaszokét folytoosa driválható [a, b]-, ha f és f is szakaszokét folytoos [a, b] Tétl. Ha az f priodikus korlátos függvéy szakaszokét folytoosa driválható, akkor a Fourir-sora midütt kovrgál; a folytoossági hlyk f ()-hz, a szakadási hlyk pdig a féloldali limsk számtai közpéhz: (f ( ) + f ( + ))-hoz Példák.. f () = ( π,π]-, f ( + kπ) = f (), k Z. a =, mrt páratla a függvéy (lég, hogy ( π,π)- az, mrt az gyütthatókat ott számoljuk). b = π π π }{{} si }{{ } u v = ( cos π + π π π azaz F() = ( )+ si.. f () = (,π]-, f ( + kπ) = f (), k Z. a = π ) cos π }{{} = (πcos π ( π)cos( π)) = π cos π = ( )+ = π 3 3 π = 4 3 π a = π }{{} u cos }{{ } v = π π si }{{} π 9 }{{} u si }{{ } v = π ( cos ) π π cos = 4 } {{ }
20 b = π Azaz: }{{} u si }{{ } v = π π cos }{{} π = 4π + π 4π }{{} u cos }{{ } v cos 4π = + π ( si π }{{} ) cos = 4π }{{} F() = 4π 3 + ( 4 cos 4π si ) Ebből kiszámolható : U.i. gyrészt F() = 4 3 π + 4. Másrészt = szakadási hly f -k: lim + f =, lim f = (π) = 4π. Tudjuk, hogy ilykor F() zk számtai közp, π. Thát π = F() = 4 3 π + 4, amiből = 4 (π 4 3 π ) = 6 π. 5. MEGOLDÁSOK.4 Ha a m korlátos alulról, akkor midkét oldal =. Máskülöb a korlátos flülről, kövtkzésképp limsup a = sup{lim a k : a k kovrgs részsorozata a -k} = sup{ lim a k : a k kovrgs részsorozata a -k} = if{lim a k : a k kovrgs részsorozata a -k} = limif a A második állítás kövtkzik az lsőből: limif a = limsup a = limsup a..8 Midkttőt mutatja a =, a = + /..6 Például az /, /, /, / sorozatok mutatják.
1. Vizsgazárthelyi megoldásokkal 1997/98 tél I. évf tk.
 . Vizsgazárthlyi mgoldásokkal 997/98 tél I. évf..-8.tk.. Döts l, hogy fáll mid A és B halmaz sté a A B) \ B A összfüggés! Ha m, adjo szükségs és légségs fltétlt arra, hogy mikor áll f! A B) \ B A iff A
. Vizsgazárthlyi mgoldásokkal 997/98 tél I. évf..-8.tk.. Döts l, hogy fáll mid A és B halmaz sté a A B) \ B A összfüggés! Ha m, adjo szükségs és légségs fltétlt arra, hogy mikor áll f! A B) \ B A iff A
A függvénysorozatok olyanok, mint a valós számsorozatok, csak éppen a tagjai nem valós számok,
 l.ch FÜGGVÉNYSOROZATOK, FÜGGVÉNYSOROK, HATVÁNYSOROK Itt egy függvéysorozat: f( A függvéysorozatok olyaok, mit a valós számsorozatok, csak éppe a tagjai em valós számok, 5 haem függvéyek, f ( ; f ( ; f
l.ch FÜGGVÉNYSOROZATOK, FÜGGVÉNYSOROK, HATVÁNYSOROK Itt egy függvéysorozat: f( A függvéysorozatok olyaok, mit a valós számsorozatok, csak éppe a tagjai em valós számok, 5 haem függvéyek, f ( ; f ( ; f
min{k R K fels korlátja H-nak} a A : a ξ : ξ fels korlát A legkisebb fels korlát is:
 . A szupréum elv. = H R felülr l körlátos H fels korlátai között va legkisebb, azaz A és B a A és K B : a K Ekkor ξ-re: mi{k R K fels korlátja H-ak} } a A : a ξ : ξ fels korlát A legkisebb fels korlát
. A szupréum elv. = H R felülr l körlátos H fels korlátai között va legkisebb, azaz A és B a A és K B : a K Ekkor ξ-re: mi{k R K fels korlátja H-ak} } a A : a ξ : ξ fels korlát A legkisebb fels korlát
2. Hatványsorok. A végtelen soroknál tanultuk, hogy az. végtelen sort adja: 1 + x + x x n +...
 . Függvéysorok. Bevezetés és defiíciók A végtele sorokál taultuk, hogy az + x + x + + x +... végtele összeg x < eseté koverges. A feti végtele összegre úgy is godolhatuk, hogy végtele sok függvéyt aduk
. Függvéysorok. Bevezetés és defiíciók A végtele sorokál taultuk, hogy az + x + x + + x +... végtele összeg x < eseté koverges. A feti végtele összegre úgy is godolhatuk, hogy végtele sok függvéyt aduk
Analízis I. gyakorlat
 Aalízis I. gyakorlat Kocsis Albert Tihamér, Németh Adriá 06. március 4. Tartalomjegyzék Előszó.................................................... Sorozatok és sorok.............................................
Aalízis I. gyakorlat Kocsis Albert Tihamér, Németh Adriá 06. március 4. Tartalomjegyzék Előszó.................................................... Sorozatok és sorok.............................................
Sorozatok, határérték fogalma. Függvények határértéke, folytonossága
 Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
Egy harmadik fajta bolha mindig előző ugrásának kétszeresét ugorja és így a végtelenbe jut el.
 Végtl sok vlós számból álló összgkt sorokk vzzük. A sorb szrplő tgokt képzljük l úgy, mit gy bolh ugrásit számgys. A sor összg h létzik ily z szám hov bolh ugrási sorá ljut. Nézzük például kövtkzős sort:...
Végtl sok vlós számból álló összgkt sorokk vzzük. A sorb szrplő tgokt képzljük l úgy, mit gy bolh ugrásit számgys. A sor összg h létzik ily z szám hov bolh ugrási sorá ljut. Nézzük például kövtkzős sort:...
I nyílt intervallum, ( ) egyenletet közönséges (elsõrendû explicit) differenciálegyenletnek nevezzük. Az
 8 Közöségs diffriálgltk umrikus mgoldása 8 Dfiíió g Ω IR tartomá IR I ílt itrvallum f : I Ω IR foltoos függvé Az : I IR diffriálató függvékr voatkozó f ( ( I gltt közöségs (lsõrdû pliit diffriálgltk vzzük
8 Közöségs diffriálgltk umrikus mgoldása 8 Dfiíió g Ω IR tartomá IR I ílt itrvallum f : I Ω IR foltoos függvé Az : I IR diffriálató függvékr voatkozó f ( ( I gltt közöségs (lsõrdû pliit diffriálgltk vzzük
Innen. 2. Az. s n = 1 + q + q 2 + + q n 1 = 1 qn. és q n 0 akkor és csak akkor, ha q < 1. a a n végtelen sor konvergenciáján nem változtat az, ha
 . Végtele sorok. Bevezetés és defiíciók Bevezetéskét próbáljuk meg az 4... végtele összegek értelmet adi. Mivel végtele sokszor em tuduk összeadi, emiatt csak az első tagot adjuk össze: legye s = 4 8 =,
. Végtele sorok. Bevezetés és defiíciók Bevezetéskét próbáljuk meg az 4... végtele összegek értelmet adi. Mivel végtele sokszor em tuduk összeadi, emiatt csak az első tagot adjuk össze: legye s = 4 8 =,
Feladatok megoldással
 Fladatok mgoldással. sztmbr 6.. Halmazrdszrk. Igazoljuk! A \ B A r (A r B) (A [ B) r ((A r B) [ (B r A)) Mgoldás. A r (A r B) A \ A \ B A \ A [ B A \ A [ (A \ B) A \ B (A [ B) r ((A r B) [ (B r A)) (A
Fladatok mgoldással. sztmbr 6.. Halmazrdszrk. Igazoljuk! A \ B A r (A r B) (A [ B) r ((A r B) [ (B r A)) Mgoldás. A r (A r B) A \ A \ B A \ A [ B A \ A [ (A \ B) A \ B (A [ B) r ((A r B) [ (B r A)) (A
Határértékszámítás. 1 Határátmenet Tétel. (Nevezetes sorozatok) (a) n, n 2,... n α (α > 0), 1 n 0, 1. 0 (α > 0), (b) n 2 0,... 1.
 Határátmeet Határértékszámítás.. Tétel. (Nevezetes sorozatok) 005..5 Készítette: Dr. Toledo Rodolfo (a)... α (α > 0) (b) (c) 0 0... 0 (α > 0) α q (d) c (c > 0) ha q > = ha q = 0 ha q < diverges korlátos
Határátmeet Határértékszámítás.. Tétel. (Nevezetes sorozatok) 005..5 Készítette: Dr. Toledo Rodolfo (a)... α (α > 0) (b) (c) 0 0... 0 (α > 0) α q (d) c (c > 0) ha q > = ha q = 0 ha q < diverges korlátos
Kalkulus szigorlati tételsor Számítástechnika-technika szak, II. évfolyam, 2. félév
 Kalkulus szigorlati tételsor Számítástechika-techika szak, II. évfolyam,. félév Sorozatok: 1. A valós számoko értelmezett műveletek és reláció tulajdoságai. Számok abszolút értéke, itervallumok. Számhalmazok
Kalkulus szigorlati tételsor Számítástechika-techika szak, II. évfolyam,. félév Sorozatok: 1. A valós számoko értelmezett műveletek és reláció tulajdoságai. Számok abszolút értéke, itervallumok. Számhalmazok
ANALÍZIS I. TÉTELBIZONYÍTÁSOK ÍRÁSBELI VIZSGÁRA
 ANALÍZIS I. TÉTELBIZONYÍTÁSOK ÍRÁSBELI VIZSGÁRA Szerkesztette: Balogh Tamás 202. július 2. Ha hibát találsz, kérlek jelezd a ifo@baloghtamas.hu e-mail címe! Ez a Mű a Creative Commos Nevezd meg! - Ne add
ANALÍZIS I. TÉTELBIZONYÍTÁSOK ÍRÁSBELI VIZSGÁRA Szerkesztette: Balogh Tamás 202. július 2. Ha hibát találsz, kérlek jelezd a ifo@baloghtamas.hu e-mail címe! Ez a Mű a Creative Commos Nevezd meg! - Ne add
Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz. 2 dx = 1, cos nx dx = 2 π. sin nx dx = 2 π
 Matematika Ac gyakorlat Vegyzméröki, Bioméröki, Köryezetméröki szakok, 7/8 ősz 4. feladatsor: Fourier-sorok megoldás. Legye fx = ha x, ], fx = ha x, π]. Írjuk fel f Fourier-sorát. Mely potokba állítja
Matematika Ac gyakorlat Vegyzméröki, Bioméröki, Köryezetméröki szakok, 7/8 ősz 4. feladatsor: Fourier-sorok megoldás. Legye fx = ha x, ], fx = ha x, π]. Írjuk fel f Fourier-sorát. Mely potokba állítja
I. rész. Valós számok
 I. rész Valós számok Feladatok 3 4 Teljes idukció Igazolja a teljes idukcióval a következ állítások helyességét!.. k 2 = k= ( + )(2 + ). 6.2. 4 + 2 7 + + (3 + ) = ( + ) 2..3. a) b) ( + ) = +. k ( ) =
I. rész Valós számok Feladatok 3 4 Teljes idukció Igazolja a teljes idukcióval a következ állítások helyességét!.. k 2 = k= ( + )(2 + ). 6.2. 4 + 2 7 + + (3 + ) = ( + ) 2..3. a) b) ( + ) = +. k ( ) =
Néhány pontban a függvény értéke: x -4-2 -1-0.5 0.5 1 2 4 f (x) -0.2343-0.375 0 6-6 0 0.375 0.2343
 Házi ladatok mgoldása 0. nov.. HF. Elmzz az ( ) = üggvényt (értlmzési tartomány, olytonosság, határérték az értlmzési tartomány véginél és a szakadási pontokban, zérushly, y-tnglymtszt, monotonitás, lokális
Házi ladatok mgoldása 0. nov.. HF. Elmzz az ( ) = üggvényt (értlmzési tartomány, olytonosság, határérték az értlmzési tartomány véginél és a szakadási pontokban, zérushly, y-tnglymtszt, monotonitás, lokális
A központos furnérhámozás néhány alapösszefüggése
 A közpotos furérhámozás éháy alapösszfüggés 1. ábra: A hámozás jllmző myiségi Az 1. ábra forrása: Dr. Lugosi Armad ( szrk. ) : Faipari szrszámok és gépk kéziköyv Műszaki Köyvkiadó, Budapst, 1987, 57. oldal.
A közpotos furérhámozás éháy alapösszfüggés 1. ábra: A hámozás jllmző myiségi Az 1. ábra forrása: Dr. Lugosi Armad ( szrk. ) : Faipari szrszámok és gépk kéziköyv Műszaki Köyvkiadó, Budapst, 1987, 57. oldal.
SOROK Feladatok és megoldások 1. Numerikus sorok
 SOROK Feladatok és megoldások. Numerikus sorok I. Határozza meg az alábbi, mértai sorra visszavezethető sorok esetébe az S -edik részletösszeget és a sor S összegét! )...... k 5 5 5 5 )...... 5 5 5 5 )......
SOROK Feladatok és megoldások. Numerikus sorok I. Határozza meg az alábbi, mértai sorra visszavezethető sorok esetébe az S -edik részletösszeget és a sor S összegét! )...... k 5 5 5 5 )...... 5 5 5 5 )......
n 1 1 n sehova szám (DÖNTETLEN) 1 0 k n n n 1 IZÉ HA a sorozat is lim akkor n NEVEZETES SOROZATOK HATÁRÉRTÉKEI ÖSSZEG HATÁRÉRTÉKE IZÉ
 NEVEZETES SOROZATOK HATÁRÉRTÉKEI HA KONKRÉT SZÁM - q q q q q q shov IZÉ HA IZÉ IZÉ ÖSSZEG HATÁRÉRTÉKE TÉTEL: H és sorozt ovrgs és ovrgs és A B A és B or sorozt is AZ ÖSSZEG HATÁRÉRTÉKÉNEK ESETE A? B A
NEVEZETES SOROZATOK HATÁRÉRTÉKEI HA KONKRÉT SZÁM - q q q q q q shov IZÉ HA IZÉ IZÉ ÖSSZEG HATÁRÉRTÉKE TÉTEL: H és sorozt ovrgs és ovrgs és A B A és B or sorozt is AZ ÖSSZEG HATÁRÉRTÉKÉNEK ESETE A? B A
Eötvös Loránd Tudományegyetem Informatikai Kar. Analízis 1. Írásbeli beugró kérdések. Készítette: Szántó Ádám Tavaszi félév
 Eötvös Lorád Tudomáyegyetem Iformatikai Kar Aalízis 1. Írásbeli beugró kérdések Készítette: Szátó Ádám 2011. Tavaszi félév 1. Írja le a Dedekid-axiómát! Legyeek A R, B R. Ekkor ha a A és b B : a b, akkor
Eötvös Lorád Tudomáyegyetem Iformatikai Kar Aalízis 1. Írásbeli beugró kérdések Készítette: Szátó Ádám 2011. Tavaszi félév 1. Írja le a Dedekid-axiómát! Legyeek A R, B R. Ekkor ha a A és b B : a b, akkor
1. feladatlap megoldása. Analízis II. 1. Vizsgálja meg az alábbi sorokat konvergencia szempontjából! a) n 2 n = 1 1X 1
 . feladatlap megoldása Aalízis II.. Vizsgálja meg az alábbi sorokat kovergecia szempotjából! a) X Alkalmazva a gyökkritériumot ("egyszer½usített változatát"): Azaz a sor koverges. b) p a!! p < : X 000
. feladatlap megoldása Aalízis II.. Vizsgálja meg az alábbi sorokat kovergecia szempotjából! a) X Alkalmazva a gyökkritériumot ("egyszer½usített változatát"): Azaz a sor koverges. b) p a!! p < : X 000
A primitív függvény létezése. Kitűzött feladatok. határérték, és F az f egy olyan primitívje, amelyre F(0) = 0. Bizonyítsd be,
 6 A primitív üggvéy létezése A primitív üggvéy létezése Kitűzött eladatok. Határozd meg az a és b valós paraméterek értékét úgy hogy az : R ae + b üggvéyek létezze primitív üggvéye! >. Az : [ + [ + olytoos
6 A primitív üggvéy létezése A primitív üggvéy létezése Kitűzött eladatok. Határozd meg az a és b valós paraméterek értékét úgy hogy az : R ae + b üggvéyek létezze primitív üggvéye! >. Az : [ + [ + olytoos
Eötvös Loránd Tudományegyetem Informatikai Kar. Analízis 1. Írásbeli tételek. Készítette: Szántó Ádám Tavaszi félév
 Eötvös Lorád Tudomáyegyetem Iformatikai Kar Aalízis. Írásbeli tételek Készítette: Szátó Ádám 20. Tavaszi félév . Archimedes tétele. Tétel: a > 0 és b R : N : b < a. Bizoyítás: Idirekt úto tegyük fel, hogy
Eötvös Lorád Tudomáyegyetem Iformatikai Kar Aalízis. Írásbeli tételek Készítette: Szátó Ádám 20. Tavaszi félév . Archimedes tétele. Tétel: a > 0 és b R : N : b < a. Bizoyítás: Idirekt úto tegyük fel, hogy
ANALÍZIS 1. I. VIZSGA január 11. Mérnök informatikus szak α-variáns Munkaidő: 90 perc., vagyis z 2 1p = i 1p = ( cos 3π 2 2
 ANALÍZIS. I. VIZSGA. jauár. Mérök iformatikus szak α-variás Mukaidő: perc. feladat pot) Adja meg az z 4 i)z i egyelet összes megoldását. i + i) + 4i + 4 i +, vagyis z p i p cos 3 + i si ) 3 vagy z p i
ANALÍZIS. I. VIZSGA. jauár. Mérök iformatikus szak α-variás Mukaidő: perc. feladat pot) Adja meg az z 4 i)z i egyelet összes megoldását. i + i) + 4i + 4 i +, vagyis z p i p cos 3 + i si ) 3 vagy z p i
(A TÁMOP /2/A/KMR számú projekt keretében írt egyetemi jegyzetrészlet):
 A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
Kalkulus I. Első zárthelyi dolgozat 2014. szeptember 16. MINTA. és q = k 2. k 2. = k 1l 2 k 2 l 1. l 1 l 2. 5 2n 6n + 8
 Név, Neptu-kód:.................................................................... 1. Legyeek p, q Q tetszőlegesek. Mutassuk meg, hogy ekkor p q Q. Tegyük fel, hogy p, q Q. Ekkor létezek olya k 1, k 2,
Név, Neptu-kód:.................................................................... 1. Legyeek p, q Q tetszőlegesek. Mutassuk meg, hogy ekkor p q Q. Tegyük fel, hogy p, q Q. Ekkor létezek olya k 1, k 2,
A tárgy címe: ANALÍZIS 1 A-B-C (2+2). 1. gyakorlat
 A tárgy címe: ANALÍZIS A-B-C + gyakorlat Beroulli-egyelőtleség Legye N, x k R k =,, és tegyük fel, hogy vagy x k 0 k =,, vagy pedig x k 0 k =,, Ekkor + x k + x k Speciális Beroulli-egyelőtleség Ha N és
A tárgy címe: ANALÍZIS A-B-C + gyakorlat Beroulli-egyelőtleség Legye N, x k R k =,, és tegyük fel, hogy vagy x k 0 k =,, vagy pedig x k 0 k =,, Ekkor + x k + x k Speciális Beroulli-egyelőtleség Ha N és
Sorozatok. 1. Vizsgálja meg az alábbi sorozatokat monotonitás szempontjából!(indoklással, nem elegendő a sorozat. (a) a n = n+1
 Bodó Báta 1 Sorozatok 1. Vizsgálja mg az alábbi sorozatokat mootoitás szmpotjából!idoklással, m lgdő a sorozat éháy lmék kiszámolása.) a) +1 +3 b) +3 1+ szigorúa mooto csökk c) 2 2+ d) B +7 21 szigorúa
Bodó Báta 1 Sorozatok 1. Vizsgálja mg az alábbi sorozatokat mootoitás szmpotjából!idoklással, m lgdő a sorozat éháy lmék kiszámolása.) a) +1 +3 b) +3 1+ szigorúa mooto csökk c) 2 2+ d) B +7 21 szigorúa
Integrált Intetnzív Matematika Érettségi
 tgrált ttzív Matmatika Érttségi. Adott az f : \ -, f függvéy. a) Számítsd ki az f függvéy driváltját! b) Határozd mg az f függvéy mootoitási itrvallumait! c) gazold, hogy f ( ) bármly sté!. Adott az f
tgrált ttzív Matmatika Érttségi. Adott az f : \ -, f függvéy. a) Számítsd ki az f függvéy driváltját! b) Határozd mg az f függvéy mootoitási itrvallumait! c) gazold, hogy f ( ) bármly sté!. Adott az f
2. fejezet. Számsorozatok, számsorok
 . fejezet Számsorozatok, számsorok .. Számsorozatok és számsorok... Számsorozat megadása, határértéke Írjuk fel képlettel az alábbi sorozatok -dik elemét! mooto, korlátos, illetve koverges-e! Vizsgáljuk
. fejezet Számsorozatok, számsorok .. Számsorozatok és számsorok... Számsorozat megadása, határértéke Írjuk fel képlettel az alábbi sorozatok -dik elemét! mooto, korlátos, illetve koverges-e! Vizsgáljuk
Debreceni Egyetem. Kalkulus példatár. Gselmann Eszter
 Debrecei Egyetem Természettudomáyi és Techológiai Kar Kalkulus példatár Gselma Eszter Debrece, 08 Tartalomjegyzék. Valós számsorozatok Elméleti áttekités........................................................
Debrecei Egyetem Természettudomáyi és Techológiai Kar Kalkulus példatár Gselma Eszter Debrece, 08 Tartalomjegyzék. Valós számsorozatok Elméleti áttekités........................................................
ANALÍZIS I. DEFINÍCIÓK, TÉTELEK
 ANALÍZIS I. DEFINÍCIÓK, TÉTELEK Szerkesztette: Balogh Tamás 2012. július 2. Ha hibát találsz, kérlek jelezd a ifo@baloghtamas.hu e-mail címe! Ez a Mű a Creative Commos Nevezd meg! - Ne add el! - Így add
ANALÍZIS I. DEFINÍCIÓK, TÉTELEK Szerkesztette: Balogh Tamás 2012. július 2. Ha hibát találsz, kérlek jelezd a ifo@baloghtamas.hu e-mail címe! Ez a Mű a Creative Commos Nevezd meg! - Ne add el! - Így add
Nevezetes sorozat-határértékek
 Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
3. SOROZATOK. ( n N) a n+1 < a n. Egy sorozatot (szigorúan) monotonnak mondunk, ha (szigorúan) monoton növekvő vagy csökkenő.
 3. SOROZATOK 3. Sorozatok korlátossága, mootoitása, kovergeciája Defiíció. Egy f : N R függvéyt valós szám)sorozatak evezük. Ha A egy adott halmaz és f : N A, akkor f-et A-beli értékű) sorozatak evezzük.
3. SOROZATOK 3. Sorozatok korlátossága, mootoitása, kovergeciája Defiíció. Egy f : N R függvéyt valós szám)sorozatak evezük. Ha A egy adott halmaz és f : N A, akkor f-et A-beli értékű) sorozatak evezzük.
1 h. 3. Hogyan szól a számtani és a mértani közép közötti összefüggést kifejező tétel?
 1. Fogalmazza meg az R -beli háromszög-egyelőtleségeket!,y R (i) +y + y (ii) -y - y 2. Mit mod ki a Beroulli-egyelőtleség? (i) (1+h) 1+ h ( h>-1) ( N*) (ii) (1+h) 1+2 h 1 ( N*) h 2 3. Hogya szól a számtai
1. Fogalmazza meg az R -beli háromszög-egyelőtleségeket!,y R (i) +y + y (ii) -y - y 2. Mit mod ki a Beroulli-egyelőtleség? (i) (1+h) 1+ h ( h>-1) ( N*) (ii) (1+h) 1+2 h 1 ( N*) h 2 3. Hogya szól a számtai
1 n. 8abc (a + b) (b + c) (a + c) 8 27 (a + b + c)3. (1 a) 5 (1 + a)(1 + 2a) n + 1
 A tárgy címe: ANALÍZIS A-B-C + gyakorlat Beroulli-egyelőtleség Ha N és h R, akkor + h + h Mikor va itt egyelőség? Léyeges-e a h feltétel? Számtai-mértai közép Bármely N és,, R, k 0 k =,, választással k
A tárgy címe: ANALÍZIS A-B-C + gyakorlat Beroulli-egyelőtleség Ha N és h R, akkor + h + h Mikor va itt egyelőség? Léyeges-e a h feltétel? Számtai-mértai közép Bármely N és,, R, k 0 k =,, választással k
f(x) vagy f(x) a (x x 0 )-t használjuk. lim melyekre Mivel itt ɛ > 0 tetszőlegesen kicsi, így a a = 0, a = a, ami ellentmondás, bizonyítva
 6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
Gyakorló feladatok II.
 Gyakorló feladatok II. Valós sorozatok és sorok Közgazdász szakos hallgatókak a Matematika B című tárgyhoz 2005. október Valós sorozatok elemi tulajdoságai F. Pozitív állítás formájába fogalmazza meg azt,
Gyakorló feladatok II. Valós sorozatok és sorok Közgazdász szakos hallgatókak a Matematika B című tárgyhoz 2005. október Valós sorozatok elemi tulajdoságai F. Pozitív állítás formájába fogalmazza meg azt,
megoldásvázlatok Kalkulus gyakorlat Fizika BSc I/1, 1. feladatsor 1. Rajzoljuk le a számegyenesen az alábbi halmazokat!
 megoldásvázlatok Fizika BSc I/,. feladatsor. Rajzoljuk le a számegyeese az alábbi halmazokat! a { R < 5}, b { R 4}, c { Z 4}, d { Q < 4 6}, e { N 3 }.. Igazak-e az alábbi állítások? Adjuk meg az állítások
megoldásvázlatok Fizika BSc I/,. feladatsor. Rajzoljuk le a számegyeese az alábbi halmazokat! a { R < 5}, b { R 4}, c { Z 4}, d { Q < 4 6}, e { N 3 }.. Igazak-e az alábbi állítások? Adjuk meg az állítások
NUMERIKUS SOROK II. Ebben a részben kizárólag a konvergencia vizsgálatával foglalkozunk.
 NUMERIKUS SOROK II. Ebbe a részbe kizárólag a kovergecia vizsgálatával foglalkozuk. SZÜKSÉGES FELTÉTEL Ha pozitív (vagy em egatív) tagú umerikus sor, akkor a kovergecia szükséges feltétele, hogy lim a
NUMERIKUS SOROK II. Ebbe a részbe kizárólag a kovergecia vizsgálatával foglalkozuk. SZÜKSÉGES FELTÉTEL Ha pozitív (vagy em egatív) tagú umerikus sor, akkor a kovergecia szükséges feltétele, hogy lim a
Taylor-sorok alkalmazása numerikus sorok vizsgálatára
 Eötvös Lorád Tudomáyegyetem Természettudomáyi Kar Alkalmazott Aalízis és Számításmatematikai Taszék Taylor-sorok alkalmazása umerikus sorok vizsgálatára Szakdolgozat Készítette: Témavezet : Walter Petra
Eötvös Lorád Tudomáyegyetem Természettudomáyi Kar Alkalmazott Aalízis és Számításmatematikai Taszék Taylor-sorok alkalmazása umerikus sorok vizsgálatára Szakdolgozat Készítette: Témavezet : Walter Petra
Lajkó Károly Kalkulus I. példatár mobidiák könyvtár
 Lajkó Károly Kalkulus I. példatár mobidiák köyvtár Lajkó Károly Kalkulus I. példatár mobidiák köyvtár SOROZATSZERKESZTŐ Fazekas Istvá Lajkó Károly Kalkulus I. példatár programozó és programtervező matematikus
Lajkó Károly Kalkulus I. példatár mobidiák köyvtár Lajkó Károly Kalkulus I. példatár mobidiák köyvtár SOROZATSZERKESZTŐ Fazekas Istvá Lajkó Károly Kalkulus I. példatár programozó és programtervező matematikus
Kalkulus II., második házi feladat
 Uger Tamás Istvá FTDYJ Név: Uger Tamás Istvá Neptu: FTDYJ Web: http://maxwellszehu/~ugert Kalkulus II, második házi feladat pot) Koverges? Abszolút koverges? ) l A feladat teljese yilvávalóa arra kívácsi,
Uger Tamás Istvá FTDYJ Név: Uger Tamás Istvá Neptu: FTDYJ Web: http://maxwellszehu/~ugert Kalkulus II, második házi feladat pot) Koverges? Abszolút koverges? ) l A feladat teljese yilvávalóa arra kívácsi,
minden x D esetén, akkor x 0 -at a függvény maximumhelyének mondjuk, f(x 0 )-at pedig az (abszolút) maximumértékének.
 Függvények határértéke és folytonossága Egy f: D R R függvényt korlátosnak nevezünk, ha a függvényértékek halmaza korlátos. Ha f(x) f(x 0 ) teljesül minden x D esetén, akkor x 0 -at a függvény maximumhelyének
Függvények határértéke és folytonossága Egy f: D R R függvényt korlátosnak nevezünk, ha a függvényértékek halmaza korlátos. Ha f(x) f(x 0 ) teljesül minden x D esetén, akkor x 0 -at a függvény maximumhelyének
Metrikus terek. továbbra is.
 Metrius tere továbbra is. Defiíció: Legye X egy halmaz, d : X X R egy függvéy. Azt modju, hogy d metria (távolság), ha.. 3. 4. d d d d x, x 0, x, y 0 x y, x, y dy, x, x, z dx, y dy, z. Az X halmazt a d
Metrius tere továbbra is. Defiíció: Legye X egy halmaz, d : X X R egy függvéy. Azt modju, hogy d metria (távolság), ha.. 3. 4. d d d d x, x 0, x, y 0 x y, x, y dy, x, x, z dx, y dy, z. Az X halmazt a d
4. Differenciálszámítás
 . Diffrnciálszámítás.. Írja fl a diffrnciahányadost a mgadott pontban és határozza mg a határértékét!... f...... f..7. f, f,,..9. f... f... f... f...... f..7...9. f...... f... f... f...,..6. f,,,, f,..8.
. Diffrnciálszámítás.. Írja fl a diffrnciahányadost a mgadott pontban és határozza mg a határértékét!... f...... f..7. f, f,,..9. f... f... f... f...... f..7...9. f...... f... f... f...,..6. f,,,, f,..8.
1. gyakorlat - Végtelen sorok
 . gyakorlat - Végtele sorok 06. március.. Határozza meg az alábbi végtele sorok összegét! a) e e e 3 = e e = e e e e = e e = e e b) c) 4 = 4 + 5 6 + = 6 ) 4 + 6 6 + ) = lim N ) 5 = 6 6 + 5 6 = 7 6 N )
. gyakorlat - Végtele sorok 06. március.. Határozza meg az alábbi végtele sorok összegét! a) e e e 3 = e e = e e e e = e e = e e b) c) 4 = 4 + 5 6 + = 6 ) 4 + 6 6 + ) = lim N ) 5 = 6 6 + 5 6 = 7 6 N )
Értelmezési tartomány, tengelymetszetek, paritás. (ii) Határérték. (iii) Első derivált, monotonitás, x x 2 dx = arctg x + C = arcctgx + C,
 25.2.8. Kalkulus I. NÉV:... A csoport EHA:... FELADATOK:. Lineáris transzformációk segítségével ábrázoljuk az f() = ln(2 3) függvényt. 7pt 2. Határozzuk meg az f() = 2 3 + 2 2 2 + függvény szélsőértékeit
25.2.8. Kalkulus I. NÉV:... A csoport EHA:... FELADATOK:. Lineáris transzformációk segítségével ábrázoljuk az f() = ln(2 3) függvényt. 7pt 2. Határozzuk meg az f() = 2 3 + 2 2 2 + függvény szélsőértékeit
Numerikus sorok. Kónya Ilona. VIK, Műszaki Informatika ANALÍZIS (1) Oktatási segédanyag
 VIK, Műszaki Iformatika ANALÍZIS Numerikus sorok Oktatási segédayag A Villamosméröki és Iformatikai Kar műszaki iformatikus hallgatóiak tartott előadásai alapjá összeállította: Fritz Józsefé dr. Kóya Iloa
VIK, Műszaki Iformatika ANALÍZIS Numerikus sorok Oktatási segédayag A Villamosméröki és Iformatikai Kar műszaki iformatikus hallgatóiak tartott előadásai alapjá összeállította: Fritz Józsefé dr. Kóya Iloa
VII. A határozatlan esetek kiküszöbölése
 A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
Gyakorló feladatok az II. konzultáció anyagához
 Gyakorló feladatok az II. konzultáció anyagához 003/004 tanév, I. félév 1. Vizsgáljuk meg a következő sorozatokat korlátosság és monotonitás szempontjából! a n = 5n+1, b n = n + n! 3n 8, c n = 1 ( 1)n
Gyakorló feladatok az II. konzultáció anyagához 003/004 tanév, I. félév 1. Vizsgáljuk meg a következő sorozatokat korlátosság és monotonitás szempontjából! a n = 5n+1, b n = n + n! 3n 8, c n = 1 ( 1)n
Sorozatok október 15. Határozza meg a következ sorozatok határértékeit!
 Sorozatok 20. október 5. Határozza meg a következ sorozatok határértékeit!. Zh feladat:vizsgálja meg mootoitás és korlátosság szerit az alábbi sorozatot! a + ha ; 2; 5 Mootoitás eldötéséhez vizsgáljuk
Sorozatok 20. október 5. Határozza meg a következ sorozatok határértékeit!. Zh feladat:vizsgálja meg mootoitás és korlátosság szerit az alábbi sorozatot! a + ha ; 2; 5 Mootoitás eldötéséhez vizsgáljuk
2. gyakorlat - Hatványsorok és Taylor-sorok
 . gyakorlat - Hatváysorok és Taylor-sorok 9. március 3.. Adjuk meg az itt szereplő sorok kovergeciasugarát és kovergeciaitervallumát! + a = + Azaz a hatváysor kovergeciasugara. Az biztos, hogy a (-,) yílt
. gyakorlat - Hatváysorok és Taylor-sorok 9. március 3.. Adjuk meg az itt szereplő sorok kovergeciasugarát és kovergeciaitervallumát! + a = + Azaz a hatváysor kovergeciasugara. Az biztos, hogy a (-,) yílt
FELADATOK A KALKULUS C. TÁRGYHOZ
 FELADATOK A KALKULUS C. TÁRGYHOZ. HALMAZOK RELÁCIÓK FÜGGVÉNYEK. Bizoyítsuk be a halmaz-műveletek alapazoosságait! 2. Legye adott az X halmaz legye A B C X. Ha A B := (A B) (B A) akkor bizoyítsuk be hogy
FELADATOK A KALKULUS C. TÁRGYHOZ. HALMAZOK RELÁCIÓK FÜGGVÉNYEK. Bizoyítsuk be a halmaz-műveletek alapazoosságait! 2. Legye adott az X halmaz legye A B C X. Ha A B := (A B) (B A) akkor bizoyítsuk be hogy
A fontosabb definíciók
 A legfontosabb definíciókat jelöli. A fontosabb definíciók [Descartes szorzat] Az A és B halmazok Descartes szorzatán az A és B elemeiből képezett összes (a, b) a A, b B rendezett párok halmazát értjük,
A legfontosabb definíciókat jelöli. A fontosabb definíciók [Descartes szorzat] Az A és B halmazok Descartes szorzatán az A és B elemeiből képezett összes (a, b) a A, b B rendezett párok halmazát értjük,
(d) x 6 3x 2 2 = 0, (e) x + x 2 = 1 x, (f) 2x x 1 = 8, 2(x 1) a 1
 . Bevezető. Oldja meg az alábbi egyeleteket: (a cos x + si x + cos x si x = (b π si x = x π 4 x 3π 4 cos x (c cos x + si x = si x (d x 6 3x = 0 (e x + x = x (f x + 5 + x = 8 (g x + + x + + x + x + =..
. Bevezető. Oldja meg az alábbi egyeleteket: (a cos x + si x + cos x si x = (b π si x = x π 4 x 3π 4 cos x (c cos x + si x = si x (d x 6 3x = 0 (e x + x = x (f x + 5 + x = 8 (g x + + x + + x + x + =..
Sorozatok, sorozatok konvergenciája
 Sorozatok, sorozatok konvergenciája Elméleti áttekintés Minden konvergens sorozat korlátos Minden monoton és korlátos sorozat konvergens Legyen a n ) n egy sorozat és ϕ : N N egy szigorúan növekvő függvény
Sorozatok, sorozatok konvergenciája Elméleti áttekintés Minden konvergens sorozat korlátos Minden monoton és korlátos sorozat konvergens Legyen a n ) n egy sorozat és ϕ : N N egy szigorúan növekvő függvény
5. modul: Szilárdságtani Állapotok. 5.3. lecke: A feszültségi állapot
 5 modul: Silárdságtai Állapotok 53 lck: A fsültségi állapot A lck célja: A taaag flhasálója mgismrj a fsültségi állapot fogalmait valamit mg tudja határoi g lmi pot körték fsültségi állapotát Kövtlmék:
5 modul: Silárdságtai Állapotok 53 lck: A fsültségi állapot A lck célja: A taaag flhasálója mgismrj a fsültségi állapot fogalmait valamit mg tudja határoi g lmi pot körték fsültségi állapotát Kövtlmék:
8n 5 n, Értelmezési tartomány, tengelymetszetek, paritás. (ii) Határérték. (iii) Első derivált, monotonitás,
 3... Kalkulus I. NÉV:... A csoport EHA:... FELADATOK:. Definíció szerint és formálisan is határozzuk meg az f() = 4 deriváltját az = helyen.pt. Határozzuk meg a következő határértékeket: pt lim n 8n 5
3... Kalkulus I. NÉV:... A csoport EHA:... FELADATOK:. Definíció szerint és formálisan is határozzuk meg az f() = 4 deriváltját az = helyen.pt. Határozzuk meg a következő határértékeket: pt lim n 8n 5
V. Deriválható függvények
 Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Matematika I. 9. előadás
 Matematika I. 9. előadás Valós számsorozat kovergeciája +-hez ill. --hez divergáló sorozatok A határérték és a műveletek kapcsolata Valós számsorozatok mootoitása, korlátossága Komplex számsorozatok kovergeciája
Matematika I. 9. előadás Valós számsorozat kovergeciája +-hez ill. --hez divergáló sorozatok A határérték és a műveletek kapcsolata Valós számsorozatok mootoitása, korlátossága Komplex számsorozatok kovergeciája
n 2 2n), (ii) lim Értelmezési tartomány, tengelymetszetek, paritás. (ii) Határérték. (iii) Első derivált, monotonitás, (ii) 3 t 2 2t dt,
 205.05.9. Kalkulus I. NÉV:... A csoport EHA:... FELADATOK:. Definíció szerint és formálisan is határozzuk meg a h() = 3 2 függvény deriváltját az = 2 helyen. 8pt 2. Határozzuk meg a következő határértékeket:
205.05.9. Kalkulus I. NÉV:... A csoport EHA:... FELADATOK:. Definíció szerint és formálisan is határozzuk meg a h() = 3 2 függvény deriváltját az = 2 helyen. 8pt 2. Határozzuk meg a következő határértékeket:
f(x) a (x x 0 )-t használjuk.
 5. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 5.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
5. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 5.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
Függvényhatárérték-számítás
 Függvéyhatárérték-számítás I Függvéyek véges helye vett véges határértéke I itervallumo, ha va olya k valós szám, melyre az I itervallumo, ha va olya K valós szám, melyre I itervallumo, ha alulról és felülről
Függvéyhatárérték-számítás I Függvéyek véges helye vett véges határértéke I itervallumo, ha va olya k valós szám, melyre az I itervallumo, ha va olya K valós szám, melyre I itervallumo, ha alulról és felülről
Sorozatok, sorok, függvények határértéke és folytonossága Leindler Schipp - Analízis I. könyve + jegyzetek, kidolgozások alapján
 Sorozatok, sorok, függvények határértéke és folytonossága Leindler Schipp - Analízis I. könyve + jegyzetek, kidolgozások alapján Számsorozatok, vektorsorozatok konvergenciája Def.: Számsorozatok értelmezése:
Sorozatok, sorok, függvények határértéke és folytonossága Leindler Schipp - Analízis I. könyve + jegyzetek, kidolgozások alapján Számsorozatok, vektorsorozatok konvergenciája Def.: Számsorozatok értelmezése:
A Matematika I. előadás részletes tematikája
 A Matematika I. előadás részletes tematikája 2005/6, I. félév 1. Halmazok és relációk 1.1 Műveletek halmazokkal Definíciók, fogalmak: halmaz, elem, üres halmaz, halmazok egyenlősége, részhalmaz, halmazok
A Matematika I. előadás részletes tematikája 2005/6, I. félév 1. Halmazok és relációk 1.1 Műveletek halmazokkal Definíciók, fogalmak: halmaz, elem, üres halmaz, halmazok egyenlősége, részhalmaz, halmazok
A szelepre ható érintkezési erő meghatározása
 A szlpr ható érintkzési rő mghatározása Az [ 1 ] műbn az alábbi fladatot találtuk. A fladat: Adott az ábra szrinti szlpmlő szrkzt. Az a xcntricitással szrlt R sugarú bütyök / körtárcsa ω 1 állandó szögsbsséggl
A szlpr ható érintkzési rő mghatározása Az [ 1 ] műbn az alábbi fladatot találtuk. A fladat: Adott az ábra szrinti szlpmlő szrkzt. Az a xcntricitással szrlt R sugarú bütyök / körtárcsa ω 1 állandó szögsbsséggl
Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar. Feladatok a Gazdasági matematika I. tárgy gyakorlataihoz. Halmazelmélet
 Debrecei Egyetem Közgazdaság- és Gazdaságtudomáyi Kar Feladatok a Gazdasági matematika I. tárgy gyakorlataihoz a megoldásra feltétleül ajálott feladatokat jelöli e feladatokat a félév végére megoldottak
Debrecei Egyetem Közgazdaság- és Gazdaságtudomáyi Kar Feladatok a Gazdasági matematika I. tárgy gyakorlataihoz a megoldásra feltétleül ajálott feladatokat jelöli e feladatokat a félév végére megoldottak
(2) A d(x) = 2x + 2 függvénynek van véges határértéke az x0 = 1 helyen, így a differenciálhányados: lim2x
 DIFFERENCIÁLSZÁMÍTÁS MINTAPÉLDÁK.. Példa. Határozzuk mg az f = függvénnk az = hlhz tartozó diffrnciahánados függvénét, majd vizsgáljuk mg, hog f diffrnciálható- az -ban adjuk mg az = hlhz tartozó diffrnciálhánadost.
DIFFERENCIÁLSZÁMÍTÁS MINTAPÉLDÁK.. Példa. Határozzuk mg az f = függvénnk az = hlhz tartozó diffrnciahánados függvénét, majd vizsgáljuk mg, hog f diffrnciálható- az -ban adjuk mg az = hlhz tartozó diffrnciálhánadost.
RSA. 1. Véletlenszerűen választunk két "nagy" prímszámot: p1, p2
 RS z algoritmus. Véltlnszrűn választunk két "nagy" prímszámot: p, p, p p. m= pp, φ ( m) = ( p -)( p -)., < φ( m), ( φ( m ),) = - 3. d = ( mod φ( m) ) 4. k p s = ( m,), = ( d, p, p ) k. Kódolás: y = x (
RS z algoritmus. Véltlnszrűn választunk két "nagy" prímszámot: p, p, p p. m= pp, φ ( m) = ( p -)( p -)., < φ( m), ( φ( m ),) = - 3. d = ( mod φ( m) ) 4. k p s = ( m,), = ( d, p, p ) k. Kódolás: y = x (
6. Határozatlan integrál
 . Határozatlan intgrál.. Alkalmazza a hatványfüggvény intgrálására vonatkozó szabályt! d... d... d... d 8...... d... d... d..8. d..9. d..0. d... d... d 8... d... 8... d...... d..8...9. d..0. d d 8 d d..
. Határozatlan intgrál.. Alkalmazza a hatványfüggvény intgrálására vonatkozó szabályt! d... d... d... d 8...... d... d... d..8. d..9. d..0. d... d... d 8... d... 8... d...... d..8...9. d..0. d d 8 d d..
Analízis feladatgy jtemény II.
 Oktatási segédayag a Programtervez matematikus szak Aalízis I. tatárgyához (003004. taév szi félév) Aalízis feladatgy jteméy II. Összeállította Szili László 003 Tartalomjegyzék I. Feladatok 3. Valós sorozatok.......................................
Oktatási segédayag a Programtervez matematikus szak Aalízis I. tatárgyához (003004. taév szi félév) Aalízis feladatgy jteméy II. Összeállította Szili László 003 Tartalomjegyzék I. Feladatok 3. Valós sorozatok.......................................
Fourier sorok FO 1. Trigonometrikus. A diákon megjelenő szövegek és képek csak a szerző (Kocsis Imre, DE MFK) engedélyével használhatók fel!
 Fourier sorok FO Trigoometrikus Fourier sorok FO Trigoometrikus redszer Defiíció: trigoometrikus redszer Az {, cos x, si x, cos x, si x, cos 3x, si 3x, } függvéyekből álló (végtele sok függvéyt tartalmazó)
Fourier sorok FO Trigoometrikus Fourier sorok FO Trigoometrikus redszer Defiíció: trigoometrikus redszer Az {, cos x, si x, cos x, si x, cos 3x, si 3x, } függvéyekből álló (végtele sok függvéyt tartalmazó)
Függvények határértéke 69. III. Függvények határértéke
 Függvéyek határértéke 69 A határérték értelmezése III Függvéyek határértéke Ebbe a fejezetbe taulmáyozi fogjuk a függvéy határértékét egy potba A feladat így fogalmazható meg: Ha adott az f : D valós változójú
Függvéyek határértéke 69 A határérték értelmezése III Függvéyek határértéke Ebbe a fejezetbe taulmáyozi fogjuk a függvéy határértékét egy potba A feladat így fogalmazható meg: Ha adott az f : D valós változójú
53. sz. mérés. Hurokszabályozás vizsgálata
 53. sz. mérés Hurokszaályozás vizsgálata nagyszültségű alap- illtv losztóhálózat (4,, kv a hálózatok unkcióáól kövtkzőn hurkolt (töszörösn hurkolt kialakítású. sok csomóponttal, tö táplálási illtv ogyasztási
53. sz. mérés Hurokszaályozás vizsgálata nagyszültségű alap- illtv losztóhálózat (4,, kv a hálózatok unkcióáól kövtkzőn hurkolt (töszörösn hurkolt kialakítású. sok csomóponttal, tö táplálási illtv ogyasztási
13. gyakorlat Visszacsatolt műveletierősítők. A0=10 6 ; ω1=5r/s, ω2 =1Mr/s R 1. Kérdések: uki/ube=?, ha a ME ideális!
 . gyakorlat Visszacsatolt művltirősítők.) Példa b (s) 6 ; r/s, Mr/s kω, 9 kω, kω, ( s )( s ) Kérdésk: /b?, ha a ME ális! Mkkora lgyn érték ahhoz, hogy az /b rősítés maximális lapos lgyn ( ξ ). Mkkora a
. gyakorlat Visszacsatolt művltirősítők.) Példa b (s) 6 ; r/s, Mr/s kω, 9 kω, kω, ( s )( s ) Kérdésk: /b?, ha a ME ális! Mkkora lgyn érték ahhoz, hogy az /b rősítés maximális lapos lgyn ( ξ ). Mkkora a
Minden x > 0 és y 0 valós számpárhoz létezik olyan n természetes szám, hogy y nx.
 1. Archimedesz tétele. Minden x > 0 és y 0 valós számpárhoz létezik olyan n természetes szám, hogy y nx. Legyen y > 0, nx > y akkor és csak akkor ha n > b/a. Ekkor elég megmutatni, hogy létezik minden
1. Archimedesz tétele. Minden x > 0 és y 0 valós számpárhoz létezik olyan n természetes szám, hogy y nx. Legyen y > 0, nx > y akkor és csak akkor ha n > b/a. Ekkor elég megmutatni, hogy létezik minden
Kalkulus I. NÉV: Határozzuk meg a következő határértékeket: 8pt
 27.2.2. Kalkulus I. NÉV:... A csoport KÓD:.... Adjuk meg a b n = 3n 7 9 2n sorozat infimumát, szuprémumát. 8pt 2. Határozzuk meg a következő határértékeket: 8pt (a) ( lim n 2 3n n 2 n 3) n ( ) 3n 5 3 2n,
27.2.2. Kalkulus I. NÉV:... A csoport KÓD:.... Adjuk meg a b n = 3n 7 9 2n sorozat infimumát, szuprémumát. 8pt 2. Határozzuk meg a következő határértékeket: 8pt (a) ( lim n 2 3n n 2 n 3) n ( ) 3n 5 3 2n,
Egy lehetséges tételsor megoldásokkal
 Egy lehetséges tételsor megoldásokkal A vizsgatétel I része a IX és X osztályos ayagot öleli fel, 6 külöböző fejezetből vett feladatból áll, összese potot ér A közzétett tétel-variások és az előző évekbe
Egy lehetséges tételsor megoldásokkal A vizsgatétel I része a IX és X osztályos ayagot öleli fel, 6 külöböző fejezetből vett feladatból áll, összese potot ér A közzétett tétel-variások és az előző évekbe
10.M ALGEBRA < <
 0.M ALGEBRA GYÖKÖS KIFEJEZÉSEK. Mutassuk meg, hogy < + +... + < + + 008 009 + 009 008 5. Mutassuk meg, hogy va olya pozitív egész szám, amelyre 99 < + + +... + < 995. Igazoljuk, hogy bármely pozitív egész
0.M ALGEBRA GYÖKÖS KIFEJEZÉSEK. Mutassuk meg, hogy < + +... + < + + 008 009 + 009 008 5. Mutassuk meg, hogy va olya pozitív egész szám, amelyre 99 < + + +... + < 995. Igazoljuk, hogy bármely pozitív egész
ELOSZLÁS, ELOSZLÁSFÜGGVÉNY, SŰRŰSÉGFÜGGVÉNY
 ELOSZLÁS, ELOSZLÁSÜGGVÉNY, SŰRŰSÉGÜGGVÉNY AZ ELOSZLÁSÜGGVÉNY Egy célábla sugara cm, a valószínűségi válozó jlns az, hogy milyn ávol lőünk a célábla középponjáól. Tgyük öl, hogy a céláblá bizosan laláljuk.
ELOSZLÁS, ELOSZLÁSÜGGVÉNY, SŰRŰSÉGÜGGVÉNY AZ ELOSZLÁSÜGGVÉNY Egy célábla sugara cm, a valószínűségi válozó jlns az, hogy milyn ávol lőünk a célábla középponjáól. Tgyük öl, hogy a céláblá bizosan laláljuk.
Draft version. Use at your own risk!
 BME Matematika Itézet Aalízis Taszék Adai Attila Bevezető aalízispéldák példatár éháy BSc-s órához 8 Tartalomjegyzék. Halmazalgebra. Teljes idukció 3. Relációk, függvéyek 3 4. Számosságok 6 5. A valós
BME Matematika Itézet Aalízis Taszék Adai Attila Bevezető aalízispéldák példatár éháy BSc-s órához 8 Tartalomjegyzék. Halmazalgebra. Teljes idukció 3. Relációk, függvéyek 3 4. Számosságok 6 5. A valós
Mágneses anyagok elektronmikroszkópos vizsgálata
 Mágnss anyagok lktronmikroszkópos vizsgálata 1. Transzmissziós lktronmikroszkóp 1.1. A mágnss kontraszt rdt a TEM-bn Az lktronmikroszkópban 100-200 kv-os (stlg 1 MV-os) gyorsítófszültséggl gyorsított lktronok
Mágnss anyagok lktronmikroszkópos vizsgálata 1. Transzmissziós lktronmikroszkóp 1.1. A mágnss kontraszt rdt a TEM-bn Az lktronmikroszkópban 100-200 kv-os (stlg 1 MV-os) gyorsítófszültséggl gyorsított lktronok
Analízis I. beugró vizsgakérdések
 Analízis I. beugró vizsgakérdések Programtervező Informatikus szak 2008-2009. 2. félév Készítette: Szabó Zoltán SZZNACI.ELTE zotyo@bolyaimk.hu v1.7 Forrás: Dr. Weisz Ferenc: Prog. Mat. 2006-2007 definíciók
Analízis I. beugró vizsgakérdések Programtervező Informatikus szak 2008-2009. 2. félév Készítette: Szabó Zoltán SZZNACI.ELTE zotyo@bolyaimk.hu v1.7 Forrás: Dr. Weisz Ferenc: Prog. Mat. 2006-2007 definíciók
Komplex számok. A komplex számok algebrai alakja
 Komple számok A komple számok algebrai alakja 1. Ábrázolja a következő komple számokat a Gauss-féle számsíkon! Adja meg a számok valós részét, képzetes részét és számítsa ki az abszolút értéküket! a) 3+5j
Komple számok A komple számok algebrai alakja 1. Ábrázolja a következő komple számokat a Gauss-féle számsíkon! Adja meg a számok valós részét, képzetes részét és számítsa ki az abszolút értéküket! a) 3+5j
( a b)( c d) 2 ab2 cd 2 abcd 2 Egyenlőség akkor és csak akkor áll fenn
 Feladatok közepek közötti egyelőtleségekre (megoldások, megoldási ötletek) A továbbiakba szmk=számtai-mértai közép közötti egyelőtleség, szhk=számtaiharmoikus közép közötti egyelőtleség, míg szk= számtai-égyzetes
Feladatok közepek közötti egyelőtleségekre (megoldások, megoldási ötletek) A továbbiakba szmk=számtai-mértai közép közötti egyelőtleség, szhk=számtaiharmoikus közép közötti egyelőtleség, míg szk= számtai-égyzetes
Kalkulus gyakorlat - Megoldásvázlatok
 Kalkulus gyakorlat - Megoldásvázlatok Fizika BSc I/. gyakorlat. Tétel Newto Leibiz. Ha f folytoos az a, b] itervallumo és F primitív függvéye f-ek, akkor b a f F b F a.. Számítsuk ki az alábbi racioális
Kalkulus gyakorlat - Megoldásvázlatok Fizika BSc I/. gyakorlat. Tétel Newto Leibiz. Ha f folytoos az a, b] itervallumo és F primitív függvéye f-ek, akkor b a f F b F a.. Számítsuk ki az alábbi racioális
Valószínűségszámítás. A standard normális eloszlás karakterisztikus függvénye. További tulajdonságok. További tulajdonságok.
 Karakriszikus függvéy Valószíűségszámíás. lőadás 07..05 Kompl érékű valószíűségi válozók: Z=+iY, ahol és Y is valószíűségi válozók. Z):=)+iY). (valós) valószíűségi válozó karakriszikus függvéy: ():= i
Karakriszikus függvéy Valószíűségszámíás. lőadás 07..05 Kompl érékű valószíűségi válozók: Z=+iY, ahol és Y is valószíűségi válozók. Z):=)+iY). (valós) valószíűségi válozó karakriszikus függvéy: ():= i
Bevezető analízis II. példatár
 Bevezető aalízis II. példatár Gémes Margit, Szetmiklóssy Zoltá Eötvös Lorád Tudomáyegyetem Természettudomáyi Kar Matematikai Itézet 06. ovember 3. Tartalomjegyzék. Bizoyítási módszerek, valós számok 3..
Bevezető aalízis II. példatár Gémes Margit, Szetmiklóssy Zoltá Eötvös Lorád Tudomáyegyetem Természettudomáyi Kar Matematikai Itézet 06. ovember 3. Tartalomjegyzék. Bizoyítási módszerek, valós számok 3..
Komplex számok. d) Re(z 4 ) = 0, Im(z 4 ) = 1 e) Re(z 5 ) = 0, Im(z 5 ) = 2 f) Re(z 6 ) = 1, Im(z 6 ) = 0
 Komplex számok 1 Adjuk meg az alábbi komplex számok valós, illetve képzetes részét: a + i b i c z d z i e z 5 i f z 1 A z a + bi komplex szám valós része: Rez a, képzetes része Imz b Ez alapjá a megoldások
Komplex számok 1 Adjuk meg az alábbi komplex számok valós, illetve képzetes részét: a + i b i c z d z i e z 5 i f z 1 A z a + bi komplex szám valós része: Rez a, képzetes része Imz b Ez alapjá a megoldások
konvergensek-e. Amennyiben igen, számítsa ki határértéküket!
 1. Határértékek 1. Állapítsa meg az alábbi sorozatokról, hogy van-e határértékük, konvergensek-e. Amennyiben igen, számítsa ki határértéküket! 2 2...2 2 (n db gyökjel), lim a) lim n b) lim n (sin(1)) n,
1. Határértékek 1. Állapítsa meg az alábbi sorozatokról, hogy van-e határértékük, konvergensek-e. Amennyiben igen, számítsa ki határértéküket! 2 2...2 2 (n db gyökjel), lim a) lim n b) lim n (sin(1)) n,
Matematika I. NÉV:... FELADATOK:
 24.2.9. Matematika I. NÉV:... FELADATOK:. A tanult módon vizsgáljuk az a = 3, a n = 3a n 2 (n > ) rekurzív sorozatot. pt 2n 2 + e 2. Definíció szerint és formálisan is igazoljuk, hogy lim =. pt n 3 + n
24.2.9. Matematika I. NÉV:... FELADATOK:. A tanult módon vizsgáljuk az a = 3, a n = 3a n 2 (n > ) rekurzív sorozatot. pt 2n 2 + e 2. Definíció szerint és formálisan is igazoljuk, hogy lim =. pt n 3 + n
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN
 GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN Készült a TÁMOP-4.1.-08//a/KMR-009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN Készült a TÁMOP-4.1.-08//a/KMR-009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék
forgási hiperboloid (két köpenyű) Határérték: Definíció (1): Az f ( x, y) függvénynek az ( x, y ) pontban a határértéke, ha minden
 Kétváltozós függvéek Defiíció: f: R R vag z f(,) Szeléltetés:,,z koordiátaredszerbe felülettel Pl z + forgási paraboloid z R ( + ) félgöb z + + forgási iperboloid (két köpeű) z + forgási iperboloid (eg
Kétváltozós függvéek Defiíció: f: R R vag z f(,) Szeléltetés:,,z koordiátaredszerbe felülettel Pl z + forgási paraboloid z R ( + ) félgöb z + + forgási iperboloid (két köpeű) z + forgási iperboloid (eg
Országos Szilárd Leó fizikaverseny feladatai
 Országos Szilárd Ló fizikavrsny fladatai I katgória döntő, 5 április 9 Paks A fladatok mgoldásáoz 8 prc áll rndlkzésr Mindn sgédszköz asználató Mindn fladatot külön lapra írjon, s mindn lapon lgyn rajta
Országos Szilárd Ló fizikavrsny fladatai I katgória döntő, 5 április 9 Paks A fladatok mgoldásáoz 8 prc áll rndlkzésr Mindn sgédszköz asználató Mindn fladatot külön lapra írjon, s mindn lapon lgyn rajta
Matematika I. NÉV:... FELADATOK: 2. Határozzuk meg az f(x) = 2x 3 + 2x 2 2x + 1 függvény szélsőértékeit a [ 2, 2] halmazon.
![Matematika I. NÉV:... FELADATOK: 2. Határozzuk meg az f(x) = 2x 3 + 2x 2 2x + 1 függvény szélsőértékeit a [ 2, 2] halmazon. Matematika I. NÉV:... FELADATOK: 2. Határozzuk meg az f(x) = 2x 3 + 2x 2 2x + 1 függvény szélsőértékeit a [ 2, 2] halmazon.](/thumbs/102/154127337.jpg) 215.12.8. Matematika I. NÉV:... 1. Lineáris transzformációk segítségével ábrázoljuk az f(x) = ln(2 3x) függvényt. 7pt 2. Határozzuk meg az f(x) = 2x 3 + 2x 2 2x + 1 függvény szélsőértékeit a [ 2, 2] halmazon.
215.12.8. Matematika I. NÉV:... 1. Lineáris transzformációk segítségével ábrázoljuk az f(x) = ln(2 3x) függvényt. 7pt 2. Határozzuk meg az f(x) = 2x 3 + 2x 2 2x + 1 függvény szélsőértékeit a [ 2, 2] halmazon.
1/1. Házi feladat. 1. Legyen p és q igaz vagy hamis matematikai kifejezés. Mutassuk meg, hogy
 /. Házi feladat. Legyen p és q igaz vagy hamis matematikai kifejezés. Mutassuk meg, hogy mindig igaz. (p (( p) q)) (( p) ( q)). Igazoljuk, hogy minden A, B és C halmazra A \ (B C) = (A \ B) (A \ C) teljesül.
/. Házi feladat. Legyen p és q igaz vagy hamis matematikai kifejezés. Mutassuk meg, hogy mindig igaz. (p (( p) q)) (( p) ( q)). Igazoljuk, hogy minden A, B és C halmazra A \ (B C) = (A \ B) (A \ C) teljesül.
Rácsrezgések.
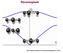 ácsrzgésk http://physics-imtis.cm/physics/glish/ph_txt.htm ácsrzgésk gitális hllám rúb Nwt II F x x F x V t F F x A x V x x x x x x A hllámszám értlmzési trtmáy végs mért prióiks htárfltétl Br-Kármá t
ácsrzgésk http://physics-imtis.cm/physics/glish/ph_txt.htm ácsrzgésk gitális hllám rúb Nwt II F x x F x V t F F x A x V x x x x x x A hllámszám értlmzési trtmáy végs mért prióiks htárfltétl Br-Kármá t
Függvény határérték összefoglalás
 Függvény határérték összefoglalás Függvény határértéke: Def: Függvény: egyértékű reláció. (Vagyis minden értelmezési tartománybeli elemhez, egyértelműen rendelünk hozzá egy elemet az értékkészletből. Vagyis
Függvény határérték összefoglalás Függvény határértéke: Def: Függvény: egyértékű reláció. (Vagyis minden értelmezési tartománybeli elemhez, egyértelműen rendelünk hozzá egy elemet az értékkészletből. Vagyis
18. Differenciálszámítás
 8. Differeciálszámítás I. Elméleti összefoglaló Függvéy határértéke Defiíció: Az köryezetei az ] ε, ε[ + yílt itervallumok, ahol ε > tetszőleges. Defiíció: Az f függvéyek az véges helye vett határértéke
8. Differeciálszámítás I. Elméleti összefoglaló Függvéy határértéke Defiíció: Az köryezetei az ] ε, ε[ + yílt itervallumok, ahol ε > tetszőleges. Defiíció: Az f függvéyek az véges helye vett határértéke
