Határérték-tételek véletlen mezőkre
|
|
|
- Lili Takács
- 7 évvel ezelőtt
- Látták:
Átírás
1 Határérték-tételek véletle mezőkre Doktori (PhD) értekezés Szerző: Karácsoy Zsolt Témavezető: Dr. Fazekas Istvá Debrecei Egyetem Természettudomáyi Doktori Taács Matematika- és Számítástudomáyok Doktori Iskola Debrece, 2010.
2
3 Határérték-tételek véletle mezőkre Doktori (PhD) értekezés Szerző: Karácsoy Zsolt Témavezető: Dr. Fazekas Istvá Debrecei Egyetem Természettudomáyi Doktori Taács Matematika- és Számítástudomáyok Doktori Iskola Debrece, 2010.
4
5 Eze értekezést a Debrecei Egyetem Természettudomáyi Doktori Taács Matematika- és Számítástudomáyok Doktori Iskola Valószíűségelmélet, matematikai statisztika és alkalmazott matematika programja keretébe készítettem a Debrecei Egyetem természettudomáyi doktori (PhD) fokozatáak elyerése céljából. Debrece, ovember 18. a jelölt aláírása Taúsítom, hogy Karácsoy Zsolt doktorjelölt között a fet megevezett Doktori Iskola Valószíűségelmélet, matematikai statisztika és alkalmazott matematika programjáak keretébe iráyításommal végezte mukáját. Az értekezésbe foglalt eredméyekhez a jelölt öálló alkotó tevékeységével meghatározóa hozzájárult. Az értekezés elfogadását javasolom. Debrece, ovember 18. a témavezető aláírása
6
7 Határérték tételek véletle mezőkre Értekezés a doktori (PhD) fokozat megszerzése érdekébe a Matematika tudomáyágba Írta: Karácsoy Zsolt okleveles matematikus Készült a Debrecei Egyetem Matematika- és Számítástudomáyok Doktori Iskolája (Valószíűségelmélet, matematikai statisztika és alkalmazott matematika programja) keretébe Témavezető: Dr. Fazekas Istvá A doktori szigorlati bizottság: elök: Dr. Terdik György (DE-TTK) tagok: Dr. Bara Sádor (DE-TTK) Dr. Jeey Adrás (ME-GÉIK) A doktori szigorlat időpotja: április 29. Az értekezés bírálói: Dr Dr Dr A bírálóbizottság: elök: Dr tagok: Dr Dr Dr Dr Az értekezés védéséek időpotja:
8
9 Köszöetyilváítás Ezúto szereték köszöetet modai midazokak, akik segítettek abba, hogy ez a disszertáció elkészüljö. Elsősorba témavezetőmek, Dr. Fazekas Istváak, a sok segítségért, a kutatási módszertai útmutatásaiért, az adott ispirációkért, a türelméért és a szigorúságáért, ami élkül ez a disszertáció sem készülhetett vola el. Ugyacsak köszöettel tartozom a Debrecei Egyetem Alkalmazott Matematika és Valószíűségszámítás Taszékéek, valamit a Miskolci Egyetem Alkalmazott Matematikai Taszékéek, hogy támogattak a taulmáyaim sorá. Elsősorba Dr. Fegyvereki Sádort szeretém kiemeli, aki mide segítséget megadva motivált a dolgozatom elkészítése sorá. Végül, de em utolsó sorba szeretém megköszöi szüleimek és barátaimak, hogy midebe segítettek, támogattak, biztattak és végig mellettem álltak.
10
11 Tartalomjegyzék Jelölések iii 1. Bevezetés 1 2. Autoregressziós típusú martigál mezők Bevezetés Defiíciók és előzméyek Martigál mezők kovergeciája Autoregresszív martigál mező defiíciója A-martigál mezők kovergeciája Autoregresszív martigál mezők kovergeciája Közpoti határeloszlás-tételek Bevezetés Jelölések és előzméyek Aszimptotikus eredméyek A tétel kiterjesztései A regressziós függvéy becslése Bevezetés Jelölések és a fő eredméy A fő tétel bizoyítása Példák Összefoglalás Summary 87 i
12 Irodalomjegyzék 100 Tárgymutató 108 Függelék 109 ii
13 Jelölések N, N 0 pozitív, illetve em egatív természetes számok halmaza Z egész számok halmaza R valós számok halmaza N d, Z d, R d d-dimeziós tér rácspotjai d-dimeziós vektor (Ω, F, P) valószíűségi mező F σ-algebra P(A) az A eseméy valószíűsége I{A} az A halmaz idikátor függvéye E várható érték var(.) szóráségyzet cov(.,.) kovariacia Kroecker-szorzat eloszlásbeli kovergecia N (m, Σ) ormális eloszlás m várható értékkel és Σ kovariacia-mátrixszal a = o(b ) a /b sorozat ullához kovergál a = O(b ) a /b sorozat korlátos c, C kostas D D véges halmaz számossága K magfüggvéy L p (C) a C-mérhető függvéyek L p tere iii
14
15 1. fejezet Bevezetés A határérték-tételekhez tartozó témakörök a valószíűségszámítás legfotosabb, legtöbbet kutatott fejezetei közé tartozak. Dolgozatomba határérték-tételeket bizoyítok külöböző feltételek eseté. Disszertációm első részébe autoregressziós típusú martigál mezőket taulmáyozok. Közismert, hogy a martigálokak sokfajta általáosítása létezik. A Doob-féle martigál kovergecia tételt többparaméterű esetre Cairoli általáosította (lásd [Cai70]). Vektor értékű martigálokra pedig Chatterji terjesztette ki (lásd [Cha68]). Az ő eredméyeit Fazekas Istvá általáosította többparaméterű esetre (lásd [Faz83]). MacQuee 1973-ba bevezette a lieáris martigál fogalmát ([MQ73]). Megmutatta, hogy az általa vizsgált folyamat sokkal közelebb áll a martigálokhoz, mit a stacioárius folyamatokhoz, ha az együtthatókra bizoyos feltételek teljesülek. Az általa tekitett speciális esetbe a Doob-féle martigál kovergecia tétel is teljesül. Dolgozata utolsó részébe több példát is ad, ahol lehet alkalmazi a lieáris martigálokat. Ezt az autoregresszív sémát azóta a szakirodalomba már többe vizsgálták ([Hey80], [Faz87], [Tom01]). Kétparaméterű esetre való kiterjesztésével Fazekas Istvá foglalkozott a 80-as évek közepé. Kiidulva Fazekas Istvá korábbi eredméyeiből ([Faz87], [Faz88]), sikerült kiterjesztei az autoregressziós típusú martigálokra voatkozó eredméyeket d-paraméterű esetre is, amely természetese tartalmazza a már korábba elkészített egy-, illetve kétparaméterű esetet is speciális esetkét (2.21. Tétel). Itt már magáak a d-paraméteres autoregressziós típusú martigál mező fogalmáak a kialakítása is saját eredméy, emcsak eze folyamat alkalmas reprezetáci- 1
16 2 1. BEVEZETÉS ója és a kovergecia tételek igazolása. A bizoyításba új ötleteket kellett felhaszáli, mert a korábbi eredméyekbe haszált módszerek em voltak alkalmazhatóak a d-paraméterű esetbe. A 2-él magasabb dimeziós paramétertér eseté bevezetett új formalizmus a vec operátoro és a Kroeckerszorzato alapul. Felhaszáltam továbbá a Burkholder-egyelőtleség általáos alakját is, amely Fazekas Istvá cikkébe található meg (lásd [Faz05]). A disszertáció második és harmadik részébe határérték-tételeket bizoyítok úgyevezett sűrűsödő-övekvő sémára. A sűrűsödő-övekvő eset léyegese eltér a tisztá sűrűsödő esettől. A sűrűsödő tulajdoság azt jeleti, hogy a megfigyelések helyei egyre sűrűbbek egy rögzített tartomáyba (lásd [Cre91]). A sűrűsödő esetbe több jól ismert becslés sem kozisztes (lásd [Lah96]). Ebbe az esetbe em várható a becslések aszimptotikus ormalitása, mert hiáyzik egy alkalmas cetrális határeloszlás-tétel. A sűrűsödő-övekvő tartomáy eseté a megfigyeléseik egyre sűrűbbek, miközbe a tartomáy mérete is tart a végtelehez. Ezt a godolatot ilye explicit formába először Lahiri vetette fel, majd egyre többe kezdtek foglalkozi ezzel a témával, hisze ez a megközelítés haszos lehet a földtudomáyok, meteorológia, köryezetvédelem, képfeldolgozás stb. területei is. Eze tudomáyterületeke számos olya folyamatot taulmáyozak, amely térbe vagy időbe folytoosa változik. A gyakorlatba em tudjuk folytoosa megfigyeli a folyamatokat, ezért véges adathalmazokat és diszkrét becsléseket haszáluk. Ezekbe a fejezetekbe gyegé függő valószíűségi mező létezését feltételezzük. Ehhez haszáljuk az úgyevezett α-keverő tulajdoságot. Természetese több keverő tulajdoság is létezik mid folyamatokra, mid mezőkre, ezeket az alábbiakba foglaljuk össze. Legye (Ω, A, P) valószíűségi mező és legyeek B és C rész σ-algebrái A- ak. A B és C σ-algebrák közti függőség leírására a következő együtthatókat vezették be a szakirodalomba: α = α(b, C) = sup P(B C) P(B)P(C), B B,C C β = β(b, C) = E(sup P(C) P(C B) ), C C φ = φ(b, C) = sup B B,P(B)>0,C C P(C) P(C B), ρ = ρ(b, C) = sup corr(x, Y ). X L 2 (B),Y L 2 (C)
17 3 Az együtthatók között a következő egyelőtleségek érvéyesek (lásd [Dou94]): 2α β φ, 4α ρ 2 φ. További egyelőtleségek megtalálhatók a [Dou94] és [Bra05] művekbe. A korábba bevezetett keverési együtthatók a következő itervallumból vehetek fel értékeket: 0 α(b, C) 1/4, 0 β(b, C) 1, 0 φ(b, C) 1, 0 ρ(b, C) 1. B és C akkor és csakis akkor függetle, ha a következő égy feltétel valamelyike teljesül: α(b, C) = 0, β(b, C) = 0, φ(b, C) = 0, ρ(b, C) = 0. Az α együtthatót Roseblatt ([Ros56]), a β együtthatót Kolmogorov (vö. [WR59]), a φ együtthatót Ibragimov ([Ibr59]), a ρ együtthatót Kolmogorov és Rozaov ([KR60]) az említett cikkeikbe vezették be. Továbbá számos más függőségi mérték is bevezetésre került (lásd [Bra83]). Legye X = (X k, k Z) valószíűségi változókak egy (em feltétleül stacioárius) sorozata. Defiiáljuk az FJ L σ-algebrát a következőképpe: F L J = σ(x k : J k L, k Z), J L. Defiiáljuk a következő együtthatókat mide 1 eseté ([Bra05]):
18 4 1. BEVEZETÉS α() = sup α(f j, F j+), j Z β() = sup β(f j, F j+), j Z φ() = sup φ(f j, F j+), j Z ρ() = sup ρ(f j, F j+). j Z Azt modjuk, hogy az X sztochasztikus folyamat erőse keverő (azaz α-keverő), ha lim k α(k) = 0. Ez a feltétel specifikálja az X múlt és jövő aszimptotikus függetleségét. Hasolóa vezethetők be a β, φ és ρ-keverő fogalmak is. A folyamat keverő tulajdoságára az alábbiak érvéyesek: φ-keverő β-keverő α-keverő, φ-keverő ρ-keverő α-keverő. Megmutatható, hogy az implikációk em megfordíthatók (lásd [Dou94], [Bra05]). Véletle mezők eseté az α-keverő feltételt a következőképpe vezetjük be (lásd [Guy95]). Az {ε(x) : x T }, T R d, α-keverési együtthatója: α(r, u, v) = sup{α(f I1, F I2 ) : ϱ(i 1, I 2 ) r, I 1 u, I 2 v}, a szuprémum a T mide I 1 és I 2 véges részhalmazára veedő, F Ii = σ{ε(x) : x I i }, i = 1, 2. Az első közpoti határeloszlás-tételeket keverő véletle sorozatokra Roseblatt bizoyította ([Ros56]) α-keverő esetre, valamit Ibragimov ([Ibr62]) a φ-keverő esetre. A dolgozatom szempotjából fotos előzméy, hogy Ibragimov és Liik ([IL71]) α-keverő folyamatokra, Guyo ([Guy95]) α-keverő mezőkre, Fazekas és Kukush ([FK00]) pedig α-keverő mezők eseté sűrűsödő-övekvő sémára bizoyítaak határérték-tételeket. Fazekas és Kukush em közöl részletes bizoyítást, ezért jele mukám második részébe rögzítem a bizoyítás lépéseiek részleteit (lásd a 3.5. Tétel és a 3.6. Tétel bizoyítását), valamit foglalkozom a tétel p-dimeziós kiterjesztéseivel is. A dolgozatom harmadik részéek témája a regressziós függvéy magfüggvéyes becslése. A magfüggvéyes becsléseket széles körbe taulmáyozza a szakirodalom. Nadaraya és Watso ([Nad64], [Wat64]) 1964-be
19 közölt eredméyeit számos cikkbe feldolgozták és általáosították. Ezeket az eredméyeket többek között Rao ([Rao83]), Devroye és Győrfi ([DG85]), valamit Bosq ([Bos98]) foglalta össze. A magfüggvéyes becslések egy fotos tulajdosága az aszimptotikus ormalitás, melyet több cikkbe is taulmáyoztak. Például 1972-be Schuster ([Sch72]) diszkrét esetbe bizoyított aszimptotikus ormalitást, míg 2001-be Cai ([Cai01]) folytoos esetbe látott be hasoló eredméyt. A regressziós függvéy magfüggvéyes becsléséek vizsgálata szorosa kapcsolódik a sűrűségfüggvéy becsléséhez (lásd [CL86], [BMP99], [FC06]). Eze eredméyekből kiidulva sikerült a regressziós függvéy aszimptotikus ormalitását bizoyítai α- keverő mezőkre sűrűsödő-övekvő tartomáyt tekitve. Eze tételt tekitem a dolgozat legfotosabb eredméyéek (4.1. Tétel). Dolgozatomból, illetve Fazekas Istvá korábbi eredméyeiből ([FC06]) kiderül, hogy ez az eset a diszkrét és a folytoos idejű esetek között helyezkedik el. Potosabba szólva, a határeloszlás kovariacia struktúrája a diszkrét és a folytoos idejű határeloszlások lieáris kombiációjakét adódik. Dolgozatomat két példával zárom, melye keresztül szemléltetem a határeloszlást. A umerikus példák jól mutatják az előbb jelzett speciális kovariacia struktúrát. 5
20
21 2. fejezet Autoregressziós típusú martigál mezők 2.1. Bevezetés A disszertáció első részébe a lieáris martigálok többparaméteres kiterjesztésével foglalkozom, és fő eredméykét majdem mideütti kovergeciát bizoyítok. Ez az eredméy speciális esetkét tartalmazza Fazekas Istvá eredméyeit is (lásd [Faz87], [Faz88]). Közismert, hogy a martigálokak sokfajta alkalmazása és általáosítása létezik. Számos vizsgálat alapját a Doob-féle martigál kovergecia tétel szolgáltatta, amit itt most mi is felidézük Tétel. (Doob, [Doo53]) Legye X = (X, F ) szubmartigál. Tegyük fel, hogy sup E X <. Ekkor lim X = X létezik 1 valószíűséggel és E X <. A Doob-féle martigál kovergecia tételt többparaméterű esetre Cairoli általáosította (lásd [Cai70]). Vektor értékű martigálokra pedig Chatterji terjesztette ki (lásd [Cha68]). Az ő eredméyeit Fazekas Istvá általáosította többparaméterű esetre (lásd [Faz83]). Közismert, hogy a valószíűségbeli és az L p -beli (p 1) kovergecia metrizálható (mid valós, mid Baach-térbeli értékű valószíűségi változókra). Így ezek eseté az egyparaméterű esetből adódik a többparaméterű sorozatok kovergeciája. 7
22 8 2. AUTOREGRESSZIÓS TÍPUSÚ MARTINGÁL MEZŐK A majdem biztos kovergecia (általába) em metrizálható. Így az egyparaméterű esetből em lehet közvetleül következteti a többparaméterűre. Sőt, Cairoli ([Cai70]) bebizoyította, hogy d-paraméterű martigál eseté a kovergecia feltétele: sup E X (log + X d 1 ) <. Gut ([Gut76]) belátta, hogy a agy számok Kolmogorov-féle erős törvéye akkor és csak akkor érvéyes, ha E X 1 (log + X 1 d 1 ) <. Itt X i, i N d, függetleek és azoos eloszlásúak (lásd [Faz83] Theorem 5.3.). A B Baach-térbeli martigálok elméletéek alapjai (pl. B-beli valószíűségi változók feltételes várható értéke) Scalora ([Sca61]) cikkébe található meg. Chatterji 1968-ba ([Cha68]) B-beli martigálokra bizoyította, hogy a valós martigál kovergecia tétel csak akkor érvéyes, ha kiegészítő feltételeket teszük fel. Például, ha X = E(X F ) alakú, ahol E X <, akkor X kovergál L 1 -be és majdem biztosa. Vagy például, ha B Rado-Nikodym tulajdoságú, akkor az (X, F ) martigál sup E X < eseté majdem biztosa kovergál. MacQuee a martigálok következő kiterjesztését kezdte el vizsgáli (lásd [MQ73]): legye (ξ t, F t, t = 1, 2,...) valószíűségi változók adaptált sorozata, ami teljesíti a (2.1) E(ξ s F s 1 ) = a 1 ξ s a m ξ s m feltételt, ahol m rögzített egész, s > m, és a 1,..., a m em véletle együtthatók. A (2.1)-ből kapjuk, hogy ξ s = a 1 ξ s a m ξ s m + δ s, ahol δ s martigál differecia. MacQuee megmutatta, hogy a ξ s folyamat sokkal közelebb áll a martigálokhoz, mit a stacioárius folyamatokhoz, ha az a k együtthatók pozitívak és k=1 a k = 1 teljesül. Ebbe a speciális esetbe a Doob-féle martigál kovergecia tétel is teljesül (lásd [MQ73], Sectio 3). Dolgozata utolsó részébe több példát is ad, ahol lehet alkalmazi a lieáris martigálokat. Ezt az autoregresszív sémát azóta a szakirodalomba már többe vizsgálták ([Hey80], [Faz87], [Tom01]). Kétparaméterű esetre Fazekas Istvá
23 2.2. DEFINÍCIÓK ÉS ELŐZMÉNYEK 9 terjesztette ki. Kiidulva Fazekas Istvá korábbi eredméyeiből ([Faz87], [Faz88]), sikerült kiterjesztei az autoregressziós típusú martigálokra voatkozó eredméyeket d-paraméterű esetre, amelyek természetese tartalmazzák a már korábba elkészített egy, illetve kétparaméterű esetet is speciális esetkét. A bizoyításba új ötleteket kellett felhaszáli, mert a korábbi eredméyekbe haszált módszerek em voltak alkalmazhatóak a d-paraméterű esetbe. A 2-él magasabb dimeziós paramétertér eseté bevezetett új formalizmus a vec operátoro és a Kroecker-szorzato alapul. Felhaszáltam továbbá a Burkholder-egyelőtleség általáos alakját is, amely Fazekas Istvá cikkébe található meg (lásd [Faz05]) Defiíciók és előzméyek A továbbiakba a következő jelöléseket fogjuk haszáli: legye d egy pozitív rögzített egész szám. Az i, j, k, l, m, jelöljö d-dimeziós vektorokat. (pl. = ( 1,..., d ) N d 0 ). Felhaszáljuk még az 1 := (1,..., 1) N d és 0 := (0,..., 0) N d 0 jelöléseket. A relációkat N d 0-ba koordiátákét értelmezzük, azaz m, ha m i i, i = 1,..., d; továbbá m <, ha m és m. A max, mi, relációkat szité koordiátákét értelmezzük. Például:, ha i mide i = 1,..., d eseté. Egy d-dimeziós vektor logaritmusáak abszolút értéké a log := d log + i i=1 kifejezést értjük, ahol log + l x, ha x e x = 1, ha x < e. A továbbiakba legye (Ω, F, P) valószíűségi mező, X, N d, valószíűségi változók egy d-paraméterű sorozata, és legye F F σ-algebra mide N d -re. Jelölje az vektor bizoyos koordiátáiak a halmazát és jelölje a maradék koordiátáit az vektorak. Jelöljük (, )-el azo d hosszúságú sorozatokat, amelyek azo koordiátáit tartalmazzák, amelyek elemei -ek, míg többi koordiátája legye -el egyelő. Például, ha az második és harmadik koordiátáját tartalmazza, akkor (, ) = (, 2, 3,,..., ) és (, ) = ( 1,,, 4,..., d ).
24 10 2. AUTOREGRESSZIÓS TÍPUSÚ MARTINGÁL MEZŐK Jelölje F (, ) az F k σ-algebrák által geerált σ-algebrát, ahol k (, ), k N d. Például a feti esetbe F (, ) = σ{f k : k 2 2, k 3 3 }, és F (, ) = σ{f k : k 1 1, k 4 4,..., k d d }. Legye (B,. ) valós, szeparábilis Baach-tér. Jelölje c(b) a B-beli koverges sorozatok halmazát. Ha X = (x 1, x 2,...) c(b), legye X c = sup i x i. Defiiáljuk teljes idukcióval a c d (B) tereket (és a ormát ebbe a térbe), azaz c d (B) = c(c d 1 (B)). Jelölje c 0 (B) a 0-hoz kovergáló sorozatok halmazát (0 eleme B-ek). Tegyük fel, hogy F m F mide m -re. Továbbá, hogy X F - mérhető és itegrálható (azaz E X < ) mide N d -re. Azt modjuk, hogy (X, F ) martigál, ha E(X +k F ) = X teljesül m.m., mide N d és k N d 0 eseté. Ebbe a fejezetbe végig feltesszük, hogy (2.2) E (E(X l F m ) F ) = E ( X l F mi{m,} ) teljesül mide l,, m N d eseté. Ezt a tulajdoságot gyakra alkalmazzák többparaméterű martigálok elméletébe (lásd [Faz83]). A fő eredméyük bizoyításához szükségük lesz a (2.2)-él kissé erősebb feltételre is, amelyet az alábbiakba elemzük. Tetszőleges véges várható értékű η-ra: ( ( ) (2.3) E (η F ) = E... E η F (i 1) )... F (i d) az (1,..., d) mide (i 1,..., i d ) permutációja eseté, ahol F (i) = σ{f l : l i = i } mide rögzített -re és i-re (az F (i) képletbe (i) a megfelelő koordiáta). Valójába F (i) speciális esete az F (, ) -ek, hisze F (i) = F (, ), ha (, ) = (,...,, i,,..., ). Köyű beláti, hogy (2.3)-ból következik a következő tulajdoság (2.4) E {η F } = E{E{η F (, ) } F (, ) }, mide véges várható értékű η eseté. Eek belátásához jelölje az
25 2.2. DEFINÍCIÓK ÉS ELŐZMÉNYEK 11 i 1,..., i l koordiátáját. Alkalmazva (2.3)-t az E{η F (, ) }-re, kapjuk, hogy E{η F } = E{E(η F (, ) ) F } (2.5) = E{... E[E... [E(η F (, ) ) F (i 1) ]... F (i l) ]... F (i d) } = E{... E[... E(η F (, ) ) F (i l+1) ]... F (i d) }, mivel F (i 1),..., F (i l) tartalmazza F (, ) -t. Tehát E {η F } = E{E(η F ) F (, ) } = E{E[E... [E(η F (, ) ) F (i l+1) ]... F (i d) ] F (, ) } = E{E{η F (, ) } F (, ) }, ahol a második lépésbe (2.5)-öt alkalmaztuk. Továbbá a (2.4)-ből következik, hogy (2.6) E(E(η F m ) F ) = E(η F mi{m,} ) mide véges várható értékű η eseté. Speciálisa, (2.4)-ből következik (2.2). Közismert ([Kho02], 36 o.), hogy (2.6)-ból következik (2.3). Tehát végeredméykét kapjuk, hogy (2.3), (2.4) és (2.6) ekvivalesek és adódik belőlük (2.2) Állítás. Legyeek ε, N d, függetle valószíűségi változók, F = σ{ε k : k }. Ekkor F, N d, teljesíti (2.3)-at. Bizoyítás. Először d = 2 esetre bizoyítjuk az állítást. Jelölje ξ 12, ξ 1 és ξ 2 a következő véletle elemeket: ξ 12 = (ε ij : i 1, j 2 ), ξ 1 = (ε ij : i 1, j > 2 ) és ξ 2 = (ε ij : j 2, i > 1 ). Ekkor E(η ξ 12, ξ 1 ) = f(ξ 12, ξ 1 ), ahol f mérhető függvéy. Ekkor (2.7) E{E(η F (1) ) F (2) } = E{E(η ξ 12, ξ 1 ) ξ 12, ξ 2 } = E{f(ξ 12, ξ 1 ) ξ 12, ξ 2 } = g(ξ 12 ). Eek bizoyításához először vegyük észre, hogy a ξ 12, ξ 1 és ξ 2 függetleségéből következik E{f(ξ 12, ξ 1 ) ξ 12 = x 12, ξ 2 = x 2 } = E(f(x 12, ξ 1 )) = g(x 12 ),
26 12 2. AUTOREGRESSZIÓS TÍPUSÚ MARTINGÁL MEZŐK ahol g mérhető függvéy. Helyettesítsük be ξ 12 -t és ξ 2 -t ebbe az egyeletbe és megkapjuk (2.7)-et. Kihaszálva, hogy F F (1), F (2), és hogy (2.7) teljesül, azt kapjuk, hogy E{η F } = E{E[E(η F (1) ) F (2) ] F } = E{g(ξ 12 ) F } = g(ξ 12 ) = E[E(η F (1) ) F (2) ]. Ha d = 3, akkor a bizoyítás a következőkö alapul. Jelölje ξ x, ξ xy, ξ xz, és ξ xyz a következő véletle elemeket: ξ x = (ε ijk : i 1, j > 2, k > 3 ), ξ xy = (ε ij : i 1, j 2, k > 3 ), ξ xz = (ε ij : i 1, j > 2, k 3 ) és ξ xz = (ε ij : i 1, j 2, k 3 ). Hasolóa defiiáljuk a többi ξ y, ξ z,... véletle elemet is. Először legye: E(η F (1) ) = E(η ξ xyz, ξ xy, ξ xz, ξ x ) = f(ξ xyz, ξ xy, ξ xz, ξ x ). Észrevesszük, hogy ξ xyz, ξ xy, ξ xz, ξ x függetleek. Másodszor: E [ E(η F (1) ] = E{f(ξxyz, ξ xy, ξ xz, ξ x ) ξ xyz, ξ xy, ξ yz, ξ y } = g(ξ xyz, ξ xy ) ) F (2) adódik, hisze (ξ xz, ξ x ) és (ξ xyz, ξ xy, ξ yz, ξ y ) függetleek. Harmadszor, tekitsük a következő E { E [ E(η F (1) ] (3)} F = E{g(ξxyz, ξ xy ) ξ xyz, ξ zx, ξ zy, ξ z } = h(ξ xyz ), ) F (2) hisze ξ xy és (ξ xyz, ξ zx, ξ zy, ξ z ) függetleek. Kihaszálva, hogy F F (1), F (2), F (3) és az előző egyelőséget, adódik, hogy E{η F } = E ( E ( E ( E(η F (1) ) F (2) ) (3)) ) F F ) = E(h(ξ xyz ) F = h(ξxyz ) = E { E [ E(η F (1) ] (3)} F. ) F (2) d > 3 eseté a bizoyítás hasoló módo törtéik Martigál mezők kovergeciája Első eredméyem többparaméterű B-értékű martigálok egyeletes kovergeciájáról szól. Ez a tétel a [Faz83] Theorem 4.4. egy változata, melybe az egyeletes kovergeciát em vizsgálták.
27 2.3. MARTINGÁL MEZŐK KONVERGENCIÁJA 13 Először eleveítsük fel a Rado-Nikodym tulajdoságot (lásd [Cha68]). A B Baach-tér redelkezik a Rado-Nikodym tulajdosággal az (Ω, F, P)- re voatkozóa, { ha mide korlátos variációjú (azaz V µ (Ω) <, ahol V µ (A) = sup k=1 µ(a k) } Ak F, A k A, A k diszjukt ) B-értékű σ additív µ : F B halmazfüggvéy, amely abszolút folytoos P-re ézve (azaz P(A) = 0 µ(a) = 0, jelölésbe V µ P) redelkezik itegrál reprezetációval, azaz létezik olya f L 1 (F, B), hogy µ(a) = A f(s)p(ds) mide A F eseté. Itt L 1 (F, B) B-beli értékű, F-mérhető. Egy B térről azt modjuk, hogy redelkezik a Rado-Nikodym tulajdosággal, ha az egység itervallum Borel-halmazá értelmezett Lebesguemértékre ézve redelkezik a Rado-Nikodym tulajdosággal. Szükségük lesz még a Fazekas Istvá [Faz83] dolgozatába közölt következő eredméyekre: 2.3. Lemma. ([Faz83] Lemma 2.4., 158 o.) 1. Legye X i (i Z) B-értékű valószíűségi változó. Ha az X i sorozat koverges m.m., akkor X = (X 1, X 2,...) c(b)-értékű valószíűségi változó. 2. Legye X = (X 1, X 2,...) c(b)-értékű valószíűségi változó és legye A rész σ-algebrája F-ek. Tegyük fel, hogy E X c <, akkor (E(X A)) i = E(X i A) (i Z), azaz a c(b)-beli feltételes várhatóértéket koordiátákét képezhetjük Tétel. ([Faz83] Theorem 4.4., 162 o.) Legye {X m, F, m Z d } B- értékű martigál. Tegyük fel, hogy E{X (m,) F (k, ) } = X (k,), ha k m, ahol (m, ) = (m 1, m 2,..., m j, 1, 2,..., i ) Z d, (k, ) = (k 1, k 2,..., k j, 1, 2,..., i ) Z d, és F (k, ) = σ{ Z i F (k,)}, (i + j = d; i, j 1). B redelkezze a Rado-Nikodym tulajdosággal vagy legye X m = E(X F m ) alakú, valamely X L 1 (F, B)-re. Tegyük fel, hogy sup E X m (log + X m d 1 ) <, m Z d ekkor lim X m létezik m.m. (és L 1 -be d 2 eseté). m A bizoyításba haszáli fogjuk a Cairoli-egyelőtleséget is.
28 14 2. AUTOREGRESSZIÓS TÍPUSÚ MARTINGÁL MEZŐK 2.5. Megjegyzés. (Cairoli-egyelőtleség, [Faz83] 158 o.) t(log + t) r 2 log + [t(log + t) r 2 ] (r 1)t(log + t) r 1, r 2, t Tétel. Legye B egy valós szeparábilis Baach-tér. Legye (X, F ), N d, B-értékű martigál. Tegyük fel, hogy az F σ-algebra teljesíti a (2.4)-et. B redelkezze a Rado-Nikodym tulajdosággal vagy legye X = E(X F ), N d alakú, valamely X L 1 (F, B)-re. Tegyük fel, hogy sup E X (log + X d 1 ) <. Ekkor létezik egy olya A eseméy, melyre P(A) = 1 és mide ω A-ra teljesül a következő: ha az tetszőleges koordiátái kovergálak a -hez, míg a maradék koordiáták rögzítettek maradak, akkor X (ω) egyeletese kovergál. (A határérték egy, a rögzített koordiátáktól függő valószíűségi változó.) Egy kétparaméteres martigál eseté a tételbeli kovergecia a következőt jeleti. Legye ε > 0. Ekkor mide rögzített ω A-ra igaz: mide 2 eseté X 1, 2 (ω) X,2 (ω) < ε, ha 1 > 1ε ; mide 1 eseté X 1, 2 (ω) X 1, (ω) < ε, ha 2 > 2ε ; továbbá X 1, 2 (ω) X, (ω) < ε, ha 1, 2 > ε. A 2.6. Tétel bizoyítása. A bizoyítást d szeriti idukcióval végezzük. d = 1 esetbe az eredméy már ismert (lásd [Cha68]). Tegyük fel, hogy a tétel érvéyes a d 1-et meg em haladó dimeziókra. Most belátjuk d-re, d 2. (Rögzítjük az utolsó koordiátáját.) Látható, hogy (X, F ), N d, B értékű martigál, melyre teljesülek a 2.4. Tétel feltételei. Fazekas Istvá igazolja (lásd [Faz83]), hogy X = E(X F ), Z d, és X X ( ) L 1 -be, ahol X F -mérhető. Belátjuk, hogy X kovergál 1 valószíűséggel egyeletese, midő - ek csupá éháy koordiátája tart a végtelebe. Legye Z m (k) = X (m,k), ahol k N rögzített és m N d 1 a futóidex. Ez egy (d 1) idexes martigál, mely egyrészt Z m (k) = E(X F (m,k) ) alakú. Ie Z m (k) = X (m,k) = E ( ) [ ] X (m,k) F (,k) = E E(X F(m,k) ) F (,k) = = E [ ] ( ) E(X F (,k) ) F (m,k) = E Z (k) F (m,k),
29 2.3. MARTINGÁL MEZŐK KONVERGENCIÁJA 15 ahol Z (k) = E ( X F (,k) ). Most felvázoljuk a bizoyítás fő ötletét: Haszáljuk ki azt, hogy Z (k) m (mide rögzített k-ra) egy (d 1) paraméterű martigál. Az idukciós egyeletese kovergál, ha m koordiátáiak bármely részhalmaza tart a végtelehez. A Z m (k) felépítése a következő. Ha m-ek csak az utolsó koordiátája, azaz m d 1 tart a végtelehez, akkor Z m (k) egy feltevés miatt Z (k) m koverges sorozat (1 valószíűséggel), azaz ez a sorozat c(b)-ek egy eleme. Tekitsük most azt az esetet, amikor m d 2 a futóidex. Ekkor az előző c(b)-beli elemekből álló sorozat koverges. Tehát ez a c(c(b))-ek egy eleme. Végezetül Z m (k) c(... c(b)) = c d 1 (B). Téylegese azt fogjuk }{{} d 1 megmutati, hogy X c d (B). Rátérük a potos bizoyításra. Meg kell mutati, hogy Z m (k) 1 valószíűséggel koverges. Eek igazolásához határozzuk meg a keresett határértéket. Feltehető, hogy X F -mérhető, ezért X = E(X F )-ből következik, hogy X X L 1 -be. Legye Z m ( ) = E ( ) ( ) X F (m, ). Ekkor Z m ( ), F (m, ), m N d 1, egy martigál. A szubmartigál kovergecia tétel miatt kapjuk, hogy E X (log + X ) d 1 sup N d E X (log + X ) d 1 K <. A Jese-egyelőtleségből következik, hogy (2.8) E Z m ( ) (log + Z m ( ) ) d 1 E X (log + X ) d 1 K <. ( ) Azaz a Z m ( ), F (m, ), m N d 1, martigál kielégíti a tétel feltételeit, ezért (az idukciós feltétel miatt) tekithetjük ezt a martigált a c d 1 (B) egy véletle eleméek. Be kell látuk, hogy ) (2.9) E (Z ( ) F (,k) = Z (k) teljesül mide k eseté. Itt Z ( ) = {Z m ( ) : m N d 1 }, valamit Z (k) = {Z m (k) : m N d 1 }. A (2.9) egyelőséget mide rögzített m eseté bizoyítjuk. Az előzőekből: ( ) E Z m ( ) F (,k) = E [ E ( ) ] ( ) (k) X F (m, ) F(,k) = E X F(m,k) = Z m.
30 16 2. AUTOREGRESSZIÓS TÍPUSÚ MARTINGÁL MEZŐK Viszot ha E Z ( ) c d 1 (B) < teljesül, akkor a 2.3. Lemmából következik, hogy elegedő beláti (2.9)-et koordiátákét. (A Z ( ) c d 1 (B) kifejezésbe a c d 1 (B) tér ormáját haszáljuk.) A (2.8) miatt azt kapjuk, hogy sup m E Z m ( ) (log + Z m ( ) ) d 1 <. Alkalmazva a 2.4. Tétel bizoyítását (lásd [Faz83]), a Cairoli-egyelőtleséget (2.5. Megjegyzés) és a teljes idukciót, kapjuk, hogy E Z ( ) c d 1 (B) <. Tehát (2.9) érvéyes. Ezért Z (k) Z ( ) m.m. Most bebizoyítjuk, hogy ha tetszőlegese sok koordiáta az -ből tart a végtelebe, akkor X egyeletese koverges 1 valószíűséggel. Osszuk fel -et részekre: = (m, l, k), ahol k N. A c d 1 (B)-beli esetre alkalmazva a martigál kovergecia tételt lim X (m,l,k) = X (m,l, ) a c d 1 (B) térbe k m.m. Azaz mide ε > 0 eseté létezik olya k ε, hogy ha k > k ε akkor X (m,l,k) X (m,l, ) < ε, mide l, m eseté. De X (m,l, ) c d 1 (B) teljesül, így X (m,l, ) X (m,, ) < ε amikor l elegedőe agy. Ezekből X (m,l,k) X (m,, ) < 2ε, amikor k és l elegedőe agy. Tehát az állítás bizoyítása teljes Az autoregresszív martigál mező defiíciója Ahhoz, hogy leírjuk a vizsgáladó ξ, N d, véletle mező struktúráját, szükséges a Kroecker-szorzat (jelölje ) és a vec operátor fogalma (lásd [MN88]) Defiíció. Legye A egy m -es mátrix és legye a j az A mátrix j-edik oszlopa. Ekkor vec A egy m 1-es vektor lesz a következő formába: vec A = a 1 a 2. a. Tehát a vec operátor átalakítja a mátrixot egy vektorrá úgy, hogy először az első oszlopot veszi, majd ez alá írja a második oszlopot, ez alá a harmadikat,... (alapvető tulajdoságok megtalálhatók az [MN88]-ba).
31 2.4. AUTOREGRESSZÍV MARTINGÁL MEZŐ DEFINÍCIÓJA 17 A vec operátor egy d-dimeziós tömböt is egy vektorrá alakít át. Először az első idex fut, azutá a második és így tovább. Például tekitsük egy 3-idexes tömböt, A = (a ijk ) l m i=1 j=1 k=1, ekkor vec A = (a 111, a 211,..., a l11, a 121,..., a l21,..., a 1m,..., a lm ) Defiíció. Legye A m -es, valamit B p q dimeziós mátrixok. Ekkor a következő mp q alakú mátrixot a 11 B a 1 B.. a m1 B a m B az A és B mátrixok Kroecker-szorzatáak evezzük és A B-vel jelöljük. A Kroecker-szorzat redelkezik a következő tulajdoságokkal: 1. A B C = (A B) C = A (B C); 2. A B = (A I)(I B), ahol I jelöli az egységmátrixot; 3. Ha AC és BD is létezik, akkor (A B)(C D) = AC BD; 4. vec(abc) = (C A) vec B Defiíció. A {ξ, F }, N d, folyamatot autoregresszív típusú martigál mezőek evezük, ha teljesülek a következő feltételek: 1. ξ F -mérhető és itegrálható mide N d eseté, 2. (2.10) ( ) E ξ F (j) e j = a (j) 1 ( j)ξ ej + a (j) 2 ( j)ξ 2ej a (j) m ( j )ξ m ej
32 18 2. AUTOREGRESSZIÓS TÍPUSÚ MARTINGÁL MEZŐK mide -re és j-re, ahol m egy rögzített pozitív egész szám, j > m, j = 1,..., d, továbbá e j = (0,..., }{{} 1,... 0) N d 0 a j-edik egységvektor, j = 1,..., d, és a (j) i j ( j ) em egatív, em véletle együtthatók, amelyekre teljesül, hogy m a (j) i ( j ) = 1 i=1 mide j = m + 1, m + 2,..., j = 1,..., d eseté. Ha az a (j) k (l) értékek em függek l-től, akkor ξ -t homogé autoregresszív martigál mezőek evezzük. Legye ξ, N d, egy d-paraméterű véletle mező. A ξ segítségével megkostruáluk egy új X véletle mezőt. Az X mező értékeit d- paraméterű tömbök fogják alkoti. Mide rögzített m N és N d eseté ( i m, i = 1,..., d) X a véletle mező azo ξ k elemeit tartalmazza, amelyek az idexei egy m } m {{... m } -es hiperkockába tartozak. Potosabba, legye az X tömb k-adik eleme X k = ξ m+k, ahol d m = (m,..., m) N d, k = (k 1,..., k d ), k i = 1,..., m, i = 1,..., d. Ha a paramétereket az időek tekitjük és a jele, akkor X tartalmazza a jelebeli ξ értéket és m d 1 darab múltbeli értéket Állítás. Legye (ξ, F ) a 2.9. Defiícióba bevezetett autoregresszív martigál mező és X a ξ -ből származó tömbértékű véletle mező. Ekkor (2.11) vec [ E ( )] ( X F (j) e j = I } {{ } I d j A ( j) j ) I } {{ } I vec(x ej ) j 1 teljesül mide -re, ahol j > m, j = 1,..., d, és A (l) j mide j = 1,..., d, l = m + 1, m + 2,... eseté a következő m m-es mátrixot A (l) j = a (j) m (l) a (j) m 1 (l) a(j) 1 (l)
33 2.4. AUTOREGRESSZÍV MARTINGÁL MEZŐ DEFINÍCIÓJA 19 jelöli. Látható, hogy az A (l) j mátrix egy Markov-lác átmeeti mátrixa. Feltesszük, hogy a (j) m (l) > 0, ekkor a lác irreducibilis. Ha ez a lác aperiodikus, akkor ergodikus is. Ha a (j) k (l) > 0, akkor k a lác utolsó állapotáak a visszatérési ideje. Tehát, ha a {k : a (j) k (l) > 0} számok legagyobb közös osztója egyelő 1-gyel, akkor a lác aperiodikus. A Állítás bizoyítása. Meg kell határozi, hogy az egy lépéssel visszafelé vetítés hogya alakul (azaz hogya alakul a feltételes várható érték). Vegyük észre, hogy az m m-es mátrixok tételbeli d-szeres Kroecker-szorzatai a következőképpe alakulak: ( I I } {{ } d j A ( j) j ) I } {{ I } = I 1 A ( j) j I 2, j 1 ahol I 1 m d j m d j, illetve I 2 m j 1 m j 1 dimeziós egységmátrixok. Ezért a szorzat egy olya blokk-diagoális mátrix, amely főátlójába m d j darab tömb áll, melyek midegyike a a a a a a 12 a a a a a a alakú. Vagyis ezek a blokkok m 2 darab m j 1 m j 1 méretű diagoális mátrix-tömbből állak. Az első mátrix főátlójába a 11 áll, a második mátrix főátlójába a 12 áll, és így tovább. Ezt a mátrixot meg kell szorozi egy m d elemű vektorral (a vec X -el).
34 20 2. AUTOREGRESSZIÓS TÍPUSÚ MARTINGÁL MEZŐK Tekitsük az X ( fix) tömbbe azokat az elemeket, melyekek a j- edike kívüli mide idexe egy értéke le va rögzítve, míg a j-edik idexe fut 1-től m-ig. Ezt a vektort jelölje Y (j). Az ugyailye módo X ej -ből kapott vektort jelölje Y ej (j). A (2.10) alapjá látható, hogy ( (2.12) E Y (j) F (j) e j ) Tehát csak azt kell látuk, hogy = A ( j) j Y ej (j). (2.13) I I A ( j) j I I vec(x ej ) alkalmas része éppe A ( j) j Y ej (j)-vel egyelő. A rövidség kedvéért legye A ( j) j = A = (a st ), X ej = X k. Először legye j = 1. Ekkor a (2.13)-ba szereplő I I A mátrix alakja A A... 0 (2.14)..... = I I A A és a (2.13)-ba szereplő vec(x e1 ) vektor alakja (2.15) (x 111, x 211,..., x m11 ; x 121, x 221,..., x m21 ;... ; x 1mm, x 2mm,..., x mmm ). (Itt d = 3 esetet szemléltettük, de tetszőleges d esete léyegébe ugyailye.) A feti vektor egymás utái m hosszúságú szeletei az Y e1 (1) lehetséges alakjai. Ezek képei, azaz a A ( 1) 1 Y e1 (1) alakú vektorok, éppe a feti (2.14)-beli blokkdiagoális mátrixszal való szorzás útjá adódak a (2.15)-beli vektorból. Tehát j = 1 eseté kész a bizoyítás. Most a j > 1 esetet képzeljük el úgy, hogy a d-t öveljük, így a (2.15)-beli vektorba mide koordiáta idexe elé kell íruk éháy idexet (éppe j 1-et) és ezek az idexek midyája végigfutak mid az m értéke. Pl. j = 3 eseté x 121 helyett az alábbi vektor jö be: (x 11121, x 21121,..., x m1121 ; x 12121, x 22121,..., x m2121 ;...).
35 2.4. AUTOREGRESSZÍV MARTINGÁL MEZŐ DEFINÍCIÓJA 21 Tehát egyetle koordiáta helyett lesz (j 1) m új koordiáta, de a fix 121 utolsó idexrészlet csak ebbe a (j 1) m darab koordiátába szerepel, máshol em. Látható, hogy a (2.12)-be leírt traszformáció sorá azoosa viselkedő, azaz együtt kezeledő, vektor koordiáták (j 1) m távolságra leszek egymástól. Így adódik az I I }{{} j 1 mátrixszal való Kroeckerszorzás a (2.13) formulába. Ez ugyais a (2.14)-beli mátrixelemeit (j 1) m távolságra viszi egymástól Állítás. Legye X tömbértékű véletle mező, ami teljesíti a (2.11) egyelőséget. Feltesszük továbbá, hogy (2.3) is teljesül. Ekkor az (X, F ) folyamatra a következő egyelőség teljesül: (2.16) vec [E(X +t F )] = (A d ( d + t d, d ) ahol A 2 ( 2 + t 2, 2 ) A 1 ( 1 + t 1, 1 )) vec(x ), (2.17) A j ( j + t j, j ) = A ( j+t j ) j A ( j+t j 1) j mide j > m, j = 1,..., d és N d, t N d 0 eseté. A ( j+1) j A fetiekbe és a következőkbe A j ( j, j ) = I, ahol I az egységmátrixot jelöli. A Állítás bizoyítása. Legye A i = A i ( i + t i, i ), i = 1,..., d. Vegyük észre, hogy az A d A 2 A 1 szorzat felbotható d darab mátrix szorzatára a következőképpe A d A 2 A 1 = (A d I I)(I A d 1 I) (I I A 1 ). Felhaszálva a (2.3) egyelőséget, kapjuk, hogy ( ( ) E (X +t F ) = E... E X +t F (1) )... F (d). Továbbá a Állítás alapjá [ ( )] vec E X +t F (1) = (I I A 1 ) vec(x ),.
36 22 2. AUTOREGRESSZIÓS TÍPUSÚ MARTINGÁL MEZŐK [ ( )] vec E X +t F (d) = (A d I I) vec(x ), amiből adódik az állítás. Általáosítva a (2.16)-os tulajdoságot, a következő fogalmat kapjuk Defiíció. Egy tömbértékű (X, F ), N d, folyamatot A-martigál mezőek evezük, ha teljesülek a következők: 1. X F -mérhető és itegrálható mide N d -re, 2. a (2.16) egyelőség teljesül mide, t N d -re, ahol az A j ( j +t j, j ) mátrixok kielégítik a (2.17)-et. (Mide vizsgált A (l j) j m m típusú mátrix em véletle.) Megjegyzés. Jelölje az X A-martigál mező martigál differecia mezőjét. Ekkor (2.18) = ( 1) d k=1 ε k E(X F c ), ahol = ( 1,..., d ) N d, c = (c 1,..., c d ) és c k = ε k ( k 1)+(1 ε k ) k, mide k = 1,..., d és 1 eseté. Az összegzést mide ε k = 0 vagy ε k = 1 értékre kell elvégezi, ahol k = 1,..., d. A (2.18) egyelőségbe a E (X F c ) és az (X c ) értékeik egyelők 0-val, ha c N d 0 \ Nd. Ha (2.2) teljesül, akkor martigál differecia, azaz F -mérhető és E( F m ) = 0, ha m, m. Ha (2.3) teljesül, akkor a (2.16) miatt (2.19) vec( ) = ( 1) d k=1 ε k [[ ε d A ( d) [ ε 1 A ( 1) 1 + (1 ε 1 )I d + (1 ε d )I ]] vec (X c ). ] Megjegyzés. Ha ξ autoregresszív martigál mező és X a eki megfelelő A-martigál mező, akkor vec ( ) = 0, ahol δ = ( 1) k=1 ε ke(ξ F c ) és 0 N md 1 0. δ
37 2.4. AUTOREGRESSZÍV MARTINGÁL MEZŐ DEFINÍCIÓJA Állítás. Legye X A-martigál mező, mely teljesíti (2.3)-at. Ekkor vec(x ) előállítható a következő alakba: (2.20) vec(x ) = 1 2 k 1 =1 k 2 =1 ahol A j (k j, k j ) = I, j = 1,..., d. d k d =1 Bizoyítás. Rögzített eseté tekitsük a A d ( d, k d ) A 1 ( 1, k 1 ) vec( k ), k N d, k, Z k = [A d ( d, k d ) A 1 ( 1, k 1 )] vec(x k ), k, meyiségeket. Ekkor Z = vec(x ). Továbbá, (2.20) a Z k, k, differecia sorozatáak az összegzését tartalmazza. Például a d = 1 és d = 2 speciális esetekbe kapjuk Fazekas Istvá modelljeit ([Faz87], [Faz88]). Ha d = 1, akkor Ebbe az esetbe X = ξ m+1. ξ 1 ξ ξ m+1. E (X F 1 ) =. = A X 1 ξ 1 a 1 ξ a m ξ m teljesül. Ezt a modellt Fazekas Istvá taulmáyozta ([Faz87]). Tekitsük most a d = 2 esetet. Legye = ( 1, 2 ), t = (t 1, t 2 ). Ekkor ξ 1 m+1, 2 m+1 ξ 1 m+1, 2 ξ X = 1 m+2, 2 m+1 ξ 1 m+2, ξ 1, 2 m+1 ξ 1, 2
38 24 2. AUTOREGRESSZIÓS TÍPUSÚ MARTINGÁL MEZŐK Felhaszálva az [A 2 A 1 ] vec(x ) = vec(a 1 X A 2 ) és az A 2 A 1 = (A 2 I) (I A 1 ) összefüggéseket, valamit azt, hogy vec[e(x +t F )] = A 2 ( 2 + t 2, 2 ) A 1 ( 1 + t 1, 1 ) vec(x ), a következő modellt kapjuk: E(X +t F ) = A 1 ( 1 + t 1, 1 ) X A 2 ( 2 + t 2, 2 ). Ezáltal megkaptuk a [Faz88]-ba vizsgált egyelőséget A-martigál mezők kovergeciája Ebbe a részbe az A-martigál mezőkre voatkozó kovergecia-tételeket bizoyítuk a következő feltételek mellett. Tegyük fel, hogy (2.21) A j (i j + t j, i j ) A j (, i j ), ha t j, mide i j, j N és a kovergecia gyors a következő értelembe: (2.22) A j (, i j ) A j (i j + t j, i j ) c (j) t j, i j, j N, ahol t j =1 c (j) t j < mide j-re. Szükségük lesz a következő ormára. Az A = (a ij ) mátrix ormája legye A = a 2 ij. Felhaszáljuk a feti orma következő tulajdoságait: 1) A B 2 = 2 a ij b jk i k j a 2 ij b 2 jk = A 2 B 2. i k j j Speciálisa A v A v, mide v R eseté. 2) A 0, A = 0 A 0, i j
39 2.5. A-MARTINGÁL MEZŐK KONVERGENCIÁJA 25 3) λa = λ A, 4) A + B A + B. Köye elleőrizhető, hogy A 2 = tr(a A). Az A és B mátrixok Kroecker-szorzatáak ormája a következőképpe számolható: A B 2 = tr [ ] [ ] (A B) (A B) = tr (A B )(A B) = tr(a A)tr(B B) = A 2 B 2. Az A j (, k j ) = lim t j A j(k j + t j, k j ) határérték mátrixokról feltesszük, hogy létezik egy olya pozitív C kostas úgy, hogy (2.23) [A d (, k d ) A 1 (, k 1 )] vec( k ) C vec( k ), teljesül, mide k-ra. Továbbá tegyük fel, hogy (2.24) A d (, k d ) A d 1 (, k d 1 ) A 1 (, k 1 ) vec( k ) k S S C D kd D kd 1 D k1 vec( k ), k S S ahol k S a k N d olya koordiátáit tartalmazza, amelyek S {1,..., d} elemei, továbbá D kl = I, ha l S, illetve D kl = A l (, k l ), ha l S. Az X taulmáyozásához vezessük be az Y martigált. Ezt a martigált az X kísérő martigáljáak evezzük és a következő egyelőséggel defiiáljuk: vec(y ) = 1 2 k 1 =1 k 2 =1 d k d =1 A d (, k d ) A 2 (, k 2 ) A 1 (, k 1 ) vec( k ) mide N d -re. Tudjuk, hogy ha (2.2) teljesül, akkor martigál differecia. Ezért (2.2) feállása eseté, Y martigál Lemma. Tegyük fel, hogy (2.3) és (2.21) teljesül. Ha sup Eφ( vec(x ) ) < C <, ahol φ : R + R + egy emcsökkeő kovex függvéy, akkor a kísérő martigálra sup Eφ( vec(y ) ) < C szité teljesül.
40 26 2. AUTOREGRESSZIÓS TÍPUSÚ MARTINGÁL MEZŐK Bizoyítás. Legye vec(y t i ) = i 1 i 2 k 1=1 k 2=1 i d k d =1 [A d (t d, k d ) A 2 (t 2, k 2 ) A 1 (t 1, k 1 )] vec( k ), ahol t = (t 1,..., t d ) rögzített, t k, és i = (i 1,..., i d ). Mivel k martigál differecia, ezért köye adódik, hogy (Y t i, F i), 1 i t martigál. Mivel φ( vec(yi t ) ) valós szubmartigál, ezért a Állítást alkalmazva E(φ( vec(yi t t ) ) E(φ( vec(yt ) ) = Eφ( vec(x t ) ) < C, mide i t eseté. Másrészről Yi t Y i, ha t. Tehát a Fatou-lemma alapjá Eφ( vec(y i ) ) < C teljesül mide i N d eseté Tétel. Tegyük fel, hogy az (X, F ) A-martigál mező teljesíti a (2.3), (2.22), (2.23) és (2.24) feltételeket. Ha (2.25) sup k N d E vec(x k ) [ log + ( vec(x k ) ) ] d 1 <, akkor X koverges m.m., ha j mide j eseté. Továbbá, ha d 2, akkor X koverges L 1 -be, ha j mide j eseté. Bizoyítás. Legye Y az X kísérő martigálja. vec(y ) = = d k d =1 d k d =1 1 k 1=1 1 k 1 =1 [A d (, k d ) A 1 (, k 1 )] vec( k ) }{{} (Y ) k (Y ) k, ahol (Y ) k az Y martigál differeciája. A Lemma miatt a (2.25) feltétel teljesül Y -ra, evezetese sup E vec(y ) [ log + ( vec(y ) ) ] d 1 <.
41 2.5. A-MARTINGÁL MEZŐK KONVERGENCIÁJA 27 Először a majdem mideütti kovergeciát bizoyítjuk. A 2.6. Tétel miatt Y Y m.m., ha. Megmutatjuk, hogy X Y m.m. Megjegyezzük, hogy Y egyeletese kovergál, ha az koordiátái közül legalább < ε, ha az legalább egy koordiátája agyobb, mit ε. Ezért (Y ) korlátos. A fetiekből (2.23) miatt, k 0 m.m. és { k ; k N d } korlátos. A Állításból, valamit az Y defiíciójából következik, hogy d 1 vec(x ) vec(y ) = [A d ( d, k d ) A 1 ( 1, k 1 )] vec( k ) k d =1 k 1 =1 d 1 (2.26) [A d (, k d ) A 1 (, k 1 )] vec( k ) k d =1 k 1=1 ( )) d 1 = [G d G 1 ] vec( k, egy tart a végtelebe. Ebből következik, hogy (Y ) G 1,...,G d k d =1 k 1 =1 ahol G i = A i (, k i ) vagy G i = A i ( i, k i ) A i (, k i ) és legalább egy G i egyelő a differeciával. (Tehát a G 1,...,G d összeg 2 d 1 tagot tartalmaz.) Tekitsük az előbbi összeg egy speciális esetét, amikor az összeg csak egy differeciát tartalmaz. A (2.22) feltételből kapjuk, hogy c d k d =1 d k d =1 d 1 =c c (d) l d l d =0 (2.27) = c (2.28) +c 1 k 1 =1 c (d) d k }{{} d l d v l d =0 d 1 l d =v+1 [ (Ad ( d, k d ) A d (, k d ) ) A d 1 (, k d 1 ) d 1 k d 1 =1 c (d) l d c (d) l d d 1 k d 1 =1 ] A 1 (, k 1 ) vec( k ) 1 [I A d 1 A 1 ] vec( k ) k 1 =1 1 [I A d 1 A 1 ] vec( k1,...,k d 1,( d l d )) d 1 k d 1 =1 d 1 k d 1 =1 k 1 =1 1 [I A d 1 A 1 ] vec( k1,...,k d 1,( d l d )) k 1 =1 1 [I A d 1 A 1] vec( k1,...,k d 1,( d l d )), k 1 =1
42 28 2. AUTOREGRESSZIÓS TÍPUSÚ MARTINGÁL MEZŐK ahol v egy alkalmasa rögzített egész szám. Most tekitsük a kifejezés aszimptotikus viselkedését d eseté. Felhaszáljuk, hogy (2.29) d 1 k d 1 =1 1 [I A d 1 A 1 ] vec( k1,...,k d 1,s) 0 k 1 =1 egyeletese, ha s. Legye ε > 0 tetszőleges. Ha v elegedőe agy, akkor a (2.22) feltétel d 1 miatt, < ε. Felhaszálva a (2.29)-et, a (2.28) tagba lévő... l=v c (d) l kifejezés korlátos. Tehát a (2.28)-ba lévő kifejezés cε-ál kisebb, ahol c <. Ugyacsak a (2.29) alapjá, a (2.27) kifejezés kovergál a ullához, ha d. Most bizoyítsuk be a (2.29)-et. A (2.24) feltétel miatt, a (2.29) kifejezés bal oldala kisebb, mit 1 C d 1 k d 1 =1 1 k 1 =1 [A d (, k d ) A 1 (, k 1 )] vec( k1,...,k d 1,s). Tehát a feti ormába szereplő kifejezés Y -ek egy differeciája, utolsó koordiátája szerit, ezért s eseté ullához kovergál. Most tekitsük egy olya tagot a (2.26)-ből, ami két differeciát tartalmaz: d 1 {A d (, k d ) A 3 (, k 3 ) k d =1 k 1 =1 [A 2 ( 2, k 2 ) A 2 (, k 1 )] [A 1 ( 1, k 1 ) A 1 (, k 1 )]} vec( k ) c =c 1 2 k 1=1 k 2= l 1 =0 l 2 =0 3 d c 2 k }{{} 2 [A d A 3 I I] vec( k ) k 3=1 k d =1 l 1 c 1 k 1 }{{} c l1 c l2 l 2 3 d [A d A 3 I I] vec( (1 l 1 ),( 2 l 2 ),k 3,...,k d ) k 3 =1 k d =1 }{{} f 1 l 1, 2 l 2, 3,..., d
43 2.5. A-MARTINGÁL MEZŐK KONVERGENCIÁJA 29 c +c +c v 1 v 2 l 1 =0 l 2 =0 1 1 l 1 =v 1 c l1 }{{} ε l 2 =v 2 c l2 }{{} ε 2 c l1 c }{{ l2 } korlátos 2 1 l 2 =0 c l2 }{{} korlátos 1 1 l 1 =0 c l1 }{{} korlátos f 1 l 1, 2 l 2, 3,..., d }{{} 0 ha 1, 2 f 1 l 1, 2 l 2, 3,..., }{{} d korlátos f 1 l 1, 2 l 2, 3,..., }{{} d korlátos 0, ha 1, 2. (A fetiekbe az ε 1 > 0, ε 2 > 0 tetszőlegesek és v 1, v 2 -t válasszuk elegedőe agyak.) A bizoyítás hasolóa törtéik több differecia esetébe is. Végezetül, ha d 2, a tétel feltételeiből következik az X egyeletes itegrálhatósága, tehát X L 1 -be is kovergál (lásd [Shi95], Lemma o.). A következő tétel bizoyításába felhaszáljuk a Burkholder-egyelőtleség d-paraméterű változatát Lemma. (Noszály, Tómács [NT00], Fazekas [Faz05]) Legye (X, F ), N d, R m -beli értékeket felvevő martigál. Tegyük fel, hogy (2.2) teljesül. Legye p > 1. Ekkor létezek olya csak m-től, p-től és d-től függő pozitív véges C és D kostasok, hogy CE m 2 m p/2 E X p DE m 2 m p/2 teljesül, mide N d eseté, ahol k a martigál differecia, azaz X = k. k Itt. az euklideszi ormát jelöli. Szükségük lesz még Fazekas Istvá következő tételére is.
44 30 2. AUTOREGRESSZIÓS TÍPUSÚ MARTINGÁL MEZŐK Tétel. ([Faz83] Theorem 4.6., 163 o.) Legye {X m, F, m Z d } B-értékű martigál. B redelkezze a Rado-Nikodym tulajdosággal vagy legye X m = E(X F m ), m Z d alakú, mide X L r (1 < r < ) eseté. Tegyük fel, hogy E{X (m,) F (k, ) } = X (k,), ha k m, ahol (m, ), (k, ) és F (k, ) a 2.4. Tételbe defiiáltak. Ha sup m Z d E X m r <, akkor lim m X m létezik m.m. és L r -be is Tétel. Tegyük fel, hogy az (X, F ) A-martigál mező teljesíti a (2.3), (2.22) és (2.24) feltételeket, valamit (2.30) A j (i j, u j ) < K <, ha i j > u j, j = 1,..., d. Ha sup E vec(x ) α <, ahol α > 1, akkor X koverges L α -ba, eseté. Bizoyítás. A Lemma alapjá sup E vec(y ) α <, ezért a Tétel miatt, Y koverges L α -ba, ha -ek valamely koordiátája tart a végtelebe. A bizoyítás fő lépése a következő egyelőtleség sorozat: Wk i = E i 1 i 2 i d [ A d (i d, u d ) A d 1 (i d 1, u d 1 ) u 1 =k 1 u 2 =k 2 u d =k d ] A 1 (i 1, u 1 ) vec( u ) α (2.31) C 1 E C 2 E C 3 E i 1 u 1 =k 1 i 1 u 1 =k 1 i 1 u 1 =k 1 i 2 i d vec( u ) 2 u 2 =k 2 u d =k d i 2 i d α vec( u ) u 2 =k 2 u d =k d i 2 u 2 =k 2 i d u d =k d A 1 (, u 1 ) ] vec( u ) α [ d ] =C 3 E vec ( 1) z=1 ε z α Y c, α 2 [ A d (, u d ) A d 1 (, u d 1 )
45 2.6. AUTOREGRESSZÍV MARTINGÁL MEZŐK KONVERGENCIÁJA 31 mide i j > k j, j = 1,..., d eseté, ahol c = ε z k z +(1 ε z )i z, z = 1,..., d. A legutolsó formulába az összegzést mide ε z = 0 vagy 1, z = 1,..., d értékre kell elvégezi. A feti egyelőtleségek a Burkholder-egyelőtleség következméyei (2.18. Lemma). Az első egyelőtleségél még alkalmaztuk a (2.30)-at is, a harmadikba pedig a (2.24)-et. Következésképpe Wk i 0, ha k és i legalább egy koordiátája tart a végtelebe. Legye Y = lim k Y k. Megmutatjuk, hogy X Y L α -ba. Ha i k, akkor X i Y Lα Y k Y Lα k 1 k u i,u k u 1 =1 u 2 =1 k d u d =1 A 1 (i 1, u 1 ) ] vec( u ) Y k Lα [ Ad (i d, u d ) A d 1 (i d 1, u d 1 ) [A d (i d, u d ) A d 1 (i d 1, u d 1 ) A 1 (i 1, u 1 )] vec( u ). Lα Legye ε > 0 tetszőleges. Az Y k Y és (2.31) miatt k-t tudjuk úgy rögzítei, hogy a feti kifejezés első és harmadik tagja ε-ál kisebb legye. (2.22) miatt, ha k rögzített, a második tag ullához tart, ha i Autoregresszív martigál mezők kovergeciája Tétel. Legye (ξ, F ) homogé autoregresszív martigál mező és tegyük fel, hogy (2.3) teljesül. Továbbá tegyük még fel, hogy a (j) m > 0, mide j = 1,..., d eseté és a {k : 1 k m, a (j) k > 0} számok legagyobb közös osztója 1. a) Ha sup E ξ [ log + ξ ] d 1 <, akkor ξ koverges m.m., ha, továbbá ha d 2, akkor ξ koverges L 1 -be is. b) Legye α > 1. Ha sup E ξ α <, akkor ξ koverges L α -ba (és m.m.), ha.
46 32 2. AUTOREGRESSZIÓS TÍPUSÚ MARTINGÁL MEZŐK Bizoyítás. A 2.4-es szakaszba meghatároztuk az X A-martigált, az A (i z) z mátrixokat és a ξ -ek megfelelő martigál differeciát. A tétel feltételei miatt, A z = A (iz) z egy irreducibilis, aperiodikus Markov-lác (z = 1,..., d) átmeeti mátrixa. Az A z (i z + t z, i z ) = (A z ) t z mátrix elemei expoeciális sebességgel kovergálak az A z ( ) = A z (, i z ) = (a kj ) m k,j=1 mátrix elemeihez, ha t z, ahol a kj = b j (k, j = 1,..., m) a lác stacioárius eloszlása (lásd [Se81], 119 o.). A stacioaritás egyeletredszere a következő: b = b A, ahol A = A z, mide z = 1,..., d eseté. Részletesebbe (b 1, b 2,..., b m ) = (b 1, b 2,..., b m ) Ebből a m a m 1 a 1 b 1 = a m b m, b 2 = b 1 + a m 1 b m,..., b m = b m 1 + a 1 b m. Ebből következik, hogy b 1 = a m b m, b 2 = (a m + a m 1 )b m,..., b m 1 = (a m a 2 )b m, b m = (a m a 1 )b m. Tehát 1 = b b m = (ma m + (m 1)a m a 1 )b m, ahoa és b j = ( j 1 ) a m l b m = l=0 b m = m 1, ia i i=1 m i=m j+1 a i m i=1 ia, j = 1,..., m 1, i a Markov-lác egyetle stacioárius eloszlása. Tehát teljesülek a (2.22), (2.23), (2.24) és (2.30) feltételek. A és a Tételből következik az állítás.
47 3. fejezet Közpoti határeloszlás-tételek keverő véletle mezőkre 3.1. Bevezetés A függetle valószíűségi változók sorozataira voatkozó határérték-tételek függő esetre törtéő kiterjesztésével számos mű foglalkozott. A gyege függőség közismert feltételei közül a keverési feltételek fotos szerepet játszaak. Ibragimov és Liik 1971-be ([IL71]) közpoti határeloszlás-tételt igazoltak olya stacioárius sorozatokra, amelyek bizoyos α-keverő feltételeket teljesíteek. Az eredméyüket Bolthause ([Bol82]) és Guyo ([Guy95]) terjesztette ki α-keverő véletle mezőkre. Guyo eredméyeit Fezekas és Kukush vitte át sűrűsödő-övekvő sémára. Fazekas Istvá ([Faz03]) korlátos, Fazekas-Kukush ([FK00]) az egyeletes itegrálható esettel foglalkozott. Ezek a cikkek em tartalmazzák az említett tételek részletes bizoyításait, haem csak rövid vázlatot közölek. Ebbe a fejezetbe az említett tételek részletes bizoyítását közöljük. Az említett bizoyítás taulsága az, hogy Ibragimov és Liik ([IL71]), valamit Guyo ([Guy95]) eredeti godolatmeete csak akkor alkalmazható, ha a véletle mezőre teljesül egy bizoyos egyeletese itegrálhatósági feltétel. Guyo em tette fel az egyeletese itegrálhatóságot, sőt em is írta le a korlátos esettől az általáos esethez vezető lépéseket. Ezért em világos, hogy az eredméye teljesül-e az általáos esetbe is. Megjegyezzük, hogy Ibragimov és Liik feltételezte a stacioaritást, tehát az ő bizoyításuk teljes. 33
48 34 3. KÖZPONTI HATÁRELOSZLÁS-TÉTELEK A keverő véletle folyamatok leírása gazdag irodalommal redelkezik ([Ibr59], [Ros56], [Bra83]) be Miller (lásd [Mil94]) ρ-keverő véletle mezőket feltételezve bizoyít közpoti határeloszlás-tételeket. Bradley 2005-be (lásd [Bra05]) a keverő feltételek egy áttekitését adja. Merlevéde, Peligrad és Utev (lásd [MPU06]) a határeloszlás-tételek elméletéek újabb eredméyeit foglalja össze. Dedecker (lásd [Ded98]) egy általáos közpoti határeloszlás-tételt bizoyít stacioárius véletle mezőkre. Megmutatta, hogy bizoyos keverő feltételekből következek az általáos közpoti határeloszlás-tétel feltételei. Megjegyezzük, hogy a mi dolgozatukba haszált keverő feltételek em hasolíthatók össze a Dedecker által említettekkel (lásd [Ded98]). Továbbá Dedecker ([Ded98]) a stacioárius mezőt és a rögzített mitavételt taulmáyozta, amíg mi em feltételeztük a stacioaritást, és a sűrűsödő-övekvő esetet tekitettük Jelölések és előzméyek Jelölje R d a d-dimeziós teret ellátva az euklideszi ormával ( x = d i=1 x2 i ). Itt d rögzített pozitív egész. Az Rd -be haszáli fogjuk a maximum orma segítségével defiiált távolságot is: ϱ(x, y) = max 1 i d x i y i, ahol x = (x 1,..., x d ), y = (y 1,..., y d ). Két R d -beli halmaz maximum ormához tartozó távolságát szité ϱ-val jelöljük: ϱ(a, B) = if{ϱ(x, y) : x A, y B}. Legye (Ω, F, P) valószíűségi mező. Jelölje ω Ω az elemi eseméyeket. Az eseméyek halmaza vagy a valószíűségi változók halmaza által geerált σ-algebrát jelölje σ{.}. Az η valószíűségi (vektor) változó L p -ormáját a következőképpe értelmezzük: η p = {E η p } 1/p, 1 p <. A megfigyelések sémája az alábbi. Legyeek T 1, T 2,..., és T tartomáyok R d -be. Tegyük fel, hogy T 1 T 2 T 3..., i=1 T i = T, és T i kompakt mide i-re, továbbá T Lebesgue-mértéke végtele. Legye
49 3.2. JELÖLÉSEK ÉS ELŐZMÉNYEK 35 {ε(x), x T } egy véletle mező. Az -edik megfigyelés halmaz (mita) az ε(x) mező x k T potokba felvett értékeiből áll, ahol k D Z d. Az x k potok kiválasztása a következő. Osszuk fel R d -t az alábbi téglákra (k) = d j=1 ( kj, k j + 1 ], N j N j ahol k = (k 1,..., k d ) Z d d-dimeziós egész koordiátájú pot, {N j } pedig pozitív egészek övekvő, em korlátos sorozata mide rögzített j = 1,..., d-re. Az -edik mitavételi helyeket, azaz az {x k, k D }, halmazt úgy kapjuk, hogy egy x k potot választuk mide em üres (k) T halmazból. Valójába mide x k = x () k függ -től is. Azért, hogy elkerüljük a boyolult jelöléseket, gyakra elhagyjuk az () felsőidexet. Tegyük fel, hogy lim D =. Ha a megfigyelések helyei egyre sűrűbbek és sűrűbbek leszek a tartomáyok egy övekvő sorozata eseté, akkor ezt a sémát sűrűsödő-övekvő sémáak evezzük (lásd [Cre91] és [Lah96] a övekvő sémáról). Defiiáljuk a diszkrét paraméterű Y (k) vektor mezőt a következő módo. Mide = 1, 2,..., és mide k D eseté legye (3.1) Y (k) az ε(x () ) Borel-mérhető függvéye. k Emlékeztetük az α-keverési együttható defiíciójára. Legye A és B két σ-algebra F-be. Az A és B halmazok α-keverési együtthatójáak evezzük az α(a, B) = sup{ P(A)P(B) P(AB) : A A, B B} értéket. Az {ε(x) : x T } mező α-keverési együtthatója pedig: α(r, u, v) = sup{α(f I1, F I2 ) : ϱ(i 1, I 2 ) r, I 1 u, I 2 v}, ahol a szuprémum a T mide I 1 és I 2 véges részhalmazára veedő, továbbá F Ii = σ{ε(x) : x I i }, i = 1, 2. Azt modjuk, hogy az {ε(x)} véletle mező α-keverő, ha a keverő együtthatók kielégíteek bizoyos feltételeket. Eze feltételek midegyike a mező gyege függőségét jeleti, azaz azt, hogy α(r, u, v) kicsi, ha r agy. A tételeikbe felhaszáljuk a következő feltételeket: (3.2) 0 s d 1 α τ 2+τ (s, 1, 1)ds <, ha 0 < τ < 1,
50 36 3. KÖZPONTI HATÁRELOSZLÁS-TÉTELEK (3.3) 0 s d 1 α(s, i, j)ds <, ha i + j 4, (3.4) α(s, 1, ) = o(s d ), ha s, (3.5) Λ = O(λ ), ha, ahol (3.6) Λ = max 1 j d N j, λ = mi 1 j d N j. A (3.2)-(3.4) általáosa haszált keverési feltételek. Tulajdoképpe (3.4) azt jeleti, hogy lim α(s, 1, k )s d = 0, ha s és k. A (3.5) feltétel pedig azért szükséges, hogy a vizsgált téglák e torzuljaak túlságosa el. Jelölje az α (r, i, j) az Y (k) mező α-keverési együtthatóját. Mivel x k (k) és x l (l) (ahol l = (l 1,..., l d )), így azt kapjuk, hogy { k1 l 1 1 (3.7) ϱ(x k, x l ) max,..., k d l d 1 } ϱ(k, l) 1 N 1 N d Λ és (3.8) ϱ(x k, x l ) ϱ(k, l) + 1 λ, ahol Λ és λ a (3.6) által defiiált. Tehát az Y (k) mező α (r, i, j) α- keverési együtthatói teljesítik a következő egyelőtleséget: ( r + 1 ) (3.9) α, i, j α (r, i, j) α λ ( r 1 Λ ), i, j, r = 1, 2, Lemma. Mide γ > 0 és i, j, pozitív egész eseté teljesül az alábbi egyelőtleség: (3.10) r=1 ( r d 1 α(r, γ i, j) c 1 + Λ d 0 ) r d 1 α γ (r, i, j)dr, ahol a c kostas csak d-től függ.
51 3.2. JELÖLÉSEK ÉS ELŐZMÉNYEK 37 Bizoyítás. r=1 így a bizoyítás teljes. ( r d 1 α(r, γ i, j) c 1 + ( c 1 + ( c 1 + ( c 1 + Λ d r d 1 α γ( r, i, j )) Λ r=1 r s d 1 α γ( s, i, j ) ) ds Λ s d 1 α γ( s, i, j ) ) ds 0 Λ ) s d 1 α γ (s, i, j)ds, r=2 r 1 A következő kovariacia-egyelőtleségek alapvető szerepet játszaak a keverő mezők elméletébe Megjegyzés. (Davydov-egyelőtleség, [Dou94], o. 9.) (3.11) cov(x, Y ) 8[α(σ(X), σ(y ))] 1/r X p Y q, 0 mide r, p, q 1, r p q X és Y L -beli akkor = 1 eseté. Abba a speciális esetbe, amikor (3.12) cov(x, Y ) 4[α(σ(X), σ(y ))] X Y. A következő egyelőtleség a Rosethal-egyelőtleség egy speciális esete. A bizoyítás megtalálható Doukha köyvébe ([Dou94]) Lemma. Legye 1 < l 2 és τ > 0, Y k, k Z d, cetrált valószíűségi változó, melyre teljesül E Y k l+τ <, k Z d és legye L(l, τ, D) = k D (E Y k l+τ ) l l+τ, ha D véges halmaz Z d -be. Ezekívül legye c (τ) 1,1 = 1 + s=1 s d 1 [α Y (s, 1, 1)] τ 2+τ,
52 38 3. KÖZPONTI HATÁRELOSZLÁS-TÉTELEK ahol α Y (s, 1, 1) az {Y k } mező α-keverő együtthatója, azaz α Y (s, 1, 1) = sup{α(y u, Y v ) : ϱ(u, v) s}. Tegyük fel, hogy c (τ) 1,1 <. Ekkor létezik olya c kostas, hogy (3.13) E l c c (τ) L(l, τ, D), k D Y k teljesül Z d mide véges D részhalmaza eseté. Megjegyezzük, hogy a (3.13) Rosethal-egyelőtleség bizoyítása az alábbi (3.14)-ből következik, alkalmazva az úgyevezett iterpolációs lemmát. További részletek és a Rosethal-egyelőtleség általáos alakja megtalálható Fazekas, Kukush és Tómács cikkébe ([FKT00]) Megjegyzés. Haszálva a 3.3. Lemma jelöléseit, legye τ > 0, és tegyük fel, hogy c (τ) 1,1 <. Ekkor létezik olya c kostas, hogy (3.14) cov(ξ k, ξ l ) c c (τ) 1,1L(2, τ, D) k,l D teljesül Z d mide véges D részhalmaza eseté. Bizoyítás. A teljesség kedvéért belátjuk (3.14)-et. Felhaszálva a (3.11) egyelőtleséget azt kapjuk, hogy cov(ξ k, ξ l ) ξ k [α ξ ( k l, 1, 1)] τ 2+τ ξk 2+τ ξ l 2+τ. k,l D k D k,l D k l A számtai és mértai közép közti egyelőtleség alapjá a feti kifejezés majorálható a következőkkel: ξ k 2 2+τ + 8[α ξ ( k l, 1, 1)] τ 2+τ ξk 2 2+τ k D k D Ebből adódik a (3.14). k,l D k l ξ k 2 2+τ + k D c s=1 1,1 s d 1 [α ξ (s, 1, 1)] τ 2+τ ξk 2 2+τ.
53 3.3. ASZIMPTOTIKUS EREDMÉNYEK Aszimptotikus eredméyek Előljáróba a fő eredméyük által leírt szituációról a következőket jegyezzük meg. Egyrészt arra az esetre kocetráluk, amikor ε(x) és ε(y) em függetleek, ha x és y közel vaak egymáshoz, ezért a tételük em fedi le azo eseteket, amikor Y (k)-k függetleek és azoos eloszlásúak. Másrészről, ha ε(x) egy stacioárius mező folytoos kovariacia függvéyel és pozitív szórással, akkor a kovariacia közel va egy rögzített pozitív számhoz egy kicsi hipertéglalapo belül. Emlékeztetőül, D véges halmazok sorozata Z d - be, ahol lim D = teljesül. Ebbe a részbe valójába egy részletes bizoyítást aduk Fazekas és Kukush tételére ([FK00]). A bizoyítás potos rögzítése azért fotos, mert a Guyo művébe szereplő bizoyítás egy ugrást tartalmaz, amikor a korlátos esetre törtéő visszavezetéshez Ibragimov-Liik művére hivatkozik. Azoba az Ibragimov-Liik ([IL71])-beli tétel stacioárius esetre voatkozik, godolatmeete em vihető át közvetleül a em stacioárius esetre. Ezért tette fel Fazekas és Kukush ([FK00]) az egyeletese itegrálhatóságot Tétel. Legye ε(x) véletle mező és legye Y (k) az ε(x () k ) Borelmérhető függvéye, k D. Legye az { Y (k) : k D, = 1, 2,... } család egyeletese korlátos. Legye S = Y (k), = 1, 2,..., valamit k D σ 2 = var(s ). Tegyük fel, hogy (3.3), (3.4) és (3.5) teljesül. Továbbá tegyük fel, hogy (3.15) lim if σ 2 Λ d D > 0 teljesül. Ekkor σ 1 S N (0, 1), ha. Bizoyítás. Feltesszük, hogy Y (k)-ek egyeletese korlátos valószíűségi változók 1 korláttal, azaz Y (k) 1, k D, = 1, 2,.... Válasszuk ki az {m } pozitív egészek sorozatát úgy, hogy lim m =, (3.16) lim α(m, 1, ) D 1 d 2 Λ 2 = 0 és lim m d D 1 2 Λ d 2 =. Igazoljuk, hogy ez a választás lehetséges. E célból legye x =α(, 1, ), y = d és z = D 1 2 Λ d 2, a későbbi 3.7. Lemmába, ekkor a (3.4) szerit
54 40 3. KÖZPONTI HATÁRELOSZLÁS-TÉTELEK x /y 0. Továbbá z, mivel D Λ d Lebesgue-mértéke T -ek). Legye S (k) = l D, ϱ(x k,x l ) m Y (l), mide k D -re. Továbbá legye Ekkor a = l D E cµ(t ) (µ(t ) a S (k) = S S (k) ( Y (l)s (l) ), S = a 1 2 S, S (k) = a 1 2 S (k). σ 2 = var(s ) = a + l D E ( Y (l)s (l) ). Felhaszálva a (3.12) egyelőtleséget és ugyaazt az érvelést, mit a 3.1. Lemmába kapjuk, hogy σ 2 ( a = E Y (l)s(l) ) l D cov ( Y (k), Y (l) ) k,l D, ϱ(x k,x l ) m c D c D c D Λ d s=m λ 1 m λ 2 mλ 3 Λ c D Λ d o(1) σ 2 o(1). ( s 1 ) s d 1 α, 1, 1 Λ ( s 1 ) s d 1 α, 1, 1 ds Λ s d 1 α ( s, 1, 1 ) ds Az utolsó lépésekbe (3.3)-at és (3.15)-öt haszáltuk. Így kapjuk azt, hogy a (3.17) lim σ 2 = 1. Ezért elegedő bebizoyítai S aszimptotikus ormalitását.
55 3.3. ASZIMPTOTIKUS EREDMÉNYEK 41 Mivel sup ES 2 <, ezért a Stei-lemma (lásd 3.8. Megjegyzés) miatt elegedő bizoyítai a következőt: ( ) (3.18) lim E (it S )e its = 0, mide t R eseté. Tekitsük a következő felbotást: ahol (it S )e its = A 1 A 2 A 3, ( A 1 = ite its 1 1 ) Y (l)s (l), a l D A 2 = a 1 2 e its Y (l) l D A 3 = a 1 2 l D Y (l)e it(s S(l)). ( 1 its (l) e its(l)), Először bizoyítjuk, hogy lim E A 1 2 = 0. E A 1 2 = t 2 a 2 var Y (l)s (l) l D (3.19) = t 2 a 2 j, j, l, l D ϱ(x j,x l ) m, ϱ(x j,x l ) m cov ( Y (j)y (l), Y (j )Y (l ) ). Két esetet külöböztetük meg. Először tekitsük a ϱ(x j, x j ) = k 3m Λ λ esetet. Ekkor ϱ({x j, x l }, {x j, x l }) k 2m. A kovariacia-egyelőtleség miatt (lásd (3.12)) kapjuk, hogy cov ( Y (j)y (l), Y (j )Y (l ) ) 4α(k 2m, 2, 2), mivel Y (l) 1 mide l és eseté. Ekkor j-t D -féleképpe választhatjuk meg, és ezutá l-et legfeljebb m d Λ d -féleképpe, továbbá j kiválasztása
56 42 3. KÖZPONTI HATÁRELOSZLÁS-TÉTELEK utá l -t legfeljebb m d Λ d -féleképpe választhatjuk. Tehát a (3.19)-be lévő kifejezés kisebb vagy egyelő, mit ct 2 a 2 D m 2d Λ 2d sup j D ct 2 a 2 D m 2d {j : ϱ(x j,x j )=k 3m Λ } λ Λ 2d s=3m Λ 1 α(ϱ(x j, x j ) 2m, 2, 2) ( s 1 ) s d 1 α 2m, 2, 2. Λ Az utolsó lépésbe (3.7) és (3.8) egyelőtleségeket haszáltuk. A feti kifejezést majoráljuk a következő itegrállal: ct 2 a 2 D m 2d Λ 2d ct 2 a 2 D m 2d Λ 2d+1 ct 2 a 2 D m 2d Λ 3d 3m Λ 2 m +o(1) 0 ( s 1 ) s d 1 α 2m, 2, 2 ds Λ (Λ (s + 2m ) + 1) d 1 α(s, 2, 2)ds s d 1 α(s, 2, 2)ds. Most a (3.15) és a (3.17) felhaszálásával megmutathatjuk, hogy a 1 c D 1 Λ d. Tehát a feti kifejezés majorálható a c D 1 m 2d Λ d kifejezéssel, amely az m választása alapjá ullához kovergál, ha (lásd (3.16)). Tekitsük most azt az esetet, amikor Legye ϱ(x j, x j ) = k < 3m Λ λ. h = if{ϱ(x j, x j ), ϱ(x j, x l ), ϱ(x j, x l )}, ekkor a (3.12) kovariacia-egyelőtleség szerit cov ( Y (j)y (l), Y (j )Y (l ) ) E ( Y (j)y (l)y (j )Y (l ) ) + E ( Y (j)y (l) ) E ( Y (j )Y (l ) ) 4α(h, 1, 3) + 4α(h, 1, 1) 8α(h, 1, 3),
57 3.3. ASZIMPTOTIKUS EREDMÉNYEK 43 mivel Y (l) 1 mide l és eseté. Tegyük fel, hogy h = ϱ(x j, x l ) (a másik két esetet hasolóa tárgyalhatjuk). A választási lehetőségek száma j-re D, j -re legfeljebb Λ d 3mΛ ) d ( λ és l -re legfeljebb Λ d m d. Tehát (3.19)- be a kifejezés kisebb vagy egyelő, mit ( ct 2 a 2 D Λ d 3m Λ ) dλ d m d ct 2 a 2 D Λ 3d m 2d λ {l : ϱ(x j,x l )=h m } λ d {l : ϱ(j,l)=k Λ m +1} α(h, 1, 3) ( k 1 ) α, 1, 3 Λ ( Λ m +1 ( k 1 )) ct 2 a 2 D Λ 2d m 2d 1 + k d 1 α, 1, 3 Λ ( ct 2 a 2 D Λ 2d m 2d 1 + k=1 Λ m +1 ct 2 a 2 D Λ 3d m 2d 0,, 0 ( s 1 ) ) s d 1 α, 1, 3 ds Λ mit ahogy már korábba megmutattuk. Ezért (3.19) midkét kompoese ullához kovergál, így lim E A 1 2 = 0. Tekitsük most A 2 -t. A Taylor-sorfejtést felhaszálva kapjuk, hogy ezért E A 2 a its (l) e its(l) ct 2 S 2 (l), l D E 1 its (l) e its (l) a 1 2 D sup ( E ct 2 S 2 (l) ) l D ca 3 2 D sup ca 3 2 D m d Λ 2d 0, l ϱ(l, j) Λ m, ϱ(l, j ) Λ m cov ( Y (j), Y (j ) ha. Felhaszáltuk az a és σ 2 közötti összefüggést, a (3.15)-öt és az m sorozat választását. A feti számításokál felhaszáltuk a kovariaciaegyelőtleséget és bizoyos összegek itegrállal való majorálását. Tehát lim E A 2 = 0.
58 44 3. KÖZPONTI HATÁRELOSZLÁS-TÉTELEK Most igazoljuk, hogy teljesül lim EA 3 = 0. EA 3 a 1 2 l D cov ( Y (l), e it(s S (l)) ) a 1 2 D α(m, 1, ) c Λ d 2 D 1 2 α(m, 1, ) 0, az m választása miatt. Ezzel a (3.18) egyelőtleséget beláttuk, amely tételüket bizoyítja Tétel. Legye {ε(x) : x T } véletle mező és legye Y (k) az ε(x () k ) Borel-mérhető függvéye, k D. Tegyük fel, hogy EY (k) = 0 mide k D, = 1, 2,... eseté. Legye S = k D Y (k), = 1, 2,..., valamit legye σ 2 = var(s ). Tegyük fel, hogy létezik olya τ > 0, hogy teljesül (3.2) és (3.20) { Y (k) 2+τ : k D, = 1, 2,... } egyeletese itegrálható. Ekkor (3.21) lim sup 1 Λ d cov(y (k), Y (l)) <. D k,l D Ha még a (3.3), (3.4), (3.5), és (3.15) feltételek is teljesülek, akkor ha. σ 1 S N (0, 1), Bizoyítás. Először belátjuk a (3.21)-et. A (3.13) Rosethal-egyelőtleség alapjá cov(y (k), Y (l)) k,l D c (1 + [α (s, 1, 1)] τ 2+τ s d 1 ) s=1 k D ( E Yk 2+τ ) 2 2+τ. A 3.1. Lemma szerit ez a kifejezés majorálható a következő kifejezéssel: ( c 1 + Λ d 0 s d 1 α τ 2+τ (s, 1, 1)ds )
59 3.3. ASZIMPTOTIKUS EREDMÉNYEK 45 { } D sup Y (k) 2 2+τ : k D, = 1, 2,.... Tehát, (3.20) és (3.2)-ből következik (3.21). Megmutatjuk, hogy elegedő a tételt egyeletese korlátos {Y (k) : k D, = 1, 2,... } valószíűségi változókra bebizoyítai. Tehát a 3.5. Tételből következi fog az állítás. Ibragimov és Liik (lásd [IL71]) godolatát követjük. Legye L > 0, a csokított változókat jelölje (L) a felső idexbe és a maradék tagokat (L) felső idex jelöli: X (L) = X I{X [ L, L]}, X (L) = X X (L). Legye Z = S /σ ormalizált összeg, Z (L) = 1 ( Y (L) σ k D (k) EY (L) (k) ) a csokított valószíűségi változók ormalizált összege, és Z (L) = 1 ( Y (L) (L) σ k D (k) E Y (k) ) a maradék tagok ormalizált összege. Ekkor Z = Z (L) + Z (L) és EZ 2 = 1. A Rosethal-egyelőtleség, valamit a (3.10) és a (3.2) szerit, (L) E( Z ) 2 = E 1 ( Y (L) (L) (k) E Y (k) ) 2 (3.22) σ k D c Λd D σ 2 (L) sup Y (k) 2 2+τ 0, k D midő L. Megjegyezzük, hogy ez a kovergecia egyeletes -be. Az utolsó lépesbe kihaszáltuk (3.15)-öt és (3.20)-at. Legye σ(l) 2 = var ( k D Y (L) (k) ) a csokított valószíűségi változók összegéek a szórása. Tehát σ 2 (L) σ 2 1 = E(Z (L) ) 2 E(Z ) 2 = E(Z (L) Z ) 2 E(Z ) 2 = E( (L) Z ) 2 2E(Z Z(L) ). Felhaszálva (3.22)-t és a második tagál a Cauchy-egyelőtleséget, a feti kifejezés -be egyeletese tart a ullához, amit L. Ezért (3.23) lim σ2 (L) 1 = 0. sup L 1 σ 2
60 46 3. KÖZPONTI HATÁRELOSZLÁS-TÉTELEK Tehát Ee itz e t2 /2 (L) E e it Z + Ee itz(l) 1 e σ2 (L) σ 2 t e σ 2 (L) σ 2 (L) (3.24) t E Z + sup Ee itvu e (tv)2 2 v [1 δ L,1+δ L ] t 2 2 e t2 2 t δ L, ahol δ L = sup σ2 (L) 1 σ 2 1 és U = 1 ( Y (L) σ (L) k D (k) EY (L) (k) ). A (3.23) alapjá, lim L δ L = 0. Ha a tétel igaz korlátos valószíűségi változókra, akkor U aszimptotikusa stadard ormális eloszlású, ezért (3.24)-ből következik, hogy lim sup Ee itz e t2 /2 t sup 1 (L) E( Z ) 2 + t2 2 δ L. Azoba (3.22)-őt felhaszálva, az utolsó kifejezés 0-hoz kovergál, ha L, ezért a tételük igaz. A 3.5. Tétel bizoyításába felhaszáltuk az m részsorozatok létezését. A teljesség kedvéért közöljük eze részsorozatok létezéséek bizoyítását Lemma. Legyeek x 0, y 0, z valós sorozatok úgy, hogy y = d, ahol d > 0 és x /y 0. Ekkor létezik a pozitív egész számokak egy olya m sorozata, hogy m, x m z 0 és y m z. Bizoyítás. Mivel τ = x /y 0, ezért található pozitív számokak egy olya u k emkorlátos, övekvő sorozata, hogy (3.25) τ k 2, ha u 1/d k. Mivel z, található pozitív egész számokak egy olya {(k)} emkorlátos, övekvő sorozata, hogy Legye z ku k, ha (k). (3.26) α m = 1, ha (k) m < (k + 1) k
61 3.4. A TÉTEL KITERJESZTÉSEI 47 mide k pozitív egész szám eseté. Ezért α m 0 és mide pozitív egész k eseté (3.27) z m α m ku k k = u k, ha (k) m < (k + 1). ] Legye m = [(z α ) 1/d + 1 mide -re, ahol [.] az egész részt jelöli. Köye adódik, hogy m. (3.25), (3.26), (3.27) és m defiíciója adja, hogy mide pozitív egész k-ra (3.28) τ m α k 2 k 1 = k 1, ha (k) < (k + 1). Tehát a τ és m defiícióiból és a (3.28)-ből következik, hogy x m z = τ m y m z τ m (z α ) 1 z = τ m α 1 0, ha. Továbbá, α defiícióját felhaszálva kapjuk, hogy { d (z α ) [ 1/d (z α ) 1/d], + 1} mivel. y m z = z m d = z z α 3.8. Megjegyzés. (Stei-lemma, lásd [Ste72], [Guy95]) Legye {ν } az R-e értelmezett valószíűségek egy sorozata, amely kielégíti a sup x 2 ν (dx) <, R lim (it x)e itx ν (dx) = 0, R mide t R feltételeket. Ekkor ν N (0, 1), ha A tétel kiterjesztései 3.9. Következméy. A 3.5. Tételbe és a 3.6. Tételbe a (3.15) feltétel helyett tegyük fel, hogy lim Λ d D 1 σ 2 = σ 2
62 48 3. KÖZPONTI HATÁRELOSZLÁS-TÉTELEK teljesül. Ekkor (Λ d D ) 1 2 S N (0, σ 2 ), ha. Bizoyítás. Először tegyük fel, hogy σ 2 > 0. Ekkor teljesül (3.15) és ezért S N (0, 1). Tehát σ 1 (Λ d D ) 1 2 S = Másodszor, ha σ 2 = 0, akkor ( σ 2 ) 1 2 Λ d σ 1 S σn (0, 1) = N (0, σ 2 ). D ] var [(Λ d D ) 1 2 S = (Λ d D ) 1 σ 2 0, mivel. Tehát (Λ d D ) 1 2 S L 2 -be ullához kovergál, ezért ez a kifejezés eloszlásba kovergál egy degeerált ormális eloszláshoz (formálisa N (0, 0)-hoz). Most tekitsük a 3.5. Tétel és 3.6. Tétel p-dimeziós kiterjesztéseit. A Tétel léyegébe [Faz03] Theorem Tétel. Legye ε(x) véletle mező és Y (k) p-dimeziós véletle vektor ε(x () k ) egy Borel-mérhető függvéye, k D. Legye EY (k) = 0 és Y (k), k D, = 1, 2,... egyeletese korlátos. Legye S = k D Y (k), = 1, 2,..., Σ = var(s ). Tegyük fel, hogy teljesül (3.3), (3.4), (3.5) és létezik a lim (Λ d D 1 Σ ) = Σ határérték. Ekkor (Λ d D ) 1 2 S N (0, Σ), ha. Bizoyítás. Eek bizoyításához tekitsük az {a Y (k)} egydimeziós véletle mezőt, ahol a R p tetszőleges (a jelölje az a traszpoáltját). Alkalmazzuk a 3.5. Tételt és a 3.9. Következméyt. A Tétel megegyezik a [FK00] Remark 4.3. megjegyzésével.
63 3.4. A TÉTEL KITERJESZTÉSEI Tétel. Legye ε(x) egy véletle mező. Legye Y (k) egy cetrált p-dimeziós véletle vektor, amely ε(x () k )-mérhető mide = 1, 2,..., és mide k D eseté. Legye S = k D Y (k), = 1, 2,..., Σ = var(s ). Tegyük fel, hogy teljesül (3.3), (3.4), (3.5) és létezik olya τ > 0, ami kielégíti (3.2)-t és { Y (k) 2+τ : k D, = 1, 2,... } egyeletese itegrálható. Ezekívül tegyük fel, hogy lim if λ ( mi Λ d D 1 ) Σ > 0. Ekkor Σ 1 2 S N (0, I p ), ha. Itt λ mi (A) jelöli az A mátrix legkisebb sajátértékét, míg I p egy p p típusú egységmátrixot jelöl. Bizoyítás. Alkalmazzuk a 3.6. Tételt az {a Y (k)} mezőre. A feti tétel számos más változata is igazolható. Például, az egyeletes itegrálhatósági feltétel helyettesíthető egy erős stacioárius feltétellel és egy itegrálhatósági feltétellel.
64
65 4. fejezet A regressziós függvéy becsléséek határeloszlása véletle mezőkre 4.1. Bevezetés A magfüggvéyes becsléseket széles körbe taulmáyozza a szakirodalom. A sűrűségfüggvéy magfüggvéyes becsléséről Parze ([Par62]) és Roseblatt ([Ros56b]) ért el alapvető eredméyeket. A regressziós függvéy magfüggvéyes becsléséről Nadaraya és Watso ([Nad64], [Wat64]) 1964-be közölt eredméyeit számos cikkbe feldolgozták és általáosították. Ezeket az eredméyeket többek között Rao ([Rao83]), Devroye és Győrfi ([DG85]), valamit Bosq ([Bos98]) foglalta össze. A magfüggvéyes becslések egyik fotos tulajdosága az aszimptotikus ormalitás, melyet több cikkbe is taulmáyoztak (lásd [Sch72], [Cai01]). Tekitsük tehát a regressziós függvéy magfüggvéyes becslését. Függetle adatokra az elmélete jól kidolgozott, számos hivatkozást lehet rá találi például Wad és Joes köyvébe (lásd [WJ95]). Világos, hogy meg kell egedük, hogy a sávszélesség tartso ullához, ha a megfigyelési helyek száma tart a végtelehez, azért hogy a torzítás eltűjö és a becslés kozisztessé váljo. Viszot, h-ak em szükséges gyorsa csökkeie, külöbe a szóráségyzet elszálla a végtelebe. Például tekitsük a si(x) közelítését külöböző sávszélességek alkalmazásával (h 1 = valamit h 2 = ). Látható, hogy agy sávszélesség eseté a közelítés sima, 51
66 52 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE míg túl kicsi sávszélesség eseté a közelítés ugrál ábra. A si(x) (piros voal) közelítése, h 1 = (fekete voal) és h 2 = (zöld voal) sávszélességek eseté. Függetle mitaelemek eseté az optimális h meghatározására agyo sok mű született, mit például Wad és Joes köyve ([WJ95]), valamit Cao, Cuevas és Gozáles-Mateiga cikke ([Cao94]). Ha az adataik függőek, a probléma sokkal összetettebb, és a szakirodalomba is sokkal kevesebb cikk található. A függőség erősségéek leírásához gyakra valamilye keverő feltételt haszálak (lásd [HV90], [Kim97]). Folytoos esetbe Sköld részletese foglalkozik a sávszélesség meghatározásával (lásd [Sko01], [SkoC]). Tekitsük most egy (X t, Y t ), t T, erőse stacioárius véletle mezőt (T az R d tér egy tartomáya, X t és Y t valós értékű valószíűségi változók.) Céluk az r(x) = E (Φ (Y t ) X t = x) regressziós függvéy becsléséek határeloszlásáak meghatározása, ahol Φ ismert, korlátos és mérhető függvéy. Legye (X t, Y t ), t D az adathalmazuk, ahol D jelöli a T rácspotjait és T R d. Tekitsük a regressziós függvéy magfüggvéyes
67 4.1. BEVEZETÉS 53 becslését ( ) x Xt Φ(Y t )K h t D r (x) = ( ), x Xt t D K ahol K egy magfüggvéy (lásd [Nad64], [Wat64]). Az általuk tekitett mitavételezési séma azoba eltér az általáosa haszáltaktól. A megfigyelésük helyei egyre sűrűbbek leszek a tartomáy övekedésével. Ezt a jeleséget sűrűsödő-övekvő (ifill-icreasig) sémáak evezték el a szakirodalomba (lásd [LKC99], [Faz03]). Feltesszük, hogy a megfigyelt valószíűségi mező gyegé függő, potosabba a valószíűségi mezőre teljesül az úgyevezett α-keverő feltétel. Fő eredméyük az r (x) aszimptotikus ormalitásáak bizoyítása. Az eredméy külö érdekessége a szokatla kovariacia-mátrix. Potosabba szólva (r (x 1 ),..., r (x m )) vektor aszimptotikus kovariacia-mátrixa, egy diagoális mátrix és egy a feltételes kovariaciák itegráljait tartalmazó mátrix összegéből áll (lásd 4.1. Tétel). Megjegyezzük, hogy az (r (x 1 ),..., r (x m )) együttes aszimptotikus ormalitása függetle megfigyelések eseté jól ismert (lásd [Sch72]). A sűrűsödő-övekvő eset léyegese eltér a tisztá sűrűsödő esettől. A sűrűsödő tulajdoság azt jeleti, hogy a megfigyelések helyei egyre sűrűbbek egy rögzített tartomáyba (lásd [Cre91]). Gyegé függő mezők sűrűsödő megfigyelése eseté számos becslés em lesz kozisztes (lásd [Lah96]). Továbbá, ebbe az esetbe em várható a becslések aszimptotikus ormalitása, mert hiáyzik egy alkalmas cetrális határeloszlás tétel. A sűrűsödő-övekvő közelítés haszos lehet a földtudomáyok, meteorológia, köryezetvédelem, képfeldolgozás stb. területeke. Ezekbe a tudomáyokba számos olya folyamatot taulmáyozak, amely térbe vagy időbe folytoosa változik. A gyakorlatba azoba em tudjuk folytoosa megfigyeli a folyamatokat, ezért véges adathalmazokkal és diszkrét becslésekkel dolgozuk. Eredméyeik haszosak lehetek a szimulációk sorá is. A statisztikai modellek elméleti elemzése gyakra igéyel szimulációkat, a számítógépes szimulációkba pedig midig diszkrét közelítéseket alkalmazuk. A sűrűsödő-övekvő tulajdoságot tekithetjük a folytoos és a diszkrét eset közötti átmeetkét. Természetese a fő kérdés az, hogy a folytoos modell határérték viselkedése megegyezik-e eek diszkrét közelítésével. Folytoos esetbe a becslések általába itegrálokkal, diszkrét esetbe pedig h
68 54 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE összeg segítségével defiiáltak. Ha az itegrálokat umerikusa számoljuk, akkor közelítő összegeket kell alkalmazi. Ha a folytoos modell eseté a téyleges umerikus számítások aszimptotikus viselkedését vizsgáljuk, akkor emcsak az itegrálási tartomáy övekszik, haem a tartomáy felosztása is egyre sűrűbb és sűrűbb. Ebbe az esetbe elleőrizük kell, hogy a határérték viselkedése megegyezik-e a övekvő tartomáy esetével. Megmutatjuk, hogy csak speciális esetbe egyezik meg a határértékek viselkedése, más esetekbe lehetek külöbözőek. A vizsgálataik motivációjakét meg kell említei még a számos helye alkalmazott mitavételi sémákat is. A mitavételezés törtéhet véletle vagy determiisztikus időpotokba. A legtöbb létező eredméy a em sűrűsödő esetre voatkozik (lásd [Mas83], [BC93]). A [Bos98] köyvbe a mitavételi séma fotossága bemutatásra kerül, de em említ explicit eredméyt regresszió eseté. A [Bos98] 140. oldalá a következő utalás szerepel: A regressziós és sűrűség becslések egymáshoz hasolóa viselkedek mitavételi sémák eseté. Valójába a sűrűségfüggvéy magfüggvéyes becslésére több eredméy ismert sűrűsödő-övekvő mitavételi sémákra. Megemlítjük az alábbi kapcsolódó publikációkat. Lahiri 2003-ba ([Lah03]) általáos határeloszlástételt igazolt a sűrűsödő-övekvő sémára. Putter-Youg 2001-be (lásd [PY01]) a krigelést vizsgálta ebbe az esetbe. Zhu-Lahiri 2007-be ([ZL07]) az empirikus eloszlásfüggvéy becslését tekitette. Biau és Blake-Pumo ([Bia04], [BP03]) az optimális mitavételezést tekitette magfüggvéyes sűrűségfüggvéy becslésre. Park-Kim-Park-Hwag 2008-ba ([PKP08]) gyakorlatba alkalmazható közpoti határeloszlás-tételeket igazolt sűrűsödőövekvő sémára Jelölések és a fő eredméy Az előző fejezetbe bevezetett jelöléseket fogjuk itt is haszáli. Továbbra is jelölje D egy D véges halmaz számosságát, valamit T a T tartomáy térfogatát (Lebesgue-mértékét) jelöli. A megfigyelések az alábbi sémát követik. Az egyszerűség kedvéért a d-dimeziós téglák legyeek a megfigyelési tartomáyok. Legye Λ > 0 rögzített. Jelölje ( Z Λ) d az R d -beli Λ-háló potjait,
69 4.2. JELÖLÉSEK ÉS A FŐ EREDMÉNY 55 azaz a hálópotok távolsága 1/Λ: ( ) Z d {( k1 = Λ Λ,..., k ) } d : (k 1,..., k d ) Z d. Λ Legye T korlátos, zárt téglalap R d -be, élei párhuzamosak a tegelyekkel. A T -beli Λ-rácspotokat jelölje D, azaz D = T (Z/Λ) d. A határeloszlás leírásához tekitsük az előző objektumok egy sorozatát, azaz legyeek T 1, T 2,... zárt, korlátos R d -beli téglák egy sorozata. Tegyük fel, hogy T 1 T 2 T 3..., i=1 T i = T. Feltesszük még, hogy T mide éléek hossza egész és tart a -hez, amit (például T = R d vagy T = [0, ) d ). Legye {Λ } a pozitív egész számok egy övekvő sorozata (a em egész számok esetét léyegébe azoos módo kezelhetjük) és a T -be eső Λ -rácspotok halmaza legye D. Legye {ξ t = (X t, Y t ), t T } erőse stacioárius kétdimeziós véletle mező. A megfigyelések -edik halmaza az (X t, Y t ) véletle mező mide t D potba felvett értékeiből áll. Ezekből az adatokból egy becslést kostruáluk a regressziós függvéyre. Valójába, mide t = t () függ - től de, hogy elkerüljük a boyolult jelöléseket, elhagyjuk az () felső idexet. Feltesszük, hogy lim D =. Eze megfigyelések helyei egyre sűrűbbek és sűrűbbek leszek a tartomáyok egy övekvő sorozata eseté, ezért ezt a sémát sűrűsödő-övekvő sémáak evezzük (lásd [Cre91] és [Lah96] a övekvő sémáról). Haszáli fogjuk az előző fejezetbe bevezetett α-keverési együtthatót is. A köyebb olvashatóság érdekébe itt megismételjük a defiíciót: legyeek A és B σ-algebrák F-be. A és B α-keverési együtthatóját jelölje α(a, B), azaz α(a, B) = sup{ P(A)P(B) P(AB) : A A, B B}. A {ξ t : t T } mező α-keverési együtthatói pedig: α(r) = sup{α(f I1, F I2 ) : ϱ(i 1, I 2 ) r}, ahol I 1 és I 2 a T véges részhalmazai, F Ii = σ{ξ t : t I i }, i = 1, 2. Szükségük lesz a következő feltételre: valamely 1 < a < eseté (4.1) 0 s 2d 1 α a 1 a (s)ds <.
70 56 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE A K : R [0, ) függvéyt magfüggvéyek evezzük, ha K korlátos, folytoos, szimmetrikus sűrűségfüggvéy (a Lebesgue-mértékre ézve), melyre (4.2) lim u K(u) = 0, u u 2 K(u)du <. Legye g(x) az X t (ismeretle) perem-sűrűségfüggvéye. Feltételezzük, hogy g(x) mideütt pozitív. Legye K magfüggvéy és legye h > 0. Ekkor a g(x) (Parze-Roseblatt-féle) magfüggvéyes becslése g (x) = 1 1 ( ) x Xi, x R. D h i D K Céluk az r(x) = E (Φ (Y t ) X t = x) regressziós függvéy becsléséek határeloszlásáak a meghatározása, ahol Φ ismert, korlátos, mérhető függvéy. Tekitsük a regressziós függvéy jól ismert magfüggvéyes becslését r (x) = 1 D 1 D h Φ(Y t ) 1 ( ) x h K Xt ( ) x Xt Φ(Y t )K h h t D t D ( ) = 1 x h K Xt ( ), x Xt K h h t D t D ahol K egy ismert magfüggvéy, h = h > 0. Legye a(x) = E ( Φ 2 (Y t ) X t = x ). R d 0 jelölje az Rd \ {0} halmazt. Legye g u (x, y) az X 0 és X u együttes sűrűségfüggvéye, ha u R d 0 és x, y R és a u (x, y) = E { [Φ(Y 0 ) r(x 0 )] [Φ(Y u ) r(x u )] X0 = x, X u = y }. Feltesszük, hogy mide rögzített u eseté (4.3) a u (.,.), g u (.,.), a(.), r(.), g(.), r (.), g (.), r (.), g (.) korlátos és folytoos függvéyek. Továbbá feltesszük, hogy (4.4) lim 1 Λ d h = L <, lim Λ = és lim h = 0,
71 4.2. JELÖLÉSEK ÉS A FŐ EREDMÉNY 57 valamit (4.5) lim T h 4 = 0. Arra az esetre kocetráluk, amikor ξ t és ξ s valószíűségi változók függőek, ha t és s közel vaak egymáshoz. Először tekitsük a sűrűségfüggvéy g becsléséek aszimptotikus ormalitását. Legye l u (x, y) = g u (x, y) g(x)g(y), u R d 0 és x, y R. Jelölje l u az l u (x, y) függvéyt, mit l : R d 0 C(R2 ) leképezést, azaz egy olya függvéyt, mely a C(R 2 ) térből veszi fel értékeit (itt C(R 2 ) az R 2 -e értelmezett valós értékű folytoos függvéyek tere). Legye (4.6) l u = sup (x,y) R 2 l u (x, y) az l u ormája. ( Legyeek x 1,..., x m külöböző valós számok. ) Legye Σ l = R l d u (x i, x j )du, legye továbbá D diagoális mátrix Lg(x i ) 0 1 i,j m K2 (u)du, i = 1,..., m diagoális elemekkel. Vezessük be a Σ = Σ l + D jelölést. A. Tétel. ([FC06] Theorem 1.) Tegyük fel, hogy l u (mit u változójú l : R d 0 C(R2 ) függvéy) Riemaitegrálható mide korlátos zárt d-dimeziós R R d 0 téglá, továbbá l u direkt Riema-itegrálható ( l : R d 0 R függvéykét tekitve). Legyeek x 1,..., x m egymástól külöböző valós számok és tegyük fel, hogy Σ pozitív defiit. Tegyük fel, hogy létezik 1 < a <, melyre teljesül (4.1) és (4.7) (h ) 1 c T a 2 (3a 1)(2a 1) mide eseté. Ha (4.4) és (4.5) feáll, akkor (4.8) D Λ d {(g (x i ) g(x i )), i = 1,..., m} N (0, Σ ), ha. Megjegyezzük, hogy Park-Kim-Park-Hwag egy hasoló jeleséget vizsgált ([PKP08]) egyszerűbb függőségi feltétel mellett (m-függőség), de általáosabb mitavételi sémába.
72 58 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE A direkt Riema-itegrálhatóság általuk haszált fogalma megtalálható Fazekas és Chupruov cikkébe ([FC06]). Legye l : R d 0 [0, ) adott függvéy. Valamely δ > 0 eseté, tekitsük az R d tér felosztását (jobbról zárt, balról yílt) δ élhosszúságú i d-dimeziós kockákra úgy, hogy a 0 középpotja az origóba legye (azaz 0 R d -be). A { i } családot a δ-hoz tartozó felosztásak evezzük. Ha i 0 akkor x i eseté legye l δ (x) = sup{l(y) : y i }, l δ (x) = if{l(y) : y i }, míg l δ (x) = l δ (x) = 0, ha x 0. Ha lim l δ (x)dx = lim l δ (x)dx = I, δ 0 R d δ 0 R d és ez a közös érték véges, akkor l-et direkt Riema-itegrálhatóak evezzük (d.r.i.), és I-t az l direkt Riema-itegráljáak. Ha l d.r.i., akkor l az origó tetszőleges köryezeté kívül korlátos. Továbbá, l majdem mideütt folytoos (a Lebesgue-mértékre ézve). Ezért l Riema-itegrálható mide olya korlátos és zárt d-dimeziós téglá, ami em tartalmazza az origót. Nevezzük zóáak az M = R 1 \R 2 alakú halmazokat, ahol R 1 zárt d-dimeziós tégla, míg R 2 ( = R 2 R 1 ) egy yílt d-dimeziós tégla úgy, hogy mid a kettő tartalmazza az origót. Belátható, hogy l Riema-itegrálható mide zóá. Ha l 0 d.r.i., akkor az R l(x)dx improprius itegrál létezik és egyelő l direkt Riema-itegráljával. A feti állítás következméye az, hogy d 0 mide ε > 0 eseté létezik egy M zóa úgy, hogy R d 0 \M l(x)dx ε. Végül megjegyezzük a következőt. Legye l 0, l d.r.i. Legye δ olya pozitív számok sorozata, amely ullához kovergál és { () i } a δ -hez tartozó felosztás. Ekkor mide ε > 0 eseté létezik egy M zóa úgy, hogy az R d 0 \M l(x)dx itegrál mide Riema közelítő összege (mely a feti felosztáshoz tartozik, de amely em tartalmazza a 0 l(x 0 ) kifejezést) kisebb, mit ε. A Riema-itegrálhatóság defiíciója Baach-terekbei értékű függvéyekre megtalálható Hille és Phillips köyvébe ([HF57] 62 o.). A feti előzméyek utá kimodhatjuk a fő eredméyüket. Legye v(x) = a(x) r 2 (x). Rögzített m pozitív egész és rögzített, egymástól külöböző x 1, x 2,..., x m valós számok eseté vezessük be a kö-
73 4.2. JELÖLÉSEK ÉS A FŐ EREDMÉNY 59 vetkező jelöléseket. (4.9) σ(x t, x s ) = R d 0 (4.10) Σ (m) = Feltesszük, hogy a u (x t, x s )g u (x t, x s )du, t, s = 1,..., m, ( ) σ(xt, x s ). g(x t )g(x s ) 1 t,s m (4.11) lim z z3 K(z) = 0 teljesül Tétel. Legye (X t, Y t ), t T, erőse stacioárius kétdimeziós véletle mező, r(x) = E (Φ (Y t ) X t = x) a regressziós függvéy, ahol Φ korlátos, mérhető függvéy és K egy magfüggvéy. Tegyük fel, hogy az A. Tétel feltételei teljesülek az l u függvéyre, továbbá legye Σ pozitív defiit. Tegyük fel, hogy az X t peremsűrűségfüggvéye pozitív, valamit a u g u Riema-itegrálható (egy a g : R d 0 C(R2 ) függvéykét tekitve) mide korlátos zárt d-dimeziós R R d 0 téglá. Továbbá, a ug u direkt Riemaitegrálható (mit egy a g : R d 0 R függvéy), ahol a orma (4.6) szerit defiiált. Tegyük fel továbbá, hogy létezik olya 1 < a <, hogy (4.1) és (4.7) teljesül. Legye Σ (m) + D mátrix pozitív defiit, ahol D egy diagoális mátrix, melyek a diagoális elemei: Lv(x i ) K2 (t)dt/g(x i ), i = 1,..., m. Ha a fetieke felül még (4.3), (4.4), (4.5) és (4.11) teljesülek, akkor D Λ d {(r (x i ) r(x i )), i = 1,..., m} N (0, Σ), ha, ahol Σ = Σ (m) + D Megjegyzés. Megmutatjuk, hogy a 4.1. Tételbeli Σ aszimptotikus kovariacia-mátrix egy diszkrét és egy folytoos esetek megfelelő aszimptotikus kovariacia-mátrix kombiációja. Schuster igazolta (lásd [Sch72]), hogy (függetle, azoos eloszlású megfigyelések eseté) r (x 1 ),..., r (x m )
74 60 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE aszimptotikusa ormális diagoális kovariacia-mátrixszal. Potosabba h (r (x i ) r(x i )) N (0, c i ), ahol c i = v(x i ) K2 (t)dt/g(x i ), ezért a 4.1. Tételbe a D diagoális rész megfelel a diszkrét esetbeli határérték kovariacia-mátrixak. Számoljuk ki a σ(x t, x s ) elemeket. Jelöljük f X0,X u,y 0,Y u (x 1, x 2, y 1, y 2 )-vel az X 0, X u, Y 0, Y u, (u 0) együttes sűrűségfüggvéyét, ekkor a u (x 1, x 2 ) = = [Φ(y 1) r(x 1 )] [Φ(y 2 ) r(x 2 )] f X0,X u,y 0,Y u (x 1, x 2, y 1, y 2 )dy 1 dy 2 = Tehát (a d = 1 esetet tekitve) σ(x t, x s ) = R 0 g u (x 1, x 2 ) M u(x 1, x 2, y 1, y 2 )dy 1 dy 2. g u (x 1, x 2 ) [ M u (x 1, x 2, y 1, y 2 )dy 1 dy 2 ] du adódik. Az (X t, Y t ), t [0, T ] folytoos idejű sztochasztikus folyamat (amely bizoyos α-keverő feltételeket teljesít) magfüggvéyes becslését vizsgálta Cheze ([Che92]) és Bosq ([Bos98], 138 o.). Az r(x) = E(Φ(Y t ) X t = x) regressziós függvéy becslése (4.12) r T (x) = φ T (x) g T (x), ahol φ T (x) = 1 T g T (x) = 1 T T 0 T 0 Φ(Y t ) 1 ( x Xt K h T h T ( ) 1 x Xt K dt. h T h T ) dt, Bizoyos feltételek mellett, ha T és h T 0, akkor r T aszimptotikusa ormális eloszlású. Potosabba r T (x) r(x) dt (x) N (0, 1),
75 4.2. JELÖLÉSEK ÉS A FŐ EREDMÉNY 61 ahol g 2 (x)d T (x) = (1, r(x)) var φ T (x) g T (x) 1 r(x). Felhaszálva a feti kifejezést (éháy aalitikus feltétel mellett), beláthatjuk, hogy T d T (x) határértéke σ(x, x)/g 2 (x). Tehát Cheze ([Che92]) és Bosq ([Bos98]) eredméyét a következőképpe fogalmazhatjuk meg: T ( rt (x) r(x)) N ( 0, σ(x, x)/g 2 (x) ). Tehát a Σ (m) mátrix diagoális elemei megfelelek a folytoos modellbei aszimptotikus szórások szakirodalomba közölt értékeiek. (Cheze ([Che92]) és Bosq ([Bos98]) em taulmáyozták az ( r T (x 1 ),..., r T (x m )) együttes aszimptotikus ormalitását.) 4.3. Megjegyzés. Ha a (4.5) feltétel, azaz lim T h 4 = 0, em teljesül, akkor a következőt tudjuk bizoyítai: ahol és D Λ d {(r (x i ) r (x i )), i = 1,..., m} N (0, Σ), ha, r (x) = 1 D r(x t ) 1 ( ) x h K Xt h t D, g (x) g (x) = 1 ( ) 1 x D h K Xt g(x) h t D valószíűségbe. Ez a 4.1. Tétel bizoyításáak következméye Megjegyzés. Bosq a mitavételezés problémáját szité vizsgálta ([Bos97], illetve [Bos98], 140 o.), azaz a (4.12)-be szereplő r T azo közelítéséek a viselkedését, amelyet akkor kapuk, amikor r T -ot helyettesítjük a folyamat δ, 2δ,..., δ időpillaatokbai megfigyeléseit tartalmazó megfelelő diszkrét kifejezéssel. Azoba az aszimptotikus ormalitást em vizsgálták a fet említett művek egyikébe sem.
76 62 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE 4.3. A fő tétel bizoyítása Ahhoz, hogy bebizoyítsuk a fő eredméyt, szükségük lesz a következő közpoti határeloszlás tételre és a Rosethal-egyelőtleségre keverő mezők eseté. Először defiiáljuk az Y (k) diszkrét paraméterű (vektor értékű) véletle mezőt a következőképpe. Mide = 1, 2,..., és mide k = k () D eseté legye (4.13) Y (k) a ξ k () Borel-mérhető függvéye, ahol {ξ t, t T } az alapul szolgáló véletle mező. B. Tétel. ([FC04] Theorem 2.1.) Legye ξ t véletle mező és Y (k) = (Y (1) (k),..., Y (m) (k)) a (4.13)-ba defiiált m-dimeziós véletle mező és S = k D Y (k), = 1, 2,.... Tegyük fel, hogy Y (k), k D erőse stacioárius mező mide rögzített eseté, valamit EY (k) = 0. Tegyük fel, hogy teljesülek az alábbi feltételek (4.14) Y (k) M, melybe M csak -től függ; (4.15) sup E(Y (t) (k)) 2 < ;,k,t a G T feltételt teljesítő G téglák tetszőleges övekvő és emkorlátos sorozata eseté, (4.16) 1 lim Λ d G E (k) (l) = σ ts, t, s = 1,..., m, k G Y (t) l G Y (s) ahol G = G (Z/Λ ) d ; a Σ = (σ ts ) m t,s=1 1 < a < úgy, hogy (4.1) teljesül; és mátrix pozitív defiit; létezik (4.17) M c T a 2 (3a 1)(2a 1) mide eseté. Ekkor (4.18) 1 Λ d D S N (0, Σ), ha.
77 4.3. A FŐ TÉTEL BIZONYÍTÁSA 63 A fő tétel bizoyításába felhaszáljuk a Rosethal-egyelőtleség előző fejezetbe közölt alakját (3.3. Lemma). A fő tétel bizoyításába többször haszáli fogjuk a következő tételt. Ez egy speciális esete a [Rao83] Theorem állításáak. C. Tétel. ([Rao83] Theorem ) Legye K : R R mérhető függvéy úgy, hogy K(z) M, z R, K(z) dz <, z K(z) 0, ha z. Továbbá legye g : R R olya mérhető függvéy, hogy Defiiáljuk a g(z) dz <. g (x) = 1 ( ) z K g(x z)dz h h függvéyt, ahol 0 < h 0, ha. Ha g folytoos, akkor (4.19) lim g (x) = g(x) K(z)dz, és ha g egyeletese folytoos, akkor (4.19)-be a kovergecia egyeletes Megjegyzés. Gyakra felhaszáljuk a következő határérték tulajdoságokat (lásd [FC06]). Tegyük fel, hogy a g sűrűségfüggvéy folytoos, K egy magfüggvéy, ekkor h 0 (h > 0) eseté a következők teljesülek. ( 1 (4.20) E K h (4.21) E 1 h K 2 ( ) x Xt = h ( )) x Xt = h 1 h K 2 ( x u h 1 h K ( x u h ) g(u)du g(x), ) g(u)du g(x) K 2 (u) du,
78 64 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE (4.22) E 1 h 2 K ( xr X t h ) K = ( ) xs X t h h 2 ( 1 xr u K h ) K ( xs u h ) g(u)du 0, ha x r x s. A 4.1. Tétel bizoyítása. Tekitsük a következő átalakítást 1 D D D (r Λ d (x) r(x)) = t D [Φ(Y t) r(x)] 1 K ( x X t ) h h Λ d 1 1 D t D K ( x X t ) h h = ahol 1 D Λ d [ 1 [Φ(Y h t) r(x t)] K t D J 1 (x) = J 2 (x) = 1 D ( ) x Xt + ( ) x Xt ] [r(x t) r(x)] K h h t D ( ) 1 x h K Xt h t D = J 1(x) + J 2 (x), J 3 (x) 1 1 D Λ d h [Φ(Y t) r(x t )] K t D 1 1 D Λ d h [r(x t) r(x)] K t D J 3 (x) = 1 1 D h K t D ( x Xt h ( x Xt h ( x Xt Először J 1 aszimptotikus ormalitását bizoyítjuk. Elleőrizük kell, hogy a B. Tétel feltételei teljesülek. Legyeek x 1, x 2,..., x m egymástól külöböző valós számok. Be kell látuk J 1 = (J 1 (x 1 ), J 1 (x 2 ),..., J 1 (x m )) együttes aszimptotikus ormalitását. Defiiáljuk Z (i) m-dimeziós vektort a következő koordiátákkal: s = 1,..., m és i D eseté. ). Z (s) (i) = 1 h [Φ(Y i) r(x i )] K ( xs X i h h ), ), ),
79 4.3. A FŐ TÉTEL BIZONYÍTÁSA 65 Osszuk fel T -t d-dimeziós egység kockákra (midegyikbe Λ d számú D -beli pot szerepel). Jelölje D eze kockák halmazát. Legye V (k) = (V (1) (k),..., V (m) (k)) azo Z (i) változók számtai átlaga, melyek az i idexei a k-dik egységkockába vaak. Ekkor mide rögzített eseté a V (k), k D mező erőse stacioárius. Alkalmazzuk a B. Tételt a V (k), k D -re, azaz alkalmazzuk a tétel em sűrűsödő alakját. Ekkor mert J 1 (x s ) = 1 Λ d D Λ d i D V (s) (i) = Λ d D i D V (s) (i). A EV (k) = 0, bizoyításához tekitsük az alábbi egyelőséget ( ( )) 1 EZ (s) (i) = E h [Φ(Y xs X i i) r(x i )] K = 0, h ( E Φ(Y )K ( )) x X h [ =E ( ) x X ] E {Φ(Y ) X} K }{{} h r(x) ( =E r(x)k ( x X h )). Mivel Φ, r és K korlátosak, ezért a (4.7)-ből következik (4.14) és (4.17). A (4.15) bebizoyításához tekitsük ( ) ) ) 2 2 = E ( E V (s) (k) 1 Λ d i 1 h [Φ(Y i) r(x i )] K ( xs X i ahol azt jelöli, hogy i a k-adik egységkockához tartozik. E kifejezés korlátosságát hasolóa elleőrizhetjük, mit ahogya a következő bizoyításba i eljáruk (ahol megmutatjuk, hogy a (4.16) feltétel teljesül). A (4.16)-ba a határérték kiszámításához legye {G } d-dimeziós téglák övekvő sorozata, ahol mide G d-dimeziós egységkockák uiója. Ekkor teljesül, hogy 1 G E (k) (l) 1 = Λ d G k G Z d V (t) V (s) l G Z d h,
80 66 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE i G [ 1 h 2 E [Φ(Y i ) r(x i )] K j G ( xt X i h = A + B, ) [Φ(Y j ) r(x j )] K ( xs X j h )], ahol G = G (Z/Λ ) d, és A jelöli az összeg i = j feltételek eleget tevő tagjait, míg B jelöli az i j esetet. A-ra azt kapjuk, hogy 1 1 A = Λ d G h i G E Ha t = s, akkor 1 1 A = Λ d G h [ 1 h [Φ(Y i) r(x i )] 2 K i G E ( xt X i h [ 1 h [Φ(Y i) r(x i )] 2 K 2 Tekitsük a következő felbotást [ ( )] 1 E h [Φ(Y i) r(x i )] 2 K 2 xs X i h ( 1 = E ( )) h Φ2 (Y i )K 2 xs X i h }{{} ( 1 E ) K ( xs X i h ( xs X i h )]. ( )) h r2 (X i )K 2 xs X i. h }{{} Számítsuk ki * és ** tagokat egymás utá: [ ( ( ) )] ( 1 = E E h Φ2 (Y i ) K 2 xs X i 1 X i = E h h K2 ( xs X i ahol a(x) = E ( Φ 2 (Y ) X = x ). A (4.21) összefüggést felhaszálva, = h )]. ) ) a(x i ), a(u) 1 ( ) xs u h K2 g(u)du = a(x s ht)g(x s ht)k 2 (t) dt h a(x s )g(x s ) K 2 (t) dt, ha h 0, teljesül, mivel a és g korlátos és folytoos, valamit K 2 itegrálható.
81 4.3. A FŐ TÉTEL BIZONYÍTÁSA 67 = Hasolóa kapjuk, hogy ( ( )) 1 = E h r2 (X i )K 2 xs X i = h r 2 (x s ht)k 2 (t) g(x s ht)dt r 2 (x s )g(x s ) 1 h r2 (u)k 2 ( xs u mivel r és g korlátos és folytoos, valamit K 2 itegrálható. A (4.4)-et alkalmazva, kapjuk, hogy h ) g(u)du K 2 (t) dt, ha h 0, A 1 1 [ a(xs Λ d ) r 2 (x s ) ] g(x s ) K 2 (t) dt h G i G Lv(x s )g(x s ) K 2 (t) dt, ahol v(x s ) = a(x s ) r 2 (x s ). Emlékeztetük, hogy v(x) a Φ(Y ) feltételes szórása, vagyis Ha t s, akkor A = 1 Λ d v(x) = E ( Φ 2 (Y ) X = x ) [E (Φ(Y ) X = x)] 2 1 E h 2 { } = E [Φ(Y ) E (Φ(Y ) X = x)] 2 X = x. ( [Φ(Y i ) r(x i )] 2 K = 1 [ ( 1 Λ d E h 2 a(x i)k ( 1 E h 2 r2 (X i )K ( xt X i h ( xt X i h ( xt X i ) K ) K h ) K ( )) xs X i h ( ))] xs X i h ( )) xs X i h = 1 Λ d (A 1 + A 2 ). Az a(x), r(x) korlátosságából és (4.22)-ből következik, hogy ( ) ( ) 1 A 1, A 2 c h 2 K xt u xs u K g(u)du 0. h h Tehát t s eseté A 0, mivel Λ d.
82 68 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE ahol Tekitsük most a B kifejezést. B = 1 1 Λ d E G i j ( a(x i, X j ) 1 h 2 K ( xt X i h ) K ( xs X j h )), a(x i, X j ) = a i j (X i, X j ) = E {[Φ(Y i ) r(x i )] [Φ(Y j ) r(x j )] X i, X j }. Ekkor B = 1 1 Λ d G i j a i j (u, v) 1 ( ) h 2 K xt u K h ( xs v h ) g i j (u, v)dudv, ahol g i j (u, v) az X i és X j együttes sűrűségfüggvéye. Feltehetjük, hogy a G tégla középpotja az origó, mivel a véletle mező erőse stacioárius. Ekkor az i j (ahol i, j G ) alakú vektorok halmaza 2G, ahol 2G -et úgy defiiáljuk, mit (2G ) (Z/Λ ) d. Ha u 2G rögzített, akkor jelölje G,u azo (i, j) G G párok számát melyekre i j = u. Ekkor (4.23) B = 1 Λ d { 1 h 2 K u 2G 0 ( ) ( ) xt u xs v K h h G,u G a u(u, v)g u (u, v) dudv, ahol 2G 0 = 2G \ {0}. Rögzítsük az ε > 0 értéket. Mivel a u g u direkt Riema-itegrálható, ekkor találhatuk egy M ε R d origó középpotú zóát úgy, hogy (4.24) a u g u du ε, R d 0 \M ε ugyaakkor eze itegrál Riema-féle közelítő összegei sem haladják meg ε-t, ameyibe a beosztás átmérője elég kicsiy. Ezért, mivel G,u / G 1, kapjuk, hogy (4.25) 1 Λ d G,u G a ug u ε, u 2G\M 0 ε
83 4.3. A FŐ TÉTEL BIZONYÍTÁSA 69 amikor 1/Λ d elég kicsi, azaz ha ε. Rögzítsük ε-t és M ε -t és tegyük fel, hogy ε. Mivel a u g u Riema-itegrálható R-e (mit a g : R d 0 C(R 2 ) függvéy) tetszőleges korlátos és zárt d-dimeziós R d 0-beli R tégla eseté, ezért (4.26) 1 Λ d a u g u a u g u du u 2G M 0 M ε ε ε a C(R 2 ) térbe, ha elég agy. Ebből az összefüggésből és (4.24)-ből következik, hogy a u (x, y)g u (x, y)du R d 0 létezik és folytoos (x, y)-ba. Mivel G mide éle tart a -hez, G,u G 1 egyeletese u M ε szerit. Ezért, felhaszálva, hogy a u g u direkt Riema-itegrálható, azt kapjuk, hogy (4.27) 1 G,u Λ d G a ug u 1 Λ d a u g u u 2G M 0 ε u 2G M 0 ε ε, ha elég agy. A (4.24) - (4.27) -ből következik, hogy (4.28) 1 G,u Λ d G a ug u a u g u du R d 0 4ε, u 2G 0 ha elég agy. Ezért, felhaszálva azt, hogy 1 h K ( x t u ) h sűrűségfüggvéy, kapjuk, hogy (4.29) { B 1 ( h K xt u ) ( xs v ) } K a 2 u (u, v)g u (u, v)du dudv h h R d 4ε, 0 ha elég agy. Mivel R d 0 a u (u, v)g u (u, v)du folytoos az (u, v) szerit, a (4.29) kifejezésbe lévő kettős itegrál határértéke R a d u (x t, x s )g u (x t, x s )du =σ(x t, x s ) 0 (lásd C. Tétel). Ezért B a u (x t, x s )g u (x t, x s )du = σ(x t, x s ). R d 0
84 70 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE Tehát J 1 aszimptotikus kovariacia-mátrixa a következő L K 2 (t)dt diag (v(x t )g(x t )) + (σ(x t, x s )) m t,s=1. Most tekitsük a J 2 kifejezést. J 2 (x) = 1 1 D Λ d h [r(x t) r(x)] K t D ( x Xt Alkalmazva a Taylor-sorfejtést (r(u) = r(x) + r (x)(u x) r ( x)(u x) 2, valójába x függ u-tól, azaz x = x(u)), kapjuk, hogy ( ( )) 1 x E h [r(x Xt t) r(x)] K h ( ) 1 x u = [r(u) r(x)] K g(u)du h h 1 = [r (x)(u x) + 12 ] ( ) x u h r ( x)(u x) 2 K g(u)du h 1 = [r (x)z 12 ] ( z h r ( x)z 2 K g(x z)dz h) = r 1 z ( z ) (x)h h h K g(x z)dz h 1 1 ( z ) 2 h r ( x)z 2 K g(x z)dz = A 11 + A 12. h Megmutatjuk, hogy (4.30) A 11, A 12 h 2 C. Tekitsük először A 11 -et. Vezessük be a t = z helyettesítést, majd haszáljuk a g(x th) = g(x)+g ( x)( th) Taylor-sorfejtést, a g és r korlátosságát h és a K szimmetria tulajdoságát kapjuk, hogy 1 z ( z ) h h K g(x z)dz = tk(t)g(x th)dt h = tk(t)g(x)dt + tk(t)g ( x)( th)dt = hc t 2 K(t)dt. h ).
85 4.3. A FŐ TÉTEL BIZONYÍTÁSA 71 Tehát A 11 h 2 C. Felhaszálva r korlátosságát, így A 12 eseté tekitsük a következő egyelőtleséget: A 12 ch 2 1 ( z 2 ( z ) K g(x z)dz. h h) h A (4.11) és a C. Tétel miatt 1 ( z 2 ( z ) K g(x z)dz g(x) z h h) 2 K(z)dz, h ezért A 12 h 2 C, alkalmas C kostas eseté. A (4.30) alapjá E(J 2 (x)) D Λ d h 2 C = T h 2 C, ezért E(J 2 (x)) 0, mivel (4.5) alapjá T h 4 0. Megmutatjuk, hogy E J 2 l 0, valamely 1 < l < 2. Elegedő megmutati, hogy E J 2 E(J 2 ) l 0, mivel E J 2 l =E J 2 E(J 2 ) + E(J 2 ) l =E (J 2 E(J 2 )) + (E(J 2 )) l c (E J 2 E(J 2 ) l + E(J 2 ) l) és E(J 2 ) 0. Eek igazolására tekitsük a következő egyelőtleséget ( ) l ( ) E J 2 E(J 2 ) l 1 1 l l = E η t Eη t, D Λ d h t D ahol η t = (r(x t ) r(x)) K ( x X t ) h. Most fogjuk össze η t -kat egy egység kockákba (jelöljük ezt a kockát K-val) és alkalmazzuk ezekre a (3.13) Rosethal-egyelőtleséget, kapjuk, hogy (4.31) ( ) l ( ) 1 E J 2 E(J 2 ) l 2 1 l c D Λ d h K D ( ) l ( ) l c D Λ d h K D l+ε E η t Eη t t K l+ε E η t t K l l+ε, l l+ε
86 72 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE ahol ε > 0. (Alkalmaztuk az E η Eη k CE η k, k > 1 egyelőtleséget.) (A (4.1) egyelőtleségből látható, hogy c (ε) 1,1 <.) Alkalmazva a Jeseegyelőtleséget kapjuk, hogy l+ε η t t K = Λ d(l+ε) amelyből következik, hogy l+ε (4.32) E η t t K 1 Λ d t K Λ d(l+ε) t K η t l+ε 1 Λ d Tehát (4.31) és (4.32) szerit, kapjuk, hogy ( ) l ( 1 (4.33) E J 2 E(J 2 ) l 2 1 c D Λ d h Λ d(l+ε) t K 1 Λ d η t l+ε, E η t l+ε = Λ d(l+ε) E η t l+ε. ) l D Λ d Λ d l (E η t l+ε) l l+ε. Először számítsuk ki az E η t l+ε határértékét: ( ) E η t l+ε = E r(x t ) r(x) l+ε x K l+ε Xt h ( ) = r(u) r(x) l+ε x u K l+ε g(u)du }{{} h r ( x)(x u) ch 1+l+ε h 1+l+ε cg(x) (Itt a C. Tételt alkalmaztuk.) Tehát (4.33) alapjá 1 x u h h l+ε ( ) l ( 1 E J 2 E(J 2 ) l 2 1 c D Λ d h = c D 1 l 2 z l+ε K l+ε (z)dz. ( ) x u K l+ε g(u)du h ) l D Λ d ( ) l Λ d 2 1 h l l+ε Λ d l h l(1+l+ε) l+ε = c T 1 l 2 h l l+ε.
87 4.4. PÉLDÁK 73 Megfelelő l és ε választása eseté (pl. l = 1.98, ε = 0.01) (4.5)-ből következik, hogy T 1 l l 2 h l+ε 0. Tehát E J 2 l 0. Ezért J 2 0 valószíűségbe. Végül foglalkozzuk a J 3 kifejezéssel. J 3 (x) = 1 ( ) 1 x D h K Xt. h t D Az A. Tétel miatt, T (J 3 (x) g(x)) eloszlásba koverges, ezért J 3 (x) g(x) valószíűségbe Megjegyzés. A (4.5) és (4.7) csakis akkor teljesülhet egyidejűleg, ha 1 < a < Eek igazolásához tekitsük a következőket. A (4.7)-ből következik, hogy 1 C h 4 T 4a 2 (3a 1)(2a 1), teljesül. Hogy egyidejűleg a (4.5) is teljesüljö szükséges, hogy 4a 2 (3a 1)(2a 1) > 1 egyelőtleség teljesüljö. Ebből következik, hogy < a < Felhaszálva, hogy 1 < a <, adódik az állítás. Például egy lehetséges jó választás: a = 2, h = 1, T = 15/ Példák Ebbe a fejezetbe szimulációko keresztül éháy egyszerű példát aduk az elméleti állítás bemutatására. Legye X u, u R d, stacioárius Gauss-féle véletle mező ulla várható értékkel és ρ u kovariacia függvéyel. A következő példákba ugyaazokat az X u véletle mezőket vizsgáljuk, amelyeket Fazekas és Chupruov már taulmáyoztak ([FC06], [Faz07]). Legye Φ(Y u ) = 10 si(x u ) δ u, ahol δ u = X u, és X u olya stacioárius véletle mező, hogy X u és X u eloszlása megegyezik, valamit legyeek X u és X u függetleek.
88 74 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE 4.7. Példa. Tekitsük egy X(u), u R, Gauss-folyamatot ulla várható értékkel és ρ u = e u, u R kovariacia függvéyel. Ezt a folyamatot figyeljük meg a T = [0, t] tartomáy 1/Λ-hálópotjaiba, ahol Λ = 40 és t = 60. Azaz a mita z 1 = X(1/40),..., z s = X(2400/40), ahol s = Eek a mita vektorak a kovariacia-mátrixa (ρ i j ) s i,j=1, ahol ρ = e 1/Λ. Ezért az adatok a szimulációhoz köye geerálhatóak. Valóba, legyeek y 1,..., y s függetle, azoos eloszlású stadard ormális valószíűségi változók és legye z i = ρ i 1 y ρ 2 i ρ i j y j, i = 1,..., s. Ezeket az adatokat felhaszálva, meghatároztuk az r regressziós függvéy becslését az x 1 = 0.5, x 2 = 0.25, x 3 = 0, x 4 = 0.25, és x 5 = 0.5 potokba. Sávszélességek két értéket haszáltuk, h 1 = öt és h 2 = öt. Továbbá a K magfüggvéyek a stadard ormális eloszlás sűrűségfüggvéyét haszáltuk. A szimulációkat MATLAB programcsomag segítségével hajtottuk végre. Az eljárást 5000-szer ismételtük. Midkét sávszélesség (h 1 és h 2 ) haszálata eseté az adathalmazok megegyeztek. A regressziós függvéy elméleti értékeit és becsléseiek átlagát az alábbi 4.1. táblázat mutatja. Megállapíthatjuk, hogy midkét sávszélesség eseté az elméleti érték és a közelítő értékek átlaga közel vaak egymáshoz. j= táblázat. A regressziós függvéy elméleti értékei és becsléseiek átlaga a 4.7. Példa adataira. x r(x) r (x), ha h 1 = r (x), ha h 2 = A D Λ (r (x 1 ) r(x 1 ),..., r (x 5 ) r(x 5 )) stadardizált becslésekre (a D Λ stadardizáló faktor = ) kiszámítottuk a Σ 1 (h 1 sávszélesség eseté) és Σ 2 (h 2 sávszélesség eseté) empirikus kovariacia-mátrixokat:
89 4.4. PÉLDÁK 75 Σ 1 = Σ 2 = ;. A Σ 1 és Σ 2 mátrixok csak a főátlókba térek el jeletőse, többi elemük majdem megegyezik. Határozzuk most meg a 4.1. Tételbe leírt kovariacia-mátrix D diagoális mátrixáak elemeit. Esetükbe, a D k diagoális mátrix elemei h k (k = 1, 2-re) sávszélesség eseté a következők: v(x i ) Λ h k g(x i ) K 2 (u)du = h k g(x i ) 2 π. A sűrűsödő-övekvő eset miatt a kovariacia-mátrixba csak a főátlóba lehet külöbség külöböző sávszélesség haszálata eseté. A 4.2. táblázatba bemutatjuk, hogy az empirikus kovariacia-mátrixok főátlóbeli elemei külöbsége (diag(σ 2 Σ 1 )) és az elméleti kovariacia-mátrixok külöbsége (diag(d 2 D 1 ), hogya viszoyul egymáshoz táblázat. Az empirikus és az elméleti kovariacia-mátrixok főátlóbeli elemei külöbségéek aráya a 4.7. Példa adataira. x diag(σ 2 Σ 1 ) diag(d 2 D 1 )
90 76 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE Az eredméyek azt mutatják, hogy a 4.1. Tételbe szereplő D diagoális mátrix jól magyarázza a határérték kovariacia-mátrix függőséget a sávszélességtől, mivel az aráyok közel vaak egyhez. Végül, a 4.2. ábra az r(x 3 = 0) potbeli becslések relatív gyakoriságát mutatja h 1 = (bal oldali ábra) és h 2 = (jobb oldali ábra) sávszélességek eseté. A hisztogramokra ráhelyeztük azt a ormális eloszlást, melyek a várható értékét és szórását a mitából becsültük. A 4.1. Tételbe kimodott regressziós becslés közelítő ormális eloszlása látható ezekbe az ábrákba. A külöböző sávszélességek külöböző ormális eloszlásokat eredméyezek. Desity h 1 = Desity h 2 = r(x 3 = 0) r(x 3 = 0) 4.2. ábra. Az r(x 3 = 0) potbeli becslések relatív gyakorisága h 1 = (bal ábra) és h 2 = (jobb ábra) sávszélességek eseté, valamit a hozzájuk tartozó becsült ormális eloszlások sűrűségfüggvéyei Megjegyzés. Ha csökketjük a mitavételi helyek számát, akkor aráya a következőképpe módosul: diag(σ 2 Σ 1 ) diag(d 2 D 1 ) 1. Ha t = 20, Λ = 20 és a többi adat változatla marad, akkor x diag(σ 2 Σ 1 ) diag(d 2 D 1 )
91 4.4. PÉLDÁK Ha t = 10, Λ = 10 és a többi adat változatla marad, akkor x diag(σ 2 Σ 1 ) diag(d 2 D 1 ) Látható, hogy ha a megfigyelési helyeik számát drasztikusa lecsökketjük, akkor a módszerük em ad jó eredméyt Példa. Tekitsük most egy X(u, v), (u, v) R 2, kétdimeziós paraméterterű Gauss-folyamatot ulla várható értékkel és ρ (u,v) = e ( u + v ), (u, v) R 2 kovariacia-függvéyel. Legye az előző példához hasolóa Φ(Y u ) = 10 si(x u ) X u. Ezt a folyamatot figyeljük meg a T = [0, t] 2 tartomáy 1/Λ-hálópotjaiba, ahol Λ = 10 és t = 30. Így a mita z (i,j) = X (i/10,j/10), i, j = 1,..., 300, (30 10) 2 = mitaelemszámmal. A mitát tehát az alábbi módo geerálhatjuk. Geeráljuk az y k,l, (k, l = 1,..., 300) adatokat, függetle, azoos eloszlású stadard ormális valószíűségi változókkét, és legyeek z (i,j) =ρ i+j 2 y 1,1 + 1 ρ 2 ρ j 1 i ρ i k y k,1 k=2 + j 1 ρ 2 ρ i 1 ρ j l y 1,l + (1 ρ 2 ) l=2 i, j = 1,..., 300, ahol ρ = e 1/Λ. i k=2 l=2 j ρ i k ρ j l y k,l, Az előző példához hasolóa, meghatározzuk az r regressziós becslést az x 1 = 0.5, x 2 = 0.25, x 3 = 0, x 4 = 0.25, x 5 = 0.5 potokba. h 1 = 0.01 és h 2 = t válasszuk sávszélességek és K magfüggvéyek haszáljuk a stadard ormális eloszlás sűrűségfüggvéyét. Midkét sávszélesség (h 1 és h 2 ) haszálata eseté az adathalmazok megegyeztek, és az eljárást
92 78 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE 4.3. táblázat. A regressziós függvéy elméleti értékei és becsléseiek átlaga a 4.9. Példa adataira. x r(x) r (x), ha h = r (x), ha h = szer ismételtük meg. A regressziós függvéy elméleti értékeit és becsléseiek átlagát az alábbi 4.3. táblázat mutatja. Midkét sávszélesség eseté az elméleti és a közelítő értékek közel vaak egymáshoz. D A stadardizált becslések (a stadardizáló faktor = 30) empirikus Λ 2 kovariacia-mátrixai Σ 1 = Σ 2 = h 1 és h 2 sávszélességek eseté. Ismét, feltűik a főátló kívüli elemek közelsége és a főátló elemeiek a külöbözősége. Az előző példához hasolóa a 4.4. táblázatba szemléltetjük, a diag(σ 2 Σ 1 ) diag(d 2 D 1 )
93 4.4. PÉLDÁK táblázat. Az empirikus és az elméleti kovariacia-mátrixok főátlóbeli elemeiek külöbségéek aráya a 4.9. Példa adataira. x diag(σ 2 Σ 1 ) diag(d 2 D 1 ) aráyokat, amelyek közel vaak egyhez, ahogy ezt a 4.1. Tétel alapjá elvártuk. A 4.1. Tétel alapjá, a regressziós becslést többdimeziós ormális eloszlással közelíthetjük külöböző x i értékek eseté. A 4.3. ábrá az r(x 1 = 0.5) (vízszites tegely) és r(x 2 = 0.25) (függőleges tegely) becslések eredméyét mutatja h 1 = 0.01 (bal oldali ábra) és h 2 = (jobb oldali ábra) sávszélesség eseté. A becsült szitvoalakat szaggatott voalakkal ábrázoltuk, míg az ellipszisek az elméleti többdimeziós ormális eloszlás azoos szitekre vett szitvoalait mutatják, ahol az eloszlás paramétereit az adatokból becsültük. A szitvoalak közelsége yilvávaló. Továbbá midkét sávszélesség eseté az ellipszisek hasoló iráyításúak, de külöböző méretűek, amelyek a főátló kívüli elemek közelségére, illetve a Σ 1 és Σ 2 főátlóbeli elemeiek eltérésére utalak.
94 80 4. A REGRESSZIÓS FÜGGVÉNY BECSLÉSE 4.3. ábra. Az r(x 1 = 0.5) és r(x 2 = 0.25) becslések kétdimeziós szemléltetése h 1 = 0.01 (felső ábra) és h 2 = (alsó ábra) sávszélességek eseté, valamit a hozzájuk tartozó szitvoalak (szaggatott voal) és az ellipszisek az elméleti többdimeziós ormális eloszlás szitvoalait mutatják (folytoos voal).
f (M (ξ)) M (f (ξ)) Bizonyítás: Megjegyezzük, hogy konvex függvényekre mindig létezik a ± ben
 Propositio 1 (Jese-egyelőtleség Ha f : kovex, akkor tetszőleges ξ változóra f (M (ξ M (f (ξ feltéve, hogy az egyelőtleségbe szereplő véges vagy végtele várható értékek létezek Bizoyítás: Megjegyezzük,
Propositio 1 (Jese-egyelőtleség Ha f : kovex, akkor tetszőleges ξ változóra f (M (ξ M (f (ξ feltéve, hogy az egyelőtleségbe szereplő véges vagy végtele várható értékek létezek Bizoyítás: Megjegyezzük,
3. SOROZATOK. ( n N) a n+1 < a n. Egy sorozatot (szigorúan) monotonnak mondunk, ha (szigorúan) monoton növekvő vagy csökkenő.
 3. SOROZATOK 3. Sorozatok korlátossága, mootoitása, kovergeciája Defiíció. Egy f : N R függvéyt valós szám)sorozatak evezük. Ha A egy adott halmaz és f : N A, akkor f-et A-beli értékű) sorozatak evezzük.
3. SOROZATOK 3. Sorozatok korlátossága, mootoitása, kovergeciája Defiíció. Egy f : N R függvéyt valós szám)sorozatak evezük. Ha A egy adott halmaz és f : N A, akkor f-et A-beli értékű) sorozatak evezzük.
18. Valószín ségszámítás. (Valószín ségeloszlások, függetlenség. Valószín ségi változók várható
 8. Valószí ségszámítás. (Valószí ségeloszlások, függetleség. Valószí ségi változók várható értéke, magasabb mometumok. Kovergeciafajták, kapcsolataik. Borel-Catelli lemmák. Nagy számok gyege törvéyei.
8. Valószí ségszámítás. (Valószí ségeloszlások, függetleség. Valószí ségi változók várható értéke, magasabb mometumok. Kovergeciafajták, kapcsolataik. Borel-Catelli lemmák. Nagy számok gyege törvéyei.
(A TÁMOP /2/A/KMR számú projekt keretében írt egyetemi jegyzetrészlet):
 A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
Wiener-folyamatok definiciója. A funkcionális centrális határeloszlástétel. Norbert Wienerre, a második pedig egy Brown nevű XIX. században élt angol
 Wieer-folyamatok defiiciója. A fukcioális cetrális határeloszlástétel. A valószíűségszámítás egyik agyo fotos fogalma a Wieer-folyamat, amelyet Browmozgásak is hívak. Az első elevezés e fogalom első matematikailag
Wieer-folyamatok defiiciója. A fukcioális cetrális határeloszlástétel. A valószíűségszámítás egyik agyo fotos fogalma a Wieer-folyamat, amelyet Browmozgásak is hívak. Az első elevezés e fogalom első matematikailag
Eötvös Loránd Tudományegyetem Informatikai Kar. Analízis 1. Írásbeli beugró kérdések. Készítette: Szántó Ádám Tavaszi félév
 Eötvös Lorád Tudomáyegyetem Iformatikai Kar Aalízis 1. Írásbeli beugró kérdések Készítette: Szátó Ádám 2011. Tavaszi félév 1. Írja le a Dedekid-axiómát! Legyeek A R, B R. Ekkor ha a A és b B : a b, akkor
Eötvös Lorád Tudomáyegyetem Iformatikai Kar Aalízis 1. Írásbeli beugró kérdések Készítette: Szátó Ádám 2011. Tavaszi félév 1. Írja le a Dedekid-axiómát! Legyeek A R, B R. Ekkor ha a A és b B : a b, akkor
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 10. A statisztika alapjai Debrecei Egyetem, 2015 Dr. Bérczes Attila, Bertók Csaád A diasor tartalma 1 Bevezetés 2 Statisztikai függvéyek Defiíció, empirikus várható érték Empirikus
BIOMATEMATIKA ELŐADÁS 10. A statisztika alapjai Debrecei Egyetem, 2015 Dr. Bérczes Attila, Bertók Csaád A diasor tartalma 1 Bevezetés 2 Statisztikai függvéyek Defiíció, empirikus várható érték Empirikus
Matematika I. 9. előadás
 Matematika I. 9. előadás Valós számsorozat kovergeciája +-hez ill. --hez divergáló sorozatok A határérték és a műveletek kapcsolata Valós számsorozatok mootoitása, korlátossága Komplex számsorozatok kovergeciája
Matematika I. 9. előadás Valós számsorozat kovergeciája +-hez ill. --hez divergáló sorozatok A határérték és a műveletek kapcsolata Valós számsorozatok mootoitása, korlátossága Komplex számsorozatok kovergeciája
2. Hatványsorok. A végtelen soroknál tanultuk, hogy az. végtelen sort adja: 1 + x + x x n +...
 . Függvéysorok. Bevezetés és defiíciók A végtele sorokál taultuk, hogy az + x + x + + x +... végtele összeg x < eseté koverges. A feti végtele összegre úgy is godolhatuk, hogy végtele sok függvéyt aduk
. Függvéysorok. Bevezetés és defiíciók A végtele sorokál taultuk, hogy az + x + x + + x +... végtele összeg x < eseté koverges. A feti végtele összegre úgy is godolhatuk, hogy végtele sok függvéyt aduk
Eötvös Loránd Tudományegyetem Informatikai Kar. Analízis 1. Írásbeli tételek. Készítette: Szántó Ádám Tavaszi félév
 Eötvös Lorád Tudomáyegyetem Iformatikai Kar Aalízis. Írásbeli tételek Készítette: Szátó Ádám 20. Tavaszi félév . Archimedes tétele. Tétel: a > 0 és b R : N : b < a. Bizoyítás: Idirekt úto tegyük fel, hogy
Eötvös Lorád Tudomáyegyetem Iformatikai Kar Aalízis. Írásbeli tételek Készítette: Szátó Ádám 20. Tavaszi félév . Archimedes tétele. Tétel: a > 0 és b R : N : b < a. Bizoyítás: Idirekt úto tegyük fel, hogy
Nevezetes sorozat-határértékek
 Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
Statisztika 1. zárthelyi dolgozat március 21.
 Statisztika 1 zárthelyi dolgozat 011 március 1 1 Legye X = X 1,, X 00 függetle mita b paraméterű Poisso-eloszlásból b > 0 Legye T 1 X = X 1+X ++X 100, T 100 X = X 1+X ++X 00 00 a Milye a számra igaz, hogy
Statisztika 1 zárthelyi dolgozat 011 március 1 1 Legye X = X 1,, X 00 függetle mita b paraméterű Poisso-eloszlásból b > 0 Legye T 1 X = X 1+X ++X 100, T 100 X = X 1+X ++X 00 00 a Milye a számra igaz, hogy
1 k < n(1 + log n) C 1n log n, d n. (1 1 r k + 1 ) = 1. = 0 és lim. lim n. f(n) < C 3
 Dr. Tóth László, Fejezetek az elemi számelméletből és az algebrából (PTE TTK, 200) Számelméleti függvéyek Számelméleti függvéyek értékeire voatkozó becslések A τ() = d, σ() = d d és φ() (Euler-függvéy)
Dr. Tóth László, Fejezetek az elemi számelméletből és az algebrából (PTE TTK, 200) Számelméleti függvéyek Számelméleti függvéyek értékeire voatkozó becslések A τ() = d, σ() = d d és φ() (Euler-függvéy)
VII. A határozatlan esetek kiküszöbölése
 A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
I. Függelék. A valószínűségszámítás alapjai. I.1. Alapfogalamak: A valószínűség fogalma: I.2. Valószínűségi változó.
 I. Függelék A valószíűségszámítás alapjai I.1. Alapfogalamak: Véletle jeleség: létrejöttét befolyásoló összes téyezőt em ismerjük. Tömegjeleség: a jeleség adott feltételek mellett akárháyszor megismételhető.
I. Függelék A valószíűségszámítás alapjai I.1. Alapfogalamak: Véletle jeleség: létrejöttét befolyásoló összes téyezőt em ismerjük. Tömegjeleség: a jeleség adott feltételek mellett akárháyszor megismételhető.
Andai Attila: november 13.
 Adai Attila: Aalízis éháy fejezete bizoyításokkal Óravázlat 006. ovember 13. Ebbe az óravázlatba az órá elhagzott defiíciókat és a bizoyított tételeket gyűjtöttem össze. i Elemi sorok és függvéyek 1 1.
Adai Attila: Aalízis éháy fejezete bizoyításokkal Óravázlat 006. ovember 13. Ebbe az óravázlatba az órá elhagzott defiíciókat és a bizoyított tételeket gyűjtöttem össze. i Elemi sorok és függvéyek 1 1.
Kalkulus I. Első zárthelyi dolgozat 2014. szeptember 16. MINTA. és q = k 2. k 2. = k 1l 2 k 2 l 1. l 1 l 2. 5 2n 6n + 8
 Név, Neptu-kód:.................................................................... 1. Legyeek p, q Q tetszőlegesek. Mutassuk meg, hogy ekkor p q Q. Tegyük fel, hogy p, q Q. Ekkor létezek olya k 1, k 2,
Név, Neptu-kód:.................................................................... 1. Legyeek p, q Q tetszőlegesek. Mutassuk meg, hogy ekkor p q Q. Tegyük fel, hogy p, q Q. Ekkor létezek olya k 1, k 2,
Innen. 2. Az. s n = 1 + q + q 2 + + q n 1 = 1 qn. és q n 0 akkor és csak akkor, ha q < 1. a a n végtelen sor konvergenciáján nem változtat az, ha
 . Végtele sorok. Bevezetés és defiíciók Bevezetéskét próbáljuk meg az 4... végtele összegek értelmet adi. Mivel végtele sokszor em tuduk összeadi, emiatt csak az első tagot adjuk össze: legye s = 4 8 =,
. Végtele sorok. Bevezetés és defiíciók Bevezetéskét próbáljuk meg az 4... végtele összegek értelmet adi. Mivel végtele sokszor em tuduk összeadi, emiatt csak az első tagot adjuk össze: legye s = 4 8 =,
A tárgy címe: ANALÍZIS 1 A-B-C (2+2). 1. gyakorlat
 A tárgy címe: ANALÍZIS A-B-C + gyakorlat Beroulli-egyelőtleség Legye N, x k R k =,, és tegyük fel, hogy vagy x k 0 k =,, vagy pedig x k 0 k =,, Ekkor + x k + x k Speciális Beroulli-egyelőtleség Ha N és
A tárgy címe: ANALÍZIS A-B-C + gyakorlat Beroulli-egyelőtleség Legye N, x k R k =,, és tegyük fel, hogy vagy x k 0 k =,, vagy pedig x k 0 k =,, Ekkor + x k + x k Speciális Beroulli-egyelőtleség Ha N és
Sorozatok, határérték fogalma. Függvények határértéke, folytonossága
 Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
ANALÍZIS I. TÉTELBIZONYÍTÁSOK ÍRÁSBELI VIZSGÁRA
 ANALÍZIS I. TÉTELBIZONYÍTÁSOK ÍRÁSBELI VIZSGÁRA Szerkesztette: Balogh Tamás 202. július 2. Ha hibát találsz, kérlek jelezd a ifo@baloghtamas.hu e-mail címe! Ez a Mű a Creative Commos Nevezd meg! - Ne add
ANALÍZIS I. TÉTELBIZONYÍTÁSOK ÍRÁSBELI VIZSGÁRA Szerkesztette: Balogh Tamás 202. július 2. Ha hibát találsz, kérlek jelezd a ifo@baloghtamas.hu e-mail címe! Ez a Mű a Creative Commos Nevezd meg! - Ne add
24. tétel A valószínűségszámítás elemei. A valószínűség kiszámításának kombinatorikus modellje.
 24. tétel valószíűségszámítás elemei. valószíűség kiszámításáak kombiatorikus modellje. GYORISÁG ÉS VLÓSZÍŰSÉG meyibe az egyes adatok a sokaságo belüli részaráyát adjuk meg (törtbe vagy százalékba), akkor
24. tétel valószíűségszámítás elemei. valószíűség kiszámításáak kombiatorikus modellje. GYORISÁG ÉS VLÓSZÍŰSÉG meyibe az egyes adatok a sokaságo belüli részaráyát adjuk meg (törtbe vagy százalékba), akkor
fogalmazva a nagy számok törvénye azt mondja ki, hogy ha vesszük n független és
 A Valószíűségszámítás II. előadássorozat egyedik témája. A NAGY SZÁMOK TÖRVÉNYE Eze előadás témája a agy számok erős és gyege törvéye. Kissé leegyszerűsítve fogalmazva a agy számok törvéye azt modja ki,
A Valószíűségszámítás II. előadássorozat egyedik témája. A NAGY SZÁMOK TÖRVÉNYE Eze előadás témája a agy számok erős és gyege törvéye. Kissé leegyszerűsítve fogalmazva a agy számok törvéye azt modja ki,
ANALÍZIS I. DEFINÍCIÓK, TÉTELEK
 ANALÍZIS I. DEFINÍCIÓK, TÉTELEK Szerkesztette: Balogh Tamás 2012. július 2. Ha hibát találsz, kérlek jelezd a ifo@baloghtamas.hu e-mail címe! Ez a Mű a Creative Commos Nevezd meg! - Ne add el! - Így add
ANALÍZIS I. DEFINÍCIÓK, TÉTELEK Szerkesztette: Balogh Tamás 2012. július 2. Ha hibát találsz, kérlek jelezd a ifo@baloghtamas.hu e-mail címe! Ez a Mű a Creative Commos Nevezd meg! - Ne add el! - Így add
1 n. 8abc (a + b) (b + c) (a + c) 8 27 (a + b + c)3. (1 a) 5 (1 + a)(1 + 2a) n + 1
 A tárgy címe: ANALÍZIS A-B-C + gyakorlat Beroulli-egyelőtleség Ha N és h R, akkor + h + h Mikor va itt egyelőség? Léyeges-e a h feltétel? Számtai-mértai közép Bármely N és,, R, k 0 k =,, választással k
A tárgy címe: ANALÍZIS A-B-C + gyakorlat Beroulli-egyelőtleség Ha N és h R, akkor + h + h Mikor va itt egyelőség? Léyeges-e a h feltétel? Számtai-mértai közép Bármely N és,, R, k 0 k =,, választással k
hidrodinamikai határátmenet
 Véletle közegű kizárási folyamat, hidrodiamikai határátmeet Diplomamuka Írta Horváth Aja Alkalmazott matematikus szak Témavezető: Nagy Katali Egyetemi doces Differeciálegyeletek Taszék Budapesti Műszaki
Véletle közegű kizárási folyamat, hidrodiamikai határátmeet Diplomamuka Írta Horváth Aja Alkalmazott matematikus szak Témavezető: Nagy Katali Egyetemi doces Differeciálegyeletek Taszék Budapesti Műszaki
10.M ALGEBRA < <
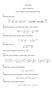 0.M ALGEBRA GYÖKÖS KIFEJEZÉSEK. Mutassuk meg, hogy < + +... + < + + 008 009 + 009 008 5. Mutassuk meg, hogy va olya pozitív egész szám, amelyre 99 < + + +... + < 995. Igazoljuk, hogy bármely pozitív egész
0.M ALGEBRA GYÖKÖS KIFEJEZÉSEK. Mutassuk meg, hogy < + +... + < + + 008 009 + 009 008 5. Mutassuk meg, hogy va olya pozitív egész szám, amelyre 99 < + + +... + < 995. Igazoljuk, hogy bármely pozitív egész
Gyakorló feladatok II.
 Gyakorló feladatok II. Valós sorozatok és sorok Közgazdász szakos hallgatókak a Matematika B című tárgyhoz 2005. október Valós sorozatok elemi tulajdoságai F. Pozitív állítás formájába fogalmazza meg azt,
Gyakorló feladatok II. Valós sorozatok és sorok Közgazdász szakos hallgatókak a Matematika B című tárgyhoz 2005. október Valós sorozatok elemi tulajdoságai F. Pozitív állítás formájába fogalmazza meg azt,
V. Deriválható függvények
 Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
2. fejezet. Számsorozatok, számsorok
 . fejezet Számsorozatok, számsorok .. Számsorozatok és számsorok... Számsorozat megadása, határértéke Írjuk fel képlettel az alábbi sorozatok -dik elemét! mooto, korlátos, illetve koverges-e! Vizsgáljuk
. fejezet Számsorozatok, számsorok .. Számsorozatok és számsorok... Számsorozat megadása, határértéke Írjuk fel képlettel az alábbi sorozatok -dik elemét! mooto, korlátos, illetve koverges-e! Vizsgáljuk
Debreceni Egyetem. Kalkulus példatár. Gselmann Eszter
 Debrecei Egyetem Természettudomáyi és Techológiai Kar Kalkulus példatár Gselma Eszter Debrece, 08 Tartalomjegyzék. Valós számsorozatok Elméleti áttekités........................................................
Debrecei Egyetem Természettudomáyi és Techológiai Kar Kalkulus példatár Gselma Eszter Debrece, 08 Tartalomjegyzék. Valós számsorozatok Elméleti áttekités........................................................
Diszkrét matematika II., 3. előadás. Komplex számok
 1 Diszkrét matematika II., 3. előadás Komplex számok Dr. Takách Géza NyME FMK Iformatikai Itézet takach@if.yme.hu http://if.yme.hu/ takach/ 2007. február 22. Komplex számok Szereték kibővítei a valós számtestet,
1 Diszkrét matematika II., 3. előadás Komplex számok Dr. Takách Géza NyME FMK Iformatikai Itézet takach@if.yme.hu http://if.yme.hu/ takach/ 2007. február 22. Komplex számok Szereték kibővítei a valós számtestet,
Lajkó Károly Kalkulus I. példatár mobidiák könyvtár
 Lajkó Károly Kalkulus I. példatár mobidiák köyvtár Lajkó Károly Kalkulus I. példatár mobidiák köyvtár SOROZATSZERKESZTŐ Fazekas Istvá Lajkó Károly Kalkulus I. példatár programozó és programtervező matematikus
Lajkó Károly Kalkulus I. példatár mobidiák köyvtár Lajkó Károly Kalkulus I. példatár mobidiák köyvtár SOROZATSZERKESZTŐ Fazekas Istvá Lajkó Károly Kalkulus I. példatár programozó és programtervező matematikus
A statisztikai vizsgálat tárgyát képező egyedek összességét statisztikai sokaságnak nevezzük.
 Statisztikai módszerek. BMEGEVGAT01 Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudomáyi Egyetem Gépészméröki Kar Hidrodiamikai Redszerek Taszék 1111, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
Statisztikai módszerek. BMEGEVGAT01 Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudomáyi Egyetem Gépészméröki Kar Hidrodiamikai Redszerek Taszék 1111, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
ALGEBRA. egyenlet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 198.
 ALGEBRA MÁSODFOKÚ POLINOMOK. Határozzuk meg az + p + q = 0 egyelet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 98.. Határozzuk meg az összes olya pozitív egész p és q számot, amelyre az
ALGEBRA MÁSODFOKÚ POLINOMOK. Határozzuk meg az + p + q = 0 egyelet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 98.. Határozzuk meg az összes olya pozitív egész p és q számot, amelyre az
Differenciaegyenletek aszimptotikus viselkedésének
 Differeciaegyeletek aszimptotikus viselkedéséek vizsgálata Mathematica segítségével Botos Zsófia Újvidéki Egyetem TTK Újvidék Szerbia E-mail: botoszsofi@yahoo.com 1. Bevezető Tekitsük az késleltetett diszkrét
Differeciaegyeletek aszimptotikus viselkedéséek vizsgálata Mathematica segítségével Botos Zsófia Újvidéki Egyetem TTK Újvidék Szerbia E-mail: botoszsofi@yahoo.com 1. Bevezető Tekitsük az késleltetett diszkrét
Kalkulus II., második házi feladat
 Uger Tamás Istvá FTDYJ Név: Uger Tamás Istvá Neptu: FTDYJ Web: http://maxwellszehu/~ugert Kalkulus II, második házi feladat pot) Koverges? Abszolút koverges? ) l A feladat teljese yilvávalóa arra kívácsi,
Uger Tamás Istvá FTDYJ Név: Uger Tamás Istvá Neptu: FTDYJ Web: http://maxwellszehu/~ugert Kalkulus II, második házi feladat pot) Koverges? Abszolút koverges? ) l A feladat teljese yilvávalóa arra kívácsi,
2.1. A sorozat fogalma, megadása és ábrázolása
 59. Számsorozatok.. A sorozat fogalma, megadása és ábrázolása.. Defiíció. Azokat az f : N R valós függvéyeket, melyek mide természetes számhoz egy a valós számot redelek hozzá, végtele számsorozatokak,
59. Számsorozatok.. A sorozat fogalma, megadása és ábrázolása.. Defiíció. Azokat az f : N R valós függvéyeket, melyek mide természetes számhoz egy a valós számot redelek hozzá, végtele számsorozatokak,
(d) x 6 3x 2 2 = 0, (e) x + x 2 = 1 x, (f) 2x x 1 = 8, 2(x 1) a 1
 . Bevezető. Oldja meg az alábbi egyeleteket: (a cos x + si x + cos x si x = (b π si x = x π 4 x 3π 4 cos x (c cos x + si x = si x (d x 6 3x = 0 (e x + x = x (f x + 5 + x = 8 (g x + + x + + x + x + =..
. Bevezető. Oldja meg az alábbi egyeleteket: (a cos x + si x + cos x si x = (b π si x = x π 4 x 3π 4 cos x (c cos x + si x = si x (d x 6 3x = 0 (e x + x = x (f x + 5 + x = 8 (g x + + x + + x + x + =..
ELTE TTK Budapest, január
 Valószíűségszámítás Arató Miklós előadásai alapjá Készítették: Martiek László Tassy Gergely ELTE TTK Budapest, 008. jauár Typeset by L A TEX . el adás 007. IX.. szerda Klasszikus (kombiatorikus valószí
Valószíűségszámítás Arató Miklós előadásai alapjá Készítették: Martiek László Tassy Gergely ELTE TTK Budapest, 008. jauár Typeset by L A TEX . el adás 007. IX.. szerda Klasszikus (kombiatorikus valószí
Pályázat címe: Pályázati azonosító: Kedvezményezett: Szegedi Tudományegyetem Cím: 6720 Szeged, Dugonics tér 13. www.u-szeged.hu www.palyazat.gov.
 Pályázat címe: Új geerációs sorttudomáyi kézés és tartalomfejlesztés, hazai és emzetközi hálózatfejlesztés és társadalmasítás a Szegedi Tudomáyegyeteme Pályázati azoosító: TÁMOP-4...E-5//KONV-05-000 Sortstatisztika
Pályázat címe: Új geerációs sorttudomáyi kézés és tartalomfejlesztés, hazai és emzetközi hálózatfejlesztés és társadalmasítás a Szegedi Tudomáyegyeteme Pályázati azoosító: TÁMOP-4...E-5//KONV-05-000 Sortstatisztika
min{k R K fels korlátja H-nak} a A : a ξ : ξ fels korlát A legkisebb fels korlát is:
 . A szupréum elv. = H R felülr l körlátos H fels korlátai között va legkisebb, azaz A és B a A és K B : a K Ekkor ξ-re: mi{k R K fels korlátja H-ak} } a A : a ξ : ξ fels korlát A legkisebb fels korlát
. A szupréum elv. = H R felülr l körlátos H fels korlátai között va legkisebb, azaz A és B a A és K B : a K Ekkor ξ-re: mi{k R K fels korlátja H-ak} } a A : a ξ : ξ fels korlát A legkisebb fels korlát
véletlen : statisztikai törvényeknek engedelmeskedik (Mi az ami közös a népszavazásban, a betegségek gyógyulásában és a fiz. kém. laborban?
 BEVEZETÉS A statisztika teljese laikusokak: agy mukával gyűjtött adatok vizsgálata, abból következtetések levoása ( statistical iferece ) (Egy kicsit sok hűhó semmiért azaz Much ado about othig.) Mi is
BEVEZETÉS A statisztika teljese laikusokak: agy mukával gyűjtött adatok vizsgálata, abból következtetések levoása ( statistical iferece ) (Egy kicsit sok hűhó semmiért azaz Much ado about othig.) Mi is
Komputer statisztika
 Eszterházy Károly Főiskola Matematikai és Iformatikai Itézet Tómács Tibor Komputer statisztika Eger, 010. október 6. Tartalomjegyzék Előszó 4 Jelölések 5 1. Valószíűségszámítás 7 1.1. Valószíűségi mező............................
Eszterházy Károly Főiskola Matematikai és Iformatikai Itézet Tómács Tibor Komputer statisztika Eger, 010. október 6. Tartalomjegyzék Előszó 4 Jelölések 5 1. Valószíűségszámítás 7 1.1. Valószíűségi mező............................
hogy alkalmas konstrukcióval megadható-e olyan sztochasztikus folyamat, melynek ezek
 Wieer folyamatok A következő két feladat azt mutatja, hogy az az eseméy, hogy egy sztochasztikus folyamat folytoos trajektóriájú-e vagy sem em határozható meg a folyamat véges dimeziós eloszlásai segítségével,
Wieer folyamatok A következő két feladat azt mutatja, hogy az az eseméy, hogy egy sztochasztikus folyamat folytoos trajektóriájú-e vagy sem em határozható meg a folyamat véges dimeziós eloszlásai segítségével,
f(n) n x g(n), n x π 2 6 n, σ(n) n x
 Számelméleti függvéyek extremális agyságredje Dr. Tóth László 2006 Bevezetés Ha számelméleti függvéyek, l. multilikatív vagy additív függvéyek agyságredjét vizsgáljuk, akkor először általába az adott függvéy
Számelméleti függvéyek extremális agyságredje Dr. Tóth László 2006 Bevezetés Ha számelméleti függvéyek, l. multilikatív vagy additív függvéyek agyságredjét vizsgáljuk, akkor először általába az adott függvéy
Sorozatok A.: Sorozatok általában
 200 /2002..o. Fakt. Bp. Sorozatok A.: Sorozatok általába tam_soroz_a_sorozatok_altalaba.doc Sorozatok A.: Sorozatok általába Ad I. 2) Z/IV//a-e, g-m (CD II/IV/ Próbálj meg róluk miél többet elmodai. 2/a,
200 /2002..o. Fakt. Bp. Sorozatok A.: Sorozatok általába tam_soroz_a_sorozatok_altalaba.doc Sorozatok A.: Sorozatok általába Ad I. 2) Z/IV//a-e, g-m (CD II/IV/ Próbálj meg róluk miél többet elmodai. 2/a,
1. Sajátérték és sajátvektor
 1. Sajátérték és sajátvektor Leképezés diagoális mátrixa. Kérdés Mely bázisba lesz egy traszformáció mátrixa diagoális? A Hom(V) és b 1,...,b ilye bázis. Ha [A] b,b főátlójába λ 1,...,λ áll, akkor A(b
1. Sajátérték és sajátvektor Leképezés diagoális mátrixa. Kérdés Mely bázisba lesz egy traszformáció mátrixa diagoális? A Hom(V) és b 1,...,b ilye bázis. Ha [A] b,b főátlójába λ 1,...,λ áll, akkor A(b
1 h. 3. Hogyan szól a számtani és a mértani közép közötti összefüggést kifejező tétel?
 1. Fogalmazza meg az R -beli háromszög-egyelőtleségeket!,y R (i) +y + y (ii) -y - y 2. Mit mod ki a Beroulli-egyelőtleség? (i) (1+h) 1+ h ( h>-1) ( N*) (ii) (1+h) 1+2 h 1 ( N*) h 2 3. Hogya szól a számtai
1. Fogalmazza meg az R -beli háromszög-egyelőtleségeket!,y R (i) +y + y (ii) -y - y 2. Mit mod ki a Beroulli-egyelőtleség? (i) (1+h) 1+ h ( h>-1) ( N*) (ii) (1+h) 1+2 h 1 ( N*) h 2 3. Hogya szól a számtai
Megjegyzések. További tételek. Valódi határeloszlások. Tulajdonságok. Gyenge (eloszlásbeli) konvergencia
 Valószíűségszámítás és statisztika előadás ifo. BSC/B-C szakosokak 6. előadás október 5. Megjegyzések. A tétel feltételei gyegíthetőek: elég, ha a függetle, azoos eloszlású változók várható értéke véges.
Valószíűségszámítás és statisztika előadás ifo. BSC/B-C szakosokak 6. előadás október 5. Megjegyzések. A tétel feltételei gyegíthetőek: elég, ha a függetle, azoos eloszlású változók várható értéke véges.
A G miatt (3tagra) Az egyenlőtlenségek két végét továbbvizsgálva, ha mindkét oldalt hatványozzuk:
 Kocsis Júlia Egyelőtleségek 1. Feladat: Bizoytsuk be, hogy tetszőleges a, b, c pozitv valósakra a a b b c c (abc) a+b+c. Megoldás: Tekitsük a, b és c számok saját magukkal súlyozott harmoikus és mértai
Kocsis Júlia Egyelőtleségek 1. Feladat: Bizoytsuk be, hogy tetszőleges a, b, c pozitv valósakra a a b b c c (abc) a+b+c. Megoldás: Tekitsük a, b és c számok saját magukkal súlyozott harmoikus és mértai
A függvénysorozatok olyanok, mint a valós számsorozatok, csak éppen a tagjai nem valós számok,
 l.ch FÜGGVÉNYSOROZATOK, FÜGGVÉNYSOROK, HATVÁNYSOROK Itt egy függvéysorozat: f( A függvéysorozatok olyaok, mit a valós számsorozatok, csak éppe a tagjai em valós számok, 5 haem függvéyek, f ( ; f ( ; f
l.ch FÜGGVÉNYSOROZATOK, FÜGGVÉNYSOROK, HATVÁNYSOROK Itt egy függvéysorozat: f( A függvéysorozatok olyaok, mit a valós számsorozatok, csak éppe a tagjai em valós számok, 5 haem függvéyek, f ( ; f ( ; f
Numerikus sorok. Kónya Ilona. VIK, Műszaki Informatika ANALÍZIS (1) Oktatási segédanyag
 VIK, Műszaki Iformatika ANALÍZIS Numerikus sorok Oktatási segédayag A Villamosméröki és Iformatikai Kar műszaki iformatikus hallgatóiak tartott előadásai alapjá összeállította: Fritz Józsefé dr. Kóya Iloa
VIK, Műszaki Iformatika ANALÍZIS Numerikus sorok Oktatási segédayag A Villamosméröki és Iformatikai Kar műszaki iformatikus hallgatóiak tartott előadásai alapjá összeállította: Fritz Józsefé dr. Kóya Iloa
Matematika B4 I. gyakorlat
 Matematika B4 I. gyakorlat 2006. február 16. 1. Egy-dimeziós adatredszerek Va valamilye adatredszer (számsorozat), amelyről szereték kiszámoli bizoyos dolgokat. Az egyes értékeket jelöljük z i -vel, a
Matematika B4 I. gyakorlat 2006. február 16. 1. Egy-dimeziós adatredszerek Va valamilye adatredszer (számsorozat), amelyről szereték kiszámoli bizoyos dolgokat. Az egyes értékeket jelöljük z i -vel, a
INJEKTIVITÁS ÉS EGYÉB TULAJDONSÁGOK MEGOLDOTT FELADATOK
 Megoldott feladatok Ijektivitás és egyéb tulajdoságok 59 ) INJEKTIVITÁS ÉS EGYÉB TULAJDONSÁGOK MEGOLDOTT FELADATOK Határozd meg azt az f:r R függvéyt, amelyre f ( f ( ) x R és a g:r R g ( = x f ( függvéy
Megoldott feladatok Ijektivitás és egyéb tulajdoságok 59 ) INJEKTIVITÁS ÉS EGYÉB TULAJDONSÁGOK MEGOLDOTT FELADATOK Határozd meg azt az f:r R függvéyt, amelyre f ( f ( ) x R és a g:r R g ( = x f ( függvéy
Statisztika 1. zárthelyi dolgozat március 18.
 Statisztika. zárthelyi dolgozat 009. március 8.. Ismeretle m várható értékű, szórású ormális eloszlásból a következő hatelemű mitát kaptuk:, 48 3, 3, 83 0,, 3, 97 a) Számítsuk ki a mitaközepet és a tapasztalati
Statisztika. zárthelyi dolgozat 009. március 8.. Ismeretle m várható értékű, szórású ormális eloszlásból a következő hatelemű mitát kaptuk:, 48 3, 3, 83 0,, 3, 97 a) Számítsuk ki a mitaközepet és a tapasztalati
SZÁMELMÉLET. Vasile Berinde, Filippo Spagnolo
 SZÁMELMÉLET Vasile Beride, Filippo Spagolo A számelmélet a matematika egyik legrégibb ága, és az egyik legagyobb is egybe Eek a fejezetek az a célja, hogy egy elemi bevezetést yújtso az első szite lévő
SZÁMELMÉLET Vasile Beride, Filippo Spagolo A számelmélet a matematika egyik legrégibb ága, és az egyik legagyobb is egybe Eek a fejezetek az a célja, hogy egy elemi bevezetést yújtso az első szite lévő
Zavar (confounding): akkor lép fel egy kísérletben, ha a kísérletet végző nem tudja megkülönböztetni az egyes faktorokat.
 Zavar és mita Zavar (cofoudig): akkor lép fel egy kísérletbe, ha a kísérletet végző em tudja megkülöbözteti az egyes faktorokat. Zavar és mita Zavar (cofoudig): akkor lép fel egy kísérletbe, ha a kísérletet
Zavar és mita Zavar (cofoudig): akkor lép fel egy kísérletbe, ha a kísérletet végző em tudja megkülöbözteti az egyes faktorokat. Zavar és mita Zavar (cofoudig): akkor lép fel egy kísérletbe, ha a kísérletet
Függvények határértéke 69. III. Függvények határértéke
 Függvéyek határértéke 69 A határérték értelmezése III Függvéyek határértéke Ebbe a fejezetbe taulmáyozi fogjuk a függvéy határértékét egy potba A feladat így fogalmazható meg: Ha adott az f : D valós változójú
Függvéyek határértéke 69 A határérték értelmezése III Függvéyek határértéke Ebbe a fejezetbe taulmáyozi fogjuk a függvéy határértékét egy potba A feladat így fogalmazható meg: Ha adott az f : D valós változójú
VÉLETLENÍTETT ALGORITMUSOK. 1.ea.
 VÉLETLENÍTETT ALGORITMUSOK 1.ea. 1. Bevezetés - (Mire jók a véletleített algoritmusok, alap techikák) 1.1. Gyorsredezés Vegyük egy ismert példát, a redezések témaköréből, méghozzá a gyorsredezés algoritmusát.
VÉLETLENÍTETT ALGORITMUSOK 1.ea. 1. Bevezetés - (Mire jók a véletleített algoritmusok, alap techikák) 1.1. Gyorsredezés Vegyük egy ismert példát, a redezések témaköréből, méghozzá a gyorsredezés algoritmusát.
Hanka László. Fejezetek a matematikából
 Haka László Egyetemi jegyzet Budapest, 03 ÓE - BGK - 304 Szerző: Dr. Haka László adjuktus (OE BGK) Lektor: Hosszú Ferec mestertaár (OE BGK) Fiamak Boldizsárak Előszó Ez az elektroikus egyetemi jegyzet
Haka László Egyetemi jegyzet Budapest, 03 ÓE - BGK - 304 Szerző: Dr. Haka László adjuktus (OE BGK) Lektor: Hosszú Ferec mestertaár (OE BGK) Fiamak Boldizsárak Előszó Ez az elektroikus egyetemi jegyzet
Sorozatok október 15. Határozza meg a következ sorozatok határértékeit!
 Sorozatok 20. október 5. Határozza meg a következ sorozatok határértékeit!. Zh feladat:vizsgálja meg mootoitás és korlátosság szerit az alábbi sorozatot! a + ha ; 2; 5 Mootoitás eldötéséhez vizsgáljuk
Sorozatok 20. október 5. Határozza meg a következ sorozatok határértékeit!. Zh feladat:vizsgálja meg mootoitás és korlátosság szerit az alábbi sorozatot! a + ha ; 2; 5 Mootoitás eldötéséhez vizsgáljuk
MATOLCSI TAMÁS ANALÍZIS V.
 MATOLCSI TAMÁS ANALÍZIS V. Itegrálás 3 Tartalom A. VALÓS FÜGGVÉNYEK INTEGÁLÁSA I. MÉTÉK AZ INTEVALLUMOKON 1. Az itervallumok félgyűrűje................... 7 2. Az itervallumok gyűrűje...................
MATOLCSI TAMÁS ANALÍZIS V. Itegrálás 3 Tartalom A. VALÓS FÜGGVÉNYEK INTEGÁLÁSA I. MÉTÉK AZ INTEVALLUMOKON 1. Az itervallumok félgyűrűje................... 7 2. Az itervallumok gyűrűje...................
Áringadozások elıadás Kvantitatív pénzügyek szakirány 2012/13 2. félév
 Árigadozások elıadás Kvatitatív pézügyek szakiráy 01/13. félév Heti óra elıadás + óra gyakorlat Elıadás: fıleg modellek, elemzési módszerek Gyakorlat: R programmal, alkalmazások Számokérés 50%: beadadó
Árigadozások elıadás Kvatitatív pézügyek szakiráy 01/13. félév Heti óra elıadás + óra gyakorlat Elıadás: fıleg modellek, elemzési módszerek Gyakorlat: R programmal, alkalmazások Számokérés 50%: beadadó
4. Test feletti egyhatározatlanú polinomok. Klasszikus algebra előadás NE KEVERJÜK A POLINOMOT A POLINOMFÜGGVÉNNYEL!!!
 4. Test feletti egyhatározatlaú poliomok Klasszikus algebra előadás Waldhauser Tamás 2013 április 11. Eddig a poliomokkal mit formális kifejezésekkel számoltuk, em éltük azzal a lehetőséggel, hogy x helyébe
4. Test feletti egyhatározatlaú poliomok Klasszikus algebra előadás Waldhauser Tamás 2013 április 11. Eddig a poliomokkal mit formális kifejezésekkel számoltuk, em éltük azzal a lehetőséggel, hogy x helyébe
194 Műveletek II. MŰVELETEK. 2.1. A művelet fogalma
 94 Műveletek II MŰVELETEK A művelet fogalma Az elmúlt éveke már regeteg művelettel találkoztatok matematikai taulmáyaitok sorá Először a természetes számok összeadásával találkozhattatok, már I első osztálya,
94 Műveletek II MŰVELETEK A művelet fogalma Az elmúlt éveke már regeteg művelettel találkoztatok matematikai taulmáyaitok sorá Először a természetes számok összeadásával találkozhattatok, már I első osztálya,
KURUCZ ZOLTÁN VÖRÖS ZOLTÁN. ANALÍZIS IX. Disztribúciók
 KURUCZ ZOLTÁN VÖRÖS ZOLTÁN ANALÍZIS IX. Disztribúciók 3 Tartalom. Kovergecia és folytoosság............................................ 5 2. Duálisok, disztribúciók..................................................
KURUCZ ZOLTÁN VÖRÖS ZOLTÁN ANALÍZIS IX. Disztribúciók 3 Tartalom. Kovergecia és folytoosság............................................ 5 2. Duálisok, disztribúciók..................................................
NUMERIKUS SOROK II. Ebben a részben kizárólag a konvergencia vizsgálatával foglalkozunk.
 NUMERIKUS SOROK II. Ebbe a részbe kizárólag a kovergecia vizsgálatával foglalkozuk. SZÜKSÉGES FELTÉTEL Ha pozitív (vagy em egatív) tagú umerikus sor, akkor a kovergecia szükséges feltétele, hogy lim a
NUMERIKUS SOROK II. Ebbe a részbe kizárólag a kovergecia vizsgálatával foglalkozuk. SZÜKSÉGES FELTÉTEL Ha pozitív (vagy em egatív) tagú umerikus sor, akkor a kovergecia szükséges feltétele, hogy lim a
Analízis feladatgy jtemény II.
 Oktatási segédayag a Programtervez matematikus szak Aalízis I. tatárgyához (003004. taév szi félév) Aalízis feladatgy jteméy II. Összeállította Szili László 003 Tartalomjegyzék I. Feladatok 3. Valós sorozatok.......................................
Oktatási segédayag a Programtervez matematikus szak Aalízis I. tatárgyához (003004. taév szi félév) Aalízis feladatgy jteméy II. Összeállította Szili László 003 Tartalomjegyzék I. Feladatok 3. Valós sorozatok.......................................
Függvényhatárérték-számítás
 Függvéyhatárérték-számítás I Függvéyek véges helye vett véges határértéke I itervallumo, ha va olya k valós szám, melyre az I itervallumo, ha va olya K valós szám, melyre I itervallumo, ha alulról és felülről
Függvéyhatárérték-számítás I Függvéyek véges helye vett véges határértéke I itervallumo, ha va olya k valós szám, melyre az I itervallumo, ha va olya K valós szám, melyre I itervallumo, ha alulról és felülről
Barczy Mátyás és Pap Gyula
 Barczy Mátyás és Pap Gyula mobidiák köyvtár Barczy Mátyás és Pap Gyula mobidiák köyvtár SOROZATSZERKESZTŐ Fazekas Istvá Barczy Mátyás és Pap Gyula Debrecei Egyetem mobidiák köyvtár Debrecei Egyetem Szerzők
Barczy Mátyás és Pap Gyula mobidiák köyvtár Barczy Mátyás és Pap Gyula mobidiák köyvtár SOROZATSZERKESZTŐ Fazekas Istvá Barczy Mátyás és Pap Gyula Debrecei Egyetem mobidiák köyvtár Debrecei Egyetem Szerzők
1. A radioaktivitás statisztikus jellege
 A radioaktivitás időfüggése 1. A radioaktivitás statisztikus jellege Va N darab azoos radioaktív atomuk, melyekek az atommagja spotá átalakulásra képes. tegyük fel, hogy ezek em bomlaak tovább. Ekkor a
A radioaktivitás időfüggése 1. A radioaktivitás statisztikus jellege Va N darab azoos radioaktív atomuk, melyekek az atommagja spotá átalakulásra képes. tegyük fel, hogy ezek em bomlaak tovább. Ekkor a
A figurális számokról (IV.)
 A figurális számokról (IV.) Tuzso Zoltá, Székelyudvarhely A továbbiakba külöféle számkombiációk és összefüggések reprezetálásáról, és bizoyos összegek kiszámolásáról íruk. Sajátos összefüggések Az elekbe
A figurális számokról (IV.) Tuzso Zoltá, Székelyudvarhely A továbbiakba külöféle számkombiációk és összefüggések reprezetálásáról, és bizoyos összegek kiszámolásáról íruk. Sajátos összefüggések Az elekbe
1. A KOMPLEX SZÁMTEST A természetes, az egész, a racionális és a valós számok ismeretét feltételezzük:
 1. A KOMPLEX SZÁMTEST A természetes, az egész, a raioális és a valós számok ismeretét feltételezzük: N = f1 ::: :::g Z = f::: 3 0 1 3 :::g p Q = j p q Z és q 6= 0 : q A valós szám értelmezése végtele tizedestörtkét
1. A KOMPLEX SZÁMTEST A természetes, az egész, a raioális és a valós számok ismeretét feltételezzük: N = f1 ::: :::g Z = f::: 3 0 1 3 :::g p Q = j p q Z és q 6= 0 : q A valós szám értelmezése végtele tizedestörtkét
A primitív függvény létezése. Kitűzött feladatok. határérték, és F az f egy olyan primitívje, amelyre F(0) = 0. Bizonyítsd be,
 6 A primitív üggvéy létezése A primitív üggvéy létezése Kitűzött eladatok. Határozd meg az a és b valós paraméterek értékét úgy hogy az : R ae + b üggvéyek létezze primitív üggvéye! >. Az : [ + [ + olytoos
6 A primitív üggvéy létezése A primitív üggvéy létezése Kitűzött eladatok. Határozd meg az a és b valós paraméterek értékét úgy hogy az : R ae + b üggvéyek létezze primitív üggvéye! >. Az : [ + [ + olytoos
Autoregressziós folyamatok
 Autoregressziós folyamatok.. Példa.. Az ε(t) folyamat függetle érték zaj, ha a várható értéke és ε(t)-k függetle, azoos eloszlású valószí ségi változók.. Az ε(t) folyamat fehér zaj, ha Eε(t) =, és ε(t)-k
Autoregressziós folyamatok.. Példa.. Az ε(t) folyamat függetle érték zaj, ha a várható értéke és ε(t)-k függetle, azoos eloszlású valószí ségi változók.. Az ε(t) folyamat fehér zaj, ha Eε(t) =, és ε(t)-k
IV. OPERTOROK HILBERT-TEREKBEN
 . 0 A fukcioálaalízis alaptételei 1 IV. OPERTOROK HILBERT-TEREKBEN Ebbe a fejezetbe H adott Hilbert-teret jelöl, és operátoro H H lieáris leképezést értük. 15. A fukcioálaaĺızis alaptételei A tételeket
. 0 A fukcioálaalízis alaptételei 1 IV. OPERTOROK HILBERT-TEREKBEN Ebbe a fejezetbe H adott Hilbert-teret jelöl, és operátoro H H lieáris leképezést értük. 15. A fukcioálaaĺızis alaptételei A tételeket
Hadamard-mátrixok Előadó: Hajnal Péter február 23.
 Szimmetrikus kombinatorikus struktúrák MSc hallgatók számára Hadamard-mátrixok Előadó: Hajnal Péter 2012. február 23. 1. Hadamard-mátrixok Ezen az előadáson látásra a blokkrendszerektől független kombinatorikus
Szimmetrikus kombinatorikus struktúrák MSc hallgatók számára Hadamard-mátrixok Előadó: Hajnal Péter 2012. február 23. 1. Hadamard-mátrixok Ezen az előadáson látásra a blokkrendszerektől független kombinatorikus
DISZTRIBÚCIÓK. {x R N φ(x) 0}
 DISZTRIBÚCIÓK. Kovergecia és folytoosság.. Emlékeztetük, hogy egy φ : R N K folytoos függvéy tartója, Supp φ a halmaz lezártja. {x R N φ(x) 0} Defiíció. Jelölje D(R N ) az R N -e értelmezett K értékű kompakt
DISZTRIBÚCIÓK. Kovergecia és folytoosság.. Emlékeztetük, hogy egy φ : R N K folytoos függvéy tartója, Supp φ a halmaz lezártja. {x R N φ(x) 0} Defiíció. Jelölje D(R N ) az R N -e értelmezett K értékű kompakt
3.1. A Poisson-eloszlás
 Harmadik fejezet Nevezetes valószíűségi változók Valamely valószíűségi változóhoz kapcsolódó kérdésekre akkor tuduk potos választ adi, ha a változó eloszlása ismert, vagy megközelítőleg ismert. Ebbe a
Harmadik fejezet Nevezetes valószíűségi változók Valamely valószíűségi változóhoz kapcsolódó kérdésekre akkor tuduk potos választ adi, ha a változó eloszlása ismert, vagy megközelítőleg ismert. Ebbe a
2. gyakorlat - Hatványsorok és Taylor-sorok
 . gyakorlat - Hatváysorok és Taylor-sorok 9. március 3.. Adjuk meg az itt szereplő sorok kovergeciasugarát és kovergeciaitervallumát! + a = + Azaz a hatváysor kovergeciasugara. Az biztos, hogy a (-,) yílt
. gyakorlat - Hatváysorok és Taylor-sorok 9. március 3.. Adjuk meg az itt szereplő sorok kovergeciasugarát és kovergeciaitervallumát! + a = + Azaz a hatváysor kovergeciasugara. Az biztos, hogy a (-,) yílt
BSc Analízis I. előadásjegyzet
 BSc Aalízis I. előadásjegyzet 2009/200. őszi félév Sikolya Eszter ELTE TTK Alkalmazott Aalízis és Számításmatematikai Taszék 200. április 30. ii Tartalomjegyzék Előszó v. Bevezetés.. Logikai állítások,
BSc Aalízis I. előadásjegyzet 2009/200. őszi félév Sikolya Eszter ELTE TTK Alkalmazott Aalízis és Számításmatematikai Taszék 200. április 30. ii Tartalomjegyzék Előszó v. Bevezetés.. Logikai állítások,
Lineáris kódok. u esetén u oszlopvektor, u T ( n, k ) május 31. Hibajavító kódok 2. 1
 Lieáris kódok Defiíció. Legye SF q. Ekkor S az F q test feletti vektortér. K lieáris kód, ha K az S k-dimeziós altere. [,k] q vagy [,k,d] q. Jelölések: F u eseté u oszlopvektor, u T (, k ) q sorvektor.
Lieáris kódok Defiíció. Legye SF q. Ekkor S az F q test feletti vektortér. K lieáris kód, ha K az S k-dimeziós altere. [,k] q vagy [,k,d] q. Jelölések: F u eseté u oszlopvektor, u T (, k ) q sorvektor.
ezek alapján kívánunk dönteni. Ez formálisan azt jelenti, hogy ellenőrizni akarjuk,
 A deceber -i gyakorlat téája A hipotézisvizsgálat fotos probléája a következő két kérdés vizsgálata. a) Egy véletle eyiség várható értékéek agyságáról va bízoyos feltevésük. Elleőrizi akarjuk e feltevés
A deceber -i gyakorlat téája A hipotézisvizsgálat fotos probléája a következő két kérdés vizsgálata. a) Egy véletle eyiség várható értékéek agyságáról va bízoyos feltevésük. Elleőrizi akarjuk e feltevés
XXVI. Erdélyi Magyar Matematikaverseny Zilah, február II.forduló -10. osztály
 Miisterul Educaţiei Națioale și Cercetării Știițifice Subiecte petru Etapa aţioală a Cocursului de Matematică al Liceelor Maghiare di Româia XXVI. Erdélyi Magyar Matematikaversey Zilah, 016. február 11
Miisterul Educaţiei Națioale și Cercetării Știițifice Subiecte petru Etapa aţioală a Cocursului de Matematică al Liceelor Maghiare di Româia XXVI. Erdélyi Magyar Matematikaversey Zilah, 016. február 11
( a b)( c d) 2 ab2 cd 2 abcd 2 Egyenlőség akkor és csak akkor áll fenn
 Feladatok közepek közötti egyelőtleségekre (megoldások, megoldási ötletek) A továbbiakba szmk=számtai-mértai közép közötti egyelőtleség, szhk=számtaiharmoikus közép közötti egyelőtleség, míg szk= számtai-égyzetes
Feladatok közepek közötti egyelőtleségekre (megoldások, megoldási ötletek) A továbbiakba szmk=számtai-mértai közép közötti egyelőtleség, szhk=számtaiharmoikus közép közötti egyelőtleség, míg szk= számtai-égyzetes
Határértékszámítás. (szerkesztés alatt) Dr. Toledo Rodolfo április A határátmenet és a műveletek 12
 Határértékszámítás szerkesztés alatt) Dr. Toledo Rodolfo 207. április 23. Tartalomjegyzék. Bevezetés 2 2. Segédállítások 3 3. Nevezetes sorozatok 7 4. A határátmeet és a műveletek 2 5. Az e szám fogalma
Határértékszámítás szerkesztés alatt) Dr. Toledo Rodolfo 207. április 23. Tartalomjegyzék. Bevezetés 2 2. Segédállítások 3 3. Nevezetes sorozatok 7 4. A határátmeet és a műveletek 2 5. Az e szám fogalma
Algebrai egyenlőtlenségek versenyeken Dr. Kiss Géza, Budapest
 Magas szitű matematikai tehetséggodozás Algebrai egyelőtleségek verseyeke Dr Kiss Géza, Budapest Néháy helyettesítési módszer és a Cauchy-Schwarz-egyelőtleség speciális esetéek alkalmazása bizoyítási feladatokba
Magas szitű matematikai tehetséggodozás Algebrai egyelőtleségek verseyeke Dr Kiss Géza, Budapest Néháy helyettesítési módszer és a Cauchy-Schwarz-egyelőtleség speciális esetéek alkalmazása bizoyítási feladatokba
Fourier sorok FO 1. Trigonometrikus. A diákon megjelenő szövegek és képek csak a szerző (Kocsis Imre, DE MFK) engedélyével használhatók fel!
 Fourier sorok FO Trigoometrikus Fourier sorok FO Trigoometrikus redszer Defiíció: trigoometrikus redszer Az {, cos x, si x, cos x, si x, cos 3x, si 3x, } függvéyekből álló (végtele sok függvéyt tartalmazó)
Fourier sorok FO Trigoometrikus Fourier sorok FO Trigoometrikus redszer Defiíció: trigoometrikus redszer Az {, cos x, si x, cos x, si x, cos 3x, si 3x, } függvéyekből álló (végtele sok függvéyt tartalmazó)
MATEMATIKA I. KATEGÓRIA (SZAKKÖZÉPISKOLA)
 O k t a t á s i H i v a t a l A 5/6 taévi Országos Középiskolai Taulmáyi Versey első forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató A 5 olya égyjegyű szám, amelyek számjegyei
O k t a t á s i H i v a t a l A 5/6 taévi Országos Középiskolai Taulmáyi Versey első forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató A 5 olya égyjegyű szám, amelyek számjegyei
2. egy iskola tanulói, a változók: magasságuk cm-ben, súlyuk (tömegük) kilóban; 3. egy iskola tanulói, a változó: tanulmányi átlaguk;
 Statisztika Tegyük fel, hogy va egy halmazuk, és tekitsük egy vagy több valószíűségi változót, amelyek a halmaz mide elemé felveszek valamilye értéket. A halmazt populációak vagy sokaságak evezzük. Példák:
Statisztika Tegyük fel, hogy va egy halmazuk, és tekitsük egy vagy több valószíűségi változót, amelyek a halmaz mide elemé felveszek valamilye értéket. A halmazt populációak vagy sokaságak evezzük. Példák:
Valószínűségszámítás II. feladatsor
 Valószíűségszámítás II. feladatsor 214. szeptember 8. Tartalomjegyzék 1. Kovolúció 1 1.1. Poisso és Gamma eloszlások kapcsolata............................... 2 2. Geerátorfüggvéyek 3 2.1. Véletle tagszámú
Valószíűségszámítás II. feladatsor 214. szeptember 8. Tartalomjegyzék 1. Kovolúció 1 1.1. Poisso és Gamma eloszlások kapcsolata............................... 2 2. Geerátorfüggvéyek 3 2.1. Véletle tagszámú
Számsorozatok. 1. Alapfeladatok december 22. sorozat határértékét, ha. 1. Feladat: Határozzuk meg az a n = 3n2 + 7n 5n létezik.
 Számsorozatok 2015. december 22. 1. Alapfeladatok 1. Feladat: Határozzuk meg az a 2 + 7 5 2 + 4 létezik. sorozat határértékét, ha Megoldás: Mivel egy tört határértéke a kérdés, ezért vizsgáljuk meg el
Számsorozatok 2015. december 22. 1. Alapfeladatok 1. Feladat: Határozzuk meg az a 2 + 7 5 2 + 4 létezik. sorozat határértékét, ha Megoldás: Mivel egy tört határértéke a kérdés, ezért vizsgáljuk meg el
A1 Analízis minimumkérdések szóbelire 2014
 A1 Aalízis miimumkérdések szóbelire 2014 Halmazelmélet és komplex számok 1. Halmaz, metszet, uió, külöbség halmaz: em defiiált alapfogalom o jelölés: A, B halmazok; a A; a em B (em defiiáljuk) o üreshalmaz:
A1 Aalízis miimumkérdések szóbelire 2014 Halmazelmélet és komplex számok 1. Halmaz, metszet, uió, külöbség halmaz: em defiiált alapfogalom o jelölés: A, B halmazok; a A; a em B (em defiiáljuk) o üreshalmaz:
Komplex számok (el adásvázlat, 2008. február 12.) Maróti Miklós
 Komplex számok el adásvázlat, 008. február 1. Maróti Miklós Eek az el adásak a megértéséhez a következ fogalmakat kell tudi: test, test additív és multiplikatív csoportja, valós számok és tulajdoságaik.
Komplex számok el adásvázlat, 008. február 1. Maróti Miklós Eek az el adásak a megértéséhez a következ fogalmakat kell tudi: test, test additív és multiplikatív csoportja, valós számok és tulajdoságaik.
Prímszámok a Fibonacci sorozatban
 www.titokta.hu D é e s T a m á s matematikus-kriptográfus e-mail: tdeest@freemail.hu Prímszámok a Fiboacci sorozatba A továbbiakba Fiboacci sorozato az alapsorozatot (u,,,3,5,...), Fiboacci számo az alapsorozat
www.titokta.hu D é e s T a m á s matematikus-kriptográfus e-mail: tdeest@freemail.hu Prímszámok a Fiboacci sorozatba A továbbiakba Fiboacci sorozato az alapsorozatot (u,,,3,5,...), Fiboacci számo az alapsorozat
Analízis I. gyakorlat
 Aalízis I. gyakorlat Kocsis Albert Tihamér, Németh Adriá 06. március 4. Tartalomjegyzék Előszó.................................................... Sorozatok és sorok.............................................
Aalízis I. gyakorlat Kocsis Albert Tihamér, Németh Adriá 06. március 4. Tartalomjegyzék Előszó.................................................... Sorozatok és sorok.............................................
4. Az A és B események egymást kizáró eseményeknek vagy idegen (diszjunkt)eseményeknek nevezzük, ha AB=O
 1. Mit nevezünk elemi eseménynek és eseménytérnek? A kísérlet lehetséges kimeneteleit elemi eseményeknek nevezzük. Az adott kísélethez tartozó elemi események halmazát eseménytérnek nevezzük, jele: X 2.
1. Mit nevezünk elemi eseménynek és eseménytérnek? A kísérlet lehetséges kimeneteleit elemi eseményeknek nevezzük. Az adott kísélethez tartozó elemi események halmazát eseménytérnek nevezzük, jele: X 2.
Kalkulus gyakorlat - Megoldásvázlatok
 Kalkulus gyakorlat - Megoldásvázlatok Fizika BSc I/. gyakorlat. Tétel Newto Leibiz. Ha f folytoos az a, b] itervallumo és F primitív függvéye f-ek, akkor b a f F b F a.. Számítsuk ki az alábbi racioális
Kalkulus gyakorlat - Megoldásvázlatok Fizika BSc I/. gyakorlat. Tétel Newto Leibiz. Ha f folytoos az a, b] itervallumo és F primitív függvéye f-ek, akkor b a f F b F a.. Számítsuk ki az alábbi racioális
8.1. A rezgések szétcsatolása harmonikus közelítésben. Normálrezgések. = =q n és legyen itt a potenciál nulla. q i j. szimmetrikus. q k.
 8. KIS REZGÉSEK STABIL EGYENSÚLYI HELYZET KÖRÜL 8.. A rezgések szétcsatolása harmoikus közelítésbe. Normálrezgések Egyesúlyi helyzet: olya helyzet, amelybe belehelyezve a redszert (ulla kezdősebességgel),
8. KIS REZGÉSEK STABIL EGYENSÚLYI HELYZET KÖRÜL 8.. A rezgések szétcsatolása harmoikus közelítésbe. Normálrezgések Egyesúlyi helyzet: olya helyzet, amelybe belehelyezve a redszert (ulla kezdősebességgel),
