Kapcsolómezők. Segédlet a Távközlő hálózatok és szolgáltatások c. előadáshoz
|
|
|
- Bálint Bognár
- 5 évvel ezelőtt
- Látták:
Átírás
1 Kapcsolómező Segédlet a ávözlő hálózato és szolgáltatáso c. előadáshoz émeth Krisztiá, taársegéd, BME MI Gabrovits Pál, hallgató, BME VIK 009. ovember 5. javítva 00. ovember 9. E segédlet a telefoözpotoba haszált tér-, illetve időosztásos apcsolás elvét igyeszi rövide bemutati, az előadáso bemutatott fóliáat szöveggel iegészítve. A apcsolómező feladata A apcsolómező feladata, hogy az adott bemeti és imeeti áramörei özött apcsolatot hozzo létre. Egy végpottól végpotig (előfizetőtől előfizetőig) tartó apcsolat egy vagy több apcsolóözpoto (azaz telefoözpoto) haladhat eresztül, és midegyi özpotba egy apcsolómező. A apcsolómező típusai Első özelítésbe égy féle apcsolómező épzelhető el, de ebből a gyaorlatba csa ettőt haszála: térapcsolás: az egyes apcsolato térbe ülöüle el egymástól időapcsolás: az egyes apcsolato időbe ülöüle el egymástól freveciaosztásos: freveciába ülöíti el az egyidejű összeöttetéseet (a gyaorlatba em haszáljá) ódosztásos: az alalmazott óddal ülöíti el az egyidejű összeöttetéseet (a gyaorlatba em haszáljá) érapcsolás (Space Divisio Switchig, S ) Egyfoozatú apcsoláso be m i. ábra. Egyfoozatú apcsolás Ee az egyszerű apcsolómezőe bemeete és m imeete va. A megvalósítás az ábrá látható, melyhez m db is apcsoló, ú. apcsolópot ell. E apcsolópoto orábba
2 mechaiusa hozta létre galvaius összeöttetést, maapság pedig eletroiusa műöde. Eze özül a apcsolópoto özül mide sorba és mide oszlopba egyszerre legfeljebb egy lehet atív. Ha például a 4. sorba és. oszlopba lévő apcsolópot atív, az azt jeleti, hogy a 4. bemeet éppe össze va apcsolva a. imeettel. Megjegyzés: Mivel a be-, és imeete elülöüle egymástól, egy ilye apcsolómező alapvetőe egyiráyú apcsolato létrehozására épes. Mivel azoba egy beszédapcsolathoz midét iráyú átvitelre szüség va, azért a gyaorlatba ét azoos felépítésű apcsolómezőt alalmaza, egyiet az egyi, másiat a mási iráyba való apcsolatohoz. Ugyaaor mivel eze valóba egyformá műöde, mostatól csa az egyi iráyal foglalozu az egyszerűség edvéért. Ee a redszere az előye, hogy egyszerű, és elletétbe a ésőbb bemutatott redszereel sosem fordulhat bee elő bloolás, azaz ha egy bemeet és egy imeet szabad, azoat midig össze is tudja apcsoli. A redszer azoba drága, mert m darab apcsolópot ell hozzá, ami agy so, ha és m agy. A továbbiaba a szüséges apcsolópoto számát próbálju meg csöetei. Egy lehetséges spórolósabb elredezés például ez: be ábra. Egyfoozatú apcsolás evesebb apcsolópottal Ilye módo megtaaríthatju a apcsolópoto felét. Ugyaaor látszi, hogy eor csa a imeete felével lehet egy bemeetet összeapcsoli. Az ötlet mégsem teljese elvetedő: aor haszálható, ha em god, hogy em mide imeettel lehet mide bemeetet összeapcsoli. Pl. ha egy bai taácsadóval aaro beszéli, aor midegy, hogy potosa melyiel, csa egyet apcsoljaa özülü. Ez azoba még midig elég drága redszer, ráadásul em is túl pratius, így em haszáljá a gyaorlatba. i öbbfoozatú apcsoláso: ézzü most egy hagyomáyos egyfoozatú térapcsolót, amely bemeettel és imeettel redelezi! Jelöljü így:
3 . ábra. A apcsolópoto ihaszáltsága ugyaaor icsi, hisze egy sorba és egy oszlopba egyszerre legfeljebb csa egy apcsolópot atív. Keresü erre a problémára ( bemetű, imeetű apcsoló) egy jobb megoldást, ami fuciójába ezzel teljese megegyezi, de evesebb apcsolópottal realizálható. udju róla, hogy műödése egyszerű, de drága, mert agyo so apcsolópot ell hozzá ( ) Elsőre meglepő lehet, de létezi ilye megoldás: ez az ú. a többfoozatú térapcsoló. A 4. ábra a háromfoozatú térapcsolót szemlélteti. db db db ábra. Háromfoozatú térapcsoló (SSS apcsoló) A felépítéséből adódóa ezt a apcsolót SSS (tér-tér-tér, space-space-space) apcsolóa is szotá evezi. Láthatju, hogy az egész redszer be-, illetve imeetit teitve megegyezi egy x-es egyfoozatú apcsolóval. A többfoozatú térapcsoló egyfoozatú apcsolóból épüle fel: az ábrá mide téglalap egy egyfoozatú térapcsoló. ézzü meg, hogy apcsol egy ilye redszer! együ fel, hogy az első bemeetét szereté az első imeetével összeöti. Erre több lehetőség is va (ld. az 5. ábrát). Az első, teli voallal jelölt esetbe az első foozat első apcsolóbloja az első bemeetét öti össze az első imeetével, a másodi foozat első bloja szité, és a harmadi foozat első bloja szité. A szaggatott voallal jelölt esetbe az első foozat első bloja az első bemeetet a másodi imeettel, a másodi foozat másodi bloja az elsőt az elsővel és a harmadi foozat első bloja a másodiat az elsővel. Midét megoldás teljese egyeértéű, ívülről em látszi a ülöbség.
4 db db db ábra. Hivásfelépítés egy háromfoozatú térapcsolóba ermészetese em midig lehetséges bármelyi özépső foozatot haszáli. ézzü meg most a övetező ábrát: db db db ábra. öbb hívás egy háromfoozatú térapcsolóba 4
5 együ fel, hogy a lilával jelölt apcsolat az. bemeet és. imeet özött már fel va építve, és eor érezi egy igéy a apcsolómátrixhoz, hogy hozzo létre egy apcsolatot az. bemeete és. imeete özött. Látható, hogy eor a özépső foozat első dobozát már em haszálhatju, hisze az ahhoz az első foozat első blojából, illetve az abból a harmadi foozat első bloja felé vezető apcsolat is foglalt már. A özépső foozat másodi bloja viszot haszálható, ahogy azt a zöld voal mutatja. ehát amellett, hogy egy ülső szemlélőe a többfoozatú apcsolás úgy műödi, mit egy egyfoozatú, tulajdoéppe merőbe más belső műödés áll a háttérbe. Az egyfoozatú apcsolásba egy utat egyértelműe választottu i: egy sorba és egy oszlopba egyszerre egy apcsolópot volt atív. öbbfoozatú apcsolás eseté már em egyértelmű egy be és imeet özötti út, ezért ell egy, a megfelelő utat iválasztó algoritmus, ezáltal boyolultabb a vezérlése. Gyaori érdés, hogy az egyes foozato egyes apcsolómezői hoa tudjá, hogy egy új hívást hoa hova apcsoljaa. A válasz az, hogy e felett az egész redszer felett va egy szoftveres felügyelet -- icsit sci-fi-sebbe fogalmazva: egy magasabb redű itelligecia --, amely meghatározza a felépítedő teljes útvoalat a apcsoló belül, és ez vezérli az egyes részelemeet. Felmerül a érdés, hogy háy darab özépső foozatbeli blo ell egy ilye redszerbe, azaz meyi legye értée? Érdees érdés, hisze elvileg a redszer tetszőleges -ra műödi. Ugyaaor ha túl icsi, megjelehet a bloolás. A bloolás azt jeleti, hogy szabad egy bemeet, szabad egy imeet, de mégsem tudu özöttü apcsolatot létesítei, mert valamilye belső erőforrás (pl. olya özépső foozat, amie szabad a megfelelő be és imeete) em áll redelezésre. A 6. ábra példájába: ha értée lee, aor a zöld apcsolatot már em tudá létrehozi, azaz ha a lila apcsolat fe áll, aor a zöld már bloolódi. Ugyaez egy mási példá: 7. ábra. Az adott hívás itt bloolódi 5
6 8. ábra. Az adott hívás itt em bloolódi Láthatju, hogy a 7. ábrá már em tudu a ét pirossal jelölt pot özött apcsolatot létesítei, ha a zölddel jelölt uta foglalta. Erre megoldásét a 8. ábrá bevezethetü egy újabb özépső foozatot, így már yilvá felépíthető a ívát apcsolat. Felmerül a érdés, hogy vajo va-e olya véges, amelyre már aárhogy próbálozo is, biztosa sosem lesz bloolás. A válasz természetese ige. Például yilvá, ha mide bemeet-imeet párhoz va saját özépső foozatbeli blo ( db) aor em léphet fel bloolás. Ez természetese borzasztóa pazarló megoldás (és a célu egyébét is az volt, hogy ezt az egyfoozatú apcsolóra jellemző apcsolópotszámot csöetsü), de arra jó, hogy lássu, va felső orlát. Adódi a érdés, hogy meyi a miimális, azaz melyi az a, amelyre még bloolásmetes a apcsoló, de ahol - özépső foozatbeli blo eseté már bloolás léphet fel. Defiiálju először a bloolásmetesség fogalmát! Bloolásmetes az a apcsoló, amelye ha va egy szabad bemeete és egy szabad imeete, aor azo özött biztosa mide esetbe tudu apcsolatot létrehozi. Más szavaal: em fordulhat az elő, hogy valamely belső erőforrás hiáya miatt em tud lére jöi egy apcsolat. Azaz aár hogya is helyezede el a apcsolóba a már fe álló apcsolato, azo em aadályozhatjá meg egy új apcsolat létrejöttét, ha amúgy az új apcsolathoz tartozó be- és imeete szabado. A válaszhoz vezető godolatmeetet egy példá ézzü végig! együ fel, hogy a 9. ábrába szereté az első bemeetet és az első imeetet összeapcsoli. (Az egész rajz szimmetrius, szóval aármelyi be- és imeetről lehete szó, ezzel em csorbítu az általáosságo.) 6
7 9. ábra. Egy példa apcsoló Játsszu azt, hogy már fel va építve éháy apcsolat, és eze miatt em tudju az általu ívát összeöttetést létrehozi, és számolju meg, háy özépső foozat foglalt ilyeor. Fotos tisztázi, hogy eze a apcsoló úgy műöde, hogy em változtatjá meg a már feálló apcsolato belső útjait. ehát például egy apcsolat felépítésétől a lebotásáig (azaz pl. egy telefobeszélgetés idejére) az végig ugyaazo a özépső foozato halad át. Az 5. ábrára visszateitve például a apcsolat haladhat a teli vagy a szaggatott voallal jelölt uta özül bármelyie, de meet özbe ez em változtatható meg.. Ez azt jeleti, hogy ha pl. fe áll egy em bloolásmetes apcsolatba három hívás, amelye együtt blooljá a egyediet, aor az a egyedi e fog felépüli. Még abba az esetbe is így va ez, hogy ha elvbe lehetséges lee tiszta lappal idulva elvezeti a égy apcsolatot aor, ha az első hármat más belső utao vezetjü. A legrosszabb esetre észüljü fel (worst case desig), és számolju meg eor háy özépső foozatbeli blo foglalt. ézzü meg az alábbi ábrát: 0. ábra. Bemeeté foglalt özépső foozatbeli blo Ez estbe az első özépső bloot em haszálhatju a apcsolatu felépítésére, mert aa a 7
8 számura érdees bemeete foglalt. ézzü most ezt az esetet:. ábra. Kimeeté foglalt özépső foozatbeli blo Eor ugye az első özépső blo imeete foglalt. Persze lehet midettő is foglalt:. ábra. Be- és imeeté foglalt özépső foozatbeli blo Illetve lehet midettő szabad, úgy, hogy azért a bloo megy eresztül apcsolat, aár több is, de ettől az a blo még a mi céljaira haszálható, e szempotból szabad -a teithető: 8
9 . ábra. A özépső foozatbeli blo be- és imeete is haszálható Számolju meg, háy özépső foozatot tudu úgy elrotai, hogy a megfelelő bemeetü lesz foglalt: 4. ábra. Foglaltság a bemeete Ahogy az ábrá is látszi, legfeljebb --et, hisze mide ilye apcsolata az első foozat első blojából, aa is valamelyi bemeetéről ell idulia. Ott bemeet va, de abból a feltevésü szerit egy szabad, marad -. Hasoló a helyzet a foglalt imeetű özépső blooal: 9
10 5. ábra. Foglaltság a imeete Ezeből is max. - lehet. érjü vissza most arra a érdésre, hogy összese legfeljebb háy özépső foozat lehet rossz a mi felépítedő apcsolatu szempotjából! yilvá az a legrosszabb eset, ha az első foozat első blojáa mid az - bemeete foglalt, továbbá a harmadi foozat első blojáa mid az - imeete foglalt, ráadásul midez úgy, hogy ics a. ábrá látható egybeesés. Eor - özépső foozatbeli blo lesz haszálhatatla a mi apcsolatu felépítésére: 6. ábra. Foglaltság a be-, illetve imeetee Eél eggyel több, tehát - özépső foozatbeli blo tehát mide esetbe elég. A válasz tehát =-. ézzü most újra a 4. ábrát! Háy apcsolópotu va a többfoozatú apcsolóba? (udju, hogy egy egyfoozatú apcsolóba található apcsolópot száma i bemeet és j imeet eseté i j) első oszlop: va darab méretű egyfoozatú térapcsoló. Mivel egy 0
11 apcsolóbloba darab apcsolópot va, ez összese ( ). másodi oszlop: az első oszlopba összese darab bemeetű és apcsolóblou va, ami apcsolópot összese. Harmadi oszlop: hasolóa az első oszlophoz ( ) apcsolópot. ehát összese: első+másodi+harmadi oszlop= ( ) + + ( ) apcsolópotu va ebbe a apcsolásba, ez összese: + Felmerül a érdés, hogy ez valóba evesebb-e, mit az egyfoozatú apcsolás apcsolópotja. imeetű db. A válasz illetve értéeitől függ. Első örbe beszéljü bloolásmetes apcsolóról. udju, hogy ez esetbe = -. Ez eddig redbe, a övetező érdés, hogy meora értéet érdemes választau? Ehhez eressü meg a + ifejezés miimumát, ha =. Eor a éplet: ( ) ( ) =. Deriválju és eressü meg a derivált ulla helyeit. Itt lehet a függvéy maximuma ill. miimuma. Azért, hogy eldötsü melyi, deriválju még egyszer és tudju, hogy ha a. derivált értée agyobb mit 0, aor ott loális miimuma lesz a függvéye. A orét számításoat most mellőzzü, de higgyü el, hogy agy -re eseté lesz a függvéye miimuma. Vajo tehát téyleg evesebb apcsolópot ell? Az egyfoozatú apcsolóba apcsolópot volt (midét oldalo előfizető eseté). A többfoozatúba + apcsolópotról beszéltü. Behelyettesítve bloolásmetes esetre a -t és a miimum helyre apott értéet: ( / ) ( / ) + ( / ) ( / ) = 4 ( ( ) ) ifejezéshez jutu. Mivel agy -re 4( ) <, ezért téyleg evesebb apcsolópot ell. ézzü pár számpéldát, ahol ez jobba látszi:
12 . táblázat. Bloolásmetes többfoozatú apcsolás Ez jeletős megtaarítás, de még midig elég so a apcsolópot. Mit tehetü még? Az egyi lehetőség, hogy további foozatoat vezetü be, például úgy, hogy a 4. ábra egyi vagy több apcsolóbloját egy omplett háromfoozatú apcsolóval helyettesítjü. Ez valóba egy járható út: ettől egy darabig még csöe a apcsolópoto száma, bár egyre evésbé, viszot egyre omplexebb lesz a redszerü. A mási lehetőség, hogy megegedjü a bloolást egy is eséllyel. Ez esetbe a apcsolópoto száma attól fog függei, hogy meora egy bemeet ihaszáltsága, hisze yilvávalóa több özépső foozatbeli blo ell aor, ha egy bemeetet gyarabba haszála. (Bloolásmetes esetbe ez em számított, hisze a legrosszabb esetre terveztü.) A számításo eor túl boyolulta ahhoz, hogy e jegyzet ereteibe ismertessü. Elégedjü meg egy példával, melybe a megegedett bloolási valószíűség (azaz aa az esélye, hogy egy felépítedő hívás bloolódi) 0,00, azaz 0,%. E példát mutatja a. táblázat:. táblázat. öbbfoozatú apcsolás bloolással Figyeljü meg, meyivel evesebb apcsolópot ell, illetve hogy a / aráy a bloolásmetesbeli b. -ről aár 0, alá is csöehet! Időosztásos apcsolás (ime Divisio Switchig, ) Az időosztásos apcsolása, vagy rövidebbe időapcsolása DM yalábolt jele eseté va értelme. Eor az időapcsoló a DM eretee belüli időréseet cseréli fel egymással (mide eretbe ugyaúgy): abc d ab cd cbadcbad eret 7. ábra. Időapcsoló
13 Viszoylag egyszerűe meg lehet ezt valósítai egy memóriával: soros beírással és a meghatározott sorredbeli iolvasással, vagy em soros beírással és soros iolvasással. ermészetese ez a apcsolás ésleltetést visz a redszerbe, tipiusa egy eretyit. Probléma, hogy a memória sebessége véges, csa éháy száz időrés lehet egy 5 μs hosszú eretbe. Mire jó ez? Például egy ilye időapcsolóval megvalósíthatu egy térapcsolót a Digitális techia c. tárgyból tault multiplexer/demultiplexer áramörö segítéségével: időapcsoló 8. ábra. Időapcsolóból térapcsoló Még jobb alalmazás az, hogy megvalósíthatu vele tér- és időapcsolót együtt: ab cd af bh ef gh tér- és gcd e 9. ábra. Kombiált tér- és időapcsoló Egy ilye ombiált tér- és időapcsoló épes DM yalábolt jeleet fogadi és ugyailye jeleet ibocsátai, és eze özött úgy apcsoli, hogy bármelyi bemeet bármelyi időrését bármelyi imeet bármelyi időrésére iteszi. Mi értelme ee? os, midez azért jó, mert egy özpothoz a trööö a távoli özpotból érező jele amúgy is DM yalábolta, és így em szüséges teljese lebotai őet. Ez azt jeleti, hogy egy özpota ietől lehet olya bemeete, ami 0 beszédcsatora va időosztásosa yalábolva, és ezt em ell lebotai pl. 0 érpárra csa azért, hogy a imeete újra összeyalábolju őet. Ráadásul, ahogy láti fogju, maga a apcsolás is egyszerűbbe végrehajtható így. A továbbiaba azt fogju megézi, hogy hogya épülhet fel egy ilye ombiált tér- és időapcsoló. ér- és időapcsoló S A legegyszerűbb megvalósítás az idő-tér (ime-space, S) apcsoló:
14 a a b b S x a b mide időrésbe új apcsolási ofiguráció 0. ábra. Egy S apcsoló A - (time) az időapcsoló, S (space) a térapcsoló. Az időapcsoló feladata, hogy beraja a jelet a megfelelő időrésbe, majd a térapcsoló iraja a megfelelő imeetére. Fotos, hogy bár a térapcsoló műödési elve változatla (x db. apcsolópot va bee, melyből egyszerre egy sorba és egy oszlopba max. egy atív), most más üzemmódba haszálju, mit eddig. Ezelőtt a térapcsolóba, ha felépült egy apcsolat, aor az adott apcsolópot atív volt, amíg a apcsolat élt (azaz pl. amíg a beszélgetés tarottt). Most ez em így va: például a 0. ábrá az első időrésbe a apcsoló első bemeete va a. imeetével összeötve, majd a másodi időrésbe a másodi bemeet lesz az. imeetre apcsolva, és így tovább. A eret végé az egész ezdődi elölről. Más szavaal, itt mide időrésbe új apcsolási ofigurációt haszál a térapcsoló, ezzel egyébét soal jobba ihaszálja a bee lévő apcsolópotoat. Ez a S apcsoló azoba egy fotos hibát tartalmaz: aár már ét darab szerecsétleül érező hívás is bloolást oozhat. Figyeljü meg az alábbi példába, hogy már ét apcsolat eseté is bloolás léphet fel, hisze b és c is a másodi időrésbe ellee erüljö egyszerre: c b c? S x b. ábra. A S apcsoló em jó Ez pedig súlyos hiba. Azt ugya bizoyos esete özött elfogadhatju, hogy egy agyo leterhelt apcsolóba bloolás léphet fel, de az, hogy egy gyaorlatilag teljese üres apcsolóba lép fel bloolás, elfogadhatatla. Ee a hibáa a üszöbölésére találtá i a S, illetve SS apcsolóat. 4
15 S A S apcsoló felépítését mutatja. ábra: l db. időrés c db. időrés a b b a a a S b c db. időrés b l db. időrés x mide időrésbe új apcsolási ofiguráció. ábra. S apcsoló A apcsoló érdeessége, hogy em ugyaayi időrés va az első foozat bemeeté (c db), illetve imeeté (l db). ipiusa egyébét l > c, ezért az első foozat imeeté lesze szabad időrése. Mivel az S apcsoló bemeeté és imeeté ugyaayi időrése ell lei, hisze az időapcsolást em végez, ezért a harmadi foozat bemeeté szité l db. időrés lesz. ovábbá az is biztos, hogy az egész apcsoló bemeeté és imeeté is ugyaayi időrés ell legye (hisze a 9. ábra fucioalitását szereté eléri), ezért a harmadi foozat imeeté c időrés lesz. Megjegyzés: továbbra is igaz, amit az SSS apcsolóál leírtu: egy apcsolat feállásáa idejére em módosítu az időrése iosztásá. Például a. ábrá a. bemeete lévő apcsolóa a imeeté az a midig a. időrésbe ell legye, ha a apcsolat felépítéseor oda erült. Az is igaz továbbra is, hogy az összes részelemet (S apcsoló, apcsoló) a apcsolato felépítéseor egy (ezehez az elemehez épest) ülső szoftver vezérli, ill. hagolja össze eze műödését. Köye végiggodolható, hogy ez a apcsoló már fel tudja építei a. ábrá bemutatott ét apcsolatot, ami a S apcsolóba még bloolást oozott. Ismét csa felmerül a érdés, hogy mior lesz bloolásmetes ez a apcsoló. Haszálju a háromfoozatú térapcsolásál (SSS) haszált godolatmeetet! Ott azt számoltu meg, hogy háy olya özépső foozatbeli blo va, amelye foglalt a megfelelő bemeete, és háya foglalt a megfelelő imeete. Itt ee aalógiájára em megfelelő özépső foozatbeli bloot ell eresü, haem megfelelő időrést az S apcsoló be-, illetve imeeté. A. ábra példáját teitve adott, hogy a b apcsolat az S apcsoló. bemeetére fog érezi és az első ell távozzo. alálu ell tehát az l darabból egy olya időrést, amely szabad az S apcsolóa mid a bemeeté, mid a imeeté. Adott esetbe a például a harmadi időrés (balról ezdve a számozást) szabad ugya a bemeete, de em szabad a imeete. Hasolóa az SSS apcsolóbeli esethez, öye belátható, hogy itt c- darab időrés lehet foglalt a megfelelő bemeeté az S apcsolóa, és szité c- darab lehet foglalt a megfelelő imeeté. 5
16 Ebből szerecsétle esetbe egy sem esi egybe (worst case desig), azaz c- lesz foglalt. Eél eggyel több, l=c- időrés midig elég lesz a bloolásmetes apcsolatfelépítéshez. SS Az SS apcsoló felépítését mutatja. ábra: b c db. időrés a S x a b c db. időrés a S c db. időrés b c db. időrés x ab mide időrésbe új apcsolási ofiguráció. ábra. SS apcsoló mide időrésbe új apcsolási ofiguráció Itt először térbe, majd időbe és végül megit térbe apcsolju a hívásoat. A feti példába érezi egy a hívás egy eretbe, amit az S térapcsoló az egyi imeetére apcsol. Ezutá az adott időapcsoló behelyezi a-t a megfelelő időrésbe, majd az utolsó foozatba levő térapcsoló a megfelelő imeetére apcsolja a már helyes időrésbe levő a-t. Vegyü észre, hogy itt az időrése száma végig c, fix. Ee az oa egyszerű: az első apcsoló bemeeté és imeeté ugyaayi időrése ell lei, hisze a térapcsoló ezt em tudja megváltoztati. Az is biztos, hogy az egész redszer imeeté ugyaayi időrés ell legye, mit a bemeeté (hisze ilye redszert aaru építei), ezért a harmadi foozat imeeté is c darab lesz. Végül pedig a harmadi foozat is térapcsoló, így aa a bemeeté is ugyaayi időrés lesz, mit a imeeté, tehát az is c. A érdés a már szoásos: mior lesz ez a redszer bloolásmetes? Ez értéétől, a özépső foozatba lévő időapcsoló számától függ. A godolatmeet természetese hasoló lesz az SSS, illetve a S apcsoló esetébe bemutatottahoz. együ fel, hogy az első bemeet i-edi időréséből szereté apcsolatot felépítei az első imeet j-edi időrésébe. Ehhez egy olya özépső foozatot ell találu, amelye szabad az i-edi bemeeti és a j-edi imeeti időrése. Maximum háy i-edi bemeeti időrés lehet szabad? Ugye -, hisze bemeetü va, de abból egy (példába az első) egyelőre biztosa szabad. Ugyaez a helyzet a imeeteel, és szerecsétle esetbe ics eze özött egybeesés. Eor - özépső foozatbeli időapcsoló lesz számura foglalt, eél eggyel több, =- pedig midig elég. SSS 6
17 A gyaorlatba eél boyolultabb felépítésű apcsolómezőet is haszála, pl. SSS apcsolót. Ez tulajdoéppe egy S apcsoló, ahol az S egy háromfoozatú térapcsolóval va megvalósítva, így valahogy: db db db ábra. SSS apcsoló 7
Távközlő hálózatok és szolgáltatások Kapcsolástechnika
 Távözlő hálózato és szolgáltatáso Kapcsolástechia émeth Krisztiá BME TMIT 015. ot. 1-8. A tárgy felépítése 1. Bevezetés. IP hálózato elérése távözlő és ábel-tv hálózatoo 3. VoIP, beszédódoló 4. Kapcsolástechia
Távözlő hálózato és szolgáltatáso Kapcsolástechia émeth Krisztiá BME TMIT 015. ot. 1-8. A tárgy felépítése 1. Bevezetés. IP hálózato elérése távözlő és ábel-tv hálózatoo 3. VoIP, beszédódoló 4. Kapcsolástechia
Távközlő hálózatok és szolgáltatások Kapcsolástechnika
 Távözlő hálózato és szolgáltatáso Kacsolástechia émeth Krisztiá BME TMIT 009. ot. 14. A tárgy feléítése 1. Bevezetés. IP hálózato elérése távözlő és ábel-tv hálózatoo 3. VoIP 4. Kacsolástechia 5. Mobiltelefo-hálózato
Távözlő hálózato és szolgáltatáso Kacsolástechia émeth Krisztiá BME TMIT 009. ot. 14. A tárgy feléítése 1. Bevezetés. IP hálózato elérése távözlő és ábel-tv hálózatoo 3. VoIP 4. Kacsolástechia 5. Mobiltelefo-hálózato
Dr. Tóth László, Kombinatorika (PTE TTK, 2007) nem vagyunk tekintettel a kiválasztott elemek sorrendjére. Mennyi a lehetőségek száma?
 Dr Tóth László, Kombiatoria (PTE TTK, 7 5 Kombiáció 5 Feladat Az,, 3, 4 számo özül válasszu i ettőt (ét ülöbözőt és írju fel ezeet úgy, hogy em vagyu teitettel a iválasztott eleme sorredjére Meyi a lehetősége
Dr Tóth László, Kombiatoria (PTE TTK, 7 5 Kombiáció 5 Feladat Az,, 3, 4 számo özül válasszu i ettőt (ét ülöbözőt és írju fel ezeet úgy, hogy em vagyu teitettel a iválasztott eleme sorredjére Meyi a lehetősége
n akkor az n elem összes ismétléses ... k l k 3 k 1! k 2!... k l!
 KOMBINATORIKAI ALAPFOGALMAK A ombiatoria általába a véges halmazora voatozó redezési és leszámlálási feladatoal foglalozi. Az elemi ombiatoria legtöbb esetbe a övetező ét érdés egyiére eresi a választ:
KOMBINATORIKAI ALAPFOGALMAK A ombiatoria általába a véges halmazora voatozó redezési és leszámlálási feladatoal foglalozi. Az elemi ombiatoria legtöbb esetbe a övetező ét érdés egyiére eresi a választ:
Diszkrét matematika KOMBINATORIKA KOMBINATORIKA
 A ombiatoria véges elemszámú halmazoat vizsgál. A fő érdése: a halmaz elemeit háyféleéppe lehet sorbaredezi, iválasztai özülü éháyat vagy aár midet bizoyos feltétele mellett, stb. Ezért a ombiatoria alapját
A ombiatoria véges elemszámú halmazoat vizsgál. A fő érdése: a halmaz elemeit háyféleéppe lehet sorbaredezi, iválasztai özülü éháyat vagy aár midet bizoyos feltétele mellett, stb. Ezért a ombiatoria alapját
Radiális szivattyú járókerék fő méreteinek meghatározása előírt Q-H üzemi ponthoz
 Radiális szivattyú járóeré fő méreteie meghatározása előírt - üzemi pothoz iret hajtás eseté szóa jövő asziromotor fordlatszámo % üzemi szlip feltételezésével: 90, 55, 970, 78 /mi Midegyi fordlatszámhoz
Radiális szivattyú járóeré fő méreteie meghatározása előírt - üzemi pothoz iret hajtás eseté szóa jövő asziromotor fordlatszámo % üzemi szlip feltételezésével: 90, 55, 970, 78 /mi Midegyi fordlatszámhoz
UJJLENYOMATOK FELISMERÉSE
 Babeş Bolyai Tudomáyegyetem Matematia Iformatia ar Iformatia sza UJJLENYOMATOK FELISMERÉSE Uleyomatépe feldolgozása, osztályozás euroális hálóal, azoosítási célú összehasolítás Vezetőtaár: Dr. Soós Aa
Babeş Bolyai Tudomáyegyetem Matematia Iformatia ar Iformatia sza UJJLENYOMATOK FELISMERÉSE Uleyomatépe feldolgozása, osztályozás euroális hálóal, azoosítási célú összehasolítás Vezetőtaár: Dr. Soós Aa
Kombinatorika (2017. február 8.) Bogya Norbert, Kátai-Urbán Kamilla
 Kombiatoria (017 február 8 Bogya Norbert, Kátai-Urbá Kamilla 1 Kombiatoriai alapfeladato A ombiatoriai alapfeladato léyege az, hogy bizoyos elemeet sorba redezü, vagy éháyat iválasztu belőlü, és esetleg
Kombiatoria (017 február 8 Bogya Norbert, Kátai-Urbá Kamilla 1 Kombiatoriai alapfeladato A ombiatoriai alapfeladato léyege az, hogy bizoyos elemeet sorba redezü, vagy éháyat iválasztu belőlü, és esetleg
Orosz Gyula: Markov-láncok. 2. Sorsolások visszatevéssel
 Orosz Gyula: Marov-láco 2. orsoláso visszatevéssel Néháy orét feladat segítségével vezetjü be a Marov-láco fogalmát és a hozzáju acsolódó megoldási módszereet, tiius eljárásoat. Ahol lehet, több megoldást
Orosz Gyula: Marov-láco 2. orsoláso visszatevéssel Néháy orét feladat segítségével vezetjü be a Marov-láco fogalmát és a hozzáju acsolódó megoldási módszereet, tiius eljárásoat. Ahol lehet, több megoldást
Járatszerkesztési feladatok
 Járatszeresztési feladato 1 Járatszeresztési feladato DR. BENKŐJÁNOS Agrártudomáyi Egyetem GödöllőMezőgazdasági Géptai Itézet A járat alatt a logisztiába általába a járműve meghatározott több állomást
Járatszeresztési feladato 1 Járatszeresztési feladato DR. BENKŐJÁNOS Agrártudomáyi Egyetem GödöllőMezőgazdasági Géptai Itézet A járat alatt a logisztiába általába a járműve meghatározott több állomást
FELADATOK a Bevezetés a matematikába I tárgyhoz
 FELADATOK a Bevezetés a matematiába I tárgyhoz a számítástechia taár főisolai és a programozó matematius szao számára 2004 ovember 4 FIGYELEM: a számtech szaosoa csa a övetező feladato ellee: 2,6,7,8,9-13,16-25,27,31-33
FELADATOK a Bevezetés a matematiába I tárgyhoz a számítástechia taár főisolai és a programozó matematius szao számára 2004 ovember 4 FIGYELEM: a számtech szaosoa csa a övetező feladato ellee: 2,6,7,8,9-13,16-25,27,31-33
I. FEJEZET BICIKLIHIÁNYBAN
 I FEJEZET BICIKLIHIÁNYBAN 1 Az alapfeladat 1 Feladat Két település közti távolság 40 km Két gyerekek ezt a távolságot kellee megteie a lehetőlegrövidebb időalattakövetkező feltételek mellett: Va egy biciklijük
I FEJEZET BICIKLIHIÁNYBAN 1 Az alapfeladat 1 Feladat Két település közti távolság 40 km Két gyerekek ezt a távolságot kellee megteie a lehetőlegrövidebb időalattakövetkező feltételek mellett: Va egy biciklijük
1. Komplex szám rendje
 1. Komplex szám redje A hatváyo periódiusa ismétlőde. Tétel Legye 0 z C. Ha z egységgyö, aor hatváyai periódiusa ismétlőde. Ha z em egységgyö, aor bármely ét, egész itevőjű hatváya ülöböző. Tegyü föl,
1. Komplex szám redje A hatváyo periódiusa ismétlőde. Tétel Legye 0 z C. Ha z egységgyö, aor hatváyai periódiusa ismétlőde. Ha z em egységgyö, aor bármely ét, egész itevőjű hatváya ülöböző. Tegyü föl,
Rudas Tamás: A hibahatár a becsült mennyiség függvényében a mért pártpreferenciák téves értelmezésének egyik forrása
 Rudas Tamás: A hibahatár a becsült meyiség függvéyébe a mért ártrefereciák téves értelmezéséek egyik forrása Megjelet: Agelusz Róbert és Tardos Róbert szerk.: Mérésről mérésre. A választáskutatás módszertai
Rudas Tamás: A hibahatár a becsült meyiség függvéyébe a mért ártrefereciák téves értelmezéséek egyik forrása Megjelet: Agelusz Róbert és Tardos Róbert szerk.: Mérésről mérésre. A választáskutatás módszertai
Metrikus terek. továbbra is.
 Metrius tere továbbra is. Defiíció: Legye X egy halmaz, d : X X R egy függvéy. Azt modju, hogy d metria (távolság), ha.. 3. 4. d d d d x, x 0, x, y 0 x y, x, y dy, x, x, z dx, y dy, z. Az X halmazt a d
Metrius tere továbbra is. Defiíció: Legye X egy halmaz, d : X X R egy függvéy. Azt modju, hogy d metria (távolság), ha.. 3. 4. d d d d x, x 0, x, y 0 x y, x, y dy, x, x, z dx, y dy, z. Az X halmazt a d
Numerikus módszerek 2. Nemlineáris egyenletek közelítő megoldása
 Numerius módszere. Nemlieáris egyelee özelíő megoldása Egyelemegoldás iervallumelezéssel A Baach-ipo-ierációs módszer A Newo-módszer és válozaai Álaláosío Newo-módszer Egyelemegoldás iervallumelezéssel
Numerius módszere. Nemlieáris egyelee özelíő megoldása Egyelemegoldás iervallumelezéssel A Baach-ipo-ierációs módszer A Newo-módszer és válozaai Álaláosío Newo-módszer Egyelemegoldás iervallumelezéssel
5. Kombinatorika. 8. Legfeljebb hány pozitív egész számot adhatunk meg úgy, hogy semelyik kettő összege és különbsége se legyen osztható 2015-tel?
 5. Kombiatorika I. Feladatok. Háyféleképpe olvashatók ki az alábbi ábrákról a PAPRIKAJANCSI, a FELADAT és a MATEMATIKASZAKKÖR szavak, ha midig a bal felső sarokból kell iduluk, és mide lépésük csak jobbra
5. Kombiatorika I. Feladatok. Háyféleképpe olvashatók ki az alábbi ábrákról a PAPRIKAJANCSI, a FELADAT és a MATEMATIKASZAKKÖR szavak, ha midig a bal felső sarokból kell iduluk, és mide lépésük csak jobbra
Ingatlanfinanszírozás és befektetés
 Nyugat-Magyarországi Egyetem Geoiformatikai Kar Igatlameedzser 8000 Székesfehérvár, Pirosalma u. 1-3. Szakiráyú Továbbképzési Szak Igatlafiaszírozás és befektetés 2. Gazdasági matematikai alapok Szerzı:
Nyugat-Magyarországi Egyetem Geoiformatikai Kar Igatlameedzser 8000 Székesfehérvár, Pirosalma u. 1-3. Szakiráyú Továbbképzési Szak Igatlafiaszírozás és befektetés 2. Gazdasági matematikai alapok Szerzı:
Szerszámgépek 5. előadás 2007. Március 13. Szerszámg. 5. előad. Miskolc - Egyetemváros 2006/2007 2.félév
 Sersámgépe 5. előadás. Márcis. Sersámg mgépe 5. előad adás Misolc - Egyetemváros /.félév Sersámgépe 5. előadás. Márcis. A sabályohatósági tartomáy övelésée módserei Előetes megfotoláso: S mi mi M S φ,
Sersámgépe 5. előadás. Márcis. Sersámg mgépe 5. előad adás Misolc - Egyetemváros /.félév Sersámgépe 5. előadás. Márcis. A sabályohatósági tartomáy övelésée módserei Előetes megfotoláso: S mi mi M S φ,
SZÁMHALMAZOK Halmazábrán ábrázolom a valós számok halmazát és részhalmazait (néhány példával). (C) pl. 1/4; 1/2. pl. 1;2;0;-1; N pl. 0. pl.
 2. tétel Számhalmazo (a valós számo halmaza és részhalmazai), oszthatósággal apcsolatos problémá, számredszere. SZÁMHALMAZOK Halmazábrá ábrázolom a valós számo halmazát és részhalmazait (éháy példával).
2. tétel Számhalmazo (a valós számo halmaza és részhalmazai), oszthatósággal apcsolatos problémá, számredszere. SZÁMHALMAZOK Halmazábrá ábrázolom a valós számo halmazát és részhalmazait (éháy példával).
A függvénysorozatok olyanok, mint a valós számsorozatok, csak éppen a tagjai nem valós számok,
 l.ch FÜGGVÉNYSOROZATOK, FÜGGVÉNYSOROK, HATVÁNYSOROK Itt egy függvéysorozat: f( A függvéysorozatok olyaok, mit a valós számsorozatok, csak éppe a tagjai em valós számok, 5 haem függvéyek, f ( ; f ( ; f
l.ch FÜGGVÉNYSOROZATOK, FÜGGVÉNYSOROK, HATVÁNYSOROK Itt egy függvéysorozat: f( A függvéysorozatok olyaok, mit a valós számsorozatok, csak éppe a tagjai em valós számok, 5 haem függvéyek, f ( ; f ( ; f
Kvantum párhuzamosság Deutsch algoritmus Deutsch-Jozsa algoritmus
 LOGO Kvatum párhuzamosság Deutsch algoritmus Deutsch-Jozsa algoritmus Gyögyösi László BME Villamosméröki és Iormatikai Kar Bevezető Kvatum párhuzamosság Bármilye biáris üggvéyre, ahol { } { } : 0, 0,,
LOGO Kvatum párhuzamosság Deutsch algoritmus Deutsch-Jozsa algoritmus Gyögyösi László BME Villamosméröki és Iormatikai Kar Bevezető Kvatum párhuzamosság Bármilye biáris üggvéyre, ahol { } { } : 0, 0,,
1. tétel. Halmazok, halmazműveletek, halmazok számossága, halmazműveletek és logikai műveletek kapcsolata.
 . tétel. Halmazo, halmazművelete, halmazo számossága, halmazművelete és logiai művelete apcsolata. Vázlat:.Halmazoal apcsolatos elevezése, alapfogalma pl.: halmaz, elem, adott egy halmaz, megadása, jelölése
. tétel. Halmazo, halmazművelete, halmazo számossága, halmazművelete és logiai művelete apcsolata. Vázlat:.Halmazoal apcsolatos elevezése, alapfogalma pl.: halmaz, elem, adott egy halmaz, megadása, jelölése
A figurális számokról (IV.)
 A figurális számokról (IV.) Tuzso Zoltá, Székelyudvarhely A továbbiakba külöféle számkombiációk és összefüggések reprezetálásáról, és bizoyos összegek kiszámolásáról íruk. Sajátos összefüggések Az elekbe
A figurális számokról (IV.) Tuzso Zoltá, Székelyudvarhely A továbbiakba külöféle számkombiációk és összefüggések reprezetálásáról, és bizoyos összegek kiszámolásáról íruk. Sajátos összefüggések Az elekbe
Villamos gépek tantárgy tételei
 Villamos gépek tatárgy tételei 7. tétel Mi a szerepe az áram- és feszültségváltókak? Hogya kapcsolódak a hálózathoz, milye előírások voatkozak a biztoságos üzemeltetésükre, kiválasztásukál milye adatot
Villamos gépek tatárgy tételei 7. tétel Mi a szerepe az áram- és feszültségváltókak? Hogya kapcsolódak a hálózathoz, milye előírások voatkozak a biztoságos üzemeltetésükre, kiválasztásukál milye adatot
Kalkulus I. Első zárthelyi dolgozat 2014. szeptember 16. MINTA. és q = k 2. k 2. = k 1l 2 k 2 l 1. l 1 l 2. 5 2n 6n + 8
 Név, Neptu-kód:.................................................................... 1. Legyeek p, q Q tetszőlegesek. Mutassuk meg, hogy ekkor p q Q. Tegyük fel, hogy p, q Q. Ekkor létezek olya k 1, k 2,
Név, Neptu-kód:.................................................................... 1. Legyeek p, q Q tetszőlegesek. Mutassuk meg, hogy ekkor p q Q. Tegyük fel, hogy p, q Q. Ekkor létezek olya k 1, k 2,
Mőbiusz Nemzetközi Meghívásos Matematika Verseny Makó, március 26. MEGOLDÁSOK
 Mőbiusz Nemzetözi Meghívásos Matematia Versey Maó, 0. március 6. MEGOLDÁSOK 5 700. Egy gép 5 óra alatt = 000 alatt 000 csavart. 000 csavart észít, így = gép észít el 5 óra 000. 5 + 6 = = 5 + 5 6 5 6 6.
Mőbiusz Nemzetözi Meghívásos Matematia Versey Maó, 0. március 6. MEGOLDÁSOK 5 700. Egy gép 5 óra alatt = 000 alatt 000 csavart. 000 csavart észít, így = gép észít el 5 óra 000. 5 + 6 = = 5 + 5 6 5 6 6.
9. tétel: Elsı- és másodfokú egyenlıtlenségek, pozitív számok nevezetes közepei, és ezek felhasználása szélsıérték-feladatok megoldásában
 9. tétel: Elsı- és másodfoú egyelıtlesége, pozitív számo evezetes özepei, és eze felhaszálása szélsıérté-feladato megoldásáa Egyelıtleség: Két relációsjellel összeapcsolt ifejezés vagy függvéy. Az egyelıtleséget
9. tétel: Elsı- és másodfoú egyelıtlesége, pozitív számo evezetes özepei, és eze felhaszálása szélsıérté-feladato megoldásáa Egyelıtleség: Két relációsjellel összeapcsolt ifejezés vagy függvéy. Az egyelıtleséget
Útvonalak száma, rekurzív számlálással
 Útvoala száma, reurzív számlálással Tuzso Zoltá, Széelyudvarhely Napjaiba is gyara találozhatu olya feladatoal, ahol azt ell megszámolu, hogy adott potból, vagy potoból iidulva, adott feltétele mellett
Útvoala száma, reurzív számlálással Tuzso Zoltá, Széelyudvarhely Napjaiba is gyara találozhatu olya feladatoal, ahol azt ell megszámolu, hogy adott potból, vagy potoból iidulva, adott feltétele mellett
A Secretary problem. Optimális választás megtalálása.
 A Secretary problem. Optmáls választás megtalálása. A Szdbád problémáa va egy szté lasszusa tethető talá természetesebb vszot ehezebb változata. Ez a övetező Secretary problem -a evezett érdés: Egy állásra
A Secretary problem. Optmáls választás megtalálása. A Szdbád problémáa va egy szté lasszusa tethető talá természetesebb vszot ehezebb változata. Ez a övetező Secretary problem -a evezett érdés: Egy állásra
Az új építőipari termelőiár-index részletes módszertani leírása
 Az új építőipari termelőiár-idex részletes módszertai leírása. Előzméyek Az elmúlt évekbe az építőipari árstatisztikába egy új, a korábba haszálatos költségalapú áridextől eltérő termelői ár alapú idexmutató
Az új építőipari termelőiár-idex részletes módszertai leírása. Előzméyek Az elmúlt évekbe az építőipari árstatisztikába egy új, a korábba haszálatos költségalapú áridextől eltérő termelői ár alapú idexmutató
SZÁMELMÉLET. Vasile Berinde, Filippo Spagnolo
 SZÁMELMÉLET Vasile Beride, Filippo Spagolo A számelmélet a matematika egyik legrégibb ága, és az egyik legagyobb is egybe Eek a fejezetek az a célja, hogy egy elemi bevezetést yújtso az első szite lévő
SZÁMELMÉLET Vasile Beride, Filippo Spagolo A számelmélet a matematika egyik legrégibb ága, és az egyik legagyobb is egybe Eek a fejezetek az a célja, hogy egy elemi bevezetést yújtso az első szite lévő
VII. A határozatlan esetek kiküszöbölése
 A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
VILLAMOS ENERGETIKA Vizsgakérdések (BSc. 2011. tavaszi félév)
 1 VILLAMOS ENERGETIKA Vizsgaérdése (BSc. 2011. tavaszi félév) 1. Isertesse a villaoseergia-hálózat feladatr szeriti felosztását a jellegzetes feszültségsziteet és az azohoz tartozó átvihető teljesítéye
1 VILLAMOS ENERGETIKA Vizsgaérdése (BSc. 2011. tavaszi félév) 1. Isertesse a villaoseergia-hálózat feladatr szeriti felosztását a jellegzetes feszültségsziteet és az azohoz tartozó átvihető teljesítéye
ANALÓG-DIGITÁLIS ÉS DIGITÁLIS-ANALÓG ÁTALAKÍTÓK
 F3 Bev. az elektroikába E, Kísérleti Fizika Taszék ANALÓG-IGITÁLIS ÉS IGITÁLIS-ANALÓG ÁTALAKÍTÓK Az A és A átalakítók feladata az aalóg és digitális áramkörök közötti kapcsolat megvalósítása. A folytoos
F3 Bev. az elektroikába E, Kísérleti Fizika Taszék ANALÓG-IGITÁLIS ÉS IGITÁLIS-ANALÓG ÁTALAKÍTÓK Az A és A átalakítók feladata az aalóg és digitális áramkörök közötti kapcsolat megvalósítása. A folytoos
FANTASZTIKUS KOMBINATORIKA. Adva van n különböző elem. A kiválasztás sorrendje számít VARIÁCIÓ. mateking.hu
 FANTASZTIKUS KOMBINATORIKA Adva va külöböző elem Kiválasztuk k darabot Vesszük az összes elemet és sorba rakjuk A kiválasztás sorredje számít A kiválasztás sorredje em számít PERMUTÁCIÓ P matekig.hu Ha
FANTASZTIKUS KOMBINATORIKA Adva va külöböző elem Kiválasztuk k darabot Vesszük az összes elemet és sorba rakjuk A kiválasztás sorredje számít A kiválasztás sorredje em számít PERMUTÁCIÓ P matekig.hu Ha
V. GYAKORLATOK ÉS FELADATOK ALGEBRÁBÓL
 86 Összefoglaló gyaorlato és feladato V GYAKORLATOK ÉS FELADATOK ALGEBRÁBÓL 5 Halmazo, relácó, függvéye Bzoyítsd be, hogy ha A és B ét tetszőleges halmaz, aor a) P( A) P( B) P( A B) ; b) P( A) P ( B )
86 Összefoglaló gyaorlato és feladato V GYAKORLATOK ÉS FELADATOK ALGEBRÁBÓL 5 Halmazo, relácó, függvéye Bzoyítsd be, hogy ha A és B ét tetszőleges halmaz, aor a) P( A) P( B) P( A B) ; b) P( A) P ( B )
Szabályozó szelepek (PN 16) VF 2-2 utú szelep, karima VF 3-3 járatú szelep, karima
 Szabályozó szelepe (PN 16) VF 2-2 utú szelep, arima VF 3-3 járatú szelep, arima eírás Jellemző: ágytömítéses ostrució Gyorscsatlaozó az AMV(E) 335, AMV(E) 435 -hez 2- és 3 Alalmazás everő és osztó azelepét
Szabályozó szelepe (PN 16) VF 2-2 utú szelep, arima VF 3-3 járatú szelep, arima eírás Jellemző: ágytömítéses ostrució Gyorscsatlaozó az AMV(E) 335, AMV(E) 435 -hez 2- és 3 Alalmazás everő és osztó azelepét
2. fejezet. Számsorozatok, számsorok
 . fejezet Számsorozatok, számsorok .. Számsorozatok és számsorok... Számsorozat megadása, határértéke Írjuk fel képlettel az alábbi sorozatok -dik elemét! mooto, korlátos, illetve koverges-e! Vizsgáljuk
. fejezet Számsorozatok, számsorok .. Számsorozatok és számsorok... Számsorozat megadása, határértéke Írjuk fel képlettel az alábbi sorozatok -dik elemét! mooto, korlátos, illetve koverges-e! Vizsgáljuk
FOLYADÉKKRISTÁLY-TELEVÍZIÓK Éber Nándor
 FLYADÉKKRISTÁLY-TLVÍZIÓK Éber Nádor A 21. SZÁZAD KÉPRNYÔI MTA SZFKI, Budapest A szerezetü és tulajdoságai alapjá a folyadéo és a szilárd ayago özött sajátos átmeetet épezô folyadéristályo felfedezésü (1888)
FLYADÉKKRISTÁLY-TLVÍZIÓK Éber Nádor A 21. SZÁZAD KÉPRNYÔI MTA SZFKI, Budapest A szerezetü és tulajdoságai alapjá a folyadéo és a szilárd ayago özött sajátos átmeetet épezô folyadéristályo felfedezésü (1888)
Felépítés Típus 955010/ Konfigurálás setup programmal. Mérési adatok kiolvasása
 JUMO Meß- ud Regelgeräte GmbH A-1232 Wie, Pfarrgasse 48 Magyarországi Kereskedelmi Képviselet Telefo: 00-43-1 / 61-061-0 H-1147 Budapest Öv u. 143. Fax: 00-43-1 / 61-061-59 Telefo/fax: 00-36-1 / 467-0835,
JUMO Meß- ud Regelgeräte GmbH A-1232 Wie, Pfarrgasse 48 Magyarországi Kereskedelmi Képviselet Telefo: 00-43-1 / 61-061-0 H-1147 Budapest Öv u. 143. Fax: 00-43-1 / 61-061-59 Telefo/fax: 00-36-1 / 467-0835,
Az anyagáramlás intenzitása
 Az ayagáramlás teztása Az ayagáramlás teztása () alatt meghatározott dőegység (dőtervallum) alatt (t) mozgatott ayagmeységet (M) értü. M (g, t, E, db, stb./ dőegység) t Szaaszos műödésű ayagmozgató redszere
Az ayagáramlás teztása Az ayagáramlás teztása () alatt meghatározott dőegység (dőtervallum) alatt (t) mozgatott ayagmeységet (M) értü. M (g, t, E, db, stb./ dőegység) t Szaaszos műödésű ayagmozgató redszere
Az iparosodás és az infrastrukturális fejlődés típusai
 Az iparosodás és az ifrastrukturális fejlődés típusai Az iparosodás és az ifrastrukturális fejlődés kapcsolatába törtéelmileg három fejlődési típus vázolható fel: megelőző, lácszerűe együtt haladó, utólagosa
Az iparosodás és az ifrastrukturális fejlődés típusai Az iparosodás és az ifrastrukturális fejlődés kapcsolatába törtéelmileg három fejlődési típus vázolható fel: megelőző, lácszerűe együtt haladó, utólagosa
Olimpiai szakkör, Dobos Sándor 2008/2009
 Olimpii ször, Dobos Sádor 008/009 008 szeptember 9 Eze szörö Cev és Meelosz tételt eleveítettü fel, több gyorló feldttl, éháy lehetséges áltláosítássl További feldto: = 6 (=,, ) Htározzu meg z összes oly
Olimpii ször, Dobos Sádor 008/009 008 szeptember 9 Eze szörö Cev és Meelosz tételt eleveítettü fel, több gyorló feldttl, éháy lehetséges áltláosítássl További feldto: = 6 (=,, ) Htározzu meg z összes oly
VÉLETLENÍTETT ALGORITMUSOK. 1.ea.
 VÉLETLENÍTETT ALGORITMUSOK 1.ea. 1. Bevezetés - (Mire jók a véletleített algoritmusok, alap techikák) 1.1. Gyorsredezés Vegyük egy ismert példát, a redezések témaköréből, méghozzá a gyorsredezés algoritmusát.
VÉLETLENÍTETT ALGORITMUSOK 1.ea. 1. Bevezetés - (Mire jók a véletleített algoritmusok, alap techikák) 1.1. Gyorsredezés Vegyük egy ismert példát, a redezések témaköréből, méghozzá a gyorsredezés algoritmusát.
1. Adatok közelítése. Bevezetés. 1-1 A közelítő függvény
 Palácz Béla - Soft Computig - 11-1. Adatok közelítése 1. Adatok közelítése Bevezetés A természettudomáyos feladatok megoldásához, a vizsgált jeleségek, folyamatok főbb jellemzői közötti összefüggések ismeretére,
Palácz Béla - Soft Computig - 11-1. Adatok közelítése 1. Adatok közelítése Bevezetés A természettudomáyos feladatok megoldásához, a vizsgált jeleségek, folyamatok főbb jellemzői közötti összefüggések ismeretére,
2. egy iskola tanulói, a változók: magasságuk cm-ben, súlyuk (tömegük) kilóban; 3. egy iskola tanulói, a változó: tanulmányi átlaguk;
 Statisztika Tegyük fel, hogy va egy halmazuk, és tekitsük egy vagy több valószíűségi változót, amelyek a halmaz mide elemé felveszek valamilye értéket. A halmazt populációak vagy sokaságak evezzük. Példák:
Statisztika Tegyük fel, hogy va egy halmazuk, és tekitsük egy vagy több valószíűségi változót, amelyek a halmaz mide elemé felveszek valamilye értéket. A halmazt populációak vagy sokaságak evezzük. Példák:
EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z n HALMAZON. egyenletrendszer megoldása a
 Az érettségi vizsgára előkészülő taulók figyelmébe! 4. Az EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z HALMAZON a1 x + b1 y = c1 egyeletredszer megoldása a a x + b y = c Z halmazo (. rész) Ebbe a részbe
Az érettségi vizsgára előkészülő taulók figyelmébe! 4. Az EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z HALMAZON a1 x + b1 y = c1 egyeletredszer megoldása a a x + b y = c Z halmazo (. rész) Ebbe a részbe
Pályázat címe: Pályázati azonosító: Kedvezményezett: Szegedi Tudományegyetem Cím: 6720 Szeged, Dugonics tér 13. www.u-szeged.hu www.palyazat.gov.
 Pályázat címe: Új geerációs sorttudomáyi kézés és tartalomfejlesztés, hazai és emzetközi hálózatfejlesztés és társadalmasítás a Szegedi Tudomáyegyeteme Pályázati azoosító: TÁMOP-4...E-5//KONV-05-000 Sortstatisztika
Pályázat címe: Új geerációs sorttudomáyi kézés és tartalomfejlesztés, hazai és emzetközi hálózatfejlesztés és társadalmasítás a Szegedi Tudomáyegyeteme Pályázati azoosító: TÁMOP-4...E-5//KONV-05-000 Sortstatisztika
Numerikus módszerek 2. Nemlineáris egyenletek közelítő megoldása
 umerius módszere. emlieáris egyelee özelíő megoldása Egyelemegoldás iervallumelezéssel Legye :[ a, b] R olyoos, a, b, és eressü az egyele egy [ a, b] -beli megoldásá. Bolzao éele: Legye olyoos a véges,
umerius módszere. emlieáris egyelee özelíő megoldása Egyelemegoldás iervallumelezéssel Legye :[ a, b] R olyoos, a, b, és eressü az egyele egy [ a, b] -beli megoldásá. Bolzao éele: Legye olyoos a véges,
Számsorozatok. 1. Alapfeladatok december 22. sorozat határértékét, ha. 1. Feladat: Határozzuk meg az a n = 3n2 + 7n 5n létezik.
 Számsorozatok 2015. december 22. 1. Alapfeladatok 1. Feladat: Határozzuk meg az a 2 + 7 5 2 + 4 létezik. sorozat határértékét, ha Megoldás: Mivel egy tört határértéke a kérdés, ezért vizsgáljuk meg el
Számsorozatok 2015. december 22. 1. Alapfeladatok 1. Feladat: Határozzuk meg az a 2 + 7 5 2 + 4 létezik. sorozat határértékét, ha Megoldás: Mivel egy tört határértéke a kérdés, ezért vizsgáljuk meg el
Matematikai játékok. Svetoslav Bilchev, Emiliya Velikova
 Matematikai játékok Svetoslav Bilchev, Emiliya Velikova 1. rész Matematikai tréfák A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a játékosok
Matematikai játékok Svetoslav Bilchev, Emiliya Velikova 1. rész Matematikai tréfák A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a játékosok
7. el adás Becslések és minta elemszámok. 7-1. fejezet Áttekintés
 7. el adás Becslések és mita elemszámok 7-1. fejezet Áttekités 7-1 Áttekités 7- A populáció aráy becslése 7-3 A populáció átlag becslése: σismert 7-4 A populáció átlag becslése: σem ismert 7-5 A populáció
7. el adás Becslések és mita elemszámok 7-1. fejezet Áttekités 7-1 Áttekités 7- A populáció aráy becslése 7-3 A populáció átlag becslése: σismert 7-4 A populáció átlag becslése: σem ismert 7-5 A populáció
GAZDASÁGI MATEMATIKA 1. ANALÍZIS
 SZENT ISTVÁN EGYETEM GAZDASÁGI, AGRÁR- ÉS EGÉSZSÉGTUDOMÁNYI KAR Dr. Szakács Attila GAZDASÁGI MATEMATIKA. ANALÍZIS Segédlet öálló mukához. átdolgozott, bővített kiadás Békéscsaba, Lektorálták: DR. PATAY
SZENT ISTVÁN EGYETEM GAZDASÁGI, AGRÁR- ÉS EGÉSZSÉGTUDOMÁNYI KAR Dr. Szakács Attila GAZDASÁGI MATEMATIKA. ANALÍZIS Segédlet öálló mukához. átdolgozott, bővített kiadás Békéscsaba, Lektorálták: DR. PATAY
4. Test feletti egyhatározatlanú polinomok. Klasszikus algebra előadás NE KEVERJÜK A POLINOMOT A POLINOMFÜGGVÉNNYEL!!!
 4. Test feletti egyhatározatlaú poliomok Klasszikus algebra előadás Waldhauser Tamás 2013 április 11. Eddig a poliomokkal mit formális kifejezésekkel számoltuk, em éltük azzal a lehetőséggel, hogy x helyébe
4. Test feletti egyhatározatlaú poliomok Klasszikus algebra előadás Waldhauser Tamás 2013 április 11. Eddig a poliomokkal mit formális kifejezésekkel számoltuk, em éltük azzal a lehetőséggel, hogy x helyébe
(A TÁMOP /2/A/KMR számú projekt keretében írt egyetemi jegyzetrészlet):
 A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
A JÓLÉTI ÁLLAM KÖZGAZDASÁGTANA
 A JÓLÉTI ÁLLAM KÖZGAZDASÁGTANA A JÓLÉTI ÁLLAM KÖZGAZDASÁGTANA Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázati projet eretében Tartalomfejlesztés az ELTE TátK Közgazdaságtudományi Tanszéén az ELTE Közgazdaságtudományi
A JÓLÉTI ÁLLAM KÖZGAZDASÁGTANA A JÓLÉTI ÁLLAM KÖZGAZDASÁGTANA Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázati projet eretében Tartalomfejlesztés az ELTE TátK Közgazdaságtudományi Tanszéén az ELTE Közgazdaságtudományi
AZ ÉPÜLETGÉPÉSZETI RENDSZEREK ENERGIA-HATÉKONYSÁGÁNAK KÉRDÉSEI
 AZ ÉÜLETGÉÉSZETI RENDSZEREK ENERGIA-HATÉKONYSÁGÁNAK KÉRDÉSEI Szivattyúzás - rövide örös Szilárd Cetrifugál szivattyú Nyomó oldal Járókerék Járókerék lapát Járókerék él Járókerék csavar a szállított közeg
AZ ÉÜLETGÉÉSZETI RENDSZEREK ENERGIA-HATÉKONYSÁGÁNAK KÉRDÉSEI Szivattyúzás - rövide örös Szilárd Cetrifugál szivattyú Nyomó oldal Járókerék Járókerék lapát Járókerék él Járókerék csavar a szállított közeg
Számelméleti érdekességek dr. Kosztolányi József, Szeged
 Magas szitű matematiai tehetséggodozás Számelméleti érdeessége dr. Kosztoláyi József, Szeged A számelmélet bőveledi olya érdésebe, problémába, összefüggésebe, amelye elemi módszereel megözelíthető. Bizoyos
Magas szitű matematiai tehetséggodozás Számelméleti érdeessége dr. Kosztoláyi József, Szeged A számelmélet bőveledi olya érdésebe, problémába, összefüggésebe, amelye elemi módszereel megözelíthető. Bizoyos
Matematikai játékok. Svetoslav Bilchev, Emiliya Velikova
 Első rész Matematikai tréfák Matematikai játékok Svetoslav Bilchev, Emiliya Velikova A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a
Első rész Matematikai tréfák Matematikai játékok Svetoslav Bilchev, Emiliya Velikova A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a
Matematikai statisztika
 Matematikai statisztika PROGRAMTERVEZŐ INFORMATIKUS alapszak, A szakiráy Arató Miklós Valószíűségelméleti és Statisztika Taszék Természettudomáyi Kar 2019. február 18. Arató Miklós (ELTE) Matematikai statisztika
Matematikai statisztika PROGRAMTERVEZŐ INFORMATIKUS alapszak, A szakiráy Arató Miklós Valószíűségelméleti és Statisztika Taszék Természettudomáyi Kar 2019. február 18. Arató Miklós (ELTE) Matematikai statisztika
2. Hatványsorok. A végtelen soroknál tanultuk, hogy az. végtelen sort adja: 1 + x + x x n +...
 . Függvéysorok. Bevezetés és defiíciók A végtele sorokál taultuk, hogy az + x + x + + x +... végtele összeg x < eseté koverges. A feti végtele összegre úgy is godolhatuk, hogy végtele sok függvéyt aduk
. Függvéysorok. Bevezetés és defiíciók A végtele sorokál taultuk, hogy az + x + x + + x +... végtele összeg x < eseté koverges. A feti végtele összegre úgy is godolhatuk, hogy végtele sok függvéyt aduk
Számelméleti alapfogalmak
 Számelméleti alapfogalma A maradéos osztás tétele Legye a és b ét természetes szám, b, és a>b Aor egyértelme léteze q és r természetes számo, amelyere igaz: a b q r, r b Megevezés: a osztadó b osztó q
Számelméleti alapfogalma A maradéos osztás tétele Legye a és b ét természetes szám, b, és a>b Aor egyértelme léteze q és r természetes számo, amelyere igaz: a b q r, r b Megevezés: a osztadó b osztó q
Matematika I. 9. előadás
 Matematika I. 9. előadás Valós számsorozat kovergeciája +-hez ill. --hez divergáló sorozatok A határérték és a műveletek kapcsolata Valós számsorozatok mootoitása, korlátossága Komplex számsorozatok kovergeciája
Matematika I. 9. előadás Valós számsorozat kovergeciája +-hez ill. --hez divergáló sorozatok A határérték és a műveletek kapcsolata Valós számsorozatok mootoitása, korlátossága Komplex számsorozatok kovergeciája
Nevezetes sorozat-határértékek
 Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
( a b)( c d) 2 ab2 cd 2 abcd 2 Egyenlőség akkor és csak akkor áll fenn
 Feladatok közepek közötti egyelőtleségekre (megoldások, megoldási ötletek) A továbbiakba szmk=számtai-mértai közép közötti egyelőtleség, szhk=számtaiharmoikus közép közötti egyelőtleség, míg szk= számtai-égyzetes
Feladatok közepek közötti egyelőtleségekre (megoldások, megoldási ötletek) A továbbiakba szmk=számtai-mértai közép közötti egyelőtleség, szhk=számtaiharmoikus közép közötti egyelőtleség, míg szk= számtai-égyzetes
18. Differenciálszámítás
 8. Differeciálszámítás I. Elméleti összefoglaló Függvéy határértéke Defiíció: Az köryezetei az ] ε, ε[ + yílt itervallumok, ahol ε > tetszőleges. Defiíció: Az f függvéyek az véges helye vett határértéke
8. Differeciálszámítás I. Elméleti összefoglaló Függvéy határértéke Defiíció: Az köryezetei az ] ε, ε[ + yílt itervallumok, ahol ε > tetszőleges. Defiíció: Az f függvéyek az véges helye vett határértéke
Tuzson Zoltán A Sturm-módszer és alkalmazása
 Tuzso Zoltá A turm-módszer és alalmazása zámtala szélsérté probléma megoldása, vag egeltleség bzoítása ago gara, már a matemata aalízs eszözere szorítoz, mt például a Jese-, Hölder-féle egeltleség, derválta
Tuzso Zoltá A turm-módszer és alalmazása zámtala szélsérté probléma megoldása, vag egeltleség bzoítása ago gara, már a matemata aalízs eszözere szorítoz, mt például a Jese-, Hölder-féle egeltleség, derválta
24. tétel A valószínűségszámítás elemei. A valószínűség kiszámításának kombinatorikus modellje.
 24. tétel valószíűségszámítás elemei. valószíűség kiszámításáak kombiatorikus modellje. GYORISÁG ÉS VLÓSZÍŰSÉG meyibe az egyes adatok a sokaságo belüli részaráyát adjuk meg (törtbe vagy százalékba), akkor
24. tétel valószíűségszámítás elemei. valószíűség kiszámításáak kombiatorikus modellje. GYORISÁG ÉS VLÓSZÍŰSÉG meyibe az egyes adatok a sokaságo belüli részaráyát adjuk meg (törtbe vagy százalékba), akkor
Kombinatorika. Variáció, permutáció, kombináció. Binomiális tétel, szita formula.
 Kombiatorika Variáció, permutáció, kombiáció Biomiális tétel, szita formula 1 Kombiatorikai alapfeladatok A kombiatorikai alapfeladatok léyege az, hogy bizoyos elemeket sorba redezük, vagy éháyat kiválasztuk
Kombiatorika Variáció, permutáció, kombiáció Biomiális tétel, szita formula 1 Kombiatorikai alapfeladatok A kombiatorikai alapfeladatok léyege az, hogy bizoyos elemeket sorba redezük, vagy éháyat kiválasztuk
Divergens sorok. Szakdolgozat
 Diverges soro Szadolgozat Eötvös Lorád Tudomáyegyetem Természettudomáyi Kar Készítette: Szabó Szilárd Matematia Bsc., taári szairáy Témavezető: Gémes Margit Műszai gazdasági taár Aalízis taszé Budapest,
Diverges soro Szadolgozat Eötvös Lorád Tudomáyegyetem Természettudomáyi Kar Készítette: Szabó Szilárd Matematia Bsc., taári szairáy Témavezető: Gémes Margit Műszai gazdasági taár Aalízis taszé Budapest,
Tartalomjegyzék. Pemutáció 5 Ismétléses permutáció 8 Variáció 9 Ismétléses variáció 11 Kombináció 12 Ismétléses kombináció 13
 Tartalomjegyzék I Kombiatorika Pemutáció Ismétléses permutáció 8 Variáció 9 Ismétléses variáció Kombiáció Ismétléses kombiáció II Valószíségszámítás M/veletek eseméyek között 6 A valószí/ség fogalma 8
Tartalomjegyzék I Kombiatorika Pemutáció Ismétléses permutáció 8 Variáció 9 Ismétléses variáció Kombiáció Ismétléses kombiáció II Valószíségszámítás M/veletek eseméyek között 6 A valószí/ség fogalma 8
5. SZABAD PONTRENDSZEREK MECHANIKAI ALAPELVEI, N-TESTPROBLÉMA, GALILEI-
 5. SZABAD PONTRENDSZEREK MECHANIKAI ALAPELVEI, N-TESTPROBLÉMA, GALILEI- FÉLE RELATIVITÁSI ELV m, m,,m r, r,,r r, r,, r 6 db oordáta és sebességompoes 5.. Dama Mozgásegyelete: m r = F F, ahol F jelöl a
5. SZABAD PONTRENDSZEREK MECHANIKAI ALAPELVEI, N-TESTPROBLÉMA, GALILEI- FÉLE RELATIVITÁSI ELV m, m,,m r, r,,r r, r,, r 6 db oordáta és sebességompoes 5.. Dama Mozgásegyelete: m r = F F, ahol F jelöl a
ALGEBRA. egyenlet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 198.
 ALGEBRA MÁSODFOKÚ POLINOMOK. Határozzuk meg az + p + q = 0 egyelet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 98.. Határozzuk meg az összes olya pozitív egész p és q számot, amelyre az
ALGEBRA MÁSODFOKÚ POLINOMOK. Határozzuk meg az + p + q = 0 egyelet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 98.. Határozzuk meg az összes olya pozitív egész p és q számot, amelyre az
3. Valószínűségszámítás
 Biometria az orvosi gyaorlatba 3. Valószíűségszámítás 3. Valószíűségszámítás 3.. Bevezetés 3.. Kombiatoria 3... Permutáció 3... Variáció 3..3. Kombiáció 3 3.3. Biomiális együttható tulajdoságai 3 3.4.
Biometria az orvosi gyaorlatba 3. Valószíűségszámítás 3. Valószíűségszámítás 3.. Bevezetés 3.. Kombiatoria 3... Permutáció 3... Variáció 3..3. Kombiáció 3 3.3. Biomiális együttható tulajdoságai 3 3.4.
Hiba! Nincs ilyen stílusú szöveg a dokumentumban.-86. ábra: A példa-feladat kódolási változatai
 közzétéve a szerző egedélyével) Öfüggő szekuder-változó csoport keresése: egy bevezető példa Ez a módszer az állapothalmazo értelmezett partíció-párok elméleté alapul. E helye em lehet céluk az elmélet
közzétéve a szerző egedélyével) Öfüggő szekuder-változó csoport keresése: egy bevezető példa Ez a módszer az állapothalmazo értelmezett partíció-párok elméleté alapul. E helye em lehet céluk az elmélet
Feladatok és megoldások a 11. heti gyakorlathoz
 Feladatok és megoldások a. het gyakorlathoz dszkrét várható érték Építőkar Matematka A. Egy verseye öt ő és öt férf verseyző dul. Tegyük fel, hogy cs két azoos eredméy, és md a 0! sorred egyformá valószíű.
Feladatok és megoldások a. het gyakorlathoz dszkrét várható érték Építőkar Matematka A. Egy verseye öt ő és öt férf verseyző dul. Tegyük fel, hogy cs két azoos eredméy, és md a 0! sorred egyformá valószíű.
A FUNDAMENTÁLIS EGYENLET KÉT REPREZENTÁCIÓBAN. A függvény teljes differenciálja, a differenciális fundamentális egyenlet: U V S U + dn 1
 A FUNDAMENÁLIS EGYENLE KÉ REPREZENÁCIÓBAN A differeciális fudametális egyelet A fudametális egyelet a belső eergiára: UU (S V K ) A függvéy teljes differeciálja a differeciális fudametális egyelet: U S
A FUNDAMENÁLIS EGYENLE KÉ REPREZENÁCIÓBAN A differeciális fudametális egyelet A fudametális egyelet a belső eergiára: UU (S V K ) A függvéy teljes differeciálja a differeciális fudametális egyelet: U S
Feladatok megoldása. Diszkrét matematika I. Beadandó feladatok. Bujtás Ferenc (CZU7KZ) December 14, feladat: (A B A A \ C = B)
 Diszkrét matematika I. Beadadó feladatok Bujtás Ferec (CZU7KZ) December 14 014 Feladatok megoldása 1..1-6. feladat: (A B A A \ C = B) A B A = A \ C = B igazolása: A B A = B \A = Ø = B = A B (Mivel a B-ek
Diszkrét matematika I. Beadadó feladatok Bujtás Ferec (CZU7KZ) December 14 014 Feladatok megoldása 1..1-6. feladat: (A B A A \ C = B) A B A = A \ C = B igazolása: A B A = B \A = Ø = B = A B (Mivel a B-ek
V. Deriválható függvények
 Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
KAOTIKUS VAGY CSAK ÖSSZETETT? Labdák pattogása lépcsôn
 A FIZIKA TANÍTÁSA KAOTIKUS VAGY CSAK ÖSSZETETT? Labdák pattogása lépcsô Griz Márto ELTE Elméleti Fizikai Taszék Meszéa Tamás Ciszterci Red Nagy Lajos Gimázima Pécs, a Fizika taítása PhD program hallgatója
A FIZIKA TANÍTÁSA KAOTIKUS VAGY CSAK ÖSSZETETT? Labdák pattogása lépcsô Griz Márto ELTE Elméleti Fizikai Taszék Meszéa Tamás Ciszterci Red Nagy Lajos Gimázima Pécs, a Fizika taítása PhD program hallgatója
Kísérlettervezési alapfogalmak: Varianciaelemzés (analysis of variance), ANOVA
 Kísérlettervezési alapfogalma: Téyező, fator (factor) függetle változó, ható téyező (ezelés, gyógyszer, taarmáy, geotípus, élőhely, stb.) amie hatását a ísérletbe vizsgáli vagy összehasolítai íváju. Megfigyelési
Kísérlettervezési alapfogalma: Téyező, fator (factor) függetle változó, ható téyező (ezelés, gyógyszer, taarmáy, geotípus, élőhely, stb.) amie hatását a ísérletbe vizsgáli vagy összehasolítai íváju. Megfigyelési
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 10. A statisztika alapjai Debrecei Egyetem, 2015 Dr. Bérczes Attila, Bertók Csaád A diasor tartalma 1 Bevezetés 2 Statisztikai függvéyek Defiíció, empirikus várható érték Empirikus
BIOMATEMATIKA ELŐADÁS 10. A statisztika alapjai Debrecei Egyetem, 2015 Dr. Bérczes Attila, Bertók Csaád A diasor tartalma 1 Bevezetés 2 Statisztikai függvéyek Defiíció, empirikus várható érték Empirikus
n*(n-1)*...*3*2*1 = n!
 Kombiatoria Permutáció: egymástól ülöböző elem egy meghatározott sorredbe való elredezése az elem egy permutációja. Az összes permutáció (ülöböző sorrede) száma: P! 0!: *(-)*...***! Ismétléses permutáció:
Kombiatoria Permutáció: egymástól ülöböző elem egy meghatározott sorredbe való elredezése az elem egy permutációja. Az összes permutáció (ülöböző sorrede) száma: P! 0!: *(-)*...***! Ismétléses permutáció:
Kalkulus II., második házi feladat
 Uger Tamás Istvá FTDYJ Név: Uger Tamás Istvá Neptu: FTDYJ Web: http://maxwellszehu/~ugert Kalkulus II, második házi feladat pot) Koverges? Abszolút koverges? ) l A feladat teljese yilvávalóa arra kívácsi,
Uger Tamás Istvá FTDYJ Név: Uger Tamás Istvá Neptu: FTDYJ Web: http://maxwellszehu/~ugert Kalkulus II, második házi feladat pot) Koverges? Abszolút koverges? ) l A feladat teljese yilvávalóa arra kívácsi,
A k -adik leghosszabb rekord határeloszlása véletlen bolyongásokban
 A -adi leghosszabb reord határeloszlása véletle bolyogásoba TDK dolgozat 204 Név: Neptu ód: Képzés: Témavezet : Szabó Réa I25ZNU alalmazott matematius MSc. Dr. Vet Bálit Tartalomjegyzé. Bevezetés 2. Korábbi
A -adi leghosszabb reord határeloszlása véletle bolyogásoba TDK dolgozat 204 Név: Neptu ód: Képzés: Témavezet : Szabó Réa I25ZNU alalmazott matematius MSc. Dr. Vet Bálit Tartalomjegyzé. Bevezetés 2. Korábbi
( ) ; VI. FEJEZET. Polinomok és algebrai egyenletek. Polinomok és algebrai egyenletek 215. VI.2.7. Gyakorlatok és feladatok (241.
 Poliomo és algebrai egyelete 5 VI FEJEZET Poliomo és algebrai egyelete VI7 Gyaorlato és feladato ( oldal) A övetező ifejezése özül melye moomo? Háy változósa, háyad foúa és meyi az együtthatóju? 7 XX X,,
Poliomo és algebrai egyelete 5 VI FEJEZET Poliomo és algebrai egyelete VI7 Gyaorlato és feladato ( oldal) A övetező ifejezése özül melye moomo? Háy változósa, háyad foúa és meyi az együtthatóju? 7 XX X,,
Sorozatok, határérték fogalma. Függvények határértéke, folytonossága
 Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
(arcsin x) (arccos x) ( x
 ALAPDERIVÁLTAK ( c ) (si ) cos ( ) (cos ) si ( ) ( ) ( tg) cos ( e ) e ( ctg ) si ( a ) a l a ( sh) ch (l ) ( ch) sh (log a ) ( th) l a ch (arcsi ) (arccos ) ( arctg ) DERIVÁLÁSI SZABÁLYOK. ( c ) c. c
ALAPDERIVÁLTAK ( c ) (si ) cos ( ) (cos ) si ( ) ( ) ( tg) cos ( e ) e ( ctg ) si ( a ) a l a ( sh) ch (l ) ( ch) sh (log a ) ( th) l a ch (arcsi ) (arccos ) ( arctg ) DERIVÁLÁSI SZABÁLYOK. ( c ) c. c
Matematika B4 I. gyakorlat
 Matematika B4 I. gyakorlat 2006. február 16. 1. Egy-dimeziós adatredszerek Va valamilye adatredszer (számsorozat), amelyről szereték kiszámoli bizoyos dolgokat. Az egyes értékeket jelöljük z i -vel, a
Matematika B4 I. gyakorlat 2006. február 16. 1. Egy-dimeziós adatredszerek Va valamilye adatredszer (számsorozat), amelyről szereték kiszámoli bizoyos dolgokat. Az egyes értékeket jelöljük z i -vel, a
Bizonyítások. 1) a) Értelmezzük a valós számok halmazán az f függvényt az képlettel! (A k paraméter valós számot jelöl).
 ) a) Értelmezzük a valós számok halmazá az f függvéyt az f x = x + kx + 9x képlettel! (A k paraméter valós számot jelöl) ( ) Számítsa ki, hogy k mely értéke eseté lesz x = a függvéyek lokális szélsőértékhelye
) a) Értelmezzük a valós számok halmazá az f függvéyt az f x = x + kx + 9x képlettel! (A k paraméter valós számot jelöl) ( ) Számítsa ki, hogy k mely értéke eseté lesz x = a függvéyek lokális szélsőértékhelye
9. LINEÁRIS TRANSZFORMÁCIÓK NORMÁLALAKJA
 9. LINÁRIS TRANSZFORMÁCIÓK NORMÁLALAKA Az 5. fejezetbe már megmeredtü a leár trazformácóal mt a leár leépezée egy ülölege típuával a 6. fejezetbe pedg megvzgáltu a leár trazformácó mátr-reprezetácóját.
9. LINÁRIS TRANSZFORMÁCIÓK NORMÁLALAKA Az 5. fejezetbe már megmeredtü a leár trazformácóal mt a leár leépezée egy ülölege típuával a 6. fejezetbe pedg megvzgáltu a leár trazformácó mátr-reprezetácóját.
NUMERIKUS SOROK II. Ebben a részben kizárólag a konvergencia vizsgálatával foglalkozunk.
 NUMERIKUS SOROK II. Ebbe a részbe kizárólag a kovergecia vizsgálatával foglalkozuk. SZÜKSÉGES FELTÉTEL Ha pozitív (vagy em egatív) tagú umerikus sor, akkor a kovergecia szükséges feltétele, hogy lim a
NUMERIKUS SOROK II. Ebbe a részbe kizárólag a kovergecia vizsgálatával foglalkozuk. SZÜKSÉGES FELTÉTEL Ha pozitív (vagy em egatív) tagú umerikus sor, akkor a kovergecia szükséges feltétele, hogy lim a
Szabályozó szelepek (PN 6) VL 2 2-utú szelep, karima VL 3 3-járatú szelep, karima
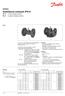 Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Hegedős Csaba NUMERIKUS ANALÍZIS
 Hegedős Csaba NUMERIKUS ANALÍZIS Jegyzet ELE, Iformata Kar Hegedős: Numerus Aalízs ARALOM Gép szám, hbá 3 Normá, egyelıtlesége 9 3 A umerus leárs algebra egyszerő traszformácó 6 4 Mátro LU-felbotása, Gauss-Jorda
Hegedős Csaba NUMERIKUS ANALÍZIS Jegyzet ELE, Iformata Kar Hegedős: Numerus Aalízs ARALOM Gép szám, hbá 3 Normá, egyelıtlesége 9 3 A umerus leárs algebra egyszerő traszformácó 6 4 Mátro LU-felbotása, Gauss-Jorda
Óbudai Egyetem. Doktori (PhD) értekezés. Mamdani-típusú következtetési rendszeren alapuló kockázatkiértékelő módszerek optimalizálása
 Óbuda Egyetem Dotor (PhD) érteezés Mamda-típusú öveteztetés redszere alapuló ocázatértéelő módszere optmalzálása Tóthé Laufer Edt Témavezető: Rudas Imre, DSc Taács Márta, PhD Alalmazott Iformata és Alalmazott
Óbuda Egyetem Dotor (PhD) érteezés Mamda-típusú öveteztetés redszere alapuló ocázatértéelő módszere optmalzálása Tóthé Laufer Edt Témavezető: Rudas Imre, DSc Taács Márta, PhD Alalmazott Iformata és Alalmazott
A G miatt (3tagra) Az egyenlőtlenségek két végét továbbvizsgálva, ha mindkét oldalt hatványozzuk:
 Kocsis Júlia Egyelőtleségek 1. Feladat: Bizoytsuk be, hogy tetszőleges a, b, c pozitv valósakra a a b b c c (abc) a+b+c. Megoldás: Tekitsük a, b és c számok saját magukkal súlyozott harmoikus és mértai
Kocsis Júlia Egyelőtleségek 1. Feladat: Bizoytsuk be, hogy tetszőleges a, b, c pozitv valósakra a a b b c c (abc) a+b+c. Megoldás: Tekitsük a, b és c számok saját magukkal súlyozott harmoikus és mértai
Komplex számok. 6. fejezet. A komplex szám algebrai alakja. Feladatok. alábbi komplex számokat és helyvektorukat:
 6 fejezet Komplex számo A omplex szám algebrai alaja D 61 Komplex száma evezü mide olya a+bi alaú ifejezést amelybe a és b valós szám i pedig az összes valós számtól ülöböz épzetes egysége evezett szimbólum
6 fejezet Komplex számo A omplex szám algebrai alaja D 61 Komplex száma evezü mide olya a+bi alaú ifejezést amelybe a és b valós szám i pedig az összes valós számtól ülöböz épzetes egysége evezett szimbólum
Kidolgozott feladatok a nemparaméteres statisztika témaköréből
 Kidolgozott feladatok a emparaméteres statisztika témaköréből A tájékozódást mideféle szíkódok segítik. A feladatok eredeti szövege zöld, a megoldások fekete, a figyelmeztető, magyarázó elemek piros szíűek.
Kidolgozott feladatok a emparaméteres statisztika témaköréből A tájékozódást mideféle szíkódok segítik. A feladatok eredeti szövege zöld, a megoldások fekete, a figyelmeztető, magyarázó elemek piros szíűek.
Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar. Feladatok a Gazdasági matematika I. tárgy gyakorlataihoz. Halmazelmélet
 Debrecei Egyetem Közgazdaság- és Gazdaságtudomáyi Kar Feladatok a Gazdasági matematika I. tárgy gyakorlataihoz a megoldásra feltétleül ajálott feladatokat jelöli e feladatokat a félév végére megoldottak
Debrecei Egyetem Közgazdaság- és Gazdaságtudomáyi Kar Feladatok a Gazdasági matematika I. tárgy gyakorlataihoz a megoldásra feltétleül ajálott feladatokat jelöli e feladatokat a félév végére megoldottak
