Érdekes geometriai számítások 9.

Átírás

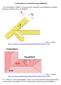
1 1 Érdekes geometriai számítások 9. Folytatjuk a sorozatot. 9. Téma: Szimmetrikus kontytető tetősíkjai lapszögének maghatározásáról Már több dolgozatunk témája volt két metsződő tetősík közbezárt szögének geometriai szóhasználattal: lapszögének meghatározása, szerkesztéssel és / vagy számítással. Hogy újra elővesszük e témát, annak az az oka, hogy találtunk néhány olyan finomságot, ami ezt indokolja. Most ezeket osztjuk meg az érdeklődő Olvasóval. A régi - új téma az internetenn talált [ 1 ] munkában bukkant fel, és erről néhány dolog eszünkbe jutott. A mondott feladat és megoldásának eredetije részben az 1. ábrán látható. ( Az orosz szöveg részletei felnagyítva könnyen olvashatóak és értelmezhetőek. ) 1. ábra [ 1 ]

2 2 A feladat feldolgozásához tekintsük a 2. ábrát is! 2. ábra Itt két sík lapszögének meghatározására emlékeztetünk. A 2. ábrán élből nézett két sík ϕ hajlásszögét úgy határozzuk meg, hogy vesszük a nor - málisaik hajlásszögét. Az S 1 sík n 1 normálvektora a két sík által közrefogott belső ( kék ) térrész, az S 2 sík n 2 normálvektora pedig a külső ( fehér ) térrész felé mutat. Ekkor a két sík ( itt M pontként megjelenő ) metszésvonala mint forgástengely körül az S 1 síkot az S 2 - be ϕ szöggel beforgatva a normálisok is ϕ szöggel fordulnak el, azaz valóban ϕ szöget zárnak be egymással. Ha nem így irányítjuk a normálisokat, hanem például mindkettő a belső térrész felé mutat, akkor a szemlélet alapján ϕ * = 180 ϕ lesz a közbezárt szögük. Az elemi vektoralgebra tanítása szerint [ 2 ] : cos=. ( 1 ) Ha most a 2. ábra jobb oldali részének megfelelően n 2 helyébe ( n 2 ) - t teszünk, akkor ( 1 ) - gyel: cos = = = cos=cos180, ( 2 ) innen ϕ * = 180 ϕ, ( 3 ) egyezésben a szemlélettel. Ezek előrebocsátása után tekintsük a 3. ábrát is! Az ( 1 ) képlet használatához tehát szert kell tennünk a metsződő síkok normálvektoraira. Ezt úgy tesszük, hogy a mondott síkokat kifeszítő két - két vektornak képezzük a vekto - riális szorzatát, úgy, hogy az így előálló normálvektorok megfeleljenek a 2. ábra bal ol - dalán mutatott irányításnak.

3 3 3. ábra A 3. ábrán a φ 1 és φ 2 hajlású tetősíkokból a metszésvonalukra merőleges segédsík által kimetszett ϕ szöget is feltüntettük, a tető jellemző a, b, c, h vonalas adatai mellett. Most alkalmazzuk az ( 1 ) képletet, az itteni jelölésekkel! cos=. ( 4 ) Részfeladat a tetősíkok normálvektorainak előállítása. Ezek a korábban mondottak szerint: =FE FD, ( 5 ) és =FC FD. ( 6 ) Utóbbiakhoz felsoroljuk a tető, mint szimmetrikus éktest csúcspontjainak helyvektorait, az ábrán is jelölt B( xyz ) koordináta - rendszerben, az ( i, j, k ) egységvektorokkal. Ezek: "0,0,0; $%,0,0; &%,',0; (0,',0; )( *,,- Most ezekkel írhatjuk, hogy,h ); /( *,,0-,h ).

4 4 //) =), innen: /) =) / =0, 2,0. ( 7 ) Majd hasonló módon: //& =&, innen: /& =& / =3 *,,- Megint így eljárva: //( =(, innen: /( =( / =3 *,,-, h 4. ( 8 ), h4. ( 9 ) Most a ( 7 ), ( 8 ), ( 9 ) képletek az egységvektorokkal is: /) = 2 5 ; ( 10 ) /& = * 6,- 5 h 7 ; ( 11 ) /( = * 6,- 5 h 7. ( 12 ) Majd ( 5 ), ( 10 ), ( 11 ) - gyel: =FE FD = * 6,- 5 h 7 4= = 2 * 5 6 2, h 5 7= =2 * 7 2,- 82 h 6=2 h 62 * 7 = 2 3h 6* 7 4, tehát: = 2 3h 6 * 7 4. ( 13 ) Hasonlóképpen: ( 6 ), ( 11 ), ( 12 ) - vel: =FC FD =3 * 6,- 5 h 7 4 3* 6,- 5 h 74= = * * 6 6 *,- 6 5* h 6 7,- * 5 6,-,- 5 5,- h 5 7 h * 7 6 h,- 7 5h h 7 7; folytatva: = *,- 6 5* h 6 7,- * 5 6,- h 5 7 h * 7 6 h,- 7 5; továbbá:

5 5 = *,- 7* h 5,- * 7,- h 6 h * 5 h,- 6; ezzel: = 6 3,- h h, * h* h4 7 3,- * *,-4= = 5 % h 7 %,-, tehát: = % 3h 5,- 74. ( 14 ) A normálvektorok abszolút értéke: = =: 2 3h 6 * h 6* 7 4= =:2 3h 6 62 h * 6 7*< = 7 74=:2 3h *< = 4=2 :h *< =, tehát: =2 :h 3 * 4. ( 15 ) Hasonlóképpen: => =:? % 3h 5,- 74@? % 3h 5,- 74@= =:% Ah 5 52 h,- 5 73, B = % :h 3,- 4, tehát: =% :h 3,- 4. ( 16 ) A normálvektorok skaláris szorzata a ( 13 ), ( 14 ) képletekkel : =?2 3h 6 * = % 2 3h 6 5h,- 7 4@? % 3h 5,- 74@= 6 7* h 7 5*, = = % 2 *,- = % 2,- =, tehát: = % 2,- =. ( 17 ) Ezután a ( 4 ), ( 15 ), ( 16 ) és ( 17 ) képletekkel

6 6 cos= = *< CDE - F tehát: cos= H < :G < 03 H < 4< - :G < 03 H < 4< * :G < 03 CDE CDE < :G < 03 CDE < 4 = H < :G < 03 H < 4< CDE <, :G < 03 CDE < 4 < 4. ( 18 ) Ámde a 3. ábra szerint: H < :G < 03 H < 4< =cosi, ( 19 ) és CDE < :G < 03 CDE < 4 =cosi J, ( 20 ) így ( 18 ), ( 19 ) és ( 20 ) szerint eredményként kapjuk, hogy cos= cosi J cosi. ( 21 ) Ez a képlet már ismerős lehet valahonnan. Valóban, egy korábbi dolgozatunkban melynek címe: Érdekes geometriai számítások 5. Egy fontos szögösszefüggés gömbháromszögtani igazolása felírtuk, illetve a szakirodalom felhasználásával bebizonyítottuk, hogy érvényes az alábbi összefüggés: cosk= cosl cosmsinl sinm cos2. ( C1 ) Itt γ jelenti az α és β hajlású (tető - )síkok lapszögét, ha c azon (eresz -)vonalak által bezárt szög, amelyekből a (tető - )síkok indulnak. Megváltoztatva jelöléseinket: K, L I J, M I, 2 Q, ( C2 ) így ( C1 ) és ( C2 ) szerint: cos= cosi J cosi sini J sini cosq. ( C3 ) Ha az ereszvonalak derékszöget zárnak be egymással, mint az itteni feladatban is, akkor Q=90 cosq=0, ( C4 ) így ( C3 ) és ( C4 ) - gyel:

7 7 cos= cosi J cosi. ( C5 ) Örömmel állapítjuk meg a ( 21 ) és ( C5 ) képletek egyezését. Megjegyzések: M1. Jó tudni, hogy a ( C3 ) képlettel nem csak szimmetrikus, hanem tetszőleges tető - kialakítás esetében is ki tudjuk számítani az összemetsződő tetősíkok egymással bezárt szögét. M2. A ( 18 ) képlet alapján belátható, hogy ~ 2<' esetén cos<0, vagyis a lapszög: tompaszög; ~ 2>' esetén cos>0, vagyis a lapszög: hegyesszög; ~ 2=' esetén cos=0, vagyis a lapszög: derékszög. M3. A ( 21 ) képletet a tetősíkok m i ( i: 1, 2 ) meredekségével is felírhatjuk. Az ismert trigonometriai azonossággal, tekintettel az M2. megjegyzésre is: cos=± J >J0VW < X, ( a ) így ( 21 ) és ( a ) szerint: ± J ±J ±J = ; ( b ) >J0VW < X >J0VW < Y Z >J0VW < Y < ( b ) - t négyzetre emelve: J = J J ; ( c ) J0VW < X J0VW < Y Z J0VW < Y < ( c ) - nek reciprokát véve: 1tg =1tg I J 1tg I ; ( d ) ( d ) jobb oldalát kifejtve: 1tg I J 1tg I =1tg I J tg I tg I J tg I ; ( e ) most ( d ) és ( e ) - vel: 1tg =1tg I J tg I tg I J tg I, innen: tg =tg I J tg I tg I J tg I ; ( f )

8 8 ( f ) - ből négyzetgyököt vonva: tg=±>tg I J tg I J tg I J tg I. ( g ) Most el kell dönteni, hogy a gyökjel előtt melyik előjel tartandó meg. Ehhez vegyük figyelembe, hogy ~ mivel 0 <I J, I <90, így 0<2]^I J,cosI <1, ~ ezért 0<2]^I J cosi <1, ~ innen 0> cosi J cosi > 1, ~ így ( 21 ) szerint 1<cos<0 ; ~ eszerint 90 <<180 ; ~ de ekkor tg<0, ~ így ( g ) - ben a negatív előjel veendő. Ezzel: tg= >tg I J tg I J tg I J tg I. ( h ) Most az _ J =tgi J, ( i ) _ =tgi ( j ) jelölésekkel és ( h ) - val: tg= >_ J J _. ( k ) ( k ) - t ( 1 ) - gyel szorozva: tg=>_ J J _. ( l ) Most figyelembe véve, hogy tg=tg =tg180, ( m ) így ( i ) és ( m ) - mel kapjuk, hogy tg180 =>_ J J _, ( n ) ( n ) - ből: 180 =arctg?>_ J J ( o ) majd ( o ) - ból: =180 arctg?>_ J J ( p )

9 9 A ( p ) képlettel közvetlenül számítható a szokásos kialakítású szimmetrikus kontytető tetősíkjainak egymással bezárt szöge, a tetősíkok ( i ) és ( j ) képletekkel adott meredek - sége ismeretében. Számpélda Egy másik korábbi dolgozatunkban melynek címe: Az ötszög keresztmetszetű élszarufa keresztmetszetének kialakításáról található az alábbi ábra - rész: 4. ábra Ezen azt szemléltettük, hogy adott I J,I, Q=90 tetőadatok esetén milyen γ 1 és γ 2 szögek alatt kell levágni az élszarufát, hogy azok pontosan illeszkedjenek a tetősíkokhoz. Az általunk itt keresett szög, valamint az ottani γ 1 és γ 2 szögek közti összefüggés a 4. ábráról is leolvashatóan: =180 γ J γ. ( P1 ) Most ( p ) és ( P1 ) összevetéséből: γ J γ = arctg?>_ J J ( P2 ) Az ottani számpélda adatai: tgi J = c, tgi =1; d = 90. ( P3 ) Az ottani eredmények: K J =17, , K =36, ( P4 ) Ezután ( P2 ) bal oldala, ( P4 ) - gyel is: γ J γ =17, , =53, ( P5 )

10 10 Most ( P2 ) jobb oldala az ( i ), ( j ) és ( P3 ) képletek szerint: arctg?>_ J J c c 14 k=53, ( P6 ) Örömmel jelenthetjük, hogy ( P5 ) és ( P6 ) pontosan ugyanazt az eredményt adja, tehát képleteink jól működnek. Végül a két sík lapszöge ( P1 ) és ( P5 ) - tel: ϕ = 126, M4. A ( 21 ) képletből adódik a =arccos cosi J cosi ( 22 ) képletalak - változat is. M5. Lehet némi félreértés a síkok hajlásszöge és a síkok lapszöge kifejezések haszná - lata során. Ezzel kapcsolatban [ 3 ] - ra utalunk. Eszerint: ~ két sík hajlásszöge nem lehet derékszögnél nagyobb; ebből adódik, hogy a tetősíkok és a vízszintes sík által bezárt hegyesszög valóban hajlásszög; ~ két sík lapszöge esetén meg kell mondani, melyik szögtartományra gondolunk, egyéb - ként a lapszög tetszőleges lehet, ahogyan azt az M2. megjegyzésben taglaltuk is. M6. Ha komolyan vesszük az M5. megjegyzésben foglaltakat, akkor a ( 20 ) képletben szereplő φ 1 szöget nem igazán nevezhetjük hajlásszögnek; hiszen az M2. megjegyzésben éppen a ( 20 ) - ban található ( b c) mennyiség előjelétől tetük függővé cos φ 1, ezzel együtt pedig cosϕ előjelét is. Márpedig M5. szerint a hajlásszög koszinusza nem lehet negatív. Eszerint azt is mondhatjuk, hogy az M5. - ben tett fogalmi korlátozás miatt akár előnyösebb is lehet a ( 18 ), mint a ( 21 ) képlet használata. M7. Az előbb vázolt problémákat áthidalhatjuk, ha egyszerűen csak a síkok közbezárt szögéről beszélünk, legyen az hajlásszög vagy lapszög. Ha szükséges, megemlítjük, hogy az éppen milyen szögtartományba esik. Ez lehet, hogy nem annyira szakszerű szóhaszná - lat, viszont talán nem okoz félreértést. M8. A [ 4 ] munkában a következőt találtuk: Két sík hajlásszögét a következőképpen határozzuk meg: ha a két sík párhuzamos, akkor hajlásszögük 0. Ha nem párhuzamosak, akkor metszésvonaluk egy tetszőleges pontjában

11 11 merőlegest állítunk e metszésvonalra mindkét síkban, s a kapott félegyenesek hajlásszögét mondjuk a két sík hajlásszögének ( 6.8. ábra). 4. ábra. 4. ábra forrása: [ 4 ] Érdekes, hogy itt nem beszélnek lapszögről, csak hajlásszögről. Viszont erről nem kötik ki, korábban sem, hogy nem lehet nagyobb a derékszögnél. Az a gyanúnk, hogy a külön - böző szerzők nem egészen ugyanazt a terminológiát alkalmazzák. Ezért aztán e sorok írójának sem fáj a feje nagyon amiatt, hogy a különféle szög - elnevezéseket egymás szinonimájaként használja. M9. A 3. ábrán a tetősíkok normálisának ábrázolásakor felhasználtuk azt a geometriai tételt, miszerint ha egy egyenes merőleges egy sík két metsző egyenesére, akkor minden egyenesére merőleges, tehát merőleges a síkra. [ 3 ]. E tétel alapján mondhatjuk, hogy a 4. ábrán jelölt szög úgy is előállítható, hogy a két sík metszésvonalára merőleges síkot állítunk, a metszésvonal egy tetszőleges pontjában. E merőleges sík a metsződő síkokból kimetsz egy - egy egyenest, melyek a keresett szöget zárják be. Ugyanis a metsződő két sík metszésvonalára külön - külön állított merőleges egyenesek egy síkot határoznak meg, és mivel ezek az egyenesek külön - külön merőlege - sek a metszésvonalra, akkor az általuk kifeszített sík is merőleges a metszésvonalra. Ezt a tényt felhasználva rajzoltuk meg a 3. ábrán a B ereszsarokból induló élgerinc mint az a és b ereszvonalakból induló, φ 1 és φ 2 hajlású tetősíkok metszésvonala merőleges metszésével adódó ϕ lapszöget. M10. A ( 3 ) képletre vezető számítást azért tettük oda, mert ezzel akartuk szemléltetni azt a körülményt, hogy a dolgozat elvi alapját képező ( 1 ) képlet használata során miért kell

12 12 nagyon ügyelni a metsződő síkok normálisának helyes felvételére. Ellenkező esetben komoly zavarok léphetnek fel az eredmény - képletekben, illetve azok értelmezésében. M11. A ( b ) egyenlet jobb oldalán is kitettük a ± jeleket, arra az esetre, ha mégis úgy döntenénk, hogy a φ 1 és φ 2 szögeket nem korlátozzuk a hajlásszög meghatározásának megfelelően. Az utána következő négyzetre emelés ezeket amúgy is eltüntette, majd pedig a ( g ) egyenletet követő választás során a φ 1 és φ 2 szögeket hajlásszög - nek vettük. A számítás részletezésének tehát nem csak az a haszna, hogy bárki könnyebben követheti, hanem az is, hogy példát ad arra is, hogy ha valaki saját képletet akar kreálni, akkor az előjelekről hogyan hozhat saját döntést. M12. E dolgozat címében a lapszög szó egyes számban szerepel. Valóban, szimmetrikus tető esetében mindegyik lapszög ugyanaz, mert a 3. ábráról leolvashatóan mindig csak φ 1 és φ 2 hajlásszögű tetősíkok metsződhetnek, ugyanazt a ϕ lapszöget eredményezve. M13. Az a tény, hogy az [ 1 ] forrás egyetemi tankönyv ( volt? ), senkit ne riasszon el a téma tanulmányozásától! Sőt! Örüljünk, hogy a kis hazánkban még nem is létező tető - geometriai szakirodalom egy újabb értékes és érdekes fejezettel bővült! Irodalom: [ 1 ] P. Sz. Mogyenov: Analityicseszkaja geometrija Izdatyelsztvo Moszkovszkogo Unyiverszityeta, 1967., sztr [ 2 ] Obádovics J. Gyula: Matematika 15. kiadás, Scolar Kiadó, Budapest, 1998., 537. o. [ 3 ] Reiman István: Matematika Typotex Kiadó, Budapest, 2011., 240. ~ 241. o. [ 4 ] Gerőcs László ~ Vancsó Ödön: Matematika Akadémiai Kiadó, Budapest, 2010., 267. o. Sződliget, június 30. Összeállította: Galgóczi Gyula mérnöktanár