A magától becsukódó ajtó működéséről

Átírás

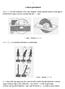
1 1 A magától becsukódó ajtó működéséről Az [ 1 ] műben találtunk egy érdekes feladatot, amit most mi is feldolgozunk. Az 1. ábrán látható az eredeti feladat másolata. A feladat kitűzése 1. ábra forrása: [ 1 ] Adott az 1. a) ábra szerinti kialakítású ajtó, az önműködő csukó - szerkezettel. Ennek lényege, hogy az ajtó C pontjához egy az ajtónyílás feletti P pontban rögzített csigán átvetett kötelet kötöttek, melynek másik végén egy m 0 tömegű nehezék lóg. Ha az ajtót a D pontbeli fogantyú meghúzásával nyitjuk, akkor a feszes kötél iránya megváltozik, és a benne ébredő F C = m 0 g nagyságú erő vízszintes összetevője az ajtót becsukni igyekszik. Amint elengedjük a D fogantyút, ez meg is történik. Az ajtó önsúlya F g = mg nagyságú. Az ajtópántok statikailag határozott kialakításúak, tehát függőleges reakció - összetevő csak az egyik itt az alsó pántban ébred, ahogyan az az 1. b) ábrarészletről leolvasható. A működés közben fellépő gyorsulásoktól eltekintünk, azaz a feladatot statikai problé - maként kezeljük. Eltekintünk a fellépő ellenállásoktól is, mint amilyen a csapsúrlódás, kötélsúrlódás, légellenállás, stb. Továbbá nem vesszük figyelembe a P pontban rögzített csiga r sugarát sem, vagyis az r 0 feltevéssel élünk.

2 2 Ezekkel a megszorításokkal keressük az ajtó lapjára merőleges F D nyitóerő nagysága, valamint a reakcióerő - komponensek kifejezését a φ ajtó - nyitási szög függvényében. A feladat megoldása Az 1. b) ábrán szemlélhető az alkalmazott Oxyz derékszögű koordináta - rendszer ( k. r. ), amelyet úgy vettünk fel, hogy annak xz síkja egyezzen az ajtó síkjával. A tengelyek menti egységvektorok: i, j, k. Az 1. b) ábrán feltüntették az ajtóra működő erőrendszert is, mely - nek egyensúlyát vizsgáljuk. Ehhez a térbeli statikai egyensúlyi feltételi egyenleteket kell alkalmaznunk. Először meghatározzuk az F C erő vektorát. Az 1. b) ábráról: Most az 1. b) és a 2. ábra szerint: ( 1 ) 2. ábra ( 2 ) ( 3 ) most ( 1 ), ( 2 ) és ( 3 ) szerint: ( 4 ) Majd kiszámítjuk a vektor abszolút értékét: ( 5 )

3 3 először a skalár szorzatot képezve: tehát: ( 6 ) Érvényesítve a kiírásban megadott ( 7 ) feltételt, ( 6 ) és ( 7 ) - tel: tehát: ( 8 ) Ezután ( 5 ) és ( 8 ) - cal: ( 9 ) Az F C vektorra fennáll, hogy ( 10 ) most ( 4 ), ( 7 ) és ( 9 ) szerint: ( 11 ) Majd ( 10 ) és ( 11 ) - gyel: ( 12 )

4 4 ahol az 1. ábra kiírása szerint: ( 13 ) A továbbiakban alkalmazzuk az alábbi egyszerűsítő jelölést:, ( 14 ) így ( 12 ) és ( 14 ) - gyel: ( 15 ) Másképpen ( 15 ) így fest: ( 16 ) ( 16 / 1 ) ( 16 / 2 ) ( 16 / 3 ) Az egyensúlyi egyenletek első csoportja: a nyomatéki egyenletek. Ezeket az A ponton átmenő, a k. r. tengelyeivel párhuzamos forgástengelyekre írjuk fel. Ennek során úgy vesszük, hogy minden keresett erő - komponens pozitív értelmű, a megfelelő nyomaték - komponens előjelét tehát a pozitív erőkomponens adott forgástengely körüli, jobbcsavar - szabály szerinti forgatásának forgásértelme szabja meg. Részletezve: ( 17 ) most ( 17 ) és ( 16 / 2 ) szerint: ( 18 ) Folytatva: majd ( 16 / 1 ), ( 16 / 3 ) és ( 18 ) szerint: innen rendezéssel:

5 5 ( 19 / 1 ) ( 19 ) ahol az 1. ábra kiírása szerint: Folytatva: ( 20 ) ( 21 ) ezután ( 16 / 2 ) és ( 21 ) szerint: innen: ( 22 ) majd ( 18 ) és ( 22 ) - vel: tehát: ( 23 / 1 ) Más alakban is felírjuk utóbbit; ( 18 ) és ( 22 ) - vel: tehát: ( 23 / 2 ) egyezésben az [ 1 ] - béli eredménnyel. Az egyensúlyi egyenletek második csoportja: a vetületi egyenletek. Részletezve: ( 24 ) most ( 16 / 1 ), ( 19 ) és ( 24 ) szerint:

6 6 ( 25 ) Folytatva: ( 26 ) Most ( 16 / 2 ), ( 23 / 1 ) és ( 26 ) szerint: ( 27 ) Folytatva: ( 28 ) Most ( 16 / 3 ), ( 23 / 1 ) és ( 26 ) szerint: innen: ( 29 ) Ezzel a közvetlen feladatot megoldottuk. Nem árt azonban még elvégezni az [ 1 ] - ben ajánlott szélsőérték - számítást is, vagyis megkeresni az F D húzóerő - nagyság szélső - értékét, a hozzá tartozó ajtónyitási szöggel együtt. Ez az alábbiak szerinti.

7 7 Először ( 13 ), ( 14 ) és ( 18 ) szerint: ( 30 ) E függvény grafikus megjelenítéséhez felhasználjuk a feladat számszerű adatait is ld.: 1. ábra : m 0 = 15 kg; g = 9,81 m / s 2 ; b = 90 cm = 0,90 m; d = 75 cm = 0,75 m. ( a ) Most ( 30 ) és ( a ) - val: ( b ) A ( b ) függvény ábráját a 3. ábrán mutatjuk meg. 3. ábra A Graph rajzoló szoftver szolgáltatása szerint a szélsőérték helye és nagysága: φ* = 52, , F D,max = 137, N. ( c ) Ezután elvégezzük a szélsőérték - számítást analitikusan is. Ehhez ( 30 ) - ból: Részletezve:

8 8 Ezt a másodfokú egyenletet a megoldó - képlettel megoldva: mivel a cos - függvény értéke nem lehet nagyobb 1 - nél, ezért a megoldást adó φ* szögre fennáll, hogy: innen: ( d ) Ez pontosan megegyezik a ( c1 ) eredménnyel.

9 9 A szélsőérték nagysága ( b ) és ( d ) - vel: ( e ) Ez gyakorlatilag pontosan megegyezik a ( c2 ) eredménnyel. Ezzel az [ 1 ] mű által kitűzött feladatokat elvégeztük. Az itteni eredmények egyeznek az [ 1 ] - ben közöltekkel. Megjegyzések: M1. Feltehető a kérdés, hogy kell - e valamire figyelni az ellensúly m 0 tömegének meg - választásakor. A válasz az, hogy az A ajtópántban ébredő F Az reakció - komponens nem lehet negatív, hiszen akkor annak az ajtót lefelé kellene visszahúznia, hogy le ne essen. Most ( 13 ), ( 14 ), ( 20 ) és ( 29 ) szerint teljesülnie kell az alábbi relációnak: innen: ( 31 ) ( 32 ) minthogy ennek már csukott ajtó φ = 0 esetén is teljesülnie kell, így ( 32 ) - ből: tehát ajánlott, hogy: ( 33 ) M2. A fenti eredményeket a súrlódás megléte befolyásolhatja, kisebb - nagyobb mérték - ben. M3. Találtunk egy sajtóhibát [ 1 ] - ben, a 180. oldalon: az vektorok 3. ko - ordinátájában az a szorzója nem 1, hanem 2.; ehhez ld. itt a ( 2 ) és ( 3 ) képleteket.

10 10 Ez az eredményeket nem módosítja, mert a mondott tagok a kivonás során kiejtik egymást. M4. Az önmagától becsukódó ajtó ilyetén megoldásával mostanság nemigen találkozni, sokkal inkább hidraulikus / pneumatikus csukószerkezeteket lehet az ajtók fölött látni. Ettől azonban még érdekes és tanulságos az itt közreadott feladat. Irodalom: [ 1 ] Hans Heinrich Gloistehn: Lehr - und Übungsbuch der Technischen Mechanik Band 1: Statik, 179 ~ 181. o. Springer Fachmedien Wiesbaden Sződliget, Összeállította: Galgóczi Gyula mérnöktanár