TERMIKUS NEUTRONFLUXUS MEGHATÁROZÁSA AKTIVÁCIÓS MÓDSZERREL
|
|
|
- Imre Kristóf Nagy
- 9 évvel ezelőtt
- Látták:
Átírás
1 TERMIKUS NEUTRONFLUXUS MEGHATÁROZÁSA AKTIVÁCIÓS MÓDSZERREL 1. BEVEZETÉS Neutronsugárzás hatására bizonyos stabil eleekben agátalakulás egy végbe, és a keletkezett radioaktív terék aktivitása egfelelő szálálórendszer segítségével érhető. A keletkező fajlagos aktivitás 1 a besugárzás helyén uralkodó neutronfluxustól és a besugárzott anyag aktivációs hatáskeresztetszetétől függ. A érés célja a neutronfluxus eghatározása. Szigorúan véve azonban nincs olyan ódszer, aely lehetővé tenné a neutronfluxus közvetlen érését. Legfeljebb arról lehet szó, hogy a neutronfluxusra a ért fajlagos aktivitásból valailyen feltevések ellett többé-kevésbé pontos becslést adjunk. Ailyen pontosan iserjük az aktivációs hatáskeresztetszetet, olyan pontosan tudjuk a neutronfluxust eghatározni. Minthogy száos olyan anyag van, elyeknek aktivációs hatáskeresztetszete ás-ás ódon függ a neutronenergiától, ezzel a ódszerrel a neutronok energia szerinti eloszlásáról is nyerhetünk néi inforációt. A jelen érés keretében aktivációs detektorok felhasználásával fogjuk a terikus neutronfluxus értékét közelítőleg eghatározni a BME oktatóreaktorának aktív zónájában. A érés két részből áll: a terikus neutronfluxus abszolút értékének becslése és helyfüggésének vizsgálata. A érés elvének egértéséhez előbb a reaktorelélet száos tételét kell egisernünk. 2. ELMÉLETI ÖSSZEFOGLALÁS 2.1. Neutronspektru, neutronfluxus eloszlása terikus reaktorokban Maghasadásban gyors neutronok keletkeznek, energia-eloszlásuk az 1. ábrán látható. Terikus reaktorokban a gyors neutronok - elsősorban a oderátor atoagjaival való ütközések révén - fokozatosan lelassulnak, és a 2. ábrán seatikusan beutatott neutronspektru alakul ki. Legyen az E és E+dE közé eső energiájú neutronok sűrűsége a reaktor r pontjának közelében n(r,e)de. Ennek felhasználásával a neutronfluxus definíciója: (, ) vnre (, ) Φ re =, (1) 1 A besugárzott anyag egy atojára (vagy töegegységére) vonatkoztatott aktivitás.
2 2 ahol v az E energiájú neutron sebessége. A neutronspektrunak érésünk szepontjából legfontosabb része a terikus spektru, aely jó közelítéssel a Maxwell-eloszlással írható le: (, ) Φ re = E E ( kt) exp 2 kt, E E th (2) ahol E th a terikus tartoány - többé-kevésbé önkényesen egválasztott - felső határa (általában 0,625 ev), k a Boltzann-állandó és T a terikus neutronspektruot jellező, hőérséklet dienziójú ennyiség. 2 Hasadási spektru spektru (önkényes egység) E (MeV) 1. ábra. A hasadási neutronok energiaspektrua 2 Általában neutronhőérsékletnek szoktuk nevezni, aely néileg agasabb, int a reaktor abszolút hőérséklete.
3 3 reaktorspektru 10 terikus neutronok (Maxwell spektru) neutronfluxus (önkényes egység /E spektru hasadási neutronok rezonanciák hatása E E E E E E E E E E E+01 E (MeV) 2. ábra. Terikus reaktor energiaspektrua (vázlatosan) Aikor terikus neutronfluxusról beszélünk, ezen az alábbi integrált értjük: aelyet gyakran a Φ th Φ th Eth () r = Φ(, ) 0 () r v.n () r th r E de, (3) =, (3a) alakban írunk fel, ahol n th a terikus neutronoknak az r helyvektorú pont körüli sűrűsége és v a terikus neutronok átlagos sebessége (lásd alább).
4 4 z a' c' y x b' 3.ábra.Téglatestalakú,csupasz,reflektornélkülireaktorzóna vázlata. Az origó a téglatestszi etriaközéppontjában van. A terikus neutronfluxus térbeli változása függ a reaktor alakjától és belső felépítésétől. Téglatest alakú, csupasz (reflektor nélküli) reaktorban (3. ábra) a terikus neutronfluxus térbeli eloszlását a reaktorelélet szerint az alábbi összefüggés adja eg: Φ th ( x, y, z ) = Φ ( ) th πx πy π 0,0,0 cos cos cos a b z c (2) ahol a, b és c rendre az aktív zónának a tényleges a, b és c fizikai éretekhez képest az ún. extrapolációs távolsággal egnövelt éretei. 3 Ha tehát a terikus neutronfluxust valaely x = x 0, y = y 0 helyen a z függvényében tekintjük, a πz Φth( x0, y0, z) = Φ0cos = Φ0ϕ () z (3) c eloszlást kapjuk. Ez a cos-alakú axiális eloszlás egyébként érvényes henger alakú reaktor esetében is, ha a henger tengelye egybeesik a koordinátarendszer z tengelyével. A reaktorok többsége azonban ne csupasz, hane az aktív zónát ún. reflektor veszi körül, aely az aktív zónából kiszökő neutronokat részben visszaszórja. 4 A kiszökő neutronok többsége a terikusnál nagyobb energiájú, ún. epiterikus neutron, aelyek a reflektorban terikus energiára lelassulnak. Mivel az ilyen energiájú neutronok szabad úthossza kisebb, int az epiterikus neutronoké, a terikus neutronfluxusnak a reflektorban helyi axiua alakul ki. Ezt a jelenséget reflektorpúpnak nevezzük, aely víz 3 A reaktorelélet alapjául szolgáló diffúzióegyenlet határfeltételei szerint a reaktor tényleges felületét az extrapolációs távolsággal kijjebb tolva kapott felületen (az ún. extrapolált határfelületen) kell egkövetelni a fluxus eltűnését. Az extrapolációs távolság értéke vízzel oderált reaktorokban néhány. Mérésünk szepontjából nincs jelentősége. 4 Innen ered a reflektor neve.
5 5 reflektor esetében indig kialakul, viszont grafit reflektor esetében általában ne. A 4. ábrán összehasonlítjuk a terikus neutronfluxusnak csupasz és reflektált reaktorban a z tengely entén kialakuló eloszlását. ter ikus neutronfluxus reflektált reaktorban neutro n fluxus ter ikus neutronfluxus csupasz reaktorban re flektor aktív zóna re flektor z 4.ábra.Ter ikus neutronfluxus eloszlása egy csupasz és egy reflektáltreaktorz koordinátája entén Mivel a reflektor lecsökkenti az aktív zónából kiszökő neutronok száát, a reflektált reaktor kritikus töege kisebb, int az azonos összetételű csupasz reaktoré. A különbséget a reflektor-egtakarítással vesszük figyelebe, aelyet a következőképpen definiáljuk. A reflektált reaktor aktív zónájában a reflektortól bizonyos távolságban ugyanolyan alakú térbeli eloszlás alakul ki, int csupasz reaktorban. Az aktív zónának ezt a részét asziptotikus tartoánynak nevezzük. Téglatest alakú aktív zónában ezt az eloszlást tehát szintén a (2) képlet adja eg, de ost az a, b és c ennyiségek a tényleges a, b és c éreteknél lényegesen nagyobbak. A különbséget nevezzük reflektor-egtakarításnak. Például, a z irányban vett reflektor-egtakarítást a 2λ z = c c (4) képlettel definiáljuk. (Az x és y irányú reflektor-egtakarítás definíciója hasonló.) Mindezt az 5. ábrán illusztrájuk. Az aktív zóna belsejében kialakuló cos-eloszlást a reflektorban folytatva, a kapott fluxus az aktív zónán kívül, a reflektor belsejében válik zérussá. Ennek a pontnak az aktív zóna határától ért távolsága a reflektor-egtakarítás. Értéke a szokásos víz oderátoros és víz reflektoros reaktorokban 7 9 c. 5 5 A reflektor-egtakarítást ne szabad összetéveszteni az extrapolációs távolsággal, hiszen az utóbbi a csupasz reaktornak a vákuual határos felületén, az utóbbi pedig az aktív zónának a reflektorral határos felületén van definiálva. Értékük is jelentősen eltér: a reflektor-egtakarítás sokkal nagyobb, int az extrapolációs távolság.
6 6 ter ikus neutro n fluxus ter ikus neutronfluxus reflektált reaktorban c/2 c'/2 re flektor λ z aktív zóna λ z re flektor z 5.ábra.A reflektor- egtakarítás eghatározása 2.2. Makroszkópikus eloszlás érése aktivációs ódszerrel A érés elve Ha egy aktivációs detektort az r helyen besugározunk, akkor abban az időegység alatt felaktiválódott atook száát, a reakciósebességet az () = ( ) σ ( ) Rr Nd Φ re, d EdE 0 (5) integrál fejezi ki, ahol σ d (E) a detektoranyag ikroszkopikus aktivációs hatáskeresztetszete 6, és N d a detektorban levő aktiválható atoagok teljes száa. A gyakorlatban csak (5) szerinti reakciósebességeket lehet érni, de a fluxust agát ne. Bizonyos feltételezésekkel azonban a ért reakciósebességekből következtethetünk a fluxusra is. Ennek érdekében definiáljuk az átlagos aktivációs hatáskeresztetszetet: σ d = Φ 0 ( re, ) σ ( ) Φ 0 d (, ) rede EdE. (6) Ez a ennyiség szigorúan véve függ attól az r helytől, ahol a besugárzás történik, hiszen a Φ(r,E) spektru is változhat helyről helyre. A reaktorelélet szerint azonban az asziptotikus tartoányban ez a függés elhanyagolható. Ilyen érteleben beszélhetünk átlagos aktivációs hatáskeresztetszetről, és hagyhatjuk el a helyfüggés feltüntetését. 6 Az aktivációs hatáskeresztetszet általában a befogási hatáskeresztetszet. Vannak azonban eltérések is. Aikor például a detektor hasadóanyag, és a hasadási terékek összaktivitását érjük, az aktivációs hatáskeresztetszet a hasadási hatáskeresztetszettel azonos.
7 7 Vannak detektorok, aelyek hatáskeresztetszete csak a terikus neutronokra száottevő, ezért ezeket terikus detektoroknak nevezzük. Egy ilyen detektorra érvényes, hogy () () Rr =Φ r σ N, (7) th d d ahol Φ th a terikus neutronfluxus (vö. (3) egyenletek). A besugárzás során az aktív agok N(r,t) száának időbeli változását a keletkezés és a bolás különbsége adja eg: (, ) dn r t dt () r N N( r, t) = Φ σ λ, (8) th d d ahol λ a keletkezett aktív agok bolási állandója, t pedig az aktiválás kezdete óta eltelt idő. A besugárzás kezdetén a besugárzandó anyag általában inaktív, tehát N(0) = 0. Ekkor a fenti differenciálegyenlet egoldása (7) figyelebevételével: N ( rt) () r R, = ( 1 exp( λ t) ). (9) λ Ha az aktiválás elég sokáig tart, az aktív agok száa eléri az R(r)/λ telítési értéket. Ha azonban a besugárzás egy véges t a ideig tart, az aktivitás a telítési értéknél kisebb: ( a ) ( ) () ( λ ) λnrt, = Rr 1 exp t. a A besugárzás befejezése utáni eltelik t idő, aíg az aktivitást egérjük. Ez alatt a érhető aktivitás exponenciálisan csökken: ( a ) ( ) ( ) () ( ) Art, = Rr 1 exp λt exp λ t. (10) Ezek az összefüggések ég ne veszik figyelebe, hogy a vizsgált anyag egyes atojait ne ugyanazzal a neutronfluxussal sugározzuk be. Ha a besugárzott inta forája a szokás szerinti fólia, aelynek a vastagsága ne elhanyagolható, akkor belsejében bekövetkező neutronabszorpció iatt az átlagos neutronfluxus ( Φ th ) kisebb, int a fólia felszínen uralkodó fluxus ( Φ o th ). Ezt az effektust nevezzük önárnyékolásnak. A (7) és (8) o képletekben szereplő fluxusnak Φ th felel eg. Tekintve, hogy a ért aktivitás alapján erre az utóbbira kívánunk következtetni, az önárnyékolást a G = Φ Φth th o
8 8 önárnyékolási tényezővel vesszük figyelebe. Ha a detektor vastagsága d, akroszkopikus totális hatáskeresztetszete Σ t, akkor izotróp neutronfluxus-eloszlás esetén a reaktorelélet szerint G a következő forulával közelíthető: ( d ) 1 G = 2E 3 Σ d Σ ahol E 3 a haradrendű exponenciális-integrál függvény. t t, (11) Végül fentiek összevonásával a detektor aktivitásának időfüggvénye: ( ) ( ) O ( ) ( ) ( ) Art, = G Φ rt, σ N 1 exp λt exp λt. (12) th d d a A terikus neutronfluxus becslése a besugárzott detektor aktivitásának iseretében A terikus neutronfluxusnak az energiától való függését a (2) alatti függvény adja eg, aely E = kt-nél veszi fel a axiuát. (Elékeztetőül egjegyezzük, hogy T a neutronhőérséklet (vö. (2) képlet).) Ez a függvény az alábbi egyszerű kapcsolatban van a terikus neutronok sebességeloszlásával: ( ) ( ) vn v dv =Φ E de, E = 2 v 2, ahol a neutron töege. Az így kapott sebességeloszlás szerinti legvalószínűbb sebesség: kt vo = 2, (13a) aint könnyen levezethetjük. Vegyük észre, hogy ez éppen az E = kt energiának egfelelő sebesség. Az átlagos sebesség azonban ettől eltér: v = 2 v o π.. (13b) Szobahőérsékleten (T = 293 K) v 0 = 2200 /s, aely az E = 0,0253 ev energiának felel eg. Terikus detektorok esetében az átlagos aktivációs hatáskeresztetszet (6) szerinti képletébe a terikus spektruot kell írni. Ez egyszerű eredényre vezet az ún. 1/v hatás-keresztetszetű detektoranyagok esetében. Ekkor ugyanis (6) így írható:
9 9 σ d C Φ( re, ) v de = 0 = Φ 0 (, ) rede (, ) C n r E de 0 (, ) vn r E de 0 = C v, (14) ahol C = v 0 σ(v 0 ) állandó. A (14) képletben kihasználtuk, hogy Φ(r,E) = vn(r,e). Ha a v 0 = 2200 /s-hoz tartozó hatáskeresztetszetet σ 0 = v 0 σ(v 0 ) -val jelöljük, a (13) képletek alapján beláthatjuk, hogy σ ( ) d T π 293 K = σ 0 2 T. (15) A besugárzott intában levő atoagok N d száának száítása: N d = M α L A d (16) ahol M - a inta töege (g), α - a detektoranyag aktiválódó izotópjának előfordulási gyakorisága, A d - az aktiválódó izotóp töegszáa, L = 6, (Loschidt szá). Az eddigi képletek egadják a (12) egyenletben szereplő inden ennyiség értékét, tehát a terikus neutronfluxust a ért A(r,t) aktivitás alapján ki tudjuk száítani, ha iserjük a terikus neutronspektruot jellező T hőérsékletet, a detektor σ 0 és σ t hatáskeresztetszeteit, továbbá jogos az a feltételezés, hogy a detektor csak a terikus neutronok hatására aktiválódik. Ha a detektor besugárzása olyan helyen történik, ahol jelentős epiterikus fluxus is jelen van, és/vagy a detektor epiterikus aktivációs hatáskeresztetszete a terikus aktivációs hatáskeresztetszet ellett jelentős, akkor a nyert aktivitás egy részéért az epiterikus neutronok felelősek. Eiatt egy korrekcióval eg kell határozni, hogy a létrehozott aktivitásnak ekkora része szárazik a terikus neutronfluxustól. Erre az ad lehetőséget, hogy a kadiu neutronabszorpciós hatáskeresztetszete terikus energiákon igen nagy (6. ábra), az epiterikus tartoányban pedig elhanyagolható. Ha tehát a detektort egfelelő vastagságú kadiual borítva sugározzuk be, akkor a burkolat a terikus neutronokat gyakorlatilag teljesen kiszűri, így a detektor aktivitása csak a 0,4 0,7 ev 7 feletti epiterikus neutronoktól szárazik. Két azonos detektort alkalazva, az egyiket csupaszon, ásikat kadiu burkolatban (azonos körülények között) besugározva, a terikus aktivitás egyszerűen nyerhető: Ath = Acs ACd (17) 7 Ez az ún. kadiu-levágási energia: a kadiu hatáskeresztetszetét ez alatti neutronenergiákra gyakorlatilag végtelennek, a felettiekre pedig nullának vesszük. Nyilvánvaló, hogy a levágási energia függ a kadiuborítás vastagságától.
10 10 ahol A cs - a csupasz detektor aktivitása, A Cd - a kadiu burkolatú detektor aktivitása. Végeredényben a következő képletet használjuk a terikus fluxus becslésére: () r (, ) (, ) 1 exp( ) A r t A r t vn σ G λt λt Φ cs Cd th = d d a ( ) exp( ), (18) ahol a nevezőben szereplő ennyiségeket rendre a (13), (16), (6) és (11) képletek alapján száítjuk ki. 1/v hatás-keresztetszetű anyag esetében ez a képlet (14) alapján egyszerűdik, hiszen ekkor v σ = 2200 s σ0, d vagyis nincs szükség a T neutronhőérséklet iseretére. A terikus neutronfluxus becslésére ezért előnyös az 1/v hatás-keresztetszetű detektoranyagok használata. 1.00E E+04 (n,γ ) hatáskeresztetszet (barn) 1.00E E E E+00 Dy-164 Cd-113 Au E E E E E E E E+03 E (ev) 6. ábra. σ c változása a neutronenergia függvényében 164 Dy, 197 Au és 113 Cd esetében A 6. ábra szerint ilyen anyag a diszpróziu 164 Dy izotópja, aelynek a befogási hatáskeresztetszete 1 ev-ig gyakorlatilag 1/v-nek tekinthető. 8 Aktiválódást követően ebben a következő reakciók játszódnak le: ( n, γ) 165 β ( 13, perc) 165 β ( 235, óra) Dy Dy Dy Ho. 8 1 ev felett a hatáskeresztetszet gyorsan csökken, 100 ev környékén pedig rezonanciái is vannak, de ez a teljes aktiválódásnak csak néhány százalékát teszi ki. Mindenesetre elegendő ahhoz, hogy a kadiu segítségével ért korrekciót figyelebe kelljen venni.
11 11 A gyakorlatban az utolsó, 2,35 órás felezési idejű bolásból szárazó β-részecskéket szoktuk egszálálni. Ennek a érésnek egvan az a hátránya, hogy általában ne isert a száláló-berendezés hatásfoka, így gyakorlatilag ne tudjuk eghatározni az A(r,t) aktivitás abszolút értékét. Erre való tekintettel a diszpróziual való érés csak relatív inforációt szolgáltat: a neutronfluxus abszolút értékét ne, legfeljebb csak térfüggésének az alakját tudjuk eghatározni. A terikus neutronfluxus abszolút értékének a eghatározása az arany aktiválása révén lehetséges. A 197 Au izotóp befogási hatáskeresztetszete szintén a 6. ábrán látható. Neutronokkal való besugárzás hatására az aranyban az alábbi reakciósor játszódik le: ( n, γ) 198 β, γ ( 64, 68 óra) Au Au Hg A 64,68 órás felezési idejű bolásban egyidejűleg keletkező β és γ részecskék külön-külön is, koincidencia szálálóban is egszálálhatók. Ennek révén az arany abszolút aktivitása eghatározható. Az 197 Au aktivációs hatáskeresztetszete a terikus neutronenergiák tartoányában közelítőleg az 1/v törvényt követi, a rezonanciatartoányban azonban száos rezonanciacsúcsa van (6. ábra). A legnagyobb rezonancia 4,47 ev-nál lép fel, ahol σ c = 9890 barn. Ezért a (17) szerinti kadiukorrekciónak itt nagy szerepe van A terikus neutronfluxus térfüggésének eghatározása A diszpróziu detektor aktivitása a fentiek szerint a terikus neutronfluxussal arányos, ezért az aktivitás érése során nyert beütésszáok közvetlenül felhasználhatók a terikus neutronfluxus térbeli eloszlásának a kísérleti eghatározásához. Ha a reaktor különböző r pontjaiban besugárzott detektorok különbözők (ás a térfogatuk, töegük stb.), ezt kalibrációs tényezőkkel kell figyelebe venni. Erre nincs szükség, ha aktiválandó intaként huzalt használunk, és a huzal egyes szakaszainak az aktivitását külön egérjük. 9 A érés folyaán azonban a inta aktivitása folyaatosan csökken, ait a érésnél kopenzálni kell, vagy a kiértékelés során boláskorrekciót kell alkalazni. A gyakorlat során az első egoldást alkalazzuk. A detektor aktivitása az egyes érések kezdeti időpontjában a (12) forula szerint írható. Abban az esetben, aikor a inta aktivitása ne nagy a érőberendezés holtidejéhez képest, a érőberendezés által szolgáltatott I(t) szálálási sebesség (intenzitás) arányos a inta aktivitásával: () Art ( ) It =η,, (19) ahol η - szálálóberendezés hatásfoka. A érés folyaán ne ezt az intenzitást, hane valaely véges t érési idő alatti összes beütésszáot lehet egkapni: 9 Hallgatólagosan feltételezzük, hogy a huzal átérője, Dy-tartala stb. a huzal entén végig azonos.
12 12 t+ t ( ) ( ) Brt, = It dt. t Tekintve, hogy a szálásái sebesség a érés közben csökken, ezt így írhatjuk: t+ t (, ) (, ) Brt = ηart e dt = t λt λt (, ) ( 1 e ) ηart (, ) ηart λ t, (20) ahol a közelítő egyenlőség arra a (gyakori) esetre vonatkozik, aikor a érési idő a boláshoz képest rövid, vagyis, aikor λt << 1. A érés során kapott beütésszáok a (12) és (20) forulák összevonás a révén hozhatók kapcsolatba a terikus neutronfluxussal: (, ) = Φ ( rt, ) Brt th λta ( 1 ) GσdNd e λ e λt λt ( e ) 1 (21) A kapcsos zárójelben szereplő kifejezés a huzal inden pontjára azonos. A beütésszáok akkor lesznek a terikus neutronfluxussal arányosak, ha az λt ( ) ( 1 ) Ft, t = e e λt (22a) függvény értéke ne függ t-től. Ezt egy ún. onitorfólia alkalazásával érhetjük el, aely biztosítja, hogy a t érési idő t-vel éppen a szükséges értékben nőjön. A onitorfóliát a huzallal együtt aktiváljuk fel, és aktivitását egy külön szálálóval, a preszet szálálóval érjük. A érőberendezés úgy van beállítva, hogy a huzal kiválasztott részének az aktivitását olyan t ideig érjük, aely alatt a onitorszálálóban egy előre beállított K beütésszá gyűlt össze. Eszerint a érési idő kielégíti az t+ t t t ( ) A e dt = A e 1 e = K (22b) λt λt λ egyenletet, ahol A valailyen, a onitorfólia aktivitását jellező állandó. Látható, hogy ezen a ódon valóban teljesül pontosan teljesül a (22a) alatti kifejezés állandósága. 10 A ódszer alkalazhatóságának fontos feltétele, hogy ind a holtidő, ind a hattér hatása elhanyagolható legyen. 3. A érési feladat 10 Könnyű belátni, hogy a ódszer akkor is alkalazható, ha a ért aktivitás ne egyetlen radioaktív izotóptól szárazik. Ennek feltétele viszont, hogy a onitor és a huzal szigorúan azonos anyagból álljon.
13 13 A gyakorlat során az aktív zóna E6 pozíciójában, függőleges egyenes entén határozzuk eg a terikus neutronfluxus relatív eloszlását az előzőekben leírt ódszerrel, ajd ennek iseretében a függőleges irányú reflektor-egtakarítást. A éréshez 10% Dy-ot tartalazó, Dy-Al ötvözetből készült huzalt használunk. A terikus neutronfluxus abszolút értékét Au fólia felaktiválása révén határozzuk eg. 7. ábra. Az aktív zóna keresztetszete a - autoata szabályzórúd; b 1, b 2 - biztonságvédeli rudak; c - gyors csőposta; d - terikus csőposták; e - függőleges besugárzó csatornák vízben; f - fűtőele-kazetták; g - grafit reflektoreleek; h - függőleges besugárzó csatornák grafitban; i - függőleges besugárzó csatorna fűtőele-kazettában; j - neutron-forrás; k - kézi szabályzórúd. 4. A éréshez szükséges eszközök, anyagok
14 14 A érés elvégzéséhez a reaktoron és a radioaktív inták kezeléséhez, éréséhez szükséges eszközökön kívül szükség van a huzalaktivitás-érő berendezésre is. Mivel ez egyedi célűszer, űködését részletesen isertetjük A éréshez szükséges eszközök, anyagok listája - reaktor + intaszállító csőposta berendezés; - plexi tartórúd a huzal száára; - szcintillációs detektor és ipulzusszáláló berendezés; - huzalaktivitásérő berendezés; - Dy-Al ötvözetből készült huzal; - Dy-Al ötvözetből készült fólia; - Au fóliák; - Al és Cd kapszulák a fóliák száára; - etalon sugárforrás ( 90 Sr- 90 Y); - sugárvédeli felszerelés (guikesztyű, csipesz stb.) A huzalaktivitás érésének elve és a érőberendezés leírása A terikus neutronfluxus térbeli eloszlásának eghatározására Dy-Al ötvözetből készült huzalt használunk. A huzal hossza entén a helyfüggő aktivitást a huzalaktivitásérő berendezéssel határozzuk eg. Mivel a huzal a z axiális koordináta entén helyezkedik el, a (21)-ben szereplő B(r,t) helyett ost B(z,t)-t írunk. A érőberendezés blokkséája a 8.ábrán látható. Működésének elve a következő. A berendezés két érőláncot tartalaz. Az effektust érő lánc (E) a érendő huzalnak a szcintillációs kristály által látott részéből érkező beütéseket (B) regisztrálja. Az időkijelző érőlánc (I) a huzallal azonos anyagból készült, és azzal egyidejűleg felaktivált fólia aktivitásával arányos beütésszáot éri. Ez a lánc preszet-szálálóban végződik, aely az előre beállított K száú ipulzus beérkezte után leállítja az effektust érő E lánc szálálóját, és egyidejűleg jelt ad arra, hogy a berendezés a érőhuzalt a beállított előtolás szerint továbbléptesse. A berendezésen 1 10 előtolás állítható. Az ipulzusszálálás és a berendezés vezérlése PC segítségével történik. 5. A érés enete 5.1. A terikus neutronfluxus relatív eloszlásának érése Az előkészületek során a érőhuzalt a plexi besugárzó tartórúd vájatába helyezzük. A plexi oderációs tulajdonságai hasonlítanak a vízéhez, így az aktív zóna fluxuseloszlásának zavarása csekély.
15 15 A besugárzó rudat az operátor az álló reaktor E6 (D5-el szoszédos) pozíciójába helyezi, ajd elvégzi a besugárzást. A besugárzás közben a D5 pozicióban lévő csőpostában a onitorfóliát is felaktiváljuk. Tekintettel arra, hogy Dy-Al ötvözettel dolgozunk, az Al zavaró aktivitásának lecsengése érdekében a besugárzás után a intákat legaléább 20 percig pihentetni kell. (Az aluíniu felezési ideje 2,24 perc.) Ezután a huzalt a tartórúdból kivesszük, és a huzalaktivitás-érő berendezés tartósínjébe helyezzük. A onitorfóliát az időkijelelő lánc detektora alatt helyezzük el. A K preszet beütésszáot az alábbi hibaszáítási egfontolások alapján egválasztva elindítjuk a érést. A érőberendezés unkapontjának beállításához szükséges adatok a éréshez ellékelt adatlapon találhatók. A érés során a 165 Dy bolásából szárazó β - részeket detektáljuk. E D y-a lhuzal S zcintillációs szá láló I Erõsítõ Nagyfesz. tápegység Ólo torony Dy-Alfólia Erõsítõ Nagyfesz. tápegység Diszkri i- nátor PC Diszkri i- nátor Szá láló P reszet szá láló Huzalvezérlés 8.ábra.H uzalaktivitás- érõ berendezés blokkvázlata 5.2. A terikus neutronfluxus abszolút értékének eghatározása Két azonos éretű és töegű arany fóliát sugárzunk be - egy csupaszt és egy kadiuos borításút - a reaktor D5 pozíciójában elhelyezkedő besugárzó csatornában. A polietilén besugárzó tokba zárt fóliákat a besugárzó csatornához csatlakozó intaszállító csőposta rendszer segítségével juttatjuk az üzeelő reaktorba. A besugárzás befejezésének időpontját jegyezzük fel, és érjük eg az egyes fóliák aktivitásának éréséig eltelt t időt. A szcintillációs szálálóberendezés segítségével egérjük a inták aktivitását. A felaktivált Au fólia β - boló, ezért aktivitását plasztik foszforral ellátott szcintillációs szálálóberendezés segítségével érjük. A szálálóberendezés β - szálálási hatásfokát (η) és a unkapontjának beállításához szükséges adatokat a éréshez ellékeljük. Mérés előtt győződjünk eg a berendezés helyes beállításáról: érjük eg egy hosszú felezési idejű etalon-preparátu beütésszáát ( 90 Sr- 90 Y, T 1/2 = 28,5 év), és hasonlítsuk össze a
16 16 egadott referencia értékekkel. Ha szükséges, korrigáljuk a hatásfokot. Mérjük eg a hátteret is, és értékét vegyük korrekcióba a fóliák beütésszáának kiértékelésénél. A (18) képletben szereplő aktivitásokat a részben írtak alapján a H háttér levonása és az η hatásfokkal való osztás után kapjuk eg: A cs = B H ηt cs cs és A Cd = B Cd H ηt Cd (23) a csupasz ( cs index), illetve a kadiuborítású ( Cd index) fóliára. Ha a t érési idő különbözik a két fóliára, ezek a képletek érteleszerűen ódosulnak. 6. A érések kiértékelése 6.1. A terikus neutronfluxus relatív eloszlásának kiértékelése A érési időt a (22b) egyenlet szerint beállítva a ért B B( z ) i = beütésszáok helyfüggése a terikus neutronfluxus-eloszlás helyfüggésével arányos (vö. (22a)). Ábrázoljuk a érési pontokat grafikusan, ajd a ért görbe középső szakaszára (3) képlet szerinti koszinusz függvényt illesztve, határozzuk eg az axiális reflektoregtakarítást a (4) képlet alapján! 11 i A relatív fluxusérés hibaszáítása A valószínűség-eléletből tudjuk, hogy a beütésszáok a Poisson-eloszlást követik. Ebből következik, hogy az egyes beütésszáok szórásnégyzete egegyezik a várható értékükkel. Az utóbbiakat agukkal a beütésszáokkal közelítjük, tehát általában igaz, hogy 2 ( ) ( ) D B = M B B. (24) i i i Ez a képlet akkor lenne alkalazható, ha a t érési idő állandó lenne. Esetünkben azonban t valószínűségi változó (vö. (22b)), ai az előbbi képlethez képest egnöveli a szórást. Meg lehet utatni [3], hogy 2 Bi D ( Bi) Bi 1 +, (25) K ahol K a preszet szálálón beállított érték. 11 Erre a feladatra általában egfelelő illesztő prograra van szükség (lásd pl. [3]).
17 17 Ez a közelítő képlet ugyanazzal a feltétellel érvényes, int aga az egész érési ódszer: ind a holtidő, ind a hattér hatása elhanyagolható. A holtidő hatásának az elhanyagolásához az szükséges, hogy indegyik beütésszára érvényes legyen, hogy B i τ/t elegendően kicsi legyen (0,01 vagy kisebb). Végül célszerű ügyelni arra, hogy a K preszet beütésszá indegyik B i -nél lényegesen nagyobb legyen. Ellenkező esetben ugyanis (25) szerint túlságosan egnő a B i beütésszánok szórása A terikus neutronfluxus abszolút értékének hibaszáítása A terikus neutronfluxus abszolút értékének a hibaszáítása lényegesen bonyolultabb feladat, int a relatív eloszlásé. Mindenekelőtt két fajta hibát kell egkülönböztetnünk: statisztikus és sziszteatikus hiba. 12 Statisztikus hiba becslése A (23)-ban felírt aktivitások relatív szórásnégyzetét az alábbi képletek alapján becsüljük: D 2 ( A ) cs = ( B H ) D ( η) D ( B H ) ( B H ) ( η) cs η cs 22 t cs η η t η t cs cs cs 22 D Bcs + H η η t cs, hiszen a beütésszáok Poisson-eloszlásúak. Megjegyezzük, hogy a t érési idő szórása általában elhanyagolható. A kadiuborítású fóliára vonatkozó képlet analóg. A (18) képletben a két fajta fólia aktivitásának a különbsége szerepel. Ennek szórásnégyzete: ( η) 2 2 D B + H + B + H D ( Acs ACd) ( Acs ACd) η η t 2 cs cs Cd Cd. (26) Az h hatásfok szórását csak egyszer kell figyelebe venni, ivel indkét fajta fóliára azonos. N d kivételével a (18) képletben szereplő többi ennyiség száított ennyiség, aelyek hibája sziszteatikus hibának inősül (lásd alább). N d iseretének a pontossága gyakorlatilag egegyezik a fóliák M töegének a pontosságával (vö. (16) képlet). 13 Ennek alapján a terikus neutronfluxus relatív szórása: 2 2 ( Φ ) ( η) ( ) D th D D M B + H + B + H + + Φ th η M 22 A A η t cs cs Cd Cd ( ) cs Cd. (27) Sziszteatikus hiba 12 A ateatikai statisztikában ezeknek a fogalaknak a neve: szórás, illetve torzítás. A fent használt elnevezések csak köznyelviek, és a ateatikában ne elfogadottak. 13 A csupasz és kadiuborítású fólia töege lehet eltérő is. Ebben az esetben a hibaszáítási képlet jóval bonyolultabb. Az egyszerűség kedvéért feltételezzük, hogy töegeik azonosak.
18 18 A (27) alatti statisztikus hiba a érés gondos végrehajtásával akár 1 2%-ra is leszorítható. Nehezebb csökkenteni a sziszteatikus hibákat, aelyek értéke akár 10% nagyságrendű is lehet. Ezek közül a legfontosabbak: - A G önárnyékolási tényező nehezen száolható ennyiség. Ennek oka egyrész az, hogy a (11) képlet csak közelítő (különösen a kadiuborítású fólia esetében), ásrészt bonyolult kiszáítani a képletben szereplő Σ t hatáskeresztetszetet. - Hasonlóan sok feltevésre van szükség a (18) képletben szereplő v σ d szorzat száításhoz. Néhány példa a felerülő probléákra: csak száításból iserjük a (14) képletbe helyettsítendő neutronspektruot, az arány hatáskeresztetszét csak véges pontossággal iserjük, stb. - A (18) képlet nevezőjében szereplő λ bolási állandót csak véges pontossággal iserjük. Ennek a hatása elérhet néhány százalékot. További pontatlanság, hogy a t a -t tartalazó aktiválási tényező feltételezi, hogy az aktiválás kezdetén a reaktor teljesíténye pillanatszerűen ugrik az aktivalási teljesítényre, ajd a végén szintén pillanatszerűen esik le 0-ra. Ez korrigálható, ha a (8) helyett egy olyan differenciálegyenletet oldunk eg, aely figyelebe veszi a neutronfluxus tényleges időfüggését. Ha az aktiválás ideje 1 óra vagy hosszabb, akkor ez a korrekció 1% alatt van. Végeredényben látjuk, hogy a száos sziszteatikus hiba iatt a neutronfluxus éréséről valójában ne beszélhetünk. Airől szó lehet, az a neturonfluxus közelítő eghatározása, de ennek eredénye erősen függ a kiértékelésben tett feltevésektől. 8. Ellenőrző kérdések 1. Mi a terikus neutronfluxus? 2. Mi a különbség az extrapolációs távolság és a reflektor-egtakarítás között? 3. Mi az átlagos aktivációs hatáskeresztetszet? 4. Mi a szerepe az önárnyékolási tényezőnek, és hogyan határozzuk eg? 5. Hogyan becsüljük a terikus neutronfluxust ért aktivitások alapján? 6. Hogyan végezzük a bolási korrekciót onitorfólia segítségével? 7. Egy onitorfólia alkalazásának i a hatása a ért beütésszáok szórására? 8. Hogyan határozzuk eg a terikus neutronfluxus abszolút értékét? 9. A terikus neutronfluxus abszolút értékének eghatározásakor ilyen statisztikus és sziszteatikus hibák lépnek fel? 9. Irodalo [1] G.I.Bell, S.Classtone: Nuclear Reactor Theory, New York etc., Van Nostrand Reinhold (1973) (Alapos, áttekintő eléleti unka) [2] J.J. Duderstadt, L.J. Hailton: Nuclear Reactor Analysis, Wiley and Sons (1976). [3] Z. Szatáry, User s Manual of Progra RFIT, Part 2. Paraeter Estiation, KFKI /G.
19 19
NEUTRON-DETEKTOROK VIZSGÁLATA. Mérési útmutató BME NTI 1997
 NEUTRON-DETEKTOROK VIZSGÁLATA Mérési útmutató Gyurkócza Csaba, Balázs László BME NTI 1997 Tartalomjegyzék 1. Bevezetés 3. 2. Elméleti összefoglalás 3. 2.1. A neutrondetektoroknál alkalmazható legfontosabb
NEUTRON-DETEKTOROK VIZSGÁLATA Mérési útmutató Gyurkócza Csaba, Balázs László BME NTI 1997 Tartalomjegyzék 1. Bevezetés 3. 2. Elméleti összefoglalás 3. 2.1. A neutrondetektoroknál alkalmazható legfontosabb
- III. 1- Az energiakarakterisztikájú gépek őse a kalapács, melynek elve a 3.1 ábrán látható. A kalapácsot egy m tömegű, v
 - III. 1- ALAKÍTÁSTECHNIKA Előadásjegyzet Prof Ziaja György III.rész. ALAKÍTÓ GÉPEK Az alakítási folyaatokhoz szükséges erőt és energiát az alakító gépek szolgáltatják. Az alakképzés többnyire az alakító
- III. 1- ALAKÍTÁSTECHNIKA Előadásjegyzet Prof Ziaja György III.rész. ALAKÍTÓ GÉPEK Az alakítási folyaatokhoz szükséges erőt és energiát az alakító gépek szolgáltatják. Az alakképzés többnyire az alakító
A megnyúlás utáni végső hosszúság: - az anyagi minőségtől ( - lineáris hőtágulási együttható) l = l0 (1 + T)
 - 1 - FIZIKA - SEGÉDANYAG - 10. osztály I. HŐTAN 1. Lineáris és térfogati hőtágulás Alapjelenség: Ha szilárd vagy folyékony halazállapotú anyagot elegítünk, a hossza ill. a térfogata növekszik, hűtés hatására
- 1 - FIZIKA - SEGÉDANYAG - 10. osztály I. HŐTAN 1. Lineáris és térfogati hőtágulás Alapjelenség: Ha szilárd vagy folyékony halazállapotú anyagot elegítünk, a hossza ill. a térfogata növekszik, hűtés hatására
III. Áramkör számítási módszerek, egyenáramú körök
 . Árakör száítás ódszerek, egyenáraú körök A vllaos ára a vllaos töltések rendezett áralása (ozgása) a fellépő erők hatására. Az áralás ránya a poztív töltéshordozók áralásának ránya, aelyek a nagyobb
. Árakör száítás ódszerek, egyenáraú körök A vllaos ára a vllaos töltések rendezett áralása (ozgása) a fellépő erők hatására. Az áralás ránya a poztív töltéshordozók áralásának ránya, aelyek a nagyobb
MUNKAANYAG. Szabó László. Áramlástani alaptörvények. A követelménymodul megnevezése:
 Szabó László Áralástani alaptörények A köetelényodul egneezése: Kőolaj- és egyipari géprendszer üzeeltetője és egyipari technikus feladatok A köetelényodul száa: 07-06 A tartaloele azonosító száa és célcsoportja:
Szabó László Áralástani alaptörények A köetelényodul egneezése: Kőolaj- és egyipari géprendszer üzeeltetője és egyipari technikus feladatok A köetelényodul száa: 07-06 A tartaloele azonosító száa és célcsoportja:
2010/2011. tanév Szakács Jenő Megyei Fizika Verseny II. forduló. 2011. január 31.
 2010/2011. tanév Szakác enő Megyei Fizika Vereny II. forduló 2011. január 31. Minden verenyzőnek a záára kijelölt négy feladatot kell egoldania. A zakközépikoláoknak az A vagy a B feladatort kell egoldani
2010/2011. tanév Szakác enő Megyei Fizika Vereny II. forduló 2011. január 31. Minden verenyzőnek a záára kijelölt négy feladatot kell egoldania. A zakközépikoláoknak az A vagy a B feladatort kell egoldani
A szállítócsigák néhány elméleti kérdése
 A szállítócsigák néhány eléleti kédése DR BEKŐJÁOS GATE Géptani Intézet Bevezetés A szállítócsigák néhány eléleti kédése A tanulány tágya az egyik legégebben alkalazott folyaatos üzeűanyagozgató gép a
A szállítócsigák néhány eléleti kédése DR BEKŐJÁOS GATE Géptani Intézet Bevezetés A szállítócsigák néhány eléleti kédése A tanulány tágya az egyik legégebben alkalazott folyaatos üzeűanyagozgató gép a
EGÉSZTESTSZÁMLÁLÁS. Mérésleírás Nukleáris környezetvédelem gyakorlat környezetmérnök hallgatók számára
 EGÉSZTESTSZÁMLÁLÁS Mérésleírás Nukleáris környezetvédelem gyakorlat környezetmérnök hallgatók számára Zagyvai Péter - Osváth Szabolcs Bódizs Dénes BME NTI, 2008 1. Bevezetés Az izotópok stabilak vagy radioaktívak
EGÉSZTESTSZÁMLÁLÁS Mérésleírás Nukleáris környezetvédelem gyakorlat környezetmérnök hallgatók számára Zagyvai Péter - Osváth Szabolcs Bódizs Dénes BME NTI, 2008 1. Bevezetés Az izotópok stabilak vagy radioaktívak
INTERFERENCIA - ÓRAI JEGYZET
 FZKA BSc,. évfolya /. félév, Optika tárgy TERFERECA - ÓRA JEGYZET (Erdei Gábor, Ph.D., 8. AJÁLOTT SZAKRODALOM: ALAPFOGALMAK Klei-Furtak, Optics Richter, Bevezetés a oder optikába Bor-Wolf, Priciples of
FZKA BSc,. évfolya /. félév, Optika tárgy TERFERECA - ÓRA JEGYZET (Erdei Gábor, Ph.D., 8. AJÁLOTT SZAKRODALOM: ALAPFOGALMAK Klei-Furtak, Optics Richter, Bevezetés a oder optikába Bor-Wolf, Priciples of
Vízműtani számítás. A vízműtani számítás készítése során az alábbi összefüggéseket használtuk fel: A csapadék intenzitása: i = a t [l/s ha]
![Vízműtani számítás. A vízműtani számítás készítése során az alábbi összefüggéseket használtuk fel: A csapadék intenzitása: i = a t [l/s ha] Vízműtani számítás. A vízműtani számítás készítése során az alábbi összefüggéseket használtuk fel: A csapadék intenzitása: i = a t [l/s ha]](/thumbs/29/13639399.jpg) Vízűtani száítás A vízűtani száítás készítése során az alábbi összefüggéseket használtuk fel: A csapadék intenzitása: i = a t [l/s ha] ahol ip a p visszatérési csapadék intenzitása, /h a a 10 perces időtartaú
Vízűtani száítás A vízűtani száítás készítése során az alábbi összefüggéseket használtuk fel: A csapadék intenzitása: i = a t [l/s ha] ahol ip a p visszatérési csapadék intenzitása, /h a a 10 perces időtartaú
MEGOLDÁSOK ÉS PONTOZÁSI ÚTMUTATÓ
 MEGOLDÁSOK ÉS PONTOZÁSI ÚTMUTATÓ. Egy kerékpáro zakazonként egyene vonalú egyenlete ozgát végez. Megtett útjának elő k hatodát 6 nagyágú ebeéggel, útjának további kétötödét 6 nagyágú ebeéggel, az h útjának
MEGOLDÁSOK ÉS PONTOZÁSI ÚTMUTATÓ. Egy kerékpáro zakazonként egyene vonalú egyenlete ozgát végez. Megtett útjának elő k hatodát 6 nagyágú ebeéggel, útjának további kétötödét 6 nagyágú ebeéggel, az h útjának
3. RADIOAKTÍV MINTÁK AKTIVITÁSÁNAK MEGHATÁROZÁSA
 3. RADIOAKTÍV MINTÁK AKTIVITÁSÁNAK MEGHATÁROZÁSA 1. Az aktivitásmérés jelentosége Modern világunk mindennapi élete számtalan helyen felhasználja azokat az ismereteket, amelyekhez a fizika az atommagok
3. RADIOAKTÍV MINTÁK AKTIVITÁSÁNAK MEGHATÁROZÁSA 1. Az aktivitásmérés jelentosége Modern világunk mindennapi élete számtalan helyen felhasználja azokat az ismereteket, amelyekhez a fizika az atommagok
1. A neutronvisszaszórási hatáskeresztmetszet
 Bevezetés Az értekezés azon munka összefoglalása, melyet 1999 februárjában még egyetemi hallgatóként kezdtem, 1999 szeptembere és 2002 augusztusa között mint PhD ösztöndíjas, 2002 szeptembere és 2003 júniusa
Bevezetés Az értekezés azon munka összefoglalása, melyet 1999 februárjában még egyetemi hallgatóként kezdtem, 1999 szeptembere és 2002 augusztusa között mint PhD ösztöndíjas, 2002 szeptembere és 2003 júniusa
Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet), A Laplace operátor derékszögű koordinátarendszerben
 Atomfizika ψ ψ ψ ψ ψ E z y x U z y x m = + + + ),, ( h ) ( ) ( ) ( ) ( r r r r ψ ψ ψ E U m = + Δ h z y x + + = Δ ),, ( ) ( z y x ψ =ψ r Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet),
Atomfizika ψ ψ ψ ψ ψ E z y x U z y x m = + + + ),, ( h ) ( ) ( ) ( ) ( r r r r ψ ψ ψ E U m = + Δ h z y x + + = Δ ),, ( ) ( z y x ψ =ψ r Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet),
6. Számitási gyakorlatok
 űvelettani érési és száítási útutató 6. Száitási gyakorlatok 6.. közegek fizikai tulajdonságainak eghatározása int iseretes, a űvelettanban, úgy egyfázisú, int többfázisú közegekkel dolgozunk. Ezek a közegek
űvelettani érési és száítási útutató 6. Száitási gyakorlatok 6.. közegek fizikai tulajdonságainak eghatározása int iseretes, a űvelettanban, úgy egyfázisú, int többfázisú közegekkel dolgozunk. Ezek a közegek
NÉV osztály. Praktikus beállítások: Oldalbeállítás: A4 (210x297 mm), álló elrendezés, első oldal eltérő
 NÉV osztály Feladat cíe Dátu Praktikus beállítások: Oldalbeállítás: A (10x97 ), álló elrendezés, első oldal eltérő Margó indenütt c. oldaltól fejléc: felül, bal oldalon név, jobb oldalon dátu alul középen
NÉV osztály Feladat cíe Dátu Praktikus beállítások: Oldalbeállítás: A (10x97 ), álló elrendezés, első oldal eltérő Margó indenütt c. oldaltól fejléc: felül, bal oldalon név, jobb oldalon dátu alul középen
Villamos kapcsolókészülékek BMEVIVEA336
 Villamos kapcsolókészülékek BMEVIVEA336 Szigetelések feladatai, igénybevételei A villamos szigetelés feladata: Az üzemszerűen vagy időszakosan különböző potenciálon lévő vezető részek (fém alkatrészek
Villamos kapcsolókészülékek BMEVIVEA336 Szigetelések feladatai, igénybevételei A villamos szigetelés feladata: Az üzemszerűen vagy időszakosan különböző potenciálon lévő vezető részek (fém alkatrészek
L Ph 1. Az Egyenlítő fölötti közelítőleg homogén földi mágneses térben a proton (a mágneses indukció
 A 2008-as bajor fizika érettségi feladatok (Leistungskurs) Munkaidő: 240 perc (A vizsgázónak két, a szakbizottság által kiválasztott feladatsort kell kidolgoznia) L Ph 1 1. Kozmikus részecskék mozgása
A 2008-as bajor fizika érettségi feladatok (Leistungskurs) Munkaidő: 240 perc (A vizsgázónak két, a szakbizottság által kiválasztott feladatsort kell kidolgoznia) L Ph 1 1. Kozmikus részecskék mozgása
A.11. Nyomott rudak. A.11.1. Bevezetés
 A.. Nyomott rudak A... Bevezetés A nyomott szerkezeti elem fogalmat általában olyan szerkezeti elemek jelölésére használjuk, amelyekre csak tengelyirányú nyomóerő hat. Ez lehet speciális terhelésű oszlop,
A.. Nyomott rudak A... Bevezetés A nyomott szerkezeti elem fogalmat általában olyan szerkezeti elemek jelölésére használjuk, amelyekre csak tengelyirányú nyomóerő hat. Ez lehet speciális terhelésű oszlop,
9. Radioaktív sugárzás mérése Geiger-Müller-csővel. Preparátum helyének meghatározása. Aktivitás mérés.
 9. Radioaktív sugárzás mérése Geiger-Müller-csővel. Preparátum helyének meghatározása. ktivitás mérés. MÉRÉS CÉLJ: Megismerkedni a radioaktív sugárzás jellemzésére szolgáló mértékegységekkel, és a sugárzás
9. Radioaktív sugárzás mérése Geiger-Müller-csővel. Preparátum helyének meghatározása. ktivitás mérés. MÉRÉS CÉLJ: Megismerkedni a radioaktív sugárzás jellemzésére szolgáló mértékegységekkel, és a sugárzás
Dinamika példatár. Szíki Gusztáv Áron
 Dinaika példatár Szíki Guztáv Áron TTLOMJEGYZÉK 4 DINMIK 4 4.1 NYGI PONT KINEMTIKÁJ 4 4.1.1 Mozgá adott pályán 4 4.1.1.1 Egyene vonalú pálya 4 4.1.1. Körpálya 1 4.1.1.3 Tetzőlege íkgörbe 19 4.1. Szabad
Dinaika példatár Szíki Guztáv Áron TTLOMJEGYZÉK 4 DINMIK 4 4.1 NYGI PONT KINEMTIKÁJ 4 4.1.1 Mozgá adott pályán 4 4.1.1.1 Egyene vonalú pálya 4 4.1.1. Körpálya 1 4.1.1.3 Tetzőlege íkgörbe 19 4.1. Szabad
TERMIKUS NEUTRONFLUXUS MEGHATÁROZÁSA AKTIVÁCIÓS MÓDSZERREL
 TERMIKUS NEUTRONFLUXUS MEGHATÁROZÁSA AKTIVÁCIÓS MÓDSZERREL 1. BEVEZETÉS Neutronsugárzás hatására bizonyos stabil elemekben magátalakulás megy végbe, és a keletkezett radioaktív termék aktivitása megfelelő
TERMIKUS NEUTRONFLUXUS MEGHATÁROZÁSA AKTIVÁCIÓS MÓDSZERREL 1. BEVEZETÉS Neutronsugárzás hatására bizonyos stabil elemekben magátalakulás megy végbe, és a keletkezett radioaktív termék aktivitása megfelelő
2. előadás: További gömbi fogalmak
 2 előadás: További gömbi fogalmak 2 előadás: További gömbi fogalmak Valamely gömbi főkör ívének α azimutja az ív egy tetszőleges pontjában az a szög, amit az ív és a meridián érintői zárnak be egymással
2 előadás: További gömbi fogalmak 2 előadás: További gömbi fogalmak Valamely gömbi főkör ívének α azimutja az ív egy tetszőleges pontjában az a szög, amit az ív és a meridián érintői zárnak be egymással
MFI mérés BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GÉPÉSZMÉRNÖKI KAR POLIMERTECHNIKA TANSZÉK HŐRE LÁGYULÓ MŰANYAGOK FOLYÓKÉPESSÉGÉNEK VIZSGÁLATA
 B1 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GÉPÉSZMÉRNÖKI KAR POLIMERTECHNIKA TANSZÉK MFI mérés HŐRE LÁGYULÓ MŰANYAGOK FOLYÓKÉPESSÉGÉNEK VIZSGÁLATA A JEGYZET ÉRVÉNYESSÉGÉT A TANSZÉKI WEB OLDALON
B1 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GÉPÉSZMÉRNÖKI KAR POLIMERTECHNIKA TANSZÉK MFI mérés HŐRE LÁGYULÓ MŰANYAGOK FOLYÓKÉPESSÉGÉNEK VIZSGÁLATA A JEGYZET ÉRVÉNYESSÉGÉT A TANSZÉKI WEB OLDALON
MFI mérés BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GÉPÉSZMÉRNÖKI KAR POLIMERTECHNIKA TANSZÉK HŐRE LÁGYULÓ MŰANYAGOK FOLYÓKÉPESSÉGÉNEK VIZSGÁLATA
 B2 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GÉPÉSZMÉRNÖKI KAR POLIMERTECHNIKA TANSZÉK MFI mérés HŐRE LÁGYULÓ MŰANYAGOK FOLYÓKÉPESSÉGÉNEK VIZSGÁLATA A JEGYZET ÉRVÉNYESSÉGÉT A TANSZÉKI WEB OLDALON
B2 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GÉPÉSZMÉRNÖKI KAR POLIMERTECHNIKA TANSZÉK MFI mérés HŐRE LÁGYULÓ MŰANYAGOK FOLYÓKÉPESSÉGÉNEK VIZSGÁLATA A JEGYZET ÉRVÉNYESSÉGÉT A TANSZÉKI WEB OLDALON
= szinkronozó nyomatékkal egyenlő.
 A 4.45. ábra jelöléseit használva, tételezzük fel, hogy gépünk túllendült és éppen a B pontban üzemel. Mivel a motor által szolgáltatott M 2 nyomaték nagyobb mint az M 1 terhelőnyomaték, a gép forgórészére
A 4.45. ábra jelöléseit használva, tételezzük fel, hogy gépünk túllendült és éppen a B pontban üzemel. Mivel a motor által szolgáltatott M 2 nyomaték nagyobb mint az M 1 terhelőnyomaték, a gép forgórészére
Doktori munka. Solymosi József: NUKLEÁRIS KÖRNYEZETELLENŐRZŐ MÉRŐRENDSZEREK. Alkotás leírása
 Doktori munka Solymosi József: NUKLEÁRIS KÖRNYEZETELLENŐRZŐ MÉRŐRENDSZEREK Alkotás leírása Budapest, 1990. 2 KÖSZÖNETNYILVÁNÍTÁS A doktori munka célja az egyéni eredmény bemutatása. Feltétlenül hangsúlyoznom
Doktori munka Solymosi József: NUKLEÁRIS KÖRNYEZETELLENŐRZŐ MÉRŐRENDSZEREK Alkotás leírása Budapest, 1990. 2 KÖSZÖNETNYILVÁNÍTÁS A doktori munka célja az egyéni eredmény bemutatása. Feltétlenül hangsúlyoznom
KÖRNYEZETVÉDELMI- VÍZGAZDÁLKODÁSI ALAPISMERETEK
 Környezetvédeli-vízgazdálkodási alaiseretek közéint ÉRETTSÉGI VIZSGA 0. október 5. KÖRNYEZETVÉDELMI- VÍZGAZDÁLKODÁSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI
Környezetvédeli-vízgazdálkodási alaiseretek közéint ÉRETTSÉGI VIZSGA 0. október 5. KÖRNYEZETVÉDELMI- VÍZGAZDÁLKODÁSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI
töltéssel rendelkező vagy semleges részecskék kinetikus energiája és (vagy) impulzusa a kondenzált közegek atomjaival ütközve megváltozhat.
 Néhány szó a neutronról Különböző részecskék, úgymint fotonok, neutronok, elektronok és más, töltéssel rendelkező vagy semleges részecskék kinetikus energiája és (vagy) impulzusa a kondenzált közegek atomjaival
Néhány szó a neutronról Különböző részecskék, úgymint fotonok, neutronok, elektronok és más, töltéssel rendelkező vagy semleges részecskék kinetikus energiája és (vagy) impulzusa a kondenzált közegek atomjaival
2. OPTIKA 2.1. Elmélet 2.1.1. Geometriai optika
 2. OPTIKA 2.1. Elmélet Az optika tudománya a látás élményéből fejlődött ki. A tárgyakat azért látjuk, mert fényt bocsátanak ki, vagy a rájuk eső fényt visszaverik, és ezt a fényt a szemünk érzékeli. A
2. OPTIKA 2.1. Elmélet Az optika tudománya a látás élményéből fejlődött ki. A tárgyakat azért látjuk, mert fényt bocsátanak ki, vagy a rájuk eső fényt visszaverik, és ezt a fényt a szemünk érzékeli. A
Gamma-spektrometria HPGe detektorral
 Gamma-spektrometria HPGe detektorral 1. Bevezetés A gamma-spektrometria az atommagból valamilyen magfolyamat következtében (radioaktív bomlás, mesterséges vagy természetes magreakció) kilépő gamma sugárzás
Gamma-spektrometria HPGe detektorral 1. Bevezetés A gamma-spektrometria az atommagból valamilyen magfolyamat következtében (radioaktív bomlás, mesterséges vagy természetes magreakció) kilépő gamma sugárzás
tel Mintavétel Az egyedek eloszlása
 Mintavételi teli ódszerek I Mintavétel tel a populáció elterjedési területe (legtöbbször túl nagy ahhoz hogy az egészet egintázzuk) intavételi terület (inden esetben kisebb, int a populáció elterjedési
Mintavételi teli ódszerek I Mintavétel tel a populáció elterjedési területe (legtöbbször túl nagy ahhoz hogy az egészet egintázzuk) intavételi terület (inden esetben kisebb, int a populáció elterjedési
6. RADIOAKTIVITÁS ÉS GEOTERMIKA
 6. RADIOAKTIVITÁS ÉS GEOTERMIKA Radioaktivitás A tapasztalat szerint a természetben előforduló néhány elem bizonyos izotópjai nem stabilak, hanem minden külső beavatkozástól mentesen radioaktív sugárzás
6. RADIOAKTIVITÁS ÉS GEOTERMIKA Radioaktivitás A tapasztalat szerint a természetben előforduló néhány elem bizonyos izotópjai nem stabilak, hanem minden külső beavatkozástól mentesen radioaktív sugárzás
Ujfalussy Balázs Idegsejtek biofizikája
 M A TTA? Ujfalussy Balázs degsejtek biofizikája Második rész A nyugali potenciál A sorozat előző cikkében nekiláttunk egfejteni az idegrendszer alapjelenségeit. Az otivált bennünket, hogy a száítógépeink
M A TTA? Ujfalussy Balázs degsejtek biofizikája Második rész A nyugali potenciál A sorozat előző cikkében nekiláttunk egfejteni az idegrendszer alapjelenségeit. Az otivált bennünket, hogy a száítógépeink
NATRII HYALURONAS. Nátrium-hialuronát
 Natrii hyaluronas Ph.Hg.VIII. Ph.Eur.6.0. - 1 01/2008:1472 NATRII HYALURONAS Nátriu-hialuronát (C 14 H 20 NNaO 11 ) n [9067-32-7] DEFINÍCIÓ A nátriu-hialuronát a hialuronsav nátriusója. A hialuronsav D-glükuronsav
Natrii hyaluronas Ph.Hg.VIII. Ph.Eur.6.0. - 1 01/2008:1472 NATRII HYALURONAS Nátriu-hialuronát (C 14 H 20 NNaO 11 ) n [9067-32-7] DEFINÍCIÓ A nátriu-hialuronát a hialuronsav nátriusója. A hialuronsav D-glükuronsav
Sűrűségmérés. 1. Szilárd test sűrűségének mérése
 Sűrűségérés. Szilárd test sűrűségének érése A sűrűség,, definíciój hoogén test esetén: test töege osztv test V térfogtávl: V A sűrűség SI értékegysége kg/, hsználtos ég kg/d, kg/l és g/c Ne hoogén testnél
Sűrűségérés. Szilárd test sűrűségének érése A sűrűség,, definíciój hoogén test esetén: test töege osztv test V térfogtávl: V A sűrűség SI értékegysége kg/, hsználtos ég kg/d, kg/l és g/c Ne hoogén testnél
FAIPARI ALAPISMERETEK
 Faipari alapiseretek középszint 1511 ÉRETTSÉGI VIZSGA 215. ájus 19. FAIPARI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIMA Fontos tudnivalók
Faipari alapiseretek középszint 1511 ÉRETTSÉGI VIZSGA 215. ájus 19. FAIPARI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIMA Fontos tudnivalók
Rezgésdiagnosztika. 1. Bevezetés. PDF created with pdffactory Pro trial version www.pdffactory.com
 Rezgésdiagnoszika. Bevezeés rezgésdiagnoszika a űszaki diagnoszika egy eghaározo erülee. gépek állapovizsgálaánál alán a legelerjedebb vizsgálai ódszer a rezgésérés. Ebben a jegyzeben először a rezgésérés
Rezgésdiagnoszika. Bevezeés rezgésdiagnoszika a űszaki diagnoszika egy eghaározo erülee. gépek állapovizsgálaánál alán a legelerjedebb vizsgálai ódszer a rezgésérés. Ebben a jegyzeben először a rezgésérés
Prizmás impulzuskompresszorok hômérsékleti stabilitásának modellezése
 Prizmás impulzuskompresszorok hômérsékleti stabilitásának modellezése Tudományos diákköri dolgozat Írta: DOMBI PÉTER Témavezetô: DR. OSVAY KÁROLY JATE Optikai és Kvantumelektronikai Tanszék Szeged 1998.
Prizmás impulzuskompresszorok hômérsékleti stabilitásának modellezése Tudományos diákköri dolgozat Írta: DOMBI PÉTER Témavezetô: DR. OSVAY KÁROLY JATE Optikai és Kvantumelektronikai Tanszék Szeged 1998.
Födémszerkezetek 2. Zsalupanelok alkalmazása
 Födészerkezetek 1. A beton Évkönyv 000-ben Dr. László Ottó és Dr. Petro Bálint egy kiváló összeoglalást adtak a beton, vasbeton és eszített vasbeton ödéekrl, elyet jól kiegészít Dr. Farkas György ejezete,
Födészerkezetek 1. A beton Évkönyv 000-ben Dr. László Ottó és Dr. Petro Bálint egy kiváló összeoglalást adtak a beton, vasbeton és eszített vasbeton ödéekrl, elyet jól kiegészít Dr. Farkas György ejezete,
Radioaktivitás. 9.2 fejezet
 Radioaktivitás 9.2 fejezet A bomlási törvény Bomlási folyamat alapjai: Értelmezés (bomlás): Azt a magfizikai folyamatot, amely során nagy tömegszámú atommagok spontán módon, azaz véletlenszerűen (statisztikailag)
Radioaktivitás 9.2 fejezet A bomlási törvény Bomlási folyamat alapjai: Értelmezés (bomlás): Azt a magfizikai folyamatot, amely során nagy tömegszámú atommagok spontán módon, azaz véletlenszerűen (statisztikailag)
Fizika belépő kérdések /Földtudományi alapszak I. Évfolyam II. félév/
 Fizika belépő kérdések /Földtudományi alapszak I. Évfolyam II. félév/. Coulomb törvény: a pontszerű töltések között ható erő (F) egyenesen arányos a töltések (Q,Q ) szorzatával és fordítottan arányos a
Fizika belépő kérdések /Földtudományi alapszak I. Évfolyam II. félév/. Coulomb törvény: a pontszerű töltések között ható erő (F) egyenesen arányos a töltések (Q,Q ) szorzatával és fordítottan arányos a
3. számú mérés Szélessávú transzformátor vizsgálata
 3. számú mérés Szélessávú transzformátor vizsgálata A mérésben a hallgatók megismerkedhetnek a szélessávú transzformátorok főbb jellemzőivel. A mérési utasítás első része a méréshez szükséges elméleti
3. számú mérés Szélessávú transzformátor vizsgálata A mérésben a hallgatók megismerkedhetnek a szélessávú transzformátorok főbb jellemzőivel. A mérési utasítás első része a méréshez szükséges elméleti
Felületi feszültség és viszkozitás mérése. I. Felületi feszültség mérése. Felületi feszültség mérés és viszkozimetria 2. Fizikai kémia gyakorlat 1
 Fizikai kémia gyakorlat 1 Felületi feszültség mérés és viszkozimetria 2 I. Felületi feszültség mérése 1. Bevezetés Felületi feszültség és viszkozitás mérése A felületi feszültség fázisok határfelületén
Fizikai kémia gyakorlat 1 Felületi feszültség mérés és viszkozimetria 2 I. Felületi feszültség mérése 1. Bevezetés Felületi feszültség és viszkozitás mérése A felületi feszültség fázisok határfelületén
Tevékenység: Olvassa el a fejezetet! Gyűjtse ki és jegyezze meg a ragasztás előnyeit és a hátrányait! VIDEO (A ragasztás ereje)
 lvassa el a fejezetet! Gyűjtse ki és jegyezze meg a ragasztás előnyeit és a hátrányait! VIDE (A ragasztás ereje) A ragasztás egyre gyakrabban alkalmazott kötéstechnológia az ipari gyakorlatban. Ennek oka,
lvassa el a fejezetet! Gyűjtse ki és jegyezze meg a ragasztás előnyeit és a hátrányait! VIDE (A ragasztás ereje) A ragasztás egyre gyakrabban alkalmazott kötéstechnológia az ipari gyakorlatban. Ennek oka,
2007/2008. tanév. Szakács Jenő Megyei Fizika Verseny I. forduló. 2007. november 9. MEGOLDÁSOK
 007/008. tané Szakác Jenő Megyei Fizika Vereny I. forduló 007. noeber 9. MEGOLDÁSOK 007-008. tané - Szakác Jenő Megyei Fizika Vereny I. forduló Megoldáok. d = 50 = 4,4 k/h = 4 / a) t =? b) r =? c) =?,
007/008. tané Szakác Jenő Megyei Fizika Vereny I. forduló 007. noeber 9. MEGOLDÁSOK 007-008. tané - Szakác Jenő Megyei Fizika Vereny I. forduló Megoldáok. d = 50 = 4,4 k/h = 4 / a) t =? b) r =? c) =?,
Ujfalussy Balázs Idegsejtek biofizikája Első rész
 Ujfalussy Balázs Idegsejtek biofizikája Első rész MI A TITA? Ez a négyrészes sorozat azt a célt szolgálja, hogy az idegsejtek űködéséről ateatikai, fizikai odellekkel alkossunk képet középiskolás iseretekre
Ujfalussy Balázs Idegsejtek biofizikája Első rész MI A TITA? Ez a négyrészes sorozat azt a célt szolgálja, hogy az idegsejtek űködéséről ateatikai, fizikai odellekkel alkossunk képet középiskolás iseretekre
II. MELLÉKLET AJÁNLATI/RÉSZVÉTELI FELHÍVÁS I. SZAKASZ: AJÁNLATKÉRŐ I.1) NÉV, CÍM ÉS KAPCSOLATTARTÁSI PONT(OK)
 II. MELLÉKLET EURÓPAI UNIÓ Az Európai Unió Hivatalos Lapjának Kiegészítő Kiadványa 2, rue Mercier, L-2985 Luxebourg Fax: (352) 29 29 42 670 E-ail: p-ojs@opoce.cec.eu.int Inforáció és on-line foranyotatványok:
II. MELLÉKLET EURÓPAI UNIÓ Az Európai Unió Hivatalos Lapjának Kiegészítő Kiadványa 2, rue Mercier, L-2985 Luxebourg Fax: (352) 29 29 42 670 E-ail: p-ojs@opoce.cec.eu.int Inforáció és on-line foranyotatványok:
Készítette: Bujnóczki Tibor Lezárva: 2005. 01. 01.
 VILÁGÍTÁSTECHNIKA Készítette: Bujnóczki Tibor Lezárva: 2005. 01. 01. ANYAGOK FELÉPÍTÉSE Az atomok felépítése: elektronhéjak: K L M N O P Q elektronok atommag W(wolfram) (Atommag = proton+neutron protonok
VILÁGÍTÁSTECHNIKA Készítette: Bujnóczki Tibor Lezárva: 2005. 01. 01. ANYAGOK FELÉPÍTÉSE Az atomok felépítése: elektronhéjak: K L M N O P Q elektronok atommag W(wolfram) (Atommag = proton+neutron protonok
VI.11. TORONY-HÁZ-TETŐ. A feladatsor jellemzői
 VI.11. TORONY-HÁZ-TETŐ Tárgy, téma A feladatsor jellemzői Szögfüggvények derékszögű háromszögben, szinusztétel, koszinusztétel, Pitagorasz-tétel. Előzmények Pitagorasz-tétel, derékszögű háromszög trigonometriája,
VI.11. TORONY-HÁZ-TETŐ Tárgy, téma A feladatsor jellemzői Szögfüggvények derékszögű háromszögben, szinusztétel, koszinusztétel, Pitagorasz-tétel. Előzmények Pitagorasz-tétel, derékszögű háromszög trigonometriája,
1. példa. 2. példa. értelemszerően. F 2.32. ábra
 . péld Htározzu meg z.. árán láthtó tégllp lú eresztmetszet és y tengelyre számított másodrendő nyomtéit! d dy (.) épler szerint y dy y d y 0 0 értelemszerően y. péld Steiner-tétel (.. éplet) llmzásávl
. péld Htározzu meg z.. árán láthtó tégllp lú eresztmetszet és y tengelyre számított másodrendő nyomtéit! d dy (.) épler szerint y dy y d y 0 0 értelemszerően y. péld Steiner-tétel (.. éplet) llmzásávl
KOVÁCS ENDRe, PARIpÁS BÉLA, FIZIkA II.
 KOVÁCS ENDRe, PARIpÁS BÉLA, FIZIkA II. 12 A MODERN FIZIKa ELEMEI XII. MAGfIZIkA ÉS RADIOAkTIVITÁS 1. AZ ATOmmAG Rutherford (1911) arra a következtetésre jutott, hogy az atom pozitív töltését hordozó anyag
KOVÁCS ENDRe, PARIpÁS BÉLA, FIZIkA II. 12 A MODERN FIZIKa ELEMEI XII. MAGfIZIkA ÉS RADIOAkTIVITÁS 1. AZ ATOmmAG Rutherford (1911) arra a következtetésre jutott, hogy az atom pozitív töltését hordozó anyag
1.3.1. Önismeretet támogató módszerek
 TÁMOP.1. -08/1/B-009-000 PÁLYÁZAT 1. SZ. ALPROJEKT 1..1. Öniseretet táogató ódszerek - Pályaoritációs ódszertani eszköztár - - vitaanyag- Készítette: Dr. Dávid Mária Dr. Hatvani Andrea Dr. Taskó Tünde
TÁMOP.1. -08/1/B-009-000 PÁLYÁZAT 1. SZ. ALPROJEKT 1..1. Öniseretet táogató ódszerek - Pályaoritációs ódszertani eszköztár - - vitaanyag- Készítette: Dr. Dávid Mária Dr. Hatvani Andrea Dr. Taskó Tünde
Az alap- és a képfelület fogalma, megadási módjai és tulajdonságai
 A VETÜLETEK ALAP- ÉS KÉPFELÜLETE Az alap- és a képfelület fogalma, megadási módjai és tulajdonságai A geodézia, a térinformatika és a térképészet a görbült földfelületen elhelyezkedő geometriai alakzatokat
A VETÜLETEK ALAP- ÉS KÉPFELÜLETE Az alap- és a képfelület fogalma, megadási módjai és tulajdonságai A geodézia, a térinformatika és a térképészet a görbült földfelületen elhelyezkedő geometriai alakzatokat
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika középszint 1413 ÉRETTSÉGI VIZSGA 015. május 5. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos tudnivalók Formai előírások:
Matematika középszint 1413 ÉRETTSÉGI VIZSGA 015. május 5. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos tudnivalók Formai előírások:
Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály, középszint
 TÁMOP-.1.4-08/2-2009-0011 A kompetencia alapú oktatás feltételeinek megteremtése Vas megye közoktatási intézményeiben Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály, középszint Vasvár,
TÁMOP-.1.4-08/2-2009-0011 A kompetencia alapú oktatás feltételeinek megteremtése Vas megye közoktatási intézményeiben Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály, középszint Vasvár,
Kecskeméti Fıiskola GAMF Kar Informatika Tanszék. Johanyák Zsolt Csaba
 Kecskeméti Fıiskola GAMF Kar Informatika Tanszék Johanyák Zsolt Csaba 003 Tartalomjegyzék. Bevezetés.... A megbízhatóság fogalmai..... A termék idıtıl függı képességei...... Használhatóság /Üzemkészség/
Kecskeméti Fıiskola GAMF Kar Informatika Tanszék Johanyák Zsolt Csaba 003 Tartalomjegyzék. Bevezetés.... A megbízhatóság fogalmai..... A termék idıtıl függı képességei...... Használhatóság /Üzemkészség/
A talliummal szennyezett NaI egykristály, mint gammasugárzás-detektor
 Bevezetés talliummal szennyezett NaI egykristály, mint gammasugárzás-detektor z ember már õsidõk óta ki van téve a radioaktív sugárzásoknak 1 1 ( α, β, γ, n, p, ν, ~,... ). Egy személy évi sugárterhelésének
Bevezetés talliummal szennyezett NaI egykristály, mint gammasugárzás-detektor z ember már õsidõk óta ki van téve a radioaktív sugárzásoknak 1 1 ( α, β, γ, n, p, ν, ~,... ). Egy személy évi sugárterhelésének
Membránsebesség-visszacsatolásos mélysugárzó direkt digitális szabályozással
 udapeti Műzaki é Gazdaágtudoányi Egyete Villaoérnöki é Inforatikai Kar TUDOMÁNYOS DIÁKKÖRI DOLGOZT Mebránebeég-vizacatoláo élyugárzó direkt digitáli zabályozáal Kézítetteték: aláz Géza V. Vill., greae@evtz.be.hu
udapeti Műzaki é Gazdaágtudoányi Egyete Villaoérnöki é Inforatikai Kar TUDOMÁNYOS DIÁKKÖRI DOLGOZT Mebránebeég-vizacatoláo élyugárzó direkt digitáli zabályozáal Kézítetteték: aláz Géza V. Vill., greae@evtz.be.hu
MAGYAR RÉZPIACI KÖZPONT. 1241 Budapest, Pf. 62 Telefon 317-2421, Fax 266-6794 e-mail: hcpc.bp@euroweb.hu
 MAGYAR RÉZPIACI KÖZPONT 1241 Budapest, Pf. 62 Telefon 317-2421, Fax 266-6794 e-mail: hcpc.bp@euroweb.hu Tartalom 1. A villamos csatlakozások és érintkezôk fajtái............................5 2. Az érintkezések
MAGYAR RÉZPIACI KÖZPONT 1241 Budapest, Pf. 62 Telefon 317-2421, Fax 266-6794 e-mail: hcpc.bp@euroweb.hu Tartalom 1. A villamos csatlakozások és érintkezôk fajtái............................5 2. Az érintkezések
RADIOAKTÍV GYÓGYSZERKÉSZÍTMÉNYEK. Radiopharmaceutica
 Radioaktív gyógyszerkészítmények Ph.Hg.VIII. Ph.Eur. 8.0. -1 01/2014:0125 RADIOAKTÍV GYÓGYSZERKÉSZÍTMÉNYEK Radiopharmaceutica DEFINÍCIÓ Radioaktív gyógyszerkészítménynek vagy radiogyógyszereknek nevezünk
Radioaktív gyógyszerkészítmények Ph.Hg.VIII. Ph.Eur. 8.0. -1 01/2014:0125 RADIOAKTÍV GYÓGYSZERKÉSZÍTMÉNYEK Radiopharmaceutica DEFINÍCIÓ Radioaktív gyógyszerkészítménynek vagy radiogyógyszereknek nevezünk
FIZIKA PRÓBAÉRETTSÉGI 2004. EMELT SZINT. 240 perc
 PRÓBAÉRETTSÉGI 2004. FIZIKA EMELT SZINT 240 perc A feladatlap megoldásához 240 perc áll rendelkezésére. Olvassa el figyelmesen a feladatok előtti utasításokat, és gondosan ossza be idejét! A feladatokat
PRÓBAÉRETTSÉGI 2004. FIZIKA EMELT SZINT 240 perc A feladatlap megoldásához 240 perc áll rendelkezésére. Olvassa el figyelmesen a feladatok előtti utasításokat, és gondosan ossza be idejét! A feladatokat
Modern Fizika Labor. Fizika BSc. Értékelés: A mérés dátuma: A mérés száma és címe: 9. mérés: Röntgen-fluoreszcencia analízis. 2008. április 22.
 Modern Fizika Labor Fizika BSc A mérés dátuma: 28. április 22. A mérés száma és címe: 9. mérés: Röntgen-fluoreszcencia analízis Értékelés: A beadás dátuma: 28. május 5. A mérést végezte: Puszta Adrián,
Modern Fizika Labor Fizika BSc A mérés dátuma: 28. április 22. A mérés száma és címe: 9. mérés: Röntgen-fluoreszcencia analízis Értékelés: A beadás dátuma: 28. május 5. A mérést végezte: Puszta Adrián,
GÁZIONIZÁCIÓS DETEKTOROK VIZSGÁLATA. Mérési útmutató. Gyurkócza Csaba
 GÁZIONIZÁCIÓS DETEKTOROK VIZSGÁLATA Mérési útmutató Gyurkócza Csaba BME NTI 1997 2 Tartalom 1. BEVEZETÉS... 3 2. ELMÉLETI ÖSSZEFOGLALÁS... 3 2.1. Töltéshordozók keletkezése (ionizáció) töltött részecskéknél...
GÁZIONIZÁCIÓS DETEKTOROK VIZSGÁLATA Mérési útmutató Gyurkócza Csaba BME NTI 1997 2 Tartalom 1. BEVEZETÉS... 3 2. ELMÉLETI ÖSSZEFOGLALÁS... 3 2.1. Töltéshordozók keletkezése (ionizáció) töltött részecskéknél...
Milyen erőtörvénnyel vehető figyelembe a folyadék belsejében a súrlódás?
 VALÓDI FOLYADÉKOK A alódi folyadékokban a belső súrlódás ne hanyagolható el. Kísérleti tapasztalat: állandó áralási keresztetszet esetén is áltozik a nyoás p csökken Az áralási sebesség az anyagegaradás
VALÓDI FOLYADÉKOK A alódi folyadékokban a belső súrlódás ne hanyagolható el. Kísérleti tapasztalat: állandó áralási keresztetszet esetén is áltozik a nyoás p csökken Az áralási sebesség az anyagegaradás
Az elektrosztatika törvényei anyag jelenlétében, dielektrikumok
 TÓTH.: Dielektrikumok (kibővített óravázlat) 1 z elektrosztatika törvényei anyag jelenlétében, dielektrikumok z elektrosztatika alatörvényeinek vizsgálata a kezdeti időkben levegőben történt, és a különféle
TÓTH.: Dielektrikumok (kibővített óravázlat) 1 z elektrosztatika törvényei anyag jelenlétében, dielektrikumok z elektrosztatika alatörvényeinek vizsgálata a kezdeti időkben levegőben történt, és a különféle
Traszformátorok Házi dolgozat
 Traszformátorok Házi dolgozat Horváth Tibor lkvm7261 2008 június 1 Traszformátorok A traszformátor olyan statikus (mozgóalkatrészeket nem tartalmazó) elektromágneses átalakító, amely adott jellemzőkkel
Traszformátorok Házi dolgozat Horváth Tibor lkvm7261 2008 június 1 Traszformátorok A traszformátor olyan statikus (mozgóalkatrészeket nem tartalmazó) elektromágneses átalakító, amely adott jellemzőkkel
Atomfizikai összefoglaló: radioaktív bomlás. Varga József. Debreceni Egyetem OEC Nukleáris Medicina Intézet 2010. 2. Kötési energia (MeV) Tömegszám
 Egy nukleonra jutó kötési energia Atomfizikai összefoglaló: radioaktív bomlás Varga József Debreceni Egyetem OEC Nukleáris Medicina Intézet Kötési energia (MeV) Tömegszám 1. 1. Áttekintés: atomfizika Varga
Egy nukleonra jutó kötési energia Atomfizikai összefoglaló: radioaktív bomlás Varga József Debreceni Egyetem OEC Nukleáris Medicina Intézet Kötési energia (MeV) Tömegszám 1. 1. Áttekintés: atomfizika Varga
Balatonfenyves Község Önkormányzata Képviselő-testületének 21/2006 (IX.15) számú rendelete (egységes szerkezetben a módosításokkal)
 Balatonfenyves Község Önkorányzata Képviselő-testületének 21/2006 (IX.15) száú rendelete (egységes szerkezetben a ódosításokkal) BALATOFENYVES KÖZSÉG HELYI ÉPÍTÉSI SZABÁLYZATÁRÓL. Balatonfenyves Község
Balatonfenyves Község Önkorányzata Képviselő-testületének 21/2006 (IX.15) száú rendelete (egységes szerkezetben a ódosításokkal) BALATOFENYVES KÖZSÉG HELYI ÉPÍTÉSI SZABÁLYZATÁRÓL. Balatonfenyves Község
R ND D ZE Z RE R LMÉLET
 0..05. RENDSZERELMÉLET Környezetgazdálodási Agrárérnö MSc Sza 3. félév A rendszer fogala A rendszer egyással ölcsönhatásban álló elee együttese A rendszer és örnyezete: a rendszer határvonalána ijelölése,
0..05. RENDSZERELMÉLET Környezetgazdálodási Agrárérnö MSc Sza 3. félév A rendszer fogala A rendszer egyással ölcsönhatásban álló elee együttese A rendszer és örnyezete: a rendszer határvonalána ijelölése,
ISMÉT FÖLDKÖZELBEN A MARS!
 nikai Vállalat, Audió, EVIG Egyesült Villamosgépgyár, Kismotor- és Gépgyár, Szerszámgép Fejlesztési Intézet (Halásztelek), Pestvidéki Gépgyár (Szigethalom), Ikladi ûszeripari ûvek (II), Kôbányai Vas- és
nikai Vállalat, Audió, EVIG Egyesült Villamosgépgyár, Kismotor- és Gépgyár, Szerszámgép Fejlesztési Intézet (Halásztelek), Pestvidéki Gépgyár (Szigethalom), Ikladi ûszeripari ûvek (II), Kôbányai Vas- és
BEVEZETÉS AZ ÁBRÁZOLÓ GEOMETRIÁBA
 Pék Johanna BEVEZETÉS AZ ÁBRÁZOLÓ GEOMETRIÁBA (Matematika tanárszakos hallgatók számára) Tartalomjegyzék Előszó ii 0. Alapismeretek 1 0.1. Térgeometriai alapok............................. 1 0.2. Az ábrázoló
Pék Johanna BEVEZETÉS AZ ÁBRÁZOLÓ GEOMETRIÁBA (Matematika tanárszakos hallgatók számára) Tartalomjegyzék Előszó ii 0. Alapismeretek 1 0.1. Térgeometriai alapok............................. 1 0.2. Az ábrázoló
1. forduló (2010. február 16. 14 17
 9. MIKOLA SÁNDOR ORSZÁGOS TEHETSÉGKUTATÓ FIZIKAVERSENY 9. frduló (. február 6. 4 7 a. A KITŰZÖTT FELADATOK: Figyele! A verenyen inden egédezköz (könyv, füzet, táblázatk, zálógép) haználható, é inden feladat
9. MIKOLA SÁNDOR ORSZÁGOS TEHETSÉGKUTATÓ FIZIKAVERSENY 9. frduló (. február 6. 4 7 a. A KITŰZÖTT FELADATOK: Figyele! A verenyen inden egédezköz (könyv, füzet, táblázatk, zálógép) haználható, é inden feladat
Fogalmi alapok Mérlegegyenletek
 1. Fogalmi alapok Mérlegegyenletek Utolsó módosítás: 2013. február 11. A transzportfolyamatokról általában 1 A természetben lezajló folyamatok leírására szolgáló összefoglaló elmélet, amely attól függetlenül
1. Fogalmi alapok Mérlegegyenletek Utolsó módosítás: 2013. február 11. A transzportfolyamatokról általában 1 A természetben lezajló folyamatok leírására szolgáló összefoglaló elmélet, amely attól függetlenül
Tető nem állandó hajlású szarufákkal
 1 Tető nem állandó hajlású szarufákkal Már korábbi dolgozatainkban is szó volt a címbeli témáról. Most azért vettük újra elő, mert szép és érdekes ábrákat találtunk az interneten, ezzel kapcsolatban, és
1 Tető nem állandó hajlású szarufákkal Már korábbi dolgozatainkban is szó volt a címbeli témáról. Most azért vettük újra elő, mert szép és érdekes ábrákat találtunk az interneten, ezzel kapcsolatban, és
Mössbauer Spektroszkópia
 Mössbauer Spektroszkópia Homa Gábor, Markó Gergely Mérés dátuma: 2008. 10. 15., 2008. 10. 22., 2008. 11. 05. Leadás dátuma: 2008. 11. 23. Figure 1: Rezonancia-abszorpció és szórás 1 Elméleti összefoglaló
Mössbauer Spektroszkópia Homa Gábor, Markó Gergely Mérés dátuma: 2008. 10. 15., 2008. 10. 22., 2008. 11. 05. Leadás dátuma: 2008. 11. 23. Figure 1: Rezonancia-abszorpció és szórás 1 Elméleti összefoglaló
A MÉRETEZÉS ALAPJAI ÉPÜLETEK TARTÓSZERKEZETI RENDSZEREI ÉS ELEMEI ÉPÜLETEK TERHEINEK SZÁMÍTÁSA AZ MSZ SZERINT
 A MÉRETEZÉS ALAPJAI ÉPÜLETEK TARTÓSZERKEZETI RENDSZEREI ÉS ELEMEI ÉPÜLETEK TERHEINEK SZÁMÍTÁSA AZ MSZ SZERINT ÉPÜLETEK TERHEINEK SZÁMÍTÁSA AZ EUROCODE SZERINT 1 ÉPÜLETEK TARTÓSZERKEZETÉNEK RÉSZEI Helyzetük
A MÉRETEZÉS ALAPJAI ÉPÜLETEK TARTÓSZERKEZETI RENDSZEREI ÉS ELEMEI ÉPÜLETEK TERHEINEK SZÁMÍTÁSA AZ MSZ SZERINT ÉPÜLETEK TERHEINEK SZÁMÍTÁSA AZ EUROCODE SZERINT 1 ÉPÜLETEK TARTÓSZERKEZETÉNEK RÉSZEI Helyzetük
EMELT SZINTŰ ÍRÁSBELI VIZSGA
 É RETTSÉGI VIZSGA 2015. október 22. FIZIKA EMELT SZINTŰ ÍRÁSBELI VIZSGA 2015. október 22. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA
É RETTSÉGI VIZSGA 2015. október 22. FIZIKA EMELT SZINTŰ ÍRÁSBELI VIZSGA 2015. október 22. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA
Széchenyi István Egyetem, 2005
 Gáspár Csaba, Molnárka Győző Lineáris algebra és többváltozós függvények Széchenyi István Egyetem, 25 Vektorterek Ebben a fejezetben a geometriai vektorfogalom ( irányított szakasz ) erős általánosítását
Gáspár Csaba, Molnárka Győző Lineáris algebra és többváltozós függvények Széchenyi István Egyetem, 25 Vektorterek Ebben a fejezetben a geometriai vektorfogalom ( irányított szakasz ) erős általánosítását
RONCSOLÁSMENTES VIZSGÁLATTECHNIKA
 RONCSOLÁSMENTES VIZSGÁLATTECHNIKA NDT TECHNICS FÉMLEMEZEK VASTAGSÁGÁNAK MÉRÉSE RÖNTGENSUGÁRZÁS SEGÍTSÉGÉVEL THICKNESS MEASURING OF METAL SHEETS WITH X-RAY METHODDS BOROMISZA LÁSZLÓ Kulcsszavak: vastagság
RONCSOLÁSMENTES VIZSGÁLATTECHNIKA NDT TECHNICS FÉMLEMEZEK VASTAGSÁGÁNAK MÉRÉSE RÖNTGENSUGÁRZÁS SEGÍTSÉGÉVEL THICKNESS MEASURING OF METAL SHEETS WITH X-RAY METHODDS BOROMISZA LÁSZLÓ Kulcsszavak: vastagság
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Műszaki Mechanikai Tanszék
 Budapesti Műszaki és Gazdaságtudoányi Egyete Gépészérnöki Kar Műszaki Mechanikai Tanszék Hiper és hipoelasztikus testek konstitutív egyenleteinek eléleti és nuerikus vizsgálata DIPLOMATERV Készítette:
Budapesti Műszaki és Gazdaságtudoányi Egyete Gépészérnöki Kar Műszaki Mechanikai Tanszék Hiper és hipoelasztikus testek konstitutív egyenleteinek eléleti és nuerikus vizsgálata DIPLOMATERV Készítette:
Abszolútértékes egyenlôtlenségek
 Abszolútértékes egyenlôtlenségek 575. a) $, $ ; b) < - vagy $, # - vagy > 4. 5 576. a) =, =- 6, 5 =, =-, 7 =, 4 = 5; b) nincs megoldás;! c), = - ; d) =-. Abszolútértékes egyenlôtlenségek 577. a) - # #,
Abszolútértékes egyenlôtlenségek 575. a) $, $ ; b) < - vagy $, # - vagy > 4. 5 576. a) =, =- 6, 5 =, =-, 7 =, 4 = 5; b) nincs megoldás;! c), = - ; d) =-. Abszolútértékes egyenlôtlenségek 577. a) - # #,
Matematika felvételi feladatok bővített levezetése 2013 (8. osztályosoknak)
 Matematika felvételi feladatok bővített levezetése 2013 (8. osztályosoknak) Erre a dokumentumra az Edemmester Gamer Blog kiadványokra vonatkozó szabályai érvényesek. 1. feladat: Határozd meg az a, b és
Matematika felvételi feladatok bővített levezetése 2013 (8. osztályosoknak) Erre a dokumentumra az Edemmester Gamer Blog kiadványokra vonatkozó szabályai érvényesek. 1. feladat: Határozd meg az a, b és
Az aperturaantennák és méréstechnikájuk
 Az aperturaantennák és méréstechnikájuk (tanulmány) Szerzők: Nagy Lajos Lénárt Ferenc Bajusz Sándor Pető Tamás Az aperturaantennák és méréstechnikájuk A vezetékmentes hírközlés, távközlés és távmérés egyik
Az aperturaantennák és méréstechnikájuk (tanulmány) Szerzők: Nagy Lajos Lénárt Ferenc Bajusz Sándor Pető Tamás Az aperturaantennák és méréstechnikájuk A vezetékmentes hírközlés, távközlés és távmérés egyik
Az ablakos problémához
 1 Az ablakos problémához A Hajdu Endre által felvetett, egy ablak akadályoztatott kinyitásával kapcsolatos probléma a következő. Helyezzünk el egy d oldalhosszúságú, álló, négyzet alapú egyenes hasábot
1 Az ablakos problémához A Hajdu Endre által felvetett, egy ablak akadályoztatott kinyitásával kapcsolatos probléma a következő. Helyezzünk el egy d oldalhosszúságú, álló, négyzet alapú egyenes hasábot
Miskolci Egyetem, Gyártástudományi Intézet, Prof. Dr. Dudás Illés
 6. MENETMEGMUNKÁLÁSOK A csavarfelületek egyrészt gépelemek összekapcsolására (kötő menetek), másrészt mechanizmusokban mozgás átadásra (kinematikai menetek) szolgálnak. 6.1. Gyártási eljárások a) Öntés
6. MENETMEGMUNKÁLÁSOK A csavarfelületek egyrészt gépelemek összekapcsolására (kötő menetek), másrészt mechanizmusokban mozgás átadásra (kinematikai menetek) szolgálnak. 6.1. Gyártási eljárások a) Öntés
A SZUPRAVEZETÉS. Fizika. A mágneses tér hatása a szupravezető állapotra
 Fizika A SZUPRAVEZETÉS A szupravezetés jelenségét 80 évvel ezelőtt fedezték fel, de az azóta eltelt idő alatt semmivel sem lankadt a fizikusok érdeklődése e témakör iránt. A szupravezetők tanulmányozása
Fizika A SZUPRAVEZETÉS A szupravezetés jelenségét 80 évvel ezelőtt fedezték fel, de az azóta eltelt idő alatt semmivel sem lankadt a fizikusok érdeklődése e témakör iránt. A szupravezetők tanulmányozása
Kristályszerkezetek és vizsgálatuk
 Kristályszerkezetek és vizsgálatuk Az anyagk tulajdnságait atmjaik fajtája, kémiai kötésük jellege és kristályszerkezete együttesen határzza meg. A fentiekre a szén egy tipikus példa. A tiszta szén gyémánt
Kristályszerkezetek és vizsgálatuk Az anyagk tulajdnságait atmjaik fajtája, kémiai kötésük jellege és kristályszerkezete együttesen határzza meg. A fentiekre a szén egy tipikus példa. A tiszta szén gyémánt
Kiegészítés a Párbeszédes Informatikai Rendszerek tantárgyhoz
 Kiegészítés a Párbeszédes Informatikai Rendszerek tantárgyhoz Fazekas István 2011 R1 Tartalomjegyzék 1. Hangtani alapok...5 1.1 Periodikus jelek...5 1.1.1 Időben periodikus jelek...5 1.1.2 Térben periodikus
Kiegészítés a Párbeszédes Informatikai Rendszerek tantárgyhoz Fazekas István 2011 R1 Tartalomjegyzék 1. Hangtani alapok...5 1.1 Periodikus jelek...5 1.1.1 Időben periodikus jelek...5 1.1.2 Térben periodikus
Nagy Sándor: Magkémia
 Nagy Sándor: Magkémia (kv1c1mg1) 07. Stabilitás & instabilitás, magmodellek, tömegparabolák Nagy Sándor honlapja ismeretterjesztő anyagokkal: http://nagysandor.eu/ A Magkémia tantárgy weboldala: http://nagysandor.eu/magkemia/
Nagy Sándor: Magkémia (kv1c1mg1) 07. Stabilitás & instabilitás, magmodellek, tömegparabolák Nagy Sándor honlapja ismeretterjesztő anyagokkal: http://nagysandor.eu/ A Magkémia tantárgy weboldala: http://nagysandor.eu/magkemia/
XXV. ELEKTROMOS VEZETÉS SZILÁRD TESTEKBEN
 2007. február 6. 1 Pálinkás József: Fizika 2. XXV. ELEKTROMOS VEZETÉS SZILÁRD TESTEKBEN Bevezetés: Az előző fejezetekben megismertük, hogy a kvantumelmélet milyen jól leírja az atomok és a molekulák felépítését.
2007. február 6. 1 Pálinkás József: Fizika 2. XXV. ELEKTROMOS VEZETÉS SZILÁRD TESTEKBEN Bevezetés: Az előző fejezetekben megismertük, hogy a kvantumelmélet milyen jól leírja az atomok és a molekulák felépítését.
Feszített vasbeton gerendatartó tervezése költségoptimumra
 newton Dr. Szalai Kálmán "Vasbetonelmélet" c. tárgya keretében elhangzott előadások alapján k 1000 km k m meter m Ft 1 1 1000 Feszített vasbeton gerendatartó tervezése költségoptimumra deg A következőkben
newton Dr. Szalai Kálmán "Vasbetonelmélet" c. tárgya keretében elhangzott előadások alapján k 1000 km k m meter m Ft 1 1 1000 Feszített vasbeton gerendatartó tervezése költségoptimumra deg A következőkben
7. VIZES OLDATOK VISZKOZITÁSÁNAK MÉRÉSE OSTWALD-FENSKE-FÉLE VISZKOZIMÉTERREL
 7. VIZES OLDATOK VISZKOZITÁSÁNAK MÉRÉSE OSTWALD-FENSKE-FÉLE VISZKOZIMÉTERREL Számos technológiai folyamat, kémiai reakció színtere gáz, vagy folyékony közeg (fluid közeg). Gondoljunk csak a fémek előállításakor
7. VIZES OLDATOK VISZKOZITÁSÁNAK MÉRÉSE OSTWALD-FENSKE-FÉLE VISZKOZIMÉTERREL Számos technológiai folyamat, kémiai reakció színtere gáz, vagy folyékony közeg (fluid közeg). Gondoljunk csak a fémek előállításakor
TARTALOMJEGYZÉK JÓVÁHAGYOTT MUNKARÉSZEK TELEPÜLÉSSZERKEZETI TERV ÉS LEÍRÁSA
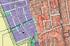 TARTALOMJEGYZÉK JÓVÁHAGYOTT MUNKARÉSZEK TELEPÜLÉSSZERKEZETI TERV ÉS LEÍRÁSA ÉS SZABÁLYOZÁSI TERV I. ÁLTALÁNOS ELŐÍRÁSOK 1 A rendelet hatálya 1 Szabályozási eleek 1 Sajátos jogintézények 2 Fogalo eghatározás
TARTALOMJEGYZÉK JÓVÁHAGYOTT MUNKARÉSZEK TELEPÜLÉSSZERKEZETI TERV ÉS LEÍRÁSA ÉS SZABÁLYOZÁSI TERV I. ÁLTALÁNOS ELŐÍRÁSOK 1 A rendelet hatálya 1 Szabályozási eleek 1 Sajátos jogintézények 2 Fogalo eghatározás
Ha vasalják a szinusz-görbét
 A dolgozat szerzőjének neve: Szabó Szilárd, Lorenzovici Zsombor Intézmény megnevezése: Bolyai Farkas Elméleti Líceum Témavezető tanár neve: Szász Ágota Beosztása: Fizika Ha vasalják a szinusz-görbét Tartalomjegyzék
A dolgozat szerzőjének neve: Szabó Szilárd, Lorenzovici Zsombor Intézmény megnevezése: Bolyai Farkas Elméleti Líceum Témavezető tanár neve: Szász Ágota Beosztása: Fizika Ha vasalják a szinusz-görbét Tartalomjegyzék
5. Mérés Transzformátorok
 5. Mérés Transzformátorok A transzformátor a váltakozó áramú villamos energia, feszültség, ill. áram értékeinek megváltoztatására (transzformálására) alkalmas villamos gép... Működési elv A villamos energia
5. Mérés Transzformátorok A transzformátor a váltakozó áramú villamos energia, feszültség, ill. áram értékeinek megváltoztatására (transzformálására) alkalmas villamos gép... Működési elv A villamos energia
23. ISMERKEDÉS A MŰVELETI ERŐSÍTŐKKEL
 23. ISMEKEDÉS A MŰVELETI EŐSÍTŐKKEL Céltűzés: A műveleti erősítők legfontosabb tlajdonságainak megismerése. I. Elméleti áttentés A műveleti erősítők (továbbiakban: ME) nagy feszültségerősítésű tranzisztorokból
23. ISMEKEDÉS A MŰVELETI EŐSÍTŐKKEL Céltűzés: A műveleti erősítők legfontosabb tlajdonságainak megismerése. I. Elméleti áttentés A műveleti erősítők (továbbiakban: ME) nagy feszültségerősítésű tranzisztorokból
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Geometria I.
 Geometria I. Alapfogalmak: Az olyan fogalmakat, amelyeket nem tudunk egyszerűbb fogalmakra visszavezetni, alapfogalmaknak nevezzük, s ezeket nem definiáljuk. Pl.: pont, egyenes, sík, tér, illeszkedés.
Geometria I. Alapfogalmak: Az olyan fogalmakat, amelyeket nem tudunk egyszerűbb fogalmakra visszavezetni, alapfogalmaknak nevezzük, s ezeket nem definiáljuk. Pl.: pont, egyenes, sík, tér, illeszkedés.
Sztochasztikus folyamatok 1. házi feladat
 Sztochasztikus folyamatok 1. házi feladat 1. Egy borfajta alkoholtartalmának meghatározására méréseket végzünk. Az egyes mérések eredményei egymástól független valószínûségi változók, melyek normális eloszlásúak,
Sztochasztikus folyamatok 1. házi feladat 1. Egy borfajta alkoholtartalmának meghatározására méréseket végzünk. Az egyes mérések eredményei egymástól független valószínûségi változók, melyek normális eloszlásúak,
Cserenkov-sugárzás, sugárzás,
 A Szilárd Leó Fizikaverseny kísérleti feladatai A verseny felépítése Selejtező (3 órás feladatsor, 10 feladat, a tanárok javítják, a továbbküldött dolgozatokat a versenybizottság felüljavítja) 350-400
A Szilárd Leó Fizikaverseny kísérleti feladatai A verseny felépítése Selejtező (3 órás feladatsor, 10 feladat, a tanárok javítják, a továbbküldött dolgozatokat a versenybizottság felüljavítja) 350-400
