A Bolyai-Lobacsevszkij-féle nem-euklideszi geometria felfedezésének és hatásának története 6.
|
|
|
- Krisztina Szilágyi
- 8 évvel ezelőtt
- Látták:
Átírás
1 A Bolyai-Lobacsvszkij-él nm-uklidszi omtria ldzésénk és hatásának történt 6. Tanács János y. adj. BME Filozóia és Tudománytörtént Tsz. MTA-BME Tudománytörtént és Tudományilozóia Kutatócsoport Eyáltalán: mi a jlntés? Fr válasza (Fr-Russll-Carnap stílusú szmantika) Mink az azonossáát állítja az Alkonycsilla azonos a Hajnalcsillaal állítás? A jlntés maa a mnvztt dolo, a rrncia. Mivl az Alkonycsilla és a Hajnalcsilla uyanarra az objktumra vonatkozik (uaz. a rrnciája), és a jlntés maa a mnvztt dolo, zért az Alkonycsilla és a Hajnalcsilla jlntés myzik Eyáltalán: mi a jlntés? Eyáltalán: mi a jlntés? Ha azonban az Alkonycsilla és a Hajnalcsilla rrnciája myzik, éspdi z, mint objktum azonos önmaával, akkor a Alkonycsilla és a Hajnalcsilla jlntés is myzik. Mí azonban Az Alkonycsilla azonos a Alkonycsillaal tautolóiának, és zért smmitmondónak tűnik, Ha azonban íy van, akkor az azonos jlntésű kijzésk salva vritat (az iazsáérték mváltozása nélkül) kicsrélhtők, lcsrélhtők. Thát: Az Alkonycsilla azonos a Alkonycsillaal állításra léphtünk addi az rdti Alkonycsilla azonos a Hajnalcsillaal állítás nm tautolóia, és nm smmitmondó, hanm tartalmas: y mpirikus tényt jz ki, mond valamit a viláról, amit l klltt ismrni vay dzni A jlntés inomabb szrkztű, l kll bontani két komponnsr: intnzió (Frnél értlm ) intraszubjktív, azaz a jbn van, introspktív, azaz maadba mélydv, blső miyléssl raadható m azonossáuk. xtnzió (Frnél jlntés) rrncia, intrszubjktív, azaz külsől is mnyilvánul, közösséil hozzáérhtő és llnőrizhtő, azonossáuk mpirikus miyléssl is tttn érhtő, mraadható. Vannak thát intnzionális és xtnzionális kijzésk és kontxtusok A jlntés két komponns: intraszubjktív (intnzió, introspktív) intrszubjktív (xtnzió, rrncia, jlölt) Eys xtnzionálisan yző kijzéskt (intnzionálisan) azonos jlntésűnk tartunk, másokat nm. Eyző xtnzió yző intnzió: 1. nős éri, érj, házas éri, husband, marrid man 2. alény, nőtln éri, unmarrid man, bachlor Eyző xtnzió különböző intnzió: 1. Tollatlan kétlábú vs. mbr 2. Szívs vs. Vsés
2 Az abszolút, a hiprbolikus és az uklidszi omtria axiomatikus lépítésbn 123. I. Illszkdési axiómák: I 1, I 2,, I 9. II. Rndzési axiómák: III. Eybváósái axiómák: IV. Folytonossái axióma(k): Co. (Olykor ) V. Párhuzamossái axióma: V1. Euklidszi párhuzamossái axióma: AX EP. V2. Hiprbolikus párhuzamossái axióma: AX BLP. A Bolyai-él abszolút omtria: az I-IV. axiómacsoport. Az uklidszi omtria: az I-IV.+ V1. axiómacsoport. A BL-él hiprbolikus omtria: az I-IV.+ V2. axiómacsoport. Az abszolút, a hiprbolikus és az uklidszi omtria 4. axiomatikus lépítésbn 124. BL-él hiprbolikus o. Bolyai-él abszolút o. Euklidszi o. + + AX BLP. AX EP. Bolyai-él abszolút Az o.: ys I-IV. axióma-csoportok axiómacsoport I. Illszkdési axiómák: I 1 : Két különböző ponthoz mindi tartozik y yns, amly mindkttőhöz illszkdik. I 2 : Két különböző ponthoz nm tartozik ynél több olyan yns, amly mindkttőhöz illszkdik II. Rndzési axiómák: O 1 : Ha a B pont az A és a C pontok között van, akkor A, B, C különböző pontok, és y yns pontjai. O 2 : Két ponthoz, A-hoz és C-hz létzik az AC ynsnk lalább y olyan B pontja, hoy C az A és B között van. III. Eybváósái axiómák: (Szakaszok, szök, valamint szök és szakaszok ybváósának ax.-i) C 1 : Ha két szakasz ybváó y harmadikkal, akkor ymással is ybváók. IV. Folytonossái axióma(k): Co. (olykor Co 1, Co 2 ) Co 1 : Arkhimédész-él szakaszlmérési ax. Co 2 : Cantor-él ymásbaskatulyázott intrvallumok ax A nm-uklidszi omtria loadásának kontxtusa: a Fr-Hilbrt vita David Hilbrt A matmatikailozóia ormalista irányzatának malapítója A matmatika ormális tudomány: a ormális, d nm jlntésnélküli szimbólumokkal A matmatikai iazsá és létzés (zisztncia) kizárólaos, szüksés és lésés kritériuma: az axiómák konzisztnciája. Hilbrt Gottlob Frhz intéztt dcmbr 29-i lvl: Ha az önkénysn kiválasztott axiómák nm mondanak llnt ymásnak vay bármly kövtkzményüknk, akkor iazak, és az általuk diniált dolok létznk. Ez számomra az iazsá és a létzés kritériuma A nm-uklidszi omtria loadásának kontxtusa: a Fr-Hilbrt vita Hilbrt a Grundlan dr Gomtri-bn is diniálásról bszél, például a második, úynvztt rndzési axiómacsoport (3. pararaus) közt lvés, között van oalma kapcsán. Ez az axiómacsoport diniálja azt az idát [oalmat], amlyt a között szó kijz Hilbrt szrint thát az axiómák dinícióként unkcionálnak ún. implicit dinícióként. Az axiómák implicit diníciók, amlyk diniálják a bnnük szrplő kijzésk (alapoalmak, primitív kijzésk) jlntését Fr llnvtési: Különbözők a Hilbrt-él axiómarndszr ys részcsoportjai kapcsán. A Hilbrt-él Grundlan második, azaz rndzési axiómacsoportja (3. parar.) kapcsán azzal érvlt, hoy: azt az azért nm tkinthtjük a között oalom diníciójának, mrt az axióma állításai nm képsk madni a jllmző tulajdonsáokat, azaz nm tljsítik azt, amit lvárunk a diníciótól, nvztsn, hoy képssé tyn bnnünkt annak ldöntésér, vajon y adott táry, dolo az úynvztt diniált oalom alá tartozik- vay sm
3 Hilbrt azonban kitartott amlltt, hoy A Hilbrt-él Grundlan lső axiómacsoportja (2. parar., az illszkdés [rajta lvés] axiómái) kapcsán pdi az volt a kioása, hoy a pont, yns, stb. szavak jlntését nm adhatják m az axiómák, hanm azoknak már lőztsn ismrtknk kll lnniük. az ys axiómacsoportok yüttsn képsk mhatározni azon kijzésk jlntését, amlyk bnnük szrplnk, és szüksé stén az axiómák lé biyszthtnénk pld., hoy a között olyan rláció, amly az yns pontjaira vonatkozik, és amlynk a kövtkző jllmző tulajdonsáai vannak: II.1. II.5. (Azaz itt yszrűn csak l kll sorolni a szóban oró axiómákat.) Ha yszr az axiómák konzisztnciája dönti l, hoy az általuk diniált dolok létznk és az axiómák iazak, akkor az axiómák yütts, mint rndszr határozza m (diniálja implicit) a bnnük szrplő kijzésk jlntését, kövtkzésképp: különböző axiómarndszrk különböző (implicit) diníciókat rdményznk, azaz különböző axiómarndszrk ormálisan azonos primitív kijzésink különbözők a jlntési A mondat a lkisbb, önmaában használható nylvi ysé: nm szavakat állítunk, hanm mondatokat, és az, amit l tudunk llnőrizni, amibn tudunk yt értni vay nm értni, az a mondat. Az lső, közvtlnül hozzáérhtő szintn a mondatoknak van, a mondatok kapnak jlntést, nm a szavak. A szavak jlntés közvttt, származtatott a mondat rammatikai szmntálása révén jön, hozható létr a szójlntés. A szmntálhatósá azonban nm yértlműn mhatározott, altrnatív ldarabolások is lképzlhtők, kövtkzésképpn a mondatjlntés lbontása szójlntésr nm yértlmű Ha a szavak címkék a oalmakon, akkor a szójlntés (azaz az intnzionális komponns) ll m a oalomnak, azaz a szójlntés ll m a oalmi taolásnak. Mivl azonban altrnatív taolások lhtsésk szavakra, zért altrnatív oalmi taolások lhtsésk nincs kivétlztt, hlys oalmi taolás, amlyhz képst a többi tévs, oalmi icamokat maában olaló. Ráadásul: Amikor y új, ddi nm használt mondatot alkotunk m, akkor viláos, hoy a mondat jlntés a bnn lőorduló szavak jlntésétől ü: abból hozzuk létr, abból alkotjuk m (kompozicionalitás). Uyanakkor a mondat használatának, iaznak tartásának körülményi hozzá is járulnak a bnn lőorduló szavak jlntéséhz A szavak jlntését az határozza m, hoy milyn iaz mondatokban ordulnak lő. A szavak kapcsolólmk: kapcsolatot trmtnk az ys ormaila, rammatikaila különböző mondatok között. Ennélova: y mondat jlntés, iazsáérték a nylv többi mondatához űződő viszonyán is múlik: a viszonyt a szavak hozzák létr, rdmény pdi az, hoy y adott mondat jlntését más, loikaila nm ütln mondatok jlntés, iazsáérték, iaznak tartásának körülményi is bolyásolnak. Összolalva: Ey nylvi ysé jlntés a nylv jlntésrndszrénk észébn lolalt hlyén múlik. Ha thát y mondat jlntés, iazsáérték mváltozik, akkor más mondatok jlntés, iazsáérték is változni o
4 Az abszolút, a hiprbolikus (nmuklidszi) és az uklidszi omtria ymáshoz való ormális viszonyai Bolyai-él abszolút omtria (AGB) axiómarndszrénk jlölés: AX AGB Az uklidszi omtria (EG) axiómarndszr: AX EG A hiprbolikus omtria (BL-omtria) axiómarndszrénk jlölés: AX BLG Az uklidszi párhuzamossái axióma jlölés: AX EP A hiprbolikus párhuzamossái axióma jlölés: AX BLP Az axiómarndszrk közötti viszony: AX EG = AX AGB + AX EP AX BLG = AX AGB + AX BLP A párhuzamossái axiómák közötti viszony ormálisan: AX EP = ~ AX BLP ~AX EP = AX BLP AX EP = AX BLP =1, szmbn azzal, hoy a klasszikus (kétértékű) loika szrint: ha p = 1, akkor ~p = 0, és ordítva Az axiómarndszrk holizmusa az abszolút, a B-L-él hiprbolikus és az uklidszi omtria axiómarndszrir Változás kövtkzik b y axiómarndszr által implicit mhatározott kijzésk jlntésébn, ha 1. az axiómarndszrt új, ütln (nm lvzthtő) axiómával bővítjük: AX AGB AX EG (=AX AGB + AX EP) átmnt, vay AX AGB AX BLG (=AX AGB + AX BLP) átmnt. 2. mváltozik az adott axiómahalmaz valamly lménk iazsáérték: AX EG AX BLG átmnt oda-vissza Az axiómarndszrk holizmusa Jlntésváltozás áll lő y adott axiómarndszr ütln axiómával történő kiészítés kövtkztébn: Mivl az uklidszi, illtv a BL-él hiprbolikus omtriát az abszolút omtria kitrjsztésiként kapjuk, zért az új (párhuzamossái) axiómák hozzáadása kövtkztébn az alapoalmak ormális azonossáa llnér jlntésük mváltozik; az uklidszi, illtől a BL-él hiprbolikus omtria alapoalmainak jlntés az abszolút omtria alapoalmainak jlntéséhz viszonyítva különböző. Jlntésváltozás az adott axiómahalmaz valamly lménk iazsáérték-változása kövtkztébn: Mivl a párhuzamossái axiómák ymásnak ormális taadásai, zért mindn további yzés llnér az uklidszi és BL-él hiprbolikus omtriában az alapoalmak jlntés ymáshoz viszonyítva a kijzésk ormális azonossáa llnér különböző Fr: Ha az axiómák diniálják a kijzésk jlntését, akkor az axiómarndszr y lménk ltávolítása, például a párhuzamossái axióma ltávolítása az uklidszi omtria axiómarndszréből, lkrülhttlnül mváltoztatja az általuk diniált kijzésk jlntését. Hilbrt: (Pontosan rről van szó.) ( ) loásom szrint lhttlnsé mkísérlni madni a pont dinícióját három sorban, mivl csak az axiómák tljs rndszr rdményz tljs diníciót. Mindn axióma hozzájárul a(z implicit) dinícióhoz, és záltal mindn új axióma változtat a oalmon. A pont az uklidszi, a nm-uklidszi, az arkhimédészi és a nm-arkhimédészi omtriák mindyikébn valamlyst különbözik Fr álláspontjának rkonstrukciója Az alapoalmak jlntés az axiómarndszrn kívülről származik, kívülről adott. A oalmak jlntés mhatározott, rözíttt és véérvénys (mir blépünk az ax. rsz.-b). A jlntés képssé tsz annak ldöntésér, hoy adott kijzés mir vonatkozik. (Ha a jlntés, ahoy Hilbrt mondja változik, akkor a BL-él hiprb. és az ukl. o. kijzési pl. az yns különbözők, ro nm uyanarra vonatkoznak, nm uyanazt írják l. Hilbrt álláspontjának rkonstrukciója Az alapoalmak jlntés nm az axiómarndszrn kívülről származik, nm kívülről adott, hanm az axiómák határozzák m implicit a jlntést. Az (alap)oalmak jlntés csak annyiban mhatározott, amnnyibn az ax. rsz. mhatározni képs. Különböző ax. rsz.-k különböző jlntést határoznak m: a jlntés változik. (Hoy mnnyir változik/ különböző, azt az ax. rsz. intrprtáción krsztül vizsálható: jlntést ténylsn az intrprtációban /modll/ nyrik l.) 139. Hoyan alkossunk újabb omtriákat? Nm is yt, Az abszolút omtria szközivl bizonyítható, hoy: Ha adott y yns és y hozzá nm illszkdő P pont, akkor az általuk mhatározott síkban létzik lalább y olyan yns, amly átmy P-n, és nm mtszi -t. Bizonyítható thát a nm mtsző ynsk létzés. Miért nm kll thát stszétválasztást csinálnunk a hiprbolikus omtria párhuzamossái axiómájának állításakor, amly az uklidszi omtria párhuzamossái axiómájának ormális taadása, és hlysn a kövtkzőképpn hanzana: Nm iaz, hoy ha adott y yns és y hozzá nm illszkdő P pont, akkor az általuk mhatározott síkban létzik pontosan y (y és csak y) olyan yns, amly átmy P-n, és nm mtszi -t
5 Hoyan alkossunk újabb omtriákat? Nm is yt, Az abszolút omtriában (a ormális taadás) thát csak az hayja nyitva, hoy pontosan y nm mtsző létzik, vay ynél több nm mtsző létzik. Kövtkzésképpn, az absz. o.-ban hamis az az állítás (llntmondásra vzt), hoy: (R) Nincsnk nm mtsző ynsk. Ha adott y yns és y hozzá nm illszkdő P pont, akkor az általuk mhatározott síkban létzik nm létzik olyan yns, amly átmy P-n, és nm mtszi -t. Nézzük m vázlatosan, hoyan lhtn bbizonyítani, hoy R hamis! 141. Hoyan alkossunk újabb omtriákat? Nm is yt, Külsőszö-tétl (T1): Az yik oldal mhosszabbításakor kltkző külső szö mindn háromszöbn nayobb, mint a két szmközti blső szö. 180º - α > ; 180º - α > γ. T2: Ha két, uyanabban a síkban kvő és ynst úy mtsz l y harmadik yns, hoy azoknak az és ynskkl alkotott llntéts irányítású (altrnáló) blső szö ynlő, akkor az rdti két és yns nm mtszi ymást. C α B γ A α 180º-α 142. Hoyan alkossunk újabb omtriákat? Nm is yt, T.. h., hoy és mtszi ymást a C pontban úy, hoy a által létrhozott α és szök ynlők. Ha és mtszné ymást a C pontban úy, hoy a által létrhozott α és szök ynlők lnnénk, akkor az yik külső szö () ynlő lnn y másik blső szöl (α): llntmondás. Thát: és nm mtszi ymást. T3: Ha két és yns mrőls uyanarra a ynsr, akkor a két yns nm mtszi ymást. C α B A 143. α * A B P α = * = 90º??? Hoyan alkossunk újabb omtriákat? Nm is yt, T4: 144. Ey adott ynshz y rajta kívül kvő pontból csak ytln mrőls yns húzható. Ha a P pontból lhtn lalább két különböző mrőlst húzni az ynshz, akkor a PAB háromszö * külső szö ynlő lnn a nm mlltt kvő α blső szöl T1 külsőszö-tétl. T5 (konstruktív bizonyítás): P-ből mrőlst bocsátva ynsr, majd P-bn az íy kapott ynsr mrőlst állítva (), és ynsk nm mtszik ymást. P Q Mit adjunk l? Mit adhatunk mé l konzisztnsn? 145. Mit adjunk l az axiómák közül, ha szrtnénk a kövtkzőt állítani és lvnni axiómáink közé? (R) Nincsnk nm mtsző ynsk. AX AGB + R yütt inkonzisztns rndszrt alkotnak. El tudunk- távolítani csupán ytln axiómát úy, hoy a mmaradók yütt konzisztns rndszrt alkossanak, azaz összérjnk az R állítással? Ki tudjuk- jlölni, vissza tudjuk- jtni az az axiómát (vay axiómákat), amly(k)től R iazsáa közvtlnül ü? 5
DIFFERENCIÁLSZÁMÍTÁS. 1. A differenciálhányados fogalma
 DIFFERENCIÁLSZÁMÍTÁS A dirnciálhánados oalma Példa: Ln adva a koordinátarndszrbn üvén raikonja (örbéj) és vizsáljuk, ho adott pontjához hoan lhtn érintőt húzni Mivl adott ( ( )) ponton át ismrt mrdkséű
DIFFERENCIÁLSZÁMÍTÁS A dirnciálhánados oalma Példa: Ln adva a koordinátarndszrbn üvén raikonja (örbéj) és vizsáljuk, ho adott pontjához hoan lhtn érintőt húzni Mivl adott ( ( )) ponton át ismrt mrdkséű
1. A keresztrejtvény megfejtésével megtudhatod, hogy mi volt első Anjou-házi királyunk születési neve.
 Nvd: Flkészítő tanárod... 7 Iskolád: Elért pontszámod:... / 92pont 1. A krsztrjtvény mfjtésévl mtudhatod, hoy mi volt lső Anjou-házi királyunk szültési nv. a) b) c) d) ) f) ) h) i) j) a) a lhatalmasabb
Nvd: Flkészítő tanárod... 7 Iskolád: Elért pontszámod:... / 92pont 1. A krsztrjtvény mfjtésévl mtudhatod, hoy mi volt lső Anjou-házi királyunk szültési nv. a) b) c) d) ) f) ) h) i) j) a) a lhatalmasabb
A Mozilla ThunderBird levelezőprogram haszálata (Készítette: Abonyi-Tóth Zsolt, SZIE ÁOTK, 2004-04-15, Version 1.1)
 A Mozilla ThundrBird lvlzőprogram haszálata (Készíttt: Abonyi-Tóth Zsolt, SZIE ÁOTK, 2004-04-15, Vrsion 1.1) Tartalomjgyzék Tartalomjgyzék...1 A Központi Lvlző Szrvr használata... 1 A ThundrBird lvlzőprogram
A Mozilla ThundrBird lvlzőprogram haszálata (Készíttt: Abonyi-Tóth Zsolt, SZIE ÁOTK, 2004-04-15, Vrsion 1.1) Tartalomjgyzék Tartalomjgyzék...1 A Központi Lvlző Szrvr használata... 1 A ThundrBird lvlzőprogram
Az Integrációs Pedagógiai Rendszer projektelemeinek beépülése
 Az Intgrációs Pdagógiai Rndszr projtlmin bépülés a Fsttics Kristóf Általános Művlődési Központ Póaszpti 1-8. évfolyamos és a Paodi 1-4. évfolyamos Általános Isola tagintézményin otató-nvlő munájába 2011/2012.
Az Intgrációs Pdagógiai Rndszr projtlmin bépülés a Fsttics Kristóf Általános Művlődési Központ Póaszpti 1-8. évfolyamos és a Paodi 1-4. évfolyamos Általános Isola tagintézményin otató-nvlő munájába 2011/2012.
6. előadás Véges automaták és reguláris nyelvek
 Formális nylvk és automaták Széchnyi István Egytm 6. lőadás Végs automaták és rguláris nylvk dr. Kallós Gábor 2017 2018 Formális nylvk és automaták Széchnyi István Egytm Tartalom Zártsági tulajdonságok
Formális nylvk és automaták Széchnyi István Egytm 6. lőadás Végs automaták és rguláris nylvk dr. Kallós Gábor 2017 2018 Formális nylvk és automaták Széchnyi István Egytm Tartalom Zártsági tulajdonságok
Mágneses anyagok elektronmikroszkópos vizsgálata
 Mágnss anyagok lktronmikroszkópos vizsgálata 1. Transzmissziós lktronmikroszkóp 1.1. A mágnss kontraszt rdt a TEM-bn Az lktronmikroszkópban 100-200 kv-os (stlg 1 MV-os) gyorsítófszültséggl gyorsított lktronok
Mágnss anyagok lktronmikroszkópos vizsgálata 1. Transzmissziós lktronmikroszkóp 1.1. A mágnss kontraszt rdt a TEM-bn Az lktronmikroszkópban 100-200 kv-os (stlg 1 MV-os) gyorsítófszültséggl gyorsított lktronok
Matematika záróvizsga Név:... osztály:... =...
 Mtmtik záróvizs 004. Név:... osztály:... 1. Számíts ki kijzésk hlyttsítési értékét! = =. + 4 =.... ( : =.... =... 0 1. =.... Mlyik átváltás hiás? A hlyskt jlöl pipávl, hiás átváltásoknál húz át z ynlőséjlt!.
Mtmtik záróvizs 004. Név:... osztály:... 1. Számíts ki kijzésk hlyttsítési értékét! = =. + 4 =.... ( : =.... =... 0 1. =.... Mlyik átváltás hiás? A hlyskt jlöl pipávl, hiás átváltásoknál húz át z ynlőséjlt!.
Nyugat-magyarországi Egyetem Regionális Pedagógiai Szolgáltató és Kutató Központ
 Nyuat-mayarorszái Eytm Rionális Pdaóiai Szoláltató és Kutató Központ Orszáos Történlm Tantáryi Vrsny 7-8. évfolyamos tanulók számára Iskolai forduló 2014/2015 Szrkszttt: Dobosné Csoknyai Ccília Mérésmtodikai
Nyuat-mayarorszái Eytm Rionális Pdaóiai Szoláltató és Kutató Központ Orszáos Történlm Tantáryi Vrsny 7-8. évfolyamos tanulók számára Iskolai forduló 2014/2015 Szrkszttt: Dobosné Csoknyai Ccília Mérésmtodikai
MINŐSÉGIRÁNYÍTÁSI KÉZIKÖNYV
 Lap: 1/145 AZ INCZÉDY GYÖRGY KÖZÉPISKOLA, SZAKISKOLA ÉS KOLLÉGIUM MINŐSÉGIRÁNYÍTÁSI E AZ MSZ EN ISO 9001 SZABVÁNY ALAPJÁN, ILLETVE MINŐSÉGIRÁNYÍTÁSI PROGRAMJA A KÖZOK-TATÁSI TÖR- VÉNY (1993. ÉVI LXXIX.)
Lap: 1/145 AZ INCZÉDY GYÖRGY KÖZÉPISKOLA, SZAKISKOLA ÉS KOLLÉGIUM MINŐSÉGIRÁNYÍTÁSI E AZ MSZ EN ISO 9001 SZABVÁNY ALAPJÁN, ILLETVE MINŐSÉGIRÁNYÍTÁSI PROGRAMJA A KÖZOK-TATÁSI TÖR- VÉNY (1993. ÉVI LXXIX.)
Áramlástechnikai gépek Hidraulikus tápegység mérése (jegyzőkönyv)
 Áramlástcnikai épk Hidraulikus tápysé mérés (jyzőkönyv) Mérés idj: 011. március. 01. Mérés ly: BME Hidrodinamikai Rndszrk Tanszék Laboratóriuma Mérésvztő: Mérőszmélyzt névsora: Budapst, 011. 0. 01. A mérés
Áramlástcnikai épk Hidraulikus tápysé mérés (jyzőkönyv) Mérés idj: 011. március. 01. Mérés ly: BME Hidrodinamikai Rndszrk Tanszék Laboratóriuma Mérésvztő: Mérőszmélyzt névsora: Budapst, 011. 0. 01. A mérés
1.2. Értelmezd a megfejtésül kapott fogalmat!.
 Orszáos Történlm Tantáryi Vrsny 7-8. osztályos tanulók számára ISKOLAI FORDULÓ Nyuat-mayarorszái Eytm Rionális Pdaóiai Szoláltató és Kutató Központ 2014/2015 Nvd: Iskolád: 1.1. Fjtsd m a középkori Európa
Orszáos Történlm Tantáryi Vrsny 7-8. osztályos tanulók számára ISKOLAI FORDULÓ Nyuat-mayarorszái Eytm Rionális Pdaóiai Szoláltató és Kutató Központ 2014/2015 Nvd: Iskolád: 1.1. Fjtsd m a középkori Európa
1. AZ MI FOGALMA. I. Bevezetés ELIZA. Első szakasz (60-as évek) Második szakasz (70-es évek) Harmadik szakasz (80-as évek)
 1. AZ MI FOGALMA I. Bvztés 1956 nyár. Darthmouth Collg-i konfrncia Kzdti cél: Az mbri gondolkodás számítógép sgítségévl történő rprodukálása. Grgorics Tibor Bvztés a mstrségs intllignciába 1 Grgorics Tibor
1. AZ MI FOGALMA I. Bvztés 1956 nyár. Darthmouth Collg-i konfrncia Kzdti cél: Az mbri gondolkodás számítógép sgítségévl történő rprodukálása. Grgorics Tibor Bvztés a mstrségs intllignciába 1 Grgorics Tibor
A művészeti galéria probléma
 A műészti galéria probléma A műészti galéria probléma (art galry problm): A műészti galéria mgfigylés kamrákkal / őrökkl. Hálózattrzés Alapjai 2007 8: Műészti Galéria Probléma Őrzési / Mgilágítási problémák
A műészti galéria probléma A műészti galéria probléma (art galry problm): A műészti galéria mgfigylés kamrákkal / őrökkl. Hálózattrzés Alapjai 2007 8: Műészti Galéria Probléma Őrzési / Mgilágítási problémák
A hőmérsékleti sugárzás
 A hőmérséklt sugárzás (Dr. Parpás Béla lőadása alapján ljgyzték a Mskolc gytm harmadévs nformatkus hallgató) Alapjlnségk Mndnnap tapasztalat, hogy a mlgíttt tstk hősugárzást (nfravörös sugárzást) bocsátanak
A hőmérséklt sugárzás (Dr. Parpás Béla lőadása alapján ljgyzték a Mskolc gytm harmadévs nformatkus hallgató) Alapjlnségk Mndnnap tapasztalat, hogy a mlgíttt tstk hősugárzást (nfravörös sugárzást) bocsátanak
Az optimális szabadalmak elméletének magatartásgazdaságtani és nemzetközi közgazdasági kiterjesztése
 Szdi Tudományym Gazdasáudományi Ka Közazdasáani Dokoi Iskola Nay Bndk Az opimális szabadalmak lmélénk maaaásazdasáani és nmzközi közazdasái kijszés Dokoi ékzés Témavzők: Pof. D. Hámoi Balázs CSc Eymi aná
Szdi Tudományym Gazdasáudományi Ka Közazdasáani Dokoi Iskola Nay Bndk Az opimális szabadalmak lmélénk maaaásazdasáani és nmzközi közazdasái kijszés Dokoi ékzés Témavzők: Pof. D. Hámoi Balázs CSc Eymi aná
ÉPÍTÕ- ÉS SZERELÕIPARI ÉPÜLETSZERKEZETEK Kõmûves szerkezetek
 Mayar Köztársasá ÉPÍTÉSÜGYI ÁGAZATI SZABVÁNY ÉPÍTÕ- ÉS SZERELÕIPARI ÉPÜLETSZERKEZETEK Kõmûvs szrkztk MSZ-04-803/1-1990 Az MSZ-04-803/1-1981 lytt G 33 BUILDING STRUCTURES FOR BUILDING AND FITTING Masonry
Mayar Köztársasá ÉPÍTÉSÜGYI ÁGAZATI SZABVÁNY ÉPÍTÕ- ÉS SZERELÕIPARI ÉPÜLETSZERKEZETEK Kõmûvs szrkztk MSZ-04-803/1-1990 Az MSZ-04-803/1-1981 lytt G 33 BUILDING STRUCTURES FOR BUILDING AND FITTING Masonry
Teherhordó üveg födémszerkezet: T gerenda ragasztott öv-gerinc kapcsolatának numerikus vizsgálata
 Tudományos Diákköri Konrncia Thrhordó üvg ödémszrkzt: T grnda ragasztott öv-grinc kapcsolatának numrikus vizsgálata Készíttt: Gál Tamás F17JCS építőmérnök hallgató Konzulns: Dr. Vigh László Grgly Egytmi
Tudományos Diákköri Konrncia Thrhordó üvg ödémszrkzt: T grnda ragasztott öv-grinc kapcsolatának numrikus vizsgálata Készíttt: Gál Tamás F17JCS építőmérnök hallgató Konzulns: Dr. Vigh László Grgly Egytmi
JT 379 www.whirlpool.com
 JT 379.hirlpool.com A HÁLÓZATRA CSATLAKOZTATÁS ELŐTT ÜZEMBE HELYEZÉS ELLENŐRIZZE, HOGY A TÖRZSLAPON jlztt fszültség mggyzik- a lakás fszültségévl. NE TÁVOLÍTSA EL A MIKROLLÁM-BEVEZETÉST VÉDŐ LEMEZEKET,
JT 379.hirlpool.com A HÁLÓZATRA CSATLAKOZTATÁS ELŐTT ÜZEMBE HELYEZÉS ELLENŐRIZZE, HOGY A TÖRZSLAPON jlztt fszültség mggyzik- a lakás fszültségévl. NE TÁVOLÍTSA EL A MIKROLLÁM-BEVEZETÉST VÉDŐ LEMEZEKET,
Villamos érintésvédelem
 Villamos érintésvédlm A villamos nrgia ipari mértű flhasználása a század ljén kzdtt gyr nagyobb mértékbn ltrjdni és zzl gyidőbn jlntkztk az áramütésből rdő balstk is. Ennk kövtkztébn nagyarányú kutatás
Villamos érintésvédlm A villamos nrgia ipari mértű flhasználása a század ljén kzdtt gyr nagyobb mértékbn ltrjdni és zzl gyidőbn jlntkztk az áramütésből rdő balstk is. Ennk kövtkztébn nagyarányú kutatás
2. A geometria alapfogalmai A geometria alapfogalmai: pont, vonal, egyenes, sík, tér.
 1. Mi z lpfoglom? Alpfoglom: olyn foglom, mit ismrtnk fogdunk l, nm tudunk más foglmk sgítségévl mghtározni, dfiniálni, lgflj szmléltsn körülírjuk. Mindn tudomány ilyn lpfoglmkr épül fl. (Egy foglmt úgy
1. Mi z lpfoglom? Alpfoglom: olyn foglom, mit ismrtnk fogdunk l, nm tudunk más foglmk sgítségévl mghtározni, dfiniálni, lgflj szmléltsn körülírjuk. Mindn tudomány ilyn lpfoglmkr épül fl. (Egy foglmt úgy
Országos Szilárd Leó fizikaverseny feladatai
 Országos Szilárd Ló fizikavrsny fladatai I katgória döntő, 5 április 9 Paks A fladatok mgoldásáoz 8 prc áll rndlkzésr Mindn sgédszköz asználató Mindn fladatot külön lapra írjon, s mindn lapon lgyn rajta
Országos Szilárd Ló fizikavrsny fladatai I katgória döntő, 5 április 9 Paks A fladatok mgoldásáoz 8 prc áll rndlkzésr Mindn sgédszköz asználató Mindn fladatot külön lapra írjon, s mindn lapon lgyn rajta
Gráfelmélet (2017. február 15.) Bogya Norbert, Kátai-Urbán Kamilla
 rálmélt (2017. ruár 15.) Boy Norrt, Káti-Urán Kmill A ráok z inormtikán ykrn lőoruló mtmtiki struktúrák. Az intrnt is lotó y ráként, kár y ott épült villmos álózt is. Az mrk közötti ismrtsék is kzltők
rálmélt (2017. ruár 15.) Boy Norrt, Káti-Urán Kmill A ráok z inormtikán ykrn lőoruló mtmtiki struktúrák. Az intrnt is lotó y ráként, kár y ott épült villmos álózt is. Az mrk közötti ismrtsék is kzltők
Modern piacelmélet. ELTE TáTK Közgazdaságtudományi Tanszék. Selei Adrienn
 Modrn piaclmélt ELTE TáTK Közgazdaságtudományi Tanszék Sli Adrinn A tananyag a Gazdasági Vrsnyhiatal Vrsnykultúra Központja és a Tudás-Ökonómia Alapítány támogatásáal készült az ELTE TáTK Közgazdaságtudományi
Modrn piaclmélt ELTE TáTK Közgazdaságtudományi Tanszék Sli Adrinn A tananyag a Gazdasági Vrsnyhiatal Vrsnykultúra Központja és a Tudás-Ökonómia Alapítány támogatásáal készült az ELTE TáTK Közgazdaságtudományi
4. Differenciálszámítás
 . Diffrnciálszámítás.. Írja fl a diffrnciahányadost a mgadott pontban és határozza mg a határértékét!... f...... f..7. f, f,,..9. f... f... f... f...... f..7...9. f...... f... f... f...,..6. f,,,, f,..8.
. Diffrnciálszámítás.. Írja fl a diffrnciahányadost a mgadott pontban és határozza mg a határértékét!... f...... f..7. f, f,,..9. f... f... f... f...... f..7...9. f...... f... f... f...,..6. f,,,, f,..8.
10. Határozatlan integrál
 0. Htároztln intrál Diníciók, lpszbályok H F =, zz F üvény rivált szármzék üvény, kkor F üvényt primitív ős üvényénk nvzzük. F mlltt bármly F+ üvény is primitív üvény -nk, hol ttszőls vlós állnó, mivl
0. Htároztln intrál Diníciók, lpszbályok H F =, zz F üvény rivált szármzék üvény, kkor F üvényt primitív ős üvényénk nvzzük. F mlltt bármly F+ üvény is primitív üvény -nk, hol ttszőls vlós állnó, mivl
MUNKAANYAG, A KORMÁNY ÁLLÁSPONTJÁT NEM TÜKRÖZI
 Az önkormányzati és trültfjlsztési minisztr../2008. (..) ÖTM rndlt a katasztrófavédlmi szrvk és az önkormányzati tűzoltóság hivatásos szolgálati viszonyban álló tagjaival kapcsolatos munkáltatói jogkörök
Az önkormányzati és trültfjlsztési minisztr../2008. (..) ÖTM rndlt a katasztrófavédlmi szrvk és az önkormányzati tűzoltóság hivatásos szolgálati viszonyban álló tagjaival kapcsolatos munkáltatói jogkörök
- 1 - A következ kben szeretnénk Önöknek a LEGO tanítási kultúráját bemutatni.
 Játékok a tanításhoz? - 1 - Tanító játékok? A Lgo kockák gészn biztosan fontos szívügyi gy gész sor gyrk és szül gnráció éltébn. Mi köz van a Lgo kockáknak a tanuláshoz? Vagy lht gyáltalán tanítani /órákat
Játékok a tanításhoz? - 1 - Tanító játékok? A Lgo kockák gészn biztosan fontos szívügyi gy gész sor gyrk és szül gnráció éltébn. Mi köz van a Lgo kockáknak a tanuláshoz? Vagy lht gyáltalán tanítani /órákat
(2) A d(x) = 2x + 2 függvénynek van véges határértéke az x0 = 1 helyen, így a differenciálhányados: lim2x
 DIFFERENCIÁLSZÁMÍTÁS MINTAPÉLDÁK.. Példa. Határozzuk mg az f = függvénnk az = hlhz tartozó diffrnciahánados függvénét, majd vizsgáljuk mg, hog f diffrnciálható- az -ban adjuk mg az = hlhz tartozó diffrnciálhánadost.
DIFFERENCIÁLSZÁMÍTÁS MINTAPÉLDÁK.. Példa. Határozzuk mg az f = függvénnk az = hlhz tartozó diffrnciahánados függvénét, majd vizsgáljuk mg, hog f diffrnciálható- az -ban adjuk mg az = hlhz tartozó diffrnciálhánadost.
ISO 9000 és ISO 20000, minőségmenedzsment és információtechnológiai szolgáltatások menedzsmentje egy szervezeten belül
 ISO 9000 és ISO 20000, minőségmndzsmnt és információtchnológiai szolgáltatások mndzsmntj gy szrvztn blül dr. Vondrviszt Lajos, Vondrviszt.Lajos@nhh.hu Nmzti Hírközlési Hatóság Előzményk A kormányzati intézményk
ISO 9000 és ISO 20000, minőségmndzsmnt és információtchnológiai szolgáltatások mndzsmntj gy szrvztn blül dr. Vondrviszt Lajos, Vondrviszt.Lajos@nhh.hu Nmzti Hírközlési Hatóság Előzményk A kormányzati intézményk
DR. JUHÁSZ MÁRTA BME Ergonómia és Pszichológia Tanszék 1111 Budapest, Egry J. u. 1. Email: juhaszm@erg.bme.hu Tel: 1/463 40 22 www.erg.bme.
 DR. JUHÁSZ MÁRTA BME Ergonómia és Pszichológia Tanszék 1111 Budapst, Egry J. u. 1. Email: juhaszm@rg.bm.hu Tl: 1/463 40 22 www.rg.bm.hu A KIVÁLASZTÁS ÉS A MUNKAKÖRI ALKALMASSÁG PSZICHOLÓGIÁJA II. Az lızı
DR. JUHÁSZ MÁRTA BME Ergonómia és Pszichológia Tanszék 1111 Budapst, Egry J. u. 1. Email: juhaszm@rg.bm.hu Tl: 1/463 40 22 www.rg.bm.hu A KIVÁLASZTÁS ÉS A MUNKAKÖRI ALKALMASSÁG PSZICHOLÓGIÁJA II. Az lızı
53. sz. mérés. Hurokszabályozás vizsgálata
 53. sz. mérés Hurokszaályozás vizsgálata nagyszültségű alap- illtv losztóhálózat (4,, kv a hálózatok unkcióáól kövtkzőn hurkolt (töszörösn hurkolt kialakítású. sok csomóponttal, tö táplálási illtv ogyasztási
53. sz. mérés Hurokszaályozás vizsgálata nagyszültségű alap- illtv losztóhálózat (4,, kv a hálózatok unkcióáól kövtkzőn hurkolt (töszörösn hurkolt kialakítású. sok csomóponttal, tö táplálási illtv ogyasztási
Város Polgármestere ELŐTERJESZTÉS
 Város Polgármstr 251 Biatorbágy, Baross Gábor utca 2/a Tlfon: 6 23 31-174/233 mllék Fax: 6 23 31-135 E-mail: bruhazas@biatorbagy.hu www.biatorbagy.hu ELŐTERJESZTÉS Budapst Balaton közötti krékpárút nyomvonalával
Város Polgármstr 251 Biatorbágy, Baross Gábor utca 2/a Tlfon: 6 23 31-174/233 mllék Fax: 6 23 31-135 E-mail: bruhazas@biatorbagy.hu www.biatorbagy.hu ELŐTERJESZTÉS Budapst Balaton közötti krékpárút nyomvonalával
Néhány pontban a függvény értéke: x -4-2 -1-0.5 0.5 1 2 4 f (x) -0.2343-0.375 0 6-6 0 0.375 0.2343
 Házi ladatok mgoldása 0. nov.. HF. Elmzz az ( ) = üggvényt (értlmzési tartomány, olytonosság, határérték az értlmzési tartomány véginél és a szakadási pontokban, zérushly, y-tnglymtszt, monotonitás, lokális
Házi ladatok mgoldása 0. nov.. HF. Elmzz az ( ) = üggvényt (értlmzési tartomány, olytonosság, határérték az értlmzési tartomány véginél és a szakadási pontokban, zérushly, y-tnglymtszt, monotonitás, lokális
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Koordináta-gomtria A szürkíttt háttrű fladatrészk nm tartoznak az érinttt témakörhöz, azonban szolgálhatnak fontos információval az érinttt fladatrészk mgoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Koordináta-gomtria A szürkíttt háttrű fladatrészk nm tartoznak az érinttt témakörhöz, azonban szolgálhatnak fontos információval az érinttt fladatrészk mgoldásához!
A szelepre ható érintkezési erő meghatározása
 A szlpr ható érintkzési rő mghatározása Az [ 1 ] műbn az alábbi fladatot találtuk. A fladat: Adott az ábra szrinti szlpmlő szrkzt. Az a xcntricitással szrlt R sugarú bütyök / körtárcsa ω 1 állandó szögsbsséggl
A szlpr ható érintkzési rő mghatározása Az [ 1 ] műbn az alábbi fladatot találtuk. A fladat: Adott az ábra szrinti szlpmlő szrkzt. Az a xcntricitással szrlt R sugarú bütyök / körtárcsa ω 1 állandó szögsbsséggl
Szerző: Böröcz Péter János H-9026, Egyetem tér 1. Győr, Magyarország
 In: Kóczy L, éánczos L, Bakó A, Prznszki J, Szgdi Z, Várlaki P (szrk.) Játéklmélt alkalmazási lhtőségi a logisztikai rndszrkbn - az gy- és többutas szállítási csomagolási szközök közötti döntéslmélti probléma
In: Kóczy L, éánczos L, Bakó A, Prznszki J, Szgdi Z, Várlaki P (szrk.) Játéklmélt alkalmazási lhtőségi a logisztikai rndszrkbn - az gy- és többutas szállítási csomagolási szközök közötti döntéslmélti probléma
FIZIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Fizika középszint 080 ÉRETTSÉGI VIZSGA 008. novmbr. FIZIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM A dolgozatokat az útmutató utasításai szrint,
Fizika középszint 080 ÉRETTSÉGI VIZSGA 008. novmbr. FIZIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM A dolgozatokat az útmutató utasításai szrint,
2011. évi intézmény-felújítás,intézményi javaslatok
 agasépítési csoport PRIORITÁSOK: BRH=biztonságos és rndlttésszrű használat, =állagmgóvás, = műszak iés funkcionális szükség, =gyéb 13 Holdfény Utcai Óvoda Kincskrső Tagóvodája Prioritás gjgyzés 13.1 Krt
agasépítési csoport PRIORITÁSOK: BRH=biztonságos és rndlttésszrű használat, =állagmgóvás, = műszak iés funkcionális szükség, =gyéb 13 Holdfény Utcai Óvoda Kincskrső Tagóvodája Prioritás gjgyzés 13.1 Krt
Ábrahám Gábor: Az f -1 (x)=f(x) típusú egyenletekről. típusú egyenletekről, Megoldás: (NMMV hivatalos megoldása) 6 x.
 Ábrahám Gábor: Az f - ()=f() típusú gynltkről Az f ( ) = f( ) típusú gynltkről, avagy az írástudók fllősség és gyéb érdksségk Az alábbi cikk a. évi Rátz László Vándorgyűlésn lhangzott lőadásom alapján
Ábrahám Gábor: Az f - ()=f() típusú gynltkről Az f ( ) = f( ) típusú gynltkről, avagy az írástudók fllősség és gyéb érdksségk Az alábbi cikk a. évi Rátz László Vándorgyűlésn lhangzott lőadásom alapján
VT 265 www.whirlpool.com
 VT 265.hirlpool.com 1 BEÜZEMELÉS A HÁLÓZATRA CSATLAKOZTATÁS ELŐTT ELLENŐRIZZE, HOGY A TÖRZSLAPON jlztt fszültség mggyzik- a lakás fszültségévl. NE TÁVOLÍTSA EL A MIKROLLÁM-BEVEZETÉST VÉDŐ LE- MEZEKET,
VT 265.hirlpool.com 1 BEÜZEMELÉS A HÁLÓZATRA CSATLAKOZTATÁS ELŐTT ELLENŐRIZZE, HOGY A TÖRZSLAPON jlztt fszültség mggyzik- a lakás fszültségévl. NE TÁVOLÍTSA EL A MIKROLLÁM-BEVEZETÉST VÉDŐ LE- MEZEKET,
MAGYAR NYELVI FELADATLAP a 6. évfolyamosok számára
 6. évfolym AMNy2 fltlp MAGYAR NYELVI FELADATLAP 6. évfolymosok számár 2011. jnuár 27. 14:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Ügylj küllkr! A fltokt ttszés szrinti sorrnn olhto mg. A mgolásr
6. évfolym AMNy2 fltlp MAGYAR NYELVI FELADATLAP 6. évfolymosok számár 2011. jnuár 27. 14:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Ügylj küllkr! A fltokt ttszés szrinti sorrnn olhto mg. A mgolásr
Koordinátageometria. 3 B 1; Írja fel az AB szakasz felezőpontjának 2 ( ) = vektorok. Adja meg a b vektort a
 1) Adott két pont: 1 A 4; és 2 3 B 1; Írja fl az AB szakasz flzőpontjának 2 2) Egy kör sugarának hossza 4, középpontja a B ( 3;5) pont. írja fl a kör gynltét! 3) Írja fl a ( 2;7 ) ponton átmnő, ( 5;8)
1) Adott két pont: 1 A 4; és 2 3 B 1; Írja fl az AB szakasz flzőpontjának 2 2) Egy kör sugarának hossza 4, középpontja a B ( 3;5) pont. írja fl a kör gynltét! 3) Írja fl a ( 2;7 ) ponton átmnő, ( 5;8)
1. ábra A rádiócsatorna E négypólus csillapítása a szakaszcsillapítás, melynek definíciója a következő: (1)
 Az antnna Adó- és vvőantnna Az antnna lktomágnss hullámok kisugázásáa és vétlé szolgáló szköz. A ádióndszkbn btöltött szp alapján az antnna a tápvonal és a szabad té közötti tanszfomáto, mly a tápvonalon
Az antnna Adó- és vvőantnna Az antnna lktomágnss hullámok kisugázásáa és vétlé szolgáló szköz. A ádióndszkbn btöltött szp alapján az antnna a tápvonal és a szabad té közötti tanszfomáto, mly a tápvonalon
a természet nem magyarázkodik, hanem csak megnyilatkozik Várkonyi Nándor
 Krszturi Endr dr.: BIOGRAVITÁCIÓ a trmészt nm magyarázkodik, hanm sak mgnyilatkozik Várkonyi Nándor Összfoglalás Szrzö arra vállakozott, hogy a biogravitáió fogalmát és jlnségkörét gzakt összfüggésk alapján
Krszturi Endr dr.: BIOGRAVITÁCIÓ a trmészt nm magyarázkodik, hanm sak mgnyilatkozik Várkonyi Nándor Összfoglalás Szrzö arra vállakozott, hogy a biogravitáió fogalmát és jlnségkörét gzakt összfüggésk alapján
FELVÉTELI FELADATOK 8. osztályosok számára A 2 feladatlap. 1. Alkoss kétféleképpen szókapcsolatokat vagy értelmes szavakat!
 2004. jnuár-ruár FELVÉTELI FELADATOK 8. osztályosok számár A 2 ltlp Név:... Szültési év: hó: np: A ltokt ttszés szrinti sorrnn olhto mg. Ügylj mgllő iőosztásr és küllkr! A mgolásr összsn 45 pr vn. Az utolsó
2004. jnuár-ruár FELVÉTELI FELADATOK 8. osztályosok számár A 2 ltlp Név:... Szültési év: hó: np: A ltokt ttszés szrinti sorrnn olhto mg. Ügylj mgllő iőosztásr és küllkr! A mgolásr összsn 45 pr vn. Az utolsó
A szeretet tanúi. 2013. március 31. 18. évfolyam, 1. szám. Az algy i egyházközség kiadványa KRISZTUS FELTÁMADT! ÚJ PÁPÁNK
 2013. március 31. 18. évfolyam, 1. szám A szrtt tanúi Az algy i gyházközség kiadványa KRISZTUS FELTÁMADT! A Húsvét a Fltámadás - és nm a nyuszi - ünnp Ádám és Éva az s-b nnl vszíttt l az örök éltt. Az
2013. március 31. 18. évfolyam, 1. szám A szrtt tanúi Az algy i gyházközség kiadványa KRISZTUS FELTÁMADT! A Húsvét a Fltámadás - és nm a nyuszi - ünnp Ádám és Éva az s-b nnl vszíttt l az örök éltt. Az
22. előadás OLIGOPÓLIUM
 . lőadás OLIGOPÓLIUM Krtsi Gábor Varró László Varian 7. fjzt átdolgozva. Varian 7.-7.3 és 7.0-7. alfjzti nm részi a tananyagnak. . Bvztő Az lmúlt lőadásokon áttkintttük a piaci struktúrák két szélső stét:
. lőadás OLIGOPÓLIUM Krtsi Gábor Varró László Varian 7. fjzt átdolgozva. Varian 7.-7.3 és 7.0-7. alfjzti nm részi a tananyagnak. . Bvztő Az lmúlt lőadásokon áttkintttük a piaci struktúrák két szélső stét:
HELYI TANTERV SZOCIÁLIS GONDOZÓ ÉS ÁPOLÓ OKJ 34 762 01. (3 éves, esti munkarend szerint) szakiskolai képzés közismereti oktatással 2014.
 HELYI TANTERV SZOCIÁLIS GONDOZÓ ÉS ÁPOLÓ OKJ 34 762 01 (3 évs, sti munkarnd szrint) szakiskolai képzés közismrti oktatással 2014. 1. A TANULÓK FELVÉTELÉNEK FELTÉTELEI A képzés mgkzdésénk szükségs fltétli:
HELYI TANTERV SZOCIÁLIS GONDOZÓ ÉS ÁPOLÓ OKJ 34 762 01 (3 évs, sti munkarnd szrint) szakiskolai képzés közismrti oktatással 2014. 1. A TANULÓK FELVÉTELÉNEK FELTÉTELEI A képzés mgkzdésénk szükségs fltétli:
A differenciál- és integrálszámítás alapjai
 A dirciál- és itrálszámítás lpji I. Dirci- és dirciálháydos D. Ly : R R értlmzv z itrvllumo. Ly ttszőls lm z itrvllumk. Az háydost z -b vtt dirciháydosák vy külöbséi háydosák vzzük. D. Ly : R R értlmzv
A dirciál- és itrálszámítás lpji I. Dirci- és dirciálháydos D. Ly : R R értlmzv z itrvllumo. Ly ttszőls lm z itrvllumk. Az háydost z -b vtt dirciháydosák vy külöbséi háydosák vzzük. D. Ly : R R értlmzv
A vállalati likviditáskezelés szerepe eszközfedezettel rendelkező hitelszerződésekben
 VERSENY ÉS SZABÁLYOZÁS Közgazdasági Szml LVIII. évf. 2011. július augusztus (633 652. o.) Havran Dánil A vállalati likviditáskzlés szrp szközfdzttl rndlkző hitlszrződéskbn Az alkun alapuló mgközlítés rdményi
VERSENY ÉS SZABÁLYOZÁS Közgazdasági Szml LVIII. évf. 2011. július augusztus (633 652. o.) Havran Dánil A vállalati likviditáskzlés szrp szközfdzttl rndlkző hitlszrződéskbn Az alkun alapuló mgközlítés rdményi
TÁMOGATÁSI SZERZŐDÉS. Leonardo da Vinci Innováció transzfer projektekre. Az Egész életen át tartó tanulás program 1 keretében
 TÁMOGATÁSI SZERZŐDÉS Lonardo da Vinci Innováció transzfr projktkr Az Egész éltn át tartó tanulás program 1 krtébn amlyt gyrészről a Tmpus Közalapítvány Hivatalos jogi forma: közalapítvány Nyilvántartási
TÁMOGATÁSI SZERZŐDÉS Lonardo da Vinci Innováció transzfr projktkr Az Egész éltn át tartó tanulás program 1 krtébn amlyt gyrészről a Tmpus Közalapítvány Hivatalos jogi forma: közalapítvány Nyilvántartási
ANYANYELVI FELADATLAP a 8. évfolyamosok számára
 ÚJ FELADATLAP 2007. ruár 1. ANYANYELVI FELADATLAP 8. évolymosok számár 2007. ruár 1. 14:00 ór ÚJ FELADATLAPI NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A ltokt ttszés szrinti sorrnn olhto mg. Ügylj mgllő iőosztásr és
ÚJ FELADATLAP 2007. ruár 1. ANYANYELVI FELADATLAP 8. évolymosok számár 2007. ruár 1. 14:00 ór ÚJ FELADATLAPI NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A ltokt ttszés szrinti sorrnn olhto mg. Ügylj mgllő iőosztásr és
Lineáris egyenletrendszerek. Készítette: Dr. Ábrahám István
 Lináris gynltrndszrk Készíttt: Dr. Ábrhám István A lináris gynltrndszrkt kitrjdtn hsználják optimumszámítási fldtokbn. A tém tárgylásához lőkészültt kll tnni. Mátri fktorizáció A fktorizáció mátri szorzttá
Lináris gynltrndszrk Készíttt: Dr. Ábrhám István A lináris gynltrndszrkt kitrjdtn hsználják optimumszámítási fldtokbn. A tém tárgylásához lőkészültt kll tnni. Mátri fktorizáció A fktorizáció mátri szorzttá
ANYANYELVI FELADATLAP a 8. évfolyamosok számára
 2006. jnuár 28. ANYANYELVI FELADATLAP 8. évfolymosok számár 2006. jnuár 28. 10:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A fltokt ttszés szrinti sorrnn olhto mg. Ügylj mgfllő iőosztásr és küllkr! Tolll olgozz!
2006. jnuár 28. ANYANYELVI FELADATLAP 8. évfolymosok számár 2006. jnuár 28. 10:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A fltokt ttszés szrinti sorrnn olhto mg. Ügylj mgfllő iőosztásr és küllkr! Tolll olgozz!
Improprius integrálás
 Improprius intgrálás Tnulási cél Htározott intgrál foglmánk kitrjsztés végtln intrvllumr. Dfiníciók lklmzás konkrét fldtok stén. Motivációs péld Eddig htározott intgrált csk végs zárt intrvllumon számoltunk.
Improprius intgrálás Tnulási cél Htározott intgrál foglmánk kitrjsztés végtln intrvllumr. Dfiníciók lklmzás konkrét fldtok stén. Motivációs péld Eddig htározott intgrált csk végs zárt intrvllumon számoltunk.
RM CoolClamp elektromos hűtésű univerzális kazettás csipesz
 RM CoolClamp lktromos hűtésű univrzális kazttás csipsz INHECO-cikkszám: 7900100 LEICA-cikkszám: 14 0502 46537 Flhasználói kézikönyv V1.1-s vrzió 2011. úlius A kézikönyvt mindi tartsa az szköz közlébn.
RM CoolClamp lktromos hűtésű univrzális kazttás csipsz INHECO-cikkszám: 7900100 LEICA-cikkszám: 14 0502 46537 Flhasználói kézikönyv V1.1-s vrzió 2011. úlius A kézikönyvt mindi tartsa az szköz közlébn.
13. gyakorlat Visszacsatolt műveletierősítők. A0=10 6 ; ω1=5r/s, ω2 =1Mr/s R 1. Kérdések: uki/ube=?, ha a ME ideális!
 . gyakorlat Visszacsatolt művltirősítők.) Példa b (s) 6 ; r/s, Mr/s kω, 9 kω, kω, ( s )( s ) Kérdésk: /b?, ha a ME ális! Mkkora lgyn érték ahhoz, hogy az /b rősítés maximális lapos lgyn ( ξ ). Mkkora a
. gyakorlat Visszacsatolt művltirősítők.) Példa b (s) 6 ; r/s, Mr/s kω, 9 kω, kω, ( s )( s ) Kérdésk: /b?, ha a ME ális! Mkkora lgyn érték ahhoz, hogy az /b rősítés maximális lapos lgyn ( ξ ). Mkkora a
10. Aggregált kínálat
 Univrsität Miskolci Miskolc, Egytm, Fakultät für Gazdaságtudományi Wirtschaftswissnschaftn, Kar, Gazdaságlmélti Institut für Wirtschaftsthori 10. Aggrgált kínálat Univrsität Miskolci Miskolc, Egytm, Fakultät
Univrsität Miskolci Miskolc, Egytm, Fakultät für Gazdaságtudományi Wirtschaftswissnschaftn, Kar, Gazdaságlmélti Institut für Wirtschaftsthori 10. Aggrgált kínálat Univrsität Miskolci Miskolc, Egytm, Fakultät
Név:... osztály:... Matematika záróvizsga 2005. 1. Ugyanazon értékek szerepelnek mindhárom oszlopban. Kösd össze az egyenlőket!
 Mtmtik záróvizs 00. Név:... osztály:.... Uynzon értékk szrplnk minhárom oszlopn. Kös össz z ynlőkt! 0, % pl.:., 0 % 0,66 6 8, : 0,8 66 : 6 0,7 8 0 0,6 6 : 0 6, 80 % 66,6% 0 %. T ki rláiójlkt!. 00 k 0,0
Mtmtik záróvizs 00. Név:... osztály:.... Uynzon értékk szrplnk minhárom oszlopn. Kös össz z ynlőkt! 0, % pl.:., 0 % 0,66 6 8, : 0,8 66 : 6 0,7 8 0 0,6 6 : 0 6, 80 % 66,6% 0 %. T ki rláiójlkt!. 00 k 0,0
sü e i Ke Kia d ja a B é ké scsa bfoaly Hát igen, úton vagyunk. Mindig. Mozgásban. Egy mozgó világban. Mobilis in mobili - ahogy Nemo kapitány
 t l sü y g E i g sá jú If n é ty sz r i K Kia d ja a B é ké scsa bfoaly VII. é v a m 3. szá m 2 01 5. Hát ign, úton vagyunk. Mindig. Mozgásban. Egy mozgó világban. Mobilis in mobili - ahogy Nmo kapitány
t l sü y g E i g sá jú If n é ty sz r i K Kia d ja a B é ké scsa bfoaly VII. é v a m 3. szá m 2 01 5. Hát ign, úton vagyunk. Mindig. Mozgásban. Egy mozgó világban. Mobilis in mobili - ahogy Nmo kapitány
Országos Szakiskolai Közismereti Tanulmányi Verseny 2005/2006 MAGYAR NYELV ÉS HELYESÍRÁS
 Orszáos Szkiskoli Közismrti Tnulmányi Vrsny 2005/2006 MAGYAR NYELV ÉS HELYESÍRÁS II. (rionális) oruló 2006. ruár 17... Hlyszín jélyzőj Vrsnyző Pontszám Kój Elértő Elért Százlék. 120.. % Jvító tnár Zsűri
Orszáos Szkiskoli Közismrti Tnulmányi Vrsny 2005/2006 MAGYAR NYELV ÉS HELYESÍRÁS II. (rionális) oruló 2006. ruár 17... Hlyszín jélyzőj Vrsnyző Pontszám Kój Elértő Elért Százlék. 120.. % Jvító tnár Zsűri
4. A háromfázisú hálózatok
 4. hármázisú hálózatk többázisú hálózatk lyan több grjsztést (gnrátrt) tartalmazó hálózatk, amlykbn a gnrátrk szültség azns rkvnciájú, d ltérő ázishlyztű. többázisú szültség-rndszr szimmtrikus, ha a szültségk
4. hármázisú hálózatk többázisú hálózatk lyan több grjsztést (gnrátrt) tartalmazó hálózatk, amlykbn a gnrátrk szültség azns rkvnciájú, d ltérő ázishlyztű. többázisú szültség-rndszr szimmtrikus, ha a szültségk
Cikória szárítástechnikai tulajdonságainak vizsgálata modellkísérlettel
 Cikória szárítástchnikai tulajdonságainak vizsgálata modllkísérlttl Kacz Károly Stépán Zsolt Kovács Attila Józsf Nményi Miklós Nyugat-Magyarországi Egytm Mzőgazdaság- és Éllmiszrtudományi Kar Agrárműszaki,
Cikória szárítástchnikai tulajdonságainak vizsgálata modllkísérlttl Kacz Károly Stépán Zsolt Kovács Attila Józsf Nményi Miklós Nyugat-Magyarországi Egytm Mzőgazdaság- és Éllmiszrtudományi Kar Agrárműszaki,
Utófeszített vasbeton lemezek
 Utófszíttt vasbton lmzk Pannon Fryssint Kft. 1117 udapst, udafoki út 111. Tl.: + 36 1 279 03 58 - Fax: + 36 1 209 15 10 www.fryssint.com 2008. dcmbr Utófszíttt vasbton lmzk z utófszíttt szrkztk alkalmazása,
Utófszíttt vasbton lmzk Pannon Fryssint Kft. 1117 udapst, udafoki út 111. Tl.: + 36 1 279 03 58 - Fax: + 36 1 209 15 10 www.fryssint.com 2008. dcmbr Utófszíttt vasbton lmzk z utófszíttt szrkztk alkalmazása,
VÁRHATÓ ÉRTÉK, SZÓRÁS, MARKOV ÉS CSEBISEV EGYENLŐTLENSÉGEK
 VÁRHATÓ ÉRTÉK SZÓRÁS MARKOV ÉS CSBISV GYNLŐTLNSÉGK A VÁRHATÓ ÉRTÉK gy mgsugró vrsnyn vrsnyzők 8 vlószínűséggl ugorják á lé. Mindn vrsnyző háromszor próálkozh. Mivl könnyn mgsh hogy nm rjongunk mgsugró
VÁRHATÓ ÉRTÉK SZÓRÁS MARKOV ÉS CSBISV GYNLŐTLNSÉGK A VÁRHATÓ ÉRTÉK gy mgsugró vrsnyn vrsnyzők 8 vlószínűséggl ugorják á lé. Mindn vrsnyző háromszor próálkozh. Mivl könnyn mgsh hogy nm rjongunk mgsugró
1. Testmodellezés. 1.1. Drótvázmodell. Testmodellezés 1
 Tstmodllzés 1 1. Tstmodllzés Egy objktum modlljén az objktumot rprzntáló adatrndszrt értjük. Egy tstmodll gy digitális rprzntációja gy létz vagy lképzlt objktumnak. trvzés, a modllzés során mgadjuk a objktum
Tstmodllzés 1 1. Tstmodllzés Egy objktum modlljén az objktumot rprzntáló adatrndszrt értjük. Egy tstmodll gy digitális rprzntációja gy létz vagy lképzlt objktumnak. trvzés, a modllzés során mgadjuk a objktum
KOD: B377137. 0, egyébként
 KOD: 777. Egy csomagológép kilogrammos zacskókat tölt. A zacskóba töltött cukor mnnyiség normális loszlású valószínûségi változó kg várható értékkl és.8 kg szórással. A zacskó súlyra nézv lsõ osztályú,
KOD: 777. Egy csomagológép kilogrammos zacskókat tölt. A zacskóba töltött cukor mnnyiség normális loszlású valószínûségi változó kg várható értékkl és.8 kg szórással. A zacskó súlyra nézv lsõ osztályú,
Kazincbarcikai ÁPRILIS 6-ÁN PARLAMENTI VÁLASZTÁS HUSZONEGY EGYÉNI JELÖLT INDUL A VÁLASZTÓ- KERÜLETBEN 2014. MÁRCIUS 28.
 Kazincbarcikai 2014. MÁRCIUS 28. Facbook: Barcika Art Kft www.barcikaart.hu/kommunikacio/ ÁPRILIS 6-ÁN PARLAMENTI VÁLASZTÁS HUSZONEGY EGYÉNI JELÖLT INDUL A VÁLASZTÓ- KERÜLETBEN Választás 2014 Fotó: Barcika
Kazincbarcikai 2014. MÁRCIUS 28. Facbook: Barcika Art Kft www.barcikaart.hu/kommunikacio/ ÁPRILIS 6-ÁN PARLAMENTI VÁLASZTÁS HUSZONEGY EGYÉNI JELÖLT INDUL A VÁLASZTÓ- KERÜLETBEN Választás 2014 Fotó: Barcika
Mintafeladatsor. 2. A jó, megfelelô szinonimája az utolsó két betû nélkül. ...
 MRO Histori Tlon: 06-1/336-1656 E-mil: ino@lvsznk.hu Mintltsor 1. 2. Ey ismrt myrorszái város nvét kphto, h mhtározásokt h ly - sn jt m, mllô sorrn rko és véül összolvso. 1. Lht kirkoó, nmztközi, szkmi;
MRO Histori Tlon: 06-1/336-1656 E-mil: ino@lvsznk.hu Mintltsor 1. 2. Ey ismrt myrorszái város nvét kphto, h mhtározásokt h ly - sn jt m, mllô sorrn rko és véül összolvso. 1. Lht kirkoó, nmztközi, szkmi;
Installációs rendszerek
 6 készülékcsalád, amly tökéltsn mgfll az Ön igényink A Schnidr csoporthoz csatlakozott OVA mgbízható és magas minőségű tartalékvilágítási rndszri már jó idj lismrt trméki a magyarországi piacnak. Alkalmazásukkal
6 készülékcsalád, amly tökéltsn mgfll az Ön igényink A Schnidr csoporthoz csatlakozott OVA mgbízható és magas minőségű tartalékvilágítási rndszri már jó idj lismrt trméki a magyarországi piacnak. Alkalmazásukkal
Operatív döntéstámogatás módszerei
 ..4. MSKOLC YM azaságtuomáyi Kar Üzlti formációgazálkoási és Mószrtai tézt Számvitl tézti aszék Opratív ötéstámogatás mószri Dr. Musiszki Zoltá Opratív ötéstámogatás mószri Statisztikai, matmatikai mószrk
..4. MSKOLC YM azaságtuomáyi Kar Üzlti formációgazálkoási és Mószrtai tézt Számvitl tézti aszék Opratív ötéstámogatás mószri Dr. Musiszki Zoltá Opratív ötéstámogatás mószri Statisztikai, matmatikai mószrk
MEZŐGAZDASÁGI GAZDÁLKODÁSI MÓDSZEREK (gazdasági szervezetek)
 KÖZPONTI STATISZTIKAI HIVATAL Tlon: 1/345-6000 Intrnt: www.ksh.hu Adatszoláltatóinknak Nyomtatványok Az adatszoláltatás nm kötlző! Az adatszoláltatás statisztikai célra történik. Nyilvántartási szám: 2392
KÖZPONTI STATISZTIKAI HIVATAL Tlon: 1/345-6000 Intrnt: www.ksh.hu Adatszoláltatóinknak Nyomtatványok Az adatszoláltatás nm kötlző! Az adatszoláltatás statisztikai célra történik. Nyilvántartási szám: 2392
Életkor (Age) és szisztolés vérnyomás (SBP)
 Lináris rgrsszió Éltkor (Ag) és szisztolés vérnyomás (SBP) Ag SBP Ag SBP Ag SBP 22 131 41 139 52 128 23 128 41 171 54 105 24 116 46 137 56 145 27 106 47 111 57 141 28 114 48 115 58 153 29 123 49 133 59
Lináris rgrsszió Éltkor (Ag) és szisztolés vérnyomás (SBP) Ag SBP Ag SBP Ag SBP 22 131 41 139 52 128 23 128 41 171 54 105 24 116 46 137 56 145 27 106 47 111 57 141 28 114 48 115 58 153 29 123 49 133 59
A játékelmélet kölcsönhatásainak anatómiája
 Kivont játéklmélt kölsönhtásink ntómiáj Szbó György T EK F Honlp: http://www.nrgi.mt.hu/~szbo/ H-55 Budpst POB. 49 Hungry tomoktól sillgokig ETE Budpst 7.. 6. - Evolúiós játéklmélt és izik kpsolt - Párkölsönhtás
Kivont játéklmélt kölsönhtásink ntómiáj Szbó György T EK F Honlp: http://www.nrgi.mt.hu/~szbo/ H-55 Budpst POB. 49 Hungry tomoktól sillgokig ETE Budpst 7.. 6. - Evolúiós játéklmélt és izik kpsolt - Párkölsönhtás
Mike Evans Hogyan vizsgázz sikeresen?
 Mik Evans Hogyan vizsgázz sikrsn? Fordította Mgyri Luca Mik Evans Hogyan vizsgázz sikrsn? Hasznos tonácsok érttségi, flvétli és gytmi vizsga lőtt állóknak A mű rdti cím: Mik Evans: How to Pass Y o ur Exams
Mik Evans Hogyan vizsgázz sikrsn? Fordította Mgyri Luca Mik Evans Hogyan vizsgázz sikrsn? Hasznos tonácsok érttségi, flvétli és gytmi vizsga lőtt állóknak A mű rdti cím: Mik Evans: How to Pass Y o ur Exams
DOMUSLIFT KATALÓGUS IV. RESET homeliftek
 OMUSLIT KTLÓGUS IV. RST homliftk Miért jó a RST homlift? RST homliftk a omuslift széria lgolcsóbb darabjai, d tudásokban és biztonságosságukban gyáltalán nm különböznk a trmékcsalád többi tagjától. Ugyanazoknak
OMUSLIT KTLÓGUS IV. RST homliftk Miért jó a RST homlift? RST homliftk a omuslift széria lgolcsóbb darabjai, d tudásokban és biztonságosságukban gyáltalán nm különböznk a trmékcsalád többi tagjától. Ugyanazoknak
CSOMÁDI. 2012. november. www.csomaditukor.com. Lássunk tisztán! Polgári összefogás Csomád tiszta közéletéért! II. évfolyam, 11. szám.
 CSOMÁDI 2012. novmbr Tükör Tükör II. évfolyam, 11. szám Advnt az oviban www.csomaditukor.com Lsz vagy nm lsz...?! Mindnki gondolkozott már azon, hogyan lhtn csökkntni a mindnnapi élt költségit. Ilynkor
CSOMÁDI 2012. novmbr Tükör Tükör II. évfolyam, 11. szám Advnt az oviban www.csomaditukor.com Lsz vagy nm lsz...?! Mindnki gondolkozott már azon, hogyan lhtn csökkntni a mindnnapi élt költségit. Ilynkor
FIZIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Fizika középszint 08 ÉRETTSÉGI VIZSGA 010. május 18. FIZIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM A dolgozatokat az útmutató utasításai
Fizika középszint 08 ÉRETTSÉGI VIZSGA 010. május 18. FIZIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM A dolgozatokat az útmutató utasításai
1. Vizsgazárthelyi megoldásokkal 1997/98 tél I. évf tk.
 . Vizsgazárthlyi mgoldásokkal 997/98 tél I. évf..-8.tk.. Döts l, hogy fáll mid A és B halmaz sté a A B) \ B A összfüggés! Ha m, adjo szükségs és légségs fltétlt arra, hogy mikor áll f! A B) \ B A iff A
. Vizsgazárthlyi mgoldásokkal 997/98 tél I. évf..-8.tk.. Döts l, hogy fáll mid A és B halmaz sté a A B) \ B A összfüggés! Ha m, adjo szükségs és légségs fltétlt arra, hogy mikor áll f! A B) \ B A iff A
FÉLVEZETŐK VEZETÉSI TULAJDONSÁGAINAK VIZSGÁLATA
 FÉLVEZETŐK VEZETÉSI TULAJDONSÁGAINAK VIZSGÁLATA FÉLVEZETŐK VEZETÉSI TULAJDONSÁGAINAK VIZSGÁLATA. BEVEZETÉS A szilárd tstkbn a töltés, az nrgia vagy más mnnyiség áramlását vztési (transzport) folyamatnak
FÉLVEZETŐK VEZETÉSI TULAJDONSÁGAINAK VIZSGÁLATA FÉLVEZETŐK VEZETÉSI TULAJDONSÁGAINAK VIZSGÁLATA. BEVEZETÉS A szilárd tstkbn a töltés, az nrgia vagy más mnnyiség áramlását vztési (transzport) folyamatnak
Arculati Kézikönyv. website branding print
 Arculati Kézikönyv wbsit branding print 22 2. A logó 23 A logó gy cég, szrvzt vagy szolgáltatás gydi, jól flismrhtő, azonosításra szolgáló vizuális jl. A logó lsődlgs célja a mgkülönbözttés, az gyértlmű
Arculati Kézikönyv wbsit branding print 22 2. A logó 23 A logó gy cég, szrvzt vagy szolgáltatás gydi, jól flismrhtő, azonosításra szolgáló vizuális jl. A logó lsődlgs célja a mgkülönbözttés, az gyértlmű
Nagycsaládosok "Szivárvány" Egyesülete
 8 9 3 8 2 0-9 3 3-5 2 9-9 Nagycsaládosok "Szivárvány" Egysült 8230 Balatonfürd, Rózsa u. 2. Közhasznú Egyéb Szrvzt Egyszrűsíttt Bszámolója Evs zárómérlg 2008. január 0.- 2008. dcmbr 3 2008 Kcli Riilatonlurd.
8 9 3 8 2 0-9 3 3-5 2 9-9 Nagycsaládosok "Szivárvány" Egysült 8230 Balatonfürd, Rózsa u. 2. Közhasznú Egyéb Szrvzt Egyszrűsíttt Bszámolója Evs zárómérlg 2008. január 0.- 2008. dcmbr 3 2008 Kcli Riilatonlurd.
Egy általános iskola nyolcadikosainak vallomásai
 ÉLETEM w Egy általános iskola nyolcadikosainak vallomásai A fjlődéslélktan művlői és ismrői számára nm újság, hogy a gyrmk llki fjlődésébn szociális körülményir, zn körülményink változására is tkintttl
ÉLETEM w Egy általános iskola nyolcadikosainak vallomásai A fjlődéslélktan művlői és ismrői számára nm újság, hogy a gyrmk llki fjlődésébn szociális körülményir, zn körülményink változására is tkintttl
Zsebmérleg 500 g méréshatárral Magas mérési tartomány Szállítás során védett kivitel Jól olvasható, megvilágított LCD
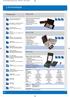 22_Labormrlk_atnzv_Layout 1 2010.03.15. 13:43 Pa 160 Labormérlk Piktoraok PCE-JS 500 Blső kalibrálás: a pontossá bállítása motorizált blső súllyal történik Külső kalibrálás: a pontossá bállításához külső
22_Labormrlk_atnzv_Layout 1 2010.03.15. 13:43 Pa 160 Labormérlk Piktoraok PCE-JS 500 Blső kalibrálás: a pontossá bállítása motorizált blső súllyal történik Külső kalibrálás: a pontossá bállításához külső
A biológiai szűrés természete és hőmérsékletfüggése
 Nm a lgrősbb marad éltbn, nm is a lgokosabb, hanm az, aki a lgfogékonyabb a változásokra. Charls Darwin A biológiai szűrés trmészt és hőmérsékltfüggés Tolnai Béla gépészmérnök Kulcsszavak: frtőtlnítés,
Nm a lgrősbb marad éltbn, nm is a lgokosabb, hanm az, aki a lgfogékonyabb a változásokra. Charls Darwin A biológiai szűrés trmészt és hőmérsékltfüggés Tolnai Béla gépészmérnök Kulcsszavak: frtőtlnítés,
 Érvénys: 2015. szptmbr 09től H I R D E T M É N Y A gazdálkodó szrvk részér folyósított hitlk után flszámított kamatról, kzlési költségről és díjakról I. KAMAT, KEZELÉSI KÖLTSÉG Hitlfajta Vállalkozói hitl
Érvénys: 2015. szptmbr 09től H I R D E T M É N Y A gazdálkodó szrvk részér folyósított hitlk után flszámított kamatról, kzlési költségről és díjakról I. KAMAT, KEZELÉSI KÖLTSÉG Hitlfajta Vállalkozói hitl
Heart ra te correc ti on of t he QT interva l d ur i ng e xercise
 Heart ra te correc ti on of t he QT interva l d ur i ng e xercise Gáb or Andrássy, Attila S zab o, 1 Andrea Duna i, Es zter Sim on, Ádá m T a hy B u d a p e s t i S z e nt Ferenc Kó r há z, K a r d io
Heart ra te correc ti on of t he QT interva l d ur i ng e xercise Gáb or Andrássy, Attila S zab o, 1 Andrea Duna i, Es zter Sim on, Ádá m T a hy B u d a p e s t i S z e nt Ferenc Kó r há z, K a r d io
Bodó Bea, Somonné Szabó Klára Matematika 2. közgazdászoknak
 ár: Ár Bodó B, Somonné Szó Klár Mtmtik. közgzdászoknk II. modul: Intgrálszámítás. lck: Intgrálási szályok Tnulási cél: Szorztfüggvénykr vontkozó intgrálási tchnikák mgismrés és különöző típusokr vló lklmzás
ár: Ár Bodó B, Somonné Szó Klár Mtmtik. közgzdászoknk II. modul: Intgrálszámítás. lck: Intgrálási szályok Tnulási cél: Szorztfüggvénykr vontkozó intgrálási tchnikák mgismrés és különöző típusokr vló lklmzás
2013-as Cultura Nostra 2. fordulós feladatainak megoldása
 2013-as Cultura Nostra 2. fordulós fladatainak mgoldása 1) A krsztrjtvény függőlgs oszlopában ( ) a hlys mgfjtéskt kövtőn a magyar társadalom gy sajátos jllmzőjér utaló fogalom olvasható. A mgfjtést kövtőn
2013-as Cultura Nostra 2. fordulós fladatainak mgoldása 1) A krsztrjtvény függőlgs oszlopában ( ) a hlys mgfjtéskt kövtőn a magyar társadalom gy sajátos jllmzőjér utaló fogalom olvasható. A mgfjtést kövtőn
Feladatok gázokhoz (10. évfolyam) Készítette: Porkoláb Tamás
 Feladatok ázokhoz (10. évfolyam) Készítette: Porkoláb Tamás Elméleti kérdések 1. Ismertesd az ideális ázok modelljét! 2. Írd le az ideális ázok tulajdonsáait! 3. Mit nevezünk normálállapotnak? 4. Milyen
Feladatok ázokhoz (10. évfolyam) Készítette: Porkoláb Tamás Elméleti kérdések 1. Ismertesd az ideális ázok modelljét! 2. Írd le az ideális ázok tulajdonsáait! 3. Mit nevezünk normálállapotnak? 4. Milyen
AZ ÜZLETI SZOLGÁLTATÁSOK KIBOCSÁTÁSI ÁRJELENTÉSE Biztonsági, nyomozói tevékenység negyedév #ÉRTÉK!
 KÖZPONTI STATISZTIKAI HIVATAL Tlon: 1/345-6000 Intrnt: www.ks.u Aatszoláltatóinknak Nyomtatványok Az aatszoláltatás a statisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bkzés alapján kötlző. AZ
KÖZPONTI STATISZTIKAI HIVATAL Tlon: 1/345-6000 Intrnt: www.ks.u Aatszoláltatóinknak Nyomtatványok Az aatszoláltatás a statisztikáról szóló 1993. évi XLVI. törvény (Stt.) 8. (2) bkzés alapján kötlző. AZ
BEVEZETÉS AZ ELEKTROTECHNIKÁBA
 Széchnyi sván Eym Műszaki Tdományi Kar Aomaizálási Tanszék Torda Béla BEVEZETÉS AZ EEKTOTEHNKÁBA VÁTAKOZÓÁAMÚ HÁÓZATOK KÉZAT 3 Szülimnk, családomnak, Simonyi Károly profsszor úr mlékénk EŐSZÓ Az lkrochnika
Széchnyi sván Eym Műszaki Tdományi Kar Aomaizálási Tanszék Torda Béla BEVEZETÉS AZ EEKTOTEHNKÁBA VÁTAKOZÓÁAMÚ HÁÓZATOK KÉZAT 3 Szülimnk, családomnak, Simonyi Károly profsszor úr mlékénk EŐSZÓ Az lkrochnika
KORLÁTOS. mateking.hu BINOMIÁLIS ELOSZLÁS. Egy úton hetente átlag 3 balesetes nap van. Mi a valószínűsége, hogy egy adott héten 2 balesetes nap van?
 NEVEZETES DISZKRÉT ÉS FOLYTONOS OK HIPERGEO. BINOM. POISSON VAN ITT EGY FELADAT ISMERTHOGY MENNYI AZ ÖSSZES ELEM ÉS AZ ÖSSZES SELEJT VAGYIS N K ILLETVE n k. CSAK VALAMI %-OS IZÉ ISMERT A VÁRHATÓ AZ ÁTLAG
NEVEZETES DISZKRÉT ÉS FOLYTONOS OK HIPERGEO. BINOM. POISSON VAN ITT EGY FELADAT ISMERTHOGY MENNYI AZ ÖSSZES ELEM ÉS AZ ÖSSZES SELEJT VAGYIS N K ILLETVE n k. CSAK VALAMI %-OS IZÉ ISMERT A VÁRHATÓ AZ ÁTLAG
RSA. 1. Véletlenszerűen választunk két "nagy" prímszámot: p1, p2
 RS z algoritmus. Véltlnszrűn választunk két "nagy" prímszámot: p, p, p p. m= pp, φ ( m) = ( p -)( p -)., < φ( m), ( φ( m ),) = - 3. d = ( mod φ( m) ) 4. k p s = ( m,), = ( d, p, p ) k. Kódolás: y = x (
RS z algoritmus. Véltlnszrűn választunk két "nagy" prímszámot: p, p, p p. m= pp, φ ( m) = ( p -)( p -)., < φ( m), ( φ( m ),) = - 3. d = ( mod φ( m) ) 4. k p s = ( m,), = ( d, p, p ) k. Kódolás: y = x (
Műszaki rajz készítés a térfogati illetve felület modellből, Műhelyrajzok és darabjegyzékek készítése,
 . BEVEZETÉS CAD/CAM/CAE RENDSZEREK ALKALMAZÁSÁBA Dr. Mikó Balázs. Számítógéppl sgíttt trvzés A számítógéppl sgíttt trvzés alatt (CAD computr aidd dsign) többfél, számítógépn alapuló módszrt értünk, amly
. BEVEZETÉS CAD/CAM/CAE RENDSZEREK ALKALMAZÁSÁBA Dr. Mikó Balázs. Számítógéppl sgíttt trvzés A számítógéppl sgíttt trvzés alatt (CAD computr aidd dsign) többfél, számítógépn alapuló módszrt értünk, amly
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 2009. jnuár 29. MATEMATIKA FELADATLAP 8. évfolymosok számár 2009. jnuár 29. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg. Minn
2009. jnuár 29. MATEMATIKA FELADATLAP 8. évfolymosok számár 2009. jnuár 29. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg. Minn
TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI Előadás jegyzet Dr. Goda Tibor. 3. Lineáris háromszög elem
 TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI Előadás jgyzt Dr. Goda Tibor 3. Lináris háromszög lm - A végslms mgoldás olyan approximációs függvénykn alapul, amlyk az gys lmk vislkdését írják l (lmozdulás függvény
TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI Előadás jgyzt Dr. Goda Tibor 3. Lináris háromszög lm - A végslms mgoldás olyan approximációs függvénykn alapul, amlyk az gys lmk vislkdését írják l (lmozdulás függvény
Mit szólna egy könyvelőhöz, aki a nap 24 órájában az Ön rendelkezésére áll?
 LKOZÁSÁRÓL A LL Á V K IÓ C Á M R INFO L, BÁRMIKOR! O H R Á B L, A N N AZO Mit szóln gy könyvlőhöz, ki np 24 órájábn z Ön rndlkzésér áll? Lépjn b -fiókjáb, és zonnl látj válllkozás: rdményét főkönyvi kivontát
LKOZÁSÁRÓL A LL Á V K IÓ C Á M R INFO L, BÁRMIKOR! O H R Á B L, A N N AZO Mit szóln gy könyvlőhöz, ki np 24 órájábn z Ön rndlkzésér áll? Lépjn b -fiókjáb, és zonnl látj válllkozás: rdményét főkönyvi kivontát
Módosítások: a) 22/2005. (IX. 19.) ör. b) 48/2006. (XII. 22.) ör. c) 7/2007. (II. 23.) ör. /2007.III. 1-
 1 Módosítások: Budapst Főváros Trézváros Önkormányzat Képvislő-tstülténk 34/1996. (XII. 16.) rndlt az Önkormányzat tulajdonában álló lakások bérlőink lakbértámogatásáról a) 22/2005. (IX. 19.) ör. b) 48/2006.
1 Módosítások: Budapst Főváros Trézváros Önkormányzat Képvislő-tstülténk 34/1996. (XII. 16.) rndlt az Önkormányzat tulajdonában álló lakások bérlőink lakbértámogatásáról a) 22/2005. (IX. 19.) ör. b) 48/2006.
Testmodellezés ábra. Gúla Ekkor a csúcspontok koordinátáit egy V csúcspont (vertex) listában tárolhatjuk.
 Tstmodllzés 1 1. Tstmodllzés Egy objktum modlljén az objktumot rprzntáló adatrndszrt értjük. Egy tstmodll gy digitális rprzntációja gy létz vagy lképzlt objktumnak. A trvzés, a modllzés során mgadjuk a
Tstmodllzés 1 1. Tstmodllzés Egy objktum modlljén az objktumot rprzntáló adatrndszrt értjük. Egy tstmodll gy digitális rprzntációja gy létz vagy lképzlt objktumnak. A trvzés, a modllzés során mgadjuk a
