KIDOLGOZÁSA - MATEMATIKA SZAK - 1. Analitikus mértan térben 2
|
|
|
- Márton Tóth
- 6 évvel ezelőtt
- Látták:
Átírás
1 ANALITIKUS MÉRTANBÓL KITŰZÖTT ÁLLAMVIZSGA TÉTELEK KIDOLGOZÁSA - MATEMATIKA SZAK - Tartalomjegyzék 1. Analitikus mértan térben 1.1. Térbeli egyenesek egyenletei Descartes-féle koordináta rendszerhez viszonyítva Egy pont és egy vektor által meghatározott egyenes egyenlete Két különböző pont által meghatározott egyenes egyenlete Egyenes megadása, mint két sít metszete Pont távolsága egyenestől (térben) Csúcspontjainak koordinátáival jellemzett háromszög területe térben és síkban Síkok egyenletei Descartes-féle koordináta rendszerhez viszonyítva Egy pont és két nem párhuzamos irány által meghatározott sík egyenlete Három nem kollineáris pont által meghatározott sík egyenlete A sík tengelymetszetes egyenlete A sík egyenlete, ha ismert egy pontja és normálvektora Pont távolsága síktól Két kitérő egyenes közös merőlegese és távolsága Két térbeli egyenes szöge Egyenes és sík szöge Két sík szöge A gömb Analitikus mértan síkban Síkbeli egyenesek egyenletei Descartes-féle koordináta rendszerhez viszonyítva Egy pont és egy vektor által meghatározott egyenes egyenlete Két különböző pont által meghatározott egyenes egyenlete Egyenes tengelymetszetes alakja Két síkbeli egyenes szöge Párhuzamos és merőleges egyenesek Párhuzamos egyenesek Merőleges egyenesek Pont távolsága egyenestől (síkban) Kúpszeletek Kör Ellipszis Hiperbola Parabola Kitűzött feladatok Analitikus mértan síkban Analitikus mértan térben
2 1. Analitikus mértan térben 1.1. Térbeli egyenesek egyenletei Descartes-féle koordináta rendszerhez viszonyítva Egy pont és egy vektor által meghatározott egyenes egyenlete Legyen R = {O, e 1, e, e 3 } egy koordináta rendszer az S háromdimenziós térben. Legyen A S egy pont és d V egy tetszőleges szabad vektor. Tudjuk, hogy egy adott pont és egy vektor (iránya) egyértelműen meghatároz egy egyenest a térben. Ez az egyenes meghatározott, ha ismerjük minden pontjának a helyzetvektorát. e e 3 r A A M d r M O e e 1 1. ábra. Az A pont és d vektor által meghatározott egyenes. Legyen tehát M egy tetszőleges pont a d vektor és az A pont által meghatározott e egyenesen. Ekkor r M = r A + AM. Mivel az AM vektor iránya megegyezik a d vektor irányával, következik, hogy létezik olyan λ R, amelyre AM = λ d. Tehát a következő egyenlethez jutunk e : r M = r A + λ d, λ R. (1) Ezt az egyenletet az e egyenes vektoriális egyenletének nevezzük, a d vektort pedig az e egyenes irányvektorának. A továbbiakban feltételezzük, hogy a d vektor felírása az R koordináta-rendszerben a következő: d = p e 1 + q e + r e 3, valamint r M = x e 1 + y e + z e 3 és r A = x 0 e 1 + y 0 e + z 0 e 3, vagyis M(x, y, z) és A(x 0, y 0, z 0 ). Behelyettesítve ezeket a vektorokat az e egyenes (1) vektoriális egyenletébe kapjuk, hogy x e 1 + y e + z e = (x 0 + λp) e 1 + (y 0 + λq) e + (z 0 + λr) e 3. Figyelembe véve az e 1, e, e 3 vektorok lineáris függetlenségét kapjuk az e egyenes parametrikus egyenleteit: e : x = x 0 + λp y = y 0 + λq z = z 0 + λr Ezekből az egyenletekből kifejezve a λ-t következik, hogy x x 0 p = y y 0 q, λ R. () = z z 0. (3) r Ezt az egyenletrendszert az e egyenes kanonikus egyenletének nevezzük és a p, q, r R valós számokat pedig az egyenes irányparamétereinek. Példa. Az A(1, 1, 0) ponton áthaladó és d(4,, 1) irányú egyenes egyenletei: 1. vektoriális egyenlet: r M = r A + λ d, λ R; x = 1 + 4λ. parametrikus egyenlet: y = 1 λ, λ R; z = λ 3. kanonikus egyenlet: x 1 4 = y + 1 = z 1.
3 1.1. Megjegyzés. Ha egy irányparaméter nulla, akkor az egyenes párhuzamos a neki megfelelő koordinátasíkkal. Példa. Az A(, 1, 3) ponton áthaladó és d( 1, 0, 1) irányú egyenes egyenletei: x = λ 1. parametrikus egyenlet: e : y = 1, λ R; z = 3 + λ. kanonikus egyenlet: e : x 1 = y 1 = z Az aránypárok tulajdonságait felhasználva ezt az egyenletet még átírhatjuk a következő alakba: e : { x = z 3 y = 1, ahonnan látszik, hogy az e egyenes benne található az y = 1 síkban, vagyis párhuzamos az (xoz) síkkal Két különböző pont által meghatározott egyenes egyenlete Legyen R = {O, e 1, e, e 3 } egy affin koordináta-rendszer és legyen M 1, M M 1 M. S két pont úgy, hogy e 3 O M 1 M e M e 1. ábra. Visszavezethetjúk az M 1 M egyenes egeynletének meghatározását az előbbi esetre, mert az M 1 M egyenest meghatározza egy pontja (például az M 1 ) és az M 1 M = r M r M vektor. Feltétezzük, hogy az M 1, M pont koordinátái: M 1 (x 1, y 1, z 1 ), M (x, y, z ), ekkor M 1 M egyenes irányvektora M 1 M (x x 1, y y 1, z z 1 ). Tehát az M 1 M egyenes vektoriális egyenlete: r M = r M1 + λ M 1 M, λ R. Behelyettesítve az M 1 M = r M r M összefüggést, kapjuk az M 1 M egyenes vektoriális egyenletét: r M = (1 λ) r M1 + λ r M, λ R. (4) Innen az M 1 M egyenes parametrikus egyenlete: x = (1 λ)x 1 + λx y = (1 λ)y 1 + λy, λ R. (5) z = (1 λ)z 1 + λz Kifejezve mindegyik egyenletből λ-t és a kapott kifejezéseket egyenlővé téve jutunk az M 1 M egyenes kanonikus egyenletéhez: x x 1 M 1 M : = y y 1 = z z 1. (6) x x 1 y y 1 z z 1
4 Egyenes megadása, mint két sít metszete 1.1. Tétel. Adott a következő egyenletrendszer: { A1 x + B 1 y + C 1 z + D 1 = 0 (7) A x + B y + C z + D = 0 ( ) A1 B úgy, hogy rang 1 C 1 D 1 =. A B C D Ekkor az (7) egyenletrendszer egy egyenest ábrázol. ( ) A1 B Bizonyítás. Mivel rang 1 C 1 D 1 =, következik, hogy létezik egy -es részmátrix, A B C D amelynek a determinánsa nem nulla, például legyen ( ) A1 B det 1 0. A B Ekkor a (7) egyenletrendszer kompatibilis és határozatlan (végtelen sok megoldása van). Tehát létezik (x 0, y 0, z 0 ) R 3 úgy, hogy { A1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 (8) A x 0 + B y 0 + C z 0 + D = 0 vagyis Az (7) és a (8) relációk megfelelő egyenleteit egymásból kivonva, kapjuk a következő egyenletrendszert: { A1 (x x 0 ) + B 1 (y y 0 ) + C 1 (z z 0 ) = 0 (9) A (x x 0 ) + B (y y 0 ) + C (z z 0 ) = 0, ( ) A1 B Mivel det 1 A B (x x 0 ) A 1 (z z 0 ) + B (y y 0 ) 1 (z z 0 ) = C 1 (x x 0 ) A (z z 0 ) + B (y y 0 ) (z z 0 ) = C. 0 a (10) egyenletrendszer egy Cramer-rendszer az x x 0 és y y 0 ismeretlenekkel. Tehát a (10) megoldásai a következők lesznek: z z 0 z z 0 x x 0 C 1 B 1 C B = z z 0 A 1 B 1 A B y y 0 A 1 C 1 A C = z z 0 A 1 B 1. A B Átrendezve ezeket az egyenleteket a következőket kapjuk: (10) x x 0 C 1 B 1 C B y y = 0 A 1 C 1 A C z z = 0 A 1 B 1 A B Észrevehetjük, hogy ez épp egy egyenes egyenlete, amely átmegy az (x 0, y 0, z 0 ) ponton és iránykomponensei: ( ) C 1 B 1 C B, A 1 C 1 A C, A 1 B 1 A B. Tehát a (7) egyenletrendszer megoldásai egy egyenes egyenletét elégítik ki. { A1 x + B 1.1. Értelmezés. Az 1 y + C 1 z + D 1 = 0 egyenletrendszert az A x + B y + C z + D = 0 egyenes általános egyenletének nevezzük, ha ( ) A1 B rang 1 C 1 D 1 =. A B C D
5 1.. Pont távolsága egyenestől (térben) Legyen R{O, i, j, k} egy descartes féle koordináta-rendszer, M 0 (x 0, y 0, z 0 ) egy rögzített pont és e : x x 1 = y y 1 = z z 1 egy egyenes. Legyen pr e (M 0 ) = M. Ekkor az M 0 pont e egyenestől való p q r távolságán az alábbi számot értjük d(m 0, e) = M 0 M. M 0 e d 7 M M 1 A 3. ábra. Az M 0 pont távolsága az e egyenestől: M 0 M. Legyen M 1 (x 1, y 1, z 1 ) és A két pont az e egyenesről úgy, hogy M 1 A = d(p, q, r), ahol d vektorral az e egyenes irányvektorát jelöltük. Ekkor az M 1 M 0 A háromszög területét kétféleképpen felírva a következő egyenlőséghez jutunk: σ(m 0 M 1 A) = 1 M 0 M M 1 A = 1 M 1 M 0 d. Ha ebből a képletből kifejezzük az M 0 M = d(m 0, e) számot kapjuk, hogy: ahol d = p + q + r és d(m 0, e) = M 1 M 0 d d, (11) M 1 M 0 d = i j k x 0 x 1 y 0 y 1 z 0 z 1 p q r = Tehát = i d(m 0, e) = y 0 y 1 z 0 z 1 q r + j y 0 y 1 z 0 z 1 q r z 0 z 1 x 0 x 1 r p + k x 0 x 1 y 0 y 1 p q + z 0 z 1 x 0 x 1 + x 0 x 1 y 0 y 1 r p p q. p + q + r Csúcspontjainak koordinátáival jellemzett háromszög területe térben és síkban Legyen {O, i, j, k} egy ortonormált jobbsodrású koordináta-rendszer és ehhez viszonyítva adottak az M 1 (x 1, y 1, z 1 ), M (x, y, z ), M 3 (x 3, y 3, z 3 ) S nem kollineáris pontok. Ekkor az M 1 M M 3 háromszög területét a következő képlettel számíthatjuk ki: T M1M M 3 = 1 M 1 M M 1 M 3 (1) A továbbiakban kifejezzük a terület képletét a pontok koordinátáival. Mivel M 1 M (x x 1, y y 1, z z 1 ) és M 1 M 3 (x 3 x 1, y 3 y 1, z 3 z 1 ) kapjuk, hogy
6 z M 1 M 3 M x O y T prxoy M 1 M M 3 4. ábra. Térbeli háromszög területe. Tehát T M1M M 3 = 1 M 1 M M 1 M 3 = = 1 M 1 M M 1 M 3 = y y 1 z z 1 y 3 y 1 z 3 z 1 i j k x x 1 y y 1 z z 1. x 3 x 1 y 3 y 1 z 3 z 1 + z z 1 x x 1 z 3 z 1 x 3 x 1 + x x 1 y y 1 x 3 x 1 y 3 y 1. Átírva a gyök alatti determinánsokat az alábbi képlethez jutunk: T M1M M 3 = 1 y 1 z 1 1 y z 1 y 3 z z 1 x 1 1 z x 1 z 3 x x 1 y 1 1 x y 1 x 3 y 3 1. (13) 1.. Megjegyzés. Ha a háromszög az (xoy) síkban található, akkor a háromszög csúcsainak koordinátái M i (x i, y i, 0), i = 1, 3 és így T M1 M M 3 = 1 x 1 y 1 1 x y 1 x 3 y 3 1 = 1 x 1 y 1 1 x y 1 x 3 y 3 1 x 1 y Megjegyzés. Észrevehetjük, hogy az x y 1 determináns értéke megadja tulajdonképpen az x 3 y 3 1 M 1 M M 3 térbeli háromszög xoy síkra eső vetületének a kétszeres területét. Hasonlóan y 1 z 1 1 y z 1 y 3 z 3 1 = T pr yoz (M 1 M M 3 ); z 1 x 1 1 z x 1 z 3 x 3 1 = T pr xoz (M 1 M M 3 ). Tehát T M1 M M 3 =. T pr yoz (M 1 M M 3 ) + T pr xoz (M 1 M M 3 ) + T pr xoy (M 1 M M 3 )
7 1.4. Síkok egyenletei Descartes-féle koordináta rendszerhez viszonyítva Egy pont és két nem párhuzamos irány által meghatározott sík egyenlete Tekintjük az A(x 0, y 0, z 0 ) S rögzített pontot és a d 1 (p 1, q 1, r 1 ), d (p, q, r ) V egymással nem párhuzamos vektorokat. Jelölje a és b a d 1 illetve a d vektorok tartóegyeneseit. Ekkor létezik egy és csakis egy a egyenes úgy, hogy a a, A a és létezik egy és csakis egy b egyenes úgy, hogy b b, A b. Ekkor dir a = dir d 1 és dir b = dir d. Mivel a b = {A} kapjuk, hogy az (a, b ) = α sík jól meghatározott. Tehát egy sík egyértelműen meghatározott egy pont és két nem párhuzamos irány által. a d 1 d α a A b b 5. ábra. Az A pont és d 1, d által meghatározott sík Egy sík egyenlete meghatározott, ha bármely M pontjának ismerjük a helyzetvektorát. Legyen M egy tetszőleges pont az A pont valamint a d 1, d vektorok által meghatározott α síkban. r A A d 1 3 d M e 3 O e r M α e 1 6. ábra. Az A pont és d 1, d vektorok által meghatározott sík Felírható, hogy r M = r A + AM. Mivel az AM vektor koplanáris a d 1, d vektorokkal, léteznek a λ, µ R valós számok úgy, hogy AM = λ d 1 + µ d. Tehát a sík vektoriális egyenlete: r M = r A + λ d 1 + µ d, λ, µ R. (14) Legyen az M(x, y, z) pont helyzetvektora az R koordináta-rendszerben r M = OM = x e 1 + y e + z e 3. Tudjuk, hogy r A = x 0 e 1 +y 0 e +z 0 e 3, d 1 = p 1 e 1 +q 1 e +r 1 e 3, d = p e 1 +q e +r e 3. Ekkor felhasználva a sík (14) egyenletét írhatjuk, hogy: x e 1 + y e + z e 3 = (x 0 + λ p 1 + µ p ) e 1 + (y 0 + λ q 1 + µ q ) e + (z 0 + λ r 1 + µ r ) e 3. Mivel az e 1, e, e 3 vektorok lineárisan függetlenek, kapjuk a következő egyenletrendszert: x = x 0 + λ p 1 + µ p y = y 0 + λ q 1 + µ q z = z 0 + λ r 1 + µ r, λ, µ R, (15)
8 amelyet a sík paraméteres egyenleteinek nevezünk. Átrendezve a kapott (15) egyenleteket írhatjuk, hogy: λ p 1 + µ p = x x 0 λ q 1 + µ q = y y 0. λ r 1 + µ r = z z 0 Ennek az egyenletrendszernek a λ és µ ismeretlenekkel akkor van megoldása (Rouché tétele szerint), ha: p 1 p x x 0 q 1 q y y 0 = 0, vagy átírva r 1 r z z 0 x x 0 y y 0 z z 0 p 1 q 1 r 1 = 0. (16) p q r Az így kapott (16) egyenletet a sík algebrai vagy kanonikus egyenletének nevezzük. Ha az (16) determinánst az első sora szerint kifejtjük, akkor az egyenletet kapjuk, ahol A(x x 0 ) + B(y y 0 ) + C(z z 0 ) = 0 (17) A = q 1 r 1 q r, B = r 1 p 1 r p, C = p 1 q 1 p q. Az (17) egyenletet az A(x 0, y 0, z 0 ) ponton áthaladó a sík algebrai egyenletének nevezzük Három nem kollineáris pont által meghatározott sík egyenlete Legyen R = {O, e 1, e, e 3 } egy affin koordináta-rendszer és M 1 (x 1, y 1, z 1 ), M (x, y, z ), M 3 (x 3, y 3, z 3 ) S három nem kollineáris pont (7. ábra). e O M 1 M M M 3 e 1 e 3 7. ábra. Ekkor az M 1, M, M 3 pontok egyértelműen meghatároznak egy (M 1 M M 3 ) = α síkot. Ha M α a sík egy tetszőleges pontja, akkor felírható, hogy ahol λ, µ R. Tehát a sík vektoriális egyenlete: r M = r M1 + M 1 M = r M1 + λ M 1 M + µ M 1 M 3 = = r M1 + λ( r M r M1 ) + µ( r M3 r M1 ) = = (1 λ µ) r M1 + λ r M + µ r M3, r M = (1 λ µ) r M1 + λ r M + µ r M3, λ, µ R. (18) Hasonlóan, mint a (15) relációban, kapjuk, hogy x = (1 λ µ)x 1 + λx + µx 3 y = (1 λ µ)y 1 + λy + µy 3 z = (1 λ µ)z 1 + λz + µz 3, λ, µ R (19)
9 amelyet a sík parametrikus egyenletének nevezünk. Ha átrendezzük a fenti rendszert kapunk λ, µ -ben egy két ismeretlenes egyenletrendszert: x x 1 = λ(x x 1 ) + µ(x 3 x 1 ) y y 1 = λ(y y 1 ) + µ(y 3 y 1 ) z z 1 = λ(z z 1 ) + µ(z 3 z 1 ) Rouché tételből következik, hogy az egyenletrendszernek akkor és csakis akkor van megoldása, ha: x x 1 y y 1 z z 1 x x 1 y y 1 z z 1 = 0. (0) x 3 x 1 y 3 y 1 z 3 z 1 Ezt az egyenletet nevezzük a három nem kollineáris ponton áthaladó sík algebrai egyenletének. Ez az egyenlet még átírható a következő alakba: x y z 1 x 1 y 1 z 1 1 x y z 1 = 0. (1) x 3 y 3 z A sík tengelymetszetes egyenlete Legyenek az A(a, 0, 0), B(0, b, 0) és a C(0, 0, c) pontok a térben. Ekkor a (0) képlet szerint az (ABC) sík egyenlete: x a y z a b 0 = 0. a 0 c e 3 C(0, 0, c) A(a, 0, 0) e 1 e B(0, b, 0) 8. ábra. : Kiszámolva a determinánst és átrendezve az egyenletet megkapjuk a sík tengelymetszetes egyenletét x a + y b + z = 1. () c A sík egyenlete, ha ismert egy pontja és normálvektora Legyen α : Ax + By + Cz + D = 0 egy sík. Ekkor létezik olyan M 0 (x 0, y 0, z 0 ) α, amelyre Ax 0 + By 0 + Cz 0 + D = 0. Kivonva a két egyenlőséget egymásból kapjuk, hogy: A(x x 0 ) + B(y y 0 ) + C(z z 0 ) = 0. (3) Legyen az N (A, B, C) egy vektor és M(x, y, z) egy tetszőleges pont az α síkban. Ekkor a (3) összefüggés ekvivalens azzal, hogy N M 0 M = 0, M α (4) vagyis N M 0 M, bármely M α pont esetén. Ez azt jelenti, hogy az N(A, B, C) vektor merőleges az α síkra.
10 z α N M 0 O M y x 9. ábra. 1.. Értelmezés. Az N (A, B, C) vektort az α : Ax + By + Cz + D = 0 sík normálvektorának nevezzük. Legyen az n = nevezzük. N N = A i + B j + C k A + B + C vektor. Az n vektort az α sík normál-egységvektorának 1.. Tétel. Az α síkot egyértelműen meghatározza egy M 0 (x 0, y 0, z 0 ) pontja és egy rá merőleges N (A, B, C) irányvektor. Ekkor a sík egyenlete: A(x x 0 ) + B(y y 0 ) + C(z z 0 ) = 0. (5) Bizonyítás. Legyen α egy sík, M 0 (x 0, y 0, z 0 ) α egy pont és N (A, B, C) úgy, hogy N α. Ekkor az N vektor merőleges az MM 0 vektorra, bármely M(x, y, z) α pont esetén, vagyis N M 0 M = 0, minden M α pontra. Felírva ezen vektorokat a komponenseik segítségével és felhasználva a skaláris szorzat kiszámítási képletét, kapjuk az α sík egyenletét: A(x x 0 ) + B(y y 0 ) + C(z z 0 ) = Pont távolsága síktól Legyen R = {O, i, j, k} egy Descartes féle ortonormált koordináta-rendszer, M 0 (x 0, y 0, z 0 ) egy pont a térben és α : Ax + By + Cz + D = 0 egy sík. Legyen M 1 = pr α (M 0 ) és N (A, B, C) a sík normálvektora. Ekkor M 0 M 1 α és M 0 M 1 N. Az M 0 pontnak az α síktól való távolságán a d(m 0, α) = M 0 M 1 számot értjük. M 0 N (A, B, C) M 1 α 10. ábra. I. Módszer. Felírjuk az M 0 ponton áthaladó α síkra merőleges d egyenes egyenletét: x x 0 A = y y 0 B = z z x = x 0 + tp 0 vagy parametrikus alakban: y = y 0 + tq. Meghatározzuk az M C 1 pont koordinátáit, amelyet a d z = z 0 + tr egyenes és az α sík metszeteként kapunk. Az M 1 pont koordinátáit tehát a következő egyenletrendszer adja: Ax + By + Cz + D = 0 x = x 0 + ta y = y 0 + tb z = z 0 + tc
11 Ebből az egyenletrendszerből kapjuk, hogy t = Ax 0 + By 0 + Cz 0 + D A + B + C. Legyenek (x 1, y 1, z 1 ) az M 1 pont koordinátái. Ekkor x 1 = x 0 A Ax 0 + By 0 + Cz 0 + D A + B + C y 1 = y 0 A Ax 0 + By 0 + Cz 0 + D A + B + C z 1 = z 0 A Ax 0 + By 0 + Cz 0 + D A + B + C Használjuk a következő jelölést: k = Ax 0 + By 0 + Cz 0 + D A + B + C. Ekkor d(m 0, α) = M 1 M 0 = A k + B k + C k = k A + B + C. Tehát az M 0 pont távolságát az α síktól a következő képlet adja meg: d(m 0, α) = Ax 0 + By 0 + Cz 0 + D A + B + C. N II. Módszer. Legyen n = N az α sík normál egységvektora. Ekkor M 1 M 0 párhuzamos a n vektorral, tehát közrezárt β szögük mértéke 0 vagy 180. Így M 1 M 0 n = M 1 M 0 n cos β = M 1 M 0 (6) Behelyettesítve az M 1 M 0 (x 1 x 0, y 1 y 0, z 1 z 0 ) és ( A n = A + B + C, összefüggéseket a fenti skaláris szorzatba, kapjuk, hogy B A + B + C, ) C A + B + C M 1 M 0 = Ax 0 + By 0 + Cz 0 Ax 1 By 1 Cz 1 A + B + C. (7) Tudjuk, hogy az M 1 pont az α síkban van, vagyis koordinátái eleget tesznek a sík egyenletének: Ax 1 +By 1 + Cz 1 + D = 0, ahonnan Ax 1 + By 1 + Cz 1 = D. Visszahelyettesítve ezt a (7) relációba, kapjuk az M 0 pont α síktól való távolságának képletét Két kitérő egyenes közös merőlegese és távolsága 1.3. Értelmezés. Legyen e 1 és e két kitérő egyenes a térben. Az e 1 és e kitérő egyenesek közös merőlegesén azt az egyenest értjük, amely merőleges mindkét egyenesre és támaszkodik rájuk Értelmezés. Legyenek az A és B pontok a közös merőleges metszéspontjai az e 1 és az e egyenesekkel. Az [AB] szakasz hosszát a két kitérő egyenes távolságának nevezzük. e 1 A e e B 11. ábra. Az e 1, e egyenesek közös merőlegese az AB egyenes
12 A közös merőleges megszerkesztése 1. Legyen a egy egyenes, amely párhuzamos az e 1 egyenessel és áthalad az e egy tetszőleges M pontján. Legyen az α az a és e egyenesek által meghatározott sík.. Legyen β az a sík, amely tartalmazza az e egyenest és merőleges az α síkra. 3. Legyen továbbá γ egy sík, amely tartalmazza az e 1 egyenest és merőleges az α síkra. 4. Ekkor a β és a γ síkok e metszésvonala merőleges lesz az α síkra és ezáltal az e 1, e egyenesekre is. Ráadásul az e támaszkodik is ezekre az egyenesekre, tehát az e egyenes lesz az e 1, e közös merőlegese. e 1 β. e... a γ N α e. 1. ábra. Az e 1, e egyenesek közös e merőlegese. A közös merőleges egyenlete Legyen R = {O, i, j, k} egy Descartes féle koordináta-rendszer a térben és legyen e 1 : x x 1 p 1 = y y 1 q 1 = z z 1 r 1 e : x x p = y y q = z z r két kitérő egyenes. Az egyenesek egyenletei alapján az M 1 (x 1, y 1, z 1 ), M (x, y, z ) pontok rajta vannak az e 1 illetve az e egyeneseken. Ekkor az α sík egyenlete: α : x x y y z z p 1 q 1 r 1 = 0. (8) p q r Ha kifejtjük a fenti determinást akkor az α sík egyenlete a következő alakba írható: α : (x x ) q 1 r 1 q r + (y y ) r 1 p 1 r p + (z z ) p 1 q 1 p q = 0. Legyen N az α sík normálvektora. Ekkor az N normálvektor irányparaméterei a következők: ( ) q1 r N 1 r, 1 p 1 p, 1 q 1. q r r p p q A β síkot meghatározza az e egyenes, vagyis az M pont és d vektor, valamint az α sík N normálvektora. Ezért egyenletét a következő képlet adja meg: β : = 0. (9) x x y y z z p q 1 r 1 q r 1 p 1 r p 1 q 1 q r r p p q
13 A γ síkot meghatározza az M 1 pont és d 1, N vektorok. Tehát egyenlete: γ : = 0. (30) x x 1 y y 1 z z 1 p 1 q 1 r 1 q 1 r 1 p 1 r 1 p 1 q 1 q r r p p q A közös merőleges egyenletét a β és a γ síkok metszete adja meg, vagyis az (9) és (30) egyenletekből alkotott egyenletrendszer Megjegyzés. A közös merőleges megszerkesztése során tulajdonképpen nincs is szükségünk az α sík egyenletére, csak annak normálvektorára. Ez a normálvektor merőleges az α síkra, tehát merőleges az e 1, e egyenesekre. Tehát a normálvektort felírhatjuk, mint a d 1 d vektorok vektori szorzata: N = d1 d = i j k p 1 q 1 r 1 = i p q r q 1 r 1 q r + j r 1 p 1 r p + k p 1 q 1 p q (31) Ezután pedig tekintjük a β síkot, amely tartalmazza az e egyenest és párhuzamos az N vektorral, majd a γ síkot, amely szintén párhuzmos az N vektorral és tartalmazza az e 1 egyenest. Ezen síkok metszete párhuzamos az N vektorral és támaszkodik az e 1, e egyenesekre, tehát az e 1, e közös merőlegese lesz. A két kitérő egyenes távolsága Az e 1 és az e egyenesek közötti távolság kiszámításánál vegyük észre, hogy az e 1 egyenes párhuzamos az e egyenest tartalmazó α síkkal, tehát: d(e 1, e ) = d(e 1, α) = d(m 1, α) = 1.7. Két térbeli egyenes szöge x 1 x y 1 y z 1 z p 1 q 1 r 1 p q r q 1 r 1 q r + r 1 p 1 r p + p 1 q 1 p q 1.5. Értelmezés. Két egyenes (hajlás)szöge alatt a tér egy tetszőleges pontján át a velük párhuzamosan húzott egyenesek által bezárt hegyesszöget vagy derékszöget értjük. Beláthatjuk, hogy ezáltal értelmezett két kitérő egyenes szöge is. Hangsúlyozzuk, hogy kitérő egyenesek lehetnek merőlegesek is egymásra, viszont ha egy pontból egy egyenesre bocsátott merőlegesről beszélünk, akkor az egyenest metsző egyenesre gondolunk. Ehhez a merőlegeshez az adott pont és egyenes síkján belül juthatunk el. Ennek a merőlegesnek a talppontja az adott pontnak az adott egyenesre eső merőleges vetülete. x x 1 Legyen d 1 : = y y 1 = z z 1 x x és d : = y y = z z két egyenes. Ekkor p 1 q 1 r 1 p q r irányvektoraiknak tekinthetjük a d 1 (p 1, q 1, r 1 ) és d (p, q, r ) vektorokat. A d 1 és d egyenesek szöge megegyezik irányvektoraik szögével, ha azok hegyesszöget vagy derékszöget zárnak be (skaláris szorzatuk nem negatív) illetve azok kiegészítő szögével, amennyiben azok tompaszöget zárnak be (skaláris szorzatuk negatív). Tehát d 1 arccos d m( d 1, d ) = d 1 d, ha d 1 d 0 d 1 π arccos d (3) d 1 d, ha d 1 d < 0. Figyelembe véve, hogy π arccos x = arccos( x), minden x [ 1, 1] esetén, majd a moduluszfüggvény értelmezését, kapjuk két egyenes szögének mértékére az alábbi összefüggést: vagy a koordináták segítségével: m( d 1, d ) = arccos m( d 1, d ) = arccos d 1 d d 1 d, (33) p 1 p + q 1 q + r 1 r p 1 + q1 + r 1 p + q +. (34) r.
14 1.8. Egyenes és sík szöge 1.6. Értelmezés. Egy egyenes és egy sík szöge alatt az egyenes síkra eső vetülete és az egyenes által bezárt szöget értjük. d α d = pr α d θ 13. ábra. Az α sík és d egyenes által bezárt θ szög Legyen α : Ax + By + Cz + D = 0 egy sík és legyen d : x x 0 = y y 0 = z z 0 egy egyenes. A sík és p q r egyenes által bezárt szöget jelöljük θ-val, az egyenes d(p, q, r) irányvektora és a sík N (A, B, C) normálvektora által bezárt szöget pedig u-val. A 14 ábra szemlélteti, hogy e két szög összege vagy különbsége egyenlő 90 - kal, a d és N vektorok helyzete alapján. d d d N d u d θ d α... α θ u ábra. Egyenes és sík szöge N Tehát π m( d, α) = m( d, N ), ha d N 0 m( π d, N ), ha d N < 0, vagyis figyelembe véve, hogy sin( π x) = cos x minden x R esetén, következik, hogy sin( d, α) = cos( d, N ) = Ap + Bq + Cr p + q + r A + B + C. Mivel egyenes és sík szögén 0és 90 közti értéket értünk, a d egyenes és α sík által bezárt szög kiszámítási képlete: Ap + Bq + Cr m( d, α) = arcsin p + q + r A + B + C. (35) Sajátos eset. A következő eseteket emeljük ki: 1.) d α egyenértékű azzal, hogy d N, vagyis A p = B q = C r ;.) d α d N d N = 0, vagyis Ap + Bq + Cr = 0; 3.) Ha d α, akkor Ap + Bq + Cr = 0 és Ax 0 + By 0 + Cz 0 + D = 0.
15 1.9. Két sík szöge 1.7. Értelmezés. Ha két sík nem párhuzamos, akkor (hajlás)szögüknek a metszésvonal egy pontjában a síkokon belül állított merőlegesek hajlásszögét nevezzük. Párhuzmos síkok hajlásszöge nullszög. Legyen α 1 : A 1 x + B 1 y + C 1 z + D 1 = 0, α : A x + B y + C z + D = 0 két sík. A két sík szögét a normálvektoraik által bezárt szög mértékének segítségével írjuk fel. A síkok normálvektorai: N 1 (A 1, B 1, C 1 ), N (A, B, C ). α α N.. N... π θ... θ θ θ α 1 α 1 N 1 N 1 N 1 N 0 N 1 N < ábra. A 15. ábra alapján is láthatjuk, hogy a két sík θ szöge megyezik a normálvektoraik szögével, ha a normálvektorok szöge hegyesszög (a skaláris szorzatuk pozitív), illetve a normálvektorok kiegészítő szögével ellenkező esetben. Tehát N 1 N arccos m( α 1, α ) = N 1 N, ha N 1 N 0 N 1 N π arccos N 1 N, ha N 1 N < 0 N 1 N arccos = N 1 N, ha N 1 N 0 N 1 N arccos N 1 N, ha N 1 N < 0 Figyelembe véve a moduluszfüggvény értelmezését, kapjuk két sík szögére az alábbi összefüggéseket a normálvektorok segítségével m( α 1, α ) = arccos valamint a síkok egyenleteinek együtthatói segítségével felírva: m( α 1, α ) = arccos N 1 N N 1 N, (36) A 1 A + B 1 B + C 1 C A 1 + B1 + C 1 A + B +. (37) C 1.5. Megjegyzés. Két sík merőlegességét és párhuzamosságát is vizsgálhatjuk a normálvektoraik segítségével. A síkok párhuamossága (merőlegessége) ekvivalens normálvektoraik párhuzamosságával (merőlegességével). Tehát α 1 α N 1 N A 1 A + B 1 B + C 1 C = 0. (38) α 1 α N 1 N A 1 A = B 1 B = C 1 C. (39)
16 z M(x, y, z) v O u r v... M (x, y, 0) y x. 16. ábra. Origó középpontú kör A gömb A gömb azon térbeli pontok mértani helye, amelyeknek egy rögzített ponttól mért távolságuk egyenlő. Az Oxyz Descartes-féle koordináta-rendszer origója legyen a gömb középpontja. Legyen M(x, y, z) egy tetszőleges pont a gömbön és ennek vetülete az xoy síkra M (x, y, 0). Ismerjük a gömb r sugarát. A paraméterek legyenek: m( xom ) = u, m(ẑom ) = v. Ekkor OM = r sin v és a gömb paraméteres egyenletei: x = r sin v cos u y = r sin v sin u, z = r cos v Az origó középpontú, r sugarú gömb algebrai egyenlete: 1.6. Megjegyzés. A gömb általános egyenlete: u [0, π), v [0, π]. (40) x + y + z = r. (41) Ax + Ay + Az Bx Cy Dz + E = 0, A 0.
17 . Analitikus mértan síkban.1. Síkbeli egyenesek egyenletei Descartes-féle koordináta rendszerhez viszonyítva Legyen R = {O, e 1, e } egy affin koordináta-rendszer a síkban Egy pont és egy vektor által meghatározott egyenes egyenlete Legyen A(x 0, y 0 ) egy rögzített pont a síkban és d(p, q) pedig egy rögzített vektor. Ekkor levezethetjük az A ponton áthaladó d irányvektorú e egyenes vektoriális egyenletét teljesen hasonlóan, mint a térbeli egyenes esetén és itt is kapjuk az egyenes egyenletének, hogy e : r M = r A + λ d, λ R, (4) ahol M(x, y) egy tetszőleges pont az e egyenesen. Behelyettesítve az r M, r A, d vektorok koordinátáit, kapjuk az e (síkbeli) egyenes paraméteres egyenleteit: { x = x0 + λp (43) y = y 0 + λq λ R. Kifejezzük a fenti egyenletrendszer mindkét egyenletéből a λ-t és egyenlővé tésszük egymással. az e (síkbeli) egyenes kanonikus egyenletéhez: Így jutunk x x 0 p = y y 0 q (44).1. Megjegyzés. Konvenció szerint, ha az egyik tört nevezője nulla, akkor a számláló is nulla. x 1 Példa. Ha az e egyenes egyenlete: = y 3, akkor ez ekvivalens azzal, hogy e : y 3 = 0, vagyis 0 az e párhuzamos az Ox tengellyel. Ha az e egyenes nem párhuzamos az Oy tengellyel (vagyis p 0), akkor az e bármely irányvektora esetén a q = m arány állandó. Ezt az arányt az e egyenes iránytényezőjének nevezzük. p Ha az R Descartes-féle koordináta-rendszer (vagyis derékszögű), akkor ahol α az e egyenesnek az Ox tengellyel bezárt szöge. m = tg α, (45) y O d(p, q) } q α }{{} p e x 17. ábra. Ha a (44) összefüggést beszorozzuk q-val, kapjuk, hogy y y 0 = q p (x x 0). (46) Tehát, az adott A(x 0, y 0 ) ponton áthaldó és adott m iránytényezőjű egyenes egyenlete y y 0 = m(x x 0 ). (47)
18 .1.. Két különböző pont által meghatározott egyenes egyenlete Legyen M 1 (x 1, y 1 ) és M (x, y ) két rögzített pont a síkban. Ekkor az M 1 és M pontokon áthaladó egyenes irányvektora M 1 M (x x 1, y y 1 ), tehát az M 1 M egyenes kanonikus egyenlete: x x 1 x x 1 = y y 1 y y 1, (48) amelyet még átírhatunk a következő könnyebben megjegyezhető alakba: x y 1 x 1 y 1 1 = 0. (49) x y Egyenes tengelymetszetes alakja Ha az egyenes a koordináta-tengelyeket az A(a, 0) és B(0, b) pontokban metszi, akkor egyenlete: x a + y b = 1... Megjegyzés. Az M 1 M nem függőleges egyenes iránytényezője:.. Két síkbeli egyenes szöge I. módszer. Legyen m M1 M = y y 1 x x 1. d 1 : a 1 x + b 1 y + c 1 = 0, d : a x + b y + c = 0 két általános egyenlettel megadott egyenes az xoy síkban. Ezt az két egyenletet átírva kanonikus alakra: x d 1 : = y + c1 b 1 x, d : = y + c b kapjuk a két egyenes irányvektorát: d1 ( b 1, a 1 ) illetve d b 1 a 1 b a ( b, a ). Felhasználva a (33) összefüggést, kapjuk, hogy cos( d 1, d ) = a 1 a + b 1 b a 1 + b 1 a + b (50) II. módszer. Legyen d 1 : y = m 1 x + n 1, d : y = m x + n két explicit egyenlettel megadott egyenes az xoy síkban. Ekkor m 1 = tgα 1 és m = tgα, ahol α 1 és α a két egyenesnek az Ox tengellyel bezárt hajlásszögét jelölik (lásd 18 ábra). y d 1 d O α φ α1 x 18. ábra. Két egyenes szöge Belátható, hogy ha φ-vel jelöljük a d 1 és d egyenesek szögét, akkor φ = α 1 α. Tehát tgφ = tg(α 1 α ) = tgα 1 tgα 1 + tgα 1 tgα = m 1 m 1 + m 1 m. (51)
19 Ha felcseréljük az m 1 és m sorrendjét, akkor a kiegészítő szög mértékét fogjuk megkapni. Mivel két egyenes szögén mindig a hegyesszöget értjük és tudjuk, hogy ennek tangense pozitív, a két síkbeli egyenes szögére levezetett összefüggést a következő alakban használjuk:.3. Párhuzamos és merőleges egyenesek.3.1. Párhuzamos egyenesek tg( d 1, d ) = m 1 m 1 + m 1 m. (5) Két párhuzamos egyenes iránya megegyezik és ezáltal iránytényezőjük is egyenlő, vagyis: d 1 d m 1 = m. (53).3. Megjegyzés. A fenti összefüggés onnan is következik, hogy Két egyenes akkor és csakis akkor párhuzamos, ha bezárt szögük 0, ami ekvivalens azzal a (5) összefüggés alapján, hogy iránytényezőik megegyeznek..3.. Merőleges egyenesek.4. Megjegyzés. Legyen d 1, d két egymásra merőleges egyenes. Ekkor irányvektoraik d 1 (p 1, q 1 ) és d (p, q ) szintén merőlegesek egymásra, ezért skaláris szorzatuk nulla. Tehát p 1 p + q 1 q = 0. Feltételezve, hogy egyik egyenes sem párhuzamos az Oy tengellyel, végigoszthajtuk ezt az egyenletet p 1 p -vel és felhasználva az iránytényező értelmezését, kapjuk, hogy d 1 d m 1 m = 1. (54).5. Megjegyzés. 1. A (54) összefüggés másként is levezethető. Ay (5) összefüggés jobboldalának nincs értelme abban az esetben, ha m 1 m = 1. Ez azt jelenti, hogy értelmetlen a tg( d 1, d ), vagyis a d 1 és d egyenesek szöge Pont távolsága egyenestől (síkban) Legyen e : ax + by + c = 0 egy egyenes az xoy síkban és M 0 (x 0, y 0 ) egy pont a síkban. Az M 0 pont távolságán az e egyenestől az [M 0 M 1 ] szakasz hosszát értjük, ahol M 1 az M 0 pont e egyenesre eső vetülete. M 0 e M ábra. Az M 0 pont távolsága az e egyenestől: M 0 M 1. Felírjuk az M 0 ponton áthaladó és az e egyenesre merőleges M 0 M 1 egyenes egyenletét: M 0 M 1 : y y 0 = 1 m e (x x 0 ), ahol m e = a b az e egyenes iránytényezője. Az M 1 pont (x 1, y 1 ) koordinátáit megkapjuk az e és M 0 M 1 egyenesek egyenleteiből alkotott { b(x x0 ) = a(y y 0 ) ax + by + cz = 0 egyenletrendszer megoldásaként: x 1 = x 0 a ax 0 + by 0 + c a + b y 1 = y 0 b ax 0 + by 0 + c a + b.
20 Kiszámítva a [M 0 M 1 ] szakasz hosszát, kapjuk, az M 0 pont távolságát az e egyenestől: d(m 0, e) = ax 0 + by 0 + c a + b. (55) Alkalmazás. Szögfelezők egyenletei (síkban). Legyen d 1 : a 1 x + b 1 y + c 1 z = 0, d : a x + b y + c z = 0 két metsző egyenes a síkban. Célunk meghatározni a két egyenes által alkotott szög (belső és külső) szögfelezőinek egyenleteit. Tudjuk, hogy a szögfelező azon pontok mértani helye, amelyeknek távolsága a szög két szárától megegyezik. Legyen M(x, y) egy tetszőleges pont a síkban. Ez a pont akkor és csakis akkor lesz a d 1 és d egyenesek szögfelezőjén, ha d(m, d 1 ) = d(m, d ), vagyis a 1 x + b 1 y + c 1 a 1 + b 1 = a x + b y + c. a + b Így a két szögfelező egyenlete: a 1 x + b 1 y + c 1 a 1 + b 1 = ± a x + b y + c. (56) a + b.5. Kúpszeletek.5.1. Kör Legyen M 0 egy rögzített pont a P síkban és legyen r > 0 egy rögzített szám..1. Értelmezés. Az M 0 középpontú és r sugarú C kör azon M pontok mértani helye a síkból, amelyeknek az M 0 ponttól vett távolsága állandó és egyenlő r-rel, vagyis Legyen xoy egy Descartes-féle koordináta-rendszer. C(M 0, r) = {M P : MM 0 = r.} (57).1. Tétel. Az M(x, y) pont akkor és csakis akkor van az M 0 (x 0, y 0 ) középpontú, r sugarú körön, ha (x x 0 ) + (y y 0 ) = r. (58) Bizonyítás. Az M pont akkor és csakis akkor van az M 0 középpontú r sugarú körön, ha MM 0 = r, vagyis (x x0 ) + (y y 0 ) = r (x x 0 ) + (y y 0 ) = r. Tehát az M 0 (x 0, y 0 ) középpontú, r sugarú kör implicit egyenlete: C : (x x 0 ) + (y y 0 ) = r... Tétel. Az (x x 0 ) +(y y 0 ) = r egyenletű kör M 1 (x 1, y 1 ) pontjában szerkesztett érintő egyenlete: (x x 0 )(x 1 x 0 ) + (y y 0 )(y 1 y 0 ) = r, (59) amelyet még a kör duplázott egyenletének is nevezünk az M 1 (x 1, y 1 ) pontban. Bizonyítás. Tudjuk, hogy a kör M 1 pontjába szerkesztett érintő merőleges az M 1 ponton áthaladó átmérőre. Felírjuk először az átmérő egyenletét: M 1 M 0 : x x 1 x 0 x 1 = y y 1 y 0 y 1 majd az erre merőleges (érintő) egyenletét, felhasználva, hogy mérintő = 1 m M1 M 0 = x 0 x 1 y 0 y 1. Tehát az érintő egyenlete: y y 1 = x 0 x 1 y 0 y 1 (x x 1 ).
21 T M 1 (x 1, y 1 ) M 0 0. ábra. Kör érintője és normálisa. ( x 0 + x 1 )(x x 1 ) (y 0 y 1 )(y y 1 ) = 0 (60) Mivel az M 1 pont rajta van a C körön, kielégíti annak egyenletét: Összeadva a (60) és (61) egyenleteket kapjuk, hogy (x 1 x 0 ) + (y 1 y 0 ) = r. (61) (y y 0 )(y 1 y 0 ) + (x x 0 )(x 1 x 0 ) = r. (6).. Értelmezés. A kör M 1 pontjába szerkesztett normálisán azt az egyenest értjük, amely áthalad az M 1 ponton és merőleges az M 1 pontba szerkesztett körérintőre. Kör esetén egy M 1 pontba szerkesztett normális megegyezik az M 1 ponton áthaladó átmérővel. Tehát egyenlete: x x 1 M 1 M 0 : = y y 1 x 0 x 1 y 0 y 1.6. Megjegyzés. Kör érintőjének egyenletét meghatározhatjuk felhasználva az analízisből jólismert eredményt is: Legyen f : I R egy deriválható függvény, I R nyílt intervallum. A függvény grafikus képéhez az M(x 1, f(x 1 ) = y 1 ) pontban szerkesztett érintő egyenlete: y y 1 = f (x 1 )(x x 1 ). Kör esetén: y = f(x) = y 0 ± r (x x 0 ), ahol az előjelet pozitívnak választjuk, ha M pont a kör felső körívén található és negatívnak ellenkező esetben..5.. Ellipszis.3. Értelmezés. Azon pontok mértani helyét a síkból, amelyeknek két rögzített ponttól mért távolságuk összege állandó, ellipszisnek nevezzük. Legyen c > 0 és F, F két rögzített pont a síkban úgy, hogy F F = c és legyen a > c. A sík azon M pontjainak mértani helyét, amelyre MF + MF = a, ellipszisnek nevezzük: E = {M P : MF + MF = a}. További elnevezések: 1. F, F : az ellipszis fókuszai. F F egyenes: fokális tengely 3. F F = c : fókusztávolság 4. [MF ] és [MF ] szakaszok: M ponthoz tartozó vezérsugarak..7. Megjegyzés. Ha c = 0, akkor az ellipszis egy a sugarú kör lesz. Legyen E egy adott ellipszis. Választunk egy xoy Descartes-féle koordináta-rendszert úgy, hogy az O pont legyen az [F F ] szakasz felezőpontja, az Ox tengely legyen a fokális tengely. Ekkor F ( c, 0) és F (0, c).
22 a y B b M a... F... F c O c a x B b 1. ábra. Ellipszis..3. Tétel. Az M(x, y) pont akkor és csakis akkor van az E ellipszisen, ha x a + y b = 1, ahol b = a c. Bizonyítás. Az M pont rajta van az E ellipszisen, ha MF + MF = a. Ekkor (x + c) + y + (x c) + y = a. (x + c) + y = (x c) + y + 4a a (x c) + y 4xc 4a = 4a (x c) + y x c xca + a 4 = a x a xc + a c + a y x (a c ) + a y = a (a c ). Bevezetjük az a c = b jelölést és végigosztva az előbbi egyenletet a b -tel kapjuk az ellipszis kanonikus egyenletét: E : x a + y = 1. (63) b.8. Megjegyzés. A B(0, b = a c ) és a B (0, b = a c ) pontok rajta vannak az ellipszisen, mégpedig az ellipszis metszéspontját jelölik az Oy tengely-lyel. Valóban, a BOF és BOF kongruens háromszögekben alkalmazva a Pithagorász tételét kapjuk, hogy a + b = c..9. Megjegyzés. Ha jelöljük A, A és B, B -tel a (63) egyenlettel megadott ellipszis metszeteit az Ox illetve Oy tengelyekkel és a > b, akkor még használjuk a következő kifejezéseket: 1. az [AA ] szakasz az ellipszis nagytengelye;. a [BB ] szakasz az ellipszis kistengelye; 3. az A(a, 0), A ( a, 0), B(0, b), B ( b, 0) pontok: az ellipszis csúcsai..10. Megjegyzés. Az ellipszis kanonikus egyenletében az x és y változók a második hatványon szerepelnek, ezért egy M(x, y) ponttal együtt az ellipszisen vannak az M 1 ( x, y), M ( x, y), M 3 (x, y) pontok is. Tehát az Ox és Oy tengelyek szimmetriatengelyei az ellipszisnek, az O pont pedig szimmetriaközéppontja..4. Tétel. Az E : x a + y b = 1 egyenletű ellipszis M 0(x 0, y 0 ) pontjába szerkesztett érintő egyenlete: xx 0 a + yy 0 b = 1, amelyet még az ellipszis duplázott egyenletének is nevezünk az M 0 pontban. Bizonyítás.Az ellipszis érintőjének meghatározására a.6 Megjegyzést használjuk fel. Az f függvény felírása érdekében az ellipszis egyenletéből kifejezzük az y-t: y = ±b 1 x a = ± b a x a.
23 Tételezzük fel, hogy az M 0 pont az ellipszis felső ívén van, vagyis y 0 0 (ellenkező esetben teljesen hasonlóan járunk el). Ekkor az f függvényt is ennek megfelelően választjuk: y = f(x) = a b a x. Az érintő egyenlete: y y 0 = f (x 0 )(x x 0 ) y y 0 = b a x 0 a x 0 (x x 0 ). (64) Mivel az M 0 (x 0, y 0 ) E, következik, hogy x 0 a + y 0 b = 1, vagyis y 0 = b a (a x 0). Feltételeztük, hogy y 0 0, tehát a x 0 = a b y 0. Visszahelyettesítve ezt a (64) összefüggésbe írhatjuk, hogy Beszorozva ezt az egyenletet y 0 -tel, kapjuk, hogy b y y 0 = b a x0 y 0 (x x 0 ). xx 0 a + yy 0 b = y 0 b + x 0 a = 1. Tehát az érintő egyenlete: xx 0 a + yy 0 b = Értelmezés. Az ellipszis M 0 pontba szerkesztett normálisa az az egyenes, amelyik áthalad az M 0 ponton és merőleges az ellipszis M 0 pontjában szerkesztett érintőre..5. Tétel. (Az ellipszis optikai tulajdonsága) Az ellipszis M 0 pontjába szerkesztett érintő és normális felezik az F M 0 és F M 0 vezéregyenesek által meghatározott szögeket. érintő y normális M 0 F O F x. ábra. Ellipszis optikai tulajdonsága. x Bizonyítás. Úgy szerkesztjük meg a koordináta-rendszert, hogy az ellipszis egyenlete legyen E : a + y b = 1, ahol b = a c és a fókuszok F ( c, 0); F (c, 0). Legyen M 0 (x 0, y 0 ) E egy tetszőleges pont. Felírjuk az F M 0 és F M 0 vezéregyenesek egyenleteit: F M 0 : x x 0 c x 0 = y y 0 y 0 F M 0 : y 0 x + (x 0 c)y + cy 0 = 0; (65) F M 0 : x x 0 c x 0 = y y 0 y 0 F M 0 : y 0 x (x 0 + c)y + cy 0 = 0. (66) F M és F M egyenesek által bezárt szögek szögfelezői (a 56 egyenlet alapján): y 0 x + (x 0 c)y + cy 0 y 0 + (x 0 c) = ± y 0x (x 0 + c)y + cy 0 y 0 + (x 0 + c) (67)
24 Kiszámítjuk a gyökjel alatti kifejezéseket: y 0 + (x 0 c) = b a (a x 0) + (x 0 c) = = a c a (a x 0) + x 0 x 0 c + c = (a cx 0 ) a. Mivel x 0 [ a, a] és 0 < c < a, következik, hogy a cx 0 0. Tehát Hasonló számítások után kapjuk, hogy Ekkor a (67), (68), (69) összefüggések alapján az y0 + (x 0 c) = a cx 0. (68) a y0 + (x 0 + c) = a + cx 0. (69) a F M 0 F szög szögfelezőinek egyenletei: y 0 x + (x 0 c)y + cy 0 a cx 0 = ± y 0x (x 0 + c)y + cy 0 a + cx 0. Két esetünk van, aszerint, hogy az egyenlőség jobboldalán melyik előjelet választjuk. Válasszuk például a + előjelet! Ekkor elvégezve a műveleteket és alkalmazva a c = a b összefüggést, kapjuk az alábbi egyenletet: a y 0 x + a x 0 y a cy + a cy 0 cx 0 y 0 x + cx 0y c x 0 y + c x 0 y 0 = = a y 0 x a x 0 y a cy + a cy 0 cx 0 y 0 x + cx 0y + c x 0 y c x 0 y 0 a y 0 x + b yx 0 + (a b )x 0 y 0 = 0. Átrendezve ezt az egyenletet észrevehetjük, hogy ez épp az M 0 pontba szerkesztett normális egyenlete. Így a másik szögfelező (a előjeles) az M 0 pontba szerkesztett érintő lesz (mert a belső és külső szögfelezők merőlegesek egymásra az M 0 pontban, akárcsak az érintő és normális)..11. Megjegyzés. A tételben kijelentett mértani tulajdonságok az alábbi optikai tulajdonságnak felel meg: az ellipszis egyik fókuszában elhelyezett fényforrásból kiinduló tetszőleges fénysugár az ellipszisről való visszaverődés után a másik fókuszon fog átmenni Hiperbola.5. Értelmezés. A hiperbola azon pontok mértani helye, amelyeknek két rögzített ponttól vett távolságuk különbsége állandó. Legyen c > 0, F, F két rögzített pont a síkban úgy, hogy F F = c és legyen a (0, c). A sík azon M pontjainak H halmazát, amelyre MF MF = a hiperbolának nevezzük: H = {M P MF MF = a}. További elnevezések: 1. F, F : a hiperbola fókuszai. F F : fokális tengely 3. F F = c: fókusztávolság 4. [MF ], [MF ] szakaszok: az M ponthoz tartozó vezérsugarak. Legyen xoy egy Descartes-féle koordináta-rendszer, amelynek origója legyen az [F F ] szakasz felezőpontja, Ox tengelye pedig a fokális tengely. Ekkor a fókuszok koordinátái: F (c, 0), F ( c, 0)..6. Tétel. A M(x, y) pont akkor és csakis akkor tartozik hozzá a H hiperbolához, ha ahol b = c a. x a y b = 1,
25 y... b a F ( c, 0) A O A... -b F (c, 0) x 3. ábra. Hiperbola Bizonyítás. A hiperbola értelmezése szerint az M pont akkor van a H hiperbolán, ha MF MF = a, vagyis MF MF = ±a (x c) + y + (x + c) + y = ±a. Négyzetreemelve mindkét oldalt kapjuk, hogy (x c) + y = 4a + (x + c) + y ± 4a (x + c) + y 4xc 4a = ±4a (x + c) + y. Újra négyzetre emelést alkalmazva és átrendezve az egyenletet következik, hogy x (c a ) a y + a (a c ) = 0. Bevezetve a b = c a jelölést és elosztva az egyenletet a b -tel, megkapjuk a hiperbola kanonikus egyenletét: H : x a y b = 1 (70).1. Megjegyzés. A hiperbola egyenletéből adódik, hogy a hiperbolának két szimmetriatengelye van; az egyik a fókuszokat összekötő egyenes, ezt a hiperbola hiperbola valós tengelyének nevezzük; a másik fókuszokat összekötő szakasz felezőmerőlegese, melyet a hiperbola képzetes tengelyének nevezünk. A két tengely O metszépontja a hiperbola szimmetria-középpontja, amit a hiperbola középpontjának is mondunk..13. Megjegyzés. Belátható, hogy az A(a, 0) és A ( a, 0) pontok rajta vannak a hiperbolán, mégpedig ott, ahol az Ox tengely metszi a hiperbolát. Ezeket a pontokat a hiperbola csúcspontjainak nevezzük. Az a, b számok a hiperbola valós és képzetes féltengelyei..7. Tétel. Az H : x a y = 1 egyenletű parabolának a van két ferde aszimptotája a ± -ben, melynek b egyenletei: Bizonyítás. Kifejezzük a hiperbola egyenletéből a y-t és legyen y = ± b x. (71) a f(x) = y = ± b a x a. f(x) Köztudott, hogy a ferde aszimptota egyenlete ± -ben: y = mx + n, ahol m = lim x ± x és n = lim (f(x) mx). A mi esetünkben kiszámolva ezeket a határértékeket kapjuk, hogy m = ± b és n = 0. x ± a
26 .8. Tétel. A H : egyenlete: x a y b = 1 egyenlettel megadott hiperbola M 0(x 0, y 0 ) pontjában szerkesztett érintő xx 0 a yy 0 = 1. (7) b Ezt az egyenletet még a hiperbola duplázott egyenletének is nevezzük az M 0 pontban. Bizonyítás. A.6 Megjegyzés alapján a hiperbola érintője az M 0 (x 0, y 0 ) pontban : y y 0 = f (x 0 )(x x 0 ), ahol f(x) = y = ± b a x a. Az f függvény előjelét azonosnak választjuk az y 0 előjelével. Feltételezve, hogy y 0 0 az érintő egyenlete: y y 0 = b a x 0 x 0 a (x x 0). (73) (Ha y 0 < 0, teljesen hasonló számítások után ugyanahhoz az egyenlethez jutunk.) Mivel az M 0 (x 0, y 0 ) H, következik, hogy x 0 a y 0 b = 1, vagyis y 0 = b a (x 0 a ). Feltételeztük, hogy y 0 0, tehát x 0 a = a b y 0. Visszahelyettesítve ezt a (73) összefüggésbe írhatjuk, hogy Beszorozva ezt az egyenletet y 0 -tel, kapjuk, hogy b Tehát az érintő egyenlete: y y 0 = b a x0 y 0 (x x 0 ). xx 0 a yy 0 b = y 0 b x 0 a = 1. xx 0 a yy 0 b = Értelmezés. Azt az egyenest, amelyik átmegy az M 0 ponton és merőleges az M 0 pontba szerkesztett érintőre, a hiperbola M 0 pontjába szerkesztett normálisnak nevezzük..9. Tétel. (A hiperbola optikai tulajdonsága) A hiperbola M 0 pontjába szerkesztett érintő és normális az F M 0 és F M 0 vezéregyenesek által meghatározott szögek szögfelezői. n y é M 0 F O F x 4. ábra. A hiperbola optikai tulajdonsága x Bizonyítás. Úgy szerkesztjük meg a koordináta-rendszert, hogy a H hiperbola egyenlete legyen a y b = 1, ahol b = c a és a fókuszok F ( c, 0); F (c, 0). Legyen M 0 (x 0, y 0 ) H egy tetszőleges pont. Felírjuk az F M 0 és F M 0 vezéregyenesek egyenleteit: F M 0 : y 0 x (x 0 c)y cy 0 = 0; (74)
27 F M és F M egyenesek által bezárt szögek szögfelezői F M 0 : y 0 x (x 0 + c)y + cy 0 = 0. (75) y 0 x (x 0 + c)y + cy 0 y 0 + (x 0 + c) = ± y 0x (x 0 c)y cy 0 y 0 + (x 0 c). (76) Kiszámoljuk a gyökjel alatti kifejezéseket: y 0 + (x 0 + c) = b ( 1 + x 0 a ) + x 0 + x 0 c + c = = ( b a + 1)x 0 + x 0 c + c b = = (b + a )x 0 a + x 0 c + a = = 1 a (c x 0 + x 0 ca + a 4 ) = 1 a (cx 0 + a ). Hasonló gondolatmenet alapján y 0 + (x 0 c) = 1 a (a cx 0 ). Ekkor a szögfelezők egyenletei: y 0 x (x 0 + c)y + cy 0 a + cx 0 = ± y 0x (x 0 c)y cy 0 a cx 0. Ha a előjeles egyenletet választjuk először, akkor az aránypárok tulajdonsága alapján írhatjuk, hogy a y 0 x a x 0 y a cy + a y 0 c cx 0 y 0 x + cx 0y + c x 0 y c x 0 y 0 = = a y 0 x + a x 0 y a cy + a cy 0 cx 0 y 0 x + cx 0y c x 0 y + c x 0 y 0 a y 0 x a x 0 y + c x 0 y c x 0 y 0 = 0 a y 0 x + b x 0 y (a + b )x 0 y 0 = 0. Tehát az egyik szögfelező egybeesik a normálissal (lásd (??) egyenletet), ami maga után vonja, hogy a másik szögfelező egybeesik az érintővel Parabola.7. Értelmezés. Azon pontok mértani helyét a síkból, amelyeknek egy rögzített ponttól és egy rögzített egyenestől mért távolságuk egyenlő parabolának nevezzük. Legyen h P egy egyenes és F h egy pont..8. Értelmezés. A sík azon M pontjainak P p halmazát, amelyekre d(m, h) = MF parabolának nevezzük: P p = {M P : d(m, h) = MF.} További elnevezések: 1. az F pont: a parabola fókusza vagy gyújtópontja;. a h egyenes: a parabola vezéregyenese; 3. az [MF ] szakasz: vezérsugár. Választunk egy Descartes-féle koordináta-rendszert, úgy, hogy az O pont legyen az [AF ] szakasz felezőpontja, ahol az A pont a fókusz h egyenesre eső vetülete és az Ox tengely pedig legyen az h-ra merőleges AF egyenes. Jelölje p = AF a fókusz és vezéregyenes közti AF távolságot. Ezt a számot a parabola paraméterének( nevezzük. p ) Ekkor F, 0 és A ( p ), 0. A h vezéregyenes egyenlete: x = p..10. Tétel. Az M(x, y) pont akkor és csakis akkor tartozik hozzá a P p parabolához, ha y = px. (77)
28 y M A - p O F p x 5. ábra. Az y = px egyenlettel megadott parabola. Bizonyítás. Az M pont akkor és csakis akkor van rajta a P p parabolán, ha d(m, h) = MF d (M, h) = MF ( x + p ) ( = x p + y ) Tehát a parabola kanonikus egyenlete: px = y. y = px..14. Megjegyzés. A parabola egyenlete alapján egy M(x, y) ponttal együtt az M 1 (x, y) pont is a parabolán van. Tehát az Ox tengely szimmetriatengelye a parabolának..11. Tétel. Az y = px egyenlettel megadott parabola M 0 (x 0, y 0 ) pontjába szerkesztett érintőjének egyenlete yy 0 = p(x + x 0 ), (78) amelyet még a parabola duplázott egyenletének is nevezünk az M 0 pontban. Bizonyítás. A.6 Megjegyzés szerint a parabola M 0 pontjába szerkesztett érintőjének egyenlete y y 0 = f (x 0 )(x x 0 ), ahol f(x) = y = ± px, ahol az f függvény előjelét azonosnak választjuk az M 0 pont y 0 ordinátájának előjelével. Tételezzük fel, hogy az M 0 pont a parabola felső ívén van, vagyis y 0 0. Ekkor még felhasználva, hogy y 0 = px 0 (mert M 0 P) kapjuk az érintő egyenletét: y y 0 = p (x x 0 ) y y 0 = p (x x 0 ) yy 0 = px + y0 px 0. px0 y 0 }{{} px 0.9. Értelmezés. Azt az egyenest, amelyik átmegy az M 0 ponton és merőleges a parabola M 0 pontba szerkesztett érintőjére, a parabola M 0 pontjába szerkesztett normálisának nevezzük..1. Tétel. (A parabola optikai tulajdonsága) A parabola tengelyével párhuzamos fénysugarak a paraboláról visszaverődve a fókuszban futnak össze vagy fordítva a parabola fókuszából kiinduló fénysugarakat a parabola a tengelyével párhuzamosan veri vissza. Az optikai tulajdonság matematikai megfogalmazása: a parabola egy M 0 pontjához tartozó érintő és normális felezi az M 0 F egyenes és az M 0 ponton át a parabola tengelyével húzott párhuzamos egyenes által bezárt szöget. Bizonyítás. Legyen y = px a parabola egyenlete. Ekkor a h egyenes egyenlete: x = p és a fókusz ( p ) koordinátái F, 0. Feltételezzük, hogy az M 0 pont koordinátái M 0 (x 0, y 0 ). Legyen B az M 0 pont vetülete ( a vezéregyenesre: B p ), y 0 Könnyen belátható, hogy a tétel kijelentése egyenértékű az alábbi állításokkal: 1. a parabola érintője az M 0 pontban a [BF ] szakasz felezőmerőlegese;. a fókusz szimmetrikusa az érintőre nézve rajta van a vezéregyenesen;
29 y M 0 B A O F x 6. ábra. A parabola optikai tulajdonsága 3. a fókusz vetülete az M 0 ponthoz tartozó érintőre a parabola csúcsérintőjén van. Ezért elég igazolni egyet ezen állításk közül. Igazoljuk például, hogy az M 0 pontban szerkesztett érintő felezőmerőlegese a [BF ] szakasznak. Az M 0 pontba szerkesztett érintő egyenlete: yy 0 = p(x + x 0 ). Tehát az érintő iránytényezője: mérintő = p y 0. (79) A BF egyenes iránytényezője: m BF = y B y F = y 0 x B x F p. (80) ( Legyen N a [BF ] szakasz felezőpontja. Ekkor N 0, y ) 0. Ez a pont rajta van az M 0 pontba szerkesztett y 0 y 0 érintőn, mert koordinátái kielégítik az érintő egyenletét: = px 0. Ekkor a (79) és (80) összefüggések alapján kapjuk, hogy az érintő a [BF ] szakasz felezőmerőlegese.
30 3. Kitűzött feladatok 3.1. Analitikus mértan síkban 1. Írjuk fel annak az egyenesnek az egyenletét, amelynek (i) iránytényezője m = 5 és átmegy az A(1, ) ponton; (ii) iránytényezője m = 8 és az Oy tengelyen egy hosszúságú szakaszt határoz meg; (iii) áthalad az A(, 3) ponton és az Ox tengellyel 60 -os szöget zár be. (iv) átmegy a B(1,7) ponton és merőleges az n(4, 3) vektorra.. Adott az ABC háromszög: A(1, 1), B(, 3), C(4, 7). Írjuk fel az oldalak valamint az A csúcshoz tartozó oldalfelező és magasság egyenleteit! E: x = 1, 3x + y 5 = Írjuk fel annak az egyenesnek az egyenletét, amely áthalad az A(1, 6) ponton és az egyenes valammint a koordinátatengelyek által meghatározott háromszög területe 150. E: 3x + 4y 60 = 0, x + 3y 30 = Az origóból egy d egyenesre húzott merőleges talppontja az A(1, ) pont. Írjuk fel a d egyenes egyenletét! E: x + y 5 = Határozzuk meg a d 1 : x + y 1 = 0 egyenes szimmetrikusát a d : x y = 0 egyenesre majd az A(, 5) pontra vonatkozóan! E: x + y 1 = 0, x y + 3 = Adott egy háromszögkét csúcsa: A( 6, ) és B(, ), valamint a H(1, ) ortocentrum. Határozzuk meg a harmadik C csúcs koordinátáit! E:C(, 4). 7. Határozzuk meg azt az A(3, 1) ponton áthaladó egyenest, amely 45 -os szöget zár be a x + 3y 1 = 0 egyenlettel megadott egyenessel. E: x 5y + = 0, 5x + y 16 = Határozzuk meg az O(0, 0), A(1, ) és B( 5, 7) pontok távolságát a 6x + 8y 15 = 0 egyenestől. E: 3, 7 10, Határozzuk meg az alábbi párhuzamos egyenesek közti távolságot ) x y + 3 = 0 és x 4y + 7 = 0; ) 3x 4y + 1 = 0 és x = 1 + 4t, y = 3t ; 3) x = t, y = 3 + t és x = s, y = 5 4s. 1 E: 1) 5. Írjuk fel annak a körnek az egyenletét, amely áthalad az A, B pontokon és középpontja rajta van a d egyenesen, ha a) A(4, 1), B(0, 3), d : x y 4 = 0; b) A(1, ), B(4,-3), d : 3x y 19 = 0. Írjuk fel a C kör P pontjába szerkesztett érintő egyenletét, ha a) C : x + y = 5, P (1, ); E: a) (x ) + (y + 1) = 8; b) (x ) + (y 1 4 ) = b) C : x + y + x 6y 15 = 0, P (3, 6). E: a) x y 5 = 0; b) 4x + 3y 30 = Adott a C kör és a d egyenes. Írjuk fel az adott egyenessel párhuzamos körérintők egyenletét, ha a) C : x + y 13 = 0, d : 4x + 6y 5 = 0; b) C : x + y + x 4y 0 = 0, d : 3x + 4y = 0. E: a) e 1 : x + 3y + 13 = 0, e : x + 3y 13 = 0; b) e 1 : 3x + 4y + 0 = 0, e : 3x + 4y 30 = Adott a C kör és a d egyenes. Írjuk fel az adott egyenesre merőleges körérintők egyenletét, ha a) C : x + y + 5x = 0, d : 4x 3y + 7 = 0; b) C : x + y 1x 8y + 47 = 0, d : x + y 4 = 0. E: a) e 1 : 3x + 4y + 0 = 0, e : 3x + 4y 5 = 0; b) e 1 : x y 3 = 0, e : x y 13 = 0.
Tartalomjegyzék. 3. Elsőfokú egyenletek és egyenlőtlenségek... 8 3.1. Elsőfokú egyenletek... 8 3.2. Valós szám abszolút értéke...
 Tartalomjegyzék 1. Műveletek valós számokkal... 1 1.1. Gyökök és hatványozás... 1 1.1.1. Hatványozás... 1 1.1.2. Gyökök... 1 1.2. Azonosságok... 2 1.3. Egyenlőtlenségek... 3 2. Függvények... 5 2.1. A függvény
Tartalomjegyzék 1. Műveletek valós számokkal... 1 1.1. Gyökök és hatványozás... 1 1.1.1. Hatványozás... 1 1.1.2. Gyökök... 1 1.2. Azonosságok... 2 1.3. Egyenlőtlenségek... 3 2. Függvények... 5 2.1. A függvény
= Y y 0. = Z z 0. u 1. = Z z 1 z 2 z 1. = Y y 1 y 2 y 1
 Egyenes és sík a térben Elméleti áttekintés Az egyenes paraméteres egyenlete: X = u 1 λ + x 0 Y = u λ + y 0, Z = u λ + z 0 ahol a λ egy valós paraméter Az u = (u 1, u, u ) az egyenes irányvektora és P
Egyenes és sík a térben Elméleti áttekintés Az egyenes paraméteres egyenlete: X = u 1 λ + x 0 Y = u λ + y 0, Z = u λ + z 0 ahol a λ egy valós paraméter Az u = (u 1, u, u ) az egyenes irányvektora és P
Az egyenes és a sík analitikus geometriája
 Az egyenes és a sík analitikus geometriája Az egyenes a kétdimenziós koordinátarendszerben A kétdimenziós koordinátarendszerben az egyenest egy n(a, B) normálvektorával és egy r 0 helyvektorú P(x 0,y 0
Az egyenes és a sík analitikus geometriája Az egyenes a kétdimenziós koordinátarendszerben A kétdimenziós koordinátarendszerben az egyenest egy n(a, B) normálvektorával és egy r 0 helyvektorú P(x 0,y 0
9. Írjuk fel annak a síknak az egyenletét, amely átmegy az M 0(1, 2, 3) ponton és. egyenessel;
 Síkok és egyenesek FELADATLAP Írjuk fel annak az egyenesnek az egyenletét, amely átmegy az M 0(,, ) ponton és a) az M(,, 0) ponton; b) párhuzamos a d(,, 5) vektorral; c) merőleges a x y + z 0 = 0 síkra;
Síkok és egyenesek FELADATLAP Írjuk fel annak az egyenesnek az egyenletét, amely átmegy az M 0(,, ) ponton és a) az M(,, 0) ponton; b) párhuzamos a d(,, 5) vektorral; c) merőleges a x y + z 0 = 0 síkra;
Síkbeli egyenesek. 2. Egy egyenes az x = 1 4t, y = 2 + t parméteres egyenletekkel adott. Határozzuk meg
 Analitikus mértan 3. FELADATLAP Síkbeli egyenesek 1. Írjuk fel annak az egyenesnek a paraméteres egyenleteit, amely (i) áthalad az M 0 (1, 2) ponton és párhuzamos a a(3, 1) vektorral; (ii) áthalad az origón
Analitikus mértan 3. FELADATLAP Síkbeli egyenesek 1. Írjuk fel annak az egyenesnek a paraméteres egyenleteit, amely (i) áthalad az M 0 (1, 2) ponton és párhuzamos a a(3, 1) vektorral; (ii) áthalad az origón
Síkbeli egyenesek Egy egyenes az x = 1 4t, y = 2 + t parméteres egyenletekkel adott. Határozzuk meg
 Analitikus mértan 5. FELADATLAP Síkbeli egyenesek 5.1. Írjuk fel annak az egyenesnek a paraméteres egyenleteit, amely (i) áthalad az M 0 (1, 2) ponton és párhuzamos a a(3, 1) vektorral; (ii) áthalad az
Analitikus mértan 5. FELADATLAP Síkbeli egyenesek 5.1. Írjuk fel annak az egyenesnek a paraméteres egyenleteit, amely (i) áthalad az M 0 (1, 2) ponton és párhuzamos a a(3, 1) vektorral; (ii) áthalad az
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT. Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. Koordináta-geometria és B 3 1; Írja fel az AB szakasz 1 3 4
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. Koordináta-geometria és B 3 1; Írja fel az AB szakasz 1 3 4
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
Koordináta-geometria II.
 Koordináta-geometria II. DEFINÍCIÓ: (Alakzat egyenlete) A síkon adott egy derékszögű koordináta rendszer. A síkban levő alakzat egyenlete olyan f (x, y) = 0 egyenlet, amelyet azoknak és csak azoknak a
Koordináta-geometria II. DEFINÍCIÓ: (Alakzat egyenlete) A síkon adott egy derékszögű koordináta rendszer. A síkban levő alakzat egyenlete olyan f (x, y) = 0 egyenlet, amelyet azoknak és csak azoknak a
Koordinátageometria Megoldások
 005-0XX Középszint Koordinátageometria Megoldások 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. és B 3 1; Írja fel az AB szakasz 1 3 + 4 + 1 3 F ; = F ;1 ) Egy kör sugarának
005-0XX Középszint Koordinátageometria Megoldások 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. és B 3 1; Írja fel az AB szakasz 1 3 + 4 + 1 3 F ; = F ;1 ) Egy kör sugarának
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
Összeállította: dr. Leitold Adrien egyetemi docens
 Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
I. Vektorok. Adott A (2; 5) és B ( - 3; 4) pontok. (ld. ábra) A két pont által meghatározott vektor:
 I. Vektorok 1. Vektorok összege Általánosan: Az ábra alapján Adott: a(4; 1) és b(; 3) a + b (4 + ; 1 + 3) = (6; ) a(a 1 ; a ) és b(b 1 ; b ) a + b(a 1 + b 1 ; a + b ). Vektorok különbsége Általánosan:
I. Vektorok 1. Vektorok összege Általánosan: Az ábra alapján Adott: a(4; 1) és b(; 3) a + b (4 + ; 1 + 3) = (6; ) a(a 1 ; a ) és b(b 1 ; b ) a + b(a 1 + b 1 ; a + b ). Vektorok különbsége Általánosan:
Vektorok és koordinátageometria
 Vektorok és koordinátageometria Vektorral kapcsolatos alapfogalmak http://zanza.tv/matematika/geometria/vektorok-bevezetese Definíció: Ha egy szakasz két végpontját megkülönböztetjük egymástól oly módon,
Vektorok és koordinátageometria Vektorral kapcsolatos alapfogalmak http://zanza.tv/matematika/geometria/vektorok-bevezetese Definíció: Ha egy szakasz két végpontját megkülönböztetjük egymástól oly módon,
, D(-1; 1). A B csúcs koordinátáit az y = + -. A trapéz BD
 Kör és egyenes kölcsönös helyzete Kör érintôje 7 9 A húr hossza: egység 9 A ( ) ponton átmenô legrövidebb húr merôleges a K szakaszra, ahol K az adott kör középpontja, feltéve, hogy a kör belsejében van
Kör és egyenes kölcsönös helyzete Kör érintôje 7 9 A húr hossza: egység 9 A ( ) ponton átmenô legrövidebb húr merôleges a K szakaszra, ahol K az adott kör középpontja, feltéve, hogy a kör belsejében van
Nagy András. Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály 2010.
 Nagy András Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály 010. Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály 1) Döntsd el, hogy a P pont illeszkedik-e az e egyenesre
Nagy András Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály 010. Feladatok a koordináta-geometria, egyenesek témaköréhez 11. osztály 1) Döntsd el, hogy a P pont illeszkedik-e az e egyenesre
10. Koordinátageometria
 I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
A kör. A kör egyenlete
 A kör egyenlete A kör A kör egyenlete 8 a) x + y 6 b) x + y c) 6x + 6y d) x + y 9 8 a) x + y 6 + 9 b) x + y c) x + y a + b 8 a) (x - ) + (y - ) 9, rendezve x + y - 8x - y + b) x + y - 6x - 6y + c) x +
A kör egyenlete A kör A kör egyenlete 8 a) x + y 6 b) x + y c) 6x + 6y d) x + y 9 8 a) x + y 6 + 9 b) x + y c) x + y a + b 8 a) (x - ) + (y - ) 9, rendezve x + y - 8x - y + b) x + y - 6x - 6y + c) x +
Skaláris szorzat: a b cos, ahol α a két vektor által bezárt szög.
 1 Összeadás: Legyen a (7; 3) és b (- 2; 4), akkor az összegük a + b (7 + (-2); 3 + 4) = (5; 7) Kivonás: Legyen a (7; 3) és b (- 2; 4), akkor a különbségük a b (7 - (-2); 3-4)=(9; - 1) Valós számmal való
1 Összeadás: Legyen a (7; 3) és b (- 2; 4), akkor az összegük a + b (7 + (-2); 3 + 4) = (5; 7) Kivonás: Legyen a (7; 3) és b (- 2; 4), akkor a különbségük a b (7 - (-2); 3-4)=(9; - 1) Valós számmal való
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. Írd fel a K (0; 2) középpontú 7 sugarú kör egyenletét! A keresett kör egyenletét felírhatjuk a képletbe való behelyettesítéssel: x 2 + (y + 2) 2 = 49. 2. Írd fel annak a körnek az egyenletét,
Megoldások 1. Írd fel a K (0; 2) középpontú 7 sugarú kör egyenletét! A keresett kör egyenletét felírhatjuk a képletbe való behelyettesítéssel: x 2 + (y + 2) 2 = 49. 2. Írd fel annak a körnek az egyenletét,
Analitikus térgeometria
 Analitikus térgeometria Wettl Ferenc el adása alapján 2015.09.21. Wettl Ferenc el adása alapján Analitikus térgeometria 2015.09.21. 1 / 23 Tartalom 1 Egyenes és sík egyenlete Egyenes Sík 2 Alakzatok közös
Analitikus térgeometria Wettl Ferenc el adása alapján 2015.09.21. Wettl Ferenc el adása alapján Analitikus térgeometria 2015.09.21. 1 / 23 Tartalom 1 Egyenes és sík egyenlete Egyenes Sík 2 Alakzatok közös
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 8 VIII VEkTOROk 1 VEkTOR Vektoron irányított szakaszt értünk Jelölése: stb Vektorok hossza A vektor abszolút értéke az irányított szakasz hossza Ha a vektor hossza egységnyi akkor
KOVÁCS BÉLA MATEmATIkA I 8 VIII VEkTOROk 1 VEkTOR Vektoron irányított szakaszt értünk Jelölése: stb Vektorok hossza A vektor abszolút értéke az irányított szakasz hossza Ha a vektor hossza egységnyi akkor
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. Tekintsük az alábbi szabályos hatszögben a következő vektorokat: a = AB és b = AF. Add meg az FO, DC, AO, AC, BE, FB, CE, DF vektorok koordinátáit az (a ; b ) koordinátarendszerben! Alkalmazzuk
Megoldások 1. Tekintsük az alábbi szabályos hatszögben a következő vektorokat: a = AB és b = AF. Add meg az FO, DC, AO, AC, BE, FB, CE, DF vektorok koordinátáit az (a ; b ) koordinátarendszerben! Alkalmazzuk
8. előadás. Kúpszeletek
 8. előadás Kúpszeletek Kör A k kört egyértelműen meghatározza C(a,b) középpontja és r sugara. A P pont pontosan akkor van k-n, ha CP=r. Vektoregyenlet: p-c = r. Koordinátás egyenlet: (X-a)2 + (Y-b)2 =
8. előadás Kúpszeletek Kör A k kört egyértelműen meghatározza C(a,b) középpontja és r sugara. A P pont pontosan akkor van k-n, ha CP=r. Vektoregyenlet: p-c = r. Koordinátás egyenlet: (X-a)2 + (Y-b)2 =
Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit
 Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit 1. Tekintsünk a térben egy P (p 1, p 2, p 3 ) pontot és egy v = (v 1, v 2, v 3 ) = 0 vektort. Ekkor pontosan egy egyenes létezik,
Vektorgeometria (2) First Prev Next Last Go Back Full Screen Close Quit 1. Tekintsünk a térben egy P (p 1, p 2, p 3 ) pontot és egy v = (v 1, v 2, v 3 ) = 0 vektort. Ekkor pontosan egy egyenes létezik,
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. Határozd meg a szakasz hosszát, ha a végpontok koordinátái: A ( 1; ) és B (5; )! A szakasz hosszához számítsuk ki a két pont távolságát: d AB = AB = (5 ( 1)) + ( ) = 6 + 1 = 7 6,08.. Határozd
Megoldások 1. Határozd meg a szakasz hosszát, ha a végpontok koordinátái: A ( 1; ) és B (5; )! A szakasz hosszához számítsuk ki a két pont távolságát: d AB = AB = (5 ( 1)) + ( ) = 6 + 1 = 7 6,08.. Határozd
15. Koordinátageometria
 I. Elméleti összefoglaló Koordinátákkal adott vektorok 15. Koordinátageometria Ha a(a ; a ) és b(b ; b ) a sík két vektora, λ valós szám, akkor az a vektor hossza: a = a + a a két vektor összege : a +
I. Elméleti összefoglaló Koordinátákkal adott vektorok 15. Koordinátageometria Ha a(a ; a ) és b(b ; b ) a sík két vektora, λ valós szám, akkor az a vektor hossza: a = a + a a két vektor összege : a +
Koordináta-geometria feladatok (középszint)
 Koordináta-geometria feladatok (középszint) 1. (KSZÉV Minta (1) 2004.05/I/4) Adott az A(2; 5) és B(1; 3) pont. Adja meg az AB szakasz felezőpontjának koordinátáit! 2. (KSZÉV Minta (2) 2004.05/I/7) Egy
Koordináta-geometria feladatok (középszint) 1. (KSZÉV Minta (1) 2004.05/I/4) Adott az A(2; 5) és B(1; 3) pont. Adja meg az AB szakasz felezőpontjának koordinátáit! 2. (KSZÉV Minta (2) 2004.05/I/7) Egy
Geometriai példatár 2.
 Geometriai példatár 2 Metrikus feladatok Baboss, Csaba, Nyugat-magyarországi Egyetem Geoinformatikai Kar Szabó, Gábor, Nyugat-Magyarországi Egyetem Geoinformatikai Kar Geometriai példatár 2: Metrikus feladatok
Geometriai példatár 2 Metrikus feladatok Baboss, Csaba, Nyugat-magyarországi Egyetem Geoinformatikai Kar Szabó, Gábor, Nyugat-Magyarországi Egyetem Geoinformatikai Kar Geometriai példatár 2: Metrikus feladatok
Vektorok összeadása, kivonása, szorzás számmal, koordináták
 Vektorok összeadása, kivonása, szorzás számmal, koordináták 1. Mik lesznek a P (3, 4, 8) pont C (3, 7, 2) pontra vonatkozó tükörképének a koordinátái? 2. Egy szabályos hatszög középpontja K (4, 1, 4),
Vektorok összeadása, kivonása, szorzás számmal, koordináták 1. Mik lesznek a P (3, 4, 8) pont C (3, 7, 2) pontra vonatkozó tükörképének a koordinátái? 2. Egy szabályos hatszög középpontja K (4, 1, 4),
3 m ; a víz sodráé sec. Bizonyítsuk be, hogy a legnagyobb szöge 120 0 -os! α =. 4cos 2
 3... Egyenes szíjhatás esetén milyen hosszú szíj szükséges 50 cmes és 6 cm-es sugarú tárcsák összekapcsolásához, ha a tárcsák tengelyeinek távolsága 335 cm? 3... Csónakkal akarunk a folyó túlsó partjára
3... Egyenes szíjhatás esetén milyen hosszú szíj szükséges 50 cmes és 6 cm-es sugarú tárcsák összekapcsolásához, ha a tárcsák tengelyeinek távolsága 335 cm? 3... Csónakkal akarunk a folyó túlsó partjára
Koordináta geometria III.
 Koordináta geometria III. TÉTEL: A P (x; y) pont akkor és csak akkor illeszkedik a K (u; v) középpontú r sugarú körre (körvonalra), ha (x u) 2 + (y v) 2 = r 2. Ez az összefüggés a K (u; v) középpontú r
Koordináta geometria III. TÉTEL: A P (x; y) pont akkor és csak akkor illeszkedik a K (u; v) középpontú r sugarú körre (körvonalra), ha (x u) 2 + (y v) 2 = r 2. Ez az összefüggés a K (u; v) középpontú r
Egyenes és sík. Wettl Ferenc szeptember 29. Wettl Ferenc () Egyenes és sík szeptember / 15
 Egyenes és sík Wettl Ferenc 2006. szeptember 29. Wettl Ferenc () Egyenes és sík 2006. szeptember 29. 1 / 15 Tartalom 1 Egyenes és szakasz Egyenes Szakasz Egyenesvonalú egyenletes mozgás Egyenes és pont
Egyenes és sík Wettl Ferenc 2006. szeptember 29. Wettl Ferenc () Egyenes és sík 2006. szeptember 29. 1 / 15 Tartalom 1 Egyenes és szakasz Egyenes Szakasz Egyenesvonalú egyenletes mozgás Egyenes és pont
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 14 XIV NEVEZETES GÖRbÉk 1 AZ EGYEnES EGYEnLETE A és pontokon átmenő egyenes egyenlete: (1), Az hányados neve iránytényező (iránytangens, meredekség) A ponton átmenő, m iránytangensű
KOVÁCS BÉLA, MATEmATIkA I 14 XIV NEVEZETES GÖRbÉk 1 AZ EGYEnES EGYEnLETE A és pontokon átmenő egyenes egyenlete: (1), Az hányados neve iránytényező (iránytangens, meredekség) A ponton átmenő, m iránytangensű
A keresett kör középpontja Ku ( ; v, ) a sugara r = 1. Az adott kör középpontjának koordinátái: K1( 4; 2)
 55 A kör 87 8 A keresett kör középpontja Ku ( ; v, ) a sugara r = Az adott kör középpontjának koordinátái: K( ; ) és a sugara r =, az adott pont P(; ) Ekkor KP = és KK = () ( u ) + ( v ) =, () ( u ) +
55 A kör 87 8 A keresett kör középpontja Ku ( ; v, ) a sugara r = Az adott kör középpontjának koordinátái: K( ; ) és a sugara r =, az adott pont P(; ) Ekkor KP = és KK = () ( u ) + ( v ) =, () ( u ) +
= 7, a 3. = 7; x - 4y =-8; x + 2y = 10; x + y = 7. C-bôl induló szögfelezô: (-2; 3). PA + PB = PA 1. (8; -7), n(7; 8), 7x + 8y = 10, x = 0 & P 0;
 98 Az egyenes egyenletei. a) A( 0) B(0 6) AB_ - 6i& n( ) x + y = b) x - y =- c) 6x - y = 0 d) 6x + y = e) x + y = f) x + y = a g) x - y = a.. A(a 0) B(0 b) AB_ -a bi n (b a) bx + ay = ab osszuk el a $
98 Az egyenes egyenletei. a) A( 0) B(0 6) AB_ - 6i& n( ) x + y = b) x - y =- c) 6x - y = 0 d) 6x + y = e) x + y = f) x + y = a g) x - y = a.. A(a 0) B(0 b) AB_ -a bi n (b a) bx + ay = ab osszuk el a $
Lineáris algebra mérnököknek
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Lineáris algebra mérnököknek BMETE93BG20 Vektorok a 2- és 3-dimenziós tér Kf87 2017-09-05
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Lineáris algebra mérnököknek BMETE93BG20 Vektorok a 2- és 3-dimenziós tér Kf87 2017-09-05
Matematika 11 Koordináta geometria. matematika és fizika szakos középiskolai tanár. > o < szeptember 27.
 Matematika 11 Koordináta geometria Juhász László matematika és fizika szakos középiskolai tanár > o < 2015. szeptember 27. copyright: c Juhász László Ennek a könyvnek a használatát szerzői jog védi. A
Matematika 11 Koordináta geometria Juhász László matematika és fizika szakos középiskolai tanár > o < 2015. szeptember 27. copyright: c Juhász László Ennek a könyvnek a használatát szerzői jog védi. A
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Bevezetés az elméleti zikába
 Bevezetés az elméleti zikába egyetemi jegyzet Kúpszeletek Lázár Zsolt, Lázár József Babe³Bolyai Tudományegyetem Fizika Kar 2011 TARTALOMJEGYZÉK 6 TARTALOMJEGYZÉK Azokat a görbéket, amelyeknek egyenlete
Bevezetés az elméleti zikába egyetemi jegyzet Kúpszeletek Lázár Zsolt, Lázár József Babe³Bolyai Tudományegyetem Fizika Kar 2011 TARTALOMJEGYZÉK 6 TARTALOMJEGYZÉK Azokat a görbéket, amelyeknek egyenlete
Koordináta-geometria feladatok (emelt szint)
 Koordináta-geometria feladatok (emelt szint) 1. (ESZÉV Minta (2) 2004.05/7) Egy ABC háromszögben CAB = 30, az ACB = 45. A háromszög két csúcsának koordinátái: A(2; 2) és C(4; 2). Határozza meg a harmadik
Koordináta-geometria feladatok (emelt szint) 1. (ESZÉV Minta (2) 2004.05/7) Egy ABC háromszögben CAB = 30, az ACB = 45. A háromszög két csúcsának koordinátái: A(2; 2) és C(4; 2). Határozza meg a harmadik
15. Koordinátageometria
 I. Elméleti összefoglaló Koordinátákkal adott vektorok 15. Koordinátageometria Ha a(a ; a ) és b(b ; b ) a sík két vektora, λ valós szám, akkor az a vektor hossza: a = a + a a két vektor összege : a +
I. Elméleti összefoglaló Koordinátákkal adott vektorok 15. Koordinátageometria Ha a(a ; a ) és b(b ; b ) a sík két vektora, λ valós szám, akkor az a vektor hossza: a = a + a a két vektor összege : a +
Helyvektorok, műveletek, vektorok a koordináta-rendszerben
 Helyvektorok, műveletek, vektorok a koordináta-rendszerben. Rajzold meg az alábbi helyvektorokat a derékszögű koordináta-rendszerben, majd számítsd ki a hosszúságukat! a) (4 ) b) ( 5 ) c) ( 6 ) d) (4 )
Helyvektorok, műveletek, vektorok a koordináta-rendszerben. Rajzold meg az alábbi helyvektorokat a derékszögű koordináta-rendszerben, majd számítsd ki a hosszúságukat! a) (4 ) b) ( 5 ) c) ( 6 ) d) (4 )
Budapesti Műszaki Főiskola, Neumann János Informatikai Kar. Vektorok. Fodor János
 Budapesti Műszaki Főiskola, Neumann János Informatikai Kar Lineáris algebra 1. témakör Vektorok Fodor János Copyright c Fodor@bmf.hu Last Revision Date: 2006. szeptember 11. Version 1.1 Table of Contents
Budapesti Műszaki Főiskola, Neumann János Informatikai Kar Lineáris algebra 1. témakör Vektorok Fodor János Copyright c Fodor@bmf.hu Last Revision Date: 2006. szeptember 11. Version 1.1 Table of Contents
5 1 6 (2x3 + 4) 7. 4 ( ctg(4x + 2)) + c = 3 4 ctg(4x + 2) + c ] 12 (2x6 + 9) 20 ln(5x4 + 17) + c ch(8x) 20 ln 5x c = 11
![5 1 6 (2x3 + 4) 7. 4 ( ctg(4x + 2)) + c = 3 4 ctg(4x + 2) + c ] 12 (2x6 + 9) 20 ln(5x4 + 17) + c ch(8x) 20 ln 5x c = 11 5 1 6 (2x3 + 4) 7. 4 ( ctg(4x + 2)) + c = 3 4 ctg(4x + 2) + c ] 12 (2x6 + 9) 20 ln(5x4 + 17) + c ch(8x) 20 ln 5x c = 11](/thumbs/93/113569557.jpg) Bodó Beáta ISMÉTLÉS. ch(6 d.. 4.. 6. 7. 8. 9..... 4.. e (8 d ch (9 + 7 d ( + 4 6 d 7 8 + d sin (4 + d cos sin d 7 ( 6 + 9 4 d INTEGRÁLSZÁMÍTÁS 7 6 sh(6 + c 8 e(8 + c 9 th(9 + 7 + c 6 ( + 4 7 + c = 7 4
Bodó Beáta ISMÉTLÉS. ch(6 d.. 4.. 6. 7. 8. 9..... 4.. e (8 d ch (9 + 7 d ( + 4 6 d 7 8 + d sin (4 + d cos sin d 7 ( 6 + 9 4 d INTEGRÁLSZÁMÍTÁS 7 6 sh(6 + c 8 e(8 + c 9 th(9 + 7 + c 6 ( + 4 7 + c = 7 4
20. tétel A kör és a parabola a koordinátasíkon, egyenessel való kölcsönös helyzetük. Másodfokú egyenlőtlenségek.
 . tétel A kör és a parabola a koordinátasíkon, egyenessel való kölcsönös helyzetük. Másodfokú egyenlőtlenségek. Először megadom a síkbeli definíciójukat, mert ez alapján vezetjük le az egyenletüket. Alakzat
. tétel A kör és a parabola a koordinátasíkon, egyenessel való kölcsönös helyzetük. Másodfokú egyenlőtlenségek. Először megadom a síkbeli definíciójukat, mert ez alapján vezetjük le az egyenletüket. Alakzat
Klár Gergely 2010/2011. tavaszi félév
 Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom Pont 1 Pont 2 3 4 5 Tartalom Pont Descartes-koordináták Homogén koordináták
Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom Pont 1 Pont 2 3 4 5 Tartalom Pont Descartes-koordináták Homogén koordináták
3. tétel Térelemek távolsága és szöge. Nevezetes ponthalmazok a síkon és a térben.
 3. tétel Térelemek távolsága és szöge. Nevezetes ponthalmazok a síkon és a térben. TÁVOLSÁG Általános definíció: két alakzat távolsága a két alakzat pontjai között húzható legrövidebb szakasz hosszaa távolság
3. tétel Térelemek távolsága és szöge. Nevezetes ponthalmazok a síkon és a térben. TÁVOLSÁG Általános definíció: két alakzat távolsága a két alakzat pontjai között húzható legrövidebb szakasz hosszaa távolság
Koordinátageometriai gyakorló feladatok I ( vektorok )
 Koordinátageometriai gyakorló feladatok I ( vektorok./ Határozd meg az AB szakasznak azt a pontját, amely a szakaszt : ha A ( ; és a B ( ; 8!./ Adott az A ( 3 ; 5 és a ( ; 6 B pont. Számítsd ki az AB vektor
Koordinátageometriai gyakorló feladatok I ( vektorok./ Határozd meg az AB szakasznak azt a pontját, amely a szakaszt : ha A ( ; és a B ( ; 8!./ Adott az A ( 3 ; 5 és a ( ; 6 B pont. Számítsd ki az AB vektor
Megoldások. Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma)
 Megoldások 1. Határozd meg az a és b vektor skaláris szorzatát, ha a = 5, b = 4 és a közbezárt szög φ = 55! Alkalmazzuk a megfelelő képletet: a b = a b cos φ = 5 4 cos 55 11,47. 2. Határozd meg a következő
Megoldások 1. Határozd meg az a és b vektor skaláris szorzatát, ha a = 5, b = 4 és a közbezárt szög φ = 55! Alkalmazzuk a megfelelő képletet: a b = a b cos φ = 5 4 cos 55 11,47. 2. Határozd meg a következő
Matematika A1a Analízis
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
A kör. A kör egyenlete
 A kör egyenlete A kör A kör egyenlete 8 a) x + y 6 b) x + y c) 6x + 6y d) x + y 9 8 a) x + y 6 + 9 b) x + y c) x + y a + b 8 a) (x - ) + (y - ) 9, rendezve x + y - 8x - 0y + 0 b) x + y - 6x - 6y + 0 c)
A kör egyenlete A kör A kör egyenlete 8 a) x + y 6 b) x + y c) 6x + 6y d) x + y 9 8 a) x + y 6 + 9 b) x + y c) x + y a + b 8 a) (x - ) + (y - ) 9, rendezve x + y - 8x - 0y + 0 b) x + y - 6x - 6y + 0 c)
Analitikus térgeometria
 5. fejezet Analitikus térgeometria Kezd és végpontjuk koordinátáival adott vektorok D 5.1 A koordináta-rendszer O kezd pontjából a P pontba mutató OP kötött vektort a P pont helyvektorának nevezzük. T
5. fejezet Analitikus térgeometria Kezd és végpontjuk koordinátáival adott vektorok D 5.1 A koordináta-rendszer O kezd pontjából a P pontba mutató OP kötött vektort a P pont helyvektorának nevezzük. T
17. előadás: Vektorok a térben
 17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
egyenletrendszert. Az egyenlő együtthatók módszerét alkalmazhatjuk. sin 2 x = 1 és cosy = 0.
 Magyar Ifjúság. X. TRIGONOMETRIKUS FÜGGVÉNYEK A trigonometrikus egyenletrendszerek megoldása során kísérletezhetünk új változók bevezetésével, azonosságok alkalmazásával, helyettesítő módszerrel vagy más,
Magyar Ifjúság. X. TRIGONOMETRIKUS FÜGGVÉNYEK A trigonometrikus egyenletrendszerek megoldása során kísérletezhetünk új változók bevezetésével, azonosságok alkalmazásával, helyettesítő módszerrel vagy más,
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Paraméter
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Paraméter A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Paraméter A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Egyenes és sík. Wettl Ferenc Wettl Ferenc () Egyenes és sík / 16
 Egyenes és sík Wettl Ferenc 2012-09-20 Wettl Ferenc () Egyenes és sík 2012-09-20 1 / 16 Tartalom 1 Egyenes és szakasz Egyenes Szakasz Egyenesvonalú egyenletes mozgás Egyenes és pont távolsága 2 Sík Sík
Egyenes és sík Wettl Ferenc 2012-09-20 Wettl Ferenc () Egyenes és sík 2012-09-20 1 / 16 Tartalom 1 Egyenes és szakasz Egyenes Szakasz Egyenesvonalú egyenletes mozgás Egyenes és pont távolsága 2 Sík Sík
9. előadás. Térbeli koordinátageometria
 9. előadás Térbeli koordinátageometria Koordinátageometria a térben Descartes-féle koordinátarendszerben dolgozunk. A legegyszerűbb alakzatokat fogjuk vizsgálni. Az ezeket leíró egyenletek első-, vagy
9. előadás Térbeli koordinátageometria Koordinátageometria a térben Descartes-féle koordinátarendszerben dolgozunk. A legegyszerűbb alakzatokat fogjuk vizsgálni. Az ezeket leíró egyenletek első-, vagy
Transzformáció a főtengelyekre és a nem főtengelyekre vonatkoztatott. Az ellipszis a sík azon pontjainak mértani helye, amelyeknek két adott pontól
 Ellipsis.tex, February 9, 01 Az ellipszis Az ellipszis leírása Az ellipszis szerkesztése és tulajdonságai Az ellipszis kanonikus egyenlete A kör vetülete ellipszis Az ellipszis polárkoordinátás egyenlete
Ellipsis.tex, February 9, 01 Az ellipszis Az ellipszis leírása Az ellipszis szerkesztése és tulajdonságai Az ellipszis kanonikus egyenlete A kör vetülete ellipszis Az ellipszis polárkoordinátás egyenlete
Síkgeometria 12. évfolyam. Szögek, szögpárok és fajtáik
 Szögek, szögpárok és fajtáik Szögfajták: Jelölés: Mindkét esetben: α + β = 180 Pótszögek: Olyan szögek, amelyeknek összege 90. Oldalak szerint csoportosítva A háromszögek Általános háromszög: Minden oldala
Szögek, szögpárok és fajtáik Szögfajták: Jelölés: Mindkét esetben: α + β = 180 Pótszögek: Olyan szögek, amelyeknek összege 90. Oldalak szerint csoportosítva A háromszögek Általános háromszög: Minden oldala
Egy sík és a koordinátasíkok metszésvonalainak meghatározása
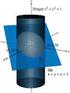 1 Egy sík és a koordinátasíkok metszésvonalainak meghatározása Ehhez tekintsük az 1. ábrát! 1. ábra Itt az ( u, v, w ) tengelymetszeteivel adott S síkot látjuk, az Oxyz térbeli derékszögű koordináta -
1 Egy sík és a koordinátasíkok metszésvonalainak meghatározása Ehhez tekintsük az 1. ábrát! 1. ábra Itt az ( u, v, w ) tengelymetszeteivel adott S síkot látjuk, az Oxyz térbeli derékszögű koordináta -
Geometria II gyakorlatok
 Geometria II gyakorlatok Kovács Zoltán Copyright c 2011 Last Revision Date: 2012. május 8. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát technikával készült, a megjelenés
Geometria II gyakorlatok Kovács Zoltán Copyright c 2011 Last Revision Date: 2012. május 8. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát technikával készült, a megjelenés
Érettségi feladatok Koordinátageometria_rendszerezve / 5
 Érettségi feladatok Koordinátageometria_rendszerezve 2005-2013 1/ 5 Vektorok 2005. május 28./12. Adottak az a (4; 3) és b ( 2; 1) vektorok. a) Adja meg az a hosszát! b) Számítsa ki az a + b koordinátáit!
Érettségi feladatok Koordinátageometria_rendszerezve 2005-2013 1/ 5 Vektorok 2005. május 28./12. Adottak az a (4; 3) és b ( 2; 1) vektorok. a) Adja meg az a hosszát! b) Számítsa ki az a + b koordinátáit!
Érettségi feladatok: Koordináta-geometria 1/5
 Érettségi feladatok: Koordináta-geometria 1/5 2003. Próba/ 13. Adott egy háromszög három csúcspontja a koordinátáival: A( 4; 4), B(4; 4) és C( 4; 8). Számítsa ki a C csúcsból induló súlyvonal és az A csúcsból
Érettségi feladatok: Koordináta-geometria 1/5 2003. Próba/ 13. Adott egy háromszög három csúcspontja a koordinátáival: A( 4; 4), B(4; 4) és C( 4; 8). Számítsa ki a C csúcsból induló súlyvonal és az A csúcsból
Trigonometria Megoldások. 1) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( )
 Trigonometria Megoldások Trigonometria - megoldások ) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( ) akkor a háromszög egyenlő szárú vagy derékszögű!
Trigonometria Megoldások Trigonometria - megoldások ) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( ) akkor a háromszög egyenlő szárú vagy derékszögű!
λ 1 u 1 + λ 2 v 1 + λ 3 w 1 = 0 λ 1 u 2 + λ 2 v 2 + λ 3 w 2 = 0 λ 1 u 3 + λ 2 v 3 + λ 3 w 3 = 0
 Vektorok a térben Egy (v 1,v 2,v 3 ) valós számokból álló hármast vektornak nevezzünk a térben (R 3 -ban). Használni fogjuk a v = (v 1,v 2,v 3 ) jelölést. A v 1,v 2,v 3 -at a v vektor komponenseinek nevezzük.
Vektorok a térben Egy (v 1,v 2,v 3 ) valós számokból álló hármast vektornak nevezzünk a térben (R 3 -ban). Használni fogjuk a v = (v 1,v 2,v 3 ) jelölést. A v 1,v 2,v 3 -at a v vektor komponenseinek nevezzük.
Szélsőérték feladatok megoldása
 Szélsőérték feladatok megoldása A z = f (x,y) függvény lokális szélsőértékének meghatározása: A. Szükséges feltétel: f x (x,y) = 0 f y (x,y) = 0 egyenletrendszer megoldása, amire a továbbiakban az x =
Szélsőérték feladatok megoldása A z = f (x,y) függvény lokális szélsőértékének meghatározása: A. Szükséges feltétel: f x (x,y) = 0 f y (x,y) = 0 egyenletrendszer megoldása, amire a továbbiakban az x =
Feladatok megoldásokkal a harmadik gyakorlathoz (érintési paraméterek, L Hospital szabály, elaszticitás) y = 1 + 2(x 1). y = 2x 1.
 Feladatok megoldásokkal a harmadik gyakorlathoz (érintési paraméterek, L Hospital szabály, elaszticitás). Feladat. Írjuk fel az f() = függvény 0 = pontbeli érintőjének egyenletét! Az érintő egyenlete y
Feladatok megoldásokkal a harmadik gyakorlathoz (érintési paraméterek, L Hospital szabály, elaszticitás). Feladat. Írjuk fel az f() = függvény 0 = pontbeli érintőjének egyenletét! Az érintő egyenlete y
Minimum követelmények matematika tantárgyból 11. évfolyamon
 Minimum követelmények matematika tantárgyból. évfolyamon A hatványozás általánosítása pozitív alap esetén racionális kitevőre. Műveletek hatványokkal. A, a 0 függvény. Az eponenciális függvény. Vizsgálata
Minimum követelmények matematika tantárgyból. évfolyamon A hatványozás általánosítása pozitív alap esetén racionális kitevőre. Műveletek hatványokkal. A, a 0 függvény. Az eponenciális függvény. Vizsgálata
9. Trigonometria. I. Nulladik ZH-ban láttuk: 1. Tegye nagyság szerint növekvő sorrendbe az alábbi értékeket! Megoldás:
 9. Trigonometria I. Nulladik ZH-ban láttuk: 1. Tegye nagyság szerint növekvő sorrendbe az alábbi értékeket! x = cos 150 ; y = sin 5 ; z = tg ( 60 ) (A) z < x < y (B) x < y < z (C) y < x < z (D) z < y
9. Trigonometria I. Nulladik ZH-ban láttuk: 1. Tegye nagyság szerint növekvő sorrendbe az alábbi értékeket! x = cos 150 ; y = sin 5 ; z = tg ( 60 ) (A) z < x < y (B) x < y < z (C) y < x < z (D) z < y
Egyenletek, egyenlőtlenségek VII.
 Egyenletek, egyenlőtlenségek VII. Magasabbfokú egyenletek: A 3, vagy annál nagyobb fokú egyenleteket magasabb fokú egyenleteknek nevezzük. Megjegyzés: Egy n - ed fokú egyenletnek legfeljebb n darab valós
Egyenletek, egyenlőtlenségek VII. Magasabbfokú egyenletek: A 3, vagy annál nagyobb fokú egyenleteket magasabb fokú egyenleteknek nevezzük. Megjegyzés: Egy n - ed fokú egyenletnek legfeljebb n darab valós
Koordináta-geometria feladatgyűjtemény
 Koordináta-geometria feladatgyűjtemény A feladatok megoldásai a dokumentum végén találhatók Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két csúcs
Koordináta-geometria feladatgyűjtemény A feladatok megoldásai a dokumentum végén találhatók Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két csúcs
3 függvény. Számítsd ki az f 4 f 3 f 3 f 4. egyenlet valós megoldásait! 3 1, 3 és 5 3 1
 Érettségi, M, I-es feladatsor, természettudomány.. Számítsd ki a C! összeget! log 4. Határozd meg a. Számítsd ki az egyenlet valós megoldásait! összeg értékét, ha és az 4. Adott az f : 0,, f. Adottak az
Érettségi, M, I-es feladatsor, természettudomány.. Számítsd ki a C! összeget! log 4. Határozd meg a. Számítsd ki az egyenlet valós megoldásait! összeg értékét, ha és az 4. Adott az f : 0,, f. Adottak az
Matematika (mesterképzés)
 Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Exponenciális és logaritmusos kifejezések, egyenletek
 Eponenciális és logaritmusos kifejezések, egyenletek. Hatványozási azonosságok. Számítsd ki a következő hatványok pontos értékét! a) 8 b) 4 c) d) 7 e) f) 9 0, g) 0, 9 h) 6 0, 7,, i) 8 j) 6 k) 4 l) 49,.
Eponenciális és logaritmusos kifejezések, egyenletek. Hatványozási azonosságok. Számítsd ki a következő hatványok pontos értékét! a) 8 b) 4 c) d) 7 e) f) 9 0, g) 0, 9 h) 6 0, 7,, i) 8 j) 6 k) 4 l) 49,.
Oktatási Hivatal. 1 pont. A feltételek alapján felírhatók az. összevonás után az. 1 pont
 Oktatási Hivatal Öt pozitív egész szám egy számtani sorozat első öt eleme A sorozatnak a különbsége prímszám Tudjuk hogy az első négy szám köbének összege megegyezik az ezen öt tag közül vett páros sorszámú
Oktatási Hivatal Öt pozitív egész szám egy számtani sorozat első öt eleme A sorozatnak a különbsége prímszám Tudjuk hogy az első négy szám köbének összege megegyezik az ezen öt tag közül vett páros sorszámú
Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit
 Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit 1. A térbeli irányított szakaszokat vektoroknak hívjuk. Két vektort egyenlőnek tekintünk, ha párhuzamos eltolással fedésbe hozhatók.
Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit 1. A térbeli irányított szakaszokat vektoroknak hívjuk. Két vektort egyenlőnek tekintünk, ha párhuzamos eltolással fedésbe hozhatók.
Az egyenlőtlenség mindkét oldalát szorozzuk meg 4 16-al:
 Bevezető matematika kémikusoknak., 04. ősz. feladatlap. Ábrázoljuk számegyenesen a következő egyenlőtlenségek megoldáshalmazát! (a) x 5 < 3 5 x < 3 x 5 < (d) 5 x
Bevezető matematika kémikusoknak., 04. ősz. feladatlap. Ábrázoljuk számegyenesen a következő egyenlőtlenségek megoldáshalmazát! (a) x 5 < 3 5 x < 3 x 5 < (d) 5 x
Geometria II gyakorlatok
 Geometria II gyakorlatok Kovács Zoltán Copyright c 2011 Last Revision Date: 2011. november 29. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát technikával készült, a megjelenés
Geometria II gyakorlatok Kovács Zoltán Copyright c 2011 Last Revision Date: 2011. november 29. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát technikával készült, a megjelenés
FELVÉTELI VIZSGA, szeptember 12.
 BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR FELVÉTELI VIZSGA, 08. szeptember. Írásbeli vizsga MATEMATIKÁBÓL FONTOS TUDNIVALÓK: A feleletválasztós feladatok,,a rész esetén egy
BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR FELVÉTELI VIZSGA, 08. szeptember. Írásbeli vizsga MATEMATIKÁBÓL FONTOS TUDNIVALÓK: A feleletválasztós feladatok,,a rész esetén egy
Geometria 1 összefoglalás o konvex szögek
 Geometria 1 összefoglalás Alapfogalmak: a pont, az egyenes és a sík Axiómák: 1. Bármely 2 pontra illeszkedik egy és csak egy egyenes. 2. Három nem egy egyenesre eső pontra illeszkedik egy és csak egy sík.
Geometria 1 összefoglalás Alapfogalmak: a pont, az egyenes és a sík Axiómák: 1. Bármely 2 pontra illeszkedik egy és csak egy egyenes. 2. Három nem egy egyenesre eső pontra illeszkedik egy és csak egy sík.
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Országos Középiskolai Tanulmányi Verseny 2011/2012 Matematika I. kategória (SZAKKÖZÉPISKOLA) 2. forduló - megoldások. 1 pont Ekkor
 Okta tási Hivatal Országos Középiskolai Tanulmányi Verseny 0/0 Matematika I. kategória (SZAKKÖZÉPISKOLA). forduló - megoldások. Az valós számra teljesül a 3 sin sin cos sin egyenlőség. Milyen értékeket
Okta tási Hivatal Országos Középiskolai Tanulmányi Verseny 0/0 Matematika I. kategória (SZAKKÖZÉPISKOLA). forduló - megoldások. Az valós számra teljesül a 3 sin sin cos sin egyenlőség. Milyen értékeket
VEKTOROK. 1. B Legyen a( 3; 2; 4), b( 2; 1; 2), c(3; 4; 5), d(8; 5; 7). (a) 2a 4c + 6d [(30; 10; 30)]
![VEKTOROK. 1. B Legyen a( 3; 2; 4), b( 2; 1; 2), c(3; 4; 5), d(8; 5; 7). (a) 2a 4c + 6d [(30; 10; 30)] VEKTOROK. 1. B Legyen a( 3; 2; 4), b( 2; 1; 2), c(3; 4; 5), d(8; 5; 7). (a) 2a 4c + 6d [(30; 10; 30)]](/thumbs/88/117769211.jpg) Bodó Beáta 1 VEKTOROK 1. B Legyen a( ; 2; 4), b( 2; 1; 2), c(; 4; 5), d(8; 5; 7). (a) 2a 4c + 6d [(0; 10; 0)] (b) c + b 7a [(18; 15; 29)] (c) 2d c + b [ (5; ; ) = 6, 56] (d) 4a + 8b 7c [ ( 49; 44; 5) =
Bodó Beáta 1 VEKTOROK 1. B Legyen a( ; 2; 4), b( 2; 1; 2), c(; 4; 5), d(8; 5; 7). (a) 2a 4c + 6d [(0; 10; 0)] (b) c + b 7a [(18; 15; 29)] (c) 2d c + b [ (5; ; ) = 6, 56] (d) 4a + 8b 7c [ ( 49; 44; 5) =
Koordináta-geometria feladatgyűjtemény (A feladatok megoldásai a dokumentum végén találhatók)
 Koordináta-geometria feladatgyűjtemény (A feladatok megoldásai a dokumentum végén találhatók) Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két
Koordináta-geometria feladatgyűjtemény (A feladatok megoldásai a dokumentum végén találhatók) Vektorok 1. Egy négyzet két szemközti csúcsának koordinátái: A( ; 7) és C(4 ; 1). Határozd meg a másik két
LINEÁRIS ALGEBRA. matematika alapszak. Euklideszi terek. SZTE Bolyai Intézet, őszi félév. Euklideszi terek LINEÁRIS ALGEBRA 1 / 40
 LINEÁRIS ALGEBRA matematika alapszak SZTE Bolyai Intézet, 2016-17. őszi félév Euklideszi terek Euklideszi terek LINEÁRIS ALGEBRA 1 / 40 Euklideszi tér Emlékeztető: A standard belső szorzás és standard
LINEÁRIS ALGEBRA matematika alapszak SZTE Bolyai Intézet, 2016-17. őszi félév Euklideszi terek Euklideszi terek LINEÁRIS ALGEBRA 1 / 40 Euklideszi tér Emlékeztető: A standard belső szorzás és standard
4 = 0 egyenlet csak. 4 = 0 egyenletből behelyettesítés és egyszerűsítés után. adódik, ennek az egyenletnek két valós megoldása van, mégpedig
 Oktatási Hivatal Az forduló feladatainak megoldása (Szakközépiskola) Melyek azok az m Z számok, amelyekre az ( m ) x mx = 0 egyenletnek legfeljebb egy, az m x + 3mx 4 = 0 egyenletnek legalább egy valós
Oktatási Hivatal Az forduló feladatainak megoldása (Szakközépiskola) Melyek azok az m Z számok, amelyekre az ( m ) x mx = 0 egyenletnek legfeljebb egy, az m x + 3mx 4 = 0 egyenletnek legalább egy valós
Lineáris algebra mérnököknek
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Lineáris algebra mérnököknek BMETE93BG20 Vektorok a 2- és 3-dimenziós tér Kf81 2018-09-04
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Lineáris algebra mérnököknek BMETE93BG20 Vektorok a 2- és 3-dimenziós tér Kf81 2018-09-04
Koordinátageometria. M veletek vektorokkal grakusan. Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1
 Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Koordinátageometria M veletek vektorokkal grakusan 1. Az ABCD négyzet oldalvektorai közül a = AB és b = BC. Adja meg az AC és BD vektorokat a
Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Koordinátageometria M veletek vektorokkal grakusan 1. Az ABCD négyzet oldalvektorai közül a = AB és b = BC. Adja meg az AC és BD vektorokat a
2014/2015. tavaszi félév
 Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
KOVÁCS BÉLA, MATEMATIKA II.
 KOVÁCS BÉLA MATEmATIkA II 6 VI TÉRGÖRbÉk 1 Alapvető ÖSSZEFÜGGÉSEk A térgörbe (1) alakú egyenletével írható le Ez a vektoregyenlet egyenértékű az (2) skaláris egyenletrendszerrel A térgörbe három nevezetes
KOVÁCS BÉLA MATEmATIkA II 6 VI TÉRGÖRbÉk 1 Alapvető ÖSSZEFÜGGÉSEk A térgörbe (1) alakú egyenletével írható le Ez a vektoregyenlet egyenértékű az (2) skaláris egyenletrendszerrel A térgörbe három nevezetes
MATEK-INFO UBB verseny április 6.
 BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATEK-INFO UBB verseny 219. április 6. Írásbeli próba matematikából FONTOS MEGJEGYZÉS: 1) Az A. részben megjelenő feleletválasztós
BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATEK-INFO UBB verseny 219. április 6. Írásbeli próba matematikából FONTOS MEGJEGYZÉS: 1) Az A. részben megjelenő feleletválasztós
Abszolútértékes és gyökös kifejezések Megoldások
 Abszolútértékes és gyökös kifejezések Megoldások ) Igazolja, hogy az alábbi négy egyenlet közül az a) és b) jelű egyenletnek pontosan egy megoldása van, a c) és d) jelű egyenletnek viszont nincs megoldása
Abszolútértékes és gyökös kifejezések Megoldások ) Igazolja, hogy az alábbi négy egyenlet közül az a) és b) jelű egyenletnek pontosan egy megoldása van, a c) és d) jelű egyenletnek viszont nincs megoldása
a) A logaritmus értelmezése alapján: x 8 0 ( x 2 2 vagy x 2 2) (1 pont) Egy szorzat értéke pontosan akkor 0, ha valamelyik szorzótényező 0.
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
Geometriai példatár 1.
 Geometriai példatár 1. Koordináta-geometria Baboss, Csaba, Nyugat-magyarországi Egyetem Geoinformatikai Kar Szabó, Gábor, Nyugat-Magyarországi Egyetem Geoinformatikai Kar Geometriai példatár 1.: Koordináta-geometria
Geometriai példatár 1. Koordináta-geometria Baboss, Csaba, Nyugat-magyarországi Egyetem Geoinformatikai Kar Szabó, Gábor, Nyugat-Magyarországi Egyetem Geoinformatikai Kar Geometriai példatár 1.: Koordináta-geometria
Számítási feladatok a Számítógépi geometria órához
 Számítási feladatok a Számítógépi geometria órához Kovács Zoltán Copyright c 2012 Last Revision Date: 2012. október 15. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát
Számítási feladatok a Számítógépi geometria órához Kovács Zoltán Copyright c 2012 Last Revision Date: 2012. október 15. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát
ANALITIKUS MÉRTAN I. VEKTORALGEBRA. 1. Adott egy ABCD tetraéder. Határozzuk meg az alábbi összegeket: a) AD + BC = BD + AC.
 ANALITIKUS MÉRTAN INFORMATIKA CSOPORT I. VEKTORALGEBRA 1. Feladatlap Műveletek vektorokkal 1. Adott egy ABCD tetraéder. Határozzuk meg az alábbi összegeket: a) AB + BD + DC; b) AD + CB + DC; c) AB + BC
ANALITIKUS MÉRTAN INFORMATIKA CSOPORT I. VEKTORALGEBRA 1. Feladatlap Műveletek vektorokkal 1. Adott egy ABCD tetraéder. Határozzuk meg az alábbi összegeket: a) AB + BD + DC; b) AD + CB + DC; c) AB + BC
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
Gyakorló feladatok javítóvizsgára szakközépiskola matematika 9. évfolyam
 Gyakorló feladatok javítóvizsgára szakközépiskola matematika 9. évfolyam Halmazok:. Adott két halmaz: A = kétjegyű pozitív, 4-gyel osztható számok B = 0-nél nagyobb, de 0-nál nem nagyobb pozitív egész
Gyakorló feladatok javítóvizsgára szakközépiskola matematika 9. évfolyam Halmazok:. Adott két halmaz: A = kétjegyű pozitív, 4-gyel osztható számok B = 0-nél nagyobb, de 0-nál nem nagyobb pozitív egész
