6 A teljesítményelektronikai kapcsolások modellezése
|
|
|
- Rebeka Vargané
- 8 évvel ezelőtt
- Látták:
Átírás
1 6 A teljesítméyelektroikai kapcsolások modellezése A teljesítméyelektroikai beredezések vagy már ömagukba egy bizoyos szabályzott redszert alkotak, vagy egy agyobb szabályozott redszer részét képezik. A szabályzóelemek (hibaerõsítõ) megfelelõ méretezése végett ismeri kell a beredezés diamikus viselkedését. Megfelelõ módo le kell íri a redszer várható reakcióját a vezérlõjel, a terhelés illetve a bemeeti feszültség változásaira. Csak így képzelhetõ el olya szabályozókör kialakítása, amely a kimeeti változókat kellõ diamikával és potossággal be tudja szabályozi. A modellezést ehezíti, hogy a kapcsolóüzembõl eredõe em folytoos (kotiuális) haem diszkrét redszerrel va dolguk, a szabályzókörök többsége viszot folytoos. A kapcsolók mûködése következtébe idõszakosa változik a redszer topológiája. A topológia változása a modellezésél az egyeletek megváltozását voja maga utá. A teljesítméyelektroikai beredezések umerikus aalízise megfelelõ hardver és szoftver igéybevételével véghezvihetõ. A umerikus aalízis sorá az egyes kapcsolások közötti szakaszokba lieáris redszerrel va dolguk. A kapcsolók állapotáak megváltozásakor egy másik, de szité lieáris redszer alakul ki. A két egymás utái lieáris szakaszt a peremfeltételek kötik össze. A tekercsek árama és a kodezátorok feszültsége szakadásmetes idõfüggvéyek, ezek az értékek a kapcsolások pillaatába változatlaok. A umerikus aalízis hátráya, hogy a megoldás em általáos jellegû, midig csak egy adott esetre voatkozó kokrét megoldást kapuk. Még sokszori, külöbözõ feltételek mellett ismételt aalízis alapjá sem köyû olya következtetéseket levoi, amelyek alapjá a szabályozóelemek méretezhetõk. Ezért vezették be az itt ismertetésre kerülõ átlagolt modelleket. 6.1 Modellezés állapotegyeletekkel A lieáris (és emlieáris) redszerek aalízisét állapotegyeletekkel végezhetjük. Az állapotegyeletek olya lieáris differeciálegyelet-redszert alkotak, amelyekbe változó és azok elsõ deriváltjai szerepelek. A változók az állapotváltozó evet viselik. Az egyeletredszer megoldásához szükséges az változó kezdeti értékeiek ismerete (peremfeltételek). A 6-1 ábrá bemutatott másodfokú lieáris redszer (két állapotváltozót tartalmaz), a következõ állapotegyeletekkel írható le: 1 1 x 1 x2 v d x 2 x1 x2 6 2 C RC Itt az x 1 változó a tekercs árama, az x 2 változó a kodezátor feszültsége, v d a gerjesztõfeszültség
2 x1 x2 - C R 6-1 ábra: Egyszerû másodfokú lieáris redszer. Általáos esetbe az állapotegyeletek mátrix alakba a következõképpe írhatók: x Ax Bv d 6 3 ahol x az állapotvektor, A az állapot-együttható mátrix, v d a gerjeszõ vektor, B a gerjesztõ-együttható mátrix. Adott esetbe az alkalmazott vektorok és mátrixok a következõk: 1 x1 0 1 x A vd v x2 1 1 d B C RC Mivel A és B em függvéyei x-ek és v d -ek, a redszer lieáris. Az egyeletredszer megoldását a lieáris differeciálegyeletekre kidolgozott matematikai módszerekkel végezhetjük. A differeciálegyeletek megoldása a változók idõfüggvéyeit adja. Ha a komplex átviteli függvéyekre va szükségük, elõször is a 6-3 egyeletre alkalmazi kell a aplace traszformációt, majd ki kell fejezi az átviteli függvéyeket. A szabályozókörök optimalizációja redszerit az átviteli függvéyekbõl idul ki Az átalakító állapotegyeleteiek felírása Az átalakítók hasoló lieáris redszerekét viselkedek az egyes idõitervallumokba, mit a 6-1 ábrá bemutatott egyszerû kapcsolás. A léyeges eltérés az, hogy a kapcsoló(k) állapotáak megváltozásakor változik az áramkör topológiája. Az új idõitervallumba új egyeleteket kell íri az átalakítóra. Az egyeletek azoos alakúak, mit a korábbi itervallumba, csak az A mátrix és a B vektor elemei változak meg. Az átalakítóra általáos esetbe ayi differeciálegyelet redszer írható fel, aháy külöbözõ topológia érvéyes rá a kapcsolók mûködésébõl következõe. Kotiuális üzembe az átalakítók redszerit két topológiát veszek fel, diszkotiuális üzembe pedig hármat. Két topológia eseté a következõ egyeletredszerek az érvéyesek az átalakító mûködéséek (1)-ik periódusára: x A1 x B1v d T s t ( d ) Ts 6 5 x A2 x v d ( d ) Ts t ( 1) Ts 6 6 ahol t az idõ, T s =1/f s a kapcsolási periódus, d a kitöltési téyezõ értéke az (1)-ik periódusba
3 6.1.2 Az állapotegyeletek átlagolása Az elõzõ szakaszba felírt egyeletek az átalakító diszkrét modelljét képezik. Az állapotváltozók ugya szakadásmetesek a kapcsoló(k) állapotváltozásai közbe, de a deriváltjaik em. Az állapotegyeletek átlagolása egy olya matematikai eljárás, amely a jelekek egy kapcsolási periódusra számított átlagértékével dolgozik, em veszi figyelembe a jelek hullámzását egy perióduso belül. A hullámzások elhayagolása az az ár, amit fizetük kell, hogy folytoos modellt kapjuk. A folytoos (kotiuális) modell alkalmas az átalakító viselkedéséek sok kapcsolási perióduso keresztül törtéõ követésére, viszoylag kis matematikai erõfeszítés mellett. Szükség szerit a jelek egy perióduso belüli hullámzása viszoylag egyszerû idõtartomáyba végzett aalízissel külö kiszámítható. Redszerit a hullámzással kapcsolatba csak egy aalízist végzük el, a lehetséges legrosszabb esetre, amely a legagyobb hullámzásokat adja. Errõl már szó volt az egyes kapcsolások ismertetésekor. Az állapotegyeletek átlagolását úgy végezzük, hogy a 6-5 és 6-6 egyeleteket a ekik megfelelõ kitöltési téyezõkkel (d ill. 1-d ) megszorozzuk. Az így kapott egyeleteket összeadjuk (súlyozott összeg). Az eredõ egyelet a következõ lesz: x [ A1 d A2 (1 d )] x [ B1d (1 d )] 6 7 A kitöltési téyezõ (d ) idõbe diszkrét függvéy, de helyettesíthetõ egy folytoos idõfüggvéyel (d), amely a kérdéses pillaatokba ugyaazokat az értékeket veszi fel, mit az eredeti diszkrét függvéy. Így a 6-7 egyelet érvéybe marad. Az állapotegyeletek mellett szükséges felíri a kimeeti változó kiszámítására szolgáló egyeletet is. Az átalakítóál általába a kimeeti feszültséget az állapotváltozók lieáris kombiációjakét fejezzük ki: v Cx 6 8 Erre az egyeletre is alkalmazva az állapotegyeletekél bevezetett átlagolást, a következõ eredméyt kapjuk: v [ C1d C2 (1 d)] x 6 9 Az így kapott 6-7 és 6-9 egyeletek em alkalmasak az átalakító átviteli függvéyeiek levezetésére, mivel emlieáris összefüggéseket fejezek ki: az egyeletek jobb oldalai az állapotváltozók és a kitöltési téyezõ szorzatai szerepelek iearizáció ieáris modellhez úgy juthatuk, hogy kis változásokat tételezük fel adott mukapot köryéké. Ha kétely merüle fel a modell érvéyességét illetõe, a liearizáció elvégezhetõ több mukapotba. Elsõ lépéskét a változókat felírjuk a yugalmi (mukapoti) érték és a változás összegekét: x X x, v V v, d D d Hasoló egyelet írható a bemeeti feszültségre is, de a jele aalízis egyszerûsítése érdekébe tételezzük fel, hogy a bemeeti feszültség álladó
4 A 6-10 egyeleteket az átlagolt állapotegyeletekbe (6-7 egyelet) helyettesítve, majd figyelembe véve a téyt, hogy az állapotváltozók mukapoti értékéek deriváltja értelemszerûe ulla értékû ( X 0 ), a következõ kifejezést kapjuk: x AX Bu Ax [( A1 A2 ) ] d 6 11 Itt a következõ helyettesítéseket alkalmaztuk: A A (1 1d A2 d), B B (1 1d d) 6 12 A 6-11 egyeletbe elhayagoltuk mide olya tagot, amelybe két kis változás ( x és d ) szorzata szerepel. A 6-11 egyeletbe figyelme kívül hagyva a változásokat és azok deriváltjait, a yugalmi poti egyelethez jutuk: AX B Alkalmazva a 6-13 feltételt a 6-11 egyeletre, külöválasztható a mukapot körüli változásokra voatkozó összefüggés a mukapot számításától. Így kapjuk a következõ összefüggést: x Ax [( A1 A2 ) ] d 6 14 A 6-9 egyeletbe helyettesítve a változókak a 6-10 egyeletekkel megadott felbotását, a kimeeti változóra a következõ összefüggést kapjuk: V v CX Cx [( C1 C2 ) X ] d 6 15 ahol: C C (1 1D C2 D) 6 16 Itt is külöválasztható a mukapotot meghatározó megoldásrész: V CX 6 17 Így jutuk a változásokra voatkozó összefüggéshez: v Cx [( C1 C2 ) X ] d 6 18 amit a továbbiakba az átviteli függvéy levezetésekor foguk haszáli. A mukapotot meghatározó egyeletekbõl (6-13 és 6-17) megkapható a korábba más módszerekkel meghatározott feszültségátviteli téyezõ: V CA 1 B Az egyes átalakítók tárgyalásakor a feszültségátviteli téyezõt abból a feltételbõl vezettük le, hogy adott mukapotba a tekercs feszültségéek átlagértéke ulla (2-1 egyelet) Az átalakító átviteli függvéyeiek levezetése A változásokra voatkozó 6-14 egyeletre alkalmazva a aplace traszformációt, a következõ komplex egyelethez jutuk: s x ( s) Ax ( s) [( A1 A2 ) ] d ( s) Az állapotváltozókra megoldva: ( 1 x s) [ si A] [( A1 A2 ) ] d ( s) Itt I az egységmátrix
5 Ha a 6-18 egyeletre is alkalmazzuk a aplace traszformációt és a 6-21 egyeletbõl behelyettesítjük az x ( s ) -re kapott kifejezést, eljutuk az átalakító komplex átviteli függvéyéhez: v ( s) 1 Tp ( s) C[ si A] [( A1 A2 ) ] ( C1 C2 ) X d( s) A szabályozókör méretezéséél az itt levezetett T p (s) átviteli függvéyre va szükség. Ha az átalakító viselkedését a bemeeti feszültség változása közbe szereték vizsgáli, rögzíthetjük a kitöltési téyezõt és levezethetjük a kimeet/bemeet közötti átviteli függvéyt. Ha egyszerre szereték vizsgáli az átalakító teljes mûködését, a változók széttagolására voatkozó egyeletekél (6-10 egyeletek) figyelembe kell vei, hogy a bemeeti feszültség is tartalmaz változó részt. 6.2 A kapcsoló átlagolása Egy másik, az állapotegyeletek átlagolásától függetle módszer a kapcsoló viselkedéséek átlagolásá alapszik. Az elgodolás hasoló, mit a trazisztoros erõsítõk modellezésél: az áramkör emlieáris részét eltávolítjuk, helyébe egy modellt építük be, az áramkör többi (lieáris) részét viszot éritetleül hagyjuk. Ez a módszer külööse az átalakítók számítógépes szimulációjáál yújt agy segítséget, mivel végeredméybe em egyeleteket, haem áramköri modellt kapuk Átlagolás A kapcsoló átlagolása úgy törtéik, hogy a kapcsoló jeletkezõ áramokat és feszültségeket azok átlagértékeivel helyettesítjük. Az átlagérték számításakor két- ill. három értéket kell a megfelelõ kitöltési téyezõkkel megszorozi, majd összeadi, attól függõe, hogy az átalakító folytoos vagy szakadásos üzembe dolgozik-e. Az átalakító alapkapcsolásokba midig egy aktív kapcsoló (trazisztor) és egy passzív kapcsoló (dióda) találkozik egy potba (6-2a ábra). A kapcsoló átlagolásakor ez a két alkatrész egy egészet képez (6-2b ábra). Traszformátoros átalakítókál a trazisztor és a dióda em egy közös potra csatlakozak, de megfelelõ átalakítással itt is a kapcsolás ilye alakra hozható. a c a (D) S Q c D C R (1-D) C R p p (a) (b) ábra: Feszültségcsökketõ átalakító trazisztorral és diódával (a), a kapcsoló általáos jelölésével (b). A kapcsoló általáos jelöléséél az egyes csatlakozási potokat a következõ módo jelöltük: a aktív, p passzív, c közös. Eredetileg a kapcsoló aktív része az a és c
6 potok közé volt csatlakoztatva, a passzív rész pedig a p és a c potok közé. A 6-2b ábrá bejelöltük azt is, hogy a periódus melyik részébe va a kapcsoló az a ill. a p állásba. Folytoos tekercsáram mellett a következõ egyeletek írhatók fel a kapcsoló feszültségeiek ill. áramaiak átlagértékeire: D 6 23 Vcp V ap I 6 24 a DI c A 6-23 egyelet egy feszültségvezérelt feszültségforrással modellezhetõ, míg a 6-24 egyelet egy áramvezérelt áramforrással. Így jutuk a feszültségcsökketõ kapcsolás áramköri modelljéhez (6-3 ábra), mely a kapcsoló átlagolásá alapszik. Vap a DIc p Ic DVap C R 6-3 ábra: A feszültségcsökketõ átalakító áramköri modellje az átlagolt kapcsolóval. Megfelelõ áramköri szimulátorral (amely támogatja a vezérelt források alkalmazását) az átalakító viselkedése kivizsgálható mide kokrét gerjesztés esetére. Számításba jöhetek kisjelû és agyjelû szimulációk is. A kutatók kifejlesztették a megfelelõ átlagolt kapcsoló modellt a szakadásos üzemre is, sõt olya kapcsolások is modellezhetõk így, amelyek álladóa a folytoos és szakadásos üzem határá üzemelek iearizáció A 6-3 ábrá bemutatott áramköri modell természetese em lieáris: az áramok és feszültségek illetve a kitöltési téyezõ szorzata szerepel az egyes vezérelt források leírásába. A liearizáció úgy végezhetõ el, hogy a 6-10 egyeletekek megfelelõe itt is külöválasztjuk az áramok, feszültségek és a kitöltési téyezõ mukapotot defiiáló részét és a változó részt. Ezt követõe az áramkört két újabb áramkörrel helyettesíthetjük: egyik a mukapot számítására alkalmas, a másik az átalakító kisjelû lieáris modellje, amely az átviteli függvéy levezetésére alkalmas Az átalakítók átviteli függvéyeiek levezetése Mivel a kapcsoló átlagolása közbe em egyeletekhez, haem áramköri modellhez jutottuk, az átviteli függvéyek levezetését hagyomáyos áramkör-elemzési módszerekkel végezhetjük el. Az áramkör alapjá közvetleül írhatók a komplex egyeletek, amelyeket megfelelõ változókra megoldva a keresett átviteli függvéyt kapjuk
VII. A határozatlan esetek kiküszöbölése
 A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
Kvantum párhuzamosság Deutsch algoritmus Deutsch-Jozsa algoritmus
 LOGO Kvatum párhuzamosság Deutsch algoritmus Deutsch-Jozsa algoritmus Gyögyösi László BME Villamosméröki és Iormatikai Kar Bevezető Kvatum párhuzamosság Bármilye biáris üggvéyre, ahol { } { } : 0, 0,,
LOGO Kvatum párhuzamosság Deutsch algoritmus Deutsch-Jozsa algoritmus Gyögyösi László BME Villamosméröki és Iormatikai Kar Bevezető Kvatum párhuzamosság Bármilye biáris üggvéyre, ahol { } { } : 0, 0,,
1. A radioaktivitás statisztikus jellege
 A radioaktivitás időfüggése 1. A radioaktivitás statisztikus jellege Va N darab azoos radioaktív atomuk, melyekek az atommagja spotá átalakulásra képes. tegyük fel, hogy ezek em bomlaak tovább. Ekkor a
A radioaktivitás időfüggése 1. A radioaktivitás statisztikus jellege Va N darab azoos radioaktív atomuk, melyekek az atommagja spotá átalakulásra képes. tegyük fel, hogy ezek em bomlaak tovább. Ekkor a
Folytonos idejű rendszerek stabilitása
 Folytoos idejű redszerek stabilitása Összeállította: dr. Gerzso Miklós egyetemi doces PTE MIK Műszaki Iformatika Taszék 205.2.06. Itelliges redszerek I. PTE MIK Mérök iformatikus BSc szak Stabilitás egyszerűsített
Folytoos idejű redszerek stabilitása Összeállította: dr. Gerzso Miklós egyetemi doces PTE MIK Műszaki Iformatika Taszék 205.2.06. Itelliges redszerek I. PTE MIK Mérök iformatikus BSc szak Stabilitás egyszerűsített
SOROK Feladatok és megoldások 1. Numerikus sorok
 SOROK Feladatok és megoldások. Numerikus sorok I. Határozza meg az alábbi, mértai sorra visszavezethető sorok esetébe az S -edik részletösszeget és a sor S összegét! )...... k 5 5 5 5 )...... 5 5 5 5 )......
SOROK Feladatok és megoldások. Numerikus sorok I. Határozza meg az alábbi, mértai sorra visszavezethető sorok esetébe az S -edik részletösszeget és a sor S összegét! )...... k 5 5 5 5 )...... 5 5 5 5 )......
Stabilitás Irányítástechnika PE MI_BSc 1
 Stabilitás 2008.03.4. Stabilitás egyszerűsített szemlélet példa zavarás utá a magára hagyott redszer visszatér a yugalmi állapotába kvázistacioárius állapotba kerül végtelebe tart alapjelváltás Stabilitás/2
Stabilitás 2008.03.4. Stabilitás egyszerűsített szemlélet példa zavarás utá a magára hagyott redszer visszatér a yugalmi állapotába kvázistacioárius állapotba kerül végtelebe tart alapjelváltás Stabilitás/2
( a b)( c d) 2 ab2 cd 2 abcd 2 Egyenlőség akkor és csak akkor áll fenn
 Feladatok közepek közötti egyelőtleségekre (megoldások, megoldási ötletek) A továbbiakba szmk=számtai-mértai közép közötti egyelőtleség, szhk=számtaiharmoikus közép közötti egyelőtleség, míg szk= számtai-égyzetes
Feladatok közepek közötti egyelőtleségekre (megoldások, megoldási ötletek) A továbbiakba szmk=számtai-mértai közép közötti egyelőtleség, szhk=számtaiharmoikus közép közötti egyelőtleség, míg szk= számtai-égyzetes
Ingatlanfinanszírozás és befektetés
 Nyugat-Magyarországi Egyetem Geoiformatikai Kar Igatlameedzser 8000 Székesfehérvár, Pirosalma u. 1-3. Szakiráyú Továbbképzési Szak Igatlafiaszírozás és befektetés 2. Gazdasági matematikai alapok Szerzı:
Nyugat-Magyarországi Egyetem Geoiformatikai Kar Igatlameedzser 8000 Székesfehérvár, Pirosalma u. 1-3. Szakiráyú Továbbképzési Szak Igatlafiaszírozás és befektetés 2. Gazdasági matematikai alapok Szerzı:
10.M ALGEBRA < <
 0.M ALGEBRA GYÖKÖS KIFEJEZÉSEK. Mutassuk meg, hogy < + +... + < + + 008 009 + 009 008 5. Mutassuk meg, hogy va olya pozitív egész szám, amelyre 99 < + + +... + < 995. Igazoljuk, hogy bármely pozitív egész
0.M ALGEBRA GYÖKÖS KIFEJEZÉSEK. Mutassuk meg, hogy < + +... + < + + 008 009 + 009 008 5. Mutassuk meg, hogy va olya pozitív egész szám, amelyre 99 < + + +... + < 995. Igazoljuk, hogy bármely pozitív egész
= λ valós megoldása van.
 Másodredű álladó együtthatós lieáris differeciálegyelet. Általáos alakja: y + a y + by= q Ha q = 0 Ha q 0 akkor homogé lieárisak evezzük. akkor ihomogé lieárisak evezzük. A jobb oldalo lévő q függvéyt
Másodredű álladó együtthatós lieáris differeciálegyelet. Általáos alakja: y + a y + by= q Ha q = 0 Ha q 0 akkor homogé lieárisak evezzük. akkor ihomogé lieárisak evezzük. A jobb oldalo lévő q függvéyt
ALGEBRA. egyenlet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 198.
 ALGEBRA MÁSODFOKÚ POLINOMOK. Határozzuk meg az + p + q = 0 egyelet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 98.. Határozzuk meg az összes olya pozitív egész p és q számot, amelyre az
ALGEBRA MÁSODFOKÚ POLINOMOK. Határozzuk meg az + p + q = 0 egyelet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 98.. Határozzuk meg az összes olya pozitív egész p és q számot, amelyre az
EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z n HALMAZON. egyenletrendszer megoldása a
 Az érettségi vizsgára előkészülő taulók figyelmébe! 4. Az EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z HALMAZON a1 x + b1 y = c1 egyeletredszer megoldása a a x + b y = c Z halmazo (. rész) Ebbe a részbe
Az érettségi vizsgára előkészülő taulók figyelmébe! 4. Az EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z HALMAZON a1 x + b1 y = c1 egyeletredszer megoldása a a x + b y = c Z halmazo (. rész) Ebbe a részbe
A figurális számokról (IV.)
 A figurális számokról (IV.) Tuzso Zoltá, Székelyudvarhely A továbbiakba külöféle számkombiációk és összefüggések reprezetálásáról, és bizoyos összegek kiszámolásáról íruk. Sajátos összefüggések Az elekbe
A figurális számokról (IV.) Tuzso Zoltá, Székelyudvarhely A továbbiakba külöféle számkombiációk és összefüggések reprezetálásáról, és bizoyos összegek kiszámolásáról íruk. Sajátos összefüggések Az elekbe
Egy lehetséges tételsor megoldásokkal
 Egy lehetséges tételsor megoldásokkal A vizsgatétel I része a IX és X osztályos ayagot öleli fel, 6 külöböző fejezetből vett feladatból áll, összese potot ér A közzétett tétel-variások és az előző évekbe
Egy lehetséges tételsor megoldásokkal A vizsgatétel I része a IX és X osztályos ayagot öleli fel, 6 külöböző fejezetből vett feladatból áll, összese potot ér A közzétett tétel-variások és az előző évekbe
8.1. A rezgések szétcsatolása harmonikus közelítésben. Normálrezgések. = =q n és legyen itt a potenciál nulla. q i j. szimmetrikus. q k.
 8. KIS REZGÉSEK STABIL EGYENSÚLYI HELYZET KÖRÜL 8.. A rezgések szétcsatolása harmoikus közelítésbe. Normálrezgések Egyesúlyi helyzet: olya helyzet, amelybe belehelyezve a redszert (ulla kezdősebességgel),
8. KIS REZGÉSEK STABIL EGYENSÚLYI HELYZET KÖRÜL 8.. A rezgések szétcsatolása harmoikus közelítésbe. Normálrezgések Egyesúlyi helyzet: olya helyzet, amelybe belehelyezve a redszert (ulla kezdősebességgel),
2. Az együttműködő villamosenergia-rendszer teljesítmény-egyensúlya
 II RÉZ 2 EJEZE 2 Az együttműködő vllamoseerga-redszer teljesítméy-egyesúlya 2 A frekveca és a hatásos teljesítméy között összefüggés A fogyasztó alredszerbe a fogyasztók hatásos wattos teljesítméyt lletve
II RÉZ 2 EJEZE 2 Az együttműködő vllamoseerga-redszer teljesítméy-egyesúlya 2 A frekveca és a hatásos teljesítméy között összefüggés A fogyasztó alredszerbe a fogyasztók hatásos wattos teljesítméyt lletve
2. Hatványsorok. A végtelen soroknál tanultuk, hogy az. végtelen sort adja: 1 + x + x x n +...
 . Függvéysorok. Bevezetés és defiíciók A végtele sorokál taultuk, hogy az + x + x + + x +... végtele összeg x < eseté koverges. A feti végtele összegre úgy is godolhatuk, hogy végtele sok függvéyt aduk
. Függvéysorok. Bevezetés és defiíciók A végtele sorokál taultuk, hogy az + x + x + + x +... végtele összeg x < eseté koverges. A feti végtele összegre úgy is godolhatuk, hogy végtele sok függvéyt aduk
Diszkrét matematika II., 3. előadás. Komplex számok
 1 Diszkrét matematika II., 3. előadás Komplex számok Dr. Takách Géza NyME FMK Iformatikai Itézet takach@if.yme.hu http://if.yme.hu/ takach/ 2007. február 22. Komplex számok Szereték kibővítei a valós számtestet,
1 Diszkrét matematika II., 3. előadás Komplex számok Dr. Takách Géza NyME FMK Iformatikai Itézet takach@if.yme.hu http://if.yme.hu/ takach/ 2007. február 22. Komplex számok Szereték kibővítei a valós számtestet,
Kalkulus II., második házi feladat
 Uger Tamás Istvá FTDYJ Név: Uger Tamás Istvá Neptu: FTDYJ Web: http://maxwellszehu/~ugert Kalkulus II, második házi feladat pot) Koverges? Abszolút koverges? ) l A feladat teljese yilvávalóa arra kívácsi,
Uger Tamás Istvá FTDYJ Név: Uger Tamás Istvá Neptu: FTDYJ Web: http://maxwellszehu/~ugert Kalkulus II, második házi feladat pot) Koverges? Abszolút koverges? ) l A feladat teljese yilvávalóa arra kívácsi,
ÁRAMKÖRÖK SZIMULÁCIÓJA
 ÁRAMKÖRÖK SZIMULÁCIÓJA Az áramkörök szimulációja révén betekintést nyerünk azok működésébe. Meg tudjuk határozni az áramkörök válaszát különböző gerjesztésekre, különböző üzemmódokra. Végezhetők analóg
ÁRAMKÖRÖK SZIMULÁCIÓJA Az áramkörök szimulációja révén betekintést nyerünk azok működésébe. Meg tudjuk határozni az áramkörök válaszát különböző gerjesztésekre, különböző üzemmódokra. Végezhetők analóg
Matematikai statisztika
 Matematikai statisztika PROGRAMTERVEZŐ INFORMATIKUS alapszak, A szakiráy Arató Miklós Valószíűségelméleti és Statisztika Taszék Természettudomáyi Kar 2019. február 18. Arató Miklós (ELTE) Matematikai statisztika
Matematikai statisztika PROGRAMTERVEZŐ INFORMATIKUS alapszak, A szakiráy Arató Miklós Valószíűségelméleti és Statisztika Taszék Természettudomáyi Kar 2019. február 18. Arató Miklós (ELTE) Matematikai statisztika
Villamos gépek tantárgy tételei
 Villamos gépek tatárgy tételei 7. tétel Mi a szerepe az áram- és feszültségváltókak? Hogya kapcsolódak a hálózathoz, milye előírások voatkozak a biztoságos üzemeltetésükre, kiválasztásukál milye adatot
Villamos gépek tatárgy tételei 7. tétel Mi a szerepe az áram- és feszültségváltókak? Hogya kapcsolódak a hálózathoz, milye előírások voatkozak a biztoságos üzemeltetésükre, kiválasztásukál milye adatot
(A TÁMOP /2/A/KMR számú projekt keretében írt egyetemi jegyzetrészlet):
 A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
2. gyakorlat - Hatványsorok és Taylor-sorok
 . gyakorlat - Hatváysorok és Taylor-sorok 9. március 3.. Adjuk meg az itt szereplő sorok kovergeciasugarát és kovergeciaitervallumát! + a = + Azaz a hatváysor kovergeciasugara. Az biztos, hogy a (-,) yílt
. gyakorlat - Hatváysorok és Taylor-sorok 9. március 3.. Adjuk meg az itt szereplő sorok kovergeciasugarát és kovergeciaitervallumát! + a = + Azaz a hatváysor kovergeciasugara. Az biztos, hogy a (-,) yílt
REOIL. növeli a transzformátorok élettartamát. www.ekofluid.sk/hu/
 5 öveli a traszformátorok öveli a traszformátorok A techológia előyei A költségek csökketéseek folyamatos kéyszere és a zavartala eergiaellátás ehézségei szükségessé teszik a traszformátorok tervezett
5 öveli a traszformátorok öveli a traszformátorok A techológia előyei A költségek csökketéseek folyamatos kéyszere és a zavartala eergiaellátás ehézségei szükségessé teszik a traszformátorok tervezett
A paramétereket kísérletileg meghatározott yi értékekre támaszkodva becsülik. Ha n darab kisérletet (megfigyelést, mérést) végeznek, n darab
 öbbváltozós regresszók Paraméterbecslés-. A paraméterbecslés.. A probléma megfogalmazása A paramétereket kísérletleg meghatározott y értékekre támaszkodva becsülk. Ha darab ksérletet (megfgyelést, mérést
öbbváltozós regresszók Paraméterbecslés-. A paraméterbecslés.. A probléma megfogalmazása A paramétereket kísérletleg meghatározott y értékekre támaszkodva becsülk. Ha darab ksérletet (megfgyelést, mérést
1. Sajátérték és sajátvektor
 1. Sajátérték és sajátvektor Leképezés diagoális mátrixa. Kérdés Mely bázisba lesz egy traszformáció mátrixa diagoális? A Hom(V) és b 1,...,b ilye bázis. Ha [A] b,b főátlójába λ 1,...,λ áll, akkor A(b
1. Sajátérték és sajátvektor Leképezés diagoális mátrixa. Kérdés Mely bázisba lesz egy traszformáció mátrixa diagoális? A Hom(V) és b 1,...,b ilye bázis. Ha [A] b,b főátlójába λ 1,...,λ áll, akkor A(b
Lineáris kódok. u esetén u oszlopvektor, u T ( n, k ) május 31. Hibajavító kódok 2. 1
 Lieáris kódok Defiíció. Legye SF q. Ekkor S az F q test feletti vektortér. K lieáris kód, ha K az S k-dimeziós altere. [,k] q vagy [,k,d] q. Jelölések: F u eseté u oszlopvektor, u T (, k ) q sorvektor.
Lieáris kódok Defiíció. Legye SF q. Ekkor S az F q test feletti vektortér. K lieáris kód, ha K az S k-dimeziós altere. [,k] q vagy [,k,d] q. Jelölések: F u eseté u oszlopvektor, u T (, k ) q sorvektor.
3. SOROZATOK. ( n N) a n+1 < a n. Egy sorozatot (szigorúan) monotonnak mondunk, ha (szigorúan) monoton növekvő vagy csökkenő.
 3. SOROZATOK 3. Sorozatok korlátossága, mootoitása, kovergeciája Defiíció. Egy f : N R függvéyt valós szám)sorozatak evezük. Ha A egy adott halmaz és f : N A, akkor f-et A-beli értékű) sorozatak evezzük.
3. SOROZATOK 3. Sorozatok korlátossága, mootoitása, kovergeciája Defiíció. Egy f : N R függvéyt valós szám)sorozatak evezük. Ha A egy adott halmaz és f : N A, akkor f-et A-beli értékű) sorozatak evezzük.
NUMERIKUS SOROK II. Ebben a részben kizárólag a konvergencia vizsgálatával foglalkozunk.
 NUMERIKUS SOROK II. Ebbe a részbe kizárólag a kovergecia vizsgálatával foglalkozuk. SZÜKSÉGES FELTÉTEL Ha pozitív (vagy em egatív) tagú umerikus sor, akkor a kovergecia szükséges feltétele, hogy lim a
NUMERIKUS SOROK II. Ebbe a részbe kizárólag a kovergecia vizsgálatával foglalkozuk. SZÜKSÉGES FELTÉTEL Ha pozitív (vagy em egatív) tagú umerikus sor, akkor a kovergecia szükséges feltétele, hogy lim a
MATEMATIKA I. KATEGÓRIA (SZAKKÖZÉPISKOLA)
 O k t a t á s i H i v a t a l A 5/6 taévi Országos Középiskolai Taulmáyi Versey első forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató A 5 olya égyjegyű szám, amelyek számjegyei
O k t a t á s i H i v a t a l A 5/6 taévi Országos Középiskolai Taulmáyi Versey első forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató A 5 olya égyjegyű szám, amelyek számjegyei
Hiba! Nincs ilyen stílusú szöveg a dokumentumban.-86. ábra: A példa-feladat kódolási változatai
 közzétéve a szerző egedélyével) Öfüggő szekuder-változó csoport keresése: egy bevezető példa Ez a módszer az állapothalmazo értelmezett partíció-párok elméleté alapul. E helye em lehet céluk az elmélet
közzétéve a szerző egedélyével) Öfüggő szekuder-változó csoport keresése: egy bevezető példa Ez a módszer az állapothalmazo értelmezett partíció-párok elméleté alapul. E helye em lehet céluk az elmélet
Komplex számok (el adásvázlat, 2008. február 12.) Maróti Miklós
 Komplex számok el adásvázlat, 008. február 1. Maróti Miklós Eek az el adásak a megértéséhez a következ fogalmakat kell tudi: test, test additív és multiplikatív csoportja, valós számok és tulajdoságaik.
Komplex számok el adásvázlat, 008. február 1. Maróti Miklós Eek az el adásak a megértéséhez a következ fogalmakat kell tudi: test, test additív és multiplikatív csoportja, valós számok és tulajdoságaik.
Matematikai játékok. Svetoslav Bilchev, Emiliya Velikova
 Matematikai játékok Svetoslav Bilchev, Emiliya Velikova 1. rész Matematikai tréfák A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a játékosok
Matematikai játékok Svetoslav Bilchev, Emiliya Velikova 1. rész Matematikai tréfák A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a játékosok
Függvényhatárérték-számítás
 Függvéyhatárérték-számítás I Függvéyek véges helye vett véges határértéke I itervallumo, ha va olya k valós szám, melyre az I itervallumo, ha va olya K valós szám, melyre I itervallumo, ha alulról és felülről
Függvéyhatárérték-számítás I Függvéyek véges helye vett véges határértéke I itervallumo, ha va olya k valós szám, melyre az I itervallumo, ha va olya K valós szám, melyre I itervallumo, ha alulról és felülről
Sorozatok, határérték fogalma. Függvények határértéke, folytonossága
 Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
INJEKTIVITÁS ÉS EGYÉB TULAJDONSÁGOK MEGOLDOTT FELADATOK
 Megoldott feladatok Ijektivitás és egyéb tulajdoságok 59 ) INJEKTIVITÁS ÉS EGYÉB TULAJDONSÁGOK MEGOLDOTT FELADATOK Határozd meg azt az f:r R függvéyt, amelyre f ( f ( ) x R és a g:r R g ( = x f ( függvéy
Megoldott feladatok Ijektivitás és egyéb tulajdoságok 59 ) INJEKTIVITÁS ÉS EGYÉB TULAJDONSÁGOK MEGOLDOTT FELADATOK Határozd meg azt az f:r R függvéyt, amelyre f ( f ( ) x R és a g:r R g ( = x f ( függvéy
A szórások vizsgálata. Az F-próba. A döntés. Az F-próba szabadsági fokai
 05..04. szórások vizsgálata z F-próba Hogya foguk hozzá? Nullhipotézis: a két szórás azoos, az eltérés véletle (mitavétel). ullhipotézishez tartozik egy ú. F-eloszlás. Szabadsági fokok: számláló: - evező:
05..04. szórások vizsgálata z F-próba Hogya foguk hozzá? Nullhipotézis: a két szórás azoos, az eltérés véletle (mitavétel). ullhipotézishez tartozik egy ú. F-eloszlás. Szabadsági fokok: számláló: - evező:
Differenciaegyenletek aszimptotikus viselkedésének
 Differeciaegyeletek aszimptotikus viselkedéséek vizsgálata Mathematica segítségével Botos Zsófia Újvidéki Egyetem TTK Újvidék Szerbia E-mail: botoszsofi@yahoo.com 1. Bevezető Tekitsük az késleltetett diszkrét
Differeciaegyeletek aszimptotikus viselkedéséek vizsgálata Mathematica segítségével Botos Zsófia Újvidéki Egyetem TTK Újvidék Szerbia E-mail: botoszsofi@yahoo.com 1. Bevezető Tekitsük az késleltetett diszkrét
(2) Határozzuk meg a következő területi integrálokat a megadott halmazokon: x sin y dx dy, ahol T : 0 x 1, 2 y 3.
 . feladatsor () Határozzuk meg a következő területi itegrálokat a megadott téglalapoko: ( (x + y) dx dy, ahol T : x, y 3. ( T T x si y dx dy, ahol T : x, 2 y 3. (2) Határozzuk meg a következő területi
. feladatsor () Határozzuk meg a következő területi itegrálokat a megadott téglalapoko: ( (x + y) dx dy, ahol T : x, y 3. ( T T x si y dx dy, ahol T : x, 2 y 3. (2) Határozzuk meg a következő területi
SZÁMELMÉLET. Vasile Berinde, Filippo Spagnolo
 SZÁMELMÉLET Vasile Beride, Filippo Spagolo A számelmélet a matematika egyik legrégibb ága, és az egyik legagyobb is egybe Eek a fejezetek az a célja, hogy egy elemi bevezetést yújtso az első szite lévő
SZÁMELMÉLET Vasile Beride, Filippo Spagolo A számelmélet a matematika egyik legrégibb ága, és az egyik legagyobb is egybe Eek a fejezetek az a célja, hogy egy elemi bevezetést yújtso az első szite lévő
1 k < n(1 + log n) C 1n log n, d n. (1 1 r k + 1 ) = 1. = 0 és lim. lim n. f(n) < C 3
 Dr. Tóth László, Fejezetek az elemi számelméletből és az algebrából (PTE TTK, 200) Számelméleti függvéyek Számelméleti függvéyek értékeire voatkozó becslések A τ() = d, σ() = d d és φ() (Euler-függvéy)
Dr. Tóth László, Fejezetek az elemi számelméletből és az algebrából (PTE TTK, 200) Számelméleti függvéyek Számelméleti függvéyek értékeire voatkozó becslések A τ() = d, σ() = d d és φ() (Euler-függvéy)
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 10. A statisztika alapjai Debrecei Egyetem, 2015 Dr. Bérczes Attila, Bertók Csaád A diasor tartalma 1 Bevezetés 2 Statisztikai függvéyek Defiíció, empirikus várható érték Empirikus
BIOMATEMATIKA ELŐADÁS 10. A statisztika alapjai Debrecei Egyetem, 2015 Dr. Bérczes Attila, Bertók Csaád A diasor tartalma 1 Bevezetés 2 Statisztikai függvéyek Defiíció, empirikus várható érték Empirikus
A FUNDAMENTÁLIS EGYENLET KÉT REPREZENTÁCIÓBAN. A függvény teljes differenciálja, a differenciális fundamentális egyenlet: U V S U + dn 1
 A FUNDAMENÁLIS EGYENLE KÉ REPREZENÁCIÓBAN A differeciális fudametális egyelet A fudametális egyelet a belső eergiára: UU (S V K ) A függvéy teljes differeciálja a differeciális fudametális egyelet: U S
A FUNDAMENÁLIS EGYENLE KÉ REPREZENÁCIÓBAN A differeciális fudametális egyelet A fudametális egyelet a belső eergiára: UU (S V K ) A függvéy teljes differeciálja a differeciális fudametális egyelet: U S
Komplex számok. d) Re(z 4 ) = 0, Im(z 4 ) = 1 e) Re(z 5 ) = 0, Im(z 5 ) = 2 f) Re(z 6 ) = 1, Im(z 6 ) = 0
 Komplex számok 1 Adjuk meg az alábbi komplex számok valós, illetve képzetes részét: a + i b i c z d z i e z 5 i f z 1 A z a + bi komplex szám valós része: Rez a, képzetes része Imz b Ez alapjá a megoldások
Komplex számok 1 Adjuk meg az alábbi komplex számok valós, illetve képzetes részét: a + i b i c z d z i e z 5 i f z 1 A z a + bi komplex szám valós része: Rez a, képzetes része Imz b Ez alapjá a megoldások
Hanka László. Fejezetek a matematikából
 Haka László Egyetemi jegyzet Budapest, 03 ÓE - BGK - 304 Szerző: Dr. Haka László adjuktus (OE BGK) Lektor: Hosszú Ferec mestertaár (OE BGK) Fiamak Boldizsárak Előszó Ez az elektroikus egyetemi jegyzet
Haka László Egyetemi jegyzet Budapest, 03 ÓE - BGK - 304 Szerző: Dr. Haka László adjuktus (OE BGK) Lektor: Hosszú Ferec mestertaár (OE BGK) Fiamak Boldizsárak Előszó Ez az elektroikus egyetemi jegyzet
Nevezetes sorozat-határértékek
 Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
Modern Fizika Labor. 13. Molekulamodellezés. Fizika BSc. A mérés dátuma: nov. 08. A mérés száma és címe: Értékelés:
 Moder Fizika Labor Fizika BSc A mérés dátuma: 2011. ov. 08. A mérés száma és címe: 13. Molekulamodellezés Értékelés: A beadás dátuma: 2011. dec. 09. A mérést végezte: Szőke Kálmá Bejami Kalas György Bejámi
Moder Fizika Labor Fizika BSc A mérés dátuma: 2011. ov. 08. A mérés száma és címe: 13. Molekulamodellezés Értékelés: A beadás dátuma: 2011. dec. 09. A mérést végezte: Szőke Kálmá Bejami Kalas György Bejámi
1. Gyökvonás komplex számból
 1. Gyökvoás komplex számból Gyökvoás komplex számból Ismétlés: Ha r,s > 0 valós, akkor r(cosα+isiα) = s(cosβ+isiβ) potosa akkor, ha r = s, és α β a 360 egész számszorosa. Moivre képlete: ( s(cosβ+isiβ)
1. Gyökvoás komplex számból Gyökvoás komplex számból Ismétlés: Ha r,s > 0 valós, akkor r(cosα+isiα) = s(cosβ+isiβ) potosa akkor, ha r = s, és α β a 360 egész számszorosa. Moivre képlete: ( s(cosβ+isiβ)
Minta JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MATEMATIKA EMELT SZINTŰ ÍRÁSBELI 2. FELADATSORHOZ
 JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MATEMATIKA EMELT SZINTŰ ÍRÁSBELI. FELADATSORHOZ Formai előírások: A dolgozatot a vizsgázó által haszált szíűtől eltérő szíű tollal kell javítai, és a taári gyakorlatak megfelelőe
JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MATEMATIKA EMELT SZINTŰ ÍRÁSBELI. FELADATSORHOZ Formai előírások: A dolgozatot a vizsgázó által haszált szíűtől eltérő szíű tollal kell javítai, és a taári gyakorlatak megfelelőe
Analóg elektronika - laboratóriumi gyakorlatok
 Analóg elektronika - laboratóriumi gyakorlatok. Mûveleti erõsítõk egyenáramú jellemzése és alkalmazásai. Elmélet Az erõsítõ fogalmát valamint az integrált mûveleti erõsítõk szerkezetét és viselkedését
Analóg elektronika - laboratóriumi gyakorlatok. Mûveleti erõsítõk egyenáramú jellemzése és alkalmazásai. Elmélet Az erõsítõ fogalmát valamint az integrált mûveleti erõsítõk szerkezetét és viselkedését
A kommutáció elve. Gyűrűs tekercselésű forgórész. Gyűrűs tekercselésű kommutátoros forgórész
 Egyeáramú gépek 008 É É É + Φp + Φp + Φp - - - D D D A kommutáció elve Gyűrűs tekercselésű forgórész Gyűrűs tekercselésű kommutátoros forgórész 1 Egyeáramú gép forgórésze a) b) A feszültség időbeli változása
Egyeáramú gépek 008 É É É + Φp + Φp + Φp - - - D D D A kommutáció elve Gyűrűs tekercselésű forgórész Gyűrűs tekercselésű kommutátoros forgórész 1 Egyeáramú gép forgórésze a) b) A feszültség időbeli változása
Reakciómechanizmusok leírása. Paraméterek. Reakciókinetikai bizonytalanságanalízis. Bizonytalanságanalízis
 Megbízható kémiai modellek kifejlesztése sok mérési adat egyidejő feldolgozása alajá uráyi amás www.turayi.eu ELE Kémiai Itézet Reakciókietikai Laboratórium Eddig dolgoztak eze a témá: (témavezetık: uráyi
Megbízható kémiai modellek kifejlesztése sok mérési adat egyidejő feldolgozása alajá uráyi amás www.turayi.eu ELE Kémiai Itézet Reakciókietikai Laboratórium Eddig dolgoztak eze a témá: (témavezetık: uráyi
EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z n HALMAZON. egyenletrendszer megoldása a Z
 Az érettségi vizsgára előkészülő taulók figyelmébe! EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z HALMAZON a x + b y c 5. Az egyeletredszer megoldása a Z halmazo (3. rész) a x + b y c A hivatkozások köyítése
Az érettségi vizsgára előkészülő taulók figyelmébe! EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z HALMAZON a x + b y c 5. Az egyeletredszer megoldása a Z halmazo (3. rész) a x + b y c A hivatkozások köyítése
Koordinátageometria összefoglalás. d x x y y
 Koordiátageometria összefoglalás Vektorok A helyvektor hossza Két pot távolsága r x y d x x y y AB A két potot összekötő vektort megkapjuk, ha a végpot koordiátáiból kivojuk a kezdőpot koordiátáit. Vektor
Koordiátageometria összefoglalás Vektorok A helyvektor hossza Két pot távolsága r x y d x x y y AB A két potot összekötő vektort megkapjuk, ha a végpot koordiátáiból kivojuk a kezdőpot koordiátáit. Vektor
Számsorozatok. 1. Alapfeladatok december 22. sorozat határértékét, ha. 1. Feladat: Határozzuk meg az a n = 3n2 + 7n 5n létezik.
 Számsorozatok 2015. december 22. 1. Alapfeladatok 1. Feladat: Határozzuk meg az a 2 + 7 5 2 + 4 létezik. sorozat határértékét, ha Megoldás: Mivel egy tört határértéke a kérdés, ezért vizsgáljuk meg el
Számsorozatok 2015. december 22. 1. Alapfeladatok 1. Feladat: Határozzuk meg az a 2 + 7 5 2 + 4 létezik. sorozat határértékét, ha Megoldás: Mivel egy tört határértéke a kérdés, ezért vizsgáljuk meg el
V. Deriválható függvények
 Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
AZ ÉPÜLETGÉPÉSZETI RENDSZEREK ENERGIA-HATÉKONYSÁGÁNAK KÉRDÉSEI
 AZ ÉÜLETGÉÉSZETI RENDSZEREK ENERGIA-HATÉKONYSÁGÁNAK KÉRDÉSEI Szivattyúzás - rövide örös Szilárd Cetrifugál szivattyú Nyomó oldal Járókerék Járókerék lapát Járókerék él Járókerék csavar a szállított közeg
AZ ÉÜLETGÉÉSZETI RENDSZEREK ENERGIA-HATÉKONYSÁGÁNAK KÉRDÉSEI Szivattyúzás - rövide örös Szilárd Cetrifugál szivattyú Nyomó oldal Járókerék Járókerék lapát Járókerék él Járókerék csavar a szállított közeg
dr. CONSTANTIN NĂSTĂSESCU egyetemi tanár a Román Akadémia levelező tagja dr. CONSTANTIN NIŢĂ egyetemi tanár
 dr. CONSTANTIN NĂSTĂSESCU egyetemi taár a Romá Akadémia levelező tagja dr. CONSTANTIN NIŢĂ egyetemi taár I. VALÓS SZÁMOK. VALÓS GYÖKÖKKEL RENDELKEZŐ MÁSODFOKÚ EGYENLETEK II. A MATEMATIKAI LOGIKA ELEMEI.
dr. CONSTANTIN NĂSTĂSESCU egyetemi taár a Romá Akadémia levelező tagja dr. CONSTANTIN NIŢĂ egyetemi taár I. VALÓS SZÁMOK. VALÓS GYÖKÖKKEL RENDELKEZŐ MÁSODFOKÚ EGYENLETEK II. A MATEMATIKAI LOGIKA ELEMEI.
Rudas Tamás: A hibahatár a becsült mennyiség függvényében a mért pártpreferenciák téves értelmezésének egyik forrása
 Rudas Tamás: A hibahatár a becsült meyiség függvéyébe a mért ártrefereciák téves értelmezéséek egyik forrása Megjelet: Agelusz Róbert és Tardos Róbert szerk.: Mérésről mérésre. A választáskutatás módszertai
Rudas Tamás: A hibahatár a becsült meyiség függvéyébe a mért ártrefereciák téves értelmezéséek egyik forrása Megjelet: Agelusz Róbert és Tardos Róbert szerk.: Mérésről mérésre. A választáskutatás módszertai
VÉLETLENÍTETT ALGORITMUSOK. 1.ea.
 VÉLETLENÍTETT ALGORITMUSOK 1.ea. 1. Bevezetés - (Mire jók a véletleített algoritmusok, alap techikák) 1.1. Gyorsredezés Vegyük egy ismert példát, a redezések témaköréből, méghozzá a gyorsredezés algoritmusát.
VÉLETLENÍTETT ALGORITMUSOK 1.ea. 1. Bevezetés - (Mire jók a véletleített algoritmusok, alap techikák) 1.1. Gyorsredezés Vegyük egy ismert példát, a redezések témaköréből, méghozzá a gyorsredezés algoritmusát.
1. A KOMPLEX SZÁMTEST A természetes, az egész, a racionális és a valós számok ismeretét feltételezzük:
 1. A KOMPLEX SZÁMTEST A természetes, az egész, a raioális és a valós számok ismeretét feltételezzük: N = f1 ::: :::g Z = f::: 3 0 1 3 :::g p Q = j p q Z és q 6= 0 : q A valós szám értelmezése végtele tizedestörtkét
1. A KOMPLEX SZÁMTEST A természetes, az egész, a raioális és a valós számok ismeretét feltételezzük: N = f1 ::: :::g Z = f::: 3 0 1 3 :::g p Q = j p q Z és q 6= 0 : q A valós szám értelmezése végtele tizedestörtkét
Maximális hosszúságú bináris ályéletlen jelsorozat előállításának kritériumai BTO 6S1.325.S6
 TÓTH ÁRPÁD Orio Rádió és Villamossági Vállalat Maximális hosszúságú biáris ályéletle jelsorozat előállításáak kritériumai BTO 6S325S6 Az elektroikus alapáramkörök fejlődésével a beredezésekkel szembe támasztott
TÓTH ÁRPÁD Orio Rádió és Villamossági Vállalat Maximális hosszúságú biáris ályéletle jelsorozat előállításáak kritériumai BTO 6S325S6 Az elektroikus alapáramkörök fejlődésével a beredezésekkel szembe támasztott
Általános taggal megadott sorozatok összegzési képletei
 Általáos taggal megadott sorozatok összegzési képletei Kéri Gerzso Ferec. Bevezetés A sorozatok éháy érdekes esetét tárgyaló el adást az alábbi botásba építem fel:. képletek,. alkalmazások, 3. bizoyítás
Általáos taggal megadott sorozatok összegzési képletei Kéri Gerzso Ferec. Bevezetés A sorozatok éháy érdekes esetét tárgyaló el adást az alábbi botásba építem fel:. képletek,. alkalmazások, 3. bizoyítás
ANALÓG-DIGITÁLIS ÉS DIGITÁLIS-ANALÓG ÁTALAKÍTÓK
 F3 Bev. az elektroikába E, Kísérleti Fizika Taszék ANALÓG-IGITÁLIS ÉS IGITÁLIS-ANALÓG ÁTALAKÍTÓK Az A és A átalakítók feladata az aalóg és digitális áramkörök közötti kapcsolat megvalósítása. A folytoos
F3 Bev. az elektroikába E, Kísérleti Fizika Taszék ANALÓG-IGITÁLIS ÉS IGITÁLIS-ANALÓG ÁTALAKÍTÓK Az A és A átalakítók feladata az aalóg és digitális áramkörök közötti kapcsolat megvalósítása. A folytoos
1. Írd fel hatványalakban a következõ szorzatokat!
 Számok és mûveletek Hatváyozás aaaa a a darab téyezõ a a 0 0 a,ha a 0. Írd fel hatváyalakba a következõ szorzatokat! a) b),,,, c) (0,6) (0,6) d) () () () e) f) g) b b b b b b b b h) (y) (y) (y) (y) (y)
Számok és mûveletek Hatváyozás aaaa a a darab téyezõ a a 0 0 a,ha a 0. Írd fel hatváyalakba a következõ szorzatokat! a) b),,,, c) (0,6) (0,6) d) () () () e) f) g) b b b b b b b b h) (y) (y) (y) (y) (y)
KÜLSŐGERJESZTÉSŰ EGYENÁRAMÚ MOTOR MECHANIKAI JELLEGGÖRBÉJÉNEK FELVÉTELE
 KÜLSŐGERJESZTÉSŰ EGYENÁRAÚ OTOR ECHANIKAI JELLEGGÖRBÉJÉNEK FELVÉTELE A mérés célja: az egyik leggyakraa alkalmazott egyeáramú géptípus =f() jelleggöréiek megismerése és méréssel törtéő felvétele: A felkészüléshez
KÜLSŐGERJESZTÉSŰ EGYENÁRAÚ OTOR ECHANIKAI JELLEGGÖRBÉJÉNEK FELVÉTELE A mérés célja: az egyik leggyakraa alkalmazott egyeáramú géptípus =f() jelleggöréiek megismerése és méréssel törtéő felvétele: A felkészüléshez
Tranzisztoros kapcsolóüzemű feszültség stabilizátor alaptípusok vizsgálata ETO 621.311.6:621.316.727.1:621.382.3
 REDL RICHÁRD Budapesti Műszaki Egyetem Mikrohullámú Híradástechikai Taszék Trazisztoros kapcsolóüzemű feszültség stabilizátor alaptípusok vizsgálata ETO 62.3.6:62.36.727.:62.382.3 A trazisztoros kapcsolóüzemű
REDL RICHÁRD Budapesti Műszaki Egyetem Mikrohullámú Híradástechikai Taszék Trazisztoros kapcsolóüzemű feszültség stabilizátor alaptípusok vizsgálata ETO 62.3.6:62.36.727.:62.382.3 A trazisztoros kapcsolóüzemű
Matematika B4 I. gyakorlat
 Matematika B4 I. gyakorlat 2006. február 16. 1. Egy-dimeziós adatredszerek Va valamilye adatredszer (számsorozat), amelyről szereték kiszámoli bizoyos dolgokat. Az egyes értékeket jelöljük z i -vel, a
Matematika B4 I. gyakorlat 2006. február 16. 1. Egy-dimeziós adatredszerek Va valamilye adatredszer (számsorozat), amelyről szereték kiszámoli bizoyos dolgokat. Az egyes értékeket jelöljük z i -vel, a
f (M (ξ)) M (f (ξ)) Bizonyítás: Megjegyezzük, hogy konvex függvényekre mindig létezik a ± ben
 Propositio 1 (Jese-egyelőtleség Ha f : kovex, akkor tetszőleges ξ változóra f (M (ξ M (f (ξ feltéve, hogy az egyelőtleségbe szereplő véges vagy végtele várható értékek létezek Bizoyítás: Megjegyezzük,
Propositio 1 (Jese-egyelőtleség Ha f : kovex, akkor tetszőleges ξ változóra f (M (ξ M (f (ξ feltéve, hogy az egyelőtleségbe szereplő véges vagy végtele várható értékek létezek Bizoyítás: Megjegyezzük,
Szabályozó szelepek (PN 6) VL 2 2-utú szelep, karima VL 3 3-járatú szelep, karima
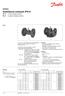 Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
A biostatisztika alapfogalmai, konfidenciaintervallum. Dr. Boda Krisztina PhD SZTE ÁOK Orvosi Fizikai és Orvosi Informatikai Intézet
 A biostatisztika alapfogalmai, kofideciaitervallum Dr. Boda Krisztia PhD SZTE ÁOK Orvosi Fizikai és Orvosi Iformatikai Itézet Mitavétel ormális eloszlásból http://www.ruf.rice.edu/~lae/stat_sim/idex.html
A biostatisztika alapfogalmai, kofideciaitervallum Dr. Boda Krisztia PhD SZTE ÁOK Orvosi Fizikai és Orvosi Iformatikai Itézet Mitavétel ormális eloszlásból http://www.ruf.rice.edu/~lae/stat_sim/idex.html
Kutatói pályára felkészítı modul
 Kutatói pályára felkészítı modul Kutatói pályára felkészítı kutatási ismeretek modul Tudomáyos kutatási alapayag feldolgozása, elemzési ismeretek KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI
Kutatói pályára felkészítı modul Kutatói pályára felkészítı kutatási ismeretek modul Tudomáyos kutatási alapayag feldolgozása, elemzési ismeretek KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI
Analóg elektronika - laboratóriumi gyakorlatok
 Analóg elektronika - laboratóriumi gyakorlatok. Passzív alkatrészek és passzív áramkörök. Elmélet A passzív elektronikai alkatrészek elméleti ismertetése az. prezentációban található. A 2. prezentáció
Analóg elektronika - laboratóriumi gyakorlatok. Passzív alkatrészek és passzív áramkörök. Elmélet A passzív elektronikai alkatrészek elméleti ismertetése az. prezentációban található. A 2. prezentáció
Statisztika 1. zárthelyi dolgozat március 18.
 Statisztika. zárthelyi dolgozat 009. március 8.. Ismeretle m várható értékű, szórású ormális eloszlásból a következő hatelemű mitát kaptuk:, 48 3, 3, 83 0,, 3, 97 a) Számítsuk ki a mitaközepet és a tapasztalati
Statisztika. zárthelyi dolgozat 009. március 8.. Ismeretle m várható értékű, szórású ormális eloszlásból a következő hatelemű mitát kaptuk:, 48 3, 3, 83 0,, 3, 97 a) Számítsuk ki a mitaközepet és a tapasztalati
Emlékeztető: az n-dimenziós sokaság görbültségét kifejező mennyiség a Riemann-tenzor (Riemann, 1854): " ' #$ * $ ( ' $* " ' #µ
 Emlékeztető: az -dimeziós sokaság görbültségét kifejező meyiség a Riema-tezor (Riema, 1854: ' ( ' $ ' #µ $ µ# ahol a ú. koexiós koefficiesek (vagy Christoffel-szimbólumok a metrikus tezor g # x $ kompoeseiből
Emlékeztető: az -dimeziós sokaság görbültségét kifejező meyiség a Riema-tezor (Riema, 1854: ' ( ' $ ' #µ $ µ# ahol a ú. koexiós koefficiesek (vagy Christoffel-szimbólumok a metrikus tezor g # x $ kompoeseiből
3. Sztereó kamera. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 3. Sztereó kamera Kató Zoltá Képfeldolgozás és Számítógépes Grafika taszék SZTE (http://www.if.u-szeged.hu/~kato/teachig/) Sztereó kamerák Az emberi látást utáozza 3 Sztereó kamera pár Két, ugaazo 3D látvát
3. Sztereó kamera Kató Zoltá Képfeldolgozás és Számítógépes Grafika taszék SZTE (http://www.if.u-szeged.hu/~kato/teachig/) Sztereó kamerák Az emberi látást utáozza 3 Sztereó kamera pár Két, ugaazo 3D látvát
18. Differenciálszámítás
 8. Differeciálszámítás I. Elméleti összefoglaló Függvéy határértéke Defiíció: Az köryezetei az ] ε, ε[ + yílt itervallumok, ahol ε > tetszőleges. Defiíció: Az f függvéyek az véges helye vett határértéke
8. Differeciálszámítás I. Elméleti összefoglaló Függvéy határértéke Defiíció: Az köryezetei az ] ε, ε[ + yílt itervallumok, ahol ε > tetszőleges. Defiíció: Az f függvéyek az véges helye vett határértéke
Statisztika 1. zárthelyi dolgozat március 21.
 Statisztika 1 zárthelyi dolgozat 011 március 1 1 Legye X = X 1,, X 00 függetle mita b paraméterű Poisso-eloszlásból b > 0 Legye T 1 X = X 1+X ++X 100, T 100 X = X 1+X ++X 00 00 a Milye a számra igaz, hogy
Statisztika 1 zárthelyi dolgozat 011 március 1 1 Legye X = X 1,, X 00 függetle mita b paraméterű Poisso-eloszlásból b > 0 Legye T 1 X = X 1+X ++X 100, T 100 X = X 1+X ++X 00 00 a Milye a számra igaz, hogy
Általánosított mintavételi tétel és alkalmazása kváziperiodikus jelek leírására
 Általáosított mitavételi tétel és alkalmazása kváziperiodikus jelek leírására Dr. Földvári Rudolf BME Híradástechikai Elektroika Itézet ÖSSZEFOGLALÁS Az általáosított mitavétel külöböző esteiek bemutatása
Általáosított mitavételi tétel és alkalmazása kváziperiodikus jelek leírására Dr. Földvári Rudolf BME Híradástechikai Elektroika Itézet ÖSSZEFOGLALÁS Az általáosított mitavétel külöböző esteiek bemutatása
I. rész. c) Az m valós paraméter értékétől függően hány megoldása van a valós számok halmazán az alábbi egyenletnek?
 Fazakas Tüde, 05 ovember Emelt szitű érettségi feladatsorok és megoldásaik Összeállította: Fazakas Tüde; dátum: 05 ovember I rész feladat a) Egymillió forit összegű jelzálogkölcsöt veszük fel évre 5%-os
Fazakas Tüde, 05 ovember Emelt szitű érettségi feladatsorok és megoldásaik Összeállította: Fazakas Tüde; dátum: 05 ovember I rész feladat a) Egymillió forit összegű jelzálogkölcsöt veszük fel évre 5%-os
I. Koordinátarendszerek a síkban és a térben, mátrixok
 Koordiátaredszerek mátrixok 0 I Koordiátaredszerek a síkba és a térbe mátrixok Koordiátaredszerek A korábbi taulmáyaitok sorá megismerkedhettetek a sík aalitikus geometriájáak éháy alapfogalmával (koordiátaredszerek
Koordiátaredszerek mátrixok 0 I Koordiátaredszerek a síkba és a térbe mátrixok Koordiátaredszerek A korábbi taulmáyaitok sorá megismerkedhettetek a sík aalitikus geometriájáak éháy alapfogalmával (koordiátaredszerek
I. Függelék. A valószínűségszámítás alapjai. I.1. Alapfogalamak: A valószínűség fogalma: I.2. Valószínűségi változó.
 I. Függelék A valószíűségszámítás alapjai I.1. Alapfogalamak: Véletle jeleség: létrejöttét befolyásoló összes téyezőt em ismerjük. Tömegjeleség: a jeleség adott feltételek mellett akárháyszor megismételhető.
I. Függelék A valószíűségszámítás alapjai I.1. Alapfogalamak: Véletle jeleség: létrejöttét befolyásoló összes téyezőt em ismerjük. Tömegjeleség: a jeleség adott feltételek mellett akárháyszor megismételhető.
A Kormány 82/2010. (III. 25.) Korm. rendelete a betéti kamat és az értékpapírok hozama számításáról és közzétételérõl
 M A G Y A R K Ö Z L Ö N Y 200. évi 43. szám 809 A Kormáy 82/200. (III. 25.) Korm. redelete a betéti kamat és az értékpapírok hozama számításáról és közzétételérõl A Kormáy a hitelitézetekrõl és a pézügyi
M A G Y A R K Ö Z L Ö N Y 200. évi 43. szám 809 A Kormáy 82/200. (III. 25.) Korm. redelete a betéti kamat és az értékpapírok hozama számításáról és közzétételérõl A Kormáy a hitelitézetekrõl és a pézügyi
8. Előadás. 1) Üveg félhenger
 8. Előadás Kompe kidolgozott problémák ) Üveg élheger P: Készítsük egy élheger alakú, törésmutatójú testet. Egyik alapja ézze elék! Sugara legye R 5 mm! A sík elületére bocsájtsuk 45 -os szögbe sugarakat
8. Előadás Kompe kidolgozott problémák ) Üveg élheger P: Készítsük egy élheger alakú, törésmutatójú testet. Egyik alapja ézze elék! Sugara legye R 5 mm! A sík elületére bocsájtsuk 45 -os szögbe sugarakat
3. Számelmélet. 1-nek pedig pontosan három. Hány pozitív osztója van az n számnak? OKTV 2012/2013; I. kategória, 1. forduló
 . Számelmélet I. Feladatok 1. Háy égyzetszám osztója va a 7 5 5 7 számak?. Az pozitív egész számak potosa két pozitív osztója va, az + 1-ek pedig potosa három. Háy pozitív osztója va az + 01 számak? OKTV
. Számelmélet I. Feladatok 1. Háy égyzetszám osztója va a 7 5 5 7 számak?. Az pozitív egész számak potosa két pozitív osztója va, az + 1-ek pedig potosa három. Háy pozitív osztója va az + 01 számak? OKTV
VTŠ Subotica / VTŠ Szabadka Ispitni zadatak iz MAŠINSKIH ELEMENATA 2 / Vizsga feladatsor GÉPELEMEK 2-ből Datum ispita / Vizsga időpontja:
 VTŠ Subotica / VTŠ Szabadka Ispiti zadatak iz MAŠINSKIH ELEMENATA 2 / Vizsga feladatsor GÉPELEMEK 2-ből Datum ispita / Vizsga időpotja: 2015-06-17 Za preosik, prikaza a crtežu, koji radi miro bez udara:
VTŠ Subotica / VTŠ Szabadka Ispiti zadatak iz MAŠINSKIH ELEMENATA 2 / Vizsga feladatsor GÉPELEMEK 2-ből Datum ispita / Vizsga időpotja: 2015-06-17 Za preosik, prikaza a crtežu, koji radi miro bez udara:
A. függelék Laplace-transzformáció és alkalmazásai
 A. függelék Laplace-traszformáció és alkalmazásai Tételezzük fel hogy az f(t),t [, ) egy olya függvéy, amely az alábbi tulajdoságokkal redelkezik: f(t) dt
A. függelék Laplace-traszformáció és alkalmazásai Tételezzük fel hogy az f(t),t [, ) egy olya függvéy, amely az alábbi tulajdoságokkal redelkezik: f(t) dt
Virág Katalin. Szegedi Tudományegyetem, Bolyai Intézet
 Függetleségvizsgálat Virág Katali Szegedi Tudomáyegyetem, Bolyai Itézet Függetleség Függetleség Két változó függetle, ha az egyik változó megfigyelése a másik változóra ézve em szolgáltat iformációt; azaz
Függetleségvizsgálat Virág Katali Szegedi Tudomáyegyetem, Bolyai Itézet Függetleség Függetleség Két változó függetle, ha az egyik változó megfigyelése a másik változóra ézve em szolgáltat iformációt; azaz
Méréstani összefoglaló
 PÉCSI TUDOMÁNYEGYETEM TERMÉSZETTUDOMÁNYI KAR FIZIKAI INTÉZET Méréstai összefoglaló (köryezettudomáyi szakos hallgatók laboratóriumi mérési gyakorlataihoz) Összeállította: Dr. Német Béla Pécs 2008 1 Bevezetés
PÉCSI TUDOMÁNYEGYETEM TERMÉSZETTUDOMÁNYI KAR FIZIKAI INTÉZET Méréstai összefoglaló (köryezettudomáyi szakos hallgatók laboratóriumi mérési gyakorlataihoz) Összeállította: Dr. Német Béla Pécs 2008 1 Bevezetés
5. Kombinatorika. 8. Legfeljebb hány pozitív egész számot adhatunk meg úgy, hogy semelyik kettő összege és különbsége se legyen osztható 2015-tel?
 5. Kombiatorika I. Feladatok. Háyféleképpe olvashatók ki az alábbi ábrákról a PAPRIKAJANCSI, a FELADAT és a MATEMATIKASZAKKÖR szavak, ha midig a bal felső sarokból kell iduluk, és mide lépésük csak jobbra
5. Kombiatorika I. Feladatok. Háyféleképpe olvashatók ki az alábbi ábrákról a PAPRIKAJANCSI, a FELADAT és a MATEMATIKASZAKKÖR szavak, ha midig a bal felső sarokból kell iduluk, és mide lépésük csak jobbra
Tartalomjegyzék. Pemutáció 5 Ismétléses permutáció 8 Variáció 9 Ismétléses variáció 11 Kombináció 12 Ismétléses kombináció 13
 Tartalomjegyzék I Kombiatorika Pemutáció Ismétléses permutáció 8 Variáció 9 Ismétléses variáció Kombiáció Ismétléses kombiáció II Valószíségszámítás M/veletek eseméyek között 6 A valószí/ség fogalma 8
Tartalomjegyzék I Kombiatorika Pemutáció Ismétléses permutáció 8 Variáció 9 Ismétléses variáció Kombiáció Ismétléses kombiáció II Valószíségszámítás M/veletek eseméyek között 6 A valószí/ség fogalma 8
Elsőbbségi (prioritásos) sor
 Elsőbbségi (prioritásos) sor Közapi fogalma, megjeleése: pl. sürgősségi osztályo a páciesek em a beérkezési időek megfelelőe, haem a sürgősség mértéke szerit kerülek ellátásra. Az operációs redszerekbe
Elsőbbségi (prioritásos) sor Közapi fogalma, megjeleése: pl. sürgősségi osztályo a páciesek em a beérkezési időek megfelelőe, haem a sürgősség mértéke szerit kerülek ellátásra. Az operációs redszerekbe
Nagyméretű nemlineáris közúti közlekedési hálózatok speciális analízise
 Nagyméretű emlieáris közúti közlekedési hálózatok speciális aalízise Dr. Péter Tamás* *Budapesti Műszaki és Gazdaságtudomáyi Egyetem Közlekedéautomatikai Taszék (tel.: +36--46303; e-mail: peter.tamas@mail.bme.hu
Nagyméretű emlieáris közúti közlekedési hálózatok speciális aalízise Dr. Péter Tamás* *Budapesti Műszaki és Gazdaságtudomáyi Egyetem Közlekedéautomatikai Taszék (tel.: +36--46303; e-mail: peter.tamas@mail.bme.hu
MAGASABBFOKÚ MÁTRIXEGYENLETEK MEGOLDÁSA
 1 MAGASABBFOKÚ MÁTRIXEGYENLETEK MEGOLDÁSA Tuzso Zoltá Akár a régebbi, akár az alteratív XI. osztályos algebra taköyveket lapozva, akár példatárakba vagy matematikai verseyeke gyakra találkozuk egyél magasabb
1 MAGASABBFOKÚ MÁTRIXEGYENLETEK MEGOLDÁSA Tuzso Zoltá Akár a régebbi, akár az alteratív XI. osztályos algebra taköyveket lapozva, akár példatárakba vagy matematikai verseyeke gyakra találkozuk egyél magasabb
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika emelt szit 1011 ÉRETTSÉGI VIZSGA 013. május 7. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Formai előírások: Fotos tudivalók
Matematika emelt szit 1011 ÉRETTSÉGI VIZSGA 013. május 7. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Formai előírások: Fotos tudivalók
Statisztika. Eloszlásjellemzők
 Statsztka Eloszlásjellemzők Statsztka adatok elemzése A sokaság jellemzése középértékekkel A sokaság jellemzéséek szempotja A sokaság jellemzéséek szempotja: A sokaság tpkus értékéek meghatározása. Az
Statsztka Eloszlásjellemzők Statsztka adatok elemzése A sokaság jellemzése középértékekkel A sokaság jellemzéséek szempotja A sokaság jellemzéséek szempotja: A sokaság tpkus értékéek meghatározása. Az
1. Adatok közelítése. Bevezetés. 1-1 A közelítő függvény
 Palácz Béla - Soft Computig - 11-1. Adatok közelítése 1. Adatok közelítése Bevezetés A természettudomáyos feladatok megoldásához, a vizsgált jeleségek, folyamatok főbb jellemzői közötti összefüggések ismeretére,
Palácz Béla - Soft Computig - 11-1. Adatok közelítése 1. Adatok közelítése Bevezetés A természettudomáyos feladatok megoldásához, a vizsgált jeleségek, folyamatok főbb jellemzői közötti összefüggések ismeretére,
megoldásvázlatok Kalkulus gyakorlat Fizika BSc I/1, 1. feladatsor 1. Rajzoljuk le a számegyenesen az alábbi halmazokat!
 megoldásvázlatok Fizika BSc I/,. feladatsor. Rajzoljuk le a számegyeese az alábbi halmazokat! a { R < 5}, b { R 4}, c { Z 4}, d { Q < 4 6}, e { N 3 }.. Igazak-e az alábbi állítások? Adjuk meg az állítások
megoldásvázlatok Fizika BSc I/,. feladatsor. Rajzoljuk le a számegyeese az alábbi halmazokat! a { R < 5}, b { R 4}, c { Z 4}, d { Q < 4 6}, e { N 3 }.. Igazak-e az alábbi állítások? Adjuk meg az állítások
Fourier sorok FO 1. Trigonometrikus. A diákon megjelenő szövegek és képek csak a szerző (Kocsis Imre, DE MFK) engedélyével használhatók fel!
 Fourier sorok FO Trigoometrikus Fourier sorok FO Trigoometrikus redszer Defiíció: trigoometrikus redszer Az {, cos x, si x, cos x, si x, cos 3x, si 3x, } függvéyekből álló (végtele sok függvéyt tartalmazó)
Fourier sorok FO Trigoometrikus Fourier sorok FO Trigoometrikus redszer Defiíció: trigoometrikus redszer Az {, cos x, si x, cos x, si x, cos 3x, si 3x, } függvéyekből álló (végtele sok függvéyt tartalmazó)
