Lineáris programozás. Ax b
|
|
|
- Krisztina Borbélyné
- 6 évvel ezelőtt
- Látták:
Átírás
1 Feladatok és kiegészítések az elmélethez Lineáris programozás Standard modell (maximumprobléma) x 0 Ax b (1) c x = z max ahol x = (x 1,..., x n ) R n 1 a keresett n dimenziós oszlopmátrix/vektor 0 = (0,..., 0) R n 1, az n dimenziós oszlop zérusvektor, az x 0 egyenlőtlenség koordinátánként (elemenként) értendő, A = (a ij ) R k n egy k n típusú (adott) mátrix, b = (b 1,..., b k ) R k 1 adott k dimenziós oszlopmátrix/vektor c = (c 1,..., c n ) R n 1 egy n dimenziós adott sorvektor, c = (c 1,..., c n ) R 1 n. Az A 1 x b 1 feltételt ekvivalens módon A 1 x b 1 -ként írhatjuk át. Az A 2 x = b 2 egyenlőség típusú feltételt ekvivalens módon A 2 x b 2 és A 2 x b 2 illetve A 2 x b 2 és A 2 x b 2 feltételként írhatjuk át. A c x = z min minimumfeltételt c x = z max-ként írhatjuk át maximumfeltétellé. Az (1) standard modell kanonikus alakján a x 0, w 0 Ax + w = b (2) c x = z max alakot értjük, ahol w = (w 1,..., w k ) R k 1 egy k dimenziós oszlopmátrix/vektor. 1
2 2 Az (1) standard feladatot x 0 Ax b (3) c x max primál feladatnak nevezzük, az ennek megfelelő duál feladat u 0 vagy u 0 u A c u b min vagy A u c vagy b u min (4) ahol u = (u 1,..., u k ) R k 1 a keresett k dimenziós oszlopmátrix/vektor,0 = (0,..., 0) R k 1 a megfelelő zérusvektor. Dualitási eredmények: Ha x = (x 1,..., x n ) R n 1 a (3) primál feladat lehetséges megoldása és u = (u 1,..., u k ) R k 1 a (4) duál feladat lehetséges megoldása akkor b 1 u b k u k c 1 x c n x n azaz a duál feladat célfüggvénye legalább akkora mint a primál feladaté. Ha x = (x 1,..., x n) R n 1 az (3) primál feladat lehetséges megoldása és u = (u 1,..., u k ) R k 1 a (4) duál feladat lehetséges megoldása melyekre b 1 u b k u k = c 1 x c n x n akkor x optimális megoldása a primál feladatnak, u optimális megoldása a duál feladatnak.
3 Dualitási tétel. Tegyük fel, hogy az (3) primál feladatnak van (véges) optimális megoldása. Ekkor a (4) duál feladatnak szintén van (véges) optimális megoldása, és a két célfüggvény optimumértékei megegyeznek. Ha primál feladatnak nincs korlátos optimuma, akkor a duál feladatnak nincs lehetséges megoldása. 3
4 4 Feladatok (1) Oldja meg (grafikusan) az alábbi kétváltozós lineáris programozási feladatokat: (a) x 1, x 2 0 x 1 + 2x 2 5 3x 1 + 3x 2 9 x 1 + x 2 6 (b) x 1, x 2 0 x 1 + x 2 3 x 1 5 x 1 8 2x 2 z = 3x 1 max z = x 1 + 4x 2 max (c) x 1, x 2 0 x 1 + 2x 2 9 x 1 + x 2 = 3 x 1 + x 2 6 (d) x 1, x 2 0 x 1 + x 2 7 x 1 3 x 1 + 3x 2 9 z = 4x x 2 max z = 2x 1 + x 2 min (2) Oldja meg a WinQSB szoftverrel az alábbi lineáris programozási feladatokat: (a) x 1, x 2, x 3 0 x 1 + 2x 2 x x 1 x 2 + 2x 3 60 x 2 + x 3 = 30 (b) x 1, x 2, x 3 0 x 1 + 2x x 1 + 4x 2 = 55 2x 1 x 3 = 0 z = 3x 1 + 2x 2 + 5x 3 min z = x 2 + 4x 3 min
5 5 (c) 0 x 1 10, 0 x x 3, 2 x 4 8 2x 1 x 2 + x 4 10 x 1 + x 2 2x 3 + x 4 0 (d) 0 x 1, x 2, x 3, x 4 10 x 1 x 2 x 3 + x x 1 + x 3 + 2x x 3 + x 4 15 z = 2x 1 + 2x 2 x 3 + x 4 max z = 4x 2 + 5x 3 min (3) (Termelési feladat) (ld. Varga J.: Gyakorlati programozás, Tankönyvkiadó, Bp. 1985, ) 1. Döntés előkészítése m 3 tölgyrönköt kell fűrészáruvá feldolgozni 4 üzemben, melyek közel azonos technikai felszereltségűek. Mindegyikben 6 féle terméket tudnak előállítani: I, II, III-adosztályú szelvényárut, dongát, parkettalécet, bányaszéldeszkát és közben fürészpor és darabos hulladék keletkezik. 2. Technológiák számszerűsítése. E termékek előállítására öt technológia van. E technológiák kihozatali mutatói próbavágások alapján az alábbiak, 1m 3 rönkre vonatkozóan, %-ban Technológiák I II III IV V I. o. szelv.áru II. o. szelv.áru III. o. szelv.áru Donga Parkettaléc Bányaszéldeszka Darabos hulladék Fürészpor
6 6 3. Technikai korlátok. Az üzemek kapacitása messzemeghaladja a feldolgozandó mennyiséget, csupán a parkettagyártó gépsor kapacitása korlátozott évi 10000m 3 -re. 4. Keresleti korlátok. Az egyes termékekből az évi kereslet/terv I.o legalább 1000m 3, II. o. legalább 5000m 3, donga legfeljebb 20000m 3, parkettaléc legalább 5000m 3 -t kell előállítani, és a hulladék (fürészpor és darabos hulladék) nem haladhatja meg a 45%-ot. 5. A célt befolyásoló adatok, a késztermékek árai: Késztermék Ft/m3 I. o. szelv.áru 3000 II. o. szelv.áru 2400 III. o. szelv.áru 1400 Donga 3500 Parkettaléc 3100 Bányaszéldeszka 1000 Darabos hulladék 500 Fürészpor 100 Így 1m 3 rönk feldolgozásával az árbevétel: Techn. Árbevételek (Ft) Össz.(Ft) I. 0, , , , , II. 0, , , , III. 0, , , IV. 0, , , , , , V. 0, , , , , , Matematikai modell.
7 Legyen x 1, x 2, x 3, x 4, x 5 az egyes technológiák szerint felvágandó rönk mennyisége m 3 -ben, akkor 7 x 1, x 2, x 3, x 4, x 5 0 nemnegativitás 0, 1x 1 + 0, 1x 4 + 0, 05x I.oszt. terv 0, 3x 1 + 0, 3x 4 + 0, 25x II.oszt. terv 0, 4x 2 + 0, 15x donga tervkorl. 0, 1x 2 + 0, 5x 3 + 0, 15x 4 + 0, 12x park.léc terv 0, 1x 2 + 0, 5x 3 + 0, 15x 4 + 0, 12x park.léc kapac. 0, 4x 1 + 0, 5x 2 + 0, 5x 3 + 0, 41x 4 + 0, 43x hulladék x 1 + x 2 + x 3 + x 4 + x 5 = teljes készlet Az árbevétel maximalizálása a cél, azaz a célfüggvény: 1440x x x x x 5 = z max Megoldás: Bevitel a WinQSB programba:(fauzem.lpp)
8 8 A megoldás a program segítségével:
9 9 Combined Report for fauzem5 13:40:22 Sunday February Decision Solution Unit Cost or Variable Value Profit c(j) Total Reduced Basis Allowable Allowable Contribution Cost Status Min. c(j) Max. c(j) 1 X1 12, , ,454, basic -M 1, X2 27, , ,363, basic 1, , X3 0 1, at bound -M 2, X4 0 1, at bound -M 1, X5 60, , ,212, basic 1, , Objective Function (Max.) = 179,030,300. Left Hand Right Hand Slack Shadow Allowable Allowable Constraint Side Direction Side or Price Min. RHS Max. Surplus RHS 1 C1 4, >= 1,000. 3, M 4, C2 18, >= 5, , M 18, C3 20, <= 20, , , C4 10, >= 5,000. 5, M 10, C5 10, <= 10, , , , C6 44, <= 45, , M 7 C7 100, = 100, , , ,136.4
10 10 A megoldás táblázatában a redukált költség nulla értékű célváltozóknál szerepel, és azt mutatja, hogy hogyan változik a célfüggvény értéke, ha az illető célváltozóra pozitív értéket követelünk meg. Például, x 3 = 0-nál a redukált költség 823, 03, ami azt jelenti, hogy ha x 3 0 helyett x 3 a 3 (> 0)-t követeljük meg, akkor az célfüggvény értéke (közelítőleg) 823, 03a 3 -mal változik. Egy feltételnél szereplő árnyékár azt mutatja meg, hogy a feltétel jobboldalán álló konstans változása hogyan hat a célfüggvény értékére. Például, a C 3 feltételnél az árnyékár 648, 48, ami azt jelenti, hogy ha C 3 jobboldalát b 3 -mal megnöveljük, (esetünkben b 3 - ra) akkor az célfüggvény értéke (közelítőleg) 648, 48b 3 -mal nő. Az utolsó két oszlop 1-5 sorai azt mutatják, hogy a célfüggvényben az illető célváltozó együtthatója milyen határok között változhat ahhoz, hogy még létezzen optimális megoldás. Az utolsó két oszlop utolsó 7 sora azt mutatja, hogy a korlátozó feltétel jobboldala milyen határok között változhat, ahhoz, hogy még létezzen optimális megoldás. A megoldás értelmezése: x 1 = első technológiával felvágandó x 2 = második technológiával felvágandó x 3 = 0 harmadik technológiával felvágandó x 4 = 0 negyedik technológiával felvágandó x 5 = ötödik technológiával felvágandó Árbevétel Ft Gyártott termékek: I.oszt. 0, , , = 4242 = 1000+többlet, II.oszt. 0, , , = 18787, 8 = többlet, III.oszt. 0, = 2424, 2,
11 Donga 0, , = 20000, Parkettaléc 0, , , , = = többlet, Bányaszéldeszka 0, 04 0 = 0, Hulladék 0, , , , , = 44545, 48 = hiány. Túlteljesítések: I.oszt II. oszt Dongából a megengedett t termeljük Parkettalécből 5000-rel túlteljesítjük a tervet, és a teljes kapacitást kihasználjuk. A hulladék 45% alatt van. 1m 3 rönköt 1790,30 Ft áron értéksítjük. 11 A modell módosításai: 1. Ha a II. oszt. árúból 13788m 3 eladhatatlan, csak adható el, akkor módosítani kell a problémát, egy új feltétel közbeiktatásával: 0, 3x 1 + 0, 3x 4 + 0, 25x Az új probléma lehet megoldhatatlan, kaphatunk új optimumot. 2. Ha pl. bányaszéldeszkából 1000m 3 -re van igény, akkor az új feltétel 0, 04x Ha a hulladékra nem teszünk kikötést akkor eggyel kevesebb feltételünk lesz, az optimális megoldás magasabb célértéket eredményezhet. 4. Az is előfordulhat, hogy az egyes fűrészüzemek technikai színvonala különböző, ekkor szét kell osztanunk a gyártandó
12 12 termékeket az üzemek között, feltéve, hogy az összkapacitásuk meghaladja a feldolgozandó nyersanyagot. (4) (Szállítási probléma) Árut kell elszállítani három telephelyről (Kecskemét, Pécs, Szombathely) öt területi raktárba, melyek Budapesten, Kaposváron, Pápán, Sopronban és Veszprémben vannak. Az áruk bármely telephelyről bármelyik raktárba elszállíthatók, de természetesen a távolabbi raktárba való szállítás többe kerül. A feladat annak meghatározása, hogy mennyi árut kell elszállítani az egyes telephelyekről az egyes raktárakba úgy, hogy a szállítási költség minimális legyen, a szükségleteket kielégítsük, és ne akarjunk sehonnan se az ott lévő készletnél elvinni. A készleteket és igényeket (mázsában) a szállítási költségeket (ezer Ft/q-ban) az alábbi táblázat adja. Készlet Bud. Kap. Pápa Sopr. Veszp. Kecsk Pécs Szomb Igény Ha a szállított mennyiségek Kecskemétről az egyes raktárakba, a felsorolt sorrendben x 1,..., x 5 Pécsről x 6,..., x 10 Szombathelyről x 11,..., x 15, akkor
13 13 x 1 + x 2 + x 3 + x 4 + x Kecskemét készlete x 6 + x 7 + x 8 + x 9 + x Pécs készlete x 11 + x 12 + x 13 + x 14 + x Szombathely készlete x 1 + x 6 + x 11 = 220 Budapest igénye x 2 + x 7 + x 12 = 200 Kaposvár igénye x 3 + x 8 + x 13 = 80 Pápa igénye x 4 + x 9 + x 14 = 180 Sopron igénye x 5 + x 10 + x 15 = 160 Veszprém igénye z = (4x 1 + 6x 2 + 8x x 4 + 5x 5 )+ (6x 6 + 4x 7 + 5x 8 + 6x 9 + 3x 10 ) +(9x x x x x 15 ) min ahol a minimalizálandó háromszor öttagú összeg a három telephelyről való szállítás összköltsége. A készletek összege 850q, az összigény 840q. Megjegyzések: 1. A feladat természetéhez jobban igazodna, ha pl a Kecskemétről az egyes raktárakba szállított mennyiségeket x 11, x 12, x 13, x 14, x 15 -tel jelölnénk, hasonló volna a x ik jelentése. Ekkor viszont a WinQSB-be LP problémaként való bevitel volna körülményes. 2. A WinQSB szoftver Network Modeling moduljában a szállítási probléma (Transportation Problem) adatai azonnal beírhatók, és a probléma megoldható anélkül, hogy átfogalmaznánk lin. prog. problémára. (5) Oldja meg az alábbi szállítási problémát! Árut kell elszállítani három telephelyről (T 1, T 2, T 3 ) négy területi raktárba (R 1, R 2, R 3, R 4 ). Az áruk bármely telephelyről bármelyik raktárba elszállíthatók, de természetesen a távolabbi raktárba való szállítás többe kerül. A feladat annak meghatározása, hogy mennyi árut kell elszállítani az egyes telephelyekről az egyes raktárakba úgy, hogy a szállítási költség minimális legyen, a szükségleteket kielégítsük, és ne akarjunk sehonnan se
14 14 az ott lévő készletnél elvinni. A készleteket és igényeket (mázsában) a szállítási költségeket (ezer Ft/q-ban) az alábbi táblázat adja. Készlet R 1 R 2 R 3 R 4 T T T Igény (6) (Optimális munkarend) Dolgozók munkarendjének kialakítása egy vidámparkban. Minden dolgozó öt egymás utáni napon dolgozik, majd két pihenőnap következik. A dolgozók napi bére azonos (a hétvégi napokra is!). Ismert, hogy a hét egyes napjain hány dolgozónak kell jelen lennie. Cél: meghatározni egy olyan munkarendet, amely esetén a hetente kifizetendő összes bér a lehető legkisebb. A jelenlegi állapotot és a napi létszámigényt az alábbi táblázat mutatja: M.rend Szabadnapok Dolgozók H K Sze Cs P Szo V I Hétfő, kedd II Kedd, szerda III Szerda, csütörtök IV Csütörtök, péntek V Péntek, szombat VI Szombat, vasárnap VII Vasárnap, hétfő Beosztva összesen: Létszámigény: A dolgozók száma 32, egy dolgozó napi bére 800 Ft, napi összbér = Ft/munkanap, heti bér (öt munkanapra számítva) = Ft. A feladat az, hogy a dolgozók létszámát és munkarendjét úgy alakítsuk ki, hogy mindig legyen elég ember, de a költség a lehető legkisebb legyen.
15 Megoldás: Jelölje rendre x 1, x 2, x 3, x 4, x 5, x 6, x 7 az I, II, III, IV,V,VI,VII munkarend szerint dolgozók számát. Ekkor létszámigénynek megfelelő feltételek, és a célfüggvény: 15 x 2 + x 3 + x 4 + x 5 + x 6 17 hétfő x 3 + x 4 + x 5 + x 6 + x 7 13 kedd x 1 + x 4 + x 5 + x 6 + x 7 14 szerda x 1 + x 2 + x 5 + x 6 + x 7 15 csütörtök x 1 + x 2 + x 3 + x 6 + x 7 18 péntek x 1 + x 2 + x 3 + x 4 + x 7 24 szombat x 1 + x 2 + x 3 + x 4 + x 5 22 vasárnap 800(x 1 + x 2 + x 3 + x 4 + x 5 + x 6 + x 7 ) = z min célfüggvény Ez egy egészértékű lineáris programozási feladat, melyet a WinQSB szoftverrel oldunk meg. Bevitel a WinQSB programba:(munkar.lpp) A megoldás a program segítségével:
16 16 Combined Report for munkarend 10:52:47 Saturday February Decision Solution Unit Cost Total Reduced Basis or Variable Value Profit c(j) Contribution Cost Status 1 X at bound 2 X at bound 3 X basic 4 X basic 5 X basic 6 X at bound 7 X basic Objective Function (Min.) = Left Hand Right Hand Slack Shadow Constraint Side Direction Side or Surplus Price 1 C1 18 >= C2 13 >= C3 14 >= C4 15 >= C5 18 >= C6 24 >= C7 23 >=
17 A megoldás értelmezése: az I, II, stb. beosztás szerint dolgozók optimális száma rendre 5, 7, 4, 6, 1, 0, 2 összesen 25 dolgozóra van szükség a működtetéshez, a többieket más munkakörbe lehet helyezni. Az optimális napi bérköltség Ft. Hogyan módosul a feladat, ha a szombati munkabér 1200 Ft-ra, a vasárnapi 1600Ft-ra nő, és mi ekkor a megoldás? (7) (Vállalati szabad pénzeszközök optimális befektetése) Ha pénzügyi vagy vezető beosztásban dolgozunk, akkor egyik legfontosabb feladatunk az, hogy a készpénzt és a rövid lejáratú befektetéseket úgy kezeljük, hogy maximalizáljuk a kamatbevételeket, miközben mindig elegendő pénz áll rendelkezésre a folyó kiadásokra. Meg kell találnunk a nagyobb kamatot kínáló hosszú távú befektetések és a rugalmasabb kezelést lehetővé tevő, de kisebb kamathozamú rövid távú befektetések között a megfelelő középutat. 1. A probléma megfogalmazása. Egy vállalatnak 40 millió készpénze felöl kell döntenünk. Az elmúlt félévben ez az összeg 1, 3 és 6 hónapos futamidejű letéti jegyekbe volt befektetve, ezek vásárlási feltételeit és kamathozamait az alábbi táblázat mutatja: Hozam Futamidő A letéti jegy vásárolható: 1 havi letéti jegy: 1.0% 1 1., 2., 3., 4., 5., 6. hónapban 3 havi letéti jegy: 4.0% 3 1. és 4. hónapban 6 havi letéti jegy: 9.0% 6 1. hónapban A jelenlegi befektetések 6 hónap folyamán, és a készpénzigények: 17
18 18 Hónapok: hó eleje Kezdő kp.: Lejárati kifiz.: Kamat: havi l.jegy: havi l.jegy: havi l.jegy: 1000 Készpénzigény: Záró készpénz: A készpénzigény rovaton lévő összeget minden hónapban elköltjük, a + előjellel szereplő összeg bevételt jelent. Minden adat ezer Ftos egységekben szerepel. Jelenleg hat hónap alatt a kamatbevétel 770 eft, a kifizetések és bevételek egyenlege: =-16000Ft Hogyan módosítanánk a befektetéseket (mikor mennyi 1, 3 és 6 hónapos futamidejű letéti jegyet veszünk) ahhoz, hogy a kamatnyereség a lehető legnagyobb legyen, de időközben a vállalat készpénzigényét (ill. a biztonsági tartalékot) mindig biztosítani tudjuk. 2. Matematikai modell. Összesen 9 összegről kell dönteni: az egy hónapos futamidejű letéti jegyekbe fektetendő összegről az első hat hónapban,x 1, x 2, x 3, x 4, x 5, x 6 a három hónapos futamidejű letéti jegyekbe fektetendő összegről az első és a negyedik hónapban,x 7, x 8 továbbá az első hónapban hat hónapos futamidejű letéti jegyekbe fektetendő összegről x 9.
19 19 Hónapok: hó eleje Kezdő kp.: t z 1 z 2 z 3 z 4 z 5 z 6 1 havi l.jegy: x 1 x 2 x 3 x 4 x 5 x 6 3 havi l.jegy: x 7 x 8 6 havi l.jegy: x 9 Lejár.+kamat: T 1 T 2 T 3 T 4 T 5 T 6 T 7 Kp.igény: k 1 k 2 k 3 k 4 k 5 k 6 Záró kp.: z 1 z 2 z 3 z 4 z 5 z 6 z 7 A modell matematikai leírása: t = 40000, kezdőösszeg x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8, x 9 0 nemnegativitás z 1 = t x 1 x 7 x 9 + k 1 1. hóvégi záróösszeg z 2 = z 1 x 2 + 1, 01x 1 + k 2 2. hóvégi záróösszeg z 3 = z 2 x 3 + 1, 01x 2 + k 3 3. hóvégi záróösszeg z 4 = z 3 x 4 x 8 + 1, 01x 3 + 1, 04x 7 + k 4 4. hóvégi záróösszeg z 5 = z 4 x 5 + 1, 01x 4 + k 5 5. hóvégi záróösszeg z 6 = z 5 x 6 + 1, 01x 5 + k 6 6. hóvégi záróösszeg z 7 = z 6 + 1, 01x 6 + 1, 04x 8 + 1, 09x 9 7. hó elején készpénz z i 0 (i = 1, 2, 3, 4, 5, 6) havi záróösszeg nemnegatív z = 0, 01(x 1 + x 2 + x 3 + x 4 + x 5 + x 6 ) + 0, 04 (x 7 + x 8 ) + 0, 09x 9 max Az első; első és második; első, második és harmadik; stb. egyenletek összeadásával kapott új egyenletek:
20 20 t = x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8, x 9 0 z 1 = t x 1 x 7 x 9 + k 1 z 2 = t + 0, 01x 1 x 2 x 7 x 9 + k 1 + k 2 z 3 = t + 0, 01(x 1 + x 2 ) x 3 x 7 x 9 + k 1 + k 2 + k 3 z 4 = t + 0, 01(x 1 + x 2 + x 3 ) + 0, 04x 7 x 4 x 9 +k 1 + k 2 + k 3 + k 4 z 5 = t + 0, 01(x 1 + x 2 + x 3 + x 4 ) + 0, 04x 7 x 9 x 8 x 5 +k 1 + k 2 + k 3 + k 4 + k 5 z 6 = t + 0, 01(x 1 + x 2 + x 3 + x 4 + x 5 ) + 0, 04x 7 x 6 x 9 x 8 +k 1 + k 2 + k 3 + k 4 + k 5 + k 6 z 7 = t + 0, 01(x 1 + x 2 + x 3 + x 4 + x 5 + x 6 ) + 0, 04(x 7 + x 8 ) + 0, 09x 9 +k 1 + k 2 + k 3 + k 4 + k 5 + k 6 z i 0 (i = 1, 2, 3, 4, 5, 6) z = 0, 01(x 1 + x 2 + x 3 + x 4 + x 5 + x 6 ) + 0, 04(x 7 + x 8 ) + 0, 09x 9 max 3. A lineáris programozási probléma: a t = 40000, k 1 = 7500, k 2 = 1000, k 3 = 2000, k 4 = 8000, k 5 = 5000, k 6 = 1500 értékeket beírva, az egyenlőtlenségeket átrendezve adódik: x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8, x 9 0 x 1 + x 7 + x , 01x 1 + x 2 + x 7 + x , 01(x 1 + x 2 ) + x 3 + x 7 + x , 01(x 1 + x 2 + x 3 ) 0, 04x 7 + x 4 + x 8 + x , 01(x 1 + x 2 + x 3 + x 4 ) 0, 04x 7 + x 5 + x 8 + x , 01(x 1 + x 2 + x 3 + x 4 + x 5 ) 0, 04x 7 + x 6 + x 8 + x , 01(x 1 + x 2 + x 3 + x 4 + x 5 + x 6 ) + 0, 04(x 7 + x 8 ) + 0, 09x 9 = z max
21 A következő alakba átírt feltételrendszer jobban mutatja e feltételek származását 21 x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8, x 9 0 x 1 + x 7 + x x 2 + x 7 + x , 01x 1 x 3 + x 7 + x , 01(x 1 + x 2 ) x 4 + x 8 + x , 01(x 1 + x 2 + x 3 ) + 0, 04x 7 x 5 + x 8 + x , 01(x 1 + x 2 + x 3 + x 4 ) + 0, 04x 7 x 6 + x 8 + x , 01(x 1 + x 2 + x 3 + x 4 + x 5 ) + 0, 04x 7 0, 01(x 1 + x 2 +x 3 + x 4 + x 5 + x 6 ) + 0, 04(x 7 + x 8 ) + 0, 09x 9 = z max 4. Megoldás a Win QSB szoftverrel (BEFEKTETES.LPP) Bevitel a WinQSB programba:(befektetes.lpp)
22 22
23 A megoldás a program segítségével: 23 Combined Report for befektet 18:48:06 Sunday March Decision Variable Solution Value Unit Cost or Profit c(j) Total Reduced Basis Allowable Allowable Contributi on Cost Status Min. c(j) Max. c(j) 1 X at bound -M X2 1, basic X3 3, basic X4 4, basic X at bound -M X6 1, basic X7 9, basic X at bound -M X9 22, , basic M Objectiv e Constrai nt Function (Max.) = 2, Left Hand Right Hand Slack Shadow Allowable Allowable Side Direction Side or Price Min. RHS Max. RHS Surplus 1 C1 32, <= 32, , , C2 33, <= 33, , ,014, C3 35, <= 35, , ,026, C4 27, <= 27, , ,028, C5 22, <= 22, , , C6 24, <= 24, , M A kamatjövedelem 2553 eft-ra nőtt, a 7. hónap elején =26553 eft a vállalat készpénze. Ez annak köszönhető, hogy
24 24 az első hónapban eft-ért hathavi befektetési jegyet, 9579 eftért háromhavi befektetési jegyet vásárolunk, és minden hónapban a lehetséges teljes összeget befektettük. Hogyan módosul a feladat, és a megoldás, ha a 7. hónap elején (a kamatjövedelmek realizálása után) a vállalatnak eft készpénzre van szüksége? (8) Oldja meg a következő döntési problémát az (a) maximin, (b) maximax módszerrel, és ha több megoldás adódik akkor azt a szempontok X 3, X 4, X 1, X 2, X 5, X 6 fontossági sorrendjével tegye egyértelművé. Az alternatívák (ajánlatok A 1, A 2, A 3, A 4, A 5 ) és szempontok X 1, X 2, X 3, X 4, X 5, X 6 táblázata a következő: X 3 -nál a legkisebb érték az ideális, az X 1, X 2, X 4 sorokban a maximális érték az ideális. Az ajánlatok táblázata: A 1 A 2 A 3 A 4 A 5 X X X X 4 7, 5 9, 5 5, 5 5, 0 5, 0 X 5 á a nj j á X 6 j á j á nj ahol na=nagyon alacsony =1 pont, a=alacsony =3 pont, á=átlagos =5 pont, j=jó =7 pont, nj=nagyon jó =9 pont veendő az utolsó két szempontban lévő adatok számszerűsítéséhez.
a = 2 + [ i] b = ahol 1 i 162 a hallgató sorszáma a csatolt névsorban, [x] az x szám
![a = 2 + [ i] b = ahol 1 i 162 a hallgató sorszáma a csatolt névsorban, [x] az x szám a = 2 + [ i] b = ahol 1 i 162 a hallgató sorszáma a csatolt névsorban, [x] az x szám](/thumbs/48/24702979.jpg) Döntéselmélet házi feladat, 2011-12 tanév II. félév A házi feladat beadása az aláírás feltétele. A házi feladatra adott minősítés az (anyag első felére vonatkozó) jegyben 40% súllyal szerepel, ennek megfelelően
Döntéselmélet házi feladat, 2011-12 tanév II. félév A házi feladat beadása az aláírás feltétele. A házi feladatra adott minősítés az (anyag első felére vonatkozó) jegyben 40% súllyal szerepel, ennek megfelelően
A DÖNTÉSELMÉLET ELEMEI
 A DÖNTÉSELMÉLET ELEMEI Irodalom: Temesi J., A döntéselmélet alapjai, Aula, 2002, Budapest Lawrence, J.A., Pasternack, B.A., Applied management science, John Wiley & Sons Inc. 2002 Stevenson, W. J., Operation
A DÖNTÉSELMÉLET ELEMEI Irodalom: Temesi J., A döntéselmélet alapjai, Aula, 2002, Budapest Lawrence, J.A., Pasternack, B.A., Applied management science, John Wiley & Sons Inc. 2002 Stevenson, W. J., Operation
Levelező tagozat. a = 3 + [ i]
![Levelező tagozat. a = 3 + [ i] Levelező tagozat. a = 3 + [ i]](/thumbs/92/108603805.jpg) Döntéselmélet házi feladat, 2012-13 tanév II. félév Levelező tagozat A házi feladat beadása az aláírás feltétele. A házi feladatra adott minősítés az (anyag első felére vonatkozó) jegyben 50% súllyal szerepel,
Döntéselmélet házi feladat, 2012-13 tanév II. félév Levelező tagozat A házi feladat beadása az aláírás feltétele. A házi feladatra adott minősítés az (anyag első felére vonatkozó) jegyben 50% súllyal szerepel,
0. BEVEZETÉS. Decision theory: web Google keresés= 27 millió találat Döntéselmélet: web Google keresés= 12 ezer találat. orvosi,
 0. BEVEZETÉS Decision theory: web Google keresés= 27 millió találat Döntéselmélet: web Google keresés= 12 ezer találat Döntéselmélet néhány területe: orvosi, ogi, bírói, közgazdasági, műszaki, egyéb. Módszerek
0. BEVEZETÉS Decision theory: web Google keresés= 27 millió találat Döntéselmélet: web Google keresés= 12 ezer találat Döntéselmélet néhány területe: orvosi, ogi, bírói, közgazdasági, műszaki, egyéb. Módszerek
A lineáris programozás alapfeladata Standard alak Az LP feladat megoldása Az LP megoldása: a szimplex algoritmus 2018/
 Operációkutatás I. 2018/2019-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Operációkutatás I. 2018/2019-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
A lineáris programozás alapfeladata Standard alak Az LP feladat megoldása Az LP megoldása: a szimplex algoritmus 2017/
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Optimumkeresés számítógépen
 C Optimumkeresés számítógépen Az optimumok megtalálása mind a gazdasági életben, mind az élet sok más területén nagy jelentőségű. A matematikában számos módszert dolgoztak ki erre a célra, például a függvények
C Optimumkeresés számítógépen Az optimumok megtalálása mind a gazdasági életben, mind az élet sok más területén nagy jelentőségű. A matematikában számos módszert dolgoztak ki erre a célra, például a függvények
KIEGÉSZÍTŽ FELADATOK. Készlet Bud. Kap. Pápa Sopr. Veszp. Kecsk. 310 4 6 8 10 5 Pécs 260 6 4 5 6 3 Szomb. 280 9 5 4 3 5 Igény 220 200 80 180 160
 KIEGÉSZÍTŽ FELADATOK (Szállítási probléma) Árut kell elszállítani három telephelyr l (Kecskemét, Pécs, Szombathely) öt területi raktárba, melyek Budapesten, Kaposváron, Pápán, Sopronban és Veszprémben
KIEGÉSZÍTŽ FELADATOK (Szállítási probléma) Árut kell elszállítani három telephelyr l (Kecskemét, Pécs, Szombathely) öt területi raktárba, melyek Budapesten, Kaposváron, Pápán, Sopronban és Veszprémben
Dualitás Dualitási tételek Általános LP feladat Komplementáris lazaság 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 7. Előadás Árazási interpretáció Tekintsük újra az erőforrás allokációs problémát (vonat
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 7. Előadás Árazási interpretáció Tekintsük újra az erőforrás allokációs problémát (vonat
Lineáris programozás. A mese
 Lineáris programozás A mese Célok Geometriai szemlélet (nem lesz matek ) Gakorlati kérdések Már megint a szendvics Kétfajta szendvicset szeretnénk készíteni, sonkásat és szalámisat. Lehetőleg minél többet.
Lineáris programozás A mese Célok Geometriai szemlélet (nem lesz matek ) Gakorlati kérdések Már megint a szendvics Kétfajta szendvicset szeretnénk készíteni, sonkásat és szalámisat. Lehetőleg minél többet.
11. Előadás. 11. előadás Bevezetés a lineáris programozásba
 11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
Operációkutatás. 4. konzultáció: Szállítási feladat. A feladat LP modellje
 Operációkutatás 1 NYME KTK, gazdálkodás szak, levelező alapképzés 2002/2003. tanév, II. évf. 2.félév Előadó: Dr. Takách Géza NyME FMK Információ Technológia Tanszék 9400 Sopron, Bajcsy Zs. u. 9. GT fszt.
Operációkutatás 1 NYME KTK, gazdálkodás szak, levelező alapképzés 2002/2003. tanév, II. évf. 2.félév Előadó: Dr. Takách Géza NyME FMK Információ Technológia Tanszék 9400 Sopron, Bajcsy Zs. u. 9. GT fszt.
Matematikai modellek megoldása számítógéppel Solver Lingo
 Matematikai modellek megoldása számítógéppel Solver Lingo Készítette: Dr. Ábrahám István A matematikai modellek számítógépes megoldásait példákkal mutatjuk be. Példa: Négy erőforrás felhasználásával négyféle
Matematikai modellek megoldása számítógéppel Solver Lingo Készítette: Dr. Ábrahám István A matematikai modellek számítógépes megoldásait példákkal mutatjuk be. Példa: Négy erőforrás felhasználásával négyféle
Egyes logisztikai feladatok megoldása lineáris programozás segítségével. - bútorgyári termelési probléma - szállítási probléma
 Egyes logisztikai feladatok megoldása lineáris programozás segítségével - bútorgyári termelési probléma - szállítási probléma Egy bútorgyár polcot, asztalt és szekrényt gyárt faforgácslapból. A kereskedelemben
Egyes logisztikai feladatok megoldása lineáris programozás segítségével - bútorgyári termelési probléma - szállítási probléma Egy bútorgyár polcot, asztalt és szekrényt gyárt faforgácslapból. A kereskedelemben
Opkut deníciók és tételek
 Opkut deníciók és tételek Készítette: Bán József Deníciók 1. Deníció (Lineáris programozási feladat). Keressük meg adott lineáris, R n értelmezési tartományú függvény, az ún. célfüggvény széls értékét
Opkut deníciók és tételek Készítette: Bán József Deníciók 1. Deníció (Lineáris programozási feladat). Keressük meg adott lineáris, R n értelmezési tartományú függvény, az ún. célfüggvény széls értékét
Érzékenységvizsgálat
 Érzékenységvizsgálat Alkalmazott operációkutatás 5. elıadás 008/009. tanév 008. október 0. Érzékenységvizsgálat x 0 A x b z= c T x max Kapacitások, együtthatók, célfüggvény együtthatók változnak => optimális
Érzékenységvizsgálat Alkalmazott operációkutatás 5. elıadás 008/009. tanév 008. október 0. Érzékenységvizsgálat x 0 A x b z= c T x max Kapacitások, együtthatók, célfüggvény együtthatók változnak => optimális
A szimplex algoritmus
 A szimplex algoritmus Ismétlés: reprezentációs tétel, az optimális megoldás és az extrém pontok kapcsolata Alapfogalmak: bázisok, bázismegoldások, megengedett bázismegoldások, degenerált bázismegoldás
A szimplex algoritmus Ismétlés: reprezentációs tétel, az optimális megoldás és az extrém pontok kapcsolata Alapfogalmak: bázisok, bázismegoldások, megengedett bázismegoldások, degenerált bázismegoldás
S Z Á L L Í T Á S I F E L A D A T
 Döntéselmélet S Z Á L L Í T Á S I F E L A D A T Szállítási feladat meghatározása Speciális lineáris programozási feladat. Legyen adott m telephely, amelyeken bizonyos fajta, tetszés szerint osztható termékből
Döntéselmélet S Z Á L L Í T Á S I F E L A D A T Szállítási feladat meghatározása Speciális lineáris programozási feladat. Legyen adott m telephely, amelyeken bizonyos fajta, tetszés szerint osztható termékből
b) Írja fel a feladat duálisát és adja meg ennek optimális megoldását!
 1. Három nemnegatív számot kell meghatározni úgy, hogy az elsőt héttel, a másodikat tizennéggyel, a harmadikat hattal szorozva és ezeket a szorzatokat összeadva az így keletkezett szám minél nagyobb legyen.
1. Három nemnegatív számot kell meghatározni úgy, hogy az elsőt héttel, a másodikat tizennéggyel, a harmadikat hattal szorozva és ezeket a szorzatokat összeadva az így keletkezett szám minél nagyobb legyen.
Operációkutatás. Vaik Zsuzsanna. ajánlott jegyzet: Szilágyi Péter: Operációkutatás
 Operációkutatás Vaik Zsuzsanna Vaik.Zsuzsanna@ymmfk.szie.hu ajánlott jegyzet: Szilágyi Péter: Operációkutatás Operációkutatás Követelmények: Aláírás feltétele: foglalkozásokon való részvétel + a félév
Operációkutatás Vaik Zsuzsanna Vaik.Zsuzsanna@ymmfk.szie.hu ajánlott jegyzet: Szilágyi Péter: Operációkutatás Operációkutatás Követelmények: Aláírás feltétele: foglalkozásokon való részvétel + a félév
Operációkutatás példatár
 1 Operációkutatás példatár 2 1. Lineáris programozási feladatok felírása és megoldása 1.1. Feladat Egy gazdálkodónak azt kell eldöntenie, hogy mennyi kukoricát és búzát vessen. Ha egységnyi földterületen
1 Operációkutatás példatár 2 1. Lineáris programozási feladatok felírása és megoldása 1.1. Feladat Egy gazdálkodónak azt kell eldöntenie, hogy mennyi kukoricát és búzát vessen. Ha egységnyi földterületen
Totális Unimodularitás és LP dualitás. Tapolcai János
 Totális Unimodularitás és LP dualitás Tapolcai János tapolcai@tmit.bme.hu 1 Optimalizálási feladat kezelése NP-nehéz Hatékony megoldás vélhetően nem létezik Jó esetben hatékony algoritmussal közelíteni
Totális Unimodularitás és LP dualitás Tapolcai János tapolcai@tmit.bme.hu 1 Optimalizálási feladat kezelése NP-nehéz Hatékony megoldás vélhetően nem létezik Jó esetben hatékony algoritmussal közelíteni
Szimplex módszer, szimplex tábla Példaként tekintsük a következ LP feladatot:
 Szimplex módszer, szimplex tábla Példaként tekintsük a következ LP feladatot: z = 5x 1 + 4x 2 + 3x 3 2x 1 + 3x 2 + x 3 5 4x 1 + x 2 + 2x 3 11 3x 1 + 4x 2 + 2x 3 8 x 1, x 2, x 3 0 = maximum, feltéve, hogy
Szimplex módszer, szimplex tábla Példaként tekintsük a következ LP feladatot: z = 5x 1 + 4x 2 + 3x 3 2x 1 + 3x 2 + x 3 5 4x 1 + x 2 + 2x 3 11 3x 1 + 4x 2 + 2x 3 8 x 1, x 2, x 3 0 = maximum, feltéve, hogy
Bevezetés az operációkutatásba A lineáris programozás alapjai
 Bevezetés az operációkutatásba A lineáris programozás alapjai Alkalmazott operációkutatás 1. elıadás 2008/2009. tanév 2008. szeptember 12. Mi az operációkutatás (operations research)? Kialakulása: II.
Bevezetés az operációkutatásba A lineáris programozás alapjai Alkalmazott operációkutatás 1. elıadás 2008/2009. tanév 2008. szeptember 12. Mi az operációkutatás (operations research)? Kialakulása: II.
A dualitás elve. Készítette: Dr. Ábrahám István
 A dalitás elve Készítette: Dr. Ábrahám István A dalitás fogalma, alapösszefüggései Definíció: Adott a lineáris programozás maimm feladata: 0 A b f()=c* ma Ekkor felírható a kővetkező minimm feladat: y
A dalitás elve Készítette: Dr. Ábrahám István A dalitás fogalma, alapösszefüggései Definíció: Adott a lineáris programozás maimm feladata: 0 A b f()=c* ma Ekkor felírható a kővetkező minimm feladat: y
Termeléstervezés és -irányítás Termelés és kapacitás tervezés Xpress-Mosel FICO Xpress Optimization Suite
 Termeléstervezés és -irányítás Termelés és kapacitás tervezés Xpress-Mosel FICO Xpress Optimization Suite Alkalmazásával 214 Monostori László egyetemi tanár Váncza József egyetemi docens 1 Probléma Igények
Termeléstervezés és -irányítás Termelés és kapacitás tervezés Xpress-Mosel FICO Xpress Optimization Suite Alkalmazásával 214 Monostori László egyetemi tanár Váncza József egyetemi docens 1 Probléma Igények
A szimplex tábla. p. 1
 A szimplex tábla Végződtetés: optimalitás és nem korlátos megoldások A szimplex algoritmus lépései A degeneráció fogalma Komplexitás (elméleti és gyakorlati) A szimplex tábla Példák megoldása a szimplex
A szimplex tábla Végződtetés: optimalitás és nem korlátos megoldások A szimplex algoritmus lépései A degeneráció fogalma Komplexitás (elméleti és gyakorlati) A szimplex tábla Példák megoldása a szimplex
Alkalmazott optimalizálás és játékelmélet Lineáris programozás Gyakorlófeladatok. Rétvári Gábor
 Alkalmazott optimalizálás és játékelmélet Lineáris programozás Gyakorlófeladatok Rétvári Gábor retvari@tmit.bme.hu Feladatok Szöveges feladatok. Egy acélgyárban négyfajta zártszelvényt gyártanak: kis,
Alkalmazott optimalizálás és játékelmélet Lineáris programozás Gyakorlófeladatok Rétvári Gábor retvari@tmit.bme.hu Feladatok Szöveges feladatok. Egy acélgyárban négyfajta zártszelvényt gyártanak: kis,
Nemlineáris programozás 2.
 Optimumszámítás Nemlineáris programozás 2. Többváltozós optimalizálás feltételek mellett. Lagrange-feladatok. Nemlineáris programozás. A Kuhn-Tucker feltételek. Konvex programozás. Sydsaeter-Hammond: 18.1-5,
Optimumszámítás Nemlineáris programozás 2. Többváltozós optimalizálás feltételek mellett. Lagrange-feladatok. Nemlineáris programozás. A Kuhn-Tucker feltételek. Konvex programozás. Sydsaeter-Hammond: 18.1-5,
0. BEVEZETÉS. Decision theory: web Google keresés= 27 millió találat Döntéselmélet: web Google keresés= 12 ezer találat
 A-PDF Merger DEMO : Purchase from www.a-pdf.com to remove the watermark 0. BEVEZETÉS Decision theory: web Google keresés= 27 millió találat Döntéselmélet: web Google keresés= 12 ezer találat Döntéselmélet
A-PDF Merger DEMO : Purchase from www.a-pdf.com to remove the watermark 0. BEVEZETÉS Decision theory: web Google keresés= 27 millió találat Döntéselmélet: web Google keresés= 12 ezer találat Döntéselmélet
Kétfázisú szimplex algoritmus és speciális esetei
 5. gyakorlat Kétfázisú szimplex algoritmus és speciális esetei. Emlékeztető Standard alak, áttérés Standard alak Minden feltétel et tartalmaz csak. A célfüggvényünket maximalizáljuk. A b vektor (jobb oldalon
5. gyakorlat Kétfázisú szimplex algoritmus és speciális esetei. Emlékeztető Standard alak, áttérés Standard alak Minden feltétel et tartalmaz csak. A célfüggvényünket maximalizáljuk. A b vektor (jobb oldalon
Követelmények Motiváció Matematikai modellezés: példák A lineáris programozás alapfeladata 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 1. Előadás Követelmények, teljesítés feltételei Vizsga anyaga Előadásokhoz tartozó diasor
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 1. Előadás Követelmények, teljesítés feltételei Vizsga anyaga Előadásokhoz tartozó diasor
Követelmények Motiváció Matematikai modellezés: példák A lineáris programozás alapfeladata 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 1. Előadás Követelmények, teljesítés feltételei Vizsga anyaga Előadásokhoz tartozó diasor
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 1. Előadás Követelmények, teljesítés feltételei Vizsga anyaga Előadásokhoz tartozó diasor
3. előadás. Termelési és optimalizálási feladatok. Dr. Szörényi Miklós, Dr. Kallós Gábor
 3. előadás Termelési és optimalizálási feladatok Dr. Szörényi Miklós, Dr. Kallós Gábor 2014 2015 1 Tartalom Matematikai alapok Matematikai modell Fontosabb feladattípusok Érzékenységvizsgálat Fontos fogalmak
3. előadás Termelési és optimalizálási feladatok Dr. Szörényi Miklós, Dr. Kallós Gábor 2014 2015 1 Tartalom Matematikai alapok Matematikai modell Fontosabb feladattípusok Érzékenységvizsgálat Fontos fogalmak
5. Előadás. (5. előadás) Mátrixegyenlet, Mátrix inverze március 6. 1 / 39
 5. Előadás (5. előadás) Mátrixegyenlet, Mátrix inverze 2019. március 6. 1 / 39 AX = B (5. előadás) Mátrixegyenlet, Mátrix inverze 2019. március 6. 2 / 39 AX = B Probléma. Legyen A (m n)-es és B (m l)-es
5. Előadás (5. előadás) Mátrixegyenlet, Mátrix inverze 2019. március 6. 1 / 39 AX = B (5. előadás) Mátrixegyenlet, Mátrix inverze 2019. március 6. 2 / 39 AX = B Probléma. Legyen A (m n)-es és B (m l)-es
1/ gyakorlat. Hiperbolikus programozási feladat megoldása. Pécsi Tudományegyetem PTI
 1/12 Operációkutatás 5. gyakorlat Hiperbolikus programozási feladat megoldása Pécsi Tudományegyetem PTI 2/12 Ha az Hiperbolikus programozási feladat feltételek teljesülése mellett a A x b x 0 z(x) = c
1/12 Operációkutatás 5. gyakorlat Hiperbolikus programozási feladat megoldása Pécsi Tudományegyetem PTI 2/12 Ha az Hiperbolikus programozási feladat feltételek teljesülése mellett a A x b x 0 z(x) = c
Előadó: Dr. Kertész Krisztián
 Előadó: Dr. Kertész Krisztián E-mail: k.krisztian@efp.hu A termelés költségei függenek a technológiától, az inputtényezők árától és a termelés mennyiségétől, de a továbbiakban a technológiának és az inputtényezők
Előadó: Dr. Kertész Krisztián E-mail: k.krisztian@efp.hu A termelés költségei függenek a technológiától, az inputtényezők árától és a termelés mennyiségétől, de a továbbiakban a technológiának és az inputtényezők
A szimplex algoritmus
 . gyakorlat A szimplex algoritmus Az előző órán bevezetett feladat optimális megoldását fogjuk megvizsgálni. Ehhez új fogalmakat, és egy algoritmust tanulunk meg. Hogy az algoritmust alkalmazni tudjuk,
. gyakorlat A szimplex algoritmus Az előző órán bevezetett feladat optimális megoldását fogjuk megvizsgálni. Ehhez új fogalmakat, és egy algoritmust tanulunk meg. Hogy az algoritmust alkalmazni tudjuk,
Operációkutatás vizsga
 Operációkutatás vizsga A csoport Budapesti Corvinus Egyetem 2007. január 9. Egyéb gyakorló és vizsgaanyagok találhatók a honlapon a Letölthető vizsgasorok, segédanyagok menüpont alatt. OPERÁCIÓKUTATÁS
Operációkutatás vizsga A csoport Budapesti Corvinus Egyetem 2007. január 9. Egyéb gyakorló és vizsgaanyagok találhatók a honlapon a Letölthető vizsgasorok, segédanyagok menüpont alatt. OPERÁCIÓKUTATÁS
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
1/ gyakorlat. Lineáris Programozási feladatok megoldása szimplex módszerrel. Pécsi Tudományegyetem PTI
 / Operációkutatás. gyakorlat Lineáris Programozási feladatok megoldása szimplex módszerrel Pécsi Tudományegyetem PTI /. Legyen adott az alábbi LP-feladat: x + 4x + x 9 x + x x + x + x 6 x, x, x x + x +
/ Operációkutatás. gyakorlat Lineáris Programozási feladatok megoldása szimplex módszerrel Pécsi Tudományegyetem PTI /. Legyen adott az alábbi LP-feladat: x + 4x + x 9 x + x x + x + x 6 x, x, x x + x +
Áttekintés LP és geometria Többcélú LP LP és egy dinamikus modell 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 6. Előadás Áttekintés Kezdjük újra a klasszikus erőforrás allokációs problémával (katonák,
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 6. Előadás Áttekintés Kezdjük újra a klasszikus erőforrás allokációs problémával (katonák,
Branch-and-Bound. 1. Az egészértéketű programozás. a korlátozás és szétválasztás módszere Bevezető Definíció. 11.
 11. gyakorlat Branch-and-Bound a korlátozás és szétválasztás módszere 1. Az egészértéketű programozás 1.1. Bevezető Bizonyos feladatok modellezése kapcsán előfordulhat olyan eset, hogy a megoldás során
11. gyakorlat Branch-and-Bound a korlátozás és szétválasztás módszere 1. Az egészértéketű programozás 1.1. Bevezető Bizonyos feladatok modellezése kapcsán előfordulhat olyan eset, hogy a megoldás során
Operációkutatási feladatok megoldása QSB-vel
 Operációkutatási feladatok megoldása QSB-vel Bevezetés A QSB a Quantitative Systems for Business (szabad fordításban: Kvantitatív módszerek a gazdaságban) kifejezés rövidítése. Ennek a programcsomagnak
Operációkutatási feladatok megoldása QSB-vel Bevezetés A QSB a Quantitative Systems for Business (szabad fordításban: Kvantitatív módszerek a gazdaságban) kifejezés rövidítése. Ennek a programcsomagnak
Pénzügyi-számviteli ügyintéző szakképesítés Számviteli ügyintéző részszakképesítés
 NEMZETGAZDASÁGI MINISZTÉRIUM TÜK szám: 49/3-116/2018 KORLÁTOZOTT TERJESZTÉSŰ Érvényességi idő: 2018. május 15. 11.15 óra Minősítő neve: Mészáros László Beosztása: főosztályvezető Készült: 1 eredeti és
NEMZETGAZDASÁGI MINISZTÉRIUM TÜK szám: 49/3-116/2018 KORLÁTOZOTT TERJESZTÉSŰ Érvényességi idő: 2018. május 15. 11.15 óra Minősítő neve: Mészáros László Beosztása: főosztályvezető Készült: 1 eredeti és
Döntéselőkészítés. I. előadás. Döntéselőkészítés. Előadó: Dr. Égertné dr. Molnár Éva. Informatika Tanszék A 602 szoba
 I. előadás Előadó: Dr. Égertné dr. Molnár Éva Informatika Tanszék A 602 szoba Tárggyal kapcsolatos anyagok megtalálhatók: http://www.sze.hu/~egertne Konzultációs idő: (páros tan. hét) csütörtök 10-11 30
I. előadás Előadó: Dr. Égertné dr. Molnár Éva Informatika Tanszék A 602 szoba Tárggyal kapcsolatos anyagok megtalálhatók: http://www.sze.hu/~egertne Konzultációs idő: (páros tan. hét) csütörtök 10-11 30
LINEÁRIS PROGRAMOZÁSI FELADATOK MEGOLDÁSA SZIMPLEX MÓDSZERREL
 LINEÁRIS PROGRAMOZÁSI FELADATOK MEGOLDÁSA SZIMPLEX MÓDSZERREL x 1-2x 2 6 -x 1-3x 3 = -7 x 1 - x 2-3x 3-2 3x 1-2x 2-2x 3 4 4x 1-2x 2 + x 3 max Alapfogalmak: feltételrendszer (narancs színnel jelölve), célfüggvény
LINEÁRIS PROGRAMOZÁSI FELADATOK MEGOLDÁSA SZIMPLEX MÓDSZERREL x 1-2x 2 6 -x 1-3x 3 = -7 x 1 - x 2-3x 3-2 3x 1-2x 2-2x 3 4 4x 1-2x 2 + x 3 max Alapfogalmak: feltételrendszer (narancs színnel jelölve), célfüggvény
Döntéselőkészítés. VII. előadás. Döntéselőkészítés. Egyszerű Kőnig-feladat (házasság feladat)
 VII. előadás Legyenek adottak Egyszerű Kőnig-feladat (házasság feladat) I, I 2,, I i,, I m személyek és a J, J 2,, J j,, J n munkák. Azt, hogy melyik személy melyik munkához ért ( melyik munkára van kvalifikálva)
VII. előadás Legyenek adottak Egyszerű Kőnig-feladat (házasság feladat) I, I 2,, I i,, I m személyek és a J, J 2,, J j,, J n munkák. Azt, hogy melyik személy melyik munkához ért ( melyik munkára van kvalifikálva)
Szöveges feladatok a mátrixaritmetika alkalmazására
 Szöveges feladatok a mátrixaritmetika alkalmazására Bevezetés: Tekintsük az alábbi -es mátrixot: A. Szorozzuk meg ezt jobbról egy alkalmas méretű (azaz -es) oszlopvektorral, amely az R tér kanonikus bázisának
Szöveges feladatok a mátrixaritmetika alkalmazására Bevezetés: Tekintsük az alábbi -es mátrixot: A. Szorozzuk meg ezt jobbról egy alkalmas méretű (azaz -es) oszlopvektorral, amely az R tér kanonikus bázisának
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Lineáris programozás. Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer
 Lineáris programozás Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer Feladat: Egy gyár kétféle terméket gyárt (A, B): /db Eladási ár 1000 800 Technológiai önköltség 400 300 Normaóraigény
Lineáris programozás Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer Feladat: Egy gyár kétféle terméket gyárt (A, B): /db Eladási ár 1000 800 Technológiai önköltség 400 300 Normaóraigény
GYAKORLÓ FELADATOK 4: KÖLTSÉGEK ÉS KÖLTSÉGFÜGGVÉNYEK
 GYAKORLÓ FELADATOK 4: KÖLTSÉGEK ÉS KÖLTSÉGFÜGGVÉNYEK 1. Egy terméket rövid távon a függvény által leírt költséggel lehet előállítani. A termelés határköltségét az összefüggés adja meg. a) Írja fel a termelés
GYAKORLÓ FELADATOK 4: KÖLTSÉGEK ÉS KÖLTSÉGFÜGGVÉNYEK 1. Egy terméket rövid távon a függvény által leírt költséggel lehet előállítani. A termelés határköltségét az összefüggés adja meg. a) Írja fel a termelés
Növényvédő szerek A B C D
 A feladat megoldása során az Excel 2010 használata a javasolt. A feladat elvégzése során a következőket fogjuk gyakorolni: Termelési és optimalizálási feladatok megoldása. Mátrixműveletek alkalmazása.
A feladat megoldása során az Excel 2010 használata a javasolt. A feladat elvégzése során a következőket fogjuk gyakorolni: Termelési és optimalizálási feladatok megoldása. Mátrixműveletek alkalmazása.
operációkutatás példatár
 operációkutatás példatár . MŰVELETEK MÁTIXOKKAL. (Megoldás a.-es gyakorló ideóban.) Itt annak ezek a mátriok illete ektorok: A c B d * E f * Végezzük el a köetkező műeleteket: A B B E B c B A A E B d..
operációkutatás példatár . MŰVELETEK MÁTIXOKKAL. (Megoldás a.-es gyakorló ideóban.) Itt annak ezek a mátriok illete ektorok: A c B d * E f * Végezzük el a köetkező műeleteket: A B B E B c B A A E B d..
Diszkrét, egészértékű és 0/1 LP feladatok
 Diszkrét, egészértékű és 0/1 LP feladatok In English Integer Programming - IP Zero/One (boolean) programming 2007.03.12 Dr. Bajalinov Erik, NyF MII 1 Diszkrét és egészértékű változókat tartalmazó feladatok
Diszkrét, egészértékű és 0/1 LP feladatok In English Integer Programming - IP Zero/One (boolean) programming 2007.03.12 Dr. Bajalinov Erik, NyF MII 1 Diszkrét és egészértékű változókat tartalmazó feladatok
A Szállítási feladat megoldása
 A Szállítási feladat megoldása Virtuális vállalat 201-2014 1. félév 4. gyakorlat Dr. Kulcsár Gyula A Szállítási feladat Adott meghatározott számú beszállító (source) a szállítható mennyiségekkel (transportation
A Szállítási feladat megoldása Virtuális vállalat 201-2014 1. félév 4. gyakorlat Dr. Kulcsár Gyula A Szállítási feladat Adott meghatározott számú beszállító (source) a szállítható mennyiségekkel (transportation
A lineáris programozás alapjai
 A lineáris programozás alapjai A konvex analízis alapjai: konvexitás, konvex kombináció, hipersíkok, félterek, extrém pontok, Poliéderek, a Minkowski-Weyl tétel (a poliéderek reprezentációs tétele) Lineáris
A lineáris programozás alapjai A konvex analízis alapjai: konvexitás, konvex kombináció, hipersíkok, félterek, extrém pontok, Poliéderek, a Minkowski-Weyl tétel (a poliéderek reprezentációs tétele) Lineáris
A Markowitz modell: kvadratikus programozás
 A Markowitz modell: kvadratikus programozás Losonczi László Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar Debrecen, 2011/12 tanév, II. félév Losonczi László (DE) A Markowitz modell 2011/12 tanév,
A Markowitz modell: kvadratikus programozás Losonczi László Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar Debrecen, 2011/12 tanév, II. félév Losonczi László (DE) A Markowitz modell 2011/12 tanév,
6. Előadás. Megyesi László: Lineáris algebra, oldal. 6. előadás Bázis, dimenzió
 6. Előadás Megyesi László: Lineáris algebra, 37. 41. oldal. Gondolkodnivalók Lineáris függetlenség 1. Gondolkodnivaló Legyen V valós számtest feletti vektortér. Igazolja, hogy ha a v 1, v 2,..., v n V
6. Előadás Megyesi László: Lineáris algebra, 37. 41. oldal. Gondolkodnivalók Lineáris függetlenség 1. Gondolkodnivaló Legyen V valós számtest feletti vektortér. Igazolja, hogy ha a v 1, v 2,..., v n V
13. A zöldborsó piacra jellemző keresleti és kínálati függvények a következők P= 600 Q, és P=100+1,5Q, ahol P Ft/kg, és a mennyiség kg-ban értendő.
 1. Minden olyan jószágkosarat, amely azonos szükségletkielégítési szintet (azonos hasznosságot) biztosít a fogyasztó számára,.. nevezzük a. költségvetési egyenesnek b. fogyasztói térnek c. közömbösségi
1. Minden olyan jószágkosarat, amely azonos szükségletkielégítési szintet (azonos hasznosságot) biztosít a fogyasztó számára,.. nevezzük a. költségvetési egyenesnek b. fogyasztói térnek c. közömbösségi
További programozási esetek Hiperbolikus, kvadratikus, integer, bináris, többcélú programozás
 További programozási esetek Hiperbolikus, kvadratikus, integer, bináris, többcélú programozás Készítette: Dr. Ábrahám István Hiperbolikus programozás Gazdasági problémák optimalizálásakor gyakori, hogy
További programozási esetek Hiperbolikus, kvadratikus, integer, bináris, többcélú programozás Készítette: Dr. Ábrahám István Hiperbolikus programozás Gazdasági problémák optimalizálásakor gyakori, hogy
Mátrixok február Feladat: Legyen A = ( ( B =
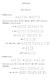 Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
1. Határozza meg, hogy az alábbi eszközök közül, melyek tartoznak a befektetett, melyek a forgóeszközök közé!
 GYAKORLÓ FELADATOK 1. Határozza meg, hogy az alábbi eszközök közül, melyek tartoznak a befektetett, melyek a forgóeszközök közé! 1. Üzemépületek Befektetett eszköz 2. Alapanyagok 3. 12 hónap futamidejű
GYAKORLÓ FELADATOK 1. Határozza meg, hogy az alábbi eszközök közül, melyek tartoznak a befektetett, melyek a forgóeszközök közé! 1. Üzemépületek Befektetett eszköz 2. Alapanyagok 3. 12 hónap futamidejű
II. évfolyam BA. Név: Neptun kód: Kurzus: Tanár neve: HÁZI DOLGOZAT 1. Számvitel 1 2013/2014. I. félév
 II. évfolyam BA Név: Neptun kód: Kurzus: Tanár neve: HÁZI DOLGOZAT 1. Számvitel 1 2013/2014 I. félév 1. Feladat (40 pont) Könyvelés Főkönyvi számlavázakon Eszközök Nyitó mérleg Források A. Befektetett
II. évfolyam BA Név: Neptun kód: Kurzus: Tanár neve: HÁZI DOLGOZAT 1. Számvitel 1 2013/2014 I. félév 1. Feladat (40 pont) Könyvelés Főkönyvi számlavázakon Eszközök Nyitó mérleg Források A. Befektetett
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 10. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Felhívás Diszkrét matematika I. középszint 2014.
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 10. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Felhívás Diszkrét matematika I. középszint 2014.
Dualitás Dualitási tételek Általános LP feladat Komplementáris lazaság 2015/2016-2. Szegedi Tudományegyetem Informatikai Tanszékcsoport
 Operációkutatás I. 2015/2016-2. Szegedi Tudományegyetem Informatikai Tanszékcsoport Számítógépes Optimalizálás Tanszék 6. Előadás Árazási interpretáció Tekintsük újra az erőforrás allokációs problémát
Operációkutatás I. 2015/2016-2. Szegedi Tudományegyetem Informatikai Tanszékcsoport Számítógépes Optimalizálás Tanszék 6. Előadás Árazási interpretáció Tekintsük újra az erőforrás allokációs problémát
Feladatlap. a hatosztályos speciális matematika tantervű osztályok írásbeli vizsgájára (2006)
 Feladatlap a hatosztályos speciális matematika tantervű osztályok írásbeli vizsgájára (2006) 1) Karcsi januárban betegség miatt háromszor hiányzott az iskolából:12-én,14-én és 24-én. Milyen napra esett
Feladatlap a hatosztályos speciális matematika tantervű osztályok írásbeli vizsgájára (2006) 1) Karcsi januárban betegség miatt háromszor hiányzott az iskolából:12-én,14-én és 24-én. Milyen napra esett
9. Előadás. Megyesi László: Lineáris algebra, oldal. 9. előadás Mátrix inverze, Leontyev-modell
 9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Tegyük fel, hogy egy elemi bázistranszformáció kezdetekor a sor- és oszlopindexek sorban helyezkednek
9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Tegyük fel, hogy egy elemi bázistranszformáció kezdetekor a sor- és oszlopindexek sorban helyezkednek
A Markowitz modell: kvadratikus programozás
 A Markowitz modell: kvadratikus programozás Harry Markowitz 1990-ben kapott Közgazdasági Nobel díjat a portfolió optimalizálási modelljéért. Ld. http://en.wikipedia.org/wiki/harry_markowitz Ennek a legegyszer
A Markowitz modell: kvadratikus programozás Harry Markowitz 1990-ben kapott Közgazdasági Nobel díjat a portfolió optimalizálási modelljéért. Ld. http://en.wikipedia.org/wiki/harry_markowitz Ennek a legegyszer
Tartalom. Matematikai alapok. Fontos fogalmak Termékgyártási példafeladat
 6. előadás Termelési és optimalizálási feladatok Dr. Szörényi Miklós, Dr. Kallós Gábor 2014 2015 1 Tartalom Matematikai alapok Matematikai modell Fontosabb feladattípusok Érzékenységvizsgálat Fontos fogalmak
6. előadás Termelési és optimalizálási feladatok Dr. Szörényi Miklós, Dr. Kallós Gábor 2014 2015 1 Tartalom Matematikai alapok Matematikai modell Fontosabb feladattípusok Érzékenységvizsgálat Fontos fogalmak
Könyvvezetési ismeretek
 1 I. évfolyam BA Név: Neptun kód: Kurzus: Tanár neve: HÁZI DOLGOZAT 2. Könyvvezetési ismeretek 2014/2015 II. félév 2 Elméleti kérdések 1. Egy vállalkozás saját tőkéjével kapcsolatosan az alábbi információkkal
1 I. évfolyam BA Név: Neptun kód: Kurzus: Tanár neve: HÁZI DOLGOZAT 2. Könyvvezetési ismeretek 2014/2015 II. félév 2 Elméleti kérdések 1. Egy vállalkozás saját tőkéjével kapcsolatosan az alábbi információkkal
Vektorterek. Wettl Ferenc február 17. Wettl Ferenc Vektorterek február / 27
 Vektorterek Wettl Ferenc 2015. február 17. Wettl Ferenc Vektorterek 2015. február 17. 1 / 27 Tartalom 1 Egyenletrendszerek 2 Algebrai struktúrák 3 Vektortér 4 Bázis, dimenzió 5 Valós mátrixok és egyenletrendszerek
Vektorterek Wettl Ferenc 2015. február 17. Wettl Ferenc Vektorterek 2015. február 17. 1 / 27 Tartalom 1 Egyenletrendszerek 2 Algebrai struktúrák 3 Vektortér 4 Bázis, dimenzió 5 Valós mátrixok és egyenletrendszerek
2018. évi. Egyszerűsített éves beszámoló
 Szervezet címe: 8181 Berhida, Veszprémi út 1-3. Nyilvántartási szám: 19-02-0002960 2018. évi Egyszerűsített éves beszámoló Berhida, 2019. május 16. Elnök 1/a melléklet MÉRLEG Fordulónap: 2018.12.31 adatok
Szervezet címe: 8181 Berhida, Veszprémi út 1-3. Nyilvántartási szám: 19-02-0002960 2018. évi Egyszerűsített éves beszámoló Berhida, 2019. május 16. Elnök 1/a melléklet MÉRLEG Fordulónap: 2018.12.31 adatok
Az érzékenységvizsgálat jelentősége
 Az érzékenységvizsgálat jelentősége (Tanulmány) Egyéb olyan fontos szempontok mellett, mint a stabilitás, rugalmasság, társadalmi elfogadottság, stb., az ipari menedzser fő célja, hogy növelje cége nyereségét.
Az érzékenységvizsgálat jelentősége (Tanulmány) Egyéb olyan fontos szempontok mellett, mint a stabilitás, rugalmasság, társadalmi elfogadottság, stb., az ipari menedzser fő célja, hogy növelje cége nyereségét.
Statisztikai számjel: Szervezet neve: Bakony és Balaton Keleti Kapuja Közhasznú Egyesület
 Statisztikai számjel: 19383578-9499-569-19 Szervezet neve: Bakony és Balaton Keleti Kapuja Közhasznú Egyesület Szervezet címe: 8181 Berhida, Veszprémi út 1-3. Nyilvántartási szám: 19-02-0002960 2017. évi
Statisztikai számjel: 19383578-9499-569-19 Szervezet neve: Bakony és Balaton Keleti Kapuja Közhasznú Egyesület Szervezet címe: 8181 Berhida, Veszprémi út 1-3. Nyilvántartási szám: 19-02-0002960 2017. évi
Matematikai modellezés
 Matematikai modellezés Bevezető A diasorozat a Döntési modellek című könyvhöz készült. Készítette: Dr. Ábrahám István Döntési folyamatok matematikai modellezése Az emberi tevékenységben meghatározó szerepe
Matematikai modellezés Bevezető A diasorozat a Döntési modellek című könyvhöz készült. Készítette: Dr. Ábrahám István Döntési folyamatok matematikai modellezése Az emberi tevékenységben meghatározó szerepe
Lineáris egyenletrendszerek
 Lineáris egyenletrendszerek 1 Alapfogalmak 1 Deníció Egy m egyenletb l álló, n-ismeretlenes lineáris egyenletrendszer általános alakja: a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
Lineáris egyenletrendszerek 1 Alapfogalmak 1 Deníció Egy m egyenletb l álló, n-ismeretlenes lineáris egyenletrendszer általános alakja: a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás)
 Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Pénzügy menedzsment. Hosszú távú pénzügyi tervezés
 Pénzügy menedzsment Hosszú távú pénzügyi tervezés Egy vállalat egyszerűsített mérlege és eredménykimutatása 2007-ben és 2008-ban a következőképpen alakult: Egyszerűsített eredménykimutatás (2008) Értékesítés
Pénzügy menedzsment Hosszú távú pénzügyi tervezés Egy vállalat egyszerűsített mérlege és eredménykimutatása 2007-ben és 2008-ban a következőképpen alakult: Egyszerűsített eredménykimutatás (2008) Értékesítés
ORSZÁGOS KÖZTERÜLETI PARKOLÁSI ZÓNAADATBÁZIS
 Város Zóna Szezon Üzemidő Üzemidő Üzemidő Hétfő - Péntek Szombat Vasárnap Max. parkolási idő Személygépkocsi díj Megjegyzés Budapest I. KERÜLET 3016 01.02-12.23 180 perc 440 Ft/óra Budapest I. KERÜLET
Város Zóna Szezon Üzemidő Üzemidő Üzemidő Hétfő - Péntek Szombat Vasárnap Max. parkolási idő Személygépkocsi díj Megjegyzés Budapest I. KERÜLET 3016 01.02-12.23 180 perc 440 Ft/óra Budapest I. KERÜLET
Optimalizálás alapfeladata Legmeredekebb lejtő Lagrange függvény Log-barrier módszer Büntetőfüggvény módszer 2017/
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 9. Előadás Az optimalizálás alapfeladata Keressük f függvény maximumát ahol f : R n R és
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 9. Előadás Az optimalizálás alapfeladata Keressük f függvény maximumát ahol f : R n R és
Esettanulmányok és modellek 2
 Esettanulmányok és modellek Kereskedelem Mezőgazdaság Készítette: Dr. Ábrahám István Kereskedelem. Kocsis Péter: Opt. döntések lin.pr. (. oldal) nyomán: Kiskereskedelmi cég négyféle üdítőt rendel, melyek
Esettanulmányok és modellek Kereskedelem Mezőgazdaság Készítette: Dr. Ábrahám István Kereskedelem. Kocsis Péter: Opt. döntések lin.pr. (. oldal) nyomán: Kiskereskedelmi cég négyféle üdítőt rendel, melyek
G Y A K O R L Ó F E L A D A T O K
 Döntéselmélet G Y A K O R L Ó F E L A D A T O K Lineáris programozás I Egy vállalat kétféle terméket gyárt, az A és B termékeket. A következő adatok ismertek: A vállalat éves munkaóra-kapacitása 1440 óra,
Döntéselmélet G Y A K O R L Ó F E L A D A T O K Lineáris programozás I Egy vállalat kétféle terméket gyárt, az A és B termékeket. A következő adatok ismertek: A vállalat éves munkaóra-kapacitása 1440 óra,
Operációkutatás. Vaik Zsuzsanna. Budapest október 10. First Prev Next Last Go Back Full Screen Close Quit
 Operációkutatás Vaik Zsuzsanna Vaik.Zsuzsanna@ymmfk.szie.hu Budapest 200. október 10. Mit tanulunk ma? Szállítási feladat Megoldása Adott: Egy árucikk, T 1, T 2, T,..., T m termelőhely, melyekben rendre
Operációkutatás Vaik Zsuzsanna Vaik.Zsuzsanna@ymmfk.szie.hu Budapest 200. október 10. Mit tanulunk ma? Szállítási feladat Megoldása Adott: Egy árucikk, T 1, T 2, T,..., T m termelőhely, melyekben rendre
Mikroökonómia előadás. Dr. Kertész Krisztián
 Mikroökonómia előadás Dr. Kertész Krisztián k.krisztian@efp.hu A TERMELÉS KÖLTSÉGEI ÁRBEVÉTEL A termelés gazdasági költsége Gazdasági Explicit költség profit Gazdasági profit Számviteli költség Implicit
Mikroökonómia előadás Dr. Kertész Krisztián k.krisztian@efp.hu A TERMELÉS KÖLTSÉGEI ÁRBEVÉTEL A termelés gazdasági költsége Gazdasági Explicit költség profit Gazdasági profit Számviteli költség Implicit
SZÁMVITELI ALAPJAI tárgyból
 BEADANDÓ FELADAT Beadási határidő: Az első zárthelyi megírásakor hozza magával, ott kell beadnia. A zárthelyi megírásának (a félév elfogadásának) előfeltétele a beadandó feladat leadása. SZÁMVITELI ALAPJAI
BEADANDÓ FELADAT Beadási határidő: Az első zárthelyi megírásakor hozza magával, ott kell beadnia. A zárthelyi megírásának (a félév elfogadásának) előfeltétele a beadandó feladat leadása. SZÁMVITELI ALAPJAI
Pénzügyi-számviteli ügyintéző szakképesítés Számviteli ügyintéző részszakképesítés
 . (vizsgázó olvasható neve) NEMZETGAZDASÁGI MINISZTÉRIUM TÜK szám: 49/3-115 /2018. (Születési hely, idő) Érvényességi idő: 2018. május 15. 9.45 óra Minősítő neve: Mészáros László Beosztása: főosztályvezető
. (vizsgázó olvasható neve) NEMZETGAZDASÁGI MINISZTÉRIUM TÜK szám: 49/3-115 /2018. (Születési hely, idő) Érvényességi idő: 2018. május 15. 9.45 óra Minősítő neve: Mészáros László Beosztása: főosztályvezető
A Z A N Y A G É S K É S Z L E T G A Z D Á L K O D Á S I R E N D S Z E R V I Z S G Á L A T A L O G I S Z T I K A I S Z E M P O N T O K A L A P J Á N
 Controlling A Z A N Y A G É S K É S Z L E T G A Z D Á L K O D Á S I R E N D S Z E R V I Z S G Á L A T A L O G I S Z T I K A I S Z E M P O N T O K A L A P J Á N Az anyagok osztályozása és számbavétele Nyersanyagnak
Controlling A Z A N Y A G É S K É S Z L E T G A Z D Á L K O D Á S I R E N D S Z E R V I Z S G Á L A T A L O G I S Z T I K A I S Z E M P O N T O K A L A P J Á N Az anyagok osztályozása és számbavétele Nyersanyagnak
Bakony és Balaton Keleti Kapuja Közhasznú Egyesület Kiegészítő melléklete a 2012. évi beszámolóhoz /Adatok: ezer Ft -ban/
 1. oldal Bakony és Balaton Keleti Kapuja Közhasznú Egyesület Kiegészítő melléklete a 2012. évi beszámolóhoz /Adatok: ezer Ft -ban/ I. Általános rész 1./ Általános háttérinformációk Bakony és Balaton Keleti
1. oldal Bakony és Balaton Keleti Kapuja Közhasznú Egyesület Kiegészítő melléklete a 2012. évi beszámolóhoz /Adatok: ezer Ft -ban/ I. Általános rész 1./ Általános háttérinformációk Bakony és Balaton Keleti
Pénzügytan szigorlat
 GF KVIFK Gazdaságtudományi Intézet Pénzügy szakcsoport Pénzügytan szigorlat 3 29,5 33 pont jeles 25,5 29 pont jó 21,5 25 pont közepes 17,5 21 pont elégséges 17 pont elégtelen Név: Elért pont: soport: Érdemjegy:
GF KVIFK Gazdaságtudományi Intézet Pénzügy szakcsoport Pénzügytan szigorlat 3 29,5 33 pont jeles 25,5 29 pont jó 21,5 25 pont közepes 17,5 21 pont elégséges 17 pont elégtelen Név: Elért pont: soport: Érdemjegy:
Lineáris egyenletrendszerek
 Lineáris egyenletrendszerek Lineáris egyenletrendszernek nevezzük az a 11 x 1 + a 12 x 2 +... +a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... +a 2n x n = b 2.. a k1 x 1 + a k2 x 2 +... +a kn x n = b k n ismeretlenes,
Lineáris egyenletrendszerek Lineáris egyenletrendszernek nevezzük az a 11 x 1 + a 12 x 2 +... +a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... +a 2n x n = b 2.. a k1 x 1 + a k2 x 2 +... +a kn x n = b k n ismeretlenes,
PÉNZÜGYI ÉS SZÁMVITELI KAR- TÁVOKTATÁSI KÖZPONT COLLEGE OF FINANCE AND ACCOUNTANCY- CENTER OF DISTANCE LEARNING 1149 BUDAPEST, BUZOGÁNY U. 10-12.
 PÉNZÜGYI ÉS SZÁMVITELI KAR- TÁVOKTATÁSI KÖZPONT COLLEGE OF FINANCE AND ACCOUNTANCY- CENTER OF DISTANCE LEARNING 1149 BUDAPEST, BUZOGÁNY U. 10-12. / FAX: 06-1-222-4584 : 06-1-469-6672 II. évfolyam BA Név:
PÉNZÜGYI ÉS SZÁMVITELI KAR- TÁVOKTATÁSI KÖZPONT COLLEGE OF FINANCE AND ACCOUNTANCY- CENTER OF DISTANCE LEARNING 1149 BUDAPEST, BUZOGÁNY U. 10-12. / FAX: 06-1-222-4584 : 06-1-469-6672 II. évfolyam BA Név:
1. Oldja meg grafikusan az alábbi feladatokat mindhárom célfüggvény esetén! a, x 1 + x 2 2 2x 1 + x 2 6 x 1 + x 2 1. x 1 0, x 2 0
 Gyakorló feladatok Operációkutatás vizsgára 1. Oldja meg grafikusan az alábbi feladatokat mindhárom célfüggvény esetén! a, b, c, d, x 1 + x 2 2 2x 1 + x 2 6 x 1 + x 2 1 x 1 2, 5 z 1 = 4x 1 3x 2 max; z
Gyakorló feladatok Operációkutatás vizsgára 1. Oldja meg grafikusan az alábbi feladatokat mindhárom célfüggvény esetén! a, b, c, d, x 1 + x 2 2 2x 1 + x 2 6 x 1 + x 2 1 x 1 2, 5 z 1 = 4x 1 3x 2 max; z
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 8. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Elemi számelmélet Diszkrét matematika I. középszint
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 8. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Elemi számelmélet Diszkrét matematika I. középszint
Stratégiai és üzleti tervezés
 PSZK Távoktatási Központ / H-1149 Budapest, Buzogány utca 10-12. / 1426 Budapest Pf.:35 IV. évfolyam GM szak Név: Neptun kód: Kurzus: Tanár neve: HÁZI DOLGOZAT 2. Stratégiai és üzleti tervezés 2013/2014
PSZK Távoktatási Központ / H-1149 Budapest, Buzogány utca 10-12. / 1426 Budapest Pf.:35 IV. évfolyam GM szak Név: Neptun kód: Kurzus: Tanár neve: HÁZI DOLGOZAT 2. Stratégiai és üzleti tervezés 2013/2014
A Készletek növekednek 200,- eft-tal, a Pénztár csökken 200,- eft-tal. A mérlegfőösszeg a gazdasági esemény hatására nem változik.
 III. GYAKORLÓ FELADATOK 1. Számszerűsítse, hogy az alábbi gazdasági események mely vagyonrészekben milyen változásokat okoznak és vizsgálja a gazdasági esemény mérlegfőösszegre gyakorolt hatását! a) Árubeszerzés
III. GYAKORLÓ FELADATOK 1. Számszerűsítse, hogy az alábbi gazdasági események mely vagyonrészekben milyen változásokat okoznak és vizsgálja a gazdasági esemény mérlegfőösszegre gyakorolt hatását! a) Árubeszerzés
Max. parkolási idő Személygépkoc Motor Kistehergépjármű Tehergépjármű Busz
 Város Zónakód Aktuális szezon munkanapon szabadnapon munkaszüneti napon Max. parkolási idő Személygépkoc Motor Kistehergépjármű Tehergépjármű Busz Ajka 8401 Jan 02 - Dec 24 07:00-17:00 07:00-12:00 - -
Város Zónakód Aktuális szezon munkanapon szabadnapon munkaszüneti napon Max. parkolási idő Személygépkoc Motor Kistehergépjármű Tehergépjármű Busz Ajka 8401 Jan 02 - Dec 24 07:00-17:00 07:00-12:00 - -
Növényvédő szerek A 500 0 0 0 0 65000 B 0 0 50 500 500 60000 C 50 25 0 50 50 12000 D 0 25 5 50 0 6000
 A feladat megoldása során az Excel 2010 használata a javasolt. A feladat elvégzése során a következőket fogjuk gyakorolni: Termelési és optimalizálási feladatok megoldása. Mátrixműveletek alkalmazása.
A feladat megoldása során az Excel 2010 használata a javasolt. A feladat elvégzése során a következőket fogjuk gyakorolni: Termelési és optimalizálási feladatok megoldása. Mátrixműveletek alkalmazása.
Bevezetés az algebrába 2 Vektor- és mátrixnorma
 Bevezetés az algebrába 2 Vektor- és mátrixnorma Wettl Ferenc Algebra Tanszék B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M 2016.
Bevezetés az algebrába 2 Vektor- és mátrixnorma Wettl Ferenc Algebra Tanszék B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M 2016.
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
