Diszkrét matematika I.
|
|
|
- Liliána Papp
- 8 évvel ezelőtt
- Látták:
Átírás
1 Diszkrét matematika I. középszint ősz 1. Diszkrét matematika I. középszint 8. előadás Mérai László diái alapján Komputeralgebra Tanszék ősz
2 Elemi számelmélet Diszkrét matematika I. középszint ősz 2. Oszthatóság Ha a és b racionális számok (b 0), akkor az a/b osztás mindig elvégezhető (és az eredmény szintén racionális). Ha a és b egész számok, az a/b osztás nem mindig végezhető el (a hányados nem feltétlenül lesz egész). Definíció Az a egész osztja a b egészet (b osztható a-val): a b, ha létezik olyan c egész, mellyel a c = b (azaz a 0 esetén b/a szintén egész). Példák 1 13, mert 1 13 = 13; 1 n, mert 1 n = n; 6 12, mert 6 2 = 12; 6 12, mert ( 6) ( 2) = 12. A definíció kiterjeszthető például a Gauss-egészekre: {a + bi : a, b Z}. Példák i 13, mert i ( 13i) = 13; 1 + i 2, mert (1 + i) (1 i) = 2.
3 Elemi számelmélet Diszkrét matematika I. középszint ősz 3. Oszthatóság tulajdonságai Álĺıtás (HF) Minden a, b, c,... Z esetén 1 a a; 2 a b és b c a c; 3 a b és b a a = ±b; 4 a b és a b aa bb ; 5 a b ac bc; 6 ac bc és c 0 a b; 7 a b 1,..., b k a c 1 b c k b k ; 8 a 0, u.i. a 0 = 0; 9 0 a a = 0; 10 1 a és 1 a; Példák 1 6 6; és ; 3 a 3 és 3 a a = ±3; és ; ; és ; 7 3 6, 9 3 6c 1 + 9c 2
4 Elemi számelmélet Diszkrét matematika I. középszint ősz 4. Egységek Definíció Ha egy ε szám bármely másiknak osztója, akkor ε-t egységnek nevezzük. Álĺıtás Az egész számok körében két egység van: 1, 1. Bizonyítás A ±1 nyilván egység. Megfordítva: ha ε egység, akkor 1 = ε q valamely q egész számra. Mivel ε 1, q 1 ε = 1, azaz ε = ±1. Példa A Gauss-egészek körében az i is egység: a + bi = i(b ai). Megjegyzés Pontosan 1 osztói az egységek.
5 Elemi számelmélet Diszkrét matematika I. középszint ősz 5. Asszociáltak Oszthatóság szempontjából nincs különbség a 12 ill. 12 között. Definíció Két szám asszociált, ha egymás egységszeresei. Megjegyzés (HF) a és b pontosan akkor asszociált, ha a b és b a. Definíció Egy számnak az asszociáltjai és az egységek a triviális osztói.
6 Elemi számelmélet Diszkrét matematika I. középszint ősz 6. Prímek, felbonthatatlanok Definíció Ha egy nem-nulla, nem egység számnak a triviális osztóin kívül nincs más osztója, akkor felbonthatatlannak (irreducibilisnek) nevezzük. Példa 2, 2, 3, 3, 5, 5 felbonthatatalnok. Példa 6 nem felbonthatatlan, mert 6 = 2 3. Definíció Egy nem-nulla, nem egység p számot prímszámnak nevezünk, ha p ab p a vagy p b. Példa 2, 2, 3, 3, 5, 5. Példa 6 nem prímszám, mert de 6 2 és 6 3.
7 Elemi számelmélet Diszkrét matematika I. középszint ősz 7. Prímek, felbonthatatlanok Álĺıtás Minden prímszám felbonthatatlan. Bizonyítás Legyen p prímszám és legyen p = ab egy felbontás. Igazolnunk kell, hogy a vagy b egység. Mivel p = ab, így p ab, ahonnan például p a. Ekkor a = pk = a(bk), azaz bk = 1, ahonnan következik, hogy b és k is egység. A fordított irány nem feltétlenül igaz: Z-ben igaz, (lásd később); {a + bi 5 : a, b Z}-ben nem igaz.
8 Elemi számelmélet Diszkrét matematika I. középszint ősz 8. Maradékos osztás A számelméletben a fő eszközünk a maradékos osztás lesz: Tétel Tetszőleges a, b 0 egész számokhoz egyértelműen léteznek q, r egészek, hogy a = bq + r és 0 r < b. Bizonyítás A tételt csak nemnegatív számok esetében bizonyítjuk. 1 Létezés: a szerinti indukcióval. Ha a < b, akkor a = b 0 + a (q = 0, r = a). Ha a b, akkor tegyük fel, hogy a-nál kisebb számok már feĺırhatók ilyen alakban. Legyen a b = bq + r. Ekkor a = b(q + 1) + r és legyen q = q + 1, r = r. 2 Egyértelműség: legyen a = bq + r = bq + r. Ekkor b(q q ) = r r. Ez csak akkor lehet, ha q = q és r = r.
9 Elemi számelmélet Diszkrét matematika I. középszint ősz 9. Maradékos osztás Definíció Legyenek a,b egész számok (b 0). Legyen a = b q + r (0 r < b ). Ekkor a mod b = r. Megjegyzés: q = a/b, ha b > 0, és q = a/b, ha b < 0. Példa 123 mod 10 = 3, 123 mod 100 = 23, 123 mod 1000 = 123; 123 mod 10 = 3, mod 10 = 7, 123 mod 100 = 77, 123 mod 1000 = 877; 123 mod 10 = 7,...
10 Elemi számelmélet Diszkrét matematika I. középszint ősz 10. Maradékos osztás Példa 1 Ha most 9 óra van, hány óra lesz 123 óra múlva? Osszuk el maradékosan 123-at 24-gyel: 123 = Tehát = 12: déli 12 óra lesz! 2 Ha most 9 óra van, hány óra lesz 116 óra múlva? Osszuk el maradékosan 116-ot 24-gyel: 116 = Tehát = 29. Újabb redukció: 29 = : hajnali 5 óra lesz! 3 Milyen napra fog esni jövőre november 11-e? Milyen napra esett három éve november 15-e? hétfő 0 kedd 1 szerda 2 csütörtök 3 péntek 4 szombat 5 vasárnap 6 Osszuk el maradékosan 365-öt 7-tel: 365 = kedd + 1 nap 1+1=2 szerda Osszuk el maradékosan -( )-ot (2012. szökőév) 7-tel: 1096 = 7 ( 157) + 3. szombat + 3 nap = 8 redukció = 1 kedd
11 Elemi számelmélet Diszkrét matematika I. középszint ősz 11. Számrendszerek 10-es számrendszerben a 123: 123 = = es számrendszerben a 123: (2) = (10) (2) = (10) Tétel Legyen q > 1 rögzített egész. Ekkor bármely n pozitív egész k egyértelműen feĺırható n = a i q i alakban, ahol 0 a i < q egészek, a k 0. i=0 Ez a feĺırás n q számrendszerben történő feĺırása. q a számrendszer alapja. a 0,..., a k az n jegyei. k = log q n.
12 Elemi számelmélet Diszkrét matematika I. középszint ősz 12. Számrendszerek n feĺırása a q alapú számrendszerben: n = Bizonyítás A tételt indukcióval bizonyítjuk. 1 n = 0 esetén a tétel igaz. k a i q i. 2 Tfh minden n-nél kisebb számot fel tudunk írni egyértelműen q alapú számrendszerben. A maradékos osztás tétele alapján létezik egyértelműen 0 a 0 < q egész, hogy q n a 0. Indukció alapján i=0 írjuk fel q alapú számrendszerben n a 0 q alapján a feĺırás egyértelmű. Ekkor n = = k a i q i 1, indukció i=1 k a i q i. i=0
13 Elemi számelmélet Diszkrét matematika I. középszint ősz 13. Számrendszerek Az előbbi bizonyítás módszert is ad a feĺırásra: Példa Írjuk fel az n = es számrendszerben feĺırt számot 2-es számrendszerben. i n n mod 2 n a i 2 jegyek
14 Elemi számelmélet Diszkrét matematika I. középszint ősz 14. Legnagyobb közös osztó Definíció Az a és b számoknak a d szám kitüntetett közös osztója (legnagyobb közös osztója), ha : d a, d b, és c a, c b c d. Figyelem! Itt a,,legnagyobb nem a szokásos rendezésre utal: Figyelem! 12-nek és 9-nek legnagyobb közös osztója lesz a 3 is. A legnagyobb közös osztó csak asszociáltság erejéig egyértelmű. Definíció Legyen (a, b) = lnko(a, b) a nemnegatív kitüntetett közös osztó! Definíció Az a és b számoknak az m szám kitüntetett közös többszöröse (legkisebb közös töbszöröse), ha : a m, b m, és a c, b c m c. Legyen [a, b] = lkkt(a, b) a nemnegatív kitüntetett közös többszörös!
15 Elemi számelmélet Diszkrét matematika I. középszint ősz 15. Legnagyobb közös osztó kiszámolása, euklideszi algoritmus Tétel Bármely két egész számnak létezik legnagyobb közös osztója, és ez meghatározható az euklideszi algoritmussal. Bizonyítás Ha valamelyik szám 0, akkor a legnagyobb közös osztó a másik szám. Tfh a, b nem-nulla számok. Végezzük el a következő osztásokat: a = bq 1 + r 1, 0 < r 1 < b, b = r 1q 2 + r 2, 0 < r 2 < r 1, r 1 = r 2q 3 + r 3, 0 < r 3 < r 2,. r n 2 = r n 1q n + r n, r n 1 = r nq n+1. 0 < r n < r n 1, Ekkor az lnko az utolsó nem-nulla maradék: (a, b) = r n. Itt a = r 1, b = r 0.
16 Elemi számelmélet Diszkrét matematika I. középszint ősz 16. Euklideszi algoritmus helyessége Bizonyítás (folyt.) a = bq 1 + r 1, 0 < r 1 < b, b = r 1q 2 + r 2, 0 < r 2 < r 1, r 1 = r 2q 3 + r 3, 0 < r 3 < r 2,. r n 2 = r n 1q n + r n, r n 1 = r nq n+1. 0 < r n < r n 1, Az algoritmus véges sok lépésben véget ér: b > r 1 > r 2 >.... Az r n maradék közös osztó: r n r n 1 r n r n 1 q n + r n = r n 2... r n b r n a. Az r n maradék a legnagyobb közös osztó: legyen c a, c b c a bq 1 = r 1 c b r 1 q 2 = r 2... c r n 2 r n 1 q n = r n.
17 Elemi számelmélet Diszkrét matematika I. középszint ősz 17. Legnagyobb közös osztó kiszámolása, euklideszi algoritmus Példa Számítsuk ki (172, 62) értékét! i r i q i r i 2 = r i 1 q i + r i = = = = = A legnagyobb közös osztó: (172, 62) = 2
18 Elemi számelmélet Diszkrét matematika I. középszint ősz 18. Legnagyobb közös osztó kiszámolása rekurzióval Tétel Legyen a 0. Ha b = 0, akkor (a, b) = a. Ha b 0, akkor (a, b) = ( b, a mod b ). Bizonyítás Ha b = 0, akkor a tétel nyilvánvaló. Mivel (a, b) = ( a, b ), feltehető, hogy a, b > 0. Ha b 0, osszuk el maradékosan a-t b-vel: a = b q + (a mod b). Ez az euklideszi algoritmus első sora. Példa Számítsuk ki (172, 62) értékét! (a, b) a mod b (172, 62) 48 (62, 48) 14 (48, 14) 6 (14, 6) 2 (6, 2) 0 A legnagyobb közös osztó: (172, 62) = 2.
19 Elemi számelmélet Diszkrét matematika I. középszint ősz 19. Legnagyobb közös osztó, további észrevételek Hasonló módon definiálható több szám legnagyobb közös osztója is (HF): (a 1, a 2,..., a n ). Álĺıtás (HF) Bármely a 1, a 2,..., a n egész számokra létezik (a 1, a 2,..., a n ) és (a 1, a 2,..., a n ) = ((... (a 1, a 2 ),..., a n 1 ), a n ). Álĺıtás (HF) Bármely a, b, c egész számokra (ca, cb) = c(a, b).
20 Elemi számelmélet Diszkrét matematika I. középszint ősz 20. Bővített euklideszi algoritmus Tétel Minden a, b egész számok esetén léteznek x, y egészek, hogy (a, b) = x a + y b. Bizonyítás Legyenek q i, r i az euklideszi algoritmussal megkapott hányadosok, maradékok. Legyen x 1 = 1, x 0 = 0 és i 1 esetén legyen x i = x i 2 q i x i 1. Hasonlóan legyen y 1 = 0, y 0 = 1 és i 1 esetén legyen y i = y i 2 q i y i 1. Ekkor i 1 esetén x i a + y i b = r i. (Biz.: HF, indukcióval) Speciálisan x n a + y n b = r n = (a, b).
21 Elemi számelmélet Diszkrét matematika I. középszint ősz 21. Bővitett euklideszi algoritmus Algoritmus: r i 2 = r i 1 q i + r i, Algoritmus: x 1 = 1, x 0 = 0, x i = x i 2 q i x i 1, Algoritmus: y 1 = 0, y 0 = 1, y i = y i 2 q i y i 1. Példa Számítsuk ki (172, 62) értékét, és oldjuk meg a 172x + 62y = (172, 62) egyenletet! i r n q n x i y i r i = 172x i + 62y i = = = ( 2) = 172 ( 1) = ( 11) = 172 ( 9) A feĺırás: 2 = 172 ( 9) , x = 9, y = 25.
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 8. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 8. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. estis képzés 017. ősz 1. Diszkrét matematika 1. estis képzés 4. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 1. estis képzés 017. ősz 1. Diszkrét matematika 1. estis képzés 4. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 9. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 9. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 8. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 8. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. estis képzés. Komputeralgebra Tanszék ősz
 Diszkrét matematika 1. estis képzés 2015. ősz 1. Diszkrét matematika 1. estis képzés 6. előadás Mérai László diái alapján Komputeralgebra Tanszék 2015. ősz Elemi számelmélet Diszkrét matematika 1. estis
Diszkrét matematika 1. estis képzés 2015. ősz 1. Diszkrét matematika 1. estis képzés 6. előadás Mérai László diái alapján Komputeralgebra Tanszék 2015. ősz Elemi számelmélet Diszkrét matematika 1. estis
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 10. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 10. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 10. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Felhívás Diszkrét matematika I. középszint 2014.
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 10. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Felhívás Diszkrét matematika I. középszint 2014.
Klasszikus algebra előadás. Waldhauser Tamás április 28.
 Klasszikus algebra előadás Waldhauser Tamás 2014. április 28. 5. Számelmélet integritástartományokban Oszthatóság Mostantól R mindig tetszőleges integritástartományt jelöl. 5.1. Definíció. Azt mondjuk,
Klasszikus algebra előadás Waldhauser Tamás 2014. április 28. 5. Számelmélet integritástartományokban Oszthatóság Mostantól R mindig tetszőleges integritástartományt jelöl. 5.1. Definíció. Azt mondjuk,
1. A maradékos osztás
 1. A maradékos osztás Egész számok osztása Példa 223 = 7 31+6. Visszaszorzunk Kivonunk 223 : 7 = 31 21 13 7 6 Állítás (számelméletből) Minden a,b Z esetén, ahol b 0, létezik olyan q,r Z, hogy a = bq +
1. A maradékos osztás Egész számok osztása Példa 223 = 7 31+6. Visszaszorzunk Kivonunk 223 : 7 = 31 21 13 7 6 Állítás (számelméletből) Minden a,b Z esetén, ahol b 0, létezik olyan q,r Z, hogy a = bq +
Számelmélet (2017. február 8.) Bogya Norbert, Kátai-Urbán Kamilla
 Számelmélet (2017 február 8) Bogya Norbert, Kátai-Urbán Kamilla 1 Oszthatóság 1 Definíció Legyen a, b Z Az a osztója b-nek, ha létezik olyan c Z egész szám, melyre ac = b Jelölése: a b 2 Példa 3 12, 2
Számelmélet (2017 február 8) Bogya Norbert, Kátai-Urbán Kamilla 1 Oszthatóság 1 Definíció Legyen a, b Z Az a osztója b-nek, ha létezik olyan c Z egész szám, melyre ac = b Jelölése: a b 2 Példa 3 12, 2
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 4. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 4. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
1. Polinomok számelmélete
 1. Polinomok számelmélete Oszthatóság, egységek. Emlékeztető Legyen R a C, R, Q, Z egyike. Azt mondjuk, hogy (1) a g R[x] polinom osztója f R[x]-nek R[x]-ben, ha létezik olyan h R[x] polinom, hogy f (x)
1. Polinomok számelmélete Oszthatóság, egységek. Emlékeztető Legyen R a C, R, Q, Z egyike. Azt mondjuk, hogy (1) a g R[x] polinom osztója f R[x]-nek R[x]-ben, ha létezik olyan h R[x] polinom, hogy f (x)
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 1. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 1. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 2. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 2. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Számelmélet. 1. Oszthatóság Prímszámok
 Számelmélet Legnagyobb közös osztó, Euklideszi algoritmus. Lineáris diofantoszi egyenletek. Számelméleti kongruenciák, kongruenciarendszerek. Euler-féle ϕ-függvény. 1. Oszthatóság 1. Definíció. Legyen
Számelmélet Legnagyobb közös osztó, Euklideszi algoritmus. Lineáris diofantoszi egyenletek. Számelméleti kongruenciák, kongruenciarendszerek. Euler-féle ϕ-függvény. 1. Oszthatóság 1. Definíció. Legyen
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2015. ősz 1. Diszkrét matematika 2.C szakirány 7. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2015.
Diszkrét matematika 2.C szakirány 2015. ősz 1. Diszkrét matematika 2.C szakirány 7. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2015.
Diszkrét matematika 2.
 Diszkrét matematika 2. 2018. november 23. 1. Diszkrét matematika 2. 9. előadás Fancsali Szabolcs Levente [email protected] www.cs.elte.hu/ nudniq Komputeralgebra Tanszék 2018. november 23. Diszkrét matematika
Diszkrét matematika 2. 2018. november 23. 1. Diszkrét matematika 2. 9. előadás Fancsali Szabolcs Levente [email protected] www.cs.elte.hu/ nudniq Komputeralgebra Tanszék 2018. november 23. Diszkrét matematika
Kongruenciák. Waldhauser Tamás
 Algebra és számelmélet 3 előadás Kongruenciák Waldhauser Tamás 2014 őszi félév Tartalom 1. Diofantoszi egyenletek 2. Kongruenciareláció, maradékosztályok 3. Lineáris kongruenciák és multiplikatív inverzek
Algebra és számelmélet 3 előadás Kongruenciák Waldhauser Tamás 2014 őszi félév Tartalom 1. Diofantoszi egyenletek 2. Kongruenciareláció, maradékosztályok 3. Lineáris kongruenciák és multiplikatív inverzek
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Számelmélet I.
 Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
1.1. Definíció. Azt mondjuk, hogy a oszója b-nek, vagy más szóval, b osztható a-val, ha létezik olyan x Z, hogy b = ax. Ennek jelölése a b.
 1. Oszthatóság, legnagyobb közös osztó Ebben a jegyzetben minden változó egész számot jelöl. 1.1. Definíció. Azt mondjuk, hogy a oszója b-nek, vagy más szóval, b osztható a-val, ha létezik olyan x Z, hogy
1. Oszthatóság, legnagyobb közös osztó Ebben a jegyzetben minden változó egész számot jelöl. 1.1. Definíció. Azt mondjuk, hogy a oszója b-nek, vagy más szóval, b osztható a-val, ha létezik olyan x Z, hogy
2. Feladatsor. N k = {(a 1,...,a k ) : a 1,...,a k N}
 2. Feladatsor Oszthatóság, legnagyobb közös osztó, prímfaktorizáció az egész számok körében 1 Kötelező házi feladat(ok) 2., Határozzuk meg a ϕ:z Z, z [ z 5] leképezés magját. Adjuk meg a ker(ϕ)-hez tartozó
2. Feladatsor Oszthatóság, legnagyobb közös osztó, prímfaktorizáció az egész számok körében 1 Kötelező házi feladat(ok) 2., Határozzuk meg a ϕ:z Z, z [ z 5] leképezés magját. Adjuk meg a ker(ϕ)-hez tartozó
1. A maradékos osztás
 1. A maradékos osztás Egész számok osztása. 223 = 7 31 + 6. Visszaszorzunk 223 : 7 = 31 21 13 7 6 Állítás (számelméletből) Minden a, b Z esetén, ahol b 0, létezik olyan q, r Z, hogy a = bq + r és r < b.
1. A maradékos osztás Egész számok osztása. 223 = 7 31 + 6. Visszaszorzunk 223 : 7 = 31 21 13 7 6 Állítás (számelméletből) Minden a, b Z esetén, ahol b 0, létezik olyan q, r Z, hogy a = bq + r és r < b.
Polinomok (el adásvázlat, április 15.) Maróti Miklós
 Polinomok (el adásvázlat, 2008 április 15) Maróti Miklós Ennek az el adásnak a megértéséhez a következ fogalmakat kell tudni: gy r, gy r additív csoportja, zéruseleme, és multiplikatív félcsoportja, egységelemes
Polinomok (el adásvázlat, 2008 április 15) Maróti Miklós Ennek az el adásnak a megértéséhez a következ fogalmakat kell tudni: gy r, gy r additív csoportja, zéruseleme, és multiplikatív félcsoportja, egységelemes
Vizsgatematika Bevezetés a matematikába II tárgyhoz tavasz esti tagozat
 8.2. Gyűrűk Fogalmak, definíciók: Gyűrű, kommutatív gyűrű, integritási tartomány, test Az (R, +, ) algebrai struktúra gyűrű, ha + és R-en binér műveletek, valamint I. (R, +) Abel-csoport, II. (R, ) félcsoport,
8.2. Gyűrűk Fogalmak, definíciók: Gyűrű, kommutatív gyűrű, integritási tartomány, test Az (R, +, ) algebrai struktúra gyűrű, ha + és R-en binér műveletek, valamint I. (R, +) Abel-csoport, II. (R, ) félcsoport,
OSZTHATÓSÁG. Osztók és többszörösök : a 3 többszörösei : a 4 többszörösei Ahol mindkét jel megtalálható a 12 többszöröseit találjuk.
 Osztók és többszörösök 1783. A megadott számok elsõ tíz többszöröse: 3: 3 6 9 12 15 18 21 24 27 30 4: 4 8 12 16 20 24 28 32 36 40 5: 5 10 15 20 25 30 35 40 45 50 6: 6 12 18 24 30 36 42 48 54 60 1784. :
Osztók és többszörösök 1783. A megadott számok elsõ tíz többszöröse: 3: 3 6 9 12 15 18 21 24 27 30 4: 4 8 12 16 20 24 28 32 36 40 5: 5 10 15 20 25 30 35 40 45 50 6: 6 12 18 24 30 36 42 48 54 60 1784. :
Bevezetés az algebrába az egész számok
 Bevezetés az algebrába az egész számok Wettl Ferenc V. 15-09-11 Wettl Ferenc Bevezetés az algebrába az egész számok V. 15-09-11 1 / 32 Jelölések 1 Egész számok és sorozataik 2 Oszthatóság 3 Közös osztók
Bevezetés az algebrába az egész számok Wettl Ferenc V. 15-09-11 Wettl Ferenc Bevezetés az algebrába az egész számok V. 15-09-11 1 / 32 Jelölések 1 Egész számok és sorozataik 2 Oszthatóság 3 Közös osztók
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 11. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Kongruenciák Diszkrét matematika I. középszint 2014.
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 11. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Kongruenciák Diszkrét matematika I. középszint 2014.
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 3. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2016. ősz 1. Diszkrét matematika 3. estis képzés 3. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Polinomok (előadásvázlat, október 21.) Maróti Miklós
 Polinomok (előadásvázlat, 2012 október 21) Maróti Miklós Ennek az előadásnak a megértéséhez a következő fogalmakat kell tudni: gyűrű, gyűrű additív csoportja, zéruseleme, és multiplikatív félcsoportja,
Polinomok (előadásvázlat, 2012 október 21) Maróti Miklós Ennek az előadásnak a megértéséhez a következő fogalmakat kell tudni: gyűrű, gyűrű additív csoportja, zéruseleme, és multiplikatív félcsoportja,
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 5. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 5. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 1. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 1. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
1. Egész együtthatós polinomok
 1. Egész együtthatós polinomok Oszthatóság egész számmal Emlékeztető (K3.1.3): Ha f,g Z[x], akkor f g akkor és csak akkor, ha van olyan h Z[x], hogy g = fh. Állítás (K3.1.6) Az f(x) Z[x] akkor és csak
1. Egész együtthatós polinomok Oszthatóság egész számmal Emlékeztető (K3.1.3): Ha f,g Z[x], akkor f g akkor és csak akkor, ha van olyan h Z[x], hogy g = fh. Állítás (K3.1.6) Az f(x) Z[x] akkor és csak
Számelméleti alapfogalmak
 1 Számelméleti alapfogalmak 1 Definíció Az a IN szám osztója a b IN számnak ha létezik c IN melyre a c = b Jelölése: a b 2 Példa a 0 bármely a számra teljesül, mivel c = 0 univerzálisan megfelel: a 0 =
1 Számelméleti alapfogalmak 1 Definíció Az a IN szám osztója a b IN számnak ha létezik c IN melyre a c = b Jelölése: a b 2 Példa a 0 bármely a számra teljesül, mivel c = 0 univerzálisan megfelel: a 0 =
Alapvető polinomalgoritmusok
 Alapvető polinomalgoritmusok Maradékos osztás Euklideszi algoritmus Bővített euklideszi algoritmus Alkalmazás: Véges testek konstrukciója Irodalom: Iványi Antal: Informatikai algoritmusok II, 18. fejezet.
Alapvető polinomalgoritmusok Maradékos osztás Euklideszi algoritmus Bővített euklideszi algoritmus Alkalmazás: Véges testek konstrukciója Irodalom: Iványi Antal: Informatikai algoritmusok II, 18. fejezet.
2017, Diszkrét matematika
 Diszkrét matematika 10. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia [email protected] 2017, őszi félév Miről volt szó az elmúlt előadáson? a prímszámtétel prímszámok,
Diszkrét matematika 10. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia [email protected] 2017, őszi félév Miről volt szó az elmúlt előadáson? a prímszámtétel prímszámok,
Hatványozás. A hatványozás azonosságai
 Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
illetve a n 3 illetve a 2n 5
 BEVEZETÉS A SZÁMELMÉLETBE 1. Határozzuk meg azokat az a természetes számokat ((a, b) számpárokat), amely(ek)re teljesülnek az alábbi feltételek: a. [a, 16] = 48 b. (a, 0) = 1 c. (a, 60) = 15 d. (a, b)
BEVEZETÉS A SZÁMELMÉLETBE 1. Határozzuk meg azokat az a természetes számokat ((a, b) számpárokat), amely(ek)re teljesülnek az alábbi feltételek: a. [a, 16] = 48 b. (a, 0) = 1 c. (a, 60) = 15 d. (a, b)
Klasszikus algebra előadás. Waldhauser Tamás március 24.
 Klasszikus algebra előadás Waldhauser Tamás 2014. március 24. Irreducibilitás 3.33. Definíció. A p T [x] polinom irreducibilis, ha legalább elsőfokú, és csak úgy bontható két polinom szorzatára, hogy az
Klasszikus algebra előadás Waldhauser Tamás 2014. március 24. Irreducibilitás 3.33. Definíció. A p T [x] polinom irreducibilis, ha legalább elsőfokú, és csak úgy bontható két polinom szorzatára, hogy az
2016, Diszkrét matematika
 Diszkrét matematika 8. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia [email protected] 2016, őszi félév Miről volt szó az elmúlt előadáson? a Fibonacci számsorozat
Diszkrét matematika 8. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia [email protected] 2016, őszi félév Miről volt szó az elmúlt előadáson? a Fibonacci számsorozat
Bevezetés az algebrába 1
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Bevezetés az algebrába 1 BMETE92AX23 Egész számok 2 H406 2016-09-13,15,18 Wettl Ferenc
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Bevezetés az algebrába 1 BMETE92AX23 Egész számok 2 H406 2016-09-13,15,18 Wettl Ferenc
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 3. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Relációk Diszkrét matematika I. középszint 2014.
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 3. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Relációk Diszkrét matematika I. középszint 2014.
Minden egész szám osztója önmagának, azaz a a minden egész a-ra.
 1. Számelmélet Definíció: Az a egész szám osztója a egész számnak, ha létezik olyan c egész szám, melyre = ac. Ezt a következőképpen jelöljük: a Tulajdonságok: Minden egész szám osztója önmagának, azaz
1. Számelmélet Definíció: Az a egész szám osztója a egész számnak, ha létezik olyan c egész szám, melyre = ac. Ezt a következőképpen jelöljük: a Tulajdonságok: Minden egész szám osztója önmagának, azaz
Diszkrét matematika 2. estis képzés
 Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 1. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 1. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 1.
 Diszkrét matematika 1. Nagy Gábor [email protected] [email protected] ELTE IK Komputeralgebra Tanszék 014. ősz 014-15 őszi félév Gyakorlat: 1. ZH tervezett időpontja: október 1.,. ZH tervezett
Diszkrét matematika 1. Nagy Gábor [email protected] [email protected] ELTE IK Komputeralgebra Tanszék 014. ősz 014-15 őszi félév Gyakorlat: 1. ZH tervezett időpontja: október 1.,. ZH tervezett
1. melléklet: A tanárokkal készített interjúk főbb kérdései
 12. Mellékletek 1. melléklet: A tanárokkal készített interjúk főbb kérdései 1. Mikor tanít számelméletet és hány órában? (Pl. 9. osztályban a nevezetes azonosságok után 4 órában.) 2. Milyen könyvet használnak
12. Mellékletek 1. melléklet: A tanárokkal készített interjúk főbb kérdései 1. Mikor tanít számelméletet és hány órában? (Pl. 9. osztályban a nevezetes azonosságok után 4 órában.) 2. Milyen könyvet használnak
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 10. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 10. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 016. ősz 1. Diszkrét matematika 1. középszint 1. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 016. ősz 1. Diszkrét matematika 1. középszint 1. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
2. Tétel (Az oszthatóság tulajdonságai). : 2. Nullát minden elem osztja, de. 3. a nulla csak a nullának osztója.
 Számelmélet és rejtjelezési eljárások. (Számelméleti alapok. RSA és alkalmazásai, Die- Hellman-Merkle kulcscsere.) A számelméletben speciálisan az egész számok, általánosan a egységelemes integritási tartomány
Számelmélet és rejtjelezési eljárások. (Számelméleti alapok. RSA és alkalmazásai, Die- Hellman-Merkle kulcscsere.) A számelméletben speciálisan az egész számok, általánosan a egységelemes integritási tartomány
Bevezetés az algebrába 1
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Bevezetés az algebrába 1 BMETE92AX23 Egész számok H406 2017-09-04,06,08,11 Wettl Ferenc
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Bevezetés az algebrába 1 BMETE92AX23 Egész számok H406 2017-09-04,06,08,11 Wettl Ferenc
7. Számelmélet. 1. Lehet-e négyzetszám az a pozitív egész szám, amelynek tízes számrendszerbeli alakjában 510 darab 1-es és valahány 0 szerepel?
 7. Számelmélet I. Nulladik ZH-ban láttuk: 1. Lehet-e négyzetszám az a pozitív egész szám, amelynek tízes számrendszerbeli alakjában 510 darab 1-es és valahány 0 szerepel? ELTE 2006. október 27. (matematika
7. Számelmélet I. Nulladik ZH-ban láttuk: 1. Lehet-e négyzetszám az a pozitív egész szám, amelynek tízes számrendszerbeli alakjában 510 darab 1-es és valahány 0 szerepel? ELTE 2006. október 27. (matematika
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 5. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 5. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 11. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 11. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2. estis képzés
 Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 4-6. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 4-6. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Következik, hogy B-nek minden prímosztója 4k + 1 alakú, de akkor B maga is 4k + 1 alakú, s ez ellentmondás.
 Prímszámok A (pozitív) prímszámok sorozata a következő: 2, 3, 5, 7, 11, 13, 17, 19,... 1. Tétel. Végtelen sok prímszám van. Első bizonyítás. (Euklidész) Tegyük fel, hogy állításunk nem igaz, tehát véges
Prímszámok A (pozitív) prímszámok sorozata a következő: 2, 3, 5, 7, 11, 13, 17, 19,... 1. Tétel. Végtelen sok prímszám van. Első bizonyítás. (Euklidész) Tegyük fel, hogy állításunk nem igaz, tehát véges
Oszthatóság. Oszthatóság definíciója (az egészek illetve a természetes számok halmazán):
 Oszthatóság Oszthatóság definíciója (az egészek illetve a természetes számok halmazán): Azt mondjuk, hogy az a osztója b-nek (jel: a b), ha van olyan c egész, amelyre ac = b. A témakörben a betűk egész
Oszthatóság Oszthatóság definíciója (az egészek illetve a természetes számok halmazán): Azt mondjuk, hogy az a osztója b-nek (jel: a b), ha van olyan c egész, amelyre ac = b. A témakörben a betűk egész
RSA algoritmus. P(M) = M e mod n. S(C) = C d mod n. A helyesség igazoláshoz szükséges számelméleti háttér. a φ(n) = 1 mod n, a (a 1,a 2,...
 RSA algoritmus 1. Vegyünk véletlenszerűen két különböző nagy prímszámot, p-t és q-t. 2. Legyen n = pq. 3. Vegyünk egy olyan kis páratlan e számot, amely relatív prím φ(n) = (p 1)(q 1)-hez. 4. Keressünk
RSA algoritmus 1. Vegyünk véletlenszerűen két különböző nagy prímszámot, p-t és q-t. 2. Legyen n = pq. 3. Vegyünk egy olyan kis páratlan e számot, amely relatív prím φ(n) = (p 1)(q 1)-hez. 4. Keressünk
Diszkrét matematika I.
 Diszkrét matematika I. - Vizsga anyag 1 EÖTVÖS LORÁND TUDOMÁNYEGYETEM INFORMATIKAI KAR Diszkrét matematika I. Vizsgaanyag Készítette: Nyilas Árpád Diszkrét matematika I. - Vizsga anyag 2 Bizonyítások 1)
Diszkrét matematika I. - Vizsga anyag 1 EÖTVÖS LORÁND TUDOMÁNYEGYETEM INFORMATIKAI KAR Diszkrét matematika I. Vizsgaanyag Készítette: Nyilas Árpád Diszkrét matematika I. - Vizsga anyag 2 Bizonyítások 1)
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 6. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 6. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 6. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 6. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 11. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 11. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján
Számelmélet. 4. Igazolja, hogy ha hat egész szám összege páratlan, akkor e számok szorzata páros!
 Számelmélet - oszthatóság definíciója - oszthatósági szabályok - maradékos osztás - prímek definíciója - összetett szám definíciója - legnagyobb közös osztó definíciója - legnagyobb közös osztó meghatározása
Számelmélet - oszthatóság definíciója - oszthatósági szabályok - maradékos osztás - prímek definíciója - összetett szám definíciója - legnagyobb közös osztó definíciója - legnagyobb közös osztó meghatározása
Algebrai alapismeretek az Algebrai síkgörbék c. tárgyhoz. 1. Integritástartományok, oszthatóság
 Algebrai alapismeretek az Algebrai síkgörbék c tárgyhoz 1 Integritástartományok, oszthatóság 11 Definíció A nullaosztómentes, egységelemes kommutatív gyűrűket integritástartománynak nevezzük 11 példa Integritástartományra
Algebrai alapismeretek az Algebrai síkgörbék c tárgyhoz 1 Integritástartományok, oszthatóság 11 Definíció A nullaosztómentes, egységelemes kommutatív gyűrűket integritástartománynak nevezzük 11 példa Integritástartományra
SE EKK EIFTI Matematikai analízis
 SE EKK EIFTI Matematikai analízis 2. Blokk A számelmélet a matematikának a számokkal foglalkozó ága. Gyakran azonban ennél sz kebb értelemben használják a számelmélet szót: az egész számok elméletét értik
SE EKK EIFTI Matematikai analízis 2. Blokk A számelmélet a matematikának a számokkal foglalkozó ága. Gyakran azonban ennél sz kebb értelemben használják a számelmélet szót: az egész számok elméletét értik
1. Hatvány és többszörös gyűrűben
 1. Hatvány és többszörös gyűrűben Hatvány és többszörös Definíció (K2.2.19) Legyen asszociatív művelet és n pozitív egész. Ekkor a n jelentse az n tényezős a a... a szorzatot. Ez az a elem n-edik hatványa.
1. Hatvány és többszörös gyűrűben Hatvány és többszörös Definíció (K2.2.19) Legyen asszociatív művelet és n pozitív egész. Ekkor a n jelentse az n tényezős a a... a szorzatot. Ez az a elem n-edik hatványa.
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2017. ősz 1. Diszkrét matematika 2.C szakirány 2. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2017.
Diszkrét matematika 2.C szakirány 2017. ősz 1. Diszkrét matematika 2.C szakirány 2. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2017.
Bizonyítási módszerek - megoldások. 1. Igazoljuk, hogy menden természetes szám esetén ha. Megoldás: 9 n n = 9k = 3 3k 3 n.
 Bizonyítási módszerek - megoldások 1. Igazoljuk, hogy menden természetes szám esetén ha (a) 9 n 3 n (b) 4 n 2 n (c) 21 n 3 n (d) 21 n 7 n (e) 5 n 25 n (f) 4 n 16 n (g) 15 n (3 n 5 n) 9 n n = 9k = 3 3k
Bizonyítási módszerek - megoldások 1. Igazoljuk, hogy menden természetes szám esetén ha (a) 9 n 3 n (b) 4 n 2 n (c) 21 n 3 n (d) 21 n 7 n (e) 5 n 25 n (f) 4 n 16 n (g) 15 n (3 n 5 n) 9 n n = 9k = 3 3k
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 2. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 2. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 5. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Számfogalom bővítése Diszkrét matematika I. középszint
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 5. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Számfogalom bővítése Diszkrét matematika I. középszint
Tartalom. Algebrai és transzcendens számok
 Nevezetes számelméleti problémák Tartalom 6. Nevezetes számelméleti problémák Számok felbontása hatványok összegére Prímszámok Algebrai és transzcendens számok 6.1. Definíció. Az (x, y, z) N 3 számhármast
Nevezetes számelméleti problémák Tartalom 6. Nevezetes számelméleti problémák Számok felbontása hatványok összegére Prímszámok Algebrai és transzcendens számok 6.1. Definíció. Az (x, y, z) N 3 számhármast
Mátrixok február Feladat: Legyen A = ( ( B =
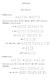 Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2013 ősz 1. Diszkrét matematika I. középszint 9. előadás Mérai László [email protected] compalg.inf.elte.hu/ merai Komputeralgebra Tanszék 2013 ősz Halmazok Diszkrét
Diszkrét matematika I. középszint 2013 ősz 1. Diszkrét matematika I. középszint 9. előadás Mérai László [email protected] compalg.inf.elte.hu/ merai Komputeralgebra Tanszék 2013 ősz Halmazok Diszkrét
Számelmélet Megoldások
 Számelmélet Megoldások 1) Egy számtani sorozat második tagja 17, harmadik tagja 1. a) Mekkora az első 150 tag összege? (5 pont) Kiszámoltuk ebben a sorozatban az első 111 tag összegét: 5 863. b) Igaz-e,
Számelmélet Megoldások 1) Egy számtani sorozat második tagja 17, harmadik tagja 1. a) Mekkora az első 150 tag összege? (5 pont) Kiszámoltuk ebben a sorozatban az első 111 tag összegét: 5 863. b) Igaz-e,
Oszthatósági problémák
 Oszthatósági problémák Érdekes kérdés, hogy egy adott számot el lehet-e osztani egy másik számmal (maradék nélkül). Ezek eldöntésére a matematika tanulmányok során néhány speciális esetre látunk is példát,
Oszthatósági problémák Érdekes kérdés, hogy egy adott számot el lehet-e osztani egy másik számmal (maradék nélkül). Ezek eldöntésére a matematika tanulmányok során néhány speciális esetre látunk is példát,
: s s t 2 s t. m m m. e f e f. a a ab a b c. a c b ac. 5. Végezzük el a kijelölt m veleteket a változók lehetséges értékei mellett!
 nomosztással a megoldást visszavezethetjük egy alacsonyabb fokú egyenlet megoldására Mivel a 4 6 8 6 egyenletben az együtthatók összege 6 8 6 ezért az egyenletnek gyöke az (mert esetén a kifejezés helyettesítési
nomosztással a megoldást visszavezethetjük egy alacsonyabb fokú egyenlet megoldására Mivel a 4 6 8 6 egyenletben az együtthatók összege 6 8 6 ezért az egyenletnek gyöke az (mert esetén a kifejezés helyettesítési
Elemi algebrai eszközökkel megoldható versenyfeladatok Ábrahám Gábor, Szeged
 Magas szintű matematikai tehetséggondozás Elemi algebrai eszközökkel megoldható versenyfeladatok Ábrahám Gábor, Szeged Ahhoz, hogy egy diák kimagasló eredményeket érhessen el matematika versenyeken, elengedhetetlenül
Magas szintű matematikai tehetséggondozás Elemi algebrai eszközökkel megoldható versenyfeladatok Ábrahám Gábor, Szeged Ahhoz, hogy egy diák kimagasló eredményeket érhessen el matematika versenyeken, elengedhetetlenül
Prezentációk készítése
 Prezentációk készítése 2009 1 / 14 Prezentációk készítése Beamer gyorstalpaló Írta: Kiss Emil [email protected] 2009 Áttekintés Prezentációk készítése 2009 2 / 14 A beamer koncepciója A beamer egy L A
Prezentációk készítése 2009 1 / 14 Prezentációk készítése Beamer gyorstalpaló Írta: Kiss Emil [email protected] 2009 Áttekintés Prezentációk készítése 2009 2 / 14 A beamer koncepciója A beamer egy L A
Matematika 7. osztály
 ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Hat évfolyamos képzés Matematika 7. osztály III. rész: Számelmélet Készítette: Balázs Ádám Budapest, 2018 2. Tartalomjegyzék Tartalomjegyzék III.
ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Hat évfolyamos képzés Matematika 7. osztály III. rész: Számelmélet Készítette: Balázs Ádám Budapest, 2018 2. Tartalomjegyzék Tartalomjegyzék III.
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 017. ősz 1. Diszkrét matematika 1. középszint. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 017. ősz 1. Diszkrét matematika 1. középszint. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Algebra es sz amelm elet 3 el oad as Nevezetes sz amelm eleti probl em ak Waldhauser Tam as 2014 oszi f el ev
 Algebra és számelmélet 3 előadás Nevezetes számelméleti problémák Waldhauser Tamás 2014 őszi félév Tartalom 1. Számok felbontása hatványok összegére 2. Prímszámok 3. Algebrai és transzcendens számok Tartalom
Algebra és számelmélet 3 előadás Nevezetes számelméleti problémák Waldhauser Tamás 2014 őszi félév Tartalom 1. Számok felbontása hatványok összegére 2. Prímszámok 3. Algebrai és transzcendens számok Tartalom
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 2. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 2. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
1. megold s: A keresett háromjegyű szám egyik számjegye a 3-as, a két ismeretlen számjegyet jelölje a és b. A feltétel szerint
 A 004{005. tan vi matematika OKTV I. kateg ria els (iskolai) fordul ja feladatainak megold sai 1. feladat Melyek azok a 10-es számrendszerbeli háromjegyű pozitív egész számok, amelyeknek számjegyei közül
A 004{005. tan vi matematika OKTV I. kateg ria els (iskolai) fordul ja feladatainak megold sai 1. feladat Melyek azok a 10-es számrendszerbeli háromjegyű pozitív egész számok, amelyeknek számjegyei közül
4. Algebrai Módszerek Klasszikus Eredmények
 4. Algebrai Módszerek Klasszikus Eredmények Igazolásában, Út az Algebrai Számelmélet felé 4.1. Maradékosztálygyűrűk egységcsoportjai szerkezete. Jelölés. Tetszőleges n > 1 egészre jelölje U n a Z n maradékosztálygyűrű
4. Algebrai Módszerek Klasszikus Eredmények Igazolásában, Út az Algebrai Számelmélet felé 4.1. Maradékosztálygyűrűk egységcsoportjai szerkezete. Jelölés. Tetszőleges n > 1 egészre jelölje U n a Z n maradékosztálygyűrű
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Számelmélet
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Számelmélet A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Számelmélet A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
5. Az Algebrai Számelmélet Elemei
 5. Az Algebrai Számelmélet Elemei 5.0. Bevezetés. Az algebrai számelmélet legegyszerűbb kérdései az ún. algebrai számtestek egészei gyűrűjének aritmetikai tulajdonságainak vizsgálata. Ezek legegyszerűbb
5. Az Algebrai Számelmélet Elemei 5.0. Bevezetés. Az algebrai számelmélet legegyszerűbb kérdései az ún. algebrai számtestek egészei gyűrűjének aritmetikai tulajdonságainak vizsgálata. Ezek legegyszerűbb
SzA XIII. gyakorlat, december. 3/5.
 SzA XIII. gyakorlat, 2013. december. 3/5. Drótos Márton 3 + 2 = 1 [email protected] 1. Határozzuk meg az Euklidészi algoritmussal lnko(504, 372)-t! Határozzuk meg lkkt(504, 372)-t! Hány osztója van 504-nek?
SzA XIII. gyakorlat, 2013. december. 3/5. Drótos Márton 3 + 2 = 1 [email protected] 1. Határozzuk meg az Euklidészi algoritmussal lnko(504, 372)-t! Határozzuk meg lkkt(504, 372)-t! Hány osztója van 504-nek?
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 207. tavasz. Diszkrét matematika 2.C szakirány 9. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 207.
Diszkrét matematika 2.C szakirány 207. tavasz. Diszkrét matematika 2.C szakirány 9. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 207.
Juhász Tibor. Diszkrét matematika
 Juhász Tibor Diszkrét matematika Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Juhász Tibor Diszkrét matematika Eger, 2013 Bíráló:??? Készült a TÁMOP-412A/1-11/2011-0038 támogatásával
Juhász Tibor Diszkrét matematika Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Juhász Tibor Diszkrét matematika Eger, 2013 Bíráló:??? Készült a TÁMOP-412A/1-11/2011-0038 támogatásával
2018, Diszkre t matematika. 10. elo ada s
 Diszkre t matematika 10. elo ada s MA RTON Gyo ngyve r [email protected] Sapientia Egyetem, Matematika-Informatika Tansze k Marosva sa rhely, Roma nia 2018, o szi fe le v MA RTON Gyo ngyve r 2018,
Diszkre t matematika 10. elo ada s MA RTON Gyo ngyve r [email protected] Sapientia Egyetem, Matematika-Informatika Tansze k Marosva sa rhely, Roma nia 2018, o szi fe le v MA RTON Gyo ngyve r 2018,
(Diszkrét idejű Markov-láncok állapotainak
 (Diszkrét idejű Markov-láncok állapotainak osztályozása) March 21, 2019 Markov-láncok A Markov-láncok anaĺızise főként a folyamat lehetséges realizációi valószínűségeinek kiszámolásával foglalkozik. Ezekben
(Diszkrét idejű Markov-láncok állapotainak osztályozása) March 21, 2019 Markov-láncok A Markov-láncok anaĺızise főként a folyamat lehetséges realizációi valószínűségeinek kiszámolásával foglalkozik. Ezekben
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Számelmélet
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Számelmélet A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Számelmélet A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Diszkrét matematika 1. estis képzés
 Diszkrét matematika 1. estis képzés 2019. tavasz 1. Diszkrét matematika 1. estis képzés 5. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 1. estis képzés 2019. tavasz 1. Diszkrét matematika 1. estis képzés 5. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 7. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 7. előadás Nagy Gábor [email protected] [email protected] compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
XXVI. Erdélyi Magyar Matematikaverseny Zilah, február II. forduló osztály
 . feladat: Szupercsiga egy függőleges falon mászik felfelé. Első nap 4 cm-t tesz meg, éjszaka cm-t visszacsúszik. Második napon 9 cm-t tesz meg, éjszaka 4 cm-t csúszik vissza, harmadik napon 6 cm-t mászik,
. feladat: Szupercsiga egy függőleges falon mászik felfelé. Első nap 4 cm-t tesz meg, éjszaka cm-t visszacsúszik. Második napon 9 cm-t tesz meg, éjszaka 4 cm-t csúszik vissza, harmadik napon 6 cm-t mászik,
