Szöveges feladatok a mátrixaritmetika alkalmazására

HTML
DOWNLOAD

Méret: px

Mutatás kezdődik a ... oldaltól:

Download "Szöveges feladatok a mátrixaritmetika alkalmazására"

Magda Hegedűsné
9 évvel ezelőtt
Látták:

1 Szöveges feladatok a mátrixaritmetika alkalmazására Bevezetés: Tekintsük az alábbi -es mátrixot: A. Szorozzuk meg ezt jobbról egy alkalmas méretű (azaz -es) oszlopvektorral, amely az R tér kanonikus bázisának első vektorával, az e vektorral azonosítható: Ae. Megfigyelhető, hogy az eredményül kapott oszlopvektor éppen az A mátrix első oszlopvektora. Hasonló módon, ha az A mátrixot az R tér kanonikus bázisának második vektorával, az e vektorral szorozzuk jobbról, akkor eredményül az A mátrix második oszlopvektorát kapjuk: Ae, és így tovább. Szorozzuk meg most az A mátrixot balról egy alkalmas méretű (azaz -as) sorvektorral, amely az R tér kanonikus bázisának első vektorával, az e vektorral azonosítható. Hangsúlyozzuk azt, hogy sorvektorral akarunk balról szorozni a transzponált jel kiírásával: e T A [ ]. Megfigyelhető, hogy az eredményül kapott sorvektor éppen az A mátrix első sorvektora. Hasonló módon, ha az A mátrixot az R tér kanonikus bázisának második vektorának megfelelő sorvektorral, azaz az e T vektorral szorozzuk balról, akkor eredményül az A mátrix második sorvektorát kapjuk: e T A [ ], és így tovább.

2 Az olyan oszlopvektorokat, amelyeknek minden eleme, összegző vektornak nevezzük. Jelölése:. Szorozzuk meg most az A mátrixot jobbról egy alkalmas méretű (azaz -es) összegző vektorral: A. Megfigyelhető, hogy egy olyan oszlopvektort kaptunk eredményül, amelynek első eleme egyenlő az A mátrix első sorában lévő elemek összegével. második eleme megegyezik az A mátrix második sorában lévő elemek összegével, míg az eredményül kapott oszlopvektor harmadik eleme az A mátrix harmadik sorában lévő elemek összegével egyenlő. Vagyis az összegző vektorral (jobbról) történő szorzás hatására összeadódtak az A mátrix soraiban az elemek. Szorozzuk meg ezután az A mátrixot balról egy alkalmas méretű (azaz -as) sorvektorral, melynek minden eleme. Ezt a vektort T -vel jelöljük, hangsúlyozva azt, hogy most sorvektorral szorzunk: T A [ ] [ 9 ]. Vegyük észre, hogy a kapott sorvektor első eleme éppen az A mátrix első oszlopában elhelyezkedő elemek összegével egyenlő, a második elem éppen az A mátrix második oszlopában lévő elemek összege, és így tovább. Végül szorozzuk meg az A mátrixot balról egy megfelelő méretű összegző vektor transzponáltjával, jobbról pedig egy alkalmas méretű összegző vektorral: T A [ ] [ 9 ] [ ]. Észrevehetjük, hogy a kapott -es mátrix egyetlen eleme egyenlő az A mátrix összes elemének összegével.

3 . Minta feladat: Tekintsük az A mátrixot. a. Mivel egyenlők az alábbi kifejezések? e T A, Ae, T A, A, e T A, T Ae (Feltételezzük, hogy a kifejezésekben szereplő sor- és oszlopvektorok olyan méretűek, hogy valamennyi szorzás elvégezhető, azaz valamennyi sorvektor -es, és valamennyi oszlopvektor -es méretű.) b. Írja fel a tanult mátrixaritmetikát alkalmazva azt a kifejezést, amely megadja az A mátrix második oszlopvektorát; az A mátrix negyedik sorvektorát; az A mátrix ötödik oszlopában lévő elemek összegét; az A mátrix első sorában lévő elemek összegét; minden egyes sorra vonatkozóan a sorokban lévő elemek összegét; minden egyes oszlopra vonatkozóan az oszlopokban lévő elemek összegét; az A mátrix összes elemének összegét! Számolja is ki a felírt kifejezéseket! Megoldás: a. Felhasználva a bevezető részben szerzett tapasztalatokat, a felírt kifejezések minimális számolással megadhatóak: Ha az e T sorvektorral szorozzuk balról az A mátrixot, akkor a második sort vágjuk ki az eredeti mátrixból: e T A [ ] [ ] Ha az e vektorral szorozzuk jobbról az A mátrixot, akkor a harmadik oszlopot vágjuk ki az eredeti mátrixból:

4 Ae Az T A kifejezés egy olyan sorvektort ad eredményül, amelyben az elemek egyenlők az A mátrix egy-egy oszlopában elhelyezkedő elemek összegével: T A Az A kifejezés eredménye egy olyan oszlopvektor, amelynek elemei egyenlők az A mátrix egy-egy sorában lévő elemek összegével: A 9 9 Az e T A kifejezésben e T A az A mátrix harmadik sorvektorával egyenlő. Ezt jobbról szorozva egy összegző vektorral, eredményül egy olyan -es mátrixot kapunk, melynek eleme az A mátrix harmadik sorában lévő elemek összegével egyenlő: e T A [ ] Az T Ae kifejezésben Ae az A mátrix első oszlopvektorával egyenlő. Ha ezt balról szorozzuk egy összegző vektor transzponáltjával, akkor eredményül egy olyan -es mátrixot kapunk, melynek eleme az A mátrix első oszlopában lévő elemek összegével egyenlő:

5 T Ae [ ] b. Írjuk fel a megfelelő kifejezéseket! Az A mátrix második oszlopvektorát úgy kapjuk meg, hogy az A mátrixot jobbról az e oszlopvektorral szorozzuk: Ae Az A mátrix negyedik sorvektorát úgy kapjuk meg, hogy az A mátrixot balról szorozzuk az e T sorvektorral: e T A [ ] Az A mátrix ötödik oszlopában lévő elemek összegét úgy kaphatjuk meg, hogy az A mátrix ötödik oszlopvektorát előállítjuk az Ae szorzattal, ezt pedig balról szorozzuk az összegző vektor transzponáltjával: T Ae [ ] Az A mátrix első sorában lévő elemek összegét úgy kaphatjuk meg, hogy az e T A szorzattal előállítjuk az A mátrix első sorvektorát, majd ezt jobbról szorozzuk az összegző vektorral:

6 e T A [ ] Minden egyes sorra vonatkozóan a sorokban lévő elemek összegét kapjuk, ha az A mátrixot jobbról az összegző vektorral szorozzuk: A 9 9 Minden egyes oszlopra vonatkozóan az oszlopokban lévő elemek összegét kapjuk, ha az A mátrixot balról szorozzuk az összegző vektor transzponáltjával: T A Az A mátrix összes elemének összegét akkor kapjuk, ha balról az összegző vektor transzponáltjával, jobbról az összegző vektorral szorzunk: T A [ ]. Minta feladat: Egy vállalat az év első négy hónapjában háromféle termékből az alábbi mennyiségeket gyártja:. termék. termék. termék Január Február Március Április

7 Az egyes termékek eladási árait tartalmazó árvektor (eft-ban): p [,, ] T. Legyen A a táblázat adataiból nyert mátrix. a. Számítsa ki és értelmezze az alábbi kifejezéseket! T Ae, A e, e T Ap. b. Írja fel és számítsa ki azokat a kifejezéseket, amelyek megadják, hogy mennyi április hónapban az egyes termékekből gyártott mennyiség; mennyi az egyes hónapokban a vállalat árbevétele: mennyi az egyes termékekből a négy hónap alatt gyártott összes mennyiség. Megoldás: a. Az Ae szorzat az A mátrix második oszlopvektorával egyenlő, azaz megadja, hogy az egyes hónapokban a vállalat mennyit gyártott a második termékből. Ha ezt még balról szorozzuk az összegző vektorral, akkor az A mátrix második oszlopában lévő elemek összegét kapjuk. Tehát az T Ae szorzat megadja, hogy a vállalat az év első négy hónapjában összesen mennyit gyártott a második termékből: [ ] T Ae [ ] [ ] Az Ae szorzat az A mátrix első oszlopvektorával egyenlő, azaz megadja, hogy az egyes hónapokban a vállalat mennyit gyártott az első termékből: Ae Az e T A szorzat az A mátrix harmadik sorvektorával egyenlő, amely megadja, hogy a vállalat márciusban mennyit gyártott az egyes termékekből. Ha ezt jobbról a p árvektorral szorozzuk, akkor megkapjuk, hogy a háromféle termékből mennyi volt a vállalat márciusi összes árbevétele (eft-ban):

8 e T Ap [ ] [ ] b. Az április hónapban az egyes termékekből gyártott mennyiségek az A mátrix negyedik sorában találhatóak, a mátrix negyedik sorvektora az e T A szorzattal kapható meg: e T A [ ] [ ] Az egyes hónapokban a vállalat árbevételét az Ap szorzat adja meg: A p Az egyes termékekből a négy hónap alatt gyártott összes mennyiségeket az T A szorzattal kapjuk: T A [ ] [ ]. Minta feladat: Egy koncertre héten keresztül négyféle kategóriában árultak jegyeket. Az alábbi táblázat az egyes heteken az egyes kategóriákban eladott jegyek számát tartalmazza:. kategória. kategória. kategória. kategória. hét. hét. hét Az egyes kategóriák jegyárait tartalmazza a következő árvektor (eft-ban): p [,.,, ] T. Legyen A a táblázat adataiból nyert mátrix.

9 a. Számítsa ki és értelmezze az alábbi kifejezéseket! T A, A e, e T Ap. b. Írja fel és számítsa ki azokat a kifejezéseket, amelyek megadják, hogy mennyi a második héten az egyes kategóriákban értékesített jegyek száma; mennyi az egyes heteken az eladott összes jegyek száma; mennyi a hét alatt a jegyek eladásából származó összes árbevétel? Megoldás: a. Az T A szorzat egy olyan sorvektort ad eredményül, amelyben oszloponként összegezzük az A mátrix elemeit, azaz megkapjuk, hogy az egyes kategóriákban hány jegyet adtak el a hét alatt összesen: T A [ ] [ 9 ] Az A e szorzat az A mátrix második oszlopvektorával egyenlő, azaz megadja, hogy a második kategóriájú jegyekből az egyes heteken hány darabot adtak el: A e Az e T A szorzat egyenlő az A mátrix első sorvektorával, azaz megadja, hogy az első héten hány jegyet adtak el az egyes kategóriákban. Ezt jobbról szorozva az árvektorral, megkapjuk az első heti árbevételt (eft-ban):,, e T Ap [ ] [ ] [ 9] b. A második héten az egyes kategóriákban értékesített jegyek számát az A mátrix második sorában találjuk, a mátrix második sorvektorát az e T A szorzat adja meg: e T A [ ] [ ] 9

10 Az egyes heteken az eladott összes jegyek számát az A szorzattal adhatjuk meg: A Az T A szorzat egy olyan sorvektort ad eredményül, amely megadja, hogy az egyes kategóriákban hány jegyet adtak el a hét alatt összesen. Ezt kell még jobbról a p árvektorral szorozni, hogy megkapjuk a hét alatt a jegyek eladásából származó összes árbevételt (eft-ban):,, T A p [ ] [ 9 ] [ ]

Hasonló dokumentumok

Mátrixok február Feladat: Legyen A = ( ( B =

Mátrixok február Feladat: Legyen A = ( ( B = 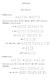Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4