5. IDŐBEN VÁLTOZÓ ELEKTROMÁGNESES TÉR

Átírás

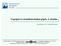
1 5 IDŐBEN VÁLTOZÓ ELEKTROMÁGNESES TÉR A koábbikbn külön, egymásól függelenül izsgáluk nyugó ölések elekomos eé és z időben állndó ám elekomos és mágneses eé Az elekomágneses é ponosbb modelljé kpjuk, h z időbeli álozások is figyelembe esszük A oábbikbn z elekomos és mágneses é éjellemzői nemcsk hely, hnem z idő szein is áloznk 5 Időben álozó mágneses é 5 Nyuglmi indukció A kísélei eedmények z muják, hogy időben álozó mágneses é elekomos ee hoz lée A kísélei eedmények állánosíásá z indukció öény fejezi ki Tekinsünk egy mjdnem zá ezeő huko, mely időben álozó mágneses ee fog köül, kko pszl szein ezeő ké ége közö feszülség méheő (5 áb), mely ányos ezeő huok fluxusánk időegység li megálozásál Az indukál feszülség iány fluxus megálozás iányához jobbcs szbály szein kpcsolódik, u i () dψ = (5) A negí előjel z jeleni, hogy fluxus időbeli megálozás és z indukál feszülség iány jobbcs szeini iánnyl ellenées 5 áb Az indukál feszülség foglm 5 áb A háomszög szein peiodikusn álozó fluxus és z indukál feszülség kpcsol Figyelembe ée ezeő huok keeszmeszeén ámenő indukció onlk, z indukál feszülség köekező összefüggéssel állíhó elő dψ () () d db ui = = B, d = d

2 4 A Iányi, Fizik-I Tekinsük z 5 ábán láhó háomszög szein peiodikusn álozó fluxus Az első negyed peiódusbn, miko fluxus lineáisn nő, z indukál feszülség negí állndó ééke esz fel A második negyed peiódusbn, miko fluxus lineáisn csökken, z indukál feszülség ugásszeűen előjele ál és mindddig pozií állndó lesz z ééke, míg fluxus nem kezd el új nöekedni Hsonló helyze lkul ki, h fluxus szinuszosn álozik () Ψ sinω Ψ =, ekko z indukál feszülség nem ugásszeűen, hnem folyonosn álozik, (53 áb) u i = Ψ ω cosω = U cos ω, hol U = ωψ Min z ábán láhó z indukál feszülség időfüggénye késik fluxus időfüggényéhez képes 53 áb Szinuszosn álozó fluxus és z indukál feszülség kpcsol 54 áb A Lenz öény éelmezése 5 Lenz öény H mjdnem zá ezeő huko bezájuk, z indukál feszölség hásá ám indul meg ezeőben Az ám iány zonbn z indukál feszülség iányál ellenées lesz (54 áb) Ez zzl mgyázhó, hogy z indukál feszülség hásá ölés-széálszás jön lée, és z ám pozií ölésől negí ölés felé folyik Az ábán bejzoluk z ám iányá, mely z R ellenállású ezeőben folyik () u i() = i R Ez z ám zonbn olyn B mágneses ee hoz lée, mely csökkeni z eedei mágneses é ééké, zz zzl ellenkező iányú ee gejesz Ez öényszeűsége, mely z indukál feszülség öényből köekezik, Lenz öénynek neezzük, és z mondj ki, hogy z indukál feszülség hásá ezeő huokbn folyó ám olyn mágneses ee hoz lée, mely z ő léehozó hás csökkeneni kj 53 Fdy indukció öény Vegyük figyelembe zá, R ellenállású ezeőben folyó i( ) feszülség hásá jön lée, u () = i() R = E dl i l ámo, melye z indukál

3 5 Fejeze, Időben álozó elekomágneses é 5 Helyeesísük z indukció öény bl oldlá kpo eedménnyel, dψ () db E, dl = = d l (5) z indukció öény állánosío lkjá, Fdy indukció öény kpjuk, mely z mondj ki, hogy z időben álozó mágneses é elekomos ee gejesz 5 A mozgási indukció H egy időben állndó mágneses ében, meőlegesen, egy ezeő dbo mozgunk, kko ezeő ké égponj közö feszülség méheő (55 áb) A jelenség Loenz eőöény lpján mgyázhó F = Q E + B, ui sebességgel mozgó ezeőben léő szbd elekonok z időben állndó mágneses ében eő h, mely öléseke széálszj, Ei = B, F = Q( B) = QEi A feni éeőssége ezeő dbjá inegál kpjuk mozgási indukcióból számzó feszülsége m ui () = Ei dl = ( B) dl (53) l l A jelenség úgy is mgyázhó, hogy sebességgel mozgó ezeő l idő l d = l felüle d Ψ = Bl fluxus onli meszi, honnn z indukál feszülség d Ψ = Bl = u i hosszúságú dbj 55 áb A mozgási indukció 56 áb Az önindukció jelensége és ekecs feszülsége Hbá nyuglmi és mozgási indukció fiziki lpj más, ké jelenség egységesen kezelheő bbn z éelemben, hogy ezeő huok fluxusánk megálozás, egyész mágneses indukció időszeini megálozás mi, másész ezeő keeszmeszeének megálozás mi jön lée, zz

4 6 A Iányi, Fizik-I dψ () () d db d () ( ) ui = = B, d = d B,, hol z egyenle jobb oldlán z uolsó elöi g nyuglmi indukcióból, z második g mozgási indukcióból számzó indukál feszülsége jeleni 53 Időben álozó ám mágneses ee 53 Önindukció jelensége Tekinsük z 56 ábán láhó ekecse H ekecsben külső foás hásá időben álozó ám folyik, z időben álozó mágneses ee gejesz, mely indukál feszülsége hoz lée ekecs ké égponj közö Figyelembe ée, ekecs L önindukció együhójá, ekecs fluxus Ψ ( ) = L i( ), és így z indukció öény éelmében z indukál feszülség dψ d di () () () u i = = Li = L A ekecs kpcsin zonbn z d () () di() u L = Ψ = L (54) ekecsfeszülsége szokuk lklmzni, mely éppen z indukál feszülséggel ellenkező iányú, így u L () u () = (55) i A ekecsfeszülség ismeeében ekecs fluxus megháozhó ( ) = u ( τ ) dτ = u ( τ ) dτ + u ( τ ) dτ = Ψ ( ) + u ( τ ) Ψ L L L L dτ, hol Ψ ekecsen pilln elői fluxus álozásból számzó fluxus, időpillnól kezdődő izsgálok kezdei feléele 53 Kölcsönös indukció jelensége Koábbn láuk, hogy egy ekecs fluxusá nemcsk sjá ám, hnem szomszéd ekecsben folyó ám, kölcsönös indukció együhón keeszül (57 áb) megálozj Ké ekecsből álló endsze eseén ekecsek fluxus (58 áb) Ψ = L i + M i, Ψ = M i + L i, (56) hol L, L ekecsek önindukció együhój, míg M kölcsönös indukció együhó Min ismeees kölcsönös indukció együhó ekecsek helyzeéől és z ámok efeenci iányáól függően lehe pozií gy negí, melye z 58 ábán ponokkl jelölünk Azz, h ké ekecsben z ámok ponokól folynk nem ponos égek felé, kko kölcsönös indukció együhó előjele pozií, ellenkező eseben negí A efeenci iányok 58 ábán ló ögzíése melle ekecsek feszülségei köekezők

5 5 Fejeze, Időben álozó elekomágneses é 7 d di di d di di = Ψ L L u L = +, = Ψ = + L (57) u 57 áb A szomszéd ekecs fluxus 58 áb Ké ekecsből álló endsze és modellje 533 Tekecsek soos és páhuzmos kpcsolás (i) Vizsgáljuk meg ké sob kpcsol ekecse, melyek ám közös (59 áb) i = i = i 59 áb Sob kpcsol csol ekecsek és eedőjük Az eedő feszülség ké feszülség összege, zz di di di di u = u + u = L ± M + ± M + L = ( L + L ± M ) di = L s, honnn ké csol ekecs eedő soos indukiiás L s = L + L M ± A pozií előjel efeenci ponoknk felel meg, negí előjel kko lép élebe, h z egyik pon ekecs másik égée keül (ii) Vizsgáljuk meg z 5 ábán láhó páhuzmosn kpcsol csol ekecseke, melyek feszülsége közös, u = u = u Az egyes ekecsek feszülsége z ámokkl kifejeze di di di di = L M u M ±, = ± + L u Fejezzük ki z ámok deiálji di

6 8 A Iányi, Fizik-I di L m M = u, L L M di L m M = u, L L M honnn z eedő ám ké ám összege, i = i + i, di = di di + = L + L L L m M M u = L p u 5 áb Páhuzmosn kpcsol csol ekecsek és eedőjük A páhuzmosn kpcsol ekecsek eedő indukiiás L L M L p = L + L m M 54 A mágneses é enegiáj 54 Tekecs enegiáj Háozzuk meg egy L indukció együhójú ekecs enegiájá, h ám idő l nulláól I ééke nő Minhogy z ám álozásál álozik ekecsben fluxus, és z ekecs pólusin méheő feszülség is u L = dψ, és így ekecs idő l fele enegiáj dψ dw = ul i = i = i dψ H ekecs ám = pillnbn null, kko idő l fele enegiáj Ψ W = i dψ, hol Ψ ekecs fluxus előző összefüggés kiéékele pillnbn A fluxus z ámml kifejeze Ψ = L i és z Ψ I W = i d = i Ldi = LI Ψ, (58) zz ekecs enegiáj

7 5 Fejeze, Időben álozó elekomágneses é 9 W LI = = Ψ I = L Ψ (59) L 54 Csol ekecsek enegiáj A csol ekecsek enegiáj z egyes ekecsek enegiájánk összege Minhogy W = ( Ψ I + ΨI ), és ekecsek fluxusi Ψ = L I + MI, Ψ = MI + LI, csol ekecs enegiáj W = L I + MII + LI (5) 543 A mágneses é enegi sűűsége Tekinsük z 5 ábán láhó elemi éfogo, melye mágneses eőonlk és z zok meőleges felüleek háolnk Az elemi éfog enegiáj dw = ΨI Az I ám gejeszési öényből bámely mágneses eőonl, és fluxus z eőonlk meőleges felülee onkozó egyenleek lpján I = H dl, Ψ = B d, l honnn z elemi éfog enegiáj, figyelembe ée, hogy s dw = IΨ = H dl B d = HB d dl = HB d l l d = d dl 5 áb Az elemi éfog enegiáj 5 áb hengees ezeő belső önindukció együhój Az elemi éfog enegiáj z egységnyi éfog onkozo w enegisűűségnek éfog e inegálj, dw = HB d = w d

8 3 A Iányi, Fizik-I honnn z elemi éfog enegisűűsége dw w = = HB [ W ] (5) m3 d 544 Belső indukció együhó A mágneses enegi és z indukiiás kpcsolánk ismeeében megháozhó belső indukció együhó, W = L = w d = H bi µ d, (5) hol µ B w = HB = H = (53) µ Alklmzzuk feni összefüggés egy l hosszúságú hengees ezeő belső indukció együhójánk megháozásá (5 áb) A gejeszési öény lklmz hengees ezeő belsejében egy eőonl I H dl = I, H π = π, l π mágnese éeősség ezeő belsejében I H () =, < < π A d = π l d elemi éfog és mágneses enegisűűség ismeeében hengees ezeő mágneses enegiáj 4 I I l W = π π l d = µ = L 4 b 4 I, = π π honnn belső indukció együhó függelen hengees ezeő sugáól, csk z nyg mágneses pemebilásáól és ezeő hosszáól függ µ l L b = (54) 8π 545 A mágneses eőhás és iuális munk ele Az elekoszikus éhez hsonlón mágneses ében fellépő eőhások is számíhók iuális munk ele lpján Hbá z enegiegyensúlyi egyenle nem álozik, dwgen = dwbelső + F ds,

9 5 Fejeze, Időben álozó elekomágneses é 3 hol geneáo áll idő l endszebe beáplál enegi endsze fluxusá álozj meg, dw = I dψ, gen k k k míg endsze belső enegiájá z indukálás soán fellépő ám megálozás eedményezi, zz dw = Ψ di belső k k k H endszebe beáplál enegi nem álozik, zz endsze fluxus állndó, iuális munk ele lpján z ds elmozdulás iányábn fellépő eőhás dw F = belső s, Ψ k = állndó, k =,, L,n (55) ds H iuális elmozdulás soán huok ám állndó, és pemebiliás függelen z indukcióól, kko F dwgen =, Ik = állndó, k =,, L n (56) ds s, 55 Időben álozó elekomos é 55 A folyonossági egyenle A ölésmegmdás ele lpján scionáius ámlás eseén z pszluk, hogy egy éfogb beámló ölések onnn el is áoznk Időben álozó elekomágneses é eseén zonbn éfogb idő l beámló dqbe, és z onnn kiámló dqki ölések különbsége éfogbn ugynzon idő l felhlmozódó dq ölésmennyiséggel egyenlő (53 áb) dqbe dq dq ki = 53 áb A folyonossági egyenle éelmezése 54 áb Gejeszési öény scionáius ében Vegyük figyelembe hogy dq be = Ibe éfogb befolyó, dq ki = Iki pedig kifolyó ám, ezzel ölésmegmdás onkozó összefüggés folyonossági egyenle köekező

10 3 A Iányi, Fizik-I I dq Iki (57) be = Az egyenle bloldl felíhó éfogo háoló zá felüleen ki és belépő ámsűűségekkel, lmin z egyenle jobb oldlán éfogbn elhelyezkedő ölések összegéel, zz I I = J d, Q = ρ d be ki A feni összefüggés lklmz és figyelembe ée, hogy éfog időben nem álozik folyonossági egyenle köekező lk hozhó d dρ J, d = ρ, d = d Némi endezés uán folyonossági egyenle szokásos lkjához juunk dρ J, d + d = (58) A folyonossági egyenle ölésmegmdás elé fejezi ki, és ezen keeszül, minhogy ölés nygi észecskék uljdonság fizik állános elé, z nygmegmdás elé epezenálj z elekomágneses eek eseében 55 Az elolási ám Időben álozó elekomágneses é eseén scionáius állpo onkozó gejeszési öény és folyonossági egyenle ellenmondás eze, dρ H dl = J d, J, d + d = l A folyonossági egyenlee éfogo háoló felülee íjuk fel Jelöljünk ki ezen felüleen egy eszőleges zá l göbé, mely felülee ké észe oszj (54 áb) Íjuk fel gejeszési öény úgy, hogy H mágneses éeőssége inegáljuk z l göbée, J ámsűűsége pedig egysze z, mjd z felülee, felülei nomálisok figyelembe éeléel H dl = J d H dl = J d l, l Minhogy bloldlon álló kifejezés mindké eseben ugynz, jobboldlk egyenlőségéből köekezik, hogy J ámsűűségnek egy zá felülee e összege, inegálj zéus J d =, folyonossági egyenle szein iszon nem Toábbá, együk figyelembe z elekoszik Guss éelé, mely szein éfogbn elhelyezkedő ölések z elolási ekonk éfogo háoló felülee e inegáljál egyenlő, ρ d = D d

11 5 Fejeze, Időben álozó elekomágneses é 33 d d dd J, d = ρ, d = D, d = d, honnn z kpjuk, hogy z ámsűűség és z elolási eko idő szeini deiáljánk összege zá felülee e inegálj d null ééke dd, J + d =, (59) és így z ellenmondás kiküszöbölése édekében gejeszési öény állános lkj köekező lesz dd H dl = J, + d, (5) l hol J = J (, ) epezenálj ezeőben folyó ezeési ámo, J e dd =, (5) pedig z elekomos é időbeli megálozásából számzó un elolási ámo képiseli Nézzük meg, hogy gejeszési öény új lkj mi jelen H dd =, J = J (, ) ezeési ám mágneses ee gejesz (55 áb), h zonbn z elolási ám nem null, dd z is léehoz egy mágneses ee és ké mágneses é összegeződik, szupeponálódik 55 áb A ezeési és z elolási ám mágneses ee 56 áb A kondenzáo ám 553 A kondenzáo ám Kpcsoljunk időben álozó u() feszülsége egy C kpciású kondenzáo A kondenzáo elekódáin időben álozó ± q ölés hlmozódik fel q () C u() = Ez úgy leheséges, hogy z egyik elekódá i ( ) ám folyik be, másikól ugynkko i ( ) ám folyik el Alklmzzuk kondenzáo folyonossági egyenlee Vegyük köül kondenzáo egy zá felüleel (5 5 áb), felüleen i ám folyik be i ám folyik ki és

12 34 A Iányi, Fizik-I i () i () () dq ki =, be = zz kondenzáo elekódáin ölések összege nem álozik, ui idő l z egyik elekódán + dq, másik elekódán dq ölés hlmozódik fel, ezek eedője zonbn null Alklmzzuk folyonossági egyenlee mos egy olyn éfog, mely csk z egyik elekódá lmzz Az felüleen mos i ( ) ám folyik be, mely ányos kondenzáo feszülségének idő szeini deiáljál () du() dq i () = = C (5) A éfog ölése z elekoszik Guss éele szein kifejezheő z elolási ekonk felülee e inegáljál Némi álkíás uán z kpjuk, hogy kondenzáo lemezei közö z elolási eko időszeini deiáljánk z felülee e inegálj, zz z elolási ámsűűségnek z inegálj, z elolási ám folyik dq () () d dd i = = D, d = d = Je() d = ie (), hol z elolási ámsűűség dd () J e =, (53) és z elolási ám dd () ie = d (54) Tehá kondenzáo elekódáihoz öléseke ezeőben folyó i ( ) ezeési ám iszi, kondenzáo lemezei közö z időben álozó elekomos é hásá z i e () elolási ámbn folyódik A kondenzáobn fellépő elolási ám ugynúgy mágneses ee hoz lée, min ezeési ám 56 Az elekomágneses é lpxiómái 56 Az elekomágneses é enegiiszonyi Vlmely éfogbn felhlmozo W ( ) elekomágneses enegi ké okból áozh z időben Az egyik, éfogbn fellépő P ( ) eljesíményű folymok, melyek P ( ) > eseén éfog elekomágneses enegiájá csökkenik, P ( ) < eseén éfog elekomágneses enegiájá nöelik, másész éfogo háoló zá felüleen áámló, gy ásugázo P s ( ) eljesímény csökkeni é enegiájá Az elekomágneses é enegimélege ezek szein dw () () + P () = + P s (55)

13 5 Fejeze, Időben álozó elekomágneses é 35 Az egyes mennyiségek kifejezheők z elemi éfog, ill felülee onkozó sűűség w, enegisűűséggel jellegű mennyiségekkel, így éfog W enegiáj W W J m ( ) = w d, w(, ) = lim, [ w] = 3 P () eljesímény p (, ) eljesímény sűűséggel P P ( ) = p d, p(, ) = lim, [ p] = 3 P s (), (56) W, (57) m míg felüleen kisugázo eljesímény z egységnyi felüleen kisugázo eljesímény sűűséggel, Poyning ekol jellemezheő Ps P () = S d, S(, ) = lim s, [ S] = W (58) m Az enegi egyensúlyi egyenle sűűségekkel köekező lkbn íhó fel dw d + p d + S d = (59) A sikus elekomos é, scionáius elekomos és mágneses é enegi és eljesímény sűűségeinek ismeeében z elekomágneses é éálozóil is felíhó z enegigeynsúlyi egyenle Az elekomágneses ében z elekomos és mágneses enegi megálozás dw dd db = E, + H, Homogén, lineáis nyg eseén, miko szigeelőnyg ε pemiiiás, és mágneses nyg µ pemebiliás nem álozik sem geomeii é ponjibn és nem függ z elekomos és mágneses é ngyságáól, D = ε E, B = µ H, z inez műele uán z elekomágneses é enegisűűsége w = D E + B H (53) A éfogbn égbemenő enegiálkukások köekezében éfogi eljesímény sűűség p = J E, mely J = σ ( E + E i ) diffeenciális Ohm öény figyelembe éeléel J p, = J Ei (53) σ lkbn dhó meg Végül, bizonyíás nékül megdjuk Poyning ekonk éálozókól ló függésé, S, = E (53) H Ezzel z enegi egyensúlyi egyenle köekező lk hozhó,

14 36 A Iányi, Fizik-I dd db J E + H d + d J Eid + σ ( E H ) d =, (533) hol z egynele bloldlán álló eső g z elekomos és mágneses é enegiájánk megálozás, második g ezeő közegekben Joule öény szein hőé áló eljesímény, hmdik g nem illmos enegi beáplálásnk figyelembe éele, míg z uolsó g felüleen kisugázo eljesímény 56 A Mxwell egyenleek Amin z koábbikbn láuk, z elekomágneses ee gejesző mennyiségek ρ (,) elekomos ölés és J (, ) illmos ám Ezek zonbn nem függelenek egymásól A közük léő kpcsolo z nyg, ill ölés-megmdási éel, folyonossági egyenle fejezi ki d J d + ρ d = (534) Az elekomágneses é éjellemzői egyész é inenziásá kifejező E (, ) elekomos éeősség eko és B (, ) mágneses indukció eko, másész é gejeszeségé megháozó D (, ) elolási eko és H (, ) mágneses éeősség eko Az elekomágneses é éálozói pszli öények állánosíásál kpo összefüggéseke Mxwell egyenleek néen foglljuk össze Az I Mxwell egyenle z állánosío gejeszési öény, dd H, dl = J, + d, (535) l mely z mondj, hogy mágneses éeősségnek egy zá göbée e inegálj (összege) göbe áll kifeszíe felüleen áhldó ámok dj Meg kell jegyezni, hogy jobb oldlon oális ám, zz ezeési és z elolási ám összege szeepel A gejeszési öény úgy éelmezhejük, hogy mind ezeési ám, mind z elolási ám mágneses ee hoz lée A II mxwell egyenle Fdy indukció öény, db E, dl = d, (536) l mely z mondj, hogy z E (, ) elekomos éeősségnek egy zá göbée e inegálj (z indukál feszülség) göbe áll köülfogo felüleen ámenő d B indukcióonlk idő szeini megálozásál egyenlő Az I és II Mxwell egyenleek nem függelenek egymásól, ui gejeszési öény jobb oldlán álló J (, ) ezeési ám léehoz egy időben álozó H (, ) mágneses ee, mely mágneses é időbeli álozás z indukció öénynek megfelelően E(, ) elekomos ee gejesz, mely zonbn z elolási ámon keeszül modósij z mágneses ee A III Mxwell egyenle mágneses indukció foásmenességé foglmzz meg,

15 5 Fejeze, Időben álozó elekomágneses é 37 B d = (537) Az mondj, hogy zá felüleen ugynnnyi mágneses eőonl lép be, min ki, zz nincsennek mágneses ölések, mágneses indukció onlk sehol nem kezdődnek és sehol nem égződnek, egyszeű eseben zá gözbé lkonk A IV Mxwell egyenle z elekoszik Guss éele, D d = ρ d, (538) mely szein z D (, ) elekomos é foás ölés Az elolási ekonk egy zá felülee e inegálj felüle áll háol éfogbn elhelyezkedő ρ (,) ölésekkel egyenlő Az V Mxwell egyenle éálozók és z nygjellemzők kpcsolá foglmzz meg Homogén, lineáis nyg eseén szigeelőnygok z ε pemiiiássl, mágneses nygok µ pemebiliássk, ezeő nygok σ ezeőképességgel jellemezheünk, D = ε E = ε E + P B = µ H = µ H + M, J = E +, (539), σ hol P szigeelőnyg polizáció eko, M feomágneses nygok mágnesezeségi eko és E i beiko éeősség, mellyel nem illmos eedeő enegiák (ölés széálszó eő) modellezünk Végül VI Mxwell egyenle z elekomágneses é enegiiszonyi d összefüggés, mely szein z elekomágneses é egységnyi éfogánk eljesíménysűűsége dw dd db p, = = E, + H,, melyből homogén, lineáis közeg eseén z elekomágneses é enegisűűsége w = D E + B H (54) E i 57 Ellenőző kédések [] Ismeesse Fdy indukció öény, [] Fogllj össze mozgási indukció jelenségé, [3] Ismeesse z állánosío gejeszési öény, [4] Ismeesse folyonossági egyenlee, [5] Fogllj össze z elekomágneses é lpxiómái 58 Gykoló feldok 58 Feld Egy R ellenállású gyűű lkú ezeő időben álozó, ében egyenlees eloszlású Ψ fluxus esz köül (57 áb) Háozz meg mekko feszülsége méünk ezeő P Q ponj közö, h olméő bloldli áb szein és h jobboldli áb szein köjük be

16 38 A Iányi, Fizik-I Megoldás dψ u A ezeőben z u i = indukál feszülség hásá i = i ám folyik A bloldli áb R szein olméő gyűű P Q ponji közöi l szkszánk R α = π R ellenállásán α fellépő u = R i = ui feszülsége méi π H zonbn jobboldli elendezés izsgáljuk, kko olméő z l szksz ellenállásán kelekeze feszülsége méi u α α = R R i = π π b u i 58 Feld 57 áb A mé feszülség szomszéd ekecs fluxus Egy sugú, d sgságú, σ ezeőképességű fémács homogén mágneses ében é iányá meőlegesen n elhelyeze (58 áb) A mágneses indukció z időben B () = B cos ( ) ω függény szein álozik A ezeő ácsá ideális szigeelő eszi köül Háozzuk meg z indukció köekezében fellépő ám hőeljesíményé Megoldás A ács sugú észén Φ () = πb( ) mágneses fluxus hld á Ennek időbeli álozás z sugú kö keülee menén éinő iányú E elekomos ee kel, mely hengeszimmei mi z sugá menén állndó Az indukció öény lklmz

17 5 Fejeze, Időben álozó elekomágneses é 39 dφ E dl = π E + l (, ) = = πb ω sin ( ω ) honnn z elekomos éeősség megháozhó E B ω = sin ( ω ) A diffeenciális Ohm öény éelmében z ámsűűség B J E ω = σ = σ sin ( ) ω A hőeljesímény Joule öény lpján számíhó, hol z elemi éfognk egy szélességű gyűü ekinünk, d = d π d J = σ B () d = σ sin( ω ) d π d = σ π 4d sin( ω ) P ω 4 Az időben álozó eljesíménynek egy peiodus e álg sin ( ω ) cos = ( ω ) összefüggés felhsználásál, és figyelembe ée, hogy ( ) álg null, = B ω σ π d, 6 P 4, B ω 8 d cos ω egy peiodus e időbeli gyis z indukció és köfekenci nágyzeéel, és sugá 4-dik hányál ányos Ennek hőé áló eljesíménynek csökkenése édekében nszfomáo smgjá mágneses indukciól páhuzmos iánybn lemezelni szokás Az indukció hásá kelekező, ezeőben záódó ámo öényámnk neezzük 58 áb A ácsábn kelekeze öényám 59 áb A mágneses ében fogó kee Az ámsűűség ismeeében megháozhó ácsábn köbe folyó ámeősség B I J d d J d d ω = = = σ sin 4 ( ω ) d = B ω σ d sin( ω ) 583 Feld

18 4 A Iányi, Fizik-I Az 59 ábán láhó kee homogén és időben állndó B indukciójú mágneses ében ω szögsebességgel foog Háozzuk meg keeben indukálódó feszülsége, h kee hossz d, szélessége h Megoldás (i) A kee fluxus, miközben α = ω szöge fodul el Φ = Bhd cos α = Bhd cosω, így z indukál feszülség dφ d u i = = Bhd cosω = Bhdω sinω (ii) A mozgási indukciólpján d hosszúságú oldl sebessége = ω h, z indukál feszülség d ui = h ( B) dl = d ω Bsinα = dhωbsinω 584 Feld,z előző eedménnyel összhngbn Az l hosszúságú úd homogén mágneses ée meőlegesen z egyik ége köül ω szögsebességgel foog (5 áb) Háozz meg mekko feszülség indukálódik úd ké égponj közö Megoldás Minhogy ud mágneses indukció meőleges iánybn mozog, benne feszülség indukálódik Az sugáon mozgó d hosszúságú szkszbn du i = ( B) dl = B d = ω B d, z egész udon pedig l l ui = ω B d = ω B feszülség lép fel 5 áb A homogén mágneses ében fogó ud 5 áb Homogén ében fogó ács 585 Feld Homogén mágneses ée meőlegesen helyezünk el egy sugú fémácsá, mely engelye köül ω szögsebeséggel foog (5 áb) Háozzuk meg mekko feszülség indukálódik ács engelye és peeme közö, h B =T, =,5 m, n = 3 fodul pec

19 5 Fejeze, Időben álozó elekomágneses é 4 Megoldás Képzeljük el, hogy ács égelen sok küllőből áll Egy küllőben z előző feld szein u i = ω B feszülség indukálódik Az egyes küllők páhuzmosn kpcsolódnk, ezé feszülségük ugynekko A numeikus dok figyelembe ée,5 u = ω i B = π = 37,7V feszülség állíhó elő 586 Feld Mekko feszülség indukálódik z 5 ábán láhó ezeőkböl álló elendezésben, h ezeők síkjá meőleges mágneses indukció B ( ) = B sin( ω ) szein álozik és z l hosszúságú ezeékdb ké ezeőel páhúzmosn ebességgel mozog Megoldás (i) Az x helyen léő ezeő áll köülzá fluxus Ψ = l xb sin( ) fluxus áll indukál feszülség megdo efeenci iány szein dψ u i = = l xω B cos ( ω ) ω Az időben álozó Az l hosszuságú ezeő sebességgel mozog, így z áll indukál feszülség efeenci iánnyl ellenkező iányú u i ( ) = Bl = lb sin, ω és így z indukál feszülség u i ( sinω xω cosω) = ui ui = B l + Vegyük még figyelembe, hogy mozgó ud indukál feszülség u i = Bl( sinω + ω cosω) x = áolságo esz meg, így keese (ii) Hsonló eedmény kpunk, h ezeő keeszmeszee áll bezá fluxus Ψ = l B sinω = B idő szeini deiáljuk, dψ u i = = d () () () () = () B () db () B d ( ) = B l ( ω cosω sinω) +

20 4 A Iányi, Fizik-I 5 áb A kee és mozgó ud 53 áb A ké hengees ezeő eőhásához 587 Feld Ké páhuzmos, kö keeszmeszeű, égelen hosszúnk ekinheő ezeék egymásól áolság helyezkedik el (53 áb) A ezeékben folyó ámok egyenlő ngyságuk és ellenekző iányúk Háozzuk meg z egyik ezeő l hosszúságú szkszá hó eő Megoldás (i) Számolhunk léehozo indukció I B = µ H = µ π df = I dl B összefőggéssel Az egyik ám áll másik helyén Ez z indukció ezeőe meőleges, így z eő jobbcs szbály lpján szíó jellegű I l F = µ π (ii) A feld megoldhó iuális munk ele lpján is Minhogy ezeők ám állndó z elmozdulás soán megálozik ezeő huok indukiiás, és így z elmozdulás iányábn fellépő eő dw dl = = I ds ds F s Minhogy keősezeék önindukció együhój µ l L = ln, π ké ezeő engelyé összeköő iánybn fellépő eőhás engelyek áolságá nöelni kj F = I dl µ li = d π (iii) Az egyes ezeőke még sugáiányú eő is h dw F = = d dl µ = li I d π

21 5 Fejeze, Időben álozó elekomágneses é 43 Vegyük figyelembe, hogy ezeők közi áolság jól ngyobb, min ezeők sug, d >>, így sugá iányú eő közelíheő F l I µ π A negí előjel z fejezi ki, hogy z eő sug csökkeneni igyekszik Ngy ámok eseén eőből számío nyomásnk z nyg sziládság áll ellen F I p µ = = π l ( π ) 588 Feld Háozzuk meg z z eőhás, mely z 54 ábán láhó égelen hosszú egyenes ezeő és ele egy síkbn fekő kee közö lép fel, h ezeők I, I ám z elmozdulás soán állndó 54 áb Az egyenes ezeő és kee helyzee Megoldás Az elendezés enegiáj kifejezheő z indukiiásokkl W = L I + LI + LII A kee bámilyen iuális elmozdulásál csk kölcsönös indukiiás álozik µ b + L = mln, π b és így iuális munk ele lpján onzóeő lép fel dw µ F x = = II m db π b + b 59 Toábbi gykoló feldok 59 Feldok [] Mekko enegiá áol z L = mh, L = 6 mh, L = 5 mh ön-, és kölcsönös indukció együhól endelkező csol ekecs melye I = A, I = 8 A ámml áplálunk

22 44 A Iányi, Fizik-I [] Mekko ámml ápláluk z z L = 8,6 mh önindukció együhójú ekecse, mely W = mw mágneses enegiá áol [3] Mekko mágneses enegiá áol z µ = mágneses pemebiliású nyg egységnyi éfog, h benne B =,8 T mágneses indukció n jelen [4] Mekko mágneses fluxus nnk z L = 5 mh önindukció együhójú ekecsnek, mely W = 38 mw mágneses enegiá áol [5] M Egy elekomágneses ee sugázó esől ngy áolságbn z elekomos és mágneses éeősség ekook egymás meőleges komponensei E x = 3cos( ω )mv/m, = 5cos( ω )µa/m Háozz meg z egységnyi felüleen áámló eljesímány H y 59 Megoldások [] Minhogy ekecsendsze enegiáj W = LklIk Il, jelen eseben csol k = l= ekecs enegiáj W = L I 776 mw,776 W + L I I + L I = = [] Minhogy ekecs enegiáj W W = LI, honnn I = =,675 A L B [3] Az egységnyi éfogbn z enegisűűség w = BH = = 7,496 Ws/m3 µ µ [4] A ekecs enegiáj W W = LI, honnn ekecs ám megháozhó I =, L W így ekecs fluxus Ψ = LI = L = WL =,95 Vs L [5] Az egységnyi felüleen áámló eljesímény Poyning eko, S = E H, így minhogy z elekomos é x iányú, mágneses é y iányú, ekoi szozból Poyning eko z iányú lesz, S E H = 5 9 W m z = x y n n