rot H = J + D div D = ρ, w = 1 2 E D H B,

Átírás

1 Ë Ð Ø Þ Ð ØÖÓÑ Ò Ø Ö Ø ÒØ Ö Ý ÒÝ Ò ÐÑ ÐÝ Ø Þ È Ú Â Þ ¾¼½ º ÒÙ Ö ½º

2 Ì ÖØ ÐÓÑ ÝÞ ½º Þ Ð ØÖÓ Ò Ñ Ø Ñ Ö Ø ÖØÓÞ Ð Ò ÓÔÓÖØÓ Ø ¾ ½º½º Þ Ð ØÖÓÑ Ò Ø Ö Ð Ø Ö Ð Ú ÐØÓÞ Ò Ô ÓÐ Ø ¾ ½º¾º ËØ Ø Ù Ø Ö d λ Ú Ý d δ º º º º º º º º º º º º º º º º º º º º º º º ½º º ÃÚ Þ Ø ÓÒ Ö Ù ÖÚ ÒÝ Ö Ñ µ Ø Ö d λ d δ º º º º º º º º º º º ½º º Ð ØÖÓÑ Ò ÙÐÐ ÑÓ d λ d δ º º º º º º º º º º º º º º º º º º ½º º ÓÑ ØÖ ÓÔØ d λ º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º º ÐÓ ÞØ ÖØ ÐÑ Þ Ø Ö Ð º º º º º º º º º º º º º º º ½º º Ú Þ Ð Ò ÐÖ Ò Þ Þ Ø ØØ º º º º º º º º º º º º º º º º º º º º ¾º Ì Ö Ó Ø ÒÝ ÑÓ ÐÐ Þ Þ ÖÚ ÒÝ Ö Ñ ÖÓÒ ÓÐ Ñ ÒØ ÒÝ ¹ Ú Þ Ð Ø Ò ¾º½º Ø Ö Ó Ø ÒÝ Ø Ð Ö ÒØ Ö Ð Ý ÒÐ Ø º º º º º º º º º º º º º º º º º ¾º¾º Ø Ö Ó Ø ÒÝ ÖÚ ÒÝ Ö Ñ Ú Ð Þ Ð Ò Þ Ñ Ø º º º º º º º º º ½ ¾º¾º½º Ñ Ò Ø Ö Ú ÐØÓÞ Ò Þ Ñ Ø º º º º º º º º º º º º º º º º ½ ¾º¾º¾º Þ ÑÔ Ò ¹Ú ÐØÓÞ Þ Ñ Ø º º º º º º º º º º º º º º º º º º º ½ ¾º¾º º Ñ Ò Ø Ö ÖØ Ò Ñ Ø ÖÓÞ Þ ÑÔ Ò ¹Ú ÐØÓÞ ÔÐ Ø Ú Ð º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ º Ë ÙÐÐ ÑÓ ½ º½º Ì ÌÅ ÔÓÐ Ö Þ ÙÐÐ ÑÓ º º º º º º º º º º º º º º º º º º º º º ½ º¾º Ë ÙÐÐ ÑÓ ÐØ Ð Þ ÐÐ ØÓØØ Ø Ð ØÑ ÒÝ º º º º º º º º º º º º º º º º º º º º ¾ º º ÙÐÐ Ñ Þ ÖØ ÐÑ Þ Ò ÒÝ Ý ÓÖÐ Ø Ð ÐÑ Þ º º º º º º ¾ º º Ö Ò ÙÐÐ Ñ Ú Ð ÒÝ Ø ÖÓÒ º º º º º º º º º º º º º º ¾ º º½º Ø Ö Ø ÖÚ ÒÝ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ º º¾º Ö Ø ÐØ ØÓÚ Ð ÙÐÐ ÑÓ ÑÔÐ Ø Ò Ñ ¹ Ø ÖÓÞ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ º º Ð ØÖÓÑ Ò ÙÐÐ ÑØ Ö Ð ÓÒØ ÙÐÐ ÑÓ Þ Ö º º º º º º º º ¾ º º½º Ø Ö Ö Ú ØÓÖÓ Ø Ö Ð ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ ÐØ º º º º º º º º º º º¾º ÙÐÐ Ñ Ý ÒÐ Ø Ñ ÓÐ Ø Ö Ð ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ Ú Ð º º º º º º Þ Å ÙÐÐ ÑØ Ö Ð Ö º º º º º º º º º º º º º º º º º º º º º º º º À Ú Ø ÓÞ Ó ½

3 ½º Þ Ø Þ Ð ØÖÓ Ò Ñ Ø Ñ Ö Ø ÖØÓÞ Ð Ò ÓÔÓÖØÓ Ø Þ Ð ØÖÓ Ò Ñ Ø Ñ Ö Ø ÖØÓÞ Ð Ò Ø Å ÜÛ Ðй Ý ÒÐ Ø Ð Ð ÖØ Ü Ñ ¹ Ö Ò Þ Ö Ð Ô Ò Ø Ö Ý Ð Ù º Þ Þ Ý ÒÐ Ø Ð Ò Ö ÞÓØÖÓÔ Þ Ò Ú Ø Þ Ð Ò Ö Ø Ð rot H = J + D t, rote = B t, divb = 0, div D = ρ, B = µ H, D = ε E, J = σ( E + Eb )+ J b, w = 1 2 E D H B, ½º½µ ½º¾µ ½º µ ½º µ ½º µ ½º µ ÓÐ E Þ Ð ØÖÓÑÓ Ø Ö Ö D Þ Ð ØÖÓÑÓ ÐØÓÐ H Ñ Ò Ø Ö Ö B Ñ Ò ÙÜÙ òöò Ú ØÓÖ º ε µ σ Þ ÒÝ ÓØ ÐÐ ÑÞ Ô ÖÑ ØØ Ú Ø Ô ÖÑ ¹ Ð Ø Ú Þ Ø Ô º J Þ Ö Ñ òöò ρ Ø ÐØ òöò Ø Ð Ð º Eb J b Ð ÓÖÖ Ó ÐØ Ð Ø ØÓØØ Ð ØÖÓÑÓ Ø Ö Ö Ö Ñ òöò º ½º½º Þ Ð ØÖÓÑ Ò Ø Ö Ð Ø Ö Ð Ú ÐØÓÞ Ò Ô ÓÐ Ø Þ ½º½µ¹ ½º µ Å ÜÛ Ðй Ý ÒÐ Ø Ø Ö Ð ¹ Ð Ô Ö Ð Ö Ú ÐØ Ø Ø ÖØ ÐÑ Þ ¹ Ö Ò Ð Ý ÒÐ Ø º Þ Ý ÒÐ Ø Ø ÖÑ Þ Ø Ð Ò Ø Ö Ð Þ Ð Ú ÐØÓÞ Ó ÝÓÖ Þ ØØ Þ Ú Òº À Ý f Ö Ú Ò Ú Ð Ú ÐØÓÞ ÐÐ Ò ÙÐØ ÐÐ ÔÓØ Ò Ð Ú Ð ØÖÓÑ Ò Åµ Ø Ö Ø Ú Þ ÐÙÒ ÓÖ ÓÑÓ Ò ÒÝ ÐÐ ÑÞ Ø Ò Þ Þ Ø ÖØÓÞ Ø Ö Ð Ú ÐØÓÞ Ó ÝÓÖ Ø Þ Ø Ð Ò λ ÙÐÐ Ñ Ó Þ Ú Þ Ø Ò ¾

4 Ô δ ØÓÐ Ñ ÐÝ ÐÐ ÑÞ º Þ ÖØ Ú Ø Þ Ñ ÓÒ Þ Ñ Ø Ø λ = 1 f µε = c f 1 δ = πfµσ ½º µ ½º µ ÓÐ c = 1 µε ÒÝ Ø Ö Þ ÓØØ Þ Ø Ð Òº Ý ÓÖÐ Ø Ò ÞÒ Ð ØÓ ÒÝ Ó Ø Ò Ñ Ñ Ò Ð Ø Ý Þ Öò Ò Ñ Ò Þ ¹ Ø Ð Ò Ø ÒØ Ò Ò ÝÓÒ Ó Ý Ð ØÖÓÑÓ Þ ÑÔÓÒØ Ð ÓÒØÓ ÒÝ Ð Ø Þ º ÁÐÝ Ò ÐÚ Þ Ø Ú Þ Ø Ö Þ Ø Ø ÖØ ÐÑ Þ ÓÐÝ Ó Þ ÓÒ Þ ÐØ Þ Ð Ö Þ Ñ¹ Ø Ø ÖØ ÐÑ Þ Þ Ø º Þ ÓÐÝ Ñ ØÓ ÑÓ ÐÐ Þ Ú Ð Ý ÓØØ Ð Ú ÐØÓÞ Þ Þ Ò Þ Ø Ò Ð Ø Ú Ð Ñ ÐÝ Ò Ø Ö Ð Ú ÐØÓÞ ÝÓÖ ¹ ÓØ Ø Ö Ø Ò º Þ Ø Ð ÒØ Ö Þ Ò ØÖ Ò ÞÔÓÖØ ÓÐÝ Ñ Ø Ò Ö ÞØÚ Ú Ó ØÙÑÓ Ø Ø ØÐ Ò Ø ÖÓÞÞ Ñ ÞØ Ó Ý Ý ÞÓÒÝÓ Ð Ú ÐØÓÞ Þ Ñ ÐÝ Ò Ø Ö Ð Ú ÐØÓÞ ÝÓÖ Ø ÖØÓÞ º Ý Ø Ø ÐÝ Ò ÒÝ Ó Ø Ò ØÙ ÙÒ ÖØ ÐÑ ÞÒ ÓÐÝ Ò Ó Þ ÐÐ ÑÞ Ø Ñ ÒØ Ñ ÐÝ Ò Ø λ δ ÓÖÑ Ò ÖØ ÐÑ ÞØ Ò Þ Ø Ð Ñ Ø Òº ØÓÚ Ò Þ Ý Þ Öò Ú ÖØ Þ Ø Ð Ö Ð Ñ Ö Ð Þ Ð Ò Þ ÐÑÓÒ ÓØØ Ø ÞÓÒ Ò ØÙ Ù Ø Ö ÞØ Ò ÓÒÝÓÐÙÐØ ÒÝ Ó Ý ¹ Ð Ñ Ú Ø Ð Ö º Å Ø Ö Ø Ö Ð Ú ÐØÓÞ Ò ÝÓÖ Ø Þ Ð Ú ÐØÓÞ ÓÒ Ú Ð Þ Ð ÐÝ Þ Ó ØÙÑÓ Ñ Ö Ø ÓÐÝ ÓÐ Ñ Þ Ú Ð Þ Å Ø Ö ÐÓ ÞÐ Ú ÐØÓÞ Ú Ø Þ ÒÝ ÐÐ ÑÞ Ø Ö Ð Ú ÐØÓÞ Ø º Þ ÒÝ ÐÐ ÑÞ Ú ÐØÓÞ Ø Ø Ö Ò Ð ÐÝ Þ ØØ Ó ØÙÑÓ Ú Þ ÐØ Ø ÖÖ Þ Ø Ô Ù Ó Ð Ð Ñ Ö Ø Ú Ð ÞÓ Ø ÐÐ Ñ ÞÒ ÞØ ØÓÚ Ò d¹ú Ð Ð Ð º ØØ Ð Ò Ó Ý Þ Å Ø Ö d¹ú Ð ÐÐ ÑÞ ØØ ÒÝ ÐÐ ÑÞ Ú ÐØÓÞ Ð ¹ ÐÐ ØÚ λ¹ú Ð Ú Ý δ¹ú Ð ÐÐ ÑÞ ØØ Ð Ú ÐØÓÞ Ð Ø Ö Ð Ú ÐØÓÞ ÝÓÖ Ó Ý Ò Ú ÞÓÒÝÙÐ ÝÑ ÓÞ Ð Ò Þ Ý Þ Öò Ø ÐØ Ø Ð Þ Ð Ð ¹ Ø Ò º Ý Þ Öò Ø ÐØ Ø Ð Þ Ð Ô Ò Þ Ð ØÖÓ Ò Ñ Ø Ú Ø Þ Ò Ø Ö Ý ÐØ Ð Ò Þ Ø Ñ Ø Ö Ð Ø Ö ØÙ Ù Ó ÞØ Ò ½ ¾ º ½º¾º ËØ Ø Ù Ø Ö d λ Ú Ý d δ ËØ Ø Ù Ø Ö Ö Ð Þ Ð Ø Ò Ò Þ Ø Ò Ñ ÓÖ Þ Ó ØÙÑÓ Ñ Ö Ø Ò ÝÓÒ ÙÐÐ Ñ Ó Þ ÓÞ Ô Ø Þ Þ d λ Ú Ý Ö ÑÐ Ø Ö Ò d δº Ö Ø ÖØÓÞÒ Þ Ð ØÖÓ Ò Ñ Ú Ø Þ Ø Ñ Ø Ö Ð Ø Ð ØÖÓ ÞØ Ø Ñ Ò ØÓ ÞØ Ø Ø ÓÒ Ö Ù Ö ÑÐ Ø Ö Ø ÓÒ Ö Ù Ö ÑÓ Ñ Ò Ø Ö Ð ÓÖÓÐØ Ø Ñ Ö Ö Þ Þ Ó Ý Ø Ö ÐÐ ÑÞ Ð Ö Ú ÐØ Ø Ð ÒÝ Óй Ù º Ð Ò Þ ½º½µ¹ ½º µ Å ÜÛ Ðй Ý ÒÐ Ø Þ Ø Ò ÓÐÝ Ò Ô Ö Ð Ö Ò ¹ Ð Ý ÒÐ Ø Ö Ñ ÐÝ Ò Ú Ý Þ Ð ØÖÓÑÓ Ú Ý Ñ Ò Ø Ö ÐÐ ÑÞ

5 Ø Ð Ð Ø º Þ Þ Ó ÒÒ Ó Ý ÐÝ Ò Ø Ò Þ Ð ØÖÓÑÓ Ñ Ò Ø Ö Ò Ò Ò ÝÑ Ð Ð Ò Ô ÓÐ Ø Òº Ý Ö ÒÝ Ô ÓÐ Ø Ô Ö Þ ÓÖ Ð Ø º È Ð ¹ ÙÐ Þ Ð ØÖÓÑÓ Ö ÑÐ Ø Ö Ò ÓÐÝ Ö ÑÓ Ñ Ò Ø Ö Ø ÓÞÒ Ð ØÖ Ú Þ Ø Ò Ò Ñ Ú Ð Ñ Ò Ø Ö Ð ÒÐ Ø Ò Ñ Ó ÓÐÝ ÓÐÒ Þ Ö ÑÐ Ø Ö Øº À Ò ÐÝÓÞÒ ÐÐ Ó Ý Ø Ø Ù Ø Ö Ø Ò Ð ÔÞ Ð Ø Ð Ú ÐØÓÞ Þ ÓÐÝ Ò Ð Ó Ý ÖÖ d λ Ú Ý d δ ÐØ Ø Ð Ðк ÁÐÝ Ò Ø Ò Þ Ð Ú ÐØÓÞ Ø Ý Ð Ø Ý Ð Ñ Ú ÒÒ Ó Ý Þ Ñ Ò Ò Ô ÐÐ Ò Ø Ò Ý¹ Ý Ø Ø Ù Ø ÖÖ ÚÓÒ Ø ÓÞ Ð ØÓØ ÓÐ ÙÒ Ñ º Ä Ò Ö Þ Ø Ò Þ Ú Ð Ò ÞØ Ð ÒØ Ó Ý Ý Ð ØÓØ ÓÐ ÙÒ Ñ ÔÓØØ Ñ ÓÐ Ø ÐÝÓÞÞÙ Þ Ò Ú ÐØÓÞ Ö ÞØ Ò Ý Ú Ðº ÒØ ÓÒ ÓÐ ØÑ Ò Ø ÓÐ Ð Ô Ð ÙÐ ÞØ Þ ÐÐ ÒØÑÓÒ Ø Ó Ý Ò Ý Ö Ú Ò Ö Ñ Ö Ò ÓÒ ÒÞ ØÓÖÓ ÓÐÝ Ò Ô Ø ÖØ Ú Ð Þ ÑÓÐÙÒ Ñ ÐÝ Ø Ð ØÖÓ¹ ÞØ Ø Ù Þ Ñ Ø Ó Ð ÔØÙÒ Ñ º Ò Þ Ø Ò Þ Ð ØÖÓ ÞØ Ø Ù Þ Ñ Ø Ó Ð ÐÑ Þ Ø ÓÞ Ù Ý Ò ÖÖ Ú Ò Þ Ò Ó Ý ÓÒ ÒÞ ØÓÖ Þ Ñ Ö ¹ Ø Þ Ô Ø Ð Ý Ò Ò ÝÓÒ Ò Ý ÙÐÐ Ñ Ó Þº ½º º ÃÚ Þ Ø ÓÒ Ö Ù ÖÚ ÒÝ Ö Ñ µ Ø Ö d λ d δ ÃÚ Þ Ø ÓÒ Ö Ù Ú Ý Ñ Ò Ú Ò ÖÚ ÒÝ Ö Ñ µ Ø ÖÖ Ð Þ Ð Ò ÓÖ Ð Ú Þ Ø ÒÝ ÓØ ÒÒ Þ Ø Ð ÖÒÝ Þ Ø Ø Ú Þ Ð Ù ÓÐÝ Ò Ö Ú Ò Ò Ñ ÐÝ Ò Ú Þ Ø Ñ Ö Ø Þ Ñ Ö Ø ØÓÐ Ñ ÐÝ Ð d δµ Ù Ý Ò ÓÖ Þ Ó Ð Þ Ø Ð Ò Þ Ñ Ø Ø ÙÐÐ Ñ Ó ÞÒ Ð d λµº ÁÐÝ Ò Ø Ò Þ ½º½µ Ó ÓÐ Ð Ò Ð Ú D Ø ÓØ ÒÝ ÓР٠к ÒÒ Ú Ø ÞØ ¹ t Ò Ú Þ Ø ÒÝ Ò Þ Ð ØÖÓÑÓ Ñ Ò Ø Ö ØÓÐ Ò Ú Ò ÝÑ Ð Þ Ò ½º½µ ½º¾µ Ý ÒÐ Ø Ò J = σe ÒÝ Ý ÒÐ ØÒ Þ Ò Ø Ò Ð ØÖÓÑÓ Ñ Ò Ø Ö ÐÐ ÑÞ Ñ Ð ÒÒ º Þ Ø Ð ÒÝ Ò Ú ÞÓÒØ Ò Ò Ð Ò ØÓÐ Ñ Ú Ð ÓØØ Þ Ð ØÖÓÑÓ Ø Ö Ò Ñ ÓÐÝ ÓÐ Ñ Ò Ø Ö Ø Ñ Ú Ð ½º½µ Ó ÓÐ Ð Ò Ò Ò Ú Þ Ø Ö Ñ Ð Ð J = J b Ý ÒÐ Ø Ð Þ Ð ØÖÓÑÓ Ø ÖØ Ð ØÐ Ò Ø Ø Ö Ñ Ðк Ú Þ Ø ÓÒ Ö Ù Ø Ö Ý ÞØ ÐÐ ÔÓØÓØ Ð ÒØ Ø Ø Ù ¹ ÙÐÐ ÑØ Ö Þ Øغ À Ò Ö Ú Ò Ú Þ Ø Ò d δ Ö Ð Ñ ØØ Ð ÙÐ Ý Ø ÓÒ Ö Ù Ö ÑÐ Ø Ö Ñ Þ Ø Ð Ò d λ ÐØ Ø Ð Ñ ØØ Ø Ø Ù Ø Ö Ð ÙÐ º Ñ ÒÒÝ Ò Ö Ú Ò Ò d δ ÐØ Ø Ð Ø Ð Ðº Þ ÞØ Ð ÒØ Ó Ý Ú Þ Ø Ò ÓÐÝ Ö ÑÓ ÒÒ Ð Ð Ø Ö ÓÒ ÒØÖ Ð Ò º Ò Þ Ø Ò Ð Þ Öò Ú Þ Ø Ø Ñ ¹ Ø Þ ÖÒ Ú Þ Ð Ò Ø ÖØÓÑ ÒÝ Ð Þ ÒÒ Ð Ð Ø Ò ÓÐÝ Ð Ð Ø Ö ÑÓ Ø Ý Ð Ñ Ú ÒÒ º À ÞØ Ø Þ ÓÖ ÙÐÐ Ñ Ð Ò Ø Ñ Ö ÙØÓØØÙÒ º ½º º Ð ØÖÓÑ Ò ÙÐÐ ÑÓ d λ d δ Ð ØÖÓÑ Ò ÙÐÐ ÑÓ Ø Ú Þ ÐÚ Å ÜÛ Ðй Ý ÒÐ Ø Ø Ð Ö Ò Þ Ö Ø ½º½µ¹ ½º µ ÐÐ Ý Ð Ñ Ú ÒÒ Ò Ñ ÓÐ ÒÙÒ º Ì Ô Ù Ò Þ Þ Ø Ñ ÖÓ ÙÐÐ Ñ Þ Þ ÒØ ÒÒ Ø º Ò Ð Þ ÓÖº Ò Þ Ø Ò Ñ Ò Ð ØÖÓÑÓ Ø Ö Þ Ø Ð Ò Ñ Ò Ø Ö ÒÝ Ò ØÓÐ Ò Ú Ò ÝÑ Ð Þ Ô ÓÐ Ø Ø Þ Ð Ø Ú Þ Å ÙÐÐ ÑÓ Ð ÙÐ Ø Ø Ö Ø Ý Þ Ú Ð ÙÐÐ Ñ Ð Ò Øº Ð Ú Þ Ø ÒÝ Ó

6 Ò Þ Ø Ò Ú Þ Ð Ø Ø ÖØÓÑ ÒÝ Ð Þ Ö Ö Ö ÐÒ Ð Ð Ø Ò ÓÐÝ Ö ÑÓ Ø Ú Þ Ý Ð Ñ º ÖÓ Þ Ú Þ Ø ÒÝ Ó Ö Ú ÞØ Ð ØÖ ÙÑ Ó ÐÑ Ò Ú Þ Ø Ú Ð Ý Ø Ô Ð Þ Ø Ð ÒØ Ø ÒØ Ò º ÀÙÐÐ ÑØ Ö Ò Ð Þ ÓÖ Ò Ø Ô Ù Ò Ò Þ ÒÙ ÞÓ Ò Ú ÐØÓÞ Å Ø Ö Ø Ú Þ ¹ ÐÙÒ º ÒÒ Ò Ð Þ Ú Ð Ý ÓØØ Ö Ú Ò Ò Ð ÙÐ Ò Ö Ú ÞÓÒÝÓ Ö ÚÓÒ Ø ÓÞ Ò ÔÙÒ ÞÒÓ Ú Ø ÞØ Ø Ø ÐÝ Ò Ô Ð ÙÐ Ý ÒØ ÒÒ Ø Ò Ñ Ò Ø Ñ¹ Ô Ò Ù ÖÞ Ö Ø Ö ÞØ Þ ÒØ ÒÒ ÒÝ Ö ÐÐ ØÚ Ù ÖÞÓØØ Ò Ö ò¹ Öò Ø ºµº Ý Ö Ú Ò Ò Ú Þ ØØ Ò Ð Þ ÞÓÒ Ò Ò Ñ ØÙ Ø Ð ÐÚ Ð Ó Ø Ø Ò Ô Ð ÙÐ ÖÖ Ó Ý Ñ ÐÝ Ò ÒØ Ö Ö Ò Ð ÙÐ Þ Ý Þ Ñ ÐÙÑÓ Þ ØØ ÑÓÒ Ù Ø ÙØ Ø Ö Ò Ò Ú Þ ØØ Ð Ò Ú Ø ÞØ Òµº ÁÐÝ Ò Ø Ò Ø Ð Ø Ò Ú Òº Þ Ý Þ Ó Ý Þ Ñ ÐÙÑÓ Ý Ð Ñ Ú Ø Ð Ú Ð Ñ ÓÐ Ø Ö Å ÜÛ Ðй Ý ÒÐ Ø Ò Ñ Ô Þ Ó Ý Ú Ú Ö Ú Ò ÖÒÝ Ò Ð Ú Ö Ú Ò¹ Ö ÐÚ ÞÞ ÖÑÓÒ Ù Ò Ð Þ Ø Ñ ÐÝ Ö Ñ ÒÝ Ø ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ Ø Ú Ð ÖØ ÐÑ Þ Ò º ½º º ÓÑ ØÖ ÓÔØ d λ Ñ ÒÒÝ Ò Þ Ó ØÙÑÓ ÐÐ ÑÞ Ñ Ö Ø Ó Ð Ò ÝÓ ÙÐÐ Ñ Ó ÞÒ Ð ÓÑ Ø¹ Ö ÓÔØ Þ ÐÝ Ð Ô Ò ØÙ Ù Ñ Ò Ð ÙÐ Å Ø Ö Øº ÁØØ Þ Ñ Ò Þ Ð Þ Ò Ø Ö Ý ÐØ Ø Ð Ò Ñ ÖÖ Ð Ú Ò Þ Ó Ý Þ Ý ÒÐ Ø Ø Ú Ð Ñ ÐÝ Ò Ñ ¹ ÓÒ Ý Þ Öò Ø ÞÓÒÝÓ Ø Ó Ð ÒÝ ÓÐ Ú Ð Ò Ñ Ó Ð Ò ÖÖ Ð Ó Ý Ý Ø ÒØ Ø ØØ Ñ ÓÐ Ð ÙÐÐ Ñ Å Ø Ö Ú Ð Ú Ò Ù Ð ÖÒ Ð Ò Øº Ý ÓØØ Ö ÒÝ Ø Ö ÙÐÐ Ñ Å ÜÛ Ðй Ý ÒÐ Ø Ý Ô Ð Ñ ÓÐ Ñ ÐÝ Ø ÞÞ Ð ÐØ Ø Ð Þ Ð ÔÙÒ Ó Ý Þ Å Ø Ö ÓØØ Ø Ö Ö ÒÝ Ö Ñ Ö Ð ¹ Ó Ò Ò Ñ Ú ÐØÓÞ º º Ö Þ Ò Ð Ø Ù Ó Ý Ð Ò Ö Þ Ø Ð Ò Ø Ø Þ Ð Ñ ÓÐ Å ÜÛ Ðй Ý ÒÐ Ø Ò Ð ÐÐ Ø Ø Ð Ò Þ Ö ÒÝÓ Ø Ö ÙÐÐ ÑÓ ÞÙÔ ÖÔÓÞ ÒØ ÔÓÒØÓ Ò Ñ Ó ÐÑ ÞÚ Ú Ø Ð Ò Ó Ý Ò ÒØ Ò Ò Ø Þ Ñ Ð Ò Ö ÙÐÐ ÑÓ Þ ÒØ ÞØ Ð Ö Ø ÙÐРѹ Ô ØÖÙÑ ÒØ Ø ÖØ Ò Ñ ¹ Ò Ú Ù º Ì ÒØ ÞØ Þ Ø Ø Ñ ÓÖ Ý ÓØØ Ö ÒÝ Ø Ö ÙÐÐ Ñ Ñ Ú Ð Ø Ý Ú ¹ Ñ Ö Øò Ø Ö Þ Ð Ð Ø Øº Ö Ø ÐØ Å Ø Ö Ð Ö Ø ÙÐÐ Ñ Ô ØÖÙÑ ÒØ Ñ ÐÝ Ô ØÖÙÑ Þ Ð ØØ Ð Ó Ò Ó Ý Ñ ÓÖ Ø Ö Þ Ð Ð Ø ÓÑ ØÖ Ñ Ö ¹ Ø º Ñ ÒÒÝ Ò Þ Þ Ñ Ö Ø ÙÐÐ Ñ Ó Þ Ð d λµ Ô ØÖÙÑ Þ Ð Ð Þ Ú ÐØÓÞ ØÓ Ö Ø ÐØ Ø Ö Ø ÔÙÒ Þ Þ Ø Ø ÖØÓÞ Þ Ð Þ Ò Ø Ö Ý ÐØ Ð ØÖÓÑ ¹ Ò ÙÐÐ ÑÓ Ø Ñ Ö º À Ú ÞÓÒØ Ø Ö Þ Ð Ð Ø Ó Ð Ò ÝÓ ÙÐÐ Ñ Ó ÞÒ Ð d λµ Ô ØÖÙÑ Ò ÝÓÒ ÒÝ Ð Þ Ý ÓÖÐ Ø Ð Ý ÙÐÐ Ñ Ð ÓØ Þصº ÞØ Ð Ò Ø Ý Ð Ø Ñ Ý Ö ÞÒ Ó Ý Ø Ö Þ Ð Ð Ø Þ Ô Ø ÖØÓÑ ÒÝ Ý Þ Ð Ø Ñ ÒØ Þ Ú Ø Ð Ò Ø ÚÓÐ Ò Ð ÒÒ ÒÒ Þ Ð Ø Ð ÙÐÐ Ñ Ó Þ 5 10¹ Þ Ö Ñ Ö Þ Ð Ø Ð Ú Ø Ð Ò Ø ÚÓÐ Ò Þ Ñ Øµ Ð Ò Þ Ô Ø ÖØÓ¹ Ñ ÒÝ Ò Ý Ú Ð Ø Ö Ñ ÒØ Þ Ý Ú Ø Ð Ò Ø Ö ò Ð Ð Ø Ö ÐØ ÚÓÐÒ Ñ Ú Ð Ø Ö º Þ Ö Ü Ð Ð Ô ØÖÙÑ ÓÑ Ò Ò ÓÑÔÓÒ Ò Öغ Ñ ÒÒÝ Ò Ð Ð Ø Ø Ð Ñ Ö Ø Ó Ð Ò ÝÓ Þ Ð Ò Ð Ú Ò ÒÝ ÙÐÐ Ñ Ó Þ Þ Ð ò ÚÒ Ð ÓÖ ÓÑ Ò Ò ÙÐÐ ÑÓÒ Ú Ð ÓÑÔÓÒ Ò Ð ÒÝ ÓÐ Ø º À Ø Ø Ö Ø Ð Ð Ð Ø Ñ Ö Ø Ó Ð Ò ÝÓ ÙÐÐ Ñ Ó ÞÒ Ð ÓÖ Ö ¹ Ð Ü Ø ÒÒÝò Þ Ð Ø Ð Ý Ð ÖÒ Ó Ý Ö Ø ÐØ Ø Ö Ø Ý Ú Ø Ð Ò Ð Ð ØÖ Ð Ú Ð Ö Ü ÒØ Ú Þ Ý Ð Ñ Þ Þ ÓÑ ØÖ ÓÔØ Þ ÐÝ Ð Ô Ò Þ Ñ Ø Ù

7 Ö Ø ÐØ ÙÐÐ Ñ Ö ÒÝ Ø Þ Ø Ò Ö Ø Ô Ý Þ Öò Ò ÐÝÓÞÞÙ Ù¹ ÖÞÓØØ Ð Ð Ø Ö Ø Ð Ð Ð Ø Ö ÒÝ Òº Þ ÓÒ ÓÐ ØÑ Ò Ø Þ Ð Ô d λ ÐØ Ø ÐÒ Ð Ø Ø Ú ÐÖ Ò Þ Ò Ð Þ Þ ÞÒ ÐØ ºÒº Ù Ö Ú Ø Ö Ý ØÖ Ò µ Þ Ñ Ø Ñ Þ Ö Ò º Î Ý ÞÖ Ó Ý d λ Ø Ò Þ ÒØ Ð Ø ØÐ Ò Ð ÒÒ Å ÜÛ Ðй Ý ÒÐ Ø Ø Ð Ñ ÓÐ Ø Ñ Ò Ñ Ú Ð Þ Ñ Ø Ø ÖØÓÑ ÒÝ Ò Ý Ò Ñ Ø ÒÒ Ð Ø Ú Ñ Þ ÒØ Ú Ø Ð Ò Þ Ñ Ø Ô Ø Ø Ò Ñ ÞØ Ó Ý Ø ÖÖ ÞØ Ý ÒÙÑ Ö Ù Ñ Þ Ö Ú Ò ÐÑ Ò Ñ Ð Ð Ò Þ Ö Ø Þ ÐÒ Ð Òº ½º º ÐÓ ÞØ ÖØ ÐÑ Þ Ø Ö Ð ÒØ ÐÓ ÞØ Ø Þ ÑÐ Ð Ø Ò ÖÞ ÐØ ØÒ ÖØ ÐÑ ÞÒ Ð Ø Þ Ý Þ Ò Ø ÖØ ¹ Ò Ò ÓÖÑ Ò Ö Ö ÑÐ Ú Ðº ËØ Ø Ù ÔÖÓ Ð Ñ Ø ÐÐ Ù Ý Ò Ú Þ ÐÒÙÒ Ò Þ Ø Ò Ð Þ Ø Ö Ø Ñ Ø ÖÓÞ Ý Ð Ñ Ú Ø Ð Ú Ð Þ ÐÖ Ò Þ Ö ÓÞ Þ Ð ØØ Ö ÞØ Ð Ò Ñ Ú ÐØÓÞ Ñ Þ ÑÓØØ Ú ¹ Òº Å Þ Ú Ð Þ Ñ Ø ØÙÒ ÖÖ Ó Ý Þ Ð Ú ÐØÓÞ Ó Ð Ð ÓÞ Ó Ý Ñ Ò Ò Ð ÐÑÓÞ ÙÐ ÙØ Ò Þ ÓØØ Ö ÞØ Þ ÒØ Þ Ø ÖØÓÞ ÐÐ Ò ÙÐØ ÐÐ ÔÓØ Ð Ö Þ Ú Ò Ð Ò º Ú Þ ØÖ ÓÒ Ö Ù Ø Ö Ò Ð ÔÔ Ò Þ ÖØ Ú Ò Þ ÑÐ Ø ØØ ØØ Ñ Þ Ö ÒØ Þ ¹ Ø Ð Ò Ø Ø Ù Ú Þ Ø Ò Ô ÙÐÐ ÑØ Ö Ú Ò Ñ ÖØ Ú Þ Ø Ò Þ Ò Ö Ø Ö¹ Ø Þ Ø Ð Ò Ñ Ö Ø ÒÝ Ø Ö Ò Ð Ð ÒØ Ò ò ØÖ Ò ÞÔÓÖØ ÓÐÝ Ñ ØÓ Ø ÖÓÞÞ Ñ º ½º º Ú Þ Ð Ò ÐÖ Ò Þ Þ Ø ØØ Ú Ð Ò Þ Ò Ð Þ Ð Ò ÐÖ Ò Þ Ò Ñ Ñ Ò Ø ÞØ Ò Ð ÓÖÓÐØ Ø Ñ Ö Ý ¹ Ø ÖØÓÞÒ º ËÓ Ð Ý ÓÖ Þ Þ Ø Ó Ý Ø Ö Þ Ñ Ø ÔÖÓ Ð Ñ Ò ÞÓÒÝÓ Ö Þ Þ Ý Ñ Ö Þ Ô Ý Ñ Ø Ñ Ö Ø ÖØÓÞÒ º Ý Ö Ò ÓÖ ÙÐ Ð Ñ ÓÐÝ Ò Ø Ñ ÓÖ Þ ÐÖ Ò Þ Ý Ñ ÒÞ Þ Ö ÒØ Ø Ø Ù ÒØ Ñ Ñ ÒÞ Þ Ö ÒØ Ô ÙÐÐ Ñ Ð Ò ÒØ Þ Ð Ø º Ì Ô Ù Ô Ð ÖÖ Þ ØÖ Ó Ü Ð Ðº ÁØØ Ð Ó ÞØ Ò ÐÝ Ö Ñ Ö Ð Ö ÒÝ Ò Ñ Ö Ø Ò ÝÓÒ ÙÐÐ Ñ Ó Þ ÓÞ Ô Øº Þ Þ Ó ÒÒ Ó Ý Ð ÐÐ Ñ Þ Ø Ø Ø Ù Þ Ñ Ø Ó Ö Ñ ÒÝ ÒØ ÔÓØØ Ó Þ Ý Ö Ô Ø Ð Ò Ù Ø Ú Ø Ð Ú Þ Ø Ð ÐÐ Ò ÐРк Ð Ú Ð Ø Ò ÐÝ Ö ÒÝ Ò Ú ÞÓÒØ Ñ Ö Ø Ú Ö ¹ Ý ÒÐ Ø Ý Ñ ÒÞ ÙÐÐ Ñ Ý ÒРص Ñ ÓÐ ÒØ Ô Ø º Å Þ Ú Ð ÞØ ÑÓÒ Ø Ù Ó Ý Ð Ó ÞØ Ò ÐÝ Ñ ÒØ Ò ÙÐÐ Ñ Ð Ò Ø ÖÖ Ñ Ö Ð Ò Ô Ø Ø Ù Ø Ö Ø ÐØ Ø Ð Þ Ò º

8 ¾º Þ Ø Ì Ö Ó Ø ÒÝ ÑÓ ÐÐ Þ Þ ÖÚ ÒÝ Ö Ñ ÖÓÒ ÓÐ Ñ ÒØ ÒÝ Ú Þ Ð Ø Ò Ò Ö Þ Ò Ý Ô Ð Ø Þ Ö ØÒ Ò ÑÙØ ØÒ ÖÖ Ó Ý Ñ ÒØ Ð Ø ÒØ Ö Ð Ý ÒÐ ¹ Ø Ø Ú Ð ÓÒÝÓÐÙÐØ Ø Ö Þ Ñ Ø ÔÖÓ Ð Ñ ÒÙÑ Ö Ù Ò Ø ÓÒÝ Ñ ÓÐ Ø Ò º ÐÙÒ ÙÔ Ò Þ Ó Ý Ð Ö ÙÒ Ý Ú Ð Ó Ñ ÖÒ ÔÖÓ Ð Ñ ÓÞ ÓÐ ÓÐÝ Ò ÒØ Ö Ð Ý ÒÐ Ø Ø Ñ ÐÝ Ò Ú ØÓÖ Ð Ú ÐØÓÞ Ø Ù Ö Ò¹ Ú ÒÝ Ø Þ¹ Ò ÐÙÒ º Þ ÒØ Ö Ð Ý ÒÐ Ø Ø ÖÓ ÐÓÑ Ò Þ ÐØ Ð Ô Ò Ö Ù Ðº Þ ÒØ Ö Ð¹ Ý ÒÐ Ø ÒÙÑ Ö Ù Ñ ÓÐ Ø Ò Ñ Ö ÞÐ Ø ÞÞ º Ø Ö Ý Ð Ò Ô Ð Ý ÓÖÐ Ø Ð ÞÒ Ð Þ ÖÚ ÒÝ Ö Ñ ÖÓÒ ÓÐ Ñ ÒØ ÒÝ ¹ Ú Þ Ð Ø ÓÞ Ô ÓÐ º Ú Þ Ð Ø Ñ Þ Ö Ð ÒÝ Ó Ý Ý Ö ÑÑ Ð Ö ÞØ ØØ Ø Ö Ø ÑÓÞ ØÙÒ Ú Þ Ð Ò Ú Þ Ø ÒÝ Ð Ð Ú ÑÙÒ Ö Ð ØØ Ø Ö Ñ Ò Ò ÔÓÞ Ò Ñ Ö ÒÒ Þ ÐØ Ø Ú Ý ÑÔ Ò Øµº Ú Þ Ð Ø Ú ¹ Ð Þ Ó Ý Ñ ÖØ ÖØ Ð Ñ Ø ÖÓÞÞÙÒ Þ ÒÝ Ò Ø Ð Ð Ø ÒÝ Ô Ö Ñ Ø Ö Ø Ñ Ö Ø Ø Ú Þ Ø Ô Ø Ø ºµº Þ Ø Ý Ö Þ Ò Ñ Ð Þ Ò Ñ Ö ÞÞ Ð Ó Ý Ñ Ð Ò ÞØ Ø ØÐ Ò ÑÙÒ Ö Ó Ø ÞÓ Ø Ð Ñ ÐÝ Ò Ú Ð Ñ ÐÝ Ò ÒÝ Ø Ð Ð Ø º Þ ÒÝ Ô Ö Ñ Ø Ö Ò Ñ Ø ÖÓÞ ÓÞ ÐØ Ø¹ Ð Ò Ð Þ Ú Ò ÖÖ Ó Ý Þ Ñ Ø Ð Ñ ØÙ Ù ÓÐÒ Ý Ñ ÖØ Ô Ö Ñ Ø Ö Ð Ö Ò Ð Þ ÒÝ Ø Ö Ñ ÖØ Ð Øº Þ Ð Ú Ø Þ Ò Ò ÑÙØ Ø Ö Ö Ð ÒØ Ö Ð Ý ÒÐ Ø Ñ ÓÐ ÔÔ Ò Ð Ñ Ø ÖÓÞ Ö ÞÓРк Þ ÒÝ Ô Ö Ñ Ø Ö Ò Ñ Ø ÖÓÞ Ý ÒØ Ý ÒÚ ÖÞ ÔÖÓ Ð Ñ Ò Ø ¹ ÒØ Ø Ñ ÐÝ Þ Ø ÖØÓÞ Ö Ø ÔÖÓ Ð Ñ Ñ ÓÐ Ö ÑÙØ ØÙÒ Ú Ø Þ Ò Ý Þ Ñ Ø ÑÓ ÐÐغ Þ ÖÚ ÒÝ Ö Ñ ÒÝ Ú Þ Ð Ø Ñ Þ ÖØ Ò ÓÐÙÐ Ý ÙÖÖ ÒØ Ì Ø Ò Ìµ Þ Ô Ö Ò Ø Ö Ø Ò ÞÒ Ð Ò Ý ÒÝ Ú Ø ÐÒ Ø ØØ Ö Ø Ù Þ Ö Þ Ø ÖÓÒ ÓÐ Ñ ÒØ Ú Þ Ð Ø Ö º ÁÐÝ Ò Ð ÐÑ Þ Ó Ôк ØÓÑÖ ØÓÖÓ Ö ¹ Ð Ò Ö Ô Ð Ô ØÙÖ Ò Ð Ô Ø Ò Ð ÓÔØ Ö ÖÓØÓÖÐ Ô Ø Ò Ø º Ú Þ Ð Ø º Ú Þ Ð Ø Ñ Þ Ö Þ ÑÙÐ Ö Ø ÖÚ Þ Ö Ð ÞÓ ØÚ Ö ÐÐÒ Ñ ÖÒ Ö Ò Ð¹ Þ Ö Þ Ð Ð ÒØ Ô Ð ÐØ Ð Ð ÞØ ØØ ÁÎ ÞÓ ØÚ Ö Ñ ÐÝÒ Ì Þ ÑÙÐ Ö ÞÓÐ Ð Ö Þ Ø ÑÙØ Ø Ö Ö Ð ÒØ Ö Ð Ý ÒÐ ØÖ Ð ÔÓÞÚ ÖØ Ñ Ð ÞØ Ð ÞØ Ò Å ¹ÀÎÌ Ö Ò Þ Ö Ò ÞÖ Ñò µº

9 σ 0, µ 0 σ, µ 0 Ì Ú Þ Ð Ì Ö Ó Ø ÒÝ Î Þ ÐØ ÑÙÒ Ö V s V d ¾º½º Ö º Ì Ú Þ Ð Ý Ø Ö Ó Ø ÒÝ Ø Ø ÖØ ÐÑ Þ ÑÙÒ Ö Ð ØØ ¾º½º Ø Ö Ó Ø ÒÝ Ø Ð Ö ÒØ Ö Ð Ý ÒÐ Ø Ì ÒØ ¾º½º Ö Ò Ð Ø Ø ÐÖ Ò Þ Ø ÓÐ Ý ÖÚ ÒÝ Ö Ñ Ú Þ Ð Ø Ð Ð Ø V s Ø Ö Ó Ø Ò Ð ÐÝ Þ Ú Þ Ð Ò ÑÙÒ Ö Ð Øغ ÑÙÒ Ö σ( r) Ú Þ Ø ¹ Ô r ÐÝÚ ØÓÖØ Ð Ð µ V d Ø Ö Ó Ø Ú Ø Ð Ú Ð Ù Ý Ò Þ Ñ Ò Ò ÓÐ ÒÒ ÖØ σ 0 Þ Þ σ( r) = σ 0, r V s \ V d µº Ø Ö Ó Ø ÒÝ ÞÓÒ V d Ø ÖÖ Þ Ò ¹ ÐÝ Þ Ð ÓÐ Ú Þ Ø Ô ÐØ Ö σ 0 ¹Ø к ÑÙÒ Ö ÒÒ Ð Ú ÒÝ ÒÝ Ò Ñ Ñ Ò Ý Þ Ô ÖÑ Ð Ø µ 0 º Ú Þ Ð Ø Ò Þ ÒÙ ÞÓ Ò Ú ÐØÓÞ ω Ö Ö Ú Ò Ö ÑÑ Ð Ö ÞØ Ð¹ Ø Ø Ð ÞÞ Ó Ý Þ ÐÖ Ò Þ Ð Ò Ö Ò Ø ÒØ Ø ÒÝ ÐÐ ÑÞ Ð Ö Ø ÖÖ Þ Ð ÐÐ Þ Ð Ú ÐØÓÞ Ø ÒØ Ø Ò Ñ Ö Ð ÙÐØ Þ ÐÐ Ò ÙÐØ ÐÐ ÔÓغ ÓÑÔÐ Ü Þ ¹ Ñ Ø Ñ Þ Ö Ð ÐÑ Þ Ú Ð ½ Ø Ö ÐÐ ÑÞ ÓÑÔÐ Ü ÖØ Ø ÞÒ Ð Ù º  РРÔк E = E( r) Þ Ð ØÖÓÑÓ Ø Ö Ö ÓÑÔÐ Ü ÖØ Ø { Þ r } ÐÝ Ò ÒÒ Ñ Ö Ø ¹ Ò Ø Ö ÐÐ ÑÞ Ú ØÓÖ Ò Ú ÒÝ Ø Ê E( r)exp(jωt) Þ Ð Ô Ø Ù Ñ ÓÐ Ê { } ÓÑÔÐ Ü Þ Ú Ð Ö Þ Ø Ð Ð º Þ ÐØÓÐ Ö Ñ Ð ÒÝ ÓÐ Ú Ð Ú Ð Ñ ÒØ J( r) Ð ØÖÓÑÓ Ö Ñ òöò E( r) Ð ØÖÓÑÓ Ø Ö Ö ÓÑÔÐ Ü ÖØ Þ ØØ Ô ÓÐ ØÓØ Ø Ö ÑØ J( r) = σ( r) E( r) ÒÝ ÐÐ ÑÞ Ö ÚÓÒ Ø ÓÞ Ý ÒÐ Ø Ý Ð Ñ Ú Ø Ð Ú Ð Ú Þ Ð Ò ÑÙÒ Ö V s Ø Ö Ó Ø Ò Þ Ð Ñ Ó Å ÜÛ Ðй Ý ÒÐ Ø Ú Ø Þ Ð Ò Ö Ø rot H( r) = σ( r) E( r), rot E( r) = jωµ 0 H( r), ÓÐ H Ñ Ò Ø Ö Ö ÓÑÔÐ Ü ÖØ Ø Ð Ð º ¾º½µ ØÖ Ò Þ Ú Ð Ô Ù rot H( r) = σ 0 E( r)+[σ( r) σ0 ] E( r) ¾º½µ ¾º¾µ ¾º µ Ð ÓØ ÓÐ Ó ÓÐ Ð Ñ Ó Ø Ø Ð Ó Ø Ù Ý Ñ ÒØ Ý Ð Ö Ñ òöò ÐÐ ò ÓÖÖ Ø Ñ ÐÝ V d Ø Ö Ó ØÖ ÓÒ ÒØÖ Ð º ÓÖÖ Ó Þ ÒÝ ÐØ Ð ÐØ ØØ Ø ÖÔ ÖØÙÖ Ø Ð ØÖ ÓÞÒ º Þ Ì Ñ Ö Ð Ø Ø Þ Ò V d Ø Ö Ó Ø Ò ÒÙÐÐ Ø Ð ÐØ Ö P( r) = [σ( r) σ 0 ] E( r), ¾º µ Òº ÒÝ Ø Ð Ö Ö Ñ Ô ÐÙ ¹ òöò ÐØ Ð ÐØ ØØ Ð ØÖÓÑ Ò Ø Ö Ñ Ø ÖÓÞ º ¾º¾µ¹ ¾º µ Ý ÒÐ Ø Ð H Þ Ð Ú Ð Ú Ø Þ Ý ÒÐ ØÖ ÙØÙÒ rotrot E( r) k 2 c E( r) = jωµ 0 P( r), ¾º µ

10 ÓÐ k 2 c = jωµ 0σ 0. ÓÒØ Ù Ð Þ Ð ØÖÓÑ Ò Ø Ö Ø Ø ÓÑÔÓÒ Ò Ö Ð Ý Ò ¾º µ E( r) = E i ( r)+ E f ( r), H( r) = H i ( r)+ H f ( r), ¾º µ ÓÐ Þ i Ð Ò Ü Þ Òº Ø ØÓØØ Ø Ö Ø Ò ÓÐÙÐ Ò ÒØ Ð µ Ð Ð Ñ ÐÝ Þ Ì Ú Þ Ð ÒÝ Ò Ð Ð ÑÙÒ Ö Ò ÐØ ØØ Ð ØÖÓÑ Ò Ø Ö Ø Ð ÒØ º Þ Ý Ô Ø Ñ Ó Ý Ø ÒØ Þ ÒÝ Ò Ð Ð ÑÙÒ Ö ÓØ σ( r) = σ 0, r V s µ Ú Þ Ð Ö Ñ Ø Ñ ÒØ Ø Ö Ø Ö ÞØ Ñ ÒÒÝ Øº Þ f Ð Ò Ü Ô Þ Òº ÒÝ Ø Ö Ø Ò ÓÐÙÐ Û Ð µ Ð Ð Ñ ÐÝ Þ ÒÝ Ð ÒÐ Ø Ú Ø ÞØ Ò Ð ØÖ Ú Ô ÖØÙÖ Ð Ø Öº ÞØ Þ Ð ØÖÓÑ Ò Ø Ö Ø Ý Ô Ù Ó Ý Ø ÒØ P( r) Ö Ñ Ô ÐÙ ¹ òöò Ñ ÒØ Ö ÞØ Ø Ö Ð ØÖ ØØ Ø Ö Ø Þ ÒÝ Ò Ð Ð ÑÙÒ ¹ Ö Ý Ð Ñ Ú Ø Ð Ú Ðº Þ ÒÝ Ø Ö Ñ Ø ÖÓÞ Ò Ð Ð Ø Þ Ö Ú Þ Ð Ð ÒÐ Ø Ø Ð ÐØ ÒØ Ò Þ Ò Ý Þ Öò Ø Ð ÐØ Ð Ò Ò Ø Ú Ø Ò Ðºµ Å Ú Ð Ø ØÓØØ Ø Ö Ø Ö ÞØ Ö Ñ V s Ø Ö Ó ØÓÒ Ú Ð ÐÝ Þ Ð Þ ÖØ E i Ú Ø Þ Ý ÒÐ Ø Ø Ð Ø V s ¹ Ò rotrot E i ( r) k 2 c E i ( r) = 0, r V s. ¾º µ P ÒÝ Ø Ð Ö Ö Ñ Ô ÐÙ ¹ òöò Ñ ÒØ ÓÖÖ ÐØ Ð ÐØ ØØ ÒÝ Ø Ö Ô Ñ ÓÐ rotrot E f ( r) k 2 c E f ( r) = jωµ 0 P( r), r Vs ¾º µ Ý ÒÐ ØÒ º Ä Ø Ø Ó Ý ¾º µ ¾º µ Þ Ú Ð Ò Ñ ¾º µ Ý ÒÐ Ø Øº Þ Ì ÐØ Ð Þ ÒÝ Ò Ð Ð ÑÙÒ Ö Ò Ö ÞØ ØØ Ø ØÓØØ Ø Ö E i ( r)µ Þ Ñ Ø Ö Ð Ò Þ Ñ Þ Ö Ñ ÖØ Þ ÖÓ ÐÓÑ Ð Ð Ôк µ ÒÒ Ö ÞÐ ¹ Ø Ú Ð ØØ Ò Ñ Ó Ð Ð ÓÞÙÒ º Á Ñ ÖØ P Ø Ò Þ ÒÝ Ø Ö Ð ÐÐ Ø Ø Ù Ö Ò¹ Ú ÒÝ Ø Ú Ð Ú Ø Þ Ñ ÓÒ E f ( r) = jωµ 0 V d G e ( r r ) P( r )d r ¾º½¼µ ÓÐ G e ( r r ) Þ Ð ØÖÓÑÓ Ø ÖÖ ÚÓÒ Ø ÓÞ Ù Ö Ò¹ Ú Òݺ Þ Þ r ÐÝ Ò Ø ¹ Ð Ð Ø ÓÒ ÒØÖ ÐØ Ö ÞØ Ø ØÖ Ò Þ ÓÖÑ Ð Þ r ÔÓÒØ Ð Ð ØÖÓÑÓ Ø Ö Ñ ÒÒÝ Ò r, r V s º Ù Ö Ò¹ Ú ÒÝ Ñ ÓÐ Ú Ø Þ Ù Ý ÒÐ ØÒ rotrotg e ( r r ) k 2 cg e ( r r ) = δ( r r )I, r, r V s, ¾º½½µ ÓÐ δ Ö ¹ Ú ÒÝØ I Þ Ý Ø ÒÞÓÖØ Ð ÒØ G e ÓÑÔÓÒ Ò G e ¹Ò Þ ÓØØ ÓÓÖ Ò Ø ¹Ö Ò Þ Ö Ý Ú ØÓÖ Ú Ð Ú ØØ Ð Ö ÞÓÖÞ ÙØ Ò ÔÓØØ Ú ØÓÖÓ µ Ð Ø Þ ÓØØ ÐÖ Ò Þ Ò Þ Ð ØÖÓÑÓ Ø ÖÖ Ñ Ó ÐÑ Þ Ø ÓÐÝØÓÒÓ ¹ Ô Ö Ñ ÐØ Ø Ð Øº Å Ý ÞÞ Ó Ý Ù Ö Ò¹ Ú ÒÝ Ñ Ý Þ Öò ÒÓÒ Ù µ ÓÑ ØÖ ÑÙÒ Ö Ó Ôк ÐØ Ö Ð Ñ Þ Ö Ø Þ ØØ Ð Ñ Þ Ò Ö Ø Ö Ø ò Ø º Ð ÑÙÒ Ö Ó µ Ø Ò Ø Ø Ñ Ú ÞÓÒÝÐ ÒÒÝ Òº Þ Ò Ø Ý ÓÖÐ Ø Ð ÒØ ÞÓÒ Ò Ò Ò Ý Ñ Ú Ð Þ Ô Ö Ò Ð ÓÖ ÙÐ Ì ÔÖÓ Ð Ñ

11 Ð ÒØ ÒÝ Ò Þ Ð Ø Ø ÑÙÒ Ö Ý Þ Öò ÓÑ ØÖ ÐÖ Ò Þ Ðº Þ Ð Ø Ð Ò Þ ÖØ Ø Ø Ñ Ñ ÖØ Þ Ì Ñ Ö Þ ÒÝ ÐØ Ð Ò Þ ÖØ Þ Ö Ñ ÒÝ Þ ÑÔÓÒØ Ð Ö Ø ÖÖ Þ Þ ÒÝ ÞÚ ØÐ Ò ÖÒÝ Þ ¹ Ø Ö ÓÒ ÒØÖ Ð Ý Ø ÖÖ Þ Ò Ð ÙÐ Ð ØÖÓÑ Ò Ø Ö Ú Ð Ò Þ Þ Ý Þ Öò Ø ØØ ÓÑ ØÖ ÐÖ Ò Þ Ò Ð ÙÐ Ø ÖØ Ðº Þ Ð ØÖÓÑÓ Ø ÖÖ ÚÓÒ Ø ÓÞ Ù Ö Ò¹ Ú ÒÝ Ñ Ø ÖÓÞ Ò Ø Ð ¾º½¼µ ÖØ Ð Ò Ý Ñ Ò Þ Ó Ý G e ( r r ) Ò Ð Ú Ú ÒÝ Þ Ò ÙÐ ¹ Ö Ó Þ r = r ÐÝ Ò Ý Þ Ñ Ø Ó ÓÖ Ò ÐØ ØÐ Ò Ð Ý Ð ÑÑ Ð ÐÐ ÖÖ Ð ÒÒ Ó Ý Þ ÒØ Ö Ð ÖØ Ð Ö Ñ Ð Ð ÒÙÑ Ö Ù Ò Ø Ð Ð ÓÖ ØÑÙ Ø ÞÒ Ð ÙÒ º Ý ÐÝ Ò Ð ÓÖ ØÑÙ Ñ Ø Ð Ð ÑÔÐ Ñ ÒØ Ð Þ Ñ Ø Ó Ý ÙÐ Ö º ¾º½¼µ Ø Ú Ð Ð Ö Ø Ù ¾º µ Ø Ð Ð ØÖÓÑÓ Ø Ö Ø Ú Ø Þ ÓÖÑ Ò E( r) = E i ( r)+jωµ 0 G e ( r r ) P( r )d r. ¾º½¾µ V d Ú Þ Ø v( r) = σ( r) σ 0, ¾º½ µ σ 0 Òº Ö Ð Ø Ú ÒÝ Ú ÒÝØ Ñ ÐÝÒ ÖØ ÒÙÐÐ Þ ÒÝ Ò Ú Ð v( r) = 0, r / V d µ V d Ø Ö Ó Ø Ò Ò Ñ ÒÙÐÐ ÖØ Ø Ú Þ Ðº È Ð ÙÐ Ò Ñ Ú Þ Ø ÒÝ Ø Ò v( r) = 1, r V d º ¾º½¾µ Ý ÒÐ Ø Ø ÞÓÖÓÞÚ σ( r) σ 0 Ú ÒÒÝ Ð Ú Ð Ñ ÒØ Ð ÞÒ ÐÚ ¾º µ ¾º½ µ ÔÐ Ø Ø Ø Ö Ó Ø ÒÝ Ø Ð Ö P( r) Ö Ñ Ô ÐÙ ¹ òöò Ö ÚÓÒ Ø ÓÞ Ñ Ó Ö ÓÐÑ Ø ÔÙ µ ÒØ Ö Ð Ý ÒÐ Ø ÞÓ Ó ÓÖÑ ÓÞ ÙØÙÒ P i ( r) = P( r)+k cv( r) 2 G e ( r r ) P( r )d r, r V d, ¾º½ µ V d ÓÐ P i Þ Ø E i Ñ Ö Ø Ò P i ( r) = [σ( r) σ 0 ] E i ( r). ¾º½ µ Ä Ø Ø Ó Ý ¾º½ µ Ð ÓÐ Ð Ó ÓÐ Ð Ñ Ò Ø Ø ÞÓÒÓ Ò ÒÙÐÐ Þ ÒÝ ¹ Ø Ö Ó Ø Ò Ú Ð Ý Þ Ò ÒØ Ö Ð Ý ÒÐ Ø Ø V d Ø Ö Ó Ø Ò ÐÐ Ñ ÓÐ Ò º Ñ ÓÐ Ð P Ñ Ö ØÐ Ò Ñ Ø ÖÓÞ Ñ Ò Ø Ú Ð Ñ Ö Þ Ñ Ø Ø Þ ÓØØ Ì Ú Þ Ð Ð Ð ¾º¾º ÔÓÒØÓصº ¾º½ µ ÒØ Ö Ð Ý ÒÐ Ø Ò Ñ Þ Ò ÙÐ Ö º Þ Ò Þ Ò ÙÐ Ö Ø Þ Ð Ù Ý¹ Ð ÖØ Ø Ú Ð Ñ ÓÐ Ø º ÒÒ ÐÐ Ò Ö Ó Ý ÔÖÓ Ð Ñ ÐÑ Ð Ø Ð Ð Ö Ð Ø ÖÓÐØ Þ ÒØ Ö Ð Ý ÒÐ Ø ÒÙÑ Ö Ù Ñ ÓÐ ÓÖ Þ Ò Þ Ò ÙÐ Ö Ø ÓÑÓÐÝ Ó ¹ Ý Ð Ø ÒÝ Ð Ý Ô Ð Ö Þ Ø Ö Ò Ø ÒÙÑ Ö Ù Ò Ø Ð Ñ ¹ ÓÐ ¾º½ µ Ý ÒÐ ØÒ º Ý Ð Ø Ñ ÓÐ Ö Ø Ð Ð Ø Ô Ð ÖÓ Ð¹ Ñ Òº Ý Ý ÓÖÐ Ø Ô Ð ÒØ Ø ÒØ ÞØ Þ Ø Ø Ñ ÓÖ Ý Ú Þ Ø Ð Ñ Þ Ò Ð ÐÝ Þ¹ ÒÝ Ð Ø Ö Ù Þ Ñ Ø Ò º Ú Þ ÐØ ÓÒ ÙÖ ¾º¾º Ö Ò Ð Ø Ø º Ð ÖØ Ð Ô Ò ¾º½ µ ÒØ Ö Ð Ý ÒÐ Ø Ñ ÓÐ ÒØ Ô Ø Ù Ñ Þ ÒÝ Ø Ö Ó Ø Ò ÖØ ÐÑ Þ ØØ P Ú ÒÝغ ¾º º Ö Ò Ø Ò Ö ÞÓÐØÙ P Ú ÒÝ x¹ Ö ÒÝ ÓÑÔÓÒ Ò Ò Ú Ð Ö Þ Ø Þ Þ t = 0 Ô ÐÐ Ò Ø Ò Ú ØØ ÖØ Øµ Ò Þ Ø Ò Ñ ÓÖ Ö ÞØ Ø Ö ÔÓÒØÓ Ò Þ ÒÝ Þ ÔÔÓÒØ Ð ØØ Ø Ð Ð Ø º ½¼

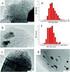
12 y r 1 r 2 Coil x c y c B Plate Flaw x Coil Plate A TOP VIEW z h z=0 l x A z=c D d z= d SIDE VIEW ¾º¾º Ö º Ì Ú Þ Ð Ý Ð Ø Ö Ó Ø ÒÝ Ø Ø ÖØ ÐÑ Þ Ð Ñ Þ Ð ØØ Ö ÔÐ Ñ ÒØ real P x (MA/m 2 ) x (mm) µ Ê ÈË Ö 0Ö ÔÐ Ñ ÒØ y (mm) { } P( r) ex z = C Ò real P x (MA/m 2 ) y (mm) µ Ê z (mm) { } P( r) ex Þ x = 0 Ò ¾º º Ö º ¾º½ µ ÒØ Ö Ð Ý ÒÐ Ø Ñ ÓÐ ÒØ ÔÓØØ P Ú ØÓÖ x¹ Ö ÒÝ ÓÑÔÓÒ Ò Þ ÒÝ Ø Ò ÖÓ ÐÓÑ Ð Ô Ò ½½

13 ¾º¾º Ø Ö Ó Ø ÒÝ ÖÚ ÒÝ Ö Ñ Ú Ð Þ Ð Ò Þ ¹ Ñ Ø ¾º½ µ Ñ ÓÐ ÒØ ÔÓØØ P ÒÝ Ø Ð Ö Ö Ñ Ô ÐÙ ¹ òöò Ñ Ö Ø Ò Ñ ØÙ Ù Ø ÖÓÞÒ Ú Þ Ð Ð Øº Ð ÔÚ Ø Ò Ø Ð Ñ Ø ÖÓÞ ÔÞ Ð Ø Ðº Þ Ð Ø Ò ÑÙÒ Ö ÓÒ Ú Ð Ð ÐÝ Þ Ñ Ò Ø Ö Ø Ñ Ö Þ ÒÞÓÖ Ð Ø ÐÐ ØÚ ÒÒ Þ ÒÝ Ø Ö Ð ØÖ Ú Ñ Ú ÐØÓÞ Ø ÐÐ Þ Ñ Ø Ò º Ñ Ð ¹ Ø Ø Þ Ñ ÓÖ Ý ÓØØ Ú Þ Ð Ø Ö Ò Ò Ù ÐØ Þ ÐØ Ò Þ ÒÝ Ð ÒÐ Ø Ð Ñ Ú ÐØÓÞ Ø ÐÐ Þ Ñ Ø Ò º Ñ Ó Ø Ò Þ Ò Ù ÐØ Þ Ðع Ú ÐØÓÞ Ø Ø Ö Ø Ö ÞØ Ö ÑÖ ÞÓ ÒÓÖÑ ÐÒ Ý Ý Ö Ò ÑÔ Ò ¹Ú ÐØÓÞ Ñ Ø ÖÓÞ Ö Ð Þ Ð Ò º Ý ÓÖÐ Ø Ò Ð ÓÖ ÙÐ Ú Þ Ð Ð Ò Þ Ñ Ø Ý Þ Öò Ò Ú Þ Ú Þ Ø Ø Þ Ò Ø Ð Ô ØÖ º Å Ý ÞÞ Ó Ý Ø ÖÑ Ö Þ ÒÞÓÖ Ð Þ Þ Ñ Ò Ø Ö ÖØ Ò Ñ Ø ÖÓÞ Ý Ú Ý ØÐ Ò ÒÝ ÔÓÒØ Ò Þ ÒØ Ò Ú Þ Ú Þ Ø Ø Ý Ú Þ Ð Ø Ö Ò Ò Ù ÐØ Þ ÐØ Ñ Ø ÖÓÞ Ö ÖÖ Ð Ð Ø Ö Ð Ñ Þ Ð Þº ¾º¾º½º Ñ Ò Ø Ö Ú ÐØÓÞ Ò Þ Ñ Ø Þ Ì Ò Ð Ú Ñ Ò Ø Ö Þ ÒÞÓÖÓ Þ ÒÝ Ú Ø ÞØ Ò Ð ØÖ Ú Ø ÖÚ Ð¹ ØÓÞ Ø Ñ Ö º Þ Þ Ø ÖÚ ÐØÓÞ Ñ ÐÝ Ø Þ ÒÝ Ø Ð Ö P Ö Ñ Ô ÐÙ ¹ òöò Ñ ÒØ Ö ÞØ ÓÞ Ð ØÖ Ò Ø ÖÖ Þ Ò ÓÐ Þ ÒÞÓÖ Ø Ð Ð Ø º ÒÒ Þ Ñ Ø Ý Þ Öò Ò Ñ Ø Ø Ñ ÒÒÝ Ò Ñ Ö ÞØ Ù Ö Ò¹ Ú ÒÝØ G m sa Ñ ÐÝ Ú Þ ÐØ ÑÙÒ Ö Ò Ø Ð Ð Ø Ö ÞØ Ø ØÖ Ò Þ ÓÖÑ Ð ÑÙÒ Ö ÓÒ Ú Ð ÐØ Ð Ò Ö ÞØ Þ Þ Ð µ Ú Þ Ð Ø ÔÓÒØ Ò Ð Ú Ñ Ò Ø Ö º Ö Ò¹ Ú ÒÝ Ð Ð ÞÓ Ó Ò Ñ Ð Ð Ò Ý Ø ÖØ Ò Ó Ý Ð Ò Ü Þ Ñ ØÓØØ Ð ØÖÓÑ Ò Ø Ö ÐÐ ÑÞ Ö ÚÓÒ Ø ÓÞ Ø Ò Ò m Þ Þ Ñ Ò Ø Ö Ö µ Þ Ð Ò Ü Øò Ô Ö Ò Ö Ö ÞØ Ú Þ Ð ÔÓÒØ ÐÝ Ø Ð Ð s ÑÙÒ Ö a ÑÙÒ Ö ÓÒ Ú Ð Ð Ú µº  РРB Þ ÒÝ Ð ÒÐ Ø Ó ÓÞØ Ñ Ò Ò Ù Ú ØÓÖ Ú ÐØÓÞ Ø Þ Þ Ò Ò ¾º µ Ý ÒÐ ØØ Ð B = B f = B B i Ý ÒÐ ØØ Ð Ø Ñ ÓÐ B Ð ÙÐØ Ñ Ò Ø Ö Ò Ù Ú ØÓÖ Ø B i Þ ÒÝ ¹ Ý Ð Ñ Ú Ø Ð Ò Ð Ð ÔÓØØ Ò Ù Ø B f Ô Þ ÒÝ Ø Ö Ð ØÖ ØØ Þ Þ P ÐØ Ð Ö ÞØ Øص Ñ Ò Ò Ù Ú ÐØÓÞ Ø Ð ÒØ º ÒØ Ð Ô Ò B Ú Ø Þ Ð Ò Ð Ö Ø B( r) = µ 0 V d G m sa ( r r ) rot P( r )d r, r V a, ¾º½ µ ÓÐ V a ÑÙÒ Ö ÓØ Ö ÐÚ Ú Ð Ú Ø Þ Þ ÞØ Ø ÖÖ ÞØ Ð Ð ÓÐ Ñ Ò Ø Ö Ú ÐØÓÞ Ø Ú Ò Ù Ñ Ø ÖÓÞÒ º Å Ú Ð r r Ð Ò Þ Ø ÖÖ Þ Ò ÐÝ Þ Ò Ð Ö Ò¹ Ú ÒÝ Ò Ñ Þ Ò ÙÐ Ö Ý ¾º½ µ ÒÙÑ Ö Ù ÖØ Ð Ñ ÖØ P Ø Ò Ý Þ Öò Ð ØÒ Ø ÒØ Ø º Î Ý ÞÖ Ó Ý ¾º½ µ Þ Ò Ö ÞØ P ÖÓØ ÒÒ Þ Ó Þ Ó Ý ¾º½ ¾º¾µ Ý ÒÐ Ø ¾º µ Ð ÓÒØ Þ Ö ÒØ Ú Þ Ø ØØ H f ¹Ö Ö Ò Þ ØØ Ð V s Ø Ö Ó Ø Ò Ú Ø Þ rotrot H f ( r) k 2 c H f ( r) = rot P( r), r V s. ¾º½ µ ½¾

14 ¾º½ µ Þ Ò Þ Ö ÔÐ G m sa Ù Ö Ò¹ Ú ÒÝ Ú Ø Þ Ù Ý ÒÐ Ø Ñ ÓÐ ÒØ Ô Ø Ñ rotrotg m sa ( r r ) k 2 0 Gm sa ( r r ) = 0, r V a, r V s, ¾º½ µ rotrotg m ss( r r ) k 2 cg m ss( r r ) = δ( r r )I, r, r V s, ¾º½ µ ÓÐ k 2 0 = ω 2 ε 0 µ 0 Ú Ð Ñ ÒØ V s Ø Ö Ó Ø V a ¹Ú Ð Ø ÖÓ Ð Ð Ø Ò G m sa G m ss ÓÑÔÓÒ Ò¹ Ò Ð Ø ÐÐ Ø ÒÒ Ñ Ò Ø ÖÖ Ñ Ó ÐÑ Þ Ø ÓÐÝØÓÒÓ ÐØ Ø Ð Ò º Å Ý ÞÞ Ó Ý ¾º½ µ Ý ÒÐ Ø Ò Ø Ð Ð Ø G e Ö Ò¹ Ú ÒÝØ ÑÓ Ø Ú ¹ Þ Ø ØØ Ð Ð Ð G e ss ÓÖÑ Ò ÐÐ Ò ÖÒ ÐÐ ØÚ ÒÒ Ñ Ø ÖÓÞ Ö ÞÒ Ð Ø Ý ÒÐ Ø ¾º½½µ ÐÝ ØØ ¾º½ ¾º½ µ Ý ÒÐ Ø Ð ÒÒ Ò ÞÞ Ð Ð Ò Ð Ó Ý Þ m Ð Ò Ü Ø e¹ö ÐÐ Ò Ö ÐÒ º Þ Øò Ö ÞØ Ð ÒØ Ó Ý Ö Ò¹ Ú ÒÝ ÓÑÔÓÒ Ò Ö Þ Ð ØÖÓÑÓ Ø ÖÖ ÚÓÒ Ø ÓÞ ÓÐÝØÓÒÓ ¹ Ô Ö Ñ ÐØ Ø Ð Ø ÐÐ ¹ Ð Ø Ò º Þ ÒØ Ö Ð Ý ÒÐ Ø Ð Ö ÓÖ Þ Ý Þ Öò Ñ ÖØ Ú ÖØ Ø ÒØ ØØ Ò Ð Þ ÐÑÓÒ ÓØØ Ö ÞÐ Ø Þ Ø Ð Þ ÖØ ÞÒ ÐØÙ G e Ð Ð Ø ¾º½½µ Ý ÒÐ Ø Øº ¾º¾º¾º Þ ÑÔ Ò ¹Ú ÐØÓÞ Þ Ñ Ø Ì ÒØ ÞØ Þ Ø Ø Ñ ÓÖ Þ Ì Ú Þ Ð Ý Ý Ú Ú Ø Ö Ð ÐÐ Ú Þ Ð Ý ÓØØ ÔÓÞ Ò Ø Ð Ð Ø ÑÙÒ Ö ÖÒÝ Þ Ø Òº Þ Ø Ö Ö Ñ Ð Ý Ò I a ÓÑÔÐ Ü ÖØ ò Þ ÒÙ ÞÓ Ö Ñ ÞØ Ú Ò Ù Ñ ÖÒ Ó Ý Ú Ú Ø Ö Ò Ò Ù ÐØ Þ ÐØ Ñ ÒÒÝ Ò Ú ÐØÓÞ ÑÙÒ Ö V d Ø ÖØÓÑ ÒÝ Ò Ø Ð Ð¹ Ø ÒÝ Ø Ö º E i ( r) Þ Ø Ö I a Ö Ñ ÐØ Ð Ñ ÒØ ÑÙÒ Ö Ò Ù ÐØ Ð ØÖÓÑÓ Ø Ö Þ Þ Ø ØÓØØ Ø Öº ÐØ Ø Ð ÞÚ Ó Ý Ú Ú Ø Ö Ö Ñ Ý I a Ö Ú Ò Ú Ð ÞÓÒÓ Ö Ú Ò I v Ø Ú Ö Ñ ÓÒÐ Ñ ÓÒ Þ Ñ Ø Ø E vi ( r) Ø Ú Ð ØÖÓÑÓ Ø Ö Ñ Ú Ú Ø Ö ÐØ Ð Ñ ÒØ ÑÙÒ Ö Ò Ù ÐØ Ð ØÖÓÑÓ Ø Ö Ø Ð ÒØ º  РРØÓÚ U v Ú Ú Ø Ö Ò Ù ÐØ Þ ÐØ Ñ Ú Ð¹ ØÓÞ Ø Ñ ÐÝ V d Ø Ö Ó Ø Ò Ø Ð Ð Ø ÒÝ Ø Ö Ò Ð ØÖ U v = U v U i v ÓÐ U v Ö ÞØ ØÐ Ò Þ Þ ÒÙÐÐ Ö Ñ µ Ú Ú Ø Ö Ò Ò Ù ÐØ Þ ÐØ Ø U i v Ô Ö ÞØ ØÐ Ò Ú Ú Ø Ö Ò Ñ ÒØ ÑÙÒ Ö ÐØ Ø Ð Þ Ø Ò Ò Ù ÐØ Þ ÐØ Ø Ð ÒØ µº Ú Ú Ø Ö Ò Ò Ù ÐØ Þ ÐØ Ñ Ú ÐØÓÞ E i E vi Ú Ð Ñ ÒØ ¾º½ µ ÒØ ¹ Ö Ð Ý ÒÐ Ø Ñ ÓÐ ÒØ ÔÓØØ P ÒÝ Ø Ð Ö Ö Ñ Ô ÐÙ ¹ òöò Ñ Ö Ø Ò Ö ÔÖÓ Ø ½¼ Ð ÞÒ Ð Ú Ð Ú Ø Þ Ñ ÓÒ Ø Ñ U v = 1 I v V d E vi ( r) P( r)d r. ¾º¾¼µ Ý Ö Ò Ð ÓÖ ÙÐ Þ Þ Ø Ñ ÓÖ Ý Ì Ò Ù Ý Ò ÞÓÒ Ø Ö Ø ÐØ Þ Ú Ú Þ Ö Ô Ø Þ Ì Ú Ð Þ ÐÒ Þ Ò Ø Ö ÑÔ Ò Ò Ñ Ú ÐØÓÞ Zµ Ø ÒØ Ø º ÁÐÝ Ò ÓÖ Ð ÞÒ ÐÚ Ó Ý I a Z = U a U a Þ Ø Ö Ò Ò¹ Ù ÐØ Þ ÐØ Ò Þ ÒÝ Ð ÒÐ Ø Ú Ø ÞØ Ò Ð ØÖ ØØ Ñ Ú ÐØÓÞ µ ¾º¾¼µ U a = U v Ð Ô Ò Þ Ì Ú Ð Þ Ð Þ ÖÓ ÐÓÑ Ð Ñ ÖØ ÓÖÑ Ò Z = 1 E i ( r) I P( r)d r, ¾º¾½µ 2 V d ÓÐ I = I a = I v Ø Ö Ö Ñ º ½

15 ¹ Ú Ú Ø Ö Ð ÐÐ Ú Þ Ð Ø Ò Þ ÒÝ Ð Ø Ú Ø Þ ÑÔ Ò ÐÐ ò Ñ ÒÒÝ ÒØ ÞÓ Ø Ñ Ò Z = U v = 1 E vi ( r) I a I a I P( r)d r. ¾º¾¾µ v V d ¾º¾¼µ ÒÒÝ Ò ÐØ Ð ÒÓ Ø Ø ÞÓ Ö Þ Ø Ö Ñ ÓÖ Ø ¹»Ú Ý Ø Ú Ú Ø Ö Ø Ð Ð Ø Þ Ì Ò ÐÐ ØÚ Ý Þ Öò Ò Þ Ð Ø Þ ÓÐÝ Ò ÓÒ ÙÖ Ñ ÐÝ Ò ÞÓÒÝÓ Ú Ú Ø Ö Ö Ò Ð Ñ Ú ÒÒ Þ Ô ÓÐÚ º Þ Ì Ú Ú Ø Ö Ò Ù ÐØ Þ ÐØ Ñ Ú ÐØÓÞ Ø ÒÒ Ò Ð Ô¹ Ò Ý Þ ÑÓÐÒ Ò Ó Ý P ÐØ Ð Ò Ö ÐØ Ð ØÖÓÑÓ Ø Ö Ö Ø ÒØ Ö ÐÒ Ò Ø Ö Ñ Ò Ø Ñ ÒØ Òº Þ Ò Ð Ö Ò Ð Ý Ó Ð Ý Þ Öò ÒÙÑ Ö Ù Ò Ø Ð Ñ ¹ ÓÐ Ø Ò ÐÒ ¾º¾¼µ ¾º¾½µ ÔÐ Ø Ñ Ú Ð Þ ÒØ Ö Ð ÖØ Ð Þ Þ ØÓ Ý ÓÖÐ Ø Ð Ñ Ö ¾º½ µ ÒØ Ö Ð Ý ÒÐ Ø Ñ ÓÐ ÓÖ Ö Ò Ð Þ Ö ÐÐÒ º Þ ÐØ ØÐ Ò Ð Ý Ú Ò ÝØ Ö Ì Ø Ò ¾º¾½µ ÐÐ ØÚ Þ Ð Ú Ú Ð ÐÐ Ì Ø Ò Ù Ý Ò ÞÓÒ Ð Ö Ñ Ø ÐØ Ð ÐÑ Þ Þ Ú Ú Ø ¹ Ö Ö Ñ ÐÝ Ø Ñ Ö Þ ÒØ Ö Ð Ý ÒÐ Ø Ñ ÓÐ Ð ØØ Ð ÐÑ ÞØÙÒ Þ Ö Þ Þ ÐÐ Þ Ñ Ø Ò Ø Ú I v Ö Ñ Ø Ò Ú Ú Ø Ö ÐØ Ð Ò Ù ÐØ E vi Ø ØÓØØ Ø Ö Ø µº Æ Ò Þ Ú ÞÓÒØ Ö Ò¹ Ú ÒÝ ÞÒ Ð Ø Ö Ñ ÒØ Ó Ý Ò Þ Ò Ð Ô Ò Ø ÖØ Ò Þ Ñ Ø Ó ÓÞ Þ Ð ØØ ÚÓÐÒ º ¾º¾¼µ ¾º¾½µ ÔÐ Ø Ñ ÖÖ Ö ÑÙØ ØÒ Ó Ý ÒÒ Ö Ò Ó Ý Þ Ì Ð Ø ÔÓÒØÓ Ò ØÙ Ù Þ Ñ Ø Ò P Ú ÒÝØ ÒØ Ö Ð ÖØ Ð Ñ Ò ÐÐ ÔÓÒØÓ Ò Ñ Ø ÖÓÞÒ º ¾º¾º º Ñ Ò Ø Ö ÖØ Ò Ñ Ø ÖÓÞ Þ ÑÔ Ò ¹ Ú ÐØÓÞ ÔÐ Ø Ú Ð Ì ÒØ Ò Ý ÒÝ ÙÖ ÓØ Ñ ÐÝ Þ Ð Ø Ð Ý Ò Ð ÐÝ Þ ÞÓÒÓ Ù Ö N Þ Ñ Ñ Ò Ø Ð Ðк À ÐÝ ÞÞ Ð ÞØ ÙÖ ÓØ Ý Ó Ý ÒÒ Þ ÔÔÓÒØ Ò ÔÓÒØ Ò Ð Ý Ò ÓÐ Ñ Ò Ø Ö ÒÝ Ú Ø ÞØ Ò Ð ØÖ Ú Ñ Ú ÐØÓÞ Ø Ú Ò Ù Ñ ÖÒ ÔÓÒØÓ Ò Ñ Ò Ø Ö ÞÓÒ ÓÑÔÓÒ Ò Ò Ñ Ú ÐØÓÞ Ø Ñ ÐÝ ÙÖÓ Ò ÒÓÖÑ Ð Ö ÒÝ º Ñ Ö ÙÖÓ A Ö ÞØÑ Ø Þ Ø Ð Ý Ò ÒÒÝ Ö Ó Ý ÐØ Ø Ð Þ Ó Ý Ñ Ò Ø Ö Þ Ð Ø Ð Ù Ý Ò Þ Þ A Ð Ð Ø Ñ Ò Ò ÔÓÒØ Òº Þ Ì Ò Ð Ú Ö ÞØ Ø Ö Ø Ð ÖØ Ñ Ö ÙÖ ÓØ Ø ÒØ Ý Ð Ú Ú Ð ÐÐ Ì Ø Ö Ò º Þ Ð Ô Ò Ñ Ö ÙÖÓ Ò Ú Ú Ø Ö Òµ Ò Ù ÐØ Þ ÐØ Ñ Ú ÐØÓÞ Ø Þ Ñ Ø Ø Ù ¾º¾¼µ ÔÐ Ø Ð Ô Òº I v ÙÖÓ Ò ÒÓÖÑ Ð Ó Ú Ö Þ ÐÝ Þ Ö ÒØ Ú ÒÒ Þ Ö Ò ÐÚ ºµ Í Ý Ò Þ ¹ Þ ÐØ Ú ÐØÓÞ Ð Ö Ø Ñ Ò Ò Ù ÙÖÓ Ò ÒÓÖÑ Ð Ö ÒÝ ÑÙØ Ø ÓÑÔÓÒ Ò Ò Þ ÒÝ Ð ÒÐ Ø Ð Ñ Ú ÐØÓÞ Ð B n µ Þ Ò Ù ¹ Ø ÖÚ ÒÝ Ø Ú Ðº Þ Ð Ô Ò Ö Ø Ù Ó Ý U v = jωan B n, ¾º¾ µ ÓÐ U v ¾º¾¼µ Ð Ô Ò ÔÓØØ Ö Ñ Òݺ ¾º¾ µ Ý ÒÐ Ø Ð Ô Ý Þ Öò Ò Þ¹ Ø Ö ØØ Ñ Ò Ò Ù Ñ Ú ÐØÓÞ B n = U v jωan. ¾º¾ µ ½

16 Ñ Ò Ò Ù Ñ Ú ÐØÓÞ Þ Ò ÔÐ Ø Ð Ô Ò Ø ÖØ Ò Þ Ñ Ø Ò Þ Ð ÒÝ Ù Ý Ò Þ Ñ ÒØ Ñ Ø Þ ÑÔ Ò ¹Ú ÐØÓÞ Þ Ñ Ø Ò Ð Þ Ñ ÒØ Ð ÖØÙÒ Ø Ø Þ Ó Ý Ò Ò Þ Ö Ò¹ Ú ÒÝ Ñ Ø ÖÓÞ Ö Ñ ÒØ Ó Ý Ò ÖÖ Þ ÚÓÐØ ¾º½ µ ÔÐ Ø Ð Ô Ò Ø ÖØ Ò Þ Ñ Ø Ø Òº Ý ÓÖÐ Ø Ò Ð ÓÖ Ò Þ ÓØØ Þ Ñ Ø ÖÒÝ Þ Ø Ø ÖÓÞÞ Ñ Ó Ý Þ ÑÔ Ò ¹Ú ÐØÓÞ Ð Ú Ð Þ Ñ Ø Ò Þ Ø Ò Ñ Ö ÙÖÓ Ø ØÓØØ Ø Ö Ø ÐÐ Þ Ñ Ø Ò µ Ú Ý ÞÚ ØÐ Ò Ñ Ò Ø Ö Þ Ñ Ø Ò Þ Ø Ò Þ Ú Ò Ñ Ð Ð Ö Ò¹ Ú ÒÝ Ö µ ÐÖ Ú Þ Ø º ½

17 º Þ Ø Ë ÙÐÐ ÑÓ Ë ÙÐÐ ÑÒ Ò Ú ÞÞ Å ÜÛ Ðй Ý ÒÐ Ø Ú Ø Ð Ò Ø Ö ò ÓÑÓ Ò Ð ØÖ Ùѹ Ñ Ð Ø ÐØ ØØ ÓÖÖ Ñ ÒØ Ø Ö Ò ÖØ ÐÑ Þ ØØ ÞÓÒÝÓ Ø ÔÙ Ñ ÓРغ Ñ ÓÐ ¹ Ó Þ ÑÓ Ý ÓÖÐ Ø Ð ÞÒ Ð Ð Ö Ò Ð ÞÒ Þ ÖØ Ö ÞÐ Ø Ú Þ Ð ØÖ Ö Ñ º Þ Ö ÙÐÐ ÑÒ Ò Ú Þ ØØ Ñ ÓÐ Ó Ö ÐÐ ÑÞ Ó Ý Þ Ð ØÖÓÑÓ Ñ Ò Ø Ö ÐÐ ÑÞ ÖØ Ý Ø ÒØ Ø ØØ Ò ÐÝØ Ð ØÐ Ò º Å Ú Ð Ú Ø Ð Ò Ø Ö ¹ ò Ø ÖØÓÑ ÒÝØ Ú Þ ÐÙÒ Ø Ö ÐÐ ÑÞ ÐÝ ØÐ Ò Ñ Ò Ò Ø ÒØ Ø ØØ Ð Ô Ö ÙÞ ÑÓ Ò Ù Ý Ò ÒÒ Ðк ÙÐÐ Ñ Òº Ø Ö Ö ÒÝ Ñ Ö Ð ¹ Ø ÒØ Ø ØØ Ö º Ñ ÖÒ Ý ÓÖÐ Ø Ò Ó ÞÓÖ ÓÐÝ Ò Ð Ø Ñ ÓÖ Ý ÙÐÐ ÑÑ Ð Ñ ¹ Ú Ð ØÓØØ Ø Ö Ý ÐØ Ð Þ ÖØ Ð ØÖÓÑ Ò Åµ Ø Ö Ø ÐÐ Ñ Ø ÖÓÞÒÙÒ º Ì Ô Ù Ò Þ Ð Ø Ñ ÓÖ Ý Ò Ý Ø ÚÓÐ Ò Ò ÝÓ Ñ ÒØ 5 10 ÙÐÐ Ñ Ó ÞÒÝ Ø ¹ ÚÓÐ Òµ Ð Ú ÒØ ÒÒ ÐØ Ð ÐØ ØØ Ø Ö Ø Þ Ö ØÒ Ò Ñ Ø ÖÓÞÒ Ý Ø Ö Ý Ú Ð Ñ ÐÝ ÖÒÝ Þ Ø Òº Ñ ÒÒÝ Ò Ø Ö Ý Ñ Ö Ø ÙÐÐ Ñ Ó Þ ÓÞ Ô Ø Ó Ð Ò ÝÓ ÒÒ Ð Ð Ø Ò Ý Ø ÖØÓÑ ÒÝ Ø ÙÐÐ Ñ Ó ÞÒ Ð Ð ÒÝ Ò Ò ÝÓ Ñ Ö Ø Ð ÐÐ ÑÞ ØØ Ó Ð Ð Ø Þ Ð Ø Ò Ó Ö Ð Ø ÖØ Ò Ö Ü Ø Ö Ñ Ú Þ ÐÒ º Þ ØØ ÐÑ Ö Ð Ð Ô Ð Ø Ø Ø Ñ Ú Ð Ø ÙÐÐ Ñ Ú Ð Ò Ú Þ Ð Ø Ð ÐÚ Ð ÞØÓØØ Ø Ð Ò Þ ÒÝ ÐÐ ÑÞ ò ÐØ Ö Ø Ö Òº ÓÒØÓ Ñ ÑÐ Ø Ò Ó Ý Þ ÒÝ Ó Ø ÐÚ Ð ÞØ ÐØ Ð Ò Ò Ñ Ô Ö ÙÞ ÑÓ ÙÐÐ Ñ Ø Ö Ö Ñ Ö Ð ¹ Ø ÒØ Ø ØØ Ð Ý ÐØ Ð ÒÓ Ø Ò Þ Òº Ö Ò ÙÐÐ Ñ Ú Ð Ø ÐÐ Ø ÒØ Ò Ò º ØÓÚ Ò Ñ ÑÙØ Ø Ù Ó Ý Å ÜÛ Ðй Ý ÒÐ Ø Ñ ÐÝ Ñ ÓÐ Ø Ò Ú ÞÞ ÙÐÐ ÑÓ Ò ÞØ Ð Ø Ù Ó Ý Ý ÓØØ ÙÐÐ ÑÓØ Ó Ý Ò Ð Ø Ý Ø Ø Þ Ð Ö ÚÓÒ Ø ÓÞØ ØÚ Ð ÓÒØ Ò Ø Ò Ú Þ Ø ÔÓÐ Ö Þ Ò ØÖ Ò ÞÚ ÖÞ Ð Ð ØÖÓÑÓ Ì µ ØÖ Ò ÞÚ ÖÞ Ð Ñ Ò Ìŵ Ø ÔÙ Ò Ò Ú Þ Øص ÙÐÐ Ñ Þ ¹ Ö º ÞØ Ú Ø Ò Ñ Ú Þ Ð Ù Ì ÌÅ ÙÐÐ ÑÓ Ú Ð Ø Ø Ð Ò Þ ÒÝ ÐÐ ÑÞ Ð Ö ÐØ Ö Ø Ö Òº Î Þ Ø Ð Ð ÖØ ÐÑ Ð Ø Ø Ø Ö ÞØ ÓÑÓ¹ Ò ÒÝ ÐÐ ÑÞ Ð Ö Ò Ð Þ Ø Ö Ò Ø Ö Ø Ø Þ Ð Å ÙÐÐ Ñ Ú Ð Ò Ú Þ Ð Ø Ö Þ ÐØ Ð Ó Ý Ñ ÑÙØ Ø Ù Ó Ý Ñ ÒØ Ð Ø Ø Ø Þ Ð ÙÐÐ ÑÓØ Ð ÖÒ ÙÐÐ ÑÓ ÞÙÔ ÖÔÓÞ Òغ º½º Ì ÌÅ ÔÓÐ Ö Þ ÙÐÐ ÑÓ Ì ÒØ Ò Ý Ú Ø Ð Ò Ø Ö ò ÓÑÓ Ò Ð Ò Ö ÞÓØÖÓÔ Ð ØÖ ÙÑÑ Ð ¹ Ø ÐØ ØØ ÓÖÖ Ñ ÒØ Ø ÖØÓÑ ÒÝغ ÐØ Ø Ð ÞÞ ØÓÚ Ó Ý Þ Å Ø Ö Ò ω Ö¹ ½

18 Ö Ú Ò Ú Ð Þ ÒÙ ÞÓ Ò Ú ÐØÓÞ ÐÐ Ò ÙÐØ ÐÐ ÔÓØ Ò Ú Ò Ú Ø Þ ÔÔ Ò Ø Ö Ð Ö ÓÞ Ø Ö ÐÐ ÑÞ ÓÑÔÐ Ü ÖØ Ø ÞÒ Ð Ù º Þ ÓØØ ÐØ Ø Ð Ñ ÐÐ ØØ Þ Ð Ñ Ó Å ÜÛ Ðй Ý ÒÐ Ø Ú Ø Þ Ð ÓØ ÐØ rot H = jωε E, rot E = jωµ H. º½µ º¾µ Å Ý ÞÞ Ó Ý ÖÑ Ò Ý Å ÜÛ Ðй Ý ÒÐ Ø ÒØ ÐØ Ø Ð Ñ ÐÐ ØØ Ö ÙÒ Ò Ñ Ú Ð ÞÓ Ñ Ô Ø º½µ º¾µ Ú Ö Ò Òغ Ã Ö ÖØ ¹ ÓÓÖ Ò Ø Ò Þ Å Ø Ö ÞÓÒ Ñ ÓÐ Ø Ñ ÐÝ z Þ Ö Ò¹ Ø Ú ÐØÓÞ e jkzz Ð º ÓÖ º½µ º¾µ Ý ÒÐ Ø Ø Ø Ö ÐÐ ÑÞ Ö Ò Þ Ö ÞÚ Ú Ø Þ Ø Ô Ù E x = 1 [ ] Hz jωε y +jk zh y, º µ E y = 1 [ H ] z jωε x jk zh x, º µ E z = 1 [ Hy jωε x H ] x. º µ y H x = 1 [ ] Ez jωµ y +jk ze y, º µ H y = 1 [ E ] z jωµ x jk ze x, º µ H z = 1 [ Ey jωµ x E ] x, º µ y º µ º µ º µ º µ Ý ÒÐ Ø ØÖ Ò Þ Ø Ý Ó Ý Ó ÓÐ Ð H z ¹Ø Ð E z ¹Ø Ð Ò Ôк º µ Ñ Ô Ø Ý Ó Ý º µ Ý ÒÐ Ø H y ÐÝ Ö ÐÝ ØØ Ø º µ Ý ÒÐ Ø Ó ÓÐ Ð Ø Ñ Þ Ö Ñ ÒÝØ Ö Ò ÞÞ E x ¹Ö µ [ 1 E x = jωµ H ] z ω 2 µε kz 2 y jk E z z, º µ x [ 1 E y = jωµ H ] z ω 2 µε kz 2 x jk E z z. º½¼µ y [ ] 1 H z H x = jk z, º½½µ H y = ω 2 µε kz 2 1 ω 2 µε kz 2 x +jωε E z y [ H z jk z y jωε E z x ], º½¾µ ÒØ Ý ÒÐ Ø Ð Ð Ø Ø Ø Ø Ó Ý ÐØ Ø Ð Ò Ñ Ð Ð Å ÙÐÐ ÑÓØ Ñ ¹ Ô Ø Ù Ø Ð Ö Ú ÒÝ E z H z Ñ Ö Ø Òº Ã Þ Ò Ú Þ ØÚ Ð ÞØ Ò Ø Ð Å Ø Ö Ø Ý Ó Ý Þ Ý Ø Ò E z = 0 Ú Ð ÞØ Ð Ñ Ø Ò Ô H z = 0 Ú Ð ÞØ Ð Ð Ò º Å Ú Ð Þ E z = 0 Ú Ð ÞØ Ø Ò Þ Ð ØÖÓÑÓ Ø ÖÒ Ò Ò z Ö ¹ ÒÝ ÓÑÔÓÒ Ò Þ ÖØ ÞØ H z 0 Ð Ö Ú ÒÝ ÐØ Ð Ð ÖØ Å Ø Ö Ø ØÖ Ò ÞÚ ÖÞ Ð Ð ØÖÓÑÓ ÔÓÐ Ö Þ Ì µ ÙÐÐ ÑÒ Ò Ú ÞÞ º À ÓÒÐ Ò Ñ ÓÖ H z = 0 Ñ ¹ Ø Ð Ð Ò Þ Òº ØÖ Ò ÞÚ ÖÞ Ð Ñ Ò ÔÓÐ Ö Þ Ìŵ ÙÐÐ Ñ ÓÞ ÙØÙÒ º E z ½

19 H z Ú ÒÝ Ò Ú Ø Þ Ò ÑÙØ Ø Ö Ö Ð Ñ Ú Ð ÞØ Ø Ò ÙÐÐ Ñ Ñ ÓÐ Ö ÙØÙÒ Þ ÖØ Ó Ù Þ Ø Ì ÌÅ ÔÓÐ Ö Þ ÙÐÐ ÑÓ Ò Ò Ú ÞÒ º ÓÒØÓ Ñ Ý ÞÒ Ó Ý Ì ÌÅ Ð ÓÒØ Ó Ñ Ò Ý Ð Ö ÓØØ Ö ÚÓ¹ Ò Ø ÓÞØ ØÚ ÖØ ÐÑ Þ Ø º Ñ Ø Ò Ò Þ z ÓÓÖ Ò Ø Ö ÒÝÖ Ñ Ö Ð xy µº Þ ÖØ ÔÓÒØÓ ÞØ ÑÓÒ Ù Ó Ý Ý ÙÐÐ Ñ z Ö ÒÝÖ Ñ Ö Ð Ö ÚÓÒ Ø ÓÞØ ØÓØØ Ì ÌÅ ÔÓÐ Ö Þ Ð ÓÒØ Ø Ù Ñ º Î Ý º¾µ Ý ÒÐ Ø ÖÓØ Ø ÐÝ ØØ Ø º½µ Ý ÒÐ Ø Øº Ö ¹ Ñ ÒÝ ÒØ H Þ Ð Ú Ð rotrote = graddive E Ú Ð Ñ ÒØ dive = 0 Ð ÞÒ Ð Ú Ð Þ E¹Ö ÚÓÒ Ø ÓÞ ÙÐÐ Ñ Ý ÒÐ Ø Ø Ô Ù E +ω 2 µε E = 0. º½ µ ÖØ ¹ ÓÓÖ Ò Ø Ö Ò Þ Ö Ò Ð ÖÚ ÞØ Þ Ý ÒÐ Ø Ø Ú Ð Ñ ÒØ Ð ÞÒ ÐÚ Þ Ð Þ Ò ÐØ Ø Ð Þ ØØ e jkzz Ð z¹ Þ Ö ÒØ ÐÝ Ø Þ E z Ö ÒÝ Ö Ò Þ Ö Ú Ø Þ Ý ÒÐ Ø Ø Ô Ù 2 E z x E z y 2 k2 z E z +ω 2 µεe z = 0. À ÓÒÐ Ñ ÓÒ Ô Ø Ù H z ¹Ö ÚÓÒ Ø ÓÞ Ý ÒÐ Ø Ø ÒÒ Ð Ú Ø Þ º½ µ 2 H z x H z y 2 k 2 zh z +ω 2 µεh z = 0. º½ µ Ã Ö º½ µ Ñ ÓÐ ÒØ E z ¹Ø ÞÓÖÞ Ø Þ Ô Ö Ú Ð Ø Ø Ð Ý Ò E z (x,y,z) = X(x)Y(y)e jkzz. º½ µ À ÐÝ ØØ Ø ÞØ Ñ ÓÐ Ø º½ µ Ý ÒÐ Ø Ñ Ó ÞÙ Ð ÔÓØØ Ý ÒÐ Ø Ø E z ¹Ú к Ö Ñ ÒÝ ÒØ Ú Ø Þ Ø Ô Ù 1 d 2 X X dx Y d 2 Y dy 2 +( k2 z +ω 2 µε) = 0. º½ µ º½ µ Ð Ø x¹ø Ð Ñ Ó Ø y¹ø Ð ÖÑ Ø Ô x¹ø Ð y¹ø Ð ØÐ Òº Ý ÐÝ Ò Ý ÒÐ Ø ÓÖ Ø Ð Ð Ø Ø Ø Þ Ð x¹ö y¹ö Þ Ð Ñ Ó Ø x¹ø Ð y¹ø Ð ØÐ Ò ÓÒ Ø Ò µ ÖØ Ø Ú Þ Ðº Á ÞÒ ÐÐ Ð ÒÒ Ø Ø Ú Ø Þ Ø Ý ÒÐ ØÒ 1 d 2 X X dx = 2 k2 x, ÓÐ k x k y Ø Ø Þ Ð ÐÐ Ò º Ñ ÓÐ 1 Y d 2 Y dy 2 = k2 y, º½ µ ÒØ Þ Ò Ö Ò Ð Ý ÒÐ Ø ÐØ Ð ÒÓ X(x) = X + e jkxx +X e jkxx, Y(x) = Y + e jkyy +Y e jkyy, º½ µ º¾¼µ ÓÐ X + X Y + Y Ø Ø Þ Ð ÓÒ Ø Ò ÖØ º º½ µ Ý ÒÐ Ø Ø º½ µ Ý ÒÐ Ø ÐÝ ØØ ØÚ Þ Òº ÞÔ ÖÞ Ý ÒÐ ØÖ ÙØÙÒ k 2 x +k 2 y +k 2 z = ω 2 µε. º¾½µ ½

20 Þ Þ ÒØ Ñ ÐÐ Ô Ø Ø Ù Ó Ý Þ Ð ØÖÓÑÓ Ø Öz Ö ÒÝ Ö Ò Þ Ú Ø Þ Ð Ð Ñ Ñ ÓÐ Ó ÞÙÔ ÖÔÓÞ ÒØ Ö Ø Ð E z (x,y,z) = E z0 e jkxx e jkyy e jkzz = E z0 e j(kxx+kyy+kzz), º¾¾µ ÓÐ Þ E z0 Ø Ø Þ Ð ÓÑÔÐ Ü ÓÒ Ø Ò k x k y k z ÖØ Ò Ð Ø ÐÐ Ø ÒÒ º¾½µ Ý ÒÐ ØÒ º Î Ý ÞÖ Ó Ý Ý k x/y/z ÖØ Ð Ø º¾½µ Ý ÒÐ Ø Ø ÓÖ ÒÒ ÐÐ ÒØ ØØ Ð Ø ÞØ Þ Þ Ôк k x = k x0 ¹Ö Þ º¾½µ ÓÖ Þ Þ Ð Þ k x = k x0 ÖØ Ö º Ã Ú Ø Þ ÔÔ Ò º¾½µ Ý ÒÐ ØÒ 8 Ñ ÓÐ Ú Ò 8 Ð Ò Þ Þ Ñ ÖÑ k x k y k z ÖØ Ò µ Ñ ÐÝ Ö Þ Þ Ó Ý k x k y k z ÞÓÐ Ø ÖØ Ù Ý Ò ÞÓ º º¾¾µ Ý ÒÐ ØØ Ð ÓØØ Ð Ñ Ñ ÓÐ Ø Ø Þ xy Ö ÚÓÒ Ø ÓÞØ ØÓØØ ÌÅ ÔÓÐ Ö Þ ÙÐÐ Ñ Ð ØÖÓÑÓ Ø Ö Ò z¹ Ö ÒÝ Ö Ò Þ Ø º ÓÒ Ö Ø Þ Ø ÖØÓÞ k x k y k z Þ Ñ ÖÑ Ø Ý Ð Ø Ôк Ñ Ø ÖÓÞÒ Ó Ý k x k y ÖØ Ø Ø Ø Þ Ð Ò Ñ Ú Ð ÞØ Ù Ñ Þ Ñ Ö Ø Ò k z ÖØ Ö Þ Ý Ñ ÓÐ Ú Ø Þ Ö Ñ Ñ ÓÐ ÒÒ Þ ÐÐ ÒØ ØØ Ð Þµ { ω2 µε kx k z = 2 ky, 2 kx 2 +ky 2 ω 2 µε, j kx 2 +k2 y ω2 µε, kx 2 +k2 y ω2 µε. º¾ µ Ä Ø Ø Ó Ý k z Ø ÞØ Ò ÔÞ Ø ÖØ Ø ÐÚ Ø Þ z¹ Ö ÒÝ ÜÔÓÒ Ò Ð Ò ¹ Ò ÑÔÐ Ø ÙÐÐ ÑÓØ Ö Ð º ÙÐÐ ÑÓ Ð Ö ÓÖ Ð Þ Öò Ú Þ ØÒ Þ Òº ÙÐÐ ÑÚ ØÓÖØ Ú Ø Þ Ò ¹ Ú Ð k = kx e x +k y e y +k z e z. º¾ µ ÓÒØÓ ÞÖ Ú ÒÒ Ó Ý k = ω µε = ω c Þ ÓØØ ÒÝ Ò Ø Ö ÒÝ Ø c Ð Ð µ Ý Þ Ö Ð Þ ÒÝ Ñ Ò Ø Ð Ö ÞØ Ö Ú Ò Ø Ð ÐÐ Ò º k = ω µε Ñ Ø Ú Ð Ò Ñ º¾½µ Ý ÒРغ ÙÐÐ ÑÚ ØÓÖÖ Ð º¾¾µ Þ Ú Ø Þ Ø Ñ Ö Ð Ò Ö Ø E z ( r) = E z0 e j k r, º¾ µ ÓÐ r ÐÝÚ ØÓÖØ Ð Ð Ñ ÖØ ¹ ÓÓÖ Ò Ø Ò r = x e x + y e y + z e z º k ÙÐÐ ÑÚ ØÓÖ ÙÐÐ Ñ Ø Ö Ö ÒÝ Ø Ð Ð Ð ØÒ Ó Ù Ù Ý Ò Ó Ý k Ö ÒÝ Ñ ¹ Ö Ð ÞÓ Ö Ó Ö Ñ ÐÝ Ñ ÒØ Ò Þ Ð ØÖÓÑÓ Ñ Ò Ø Ö Ö ÖØ ÐÐ Ò º º½ µ Ý ÒÐ Ø Ð Ò ÙÐÚ Ø Ð Ò Ò Ð Ñ ÓÒ Ô Ø Ñ H z Þ H z ( r) = H z0 e j k r. º¾ µ ÐÝ ØØ ØÚ Þ ÞÓÒÓ k ÙÐÐ ÑÚ ØÓÖÓ ÓÞ Ø ÖØÓÞ º¾ µ¹ º¾ µ Þ Ø º µ¹ º½¾µ Ý ÒÐ Ø Ñ Ô Ù Þ ÓØØ ÙÐÐ ÑÚ ØÓÖ ÓÞ Ø ÖØÓÞ ÙÐÐ Ñ Ð ØÖÓÑÓ ½

21 Ñ Ò Ø Ö Ö Ò Ö Ò Þ Ø ( E x ( r) = k xk z kx 2 +k2 y E y ( r) = E z ( r) = E z0 e j k r, ( ωεky H x ( r) = H y ( r) = H z ( r) = H z0 e j k r. E z0 ωµk y H kx 2 z0 )e j k r, º¾ µ +k2 y ( k yk z E kx 2 +ky 2 z0 + ωµk x H kx 2 +ky 2 z0 )e j k r, º¾ µ E kx 2 z0 k xk z +k2 y kx 2 +k2 y º¾ µ H z0 )e j k r, º ¼µ ( ωεk x E kx 2 z0 k yk z H +k2 y kx 2 z0 )e j k r, º ½µ +k2 y º ¾µ ÒØ Þ Ò ÒÒÝ Ò Þ Ô Ö Ð Ø Ì ÌÅ ÔÓÐ Ö Þ Ö Þ Þ Ò Ì ÓÑÔÓÒ Ò Þ ÙØÙÒ Þ E z0 = 0 Ú Ð ÞØ Ð Ñ H z0 = 0 Ú Ð ÞØ ÙÐÐ Ñ ÌÅ ÓÑÔÓÒ Ò Ø Ö Ð º º½º º¾º Ö ÓÒ Ì ÌÅ ÔÓÐ Ö Þ ÙÐÐ ÑÓ Ø ÐÐ ÑÞ Ú ØÓÖÓ Þ Òº Ð Ø Ø º Å Ò Ø ÔÓÐ Ö Þ ÙÐÐ ÑÖ Þ Ú Ø Þ µ k Ú ØÓÖ z = 0 ÒÓÖÑ Ð Þ Þ Þ e z µ ÐØ Ð Ñ Ø ÖÓÞÓØØ ÞØ ÓØ Þ e z Þ e xy = kx k 2 x + x +ky e ky 2 k 2 y ÝÑ Ö Ñ Ö Ð Ý Ú ØÓÖÓ x +ky e 2 Þ Ø µ z = 0 ÝÑ Ö Ñ Ö Ð µ Þ E H k ÝÑ Ö Ñ Ö Ð Ó Ó Ö Ö Ò Þ ÖØ Ð ÓØÒ E E H H µ Úµ Þ α Þ = k k k e z Ú ØÓÖÓ ÐØ Ð Þ ÖØ Þ º Ì ÔÓÐ Ö Þ ÙÐÐ Ñ Ø Ò H Ú ØÓÖ Ò Þ E Ú ØÓÖ z = 0 Ò Þ Ñ ÌÅ ÔÓÐ Ö Þ Ö Þ Þ Ó Ý Þ E Ú ØÓÖ Ò H Ú ØÓÖ Ô z = 0 Ò Þ º Å ÜÛ Ðй Ý ÒÐ Ø ÙÐÐ Ñ Ø ÔÙ Ñ ÓÐ Ø Þ Þ ÙÐÐ ÑÓØ Ø Ø Ý Ô ØÙÒ Ó Ý Ú Ð ÞØÙÒ Ý k ÙÐÐ ÑÚ ØÓÖØ Ñ ÐÝÖ Þ Ó Ý k = ω µε ÖØ Ø ÙÒ Þ E z0 H z0 ÓÑÔÐ Ü Þ ÑÓ Ò Þ Ñ Ö Ø Ò Ù Ý Ò º¾ µ¹ º ¾µ ÔÐ Ø Ñ ÙÐÐ Ñ Ð ØÖÓÑÓ Ñ Ò Ø Ö Ö Ø Ø Ö Ñ Ò Ò ÔÓÒØ Òº Î Ý ÞÖ Ó Ý º¾ µ¹ º ¾µ Þ k x = k y = 0 Ø Ò Ò Ñ ÖØ ÐÑ Þ¹ Ø º Þ Ú Ð Ò Ý z Ö ÒÝ Ø Ö ÙÐÐ ÑÓØ Ð ÒØ Ñ ÐÝ Ø Ò Ñ Ö Ø Ó Ý Þ Ð ØÖÓÑÓ Ñ Ò Ø ÖÒ Þ ÖÙ z Ö ÒÝ Ö Ò Þ º Þ ÐÝ Ò ¹ ÙÐÐ ÑÓØ Ì Å ØÖ Ò ÞÚ ÖÞ Ð Ð ØÖÓÑÓ Ñ Ò µ ÙÐÐ ÑÒ ÞÓ Ø Ò Ú ÞÒ º Å ÐÐ Ô Ø Ø Ù Ø Ø Ó Ý Ì ÌÅ Ð ÓÒØ Ö Ð ÓÖ Ð Ø Þ ÐÒ Þ Ñ ÐÝÖ ÚÓÒ Ø ÓÞ Ò ÙÐÐ ÑÓØ Ð ÓÒØ Ò Ú Ò Ù Ò Ñ Ñ Ö Ð Ø Ö Ö ÒÝ Ö ÐÝ Ò ÓÖ Ö Ò Ø Ö ÙÐÐ ÑÖ Ð Þ Ð Ò º ÒØ Ð Ô Ò Ð Ò ÐÐ Þ ÐÒ Ò Þ z = 0 Ö ÚÓÒ Ø ÓÞØ ØÓØØ Ì Å ÔÓÐ Ö Þ ¹ Þ Þ z = 0 Ö Ñ Ö Ð Ò Ø Ö ÙÐÐ Ñ Ø Øº ÓÖ k = k z e z = ω µε e z Ñ ÐÝ Ð Ú Ø Þ Ó Ý k x = k y = 0 Þ Þ Ó Ý = = 0º À ÞÒ Ð Ù Þ x y E x0 = E x (x = 0,y = 0,z = 0) E y0 = E y (x = 0,y = 0,z = 0) ÓÑÔÐ Ü ÓÒ Ø Ò Ó Ø Å Ø Ö Ð Ö Ö ½ ÐÝ ØØ Ø Þ Ø º µ¹ º µ Ý ÒÐ Ø º Ö Ñ ÒÝ ÒØ H y º ½ À ÓÒÐ Ò ÞÒ Ð ØÒ Ò ÖÑ ÐÝ ØØ Ø Þ Å Ø Ö Ú Ø Þ Ò Ý Ö Ò Þ Þ Ð E x E y H x ¾¼

22 xy k z ϑ E H z0 z k H k 2 x +k 2 y µ Ú ØÓÖÓ Ñ Ð Ò Ø Ú Ð Ñ ÒØ ¹ Ö Ñ Ö Ð z = 0 Ó µ Ú ØÓÖÓ ¾ Ñ Ð Ò Ø Ò º½º Ö º Ö Ò z = 0 Ö ÚÓÒ Ø ÓÞØ ØÓØØ Ì ÔÓÐ Ö Þ ÙÐРѺ H Ú ØÓÖ Ò Þ E Ú ØÓÖ z = 0 Ò Þ º E xy k z E z0 ϑ H z k k 2 x +k 2 y µ Ú ØÓÖÓ Ñ Ð Ò Ø Ú Ð Ñ ÒØ ¹ Ö Ñ Ö Ð z = 0 Ó µ Ú ØÓÖÓ ¾ Ñ Ð Ò Ø Ò º¾º Ö º Ö Ò z = 0 Ö ÚÓÒ Ø ÓÞØ ØÓØØ ÌÅ ÔÓÐ Ö Þ ÙÐРѺ Þ E Ú ØÓÖ Ò H Ú ØÓÖ z = 0 Ò Þ º Ì Å ÙÐÐ Ñ Ø Ö Ö ÖØ ÓÓÖ Ò Ø Ò Ú Ø Þ Ð Ñ ÖØ ÔÐ Ø Ø Ô Ù ¾½

23 E x ( x,y,z) = E x0 e jkzz, E y (x,y,z) = E y0 e jkzz, E z (x,y,z) = 0, º µ H x (x,y,z) = k z ωµ E y0e jkzz, H y (x,y,z) = k z ωµ E x0e jkzz, H z (x,y,z) = 0. º µ Î Ý ÞÖ Ó Ý kz = ε = 1 ωµ µ Z 0 ÓÐ Z 0 Þ ÙÐÐ Ñ ÑÔ Ò º Ä ØØÙ Ó Ý ÓØØ ÙÐÐ ÑÚ ØÓÖ Ø Ò Ø Ð Ö ÐÐ Ò Ð Ò ÙÐÐ Ñ Ð ØÖÓÑ Ò Ø Ö Ò Ð Ö Ö º Þ ÓÒ Ø Ò Ó Þ Ø Ö Ý ÐØ E z0 H z0 ÐÝ ØØ Ö Ò Ø Ö ÙÐÐ ÑÓ Ø Ò Ð ØÒ Ôк Ø Ö Ý ÔÓÒØ Ò Ø Ô Ù Ò Þ ÓÖ Òµ Þ Ð ØÖÓÑÓ Ø Ö x y Ö ÒÝ Ö Ò Þ Ú Ý Ñ Ò Ø Ö x y Ö ÒÝ Ö Ò Þ Ú Ý Ð ØÒ Ò ÔÔ Ò Þ Ð ØÖÓÑÓ Ñ Ò Ø Öx¹ Ú Ýy¹ Ö ÒÝ Ö Ò Þ Ø º È Ð ÒØ ÓÒÐ Ò Ì Å ÙÐÐ ÑÓ Ò Ð Ð ÖØ ÓÞ Ú Ð ÞÙ ÞØ Ó Ý Þ E x0 = E x (x = 0,y = 0,z = 0) E y0 = E y (x = 0,y = 0,z = 0) ÓÑÔÐ Ü ÓÒ Ø Ò Ó Ø ÞÒ Ð Ù Þ Å Ø Ö Ð Ö ÓÞº ÓÖ º¾ µ º¾ µ Ð ÞÒ Ð Ú Ð Ö Ø Ù Ó Ý E x0 = k xk z E kx 2 z0 ωµk y H +k2 y kx 2 z0, +k2 y E y0 = k yk z E kx 2 +ky 2 z0 + ωµk x H kx 2 +ky 2 z0. º µ º µ ÒØ Ý ÒÐ Ø Ð ÞÚ Þ E z0 H z0 ÖØ Ø Ñ Ú Þ ÐÝ ØØ ØÚ ÞÓ Ø º¾ µ ¹ º ¾µ Ý ÒÐ Ø ÙÐÐ Ñ Ø Ö ÓÑÔÓÒ Ò Ò Ú Ø Þ Þ Ø Ô¹ Ù E x ( r) = E x0 e j k r, E y ( r) = E y0 e j k r, ( E z ( r) = k x E x0 k ) y E y0 e j k r, k z k z ( H x ( r) = k xk y E x0 k2 y +k2 z E y0 ωµk z ωµk z ( k 2 H y ( r) = x +kz 2 E x0 + k xk y E y0 ωµk z ωµk ( z H z ( r) = k y ωµ E x0 + k ) x ωµ E y0 e j k r. ) e j k r, ) e j k r, º µ º µ º µ º ¼µ º ½µ º ¾µ Î Ý ÞÖ Ó Ý Þ ÙØ Ý ÒÐ Ø Ñ Ö ÞÒ Ð Ø z¹ Ö ÒÝ Ø Ö Ì Å ¹ ÙÐÐ Ñ Ð Ö Ö ¾ ÞÞ Ð Þ Ñ Ò Ò Ñ Ð ÐÑ Þ xy Ò Ú ÙÐÐ ÑÚ ØÓÖÖ Ð k z = 0µ Ð Ö Ø ÙÐÐ ÑÓ ÐÐ ÑÞ Ö º ÑÐ ÞØ Ø Ò ÖÖ Ó Ý k x k y k z Þ Ñ ÖÑ Ö Þ Ý ØÐ Ò Ñ Ø Ò º¾½µ ÞÔ ÖÞ Ý ÒÐ Ø Ð Ú Ø Þ Ò ØØ Ø ÖÓÑ Þ Ñ Ð Þ ÓÒ Ú Ð ÞØ ØÙÒ Ñ ÖÑ Ô º Ý ÓÖÐ Ø Ò ÓÒØÓ Ø Þ Ñ ÓÖ k x k y ÖØ Ø Ø Ø Þ Ð Ú Ð Ò Ú Ð ÞØ Ù ÓÖ k z º¾ µ Ð Ô Ò Ú Ð Ò Ú Ý Ø ÞØ ÔÞ Ø Ò º Ø ÖÚ ØÓÖÓ º¾ µ¹ º ¾µ º µ¹ º ¾µ Þ Ø ÖÑ Þ Ø Ò Þ ÓÖ ¾ º µ¹ º ¾µ Ý ÒÐ Ø Ð º µ º µ Ñ Ô Ø k x = k y = 0 k = k z e z ÐÝ ØØ Ø Ðº ¾¾

24 k z Ø ÞØ Ò ÔÞ Ø º ÒÒ Þ ØÒ Þ Ý Þ Öò ÖØ ÐÑ Þ Ö Ò Ö Ù Ð Ôк º¾ µ Þ Ø Ñ Ø k z = jα α ÔÓÞ Ø Ú Ú Ð µ Ð Ð Ú Þ Ø Ú Ð ( jαkx E x (x,y,z) = E kx 2 z0 ωµk y H +k2 y kx 2 z0 )e j(kxx+kyy) e αz. º µ +k2 y À ÓÒÐ ÐÐ ò Þ Ø ÔÙÒ Ø Ø Ö ÓÑÔÓÒ Ò Ö º Ä Ø Ø Ó Ý Ò Þ Ø Ò Ñ Ö Ø Ö Ö ÒÝ Ò Þ Ð Þ Ò Ñ Ó Ð¹ Ñ ÞÓØØ ÖØ ÐÑ Þ Ò Þ Ø Þ º Þ Å Ø Ö ÑÔÐ Ø Ù Ý Ò z¹ Ö ÒÝ ÜÔÓÒ Ò Ð Ò Ò k = kx e x +k y e y Ö ÒÝ Ò Ô Ú ÐØÓÞ ØÐ Ò Ú Ý ÞÖ Ó Ý k k = ω µǫµº Þ ÞÓÒÓ Þ Ó k Ú ØÓÖÖ Ñ Ö Ð Ó Ð ÞÒ ÑÐ Þ¹ Ø Ø Ò ÖÖ Ó Ý Ú Ð k z Ø Ò Þ ÞÓÒÓ Þ Ó k ÙÐÐ Ñ Ú ØÓÖÖ Ñ Ö Ð µº Þ Þ ÒØ Ñ ÐÐ Ô Ø Ø Ù Ó Ý ÔÞ Ø k z Ø Ò Ý z¹ Ö ÒÝ Ò ÜÔÓÒ Ò Ð ¹ Ò ÐÐ ÔÓ Å Ø Ö Ø ÔÙÒ Ñ ÐÝ Ø ØÓÚ Ö ÙÐÐ ÑÒ Ò Ú Þ Ò Ø Þ ÞØ ÒÒ ÐÐ Ò Ö Ó Ý ÒÒ Þ Å Ø ÖÒ ØÙÐ ÓÒ Ó Þ ÑÔÓÒØ Ð Ð Ò ÞÒ Ú Ð ÙÐÐ ÑÚ ØÓÖ¹ ÓÑÔÓÒ Ò Ð Ö Ò Ð Þ ÙÐÐ ÑÓ ØÙÐ ÓÒ Ø Ðº ÔÞ Ø k z ¹Ú Ð Ð ÖØ ÙÐÐ ÑÓ Ø z Ö ÒÝ Ò Ò Ñ Ø Ö Ò z Ö ÒÝ Ò ÐØòÒ Ò µ ÞÓ ØÙ Ò Ú ÞÒ º º¾º Ë ÙÐÐ ÑÓ ÐØ Ð Þ ÐÐ ØÓØØ Ø Ð ØÑ ÒÝ ÁÒ ÙÐ ÙÒ º¾ µ¹ º ¾µ ÔÐ Ø Ð ÓØØ Ì ÌÅ ÔÓÐ Ö Þ ÙÐÐ ÑÓ ÞÙÔ ÖÔÓÞ ÒØ Ð ÐÐ ÙÐÐ ÑÐ Ö Ð ÐØ Ø Ð ÞÞ Ó Ý ÙÐÐ ÑÚ ØÓÖ Ú Ð Þ Þ k x k y k z Ú Ð Þ ÑÓ µº ÔÐ Ø Ø Ú Ð Ð Ö Ø Ù ÓÑÔÐ Ü ÈÓÝÒØ Ò ¹ Ú ØÓÖØ Ñ ÐÝ Ú Ø Þ Ð Ð Þ S = 1 [ E 2 H 1 ωµ = H 2kx 2 +ky 2 z ωε E 2kx 2 +ky 2 z0 ] 2 k, ÓÐ ÓÑÔÐ Ü ÓÒ Ù ÐØ Ø Ð ÒØ º Ñ ÒÒÝ Ò ÙÐÐ Ñ º µ¹ º ¾µ Þ Ð ÓØØ Ð Ö Ð Ò ÙÐÙÒ ÓÑÔÐ Ü ÈÓÝÒØ Ò ¹Ú ØÓÖ Ú Ø Þ Ð Ø Ô Ù Ú Ð ÙÐÐ ÑÚ ØÓÖ Ø Ò S = 1 [ (k 2 2ωµkz 2 x +kz) E 2 x0 2 +(ky 2 +kz) E 2 y0 2 +2k x k y Ê {Ex0E y0 } ] k, ÓÐ Ê { } ÓÑÔÐ Ü Þ Ñ Ú Ð Ö Þ Ø Ð Ð º Ð Þ Ð Ð Þ ÖÑ ÞØ Ø Ø Þ Ô Ð Ø Ñ ÓÖ ÙÐÐ Ñ z¹ Ö ÒÝ Ò Þ Ø Ò Ù Ý Ò Ò Ñ Þ¹ Ò Ð Ø µ ÐÝ Ò ÓÖ Ð ÞÒ ÐÚ k x = 0 k y = 0 k = k z e z = ω µε e z ÞÓÒÓ Ó Ø Ú Ø Þ Þ Ø Ô Ù S = 1 [ Ex0 2 + E ] y0 2 e z, 2 Z 0 Z 0 ÓÐ Z 0 = µ Þ ÙÐÐ Ñ ÐÐ Ò ÐÐ º ε ÈÓÝÒØ Ò ¹Ú ØÓÖÖ ÔÓØØ Þ Ð Ø Þ ØØ Ú Ø Þ Ñ ÐÐ Ô Ø ¹ Ó Ø ÓÐÚ Ø Ù Ø Ö Þ Þ Ú Ð ÙÐÐ ÑÚ ØÓÖÖ Ð Ð Ö Ø µ ÙÐÐ ÑÓ Ö ÚÓÒ Ø Ó¹ Þ Ò ¾

25 ÈÓÝÒØ Ò ¹Ú ØÓÖ Ø Ö Ñ Ò Ò Ý ÓÓÖ Ò Ø Ò ÞÓÒÓ Ú Ò Ý ÈÓÝÒØ Ò ¹Ú ØÓÖ Ú Ð Ø Ø Ø Ó Ø Ð ØÑ ÒÝ Ö ÑÐ Ú Ò ÈÓÝÒØ Ò ¹Ú ØÓÖ ÙÐÐ ÑÚ ØÓÖ Ö ÒÝ ÑÙØ Ø ÙÐÐ Ñ Ò Ø Ø Þ Ò Ö Ø Ö Ò Ö ÒÝ Ý Ø Ö Ö ÒÝ Ú Ð Ý ÙÐÐ ÑÓØ Ì ÌÅ ÔÓÐ Ö Þ ÙÐÐ ÑÓ Ö ÓÒØÙÒ ÓÖ Þ Ö Þ Ó Ý Þ Ý ÔÓÐ Ö Þ ÓÑÔÓÒ Ò ÐØ Ð Þ ÐÐ ØÓØØ Ò Ö ÝÑ Ø Ð ¹ ØÐ Ò Ö Ú Ò ÞØ Ý ÞÓ Ø ÞÒ Ó Ý Ì ÌÅ ÔÓÐ Ö Þ ÙÐÐ ÑÓ ÓÖØÓ ÓÒ Ð ÝÑ Ö Ñ Ú Ð Ý ÙÐÐ Ñ ÐØ Ð Þ ÐÐ ØÓØØ Ò Ö òöò Ú Þ ÖØ Ø Ö Ø ØØ Ó ÞØ Ú Ø Ð Ò ÓÒ Ø Ð Ø Ð ØÑ ÒÝ Ú Ø Ð Ò Ñ ÒÒÝ Ò ÙÐÐ ÑÚ ØÓÖÒ Ú Ò Ö Ñ Ö Ð ÓÑÔÓÒ Ò º ÈÓÝÒØ Ò ¹Ú ØÓÖÖ ÔÓØØ ¹ Þ Ñ Ó ÙÐÒ Ò Þ Ø Ò Ñ ÓÖ k z ÔÞ Ø º k z = jα α ÔÓÞ Ø Ú Ú Ð µ Ð Ð Ð ÞÒ Ð Ú Ð Ú Ø Þ Þ Ø Ô Ù Ú Ý ÞÖ Ó Ý e j(kxx+kyy jαz)[ e j(kxx+kyy jαz)] = e 2αz µ [ 1 ωµk x S = e x H 2kx 2 +ky 2 z ωεk x 2kx 2 +ky 2 [ 1 ωµk y e y H 2kx 2 z ωεk y +k2 y 2kx 2 +k2 y [ 1 jαωµ e z H 2kx 2 +ky 2 z0 2 1 jαωε E 2kx 2 +ky 2 z0 ]e 2 2αz. E z0 2 + jαk ] y E kx 2 +ky 2 z0 Hz0 e 2αz + ] E z0 2 + jαk x E kx 2 z0 H +k2 z0 y e 2αz + ÔÓØØ Ö Ñ ÒÝ Ð Ô Ò Ú Ø Þ Ñ ÐÐ Ô Ø Ó Ø Ø Ø z¹ Ö ÒÝ Ò ÐØòÒ ÙÐÐ ÑÓ Ö ÚÓÒ Ø ÓÞ Ò ÈÓÝÒØ Ò ¹Ú ØÓÖ z ÓÓÖ Ò Ø ÔÓÞ Ø Ú Ö ÒÝ Ò ÜÔÓÒ Ò Ð Ò Ò Ñ z ÓÓÖ Ò Ø Ò Ø Ú Ö ÒÝ Ò ÜÔÓÒ Ò Ð Ò Ò ÈÓÝÒØ Ò ¹Ú ØÓÖ z Ö ÒÝ Ö Ò Þ Ø ÞØ Ò ÔÞ Ø Ø Ø z Ö ÒÝ Ò Ò Ò Ø Ó Ø Ð ØÑ ÒÝ Ö ÑÐ ÈÓÝÒØ Ò ¹Ú ØÓÖ Ú Ð Ö Þ Ø Ó Ø Ð ØÑ ÒÝ Ö ÑÐ Ö ÒÝ µ z ÓÓÖ Ò Ø Ö ÒÝ Ö Ñ Ö Ð Ò Ñ ÐØ ØÐ Ò Ð Ý k x e x +k y e y Ö ÒÒÝ Ð ÙÐÐ Ñ Ì ÌÅ ÔÓÐ Ö Þ ÓÑÔÓÒ Ò ÐØ Ð Þ ÐÐ ØÓØØ Ò Ö ÝÑ ¹ Ø Ð Ò Ñ ØÐ Ò Ì ÌÅ ÔÓÐ Ö Þ ÙÐÐ ÑÓ Ò Þ Ø Ò Ò Ñ ÓÖØÓ ÓÒ Ð ÝÑ Ö z Ø Ò ÐÐÝ Ð Ô Ö ÙÞ ÑÓ Ú Ø Ð Ò Ó ÓÒ Ø Ð Ø Ó Ø Ð ØÑ ÒÝ Ú Ø Ð Ò Ú Ú ÞØ Þ Ý ÓØ Ñ ÐÝ Ñ Ò Ó Ð Ð ÈÓÝÒØ Ò ¹Ú ØÓÖغ Ð ØÙÐ ÓÒ Ð Ð Ø Ø Ó Ý Þ ÐÝ Ò Ø ÔÙ ÙÐÐ Ñ Þ Ð z ÓÓÖ Ò Ø Ý ÓØØ ÒØ ÖÚ ÐÐÙÑ Ò ØÐ Ý Ð Þ ÖØ ÒØ ÖÚ ÐÐÙÑ Ò ¹ Ø Ö Þ ÑÔÓÒØ Ð Ý ÐØ Ö Òµ Ð Ø Þ Ø Þ Ò Ý ÔÞ Ð Ø Ð Ó Ý Ñ Ò Ò ÓÐ Ú Ð Ý Ò ÈÓÝÒØ Ò ¹Ú ØÓÖ Ò Ý º ¾

26 º º ÙÐÐ Ñ Þ ÖØ ÐÑ Þ Ò ÒÝ Ý ÓÖÐ Ø Ð ÐÑ Þ Þ Ð Þ Þ Þ Ñ ÐÐ Ô Ø Ð Ð Ø Ø Ù Ó Ý ÙÐÐ Ñ Ý ÞØÖ ÐÝ Ò Å Ø Ö Ú Ð Ò Ò Ò Ò Ò Ù Ý Ò Ú Ø Ð Ò Ø Ó Ø Ð ØÑ ÒÝØ Þ ÐÐ Ø Ú Ð ¹ Ó Å Ø Öµº Ý Ñ ÓÒØÓ Ð Ñ Ñ Þ Ð Þ Ð ÒØ Ø Ø Ñ ÞØ Ð Þ Ó Ý Ò Ñ Ð Ø ÖØ ÐÑ Ò Ñ Ó ÐÑ ÞÒ ÓÐÝ Ò Ô Ö Ñ ÐØ Ø Ð Ø Ñ ÐÝ Ø ÙÐÐ Ñ Ð Øº ÞØ Ñ Ö ÓÖ Ý Ò Ø Ò Ð Ø ØØ Ñ ÓÖ Ð ÒØ ØØ Ó Ý ÙÐÐ Ñ Ö¹ Ö Ð Ñ ÓÒ Ú Ø Ð Ò Ø Ð ØÑ ÒÝ Ö ÑÐ Ð Ö Þ Ò Þ Ý ÖØ ÐÑò Ø Ý Þ Ý ÖØ ÐÑò Þ Þ Ô Ö Ñ ÐØ Ø Ð Ø ÔÔ Ò Ò Ö Ø Ñ ÓÒ ÓÐ Ó Ð Ô¹ Ò ÞÓÒÝ ØÓØØÙ º Ä Ø Ø Ó Ý ÙÐÐ ÑÚ ØÓÖ Ö ÒÝ Ò ÙÐÐ Ñ Ù Ý Ò Ð Ø Ù ÖÞ ÐØ Ø ÐØ Ú Ø Ð Ò Ø ÖÖ ÞÖ ÚÓÒ Ø ÓÞ Ô Ö Ñ ÐØ Ø Ðص Ò Ñ Ð Ø ÞØ Ø Ö Ö Ñ Ö Ð Ø Ö Ö ÒÝ Ú Ð ÐÐ ÒØ Ø Ö ÒÝÓ Ò Ý Þ Ñ ÓÐ Þ Ð Ò Ñ Ð Ø Þ ÐÖ Ò Þ Þ Ø ÖØÓÞ º ÒØ ÐÐ Ò Ö ÙÐÐ Ñ Ý ÓÖÐ Ø Ò Ð ÓÖ ÙÐ Ø Ö ÔÖÓ Ð Ñ Ð Ö ¹ Ò Ð Ò ÞÒ ÐØ Þ Þ º Å Ò Þ Þ ÖØ Ú Ò Ý Ñ ÖØ Ø Ø Þ Ð ÒØ ÒÒ ÒØ ÒÒ ¹ Ö Ò Þ Öµ Ø ÚÓÐ Ø Ö ÐÓ Ð Ò ÙÐÐ ÑÑ Ð Þ Ð Ø Ø º Þ ÞØ Ð ÒØ Ó Ý Þ ÒØ ÒÒ Ø Ð ÐÐ Ò Ø ÚÓÐ Þ ÒØ ÒÒ Ó Ð Ð Ñ Ö Ø Ò ÙÐÐ Ñ Ó Þ Ò Ý Ò Ó ÞÓÖÓ Ø ÚÓÐ Òµ Ý Ú Ñ Ö Øò Þ ÒØ ÒÒ Ø Ú Þ Ð ÔÓÒØÓØ Þ Ø Ù ÖÖ Ñ Ö Ð ¹ Ð Ð Ø Ò Þ Å Ø Ö Ý Ø ÒØ Ø Ñ ÒØ Þ Ý Ù Ö Ö ÒÝ Ø Ö ÙÐÐ Ñ Ð ÒÒ º Þ ÐÐ Ø ÒÒÝ Ò Ð Ø Ø Ý Ó Ý Ý Ð Ñ Ú Þ ÞØ Ó Ý Ø Ø Þ Ð ¹ ÒØ ÒÒ À ÖØÞ¹ Ô ÐÙ Ó ÞÙÔ ÖÔÓÞ ÒØ Ð ÐÐ Ø Ø Ý ÒÒ Ø ÚÓÐ Ø Ö À ÖØÞ¹ Ô ÐÙ Ó Ø ÚÓÐ Ø Ö Ò ÞÙÔ ÖÔÓÞ ÒØ ÐÐ Ð ºµ Þ Ð Ø Ó Ø Ð Ý Ð Ð Ø Ò Ñ Ð Ð Ø Ý ÔÓÒØ Ò ÒØ ÒÒ Ø Ð Ñ ÖØ Ø ÚÓÐ ÙÐÐ Ñ Ó Þ Ø Ö Ò Ð Ñ ÖØ Ò Ú ÐØÓÞ Ø Ð Ð Ð Ø Ò º Ð Ø Ø Ó Ý Ò Ý Ø ÚÓй Ò Ð Ú ÒØ ÒÒ Ø Ò Þ Ñ Ö Ø Ñ Ò ÒÝ ÙÐÐ Ñ Ó Þ Ø Ò Ð ÒØ Ð Ø Ôк Ý 10km Ø ÚÓÐ Ò Ð Ú 3GHz Ö Ú Ò Ò Ñò ÒØ ÒÒ Ø Ò ÒÒ Ú Ò Þ ÓÐ Ð Ó Þ 10m¹ Ò Ý Ö Ò º Ã Þ Ò Ú Ó Ý Þ ÒØ ÒÒ Ø ÚÓÐ Ø Ö Ò ÙÐÐ Ñ Þ Ð Ø Ð ÐÑ Þ Ø Ò Þ Ø Ò Ñ ÓÖ Ú Ò Ñ Ñ Ö Ð Þ ÒØ ÒÒ Ð Ò ØÓØØ Ù ÖÖ Ò Þ Ø Ò ÙÐÐ Ñ Ø Ö Ö ÒÝ Ú Þ ÐØ Ð Ð Ø ÒÓÖÑ Ð Ò Ñ Ý Ö ÒÝ ÑÙ¹ Ø ØÒ º Þ Þ Òº Ö Ò ÙÐÐ ÑÓ Ö Ü Ò Ø Ö Ú Þ Ø ÞØ Ð Ò Ø ØÓÚ Ò Ö ÞÐ Ø Ò Ú Þ ÐÒ Ó ÙÒ º Å ÐÐ Ô Ø Ø Ù Ø Ø Ó Ý Ñ ÖÒ Ý ¹ ÓÖÐ Ø Ò Ú Þ ÐØ Ø Ò Ò Ý ÒÝ Ò Ø ÒØ Ø Ñ Ú Ð Ø Ø Ö Ø ÐÓ Ð Ò ÙÐÐ ÑÒ Þ Þ Ó ÒÒ Ó Ý ÙÐРѹ ÞØÖ Ö ÞÐ Ø Ú Þ Ð Ø Ö Ð Ú Ò º ÙÐÐ ÑÓ Ð Ú Ð Ø Ó Ð Ð ÓÞ Ñ Ó Þ Ó Ý º ÔÓÒØ Ò ÑÙ¹ Ø Ø Ö Ö Ð ÖÚ Ð Ð Ô Ò Ð Ø Ø Ó Ý Ñ Ò Ò ÓÑÓ Ò ÓÖÖ Ñ ÒØ Ø ÖØÓ¹ Ñ ÒÝ Ò Ð ÙÐ Å ÙÐÐ ÑØ Ö Ø Ð Ð Ø ÖÒ Ð Ò Þ Ö ÒÝ Ò Ø Ö ÙÐÐ ÑÓ ÞÙÔ ÖÔÓÞ Òغ Ð Ò Ø Ø ÙÐÐ ÑÓ Ö ÔÓØØ Ö Ñ ÒÝ ÐØ Ð ÒÓ¹ Ø Ø º Þ Ð Ô Ò Ôк Ø Ø Þ Ð Ñ Ú Ð Ø Å ÙÐÐ Ñ Þ Ö Ø Ø ÒØ Ø Ý Ñ ÒØ Ñ Ú Ð Ø Ø Ð ÓØ ÙÐÐ ÑÓ Þ Ö Ò ÞÙÔ ÖÔÓÞ Øº ÙÐÐ Ñ Ó Þ Ø Ö Ð ØØ Ñ Ò Ò ÓÖ ÔÓÒØÓ Ú Ø ÐÑ ÒÝ Ø Ý Ð Ñ Ú Ú ÖØ Ø Ö¹ Ø Ò λ/32...λ/16 Ú Ð ÞØ ÐØ Ð Ò Ñ Ð Ð º ËÞ Ö Ð ØØ ÓØØ Ñ Ú Ð Ø Å ÙÐÐ ÑÒ Ý Ñ ÖØ Ó ØÙÑ Ð ÒÐ Ø Ø Ö Ø ÖØ Ò Ñ Ú ÐØÓÞ Ø ÖØ º ¾

27 º º Ö Ò ÙÐÐ Ñ Ú Ð ÒÝ Ø ÖÓÒ Ì ÒØ Ò Ø Ð Ò Þ ÒÝ ÐØ Ö Ø Ñ ÐÝ Ø z = 0 Ú Ð ÞØ Ð ÝÑ ¹ Ø Ðº Å Ò Ø Þ ÒÝ Ò Ô ÖÑ Ð Ø Ð Ý Ò µ 0 Þ Ð Þ Ô ÖÑ ØØ Ú Ø ¹ Ð Ý Ò ε 1 Ñ Ó ε 2 º Î Ð Ø Ñ Ø Ö Ð Ð Ø Ø Þ Ð Þ Ò Ø Ö k + 1 = k x e x +k y e y +k z,1 e z ÙÐÐ ÑÚ ØÓÖÖ Ð Ð ÖØ ÙÐРѺ Ñ Ú Ð Ø Ø Ý ÖØ ÐÑò Ò Ñ ØÙ º¾ µ¹ º ¾µ ÔÐ Ø Þ Ö ÒØ Ð Ö Ø Ý Ð Ñ Ú Ú ÙÐÐ ÑÚ ØÓÖÓÒ Ø Ð Ñ ØÙ H z0 E z0 ÓÑÔÐ Ü ÓÒ Ø Ò Ó Øº ÖØ Ð Ñ Þ Öò Ò Ñ ÒÒÝ Ò Ùй Ð Ñ º µ¹ º ¾µ Þ Ð ÓØØ Ð Ö Ð Ò ÙÐÙÒ Þ E x0 E y0 ÓÒ Ø Ò Ó Ø ÐÐ Ñ ÖÒ Ò Ñ Ú Ð Ø Ý ÖØ ÐÑò Ñ ÓÞºµ ÐÙÒ Þ Ó Ý Ñ Ú Ð Ø ÙÐÐ Ñ Ñ Ö Ø Ò Ñ Ø ÖÓÞÞÙ Ð ÙÐ Å Ø Ö Øº º º½º Ø Ö Ø ÖÚ ÒÝ ÙÐÐ Ñ Ñ Ú Ð Ø Ø Ö Å ÜÛ Ðй Ý ÒÐ Ø Ð Ð Ú Þ Ø Ø Ø Ö ÐØ Ø Ð ¹ Ò Ñ Ð Ð Å Ø Ö Ó Ð ÙÐÒ Þ Þ Ö ÒØ Þ ÐÚ Ð ÞØ Ñ Ò Ø ÓÐ Ð Ò Þ Ð ØÖÓÑÓ Ñ Ò Ø Ö Ö Ø Ò Ò Ð ÓÑÔÓÒ Ò Ò Ý Ð Ò ÐÐ Ð ÒÒ º Ø Ö ÐØ Ø Ð Ð Ú Ø Þ Ó Ý z = 0 Ñ Ò Ø ÓÐ Ð Ò Ù Ý ÒÓÐÝ Ò Ø Ö Ð Ú ÒÝ Þ Ö ÒØ ÐÐ Þ Ð ØÖÓÑÓ Ñ Ò Ø ÖÒ Ú ÐØÓÞÒ º Å Ú Ð Ñ Ú Ð Ø ÙÐÐ Ñ x y Þ Ö ÒØ Ø Ö Ð e j(kxx+kyy) Ý Ø ÓÐ ÐÓÒ ÓÖ Ð Ø¹ Ò Ý Ð Ø Ò Ò Ð ÓÑÔÓÒ Ò Ñ Ò Ø ÓÐ ÐÓÒ Þ x y Þ Ö ÒØ e j(kxx+kyy) Ð Ð Þ º Ã Ú Ø Þ ÔÔ Ò ÙÐÐ ÑÓ Ð ØÒ Þ Ý Ø ÖÖ Þ ¹ Ò Ð Ø ÙÐÐ ÑÓ ÙÐÐ ÑÚ ØÓÖ Ò x y ÓÑÔÓÒ Ò Ñ Ò Ø Þ Ò Ù Ý Ò ÞÓ k x k y Ñ ÐÝ Ñ Ý ÞÒ Ñ Ú Ð Ø ÙÐÐ Ñ ÙÐÐ ÑÚ ØÓÖ Ò x y ÓÑÔÓÒ Ò Ú Ðº Þ Ð Þ Ò Ð ØØÙ Ó Ý Ñ ÒÒÝ Ò Ý Þ Ò k x k y ÓØØ k z º¾½µ Ý ÒÐ Ø Ðº k z ¹Ö Þ Ð Þ Ò Ø Ñ ÓÐ Ô Ø Ñ ¹ ÐÝ ÝÑ Ò ÐÐ ÒØ ØØ Þ Ø + Ð Ò Ü Ð Ð Ò ÞØ Ø Ñ º Å Ú Ð Ñ Ú Ð Ø ÙÐÐ Ñ Ø Ö Ú Ð ÙÐÐ ÑÚ ØÓÖÖ Ð Ð Öص Ð Ø k z ÖØ Ú Ø Þ k z,1 + = k z,1 = ω 2 µ 0 ε 1 kx 2 ky, 2 kz,1 = k z,1 = ω 2 µ 0 ε 1 kx 2 ky 2 = k z,1. + Ä Ø Ø Ó Ý Þ Ð Þ Ò Þ Ö Ø Ñ Ú Ð Ø ÙÐÐ ÑÓÒ Ú Ð Ð ÙÐ Ø Ñ Ý ÝÒ Ú Þ ØØ Ö Ø ÐØ ÙÐÐ Ñ Ñ ÐÝÒ ÙÐÐ ÑÚ ØÓÖ k1 = k x e x +k y e y k z,1 e z º Å Ú Ð k x k y ÖØ Ñ Ú Ð Ø ÐØ Ð Ñ Ó Þ Ò ÓØØ Þ ØØ Ð ÙÐ ÙÐÐ ÑÓ ÙÐÐ ÑÚ ØÓÖ Ò z ÓÑÔÓÒ Ò Ú Ø Þ ÖØ Ø Ú Ø Ð { k z,2 ± = ±k ω2 µ z,2 = ± 0 ε 2 kx 2 ky, 2 kx 2 +ky 2 ω 2 µ 0 ε 2, j kx 2 +k2 y ω2 µ 0 ε 2, kx 2 +k2 y. ω2 µ 0 ε 2, Å Ú Ð Ñ Ó Þ z¹ Ö ÒÝ Ò Ú Ø Ð Ò Ú Ø Ð Ò Ð Ö Ø ÐØ ÙÐÐ Ñ Ù ÖÞ ÐØ Ø Ð Ñ ØØ Ò Ñ Ð Ø Þ Þ ÖØ Ñ Ó Þ Ò ÔÓÞ Ø Ú Ð ÐÐ Ð ÔÓØØ k z,2 ¹Ò Ñ Ð Ð ÙÐÐ Ñ Ð ÙÐ Þ Þ Ñ Ó Þ Ò Ý Ð k + 2 = k x e x +k y e y +k z,2 e z ÙÐÐ ÑÚ ØÓÖÖ Ð Ð Ö Ø ÙÐÐ Ñ Ð Þº Ñ ÒÒÝ Ò Ð Ô Ò k z,2 Ú Ð Ò Ñ Ó Þ Ò Ø Ö Ùй Ð Ñ Ó Ð ÙÐÒ ÓÖ Ñ Ú Ð ÙÐÐ Ñ Ö ÒÝ Ò Ñ Ð Þ Ñ Ú Ð Ø ÙÐÐ Ñ Ú Ð Î Ý ÞÖ Ó Ý Þ ÐÚ Ð ÞØ Ò z = ÓÒ Ø Ò Ý Þ Å Ø Ö z Þ Ö ÒØ Ö Ø Ö Ð¹ Ø Ø Ð Ò Ñ Ø ÞÒ Ñ Ø Øº ¾

28 xy xy xy k 1 k + 2 k 1 k = kx e x +k y e y k 1 k + ϑ 1 ϑ 2 ϑ 1 2 z ϑ 1 ϑ 2 ϑ 1 z ϑ 1 ϑ 2 ϑ 1 z k + 1 µ 0,ε 1 µ 0,ε 2 µ ε 1 < ε 2 k + 1 µ 0,ε 1 µ 0,ε 2 µ ε 1 > ε 2 k 2 x +k 2 y < ω 2 µ 0 ε 2 k + 1 µ 0,ε 1 µ 0,ε 2 µ ε 1 > ε 2 k 2 x +k 2 y > ω 2 µ 0 ε 2 º º Ö º Ö Ò ÙÐÐ Ñ Ú Þ Ú Ö Ø Ö Ø ÒÝ ÓØ ÐÚ Ð ÞØ z = 0 Ø Ö Ð Ð Ø Ò Ò Ö ÞÓÐÚ º Þ xy Ø Ò ÐÝ Ö ÒÝ ÑÙØ Ø Ý Ú ØÓÖ e xy = kx k 2 x +ky e 2 x + ky k 2 x +ky e 2 y ÙÐÐ ÑÚ ØÓÖÓ xy Ö Ú Ø Ð Ø Ò Ö ÒÝ ÑÙØ Øº Ý Þ Ø Ö Ö Ð Þ Ð Ò º Ò Þ Ø Ò Ø Ó Ø Ð ØÑ ÒÝ Ö ÑÐ Þ ÐÚ Ð ÞØ Ð Ð Ø Ò Ö ÞØ Ð Ñ Ó Þ º À Ú ÞÓÒØ Ð Ô Òk z,2 ÔÞ Ø Ò Ñ Ó Þ Ò z Ö ÒÝ ÐØòÒ ÙÐÐ Ñ Ð ÙÐ ÐÝ Ò ÓÖ Ø Ð Ú Þ Ú Ö Ø ÐÐ Ð º ÓÖ Ù Ý Ò Ø Ó Ø Ð ØÑ ÒÝ Ò Ñ Ó Ø Ö ÑÐ Ò Þ Ð Þ Ð Ñ Ó Ý Ø Ó Ø Ð ØÑ ÒÝ ÙÔ Ò Þ xy Ð Ô Ö ÙÞ ÑÓ Ò Ó Ø Ö Ò Ñ Ò Ø Þ Òº º Ö Ò ÙÐÐ ÑÚ ØÓÖÓ Ø Ö ÞÓÐØÙ ÖÓÑ Ð Ò Þ Ø Òº º º Ö ÓÒ Ø Ö Ø Ø ÑÙØ Ø Ù ÓÐ ØÓÚ Ð ÙÐÐ ÑÓ ÙÐÐ ÑÚ ØÓ¹ Ö Ò Ñ Ö Ð Ð Þ ÖØ Þ Ö ϑ 1 ϑ 2 µ Þ Ñ ÖØ ËÒ ÐÐ Ù ÖØ Ø Ö Ø ÖÚ ÒÝ ÖÚ ÒÝ Ðº Þ ÐÑÓÒ ÓØØ Ð ÞØ Ñ ÒÒÝ Ò Ð Ú Þ Ø Ø Ð ÞÒ Ð Ù Ó Ý k 2 x +ky 2 k 2 sinϑ 1 = ω x +ky 2, sinϑ 2 = µ 0 ε 1 ω, º ¼µ µ 0 ε 2 Ý Ð Ñ Ú Þ Ó Ý n 1 = ε 1r n 2 = ε 2r Þ Ý Þ Ø Ö ÑÙØ Ø ÓÐ ε 1r ε 2r Þ Ö Ð Ø Ú Ô ÖÑ ØØ Ú Ø Ø Ð Ð º Ö Ñ ÒÝ ÒØ º ¼µ Ý ÒÐ Ø Ð Ñ ÞÓ ÓØØ ÓÖÑ Ò Ø Ö Ø ÖÚ ÒÝ sinϑ 1 sinϑ 2 = n 2 n 1. º ½µ Þ Ø ÖÚ ÒÝ Ø ÖÑ Þ Ø Ò ÓÖ Ð ÐÑ Þ Ø Ñ ÓÖ Ñ Ó Þ Ò Ø Ö ÙÐÐ Ñ Ð ÙÐ º Ø Ð Ú Þ Ú Ö Ø ÞØ ÑÙØ Ø º Ö Ö ÓÖ Ð ÒØ Þ Ñ Ó Þ Ô ÖÑ ØØ Ú Ø Ø Ö ÑÙØ Ø µ Þ Ð Þ Ô ÖÑ ØØ Ú Ø Ò Ð Ñ Ú Ð Ø ÙÐÐ Ñ Þ Ò ÝÓ Þ ϑ kr 1 = arcsin n 2 n 1 Ö Ø Ù Þ Ò Ðº º º¾º Ö Ø ÐØ ØÓÚ Ð ÙÐÐ ÑÓ ÑÔÐ Ø Ò Ñ Ø ÖÓÞ ØÓÚ Ò Ñ Ø ÖÓÞÞÙ Ö Ø ÐØ k z,1 Ö ÒÝ Ð µ Ñ Ó Þ Ò ØÓÚ Ð k + z,2 Ö ÒÝ Ø Ö µ ÙÐÐ ÑÓ ÑÔÐ Ø Ø Ñ Ú Ð Ø ÙÐÐ Ñ ¾

29 k z,1 + Ö ÒÝ µ ÑÔÐ Ø Ò Ñ Ö Ø Òº Ð Ð Ô ÒØ Þ Ý Þ Öò Þ Ö Ò Ö Ù Ø ÙÐÐ Ñ Å Ø Ö Ò º¾ µ¹ º ¾µ ÔÐ Ø Ð ÓØØ Ð Ö Ø Ð Ð Ðº Å Ò Ò Ð ØØ Ö Ù Ð k = k x e x +k y e y +k z e z ÙÐÐ ÑÚ ØÓÖ Ö Ò Þ Ø Ñ ÓÓÖ Ò Ø k = k e r +ϑ e ϑ +ϕ e ϕ Ø Ú Ð k x = ksinϑcosϕ, k y = ksinϑsinϕ, k z = kcosϑ, º ¾µ ÓÐk = ω µε ÙÐÐ ÑÚ ØÓÖ ÞÓÐ Ø ÖØ ϑ k Ú ØÓÖ z Ø Ò ÐÐÝ Ð Þ ÖØ Þ ϕ k Ú ØÓÖ xy Ö Ú ØØ Ú Ø Ð Ø Ò x Ø Ò ÐÐÝ Ð Þ ÖØ Þ º k ϑ ϕ ÖØ ÐÑ Þ Þ Ð Ñ º½ º¾ Ö Øºµ Î Þ ØÓÚ Þ E TE = ωµ k k 2 x +kyh 2 z0 = k 2 x +ky 2 Z 0 H z0 = 1 sinϑ Z 0H z0, º µ k z E TM = k 2 x +kye 2 z0 = Ø ϑe z0 µ Ð Ð Ø ÓÐ Z 0 = Ø Ö ÙÐÐ Ñ ÑÔ Ò º Î Ð Ú Þ Ú Ø Þ ε ÑÔ Ò ÐÐ ò Ñ ÒÒÝ Ø Z TE = ωµ = ω µε Z 0 = k 1 Z 0 = Z 0 k z k z k z cosϑ, Z TM = k z ωε = k z ω µε Z 0 = k z k Z 0 = Z 0 cosϑ. Å Ý ÞÞ Ó Ý ÞÓ Þ Ñ ÐÝ Ò ϑ Ñ Ð Ò ÓÖ ÞÒ Ð¹ Ø Ø Ö ÙÐÐ ÑÖ Ð Ú Ò Þ º z Ö ÒÝ Ò ÐØòÒ ÙÐÐ ÑÓ ÔÞ Ø k z µ Ø Ò k z ¹Ø Ø ÖØ ÐÑ Þ Þ ÞÒ Ð Ø º Å ÐÐ Ô Ø Ø Ù ØÓÚ ÞØ Ó Ý Ú Þ ÐØ Ð ØÒ Ð Ð ÙÐ ÙÐÐ ÑÓ ÙÐÐ ÑÚ ØÓÖ Ò k + z,1 k z,1 k + z,2µ ϕ Þ Ù Ý Ò Þ Ñ Ú Ð Ñ Ò ÖÓÑ ÙÐÐ ÑÚ ØÓÖ Ò Ú Òº Ú Þ Ø ØØ Ð Ð Ð ÙÐÐ Ñ Ì ÔÓÐ Ö Þ ÓÑÔÓÒ Ò Ò Å Ø Ö Ú Ø Þ Ð Ò Ö Ø E x ( r) = k y k 2 x +k 2 ye TE e j k r = sinϕe TE e j k r, k x E y ( r) = k 2 x +kye 2 TE e j k r = cosϕe TE e j k r, E z ( r) = 0, k x E H x ( r) = TE e j k r = cosϕ E TE e j k r, k 2 x +ky 2 Z TE Z TE º ¼µ H y ( r) = k y E TE e j k r = sinϕ E TE e j k r, k 2 x +ky 2 Z TE Z TE º ½µ H z ( r) = k 2 x +k 2 y k z E TE Z TE e j k r = Ø ϑ E TE Z TE e j k r. º ¾µ ϑ ÙÐÐ Ñ z = ÐÐ Ò Ö ÚÓÒ Ø ÓÞØ ØÓØØ Þ Ý Ò Þ Þ cosϑ = kz k ϕ z = ÐÐ Ò Ó Ñ Ø Þ ÚÓÒ Ð Ò Þ x Ø Ò ÐÐÝ Ð Þ ÖØ Þ Þ Þ Ø ϕ = ky k x ¾

30 ÙÐÐ Ñ ÌÅ ÔÓÐ Ö Þ ÓÑÔÓÒ Ò Ò Å Ø Ö Ô Ú Ø Þ Ð Ò Ö Ø E x ( r) = E y ( r) = k x k 2 x +k 2 ye TM e j k r = cosϕe TM e j k r, º µ k y k 2 x +k 2 ye TM e j k r = sinϕe TM e j k r, k 2 x +ky 2 E z ( r) = E TM e j k r = Ø ϑe TM e j k r, k z k y E H x ( r) = TM e j k r = sinϕ E TM e j k r, k 2 x +ky 2 Z TM Z TM H y ( r) = H z ( r) = 0. k x E TM e j k r = cosϕ E TM e j k r, k 2 x +ky 2 Z TM Z TM Â Ð Ð Ì ÌÅ ÔÓÐ Ö Þ ÙÐÐ Ñ ÓÑÔÓÒ Ò z = 0 Þ Þ Ø Ò Ò Ð µ Ð ØÖÓÑÓ Ñ Ò Ø Ö Ö Ø Ö Ò Ö E t TE TM TE TM E t H t H t Þ Ñ ¹ ÐÙÑÓ Ð Þ Þ ¹ Ý ÒÐ Ø Ð Ú Ø Þ E TE t = sinϕe TE e x cosϕe TE e y, H TE t = cosϕ E TE Z TE e x +sinϕ E TE Z TE e y, º ¼µ E TM t = cosϕe TM e x +sinϕe TM e y, º ½µ H TM t = sinϕ E TM Z TM e x +cosϕ E TM Z TM e y. º ¾µ ¹ º ¾µ Ý ÒÐ Ø Ú Þ Ð Ø Ð Ô Ò z = 0 Ò Ø Ö Ö Ö ÚÓÒ Ø Ó¹ Þ Ò Ú Ø Þ ÓÒØÓ Ñ ÐÐ Ô Ø Ó Ø Ø Ø Ú Ý ÞÖ Ó Ý Ý ÙÐÐ Ñ Ò z = 0 Ò Ñ Ø ÒØ Ø ØØ Ý Þ Ñ ÐÐ Ô Ø Ó ÓÒÐ Ò Ñ Ó ÐÑ Þ Ø ÖÑ ÐÝ z = ÐÐ Ò Ò µ E TE t = E TE E t TM = E TM H TE t = 1 Z TE E TE t = E TE Z TE H TM t = 1 E Z t TM TM = E TM Z TM E TE t H TE t = 0 E TM t H TM t = 0 E TE t E TM t = 0 H TE t H TM t = 0º ¾

31 xy xy E = E t = E TE E ϑ E t E t = E TE E = E t k ϑ H t ϑ H z k ϑ H = H t z H = H t = E TM Z TM H t = E TE Z TE µ Ì ÔÓÐ Ö Þ ÙÐÐ ÑÓØ ÐÐ ÑÞ Ú ØÓ¹ ÖÓ Ö ÞÓÐ Ò µ ÌÅ ÔÓÐ Ö Þ ÙÐÐ ÑÓØ ÐÐ ÑÞ Ú ¹ ØÓÖÓ Ö ÞÓÐ Ò º º Ö º Ö Ò z = 0 Ö ÚÓÒ Ø ÓÞØ ØÓØØ Ì ÌÅ ÔÓÐ Ö Þ ÙÐÐ Ñ ÐÐ ÑÞ Ö ÞÒ ÐØ Ð Ð Ñ Ý Ö Þ Ø ØØ Þ Ð Ð Ú ØÓÖ Ó Þ Ø Ò Ñ Ý ÓÑÔÐ Ü Þ Ñ ÞÓÐ Ø ÖØ Ø Ð Ð µº ËÞ Ú Ò ÒØ Ñ ÐÐ Ô Ø Ó Ð ÒÝ ÝÖ ÞØ Þ Ó Ý Þ Ý ÔÓÐ Ö Þ ¹ ÙÐÐ ÑÓ E H Ø Ö Ò xy Ð ÓÑÔÓÒ Ò Ñ Ö Ð ÝÑ Ö Þ ÒÝ Ó Z TE Z TM ÐÐ Ò º Å Ö ÞØ Ô Þ Ó Ý Þ Ý ÔÓÐ Ö Þ Ð ØÖÓÑÓ Ø ÖÚ ¹ ØÓÖ Ò Ø Ò Ò Ð ÓÑÔÓÒ Ò Ñ Ö Ð ÝÑ Ö ÓÒÐ Ñ ÐÐ Ô Ø Ø Ø Ñ Ò Ø Ö Ö Ú ØÓÖÓ Ö º ÒØ Ñ ÐÐ Ô Ø Ó Ø Þ ÑÐ ÐØ Ø º Ö Ñ ÐÝ Ø Ú Ð Ú Þ Ø ØØ Ð Ð Ý Þ Öò Ò ÖØ ÐÑ Þ Ø º Ó Ý Ò ÞØ Ñ Ö ÒØ ÑÐ Ø ØØ Ú Þ ÐØ Ð Ø Ò Ö Ò ÙÐÐ Ñ Ú Ð Ø Ð Ò Þ ÒÝ ÐÐ ÑÞ ò Ø ÖÖ Þ Ø Ö Òµ ÓÐÝ Ò Å Ø Ö Ð ÙÐ Ñ ÐÝ Ð Ø Ø Þ z = 0 Ò Å ÜÛ Ðй Ý ÒÐ Ø ÐØ Ð Ø ÐØ ÓÐÝØÓÒÓ ÐØ Ø Ð ¹ Ò Þ Þ Þ Ð ØÖÓÑÓ Ñ Ò Ø Ö Ø Ò Ò Ð ÓÑÔÓÒ Ò ÓÐÝØÓÒÓ z = 0 Òº Ð ÐØ Ø Ð Ð Ú Þ ØØ Ð Ð ÙÐ ÙÐÐ ÑÓ ÙÐÐ ÑÚ ØÓÖ Ö ÚÓÒ Ø ÓÞ º ½µ Ø Ö Ø ÖÚ ÒÝØ Ú Ø Þ Ò ÙÐÐ ÑÓ ÑÔÐ Ø Ö ÚÓÒ Ø ÓÞ Ø ÖÚ ÒÝØ Ó Ù Ð ÖÒ º ÞØ Ì ÌÅ ÔÓÐ Ö Þ ÙÐÐ Ñ ÓÑÔÓÒ Ò Ö Ð Ò¹ Ð Ò Ø Ø¹ Ñ Ñ Ú Ð Ð ØØÙ Ó Ý Ì ÌÅ ÔÓÐ Ö Þ Ñ Ð Ð Ø Ö Ö ¹ ÓÑÔÓÒ Ò Ñ Ö Ð ÝÑ Ö ØÓÚ ÓÐÝØÓÒÓ ÐØ Ø Ð Ò Ñ Ú ÐØÓÞØ ØÒ Ø Ò Ò Ð ÓÑÔÓÒ Ò Ö ÒÝ Ò Ý Ö Ü ÔÖÓ Ð Ñ ÓÖ Ò Ì ÌÅ ÔÓÐ Ö Þ ÙÐÐ ÑÓ Ò Ñ ØÓÐ Ò ÝÑ Ð Ú Ø Þ ÔÔ Ò ÝÑ Ø Ð ØÐ Ò Ð Þ Ð Ø º Â Ð Ð Ö Ò Ö E TE,1 + E TE,1 E+ TE,2 k 1 + k 1 k 2 + ÙÐÐ ÑÚ ØÓÖÖ Ð Ð ÖØ ÙÐÐ ÑÓ Ì ÔÓÐ Ö Þ ÓÑÔÓÒ Ò Ò ÑÔÐ Ø Øº Þ Ø Ú Ð Ì ÔÓÐ Ö Þ ÙÐÐ Ñ ÓÑÔÓÒ Ò Ö ÚÓÒ Ø ÓÞ ÓÐÝØÓÒÓ ÐØ Ø Ð z = 0 Ò Ú Ø Þ Ñ ÓÒ Þ Ø E + TE,1 +E TE,1 = E+ TE,2, E + TE,1 Z TE,1 E TE,1 Z TE,1 = E+ TE,2 Z TE,2, º µ ÓÐ Z TE,1 Ý ÒÐ Ø Ð Þ Ñ Ø Ø Þ ε = ε 1 µ = µ 0 k z = k z,1 ÐÝ ØØ Ø Ð ¼

32 ÓÒÐ Ò Ô Ø Ñ Z TE,2 Þ ε = ε 2 µ = µ 0 k z = k z,2 Ð ÞÒ Ð Ú Ðº Î Ý Þ¹ Ö Ó Ý k 1 ÙÐÐ ÑÚ ØÓÖ ÓÞ Ø ÖØÓÞ ÙÐÐ Ñ Ñ Ò Ø Ö Ö E TE,1 Z TE,1 ÖØ òº Þ Þ ÖØ Ú Ò Ý Ñ ÖØ k 1 ÙÐÐ ÑÚ ØÓÖ z Ö ÒÝ ÓÑÔÓÒ Ò ÐÐ ÒØ ØØ k + 1 ÙÐÐ ÑÚ ØÓÖ z Ö ÒÝ ÓÑÔÓÒ Ò Ò Ð Ò Ð Ô Ò Þ Ñ ØÓØØ ÖØ ÐÐ ÒØ ØØ Ð ÞÒ ÝÑ Ò Z TE,1 k + 1 ÙÐÐ ÑÚ ØÓÖ ÓÞ Þ Ñ ØÓØØ ÖØ µ º ÌÅ ÔÓÐ Ö Þ ÙÐÐ Ñ ÓÑÔÓÒ Ò Ö ÓÐÝØÓÒÓ ÐØ Ø Ð Ú Ø Þ Ý Ò¹ Ð ØÖ Ú Þ Ø E + TM,1 +E TM,1 = E+ TM,2, E + TM,1 Z TM,1 E TM,1 Z TM,1 = E+ TM,2 Z TM,2, ÓÐ E TM,1 + E TM,1 E+ TM,2 k 1 + k 1 k 2 + ÙÐÐ ÑÚ ØÓÖÖ Ð Ð ÖØ ÙÐÐ ÑÓ ÌÅ ÔÓ¹ Ð Ö Þ ÓÑÔÓÒ Ò Ò ÑÔÐ Ø Ø Ð Ð Ú Ð Ñ ÒØ Z TM,1 Z TM,2 ÖØ Ð Ñ Þ Öò Ò Ô Ø Þ Ðº ÓØØ Ñ Ú Ð Ø ÙÐÐ Ñ Ø Ò Ö Ø ÐØ ØÓÚ Ð ÙÐÐ Ñ ÑÔÐ ¹ Ø Ø Ý Ø ÖÓÞ Ø Ù Ñ Ó Ý Ð ÓÒØ Ù Ñ Ú Ð Ø Ø Ì ÌÅ ÔÓÐ Ö Þ ÓÑÔÓÒ Ò Ö Þ Þ Ñ Ø ÖÓÞÞÙ E + TE,1 E+ TM,1 ÖØ Øº ÞØ Ñ Ø Ø Ôк Ø Ö Ö z Ö ÒÝ ÓÑÔÓÒ Ò Ò Ñ Ö Ø Ò º µ ÔÐ Ø Ð ÞÒ Ð ¹ Ú Ðºµ Þ Ø Ð ÞÒ ÐÚ º µ¹ ØÖ Ò Þ Ú Ð Ú Ø Þ Ö Ñ ÒÝØ Ô Ù Ö Ø ÐØ ØÓÚ Ð ÙÐÐ ÑÓ Ì ÌÅ ÓÑÔÓÒ Ò Ò ÑÔÐ Ø Ö E TE,1 = Z TE,2 Z TE,1 Z TE,2 +Z TE,1 E + TE,1, E+ TE,2 = 2Z TE,2 Z TE,2 +Z TE,1 E + TE,1, E TM,1 =Z TM,2 Z TM,1 Z TM,2 +Z TM,1 E + TM,1, E+ TM,2 = 2Z TM,2 Z TM,2 +Z TM,1 E + TM,1. º º Ð ØÖÓÑ Ò ÙÐÐ ÑØ Ö Ð ÓÒØ ÙÐÐ ÑÓ Þ Ö Ì ÒØ Ò º º Ö Ò Ð Ø Ø Ô Ö ÙÞ ÑÓ Ó ÐØ Ð Ø ÖÓÐØ ÓÑÓ Ò Ð Ò Ö ÞÓØÖÓÔ Ð ØÖ ÙÑÑ Ð Ø ÐØ ØØ ÓÖÖ Ñ ÒØ Ø ÖØÓÑ ÒÝغ ÐØ Ø Ð ÞÞ ØÓÚ Ó Ý Þ Å Ø Ö Ò ω Ö Ö Ú Ò Ú Ð Þ ÒÙ ÞÓ Ò Ú ÐØÓÞ ÐÐ Ò ÙÐØ ÐÐ ÔÓØ Ò Ú Ò Ý ØÓÚ Ò Ø Ö ÐÐ ÑÞ ÓÑÔÐ Ü ÖØ Ø ÞÒ Ð Ù Ø Ö Ð Ö Ö º Þ Ð Ñ Ó Å ÜÛ Ðй Ý ÒÐ Ø Ð º½µ º¾µ Ñ Ò Ø Ö Ö Þ Ð Ú Ð ÙØÙÒ Þ Ð ØÖÓÑÓ Ø Ö Ö Ö Ð ÖØ ÓÑÓ Ò ÙÐÐ Ñ Ý ÒÐ ØÖ E +k 2 E = 0, ÓÐ k 2 = ω 2 µεº º Ö Ð Ô Ò Ð Ø Þ Ó Ý Þ ÓØØ Ö ÞÓÐØ k Ú ØÓÖ ÓÞ Ø ÖØÓÞ Ö Ø ÐØ ÙÐÐ Ñ Ø Ò Ò¹ Ð Ñ Ò Ø Ö ÐÐ ÒØ Ø Ö ÒÝ Ð Þ Ñ ÒÒÝ Ò Ö Ø ÐØ ÙÐÐ Ñ Ð ØÖÓÑÓ Ø Ö Ò Ö ÒÝ Ñ Ý Þ Þ Ö ÞÓÐØ k Ú ØÓÖ ÓÞ Ø ÖØÓÞ Ð ØÖÓÑÓ Ø ÖÖ Ðº À ÓÒÐ Ñ ÐÐ Ô Ø Ø Ø Ø Ò Þ Ð Ð Ñ ÓÖ ÙÐ Ö ÌÅ ÔÓÐ Ö Þ ÙÐÐ ÑÓ Ö ÚÓÒ Ø ÓÞ Ò º ½

33 x ε,µ 0 z y º º Ö º È Ö ÙÞ ÑÓ Ó Ð Ø ÖÓÐØ ÓÑÓ Ò Ø ÖÖ Þº º º½º Ø Ö Ö Ú ØÓÖÓ Ø Ö Ð ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ ÐØ Ð Ð Ô ÒØ Ú Þ Ø Ø Ö Ö Ø Ö Ð ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ ÐØ Øº Ò Ð Ù Þ E Ð ØÖÓÑÓ Ø Ö Ö Ú ØÓÖ z Ö ÒÝ Ö Ò Þ Ò x Ú ÐØÓÞ Þ Ö ÒØ Ø Ö Ð ÓÙÖ Ö¹ ØÖ Ò Þ ÓÖÑ ÐØ Ø ÒÚ ÖÞ Ø Ú Ø Þ Ñ ÓÒ F x {E z } = 1 2π E z = F 1 x {F x {E z }} = E z e jkxx dx, F x {E z }e jkxx dk x, º ¼µ º ½µ ÓÐ k x Þ x Ø Ö Ð ÓÓÖ Ò Ø Ô ØÖÙÑ Ð Ô Ö ½¼ º À ÓÒÐ Ò ÖØ ÐÑ ÞÞ Þ y ÓÓÖ¹ Ò Ø Þ Ö ÒØ ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ ÐØ Ø F y {E z } = 1 2π E z = F 1 y {F y {E z }} = E z e jkyy dy, F y {E z }e jkyy dk y, º ¾µ º µ ÓÐ k y Ô Þ y Ø Ö Ð ÓÓÖ Ò Ø Ô ØÖÙÑ Ð Ô Ö º Ý Ú ØÓÖ Ú Ð Ñ ÐÝ Ö ÒÝ Ö Ò Þ Ò Ø Ñ ÒÞ Ø Ö Ð ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ ÐØ ÖØ ÐÑ Þ Ø Þ Ý Ñ ÒÞ ØÖ Ò Þ ÓÖÑ ÐØ Ð Ô Òº ØÓÚ Ò Ø Ö Ð µ ÓÙÖ Ö¹ ØÖ Ò Þ ÓÖÑ Ð ØØ Ø Ñ ÒÞ Ø Ö Ð ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ Ø ÖØ º Þ E Ú ØÓÖ z Ö ÒÝ Ö Ò Þ x y Ú ÐØÓÞ Þ Ö ÒØ Ø Ö Ð ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ ÐØ Ò ÒÚ ÖÞ Ò ½¼ Î Ý ÞÖ Ó Ý ØØ Þ Þ Ö ÒØ ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ ÐØ Ò Ð Ñ ÞÓ ÓØØ ÓÞ Ô Ø Ð Ö ÐØ ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ ÒÒ ÒÚ ÖÞ Ò Ò Øº ÞØ Þ ÓÒ Ñ Ø Ø ÖÖ Þ ÖØ Ú Ò Þ Ò Ñ ÖØ Ý ØÙ Ù Ñ Ø Ö Ð ÓÙÖ Ø¹ØÖ Ò Þ ÓÖÑ ÐØ Þ ÖØ ÐÑ Þ Ø Ý Þ Öò Ò Ñ Ò º ¾