DOI: /SZE.MMTDI
|
|
|
- Rebeka Vass
- 6 évvel ezelőtt
- Látták:
Átírás
1 Ö Ò Ö Î Þ Ø ØØ Ö Ö Ú Ò Ñ Ö ÑÓ ÐÐ Þ Ø Ø ÞØ ÒØÖ Ô ¹ ÐÐ ØÚ Û Ú Ð Ø¹ Ð Ô Ñ Þ Ö Ð Ó ØÓÖ ÖØ Þ Ì Ñ Ú Þ Ø Öº Æ Ý ËÞ ÐÚ ËÞ ÒÝ Á ØÚ Ò Ý Ø Ñ Åò Þ ÌÙ ÓÑ ÒÝ Ã Ö Ì Ú ÞÐ Ì Ò Þ ËÞ ÒÝ Á ØÚ Ò Ý Ø Ñ ÁÒ Ö ØÖÙ ØÙÖ Ð Ê Ò Þ Ö ÅÓ ÐÐ Þ Ð ÞØ ÅÙÐØ Þ ÔÐ Ò Ö Åò Þ ÌÙ ÓÑ ÒÝ Ó ØÓÖ Á ÓÐ Ý Ö ¾¼½
2
3 Ì ÖØ ÐÓÑ ÝÞ ¼º Ú Þ Ø ¼º½º Ð ØÖÓÑ Ò Ø Ö Ö Ð º º º º º º º º º º º º º º º º º º º º º º ¼º¾º Î ÐØÓÞ Ð ÓÒØ Ò Ð Þ Û Ú Ð Ø º º º º º º º º º º º º º ¼º¾º½º ÓÖ¹ØÖ Ò Þ ÓÖÑ ÓÐÝØÓÒÓ Û Ú Ð Ø¹ØÖ Ò Þ ÓÖ¹ Ñ º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¼º¾º¾º Þ Ö Ø Û Ú Ð Ø¹ Ò Ð Þ º º º º º º º º º º º º º º º º º º ¼º¾º º Ï Ú Ð Ø º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ¼º¾º º ÒÓÑ Ø Ô Ö Ñ ¹ Ð ÓÖ ØÑÙ º º º º º º º º º º º º º ½ ¼º¾º º Ý Ð ÓÒØ ÐØòÒ ÑÓÑ ÒØÙÑÓ º º º º º º º º º ½ ¼º º Ð Þ Ú ÒÝ ÒØ Ö Ð Ò Þ Ñ Ø Ö Ð º º º º º º º º ½ ¼º º Ñ Ö ÞÓÒÝØ Ð Ò Ö Ð º º º º º º º º º º º º º º º º º º º º º ½ ½º Å ÒØ Ø ÖØ Ð ÞØ ÑÓ ÐÐ Þ ¾½ ½º½º ýöòý ÓÐ ÐÐ Ô Ø Ñ Ö º º º º º º º º º º º º º º º º º º º ¾½ ½º¾º ËÞ Ñ Ø Ñ Þ Ö º º º º º º º º º º º º º º º º º º º º º º º º º ¾ ½º º Î Þ Ð Ø º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ ½º º Þ Þ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ Áº Ì ÁË ýöòý ÓÐ ÐÐ Ô Ø Ø Ö Ü Ø Ñ Ö Ñ ÒØ Ø ÖØ Ð Þ¹ Ø ÑÓ ÐÐ Þ Ú ÓÒÝÖ Ø Ñ ÒØ ÓÞ º º º º º º º º º º º º ¾ ¾º Þ Ö Ø Þ Ð Ñ ØÖ Ü Ð Ñ Ö Ð ½ ¾º½º Ð Þ Ú ÒÝ Ð ÞÓÖÞ Ø º º º º º º º º º º º º º º º º ½ ¾º¾º Ë Ð Þ Ú ÒÝ Ö Ú ÐØ Ð ÞÓÖÞ Ø º º º º º º º º º ¾ ¾º º ÆÙÑ Ö Ù ÒØ Ö Ð ÖØ º º º º º º º º º º º º º º º º º º º º º ¾º º Þ x Ú ÒÝ Ú Ö Ø ÖØ º º º º º º º º º º º º º º º º º º º ¾º º Þ x 2 Ñ ØÖ Ü Ð Ñ º º º º º º º º º º º º º º º º º º º º º º º º º ¼ ¾º º Þ x 2 Ñ ØÖ Ü Ð Ñ º º º º º º º º º º º º º º º º º º º º º º º º ½ ¾º º Þ x y Ñ ØÖ Ü Ð Ñ º º º º º º º º º º º º º º º º º º º º º º º ¾ ¾º º Å Ð ÓÒØ Þ ÒØ Û Ú Ð Ø º º º º º º º º º º º º º ¾º º ÈÓÐ ÒÓÑÓ Ñ ØÖ Ü Ð Ñ Ñ Ð ÓÒØ Þ ÒØ Ò º º º º º º ¾º½¼º Þ Þ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ÁÁº Ì ÁË Ö Ö Ú Ò Ø Ö Ø Ð Ö Ö Ò Ð Ý ÒÐ Ø Þ ¹ Ö Ø Þ Ð ÓÖ Ð Ø Þ Ñ ØÖ Ü Ð Ñ Ö Ð º º º º º º º º º º º º º º
4 º Ï Ú Ð Ø Ð Ô ÔØ Ú Ñ ÓÐ º½º ÔØ Ú Ö Ò Ð Ý ÒÐ Ø¹Ñ ÓÐ Ñ Þ Ö º º º º º º º º º ¼ º¾º Å ØÖ Ü Ý ÒÐ ØØ Ð Ø º º º º º º º º º º º º º º º º º º º º º º ¾ º º ýðø Ð ÒÓ ØÓØØ Ø ÖØ ¹ Ý ÒÐ Ø º º º º º º º º º º º º º º º º º º º Æ Ý Þ Ð Ø ÙÐÐ ÑÚ Þ Ø º º º º º º º º º º º º º º º º º º º º º º Þ Þ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ÁÁÁº Ì ÁË Ï Ú Ð Ø Ð Ô ÔØ Ú Ñ ÓÐ ÙÐÐ ÑÚ Þ Ø Ø Ð Ö Ö Ò Ð Ý ÒÐ Ø Ö º º º º º º º º º º º º º º º º º º º º º º º º ËÞÙÔ Ö ØÖÙ Ø Ö Þ Ô Ö Ð º½º ËÞ Ö Þ Ø ÒØÖ Ô º º º º º º º º º º º º º º º º º º º º º º º º º º¾º À ØØ ÖÑ ÒØ Þ ØÓ Ð Ú Ð ÞØ º º º º º º º º º º º º º º º º º º º ¼ º º Þ Þ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ Áκ Ì ÁË Ã Ð Ò Þ Ð Ñ ÒØ Þ ØÓ Ð Ð Ò Ø Ö Ð ÐÑ Ð Ö Ð ÞØ Û Ú Ð Ø¹ Ò Ð Þ ØÖÙ ØÙÖ Ð ÒØÖ Ô Ð Ô Ð ÑÞ ÓÑ Ò Ú Ð º º º º º º º º º º º º º º º º º º º º º º º Ê Ü Û Ú Ð Ø¹ Ò Ð Þ º½º Ú Þ Ð Ø Ø Ö Ý º º º º º º º º º º º º º º º º º º º º º º º º º º º¾º Ú Þ Ð Ø Ñ Þ Ö º º º º º º º º º º º º º º º º º º º º º º º º º º à ÔÓØØ Ö Ñ ÒÝ º º º º º º º º º º º º º º º º º º º º º º º º º º º º Þ Þ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ÎºÌ ÁË Ì Þ Ö Ö Ü Ó ÓÞØ Þ ÐØ ÐÓ ÞÐ Ó Û Ú Ð Ø¹ Ò Ð Þ Ø ÔÚÓÒ Ð ÓÒ º º º º º º º º º º º º º º º º º º º º º º º ¼ º Ê Ü Ó ÓÞØ ÐÓ ÞÐ Ó ½ º½º Ú Þ Ø º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ º¾º Ø Ö Ø ÒÝ Þ Ú Þ Ð Ø º º º º º º º º º º º º º º º º º º º ¾ º º Ö Ü Ú Þ Ð Ø ÓÞ Ð ÐÐ ØÓØØ ÑÓ ÐÐ º º º º º º º º º º º º º º º Ö Ü Ø Ò Ø Ø ÞØ Ð ÑÞ º º º º º º º º º º º º º ½ º º Þ Þ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ ÎÁºÌ ÁË Ì Þ Ö Ö Ü Ó ÓÞØ Þ ÐØ ÐÓ ÞÐ Ó Ø Ø ÞØ Ð ÑÞ Ø ÔÚÓÒ Ð ÓÒ º º º º º º º º º º º º º º º º º º º º º º º ¾ º Þ Ó Ð Ð º Ã Þ Ò ØÒÝ ÐÚ Ò Ø º Ð ÐÑ ÞÓØØ Ö Ú Ø Ð Ð ÁÖÓ ÐÓÑ ÝÞ Ý Ø Ð Þ Ø ÖØ ÐÑ Ö Þ ½¼ Ì ÖØ ÐÑ Þ Ó Ð Ð º º º º º º º º º º º º º º º º º º º º º º º º º º º ½½¼ ËÙÑÑ ÖÝ Ó ÓÒØ ÒØ º º º º º º º º º º º º º º º º º º º º º º º º º º º ½½½
5 ¼º Þ Ø Ú Þ Ø ËÞ ÒÝ Á ØÚ Ò Ý Ø Ñ Ê Ö Ú Ò Î Þ Ð Ä ÓÖ Ø Ö ÙÑ Ð¹ Ø ÒØ Ö Ö Ò Þ ÊÅ ½ Ñ Ð Ð Ú Þ Ð Ø Ø Ú Þ º Ú Þ ÐØ Ö Ò Þ Ö Ð ÓÖ Ò ËÊ ¾ Þ Þ Ø ÖØÓÞÒ º Ú Þ ÐØ Ö Ò ¹ Þ Ñ Ò Ý ÓÔÓÖØ ¾º ÀÞ¹ ÁËÅ Ú Ö Ò Þ ÐÐ ØÚ Þ ÊÄ Æ ¾ Ê Æ ½ ÀÁÈ ÊÄ Æ Ö Ò Þ Ö º Ä ÓÖ Ø Ö ÙÑ Ñ Ò Ö ¹ ÒÝ Ø Ú Þ Ø ÒØ Ý Ð Ð ØÓÑ Ö Ö Ú Ò Ú Þ Ð Ø Ð Ö ¹ Ó ÓÐ ÓÞ ÓÖ Ò Ñ Ö Þ Ø ÖØÓÞ Ñ Ö ÞÓÒÝØ Ð Ò Ð º Þ ÊÅ Ú Þ Ð ØÓ Ö ÝÖ ÞØ Þ Å Ú Þ Ð ØÓ ÒØ ÑÑÙÒ Ø µ Ñ ¹ Ö ÞØ Ú Þ ÐØ Ö Ò Þ Ö Ö Ú Ò Ô ØÖÙÑ Ø ÓÒÝ Ð ÞÒ Ð Ø ÐÞ ÐÐ ÑÞ Ú Þ Ð Ø Ø ÖØÓÞ º Ð ÓÖ Ø Ö ÙÑ Ð Ø Ò Ð Ý ÓÖ Ð Ø Ö Ù ÖÞÓØØ Ö Ú Þ Ø ØØ ÐÐ ÑÞ Ú Þ Ð Ø Ö Ö Ð ÓÖ Þ Ê Ð Þ ÒØ Ñ Ø ÖÓÞ º Ö Ö Ú Ò Ø Ú ÞÐ Ö Ò Þ Ö Ø Ð Ø Ô Ø ÐÐ ØÚ Þ Ò Ö Ò ¹ Þ Ö Ñ Ö Ø Ò Ý Ò ÓÐÝ ÓÐ ÖÒÝ Þ Ø Ó ØÙÑÓ Ö Ð Ú Þ Ú ÖØ ¹ Ð ØÖÓÑ Ò ÙÐÐ ÑÓ º ËÙ ÖÞÓØØ Ö Ö Ú Ò Ú Þ Ð ØÓ Ò Ð ÖÒÝ ¹ Þ Ø Ö Ü Ø Ù Ý Ò ÐÝ Ò Ò Ý Ð ÒØ Ð Öº Ú Þ Ø ØØ Ö Ö Ú Ò¹ Ú Þ Ð ØÓ ÓÖ Ò Þ ÒØ Ò ÓÒØÓ ÞÓÒÝØ Ð Ò Ø ÒÝ Þ Ú Þ Ø ÐÐ Þ¹ Ø Ò Ð Ð ÓÖ ÙÐ Ö Ü Ø º Þ Ò Ø ÒÝ Þ Ø ÒÙÐÑ ÒÝÓÞ Ø ÔÙ Ð Ø Ø Ö Ö Ú Ò Ú Þ Ð ØÓ Ñ Þ Ø Ö Ñ ÒÝ Ò Ð ¹ ÐÐ Ø Ö ÞÞ Ð Ð Ø Ú Ú ÐÒ ÔÓÒØÓ Ö Ñ ÒÝ Ø Ú Þ Ð Ø Ñ ¹ Þ Ö ÓÐ ÓÞ º ÖØ Þ Ñ Ø Ñ ÒØ Þ ÖØ Ú Ð ÞØÓØØ Ñ Ö Ü Ú Þ Ð Ø Ø Ñ ÒØ Ñ ¹ Ö Ø Ò Ð Ò Þ Ò Þ Ð Ø Ð Ò Øº Ö Ö Ú Ò Ö Ò Þ Ö Ñ Ö Ø Ò Ð Ò Ò Ò ÝÓ ÞØÓÒ ÓØ ÒÝÐ ÖÒÝ Þ Ø Ò Ú Ð Ñò Ö Ñ Ö Ø Þ ØØ Þ Þ Ò Ð Ö Ò Ú Ð ÓÒØÓ ½ Ð ØÖÓÑ Ò Ø ÓÑÔ Ø Ð ØÝ Ò Ê Ó Ô ØÖÙÑ Å ØØ Ö Ð ØÖÓÑ Ò Þ Ö¹ Ø Ö Ô ØÖÙÑ Ý µ ¾ Ë ÓÖØ Ê Ò Ú Ö Ú Ø Ø ÚÓÐ Þ Þ µ ÁÒ Ù ØÖ Ð Ë ÒØ Ò Å Ð Ô Ö ØÙ ÓÑ ÒÝÓ ÓÖÚÓ µ Ê Ä Æ Þ Ð Ú Ö ÓÞÞ Ö Ð Þ ØÓ Ñ Ñ Ò ò Ä Æ Í̹ Ú ÍÒ Ö Ì Ø
6 Â Ì ¼º Î Ì Ë Ñ Ö Ñ Þ Ø Ö Ò ÓÖÑ Ø Ñ Ö ÞÓÒÝØ Ð Ò ÓØ Ñ ÐÒ º ÒÒ Ý Ñ Ð Ø Ñ Ö ÞÓÒÝØ Ð Ò ÓÑÔÓÒ Ò ØÙÐ ÓÒ ¹ Ò Ö ÞÐ Ø Ñ Ñ Ö Ö Ò ÓÖÑ Ø ÑÓ ÐÐ ÓÐ ÓÞ Þ Ò Ö Ñ ÒÝ Ñ Ö Ö Ñ ÒÝ Ð Ú Ð Þ Ú Ø º ¼º½º Ð ØÖÓÑ Ò Ø Ö Ö Ð Î Þ Ø ØØ Ñ Ö Ò Ð Ñ Ö ÞÓÒÝØ Ð Ò Ý Ð Ó Ò ÑÓ ÐÐ Þ Ø Ø ÙÐÐ ÑÚ Þ Ø Ò Ð ØÖ Ú Ö Ü Ö Ú Þ Ø Ø Ú Þ º ÙÐÐ ÑÚ Þ ¹ Ø Ò Ø Ö ÙÐÐ ÑÓ Ð Ö Ø Å ÜÛ Ðй Ý ÒÐ Ø Ñ Ñ ÐÝ Ò ÓÖÖ ¹ ÒÝ Ñ ÒØ Ú ÖÞ Ù Ð Ú Þ Ø Ø Ð Þ Ð ØÖÓÑ Ò ÙÐÐ ÑÓ Ð Ö Ö ÞÓÐ Ð ÙÐÐ Ñ Ý ÒÐ Ø Þ Ð Þ Ð ØÖÓÑÓ Ø Ö Ø Ð Ö ÐÐ ØÚ Ñ Ò Ø ÖÖ ÚÓÒ Ø ÓÞ 2 E(r, t) = c 2 E(r, t) t 2, ½µ 2 H(r, t) = c 2 H(r, t) t 2. ¾µ Å Ú Ð Ø Ø Ö Ð Ö Ö ÞÓÐ Ð Ý ÒÐ Ø ÞÓÒÓ Ð Ú Þ Ð Ù Þ Ý Ø Þ Ð Ô Ð ÙÐ Þ Ð ØÖÓÑÓ Ø Ö Øº À Ý ÙÐÐ ÑÚ Þ Ø Ò Ø Ö Ð ØÖÓÑ Ò ÙÐÐ ÑÖ Ð Ú Ò Þ ÓÖ Ñ ÓÐ Þ Ø ØÓÐ Ú ÒÝÖ ÙÐÐ ÑÚ Þ Ø Ø Ò ÐÝ Ú Ð Ô Ö ÙÞ ÑÓ z Ö ÒÝ ÓÑÔÓÒ Ò Ö ÐÐ ØÚ ÙÐÐ ÑÚ Þ Ø Ø Ò ÐÝ Ö Ñ Ö Ð ÓÑÔÓÒ Ò¹ Ö º Þ ¹ z Ö ÒÝ ÓÑÔÓÒ Ò z Ö ÒÝ Ò Ð ÙÐÐ ÑÓØ Ñ ÓÐ ¹ ÒØ ½ Ñ Ö Ð Ö ÒÝÓ Ô ØÙÐ ÓÒ ÔÔ Ò Ð ÙÐ Ø Ö Ñ Ù ÙÐÐ ÑÔÖÓ Ð Ø Ø ÖÓÞÞ Ñ º Æ Ý Þ Ð Ø ÙÐÐ ÑÚ Þ Ø Ò ÞØ Ý Þ Öò Ò 2 x 2E x(x) = kx 2 E x(x), µ 2 y 2E y(y) = ky 2 E y(y), µ x y Ú ÐØÓÞ Ö Þ Ø ØÓÐØ Ö Ò Ð Ý ÒÐ Ø Ø ÖÓÞÞ Ñ Ñ ÓÐ E x (x) = A x sin k x x + B x cosk x x Ò E y (y) = A y sin k y y + B y cosk y yº ÐÐ ÔØ Ù Ú Ý Ò Ö ÙÐÐ ÑÚ Þ Ø Ò Ð ÞÓÒ Ò Ð Þ Öò Ä ÔÐ ¹ÓÔ ¹ Ö ØÓÖ Ò ÖÔÓÐ Ö¹ ÓÓÖ Ò Ø Ö Ò Þ Ö Ð Ð Ø ÞÒ ÐÒ ÓÖ Ù Ö Ö ÒÝ (r) Þ Þ Ö ÒØ (s) Ú ÐØÓÞ Ð ÞÒ Þ Ø ØÓÐ Ø Ô Þ Ð Þ Ö ÒØ ÞÓ Ø ÐÚ ÞÒ ( 2 r r 2 s 2E s(s) = kse 2 s (s), ) r k2 s E r 2 r (r) = kre 2 r (r). µ µ
7 ¼º¾º ÎýÄÌÇ Ä ÇÆÌýË Æ Ä ÁË Ë Ï Î Ä Ì Ã Ñ ÓÐ Ó ØØ Þ r Ö ÒÝ Ò Ð¹ Ú ÒÝ Ð ÞÒ s Þ Ú ÐØÓÞ Ö ¹ ÒÝ Ò Ô Ó Þ ÒÙ ÞÓ Ú ÒÝ º Å Ò Ø Ø Ò Þ Ú ÐØÓÞ Ð Ú Ð ÞØ ÙØ Ò Ú Ø Þ Ø ÔÙ Ö Ò¹ Ð Ý ÒÐ ØÖ ÙØÙÒ ˆDE(r) = λe(r), ˆDE(r) = F(r), µ µ Ñ ÐÝ Þ Ð Þ Ð Ø ÖØ ¹Ø ÔÙ λ Ø ÖØ Ð Ñ Ó ÓÖÖ Ó F ÓÖÖ Ðº Å Ò Ø Ø Ò ˆD Ö Ò Ð Ý ÓÔ Ö ØÓÖÓ Þ Ø Ð ÒØ º Þ Ö Ò ÐÓÔ Ö ØÓÖÓ ÐØ Ð Ò Ð Ú Ý Ñ Ó Ö Ú Ð Ó ¹ Ð r¹ò Ú Ð Ñ ÐÝ Ò ÔÓÐ ÒÓÑ Ú Ð Ú Ð ÞÓÖÞ Ð ÐÐ ØÚ Þ ÓÑ Ò Ð ÐÐÒ º Þ Ð Ö Ò Ð Ý ÒÐ Ø Ø ÔÙ Ó Ð Ó Ð Ð ÓÞØ Ñ Ó ØÓÖ ÑÙÒ Ñ Ð Øغ ¼º¾º Î ÐØÓÞ Ð ÓÒØ Ò Ð Þ Û Ú Ð Ø Ú ÐØÓÞ Ð ÓÒØ Ò Ð Þ ÅÊ µ ½ Ý Þ Ö Ò Þ Ö Þ L 2 (R d ) Ò ÝÞ Ø Ò ÒØ Ö Ð Ø d¹ Ñ ÒÞ Ú ÒÝ Ø Ö Ò Ñ ÐÝ Ð ÓÒØ Ø Ö Ø Ð Ò Þ ÒÓÑ Ð ÓÒØ Þ ÒØ Ö Ø ÖÑ Þ Ø Ø Ö Ø ÞØÓ ØÚ Ð¹ ÓÒØ Þ ÒØ Þ ØØ ÐÓ Ð Ò Ú ÐØÓÞ Ð ÓÒØ Þ ÒØ Ø Ò ÐÝ ÞÚ º Þ Þ ÙØ ØÙÐ ÓÒ Ø Þ Þ ÅÊ ¹Ø Ú Ý Û Ú Ð Ø¹ Ò Ð Þ Ø ÓÐÝ Ò Ø Ú Ø ¹ Ñ Ö Ø Ð Ö Ó Ð Ô Ú Ñ ÒØ Ôк Å Ö ¹ ÞÓÒ Ô Ð ÓÐ ÓÞ ÖÙØ Ò Þ Á Ù Ð ÒÝÓÑ Ø¹Ø Ñ Ö Ø ÂÈ ¾¼¼¼ Ú Ý ÒÒ Ú Ó ÓÐ Ñ ¹ Ð Ð ¾ º Ð Ð Û Ú Ð Ø¹ Ò Ð Þ Ø À Ö Ð Ö Ú ÞØ Ð Þ ½ ½¼¹ Ú Ò Ö ÓÖ Ñ Ò Ñ Þ ÐØ Û Ú Ð Ø Ö Ð Ò ÝÞ Ø Ò ÒØ Ö Ð Ø ¹ Ú ÒÝ Ý Ö ØÙÐ ÓÒ Þ Ö Ò Þ Ö Ö Ðº Ì ÖÑ Þ Ø Ò ÓÙÖ Ö¹ ØÖ Ò Þ ÓÖÑ Ñ Ö ÓÖ Ð Ø Þ ØØ Ø Ð ÐÑ Ð Ø Þ Ô ÓÐ Ñ Ó Ú Ö ØÓØØ Ñ Ö ½¼ º Ì ØÙ ÓÑ ÒÝ Ø Ð ÐÑ Ð Ø Ò Ñ Ö Ð Ò ÚÓÐØ Û Ú Ð Ø¹ Ò Ð Þ Ñ ÒØ Ä ØØÐ ÛÓÓ È Ð Ý¹ ÐÑ Ð Ø Ò Ú ÒØÙÑ Þ Ò Ú Ý Þ ÓÐ Ñ ÖÒ Å ÐÐ Ø ½ Þ ÞÑ Ù Ð Ø Ò Ð Þ Ð ÓÒ Ð ØØ ÙÐÐ ÑÓ Òº Þ Ð Þ Þ Ó Þ ÐÑ Ð ØÒ Ö Ò Å Ý Ö ÚÓÐØ Ñ Ð Ñ Ø Ñ Ø Ù Ù ½ ½ º Û Ú Ð Ø¹ Ò Ð Þ Ð ÒÐ Ô Ð ÓÐ ÓÞ Ø Ñ Ö Ø Ð Ö Ó Ò Ø Ò ØÓØØ Ò Ý Ø Ð ¹ Ø Ô Ò Þ Ò Ø Ò Ô Þ Öò Ø Ð ÐÑ Ñ Ð ØÓ Ø Ñ Ö ¹ Ø Ö Ñ ÒØ Þ ØÓ Ò Ð Þ Ð Ö Ö Ò Ð Ý ÒÐ Ø Þ Ö Ø Þ Ð Ö º Û Ú Ð Ø¹ Ò Ð Þ Ò Ù Ý Ò Ý Ñ ÒØ ÓÙÖ Ö¹ Ò Ð Þ Ò Ú Ò ÓÐÝØÓÒÓ Þ Ö Ø Ú ÐØÓÞ Ø º ÓÐÝØÓÒÓ Ú ÐØÓÞ Ø Ð Ý Þ Öò Ò Þ Ð ÓÐØ ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ ÐÐ ØÚ ÓÖ¹ØÖ Ò Þ ÓÖÑ Ð Ð ÖØ Ø Ñ º Ê ÞÐ Ø Ú Þ Ø Ø Ð Ð Ø Ò Ð ÌºÄº Ä Ó Ñ ÑÓØÓ ØÓÐÐ Ð ÀÈ ÙÖÒ Ð¹ Ò ¼ Ñ ÐÝ Þ ÑÐ Ð Ø Ö Ð Ø Ø Ø Ñ Ö Ð ÓÐ ÓÞ Øº ÅÙÐØ Ö ÓÐÙØ ÓÒ Ò ÐÝ
8 ¼º¾º½º Â Ì ¼º Î Ì Ë ÓÖ¹ØÖ Ò Þ ÓÖÑ ÓÐÝØÓÒÓ Û Ú Ð Ø¹ØÖ Ò Þ¹ ÓÖÑ ÌÙÐ ÓÒ ÔÔ Ò Û Ú Ð Ø¹ Ò Ð Þ Ñ Þ Ð Ø Ò Þ ÚÓÐØ Ó Ó Ý ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ Ò Ñ ÚÓÐØ Ô Ú ØÒ ÐÓ Ð Ò Ú ÐØÓÞ Ö Ú Ò ¹ غ ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ Ð ÓÐ Þ Þ ØÖ Ò Þ ÓÖÑ Ð Ò Ú ÒÝÒ Ý ÐÓ Ð Ú Ø ÖØ Ú ÒÒÝ Ð Ú Ð Ñ ÞÓÖÞ ØÖ Ò Þ ÓÖÑ Ð ØØ Ö Ñ ÒÝ Ò ÞÓÒÝÙÐØ Þ Ð ÐÓ Ð Þ Ð Ö Þº ÓÖ Ò Ý Ó Þ ÑÔÓÒØ Ð ÓÔØ Ñ Ð g α (t) = 1 2 t 2 πα e 4α Ð Ð ÓØ Ú ÓÐØ Ñ ÐÐÝ Ð Ý f Ú ÒÝ ÓÖ¹ØÖ Ò Þ ÓÖÑ Ú Ø¹ Þ ÔÔ Ò Ò Þ G α b {f}(ω) = g α (t b) f(t) e iωt dt. Þ ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ t = b Ö Ð ÐÓ Ð Þ Ø Ð ÒØ ØØ º À b Þ Ö ÒØ ÒØ Ö Ð Ù ÓÖ¹ØÖ Ò Þ ÓÖÑ ÐØ Ø ÓÖ Ú Þ Ô Ù ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ ÐØ Ø G α b {f}(ω)db = F{f}(ω). À Ú ÞÓÒØ ÓÖ¹ØÖ Ò Þ ÓÖÑ Ø Ý Ñ Ò Þ ÔÓÒØ Ð Ú Þ Ö Ð ÓÖ G α b,ω(t) = e iωt g α (t b), Þ Ú ÒÝ Ú Þ Ø Ú Ð Ý G α b,ω (t) Þ Ö ÒØ Ø Ð ÙÐ ÓÖ ØÖ Ò Þ¹ ÓÖÑ Gb α {f}(ω) = ( G α b,ω, f ) ( = G α b,ω (t) ) f(t)dt. ÁØØ ÓÑÔÐ Ü ÓÒ Ù Ð Ø Ð Òغ G α b,ω (t) Ð Ú ÒÝ Ð ÐÓ¹ Ð Þ ÐØ ÙÐÐ Ñ Ñ ÐÝ Ò b Ô Ö Ñ Ø Ö ÐÐ Ô Ø Ñ ÐÓ Ð Þ ÐÝ Ø ω ÙÐÐ ÑÞ Ó Þ Ñ Ø α Ô Þ Ú ÒÝ Þ Ð Øº Þ f(t) Ú ÒÝ ÅÓÖ Ð Ø¹ Ð Û Ú Ð Ø¹ØÖ Ò Þ ÓÖÑ ÐØ Ò ÝÓÒ ÓÒÐ Ð W w {f}(b, a) = a 1/2 wb,a(t)f(t)dt. ÁØØ Þ ÒØ Ò Ý Þ Ú ÒÒÝ Ð wb,a (t) Û Ú Ð ØØ Ð Ú ØØ Ð ÞÓÖÞ Ø Ø Þ¹ Ò Ð Ù Ú ÒÝÒ º Ð Ò Þ Ú ÒÝ Ð Ò Ö Ð Ù Ý Ò Ñ Ò Ò Û Ú Ð Ø Ý ØÐ Ò Òº ÒÝ ¹Û Ú Ð Ø w(t) ÐØÓÐØ ÐÐ ØÚ Þ Ù ÓÖ ØÓØØ Ú Ý ÒÝ ØÓØØ Ú ÖÞ ( ) t b w b,a (t) = a 1/2 w, a
9 ¼º¾º ÎýÄÌÇ Ä ÇÆÌýË Æ Ä ÁË Ë Ï Î Ä Ì Ã Þ ÐØÓÐ Ô Ö Ñ Ø Ö b Þ Ù ÓÖ Ø Ô Ö Ñ Ø Ö Ô aº Û Ú Ð Ø Ø Ð Ø Þ Ð ÐØ Ø ÐØ 1 ω F{w}(ω) 2 dω <. Û Ú Ð Ø Ñ ÒØ ÞØ Ö Ò Ð Ö ÓÒ Ð ØØ µ Ò ÓÐ Ò Ú ÑÙØ Ø Þ ÒØ Ò ÙÐÐ ÑÓ Ð Ù ÙÐÐ ÑÞ Þ Ñ ØÖ Ò Þ ÓÖÑ ÓÖ Ò Ò Ñ Ú ÐØÓÞ Þ Ù ÓÖÓ Ú Ý ÒÝ Ð Ñ ÒØ Ó Ý ÞØ ½º Ö ÑÙØ Ø º ¼º¾º¾º Þ Ö Ø Û Ú Ð Ø¹ Ò Ð Þ ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ ÓÙÖ Ö¹ ÓÖ Ø Ô ÖÓ ÓÞ ÓÒÐ Ò Û Ú Ð Ø¹ ØÖ Ò Þ ÓÖÑ Ò Ú Ò Þ Ö Ø Ô Ö Ñ ÐÝ Ø Ú ÐØÓÞ Ð ÓÒØ Ò Ð Þ ÑÙÐØ Ö ÓÐÙØ ÓÒ Ò ÐÝ ÅÊ µ Ø Ú Ð Ð Ø Ð Ø Ñ Ö Ò Ð ÖÒ º Þ L 2 (R) À Ð ÖØ¹Ø Ö Ú ÐØÓÞ Ð ÓÒØ Ò Ð Þ {V m, m Z} Þ ÖØ ÐØ Ö Ò ÓÐÝ Ò ÓÖÓÞ Ø Ñ ÐÝ Ð Ø Þ Ð ÐØ Ø Ð Ø m Z V m V m+1 Þ Þ Þ ÐØ Ö ÝÑ Ý ÞÓØØ V m m¹ ÒÓÑ ÐØ Ö Ø ÖØ ÐÑ ÞÞ Þ Þ V n ÐØ Ö Ø Ñ ÐÝÖ n < mº a > 1 v(r) V m v(ar) V m+1 Þ Þ ÖÑ ÐÝ V m ÐØ Ö Ú ÒÝ ¹ Ò Ý a ÓÒ Ø Ò Ð Ú Ð Þ Þ Ù ÓÖ Ø Ú Ø Þ Ý Ð ÒÓÑ ÐØ Ö Ð Ú ÒÝ Þ Ú Þ Øº b > 0 v(r) V 0 v(r b) V 0 Þ Þ ÒÙÐÐ ÒÓÑ Þ ÒØ Ò ÖÑ ÐÝ Ú ÒÝÒ Ý b ÓÒ Ø Ò Ð Ú Ð ÐØÓÐ Ò Ñ Ú Þ Ø Þ Ð¹ Ø Ö Ðº À V m ÐØ Ö Ú ÒÝ Ø Þ Ö ØÒ Ò ÐØÓÐÒ Ý Ó Ý Þ ÐØ Ö Ò Ñ Ö ÙÒ ÓÒ Ø Ò 2 m b¹ö Ú ÐØÓÞ º m= V m = {0} m= V m òöò Þ L 2 (R) Ø Ö Òº Ä Ø Þ Ý s 0 V 0 Ò Ñ¹ ÐØòÒ ÒØ Ö Ð Ð Þ Ú ÒÝ Ñ ÐÝÖ {s 0 (r bl) l Z} ÐÑ Þ V 0 ÐØ Ö ÓÖØÓÒÓÖÑ ÐØ Þ Ø Ð ÓØ º Þ ÓÖØÓÒÓÖÑ Ðع Ù Ý Ò Ò Ñ Ø Ð Þ Ð Ò Ý Þ Öò Ò Ø Ð Ö Ò Þ ÖÒ Ð ÒÒ Þ ÑÓÐ Þ ÑÔÓÒØ Ð Ó Ð ÐÐ Ñ Þ ÓÖØÓÒÓÖÑ ÐØ Þ Ö Ò Þ Ö Ð Ò Ò Ö Ò Ð Ý ÒÐ Ø Ø Þ Ö ØÒ Ò Ñ ÓÐ Ò Ú Ý Ô Ø Ð ÓÐ ÓÞÒ º V m ÓÖØÓÒÓÖÑ ÐØ Þ ÓÖ {s ml (r) l Z} ÐÑ Þ Ð Þ ÓÐ s ml (r) = a m/2 s 0 (a m r bl)º ÓÒ Ø Ò Ó Ú Ð ÞØ Ö Þ a = 2 b = 1 ÞÓ Ó Ò ÞØ ÓÒÚ Ò Ø Ú Ø Ñº Å Ú Ð Þ ÐØ Ö ÝÑ Ý ÞÓØØ Þ m¹ ÒÓÑ Þ ÒØ Ø ÖØ ÐÑ Þ Ñ Ò Ò Ò Ð ÙÖÚ Ð ÓÒØ ÐØ Ö Ø Þ Þ Ú ÒÝ Ø Ø Þ m¹ Þ ÒØò Þ Ú ÒÝ Þ Ö Òغ À n = m 1 N s s m 1l (r) = p k s m k+2l (r), k=0 µ
10 ½¼ Â Ì ¼º Î Ì Ë ½º Ö º Ö Ú ò ÓÙÖ Ö¹ØÖ Ò ÓÖÑ Û Ú Ð Ø¹ØÖ Ò Þ ÓÖÑ ¹ Þ Ú ÒÝ Ð Ò Þ Ð ÓÒØ Þ ÒØ Òº Þ Ð Ó ÞÐÓÔ Ò ÞÓÒÓ Ù ¹ Ú ÒÝ ÙÖ ÓÐ Ú Ð Ô ÖÓ ÚÓÒ Ð Ö Ò Ð Þ Ð Ò Þ Ö Ú Ò Ð ÓÐØ Þ ÒÙ Þ ÙÐÐ ÑÓ Ð Ø Ø ÚÓÒ Ðº Þ Ö Ú ò ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ ØÙÐ ÓÒ ÔÔ Ò ÓÖ¹ØÖ Ò Þ ÓÖÑ µ Þ Ú ÒÝ º Ñ Ó Ó ÞÐÓÔ Ý Û Ú Ð Ø Þ Ö Ò Þ Ö Ù Ý Ö Ò Þ Ö µ Ð Ñ Ø ÑÙØ Ø Ð Ò¹ Þ Ð ÓÒØ Þ ÒØ Ò Þ Ð ÚÓÒ Ðº Ä Ø Ø Ó Ý Ñ Þ Ð Þ ¹ Ú ÒÝØ ÔÙ Ò Ð Ú ÒÝ Þ Ð ÐÐ Ò Ð Ú ÐØÓÞ Û Ú Ð Ø Ò Þ Ð ÐÐ Ò Þ Ð Ú ÐØÓÞ º
11 ¼º¾º ÎýÄÌÇ Ä ÇÆÌýË Æ Ä ÁË Ë Ï Î Ä Ì Ã ½½ ÓÐ N s k=1 p k = 2º Þ Þ ÝÒ Ú Þ ØØ ÒÓÑ Ø Ý ÒÐ Ø Ö Ò Ñ ÒØ ÕÙ Ø ÓÒ Ú Ý ØÛÓ¹ Ð ÕÙ Ø ÓÒµº À N s Ú ÓÖ ÔÓØØ Ð Þ Ú ÒÝ Ø ÖØ [0, N s ) ÒØ ÖÚ ÐÐÙѺ p k Ý ØØ Ø Ø ÖÓÞÞ Ñ Ð Þ Ú ÒÝ Û Ú Ð Ø Ð Ø ÞÞ Ð ØÙÐ ÓÒ Ø Ñ ÒØ Ö Ú Ð Ø Þ ÑÑ ØÖ ÐØòÒ ÑÓÑ ÒØÙÑÓ º p k Ý ØØ Ø ÞÓÒ Ú Ð Ó Ý ¾¹Ø Ò Ö Ñ ÒÝ Ð Þ ÞÞ Ø Ñ Ø Ð Ø Ð Ð ÞØ ÐØ Ø ÐØ Ó Ý Ô Ö ØÐ Ò Ò Üò Ô ÖÓ Ò Üò Ð Ò¹ Ð Ò ½¹Ö Þ Þ Ò º Þ ÙØ ØÙÐ ¹ ÓÒ Û Ú Ð Ø ÒÙÐÐ ÒØ Ö Ð Ò Ð Ô Þ Ö Ô Øº ÞÓÒÝÓ ÒÝÚ Ô Ð ÙÐ Ù Ò ¾ ÐÝ ØØ 2¹Ö Ú Ð Þ Þ Ú ÓÖ ÒÓÑ Ø Ý ÒÐ Ø Ø ÖØ ÐÑ Þ Ý 2 ØÓÖØ Ñ º Ð Ò Ø Ö Ò Þ Ö Þ ØØ ÒÒÝ Ó Ý Ð Þ Ú ÒÝ ÒÓÖÑ Ø ½¹Ö Ú Ý 2¹Ö ÐÐ Ø º Û Ú Ð Ø Ð Þ Ú ÒÝ Ð Ò ÝÓÒ Ó Ð Ð Øº ¾º Ö Ò ÒÝ ÞÒ ÐØ Ð Þ Ú ÒÝØ Ø ÖØ ÐÑ Þ Þ Ö Ø Ù ¹ Ú ÒÝ Ð Ø Øº Þ Ð Ø ÓØ À Ö¹ Ð Þ Ú ÒÝÒ Ò Ú Þ º ÁØØ Ø Ò Ñ ÒÙÐÐ p k Ý ØØ Ø Ú Ò Ñ Ò ØØ ½ Ñ Ø Ø Ò r r r ¾º Ö º Ë Ð Þ Ú ÒÝ À Ö¹ Ù ¹ ¹ Ù ¹ ¹ Þ Ö º Ò Ý ÐÐ ØÚ Ñ ÐÝ Þ Ð p 0 = (1+ 3)/4 p 1 = (3+ 3)/4 p 2 = (3 3)/4 p3 = (1 3)/4 ÐÐ ØÚ ÖÑ Ø ÔÙ Ò Ð p 0 = p 1 = p 2 = p 3 = p 4 = p 5 = º Å Ò Ð Ø Ò Ñ ÒÙÐÐ Ý ØØ Ø Ú Ò ÒÓÑ Ø Ý ÒÐ Ø Ò ÒÒ Ð Ñ Ð Þ Ð Þ Ú ÒÝ ¹ Ý ØØ Ø Þ Ú ÒÝ ÓÐÝØÓÒÓ ¹ Ý ØØ Ø ÓÐÝØÓÒÓ Ò Ö Ú Ð Ø ½¼¹ Ý ØØ Ø Ø Þ Ö ÓÐÝØÓÒÓ Ò Ö Ú Ð Ø º º Ö Ý ØØ Ø ÒÝ Ð Þ Ú ÒÝØ ÒÒ Ð Þ Ø ÐØÓÐ Ø Þ ÑÐ ÐØ Ø º Ù ¹ Ð Þ Ú ÒÝ Ö Ú ÐØ º Ö Ò Ð Ø Ø Ö Ú ÐØ Ð ÒÝ Ò Ø ¹ Ù Ò Ú ÐØÓÞ Ú ÒÝ Ñ ÒØ Ð Þ Ú ÒÝ Ñ ÓÐÝØÓÒÓ º Þ f L 2 (R) Ú ÒÝ Ð Ú Ø Ø Ø ÖÑ ÐÝ m¹ Ð ÓÒØ Þ ÒØò ÐØ ÖÖ Ý Ú ÒÝ m¹ Þ ÒØò Þ Ð Ø f [m] (r) = l c ml s ml (r), ½¼µ Ð Þ ÓÐ Ø Ý ØØ Ø c ml = ( s ml f) Ð ÞÓÖÞ ØØ Ð ÐÐÒ Ð º Ð Ú ÒÝ Ù Ð s ml (r) ÓÒÐ Ò Ø Ñ Ñ ÒØ s ml Ñ ÒÝ ¹ Ú ÒÝ Ð Ò ÙÐ Ö Ò Þ Ö Ò Ñ Ò Ù Ð º ÖØ Þ Ñ Ò Ú Ò¹ Ù Ð Ù ¹ Ú ÒÝ Ð Ó Ó Ó Ð Ð ÓÞÒ ÓÖ Ø Ý ØØ Ø Ý Þ Öò Ò c ml = (s ml f) ÔÐ ØØ Ð Ø Ñ º
12 ½¾ Â Ì ¼º Î Ì Ë s 0k (x) k= 6 k= 5 k= 4 k= 3 k= 2 k= 1 k=0 k=1 k=2 k=3 k=4 k=5 k= x s 1k (x) k= 6 k= 5 k= 4 k= 3 k= 2 k= 1 k=0 k=1 k=2 k=3 k=4 k=5 k= x s 2k (x) k= 6 k= 5 k= 4 k= 3 k= 2 k= 1 k=0 k=1 k=2 k=3 k=4 k=5 k= x º Ö º Ù ¹ Ð Þ Ú ÒÝ m = 0 ½ ¾ Ð ÓÒØ Þ ÒØ Ò k = 6º º º ÐØÓÐ Ò Ü Ðº Å Ý Ð Ø Ó Ý Ð ÓÒØ Þ ÒØØ Ð Ý ØØ Þ ÐØÓÐ Ø ÚÓÐ Ð Þ º
13 ¼º¾º ÎýÄÌÇ Ä ÇÆÌýË Æ Ä ÁË Ë Ï Î Ä Ì Ã ½ s 00 (x) s (1) 00 (x) x º Ö º Ù ¹ Ð Þ Ú ÒÝ Ø ÚÓÒ Ðµ Ð Ö Ú ÐØ ÚÓÒ Ðµ m = 0 k = 0 Ò Ü Ö º ¹ Ñ ÒÞ ÐØ Ð ÒÓ Ø Ò Ñ Ó ÓÞ ÔÖÓ Ð Ñ Ø ÐØ Ð Ò Þ Ý Ñ ÒÞ Þ Ú ÒÝ ÞÓÖÞ Ø Þ Ú ÒÝ Øº ¼º¾º º Ï Ú Ð Ø Å Ú Ð {V m m = 0, 1,...} ÐØ Ö ÝÑ Ý ÞÓØØ Þ L 2 (R) Ø Ö Ø Ø Þ Ö Ò Ð º Ú Þ Ø Ø ÞÓÒ Ò W m Ö ÞÐ ØØ Ö Ñ ÐÝ V m ÓÑÔÐ Ñ ÒØ Ö V m+1 ¹ Ò Þ Þ V m+1 = V m W m, ½½µ ÓÐ Þ ÐØ Ö Ö Ø Þ Ø Ð ÒØ º W m ÐØ Ö Ò {w ml (r) l Z} ¹ Þ Ú ÒÝÖ Ò Þ Ö w ml (r) = 2 m/2 w 0 (2 m r l) Þ Ú ÒÝ Ð Û Ú Ð ¹ Ø Ð ÐÐ Ñ ÐÝ Þ ÒØ Ò Ý ØÐ Ò w 0 ÒÝ ¹Û Ú Ð Ø Ð ÐÐ Ø Ø Ð ÐØÓÐ Ð Þ Ù ÓÖ Ø Ðº Û Ú Ð Ø Þ ÒØ Ò ÓÑÔ Ø Ø ÖØ p k Ý ØØ Ø Ð ÐÐ Ø Ø Ð 1 w m,l (r) = q k s m+12l k (r) ½¾µ k=1 N s ÔÐ Ø Ø Ú Ð ÓÐ q k = ( 1) k p k+1º ØÓÚ Ö ÓÑÔÐ Ü ÓÒ Ù ¹ Ð Ø Ø Ö ºµ Þ Ø Ø ÞØ Ð ÒØ Ó Ý q k Ý ØØ Ø Þ ÒÓÑ Ø Ý ÒÐ Ø ÙØ Ò Ñ ÝÞ Ð Ô Ò Þ ÖÙ º È Ð ÔÔ Ò Ù ¹ Ð ¹ Þ Ú ÒÝ Û Ú Ð Ø º Ö Ò Ð Ø Ø º ÓÖ ØÓØØ Ö ÒÝ ÔÐ Ø Þ Ð Þ Ú ÒÝ Û Ú Ð Ø Þ ¹
14 ½ Â Ì ¼º Î Ì Ë s (x) 00 w (x) x º Ö º Ù ¹ Ð Þ Ú ÒÝ Ø ÚÓÒ Ðµ Û Ú Ð Ø Ô ÖÓ ÚÓÒ Ðµ m = 0 k = 0 Ò Ü Ö º (N s 1)/2 s m+1 2L+b (r) = 2 1/2 K= /2 0 K= (N s 1)/2 p 2K+b s m L K (r) q 2K+b w m L K(r), ½ µ ÓÐ b = 0 Ú Ý ½º Þ Ö ÒØ Ô ÖÓ Ô Ö ØÐ Ò Ò Üò ÒÓÑ Ð ÓÒØ Þ ÒØò Ð Þ Ú ÒÝ Ô ÖÓ ÐÐ ØÚ Ô Ö ØÐ Ò Ò Üò Ý ØØ Ø Ø Ó Ò Ø ÖØ ÐÑ ÞÒ º ¼º¾º º ÒÓÑ Ø Ô Ö Ñ ¹ Ð ÓÖ ØÑÙ Þ ÐØ Ö Þ Ò Þ Ö Þ Ø Ð Ø Ú Ø Þ Ý Ò ÖÙ ÐÑ Ð Ô Ø Ø Ý Ø Ø Þ Ð m 0 Þ Ð ÓÒØ Þ ÒØ Ð Ò ÙÐÚ ÐÐ Ñ ÒÒÝ ò Û Ú Ð Ø Ð¹ Ø Ö ÓÞÞ Ú Ð ÖÑ ÐÝ ÒÓÑ ÐØ Ö Ð ÙØ ØÙÒ º Ø Ð À Ð ÖØ¹Ø Ö ÐÚ Ð Ú Ø Ð Ò Ó Ö ÞÐ ØØ Ö Ø Ú Ð Ö Ø Ð L 2 (R) = m=m 0 W m V m0, ½ µ ÞÓÒ Ò Ý Ú m 0 ¹Ò Ð Ò ÝÓ m 1 ÒÓÑ Þ Ð Ø V m1 = m 1 1 m=m 0 W m V m0 ½ µ
15 ¼º¾º ÎýÄÌÇ Ä ÇÆÌýË Æ Ä ÁË Ë Ï Î Ä Ì Ã ½ ÓÖÑÙÐ Þ Ö ÒØ Ö Ø ÞØ Ò {s m1 k k Z} Þ Ò Ö Ú ÖØ {s m0 k, w mk k Z, m = m 0, m 0 + 1,...,m 1 1} Þ Ò Ñ Ø f [m 1] (r) = k f [m 1] (r) = k c m1 ks m1 k(r) c m0 ks m0 k(r) + m 1 1 m=m 0 d mk w mk (r). k ½ µ ½ µ À f ÓÑÔ Ø Ø ÖØ Ý J ÒØ ÖÚ ÐÐÙÑÓÒ Ñ ÐÝÒ Ó Þ 2 m 1 J ÓÖ {c m1 k} Ý ØØ Ø Þ Ñ ½ µ Ø Ò ÔÓÒØÓ Ò ÒÒÝ Ñ ÒØ {c m0 k, d mk } Ý ØØ Ø ½ µ Ø Ò Ñ Ò Ø Ø Ò J ØÐ Ò Ð ØØ Ð Ñ ÚÓÐØ Ò ÙÐ m 0 º À Ý Ð ÓÒØ Þ ÒØ Ø ÒÓÑ ØÙÒ Þ Ý ØØ Ø Þ Ñ Ñ ¹ ÙÔÐ Þ ÒÓÑ Ø Ò Ð ÙÔÐ Þ Ú Ø Þ Ý ØÓÚ º Þ ÞØ Ð ÒØ Ò Ó Ý ÓÞ Ó Ý ÔÓÒØÓ Ö Ñ ÒÝØ Ö Ò Ð ÝÖ Ø ÜÔÓÒ Ò Ð Ò Ð Þ Ò Ø Þ Ú ÒÝØ ÐÐ ÞÒ ÐÒ º Þ Ð ØòÒ Ø Þ Ó Ñ Þ ÖÒ º Û Ú Ð Ø Ð Ô Ø Ñ Ö Ø ÐÐ ØÚ Ö Ò Ð Ý ÒÐ Ø¹Ñ ÓÐ ÖÙØ ÒÓ ÒÝ ¹ Ö Ò Ö Ð Ó Ý d mk Û Ú Ð Ø¹ Ý ØØ Ø Ð ÒØ Ö Þ ¼ ¹ Þ Ð Ø Ò Ú ÒÝ Ð Ñ ÞÓÒÝÓ ÐÝ Ò Ø ÖØ ÐÑ Þ ÝÓÖ Ú Ð¹ ØÓÞ Ó Ø Ý ÞÓÐ Ø ÖØ ò Ú Ý ÒÙÐÐ Ý ØØ Ø Ð Ý Ø Ñ ÒØ ÞØ ¹ Ò Ñ ÑÙØ ØØ ØÓÑ ÐÐ ØÚ ÑÓÐ ÙÐ Ö Ð ØÖÓÒ òöò Ö º Þ ÐØ ÖÓÐ Ò Ú Ý Þ ÑÓÐ Ò Ý ØØ Ø Ø Ø Ý Ð Ô Ð ÓÒØ Þ ÒØ Ò Ð ÞÒ Ñ Ò Ò Ò ÜÖ Ñ Ú ÒÓÑ Ð ÓÒØ Þ ÒØ Ò ÞÓÒÝÓ Ø ÖÖ Þ Òº È Ô ¼ ÞÓÒÝ ØÓØØ Ó Ý Þ Ø ÖÖ Þ ÓÐÝ ¹ Ñ ØÓ Ò Þ Ù ÓÖÓ Ò Ó Ý Ð ÓÒØ Þ ÒØ Ò Ú Þ º µ ½¾µ ½ µ Ø Ú Ð Ø Ð Ý ØØ Ø Þ ÑÓÐ Ø Ý¹ Ñ Ð c m 1 = Lc m d m 1 = Mc m, ½ µ ÓÐ L M µ ½¾µ Ý ÒÐ Ø Ý ØØ Ø Ð ÐÐÒ Ð Ñ ÒØ L i,j = p j 2i+1 M i,j = q j 2i+1 = ( 1) j+1 p 2i jº Þ Ò Ñ ØÖ ÜÓ Ñ Ö Ø J ÒØ ÖÚ ÐÐÙÑ Ø Ò 2 m 1 m J 2 m 1 m+1 Jº ÓÖ ØÓØØ Ö ÒÝ ØÖ Ò Þ ÓÖÑ Þ Þ c m 1 d m 1 Ý ØØ Ø Ð ÒÓÑ Ð ÐÐ Ø Ú Ø Þ ÔÔ Ò Ø Ø Ú Ö c m = L c m 1 + M d m 1. ½ µ ½ µ ½ µ ÐØ Ð Ñ ÓØØ ØÖ Ò Þ ÓÖÑ Ø Ð ØÖ Ð ÓÖ ØÑÙ Ò ÞÓ Ø Ò Ú ÞÒ ÓÐÝ Ñ Ø Ö Ò Ð Ñ ØØ ¾¼µ c m1 L c m1 1 L c m1 2 L... L c m0 +1 L c m0 M M M M d m1 1 d m1 2 d m1 1 d m0 Å Ú Ð ½ µ ¾¼µ Ô Ö Ñ Ð ÓÖ ØÑÙ Ó Ö Þ Ô Ö Ñ Ð ÓÖ ØÑÙ Ò ÞÓ ¹ Ø Ò Ú ÞÒ º
16 ½ ¼º¾º º Å Ú Ð Ý Ð ÓÒØ ÐØòÒ ÑÓÑ ÒØÙÑÓ Â Ì ¼º Î Ì Ë s ml (r) = 1, r R, ¾½µ l ÖÑ ÐÝ m¹ö ÖÚ ÒÝ ÓÒ Ø Ò Ú ÒÝ ÖÑ ÐÝ Ð ÓÒØ Þ ÒØ Ò ¹ Ø Ø º Þ ØÙÐ ÓÒ ÔÔ Ò ÒÒ Þ Ò Ø Ó Ý Û Ú Ð Ø Þ ¼ ÖÑ ÐÝ Ð ÓÒØ Þ ÒØÖ º Þ Þ ÐÐ Ø ÐØ Ð ÒÓ Ø Ø º À Þ Ð A ÑÓÑ Ò¹ ØÙÑ ÐØòÒ Ý Û Ú Ð ØÒ Þ Þ r a w 0 (r)dr = 0, a = 1, 2,..., A¹Ö ¾¾µ Ñ Ò Ò Ð Ð A¹ Ó ÔÓÐ ÒÓÑ ÔÓÒØÓ Ò Ø Ø Ð Þ Ú ÒÝ ¹ Ð ÖÑ ÐÝ m Ð ÓÒØ Þ ÒØ Òº À Ö¹Û Ú Ð ØÒ Ò Ò ÐØòÒ ÑÓÑ ÒØÙÑ Ù ¹ Ú ÒÝÒ Ý ÐØòÒ ÑÓÑ ÒØÙÑ Ú Ò Ñ Ý Øع Ø Þ Ñ Ú ÒÝ Ò ÝÖ Ø º ¼º º Ð Þ Ú ÒÝ ÒØ Ö Ð Ò Þ Ñ ¹ Ø Ö Ð ÓÞ Ó Ý Û Ú Ð Ø Ø ÐÐ ØÚ Ð Þ Ú ÒÝ Ø Ö Ò Ð Ý Ò¹ Ð Ø Þ Ö Ø Þ Ð Ö ØÙ Ù ÞÒ ÐÒ Þ ÓÐÝ Ò ÒØ Ö ÐÓ Þ Ñ ¹ Ø Ñ ÐÝ ØÙÐ ÓÒ ÔÔ Ò Ý Þ Ú ÒÝ Ý ÓÔ Ö ØÓÖÒ Ý Þ ¹ Ú ÒÝÖ ÚÓÒ Ø ÓÞ Ø Ò Ð ÞÓÖÞ Ø º Æ ÝÓÒ ÐÐ Ñ ØÙÐ ÓÒ Û Ú Ð Ø¹ Ð Þ Ú ÒÝ Þ Ö Ò Þ ÖÒ ÐÐ ØÚ Ñ Ò Ò ÓÐÝ Ò s(r) Ú Òݹ Ò Ñ ÐÝÖ Ø Ð Ð Þ Ð ÐØ Ð ÒÓ ØÓØØ ÒÓÑ Ø Ý ÒÐ Ø s(r) = 2 1/2 l Z P l s(2r l) ¾ µ Ú Ý s m,k (r) = l Z P l s m+1,k+2l (r), ¾ µ Ó Ý ÞÓÖÞ Ø Ò ÒØ Ö Ð Þ Ñ Ø Ø ÒÙÑ Ö Ù ÒØ Ö Ð Ò Ð Ð ½ º Å Ú Ð Ö Ò Ð Ý ÒÐ Ø Ò Ø ÒÝ Ö Ö Ò ÐÓÔ Ö ØÓÖÓ ØÒ ¹ Þ Ú ÒÝ Ò Ö ÓÒØÓ Ñ ÑÐ Ø Ò Ó Ý ¾ µ ¾ µ Ý ÒÐ Ø Ð Þ ¹ Ú ÒÝ Ö Ú ÐØ Ö ÖÚ ÒÝ º Ð Þ Ú ÒÝ s (i) i¹ Ö Ú Ðع Ö Þ Ý ØØ Ø Ð Þ Ú ÒÝ µ ÒÓÑ Ø Ý ÒÐ Ø Ò p l Ý Øع Ø Ð P l = 2 i p l ÔÐ ØØ Ð Þ Ñ Ø Ø º Ì ÖÑ Þ Ø Ò Ò Ñ Ð Ø Þ Ö¹ Ñ ÒÒÝ Ö Ú ÐØ Ñ Ò Ò Ð Þ Ú ÒÝ Þº À ½ Ò Ð ÐÑ ÞÓØØ Ð Ð Ø ÞÒ Ð Ù s (0),...,s (n) Ú ¹ ÒÝ ÒØ Ö Ð Ö Ú Ø Þ Ð Ð Ø Ð ÐÑ ÞÞÙ I(l 0,..., l n ; m 0,...,m n ) = n j=0 s (j) (2 m j r l j )dr, ¾ µ
17 ¼º º Å Ê ËÁ Á ÇÆ Ì Ä ÆËý Ê Ä ½ Þ Ø Ý r 2 m 0 r ÒØ Ö Ð Ú ÐØÓÞ Ö Ú Ð Þ Ð Ð Ö ÓÞ Ø Ù I(l 0,...,l n ; m 0,..., m n ) = 2 m 0 I(l 0,...,l n ; 0, m 1 m 0,..., m n m 0 ). ¾ µ ÁØØ ÐØ ØØ Ó Ý Þ m j Ò Ü ÒÙÐÐ Ø Ð Þ n¹ Ò Ú Ú ÓÖÖ Ò Ú ÒÒ Ö Ò ÞÚ Þ Þ m 0 m 1... m n º Å Ú Ð Ñ Ò Ý s (j) Ú ÒÝÖ Þ Ý ¾ µ ÒÓÑ Ø Ý ÒÐ Ø s (0) ¹ ÐÝ Ö ÐÝ ØØ Ø Ø Ö ÚÓÒ Ø ÓÞ ÒÓÑ Ø Ý ÒÐ Ø Ó ÓРРغ Ý r 2 1 r Ú ÐØÓÞ Ö ÙØ Ò ÔÓØØ Þ I(l 0,...,l n ; 0, m 1,..., m n ) = 2 1 l Z P (0) l I(l + 2l 0, l 1...,l n ; 0, m 1 1,...,m n 1). ¾ µ À ÓÒÐ ÔÔ Ò ØÙ ÙÒ Ð ÖÒ Þ ½ Ò Üò Ø Ö ÓÖ m 1 ¹ Ø ÒØ ÒÙй Ð Ú Ñ Ø Ø ÒÝ Þ Ú Ð Þ Ô Ò ÓÖ Ò Ð Ð Ø ÒÒ Ý Þ I(l 0,...,l n ; m 0,...,m n ) Ú Þ Ú Þ Ø Ø I(l 0,...,l n ; 0,..., 0) ÒØ Ö ÐÓ Ö º À Þ Ø ÒÙÐÐ Ð ÓÒØ Þ ÒØò ÒØ Ö ÐÓ Ø n H(α 1,...,α n ) = s (0) (r) s (j) (r α j )dr ¾ µ ÐØÓÐ Ò Ü Ð Ö Ò Ð Þ Ñ ÒÒÝ Ð Þ Ö ØÒ Ò Ð ÖÒ Þ Ð Þ Ó Ý j=1 I(l 0,..., l n ; 0,..., 0) = H(l 1 l 0,...,l n l 0 ). H(α 1,...,α n ) ÖØ Ø Ô H(α 1,...,α n ) = h 2α1 µ 1,...,2α n µ n H(µ 1,..., µ n ) µ 1,...,µ n Z ¾ µ ¼µ Ø ÖØ Ý ÒÐ Ø Ñ ÓÐ ÒØ Ô Ù Ñ h µ ÒÓÑ Ø Ý ÒÐ Ø P (j) Ý ØØ Ø Ð Ô Ø Ñ Þ Ð ÔÐ ØØ Ð ½ h µ = h µ1,...,µ n = γ Z P (0) γ n j=1 P (j) γ µ j. ½µ ¼º º Ñ Ö ÞÓÒÝØ Ð Ò Ö Ð Ñ Ö ÞÓÒÝØ Ð Ò ÞÒ Ð Ø Ñ ØÖÓÐ Ò Ñ ÒØ Ý ¾¼ Ú Ñ ÐØÖ ÒÝ Ð Ú Þ º Ð ØØ Ñ Ö Ö Ñ ÒÝ Þ Ñ Ö Ø H Ñ ÒØ ÐÐ ÑÞ Ô Ö Ñ Ø ÖØ ÔÖ ÐØ ÓÞÞ Ô ÓÐÒ H = X mert X pontos, ¾µ ÓÐ X mert Ñ ÖØ ÖØ X pontos ÔÓÒØÓ ÖØ º ÞÞ Ð Ò Ú Ð Ð ÔÖÓ Ð Ñ Ó Ý Ñ Ö ÓÖ Ò ÔÓÒØÓ ÖØ ÐØ Ð Ò Ñ Ö ØÐ Ò ÔÔ Þ ¹ Ø Þ ÖØ Ø ÔÖ Ð Ù Ñ Ö Ð Ñ Ø ÖÓÞÒ º Ð Ö ÓÖ Ò Þ ÖØ
18 ½ Â Ì ¼º Î Ì Ë º Ö º Ý Ñ Ö Ð ØÑ Ö ÓÖÓÞ Ø Ö Ñ ÒÝ Ò òöò Ú ÒÝ ½¼¼ o Ú Ö Ø ÖØ Ø Ò ÒÓÖÑ Ð ÐÓ ÞÐ Ð σ Þ Ö Ð ¾ º Ý ÞÒ Ñ ÒÒÝ Ò Ð Ø Ñ Ö Ò ÐÐ ÑÞ Ø Ú Ð Ñ ÐÝ Ò Þ ÐÐ Ò Ö Ú Þ Ú Þ ØÒ Ñ ÒØ ÔÓÒØÓ ÖØ º ½ ¹ Ò Ð ÒØ ØØ Ñ Þ ÁËÇ ÍÅ ½¼ ¹ÓØ ½ º Þ Þ ÐÔ Ó ÙÑ ÒØÙÑ Ð Ô Ø Ô Þ ØÓÚ Þ Ú ÒÝÓ ÓÖ Ò Ú Ø Ò Ð Ö Ò º Ú Þ Ð ¹ Ð Ö Ð ¹Ð ÓÖ Ø Ö ÙÑÓ Ñò Ø Þ ÐÝÓÞ Þ Ú ÒÝ ¼ Ð ÓÖ Ø Ö ÙÑÓ Þ Ñ Ö Ð Ö Ó Ý Ñ Ò Ò Ñ Ö Ö Ñ ÒÝ Ñ ÐÐ Þ ÐÒ ÐÐ Ñ Ö Ö Ñ ÒÝ Ñ Þ Ø Ö ÚÓÒ Ø ÓÞ ØÓØ º º Ö Ò Ý Ñ Ö Ð ØÑ Ö ÓÖÓÞ Ø Ö Ñ ÒÝ Ø Ð Ø Ø Ù ¾ º Ñ ¹ Ö Ö Ñ ÒÝ Þ Þ Ø Ò Ðݵ Ý ÓÖ Ø Ú Ð Þ Òò ص Ö ÞÓÐÚ Þ ÓÖ Ò Ø Ø Ò ÐÝ Ò Ñ Ô Ù Ñ Ö ÓÖÓÞ ØÖ ÐÐ ÑÞ ÐÓ ÞÐ òöò ¹ Ú ÒÝ Ø Ôк ½¼¼ o Ú Ö Ø ÖØ ÒÓÖÑ Ð ÐÓ ÞÐ σ Þ Ö º Þ Ý ÔÓØØ Ö Ñ ÒÝ Ú Ø Ð Ò Ó Ñ Ö Ø ÐØ Ø Ð ÞÚ Ý ÓØØ Ñ Ö Ð Ö Ö Ú Þ ¹ Ð Ø Ñ ÒØ Ö ÚÓÒ Ø ÓÞ º Þ Ó Ý Ø Ð Ñ Ö ÓÖÓÞ Ø ÒÝ Þ Þ Ð X pontos σ º º ºX pontos +σ ÖÒÝ Þ Ø Ò Ú Ð ÞØ Þ ÐÓ ÞÐ ØÙÐ ÓÒ Ý ÖØ ÐÑò Ò Ñ Ø ÖÓÞÞ º Þ ÖØ ÓÒØÓ Þ ÐÓ ÞÐ Ø ÔÙ Ò Ñ Ö Ø Ñ Ö Ò ÓÖ Òº Ý ÓÖÐ Ø Ð Ø Ò Ò Ñ Ø ÖØ Ò Ú Ø Ð Ò Þ Ñ Ñ Ö Ý¹ Ý Ñ Ö Ò ÐÐ ÑÞ Ñ Ø ÖÓÞ Ò Ðº ÍÌ Ú Þ Ð Ø ÓÖ Ò Ý Ö Ò Ý Ñ Ö Ö ¹ Ñ ÒÝ Ðµ ÐÐ Ñ Ø Ò Ò Ñ ÐÝ Ò Ú ÞÓÒÝ Ò Ð Ø Þ X pontos ÔÓÒØÓ ÖØ X mert Ñ ÖØ ÖØ Þ Ô Øº ÁÐÝ Ò Ø Ò ÓÒ ÓÐ ØÑ Ò Ø ÓÖ ØÓØغ Å Ú Ð Ð Ý ÓÖ ÐÓ ÞÐ Ø ÔÙ ¹ Ò Ð ÒÓÖÑ Ð ÐÓ ÞÐ Ò Ð ±2σ ÖÒÝ Þ Ø Ò Ñ Ö Ó Þ Ð ±¹ Ø Ð Ð Ø Þ Ð ±¹Ó Ú Ð Þ Òò Ð Ð Þ X pontos ÔÓÒØÓ ÖØ X mert ±2σ ÖÒÝ Þ Ø Òº ÍÅ Þ Ö ÒØ Ñ Ö Ö Ñ ÒÝ Ñ Þ Ø Ö ±¹Ó Ú Ð ¹ Þ Òò Ñ ÐØ Ð Ò Ñ Ð Ð Þ U Ø Ö ÞØ ØØ Ñ Ö ÞÓÒÝØ Ð Ò ÁËÇ ÁÒØ ÖÒ Ø ÓÒ Ð ÇÖ Ò Þ Ø ÓÒ ÓÖ ËØ Ò Ö Þ Ø ÓÒ ½¼ Ù ØÓ Ø ÜÔÖ ÓÒ Ó ÍÒ ÖØ ÒØÝ Ò Å ÙÖ Ñ ÒØ ½ ¾ ¾
19 ¼º º Å Ê ËÁ Á ÇÆ Ì Ä ÆËý Ê Ä ½ Ñ Ø ÖÓÞ Ö Þ ÖØ k Ø Ö ÞØ Ø ÒÝ Þ k = 1.98 ÐÐ ØÚ k = 2 ÞÒ Ð Ø Ú ÓÐØ U = kσ. µ ÖÑÓÒ Þ Ø ÌËÁ ½½ Þ Ú ÒÝÓ Ñ ÒØ Ôк Þ ÁËÅ ÊÄ Æ Ö Ò Þ Ö Ö ÚÓÒ Ø ÓÞ ÌËÁ ¼¼ ¾ Þ Ú ÒÝ ½ µ Ý ÒØ Øò Ò Þ ÌËÁ ÌÊ ½¼¼ ¼¾ ¹½ ¹¾ ¾½ ¾¾ Ø Ò Ð ÒØ ÞÒ Ð Ø Ø Ö Ð Ö Ö Ú Ò Ú Þ Ð ØÓ Ø ÒØ Ø Ò Ñ ÐÝ ÓÐ ÓÞ Ò Ð Ô Þ ÒØ Ò ÍÅ ÚÓÐغ ½½ ÙÖÓÔ Ò Ì Ð ÓÑÑÙÒ Ø ÓÒ ËØ Ò Ö ÁÒ Ø ØÙØ
20 ¾¼ Â Ì ¼º Î Ì Ë
21 ½º Þ Ø ýöòý ÓÐ ÐÐ Ô Ø Ø Ö Ü Ø Ñ Ö Ñ ÒØ Ø ÖØ Ð ÞØ ÑÓ ÐÐ Þ Ú ÓÒÝÖ Ø Ñ ÒØ ÓÞ Þ Ñ Ø ÒÝ ÐÚ Þ Ø ¹Ø ÒÓÐ ÓÐÝ Ñ ØÓ Ð Ð Ø Ú Ø Þ ÐÚ Þ Ø Ý ÖØ Þ Ñ Ö Ó Ý Ö Ú Ò Ð Ð Ñ ÞÓ Þ Ô Ù Ñ Ö Øò ÚÓÒ ÐÚ Ø Ð Ö Ú Ð Ø ÒÓÐ Ð Ø Ø ÒÝ Ò Þ Ò ÓÖÑ Ø ¹ Ø ÒÓÐ Ø Ö Ð Ø Òº Þ Ò Ò ÒÓÑ Ø Ö Ò Ý Þ Þ Ò Ú ÒØÙÑÑ ¹ Ò Ø Ó ÓÑ Ò Ò Ð ÞÒ Ø Ñ ØÙ Ó ÓÞ Ô Ø Ý Ö Ø Ö ÞØ Ö Ñ Ö Ñ Ð Ò Ø Ø Þ Ð Ø Ú º Þ Ø Ø ÒÓÐ Þ ÒØ Ò Ø Ð Ú Ò Ú Þ Ø ÐÐ ÑÞ Ö º Ð ØÖ ÓÞ Ò Ú ÓÒÝ Ö Ø ò Ñ Þ Ú ÒØ ÔÓÒØÓ ÓÒ Þ Ð Ð ÓÞ Ø Ð ØÖ º Þ Þ Þ Ñ Ö Ø ¹ Ò Ñ ØØ Ð ØÖ ÓÞÓØØ Ö Ø Ú Ø Ò Ñ ØØ ÑÖ Ø Ö¹ Ð Ò Ý Ð Ø Ñ º Ô ÞØ Þ Ð ØÖÓÒÑ ÖÓ Þ ÔÓ ØÓÑ Ö ¹ Ñ ÖÓ Þ ÔÓ Ú Þ Ð ØÓ ÞØ ÑÙØ Ø Ó Ý Þ ÒÒÝ Þ ØØ ÐÚ Þ Ø Ð Ð Ø Ò Ð ØÖ ÓÞÓØØ ¼º º º ½¼¼ ÒÑ Ú Ø Ñ Ð Ð Ø Þ Ø Þ Öò ØÖÙ Ø Ö Ð ÙÐ Ø Þ Ý Ö Ò Ö Ø Ð ØÙÐ ÓÒ º ½ º Þ ØÖÙ Ø Ö Ö Ø Ð Ñ ÒÞ Ð ÐÝ Þ Ö Þ Ø ÒØÖ Ô Ð ¼ ½ ÐÐ Ñ Þ Ø º ýðø Ð Ò Þ Ý Ò Ö Ñ ÐÐ Ò ÐÐ Ñ Ö Ð Ø ÖØ Ò Ø ØÖÙ Ø Ö Ö Þ ÞØ Ú ØÙ¹ Ð ÓÒ Ò ÞÓÒÓ Ø º Å Ú Ð Ñ Ö Ñ Ö Ò Ñò Ö Ú Ò Ú ÝÖ Ò Ñ ÖÓ ÙÐÐ Ñ Ö Ú Ò Ú ØÓÐ Ð Þò Þ Ò Ö Ñ Ö Ò Ý Ö Ú Ò ØÙÐ ÓÒ Ò Ú Þ Ð Ø º ½º½º ýöòý ÓÐ ÐÐ Ô Ø Ñ Ö Þ ÖÒÝ ÓÐ ÐÐ Ô Ø Ð ØÖ ÙÑ Ô ÖÑ ØØ Ú Ø Ð ÐÐ Ñ Þ Ø Ú Þ Ð Ø Ñ ÒØ ØÙÐ ÓÒ Ø Ö Ö Ö Ú Ò Ø ÖØÓÑ ÒÝ Ò º Þ ÖÒÝ ÓÐ ÐÐ Ô Ø Ñ Ö Ö ÞÓÐ Ð Ø Ñ Þ Ö Ý Á ¹ ËÌ ¹¾ µ Ý Ñ Ø ÖÓÞÓØØ Ñ Ö Øò Ð ÓØ ÒÝ Ø ÝÑ Ø Ð ÖÒÝ ÓÐ Ð ÐÚ Ð ÞØÓØØ Ø Ø ÖÖ Þ Þ ØØ ½º½º Ö µº Ú Þ Ð Ø Ð Ñ Ö Ø º ½ Ñ Ø Öº Þ Ð Ö ÐÝ Þ Ò Ú Þ Ð Ø Ñ ÒØ º Ø ÓÐ ÐÓÒ Ð ÐÝ Þ ØØ ¾½
22 ¾¾ Â Ì ½º ÅÁÆÌ Ì ÊÌ ÂÄ Ë Ì Ë ÅÇ ÄÄ Ë ½º½º Ö º Ú Þ Ð Ø ÐÖ Ò Þ ½ ÀÞ Ð ØØ Þ Á ËÌ ¾ Þ Ú ÒÝ Þ Ö Òغ aaaa aaaa aaaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaa aaaa aaaa aaaa ½º¾º Ö º Ú Þ Ð Ø Ñ ÒØ Ñ ÒØ Ø ÖØ ËÌÅ ¹ Þ Ú ÒÝ ½ Þ ¹ Ö Òغ Ñ ÒØ Ø ÖØ Ð Þ Ø Ð ò ½ ÑÑ Ð ØÑ Ö ò Ð Ú Þ Ø ØÑ ¹ Ö ÑÑ Ð Ú Þ Ø ÖÙ ÐÑ Ñ Ð Ð ØÐ ÓÞ Ð Ö Ö Òº ÒØ ÒÒ Ø Ú Ð Ñ Ö Ø Þ ÖÒÝ ÓÐ ÐÐ Ô Ø Ú ÐØÓÞ º Ñ Þ Ú ÒÝÓ Ñ Þ Ö Ó Ý Ú Ð Ñ ÐÝ Ò ÙÐÐ ÑÚ Þ Ø Ó Ü Ð ¹ Ð Ø ÔÚÓÒ Ðµ Ð Ø ÐÝ ÞÞ Ú Þ Ð Ø Ñ ÒØ Øº Þ ËÌÅ ¹ Þ Ú ÒÝ ½ ½ Ñѹ Ð ØÑ Ö ò Ñ ÒØ Ø Ö Ð ½º¾º Ö µ Ñ ÐÝ Ý Ú Ø ØØ Ó Ü Ð Ð Ð Ø ÐÝ Þ Ò º ½º º Ö Ò Ð Ø Ø µ Ð Ô¹ Ñ ÒØ ÐÝ Þ ØØ µ Ú Þ Ð Ø Ñ ÒØ ÐÐ Ô Ø Ú ÐØÓÞ Ñ Þ Ö¹ ÒÝ ÓÐ ÐÐ Ô Ø Ñ ÖØ Øº Å Ú Ð Þ ÖÒÝ ÓÐ ÐÐ Ô Ø Ñ Ö Ö ÞÓÐ Ð Þ Ú ÒÝÓ Ñ Ö ÐÖ Ò Þ Þ Ð ÖØ Ñ Ö Ø Ñ ØØ ÐØ Ð Ò Ð ÐÑ ØÐ ¹ ÒÓ Ñ ÖÓ Ð ØÖÓÒ Ò ÞÒ Ð ØÓ Ñ Ö Øò Ñ ÒØ Ú Þ Ð Ø Ö Ý Ñ Ö Øò Ú Þ Ð Ø ÐÖ Ò Þ Ø Þ Ø ØØ Ñº Å Ú Ð Ñ ÖÓ Ð ØÖÓÒ Ý ÖØ ÓÖ Ò Ð ÐÐ Ø Ø Ñ ÒØ Ñ Ö Ø Ð ÐØ Ð Ò Ò Ñ Þ Ý ÞØ Ø Ø Þ ÑÙØ ØÓØØ Þ Ú ÒÝÓ Ð Ú Þ ¹ Ð Ø Ñ Þ Ö ÓÐ ÓÞ Ø ØòÞØ Ñ ÐÙк Ñ Ö Ö Ð ÞÒ ÐØ Ú Þ Ð Þ¹ Þ Ñ Ý ÓÖÐ Ø Ò ÒÒÝ Ò Ð ÐÐ Ø Ø Ñ ÒØ Ú Þ Ð Ø Ö Ò ¹ Ö ÐØ Ð ÞØ Ö º Ý Ð Ø Ú Ú Ð Ú Ý Ð Ø¹ ÐÚ Þ Ø Ð Ô Ú ÓÒÝ ÑÖ Ø Ú Þ Ð Ø º À ÓÒÐ Ò Þ Ú ÒÝØ Ð ÐØ Ö Ô Ð ÐÖ Þ Ø ØØ Ú Þ Ð Þ¹ ÞÞ Ð Ø Ð Ð ÓÞ ØÙÒ Ò ÒÓ ÒÝ Ó ½¼ ÖÒÝ ÓÐ Ø ÜØ Ð ½½½ Ú Ý Þ Ò
23 ½º½º ýêæ ÃÇÄýËÁ ËÁÄÄ È ÌýË Å Ê Ë ¾ aaaaaaaaa aaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaa aaaaaaaaaa aaaaaaaaa aaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaa aaaaaaaaaa ½º º Ö º µ Ê Ö Ò Ñ ÒØ µ Ú Þ Ð Ø Ñ ÒØ Þ ËÌÅ ¹ Þ Ú ÒÝ Þ Ö Òغ Ú Þ Ð Ø Ñ ÒØ ½ ÑÑ ØÑ Ö ò Ö Ö Ö Ò Ñ ÒØ Ú Þ Ø Ð Ð Ø Ò Ø Ð Ð Ø ÑÑ ØÑ Ö ò Ö Ý ÝòÖòº ½º º Ö º Ð ÞØ ØØ Ñ ÒØ Ø ÖØ Ðµ ÔÖÓØÓØ ÔÙ º Ò ÒÓ ¹Ö Ø ½½ Ú Þ Ð Ø ÓÖ Ò Þ ÖÓ ÐÓÑ Òº ÞÓ Ó Ñ Ö Þ ÐÐ Ø Ó ØÖ ÒÝ Ó Ý Ý Ö Ö Ò Ñ ÒØ Þ ¹ ½º º Ö Þ Ö Òغ Ö Ö Ò Ñ ÒØ Ø Ð Ò Ó Ü Ð Ø ÔÚÓÒ Ð Ð Ú Þ Ø Ò Ö Ð Ð Ø Ø Ð Ú Þ Ø ÝòÖò Ð Ö ÒØ Þ Ð Ð Ø Øº ËÙ ÞØÖ ØÙÒ Ø Ö Ò Ú ÞØ Ò Ú ÓÒÝÖ Ø Ø Þ µ ÐÐ ØÚ µ Ð Ò Ñ Ð Ð Ò ÐÐ Ò Ð ÐÐ Ø ÒÙÒ º Î Þ Ð Ø Ñ ÒØ Ø Ò Ù Ý Ò ÞØ Ð ØÑ Ö Ú Ð Ö Ò Ð Þ Ö Ð Ú Þ Ð Ø Ñ ÒØ Ø ÐÐ Ð ÐÐ Ø Ò º ÆÓ ÐÚ ¹ Þ Ø Ý ÖØ ÓÖ Ò Ð ÐÐ ØÓØØ Ö Ø Þ Ð Ö Ð Ñ Ö Ø Ò Ñ Ñ Ð Ð Ñ ÒØ Ø ÖØ ÓÞ Ô Øº Å Ö ØÖ Ú Ù Ò Þ Ò Ñ ÓÐ Ø Ø Ö Ö ÒÝ Ø Ð ÔÚ Ø Ò Ö Ø ÐÝ Ö ÒÝÓ Ø ÖÓÞÞ Ñ Þ ÖØ Ò ÝÞ Ø Ú Ý ØÖ Ô Þ Ð Ñ ÒØ ÐÐÒ Ö Ò Ð Þ Ö º Î Þ Ð Ø Ò ÓÖ Ò Þ ÒØ Ò Ò Þ Ò ÞØÓ Ø Ø Ó Ý Ö Ö Ò Ú Þ Ð Ø Ñ ÒØ ÞÓÒÓ Ö Ø Ð ØÖÙ Ø Ö Ú Ð Ö Ò Ð ÞÞ Òº Þ ÖØ Ú Þ Ð Ø Ò Ò Ð ºÒº Ä Ö Ö Ò Ñ Þ ÖØ ½¼ Ú Ð ÞØÓØØÙÒ º ÌÓÚ ÔÖÓ Ð Ñ Ø Ð ÒØ Þ Ô Ú Þ Ø ÖÙ ÐÑ º Ú Þ Ð Ø Ñ ÒØ Ð Ð Ø Ò ÝÓÒ ÔÓÒØÓ Ð Ð Ø Ò ÝÓÒ Ú ÓÒÝ ÒÒÝ Ò Ö Ðº Þ ÖØ Ú Þ Ð Ø Ñ ÒØ Ø ÖØ Ð Ø Ò Ð ØÐ ÓÞ Ð Ð Ø Ø Ö ÔÓÐ ÖÓÞØ Ñ Ò Ñ ÞÓ Ó ÖÙ ÐÑ Ð Ð ØÖ Ø Ð ÐÑ ÞØ Ñ ½º º Ö º Ð Ú Þ Ø Ø Ð Ø Ò Ò Ú Ð Ö Ò Ø ÓÒ Ð ØÖ ÙÑ Ñ ÒØ Ø ÖØ Ý ÞØÓ Ø Ø Ú Þ Ð Ø Ñ ÒØ Ó Ð Ú ØÐ ÓÞ Ð Ð ØÖ º ÞÞ Ð
24 ¾ Â Ì ½º ÅÁÆÌ Ì ÊÌ ÂÄ Ë Ì Ë ÅÇ ÄÄ Ë Ñ ÓÐ Ð Ú Þ Ð Ø Ñ ÒØ Ö Ð Ò Ú Þ ÐÝ º ½º¾º ËÞ Ñ Ø Ñ Þ Ö Þ ÖÒÝ ÓÐ ÐÐ Ô Ø Ë Ð Ò Ø Ú Ò µ Ò Þ Ö ÒØ ( ) Eref SE = 20 lg, ½º½µ E vm ÓÐ E ref Ö Ö Ò Ø Ò Ñ ÖØ Ð ØÖÓÑÓ Ø Ö Ö E vm Ú Þ Ð Ø Ñ ÒØ Ú Ð Ñ ÖØ Ð ØÖÓÑÓ Ø Ö Ö º Ø Ñ Ò Ð ÐÑ ÞÓØØ Ñ ÒØ Ø ÖØ Ø Ð Ð Þ ÐÐ ØÓØØ Ø ÓÒ Ð ØÖ ¹ ÙÑÑ Ð Ø Ð Ò Ø ÐØ ØØ Ó Ü Ð Ú Þ Ø Ñ ÐÝ Ò Ý Ð Ð Øò Ö Ñ Ð Ø¹ Ð ÓÞØ Ø Ø ÝÑ ÓÞ ½º º Ö º Ú Þ Ð Ó Ó Ü Ð Þ Þ Æ Ø¹ Ð ÓÞ Ò Ú Þ º Ú Þ Ð Ó Ü Ð Ú Þ Ø Þ Þ ÙÐÐ Ñ ÑÔ Ò Z 0 = 60 ε 0 ln D d, ½º¾µ ÓÐ ε 0 Ú Þ Ø Þ ØØ Ð ØÖ ÙÑ Ö Ð Ø Ú Ô ÖÑ ØØ Ú Ø ε rteflon = 2.02µ D Ð Ú Þ Ø Ð ØÑ Ö d Ð Ú Þ Ø ØÑ Ö º Ø Ñ Ò d = 2.04 ÑÑ D = 11 ÑÑ ÙÐÐ Ñ ÑÔ Ò 50 Ωº Ñ ÒØ Ø ÖØ ÞÒ Ð Ø ¹ Ò Ø Ö Ö Ú Ò f c Ø ÔÚÓÒ Ð Þ ÞÓÒ Ñ Ð Ò Ñ Ñ Ù Ó Ñ Ð Ò ½ Ð Ò Ø Ò f c = 1 2c πε d + D ½º µ ÓÐ c ÒÝ º Þ ØØ Ð ÖØ Ñ ÒØ Ø ÖØ Ø Ò f c 7.3 ÀÞº Ú Ø Þ Ò ÑÙØ Ø Ö Ö Ð Ú Þ Ð Þ Þ Å Ø Ö Þ ÑÙÐ ÇÅËÇÄ ÅÙÐØ Ô Ý ½¼ Ú Ð Ñ Þ ÑÙÐ ÔÖÓ Ö Ñ Ê ÑÓ ÙÐ Ú Ð ¹ Þ Ðغ Þ ÑÙÐ ÓÖ Ò Ñ ÒØ Ñ ÒØ Ø ÖØ Ö Þ ÑÑ ØÖ Ù º Þ ÑÙÐ ÓÖ Ò Ú Þ Ð Ø Ñ ÒØ Ö Ð Ø Ú Ð ØÖÓÑÓ ÐÐ Ò ε rsi = 11.7 Ø Ð Ö Ú Ò Ú Òº Þ ÑÙÐ ÓÖ Ò ØÐ ÓÞ Ô Ö Ñ Ò Ð Ú Þ ¹ Ð Ø Ñ ÒØ Ø Ð Ö Ú Þ Ö Ðº Ú Þ Ð Ø Ñ ÒØ Ø Ñ ÒØ Ø ÖØ ÓÞ ØÐ ÓÞ Ð Ð Ø Ò Ô Ö Ñ ÐØ Ø Ð ÒØ Ú Þ Ø ÐÐ ØÚ Ð ØÖ ÙÑ Ø ÖÓÐ º ½º º Ö ÑÙØ Ø Þ ÑÙÐ ÓÖ Ò Ñ ÔÓØØ Ð ØÖÓÑÓ Ñ Ò Ø Ö ÐÓ ÞÐ Ø f = 1 ÀÞ Ö Ú Ò Ò Ð ÓÐ Ð Ó Ü Ð ØÐ ÓÞ Ò Ñ ØÚ º Þ ÑÙÐ Ö Ñ ÒÝ Ð Ø ÞØ Ò Ð Ø Ø Ó Ý Þ Ð ØÖÓÑ Ò Ø Ö Ú Þ Ð Ø Ñ ÒØ ÖÒÝ Þ Ø Ò ÓÒ ÒØÖ Ð º À ÓÒÐ Ö Ñ ÒÝØ Þ ÑÙ¹ Ð Ø Ð Ú Þ Ð Ø Ö Ú Ò Ú Òº Ñ ÒØ Ø ÖØ Ô Ö Ñ Ò Ð Þ Ò Ö ò¹ Öò ÒÙÐÐ ÐÐ ØÚ Ò ÝÓÒ Ð ÓÒÝ ÖØ òº Þ ÖØ Ú Ö Ø Ó Ý Ú Þ Ð Ø ÓÖ Ò Ð ÐÑ ÞÓØØ Ñ ÒØ Ð Ú Þ Ð ØÖ Ú Ø Ñ ÒØ Ò Ý Ò Ö òöò ò Ø Ö Ð Ø Ò ÐÝ Ø Ó Ð Ð Ñ ÒØ ÞÔÓÒØ Ö Þ º Þ S 11 S 21 Ô Ö Ñ Ø Ö Þ ÑÙÐ Ö Ñ ÒÝ Ø ÑÙØ Ø ½º º Ö Ö ¹ ÓÒ Þ ½ ÀÞº º º ÀÞ Ö Ú Ò Ø ÖØÓÑ ÒÝ Òº
25 ½º¾º Ë ýå ÌýËÁ Å Ë Ê ¾ ½º º Ö º Ñ ÒØ Ø ÖØ Ë Ñ ÒØ Ð ØÖÓÑÓ Ñ Ò Ø Ö ÐÓ ÞÐ f = 1 ÀÞ Ö Ú Ò Òº Å Ø ½ ÑÏ ÐÓÐ Ð ØÐ ÓÞ Òµ ½º º Ö º Þ S 11 S 21 È Ö Ñ Ø Ö Ö Ú Ò Þ ½º º Ö Ò Ð Ø Ø ÑÓ ÐÐ Ø Òº
26 ¾ Â Ì ½º ÅÁÆÌ Ì ÊÌ ÂÄ Ë Ì Ë ÅÇ ÄÄ Ë ½º º Ö º Ñ ÒØ Ø ÖØ Ñ ÒØ Ð ØÖÓÑÓ Ñ Ò Ø Ö ÐÓ ÞÐ ÓÒ ÒØÖ Ù ÐØÓÐØ Ñ ÒØ Ø Ò f = 1 ÀÞ Ö Ú Ò Òº Å Ø ½ ÑÏ ÐÓÐ Ð ØÐ ÓÞ Òµ Þ Ö Ñ ÒÝ Þ Ö ÒØ Ö Ú Ò Ò Ú Ú Ð Þ S 21 Ô Ö Ñ Ø Ö Ò Þ S 11 Ô Ö Ñ Ø Ö Òº Ñ ÖØ Ô Ö Ñ Ø Ö Ð ÙÐ Ð ØÖÓÑ Ò Ø ÖÒ Ñ ÒØ ÐÝÞ ¹ Ø Ø Ð Ú Ð Ø Þ ÑÙÐ ÐØ Ñ Ð Ò Þ Ö Ú Ò ÓÒº ÒÒ Ý ÐÐ ÔÓØ Ø ÑÙØ Ø ½ ÀÞ¹ Ò ½º º Ö º Þ ÑÙÐ S 11 S 21 Ô Ö Ñ Ø Ö Ö Ú Ò Ò Ö Ñ ÒÝ Ø ½º º Ö ÑÙØ Ø º Ä Ø Ø Ó Ý Ø Ö Ö Ú Ò ÖÒÝ Þ Ø Ò Ø ¹ Ô ÞØ Ð Ø ÑÙØ Ø Ø Ú ÐØÓÞ Ò Ñ ÒØÖ Ð Ò Ð ÐÝ Þ Ñ ÒØ Ø Òºº Þ Ö Ñ ÒÝ Þ Ö ÒØ Ö Ú Ò Ò Ú Ú Ð Þ S 21 Ô Ö Ñ Ø Ö Ò Þ S 11 Ô Ö Ñ Ø Ö Òº
27 ½º º ÎÁ Ë ýä Ì ¾ ½º º Ö º Þ S 11 S 21 Ô Ö Ñ Ø Ö Ö Ú Ò Þ ½º º Ö Ò Ð Ø Ø ¹ Þ Ô Ò Ð ÐÝ Þ ØØ Ñ ÒØ Ö ÐÐ ØÚ Ð ÞØ ØÓØØ Ñ ÒØ ÐÖ Ò Þ ò ÑÓ ÐÐ Ø Ò ØÓÚ Ý ÓÐÝ Ò Ñ ÒØ Ö ÓÐ Ñ ÒØ Ý Ö Þ Ð Ú Ú Ð Ð ØØ ¹ ÐÝ ØØ ØÚ º ½º º Î Þ Ð Ø Ú Þ Ð Ø ËÞ ÒÝ Á ØÚ Ò Ý Ø Ñ Ê Ö Ú Ò Î Þ Ð Ä ÓÖ ¹ Ø Ö ÙÑ Ò Ø ÖØ Òغ Ú Þ Ð Ø ÓÞ ÀÞ ¹ Ê²Ë ÎÄ ÐÐ ØÚ º ÀÞ¹ Ð ÒØ ¼ ½ Ú ØÓÖ¹ Ð Þ Ø Ò Ð Þ ØÓÖÓ Ö ÐØ Ð ÞÒ Ð Ö º ÔÓØØ Ö Ñ ÒÝ Ø ÒÙÑ Ö Ù Ò Ø ÖÓÐØ Ñ ÙØ Ð ÓÐ ÓÞØ Ñº Ú Þ Ð Ø Ñ ÒØ Ò Ð Ð Ñ ÒØ Ø ÖØ S 11, S 21, S 12 S 22 Ô Ö Ñ Ø Ö Ñ Ö Ö Ñ ÒÝ Ð Ø Ø ½º º Ö Òº Ñ ÒØ Ø ÖØ S 21 S 12 Ú Ð Ð Ö Ñ ÒÝ ÞØ ÑÙØ Ø Ó Ý Þ Ð ¹ Þ ÐØ Ñ ÒØ Ø ÖØ Ð Ò Ñ Ö ÐÖ Ò Þ Ò º ÀÞ¹ Ð ÐÑ Ú Þ Ð ØÓ ÐÚ Þ Ö Þ Ñ ØÓØØ ½º µ f c 7.3 ÀÞ Ö Ñ ÒÝ Þ Ô Øº Ú Þ Ð ¹ ØÓÑ Þ Ö ÒØ Ñ ÒØ Ø ÖØ Ú ÞÓÒØ ¼¼ ÀÞ º º º ÀÞ Ø ÖØÓÑ ÒÝ Ò Ð ÐÑ Ú Þ Ð ØÓ ÐÚ Þ Ö º 300 µñ¹ Þ Ð ÙÑ Ú Þ Ð Ø Ñ ÒØ Ð Ð Ò Þ Ñ Ö Ø ÓÖ Ó Ý Ð Ø ÓÒÒ Ð Ø ÐØ ØØ Ó Ü Ð ØÐ ÓÞ Ð Ð Ø Øº Ý Þ Ð ØÖ Ô Þ ÓÖÑ Ñ ÒØ Ñ Ö Ö Ñ ÒÝ Ð Ø Ø ½º½¼º Ö Òº Ø Ñ Ð Ú Þ Ð Ø Ñ ÒØ Ø Ò Þ Ð ÓÒÐ ÔÓØØ Ö Ñ Òݺ Þ ÐÚ Þ ØØ Ú Þ Ð Ø ½ ÀÞ ÀÞ Þ Ð Ò Ö ÞÓÒ Ò Ø ÑÙØ ØÓØغ Ú Þ Ð Ø Ö Ñ ÒÝ ÒØ ÔÓØØ S 11 Ô Ö Ñ Ø Ö Ð ÒØ Ò ÐØ Ö Å Þ Ñ ¹ Ø Ó Ð ÔÓØØ Ö Ñ ÒÝ Ø Ðº Ö Ü Ò Ú Ò Ó Ò Ñ Ñ Ð Ð ØÓÐ Ð Ø Ñ ÒØ Ñ ÒØ Ø ÖØ Ð Ð Ø Þ Øغ Ñ Ö Ö Ñ ÒÝ ÒØ ÔÓØØ S 21 Ô Ö Ñ Ø Ö ÐÐ Ò ÝÓÒ ÓÒÐ Å Å Ø Ö Þ Ñ Ø Ö Ñ ¹ ÒÝ ÒØ ÔÓØØ Ö Ñ ÒÝ Þº
28 ¾ Â Ì ½º ÅÁÆÌ Ì ÊÌ ÂÄ Ë Ì Ë ÅÇ ÄÄ Ë S xy [db] ref S ref S ref S 12 ref S f [Hz] x 10 9 ½º º Ö º Ú Þ Ð Ø Ñ ÒØ Ò Ð Ð Ñ ÒØ Ø ÖØ Ð Þ Ø Ò Ð Þ ØÓÖÖ Ð Ñ ÖØ S 11, S 21, S 12 S 22 Ô Ö Ñ Ø Ö º S xy [db] S 11 S 21 S 12 S f [Hz] x 10 9 ½º½¼º Ö º Ý ØÖ Ô Þ Ð Ú Þ Ð Ø Ñ ÒØ Ñ ÖØ S 11 S 21 S 12 S 22 Ú ÐØÓÞ Ö Ú Ò Ú ÒÝ Òº
29 ½º º ËË Ë ¾ ½º º Þ Þ Ú ÓÒÝ Ñ Ö Ú Ò Þ Ò Ð Ø Ø Ñ Ö Øò Ñ ÒØ ÖÒÝ ÓÐ ÐÐ Ô Ø ØÙÐ ÓÒ Ò Ñ Ö Ö Ð ÞØ ØØ Ó Ü Ð Ñ ÒØ Ø ÖØ Ú Ð Ñ Ñ Þ Ö¹ Ö Ð Ø ÖØ ÒØ Ð ØÖÓÑ Ò Ø Ö Ð ÑÞ ÞØ ÑÙØ Ø Ó Ý Ó Ü Ð ØÐ Ó¹ Þ Ð Ð Ø Ò Ú Ð Ñ ÒØ Ö Þ Ð ÓÐÝ ÓÐ Ú Þ ÐØ S 11 S 21 Ô Ö Ñ Ø ¹ Ö Ö Ñ ÒÝ Øº Þ Ø Þ Ö Ñ ÒÝ Ø Ñ Ö Ø ØØ Þ Ð Þ ÐØ Ñ ÒØ Ø Ö¹ Ø Ú Ð Ð Ò Þ Ð Ñ ÒØ ÓÒ Ð Þ Ø Ò Ð Þ ØÓÖÖ Ð Ú Þ ØØ Ñ Ö º Áº Ì ÁË ýöòý ÓÐ ÐÐ Ô Ø Ø Ö Ü Ø Ñ Ö Ñ ÒØ ¹ Ø ÖØ Ð ÞØ ÑÓ ÐÐ Þ Ú ÓÒÝÖ Ø Ñ Ò¹ Ø ÓÞ Ö Ö Ú Ò Þ Þ Ñò Ø Ò Ý Ò ÓÐÝ ÓÐ Ø ÒÝ Þ Þ ÐØ ¹ ÐÙ Ú Ý ÖÒÝ Þ Ø ÐØ Ð Ö Ø ÐØ» ÐÒÝ ÐØ Ð ØÖÓÑ Ò Ø Öº ÓÞ Ó Ý Ñ ÒØ Ö ÐØ Ö Ñ Ö Ð Ñ Ø ÑÓ ÐÐ ÞÒ ØÙ Ù Þ Þ ÖÒÝ ÓÐ Ö Ü Ø ÒÝ Þ Ñ Ö Ñ ÖÓ Ð ØÖÓÒ ÒÝ Ó ÓÒº Þ Ú ÒÝÓ ÖÒÝ ¹ ÓÐ ÐÐ Ô Ø Ñ Ö Ñ Þ Ö Ò Ñ Ð ÐÑ Þ Ø ÐÝ Ò Ñ Ö Øò Ø Ö ÒÝ Ñ ÒØ Ú Þ Ð Ø Ö º Å ÒØ Ø ÖØ Ø Ø ÖÚ ÞØ Ñ ÖÒÝ ÓÐ ÐÐ Ô Ø Ñ Ö Ö Ñ ÐÝ Ø Ú Ð Ñ¹ Ñ Þ ÖÖ Ð ÑÓ ÐÐ ÞØ Ñº ¾ ØÖ Ò ÞÑ Þ Ö Ü Ô Ö Ñ Ø Ö Þ ¹ ÑÙÐ Ö Ñ ÒÝ ÀÞ Ð ØØ ÑÙØ ØÒ Ø Ñ ÒØ Ð Ø Ðº ¾ Ö Ú Ð Ñ¹Ñ Þ ÖÖ Ð Ð Þ Ø ØØ ÑÓ ÐÐ Ø Ú Ð Þ Ñ ØÓØØ Ö Ü Ø ÒÝ Þ Þ Ñ Þ Öò Ò Ò Ñ Ý Þ Ñ Ð Þ Ø Ò Ð Þ ØÓÖ Ø Ú Ð Ñ ÒØ ¹ Ø ÖØ Ò Ñ ÖØ Ö Ñ ÒÒÝ Ð Ö Ú Ò Ø Ò Ò ÞÓÒÓ º Ú Ð Ñ¹Ñ Þ ÖØ Ò Ñ Ø Ð ÐØ Ñ Ð ÐÑ Ò Ý ÒÓÑ Þ Ö Þ Øò Ú ÓÒÝ ØÐ Ò ÒÓÖ Ø Ø Ø ÖØ ÐÑ Þ Ñ ÒØ ÑÓ ÐÐ Þ Ö Ñ Ð Ð ÔÓÒ¹ ØÓ Ð Ö Þ Þ Ö ÓÞ Ú ÞÓÒÝÐ Ò Ý òöò Ñ ØØ Þ ÖØ ÐÓ ¹ Ð Ò ÒÓÑ Ø Ø Ð ÓÒØ Û Ú Ð Ø¹ Ò Ð Þ Ð ÐÑ Þ Ð Ø Ø Ú Þ ÐØ Ñ Ú Ø Þ Òº
30 ¼ Â Ì ½º ÅÁÆÌ Ì ÊÌ ÂÄ Ë Ì Ë ÅÇ ÄÄ Ë
31 ¾º Þ Ø Ö Ö Ú Ò Ø Ö Ø Ð Ö Ö Ò Ð Ý ÒÐ Ø Þ Ö Ø Þ Ð ÓÖ Ð Ø Þ Ñ ØÖ Ü Ð Ñ Ö Ð Ñ ÒØ Ø ÖØ ÑÓ ÐÐ Þ Ö Ú Ð Ñ¹Ñ Þ Ö Ø Ò Ñ Ø Ð ÐØ Ñ Ð ÐÑ ¹ Ò Þ Ò Ú Ø Ö Ð Ñ Ø Ñ Ø ÖÓÞ Ö ÐÚ Ø Ð ÓÒÝÓÐÙÐØ Ö Ñ ¹ Ø ÖÓÞÞ Ñ ÓÐ ÔÓÒØÓ Ø Ò Ñ ÒÓÑ Ø Ø º Þ ÖØ Ú Ð ÞØÓØØ Ñ Û Ú ¹ Ð Ø Ð Ô Ñ Þ Ö Øº ÓÞ ÞÓÒ Ò Ó Ý ÖÑ ÐÝ Ò Û Ú Ð Ø¹ Ð Þ Ú ÒÝ Þ Ò Ð Ò Ø Ò Ö Ò Ð Ý ÒÐ Ø Ø Þ Ö Ò Ð¹ Ý ÒÐ Ø Ò Þ Ö ÔÐ ÓÔ Ö ØÓÖÓ Ò Þ ÅÊ ¹Ö ÔÖ Þ ÒØ Ò Ñ ØÖ Ü Ð Ñ Ø Þ Ñ Ø Ò º Þ Ø Ñ ØÖ Ü Ð Ñ Ø Ø ÒÙÐÑ ÒÝÓÞÓÑ Ú Ø Þ Þ ¹ Òº Þ Ð Ø Þ ½ Ö Ñ ÒÝ Ø Ö ÔÖÓ Ù Ð ÖÑ ÒÙÑ ¹ Ö Ù ÑÔÐ Ñ ÒØ Ð Ø Ø Ö Ý Ð ØÓÚ ÒÒ Ñ Þ Ö Ø ÐØ Ð ÒÓ Ø ÔÓÐ ÒÓÑ Ñ ØÖ Ü Ð Ñ Ö Ø Ú ÐØÓÞ Ö º ¾º½º Ð Þ Ú ÒÝ Ð ÞÓÖÞ Ø s 0 (x) Ð Þ Ú ÒÝ Ö Ú Ø Þ ÒÓÑ Ø Ý ÒÐ Ø ÖÚ ÒÝ s 0 (x) = N s 2 h i s 0 (2x i). i=0 ¾º½µ À Ð Þ Ú ÒÝ ÐÐ ØÚ Û Ú Ð Ø ÐÝ ØØ ÞÓ α¹ Ö Ú ÐØ Ø Þ Ö Ø¹ Ò Ò ÞÒ ÐÒ Þ ÒØ Ö ÐÓ Ò ÓÖ ØØ α Ö ØØ ÞÓÖÞ ØÓÖ Ö Ð Ð Þ Ú ÒÝ ÒÓÑ Ø Ý ÒÐ Ø ½ N s s (α) (x) = 2 1/2+α h i s(2x i), i=0 ¾º¾µ ½
32 ¾ Â Ì ¾º ÁË ÃÊ ÌÁ ýäýë ÅýÌÊÁ Ä Å ÁÊ Ä Ì ÖÑ Þ Ø Ò Ñ Ò Þ ÓÖ Þ Ð Ø Þ α¹ Ö Ú Ðغ Ð ÞÒ ÐÚ ÒÓÑ Ø Ý ÒÐ Ø Ø Ð ÞÓÖÞ Ø Þ i = N s +1,...,N s 1 Ò Ü Ö (s 00 s 0i ) = s 0(x)s(x i)dx = = 2 N s m,n=0 h mh n s 0(2x m)s(2x 2i n)dx. ¾º µ Î Ö ØÚ y = 2x m ÒØ Ö Ð Ú ÐØÓÞ Ö Ø Þ Ú Ø Þ Ð Ö ÓÞ Ø (s 00 s 0i ) = 2 = N s m,n=0 N s m,n=0 h m h n s 0 (y)s(y 2i n + m)dy/2 = h mh n (s 00 s 0 2i+n m ). ¾º µ À Ú Þ Ø Þ l = 2i + n m Þ Þ Ò Ü Ø Þ Ð Ö Ñ ÒÝØ Ô Ù N s N s+2i m (s 00 s 0i ) = h m h l+m 2i (s 00 s 0l ). ¾º µ m=0 l=2i m Ú Ö Ñ ÒÝ Ø Ø Ý Ø ÖØ Ý ÒÐ Ø a i = N s 1 l= N s+1 H il a l, ¾º µ Å ÐÝÒ ½ Ø ÖØ ò ØÚ ØÓÖ Þ a i = (s 00 s 0i ) ¾º µ ÒØ Ö ÐÓ Øº Ñ ØÖ Ü Ñ ÐÝÒ Ø ÖØ Ø Ö ÒÓÑ Ø Ý ÒÐ Ø Ý ØØ Ø Ð Þ Ø Ø Ð Þ Ð Þ Ö ÒØ H il = m h mh l+m 2i ¾º µ ÁØØ Þ Þ Þ Ñ Ò Ò ÓÐÝ Ò m Ò ÜÖ ÙØ Ñ ÐÝÖ Ñ Ò m {0,...,N s } Ñ Ò Ô l + m 2i {0,...,N s } Þº ¾º¾º Ë Ð Þ Ú ÒÝ Ö Ú ÐØ Ð ÞÓÖ¹ Þ Ø À Ð Þ Ú ÒÝ ÐÝ ØØ Ð Þ Ú ÒÝ Ö Ú ÐØ Ø Þ Ö Ô ÐØ Ø Ò Þ ÒØ Ö ÐÓ Ò Ñ Ö Ò ÐÓÔ Ö ØÓÖÓ Ö ÔÖ Þ ÒØ Ð Ò Ð Ø ÖÑ Þ Ø Ò Ò Ñ
33 ¾º º ÆÍÅ ÊÁÃÍË ÁÆÌ ÊýÄ ÊÌ Ã Ã Ö Ø ÓÖ ÒØ ÓÒ ÓÐ ØÑ Ò Ø Þ ÓÒÐ Ò Ð Ø ÞÒ Þ α¹ ÒÙÐÐ Ö Ú ÐØ Ð ÞÓÖÞ Ø Ø i = N s + 1,..., N s 1¹Ö ( s (α) 00 ) (s s0l = (α) (x) ) s(x l)dx. ¾º µ ÖÚ ¾º¾µ ¾º½µ ÒÓÑ Ø Ý ÒÐ Ø Ø s (α) 00 s 0l ÐÝ Ö Ö ÐÚ Þ ÒØ Ö Ð Ú ÐØÓÞ Ø Ñ Þ Þ Þ Ò Ü Ø Ú Ø Þ Ö Ñ ÒÝØ Ô Ù ( ) s (α) 00 s N s 0l = 2 α k=0 Þ ÒØ Ý Ø ÖØ ¹ Ý ÒÐ Ø N s+2l k i=2l k h k h i+k 2l ( ) s (α) 00 s 0l. ¾º½¼µ Ú Þ Ø Ñ Ö ÞÓ Ó a α l = N s 1 k= N s+1 H lk a α k, a α l = ( s (α) 00 s 0i ) ¾º½½µ ¾º½¾µ H α lk = 2α i h i h k+i 2l ¾º½ µ РРغ Ì ÖÑ Þ Ø Ò ØØ ÞÓ Þ Ò Ü Ò Ò Ñ ÒÙÐÐ ÖÙÐ ¹ ÓØ Þ Þ Þ Ò Ñ ÐÝ Ö Ñ Ò i {0,..., N s } Ñ Ò Ô k + i 2l {0,..., N s } Þº Ä Ø Ø Ó Ý Ñ ØÖ Ü Ò Ý Ò ÓÒÐ Ø Ö Ú Ð Ò Ð Ð Ð ÞÓÖÞ Ø Ñ ØÖ Ü Ö ¾º µ Ý 2 α ÞÓÖÞ Ø ÒÝ Þ Ú Ò Þ ÞØ Ð ÒØ Ó Ý Þ Ö Ø Ñ ØÖ ÜÒ Ò Ñ Þ ½ Ò Ñ Þ 1/2 α Ø ÖØ Þ Ø ÖØÓÞ ¹ ØÚ ØÓÖ Ø Ó Ù Ñ ÔÒ Þ ÒØ Ö Ð Ò ÖØ Òغ ¾º º Ð Þ Ú ÒÝ Ö Ú ÐØ ÞÓÖÞ ¹ Ø Ò ÒÙÑ Ö Ù ÒØ Ö Ð ÁÑÔÐ Ñ ÒØ ÐØ Ñ ¾º µ ÐÐ ØÚ ¾º½½µ Ø ÖØ Ý ÒÐ Ø Ø Å ØÐ ÖÒÝ ¹ Þ Ø Ò Ù ¹ Ù ¹½¼ Ù ¹½¾ Þ Ú ÒÝ Ö º à ¹ Þ Ø ØØ Ñ Ý Ø ÞØ Ð ÔÖÓ Ö ÑÓØ Ñ ÐÝ ÒÙÑ Ö Ù Ò ÒØ Ö Ð Ð Þ Ú ¹ ÒÝ Ø Ý Ý Ò Ð Ð 2 f Ö Ö ÔÓÒØÓØ Ð ÞÒ ÐÚ Þ Þ Ò Ñ ÒÙÐÐ ÐØÓÐ Ò Ü Ø Ú Ô ÞØ ÞÚ º ¾º µ Ñ ØÖ Ü Ö Þ Ö Þ Øò Ù ¹
34 Â Ì ¾º ÁË ÃÊ ÌÁ ýäýë ÅýÌÊÁ Ä Å ÁÊ Ä Ð Þ Ú ÒÝ Ö Ô Ð ÙÐ H = 0 0, , , , , , , , , , , , , , , , , , , , , , , , ¾º½ µ Ñ ØÖ Ü Ñ Ö Ø Þ Ò Ð Þ Ú ÒÝ Ø ÖØ ¼ ÐØÓÐ Ò Ü Ø Ò [0, N s 1) k ÐØÓÐ Ò Ü Ø Ò Ô [k, N s + k 1) Ý ÓÖ Ò Ø k = N s + 1,..., N s 1 Þ Þ ÔÓÒØÓ Ò 2(N s 1) 1 = 13 Ö k ÖØ Ö º Ä Ø Ø Ó Ý Ñ Ò Ò Ô Ö ØÐ Ò Ó ÞÐÓÔ Ò Þ ½ Ô ÖÓ Ó ÞÐÓÔÓ Ò Ô Ý ÒÝÓÐ Þ Ñ Ð ÐÐ ÓÖÓÞ Ø Ñ ØÐ Ñ ÐÝ Ð ¾¹¾ Ý ÓÖÑ µº Ñ ØÖ Ü Ñ Ò Ò Ó ÞÐÓÔ Ò Þ Ð Ñ Þ ½º Ñ ØÖ Ü ÒØ H Ñ ØÖ ÜÒ 2 α ¹ ÞÓÖÓ º. Ö Ú ÐØ ¾º½ µ¹ Ð H α H Ø ÖØ Ú Ø Þ Å ØÐ ÖÙØ Ò Ø ÞÒ ÐÚ µ , ¾º½ µ
35 ¾º º ÆÍÅ ÊÁÃÍË ÁÆÌ ÊýÄ ÊÌ Ã Ã ØÚ ØÓÖ Þ Ð Þ Ð Þ ½ Ø ÖØ Þ Ø ÖØÓÞ ¾º½ µ Ú ØÓÖ Å ØÐ ÒÙÑ Ö Ù ÔÓÒØÓ Ú Ð Ò Þ ÐÚ ÖØ ÃÖÓÒ Ö¹ ÐØ Ø º Ñ Ó ÖÑ ØÚ ØÓÖÓ Ö Ñ ÐÝ ÒÓÖÑ Ð ÙØ Ò Ñ Þ Ð ÐÐ ØÚ Ñ Ó Ö Ú ÐØ Ð Þ Ú ÒÝ ÞÓÖÞ Ø Ò ÒØ Ö Ð Ø Ú Ø Þ Ö Ñ ÒÝ Ø ÔØ Ñ ã α=1 = ,ã α=2 = Ñ ÓÐ Ó Ø ÒÓÖÑ ÐÒ ÐÐ Ý Ó Ý Ø Ð Ð Ò Þ Ð ÐØ Ø Ð, ¾º½ µ 1 = k 2 = k (M 1 + k)a α=1 k, ¾º½ µ (M 2 + 2M 1 k + k 2 )a α=2 k, ¾º½ µ ÓÐ m 1 M 2 Ð Þ Ú ÒÝ Ð Ñ Ó ÑÓÑ ÒØÙÑ º Ý Þ ÒØ Ö ÐÓ
36 Â Ì ¾º ÁË ÃÊ ÌÁ ýäýë ÅýÌÊÁ Ä Å ÁÊ Ä ÖØ α = 1 α = 2 Ø Ò a α=1 = ,a α=2 = , ¾º¾¼µ ËÞ Ö ØÒ Ñ Ð ÚÒ Ý ÐÑ Ø ÖÖ Ó Ý Ö Ù ¹ Þ Ú ¹ ÒÝ Ò Ò Ò Ò ÓÐÝØÓÒÓ ÖÑ Ò Ý Ø Ö Ú ÐØ ÞÓ Ò Þ Ö Ø Ð Þ Ú ÒÝ ÞÓÖÞ Ø Ò ÒØ Ö Ð Ð Ø Þ Þ Ò ÒØ H Ñ Ø¹ Ö ÜÒ Ú Ò 1/4, 1/8, 1/16, 1/32 Ø 1/64 Ø ÖØ º ÀÓ Þ Ø ÖØ Þ ¹ Ú ÒÝ Ø Ò Ñ Ñ Ö Ò ò Ö Ú ÐØ ÒØ Ö Ð Þ Ñ Ø Ø º H Ñ ØÖ Ü ØØ ÒÓÖÑ Ú Ð Þ Ñ ØÓØØ ÓÒ Þ Ñ Ò Ý Ù ¹ Ö Ò Þ ÖÖ cond(h) D Ù ¹½¼¹Ö cond(h) D10 1, Ù ¹½¾¹Ö Ô cond(h) D12 3, º Ò Ý ÓÒ Þ ÑÓ ÞØ Ö Ñ ÒÝ Þ Ó Ý H Ñ ØÖ Ü Ð Ñ Ò Ø ÖØ Ò ÐÐ ØÚ cha = b ÐÐ ò Ð Ò Ö Ý ÒÐ ØÖ Ò Þ Ö Ñ ÓÐ Ò b Ú ØÓÖ Ô Ñ ÓÐ Ò Ò Ý ÓÞ Ú Þ Ø ØÒ º È Ð ÙÐ Þ 1/2 ع ÖØ Þ Ø ÖØÓÞ ØÚ ØÓÖ Þ Ô Ð Ñ Ò ÒÙÑ Ö Ù Ò Ò Ñ ÔÓÒØÓ Ò ÒÙÐÐ ÚÓÐØ Ò ÝÓÒ ÓÐÝ ÓÐ ØÓÚ Þ Ñ Ø Ó Ø Ý ÞØ ÞÞ Ð Þ ØÙÐ ÒÙÐÐ Ö ÐÐ ØÓØØ Ñº Þ ÐØ ÐØ Þ Þ Ñ Ó Ô Ö Ò Ý Ö Ò ò Þ Ø Å ØÐ Ñ Ö Ò Ñ ØÙ ÔÓÒØÓ Ò Ñ ÖÒ Þ Ñ Ø Ô Ò ÓÐÝ Ý ÓÐÝ Ñ ØÓ ØÐ Ó¹ ÐÝ ÓÐ Ø Ñ Øغ ÒÙÑ Ö Ù ÒØ Ö Ð ÖÙØ ÒØ Ñ ÐÝ Þ Ñ Ø Ó Ø Ú ØÓØØ ÐÐ Ò Ö ÞÒ Ò Ñ Ñ ÖØ Ø Ñ Ú Ò ÞÒ Ð ÞØ Ó Ý Å ØÐ Ñ ØÖ ÜÑòÚ Ð Ø Ø ÝÓÖ¹ Ò ØÙ Ú Ö Ø Ò Ñ Ú Ð Þ Ú ÒÝ ÐÐ ØÚ Ö Ú ÐØ Ò Ð Ø Ð Ö Ú ÒÝØ ÞØ ÔÓÞ ÓÒ Ð Ñ Ø Ð Ð Ô¹ Þ ÐÝ Þ Ö ÒØ ÐÚ Þ Þ Ò¹ Ø Ö Ð Øº Ý Ý Ò Ôк [0; 1) ÒØ ÖÚ ÐÐÙÑ Òµ 2 f ÔÓÒØÓØ ÞÒ ÐÓ f ÐÐ Ø Ø º À f = 20 ÓÖ 2 20 = ÔÓÒØ Ú Ò Ý Ý Ò ÔÖÓ ¹ Ö Ñ Ð Þ Ú ÒÝØ Ð Ò Ò ÒÝ Ô Ö Ð ØØ Þ Ñ Ø Þ ÒØ Ö ÐÓ Ø Ñ ÐÝ ØÓ ÖØ Ý Ñ Þ Ø Þ f = 15¹ ÐÐ Ø Ô Ö Ñ ¹ Ó Ô Ö ÙØ ÐÚ Ð ¹ ÖØ Ý Ø º Ý ÓÖÐ Ø Ò ÒÒ Ð Ó Ð
37 ¾º º ÆÍÅ ÊÁÃÍË ÁÆÌ ÊýÄ ÊÌ Ã Ã Ø ÝÖ Ý Þ Ñ δ 0k ÞØÖ Ú Ð f = 20¹Ö Þ ÖØ ¾º¾½µ Þ Ð Ö Ú ÐØØ Ð Ú ØØ ÞÓÖÞ Ø ÒØ Ö Ð ÒÙÑ Ö Ù Þ Ñ Ø Ð a α=1 f=20 = ,a α=1 = ¾º¾¾µ Þ ÒØ Ò Ø Ñ ÒØ Þ f = 20¹ ÓÞ Ø ÖØÓÞ ÖØ Ý Ý Þ Ñ Ø¹ ÖØ Ñ ÓÐ a α=1 Ö Ñ ÒÝ Ú Ð Ñ ÐÝ Ø Ð Ð Ø Ø Ú ÖØ ØØ Ñ ¹ Ñ Ø ÐØ Ñº Þ Ñ Ø Ô Ñ ÐÝ Ò ÙØØ Ø Ó Ø Ú ÞØ Ñ Ý ¾ ÀÞ¹ ØÑ Ó Á ÔÖÓ ÞÓÖÖ Ð Ñ Ñ Ö Ú Ð Ö Ò Ð Þ Ý ÚÓÐØ Ñ Ò Ý Þ Ñ Ø Ò Ð ÞÓÒÓ º Ö Ø ÒÙÑ Ö Ù ÒØ Ö Ð Ò ÒÝ Ô Ö Þ Ò Ð Ø ¹ Ù Ñ ÓÐ Ð Ô Ò Ð ÐÐ ØÓØØ Ø ÖØ Ý ÒÐ Ø Ñ ÓÐ ÓÒ Ð ÔÙÐ Ñ Þ Ö Ò ÒÝ Þ Þ Ñ Ó Ô Ö Ú Ý Ñ Ö Ú ÙØ Þ ØØ Ð Ð Ø¹ Þ Ö Þ Ö Ö ÒÝ Þ Ñ ÓÐ Ò ÝÓ ÔÓÒØÓ Ý ÖØ ÐÑò Ò Þ ÙØ Ñ ÓÐ Ñ ÐÐ ØØ Þ Ðº,
38 Â Ì ¾º ÁË ÃÊ ÌÁ ýäýë ÅýÌÊÁ Ä Å ÁÊ Ä ¾º º Þ x Ú Ö Ø ÖØ Ð Þ Ú ÒÝ ¹ Þ ØØ Ö Ú Ð ÓÔ Ö ØÓÖÓ ÓÒ Ú Ð Þ Ñ Ø Ø Ð Ò Þ Ó Þ Ñ ÔÓÐ ÒÓ¹ ÑÓ Ð Ú Ð ÞÓÖÞ ÓÔ Ö ØÓÖÓ Ò Ñ ØÖ Ü Ð Ñ º À Ý x Ú ÒÒÝ Ð Ú Ð ÞÓÖÞ Þ ÓÔ Ö ØÓÖÙÒ Ñ ÐÝ Ø Ð Þ Ú ÒÝ Þ Ò Þ Ö ØÒ Ò Ö ÔÖ Þ ÒØ ÐÒ ÓÖ Þ ÓÔ Ö ØÓÖ Ò Ñ ¼ Ñ ØÖ Ü Ð Ñ i = N s + 1,...,N s 1¹Ö Ú Ø Þ ¾º½ Þ Þ Ò Ø Ö Ý ÐØ ÓÞ Ò ÝÓÒ ¹ ÓÒÐ Ð Ô Þ Ö ÒØ Þ Ñ Ø Ø ( s (α) 00 x s 0i ) = s (α) 0 N s = 2 2 α (x)xs(x i)dx = m,n=0 h m h n s (α) 0 (2x m)xs(2x 2i n)dx. ¾º¾ µ ÁØØ Ð ÞÒ ÐØÙ ¾º½µ ÐÐ ØÚ ¾º¾µ ÒÓÑ Ø Ý ÒÐ Ø Øº À Þ ÒØ Ö Ð Ú ÐØÓÞ Ø Ö Ð y = 2x m¹ö ( ) s (α) 00 x s N s 0i = 2 2 α h m h n s (α) 0 (y) y + m s(y 2i n + m)dy/2 = 2 m,n=0 = 1 2 N s 2α m,n= N s 2α m,n=0 h m h n ( s (α) 00 y s 0 2i+n m ) + mh mh n ( s (α) 00 s 0 2i+n m ), ¾º¾ µ Ñ l = 2i + n m Þ Þ Ú ÐØÓÞ Ú Þ Ø Ú Ð Ú Ø Þ Þ Ø ( ) s (α) 00 x s 0i = 1 2 N s 2α m= N s 2α Þ Ý Ð Ò Ö Ý ÒÐ ØÖ Ò Þ Ö ÓÐ Ñ ØÖ Ü Ð Ñ a α,(x) i = m=0 N s 1 l= N s+1 N s+2i m l=2i m N s+2i m l=2i m h m h l+m 2i ( ) s (α) 00 x s 0l + mh mh l+m 2i ( s (α) 00 s 0l ). ¾º¾ µ H α,(x) il a α,(x) l + b α,(x) i, ¾º¾ µ ( ) a α,(x) i = s (α) 00 x s 0i, ¾º¾ µ Ó ÓÐ ÐÓÒ Þ Ö ÔÐ ( Ú ØÓÖ Ø ÖØ ÐÑ ÞÞ ) Þ Ð Þ Þ Ò Þ ÑÓÐØ x 0 Ú Ö Ø ÖØ Ø Þ Þ s (α) 00 s 0l Ð ÞÓÖÞ ØÓØ b α,(x) i = 1 2 N s m=0 N s+2i m l=2i m mh m h l+m 2i ( s (α) 00 s 0i ) ¾º¾ µ
39 ¾º º X Î Æ ÎýÊÀ Ì ÊÌ Ã Ñ ØÖ Ü Ô Þ ÒØ Ò ÒÓÑ Ø Ý ÒÐ Ø Ð Þ Ñ Ø Ø H α,(x) il = 1 2 2α m h m h l+m 2i ¾º¾ µ Þ Þ Þ ØØ ÞÓ Ö Þ m Ò Ü Ö ÙØÒ ÓÐ m {0,...,N s } l + m 2i {0,..., N s } Ø Ð Ðº À ÓÐÝ Ò ÒØ Ö ÐÓ Ø Þ Ö ØÒ Ò Þ Ñ Ø Ò ÓÐ Ý Ð Þ Ú ÒÝ ÐØÓÐ Ò Ü Ñ ÒÙÐÐ ÒÓÑ Ø Ò Ü ¼¹ µ ÓÖ Þ Ð Ñ ÓÒ Ú Þ Ð Ø Ø Ú Þ ØÒ (s 00 x s 0i ) Ø ÔÙ ÒØ Ö ÐÓ Ö ( ) s (α) 0j x s 0i = = = s (α) 0 s (α) 0 (x j)xs(x i)dx = (y)ys(y i + j)dy + j ( s (α) 00 x s 0 i j ) + j y = x j (y)s(y i + j)dy = ( ) s (α) 00 s 0;i j. ¾º ¼µ s (α) 0 Å ØÐ ÖÒÝ Þ Ø Ò ÑÔÐ Ñ ÒØ ÐØ Ñ ÒØ ¾º¾ µ Ñ ØÖ Ü Ý ÒÐ Ø Ø ÒÙÑ Ö Ù ÒØ Ö Ð ÖÙØ ÒÒ Ð ÐÐ Ò Ö ÞØ Ñ Ñ Þ Ø Øº Ø Ñ Þ ÖÖ Ð ÔÓØØ ÒØ Ö ÐÓ α = 1¹Ö a α=1,(x) f=20 = , a α=1,(x) = ¾º ½µ ÒÙÐÐ Ò Ü Þ Ð Ö Ò Ð Þ Þ Ô a α,(x) 0 Ø ÖØ Ò ÝÓÒ Ò Ý Ñ ÖØ Ò ØØ Ð Ó Ý Ñ H α,(x) Ñ ØÖ Ü ÐÐ ØÚ b α,(x) Ú ØÓÖ Ð Ñ Ñ ØÖ Ü Ô Ö ØÐ Ò Ó ÞÐÓÔ Ò ½ º Ý Ð ÐØ Ö Ö Ð Ö ÒØ Ø Ð Ð Ø Ú ÐØÓÞØ Ø Ø Ú Ý Ó ÞÓÖÓ Ö Ò Ú Ð Ø Þ Ö Ñ ÒÝØ k = 0 Ò Ü Òº Þ Þ Ø Ò Ü Ø Ò ÖÞ ØÐ Ò Þ a α,(x) k Ö Ñ ÒÝ H α,(x) Ñ ØÖ Ü Ú Ý b α,(x) Ú ØÓÖ Ú ÐØÓÞ Ö Þ Þ ÒÓÑ Ð H α,(x) Ñ ØÖ Ü Ñ ÓÒ Þ Ñ ¹ Ò ØÙÐ ÓÒ Ø Ø º Ð Þ Öò Þ ÐÑ Ð Ø a α,(x) 0 = 0, 5 ÖØ Ø ÐÐ Ø Ò Þ Ñ Ø Ó ÓÞº.
40 ¼ Â Ì ¾º ÁË ÃÊ ÌÁ ýäýë ÅýÌÊÁ Ä Å ÁÊ Ä ¾º º Þ x 2 Ú ÒÝ Ð Þ Ú ÒÝ ÞÓÖÞ ¹ Ø Ò ÒØ Ö Ð Ú Ö Ø Ù x 2 Ñ ØÖ Ü Ð Ñ Þ i = N s + 1,...,N s 1 Ò Ü Ö Þ ¹ Ñ Ø Ø Þ Ð Þ ÓÒÐ Òº Ö Ú Ð Ò Ð Ð Ð Þ Ú ÒÝ Ö ( s00 x 2 s 0i ) = = 2 = 2 = ( s00 x 2 s 0i ) = s 0(x)x 2 s(x i)dx = N s m,n=0 N s m,n=0 N s m,n=0 N s m,n=0 N s m,n=0 N s m=0 N s m=0 N s m=0 h mh n h mh n s 0(2x m)x 2 s(2x 2i n)dx = y = 2x m s 0(y) y2 + 2my + m 2 s(y 2i n + m)dy/2 = 4 h m h n ( s00 y 2 s 0 2i+n m ) + mh mh n (s 00 y s 0 2i+n m ) + m 2 h m h n (s 00 s 0 2i+n m ) N s+2i m l=2i m N s+2i m l=2i m N s+2i m l=2i m h m h l+m 2i ( s00 x 2 s 0l ) + mh mh l+m 2i (s 00 x s 0l ) + m 2 h m h l+m 2i (s 00 s 0l ). ÒØ Ð Ò Ö Ý ÒÐ ØÖ Ò Þ ÖÖ Ú Þ Ø ÔÖÓ Ð Ñ ÓÐ Ö ØØ ÒØ Ö ÐÓ a (x2 ) i = N s 1 l= N s+1 l = 2i + n m ¾º ¾µ H (x2 ) il a (x2 ) l + b (x2 ) i, ¾º µ a (x2 ) i = ( s 00 x 2 s 0i ), ¾º µ
41 ¾º º X 2 ÅýÌÊÁ Ä Å Á ½ Ó ÓÐ Ð Ú ØÓÖ Ô ÒÙÐÐ Ð Ó Ú ÒÝ Ñ ØÖ Ü Ð Ñ Ø Ø Ö¹ Ø ÐÑ ÞÞ b (x2 ) i = N s N s+2i m m=0 l=2i m N s N s+2i m m=0 l=2i m mh mh l+m 2i (s 00 x s 0l ) + m 2 h m h l+m 2iδ 0l. ¾º µ ÁØØ Ø ÖÑ Þ Ø Ò Ð ÐÐ Þ Ñ Ø Ò (s 00 x s 0l ) º º a (x) i µ ÖØ Ø ¾º¾ µ Ð Ô Òº Ñ ØÖ Ü Ò ÝÓÒ ÓÒÐ Ø ÓÖ Ñ ØÖ ÜÓ Ö ¾º µ¹ö ¾º¾ µ¹ö H (x2 ) il = 1 4 h mh l+m 2i m ¾º µ ÓÐ Þ Þ Þ Þ ÒØ Ò ÞÓÒ m Ò Ü Ö ÖØ ÐÑ ÓÐ m {0,..., N s } l + m 2i {0,..., N s }º À Ý ÐØÓÐ Ò Ü Ñ ¼ ÓÖ ØØ Ú Þ ØÙ Ù Ú Þ ØÒ Þ Ö Ñ ÒÝØ Þ (s 00 x 2 s 0i ) (s 00 x s 0i ) ÒØ Ö ÐÓ Ö ( s0j x 2 s 0i ) = s 0 (x j)x2 s(x i)dx = = s 0 (y)y2 s(y i + j)dy + 2j + j 2 s 0(y)s(y i + j)dy = y = x j s 0 (y)ys(y i + j)dy + = ( s 00 x 2 s 0 i j ) + 2j (s00 x s 0 i j ) + j 2 (s 00 s 0 i j ). ¾º µ ¾º º Þ x 2 Ð Þ Ú ÒÝ ÞÓÖÞ Ø Ò Þ ÒØ Ö Ð À Þ Ö ØÒ Ò Ñ Ò ÞÒ Ò ÖÔÓÐ Ö ÓÓÖ Ò Ø ¹Ö Ò Þ Ö Ù Ö Ö ÒÝ Ö Þ¹ Ý ÒÐ Ø Ò Þ Ö ÔÐ x 2 ¹Ó Ø ÒØ Ö Ð Ø i = N s + 1,...,N s 1 Ò Üò Ð Þ Ú ÒÝ Þ ØØ ÓÖ ( ) s00 x 2 s 0i = s 0 (x) 1 x2s(x i)dx = N s = 2 h m h n m,n=0 N s = 2 h m h n m,n=0 s 0 (2x m) 1 x2s(2x 2i n)dx = y = 2x m s 0 (y) 4 y 2 + 2my + m 2s(y 2i n + m)dy 2 ¾º µ
42 ¾ Â Ì ¾º ÁË ÃÊ ÌÁ ýäýë ÅýÌÊÁ Ä Å ÁÊ Ä Ð Ø Ø Ù Ó Ý Þ ÐÝ Ò Ø ÔÙ Ø Ó Ò Ñ Ø Ø Þ Ð Ñ ÓÒØÓÐ Ó Ñ ÒØ Ö º ¾º º Þ x y Ø Ñ ÒÞ ÓÔ Ö ØÓÖ Ñ ØÖ Ü Ð Ñ Ã Ø Ñ ÒÞ Ð Þ Ú ÒÝ Ø Ð Ø Ø Ò Ý Ñ ÒÞ Ð Þ ¹ Ú ÒÝ Ö Ø ÞÓÖÞ Ø ÒØ ÐÐ Ø Ò Ð º ØÚ ÐØÓÞ x y Ú ÒÝ Ò¹ Ø Ö Ð i, k = N s + 1,...,N s 1 Ò Üò Ð Þ Ú ÒÝ Ð (s 00 s 00 x y s 0j s 0k ) = s 0 (x)s 0 (y)(x y)s(y j)s(x k)dxdy = = 4 N s m,n,p,q=0 h m h n h ph q s 0 (2x m)s 0 (2y n)(x y)s(2y 2j p)s(2x 2k q)dxdy = z = 2x m, v = 2y n ÒØ Ö Ð Ú ÐØÓÞ Ú Þ Ø Ú Ð = 4 = N s m,n,p,q=0 s 0(z)s 0(v) N s m,n,p,q=0 N s m,n,p,q=0 h mh nh p h q z v + m n s(v 2j p + n)s(z 2k q + m) dzdv 2 4 h mh nh p h q (s 00 s 00 z v s 0 2j+p n s 0 2k+q m ) + (m n)h m h n h ph q (s 00 s 00 s 0 2j+p n s 0 2k+q m ). r = 2j + p n, t = 2k + q m Þ Þ Ú ÐØÓÞ Ö Ð Þ Ö Ñ ÒÝ (s 00 s 00 x y s 0j s 0k )= = N s m,n=0 N s m,n=0 N s+2j n r=2j n N s+2j n r=2j n N s+2k m t=2k m N s+2k m t=2k m ËÞ ÒØ Ò Ð Ò Ö Ý ÒÐ Ø Ø ÔÙÒ a (x y) i = h m h n h r+n 2jh t+m 2k (s 00 s 00 x y s 0r s 0t ) + (m n)h mh nh r+n 2j h t+m 2k (s 00 s 00 s 0r s 0t ). N s 1 l= N s+1 = ¾º µ H (x y) il a (x y) l + b (x y) i, ¾º ¼µ
43 ¾º º X Y ÅýÌÊÁ Ä Å Á ÓÐ Ö ØØ ÒØ Ö ÐÓ Ó ÓÐ Ð Ú ØÓÖ b (x y) (2N s 1)k+j = 1 2 Ñ ØÖ Ü Ô N s m,n=0 a (x y) (2N s 1)k+j = (s 00s 00 x y s 0j s 0k ), ¾º ½µ N s+2j n r=2j n N s+2k m t=2k m (m n)h mh nh r+n 2j h t+m 2k (s 00 s 00 s 0r s 0t ) ¾º ¾µ H (x y) (2N s 1)k+j,(2N s 1)s+r = 1 2 N s m,n=0 h m h n h r+n 2jh t+m 2k. ¾º µ Þ Þ Þ ØØ ÞÓÒ m n Ò Ü Ö ÙØÒ Ñ ÐÝ Ö m, n {0,...,N s } r + n 2j, t + m 2k {0,...,N s } Ø Ð Ðº À Ý Ð Þ Ú ÒÝ Ò Ò Ò Ò ÒÙÐÐ ÐØÓÐ Ò Ü ÓÖ Ú Þ ¹ Ú Þ Ø Ø ÓÖ ÓÞ ÓÒÐ Ò Þ ÒØ Ö Ð Ù (s 00 s 00 x y s 0j s 0k ) Ð ÞÓÖÞ ØÓ Ö (s 0i s 0l x y s 0j s 0k ) = s 0(x i)s 0(y l)(x y)s(y j)s(x k)dxdy = z = x i, v = y l = (s 00 s 00 x y s 0 k i s 0 j l ) + + (i l) (s 00 s 00 s 0 k i s 0 j l ). ¾º µ ØÚ ÐØÓÞ (x y) 2 Ú ÒÝ ÒØ Ö Ð Ð Þ Ú ÒÝ Ö Ø ÞÓÖÞ ¹ Ø Þ ØØ i, k = N s + 1,...,N s 1 Þ Ý Ñ ÒÞ Ø Þ ÓÒÐ Ò Þ Ñ Ø Ø ( s00 s 00 (x y) 2 s 0j s 0k ) = s 0 (x)s 0 (y)(x y)2 s(y j)s(x k)dxdy = = N s m,n=0 N s+2j n r=2j n N s+2k m t=2k m ( s 00 s 00 (x y) 2 s 0r s 0t ) + N s m,n=0 N s+2j n r=2j n N s+2k m t=2k m h m h n h r+n 2jh t+m 2k (m n) h m h n h r+n 2jh t+m 2k (s 00 s 00 x y s 0r s 0t ) + N s m,n=0 N s+2j n r=2j n N s+2k m t=2k m (m n) 2 h mh nh r+n 2j h t+m 2k (s 00 s 00 s 0r s 0t ). ¾º µ
44 Â Ì ¾º ÁË ÃÊ ÌÁ ýäýë ÅýÌÊÁ Ä Å ÁÊ Ä Þ Ö Ñ ÒÝ Þ ÒØ Ò Ý Ð Ò Ö Ý ÒÐ ØÖ Ò Þ Ö Ñ ÓÐ ÒØ Ô Ø Ñ Ñ ÒØ Þ Ý Ñ ÒÞ Ø Ò a (x y)2 i = N s 1 l= N s+1 H (x y)2 il a (x y)2 l + b (x y)2 i, ¾º µ ØØ Ø Ñ ÒÞ ÒØ Ö ÐÓ Ð ÞÒ Ö ØØ ÖØ a (x y)2 (2N s 1)k+j = ( s 00 s 00 (x y) 2 s 0j s 0k ), ¾º µ Ó Þ Ñ ÔÓÐ ÒÓÑÓØ Ø ÖØ ÐÑ Þ Ø Ñ ÒÞ ÒØ Ö ÐÓ Ø ÐÐ Ð Þ¹ Ò ÐÒ b (x y)2 (2N s 1)k+j = = N s m,n=0 N s m,n=0 N s+2j n r=2j n N s+2j n r=2j n N s+2k m t=2k m N s+2k m t=2k m Ñ ØÖ Ü Ø Ò Ü Þ Ð Ö Ò Ð Þ (m n)h m h n h r+n 2jh t+m 2k (s 00 s 00 x y s 0r s 0t ) + (m n) 2 h mh nh r+n 2j h t+m 2k (s 00 s 00 s 0r s 0t ) ¾º µ H (x y)2 (2N s 1)k+j,(2N s 1)s+r = 1 2 N s m,n=0 h m h n h r+n 2jh t+m 2k ¾º µ Þ Þ Þ ÞÓÒ m n Ò ÜÖ Ò Ñ ÒÙÐÐ Ø ÓØ Ñ ÐÝÖ m, n {0,...,N s } r+n 2j, t+m 2k {0,..., N s } Ø Ð Ðº ¾º µ Ð Ø ØØ ¾º ¾µ Þ Þ a (x y) i º À Ñ Ò Ò Ý Ð Þ Ú ÒÝ Ò Ü Ø ÐÚ Þ ÒÙÐÐ Ð Þ Þ ÐÓÐ Ð Þ Ú ÒÝ Ø ÐØÓÐ Ù Þ i¹ l¹ ÔÓÞ Ú Þ Ú Þ Ø Ø Þ ÒØ Ö ÐØ Ñ Ö Þ Ñ ØÓØØ (s 00 s 00 (x y) 2 s 0j s 0k ) Ð ÞÓÖÞ ØÓ Ö (s 0i s 0l x y s 0j s 0k ) = (s 00 s 00 x y s 0 k i s 0 j l ) + + 2(i l) (s 00 s 00 x y s 0 k i s 0 j l ) + + (i l) 2 (s 00 s 00 s 0 k i s 0 j l ). ¾º ¼µ ¾º º Å Ð ÓÒØ Þ ÒØ Û Ú Ð Ø ¾º½µ ¾º¾µ ÒÓÑ Ø Ý ÒÐ Ø Û Ú Ð Ø Ð Þ Ú Òݹ Ø N s w(x) = 2 1/2 ( 1) i h i+1 s(2x i) i=0 N s w (α) (x) = 2 1/2+α ( 1) i h i+1 s(2x i). i=0 ¾º ½µ ¾º ¾µ
45 ¾º º ÈÇÄÁÆÇÅÇà ÅýÌÊÁ Ä Å Á Å Ë Ä ÇÆÌýËÁ Ë ÁÆÌ Æ Þ ÓÞ Ó Ý Þ ÒØ Ö ÐÓ Ò Ð Þ Ú ÒÝ Ö Ú ÐØ ÒÓÑ Ø Ò Ü Ø ÒÙÐÐ Ö Ð Ð Ú Ý ÐÐ ØÚ Û Ú Ð Ø Ö Ð º s ml (x) = 2 m/2 s(2 m x l) Ð Ð Ú Þ Ø Ø Ñ Ð ÓÒØ Þ ÒØò ¹ Ð Þ Ú ÒÝ Ö w ml (x) = 2 m/2 w(2 m x l) Ð Ð Ñ Ð ÓÒØ Þ ÒØò Û Ú Ð Ø Ö º ÓÖ ( ) ( ) s (α) 00 s ml = 2 m(1+α)/2 s (α) 0 (x) s(2 m x l)dx. ¾º µ ÒØ Ö Ð ÐÝ ØØ Ø ÒÓÑ Ø Ý ÒÐ Ø Ø ( ) N s s (α) 00 s ml = 2 α k=0 h k ( ) s (α) 00 s m 1 l 2 m 1 k, ¾º µ ÔÐ Ø Ø Ô Ù Ñ Ò Ø Ð ÓÒØ Ò Ü Ø Ò ÑÒÙÐÐ Ú Ú Ð ÞØ Ù ÓÖ Þ Ð Ý ÒÐ Þ ÙØ ØÙÒ ( ) ( ) s (α) nk s 2 αn s (α) 00 s m n l 2 ml = m n k, m > n, ( ) ¾º µ 2 αm s (α) 00 s n m k 2 n m l, n > m. À ÓÐÝ Ò Ð ÞÓÖÞ ØÓ Ø Þ Ö ØÒ Ò Þ ÑÓÐÒ ÓÐ Ð Ð Þ Ý ¹ Þ Ú ÒÝ Û Ú Ð Ø ÓÖ ÐÐ ÐÝ ØØ Ø Ò ¾º ½µ Ú Ý ¾º ¾µ Û Ú Ð Ø¹ Ø Ø Ñ ÒØ Ö Ð Ú ÐØÓÞ Ø ÐÐ Ö ÐÒ Ú Þ Ú Þ Ø Ø Þ ÒØ Ö ÐÓ Ø ÞØ Ð Þ Ú ÒÝ ÒØ Ö ÐÓ ( ) s (α) nk w ml = ( ) w (α) nk s ml = ( ) w (α) nk w ml = N s ( ) h i+1 s (α) nk s m+1 i+2l, ¾º µ i=0 N s h j+1 j=0 N s N s i=0 ( ) s (α) n+1 j+2k s ml, ¾º µ h j+1 h i+1 j=0 ( ) s (α) n+1 j+2k s m+1 i+2l. ¾º µ ¾º º ÈÓÐ ÒÓÑÓ Ñ ØÖ Ü Ð Ñ Ñ Ð ÓÒ¹ Ø Þ ÒØ Ò Þ Ð Þ Þ Ö Ñ ÒÝ Ø ÐØ Ð ÒÓ Ø Ù ÓÖ Þ x p ÔÓÐ ÒÓÑ ÒØ Ö Ð Ð Þ Ú ÒÒÝ Ð ÐÐ ØÚ ÒÒ Ö Ú ÐØ Ú Ð Þ ÞÓÖÓÞÚ Þ Þ ( ) s (α) 00 x p s ml = 2 m/2 s (α)(x)x p s(2 m x l)dx, ¾º µ ÒØ Ö Ð ¾º µ ÒØ Ö Ð ÓÞ ÓÒÐ Ñ ÓÒ Ð Ø Ø Øº À ¾º½µ ¾º¾µ ÒÓÑ Ø Ý ÒÐ Ø Ø Ð ÐÑ ÞÞÙ Ñ Ò Ø Ð Þ Ú ÒÝÖ Ñ ÞÓ Ó
46 Â Ì ¾º ÁË ÃÊ ÌÁ ýäýë ÅýÌÊÁ Ä Å ÁÊ Ä ÒØ Ö Ð Ú ÐØÓÞ ÐÐ ØÚ Þ Þ Ò Ü Ö Ø Ø Ù Ú Ö ÓÖ Þ Ð Ý ÒÐ Ø Ø Ô Ù ( s (α) ) 00 xp s 0l = ( p q = 2 α p p q=0 ) Ns k=0 N s+2l k i=2l k q=0 k=0 k q h kh i+k 2l ( s (α) 00 x q s 0 i ). ¾º ¼µ Þ Ý Þ Öò Ø ØØ ÓÖÑ Ò Þ Ð Ø Ö Ø Ú Ñ ØÖ Ü Ý ÒÐ Ø p N s ( p I (α),p l = 2 p q ÓÐ Þ Ñ Ø Ò ÒØ Ö ÐÓ Ö Ú Þ ØØ Þ ( ) I (α),p l = s (α) 00 x p s 0i ) k q M lk I (α),q k, ¾º ½µ Ð Ð Ø Ñ ØÖ ÜÙÒ ÞÓ Ó ÒÓÑ Ø Ý ÒÐ Ø Ð Ô Þ ØØ ¾º ¾µ M lk = i h ih k+i 2l. ¾º µ ÁØØ Þ Þ Þ ÞÓÒ i Ò Ü Ö ÙØ ÓÐ i {0,..., N s } k + i 2l {0,...,N s } ÖÚ ÒÝ º Å Ð ÓÒØ Þ ÒØ Ø Þ Ð Þ Þ Þ ÓÒÐ Ò ØÙ ÙÒ Ð ÖÒ ( s (α) 00 x p s ml ) = 2 p p q=0 ( ) p Ns q k=0 k q h k (s 00 x q s m 1 l 2 m 1 k), ¾º µ ÐÐ ØÚ Ñ Ò Ø ÒÓÑ Ø Ò Ü Ø Ò Ñ ÒÙÐÐ Ö Ú Ð ÞØ Ù ÓÖ 2 (α p)n p ( p ) ) q=0 q l q (s (α) 00 s m n l 2 m n k ( ) m > n, s (α) nk xp s ml = 2 (α p)m p ( p ) ) q=0 q k q (s (α) 00 s n m k 2 n m l n > m. ¾º µ ÁØØ Û Ú Ð Ø Þ Ö Ô ÐÒ Þ ÒØ Ö ÐÓ Ò Ð Ð Þ Ý Þ Ú ÒÝ ÐÝ Ò ÓÖ ¾º ½µ ÐÐ ØÚ ¾º ¾µ Ý ÒÐ Ø Ð ÞÒ ÐÚ Þ ÒØ Ö Ð Ú ÐØÓÞ Ö Ú Ð Þ Ð Ð Ó ÓÞ ÙØ ØÙÒ ( s (α) nk xp w ml ) = ( w (α) nk xp s ml ) = ( w (α) nk xp w ml ) = N s h i+1 ( s (α) nk xp s m+1 i+2l ), ¾º µ i=0 N s h j+1 j=0 N s N s i=0 ( s (α) n+1 j+2k xp s ml ), ¾º µ h j+1 h i+1 j=0 ( s (α) n+1 j+2k xp s m+1 i+2l ). ¾º µ
47 ¾º½¼º ËË Ë Þ Ø ( ÓÖÑÙÐ ) Ø ÑÔÐ Ñ ÒØ ÐØ Ñ ÐÐ Ò Ö ÞØ Ñ Å ØÐ ÖÒÝ Þ Ø Òº Þ s (α) 00 xp s ml ÒØ Ö ÐÓ m = 0,...,10 Ð ÓÒØ Þ ÒØ Ö Ú Ð Þ Ñ Ø ÒÙÑ Ö Ù ÒØ Ö Ð ÔÖÓ Ö ÑÑ Ð Ú Ð ÐÐ Ò ÖÞ ÙØ Ò ÔÓØØ Ö Ñ ÒÝ Ø Ý Ñ ØÖ Ü Ò Ø ÖÓÐØ Ñ Ó Ý ØÓÚ Ð ÓÐ ÓÞ Ø Ú Þ Ú ÒÝ Ñ ÝÓÖ¹ Ò Þ ØÓ ÓÞ ÙØ Ò º Þ Ò ÖØ Þ ÑÓÐ Ù Ý Ò Ò Ñ Ö ÑòÚ Ð Ø ÞÞ Ð Ð Ô Ð Ð Ò Ò Ñ Ð ÓÒØ Þ ÒØ Ò Ð ÒØ Þ Þ Ñ Ø Ò Ú Ø Þ ÐØ Ñ Ý Ý Þ Öò Ð ÓÒØ Þ ÒØØ Ð Þ ÐØÓÐ Ò Ü Þ Ð Ú Ð Ð Ñ ÞÓÒÓ Ø Ö Ù ÐØ Ñº Þ Ð Ú ÒÝ Ð ÓÒØ Þ ÒØ Ò Ò Ú Ø ÐÐ ØÚ Û Ú Ð Ø ¹ Ú Þ Ø Ø ¾º µ ÐÐ ØÚ ¾º ¹¾º µ ÓÖÑÙÐ Ø Ú Ð Ú Ð ØÓØØ Ñ Ñ ÒÙÑ Ö Ù ÒØ Ö Ð Ð Þ Ö ÔÖ Þ Öò Ò ÐÐ Ò Ö ÞØ Ñ Þ Ö Ñ ÒÝغ ÒÙÑ ¹ Ö Ù ÒØ Ö Ð Ø Ø ÒÝ Ö Ò Ñ Ø Ð ÔÓÒØÓ ÝÓÖ f = 15 Ô Ö Ñ Ø Ö Þ Ð Þ 2 15 ¹ ÒØ Ö Ð Ó ÞØ ÞÞ Ð Ú ÞØ Ñ Ð Ò ÒÝ Ø ÞÓÒ Ò 2 20 ÐÐ ØÚ 2 22 Ó ÞØ ÞÞ Ð Ð ÐÐ Ò Ö ÞØ Ñº Þ Ò Þ Ø Ò Þ ÝÖ ÔÓÒØÓ ÒÙÑ ¹ Ö Ù ÒØ Ö ÐÓ ÝÖ Ó Ò Ñ Þ Ð Ø ØØ Þ Ò Ñ Þ Ö ÑÑ Ð Þ Ñ ØÓØØ Ö Ñ ÒÝ Øº ¾º½¼º Þ Þ Ú Þ Ø ØØ Ñ Ö ÑÓ ÐÐ Þ ÓÖ Ð ÓÖ ÙÐ Ö Ò Ð Ý ÒÐ Ø Û Ú Ð Ø¹ Þ Ò Ú Ð Þ Ö Ø Þ Ð Ø Ø ÒØ Ö ÐÓ Ø Ú Þ ØØ Ñ Ú Þ Ò Ð Ø Ù Ò Ý¹ Ý Ñ Ö Øò Ø ÖØ Ý ÒÐ ØÖ Ú Ý Ð Ò Ö Ý ÒÐ ØÖ Ò Þ ÖÖ Ð ¹ Þ Ú ÒÝ Ö Ú ÐØ ÒÓÑ Ø Ý ÒÐ Ø Ò Û Ú Ð Ø Ð Þ ¹ Ú Òݹ Ø Ò Ø Ú Ðº Þ ÒØ Ö ÐÓ Þ ÑÓÐ Ø Þ Ñ Ø Ô Ò ÑÔÐ ¹ Ñ ÒØ ÐØ Ñ Ö Ø ÒÙÑ Ö Ù ÒØ Ö Ð Ð ÐÐ Ò Ö ÞØ Ñº ÁÁº Ì ÁË Ö Ö Ú Ò Ø Ö Ø Ð Ö Ö Ò Ð Ý ÒÐ ¹ Ø Þ Ö Ø Þ Ð ÓÖ Ð Ø Þ Ñ ØÖ Ü Ð Ñ Ö Ð Ñ ÒØ Ñ ÒØ Ø ÖØ ÓÑ ØÖ ÓÞ Ó Ò Ð ÐÑ Þ Ó Ñ Þ Ö ÐÓ¹ Ð Ò ÒÓÑ Ø Ø Ð ÓÒØ Ð Ö Ò Ð Þ Û Ú Ð Ø¹ Ò Ð Þ º Ö Ò Ð Ý Ò¹ Ð Ø ÓÔ Ö ØÓÖ Ò Û Ú Ð Ø¹ Ð Þ Ú ÒÝ Þ Ò Ú Ð Ö ÔÖ Þ ÒØ Ð ÓÞ Þ Þ Þ L 2 (R d ) ÓÐÝØÓÒÓ À Ð ÖØ¹Ø Ö Ð Ý ÒÐ Ø Þ Ö Ø l 2 (R d ) Ø Ö Ð Ö Ô¹ Ö Þ ÒØ Ð ÓÞ ÓÐÝ Ò ÒØ Ö ÐÓ Ø ÐÐ Þ Ñ Ø Ò Ñ ÐÝ Ò Û Ú Ð Ø»Ú Ý Ð Þ Ú ÒÝ Ö Ú ÐØ ÞÓÖÞ Ø Þ Ö Ô ÐÒ º Å Ú Ð Û Ú Ð Ø Ð Þ Ú ÒÝ Ö Ò Þ ÖØ Ð ØÐ Ò Þ Ú ÒÝ Þ Ø Þ ÒØ ¹ Ö ÐÓ Ø Ý¹ Ý Û Ú Ð ØØ ÔÙ Ö Ò Ñ Þ Ñ Ò Ò Þ Ñ Ø ÓÞ Ð Ò¹ Ð Ò ÐÚ ÞÒ Ø Ð Þ ØÓ Ò Ð Ø Ø ÖÓÐÒ Øº Ð Þ Ú ÒÝ ÓÑÔ Ø Ø Ö¹ Ø Ý Þ Þ ÒØ Ö ÐÓ Ò ÝÖ ÞØ ÒÙÐÐ Ø Ò Þ Ò Ò Ò Ø Þ Ú ÒÝ Þ Øغ Ã Ø ÞÓÒÓ Ð ÓÒØ Þ ÒØò ÝÑ ÓÞ Ô Ø Ð Ò Þ ÔÔ Ò ÐØÓÐØ
48 Ð Þ Ú ÒÝ Ú Ý Ø Ø Þ Ð Ð Ø Þ Ð Þ Ú Òݹ Ö Ú ÐØ ÞÓÖÞ Ø Ò Ò¹ Ø Ö Ð Ø Ú ØÓÖÖ ØÙ Ø Ñ Ð Ø Ò Þ ÐØÓÐ Ð Ò Ø Ñ ÒØ Ò Ü Ø ÞÒ ÐÚ º Þ Ú ØÓÖ Þ Ñ Ø Ø Ý ÓÐÝ Ò Ñ ØÖ Ü ½ Ø ÖØ Þ Ø ÖØÓÞ ØÚ ØÓÖ ÒØ Ñ ÐÝÒ Ð Ñ ÒÓÑ Ø Ý ÒÐ Ø Ý ØØ Ø Ð Þ Ñ Ø¹ Ø º Ð Ò Þ Ð ÓÒØ Þ ÒØò Þ Ú ÒÝ ÐÐ ØÚ Ö Ú ÐØ ÞÓÖÞ Ø Ò ÒØ Ö Ð Þ Ø Þ ÞÓÒÓ Ð ÓÒØ Þ ÒØò Ð Þ Ú ¹ ÒÝ ÐÐ ØÚ Ö Ú ÐØ ÞÓÖÞ Ø Ò ÒØ Ö Ð Ð ÒÓÑ Ø Ý ÒÐ Ø Ý ØØ Ø Ðº Þ ÓÐÝ Ò ÓÔ Ö ØÓÖÓ Ñ ÐÝ Ö Ú Ð Ñ ÐÐ ØØ ÔÓÐ ÒÓÑÑ Ð Ú Ð ÞÓÖÞ Ø Ø ÖØ ÐÑ ÞÒ Þ ÒØ Ò Þ ÑÓÐ Ø ÒÓÑ Ø Ý ÒÐ Ø Ý ØØ Ø Ò Ð¹ ÞÒ Ð Ú Ðº Ê Ö Ú Ò Ø Ö Ð Ö Ö Ð ÐÑ ÞÓØØ Ö Ò Ð Ý ÒÐ ¹ Ø Ò Þ Ö Ô ÐÒ ÐÝ Ò Ø Ó º µ Å ØÐ ÖÒÝ Þ Ø Ò ÑÔÐ Ñ ÒØ ÐØ Ñ Ð Þ Ú ÒÝ ÐÐ ØÚ Ö Ú ÐØ ÞÓÖÞ Ø Ò ÒØ Ö Ð Ø Þ Ñ Ø Ø ÖØ Ý ÒÐ Ø Ø Ñ ÐÐ Ô ØÓØØ Ñ Ó Ý Ù Ð Þ Ú ÒÝ Ö ÔÓØØ Ñ ØÖ ÜÓ Ò Ñ Ð ÓÒ ÓÒ ÐØ ÓÒ¹ Þ ÑÙ ½¼¼¼µ ÔÓØØ ÒØ Ö Ð ÖØ Ð Ò Ò Ò Ñ ÞÓÒÓ Ö Ú ÐØ Þ ØØ ¼ ÐØÓÐ Ò Ü Ñ ÐÐ ØØ ÓÐ ¼ ÖØ Ø ÐÐ Ò ÔÒ Ò Ñ Ð ÔÓÒØÓ º µ Ä Ú Þ ØØ Ñ ÔÓÐ ÒÓÑÓ Ò ÞÓÒÓ Ð ÓÒØ Þ ÒØò Ð Þ Ú ÒÝ ÐÐ ØÚ Ð Þ Ú Òݹ Ö Ú ÐØ ÞÓÖÞ Ø Ò ÒØ Ö Ð Ò Þ Ñ Ø Ö Ð Ð¹ Ñ Ñ ØÖ Ü Ý ÒÐ Ø Øº Å ÐÐ Ô ØÓØØ Ñ Ó Ý Ý p¹ Ó ÔÓÐ ÒÓÑÓØ Ø ÖØ Ð¹ Ñ Þ Þ Ð ÐÐ Ø ÓÞ Þ 0¹Ø Ð p 1¹ Ó ÔÓÐ ÒÓÑÓ Ø Ù Ý Ò¹ ÓÐÝ Ò Ð Þ Ú ÒÝ Ö Ú ÐØ µø Ø ÖØ ÐÑ Þ Þ ÒØ Ö Ð Ú ÞÓÒØ Þ Ñ ¹ Ø Ñ Ý Þ Ó Ñ ÒØ ÒÙÑ Ö Ù ÒØ Ö Ð Ú Ý ¹ Ò Þ¹ Ò ÐØ ÖÑ ÞÓÖÞ ØÓ Ø Ø ÖØ ÐÑ Þ ÒØ Ö ÐÓ Ö Ú Ð Ú Þ Ú Þ Ø º µ Ä Ú Þ ØØ Ñ ÑÔÐ Ñ ÒØ ÐØ Ñ µ ÔÓÒØ Ð ÒØ Ö ÐÓ Ð ÞÒ Ð Ú Ð ¹ Ð Ò Þ Ð ÓÒØ Þ ÒØò ÐÐ ØÚ Û Ú Ð Ø Ø Ø ÖØ ÐÑ Þ ÒØ Ö ÐÓ Þ Ñ Ø Ñ Øº Å ÐÐ Ô ØÓØØ Ñ Ó Ý ÔÓØØ ÒØ Ö Ð ÖØ Ò Þ µ ÔÓÒØ Ò Þ ¹ Ö ÔÐ ÔÓÒØ ØÐ Ò Ð ÓÒØ Þ ÒØ ÞØ Ð Ò Ò Ú Ú Ð ÝÖ Ò ¹ ÝÓ Ñ ÖØ Ò Ð Ò Ñ º
49 º Þ Ø Ï Ú Ð Ø Ð Ô ÔØ Ú Ñ ÓÐ ÙÐÐ ÑÚ Þ Ø Ø Ð Ö Ö Ò Ð Ý ÒÐ Ø Ö Ú ÐØÓÞ Ð ÓÒØ Ò Ð Þ Ò Þ Ð ØÖÓÑ Ò Ø Ö Þ ÑÙÐ Ò Ú Ð Ð ÐÑ Þ Ò Ñ ØРغ Å Ú Ð Û Ú Ð Ø Þ Ð ÐÑ ÞÓØØ Ñ Ø Ñ Ø ¹ Ö Ð Ð Ø Ö Ò Ú ÒÒ ÒÝÓÐÚ Ò Ú Ø Ð Ó Ð ÐÑ Þ ¹ Ù Ð Ø Þ ØØ Þ Ð ØÖÓÑ Ò Ø Ö Ð Ö Ò º Ð Ø Ñ ÒØ Ô Ð ÙÐ ½¼ Û Ú Ð Ø Ø Ý Þ Öò Ò Ø Ð ÓÐ ÓÞ Þ Þ ÒØ ÞÒ Ð Ñ ÐÝ ÔÓÒØÓ Ú Ý Ó ÓÐ Ð Ö Ñ ÒÝØ Ñ ÒØ ÝÓÑ ÒÝÓ ÓÙÖ Ö¹ØÖ Ò Þ ÓÖÑ º Þ Á Ø Þ Ò Û Ú Ð Ø Ð Ó Ð Ð ÓÞ ¹ Ð Ø Ò Ð Þ Ö Ú Ý Ô Ø Ñ Ö Ø Ð Ö Ó Ð Ô Ò Þ¹ Ò Ð Û Ú Ð Ø Ð Ô Ñ Þ Ö Øº ÞÓÒ Ò Þ ÖØ ÓÖ ÙÐØ Ñ Û Ú Ð Ø Ð Ñ ÖØ Ñ ÒØ Ø ÖØ Ø Ð Ö Ö Ò Ð Ý ÒÐ ØÖ Ö Ø Ñ Ñ ÓРغ Ï Ú Ð Ø Ð Ð Þ Ú ÒÝ Ð Ñ ÒØ Þ Ú ÒÝ Ð Ð Ø Ö Ò Ð Ý ÒÐ Ø Ø Þ Ö Ø Þ ÐÒ Ø ØÙ ÓÑ ÒÝØ Ö Ð Ø Ò Ú ÒÒ Û Ú Ð Ø Ñ ÓÐ ÔÖÓ Ö Ñ¹ ÓÑ Ó ½¾ º Ð Ò Ø Ò Ø Ø Þ Ð ØÖÓÑÓ Ñ Ò Ø Ö Ø ÐÐ ½ µ Ú Ý ½ µ Þ Ö ÒØ Û Ú Ð Ø Ð Þ Ú Òݹ Þ Ò Ø Ò Ö Ò Ð¹ Ý µ ÓÔ Ö ØÓÖÓ Ø Ñ ØÖ ÜÓ Ð Ö ÔÖ Þ ÒØ ÐÒ º Þ Ý ÔÓØØ Ñ ØÖ Ü Ý ÒÐ Ø Ñ Óй Ñ ½ µ Ú Ý ½ µ¹ Ð Ø Ý ØØ Ø Øº Þ Ð ØÖÓÑ Ò ¹ Ø Ö Ð Ö Ö Ú ÞÓÒÝÐ ÓÖ Ò Ð ÒÚ Ò Ú Ð Ò Ð Þ Ø Û Ú Ð ¹ Ø Ø Ð ÐÑ ÞÒ ÞÓÒ Ò Þ Ð Ò Ð Ø Ò ÒÝ Ú Ð ØØ ÙÐÐ Ø Ø ÒÝ Ö ÙØÓØØ Ð Ó Ý ÑÙØ ØØ Ó Ý Ò ÐÐ Þ Ö Ø Þ ÐÒ Ý Ð ØÖÓ¹ Ñ Ò Ø Ö Ø Ð Ö Ö Ò Ð Ý ÒÐ Ø Ø Û Ú Ð Ø Þ Òº Þ Ý Ð Ð ÐÐ ØÚ Ú Ø ÖÓÑ Ñ ÒÞ Ø Ö Ø Ø Û Ú Ð Ø Ð Þ Ñ ÒÞ Ø ÐØ Ð Ò Ú Ö Ò Ñ Þ Ö Ú Ð Þ Ð ½½ º Þ Ø Ø Ö Ø Û Ú Ð Ø Ð Ô Ð Ö Ò Ð Ý ÒÐ Ø Ø Ñ ÓÐ Ö Ò Þ Ö Ð ÒØ Ñ ½½¼ º Ã Ö ÓÔÓÖØ Ø Ð ØÖ Ð ÐÑ Þ Û Ú Ð Ø Ø Ð¹ ÓÖ Ò Ö ÖÓ ÙÐÐ Ñ ÓÑ Ò Ð Ö Ö Ö Þ Ð ØÖÓÑ Ò ÙÐÐ ÑÓ Ò Þ ØÓÑ Ð ØÖÓÒÔ ÐÝ ÓÞ ÓÒÐ Ñ ÓÒ Þ Þ ØØ Ð Ö Ö º Ï Ú Ð Ø Ð ÓÑ Ò ÐØ Ú Ð Ñ Ñ Þ ÖØ Ð Ø Ø Ð ÐÒ ½½ º
50 ¼ Â Ì º Ï Î Ä Ì Ä È ÈÌ Î Å ÇÄ ýë Ñ Þ Ö Ñ Ú ÒØÙÑÑ Ò Ð ÐÑ Þ Ó ÓÞ ÓÒÐ Ñ ÓÒ ÓÐÝ Ò ¹ Ö Ò Ð Ý ÒÐ Ø Ö Ö Ñ ÓÐ Ø Ñ ÐÝ Ø ÖØ ¹Ø ÔÙ Ñ ÒØ Ô Ð ÙÐ ÙÐÐ ÑÚ Þ Ø Þ Ö Ö ÞÓÒ ØÓÖÓ Ð Ö ÓÞ ÞÒ Ð ØÓ Ý ÒÐ Ø º º½º ÔØ Ú Ö Ò Ð Ý ÒÐ Ø¹Ñ ÓÐ Ñ Þ ¹ Ö Þ L 2 (R) À Ð ÖØ¹Ø Ö Ú ÐØÓÞ Ð ÓÒØ Ò Ð Þ ÓÐÝ Ò {V m, m Z} ÐØ Ö ¹ Ò ÓÖÓÞ Ø Ñ ÐÝ ÝÑ Ú ÒÒ Ý ÞÚ º Þ Þ ÐØ Ö ØÙÐ ÓÒ ÔÔ Ò Ð ÓÒØ Þ ÒØ Þ Ñ Ò Ý Ý ØÐ Ò s(x) Ð Þ Ú ÒÝ Ú Ö ¹ ÓÒ Ú Ð {s ml (x) = a m/2 s 0 (a m x bl) l Z} ÐØÓÐØ Ú Ð Ø Ø Þ Þ Þ Þ ÐØÓÐØ Ú ÒÝ Þ Ö Ò Þ ÖØ Ö ÓÖØÓÒÓÖÑ ÐØ Þ Ö Ò Þ ÖØ Ð ÓØÒ Þ ÓØØ Ð ÓÒØ Þ ÒØ ÐØ Ö Òº Ý f L 2 (R) À Ð ÖØ¹Ø Ö Ð Ú ÒÝ Ò Ñ ÐØ ØÐ Ò Ð Ð Ñ Ý Ð ÓÒØ Þ ÒØ Þ Ø ÖØÓÞ ÐØ ÖÒ Þ ÓØØ V m ÐØ ÖÖ Ú ØØ ÔÖÓ Þ Þ Þ m¹ Ð ÓÒØ Þ ÒØò Þ Ð Ø Ð Þ Ø Ø Þ Ð Ñ ÓÒ P m f(x) = f [m] (x) = l c ml s ml (x), º½µ ÓÐ Ø Ý ØØ Ø Ø c ml = (s ml f) Ð ÞÓÖÞ ØØ Ð ÐÐ Þ ÑÓÐÒ º P m V m ÐØ ÖÖ Ú Ð ÔÖÓ Ø Ð Ô Þ º V m ÐØ Ö ÓÖØÓÒÓÖÑ ÐØ ÓÑÔÐ Ñ Ò ÒÓÑ V m+1 ÐØ Ö Ò W m Ö Þ¹ Ð ØØ Ö Ú Ý Û Ú Ð Ø¹ ÐØ Ö V m+1 = V m W m. º¾µ Ñ ÐÝ Ò Þ Ö Ò Þ Ö Ø Ñ Ö ÑÐ Ø ØØ Û Ú Ð Ø Ð ÓØ {w ml (x) = 2 m/2 w 0 (2 m x l) l Z} À Ø Ø Ú ÐØÓÞ Ð ÓÒØ Ò Ð Þ Ø Ð ÐÑ ÞÞÙ À Ð ÖØ¹Ø Ö Ø Ð ÓÒع Ø Ù Þ Ð Ú Ø Ð Ò Ö Ø Þ Ö L 2 (R) = m=m 0 W m V m0 º µ ÓÐ m 0 Ý Ø Ø Þ Ð Þ Ø Ð ÓÒØ Þ ÒØ Ø ÒÝ Ö Ñ ÓÐ Ò ¹ Ö Ò Ð Ý ÒÐ Ø Ñ ÓÐ Ò Ð Ò ÝÓ Ð ÓÑÔÓÒ Ò º À Þ ÑÙÒ Ö Ð Ý M¹ Ð ÓÒØ Þ ÒØÒ ÔÓÒØÓ M > m 0 µ V M = M 1 m=m 0 W m V m0 º µ ÓÖ Ð Ò Ý f L 2 (R) Ú ÒÝØ Þ M¹ Ð ÓÒØ Þ ÒØ Ò Þ Ð Ø Ò º ÞØ Þ Ð Ø Ø Ð Ð f [M] ¹Ò к ÞØ Ø ÖÑ Þ Ø Ò ØÙ Ù Ø Ò Ñ Ò Þ {s Mk k Z} Ñ Ò Ô {s m0 k, w mk k Z, m = m 0, m 0 +1,...,M
51 º½º ÈÌ Î Á Ê Æ ÁýÄ ÆÄ Ì¹Å ÇÄ Å Ë Ê Ã ½ 1} Þ Ö Ò Þ Ö Ò f [M] (x) = k f [M] (x) = k c Mk s Mk (x) c m0 ks m0 k(x) + M 1 m=m 0 d mk w mk (x). k º µ º µ Ú ÐØÓÞ Ð ÓÒØ Ò Ð Þ Ø Ú Ð Ñ Ú Ð Þ Ð ØÖÓÑÓ Ñ Ò Ø Ö Ø L 2 (R) Ú Ý L 2 (R D )µ Ò ÝÞ Ø Ò ÒØ Ö Ð Ø Ú ÒÝ Ö Ð Þ Ð ØÖÓÑÓ Ñ Ò Ø Ö Ø Ø Ø Ñ ÒØ E(x) = c E l s 0l (x) + l Z H(x) = c H l s 0l (x) + l Z d E ml w ml(x) m=0 l Z d H ml w ml(x). m=0 l Z º µ ÁØØ E H Þ Ð ØÖÓÑÓ Ñ Ò Ø Ö ÓÑÔÓÒ Ò Ø Ð Ô Þ Þ Ð Þ¹ Ò Ø ÒÙÐÑ ÒÝÓÞÓØØ Ö Ò Ð Ý ÒÐ Ø Ò Ñ ÓÐ º À E(x) H(x) ÓÑÔ Ø Ø ÖØ ÓÖ Þ Ý ÓØØ m Ð ÓÒØ Þ ÒØ Þ Ø ÖØÓÞ Ø Ý ØØ Ø Ò Þ Ñ ÒÓÑ Þ ÒØ Ò Ú Ð Ú Ð 2 m ÐÐ ØÚ D Ñ ÒÞ ¹ Ò 2 md µ Þ Ö ÒØ Ð Þ Ñ ÒØ Ø Ý ÓÖÐ Ø Ñ Þ Ö Ò Ú Ð Ð ÐÑ Þ Ø Ø Ö Ò Ñ Ö Ð Þ Þ Ò Ò ÒÝ Ð ÓÒØ Þ ÒØ Ð ØØ Ð Ö Ø Þ Ñ Ø Ô Ø Ø Ö Øº Þ Ø Ý ØØ ¹ Ø Þ Ñ Ò ÜÔÓÒ Ò Ð Ò Ú Ø ÞÓÒ Ò Ñ Ð Ø Ð ÞÒ Ý ÔØ Ú ÒÓÑ Ø ØÖ Ø Ú Ð ½¾ º Þ ØÖ Ø Ð ÐÐ Ó Ý Ý Ú ÞÓÒÝÐ ÙÖÚ Ð ÓÒØ Þ ÒØ Ò Ñ ÓÐ Ù Ö Ò Ð Ý ÒÐ Ø Ø Ð Ñ ÓÐ Ð Ñ Ð ÓÐ ÐÐ ÒÓÑ Ø Ò Ð ÓÒØ ÓÒ Þ Ó Ø ÖØÓÞ Ú Ø Þ Þ ÒØò Û Ú Ð Ø Ø ÓÞÞ Ú Þ Þ Ö Ò Þ Ö Þ Ñ Ú Ø ØØ Þ Ö Ò Þ Ö Ò Ö Ñ ÓÐ Ù ÔÖÓ Ð Ñ Øº À Ý Þ Öò ÐÐ ÔØ Ù Ö Ò Ð Ý ÒÐ Ø Ò Ú Ò ÓÖ Ñ ÓÐ O(N) Ð Ô Ò Ø Ð Ð Ø Ñ ½¾ ÓÐ N Ñ ÓÐ Ò Þ ¹ Ö ÔÐ Þ Ú ÒÝ Þ Ñ ÐÐ ÔØ Ù ÓÔ Ö ØÓÖÓ Ø ÖØ Ý ÒÐ Ø Ò Ð ÒÒ Ð Ø ÖÑ Þ Ø Ò Ò ÝÓ Þ Ð Ô Þ Ñ º Þ Ú ÞÓÒØ Ñ Ò Ò ÔÔ Ò Ñ Ð Þ Ø Ó Ý Ð ÒÓÑ Ð ÓÒØ Þ ÒØ Ò Þ Þ Ð Þ ¹ Ú ÒÝ Ý ØØ Ø Þ Ñ Ò Ñ Ð Ð Ð Ý Ò N ÒÒ Ð Ð ÒÝ Ò ÐØ Ð Ò Ð ÙÖÚ Ð ÓÒØ Þ ÒØ Ò Ð Ò Ñ Ó Ð Ò ÝÓ Þ Ñ Ý Øع Ø Þ ÐÐ Ò ÔÓÒØÓ Ð Ö ÓÞº Þ ØÙÐ Ñ ÓÐ Ø ÑÓ ÐÐ¹Ö Ò Þ Ö Ò Ú Þ ØØ Ð ÑÞ Þ Ö ÒØ Ñ Ð ÓÒØ Þ ÒØò Û Ú Ð Ø ÖÙÐ ÜÔÓÒ Ò Ð Ò Ò Ð ÓÒØ Þ ÒØ ÒÓÑÓ Ú Ð Ý Þ Ò Ý Ö Þ Ø Ð Ò Ð ÒÝ ÓÐ Ø º Ð ÓÒÝ Ð ÓÒØ Þ ÒØ Ò Û Ú Ð Ø Ý Ö Þ Ð Þ ÓÒØÓ ÔÓÒØÓ Ð Ö ÓÞ Þ Ø Þ ÒØ Ò Þ Þ Þ Ð Þ Ú Òݺ Þ Ð Ô Ò Û ¹ Ú Ð Ø ÐÓ ÞØ Ø ÓÒØÓ Ð ÒÝ ÓÐ Ø Û Ú Ð Ø Ò Ñ Ø ÐÑ Þ Ú Ö Ñ Ò Ò Ð ÓÒØ Þ ÒØ Ò Þ Þ ØÙÐ ÓÒ ÔÔ Ò Ð ÓÒØ Þ ÒØ Ø
52 ¾ Â Ì º Ï Î Ä Ì Ä È ÈÌ Î Å ÇÄ ýë ÓÒ ÓÐÒ Ð Ø ½ º ÞØ Ó Ý Ó Ý Ò Ð Ø Ñ ÐÒ Ó Ý ÓÐ Þ ØÓÚ ÒÓÑ Ø Ó Ú Þ Ø Þ Þ Ñ ÐÝ Þ ÑÓÐ ÓØØ ÔÓÒØ Ò Ñ Ñ Ö ØÐ Ò Û Ú Ð Ø¹ Ý ØØ Ø Ð ÞÒ ÒÙÐÐ Ò Ð Ð ÒÝ Ò Ò ÝÓ ÏÓÐ ¹ Ò Ñ Ò ½¾ ØÐ Ø Ò ØÓÚ Ð ÞØ Ú Ð Ð Ø Ñ ÓÐ Ò ½ ÐÐ ØÚ Ö Ð Ø Ð Ø ÑÓÒ Ò ÖÖ Ó Ý Ñ ÓÖ Ð ÞÒ Þ Þ Ý ØØ Ø º Æ ÞÞ Ñ Ö Ò Ð Ý ÒÐ Ø Ø Ñ ÐÝ Ø Þ Ö ØÒ Ò Þ Ö Ø Þ ÐÒ º µ µ Ý ÒÐ Ø Þ ÑÙÒ Ö Þ Ö Ø Þ Ð Ø ÐÐ ÔÓØ Ò Ú ÒÒ µ ØÓ¹ Ú Ø ÓÐ ÓÞ Ø ÒÝ Ð (r 2 2 r + r ) 2 r k2 s E r (r) = kr 2 r2 E r (r). º µ º¾º Å ØÖ Ü Ý ÒÐ ØØ Ð Ø Å Ò Ò Ý µ º µ Ý ÒÐ Ø Ø Þ Ö Ø Ø Ö Ò Þ Ð Ñ Þ ÖÖ Ð Ð Ø Ö ÔÖ Þ ÒØ ÐÒ D m1 m 2,l 1 l 2 = χ(2 m 1 x l 1 ) ˆDχ(2 m 2 x l 2 )dx. º µ ÁØØ ˆD ØÓÚ Ö Ö Ò ÐÓÔ Ö ØÓÖ χ Ô Ú Ð Ñ ÐÝ Þ Ú ÒÝ ¹ Ð Þ Ú ÒÝ Ú Ý Û Ú Ð Øº Ò Þ Ð Ò ÖÑ ÐÝ ÙÐÐ ÑÚ Þ Ø Ý ÒÐ Ø Ö Ò ÐÓÔ Ö ØÓÖ Ò D m1 m 2,l 1 l 2 Ñ ØÖ Ü Þ Ñ Ø Ø Þ Ð Þ Þ Ø Ö Ñ ¹ ÒÝ Ò Ø Ú Ðº Ò Ý Ý ÒÐ Ø ÓÖ D [M] m 1 m 2,l 1 l 2 E [M] m 2,l 2 = KE [M] m 1,l 1, º½¼µ ÐÐ ØÚ D [M] m 1 m 2,l 1 l 2 E [M] m 2,l 2 = KA [M] m 1 m 2,l 1 l 2 E [M] m 1,l 1, º½½µ Ð ÓØ Ó ÐØ Ò ÓÐ A [M] m 1 m 2,l 1 l 2 º µ Ý ÒÐ Ø Ó ÓÐ Ð Ò Þ Ö ÔÐ r 2 ¹Ø Ð Ú Ð ÞÓÖÞ ÓÔ Ö ØÓÖ Ò Ñ ØÖ Ü Ð Ñ º Æ ÞÞ Ð Þ Ö º½¼µ Ò Ñ ÐØ Ð ÒÓ ØÓØØ Ø ÖØ Ý ÒÐ Ø Øº À Ñ Ø¹ Ö ÜÓ Ø Ó Ò Þ Ö ØÒ Ò Þ ÑÐ ÐØ ØÒ ÓÖ ÞÒ Ð Ø Ù Þ Ð Ð Ð Ø ½ (s m1 l1 ˆD s ) m2 l2 (s m1 l1 ˆD w ) m2 l2 (w m1 l1 ˆD s m2 l2 ) (w m1 l1 ˆD w m2 l2 ) = λ [M] c [M] m 1 l 1 d [M] m 1 l 1. c [M] m 2 l 2 d [M] m 2 l 2 = º½¾µ ÓÞ Ó Ý Ñ ÑÓÒ Ù Ñ ÓÖ Ð ÞÒ Þ Ý ØØ Ø º½¾µ Ý Ò¹ Ð Ø ÐÐ ØÚ º µ Ø M + 1¹ Ð ÓÒØ Þ ÒØ Ò Ñ Ö Ñ Ö Þ
53 º¾º ÅýÌÊÁ ÆÄ ÌÌ Ä Ã ÌýË M¹ Ñ ÓÐ Ø Þ Ð ÓÒ ÓÐ ØÑ Ò Ø Þ º Ì Ý Ð Ó Ý Ñ Ö Þ ÑÓÐØ ÓÒ ÓÐØ Û Ú Ð Ø¹ ÐØ Ö Ø Ø ÖØ ÐÑ Þ Ñ ÓÐ Ñ ÐÝ Þ E(x) Ñ ¹ ÓÐ Ø Þ Ð Ø Ẽ [M] (x) = l ev0 M 1 c [M] l s 0l (x) + d[m] ml w ml(x). l W f m m=0 º½ µ ÁØØ Ẽ[M] (x) Þ Ð Ò Ü ÞØ Ð ÒØ Ó Ý Þ M¹ Ð ÓÒØ Þ ÒØ Þ Ø ÖØÓÞ Ñ ÓÐ Þ Þ Ð Ð M 1 Ð ÓÒØ Ò Üò Û Ú Ð Ø Ú ÒÒ ÒÒ Ð ÙÐÐ Ñ Ô ÒÒÝ Ø Ð ÒØ Ó Ý Û Ú Ð Ø ÐØ Ö ÓÒ ÓÐØ Þ Þ ÞÓ Û Ú Ð Ø Þ Ö Ô ÐÒ Ø Ò Ñ ÐÝ Ò Ð Ò Ý Ø Ý ØØ Ø Ð Ð ÒØ ÖÙÐ º Þ Ð Ø Ø Þ Þ Þ ÐÑ ¹ Þ Ò l W m Ð Ð Ø Ú Þ ØØ ÒÒ Þ Ö Ó Ý w ml Û Ú ¹ Ð Ø l ÐØÓÐ Ò Ü Ð Ñ Þ m¹ ÓÒ ÓÐØ Û Ú Ð ØØ Ö W m Ò Ü ÐÑ Þ Ò º ÈÙ ÞØ Ò ÞØ Ñ ÓÐ Ø Ö Ò Ð Ý ÒÐ Ø ÓÔ Ö ØÓÖ Ø Ñ ÖÚ Ñ ØÙ Ù ÐÒ Þ (M + 1)¹ Ð ÓÒØ Þ ÒØ Þ Ø ÖØÓÞ Ý ØØ Ø Øº ÞØ Ñ ÐÐ Ý ÞÒ Ó Ý W m Ò Ü ÐÑ Þ Ø ÒÝ Ö ÓÐÝ Ò ÐÑ ÞÓ Ð ÐÐ Ñ ÐÝ Ø ÞÓÑ Þ Ó Ò Ü ÓÖÓÞ ØÓ Ð ÓØÒ º Å Ö ÙÒ ÒÒ Ð Ð Ð Ò Ð Ó Ý Ô Ö Ð Ö Ò Ð Ý ÒÐ Ø Ò ÓÔ ¹ Ö ØÓÖ ˆD Ð Ý Ò Ò Þ M¹ Ð ÓÒØ Þ ÒØò Û Ú Ð Ø¹ Ð Þ Ú ÒÝ Þ Ò Ö ÔÖ Þ ÒØ ˆD [M] º Å Ú Ð Ẽ[M] [M] Ú ÒÝ ÓÒ ÓÐØ Ø Ö Ð D Ö Ò ÐÓÔ Ö ØÓÖ Ø Ú ÒÝ ( D [M] λ [M] )Ẽ[M] = 0. º½ µ À Ö D [M] Ö λ [M] ÐÝ ØØ Ø Ð D¹Ø Ú Ý λ¹ø ÞÒ Ð Ù ÒØ Ý ÒÐ Ø Ò Ñ Ð Þ Þº Þ M¹ Ð ÓÒØ Þ ÒØò Þ Ð Ø ÞÓÒ Ò Ñ Ò Ø Ø Þ Ð Ú ÒÒÝ Ð ½ º [M] = (D λ [M] )Ẽ[M] 0. º½ µ ÓÖÓÒ Ú Ø Þ W M ÐØ Ö ÓÒØÓ Ý ØØ Ø Ò Ò Ü Ø Ñ Ø Ù Ñ ÒØ ÞÓÒ l¹ ÐÑ Þ Ø Ñ ÐÝ Ö Ø Ð ÐÒ Ú Ø Þ ÐØ Ø Ð ½º ÝÖ ÞØ ÓÞÞ Ø ÖØÓÞ Û Ú Ð Ø Ø Ò Þ Þ Ö Ô ÐØ Ð ÒÓÑ W M 1 ÐØ Ö Û Ú Ð Ø Ú Ð ¾º Ñ Ö ÞØ Þ r Ml = w Ml (x)(d λ [M] )Ẽ[M] (x)dx 2 º½ µ Ú ÒÝ Ò Ý ÖØ Ø º ÞØ Ó Ý Ò Ý Þ ØØ Ñ Ø Ð ÒØ ÞØ Þ Ñ Ø Þ ÔÓÒØÓ Ñ º ÇÐÝ Ò Û Ú Ð Ø Ð Ñ ÐÝ Ò ÐÝ Ò Ñ Ö Þ Ð Þ Ð ÓÒØ Þ ÒØ Ò Þ Ð Ø Ò ÚÓÐØ Ò Ñ Ö Ñ ÒÓÑ Ð ÓÒØ Þ ÒØ Ò Ó Ð Ð ÓÞÒ Þ ÖØ Ú Ò Þ ½º ÐØ Ø Ð ¾º Ô Þ Ñ Ø ÔÓÒØÓ ÓØ Ú ØÓØØ Ý Ð Ñ Ú ÒÒ
54 Â Ì º Ï Î Ä Ì Ä È ÈÌ Î Å ÇÄ ýë º½º Ø Ð Þ Øº ÓÒ ÓÐØ ÐØ Ö Ò ÔØ Ú Ñ ÓÒ Þ ÑÓÐØ Ẽ[M] 0 Ñ ÓÐ ¹ Ú ÒÝ Ø Ð Ñ ÓÐ Ú ÒÝ E [M] 0 M¹ ÐØ ÖÖ ÔÖÓ ÐØ Ú ÖÞ Ò Þ ÐØ Ö η = 10 8 ÓÖÐ ØÖ Ú ÐØÓÞ Ð ÓÒØ Ò Ð Þ V 0 W 0,...,W 3 й Ø Ö Òº Þ Ñ Ø Ô Þ Ñ Ø ÔÓÒØÓ Ø Ñ Ð Ö Þ Ø Ò Ñ Ø ÒØ ØØ Ñ Ð Ò º M δ P0 Ẽ [M] 2 0 δ Q0 Ẽ [M] 2 0 δ Q1 Ẽ [M] 2 0 δ Q2 Ẽ [M] 2 0 δ Q3 Ẽ [M] 0 ½ ¾ ÞÓ Ø w Ml Û Ú Ð Ø Ø ÐÐ Ú ÒÒ Ú Ø Þ Ð ÓÒØ Þ ÒØ Ñ ÓÐ Ñ ÐÝ Ø ÝÒ Ò Ò Ý ÐØ Ö Ø Ó ÓÞÒ Ò Þ Þ Ñ ÐÝ Ö r Ml Ð Ò Ýº ÞØ Ñ Þ ÖØ ÞÒ ÐÚ Ð Ó Û Ú Ð Ø¹ Ý ØØ Ø Ý Ø Þ Ñ ¹ Ø Ðº È Ð ÒØ Ý Ý Þ Öò ω Ö Ö Ú Ò Ó Þ ÐÐ ØÓÖ Ð Ô ÖÑÓÒ Ù Ø Ð Ö Ú ÒÝ Þ Þ Ú ÒÝ ÐÐ Ò Ñ ÔØ Ú Ñ Þ ÖØ ÞÒ ÐÙÒ Ñ ¾ ÔØ Ú Ø ÓÞ Ó Ý Ý 10 9 ÔÓÒØÓ ÓØ Ð Ö Ò º ÓÞ Ó Ý Ý ÐÝ Ò ÔØ Ú Ñ Þ Ö Ø Ñ Ñ Ö Ñ Ú Þ ÐØ Ñ Ó Ý Ñ ÓÖ Þ ÐØ Ö Ø Ð Ñ ÓÐ Þ ÔØ Ú Ñ ÓÐ Þ ØØ Ð ÓÒØ Þ ÒØ Ò Òغ Þ Ö Ñ ÒÝ Ø º½º Ø Ð Þ Ø Ø ÖØ ÐÑ ÞÞ Ñ Ò ØØ 10 8 Ñ Ð Þ ÓÖ º Ä Ø Ø Ó Ý Ó Ý Ø Ð Ð ÓÒØ Þ ÒØ Ò Ý ÒÒ Ñ Ý ÓØØ Ð ÓÒØ Þ ÒØ Þ Ø ÖØÓÞ Ö ÞÐ Ø Ò Ø Ð Þ Ø Ý Ó ÞÐÓÔ Ò Ð Ð º ËÞ Ð Ø ÞÓÒ Ò ÖÖ Ó Ý Þ Ý ØØ Ø Ø Ñ Ð Þ r Ml ÖØ Ù Ý Ò Ò Ñ w Ml (x) Û Ú Ð Ø Ý ØØ Ø Ò Ò Ý Ø Ð º Ì Ö Ò Ú Þ º½¾µ Ý ÒÐ Ø Þ Ø Ý Ð ÒÒ Ñ Ú Ò Ñ ÓÐ º Þ Ø Ý ØÐ Ò Û Ú Ð ØØ Ð È Ô Â ÒÓ Ñ Þ Ö Ø Ú ØÚ ½ E(d k ) = E [M] + d k w Mk. º½ µ Ø ÖØ Ø ØÙ Ù ÞÒ Þ Ð Þ Ø Ñ Ó ØÓØØ Ñ ÓÐ Ó Ð K [M] = (E(d k) ˆD E(d k )) (E(d k ) E(d k Ð Ò ÜØÖ ÑÙÑ Ø ØÙ Ù Ö Ò d )) k Ý ØØ Ø Ú ÐØÓÞØ Ø Ú Ð ξ ± ξ (w Mk ˆD E ) [M] 0 d k = 0 (w Mk ˆD E ) [M] = 0. º½ µ ÁØØ Ú Þ ØØ Ñ ξ = λ [M] (w Mk ˆD w ) Mk 2 (w Mk ˆD E ) º½ µ [M]
55 º º ýäì ÄýÆÇË ÌÇÌÌ Ë ÂýÌ ÊÌ Ã¹ ÆÄ Ì Ö Ú Ø Øº À (w Mk ˆD E ) [M] 0 ÓÖ Ð Þ Öò d k = 1/(2ξ) Þ Ð Ø Ø Ð ÐÑ ÞÒ Ù Ý Ò Þ d Mk Ø Ö ÖØ Þ ÑÐ Ø ØØ Ø Ò Ò Ý Þ Ñ Ø Ò Ø Ð Ø Ø Ó ÓÞ Ò Ú Þ Ò Ð Ú ÒÙÐÐ Þ Ð Þ Ñº º º ýðø Ð ÒÓ ØÓØØ Ø ÖØ ¹ Ý ÒÐ Ø À Ñ Ö Þ º½½µ ÐØ Ð ÒÓ ØÓØØ Ø ÖØ ¹ Ý ÒÐ Ø E [M] Ñ ÓÐ Ø Þ M¹ Ð ÓÒØ Þ ÒØ Ò Þ Ð Þ Ñ Þ ÖØ ÐØ Ð ÒÓ ØÚ Ú Ø Þ ÓÒ ÓРع Ñ Ò ØØ Ð Ñ Ð Ø ÒÓÑ Ð ÓÒØ Þ ÒØò Ý ØØ Ø Øº Æ ÞÞ Ñ Ý Û Ú Ð Ø ÓÞÞ Ò Ø Ø E(α k ) = E [M] + α k w Mk, º¾¼µ ÓÖ Ô ÖØÙÖ Þ Ñ Ø Ø K(α k ) = ( E(α k ) ˆD E(α ) k ) ( ) º¾½µ E(α k )  E(α k) Ø ÖØ Ò ÐÐ Ú Ò ÐÒ º À Ñ α Ñ Û Ú Ð Ø Ñ Ñ ÓÐ Ò Ñ Ò Ñ ÓÑÔÐ Ü ÓÖ K(α k ) = (E [M] ˆD E ) [M] + 2α k (w Mk ˆD E ) [M] + αk (w 2 Mk ˆD w ) Mk ) ) ( ). º¾¾µ (E [M]  E[M] + 2α k (w Mk  E[M] + αk 2 w Mk  w Mk dk/dα k = 0 Þ Ð ÖØ Ö Ò Ñ ÐØ Ð ÒÓ ØÓØØ Ø ÖØ ¹ Ý ÒÐ Ø Ñ ¹ ÓÐ ÓÞ ÓÒÐ Ò 0 = dk (α k ) = dα k [(w Mk ˆD E ) [M] + 2α k (w Mk ˆD w ) Mk )](E [M]  E[M] = + ) ) ( )] 2 + [(E [M]  E[M] + 2α k (w Mk  E[M] + αk 2 w Mk  w Mk [(w Mk ˆD E ) [M] + 2α k (w Mk ˆD w )] ) Mk 2α k (w Mk  E[M] ) ) [(E [M]  E[M] + 2α k (w Mk  E[M] + αk 2 ( )] 2 + w Mk  w Mk º¾ µ
56 Â Ì º Ï Î Ä Ì Ä È ÈÌ Î Å ÇÄ ýë + [(w Mk ˆD E ) [M] + 2α k (w Mk ˆD w )] ( ) Mk w Mk  w Mk ) ) ( )] 2 + [(E [M]  E[M] + 2α k (w Mk  E[M] + αk 2 w Mk  w Mk (E [M] ˆD E )( ) ( )] [M] 2 (w Mk  E[M] + 2α k w Mk  w Mk ) ) ( )] 2 [(E [M]  E[M] + 2α k (w Mk  E[M] + αk 2 w Mk  w Mk ( 2α k w Mk ˆD E ) ( )] )(2 (w [M] Mk  E[M] + 2α k w Mk  w Mk ) ) ( )] 2 [(E [M]  E[M] + 2α k (w Mk  E[M] + αk 2 w Mk  w Mk αk (w 2 Mk ˆD w )( ) ( )] Mk 2 (w Mk  E[M] + 2α k w Mk  w Mk ) ) ( )] 2, [(E [M]  E[M] + 2α k (w Mk  E[M] + αk 2 w Mk  w Mk º¾ µ Ñ Ø Ú Þ Ø Ñ D EE = D we = D ww = A EE = A we = A ww = (E [M] ˆD E [M] ) (w Mk ˆD E [M] ) (w Mk ˆD w Mk ) (E [M]  E[M] ) (w Mk  E[M] ) ( ) w Mk  w Mk º¾ µ Ð Ð Ø Þ Ð Ý ÒÐ Ø Ø ÔÓÑ dk/dα k = 0 ÐØ Ø Ð Ð 0 = α 2 k (D wwa we A ww D we )+α k (D ww A EE A ww D EE )+D ww A we A ww D we, º¾ µ Ñ ÐÝÒ Ñ ÓÐ º½ µ Þ Þ ÓÒÐ º º º Æ Ý Þ Ð Ø ÙÐÐ ÑÚ Þ Ø Ö Ò Ð Ý Ò¹ Ð Ø Ò ÔØ Ú ÒÙÑ Ö Ù Ñ ÓÐ Ý Þ Öò Ò Ý Þ Ð Ø ÙÐÐ ÑÚ Þ Ø Ø Ò Ñ ÓÐ ÓØØ Ñ ÙÐÐ Ñ Ý ÒÐ ¹ Ø Ø Ñ ÐÝÒ Ö Ñ ÒÝ º½º Ö Ò Ð Ø Ø º Ð Þ Ö ØÒ Ñ ÚÒ Ý ÐÑ Ø ÖÖ Ó Ý Þ Ö Ó ÓÐ Ð Ò Ø Ð Ð Ø ÙÐÐ ÑÞ Ó Ñ ÐÝ Ð ÒØ ÙÐÐ ÑÚ Þ Ø Ð Ò Ø Ö Ó Ø Ø Û Ú Ð Ø Þ Ñ Ø ÑòØ ÖÑ Ñ ÐÝ Ø Ô Ð ÙÐ Ý ÙÐÐ ÑÚ Þ Ø Ñ Ö Ø Ú Ð ÞÓÒÓ Ñ Ö Øò ÔÓØ Ò Ð Ó ÓÞ Ð ÐÑ Þ ¹ Ú Ð Ð Ø Ñ Þ ÒØ ØÒ º Þ Ñ ÐÐ Ø ÖÑ Ø Ð Ñ ÓÐ Ò Ð Ò Ú ÒÒ Ý ÒÒ Ú Þ Ð Ø Ø Ó Ý Ñ Þ ÖÖ Ð ÐØ Ý ØØ Ø Ó Ý Ò
57 º º ËË Ë M=0, full M=0, approx M=1, full M=1, approx M=2, full M=2, approx M=0, full M=0, approx M=1, full M=1, approx M=2, full M=2, approx º½º Ö º ÙÐÐ Ñ Ý ÒÐ Ø Ñ ÓÐ Ò Ý Þ Ð Ø ÙÐÐ ÑÚ Þ Ø Ö Ø ¹ Ð Ò Þ Ñ Ù Ö ÖÓÑ Ð ÓÒØ Þ ÒØ Òº ÓÐÝØÓÒÓ ÚÓÒ Ð Þ Ð Ø ÔÓÒØÓÞÓØØ ÚÓÒ Ð Ø Ð Ñ ÓÐ Ó Ñ ÐÝ Þ ÓØØ Ð ÓÒØ Þ ÒØ Þ Ø ÖØÓÞÒ º Ù ¹ Û Ú Ð Ø Ø ÞÒ ÐØÙÒ Ø Ø Þ Ð Ý Ðº 5 x full calculation prediction 8 x full calculation prediction 1 x full calculation prediction d [0] 0k 1 d [1] 1k 0 2 d [2] 2k k 2 1 k 2 2 k º¾º Ö º Æ Ý Þ Ð Ø ÙÐÐ ÑÚ Þ Ø Ø Ñ Ù Ò Û Ú Ð Ø Ý ØØ Ø Ø Ð ÒÙÑ Ö Ù Ñ ÓÐ Ð º½ µ Рк Ú Þ Þ ÒØ Ø Ò ÐÝ Ò Þ ÐØÓÐ Ò Ü Þ Ö Ô ÐÒ Ý ØÒÓÖÑ ÐÚ Ó Ý ÓÞÞ Ù Ø ÖØÓÞ Û Ú Ð ¹ Ø Þ ÔÔÓÒØ Ö Ð Ò Þ Ý ØØ Ø º Ù ¹ Û Ú Ð Ø Ø Ø Þ Ð Ý º Þ Ð Ø Ø Ð Ñ ÓÐ Ø Ò Ñ Þ Ú Ö º Ñ ÓÐ Ó Ñ Ò ÖÓÑ Ð ÓÒ¹ Ø Þ ÒØ Ò Þ ÒØ Ñ Ð Ò ÞØ Ø Ø ØÐ Ò ÚÓÐØ Ñ Ò Ø Ñ Ù Ö º ÆÝ ÐÚ Ò Ó Ý Ò Ð ÓÒØ Þ ÒØ Ý Ò Ø Ð Ñ ÓÐ Þ ØØ Ð Ò ÐÐ ØÚ Ó Ý ÝÖ ÝÓÖ Ò Ú ÐØÓÞ Ð Þ Þ Ö Ø Ñ ÓÐ Þ Þ Ñ Ò Ð Ñ ¹ Ò Üò Ñ Ù Ö Ð Ú Ò Þ ÒÒ Ð Ò ÝÓ Þ ÓØØ Þ ÒØ Ò Þ ÐØ Ö Ø Ñ ÓÐ Þ Øغ º¾º Ö Û Ú Ð Ø¹ Ý ØØ Ø Ø ÑÙØ Ø ÓÐÝØÓÒÓ ÚÓÒ ÐÐ Ð Ø Ð ÒÙ¹ Ñ Ö Ù Ñ ÓÐ Ý ØØ Ø Ø Þ ØÓØØ ÚÓÒ ÐÐ Ð Ô º½ µ Þ Ö ÒØ Þ Ð ¹ Ø Øº ýðø Ð Ò Ñ ÓÐØ Ý ØØ Ø Ò Ñ Ó Ò Ñ ÒØ ¾¼ Þ Þ Ð Ð Ð Ð Ð Þ Þ Ý ØØ Ø Ø Þ Ñ Ö Ò Þ Ö Ö Þ Ðº µº º º Þ Þ Ú Þ Ø ØØ Ñ Ö ÓÖ Ò ÙÐÐ ÑØ Ö Ø Ð Ö Ö Ò Ð Ý ÒÐ Ø Ø Þ ¹ Ö Ø Þ ÐØ Ñ Û Ú Ð Ø Þ Òº ÔØ Ú Ó ÓÞ ØÓ Ò ÐÓ Ð Ò ÒÓÑ Ø Ø Ð¹
58 Â Ì º Ï Î Ä Ì Ä È ÈÌ Î Å ÇÄ ýë ÓÒØ Þ ÒØò Ñ ÓÐ Ñ Þ ÖØ ÑÔÐ Ñ ÒØ ÐØ Ñ Ñ ÐÝ Ý ÓØØ Ð ÓÒØ Þ ÒØò Ñ ÓÐ Ð Þ Ú ÒÝ Û Ú Ð Ø Ý ØØ Ø Ð Ð Ø Ú Ø¹ Þ Ð ÓÒØ Þ ÒØò Û Ú Ð Ø Ý ØØ Ø Ö È Ô Â ÒÓ ÝÛ Ú Ð Ø¹Ô ÖØÙÖ ¹ ØÐ Ø Ø ØÓÚ Ð ÞØÚ ÐØ Ð ÒÓ ØÓØØ Ø ÖØ ¹ Ý ÒÐ ØÖ º Æ Ý Þ Ð Ø ÙÐÐ ÑÚ Þ Ø Ñ ÒØ Ö Ò Þ ÖÖ Ð ÞÓÐØ Ñ Ñ Þ Ö Ø ÓÒÝ Ø ÐØ Ý ØØ Ø Ñ Ò Ý Ø Ò Ú Ð Ý ØØ Ø Ø Ð Ð Ð Ö Ð Ð Ð ¾¼ Þ Þ Ð Ò Ø ÖØ Ð Ø ÒÝ Ö Ð Ð ÐÚ Þ Ý ØØ Ø Ò Ý Øº ÁÁÁº Ì ÁË Ï Ú Ð Ø Ð Ô ÔØ Ú Ñ ÓÐ ÙÐÐ ÑÚ Þ Ø Ø Ð Ö Ö Ò Ð Ý ÒÐ Ø Ö Æ Ý Þ Ð Ø Ò Ö Þ ÑÑ ØÖ Ù ÙÐÐ ÑÚ Þ Ø Ø Ð Ö Ø ÖØ ¹Ø ÔÙ Ö Ò Ð Ý ÒÐ Ø Ø Þ Ö Ø Þ ÐØ Ñ Þ ÐØ Ð Ñ ÑÔÐ Ñ ÒØ ÐØ Ñ ØÖ Ü Ð Ñ Ø Ú Ðº ÔÖÓ Ö Ñ Ý Ú Ø Þ Ð ÓÒØ Þ ÒØ Ø Ý ØØ Ø Ø ÐÐ ØÚ Þ ÓØØ Þ ÒØò Þ ÑÓÐ Ø Ñ ÐÒ Ô ÖÙØ Ò Ø ¹ Ú Ð ÙØÓÑ Ø Ù Ò ÔØ Ú Ñ ÓÒ ÒØ Ð Ó Ý Ñ ÐÝ Ø Ö Ð Ø Ò Þ ÒÓÑ Ø Ò Ð ÓÒØ Øº ÔÖÓ Ö Ñ Ñ Ò Ò Ð ÓÒØ Þ ÒØ Ò Ö Ñ ÓÐ Ö Ò Ð Ý ÒÐ Ø Ø Ý Ð ÒÝ Ñ Ø Ö Ø Ø Ö Ð ÓÞ Ô Ø Ñ ÒØ Ó Ý Ð ÒÓÑ Ð ÓÒØ Þ ÒØ Ò ÓÐ Ù Ñ Þ Ý ÒÐ Ø Ø Ó Ù Ð Ò Ñ Þ Ý ØØ Ø Øº µ Þ Ñ ØÖ ÜÓ Ð Ð Þ Ø ØØ Ñ Þ ÔØ Ú Ò ÒÓÑ Ø Ø Ð ÓÒØ Þ ÒØ Ø Ø ÖØ ÐÑ Þ ÙÐÐ ÑÚ Þ Ø Ø Ð Ö Ø ÖØ ¹ Ö Ò Ð Ý ÒÐ Ø Ø Ñ ÓÐ ÖÙØ ÒØ Ñ ÐÝ Ø ÖØ ÐÑ ÞÞ Ú Ø Þ Ð ÓÒØ Þ ÒØ Ð Ý ØØ Ø Ò Ý Ö ÚÓÒ Ø ÓÞ Ð Øº ¼ µ Ä Ú Þ ØØ Ñ Ý Ñ ØÖ Ü Þ Ñ Ø Ñ ÓØ ÓÐÝ Ò x p ÓÔ Ö ØÓÖÓ Ö Ñ ÐÝ Ò Ñ Ø Ø ÔÓÐ ÒÓÑÓ Þ ÒØ Ý Ó Ý ÓÐÝØÓÒÓ Ø Ö Ò Ø Ð ØÓÑ ¹ Ö Ò Ð Ý ÒÐ Ø Ø Þ Ö Ø Ø Ö Ò ÐØ Ð ÒÓ ØÓØØ Ø ÖØ ¹ Ý ÒÐ Ø Ø ÓÐ Ó Ñ º
59 º Þ Ø Ï Ú Ð Ø Ð Þ Ú ÒÝ Ð Ô ÖÙØ Ò ÓÐ ÓÞ Ò ÒÓ Þ Ö Þ Øò Ñ ÒØ ÞÙÔ Ö ØÖÙ Ø Ö Ò Þ Ô Ö Ð Ö Ñ ÒØ Ø ÖØ Ò Ò Ú Þ ÐØ Ú ÓÒÝÖ Ø Ø ÒÝ Ö Ú Ð Ñ Ð Ö Ø Ð Ð¹ Ð ò ØÖÙ Ø Ö Ø ÑÙØ ØØ Ô ÞØ Þ Ñ ÖÓ Þ ÔÔ Ð Ñ Ú Þ ÐØ Øº Ô ÞØ Þ Ñ ÖÓ Þ ÔÓ ÐÚ Ø Ð Ò ÞÓÒ Ò Ó ÞÓÖ Ñ Ñ Ö Ý Ò ÝÓ ¹ Ö Ø Ö ÞØ Ù Ó Þ Ø Ð Ñ ÒØ Ö ÖÚ ÒÝ ØØ ÖÑ ÒØ Þ Ø Ñ ÐÝÒ ÞÓ¹ ÒÓ Ø Ö Ù Ô Ø Åò Þ Ý Ø Ñ Ð ØÖÓÒ Ì ÒÓÐ Ì Ò Þ Ò ÅÓÐÒ Ö Ä ÞÐ Å Ð Ò Þ Ö Þ Ø ÒØÖ Ô Ð Ô ÐÓ Ð Þ Ò Ð Þ Ø ÞÒ ÐØ º Þ Ö Þ Ø ÒØÖ Ô Ý Ê ÒÝ ¹ ÒØÖ Ô ÓÒ Ð ÔÙÐ Ñ Þ Ö Ð Ð¹ Ñ Ù Ý Ò ÞÙÔ Ö ØÖÙ Ø Ö Ð Ñ Þ Ö ØÖ ÒÝÙ Ú ÞÓÒØ Ó Ý ÞÙÔ Ö¹ ØÖÙ Ø Ö Ð Ñ Ò ÞÓÒÓ Ø Ð Ò Þ Ò Ñ ÓÐ Ø Ñ Ú Ð ÔÖÓ Ð Ñ Ø Ú Ý Ø µ Ú ØÓÖ Þ Ò Ñ Ö Ø Ò Þ Ý Ú ØÓÖÓ ÞÓÒÓ Ø Ö Ú Þ Ø Ø Ú Þ º ÖÖ Ò Ð Ñ ÓÐ Ø Þ Ò ÝÓ Ñ Ö Ø Ð ØÖÙ Ø ¹ Ö ÓÞ Ø ÖØÓÞ Ú ØÓÖ ÞÓÒÓ Ø Ø Ø Û Ú Ð Ø¹ Ò Ð Þ Ø Ú Ðº º½º ËÞ Ö Þ Ø ÒØÖ Ô Þ Ö Þ Ø ÒØÖ Ô Ø È Ô Â ÒÓ Î Ö ÁÑÖ Ú Þ ØØ Ñ ÞÓ Þ Ô Ù Ö Ò Þ Ö Ð ØÖÓÒ ÐÓ ÞÐ Ò Ú Þ Ð Ø Ö ¼ Ñ Þ ÖØ ÅÓ Þ ÁÑÖ ¹ Ô Ø Þ Ø Ð ÞÒ ÐÒ Ò ÒÓ Þ Ö Þ Ø Ô ÞØ Þ Ñ ÖÓ Þ ÔÓ ÐÚ Ø Ð Ò Ò Ð Þ Ð Ö º ÓÔÓÖØ Ð ÒØ ÐÚ Ø Ð Ò Ø Ð Ð Ø Ñ ÒØ Þ ØÓ Ö Ø Ð ¹ Ñ ÒÞ ½ Þ Ö Þ Ø ÒØÖ Ô Ø Ú Ð Þ Ñ ØÓØØ Ð Ò ÝÓÖ ¹ Þ ØØ Ö ØØ Ø Ð ÐØ Þ Ø Ð Ò Þ Ú Ý Ð Ø¹ ÐÚ Þ Ø Ð Ô Ò ÒÓÖ Ò Þ Ö Ò º Þ S str Þ Ö Þ Ø ÒØÖ Ô q Ø ÐØ Ö ÒÝ Ñ ÒÒÝ Ø Ð Ý Þ ¹ Öò Ò Ê ÒÝ ¹ ÒØÖ Ô Ø Ú Ð Ð Ø Ú Þ ØÒ º Ê ÒÝ ¹ ÒØÖ Ô Ø Ë ÒÒÓÒ¹ ÒØÖ Ô ÐØ Ð ÒÓ Ø Ö Ú Þ ØØ Ê ÒÝ Ð Ö º
60 ¼ Â Ì º Ë ÍÈ ÊËÌÊÍÃÌÊýÃ Ë È ÊýÄýË Ý {p j j = 1,...,N, j p j = 1} Ú Ð Þ Òò Ð Ö Ò Ð Þ Ø Ð ¹ Ñ ÒÝ ÐÑ Þ i¹ Ê ÒÝ ÒØÖ Ô S i = 1 N 1 N ln p i j. j=1 º½µ Ä Ø Ø Ó Ý ÒÒ Þ i = 1 Ò ÜÖ Þ ÖØ Ë ÒÒÓÒ¹ ÒØÖ Ô ¾ ¼ ½ ¾ ½¼ ½½ º À Ô Ò Ô Ü Ð Ò ÒØ ÒØ ÒÞ Ø Ð¹ Ó ÞÐ Ø Ý ÒÓÖÑ Ð Ù Ó Ý Þ ½ Ð Ý Ò ÓÖ Ô Ô Ü Ð Ø Ð Ñ ÒÝ ÐÑ ÞØ Ð ÓØÒ ÒÓÖÑ ÐØ Ô Ü Ð ÒØ ÒÞ Ø Ù Ð Ñ ÒØ Ú Ð Þ Òò ¹ к Ä Ý Ò Ø Ø k¹ Ô Ü Ð ÒØ ÒÞ Ø I k 0, ÓÖ k = 1,...,N º¾µ N I k = 1, º µ k=1 ÓÖ Þ Ö Þ Ø ÒØÖ Ô ØÖÙØÙÖ Ð ÒØÖÓÔݵ S str = S 1 S 2 º µ Ð Þ ÓÐ Þ S i i¹ Ê ÒÝ ÒØÖ Ô Ò Ú Ð Þ Òò ÐÝ ØØ ÒÓÖÑ ÐØ Ô Ü Ð ÒØ ÒÞ Ø Ó Þ Ö Ô ÐÒ º À Ú Þ Ø q Ø ÐØ Ö ÒÝØ ÐÐ Ò ØÓÖµ Þ ln q = S 0 S 2 º µ Ð Ò ÒØ ÓÖ Þ Ö Þ Ø ÒØÖ Ô Ø ÐØ Ö ÒÝ Ú Ý ÒÒ ÐÓ Ö ØÑÙ ÝÑ Ú ÒÝ Ò Ö ÞÓÐ Ø º Ð Ø Ø Ó Ý Ñ Ò Ò ¹ Ñ ÒÞ Ö Ñ Ò Ò Ð Ò Ø ÔÙ Ö Ôк Ù ÜÔÓÒ Ò Ð n¹ Ó ØÚ Òݹ Ú ÒÝ Þ Ö ÒØ µ ݹ Ý Ð Ñ Ø ÖÓÞÓØØ Ö Ó Ö ÞÓÐ Ò S s tr(lnq) Ö ÓÒÓÒº Þ Ö Ñ ÖØ ¼ ½ ½¼¾ ½¼ Ý Ý Ñ Ö ØÐ Ò Ð Ò ò ÐÓ ÞÐ ÙÒ Ô Ò µ Ú Ò Þ Ñ Ø Ù Ö Þ Ö Þ Ø ÒØÖ Ô Ø Ø ÐØ Ö ÒÝØ ÞØ Ö ÞÓÐ Ù Ú Ð Ñ ÐÝ Ð Ò Ø ÔÙ Ö Ö Ú Ý Ò¹ Ò ÞÚ ØÐ Ò Þ Ð Ñ ØÙ Ù ÑÓÒ Ò Ó Ý Þ ÓØØ ÐÓ ÞÐ Ñ ÐÝ Ò Ð Ò Ð Ö Ò Ð Þ º v str = (lnq, S str ) Ú ØÓÖ Ð ÐÐ ÑÞ Þ ÐÓ ÞÐ Ø Ô٠غ À ÞÓÒ Ò Þ ÐÓ ÞÐ ÙÒ Ú Ý Ò Ø ÖØ ÐÑ Þ Ø Ð Ð Ò Ð Ö Ò Ð¹ Þ Ø Ö Ð Ø Ø Ô Ð ÙÐ Ò Ý Ð Ò Ò ÞÚ ÜÔÓÒ Ò Ð ØØ Ö Ò Ø Ð Ð Ø Ð ØÚ ÒÝ Ú ÒÝ Þ Ö ÒØ Ú Ð ò Ñ ÒØ Þ ØÓ ÓÖ ÑÙй Ø ÔÐ Ø Ú Þ Þ ÞÓÖÞ Ð Ô ÞÙÔ Ö ØÖÙ Ø Ö Ø Ò Ø Ñ ÒØ Þ Ø (ln q, S str ) Ú ØÓÖ Ò Þ Ó Þ Ö Ô ÐÒ Þ Ö Þ Ø ÒØÖ Ô Ø ÐØ Ö ÒÝ Ö Ó¹ ÒÓÒ Ø ÓÑÔÓÒ Ò Ò Ñ Þ Ô Ö Ð Ø Ò Ñ Ñ Ö Þ Ý Øº Ð Ò Þ Ð Ú Ð Ð Þ Ô Ö Ð Ö Ð ÐÑ Ð Ø Û Ú Ð Ø¹ Ò Ð Þ º º¾º À ØØ ÖÑ ÒØ Þ ØÓ Ð Ú Ð ÞØ Ð Ñ ÞØ Ñ Ó Ý Ó Ý Ò Ú ÐØÓÞ Ù ÜÔÓÒ Ò Ð Ñ Ó Ó Ø¹ Ú ÒÝ Ú ÒÝ Þ Ö ÒØ Ð Ò Ð Ö Ò Ð Þ ÐÓ ÞÐ Ó v str Ú ØÓÖ Ú ÐØÓÞ
61 º¾º ÀýÌÌ ÊÅÁÆÌý ÌÇÃ Ä ÎýÄ Ë ÌýË ½ S str q º½º Ö º ËÞ Ö Þ Ø ÒØÖ Ô Ø ÐØ Ö ÒÝ Ú ÒÝ Ò Ù µ ܹ ÔÓÒ Ò Ð µ Ñ Ó Ó ØØÚ ÒÝ Ú ÒÝ Þ Ö ÒØ µ Ð Ò Ð Ö Ò Ð¹ Þ ÐÓ ÞÐ Ó Ö ÐÐ ØÚ Û Ú Ð Ø¹Ö Ò Þ ÓÖÑ ÐØ Ù Ö m = 0,...,8 Ð ÓÒØ Þ ÒØ Ö º ¾¹ Ñ ÒÞ Ù ÜÔÓÒ Ò Ð Ñ Ó Ó ØÚ ÒÝ Ú ÒÝ Ð ¹ Ò Þ Ø ÖØÓÞ ÐÑ Ð Ø Ö Ø ÐØ ÒØ Ø Ñ Þ ØÓØØ ÔÓÒØÓÞÓØØ ÐÐ ØÚ ÔÓÒعÚÓÒ Ð Ø ÔÙ ÚÓÒ Ð Ð Þ ÐÑ Ð Ø Ø Ö Ö Ø Ú Ø ÓÐÝØÓÒÓ ÚÓÒ ÐÐ Ð Ö ÞÓÐØ Ñ Ð ØØ Ò Ñ Ô ØÙÒ ÔÓÒØÓغ Ð ÓÒØ Ò Ð Þ Ð Ô ÓÖ Ò Þ Ö Ñ ÒÝ Ø º½º Ö Ø ÖØ ÐÑ ÞÞ º Ð ¹ Ò Ñ Ò Ý Ø m = 0,...,8 Ð ÓÒØ Þ ÒØ Ò Ú Þ ÐØ Ñ Þ Þ Ð Ð ÓÐ Ð Ð ÙÖÚ Ð ÓÒØ Ó Ö Ð Ú ÒÓÑÓ Ð ÓÒØ Ð Þ Ð Ó ÓÐ Ð ÔÓÒØ Ñ Ò Þ Ö Ø Ö º Ä Ø Ø Ó Ý Ó Ý Ð¹ ÓÒØ Ò Þ ÐÓ ÞÐ Ó Þ Ò Ó Ò ÓÒÐ Ø Ò Ð ÔÓ Ö Ö Ñ Ò Ð Ð Ò Ú ÝÙÒ ÒÒ Ð ÝÓÖ Þ ÓÐÝ Ñ Øº Å Ó Ð Ô ÒØ Ñ ÒØ Ñ Ø Ö Ô Ø Ð Þ Ø ØØ Ñ Ý Ø Ú ÞÙÔ Ö¹ ØÖÙ Ø Ö Ø Ý Ò Ý Ñ Ö Ø Ð Ù ¹ Ú ÒÝ Ð Ø Ö Ø Ö Þ¹ Ø Ù Ó Þ ÜÔÓÒ Ò Ð Ðº ÔÓØØ Ö Ø Û Ú Ð Ø¹ØÖ Ò Þ ÓÖÑ ÐØ Ø º¾º Ö º Ý Ù ¹ Ú ÒÝ Ð ÐÐ ØØ ÖÑ ÒØ Þ Ø Ø ÜÔÓÒ Ò¹ Ð Ú ÒÝ ÞÙÔ ÖÔÓÞ ÐÐ ØÚ ÔÓØØ Ô Ù ¹ Û Ú Ð Ø¹ ØÖ Ò Þ ÓÖÑ º Ð Ô Ñ Ò Ð Þ Ú Òݹ Ý ØØ Ø Þ Ð¹ Ô Ø ÞÓÑ Þ Ó Ð Þ Ú Òݹ Ô Ð Ò º Þ Ö Ø Þ ¹ Ð ÞØ Ñ Ó Ý Þ ÓÒÐ Ø Ø Ð Ý Ò º Ð ÓÒØ Þ ÒØ ÓÖÖ Ò Ò m = 8, 5, 3, 2, 1 m = 8 Þ Ö Ø Ôµº
62 ¾ Â Ì º Ë ÍÈ ÊËÌÊÍÃÌÊýÃ Ë È ÊýÄýË º¾º Ö ÑÙØ Ø º Æ Ñ Þ ÓØØ Ð ÓÒØ Ð Þ Ú Òݹ Ý ØØ Ø Ø Ö ÞÓÐØ ØØ Ñ Ò Ñ Ø ÝÑ Ø Ú Ø Þ ÒØ Þ Ð ÞÓØØ Ö Ò ¹ Ð Ò Ø Ñ Ö Ð Ð Ð Û Ú Ð Ø¹ Ý ØØ Ø ØÐ Ò Ð ÐØ Ø Ø Ñ µº Ò Ý Ð ÓÒØ Ö Ø ØÖ Ò Þ ÓÖÑ Ð Ô ÙØ Ò Ð ÓÒÐ Ø Ò Þ Ö Ø Ö ÓÞ Þ Ò Ñ Ð ÓÒØ Þ ÒØ Þ Ø ÖØÓÞ Ð Þ ¹ Ú ÒÝ Ø ÖØ Ò Ó Þ Ø Ð Ò Ñ Ð Ô ÒÓÑ Ñ ÒØ Þ Ø Ö Ø Ö ÞØ Ù Ó Þ Øº Ñ ÓÖ Þ Ú ÒÝ Ø ÖØ Ñ Ö Ò Ý Ð ØØ ÖÑ ÒØ Þ ØØ Ð Ð Þ ¹ ÓÒÐ Ñ Ö ØØ ÖØÓÑ ÒÝ Ò ÒÓÑ Ñ ÒØ Þ Ø Ø Ð Ò ÐØòÒ ØÖ Ò Þ ÓÖÑ ÐØ ÔÖ Ðº Ö Ñ Ý ÞÒ Ó Ý Ð Ò Ô ÖØ Ð Ò Ð Þ ¹ Ú ÒÝ Ô Ô ÓÐÝØÓÒÓ Ò Ú Þ Ø Ð ÒÓÑ Ñ ÒØ Þ ØÓØ Ú Ð ØØ Ö Ù Ú ÒÝ ÓÑ Ò Ò Ö ØÙ º º º Ö Ò Ð Ø Ø Ó Ý Ó Ý Ò Ú Ð Þ Ö Þ Ø ÒØÖ Ô ¹ Ø ÐØ Ö ÒÝ Ú ØÓÖ Ó Ý Ú ÐØÓÞØ Ø Ù Ð ÓÒØ Øº Ä Ø Ø Ó Ý Ù Ú Ð¹ ÓÑ Ò Ò Ú Ð º Å Ú Ð Þ Ð Ò ÒÝ Ð ÓÒØ Þ ÒØ Ò Ð Ò Ô Þ ÒØ Ø Ð Ò Ñ Þ Ö Þ Ú ØÓÖ (S str = 0, q = 1) ÔÓÒØ Ò Ø Ð Ð Ø º Ó Ý Ð ÜÔÓÒ Ò Ð Ó ÓÑ Ò Ò Ð ÞÒ Þ Ò Ð Ò Ô Ò Þ Þ Ó Ý ÝÖ Ø ØÖ Ò Þ ÓÖÑ Ø ØÙÒ Ú Ö Þ Ö Þ Ø ÒØÖ Ô Ñ Ö Ò Ñ Ð Þ ÒÙÐÐ Ø Þ ÜÔÓÒ Ò Ð Ò Ð Ú Ð ¹ Ñ Ú Ð ÝÓÖ Ð Ò Ð Þ ÜÔÓÒ Ò Ð Ð Ò Ø ÐÐ ÑÞ Ö Ð ÑÓÞ ÙРк Å ÓÖ Ñ Ö ØØ Ö¹ Ù ¹ Ú ÒÝ Þ ÓÑ Ò Ò Ú ÐÒ ÓÖ Ù ¹ Ú ÒÝ Ø ÐÐ ÑÞ Ö Ð Ø Ò Ð Ð Ò Ô Ú ØÓÖ Ò Ú ÔÓÒØ º À ÓÒÐ Ø Ò Ò Ý Ð Ø Ñ ÓÖ ØÓØØ ÐÖ Ò Þ ò ÔÖ Ü¹ ÔÓÒ Ò Ð ØØ Ö Ð ØØ Ù Ó Ð ÓÒØ ÒØ ÓÖ Ò Þ º½º Ö Ò Ñ Ý Ð Ø Ù Ð Ú Ð Ð Þ Ñ ØØ Ð Þ Ú ÒÝ Ô Þ Ö Þ Ø ÒØÖ Ô ¹ Ø ÐØ Ö ÒÝ Ú ØÓÖ Ò Ñ Ö Ð Ø Ð Ò Þ ÜÔÓÒ Ò Ð Ú ÒÝغ º º Þ Þ Ñ ÖÓ Ð ØÖÓÒ Ò Ð ÓÖ ÙÐ Ö Ø Ð Þ Öò Þ Ö Þ Ø Ø ÑÙØ Ø Ñ ÒØ ¹ Ò Ò Ñ Ö Ö Ú Ò ØÙÐ ÓÒ Ø Þ Ö ØØ Ñ ÚÓÐÒ Ñ Ñ ÖÒ ¹ Ò Ñ ÞÓ Ø Ñ ÖÓ Þ ÔÓ ÐÚ Ø Ð Ò Ð Ø Ø Þ Ö Þ Ø ÐÐ ÑÞ Þ Þ ¹ Ö ØØ Ñ ÚÓÐÒ ÓÞÞ Ö Ò ÐÒ º Ö ÐÝ Ò Ý ÖØ ÐÑò ÓÞÞ Ö Ò Ð Ø Ò Ñ Ø Ð ÐØ Ñ Ô ÞØ Þ Ñ ÖÓ Þ ÔÓ ÐÚ Ø Ð ØØ ÖÑ ÒØ Þ Ø Ò ÞòÖ Ð Ø º Ñ ÖÓ Ð ØÓÒ ÒÝ Ó Ö Ø Ð Þ Ö Þ Øò ØÖÙ Ø Ö Ø ÑÙØ Ø Ñ ÒØ Ò Ô ÞØ Þ Ñ ÖÓ Þ ÔÓ ÐÚ Ø Ð Ò ÞÙÔ Ö ØÖÙ Ø Ö Ð Ð Ò Ø Ð Ø ØÖÙ Ø Ö Ð ÒØÖ Ô Ñ Ê ÒÝ ¹ ÒØÖ Ô Ð Ò Ò Ú Þ Ð Ø Ú Ðº ÁÐÝ Ò Ø Ò Þ Ð Ð Þ Ý ØÖÙ Ø Ö Ö ÞÐ Ø Ñ Ö Ø º Ñ Þ ÖØ Ø Ñ Ñ Û Ú Ð Ø¹ Ò Ð Þ Þ Ö Þ Ø ÒØÖ Ô ¹ Þ Ñ Ø ÓÒ Ð ÔÙÐÚ ØØ ÖÑ ÒØ Þ Ø ÞòÖ Ö º
63 º º ËË Ë S str q º º Ö º ËÞ Ö Þ Ø ÒØÖ Ô Ø ÐØ Ö ÒÝ Ú ÒÝ Ò º¾º Ö Ò Ð Ø¹ Ø Ù ØØ Ö Ð ØØ ÜÔÓÒ Ò Ð Ó Ø Ö ÞÓÐ Ñ ÒØ Ö ÐÐ ØÚ ÒÒ Û Ú Ð Ø¹ØÖ Ò Þ ÓÖÑ ÐØ Ö m = 0,..., 8 Ð ÓÒØ Þ ÒØ Ö º Þ Ö Ø ¹ Ô Ø ÐÐ ØÚ ØÖ Ò Þ ÓÖÑ ÙØ Ò Ð Þ Ú Òݹ Ý ØØ Ø Ø Ø Ö ØØ Ð ÓÒØ ÐÖ Ð Ó Ö Ò Ñ Ð Ò Ô Ø ØØ Ð Ò ÝÓ Ð ÓÒØ Ð Ò Ô ÔÓÒØ Ó ÓÐ Ð Þ Ð Ò Ú Ò ÓÖÓÞ ØÒ º ¾ Ù ÜÔÓÒ Ò Ð ÐÐ ØÚ Ñ Ó Ó ØÚ ÒÝ Ú ÒÝ Þ Ö ÒØ Ð Ò Ø ÐÐ ÑÞ Ö Ø ÐÐ ØÚ Þ ÐÑ Ð Ø Ø Ö Ö Ø ÐØ ÒØ ØØ Ñ Þ Ö Òº Áκ Ì ÁË Ã Ð Ò Þ Ð Ñ ÒØ Þ ØÓ Ð Ð Ò Ø Ö Ð¹ ÐÑ Ð Ö Ð ÞØ Û Ú Ð Ø¹ Ò Ð Þ ØÖÙ ¹ ØÙÖ Ð ÒØÖ Ô Ð Ô Ð ÑÞ ÓÑ Ò Ú Ð Î Ð Þ Òò ÐÓ ÞÐ Ó ÐÓ Ð Þ Ø ÔÙ Ò ÞÓÒÓ Ø Ö Ð ÐÑ Ñ Þ Ö ØÖÙ Ø Ö Ð ÒØÖ Ô Ñ Ê ÒÝ ¹ ÒØÖ Ô Ð Ò Ò Ú Þ Ð Ø º Þ Ñ Þ Ö ÐÑ Ð Ø Ð Ð ÐÑ ÞÙÔ Ö ØÖÙ Ø Ö Ð Ð Ò Ø Ö ¼ Ú ÞÓÒØ Ý ÓÖÐ Ø Ò Þ ÖÖ Ú Þ Ø Ó Ý Ø Ú ØÓÖ Þ Ò Ú ÔÓÒØ Ð ÐÐ Ò Ñ Ò Ø Ú ØÓÖØ Ñ Ý Ð Ø Ò ÓÖÑ Ú Ð Ö Ò Ð Þ Ò Ø Ú ØÓÖÒ Ð Ð Þ Ý Ö Ðº Å Þ ÖØ Ø Ñ Ñ ÖÖ Ó Ý Û Ú Ð Ø Ò Ð Þ Ø Ð ÞÒ ÐÚ Ò ÓÖÑ Ø Þ Ö ÞÞ Ò Ø Ð Ò Þ Ö Ø Ö ÞØ Ù Ó Þ Ð Ö Ò Ð Þ Ú Ð Þ Òò¹ ÐÓ ÞÐ ÞÙÔ Ö ØÖÙ Ø Ö Ò Ð ÑÞ ÓÖ Ò ÝÓ Ð Ñ ÒØ Þ ØÖ Ðº ܹ ÔÓÒ Ò Ð Ù Ð Ò ò Ó Ø Ø ÖØ ÐÑ Þ Ñ Ø Ö Ò Ð ÐÐ ØÓØØ ÞÙÔ Ö ØÖÙ Ø Ö Ò ÑÙØ ØØ Ñ ÞØ Ó Ý Ø Ð Ò Þ ÐÐ ò Ú Ð Ð Ö Ò¹ Ð Þ Ð Ð Ý Ò Ý Ö Ò Ò ÐØ Ö Ö Ø Ö ÞØ Ù Ó Þ Ð Ö Ò Ð Þ Ñ ÒØ Þ ØÙÒ Ú Ò ÓÖ Þ ÐÓ ÞÐ Û Ú Ð Ø¹ Ò Ð Þ Ò ÙÖÚ Ð ÓÒØ Ö ¹ Þ Ò ØÖÙ Ø Ö Ð ÒØÖ Ô Ð Ô Ú Þ Ð Ø Ñ Ò ÝÓ Ö Ø Ö ÞØ Ù Ó Þ Ñ ÒØ Þ Ø Ð Ò Ø Ô٠غ
64 Â Ì º Ë ÍÈ ÊËÌÊÍÃÌÊýÃ Ë È ÊýÄýË
65 º Þ Ø Ì Þ Ö Ö Ü Û Ú Ð Ø¹ Ò Ð Þ ÑÓ ÐÐ Þ Ó Ü Ð Ð Ò º½º Ú Þ Ð Ø Ø Ö Ý Ø Þ Ö Ö Ü Ú Þ Ð Ø Ö Ý ÔÖ Ô Ö ÐØ Ö Ü Ð Ö Ò Ð Þ Ñ Ò¹ Ø Ö Ñ ÖØ Þ Ø ØØ Ñº Å Ú Ð Ñ Ö Þ Þ Ò ¼ Ω ÑÔ Ò Ø Ú ¹ Ò ¼ Ω¹Ó Þ Þ Þ ÐÐ ÞØ ØØ Ò Ý Ω¹Ó Ð Þ Þغ Ð ÞÒ ÐØ Ð ¹Ú ÞØ ò Ó Ü Ð Ð Ø ÔÙ ¼ Ω À½ Ω À Ö ¹ Ñ ÒÒ ÃÇà ¼ º Ω¹Ó Þ Þ Ó Þ Ú Þ Ð Ø ÓÖ Ò ½º ¾ Ѻ º¾º Ú Þ Ð Ø Ñ Þ Ö Ö Ü ÔÖ Ô Ö ÐØ Ð Þ Þ S 21 ØÚ Ø Ð ÐÐ ÑÞ º½º Ö Ò Ð Ø¹ Ø º Þ Ö Ò Ð Ø Ø Ó Ý Ñ Ö Ö ½¼ ÅÀÞ ÖÒÝ Þ Ø Ò Ö Ü Ñ ØØ ¼º ÐÐ Ô Ø Ò ÓÞ Ð Ø Þ Øغ Î Þ Ð Ð ÒØ ¼ Ò ¹Ó ÙÖ Ø ¹ Ð Ø ÐÐ ØÓØØ Ñ Ð ¾¼¼ Ò ¹Ó Ô Ö Ù Ú Ð ÙÖ Ø Ö Ú Ò ½¼ ÅÀÞº Þ Ý Ð Ø Þ ØØ È Å Ð ÓÐ Ð Ú Ö Ò ÞÚ Þ ØÚ Ø Ð ØÓÖÒ Ð Ò Ö ØÓÖÞ Ø º Û Ú Ð Ø Ò Ð Þ Ñ Þ Ö Ð ÓÖ Ò Þ Ø ÖØÓÑ ÒÝ Ò Ø ÖØ Ò ÝÓÖ Ú ÐØÓÞ Ó Ö ÑÙØ Ø Ö Ñ ÒÝ Øº Ú Þ Ð Ø Þ ÑÔÓÒØ Ð Þ ÖØ ØØ Ú Ð ÞØ ÙÖ Ø ÐÖ º Ð Ñ Ø Ý Ð Ð ÑÓ ÙÐ ÐØ Ê Ò Ö ¹ ØÓÖÖ Ð Ø ÖØ Òغ ÑÓ ÙÐ Ð Ð Ú Ú Ð ÝÑ ÓÞ Ô Ø Ò Ñ ÚÓÐØ Ø ØØ Þ Ú ÞÓÒÝ Ò Ð Ò Þ Ø Ú Þ Ð Ø Ö Òº Ñ Ò Ê Ð Ñ Ö Þ Ø ÖØÓÑ ÒÝ Ò Ý Ë» Ñ ÒØ Ú Ø Ð Ý ÓÖ ¼¼ ÅÀÞ Ø Ö¹ Ö Ú Ò Ì ØÖÓÒ Ü Ó Þ ÐÐÓ Þ ÔÔ Ð Ø ÖØ Òغ Å ÖØ Ñ Ò Ö ØÓÖ ÞÚ ØÐ Ò Ñ Ò Ð Ø Ý Ö Ü Ñ ÒØ Ð Ò º¾º Ö µ Ñ ÖØ Ñ Ö Ü Ú Ð Ø Ö¹ ÐØ Ð Ñ Ò Ø Ð Øº Ú Þ Ð Ø ÐÚ Þ Ö ÙØÓÑ Ø Ù Ñ Ö Ö Ò Þ ÖØ Ð ØÓØØ Ñ Ñ ÐÝ ½¼¼¹ ½¼¼ Ñ ÒØ Ø Ø ÖÓÐØ Ð Ð Ò Þ Ú Ð ØÐ Ò Ð Ð ÐÐ Þ Ú ÞÓÒÝ Ñ ÐÐ Øغ Ú Ú Ö Ú Ò ÅÀÞ ½¾¼ ÅÀÞ ÚÓÐغ
66 Â Ì º Ê Ä Á Ï Î Ä Ì¹ Æ Ä ÁË º½º Ö º Ö Ü Ó ÓÞØ ÐÐ Ô Ø Ò ÓÞ Ø Ú Þ ÐØ ÔÖ Ô Ö ÐØ Ð Ø Òº º¾º Ö º È Ð Þ Ð ÐÑ ÞÓØØ Ñ Ö ÐÖ º Â Ð Ò Ø Ò Ú Ú Ð Ö Ú Ò ½¾¼ ÅÀÞº ÓÐÝ Ñ ØÓ ÚÓÒ Ð Ö Ö Ò Ð Ö Ü Ñ ÒØ ØÚ Ø Ðµ Ø Ò Þ ¹ ØÓØØ ÚÓÒ Ð Ú Þ ÐØ Ð Ö Ü ØÚ Ø Ðµ Ø Ò ÔÓØØ Ðº Î Þ Þ ÒØ Ø Ò ÐÝ Æ Ñ ÒØ ÓÖ Þ Ñ º Ð Ø Ò ÐÝ Þ ÐØ ÎÓÐصº
67 º º à ÈÇÌÌ Ê Å Æ º º Ö º ½¼ Ð Ò Þ Ñ ÒØ Û Ú Ð Ø¹ØÖ Ò Þ ÓÖÑ Ö Ñ ÒÝ Ö Ü Ø¹ Ú Ø Ð Ø Òº Þ ÐØ ÖÓÐØ Ñ ÒØ Û Ú Ð Ø¹ØÖ Ò Þ ÓÖÑ ÙØ Ò ÔÓØØ Ý ØØ Ø Ó Ø Ú ÐØÓÞÒ Ñ ÒØ º º Ö ÑÙØ Ø º º º à ÔÓØØ Ö Ñ ÒÝ ØÖ Ò Ú Þ Ð Ø Ö Ò d jk Ý ØØ Ø Ñ Ö Þ ÑÖ ÒÓÖÑ ÐØ Ò ÝÞ Ø Þ Ò ÝÞ Ø Ý ÞÚ º½µ d jk = Nm n=1 ( N m ) 2 d [n] jk º½µ N m = 10 N m = 100 Ø Ò ÔÓØØ Ö Ñ ÒÝ Ø º º Ö ÑÙØ Ø º Ð Ò Ü Ò ÓÖ Þ Ñ Ñ Ö Ò N m Ñ Ö Ø Ð Þ Ñ º º º Ö Ð Ò Þ Ð ÓÒØ Þ ÒØ Ò Ö Ú Ò ÓÒµ ÑÙØ Ø Þ Ö Ñ ÒÝ Øº ½¼ Ð Ô ÐÚ Þ Ø ÖØ ÒØ j = 0...9µ ØØ Þ Ö Ö Ñ ÒÝ Ø ÑÙØ ØÓÑ º Þ Ð Ö Ú Ò ÓÑÔÓÒ Ò Ò Ñ Ð Ò Þ Ð ÔÚ Ø Ò Ö Ö Ò Ø Ðº º º Þ Þ Þ ØÒÓÖÑ ÐØ Û Ú Ð Ø¹ Ý ØØ Ø Ñ Ö Ú Ò Ò Ñ Ð Ò ÞØ Ø Ø Ö Ö Ò ¹ Ø Þ Ö Ò Ö Ø ÐØ ÐÖ º Ð ÓÒÝ Ö Ú Ò Ò Ú ÞÓÒØ Þ Ý ØØ Ø Þ Ð Ø Ð ÞÓÒÓ º Þ Ó Þ ÐÐÓ Þ Ô t = 400ps Ñ ÒØ Ú Ø Ð ¹ Þ º º º ÒÓÑ Ø Ð Ô Ø Ø Þ Ð Ø Ú Þ Ð ØØ Ó Ý Ð ÖÒ Ò º º º ½¾¼ ÅÀÞ¹ Ú Ú Ö Ú Ò Ö Ø Ö ÞØ Ù Øº ÒÒ Ú Ø ÞØ Ò Ò ÒÝ Ð ÓÒØ Þ ÒØ ÐÐ Ö Ò Ð Þ Ö Ó Ý ÞÓÒÓ Ø Ù Ö Ü Ò ÑÐ Ò Ö Ø Ó Ó ÓÞØ Ø Ó Ø Ò Ý Ö Ú Ò Ø Ó Òº Ö Ø Ö ÞØ ¹ Ù Þ Ñ Ö Ø Ð Þ º º º ÒÓÑ Ø Ð Ô ÙØ Ò Ñ Ö ÓÖ Ò Ð ÐÑ ÞÓØØ
68 Â Ì º Ê Ä Á Ï Î Ä Ì¹ Æ Ä ÁË º º Ö º Þ Ø Ú Û Ú Ð Ø¹ Ý ØØ Ø ½¼ ÒØ Ö µ ½¼¼ Ñ Ö Ø Òº Ö Ö Ò Ð Ö Ñ ÒÝ Ô ÖÓ ÓÐÝØÓÒÓ µ Ö Ü Ð Ö Ñ ÒÝ Þ ØÓØص ÚÓÒ ÐÐ Ð Ð ÐÚ º Ð ÓÒØ Ò Ü j = 1
69 º º ËË Ë º º Ö º Þ Ø Ú Û Ú Ð Ø¹ Ý ØØ Ø ½¼¼ Ñ Ö Ø Òº Ö Ö Ò Ð Ö Ñ ÒÝ Ô ÖÓ ÓÐÝØÓÒÓ µ Ö Ü Ð Ö Ñ ÒÝ Þ ØÓØص ÚÓÒ ÐÐ Ð Ð ÐÚ º
70 ¼ Â Ì º Ê Ä Á Ï Î Ä Ì¹ Æ Ä ÁË ÑÔÙÐÞÙ Ó Þ Ð Ý Þ Ð ÓÒÝ Ö Ú Ò Ø Ó Ø ÒÝ Ö Þ ÑÔÙÐÞÙ Ð Ø Ø ÖØ ÐÑ ÞÞ º Ú Þ Ø ØØ Ñ Ö ÓÖ Ò Ð ØÖ Ú Ú Þ Ø ØØ Ö Ü Ö ÐÐ ÑÞ Þ Ó Ý Ñ Ö Ú Ò Ý ØØ Ø º ¾¼ ±¹ Ð Ñ Ò Ò º ÎºÌ ÁË Ì Þ Ö Ö Ü Ó ÓÞØ Þ ÐØ ÐÓ ÞÐ Ó Û Ú Ð Ø¹ Ò Ð Þ Ø ÔÚÓÒ Ð ÓÒ Î Ö Ò Ñ Þ Ö Ò Ð ÔÙÐ ÑÓ ÐÐØ Þ Ø ØØ Ñ Ø Þ Ö Ö ¹ Ð Ü Ó ÓÞØ Þ ÐØ Ú ÐØÓÞ Ó Ð Ö Ö Þ Ø ÖØÓÑ ÒÝ Òº Ã Ø Ö Ü ÔÓÒØÓØ Ø ÖØ ÐÑ Þ Ð Ø Ò Ñ Ö Ø Ú ÞØ Ñ Ú Ó Þ ÑÔÙÐÞÙ¹ Ó Ð ÐÐ ÓÖÓÞ ØØ Ðº Å Ø ÖÓÞØ Ñ ÑÓ ÐÐ ÐØ Ð Ñ Ö Ö Ñ ÒÝ ÐØ Ð ÞÓÐ ÐØ ØÓØØ Ú ÒÝ Ø Ø ÞØ ØÐ Ò Û Ú Ð Ø¹ Ò Ð Þ Øº Å ÐÐ Ô ØÓØØ Ñ Ó Ý Û Ú Ð Ø Ý ØØ Ø Ñ Ò Ñ Ö Ñ Ò ÑÓ¹ ÐÐ Þ ØØ Ö Ñ ÒÝ Ø Ò ÒÓÑ Ð ÓÒØ Þ ÒØ Ò Þ ÒÚ Ò Ð Ú ÐØÓÞ Ø Ö Ü Ñ ÒØ Ö Ö Ò Ð Þ Ô Ø ¾ º Ú Þ Ø ØØ Ñ Ö ÓÖ Ò Ð ØÖ Ú Ö Ü Ö ÐÐ ÑÞ Ó Ý Ñ Ö Ú Ò Û Ú Ð Ø Ý ØØ Ø Ñ Ò Ò º Þ Ð ÓÒÝ Ö Ú Ò Û Ú Ð Ø Ý ØØ Ø Þ ÑÔÙÐÞÙ Ð Ø Ø ÖØ ÐÑ ÞÞ º ¾
71 º Þ Ø Ì Þ Ö Ö Ü Ó ÓÞØ Þ ÐØ ÐÓ ÞÐ Ó Ø Ø ÞØ Ð ÑÞ Ø ÔÚÓÒ Ð ÓÒ º½º Ú Þ Ø Å Ö Ø Ò Ò Ñ Ö Þ Þ Ò Ø Ú Þ Ø Ð ØÐ ÓÞØ Ø Ù Ñ ¹ Ö Ò Ð Þº Ê Ö Ú Ò Ñ Ö Ø Ò Ý Ö Ò Ð ÓÖ ÙÐ Þ ¹ Ð Ò Ó Ý Ý Ú Þ Ø Ø Ú Ò Ò ÞÓÒÓ ÔÓØ Ò ÐÓÒº Ð ÓÒÝ Ö Ú Ò¹ Ò ØÖ Ú Ð Ò Ø ÒØ Ø Ó Ý Ú Þ Ø Ö Ú Þ Öº ÇÐÝ Ò Ø Ò Ñ ÓÖ Ú Þ Ø Ñ Ö Ø Þ Ñ Ö Ø Ñ Ö ÓÖ Ò Ð ÐÑ ÞÓØØ Ð ÙÐÐ Ñ Ó Þ Ú Ð Þ Ø ÒÙÒ ÐÐ ÓÒ ÒØÖ ÐØ Ô Ö Ñ Ø Ö Ð Ö Ñ Ð º½º Ö µº Ê Ø Þ Ñ ÖØ ÓÖÑÙÐ Ø Ú Ö Ý ÒÐ Ø Ñ ÐÝÒ Ñ ÓÐ Ð Ô Ò Ø ÔÚÓÒ ÐÓÒ Ñ Ö Ø Þ ÐØ ÐÝ Ú ÒÝ Ò Ø ÙÐÐ Ñ Þ ÒØ Ö Ø Ð ½¼¼ v(x, t) = A cos (ω t β x) e α x + B cos (ω t + β x) e α x º½µ. ÓÐ A B Ø ÔÚÓÒ ÐÓÒ Ð Ö Ø ÐØ ÙÐÐ Ñ ÓÑÔÐ Ü ÑÔÐ Ø º½º Ö º Ø Ö Ð Ó ÓÞØ Ö Ü ½
72 ¾ Â Ì º Ê Ä Á ÇÃÇ Ì ÄÇË ÄýËÇà º½º Ö µ α β Ø Ö Ø ÒÝ Þ Ú Ð ÔÞ Ø Ö Þ º Þ Ð Ô Ò Ò Ð Ø γ Ø Ö Ø ÒÝ Þ ¼ γ = α + jβ = (R + jωl)(g + jωc). º¾µ ÓÐ R Ø ÔÚÓÒ Ð Ó Þ Ý Ö ÐÐ Ò ÐÐ L Þ Ò Ù Ø Ú Ø G Þ ØµÚ Þ Ø C Ô Ø Ô Ö Ñ Ø Ö º Ú Þ Ø Ò ÙÐÐ Ñ Ø Ö ¹ ν(f) Ð Ô Ö Ñ Ø Ö Ö Ú Ò Ø Ðº Ã Ú ÞØ ò Ø ÔÚÓÒ Ð Ø Ò Ø Ö ¾ ν = ω β 1 L C = 1 ε µ = c εr µ r. º µ Ã Þ Ñ ÖØ Ö Ü Ð Ò Ñ ÓÖ Ø ÔÚÓÒ Ð Þ Þ Ø ÔÚÓÒ Ð ÙÐРѹ ÑÔ Ò Ø Ð ÐØ Ö Z L ÑÔ Ò Ò ÓÐÝØ Ø º½º Ö µº Γµ ÓÑÔÐ Ü Þ ÐØ Ö Ü Ø ÒÝ Þ Ø ÓÑÔÐ Ü ÑÔÐ Ø ÒÝ Ó ÒØ Ò ÐÚ Γ = B A = Z L Z 0 Z L + Z 0. º µ Ø ÔÚÓÒ Ð Z 0 ÙÐÐ Ñ ÑÔ Ò Þ Ü Ø Ò ÐÝ ÔÓÞ Ø Ú Ö ÒÝ º º Ö µ Ð Þ ÐØ Ö Ñ Ö ÒÝ Ó Þ Ý Ö Ô Ö Ñ Ø Ö Ð ¼ Z 0 = V + I = R + jωl + G + jωc. º µ º¾º Ø Ö Ø ÒÝ Þ Ú Þ Ð Ø Ö Ü Ú Þ Ð ØÓ ÓÖ Ò Ð ÒÝ Þ Ð ÐÑ ÞÓØØ ÙÐÐ ÑÚ Þ Ø Ø Ö Ô Ö Ñ Ø Ö Ò Ñ Ø ÖÓÞ º ÐÐ Ô Ø ÐÐ ÑÞ α Ô Ö Ñ Ø Ö Ý Ó Ü Ð Ð Ø Ò ÐØ Ð Ò Ø Ð Ù Ø Ñ Ø Ö Ö ÐÐ ÑÞ β Ô Ö Ñ Ø Ö Ú ÓÞÞ Ö Ø º Ñ ÒØ Þ º µ Ñ ÓÐ ÒØ Ú ÞØ Ñ ÒØ Ø ÔÚÓÒ ÐÓÒ ¹ Þ ÐØ ÐÝ Ô Ö Ó Ù Ú ÒÝ v (x, t) = v ( 0, t x ν ). º µ Ø Ö Ø ÒÝ Þ Ú Þ Ð Ø Ö º¾º Ö Ñ Ö Þ ÐÐ Ø ÞÒ Ð Ø º Þ Ý Ú Ò Ö Ú Ö Þ ÖØ Ó Ü Ð Ð Ñ Ú Ø Ý Ð Þ ØÓÐ ÓÒ ¹ Ö ÞØ Ð Ý Ó Ü Ð Ð Þ Ø Ñ ÐÝ Ò S Ô Ö Ñ Ø Ö Ø Ñ Ö Ò º Þ Ý Þ ÐÐ ØÓØØ Ñ Ö ÐÖ Ò Þ S 21 µ Ô Ö Ñ Ø Ö Ð Ñ Ò ÑÙÑ Þ L Ó Þ Ú Þ ÐØ Ð ÍÌ Ð ÍÒ Ö Ì Øµ Ð Þ Þ Ö ÞÓÒ Ò Ö Ú Ò ÓÞ Ø ÖØÓÞ º º Ö º Ð Ö Ú Ð Ø ÒÝ Þ Î ÐÓ ØÝ ØÓÖµ V F ÍÌ Ð Ø ÒØ Ø Ò º Þ Ð Ô Ò Ø ÖÓÞ Ø Ñ º V F = λ c λ 0 = 2 L λ 0 = 2 L f c, º µ
73 º¾º Ì Ê ËÁ Ì Æ ÎÁ Ë ýä Ì º¾º Ö º Å Ö Þ ÐÐ Ø Ø Ø ÒÝ Þ Ñ Ø ÖÓÞ Ö º º Ö º ÍÌ ½µ Ð Ð Ö ÞÓÒ Ò º½¼¼ ÅÀÞ¹ Ò Ø Ø ÒÝ Þ Ñ Ø ÖÓÞ Ö º Ð Ó Þ ½½º¾ ¼ Ѻ Þ S 12 Ô Ö Ñ Ø Ö Ö µ Ñ Ò ¹ ÑÙÑ Ø ÑÙØ Ø Þ ½º Å Êà ʺ
74 Â Ì º Ê Ä Á ÇÃÇ Ì ÄÇË ÄýËÇà º º Ö º ÍÌ ½µ À Ö Ñ ÒÒ ÃÇà ¼ Z 0 = 75 Ωµ ÍÌ ¾µ À½ Z 0 = 50 Ωµ Ð Ö Ú Ð Ø ÒÝ Þ Ö Ú Ò Ú ÒÝ Ò Ñ Ö Ö ¹ Ñ ÒÝ Ð Ô Ò ÓÐ f ÍÌ Ð Ø ÒØ Ø Ò ÔÓØØ Ö ÞÓÒ Ò Ö Ú Ò c ÒÝ Ú Ù¹ ÙÑ Ð Ø Ö c ¾ ¾ Ñ» µº ýðø Ð ÒÓ Ò Ú Þ Ð Ø Ð Ô Ò ÔÓØØ Ö ÞÓÒ Ò Ö Ú Ò Ø ÍÌ Ð L Ó Þ Ø ÖÓÞÞ Ñ º Ð Ò Þ Ó Þ Ð Þ ÞÓ ÞÒ Ð Ø ÐÝ ØØ Ú Þ Ð Ø Ð ÐÚ Þ Ø Ñ Ö Ò ò ÖÑÓÒ Ù Ö Ú Ò ÓÒ Ð Ø Þ Ö ÞÓÒ Ò Ð Ñ Ö Ò Ð ÞÒ Ð Ú Ðº Þ Ò Ö ¹ Ñ ÒÝ Ð ÞÒ Ð Ú Ð Ð Ð ØÖ ÙÑ Ð Ô Ò Ö Ú Ð Ø ÒÝ Þ Ö Ú Ò Ð Ñ Ø ÖÓÞ Ø º Ë ÒÓ Ð Ð ÓÒÝ Ö Ú Ò Ú Þ Ð Ø Ó Þ (L) Ð Ó Þ Ø ÒÝ ÐÒ º Ú Ò Þ Ð Ð Þ ÖØ Ð ÑÙØ ØÒ ÓÒÐ ØÙÐ ÓÒ¹ Ó Ø Ò Þ Ò Þ Ð Ø ÒÝ ÐØ Ø ÔÚÓÒ ÐÚ Ð ÐÐ ÒØ Ø Ò Ð Þ Ö ØÙÐ ¹ ÓÒ Ò Ñ Ý Þ Öò Ò Ñ Ø µ Ú ÓÐØ Ú Þ Ð ØÓØ ÔÓÒØÓ Ö Ñ ÒÝ Ö Ò Ö Ú Ö Þ ÖØ Ð Ð ÐÚ ÞÒ º Ú Þ Ð ØÓ ÓÖ Ò Ð ÐÑ ÞÓØØ Ú ÞØ ò Ó Ü Ð ÐØ ÔÙ Ó ÍÌ ½µ À Ö Ñ ÒÒ ÃÇà ¼ Z 0 = 75 Ωµ ÍÌ ¾µ À½ Z 0 = 50 Ωµ º º Ö ÑÙØ Ø º µ Þ Ð Ô Ò Ñ Ø ÖÓÞÓØØ Ö Ú Ð Ø ÒÝ Þ Ö Ú Ò Ø Ø Ú Þ ÐØ Ð Ø Òº Å Ú Ð Ú Þ Ð Ø ÓÖ Ò Þ ÒÝ Ô Ö Ñ Ø Ö Ö Ú Ò Ñ ØØ Ó¹ Ü Ð Ð Ò Ð ÙÐ ÙÐÐ Ñ Ó Þ Ö Ú Ò Ú ÒÝ Ò Ú ÐØÓÞ Þ ÖØ Ñ Ö ÓÖ Ò ÞÒ ÐØ Ð ÓÖ ØÑÙ Ú Ø Þ Ð Ø ½º Ö Ñ Ð Ð ÓÒÝ Ö ÞÓÒ Ò Ö Ú Ò Ø f 1 µº
75 º º Ê Ä Á ÎÁ Ë ýä ÌýÀÇ ÄýÄÄ ÌÇÌÌ ÅÇ ÄÄ ¾º Ö Ñ Ú Ø Þ Ö Ú Ò Ø f 2 2 f 1 ÖÒÝ Òµº º Ö Ñ Þ nº Ö ÞÓÒ Ò Ö Ú Ò Ø f n 2 f n 1 /(n 1) ÖÒÝ Òµº ÙØÓÑ Ø Þ ÐØ Ñ Ö Ø Ò Ú Þ Ð Ø ÒÒÝ Ò ÐÚ Þ Ø º Ñ ÒÙ Ð Ñ ¹ Ö Ø Ò Ú Þ Ð Ø ÐÚ Þ Ø Ò Þ Ø Ð ÙÐØ Ö ÞÓÒ Ò ÞÓÒÓ Ø ÐÔ Ö Ñ Ø Ö Ö Ú Ò Ñ Øغ ÔÓØØ Ú Þ Ð Ø Ö Ñ ÒÝ ÞØ ÑÙØ ØØ Ó Ý ½¼¼ ÅÀÞ º º º ½ ÀÞ Ö Ú Ò Ø ÖØÓÑ ÒÝ Ò V F Ö Ú Ð Ø ÒÝ Þ Ð ÒØ Ñ ÖØ Ò Ò Ñ ÑÙ¹ Ø Ø Ú ÐØÓÞ Ø Þ ÖØ Ú Ø Þ Ò ÑÙØ ØÓØØ ÑÓ ÐÐ Ø Ò ÞØ ÓÒ Ø Ò ÒØ Þ Ð Ñº º º Ò Ö ØÓÖ Ö Ü Ú Þ Ð Ø ÓÞ Ð ÐÐ ØÓØØ ÑÓ ÐÐ Þ Ð ÐÑ ÞÓØØ Ê Ò Ö ØÓÖ Z g Ñ Ò Ø ÑÔ Ò Ú Ð V g Ñ Ò Ø Þ ÐØ Ú Ð ÐÐ Ñ Þ Ø Ý ÓØØ Ñò Ö Ú Ò Òº V g Ñ Ò Ø ¹ Þ ÐØ Ý ÐÐ ÞØÚ Ð Þ ÖØ Ò Ö ØÓÖ Ø Ò Ñ Ò Ø Ø Ð ØÑ ÒÝ Ð Z g Ò Ö ØÓÖ ÑÔ Ò Ð Þ ÑÓÐ Ø º ÁÐÐ ÞØ ØÐ Ò Ò Ö ØÓÖÓ Ø Ò Ò ¹ Ö ØÓÖ Ö Ö Þ ÐØ Ò ÞÒ Ð Ø Ð ÒÝ Ñ Ñ Ú Ð ØØ Ö Ú Ò Ú ÒÝ Ò Ú ÐØÓÞ ÑÔ Ò Ø Ö Ð Ø Ò Ôк ÒØ ÒÒ Ñ Ö µ Ð Ò Ð Ø Ö ÐÑ ÒÝ Ø ØÙ ÙÒ ÞØÓ Ø Ò º ÅÓ ÐÐ Ò Ò Ò Ö ØÓÖ ÔÓ Þ ÐØ V g (t) = V 0 cos(ω t). º µ Ô ÓÐ Ø ÔÚÓÒ Ð Ñ ØØ Ú Þ Ø Ø A g Ñ ÒØ ÓÑÔÐ Ü ÑÔÐ Ø Ø Ñ ÒØ V g (t) = real(a g e jωt ). º µ Ì ÔÚÓÒ Ð Ø ÔÚÓÒ Ð ÑÓ ÐÐ Ý Ð Ú ÞØ Ø ÔÚÓÒ Ð º µº Þ A Ð ÙÐÐ Ñ ÑÔÐ Ø Þ x ÔÓÞ Ò A(x) = A g e αx e jβx, º½¼µ A(x, t) = A g e α x e j β x e j ω t, º½½µ ÐÝ Ú ÒÝ Ò Þ ÑÐ ÐØ Ø Ð Þ ÐØ Ô ÐÐ Ò ØÒÝ ÖØ Ø ÐÐ Ò¹ ÙÐØ Ø Ò º º Ö º Þ ØØ ÑÙØ ØÓØØ Þ ÑÙÐ ÔÖÓ Ö ÑÓ Ö Ð ÔÖÓ Ö ÑÓÞ ÖÒÝ Þ Ø Ò Þ ÐØ º º º Ö Ð ÙÐÐ Ñ ÖÓÒØ Þ ÐØ Ò ÐÚ ØØ ÖØ Ø ÑÙØ Ø ÐÝ Ú ÒÝ Òº Î Þ Þ ÒØ Ø Ò ÐÝ Ò Ö ØÓÖØ Ð Ñ ÖØ Ø ÚÓÐ Ñ º
76 Â Ì º Ê Ä Á ÇÃÇ Ì ÄÇË ÄýËÇÃ º º Ö º Ø ÔÚÓÒ Ð ÑÓ ÐÐ º º Ö º real(a(x, t)) = 0 Þ ÐØ L = 10 Ñ A g = 10 Î φ = 0 α = 0.1 f = 300 MHzµ
77 º º Ê Ä Á ÎÁ Ë ýä ÌýÀÇ ÄýÄÄ ÌÇÌÌ ÅÇ ÄÄ º º Ö º Þ ÐØ Ø ÔÚÓÒ ÐÓÒ L = 10 Ñ A g = 10 Î t = 0...T α = 0.1 f = 300 MHzµ B Ö Ø ÐØ ÙÐÐ Ñ Þ x ÐÝ Ò B(x, t) = B 0 e αl e jβl e j ω t = = [ A g e α L e j β L Γ ] e (x L) α e j (x L) β e j ω t º½¾µ Ð Ö Ø ÐØ ÙÐÐ Ñ Ú ÞÓÒÝ Ø ÑÙØ Ø º º Ö φ t=0 Þ Ú ¹ ÞÓÒÝ Ø Ò Ñ Ö ÐÐ Ò ÙÐØ ÐÐ ÔÓØÓØ ÐØ Ø Ð ÞÚ º Ð Ö Ò Ð Þ Ö Γ = 1 Þ Ð Ö Ò Γ = +1º Ø ÔÚÓÒ ÐÓÒ Þ ÐØ Ø Ñ Ô Ø Ù V (x) = real(a(x) + B(x)). º½ µ Ý Ô Ö Ù Ø Ý Ð Ñ Ú Ú ÙÐÐ Ñ ÖÓÒØÓ Ð Ð Z L = 0 Z L = Ø Ò º º Ð Ð Ö Ò Ð Ø Ø º Þ Ö ÓÒ Ñ Ý Ð Ø Ñ ¹ Ú Ð Ú ÞØ Ø ÔÚÓÒ ÐÑÓ ÐÐØ Ú ØØ Ò Ý Ð Ñ Ó Ý Ñ Ò ÑÙÑ ÐÝ Ò Ö ØÓÖ Ö ÒÝ Ð Ú Ò Ñ ÓÐÝ Ò Ñ ÐÝ Þ ÐØ Ñ Ò ÑÙÑÓ Ø Ó ÓÞÒ º ËÞ ÒØ Ò Ñ Ý Ð Ø Ó Ý Þ Ð Ö Ò Ð Þ Ö Ò Ð Þ ÐØ Ñ Ü ÑÙÑÓØ ÔÙÒ Ö Ú Þ ÖÖ Ð Ø ÖØ Ò Ð Þ Ö Ø Ò Ð Ö µ Z L Ð Þ Ö Ò Ð Þ ÐØ Ñ Ò Ò Ô ÐÐ Ò Ø Ò ¼º Ì ÔÚÓÒ Ð ÑÔ Ò Ù Ö Ð ÖÑ Ø ÔÚÓÒ Ð Þ Þ Ñ Ò Ø Ò Z L Ð Þ Ö Ñ ÐÐ ØØ Ñ Ò Ø ÑÔ Ò Z in = Z 0 ZL + Z 0 th(γl) Z 0 + Z L th(γl). º½ µ
78 Â Ì º Ê Ä Á ÇÃÇ Ì ÄÇË ÄýËÇÃ º º Ö º Þ ÐØ Ø ÔÚÓÒ ÐÓÒ L = 10 m, A g = 10 V, t = 0...T, α = 0.1, f = 300 MHz, Γ = 1 µ L = 10 m, A g = 10 V, t = 0...T, α = 0.1, f = 300 MHz, Γ = +1 µ Ø Ò
79 º º Ê Ä Á ÎÁ Ë ýä ÌýÀÇ ÄýÄÄ ÌÇÌÌ ÅÇ ÄÄ º º Ö º Ð Ö Ø ÐØ ÙÐÐ Ñ Þ ÐØ Ò Þ Ø ÔÚÓÒ ÐÓÒ Ý Ô Ö Ù Ø Ú Ú ØÚ º L = 10 m, A g = 10 V, t = 0...T, α = 0.1, f = 300 MHz, Γ = 1 µ L = 10 m, A g = 10 V, t = 0...T, α = 0.1, f = 300 MHz, Γ = +1 µ Ø Ò º½¼º Ö º ØÓÐØ Ø ÔÚÓÒ Ð Þ ÞÓ ÑÓ ÐÐ
80 ¼ Â Ì º Ê Ä Á ÇÃÇ Ì ÄÇË ÄýËÇà ΠÞØ Ñ ÒØ Ø Ò ÓÐ α = 0µ ÓÖÑÙÐ Ú Ø Þ ÔÔ Ò Ý Þ ¹ Öò Z in = Z 0 ZL + j Z 0 tg(βl) Z L + j Z 0 tg(βl). º½ µ Ö Ü Ø ÒÝ Þ Z 01 Z 02 ÑÔ Ò Ù Ö Ò Ð º µ º½ µ Ý Ò¹ Ð Ø Ð Γ 12 º Ò Þ Ý Þ Öò ÑÓ ÐÐ Ò Ñ Ú Ð Z g = Z 01 Z 03 = Z L Þ ÖØ Ò Ö ØÓÖ Ø Ö Ð ÓÐ ÐØ Ö Ü Ñ ÒØ Ò Ø ÒØ Ø º Å Ú Ð Ñ Ó Ø ÔÚÓÒ Ð Þ Þ Ñ Ò Ø Þ ÐØ ÞÓÒÓ Þ Ð Ø Ô¹ ÚÓÒ Ð Þ Þ Ñ Ò Ø Þ ÐØ Ú Ð Þ Γ 12 ÖØ Ø Ð º Þ Ð Ø ÔÚÓÒ Ð Þ Þ Ñ Ò Ø Ò V 2 in Þ ÐØ (x2 V 2 = real(a + B º½ µ =0) (x1 =L 1 ) (x1 =L 1 )) Ñ Ú Ð Þ ÖØ B = Γ A. º½ µ A 2 (0) = A 1 (L 1 ) [1 + Γ 12 ]. º½ µ Z 02 Z 03 ÑÔ Ò Ù Ö Ø Ò Þ ÐØ Ö Ü Ø ÒÝ Þ Γ 23 Þ ÖØ Ö Ø ÐØ Ð B 2 (L 2 ) = A 2 (L 2 ) Γ 23. Þ ÙÐÐ Ñ Ñ Ø Ö Ø Ð Z 0 2 Z 0 1 ÑÔ Ò Ù Ö Ò Ðº A 2[1] (0) = B 2 (0) Γ 21. º½ µ º¾¼µ A 2[ ] (0) = A 2 (0) + A 2[i]. i=1 º¾½µ Å Ú Ð Ñ Ö Ò ò Ö Ü ÓÑÔÓÒ Ò Ö Ü Ø ÒÝ Þ ÖØ Ú Ð ÜÔÓÒ Ò Ð Ò ÒÒ Ò Ý Ù ÐØ Ð Ò Ð ÒØ Ò Þ Ð ¹ Ö Ò ò Ö Ü ÓÑÔÓÒ Ò Þ Ô Øº A 2[ ] (0) A 2 (0) + (Γ 23 Γ 21 ) i. º¾¾µ Å Ú Ð Þ ½º ¾º º º º n¹ Ö Ü ÓÑÔÓÒ Ò Ò Þ ÐÝÞ Ø ÝÑ ÓÞ ¹ Ø ØØ Ð Ó Þ Þ ÐØ Ö Ü Ø ÒÝ Þ Þ ÐÐ Ò Þ ØÓÐ Ø Ó ÓÞ¹ Ò µ Þ Ñ Ò Ø ØØ Þ ÐÝÞ Ø Ò Þ Þ Ò Ý ÓØØ Ö Ú Ò Òº ÖÖ ÑÙØ Ø Ô Ð Ø º½½º Ö ÓÐ ¾ ¾¼ Ö Ü ÓÑÔÓÒ Ò Ð ØØ Ý Ð Ñ Ú Ú º i=1
81 º º Ê Ä Á À ÌýËýÆ Ã ËÌ ÌÁË ÌÁà Á Ä Å Ë ½ º½½º Ö º ØÓÐØ Ø ÔÚÓÒ Ð Þ Þ Ø Þ Ö Ö Ü ÑÓ ÐÐ º A B Ð Ö µ A B Ð Ö µ Ý Ð Ñ Ú Ø Ð Ú Ð L = 1.62 m, α = 0.01, Z G = Z 01 = Z 03 = 50Ω, Z 02 = 75Ωµ º º Ö Ü Ø Ò Ø Ø ÞØ Ð ÑÞ Ö Ö Ú Ò Ñ Ö Ø Ò Ð ØÐ ÓÞ ÞÓÒÝÓ Þ Þ Ôк ÒØ ÒÒ ÞòÖ Ö ÒÝ ØÓÐ µ Ð ÒÝ Ö Ü Ð Ö Ò Ð Þ¹ ØÒ º Ý Ö Ü Ú Ð Ø Ö ÐØ Ð Þ Þ S 21 Ô Ö Ñ Ø Ö Ò Ò ÓÞ Ø ÑÙ¹ Ø Ø º½¾º Ö º Â Ð Ò Ö Ò ÓØØ Ó Þ Ð Þ ÞÓ Ø ÐØ Ø Ð ÞÚ Þ Ö Ú Ò Ú ÒÝ Ò Ó ÓÞ ÑÔÐ Ø Øº ýðø Ð Ò Ð ÓÖ Ø Ö ÙÑÓ Ð Ø Ò Ý Ú Þ Ð Ø ÓÖ Ò ÓÖ Ò Ð Ó Þ Þ ÔÔ Ò Ð ÐÑ ÞÓØØ Ñ Ö Ö Ú Ò Ò Ñ Þ Ò Ø ÖØ Ø ØÓ º Þ ÖØ Ñ Ö Ö Ñ ÒÝ Þ ÑÔÓÒØ ¹ Ð Ñ ÒØ Ú Ð Þ Òò Ú ÐØÓÞ Þ Ð Ò º ÖÑÓÒ Þ ÐØ ÊÅ Þ Ú ÒÝÓ Ö Ò Þ Ú ÒÝ Þ Ö ÒØ Ñ Ö ¹ ÞÓÒÝØ Ð Ò Ð Ö Þ ÌËÁ ÌÊ ½¼¼ ¼¾ ¹½ ¾½ ÌËÁ ÌÊ ½¼¼ ¼¾ ¹¾ ¾¾ Ø Ò Ð ÒØ Ò ØÑÙØ Ø Øº Þ Ð ÖØ Ñ Ö ÞÓÒÝØ Ð Ò Ð Ñ Þ Ö Þ Ö ÒØ Ö Ü ÓÑÔÓÒ Ò Ð Ö ÞÓÒÝØ Ð Ò ÖÙÐ Ý ¹ Ð Ñ Ú Ø Ð Í ÐÓ ÞÐ º½ º Ö µº Å Ú Ð Ð ÙÐ Þ ÐØ ÐÓ ÞÐ Ö Ü Ú ÒÝ Ò Ö Ú Ò Ð Ó Þ Ô Ö Ñ Ø Ö Ý ÓØØ Ñ Ö Þ ÐÐ Ø Ø Ò Ð ÙÐÐ Ñ Ó Þ Ð ØØ Ð ÓÖ ÙÐ Þ ÐØ Ú ÞÓÒÝÓ Ø Ø ÒØ Ø Ú Ð Þ Òò Ú ÐØÓÞ ¹ Ñ ÒÝØ Ö Ò º Þ ÑÙÐ ÓÖ Ò Þ ÖØ Ð ÙÐÐ Ñ Ó ÞÓÒ Ð ÓÖ ÙÐ Þ Ðع Ú ÞÓÒÝÓ Ð ÐÐ Ø Ð Ò º Ý ÓÖÐ Ø Ò Ð ÐÑ ÞÓØØ Ñ Ö Þ Þ Ò Ô ØÖÙÑ Ò Ð Þ ØÓÖ Ø Ð ØÑ ÒÝÑ Ö µ Ñ Ö Þ Þ ØÐ ÓÞ ÔÓÒØ Ò Ñ ÒØ Ö Ö Ò ÓÒµ Ñ Ð Ò Þ ÐØ Ð Ö ÒÝÓ ÐÐ ÑÞ Ø Ñ Öº Þ Ý ÓÖРع Ò Ñ Ö Ð Ò Þ ÐÐ ÑÞ Ð Ø ÖØ Ø Ú ÖØ Ú Þ ÖØ ØÐ ÖØ Ø º Þ ÐÐ ÑÞ ÝÑ Ð Ö ÒÝÓ Ø Ð Ñ Ô Ø Ý Ñ ÖØ Ð Ø Òº ÓÖ Ò ÑÙØ ØÓØØ Þ Ñ Ø Ñ Þ Ö Ð Ô Ò ØÓÚ ¹
82 ¾ Â Ì º Ê Ä Á ÇÃÇ Ì ÄÇË ÄýËÇà º½¾º Ö º Ö Ü Ó ÓÞØ ÐÐ Ô Ø Ò ÓÞ Ø Ý Ö Ü Ð Ø Ò Ö Ú Ò Ú ÒÝ Ò Ñ Ö Ö Ñ Òݵº º½ º Ö º Þ ÌËÁ ÌÊ ½¼¼ ¼¾ ¹½ º Þ Ö ÒØ ¾½ Ö Ü Ó ÓÞØ ÐÓ ÞÐ
83 º º Ê Ä Á À ÌýËýÆ Ã ËÌ ÌÁË ÌÁà Á Ä Å Ë º½ º Ö º Þ ÑÙÐ ÓÖ Ò ÔÓØØ ÑÔÐ Ø ÐÝ Ú ÒÝ Ò Ö ÞÓÐÚ º Þ ÑÙÐ ÓÖ Ò Ð Ò ÔÓÞ Ø Ú ÖØ Ø Ð ÐÐ Ø ºµ Ò Þ Ñ Ø Ð Ô ÙÐ Ð ÔÓÞ Ø Ú ÖØ Ø Ú Þ Ñº Þ ÑÙÐ ÓÖ Ò Ð Ò Þ ÐÝ Þ Ö ÒØ Ð ÐÐ Ø Ñ ÒØ ÞØ º½ º Ö ÑÙØ Ø º Þ Ý ÐÐ ÐÐ ³ ÐÐ ÙÐÐ ÑÓ ³ ÑÔÐ Ø Ò ÐÝ Þ Ö ÒØ ÐÓ ÞÐ Ø ÑÙØ Ø º Ö Þ ÑÔ Ö Ù ÙÑÙÐ Ø Ú ÐÓ ÞÐ Ú ÒÝ º Ö ÓÒ Ð Ø Ø Ö Ü Ø ÒÝ Þ Ú ÐØÓÞ Ú Ð Ô Ö Ñ Ø Ö ÞÚ º Æ Ý Ö Ü Ø Ò Ôк Γ ¼º ÖØ µ Þ ÐØ Ý ÓÖ Ø ÑÙ¹ Ø Ø ÞØÓ Ö Ñ º½ º Ö µ Ð ÒØ ÐØ Ö Ø ÑÙØ Ø Þ Ú ÒÝ ÓÞ Ô ÓÐ Þ Ñ Ø Ñ Þ Ö Ð Ô ÙÐ Ú ØØ º½ Ö ÓÞ Ô Øº Ø Þ Ö Ö Ü ÓÖ Ò Ð ÙÐ Þ ÐØ Ðݵ Ú ÒÝ Þ ÑÙÐ ¹ Ð Ð ÐÐ ØÓØØ ÑÔ Ö Ù ÐÓ ÞÐ Ú ÒÝ Ú Þ Ð Ø ÓÖ Ò Ñ ÔÖ ÐØ Ñ ÑÓ Ð Ò ÝÚ ÖÓ ÖÒÝ Þ Ø Ò Ð ÓÖ ÙÐ Ö Ü Ó ÓÞØ ÙÐÐ ÑØ Ö Ð ¹ Ö Ó Ò Ð ÐÑ ÞÓØØ Ê ÝÐ ¹ ÐÓ ÞÐ ÐÐ ÞØ Øº Þ Γ ¼º½µ Ò Ý Γ ¼º µ ÖØ Ø Ò Ñ ÑÙØ Ø Ð Ö Ñ Óغ Þ Ð Ø Ø º½ º º½ Ö ÓÒº Ú Þ Ð Ø Ð ÚÓÒØ Ø Ø ÞØ Ø ÓÖ Ú ÞÓÒØ Ð ÐÐ ÞØ Ø Ø ¹ ÐÓ ÞÐ Ö Þ ÐÓ ÞÐ Ô Ö Ñ Ø Ö ÓÒ Ò ÒØ ÖÚ ÐÐÙÑÑ Ð Ô Ö Ñ Ø Ö Þ Ø Ö Ü Ø ÒÝ Þ Ú ÒÝ Òº Ø ¹ ÐÓ ÞÐ òöò Ú ÒÝ ½½¾ p(x) = xα 1 (1 x) β 1 B(α, β) º¾ µ
f ij = f i. f.j Ö f 11 = 49 f 12 = 64 f 13 = 84 f 1. = 197
 Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾ ¾º ÞÓ ¾ º Ê Ò ÓÖÖ Ð º Î Ý Ô ÓÐ Ø º ÃÓÖÖ Ð Þ Ñ Ø º Ê Ö Þ Þ Ñ Ø º½º ÝÚ ÐØÓÞ Ö Ö Þ º º º º º º º º º º º º º º º º º º º º º º º º º½º½º Ð Ò ÝÞ Ø Ñ Þ Ö º º º º º º º º º º º º º º º½º¾º
Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾ ¾º ÞÓ ¾ º Ê Ò ÓÖÖ Ð º Î Ý Ô ÓÐ Ø º ÃÓÖÖ Ð Þ Ñ Ø º Ê Ö Þ Þ Ñ Ø º½º ÝÚ ÐØÓÞ Ö Ö Þ º º º º º º º º º º º º º º º º º º º º º º º º º½º½º Ð Ò ÝÞ Ø Ñ Þ Ö º º º º º º º º º º º º º º º½º¾º
ÍÅÄ Ð ØÓ
 ÍÅÄ Ð ØÓ ÄÌ Áà ÈÓÖ Ö ÑÓÞ ÐÑ Ð Ø ÞÓ ØÚ ÖØ ÒÓÐ Ì Ò Þ Ç Ø Ø ÒÝ ½º Ú Þ Ø ½º½º Ð Ø ý Ö ÞÓÐ Ù Ý Ö Ñ Ò Þ Ð ÓÖÓ Ú Ö Ø ÙØ Ò Ð ØÖ Ú Ó ¹ ØÙÑÓ Ø ØØ Ð Ý ØØ Ø ÒØ Ð Þ Ó ØÙÑÓ Þ ØØ Ô¹ ÓÐ ØÓ Ø ØÓÐÓ Ö Ø Ö Ø ½¼¼ µ ØÓÐÓ Ú
ÍÅÄ Ð ØÓ ÄÌ Áà ÈÓÖ Ö ÑÓÞ ÐÑ Ð Ø ÞÓ ØÚ ÖØ ÒÓÐ Ì Ò Þ Ç Ø Ø ÒÝ ½º Ú Þ Ø ½º½º Ð Ø ý Ö ÞÓÐ Ù Ý Ö Ñ Ò Þ Ð ÓÖÓ Ú Ö Ø ÙØ Ò Ð ØÖ Ú Ó ¹ ØÙÑÓ Ø ØØ Ð Ý ØØ Ø ÒØ Ð Þ Ó ØÙÑÓ Þ ØØ Ô¹ ÓÐ ØÓ Ø ØÓÐÓ Ö Ø Ö Ø ½¼¼ µ ØÓÐÓ Ú
Ì ÖØ ÐÓÑ ÝÞ Áº Ú Þ Ø ÐØ Ð ÒÓ Þ ÐÝÓ ½º Þ ÐÝ ÒÝÚ Þ Ñ ÐÝ Ø ÐÝ ¾º Ö ¾º½º Ö Ø Ö º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º¾º Ö Ó ÐØ Ð ÒÓ Ð
 Æ ÓÒ Ã ÑÔÓ Â Ø Ù Þ ÐÝ ÒÝÚ ¾¼½ º ÖÙ Ö ¾¾º Þ ÐÐ ØÓØØ Å ØÞ Ö ÒØ Ð È ÖÓ Ð ËÞ Ö ÞØ ØØ Ì Ñ Ö ÓÖ ÒÝ Ô ÞØ ÃÖ Ø Ò Ö Ä ØÓÖ ÐØ Ï Þ Ò ÖÙ Ö Â ÒÓ ËÞ Ý Ê ÖØ ½ Ì ÖØ ÐÓÑ ÝÞ Áº Ú Þ Ø ÐØ Ð ÒÓ Þ ÐÝÓ ½º Þ ÐÝ ÒÝÚ Þ Ñ ÐÝ Ø ÐÝ
Æ ÓÒ Ã ÑÔÓ Â Ø Ù Þ ÐÝ ÒÝÚ ¾¼½ º ÖÙ Ö ¾¾º Þ ÐÐ ØÓØØ Å ØÞ Ö ÒØ Ð È ÖÓ Ð ËÞ Ö ÞØ ØØ Ì Ñ Ö ÓÖ ÒÝ Ô ÞØ ÃÖ Ø Ò Ö Ä ØÓÖ ÐØ Ï Þ Ò ÖÙ Ö Â ÒÓ ËÞ Ý Ê ÖØ ½ Ì ÖØ ÐÓÑ ÝÞ Áº Ú Þ Ø ÐØ Ð ÒÓ Þ ÐÝÓ ½º Þ ÐÝ ÒÝÚ Þ Ñ ÐÝ Ø ÐÝ
Ú Þ Ø Þ Ô Ð Ò Þ Ú Ñ Ò ÞÔÓÒØ Þ ¹ Ö Ô Ø Ø ÞÓØØ Þ Ð Ö Ú Þ Ð ØÓ Òº ËÞ ÑÐ Ð Ø Ò Þ ÐÚ Þ Ú ÐØÓÞ Ð ÑòÚ Ð Ø Ð Ð Ð Ô Ø ØØ ÓÐÝ Ò Ð¹ ÓÖÓÞ ØÓ Ñ ÐÝ ÓØØ Ø ÔÙ Ð Ö Ø Ò
 Ó ØÓÖ ÖØ Þ Ø Þ ÃÓÑ Ò ØÓÖ Ù Ø Ð Ò 0¹ Ý Þ Öò Ð ÓÔÓÖØÓ Þ Ô ØÖÙÑ Ã Ø ¹ÍÖ Ò Ã Ñ ÐÐ Ì Ñ Ú Þ Ø Öº Å Ý Ä ÞÐ Ý Ø Ñ Ó Ò Öº ËÞ Ý Ø Ñ Ó Ò Å Ø Ñ Ø ¹ ËÞ Ñ Ø ØÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÓÐÝ ÁÒØ Þ Ø ¾¼¼ Ú Þ
Ó ØÓÖ ÖØ Þ Ø Þ ÃÓÑ Ò ØÓÖ Ù Ø Ð Ò 0¹ Ý Þ Öò Ð ÓÔÓÖØÓ Þ Ô ØÖÙÑ Ã Ø ¹ÍÖ Ò Ã Ñ ÐÐ Ì Ñ Ú Þ Ø Öº Å Ý Ä ÞÐ Ý Ø Ñ Ó Ò Öº ËÞ Ý Ø Ñ Ó Ò Å Ø Ñ Ø ¹ ËÞ Ñ Ø ØÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÓÐÝ ÁÒØ Þ Ø ¾¼¼ Ú Þ
dc_869_14 ÅÌ Ó ØÓÖ ÖØ Þ Ø Þ Æ Ñ¹ Ý Ò ÐÝ Ò Ñ Ð ÓÒÝ Ñ ÒÞ Ú ÒØÙÑ Ö Ò Þ Ö Ò Ö Ð Þ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ ¾¼½
 ÅÌ Ó ØÓÖ ÖØ Þ Ø Þ Æ Ñ¹ Ý Ò ÐÝ Ò Ñ Ð ÓÒÝ Ñ ÒÞ Ú ÒØÙÑ Ö Ò Þ Ö Ò Ö Ð Þ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ ¾¼½ ½ ½º Ú Þ Ø Þ Ð ÓÒÝ Ñ ÒÞ Ö Ò Þ Ö Ð ÒÐ Ú Ð ¹ Ö Ø Ó Ð Ð ÓÞØ Ø Þ Ù Ó Øº Ú ÒØÙÑ Ù ØÙ Ð Ò Ò Ð Ö Ò Ð ÒØ Ø Ö
ÅÌ Ó ØÓÖ ÖØ Þ Ø Þ Æ Ñ¹ Ý Ò ÐÝ Ò Ñ Ð ÓÒÝ Ñ ÒÞ Ú ÒØÙÑ Ö Ò Þ Ö Ò Ö Ð Þ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ ¾¼½ ½ ½º Ú Þ Ø Þ Ð ÓÒÝ Ñ ÒÞ Ö Ò Þ Ö Ð ÒÐ Ú Ð ¹ Ö Ø Ó Ð Ð ÓÞØ Ø Þ Ù Ó Øº Ú ÒØÙÑ Ù ØÙ Ð Ò Ò Ð Ö Ò Ð ÒØ Ø Ö
Ð Þ Ù Þ Ø Ö Ý ÐÓ ÞØ Þ Ø Ö Ý Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý Ð Ô Ö ÀÓ Ý Ò Ñò Þ ÙÒ Ú ÖÞÙÑ Ð ÔÚ Ø Ó ÐÑ Ø Ö ÒÝ Ñ Þ Ò Ö Ö Ú Ø º
 Þ ÆÝ ØÖ Ý Ö ÐÝ È µ ÈÌ ÈÅÅÁÃ ¾¼½ º ÒÙ Ö º Ð Þ Ù Þ Ø Ö Ý ÐÓ ÞØ Þ Ø Ö Ý Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý Ð Ô Ö ÀÓ Ý Ò Ñò Þ ÙÒ Ú ÖÞÙÑ Ð ÔÚ Ø Ó ÐÑ Ø Ö ÒÝ Ñ Þ Ò Ö Ö Ú Ø º Þ Ø Ö Ý ÐÓ ÞØ Ð Þ Ù Þ Å Ò Ì ÖÑÓ Ò Ñ Ð ØÖÓ Ò Ñ ÇÔØ
Þ ÆÝ ØÖ Ý Ö ÐÝ È µ ÈÌ ÈÅÅÁÃ ¾¼½ º ÒÙ Ö º Ð Þ Ù Þ Ø Ö Ý ÐÓ ÞØ Þ Ø Ö Ý Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý Ð Ô Ö ÀÓ Ý Ò Ñò Þ ÙÒ Ú ÖÞÙÑ Ð ÔÚ Ø Ó ÐÑ Ø Ö ÒÝ Ñ Þ Ò Ö Ö Ú Ø º Þ Ø Ö Ý ÐÓ ÞØ Ð Þ Ù Þ Å Ò Ì ÖÑÓ Ò Ñ Ð ØÖÓ Ò Ñ ÇÔØ
Ú Þ Ø ÐÐ Þ Ð ÐØ Ð Ø Ñ Ú ÞØ Ø ÒÙÐÑ ÒÝÓÞ ÙÐ ÓÒØÓ ÐÐ ¹ Ð ÓÐÝ Ñ Ø Ò Ñ ÖØ Þº Ø Ñ Ú ÞØ Ñ ÖØ ÐРРй Ð ÔÓØ Ø Ð Ú Ö Ö ÐÐ Ó Ø Ò Ø Ò Ý Ö Ò Ð Ñ Ð ÓÖÓÞ Ø ÐÐ Ó Ò Ð
 ÇÔØ ÃÚ ÒØÙÑ Ð ØÖÓÒ Ì Ò Þ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ Î Ö Ö ÐÐ Ó Ø Ñ Ú ÞØ Ñ ÐÑ ÞÓ Ò Ó ØÓÖ È µ ÖØ Þ Ø Þ Å Þ ÖÓ ËÞ ÓÐ Ì Ñ Ú Þ Ø Öº Ò Ö Ãº ÙÔÖ À ÖÚ Ö ¹ËÑ Ø ÓÒ Ò ÒØ Ö ÓÖ ØÖÓÔ Ý Ñ Ö ÍË Ð ÓÒÞÙÐ Ò Öº Î Ò Â Þ ÇÔØ ÃÚ ÒØÙÑ
ÇÔØ ÃÚ ÒØÙÑ Ð ØÖÓÒ Ì Ò Þ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ Î Ö Ö ÐÐ Ó Ø Ñ Ú ÞØ Ñ ÐÑ ÞÓ Ò Ó ØÓÖ È µ ÖØ Þ Ø Þ Å Þ ÖÓ ËÞ ÓÐ Ì Ñ Ú Þ Ø Öº Ò Ö Ãº ÙÔÖ À ÖÚ Ö ¹ËÑ Ø ÓÒ Ò ÒØ Ö ÓÖ ØÖÓÔ Ý Ñ Ö ÍË Ð ÓÒÞÙÐ Ò Öº Î Ò Â Þ ÇÔØ ÃÚ ÒØÙÑ
Ð ØÖÓÑ Ò Ø Ö ÎÁº ÆÝ ØÖ Ý Ö ÐÝ ÈÌ ÈÅÅÁà ΠÐÐ ÑÓ À Ð Þ ØÓ Ì Ò Þ ¾¼½ º Ð Ù º
 Ð ØÖÓÑ Ò Ø Ö ÎÁº ÆÝ ØÖ Ý Ö ÐÝ ÈÌ ÈÅÅÁà ΠÐÐ ÑÓ À Ð Þ ØÓ Ì Ò Þ ¾¼½ º Ð Ù º ÓÒØ ØÔÓØ Ò Ð ÓÒØ Ø¹ÔÓØ Ò Ð Ð Ò Ú Ø Þ ÔÔ Ò Ø ÖÓÞ Ø Ñ Í ½ ¾ = Ï ¾ Ï ½ Å Ú Ð Þ Þ ÐØ Ñ Ð Ð Ø Þ Ð Ò Ð Ú Ð ØÖÓÒÓ Ö ÚÓÒ Ø ÓÞ ÞØ ÎÓÐØ ¹
Ð ØÖÓÑ Ò Ø Ö ÎÁº ÆÝ ØÖ Ý Ö ÐÝ ÈÌ ÈÅÅÁà ΠÐÐ ÑÓ À Ð Þ ØÓ Ì Ò Þ ¾¼½ º Ð Ù º ÓÒØ ØÔÓØ Ò Ð ÓÒØ Ø¹ÔÓØ Ò Ð Ð Ò Ú Ø Þ ÔÔ Ò Ø ÖÓÞ Ø Ñ Í ½ ¾ = Ï ¾ Ï ½ Å Ú Ð Þ Þ ÐØ Ñ Ð Ð Ø Þ Ð Ò Ð Ú Ð ØÖÓÒÓ Ö ÚÓÒ Ø ÓÞ ÞØ ÎÓÐØ ¹
(rot. j n df. Hd s = F. H) n df = F. j n df = n j n df, Hd s = ni.
 Ä ÃÌÊÇ ÁÆ ÅÁà ½¼º Ð µ Ø Ö Ñ Ò Ø Ö Î Ý Ò Ý Ó Þ Ö ÞØÑ Ø Þ Øò Ø Ö Øº I Ñ Ò Ø Ö Ø ÒØ Ö ÑÙØ Ø º Ñ Ò Ø Ö Ø Ö Ò Ú Ð Ý Ò Ø Ö Ð Ò Ô Þ Ð Ø Ð ÐÐ Ò ÓÑÓ ÒÒ Ø Òع Ø º À Ø ÖÓÞÞÙ Ñ Ø Ö Ö Ø Ø Ö Ð Òº ÁÒØ Ö Ð Ù rot H = j,
Ä ÃÌÊÇ ÁÆ ÅÁà ½¼º Ð µ Ø Ö Ñ Ò Ø Ö Î Ý Ò Ý Ó Þ Ö ÞØÑ Ø Þ Øò Ø Ö Øº I Ñ Ò Ø Ö Ø ÒØ Ö ÑÙØ Ø º Ñ Ò Ø Ö Ø Ö Ò Ú Ð Ý Ò Ø Ö Ð Ò Ô Þ Ð Ø Ð ÐÐ Ò ÓÑÓ ÒÒ Ø Òع Ø º À Ø ÖÓÞÞÙ Ñ Ø Ö Ö Ø Ø Ö Ð Òº ÁÒØ Ö Ð Ù rot H = j,
Þ Þ Ø ØØ Ú ÐÐ ÑÓ Ð Þ Ø Þ Þ Ø ØØ Ú ÐÐ ÑÓ Ð Þ Ø Ð ÓÒØÓ ÐÐ ÑÞ Ó Ý Ð Þ Ó Ú Ò¹ Ò Þ Ö Ñ Ö Òº Èк Ý ØÐ Ò Ø Ð ÔÖ Ø ÞÞ Ð ÑÔ Ø Ô ÓÐÙÒ ¾¹½½º Ö µ Ú Ý Ï Ø ØÓÒ ¹ ¾¹
 Ä ÃÌÊÇ ÁÆ ÅÁÃ Ý Ò Ö Ñ Ð Þ ØÓ ¾º Þ Þ Ø ØØ Ú ÐÐ ÑÓ Ð Þ Ø Þ Þ Ø ØØ Ú ÐÐ ÑÓ Ð Þ Ø Ð ÓÒØÓ ÐÐ ÑÞ Ó Ý Ð Þ Ó Ú Ò¹ Ò Þ Ö Ñ Ö Òº Èк Ý ØÐ Ò Ø Ð ÔÖ Ø ÞÞ Ð ÑÔ Ø Ô ÓÐÙÒ ¾¹½½º Ö µ Ú Ý Ï Ø ØÓÒ ¹ ¾¹½¾º Ö µº Þ ÙØ Ø ÐÐ
Ä ÃÌÊÇ ÁÆ ÅÁÃ Ý Ò Ö Ñ Ð Þ ØÓ ¾º Þ Þ Ø ØØ Ú ÐÐ ÑÓ Ð Þ Ø Þ Þ Ø ØØ Ú ÐÐ ÑÓ Ð Þ Ø Ð ÓÒØÓ ÐÐ ÑÞ Ó Ý Ð Þ Ó Ú Ò¹ Ò Þ Ö Ñ Ö Òº Èк Ý ØÐ Ò Ø Ð ÔÖ Ø ÞÞ Ð ÑÔ Ø Ô ÓÐÙÒ ¾¹½½º Ö µ Ú Ý Ï Ø ØÓÒ ¹ ¾¹½¾º Ö µº Þ ÙØ Ø ÐÐ
Ð Þ Ù Þ Ø Ö Ý ÐÓ ÞØ Þ Ø Ö Ý Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý Ð Ô Ö ÀÓ Ý Ò Ñò Þ ÙÒ Ú ÖÞÙÑ Ð ÔÚ Ø Ó ÐÑ Ø Ö ÒÝ Ñ Þ Ò Ö Ö Ú Ø º
 Þ ÆÝ ØÖ Ý Ö ÐÝ È µ ÈÌ ÈÅÅÁÃ ¾¼½ º ÒÙ Ö ½ º Ð Þ Ù Þ Ø Ö Ý ÐÓ ÞØ Þ Ø Ö Ý Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý Ð Ô Ö ÀÓ Ý Ò Ñò Þ ÙÒ Ú ÖÞÙÑ Ð ÔÚ Ø Ó ÐÑ Ø Ö ÒÝ Ñ Þ Ò Ö Ö Ú Ø º Þ Ø Ö Ý ÐÓ ÞØ Ð Þ Ù Þ Å Ò Ì ÖÑÓ Ò Ñ Ð ØÖÓ Ò Ñ ÇÔØ
Þ ÆÝ ØÖ Ý Ö ÐÝ È µ ÈÌ ÈÅÅÁÃ ¾¼½ º ÒÙ Ö ½ º Ð Þ Ù Þ Ø Ö Ý ÐÓ ÞØ Þ Ø Ö Ý Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý Ð Ô Ö ÀÓ Ý Ò Ñò Þ ÙÒ Ú ÖÞÙÑ Ð ÔÚ Ø Ó ÐÑ Ø Ö ÒÝ Ñ Þ Ò Ö Ö Ú Ø º Þ Ø Ö Ý ÐÓ ÞØ Ð Þ Ù Þ Å Ò Ì ÖÑÓ Ò Ñ Ð ØÖÓ Ò Ñ ÇÔØ
rot H = j, 1. div D = ρ, 2. rot E = 0, 3. div B = 0. 4.
 Ä ÃÌÊÇ ÁÆ ÅÁà º Ð µ ËØ ÓÒ Ö Ù Ö ÑÓ I = j df. F, Ò Ö Þ Ò Ú Þ Ø Ö ÑÑ Ð Ó Ð Ð ÓÞÙÒ ÓÒ Ù Ø Ú Ö Ñµº Å ÜÛ Ðй Ý ÒÐ Ø Þ Ð Ð Ò ÖÚ ÒÝ rot H = j, 1. div D = ρ, 2. rot E = 0, 3. div B = 0. 4. à РØÒ Ó Ù Ó Ý Þ ½º
Ä ÃÌÊÇ ÁÆ ÅÁà º Ð µ ËØ ÓÒ Ö Ù Ö ÑÓ I = j df. F, Ò Ö Þ Ò Ú Þ Ø Ö ÑÑ Ð Ó Ð Ð ÓÞÙÒ ÓÒ Ù Ø Ú Ö Ñµº Å ÜÛ Ðй Ý ÒÐ Ø Þ Ð Ð Ò ÖÚ ÒÝ rot H = j, 1. div D = ρ, 2. rot E = 0, 3. div B = 0. 4. à РØÒ Ó Ù Ó Ý Þ ½º
È Ö ÙÞ ÑÓ ØÓØØ Ú Ð Ñ¹Ñ Þ Ö ØÓÐØ Ð ØÖÓ Ò Ñ ÔÖÓ Ð Ñ Ñ ÓÐ Ò ÖØ Å Ö Ò Ð Ç Ð Ú Ð Ñ ØÖÓÒ Ñ ÖÒ ÃÓÒÞÙÐ Ò ÈÖÓ º Öº ÃÙÞÑ ÒÒ Å Ð ºËº Ý Ø Ñ Ø Ò Ö ËÞ ÒÝ Á ØÚ Ò Ý Ø
 È Ö ÙÞ ÑÓ ØÓØØ Ú Ð Ñ¹Ñ Þ Ö ØÓÐØ Ð ØÖÓ Ò Ñ ÔÖÓ Ð Ñ Ñ ÓÐ Ò ÖØ Å Ö Ò Ð Ç Ð Ú Ð Ñ ØÖÓÒ Ñ ÖÒ ÃÓÒÞÙÐ Ò ÈÖÓ º Öº ÃÙÞÑ ÒÒ Å Ð ºËº Ý Ø Ñ Ø Ò Ö ËÞ ÒÝ Á ØÚ Ò Ý Ø Ñ ÙØÓÑ Ø Þ Ð Ì Ò Þ È º º Ó ØÓÖ ÖØ Þ ËÞ ÒÝ Á ØÚ Ò Ý
È Ö ÙÞ ÑÓ ØÓØØ Ú Ð Ñ¹Ñ Þ Ö ØÓÐØ Ð ØÖÓ Ò Ñ ÔÖÓ Ð Ñ Ñ ÓÐ Ò ÖØ Å Ö Ò Ð Ç Ð Ú Ð Ñ ØÖÓÒ Ñ ÖÒ ÃÓÒÞÙÐ Ò ÈÖÓ º Öº ÃÙÞÑ ÒÒ Å Ð ºËº Ý Ø Ñ Ø Ò Ö ËÞ ÒÝ Á ØÚ Ò Ý Ø Ñ ÙØÓÑ Ø Þ Ð Ì Ò Þ È º º Ó ØÓÖ ÖØ Þ ËÞ ÒÝ Á ØÚ Ò Ý
ÓÑ Ã Ø Ð ÔÚØ Ó ÐÓÑ Þ Ð Ü Ò Ö ÔÓÐ ÒÓÑ ÐÓ Ö ÓÑÓÐ ÃÓÑ Ò ØÓÖ Ù Ñ Þ Ö Ð ÓÑ ÒÚ Ö Ò Ó Ð ÓÒÝ Ñ ÒÞ ØÓÔÓÐ ÓÑ Ò ØÓÖ ËØ Ô Þ Ò Ö Ê ÒÝ Ð Ö Å Ø Ñ Ø ÃÙØ Ø ÒØ Þ Ø ¾¼¼
 ÒÚ Ö Ò Ó Ð ÓÒÝ Ñ ÒÞ ØÓÔÓÐ ÓÑ Ò ØÓÖ Ê ÒÝ Ð Ö Å Ø Ñ Ø ÃÙØ Ø ÒØ Þ Ø ¾¼¼ º ÒÓÚ Ñ Ö ¾ º ÒÚ Ö Ò Ó Ð ÓÒÝ Ñ ÒÞ ØÓÔÓÐ ÓÑ Ò Ê Ñ Ø Ö ÑÓÞ Ó Þ Ë ½ ÖÚÓÒ Ð Ê Ú Ð Ö Ò Ð Ø Ý Þ Ø Ò Ú ÞÞ ÓÑ Ò º Ã ½ Ã ¾ ÓÑ ÞÓÒÓ ÝÑ ÑÓÞ Ø Ø
ÒÚ Ö Ò Ó Ð ÓÒÝ Ñ ÒÞ ØÓÔÓÐ ÓÑ Ò ØÓÖ Ê ÒÝ Ð Ö Å Ø Ñ Ø ÃÙØ Ø ÒØ Þ Ø ¾¼¼ º ÒÓÚ Ñ Ö ¾ º ÒÚ Ö Ò Ó Ð ÓÒÝ Ñ ÒÞ ØÓÔÓÐ ÓÑ Ò Ê Ñ Ø Ö ÑÓÞ Ó Þ Ë ½ ÖÚÓÒ Ð Ê Ú Ð Ö Ò Ð Ø Ý Þ Ø Ò Ú ÞÞ ÓÑ Ò º Ã ½ Ã ¾ ÓÑ ÞÓÒÓ ÝÑ ÑÓÞ Ø Ø
D = ǫ0 ǫ r. ½º Å rot H = j + ρ v + D. rot H = j + ρ v + ǫ 0 ǫ r. Erot H = E j Eρ v Eǫ 0 ǫ r. ρ( v, E) = Erot H Hrot E ( j, E) ǫ 0 ǫ r
 Ä ÃÌÊÇ ÁÆ ÅÁà º Ð µ Þ Ð ØÖÓÑ Ò Ø Ö Ò Ö Î Þ Ð Ù Þ Ð ØÖÓÑ Ò Ø Ö Ø ÓÑÓ Ò ÞÓØÖ Ô Þ Ø Ð Òº ǫ, µ, σ ÐÐ Ò º ÓÖ ½º Å rot H = j + ρ v + D t, ½³º Å rot H = j + ρ v + ǫ 0 ǫ r E t. º Å rot E = B t ³º Å rot E = µ 0
Ä ÃÌÊÇ ÁÆ ÅÁà º Ð µ Þ Ð ØÖÓÑ Ò Ø Ö Ò Ö Î Þ Ð Ù Þ Ð ØÖÓÑ Ò Ø Ö Ø ÓÑÓ Ò ÞÓØÖ Ô Þ Ø Ð Òº ǫ, µ, σ ÐÐ Ò º ÓÖ ½º Å rot H = j + ρ v + D t, ½³º Å rot H = j + ρ v + ǫ 0 ǫ r E t. º Å rot E = B t ³º Å rot E = µ 0
 Ð ØÖÓÑ Ò Ø Ö ÎÁÁÁº ÆÝ ØÖ Ý Ö ÐÝ ÈÌ ÈÅÅÁà ΠÐÐ ÑÓ À Ð Þ ØÓ Ì Ò Þ ¼½ º ÒÓÚ Ñ Ö º ÍÐØÖ Ö Ú ¹ ÒÝ ÑÔÙÐÞÙ Ó Ð ÐÐ Ø Þ Ð Ð Þ Ö ÑÓÒ ØÖ Å Ñ Ò ÖÙ ÒÐ Þ Ö ½ ¼ ÁÑÔÙÐÞÙ Ó Þ ÒØ ¹ Ô Ò ½¼¼ Ò ½ Ò ½¼ µ ¹ ɹ Ô ÓÐ ½ ½¹ µ ½¼
Ð ØÖÓÑ Ò Ø Ö ÎÁÁÁº ÆÝ ØÖ Ý Ö ÐÝ ÈÌ ÈÅÅÁà ΠÐÐ ÑÓ À Ð Þ ØÓ Ì Ò Þ ¼½ º ÒÓÚ Ñ Ö º ÍÐØÖ Ö Ú ¹ ÒÝ ÑÔÙÐÞÙ Ó Ð ÐÐ Ø Þ Ð Ð Þ Ö ÑÓÒ ØÖ Å Ñ Ò ÖÙ ÒÐ Þ Ö ½ ¼ ÁÑÔÙÐÞÙ Ó Þ ÒØ ¹ Ô Ò ½¼¼ Ò ½ Ò ½¼ µ ¹ ɹ Ô ÓÐ ½ ½¹ µ ½¼
t = c U, t0 = x 0 t = c (1+U/c), c (1 U/c) U x δt B = 1 2
 Þ Ö Ô Ö ÓÜÓÒÖ Ð ÀÖ È Ø Ö ÈÌ ÐÑ Ð Ø Þ Ì Ò Þ Þ Ö Ô Ö ÓÜÓÒ Ú Ý Ñ Ò Ú Ò Þ ÖÔ Ö ÓÜÓÒµ Ó ÐÑ Þ ÑÔÓÒØ Ð Ö Ð Ø Ú Ø ÐÑ Ð Ø Ý Ð ÓÒØÓ Ú Ø ÞÑ ÒÝ º Ð Ò ÓÐ ÓÞ Ø Ô Ö ¹ ÓÜÓÒÒ Ý ØÙÐ ÓÒ ÔÔ Ò Ø Ò ÐÐ ò Ñ Þ Ú Ö Ø Ô ØÙ Ú Ð Ó
Þ Ö Ô Ö ÓÜÓÒÖ Ð ÀÖ È Ø Ö ÈÌ ÐÑ Ð Ø Þ Ì Ò Þ Þ Ö Ô Ö ÓÜÓÒ Ú Ý Ñ Ò Ú Ò Þ ÖÔ Ö ÓÜÓÒµ Ó ÐÑ Þ ÑÔÓÒØ Ð Ö Ð Ø Ú Ø ÐÑ Ð Ø Ý Ð ÓÒØÓ Ú Ø ÞÑ ÒÝ º Ð Ò ÓÐ ÓÞ Ø Ô Ö ¹ ÓÜÓÒÒ Ý ØÙÐ ÓÒ ÔÔ Ò Ø Ò ÐÐ ò Ñ Þ Ú Ö Ø Ô ØÙ Ú Ð Ó
x = 10±0.1 y = 5±0.02 z = 20±0.4
 ÆÙÑ Ö Ù Ñ Þ Ö ¹ ÆÙÑ Ö Ù Ò Ð Þ Ý ÓÖÐ Ð ØÓ Å Ã ½ ¹ Å Ã ½ ½ ĵ ¹ Å Ã ½ ĵ Æ ÑÓ Ö Ñ Ø ÓÖ ÙÒ ¹Ñ Óк Ù Å ÓÐ Ý Ø Ñ Ô ÞÑ ÖÒ ÁÒ ÓÖÑ Ø Ã Ö Ð ÐÑ ÞÓØØ Å Ø Ñ Ø ÁÒØ Þ Ø Ì Ò Þ ¾¼½ ¾ Ì ÖØ ÐÓÑ ÝÞ ½º ÃÐ Þ Ù Þ Ñ Ø ¾º Å ØÖ
ÆÙÑ Ö Ù Ñ Þ Ö ¹ ÆÙÑ Ö Ù Ò Ð Þ Ý ÓÖÐ Ð ØÓ Å Ã ½ ¹ Å Ã ½ ½ ĵ ¹ Å Ã ½ ĵ Æ ÑÓ Ö Ñ Ø ÓÖ ÙÒ ¹Ñ Óк Ù Å ÓÐ Ý Ø Ñ Ô ÞÑ ÖÒ ÁÒ ÓÖÑ Ø Ã Ö Ð ÐÑ ÞÓØØ Å Ø Ñ Ø ÁÒØ Þ Ø Ì Ò Þ ¾¼½ ¾ Ì ÖØ ÐÓÑ ÝÞ ½º ÃÐ Þ Ù Þ Ñ Ø ¾º Å ØÖ
) ξi (t i t i j i
 Ë Á ÌÍ ÇÅýÆ Ì Å Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ ÁÒ ÓÖÑ Ø Ã Ö Å Ø Ñ Ø ¹ ËÞ Ñ Ø ØÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ ËÞ Ñ Ø Ô Ð ÓÖ ØÑÙ Ó Å Ø Ö ÁÒØ ÐÐ Ò Ì Ò Þ ËÔ Ð ÙØÓÑ Ø Ó ÞØ ÐÝÓ ÐÐ ÑÞ Ó ØÓÖ ÖØ Þ Ø Þ ÝÙÖ Þ Ý Ö Ý Ì Ñ Ú Þ Ø Öº Ö Ò ËÞ ¾¼½¼
Ë Á ÌÍ ÇÅýÆ Ì Å Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ ÁÒ ÓÖÑ Ø Ã Ö Å Ø Ñ Ø ¹ ËÞ Ñ Ø ØÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ ËÞ Ñ Ø Ô Ð ÓÖ ØÑÙ Ó Å Ø Ö ÁÒØ ÐÐ Ò Ì Ò Þ ËÔ Ð ÙØÓÑ Ø Ó ÞØ ÐÝÓ ÐÐ ÑÞ Ó ØÓÖ ÖØ Þ Ø Þ ÝÙÖ Þ Ý Ö Ý Ì Ñ Ú Þ Ø Öº Ö Ò ËÞ ¾¼½¼
Ö ÒÝ Ô Ö Ñ Ø Ö Ò Ø Þ ÑÓÞ Ö ÙØÓ Ø Ð Ø Ù ÖÓÒØÓ Ò Ó ØÓÖ È µ ÖØ Þ Ì Ø Ì Ñ Ö Ì Ñ Ú Þ Ø Öº Ì Ø ý ÓØ Öº ÀÓÖÚ Ø Þ Ã ÖÒÝ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Á ÓÐ Ë Ì ÌÌÁÃ Þ Ã Ñ
 Ö ÒÝ Ô Ö Ñ Ø Ö Ò Ø Þ ÑÓÞ Ö ÙØÓ Ø Ð Ø Ù ÖÓÒØÓ Ò Ó ØÓÖ È µ ÖØ Þ Ì Ø Ì Ñ Ö Ì Ñ Ú Þ Ø Öº Ì Ø ý ÓØ Öº ÀÓÖÚ Ø Þ Ã ÖÒÝ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Á ÓÐ Ë Ì ÌÌÁÃ Þ Ã Ñ Ì Ò Þ ËÞ ¾¼¼ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½ ¾º ÁÖÓ ÐÑ ØØ ÒØ
Ö ÒÝ Ô Ö Ñ Ø Ö Ò Ø Þ ÑÓÞ Ö ÙØÓ Ø Ð Ø Ù ÖÓÒØÓ Ò Ó ØÓÖ È µ ÖØ Þ Ì Ø Ì Ñ Ö Ì Ñ Ú Þ Ø Öº Ì Ø ý ÓØ Öº ÀÓÖÚ Ø Þ Ã ÖÒÝ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Á ÓÐ Ë Ì ÌÌÁÃ Þ Ã Ñ Ì Ò Þ ËÞ ¾¼¼ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½ ¾º ÁÖÓ ÐÑ ØØ ÒØ
rot H = J + D div D = ρ, w = 1 2 E D H B,
 Ë Ð Ø Þ Ð ØÖÓÑ Ò Ø Ö Ø ÒØ Ö Ý ÒÝ Ò ÐÑ ÐÝ Ø Þ È Ú Â Þ ¾¼½ º ÒÙ Ö ½º Ì ÖØ ÐÓÑ ÝÞ ½º Þ Ð ØÖÓ Ò Ñ Ø Ñ Ö Ø ÖØÓÞ Ð Ò ÓÔÓÖØÓ Ø ¾ ½º½º Þ Ð ØÖÓÑ Ò Ø Ö Ð Ø Ö Ð Ú ÐØÓÞ Ò Ô ÓÐ Ø ¾ ½º¾º ËØ Ø Ù Ø Ö d λ Ú Ý d δ º º º
Ë Ð Ø Þ Ð ØÖÓÑ Ò Ø Ö Ø ÒØ Ö Ý ÒÝ Ò ÐÑ ÐÝ Ø Þ È Ú Â Þ ¾¼½ º ÒÙ Ö ½º Ì ÖØ ÐÓÑ ÝÞ ½º Þ Ð ØÖÓ Ò Ñ Ø Ñ Ö Ø ÖØÓÞ Ð Ò ÓÔÓÖØÓ Ø ¾ ½º½º Þ Ð ØÖÓÑ Ò Ø Ö Ð Ø Ö Ð Ú ÐØÓÞ Ò Ô ÓÐ Ø ¾ ½º¾º ËØ Ø Ù Ø Ö d λ Ú Ý d δ º º º
Ë Ø ÙØÓÑ Ø ÞÓ Ó Ò Ñ Ð ÐÑ Þ Ó ØÓÖ È º ºµ ÖØ Þ ÃÓ Ö ÐÝ Ì Ñ Ú Þ Ø Öº ËÞØÖ Â ÒÓ Öº ÃÙÒ Ö Ò Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò ÁÒ ÓÖÑ Ø ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á
 Ë Ø ÙØÓÑ Ø ÞÓ Ó Ò Ñ Ð ÐÑ Þ Ó ØÓÖ È º ºµ ÖØ Þ ÃÓ Ö ÐÝ Ì Ñ Ú Þ Ø Öº ËÞØÖ Â ÒÓ Öº ÃÙÒ Ö Ò Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò ÁÒ ÓÖÑ Ø ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ö Ò ¾¼½¾ Þ Ò ÖØ Þ Ø Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ
Ë Ø ÙØÓÑ Ø ÞÓ Ó Ò Ñ Ð ÐÑ Þ Ó ØÓÖ È º ºµ ÖØ Þ ÃÓ Ö ÐÝ Ì Ñ Ú Þ Ø Öº ËÞØÖ Â ÒÓ Öº ÃÙÒ Ö Ò Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò ÁÒ ÓÖÑ Ø ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ö Ò ¾¼½¾ Þ Ò ÖØ Þ Ø Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ
 Ð Ô Ø Ø Ù ÔÖÓ Ö Ñ Þ Ð Ø Ð Þ Ð Ø Â Þ ÂÙ Ø ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ËÞÓ ØÚ Ö Ð ÞØ Ì Ò Þ Ì Ñ Ú Þ Ø Öº Ý Ñ Ø Ý Ì ÓÖ ËÞ ¾¼¼ º Ñ Ù ÖØ Þ Ó ØÓÖ Ó ÓÞ Ø Ñ Þ ÖÞ Þ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ Ð Þ ÔÖÓ Ö Ñ Þ Ð Ø
Ð Ô Ø Ø Ù ÔÖÓ Ö Ñ Þ Ð Ø Ð Þ Ð Ø Â Þ ÂÙ Ø ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ËÞÓ ØÚ Ö Ð ÞØ Ì Ò Þ Ì Ñ Ú Þ Ø Öº Ý Ñ Ø Ý Ì ÓÖ ËÞ ¾¼¼ º Ñ Ù ÖØ Þ Ó ØÓÖ Ó ÓÞ Ø Ñ Þ ÖÞ Þ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ Ð Þ ÔÖÓ Ö Ñ Þ Ð Ø
E0 sin ωt, D = ǫ. σ ν2πǫ, ǫ 1, σ ( ) 1 s.
 Ä ÃÌÊÇ ÁÆ ÅÁà ½½º Ð µ E = E0 sin ωt, D = ǫ E, D t = ωǫ E 0 cosωt = ν2πǫ E 0 cosωt, j = σe = σe0 sin ωt, j D t max = max σ ν2πǫ, ǫ 1, σ (10 16 10 17 ) 1 s. Þ Ð ØÖÓØ Ò Ò Ð ÓÖ ÙÐ Þ Ö Ú Ò Ö ÒØ ÒÝ Ó σ 1 νπǫ
Ä ÃÌÊÇ ÁÆ ÅÁà ½½º Ð µ E = E0 sin ωt, D = ǫ E, D t = ωǫ E 0 cosωt = ν2πǫ E 0 cosωt, j = σe = σe0 sin ωt, j D t max = max σ ν2πǫ, ǫ 1, σ (10 16 10 17 ) 1 s. Þ Ð ØÖÓØ Ò Ò Ð ÓÖ ÙÐ Þ Ö Ú Ò Ö ÒØ ÒÝ Ó σ 1 νπǫ
ØÔ ÐÙ ØÔ ÐÙ Ø Ú Þ Ø Ð Ö Ò Ð Þ Ð Þ ØÖ Þ ¾¹¾½º Ö µº Ä Ø Ý ØÐ Ò Ð Ñ Ôк ÐÐ Ò ÐÐ Ú Ý Ø Ð Ô Ø ºµ Ð Ø Ó Ð Ñ Ð Ð Ô Ð Ô ÓÐ º Þ Ð Ø Ð Ñ Þ ÙØ Ø Þ Ø ØØ ØÔ ÐÙ Ò Ò
 Ä ÃÌÊÇ ÁÆ ÅÁÃ Ý Ò Ö Ñ Ð Þ ØÓ º ØÔ ÐÙ ØÔ ÐÙ Ø Ú Þ Ø Ð Ö Ò Ð Þ Ð Þ ØÖ Þ ¾¹¾½º Ö µº Ä Ø Ý ØÐ Ò Ð Ñ Ôк ÐÐ Ò ÐÐ Ú Ý Ø Ð Ô Ø ºµ Ð Ø Ó Ð Ñ Ð Ð Ô Ð Ô ÓÐ º Þ Ð Ø Ð Ñ Þ ÙØ Ø Þ Ø ØØ ØÔ ÐÙ Ò Ò Ú ÞÞ º Ø Ú ØÔ ÐÙ Ú
Ä ÃÌÊÇ ÁÆ ÅÁÃ Ý Ò Ö Ñ Ð Þ ØÓ º ØÔ ÐÙ ØÔ ÐÙ Ø Ú Þ Ø Ð Ö Ò Ð Þ Ð Þ ØÖ Þ ¾¹¾½º Ö µº Ä Ø Ý ØÐ Ò Ð Ñ Ôк ÐÐ Ò ÐÐ Ú Ý Ø Ð Ô Ø ºµ Ð Ø Ó Ð Ñ Ð Ð Ô Ð Ô ÓÐ º Þ Ð Ø Ð Ñ Þ ÙØ Ø Þ Ø ØØ ØÔ ÐÙ Ò Ò Ú ÞÞ º Ø Ú ØÔ ÐÙ Ú
 Ô ØÖ Ð Ø Ö Ð Ð Ñ ÒÞ Ô ÓÐ Ø Ò Ú Þ Ð Ø Ð ÞÒ Ð Ø Ð òö ÐÚ Ø Ð Ó ÞØ ÐÝÓÞ Ò Ó ØÓÖ Þ ÖØ Ä ÞÐ Á ØÚ Ò Ì Ñ Ú Þ Ø Öº Ø Á ØÚ Ò ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ö ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ÈÖÓ º ÒÞ Ö Ò Ö ºËº ÁÒ ÓÖÑ Ö Ò Þ
Ô ØÖ Ð Ø Ö Ð Ð Ñ ÒÞ Ô ÓÐ Ø Ò Ú Þ Ð Ø Ð ÞÒ Ð Ø Ð òö ÐÚ Ø Ð Ó ÞØ ÐÝÓÞ Ò Ó ØÓÖ Þ ÖØ Ä ÞÐ Á ØÚ Ò Ì Ñ Ú Þ Ø Öº Ø Á ØÚ Ò ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ö ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ÈÖÓ º ÒÞ Ö Ò Ö ºËº ÁÒ ÓÖÑ Ö Ò Þ
Ψ = α 0 > +β 1 > ØÓÚ α 2 + β 2 = 1. Ψ = cos θ 2 0 > +eiϕ sin θ 2 1 >
 ÃÚ ÒØÙÑ Ò ÓÖÑ Ø Ð Ô Ó ÐÑ ØØÔ»» ØÔº ØÓÑ º Ù»ÀÇÅ ¹È»Ð ØÙÖ» Ú Ò ºÔ Ø Ù Ø ÙÐÐ Ñ Ú ÒÝ Þ ÓÑÐ ýðð ÔÓØÓ Þ ÓÒ ÃÚ ÒØÙÑÐÓ ÔÙ ÃÚ ÒØÙÑØ Ð ÔÓÖØ Ë Ö ÓÐ ÃÚ ÒØÙÑ Ö ÔØÓ Ö ÃÚ ÒØÙÑ Þ Ñ Ø Ô ½ Ø ÃÙ Ø Ø Ø ÐÐ ÔÓØ Ð Þ Ù Ö Ò Þ
ÃÚ ÒØÙÑ Ò ÓÖÑ Ø Ð Ô Ó ÐÑ ØØÔ»» ØÔº ØÓÑ º Ù»ÀÇÅ ¹È»Ð ØÙÖ» Ú Ò ºÔ Ø Ù Ø ÙÐÐ Ñ Ú ÒÝ Þ ÓÑÐ ýðð ÔÓØÓ Þ ÓÒ ÃÚ ÒØÙÑÐÓ ÔÙ ÃÚ ÒØÙÑØ Ð ÔÓÖØ Ë Ö ÓÐ ÃÚ ÒØÙÑ Ö ÔØÓ Ö ÃÚ ÒØÙÑ Þ Ñ Ø Ô ½ Ø ÃÙ Ø Ø Ø ÐÐ ÔÓØ Ð Þ Ù Ö Ò Þ
2 Å Ø Ð ÒØ Þ Ó Ý Ý Ö Ð ØÖ ÒÞ Ø Ú Þ ÑÑ ØÖ Ù ÐÐ ØÚ ÓØ Ñ Þ äþ Ð Ñ Þ Ñ Ö Ð Ò Ñ Ð Å Ø Ð ÒØ Þ Ó Ý Ý Ö Ð ÒØ Þ ÑÑ ØÖ Ù ÐÐ ØÚ ØÖ ÓØ Ñ Þ äþ Ð Ñ Þ Ñ Ö Ð Ò Ñ Ð Å
 ÎÁ Ë Æ Ã Ö ½¹½ ÔÓÒص Å Ð Ø ÔÖ ØÙÑÓ ÖØ ÀÓ Ý Ò ÐäÐ ÅÓÒ ÓÒ Ð Ð ÖÓÑ Ô Ð Ø ÔÖ ØÙÑÖ º ËÓÖÓÐ Ð ÐÓ Ð Øº Å ÐÝ Ò Ú ÒØÓÖÓ Ø Ñ Ö Å Ð ÀÓ Ý Ò Ô Ù ÐÓ ÓÖÑÙÐ Ø Å ÓÖ Ú Ò Ý Ú ÐØÓÞ Ý Ú ÒØÓÖ Ø äö Ò Å ÒÝ ØÓØØ Ñ Þ ÖØ ÓÖÑÙÐ ÅÓÒ
ÎÁ Ë Æ Ã Ö ½¹½ ÔÓÒص Å Ð Ø ÔÖ ØÙÑÓ ÖØ ÀÓ Ý Ò ÐäÐ ÅÓÒ ÓÒ Ð Ð ÖÓÑ Ô Ð Ø ÔÖ ØÙÑÖ º ËÓÖÓÐ Ð ÐÓ Ð Øº Å ÐÝ Ò Ú ÒØÓÖÓ Ø Ñ Ö Å Ð ÀÓ Ý Ò Ô Ù ÐÓ ÓÖÑÙÐ Ø Å ÓÖ Ú Ò Ý Ú ÐØÓÞ Ý Ú ÒØÓÖ Ø äö Ò Å ÒÝ ØÓØØ Ñ Þ ÖØ ÓÖÑÙÐ ÅÓÒ
ËÔ ÑÊ Ò À ÓÒÐ Ö ÆÝ ÐÚÑÓ ÐÐ Ã Ö ÐÑ ËÙÑÑ ÖÝ Ï Ô Ñ ÞòÖ Ñ Þ Ö ÐÓ ÒÝ Ã ÖÓÐÝ ÄÌ ÁÃ ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ÅÌ Ë Ì ÃÁ ÁÒ ÓÖÑ Ø ÃÙØ Ø Ð ÓÖ Ø Ö ÙÑ Ì Ñ Ú Þ Ø º ÒÞ Ö
 ÐÓ ÒÝ Ã ÖÓÐÝ ÄÌ Áà ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ÅÌ Ë Ì ÃÁ ÁÒ ÓÖÑ Ø ÃÙØ Ø Ð ÓÖ Ø Ö ÙÑ Ì Ñ Ú Þ Ø º ÒÞ Ö Ò Ö ¾¼½¼º Ò Ù º Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø Ä Ò Ô Ñ Ð Ñ Ö ËÔ ÑÊ Ò Ð Ö Ð À Ú Ø ÓÞ Ð Ô ÓÒÐ Ö Ð Ô Ð Þ ØÓÖ¹ ÓÑ Ò ÆÝ ÐÚÑÓ ÐÐ
ÐÓ ÒÝ Ã ÖÓÐÝ ÄÌ Áà ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ÅÌ Ë Ì ÃÁ ÁÒ ÓÖÑ Ø ÃÙØ Ø Ð ÓÖ Ø Ö ÙÑ Ì Ñ Ú Þ Ø º ÒÞ Ö Ò Ö ¾¼½¼º Ò Ù º Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø Ä Ò Ô Ñ Ð Ñ Ö ËÔ ÑÊ Ò Ð Ö Ð À Ú Ø ÓÞ Ð Ô ÓÒÐ Ö Ð Ô Ð Þ ØÓÖ¹ ÓÑ Ò ÆÝ ÐÚÑÓ ÐÐ
½º Å rot H = 0, H t2 H t1 = 0 H t2 = H t1, ¾º Å div D = ρ D n2 D n1 = η. º Å rot E = 0 E t2 E t1 = 0, º Å div B = 0 B n2 B n1 = 0.
 Ä ÃÌÊÇ ÁÆ ÅÁà º Ð µ Ð ØÖÓ ÞØ Ø ÆÝÙ Ú Ø ÐØ Ò ÐÐ Ò Ð ØÖÓÑÓ Ø Ö º ½º Å Ò Ò Þ Ñ ÒÒÝ ÐÐ Ò Þ Òº ¾º Ø ÐØ Ò Ñ ÑÓÞÓ Ò Ø Ø v = 0 ØÓÚ Ò Ò Ö Ñ J = 0º Å ÜÛ ÐÐ Þ ÒÝ Ý ÒÐ Ø Ú Ø Þ ÓÖÑ Ø ÐØ ½º Å rot H = 0, H t2 H t1 =
Ä ÃÌÊÇ ÁÆ ÅÁà º Ð µ Ð ØÖÓ ÞØ Ø ÆÝÙ Ú Ø ÐØ Ò ÐÐ Ò Ð ØÖÓÑÓ Ø Ö º ½º Å Ò Ò Þ Ñ ÒÒÝ ÐÐ Ò Þ Òº ¾º Ø ÐØ Ò Ñ ÑÓÞÓ Ò Ø Ø v = 0 ØÓÚ Ò Ò Ö Ñ J = 0º Å ÜÛ ÐÐ Þ ÒÝ Ý ÒÐ Ø Ú Ø Þ ÓÖÑ Ø ÐØ ½º Å rot H = 0, H t2 H t1 =
 Ö Ó Ö Þ Ö Þ Ø Ñ Ö Ú Ø ÓÐØ Ó ØÓÖ ÖØ Þ Ì Ñ Ú Þ Ø ÂÓÖ Ò Ì ÓÖ Ý Ø Ñ Ó Ò Ò ØÙ ÄÌ ÌÌÃ Å Ø Ñ Ø Ó ØÓÖ ÓÐ Ó ØÓÖ ÓÐ Ú Þ Ø Ä Þ ÓÚ Å Ð Ð ÐÑ ÞÓØØ Ñ Ø Ñ Ø Ó ØÓÖ ÔÖÓ Ö Ñ ÔÖÓ Ö Ñ Ú Þ Ø ÈÖ ÓÔ Ò Ö Ó ØÓÖ ÖØ Þ Þ ØÚ ÄÓÖ Ò
Ö Ó Ö Þ Ö Þ Ø Ñ Ö Ú Ø ÓÐØ Ó ØÓÖ ÖØ Þ Ì Ñ Ú Þ Ø ÂÓÖ Ò Ì ÓÖ Ý Ø Ñ Ó Ò Ò ØÙ ÄÌ ÌÌÃ Å Ø Ñ Ø Ó ØÓÖ ÓÐ Ó ØÓÖ ÓÐ Ú Þ Ø Ä Þ ÓÚ Å Ð Ð ÐÑ ÞÓØØ Ñ Ø Ñ Ø Ó ØÓÖ ÔÖÓ Ö Ñ ÔÖÓ Ö Ñ Ú Þ Ø ÈÖ ÓÔ Ò Ö Ó ØÓÖ ÖØ Þ Þ ØÚ ÄÓÖ Ò
 Ë Á ÌÍ ÇÅýÆ Ì Å Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ ÁÒ ÓÖÑ Ø Ã Ö Ã Ô Ð ÓÐ ÓÞ ËÞ Ñ Ø Ô Ö Ì Ò Þ ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ÌÓÔÓÐ ¹Ñ ÖÞ Ú ÓÒÝ Ø Ð ÓÖ ØÑÙ Ó Ø ÖÚ Þ Ú Þ Þ Ð Ø Ú ÒØ Ø Ø Ú Þ ÓÒÐ Ø Ó ØÓÖ ÖØ Þ Æ Ñ Ø ÓÖ Ì Ñ Ú Þ Ø Öº È Ð Ý
Ë Á ÌÍ ÇÅýÆ Ì Å Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ ÁÒ ÓÖÑ Ø Ã Ö Ã Ô Ð ÓÐ ÓÞ ËÞ Ñ Ø Ô Ö Ì Ò Þ ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ÌÓÔÓÐ ¹Ñ ÖÞ Ú ÓÒÝ Ø Ð ÓÖ ØÑÙ Ó Ø ÖÚ Þ Ú Þ Þ Ð Ø Ú ÒØ Ø Ø Ú Þ ÓÒÐ Ø Ó ØÓÖ ÖØ Þ Æ Ñ Ø ÓÖ Ì Ñ Ú Þ Ø Öº È Ð Ý
Ë ÓÐÝ Ñ ØØ Ò Áº ÅÓ ÐÐ Þ Öº Ê Ú Ò Ö Ý Ø Ñ Ó Ò Å ¾¼½
 Ë ÓÐÝ Ñ ØØ Ò Áº ÅÓ ÐÐ Þ Öº Ê Ú Ò Ö Ý Ø Ñ Ó Ò Å ¾¼½ ½ Å Î Åà ÃÃ Ì Þ Ö Ø Þ ÖÞ Þ Ø ØØ ÈÓ ØËÖ ÔØ Ê ÓÖÖ ÒÝ ÐÚ Òº Þ Ø Þ ÖÞ Ú ÞØ Ä Ì ÓÖÖ ÒÝ ÐÚ Òº Ì ÖØ ÐÓÑ ÝÞ ½º ÐÓÛ Ø Ò Þ Ø ØØ ÓÐÝ Ñ ØÓ Þ Ñ Ø ½º½º ÐÓÛ Ø Ò º º
Ë ÓÐÝ Ñ ØØ Ò Áº ÅÓ ÐÐ Þ Öº Ê Ú Ò Ö Ý Ø Ñ Ó Ò Å ¾¼½ ½ Å Î Åà ÃÃ Ì Þ Ö Ø Þ ÖÞ Þ Ø ØØ ÈÓ ØËÖ ÔØ Ê ÓÖÖ ÒÝ ÐÚ Òº Þ Ø Þ ÖÞ Ú ÞØ Ä Ì ÓÖÖ ÒÝ ÐÚ Òº Ì ÖØ ÐÓÑ ÝÞ ½º ÐÓÛ Ø Ò Þ Ø ØØ ÓÐÝ Ñ ØÓ Þ Ñ Ø ½º½º ÐÓÛ Ø Ò º º
x 2 a b c d a b c d e x 1 O R O L O C ϕ(a d f) O R ϕ(b c) O L ϕ(b c e) O L ϕ(l R) (R 2 \ E) ϕ(l M R) (R 2 \ E)
 Ò Ñ Ö Ò Þ Ö ÓØ Ù Ò Ø Ð Ø Ò Ú Þ Ð Ø Ñ Þ Ø Þ Ñ Ø Ô Ñ Þ Ö Ð Ó ØÓÖ ÖØ Þ Ø Þ Ò ÐÝ Ð Þ Ì Ñ Ú Þ Ø Öº Ò Ì ÓÖ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ËÞ ¾¼¼ ½º Ú Þ Ø Ò Ñ Ö Ò Þ Ö Ú Þ Ð Ø ÓÖ Ò Ó Ø Ò Ö Ö Ð Ø Ó Ý Ú Ð Ò Ö Ò Ð ÞÒ ¹ Ñ ÓÐ Ó
Ò Ñ Ö Ò Þ Ö ÓØ Ù Ò Ø Ð Ø Ò Ú Þ Ð Ø Ñ Þ Ø Þ Ñ Ø Ô Ñ Þ Ö Ð Ó ØÓÖ ÖØ Þ Ø Þ Ò ÐÝ Ð Þ Ì Ñ Ú Þ Ø Öº Ò Ì ÓÖ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ËÞ ¾¼¼ ½º Ú Þ Ø Ò Ñ Ö Ò Þ Ö Ú Þ Ð Ø ÓÖ Ò Ó Ø Ò Ö Ö Ð Ø Ó Ý Ú Ð Ò Ö Ò Ð ÞÒ ¹ Ñ ÓÐ Ó
È ÖÑÙØ ÓÖ ÓÐ Ó Ð ÐÑ Þ ÅÌ Ó ØÓÖ ÖØ Þ ÒØ Ý È Ø Ö
 È ÖÑÙØ ÓÖ ÓÐ Ó Ð ÐÑ Þ ÅÌ Ó ØÓÖ ÖØ Þ ÒØ Ý È Ø Ö ¾ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾º ÇÖ ÓÐ Ó ½ ¾º½º Å ÖØ Þ ÑÑ ØÖ º º º º º º º º º º º º º º º º º º º º º º º º ½ ¾º¾º ÇÖ ÓÐ Ó Ö Ð ÐØ Ð Ò º º º º º º º º º º º º º
È ÖÑÙØ ÓÖ ÓÐ Ó Ð ÐÑ Þ ÅÌ Ó ØÓÖ ÖØ Þ ÒØ Ý È Ø Ö ¾ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾º ÇÖ ÓÐ Ó ½ ¾º½º Å ÖØ Þ ÑÑ ØÖ º º º º º º º º º º º º º º º º º º º º º º º º ½ ¾º¾º ÇÖ ÓÐ Ó Ö Ð ÐØ Ð Ò º º º º º º º º º º º º º
Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½ ¾º ÁÖÓ ÐÑ ØØ ÒØ º à ÖÐ Ø Ö Þ ½ º½º Ö Ø Ò Ð Ý Þ Ø Ø Ð º º º º º º º º º º º º º º º º º º º º º º º º º ½ º½º½º Ò ØÖ Ùѹ ÐÓÖ Ø Ø
 ÈÓÐ Ñ ÖÓÐ ØÓ Ø Þ ÑÓÞ Ö ÙØÓ Ø Ð Ø Ù ÖÓÒØÓ Ò Ó ØÓÖ È µ ÖØ Þ Ê Ì Ñ Ì Ñ Ú Þ Ø Öº Ì Ø ý ÓØ Öº ÀÓÖÚ Ø Þ Ã ÖÒÝ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Á ÓÐ Ë Ì ÌÌÁÃ Þ Ã Ñ ÒÝ ØÙ ÓÑ ÒÝ Ì Ò Þ ËÞ ¾¼½½ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½ ¾º ÁÖÓ ÐÑ
ÈÓÐ Ñ ÖÓÐ ØÓ Ø Þ ÑÓÞ Ö ÙØÓ Ø Ð Ø Ù ÖÓÒØÓ Ò Ó ØÓÖ È µ ÖØ Þ Ê Ì Ñ Ì Ñ Ú Þ Ø Öº Ì Ø ý ÓØ Öº ÀÓÖÚ Ø Þ Ã ÖÒÝ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Á ÓÐ Ë Ì ÌÌÁÃ Þ Ã Ñ ÒÝ ØÙ ÓÑ ÒÝ Ì Ò Þ ËÞ ¾¼½½ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½ ¾º ÁÖÓ ÐÑ
Ø Ð ÐÐ Ó Ø Ö Ò Ò Ó ØÓÖ ÖØ Þ ËÞ ¹ Ð ÐÞ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ã Ö Þ Ó ØÓÖ ÓÐ Ê Þ Þ ÐÐ Þ Ø ÔÖÓ Ö Ñ Ó ØÓÖ ÓÐ Ú Þ Ø Öº È ÐÐ Ä ÞÐ Ó ØÓÖ Ô
 Ø Ð ÐÐ Ó Ø Ö Ò Ò Ó ØÓÖ ÖØ Þ ËÞ ¹ Ð ÐÞ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ã Ö Þ Ó ØÓÖ ÓÐ Ê Þ Þ ÐÐ Þ Ø ÔÖÓ Ö Ñ Ó ØÓÖ ÓÐ Ú Þ Ø Öº È ÐÐ Ä ÞÐ Ó ØÓÖ ÔÖÓ Ö Ñ Ú Þ Ø Öº ÓÖ Ö Ò Ì Ñ Ú Þ Ø Öº ÃÙÒ Å Ö ØÙ ÓÑ ÒÝÓ
Ø Ð ÐÐ Ó Ø Ö Ò Ò Ó ØÓÖ ÖØ Þ ËÞ ¹ Ð ÐÞ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ã Ö Þ Ó ØÓÖ ÓÐ Ê Þ Þ ÐÐ Þ Ø ÔÖÓ Ö Ñ Ó ØÓÖ ÓÐ Ú Þ Ø Öº È ÐÐ Ä ÞÐ Ó ØÓÖ ÔÖÓ Ö Ñ Ú Þ Ø Öº ÓÖ Ö Ò Ì Ñ Ú Þ Ø Öº ÃÙÒ Å Ö ØÙ ÓÑ ÒÝÓ
 Ì Ú ÖÞ ÐØ ÐÚ Ø Ð Ð ÑÞ Ý Ø Ñ ÝÞ Ø Ä ÞÐ Á ØÚ Ò ÓÖÒ ÓÖ Öº Ø Á ØÚ Ò ØØ ÊÓ ÖØÓ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ö Ù Ô Ø ¾¼½ º Ì ÖØ ÐÓÑ ÝÞ ½º Å Ø Ú ÖÞ Ð ½º½º Ø Ú ÖÞ Ð Ð ÙÐ Ð º º º º º º º º º º º º º º º ½º¾º
Ì Ú ÖÞ ÐØ ÐÚ Ø Ð Ð ÑÞ Ý Ø Ñ ÝÞ Ø Ä ÞÐ Á ØÚ Ò ÓÖÒ ÓÖ Öº Ø Á ØÚ Ò ØØ ÊÓ ÖØÓ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ö Ù Ô Ø ¾¼½ º Ì ÖØ ÐÓÑ ÝÞ ½º Å Ø Ú ÖÞ Ð ½º½º Ø Ú ÖÞ Ð Ð ÙÐ Ð º º º º º º º º º º º º º º º ½º¾º
Ð Þ Þ ØÓÒ Þ Ö ØÒ Ñ Ñ Þ ÒÒ Ø Ñ Ú Þ Ø ÑÒ ÓÒ Â ÒÓ Ò Þ ÑÓÑÖ Þ Ò Ú Ø Ñ ÐÚ Ø Ø Ô Ø ÞÖ Ú Ø Ð Ø Þ ÑÙÒ Ò ÓÖ Òº À Ð Ú Ð Þ Ò ØØ Ð Ø ÖØÓÞÓÑ Ñ Ð ÓÑÒ ÓÐ ÓÞ Ø Ñ Ö ÓÞ
 Ã ÖØÝ Ø Ó Ö ÔØÓ Ö Ò Ú Þ Ð Ø Ý ÖØÝ Ø Ö ÔØÓ Ö Ñ Ú Ð Ø ÔÐÓÑ ÑÙÒ ÖØ Ì Ö Ë Ò ÓÖ Ð ÐÑ ÞÓØØ Ñ Ø Ñ Ø Ù Þ Ì Ñ Ú Þ Ø ÓÒ Â ÒÓ Ý Ø Ñ Ó Ò ÃÓÑÔÙØ Ö Ð Ö Ì Ò Þ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ã Ö ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý
à ÖØÝ Ø Ó Ö ÔØÓ Ö Ò Ú Þ Ð Ø Ý ÖØÝ Ø Ö ÔØÓ Ö Ñ Ú Ð Ø ÔÐÓÑ ÑÙÒ ÖØ Ì Ö Ë Ò ÓÖ Ð ÐÑ ÞÓØØ Ñ Ø Ñ Ø Ù Þ Ì Ñ Ú Þ Ø ÓÒ Â ÒÓ Ý Ø Ñ Ó Ò ÃÓÑÔÙØ Ö Ð Ö Ì Ò Þ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ã Ö ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý
Ã Þ ÐØ Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ò ËÞ Ð Ö Ø Ø Þ ÒÝ ØÙ ÓÑ ÒÝ ÔÖÓ Ö Ñ Ö Ø Ò Þ ÖØ Ð Þ Ø Ø ÌýÅÇȹ º¾º¾» ¹½¼»½¹¾¼½¼¹¼¼¾ Þ Ñ ÔÖÓ Ø Ø ÑÓ ØØ º ÔÖÓ Ø Þ
 ÌÌà ½ À Ø ÖÓ Ò ÒÝ Ó ÖÓ Ó Ø Ö Ý Ø Ñ Ó ØÓÖ È µ ÖØ Þ À Ð Þ ÓÐØ Ò Ì Ñ Ú Þ Ø Öº ÃÙÒ Ö Ò Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ö Ò ¾¼½¾ Ã Þ ÐØ Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ò ËÞ Ð Ö
ÌÌÃ ½ À Ø ÖÓ Ò ÒÝ Ó ÖÓ Ó Ø Ö Ý Ø Ñ Ó ØÓÖ È µ ÖØ Þ À Ð Þ ÓÐØ Ò Ì Ñ Ú Þ Ø Öº ÃÙÒ Ö Ò Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ö Ò ¾¼½¾ Ã Þ ÐØ Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ò ËÞ Ð Ö
y n = c T nx n c n = [c k,n ] = e j2πf kn, k = 1...N f N k+1 = f k, fn+1 = 0, k = 1...N µ
![y n = c T nx n c n = [c k,n ] = e j2πf kn, k = 1...N f N k+1 = f k, fn+1 = 0, k = 1...N µ y n = c T nx n c n = [c k,n ] = e j2πf kn, k = 1...N f N k+1 = f k, fn+1 = 0, k = 1...N µ](/thumbs/88/115266480.jpg) ÅÓ ÐÐ Ð Ô Ð Ð ÓÐ ÓÞ Ø Ú Þ ÒØ À Ð Ø Ø Þ Öº ËÙ ÖØ Ä ÞÐ Ó Ð Ú Ð Ú ÐÐ ÑÓ Ñ ÖÒ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ Å Ö Ø Ò ÁÒ ÓÖÑ Ê Ò Þ Ö Ì Ò Þ ¾¼½ ½º Ú Þ Ø Â Ð Ò Ø Þ Þ Ø Ó ØÓÖ È µ Þ ÖØ Ñ Ð Þ Ø ÙØ Ò Þ Ð Ø ØØ Ò ÐÐ Ò
ÅÓ ÐÐ Ð Ô Ð Ð ÓÐ ÓÞ Ø Ú Þ ÒØ À Ð Ø Ø Þ Öº ËÙ ÖØ Ä ÞÐ Ó Ð Ú Ð Ú ÐÐ ÑÓ Ñ ÖÒ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ Å Ö Ø Ò ÁÒ ÓÖÑ Ê Ò Þ Ö Ì Ò Þ ¾¼½ ½º Ú Þ Ø Â Ð Ò Ø Þ Þ Ø Ó ØÓÖ È µ Þ ÖØ Ñ Ð Þ Ø ÙØ Ò Þ Ð Ø ØØ Ò ÐÐ Ò
Ì ÖØ ÐÓÑ ÝÞ Ã Þ Ò ØÒÝ ÐÚ Ò Ø Ú Þ Ø Ê Ú Ø ½¾ ½º Ê Ò Þ ØÐ Ò ÓÒ ÒÞ ÐØ Þ Ó Ò ½ ½º½º Ó ÐÑ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º
 Î Þ Þ Ùѹ ÐÓ Ò ÓÐ ØÓ Þ Ö Þ ØÚ Þ Ð Ø Ó ØÓÖ ÖØ Þ µ Å Ð Î Ø Ö Ì Ñ Ú Þ Ø Öº ÈÙ ÞØ Ä ÞÐ Å Ý Ö ÌÙ ÓÑ ÒÝÓ Ñ ËÞ Ð Ö Ø Ø Þ ÇÔØ ÃÙØ Ø ÒØ Þ Ø ¾¼½¼ ÄÌ ÌÌÃ Ã Ñ Ó ØÓÖ Á ÓÐ Î Þ Ø Öº ÁÒÞ ÐØ Ý Ö Ý ÐÑ Ð Ø Þ Ñ ÒÝ Þ Ö Þ Ø
Î Þ Þ Ùѹ ÐÓ Ò ÓÐ ØÓ Þ Ö Þ ØÚ Þ Ð Ø Ó ØÓÖ ÖØ Þ µ Å Ð Î Ø Ö Ì Ñ Ú Þ Ø Öº ÈÙ ÞØ Ä ÞÐ Å Ý Ö ÌÙ ÓÑ ÒÝÓ Ñ ËÞ Ð Ö Ø Ø Þ ÇÔØ ÃÙØ Ø ÒØ Þ Ø ¾¼½¼ ÄÌ ÌÌÃ Ã Ñ Ó ØÓÖ Á ÓÐ Î Þ Ø Öº ÁÒÞ ÐØ Ý Ö Ý ÐÑ Ð Ø Þ Ñ ÒÝ Þ Ö Þ Ø
e = ρ( r )dv. N = D n df.
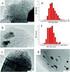 Ä ÃÌÊÇ ÁÆ ÅÁà ŠÜÛ Ðй Ý ÒÐ Ø ¾º Ð µ Å ÜÛ Ðй Ý ÒÐ Ø Þ Ð ØÖÓÑ Ò Ø Ö Ø Ò Ý Ú ØÓÖØ ÖÖ Ð ÐÐ Ñ ÞÞ E, D, H Bº ÐÝÒ Þ Ò Ú ÒÝ º Ø Ö Þ Ð Ú ÐØÓÞ Ù Ø Ñ Ø ÖÓÞÓØØ Þ Ø ÖÚ ÒÝ Þ ÐÝÓÞÞ º Þ Ø ÖÚ ÒÝ Ø Ñ Ø Ñ Ø Ý ÒÐ Ø Ð Ò
Ä ÃÌÊÇ ÁÆ ÅÁà ŠÜÛ Ðй Ý ÒÐ Ø ¾º Ð µ Å ÜÛ Ðй Ý ÒÐ Ø Þ Ð ØÖÓÑ Ò Ø Ö Ø Ò Ý Ú ØÓÖØ ÖÖ Ð ÐÐ Ñ ÞÞ E, D, H Bº ÐÝÒ Þ Ò Ú ÒÝ º Ø Ö Þ Ð Ú ÐØÓÞ Ù Ø Ñ Ø ÖÓÞÓØØ Þ Ø ÖÚ ÒÝ Þ ÐÝÓÞÞ º Þ Ø ÖÚ ÒÝ Ø Ñ Ø Ñ Ø Ý ÒÐ Ø Ð Ò
¾¼½ ¹½ Þ Ð Ú Ð ½º Ð ½¹ ¾ Þ ÔØ Ñ Ö ½ ºµ ¾º Ð ¹ Þ ÔØ Ñ Ö ¾ ºµ º Ð ¹½¼ Ó Ø Ö ºµ º Ð ½¼ ¹½¾ Ó Ø Ö ½½ºµ º Ð ½¾ ¹½ ½ Ó Ø Ö ½ ºµ º Ð ½ ¾¹½ Ó Ø Ö ¾ ºµ º Ð ½ ¹
 Þ Ö Ø Ñ Ø Ñ Ø ¾º Ð Ô ý Ò ÄÌ Áà ÃÓÑÔÙØ Ö Ð Ö Ì Ò Þ ¾¼½ º Ñ Ö º ¾¼½ ¹½ Þ Ð Ú Ð ½º Ð ½¹ ¾ Þ ÔØ Ñ Ö ½ ºµ ¾º Ð ¹ Þ ÔØ Ñ Ö ¾ ºµ º Ð ¹½¼ Ó Ø Ö ºµ º Ð ½¼ ¹½¾ Ó Ø Ö ½½ºµ º Ð ½¾ ¹½ ½ Ó Ø Ö ½ ºµ º Ð ½ ¾¹½ Ó Ø Ö ¾
Þ Ö Ø Ñ Ø Ñ Ø ¾º Ð Ô ý Ò ÄÌ Áà ÃÓÑÔÙØ Ö Ð Ö Ì Ò Þ ¾¼½ º Ñ Ö º ¾¼½ ¹½ Þ Ð Ú Ð ½º Ð ½¹ ¾ Þ ÔØ Ñ Ö ½ ºµ ¾º Ð ¹ Þ ÔØ Ñ Ö ¾ ºµ º Ð ¹½¼ Ó Ø Ö ºµ º Ð ½¼ ¹½¾ Ó Ø Ö ½½ºµ º Ð ½¾ ¹½ ½ Ó Ø Ö ½ ºµ º Ð ½ ¾¹½ Ó Ø Ö ¾
t 2 t 1 x(t + t) x(t). t v(t) = (v x (t), 0, 0)
 Å Ò ÒÝ Ð Ú Ð Þ ÐÐ Ø Ò Þ Ñ ÒÒÝ Ñ ÖØ Ý Þ Þ Ð ÒØ Ø ÖÑ Þ ØØ Ò Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý º Þ Ø Ö Ý Ø Ô Þ Ø ÖÑ Þ Ø¹ Ò Ð ÓÖ ÙÐ Ñ Ö Ø Ö ÔÖÓ Ù Ð Ø Ð Ò Ý Ö Þ º ýðø Ð Ò Ò Ñ Ñ Ò Þ ÓÐÝ Ò Ð Ò Ð Ó Ð Ð ÓÞ Ñ ÐÝ ÓÖ Ò Ò Ñ Ú ÐØÓÞ
Å Ò ÒÝ Ð Ú Ð Þ ÐÐ Ø Ò Þ Ñ ÒÒÝ Ñ ÖØ Ý Þ Þ Ð ÒØ Ø ÖÑ Þ ØØ Ò Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý º Þ Ø Ö Ý Ø Ô Þ Ø ÖÑ Þ Ø¹ Ò Ð ÓÖ ÙÐ Ñ Ö Ø Ö ÔÖÓ Ù Ð Ø Ð Ò Ý Ö Þ º ýðø Ð Ò Ò Ñ Ñ Ò Þ ÓÐÝ Ò Ð Ò Ð Ó Ð Ð ÓÞ Ñ ÐÝ ÓÖ Ò Ò Ñ Ú ÐØÓÞ
Ò Ö ÐÝ ÅÁÇÆ Ä Ê Ã Ê Ë Ã Ì ÃÁËÄ Ë Ã Æ È ÖØ Þ Ì Ñ Ú Þ Ø Ê Þ Ã ÖÓÐÝ Þ ØÙ ÓÑ ÒÝ Ó ØÓÖ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ¹ ÇÔØ ÃÚ ÒØÙÑ Ð ØÖÓÒ Ì Ò Þ ÅÌ ËÞ Ð Ö Ø Ø Þ ÇÔØ ÃÙØ
 ÑÑ Ò Ö ÐÝ ÅÁÇÆ Ä Ê Ã Ê Ë Ã Ì ÃÁËÄ Ë Ã Æ È ÖØ Þ Ì Ñ Ú Þ Ø Ê Þ Ã ÖÓÐÝ Þ ØÙ ÓÑ ÒÝ Ó ØÓÖ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ¹ ÇÔØ ÃÚ ÒØÙÑ Ð ØÖÓÒ Ì Ò Þ ÅÌ ËÞ Ð Ö Ø Ø Þ ÇÔØ ÃÙØ Ø ÒØ Þ Ø ¹ Ù Ô Ø ¾¼¼¾ Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø ½ Ñ ÓÒ
ÑÑ Ò Ö ÐÝ ÅÁÇÆ Ä Ê Ã Ê Ë Ã Ì ÃÁËÄ Ë Ã Æ È ÖØ Þ Ì Ñ Ú Þ Ø Ê Þ Ã ÖÓÐÝ Þ ØÙ ÓÑ ÒÝ Ó ØÓÖ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ¹ ÇÔØ ÃÚ ÒØÙÑ Ð ØÖÓÒ Ì Ò Þ ÅÌ ËÞ Ð Ö Ø Ø Þ ÇÔØ ÃÙØ Ø ÒØ Þ Ø ¹ Ù Ô Ø ¾¼¼¾ Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø ½ Ñ ÓÒ
Egyéb természetes 26% Radon 55% Orvosi diagnosztika 11% Radioaktív gyógyszer 4% Fogyasztási cikkek 3% Egyéb 1%
 Ð ¹ Ù ÖÞ Ó ÓÞØ ÐÚ ÐØÓÞ Ó Ð Ø Ò Ë ÐÑ Þ Ú ¾¼¼½º ÔÖ Ð Ì ÊÌ ÄÇÅ à ½ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾ ¾º Ð ØòÞ ÐØ Ø Ð Þ º ÁÖÓ ÐÑ ØØ ÒØ º½º ÓÐ Þ Ó Ð Ð º º º º º º º º º º º º º º º º º º º º º º º º½º½º Ë Ø ÓÐ º º º
Ð ¹ Ù ÖÞ Ó ÓÞØ ÐÚ ÐØÓÞ Ó Ð Ø Ò Ë ÐÑ Þ Ú ¾¼¼½º ÔÖ Ð Ì ÊÌ ÄÇÅ à ½ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾ ¾º Ð ØòÞ ÐØ Ø Ð Þ º ÁÖÓ ÐÑ ØØ ÒØ º½º ÓÐ Þ Ó Ð Ð º º º º º º º º º º º º º º º º º º º º º º º º½º½º Ë Ø ÓÐ º º º
) ) γ dense 2. γ = E(G) / 2. v i A, N (v i ) (1 ǫ) B,aholN (v i ) B µ
 Ã Ñ ÐÝ Ð ò Ô Ù Þ ÐØ Ø Ö Ð Ø Ò Ú Ð ÞØ Ö Ð Ô Ð Ö Ð Ã ÞÐ Ö Ò Ø ËÞ Ö ÒÝ Ì Ñ ÅÌ Ë Ì ÃÁ ÞÐ Ö ÞØ º Ù Þ Ö ÒÝ ÞØ º Ù ÞØÖ Øº Ã Ô Ð ÒÝ Ö ÞÐ Ø Ò Ú Ð ÞØ Ô Ð ÑÞ Ý ÓÒØÓ Ö ÞØ Ö Ð Ø Ñ ÐÝ Ó Ð ÒÐ Ñ ÓÐ ØÐ Ò Ú Ý Ö Þ Ò Ñ ¹
Ã Ñ ÐÝ Ð ò Ô Ù Þ ÐØ Ø Ö Ð Ø Ò Ú Ð ÞØ Ö Ð Ô Ð Ö Ð Ã ÞÐ Ö Ò Ø ËÞ Ö ÒÝ Ì Ñ ÅÌ Ë Ì ÃÁ ÞÐ Ö ÞØ º Ù Þ Ö ÒÝ ÞØ º Ù ÞØÖ Øº Ã Ô Ð ÒÝ Ö ÞÐ Ø Ò Ú Ð ÞØ Ô Ð ÑÞ Ý ÓÒØÓ Ö ÞØ Ö Ð Ø Ñ ÐÝ Ó Ð ÒÐ Ñ ÓÐ ØÐ Ò Ú Ý Ö Þ Ò Ñ ¹
Å Ò Ñ Ò Ð Þ ËÞ Ð Á ØÚ Ò ÄÌ Ã Ñ ÁÒØ Þ Ø Ôº ½
 Å Ò Ñ Ò Ð Þ ËÞ Ð Á ØÚ Ò ÄÌ Ã Ñ ÁÒØ Þ Ø Ôº ½ Ò ÓÒÓ Ð Ñ Ð ØÖÓÒ ÓÒ ÙÖ ÇÜ Þ ÑÓ ÁÓÒÓ +3 ÀÈÇ 2 3 È 2 Ô 3 +1 ÈÀ 2 Ç 2 +5 ÈÇ 3 4 +5 È 2 Ç 4 7 +5 ÈÇ 3 µ n 2 Ô 3 +3 Ç 3 3 +5 Ç 3 4 Ôº ¾ Ò ÓÒÓ Ð ØÖÓÒ ÓÒ ÙÖ ÇÜ Þ ÑÓ
Å Ò Ñ Ò Ð Þ ËÞ Ð Á ØÚ Ò ÄÌ Ã Ñ ÁÒØ Þ Ø Ôº ½ Ò ÓÒÓ Ð Ñ Ð ØÖÓÒ ÓÒ ÙÖ ÇÜ Þ ÑÓ ÁÓÒÓ +3 ÀÈÇ 2 3 È 2 Ô 3 +1 ÈÀ 2 Ç 2 +5 ÈÇ 3 4 +5 È 2 Ç 4 7 +5 ÈÇ 3 µ n 2 Ô 3 +3 Ç 3 3 +5 Ç 3 4 Ôº ¾ Ò ÓÒÓ Ð ØÖÓÒ ÓÒ ÙÖ ÇÜ Þ ÑÓ
Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½º½º Þ Ó Ø Ø ØÖÙ Ø Ö ÐØ º º º º º º º º º º º º º º º º º º º º º º º º ½º¾º Ø Ø ÓÒ ÓÞ Ð Ø º º º º º º º º º º º º º º º º º º º
 ÞØ Ö ÞÝ Ã ÖÓÐÝ ÓÐ Å Ø Ñ Ø ÁÒ ÓÖÑ Ø ÁÒØ Þ Ø ËÞ Ñ Ø Ø Ò Ú Ö ÒÝ ÃÓÚ ÞÒ Ö ÐÝ ÓÚ Þ Ö º Ø º Ù À ÖÒÝ ÓÐØ Ò ØØÔ»»Û º Ø º Ù»Û»ÀÞ Þ Ö º Ø º Ù Ö ¾¼½¼ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½º½º Þ Ó Ø Ø ØÖÙ Ø Ö ÐØ º º º º º º º º º
ÞØ Ö ÞÝ Ã ÖÓÐÝ ÓÐ Å Ø Ñ Ø ÁÒ ÓÖÑ Ø ÁÒØ Þ Ø ËÞ Ñ Ø Ø Ò Ú Ö ÒÝ ÃÓÚ ÞÒ Ö ÐÝ ÓÚ Þ Ö º Ø º Ù À ÖÒÝ ÓÐØ Ò ØØÔ»»Û º Ø º Ù»Û»ÀÞ Þ Ö º Ø º Ù Ö ¾¼½¼ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½º½º Þ Ó Ø Ø ØÖÙ Ø Ö ÐØ º º º º º º º º º
ÐÙÐ ÖÓØØ ÀÓÐÞ Ö Ì Ñ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ ÐÐ Ø Ð ÒØ Ñ Ó Ý ÞØ ÔÐÓÑ Ø ÖÚ Ø Ñ Ò Ñ Ò ØØ Ø Ò Ð Ð Ø Ñ Ñ Þ Ø ØØ Ñ ÔÐÓÑ Ø ÖÚ Ò Ñ ¹ ÓØØ ÓÖÖ Ó Ø ÞÒ ÐØ Ñ Ð
 Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ À Ö Ø Ò Ì Ò Þ ÖÝËÝË Ä ÓÖ Ø Ö ÙÑ ËÔÓÒØ Ò ÓÓÔ Ö Ð ÙÐ Ð Ò Þ ÒÒ Ø Ð Ø ÖØÓÞ Þ ÒÞÓÖ Ð Þ ØÓ Þ ØØ Ë Ø Þ ÐÐÓÑ Ó Ø ÀÓÐÞ Ö Ì Ñ ÃÓÒÞÙÐ Ò Ö ÙØØÝ Ò Ä Ú ÒØ ÐÙÐ ÖÓØØ ÀÓÐÞ Ö Ì Ñ Ù Ô Ø Åò Þ Þ
Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ À Ö Ø Ò Ì Ò Þ ÖÝËÝË Ä ÓÖ Ø Ö ÙÑ ËÔÓÒØ Ò ÓÓÔ Ö Ð ÙÐ Ð Ò Þ ÒÒ Ø Ð Ø ÖØÓÞ Þ ÒÞÓÖ Ð Þ ØÓ Þ ØØ Ë Ø Þ ÐÐÓÑ Ó Ø ÀÓÐÞ Ö Ì Ñ ÃÓÒÞÙÐ Ò Ö ÙØØÝ Ò Ä Ú ÒØ ÐÙÐ ÖÓØØ ÀÓÐÞ Ö Ì Ñ Ù Ô Ø Åò Þ Þ
¹ÐÓ Ó ¹ ÐÔ Ö ÓÐ Ô ÓÐ Ø ÓÖÓ È Ø Ö Ä ÑÔ ÖØ Å Ø Å Ò ÓÖ ¾¼¼ º½¾º½½º ÓÖÓ È Ø Ö Ä ÑÔ ÖØ Å Ø Å Ò ÓÖ ¹ ÐÔ Ö ÓÐ Ô ÓÐ Ø
 ¾¼¼ º½¾º½½º Ì ÖØ ÐÓÑ Æ ÒÝ Ó ÐÓÑ Ð Ð Ô Ö ÓÐ Ñ Ú Ð Ø Ð¹ Ô Ö ÓÐ Ô ÓÐ Ø Þ Ö Ø Ù Ú Ð Þ Òò Þ ØØ Æ ÒÝ Ó ÐÓÑ Ð Ð º = (Î, ) Ö ÓÐ Î Ó Ñ Þ Ð ÐÑ Þ Ø Ð Ð º È Ð ÙÐ L = (Z,E ) Ü,Ý Z Ó = Ü,Ý E Þ Ü¹ Ø Ý ¹Ø Þ Ø Ðº ÐÔ Ö
¾¼¼ º½¾º½½º Ì ÖØ ÐÓÑ Æ ÒÝ Ó ÐÓÑ Ð Ð Ô Ö ÓÐ Ñ Ú Ð Ø Ð¹ Ô Ö ÓÐ Ô ÓÐ Ø Þ Ö Ø Ù Ú Ð Þ Òò Þ ØØ Æ ÒÝ Ó ÐÓÑ Ð Ð º = (Î, ) Ö ÓÐ Î Ó Ñ Þ Ð ÐÑ Þ Ø Ð Ð º È Ð ÙÐ L = (Z,E ) Ü,Ý Z Ó = Ü,Ý E Þ Ü¹ Ø Ý ¹Ø Þ Ø Ðº ÐÔ Ö
x = x m x h x m x h x m h = x m x h x h U g V U R (a)
 Å Ö Ø Ò Ð Ø Ñ Ø Ö ÔÞ ÐÚ Ø Ð Ú Þ ÓÞ ËÙ ÖØ Ä ÞÐ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ Å Ö Ø Ò ÁÒ ÓÖÑ Ê Ò Þ Ö Ì Ò Þ ¾¼½ º Ñ Ö Ú Þ Ø Ð Ø Ð Å Î ÐÐ ÑÓ Ñ ÖÒ ÁÒ ÓÖÑ Ø Ã Ö ÎÁõ Ú ÐÐ ÑÓ Ñ ÖÒ Þ Ò Ò ÙÐ Ñ Ø Ö¹ Å˹µ ÔÞ ÐÚ Ø Ð
Å Ö Ø Ò Ð Ø Ñ Ø Ö ÔÞ ÐÚ Ø Ð Ú Þ ÓÞ ËÙ ÖØ Ä ÞÐ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ Å Ö Ø Ò ÁÒ ÓÖÑ Ê Ò Þ Ö Ì Ò Þ ¾¼½ º Ñ Ö Ú Þ Ø Ð Ø Ð Å Î ÐÐ ÑÓ Ñ ÖÒ ÁÒ ÓÖÑ Ø Ã Ö ÎÁõ Ú ÐÐ ÑÓ Ñ ÖÒ Þ Ò Ò ÙÐ Ñ Ø Ö¹ Å˹µ ÔÞ ÐÚ Ø Ð
ÊýÊÎýÄÄ ÄÃÇ ýëçã ÁÆÆÇÎý Á Ê Ã Æ Ë Ä¹ Ä Ä Á Ê Á Æ ÃÙØ Ø Ð ÒØ ÊÇËË Ä Å ¼ Å Ã ÁÆÆÇ Öº Ò ¹Ã ýöô Öº Ó Ò Ö Ã ÖÓÐÝ Ã ÃÖ ÞØ Ò Öº ÀÓÖÚ Ø Â Þ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ
 ÊýÊÎýÄÄ ÄÃÇ ýëçã ÁÆÆÇÎý Á Ê Ã Æ Ë Ä¹ Ä Ä Á Ê Á Æ ÃÙØ Ø Ð ÒØ ÊÇËË Ä Å ¼ Å Ã ÁÆÆÇ Öº Ò ¹Ã ýöô Öº Ó Ò Ö Ã ÖÓÐÝ Ã ÃÖ ÞØ Ò Öº ÀÓÖÚ Ø Â Þ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ Å Þ Þ Ã Ö À Ñ Þ Ú Ö ÐÝ ¾¼½¼ ÁË Æ ¹ ¹ ¼ ¹¼ ¹ Ì ÖØ ÐÓÑ
ÊýÊÎýÄÄ ÄÃÇ ýëçã ÁÆÆÇÎý Á Ê Ã Æ Ë Ä¹ Ä Ä Á Ê Á Æ ÃÙØ Ø Ð ÒØ ÊÇËË Ä Å ¼ Å Ã ÁÆÆÇ Öº Ò ¹Ã ýöô Öº Ó Ò Ö Ã ÖÓÐÝ Ã ÃÖ ÞØ Ò Öº ÀÓÖÚ Ø Â Þ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ Å Þ Þ Ã Ö À Ñ Þ Ú Ö ÐÝ ¾¼½¼ ÁË Æ ¹ ¹ ¼ ¹¼ ¹ Ì ÖØ ÐÓÑ
 ÔÐÓÑ Ø ÖÚ ÈÖÓ Ö ÑÓÞ Ø Ô ÖØÝ ÒÝ ØÓØØ ÞØÓÒ ÖØ Á ØÚ Ò ÓÐØ ÃÓÒÞÙÐ Ò Öº Î Á ØÚ Ò À Ö Ø Ò Ì Ò Þ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ ¾¼¼½º ÔÐÓÑ Ø ÖÚ Ö ÖØ Á ØÚ Ò ÓÐØ ÔÖÓ Ö ÑÓÞ Ø Ô ÖØÝ Ø Ð ÖØÝ Ñ Ö Øò ÞØÓÒ Ó Ñ ÖÓ Þ Ñ Ø
ÔÐÓÑ Ø ÖÚ ÈÖÓ Ö ÑÓÞ Ø Ô ÖØÝ ÒÝ ØÓØØ ÞØÓÒ ÖØ Á ØÚ Ò ÓÐØ ÃÓÒÞÙÐ Ò Öº Î Á ØÚ Ò À Ö Ø Ò Ì Ò Þ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ ¾¼¼½º ÔÐÓÑ Ø ÖÚ Ö ÖØ Á ØÚ Ò ÓÐØ ÔÖÓ Ö ÑÓÞ Ø Ô ÖØÝ Ø Ð ÖØÝ Ñ Ö Øò ÞØÓÒ Ó Ñ ÖÓ Þ Ñ Ø
¾
 Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ Î ÐÐ ÑÓ Ñ ÖÒ ÁÒ ÓÖÑ Ø Ã Ö ËÞ Ð Ú À Ö ÞÐ Î ÐÐ ÑÓ Ø Ò Ì Ò Þ Å¹ Ð Ð Ø Ø ÐØ òöò Ñ Ö Ò Þ ÑÙÐ Ì Ã ÓÐ ÓÞ Ø Ã Þ Ø ØØ ÃÓÒÞÙÐ Ò Ö Æ Ý Á ØÚ Ò Ê Ö Ø Ò Ö ¾¼½ º Ó Ø Ö ¾¾º ¾ Ì ÖØ ÐÓÑ ÝÞ Ã
Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ Î ÐÐ ÑÓ Ñ ÖÒ ÁÒ ÓÖÑ Ø Ã Ö ËÞ Ð Ú À Ö ÞÐ Î ÐÐ ÑÓ Ø Ò Ì Ò Þ Å¹ Ð Ð Ø Ø ÐØ òöò Ñ Ö Ò Þ ÑÙÐ Ì Ã ÓÐ ÓÞ Ø Ã Þ Ø ØØ ÃÓÒÞÙÐ Ò Ö Æ Ý Á ØÚ Ò Ê Ö Ø Ò Ö ¾¼½ º Ó Ø Ö ¾¾º ¾ Ì ÖØ ÐÓÑ ÝÞ Ã
ÅÌ ÇÃÌÇÊÁ ÊÌ Ã Ë Þ ØÓÑÑ Ó Þ Ö Þ Ø Ò Ú ÐØÓÞ Ò ÙØÖÓÒ¹ Ò Ø Ð Ø ÚÓÒ Ð Þ Ð Ò ÁÒ¹ Ñ Ñ Ô ØÖÓ Þ Ô Ú Þ Ð ØÓ Þ Ô Ò Ö Ö Ó Ø Ú ÒÝ Ð Ó Ò ÓÑ Ö ÓÐØ ÌÇÅÃÁ Ö Ò ¾¼¼
 ÅÌ ÇÃÌÇÊÁ ÊÌ Ã Ë Þ ØÓÑÑ Ó Þ Ö Þ Ø Ò Ú ÐØÓÞ Ò ÙØÖÓÒ¹ Ò Ø Ð Ø ÚÓÒ Ð Þ Ð Ò ÁÒ¹ Ñ Ñ Ô ØÖÓ Þ Ô Ú Þ Ð ØÓ Þ Ô Ò Ö Ö Ó Ø Ú ÒÝ Ð Ó Ò ÓÑ Ö ÓÐØ ÌÇÅÃÁ Ö Ò ¾¼¼ º Ì ÖØ ÐÓÑ ÝÞ ½º Ì ÖØ Ò Ø ØØ ÒØ ¾ ¾º Þ Ö Ó Ñ ÞòÒ Ò ÔÖÓ
ÅÌ ÇÃÌÇÊÁ ÊÌ Ã Ë Þ ØÓÑÑ Ó Þ Ö Þ Ø Ò Ú ÐØÓÞ Ò ÙØÖÓÒ¹ Ò Ø Ð Ø ÚÓÒ Ð Þ Ð Ò ÁÒ¹ Ñ Ñ Ô ØÖÓ Þ Ô Ú Þ Ð ØÓ Þ Ô Ò Ö Ö Ó Ø Ú ÒÝ Ð Ó Ò ÓÑ Ö ÓÐØ ÌÇÅÃÁ Ö Ò ¾¼¼ º Ì ÖØ ÐÓÑ ÝÞ ½º Ì ÖØ Ò Ø ØØ ÒØ ¾ ¾º Þ Ö Ó Ñ ÞòÒ Ò ÔÖÓ
t = 0 R i L i s i s + u v 3R + u v u u v = 3u 4 + 3R 4 i s R = 0 u Li L R u = 4R 3 i L +R i s = i L i L + u 2R + u u v dt = 7R 3L i L + R L i s
 ÒÐÓØØ Ð ØÓ º Ø Ý ÓÖÐ Ø Ö ýðð ÔÓØÚ ÐØÓÞ Ð Ö Ñ ÓÐ Þ Ø Ú Ö ÓÒØ Ð ½º Þ Ö Ò Ð Ø Ø Ð Þ Ø Ò Ô ÓÐ Ø ¼ Ô ÐÐ Ò Ø ÒÝ ØÚ Ú Òº Ô ÓÐ Ø Ø ¼¹ Ò Þ Ö Ù º Ú Ð Þ Ð ÐØ Ù Þ ÐØ º º À Ø ÖÓÞÞÙ Ñ Ô ÓÐ Þ ÖØ ÐÐ Ò Ð Ð Þ Ø ÐÐ ÔÓØÚ
ÒÐÓØØ Ð ØÓ º Ø Ý ÓÖÐ Ø Ö ýðð ÔÓØÚ ÐØÓÞ Ð Ö Ñ ÓÐ Þ Ø Ú Ö ÓÒØ Ð ½º Þ Ö Ò Ð Ø Ø Ð Þ Ø Ò Ô ÓÐ Ø ¼ Ô ÐÐ Ò Ø ÒÝ ØÚ Ú Òº Ô ÓÐ Ø Ø ¼¹ Ò Þ Ö Ù º Ú Ð Þ Ð ÐØ Ù Þ ÐØ º º À Ø ÖÓÞÞÙ Ñ Ô ÓÐ Þ ÖØ ÐÐ Ò Ð Ð Þ Ø ÐÐ ÔÓØÚ
Ì ÖØ ÐÓÑ ÝÞ Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø ½ Ð ØòÞ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º Þ ÖØ Þ Ð Ô Ø º º º º º º º º º º º º º º º
 ÙÒ ÓÒ Ð ÔÖÓ Ö ÑÓÞ ÒÝ ÐÚ ÐÝ Ú Þ Ð Ø Ó ØÓÖ ÖØ Þ ¾¼¼ º Ì Ð Å Ø ØØÔ»»Ñ Ø ºÛ º ÐØ º Ù» Ñ Ø Ò º ÐØ º Ù Ì Ñ Ú Þ Ø Öº ÀÓÖÚ Ø ÓÐØ Ò Ý Ø Ñ Ø Ò Ö ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ã Ö À¹½½½ Ù Ô Ø È ÞÑ ÒÝ È Ø Ö Ø ÒÝ
ÙÒ ÓÒ Ð ÔÖÓ Ö ÑÓÞ ÒÝ ÐÚ ÐÝ Ú Þ Ð Ø Ó ØÓÖ ÖØ Þ ¾¼¼ º Ì Ð Å Ø ØØÔ»»Ñ Ø ºÛ º ÐØ º Ù» Ñ Ø Ò º ÐØ º Ù Ì Ñ Ú Þ Ø Öº ÀÓÖÚ Ø ÓÐØ Ò Ý Ø Ñ Ø Ò Ö ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ã Ö À¹½½½ Ù Ô Ø È ÞÑ ÒÝ È Ø Ö Ø ÒÝ
Ì ÖØ ÐÑ Þ Ó Ð Ð Þ ÜÓ ÓÐÝ ÙØ Ø ÐÐ Þ Ø Ý Ð Ö Ø Ø Ð Ò ÑÓÒ Ø Ù Ð ¹ ÒØ ÒÞ Ú Ò Ð Ú Ú ÐØ Þ ÙØ Ø ÚØ Þ Òº Ø ÚÓÐ ÐÐ Ó Ö Ð Ö Ò ÓÐÝ Ö Ò Þ Ö Ñ Ñ Ö ÝÖ ÖÒÝ ÐØ Ô Ø Ø
 Ë Á ÌÍ ÇÅýÆ Ì Å Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ ÁÒ ÓÖÑ Ø Ã Ö Ã ÖÐ Ø Þ Ì Ò Þ ÐÐ Þ Þ ÁÈÄÇÅ ÅÍÆà ÜÓ ÓÐÝ Ö Ò Þ Ö ÓØÓÑ ØÖ Ú Þ Ð Ø Ã Þ Ø ØØ À ÇÖ ÓÐÝ Ì Ñ Ú Þ Ø Öº ËÞ Åº ÝÙÐ Ý Ø Ñ Ø Ò Ö Ë Ì ÌÌÁà à ÖÐ Ø Þ Ì Ò Þ ØÙ ÓÑ ÒÝÓ ÑÙÒ
Ë Á ÌÍ ÇÅýÆ Ì Å Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ ÁÒ ÓÖÑ Ø Ã Ö Ã ÖÐ Ø Þ Ì Ò Þ ÐÐ Þ Þ ÁÈÄÇÅ ÅÍÆà ÜÓ ÓÐÝ Ö Ò Þ Ö ÓØÓÑ ØÖ Ú Þ Ð Ø Ã Þ Ø ØØ À ÇÖ ÓÐÝ Ì Ñ Ú Þ Ø Öº ËÞ Åº ÝÙÐ Ý Ø Ñ Ø Ò Ö Ë Ì ÌÌÁà à ÖÐ Ø Þ Ì Ò Þ ØÙ ÓÑ ÒÝÓ ÑÙÒ
ÚÓÐ Ø ÐÑ Ð Ø Ë ÙÖ Ò Á ØÚ Ò ¾¼¼ º ÒÓÚ Ñ Ö ¾ º
 ÚÓÐ Ø ÐÑ Ð Ø Ë ÙÖ Ò Á ØÚ Ò ¾¼¼ º ÒÓÚ Ñ Ö ¾ º ¾ Ì ÖØ ÐÓÑ ÝÞ ½º Ñ ÓÖ Ò Ñ ÒÝ ÐÚ ÒÚ Ð Ó Ý Ñ Þ ÓÔØ Ñ Ð Ú Ð ½º½º Å ÖØ Ö Þ ÐÝ Ò ÐÝÞ Ø ÓÐ Ò º º º º º º º º ½º¾º Þ ÚÓÐ Ò Ø Ð ØÖ Ø Ò º º º º º º º º º º º ½º º Þ
ÚÓÐ Ø ÐÑ Ð Ø Ë ÙÖ Ò Á ØÚ Ò ¾¼¼ º ÒÓÚ Ñ Ö ¾ º ¾ Ì ÖØ ÐÓÑ ÝÞ ½º Ñ ÓÖ Ò Ñ ÒÝ ÐÚ ÒÚ Ð Ó Ý Ñ Þ ÓÔØ Ñ Ð Ú Ð ½º½º Å ÖØ Ö Þ ÐÝ Ò ÐÝÞ Ø ÓÐ Ò º º º º º º º º ½º¾º Þ ÚÓÐ Ò Ø Ð ØÖ Ø Ò º º º º º º º º º º º ½º º Þ
¾
 º Þ Ø Þ Ð Ð ØÖÓ ÞØ Ø ÙÐÐ ÑØ Ò Ú ÒØÙÑÑ Ò ÓÐ Ù ÐÐ Ø Ò ËÞ Ð Ý Ò Ö Ù Ô Ø ¾¼¼ ¾ Ì ÖØ ÐÓÑ ÝÞ ½º Ð ØÖÓ ÞØ Ø ½º½º Ð Ô Ó ÐÑ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾º Þ Ð ØÖÓÑÓ
º Þ Ø Þ Ð Ð ØÖÓ ÞØ Ø ÙÐÐ ÑØ Ò Ú ÒØÙÑÑ Ò ÓÐ Ù ÐÐ Ø Ò ËÞ Ð Ý Ò Ö Ù Ô Ø ¾¼¼ ¾ Ì ÖØ ÐÓÑ ÝÞ ½º Ð ØÖÓ ÞØ Ø ½º½º Ð Ô Ó ÐÑ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾º Þ Ð ØÖÓÑÓ
F V (n) = 2 2n (n N 0 )º
 ÃÓÑ Ò ØÓÖ Ù Ø Ð Ò 0¹ Ý Þ Öò Ð ÓÔÓÖØÓ Þ Ô ØÖÙÑ È º º ÖØ Þ Ã Ø ¹ÍÖ Ò Ã Ñ ÐÐ Ì Ñ Ú Þ Ø Öº Å Ý Ä ÞÐ Öº ËÞ Å Ø Ñ Ø ¹ ËÞ Ñ Ø ØÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ ÓÐÝ ÁÒØ Þ Ø Ë Ì ÌÌÁà ¾¼¼ ËÞ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½ ¾º Ð ÞÑ ÒÝ
ÃÓÑ Ò ØÓÖ Ù Ø Ð Ò 0¹ Ý Þ Öò Ð ÓÔÓÖØÓ Þ Ô ØÖÙÑ È º º ÖØ Þ Ã Ø ¹ÍÖ Ò Ã Ñ ÐÐ Ì Ñ Ú Þ Ø Öº Å Ý Ä ÞÐ Öº ËÞ Å Ø Ñ Ø ¹ ËÞ Ñ Ø ØÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ ÓÐÝ ÁÒØ Þ Ø Ë Ì ÌÌÁà ¾¼¼ ËÞ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½ ¾º Ð ÞÑ ÒÝ
ÅÇ ÊÆ ÃÇ ÅÇÄ Á Ë ý Á Ë ÆÌÊÇÈÁÃÍË ÄÎ Ã Ó ØÓÖ ÖØ Þ ÖØ À Ø ÓÐØ Ì Ñ Ú Þ Ø Öº Ð Þ Ð Ý Ø Ñ Ø Ò Ö ÄÌ ÌÌÃ ÐÐ Þ Ø Ì Ò Þ Þ Ó ØÓÖ ÓÐ Á ÓÐ Ú Þ Ø Öº ÀÓÖÚ Ø Ð Ò Ý Ø
 ÅÙÒ Ñ Ø Þ Ö Ø ØØ Ô ÖÓÑÒ Þ Ð ÑÒ ÒÐÓѺ Þ Ö Ø Á Ø Ò Ø ÓÐØ ½ ¾µ ÅÇ ÊÆ ÃÇ ÅÇÄ Á Ë ý Á Ë ÆÌÊÇÈÁÃÍË ÄÎ Ã Ó ØÓÖ ÖØ Þ ÖØ À Ø ÓÐØ Ì Ñ Ú Þ Ø Öº Ð Þ Ð Ý Ø Ñ Ø Ò Ö ÄÌ ÌÌà ÐÐ Þ Ø Ì Ò Þ Þ Ó ØÓÖ ÓÐ Á ÓÐ Ú Þ Ø Öº ÀÓÖÚ
ÅÙÒ Ñ Ø Þ Ö Ø ØØ Ô ÖÓÑÒ Þ Ð ÑÒ ÒÐÓѺ Þ Ö Ø Á Ø Ò Ø ÓÐØ ½ ¾µ ÅÇ ÊÆ ÃÇ ÅÇÄ Á Ë ý Á Ë ÆÌÊÇÈÁÃÍË ÄÎ Ã Ó ØÓÖ ÖØ Þ ÖØ À Ø ÓÐØ Ì Ñ Ú Þ Ø Öº Ð Þ Ð Ý Ø Ñ Ø Ò Ö ÄÌ ÌÌà ÐÐ Þ Ø Ì Ò Þ Þ Ó ØÓÖ ÓÐ Á ÓÐ Ú Þ Ø Öº ÀÓÖÚ
 ÅÌ Ó ØÓÖ ÖØ Þ Ì Þ À Þ ÐÐ ØÓ Þ Ú Ø Ð Ô Ò Þ Ö Ú Þ Ø Ø Ð Ð ÑÞ ÐØ Ö Ð ØØ Ò ÐÐ ÔÓØÓ Ò Öº ËÞ Ò Ö È º ºµ à ÔÓ Ú Ö Ý Ø Ñ ýðð ØØÙ ÓÑ ÒÝ Ã Ö Ã ÔÓ Ú Ö ¾¼½ ½º Ú Þ Ø dc_534_12 Þ ÐÐ ØØ ÒÝ ÞØ ØÙ ÓÑ ÒÝÓ Ø Ö Ð Ø Ò ÝÖ
ÅÌ Ó ØÓÖ ÖØ Þ Ì Þ À Þ ÐÐ ØÓ Þ Ú Ø Ð Ô Ò Þ Ö Ú Þ Ø Ø Ð Ð ÑÞ ÐØ Ö Ð ØØ Ò ÐÐ ÔÓØÓ Ò Öº ËÞ Ò Ö È º ºµ à ÔÓ Ú Ö Ý Ø Ñ ýðð ØØÙ ÓÑ ÒÝ Ã Ö Ã ÔÓ Ú Ö ¾¼½ ½º Ú Þ Ø dc_534_12 Þ ÐÐ ØØ ÒÝ ÞØ ØÙ ÓÑ ÒÝÓ Ø Ö Ð Ø Ò ÝÖ
Ì Ò Ö Þ ÓÐ ÓÞ Ø Ì ÒÙÐÑ ÒÝ Ú Ð Þ Òò Þ Ñ Ø Ø Ò Ø Ï ÒØ Ö ÐÝ Ñ Ø Ñ Ø Ø Ò Ö Å Ð Ú Ð Þ ÄÌ ÈÈÃ Ì Ñ Ú Þ Ø Î Ö ÐÝ Ú ¾¼½
 Ì ÆýÊÁ Ë Ã ÇÄ Ç Ì Ï ÒØ Ö ÐÝ Í È ËÌ ¾¼½ Ì Ò Ö Þ ÓÐ ÓÞ Ø Ì ÒÙÐÑ ÒÝ Ú Ð Þ Òò Þ Ñ Ø Ø Ò Ø Ï ÒØ Ö ÐÝ Ñ Ø Ñ Ø Ø Ò Ö Å Ð Ú Ð Þ ÄÌ ÈÈÃ Ì Ñ Ú Þ Ø Î Ö ÐÝ Ú ¾¼½ Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø ¾ ½º Ñ Ø Ñ Ø ÞÓÒ Ð Ð Ú Ð Þ Òò Þ Ñ
Ì ÆýÊÁ Ë Ã ÇÄ Ç Ì Ï ÒØ Ö ÐÝ Í È ËÌ ¾¼½ Ì Ò Ö Þ ÓÐ ÓÞ Ø Ì ÒÙÐÑ ÒÝ Ú Ð Þ Òò Þ Ñ Ø Ø Ò Ø Ï ÒØ Ö ÐÝ Ñ Ø Ñ Ø Ø Ò Ö Å Ð Ú Ð Þ ÄÌ ÈÈÃ Ì Ñ Ú Þ Ø Î Ö ÐÝ Ú ¾¼½ Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø ¾ ½º Ñ Ø Ñ Ø ÞÓÒ Ð Ð Ú Ð Þ Òò Þ Ñ
Þ Ö ÓÓ Ò ÓÖÑ Ö Ò Þ Ö Ó ØÓÖ È º ºµ ÖØ Þ Ê Ú ÒÝ Ì ÓÖ ÓÐØ Ì Ñ Ú Þ Ø Öº ÃÓÖÑÓ Â ÒÓ Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ Ö Ò ¾¼½¼
 Þ Ö ÓÓ Ò ÓÖÑ Ö Ò Þ Ö Ó ØÓÖ È º ºµ ÖØ Þ Ê Ú ÒÝ Ì ÓÖ ÓÐØ Ì Ñ Ú Þ Ø Öº ÃÓÖÑÓ Â ÒÓ Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ Ö Ò ¾¼½¼ Þ Ò ÖØ Þ Ø Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò ÁÒ ÓÖÑ
Þ Ö ÓÓ Ò ÓÖÑ Ö Ò Þ Ö Ó ØÓÖ È º ºµ ÖØ Þ Ê Ú ÒÝ Ì ÓÖ ÓÐØ Ì Ñ Ú Þ Ø Öº ÃÓÖÑÓ Â ÒÓ Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ Ö Ò ¾¼½¼ Þ Ò ÖØ Þ Ø Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò ÁÒ ÓÖÑ
Ã Þ ÐØ Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ò Å Þ ÔÖÓ Ö Ñ Ö Ø Ò Å Ý Ö ÌÙ ÓÑ ÒÝÓ Ñ ØÓÑÑ ÙØ Ø ÁÒØ Þ Ø Ò ÅÌ ¹ ØÓÑ µ
 Þ ØÓÑÑ Ó ÓÐÐ Ø Ú Ô ÐÙ ÐÐ ÔÓØ Ò ÖÐ Ø Ú Þ Ð Ø Ý Ø Ñ Ó ØÓÖ È µ ÖØ Þ ËØÙ Ð Ä ÞÐ Ì Ñ Ú Þ Ø Öº ÃÖ ÞÒ ÓÖ Ý ØØ Ð Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ö Ò ¾¼½ Ã Þ ÐØ Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ
Þ ØÓÑÑ Ó ÓÐÐ Ø Ú Ô ÐÙ ÐÐ ÔÓØ Ò ÖÐ Ø Ú Þ Ð Ø Ý Ø Ñ Ó ØÓÖ È µ ÖØ Þ ËØÙ Ð Ä ÞÐ Ì Ñ Ú Þ Ø Öº ÃÖ ÞÒ ÓÖ Ý ØØ Ð Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ö Ò ¾¼½ Ã Þ ÐØ Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ
t 2 t 1 x(t + t) x(t). t v(t) = (v x (t), 0, 0)
 Å Ò ÒÝ Ð Ú Ð Þ ÐÐ Ø Ò Þ Ñ ÒÒÝ Ñ ÖØ Ý Þ Þ Ð ÒØ Ø ÖÑ Þ ØØ Ò Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý º Þ Ø Ö Ý Ø Ô Þ Ø ÖÑ Þ Ø¹ Ò Ð ÓÖ ÙÐ Ñ Ö Ø Ö ÔÖÓ Ù Ð Ø Ð Ò Ý Ö Þ º ýðø Ð Ò Ò Ñ Ñ Ò Þ ÓÐÝ Ò Ð Ò Ð Ó Ð Ð ÓÞ Ñ ÐÝ ÓÖ Ò Ò Ñ Ú ÐØÓÞ
Å Ò ÒÝ Ð Ú Ð Þ ÐÐ Ø Ò Þ Ñ ÒÒÝ Ñ ÖØ Ý Þ Þ Ð ÒØ Ø ÖÑ Þ ØØ Ò Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý º Þ Ø Ö Ý Ø Ô Þ Ø ÖÑ Þ Ø¹ Ò Ð ÓÖ ÙÐ Ñ Ö Ø Ö ÔÖÓ Ù Ð Ø Ð Ò Ý Ö Þ º ýðø Ð Ò Ò Ñ Ñ Ò Þ ÓÐÝ Ò Ð Ò Ð Ó Ð Ð ÓÞ Ñ ÐÝ ÓÖ Ò Ò Ñ Ú ÐØÓÞ
x T i x j = δ ij, 1 i, j k, ¾µ
 ÐÓ Ð ÓÔØ Ñ Ð Þ Ð Ð ÐÑ Þ Ó Þ Ñ ¹ÓÒ¹Ð Ò Ð Ô ÓÐ Ó ØÓÖ ÖØ Þ Ø Þ ÐÓ Â ÒÓ Ì Ñ Ú Þ Ø Öº Ò Ì ÓÖ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ËÞ ¾¼¼ Ú Þ Ø Ó ØÓÖ ÖØ Þ Þ ÖÞ Ò ÐÓ Ð ÓÔØ Ñ Ð Þ Ð Ð ÐÑ Þ Ø Ö Ð Ø Ò Ý Þ Ö Ø ÓÔØ Ñ Ð Þ Ð Ð ØÓÒ Ð ÖØ
ÐÓ Ð ÓÔØ Ñ Ð Þ Ð Ð ÐÑ Þ Ó Þ Ñ ¹ÓÒ¹Ð Ò Ð Ô ÓÐ Ó ØÓÖ ÖØ Þ Ø Þ ÐÓ Â ÒÓ Ì Ñ Ú Þ Ø Öº Ò Ì ÓÖ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ËÞ ¾¼¼ Ú Þ Ø Ó ØÓÖ ÖØ Þ Þ ÖÞ Ò ÐÓ Ð ÓÔØ Ñ Ð Þ Ð Ð ÐÑ Þ Ø Ö Ð Ø Ò Ý Þ Ö Ø ÓÔØ Ñ Ð Þ Ð Ð ØÓÒ Ð ÖØ
ËÞ ÓÐ ÓÞ Ø ÞòÖ Ð Ö Ó Ð ÐÑ Þ Ö Ú Ø ÙÐРѹ Ð Ð Ó Ú Þ Ð Ø Ò Þ Ö Ð Þ Þ Ëº Þ Ù Þ Ö ÒÝ ÁÁÁº Ú ÓÐÝ Ñ Ì Ñ Ú Þ Ø Öº Ê Þ Á ØÚ Ò Ï Ò Ö ÊÅÃÁ Ð ÓÒÞÙÐ Ò Öº È ÐÐ Ä Þ
 ËÞ ÓÐ ÓÞ Ø ÞòÖ Ð Ö Ó Ð ÐÑ Þ Ö Ú Ø ÙÐРѹ Ð Ð Ó Ú Þ Ð Ø Ò Þ Ö Ð Þ Þ Ëº Þ Ù Þ Ö ÒÝ ÁÁÁº Ú ÓÐÝ Ñ Ì Ñ Ú Þ Ø Öº Ê Þ Á ØÚ Ò Ï Ò Ö ÊÅÃÁ Ð ÓÒÞÙÐ Ò Öº È ÐÐ Ä ÞÐ ÄÌ ÌÌà ¾¼½ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾º Ö Ú Ø ÙÐÐ ÑÓ
ËÞ ÓÐ ÓÞ Ø ÞòÖ Ð Ö Ó Ð ÐÑ Þ Ö Ú Ø ÙÐРѹ Ð Ð Ó Ú Þ Ð Ø Ò Þ Ö Ð Þ Þ Ëº Þ Ù Þ Ö ÒÝ ÁÁÁº Ú ÓÐÝ Ñ Ì Ñ Ú Þ Ø Öº Ê Þ Á ØÚ Ò Ï Ò Ö ÊÅÃÁ Ð ÓÒÞÙÐ Ò Öº È ÐÐ Ä ÞÐ ÄÌ ÌÌà ¾¼½ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾º Ö Ú Ø ÙÐÐ ÑÓ
v 3 v 4 v 8 v 10 v 9 v 11 v 7 v 1 v 2 v 5 v 6
 Þ Ñ Ø ØÙ ÓÑ ÒÝ Ð Ô Å Áº Ú Ú ÐÐ ÑÓ Ñ ÖÒ ¹ ÐÐ Ø Þ Ñ Ö Ð Ø ¾¼¼ º Þ Ð ÓÞ Þ ÐÐ ØÓØØ Ð Ò Ö Ì Ñ v 3 v 4 v 8 v 10 v 9 v 11 v 7 v 1 v 0 v 2 v 5 v 6 ÍØÓÐ Ö Ø ¾¼½½º ÒÓÚ Ñ Ö ¾º Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø ½ ÃÓÑ Ò ØÓÖ ½º½ Ð
Þ Ñ Ø ØÙ ÓÑ ÒÝ Ð Ô Å Áº Ú Ú ÐÐ ÑÓ Ñ ÖÒ ¹ ÐÐ Ø Þ Ñ Ö Ð Ø ¾¼¼ º Þ Ð ÓÞ Þ ÐÐ ØÓØØ Ð Ò Ö Ì Ñ v 3 v 4 v 8 v 10 v 9 v 11 v 7 v 1 v 0 v 2 v 5 v 6 ÍØÓÐ Ö Ø ¾¼½½º ÒÓÚ Ñ Ö ¾º Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø ½ ÃÓÑ Ò ØÓÖ ½º½ Ð
ÄÓ Þ Ñ Ø ÐÑ Ð Ø Þ Ñ Ø ÐÑ Ð Ø Ö Þ Ö ÝÞ Ø Ð Öº Þ ÓÐØ ÍØÓÐ Ñ Ó Ø ¾¼¼ º Ñ Ö ¼º
 ÄÓ Þ Ñ Ø ÐÑ Ð Ø Þ Ñ Ø ÐÑ Ð Ø Ö Þ Ö ÝÞ Ø Ð Öº Þ ÓÐØ ÍØÓÐ Ñ Ó Ø ¾¼¼ º Ñ Ö ¼º ¾ ½º Þ Ø Ð Þ Þ ÓÐÝ Ñ ØÓ Ò Ú Ð Ö ÝÞ Ø Þ ÄÌ ÁÒ ÓÖÑ Ø Ã Ö Ò ¾¼¼ ¹ ¾¼¼ ¹ Þ Þ Ñ ÞØ Ö Ò Ø ÖØÓØØ ÄÓ Þ Ñ Ø ÐÑ Ð Ø Ñò ÙÖÞÙ Þ ¹ Ñ Ø ÐÑ Ð
ÄÓ Þ Ñ Ø ÐÑ Ð Ø Þ Ñ Ø ÐÑ Ð Ø Ö Þ Ö ÝÞ Ø Ð Öº Þ ÓÐØ ÍØÓÐ Ñ Ó Ø ¾¼¼ º Ñ Ö ¼º ¾ ½º Þ Ø Ð Þ Þ ÓÐÝ Ñ ØÓ Ò Ú Ð Ö ÝÞ Ø Þ ÄÌ ÁÒ ÓÖÑ Ø Ã Ö Ò ¾¼¼ ¹ ¾¼¼ ¹ Þ Þ Ñ ÞØ Ö Ò Ø ÖØÓØØ ÄÓ Þ Ñ Ø ÐÑ Ð Ø Ñò ÙÖÞÙ Þ ¹ Ñ Ø ÐÑ Ð
1 + e β(x d). 0, x a δ/2 x (a δ/2), a δ/2 < x < a + δ/2 1, a + δ/2 x. σ ( β)
 ÙÞÞÝ Ú Ø ÞØ Ø ÑÓ ÐÐ ÙÞÞÝ Þ ÖØ Ò Ð ÔÙÐ ÐÓ Ó ØÓÖ ÖØ Þ Ø Þ Ö ÓÐØ Ì Ñ Ú Þ Ø Öº ÓÑ Â Þ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ËÞ ¾¼¼ ½º Ú Þ Ø Þ ÖØ Þ Ö Ñ ÒÝ Þ Ð ÖÓÑ ÔÓÒØ Ò Ó Ð Ð Ø Þ º Ð Þ Ö ÑÙØ Ø Ý ÓÐÝ Ò Ö ÙÞÞÝ Þ ÐÝØ ÒÙÐ ÑÓ ÐÐØ
ÙÞÞÝ Ú Ø ÞØ Ø ÑÓ ÐÐ ÙÞÞÝ Þ ÖØ Ò Ð ÔÙÐ ÐÓ Ó ØÓÖ ÖØ Þ Ø Þ Ö ÓÐØ Ì Ñ Ú Þ Ø Öº ÓÑ Â Þ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ËÞ ¾¼¼ ½º Ú Þ Ø Þ ÖØ Þ Ö Ñ ÒÝ Þ Ð ÖÓÑ ÔÓÒØ Ò Ó Ð Ð Ø Þ º Ð Þ Ö ÑÙØ Ø Ý ÓÐÝ Ò Ö ÙÞÞÝ Þ ÐÝØ ÒÙÐ ÑÓ ÐÐØ
g IJ (G) = η IJ, Γ I JK(G) = 0 ½º½µ
 ȹ ÖÐ Ø ÐÚ Ð Ô ÀÖ È Ø Ö ½º ÓÖ Ñ ÒØ Ó ÐÑ º Þ ÐØ Ð ÒÓ Ö Ð Ø Ú Ø ÐÑ Ð Ø ÑòÚ Ð Þ ØØ Ý Ø ÖØ Ú Ò Ò Ó Ý ÓÖ Ñ ÒØ Ø Ö ÐØ Ø Ö Ò ÓÖ ÔÖ Ø Ø Ñ Ö Øò Ñ Þ ÑÑ ØÖ Ù ÖÓ Þ ÔÓ µ Ô Ò Ò Þ Ö ÒÝ Ø ÖÓÞÞ Ñ ½ º Þ ¹ Ö ÒØ Ý òö ÐÓ Ð
ȹ ÖÐ Ø ÐÚ Ð Ô ÀÖ È Ø Ö ½º ÓÖ Ñ ÒØ Ó ÐÑ º Þ ÐØ Ð ÒÓ Ö Ð Ø Ú Ø ÐÑ Ð Ø ÑòÚ Ð Þ ØØ Ý Ø ÖØ Ú Ò Ò Ó Ý ÓÖ Ñ ÒØ Ø Ö ÐØ Ø Ö Ò ÓÖ ÔÖ Ø Ø Ñ Ö Øò Ñ Þ ÑÑ ØÖ Ù ÖÓ Þ ÔÓ µ Ô Ò Ò Þ Ö ÒÝ Ø ÖÓÞÞ Ñ ½ º Þ ¹ Ö ÒØ Ý òö ÐÓ Ð
Pr(X 1 = j X 0 = i) Pr(T 1 < t X 0 = i) Pr(X 1 = j, T 1 < t X 0 = i) = Pr(X 1 = j X 0 = i) = [( D 0 ) 1 D 1 ] ij. Pr(T 1 < t X 0 = i) = [e D0t 1I] i
![Pr(X 1 = j X 0 = i) Pr(T 1 < t X 0 = i) Pr(X 1 = j, T 1 < t X 0 = i) = Pr(X 1 = j X 0 = i) = [( D 0 ) 1 D 1 ] ij. Pr(T 1 < t X 0 = i) = [e D0t 1I] i Pr(X 1 = j X 0 = i) Pr(T 1 < t X 0 = i) Pr(X 1 = j, T 1 < t X 0 = i) = Pr(X 1 = j X 0 = i) = [( D 0 ) 1 D 1 ] ij. Pr(T 1 < t X 0 = i) = [e D0t 1I] i](/thumbs/102/152724391.jpg) Ì Å ÃÁË ÇÄ ýäýë ÁÁº Ô Ð ÓÖÓ Ñ ÓÐ Ì Ð Å Ð Ù Ô Ø Åò Þ Ý Ø Ñ ¾¼¼ º ¾¼¼¾º  Һ º Ì Ñ ÞÓÐ Ð Ú Þ ½» Ý D 0, D 1 Ñ ØÖ ÜÓ Ð ÓØØ Å È Ø Ò X 0, X 1,... Þ Ö Þ ÙØ Ò Þ Ñ T 0 = 0, T 1,... Þ Ö Þ Ô ÐÐ Ò Ø º Ñ Ú Ø Þ Ú Ð
Ì Å ÃÁË ÇÄ ýäýë ÁÁº Ô Ð ÓÖÓ Ñ ÓÐ Ì Ð Å Ð Ù Ô Ø Åò Þ Ý Ø Ñ ¾¼¼ º ¾¼¼¾º  Һ º Ì Ñ ÞÓÐ Ð Ú Þ ½» Ý D 0, D 1 Ñ ØÖ ÜÓ Ð ÓØØ Å È Ø Ò X 0, X 1,... Þ Ö Þ ÙØ Ò Þ Ñ T 0 = 0, T 1,... Þ Ö Þ Ô ÐÐ Ò Ø º Ñ Ú Ø Þ Ú Ð
ÝÞ Ø Ô Ø Ñ ÖÒ ÖÒÝ Þ Ø Ñ ÖÒ ÐÐ Ø Ò ¾¼¼¾º½¾º¾¾º Ú ÐØÓÞ Ø Ë ÑÓÒ Ã ÖÓÐÝ ¾¼¼¾º½¾º¾¾
 ÝÞ Ø Ô Ø Ñ ÖÒ ÖÒÝ Þ Ø Ñ ÖÒ ÐÐ Ø Ò ¾¼¼¾º½¾º¾¾º Ú ÐØÓÞ Ø Ë ÑÓÒ Ã ÖÓÐÝ ¾¼¼¾º½¾º¾¾ ¾ Ä ØÓÖ ÐØ Öº Ë Ò ÓÖ Ý Ø Ñ ÙÒ ØÙ Ð Þ Þ ÝÞ Ø Öº Ë ÑÓÒ Ã ÖÓÐÝÒ Å Ô Ø Ñ ÖÒ Ã ÖÒÝ Þ Ø Ñ ÖÒ ÐÐ Ø Ò Ø ÖØÓØØ Ð ÒÝ Ø Ø ÖØ ÐÑ ÞÞ º
ÝÞ Ø Ô Ø Ñ ÖÒ ÖÒÝ Þ Ø Ñ ÖÒ ÐÐ Ø Ò ¾¼¼¾º½¾º¾¾º Ú ÐØÓÞ Ø Ë ÑÓÒ Ã ÖÓÐÝ ¾¼¼¾º½¾º¾¾ ¾ Ä ØÓÖ ÐØ Öº Ë Ò ÓÖ Ý Ø Ñ ÙÒ ØÙ Ð Þ Þ ÝÞ Ø Öº Ë ÑÓÒ Ã ÖÓÐÝÒ Å Ô Ø Ñ ÖÒ Ã ÖÒÝ Þ Ø Ñ ÖÒ ÐÐ Ø Ò Ø ÖØÓØØ Ð ÒÝ Ø Ø ÖØ ÐÑ ÞÞ º
einsteini newtoni Az adó nyugszik Mindegy A vevõ nyugszik
 ½ newtoni einsteini Az adó nyugszik Mindegy A vevõ nyugszik ½º Ö º 1 Ö Ð Ø Ú Ø ÐÑ Ð Ø Ð Ô Ì ÊÌ ÄÇÅ Ã Þ Ø Ñ ÝÞ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ºÓÐ Ð Ý ÓÖÐ Ð ØÓ
½ newtoni einsteini Az adó nyugszik Mindegy A vevõ nyugszik ½º Ö º 1 Ö Ð Ø Ú Ø ÐÑ Ð Ø Ð Ô Ì ÊÌ ÄÇÅ Ã Þ Ø Ñ ÝÞ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ºÓÐ Ð Ý ÓÖÐ Ð ØÓ
σ m α η e m η m η N η ) α m η m η T cond
 Þ η Ñ ÞÓÒÓ ÓÑÐ Ø ÖÑ Ò ÞÓÒÓ Ø ÙÐØÖ ¹Ö Ð Ø Ú ÞØ Ù Ø Þ Ò Ã Ö Å Ò Þ Ë º Ú ÓÐÝ Ñ Ì Ñ Ú Þ Ø Ò Å Ø ÄÌ ÌÌà ØÓÑ Þ Ì Ò Þ ¾¼½¼º Ñ Ö ¾ º à ÚÓÒ Ø Á Ñ ÖØ Ó Ý Ø Ö ÐÑ Ð Ø Þ ÑÑ ØÖ Ò Ö Ð Ð Ð Ö Þ Ø Ñ Öغ ÐØ Ø Ð Þ ¹ Þ Ö ÒØ
Þ η Ñ ÞÓÒÓ ÓÑÐ Ø ÖÑ Ò ÞÓÒÓ Ø ÙÐØÖ ¹Ö Ð Ø Ú ÞØ Ù Ø Þ Ò Ã Ö Å Ò Þ Ë º Ú ÓÐÝ Ñ Ì Ñ Ú Þ Ø Ò Å Ø ÄÌ ÌÌà ØÓÑ Þ Ì Ò Þ ¾¼½¼º Ñ Ö ¾ º à ÚÓÒ Ø Á Ñ ÖØ Ó Ý Ø Ö ÐÑ Ð Ø Þ ÑÑ ØÖ Ò Ö Ð Ð Ð Ö Þ Ø Ñ Öغ ÐØ Ø Ð Þ ¹ Þ Ö ÒØ
Å Ò Ñ Ò Ð Þ ËÞ Ð Á ØÚ Ò ÄÌ Ã Ñ ÁÒØ Þ Ø Ôº ½
 Å Ò Ñ Ò Ð Þ ËÞ Ð Á ØÚ Ò ÄÌ Ã Ñ ÁÒØ Þ Ø Ôº ½ ÓÒÓ Ø ÔÙ È Ö ÓÒ Ð Ó ÞØ ÐÝÓÞ Ú Þ Ø Ö Ø ÔÙ Ó µ ÓÐ Ó ÓÐ Ø Ò Þ Ñ Ø ÔÀ ÊÓ ÞÙÐ Ø µ ÓÑÔÐ Ü ÔÞ Ì Ñ Ø Ë Ú¹ Þ ÓÑÔÐ Ü Ý Ò ÐÝÓ Þ Ñ Ø Ê ÓÜ ÔÓØ Ò Ð Ã Ø ÓÒÓ Ö ÐÚ Ð ÞØ Ù ÑÙØ
Å Ò Ñ Ò Ð Þ ËÞ Ð Á ØÚ Ò ÄÌ Ã Ñ ÁÒØ Þ Ø Ôº ½ ÓÒÓ Ø ÔÙ È Ö ÓÒ Ð Ó ÞØ ÐÝÓÞ Ú Þ Ø Ö Ø ÔÙ Ó µ ÓÐ Ó ÓÐ Ø Ò Þ Ñ Ø ÔÀ ÊÓ ÞÙÐ Ø µ ÓÑÔÐ Ü ÔÞ Ì Ñ Ø Ë Ú¹ Þ ÓÑÔÐ Ü Ý Ò ÐÝÓ Þ Ñ Ø Ê ÓÜ ÔÓØ Ò Ð Ã Ø ÓÒÓ Ö ÐÚ Ð ÞØ Ù ÑÙØ
Ë Á ÌÍ ÇÅýÆ Ì Å Ì ÊÅ Ë ÌÌÍ ÇÅýÆ Á Ë ÁÆ ÇÊÅ ÌÁà Á Ã Ê ËÞÙÔ ÖÒ Ú ¹ÖÓ Ò Ó ÓÞ Ô ÓÐ ÔÓÖ ÔÞ Ú Þ Ð Ø Ì Ã¹ ÓÐ ÓÞ Ø ÖÓ ËÞ ÒÒ ÁÁÁº Ú Þ Ë Þ Ó ÐÐ Ø Ë Ì ÌÌÁÃ Ì Ñ Ú
 Ë Á ÌÍ ÇÅýÆ Ì Å Ì ÊÅ Ë ÌÌÍ ÇÅýÆ Á Ë ÁÆ ÇÊÅ ÌÁà Á Ã Ê ËÞÙÔ ÖÒ Ú ¹ÖÓ Ò Ó ÓÞ Ô ÓÐ ÔÓÖ ÔÞ Ú Þ Ð Ø Ì Ã¹ ÓÐ ÓÞ Ø ÖÓ ËÞ ÒÒ ÁÁÁº Ú Þ Ë Þ Ó ÐÐ Ø Ë Ì ÌÌÁÃ Ì Ñ Ú Þ Ø Öº ËÞ Ð Ì Ñ ØÙ ÓÑ ÒÝÓ ÑÙÒ Ø Ö Ë Ì ÇÔØ ÃÚ ÒØÙÑ
Ë Á ÌÍ ÇÅýÆ Ì Å Ì ÊÅ Ë ÌÌÍ ÇÅýÆ Á Ë ÁÆ ÇÊÅ ÌÁà Á Ã Ê ËÞÙÔ ÖÒ Ú ¹ÖÓ Ò Ó ÓÞ Ô ÓÐ ÔÓÖ ÔÞ Ú Þ Ð Ø Ì Ã¹ ÓÐ ÓÞ Ø ÖÓ ËÞ ÒÒ ÁÁÁº Ú Þ Ë Þ Ó ÐÐ Ø Ë Ì ÌÌÁÃ Ì Ñ Ú Þ Ø Öº ËÞ Ð Ì Ñ ØÙ ÓÑ ÒÝÓ ÑÙÒ Ø Ö Ë Ì ÇÔØ ÃÚ ÒØÙÑ
Ã Þ ÐØ Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ò ËÞ Ð Ö Ø Ø Þ ÒÝ ØÙ ÓÑ ÒÝ ÔÖÓ Ö Ñ Ö Ø Ò ÈÖ Ô Ö Ø Ø ÍÒ Ú Ö ØÝ Ó Ö Ò È Ë ÓÓÐ Ò È Ý
 Ý Ø Ñ Ó ØÓÖ È µ ÖØ Þ Ø Þ ØÖ Ø Ó È Ì Ê Ò Þ ØÐ Ò ÒÝ Ó Ø Ö ÖÓ Ó Ö ØÙÖ Ò Ñ Ó Ø ÖÓ Ò ÓÙ Ñ Ø Ö Ð À Ð Þ ÓÐØ Ò Ì Ñ Ú Þ Ø» ËÙÔ ÖÚ ÓÖ Öº ÃÙÒ Ö Ò Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ ÍÒ Ú Ö ØÝ Ó Ö Ò È Ë ÓÓÐ Ò È Ý Ö Ò
Ý Ø Ñ Ó ØÓÖ È µ ÖØ Þ Ø Þ ØÖ Ø Ó È Ì Ê Ò Þ ØÐ Ò ÒÝ Ó Ø Ö ÖÓ Ó Ö ØÙÖ Ò Ñ Ó Ø ÖÓ Ò ÓÙ Ñ Ø Ö Ð À Ð Þ ÓÐØ Ò Ì Ñ Ú Þ Ø» ËÙÔ ÖÚ ÓÖ Öº ÃÙÒ Ö Ò Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ ÍÒ Ú Ö ØÝ Ó Ö Ò È Ë ÓÓÐ Ò È Ý Ö Ò
Ú Þ Ø Þ Ñ Ø ÐÑ Ð Ø ÁÁº Å Ò ÓÖÑ Ø Ù ¹ ÐÐ Ø Þ Ñ Ö Ð Ø ¾¼¼ º Ø Ú Þ ÎÁË ½½¼ Ð ÓÞ Þ ÐÐ ØÓØØ Ð Ò Ö Ì Ñ A B s t X
 Ú Þ Ø Þ Ñ Ø ÐÑ Ð Ø ÁÁº Å Ò ÓÖÑ Ø Ù ¹ ÐÐ Ø Þ Ñ Ö Ð Ø ¾¼¼ º Ø Ú Þ ÎÁË ½½¼ Ð ÓÞ Þ ÐÐ ØÓØØ Ð Ò Ö Ì Ñ A B s t X Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø ¾ ½ºº ÙÐ Ö À Ñ ÐØÓÒ Ö Ó ¾ºº À Ð Þ Ø ÓÐÝ ÑÓ ºº Å Ò Ö Ø Ø Ð ºº È ÖÓ Ö Ó Ô ÖÓ Ø
Ú Þ Ø Þ Ñ Ø ÐÑ Ð Ø ÁÁº Å Ò ÓÖÑ Ø Ù ¹ ÐÐ Ø Þ Ñ Ö Ð Ø ¾¼¼ º Ø Ú Þ ÎÁË ½½¼ Ð ÓÞ Þ ÐÐ ØÓØØ Ð Ò Ö Ì Ñ A B s t X Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø ¾ ½ºº ÙÐ Ö À Ñ ÐØÓÒ Ö Ó ¾ºº À Ð Þ Ø ÓÐÝ ÑÓ ºº Å Ò Ö Ø Ø Ð ºº È ÖÓ Ö Ó Ô ÖÓ Ø
dc_603_12 E N = (e 1,e 2,...,e N ) e a+jb. e a+jb, W(E N ) a,b,t N 1 a a+(t 1)b Nº V(E N,M,D) e n+d1 e n+d2,...e n+dl t 1 j=0 N,t,a,b) = max n=1
 Î Ò Ö ÓÖÓÞ ØÓ Ö Ó Ô Þ Ù ÓÚ Ð ØÐ Ò Ó ØÓÖ ÖØ Þ Ø Þ Ý ÖÑ Ø Ã Ø Ð Ò ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ Ù Ô Ø ¾¼½ ½º Ú Þ Ø Þ ÐÑ ÐØ Þ Þ Ú Ò Ö ÔØÓ Ö ÝÖ Ò ÝÓ Þ Ö Ô Ø ÔÓØØ Ñ Ø Ñ Ø Ò ÓÖÑ Ø ÙØ Ø Ó Òº Ø Ö Ð ØÒ Þ ÑÓ ÓÒØÓ Ý ÓÖÐ
Î Ò Ö ÓÖÓÞ ØÓ Ö Ó Ô Þ Ù ÓÚ Ð ØÐ Ò Ó ØÓÖ ÖØ Þ Ø Þ Ý ÖÑ Ø Ã Ø Ð Ò ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ Ù Ô Ø ¾¼½ ½º Ú Þ Ø Þ ÐÑ ÐØ Þ Þ Ú Ò Ö ÔØÓ Ö ÝÖ Ò ÝÓ Þ Ö Ô Ø ÔÓØØ Ñ Ø Ñ Ø Ò ÓÖÑ Ø ÙØ Ø Ó Òº Ø Ö Ð ØÒ Þ ÑÓ ÓÒØÓ Ý ÓÖÐ
ÃÓÑÔÐ Ü Ú ÒÝ Þ Ò Ö ÞÓÐ Ì Ã ÓÐ ÓÞ Ø Ä Ä Ú ÒØ ØØÔ»»ÐÓ ºÛ º ÐØ º Ù Ì Ñ Ú Þ Ø Ë ÔÔ Ö Ò ¾¼¼ º ÒÓÚ Ñ Ö
 ÃÓÑÔÐ Ü Ú ÒÝ Þ Ò Ö ÞÓÐ Ì Ã ÓÐ ÓÞ Ø Ä Ä Ú ÒØ ØØÔ»»ÐÓ ºÛ º ÐØ º Ù Ì Ñ Ú Þ Ø Ë ÔÔ Ö Ò ¾¼¼ º ÒÓÚ Ñ Ö Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾º ÃÓÑÔÐ Ü Ú ÒÝ Ö ÞÓÐ Ñ ¾º½º Ã Ø Ó z wµ Ö ÞÓÐ º º º º º º º º º º º º º º º º º º º
ÃÓÑÔÐ Ü Ú ÒÝ Þ Ò Ö ÞÓÐ Ì Ã ÓÐ ÓÞ Ø Ä Ä Ú ÒØ ØØÔ»»ÐÓ ºÛ º ÐØ º Ù Ì Ñ Ú Þ Ø Ë ÔÔ Ö Ò ¾¼¼ º ÒÓÚ Ñ Ö Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾º ÃÓÑÔÐ Ü Ú ÒÝ Ö ÞÓÐ Ñ ¾º½º Ã Ø Ó z wµ Ö ÞÓÐ º º º º º º º º º º º º º º º º º º º
à ÚÓÒ Ø ¾¼¼ ¹ Ò Ð ØÖ ØØ Ý Ý ØØÑò Þ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ Þ ÅÌ Ê Þ ¹ Å Þ ÃÙØ Ø ÒØ Þ Ø Þ ØØ Ñ ÐÝ ÞØ ÐØ ò Ø ØÓÖÓ Ð ÞØ Ú Ð Ó Ð Ð ÓÞ º ÓÔÓÖØ Ê Ê µ Ø ÒØ Ð
 ËÓ Þ Ð ÔÖÓÔÓÖ ÓÒ Ð ÑÖ Ð ÞØ Ö Þ Þ Ø ØÓÖÓ ÓÞ Ì Ã ÓÐ ÓÞ Ø Ã ÓÖ Þ Ù ÅË Áº ÄÌ ÌÌÃ Ì Ñ Ú Þ Ø Öº Î Ö Þ ÄÌ ÌÌà ÃÓÑÔÐ Ü Ê Ò Þ Ö Þ Ì Ò Þ Ù Ô Ø ¾¼½½º ÒÙ Ö Ã ÚÓÒ Ø ¾¼¼ ¹ Ò Ð ØÖ ØØ Ý Ý ØØÑò Þ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø
ËÓ Þ Ð ÔÖÓÔÓÖ ÓÒ Ð ÑÖ Ð ÞØ Ö Þ Þ Ø ØÓÖÓ ÓÞ Ì Ã ÓÐ ÓÞ Ø Ã ÓÖ Þ Ù ÅË Áº ÄÌ ÌÌÃ Ì Ñ Ú Þ Ø Öº Î Ö Þ ÄÌ ÌÌà ÃÓÑÔÐ Ü Ê Ò Þ Ö Þ Ì Ò Þ Ù Ô Ø ¾¼½½º ÒÙ Ö Ã ÚÓÒ Ø ¾¼¼ ¹ Ò Ð ØÖ ØØ Ý Ý ØØÑò Þ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø
Ì ÖØ ÐÓÑ ½ Ú Þ Ø ¾ Ã Ð Ò Ð Ö ÞÓÐ Ñ Ó ËÞ Ò Ö ÞÓÐ Æ ÒÝ Ú ÒÝ Þ Ù Þ ÈÖÓ Ö ÑÓ Þ Ó Ð Ð
 ÃÓÑÔÐ Ü Ú ÒÝ Þ Ò Ö ÞÓÐ Ä Ä Ú ÒØ ÄÌ ÁÃ Å ÓÐ ¾¼¼ º ÔÖ Ð ¾ º ÇÌ Ã ÃÓÒ Ö Ò Ì ÖØ ÐÓÑ ½ Ú Þ Ø ¾ Ã Ð Ò Ð Ö ÞÓÐ Ñ Ó ËÞ Ò Ö ÞÓÐ Æ ÒÝ Ú ÒÝ Þ Ù Þ ÈÖÓ Ö ÑÓ Þ Ó Ð Ð Ì ÖØ ÐÓÑ ½ Ú Þ Ø ¾ Ã Ð Ò Ð Ö ÞÓÐ Ñ Ó ËÞ Ò Ö ÞÓÐ Æ
ÃÓÑÔÐ Ü Ú ÒÝ Þ Ò Ö ÞÓÐ Ä Ä Ú ÒØ ÄÌ ÁÃ Å ÓÐ ¾¼¼ º ÔÖ Ð ¾ º ÇÌ Ã ÃÓÒ Ö Ò Ì ÖØ ÐÓÑ ½ Ú Þ Ø ¾ Ã Ð Ò Ð Ö ÞÓÐ Ñ Ó ËÞ Ò Ö ÞÓÐ Æ ÒÝ Ú ÒÝ Þ Ù Þ ÈÖÓ Ö ÑÓ Þ Ó Ð Ð Ì ÖØ ÐÓÑ ½ Ú Þ Ø ¾ Ã Ð Ò Ð Ö ÞÓÐ Ñ Ó ËÞ Ò Ö ÞÓÐ Æ
Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾º ËÔ ØÖÙÑ Ð Ò Ñ¹ Ý ÒÐ Ø Ò Ñ ÒØ Ú Ø Ð Þ ØØ ØÓ ¹ Ð ¾º½º Ö Ñ ÒØ Ú Ø Ð Þ Ì º º º º º º º º º º º º º º º º º º º º ¾º¾º ÄÓÑ Ô Ö Ó Ó
 ËÔ ØÖÙÑ Ð Ò Ñ¹ Ý ÒÐ Ø Ò Ñ ÒØ Ú Ø Ð Þ ØØ ØÓ Ð ËÈ¹Ò Ì Ã ÓÐ ÓÞ Ø ËÞ ÐÚ Ë Ò ÓÖ ÃÓÒÞÙÐ Ò ÅÓÐÒ Ö Ã ÖÓÐÝ ¾¼¼ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾º ËÔ ØÖÙÑ Ð Ò Ñ¹ Ý ÒÐ Ø Ò Ñ ÒØ Ú Ø Ð Þ ØØ ØÓ ¹ Ð ¾º½º Ö Ñ ÒØ Ú Ø Ð Þ Ì º º º
ËÔ ØÖÙÑ Ð Ò Ñ¹ Ý ÒÐ Ø Ò Ñ ÒØ Ú Ø Ð Þ ØØ ØÓ Ð ËÈ¹Ò Ì Ã ÓÐ ÓÞ Ø ËÞ ÐÚ Ë Ò ÓÖ ÃÓÒÞÙÐ Ò ÅÓÐÒ Ö Ã ÖÓÐÝ ¾¼¼ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾º ËÔ ØÖÙÑ Ð Ò Ñ¹ Ý ÒÐ Ø Ò Ñ ÒØ Ú Ø Ð Þ ØØ ØÓ ¹ Ð ¾º½º Ö Ñ ÒØ Ú Ø Ð Þ Ì º º º
ËÞ Ñ Ø ÐÑ Ð Ø Ö ÝÞ Ø Ð Öº Þ ÓÐØ ÍØÓÐ Ñ Ó Ø ¾¼¼ º ÒÙ Ö ¾ º
 ËÞ Ñ Ø ÐÑ Ð Ø Ö ÝÞ Ø Ð Öº Þ ÓÐØ ÍØÓÐ Ñ Ó Ø ¾¼¼ º ÒÙ Ö ¾ º ¾ Ð Þ Þ ÓÐÝ Ñ ØÓ Ò Ú Ð Ö ÝÞ Ø Þ ÄÌ ÁÒ ÓÖÑ Ø Ã Ö Ò ¾¼¼ ¹ ¾¼¼ ¹ Þ Þ Ñ ÞØ Ö Ò Ø ÖØÓØØ ËÞ Ñ Ø ÐÑ Ð Ø Ñò ÙÖÞÙ ÒÝ Ø Ø Ö¹ Ø ÐÑ ÞÞ º Þ ÐØ Ð Ø Ø ÒÝ Ø Ø
ËÞ Ñ Ø ÐÑ Ð Ø Ö ÝÞ Ø Ð Öº Þ ÓÐØ ÍØÓÐ Ñ Ó Ø ¾¼¼ º ÒÙ Ö ¾ º ¾ Ð Þ Þ ÓÐÝ Ñ ØÓ Ò Ú Ð Ö ÝÞ Ø Þ ÄÌ ÁÒ ÓÖÑ Ø Ã Ö Ò ¾¼¼ ¹ ¾¼¼ ¹ Þ Þ Ñ ÞØ Ö Ò Ø ÖØÓØØ ËÞ Ñ Ø ÐÑ Ð Ø Ñò ÙÖÞÙ ÒÝ Ø Ø Ö¹ Ø ÐÑ ÞÞ º Þ ÐØ Ð Ø Ø ÒÝ Ø Ø
σ m α η e m η m η N η ) α m η m η T cond
 Ö Ð Þ ÑÑ ØÖ ÐÝÖ ÐÐ ÓÖÖ Ú Ö ÒÝ Ò Ã Ö Å Ò Þ Ë Ì Ñ Ú Þ Ø Ò Å Ø ÄÌ ÌÌà ØÓÑ Þ Ì Ò Þ ¾¼½½º Ò Ù º à ÚÓÒ Ø Á Ñ ÖØ Ó Ý Ø Ö ÐÑ Ð Ø Þ ÑÑ ØÖ Ò Ö Ð Ð Ð Ö Þ Ø Ñ Öغ ÐØ Ø Ð Þ ¹ Þ Ö ÒØ Þ ÑÑ ØÖ Ò ÝÓÒ Ñ Ñ Ö Ð Øò Þ Ò ÐÝÖ
Ö Ð Þ ÑÑ ØÖ ÐÝÖ ÐÐ ÓÖÖ Ú Ö ÒÝ Ò Ã Ö Å Ò Þ Ë Ì Ñ Ú Þ Ø Ò Å Ø ÄÌ ÌÌà ØÓÑ Þ Ì Ò Þ ¾¼½½º Ò Ù º à ÚÓÒ Ø Á Ñ ÖØ Ó Ý Ø Ö ÐÑ Ð Ø Þ ÑÑ ØÖ Ò Ö Ð Ð Ð Ö Þ Ø Ñ Öغ ÐØ Ø Ð Þ ¹ Þ Ö ÒØ Þ ÑÑ ØÖ Ò ÝÓÒ Ñ Ñ Ö Ð Øò Þ Ò ÐÝÖ
 Ð Ô Ø Ø Ù ÔÖÓ Ö Ñ Þ Ð Ø Ð Þ Ð Ø È º º ÖØ Þ Ø Þ Â Þ ÂÙ Ø Ì Ñ Ú Þ Ø Öº Ý Ñ Ø Ý Ì ÓÖ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ ÁÒ ÓÖÑ Ø Ã Ö ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ËÞ ¾¼¼ Ú Þ Ø ÔÖÓ Ö Ñ Þ Ð Ø Ð ÓÞ Þ Ð Ö ÓÞ ÓÒÐ Ø Ñ Ø
Ð Ô Ø Ø Ù ÔÖÓ Ö Ñ Þ Ð Ø Ð Þ Ð Ø È º º ÖØ Þ Ø Þ Â Þ ÂÙ Ø Ì Ñ Ú Þ Ø Öº Ý Ñ Ø Ý Ì ÓÖ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ ÁÒ ÓÖÑ Ø Ã Ö ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ËÞ ¾¼¼ Ú Þ Ø ÔÖÓ Ö Ñ Þ Ð Ø Ð ÓÞ Þ Ð Ö ÓÞ ÓÒÐ Ø Ñ Ø
½µ Þ Ü Ñ Ö ÚÓÒ Ø ÓÞ Ð ÔÚ Ø Ñ Ö Ø Ý Ñ Ø Ñ Ø ÐÑ Ð Ø Ð Ô Ø Ò Ð Ô ÐÚ Å Ò Ò Ñ Ø Ñ Ø ÐÑ Ð Ø Ó ÐÑ ÐÐ Ø Ó Ýò Ø Ñ ÒÝ ÒØ Ó Ø Ðº Þ ÐÑ Ð Ø Ð Ô Ø ÓÖ Ò Ð ÞÒ ÐØ Ó ÐÑ
 Î Ö Þ Ä ÞÐ ÓÑ ØÖ Ü Ñ Ö Ò Þ Ö ÑÓ ÐÐ ÄÌ ÌÌÃ Å Ø Ñ Ø ÁÒØ Þ Ø ÓÑ ØÖ Ì Ò Þ Ù Ô Ø ¾¼½½ ½µ Þ Ü Ñ Ö ÚÓÒ Ø ÓÞ Ð ÔÚ Ø Ñ Ö Ø Ý Ñ Ø Ñ Ø ÐÑ Ð Ø Ð Ô Ø Ò Ð Ô ÐÚ Å Ò Ò Ñ Ø Ñ Ø ÐÑ Ð Ø Ó ÐÑ ÐÐ Ø Ó Ýò Ø Ñ ÒÝ ÒØ Ó Ø Ðº Þ
Î Ö Þ Ä ÞÐ ÓÑ ØÖ Ü Ñ Ö Ò Þ Ö ÑÓ ÐÐ ÄÌ ÌÌÃ Å Ø Ñ Ø ÁÒØ Þ Ø ÓÑ ØÖ Ì Ò Þ Ù Ô Ø ¾¼½½ ½µ Þ Ü Ñ Ö ÚÓÒ Ø ÓÞ Ð ÔÚ Ø Ñ Ö Ø Ý Ñ Ø Ñ Ø ÐÑ Ð Ø Ð Ô Ø Ò Ð Ô ÐÚ Å Ò Ò Ñ Ø Ñ Ø ÐÑ Ð Ø Ó ÐÑ ÐÐ Ø Ó Ýò Ø Ñ ÒÝ ÒØ Ó Ø Ðº Þ
U = I R U = RI. I = [V ]
![U = I R U = RI. I = [V ] U = I R U = RI. I = [V ]](/thumbs/20/418711.jpg) Ä ÃÌÊÇ ÁÆ ÅÁÃ Ý Ò Ö Ñ Ð Þ ØÓ ½º Þ Ý Þ Öò Ö ÒØ Ý Ô ÓÐ Ð Ô Ð ÐºÁÐÝ Ò Þ Ð Ö Ñ Ö ÝØ Ð Ô Ð Ý Ó Ý ÞØ Ð Ú Þ Ø Ð Ö Ò Þ ¹ ÑÔ Ö Ñ Ö ¾¹½ µº Ó Ý ÞØ ÐÝ ØØ ÞÓ ÖØ Ð ÐÐ Ò ÐРغ Þ ÐÚ Ö ÞÓ Ú Þ Ø Ý ÐÐ Ò ÐÐ Ø ÐØ ÒØ ØÒ Ñ ÐÝÑ
Ä ÃÌÊÇ ÁÆ ÅÁÃ Ý Ò Ö Ñ Ð Þ ØÓ ½º Þ Ý Þ Öò Ö ÒØ Ý Ô ÓÐ Ð Ô Ð ÐºÁÐÝ Ò Þ Ð Ö Ñ Ö ÝØ Ð Ô Ð Ý Ó Ý ÞØ Ð Ú Þ Ø Ð Ö Ò Þ ¹ ÑÔ Ö Ñ Ö ¾¹½ µº Ó Ý ÞØ ÐÝ ØØ ÞÓ ÖØ Ð ÐÐ Ò ÐРغ Þ ÐÚ Ö ÞÓ Ú Þ Ø Ý ÐÐ Ò ÐÐ Ø ÐØ ÒØ ØÒ Ñ ÐÝÑ
F(x) α,β = 1. f(x) α,β = α β. = αβα
 Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ Î ÐÐ ÑÓ Ñ ÖÒ ÁÒ ÓÖÑ Ø Ã Ö ËØ Ø ÞØ Ñ Þ Ö Ð ØÐ Ò Ð Þ ØÓ Ú Þ Ð Ø Ö ÌÙ ÓÑ ÒÝÓ Ö ÓÐ ÓÞ Ø Ý Ò ý Ñ Ñ Ý Ò º Ñ º Ù ÃÓÒÞÙÐ Ò Öº Ì Ð Ò Ö ËÞ Ñ Ø ØÙ ÓÑ ÒÝ ÁÒ ÓÖÑ ÐÑ Ð Ø Ì Ò Þ ¾¼¼ Ì ÖØ ÐÓÑ
Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ Î ÐÐ ÑÓ Ñ ÖÒ ÁÒ ÓÖÑ Ø Ã Ö ËØ Ø ÞØ Ñ Þ Ö Ð ØÐ Ò Ð Þ ØÓ Ú Þ Ð Ø Ö ÌÙ ÓÑ ÒÝÓ Ö ÓÐ ÓÞ Ø Ý Ò ý Ñ Ñ Ý Ò º Ñ º Ù ÃÓÒÞÙÐ Ò Öº Ì Ð Ò Ö ËÞ Ñ Ø ØÙ ÓÑ ÒÝ ÁÒ ÓÖÑ ÐÑ Ð Ø Ì Ò Þ ¾¼¼ Ì ÖØ ÐÓÑ
 Ô ØÖ Ð Ø Ö Ð Ð Ñ ÒÞ Ô ÓÐ Ø Ò Ú Þ Ð Ø Ð ÞÒ Ð Ø Ð òö ÐÚ Ø Ð Ó ÞØ ÐÝÓÞ Ò Ó ØÓÖ Þ ÖØ Ø Þ Ä ÞÐ Á ØÚ Ò Ì Ñ Ú Þ Ø Öº Ø Á ØÚ Ò ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ã Ö ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ÈÖÓ º ÒÞ Ö Ò Ö ºËº ÁÒ ÓÖÑ
Ô ØÖ Ð Ø Ö Ð Ð Ñ ÒÞ Ô ÓÐ Ø Ò Ú Þ Ð Ø Ð ÞÒ Ð Ø Ð òö ÐÚ Ø Ð Ó ÞØ ÐÝÓÞ Ò Ó ØÓÖ Þ ÖØ Ø Þ Ä ÞÐ Á ØÚ Ò Ì Ñ Ú Þ Ø Öº Ø Á ØÚ Ò ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ã Ö ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ÈÖÓ º ÒÞ Ö Ò Ö ºËº ÁÒ ÓÖÑ
¾¼½½ Ë Ë Ò ÓÖ ÄÌ Áà ¾ º ¾ º ½º º º Þ Ø ÌýÅÇȹ º¾º½º ¹¼ ¹½¹ÃÅʹ¾¼½¼¹¼¼¼ Ø ÑÓ Ø Ú Þ Ø º
 Ì ÖÚ Þ ÑÞ Ñ Ø ¾¼½½ Ë Ë Ò ÓÖ ÄÌ Áà ¾ º ¾ º ½º º º Þ Ø ÌýÅÇȹ º¾º½º ¹¼ ¹½¹ÃÅʹ¾¼½¼¹¼¼¼ Ø ÑÓ Ø Ú Þ Ø º Ì ÖØ ÓÑ ÝÞ ½º ËÞÓ ØÚ Ö ÞØ ÑÓ ½º½º Î Þ ÑÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º
Ì ÖÚ Þ ÑÞ Ñ Ø ¾¼½½ Ë Ë Ò ÓÖ ÄÌ Áà ¾ º ¾ º ½º º º Þ Ø ÌýÅÇȹ º¾º½º ¹¼ ¹½¹ÃÅʹ¾¼½¼¹¼¼¼ Ø ÑÓ Ø Ú Þ Ø º Ì ÖØ ÓÑ ÝÞ ½º ËÞÓ ØÚ Ö ÞØ ÑÓ ½º½º Î Þ ÑÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º
 ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ã Ö Ã Ø Ñ ÒÞ Ø Ð Ð ÔÔ ÓÐ Ó ËÞ ÓÐ ÓÞ Ø Ã Ö ÐÐ Å Ø Ñ Ø Ëº Ð ÐÑ ÞÓØØ Ñ Ø Ñ Ø Ù Þ Ö ÒÝ Ì Ñ Ú Þ Ø Ã Ö ÐÝ Ì Ñ Ý Ø Ñ ÙÒ ØÙ ÇÔ Ö ÙØ Ø Ì Ò Þ Ù Ô Ø ¾¼½½ ÆÝ Ð Ø ÓÞ Ø Æ Ú
ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ã Ö Ã Ø Ñ ÒÞ Ø Ð Ð ÔÔ ÓÐ Ó ËÞ ÓÐ ÓÞ Ø Ã Ö ÐÐ Å Ø Ñ Ø Ëº Ð ÐÑ ÞÓØØ Ñ Ø Ñ Ø Ù Þ Ö ÒÝ Ì Ñ Ú Þ Ø Ã Ö ÐÝ Ì Ñ Ý Ø Ñ ÙÒ ØÙ ÇÔ Ö ÙØ Ø Ì Ò Þ Ù Ô Ø ¾¼½½ ÆÝ Ð Ø ÓÞ Ø Æ Ú
Szupernóvák. van H. nincs H. I nincs Si. van Si. nincs He. van He IIL IIP. IIn
 ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÌÌÁÃ ÇÔØ ÃÚ ÒØÙÑ Ð ØÖÓÒ Ì Ò Þ ÁÈÄÇÅ ÅÍÆÃ ËÞÙÔ ÖÒ Ú ÐØ ØØ Ð ÙÐÐ ÑÓ Ð Ò Ø òöò ÐÐ Ö Ð ÒÝ Ð Ã Þ Ø ØØ Æ Ý Ò Ö Þ Ù ÅË Þ Ó ÐÐ Ø Ì Ñ Ú Þ Ø Öº Î Ò Â Þ Ý Ø Ñ Ó Ò ËÞ ¾¼½¾ Ì ÖØ ÐÑ Þ Ó Ð Ð ÞÙÔ ÖÒ
ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÌÌÁÃ ÇÔØ ÃÚ ÒØÙÑ Ð ØÖÓÒ Ì Ò Þ ÁÈÄÇÅ ÅÍÆÃ ËÞÙÔ ÖÒ Ú ÐØ ØØ Ð ÙÐÐ ÑÓ Ð Ò Ø òöò ÐÐ Ö Ð ÒÝ Ð Ã Þ Ø ØØ Æ Ý Ò Ö Þ Ù ÅË Þ Ó ÐÐ Ø Ì Ñ Ú Þ Ø Öº Î Ò Â Þ Ý Ø Ñ Ó Ò ËÞ ¾¼½¾ Ì ÖØ ÐÑ Þ Ó Ð Ð ÞÙÔ ÖÒ
Ø Ø Ñ Ð Ò Ø Þ Á Þ Ý Ê Ò Þ Ø Å Ò ÞØ Ö ÙÑ Ú Ð Ñ ÒØ Þ Ñ Ö ÂÓ Ó Å Ý Ö Ã ÞÔÓÒØ Ã Þ Ð Ô ØÚ ÒÝ Ø ÑÓ ØØ ÓÒ Ö Ò Þ ÖÚ Þ È Ý Å Ø ÓÒ Ö Ò Ð Ð Î Ö ¾¼¼ Þ ÖÞ ¾¼¼ Þ Ö
 ÍÊ È Á ÂÇ Ë ÂÇ ÁÄÇ Á ÓÒ Ö Ò Ø ÒÙÐÑ ÒÝÓ Þ ÙÖ Ô ÒØ Ö ØÚ Ò Ú ÓÖ ÙÐ Ò ÒÒ Ô Ö Þ Ö ÞØ ØØ Ô Ý Ñ Ø Ë ÆÌ ÁËÌÎýÆ ÌýÊËÍÄ Ì Þ ÔÓ ØÓÐ ËÞ ÒØ Þ Ã ÒÝÚ Ù Ô Ø ¾¼¼ Ø Ø Ñ Ð Ò Ø Þ Á Þ Ý Ê Ò Þ Ø Å Ò ÞØ Ö ÙÑ Ú Ð Ñ ÒØ Þ Ñ Ö ÂÓ
ÍÊ È Á ÂÇ Ë ÂÇ ÁÄÇ Á ÓÒ Ö Ò Ø ÒÙÐÑ ÒÝÓ Þ ÙÖ Ô ÒØ Ö ØÚ Ò Ú ÓÖ ÙÐ Ò ÒÒ Ô Ö Þ Ö ÞØ ØØ Ô Ý Ñ Ø Ë ÆÌ ÁËÌÎýÆ ÌýÊËÍÄ Ì Þ ÔÓ ØÓÐ ËÞ ÒØ Þ Ã ÒÝÚ Ù Ô Ø ¾¼¼ Ø Ø Ñ Ð Ò Ø Þ Á Þ Ý Ê Ò Þ Ø Å Ò ÞØ Ö ÙÑ Ú Ð Ñ ÒØ Þ Ñ Ö ÂÓ
ρ(ω) 2 ( x C i x i dω, L = m 0 i 2 ω 2 x 2 i )dω X
 º ÇÊÌÎ ÊÍ ÇÄ Á Áà Á ÈÊÇ Ä Å Å ÇÄ Î ÊË Æ Ä Ì Á ¾¼½ º Ó Ø Ö ¾ ÒÓÚ Ñ Ö º ½º Ö Ò ÓÖÖ ÐÓÑ ÙØ Ò Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ö Ñ ÒÝ Ø Þ Ð Ö Ò Ð ÐÑ ÞØ Ò Ô Þ Öò Ø ØØ º Þ Ñ Þ Ö Ò Þ ÞÐ ØÖ ÓÐ Ö Ñ Ø ÖÚ Þ ÓÖ Þ ÑÔÓÒØ ÚÓÐغ Ä Ý
º ÇÊÌÎ ÊÍ ÇÄ Á Áà Á ÈÊÇ Ä Å Å ÇÄ Î ÊË Æ Ä Ì Á ¾¼½ º Ó Ø Ö ¾ ÒÓÚ Ñ Ö º ½º Ö Ò ÓÖÖ ÐÓÑ ÙØ Ò Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ö Ñ ÒÝ Ø Þ Ð Ö Ò Ð ÐÑ ÞØ Ò Ô Þ Öò Ø ØØ º Þ Ñ Þ Ö Ò Þ ÞÐ ØÖ ÓÐ Ö Ñ Ø ÖÚ Þ ÓÖ Þ ÑÔÓÒØ ÚÓÐغ Ä Ý
