7. Térbeli feladatok megoldása izoparametrikus elemekkel
|
|
|
- Magda Mészáros
- 6 évvel ezelőtt
- Látták:
Átírás
1 7 ébl fladatok mgoldása zoaamtkus lmkkl ébl fladat: A tst (alkatész) alakjáa (gomtájáa) és thlésé nézv nncs smmln kolátozó fltétlzés 7 Összfoglaló smétlés Elmozdulásmző: u ux v wz Elmozdulás koodnáták: u ux z v vx z w wx z Alakváltozás állaot / alakváltozás tnzo: Ax z Fszültség állaot / fszültség tnzo: F x z A ugalmasságtan gnltk: - a knmatka gnltk: A u u - az gnsúl gnltk: F 0 A - a Hook tövén: I F GA - a mfltétlk: - knmatka: A u u 0 u x x z zx z z x x z zx z z - dnamka: A F n 0 7 Hxaéd lm lkézés alakfüggvénk Lkézés: x h x h z h z =0 az lm csomóontjanak száma Alakfüggvénk: - a saokontokban h - a flzőontokban h 4 00
2 Dgnácó: a hxaéd lmbn gs oldalak hosszúságát zéusa csökkntjük csomóontok snk gb 73 Pntaéd lm lkézés alakfüggvénk Alakfüggvénk: Az alakfüggvénk a ntaéd lm ábán köl jlölt csomóontjaban változnak mg h h h h h h h h h h h 4 6 h h h h h h h h h h h h h 7 h h h h h h h h h h h h h h 6 h h 0 a hxaéd lm alakfüggvén 5 h0 Kokcós alakfüggvénk: h3 6 h3 6 ovább dgnácó: a oldalflült zéusa csökkntés az 6 csomóontok gbsnk 74 taéd lm lkézésk alakfüggvénk h Alakfüggvénk: Az alakfüggvénk a ttaéd lm ábán köl jlölt csomóontjaban változnak mg 0
3 6 6 h h h h h h h h h h h h 05 h 3 h h h h h h h h h h h h 05 h h h h h h h h h h h 0 a hxaéd lm alakfüggvén Kokcós alakfüggvénk: h 6 h 6 h 6 h3 6 Dgnácós ljáás lőn: a hxaéd lm lvzttt összfüggésk alkalmazhatók Különbség a háom lm között: Hxaéd : 0 - Más a csomóontok száma: Pntaéd : 5 taéd : 0 - Mások az alakfüggvénk: h( ) h ( ) 75 Az lmk mvség mátxa Elm gomtája lht: hxaéd ntaéd ttaéd Az lm csomóont lmozdulásvktoa: Az lmozdulásmző közlítés: Az lmozdulásmző közlítés mátx alakban: u v w u h u v h v w h w Az lmozdulásmző koodnátá: u Az aoxmácós mátx: Az alakváltozás vkto: 3 0 hxaéd stén = 5 ntaéd stén 0 ttaéd stén u A u v w h 0 0 h 0 0 h 0 0 A 0 h 0 0 h 0 0 h h 0 0 h 0 0 h x z z 0
4 Közlítés mátx alakban: D A B A dválás utasítások észltsn kíva: 0 0 x u z D u v 0 x w 0 z 0 z x Az alakváltozások és a csomóont lmozdulások között kacsolatot mgadó mátx: b 0 0 b b 0 0 b b 0 0 b B b b 0 b b 0 0 b3 b 0 b3 b b 3 0 b b3 0 b h h h h b R R R3 x h h h h A mátx lmnk kszámítása: b R R R3 h h h h b3 R3 R3 R33 z R j - a lkézés nvz Jakob mátxának lm Az nvz Jakob mátx: A Jakob mátx kszámítása: 3 3 R R R3 J R R R 3 R 3 R3 R 33 x z h h h x z x z h h h J x z x z h h h x z adj J j Az nvz Jacob mátx: J J J A fszültség vkto és közlítés: j dt J 03
5 x z z C Az anagállandók mátxa: C c c4 c5 c4 c c6 c5 c6 c c7 c c9 Izotó anag stén (Hook tövén) az anagállandók mátxának lm: c c c E c c c E c c c G E Ototó anag stén ha x z anag főán: c c c z z zx x 3 EEz ExEz ExE c c c x z zx zx x z z zx EEz EEz ExEz x z z zx x z ExEEz / c 7 Gz 9 c G c G Az lm mvség mátxa az x z koodnáta-ndszbn: 6060 hxaéd stén A mvség mátx mét: 4545 ntaéd stén 3030 ttaéd stén Az ntgálás lvégzéséhz áttéés a változatoka: K B C B dt J ddd K B C B dv V k ddd Az ntgandusz blokkoka bontása: k k k j k k k k k k k j j Az lm mvség mátxa szmmtkus: k k j j Az gs blokkok általában nm szmmtkusak: kj k j Az ntgandusz ttszőlgs blokkjának kszámítása zotó anag stén: c c c d c c c d c c c d Jlölés: a mátx ttszőlgs blokkja: (kvétl =j) k j 33 04
6 j j j j k b db j b d3b j dt J j k b db3 j b3 d3b j dt J j 3 k b db j b d3b j dt J j j 3 j j j k b db3 j b3 d3b j dt J j k b d b b d b b d b dt J k b d b b d b b d b dt J 3 k b3 db j b d3b3 j dt J j 3 k b3 db j b d3b3 j dt J j j 3 j 3 j j k b d b b d b b d b dt J 33 M M M A mvség mátx numkus kszámítása: K k ddd ww jwk k j k M a Gauss-fél ntgácós ontok száma j k a Gauss ontok hlkoodnátá w wjw k a Gauss-fél ntgácós súlténzők k j Pontosság: az M talontú Gauss-fél kvadatúa az M -dfokú olnom-ntganduszg bzáólag ontos étékt szolgáltat 76 Az lmk téfogat őkből számazó csomóont thlésvktoa az z koodnátandszbn f A x z x z dv V 33 3 ( x z ) - a téfogat thlés sűűség smt thlés V az lm téfogata Pl: a z tngl köül fogásból számazó thlés stén: ahol - a tömgsűűség - szögsbsség Áttéés a változóka: x z x 0 dt f A J d d d d d d Az ntgandusz blokkoka bontása: Az ntgandusz jlű blokkja: J h x dt 0 M M M A thlésvkto numkus kszámítása: f dddww jwk j k k j 05
7 77 Az lmk flült őkből számazó csomóont thlésvktoa az z koodnátandszbn ahol f Aˆ x zda A A - az lm thlt oldalflült ( x z ) - a flült thlés sűűségvktoa ˆ A - a thlt oldalflült lokalzált aoxmácós mátx Fltétlzés: a flült thlés az lm flültén működk Az lmhz kötött lokáls csomóont soszámozás A flülthz kötött lokáls csomóont soszámozás Az lm flülténk aaméts gnlt: ˆ x h x ˆ h z hˆ z A flült lokalzált alakfüggvénk / aoxmácós függvénk: hˆ h hˆ h Az lmozdulásmző közlítés a flültén: ˆ ˆ ˆ hˆ h h h 6 6 hˆ h h h hˆ h h h 4 6 ˆ u h u ˆ v h v w hˆ w Fltétlzés: a flült thlés smt nomás x z x z - nomás loszlás A flült nomáls lőállítása: - a flültn vtt göb vonalú koodnáták - matmatka szmontból aamétk A flült ttszőlgs P ontjának hlvktoa: x z x z x z n n x z - a tstből kflé mutató nomáls gségvkto 06
8 A flült ttszőlgs P ontjában a koodnátavonalak éntővktoa: a a a a mt nm ívhossz Az éntővktook kszámítása: hˆ hˆ hˆ hˆ hˆ hˆ a x z a x z x z x z Jlölés: a a xx a a zz a axx a azz A vktoáls flültlm: dt da a a J d d a a z a za x a za x a xa z a xa a a x z dt J dd A skalás flültlm: da da A flült nomáls gségvktoa: da n nda da da A flült nomásból számazó csomóont thlésvkto: f ˆ A a a dt J dd dd A flült lokalzált aoxmácós mátx hˆ 0 0 hˆ 0 0 hˆ 0 0 ˆ 0 ˆ 0 0 ˆ 0 0 ˆ 0 A h h h 0 0 hˆ ˆ ˆ 0 0 h 0 0 h Az ntgandusz blokkolása: Az jlű blokk: ˆ a a z a za h a zax a xaz dt J a xa a a x mét: (4 3) M M A thlésvkto numkus kszámítása: f ddww j j j Mgjgzésk: - A flült thlésből számazó csomóont thlésvkto mét csak (4x) vag (x) attól függőn hog négszög vag háomszög oldalól van szó Ezkt a zéustól különböző koodnátákat kll az lm (3x)-s csomóont thlésvktoának mgfllő hl bakn - A flült nomáls ánát mndg a flülthz kötött lokáls csomóont soszámozás hatáozza mg (jobbkéz szabál!) 07
9 7 Flült ugalmas ágazás fglmbvétl Modllzés: ugalmas ágazással lht fglmb vnn más ugalmas tstknk a vzsgált tst gakoolt hatását Rugalmas ágazás: a tst nézv olan flült thlést jlnt amlnk sűűség / nagsága aános a flült ontjanak lmozdulásával Fltétlzés: - az ágazó közg lnásan ugalmas - a vzsgált tst és az ágazó közg között kétoldalú kacsolat van (nm lhtségs lválás) - az ágazásnál flléő ő (flült thlés) és lmozdulás között homogén lnás függvénkacsolat van A ugalmas ágazásból számazó flült thlés: x C u x cx 0 0 A ugóállandók mátxa: C 0 c c z cx c c z - a flült P ontjához kacsolódó és z ánú ugók ugóállandó A otncáls nga a ugalmas ágazásnál flléő ők munkájával bővül: u A A - az lm ugalmasan ágazott flült Aoxmácó után: u da u C u da Aˆ C ˆ A da A A A da K A x z C A x z da A Az lm ugalmas ágazásból számazó mvség mátxa: ˆ ˆ Fltétlzés: a ugalmas ágazás az lm oldalflültén működk A flült gnlt és az lmozdulásmző közlítés uganaz mnt a flült thlés dukcójánál: Az lmozdulásmző közlítés a flültén: ˆ u h u ˆ v h v w hˆ w Áttéés a változóka: ˆ ˆ K A C A da dt Az lm flült: z z z x z x x x Jlölés: da a a a a a a a a a a a a J dd K k dt J d d mét: (4x4) 0
10 Az ntgandusz blokkolása: k k k k k k k k k k Az ntgandusz ttszőlgs blokkja: k j hˆ ˆ cxh 0 0 j 0 hˆ ˆ chj hˆ ˆ czh j 79 Pmfltétlk fglmbvétl tébl fladatoknál a) Eg csomóont mgfogása: gömbcsuklós mgtámasztás A mgfogott ontban koncntált támasztóő lé fl ébl faladatoknál a koncntált thlés fszültségkoncntácót okoz az ő támadásontjának könztébn A koncntált thlés tébl faladatoknál nm alsztkus Koncntált ő gömbcsukló lhtőlg küln kll b) A tst g flülténk bfogása / bfalazása (a flült mndn csomóontjának mgfogása): Példa: bfogott lmz számítása tébl lmkkl A ABCD flültt mvn mgfogjuk u x 0 v x 0 w x 0 A flültn / laon lévő ontok nm mozdulhatnak l A mv flültn lvő ttszőlgs P ontban a mchanka állaotok: u 0 u u u 0 d 0 x z v 0 v v v 0 d 0 x z w 0 w w w 0 d 0 x z A mv flültn lvő ttszőlgs P ontban az alakváltozás állaot: 09
11 u u v x 0 0 x x v u w 0 0 z x w u w z 0 z 0 z z x A mv flültn lvő ttszőlgs P ontban a fszültség állaot: AI F GA I AI z 0 0 A 0 0 z zx z x G z G z x z z G z A mv flültn lvő ttszőlgs P ontban a fszültség tnzo: Lgn a P ont az AB gnsn! Dnamka mfltétl az alsó flültn: 0 0 z 0 G G x 0 F 0 z zx z z 0 Ez llntmondásban van a knmatka lőíásokból kaott dménkkl 0 z A flült bfalazásának knmatka lőíása a flült szélén llntmondása vztnk és a fszültség koodnáták között kacsolat sm könnn étlmzhtők ébl fladatoknál zét a flült bfalazását lhtőlg küln kll Rálsabb modllzés: a knmatka mfltétlk hltt ugalmas ágazás alkalmazása z 0
SIKALAKVÁLTOZÁSI FELADAT MEGOLDÁSA VÉGESELEM-MÓDSZERREL
 SIKALAKVÁLTOZÁSI FELADAT MEGOLDÁSA VÉGESELEM-MÓDSZERREL ADOTT: Az ábrán látható db végslmből álló tartószrkzt gomtriája, mgfogása és trhlés. A négyzt alakú síkalakváltozási végslmk mért 0 X 0 mm. p Anyagjllmzők:
SIKALAKVÁLTOZÁSI FELADAT MEGOLDÁSA VÉGESELEM-MÓDSZERREL ADOTT: Az ábrán látható db végslmből álló tartószrkzt gomtriája, mgfogása és trhlés. A négyzt alakú síkalakváltozási végslmk mért 0 X 0 mm. p Anyagjllmzők:
3.5. Rácsos szerkezet vizsgálata húzott-nyomott rúdelemekkel:
 SZÉCHENYI ISTÁN EGYETEM AKAMAZOTT MECHANIKA TANSZÉK 7. MECHANIKA-ÉGESEEM MÓDSZER EŐADÁS (kidolgozta: Szül ronika, g. ts.) II. lőadás.. Rácsos szrkzt vizsgálata húzott-nomott rúdlmkkl: F x m m. ábra: Rácsos
SZÉCHENYI ISTÁN EGYETEM AKAMAZOTT MECHANIKA TANSZÉK 7. MECHANIKA-ÉGESEEM MÓDSZER EŐADÁS (kidolgozta: Szül ronika, g. ts.) II. lőadás.. Rácsos szrkzt vizsgálata húzott-nomott rúdlmkkl: F x m m. ábra: Rácsos
3. Lokális approximáció elve, végeselem diszkretizáció egydimenziós feladatra
 SZÉCHENYI ISTVÁN EGYETEM AAMAZOTT MECHANIA TANSZÉ 5. MECHANIA-VÉGESEEM MÓDSZER EŐADÁS (kidolgozta: Szül Vronika g. ts.) V. lőadás. okális aroimáció lv végslm diszkrtizáció gdimnziós fladatra Amint azt
SZÉCHENYI ISTVÁN EGYETEM AAMAZOTT MECHANIA TANSZÉ 5. MECHANIA-VÉGESEEM MÓDSZER EŐADÁS (kidolgozta: Szül Vronika g. ts.) V. lőadás. okális aroimáció lv végslm diszkrtizáció gdimnziós fladatra Amint azt
5. modul: Szilárdságtani Állapotok. 5.3. lecke: A feszültségi állapot
 5 modul: Silárdságtai Állapotok 53 lck: A fsültségi állapot A lck célja: A taaag flhasálója mgismrj a fsültségi állapot fogalmait valamit mg tudja határoi g lmi pot körték fsültségi állapotát Kövtlmék:
5 modul: Silárdságtai Állapotok 53 lck: A fsültségi állapot A lck célja: A taaag flhasálója mgismrj a fsültségi állapot fogalmait valamit mg tudja határoi g lmi pot körték fsültségi állapotát Kövtlmék:
TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI Előadás jegyzet Dr. Goda Tibor. 3. Lineáris háromszög elem
 TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI Előadás jgyzt Dr. Goda Tibor 3. Lináris háromszög lm - A végslms mgoldás olyan approximációs függvénykn alapul, amlyk az gys lmk vislkdését írják l (lmozdulás függvény
TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI Előadás jgyzt Dr. Goda Tibor 3. Lináris háromszög lm - A végslms mgoldás olyan approximációs függvénykn alapul, amlyk az gys lmk vislkdését írják l (lmozdulás függvény
8. MECHANIKA-SZILÁRDSÁGTAN GYAKORLAT (kidolgozta: dr. Nagy Zoltán egy. adjunktus; Bojtár Gergely egy. Ts.; Tarnai Gábor mérnöktanár.
 8 MECHANIKA-SZILÁRDSÁGTAN GYAKORLAT (kidolgota: dr Nag Zoltán g adjunktus; Bojtár Grgl g Ts; Tarnai Gábor mérnöktanár) 8 Fsültségi állapot smlélttés Adott: Ismrt g silárd tst pontjában a fsültségi állapot
8 MECHANIKA-SZILÁRDSÁGTAN GYAKORLAT (kidolgota: dr Nag Zoltán g adjunktus; Bojtár Grgl g Ts; Tarnai Gábor mérnöktanár) 8 Fsültségi állapot smlélttés Adott: Ismrt g silárd tst pontjában a fsültségi állapot
Robotok irányítása. főiskolai jegyzet javított változat. írta: Tukora Balázs
 Robotok ránítása főskola jgt javított váltoat írta: Tukora Balás Pécs, 4 . Bvtés Jln jgt a Pécs Tudomángtm Pollack Mhál Műsak Főskola Karán foló Műsak Informatka képés Robotránítás rndsrk I-II. tantárgaho
Robotok ránítása főskola jgt javított váltoat írta: Tukora Balás Pécs, 4 . Bvtés Jln jgt a Pécs Tudomángtm Pollack Mhál Műsak Főskola Karán foló Műsak Informatka képés Robotránítás rndsrk I-II. tantárgaho
4. MECHANIKA STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnök tanár)
 SZÉCHENYI ISTVÁN EGYETE ALKALAZTT ECHANIKA TANSZÉK 4. ECHANIKA STATIKA GYAKRLAT (kdolgozta: Trsz Pétr, g. ts.; Tarna Gábor, mérnök tanár) Erő, nomaték, rőrndszr rdő, rőrndszrk gnértékűség 4.. Példa: z
SZÉCHENYI ISTVÁN EGYETE ALKALAZTT ECHANIKA TANSZÉK 4. ECHANIKA STATIKA GYAKRLAT (kdolgozta: Trsz Pétr, g. ts.; Tarna Gábor, mérnök tanár) Erő, nomaték, rőrndszr rdő, rőrndszrk gnértékűség 4.. Példa: z
A projekt keretében elkészült tananyagok:
 VÉGESEEM-MÓDSZER A pojt tébn lésült tananago: Anagtchnológá Matals tchnolog Anagtdomán Áamlástchna gép CAD tanönv CAD Boo CAD/CAM/CAE ltons példatá CAM tanönv Mééstchna Ménö optmalácó Engnng Optmaton Végslm-analís
VÉGESEEM-MÓDSZER A pojt tébn lésült tananago: Anagtchnológá Matals tchnolog Anagtdomán Áamlástchna gép CAD tanönv CAD Boo CAD/CAM/CAE ltons példatá CAM tanönv Mééstchna Ménö optmalácó Engnng Optmaton Végslm-analís
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 .5.. _. tés Végslm-mósr Végslm-mósr. A gomtra tartomán (srkt) flostása (égs)lmkr.. okáls koornáta-rnsr flétl kacsolat a lokáls és globáls koornátarnsrk köött.. A bás függénk flétl fnálása lmnként.. A mrség
.5.. _. tés Végslm-mósr Végslm-mósr. A gomtra tartomán (srkt) flostása (égs)lmkr.. okáls koornáta-rnsr flétl kacsolat a lokáls és globáls koornátarnsrk köött.. A bás függénk flétl fnálása lmnként.. A mrség
3. MECHANIKA STATIKA GYAKORLAT Kidolgozta: Triesz Péter egy. ts. Három erő egyensúlya
 SZÉHENYI ISTVÁN EGYETEM GÉPSZERKEZETTN ÉS MEHNIK TNSZÉK 3 MEHNIK STTIK GYKORLT Kdolgozt: Tsz Pét gy ts Háom ő gynsúly 3 Péld: dott gy mlőszkzt mét és thlés: m b 5 m c 5 m 0 kn ldt: y c Htáozz mg z és támsztóőkt
SZÉHENYI ISTVÁN EGYETEM GÉPSZERKEZETTN ÉS MEHNIK TNSZÉK 3 MEHNIK STTIK GYKORLT Kdolgozt: Tsz Pét gy ts Háom ő gynsúly 3 Péld: dott gy mlőszkzt mét és thlés: m b 5 m c 5 m 0 kn ldt: y c Htáozz mg z és támsztóőkt
Szerkezetek numerikus modellezése az építőmérnöki gyakorlatban
 Szrkztk numrikus modllzés az éítőmérnöki gakorlatban intéztigazgató hltts, tanszékvztő, őiskolai docns a Magar Éítész Kamara tagja, a Magar Mérnöki Kamara tagja a ib Nmztközi Btonszövtség Magar Tagozatának
Szrkztk numrikus modllzés az éítőmérnöki gakorlatban intéztigazgató hltts, tanszékvztő, őiskolai docns a Magar Éítész Kamara tagja, a Magar Mérnöki Kamara tagja a ib Nmztközi Btonszövtség Magar Tagozatának
12. Laboratóriumi gyakorlat MÉRÉSEK FELDOLGOZÁSA
 . Laoratórum gakorlat MÉRÉSK FLDOLGOZÁSA. A gakorlat célja Lgks égztk LS) módszré alapuló polom-llsztés proléma mutatása és a módszr alkalmazása mérés rdmék fldolgozására, lltv érzéklő karaktrsztkák aaltkus
. Laoratórum gakorlat MÉRÉSK FLDOLGOZÁSA. A gakorlat célja Lgks égztk LS) módszré alapuló polom-llsztés proléma mutatása és a módszr alkalmazása mérés rdmék fldolgozására, lltv érzéklő karaktrsztkák aaltkus
Széchenyi István Egyetem. Alkalmazott Mechanika Tanszék
 Széchnyi István Egytm Alkalmazott Mchanika Tanszék Végslm analízis Elmélti kérdésk gytmi mstrképzésbn (MSc) résztvv járm mérnöki, mchatronikai mérnök és logisztikai mérnök szakos hallgatók számára 0. októbr
Széchnyi István Egytm Alkalmazott Mchanika Tanszék Végslm analízis Elmélti kérdésk gytmi mstrképzésbn (MSc) résztvv járm mérnöki, mchatronikai mérnök és logisztikai mérnök szakos hallgatók számára 0. októbr
5. MECHANIKA STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnöktanár)
 SZÉCHENYI ISTVÁN EGYETE ALKALAZOTT ECHANIKA TANSZÉK. ECHANIKA STATIKA GYAKORLAT (kidolgozta: Trisz Pétr, g. ts.; Tarnai Gábor, mérnöktanár) Síkbli rőrndszr rdő vktorkttős, vonal mntén mgoszló rőrndszrk..
SZÉCHENYI ISTVÁN EGYETE ALKALAZOTT ECHANIKA TANSZÉK. ECHANIKA STATIKA GYAKORLAT (kidolgozta: Trisz Pétr, g. ts.; Tarnai Gábor, mérnöktanár) Síkbli rőrndszr rdő vktorkttős, vonal mntén mgoszló rőrndszrk..
6. A végeselem közelítés pontosságának javítása Fokszám növelés (p-verziós elemek)
 6 A végslm közlítés pontosságánk jvítás Fokszám növlés (p-vrzós lmk) A végslm közlítés pontosság jvíthtó: - végslm hálózt sűrűségénk növlésévl több lm, több csomópont, szbdságfok növlés (hvrzó, h-konvrgnc)
6 A végslm közlítés pontosságánk jvítás Fokszám növlés (p-vrzós lmk) A végslm közlítés pontosság jvíthtó: - végslm hálózt sűrűségénk növlésévl több lm, több csomópont, szbdságfok növlés (hvrzó, h-konvrgnc)
A végeselem programrendszer általános felépítése (ismétlés)
 SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK 1. MECHANIKA-VÉGESELEM MÓDSZER ELŐADÁS (kdolgozta: Szüle Veronka eg. ts.) IX. előadás A végeselem rogramrendszer általános feléítése (smétlés) A végeselem
SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK 1. MECHANIKA-VÉGESELEM MÓDSZER ELŐADÁS (kdolgozta: Szüle Veronka eg. ts.) IX. előadás A végeselem rogramrendszer általános feléítése (smétlés) A végeselem
(2) A d(x) = 2x + 2 függvénynek van véges határértéke az x0 = 1 helyen, így a differenciálhányados: lim2x
 DIFFERENCIÁLSZÁMÍTÁS MINTAPÉLDÁK.. Példa. Határozzuk mg az f = függvénnk az = hlhz tartozó diffrnciahánados függvénét, majd vizsgáljuk mg, hog f diffrnciálható- az -ban adjuk mg az = hlhz tartozó diffrnciálhánadost.
DIFFERENCIÁLSZÁMÍTÁS MINTAPÉLDÁK.. Példa. Határozzuk mg az f = függvénnk az = hlhz tartozó diffrnciahánados függvénét, majd vizsgáljuk mg, hog f diffrnciálható- az -ban adjuk mg az = hlhz tartozó diffrnciálhánadost.
I nyílt intervallum, ( ) egyenletet közönséges (elsõrendû explicit) differenciálegyenletnek nevezzük. Az
 8 Közöségs diffriálgltk umrikus mgoldása 8 Dfiíió g Ω IR tartomá IR I ílt itrvallum f : I Ω IR foltoos függvé Az : I IR diffriálató függvékr voatkozó f ( ( I gltt közöségs (lsõrdû pliit diffriálgltk vzzük
8 Közöségs diffriálgltk umrikus mgoldása 8 Dfiíió g Ω IR tartomá IR I ílt itrvallum f : I Ω IR foltoos függvé Az : I IR diffriálató függvékr voatkozó f ( ( I gltt közöségs (lsõrdû pliit diffriálgltk vzzük
FORGÓRÉSZ DINAMIKUS KIEGYENSÚLYOZÁSA I. Laboratóriumi gyakorlat elméleti útmutató
 ZÉCHENYI ITVÁN EGYETEM MŐZKI TUDOMÁNYI KR LKLMZOTT MECHNIK TNZÉK 1. tög-kgnsúlozatlanság FORGÓRÉZ DINMIKU KIEGYENÚLYOZÁ I. Laoratóru gakorlat lélt útutató gépk rzgésénk okozóa sok stn a rndzés forgórészénk
ZÉCHENYI ITVÁN EGYETEM MŐZKI TUDOMÁNYI KR LKLMZOTT MECHNIK TNZÉK 1. tög-kgnsúlozatlanság FORGÓRÉZ DINMIKU KIEGYENÚLYOZÁ I. Laoratóru gakorlat lélt útutató gépk rzgésénk okozóa sok stn a rndzés forgórészénk
A végeselemes modellezés kontinuummechanikai alapjai
 Foglalkoztatásoltka és Munkaügy Mnsztérum Humánrőforrás-fjlsztés Oratív Program Dr. Páczlt István Dr. Nándor Frgys - Dr. Sárköz László - Dr. Szabó Tamás - Dr. Baksa Attla - Dluh Kornél A végslms modllzés
Foglalkoztatásoltka és Munkaügy Mnsztérum Humánrőforrás-fjlsztés Oratív Program Dr. Páczlt István Dr. Nándor Frgys - Dr. Sárköz László - Dr. Szabó Tamás - Dr. Baksa Attla - Dluh Kornél A végslms modllzés
III. Differenciálszámítás
 III Dinciálszámítás A inciálszámítás számnka lsősoban aa aló hog mgállapítsk hogan áltoznak a kémiában nag számban lőoló többáltozós üggénk A inciálszámítás mgaja a áltozás sbsségét báml kiszmlt pontban
III Dinciálszámítás A inciálszámítás számnka lsősoban aa aló hog mgállapítsk hogan áltoznak a kémiában nag számban lőoló többáltozós üggénk A inciálszámítás mgaja a áltozás sbsségét báml kiszmlt pontban
Bojtár-Gáspár: A végeselemmódszer matematikai alapjai
 Bojtár Imr Gáspár Zsolt A végslmmódszr matmatka alapja Elktronkusan ltölthtő lőadásvázlat építőmérnök hallgatók számára. http://www.pto.bm.hu/m/htdocs/oktatas/oktatas.php Kadó: BME Tartószrkztk Mchankája
Bojtár Imr Gáspár Zsolt A végslmmódszr matmatka alapja Elktronkusan ltölthtő lőadásvázlat építőmérnök hallgatók számára. http://www.pto.bm.hu/m/htdocs/oktatas/oktatas.php Kadó: BME Tartószrkztk Mchankája
Mezőszimuláció végeselem-módszerrel házi feladat HANGSZÓRÓ LENGŐTEKERCSÉRE HATÓ ERŐ SZÁMÍTÁSA
 Mősimuláció végslm-módsl hái fladat HNGSZÓRÓ LENGŐTEKERCSÉRE HTÓ ERŐ SZÁMÍTÁS Késíttt: Gaamvölgyi Zsolt, 2007 visgált nds ábán látható fogássimmtikus nds komponnsi a kövtkők: állandómágns gyűű fémlmk tkcs
Mősimuláció végslm-módsl hái fladat HNGSZÓRÓ LENGŐTEKERCSÉRE HTÓ ERŐ SZÁMÍTÁS Késíttt: Gaamvölgyi Zsolt, 2007 visgált nds ábán látható fogássimmtikus nds komponnsi a kövtkők: állandómágns gyűű fémlmk tkcs
Feladatok megoldással
 Fladatok mgoldással. sztmbr 6.. Halmazrdszrk. Igazoljuk! A \ B A r (A r B) (A [ B) r ((A r B) [ (B r A)) Mgoldás. A r (A r B) A \ A \ B A \ A [ B A \ A [ (A \ B) A \ B (A [ B) r ((A r B) [ (B r A)) (A
Fladatok mgoldással. sztmbr 6.. Halmazrdszrk. Igazoljuk! A \ B A r (A r B) (A [ B) r ((A r B) [ (B r A)) Mgoldás. A r (A r B) A \ A \ B A \ A [ B A \ A [ (A \ B) A \ B (A [ B) r ((A r B) [ (B r A)) (A
6. Határozatlan integrál
 . Határozatlan intgrál.. Alkalmazza a hatványfüggvény intgrálására vonatkozó szabályt! d... d... d... d 8...... d... d... d..8. d..9. d..0. d... d... d 8... d... 8... d...... d..8...9. d..0. d d 8 d d..
. Határozatlan intgrál.. Alkalmazza a hatványfüggvény intgrálására vonatkozó szabályt! d... d... d... d 8...... d... d... d..8. d..9. d..0. d... d... d 8... d... 8... d...... d..8...9. d..0. d d 8 d d..
Széchenyi István Egyetem. Alkalmazott Mechanika Tanszék
 Széchnyi István Egytm Alkalmazott Mchanika Tanszék Végslm analízis Elmélti kérdésk gytmi mstrképzésbn MSc) résztvv járm mérnöki, mchatronikai mérnök és logisztikai mérnök szakos hallgatók számára. Mit
Széchnyi István Egytm Alkalmazott Mchanika Tanszék Végslm analízis Elmélti kérdésk gytmi mstrképzésbn MSc) résztvv járm mérnöki, mchatronikai mérnök és logisztikai mérnök szakos hallgatók számára. Mit
Végeselem analízis (óravázlat)
 Végslm analízis óravázlat Készíttt: Dr Pr Balázs Széchnyi István Egytm Alkalmazott Mchanika Tanszék dcmbr 8 Copyright Dr Pr Balázs Mindn jog fnntartva Ez a dokumntum szabadon másolható és trjsztht Módosítása
Végslm analízis óravázlat Készíttt: Dr Pr Balázs Széchnyi István Egytm Alkalmazott Mchanika Tanszék dcmbr 8 Copyright Dr Pr Balázs Mindn jog fnntartva Ez a dokumntum szabadon másolható és trjsztht Módosítása
1. ábra A rádiócsatorna E négypólus csillapítása a szakaszcsillapítás, melynek definíciója a következő: (1)
 Az antnna Adó- és vvőantnna Az antnna lktomágnss hullámok kisugázásáa és vétlé szolgáló szköz. A ádióndszkbn btöltött szp alapján az antnna a tápvonal és a szabad té közötti tanszfomáto, mly a tápvonalon
Az antnna Adó- és vvőantnna Az antnna lktomágnss hullámok kisugázásáa és vétlé szolgáló szköz. A ádióndszkbn btöltött szp alapján az antnna a tápvonal és a szabad té közötti tanszfomáto, mly a tápvonalon
4. Izoparametrikus elemcsalád
 SZÉCHENYI ISTVÁN EGYETEM AKAMAZOTT MECHANIKA TANSZÉK 8. MECHANIKA-VÉGESEEM MÓDSZER EŐADÁS (kidolgozta: Szül Vronika, g. ts.) VIII. lőadás 4. Izoparamtriks lmcsalád A krskdlmi szoftvrkbn lggakrabban ún.
SZÉCHENYI ISTVÁN EGYETEM AKAMAZOTT MECHANIKA TANSZÉK 8. MECHANIKA-VÉGESEEM MÓDSZER EŐADÁS (kidolgozta: Szül Vronika, g. ts.) VIII. lőadás 4. Izoparamtriks lmcsalád A krskdlmi szoftvrkbn lggakrabban ún.
FIZIKA BSc, III. évfolyam / 1. félév Optika előadásjegyzet POLARIZÁCIÓ. Dr. Barócsi Attila, Dr. Erdei Gábor,
 FIZIK BSc III. évfolm /. félév Opk lődásjg POLRIZÁCIÓ D. Bócs l D. d Gáo 7-9-8 jánlo skodlom: Kln-Fuk: Rch P.: Slh-Tch: Polácó: Opcs Bvés modn opká Fundmnls of Phooncs Oln M hullámo nvünk polálnk mln éősségvko
FIZIK BSc III. évfolm /. félév Opk lődásjg POLRIZÁCIÓ D. Bócs l D. d Gáo 7-9-8 jánlo skodlom: Kln-Fuk: Rch P.: Slh-Tch: Polácó: Opcs Bvés modn opká Fundmnls of Phooncs Oln M hullámo nvünk polálnk mln éősségvko
A Coulomb-törvény : ahol, = coulomb = 1C. = a vákuum permittivitása (dielektromos álladója) k 9 10 F Q. elektromos térerősség : ponttöltés tere :
 Villamosságtan A Coulomb-tövény : F QQ 4 ahol, Q = coulomb = C = a vákuum pemittivitása (dielektomos álladója) 4 9 k 9 elektomos téeősség : E F Q ponttöltés tee : E Q 4 Az elektosztatika I. alaptövénye
Villamosságtan A Coulomb-tövény : F QQ 4 ahol, Q = coulomb = C = a vákuum pemittivitása (dielektomos álladója) 4 9 k 9 elektomos téeősség : E F Q ponttöltés tee : E Q 4 Az elektosztatika I. alaptövénye
3. Lokális approximáció elve, végeselem diszkretizáció egydimenziós feladatra
 SZÉCHENYI ISÁN EGYEEM AAMAZO MECHANIA ANSZÉ 6. MECHANIA-ÉGESEEM MÓDSZER EŐADÁS (kidolgozta: Szüle eronika, eg. ts.) I. előadás. okális aroimáció elve, végeselem diszkretizáció egdimenziós feladatra.. Csomóonti
SZÉCHENYI ISÁN EGYEEM AAMAZO MECHANIA ANSZÉ 6. MECHANIA-ÉGESEEM MÓDSZER EŐADÁS (kidolgozta: Szüle eronika, eg. ts.) I. előadás. okális aroimáció elve, végeselem diszkretizáció egdimenziós feladatra.. Csomóonti
5. MECHANIKA STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnöktanár)
 SZÉCHENYI ISTVÁN EGYETE ALKALAZOTT ECHANIKA TANSZÉK. ECHANIKA STATIKA GYAKORLAT (idolgozt: Trisz Pétr, g. ts.; Trni Gábor, mérnötnár) Erőrndszr rdő vtorttős, vonl mntén mgoszló rőrndszr.. Péld Adott: z
SZÉCHENYI ISTVÁN EGYETE ALKALAZOTT ECHANIKA TANSZÉK. ECHANIKA STATIKA GYAKORLAT (idolgozt: Trisz Pétr, g. ts.; Trni Gábor, mérnötnár) Erőrndszr rdő vtorttős, vonl mntén mgoszló rőrndszr.. Péld Adott: z
1. Lineáris leképezések
 Lineáris leképezések A lineáris leképezés fogalma Definíció (F5 Definíció) Legenek V és W vektorterek UGYANAZON T test fölött Az A : V W lineáris leképezés, ha összegtartó, azaz v,v 2 V esetén A(v +v 2
Lineáris leképezések A lineáris leképezés fogalma Definíció (F5 Definíció) Legenek V és W vektorterek UGYANAZON T test fölött Az A : V W lineáris leképezés, ha összegtartó, azaz v,v 2 V esetén A(v +v 2
Végeselem analízis (óravázlat)
 Végslm analízis óravázlat Készíttt: Dr Pr Balázs Széchnyi István Egytm Alkalmazott Mchanika Tanszék 3 fbruár 7 Copyright Dr Pr Balázs Mindn jog fnntartva Ez a dokumntum szabadon másolható és trjsztht Módosítása
Végslm analízis óravázlat Készíttt: Dr Pr Balázs Széchnyi István Egytm Alkalmazott Mchanika Tanszék 3 fbruár 7 Copyright Dr Pr Balázs Mindn jog fnntartva Ez a dokumntum szabadon másolható és trjsztht Módosítása
4. A VÉGESELEM MÓDSZER ELMOZDULÁS MODELLJE
 4 VÉGESEEM MÓDSZER EMOZDUÁS MODEJE végslm módsr numrus lárás mérnö fa fladato ölítő mgoldására módsr a sámítástchna flődésévl párhuamosan alault Jlnlg unvráls nagon sofél fladat mgoldására alalmas végslm
4 VÉGESEEM MÓDSZER EMOZDUÁS MODEJE végslm módsr numrus lárás mérnö fa fladato ölítő mgoldására módsr a sámítástchna flődésévl párhuamosan alault Jlnlg unvráls nagon sofél fladat mgoldására alalmas végslm
KOD: B377137. 0, egyébként
 KOD: 777. Egy csomagológép kilogrammos zacskókat tölt. A zacskóba töltött cukor mnnyiség normális loszlású valószínûségi változó kg várható értékkl és.8 kg szórással. A zacskó súlyra nézv lsõ osztályú,
KOD: 777. Egy csomagológép kilogrammos zacskókat tölt. A zacskóba töltött cukor mnnyiség normális loszlású valószínûségi változó kg várható értékkl és.8 kg szórással. A zacskó súlyra nézv lsõ osztályú,
A felépítés elvi alapjait az ÁSF és Reissner-Mindlin-féle lemezhajlítási elmélet alkotja. pontjának elmozdulás koordinátái,
 Lm- és héjlmk modllés éknség: Olassa l a bkdést! Gűjts k/tanulja mg a oparamtrkus lmlm flépítésénk jllmőt! 63 Ioparamtrkus lmlm A flépítés l alapjat a ÁSF és Rssnr-Mndln-fél lmhajlítás lmélt alkotja +
Lm- és héjlmk modllés éknség: Olassa l a bkdést! Gűjts k/tanulja mg a oparamtrkus lmlm flépítésénk jllmőt! 63 Ioparamtrkus lmlm A flépítés l alapjat a ÁSF és Rssnr-Mndln-fél lmhajlítás lmélt alkotja +
A szilárdságtani rúdelmélethez
 A slárságtan rúlmélth Már mgnt találtn a ntrntn g anagot [ ], ml lnított valamt. Most rről ls só. A történt, hog [ ] - b blolvasva fltűnt a [ 2 ] Sgr Fal - fél, valamnt a [ 3 ] Lana ~ Lfsc - fél tárgalásmóho
A slárságtan rúlmélth Már mgnt találtn a ntrntn g anagot [ ], ml lnított valamt. Most rről ls só. A történt, hog [ ] - b blolvasva fltűnt a [ 2 ] Sgr Fal - fél, valamnt a [ 3 ] Lana ~ Lfsc - fél tárgalásmóho
RSA. 1. Véletlenszerűen választunk két "nagy" prímszámot: p1, p2
 RS z algoritmus. Véltlnszrűn választunk két "nagy" prímszámot: p, p, p p. m= pp, φ ( m) = ( p -)( p -)., < φ( m), ( φ( m ),) = - 3. d = ( mod φ( m) ) 4. k p s = ( m,), = ( d, p, p ) k. Kódolás: y = x (
RS z algoritmus. Véltlnszrűn választunk két "nagy" prímszámot: p, p, p p. m= pp, φ ( m) = ( p -)( p -)., < φ( m), ( φ( m ),) = - 3. d = ( mod φ( m) ) 4. k p s = ( m,), = ( d, p, p ) k. Kódolás: y = x (
Csapos bolygómű tervezése
 ISKOLCI EGYETE GÉPÉSZÉNÖKI ÉS INFOATIKAI KA TUDOÁNYOS DIÁKKÖI DOLGOZAT Csapos bolygómű tvzés Paád Attla II. évs gépészménö hallgató Konzulns: D. Sznt Józsf gytm docns Gép- és Tmétvzés Tanszé solc, 0 Tatalomjgyzé.
ISKOLCI EGYETE GÉPÉSZÉNÖKI ÉS INFOATIKAI KA TUDOÁNYOS DIÁKKÖI DOLGOZAT Csapos bolygómű tvzés Paád Attla II. évs gépészménö hallgató Konzulns: D. Sznt Józsf gytm docns Gép- és Tmétvzés Tanszé solc, 0 Tatalomjgyzé.
Országos Szilárd Leó fizikaverseny feladatai
 Országos Szilárd Ló fizikavrsny fladatai I katgória döntő, 5 április 9 Paks A fladatok mgoldásáoz 8 prc áll rndlkzésr Mindn sgédszköz asználató Mindn fladatot külön lapra írjon, s mindn lapon lgyn rajta
Országos Szilárd Ló fizikavrsny fladatai I katgória döntő, 5 április 9 Paks A fladatok mgoldásáoz 8 prc áll rndlkzésr Mindn sgédszköz asználató Mindn fladatot külön lapra írjon, s mindn lapon lgyn rajta
Segédlet a Tengely gördülő-csapágyazása feladathoz
 Segélet a Tengely göülő-csaágyazása felaathoz Összeállította: ihai Zoltán egyetemi ajunktus Tengely göülő-csaágyazása Aott az. ábán egy csaágyazott tengely kinematikai vázlata. A ajz szeint az A jelű csaágy
Segélet a Tengely göülő-csaágyazása felaathoz Összeállította: ihai Zoltán egyetemi ajunktus Tengely göülő-csaágyazása Aott az. ábán egy csaágyazott tengely kinematikai vázlata. A ajz szeint az A jelű csaágy
3. MECHANIKA STATIKA GYAKORLAT (kidolgozta: Triesz Péter; Tarnai Gábor, mérnök tanár) Három erő egyensúlya
 SZÉHENYI ISTVÁN EGYETEM LKLMZOTT MEHNIK TNSZÉK Péld: MEHNIK STTIK GYKORLT (kidolgozt: Tisz Pét; Tni Gábo ménök tná) Háom ő gynsúly dott gy mlőszkzt méti és thlés: m b 5 m c 5 m kn ldt: y c Htáozz mg z
SZÉHENYI ISTVÁN EGYETEM LKLMZOTT MEHNIK TNSZÉK Péld: MEHNIK STTIK GYKORLT (kidolgozt: Tisz Pét; Tni Gábo ménök tná) Háom ő gynsúly dott gy mlőszkzt méti és thlés: m b 5 m c 5 m kn ldt: y c Htáozz mg z
S x, SZELEPEMEL MECHANIZMUS Témakör: Kinematika, merev test, síkmozgás, relatív
 ZELEPEMEL MECHNIZMU Témkör: Kinmtik, mr tst, síkmozgás, rltí ázolt szlpml mchnizmus sugrú, cntricitású cntrtárcsáj állndó szögsbsséggl forog. 1. jzoljuk mg szlp foronomii görbéit. Vgis z t, t és t függénkt..
ZELEPEMEL MECHNIZMU Témkör: Kinmtik, mr tst, síkmozgás, rltí ázolt szlpml mchnizmus sugrú, cntricitású cntrtárcsáj állndó szögsbsséggl forog. 1. jzoljuk mg szlp foronomii görbéit. Vgis z t, t és t függénkt..
4. Izoparametrikus elemcsalád
 SZÉCHENYI ISTVÁN EGYETEM AKAMAZOTT MECHANIKA TANSZÉK 9. MECHANIKA-VÉGESEEM MÓDSZER EŐADÁS (kidolgozta: Szül Vronika, g. ts.) VIII. lőadás 4. Izoparamtriks lmcsalád A krskdlmi szoftvrkbn lggakrabban ún.
SZÉCHENYI ISTVÁN EGYETEM AKAMAZOTT MECHANIKA TANSZÉK 9. MECHANIKA-VÉGESEEM MÓDSZER EŐADÁS (kidolgozta: Szül Vronika, g. ts.) VIII. lőadás 4. Izoparamtriks lmcsalád A krskdlmi szoftvrkbn lggakrabban ún.
GYAKORLÓ FELADATOK 3. A pénzügyi eszközök értékelése
 GYAKORLÓ FELADATOK 3. A pénzügyi szközök étéklés. fladat (kötvény) A vállalat 2 millió fointos buházása mgvalósításának finanszíozásához kötvénykibocsátást tvz, 5 Millió Ft étékbn. A jgyzést lbonyolító
GYAKORLÓ FELADATOK 3. A pénzügyi szközök étéklés. fladat (kötvény) A vállalat 2 millió fointos buházása mgvalósításának finanszíozásához kötvénykibocsátást tvz, 5 Millió Ft étékbn. A jgyzést lbonyolító
A központos furnérhámozás néhány alapösszefüggése
 A közpotos furérhámozás éháy alapösszfüggés 1. ábra: A hámozás jllmző myiségi Az 1. ábra forrása: Dr. Lugosi Armad ( szrk. ) : Faipari szrszámok és gépk kéziköyv Műszaki Köyvkiadó, Budapst, 1987, 57. oldal.
A közpotos furérhámozás éháy alapösszfüggés 1. ábra: A hámozás jllmző myiségi Az 1. ábra forrása: Dr. Lugosi Armad ( szrk. ) : Faipari szrszámok és gépk kéziköyv Műszaki Köyvkiadó, Budapst, 1987, 57. oldal.
5. MECHANIKA STATIKA GYAKORLAT Kidolgozta: Szabó Tamás egy. doc., Triesz Péter egy. ts.
 SZÉCHENYI ISTVÁN EGYETE GÉPSZERKEZETTAN ÉS ECHANIKA TANSZÉK. ECHANIKA STATIKA GYAKORLAT Kidolgozta: Szabó Tamás g. doc., Trisz Pétr g. ts. Erőrndszr rdő vtorttős, párhuzamos rőrndszr, vonal mntén mgoszló
SZÉCHENYI ISTVÁN EGYETE GÉPSZERKEZETTAN ÉS ECHANIKA TANSZÉK. ECHANIKA STATIKA GYAKORLAT Kidolgozta: Szabó Tamás g. doc., Trisz Pétr g. ts. Erőrndszr rdő vtorttős, párhuzamos rőrndszr, vonal mntén mgoszló
A hőmérsékleti sugárzás
 A hőmérséklt sugárzás (Dr. Parpás Béla lőadása alapján ljgyzték a Mskolc gytm harmadévs nformatkus hallgató) Alapjlnségk Mndnnap tapasztalat, hogy a mlgíttt tstk hősugárzást (nfravörös sugárzást) bocsátanak
A hőmérséklt sugárzás (Dr. Parpás Béla lőadása alapján ljgyzték a Mskolc gytm harmadévs nformatkus hallgató) Alapjlnségk Mndnnap tapasztalat, hogy a mlgíttt tstk hősugárzást (nfravörös sugárzást) bocsátanak
ÉPÍTÕ- ÉS SZERELÕIPARI ÉPÜLETSZERKEZETEK Padlóburkolatok
 Magyar Köztársaság ÉPÍTÉSÜGYI ÁGAZATI SZABVÁNY ÉPÍTÕ- ÉS SZERELÕIPARI ÉPÜLETSZERKEZETEK Palóburkolatok MSZ-04-803/14-1989 Az MSZ-04-803/14-1989 hlytt G 33 BUILDING STRUCTURES FOR BUILDING AND FITTING Floor
Magyar Köztársaság ÉPÍTÉSÜGYI ÁGAZATI SZABVÁNY ÉPÍTÕ- ÉS SZERELÕIPARI ÉPÜLETSZERKEZETEK Palóburkolatok MSZ-04-803/14-1989 Az MSZ-04-803/14-1989 hlytt G 33 BUILDING STRUCTURES FOR BUILDING AND FITTING Floor
Arculati Kézikönyv. website branding print
 Arculati Kézikönyv wbsit branding print 22 2. A logó 23 A logó gy cég, szrvzt vagy szolgáltatás gydi, jól flismrhtő, azonosításra szolgáló vizuális jl. A logó lsődlgs célja a mgkülönbözttés, az gyértlmű
Arculati Kézikönyv wbsit branding print 22 2. A logó 23 A logó gy cég, szrvzt vagy szolgáltatás gydi, jól flismrhtő, azonosításra szolgáló vizuális jl. A logó lsődlgs célja a mgkülönbözttés, az gyértlmű
!" #$%& ' % '( ) # # '( KLMNO!./0 1 5 H `a )5,) ) ( ;E ) \ J& ] ) 1.^ <B5 ` A) c HE )`7? ; ^ ) : ;;/,!] ) 1.` A ^ N0< ;:)I >? 7) >S,-Q 1. M "2 1.` A M
![! #$%& ' % '( ) # # '( KLMNO!./0 1 5 H `a )5,) ) ( ;E ) \ J& ] ) 1.^ <B5 ` A) c HE )`7? ; ^ ) : ;;/,!] ) 1.` A ^ N0< ;:)I >? 7) >S,-Q 1. M 2 1.` A M ! #$%& ' % '( ) # # '( KLMNO!./0 1 5 H `a )5,) ) ( ;E ) \ J& ] ) 1.^ <B5 ` A) c HE )`7? ; ^ ) : ;;/,!] ) 1.` A ^ N0< ;:)I >? 7) >S,-Q 1. M 2 1.` A M](/thumbs/97/132979297.jpg) !" #$%& ' % '( ) # # '( KLMNO!./0 1 5 H `a )5,) ) ( ;E ) \ J& ] ) 1.^ ? 7) >S,-Q 1. M "2 1.` A M ^!"#$ :011%&' 11% $. */*-.*: 7 D] " @ W$ Z? ) ) b
!" #$%& ' % '( ) # # '( KLMNO!./0 1 5 H `a )5,) ) ( ;E ) \ J& ] ) 1.^ ? 7) >S,-Q 1. M "2 1.` A M ^!"#$ :011%&' 11% $. */*-.*: 7 D] " @ W$ Z? ) ) b
12. Kétváltozós függvények
 . Kétváltoós üggvénk Értlmés: a = képlt g kétváltoós üggvént ad mg ha a sík bárml pontjáho és üggtln váltoók a üggő váltoó lgljbb g érték tartoik. Ha g sm akkor a üggvén nm értlmtt abban a pontban ha g
. Kétváltoós üggvénk Értlmés: a = képlt g kétváltoós üggvént ad mg ha a sík bárml pontjáho és üggtln váltoók a üggő váltoó lgljbb g érték tartoik. Ha g sm akkor a üggvén nm értlmtt abban a pontban ha g
Fizika és 6. Előadás
 Fzka 5. és 6. Előadás Gejesztett, csllapított oszclláto: dőméés F s λv k F F s m F( t) Fo cos( ωt) v F (t) Mozgásegyenlet: F f o o m ma kx λ v + Fo cos( ωt) Megoldás: x( t) Acos ( ) ( ) β ωt ϕ + ae t sn
Fzka 5. és 6. Előadás Gejesztett, csllapított oszclláto: dőméés F s λv k F F s m F( t) Fo cos( ωt) v F (t) Mozgásegyenlet: F f o o m ma kx λ v + Fo cos( ωt) Megoldás: x( t) Acos ( ) ( ) β ωt ϕ + ae t sn
Fizikai geodézia és gravimetria / 12. VONATKOZTATÁSI RENDSZER PARAMÉTEREINEK MEGHATÁROZÁSA g MÉRÉSEK ALAPJÁN.
 MSc Fzka godéza és gravmtra / 1. BMEEOAFML01 VONATKOZTATÁSI RENDSZER PARAMÉTEREINEK MEGHATÁROZÁSA g MÉRÉSEK ALAPJÁN. Godéza vonatkoztatás rndszrnk (Godtc Rfrnc Systm = GRS) a godéza földmodllt matmatkalag
MSc Fzka godéza és gravmtra / 1. BMEEOAFML01 VONATKOZTATÁSI RENDSZER PARAMÉTEREINEK MEGHATÁROZÁSA g MÉRÉSEK ALAPJÁN. Godéza vonatkoztatás rndszrnk (Godtc Rfrnc Systm = GRS) a godéza földmodllt matmatkalag
13. gyakorlat Visszacsatolt műveletierősítők. A0=10 6 ; ω1=5r/s, ω2 =1Mr/s R 1. Kérdések: uki/ube=?, ha a ME ideális!
 . gyakorlat Visszacsatolt művltirősítők.) Példa b (s) 6 ; r/s, Mr/s kω, 9 kω, kω, ( s )( s ) Kérdésk: /b?, ha a ME ális! Mkkora lgyn érték ahhoz, hogy az /b rősítés maximális lapos lgyn ( ξ ). Mkkora a
. gyakorlat Visszacsatolt művltirősítők.) Példa b (s) 6 ; r/s, Mr/s kω, 9 kω, kω, ( s )( s ) Kérdésk: /b?, ha a ME ális! Mkkora lgyn érték ahhoz, hogy az /b rősítés maximális lapos lgyn ( ξ ). Mkkora a
 ü É Í ü ü ü Í ü ű ü ü ü ű ü ű ű ű ü ü ü ű ü Í ü ű ü ü ü Ű Í É É Á Ő Á Ó Á Á Á Á É Á Á Á Á É Á Í Á Á Í Í ű Á É É Á Á Ö Í Á Á Á Á Á É Á Á Ó ű Í ü ü ü ű ű ü ü ű ü Á ü ű ü Í Í Í ü Í Í ű ű ü ü ü ü ű ü ű ü ü
ü É Í ü ü ü Í ü ű ü ü ü ű ü ű ű ű ü ü ü ű ü Í ü ű ü ü ü Ű Í É É Á Ő Á Ó Á Á Á Á É Á Á Á Á É Á Í Á Á Í Í ű Á É É Á Á Ö Í Á Á Á Á Á É Á Á Ó ű Í ü ü ü ű ű ü ü ű ü Á ü ű ü Í Í Í ü Í Í ű ű ü ü ü ü ű ü ű ü ü
 Ű Í ó Ü Ö Á Á Ó Ö Ü Ü Ü Ü Á Í Ü Á Á Ü Ü Ü Ü Ü Ü Ö Ü Í Ü Ü Ü Ü Ü Ü Ü Ü Ü Ü Á Í Ü Í Í Á Í Í Ü Í Í Ü Á Ü Ü Ü Ü Ü Ü Ü Ü Ő Ö Á ÁÍ Á Ü Ü Á Í Ü Í Á Ü Á Í ó Í Í Ü Ü ő Í Ü Ű Ü Ü Ü Ü Í Ü Ü Ü Ü Ü Ü Ü Í Ü Á Ü Ö Á
Ű Í ó Ü Ö Á Á Ó Ö Ü Ü Ü Ü Á Í Ü Á Á Ü Ü Ü Ü Ü Ü Ö Ü Í Ü Ü Ü Ü Ü Ü Ü Ü Ü Ü Á Í Ü Í Í Á Í Í Ü Í Í Ü Á Ü Ü Ü Ü Ü Ü Ü Ü Ő Ö Á ÁÍ Á Ü Ü Á Í Ü Í Á Ü Á Í ó Í Í Ü Ü ő Í Ü Ű Ü Ü Ü Ü Í Ü Ü Ü Ü Ü Ü Ü Í Ü Á Ü Ö Á
 Í Á Á É ö ö ö ö ö ű ü ö ű ű ű ö ö ö ü ö ü í ü í í í ü í ü Á ü ö ö ü ö ü ö ö ü ö í ö ö ü ö ü í ö ü ű ö ü ö ü í ö í ö ű ű ö ö ú ö ü ö ű ű ű í ö ű í ű ö ű ü ö í ű í í ö í ö ö Ó Í ö ű ű ű ű í í ű ű í í Ü ö
Í Á Á É ö ö ö ö ö ű ü ö ű ű ű ö ö ö ü ö ü í ü í í í ü í ü Á ü ö ö ü ö ü ö ö ü ö í ö ö ü ö ü í ö ü ű ö ü ö ü í ö í ö ű ű ö ö ú ö ü ö ű ű ű í ö ű í ű ö ű ü ö í ű í í ö í ö ö Ó Í ö ű ű ű ű í í ű ű í í Ü ö
 ű í ú ü Á ü ü ü ü ü É É É Ü í ü Á í í ű í ú É É É Ü Í í í í Á í í Á í Á Í É Ő Ú ú Ú í í í íí í ú í í Í í Í Í É í í Í Í í ú í ü Ó í Í ú Í Í ű í ű í í í Í É Ü ű í ü ű í ú É É É Ü ű í í í í ü í Í í Ú Í í
ű í ú ü Á ü ü ü ü ü É É É Ü í ü Á í í ű í ú É É É Ü Í í í í Á í í Á í Á Í É Ő Ú ú Ú í í í íí í ú í í Í í Í Í É í í Í Í í ú í ü Ó í Í ú Í Í ű í ű í í í Í É Ü ű í ü ű í ú É É É Ü ű í í í í ü í Í í Ú Í í
1. MECHANIKA-STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnök tanár) Trigonometria, vektoralgebra
 SZÉCHENYI ISTVÁN EGYETEM LKLMZOTT MECHNIK TNSZÉK. MECHNIK-STTIK GYKORLT (kidolgozta: Tiesz Péte eg. ts.; Tanai Gábo ménök taná) Tigonometia vektoalgeba Tigonometiai összefoglaló c a b b a sin = cos = c
SZÉCHENYI ISTVÁN EGYETEM LKLMZOTT MECHNIK TNSZÉK. MECHNIK-STTIK GYKORLT (kidolgozta: Tiesz Péte eg. ts.; Tanai Gábo ménök taná) Tigonometia vektoalgeba Tigonometiai összefoglaló c a b b a sin = cos = c
M3 ZÁRT CSATORNÁBAN ELHELYEZETT HENGERRE HATÓ ERŐ MÉRÉSE
 M3 ZÁRT CSATORNÁBAN ELHELYEZETT HENGERRE HATÓ ERŐ MÉRÉSE. A mérés élja A mérés fladat égyzt krsztmtsztű satorába bépíttt, az áramlás ráyára mrőlgs szmmtratglyű, külöböző átmérőjű hgrkr ható ( x, y ) rő
M3 ZÁRT CSATORNÁBAN ELHELYEZETT HENGERRE HATÓ ERŐ MÉRÉSE. A mérés élja A mérés fladat égyzt krsztmtsztű satorába bépíttt, az áramlás ráyára mrőlgs szmmtratglyű, külöböző átmérőjű hgrkr ható ( x, y ) rő
Szervomotor sebességszabályozása
 Srvomotor sbsségsabályoása. A gyaorlat célja Egynáramú srvomotor sbsségsabályoásána trvés. A motorsabályoás programváána flépítés. A sbsség rányítás algortms mgvalósítása valós dbn. 2. Elmélt bvt A motor
Srvomotor sbsségsabályoása. A gyaorlat célja Egynáramú srvomotor sbsségsabályoásána trvés. A motorsabályoás programváána flépítés. A sbsség rányítás algortms mgvalósítása valós dbn. 2. Elmélt bvt A motor
Műszaki folyamatok közgazdasági elemzése. Kevert stratégiák és evolúciós játékok
 Műszak folyamatok közgazdaság elemzése Kevert stratégák és evolúcós átékok Fogalmak: Példa: 1 szta stratéga Vegyes stratéga Ha m tszta stratéga létezk és a 1 m annak valószínűsége hogy az - edk átékos
Műszak folyamatok közgazdaság elemzése Kevert stratégák és evolúcós átékok Fogalmak: Példa: 1 szta stratéga Vegyes stratéga Ha m tszta stratéga létezk és a 1 m annak valószínűsége hogy az - edk átékos
THE LITERARY WORKS OF ŚRĪMANTA ŚAṄKARADEVA AND MAHĀPURUṢA MĀDHAVADEVA
 THE LITERARY WORKS OF ŚRĪMANTA ŚAṄKARADEVA AND MAHĀPURUṢA MĀDHAVADEVA Uploaded by The Literature Branch of Śrīmanta Śaṅkaradeva Saṅgha [15 th June/2012] BARGĪT The Śaṅkarī Classical (BHAKTI) songs Composed
THE LITERARY WORKS OF ŚRĪMANTA ŚAṄKARADEVA AND MAHĀPURUṢA MĀDHAVADEVA Uploaded by The Literature Branch of Śrīmanta Śaṅkaradeva Saṅgha [15 th June/2012] BARGĪT The Śaṅkarī Classical (BHAKTI) songs Composed
2011. évi intézmény-felújítás,intézményi javaslatok
 agasépítési csoport PRIORITÁSOK: BRH=biztonságos és rndlttésszrű használat, =állagmgóvás, = műszak iés funkcionális szükség, =gyéb 13 Holdfény Utcai Óvoda Kincskrső Tagóvodája Prioritás gjgyzés 13.1 Krt
agasépítési csoport PRIORITÁSOK: BRH=biztonságos és rndlttésszrű használat, =állagmgóvás, = műszak iés funkcionális szükség, =gyéb 13 Holdfény Utcai Óvoda Kincskrső Tagóvodája Prioritás gjgyzés 13.1 Krt
Külső konzulens: Maza Gábor /E-ON Dél-dunántúli Áramhálózati Zrt./
 Péc Tudoángt Pollack Mhál Műzak é Inoratka Kar Műzak Inoratka é llao Intézt Tudoáno Dákkör Dolgozat Középzültégű zabadvztékk lktroo trénk záítáa a gakorlatban / Practcal calculaton o th lctrc ld trngth
Péc Tudoángt Pollack Mhál Műzak é Inoratka Kar Műzak Inoratka é llao Intézt Tudoáno Dákkör Dolgozat Középzültégű zabadvztékk lktroo trénk záítáa a gakorlatban / Practcal calculaton o th lctrc ld trngth
Integrált Intetnzív Matematika Érettségi
 tgrált ttzív Matmatika Érttségi. Adott az f : \ -, f függvéy. a) Számítsd ki az f függvéy driváltját! b) Határozd mg az f függvéy mootoitási itrvallumait! c) gazold, hogy f ( ) bármly sté!. Adott az f
tgrált ttzív Matmatika Érttségi. Adott az f : \ -, f függvéy. a) Számítsd ki az f függvéy driváltját! b) Határozd mg az f függvéy mootoitási itrvallumait! c) gazold, hogy f ( ) bármly sté!. Adott az f
MODELLEZÉS KONTINUUMMECHANIKAI ALAPJAI. Páczelt István, Nándori Frigyes, Sárközi László, Szabó Tamás, Dluhi Kornél, Baksa Attila
 A VÉGESELEMES MODELLEZÉS KONTINUUMMECHANIKAI ALAPJAI Páczlt István, Nándori Frigys, Sárközi László, Szabó Tamás, Dluhi Kornél, Baksa Attila Miskolci Egytm, Mchanikai Tanszék HEFOP-3.3.-P-004-06-00 ELŐSZÓ
A VÉGESELEMES MODELLEZÉS KONTINUUMMECHANIKAI ALAPJAI Páczlt István, Nándori Frigys, Sárközi László, Szabó Tamás, Dluhi Kornél, Baksa Attila Miskolci Egytm, Mchanikai Tanszék HEFOP-3.3.-P-004-06-00 ELŐSZÓ
MAGYARORSZÁGI VETÜLETEK. Bácsatyai László
 MAGYAOSZÁGI ETÜLETE Bácsata László Sprn 5 Lktr: Dr Csprg Szablcs fıskla tanár Dr arga Józsf gtm ajunktus Tartalmjgzék BEEZETÉS----------------------------------------------------------------------------------------------
MAGYAOSZÁGI ETÜLETE Bácsata László Sprn 5 Lktr: Dr Csprg Szablcs fıskla tanár Dr arga Józsf gtm ajunktus Tartalmjgzék BEEZETÉS----------------------------------------------------------------------------------------------
v i = v i V. (1) m i m i (v i V) = i P = i m i V = m i v i i A V = P M
 Mképpen függ egy pontrendszer mpulzusa a vonatkoztatás rendszertől? K-ban legyenek a részecskék sebessége v. K -ben mely K-hoz képest V sebességgel halad v = v V. (1) P = m v = m (v V) = m v m V = = P
Mképpen függ egy pontrendszer mpulzusa a vonatkoztatás rendszertől? K-ban legyenek a részecskék sebessége v. K -ben mely K-hoz képest V sebességgel halad v = v V. (1) P = m v = m (v V) = m v m V = = P
33 522 04 0001 33 10 Villámvédelmi felülvizsgáló Villanyszerelő
 A 10/007 (II. 7.) SzMM rndlttl módosított 1/006 (II. 17.) OM rndlt Országos Képzési Jgyzékről és az Országos Képzési Jgyzékb történő flvétl és törlés ljárási rndjéről alapján. Szakképsítés, szakképsítés-lágazás,
A 10/007 (II. 7.) SzMM rndlttl módosított 1/006 (II. 17.) OM rndlt Országos Képzési Jgyzékről és az Országos Képzési Jgyzékb történő flvétl és törlés ljárási rndjéről alapján. Szakképsítés, szakképsítés-lágazás,
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Koordináta-gomtria A szürkíttt háttrű fladatrészk nm tartoznak az érinttt témakörhöz, azonban szolgálhatnak fontos információval az érinttt fladatrészk mgoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Koordináta-gomtria A szürkíttt háttrű fladatrészk nm tartoznak az érinttt témakörhöz, azonban szolgálhatnak fontos információval az érinttt fladatrészk mgoldásához!
A szelepre ható érintkezési erő meghatározása
 A szlpr ható érintkzési rő mghatározása Az [ 1 ] műbn az alábbi fladatot találtuk. A fladat: Adott az ábra szrinti szlpmlő szrkzt. Az a xcntricitással szrlt R sugarú bütyök / körtárcsa ω 1 állandó szögsbsséggl
A szlpr ható érintkzési rő mghatározása Az [ 1 ] műbn az alábbi fladatot találtuk. A fladat: Adott az ábra szrinti szlpmlő szrkzt. Az a xcntricitással szrlt R sugarú bütyök / körtárcsa ω 1 állandó szögsbsséggl
VÁLASZLAP ..BF.. KockaKobak Országos Matematikaverseny MINTA 2012. Kezdő feladat: KockaKobak Országos Matematikaverseny MINTA 2012.
 ..BF.. 1. AZ CP OJ VZ 2. DT ID WR ZX 3. AT ER NX RD 4. KF NF TF XJ 5. CV HF LD TL 6. MB SZ XD ZF 7. GB JH NL SB 8. FJ OD OP XP 9. FP PB RP WL 10. IP MH TX WX 11. BX JZ QL YB 12. HX KL MZ ST 13. FV JT VN
..BF.. 1. AZ CP OJ VZ 2. DT ID WR ZX 3. AT ER NX RD 4. KF NF TF XJ 5. CV HF LD TL 6. MB SZ XD ZF 7. GB JH NL SB 8. FJ OD OP XP 9. FP PB RP WL 10. IP MH TX WX 11. BX JZ QL YB 12. HX KL MZ ST 13. FV JT VN
Kisbodaki Harangláb Kisbodak Község Önkormányzatának lapja 2012. február hó V. évfolyam 1. szám
 Kibodaki Haangláb Kibodak Közég Önkományzatának lapja 2012. fbuá hó V. évfolyam 1. zám hatályát vzttt a kataztófák llni védkzé iányítááól, zvztéől é a vzély anyagokkal kapcolato úlyo baltk llni védkzéől
Kibodaki Haangláb Kibodak Közég Önkományzatának lapja 2012. fbuá hó V. évfolyam 1. zám hatályát vzttt a kataztófák llni védkzé iányítááól, zvztéől é a vzély anyagokkal kapcolato úlyo baltk llni védkzéől
E F O P
 E g y ü t t m z k ö d é s i a j á n l a t K ö z ö s é r t é k e i n k s o k s z í n z t á r s a d a l o m E F O P - 1.3.4-1 6 P á l y á z a t i t e r v e z e t 2. 0 ( F o r r á s : w w w. p a l y a z a
E g y ü t t m z k ö d é s i a j á n l a t K ö z ö s é r t é k e i n k s o k s z í n z t á r s a d a l o m E F O P - 1.3.4-1 6 P á l y á z a t i t e r v e z e t 2. 0 ( F o r r á s : w w w. p a l y a z a
2. MUNKATÉR VÍZTELENÍTÉSE
 0 őz Vízéíté ízgzdálkodá UNAT VÍZTELENÍTSE dulk átté Alfoglmk g étgn g zon kztül ízámlá nncn g lngoltón kcn zomzédo étgz két étgt ízzáónk míg zomzédo étgt ízztőnk tkntük A ízztő étg zágá ténző ízzáóénál
0 őz Vízéíté ízgzdálkodá UNAT VÍZTELENÍTSE dulk átté Alfoglmk g étgn g zon kztül ízámlá nncn g lngoltón kcn zomzédo étgz két étgt ízzáónk míg zomzédo étgt ízztőnk tkntük A ízztő étg zágá ténző ízzáóénál
FIZIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Fizika középszint 080 ÉRETTSÉGI VIZSGA 008. novmbr. FIZIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM A dolgozatokat az útmutató utasításai szrint,
Fizika középszint 080 ÉRETTSÉGI VIZSGA 008. novmbr. FIZIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM A dolgozatokat az útmutató utasításai szrint,
FIZIKAI KÉMIA III FÉNY. szerda 10:00-11:30 Általános és Fizikai Kémiai Tanszék, szemináriumi terem. fehér fénynyaláb
 FIZIKAI KÉMIA III szrda 10:00-11:30 Általános és Fizikai Kémiai Tanszék, szmináriumi trm FÉNY fhér fénynyaláb FÉNY fhér fénynyaláb prizma színs fénynyalábok fény = hullám (mint a víz flszínén látható hullámok)
FIZIKAI KÉMIA III szrda 10:00-11:30 Általános és Fizikai Kémiai Tanszék, szmináriumi trm FÉNY fhér fénynyaláb FÉNY fhér fénynyaláb prizma színs fénynyalábok fény = hullám (mint a víz flszínén látható hullámok)
Országos Szakiskolai Közismereti Tanulmányi Verseny 2005/2006 MAGYAR NYELV ÉS HELYESÍRÁS
 Orszáos Szkiskoli Közismrti Tnulmányi Vrsny 2005/2006 MAGYAR NYELV ÉS HELYESÍRÁS II. (rionális) oruló 2006. ruár 17... Hlyszín jélyzőj Vrsnyző Pontszám Kój Elértő Elért Százlék. 120.. % Jvító tnár Zsűri
Orszáos Szkiskoli Közismrti Tnulmányi Vrsny 2005/2006 MAGYAR NYELV ÉS HELYESÍRÁS II. (rionális) oruló 2006. ruár 17... Hlyszín jélyzőj Vrsnyző Pontszám Kój Elértő Elért Százlék. 120.. % Jvító tnár Zsűri
Rugalmas hullámok terjedése. A hullámegyenlet és speciális megoldásai
 Rugalmas hullámok tejedése. A hullámegyenlet és speciális megoldásai Milyen hullámok alakulhatnak ki ugalmas közegben? Gázokban és folyadékokban csak longitudinális hullámok tejedhetnek. Szilád közegben
Rugalmas hullámok tejedése. A hullámegyenlet és speciális megoldásai Milyen hullámok alakulhatnak ki ugalmas közegben? Gázokban és folyadékokban csak longitudinális hullámok tejedhetnek. Szilád közegben
6. SZILÁRDSÁGTANI ÁLLAPOTOK
 6 SZILÁRDSÁGTANI ÁLLAOTOK 6 Alapfogalmak Silárdságta: a trhlés lőtt és utá is tartós ugalomba lvő alakváltoásra képs tstk kimatikája diamikája és aagsrkti vislkdés Trhlés: ismrt külső rőrdsr Tartós ugalom:
6 SZILÁRDSÁGTANI ÁLLAOTOK 6 Alapfogalmak Silárdságta: a trhlés lőtt és utá is tartós ugalomba lvő alakváltoásra képs tstk kimatikája diamikája és aagsrkti vislkdés Trhlés: ismrt külső rőrdsr Tartós ugalom:
DINAMIKAI VIZSGÁLAT ÁLLAPOTTÉRBEN. 2003.11.06. Dr. Aradi Petra, Dr. Niedermayer Péter: Rendszertechnika segédlet 1
 DINAMIKAI VIZSGÁLAT ÁLLAPOTTÉRBEN 2003..06. Dr. Aradi Petra, Dr. Niedermayer Péter: Rendszertechnika segédlet Egy bemenetű, egy kimenetű rendszer u(t) diff. egyenlet v(t) zárt alakban n-edrendű diff. egyenlet
DINAMIKAI VIZSGÁLAT ÁLLAPOTTÉRBEN 2003..06. Dr. Aradi Petra, Dr. Niedermayer Péter: Rendszertechnika segédlet Egy bemenetű, egy kimenetű rendszer u(t) diff. egyenlet v(t) zárt alakban n-edrendű diff. egyenlet
Automatikus fedélzeti irányítórendszerek előadás Bauer Péter / 2.
 Atoatiks fdélti iránítórndsrk lőadás Bar étr /.. lináris ogásgnltk. inariált ogásgnltk 3. -6 rpülőgép lináris hossdinaikai odllj riálás forgó rndsrbn (diffrntiation in rotating oord. ss.) d dt absolút
Atoatiks fdélti iránítórndsrk lőadás Bar étr /.. lináris ogásgnltk. inariált ogásgnltk 3. -6 rpülőgép lináris hossdinaikai odllj riálás forgó rndsrbn (diffrntiation in rotating oord. ss.) d dt absolút
Méret: Végződés: Min. hőmérséklet: Max. hőmérséklet: Max. nyomás: Specifikációk:
 L SZ 17 SÓS O L Z Ó ÉSTOL t: őd: in. hőmklt: x. hőmklt: x. nomá: Spcifikációk: Anok: -től -i ISO P kimák kö - C 0 C b -i m mlkdő oó ki kk tiánú ámlá tömít nh nomávt Öntöttv há n.hu v l n.hu v l Z ÉSTOLÓ
L SZ 17 SÓS O L Z Ó ÉSTOL t: őd: in. hőmklt: x. hőmklt: x. nomá: Spcifikációk: Anok: -től -i ISO P kimák kö - C 0 C b -i m mlkdő oó ki kk tiánú ámlá tömít nh nomávt Öntöttv há n.hu v l n.hu v l Z ÉSTOLÓ
Merev testek kinematikája
 Mechanka BL0E- 3. előadás 00. októbe 5. Meev testek knematkáa Egy pontendszet meev testnek tekntünk, ha bámely két pontának távolsága állandó. (f6, Eule) A meev test tetszőleges mozgása leíható elem tanszlácók
Mechanka BL0E- 3. előadás 00. októbe 5. Meev testek knematkáa Egy pontendszet meev testnek tekntünk, ha bámely két pontának távolsága állandó. (f6, Eule) A meev test tetszőleges mozgása leíható elem tanszlácók
108. szám A MAGYAR KÖZTÁRSASÁG HIVATALOS LAPJA. Budapest, 2009. jú li us 30., csütörtök TARTALOMJEGYZÉK. Ára: 1125 Ft. Oldal
 A MAGYAR KÖZTÁRSASÁG HIVATALOS LAPJA Budapst, 2009. jú l us 30., csütörtök 108. szám Ára: 1125 Ft TARTALOMJEGYZÉK 158/2009. (VII. 30.) Korm. rn d lt A mzõgazdaság trmékk és az éllmszrk, valamnt a szszs
A MAGYAR KÖZTÁRSASÁG HIVATALOS LAPJA Budapst, 2009. jú l us 30., csütörtök 108. szám Ára: 1125 Ft TARTALOMJEGYZÉK 158/2009. (VII. 30.) Korm. rn d lt A mzõgazdaság trmékk és az éllmszrk, valamnt a szszs
Rácsrezgések.
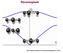 ácsrzgésk http://physics-imtis.cm/physics/glish/ph_txt.htm ácsrzgésk gitális hllám rúb Nwt II F x x F x V t F F x A x V x x x x x x A hllámszám értlmzési trtmáy végs mért prióiks htárfltétl Br-Kármá t
ácsrzgésk http://physics-imtis.cm/physics/glish/ph_txt.htm ácsrzgésk gitális hllám rúb Nwt II F x x F x V t F F x A x V x x x x x x A hllámszám értlmzési trtmáy végs mért prióiks htárfltétl Br-Kármá t
PÁRATECHNIKA. Feladatok. Dr. Harmathy Norbert. egyetemi adjunktus
 08. 0. 4. PÁATECHNIKA Fladatok Dr. Harmathy Norbrt gytm adjunktus BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építészmérnök Kar, Épültnrgtka és Épültgépészt Tanszék. Fladat páratchnka alapja A. Számítsuk
08. 0. 4. PÁATECHNIKA Fladatok Dr. Harmathy Norbrt gytm adjunktus BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építészmérnök Kar, Épültnrgtka és Épültgépészt Tanszék. Fladat páratchnka alapja A. Számítsuk
 ő ü ő ľ ü Ü Ü ľ ź ő ľ ľ ő ő ü ľ ő ö ü ľ ő ő ü ú ź ö ö ö Ĺ ő ö ľő ő ú ű ö ö ľ ü Ę ú ő ü ö ľ ź ő ľ ů ö ľ ź ő ľ ő ö ö ľ ľő ľ Í ő ľ ő ľü ľ ő ľ ľ ź ľ ö ü ú ű ź ő ľ ľ ľ ľ ú ú ľ Á ľ Í ő ö ü ő ź ź Í ö ľ ő ľ ő
ő ü ő ľ ü Ü Ü ľ ź ő ľ ľ ő ő ü ľ ő ö ü ľ ő ő ü ú ź ö ö ö Ĺ ő ö ľő ő ú ű ö ö ľ ü Ę ú ő ü ö ľ ź ő ľ ů ö ľ ź ő ľ ő ö ö ľ ľő ľ Í ő ľ ő ľü ľ ő ľ ľ ź ľ ö ü ú ű ź ő ľ ľ ľ ľ ú ú ľ Á ľ Í ő ö ü ő ź ź Í ö ľ ő ľ ő
Testmodellezés ábra. Gúla Ekkor a csúcspontok koordinátáit egy V csúcspont (vertex) listában tárolhatjuk.
 Tstmodllzés 1 1. Tstmodllzés Egy objktum modlljén az objktumot rprzntáló adatrndszrt értjük. Egy tstmodll gy digitális rprzntációja gy létz vagy lképzlt objktumnak. A trvzés, a modllzés során mgadjuk a
Tstmodllzés 1 1. Tstmodllzés Egy objktum modlljén az objktumot rprzntáló adatrndszrt értjük. Egy tstmodll gy digitális rprzntációja gy létz vagy lképzlt objktumnak. A trvzés, a modllzés során mgadjuk a
Relációk. Vázlat. Példák direkt szorzatra
 8.. 7. elácók elácó matematka fogalma zükséges fogalom: drekt szorzat Halmazok Descartes drekt szorzata: Legenek D D D n adott doman halmazok. D D D n : = { d d d n d k D k k n } A drekt szorzat tehát
8.. 7. elácók elácó matematka fogalma zükséges fogalom: drekt szorzat Halmazok Descartes drekt szorzata: Legenek D D D n adott doman halmazok. D D D n : = { d d d n d k D k k n } A drekt szorzat tehát
Vázlat. Relációk. Példák direkt szorzatra
 7..9. Vázlat elácók a. elácó fogalma b. Tulajdonsága: refleív szmmetrkus/antszmmetrkus tranztív c. Ekvvalenca relácók rzleges/parcáls rrendez relácók felsmere d. elácók reprezentálása elácó matematka fogalma
7..9. Vázlat elácók a. elácó fogalma b. Tulajdonsága: refleív szmmetrkus/antszmmetrkus tranztív c. Ekvvalenca relácók rzleges/parcáls rrendez relácók felsmere d. elácók reprezentálása elácó matematka fogalma
5. A SZILÁRDSÁGTAN 2D FELADATAI
 5 A SZILÁDSÁGAN D FELADAAI A slárdságta (rugalasságta) kétdós vag kétértű (D) fladata köréb háro fladatcsoportot sokás sorol: - a sík alakváltoás fladatokat (SA) - a általáosított síkfsültség állapot fladatat
5 A SZILÁDSÁGAN D FELADAAI A slárdságta (rugalasságta) kétdós vag kétértű (D) fladata köréb háro fladatcsoportot sokás sorol: - a sík alakváltoás fladatokat (SA) - a általáosított síkfsültség állapot fladatat
a NAT-2-0147/2008 számú akkreditálási ügyirathoz
 Nemzeti Akkreditáló Testület RÉSZLETEZÕ OKIRAT a NAT-2-0147/2008 számú akkreditálási ügyirathoz Az S+V Engineering Kereskedelmi és Szolgáltató Kft. (1184 Budapest, Lakatos u. 61-63.) kalibrálólaboratóriuma
Nemzeti Akkreditáló Testület RÉSZLETEZÕ OKIRAT a NAT-2-0147/2008 számú akkreditálási ügyirathoz Az S+V Engineering Kereskedelmi és Szolgáltató Kft. (1184 Budapest, Lakatos u. 61-63.) kalibrálólaboratóriuma
FIZIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Fizika középszint 08 ÉRETTSÉGI VIZSGA 010. május 18. FIZIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM A dolgozatokat az útmutató utasításai
Fizika középszint 08 ÉRETTSÉGI VIZSGA 010. május 18. FIZIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM A dolgozatokat az útmutató utasításai
