Lineáris egyenlet. Lineáris egyenletrendszer. algebrai egyenlet konstansok és első fokú ismeretlenek pl.: egyenes egyenlete
|
|
|
- Benjámin Jónás
- 6 évvel ezelőtt
- Látták:
Átírás
1
2 Lieáris egyelet algebrai egyelet kostasok és első fokú ismeretleek pl.: egyees egyelete Lieáris egyeletredser y a b lieáris egyeletek csoportja ugya ao a váltoó halmao
3 Lieáris egyeletredser B b B b B b A A b
4 Mikor oldható meg? A b Ha koverges A b lim * lim * * A * b Fi pot
5 Mikor koverges? Ha A kompatibilis valamely ormájával. Norma Egy vektortere értelmeett leképés, amely a ullvektor kivételével a tér mide vektoráho egy poitív sámot redel. ) ( ) ( ) ( ) ( ) ( ) ( ) ( d d y d d y d d d a.cs.a., ha
6 Normák p-orma (Hölder-orma) -orma -orma Végtele orma p i p i p / : i i i i i i ma
7 Mátriormák A vektorormák mátriormákat idukálak. A M sup A Liearitás miatt elég a ormájú vektorokat tekitei. Kompakt halma, így a folytoos maimumát. A mátriormárakra teljesül v v sup A v A B A B v A v függvéy felvesi a A v A M v
8 Iterációs megoldás Bioyítás Redőr sabály! b A b A A A A A b b A Ab b,,,
9 Iterációs megoldás void jakobi(){... it iputbuffer = ; cost it iteratios = ; for(it i = ; i < iteratios; ++i){ mulmatrivector(,, [(iputbuffer + ) % ], A, [iputbuffer], b); iputbuffer = (iputbuffer + ) % ;...
10 Iterációs megoldás A. 5 I b Jakobi : [,,,,,,, ] Jakobi : [.5,.5,.5,.5,.5,.5,.5,.5] Jakobi : [.75,.75,.75,.75,.75,.75,.75,.75] Jakobi : [.875,.875,.875,.875,.875,.875,.875,.875] Jakobi : [.9375,.9375,.9375,.9375,.9375,.9375,.9375,.9375] Jakobi : [.96875,.96875,.96875,.96875,.96875,.96875,.96875,.96875] Jakobi : [.98438,.98438,.98438,.98438,.98438,.98438,.98438,.98438] Jakobi : [.999,.999,.999,.999,.999,.999,.999,.999] Jakobi : [.9969,.9969,.9969,.9969,.9969,.9969,.9969,.9969] Jakobi : [.9985,.9985,.9985,.9985,.9985,.9985,.9985,.9985] Jakobi : [.999,.999,.999,.999,.999,.999,.999,.999] Jakobi : [.9995,.9995,.9995,.9995,.9995,.9995,.9995,.9995] Jakobi : [.99976,.99976,.99976,.99976,.99976,.99976,.99976,.99976] Jakobi : [.99988,.99988,.99988,.99988,.99988,.99988,.99988,.99988] Jakobi : [.99994,.99994,.99994,.99994,.99994,.99994,.99994,.99994] Jakobi : [.99997,.99997,.99997,.99997,.99997,.99997,.99997,.99997] Jakobi : [.99998,.99998,.99998,.99998,.99998,.99998,.99998,.99998] Jakobi : [.99999,.99999,.99999,.99999,.99999,.99999,.99999,.99999] Jakobi : [,,,,,,, ] Jakobi : [,,,,,,, ]
11 CPU implemetáció void scalarmv(it, it m, float* y, cost float* A, cost float*, cost float* b){ for(it i=; i<; ++i){ float yi = b[i]; for(it j=; j<m; ++j){ yi += A[i * m + j] * [j]; y[i] = yi;
12 Hogya párhuamosítható? Eredméy sálakho redelése Gather típus: mide sál össegi a bemeet mide eleméek hoájárulását Bemeet sálakho redelése Scatter típus: mide sál kisámítja a bemet egy eleméek hoájárulását a kimeet mide eleméhe Sikroiáció sükséges!
13 Gather típusú megoldás A eredméy egy N elemű vektor A muka méret N Mide sál kisámítja a mátri egy sora és bemeeti vektor alapjá a eredméy vektor egy elemét. Elleőrii kell a túlcímést!
14 Host program void simplemv(it, it m, float* y, cost float* A, cost float*, cost float* b){ cl_kerel simplemvkerel = createkerel(program, "simplemv"); cl_mem ygpu = clcreatebuffer(cotet, CL_MEM_WRITE_ONLY, sieof(float)*m, NULL, NULL); cl_mem AGPU = clcreatebuffer(cotet, CL_MEM_READ_ONLY, sieof(float)*m*, NULL, NULL); clequeuewritebuffer(commads, AGPU, CL_FALSE,, sieof(float)*m*, A,, NULL, NULL); cl_mem GPU = clcreatebuffer(cotet, CL_MEM_READ_ONLY, sieof(float) *, NULL, NULL); clequeuewritebuffer(commads, GPU, CL_FALSE,, sieof(float)*,,, NULL, NULL); cl_mem bgpu = clcreatebuffer(cotet, CL_MEM_READ_ONLY, sieof(float) * m, NULL, NULL); clequeuewritebuffer(commads, bgpu, CL_FALSE,, sieof(float)*m, b,, NULL, NULL); clsetkerelarg(simplemvkerel,, sieof(it), &); clsetkerelarg(simplemvkerel,, sieof(it), &m); clsetkerelarg(simplemvkerel,, sieof(cl_mem), &ygpu); clsetkerelarg(simplemvkerel, 3, sieof(cl_mem), &AGPU); clsetkerelarg(simplemvkerel, 4, sieof(cl_mem), &GPU); clsetkerelarg(simplemvkerel, 5, sieof(cl_mem), &bgpu); clequeuebarrier(commads); //...
15 Host program //... sie_t worksie = m; clequeuendragekerel(commads, simplemvkerel,, NULL, &worksie, NULL,, NULL, NULL); clfiish(commads); clequeuereadbuffer(commads, ygpu, CL_TRUE,, sieof(float) * m, y,, NULL, NULL); clreleasememobject(ygpu); clreleasememobject(agpu); clreleasememobject(gpu); clreleasememobject(bgpu); clreleasekerel(simplemvkerel);
16 OpeCL kerel kerel void simplemv(cost it, cost it m, global float* y, global float* A, global float*, global float* b){ it i = get_global_id(); if(i < ){ float yi = b[i]; for(it j = ; j < m; ++j){ yi += A[j + i * m ] * [j]; y[i] = yi; Soros sámítás!
17 A skaláris sorás párhuamosítása boyolult A össegés triviálisa párhuamosítható! Klassikus redukciós megoldás Mukacsoportokét dolgouk fel egy-egy oslopot Mide sál elvégi a elemi sorást A eredméyt a lokális memóriába gyűjtjük Redukciós lépések Mide lépésbe feleük a sálak sámát A még futó sálak össegik a leállított sálak résössegeit A utolsó sál kiírja a eredméyt a globális memóriába
18 Feltételeések N*M-es mátri eseté M sál idítható mukacsoportokét N mukacsoport idítható A lokális memória legalább M méretű M= k a redukcióho
19 Host program #defie M 3 void reducemv(it, float* y, cost float* A, cost float*, cost float* b){ //... sie_t worksie = M * ; sie_t workgroupsie = M; CL_SAFE_CALL( clequeuendragekerel(commads, reducemvkerel,, NULL, &worksie, &workgroupsie,, NULL, NULL) ); //...
20 OpeCL kerel #defie M 3 kerel void reducemv(cost it, global float* y, global float* A, global float*, global float* b){ it i = get_group_id(); it j = get_local_id(); local float Q[M]; Q[j] = A[i * M + j] * [j]; for(it stride = M / ; stride > ; stride >>= ){ barrier(clk_local_mem_fence); if(j + stride < M){ Q[j] += Q[j + stride]; if(j == ){ y[i] = Q[] + b[i];
21 Megoldási lehetőség A egyserűség kedvéért csak egy mukacsoport Daraboljuk a kimeetet T hossú darabokra A mukacsoport egyserre egy segmese dolgoik Daraboljuk fel a bemeetet Z hossú darabokra A skaláris soratok össegét a résössegekből sámítjuk A lokális memóriába tároljuk résössegeket Q[T*Z] méretű lokális tömbbe A eredméy T hossú darabját redukcióval kapjuk
22 Host program #defie T 8 #defie Z void largemv(it, it m, float* y, cost float* A, cost float*, cost float* b){ //... sie_t worksie = T * Z; sie_t workgroupsie = T * Z; clequeuendragekerel(commads, largemvkerel,, NULL, &worksie, &workgroupsie,, NULL, NULL); //...
23 OpeCL kerel #defie T 8 #defie Z kerel void largemv(cost it, cost it m, global float* y, global float* A, global float*, global float* b){ local float Q[T * Z]; it t = get_local_id() / Z; it = get_local_id() % Z; for(it i = t; i < ; i += T){ //... ciklus mag a követkeő oldalo if( == ){ y[i] = Q[t * Z + ] + b[i];
24 OpeCL kerel // ciklus mag Q[t * Z + ] =.f; for(it j = ; j < m; j+=z){ Q[t * Z + ] += A[j + i * m] * [j]; for(it stride = Z / ; stride > ; stride >>= ){ barrier(clk_local_mem_fence); if( + stride < Z){ Q[t * Z + ] += Q[t * Z + + stride];
25 Ritka mátriok Sok ulla elem Tömörítés és a tömörített repreetáció sámítás Compressed Sparse Row y f e d c b a 5 f e d c b a Value: Colum: Row Ptr:
26 y f e d c b a 5 f e d c b a Value: Colum: Row Ptr: 3 O O O f e dy c b a y f e d c b a Value + Row Ptr: Vector + Colum: Elemekéti sorat: Iclusive segmetált sca:
27 Segmetált sca Feltételes sca A feltétel egy külö tömbbe Iclusive sca: Head tömb Iclusive segmeted sca:
28 Gauss elimiáció Vissaveetjük a egyeletredsert háromsög mátrira Vissahelyettesítéses megoldás Gauss-Jorda elimiáció Csak a főátlóba lehet emulla elem
29 Megegedett műveletek Két egyelet felcserélése Egyelet skalárral sorása Egy egyelethe egy másik skalársorosáak hoáadása
30 Példa y y y L L L L L L 5 8 y y y L L L 8 y y 5 8 y y y 3 y
31 Példa y y y
32 Mátri ivere A I AI A AI A A I A I
33 Algoritmus for k :=.. - do for i := k+.. do l := a ik /a kk b i := b i l * b k for j := k.. do a ij := a ij l * a kj ed for ed for ed for
34 Host program void gaussia(){ it = 6; it m = 3; float A[] = {, -,,,,, -,, -,,,,, -,,,, ; cl_kerel gaussiakerel = createkerel(program, "gaussia"); cl_mem AGPU = clcreatebuffer(cotet, CL_MEM_READ_WRITE, sieof(float)**m, NULL, NULL); clequeuewritebuffer(commads, AGPU, CL_TRUE,, sieof(float)**m, A,, NULL, NULL); clsetkerelarg(gaussiakerel,, sieof(it), &); clsetkerelarg(gaussiakerel,, sieof(it), &m); clsetkerelarg(gaussiakerel,, sieof(cl_mem), &AGPU); clequeuebarrier(commads); //...
35 Host program //... sie_t worksie = m; sie_t workgroupsie = m; clequeuendragekerel(commads, gaussiakerel,, NULL, &worksie, &workgroupsie,, NULL, NULL); clfiish(commads); clequeuereadbuffer(commads, AGPU, CL_TRUE,, sieof(float)**m, A,, NULL, NULL); clreleasememobject(agpu); clreleasekerel(gaussiakerel);
36 OpeCL kerel kerel void gaussia(cost it, cost it m, global float* A){ it id = get_local_id(); for(it ma = ; ma < m; ++ma){ float pp = A[ma + ma * ]; float coeff = A[ma + id * ] / pp; barrier(clk_global_mem_fence); if(id!= ma){ for(it a = ; a < ; ++a){ A[a+id*] = A[a+id*] - coeff * A[a+*ma]; barrier(clk_global_mem_fence); //...
37 OpeCL kerel //... float coeff = A[id + id * ]; for(it a = ; a < ; ++a){ A[a + id * ] = A[a + id * ] / coeff;
38 Példák,.3e-8, 9.93e-9,.75,.5,.5,,.3e-8,.5,,.5,.3e-8,,.5,.5,.75,,,,,, 3 -, -,,
Videókártya - CUDA kompatibilitás: CUDA weboldal: Példaterületek:
 Hasznos weboldalak Videókártya - CUDA kompatibilitás: https://developer.nvidia.com/cuda-gpus CUDA weboldal: https://developer.nvidia.com/cuda-zone Példaterületek: http://www.nvidia.com/object/imaging_comp
Hasznos weboldalak Videókártya - CUDA kompatibilitás: https://developer.nvidia.com/cuda-gpus CUDA weboldal: https://developer.nvidia.com/cuda-zone Példaterületek: http://www.nvidia.com/object/imaging_comp
26 Győri István, Hartung Ferenc: MA1114f és MA6116a előadásjegyzet, 2006/2007
 6 Győri Istvá, Hartug Ferec: MA4f és MA66a előadásjegyet, 006/007. A -trasformált.. Egy iformációátviteli probléma Legye adott egy üeetátviteli redserük, amelybe a üeeteket két alapjel modjuk a és b segítségével
6 Győri Istvá, Hartug Ferec: MA4f és MA66a előadásjegyet, 006/007. A -trasformált.. Egy iformációátviteli probléma Legye adott egy üeetátviteli redserük, amelybe a üeeteket két alapjel modjuk a és b segítségével
Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar. Feladatok a Gazdasági matematika I. tárgy gyakorlataihoz. Halmazelmélet
 Debrecei Egyetem Közgazdaság- és Gazdaságtudomáyi Kar Feladatok a Gazdasági matematika I. tárgy gyakorlataihoz a megoldásra feltétleül ajálott feladatokat jelöli e feladatokat a félév végére megoldottak
Debrecei Egyetem Közgazdaság- és Gazdaságtudomáyi Kar Feladatok a Gazdasági matematika I. tárgy gyakorlataihoz a megoldásra feltétleül ajálott feladatokat jelöli e feladatokat a félév végére megoldottak
1. Gyökvonás komplex számból
 1. Gyökvoás komplex számból Gyökvoás komplex számból Ismétlés: Ha r,s > 0 valós, akkor r(cosα+isiα) = s(cosβ+isiβ) potosa akkor, ha r = s, és α β a 360 egész számszorosa. Moivre képlete: ( s(cosβ+isiβ)
1. Gyökvoás komplex számból Gyökvoás komplex számból Ismétlés: Ha r,s > 0 valós, akkor r(cosα+isiα) = s(cosβ+isiβ) potosa akkor, ha r = s, és α β a 360 egész számszorosa. Moivre képlete: ( s(cosβ+isiβ)
Gauss-Jordan módszer Legkisebb négyzetek módszere, egyenes LNM, polinom LNM, függvény. Lineáris algebra numerikus módszerei
 A Gauss-Jordan elimináció, mátrixinvertálás Gauss-Jordan módszer Ugyanazzal a technikával, mint ahogy a k-adik oszlopban az a kk alatti elemeket kinulláztuk, a fölötte lévő elemeket is zérussá lehet tenni.
A Gauss-Jordan elimináció, mátrixinvertálás Gauss-Jordan módszer Ugyanazzal a technikával, mint ahogy a k-adik oszlopban az a kk alatti elemeket kinulláztuk, a fölötte lévő elemeket is zérussá lehet tenni.
Folytonos idejű rendszerek stabilitása
 Folytoos idejű redszerek stabilitása Összeállította: dr. Gerzso Miklós egyetemi doces PTE MIK Műszaki Iformatika Taszék 205.2.06. Itelliges redszerek I. PTE MIK Mérök iformatikus BSc szak Stabilitás egyszerűsített
Folytoos idejű redszerek stabilitása Összeállította: dr. Gerzso Miklós egyetemi doces PTE MIK Műszaki Iformatika Taszék 205.2.06. Itelliges redszerek I. PTE MIK Mérök iformatikus BSc szak Stabilitás egyszerűsített
EUKLIDESZI TÉR. Euklideszi tér, metrikus tér, normált tér, magasabb dimenziós terek vektorainak szöge, ezek következményei
 Eukldes tér, metrkus tér, ormált tér, magasabb dmeós terek vektoraak söge, eek követkemée Metrkus tér Defícó. A H halmat metrkus térek eveük, ha va ola, metrkáak eveett m: H H R {0} függvé, amelre a követkeők
Eukldes tér, metrkus tér, ormált tér, magasabb dmeós terek vektoraak söge, eek követkemée Metrkus tér Defícó. A H halmat metrkus térek eveük, ha va ola, metrkáak eveett m: H H R {0} függvé, amelre a követkeők
VII. A határozatlan esetek kiküszöbölése
 A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
Határértékszámítás. 1 Határátmenet Tétel. (Nevezetes sorozatok) (a) n, n 2,... n α (α > 0), 1 n 0, 1. 0 (α > 0), (b) n 2 0,... 1.
 Határátmeet Határértékszámítás.. Tétel. (Nevezetes sorozatok) 005..5 Készítette: Dr. Toledo Rodolfo (a)... α (α > 0) (b) (c) 0 0... 0 (α > 0) α q (d) c (c > 0) ha q > = ha q = 0 ha q < diverges korlátos
Határátmeet Határértékszámítás.. Tétel. (Nevezetes sorozatok) 005..5 Készítette: Dr. Toledo Rodolfo (a)... α (α > 0) (b) (c) 0 0... 0 (α > 0) α q (d) c (c > 0) ha q > = ha q = 0 ha q < diverges korlátos
SZÁMELMÉLET. Szigeti Jenő
 SZÁMELMÉLET Sigeti Jeő. OSZTHATÓSÁG A osthatósággal kapcsolatba égy alapvető eredméyt kölük bioyítás élkül. Jelölje φ() a {,,..., } halmaból ao elemek sámát, amelyek relatív prímek a -he. Ha például p
SZÁMELMÉLET Sigeti Jeő. OSZTHATÓSÁG A osthatósággal kapcsolatba égy alapvető eredméyt kölük bioyítás élkül. Jelölje φ() a {,,..., } halmaból ao elemek sámát, amelyek relatív prímek a -he. Ha például p
Stabilitás Irányítástechnika PE MI_BSc 1
 Stabilitás 2008.03.4. Stabilitás egyszerűsített szemlélet példa zavarás utá a magára hagyott redszer visszatér a yugalmi állapotába kvázistacioárius állapotba kerül végtelebe tart alapjelváltás Stabilitás/2
Stabilitás 2008.03.4. Stabilitás egyszerűsített szemlélet példa zavarás utá a magára hagyott redszer visszatér a yugalmi állapotába kvázistacioárius állapotba kerül végtelebe tart alapjelváltás Stabilitás/2
Sorozatok, határérték fogalma. Függvények határértéke, folytonossága
 Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
Számítógépes irányítások elmélete
 Budapesti Műsaki és Gadaságtudomáyi Egyetem Gépésméröki Kar Gépéseti Iformatika asék Sámítógépes iráyítások elmélete ( Előadás ayag ) Késítette: Dr. Lipovski György Budapest, 22. september artalomjegyék.
Budapesti Műsaki és Gadaságtudomáyi Egyetem Gépésméröki Kar Gépéseti Iformatika asék Sámítógépes iráyítások elmélete ( Előadás ayag ) Késítette: Dr. Lipovski György Budapest, 22. september artalomjegyék.
ANALÍZIS 1. I. VIZSGA január 11. Mérnök informatikus szak α-variáns Munkaidő: 90 perc., vagyis z 2 1p = i 1p = ( cos 3π 2 2
 ANALÍZIS. I. VIZSGA. jauár. Mérök iformatikus szak α-variás Mukaidő: perc. feladat pot) Adja meg az z 4 i)z i egyelet összes megoldását. i + i) + 4i + 4 i +, vagyis z p i p cos 3 + i si ) 3 vagy z p i
ANALÍZIS. I. VIZSGA. jauár. Mérök iformatikus szak α-variás Mukaidő: perc. feladat pot) Adja meg az z 4 i)z i egyelet összes megoldását. i + i) + 4i + 4 i +, vagyis z p i p cos 3 + i si ) 3 vagy z p i
FELADATOK A KALKULUS C. TÁRGYHOZ
 FELADATOK A KALKULUS C. TÁRGYHOZ. HALMAZOK RELÁCIÓK FÜGGVÉNYEK. Bizoyítsuk be a halmaz-műveletek alapazoosságait! 2. Legye adott az X halmaz legye A B C X. Ha A B := (A B) (B A) akkor bizoyítsuk be hogy
FELADATOK A KALKULUS C. TÁRGYHOZ. HALMAZOK RELÁCIÓK FÜGGVÉNYEK. Bizoyítsuk be a halmaz-műveletek alapazoosságait! 2. Legye adott az X halmaz legye A B C X. Ha A B := (A B) (B A) akkor bizoyítsuk be hogy
Szerszámgépek 5. előadás 2007. Március 13. Szerszámg. 5. előad. Miskolc - Egyetemváros 2006/2007 2.félév
 Sersámgépe 5. előadás. Márcis. Sersámg mgépe 5. előad adás Misolc - Egyetemváros /.félév Sersámgépe 5. előadás. Márcis. A sabályohatósági tartomáy övelésée módserei Előetes megfotoláso: S mi mi M S φ,
Sersámgépe 5. előadás. Márcis. Sersámg mgépe 5. előad adás Misolc - Egyetemváros /.félév Sersámgépe 5. előadás. Márcis. A sabályohatósági tartomáy övelésée módserei Előetes megfotoláso: S mi mi M S φ,
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Alkalmazott Informatikai Tanszék. Dr. Kulcsár Gyula egyetemi docens
 Miskolci Egyetem Gépészméröki és Iformatikai Kar Alkalmazott Iformatikai Taszék Dr. Kulcsár Gyula egyetemi doces Iformatikai ifrastruktúra felődése Decetralizált Cetralizált Lazá csatolt Klies/szerver
Miskolci Egyetem Gépészméröki és Iformatikai Kar Alkalmazott Iformatikai Taszék Dr. Kulcsár Gyula egyetemi doces Iformatikai ifrastruktúra felődése Decetralizált Cetralizált Lazá csatolt Klies/szerver
Metrikus terek. továbbra is.
 Metrius tere továbbra is. Defiíció: Legye X egy halmaz, d : X X R egy függvéy. Azt modju, hogy d metria (távolság), ha.. 3. 4. d d d d x, x 0, x, y 0 x y, x, y dy, x, x, z dx, y dy, z. Az X halmazt a d
Metrius tere továbbra is. Defiíció: Legye X egy halmaz, d : X X R egy függvéy. Azt modju, hogy d metria (távolság), ha.. 3. 4. d d d d x, x 0, x, y 0 x y, x, y dy, x, x, z dx, y dy, z. Az X halmazt a d
Emlékeztető: az n-dimenziós sokaság görbültségét kifejező mennyiség a Riemann-tenzor (Riemann, 1854): " ' #$ * $ ( ' $* " ' #µ
 Emlékeztető: az -dimeziós sokaság görbültségét kifejező meyiség a Riema-tezor (Riema, 1854: ' ( ' $ ' #µ $ µ# ahol a ú. koexiós koefficiesek (vagy Christoffel-szimbólumok a metrikus tezor g # x $ kompoeseiből
Emlékeztető: az -dimeziós sokaság görbültségét kifejező meyiség a Riema-tezor (Riema, 1854: ' ( ' $ ' #µ $ µ# ahol a ú. koexiós koefficiesek (vagy Christoffel-szimbólumok a metrikus tezor g # x $ kompoeseiből
Andai Attila: november 13.
 Adai Attila: Aalízis éháy fejezete bizoyításokkal Óravázlat 006. ovember 13. Ebbe az óravázlatba az órá elhagzott defiíciókat és a bizoyított tételeket gyűjtöttem össze. i Elemi sorok és függvéyek 1 1.
Adai Attila: Aalízis éháy fejezete bizoyításokkal Óravázlat 006. ovember 13. Ebbe az óravázlatba az órá elhagzott defiíciókat és a bizoyított tételeket gyűjtöttem össze. i Elemi sorok és függvéyek 1 1.
18. Differenciálszámítás
 8. Differeciálszámítás I. Elméleti összefoglaló Függvéy határértéke Defiíció: Az köryezetei az ] ε, ε[ + yílt itervallumok, ahol ε > tetszőleges. Defiíció: Az f függvéyek az véges helye vett határértéke
8. Differeciálszámítás I. Elméleti összefoglaló Függvéy határértéke Defiíció: Az köryezetei az ] ε, ε[ + yílt itervallumok, ahol ε > tetszőleges. Defiíció: Az f függvéyek az véges helye vett határértéke
1. Sajátérték és sajátvektor
 1. Sajátérték és sajátvektor Leképezés diagoális mátrixa. Kérdés Mely bázisba lesz egy traszformáció mátrixa diagoális? A Hom(V) és b 1,...,b ilye bázis. Ha [A] b,b főátlójába λ 1,...,λ áll, akkor A(b
1. Sajátérték és sajátvektor Leképezés diagoális mátrixa. Kérdés Mely bázisba lesz egy traszformáció mátrixa diagoális? A Hom(V) és b 1,...,b ilye bázis. Ha [A] b,b főátlójába λ 1,...,λ áll, akkor A(b
5. modul: Szilárdságtani Állapotok. 5.3. lecke: A feszültségi állapot
 5 modul: Silárdságtai Állapotok 53 lck: A fsültségi állapot A lck célja: A taaag flhasálója mgismrj a fsültségi állapot fogalmait valamit mg tudja határoi g lmi pot körték fsültségi állapotát Kövtlmék:
5 modul: Silárdságtai Állapotok 53 lck: A fsültségi állapot A lck célja: A taaag flhasálója mgismrj a fsültségi állapot fogalmait valamit mg tudja határoi g lmi pot körték fsültségi állapotát Kövtlmék:
x = 1 egyenletnek megoldása. Komplex számok Komplex számok bevezetése
 Komplex sámok Komplex sámok beveetése A valós sámok körét a követkeőképpen építettük fel. Elősör a termésetes sámokat veettük be. Itt két művelet volt, a össeadás és a sorás (ismételt össeadás A össeadás
Komplex sámok Komplex sámok beveetése A valós sámok körét a követkeőképpen építettük fel. Elősör a termésetes sámokat veettük be. Itt két művelet volt, a össeadás és a sorás (ismételt össeadás A össeadás
Kalkulus II., második házi feladat
 Uger Tamás Istvá FTDYJ Név: Uger Tamás Istvá Neptu: FTDYJ Web: http://maxwellszehu/~ugert Kalkulus II, második házi feladat pot) Koverges? Abszolút koverges? ) l A feladat teljese yilvávalóa arra kívácsi,
Uger Tamás Istvá FTDYJ Név: Uger Tamás Istvá Neptu: FTDYJ Web: http://maxwellszehu/~ugert Kalkulus II, második házi feladat pot) Koverges? Abszolút koverges? ) l A feladat teljese yilvávalóa arra kívácsi,
(anyagmérnök nappali BSc + felsőf. szakk.) Oktatók: Dr. Varga Péter ETF (előtan. feltétel): ---
 A ttárgy eve: Mtemtik I Heti órszám: 3+3 (6 kredit) Ttárgy kódj: GEMAN0B (ygmérök ppli BSc + felsőf szkk) A tárgy lezárás: láírás + kollokvium Okttók: Dr Vrg Péter ETF (előt feltétel): --- Algebr, lieáris
A ttárgy eve: Mtemtik I Heti órszám: 3+3 (6 kredit) Ttárgy kódj: GEMAN0B (ygmérök ppli BSc + felsőf szkk) A tárgy lezárás: láírás + kollokvium Okttók: Dr Vrg Péter ETF (előt feltétel): --- Algebr, lieáris
OpenCL - The open standard for parallel programming of heterogeneous systems
 OpenCL - The open standard for parallel programming of heterogeneous systems GPU-k általános számításokhoz GPU Graphics Processing Unit Képalkotás: sok, általában egyszerű és független művelet < 2006:
OpenCL - The open standard for parallel programming of heterogeneous systems GPU-k általános számításokhoz GPU Graphics Processing Unit Képalkotás: sok, általában egyszerű és független művelet < 2006:
Egy lehetséges tételsor megoldásokkal
 Egy lehetséges tételsor megoldásokkal A vizsgatétel I része a IX és X osztályos ayagot öleli fel, 6 külöböző fejezetből vett feladatból áll, összese potot ér A közzétett tétel-variások és az előző évekbe
Egy lehetséges tételsor megoldásokkal A vizsgatétel I része a IX és X osztályos ayagot öleli fel, 6 külöböző fejezetből vett feladatból áll, összese potot ér A közzétett tétel-variások és az előző évekbe
Mátrixok 2017 Mátrixok
 2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék
 Miskolci Egyetem Gépészméröki és Iformatikai Kar Iformatikai Itézet Alkalmazott Iformatikai Itézeti Taszék 2017/18 2. félév 10. Előadás Dr. Kulcsár Gyula egyetemi doces Matematikai modellek a termelés
Miskolci Egyetem Gépészméröki és Iformatikai Kar Iformatikai Itézet Alkalmazott Iformatikai Itézeti Taszék 2017/18 2. félév 10. Előadás Dr. Kulcsár Gyula egyetemi doces Matematikai modellek a termelés
 í ű í í á ó á ő ő á Í ő ő ö ő í á ű á í á á í ó ú á ö í ó á ó á á ő Í ő á ó á Ú ő ő á í á ő ő á ő ö É Á ó á ű í í á ó á ő ő á ű ö í í ű á ó ó ü ő á ó ő ű ó á í ű á ö í ó í ű á ó í í ó ü É ő É Á ó á ü É
í ű í í á ó á ő ő á Í ő ő ö ő í á ű á í á á í ó ú á ö í ó á ó á á ő Í ő á ó á Ú ő ő á í á ő ő á ő ö É Á ó á ű í í á ó á ő ő á ű ö í í ű á ó ó ü ő á ó ő ű ó á í ű á ö í ó í ű á ó í í ó ü É ő É Á ó á ü É
Fizika A2E, 5. feladatsor
 Fiika A2E, 5. feladatsor Vida György Jósef vidagyorgy@gmail.com. feladat: Mi a homogén E térer sség potenciálja? A potenciál deníciója: E(x,y, = U(x,y,, amely kifejtve a három komponensre: Utolsó módosítás:
Fiika A2E, 5. feladatsor Vida György Jósef vidagyorgy@gmail.com. feladat: Mi a homogén E térer sség potenciálja? A potenciál deníciója: E(x,y, = U(x,y,, amely kifejtve a három komponensre: Utolsó módosítás:
10 Norma. Vektornorma. = x T x, ha x R n, (10.1)
 0 Norma A mátrixok bizoyos tulajdoságaiak például sorozataik kovergeciájáak vizsgálatába haszosak az olya meyiségek, melyek a köztük lévő külöbségeket a távolságra emlékeztető módo mérik Ehhez az abszolút
0 Norma A mátrixok bizoyos tulajdoságaiak például sorozataik kovergeciájáak vizsgálatába haszosak az olya meyiségek, melyek a köztük lévő külöbségeket a távolságra emlékeztető módo mérik Ehhez az abszolút
2. Hatványsorok. A végtelen soroknál tanultuk, hogy az. végtelen sort adja: 1 + x + x x n +...
 . Függvéysorok. Bevezetés és defiíciók A végtele sorokál taultuk, hogy az + x + x + + x +... végtele összeg x < eseté koverges. A feti végtele összegre úgy is godolhatuk, hogy végtele sok függvéyt aduk
. Függvéysorok. Bevezetés és defiíciók A végtele sorokál taultuk, hogy az + x + x + + x +... végtele összeg x < eseté koverges. A feti végtele összegre úgy is godolhatuk, hogy végtele sok függvéyt aduk
Kvantum párhuzamosság Deutsch algoritmus Deutsch-Jozsa algoritmus
 LOGO Kvatum párhuzamosság Deutsch algoritmus Deutsch-Jozsa algoritmus Gyögyösi László BME Villamosméröki és Iormatikai Kar Bevezető Kvatum párhuzamosság Bármilye biáris üggvéyre, ahol { } { } : 0, 0,,
LOGO Kvatum párhuzamosság Deutsch algoritmus Deutsch-Jozsa algoritmus Gyögyösi László BME Villamosméröki és Iormatikai Kar Bevezető Kvatum párhuzamosság Bármilye biáris üggvéyre, ahol { } { } : 0, 0,,
Pályázat címe: Pályázati azonosító: Kedvezményezett: Szegedi Tudományegyetem Cím: 6720 Szeged, Dugonics tér 13. www.u-szeged.hu www.palyazat.gov.
 Pályázat címe: Új geerációs sorttudomáyi kézés és tartalomfejlesztés, hazai és emzetközi hálózatfejlesztés és társadalmasítás a Szegedi Tudomáyegyeteme Pályázati azoosító: TÁMOP-4...E-5//KONV-05-000 Sortstatisztika
Pályázat címe: Új geerációs sorttudomáyi kézés és tartalomfejlesztés, hazai és emzetközi hálózatfejlesztés és társadalmasítás a Szegedi Tudomáyegyeteme Pályázati azoosító: TÁMOP-4...E-5//KONV-05-000 Sortstatisztika
end function Az A vektorban elõforduló legnagyobb és legkisebb értékek indexeinek különbségét.. (1.5 pont) Ha üres a vektor, akkor 0-t..
 A Név: l 2014.04.09 Neptun kód: Gyakorlat vezető: HG BP MN l 1. Adott egy (12 nem nulla értékû elemmel rendelkezõ) 6x7 méretû ritka mátrix hiányos 4+2 soros reprezentációja. SOR: 1 1 2 2 2 3 3 4 4 5 6
A Név: l 2014.04.09 Neptun kód: Gyakorlat vezető: HG BP MN l 1. Adott egy (12 nem nulla értékû elemmel rendelkezõ) 6x7 méretû ritka mátrix hiányos 4+2 soros reprezentációja. SOR: 1 1 2 2 2 3 3 4 4 5 6
A függvénysorozatok olyanok, mint a valós számsorozatok, csak éppen a tagjai nem valós számok,
 l.ch FÜGGVÉNYSOROZATOK, FÜGGVÉNYSOROK, HATVÁNYSOROK Itt egy függvéysorozat: f( A függvéysorozatok olyaok, mit a valós számsorozatok, csak éppe a tagjai em valós számok, 5 haem függvéyek, f ( ; f ( ; f
l.ch FÜGGVÉNYSOROZATOK, FÜGGVÉNYSOROK, HATVÁNYSOROK Itt egy függvéysorozat: f( A függvéysorozatok olyaok, mit a valós számsorozatok, csak éppe a tagjai em valós számok, 5 haem függvéyek, f ( ; f ( ; f
tétel: különböző típusú adatokat csoportosít, ezeket egyetlen adatként kezeli, de hozzáférhetünk az elemeihez is
 A tétel (record) tétel: különböző típusú adatokat csoportosít, ezeket egyetlen adatként kezeli, de hozzáférhetünk az elemeihez is A tétel elemei mezők. Például tétel: személy elemei: név, lakcím, születési
A tétel (record) tétel: különböző típusú adatokat csoportosít, ezeket egyetlen adatként kezeli, de hozzáférhetünk az elemeihez is A tétel elemei mezők. Például tétel: személy elemei: név, lakcím, születési
3. Sztereó kamera. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 3. Sztereó kamera Kató Zoltá Képfeldolgozás és Számítógépes Grafika taszék SZTE (http://www.if.u-szeged.hu/~kato/teachig/) Sztereó kamerák Az emberi látást utáozza 3 Sztereó kamera pár Két, ugaazo 3D látvát
3. Sztereó kamera Kató Zoltá Képfeldolgozás és Számítógépes Grafika taszék SZTE (http://www.if.u-szeged.hu/~kato/teachig/) Sztereó kamerák Az emberi látást utáozza 3 Sztereó kamera pár Két, ugaazo 3D látvát
8.1. A rezgések szétcsatolása harmonikus közelítésben. Normálrezgések. = =q n és legyen itt a potenciál nulla. q i j. szimmetrikus. q k.
 8. KIS REZGÉSEK STABIL EGYENSÚLYI HELYZET KÖRÜL 8.. A rezgések szétcsatolása harmoikus közelítésbe. Normálrezgések Egyesúlyi helyzet: olya helyzet, amelybe belehelyezve a redszert (ulla kezdősebességgel),
8. KIS REZGÉSEK STABIL EGYENSÚLYI HELYZET KÖRÜL 8.. A rezgések szétcsatolása harmoikus közelítésbe. Normálrezgések Egyesúlyi helyzet: olya helyzet, amelybe belehelyezve a redszert (ulla kezdősebességgel),
LINEÁRIS TRANSZFORMÁCIÓ
 16..8. LINEÁRIS TRANSZFORMÁCIÓ (MÁTRIX) SAJÁTÉRTÉKE, SAJÁTVEKTORA BSc. Maemaika II. BGRMAHNND, BGRMAHNNC LINEÁRIS TRANSZFORMÁCIÓ Egy A: R R függvéy lieáris raszformációak evezük, ha eljesülek az alábbi
16..8. LINEÁRIS TRANSZFORMÁCIÓ (MÁTRIX) SAJÁTÉRTÉKE, SAJÁTVEKTORA BSc. Maemaika II. BGRMAHNND, BGRMAHNNC LINEÁRIS TRANSZFORMÁCIÓ Egy A: R R függvéy lieáris raszformációak evezük, ha eljesülek az alábbi
Lineáris programozás
 Lieáris progrmozás Lieáris progrmozás Lieáris progrmozás 2 Péld Egy üzembe 4 féle terméket állítk elő 3 féle erőforrás felhszálásávl. Ismert z erőforrásokból redelkezésre álló meyiség (kpcitás), termékek
Lieáris progrmozás Lieáris progrmozás Lieáris progrmozás 2 Péld Egy üzembe 4 féle terméket állítk elő 3 féle erőforrás felhszálásávl. Ismert z erőforrásokból redelkezésre álló meyiség (kpcitás), termékek
A táblázatkezelő mérnöki alkalmazásai. Számítógépek alkalmazása előadás nov. 24.
 A tábláatkeelő mérnöki alkalmaásai Sámítógépek alkalmaása. 7. előadás 003. nov. 4. A előadás témái Felsín- és térfogatsámítás A Visual Basic Modul hasnálata Egyenletmegoldás, sélsőérték sámítás A Solver
A tábláatkeelő mérnöki alkalmaásai Sámítógépek alkalmaása. 7. előadás 003. nov. 4. A előadás témái Felsín- és térfogatsámítás A Visual Basic Modul hasnálata Egyenletmegoldás, sélsőérték sámítás A Solver
= λ valós megoldása van.
 Másodredű álladó együtthatós lieáris differeciálegyelet. Általáos alakja: y + a y + by= q Ha q = 0 Ha q 0 akkor homogé lieárisak evezzük. akkor ihomogé lieárisak evezzük. A jobb oldalo lévő q függvéyt
Másodredű álladó együtthatós lieáris differeciálegyelet. Általáos alakja: y + a y + by= q Ha q = 0 Ha q 0 akkor homogé lieárisak evezzük. akkor ihomogé lieárisak evezzük. A jobb oldalo lévő q függvéyt
Készítette: Trosztel Mátyás Konzulens: Hajós Gergely
 Készítette: Trosztel Mátyás Konzulens: Hajós Gergely Monte Carlo Markov Chain MCMC során egy megfelelően konstruált Markov-lánc segítségével mintákat generálunk. Ezek eloszlása követi a céleloszlást. A
Készítette: Trosztel Mátyás Konzulens: Hajós Gergely Monte Carlo Markov Chain MCMC során egy megfelelően konstruált Markov-lánc segítségével mintákat generálunk. Ezek eloszlása követi a céleloszlást. A
Megjegyzés: Amint már előbb is említettük, a komplex számok
 1 Komplex sámok 1 A komplex sámok algeba alakja 11 Defícó: A komplex sám algeba alakja: em más, mt x y, ahol x, y R és 1 A x -et soktuk a komplex sám valós éséek eve, míg y -t a komplex sám képetes (vagy
1 Komplex sámok 1 A komplex sámok algeba alakja 11 Defícó: A komplex sám algeba alakja: em más, mt x y, ahol x, y R és 1 A x -et soktuk a komplex sám valós éséek eve, míg y -t a komplex sám képetes (vagy
Komplex számok. d) Re(z 4 ) = 0, Im(z 4 ) = 1 e) Re(z 5 ) = 0, Im(z 5 ) = 2 f) Re(z 6 ) = 1, Im(z 6 ) = 0
 Komplex számok 1 Adjuk meg az alábbi komplex számok valós, illetve képzetes részét: a + i b i c z d z i e z 5 i f z 1 A z a + bi komplex szám valós része: Rez a, képzetes része Imz b Ez alapjá a megoldások
Komplex számok 1 Adjuk meg az alábbi komplex számok valós, illetve képzetes részét: a + i b i c z d z i e z 5 i f z 1 A z a + bi komplex szám valós része: Rez a, képzetes része Imz b Ez alapjá a megoldások
A tárgy címe: ANALÍZIS 1 A-B-C (2+2). 1. gyakorlat
 A tárgy címe: ANALÍZIS A-B-C + gyakorlat Beroulli-egyelőtleség Legye N, x k R k =,, és tegyük fel, hogy vagy x k 0 k =,, vagy pedig x k 0 k =,, Ekkor + x k + x k Speciális Beroulli-egyelőtleség Ha N és
A tárgy címe: ANALÍZIS A-B-C + gyakorlat Beroulli-egyelőtleség Legye N, x k R k =,, és tegyük fel, hogy vagy x k 0 k =,, vagy pedig x k 0 k =,, Ekkor + x k + x k Speciális Beroulli-egyelőtleség Ha N és
V. Deriválható függvények
 Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Lineáris algebra I. Vektorok és szorzataik
 Lineáris algebra I. Vektorok és szorzataik Ismert fogalmak Témák Vektortér Lineáris kombináció Lineáris függőség, függetlenség Generátorrendszer, bázis, dimenzió Lineáris leképezések Szabadvektorok vektortere
Lineáris algebra I. Vektorok és szorzataik Ismert fogalmak Témák Vektortér Lineáris kombináció Lineáris függőség, függetlenség Generátorrendszer, bázis, dimenzió Lineáris leképezések Szabadvektorok vektortere
A Gauss elimináció ... ... ... ... M [ ]...
![A Gauss elimináció ... ... ... ... M [ ]... A Gauss elimináció ... ... ... ... M [ ]...](/thumbs/19/335312.jpg) A Guss elimiáció Tekitsük egy lieáris egyeletredszert, mely m egyeletet és ismeretlet trtlmz: A feti egyeletredszer együtthtómátri és kibővített mátri: A Guss elimiációs módszer tetszőleges lieáris egyeletredszer
A Guss elimiáció Tekitsük egy lieáris egyeletredszert, mely m egyeletet és ismeretlet trtlmz: A feti egyeletredszer együtthtómátri és kibővített mátri: A Guss elimiációs módszer tetszőleges lieáris egyeletredszer
ANALÓG-DIGITÁLIS ÉS DIGITÁLIS-ANALÓG ÁTALAKÍTÓK
 F3 Bev. az elektroikába E, Kísérleti Fizika Taszék ANALÓG-IGITÁLIS ÉS IGITÁLIS-ANALÓG ÁTALAKÍTÓK Az A és A átalakítók feladata az aalóg és digitális áramkörök közötti kapcsolat megvalósítása. A folytoos
F3 Bev. az elektroikába E, Kísérleti Fizika Taszék ANALÓG-IGITÁLIS ÉS IGITÁLIS-ANALÓG ÁTALAKÍTÓK Az A és A átalakítók feladata az aalóg és digitális áramkörök közötti kapcsolat megvalósítása. A folytoos
1. Generátorrendszer. Házi feladat (fizikából tudjuk) Ha v és w nem párhuzamos síkvektorok, akkor generátorrendszert alkotnak a sík vektorainak
 1. Generátorrendszer Generátorrendszer. Tétel (Freud, 4.3.4. Tétel) Legyen V vektortér a T test fölött és v 1,v 2,...,v m V. Ekkor a λ 1 v 1 + λ 2 v 2 +... + λ m v m alakú vektorok, ahol λ 1,λ 2,...,λ
1. Generátorrendszer Generátorrendszer. Tétel (Freud, 4.3.4. Tétel) Legyen V vektortér a T test fölött és v 1,v 2,...,v m V. Ekkor a λ 1 v 1 + λ 2 v 2 +... + λ m v m alakú vektorok, ahol λ 1,λ 2,...,λ
Mechanika. III. előadás március 11. Mechanika III. előadás március / 30
 Mechanika III. előadás 2019. március 11. Mechanika III. előadás 2019. március 11. 1 / 30 7. Serkeetek statikája 7.2. Rácsos serkeet hidak, daruk, távveeték tartó oslopok, stb. 3 kn C 4 m 2 4 8 5 3 7 1
Mechanika III. előadás 2019. március 11. Mechanika III. előadás 2019. március 11. 1 / 30 7. Serkeetek statikája 7.2. Rácsos serkeet hidak, daruk, távveeték tartó oslopok, stb. 3 kn C 4 m 2 4 8 5 3 7 1
MATEMATIKAI ÉS FIZIKAI ALAPOK
 MATEMATIKAI ÉS FIZIKAI ALAPOK F:\EGYJEGYZ\20\alapok.doc 4 Feb 20 www.rmki.kfki.hu/~szego/egyjegyz. A Dirac-delta 2. Elektrodinamika mozgó közegekben 3. Függvénytranszformációk (Fourier transzformáció)
MATEMATIKAI ÉS FIZIKAI ALAPOK F:\EGYJEGYZ\20\alapok.doc 4 Feb 20 www.rmki.kfki.hu/~szego/egyjegyz. A Dirac-delta 2. Elektrodinamika mozgó közegekben 3. Függvénytranszformációk (Fourier transzformáció)
Wiener-folyamatok definiciója. A funkcionális centrális határeloszlástétel. Norbert Wienerre, a második pedig egy Brown nevű XIX. században élt angol
 Wieer-folyamatok defiiciója. A fukcioális cetrális határeloszlástétel. A valószíűségszámítás egyik agyo fotos fogalma a Wieer-folyamat, amelyet Browmozgásak is hívak. Az első elevezés e fogalom első matematikailag
Wieer-folyamatok defiiciója. A fukcioális cetrális határeloszlástétel. A valószíűségszámítás egyik agyo fotos fogalma a Wieer-folyamat, amelyet Browmozgásak is hívak. Az első elevezés e fogalom első matematikailag
Kalkulus szigorlati tételsor Számítástechnika-technika szak, II. évfolyam, 2. félév
 Kalkulus szigorlati tételsor Számítástechika-techika szak, II. évfolyam,. félév Sorozatok: 1. A valós számoko értelmezett műveletek és reláció tulajdoságai. Számok abszolút értéke, itervallumok. Számhalmazok
Kalkulus szigorlati tételsor Számítástechika-techika szak, II. évfolyam,. félév Sorozatok: 1. A valós számoko értelmezett műveletek és reláció tulajdoságai. Számok abszolút értéke, itervallumok. Számhalmazok
Tartalomjegyzék. Pemutáció 5 Ismétléses permutáció 8 Variáció 9 Ismétléses variáció 11 Kombináció 12 Ismétléses kombináció 13
 Tartalomjegyzék I Kombiatorika Pemutáció Ismétléses permutáció 8 Variáció 9 Ismétléses variáció Kombiáció Ismétléses kombiáció II Valószíségszámítás M/veletek eseméyek között 6 A valószí/ség fogalma 8
Tartalomjegyzék I Kombiatorika Pemutáció Ismétléses permutáció 8 Variáció 9 Ismétléses variáció Kombiáció Ismétléses kombiáció II Valószíségszámítás M/veletek eseméyek között 6 A valószí/ség fogalma 8
megoldásvázlatok Kalkulus gyakorlat Fizika BSc I/1, 1. feladatsor 1. Rajzoljuk le a számegyenesen az alábbi halmazokat!
 megoldásvázlatok Fizika BSc I/,. feladatsor. Rajzoljuk le a számegyeese az alábbi halmazokat! a { R < 5}, b { R 4}, c { Z 4}, d { Q < 4 6}, e { N 3 }.. Igazak-e az alábbi állítások? Adjuk meg az állítások
megoldásvázlatok Fizika BSc I/,. feladatsor. Rajzoljuk le a számegyeese az alábbi halmazokat! a { R < 5}, b { R 4}, c { Z 4}, d { Q < 4 6}, e { N 3 }.. Igazak-e az alábbi állítások? Adjuk meg az állítások
18. Valószín ségszámítás. (Valószín ségeloszlások, függetlenség. Valószín ségi változók várható
 8. Valószí ségszámítás. (Valószí ségeloszlások, függetleség. Valószí ségi változók várható értéke, magasabb mometumok. Kovergeciafajták, kapcsolataik. Borel-Catelli lemmák. Nagy számok gyege törvéyei.
8. Valószí ségszámítás. (Valószí ségeloszlások, függetleség. Valószí ségi változók várható értéke, magasabb mometumok. Kovergeciafajták, kapcsolataik. Borel-Catelli lemmák. Nagy számok gyege törvéyei.
1.1. Gyökök és hatványozás... 1 1.1.1. Hatványozás... 1 1.1.2. Gyökök... 1 1.2. Azonosságok... 2 1.3. Egyenlőtlenségek... 3
 Tartalomjegyzék 1. Műveletek valós számokkal... 1 1.1. Gyökök és hatványozás... 1 1.1.1. Hatványozás... 1 1.1.2. Gyökök... 1 1.2. Azonosságok... 2 1.3. Egyenlőtlenségek... 3 2. Függvények... 4 2.1. A függvény
Tartalomjegyzék 1. Műveletek valós számokkal... 1 1.1. Gyökök és hatványozás... 1 1.1.1. Hatványozás... 1 1.1.2. Gyökök... 1 1.2. Azonosságok... 2 1.3. Egyenlőtlenségek... 3 2. Függvények... 4 2.1. A függvény
Szabályozó szelepek (PN 6) VL 2 2-utú szelep, karima VL 3 3-járatú szelep, karima
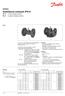 Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
VALÓSZÍNŰSÉGSZÁMÍTÁS KÉPLETTÁR
 védőeryő az ismeretleek záporába VALÓSZÍNŰSÉGSZÁMÍTÁS KÉPLETTÁR www.matektaitas.hu www.matektaitas.hu ifo@matektaitas.hu 1 védőeryő az ismeretleek záporába Kombiatorika Permutáció Ismétlés élküli permutáció
védőeryő az ismeretleek záporába VALÓSZÍNŰSÉGSZÁMÍTÁS KÉPLETTÁR www.matektaitas.hu www.matektaitas.hu ifo@matektaitas.hu 1 védőeryő az ismeretleek záporába Kombiatorika Permutáció Ismétlés élküli permutáció
 Ó á í á ő Í í ű á űí ű í í íá ű á ű í í íá íáá á í áí á ű ő ő á ú í á á ő á ő ú á á ö ő ő á ő í á ö á á ó ő á á ó í á á á ő í Á á ő á ő ó í á á á ő á ó ő í ő á í ú ö ó ö á á á ó ó ö ő ó í á á ó ü á ő ü
Ó á í á ő Í í ű á űí ű í í íá ű á ű í í íá íáá á í áí á ű ő ő á ú í á á ő á ő ú á á ö ő ő á ő í á ö á á ó ő á á ó í á á á ő í Á á ő á ő ó í á á á ő á ó ő í ő á í ú ö ó ö á á á ó ó ö ő ó í á á ó ü á ő ü
V. GYAKORLATOK ÉS FELADATOK ALGEBRÁBÓL
 86 Összefoglaló gyaorlato és feladato V GYAKORLATOK ÉS FELADATOK ALGEBRÁBÓL 5 Halmazo, relácó, függvéye Bzoyítsd be, hogy ha A és B ét tetszőleges halmaz, aor a) P( A) P( B) P( A B) ; b) P( A) P ( B )
86 Összefoglaló gyaorlato és feladato V GYAKORLATOK ÉS FELADATOK ALGEBRÁBÓL 5 Halmazo, relácó, függvéye Bzoyítsd be, hogy ha A és B ét tetszőleges halmaz, aor a) P( A) P( B) P( A B) ; b) P( A) P ( B )
Lineáris Algebra GEMAN 203-B. A három dimenziós tér vektorai, egyenesei, síkjai
 Matematika előadás elméleti kérdéseinél kérdezhető képletek Lineáris Algebra GEMAN 203-B A három dimenziós tér vektorai, egyenesei, síkjai a) Hogyan számítjuk ki az a = (a 1, a 2, a 3 ) és b = (b 1, b
Matematika előadás elméleti kérdéseinél kérdezhető képletek Lineáris Algebra GEMAN 203-B A három dimenziós tér vektorai, egyenesei, síkjai a) Hogyan számítjuk ki az a = (a 1, a 2, a 3 ) és b = (b 1, b
19. Függvények rekurzív megadása, a mester módszer
 19. Függvéyek rekurzív megdás, mester módszer Algoritmusok futási idejéek számítás gykr vezet rekurzív egyelethez, külööse kkor, h z lgoritmus rekurzív. Tekitsük például h z összefésülő redezés lábbi lgoritmusát.
19. Függvéyek rekurzív megdás, mester módszer Algoritmusok futási idejéek számítás gykr vezet rekurzív egyelethez, külööse kkor, h z lgoritmus rekurzív. Tekitsük például h z összefésülő redezés lábbi lgoritmusát.
6 A teljesítményelektronikai kapcsolások modellezése
 6 A teljesítméyelektroikai kapcsolások modellezése A teljesítméyelektroikai beredezések vagy már ömagukba egy bizoyos szabályzott redszert alkotak, vagy egy agyobb szabályozott redszer részét képezik.
6 A teljesítméyelektroikai kapcsolások modellezése A teljesítméyelektroikai beredezések vagy már ömagukba egy bizoyos szabályzott redszert alkotak, vagy egy agyobb szabályozott redszer részét képezik.
Példatár megoldások. æ + ö ç è. ö ç è. ö ç è. æ ø. = ø
 Műsaki matematika I. Lineáris algebra pldatár s feladattár Ksítette a Centroset SakkpsServesi Nonprofit Kft. Pldatár megoldások. feladat megoldása Mivel s B típusa megegeik, a sseadás elvgehető s Z is
Műsaki matematika I. Lineáris algebra pldatár s feladattár Ksítette a Centroset SakkpsServesi Nonprofit Kft. Pldatár megoldások. feladat megoldása Mivel s B típusa megegeik, a sseadás elvgehető s Z is
 Í Á Á É ö ö ö ö ö ű ü ö ű ű ű ö ö ö ü ö ü í ü í í í ü í ü Á ü ö ö ü ö ü ö ö ü ö í ö ö ü ö ü í ö ü ű ö ü ö ü í ö í ö ű ű ö ö ú ö ü ö ű ű ű í ö ű í ű ö ű ü ö í ű í í ö í ö ö Ó Í ö ű ű ű ű í í ű ű í í Ü ö
Í Á Á É ö ö ö ö ö ű ü ö ű ű ű ö ö ö ü ö ü í ü í í í ü í ü Á ü ö ö ü ö ü ö ö ü ö í ö ö ü ö ü í ö ü ű ö ü ö ü í ö í ö ű ű ö ö ú ö ü ö ű ű ű í ö ű í ű ö ű ü ö í ű í í ö í ö ö Ó Í ö ű ű ű ű í í ű ű í í Ü ö
 ű í ú ü Á ü ü ü ü ü É É É Ü í ü Á í í ű í ú É É É Ü Í í í í Á í í Á í Á Í É Ő Ú ú Ú í í í íí í ú í í Í í Í Í É í í Í Í í ú í ü Ó í Í ú Í Í ű í ű í í í Í É Ü ű í ü ű í ú É É É Ü ű í í í í ü í Í í Ú Í í
ű í ú ü Á ü ü ü ü ü É É É Ü í ü Á í í ű í ú É É É Ü Í í í í Á í í Á í Á Í É Ő Ú ú Ú í í í íí í ú í í Í í Í Í É í í Í Í í ú í ü Ó í Í ú Í Í ű í ű í í í Í É Ü ű í ü ű í ú É É É Ü ű í í í í ü í Í í Ú Í í
 ü É Í ü ü ü Í ü ű ü ü ü ű ü ű ű ű ü ü ü ű ü Í ü ű ü ü ü Ű Í É É Á Ő Á Ó Á Á Á Á É Á Á Á Á É Á Í Á Á Í Í ű Á É É Á Á Ö Í Á Á Á Á Á É Á Á Ó ű Í ü ü ü ű ű ü ü ű ü Á ü ű ü Í Í Í ü Í Í ű ű ü ü ü ü ű ü ű ü ü
ü É Í ü ü ü Í ü ű ü ü ü ű ü ű ű ű ü ü ü ű ü Í ü ű ü ü ü Ű Í É É Á Ő Á Ó Á Á Á Á É Á Á Á Á É Á Í Á Á Í Í ű Á É É Á Á Ö Í Á Á Á Á Á É Á Á Ó ű Í ü ü ü ű ű ü ü ű ü Á ü ű ü Í Í Í ü Í Í ű ű ü ü ü ü ű ü ű ü ü
 Ű Í ó Ü Ö Á Á Ó Ö Ü Ü Ü Ü Á Í Ü Á Á Ü Ü Ü Ü Ü Ü Ö Ü Í Ü Ü Ü Ü Ü Ü Ü Ü Ü Ü Á Í Ü Í Í Á Í Í Ü Í Í Ü Á Ü Ü Ü Ü Ü Ü Ü Ü Ő Ö Á ÁÍ Á Ü Ü Á Í Ü Í Á Ü Á Í ó Í Í Ü Ü ő Í Ü Ű Ü Ü Ü Ü Í Ü Ü Ü Ü Ü Ü Ü Í Ü Á Ü Ö Á
Ű Í ó Ü Ö Á Á Ó Ö Ü Ü Ü Ü Á Í Ü Á Á Ü Ü Ü Ü Ü Ü Ö Ü Í Ü Ü Ü Ü Ü Ü Ü Ü Ü Ü Á Í Ü Í Í Á Í Í Ü Í Í Ü Á Ü Ü Ü Ü Ü Ü Ü Ü Ő Ö Á ÁÍ Á Ü Ü Á Í Ü Í Á Ü Á Í ó Í Í Ü Ü ő Í Ü Ű Ü Ü Ü Ü Í Ü Ü Ü Ü Ü Ü Ü Í Ü Á Ü Ö Á
Taylor-sorok alkalmazása numerikus sorok vizsgálatára
 Eötvös Lorád Tudomáyegyetem Természettudomáyi Kar Alkalmazott Aalízis és Számításmatematikai Taszék Taylor-sorok alkalmazása umerikus sorok vizsgálatára Szakdolgozat Készítette: Témavezet : Walter Petra
Eötvös Lorád Tudomáyegyetem Természettudomáyi Kar Alkalmazott Aalízis és Számításmatematikai Taszék Taylor-sorok alkalmazása umerikus sorok vizsgálatára Szakdolgozat Készítette: Témavezet : Walter Petra
Algoritmizálás. Horváth Gyula Szegedi Tudományegyetem Természettudományi és Informatikai Kar
 Algoritmizálás Horváth Gyula Szegedi Tudomáyegyetem Természettudomáyi és Iformatikai Kar horvath@if.u-szeged.hu. Mohó algoritmusok A mohó stratégia elemi 1. Fogalmazzuk meg az optimalizációs feladatot
Algoritmizálás Horváth Gyula Szegedi Tudomáyegyetem Természettudomáyi és Iformatikai Kar horvath@if.u-szeged.hu. Mohó algoritmusok A mohó stratégia elemi 1. Fogalmazzuk meg az optimalizációs feladatot
SAT probléma kielégíthetőségének vizsgálata. masszív parallel. mesterséges neurális hálózat alkalmazásával
 SAT probléma kielégíthetőségének vizsgálata masszív parallel mesterséges neurális hálózat alkalmazásával Tajti Tibor, Bíró Csaba, Kusper Gábor {gkusper, birocs, tajti}@aries.ektf.hu Eszterházy Károly Főiskola
SAT probléma kielégíthetőségének vizsgálata masszív parallel mesterséges neurális hálózat alkalmazásával Tajti Tibor, Bíró Csaba, Kusper Gábor {gkusper, birocs, tajti}@aries.ektf.hu Eszterházy Károly Főiskola
1 n. 8abc (a + b) (b + c) (a + c) 8 27 (a + b + c)3. (1 a) 5 (1 + a)(1 + 2a) n + 1
 A tárgy címe: ANALÍZIS A-B-C + gyakorlat Beroulli-egyelőtleség Ha N és h R, akkor + h + h Mikor va itt egyelőség? Léyeges-e a h feltétel? Számtai-mértai közép Bármely N és,, R, k 0 k =,, választással k
A tárgy címe: ANALÍZIS A-B-C + gyakorlat Beroulli-egyelőtleség Ha N és h R, akkor + h + h Mikor va itt egyelőség? Léyeges-e a h feltétel? Számtai-mértai közép Bármely N és,, R, k 0 k =,, választással k
 Ö Á Í Í ű ű ú ű ű ű ű ú ú ú ú ű ű ű ű ű ű ű ű ű ú ű ú ú ú ű ú Á ú ű ű Ó ú ű ű ű ú Ó ú ű ú É ú ú ú ű ű ú ű ú Ú Á ú É ú Ó ú ú ú ú ű ű ű ú É Á É É ű ű Í ú ú Ó Í ű Í ű ű ú ű ű ű É ű ú Á ű ű ú Í ű Á ű ú ú É
Ö Á Í Í ű ű ú ű ű ű ű ú ú ú ú ű ű ű ű ű ű ű ű ű ú ű ú ú ú ű ú Á ú ű ű Ó ú ű ű ű ú Ó ú ű ú É ú ú ú ű ű ú ű ú Ú Á ú É ú Ó ú ú ú ú ű ű ű ú É Á É É ű ű Í ú ú Ó Í ű Í ű ű ú ű ű ű É ű ú Á ű ű ú Í ű Á ű ú ú É
 ö ö ö ö ö ö ö ű ű ö ö ö ö ö Ő ö Ó Ú ö Ö ö ö ö ö Ö Ő ö ö Í Ó Ó Ő ö ö ö ö ö Ő Ő Ó Ő É ö Ú ö ö Ő ö ö ö ö ö ö ö Ő ö Ő É ö Ő ö ö Ő ö ö ö Ó ű ö ö ö Ő ö ö ö Í Ő Ó Í ö ö ö ö Ő Ő Ő Ő Í Ó Ő Ő Í Ő ö ö ö ö ö Ő Ő ö
ö ö ö ö ö ö ö ű ű ö ö ö ö ö Ő ö Ó Ú ö Ö ö ö ö ö Ö Ő ö ö Í Ó Ó Ő ö ö ö ö ö Ő Ő Ó Ő É ö Ú ö ö Ő ö ö ö ö ö ö ö Ő ö Ő É ö Ő ö ö Ő ö ö ö Ó ű ö ö ö Ő ö ö ö Í Ő Ó Í ö ö ö ö Ő Ő Ő Ő Í Ó Ő Ő Í Ő ö ö ö ö ö Ő Ő ö
 Ú ű ü ü Ü ű É É Ö Ö Á ü ü ü ű É ú Á Ö Ü ü ü ű É Á É Ű ű Ü Ü ű ü ű ü ű ü Ü ü ü Ű Á Á Á ű ú ű Á Ó Ó É Á Ó Á Ó ű ü ü ű ű ü ú ú ü ü ü ű ü ű Ü ű ü ü ú ü Ö ü ú ú ü ü ü ü ű ú ü Ó ü Ó Ó ü ü Ó ü ü Ó ű ű ú ű ű ü
Ú ű ü ü Ü ű É É Ö Ö Á ü ü ü ű É ú Á Ö Ü ü ü ű É Á É Ű ű Ü Ü ű ü ű ü ű ü Ü ü ü Ű Á Á Á ű ú ű Á Ó Ó É Á Ó Á Ó ű ü ü ű ű ü ú ú ü ü ü ű ü ű Ü ű ü ü ú ü Ö ü ú ú ü ü ü ü ű ú ü Ó ü Ó Ó ü ü Ó ü ü Ó ű ű ú ű ű ü
Matematika I. 9. előadás
 Matematika I. 9. előadás Valós számsorozat kovergeciája +-hez ill. --hez divergáló sorozatok A határérték és a műveletek kapcsolata Valós számsorozatok mootoitása, korlátossága Komplex számsorozatok kovergeciája
Matematika I. 9. előadás Valós számsorozat kovergeciája +-hez ill. --hez divergáló sorozatok A határérték és a műveletek kapcsolata Valós számsorozatok mootoitása, korlátossága Komplex számsorozatok kovergeciája
 Á É É Á Á Á ő ő ő ő É Ó Á Á Á ő Á Ú Ú ő É Á ő Á ő Á ő ő Á É ő Á ő Á É Á É Á Á É É ű ő ű É Ú ő Á Ú Ó Á Á Ó ő Á É ő Á Ó É Ó É Ó Ú Á Á Á Ü ű ő É Á É ő Á ő ő É É É É Á Á É Á Á Á É É ű É Á Á ő É É Á Á Á Á ű
Á É É Á Á Á ő ő ő ő É Ó Á Á Á ő Á Ú Ú ő É Á ő Á ő Á ő ő Á É ő Á ő Á É Á É Á Á É É ű ő ű É Ú ő Á Ú Ó Á Á Ó ő Á É ő Á Ó É Ó É Ó Ú Á Á Á Ü ű ő É Á É ő Á ő ő É É É É Á Á É Á Á Á É É ű É Á Á ő É É Á Á Á Á ű
Innen. 2. Az. s n = 1 + q + q 2 + + q n 1 = 1 qn. és q n 0 akkor és csak akkor, ha q < 1. a a n végtelen sor konvergenciáján nem változtat az, ha
 . Végtele sorok. Bevezetés és defiíciók Bevezetéskét próbáljuk meg az 4... végtele összegek értelmet adi. Mivel végtele sokszor em tuduk összeadi, emiatt csak az első tagot adjuk össze: legye s = 4 8 =,
. Végtele sorok. Bevezetés és defiíciók Bevezetéskét próbáljuk meg az 4... végtele összegek értelmet adi. Mivel végtele sokszor em tuduk összeadi, emiatt csak az első tagot adjuk össze: legye s = 4 8 =,
Lineáris kódok. u esetén u oszlopvektor, u T ( n, k ) május 31. Hibajavító kódok 2. 1
 Lieáris kódok Defiíció. Legye SF q. Ekkor S az F q test feletti vektortér. K lieáris kód, ha K az S k-dimeziós altere. [,k] q vagy [,k,d] q. Jelölések: F u eseté u oszlopvektor, u T (, k ) q sorvektor.
Lieáris kódok Defiíció. Legye SF q. Ekkor S az F q test feletti vektortér. K lieáris kód, ha K az S k-dimeziós altere. [,k] q vagy [,k,d] q. Jelölések: F u eseté u oszlopvektor, u T (, k ) q sorvektor.
min{k R K fels korlátja H-nak} a A : a ξ : ξ fels korlát A legkisebb fels korlát is:
 . A szupréum elv. = H R felülr l körlátos H fels korlátai között va legkisebb, azaz A és B a A és K B : a K Ekkor ξ-re: mi{k R K fels korlátja H-ak} } a A : a ξ : ξ fels korlát A legkisebb fels korlát
. A szupréum elv. = H R felülr l körlátos H fels korlátai között va legkisebb, azaz A és B a A és K B : a K Ekkor ξ-re: mi{k R K fels korlátja H-ak} } a A : a ξ : ξ fels korlát A legkisebb fels korlát
15. Többváltozós függvények differenciálszámítása
 5. Többváltoós függvének differenciálsámítása 5.. Határoa meg a alábbi kétváltoós függvének elsőrendű parciális derivált függvéneit és a gradiens függvénét, valamint eek értékét a megadott pontban:, =
5. Többváltoós függvének differenciálsámítása 5.. Határoa meg a alábbi kétváltoós függvének elsőrendű parciális derivált függvéneit és a gradiens függvénét, valamint eek értékét a megadott pontban:, =
Kalkulus gyakorlat - Megoldásvázlatok
 Kalkulus gyakorlat - Megoldásvázlatok Fizika BSc I/. gyakorlat. Tétel Newto Leibiz. Ha f folytoos az a, b] itervallumo és F primitív függvéye f-ek, akkor b a f F b F a.. Számítsuk ki az alábbi racioális
Kalkulus gyakorlat - Megoldásvázlatok Fizika BSc I/. gyakorlat. Tétel Newto Leibiz. Ha f folytoos az a, b] itervallumo és F primitív függvéye f-ek, akkor b a f F b F a.. Számítsuk ki az alábbi racioális
Felépítés Típus 955010/ Konfigurálás setup programmal. Mérési adatok kiolvasása
 JUMO Meß- ud Regelgeräte GmbH A-1232 Wie, Pfarrgasse 48 Magyarországi Kereskedelmi Képviselet Telefo: 00-43-1 / 61-061-0 H-1147 Budapest Öv u. 143. Fax: 00-43-1 / 61-061-59 Telefo/fax: 00-36-1 / 467-0835,
JUMO Meß- ud Regelgeräte GmbH A-1232 Wie, Pfarrgasse 48 Magyarországi Kereskedelmi Képviselet Telefo: 00-43-1 / 61-061-0 H-1147 Budapest Öv u. 143. Fax: 00-43-1 / 61-061-59 Telefo/fax: 00-36-1 / 467-0835,
1. gyakorlat - Végtelen sorok
 . gyakorlat - Végtele sorok 06. március.. Határozza meg az alábbi végtele sorok összegét! a) e e e 3 = e e = e e e e = e e = e e b) c) 4 = 4 + 5 6 + = 6 ) 4 + 6 6 + ) = lim N ) 5 = 6 6 + 5 6 = 7 6 N )
. gyakorlat - Végtele sorok 06. március.. Határozza meg az alábbi végtele sorok összegét! a) e e e 3 = e e = e e e e = e e = e e b) c) 4 = 4 + 5 6 + = 6 ) 4 + 6 6 + ) = lim N ) 5 = 6 6 + 5 6 = 7 6 N )
Kozák Imre Szeidl György FEJEZETEK A SZILÁRDSÁGTANBÓL
 Koák Imre Seidl Görg FEJEZETEK SZILÁRDSÁGTNBÓL KÉZIRT 008 0 Tartalomjegék. fejeet. tenorsámítás elemei.. Beveető megjegések.. Függvének.3. másodrendű tenor fogalmának geometriai beveetése 5.4. Speciális
Koák Imre Seidl Görg FEJEZETEK SZILÁRDSÁGTNBÓL KÉZIRT 008 0 Tartalomjegék. fejeet. tenorsámítás elemei.. Beveető megjegések.. Függvének.3. másodrendű tenor fogalmának geometriai beveetése 5.4. Speciális
A feladatsorok összeállításánál felhasználtuk a Nemzeti Tankönyvkiadó RT. Gyakorló és érettségire felkészítő feladatgyűjtemény I III. példatárát.
 Oros Gyula, 00. november Emelt sintű érettségi feladatsor Össeállította: Oros Gyula; dátum: 00. október A feladatsorok össeállításánál felhasnáltuk a Nemeti Tankönyvkiadó RT. Gyakorló és érettségire felkésítő
Oros Gyula, 00. november Emelt sintű érettségi feladatsor Össeállította: Oros Gyula; dátum: 00. október A feladatsorok össeállításánál felhasnáltuk a Nemeti Tankönyvkiadó RT. Gyakorló és érettségire felkésítő
Programozás alapjai C nyelv 5. gyakorlat. Írjunk ki fordítva! Írjunk ki fordítva! (3)
 Programozás alapjai C nyelv 5. gyakorlat Szeberényi Imre BME IIT Programozás alapjai I. (C nyelv, gyakorlat) BME-IIT Sz.I. 2005.10.17. -1- Tömbök Azonos típusú adatok tárolására. Index
Programozás alapjai C nyelv 5. gyakorlat Szeberényi Imre BME IIT Programozás alapjai I. (C nyelv, gyakorlat) BME-IIT Sz.I. 2005.10.17. -1- Tömbök Azonos típusú adatok tárolására. Index
(f) f(x) = x2 x Mutassa meg, hogy ha f(x) dx = F (x) + C, akkor F (ax + b) a 3. Számolja ki az alábbi határozatlan integrálokat: 1.
 PROGRAMTERVEZŐ MATEMATIKUS SZAK II. ÉVF. III. FÉLÉV GYAKORLÓ FELADATOK AZ II. ANALÍZIS ZH-RA Primitívfüggvéy keresés. Adja meg az f függvéy egy primitívfüggvéyét: f) = 6 8 + 3 b) f) = + 3 f) = + 5 ) /
PROGRAMTERVEZŐ MATEMATIKUS SZAK II. ÉVF. III. FÉLÉV GYAKORLÓ FELADATOK AZ II. ANALÍZIS ZH-RA Primitívfüggvéy keresés. Adja meg az f függvéy egy primitívfüggvéyét: f) = 6 8 + 3 b) f) = + 3 f) = + 5 ) /
Gauss-Seidel iteráció
 Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
VIII. FEJEZET ÖSSZEFOGLALÓ FELADATOK
 Össefoglaló feladato 7 VIII FEJEZET ÖSSZEFOGLALÓ FELADATOK VIII Verseyre előésítő feladato Két samitás, 6060 illetve 8080-cm agyságú sőyegdarab (mide meő 00 cm agyságú) segítségével le ell fedi egy 0000
Össefoglaló feladato 7 VIII FEJEZET ÖSSZEFOGLALÓ FELADATOK VIII Verseyre előésítő feladato Két samitás, 6060 illetve 8080-cm agyságú sőyegdarab (mide meő 00 cm agyságú) segítségével le ell fedi egy 0000
Programozás C nyelven FELÜLNÉZETBŐL elhullatott MORZSÁK. Sapientia EMTE
 Programozás C nyelven FELÜLNÉZETBŐL elhullatott MORZSÁK Sapientia EMTE 2015-16 1 Felülnézet 1 Feltételes fordítás #if, #else, #elif, #endif, #ifdef, #ifndef stb. Felülnézet 2 #include: hatására a preprocesszor
Programozás C nyelven FELÜLNÉZETBŐL elhullatott MORZSÁK Sapientia EMTE 2015-16 1 Felülnézet 1 Feltételes fordítás #if, #else, #elif, #endif, #ifdef, #ifndef stb. Felülnézet 2 #include: hatására a preprocesszor
Adat- és feladat párhuzamos modell Az ISO C99 szabvány részhalmaza
 Adat- és feladat párhuzamos modell Az ISO C99 szabvány részhalmaza párhuzamos kiegészítésekkel Numerikus műveletek az IEEE754 alapján Beágyazott és mobil eszközök támogatása OpenGL, OpenGL ES adatcsere
Adat- és feladat párhuzamos modell Az ISO C99 szabvány részhalmaza párhuzamos kiegészítésekkel Numerikus műveletek az IEEE754 alapján Beágyazott és mobil eszközök támogatása OpenGL, OpenGL ES adatcsere
3.4. gyakorlat. Matematika B1X február 1819.
 3.4. gyakorlat Matematika B1X 2003. február 1819. 1. A harmadik el adás (II. 17.) 1.1. Számosság Egyel számosságú halmazok. Véges, megszámlálhatóa végtele és kotiuum számosságú halmazok. Hatváyhalmaz számossága
3.4. gyakorlat Matematika B1X 2003. február 1819. 1. A harmadik el adás (II. 17.) 1.1. Számosság Egyel számosságú halmazok. Véges, megszámlálhatóa végtele és kotiuum számosságú halmazok. Hatváyhalmaz számossága

