ACÉLSZERKEZETÛ TERMÉNYTÁROLÓ SILÓK MÉRETEZÉSE
|
|
|
- Petra Juhász
- 6 évvel ezelőtt
- Látták:
Átírás
1 ÉPÍTÉSÜGY ÁGAZAT MÛSZAK RÁNYELV M ACÉLSZERKEZETÛ TERMÉNYTÁROLÓ SLÓK MÉRETEZÉSE ÉPÍTÉSÜGY TÁJÉKOZATÁS KÖZPONT
2 BUDAPEST, 978 Készült az ÉVM Mûszaki Fejlesztési Fõosztál megbízásából Kidolgozta DR. HUNYAD FERENC FT 30-60/50 DR. NAGY SÁNDOR BME 664-0/-76 az Építésügi Szabánosítási Központ részérõl közremûködött BARSA ÁRPÁD ÉSZK 85-5/44
3
4 ÉPÍTÉSÜGY ÁGAZAT MÛSZAK RÁNYELV ACÉLSZERKEZETÛ TERMÉNYTÁROLÓ SLÓK MÉRETEZÉSE M G0 ÉPÍTÉSÜGY SZABVÁNYOSÍTÁS KÖZPONT Ez az építésügi ágazati Mûszaki ránel (a köetkezõkben: ránel) olan acélszerkezetû silók számítási és méretezési feladataira onatkozik, amelek gabona ag egéb szemestermén, illete dercés, ag összetapadásra hajlamos, porszerû terménanagok (liszt, gríz, porcukor stb.) tárolására szolgálnak és amelek függõleges oldalfalakkal rendelkeznek. A függõleges oldalfalakra onatkozó számítási eljárások feltételezik, hog a tárolt anag a ízszintes fenékben mûködõ szerkezettel üríthetõ. Ez az ránel a tölcsér erõjátékára és a tölcsér okozta hatások izsgálatára nem onatkozik. A silók acél anagára onatkozóan az MSZ 504/ elõírásait kell alkalmazni, az ott felsoroltaknál gengébb minõségû acélanagot csak a határfeszültségek megfelelõ csökkentése mellett és csak kiételesen lehet felhasználni. Ez az ránel csak olan speciális izsgálatokat érint, ameleket az MSZ 504/ nem tartalmaz. Ezek mellett minden olan izsgálatot is el kell égezni, amelet az MSZ 504/ felsorol. A jóáhagás idõpontja: 978. május hó A hatálbalépés idõpontja: 978. szeptember.
5 5 M TARTALOMJEGYZÉK. Fogalmak, meghatározások...7. A tárolt anagok által okozott nomások számítása A szélnomás figelembeétele A hõmérsékletáltozás figelembeétele A mértékadó terhelési állapot számítása A silócella függõleges falaiban fellépõ igénbeételek számítása Összehasonlító feszültség számítása Kapcsolatok számítása Korrózióédelem...4
6 M FOGALMAK, MEGHATÁROZÁSOK.. Átboltozódás A tárolt anag azon tulajdonsága, hog a siló-oldalfalakon kifejtett nomóerõ köetkeztében, boltíszerûen dolgozó nomott zóna fejlõdik ki benne, s az ürítéskor a nomott zóna alól kifolán a tárolt anag, az oldalfalakra kifejtett nomás heli jelleggel, nag értékkel alakul ki... Szimmetrikus az átboltozódás, ha az oldalfalakra kifejtett nomás körszimmetrikus ag kettõsen szimmetrikus... Aszimmetrikus az átboltozódás, ha a nomott zóna felülrõl néze nem körszimmetrikus, sõt eges pontokban hiánozhat is a nomott zóna és íg térbeli átboltozódás alakul ki... Pneumatikus ürítés Ha a tárolt anag saját súla réén nem, ag csak részben üríthetõ, mert a belsõ súrlódási szög miatti oldalhatás ezt megakadálozza, leegõt kell - arra alkalmas módon - befúatni, miáltal a tárolt anag foladékszerûen iselkedik és minteg kifolik a silóból... Homogenizálás A pneumatikus ürítés során elõálló azon állapot, amikor a tárolt anag a leegõel elkeeredik.
7 7 M Metszeterõ A silófalban fellépõ, a kerület mentén megoszló fajlagos terhelés Mp/m..4. Hirtelen hõmérsékletcsökkenés A lassú hõmérsékletingadozás északok áltozása során alakul ki. Ezt a jelenséget az MSZ 50/-75 szabán tárgalja. Hirtelen hõmérsékletcsökkenés új fogalom: a napsütéstõl felmelegedett acélpalást hírtelen hül le (pl. nári idõszakban jégesõ, ag meleg nappali hõmérséklet után nagmérû éjszakai lehülés télen ag akár náron), összehúzódik, de a tárolt anag - tömege miatt - nem tud lehûlni ilen hírtelen, tehát csak a palást közelében tömörödik, uganakkor jelentéken többletfeszültséget eredménez a palástban..5. Hidraulikus sugár (r h ) A cella keresztmetszeti területének (F) és a cella keresztmetszeti kerületének (K) hánadosa: r h K F
8 M TÁROLT ANYAG ÁLTAL OKOZOTT NYOMÁSOK SZÁMÍTÁSA.. A nomások számításánál az oldalfalon aló súrlódás hatását figelembe kell enni, ha a silópalást magasságának (H), illete a cella keresztmetszeti területének (F) arána: H 5, F.. Ennél alacsonabb silóknál is kell súrlódással számolni, ha a silófal hullámosított lemezbõl, ag belsõ ízszintes bordákkal készült. Ez esetben a H F tg ϕ képlet érénes, ahol ϕ a tárolt anag belsõ súrlódási szöge. H < F tg ϕ esetén függõleges súrlódással nem kell számolni..3. A tárolt anagból származó nomások alapértékeit a köetkezõ képletek segítségéel lehet számítani: a függõleges nomás: a ízszintes nomás: p z γ( e o z zo ) p h kp kz γ( e a függõleges falon a súrlódó nomás: p µ p s h o z zo µ kz γ( e o ) z zo )
9 A nomások eloszlását az. ábra tünteti fel. E képletekben γ a tárolt anag térfogatsúla z F K r h 9 M a tárolt anag felsõ szintjétõl mért táolság a. ábra szerinti értelmezéssel F zo r h µ k K µ k F r h K a cella keresztmetszet területe a cella keresztmetszet kerülete a hidraulikus sugár. ábra
10 M p µ p s h p k p h a falon aló súrlódási ténezõ, illete a súrlódó és ízszintes nomás iszona, amelnek értéke nemcsak az anag belsõ súrlódási szögétõl függ, hanem attól is, hog töltés ag ürítés történik. a ízszintes és függõleges nomás iszona A legnagobb nomások z helen p p p max h max smax Fγ zoγ µ kk Fγ kzoγ µ K Fγ µ kzoγ K. ábra
11 M A k ténezõ értékére a tárolt anag belsõ súrlódási szögétõl (ϕ) függõen a köetkezõ képletek használhatók: Gabonasilóknál töltéskor: ürítéskor k t sin ϕ k ü Egéb ömlesztett anagoknál töltéskor: k sin + sin t k ü ϕ ϕ ürítéskor.5. Az µ ténezõ az anag belsõ súrlódási szögétõl és a töltési ag ürítési folamattól függ. A falon aló súrlódási ténezõ: µ tg( ε ϕ) A számítás gakorlati égrehajtásához - amenniben mért értékek nem állnak rendelkezésre - a γ, ϕ és µ ténezõk átlagos értékei az. sz. táblázatból, míg ε (folamat ténezõ) értékei a. sz. táblázatból ehetõk. Gabona esetében a folamat ténezõ ε t 0,75 (töltés) ε ü 0,60 (ürítés) A méretezés során a töltést és ürítést is figelembe kell enni.
12 M A tárolt anag átboltozásából származó nomások Összetapadásra hajlamos porszerû termének (liszt, gríz, porcukor) esetében a töltés izsgálata során karcsú silóknál (kis cellakeresztmetszet és nag cellamagasság) az átboltozódásból származó p h ízszintes nomási alapértéket kell figelembe enni. A cella felsõ 3 m-es szakaszán p h értéke megegezik a.3. pontban adott p h értékkel. A cella felsõ 3.0 m-es szakasza alatt a p' h γ µ b állandó értékkel kell számolni, ahol b a cella átmérõje, illete kisebb oldalhossza.
13 3 M Térfogatsúl. táblázat Súrlódási ténezõ a silófalon Az ömlesztett anag megneezése γ kp/m 3 statikai számításhoz befogadóképesség kiszámításához γ kp/m 3 Belsõ súrlódási szög töltéskor µ t ürítéskor µ ü Mezõgazdasági termékek (4%-nál kisebb íztartalom feltételezése esetén) Gabonafélék általában ,44 0,35 Búza, rozs, kukorica (morzsolt) ,44 0,35 Árpa, köles, rizs (hántolt) ,44 0,35 Bab, rizs (hántolatlan) ,44 0,35 Hüelesek (borsó) ,349 0,68 Olajosmagak ,349 0,68 Takarmánkeerék Koncentrált takarmán, olajpogácsa ,668 0,50 Darált szemestermén ,668 0,50 Korpa ,668 0,50 Burgona ,44 0,35 Élelmiszerek Liszt ,38 0,3 Gríz (dara, búzadara) ,493 0,384 Porcukor (fehércukor) ,493 0,384 Maláta ,68 0,3
14 M táblázat d (mm) szemnagság töltéskor ε folamat ténezõ ürítéskor d 0,06,00,00 0,06<d<0, (,-,78d) (,7-,85d) d>0, 0,75 0,60.7. Silónomás pneumatikus ürítésnél Ha a silóban a tárolt anagot sûrített leegõel állandóan keerik (homogenizálás), akkor a leegõel keert anag foladékszerûen iselkedik ezért a nomásiszonokat foladéknomáshoz hasonlóan számítjuk. A nomások alapértékeit a p h p 0,6γz képlettel lehet meghatározni. A z mélséget azonban ebben az esetben a silótetõ kúpjának legmagasabb pontjától kell számítani (3. ábra). A cellafalra ható leegõ-túlnomás nagságát is figelembe kell enni. Értéke hozzáadandó a p h p 0,6γz értékéhez. A silóra ható mértékadó igénbeételek meghatározásánál a homogenizálás nélkül számított, illete a homogenizálás és leegõ túlnomás egüttes hatása esetén számított értékek közül a nagobbikat kell figelembe enni.
15 5 M A pneumatikus ürítésre onatkozó elõírások nem onatkoznak arra az esetre, ha a leegõt kizárólag csak az ürítõnílás mellett fúatják be, az ürítés megkönnítése céljából és felül leegõkibocsátó nílás an. 3. ábra A tárolt anagból számított nomások alapértékeit a mértékadó igénbeétel meghatározása során az MSZ 50/ szerint k e,3 biztonsági ténezõel kell szorozni. A fenék körnezetében az ürítés közbeni állapotra onatkozó oldalnomás értéket a 4. ábra szerint csökkenteni lehet. 4. ábra
16 M A SZÉLNYOMÁS FGYELEMBEVÉTELE 3.. Teljesen töltött, nem állánon álló fémsilók esetén a szélnomás hatását nem kell figelembe enni. 3.. Üres fémsilók esetében a szélnomás hatását figelembe kell enni. 3.. Négzetes silócella esetén a szél hatását eg alul befogott konzolként mûködõ tartó erõjátékáal lehet jellemezni. Ez esetben a szélteher alaki ténezõi az MSZ 50/ szerint eendõk fel. 3.. Hengerhéj palásttal rendelkezõ silóknál feltételezhetõ a héjelmélet szerinti erõjáték kialakulása. A metszeterõk maximális értékei ez esetben függõleges fajlagos normálerõ: z N x 3,9pt (kp/ m) R ízszintes fajlagos normálerõ: N,505p R (kp/ m) t fajlagos níróerõ: N 3,3p z (kp /m) x t ahol H' + 0 H' + 50 p t 80 kp/ m H a siló teljes magassága z a palást felsõ szélétõl lefelé mért táolság (6. ábra)
17 7 M A metszeterõk az MSZ 50/-7 szabán szerinti illete c, 75cos ψ 0, 75 (0 ψ 0 ) c-0,5 (0 ψ 80 ) alaki ténezõk figelembeétele helett a c, 44 cos ψ + 0, 65cos ψ -, 065 képlettel számításba ett alaki ténezõel adódtak. (5. ábra) 5. ábra Ha a siló szerkezeti kialakítása miatt az üres siló erõjátéka nem a héjelmélet szerint alakul, akkor a szélterhelésbõl keletkezõ igénbeételeket a héjak hajlítási elmélete alapján is meg lehet határozni, a szerkezeti köetelmének figelembeételéel.
18 M A szélnomásból számított igénbeételek alapértékeinek biztonsági ténezõje k e, 3.4. A szélnomásból származó rezgések figelembeételére az MSZ 50/ elõírásai onatkoznak, ameleket csak üres silók esetében kell figelembe enni.
19 9 M A HÕMÉRSÉKLETVÁLTOZÁS FGYELEMBEVÉTELE 4.. Hõmérsékletáltozásként csak a hírtelen hõmérsékletcsökkenés esetét kell izsgálni, mert csak ez nöeli a radiális silónomást. 4.. A hírtelen hõmérsékletcsökkenés hengeres silóknál a silópalástban ízszintes húzó igénbeételt okoz, melnek számításához a hírtelen hõmérsékletcsökkenésbõl származó radiális többletnomás alapértéke a p T α Eg T D Eg + µ g E a képlettel számítható, ahol α E g E a D a siló szerkezeti anagának hõtágulási egütthatója a tárolt anag rugalmassági modulusa a siló szerkezeti anagának rugalmassági modulusa a silócella átmérõje a silócella falastagsága µ g a tárolt anag Poisson ténezõje T a hírtelen hõmérsékletcsökkenés, amelre 0 C-t kell felenni. Gabona tárolása esetén E µ g g 700kp / cm 0,4 ehetõ fel. Egéb anag tárolása esetén kísérleti ag irodalmi adatokkal alátámasztott anagjellemzõkkel kell számolni.
20 M Négzetalaprajzú silócelláknál a hírtelen hõmérsékletcsökkenés okozta ízszintes többletnomás p T α Eg T 4 l Eg + 0,03 µ aj E g ahol az elõbbieken kíül a l J a cella oldalhossza a ízszintes mereítések közti függõleges táolság az l támaszközû panelfal egségni szélességre ett függõleges iránú fajlagos inercianomatéka 4.4. A hõmérsékletáltozásból számított igénbeételek alapértékének biztonsági ténezõje k e,
21 M A MÉRTÉKADÓ TERHELÉS ÁLLAPOT SZÁMÍTÁSA 5.. A mértékadó hatást az MSZ 50/-7 szerint kell számítani. 5.. A különbözõ teherfajták egidejûségi ténezõje: hó: 0,6 szél: 0,6 hõmérsékletáltozás: 0,6 silónomás: 0, A mértékadó nomások számításakor azt is fel kell tételezni, hog a tárolt anag belsõ súrlódási szöge ±0%-os értékkel áltozik. A belsõ súrlódási szög áltozását minden izsgálatnál a kedezõtlenebb értelemben kell figelembe enni.
22 M A SLÓCELLA FÜGGÕLEGES FALABAN FELLÉPÕ GÉNYBEVÉTELEK SZÁMÍTÁSA 6.. Vízszintes húzóerõ számítása 6.. Négszög alakú celláknál a maximális nomatékkal egidejû fajlagos húzóerõ: b a N ph a b N p h itt a és b az oldalhosszak, és p h a.3 pont szerint számított ízszintes nomás. 6.. Szabálos sokszög alakú celláknál a fal közepén: a sarokpontokban: tt r a beírt R a körülírt kör sugara 6.3. Köralakú celláknál N N N p r h p R h p D / itt p h a ízszintes nomás D a cellakeresztmetszet belsõ átmérõje h
23 3 M Több, érintkezõ szomszédos cella egmásra hatását értelemszerûen kell figelembe enni, a töltött és az üres állapot legkedezõtlenebb ariációi alapján. 6.. Függõleges igénbeételek miatti horpadásizsgálat 6.. Négszög és szabálos sokszög alakú celláknál a silófalban fellépõ függõeleges nomóigénbeétel a fal horpadását idézheti elõ. A horpadási izsgálat során ki kell mutatni, hog a cellafalban keletkezõ nomófeszültség σn σ bh ahol σ bh az MSZ 504/ 9. táblázat szerinti érték, melhez a lemezkarcsúságot képlettel kell számítani. λ o 3,3 b k tt b a izsgált lemezmezõ szélessége a izsgált lemez astagsága k horpadási ténezõ Vízszintes bordákkal aló mereítés esetén - a függõleges iránban áltozó feszültségértékek helett - átlagos feszültséggel szabad számolni a horpadási izsgálatnál. Az átlagos feszültség a izsgált mezõ alsó és felsõ szélére onatkozó feszültségek számtani közepe zotróp lemez A horpadási ténezõ k a lemez a α iszonszámtól és az egidejû, b ízszintes húzás nagságától (N ) függ (6. ábra), ahol a a izsgált oldalszakasz ízszintes megtámasztásainak táolsága, b a izsgált oldalfal szélessége, toábbá N x és N z mélségtõl függõen, fajlagos metszeterõk.
24 M Ha 6.. Ortotróp lemez α 6. ábra 4 + β, akkor k ( + + β). Ha, akkor α < 4 + β, k ( + α) + α β α N b σ b β, ( ), ( ) E E ahol E a silópalást anagának rugalmassági modulusa Ha a síklemez függõleges és ízszintes bordákkal mereített ag egéb módon an ortotróppá tée, akkor a lemezkarcsúság értéke: λ o ahol b a mereített lemez szélessége; toábbá α 4 illete α < 4 D x esetén D * k* Dx D esetén k* D * α b k * ( D D * + D ) x x + D x x EF, + D * α EF
25 5 M tt D x az ortotróp lemez függõleges hajlító; D az ortotróp lemez ízszintes hajlító; D x az ortotróp lemez csaarási hajlító meresége, melnek értéke F E ( Dx + D ) µ+ ( ) DxD D x µ N b D * D + π a nomás iselésében b szélességben részteõ függõleges elemek keresztmetszeti területe és a b szélesség hánadosa (ha az erõsítés területét nem kíánjuk figelembe enni, akkor F ); a silófal anagának rugalmassági modulusa µ 0,3 (Poisson ténezõ) A különbözõ lemezastagások izsgálatáal az ahhoz tartozó legnagobb N érték eendõ figelembe a D * számításánál Ha az ortotrópiát kétiránú bordázás okozza, a 6.. szerinti képletek az alábbiak szerint módusulnak x 3 feltételezéséel (7. ábra): 7. ábra
26 M Ha α 4 x * x Ha α < 4, akkor * b bx x + a b N b * + π E k* Fbx, akkor b k* 3 * + x 3 x + + α F α 6 * bx + b 6.4. Bordaközi kazetta izsgálata Annak feltétele, hog a derékszögû bordázás esetén a bordaközi kazetta nem horpad ki elõbb, mint a teljes izsgált lemezmezõ: ahol b ϕ + F bx, + ϕ b ϕ 0,89 bx b és a b 6.5. Ha az ortotrópiát parabolikus hullámosítás okozza, akkor (8. ábra). 8. ábra
27 7 M h: a lemez középfelületei között mért hullámmagasság (lásd 8. ábrát). Ha + φ α 4, akkor k * ( + ( + φ )( + β )) + β 6 Ha + φ + φ α 4, akkor k * + + α + β α ( + β ) ahol 3 φo 5 h és β Trapéz hullámosítás esetén N b 3 π E a képletekben +φ helett a h h s 3 h + s kifejezés használandó, ahol h a trapéz középfelületei közti magasság s a trapéz kétszeres közép oldalhossza 6.. Köralakú celláknál a hengerhéjpalást kihorpadhat az axiális igénbeétel hatására. A izsgálat során ki kell mutatni, hog a cellafalban ébredõ függõleges nomófeszültség: σn σ KH,héj ahol σ KH, héj : a λ héj és a σ gûrûfeszültség függénében a 3. táblázatból ehetõ ki. (csak húzó gûrûfeszültséget szabad figelembe enni)
28 M es anag 3/a táblázat λ héj σ kp/cm A táblázat foltatódik
29 9 M es anag 3/a táblázat λ héj σ kp/cm
30 M es anag 3/b táblázat λ héj σ kp/cm A táblázat foltatódik
31 3 M es anag A 3/b táblázat foltatása λ héj σ kp/cm A táblázat foltatása
32 M es anag A 3/b táblázat foltatása λ héj σ kp/cm A táblázat foltatódik
33 33 M es anag A 3/b táblázat foltatása λ héj σ kp/cm
34 M zotróp hengerhéjnál R λ héj ahol R a henger sugara a palást astagsága 6.. Ortotróp hengerhéj esetén λ héj R i ahol i eg fiktí lemezastagság, mel az adott feladatból számítható. 6.. Bordázott ortotróp hengerhéj esetén (9. ábra) 9. ábra
35 35 M Ha x bo b F R E N + akkor x bo i b F 3 3 +, Ha x bo b F R E N + < akkor E N R,65 b F 3,3 x x bo i tt b 3 bx x + a 3 b + F bo az F bx és F b közül a kisebbik. 6.. Hullámosított ortotróp lemez Ha az ortotrópia hullámosítás útján áll elõ (gûrû-iránban futó hullámosítás (0. ábra), akkor a fiktí lemezastagság: 0. ábra 5 i 5 R
36 M Axiális bordákkal mereített (. ábra), hullámosított hengerhéj esetén Ha Akkor Ha Akkor N i N E R x i 3,3 E < R x x. ábra 3, , + 3 x + 3 ( + φ) ( + φ) x N R E A képletekben a izsgált lemezastagsághoz tartozó legnagobb N eendõ figelembe. E képletekben 6.3. Bordaközi kazetta izsgálata 3 φ 5 b h bx x + 3
37 37 M Annak feltétele, hog a bordák közti lemezkazetta nem eszti el elõbb a stabilitását, mint a teljes hengerhéj: a) Kétiránú bordázás esetén (0. ábra) egrészt a b 33 πa R a egenlõség fennállása. Az összefüggés minimuma alkotóiránban: a, 73 R gûrûiránban: 3, 46 R másrészt a b b, R bx ab + b b) Ha csak függõleges bordák annak, akkor a feltétel: b, 4 R c) Axiálisan bordázott, hullámosított hengerhéj esetén: b, 45 + R + φ 6.3. Ha a felsorolt feltételek nem állanak fenn, akkor a bordaközi kazetta kihorpad. Ezzel azonban a hengerhéj nem eszti el a teherhordó képességét, csak az erõjáték rendezõdik át: a lemez csupán a gûrûfeszültségeket eszi fel, axiálisan csak közetíti a súrlódó erõket a bordákhoz, míg az axiális bordák nomott rudakként a teljes függõleges igénbeételt hordják. Ekkor a bordák kihajlási izsgálatához a (. ábra) λ i 4 4 π R F 4 b bx bx
38 M karcsúság függénében az MSZ 504/. táblázata szerint kell a σ KH kihajlási határfeszültséget meghatározni. A borda megfelel, ha σ x,b N x b σ F bx KH. ábra
39 39 M ÖSSZEHASONLÍTÓ FESZÜLTSÉG SZÁMÍTÁSA A silócella falának olan pontjaiban, melekben egidejûleg lép fel a függõleges iránú (σ x ), és a kerület menti (σ ) normálfeszültség, alamint τ x ) nírófeszültség, kiszámítandó az összehasonlító feszültség az alábbi képlettel σ ö σ x + σ σ σ x + 3τ x (A normálfeszültségeket elõjeles menniségként kell kezelni.) Szükséges, hog a σö σ öh feltétel teljesüljön. itt σ a 504/ szerint az összehasonlító feszültségre elõírt határérték. öh
40 M KAPOCSOLATOK SZÁMÍTÁSA A kapcsolóelemek fajtáira, anagára és erõtani számításaira onatkozóan az MSZ 504/ elõírásait kell alkalmazni. 3 mm-nél ékonabb lemezek csaarkapcsolati teherbírásának megállapítása esetenkénti szakítókísérletek alapján történhet. Az íg megállapított kapcsolati határerõk az MSZ 504/ által elõírt értékeknél nagobbak is lehetnek. 9. KORRÓZÓVÉDELEM A silók korrózióédelmét az MSZ szabánsorozat szerint kell megterezni.
41 4 M A TÁRGGYAL KAPCSOLATOS FONTOSABB ELÕÍRÁSOK MSZ 504/ MSZ-04.88/ MSZ 89/ M 800 M 8830 M 8868 M MSZ 886/ M Építmének teherhordó szerkezeteinek erõtani terezése. Acélszerkezetek Építménszerkezetek korrózióédelme Acélfelületek elõkészítése felületédelemhez Acélfelületek korrózióédelme, festék és kombinált beonatrendszerek Fémszórás általános iránelei Acélszerkezetek tüzihorganzása Fémfelületek elõkezelése festéshez Korrózióédõ szórt fémbeonatok Fémfelületek elõkészítése szemcseszórással
Gyakorló feladatok a 2. zárthelyihez. Kidolgozott feladatok
 Gakorló feladatok a. zárthelihez Kidolgozott feladatok. a) Határozzuk meg a függesztőrúd négzetkeresztmetszetének a oldalhosszát cm-re kerekítve úg, hog a függesztőrúdban ébredő normálfeszültség ne érje
Gakorló feladatok a. zárthelihez Kidolgozott feladatok. a) Határozzuk meg a függesztőrúd négzetkeresztmetszetének a oldalhosszát cm-re kerekítve úg, hog a függesztőrúdban ébredő normálfeszültség ne érje
A= a keresztmetszeti felület cm 2 ɣ = biztonsági tényező
 Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
Határfeszültségek alapanyag: σ H = 200 N/mm 2, σ ph = 350 N/mm 2 ; szegecs: τ H = 160 N/mm 2, σ ph = 350 N/mm 2. Egy szegecs teherbírása:
 ervezze meg az L10.10.1-es szögacélpár eltolt illesztését L100.100.1-es hevederekkel és Ø1 mm-es szegecsekkel. nyagminőség: 8, szegecs: SZ. atárfeszültségek alapanyag: 00 /mm, p 50 /mm szegecs: τ 160 /mm,
ervezze meg az L10.10.1-es szögacélpár eltolt illesztését L100.100.1-es hevederekkel és Ø1 mm-es szegecsekkel. nyagminőség: 8, szegecs: SZ. atárfeszültségek alapanyag: 00 /mm, p 50 /mm szegecs: τ 160 /mm,
Acél tartószerkezetek
 Acél tartószerkezetek laborvizsgálatok összefoglalója 217 szept 28 Az Acél tartószerkezetek tárg keretében laborvizsgálatokat végeztünk melek során a hallgatók tapasztalatokat szerezhettek az acélszerkezetek
Acél tartószerkezetek laborvizsgálatok összefoglalója 217 szept 28 Az Acél tartószerkezetek tárg keretében laborvizsgálatokat végeztünk melek során a hallgatók tapasztalatokat szerezhettek az acélszerkezetek
Acélszerkezetek I. Gyakorlati óravázlat. BMEEOHSSI03 és BMEEOHSAT17. Jakab Gábor
 Acélszerkezetek I. BMEEOHSSI0 és BMEEOHSAT17 Gakorlati óravázlat Készítette: Dr. Kovács Nauzika Jakab Gábor A gakorlatok témája: 1. A félév gakorlati oktatásának felépítése. A szerkezeti acélanagok fajtái,
Acélszerkezetek I. BMEEOHSSI0 és BMEEOHSAT17 Gakorlati óravázlat Készítette: Dr. Kovács Nauzika Jakab Gábor A gakorlatok témája: 1. A félév gakorlati oktatásának felépítése. A szerkezeti acélanagok fajtái,
Hegesztett gerinclemezes tartók
 Hegesztett gerinclemezes tartók Lemezhorpadások kezelése EC szerint dr. Horváth László BME Hidak és Szerkezetek Tanszéke Bevezetés Gerinclemezes tartók vékony lemezekből: Bevezetés Összetett szelvények,
Hegesztett gerinclemezes tartók Lemezhorpadások kezelése EC szerint dr. Horváth László BME Hidak és Szerkezetek Tanszéke Bevezetés Gerinclemezes tartók vékony lemezekből: Bevezetés Összetett szelvények,
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK. Acélszerkezetek II. VI. Előadás. Rácsos tartók hegesztett kapcsolatai.
 DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II VI. Előadás Rácsos tartók hegesztett kapcsolatai. - Tönkremeneteli módok - Méretezési kérdések - Csomóponti kialakítások Összeállította:
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II VI. Előadás Rácsos tartók hegesztett kapcsolatai. - Tönkremeneteli módok - Méretezési kérdések - Csomóponti kialakítások Összeállította:
6. ELŐADÁS E 06 TARTÓSZERKEZETEK III. SZÉCHENYI ISTVÁN EGYETEM. Az ábrák forrása:
 SZÉCHNYI ISTVÁN GYT Az ábrák orrása: 6. LŐADÁS [1] Dr. Németh Görg: Tartószerkezetek III., Acélszerkezetek méretezésének alapjai [2] Halász Ottó - Platth Pál: Acélszerkezetek [3] Ádán Sándor - Dulácska
SZÉCHNYI ISTVÁN GYT Az ábrák orrása: 6. LŐADÁS [1] Dr. Németh Görg: Tartószerkezetek III., Acélszerkezetek méretezésének alapjai [2] Halász Ottó - Platth Pál: Acélszerkezetek [3] Ádán Sándor - Dulácska
Fa- és Acélszerkezetek I. 11. Előadás Faszerkezetek II. Dr. Szalai József Főiskolai adjunktus
 Fa- és Acélszerkezetek I. 11. Előadás Faszerkezetek II. Dr. Szalai József Főiskolai adjunktus Tartalom Méretezés az Eurocode szabványrendszer szerint áttekintés Teherbírási határállapotok Húzás Nyomás
Fa- és Acélszerkezetek I. 11. Előadás Faszerkezetek II. Dr. Szalai József Főiskolai adjunktus Tartalom Méretezés az Eurocode szabványrendszer szerint áttekintés Teherbírási határállapotok Húzás Nyomás
Központosan nyomott vasbeton oszlop méretezése:
 Központosan nyomott vasbeton oszlop méretezése: Központosan nyomott oszlopok ellenőrzése: A beton által felvehető nyomóerő: N cd = A ctot f cd Az acélbetétek által felvehető nyomóerő: N sd = A s f yd -
Központosan nyomott vasbeton oszlop méretezése: Központosan nyomott oszlopok ellenőrzése: A beton által felvehető nyomóerő: N cd = A ctot f cd Az acélbetétek által felvehető nyomóerő: N sd = A s f yd -
Leggyakoribb fa rácsos tartó kialakítások
 Fa rácsostartók vizsgálata 1. Dr. Koris Kálmán, Dr. Bódi István BME Hidak és Szerkezetek Tanszék Leggakoribb fa rácsos tartó kialakítások Változó magasságú Állandó magasságú Kis mértékben változó magasságú
Fa rácsostartók vizsgálata 1. Dr. Koris Kálmán, Dr. Bódi István BME Hidak és Szerkezetek Tanszék Leggakoribb fa rácsos tartó kialakítások Változó magasságú Állandó magasságú Kis mértékben változó magasságú
Használhatósági határállapotok. Alakváltozások ellenőrzése
 1.GYAKORLAT Használhatósági határállapotok A használhatósági határállapotokhoz tartozó teherkombinációk: Karakterisztikus (repedésmentesség igazolása) Gyakori (feszített szerkezetek repedés korlátozása)
1.GYAKORLAT Használhatósági határállapotok A használhatósági határállapotokhoz tartozó teherkombinációk: Karakterisztikus (repedésmentesség igazolása) Gyakori (feszített szerkezetek repedés korlátozása)
KERESZTMETSZETI JELLEMZŐK
 web-lap : www.hild.gor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 50. KERESZTMETSZETI JELLEMZŐK A TARTÓK MÉRETEZÉSE SORÁN SZÁMOS ESETBEN SZÜKSÉGÜNK VAN OLYAN ADATOKRA,
web-lap : www.hild.gor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 50. KERESZTMETSZETI JELLEMZŐK A TARTÓK MÉRETEZÉSE SORÁN SZÁMOS ESETBEN SZÜKSÉGÜNK VAN OLYAN ADATOKRA,
ACÉLSZERKEZETEK I. LEHÓCZKI Bettina. Debreceni Egyetem Műszaki Kar, Építőmérnöki Tanszék. [1]
![ACÉLSZERKEZETEK I. LEHÓCZKI Bettina. Debreceni Egyetem Műszaki Kar, Építőmérnöki Tanszék. [1] ACÉLSZERKEZETEK I. LEHÓCZKI Bettina. Debreceni Egyetem Műszaki Kar, Építőmérnöki Tanszék. [1]](/thumbs/59/43903450.jpg) ACÉLSZERKEZETEK I. LEHÓCZKI Bettina Debreceni Egyetem Műszaki Kar Építőmérnöki Tanszék E-mail: lehoczki.betti@gmail.com [1] ACÉLSZERKEZETEK I. Gyakorlati órák időpontjai: szeptember 25. október 16. november
ACÉLSZERKEZETEK I. LEHÓCZKI Bettina Debreceni Egyetem Műszaki Kar Építőmérnöki Tanszék E-mail: lehoczki.betti@gmail.com [1] ACÉLSZERKEZETEK I. Gyakorlati órák időpontjai: szeptember 25. október 16. november
Csavarorsós emelőbak tervezési feladat Gépészmérnök, Járműmérnök, Mechatronikai mérnök, Logisztikai mérnök, Mérnöktanár (osztatlan) BSC szak
 Csavarorsós emelőbak tervezési feladat Gépészmérnök, Járműmérnök, Mechatronikai mérnök, Logisztikai mérnök, Mérnöktanár (osztatlan) BSC szak A feladat részletezése: Név:.. Csoport:... A számításnak (órai)
Csavarorsós emelőbak tervezési feladat Gépészmérnök, Járműmérnök, Mechatronikai mérnök, Logisztikai mérnök, Mérnöktanár (osztatlan) BSC szak A feladat részletezése: Név:.. Csoport:... A számításnak (órai)
Gyakorló feladatok síkalakváltozás alkalmazására forgásszimmetrikus esetben térfogati terhelés nélkül és térfogati terheléssel.
 Alkalmazások síkalakváltozásra: Gakorló feladatok síkalakváltozás alkalmazására forgásszimmetrikus esetben térfogati terhelés nélkül és térfogati terheléssel. SAF1. Az ábrán vázolt zárt vastagfal csövet
Alkalmazások síkalakváltozásra: Gakorló feladatok síkalakváltozás alkalmazására forgásszimmetrikus esetben térfogati terhelés nélkül és térfogati terheléssel. SAF1. Az ábrán vázolt zárt vastagfal csövet
Szabadsugár. A fenti feltételekkel a folyadék áramlását leíró mozgásegyenlet és a kontinuitási egyenlet az alábbi egyszerű alakú: (1) .
 Szabadsugár Tekintsük az alábbi ábrán látható b magasságú résből kiáramló U sebességű sugarat. A résből kiáramló és a függőleges fal melletti térben lévő foladék azonos. A rajz síkjára merőleges iránban
Szabadsugár Tekintsük az alábbi ábrán látható b magasságú résből kiáramló U sebességű sugarat. A résből kiáramló és a függőleges fal melletti térben lévő foladék azonos. A rajz síkjára merőleges iránban
1 2 φ6. φ10. l=4,0m α. x 5,0m. 5-x. Statikai váz: 5,0 m. 3,0 m. 60 2,940m +5, ,81 m. 1,05 3,81=4,0 m 0,5. T=2m². 3,00 m. 1 fm 0,5 = = = B = =
 I. Központos húzás Központos húzás I I. Központos húzás a) Határozza meg az teher helét, hog a gerenda vízszintes maradjon! b) Számítsa ki a függesztő acélszálakban keletkező feszültséget és a szálak megnúlását
I. Központos húzás Központos húzás I I. Központos húzás a) Határozza meg az teher helét, hog a gerenda vízszintes maradjon! b) Számítsa ki a függesztő acélszálakban keletkező feszültséget és a szálak megnúlását
Statika gyakorló teszt II.
 Statika gakorló teszt II. Készítette: Gönczi Dávid Témakörök: (I) Egszerű szerkezetek síkbeli statikai feladatai (II) Megoszló terhelésekkel kapcsolatos számítások (III) Összetett szerkezetek síkbeli statikai
Statika gakorló teszt II. Készítette: Gönczi Dávid Témakörök: (I) Egszerű szerkezetek síkbeli statikai feladatai (II) Megoszló terhelésekkel kapcsolatos számítások (III) Összetett szerkezetek síkbeli statikai
Statika gyakorló teszt I.
 Statika gakorló teszt I. Készítette: Gönczi Dávid Témakörök: (I) közös ponton támadó erőrendszerek síkbeli és térbeli feladatai (1.1-1.6) (II) merev testre ható síkbeli és térbeli erőrendszerek (1.7-1.13)
Statika gakorló teszt I. Készítette: Gönczi Dávid Témakörök: (I) közös ponton támadó erőrendszerek síkbeli és térbeli feladatai (1.1-1.6) (II) merev testre ható síkbeli és térbeli erőrendszerek (1.7-1.13)
Tevékenység: Tanulmányozza a ábrát és a levezetést! Tanulja meg a fajlagos nyúlás mértékének meghatározásának módját hajlításnál!
 Tanulmányozza a.3.6. ábrát és a levezetést! Tanulja meg a fajlagos nyúlás mértékének meghatározásának módját hajlításnál! Az alakváltozás mértéke hajlításnál Hajlításnál az alakváltozást mérnöki alakváltozási
Tanulmányozza a.3.6. ábrát és a levezetést! Tanulja meg a fajlagos nyúlás mértékének meghatározásának módját hajlításnál! Az alakváltozás mértéke hajlításnál Hajlításnál az alakváltozást mérnöki alakváltozási
Mechanika. II. előadás március 4. Mechanika II. előadás március 4. 1 / 31
 Mechanika II. előadás 219. március 4. Mechanika II. előadás 219. március 4. 1 / 31 4. Merev test megtámasztásai, statikai feladatok megtámasztás: testek érintkezése útján jön létre, az érintkezés során
Mechanika II. előadás 219. március 4. Mechanika II. előadás 219. március 4. 1 / 31 4. Merev test megtámasztásai, statikai feladatok megtámasztás: testek érintkezése útján jön létre, az érintkezés során
Gyakorlat 04 Keresztmetszetek III.
 Gyakorlat 04 Keresztmetszetek III. 1. Feladat Hajlítás és nyírás Végezzük el az alábbi gerenda keresztmetszeti vizsgálatait (tiszta esetek és lehetséges kölcsönhatások) kétféle anyaggal: S235; S355! (1)
Gyakorlat 04 Keresztmetszetek III. 1. Feladat Hajlítás és nyírás Végezzük el az alábbi gerenda keresztmetszeti vizsgálatait (tiszta esetek és lehetséges kölcsönhatások) kétféle anyaggal: S235; S355! (1)
A FERIHEGYI IRÁNYÍTÓTORONY ÚJ RADARKUPOLÁJA LEERÕSÍTÉSÉNEK STATIKAI VIZSGÁLATA TARTALOM
 A FERIHEGYI IRÁYÍTÓTOROY ÚJ RADARKUPOLÁJA LEERÕSÍTÉSÉEK STATIKAI VIZSGÁLATA TARTALOM 1. KIIDULÁSI ADATOK 3. 2. TERHEK 6. 3. A teherbírás igazolása 9. 2 / 23 A ferihegyi irányítótorony tetején elhelyezett
A FERIHEGYI IRÁYÍTÓTOROY ÚJ RADARKUPOLÁJA LEERÕSÍTÉSÉEK STATIKAI VIZSGÁLATA TARTALOM 1. KIIDULÁSI ADATOK 3. 2. TERHEK 6. 3. A teherbírás igazolása 9. 2 / 23 A ferihegyi irányítótorony tetején elhelyezett
Erőtani számítás Szombathely Markusovszky utcai Gyöngyös-patak hídjának ellenőrzéséhez
 Erőtani számítás Szombathely Markusovszky utcai Gyöngyös-patak hídjának ellenőrzéséhez Pécs, 2015. június . - 2 - Tartalomjegyzék 1. Felhasznált irodalom... 3 2. Feltételezések... 3 3. Anyagminőség...
Erőtani számítás Szombathely Markusovszky utcai Gyöngyös-patak hídjának ellenőrzéséhez Pécs, 2015. június . - 2 - Tartalomjegyzék 1. Felhasznált irodalom... 3 2. Feltételezések... 3 3. Anyagminőség...
Szerkezeti elemek globális stabilitási ellenállása
 Szerkezetépítés II. 014/015 II. élév Előadás / 015. ebruár 11. (szerda) 9 50 B- terem Szerkezeti elemek globális stabilitási ellenállása előadó: Papp Ferenc Ph.D. Dr.habil eg. docens Szerkezetépítés II.
Szerkezetépítés II. 014/015 II. élév Előadás / 015. ebruár 11. (szerda) 9 50 B- terem Szerkezeti elemek globális stabilitási ellenállása előadó: Papp Ferenc Ph.D. Dr.habil eg. docens Szerkezetépítés II.
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 Vasalt falak: 4. Vasalt falazott szerkezetek méretezési mószerei Vasalt falak 1. Vasalás fekvőhézagban vagy falazott üregben horonyban, falazóelem lyukban. 1 2 1 Vasalt falak: Vasalás fekvőhézagban vagy
Vasalt falak: 4. Vasalt falazott szerkezetek méretezési mószerei Vasalt falak 1. Vasalás fekvőhézagban vagy falazott üregben horonyban, falazóelem lyukban. 1 2 1 Vasalt falak: Vasalás fekvőhézagban vagy
MŰSZAKI MECHANIKA II SZILÁRDSÁGTAN A legfontosabb fogalmak jegyzéke a fogalmak felsorolása (2009/2010)
 MŰSZAKI MECHANIKA II SZILÁRDSÁGTAN A legfontosabb fogalmak jegzéke a fogalmak felsorolása (2009/2010) Műszaki Mechanika II Pontszám 1. A másodrendű tenzor értelmezése (2) 2. A másodrendű tenzor transzponáltjának
MŰSZAKI MECHANIKA II SZILÁRDSÁGTAN A legfontosabb fogalmak jegzéke a fogalmak felsorolása (2009/2010) Műszaki Mechanika II Pontszám 1. A másodrendű tenzor értelmezése (2) 2. A másodrendű tenzor transzponáltjának
Határérték. Wettl Ferenc el adása alapján és Wettl Ferenc el adása alapján Határérték és
 2015.09.28. és 2015.09.30. 2015.09.28. és 2015.09.30. 1 / Tartalom 1 A valós függvén fogalma 2 A határérték fogalma a végtelenben véges pontban Végtelen határértékek 3 A határértékek kiszámítása A rend
2015.09.28. és 2015.09.30. 2015.09.28. és 2015.09.30. 1 / Tartalom 1 A valós függvén fogalma 2 A határérték fogalma a végtelenben véges pontban Végtelen határértékek 3 A határértékek kiszámítása A rend
BME Gépészmérnöki Kar 3. vizsga (112A) Név: 1 Műszaki Mechanikai Tanszék január 11. Neptun: 2 Szilárdságtan Aláírás: 3
 BME Gépészmérnöki Kar 3. vizsga (2A) Név: Műszaki Mechanikai Tanszék 2. január. Neptun: 2 Szilárdságtan Aláírás: 3. feladat (2 pont) A vázolt befogott tartót a p intenzitású megoszló erőrendszer, az F
BME Gépészmérnöki Kar 3. vizsga (2A) Név: Műszaki Mechanikai Tanszék 2. január. Neptun: 2 Szilárdságtan Aláírás: 3. feladat (2 pont) A vázolt befogott tartót a p intenzitású megoszló erőrendszer, az F
Vasbeton tartók méretezése hajlításra
 Vasbeton tartók méretezése hajlításra Képlékenység-tani méretezés: A vasbeton keresztmetszet teherbírásának számításánál a III. feszültségi állapotot vesszük alapul, amelyre az jellemző, hogy a hajlításból
Vasbeton tartók méretezése hajlításra Képlékenység-tani méretezés: A vasbeton keresztmetszet teherbírásának számításánál a III. feszültségi állapotot vesszük alapul, amelyre az jellemző, hogy a hajlításból
I/2 Egy 20/20mm km. rúd fajlagos megnyúlása ε = 0, 001. Adott: F a. a) vízszintes, ha l1 = l2. l = Alapértékek: F1, a F 2
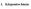 . Központos húzás / Központos húzás a) atározza meg az F teher helét, hog a gerenda vízszintes maradjon! b) zámítsa ki a függesztő acélszálakban keletkező feszültségét és a szálak megnúlását is! l,0m α
. Központos húzás / Központos húzás a) atározza meg az F teher helét, hog a gerenda vízszintes maradjon! b) zámítsa ki a függesztő acélszálakban keletkező feszültségét és a szálak megnúlását is! l,0m α
TARTALOMJEGYZÉK. 1. KIINDULÁSI ADATOK 3. 1.1 Geometria 3. 1.2 Anyagminőségek 6. 2. ALKALMAZOTT SZABVÁNYOK 6.
 statikai számítás Tsz.: 51.89/506 TARTALOMJEGYZÉK 1. KIINDULÁSI ADATOK 3. 1.1 Geometria 3. 1. Anyagminőségek 6.. ALKALMAZOTT SZABVÁNYOK 6. 3. A VASBETON LEMEZ VIZSGÁLATA 7. 3.1 Terhek 7. 3. Igénybevételek
statikai számítás Tsz.: 51.89/506 TARTALOMJEGYZÉK 1. KIINDULÁSI ADATOK 3. 1.1 Geometria 3. 1. Anyagminőségek 6.. ALKALMAZOTT SZABVÁNYOK 6. 3. A VASBETON LEMEZ VIZSGÁLATA 7. 3.1 Terhek 7. 3. Igénybevételek
Acélszerkezetek tervezése tűzhatásra Analízis és méretezés
 Előadás /6 2015. március 11., szerda, 9 50-11 30, B-2 terem Acélszerkezetek tervezése tűzhatásra Analízis és méretezés Detroit Marseille előadó: Dr. habil Papp Ferenc eg. docens Szabvánok MSZ EN 1990:2005
Előadás /6 2015. március 11., szerda, 9 50-11 30, B-2 terem Acélszerkezetek tervezése tűzhatásra Analízis és méretezés Detroit Marseille előadó: Dr. habil Papp Ferenc eg. docens Szabvánok MSZ EN 1990:2005
Acélszerkezetek méretezése Eurocode 3 szerint
 Acélszerkezetek méretezése Eurocode 3 szerint Gakorlati útmutató Dunai László, Horváth László, Kovács Nauzika, Varga Géza, Verőci Béla (az Útmutató jelen készültségi szintjén a Tartalomjegzékben dőlt betűvel
Acélszerkezetek méretezése Eurocode 3 szerint Gakorlati útmutató Dunai László, Horváth László, Kovács Nauzika, Varga Géza, Verőci Béla (az Útmutató jelen készültségi szintjén a Tartalomjegzékben dőlt betűvel
Földstatikai feladatok megoldási módszerei
 Földstatikai feladatok megoldási módszerei Földstatikai alapfeladatok Földnyomások számítása Általános állékonyság vizsgálata Alaptörés parciális terhelés alatt Süllyedésszámítások Komplex terhelési esetek
Földstatikai feladatok megoldási módszerei Földstatikai alapfeladatok Földnyomások számítása Általános állékonyság vizsgálata Alaptörés parciális terhelés alatt Süllyedésszámítások Komplex terhelési esetek
MECHANIKA I. rész: Szilárd testek mechanikája
 Egészségügyi mérnökképzés MECHNIK I. rész: Szilárd testek mechanikája készítette: Németh Róbert Igénybevételek térben I. z alapelv ugyanaz, mint síkban: a keresztmetszet egyik oldalán levő szerkezetrészre
Egészségügyi mérnökképzés MECHNIK I. rész: Szilárd testek mechanikája készítette: Németh Róbert Igénybevételek térben I. z alapelv ugyanaz, mint síkban: a keresztmetszet egyik oldalán levő szerkezetrészre
A BP. XIV. ker., KOLOSVÁRY út 48. sz. ALATT (hrsz. 1956/23) ÉPÜLŐ RAKTÁRÉPÜLET FÖDÉMSZERKEZETÉNEK STATIKAI SZÁMÍTÁSA
 A BP. XIV. ker., KOLOSVÁRY út 48. sz. ALATT (hrsz. 1956/23) ÉPÜLŐ RAKTÁRÉPÜLET FÖDÉMSZERKEZETÉNEK STATIKAI SZÁMÍTÁSA A FÖDÉMSZERKEZET: helyszíni vasbeton gerendákkal alátámasztott PK pallók. STATIKAI VÁZ:
A BP. XIV. ker., KOLOSVÁRY út 48. sz. ALATT (hrsz. 1956/23) ÉPÜLŐ RAKTÁRÉPÜLET FÖDÉMSZERKEZETÉNEK STATIKAI SZÁMÍTÁSA A FÖDÉMSZERKEZET: helyszíni vasbeton gerendákkal alátámasztott PK pallók. STATIKAI VÁZ:
SZILÁRDSÁGTAN A minimum teszt kérdései a gépészmérnöki szak egyetemi ágon tanuló hallgatói részére (2004/2005 tavaszi félév, szigorlat)
 SILÁRDSÁGTAN A minimum teszt kérdései a gépészmérnöki szak egetemi ágon tanuló hallgatói részére (2004/2005 tavaszi félév, szigorlat) Szilárdságtan Pontszám 1. A másodrendű tenzor értelmezése (2) 2. A
SILÁRDSÁGTAN A minimum teszt kérdései a gépészmérnöki szak egetemi ágon tanuló hallgatói részére (2004/2005 tavaszi félév, szigorlat) Szilárdságtan Pontszám 1. A másodrendű tenzor értelmezése (2) 2. A
Acélszerkezetek méretezése Eurocode 3 szerint
 Acélszerkezetek méretezése Eurocode 3 szerint Gakorlati útmutató Dunai László, Horváth László, Kovács auzika, Varga Géza, Verőci Béla (az Útmutató jelen készültségi szintjén a Tartalomjegzékben dőlt betűvel
Acélszerkezetek méretezése Eurocode 3 szerint Gakorlati útmutató Dunai László, Horváth László, Kovács auzika, Varga Géza, Verőci Béla (az Útmutató jelen készültségi szintjén a Tartalomjegzékben dőlt betűvel
MŰSZAKI MECHANIKAII SZILÁRDSÁGTAN A legfontosabb fogalmak jegyzéke a fogalmak felsorolása (2007/2008)
 MŰSZAKI MECHANIKAII SZILÁRDSÁGTAN A legfontosabb fogalmak jegzéke a fogalmak felsorolása (2007/2008) Műszaki Mechanika II Pontszám 1. A másodrendű tenzor értelmezése (2) 2. A másodrendű tenzor transzponáltjának
MŰSZAKI MECHANIKAII SZILÁRDSÁGTAN A legfontosabb fogalmak jegzéke a fogalmak felsorolása (2007/2008) Műszaki Mechanika II Pontszám 1. A másodrendű tenzor értelmezése (2) 2. A másodrendű tenzor transzponáltjának
VASBETON LEMEZEK. Oktatási segédlet v1.0. Összeállította: Dr. Bódi István - Dr. Farkas György. Budapest, 2001. május hó
 BUDAPEST MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építőmérnöki Kar Hidak és Szerkezetek Tanszéke VASBETON LEMEZEK Oktatási segédlet v1.0 Összeállította: Dr. Bódi István - Dr. Farkas Görg Budapest, 001. május
BUDAPEST MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építőmérnöki Kar Hidak és Szerkezetek Tanszéke VASBETON LEMEZEK Oktatási segédlet v1.0 Összeállította: Dr. Bódi István - Dr. Farkas Görg Budapest, 001. május
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet
 Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
SZERKEZETI MŰSZAKI LEÍRÁS + STATIKAI SZÁMÍTÁS
 454 Iváncsa, Arany János utca Hrsz: 16/8 Iváncsa Faluház felújítás 454 Iváncsa, Arany János utca Hrsz.: 16/8 Építtető: Iváncsa Község Önkormányzata Iváncsa, Fő utca 61/b. Fedélszék ellenőrző számítása
454 Iváncsa, Arany János utca Hrsz: 16/8 Iváncsa Faluház felújítás 454 Iváncsa, Arany János utca Hrsz.: 16/8 Építtető: Iváncsa Község Önkormányzata Iváncsa, Fő utca 61/b. Fedélszék ellenőrző számítása
László István, Fizika A2 (Budapest, 2013) Előadás
 László István, Fizika A (Budapest, 13) 1 14.A Maxwell-egenletek. Az elektromágneses hullámok Tartalmi kiemelés 1.Maxwell általánosította Ampère törvénét bevezetve az eltolási áramot. szerint ha a térben
László István, Fizika A (Budapest, 13) 1 14.A Maxwell-egenletek. Az elektromágneses hullámok Tartalmi kiemelés 1.Maxwell általánosította Ampère törvénét bevezetve az eltolási áramot. szerint ha a térben
SZÉLTEHER. Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 Szakmérnöki tanfolyam SZÉLTEHER Erdélyi Tamás egy. tanársegéd BME Építészmérnöki kar Szilárdságtani és Tartószerkezeti Tanszék 2014. február 27. Szabványok MSZ EN 1991-1-4: 2005. Wind actions pren 1991-1-4
Szakmérnöki tanfolyam SZÉLTEHER Erdélyi Tamás egy. tanársegéd BME Építészmérnöki kar Szilárdságtani és Tartószerkezeti Tanszék 2014. február 27. Szabványok MSZ EN 1991-1-4: 2005. Wind actions pren 1991-1-4
Fa- és Acélszerkezetek I. 1. Előadás Bevezetés. Dr. Szalai József Főiskolai adjunktus
 Fa- és Acélszerkezetek I. 1. Előadás Bevezetés Dr. Szalai József Főiskolai adjunktus Okt. Hét 1. Téma Bevezetés acélszerkezetek méretezésébe, elhelyezés a tananyagban Acélszerkezetek használati területei
Fa- és Acélszerkezetek I. 1. Előadás Bevezetés Dr. Szalai József Főiskolai adjunktus Okt. Hét 1. Téma Bevezetés acélszerkezetek méretezésébe, elhelyezés a tananyagban Acélszerkezetek használati területei
Építészeti tartószerkezetek II.
 Építészeti tartószerkezetek II. Vasbeton szerkezetek Dr. Szép János Egyetemi docens 2019. 05. 03. Vasbeton szerkezetek I. rész o Előadás: Vasbeton lemezek o Gyakorlat: Súlyelemzés, modellfelvétel (AxisVM)
Építészeti tartószerkezetek II. Vasbeton szerkezetek Dr. Szép János Egyetemi docens 2019. 05. 03. Vasbeton szerkezetek I. rész o Előadás: Vasbeton lemezek o Gyakorlat: Súlyelemzés, modellfelvétel (AxisVM)
Öszvér oszlopok kialakítása, THÁ, nyírt kapcsolatok, erőbevezetés környezete. 2. mintapélda - oszlop méretezése.
 Öszvérszerkezetek 4. előadás Öszvér oszlopok kialakítása, THÁ, nyírt kapcsolatok, erőbevezetés környezete. 2. mintapélda - oszlop méretezése. készítette: 2012.10.27. Tartalom Öszvér oszlopok szerkezeti
Öszvérszerkezetek 4. előadás Öszvér oszlopok kialakítása, THÁ, nyírt kapcsolatok, erőbevezetés környezete. 2. mintapélda - oszlop méretezése. készítette: 2012.10.27. Tartalom Öszvér oszlopok szerkezeti
Y 10. S x. 1. ábra. A rúd keresztmetszete.
 zilárdságtan mintafeladatok: tehetetlenségi tenzor meghatározása, a tehetetlenségi tenzor főtengelproblémájának megoldása két mintafeladaton keresztül Először is oldjuk meg a gakorlatokon is elhangzott
zilárdságtan mintafeladatok: tehetetlenségi tenzor meghatározása, a tehetetlenségi tenzor főtengelproblémájának megoldása két mintafeladaton keresztül Először is oldjuk meg a gakorlatokon is elhangzott
KRITIKUS KÉRDÉS: ACÉL ELEMEK
 KRITIKUS KÉRDÉS: ACÉL ELEMEK KRITIKUS HŐMÉRSÉKLETE Dr. Horváth László egyetem docens Acélszerkezetek tűzvédelmi tervezése workshop, 2018. 11.09 TARTALOM Acél elemek tönkremeneteli folyamata tűzhatás alatt
KRITIKUS KÉRDÉS: ACÉL ELEMEK KRITIKUS HŐMÉRSÉKLETE Dr. Horváth László egyetem docens Acélszerkezetek tűzvédelmi tervezése workshop, 2018. 11.09 TARTALOM Acél elemek tönkremeneteli folyamata tűzhatás alatt
A kerék-sín között fellépő Hertz-féle érintkezési feszültség vizsgálata
 A keréksín között fellépő Hertzféle érintkezési feszültség vizsgálata közúti vasúti felépítmények esetében Dr. Kazinczy László PhD. egyetemi docens i Műszaki és Gazdaságtudományi gyetem, Út és Vasútépítési
A keréksín között fellépő Hertzféle érintkezési feszültség vizsgálata közúti vasúti felépítmények esetében Dr. Kazinczy László PhD. egyetemi docens i Műszaki és Gazdaságtudományi gyetem, Út és Vasútépítési
Keresztmetszet másodrendű nyomatékainak meghatározása
 BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
1. Határozzuk meg az alábbi tartó vasalását, majd ellenőrizzük a tartót használhatósági határállapotokra!
 1. Határozzuk meg az alábbi tartó vasalását majd ellenőrizzük a tartót használhatósági határállapotokra! Beton: beton minőség: beton nyomószilárdságnak tervezési értéke: beton húzószilárdságának várható
1. Határozzuk meg az alábbi tartó vasalását majd ellenőrizzük a tartót használhatósági határállapotokra! Beton: beton minőség: beton nyomószilárdságnak tervezési értéke: beton húzószilárdságának várható
a térerősség mindig az üreg falára merőleges, ezért a tér ott nem gömbszimmetrikus.
 2. Gyakorlat 25A-0 Tekintsünk egy l0 cm sugarú üreges fémgömböt, amelyen +0 µc töltés van. Legyen a gömb középpontja a koordinátarendszer origójában. A gömb belsejében az x = 5 cm pontban legyen egy 3
2. Gyakorlat 25A-0 Tekintsünk egy l0 cm sugarú üreges fémgömböt, amelyen +0 µc töltés van. Legyen a gömb középpontja a koordinátarendszer origójában. A gömb belsejében az x = 5 cm pontban legyen egy 3
Kizárólag oktatási célra használható fel!
 DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II III. Előadás Vékonyfalú keresztmetszetek nyírófeszültségei - Nyírófolyam - Nyírási középpont - Shear lag hatás - Csavarás Összeállította:
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II III. Előadás Vékonyfalú keresztmetszetek nyírófeszültségei - Nyírófolyam - Nyírási középpont - Shear lag hatás - Csavarás Összeállította:
Utak és környezetük tervezése
 Dr. Fi István Utak és környezetük tervezése 3A előadás: Vonalvezetési elvek Vonalvezetési elvek Vonalvezetés az útvonalat alkotó egyenesek és ívek elrendezése. A vonalvezetés ismérve az ívesség (I) (lásd
Dr. Fi István Utak és környezetük tervezése 3A előadás: Vonalvezetési elvek Vonalvezetési elvek Vonalvezetés az útvonalat alkotó egyenesek és ívek elrendezése. A vonalvezetés ismérve az ívesség (I) (lásd
Hajlított elemek kifordulása. Stabilitásvesztési módok
 Hajlított elemek kifordulása Stabilitásvesztési módok Stabilitásvesztés (3.3.fejezet) Globális: Nyomott rudak kihajlása Hajlított tartók kifordulása Lemezhorpadás (lokális stabilitásvesztés): Nyomott és/vagy
Hajlított elemek kifordulása Stabilitásvesztési módok Stabilitásvesztés (3.3.fejezet) Globális: Nyomott rudak kihajlása Hajlított tartók kifordulása Lemezhorpadás (lokális stabilitásvesztés): Nyomott és/vagy
V. fejezet: Vasbeton keresztmetszet ellenõrzése nyírásra
 : Vasbeton keresztmetszet ellenõrzése nyírásra 5.. Koncentrált erõvel tehelt konzol ellenõrzése nyírásra φ0/00 Q=0 kn φ0 φ0 Anyagok : Beton: C5/30 Betonacél: B60.0 Betonfedés:0 mm Kedv.elm.: 0 mm Kengy.táv:
: Vasbeton keresztmetszet ellenõrzése nyírásra 5.. Koncentrált erõvel tehelt konzol ellenõrzése nyírásra φ0/00 Q=0 kn φ0 φ0 Anyagok : Beton: C5/30 Betonacél: B60.0 Betonfedés:0 mm Kedv.elm.: 0 mm Kengy.táv:
- Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági
 1. - Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági vizsgálatát. - Jellemezze a vasbeton három feszültségi
1. - Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági vizsgálatát. - Jellemezze a vasbeton három feszültségi
Tartószerkezetek I. (Vasbeton szilárdságtan)
 Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.10.11. Vasbeton külpontos nyomása Az eső ágú σ-ε diagram miatt elvileg minden egyes esethez külön kell meghatározni a szélső szál összenyomódását.
Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.10.11. Vasbeton külpontos nyomása Az eső ágú σ-ε diagram miatt elvileg minden egyes esethez külön kell meghatározni a szélső szál összenyomódását.
TARTÓSZERKEZETEK II. NGB_se004_02 Vasbetonszerkezetek
 Széchenyi István Egyetem Szerkezetépítési és Geotechnikai Tanszék TARTÓSZERKEZETEK II. NGB_se004_0 Vasbetonszerkezetek Monolit vasbetonvázas épület födémlemezének tervezése című házi feladat részletes
Széchenyi István Egyetem Szerkezetépítési és Geotechnikai Tanszék TARTÓSZERKEZETEK II. NGB_se004_0 Vasbetonszerkezetek Monolit vasbetonvázas épület födémlemezének tervezése című házi feladat részletes
Segédlet: Kihajlás. Készítette: Dr. Kossa Attila BME, Műszaki Mechanikai Tanszék május 15.
 Segédlet: Kihajlás Készítette: Dr. Kossa ttila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2012. május 15. Jelen segédlet célja tömören összefoglalni a hosszú nyomott rudak kihajlásra történő ellenőrzését.
Segédlet: Kihajlás Készítette: Dr. Kossa ttila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2012. május 15. Jelen segédlet célja tömören összefoglalni a hosszú nyomott rudak kihajlásra történő ellenőrzését.
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 SZÉLTEHER Erdélyi Tamás BME Építészmérnöki kar Szilárdságtani és Tartószerkezeti Tanszék 2016. február 26. Szakmérnöki tanfolyam Szabványok MSZ EN 1991-1-4: 2005. Wind actions pren 1991-1-4 2004. January
SZÉLTEHER Erdélyi Tamás BME Építészmérnöki kar Szilárdságtani és Tartószerkezeti Tanszék 2016. február 26. Szakmérnöki tanfolyam Szabványok MSZ EN 1991-1-4: 2005. Wind actions pren 1991-1-4 2004. January
6. MECHANIKA-STATIKA GYAKORLAT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya, Culmann-szerkesztés, Ritter-számítás
 ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
SZENT ISTVÁN EGYETEM YBL MIKLÓS ÉPÍTÉSTUDOMÁNYI KAR EUROCODE SEGÉDLETEK A MÉRETEZÉS ALAPJAI C. TÁRGYHOZ
 SZENT ISTVÁN EGYETEM YBL MIKLÓS ÉPÍTÉSTUDOMÁNYI KAR EUROCODE SEGÉDLETEK A MÉRETEZÉS ALAPJAI C. TÁRGYHOZ A segédlet nem helyettesíti az építmények teherhordó szerkezeteinek erőtani tervezésére vonatkozó
SZENT ISTVÁN EGYETEM YBL MIKLÓS ÉPÍTÉSTUDOMÁNYI KAR EUROCODE SEGÉDLETEK A MÉRETEZÉS ALAPJAI C. TÁRGYHOZ A segédlet nem helyettesíti az építmények teherhordó szerkezeteinek erőtani tervezésére vonatkozó
Matematika OKTV I. kategória 2017/2018 második forduló szakgimnázium-szakközépiskola
 O k t a t á s i H i v a t a l A 017/018. tanévi Országos Középiskolai Tanulmáni Versen második forduló MATEMATIKA I. KATEGÓRIA (SZAKGIMNÁZIUM, SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató 1. Adja meg
O k t a t á s i H i v a t a l A 017/018. tanévi Országos Középiskolai Tanulmáni Versen második forduló MATEMATIKA I. KATEGÓRIA (SZAKGIMNÁZIUM, SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató 1. Adja meg
- Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági
 1. - Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági vizsgálatát. - Jellemezze a vasbeton három feszültségi
1. - Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági vizsgálatát. - Jellemezze a vasbeton három feszültségi
1. MÁSODRENDŰ NYOMATÉK
 Gak 01 Mechanka. Szlárdságtan 016 01 Segédlet MECHNK. TNNYG SMÉTLÉSE Tartalom 1. MÁSODRENDŰ NYOMTÉK... 1. RÁCSOS TRTÓ.... GÉNYEVÉTEL ÁRÁK... 5. TÉREL TRTÓK GÉNYEVÉTEL ÁRÁ... 8 Ez a Segédlet a 015, 016
Gak 01 Mechanka. Szlárdságtan 016 01 Segédlet MECHNK. TNNYG SMÉTLÉSE Tartalom 1. MÁSODRENDŰ NYOMTÉK... 1. RÁCSOS TRTÓ.... GÉNYEVÉTEL ÁRÁK... 5. TÉREL TRTÓK GÉNYEVÉTEL ÁRÁ... 8 Ez a Segédlet a 015, 016
Szilárdsági számítások. Kazánok és Tüzelőberendezések
 Szilárdsági számítások Kazánok és Tüzelőberendezések Tartalom Ellenőrző számítások: Hőtechnikai számítások, sugárzásos és konvektív hőátadó felületek számításai már ismertek Áramlástechnikai számítások
Szilárdsági számítások Kazánok és Tüzelőberendezések Tartalom Ellenőrző számítások: Hőtechnikai számítások, sugárzásos és konvektív hőátadó felületek számításai már ismertek Áramlástechnikai számítások
Szádfal szerkezet ellenőrzés Adatbev.
 Szádfal szerkezet ellenőrzés Adatbev. Projekt Dátum : 8.0.05 Beállítások (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : Acél szerkezetek : Acél keresztmetszet teherbírásának
Szádfal szerkezet ellenőrzés Adatbev. Projekt Dátum : 8.0.05 Beállítások (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : Acél szerkezetek : Acél keresztmetszet teherbírásának
ÜVEGEZETT FELVONÓ AKNABURKOLATOK MÉRETEZÉSE
 ÜVEGEZETT FELVONÓ AKNABURKOLATOK MÉRETEZÉSE EGYSZERŰSÍTETT SZÁMÍTÁS AZ MSZ EN81-0:014 SZABVÁNY ELŐÍRÁSAINAK FIGYELEMBEVÉTELÉVEL. MAKOVSKY ZSOLT. Üvegszerkezetek .Követelmények: MSZ EN81-0:014.1 A felvonóakna
ÜVEGEZETT FELVONÓ AKNABURKOLATOK MÉRETEZÉSE EGYSZERŰSÍTETT SZÁMÍTÁS AZ MSZ EN81-0:014 SZABVÁNY ELŐÍRÁSAINAK FIGYELEMBEVÉTELÉVEL. MAKOVSKY ZSOLT. Üvegszerkezetek .Követelmények: MSZ EN81-0:014.1 A felvonóakna
Gyakorlat 03 Keresztmetszetek II.
 Gyakorlat 03 Keresztmetszetek II. 1. Feladat Keresztmetszetek osztályzása Végezzük el a keresztmetszet osztályzását tiszta nyomás és hajlítás esetére! Monoszimmetrikus, hegesztett I szelvény (GY02 1. példája)
Gyakorlat 03 Keresztmetszetek II. 1. Feladat Keresztmetszetek osztályzása Végezzük el a keresztmetszet osztályzását tiszta nyomás és hajlítás esetére! Monoszimmetrikus, hegesztett I szelvény (GY02 1. példája)
= Φ B(t = t) Φ B (t = 0) t
 4. Gyakorlat 32B-3 Egy ellenállású, r sugarú köralakú huzalhurok a B homogén mágneses erőtér irányára merőleges felületen fekszik. A hurkot gyorsan, t idő alatt 180 o -kal átforditjuk. Számitsuk ki, hogy
4. Gyakorlat 32B-3 Egy ellenállású, r sugarú köralakú huzalhurok a B homogén mágneses erőtér irányára merőleges felületen fekszik. A hurkot gyorsan, t idő alatt 180 o -kal átforditjuk. Számitsuk ki, hogy
11. MECHANIKA-STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnöktanár)
 SZÉHENYI ISTVÁN EGYETEM LKLMZOTT MEHNIK TNSZÉK.. Példa:. MEHNIK-STTIK GYKORLT (kidolgozta: Triesz Péter, eg. ts.; Tarnai Gábor, mérnöktanár) Összetett szerkezetek statikája (három csuklós ív, Gerber tartó)
SZÉHENYI ISTVÁN EGYETEM LKLMZOTT MEHNIK TNSZÉK.. Példa:. MEHNIK-STTIK GYKORLT (kidolgozta: Triesz Péter, eg. ts.; Tarnai Gábor, mérnöktanár) Összetett szerkezetek statikája (három csuklós ív, Gerber tartó)
Téma: A szerkezeti acélanyagok fajtái, jelölésük. Mechanikai tulajdonságok. Acélszerkezeti termékek. Keresztmetszeti jellemzők számítása
 1. gakorlat: Téma: A szerkezeti acélanagok fajtái, jelölésük. echanikai tulajdonságok. Acélszerkezeti termékek. Keresztmetszeti jellemzők számítása A szerkezeti acélanagok fajtái, jelölésük: Ádán Dulácska-Dunai-Fernezeli-Horváth:
1. gakorlat: Téma: A szerkezeti acélanagok fajtái, jelölésük. echanikai tulajdonságok. Acélszerkezeti termékek. Keresztmetszeti jellemzők számítása A szerkezeti acélanagok fajtái, jelölésük: Ádán Dulácska-Dunai-Fernezeli-Horváth:
Vasbeton födémek tűz alatti viselkedése Egyszerű tervezési eljárás
 tűz alatti eljárás A módszer célja 2 3 Az előadás tartalma Öszvérfödém szerkezetek tűz esetén egyszerű módszere 20 C Födém modell Tönkremeneteli módok Öszvérfödémek egyszerű eljárása magas Kiterjesztés
tűz alatti eljárás A módszer célja 2 3 Az előadás tartalma Öszvérfödém szerkezetek tűz esetén egyszerű módszere 20 C Födém modell Tönkremeneteli módok Öszvérfödémek egyszerű eljárása magas Kiterjesztés
0,00 0,01 0,02 0,03 0,04 0,05 0,06 Q
 1. Az ábrában látható kapcsolási vázlat szerinti berendezés két üzemállapotban működhet. A maximális vízszint esetében a T jelű tolózár nyitott helyzetben van, míg a minimális vízszint esetén az automatikus
1. Az ábrában látható kapcsolási vázlat szerinti berendezés két üzemállapotban működhet. A maximális vízszint esetében a T jelű tolózár nyitott helyzetben van, míg a minimális vízszint esetén az automatikus
4. feladat Géprajz-Gépelemek (GEGET224B) c. tárgyból a Műszaki Anyagtudományi Kar, nappali tagozatos hallgatói számára
 4. feladat Géprajz-Gépelemek (GEGET4B) c. tárgyból a űszaki Anyagtudományi Kar, nappali tagozatos hallgatói számára TOKOS TENGELYKAPCSOLÓ méretezése és szerkesztése útmutató segítségével 1. Villamos motorról
4. feladat Géprajz-Gépelemek (GEGET4B) c. tárgyból a űszaki Anyagtudományi Kar, nappali tagozatos hallgatói számára TOKOS TENGELYKAPCSOLÓ méretezése és szerkesztése útmutató segítségével 1. Villamos motorról
A HELIKOPTER FÜGGÉSI ÉS FÜGGŐLEGES EMELKEDÉSI ÜZEMMÓDJÁNAK VIZSGÁLATA
 Szolnoki Tudomános Közlemének XIII. Szolnok, 009. Dr. BÉKÉSI LÁSZLÓ 1 A HELIKOPTER VONÓEREJÉNEK CSÖKKENÉSE A SÁRKÁNYSZERKEZET MEGFÚVÁSA MIATT A helikopter repülésekor a függés és a függőleges emelkedés
Szolnoki Tudomános Közlemének XIII. Szolnok, 009. Dr. BÉKÉSI LÁSZLÓ 1 A HELIKOPTER VONÓEREJÉNEK CSÖKKENÉSE A SÁRKÁNYSZERKEZET MEGFÚVÁSA MIATT A helikopter repülésekor a függés és a függőleges emelkedés
Kirchhoff 2. törvénye (huroktörvény) szerint az áramkörben levő elektromotoros erők. E i = U j (3.1)
 3. Gyakorlat 29A-34 Egy C kapacitású kondenzátort R ellenálláson keresztül sütünk ki. Mennyi idő alatt csökken a kondenzátor töltése a kezdeti érték 1/e 2 ed részére? Kirchhoff 2. törvénye (huroktörvény)
3. Gyakorlat 29A-34 Egy C kapacitású kondenzátort R ellenálláson keresztül sütünk ki. Mennyi idő alatt csökken a kondenzátor töltése a kezdeti érték 1/e 2 ed részére? Kirchhoff 2. törvénye (huroktörvény)
Nyomott oszlopok számítása EC2 szerint (mintapéldák)
 zéhenyi István Egyetem zerkezetépítési és Geotehnikai Tanszék yomott oszlopok számítása E szerint 1. Központosan nyomott oszlop Központosan nyomott az oszlop ha e = 0 (e : elsőrendű, vagy kezdeti külpontosság).
zéhenyi István Egyetem zerkezetépítési és Geotehnikai Tanszék yomott oszlopok számítása E szerint 1. Központosan nyomott oszlop Központosan nyomott az oszlop ha e = 0 (e : elsőrendű, vagy kezdeti külpontosság).
A statika és dinamika alapjai 11,0
 FA Házi feladatok (A. gakorlat) Adottak az alábbi vektorok: a=[ 2,0 6,0,2] [ 5,2,b= 8,5 3,9] [ 4,2,c= 0,9 4,8] [,0 ],d= 3,0 5,2 Számítsa ki az alábbi vektorokat! e=a+b+d, f =b+c d Számítsa ki az e f vektort
FA Házi feladatok (A. gakorlat) Adottak az alábbi vektorok: a=[ 2,0 6,0,2] [ 5,2,b= 8,5 3,9] [ 4,2,c= 0,9 4,8] [,0 ],d= 3,0 5,2 Számítsa ki az alábbi vektorokat! e=a+b+d, f =b+c d Számítsa ki az e f vektort
TARTÓSZERKEZETEK II. NGB_se004_02 Vasbetonszerkezetek
 Széchenyi István Egyetem Szerkezetépítési és Geotechnikai Tanszék TARTÓSZERKEZETEK II. NGB_se004_0 Vasbetonszerkezetek Monolit vasbetonvázas épület födémlemezének tervezése című házi feladat részletes
Széchenyi István Egyetem Szerkezetépítési és Geotechnikai Tanszék TARTÓSZERKEZETEK II. NGB_se004_0 Vasbetonszerkezetek Monolit vasbetonvázas épület födémlemezének tervezése című házi feladat részletes
NE HABOZZ! KÍSÉRLETEZZ!
 NE HABOZZ! KÍSÉRLETEZZ! FOLYADÉKOK FELSZÍNI TULAJDONSÁGAINAK VIZSGÁLATA KICSIKNEK ÉS NAGYOKNAK Országos Fizikatanári Ankét és Eszközbemutató Gödöllő 2017. Ötletbörze Kicsiknek 1. feladat: Rakj három 10
NE HABOZZ! KÍSÉRLETEZZ! FOLYADÉKOK FELSZÍNI TULAJDONSÁGAINAK VIZSGÁLATA KICSIKNEK ÉS NAGYOKNAK Országos Fizikatanári Ankét és Eszközbemutató Gödöllő 2017. Ötletbörze Kicsiknek 1. feladat: Rakj három 10
Magasépítési acélszerkezetek
 Magasépítési acélszerkezetek Egyhajós acélszerkezetű csarnok tervezése Szabó Imre Gábor Pécsi Tudományegyetem Műszaki és Informatikai Kar Építőmérnök Tanszék 1. ábra. Acél csarnoképület tipikus hierarchikus
Magasépítési acélszerkezetek Egyhajós acélszerkezetű csarnok tervezése Szabó Imre Gábor Pécsi Tudományegyetem Műszaki és Informatikai Kar Építőmérnök Tanszék 1. ábra. Acél csarnoképület tipikus hierarchikus
Számítási dokumentáció. Megnevezés: Félév: 2008/2009 I. félév. Lapok száma: 10. Tervezési feladat I. Autóemelő. Név: Katona Géza. Neptun kód: L0I8ZH
 Megnevezés: Tervezési feladat I. Autóemelő Számítási dokumentáció Félév: 008/009 I. félév Név: Katona Géza Lapok száma: 10 Neptun kód: L0I8ZH Bevezető Ezen autóemelő szerkezettel Renault típusú személygépkocsit
Megnevezés: Tervezési feladat I. Autóemelő Számítási dokumentáció Félév: 008/009 I. félév Név: Katona Géza Lapok száma: 10 Neptun kód: L0I8ZH Bevezető Ezen autóemelő szerkezettel Renault típusú személygépkocsit
a.) b.) c.) d.) e.) össz. 4 pont 2 pont 4 pont 2 pont 3 pont 15 pont
 1. Az alábbi feladatok egszerűek, akár fejben is kiszámíthatóak, de a piszkozatpapíron is gondolkodhat. A megoldásokat azonban erre a papírra írja! a.) A 2x 2 5x 3 0 egenlet megoldása nélkül határozza
1. Az alábbi feladatok egszerűek, akár fejben is kiszámíthatóak, de a piszkozatpapíron is gondolkodhat. A megoldásokat azonban erre a papírra írja! a.) A 2x 2 5x 3 0 egenlet megoldása nélkül határozza
Navier-formula. Frissítve: Egyenes hajlítás
 Navier-formula Akkor beszélünk egyenes hajlításról, ha a nyomatékvektor egybeesik valamelyik fő-másodrendű nyomatéki tengellyel. A hajlítást mindig súlyponti koordinátarendszerben értelmezzük. Ez még a
Navier-formula Akkor beszélünk egyenes hajlításról, ha a nyomatékvektor egybeesik valamelyik fő-másodrendű nyomatéki tengellyel. A hajlítást mindig súlyponti koordinátarendszerben értelmezzük. Ez még a
Végeselem analízis 5. gyakorlat (kidolgozta: Bojtár Gergely egyetemi tanársegéd)
 p 0 v =0 SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Végeselem analízis. gakorlat (kidolgozta: Bojtár Gergel egetemi tanársegéd) Feladat: Tengelszimmetrikus héj (hengeres tartál) Adott: A hengeres
p 0 v =0 SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Végeselem analízis. gakorlat (kidolgozta: Bojtár Gergel egetemi tanársegéd) Feladat: Tengelszimmetrikus héj (hengeres tartál) Adott: A hengeres
A diplomaterv keretében megvalósítandó feladatok összefoglalása
 A diplomaterv keretében megvalósítandó feladatok összefoglalása Diplomaterv céljai: 1 Sclieren résoptikai módszer numerikus szimulációk validálására való felhasználhatóságának vizsgálata 2 Lamináris előkevert
A diplomaterv keretében megvalósítandó feladatok összefoglalása Diplomaterv céljai: 1 Sclieren résoptikai módszer numerikus szimulációk validálására való felhasználhatóságának vizsgálata 2 Lamináris előkevert
ÜVEG FIZIKAI TULAJDONSÁGAI,
 ÜVEG FIZIKAI TULAJDONSÁGAI, ÜVEGTERMÉKEK Erdélyi Tamás egyetemi tanársegéd BME Építészmérnöki é kar Szilárdságtani és Tartószerkezeti Tanszék 2013. február 28. Tematika alkal om 1. 2. 3. 4. 5. nap 02.28.
ÜVEG FIZIKAI TULAJDONSÁGAI, ÜVEGTERMÉKEK Erdélyi Tamás egyetemi tanársegéd BME Építészmérnöki é kar Szilárdságtani és Tartószerkezeti Tanszék 2013. február 28. Tematika alkal om 1. 2. 3. 4. 5. nap 02.28.
PONTOKON MEGTÁMASZTOTT SÍKLEMEZ FÖDÉMEK ÁTSZÚRÓDÁSA
 PONTOKON MEGTÁMASZTOTT SÍKLEMEZ FÖDÉMEK ÁTSZÚRÓDÁSA A pontokon megtámasztott síklemez födémek a megtámasztások környezetében helyi igénybevételre nyírásra is tönkremehetnek. Ezt a jelenséget: Nyíróerı
PONTOKON MEGTÁMASZTOTT SÍKLEMEZ FÖDÉMEK ÁTSZÚRÓDÁSA A pontokon megtámasztott síklemez födémek a megtámasztások környezetében helyi igénybevételre nyírásra is tönkremehetnek. Ezt a jelenséget: Nyíróerı
l = 1 m c) Mekkora a megnyúlás, ha közben a rúd hőmérséklete ΔT = 30 C-kal megváltozik? (a lineáris hőtágulási együtható: α = 1, C -1 )
 5. TIZTA HÚZÁ-NYOMÁ, PÉLDÁK I. 1. a) Határouk meg a függestőrúd négetkerestmetsetének a oldalhossát cm-re kerekítve úg, hog a függestőrúdban ébredő normálfesültség ne érje el a σ e = 180 MPa-t! 3 m 1 C
5. TIZTA HÚZÁ-NYOMÁ, PÉLDÁK I. 1. a) Határouk meg a függestőrúd négetkerestmetsetének a oldalhossát cm-re kerekítve úg, hog a függestőrúdban ébredő normálfesültség ne érje el a σ e = 180 MPa-t! 3 m 1 C
SIÓFOK VÁROS ÖNKORMÁNYZATA POLGÁRMESTER
 SIÓFOK VÁROS ÖNKORMÁNYZATA POLGÁRMESTER 8600 SIÓFOK, FŐ TÉR 1. TELEFON +36 84 504100 FAX: +36 84 504103 Az előjesztés törénességi szempontból megfelelő. Siófok, 2014. noember Kónáné Dr. Zsarnoszk Judit
SIÓFOK VÁROS ÖNKORMÁNYZATA POLGÁRMESTER 8600 SIÓFOK, FŐ TÉR 1. TELEFON +36 84 504100 FAX: +36 84 504103 Az előjesztés törénességi szempontból megfelelő. Siófok, 2014. noember Kónáné Dr. Zsarnoszk Judit
3. feladat Géprajz-Gépelemek (GEGET224B) c. tárgyból a Műszaki Anyagtudományi Kar, nappali tagozatos hallgatói számára
 3. feladat Géprajz-Gépelemek (GEGET224B) c. tárgyból a Műszaki Anyagtudományi Kar, nappali tagozatos hallgatói számára TENGELYVÉG CSAPÁGYAZÁSA, útmutató segítségével d. A táblázatban szereplő adatok alapján
3. feladat Géprajz-Gépelemek (GEGET224B) c. tárgyból a Műszaki Anyagtudományi Kar, nappali tagozatos hallgatói számára TENGELYVÉG CSAPÁGYAZÁSA, útmutató segítségével d. A táblázatban szereplő adatok alapján
3. Lokális approximáció elve, végeselem diszkretizáció egydimenziós feladatra
 SZÉCHENYI ISÁN EGYEEM AAMAZO MECHANIA ANSZÉ 6. MECHANIA-ÉGESEEM MÓDSZER EŐADÁS (kidolgozta: Szüle eronika, eg. ts.) I. előadás. okális aroimáció elve, végeselem diszkretizáció egdimenziós feladatra.. Csomóonti
SZÉCHENYI ISÁN EGYEEM AAMAZO MECHANIA ANSZÉ 6. MECHANIA-ÉGESEEM MÓDSZER EŐADÁS (kidolgozta: Szüle eronika, eg. ts.) I. előadás. okális aroimáció elve, végeselem diszkretizáció egdimenziós feladatra.. Csomóonti
BI/1 feladat megoldása Meghatározzuk a hőátbocsátási tényezőt 3 különböző szigetelés vastagság (0, 3 és 6 cm) mellett.
 BI/1 feladat megoldása Meghatározzuk a hőátbocsátási tényezőt 3 különböző szigetelés vastagság (0, 3 és 6 cm) mellett. 1 1 2 U6 cm = = = 0,4387 W/ m K 1 d 1 1 0,015 0,06 0,3 0,015 1 + + + + + + + α λ α
BI/1 feladat megoldása Meghatározzuk a hőátbocsátási tényezőt 3 különböző szigetelés vastagság (0, 3 és 6 cm) mellett. 1 1 2 U6 cm = = = 0,4387 W/ m K 1 d 1 1 0,015 0,06 0,3 0,015 1 + + + + + + + α λ α
