VASBETON LEMEZEK. Oktatási segédlet v1.0. Összeállította: Dr. Bódi István - Dr. Farkas György. Budapest, május hó
|
|
|
- Laura Boros
- 9 évvel ezelőtt
- Látták:
Átírás
1 BUDAPEST MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építőmérnöki Kar Hidak és Szerkezetek Tanszéke VASBETON LEMEZEK Oktatási segédlet v1.0 Összeállította: Dr. Bódi István - Dr. Farkas Görg Budapest, 001. május hó
2 VASBETON LEMEZEK TARTALOM 1. A rugalmas lemezelmélet alapjai. Lemez és gerenda viselkedésének összehasonlítása 3. Speiális kérdések 3.1 Derékszögű négszög alakú lemez reakiói 3. Egiránban teherviselő lemezek 3.3 Konentrált terhek esete 3.. Konentrált erővel terhelt konzolos lemezek 3.5.A lemez vasalásának meghatározása a rugalmas igénbevételek alapján. Derékszögű négszög alakú lemezek igénbevételei, vasalása.1 Az igénbevételek meghatározása grafikonok segítségével. A maimális igénbevételek közelítő számítása.1 Tartókereszt eljárás. Marus módszere 5. Lemezrendszerek közelítő vizsgálata 6. Gombafödémek, síklemez födémek 6.1 Általánosságok 6. Hajlítási méretezés 6.3 Átszúródási vizsgálat BEVEZETÉS VASBETON LEMEZEK A lemez olan sík tartóelem, melnek vastagsága a másik kétiránú kiterjedéshez képest kisi és amelnek terhei a középfelület síkjára merőlegesen működnek. A vasbeton lemez mind a magas, mind a mél, mind pedig a hídépítésben rendkívül gakran előforduló szerkezeti elem. Alakja a legtöbb esetben szabálos (derékszögű négszög, rombusz, romboid, kör vag körgűrű), de néha szabáltalan is lehet (sokszög, vag tetszőleges íves vonalakkal határolt, esetenként nílásokkal áttört). Eg lemezszerkezet alátámasztása lehet pontszerű, vonal vag felület mentén történő fi vag rugalmas megtámasztás, illetve ezek kombináiója. Ebben a fejezetben sak a gakorlatban legtöbbször előforduló, derékszögű négszög alakú, szabálos elrendezésben kialakított vonalak vag pontok mentén fien megtámasztott, vékon vasbeton lemezek rugalmas igénbevételeinek meghatározásával és vasalásának kialakításával foglalkozunk.
3 1. A RUGALMAS LEMEZELMÉLET ALAPJAI A lemezre működő terhelés hatására annak eredetileg sík középfelülete, általában a derékszögű koordináta rendszer mindkét iránában görbült felületté alakul át. Ha a lemez felületét képzeletben az és tengelekkel párhuzamos lemezsávokra bontjuk, akkor látható, hog az alakváltozás hatására, az oldalaik mentén satlakozó, egmást keresztező, önálló gerendáknak tekinthető lemezsávok nem sak hajlítási alakváltozást szenvednek, hanem el is savarodnak. A terhelés hatására bekövetkező alakváltozások figelembe vételével, és elemi rugalmasságtani ismereteink alapján, eg t vastagságú lemez felületéből kivágott d, valamint d oldalhosszúságú lemezre működő igénbevételek az és iránú m illetve m fajlagos hajlítónomatékok, a v és v fajlagos níróerők, valamint a felserélhetőségi tétel miatt azonos m m fajlagos savarónomaték A rugalmas lemez igénbevételeit a klasszikus, Kirhoff féle hajlításelmélet felhasználásával határozhatjuk meg. Ennek alapfeltevései a következők: - a lemez vastagsága állandó és egéb méreteihez képest kisi, azaz l min /t>5, ahol l min a legkisebb támaszköz, - a lemez középsíkjában fekvő pontok sak a középsíkra merőlegesen tolódnak el és a maimális eltolódás a lemez vastagságához képest kisi, azaz t/w ma >5, - a lemez anaga homogén, izotrop és lineárisan rugalmas, - a középsík normálisán fekvő pontok az alakváltozások után is a középfelület azonos normálisán maradnak, vagis érvénes a Bernoulli-Navier feltétel - a középfelületre merőleges feszültségek elhanagolhatók, - a lemez síkjában az elmozdulások szabadon létrejöhetnek. Megjegzés Az előző feltételek vasbeton lemezeknél sak közelítően teljesülnek, minthog például két, egmásra merőleges iránban vasalt vasbeton lemez esetében, a kétiránú vasalás eltérő volta következtében, az egségni szélességű lemezsávok ideális inerianomatékai a vasalási iránokban általában némileg különbözőek. Valamel iránban berepedt lemez esetén a különböző iránok szerint számítható inerianomatékok eltérése jelentős is lehet. Gakorlati tapasztalatok szerint, ennek ellenére, a rugalmas elmélet alapján számítható igénbevételek, elsősorban használati határállapotok szerinti vizsgálatoknál, elegendően pontosak. A lemez ténleges törési állapotához közeledve a repedések egre jobban megnílnak, az igénbevételek átrendeződnek és ekkor a képléken lemezelmélet alkalmazásával lehet a szerkezet teherbírását megbesülni. A gakorlati esetek döntő többségében a használati állapotban rugalmas elmélet szerint méretezett lemezek a teherbírási határállapotra is megfelelnek.
4 Az előzőekben megfogalmazott alapfeltevések teljesülése esetén a (,) teherrel terhelt lemez eg d,d eleme egensúlának vizsgálata alapján a szerkezet egensúlát leíró összefüggés az, derékszögű koordinátarendszerben az alábbi alakban írható: m m m Ez az egensúli egenlet a σ E 1- µ E ( ε + µ ε ); σ ( ε µ ε ) + ; τ 1- µ E γ 1 + ( µ ) fizikai, valamint az w w ε z ;ε z ;γ z w összeférhetőségi egenletek felhasználásával a w w w + + k alakú Lagrange féle negedrendű, pariális, inhomogén differeniálegenletté alakítható, mel a rugalmas lemezelmélet alapegenlete derékszögű koordinátarendszerben. A fenti összefüggésekben: - - E a lemez anagának, vasbeton lemez esetén a beton rugalmassági modulusa, - µ a harántnúlási ténező (a Poisson szám reiproka), melnek értéke vasbeton lemeznél µ 0,15 ~ 0,0 3 E t K 1 1- µ ( ) a lemez hajlítómerevsége. A lemez középfelületére merőleges (,) teherfüggvén akkor pozitív, ha a pozitív w(,) eltolódásfüggvénnel azonos iránban működik. A Lagrange féle lemezegenlet elegendő számú peremfeltétel esetén egértelműen leírja a terhelés hatására kialakuló lehajlásfüggvént. A kétváltozós negedrendű differeniálegenlet megoldásának matematikai határozottságához minden perempontban két peremfeltételt kell előírni. Ezek a lemez megtámasztási viszonai alapján határozhatók meg. A mérnöki feladatoknál leggakrabban előforduló megtámasztások esetén felírható peremfeltételek, ha n inde jelöli a megtámasztás vonalára merőleges, t pedig az azzal párhuzamos iránt, az alátámasztás vonalában az alábbiak:
5 - suklós megtámasztás (pl. falra feltámaszkodó lemez): lehajlás w 0 a támasz vonalára merőleges hajlítónomaték m n 0 - tökéletes befogás (pl. nag merevségű gerendába befogott perem): lehajlás w 0 normális iránú szögelfordulás w n 0 - rugalmas befogás (pl. koszorúgerendába befogott perem): - szabad peremű lemez: lehajlás w 0 a normális iránú szögelfordulás arános a w 1 nomatékkal n n m rugóállandó normális iránú nomaték m n 0 perem reakióerő r 0 Téglalap alakú lemezeknél a peremfeltételeket is kielégítő analitikus megoldás például az ismeretlen w(,) lehajlásfüggvén és az ismert (,) teherfüggvén Fourier sorba fejtése után és az egenes Fourier tagok egeztetése révén meghatározott Fourier egütthatók felhasználásával a következő alakban írható m w (, n ) a sin π a sin π mn b m 1 n1 Mivel a Fourier sor alakjában keresett megoldás meglehetősen gorsan konvergál, az igénbevételeknek a gakorlat számára pontos meghatározásához elegendő a sor első -3 tagját figelembe venni. A lemez vasalásának meghatározására szolgáló igénbevételeket a lehajlás- függvén ismeretében a klasszikus rugalmasságtan elvei szerint lehet meghatározni, az egmásra merőleges iránoknak a harántnúlási ténező miatt kialakuló egmásrahatását is figelembe véve. A legtöbb gakorlati esetre az analitikus megoldások alapján táblázatokat, grafikonokat dolgoztak ki a lemez kritikus keresztmetszeteinek maimális igénbevételei meghatározására, melek segítségével a méretezés alapjául szolgáló fő igénbevételek egszerűen megbesülhetők. Bonolultabb esetekben a lemezszerkezet igénbevételeinek meghatározásához a differenia módszeren, vag a véges elemek módszerén alapuló számítógépi programokat lehet használni.
6 . A LEMEZ ÉS GERENDA VISELKEDÉSÉNEK ÖSSZEHASONLITÁSA A lemez és a gerenda viselkedése közötti alapvető különbség, hog míg eg gerendában sak annak tengele iránában, addig eg lemezben a lemez síkjának minden iránában keletkeznek igénbevételek. Vasbeton lemez esetén ezért az igénbevételekből keletkező húzóerők felvétele egiránú vasalással általában nem oldható meg. A lemezekben a hajlítónomatékon kívül, savarónomaték is ébred a külső teher w hatására. A savarás hatását a Lagrange féle lemezegenletben a középső, tag veszi figelembe, valamel iránban két egmás mögött elhelezkedő keresztmetszet relatív elfordulásának függvénében. tg tg w1 φ 1 φ 1 φ 1 d 1 φ + φ d φ 1 + w 1 Ha két, egmást merőlegesen keresztező gerendarendszer kereszteződési pontjaiban suklós kapsolatot tételezzük fel, akkor a külső terhelés hatására a rúdelemekben nem keletkezik savarónomaték, mivel az egik iránú rúdelem alakváltozása nem kénszeríti a másik iránú rudat elsavarodásra. Ekkor a Lagrange féle differeniálegenlet az alábbi alakúra egszerűsödik w + w k A µ harántnúlási ténező a gerendák igénbevételét nem befolásolja, de a lemezek igénbevételeit jelentősen módosítja. Eg a peremei mentén suklósan megtámasztott négzet alakú lemez maimális hajlítónomatékai a lemezmező középpontjában µ különböző értékei esetén egenletesen megoszló teher hatására az alábbiak µ 0 m ma l ; µ 7, 015, m ma l ; µ 3,6 03, m ma l 0,9 A maimális nomaték ekkor 1+ µ a változás mértéke is eltérő. -vel aránosan változik. Más oldalaránú lemeznél
7 Az alábbi táblázatban a lemezek illetve a gerendák viselkedését leíró analóg összefüggéseket hasonlítottuk össze. Jellemző menniség állandó t vastagságú lemez gerenda teher felületen működő (,) vonal mentén működő () lehajlás alapegenlet hajlítási merevség w + w + w k K E I 1 µ 3 ; I t 1 w w hajlító nomaték m K + µ savaró nomaték níróerő níróerő - hajlítónomaték összefüggés níróerő - teher összefüggés hajlítónomaték - teher összefüggés m w w K + µ m m K ( 1 µ ) v w w w K + w w v K + m m v + m m v + w w m m m kn/m K` E I w K ` ; I b h 3 1 M K d w ` d M 0 M 0 ha a teher a szim. tengelben hat V K d 3 w ` 3 d 0 V V V dm d 0 dv + 0 d d M + 0 d kn/m megoszló teher dim. nomaték dim. knm/m knm níróerő dim. kn/m kn
8 3. SPECIÁLIS KÉRDÉSEK 3.1 Derékszögű négszög alakú lemez reakiói A peremei mentén szabadon fekvő lemez reakióerő megoszlása a támaszok vonalában nem azonos a támasz feletti ténleges v vag v nomóerővel, mivel az tengellel párhozamos alátámasztás vonalában, a savarásból származó m fajlagos níróerővel módosítani kell. Az tengellel párhuzamos perem mentén ezzel a redukált níróerő, illetve támaszreakió megoszlása az előző táblázatban feltüntetett menniségek figelembe- vételével 3 3 m w w v red r v K 3 + ( ) µ mel értéket Kirhoff féle peremerőnek nevezzük. Az ábrán a lemez egik sarkát tüntettük fel úg, hog a perem elemi szakaszára működő m savarónomatékokat m d/d m értékű ellentett erőkből álló erőpárokkal helettesítettük. Az ábrákból látható, hog a lemez sarokpontjában, a satlakozó peremekre működő savarónomatékok előjele következtében, felfelé mutató konentrált reakióerő ébred, melnek értéke merőlegesen satlakozó peremek esetén: R o m A b, ábra a sarkaiban leterheletlen négzet alakú lemez alakváltozását, a, ábra pedig a níróerő és a reakió eloszlását mutatja µ 0 esetben. Látható, hog amenniben a lemez pereme nins leterhelve vag lekötve, úg a lemezsarok felemelkedik. Ha a lemez a peremei mentén befogott, akkor pl. az tengellel párhuzamos perem mentén érvénes w w 0 peremfeltétel miatt a derivált ugansak zérus értékű, tehát a befogott peremen az m savarónomaték zérus. Ebből következik, hog befogott peremhez satlakozó sarokpontban nem lép fel konentrált reakióerő, és a befogott perem mentén a reakióerő és a níróerő eloszlása azonos.
9 3. Egiránban teherviselő lemezek Vizsgáljuk eg olan, az iránban végtelen kiterjedésűnek tekintett lemezt, melnek terhelése az változótól független és az tengellel párhuzamos peremei mentén van megtámasztva Ekkor a lemez hengeres alakváltozást szenved, vagis a w lehajlásfüggvén sak -től függő lesz, és az azt leíró Lagrange féle differeniálegenlet a w ( ) egszerű alakot ölti. Ennek megoldása analóg eg hajlított gerenda K rugalmas vonalának megoldásával. A lehajlásfüggvén alapján számítható nomatékok m w w K + µ 0 és m K 0 + µ µ m alakban kaphatók, vagis az tengel, másképpen a teherbírás iránában számítható nomatékok az tengel iránú lemezsávokon mint egségni széles gerendákon keletkező nomatékokkal azonosak, míg az erre merőleges iránban keletkező nomaték ennek µ - szerese Ez indokolja, hog bármel lemezben a fő teherbírás iránára merőlegesen legalább a főiránban szükséges vasalás 0 %-át élszerű alkalmazni. Megjegezzük, hog gakorlatilag egiránban teherviselőnek tekinthető az a derékszögű négszög alakú lemez, melnek hosszabbik oldala nagobb a rövidebbik oldala kétszeresénél és terhelése a felületén egenletesen megoszló teher. Az ilen lemezeknél uganis a pontos lemezelmélet alapján számítható kétiránú nomatékok arána már 5-nél nagobbra adódik, íg minthog a mellék iránban a főirán vasalásának 0 %-át mindenképpen alkalmazni kell, felesleges az igénbevételeket a pontosabb, kétiránban teherviselő lemezelmélet alapján meghatározni. 3.3 Konentrált terhek esete Konentrált erővel terhelt lemezek esetén a Fourier sorba fejtett megoldás nagon lassan konvergál és sak több száz tag figelembe vételével vezet elegendően pontos eredménre. A konentrált terhek hatására keletkező igénbevételek gakorlati meghatározására sak II. világháború után, Puher osztrák professzor által kidolgozott hatásfelületek elterjedésével nílt lehetőség. A hatásfelületek meghatározása a Mawell féle felserélhetőségi tételen alapul, mel szerint a lemezfelület eg adott pontjában működő egségni konentrált erő hatására a lemez eg tetszőleges másik pontjának lehajlása megegezik az utóbbi pontra állított egségből az eredeti pontban számítható lehajlással. A lemez valamel kritikus keresztmetszete hatásfelületének előállításához tehát elegendő az adott keresztmetszetre állított egségerőből meghatározni a lehajlásfüggvént, és az íg előállított hatásfelület alapján ismert összefüggésekből számíthatók az igénbevételek. Eg a peremei mentén szabadon felfekvő lemez középső keresztmetszete görbületi, illetve az azzal arános hajlítónomtéki hatásfelületét, valamint annak szintvonalas ábrázolását mutatja az alábbi bra. Látható, hog a keresztmetszet felett álló konentrált erőből a keresztmetszetben keletkező nomaték értéke elvileg végtelen. A gakorlatban azonban ténleges konentrált erő nem létezik, sak kis felületen megoszló teher. Ennek
10 alapján a vizsgált hatás az A terhelt felület fölötti hatásfelületrész V térfogatának meghatározása után kapható. V η da A Ha a konentrált erő hatására keletkező igénbevételeket véges elemes számítógépi programmal határozzuk meg, akkor a kis felületen megoszló teher körnezetében a véges elemes hálózat felosztását megfelelően sűríteni kell. 3.. Konentrált erővel terhelt konzolos lemezek Eg a szabad szélén P konentrált erővel terhelt, iránban elegendően hosszú és az 0 peremén befogott, állandó vastagságú konzollemez maimális fajlagos befogási nomatéka a rugalmas lemezelmélet szerint meghatározva m ma - 0,65 P [knm/m] Hasonlítsuk össze ezt az eredmént eg olan közelítő eljárással számított befogási nomatékkal, melnél azt a feltételezést tettük, hog a konentrált erőből származó hatás szétterjedése 5 o. Ezzel a befogási keresztmetszetben számítható fajlagos nomaték értéke m ma - ( P l ) / ( l ) P [knm/m] Látható, hog ezzel az egszerű közelítéssel a pontos eredméntől mindössze 7,5 %- kal a biztonság javára eltérő nomatékot kaptunk. Meg kell jegezni, hog amenniben a lemez szabad pereme gerendával erősített, úg az igénbevétel 5 o -nál nagobb szög alatt terjed szét, ezáltal a befogási nomaték az előzőnél kisebb lesz. Ha a lemez vastagsága a befogási keresztmetszet felé növekszik, akkor az igénbevételek szétterjedésének szöge kisebb, tehát a befogási nomaték nagobb lesz. 3.5 A lemez vasalásának meghatározása a rugalmas igénbevételek alapján A rugalmas lemezelmélet alapján a lemez bármel pontjában meghatározhatók az m és m fajlagos hajlító és az m fajlagos savarónomatékok. Ezek felhasználásával a lemezben keletkező főnomatékok az alábbi összefüggéssel számíthatók: m 1, ( ) m + m m m ± + m A főnomatékok irána a lemez felületén pontról pontra változik és az un. trajektória vonalakkal jellemezhető. A főnomatéki iránokhoz tartozó metszetekben a savarónomaték zérus. A nomatékokból származó húzóerők felvétele szempontjából a trajektória iránú vasalás alkalmazása lenne a leghatékonabb, ennek gakorlati kivitelezése azonban általában lehetetlen. Ezért a legtöbb esetben a lemez vasalását egmást merőlegesen keresztező vasbetétekkel alakítják ki. Ha az és tengelekkel párhuzamos iránú vasaláshoz tartozó fajlagos határnomatékok értékei m H és m H, akkor az tengellel szöget bezáró iránban a határnomaték Johansen szerint az mα H mh os α + m Hsin α összefüggéssel számítható.
11 Ennek felhasználásával levezethető, hog az illetve iránban szükséges vasalást a biztonság javára szolgáló közelítéssel, a lemez minden pontjában az m +m illetve m +m fajlagos nomatékok alapján kell meghatározni. A vasbeton lemezek méreteire és vasalására vonatkozóan az alábbi legfontosabb szerkesztési szabálokat kell betartani: - a lemez vastagsága minimálisan 60 mm, konzolos lemez befogási keresztmetszetében legalább 100 mm legen, - a lemezben elhelezett aélbetétek minimális átmérője 5 mm, hegesztett hálós vasalás esetén, mm lehet, és a vasátmérő ne legen nagobb a lemezvastagság egnoladánál, - az aélbetétek egmástól való maimális távolsága az egik iránban 00 mm, a másik iránban 00 mm, illetve a lemezvastagság kétszerese (a két érték közül a nagobb) lehet, A - a fő teherviselési iránban a minimális aélmenniség az A s min 016, f t, eff δ s összefüggéssel számítható, ahol δ s az aélbetétben megengedett feszültség, de A s,min ne legen 0,0015 A -nél kisebb, - a mellékiránban legalább a főiránban a méretezés, vag a szerkesztési szabálok által meghatározott vasmenniség 0 %-át kell betervezni, - az eges lemezmezőkben a legnagobb mezőnomaték felvételéhez szükséges húzott vasalásnak legalább a felét végig kell vezetni a teljes lemezmezőn úg, hog a támasz középvonala mögött legen lehorgonozva. Ha a támasztónomatékok felvételére alkalmazott vasalás keresztmetszete legalább a végig vezetett vasak keresztmetszetének egharmada, úg elegendő a maimális mezőnomaték felvételéhez szükséges vasalás egharmadát végig vezetni, - a lemez szabad szélén, azzal párhuzamosan, szegél aélbetéteket kell elhelezni. Ezek a perem sarkaiban vezetett legalább 5 mm átmérőjű vasak legenek, meleket a lemezszélre merőlegesen kifutó aélbetétek visszahajtásával, vag külön hajtűvasakkal kell összefogni. Ezek távolsága 00 mm vag a lemezvastagság kétszerese lehet.. DERÉKSZÖGŰ NÉGYSZÖG ALAKÚ LEMEZEK IGÉNYBEVÉTELEI, VASALÁSA.1 Az igénbevételek meghatározása grafikonok segítségével Egenletesen megoszló teherrel terhelt, a peremei mentén feltámaszkodó, illetve befogott lemezek maimális hajlító-igénbevételeinek és lehajlásának meghatározására grafikusan feldolgozott eredméneket, görbesereget alkalmazunk. A görbesereg görbéi R. Bares analitikus megoldáson alapuló táblázatainak eredménét foglalják össze. A maimális mezőnomatékok a lemez szimmetriatengeleiben alakulnak ki. Itt a savarónomatékok zérus értékűek, tehát a vasalás itt közvetlenül a hajlítónomatékokból számítható. A feltámaszkodó peremű lemez sarkain fellépő savarónomatékok miatt, a sarok körnezetében keletkező negatív főnomatékra a lemez felső síkját is meg kell vasalni. Derékszögű négszög alakú lemezek vasalásának elvi kialakítását mutatják a következő. ábrák hagomános, egenes vasakból kialakított, illetve hálós vasalás esetén.
12
13
14 .. A maimális igénbevételek közelítő számítása Az igénbevételek egszerű megfontolásokon alapuló, közelítő meghatározására egrészt a pontosabb, esetleg gépi számítási eredmének ellenőrzésekor, másrészt a szerkezetek előméretezésekor lehet szükség. A továbbiakban két egszerű módszert ismertetünk derékszögű négszög alakú lemezek maimális hajlítónomatékainak közelítő számítására..1 Tartókereszt eljárás Az eljárást sávmódszernek is nevezik, és alapötlete az, hog a lemezből a maimális lehajlás helén és iránában eg-eg egmást keresztező, egségni szélességű lemezsávot vágunk ki, meleket a saját iránukban önállóan működő gerendáknak tekintünk. Ezzel, a savarási ellenállást figelembe vevő tag elhanagolása miatt, a rugalmas lemezek Lagrange féle differeniálegenlete: w + w k alakúra egszerűsödik, ahol a baloldal első tagja egségni szélességű iránú, a második pedig szintén egségni szélességű, de iránú gerenda alakváltozás-teher összefüggéseként értelmezhető. Ha az -es iránú tartók által viselt megoszló teherrész és, és a lemez felületére egenletesen megoszló teher működik, akkor az egensúl alapján + onst. Minthog a két sáv kereszteződési pontjában a lehajlás azonos értékű, ezért a kompatibilitási feltétel w w A lemezsávok rugalmas vonalának differeniálegenlete alapján w a l és w a l E I E I ahol az a és a értékek a lemez megtámasztási viszonaitól függő ténezők, az ábra szerint.
15 Állandó vastagságú lemeznél I I felhasználásával, és az ε l / l valamint m a /a paraméterek bevezetésével a kompatibilitási egenlet ε m m, illetve alakra hozható, mel értékeket az egensúli ε ε egenletbe beírva a kétiránú lemezsávra jutó teherrészekre a és m + ε m összefüggéseket kapjuk. m + ε A lemezsávok maimális nomatékai ezután az adott iránú sávra működő teherrészből a megtámasztási viszonok függvénében számíthatók. A kétiránú teherviselést mindkét iránban azonos megtámasztású lemezsávok esetén sak 05, < ε < esetben érdemes figelembe venni, mivel ha ε és m 1 akkor 16 a teljes teher 9 %-a és 17 1 a teljes tehernek sak 6 %-a 17 A sávmódszer elhanagolja a keresztező lemezsávok egmásra gakorolt hatásából fellépő savarónomatékokat, ezért a hajlítónomatékokat a biztonság javára szolgáló közelítéssel állapítja meg.. Marus módszere Az eljárást Marus dolgozta ki a sávmódszer alapján, de az ott elhanagolt savarónomaték hatásának figelembevételével. A megoldás alapesete a nég peremén feltámaszkodó, egenletesen megoszló teherrel terhelt négszöglemez. A lemezre működő terheket Marus az egmást keresztező lemezsávokra értelmezett módon `+ `+ ``+ `` onst. alakban bontotta fel, ahol a ``+ `` tag a savarási ellenállásnak megfelelő teherrészt veszi figelembe. A savarási teherhánad meghatározására a l m `` 5 5 l m l ; `` 6 m 0 l 6 m 0 összefüggéseket vezette le, ahol - m és m a sávmódszerrel meghatározható mezőközépi fajlagos hajlítónomatékok, - m o és m o a kéttámaszúnak tekintett és iránú lemezsávok maimális nomatékai a teljes teherből, - és a sávmódszerrel meghatározható teherrészek. Fentiek alapján a ` és ` hajlítási teherhánadok a ` `` és ` `` kifejezések segítségével számíthatók, melekből a lemez hajlítónomatékai a megtámasztási viszonoktól függően határozhatók meg.
16 A savarási taggal módosított hajlítási teherhánad, illetve az abból számítható nomatékok meghatározására Marus az alábbi ábrán feltüntetett alapesetekre dolgozott ki táblázatokat. 5LEMEZRENDSZEREK KÖZELÍTŐ VIZSGÁLATA A mérnöki gakorlatban sokszor előforduló feladat az eg vag mindkét iránban többtámaszú lemezrendszerek méretezése mezőnként egenletesen megoszló teherre. A lemezrendszer terhelése a önsúl és a lemezmezőnként függetlenül működtethető p hasznos teher. A többtámaszú, kétiránban teherviselő lemezrendszer eg mezőjének maimális nomatékai közelítően eg, a vizsgált mezővel azonos méretű, különálló lemezen határozhatók meg, ha az alábbi feltételek teljesülnek: - a lemezvastagság minden mezőben azonos, - a lemezmezők peremei megtámasztásának módja nem befolásolja a lemez igénbevételeit, - a lemezmezők hajlításra mereven kapsolódnak egmáshoz, de a megtámasztási vonalak mentén szabadon elfordulhatnak, - a szomszédos lemezmezők fesztávolságainak arána mindkét iránban 0,8 és 1,5 között van. A maimális és minimális mezőnomatékok számításához az önsúl teherrel a teljes lemezrendszert, míg a hasznos teherrel sakktábla szerűen, minden második lemezmezőt kell leterhelni. Ennek figelembe vételével a mezőnomatékok az összes mezőben mindkét iránban úg határozhatók meg, hog a különálló lemezek egmáshoz satlakozó peremein a g + p/ terhelésre merev befogást, míg a mezőnként változó ± p/ terhelésre szabadon elforduló megtámasztást tételezünk fel az ábra szerint. A legnagobb mezőnomatékok ekkor a két tehersoporthoz tartozó ( + g + p) nomatékok összegéből, míg a legkisebb mezőnomatékok a két tehersoporthoz tartozó ( g) nomatékok különbségéből kaphatók. Lemezrendszer mértékadó leterhelése mezőnomatékra, p g+, p g+,, p ±,, p +
17 A legnagobb támasztónomaték meghatározásához az önsúllal a teljes lemezrendszert, a hasznos teherrel pedig a vizsgált támasz melletti lemezmezőket kell leterhelni. A támasztónomaték számításához az előzőekben definiált teherből a támaszok vonalában tökéletes befogást feltételezve, míg a teherből a vizsgált támaszon az alábbi ábra szerint befogást, a többi peremen pedig szabadon elforduló megtámasztást figelembe véve határozzuk meg az igénbevételeket. A satlakozó lemezekre vonatkozó támasznomaték a kétféle leterhelésből meghatározható nomatékok összege. Lemezrendszer mértékadó leterhelése támasznomatékra, p g+,, p g±, p g+,, p + A támasz feletti vasalás szempontjából a satlakozó lemezelemek alapján számítható, és a legtöbb esetben egmástól eltérő támasznomatékok átlaga tekinthető mértékadónak.
18 6. GOMBAFÖDÉMEK, SIKLEMEZ FÖDÉMEK 6.1. Általánosságok A magas és mélépítésben is igen gakran alkalmazott szerkezettípus a gomba vag síklemez födém, melnél a vasbeton lemez közvetlenül, tartógerendák közbeiktatása nélkül támaszkodik az oszlopokra. A klasszikus, régebbi szerkezeteknél az oszlopok kiszélesedő oszlopfővel, gombafejjel satlakoznak a lemezhez. Újabban széles körben elterjedt a fejnélküli gombafödémek, vag síklemez födémek alkalmazása. Hasonlóan, de a födémekhez képest ellentett terhelési és igénbevételi viszonokkal működnek az oszlopok közvetlen alátámasztását szolgáló lemezalapok is. ' ' l1 l1 l l 3 3 ' l3 l3 3 m elméleti oszlopmagasság l elméleti támaszköz A gomba és síklemez födémek alkalmazásának előnei: - egszerű, gors zsaluzás, állvánozás, vasszerelés, - jobb térkihasználás a gerendák elmaradása miatt, - kisebb kötöttségek az alaprajzi elrendezésben, - jobb természetes levilágítás. és hátránai: - bonolultabb erőjáték, az igénbevételek pontos számítása nehézkesebb, - a közelítő módszerek túlméretezéshez vezethetnek, - nagobb alakváltozások, - a lemez és oszlop kapsolatának modellezése bizontalan.
19 A felsorolt hátránok kevésbé jelentkeznek nag alapterületű, szabálos derékszögű hálózatban alátámasztott és kiegenlített terhelésű födémeknél. Az alakváltozások korlátozása érdekében a lemez vastagságát az l/t 5 feltétel alapján élszerű megválasztani. A gomba és síklemez födémek vizsgálatánál általában két alapvető feladatot, a hajlítási méretezést és az átszúródásvizsgálatot kell elvégezni. 6. Hajlítási méretezés Itt sak a födémet közvetlenül terhelő, függőleges, egenletesen megoszló terhekből származó hajlítónomatékok közelítő meghatározásával foglalkozunk, feltételezve, hog az épületre működő vízszintes terheket a külön erre a élra kialakított merevítőrendszer veszi fel. Amenniben ilen merevítőrendszert nem alakítottak ki, úg a vízszintes terhelésből a lemez többlet igénbevételeit például eg olan helettesítő keretszerkezeten lehet meghatározni, melnek a gerendája eg, az oszlopokkal egüttdolgozónak tekintett, fiktív szélességű és t vastagságú lemezsáv. Az egenletesen megoszló teherrel terhelt, gomba vag síklemez födémek igénbevételei, általánosan a rugalmas lemezelmélet alapján felírható differeniálegenlet analitikus vag numerikus megoldásával állíthatók elő. A megoldás során általában feltételezik, hog az oszlopreakió a gombafej felületén egenletesen oszlik meg. A pontos rugalmas elmélet alapján számított eredmének felhasználásával, táblázatokat dolgoztak ki, a gakorlatban legtöbbször előforduló, szabálos alaprajzi elrendezésben megtámasztott födémlemezek fajlagos hajlítónomatékainak meghatározására a kritikus keresztmetszetekben. Eg ilen táblázatra mutatunk be példát az alábbiakban: egenletesen megoszló teher 3 E I E t B 1 µ 1 1 µ ( ) oszlopméret: 0,05l 0,05l A ténezők értékeit az ( µ 0 Poisson ténező feltételezésével) az a maimális lehajlás, az m és m nomatékok, valamint az R reakióerő meghatározásához a következő táblázatból vehetjük:
20 l l 05. l l 10. l l 0. A B C D A B C D A B C D 1 0,000 0,11 0,000 0,091 0,000 0,639 0,000 0,177 0,000,33 0,000 0,80,089,067,016 1,990 0,617 1,018 0,66 0,611 0,10,01 0,303 0,36 3 0,000 0,30 0,000 0,19 0,000 0,700 0,000 0,1 0,000,153 0,000 0,95 a 0,69 0,736 0,678 0,67 0,70 0,70 0,89 0,36 0,11,118 0,150 0,53 5 0,000 0,58 0,000 0,103 0,000 0,630 0,000 0,17 0,000,11 0,000 0,37 1,00 7,16-15,68,1,00 8,70-19,15,16,00 1,1 -,95,6,00 1,13 -,09 -,9,00 5,33-3,19,8,00 13,7-1,38 3,77 3,00 8,65 -,98 5,9,00 9,51 --5,38,80,00 1,53-7,57,75 m,00 1,0 -, -,6,00 5,76-3,70,5,00 1,18-13,37,5 5,00 6,51-15,8 3,91,00 8,13-17,93 3,6,00 1,7-3,60,39 1,00,00,00,00,00,00,00,00,00,00,00,00 13,80 13,1 1,10 1,05 8,56 5,08 9,19 5,9 7, 1,16 8,33 1,38 3-6,5-13,1-9,17-15,6-0,11-3,31-5,60 -,31-16,5,09 -, -,01 m 6,63 5,87 6,86 6,75 5,00 1,3 5,36 1,8,76 -, 5,53 -,9 5-17,8-8,9-19,09-9,9-1,75 -,6-17,18 -,7-1,58 -,69-18, -, ,5,31 16,68,60 16,85 5,3 3 7,07 13,96 6,8 13,1 5,65 10,81 R 5 36,06 99,6 37,11 101,09 38,5 10,1 Derékszögű négszög hálózatban megtámasztott gomba, vag síklemez födémeknél, ha az alátámasztások távolságainak arána mindkét iránban 0,8 és 1,5 között van, a maimális igénbevételek meghatározására alkalmazható az alábbi közelítő eljárás. A gombafödém lemezének nomatékait eg olan,, illetve iránú helettesítő gerendán határozzuk meg, melnek szélessége a képzelt gerenda tengelére merőleges két szomszédos oszlop l tengeltávolságával egezik meg és a gerenda tengelével párhuzamos iránban egmástól az ábrán jelölt l elméleti távolságra lévő pontokban van megtámasztva. Az egmást keresztező lemezsávokra külön-külön, az adott iránnak megfelelő, teljes l lemezszélességnek megfelelő terhelést kell figelembe venni. Az íg kialakított helettesítő gerendákon meghatározott nomatékokat az ábra szerint kell eg 0,5 l szélességű lemezsáv és eg ugansak 0,5 l szélességű oszlopsáv között szét-osztani. Az ábra szerint valamel iránban a gerendán számítható mezőnomaték 5 %-át a lemezsáv, míg 55 %-át az oszlopsáv veszi fel. Uganakkor a támasztónomatéknak 5 %-a lemezsávra, 75 %-a pedig az oszlopsávra jut, és a lemez hajlítási vasalását ennek megfelelően kell kialakítani:
21 Fejnélküli, síklemez födém maimális nomatékait is hasonló közelítéssel lehet meghatározni. Ekkor azonban a kis feltámaszkodási felület következtében az igénbevételek még inkább az oszlopok körnezetére konentrálódnak, ezért ekkor az oszlopsáv szélességét 0, l-re, a lemezsávét pedig 0,6 l-re kell felvenni, és a helettesítő gerenda mező, illetve támasztónomatékait az alábbi ábrán bemutatott módon kell a lemezsáv és az oszlopsáv között felosztani. Eg síklemez födém belső mezőjének általános vasalását az előbbiek szerint meghatározott nomatékokalapján a következő ábrán mutatjuk be:
22
23 7.3. Átszúródási vizsgálat A kis felületen átadódó reakióerő következtében különösen a síklemez födémek átszúródási teherbírása kritikus. Kísérleti tapasztalatok szerint az átszúródás központos oszlopreakió esetén eg sonka gúla, vag sonka kúp alakú idomnak a lemezből az oszlop körnékén való kiszakadása formájában következik be. A kiszakadó gúla vag kúp β hajlásszöge az ábra szerint vasalatlan lemez esetén ~ 5 o, míg hajlításra megvasalt lemeznél kb. 30 o. Eg lemez átszúródásra való ellenőrzésekor igazolni kell, hog a b w kritikus átszúródási vonal mentén fellépő fajlagos mértékadó V sd níróerő nem haladja meg a lemez d hasznos vastagságától, a beton húzószilárdságától és az átszúródási ellenállás szempontjából figelembe vehető vasalástól függő V Rd határníróerőt. Központos oszlopreakió esetén a mértékadó fajlagos níróerő a következő összefüggéssel számítható: Vsd vsd u ahol V sd a mértékadó oszlopreakió, u pedig az átszúródási vonal kerülete. A mértékadó oszlopreakió meghatározásánál a lemezre ható terheknek a u kerületen belülre eső részét nem kell figelembe venni. Különböző oszlopkeresztmetszetek esetén, valamint az oszlopnak a lemez szabad széléhez viszonított helzetétől függően az átszúródási vonalat a következő módon szabad felvenni: Alapelv, hog az átszúródási vonal az oszlop kerületétől mindenütt 1,5 d távolságra van, ahol d a vasalt lemez hasznos magassága, a vonal konve és a sarkai lekerekítettek. Nújtott oszlopkeresztmetszet (pengepillér) esetén ha a keresztmetszet hosszabbik oldala nagobb a rövidebbik oldal négszeresénél, akkor az átszúródási vonal szakaszos (mivel a hosszabbik oldal közepe táján a níróerő jelentősen lesökken, sőt előjelet is válthat). Szabad peremek, illetve lemezsarkok közelében az átszúródási vonal kifuthat a lemez szélére. Külpontos oszlopreakió esetén az átszúródási vonal mentén fellépő fajlagos mértékadó níróerő eloszlása nem egenletes. Maimális értéke ekkor az alábbi közelítő összefüggéssel határozható meg, v Sd V u Sd M ± I Sd u
24 ahol M Sd a V Sd mértékadó reakióerővel egidejűleg működő maimális hajlítónomaték az oszlopvégen, I u az átszúródási vonal tehetetlenségi nomatéka a hajlítás tengelére, és az átszúródási vonal vizsgált pontjának távolsága a hajlítási tengeltől. Az I u tehetetlenségi nomaték értékei: - téglalap alakú átszúródási vonal esetén b a b Iu ; vag a b a Iu ahol a és b a téglalap oldalainak hosszúsága - a oldalú négzet alakú átszúródási vonal esetén I u 3 - r sugarú kör alakú beszúródási vonal esetén a 3 Iu r 3 Π Külpontos oszlopreakió esetén az EC- szerint az átszúródási vonal mentén keletkező fajlagos níróerő közelítően a v Sd V β u Sd összefüggéssel besülhető, ahol ß 1,15 belső oszlop ß 1,0 szélső oszlop, és ß 1,50 sarokoszlop esetén. Az átszúródási ellenállás számítása és a nírási vasalás kialakítása Az átszúródással szembeni ellenállás pontosabb, háromdimenziós számítási modell alkalmazásának hiánában, az EC- alapján a vasbeton gerendák nírási teherbírásának számításához hasonló elven határozható meg. A kritikus átszúródási kerület mentén számításba vehető fajlagos nírási ellenállás nírási vasalás nélkül ahol: τ Rd a beton nírási határfeszültsége (, ρ ) vrd1 τrd k 1+ 0 l d
25 k 1,6 - d 1, (d méterben behelettesítve) ρ l ρl ρl 0,015 ρ l és ρ l az és iránú lemezvasalás betonkeresztmetszetre vonatkoztatott fajlagos értéke d 0,5(d + d ), d és d az ill. az iránú lemezvasalás alapján számítható hatékon lemezvastagság Tapasztalatok alapján a fajlagos nírási ellenállás felső korlátja az alábbi: v Rd 1, 6 v Rd 1 v Rd1 < v Sd v Rd esetén az átszúródási ellenállás biztosítására nírási vasalást kell alkalmazni. A fajlagos átszúródási ellenállás ekkor a v Rd 3 v Rd 1 A + sw f u d sinα összefüggéssel számítható, ahol a ΣA sw f d sinα menniség az a kritikus kerületet átmetsző összes nírási aélbetét nírási ellenállása. α a nírási vasak tengelének a lemez középfelületével bezárt szöge. A beton és az aélbetétek teherbírásának egmásráhalmozása miatt, a kompatibilitási feltételek teljesülése érdekében ajánlott az aélbetétek feszültségét σ 0,5 f d értékére korlátozni. Az ismertetett módszer feltételezi, hog a lemez síkjában mindkét iránban futó hajlítási vasalás van az oszlop fölött. A vasalás mértéke legen legalább a hatékon betonkeresztmetszet 0,5%-a. v Sd > v Rd1 esetén az átszúródási teherbírást biztosító nírási vasalás minimális keresztmetszeti területe ΣA sw sinα 0,6 ρ wmin (A rit - A terh ), ill. ρ wmin az EC- szerinti minimális fajlagos vasalás, A rit az u kerület által körülírt kritikus lemezfelület, A terh pedig a közvetlenül terhelt lemezterület. Az alakváltozási pont körnezetében a lemez átszúródási vasalása az ábra szerint nírókosárral (a. ábra), tangeniális iránban elhelezett függőleges kengelekkel (b. ábra), rúdszerű nírási vasalással (. ábra), idomaélokból hegesztett merev vázzal (d. ábra), vag aéllemezre hegesztett nírósapokkal (e. ábra) alakítható ki.
26 Külpontos erővel terhelt oszlop - lemez kapsolat esetén az átszúródással szembeni ellenállás biztosítása érdekében a lemezt a külpontosságból adódó hajlítónomatékra is meg kell vasalni. Az illetve iránú szükséges vasalást az m Sd, (vag m Sd, ) η V Sd fajlagos hajlítónomatékokból lehet meghatározni, ahol V Sd az átszúródást okozó teljes níróerő és az η ténező az alábbi táblázatból határozható meg az alátámasztás helzetétől függően. A nomatékokból számítható húzott vasalást az ábrában definiált b illetve b hatékon lemezsávokban kell egenletesen kiosztani.
27 Az oszlop helzete az m Sd, nomatéki ténezők η felső alsó b vasalat vasalás az m Sd, nomatéki ténezők η felső alsó b vasalat vasalás Belső oszlop -0,15 0 0,30 l -0,15 0 0,30 l Az tengellel párhuzamos -0,50 0 0,15 l -0,15 0 * szélen lévő oszlop Az tengellel párhuzamos -0,15 +0,50 * -0,50 * 0,15 l szélen lévő oszlop Sarok oszlop -0,500 +0,500 * -0,500 +0,500 * * a vasalást a keresztező sávszélességben kell egenletesen kiosztani
Vasbetonszerkezetek II. STNA252
 Szilárdságtan és Tartószerkezet Tanszéke Vasbetonszerkezetek II. STNA5 Pécs, 007. november STNA5 Szerző: Kiss Rita M. Műszaki rajzoló: Szabó Imre Gábor ISBN szám: Kézirat lezárva: 007. november 30. STNA5
Szilárdságtan és Tartószerkezet Tanszéke Vasbetonszerkezetek II. STNA5 Pécs, 007. november STNA5 Szerző: Kiss Rita M. Műszaki rajzoló: Szabó Imre Gábor ISBN szám: Kézirat lezárva: 007. november 30. STNA5
TARTÓSZERKEZETEK II. VASBETONSZERKEZETEK 2013.02.11.
 TARTÓSZERKEZETEK II. VASBETONSZERKEZETEK 2013.02.11. A felületszerkezetek csoportosítása Felületszerkezetek Sík középfelület Görbült középfelület (héjszerkezet) Tárcsa Lemez Egyszeresen görbült Kétszeresen
TARTÓSZERKEZETEK II. VASBETONSZERKEZETEK 2013.02.11. A felületszerkezetek csoportosítása Felületszerkezetek Sík középfelület Görbült középfelület (héjszerkezet) Tárcsa Lemez Egyszeresen görbült Kétszeresen
Téma: A szerkezeti acélanyagok fajtái, jelölésük. Mechanikai tulajdonságok. Acélszerkezeti termékek. Keresztmetszeti jellemzők számítása
 1. gakorlat: Téma: A szerkezeti acélanagok fajtái, jelölésük. echanikai tulajdonságok. Acélszerkezeti termékek. Keresztmetszeti jellemzők számítása A szerkezeti acélanagok fajtái, jelölésük: Ádán Dulácska-Dunai-Fernezeli-Horváth:
1. gakorlat: Téma: A szerkezeti acélanagok fajtái, jelölésük. echanikai tulajdonságok. Acélszerkezeti termékek. Keresztmetszeti jellemzők számítása A szerkezeti acélanagok fajtái, jelölésük: Ádán Dulácska-Dunai-Fernezeli-Horváth:
SZILÁRDSÁGTAN A minimum teszt kérdései a gépészmérnöki szak egyetemi ágon tanuló hallgatói részére (2004/2005 tavaszi félév, szigorlat)
 SILÁRDSÁGTAN A minimum teszt kérdései a gépészmérnöki szak egetemi ágon tanuló hallgatói részére (2004/2005 tavaszi félév, szigorlat) Szilárdságtan Pontszám 1. A másodrendű tenzor értelmezése (2) 2. A
SILÁRDSÁGTAN A minimum teszt kérdései a gépészmérnöki szak egetemi ágon tanuló hallgatói részére (2004/2005 tavaszi félév, szigorlat) Szilárdságtan Pontszám 1. A másodrendű tenzor értelmezése (2) 2. A
Mechanika II. Szilárdságtan
 echanika II. Szilárdságtan Zalka Károl / q / B Budapest, 05 Zalka Károl, 05, e-kiadás Szabad ezt a kiadvánt sokszorosítani, terjeszteni és elektronikus vag bármel formában tárolni. Tilos viszont a kiadvánt
echanika II. Szilárdságtan Zalka Károl / q / B Budapest, 05 Zalka Károl, 05, e-kiadás Szabad ezt a kiadvánt sokszorosítani, terjeszteni és elektronikus vag bármel formában tárolni. Tilos viszont a kiadvánt
Előadó: Dr. Bukovics Ádám
 SZÉCHYI ISTVÁ GYT TARTÓSZRKZTK III. lőadó: Dr. Bukovics Ádám Az ábrák forrása: 6. LŐADÁS [] Dr. émeth Görg: Tartószerkezetek III., Acélszerkezetek méretezésének alapjai [2] Halász Ottó - Platth Pál: Acélszerkezetek
SZÉCHYI ISTVÁ GYT TARTÓSZRKZTK III. lőadó: Dr. Bukovics Ádám Az ábrák forrása: 6. LŐADÁS [] Dr. émeth Görg: Tartószerkezetek III., Acélszerkezetek méretezésének alapjai [2] Halász Ottó - Platth Pál: Acélszerkezetek
Szilárdságtan. Miskolci Egyetem GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR
 Miskolci Egetem GÉÉMÉRNÖKI É INORMTIKI KR ilárságtan (Oktatási segélet a Gépésmérnöki és Informatikai Kar sc leveleős hallgatói résére) Késítette: Nánori riges, irbik ánor Miskolc, 2008. Een kéirat a Gépésmérnöki
Miskolci Egetem GÉÉMÉRNÖKI É INORMTIKI KR ilárságtan (Oktatási segélet a Gépésmérnöki és Informatikai Kar sc leveleős hallgatói résére) Késítette: Nánori riges, irbik ánor Miskolc, 2008. Een kéirat a Gépésmérnöki
KERETSZERKEZETEK. Definíciók, Keretek igénybevételei, méretezése. 10. előadás
 KERETSZERKEZETEK Definíciók, Keretek igénybevételei, méretezése 10. előadás Definíciók: Oszlop definíciója: Az oszlop vonalas tartószerkezet, két keresztmetszeti mérete (h, b) lényegesen kisebb, mint a
KERETSZERKEZETEK Definíciók, Keretek igénybevételei, méretezése 10. előadás Definíciók: Oszlop definíciója: Az oszlop vonalas tartószerkezet, két keresztmetszeti mérete (h, b) lényegesen kisebb, mint a
A.11. Nyomott rudak. A.11.1. Bevezetés
 A.. Nyomott rudak A... Bevezetés A nyomott szerkezeti elem fogalmat általában olyan szerkezeti elemek jelölésére használjuk, amelyekre csak tengelyirányú nyomóerő hat. Ez lehet speciális terhelésű oszlop,
A.. Nyomott rudak A... Bevezetés A nyomott szerkezeti elem fogalmat általában olyan szerkezeti elemek jelölésére használjuk, amelyekre csak tengelyirányú nyomóerő hat. Ez lehet speciális terhelésű oszlop,
A.14. Oldalirányban megtámasztott gerendák
 A.14. Oldalirányban megtámasztott gerendák A.14.1. Bevezetés A gerendák talán a legalapvetőbb szerkezeti elemek. A gerendák különböző típusúak lehetnek és sokféle alakú keresztmetszettel rendelkezhetnek
A.14. Oldalirányban megtámasztott gerendák A.14.1. Bevezetés A gerendák talán a legalapvetőbb szerkezeti elemek. A gerendák különböző típusúak lehetnek és sokféle alakú keresztmetszettel rendelkezhetnek
Feszített vasbeton gerendatartó tervezése költségoptimumra
 newton Dr. Szalai Kálmán "Vasbetonelmélet" c. tárgya keretében elhangzott előadások alapján k 1000 km k m meter m Ft 1 1 1000 Feszített vasbeton gerendatartó tervezése költségoptimumra deg A következőkben
newton Dr. Szalai Kálmán "Vasbetonelmélet" c. tárgya keretében elhangzott előadások alapján k 1000 km k m meter m Ft 1 1 1000 Feszített vasbeton gerendatartó tervezése költségoptimumra deg A következőkben
LINDAB Floor könnyűszerkezetes födém-rendszer Tervezési útmutató teherbírási táblázatok
 LINDAB Floor könnyűszerkezetes födém-rendszer Tervezési útmutató teherbírási táblázatok Budapest, 2004. 1 Tartalom 1. BEVEZETÉS... 4 1.1. A tervezési útmutató tárgya... 4 1.2. Az alkalmazott szabványok...
LINDAB Floor könnyűszerkezetes födém-rendszer Tervezési útmutató teherbírási táblázatok Budapest, 2004. 1 Tartalom 1. BEVEZETÉS... 4 1.1. A tervezési útmutató tárgya... 4 1.2. Az alkalmazott szabványok...
Néhány érdekes függvényről és alkalmazásukról
 Néhán érdekes függvénről és alkalmazásukról Bevezetés Meglehet, a középiskola óta nem kedveltük az abszolútérték - függvént; most itt az ideje, hog változtassunk ezen. Erre az adhat okot, hog belátjuk:
Néhán érdekes függvénről és alkalmazásukról Bevezetés Meglehet, a középiskola óta nem kedveltük az abszolútérték - függvént; most itt az ideje, hog változtassunk ezen. Erre az adhat okot, hog belátjuk:
10. OPTIMÁLÁSI LEHETŐSÉGEK A MŰVELET-ELEMEK TERVEZÉSEKOR
 10. OPIMÁLÁSI LEHEŐSÉGEK A MŰVELE-ELEMEK ERVEZÉSEKOR A technológiai terezés ezen szintén a fő feladatok a köetkezők: a forgácsolási paraméterek meghatározása, a szerszám mozgásciklusok (üresárati, munkautak)
10. OPIMÁLÁSI LEHEŐSÉGEK A MŰVELE-ELEMEK ERVEZÉSEKOR A technológiai terezés ezen szintén a fő feladatok a köetkezők: a forgácsolási paraméterek meghatározása, a szerszám mozgásciklusok (üresárati, munkautak)
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 6.2. fejezet 483 FEJEZET BEVEZETŐ 6.2. fejezet: Síkalapozás (vb. lemezalapozás) Az irodaház szerkezete, geometriája, a helyszín és a geotechnikai adottságok is megegyeznek az előző (6.1-es) fejezetben
6.2. fejezet 483 FEJEZET BEVEZETŐ 6.2. fejezet: Síkalapozás (vb. lemezalapozás) Az irodaház szerkezete, geometriája, a helyszín és a geotechnikai adottságok is megegyeznek az előző (6.1-es) fejezetben
Használhatósági határállapotok
 Használhatósági határállapotok Repedéstágasság ellenőrzése Alakváltozás ellenőrzése 10. előadás Definíciók Határállapot: A tartószerkezet olyan állapotai, amelyeken túl már nem teljesülnek a vonatkozó
Használhatósági határállapotok Repedéstágasság ellenőrzése Alakváltozás ellenőrzése 10. előadás Definíciók Határállapot: A tartószerkezet olyan állapotai, amelyeken túl már nem teljesülnek a vonatkozó
ELŐFESZÍTETT VASBETON TARTÓ TERVEZÉSE AZ EUROCODE SZERINT
 BUDAPEST MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építőmérnöki Kar Hidak és Szerkezetek Tanszéke ELŐFESZÍTETT VASBETON TARTÓ TERVEZÉSE AZ EUROCODE SZERINT Segédlet v1.14 Összeállította: Koris Kálmán Budapest,
BUDAPEST MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építőmérnöki Kar Hidak és Szerkezetek Tanszéke ELŐFESZÍTETT VASBETON TARTÓ TERVEZÉSE AZ EUROCODE SZERINT Segédlet v1.14 Összeállította: Koris Kálmán Budapest,
BMEEOHSAT17 segédlet a BME Építőmérnöki Kar hallgatói részére. Az építész- és az építőmérnök képzés szerkezeti és tartalmi fejlesztése
 EURÓPAI UNIÓ STRUKTURÁLIS ALAPOK A C É L S Z E R K E Z E T E K I. BMEEOHSAT17 segédlet a BME Építőmérnöki Kar hallgatói részére Az építész- és az építőmérnök képzés szerkezeti és tartalmi ejlesztése HEFOP/004/3.3.1/0001.01
EURÓPAI UNIÓ STRUKTURÁLIS ALAPOK A C É L S Z E R K E Z E T E K I. BMEEOHSAT17 segédlet a BME Építőmérnöki Kar hallgatói részére Az építész- és az építőmérnök képzés szerkezeti és tartalmi ejlesztése HEFOP/004/3.3.1/0001.01
Vasbetontartók vizsgálata az Eurocode és a hazai szabvány szerint
 Vasbetontartók vizsgálata az Eurocoe és a hazai szabvány szerint Dr. Kiss Zoltán Kolozsvári Műszaki Egyetem 1. Bevezetés A méretezési előírasok betartása minenhol kötelező volt régen is, kötelező ma is.
Vasbetontartók vizsgálata az Eurocoe és a hazai szabvány szerint Dr. Kiss Zoltán Kolozsvári Műszaki Egyetem 1. Bevezetés A méretezési előírasok betartása minenhol kötelező volt régen is, kötelező ma is.
7. előad. szló 2012.
 7. előad adás Kis LászlL szló 2012. Előadás vázlat Lemez hidak, bordás hidak Lemez hidak Lemezhidak fogalma, osztályozása, Lemezhíd típusok bemutatása, Lemezhidak számítása, vasalása. Bordás hidak Bordás
7. előad adás Kis LászlL szló 2012. Előadás vázlat Lemez hidak, bordás hidak Lemez hidak Lemezhidak fogalma, osztályozása, Lemezhíd típusok bemutatása, Lemezhidak számítása, vasalása. Bordás hidak Bordás
10.3. A MÁSODFOKÚ EGYENLET
 .. A MÁSODFOKÚ EGYENLET A másodfokú egenlet és függvén megoldások w9 a) ( ) + ; b) ( ) + ; c) ( + ) ; d) ( 6) ; e) ( + 8) 6; f) ( ) 9; g) (,),; h) ( +,),; i) ( ) + ; j) ( ) ; k) ( + ) + 7; l) ( ) + 9.
.. A MÁSODFOKÚ EGYENLET A másodfokú egenlet és függvén megoldások w9 a) ( ) + ; b) ( ) + ; c) ( + ) ; d) ( 6) ; e) ( + 8) 6; f) ( ) 9; g) (,),; h) ( +,),; i) ( ) + ; j) ( ) ; k) ( + ) + 7; l) ( ) + 9.
3. MÉRETEZÉS, ELLENŐRZÉS STATIKUS TERHELÉS ESETÉN
 ÉRETEZÉS ELLENŐRZÉS STATIUS TERHELÉS ESETÉN A méreteés ellenőrés célkitűése: Annak elérése hog a serkeet rendeltetésserű hasnálat esetén előírt ideig és előírt bitonsággal elviselje a adott terhelést anélkül
ÉRETEZÉS ELLENŐRZÉS STATIUS TERHELÉS ESETÉN A méreteés ellenőrés célkitűése: Annak elérése hog a serkeet rendeltetésserű hasnálat esetén előírt ideig és előírt bitonsággal elviselje a adott terhelést anélkül
VII. Gyakorlat: Használhatósági határállapotok MSZ EN 1992 alapján Betonszerkezetek alakváltozása és repedéstágassága
 VII. Gyakorlat: Használhatósági határállapotok MSZ EN 199 alapján Betonszerkezetek alakváltozása és repedéstágassága Készítették: Kovács Tamás és Völgyi István -1- Készítették: Kovács Tamás, Völgyi István
VII. Gyakorlat: Használhatósági határállapotok MSZ EN 199 alapján Betonszerkezetek alakváltozása és repedéstágassága Készítették: Kovács Tamás és Völgyi István -1- Készítették: Kovács Tamás, Völgyi István
A MÉRETEZÉS ALAPJAI ÉPÜLETEK TARTÓSZERKEZETI RENDSZEREI ÉS ELEMEI ÉPÜLETEK TERHEINEK SZÁMÍTÁSA AZ MSZ SZERINT
 A MÉRETEZÉS ALAPJAI ÉPÜLETEK TARTÓSZERKEZETI RENDSZEREI ÉS ELEMEI ÉPÜLETEK TERHEINEK SZÁMÍTÁSA AZ MSZ SZERINT ÉPÜLETEK TERHEINEK SZÁMÍTÁSA AZ EUROCODE SZERINT 1 ÉPÜLETEK TARTÓSZERKEZETÉNEK RÉSZEI Helyzetük
A MÉRETEZÉS ALAPJAI ÉPÜLETEK TARTÓSZERKEZETI RENDSZEREI ÉS ELEMEI ÉPÜLETEK TERHEINEK SZÁMÍTÁSA AZ MSZ SZERINT ÉPÜLETEK TERHEINEK SZÁMÍTÁSA AZ EUROCODE SZERINT 1 ÉPÜLETEK TARTÓSZERKEZETÉNEK RÉSZEI Helyzetük
A.15. Oldalirányban nem megtámasztott gerendák
 A.15. Oldalirányban nem megtámasztott gerendák A.15.1. Bevezetés Amikor egy karcsú szerkezeti elemet a nagyobb merevségű síkjában terhelünk, mindig fennáll annak lehetősége, hogy egy hajlékonyabb síkban
A.15. Oldalirányban nem megtámasztott gerendák A.15.1. Bevezetés Amikor egy karcsú szerkezeti elemet a nagyobb merevségű síkjában terhelünk, mindig fennáll annak lehetősége, hogy egy hajlékonyabb síkban
BMEEOHSASA4 segédlet a BME Építőmérnöki Kar hallgatói részére. Az építész- és az építőmérnök képzés szerkezeti és tartalmi fejlesztése
 EURÓPAI UNIÓ STRUKTURÁLIS ALAPOK S Z E R K E Z E T E K M E G E R Ő S Í T É S E BMEEOHSASA4 segédlet a BME Építőmérnöki Kar hallgatói részére Az építész- és az építőmérnök képzés szerkezeti és tartalmi
EURÓPAI UNIÓ STRUKTURÁLIS ALAPOK S Z E R K E Z E T E K M E G E R Ő S Í T É S E BMEEOHSASA4 segédlet a BME Építőmérnöki Kar hallgatói részére Az építész- és az építőmérnök képzés szerkezeti és tartalmi
Központi értékesítés: 2339 Majosháza Tóközi u. 10. Tel.: 24 620 406 Fax: 24 620 415 vallalkozas@sw-umwelttechnik.hu www.sw-umwelttechnik.
 Központi értékesítés: 2339 Majosháza Tóközi u. 10. Tel.: 24 620 406 Fax: 24 620 415 vallalkozas@sw-umwelttechnik.hu www.sw-umwelttechnik.hu Termékeink cementtel készülnek Helyszíni felbetonnal együttdolgozó
Központi értékesítés: 2339 Majosháza Tóközi u. 10. Tel.: 24 620 406 Fax: 24 620 415 vallalkozas@sw-umwelttechnik.hu www.sw-umwelttechnik.hu Termékeink cementtel készülnek Helyszíni felbetonnal együttdolgozó
Csatlakozási lehetőségek 11. Méretek 12-13. A dilatációs tüske méretezésének a folyamata 14. Acél teherbírása 15
 Schöck Dorn Schöck Dorn Tartalom Oldal Termékleírás 10 Csatlakozási lehetőségek 11 Méretek 12-13 A dilatációs tüske méretezésének a folyamata 14 Acél teherbírása 15 Minimális szerkezeti méretek és tüsketávolságok
Schöck Dorn Schöck Dorn Tartalom Oldal Termékleírás 10 Csatlakozási lehetőségek 11 Méretek 12-13 A dilatációs tüske méretezésének a folyamata 14 Acél teherbírása 15 Minimális szerkezeti méretek és tüsketávolságok
18. előadás ÁLLANDÓ KÖLTSÉGEK ÉS A KÖLTSÉGGÖRBÉK
 18. előadás ÁLLANDÓ KÖLTSÉGEK ÉS A KÖLTSÉGGÖRBÉK Kertesi Gábor Világi Balázs Varian 21. fejezete átdolgozva 18.1 Bevezető A vállalati technológiák sajátosságainak vizsgálatát eg igen fontos elemzési eszköz,
18. előadás ÁLLANDÓ KÖLTSÉGEK ÉS A KÖLTSÉGGÖRBÉK Kertesi Gábor Világi Balázs Varian 21. fejezete átdolgozva 18.1 Bevezető A vállalati technológiák sajátosságainak vizsgálatát eg igen fontos elemzési eszköz,
Acélszerkezetek. 2. előadás 2012.02.17.
 Acélszerkezetek 2. előadás 2012.02.17. Méretezési eladat Tervezés: új eladat Keresztmetszeti méretek, szerkezet, kapcsolatok a tervező által meghatározandóak Gazdasági, műszaki, esztétikai érdekek Ellenőrzés:
Acélszerkezetek 2. előadás 2012.02.17. Méretezési eladat Tervezés: új eladat Keresztmetszeti méretek, szerkezet, kapcsolatok a tervező által meghatározandóak Gazdasági, műszaki, esztétikai érdekek Ellenőrzés:
V. Gyakorlat: Vasbeton gerendák nyírásvizsgálata Készítették: Friedman Noémi és Dr. Huszár Zsolt
 . Gyakorlat: asbeton gerenák nyírásvizsgálata Készítették: Frieman Noémi és Dr. Huszár Zsolt -- A nyírási teherbírás vizsgálata A nyírási teherbírás megfelelő, ha a következő követelmények minegyike egyiejűleg
. Gyakorlat: asbeton gerenák nyírásvizsgálata Készítették: Frieman Noémi és Dr. Huszár Zsolt -- A nyírási teherbírás vizsgálata A nyírási teherbírás megfelelő, ha a következő követelmények minegyike egyiejűleg
ÉPÍTMÉNYEK FALAZOTT TEHERHORDÓ SZERKEZETEINEK ERÕTANI TERVEZÉSE
 Magyar Népköztársaság Országos Szabvány ÉPÍTMÉNYEK FALAZOTT TEHERHORDÓ SZERKEZETEINEK ERÕTANI TERVEZÉSE MSZ 15023-87 Az MSZ 15023/1-76 helyett G 02 624.042 Statical desing of load carrying masonry constructions
Magyar Népköztársaság Országos Szabvány ÉPÍTMÉNYEK FALAZOTT TEHERHORDÓ SZERKEZETEINEK ERÕTANI TERVEZÉSE MSZ 15023-87 Az MSZ 15023/1-76 helyett G 02 624.042 Statical desing of load carrying masonry constructions
MEREVSZÁRNYÚ REPÜLŐGÉPEK VEZÉRSÍK-RENDSZEREINEK KIALAKÍTÁSA 3 REPÜLŐKÉPESSÉG
 Dr. Óvári Gula 1 - Dr. Urbán István 2 MEREVSZÁRNYÚ REPÜLŐGÉPEK VEZÉRSÍK-RENDSZEREINEK KILKÍTÁS 3 cikk(soroatban)ben a merev sárnú repülőgépek veérsík rendserinek terveését és építését követheti nomon lépésről
Dr. Óvári Gula 1 - Dr. Urbán István 2 MEREVSZÁRNYÚ REPÜLŐGÉPEK VEZÉRSÍK-RENDSZEREINEK KILKÍTÁS 3 cikk(soroatban)ben a merev sárnú repülőgépek veérsík rendserinek terveését és építését követheti nomon lépésről
A nyírás ellenőrzése
 A nyírás ellenőrzése A nyírási ellenállás számítása Ellenőrzés és tervezés nyírásra 7. előadás Nyírásvizsgálat repedésmentes állapotban (I. feszültségi állapotban) A feszültségek az ideális keresztmetszetet
A nyírás ellenőrzése A nyírási ellenállás számítása Ellenőrzés és tervezés nyírásra 7. előadás Nyírásvizsgálat repedésmentes állapotban (I. feszültségi állapotban) A feszültségek az ideális keresztmetszetet
 A méretezés alapjai II. Épületek terheinek számítása az MSZ szerint SZIE-YMMF 1. Erőtani tervezés 1.1. Tartószerkezeti szabványok Magyar Szabvány: MSZ 510 MSZ 15012/1 MSZ 15012/2 MSZ 15020 MSZ 15021/1
A méretezés alapjai II. Épületek terheinek számítása az MSZ szerint SZIE-YMMF 1. Erőtani tervezés 1.1. Tartószerkezeti szabványok Magyar Szabvány: MSZ 510 MSZ 15012/1 MSZ 15012/2 MSZ 15020 MSZ 15021/1
Lepárlás. 8. Lepárlás
 eárlás 8. eárlás csefolós elegek szétválasztására leggakrabban használt művelet a leárlás. Míg az egszeri leárlás desztilláció néven is ismerjük az ismételt leárlás vag ismételt desztillációt rektifikálásnak
eárlás 8. eárlás csefolós elegek szétválasztására leggakrabban használt művelet a leárlás. Míg az egszeri leárlás desztilláció néven is ismerjük az ismételt leárlás vag ismételt desztillációt rektifikálásnak
 A méretezés alapjai I. Épületek terheinek számítása az MSZ szerint SZIE-YMMF BSc Építőmérnök szak I. évfolyam Nappali tagozat 1. Bevezetés 1.1. Épületek tartószerkezetének részei Helyzetük szerint: vízszintes:
A méretezés alapjai I. Épületek terheinek számítása az MSZ szerint SZIE-YMMF BSc Építőmérnök szak I. évfolyam Nappali tagozat 1. Bevezetés 1.1. Épületek tartószerkezetének részei Helyzetük szerint: vízszintes:
BME Szilárdságtani és Tartószerkezeti Tanszék LEMEZEK. ;2 ) = 2,52 m. 8 = 96 mm. d = 120 20-2. a s,min = ρ min bd = 0,0013 1000 96 = 125 mm 2,
 . fejezet:.1. Hajlított lemezkeresztmetszet ellenőrzése Adatok C0/5 4/K beton f cd 13,3 N/mm B0.50 betonacél f yd 435 N/mm c nom 0 mm betonfedés Terhelés: p Ed 1 kn/m Alsó lemezvasalás y irányban : Ø8/150
. fejezet:.1. Hajlított lemezkeresztmetszet ellenőrzése Adatok C0/5 4/K beton f cd 13,3 N/mm B0.50 betonacél f yd 435 N/mm c nom 0 mm betonfedés Terhelés: p Ed 1 kn/m Alsó lemezvasalás y irányban : Ø8/150
AutoN cr. Automatikus Kihajlási Hossz számítás AxisVM-ben. elméleti háttér és szemléltető példák. 2016. február
 AutoN cr Automatikus Kihajlási Hossz számítás AxisVM-ben elméleti háttér és szemléltető példák 2016. február Tartalomjegyzék 1 Bevezető... 3 2 Célkitűzések és alkalmazási korlátok... 4 3 Módszertan...
AutoN cr Automatikus Kihajlási Hossz számítás AxisVM-ben elméleti háttér és szemléltető példák 2016. február Tartalomjegyzék 1 Bevezető... 3 2 Célkitűzések és alkalmazási korlátok... 4 3 Módszertan...
Draskóczy András VASBETONSZERKEZETEK PÉLDATÁR az Eurocode előírásai alapján
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építészmérnöki Kar SZILÁRDSÁGTANI ÉS TARTÓSZERKEZETI TANSZÉK Draskóczy András VASBETONSZERKEZETEK PÉLDATÁR az Eurocode előírásai alapján LEMEZEK OSZLOPOK,
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építészmérnöki Kar SZILÁRDSÁGTANI ÉS TARTÓSZERKEZETI TANSZÉK Draskóczy András VASBETONSZERKEZETEK PÉLDATÁR az Eurocode előírásai alapján LEMEZEK OSZLOPOK,
Közgazdaságtan - 3. elıadás
 Közgazdaságtan - 3. elıadás A FOGYASZTÓI DÖNTÉS TÉNYEZİI 1 A FOGYASZTÓI DÖNTÉS ELEMEI Példa: Eg személ naponta 2000 Ft jövedelmet költhet el pogácsára és szendvicsre. Melikbıl mennit tud venni? 1 db pogácsa
Közgazdaságtan - 3. elıadás A FOGYASZTÓI DÖNTÉS TÉNYEZİI 1 A FOGYASZTÓI DÖNTÉS ELEMEI Példa: Eg személ naponta 2000 Ft jövedelmet költhet el pogácsára és szendvicsre. Melikbıl mennit tud venni? 1 db pogácsa
Analízis I. jegyzet. László István. 2008. november 3.
 Analízis I. jegzet László István 2008. november 3. Tartalomjegzék 1. Halmazok 5 1.1. Halmaz fogalma............................ 5 1.2. Halmaz megadása........................... 6 1.2.1. Eplicit megadás.......................
Analízis I. jegzet László István 2008. november 3. Tartalomjegzék 1. Halmazok 5 1.1. Halmaz fogalma............................ 5 1.2. Halmaz megadása........................... 6 1.2.1. Eplicit megadás.......................
Acélszerkezetek I. Gyakorlati óravázlat. BMEEOHSSI03 és BMEEOHSAT17. Jakab Gábor
 Acélszerkezetek I. BMEEOHSSI0 és BMEEOHSAT17 Gakorlati óravázlat Készítette: Dr. Kovács Nauzika Jakab Gábor A gakorlatok témája: 1. A félév gakorlati oktatásának felépítése. A szerkezeti acélanagok fajtái,
Acélszerkezetek I. BMEEOHSSI0 és BMEEOHSAT17 Gakorlati óravázlat Készítette: Dr. Kovács Nauzika Jakab Gábor A gakorlatok témája: 1. A félév gakorlati oktatásának felépítése. A szerkezeti acélanagok fajtái,
MECHANIKA-SZILÁRDSÁGTAN 12. hét gyakorlati anyaga (kidolgozta : dr. Nagy Zoltán egy.adjunktus, Bojtár Gergely egy.tanársegéd)
 ZÉHENY TVÁN EGYETE LKLZOTT EHNK TNZÉK EHNK-ZLÁRÁGTN 1. hét gakorlati anaga (kidolgota : dr. Nag Zoltán eg.adjunktus, ojtár Gergel eg.tanársegéd) 1.1 feladat : Primatikus rudak össetett igénbevételei (
ZÉHENY TVÁN EGYETE LKLZOTT EHNK TNZÉK EHNK-ZLÁRÁGTN 1. hét gakorlati anaga (kidolgota : dr. Nag Zoltán eg.adjunktus, ojtár Gergel eg.tanársegéd) 1.1 feladat : Primatikus rudak össetett igénbevételei (
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 Építészeti és építési alapismeretek középszint 1211 ÉRETTSÉGI VIZSGA 2013. május 23. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK
Építészeti és építési alapismeretek középszint 1211 ÉRETTSÉGI VIZSGA 2013. május 23. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK
Oktatási segédlet. Acél- és alumínium-szerkezetek hegesztett kapcsolatainak méretezése fáradásra. Dr. Jármai Károly.
 Oktatási segédlet Acél- és alumínium-szerkezetek hegesztett kapcsolatainak méretezése fáradásra a Létesítmények acélszerkezetei tárgy hallgatóinak Dr. Jármai Károly Miskolci Egyetem 013 1 Acél- és alumínium-szerkezetek
Oktatási segédlet Acél- és alumínium-szerkezetek hegesztett kapcsolatainak méretezése fáradásra a Létesítmények acélszerkezetei tárgy hallgatóinak Dr. Jármai Károly Miskolci Egyetem 013 1 Acél- és alumínium-szerkezetek
SCHÖCK BOLE MŰSZAKI INFORMÁCIÓK 2005. NOVEMBER
 SCHÖCK BOLE MŰSZAKI INFORMÁCIÓK 2005. NOVEMBER SCHÖCK BOLE ÁTSZÚRÓDÁSI VASALÁS Schöck BOLE előnyei az építés helyszínén Egyszerű beépíthetőség A statikai igénybevétel szerint összeszerelt beépítéskész
SCHÖCK BOLE MŰSZAKI INFORMÁCIÓK 2005. NOVEMBER SCHÖCK BOLE ÁTSZÚRÓDÁSI VASALÁS Schöck BOLE előnyei az építés helyszínén Egyszerű beépíthetőség A statikai igénybevétel szerint összeszerelt beépítéskész
5. ROBOTOK IRÁNYÍTÓ RENDSZERE. 5.1. Robotok belső adatfeldolgozásának struktúrája
 TARTALOM 5. ROBOTOK IRÁNYÍTÓ RENDSZERE... 7 5.. Robotok belső adatfeldolgozásának struktúrája... 7 5.. Koordináta transzformációk... 5... Forgatás... 5... R-P-Y szögek... 5... Homogén transzformációk...
TARTALOM 5. ROBOTOK IRÁNYÍTÓ RENDSZERE... 7 5.. Robotok belső adatfeldolgozásának struktúrája... 7 5.. Koordináta transzformációk... 5... Forgatás... 5... R-P-Y szögek... 5... Homogén transzformációk...
Ytong tervezési segédlet
 Ytong tervezési segédlet Tartalom Statika Falazott szerkezetek 4 Áthidalások Pu zsaluelemekkel 8 Pu 20/25 jelű Ytong kiváltógerenda 9 Pu 20/30 jelű Ytong kiváltógerenda 10 Pu 20/37,5 jelű Ytong kiváltógerenda
Ytong tervezési segédlet Tartalom Statika Falazott szerkezetek 4 Áthidalások Pu zsaluelemekkel 8 Pu 20/25 jelű Ytong kiváltógerenda 9 Pu 20/30 jelű Ytong kiváltógerenda 10 Pu 20/37,5 jelű Ytong kiváltógerenda
TERVEZÉSI SEGÉDLET. Helyszíni felbetonnal együttdolgozó felülbordás zsaluzópanel. SW UMWELTTECHNIK Magyarország. Kft 2339.
 TERVEZÉSI SEGÉDLET Helyszíni felbetonnal együttdolgozó felülbordás zsaluzópanel Készítette: SW UMWELTTECHNIK Magyarország. Kft 2339. Majosháza Majosháza, 2007. február TARTALOMJEGYZÉK: STATIKAI MŰSZAKI
TERVEZÉSI SEGÉDLET Helyszíni felbetonnal együttdolgozó felülbordás zsaluzópanel Készítette: SW UMWELTTECHNIK Magyarország. Kft 2339. Majosháza Majosháza, 2007. február TARTALOMJEGYZÉK: STATIKAI MŰSZAKI
13. Tárcsák számítása. 1. A felületszerkezetek. A felületszerkezetek típusai
 Tárcsák számítása A felületszerkezetek A felületszerkezetek típusa A tartószerkezeteket geometra méretek alapjá osztálozzuk Az eddg taulmáakba szereplı rúdszerkezetek rúdjara az a jellemzı hog a hosszuk
Tárcsák számítása A felületszerkezetek A felületszerkezetek típusa A tartószerkezeteket geometra méretek alapjá osztálozzuk Az eddg taulmáakba szereplı rúdszerkezetek rúdjara az a jellemzı hog a hosszuk
TÁJÉKOZTATÓ. az MSZ EN 1998-5 (EC8-5) szerinti földrengésre történő alapozás tervezéshez. Összeállította: Dr. Dulácska Endre
 Magyar Mérnöki Kamara Tartószerkezeti Tagozat TÁJÉKOZTATÓ az MSZ EN 1998-5 (EC8-5) szerinti földrengésre történő alapozás tervezéshez Összeállította: Dr. Dulácska Endre A tájékoztatót a MMK-TT következő
Magyar Mérnöki Kamara Tartószerkezeti Tagozat TÁJÉKOZTATÓ az MSZ EN 1998-5 (EC8-5) szerinti földrengésre történő alapozás tervezéshez Összeállította: Dr. Dulácska Endre A tájékoztatót a MMK-TT következő
Oktatási segédlet ACÉLSZERKEZETI ELEMEK TERVEZÉSE TŰZTEHERRE AZ EUROCODE SZERINT. Dr. Jármai Károly. Miskolci Egyetem
 Oktatási segédlet ACÉLSZERKEZETI ELEMEK TERVEZÉSE TŰZTEHERRE AZ EUROCODE SZERINT a Nemzetközi Hegesztett Szerkezettervező mérnök képzés hallgatóinak Dr. Jármai Károly Miskolci Egyetem 2014-1 - 1 Bevezetés
Oktatási segédlet ACÉLSZERKEZETI ELEMEK TERVEZÉSE TŰZTEHERRE AZ EUROCODE SZERINT a Nemzetközi Hegesztett Szerkezettervező mérnök képzés hallgatóinak Dr. Jármai Károly Miskolci Egyetem 2014-1 - 1 Bevezetés
ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS
 Miskolci Egyetem Bányászati és Geotechnikai Intézet Bányászati és Geotechnikai Intézeti Tanszék ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS Oktatási segédlet Szerző: Dr. Somosvári Zsolt DSc professzor emeritus Szerkesztette:
Miskolci Egyetem Bányászati és Geotechnikai Intézet Bányászati és Geotechnikai Intézeti Tanszék ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS Oktatási segédlet Szerző: Dr. Somosvári Zsolt DSc professzor emeritus Szerkesztette:
Födémszerkezetek 2. Zsalupanelok alkalmazása
 Födészerkezetek 1. A beton Évkönyv 000-ben Dr. László Ottó és Dr. Petro Bálint egy kiváló összeoglalást adtak a beton, vasbeton és eszített vasbeton ödéekrl, elyet jól kiegészít Dr. Farkas György ejezete,
Födészerkezetek 1. A beton Évkönyv 000-ben Dr. László Ottó és Dr. Petro Bálint egy kiváló összeoglalást adtak a beton, vasbeton és eszített vasbeton ödéekrl, elyet jól kiegészít Dr. Farkas György ejezete,
KÉRDÉSEK_GÉPELEMEKBŐL_TKK_2016.
 KÉRDÉSEK_GÉPELEMEKBŐL_TKK_2016. 1.Tűréseknek nevezzük: 2 a) az anyagkiválasztás és a megmunkálási eljárások előírásait b) a gépelemek nagyságának és alakjának előírásai c) a megengedett eltéréseket az
KÉRDÉSEK_GÉPELEMEKBŐL_TKK_2016. 1.Tűréseknek nevezzük: 2 a) az anyagkiválasztás és a megmunkálási eljárások előírásait b) a gépelemek nagyságának és alakjának előírásai c) a megengedett eltéréseket az
Hajlított vasbeton keresztmetszet ellenőrzése III. feszültségi állapotban
 Hajlított vasbeton keresztmetszet ellenőrzése III. feszültségi állapotban /Határnyomaték számítás/ 4. előadás A számítást III. feszültségi állapotban végezzük. A számításokban feltételezzük, hogy: -a rúd
Hajlított vasbeton keresztmetszet ellenőrzése III. feszültségi állapotban /Határnyomaték számítás/ 4. előadás A számítást III. feszültségi állapotban végezzük. A számításokban feltételezzük, hogy: -a rúd
8. előadás Kis László Szabó Balázs 2012.
 8.. előad adás Kis LászlL szló Szabó Balázs 2012. Kerethidak Előadás vázlat Csoportosítás statikai váz alapján, Viselkedésük, Megépült példák. Szekrény keresztmetszetű hidak Csoportosítás km. kialakítás
8.. előad adás Kis LászlL szló Szabó Balázs 2012. Kerethidak Előadás vázlat Csoportosítás statikai váz alapján, Viselkedésük, Megépült példák. Szekrény keresztmetszetű hidak Csoportosítás km. kialakítás
Többváltozós függvények Riemann integrálja
 Többváltozós üggvének Riemann integrálja Többváltozós üggvének Riemann integrálja Többváltozós üggvének Riemann integrálja Az integrál konstrukciója tetszőleges változószám esetén Deiníció: n dimenziós
Többváltozós üggvének Riemann integrálja Többváltozós üggvének Riemann integrálja Többváltozós üggvének Riemann integrálja Az integrál konstrukciója tetszőleges változószám esetén Deiníció: n dimenziós
A SOPRONI TÛZTORONY HELYREÁLLÍTÁSÁNAK BEMUTATÁSA 2.
 A SOPRONI TÛZTORONY HELYREÁLLÍTÁSÁNAK BEMUTATÁSA 2. Dr. Almási József Dr. Oláh M. Zoltán Nemes Bálint Petik Árpád Petik Csaba A Soproni Tűztorony mai formáját az 1676. évi tűzvészt követően nyerte el.
A SOPRONI TÛZTORONY HELYREÁLLÍTÁSÁNAK BEMUTATÁSA 2. Dr. Almási József Dr. Oláh M. Zoltán Nemes Bálint Petik Árpád Petik Csaba A Soproni Tűztorony mai formáját az 1676. évi tűzvészt követően nyerte el.
MAGYAR RÉZPIACI KÖZPONT. 1241 Budapest, Pf. 62 Telefon 317-2421, Fax 266-6794 e-mail: hcpc.bp@euroweb.hu
 MAGYAR RÉZPIACI KÖZPONT 1241 Budapest, Pf. 62 Telefon 317-2421, Fax 266-6794 e-mail: hcpc.bp@euroweb.hu Tartalom 1. A villamos csatlakozások és érintkezôk fajtái............................5 2. Az érintkezések
MAGYAR RÉZPIACI KÖZPONT 1241 Budapest, Pf. 62 Telefon 317-2421, Fax 266-6794 e-mail: hcpc.bp@euroweb.hu Tartalom 1. A villamos csatlakozások és érintkezôk fajtái............................5 2. Az érintkezések
Miskolci Egyetem, Gyártástudományi Intézet, Prof. Dr. Dudás Illés
 6. MENETMEGMUNKÁLÁSOK A csavarfelületek egyrészt gépelemek összekapcsolására (kötő menetek), másrészt mechanizmusokban mozgás átadásra (kinematikai menetek) szolgálnak. 6.1. Gyártási eljárások a) Öntés
6. MENETMEGMUNKÁLÁSOK A csavarfelületek egyrészt gépelemek összekapcsolására (kötő menetek), másrészt mechanizmusokban mozgás átadásra (kinematikai menetek) szolgálnak. 6.1. Gyártási eljárások a) Öntés
KULCS_GÉPELEMEKBŐL III.
 KULCS_GÉPELEMEKBŐL III. 1.Tűréseknek nevezzük: 2 a) az anyagkiválasztás és a megmunkálási eljárások előírásait b) a gépelemek nagyságának és alakjának előírásai c) a megengedett eltéréseket az adott mérettől
KULCS_GÉPELEMEKBŐL III. 1.Tűréseknek nevezzük: 2 a) az anyagkiválasztás és a megmunkálási eljárások előírásait b) a gépelemek nagyságának és alakjának előírásai c) a megengedett eltéréseket az adott mérettől
Legkisebb keresztmetszeti méretek: 25 cm-es falnál 60 25 cm (egy teljes falazó elem) 30 cm-es falnál 50 30 cm 37,5 cm-es falnál 40 37,5 cm.
 Statika Tartalom Falazott szerkezetek...4 Áthidalások Pu zsaluelemekkel...8 Pu 20/25 jelű YTONG kiváltógerenda...9 Pu 20/30 jelű YTONG kiváltógerenda...10 Pu 20/37,5 jelű YTONG kiváltógerenda...11 Pu
Statika Tartalom Falazott szerkezetek...4 Áthidalások Pu zsaluelemekkel...8 Pu 20/25 jelű YTONG kiváltógerenda...9 Pu 20/30 jelű YTONG kiváltógerenda...10 Pu 20/37,5 jelű YTONG kiváltógerenda...11 Pu
Magasépítési vasbetonszerkezetek
 Magasépítési vasbetonszerkezetek k Egyhajós daruzott vasbetoncsarnok tervezése Szabó Imre Gábor Pécsi Tudományegyetem Műszaki és Informatikai Kar Szilárdságtan és Tartószerkezetek Tanszék Rövid főtartó
Magasépítési vasbetonszerkezetek k Egyhajós daruzott vasbetoncsarnok tervezése Szabó Imre Gábor Pécsi Tudományegyetem Műszaki és Informatikai Kar Szilárdságtan és Tartószerkezetek Tanszék Rövid főtartó
Lindab vékonyfalú profilok méretezése DimRoof statikai szoftverrel
 indab Profil oktatási program 010 indab vékonyfalú profilok méretezése DimRoof statikai szoftverrel indab Kft. 1 1. A statikai tervezés eszközei a indabnál indab vékonyfalú acélszelvények (burkolati lemezek
indab Profil oktatási program 010 indab vékonyfalú profilok méretezése DimRoof statikai szoftverrel indab Kft. 1 1. A statikai tervezés eszközei a indabnál indab vékonyfalú acélszelvények (burkolati lemezek
FAUR KRISZTINA BEÁTA, SZAbÓ IMRE, GEOTECHNIkA
 FAUR KRISZTINA BEÁTA, SZAbÓ IMRE, GEOTECHNIkA 7 VII. A földművek, lejtők ÁLLÉkONYSÁgA 1. Földművek, lejtők ÁLLÉkONYSÁgA Valamely földművet, feltöltést vagy bevágást építve, annak határoló felületei nem
FAUR KRISZTINA BEÁTA, SZAbÓ IMRE, GEOTECHNIkA 7 VII. A földművek, lejtők ÁLLÉkONYSÁgA 1. Földművek, lejtők ÁLLÉkONYSÁgA Valamely földművet, feltöltést vagy bevágást építve, annak határoló felületei nem
Csavarkötés mérése ), (5) μ m a menetes kapcsolat súrlódási tényezője, β a menet élszöge. 1. Elméleti alapok
 GEGE-AGG labormérések Csavarkötés mérése. Elméleti alapok Csavarkötéseknél az összekapcsolt alkatrészek terhelés alatti elmozdulásának megakadályozása céljából előfeszítést kell alkalmazni, amelynek nagyságát
GEGE-AGG labormérések Csavarkötés mérése. Elméleti alapok Csavarkötéseknél az összekapcsolt alkatrészek terhelés alatti elmozdulásának megakadályozása céljából előfeszítést kell alkalmazni, amelynek nagyságát
Segédlet és méretezési táblázatok Segédlet az Eurocode használatához, méretezési táblázatok profillemezekhez és falkazettákhoz
 Segédlet az Eurocode használatához, méretezési táblázatok profillemezekhez és falkazettákhoz A trapézprofilokat magas minőség, tartósság és formai változatosság jellemzi. Mind a legmagasabb minőséget képviselő
Segédlet az Eurocode használatához, méretezési táblázatok profillemezekhez és falkazettákhoz A trapézprofilokat magas minőség, tartósság és formai változatosság jellemzi. Mind a legmagasabb minőséget képviselő
Ikerház téglafalainak ellenőrző erőtani számítása
 BME Hidak és Szerkezeek Tanszék Fa-, falazo és kőszerkezeek (BMEEOHSAT19) Ikerház églafalainak ellenőrző erőani számíása segédle a falaza ervezési feladahoz v3. Dr. Varga László, Dr. Koris Kálmán, Dr.
BME Hidak és Szerkezeek Tanszék Fa-, falazo és kőszerkezeek (BMEEOHSAT19) Ikerház églafalainak ellenőrző erőani számíása segédle a falaza ervezési feladahoz v3. Dr. Varga László, Dr. Koris Kálmán, Dr.
Födémszerkezetek megerősítése
 Födémszerkezetek megerősítése FÖDÉMEK MEGERŐSÍTÉSE FASZERKEZETŰ TARTÓK CSAPOS GERENDAFÖDÉM A csapos gerendafödémek károsodása a falazatra felfekvő végek bütüinek és az 50..10 cm hosszra kiterjedő felső
Födémszerkezetek megerősítése FÖDÉMEK MEGERŐSÍTÉSE FASZERKEZETŰ TARTÓK CSAPOS GERENDAFÖDÉM A csapos gerendafödémek károsodása a falazatra felfekvő végek bütüinek és az 50..10 cm hosszra kiterjedő felső
Tevékenység: Gyűjtse ki és tanulja meg a kötőcsavarok szilárdsági tulajdonságainak jelölési módját!
 Csavarkötés egy külső ( orsó ) és egy belső ( anya ) csavarmenet kapcsolódását jelenti. A következő képek a motor forgattyúsházában a főcsapágycsavarokat és a hajtókarcsavarokat mutatják. 1. Kötőcsavarok
Csavarkötés egy külső ( orsó ) és egy belső ( anya ) csavarmenet kapcsolódását jelenti. A következő képek a motor forgattyúsházában a főcsapágycsavarokat és a hajtókarcsavarokat mutatják. 1. Kötőcsavarok
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet
 Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
GEOMETRIAI OPTIKA - ÓRAI JEGYZET
 ε ε hullámegelet: Mérökizikus szak, Optika modul, III. évolam /. élév, Optika I. tárg GEOMETRIAI OPTIKA - ÓRAI JEGYZET (Erdei Gábor, Ph.D., 6. AJÁNLOTT SZAKIRODALOM: ELMÉLETI ALAPOK Maxwell egeletek E(
ε ε hullámegelet: Mérökizikus szak, Optika modul, III. évolam /. élév, Optika I. tárg GEOMETRIAI OPTIKA - ÓRAI JEGYZET (Erdei Gábor, Ph.D., 6. AJÁNLOTT SZAKIRODALOM: ELMÉLETI ALAPOK Maxwell egeletek E(
HUNYADI MÁTYÁS ÁLTALÁNOS ISKOLA BŐVÍTÉSE MELEGÍTŐ KONYHÁVAL ÉS ÉTKEZŐVEL 3021 LŐRINCI, SZABADSÁG TÉR 18. Hrsz: 1050 KIVITELI TERV STATIKAI MUNKARÉSZ
 . HUNYADI MÁTYÁS ÁLTALÁNOS ISKOLA BŐVÍTÉSE MELEGÍTŐ KONYHÁVAL ÉS ÉTKEZŐVEL 3021 LŐRINCI, SZABADSÁG TÉR 18. Hrsz: 1050 KIVITELI TERV STATIKAI MUNKARÉSZ ÉPÍTTETŐ: LŐRINCI VÁROS ÖNKORMÁNYZATA 3021 LŐRINCI,
. HUNYADI MÁTYÁS ÁLTALÁNOS ISKOLA BŐVÍTÉSE MELEGÍTŐ KONYHÁVAL ÉS ÉTKEZŐVEL 3021 LŐRINCI, SZABADSÁG TÉR 18. Hrsz: 1050 KIVITELI TERV STATIKAI MUNKARÉSZ ÉPÍTTETŐ: LŐRINCI VÁROS ÖNKORMÁNYZATA 3021 LŐRINCI,
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 Építészeti és építési alapismeretek középszint 1411 ÉRETTSÉGI VIZSGA 2016. május 18. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK
Építészeti és építési alapismeretek középszint 1411 ÉRETTSÉGI VIZSGA 2016. május 18. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK
Falazott szerkezetek méretezése
 Falazo szerkezeek méreezése A falazaok alkalmazásának előnyei: - Épíészei szemponból: szabadon kialakíhaó alaprajzi megoldások, válozaos homlokzai megjelenés leheőségei - Tarószerkezei szemponból: arós
Falazo szerkezeek méreezése A falazaok alkalmazásának előnyei: - Épíészei szemponból: szabadon kialakíhaó alaprajzi megoldások, válozaos homlokzai megjelenés leheőségei - Tarószerkezei szemponból: arós
5. gyakorlat. Szabó Imre Gábor. Szilárdságtan és Tartószerkezetek Tanszék
 Acélszerkezetek (I.) 5. gyakorlat Csavarozott és hegesztett tt kapcsolatok k Szabó Imre Gábor Pécsi Tudományegyetem Műszaki és Informatikai Kar Szilárdságtan és Tartószerkezetek Tanszék A kapcsolatok kialakítására
Acélszerkezetek (I.) 5. gyakorlat Csavarozott és hegesztett tt kapcsolatok k Szabó Imre Gábor Pécsi Tudományegyetem Műszaki és Informatikai Kar Szilárdságtan és Tartószerkezetek Tanszék A kapcsolatok kialakítására
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 Építészeti és építési alapismeretek emelt szint 0911 ÉRETTSÉGI VIZSGA 2009. október 19. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI
Építészeti és építési alapismeretek emelt szint 0911 ÉRETTSÉGI VIZSGA 2009. október 19. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI
MUNKAANYAG. Szabó László. Szilárdságtan. A követelménymodul megnevezése:
 Szabó László Szilárdságtan A követelménymodul megnevezése: Kőolaj- és vegyipari géprendszer üzemeltetője és vegyipari technikus feladatok A követelménymodul száma: 047-06 A tartalomelem azonosító száma
Szabó László Szilárdságtan A követelménymodul megnevezése: Kőolaj- és vegyipari géprendszer üzemeltetője és vegyipari technikus feladatok A követelménymodul száma: 047-06 A tartalomelem azonosító száma
Schöck Isokorb KX-HV, KX-WO, KX-WU és KX-BH
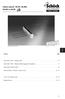 Schöck Isokorb, WO, WU és BH SCHÖCK ISOKORB Ábra: Schöck Isokorb KX 10/7 10 ÚJ! Már minen teherbírási osztály kapható HTE moullal. Tartalom olal Schöck Isokorb föémugrás lefelé..........................................................
Schöck Isokorb, WO, WU és BH SCHÖCK ISOKORB Ábra: Schöck Isokorb KX 10/7 10 ÚJ! Már minen teherbírási osztály kapható HTE moullal. Tartalom olal Schöck Isokorb föémugrás lefelé..........................................................
Előadó: Dr. Bukovics Ádám 9. ELŐADÁS
 SZÉCHNYI ISTVÁN GYTM TARTÓSZRKZTK III. lőadó: Dr. ukovics Ádám 9. LŐADÁS Az ábrák forrása: [1] Dr. Németh György: Tartószerkezetek III., Acélszerkezetek méretezésének alapjai [] Halász Ottó Platthy Pál:
SZÉCHNYI ISTVÁN GYTM TARTÓSZRKZTK III. lőadó: Dr. ukovics Ádám 9. LŐADÁS Az ábrák forrása: [1] Dr. Németh György: Tartószerkezetek III., Acélszerkezetek méretezésének alapjai [] Halász Ottó Platthy Pál:
Schöck Tronsole AZT típus SCHÖCK TRONSOLE
 Schöck Tronsole típus SCHÖCK TRONSOLE Monolit vasbeton pihenő és lépcsőházi fal közötti lépéshangszigetelés (beépítéskész teherhordó elemmel) Schöck Tronsole típus Lépcsőpihenő: Monolit vasbeton Lépcsőházi
Schöck Tronsole típus SCHÖCK TRONSOLE Monolit vasbeton pihenő és lépcsőházi fal közötti lépéshangszigetelés (beépítéskész teherhordó elemmel) Schöck Tronsole típus Lépcsőpihenő: Monolit vasbeton Lépcsőházi
Elektromágneses hullámok
 KÁLMÁN P.-TÓT.: ullámok/4 5 5..5. (kibőíe óraála) lekromágneses hullámok elekromágneses elenségek árgalásánál láuk, hog áloó mágneses erőér elekromos erőere (elekromágneses inukció), áloó elekromos erőér
KÁLMÁN P.-TÓT.: ullámok/4 5 5..5. (kibőíe óraála) lekromágneses hullámok elekromágneses elenségek árgalásánál láuk, hog áloó mágneses erőér elekromos erőere (elekromágneses inukció), áloó elekromos erőér
Segédlet Egyfokozatú fogaskerék-áthajtómű méretezéséhez
 Pécsi Tudományegyetem Pollack Mihály Műszaki Kar Gépszerkezettan tanszék Segédlet Egyfokozatú fogaskerék-áthajtómű méretezéséhez Összeállította: Dr. Stampfer Mihály Pécs, 0. . A fogaskerekek előtervezése.
Pécsi Tudományegyetem Pollack Mihály Műszaki Kar Gépszerkezettan tanszék Segédlet Egyfokozatú fogaskerék-áthajtómű méretezéséhez Összeállította: Dr. Stampfer Mihály Pécs, 0. . A fogaskerekek előtervezése.
Dr. habil JANKÓ LÁSZLÓ. VASBETON SZILÁRDSÁGTAN az EUROCODE 2 szerint (magasépítés) Az EC és az MSZ összehasonlítása is TANKÖNYV I. AZ ÁBRÁK.
 Dr. habil JANKÓ LÁSZLÓ VASBETON SZILÁRDSÁGTAN az EUROCODE 2 szerint (magasépítés) Az és az összehasonlítása is TANKÖNYV I. AZ ÁBRÁK N Ed M Edo (alapérték, elsőrendű elmélet) Mekkora az N Rd határerő? l
Dr. habil JANKÓ LÁSZLÓ VASBETON SZILÁRDSÁGTAN az EUROCODE 2 szerint (magasépítés) Az és az összehasonlítása is TANKÖNYV I. AZ ÁBRÁK N Ed M Edo (alapérték, elsőrendű elmélet) Mekkora az N Rd határerő? l
Államvizsga kérdések Geotechnika Szakirány
 Államvizsga kérdések Geotechnika Szakirány 1. Ismertesse az állékonyság alapkérdését. 2. Ismertesse szabadon álló és megtámasztott földtestek egyensúlyi kérdését! 3. Ismertesse a földmunkák végzése során
Államvizsga kérdések Geotechnika Szakirány 1. Ismertesse az állékonyság alapkérdését. 2. Ismertesse szabadon álló és megtámasztott földtestek egyensúlyi kérdését! 3. Ismertesse a földmunkák végzése során
ADDITÍV KONVOLÚCIÓS ÖSSZEGEK SPEKTRÁLIS FELBONTÁSA
 ADDITÍV KONVOLÚCIÓS ÖSSZEGEK SPEKTRÁLIS FELBONTÁSA HARCOS GERGELY Ha a(n) eg számelméleti függvén, akkor természetes feladat a a(m)a(n)w(m, n) m±nh alakú additív konvolúciós összegek vizsgálata. Ha W :
ADDITÍV KONVOLÚCIÓS ÖSSZEGEK SPEKTRÁLIS FELBONTÁSA HARCOS GERGELY Ha a(n) eg számelméleti függvén, akkor természetes feladat a a(m)a(n)w(m, n) m±nh alakú additív konvolúciós összegek vizsgálata. Ha W :
T E R V E Z É S I S E G É D L E T
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM HIDAK ÉS SZERKEZETEK TANSZÉK T E R V E Z É S I S E G É D L E T a Magasépítési Vasbetonszerkezetek című tantárgy féléves gyakorlati feladatához (BSc. képzés)
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM HIDAK ÉS SZERKEZETEK TANSZÉK T E R V E Z É S I S E G É D L E T a Magasépítési Vasbetonszerkezetek című tantárgy féléves gyakorlati feladatához (BSc. képzés)
Matematika OKTV I. kategória 2017/2018 második forduló szakgimnázium-szakközépiskola
 O k t a t á s i H i v a t a l A 017/018. tanévi Országos Középiskolai Tanulmáni Versen második forduló MATEMATIKA I. KATEGÓRIA (SZAKGIMNÁZIUM, SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató 1. Adja meg
O k t a t á s i H i v a t a l A 017/018. tanévi Országos Középiskolai Tanulmáni Versen második forduló MATEMATIKA I. KATEGÓRIA (SZAKGIMNÁZIUM, SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató 1. Adja meg
Fa- és Acélszerkezetek I. 6. Előadás Stabilitás II. Dr. Szalai József Főiskolai adjunktus
 Fa- és Acélszerkezetek I. 6. Előadás Stabilitás II. Dr. Szalai József Főiskolai adjunktus Tartalom Kifordulás jelensége Rugalmas hajlított gerenda kritikus nyomatéka Valódi hajlított gerendák viselkedése
Fa- és Acélszerkezetek I. 6. Előadás Stabilitás II. Dr. Szalai József Főiskolai adjunktus Tartalom Kifordulás jelensége Rugalmas hajlított gerenda kritikus nyomatéka Valódi hajlított gerendák viselkedése
Födémrendszerek Alkalmazástechnika. www.leier.eu
 Födémrendszerek Alkalmazástechnika MAGASÉPÍTÉS LEIER ÉPÍTŐANYAG-ÜZEMEK Devecser-Téglagyár 8460 Devecser, Sümegi út telefon: 88/512-600 fax: 88/512-619 e-mail: devecser@leier.hu Gönyű-Betonelemgyár 9071
Födémrendszerek Alkalmazástechnika MAGASÉPÍTÉS LEIER ÉPÍTŐANYAG-ÜZEMEK Devecser-Téglagyár 8460 Devecser, Sümegi út telefon: 88/512-600 fax: 88/512-619 e-mail: devecser@leier.hu Gönyű-Betonelemgyár 9071
Szóbeli vizsgatantárgyak. 1. Mélyépítéstan 2. Szilárdságtan 3. Szervezési és vállalkozási ismeretek
 Szóbeli vizsgatantárgyak 1. Mélyépítéstan 2. Szilárdságtan 3. Szervezési és vállalkozási ismeretek Megjegyzések: 1. A Mélyépítéstan vizsgatantárgy szóbeli tételei szóban és vázlatrajzokkal megválaszolható
Szóbeli vizsgatantárgyak 1. Mélyépítéstan 2. Szilárdságtan 3. Szervezési és vállalkozási ismeretek Megjegyzések: 1. A Mélyépítéstan vizsgatantárgy szóbeli tételei szóban és vázlatrajzokkal megválaszolható
HOSSZTARTÓ TERVEZÉSE HEGESZTETT GERINCLEMEZES TARTÓBÓL
 HOSSZARÓ ERVEZÉSE HEGESZE GERNCLEMEZES ARÓBÓL 9 Anyaminőséek: Acél: A 8 σ H 00 N/ mm [99] H 115 N/ mm [99] σ ph 50 N /mm [99] Csaar: M 0 és M ill. 5. H 195 N/ mm [100] σ ph 90 N /mm [100] Varrrat:.o. sarok.
HOSSZARÓ ERVEZÉSE HEGESZE GERNCLEMEZES ARÓBÓL 9 Anyaminőséek: Acél: A 8 σ H 00 N/ mm [99] H 115 N/ mm [99] σ ph 50 N /mm [99] Csaar: M 0 és M ill. 5. H 195 N/ mm [100] σ ph 90 N /mm [100] Varrrat:.o. sarok.
Alkalmazástechnikai és tervezési útmutató
 BAKONYTHERM Alkalmazástechnikai és tervezési útmutató Alkalmazási előnyök természetes anyagokból készül, költségtakarékos beépítés, a 12,0 cm-es szélességi méretből adódóan kevesebb áthidalóval megoldható
BAKONYTHERM Alkalmazástechnikai és tervezési útmutató Alkalmazási előnyök természetes anyagokból készül, költségtakarékos beépítés, a 12,0 cm-es szélességi méretből adódóan kevesebb áthidalóval megoldható
Harántfalas épület két- és többtámaszú monolit vasbeton födémlemezének tervezése kiadott feladatlap alapján.
 TERVEZÉSI FELADAT: Harántfalas épület két- és többtámaszú monolit vasbeton födémlemezének tervezése kiadott feladatlap alapján. Feladatok: 1. Tervezzük meg a harántfalas épület egyirányban teherhordó monolit
TERVEZÉSI FELADAT: Harántfalas épület két- és többtámaszú monolit vasbeton födémlemezének tervezése kiadott feladatlap alapján. Feladatok: 1. Tervezzük meg a harántfalas épület egyirányban teherhordó monolit
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 Építészeti és építési alapismeretek középszint 1521 ÉRETTSÉGI VIZSGA 2015. október 12. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK
Építészeti és építési alapismeretek középszint 1521 ÉRETTSÉGI VIZSGA 2015. október 12. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK
III. FEJEZET FÜGGVÉNYEK ÉS TULAJDONSÁGAIK
 Függvéek és tulajdoságaik 69 III FEJEZET FÜGGVÉNYEK ÉS TULAJDONSÁGAIK 6 Gakorlatok és feladatok ( oldal) Írd egszerűbb alakba: a) tg( arctg ) ; c) b) cos( arccos ) ; d) Megoldás a) Bármel f : A B cos ar
Függvéek és tulajdoságaik 69 III FEJEZET FÜGGVÉNYEK ÉS TULAJDONSÁGAIK 6 Gakorlatok és feladatok ( oldal) Írd egszerűbb alakba: a) tg( arctg ) ; c) b) cos( arccos ) ; d) Megoldás a) Bármel f : A B cos ar
KÖTÉLSZERKEZETEK. Különleges Tartószerkezetek Hegyi Dezső Jegyzet kézirat 2012. v1 Kötélszerkezetek
 KÖTÉLSZERKEZETEK A kötélszerkezetek olyan szerkezeti elemekből épülnek fel, melyek csak húzószilárdsággal rendelkeznek. Ez a valóságban azt jelenti, hogy a szerkezeti elemeink a geometriai kialakításuk
KÖTÉLSZERKEZETEK A kötélszerkezetek olyan szerkezeti elemekből épülnek fel, melyek csak húzószilárdsággal rendelkeznek. Ez a valóságban azt jelenti, hogy a szerkezeti elemeink a geometriai kialakításuk
