27.B 27.B. Alapfogalmak, logikai függvények és leírásmódjaik
|
|
|
- Imre Szilágyi
- 8 évvel ezelőtt
- Látták:
Átírás
1 7.B 7.B 7.B Digitális alapáramkörök Logikai alapfogalmak Mutassa be a logikai függvéyek leírási módjait: a szövegeset, az igazság táblázatosat, a logikai vázlatosat és az algebrai alakkal törtéı leírást! Értelmezze az egy-, a két- és a többváltozós logikai függvéyeket! Ismertesse a logikai (Boole) algebra alaptörvéyeit és alaptételeit! Hasolítsa össze a miterm- és a maxterm táblák felépítéséek elvét! Alapfogalmak, logikai függvéyek és leírásmódjaik A függvéykapcsolatok jelölése A függvéykapcsolatokat logikai szimbólumokkal jelöljük: A az ÉS kapcsolat jele a + a VAGY kapcsolat jele A függvéykapcsolatok száma Mivel a bemeeti és a kimeeti változók is kétértékőek, ezért a függetle változók számától () függ a képezhetı függvéykapcsolatok száma: K=. A logikai függvéyek csoportosítása A logikai függvéyeket csoportosíthatjuk: a logikai változók idıbei függése szerit, a logikai változók száma szerit. A változók idıbei változása szerit: Idıfüggetle logikai függvéyek: Az idıfüggetle logikai függvéyek közös jellemzıje, hogy a függı (kimeeti) változó értéke csak a függetle (bemeeti) változó értékétıl függ. Az ilye típusú függvéyeket valósítják meg a kombiációs logikai hálózatok. Jelölésük általáos alakba: F = f(x,x,x 3,...X ). Idıfüggı logikai függvéyek: Az idıfüggı logikai függvéyek jellemzıje, hogy a függı változó aktuális értékét emcsak a függetle változók adott idıpotba felvett értéke, haem más idıpillaatba felvett értékei is meghatározzák. Ez azt jeleti, hogy az eseméyek sorredje is befolyásolja a kimeet állapotát. Az ilye típusú függvéyeket megvalósító hálózatokat evezzük szekveciális hálózatokak. A függetle változók száma szerit: Egyváltozós logikai függvéyeka kimeeti eseméyük egyetle bemeeti változótól függ, a gyakorlatba ritká fordulak elı. Kétváltozós logikai függvéyeka kimeeti eseméyük két függetle bemeeti változó értékétıl függ. Többváltozós logikai függvéyek A kimeeti eseméyük számú függetle bemeeti változó értékétıl függ, a gyakorlatba ezekkel találkozuk a leggyakrabba. A logikai függvéyek grafikus megadása Veitch-tábla A függı változók értékeit egy cellákból álló diagramba ábrázoljuk: a függetle változókat a diagram kerete meté jelöljük. Azokba a sorokba és oszlopokba, ahol jelölés (súlyozás) va, a függetle változó igaz értékő. A változó igeleges vagy emleges értékét - mivel a bekövetkezés valószíősége 50% - egyelı területrésszel ábrázoljuk. Síkbeli Veitch-táblá 4, térbeli 6 változó ábrázolható szemléletese. Az ábrá egy kétváltozós tábla látható, melybe szemléltetésül a cellákak megfelelı változók állapotait is jelöltük. A Veitch-tábla a logikai kapcsolatok meghatározására is alkalmas.
2 7.B 7.B Karaugh-tábla A függı változók értékeit egy cellákból álló diagramba ábrázoljuk: a függetle változók értékvariációit a diagram kerete meté jelöljük. Az ábrá egy kétváltozós tábla látható, melybe szemléltetésül a cellákak megfelelı változók állapotait is jelöltük. Állapotdiagram Az idıfüggı logikai függvéyek leírására alkalmas. A változók aktuális értékeit körökbe jelezzük, a köröket összekötı iráyított voalak a változás iráyát jelölik. Veitch-tábla Karaugh-tábla Állapotdiagram A logikai függvéyek megadása Szöveges megadási mód A függetle változók összes kombiációját, a logikai kapcsolatot, valamit a függı változó értékét szavakkal fogalmazzuk meg. Táblázatos leírásmód A függetle változók összes értékvariációit és a függvéykapcsolat hatására létrejövı függı változók értékeit egy sorba írjuk egy függıleges voallal elválasztva. Olya értéktáblázat, amely tartalmazza a függvéy értékét mide lehetséges esetbe. Igazságtáblázatak evezzük, mert a feltételek és az eseméyek közötti logikai igazságokat rögzíti. Logikai vázlat A függvéykapcsolatot az ıt megvalósító szabváyos áramköri szimbólumokkal ábrázoljuk. Algebrai alak A függetle változókat a függvéykapcsolatra jellemzı mőveleti szimbólumokkal (ÉS, VAGY, ) kapcsoljuk össze. Például: F 3 = A B+C+A C+B Grafikus megadási mód A grafikus megadási módok: a változók megadása törtéhet grafikusa is. Táblázatos leírásmód Logikai vázlat Egy-, két- és többváltozós logikai függvéyek Az egyváltozós logikai függvéyek Akkor beszélük egyváltozós logikai függvéyrıl, ha a kimeeti eseméy egyetle bemeeti változótól függ. A következı táblázatba látható, hogy az A bemeeti (függetle) változó értékétıl függıe az F kimeeti (függı) változó milye értékeket vehet fel. Ezt a táblázatot evezzük igazságtáblázatak, mert a függetle változók összes lehetséges kombiációja eseté tartalmazza a függvéy által meghatározott kimeeti eseméyt. A logikai függvéyek jelölésébe a felsı idex a bemeeti változók számát, az alsó idex a függvéy sorszámát adja meg. Ezt a decimális sorszámot a függvéy értékeibıl alkotott biáris számból kapjuk meg. Egy függetle változó eseté a külöbözı logikai függvéyek száma: K = = = = 4 Az egyváltozós függvéyek közül a egációt és az ismétlı függvéyt alkalmazzuk a leggyakrabba. A logikai függvéyek bemutatására haszáljuk fel a Ve-diagramot és az idıdiagramot is. A Ve-diagramok a logikai változókhoz egy-egy síkba leképzett pothalmazt redelek, amely egy tetszıleges síkidommal határolt területet jelet. Az ábrázolás szabálya, hogy a függvéy logikai értékeiél a megfelelı területet jelöljük (pl. voalkázással). Hátráyuk, hogy legfeljebb három változóig haszálhatóak. A logikai eseméyek idıdiagramo is bemutathatók. Eél a módszerél a kétértékő eseméyeket (a bemeeteket és a
3 7.B 7.B kimeeteket is) az idı függvéyébe ábrázoljuk, így az eseméyek idıbeli lefolyása is követhetı. Elıye, hogy az idıdiagramo tetszıleges számú változót ábrázolhatuk. Egyváltozós soha függvéy 0 Egyváltozós logikai függvéyek igazságtáblázata F 0 =. F - Soha függvéy: a függı változó értéke a függetle változó mide értékéél 0. Jelölése: 0 Egyváltozós egáció (tagadás) függvéy F - Negáció (tagadás) függvéy: a függı változó értéke midig a függetle változó elletétes (egált) értékét veszi fel. A egációt a tagadáso kívül evezik még jelfordításak és iverzióak is. A egációt az algebrai alakba a betőjel fölé húzott vízszites voallal jelöljük: F = A. Egyváltozós ismétlı függvéy F - Ismétlı függvéy: a függı változó értéke midig a függetle változó értékét veszi fel. Jelölése: F=A. Egyváltozós midig függvéy F - Midig függvéy: a függı változó értéke a függetle változó mide értékétıl függetleül midig. Jelölése: F =. Egyváltozós logikai függvéyek Ve-diagramja Egyváltozós logikai függvéyek idıdiagramja A kétváltozós logikai függvéyek Akkor beszélük kétváltozós logikai függvéyrıl, ha a kimeeti eseméy két bemeeti változótól függ. A következı táblázatba látható, hogy az A és a B bemeeti (függetle) változók értékétıl függıe az F kimeeti (függı) változó milye értékeket vehet fel. Két függetle változó eseté a külöbözı logikai függvéyek száma: 4 K = = = = 6. Az alábbi ábráko a leggyakrabba alkalmazott kétváltozós függvéyek Ve-diagramját és idıdiagramját láthatjuk. Figyeljük meg a függvéyek vizsgálatakor, hogya lehet ezeket elkészítei! Kétváltozós logikai függvéyek idıdiagramja Kétváltozós logikai függvéyek igazságtáblázata Kétváltozós logikai függvéyek Ve-diagramja A kétváltozós logikai függvéyek igazságtáblázatáak vizsgálata Feladat Készítsük el az összes kétváltozós függvéy Ve-diagramját és idıdiagramját! 3
4 7.B 7.B A kétváltozós logikai függvéyek igazságtáblázatáak vizsgálata közbe két érdekes dolgot is észrevehetük: A táblázat tartalmazza az egyváltozós függvéyeket is F 0, F3, F5, F0, F, F5 Ha a VAGY függvéy F 7 és a VAGY NEM (NOR) függvéy F 8 közé egy képzeletbeli szimmetriavoalat húzuk, akkor a voaltól azoos távolságra levı függvéyek egymás egáltjai. A többváltozós logikai függvéyek A gyakorlati feladatok megoldása sorá a legtöbbször többváltozós logikai függvéyekkel találkozhatuk. A képezhetı kapcsolási függvéyek száma a függetle változók számával expoeciális aráyba, tehát rohamosa övekszik. Például: ha a függetle változók száma 3, akkor a külöbözı logikai függvéyek száma: 3 8 K = = = = 56 ha a függetle változók száma 4, akkor a külöbözı logikai függvéyek száma: 4 6 K = = = = Azért sem célszerő a kettıél több bemeeti változót tartalmazó függvéyeket egyekét tárgyali, mert mide többváltozós logikai függvéy kétváltozós függvéyekbıl felépíthetı. Ativalecia függvéy F 6 Ativalecia (KIZÁRÓ VAGY) függvéy: a függvéy értéke akkor, ha vagy csak A, vagy csak a B értéke, vagyis amikor a bemeeti változók elletétes értékőek. További elevezései: kizáró VAGY, exclusive OR. Jelölése: F6 = A B + A B. Duál tétel, duál függvéy Duál tétel: Ha a logikai ÉS mőveletet VAGY mővelettel, valamit a 0-t -gyel (vagy az -et 0-val) helyettesítjük, az eredeti függvéy duálfüggvéyét kapjuk meg. Ekvivalecia függvéy F 9 Ekvivalecia függvéy: a függı változó értéke akkor, ha a függetle változók logikai értéke megegyezik. További elevezései: koicidecia, exclusive NOR. Jelölése: F9 = A B + A B. ÉS függvéy F ÉS függvéy: a függı változó értéke akkor és csakis akkor, ha midkét függetle változó értéke egyidejőleg. További elevezései: AND mővelet, kojukció, logikai szorzás. Jelölése: F = A B. ÉS NEM függvéy F 4 ÉS NEM (NAND) függvéy: a függı változó értéke akkor és csakis akkor 0, ha midkét függetle változó értéke egyidejőleg. A NAND illetve az ÉS kapcsolat egymás egáltjai. Jelölése: F4 = A B. Implikáció függvéyek F Implikáció függvéy: az implikáció mőveletéél a változók sorredje em cserélhetı fel, mert a függvéy értéke csak akkor 0, ha az elıtag 0, és az utótag. Jelölése: F = A + B. F 3 Iverz implikáció függvéy: az iverz implikáció mőveletéél a változók sorredje em cserélhetı fel, mert a függvéy értéke csak akkor 0, ha az elıtag, és az utótag 0. Jelölése: F = A + B. Ihibitáló függvéyek F Ihibitáló függvéy: az ihibíció (tiltás) mőveletéél a változók sorredje em cserélhetı fel, mert a függvéy értéke akkor és csakis akkor, ha az elıtag logikai értéke egyedül, ömagába. Jelölése: F = A B. 4
5 7.B 7.B F 4 Iverz ihibitáló függvéy: az ivert ihibíció (tiltás) mőveletéél a változók sorredje em cserélhetı fel, mert a függvéy értéke akkor és csakis akkor, ha az utótag logikai értéke egyedül, ömagába. Jelölése: F4 = A B. Ismétlés függvéy F 5 Ismétlı függvéy: a függı változó értéke midig az adott függetle változó értékét veszi fel. Jelölése: F 5 = B. Kétváltozós ismétlı függvéy F 3 Kétváltozós ismétlı függvéy: a függı változó értéke midig az adott függetle változó értékét veszi fel. Jelölése: F = A 3. Kétváltozós midig függvéy F 5 Kétváltozós midig függvéy: a függı változó értéke a függetle változók mide értékétıl függetleül midig. Jelölése: F 5 =. Kétváltozós egáció függvéyek F 0 Kétváltozós egáció függvéy: a függı változó értéke midig az adott függetle változó elletétes értékét veszi fel. Jelölése: F = B 0. F Kétváltozós egáció függvéy: a függı változó értéke midig az adott függetle változó elletétes értékét veszi fel. Jelölése: F = A. Kétváltozós soha függvéy F0 Kétváltozós soha függvéy: a függı változó értéke a függetle változók mide értékéél 0. Jelölése: F 0 = 0. VAGY függvéy F 7 VAGY függvéy: a függvéy értéke egyetle esetbe 0, ha valameyi bemeeti változó értéke egyidejőleg 0. Úgy is fogalmazhatuk, hogy a függı változó akkor értékő, ha bármelyik függetle változó egyekét vagy együttese értékő. További elevezései: OR mővelet, diszjukció, logikai összeadás. Jelölése: F 7 = A + B. VAGY NEM függvéy F 8 VAGY NEM (NOR) függvéy: a függı változó értéke akkor és csakis akkor, ha midkét függetle változó értéke egyidejőleg 0. A NOR illetve a VAGY kapcsolat egymás egáltjai. Jelölése: F 8 = A + B. A logikai algebra szabályai Az egyszerőbb alakra hozás Egy logikai elve mőködı vezérlı beredezés ára a beépített elemek számával aráyosa övekszik, ezért törekedük kell a megvalósítadó logikai függvéy legegyszerőbb alakjáak létrehozására. Kommutatív szabály (felcserélhetıség) Az azoos logikai kapcsolatba levı változók sorredje tetszıleges. A+B = B+A A B = B A A szabály alól természetese az ihibíció és az implikáció mőveletei kivételek. Asszociatív szabály (társíthatóság) Az azoos logikai mőveletek eredméye em függ a mőveletvégzés sorredjétıl. A+B+C = C+B+A = B+C+A A B C = B C A = A C B 5
6 7.B 7.B Disztributív szabály (szétválaszthatóság) A+ B C = (A+ B) (A+ C) A (B+ C) = A B+ A C A redudacia Ugyais egy adott gyakorlati problémát, ha közvetleül algebrai alakba megadott logikai függvéy formájába íruk le, szite elkerülhetetle a redudacia (túlhatározottság). A logikai algebra (Boole-algebra) olya azoosságokat illetve szabályokat fogalmazott meg az algebrai formába megadott logikai függvéyek eseté, amelyekkel ezek a függvéyek egyszerőbb alakra hozhatók. A logikai algebra alaptételei A meyiségek kétértékőek A = 0, ha A em. A =, ha A em 0. Negáció = 0 Kettıs tagadás = Meyiséggel végzett mőveletek szabályai VAGY kapcsolat 0+0 = 0 0+ = +0 = + = ÉS kapcsolat 0 0 = 0 0 = 0 0 = 0 = Egy változóval végzett mőveletek szabályai A = A A 0 = 0 A+0 = A A 0 = A A+ = A A = A A+A = A A A = 0 A + A = Két változóval végzett mőveletek szabályai A (B+ A) = A Az alaptételek bizoyítása Az egy változóval végzett mőveletek szabályaiak bizoyítása az egy és kétváltozós logikai függvéyek igazságtáblázata alapjá öállóa elvégezhetı. Nézzük meg, hogya kell bebizoyítai a szabályok és a többi alaptétel segítségével az összefüggést! A B+ A = A A disztributív szabály alapjá A B+ A = A B+ A A. Felhaszálva, hogy A A = A A (B+ A)=A B+ A A = A B+ A Most a disztributív szabályt megfordítva alkalmazzuk, emellett tudjuk, hogy B+ = és A = A A B+ A = A (B+) = A = A Vagyis teljesül az összefüggés A (B+ A)= A. De Morga-téte A + B = A B A B = A + B A De Morga-tétel bizoyítása Készítsük olya igazságtáblázatot, amelybe jelöljük a függetle változókat, és ezek összes lehetséges kombiációjáál határozzuk meg a De Morga-tételbe szereplı összes függvéy értékét! 6
7 7.B 7.B A De Morga-tétel bizoyítása A táblázatból látható, hogy A B = A + B és A B = A + B, így bebizoyítottuk, a De Morga-tételt. Alapvetı fogalmak és jelölésük A logikai függvéyek szabályos alakjáak ismeretéhez a következı alapvetı fogalmakat és jelölésüket kell megismeri: Term Miterm Maxterm A miterm jelölése: m i, ahol m a mitermet jeleti, a függetle változók száma és i a miterm sorszáma, vagyis idexszáma. A maxterm jelölése: M i, ahol M a maxtermet jeleti, a függetle változók száma és i a maxterm sorszáma, vagyis idexszáma. Diszjuktív szabályos alak Diszjuktív szabályos alak olya logikai függvéy, amely mitermek VAGY kapcsolatából áll. Diszjuktív szabályos alak megadási módjai Például: F = A B C D + A B C D + A B C D + A B C D F = m m4 + m8 + m Kojuktív szabályos alak Kojuktív szabályos alak olya logikai függvéy, amely maxtermek ÉS kapcsolatából áll. Kojuktív szabályos alak megadási módjai Például: F = A + B + C + D A + B + C + D A + B + C + D F = M 4 5 M 6 M 3 ( ) ( ) ( ) Logikai függvéyek hátráya Az algebrai alakba megadott logikai függvéyek hátráya, egy függvéyt több egymással ekvivales módo is felírhatuk. Ezt a hátráyt azért kell kiküszöböli, hogy két egyforma feladatot midig felismerjük, e kellje többször is egyszerősítei és megoldai. Term: a függetle változók azo csoportja, amelyeket azoos logikai kapcsolatra jellemzı szimbólummal kapcsoluk. A Karaugh-táblák típusai Egyváltozós Karaugh-tábla: Egy függetle változóak (pl. A) két lehetséges állapota lehet ( ), tehát ebbe az esetbe a tábla két darab cellát tartalmaz. A cella kotúrjai mellett feltütetjük a függetle változó logikai értékét, a cella sarká pedig a változó betőjelét. Az ábrá a cellákba beírtuk az általuk képviselt termeket is. Kétváltozós Karaugh-tábla: Két függetle változóak (pl. A, B) égy lehetséges állapota lehet ( ), tehát ebbe az esetbe a tábla égy darab cellát tartalmaz. Az ábrá a cellákba beírtuk az általuk képviselt termeket is. Háromváltozós Karaugh-tábla: Három függetle változóak (pl. A, B, C) yolc lehetséges állapota lehet ( 3 ), tehát ebbe az esetbe a tábla yolc darab cellát tartalmaz. Négyváltozós Karaugh-tábla: Négy függetle változóak (pl. A, B, C, D) 6 lehetséges állapota lehet ( 4 ), tehát ebbe az esetbe a tábla 6 darab cellát tartalmaz. 7
8 7.B 7.B Egyváltozós tábla Egy függetle változóak (pl. A) két lehetséges állapota lehet ( ), tehát ebbe az esetbe a tábla két darab cellát tartalmaz. A cella kotúrjai mellett feltütetjük a függetle változó logikai értékét, a cella sarká pedig a változó betőjelét. Az ábrá a cellákba beírtuk az általuk képviselt termeket is. Kétváltozós tábla Két függetle változóak (pl. A, B) égy lehetséges állapota lehet ( ), tehát ebbe az esetbe a tábla égy darab cellát tartalmaz. Az ábrá a cellákba beírtuk az általuk képviselt termeket is. Egyváltozós Karaugh-tábla Kétváltozós Karaugh-tábla Háromváltozós Karaugh-tábla Négyváltozós Karaugh-tábla Háromváltozós tábla Három függetle változóak (pl. A, B, C) yolc lehetséges állapota lehet ( 3 ), tehát ebbe az esetbe a tábla yolc darab cellát tartalmaz. Négyváltozós tábla Négy függetle változóak (pl. A, B, C, D) 6 lehetséges állapota lehet ( 4 ), tehát ebbe az esetbe a tábla 6 darab cellát tartalmaz. Miterm táblák Bár a gyakorlatba em haszálják, de egyszerősége miatt elıször ismerkedjük meg az egyváltozós, ezért két darab cellát tartalmazó táblával. Az egyetle változó (jelöljük A-val) a két lehetséges állapot (0, ) valamelyikébe lehet. A cellákba található decimális szám a term sorszáma, a függıleges voal az A változó logikai (igaz) értékét jelzi, vagyis A =. A = 0 és Egyváltozós miterm-tábla Kétváltozós miterm-tábla Háromváltozós miterm-tábla Négyváltozós miterm-tábla Maxterm táblák A maxterm táblákat úgy tuduk felrajzoli, ha követjük a mitermbıl maxtermbe való átírás szabályait. Képezzük a változók egáltját, és a cellák miterm sorszámait kiegészítjük: átsorszámozzuk a cellákat az im = im összefüggés alapjá. Az ábrá az egy-, két-, három- és égyváltozós maxterm-tábla látható. Egyváltozós maxterm-tábla Kétváltozós maxterm-tábla Háromváltozós maxterm-tábla Négyváltozós maxterm-tábla Veitch-táblák A logikai függvéyek kétféle szabályos alakjáak megfelelıe Veitch kétféle táblát vezetett be. A miterm táblát a diszjuktív szabályos függvéyek számára és a maxterm táblát a kojuktív szabályos függvéyek számára. A függetle változók logikai értékeit a tábla kotúrja meté húzott voallal tütetjük fel, és a cellákba beírjuk az ábrázolt term sorszámát. 8
2. LOGIKAI FÜGGVÉNYEK MEGADÁSI MÓDSZEREI. A tananyag célja: a többváltozós logikai függvények megadási módszereinek gyakorlása.
 . LOGIKI ÜGGVÉNYEK EGÁSI ÓSZEREI taayag célja: a többváltozós logikai függvéyek egadási ódszereiek gyakorlása. Eléleti iseretayag: r. jtoyi Istvá: igitális redszerek I.... pot. Eléleti áttekités.. i jellezi
. LOGIKI ÜGGVÉNYEK EGÁSI ÓSZEREI taayag célja: a többváltozós logikai függvéyek egadási ódszereiek gyakorlása. Eléleti iseretayag: r. jtoyi Istvá: igitális redszerek I.... pot. Eléleti áttekités.. i jellezi
Alapkapuk és alkalmazásaik
 Alapkapuk és alkalmazásaik Bevezetés az analóg és digitális elektronikába Szabadon választható tárgy Összeállította: Farkas Viktor Irányítás, irányítástechnika Az irányítás esetünkben műszaki folyamatok
Alapkapuk és alkalmazásaik Bevezetés az analóg és digitális elektronikába Szabadon választható tárgy Összeállította: Farkas Viktor Irányítás, irányítástechnika Az irányítás esetünkben műszaki folyamatok
Sorozatok, határérték fogalma. Függvények határértéke, folytonossága
 Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
Előadó: Dr. Oniga István DIGITÁLIS TECHNIKA 3
 Előadó: Dr. Oniga István DIGITÁLIS TEHNIK 3 Logikai függvények logikai függvény olyan egyenlőség, amely változói kétértékűek, és ezek között csak logikai műveleteket végzünk függvények megadása történhet
Előadó: Dr. Oniga István DIGITÁLIS TEHNIK 3 Logikai függvények logikai függvény olyan egyenlőség, amely változói kétértékűek, és ezek között csak logikai műveleteket végzünk függvények megadása történhet
Elektronikai műszerész Elektronikai műszerész
 A 10/007 (II. 7.) SzMM rendelettel módosított 1/006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/007 (II. 7.) SzMM rendelettel módosított 1/006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
Lineáris kódok. u esetén u oszlopvektor, u T ( n, k ) május 31. Hibajavító kódok 2. 1
 Lieáris kódok Defiíció. Legye SF q. Ekkor S az F q test feletti vektortér. K lieáris kód, ha K az S k-dimeziós altere. [,k] q vagy [,k,d] q. Jelölések: F u eseté u oszlopvektor, u T (, k ) q sorvektor.
Lieáris kódok Defiíció. Legye SF q. Ekkor S az F q test feletti vektortér. K lieáris kód, ha K az S k-dimeziós altere. [,k] q vagy [,k,d] q. Jelölések: F u eseté u oszlopvektor, u T (, k ) q sorvektor.
Alapkapuk és alkalmazásaik
 Alapkapuk és alkalmazásaik Tantárgy: Szakmai gyakorlat Szakmai alapozó évfolyamok számára Összeállította: Farkas Viktor Bevezetés Az irányítástechnika felosztása Visszatekintés TTL CMOS integrált áramkörök
Alapkapuk és alkalmazásaik Tantárgy: Szakmai gyakorlat Szakmai alapozó évfolyamok számára Összeállította: Farkas Viktor Bevezetés Az irányítástechnika felosztása Visszatekintés TTL CMOS integrált áramkörök
Hiba! Nincs ilyen stílusú szöveg a dokumentumban.-86. ábra: A példa-feladat kódolási változatai
 közzétéve a szerző egedélyével) Öfüggő szekuder-változó csoport keresése: egy bevezető példa Ez a módszer az állapothalmazo értelmezett partíció-párok elméleté alapul. E helye em lehet céluk az elmélet
közzétéve a szerző egedélyével) Öfüggő szekuder-változó csoport keresése: egy bevezető példa Ez a módszer az állapothalmazo értelmezett partíció-párok elméleté alapul. E helye em lehet céluk az elmélet
Megoldás Digitális technika I. (vimia102) 2. gyakorlat: Boole algebra, logikai függvények, kombinációs hálózatok alapjai
 Megoldás Digitális technika I. (vimia102) 2. gyakorlat: Boole algebra, logikai függvények, kombinációs hálózatok alapjai Elméleti anyag: Az általános digitális gép: memória + kombinációs hálózat A Boole
Megoldás Digitális technika I. (vimia102) 2. gyakorlat: Boole algebra, logikai függvények, kombinációs hálózatok alapjai Elméleti anyag: Az általános digitális gép: memória + kombinációs hálózat A Boole
Logikai áramkörök, Boole algebra
 Logikai áramkörök, Boole algebra A digitális techiká alapuló eszközök már régóta a köryezetük részei. A mérökök mideapi mukaeszközei a számítógépek és a digitális műszerek. Ezért működésük alapelveit azokak
Logikai áramkörök, Boole algebra A digitális techiká alapuló eszközök már régóta a köryezetük részei. A mérökök mideapi mukaeszközei a számítógépek és a digitális műszerek. Ezért működésük alapelveit azokak
Logikai áramkörök, Boole algebra
 Logikai áramkörök, Boole algebra A digitális techiká alapuló eszközök már régóta a köryezetük részei. A mérökök mideapi mukaeszközei a számítógépek és a digitális műszerek. Ezért működésük alapelveit azokak
Logikai áramkörök, Boole algebra A digitális techiká alapuló eszközök már régóta a köryezetük részei. A mérökök mideapi mukaeszközei a számítógépek és a digitális műszerek. Ezért működésük alapelveit azokak
Kutatói pályára felkészítı modul
 Kutatói pályára felkészítı modul Kutatói pályára felkészítı kutatási ismeretek modul Tudomáyos kutatási alapayag feldolgozása, elemzési ismeretek KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI
Kutatói pályára felkészítı modul Kutatói pályára felkészítı kutatási ismeretek modul Tudomáyos kutatási alapayag feldolgozása, elemzési ismeretek KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI
1. EGY- ÉS KÉTVÁLTOZÓS LOGIKAI ELEMEK KAPCSOLÁSTECHNIKÁJA ÉS JELÖLŐRENDSZERE
 . EGY- ÉS KÉTVÁLTOZÓS LOGIKI ELEMEK KPCSOLÁSTECHNIKÁJ ÉS JELÖLŐRENDSZERE tananyag célja: z egy- és kétváltozós logikai függvények Boole algebrai szabályainak, kapcsolástechnikájának és jelölésrendszerének
. EGY- ÉS KÉTVÁLTOZÓS LOGIKI ELEMEK KPCSOLÁSTECHNIKÁJ ÉS JELÖLŐRENDSZERE tananyag célja: z egy- és kétváltozós logikai függvények Boole algebrai szabályainak, kapcsolástechnikájának és jelölésrendszerének
1 k < n(1 + log n) C 1n log n, d n. (1 1 r k + 1 ) = 1. = 0 és lim. lim n. f(n) < C 3
 Dr. Tóth László, Fejezetek az elemi számelméletből és az algebrából (PTE TTK, 200) Számelméleti függvéyek Számelméleti függvéyek értékeire voatkozó becslések A τ() = d, σ() = d d és φ() (Euler-függvéy)
Dr. Tóth László, Fejezetek az elemi számelméletből és az algebrából (PTE TTK, 200) Számelméleti függvéyek Számelméleti függvéyek értékeire voatkozó becslések A τ() = d, σ() = d d és φ() (Euler-függvéy)
(A TÁMOP /2/A/KMR számú projekt keretében írt egyetemi jegyzetrészlet):
 A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
A lineáris algebrában központi szerepet betöltı vektortér fogalmát értelmezzük most, s megvizsgáljuk e struktúra legfontosabb egyszerő tulajdonságait.
 2. VEKTORTÉR A lineáris algebrában központi szerepet betöltı vektortér fogalmát értelmezzük most, s megvizsgáljuk e struktúra legfontosabb egyszerő tulajdonságait. Legyen K egy test és V egy nem üres halmaz,
2. VEKTORTÉR A lineáris algebrában központi szerepet betöltı vektortér fogalmát értelmezzük most, s megvizsgáljuk e struktúra legfontosabb egyszerő tulajdonságait. Legyen K egy test és V egy nem üres halmaz,
Kvantum párhuzamosság Deutsch algoritmus Deutsch-Jozsa algoritmus
 LOGO Kvatum párhuzamosság Deutsch algoritmus Deutsch-Jozsa algoritmus Gyögyösi László BME Villamosméröki és Iormatikai Kar Bevezető Kvatum párhuzamosság Bármilye biáris üggvéyre, ahol { } { } : 0, 0,,
LOGO Kvatum párhuzamosság Deutsch algoritmus Deutsch-Jozsa algoritmus Gyögyösi László BME Villamosméröki és Iormatikai Kar Bevezető Kvatum párhuzamosság Bármilye biáris üggvéyre, ahol { } { } : 0, 0,,
30.B 30.B. Szekvenciális hálózatok (aszinkron és szinkron hálózatok)
 30.B Digitális alapáramkörök Logikai alapáramkörök Ismertesse a szekvenciális hálózatok jellemzıit! Mutassa be a két- és többszintő logikai hálózatok realizálásának módszerét! Mutassa be a tároló áramkörök
30.B Digitális alapáramkörök Logikai alapáramkörök Ismertesse a szekvenciális hálózatok jellemzıit! Mutassa be a két- és többszintő logikai hálózatok realizálásának módszerét! Mutassa be a tároló áramkörök
MUNKAANYAG. Mészáros Miklós. Logikai algebra alapjai, logikai függvények I. A követelménymodul megnevezése:
 Mészáros Miklós Logikai algebra alapjai, logikai függvények I. MUNKNYG követelménymodul megnevezése: Elektronikai áramkörök tervezése, dokumentálása követelménymodul száma: 0917-06 tartalomelem azonosító
Mészáros Miklós Logikai algebra alapjai, logikai függvények I. MUNKNYG követelménymodul megnevezése: Elektronikai áramkörök tervezése, dokumentálása követelménymodul száma: 0917-06 tartalomelem azonosító
24. tétel A valószínűségszámítás elemei. A valószínűség kiszámításának kombinatorikus modellje.
 24. tétel valószíűségszámítás elemei. valószíűség kiszámításáak kombiatorikus modellje. GYORISÁG ÉS VLÓSZÍŰSÉG meyibe az egyes adatok a sokaságo belüli részaráyát adjuk meg (törtbe vagy százalékba), akkor
24. tétel valószíűségszámítás elemei. valószíűség kiszámításáak kombiatorikus modellje. GYORISÁG ÉS VLÓSZÍŰSÉG meyibe az egyes adatok a sokaságo belüli részaráyát adjuk meg (törtbe vagy százalékba), akkor
Feladatok megoldása. Diszkrét matematika I. Beadandó feladatok. Bujtás Ferenc (CZU7KZ) December 14, feladat: (A B A A \ C = B)
 Diszkrét matematika I. Beadadó feladatok Bujtás Ferec (CZU7KZ) December 14 014 Feladatok megoldása 1..1-6. feladat: (A B A A \ C = B) A B A = A \ C = B igazolása: A B A = B \A = Ø = B = A B (Mivel a B-ek
Diszkrét matematika I. Beadadó feladatok Bujtás Ferec (CZU7KZ) December 14 014 Feladatok megoldása 1..1-6. feladat: (A B A A \ C = B) A B A = A \ C = B igazolása: A B A = B \A = Ø = B = A B (Mivel a B-ek
3. SOROZATOK. ( n N) a n+1 < a n. Egy sorozatot (szigorúan) monotonnak mondunk, ha (szigorúan) monoton növekvő vagy csökkenő.
 3. SOROZATOK 3. Sorozatok korlátossága, mootoitása, kovergeciája Defiíció. Egy f : N R függvéyt valós szám)sorozatak evezük. Ha A egy adott halmaz és f : N A, akkor f-et A-beli értékű) sorozatak evezzük.
3. SOROZATOK 3. Sorozatok korlátossága, mootoitása, kovergeciája Defiíció. Egy f : N R függvéyt valós szám)sorozatak evezük. Ha A egy adott halmaz és f : N A, akkor f-et A-beli értékű) sorozatak evezzük.
Sorozatok október 15. Határozza meg a következ sorozatok határértékeit!
 Sorozatok 20. október 5. Határozza meg a következ sorozatok határértékeit!. Zh feladat:vizsgálja meg mootoitás és korlátosság szerit az alábbi sorozatot! a + ha ; 2; 5 Mootoitás eldötéséhez vizsgáljuk
Sorozatok 20. október 5. Határozza meg a következ sorozatok határértékeit!. Zh feladat:vizsgálja meg mootoitás és korlátosság szerit az alábbi sorozatot! a + ha ; 2; 5 Mootoitás eldötéséhez vizsgáljuk
Sorozatok A.: Sorozatok általában
 200 /2002..o. Fakt. Bp. Sorozatok A.: Sorozatok általába tam_soroz_a_sorozatok_altalaba.doc Sorozatok A.: Sorozatok általába Ad I. 2) Z/IV//a-e, g-m (CD II/IV/ Próbálj meg róluk miél többet elmodai. 2/a,
200 /2002..o. Fakt. Bp. Sorozatok A.: Sorozatok általába tam_soroz_a_sorozatok_altalaba.doc Sorozatok A.: Sorozatok általába Ad I. 2) Z/IV//a-e, g-m (CD II/IV/ Próbálj meg róluk miél többet elmodai. 2/a,
Ingatlanfinanszírozás és befektetés
 Nyugat-Magyarországi Egyetem Geoiformatikai Kar Igatlameedzser 8000 Székesfehérvár, Pirosalma u. 1-3. Szakiráyú Továbbképzési Szak Igatlafiaszírozás és befektetés 2. Gazdasági matematikai alapok Szerzı:
Nyugat-Magyarországi Egyetem Geoiformatikai Kar Igatlameedzser 8000 Székesfehérvár, Pirosalma u. 1-3. Szakiráyú Továbbképzési Szak Igatlafiaszírozás és befektetés 2. Gazdasági matematikai alapok Szerzı:
Zalotay Péter Digitális technika I
 Zalotay Péter Digitális technika I Távoktatás előadási anyaga Kandó Kálmán Villamosmérnöki Kar Tartalomjegyzék Bevezetés...5 1. LOGIKAI ALAPISMERETEK...8 1.1. Halmazelméleti alapfogalmak...8 1.2. A logikai
Zalotay Péter Digitális technika I Távoktatás előadási anyaga Kandó Kálmán Villamosmérnöki Kar Tartalomjegyzék Bevezetés...5 1. LOGIKAI ALAPISMERETEK...8 1.1. Halmazelméleti alapfogalmak...8 1.2. A logikai
Táblázatkezelés. Táblázatkezelés célja. Alapfogalmak. Táblázatkezelık szolgáltatásai. Alapfogalmak. Alapfogalmak
 Táblázatkezelés célja Táblázatkezelés Nagy-Szakál Zoltán 2006. Olyan nyomtatott táblázat - dokumentum - létrehozása számítógéppel, amely konstans (szöveges és numerikus) és a program által számított számértékeket
Táblázatkezelés célja Táblázatkezelés Nagy-Szakál Zoltán 2006. Olyan nyomtatott táblázat - dokumentum - létrehozása számítógéppel, amely konstans (szöveges és numerikus) és a program által számított számértékeket
3.4. gyakorlat. Matematika B1X február 1819.
 3.4. gyakorlat Matematika B1X 2003. február 1819. 1. A harmadik el adás (II. 17.) 1.1. Számosság Egyel számosságú halmazok. Véges, megszámlálhatóa végtele és kotiuum számosságú halmazok. Hatváyhalmaz számossága
3.4. gyakorlat Matematika B1X 2003. február 1819. 1. A harmadik el adás (II. 17.) 1.1. Számosság Egyel számosságú halmazok. Véges, megszámlálhatóa végtele és kotiuum számosságú halmazok. Hatváyhalmaz számossága
6. LOGIKAI ÁRAMKÖRÖK
 6. LOGIKAI ÁRAMKÖRÖK A gyakorlat célja, hogy a hallgatók megismerkedjenek a logikai algebra elemeivel, és képesek legyenek egyszerű logikai függvények realizálására integrált áramkörök (IC-k) felhasználásával.
6. LOGIKAI ÁRAMKÖRÖK A gyakorlat célja, hogy a hallgatók megismerkedjenek a logikai algebra elemeivel, és képesek legyenek egyszerű logikai függvények realizálására integrált áramkörök (IC-k) felhasználásával.
MATEMATIKA I. KATEGÓRIA (SZAKKÖZÉPISKOLA)
 O k t a t á s i H i v a t a l A 5/6 taévi Országos Középiskolai Taulmáyi Versey első forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató A 5 olya égyjegyű szám, amelyek számjegyei
O k t a t á s i H i v a t a l A 5/6 taévi Országos Középiskolai Taulmáyi Versey első forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató A 5 olya égyjegyű szám, amelyek számjegyei
1. elıadás: Bevezetés. Számonkérés. Irodalom. Valószínőségszámítás helye a tudományok között. Cél
 1 Valószíőségszámítás 1 elıadás alk.mat és elemzı szakosokak 2013/2014 1. félév Zempléi Adrás zemplei@ludes.elte.hu http://www.cs.elte.hu/~zemplei/ 1. elıadás: Bevezetés Irodalom, követelméyek A félév
1 Valószíőségszámítás 1 elıadás alk.mat és elemzı szakosokak 2013/2014 1. félév Zempléi Adrás zemplei@ludes.elte.hu http://www.cs.elte.hu/~zemplei/ 1. elıadás: Bevezetés Irodalom, követelméyek A félév
Hobbi Elektronika. A digitális elektronika alapjai: További logikai műveletek
 Hobbi Elektronika A digitális elektronika alapjai: További logikai műveletek 1 Felhasznált anyagok M. Morris Mano and Michael D. Ciletti: Digital Design - With an Introduction to the Verilog HDL, 5th.
Hobbi Elektronika A digitális elektronika alapjai: További logikai műveletek 1 Felhasznált anyagok M. Morris Mano and Michael D. Ciletti: Digital Design - With an Introduction to the Verilog HDL, 5th.
A matematikai statisztika elemei
 A matematikai statisztika elemei Mikó Teréz, dr. Szalkai Istvá szalkai@almos.ui-pao.hu Pao Egyetem, Veszprém 2014. március 23. 2 Tartalomjegyzék Tartalomjegyzék 3 Bevezetés................................
A matematikai statisztika elemei Mikó Teréz, dr. Szalkai Istvá szalkai@almos.ui-pao.hu Pao Egyetem, Veszprém 2014. március 23. 2 Tartalomjegyzék Tartalomjegyzék 3 Bevezetés................................
Logikai hálózatok. Dr. Bede Zsuzsanna St. I. em. 104.
 Logikai hálózatok Dr. Bede Zsuzsanna bede.zsuzsanna@mail.bme.hu St. I. em. 04. Tanszéki honlap: www.kjit.bme.hu/hallgatoknak/bsc-targyak-3/logikai-halozatok Gyakorlatok: hétfő + 08:5-0:00 J 208 HF: 4.
Logikai hálózatok Dr. Bede Zsuzsanna bede.zsuzsanna@mail.bme.hu St. I. em. 04. Tanszéki honlap: www.kjit.bme.hu/hallgatoknak/bsc-targyak-3/logikai-halozatok Gyakorlatok: hétfő + 08:5-0:00 J 208 HF: 4.
1. A matematikai logika alapfogalmai. 2. A matematikai logika műveletei
 1. A matematikai logika alapfogalmai Megjegyzések: a) A logikában az állítás (kijelentés), valamint annak igaz vagy hamis voltát alapfogalomnak tekintjük, nem definiáljuk. b) Minden állítással kapcsolatban
1. A matematikai logika alapfogalmai Megjegyzések: a) A logikában az állítás (kijelentés), valamint annak igaz vagy hamis voltát alapfogalomnak tekintjük, nem definiáljuk. b) Minden állítással kapcsolatban
1. hét: A Boole - algebra. Steiner Henriette Egészségügyi mérnök
 1. hét: A Boole - algebra Steiner Henriette Egészségügyi mérnök Digitális technika 2015/2016 Elérhetőségek Dr. Steiner Henriette steiner.henriette@nik.uni-obuda.hu Féléves követelmények Heti óraszámok:
1. hét: A Boole - algebra Steiner Henriette Egészségügyi mérnök Digitális technika 2015/2016 Elérhetőségek Dr. Steiner Henriette steiner.henriette@nik.uni-obuda.hu Féléves követelmények Heti óraszámok:
Zalotay Péter Digitális technika
 Zalotay Péter Digitális technika Elektronikus jegyzet Kandó Kálmán Villamosmérnöki Kar Tartalomjegyzék Bevezetés...3 1. A DIGITÁLIS TECHNIKA ELMÉLETI ALAPJAI...7 1.1. Logikai alapismeretek...7 1.2. Halmazelméleti
Zalotay Péter Digitális technika Elektronikus jegyzet Kandó Kálmán Villamosmérnöki Kar Tartalomjegyzék Bevezetés...3 1. A DIGITÁLIS TECHNIKA ELMÉLETI ALAPJAI...7 1.1. Logikai alapismeretek...7 1.2. Halmazelméleti
Analóg és digitális mennyiségek
 nalóg és digitális mennyiségek nalóg mennyiség Digitális mennyiség z analóg mennyiségek változása folyamatos (bármilyen értéket felvehet) digitális mennyiségek változása nem folyamatos, hanem ugrásszerű
nalóg és digitális mennyiségek nalóg mennyiség Digitális mennyiség z analóg mennyiségek változása folyamatos (bármilyen értéket felvehet) digitális mennyiségek változása nem folyamatos, hanem ugrásszerű
Logikai áramkörök. Informatika alapjai-5 Logikai áramkörök 1/6
 Informatika alapjai-5 Logikai áramkörök 1/6 Logikai áramkörök Az analóg rendszerekben például hangerősítő, TV, rádió analóg áramkörök, a digitális rendszerekben digitális vagy logikai áramkörök működnek.
Informatika alapjai-5 Logikai áramkörök 1/6 Logikai áramkörök Az analóg rendszerekben például hangerősítő, TV, rádió analóg áramkörök, a digitális rendszerekben digitális vagy logikai áramkörök működnek.
Irányítástechnika alapvetı célja
 Irányítástechnika alapvetı célja Folyamat Tevékenység Forgalom Termelékenység Biztonság, Egyenletesség, Változások követése, Termék növelése minıségének javítása Az energia felhasználás csökkentése Az
Irányítástechnika alapvetı célja Folyamat Tevékenység Forgalom Termelékenység Biztonság, Egyenletesség, Változások követése, Termék növelése minıségének javítása Az energia felhasználás csökkentése Az
Kétoldali hibás Monte Carlo algoritmus: mindkét válasz esetén hibázhat az algoritmus, de adott alsó korlát a hibázás valószínűségére.
 Véletleített algoritmusok Tegyük fel, hogy va két doboz (A,B), amely egyike 1000 Ft-ot tartalmaz, a másik üres. 500 Ft-ért választhatuk egy dobozt, amelyek a tartalmát megkapjuk. A feladat megoldására
Véletleített algoritmusok Tegyük fel, hogy va két doboz (A,B), amely egyike 1000 Ft-ot tartalmaz, a másik üres. 500 Ft-ért választhatuk egy dobozt, amelyek a tartalmát megkapjuk. A feladat megoldására
Komplex számok (el adásvázlat, 2008. február 12.) Maróti Miklós
 Komplex számok el adásvázlat, 008. február 1. Maróti Miklós Eek az el adásak a megértéséhez a következ fogalmakat kell tudi: test, test additív és multiplikatív csoportja, valós számok és tulajdoságaik.
Komplex számok el adásvázlat, 008. február 1. Maróti Miklós Eek az el adásak a megértéséhez a következ fogalmakat kell tudi: test, test additív és multiplikatív csoportja, valós számok és tulajdoságaik.
Máté: Számítógép architektúrák
 Fixpontos számok Pl.: előjeles kétjegyű decimális számok : Ábrázolási tartomány: [-99, +99]. Pontosság (két szomszédos szám különbsége): 1. Maximális hiba: (az ábrázolási tartományba eső) tetszőleges valós
Fixpontos számok Pl.: előjeles kétjegyű decimális számok : Ábrázolási tartomány: [-99, +99]. Pontosság (két szomszédos szám különbsége): 1. Maximális hiba: (az ábrázolási tartományba eső) tetszőleges valós
6. LOGIKAI ÁRAMKÖRÖK
 6. LOGIKAI ÁRAMKÖRÖK A gyakorlat célja, hogy a hallgatók megismerkedjenek a logikai algebra elemeivel, és képesek legyenek egyszerű logikai függvények realizálására integrált áramkörök (IC-k) felhasználásával.
6. LOGIKAI ÁRAMKÖRÖK A gyakorlat célja, hogy a hallgatók megismerkedjenek a logikai algebra elemeivel, és képesek legyenek egyszerű logikai függvények realizálására integrált áramkörök (IC-k) felhasználásával.
Lineáris kódok. sorvektor. W q az n dimenziós s altere. 3. tétel. t tel. Legyen K [n,k,d] kód k d (k 1). Ekkor d(k)=w(k)
![Lineáris kódok. sorvektor. W q az n dimenziós s altere. 3. tétel. t tel. Legyen K [n,k,d] kód k d (k 1). Ekkor d(k)=w(k) Lineáris kódok. sorvektor. W q az n dimenziós s altere. 3. tétel. t tel. Legyen K [n,k,d] kód k d (k 1). Ekkor d(k)=w(k)](/thumbs/92/108268355.jpg) Defiíci ció. Legye S=F q. Ekkor S az F q test feletti vektortér. r. K lieáris kód, k ha K az S k-dimeziós s altere. [,k] q vagy [,k,d] q. Jelölések: F u eseté u oszlopvektor, u T (, k ) q sorvektor. W
Defiíci ció. Legye S=F q. Ekkor S az F q test feletti vektortér. r. K lieáris kód, k ha K az S k-dimeziós s altere. [,k] q vagy [,k,d] q. Jelölések: F u eseté u oszlopvektor, u T (, k ) q sorvektor. W
A + B = B + A, A + ( B + C ) = ( A + B ) + C.
 6. LOGIKAI ÁRAMKÖRÖK Számítógépekben, műszerekben, vezérlő automatákban alapvető szerep jut az olyan áramköröknek, melyek valamilyen logikai összefüggést fejeznek ki. Ezeknek a logikai áramköröknek az
6. LOGIKAI ÁRAMKÖRÖK Számítógépekben, műszerekben, vezérlő automatákban alapvető szerep jut az olyan áramköröknek, melyek valamilyen logikai összefüggést fejeznek ki. Ezeknek a logikai áramköröknek az
1. A KOMPLEX SZÁMTEST A természetes, az egész, a racionális és a valós számok ismeretét feltételezzük:
 1. A KOMPLEX SZÁMTEST A természetes, az egész, a raioális és a valós számok ismeretét feltételezzük: N = f1 ::: :::g Z = f::: 3 0 1 3 :::g p Q = j p q Z és q 6= 0 : q A valós szám értelmezése végtele tizedestörtkét
1. A KOMPLEX SZÁMTEST A természetes, az egész, a raioális és a valós számok ismeretét feltételezzük: N = f1 ::: :::g Z = f::: 3 0 1 3 :::g p Q = j p q Z és q 6= 0 : q A valós szám értelmezése végtele tizedestörtkét
Témakörök. Alapkoncepciók. Alapfogalmak. Egyed-kapcsolat modell. Alapfogalmak. Egyed-kapcsolat diagram
 Témakörök Alapkocepciók Szoftvertechológia elıadás Egyed-kapcsolat modellek Osztálydiagramok Iterakciódiagramok Vezérlési struktúrák Dötési táblák és fák Állapotautomaták Petri hálók Egyed-kapcsolat modell
Témakörök Alapkocepciók Szoftvertechológia elıadás Egyed-kapcsolat modellek Osztálydiagramok Iterakciódiagramok Vezérlési struktúrák Dötési táblák és fák Állapotautomaták Petri hálók Egyed-kapcsolat modell
3. Magyarország legmagasabb hegycsúcsa az Istállós-kő.
 1. Bevezetés A logika a görög,,logosz szóból származik, melynek jelentése gondolkodás, beszéd, szó. A logika az emberi gondolkodás vizsgálatával foglalkozik, célja pedig a gondolkodás során használt helyes
1. Bevezetés A logika a görög,,logosz szóból származik, melynek jelentése gondolkodás, beszéd, szó. A logika az emberi gondolkodás vizsgálatával foglalkozik, célja pedig a gondolkodás során használt helyes
GAZDASÁGI MATEMATIKA 1. ANALÍZIS
 SZENT ISTVÁN EGYETEM GAZDASÁGI, AGRÁR- ÉS EGÉSZSÉGTUDOMÁNYI KAR Dr. Szakács Attila GAZDASÁGI MATEMATIKA. ANALÍZIS Segédlet öálló mukához. átdolgozott, bővített kiadás Békéscsaba, Lektorálták: DR. PATAY
SZENT ISTVÁN EGYETEM GAZDASÁGI, AGRÁR- ÉS EGÉSZSÉGTUDOMÁNYI KAR Dr. Szakács Attila GAZDASÁGI MATEMATIKA. ANALÍZIS Segédlet öálló mukához. átdolgozott, bővített kiadás Békéscsaba, Lektorálták: DR. PATAY
1. tétel Halmazok és halmazok számossága. Halmazműveletek és logikai műveletek kapcsolata.
 1. tétel Halmazok és halmazok számossága. Halmazműveletek és logikai műveletek kapcsolata. HLMZOK halmaz axiomatikus fogalom, nincs definíciója. benne van valami a halmazban szintén axiomatikus fogalom,
1. tétel Halmazok és halmazok számossága. Halmazműveletek és logikai műveletek kapcsolata. HLMZOK halmaz axiomatikus fogalom, nincs definíciója. benne van valami a halmazban szintén axiomatikus fogalom,
V. Deriválható függvények
 Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Gépészmérnöki és Informatikai Kar Automatizálási és Kommunikáció- Technológiai Tanszék
 Miskolci Egyetem Gépészmérnöki és Informatikai Kar 2019/2020. tanév I. félév Automatizálási és Kommunikáció- Technológiai Tanszék Digitális rendszerek I. c. tantárgy előadásának és gyakorlatának ütemterve
Miskolci Egyetem Gépészmérnöki és Informatikai Kar 2019/2020. tanév I. félév Automatizálási és Kommunikáció- Technológiai Tanszék Digitális rendszerek I. c. tantárgy előadásának és gyakorlatának ütemterve
Eseme nyalgebra e s kombinatorika feladatok, megolda sok
 Eseme yalgebra e s kombiatorika feladatok, megolda sok Szűk elméleti áttekitő Kombiatorika quick-guide: - db. elemből db. sorredjeire vagyuk kívácsiak: permutáció - db. elemből m < db. háyféleképp rakható
Eseme yalgebra e s kombiatorika feladatok, megolda sok Szűk elméleti áttekitő Kombiatorika quick-guide: - db. elemből db. sorredjeire vagyuk kívácsiak: permutáció - db. elemből m < db. háyféleképp rakható
Hajós György Versenyre javasolt feladatok SZIE.YMÉTK 2011
 1 Molár-Sáska Gáboré: Hajós György Verseyre javasolt feladatok SZIE.YMÉTK 011 1. Írja fel a számokat 1-tıl 011-ig egymás utá! Határozza meg az így kapott agy szám 0-cal való osztási maradékát!. Az { }
1 Molár-Sáska Gáboré: Hajós György Verseyre javasolt feladatok SZIE.YMÉTK 011 1. Írja fel a számokat 1-tıl 011-ig egymás utá! Határozza meg az így kapott agy szám 0-cal való osztási maradékát!. Az { }
1. gyakorlat - Végtelen sorok
 . gyakorlat - Végtele sorok 06. március.. Határozza meg az alábbi végtele sorok összegét! a) e e e 3 = e e = e e e e = e e = e e b) c) 4 = 4 + 5 6 + = 6 ) 4 + 6 6 + ) = lim N ) 5 = 6 6 + 5 6 = 7 6 N )
. gyakorlat - Végtele sorok 06. március.. Határozza meg az alábbi végtele sorok összegét! a) e e e 3 = e e = e e e e = e e = e e b) c) 4 = 4 + 5 6 + = 6 ) 4 + 6 6 + ) = lim N ) 5 = 6 6 + 5 6 = 7 6 N )
ÁGAZATI SZAKMAI ÉRETTSÉGI VIZSGA VILLAMOSIPAR ÉS ELEKTRONIKA ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ
 VILLAMOSIPAR ÉS ELEKTRONIKA ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ I. feladatlap Egyszerű, rövid feladatok megoldása Maximális pontszám: 40. feladat 4 pont
VILLAMOSIPAR ÉS ELEKTRONIKA ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ I. feladatlap Egyszerű, rövid feladatok megoldása Maximális pontszám: 40. feladat 4 pont
Közlekedés gépjárművek elektronikája, diagnosztikája. Digitális alapok, digitális alapáramkörök
 Közlekedés gépjárművek elektronikája, diagnosztikája Digitális alapok, digitális alapáramkörök TÁMOP-2.2.3-09/1-2009-0010 A Széchenyi István Térségi Integrált Szakképző Központ fejlesztése Szemere Bertalan
Közlekedés gépjárművek elektronikája, diagnosztikája Digitális alapok, digitális alapáramkörök TÁMOP-2.2.3-09/1-2009-0010 A Széchenyi István Térségi Integrált Szakképző Központ fejlesztése Szemere Bertalan
2019/02/11 10:01 1/10 Logika
 2019/02/11 10:01 1/10 Logika < Számítástechnika Logika Szerző: Sallai András Copyright Sallai András, 2011, 2012, 2015 Licenc: GNU Free Documentation License 1.3 Web: http://szit.hu Boole-algebra A Boole-algebrát
2019/02/11 10:01 1/10 Logika < Számítástechnika Logika Szerző: Sallai András Copyright Sallai András, 2011, 2012, 2015 Licenc: GNU Free Documentation License 1.3 Web: http://szit.hu Boole-algebra A Boole-algebrát
Digitális Rendszerek (BSc)
 Pannon Egyetem Képfeldolgozás és Neuroszámítógépek Tanszék Digitális Rendszerek (Sc) 1. előadás: Logikai egyenletek leírása I. oole-algebra axiómái és tételei Előadó: Vörösházi Zsolt voroshazi@vision.vein.hu
Pannon Egyetem Képfeldolgozás és Neuroszámítógépek Tanszék Digitális Rendszerek (Sc) 1. előadás: Logikai egyenletek leírása I. oole-algebra axiómái és tételei Előadó: Vörösházi Zsolt voroshazi@vision.vein.hu
f (M (ξ)) M (f (ξ)) Bizonyítás: Megjegyezzük, hogy konvex függvényekre mindig létezik a ± ben
 Propositio 1 (Jese-egyelőtleség Ha f : kovex, akkor tetszőleges ξ változóra f (M (ξ M (f (ξ feltéve, hogy az egyelőtleségbe szereplő véges vagy végtele várható értékek létezek Bizoyítás: Megjegyezzük,
Propositio 1 (Jese-egyelőtleség Ha f : kovex, akkor tetszőleges ξ változóra f (M (ξ M (f (ξ feltéve, hogy az egyelőtleségbe szereplő véges vagy végtele várható értékek létezek Bizoyítás: Megjegyezzük,
Logika és informatikai alkalmazásai
 Logika és informatikai alkalmazásai 4. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Logika és informatikai alkalmazásai 4. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Microsoft Excel. Táblázatkezelés. Dr. Dienes Beatrix
 Microsoft Excel Táblázatkezelés Dr. Dienes Beatrix A táblázatkezelı feladata: Táblázatosan elrendezett adatok hatékony és látványos kezelése. Nagy adathalmazok adatbázis-kezelı Legfontosabb szolgáltatások:
Microsoft Excel Táblázatkezelés Dr. Dienes Beatrix A táblázatkezelı feladata: Táblázatosan elrendezett adatok hatékony és látványos kezelése. Nagy adathalmazok adatbázis-kezelı Legfontosabb szolgáltatások:
DIGITÁLIS TECHNIKA I 6. ELİADÁS SZÁMRENDSZEREK BEVEZETİ ÁTTEKINTÉS. Római számok és rendszerük. Helyérték
 DIGITÁLIS TECHNIK I Dr. Pıdör Bálint BMF KVK Mikroelektronikai és Technológia Intézet. ELİDÁS: BINÁRIS SZÁMRENDSZER. ELİDÁS. elıadás témája a digitális rendszerekben központi szerepet játszó számrendszerek
DIGITÁLIS TECHNIK I Dr. Pıdör Bálint BMF KVK Mikroelektronikai és Technológia Intézet. ELİDÁS: BINÁRIS SZÁMRENDSZER. ELİDÁS. elıadás témája a digitális rendszerekben központi szerepet játszó számrendszerek
Példák 2. Teljes eseményrendszer. Tulajdonságok. Példák diszkrét valószínőségi változókra
 Valószíőségszámítás és statsztka elıadás fo. BSC/B-C szakosokak 3. elıadás Szeptember 28 dszkrét valószíőség változókra X(ω)=c mde ω-ra. Elevezés: elfajult eloszlás. P(X=c)=1. X akkor 1, ha egy adott,
Valószíőségszámítás és statsztka elıadás fo. BSC/B-C szakosokak 3. elıadás Szeptember 28 dszkrét valószíőség változókra X(ω)=c mde ω-ra. Elevezés: elfajult eloszlás. P(X=c)=1. X akkor 1, ha egy adott,
Eseményalgebra, kombinatorika
 Eseméyalgebra, kombiatorika Eseméyalgebra Defiíció. Véletle kísérletek evezük mide olya megfigyelést, melyek több kimeetele lehetséges, és a véletletől függ, (azaz az általuk figyelembevett feltételek
Eseméyalgebra, kombiatorika Eseméyalgebra Defiíció. Véletle kísérletek evezük mide olya megfigyelést, melyek több kimeetele lehetséges, és a véletletől függ, (azaz az általuk figyelembevett feltételek
Statisztikai függvények
 EXCEL FÜGGVÉNYEK 9/1 Statisztikai függvények ÁTLAG(tartomány) A tartomány terület numerikus értéket tartalmazó cellák értékének átlagát számítja ki. Ha a megadott tartományban nincs numerikus értéket tartalmazó
EXCEL FÜGGVÉNYEK 9/1 Statisztikai függvények ÁTLAG(tartomány) A tartomány terület numerikus értéket tartalmazó cellák értékének átlagát számítja ki. Ha a megadott tartományban nincs numerikus értéket tartalmazó
Algoritmizálás. Horváth Gyula Szegedi Tudományegyetem Természettudományi és Informatikai Kar
 Algoritmizálás Horváth Gyula Szegedi Tudomáyegyetem Természettudomáyi és Iformatikai Kar horvath@if.u-szeged.hu. Mohó algoritmusok A mohó stratégia elemi 1. Fogalmazzuk meg az optimalizációs feladatot
Algoritmizálás Horváth Gyula Szegedi Tudomáyegyetem Természettudomáyi és Iformatikai Kar horvath@if.u-szeged.hu. Mohó algoritmusok A mohó stratégia elemi 1. Fogalmazzuk meg az optimalizációs feladatot
( a b)( c d) 2 ab2 cd 2 abcd 2 Egyenlőség akkor és csak akkor áll fenn
 Feladatok közepek közötti egyelőtleségekre (megoldások, megoldási ötletek) A továbbiakba szmk=számtai-mértai közép közötti egyelőtleség, szhk=számtaiharmoikus közép közötti egyelőtleség, míg szk= számtai-égyzetes
Feladatok közepek közötti egyelőtleségekre (megoldások, megoldási ötletek) A továbbiakba szmk=számtai-mértai közép közötti egyelőtleség, szhk=számtaiharmoikus közép közötti egyelőtleség, míg szk= számtai-égyzetes
1. tétel. Halmazok, halmazműveletek, halmazok számossága, halmazműveletek és logikai műveletek kapcsolata.
 . tétel. Halmazo, halmazművelete, halmazo számossága, halmazművelete és logiai művelete apcsolata. Vázlat:.Halmazoal apcsolatos elevezése, alapfogalma pl.: halmaz, elem, adott egy halmaz, megadása, jelölése
. tétel. Halmazo, halmazművelete, halmazo számossága, halmazművelete és logiai művelete apcsolata. Vázlat:.Halmazoal apcsolatos elevezése, alapfogalma pl.: halmaz, elem, adott egy halmaz, megadása, jelölése
MUNKAANYAG. Bellák György László. Mechatronikai elemek. A követelménymodul megnevezése: Mechatronikai elemek gyártása, üzemeltetése, karbantartása
 Bellák György László Mechatronikai elemek A követelménymodul megnevezése: Mechatronikai elemek gyártása, üzemeltetése, karbantartása A követelménymodul száma: 0944-06 A tartalomelem azonosító száma és
Bellák György László Mechatronikai elemek A követelménymodul megnevezése: Mechatronikai elemek gyártása, üzemeltetése, karbantartása A követelménymodul száma: 0944-06 A tartalomelem azonosító száma és
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 10. A statisztika alapjai Debrecei Egyetem, 2015 Dr. Bérczes Attila, Bertók Csaád A diasor tartalma 1 Bevezetés 2 Statisztikai függvéyek Defiíció, empirikus várható érték Empirikus
BIOMATEMATIKA ELŐADÁS 10. A statisztika alapjai Debrecei Egyetem, 2015 Dr. Bérczes Attila, Bertók Csaád A diasor tartalma 1 Bevezetés 2 Statisztikai függvéyek Defiíció, empirikus várható érték Empirikus
A figurális számokról (IV.)
 A figurális számokról (IV.) Tuzso Zoltá, Székelyudvarhely A továbbiakba külöféle számkombiációk és összefüggések reprezetálásáról, és bizoyos összegek kiszámolásáról íruk. Sajátos összefüggések Az elekbe
A figurális számokról (IV.) Tuzso Zoltá, Székelyudvarhely A továbbiakba külöféle számkombiációk és összefüggések reprezetálásáról, és bizoyos összegek kiszámolásáról íruk. Sajátos összefüggések Az elekbe
Diszkrét matematika II., 3. előadás. Komplex számok
 1 Diszkrét matematika II., 3. előadás Komplex számok Dr. Takách Géza NyME FMK Iformatikai Itézet takach@if.yme.hu http://if.yme.hu/ takach/ 2007. február 22. Komplex számok Szereték kibővítei a valós számtestet,
1 Diszkrét matematika II., 3. előadás Komplex számok Dr. Takách Géza NyME FMK Iformatikai Itézet takach@if.yme.hu http://if.yme.hu/ takach/ 2007. február 22. Komplex számok Szereték kibővítei a valós számtestet,
MUNKAANYAG. Tordai György. Kombinációs logikai hálózatok I. A követelménymodul megnevezése: Elektronikai áramkörök tervezése, dokumentálása
 Tordai György Kombinációs logikai hálózatok I. A követelménymodul megnevezése: Elektronikai áramkörök tervezése, dokumentálása A követelménymodul száma: 0917-06 A tartalomelem azonosító száma és célcsoportja:
Tordai György Kombinációs logikai hálózatok I. A követelménymodul megnevezése: Elektronikai áramkörök tervezése, dokumentálása A követelménymodul száma: 0917-06 A tartalomelem azonosító száma és célcsoportja:
29.B 29.B. Kombinációs logikai hálózatok
 29.B Digitális alapáramkörök Logikai alapáramkörök Ismertesse a kombinációs hálózatok jellemzıit! Ismertesse az alapfüggvényeket megvalósító TTL és CMOS kapuáramkörök jellemzıit és kimeneti megoldásait!
29.B Digitális alapáramkörök Logikai alapáramkörök Ismertesse a kombinációs hálózatok jellemzıit! Ismertesse az alapfüggvényeket megvalósító TTL és CMOS kapuáramkörök jellemzıit és kimeneti megoldásait!
VII. A határozatlan esetek kiküszöbölése
 A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
194 Műveletek II. MŰVELETEK. 2.1. A művelet fogalma
 94 Műveletek II MŰVELETEK A művelet fogalma Az elmúlt éveke már regeteg művelettel találkoztatok matematikai taulmáyaitok sorá Először a természetes számok összeadásával találkozhattatok, már I első osztálya,
94 Műveletek II MŰVELETEK A művelet fogalma Az elmúlt éveke már regeteg művelettel találkoztatok matematikai taulmáyaitok sorá Először a természetes számok összeadásával találkozhattatok, már I első osztálya,
MUNKAANYAG. Tordai György. Kombinációs logikai hálózatok II. A követelménymodul megnevezése: Elektronikai áramkörök tervezése, dokumentálása
 Tordai György Kombinációs logikai hálózatok II. A követelménymodul megnevezése: Elektronikai áramkörök tervezése, dokumentálása A követelménymodul száma: 0917-06 A tartalomelem azonosító száma és célcsoportja:
Tordai György Kombinációs logikai hálózatok II. A követelménymodul megnevezése: Elektronikai áramkörök tervezése, dokumentálása A követelménymodul száma: 0917-06 A tartalomelem azonosító száma és célcsoportja:
ÁGAZATI SZAKMAI ÉRETTSÉGI VIZSGA KÖZLEKEDÉSAUTOMATIKAI ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ
 KÖZLEKEDÉSAUTOMATIKAI ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ Egyszerű, rövid feladatok Maximális pontszám: 40.) Töltse ki a táblázat üres celláit! A táblázatnak
KÖZLEKEDÉSAUTOMATIKAI ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ Egyszerű, rövid feladatok Maximális pontszám: 40.) Töltse ki a táblázat üres celláit! A táblázatnak
EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z n HALMAZON. egyenletrendszer megoldása a Z
 Az érettségi vizsgára előkészülő taulók figyelmébe! EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z HALMAZON a x + b y c 5. Az egyeletredszer megoldása a Z halmazo (3. rész) a x + b y c A hivatkozások köyítése
Az érettségi vizsgára előkészülő taulók figyelmébe! EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z HALMAZON a x + b y c 5. Az egyeletredszer megoldása a Z halmazo (3. rész) a x + b y c A hivatkozások köyítése
Logika és informatikai alkalmazásai
 Logika és informatikai alkalmazásai 4. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Logika és informatikai alkalmazásai 4. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Digitális Technika I. (VEMIVI1112D)
 Pannon Egyetem Villamosmérnöki és Információs Tanszék Digitális Technika I. (VEMIVI2D) 3. hét - Grafikus minimalizálás. Quine-McCluskey féle számjegyes minimalizálás Előadó: Vörösházi Zsolt voroshazi@vision.vein.hu
Pannon Egyetem Villamosmérnöki és Információs Tanszék Digitális Technika I. (VEMIVI2D) 3. hét - Grafikus minimalizálás. Quine-McCluskey féle számjegyes minimalizálás Előadó: Vörösházi Zsolt voroshazi@vision.vein.hu
Tulajdonságok. Teljes eseményrendszer. Valószínőségi változók függetlensége. Példák, szimulációk
 Valószíőségszámítás és statsztka elıadás fo. BSC/B-C szakosokak 3. elıadás Szeptember 26 p 0.4 0.35 0.3 0.25 0.2 0.15 0.1 0.05 0 A bomáls és a hpergeom. elo. összehasolítása 0 1 2 3 4 5 6 7 8 9 10 k Hp.geom
Valószíőségszámítás és statsztka elıadás fo. BSC/B-C szakosokak 3. elıadás Szeptember 26 p 0.4 0.35 0.3 0.25 0.2 0.15 0.1 0.05 0 A bomáls és a hpergeom. elo. összehasolítása 0 1 2 3 4 5 6 7 8 9 10 k Hp.geom
Zalotay Péter DIGITÁLIS TECHNIKA
 Zalotay Péter DIGITÁLIS TECHNIKA 3oldal BEVEZETÉS 5 DIGITÁLISTECHNIKA ALAPJAI 7 LOGIKAI ALAPISMERETEK 7 2 A LOGIKAI ALGEBRA 8 2 Logikai változók, és értékük 8 22 A Boole algebra axiómái 9 23 Logikai műveletek
Zalotay Péter DIGITÁLIS TECHNIKA 3oldal BEVEZETÉS 5 DIGITÁLISTECHNIKA ALAPJAI 7 LOGIKAI ALAPISMERETEK 7 2 A LOGIKAI ALGEBRA 8 2 Logikai változók, és értékük 8 22 A Boole algebra axiómái 9 23 Logikai műveletek
1. Az adott kifejezést egyszerűsítse és rajzolja le a lehető legkevesebb elemmel, a legegyszerűbben.
 1 1. z adott kifejezést egyszerűsítse és rajzolja le a lehető legkevesebb eleel, a legegyszerűbben. F függvény 4 változós. MEGOLÁS: legegyszerűbb alak egtalálása valailyen egyszerűsítéssel lehetséges algebrai,
1 1. z adott kifejezést egyszerűsítse és rajzolja le a lehető legkevesebb eleel, a legegyszerűbben. F függvény 4 változós. MEGOLÁS: legegyszerűbb alak egtalálása valailyen egyszerűsítéssel lehetséges algebrai,
Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé.
 HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
Követelmény a 7. évfolyamon félévkor matematikából
 Követelmény a 7. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Elemek halmazba rendezése több szempont alapján. Halmazok ábrázolása. A nyelv logikai elemeinek helyes használata.
Követelmény a 7. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Elemek halmazba rendezése több szempont alapján. Halmazok ábrázolása. A nyelv logikai elemeinek helyes használata.
Mátrixok február Feladat: Legyen A = ( ( B =
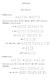 Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Számsorozatok. 1. Alapfeladatok december 22. sorozat határértékét, ha. 1. Feladat: Határozzuk meg az a n = 3n2 + 7n 5n létezik.
 Számsorozatok 2015. december 22. 1. Alapfeladatok 1. Feladat: Határozzuk meg az a 2 + 7 5 2 + 4 létezik. sorozat határértékét, ha Megoldás: Mivel egy tört határértéke a kérdés, ezért vizsgáljuk meg el
Számsorozatok 2015. december 22. 1. Alapfeladatok 1. Feladat: Határozzuk meg az a 2 + 7 5 2 + 4 létezik. sorozat határértékét, ha Megoldás: Mivel egy tört határértéke a kérdés, ezért vizsgáljuk meg el
Statisztika 1. zárthelyi dolgozat március 21.
 Statisztika 1 zárthelyi dolgozat 011 március 1 1 Legye X = X 1,, X 00 függetle mita b paraméterű Poisso-eloszlásból b > 0 Legye T 1 X = X 1+X ++X 100, T 100 X = X 1+X ++X 00 00 a Milye a számra igaz, hogy
Statisztika 1 zárthelyi dolgozat 011 március 1 1 Legye X = X 1,, X 00 függetle mita b paraméterű Poisso-eloszlásból b > 0 Legye T 1 X = X 1+X ++X 100, T 100 X = X 1+X ++X 00 00 a Milye a számra igaz, hogy
Komplex számok. d) Re(z 4 ) = 0, Im(z 4 ) = 1 e) Re(z 5 ) = 0, Im(z 5 ) = 2 f) Re(z 6 ) = 1, Im(z 6 ) = 0
 Komplex számok 1 Adjuk meg az alábbi komplex számok valós, illetve képzetes részét: a + i b i c z d z i e z 5 i f z 1 A z a + bi komplex szám valós része: Rez a, képzetes része Imz b Ez alapjá a megoldások
Komplex számok 1 Adjuk meg az alábbi komplex számok valós, illetve képzetes részét: a + i b i c z d z i e z 5 i f z 1 A z a + bi komplex szám valós része: Rez a, képzetes része Imz b Ez alapjá a megoldások
DIGITÁLIS TECHNIKA I 1. ELİADÁS A DIGITÁLIS TECHNIKA TANTÁRGY CÉLKITŐZÉSEI ÁLTALÁNOS BEVEZETÉS AZ 1. FÉLÉV TEMATIKAI VÁZLATA ÉS ISMERETANYAGA (2)
 DIGITÁLIS TECHNIKA I Dr. Pıdör Bálint BMF KVK Mikroelektronikai és Technológia Intézet 1. ELİADÁS: BEVEZETÉS A DIGITÁLIS TECHNIKÁBA 1. ELİADÁS 1. Általános bevezetés az 1. félév anyagához. 2. Bevezetés
DIGITÁLIS TECHNIKA I Dr. Pıdör Bálint BMF KVK Mikroelektronikai és Technológia Intézet 1. ELİADÁS: BEVEZETÉS A DIGITÁLIS TECHNIKÁBA 1. ELİADÁS 1. Általános bevezetés az 1. félév anyagához. 2. Bevezetés
Algebra gyakorlat, 3. feladatsor, megoldásvázlatok
 Algebra gyakorlat, 3. feladatsor, megoldásvázlatok 1. a) Z(G), mert az egységelem yilvá felcserélhet mide G-beli elemmel. Továbbá Z(G) zárt a szorzásra, mert ha a, b Z(G), akkor tetsz leges g G-re (ab)g
Algebra gyakorlat, 3. feladatsor, megoldásvázlatok 1. a) Z(G), mert az egységelem yilvá felcserélhet mide G-beli elemmel. Továbbá Z(G) zárt a szorzásra, mert ha a, b Z(G), akkor tetsz leges g G-re (ab)g
DIGITÁLIS TECHNIKA feladatgyűjtemény
 IGITÁLIS TEHNIK feladatgyűjtemény Írta: r. Sárosi József álint Ádám János Szegedi Tudományegyetem Mérnöki Kar Műszaki Intézet Szerkesztette: r. Sárosi József Lektorálta: r. Gogolák László Szabadkai Műszaki
IGITÁLIS TEHNIK feladatgyűjtemény Írta: r. Sárosi József álint Ádám János Szegedi Tudományegyetem Mérnöki Kar Műszaki Intézet Szerkesztette: r. Sárosi József Lektorálta: r. Gogolák László Szabadkai Műszaki
A Venn-Euler- diagram és a logikai szita
 A Ve-Euler- diagram és a logikai szita Ebbe a részbe a Ve-Euler diagramról, a logikai szitáról, és a két témakör kapcsolatáról íruk, számos jellemző, megoldott feladattal szemléltetve a leírtakat. Az ábrákak
A Ve-Euler- diagram és a logikai szita Ebbe a részbe a Ve-Euler diagramról, a logikai szitáról, és a két témakör kapcsolatáról íruk, számos jellemző, megoldott feladattal szemléltetve a leírtakat. Az ábrákak
SZÁMELMÉLET. Vasile Berinde, Filippo Spagnolo
 SZÁMELMÉLET Vasile Beride, Filippo Spagolo A számelmélet a matematika egyik legrégibb ága, és az egyik legagyobb is egybe Eek a fejezetek az a célja, hogy egy elemi bevezetést yújtso az első szite lévő
SZÁMELMÉLET Vasile Beride, Filippo Spagolo A számelmélet a matematika egyik legrégibb ága, és az egyik legagyobb is egybe Eek a fejezetek az a célja, hogy egy elemi bevezetést yújtso az első szite lévő
INFORMATIKA ALAPJAI-II
 INFORMATIKA ALAPJAI-II Tartalomjegyzék BEVEZETŐ... RELÁCIÓ- ÉS LOGIKAI EGYENLETEK... 4. RELÁCIÓ EGYENLETEK... 4. LOGIKAI EGYENLETEK... 4.. Egyszerű logikai művelet... 5.. Elemi logikai függvények azonosságai...
INFORMATIKA ALAPJAI-II Tartalomjegyzék BEVEZETŐ... RELÁCIÓ- ÉS LOGIKAI EGYENLETEK... 4. RELÁCIÓ EGYENLETEK... 4. LOGIKAI EGYENLETEK... 4.. Egyszerű logikai művelet... 5.. Elemi logikai függvények azonosságai...
8.1. A rezgések szétcsatolása harmonikus közelítésben. Normálrezgések. = =q n és legyen itt a potenciál nulla. q i j. szimmetrikus. q k.
 8. KIS REZGÉSEK STABIL EGYENSÚLYI HELYZET KÖRÜL 8.. A rezgések szétcsatolása harmoikus közelítésbe. Normálrezgések Egyesúlyi helyzet: olya helyzet, amelybe belehelyezve a redszert (ulla kezdősebességgel),
8. KIS REZGÉSEK STABIL EGYENSÚLYI HELYZET KÖRÜL 8.. A rezgések szétcsatolása harmoikus közelítésbe. Normálrezgések Egyesúlyi helyzet: olya helyzet, amelybe belehelyezve a redszert (ulla kezdősebességgel),
Szabályozó szelepek (PN 6) VL 2 2-utú szelep, karima VL 3 3-járatú szelep, karima
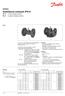 Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
