Bevezető Mi a statisztika? Mérés Feldolgozás Adatok rendezése Adatok jellemzése Időbeli elemzés Feladatok. Statisztika I.
|
|
|
- Erik Boros
- 9 évvel ezelőtt
- Látták:
Átírás
1 Statisztika I. 1. előadás: A statisztika alapfogalmai Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet Óbudai Egyetem
2 A kurzusról A kurzus célja A statisztika I. az adatok felvételével, főbb jellemzőivel foglalkozik. A végén megismerkedünk a statisztikai minta fogalmával, felvételével és a mintából az alapsokaságra való következtetéssel. A tárgy kreditpontszáma: 3 Heti óraszám: 1 előadás + 2 gyakorlat A kurzus weboldala: Tematika Előadások fóliái Házifeladatok Régi vizsgafeladatok
3 Oktatók Előadó Kóczy Á. László Fogadóóra: kedd 11:15 11:30, TC212 Gyakorlatvezetők KM: GM: Nagy Viktor Mikor és milyen problémákban tudunk segíteni 1 Nem ért valamit megkérdezni előadás közben, gyakorlaton 2 Házi leadás gyakorlaton 3 Egyéni tanrend/felmetés/igazolás írásbeli kérvény előadás után/fogadóórán 4 Megnézné a ZH dolgozatát fogadóórán 5 TDK-zni szeretne előzetes egyeztetés alapján 6 Egyéb óhaj-sóhaj lehetőleg fogadóórán
4 Oktatók Előadó Kóczy Á. László Fogadóóra: kedd 11:15 11:30, TC212 Gyakorlatvezetők KM: GM: Nagy Viktor Mikor és milyen problémákban tudunk segíteni 1 Nem ért valamit megkérdezni előadás közben, gyakorlaton 2 Házi leadás gyakorlaton 3 Egyéni tanrend/felmetés/igazolás írásbeli kérvény előadás után/fogadóórán 4 Megnézné a ZH dolgozatát fogadóórán 5 TDK-zni szeretne előzetes egyeztetés alapján 6 Egyéb óhaj-sóhaj lehetőleg fogadóórán
5 Jegyzet Általános Statisztika I-II. Szerkesztette: Korpás Attiláné dr. Nemzeti Tankönyvkiadó, Budapest Általános Statisztika Példatár I-II. Szerkesztette: Molnár Máténé dr Tóth Mártonné dr. Nemzeti Tankönyvkiadó, Budapest Hogyan használjuk? Kurzus = könyv, elejétől a végéig tudni kell Érteni, nem bemagolni ZH-k a könyv és a feladatgyűjtemény feladatai alapján Minden gyakorlat után vegyünk át 4-5 típuspéldát.
6 Jegyzet Általános Statisztika I-II. Szerkesztette: Korpás Attiláné dr. Nemzeti Tankönyvkiadó, Budapest Általános Statisztika Példatár I-II. Szerkesztette: Molnár Máténé dr Tóth Mártonné dr. Nemzeti Tankönyvkiadó, Budapest Hogyan használjuk? Kurzus = könyv, elejétől a végéig tudni kell Érteni, nem bemagolni ZH-k a könyv és a feladatgyűjtemény feladatai alapján Minden gyakorlat után vegyünk át 4-5 típuspéldát.
7 Követelmények és számonkérés A hallgató 1 Részt vesz a gyakorlatokon (min. 70%). 2 Legalább 1 zh-t ír a szorgalmi időszakban. 3 A két legjobban zh összesen 50+ pontos VAGY a pót zh 25+ pontos VAGY 4 a pót-pót zh 25+ pontos. 5 Egyéni tanrend: Csak az 1. alól felmentve. Ha 1 3. nem teljesül: letiltva nincs javítás Ha 1 3. teljesül, 4. nem: megtagadva Ha ezután 5. sem teljesül: letiltva Ha 5. teljesül: aláírás. Ha 1 4. teljesül: aláírás.
8 Követelmények és számonkérés A hallgató 1 Részt vesz a gyakorlatokon (min. 70%). 2 Legalább 1 zh-t ír a szorgalmi időszakban. 3 A két legjobban zh összesen 50+ pontos VAGY a pót zh 25+ pontos VAGY 4 a pót-pót zh 25+ pontos. 5 Egyéni tanrend: Csak az 1. alól felmentve. Ha 1 3. nem teljesül: letiltva nincs javítás Ha 1 3. teljesül, 4. nem: megtagadva Ha ezután 5. sem teljesül: letiltva Ha 5. teljesül: aláírás. Ha 1 4. teljesül: aláírás.
9 Értékelés A hallgató ponteredménye = A két legjobb ZH pontszámának összege, VAGY A pót-zh pontszámának kétszerese, VAGY A pót-pót-zh pontszámának kétszerese 0 49 elégtelen (1) elégséges (2) közepes (3) jó (4) jeles (5) Statisztika TDK, szakdolgozat, tudományos kutatás pluszpontot érhet.
10 Mibe kerül egy ingatlan?
11 Mibe kerül egy ingatlan? Az attól függ...
12 Mibe kerül egy ingatlan? Az attól függ... Típus, méret, szobák száma, elhelyezkedés, fűtés típusa, emelet, terasz, lift, extrák...
13 Mibe kerül egy ingatlan? Az attól függ... Típus, méret, szobák száma, elhelyezkedés, fűtés típusa, emelet, terasz, lift, extrák...
14 Mibe kerül egy ingatlan? Az attól függ... Típus, méret, szobák száma, elhelyezkedés, fűtés típusa, emelet, terasz, lift, extrák... Statisztika A valóság tömör, számszerű jellemzésére szolgáló tudományos módszertan, illetve gyakorlati tevékenység.
15 A statisztika fajtái Statisztika, mint gyakorlati tevékenység A tömeges jelenségek egyedeire vonatkozó információk gyűjtése, feldolgozása, elemzése, a vizsgált jelenség tömör számszerű jellemzése.
16 A statisztika fajtái Statisztika, mint gyakorlati tevékenység A tömeges jelenségek egyedeire vonatkozó információk gyűjtése, feldolgozása, elemzése, a vizsgált jelenség tömör számszerű jellemzése.
17 A statisztika fajtái eladott budai kétszobás lakások száma? VIII. kerületi négyzetméterár?
18 A statisztika fajtái eladott budai kétszobás lakások száma? VIII. kerületi négyzetméterár? Leíró statisztika: Információk összegyűjtése, összegzése, rendszerezése
19 A statisztika fajtái eladott budai kétszobás lakások száma? VIII. kerületi négyzetméterár? Leíró statisztika: Információk összegyűjtése, összegzése, rendszerezése Statisztikai következtetés: Szűkebb csoport megfigyeléséből következtetés az egészre
20 A statisztika fajtái eladott budai kétszobás lakások száma? VIII. kerületi négyzetméterár? Leíró statisztika: Információk összegyűjtése, összegzése, rendszerezése Statisztikai következtetés: Szűkebb csoport megfigyeléséből következtetés az egészre eladott lakások átlagára átlagos érték mennyit kérhetek? I. félévi árak érdemes most eladni? megéri-e eladás előtt ablakot cserélni?
21 Sokaság Statisztikai sokaság A megfigyelés tárgyát képező egyedek (pl. ingatlanok) összessége, halmaza. Az egyedeket a sokaság egységeinek nevezzük. A sokaság lehet
22 Sokaság Statisztikai sokaság A megfigyelés tárgyát képező egyedek (pl. ingatlanok) összessége, halmaza. Az egyedeket a sokaság egységeinek nevezzük. A sokaság lehet diszkrét vagy folytonos
23 Sokaság Statisztikai sokaság A megfigyelés tárgyát képező egyedek (pl. ingatlanok) összessége, halmaza. Az egyedeket a sokaság egységeinek nevezzük. A sokaság lehet álló vagy mozgó diszkrét vagy folytonos
24 Sokaság Statisztikai sokaság A megfigyelés tárgyát képező egyedek (pl. ingatlanok) összessége, halmaza. Az egyedeket a sokaság egységeinek nevezzük. A sokaság lehet álló vagy mozgó diszkrét vagy folytonos lakosság
25 Sokaság Statisztikai sokaság A megfigyelés tárgyát képező egyedek (pl. ingatlanok) összessége, halmaza. Az egyedeket a sokaság egységeinek nevezzük. A sokaság lehet álló vagy mozgó diszkrét vagy folytonos lakosság látogatók
26 Sokaság Statisztikai sokaság A megfigyelés tárgyát képező egyedek (pl. ingatlanok) összessége, halmaza. Az egyedeket a sokaság egységeinek nevezzük. A sokaság lehet diszkrét vagy folytonos álló lakosság hitelállomány vagy mozgó látogatók
27 Sokaság Statisztikai sokaság A megfigyelés tárgyát képező egyedek (pl. ingatlanok) összessége, halmaza. Az egyedeket a sokaság egységeinek nevezzük. A sokaság lehet diszkrét vagy folytonos álló lakosság hitelállomány vagy mozgó látogatók gázfogyasztás
28 A statisztikai ismérv Statisztikai ismérv A statisztikai sokaság egyedeit jellemző tulajdonság. Az ismérv lehetséges kimenetelei az ismérvváltozatok. alternatív Kétféle értéket vehet fel. Pl férfi/nő. közös A sokaság minden tagjára jellemző megkülönböztető a sokaság tagjait megkülönbözteti egymástól időbeli idő(szako)t jelző ismérv területi minőségi számszerűen nem mérhető tulajdonság mennyiségi számszerűen mérhető/megszámlálható tulajdonság ismérvértékek
29 A statisztikai ismérv Statisztikai ismérv A statisztikai sokaság egyedeit jellemző tulajdonság. Az ismérv lehetséges kimenetelei az ismérvváltozatok. alternatív Kétféle értéket vehet fel. Pl férfi/nő. közös A sokaság minden tagjára jellemző megkülönböztető a sokaság tagjait megkülönbözteti egymástól időbeli idő(szako)t jelző ismérv területi minőségi számszerűen nem mérhető tulajdonság mennyiségi számszerűen mérhető/megszámlálható tulajdonság ismérvértékek
30 Ismérvek fajtái
31 Ismérvek fajtái Cím területi ismérv (mindig minőségi) Típus minőségi, megkülönböztető ismérv Szobák mennyiségi ismérv Nm mennyiségi ismérv Emelet, állapot, kilátás, fekvés minőségi ismérv Erkély, lift alternatív ismérv Mióta eladó, mikor épült időbeli ismérv
32 A statisztikai mérés, adat és mutatószám Mérés Számok szabályok szerinti hozzárendelése jelenségekhez, illetve tulajdonságaikhoz. 4-féle mérési szint, ill. skála névleges Számok kötetlen hozzárendelése. sorrendi Rangsor szerinti hozzárendelés. különbségi Önkényes 0. Különbség számolható. arányskála Valódi 0. Arány is számolható. A statisztikai adat Sokaság elemeinek száma v. másféle jellemzője, mérési eredménye. alap-, vagy leszármaztatott adatok A statisztikai mutatószám Rendszeresen ismétlődő jelenség statisztikai jellemzője.
33 A statisztikai mérés, adat és mutatószám Mérés Számok szabályok szerinti hozzárendelése jelenségekhez, illetve tulajdonságaikhoz. 4-féle mérési szint, ill. skála névleges Számok kötetlen hozzárendelése. Rendszám, irsz. Címke! sorrendi Rangsor szerinti hozzárendelés. különbségi Önkényes 0. Különbség számolható. (hőmérséklet) arányskála Valódi 0. Arány is számolható. (hosszúság, jövedelem,..) A statisztikai adat Sokaság elemeinek száma v. másféle jellemzője, mérési eredménye. alap-, vagy leszármaztatott adatok
34 A statisztikai mérés, adat és mutatószám Mérés Számok szabályok szerinti hozzárendelése jelenségekhez, illetve tulajdonságaikhoz. 4-féle mérési szint, ill. skála névleges Számok kötetlen hozzárendelése. sorrendi Rangsor szerinti hozzárendelés. különbségi Önkényes 0. Különbség számolható. arányskála Valódi 0. Arány is számolható. A statisztikai adat Sokaság elemeinek száma v. másféle jellemzője, mérési eredménye. alap-, vagy leszármaztatott adatok A statisztikai mutatószám Rendszeresen ismétlődő jelenség statisztikai jellemzője.
35 Adatgyűjtés gyorsaság elfogadható pontosság gazdaságosság teljes körű v. részleges Reprezentatív Monográfia egyéni kérdőív v. lajstrom önszámlálás v. kikérdezés
36 Hiba Adatfeldolgozás, adatközlés során, v. mintavételben Abszolút hiba a = A Â, ahol A = valóságos, Â = mért adat Abszolút hibakorlát (â). A Â ± â. Relatív hiba α = a A Relatív hibakorlát: ˆα = ââ.
37 Statisztikai csoportosítás Csoportosítás A sokaság átfedésmentes és teljes felosztása egy megkülönböztető ismérv szerint. Csoportosító sor Osztály Egységek száma C 1 f 1 C 2 f 2. C i. C k Összesen. f i. f k N A csoportosító sor lehet minőségi mennyiségi területi idősor kombinatív
38 Összehasonĺıtás A csoportosítás Két, vagy több statisztikai adat viszonyítása. Sorba rendezve: Összehasonĺıtó sor Különböző időpontok: idősor Területi alapon: összehasonĺıtó területi sor
39 Viszonyszámok Viszonyszám Két, logikai kapcsolatban álló statisztikai adat hányadosa. Azonos fajta adatokból számolva Megoszlási: részsokaságok aránya az egészhez Koordinációs: részsokaságok aránya egymáshoz Dinamikus: két idősza/időpont adatainak hányadosa Különböző fajta, mértékegységű adatokból számolva intenzitási (telefon/1000 lakás)
40 Átlagok Átlagok Azonos fajta adatok tömör jellemzésére használjuk. Átlagolandó értékek: X 1, X 2, X 3,..., X N. Számtani: X = Súlyozott számtani: X = N i=1 X i N k i=1 f i X i k i=1 f i Harmonikus: X h = N N i=1 1 X i = k i=1 f i k f i i=1 X i Mértani: X g = N N i=1 X i = k i=1 f i k i=1 X f i Négyzetes: X q = X min X h X g X X q X max N k i=1 X i 2 i=1 N = f i Xi 2 k i=1 f i i
41 Átlagok Átlagok Azonos fajta adatok tömör jellemzésére használjuk. Átlagolandó értékek: X 1, X 2, X 3,..., X N. Számtani: X = Súlyozott számtani: X = N i=1 X i N k i=1 f i X i k i=1 f i Harmonikus: X h = N N i=1 1 X i = k i=1 f i k f i i=1 X i Mértani: X g = N N i=1 X i = k i=1 f i k i=1 X f i Négyzetes: X q = X min X h X g X X q X max N k i=1 X i 2 i=1 N = f i Xi 2 k i=1 f i i
42 Ismérv szerinti rendezés
43 Ismérv szerinti rendezés Hogyan rendszerezzünk ennyi lakást?
44 Ismérv szerinti rendezés cím, emelet, komfort, fekvés szobák száma alapterület, ár, rezsi, gázfogyasztás
45 Ismérv szerinti rendezés Minőségi: cím, emelet, komfort, fekvés Mennyiségi: szobák száma alapterület, ár, rezsi, gázfogyasztás
46 Ismérv szerinti rendezés Minőségi: cím, emelet, komfort, fekvés Mennyiségi: diszkrét: szobák száma folytonos: alapterület, ár, rezsi, gázfogyasztás
47 Ismérv szerinti rendezés Minőségi: cím, emelet, komfort, fekvés Mennyiségi: diszkrét: szobák száma véges, v megszámlálhatóan végtelen értéket vehet fel folytonos: alapterület, ár, rezsi, gázfogyasztás bármilyen értéket felvehet: egy 54ñm-es lakás lehet 53,78, vagy 54,003ñm-es, bármi 53,5 és 54.5 között. (a pontosság kedvéért: minden racionális szám (a tizedestörttel feĺırhatók is ide tartoznak) megszámlálható, a gond az irracionális számokkal van, pl ha a lakás kör alapterületű.)
48 Ismérv szerinti rendezés Minőségi: cím, emelet, komfort, fekvés Mennyiségi: diszkrét: szobák száma véges, v megszámlálhatóan végtelen értéket vehet fel folytonos: alapterület, ár, rezsi, gázfogyasztás bármilyen értéket felvehet: egy 54ñm-es lakás lehet 53,78, vagy 54,003ñm-es, bármi 53,5 és 54.5 között. (a pontosság kedvéért: minden racionális szám (a tizedestörttel feĺırhatók is ide tartoznak) megszámlálható, a gond az irracionális számokkal van, pl ha a lakás kör alapterületű.) Rangsor Mennyiségi ismérv értékeinek monoton sorozata.
49 Gyakorisági sorok
50 Gyakorisági sorok Csoportosító sor A sokaság egységeinek mennyiségi ismérv szerinti osztályozása. HA az ismérvváltozatok száma kicsi, 1-1 ismérvváltozat szerint. HA nagy, több ismérvértéket magukba foglaló intervallumok, ún. osztályközök szerint. Gyakoriság (f i ) Az egy-egy csoportba/osztályközbe tartozó egységek száma. Relatív gyakoriság (g i = f i N ) Az egy csoportba/osztályközbe tartozó egységek (százalékos) részesedése. Ha az osztályok 1 ismérvértékből állnak, (gyakorisági) eloszlás, osztályközök esetén (gyakorisági) megoszlás.
51 Gyakorisági sorok Csoportosító sor A sokaság egységeinek mennyiségi ismérv szerinti osztályozása. HA az ismérvváltozatok száma kicsi, 1-1 ismérvváltozat szerint. HA nagy, több ismérvértéket magukba foglaló intervallumok, ún. osztályközök szerint. Gyakoriság (f i ) Az egy-egy csoportba/osztályközbe tartozó egységek száma. Relatív gyakoriság (g i = f i N ) Az egy csoportba/osztályközbe tartozó egységek (százalékos) részesedése. Ha az osztályok 1 ismérvértékből állnak, (gyakorisági) eloszlás, osztályközök esetén (gyakorisági) megoszlás.
52 Gyakorisági sorok Csoportosító sor A sokaság egységeinek mennyiségi ismérv szerinti osztályozása. HA az ismérvváltozatok száma kicsi, 1-1 ismérvváltozat szerint. HA nagy, több ismérvértéket magukba foglaló intervallumok, ún. osztályközök szerint. Gyakoriság (f i ) Az egy-egy csoportba/osztályközbe tartozó egységek száma. Relatív gyakoriság (g i = f i N ) Az egy csoportba/osztályközbe tartozó egységek (százalékos) részesedése. Ha az osztályok 1 ismérvértékből állnak, (gyakorisági) eloszlás, osztályközök esetén (gyakorisági) megoszlás.
53 Gyakorisági sorok általános sémája Ismérvérték X i Gyakoriság f i X 1 f 1 X 2 f 2. X i. X k Összesen. f i. f k N
54 Gyakorisági sorok általános sémája Az osztályközök Gyakoriság Alsó határa Felső határa f i X 1 X 1 f 1 X 2 X 2 f 2... X i X i f i... X k X k f k Összesen N
55 Gyakorisági sorok általános sémája Ismérvérték X i Relatív gyakoriság g i X 1 g 1 X 2 g 2. X i. X k. g i. g k Összesen 1
56 Gyakorisági sorok általános sémája Az osztályközök Relatív gyakoriság Alsó határa Felső határa g i X 1 X 1 g 1 X 2 X 2 g 2... X i X i g i... X k X k g k Összesen 1
57 Osztályközök Az osztályközök meghatározása Minden ismérvérték pontosan 1 osztályba tartozzon Az osztályközök megadása Valódi határok : Hézagmentesen illeszkednek (45 50, 50 55,...). Minden ismérvérték besorolásra kerül. Közölt határok : Az intervallumok kezdőértékeit a mérési pontosság egységével eltoljuk ( 20.0, ,...). Egyértelmű besorolhatóság
58 Osztályközök Az osztályközök meghatározása Minden ismérvérték pontosan 1 osztályba tartozzon Számuk a legkisebb k, melyre 2 k > N Az osztályközök megadása Valódi határok : Hézagmentesen illeszkednek (45 50, 50 55,...). Minden ismérvérték besorolásra kerül. Közölt határok : Az intervallumok kezdőértékeit a mérési pontosság egységével eltoljuk ( 20.0, ,...). Egyértelmű besorolhatóság
59 Osztályközök Az osztályközök meghatározása Minden ismérvérték pontosan 1 osztályba tartozzon Számuk a legkisebb k, melyre 2 k > N Hosszuk h = Xmax X min k Az osztályközök megadása Valódi határok : Hézagmentesen illeszkednek (45 50, 50 55,...). Minden ismérvérték besorolásra kerül. Közölt határok : Az intervallumok kezdőértékeit a mérési pontosság egységével eltoljuk ( 20.0, ,...). Egyértelmű besorolhatóság
60 Osztályközök Az osztályközök meghatározása Minden ismérvérték pontosan 1 osztályba tartozzon Számuk a legkisebb k, melyre 2 k > N Hosszuk h = Xmax X min k
61 Osztályközök Az osztályközök meghatározása Minden ismérvérték pontosan 1 osztályba tartozzon Számuk a legkisebb k, melyre 2 k > N Hosszuk h = Xmax X min k Nagy X max X min különbség, egyenetlen eloszlás esetén nem egyforma osztályközök. Az osztályközök megadása Valódi határok : Hézagmentesen illeszkednek (45 50, 50 55,...). Minden ismérvérték besorolásra kerül. Közölt határok : Az intervallumok kezdőértékeit a mérési pontosság egységével eltoljuk ( 20.0, ,...). Egyértelmű besorolhatóság
62 Osztályközök Az osztályközök meghatározása Minden ismérvérték pontosan 1 osztályba tartozzon Számuk a legkisebb k, melyre 2 k > N Hosszuk h = Xmax X min k Nagy X max X min különbség, egyenetlen eloszlás esetén nem egyforma osztályközök. Az osztályközök megadása Valódi határok : Hézagmentesen illeszkednek (45 50, 50 55,...). Minden ismérvérték besorolásra kerül. Közölt határok : Az intervallumok kezdőértékeit a mérési pontosság egységével eltoljuk ( 20.0, ,...). Egyértelmű besorolhatóság Nyitott osztályköz : Egyik határa hiányzik; számolásokban ugyanolyan hosszú, mint a többi
63 Kumulatív gyakoriság Kumulatív gyakoriság (f i ) A felső értékhatárnak megfelelő, vagy kisebb ismérvértékek előfordulásának száma. Kumulatív relatív gyakoriság (g i ) A felső értékhatárnak megfelelő, vagy kisebb ismérvértékek előfordulásának aránya. Lefelé kumulatív (relatív) gyakoriság (f i (g i )) Az alsó értékhatárnak megfelelő, vagy nagyobb ismérvértékek előfordulásának száma (aránya).
64 Értékösszegsorok Értékösszegsor A mennyiség ismérv alapján kialakított osztályokhoz az odatartozó egységek ismérvértékeinek összegét (S i ) rendeli. A sokaság teljes értékösszege S = k i=1 f i X i. Osztályközös gyakoriság esetén... a tényleges értékösszeg csak az eloszlás ismeretében határozható meg. egyébként az osztályközépsőből (X i = x i +x i 2 ) becsüljük. A relatív értékösszeg az a megoszlási viszonyszám, ami az osztályok értékösszegét (S i ) a teljes értékösszeghez (S) viszonyítja.
65 Grafikus ábrázolás: Definíciók Hisztogram Hézagmentesen illesztett téglalapokkal szemléltet. Egyenlő osztályközök esetén területük arányos a relatív gyakorisággal. Különböző osztályközhosszúságok esetén magasságuk az egységnyi osztályközhosszra jutó gyakoriság (( fi h i ), vagy ( gi h i )) sűrűséghisztogram. Gyakorisági poligon Az osztályközepeknél felmért gyakoriságok pontjait egyenes szakaszokkal összekötő vonaldiagram.
66 Gyakorisági sorok grafikus ábrázolása Osztályok: bot-ábra Osztályközök: hisztogram
67 Gyakorisági sorok grafikus ábrázolása Osztályok: bot-ábra Osztályközök: gyakorisági poligon
68 Helyzetmutatók: Módusz Módusz (Mo) A leggyakoribb elem a sokaságban tipikus érték Mo Nyers módusz: a gyakorisági poligon maximumhelye. Folytonos/sokváltozatos mennyiségi ismérv esetén modális osztályköz. A modális osztályköz közepe: nyers módusz
69 Helyzetmutatók: Módusz Módusz (Mo) A leggyakoribb elem a sokaságban tipikus érték Mo Nyers módusz: a gyakorisági poligon maximumhelye. Folytonos/sokváltozatos mennyiségi ismérv esetén modális osztályköz. A modális osztályköz közepe: nyers módusz
70 Helyzetmutatók: Módusz Módusz (Mo) A leggyakoribb elem a sokaságban tipikus érték Mo Nyers módusz: a gyakorisági poligon maximumhelye. Folytonos/sokváltozatos mennyiségi ismérv esetén modális osztályköz. A modális osztályköz közepe: nyers módusz
71 Helyzetmutatók: Módusz Módusz (Mo) A leggyakoribb elem a sokaságban tipikus érték Szimmetrikus a megoszlás: modális osztályköz közepe.
72 Helyzetmutatók: Módusz Módusz (Mo) A leggyakoribb elem a sokaságban tipikus érték Szimmetrikus a megoszlás: modális osztályköz közepe. Amúgy Mo = mo + k 1 k 1 + k 2 h mo: a mod. osztályköz alsó határa k 1 (k 2 ): a mod. és megelőző (követő) osztályköz gyakorisága különbsége h: a modális osztályköz hossza.
73 Helyzetmutatók: Módusz Módusz (Mo) A leggyakoribb elem a sokaságban tipikus érték Szimmetrikus a megoszlás: modális osztályköz közepe. Amúgy Mo = mo + k 1 k 1 + k 2 h mo: a mod. osztályköz alsó határa k 1 (k 2 ): a mod. és megelőző (követő) osztályköz gyakorisága különbsége h: a modális osztályköz hossza.
74 Medián Medián (Me) Ugyanannyi kisebb és nagyobb érték. A = Me minimalizálja a N i=1 X i A -t Ha az elemszám páratlan a medián -edik ismérvérték. Ha páros, az N 2 és N edik ismérvértékek átlaga az N+1 2
75 Medián Medián (Me) Ugyanannyi kisebb és nagyobb érték. A = Me minimalizálja a N i=1 X i A -t Ha az elemszám páratlan a medián -edik ismérvérték. Ha páros, az N 2 és N edik ismérvértékek átlaga az N+1 2
76 Medián Medián (Me) Ugyanannyi kisebb és nagyobb érték. A = Me minimalizálja a N i=1 X i A -t Ha az elemszám páratlan a medián -edik ismérvérték. Ha páros, az N 2 és N edik ismérvértékek átlaga az N+1 2
77 Medián Medián (Me) Ugyanannyi kisebb és nagyobb érték. Osztályközös gyakoriság esetén az i-edik osztályköz tartalmazza, ha f i 1 N 2 f i Egyenletes elhelyezkedés esetén: Me = me + N 2 f me 1 f me h me: a med. osztályköz alsó határa f kumulált gyakoriság h: a mediánt tartalmazó osztályköz hossza.
78 Medián Medián (Me) Ugyanannyi kisebb és nagyobb érték. Osztályközös gyakoriság esetén az i-edik osztályköz tartalmazza, ha f i 1 N 2 f i Egyenletes elhelyezkedés esetén: Me = me + N 2 f me 1 f me h me: a med. osztályköz alsó határa f kumulált gyakoriság h: a mediánt tartalmazó osztályköz hossza.
79 Átlag Átlag (X ) Az ismérvértékek összegének és a sokaság elemszámának hányadosa; az ismérvértékek számtani átlaga. X = N i=1 X i N Gyakorisági sor esetén súlyozott átlag X = N i=1 f i X i N i=1 f i Megoszlásból becsült érték, súlyozott harmonikus átlag: X = N i=1 S i N S i i=1 X i (X i az osztályközép, S i az i-edik értékösszeg.)
80 Átlag Átlag (X ) Az ismérvértékek összegének és a sokaság elemszámának hányadosa; az ismérvértékek számtani átlaga. X = N i=1 X i N Gyakorisági sor esetén súlyozott átlag X = N i=1 f i X i N i=1 f i Megoszlásból becsült érték, súlyozott harmonikus átlag: X = N i=1 S i N S i i=1 X i (X i az osztályközép, S i az i-edik értékösszeg.)
81 Átlag Átlag (X ) Az ismérvértékek összegének és a sokaság elemszámának hányadosa; az ismérvértékek számtani átlaga. X = N i=1 X i N Gyakorisági sor esetén súlyozott átlag X = N i=1 f i X i N i=1 f i Megoszlásból becsült érték, súlyozott harmonikus átlag: X = N i=1 S i N S i i=1 X i (X i az osztályközép, S i az i-edik értékösszeg.)
82 Kvantilisek q-ad rendű, vagy q-adik kvantilis (Q q ) Az ismérvértékek rangsorát q : (1 q) arányban osztó ismérvérték Q q = X i, ha f i 1 N q f i Gyakori kvantilisek: Tercilisek: Q 1 3 Kvartilisek: Q 1 4 Q 3 4 = T 2 (felső kvartilis) Kvintilisek: Q i 5 Decilisek: Q i 10 = T 1 (alsó tercilis), Q 2 3 = Q 1 (alsó kvartilis), Q 2 4 = K i = D i Percentilisek: Q i 100 = P i = T 2 (felső tercilis) = Me (medián),
83 Kvantilisek q-ad rendű, vagy q-adik kvantilis (Q q ) Az ismérvértékek rangsorát q : (1 q) arányban osztó ismérvérték Q q = X i, ha f i 1 N q f i Gyakori kvantilisek: Tercilisek: Q 1 3 Kvartilisek: Q 1 4 Q 3 4 = T 2 (felső kvartilis) Kvintilisek: Q i 5 Decilisek: Q i 10 = T 1 (alsó tercilis), Q 2 3 = Q 1 (alsó kvartilis), Q 2 4 = K i = D i Percentilisek: Q i 100 = P i = T 2 (felső tercilis) = Me (medián),
84 Kvantilisek q-ad rendű, vagy q-adik kvantilis (Q q ) Az ismérvértékek rangsorát q : (1 q) arányban osztó ismérvérték Q j k meghatározása, mint a mediáné: Rangsorból [ kiindulva ] m = j k (N + 1) X m az { m-edik elem } a rangsorban t = j k (N + 1) = j k (N +1) m. Ekkor = X m + t(x m+1 X m ) Q j k
85 Szóródás Szóródás Azonos fajta számszerű adatok különbözősége. Léteznek abszolút és relatív mutatói. Gyakran használt mérőszámok: a szóródás terjedelme az átlagos eltérés szórás átlagos különbség relatív szórás
86 A szóródás terjedelme Szóródás terjedelme (R) Az előforduló legnagyobb és legkisebb ismérvérték különbsége: R = X max X min. Interkvantilis terjedelemmutatók A két szélső kvantilis különbsége. Pl. D 9 D 1.
87 A szóródás terjedelme Szóródás terjedelme (R) Az előforduló legnagyobb és legkisebb ismérvérték különbsége: R = X max X min. Interkvantilis terjedelemmutatók A két szélső kvantilis különbsége. Pl. D 9 D 1.
88 Átlagos eltérés Átlagos eltérés (δ) Az értékek számtani átlagtól vett abszolút eltérésének átlaga. Ha d i = X i X, illetve δ = N i=1 X i X = N k i=1 δ = f i X i X k i=1 f = i N i=1 d i, N k i=1 f i d i k i=1 f. i
89 Szórás Szórás (σ) Az értékek számtani átlagtól vett eltérésének négyzetes átlaga. Ha d i = X i X, σ = σ = N i=1(x i X) 2 N i=1 N = d2 i N k i=1 f i(x i X) 2 k = i=1 f i, illetve k i=1 f i di 2 k. i=1 f i A szórásnégyzet (σ 2 ) más néven variancia. Eltérés-négyzetösszeg: SS = N ( i=1 Xi X ) 2, illetve SS = N i=1 f ( i Xi X ) 2. Relatív szórás V = σ X
90 Szórás Szórás (σ) Az értékek számtani átlagtól vett eltérésének négyzetes átlaga. Ha d i = X i X, σ = σ = N i=1(x i X) 2 N i=1 N = d2 i N k i=1 f i(x i X) 2 k = i=1 f i, illetve k i=1 f i di 2 k. i=1 f i A szórásnégyzet (σ 2 ) más néven variancia. Eltérés-négyzetösszeg: SS = N ( i=1 Xi X ) 2, illetve SS = N i=1 f ( i Xi X ) 2. Relatív szórás V = σ X
91 Szórás Szórás (σ) Az értékek számtani átlagtól vett eltérésének négyzetes átlaga. Ha d i = X i X, σ = σ = N i=1(x i X) 2 N i=1 N = d2 i N k i=1 f i(x i X) 2 k = i=1 f i, illetve k i=1 f i di 2 k. i=1 f i A szórásnégyzet (σ 2 ) más néven variancia. Eltérés-négyzetösszeg: SS = N ( i=1 Xi X ) 2, illetve SS = N i=1 f ( i Xi X ) 2. Relatív szórás V = σ X
92 Szórás tulajdonságai δ σ. σ Xi +A = σ Xi σ B Xi = B σ B Xi 2 2 σ = X q X
93 Szórás tulajdonságai δ σ. σ Xi +A = σ Xi σ B Xi = B σ B Xi 2 2 σ = X q X
94 Átlagos különbség Átlagos különbség vagy Gini-féle szóródási mérőszám (G) Az ismérvértékek egymástól számított abszolút különbségeinek számtani átlaga. G = N N i=1 j=1 X i X j k k i=1 j=1 N 2 illetve G = f if j X i X j N 2
95 Az aszimmetria és mérőszámai bal oldali szimmetrikus jobb oldali aszimmetria eloszlás aszimmetria Mo < Me < X Mo = Me = X Mo > Me > X Q 3 Me > Me Q 1 Q 3 Me = Me Q 1 Q 3 Me < Me Q 1
96 Az aszimmetria és mérőszámai bal oldali szimmetrikus jobb oldali aszimmetria eloszlás aszimmetria Mo < Me < X Mo = Me = X Mo > Me > X Q 3 Me > Me Q 1 Q 3 Me = Me Q 1 Q 3 Me < Me Q 1 A > 0 A = 0 A < 0 Pearson-féle mutató A számtani átlag és a módusz viszonyán alapul: A = X Mo σ
97 Az aszimmetria és mérőszámai bal oldali szimmetrikus jobb oldali aszimmetria eloszlás aszimmetria Mo < Me < X Mo = Me = X Mo > Me > X Q 3 Me > Me Q 1 Q 3 Me = Me Q 1 Q 3 Me < Me Q 1 A > 0 A = 0 A < 0 F > 0 F = 0 F < 0 F-mutató Az alsó és felső kvartilis mediántól való eltérésének egymáshoz viszonyított nagyságán alapul: F = (Q 3 Me) (Me Q 1 ) (Q 3 Me) + (Me Q 1 ) Kiszámítható más kvantilisből, pl. decilisekből is. Többmóduszú eloszlásoknál is alkalmazható
98 Koncentráció Koncentráció A sokasághoz tartozó teljes értékösszeg jelentős része kevés egységre összpontosul. (Általában: tömörülés, összpontosulás) A relatív gyakoriságok (g i ) és relatív értékösszegek (Z i ) összehasonĺıtásával mutatható ki. Lorenz-görbe kumulált relatív értékösszeg a kum. gyakoriságok függvényében. Koncentrációs együttható (K) koncentrációs terület aránya az átló alatti területhez. K = G 2X.
99 Koncentráció Koncentráció A sokasághoz tartozó teljes értékösszeg jelentős része kevés egységre összpontosul. (Általában: tömörülés, összpontosulás) A relatív gyakoriságok (g i ) és relatív értékösszegek (Z i ) összehasonĺıtásával mutatható ki. Lorenz-görbe kumulált relatív értékösszeg a kum. gyakoriságok függvényében. Koncentrációs együttható (K) koncentrációs terület aránya az átló alatti területhez. K = G 2X.
100 Koncentráció Koncentráció A sokasághoz tartozó teljes értékösszeg jelentős része kevés egységre összpontosul. (Általában: tömörülés, összpontosulás) A relatív gyakoriságok (g i ) és relatív értékösszegek (Z i ) összehasonĺıtásával mutatható ki. Lorenz-görbe kumulált relatív értékösszeg a kum. gyakoriságok függvényében. Koncentrációs együttható (K) koncentrációs terület aránya az átló alatti területhez. K = G 2X.
101 Idősorok Idősor (Y 1, Y 2,..., Y t,..., Y n ) Társadalmi/gazdasági jelenség egyenlő időközönként mért értékei. állapotidősor, v. tartamidősor
102 Idősorok Idősor (Y 1, Y 2,..., Y t,..., Y n ) Társadalmi/gazdasági jelenség egyenlő időközönként mért értékei. állapotidősor : álló sokaságok időbeli változását mutatja; állapotfelvételek eredménye. tartamidősor: mozgó sokaságok időbeli változását mutatja; időtartam folyamán bekövetkezett események.
103 Idősorok Idősor (Y 1, Y 2,..., Y t,..., Y n ) Társadalmi/gazdasági jelenség egyenlő időközönként mért értékei. állapotidősor tartamidősor Dinamikus viszonyszámok Bázisviszonyszám b t = Yt Y b Láncviszonyszám l t = Yt Y t 1
104 Idősorok Idősor (Y 1, Y 2,..., Y t,..., Y n ) Társadalmi/gazdasági jelenség egyenlő időközönként mért értékei. állapotidősor tartamidősor Dinamikus viszonyszámok Bázisviszonyszám b t = Yt Y b b t = l b+1 l b+2... l t = t i=b+1 l i Láncviszonyszám l t = Yt l t = Y t 1 bt b t 1
105 Idősorok grafikus ábrázolása Vonaldiagrammal, a vízszintes tengelyen az időszakok, a függőleges tengelyen az idősor adatai.
106 Idősorok elemzése: Átlagos értékek Tartamidősorok Az adatok összegezhetők. n t=1 Y = Y t n A jelenség egy időszakra jutó átlagos értéke. (Pl. egy weboldal átlagos látogatottsága) Állapotidősorok Az összegzésnek nincs értelme: kronologikus átlag Y k = Y k = Y 1 +Y Y n 1+Y n 2 n 1 Y n 1 t=2 Y t + Yn 2 n 1 Egyfajta súlyozott átlag.
107 Idősorok elemzése: Átlagos változás vizsgálata Fejlődés átlagos mértéke A bekövetkezett átlagos abszolút változás d = (Y 2 Y 1 ) + (Y 3 Y 2 ) + + (Y n Y n 1 ) n 1 = Y n Y 1 n 1 Fejlődés átlagos üteme A bekövetkezett átlagos relatív változás l = n 1 l 2 l 3 l n = n 1 n t=2 l t = n 1 Yn Y 1
108 Idősorok elemzése: Átlagos változás vizsgálata Fejlődés átlagos mértéke A bekövetkezett átlagos abszolút nominális változás d = (Y 2 Y 1 ) + (Y 3 Y 2 ) + + (Y n Y n 1 ) n 1 = Y n Y 1 n 1 Fejlődés átlagos üteme A bekövetkezett átlagos relatív változás l = n 1 l 2 l 3 l n = n 1 n t=2 l t = n 1 Yn Y 1
109 Idősorok elemzése: Átlagos változás vizsgálata Fejlődés átlagos mértéke A bekövetkezett átlagos abszolút nominális változás d = (Y 2 Y 1 ) + (Y 3 Y 2 ) + + (Y n Y n 1 ) n 1 = Y n Y 1 n 1 Fejlődés átlagos üteme A bekövetkezett átlagos relatív változás l = n 1 l 2 l 3 l n = n 1 n t=2 l t = n 1 Yn Y 1
110 1/2. feladat (részlet) Néhány sokaság a Az 1994-ben Magyarországon kiadott könyvek összessége. b Az iskolai könyvtárak könyvállománya január 5.-én. c Üzembe helyezett beruházások nagysága 1994-ben Nevezzük meg a sokaságok típusát!
111 1/2. feladat (részlet) Néhány sokaság a Az 1994-ben Magyarországon kiadott könyvek összessége. Természetes az egység (kötet), összegzés, tehát diszkrét, mozgó. b Az iskolai könyvtárak könyvállománya január 5.-én. c Üzembe helyezett beruházások nagysága 1994-ben Nevezzük meg a sokaságok típusát!
112 1/2. feladat (részlet) Néhány sokaság a Az 1994-ben Magyarországon kiadott könyvek összessége. Természetes az egység (kötet), összegzés, tehát diszkrét, mozgó. b Az iskolai könyvtárak könyvállománya január 5.-én. c Természetes az egység (kötet), pillanatfelvétel, tehát diszkrét, álló. Üzembe helyezett beruházások nagysága 1994-ben Nevezzük meg a sokaságok típusát!
113 1/2. feladat (részlet) Néhány sokaság a Az 1994-ben Magyarországon kiadott könyvek összessége. Természetes az egység (kötet), összegzés, tehát diszkrét, mozgó. b Az iskolai könyvtárak könyvállománya január 5.-én. c Természetes az egység (kötet), pillanatfelvétel, tehát diszkrét, álló. Üzembe helyezett beruházások nagysága 1994-ben Forintban, vagy euróban? Nincs természetes egység, összegzés, tehát folytonos, mozgó. Nevezzük meg a sokaságok típusát!
114 1/5. feladat A hazánkba érkező turisták közül legtöbben Romániából (5498 ezer fő), Németországból (2838 ezer fő) és Jugoszlávia utódállamaiból (2585 ezer fő) érkeztek 1992-ben. Ismerjük továbbá, hogy Európából összesen ezer fő, Ázsiából 151 ezer fő, Afrikából 20 ezer fő, Amerikából 304 ezer fő, Ausztráliából és Óceániából pedig 25 ezer turista érkezett. Rendezzük az adatokat statisztikai sorokba! Terület ezer fő Románia 5498 Németország 2838 volt Jugoszlávia 2585 Európa Ázsia 151 Afrika 20 Amerika 304 Ausztrália és Óceánia 25
115 1/5. feladat A legtöbben Romániából (5498), Németországból (2838) és Jugoszlávia (2585) Európából összesen 16688, Ázsiából 151, Afrikából 20, Amerikából 304, Ausztráliából és Óceániából 25. Rendezzük az adatokat statisztikai sorokba! Terület ezer fő Románia 5498 Németország 2838 volt Jugoszlávia 2585 Európa Ázsia 151 Afrika 20 Amerika 304 Ausztrália és Óceánia 25 A felbontás nem szerencsés, hiszen pl a romániai adatok kétszer szerepelnek.
116 1/5. feladat A legtöbben Romániából (5498), Németországból (2838) és Jugoszlávia (2585) Európából összesen 16688, Ázsiából 151, Afrikából 20, Amerikából 304, Ausztráliából és Óceániából 25. Rendezzük az adatokat statisztikai sorokba! Terület ezer fő Románia 5498 Németország 2838 volt Jugoszlávia 2585 egyéb Európa 5767 Ázsia 151 Afrika 20 Amerika 304 Ausztrália és Óceánia 25 A felbontás nem szerencsés, hiszen pl a romániai adatok kétszer szerepelnek.
117 1/7. feladat érték súly a) Számítsuk ki a súlyozott számtani, harmonikus, mértani és négyzetes átlagát! b) Állapítsuk meg az átlagok nagyságrendjét! c) Határozzuk meg a f i (X i A) 2 kifejezés értékeit a következő A értékek mellett: 5, 6, 8, és X! Súlyozott számtani közép: k i=1 f i X i = = = 10, 4 k i=1 f i Súlyozott harmonikus közép: k i=1 f i k f i = i=1 X i = 10 1,2375 = 8, 08.
118 1/7. feladat érték X i súly f i a) Számítsuk ki a súlyozott számtani, harmonikus, mértani és négyzetes átlagát! b) Állapítsuk meg az átlagok nagyságrendjét! c) Határozzuk meg a f i (X i A) 2 kifejezés értékeit a következő A értékek mellett: 5, 6, 8, és X! Súlyozott számtani közép: k i=1 f i X i = = = 10, 4 k i=1 f i Súlyozott harmonikus közép: k i=1 f i k f i = i=1 X i = 10 1,2375 = 8, 08.
119 1/7. feladat érték X i súly f i a) Számítsuk ki a súlyozott számtani, harmonikus, mértani és négyzetes átlagát! b) Állapítsuk meg az átlagok nagyságrendjét! c) Határozzuk meg a f i (X i A) 2 kifejezés értékeit a következő A értékek mellett: 5, 6, 8, és X! Súlyozott számtani közép: k i=1 f i X i k = i=1 f = = 10, 4 i Szorzat összege összeg szorzata!!! Súlyozott harmonikus közép: k i=1 f i k f i = i=1 X i = 10 1,2375 = 8, 08.
120 1/7. feladat érték X i súly f i a) Számítsuk ki a súlyozott számtani, harmonikus, mértani és négyzetes átlagát! b) Állapítsuk meg az átlagok nagyságrendjét! c) Határozzuk meg a f i (X i A) 2 kifejezés értékeit a következő A értékek mellett: 5, 6, 8, és X! Súlyozott számtani közép: k i=1 f i X i = = = 10, 4 k i=1 f i Súlyozott harmonikus közép: k i=1 f i k f i = i=1 X i = 10 1,2375 = 8, 08.
121 1/7. feladat - a) folytatás + b) Súlyozott mértani közép: ki=1 f i k i=1 X f i i = = = 9, 08. Súlyozott négyzetes közép: k i=1 f i Xi 2 k i=1 f i = = = 11, 76. Sorrend: 8, 08 < 9, 08 < 10, 4 < 11, 76.
122 1/7. feladat - a) folytatás + b) Súlyozott mértani közép: ki=1 f i k i=1 X f i i = = = 9, 08. Súlyozott négyzetes közép: k i=1 f i Xi 2 k i=1 f i = = = 11, 76. Sorrend: 8, 08 < 9, 08 < 10, 4 < 11, 76.
123 1/7. feladat - a) folytatás + b) Súlyozott mértani közép: ki=1 f i k i=1 X f i i = = = 9, 08. Súlyozott négyzetes közép: k i=1 f i Xi 2 k i=1 f i = = = 11, 76. Sorrend: 8, 08 < 9, 08 < 10, 4 < 11, 76.
124 1/7. feladat - a) folytatás + b) Súlyozott mértani közép: ki=1 f i k i=1 X f i i = = = 9, 08. Súlyozott négyzetes közép: k i=1 f i Xi 2 k i=1 f i = = = 11, 76. Sorrend: harmonikus < mértani < számtani < négyzetes.
125 1/7. feladat c) fi (X i A) 2 = 6 (6 5) (16 5) (20 5) 2 = = 599. Ugyanez A = 6, 8 és 10, 4-re számolva 502, 368, és 312,8: fi (X i A) 2 = 6 (6 6) (16 6) (20 6) 2 = = 502. fi (X i A) 2 = 6 (6 8) (16 8) (20 8) 2 = = 368. fi (X i A) 2 = 6 (6 10, 4) 2 +3 (16 10, 4) 2 +1 (20 10, 4) 2 = 6 19, , , 16 = 312, 8.
126 2. Feladat/3. Medián, átlag A mediánt tartalmazó osztályköz ahol elérjük a = 18. elemet: Medián Me = me + N 2 f me 1 f me h = = 44, 2 (Súlyozott) átlag X = 46, 86. N i=1 f i X i N i=1 f i = 9x20+12x40+7x60+7x = =
127 2. Feladat/3. Medián, átlag A mediánt tartalmazó osztályköz ahol elérjük a = 18. elemet: Medián Me = me + N 2 f me 1 f me h = = 44, 2 (Súlyozott) átlag X = 46, 86. N i=1 f i X i N i=1 f i = 9x20+12x40+7x60+7x = =
128 2. Feladat/3. Medián, átlag A mediánt tartalmazó osztályköz ahol elérjük a = 18. elemet: Medián Me = me + N 2 f me 1 f me h = = 44, 2 (Súlyozott) átlag X = 46, 86. N i=1 f i X i N i=1 f i = 9x20+12x40+7x60+7x = =
129 2. Feladat/4. Kvantilisek (Kvadrilisek) Alsó kvartilis ( j k = 1 4 ): 0 = f 0 < j k N = = 8.75 < f 1 = 9 Q 1 = a 1 + N 4 f 1 1 f 1 h = = 19, 44 Felső kvartilis ( j k = 3 4 ): 21 = f 2 < j k N = = 26, 25 < f 3 = 28 Q 3 = a 1 + 3N 4 f 2 h = x = 65 f 3
130 2. Feladat/4. Kvantilisek (Kvadrilisek) Alsó kvartilis ( j k = 1 4 ): 0 = f 0 < j k N = = 8.75 < f 1 = 9 Q 1 = a 1 + N 4 f 1 1 f 1 h = = 19, 44 Felső kvartilis ( j k = 3 4 ): 21 = f 2 < j k N = = 26, 25 < f 3 = 28 Q 3 = a 1 + 3N 4 f 2 h = x = 65 f 3
131 2. Feladat/4. Kvantilisek (Kvadrilisek) Alsó kvartilis ( j k = 1 4 ): 0 = f 0 < j k N = = 8.75 < f 1 = 9 Q 1 = a 1 + N 4 f 1 1 f 1 h = = 19, 44 Felső kvartilis ( j k = 3 4 ): 21 = f 2 < j k N = = 26, 25 < f 3 = 28 Q 3 = a 1 + 3N 4 f 2 h = x = 65 f 3
132 2. Feladat/4. Kvantilisek (Kvadrilisek) Alsó kvartilis ( j k = 1 4 ): 0 = f 0 < j k N = = 8.75 < f 1 = 9 Q 1 = a 1 + N 4 f 1 1 f 1 h = = 19, 44 Felső kvartilis ( j k = 3 4 ): 21 = f 2 < j k N = = 26, 25 < f 3 = 28 Q 3 = a 1 + 3N 4 f 2 h = x = 65 f 3
133 2. Feladat/5. Szórás, aszimmetria Szórás σ = k = 9(20 46,86) (80 46,86) = i=1 f i(x i X) 2 k i=1 f i = 7, 63. Pearson-féle mutató A = X Mo σ F-mutató F = (Q 3 Me) (Me Q 1 ) = 46,86 37,5 7,63 = 1, 23 (Q 3 Me)+(Me Q 1 ) = (65 44,2) (44,2 19,44) (65 44,2)+(44,2 19,44) = 20,8 24,76 20,8+24,76 = 3,96 45,56 = 0, 0869
134 2. Feladat/5. Szórás, aszimmetria Szórás σ = k = 9(20 46,86) (80 46,86) = i=1 f i(x i X) 2 k i=1 f i = 7, 63. Pearson-féle mutató A = X Mo σ F-mutató F = (Q 3 Me) (Me Q 1 ) = 46,86 37,5 7,63 = 1, 23 (Q 3 Me)+(Me Q 1 ) = (65 44,2) (44,2 19,44) (65 44,2)+(44,2 19,44) = 20,8 24,76 20,8+24,76 = 3,96 45,56 = 0, 0869
135 2. Feladat/5. Szórás, aszimmetria Szórás σ = k = 9(20 46,86) (80 46,86) = i=1 f i(x i X) 2 k i=1 f i = 7, 63. Pearson-féle mutató A = X Mo σ F-mutató F = (Q 3 Me) (Me Q 1 ) = 46,86 37,5 7,63 = 1, 23 (Q 3 Me)+(Me Q 1 ) = (65 44,2) (44,2 19,44) (65 44,2)+(44,2 19,44) = 20,8 24,76 20,8+24,76 = 3,96 45,56 = 0, 0869
GAZDASÁGI STATISZTIKA
 GAZDASÁGI STATISZTIKA Dr. Kun István GÁBOR DÉNES FŐISKOLA Tantárgy: Gazdasági statisztika Kódszám: 224 Lapszám: 1 TÉMAKÖRÖK A STATISZTIKA ALAPFOGALMAI STATISZTIKAI SOROK STATISZTIKAI TÁBLÁK ÖSSZETETT VISZONYSZÁMOK
GAZDASÁGI STATISZTIKA Dr. Kun István GÁBOR DÉNES FŐISKOLA Tantárgy: Gazdasági statisztika Kódszám: 224 Lapszám: 1 TÉMAKÖRÖK A STATISZTIKA ALAPFOGALMAI STATISZTIKAI SOROK STATISZTIKAI TÁBLÁK ÖSSZETETT VISZONYSZÁMOK
Bevezető Adatok rendezése Adatok jellemzése Időbeli elemzés. Gazdaságstatisztika KGK VMI
 Gazdaságstatisztika 2. előadás Egy ismérv szerinti rendezés Kóczy Á. László KGK VMI Áttekintés Gyakorisági sorok Grafikus ábrázolásuk Helyzetmutatók Szóródási mutatók Az aszimmetria mérőszámai Koncentráció
Gazdaságstatisztika 2. előadás Egy ismérv szerinti rendezés Kóczy Á. László KGK VMI Áttekintés Gyakorisági sorok Grafikus ábrázolásuk Helyzetmutatók Szóródási mutatók Az aszimmetria mérőszámai Koncentráció
Bevezető Adatok rendezése Adatok jellemzése Időbeli elemzés
 Gazdaságstatisztika 2. előadás Egy ismérv szerinti rendezés Kóczy Á. László KGK VMI Áttekintés Gyakorisági sorok Grafikus ábrázolásuk Helyzetmutatók Szóródási mutatók Az aszimmetria mérőszámai Koncentráció
Gazdaságstatisztika 2. előadás Egy ismérv szerinti rendezés Kóczy Á. László KGK VMI Áttekintés Gyakorisági sorok Grafikus ábrázolásuk Helyzetmutatók Szóródási mutatók Az aszimmetria mérőszámai Koncentráció
Nyugat-magyarországi Egyetem Geoinformatikai Kara. Prof. Dr. Závoti József. Matematika III. 7. MA3-7 modul. Helyzetmutatók, átlagok, kvantilisek
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematika III. 7. MA3-7 modul Helyzetmutatók, átlagok, kvantilisek SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról
Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematika III. 7. MA3-7 modul Helyzetmutatók, átlagok, kvantilisek SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról
Matematikai statisztikai elemzések 2.
 Matematikai statisztikai elemzések 2. Helyzetmutatók, átlagok, kvantilisek. A szórás és szóródás Prof. Dr. Závoti, József Matematikai statisztikai elemzések 2.: Helyzetmutatók, átlagok, Prof. Dr. Závoti,
Matematikai statisztikai elemzések 2. Helyzetmutatók, átlagok, kvantilisek. A szórás és szóródás Prof. Dr. Závoti, József Matematikai statisztikai elemzések 2.: Helyzetmutatók, átlagok, Prof. Dr. Závoti,
Bevezető Mi a statisztika? Mérés Feldolgozás Adatok rendezése Adatok jellemzése Időbeli elemzés Feladatok. Statisztika I.
 Statisztika I. 1. előadás: A statisztika alapfogalmai Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet Óbudai Egyetem A kurzusról A kurzus célja
Statisztika I. 1. előadás: A statisztika alapfogalmai Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet Óbudai Egyetem A kurzusról A kurzus célja
Tantárgyi útmutató. 1. A tantárgy helye a szaki hálóban. 2. A tantárgyi program általános célja. Statisztika 1.
 Tantárgyi útmutató 1. A tantárgy helye a szaki hálóban Gazdálkodási és menedzsment szakirány áttekintő tanterv Nagyításhoz kattintson a képre! Turizmus - vendéglátás szakirány áttekintő tanterv Nagyításhoz
Tantárgyi útmutató 1. A tantárgy helye a szaki hálóban Gazdálkodási és menedzsment szakirány áttekintő tanterv Nagyításhoz kattintson a képre! Turizmus - vendéglátás szakirány áttekintő tanterv Nagyításhoz
Statisztika gyakorlat
 Félévi követelményrendszer tatisztika gyakorlat. Gazdasági agrármérnök szak II. évolyam 007.0.. Heti óraszám: + Aláírás eltételei: az elıadásokon való részvétel nem kötelezı, de AJÁNLOTT! a gyakorlatokon
Félévi követelményrendszer tatisztika gyakorlat. Gazdasági agrármérnök szak II. évolyam 007.0.. Heti óraszám: + Aláírás eltételei: az elıadásokon való részvétel nem kötelezı, de AJÁNLOTT! a gyakorlatokon
Statisztika I. 6. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 6. előadás Előadó: Dr. Ertsey Imre GYAKORISÁGI SOROK ELOSZLÁSA KONCENTRÁCIÓ ELEMZÉSE GYAKORISÁGI SOROK ELOSZLÁSA KONCENTRÁCIÓ ELEMZÉSE szorosan kapcsolódik a szóródás elemzéshez, elméleti
Statisztika I. 6. előadás Előadó: Dr. Ertsey Imre GYAKORISÁGI SOROK ELOSZLÁSA KONCENTRÁCIÓ ELEMZÉSE GYAKORISÁGI SOROK ELOSZLÁSA KONCENTRÁCIÓ ELEMZÉSE szorosan kapcsolódik a szóródás elemzéshez, elméleti
Adatok gyűjtésének és értékelésének módszerei Domokos, Endre Csom, Veronika
 Adatok gyűjtésének és értékelésének módszerei Domokos, Endre Csom, Veronika Adatok gyűjtésének és értékelésének módszerei Domokos, Endre Csom, Veronika Tartalom 1. Jelmagyarázat és rövidítésjegyzék...
Adatok gyűjtésének és értékelésének módszerei Domokos, Endre Csom, Veronika Adatok gyűjtésének és értékelésének módszerei Domokos, Endre Csom, Veronika Tartalom 1. Jelmagyarázat és rövidítésjegyzék...
Bevezető Mi a statisztika? Mérés Csoportosítás
 Gazdaságstatisztika 1. előadás Kóczy Á. László Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet Oktatók Előadó Kóczy Á. László (koczy.laszlo@kgk.bmf.hu) Fogadóóra: szerda 11:30 11:55, TA125 Gyakorlatvezető
Gazdaságstatisztika 1. előadás Kóczy Á. László Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet Oktatók Előadó Kóczy Á. László (koczy.laszlo@kgk.bmf.hu) Fogadóóra: szerda 11:30 11:55, TA125 Gyakorlatvezető
[GVMGS11MNC] Gazdaságstatisztika
![[GVMGS11MNC] Gazdaságstatisztika [GVMGS11MNC] Gazdaságstatisztika](/thumbs/54/34260531.jpg) [GVMGS11MNC] Gazdaságstatisztika 1. előadás Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet Óbudai Egyetem Oktatók Előadó Kóczy Á. László (koczy.laszlo@kgk.uni-obuda.hu)
[GVMGS11MNC] Gazdaságstatisztika 1. előadás Kóczy Á. László koczy.laszlo@kgk.uni-obuda.hu Keleti Károly Gazdasági Kar Vállalkozásmenedzsment Intézet Óbudai Egyetem Oktatók Előadó Kóczy Á. László (koczy.laszlo@kgk.uni-obuda.hu)
Véletlenszám-generátorok
 Véletlenszám-generátorok 1. Lineáris kongruencia generátor megvalósítása: (a) Készítsen lineáris kongruencia generátort az paraméterekkel, rnd_lcg néven. (b) Nyomtasson ki 20 értéket. legyen. (a, c, m,
Véletlenszám-generátorok 1. Lineáris kongruencia generátor megvalósítása: (a) Készítsen lineáris kongruencia generátort az paraméterekkel, rnd_lcg néven. (b) Nyomtasson ki 20 értéket. legyen. (a, c, m,
Az oszlopdiagram kinézhet például úgy, mint a bal oldali ábra. 1,2 1,0 0,8 0,6 0,4 0,2. Kategória busz teherautó furgon személyautó összesen
 STATISZTIKA 9.7. STATISZTIKA Az adatok ábrázolása megoldások wx76 Az oszlopdiagram kinézhet például úgy, mint a bal oldali ábra. Napi futásteljesítmény Almafajták megtett kilométerek 9 7 6 hétfô kedd szerda
STATISZTIKA 9.7. STATISZTIKA Az adatok ábrázolása megoldások wx76 Az oszlopdiagram kinézhet például úgy, mint a bal oldali ábra. Napi futásteljesítmény Almafajták megtett kilométerek 9 7 6 hétfô kedd szerda
KVANTITATÍV MÓDSZEREK
 KVANTITATÍV MÓDSZEREK Dr. Kövesi János Tóth Zsuzsanna Eszter 6 Tartalomjegyzék Kvantitatív módszerek. Valószínűségszámítási tételek. eltételes valószínűség. Események függetlensége.... 3.. eltételes valószínűség...
KVANTITATÍV MÓDSZEREK Dr. Kövesi János Tóth Zsuzsanna Eszter 6 Tartalomjegyzék Kvantitatív módszerek. Valószínűségszámítási tételek. eltételes valószínűség. Események függetlensége.... 3.. eltételes valószínűség...
Matematikai statisztikai elemzések 1.
 Matematikai statisztikai elemzések 1. A statisztika alapfogalmai, feladatai, Prof. Dr. Závoti, József Matematikai statisztikai elemzések 1.: A statisztika alapfogalmai, feladatai, statisztika, osztályozás,
Matematikai statisztikai elemzések 1. A statisztika alapfogalmai, feladatai, Prof. Dr. Závoti, József Matematikai statisztikai elemzések 1.: A statisztika alapfogalmai, feladatai, statisztika, osztályozás,
Nyugat-magyarországi Egyetem Geoinformatikai Kara. Prof. Dr. Závoti József. Matematika III. 6. MA3-6 modul. A statisztika alapfogalmai
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematika III. 6. MA3-6 modul A statisztika alapfogalmai SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról szóló 1999.
Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematika III. 6. MA3-6 modul A statisztika alapfogalmai SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról szóló 1999.
Matematika III. 8. A szórás és a szóródás egyéb mérőszámai Prof. Dr. Závoti, József
 Matematika III. 8. A szórás és a szóródás egyéb Prof. Dr. Závoti, József Matematika III. 8. : A szórás és a szóródás egyéb Prof. Dr. Závoti, József Lektor : Bischof, Annamária Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
Matematika III. 8. A szórás és a szóródás egyéb Prof. Dr. Závoti, József Matematika III. 8. : A szórás és a szóródás egyéb Prof. Dr. Závoti, József Lektor : Bischof, Annamária Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
KÖZPONTI STATISZTIKAI HIVATAL. Szóbeli vizsgatevékenység
 KÖZPONTI STATISZTIKAI HIVATAL A vizsgarészhez rendelt követelménymodul azonosító száma, megnevezése: 2143-06 Statisztikai feladatok A vizsgarészhez rendelt vizsgafeladat megnevezése: A statisztikai elemzés
KÖZPONTI STATISZTIKAI HIVATAL A vizsgarészhez rendelt követelménymodul azonosító száma, megnevezése: 2143-06 Statisztikai feladatok A vizsgarészhez rendelt vizsgafeladat megnevezése: A statisztikai elemzés
GAZDASÁGSTATISZTIKA. Készítette: Bíró Anikó. Szakmai felelős: Bíró Anikó. 2010. június
 GAZDASÁGSTATISZTIKA Készült a TÁMOP-4.1.2-8/2/A/KMR-29-41pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén, az ELTE Közgazdaságtudományi Tanszék, az MTA Közgazdaságtudományi
GAZDASÁGSTATISZTIKA Készült a TÁMOP-4.1.2-8/2/A/KMR-29-41pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén, az ELTE Közgazdaságtudományi Tanszék, az MTA Közgazdaságtudományi
S a t ti a s ti z s ti z k ti a k i a i soka k s a ág Megfigyelési egység Statisztikai ismérv
 Üzleti gazdaságtan Ismétlés statisztika A statisztikai alapfogalmak A statisztikaa társadalom és a gazdasági élet jelenségeinek, folyamatainak számadatok segítségével történő megismerésével, leírásával,
Üzleti gazdaságtan Ismétlés statisztika A statisztikai alapfogalmak A statisztikaa társadalom és a gazdasági élet jelenségeinek, folyamatainak számadatok segítségével történő megismerésével, leírásával,
Elméleti összefoglalók dr. Kovács Péter
 Elméleti összefoglalók dr. Kovács Péter 1. Adatállományok létrehozása, kezelése... 2 2. Leíró statisztikai eljárások... 3 3. Várható értékek (átlagok) vizsgálatára irányuló próbák... 5 4. Eloszlások vizsgálata...
Elméleti összefoglalók dr. Kovács Péter 1. Adatállományok létrehozása, kezelése... 2 2. Leíró statisztikai eljárások... 3 3. Várható értékek (átlagok) vizsgálatára irányuló próbák... 5 4. Eloszlások vizsgálata...
INTELLIGENS ADATELEMZÉS
 Írta: FOGARASSYNÉ VATHY ÁGNES STARKNÉ WERNER ÁGNES INTELLIGENS ADATELEMZÉS Egyetemi tananyag 2011 COPYRIGHT: 2011 2016, Dr. Fogarassyné Dr. Vathy Ágnes, Pannon Egyetem Műszaki Informatikai Kar Matematika
Írta: FOGARASSYNÉ VATHY ÁGNES STARKNÉ WERNER ÁGNES INTELLIGENS ADATELEMZÉS Egyetemi tananyag 2011 COPYRIGHT: 2011 2016, Dr. Fogarassyné Dr. Vathy Ágnes, Pannon Egyetem Műszaki Informatikai Kar Matematika
Csicsman József-Sipos Szabó Eszter csicsman@calculus.hu, siposeszti@gmail.com. Matematikai alapok az adatbányászati szoftverek első megismeréséhez
 Csicsman József-Sipos Szabó Eszter csicsman@calculus.hu, siposeszti@gmail.com Matematikai alapok az adatbányászati szoftverek első megismeréséhez 1.1 A statisztikai sokaság A statisztika a valóság számszerű
Csicsman József-Sipos Szabó Eszter csicsman@calculus.hu, siposeszti@gmail.com Matematikai alapok az adatbányászati szoftverek első megismeréséhez 1.1 A statisztikai sokaság A statisztika a valóság számszerű
MATEMATIKA Kiss Árpád Országos Közoktatási Szolgáltató Intézmény Vizsgafejlesztő Központ
 MATEMATIKA Kiss Árpád Országos Közoktatási Szolgáltató Intézmény Vizsgafejlesztő Központ I. RÉSZLETES ÉRETTSÉGI VIZSGAKÖVETELMÉNY Az érettségi követelményeit két szinten határozzuk meg: középszinten a
MATEMATIKA Kiss Árpád Országos Közoktatási Szolgáltató Intézmény Vizsgafejlesztő Központ I. RÉSZLETES ÉRETTSÉGI VIZSGAKÖVETELMÉNY Az érettségi követelményeit két szinten határozzuk meg: középszinten a
ELEMI VALÓSZÍNŰSÉGSZÁMÍTÁS és STATISZTIKAI MÓDSZEREK A FIZIKÁBAN
 ELEMI VALÓSZÍNŰSÉGSZÁMÍTÁS és STATISZTIKAI MÓDSZEREK A FIZIKÁBAN SINKOVICZ PÉTER (PhD hallgató) MTA WIGNER FIZIKAI KUTATÓKÖZPONT (2013) a TARTALOMJEGYZÉK A VALÓSÁG STATISZTIKAI LEKÉPEZÉSE 1. Alapfogalmak
ELEMI VALÓSZÍNŰSÉGSZÁMÍTÁS és STATISZTIKAI MÓDSZEREK A FIZIKÁBAN SINKOVICZ PÉTER (PhD hallgató) MTA WIGNER FIZIKAI KUTATÓKÖZPONT (2013) a TARTALOMJEGYZÉK A VALÓSÁG STATISZTIKAI LEKÉPEZÉSE 1. Alapfogalmak
Halmazok Halmazok, részhalmaz, halmazműveletek, halmazok elemszáma
 Az osztályozóvizsgák követelményrendszere 9.Ny osztály Halmazok Halmazok, részhalmaz, halmazműveletek, halmazok elemszáma Algebra és számelmélet Alapműveletek az egész és törtszámok körében Műveleti sorrend,
Az osztályozóvizsgák követelményrendszere 9.Ny osztály Halmazok Halmazok, részhalmaz, halmazműveletek, halmazok elemszáma Algebra és számelmélet Alapműveletek az egész és törtszámok körében Műveleti sorrend,
2) = 0 ahol x 1 és x 2 az ax 2 + bx + c = 0 ( a,b, c R és a 0 )
 Fogalom gyűjtemény Abszcissza: az x tengely Abszolút értékes egyenletek: azok az egyenletek, amelyekben abszolút érték jel szerepel. Abszolútérték-függvény: egy elemi egyváltozós valós függvény, mely minden
Fogalom gyűjtemény Abszcissza: az x tengely Abszolút értékes egyenletek: azok az egyenletek, amelyekben abszolút érték jel szerepel. Abszolútérték-függvény: egy elemi egyváltozós valós függvény, mely minden
JANUS PANNONIUS TUDOMÁNYEGYETEM. Schipp Ferenc ANALÍZIS I. Sorozatok és sorok
 JANUS PANNONIUS TUDOMÁNYEGYETEM Schipp Ferenc ANALÍZIS I. Sorozatok és sorok Pécs, 1994 Lektorok: Dr. FEHÉR JÁNOS egyetemi docens, kandidtus. Dr. SIMON PÉTER egyetemi docens, kandidtus 1 Előszó Ez a jegyzet
JANUS PANNONIUS TUDOMÁNYEGYETEM Schipp Ferenc ANALÍZIS I. Sorozatok és sorok Pécs, 1994 Lektorok: Dr. FEHÉR JÁNOS egyetemi docens, kandidtus. Dr. SIMON PÉTER egyetemi docens, kandidtus 1 Előszó Ez a jegyzet
Árvainé Libor Ildikó Murátiné Szél Edit. Tanítói kézikönyv. tanmenetjavaslattal. Sokszínû matematika. 4
 Árvainé Libor Ildikó Murátiné Szél Edit Tanítói kézikönyv tanmenetjavaslattal Sokszínû matematika. 4 Mozaik Kiadó - Szeged, 2007 Készítette: ÁRVAINÉ LIBOR ILDIKÓ szakvezetõ tanító MURÁTINÉ SZÉL EDIT szakvezetõ
Árvainé Libor Ildikó Murátiné Szél Edit Tanítói kézikönyv tanmenetjavaslattal Sokszínû matematika. 4 Mozaik Kiadó - Szeged, 2007 Készítette: ÁRVAINÉ LIBOR ILDIKÓ szakvezetõ tanító MURÁTINÉ SZÉL EDIT szakvezetõ
Beadható feladatok. 2006. december 4. 1. Add meg az alábbi probléma állapottér-reprezentációját!
 Beadható feladatok 2006. december 4. 1. Feladatok 2006. szeptember 13-án kitűzött feladat: 1. Add meg az alábbi probléma állapottér-reprezentációját! Adott I 1,..., I n [0, 1] intervallumokból szeretnénk
Beadható feladatok 2006. december 4. 1. Feladatok 2006. szeptember 13-án kitűzött feladat: 1. Add meg az alábbi probléma állapottér-reprezentációját! Adott I 1,..., I n [0, 1] intervallumokból szeretnénk
Definíció. Definíció. 2. El adás (folytatása) Az adatok leírása, megismerése és összehasonlítása. 2-5. fejezet. A variabilitás mér számai 3.
 . El adás (folytatása) Az adatok leírása, megismerése és összehasonlítása -1 Áttekintés - Gyakoriság eloszlások -3 Az adatok vizualizációja -4 A centrum mérıszámai -5 A szórás mérıszámai -6 A relatív elhelyezkedés
. El adás (folytatása) Az adatok leírása, megismerése és összehasonlítása -1 Áttekintés - Gyakoriság eloszlások -3 Az adatok vizualizációja -4 A centrum mérıszámai -5 A szórás mérıszámai -6 A relatív elhelyezkedés
Nevezetes függvények
 Nevezetes függvények Függvények értelmezése Legyen adott az A és B két nem üres halmaz. Az A halmaz minden egyes eleméhez rendeljük hozzá a B halmaz egy-egy elemét. Ez a hozzárendelés egyértelmű, és ezt
Nevezetes függvények Függvények értelmezése Legyen adott az A és B két nem üres halmaz. Az A halmaz minden egyes eleméhez rendeljük hozzá a B halmaz egy-egy elemét. Ez a hozzárendelés egyértelmű, és ezt
Középszintű érettségi feladatsorok és megoldásaik Összeállította: Pataki János; dátum: 2005. november. I. rész
 Pataki János, 005. november Középszintű érettségi feladatsorok és megoldásaik Összeállította: Pataki János; dátum: 005. november I. rész. feladat Egy liter 0%-os alkoholhoz / liter 40%-os alkoholt keverünk.
Pataki János, 005. november Középszintű érettségi feladatsorok és megoldásaik Összeállította: Pataki János; dátum: 005. november I. rész. feladat Egy liter 0%-os alkoholhoz / liter 40%-os alkoholt keverünk.
Statisztika, próbák Mérési hiba
 Statisztika, próbák Mérési hiba ÁTLAG SZÓRÁS KICSI, NAGY MIN, MAX LIN.ILL LOG.ILL MEREDEKSÉG METSZ T.PROBA TREND NÖV Statisztikai függvények Statisztikailag fontos értékek Számtani átlag: ŷ= i y i /n Medián:
Statisztika, próbák Mérési hiba ÁTLAG SZÓRÁS KICSI, NAGY MIN, MAX LIN.ILL LOG.ILL MEREDEKSÉG METSZ T.PROBA TREND NÖV Statisztikai függvények Statisztikailag fontos értékek Számtani átlag: ŷ= i y i /n Medián:
2. Hatványozás, gyökvonás
 2. Hatványozás, gyökvonás I. Elméleti összefoglaló Egész kitevőjű hatvány értelmezése: a 1, ha a R; a 0; a a, ha a R. Ha a R és n N; n > 1, akkor a olyan n tényezős szorzatot jelöl, aminek minden tényezője
2. Hatványozás, gyökvonás I. Elméleti összefoglaló Egész kitevőjű hatvány értelmezése: a 1, ha a R; a 0; a a, ha a R. Ha a R és n N; n > 1, akkor a olyan n tényezős szorzatot jelöl, aminek minden tényezője
I. Gondolkodási módszerek: (6 óra) 1. Gondolkodási módszerek, a halmazelmélet elemei, a logika elemei. 1. Számfogalom, műveletek (4 óra)
 MATEMATIKA NYEK-humán tanterv Matematika előkészítő év Óraszám: 36 óra Tanítási ciklus 1 óra / 1 hét Részletes felsorolás A tananyag felosztása: I. Gondolkodási módszerek: (6 óra) 1. Gondolkodási módszerek,
MATEMATIKA NYEK-humán tanterv Matematika előkészítő év Óraszám: 36 óra Tanítási ciklus 1 óra / 1 hét Részletes felsorolás A tananyag felosztása: I. Gondolkodási módszerek: (6 óra) 1. Gondolkodási módszerek,
9. ÉVFOLYAM. Tájékozottság a racionális számkörben. Az azonosságok ismerete és alkalmazásuk. Számok abszolútértéke, normál alakja.
 9. ÉVFOLYAM Gondolkodási módszerek A szemléletes fogalmak definiálása, tudatosítása. Módszer keresése az összes eset áttekintéséhez. A szükséges és elégséges feltétel megkülönböztetése. A megismert számhalmazok
9. ÉVFOLYAM Gondolkodási módszerek A szemléletes fogalmak definiálása, tudatosítása. Módszer keresése az összes eset áttekintéséhez. A szükséges és elégséges feltétel megkülönböztetése. A megismert számhalmazok
Leggyakrabban használt adatbányászási technikák. Vezetői információs rendszerek
 Leggyakrabban használt adatbányászási technikák ADATBÁNYÁSZÁS II. 1. A társításelemzés társítási szabályok (asszociációs szabályok) feltárását jelenti. Azt vizsgájuk, hogy az adatbázis elemei között létezik-e
Leggyakrabban használt adatbányászási technikák ADATBÁNYÁSZÁS II. 1. A társításelemzés társítási szabályok (asszociációs szabályok) feltárását jelenti. Azt vizsgájuk, hogy az adatbázis elemei között létezik-e
Matematikai statisztikai elemzések 5.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematikai statisztikai elemzések. MSTE modul Kapcsolatvizsgálat: asszociáció vegyes kapcsolat korrelációszámítás. Varianciaanalízis
Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematikai statisztikai elemzések. MSTE modul Kapcsolatvizsgálat: asszociáció vegyes kapcsolat korrelációszámítás. Varianciaanalízis
Bánhalmi Árpád * Bakos Viktor ** MIÉRT BUKNAK MEG STATISZTIKÁBÓL A JÓ MATEKOSOK?
 Bánhalmi Árpád * Bakos Viktor ** MIÉRT BUKNAK MEG STATISZTIKÁBÓL A JÓ MATEKOSOK? A BGF KKFK Nemzetközi gazdálkodás és Kereskedelem és marketing szakjain a hallgatók tanrendjében statisztikai és matematikai
Bánhalmi Árpád * Bakos Viktor ** MIÉRT BUKNAK MEG STATISZTIKÁBÓL A JÓ MATEKOSOK? A BGF KKFK Nemzetközi gazdálkodás és Kereskedelem és marketing szakjain a hallgatók tanrendjében statisztikai és matematikai
Az osztályozó, javító és különbözeti vizsgák (tanulmányok alatti vizsgák) témakörei matematika tantárgyból
 Az osztályozó, javító és különbözeti vizsgák (tanulmányok alatti vizsgák) témakörei matematika tantárgyból A vizsga formája: Feladatlap az adott évfolyam anyagából, a megoldásra fordítható idő 60 perc.
Az osztályozó, javító és különbözeti vizsgák (tanulmányok alatti vizsgák) témakörei matematika tantárgyból A vizsga formája: Feladatlap az adott évfolyam anyagából, a megoldásra fordítható idő 60 perc.
Módszertani Intézeti Tanszéki Osztály
 BGF Módszertani ntézeti Tanszéki Osztály Budaest,. Név:... ód:...... Eredmény:..... STATSZTA. ZSGA; NG M ÉS G TQM SZAOON MNTAZSGA Feladatok.. 3. 4. 5. 6. Összesen Szerezhető ontszám 8 7 8 6 Elért ontszám
BGF Módszertani ntézeti Tanszéki Osztály Budaest,. Név:... ód:...... Eredmény:..... STATSZTA. ZSGA; NG M ÉS G TQM SZAOON MNTAZSGA Feladatok.. 3. 4. 5. 6. Összesen Szerezhető ontszám 8 7 8 6 Elért ontszám
Tanmenet Matematika 8. osztály HETI ÓRASZÁM: 3,5 óra ( 4-3) ÉVES ÓRASZÁM: 126 óra
 Tanmenet Matematika 8. osztály HETI ÓRASZÁM: 3,5 óra ( 4-3) ÉVES ÓRASZÁM: 126 óra A Kiadó javaslata alapján összeállította: Látta:...... Harmath Lajos munkaközösség vezető tanár Jóváhagyta:... igazgató
Tanmenet Matematika 8. osztály HETI ÓRASZÁM: 3,5 óra ( 4-3) ÉVES ÓRASZÁM: 126 óra A Kiadó javaslata alapján összeállította: Látta:...... Harmath Lajos munkaközösség vezető tanár Jóváhagyta:... igazgató
Alapfogalmak áttekintése. Pszichológiai statisztika, 1. alkalom
 Alapfogalmak áttekintése Pszichológiai statisztika, 1. alkalom Hipotézisek Milyen a jó null hipotézis?? H0: Léteznek kitőnı tanuló diszlexiások.? H1: Nem léteznek. Sokkal inkább: H0: Nincs diszlexiás kitőnı
Alapfogalmak áttekintése Pszichológiai statisztika, 1. alkalom Hipotézisek Milyen a jó null hipotézis?? H0: Léteznek kitőnı tanuló diszlexiások.? H1: Nem léteznek. Sokkal inkább: H0: Nincs diszlexiás kitőnı
ÚTMUTATÓ A MÓDSZERTANI SZIGORLAT LETÉTELÉHEZ
 Szolnoki Főiskola Üzleti Fakultás, 5000 Szolnok, Tiszaligeti sétány ÚTMUTATÓ A MÓDSZERTANI SZIGORLAT LETÉTELÉHEZ A 4/1996. (I. 18.) Korm. rendelet a közgazdasági felsőoktatás alapképzési szakjainak képesítési
Szolnoki Főiskola Üzleti Fakultás, 5000 Szolnok, Tiszaligeti sétány ÚTMUTATÓ A MÓDSZERTANI SZIGORLAT LETÉTELÉHEZ A 4/1996. (I. 18.) Korm. rendelet a közgazdasági felsőoktatás alapképzési szakjainak képesítési
Ittfoglalomösszea legfontosabbtudnivalókat, részleteka honlapon, illetvea gyakorlatvezetőtől is kaptok információkat.
 1 Ittfoglalomösszea legfontosabbtudnivalókat, részleteka honlapon, illetvea gyakorlatvezetőtől is kaptok információkat. A statisztika tanulásához a legtöbb infomrációkat az előadásokon és számítógépes
1 Ittfoglalomösszea legfontosabbtudnivalókat, részleteka honlapon, illetvea gyakorlatvezetőtől is kaptok információkat. A statisztika tanulásához a legtöbb infomrációkat az előadásokon és számítógépes
Miskolci Egyetem. Diszkrét matek I. Vizsga-jegyzet. Hegedűs Ádám Imre 2010.12.28.
 Miskolci Egyetem Diszkrét matek I. Vizsga-jegyzet Hegedűs Ádám Imre 2010.12.28. KOMBINATORIKA Permutáció Ismétlés nélküli permutáció alatt néhány különböző dolognak a sorba rendezését értjük. Az "ismétlés
Miskolci Egyetem Diszkrét matek I. Vizsga-jegyzet Hegedűs Ádám Imre 2010.12.28. KOMBINATORIKA Permutáció Ismétlés nélküli permutáció alatt néhány különböző dolognak a sorba rendezését értjük. Az "ismétlés
Költségvetési szabályzat
 Budapesti Műszaki és Gazdaságtudományi Egyetem Építészmérnöki Kar Költségvetési szabályzat Az Építészmérnöki Kar költségvetése a kar alapvető gazdálkodási döntéseit tartalmazza. Célja a várható bevételek
Budapesti Műszaki és Gazdaságtudományi Egyetem Építészmérnöki Kar Költségvetési szabályzat Az Építészmérnöki Kar költségvetése a kar alapvető gazdálkodási döntéseit tartalmazza. Célja a várható bevételek
MATEMATIKA ÉRETTSÉGI 2012. május 8. EMELT SZINT I.
 MATEMATIKA ÉRETTSÉGI 01. május 8. EMELT SZINT I. 1) Egy 011-ben készült statisztikai összehasonlításban az alábbiakat olvashatjuk: Ha New York-ban az átlagfizetést és az átlagos árszínvonalat egyaránt
MATEMATIKA ÉRETTSÉGI 01. május 8. EMELT SZINT I. 1) Egy 011-ben készült statisztikai összehasonlításban az alábbiakat olvashatjuk: Ha New York-ban az átlagfizetést és az átlagos árszínvonalat egyaránt
2.3.2.2.1.2.1 Visszatérítő nyomaték és visszatérítő kar
 2.3.2.2.1.2 Keresztirányú stabilitás nagy dőlésszögeknél A keresztirányú stabilitás számszerűsítésénél, amint korábban láttuk, korlátozott a metacentrikus magasságra való támaszkodás lehetősége. Csak olyankor
2.3.2.2.1.2 Keresztirányú stabilitás nagy dőlésszögeknél A keresztirányú stabilitás számszerűsítésénél, amint korábban láttuk, korlátozott a metacentrikus magasságra való támaszkodás lehetősége. Csak olyankor
Adatok statisztikai feldolgozása
 Adatok statisztikai feldolgozása Kaszaki József Ph.D Szegedi Tudományegyetem Sebészeti Műtéttani Intézet Szeged A mérési adatok kiértékelése, statisztikai analízis A mért adatok konvertálása adatbázis
Adatok statisztikai feldolgozása Kaszaki József Ph.D Szegedi Tudományegyetem Sebészeti Műtéttani Intézet Szeged A mérési adatok kiértékelése, statisztikai analízis A mért adatok konvertálása adatbázis
Tanmenetjavaslat a 6. osztályos matematika kísérleti tankönyvhöz
 MATEMATIKA 6. Tanmenetjavaslat a 6. osztályos matematika kísérleti tankönyvhöz Témák 1. Játékos feladatok Egyszerű, matematikailag is értelmezhető hétköznapi szituációk megfogalmazása szóban és írásban.
MATEMATIKA 6. Tanmenetjavaslat a 6. osztályos matematika kísérleti tankönyvhöz Témák 1. Játékos feladatok Egyszerű, matematikailag is értelmezhető hétköznapi szituációk megfogalmazása szóban és írásban.
Biostatisztika Bevezetés. Boda Krisztina előadása alapján ma Bari Ferenc SZTE ÁOK Orvosi Fizikai és Orvosi Informatikai Intézet
 Biostatisztika Bevezetés Boda Krisztina előadása alapján ma Bari Ferenc SZTE ÁOK Orvosi Fizikai és Orvosi Informatikai Intézet Az orvosi, biológiai kutatások egyik jellemzője, hogy a vizsgálatok eredményeként
Biostatisztika Bevezetés Boda Krisztina előadása alapján ma Bari Ferenc SZTE ÁOK Orvosi Fizikai és Orvosi Informatikai Intézet Az orvosi, biológiai kutatások egyik jellemzője, hogy a vizsgálatok eredményeként
Statisztikai. Statisztika Sportszervező BSc képzés (levelező tagozat) Témakörök. Statisztikai alapfogalmak. Statisztika fogalma. Statisztika fogalma
 Témakörök Statsztka Sortszerező BSc kézés (leelező tagozat) 2-2-es tané félé Oktató: Dr Csáfor Hajnalka főskola docens Vállalkozás-gazdaságtan Tsz E-mal: hcsafor@ektfhu Statsztka fogalmak Statsztka elemzések
Témakörök Statsztka Sortszerező BSc kézés (leelező tagozat) 2-2-es tané félé Oktató: Dr Csáfor Hajnalka főskola docens Vállalkozás-gazdaságtan Tsz E-mal: hcsafor@ektfhu Statsztka fogalmak Statsztka elemzések
11. Matematikai statisztika
 11. Matematikai statisztika 11.1. Alapfogalmak A statisztikai minta valamely valószínűségi változóra vonatkozó véges számú független kisérlet eredménye. Ez véges sok, azonos eloszlású valószínűségi változó
11. Matematikai statisztika 11.1. Alapfogalmak A statisztikai minta valamely valószínűségi változóra vonatkozó véges számú független kisérlet eredménye. Ez véges sok, azonos eloszlású valószínűségi változó
TANMENET javaslat. a szorobánnal számoló. osztály számára. Vajdáné Bárdi Magdolna tanítónő
 2 TANMENET javaslat a szorobánnal számoló 2. osztály számára Szerkesztette: Dr. Vajda József - Összeállította az Első Szorobán Alapítvány megbízásából: Vajdáné Bárdi Magdolna tanítónő Makó, 2001. 2010.
2 TANMENET javaslat a szorobánnal számoló 2. osztály számára Szerkesztette: Dr. Vajda József - Összeállította az Első Szorobán Alapítvány megbízásából: Vajdáné Bárdi Magdolna tanítónő Makó, 2001. 2010.
Analízis 1. (BSc) vizsgakérdések Programtervez informatikus szak 2008-2009. tanév 2. félév
 Analízis 1. (BSc) vizsgakérdések Programtervez informatikus szak 2008-2009. tanév 2. félév Valós számok 1. Hogyan szól a Bernoulli-egyenl tlenség? Mikor van egyenl ség? Válasz. Minden h 1 valós számra
Analízis 1. (BSc) vizsgakérdések Programtervez informatikus szak 2008-2009. tanév 2. félév Valós számok 1. Hogyan szól a Bernoulli-egyenl tlenség? Mikor van egyenl ség? Válasz. Minden h 1 valós számra
Matematika. 5. 8. évfolyam
 Matematika 5. 8. évfolyam 5. 6. évfolyam Éves órakeret: 148 Heti óraszám: 4 Témakörök Óraszámok Gondolkodási és megismerési módszerek folyamatos Számtan, algebra 65 Összefüggések, függvények, sorozatok
Matematika 5. 8. évfolyam 5. 6. évfolyam Éves órakeret: 148 Heti óraszám: 4 Témakörök Óraszámok Gondolkodási és megismerési módszerek folyamatos Számtan, algebra 65 Összefüggések, függvények, sorozatok
Komputer statisztika gyakorlatok
 Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Tómács Tibor Komputer statisztika gyakorlatok Eger, 2010. október 26. Tartalomjegyzék Előszó 4 Jelölések 5 1. Mintagenerálás 7 1.1. Egyenletes
Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Tómács Tibor Komputer statisztika gyakorlatok Eger, 2010. október 26. Tartalomjegyzék Előszó 4 Jelölések 5 1. Mintagenerálás 7 1.1. Egyenletes
Statisztika 2. Dr Gősi Zsuzsanna Egyetemi adjunktus
 Statisztika 2. Dr Gősi Zsuzsanna Egyetemi adjunktus Gyakorisági sorok Mennyiségi ismérv jellemző rangsor készítünk. (pl. napi jegyeladások száma) A gyakorisági sor képzése igazából tömörítést jelent Nagyszámú
Statisztika 2. Dr Gősi Zsuzsanna Egyetemi adjunktus Gyakorisági sorok Mennyiségi ismérv jellemző rangsor készítünk. (pl. napi jegyeladások száma) A gyakorisági sor képzése igazából tömörítést jelent Nagyszámú
MATEMATIKA ÉRETTSÉGI VIZSGA ÁLTALÁNOS KÖVETELMÉNYEI
 A vizsga formája Középszinten: írásbeli. Emelt szinten: írásbeli és szóbeli. MATEMATIKA ÉRETTSÉGI VIZSGA ÁLTALÁNOS KÖVETELMÉNYEI A matematika érettségi vizsga célja A matematika érettségi vizsga célja
A vizsga formája Középszinten: írásbeli. Emelt szinten: írásbeli és szóbeli. MATEMATIKA ÉRETTSÉGI VIZSGA ÁLTALÁNOS KÖVETELMÉNYEI A matematika érettségi vizsga célja A matematika érettségi vizsga célja
MATEMATIKA TANTERV Bevezetés Összesen: 432 óra Célok és feladatok
 MATEMATIKA TANTERV Bevezetés A matematika tanítását minden szakmacsoportban és minden évfolyamon egységesen heti három órában tervezzük Az elsı évfolyamon mindhárom órát osztálybontásban tartjuk, segítve
MATEMATIKA TANTERV Bevezetés A matematika tanítását minden szakmacsoportban és minden évfolyamon egységesen heti három órában tervezzük Az elsı évfolyamon mindhárom órát osztálybontásban tartjuk, segítve
Működési kockázati önértékelések veszteségeloszlás-alapú modellezése
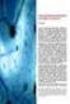 506 HITELINTÉZETI SZEMLE HAJNAL BÉLA KÁLLAI ZOLTÁN NAGY GÁBOR Működési kockázati önértékelések veszteségeloszlás-alapú modellezése Tanulmányunkban a működési kockázatok önértékelésen alapuló modellezését
506 HITELINTÉZETI SZEMLE HAJNAL BÉLA KÁLLAI ZOLTÁN NAGY GÁBOR Működési kockázati önértékelések veszteségeloszlás-alapú modellezése Tanulmányunkban a működési kockázatok önértékelésen alapuló modellezését
Matematikai és matematikai statisztikai alapismeretek
 Kézirat a Matematikai és matematikai statisztikai alapismeretek című előadáshoz Dr. Győri István NEVELÉSTUDOMÁNYI PH.D. PROGRM 1999/2000 1 1. MTEMTIKI LPOGLMK 1.1. Halmazok Halmazon mindig bizonyos dolgok
Kézirat a Matematikai és matematikai statisztikai alapismeretek című előadáshoz Dr. Győri István NEVELÉSTUDOMÁNYI PH.D. PROGRM 1999/2000 1 1. MTEMTIKI LPOGLMK 1.1. Halmazok Halmazon mindig bizonyos dolgok
hogy a megismert fogalmakat és tételeket változatos területeken használhatjuk Az adatok, táblázatok, grafikonok értelmezésének megismerése nagyban
 MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
Analízis előadás és gyakorlat vázlat
 Analízis előadás és gyakorlat vázlat Készült a PTE TTK GI szakos hallgatóinak Király Balázs 00-. I. Félév . fejezet Számhalmazok és tulajdonságaik.. Nevezetes számhalmazok ➀ a) jelölése: N b) elemei:
Analízis előadás és gyakorlat vázlat Készült a PTE TTK GI szakos hallgatóinak Király Balázs 00-. I. Félév . fejezet Számhalmazok és tulajdonságaik.. Nevezetes számhalmazok ➀ a) jelölése: N b) elemei:
II. A következtetési statisztika alapfogalmai
 II. A következtetési statisztika alapfogalmai Tartalom Statisztikai következtetések A véletlen minta fogalma Pontbecslés és hibája Intervallumbecslés A hipotézisvizsgálat alapfogalmai A legegyszerűbb statisztikai
II. A következtetési statisztika alapfogalmai Tartalom Statisztikai következtetések A véletlen minta fogalma Pontbecslés és hibája Intervallumbecslés A hipotézisvizsgálat alapfogalmai A legegyszerűbb statisztikai
Egyszerű programozási tételek
 Egyszerű programozási tételek Sorozatszámítás tétele Például az X tömbben kövek súlyát tároljuk. Ha ki kellene számolni az összsúlyt, akkor az S = f(s, X(i)) helyére S = S + X(i) kell írni. Az f0 tartalmazza
Egyszerű programozási tételek Sorozatszámítás tétele Például az X tömbben kövek súlyát tároljuk. Ha ki kellene számolni az összsúlyt, akkor az S = f(s, X(i)) helyére S = S + X(i) kell írni. Az f0 tartalmazza
10. Valószínűségszámítás
 . Valószínűségszámítás.. Események A valószínűségszámítás nagyon leegyszerűsítve események bekövetkezésének valószínűségével foglalkozik. Példák: Ha egy játékban egy dobókockával dobunk, akkor a kockadobás
. Valószínűségszámítás.. Események A valószínűségszámítás nagyon leegyszerűsítve események bekövetkezésének valószínűségével foglalkozik. Példák: Ha egy játékban egy dobókockával dobunk, akkor a kockadobás
Nemzeti alaptanterv 2012 MATEMATIKA
 ALAPELVEK, CÉLOK Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
ALAPELVEK, CÉLOK Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
különösen a média közleményeiben való reális tájékozódást. Mindehhez elengedhetetlen egyszerű matematikai szövegek értelmezése, elemzése.
 MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
Gyakorlatok. P (n) = P (n 1) + 2P (n 2) + P (n 3) ha n 4, (utolsó lépésként l, hl, u, hu-t léphetünk).
 Gyakorlatok Din 1 Jelölje P (n) azt a számot, ahányféleképpen mehetünk le egy n lépcsőfokból álló lépcsőn a következő mozgáselemek egy sorozatával (zárójelben, hogy mennyit mozgunk az adott elemmel): lépés
Gyakorlatok Din 1 Jelölje P (n) azt a számot, ahányféleképpen mehetünk le egy n lépcsőfokból álló lépcsőn a következő mozgáselemek egy sorozatával (zárójelben, hogy mennyit mozgunk az adott elemmel): lépés
különösen a média közleményeiben való reális tájékozódást. Mindehhez elengedhetetlen egyszerű matematikai szövegek értelmezése, elemzése.
 MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson amatematikáról, mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson amatematikáról, mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
RENDELKEZÉSRE ÁLLÓ SZÉLENERGIA TENDENCIÁI HAZÁNKBAN A XXI. SZÁZAD SORÁN
 RENDELKEZÉSRE ÁLLÓ SZÉLENERGIA TENDENCIÁI HAZÁNKBAN A XXI. SZÁZAD SORÁN Péliné Németh Csilla 1,2 Radics Kornélia 1,2 Bartholy Judit 2 1 MH Geoinformációs Szolgálat 2 ELTE Meteorológiai Tanszék Vázlat 1.
RENDELKEZÉSRE ÁLLÓ SZÉLENERGIA TENDENCIÁI HAZÁNKBAN A XXI. SZÁZAD SORÁN Péliné Németh Csilla 1,2 Radics Kornélia 1,2 Bartholy Judit 2 1 MH Geoinformációs Szolgálat 2 ELTE Meteorológiai Tanszék Vázlat 1.
NT-17102 Matematika 9. (Heuréka) Tanmenetjavaslat
 NT-17102 Matematika 9. (Heuréka) Tanmenetjavaslat Ezzel a segédanyaggal szeretnék segítséget nyújtani a középiskolák azon matematikatanárainak, akik a matematikai oktatáshoz és neveléshez Dr. Fried Katalin
NT-17102 Matematika 9. (Heuréka) Tanmenetjavaslat Ezzel a segédanyaggal szeretnék segítséget nyújtani a középiskolák azon matematikatanárainak, akik a matematikai oktatáshoz és neveléshez Dr. Fried Katalin
VONALVEZETÉS TERVEZÉSE
 VONALVEZETÉS TERVEZÉSE A vonalvezetés tervezésének általános követelményei A tervezési sebesség Látótávolságok Vízszintes vonalvezetés Magassági vonalvezetés Burkolatszélek vonalvezetése Térbeli tervezés
VONALVEZETÉS TERVEZÉSE A vonalvezetés tervezésének általános követelményei A tervezési sebesség Látótávolságok Vízszintes vonalvezetés Magassági vonalvezetés Burkolatszélek vonalvezetése Térbeli tervezés
SZÁMVITEL TÁRGYAK 2005/2006 1. FÉLÉV
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gazdaság- és Társadalomtudományi Kar Pénzügy és Számvitel Tanszék SZÁMVITEL TÁRGYAK 2005/2006 1. FÉLÉV - az év elején kiadott követelményrendszer módosításai
Budapesti Műszaki és Gazdaságtudományi Egyetem Gazdaság- és Társadalomtudományi Kar Pénzügy és Számvitel Tanszék SZÁMVITEL TÁRGYAK 2005/2006 1. FÉLÉV - az év elején kiadott követelményrendszer módosításai
Apor Vilmos Katolikus Iskolaközpont. Helyi tanterv. Matematika. készült. a 51/2012. (XII. 21.) EMMI rendelet 1. sz. melléklet 1-4./1.2.3.
 1 Apor Vilmos Katolikus Iskolaközpont Helyi tanterv Matematika készült a 51/2012. (XII. 21.) EMMI rendelet 1. sz. melléklet 1-4./1.2.3. alapján 1-4. évfolyam 2 MATEMATIKA Az iskolai matematikatanítás célja,
1 Apor Vilmos Katolikus Iskolaközpont Helyi tanterv Matematika készült a 51/2012. (XII. 21.) EMMI rendelet 1. sz. melléklet 1-4./1.2.3. alapján 1-4. évfolyam 2 MATEMATIKA Az iskolai matematikatanítás célja,
MATEMATIKA TAGOZAT 5-8. BEVEZETŐ. 5. évfolyam
 BEVEZETŐ Ez a helyi tanterv a kerettanterv Emelet matematika A változata alapján készült. Az emelt oktatás során olyan tanulóknak kívánunk magasabb szintű ismerteket nyújtani, akik matematikából átlag
BEVEZETŐ Ez a helyi tanterv a kerettanterv Emelet matematika A változata alapján készült. Az emelt oktatás során olyan tanulóknak kívánunk magasabb szintű ismerteket nyújtani, akik matematikából átlag
Kaposvár Megyei Jogú Város Önkormányzata 14/2014. (IV. 28.) önkormányzati rendelete
 Kaposvár Megyei Jogú Város Önkormányzata 14/2014. (IV. 28.) önkormányzati rendelete Kaposvár Építési Szabályzatának és Szabályozási Tervének megállapításáról szóló 70/2005. (XII. 15.) önkormányzati rendelet
Kaposvár Megyei Jogú Város Önkormányzata 14/2014. (IV. 28.) önkormányzati rendelete Kaposvár Építési Szabályzatának és Szabályozási Tervének megállapításáról szóló 70/2005. (XII. 15.) önkormányzati rendelet
VALÓSZÍNŰSÉG, STATISZTIKA
 0893. MODUL VALÓSZÍNŰSÉG, STATISZTIKA Felmérés Készítette: Pintér Klára Matematika A 8. évfolyam 0892. modul: Valószínűség, statisztika Felmérés 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
0893. MODUL VALÓSZÍNŰSÉG, STATISZTIKA Felmérés Készítette: Pintér Klára Matematika A 8. évfolyam 0892. modul: Valószínűség, statisztika Felmérés 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
MATEMATIKA 9. osztály Segédanyag 4 óra/hét
 MATEMATIKA 9. osztály Segédanyag 4 óra/hét - 1 - Az óraszámok az AROMOBAN követhetőek nyomon! A tananyag feldolgozása a SOKSZÍNŰ MATEMATIKA (Mozaik, 013) tankönyv és a SOKSZÍNŰ MATEMATIKA FELADATGYŰJTEMÉNY
MATEMATIKA 9. osztály Segédanyag 4 óra/hét - 1 - Az óraszámok az AROMOBAN követhetőek nyomon! A tananyag feldolgozása a SOKSZÍNŰ MATEMATIKA (Mozaik, 013) tankönyv és a SOKSZÍNŰ MATEMATIKA FELADATGYŰJTEMÉNY
matematikai statisztika 2006. október 24.
 Valószínűségszámítás és matematikai statisztika 2006. október 24. ii Tartalomjegyzék I. Valószínűségszámítás 1 1. Véletlen jelenségek matematikai modellje 3 1.1. Valószínűségi mező..............................
Valószínűségszámítás és matematikai statisztika 2006. október 24. ii Tartalomjegyzék I. Valószínűségszámítás 1 1. Véletlen jelenségek matematikai modellje 3 1.1. Valószínűségi mező..............................
A térinformatika t. Az informáci. ciós s rendszerek funkciói. Az adatok vizsgálata
 Térinformatika Elemzések 1. Az informáci ciós s rendszerek funkciói adatnyerés s (input) adatkezelés s (management) adatelemzés s (analysis) adatmegjelenítés s (presentation) Összeállította: Dr. Szűcs
Térinformatika Elemzések 1. Az informáci ciós s rendszerek funkciói adatnyerés s (input) adatkezelés s (management) adatelemzés s (analysis) adatmegjelenítés s (presentation) Összeállította: Dr. Szűcs
Budapesti Műszaki és Gazdaságtudományi Egyetem Gazdaság- és Társadalomtudományi Kar
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gazdaság- és Társadalomtudományi Kar Dr. Kövesi János Erdei János Nagy Jenő Bence Dr. Tóth Zsuzsanna Eszter Gazdaságstatisztika Oktatási segédanyag a Gazdaságstatisztika
Budapesti Műszaki és Gazdaságtudományi Egyetem Gazdaság- és Társadalomtudományi Kar Dr. Kövesi János Erdei János Nagy Jenő Bence Dr. Tóth Zsuzsanna Eszter Gazdaságstatisztika Oktatási segédanyag a Gazdaságstatisztika
Felszín- és térfogatszámítás (emelt szint)
 Felszín- és térfogatszámítás (emelt szint) (ESZÉV 2004.minta III./7) Egy négyoldalú gúla alaplapja rombusz. A gúla csúcsa a rombusz középpontja felett van, attól 82 cm távolságra. A rombusz oldalának hossza
Felszín- és térfogatszámítás (emelt szint) (ESZÉV 2004.minta III./7) Egy négyoldalú gúla alaplapja rombusz. A gúla csúcsa a rombusz középpontja felett van, attól 82 cm távolságra. A rombusz oldalának hossza
Számtani- és mértani sorozatos feladatok (középszint)
 Számtani- és mértani sorozatos feladatok (középszint) (KSZÉV Minta (2) 2004.05/II/16) a) Egy számtani sorozat első tagja 9, különbsége pedig 4. Adja meg e számtani sorozat első 5 tagjának az összegét!
Számtani- és mértani sorozatos feladatok (középszint) (KSZÉV Minta (2) 2004.05/II/16) a) Egy számtani sorozat első tagja 9, különbsége pedig 4. Adja meg e számtani sorozat első 5 tagjának az összegét!
különösen a média közleményeiben való reális tájékozódást. Mindehhez elengedhetetlen egyszerű matematikai szövegek értelmezése, elemzése.
 MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról, mint tudásrendszerről, és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról, mint tudásrendszerről, és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
Oktatáskutató és Fejlesztő Intézet TÁMOP-3.1.1-11/1-2012-0001 XXI. századi közoktatás (fejlesztés, koordináció) II. szakasz. Fejlesztőfeladatok
 Oktatáskutató és Fejlesztő Intézet TÁMOP-3.1.1-11/1-2012-0001 XXI. századi közoktatás (fejlesztés, koordináció) II. szakasz Fejlesztőfeladatok MATEMATIKA 4. szint 2015 Oktatáskutató és Fejlesztő Intézet
Oktatáskutató és Fejlesztő Intézet TÁMOP-3.1.1-11/1-2012-0001 XXI. századi közoktatás (fejlesztés, koordináció) II. szakasz Fejlesztőfeladatok MATEMATIKA 4. szint 2015 Oktatáskutató és Fejlesztő Intézet
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika emelt szint 0613 ÉRETTSÉGI VIZSGA 007. május 8. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Formai előírások: Fontos tudnivalók
Matematika emelt szint 0613 ÉRETTSÉGI VIZSGA 007. május 8. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Formai előírások: Fontos tudnivalók
MATEMATIKA 1-2.osztály
 MATEMATIKA 1-2.osztály A matematikatanítás feladata a matematika különböző arculatainak bemutatása. A tanulók matematikai gondolkodásának fejlesztése során alapvető cél, hogy mind inkább ki tudják választani
MATEMATIKA 1-2.osztály A matematikatanítás feladata a matematika különböző arculatainak bemutatása. A tanulók matematikai gondolkodásának fejlesztése során alapvető cél, hogy mind inkább ki tudják választani
JOGSZABÁLY. LI. ÉVFOLYAM, 15. SZÁM Ára: 693 Ft 2007. JÚNIUS 5. TARTALOM. 1. (1) A rendelet hatálya fenntartótól függetlenül
 LI. ÉVFOLYAM, 15. SZÁM Ára: 693 Ft 2007. JÚNIUS 5. oldal JOGSZABÁLY 24/2007. (IV. 2.) OKM rendelet a közoktatás minõségbiztosításáról és minõségfejlesztésérõl szóló 3/2002. (II. 15.) OM rendelet módosításáról...
LI. ÉVFOLYAM, 15. SZÁM Ára: 693 Ft 2007. JÚNIUS 5. oldal JOGSZABÁLY 24/2007. (IV. 2.) OKM rendelet a közoktatás minõségbiztosításáról és minõségfejlesztésérõl szóló 3/2002. (II. 15.) OM rendelet módosításáról...
STATISZTIKAI ADATOK. Összeállította fazekas károly köllő jános lakatos judit lázár györgy
 STATISZTIKAI ADATOK Összeállította fazekas károly köllő jános lakatos judit lázár györgy statisztikai adatok 1. Alapvető gazdasági adatok 2. Népesség 3. Gazdasági aktivitás 4. Foglalkoztatottak 5. Munkanélküliek
STATISZTIKAI ADATOK Összeállította fazekas károly köllő jános lakatos judit lázár györgy statisztikai adatok 1. Alapvető gazdasági adatok 2. Népesség 3. Gazdasági aktivitás 4. Foglalkoztatottak 5. Munkanélküliek
Munkafüzet megoldások 7. osztályos tanulók számára. Makara Ágnes Bankáné Mező Katalin Argayné Magyar Bernadette Vépy-Benyhe Judit
 Kalandtúra 7. unkafüzet megoldások 7. osztályos tanulók számára akara Ágnes Bankáné ező Katalin Argayné agyar Bernadette Vépy-Benyhe Judit BEELEGÍTŐ GONDOLKODÁS. SZÓRAKOZTATÓ FELADVÁNYOK. oldal. 6... 6.
Kalandtúra 7. unkafüzet megoldások 7. osztályos tanulók számára akara Ágnes Bankáné ező Katalin Argayné agyar Bernadette Vépy-Benyhe Judit BEELEGÍTŐ GONDOLKODÁS. SZÓRAKOZTATÓ FELADVÁNYOK. oldal. 6... 6.
ÚTMUTATÓ a külterületi közúthálózati fejlesztések költség-haszon vizsgálatához
 Gazdasági és Közlekedési Minisztérium Közúti Főosztály ÚTMUTATÓ a külterületi közúthálózati fejlesztések költség-haszon vizsgálatához I. 2002. december 2002. december 2. Útmutató a külterületi közúthálózati
Gazdasági és Közlekedési Minisztérium Közúti Főosztály ÚTMUTATÓ a külterületi közúthálózati fejlesztések költség-haszon vizsgálatához I. 2002. december 2002. december 2. Útmutató a külterületi közúthálózati
TARTALOMJEGYZÉK ELŐSZÓ... 7 1. GONDOLKOZZ ÉS SZÁMOLJ!... 9 2. HOZZÁRENDELÉS, FÜGGVÉNY... 69
 TARTALOMJEGYZÉK ELŐSZÓ............................................................ 7 1. GONDOLKOZZ ÉS SZÁMOLJ!............................. 9 Mit tanultunk a számokról?............................................
TARTALOMJEGYZÉK ELŐSZÓ............................................................ 7 1. GONDOLKOZZ ÉS SZÁMOLJ!............................. 9 Mit tanultunk a számokról?............................................
MINİSÉGSZABÁLYOZÁS. Dr. Drégelyi-Kiss Ágota e-mail: dregelyi.agota@bgk.uni-obuda.hu http://uni-obuda.hu/users/dregelyia
 MINİSÉGSZABÁLYOZÁS A GÉPIPARBAN Dr. Drégelyi-Kiss Ágota e-mail: dregelyi.agota@bgk.uni-obuda.hu http://uni-obuda.hu/users/dregelyia ISO 9000:2008 A STATISZTIKAI MÓDSZEREK HASZNÁLATÁRÓL A statisztikai módszerek
MINİSÉGSZABÁLYOZÁS A GÉPIPARBAN Dr. Drégelyi-Kiss Ágota e-mail: dregelyi.agota@bgk.uni-obuda.hu http://uni-obuda.hu/users/dregelyia ISO 9000:2008 A STATISZTIKAI MÓDSZEREK HASZNÁLATÁRÓL A statisztikai módszerek
Fazekas nyílt verseny matematikából 8. osztály, speciális kategória
 Fazekas nyílt verseny matematikából 8. osztály, speciális kategória 2005. január 12. feladatok kidolgozására két óra áll rendelkezésre. Számológép nem használható. példák tetszőleges sorrendben megoldhatók.
Fazekas nyílt verseny matematikából 8. osztály, speciális kategória 2005. január 12. feladatok kidolgozására két óra áll rendelkezésre. Számológép nem használható. példák tetszőleges sorrendben megoldhatók.

