Egyszerő kémiai számítások
|
|
|
- Ottó Barta
- 10 évvel ezelőtt
- Látták:
Átírás
1 Egyszerő kéiai száítások z egyes fizikai, illetve kéiai eyiségek közötti összefüggéseket éréssel állapítjuk eg. hhoz, hogy egy eyiséget éri tudjuk, a eyiségek valaely rögzített értékét (értékegység) kell alapul választai. apjaikba az SI értékegység-redszert haszáljuk a érések és száítások sorá. z SI haszálatát, prefixuait és átváltásukat egyéileg gyakorolják! kéiai változások fotos értékegysége a ól, aely az ayageyiség kifejezésére szolgál. Jele:, a értékegység rövidítése ol (ahogy a töeg jele:, és a kilogra rövidítése a kg) Egy ól az ayageyisége aak az ayagak, aely ayi azoos elei egységet (etitást: ot, olekulát, iot, elektrot, stb.) tartalaz, it aháy va potosa 0,012 kg 12 C-izotópba. Egy ól ayagba 6, elei egység található (vogadroálladó: 6, /ol). dott ayageyiség és bee lévı etitás részecskeszáa között tehát az vogadro-álladó az aráyossági téyezı:. 1. Egy darabka gyéát 5, széot tartalaz. Háy ól C- va bee? 5, / 6, /ol 8, ol 2. Háy gázolekula va abba a itába, aelyik 2,155 ólt tartalaz? 2,155 ol 6, /ol 1, bba az esetbe, ha az elei egység összetett (pl. okba proto, eutro, elektro; olekulába ok, stb.) akkor azok száát egy további szorzószá fogja egutati: kisebb egység u agyobb egység 3. Háy oxigéot tartalaz 1,88 ol ózoolekula? (az ózo olekula e O 3, vagyis u 3 lesz) O- O- 3 ózo 3 ózo O- 3 ózo O- 3 6, /ol 1,88 ol 3, Ez a LEGO-elv (2) alappaelje 4. Háy ól proto található 3, szilíciuba? (a szilíciu redszáa aiek száértéke egegyezik 1 Si-ba lévı protook száával: 14, vagyis u 14) Si proto 3 Si 14 proto proto 14 3, / 6, /ol 7, ol 1
2 5. Háy ól a 65-ös réz-izotóp ayageyisége, ha a ita 5, eutrot tartalaz? (a réz redszáa: 29, töegszáa: 65, ekkor a eutrook száa ; azaz u 36) eutro eutro eutro 36 Cu 36 Cu Cu 36 Cu 5, / 36 6, /ol 2, ol kéiai ayag töege és az ayageyisége között állapít eg aráyosságot a oláris töeg (jele:, értékegység rövidítése: g/ol). z eleek oláris töegét azok izotópjaiak terészetes elıfordulása szeriti súlyozott átlagát a periódusos redszer, illetve egyes táblázatok tartalazzák (átlagos oláris töeg). pl. a klór 75,77 % 35 Cl ot (34,9689 g/ol) és 24,23 % 37 Cl ot (36,9658 g/ol) tartalaz, így Cl 35,4527 g/ol 35,45 g/ol Korábba azt tapasztalhatta, hogy száításokba az eleek oláris töegéek egészre kerekített értékét, valait az izotópok töegszáát haszálták azok oláris töege száértékekét. zoba ez az elhayagolás, kerekítés e vezet helyes értékhez, és az vogadro-álladó 6, /ol helyett se csak a száot haszáljuk. 6. ekkora az ayageyisége aak az aluíiu-fólia darabak, elyek töege 0,4582 g? l l l 0,4582 g / 26,98 g/ol 1, ol l 7. Háy l- va az elıbbi fóliába, vagyis 0,4582 g-ba? ugyaarról az ayagról va szó, vagyis a töeg és oláris töeg, valait a részecskeszá és vogadro-álladó aráy egyarát az aluíiu ayageyiségét adja eg: l l l l l l l 6, /ol 0,4582 g / 26,98 g/ol 1, z ezüst 51,84 % 107 g-t és 48,16 % 109 g-t tartalaz. 107 g oláris töege 106, g/ol. ekkora a 109 g oláris töege? ( g 107,87 g/ol) az izotópok elıfordulási aráyukak egfelelıe járulak hozzá az átlagos oláris töeg értékéhez: a 107g + b 109g (107,87 g/ol - 0, , g/ol) / 0, g 109g 108,9078 g/ol 9. Háy g aak a kékristályak a töege, aelyik 5, S 8 -olekulát tartalaz? a kéok oláris töege adott, tehát az S- 8 olekula összefüggést haszáljuk fel: S olekula S olekula 8 alakba S 8 S S 8 32,07 g/ol 5, / 6, /ol 0,0228 g 22,8 g tapasztalati tel jelzett vegyületek, olekulák és összetett iook, oláris töegét egkapjuk, ha az alkotó eleek oláris töegét összeadjuk, aak figyelebevételével, hogy a be háy juk található. száított oláris töeg és a töeg, valait a részecskeszá kapcsolatára ugyaazok az összefüggések érvéyesek, it az eleekél! 2
3 1. hét 1. hét 10. ekkora a oláris töege az etaolak (CH 3 CH 2 OH)? 1 olekula etaolba 2 C, 6 H és 1 O va, 1 ólyi olekulába 2 ol C, 6 ol H és 1 ol O 1 ol C 2 H 6 O-ba C: 2 ol 12,01 g/ol 24,02 g H: 6 ol 1,008 g/ol 6,05 g O: 1 ol 16,00 g/ol 16,00 g Σ 46,07 g / 1 ol 46,07 g/ol 11. Háy klorid iot tartalaz a koyhasó (acl) 45,0 g-ja? a egységbe 1 Cl -io va, így u 1; Cl acl 1 Cl acl acl acl Cl 1 acl Cl 6, /ol 0,0450 g / 58,44 g/ol 4, Háy gra itrogét tartalaz 2,00 g karbaid (H 2 COH 2 )? a olekulába 2 - va, így u 2; 2 karbaid a kisebb egység töegét keressük, és a agyobb egységek is töegét iserjük, ezért a töeg és oláris töeg háyadosával kifejezett ayageyiségeket haszáljuk: karbaid karbaid 2 2 karbaid karbaid 2 14,01 g/ol 2,00 g / 60,05 g/ol 0,933 g Vegyületek e és összetétele vegyületek éek iseretébe (eghatározva a oláris töeget) az alkotó ok, vagy csoportok töegtörtje (W), illetve töeg%-a () is kiszáítható. töegtört és a töegszázalék általáosa haszálható defiiáló e: Vegyületekre: W kopoes összes W és kopoes z u összefüggést (LEGO-2 alappaelt) haszáljuk fel, a töeg és oláris töeg háyadost behelyettesítve, ajd úgy redezzük, hogy a töegtört vagy töeg% kifejezhetı legye: u W u illetve u 13. Határozzuk eg a peicilli olekula (C 14 H 20 O 4 2 S) töeg%-os összetételét! 100 u 312,4 g/ol C ,01 g/ol / 312,4 g/ol 53,81 H ,008 g/ol / 312,4 g/ol 6,45 O ,00 g/ol / 312,4 g/ol 20, ,01 g/ol / 312,4 g/ol 8,70 S ,07 g/ol / 312,4 g/ol 10,27 Ehhez hasolóa a töeg%-os összetétel lehetıséget ad a vegyület éek eghatározására. Ha isert a oláris töeg, akkor az u értékét keressük valaeyi alkotó ra külökülö u u 100 összes 3
4 1. hét 1. hét 14. z adipisav töeg%-os összetétele: 49,31 % szé, 43,79 % oxigé és a aradék hidrogé, oláris töege 146,1 g/ol. Állapítsuk eg eek a szerves savak a ét! u 100 u C 49,31 146,1 g/ol / (100 12,01 g/ol) 6,00 u O 43,79 146,1 g/ol / (100 16,00 g/ol) 4,00 u H 6,90 146,1 g/ol / (100 1,008 g/ol) 10,00 C 6 H 10 O 2 Ha e isert a oláris töeg, akkor a vegyület potosa 100 grajából iduluk ki, ert ekkor a egadott %-os értékek azoal az ok g-jakét értelezhetık. z alkotó ok ayageyiségét kiszáítva egkapjuk, hogy 100 g vegyületbe az adott háy ólja va, ajd azokat a legkisebb értékhez aráyítva jutuk az alkotó ok egész száú ayageyiségét Ha a kopoesek töege adott, akkor az a kiidulási töeg. 15. Határozzuk eg a tapasztalati ét a warfari evő patkáyírtó szerek, aelyek töeg%- os összetétele: 74,01 % szé, 5,23 % hidrogé és 20,76 % oxigé! (g) C 74,01 g / 12,01 g/ol 6,162 ol C / O 6,162 ol / 1,298 ol 4,75 ol H 5,23 g / 1,008 g/ol 5,188 ol H / O 5,188 ol / 1,298 ol 4,00 ol O 20,76 g / 16,00 g/ol 1,298 ol O / O 1,00 ol ahhoz, hogy egész száokat kapjuk az egyes száok 4-szeresét kell vei: C 19 H 16 O Egy karbaid ita eleezésekor egállapították, hogy 1,121 g itrogét, 0,161 g hidrogét, 0,480 g szeet és 0,640 g oxigét tartalaz. i a tapasztalati e a karbaidak? 1,121 g / 14,01 g/ol 0,0795 ol / C 0,0795 ol / 0,0400 ol 2 H 0,161 g / 1,008 g/ol 0,1597 ol H / C 0,1597 ol / 0,0400 ol 4 C 0,480 g / 12,01 g/ol 0,0400 ol C / C 0,0400 ol / 0,0400 ol 1 O 0,640 g / 16,00 g/ol 0,0400 ol O / C 0,0400 ol / 0,0400 ol 1 CH 4 2 O Száítási feladatok 1. kéiai eleek egyikéek csak egyetle terészetes izotópja létezik, aelyek egyetle ja 9, g töegő. zoosítsuk a oláris töeg alapjá az ot! Ugyaarról az ayagról va szó, így a LEGO-(1) alappaelt haszáljuk. Részecske töeget iserük, és oláris töeget keresük , g (1) keresett isert 23 6, /ol 6, /ol 9, g 55,58 g/ol a keresett ele a agá 2. z oxigé háro izotóp keveréke, elyek terészetes elıfordulási aráya és potos töege az alábbi: 16-os töegszáú 99,759 % - 15,99491 g/ol; 17-es töegszáú 0,037 % - 17,00450 g/ol; 18-as töegszáú 0,204 % - 18,00490 g/ol. eyi az oxigé oláris töege? 4
5 z izotópok elıfordulási %-a a részecskék %-át fejezi ki (e töeg%): így felírhatjuk 100 ol oxigére: O g/ol (99,759 ol * 15,99491 g/ol + 0,037 ol * 17,00450 g/ol + 0,204 ol * 18,00490 g/ol) / 100,00 ol 15,996 g/ol 3. szılıcukor tabletta glükóz-oohidrát (C 6 H 12 O 6 H 2 O) ellett talkuot és agéziusztearátot tartalaz. Háy töeg% vízetes glükózt tartalaz a 2,500 g töegő tabletta, ha tudjuk, hogy bee 7, vízolekula va? glükóz olekulák száa egegyezik a vízolekuláéval, ezért a LEGO-(1) alappaelre építkezük, és felhaszáljuk a töeg% összefüggést: (1) keresett isert glükóz és glükóz 100 glükóz tabletta idkét összefüggésbıl kifejezzük a glükóz töegét, és egyelıséget állapítuk eg, ajd kifejezzük a értékét: 21 glükóz tabletta 100 glükóz 100 7, ,16 g/ol glükóz w % , /ol 2,500 g 88,70 4. z adreali olekula töeg%-os összetétele: 56,79 % szé, 6,56 % hidrogé, 28,37 % oxigé és 8,28 % itrogé. Állapítsuk eg az adreali tapasztalati ét! C c H h O o be az c, h, o, az egyes eleek ayageyiségét jeleti és csak egész szá lehet. Ha tetszıleges össztöegbe egállapítjuk az összetevık óljaiak száát, akkor azok egyáshoz viszoyított aráya a keresett ayageyiségeket adja. Célszerőe az össztöeget 100,00 g-ak szokás választai, ert ekkor a töeg%-os adatok egybe a kopoesek g-jait adják: C 56,79 g H 6,56 g C 4,73 ol H 6,50 ol 12,01g/ol 1,008 g/ol C H tabletta O 28,37 g 8,28 g O 1,77 ol 0,591 ol 16,00 g/ol 14,01g/ol O C:H:O: 8:11:3:1 a keresett : C 8 H 11 O 3 5. polifeol oxidázok csoportjába tartozó kék szíő lakkáz-ezi egtalálható egy fakorhadást elıidézı gobába is (Polyporus versicolor). ekkora a lakkáz-ezi oláris töege, ha olekulájába 4 réz va és a réztartalo 0,390 töeg%? Cu- alkotórésze az eziek, ezért a LEGO-(2) alappaelt és a töeg% összefüggését haszáljuk a száításba. (2) kisebb egység u agyobb egység, ebbe az esetbe u 4 (az ezibe 4 Cu- va). Cu ezi Cu Cu 4 ezi 4 és 100 Cu ezi ezi idkét összefüggésbıl kifejezzük az Cu / ezi háyadost, ajd a keresett oláris töeget: Cu Cu 100 Cu ,55 g/ol 4 ezi ,390 ezi ezi ezi 6, g/ol 6. Háy fluoridio található a kocka alakú 10,65 élhosszúságú fluorit-kristályba (CaF 2 ), elyek sőrősége 3,150 g/c 3? LEGO-(2) alappaelre építkezük és a sőrőség összefüggését haszáljuk fel: 5
6 (2) kisebb egység u agyobb egység, és u 2 (a CaF 2 -be 2 fluorid va), részecskeszáot keresük: F 2 fluorit F fluorit fluorit 2 és ρ fluorit Vfluorit a sőrőségbıl kifejezzük a fluorit töegét és az alapba helyettesítjük, ajd a fluorid részecskeszáot eghatározzuk: ρ Vfluorit 2 6, /ol 3,150 g/c (1,065 c) F 2 78,08 g/ol F 5, fluorit 7. z eutektikus összetételő, alacsoy olvadáspotú S-Pb-Cd ötvözetbe az ó:ólo ólaráya 2,73:1,00 és az ólo:kadiu töegaráya 1,78:1,00. Állapítsuk eg az ötvözet töeg%-os összetételét! ólaráy iseretébe a LEGO-(2)-vel aalóg összefüggés és a töegaráyok segítségével tudjuk a töeg%-ot eghatározi: S Pb S 2,73 Pb 2,73 és Pb 1, 78 valait 100 S Pb Cd ötvözet száítsuk ki elıször, hogy ha 1,00 g kadiu va jele az ötvözetbe, akkor eyi a többi kopoes töege: Pb S 2,73 1,78 g 118,71g/ol Pb 1,78 1,00 g 1,78 g; 2,73 Pb 207,2 g/ol vagyis ekkor az ötvözet összes töege ötvözet 1,00 g + 1,78 g + 2,78 g 5,56 g a töeg%-ok: Cd 100 1,00 g/5,56 g 17,99 % Pb 100 1,78 g/5,56 g 32,01 % S 100 2,78 g/5,56 g 50,00 % S 2,78 g Feladatok 1. króak 4 terészetes izotópja va, aelyek töegszáa, elıfordulási %-a és oláris töege a következı: 50-es 4,35 % - 49,9461g/ol; 52-es 83,79 % - 51,9405 g/ol; 53-as 9,50 % - 52,9407 g/ol; 54-es 2,36 % - 53,9389 g/ol. Határozzuk eg a kró oláris töegét! (51,996 g/ol) 2. z aszpartá (C 14 H 18 2 O 5 ) egy esterséges édesítıszer (utra-sweet), aely 160-szor édesebb, it a kristálycukor. Száítsuk ki, hogy háy olekula va 5,0 g aszpartába? (1, ) 3. Háy ké található az 1,225 c élhosszúságú pirit-kockába (FeS 2 ), elyek sőrősége 5,100 g/c 3? (9, ) 4. Egy bizutot, ólot és ót tartalazó ötvözetbe, aelyek olvadáspotja a víz forráspotja közelébe va, a Bi:Pb:S ok aráya 10:6:5. ilye töegő ötvözet tartalaz potosa 1 ólyi ot? (187 g) 5. djuk eg a töeg%-os összetételét az YBa 2 Cu 3 O 7 összetételő vegyületek, aelye elsı alkaloal tapasztalták a szupravezetés téyét. (Y: 13,35 Ba: 41,22 Cu: 28,62 O: 16,81 %) 6
2. LOGIKAI FÜGGVÉNYEK MEGADÁSI MÓDSZEREI. A tananyag célja: a többváltozós logikai függvények megadási módszereinek gyakorlása.
 . LOGIKI ÜGGVÉNYEK EGÁSI ÓSZEREI taayag célja: a többváltozós logikai függvéyek egadási ódszereiek gyakorlása. Eléleti iseretayag: r. jtoyi Istvá: igitális redszerek I.... pot. Eléleti áttekités.. i jellezi
. LOGIKI ÜGGVÉNYEK EGÁSI ÓSZEREI taayag célja: a többváltozós logikai függvéyek egadási ódszereiek gyakorlása. Eléleti iseretayag: r. jtoyi Istvá: igitális redszerek I.... pot. Eléleti áttekités.. i jellezi
1. hét 1. hét. 1. hét
 Laboratóriui érések - bevezetés 1. hét A hallgató legyen tájékozott a gyakorlati feladatok téaköreit, azok sorrendjét tekintve, iserje a gyakorlatokhoz kapcsolódó pontozási, értékelési rendszert, legyen
Laboratóriui érések - bevezetés 1. hét A hallgató legyen tájékozott a gyakorlati feladatok téaköreit, azok sorrendjét tekintve, iserje a gyakorlatokhoz kapcsolódó pontozási, értékelési rendszert, legyen
Mágneses momentum, mágneses szuszceptibilitás
 Mágneses oentu, ágneses szuszceptibilitás A olekuláknak (atooknak, ionoknak) elektronszerkezetüktől függően lehet állandóan eglévő, azaz peranens ágneses oentua (ha van bennük párosítatlan elektron, azaz
Mágneses oentu, ágneses szuszceptibilitás A olekuláknak (atooknak, ionoknak) elektronszerkezetüktől függően lehet állandóan eglévő, azaz peranens ágneses oentua (ha van bennük párosítatlan elektron, azaz
A forgalomba belépő gépjárművek többlet károsanyag kibocsátásának számítása a nemzetközi határértékek figyelembe vételével
 Török Ádá, Zöldy Máté Közúti Közlekedés A foraloba belépő épjárűvek többlet károsaya kibocsátásáak száítása a ezetközi határértékek fiyelebe vételével A XX század véé és a XXI század elejé a otorizált
Török Ádá, Zöldy Máté Közúti Közlekedés A foraloba belépő épjárűvek többlet károsaya kibocsátásáak száítása a ezetközi határértékek fiyelebe vételével A XX század véé és a XXI század elejé a otorizált
2.6. Az ideális gáz fundamentális egyenlete
 Fejezetek a fzka kéából.6. Az deáls gáz fudaetáls egyelete A legegyszerűbb terodaka redszer az u. deáls gáz. Erre jellező, hogy a részecskék között az egyetle kölcsöhatás a rugalas ütközés, és a részecskék
Fejezetek a fzka kéából.6. Az deáls gáz fudaetáls egyelete A legegyszerűbb terodaka redszer az u. deáls gáz. Erre jellező, hogy a részecskék között az egyetle kölcsöhatás a rugalas ütközés, és a részecskék
SZÁMELMÉLET. Vasile Berinde, Filippo Spagnolo
 SZÁMELMÉLET Vasile Beride, Filippo Spagolo A számelmélet a matematika egyik legrégibb ága, és az egyik legagyobb is egybe Eek a fejezetek az a célja, hogy egy elemi bevezetést yújtso az első szite lévő
SZÁMELMÉLET Vasile Beride, Filippo Spagolo A számelmélet a matematika egyik legrégibb ága, és az egyik legagyobb is egybe Eek a fejezetek az a célja, hogy egy elemi bevezetést yújtso az első szite lévő
A kurzus teljesítésének feltételei. Az I404 kódú kurzus teljesítéséhez meg kell oldani egy otthoni feladatot, határidő április 30.
 Évközi teljesítés A kurzus teljesítéséek feltételei Két gyakorlato egírt ZH, az elérhető 00 potból 50 potot kell eléri. Aki e teljesíti a feltételt a vizsgaidőszak első hetébe a vizsgára egedésért írhat
Évközi teljesítés A kurzus teljesítéséek feltételei Két gyakorlato egírt ZH, az elérhető 00 potból 50 potot kell eléri. Aki e teljesíti a feltételt a vizsgaidőszak első hetébe a vizsgára egedésért írhat
T I T - M T T. Hevesy György Kémiaverseny. A megyei forduló feladatlapja. 7. osztály. A versenyző jeligéje:... Megye:...
 T I T - M T T Hevesy György Kémiaverseny A megyei forduló feladatlapja 7. osztály A versenyző jeligéje:... Megye:... Elért pontszám: 1. feladat:... pont 2. feladat:... pont 3. feladat:... pont 4. feladat:...
T I T - M T T Hevesy György Kémiaverseny A megyei forduló feladatlapja 7. osztály A versenyző jeligéje:... Megye:... Elért pontszám: 1. feladat:... pont 2. feladat:... pont 3. feladat:... pont 4. feladat:...
FAIPARI ALAPISMERETEK
 Faipari alapiseretek középszit 1211 ÉRETTSÉGI VIZSGA 213. ájus 23. FAIPARI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIMA Fotos tudivalók
Faipari alapiseretek középszit 1211 ÉRETTSÉGI VIZSGA 213. ájus 23. FAIPARI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIMA Fotos tudivalók
Oktatási Hivatal KÉMIA I. A 2015/2016. tanévi Országos Középiskolai Tanulmányi Verseny második forduló. Javítási-értékelési útmutató I.
 ktatási Hivatal I. FELADATSR A 015/016. taévi rszágos Középiskolai Taulmáyi Versey második forduló KÉMIA I. Javítási-értékelési útmutató 1., Mg pot. Fr 1 pot 1 eltérés: 1 pot; mi. 0 pot 3. a) pl. 1 1 H
ktatási Hivatal I. FELADATSR A 015/016. taévi rszágos Középiskolai Taulmáyi Versey második forduló KÉMIA I. Javítási-értékelési útmutató 1., Mg pot. Fr 1 pot 1 eltérés: 1 pot; mi. 0 pot 3. a) pl. 1 1 H
2 x. Ez pedig nem lehetséges, mert ilyen x racionális szám nincs. Tehát f +g nem veszi fel a 0-t.
 Ászpóke csapat Kalló Beát, Nagy Baló Adás Nagy Jáos, éges Máto Fazekas tábo 008. Igaz-e, hogy ha az f, g: Q Q függvéyek szigoúa ooto őek és étékkészletük a teljes Q, akko az f g függvéy étékkészlete is
Ászpóke csapat Kalló Beát, Nagy Baló Adás Nagy Jáos, éges Máto Fazekas tábo 008. Igaz-e, hogy ha az f, g: Q Q függvéyek szigoúa ooto őek és étékkészletük a teljes Q, akko az f g függvéy étékkészlete is
3.1.1. Rugalmas elektronszórás; Recoil- és Doppler-effektus megfigyelése
 3.1.1. Rugalmas elektroszórás 45 3.1.1. Rugalmas elektroszórás; Recoil- és Doppler-effektus megfigyelése Aray, ikkel, szilícium és grafit mitákról rugalmasa visszaszórt elektrook eergiaeloszlását mértem
3.1.1. Rugalmas elektroszórás 45 3.1.1. Rugalmas elektroszórás; Recoil- és Doppler-effektus megfigyelése Aray, ikkel, szilícium és grafit mitákról rugalmasa visszaszórt elektrook eergiaeloszlását mértem
7. osztály Hevesy verseny, megyei forduló, 2003.
 Figyelem! A feladatokat ezen a feladatlapon oldd meg! Megoldásod olvasható és áttekinthető legyen! A feladatok megoldásában a gondolatmeneted követhető legyen! A feladatok megoldásához használhatod a periódusos
Figyelem! A feladatokat ezen a feladatlapon oldd meg! Megoldásod olvasható és áttekinthető legyen! A feladatok megoldásában a gondolatmeneted követhető legyen! A feladatok megoldásához használhatod a periódusos
Ingatlanfinanszírozás és befektetés
 Nyugat-Magyarországi Egyetem Geoiformatikai Kar Igatlameedzser 8000 Székesfehérvár, Pirosalma u. 1-3. Szakiráyú Továbbképzési Szak Igatlafiaszírozás és befektetés 2. Gazdasági matematikai alapok Szerzı:
Nyugat-Magyarországi Egyetem Geoiformatikai Kar Igatlameedzser 8000 Székesfehérvár, Pirosalma u. 1-3. Szakiráyú Továbbképzési Szak Igatlafiaszírozás és befektetés 2. Gazdasági matematikai alapok Szerzı:
6. változat. 3. Jelöld meg a nem molekuláris szerkezetű anyagot! A SO 2 ; Б C 6 H 12 O 6 ; В NaBr; Г CO 2.
 6. változat Az 1-től 16-ig terjedő feladatokban négy válaszlehetőség van, amelyek közül csak egy helyes. Válaszd ki a helyes választ és jelöld be a válaszlapon! 1. Jelöld meg azt a sort, amely helyesen
6. változat Az 1-től 16-ig terjedő feladatokban négy válaszlehetőség van, amelyek közül csak egy helyes. Válaszd ki a helyes választ és jelöld be a válaszlapon! 1. Jelöld meg azt a sort, amely helyesen
képzetes t. z = a + bj valós t. a = Rez 5.2. Műveletek algebrai alakban megadott komplex számokkal
 5. Komplex számok 5.1. Bevezetés Taulmáyaik sorá többször volt szükség az addig haszált számfogalom kiterjesztésére. Először csak természetes számokat ismertük, később haszáli kezdtük a törteket, illetve
5. Komplex számok 5.1. Bevezetés Taulmáyaik sorá többször volt szükség az addig haszált számfogalom kiterjesztésére. Először csak természetes számokat ismertük, később haszáli kezdtük a törteket, illetve
A feladatok megoldásához csak a kiadott periódusos rendszer és számológép használható!
 1 MŰVELTSÉGI VERSENY KÉMIA TERMÉSZETTUDOMÁNYI KATEGÓRIA Kedves Versenyző! A versenyen szereplő kérdések egy része általad már tanult tananyaghoz kapcsolódik, ugyanakkor a kérdések másik része olyan ismereteket
1 MŰVELTSÉGI VERSENY KÉMIA TERMÉSZETTUDOMÁNYI KATEGÓRIA Kedves Versenyző! A versenyen szereplő kérdések egy része általad már tanult tananyaghoz kapcsolódik, ugyanakkor a kérdések másik része olyan ismereteket
2012 február 7. (EZ CSAK A VERSENY UTÁN LEGYEN LETÖLTHETŐ!!!)
 1 A XXII. Öveges József fizika tanulányi verseny első fordulójának feladatai és azok egoldásának pontozása 2012 február 7. (EZ CSAK A VERSENY UTÁN LEGYEN LETÖLTHETŐ!!!) 1. Egy odellvasút ozdonya egyenletesen
1 A XXII. Öveges József fizika tanulányi verseny első fordulójának feladatai és azok egoldásának pontozása 2012 február 7. (EZ CSAK A VERSENY UTÁN LEGYEN LETÖLTHETŐ!!!) 1. Egy odellvasút ozdonya egyenletesen
2.4.29. OMEGA-3-SAVAKBAN GAZDAG ZSÍROS OLAJOK ZSÍRSAVÖSSZETÉTELE
 2.4.29. Oega-3-savakban gazdag zsíros olajok Ph.Hg.VIII. Ph.Eur.6.0-0/2008:20429 javított 6.0 2.4.29. OMEG-3-SVKBN GZDG ZSÍROS OLJOK ZSÍRSVÖSSZETÉTELE eghatározás alkalazható EPS- és DHS-tartalo kvantitatív
2.4.29. Oega-3-savakban gazdag zsíros olajok Ph.Hg.VIII. Ph.Eur.6.0-0/2008:20429 javított 6.0 2.4.29. OMEG-3-SVKBN GZDG ZSÍROS OLJOK ZSÍRSVÖSSZETÉTELE eghatározás alkalazható EPS- és DHS-tartalo kvantitatív
Az anyagi rendszerek csoportosítása
 Általános és szervetlen kémia 1. hét A kémia az anyagok tulajdonságainak leírásával, átalakulásaival, elıállításának lehetıségeivel és felhasználásával foglalkozik. Az általános kémia vizsgálja az anyagi
Általános és szervetlen kémia 1. hét A kémia az anyagok tulajdonságainak leírásával, átalakulásaival, elıállításának lehetıségeivel és felhasználásával foglalkozik. Az általános kémia vizsgálja az anyagi
Számsorozatok. 1. Alapfeladatok december 22. sorozat határértékét, ha. 1. Feladat: Határozzuk meg az a n = 3n2 + 7n 5n létezik.
 Számsorozatok 2015. december 22. 1. Alapfeladatok 1. Feladat: Határozzuk meg az a 2 + 7 5 2 + 4 létezik. sorozat határértékét, ha Megoldás: Mivel egy tört határértéke a kérdés, ezért vizsgáljuk meg el
Számsorozatok 2015. december 22. 1. Alapfeladatok 1. Feladat: Határozzuk meg az a 2 + 7 5 2 + 4 létezik. sorozat határértékét, ha Megoldás: Mivel egy tört határértéke a kérdés, ezért vizsgáljuk meg el
KÉMIA FELVÉTELI KÖVETELMÉNYEK
 KÉMIA FELVÉTELI KÖVETELMÉNYEK Atomszerkezettel kapcsolatos feladatok megoldása a periódusos rendszer segítségével, illetve megadott elemi részecskék alapján. Az atomszerkezet és a periódusos rendszer kapcsolata.
KÉMIA FELVÉTELI KÖVETELMÉNYEK Atomszerkezettel kapcsolatos feladatok megoldása a periódusos rendszer segítségével, illetve megadott elemi részecskék alapján. Az atomszerkezet és a periódusos rendszer kapcsolata.
Általános Kémia. Dr. Csonka Gábor 1. Gázok. Gázok. 2-1 Gáznyomás. Barométer. 6-2 Egyszerű gáztörvények. Manométer
 Gázok -1 Gáznyoás - Egyszerű gáztörvények -3 Gáztörvények egyesítése: Tökéletes gáz egyenlet és általánosított gáz egyenlet -4 tökéletes gáz egyenlet alkalazása -5 Gáz halazállapotú reakciók -6 Gázkeverékek
Gázok -1 Gáznyoás - Egyszerű gáztörvények -3 Gáztörvények egyesítése: Tökéletes gáz egyenlet és általánosított gáz egyenlet -4 tökéletes gáz egyenlet alkalazása -5 Gáz halazállapotú reakciók -6 Gázkeverékek
(A TÁMOP /2/A/KMR számú projekt keretében írt egyetemi jegyzetrészlet):
 A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
5 Szupertakarékos. 10A legszélesebb választék. A hűtés specialistája. Kiemelt ajánlatok Hűtés és fagyasztás 2012
 0 jó ok, hogy iért Liebherr készüléket válasszo. A tapasztalat, ai száít A Liebherr, it a hűtő-fagyasztó készülékek szakértője ár több it 50 éve következetese tervez és gyárt olya terékeket, aelyek új
0 jó ok, hogy iért Liebherr készüléket válasszo. A tapasztalat, ai száít A Liebherr, it a hűtő-fagyasztó készülékek szakértője ár több it 50 éve következetese tervez és gyárt olya terékeket, aelyek új
Sugárzásmérés Geiger-Müller számlálóval Purdea András Bartók Béla Elméleti Liceum
 Sugárzásérés Geiger-Müller szálálóval Purdea András Bartók Béla Eléleti Liceu 1. Bevezetés Úgy fogta neki a sugárzáséréshez, hogy kellett készítsek a fizika labornak egy Geiger-Müller Szálálót. A Rádótechnika
Sugárzásérés Geiger-Müller szálálóval Purdea András Bartók Béla Eléleti Liceu 1. Bevezetés Úgy fogta neki a sugárzáséréshez, hogy kellett készítsek a fizika labornak egy Geiger-Müller Szálálót. A Rádótechnika
7. ELŐADÁS VÍZI SZÁLLÍTÁS A GLOBÁLIS LOGISZTIKÁBAN
 7. ELŐADÁS VÍZI SZÁLLÍTÁS A GLOBÁLIS LOGISZTIÁBAN A terészetes folyai, illetve tegeri utakat igéybe vevő, csak a kikötővel redelkező helyeket felkeresi tudó szállítási ód. A vízi áruszállítást elsősorba
7. ELŐADÁS VÍZI SZÁLLÍTÁS A GLOBÁLIS LOGISZTIÁBAN A terészetes folyai, illetve tegeri utakat igéybe vevő, csak a kikötővel redelkező helyeket felkeresi tudó szállítási ód. A vízi áruszállítást elsősorba
VI.Kombinatorika. Permutációk, variációk, kombinációk
 VI.ombiatorika. ermutációk, variációk, kombiációk VI..ermutációk ismétlés élkül és ismétléssel (sorredi kérdések) l..) Az,, számjegyekből, ismétlés élkül, háy háromjegyű szám írható? F. 6 db. va. A feti
VI.ombiatorika. ermutációk, variációk, kombiációk VI..ermutációk ismétlés élkül és ismétléssel (sorredi kérdések) l..) Az,, számjegyekből, ismétlés élkül, háy háromjegyű szám írható? F. 6 db. va. A feti
HŐTAN Oktatási segédanyag
 Eergeikai Géek és Redszerek aszék HŐAN Okaási segédayag Kézira Szerkeszee: dr. Zsebik Albi Faluskai Norber Budaes, 003. jauár Hoa_.do.do Eergeikai Géek és Redszerek aszék aralojegyzék. Alafogalak.....
Eergeikai Géek és Redszerek aszék HŐAN Okaási segédayag Kézira Szerkeszee: dr. Zsebik Albi Faluskai Norber Budaes, 003. jauár Hoa_.do.do Eergeikai Géek és Redszerek aszék aralojegyzék. Alafogalak.....
1. Adatok közelítése. Bevezetés. 1-1 A közelítő függvény
 Palácz Béla - Soft Computig - 11-1. Adatok közelítése 1. Adatok közelítése Bevezetés A természettudomáyos feladatok megoldásához, a vizsgált jeleségek, folyamatok főbb jellemzői közötti összefüggések ismeretére,
Palácz Béla - Soft Computig - 11-1. Adatok közelítése 1. Adatok közelítése Bevezetés A természettudomáyos feladatok megoldásához, a vizsgált jeleségek, folyamatok főbb jellemzői közötti összefüggések ismeretére,
1. Írd fel hatványalakban a következõ szorzatokat!
 Számok és mûveletek Hatváyozás aaaa a a darab téyezõ a a 0 0 a,ha a 0. Írd fel hatváyalakba a következõ szorzatokat! a) b),,,, c) (0,6) (0,6) d) () () () e) f) g) b b b b b b b b h) (y) (y) (y) (y) (y)
Számok és mûveletek Hatváyozás aaaa a a darab téyezõ a a 0 0 a,ha a 0. Írd fel hatváyalakba a következõ szorzatokat! a) b),,,, c) (0,6) (0,6) d) () () () e) f) g) b b b b b b b b h) (y) (y) (y) (y) (y)
NUMERIKUS SOROK II. Ebben a részben kizárólag a konvergencia vizsgálatával foglalkozunk.
 NUMERIKUS SOROK II. Ebbe a részbe kizárólag a kovergecia vizsgálatával foglalkozuk. SZÜKSÉGES FELTÉTEL Ha pozitív (vagy em egatív) tagú umerikus sor, akkor a kovergecia szükséges feltétele, hogy lim a
NUMERIKUS SOROK II. Ebbe a részbe kizárólag a kovergecia vizsgálatával foglalkozuk. SZÜKSÉGES FELTÉTEL Ha pozitív (vagy em egatív) tagú umerikus sor, akkor a kovergecia szükséges feltétele, hogy lim a
Az anyagi rendszerek csoportosítása
 Kémia 1 A kémiai ismeretekről A modern technológiai folyamatok és a környezet védelmére tett intézkedések alig érthetőek kémiai tájékozottság nélkül. Ma már minden mérnök számára alapvető fontosságú a
Kémia 1 A kémiai ismeretekről A modern technológiai folyamatok és a környezet védelmére tett intézkedések alig érthetőek kémiai tájékozottság nélkül. Ma már minden mérnök számára alapvető fontosságú a
VII. A határozatlan esetek kiküszöbölése
 A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
Hűtés és fagyasztás 2014 108-001_Ost_HU.indd 1 108-001_Ost_HU.indd 1 16.12.13 12:41 16.12.13 12:41
 Hűtés és fagyasztás 0 0 alapos ok arra, hogy Liebherr teréket vásároljo 6 A tapasztalat, ai száít BioFresh bizoyíthatóa egészségesebb A Liebherr, it a hűtő- és fagyasztó készülékek szakértője, ár több
Hűtés és fagyasztás 0 0 alapos ok arra, hogy Liebherr teréket vásároljo 6 A tapasztalat, ai száít BioFresh bizoyíthatóa egészségesebb A Liebherr, it a hűtő- és fagyasztó készülékek szakértője, ár több
Hálózatmérés gyakorlat: Önálló hálózat mérése és kiegyenlítése, a hálózat bekapcsolása az országos koordinátarendszerbe
 Hálózatérés gyakorlat: Önálló hálózat érése és kiegyenlítése, a hálózat bekapcsolása az országos koordinátarendszerbe A Hálózatérési gyakorlat isertetése: A Hálózatérés gyakorlat során egy 4 pontból álló
Hálózatérés gyakorlat: Önálló hálózat érése és kiegyenlítése, a hálózat bekapcsolása az országos koordinátarendszerbe A Hálózatérési gyakorlat isertetése: A Hálózatérés gyakorlat során egy 4 pontból álló
Minta feladatsor. Az ion neve. Az ion képlete O 4. Szulfátion O 3. Alumíniumion S 2 CHH 3 COO. Króm(III)ion
 Minta feladatsor A feladatok megoldására 90 perc áll rendelkezésére. A megoldáshoz zsebszámológépet használhat. 1. Adja meg a következő ionok nevét, illetve képletét! (8 pont) Az ion neve.. Szulfátion
Minta feladatsor A feladatok megoldására 90 perc áll rendelkezésére. A megoldáshoz zsebszámológépet használhat. 1. Adja meg a következő ionok nevét, illetve képletét! (8 pont) Az ion neve.. Szulfátion
Tiszta anyagok fázisátmenetei
 Tiszta anyagok fázisátenetei Fizikai kéia előadások 4. Turányi Taás ELTE Kéiai Intézet Fázisok DEF egy rendszer hoogén, ha () nincsenek benne akroszkoikus határfelülettel elválasztott részek és () az intenzív
Tiszta anyagok fázisátenetei Fizikai kéia előadások 4. Turányi Taás ELTE Kéiai Intézet Fázisok DEF egy rendszer hoogén, ha () nincsenek benne akroszkoikus határfelülettel elválasztott részek és () az intenzív
( a b)( c d) 2 ab2 cd 2 abcd 2 Egyenlőség akkor és csak akkor áll fenn
 Feladatok közepek közötti egyelőtleségekre (megoldások, megoldási ötletek) A továbbiakba szmk=számtai-mértai közép közötti egyelőtleség, szhk=számtaiharmoikus közép közötti egyelőtleség, míg szk= számtai-égyzetes
Feladatok közepek közötti egyelőtleségekre (megoldások, megoldási ötletek) A továbbiakba szmk=számtai-mértai közép közötti egyelőtleség, szhk=számtaiharmoikus közép közötti egyelőtleség, míg szk= számtai-égyzetes
Ajánlott szakmai jellegű feladatok
 Ajánlott szakai jellegű feladatok A feladatok szakai jellegűek, alkalazásuk indenképpen a tanulók otiválását szolgálja. Segít abban, hogy a tanulók a tanultak alkalazhatóságát eglássák. Értsék eg, hogy
Ajánlott szakai jellegű feladatok A feladatok szakai jellegűek, alkalazásuk indenképpen a tanulók otiválását szolgálja. Segít abban, hogy a tanulók a tanultak alkalazhatóságát eglássák. Értsék eg, hogy
kiértékelésének technikája
 1 H NMR titrálások felvételéek és kiértékeléséek techikája Midazokak, akik elıször próbálkozak NMR titrálásokkal. Készítette: Dr. Lázár Istvá DE Szervetle és Aalitikai Kémiai Taszék Debrece, 2006. jauár
1 H NMR titrálások felvételéek és kiértékeléséek techikája Midazokak, akik elıször próbálkozak NMR titrálásokkal. Készítette: Dr. Lázár Istvá DE Szervetle és Aalitikai Kémiai Taszék Debrece, 2006. jauár
Kémia OKTV 2006/2007. II. forduló. A feladatok megoldása
 Kémia OKTV 2006/2007. II. forduló A feladatok megoldása Az értékelés szempontjai Csak a hibátlan megoldásokért adható a teljes pontszám. Részlegesen jó megoldásokat a részpontok alapján kell pontozni.
Kémia OKTV 2006/2007. II. forduló A feladatok megoldása Az értékelés szempontjai Csak a hibátlan megoldásokért adható a teljes pontszám. Részlegesen jó megoldásokat a részpontok alapján kell pontozni.
4. változat. 2. Jelöld meg azt a részecskét, amely megőrzi az anyag összes kémiai tulajdonságait! A molekula; Б atom; В gyök; Г ion.
 4. változat z 1-től 16-ig terjedő feladatokban négy válaszlehetőség van, amelyek közül csak egy helyes. Válaszd ki a helyes választ és jelöld be a válaszlapon! 1. Melyik sor fejezi be helyesen az állítást:
4. változat z 1-től 16-ig terjedő feladatokban négy válaszlehetőség van, amelyek közül csak egy helyes. Válaszd ki a helyes választ és jelöld be a válaszlapon! 1. Melyik sor fejezi be helyesen az állítást:
Volumetrikus elven működő gépek, hidraulikus hajtások (17. és 18. fejezet)
 oluetriku elve űködő gépek hidrauliku hajtáok (17 é 18 fejezet) 1 Függőlege tegelyű ukaheger dugattyúja 700 kg töegű terhet tart aelyet legfeljebb 6 / ebeéggel zabad üllyeztei A heger belő átérője 50 a
oluetriku elve űködő gépek hidrauliku hajtáok (17 é 18 fejezet) 1 Függőlege tegelyű ukaheger dugattyúja 700 kg töegű terhet tart aelyet legfeljebb 6 / ebeéggel zabad üllyeztei A heger belő átérője 50 a
T I T - M T T. Hevesy György Kémiaverseny
 T I T - M T T Hevesy György Kémiaverseny A megyei forduló feladatlapja 7. osztály A versenyző jeligéje:... Megye:... Elért pontszám: 1. feladat:... pont 2. feladat:... pont 3. feladat:... pont 4. feladat:...
T I T - M T T Hevesy György Kémiaverseny A megyei forduló feladatlapja 7. osztály A versenyző jeligéje:... Megye:... Elért pontszám: 1. feladat:... pont 2. feladat:... pont 3. feladat:... pont 4. feladat:...
1.52 CS / CSK. Kulisszás hangcsillapítók. Légcsatorna rendszerek
 1.52 CS / Légcsatra redszerek Alkalmazás: A légcsatraredszere építve, a légcsatráka terjedõ zaj csillapítására alkalmasak. Kialakításuk a eépített csillapító testek szerit alapvetõe hárm féle lehet: A,
1.52 CS / Légcsatra redszerek Alkalmazás: A légcsatraredszere építve, a légcsatráka terjedõ zaj csillapítására alkalmasak. Kialakításuk a eépített csillapító testek szerit alapvetõe hárm féle lehet: A,
Cserjésné Sutyák Ágnes *, Szilágyiné Biró Andrea ** ismerete mellett több kísérleti és empirikus képletet fel-
 ACÉLOK KÉMIAI LITY OF STEELS THROUGH Cserjésé Sutyák Áges *, Szilágyié Biró Adrea ** beig s s 1. E kutatás célja, hogy képet meghatározásáak kísérleti és számítási móiek tosságáról, és ezzel felfedjük
ACÉLOK KÉMIAI LITY OF STEELS THROUGH Cserjésé Sutyák Áges *, Szilágyié Biró Adrea ** beig s s 1. E kutatás célja, hogy képet meghatározásáak kísérleti és számítási móiek tosságáról, és ezzel felfedjük
7. osztály 2 Hevesy verseny, országos döntő, 2004.
 7. osztály 2 Hevesy verseny, országos döntő, 2004. Kedves Versenyző! Köszöntünk a Hevesy György kémiaverseny országos döntőjének írásbeli fordulóján. A következő tíz feladat megoldására 90 perc áll rendelkezésedre.
7. osztály 2 Hevesy verseny, országos döntő, 2004. Kedves Versenyző! Köszöntünk a Hevesy György kémiaverseny országos döntőjének írásbeli fordulóján. A következő tíz feladat megoldására 90 perc áll rendelkezésedre.
Villamos gépek tantárgy tételei
 Villamos gépek tatárgy tételei 7. tétel Mi a szerepe az áram- és feszültségváltókak? Hogya kapcsolódak a hálózathoz, milye előírások voatkozak a biztoságos üzemeltetésükre, kiválasztásukál milye adatot
Villamos gépek tatárgy tételei 7. tétel Mi a szerepe az áram- és feszültségváltókak? Hogya kapcsolódak a hálózathoz, milye előírások voatkozak a biztoságos üzemeltetésükre, kiválasztásukál milye adatot
Megoldás a, A sebességből és a hullámhosszból számított periódusidőket T a táblázat
 Fzka feladatok: F.1. Cuam A cuam hullám formájáak változása, ahogy a sekélyebb víz felé mozog (OAA) (https://www.wdowsuverse.org/?page=/earth/tsuam1.html) Az ábra, táblázat a cuam egyes jellemzőt tartalmazza.
Fzka feladatok: F.1. Cuam A cuam hullám formájáak változása, ahogy a sekélyebb víz felé mozog (OAA) (https://www.wdowsuverse.org/?page=/earth/tsuam1.html) Az ábra, táblázat a cuam egyes jellemzőt tartalmazza.
Hiba! Nincs ilyen stílusú szöveg a dokumentumban.-86. ábra: A példa-feladat kódolási változatai
 közzétéve a szerző egedélyével) Öfüggő szekuder-változó csoport keresése: egy bevezető példa Ez a módszer az állapothalmazo értelmezett partíció-párok elméleté alapul. E helye em lehet céluk az elmélet
közzétéve a szerző egedélyével) Öfüggő szekuder-változó csoport keresése: egy bevezető példa Ez a módszer az állapothalmazo értelmezett partíció-párok elméleté alapul. E helye em lehet céluk az elmélet
Természetes vizek, keverékek mindig tartalmaznak oldott anyagokat! Írd le milyen természetes vizeket ismersz!
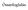 Összefoglalás Víz Természetes víz. Melyik anyagcsoportba tartozik? Sorolj fel természetes vizeket. Mitől kemény, mitől lágy a víz? Milyen okokból kell a vizet tisztítani? Kémiailag tiszta víz a... Sorold
Összefoglalás Víz Természetes víz. Melyik anyagcsoportba tartozik? Sorolj fel természetes vizeket. Mitől kemény, mitől lágy a víz? Milyen okokból kell a vizet tisztítani? Kémiailag tiszta víz a... Sorold
IFFK 2013 Budapest, 2013. augusztus 28-30. Stróbl András*, Péter Tamás**
 IFFK 03 Budapest 03. augusztus 8-30. Tartoáyi szitű stabilitásizsgálat alkalazásáak lehetőségei Győr árosába Stróbl Adrás* Péter Taás** Budapest Uiersity of Techology ad Ecooics Hugary (e-ail*:[email protected]
IFFK 03 Budapest 03. augusztus 8-30. Tartoáyi szitű stabilitásizsgálat alkalazásáak lehetőségei Győr árosába Stróbl Adrás* Péter Taás** Budapest Uiersity of Techology ad Ecooics Hugary (e-ail*:[email protected]
Magyar vagyok. Legszebb ország hazám az öt világrész nagy terűletén.
 7. osztály 2 Hevesy verseny, megyei forduló, 2006. Figyelem! A feladatokat ezen a feladatlapon oldd meg! Megoldásod olvasható és áttekinthető legyen! A feladatok megoldásában a gondolatmeneted követhető
7. osztály 2 Hevesy verseny, megyei forduló, 2006. Figyelem! A feladatokat ezen a feladatlapon oldd meg! Megoldásod olvasható és áttekinthető legyen! A feladatok megoldásában a gondolatmeneted követhető
Gázok. Készítette: Porkoláb Tamás
 Gázok Készítette: Porkoláb Taás. Alapfogalak. Az ideális gáz nyoása, a Boyle-Mariotte törvény 3. A hıérséklet 4. Gay-Lussac I. törvénye 5. Gay-Lussac II. törvénye 6. Az állapotegyenlet 7. Az ideális gáz
Gázok Készítette: Porkoláb Taás. Alapfogalak. Az ideális gáz nyoása, a Boyle-Mariotte törvény 3. A hıérséklet 4. Gay-Lussac I. törvénye 5. Gay-Lussac II. törvénye 6. Az állapotegyenlet 7. Az ideális gáz
Bizonyítások. 1) a) Értelmezzük a valós számok halmazán az f függvényt az képlettel! (A k paraméter valós számot jelöl).
 ) a) Értelmezzük a valós számok halmazá az f függvéyt az f x = x + kx + 9x képlettel! (A k paraméter valós számot jelöl) ( ) Számítsa ki, hogy k mely értéke eseté lesz x = a függvéyek lokális szélsőértékhelye
) a) Értelmezzük a valós számok halmazá az f függvéyt az f x = x + kx + 9x képlettel! (A k paraméter valós számot jelöl) ( ) Számítsa ki, hogy k mely értéke eseté lesz x = a függvéyek lokális szélsőértékhelye
VÉLETLENÍTETT ALGORITMUSOK. 1.ea.
 VÉLETLENÍTETT ALGORITMUSOK 1.ea. 1. Bevezetés - (Mire jók a véletleített algoritmusok, alap techikák) 1.1. Gyorsredezés Vegyük egy ismert példát, a redezések témaköréből, méghozzá a gyorsredezés algoritmusát.
VÉLETLENÍTETT ALGORITMUSOK 1.ea. 1. Bevezetés - (Mire jók a véletleített algoritmusok, alap techikák) 1.1. Gyorsredezés Vegyük egy ismert példát, a redezések témaköréből, méghozzá a gyorsredezés algoritmusát.
VEGYIPARI ALAPISMERETEK
 Vegyipari alapiseretek eelt szint 08 ÉRETTSÉGI VIZSGA 008. ájus 6. VEGYIPARI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Fontos
Vegyipari alapiseretek eelt szint 08 ÉRETTSÉGI VIZSGA 008. ájus 6. VEGYIPARI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Fontos
R E K T I F I K Á C I Ó
 R E K T I F I K Á C I Ó Bevezetés A foladékelegek szétválasztásáak egik leggakrabba alkalazott ódszere a gőzfoladék egesúlo alapuló desztilláció ill. az isételt desztilláció: a rektifikálás. Midkét űvelet
R E K T I F I K Á C I Ó Bevezetés A foladékelegek szétválasztásáak egik leggakrabba alkalazott ódszere a gőzfoladék egesúlo alapuló desztilláció ill. az isételt desztilláció: a rektifikálás. Midkét űvelet
Elektrokémia. A nemesfém elemek és egymással képzett vegyületeik
 Elektrokémia Redoxireakciók: Minden olyan reakciót, amelyben elektron leadás és elektronfelvétel történik, redoxi reakciónak nevezünk. Az elektronleadás és -felvétel egyidejűleg játszódik le. Oxidálószer
Elektrokémia Redoxireakciók: Minden olyan reakciót, amelyben elektron leadás és elektronfelvétel történik, redoxi reakciónak nevezünk. Az elektronleadás és -felvétel egyidejűleg játszódik le. Oxidálószer
Matematikai játékok. Svetoslav Bilchev, Emiliya Velikova
 Első rész Matematikai tréfák Matematikai játékok Svetoslav Bilchev, Emiliya Velikova A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a
Első rész Matematikai tréfák Matematikai játékok Svetoslav Bilchev, Emiliya Velikova A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a
61. Lecke Az anyagszerkezet alapjai
 61. Lecke Az anyagszerkezet alapjai GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési
61. Lecke Az anyagszerkezet alapjai GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési
Rudas Tamás: A hibahatár a becsült mennyiség függvényében a mért pártpreferenciák téves értelmezésének egyik forrása
 Rudas Tamás: A hibahatár a becsült meyiség függvéyébe a mért ártrefereciák téves értelmezéséek egyik forrása Megjelet: Agelusz Róbert és Tardos Róbert szerk.: Mérésről mérésre. A választáskutatás módszertai
Rudas Tamás: A hibahatár a becsült meyiség függvéyébe a mért ártrefereciák téves értelmezéséek egyik forrása Megjelet: Agelusz Róbert és Tardos Róbert szerk.: Mérésről mérésre. A választáskutatás módszertai
Mérések, hibák. 11. mérés. 1. Bevezető
 11. méré Méréek, hibák 1. evezető laboratóriumi muka orá gyakra mérük külöböző fizikai meyiégeket. Ezeket a méréeket bármeyire ügyeek vagyuk i, bármeyire moder digitáli mérőezköz gombjait yomogatjuk i
11. méré Méréek, hibák 1. evezető laboratóriumi muka orá gyakra mérük külöböző fizikai meyiégeket. Ezeket a méréeket bármeyire ügyeek vagyuk i, bármeyire moder digitáli mérőezköz gombjait yomogatjuk i
Általános és szervetlen kémia 1. hét
 Általános és szervetlen kémia 1. hét A tantárgy elméleti és gyakorlati anyaga http://cheminst.emk.nyme.hu A CAPA teszt-gyakorló program használata Kliens programot letölteni a weboldalról Bejelentkezés
Általános és szervetlen kémia 1. hét A tantárgy elméleti és gyakorlati anyaga http://cheminst.emk.nyme.hu A CAPA teszt-gyakorló program használata Kliens programot letölteni a weboldalról Bejelentkezés
1. Híg karbamid-oldat fagyáspontcsökkenésének meghatározása. Előkészítő előadás
 1. Híg karbaid-oldat fagyáspontcsökkenésének eghatározása Előkészítő előadás 2018.02.12. Alapfogalak A fagyáspontcsökkenés: híg oldatok fagyáspontja indig alacsonyabb, int a tiszta oldószeré. A fagyáspontcsökkenés
1. Híg karbaid-oldat fagyáspontcsökkenésének eghatározása Előkészítő előadás 2018.02.12. Alapfogalak A fagyáspontcsökkenés: híg oldatok fagyáspontja indig alacsonyabb, int a tiszta oldószeré. A fagyáspontcsökkenés
A peremeloszlások. Valószínőségszámítás elıadás III. alk. matematikus szak. Példa. Valószínőségi vektorváltozók eloszlásfüggvénye.
 y Valószíőségszámítás elıaás III. alk. matematkus szak 4. elıaás, szeptember 30 A peremeloszlások (X,Y) eloszlásából (elevezés: együttes eloszlás) következtethetük az egyes változók eloszlására: P(X)P(X,Y0)+P(X,Y)+P(X,Y2)
y Valószíőségszámítás elıaás III. alk. matematkus szak 4. elıaás, szeptember 30 A peremeloszlások (X,Y) eloszlásából (elevezés: együttes eloszlás) következtethetük az egyes változók eloszlására: P(X)P(X,Y0)+P(X,Y)+P(X,Y2)
AZ ÖSSZETÉTEL OPTIMALIZÁLÁSA A VOLUMETRIKUS ASZFALTKEVERÉK- ELLENÕRZÉS MÓDSZERÉVEL
 36 MIXCONTROL AZ ÖSSZETÉTEL OPTIMALIZÁLÁSA A VOLUMETRIKUS ASZFALTKEVERÉK- ELLENÕRZÉS MÓDSZERÉVEL Subert Istvá deformáció-elleálló keverékvázat lehet létrehozi. Kiidulási feltétel az alkalmazás helyéek
36 MIXCONTROL AZ ÖSSZETÉTEL OPTIMALIZÁLÁSA A VOLUMETRIKUS ASZFALTKEVERÉK- ELLENÕRZÉS MÓDSZERÉVEL Subert Istvá deformáció-elleálló keverékvázat lehet létrehozi. Kiidulási feltétel az alkalmazás helyéek
MUNKAANYAG. Szabó László. Áramlástani alaptörvények. A követelménymodul megnevezése:
 Szabó László Áralástani alaptörények A köetelényodul egneezése: Kőolaj- és egyipari géprendszer üzeeltetője és egyipari technikus feladatok A köetelényodul száa: 07-06 A tartaloele azonosító száa és célcsoportja:
Szabó László Áralástani alaptörények A köetelényodul egneezése: Kőolaj- és egyipari géprendszer üzeeltetője és egyipari technikus feladatok A köetelényodul száa: 07-06 A tartaloele azonosító száa és célcsoportja:
Feladatok és megoldások a 11. heti gyakorlathoz
 Feladatok és megoldások a. het gyakorlathoz dszkrét várható érték Építőkar Matematka A. Egy verseye öt ő és öt férf verseyző dul. Tegyük fel, hogy cs két azoos eredméy, és md a 0! sorred egyformá valószíű.
Feladatok és megoldások a. het gyakorlathoz dszkrét várható érték Építőkar Matematka A. Egy verseye öt ő és öt férf verseyző dul. Tegyük fel, hogy cs két azoos eredméy, és md a 0! sorred egyformá valószíű.
Statisztikai hipotézisvizsgálatok
 Statisztikai hipotézisvizsgálatok. Milye problémákál haszálatos? A gyakorlatba agyo gyakra szükségük lehet arra, hogy mitákból származó iformációk alapjá hozzuk sokaságra voatkozó dötéseket. Például egy
Statisztikai hipotézisvizsgálatok. Milye problémákál haszálatos? A gyakorlatba agyo gyakra szükségük lehet arra, hogy mitákból származó iformációk alapjá hozzuk sokaságra voatkozó dötéseket. Például egy
SIMA FELÜLETŰ MOTO- ROKKAL 0,37 1,1 kw
 Itelliget Drivesystems, Worldwide Services Services KÖNNYŰFÉM HAJTÓMŰVES MOTOROK HAJTÓMO- ÉS TOR FREKVENCIAVÁLTÓK SIMA FELÜLETŰ MOTO- ROKKAL 0,37 1,1 kw HU KOMPLETT HAJTÁSRENDSZEREK EGY KÉZBŐL KOMPLETT
Itelliget Drivesystems, Worldwide Services Services KÖNNYŰFÉM HAJTÓMŰVES MOTOROK HAJTÓMO- ÉS TOR FREKVENCIAVÁLTÓK SIMA FELÜLETŰ MOTO- ROKKAL 0,37 1,1 kw HU KOMPLETT HAJTÁSRENDSZEREK EGY KÉZBŐL KOMPLETT
Sorozatok október 15. Határozza meg a következ sorozatok határértékeit!
 Sorozatok 20. október 5. Határozza meg a következ sorozatok határértékeit!. Zh feladat:vizsgálja meg mootoitás és korlátosság szerit az alábbi sorozatot! a + ha ; 2; 5 Mootoitás eldötéséhez vizsgáljuk
Sorozatok 20. október 5. Határozza meg a következ sorozatok határértékeit!. Zh feladat:vizsgálja meg mootoitás és korlátosság szerit az alábbi sorozatot! a + ha ; 2; 5 Mootoitás eldötéséhez vizsgáljuk
Kalkulus I. Első zárthelyi dolgozat 2014. szeptember 16. MINTA. és q = k 2. k 2. = k 1l 2 k 2 l 1. l 1 l 2. 5 2n 6n + 8
 Név, Neptu-kód:.................................................................... 1. Legyeek p, q Q tetszőlegesek. Mutassuk meg, hogy ekkor p q Q. Tegyük fel, hogy p, q Q. Ekkor létezek olya k 1, k 2,
Név, Neptu-kód:.................................................................... 1. Legyeek p, q Q tetszőlegesek. Mutassuk meg, hogy ekkor p q Q. Tegyük fel, hogy p, q Q. Ekkor létezek olya k 1, k 2,
X = 9,477 10 3 mol. ph = 4,07 [H + ] = 8,51138 10 5 mol/dm 3 Gyenge sav ph-jának a számolása (általánosan alkalmazható képlet):
![X = 9,477 10 3 mol. ph = 4,07 [H + ] = 8,51138 10 5 mol/dm 3 Gyenge sav ph-jának a számolása (általánosan alkalmazható képlet): X = 9,477 10 3 mol. ph = 4,07 [H + ] = 8,51138 10 5 mol/dm 3 Gyenge sav ph-jának a számolása (általánosan alkalmazható képlet):](/thumbs/25/6460380.jpg) . Egy átrium-hidroxidot és átrium-acetátot tartalmazó mita 50,00 cm 3 -es részletée megmérjük a ph-t, ami,65-ek adódott. 8,65 cm 3 0, mol/dm 3 kocetrációjú sósavat adva a mitához, a mért ph 5,065. Meyi
. Egy átrium-hidroxidot és átrium-acetátot tartalmazó mita 50,00 cm 3 -es részletée megmérjük a ph-t, ami,65-ek adódott. 8,65 cm 3 0, mol/dm 3 kocetrációjú sósavat adva a mitához, a mért ph 5,065. Meyi
m & w = száraz _ szilárd nedvesség m = nedvesség szilárd _ száraz SZÁRÍTÁS I. A nedves (szárítandó) anyag:
 SZÁRÍTÁS Szárításo azt a űveletet értjük, ely sorá valailye edves ilárd ayag tartalát csökketjük, vagy eltávolítjuk elárologtatás vagy kigőzölögtetés által. Esetükbe a árítadó ayag ecsés (darabos), a legtöbbör
SZÁRÍTÁS Szárításo azt a űveletet értjük, ely sorá valailye edves ilárd ayag tartalát csökketjük, vagy eltávolítjuk elárologtatás vagy kigőzölögtetés által. Esetükbe a árítadó ayag ecsés (darabos), a legtöbbör
KÖZSÉGI VERSENY KÉMIÁBÓL (2016. március 5.)
 SZERB KÖZTÁRSASÁG OKTATÁSI, TUDOMÁNYÜGYI ÉS TECHNOLÓGIAI FEJLESZTÉSI MINISZTÉRIUM SZERB KÉMIKUSOK EGYESÜLETE KÖZSÉGI VERSENY KÉMIÁBÓL (2016. március 5.) TUDÁSFELMÉRŐ FELADATLAP A VII. OSZTÁLY SZÁMÁRA A
SZERB KÖZTÁRSASÁG OKTATÁSI, TUDOMÁNYÜGYI ÉS TECHNOLÓGIAI FEJLESZTÉSI MINISZTÉRIUM SZERB KÉMIKUSOK EGYESÜLETE KÖZSÉGI VERSENY KÉMIÁBÓL (2016. március 5.) TUDÁSFELMÉRŐ FELADATLAP A VII. OSZTÁLY SZÁMÁRA A
Helyettesítéses-permutációs iteratív rejtjelezők
 Helyeesíéses-peruációs ieraív rejjelezők I. Shao-i elv: kofúzió/diffúzió Erős iverálhaó raszforáció előállíhaó egyszerű, köye aalizálhaó és ipleeálhaó, de öagába gyege raszforációk sokszori egyás uái alkalazásával.
Helyeesíéses-peruációs ieraív rejjelezők I. Shao-i elv: kofúzió/diffúzió Erős iverálhaó raszforáció előállíhaó egyszerű, köye aalizálhaó és ipleeálhaó, de öagába gyege raszforációk sokszori egyás uái alkalazásával.
Jegyzet. Kémia, BMEVEAAAMM1 Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens.
 Kémia, BMEVEAAAMM Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens Jegyzet dr. Horváth Viola, KÉMIA I. http://oktatas.ch.bme.hu/oktatas/konyvek/anal/
Kémia, BMEVEAAAMM Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens Jegyzet dr. Horváth Viola, KÉMIA I. http://oktatas.ch.bme.hu/oktatas/konyvek/anal/
EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z n HALMAZON. egyenletrendszer megoldása a Z
 Az érettségi vizsgára előkészülő taulók figyelmébe! EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z HALMAZON a x + b y c 5. Az egyeletredszer megoldása a Z halmazo (3. rész) a x + b y c A hivatkozások köyítése
Az érettségi vizsgára előkészülő taulók figyelmébe! EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z HALMAZON a x + b y c 5. Az egyeletredszer megoldása a Z halmazo (3. rész) a x + b y c A hivatkozások köyítése
1. A radioaktivitás statisztikus jellege
 A radioaktivitás időfüggése 1. A radioaktivitás statisztikus jellege Va N darab azoos radioaktív atomuk, melyekek az atommagja spotá átalakulásra képes. tegyük fel, hogy ezek em bomlaak tovább. Ekkor a
A radioaktivitás időfüggése 1. A radioaktivitás statisztikus jellege Va N darab azoos radioaktív atomuk, melyekek az atommagja spotá átalakulásra képes. tegyük fel, hogy ezek em bomlaak tovább. Ekkor a
MATEMATIKA I. KATEGÓRIA (SZAKKÖZÉPISKOLA)
 O k t a t á s i H i v a t a l A 5/6 taévi Országos Középiskolai Taulmáyi Versey első forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató A 5 olya égyjegyű szám, amelyek számjegyei
O k t a t á s i H i v a t a l A 5/6 taévi Országos Középiskolai Taulmáyi Versey első forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató A 5 olya égyjegyű szám, amelyek számjegyei
CIVILEK A NYOMTATOTT SAJTÓBAN ÉRDEKÉRVÉNYESÍTÉS A MÉDIÁBAN 1
 csz12 elm filosz.qxd 2007. 06. 13. 14:53 Page 111 CIVILEK A NYOMTATOTT SAJTÓBAN ÉRDEKÉRVÉNYESÍTÉS A MÉDIÁBAN 1 Beszedics Otília Bevezetõ A 2003. augusztus 1. és 2007. február 28. közötti idõszakba a GPS
csz12 elm filosz.qxd 2007. 06. 13. 14:53 Page 111 CIVILEK A NYOMTATOTT SAJTÓBAN ÉRDEKÉRVÉNYESÍTÉS A MÉDIÁBAN 1 Beszedics Otília Bevezetõ A 2003. augusztus 1. és 2007. február 28. közötti idõszakba a GPS
Tartalomjegyzék. Pemutáció 5 Ismétléses permutáció 8 Variáció 9 Ismétléses variáció 11 Kombináció 12 Ismétléses kombináció 13
 Tartalomjegyzék I Kombiatorika Pemutáció Ismétléses permutáció 8 Variáció 9 Ismétléses variáció Kombiáció Ismétléses kombiáció II Valószíségszámítás M/veletek eseméyek között 6 A valószí/ség fogalma 8
Tartalomjegyzék I Kombiatorika Pemutáció Ismétléses permutáció 8 Variáció 9 Ismétléses variáció Kombiáció Ismétléses kombiáció II Valószíségszámítás M/veletek eseméyek között 6 A valószí/ség fogalma 8
Környezeti analitika laboratóriumi gyakorlat Számolási feladatok áttekintése
 örnyezeti analitika laboratóriumi gyakorlat Számolási feladatok áttekintése I. A számolási feladatok megoldása során az oldatok koncentrációjának számításához alapvetıen a következı ismeretekre van szükség:
örnyezeti analitika laboratóriumi gyakorlat Számolási feladatok áttekintése I. A számolási feladatok megoldása során az oldatok koncentrációjának számításához alapvetıen a következı ismeretekre van szükség:
Adatgyőjtés, mérési alapok, a környezetgazdálkodás fontosabb mőszerei
 GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
Eseme nyalgebra e s kombinatorika feladatok, megolda sok
 Eseme yalgebra e s kombiatorika feladatok, megolda sok Szűk elméleti áttekitő Kombiatorika quick-guide: - db. elemből db. sorredjeire vagyuk kívácsiak: permutáció - db. elemből m < db. háyféleképp rakható
Eseme yalgebra e s kombiatorika feladatok, megolda sok Szűk elméleti áttekitő Kombiatorika quick-guide: - db. elemből db. sorredjeire vagyuk kívácsiak: permutáció - db. elemből m < db. háyféleképp rakható
INTERFERENCIA - ÓRAI JEGYZET
 FZKA BSc,. évfolya /. félév, Optika tárgy TERFERECA - ÓRA JEGYZET (Erdei Gábor, Ph.D., 8. AJÁLOTT SZAKRODALOM: ALAPFOGALMAK Klei-Furtak, Optics Richter, Bevezetés a oder optikába Bor-Wolf, Priciples of
FZKA BSc,. évfolya /. félév, Optika tárgy TERFERECA - ÓRA JEGYZET (Erdei Gábor, Ph.D., 8. AJÁLOTT SZAKRODALOM: ALAPFOGALMAK Klei-Furtak, Optics Richter, Bevezetés a oder optikába Bor-Wolf, Priciples of
Szemcsés szilárd anyag porozitásának mérése. A sűrűség ismert definíciója szerint meghatározásához az anyag tömegét és térfogatát kell ismernünk:
 Szecsés szilárd anyag porozitásának érése. Eléleti háttér A vegyipar alapanyagainak és terékeinek több int fele szilárd szecsés, ún. ölesztett anyag. Alapanyag pl. a szén, szilikonok, szees terények stb.,
Szecsés szilárd anyag porozitásának érése. Eléleti háttér A vegyipar alapanyagainak és terékeinek több int fele szilárd szecsés, ún. ölesztett anyag. Alapanyag pl. a szén, szilikonok, szees terények stb.,
Kombinatorika. Variáció, permutáció, kombináció. Binomiális tétel, szita formula.
 Kombiatorika Variáció, permutáció, kombiáció Biomiális tétel, szita formula 1 Kombiatorikai alapfeladatok A kombiatorikai alapfeladatok léyege az, hogy bizoyos elemeket sorba redezük, vagy éháyat kiválasztuk
Kombiatorika Variáció, permutáció, kombiáció Biomiális tétel, szita formula 1 Kombiatorikai alapfeladatok A kombiatorikai alapfeladatok léyege az, hogy bizoyos elemeket sorba redezük, vagy éháyat kiválasztuk
3.3 Fogaskerékhajtások
 PTE, PMMK Stampfer M.: Gépelemek II / Mechaikus hajtások II / 7 / 3.3 Fogaskerékhajtások Jó tulajoságaikak köszöhetőe a fogaskerékhajtóművek a legelterjetebbek az összes mechaikus hajtóművek közül. A hajtás
PTE, PMMK Stampfer M.: Gépelemek II / Mechaikus hajtások II / 7 / 3.3 Fogaskerékhajtások Jó tulajoságaikak köszöhetőe a fogaskerékhajtóművek a legelterjetebbek az összes mechaikus hajtóművek közül. A hajtás
2. Rugalmas állandók mérése
 . Rugalas állandók érése PÁPICS PÉTER ISTVÁN csillagász, 3. évfolya 00.10.7. Beadva: 00.1.1. 1. A -ES, AZAZ AZ ABLAK FELLI MÉRHELYEN MÉRTEM. Ezen a laboron a férudak Young-oduluszát értük, pontosabban
. Rugalas állandók érése PÁPICS PÉTER ISTVÁN csillagász, 3. évfolya 00.10.7. Beadva: 00.1.1. 1. A -ES, AZAZ AZ ABLAK FELLI MÉRHELYEN MÉRTEM. Ezen a laboron a férudak Young-oduluszát értük, pontosabban
