kiértékelésének technikája
|
|
|
- Ádám Borbély
- 10 évvel ezelőtt
- Látták:
Átírás
1 1 H NMR titrálások felvételéek és kiértékeléséek techikája Midazokak, akik elıször próbálkozak NMR titrálásokkal. Készítette: Dr. Lázár Istvá DE Szervetle és Aalitikai Kémiai Taszék Debrece, jauár 16.
2 Milye területeke látjuk haszát az NMR titrálásokak? Két agy területet lehet kiemeli, amelyekbe külööse fotos a protoálódási álladók ismerete. Koordiációs kémia: az egész kutatási területe belül alapvetı fotosságú a komplexképzı vegyületek protoálódási tulajdoságaiak miél szélesebb körő ismerete. Gyógyszerkutatás: bármilye amiocsoportot vagy karboxilátcsoportot tartalmazó hatóayag felszívódási tulajdoságait alapvetıe meghatározzák az adott vegyület protoálódási tulajdoságai, így azok ismerete élkülözhetetle. Milye iformációkat yerhetük egy 1 H NMR titrálásból? Meghatározhatjuk az általuk vizsgált ayag lépcsızetes protoálódási álladóit akkor is, ha em áll redelkezésükre potos ph-poteciometriás mérésekhez haszálható titráló beredezés és a számításhoz speciális számítógépes program. Meghatározhatjuk azt, hogy az egyes protoáltsági állapotokba (azaz pl. egy kiszemelt ph-) a molekulá belüli protoálható csoportok (leggyakrabba az amio ill. karboxilát csoportok) melyike és milye mértékbe va protoálódva. Eek a meghatározására a ph-poteciometria em alkalmas. Milye további elıyei vaak az NMR titrálásokak? A legagyobb elıye az, hogy szeyezett ayagokat is haszálhatuk a titrálásokhoz, feltéve, ha a vizsgált kompoes jelei elkülöíthetık a szeyezések jeleitıl. Mivel a szitetikus kémiai mukák sorá a kutatások kezdeté az új vegyületek a leggyakrabba még csak szeyezett formába állak redelkezésre, jeletıse meggyorsíthatja az új ligadumok fejlesztését az, hogy em kell az elsı eredméyekre a megfelelı tisztasági fok eléréséig vári. Redkívül fotos, hogy az NMR titrálásokhoz em kell ismeri az illetı ayag moláris tömegét, így teljese ismeretle ayagok eseté is tuduk protoálódási álladót meghatározi. Eek külööse olya esetekbe va jeletısége, amikor az extrakciós tulajdoságok beállításához va szükségük arra, hogy tudjuk, milye ph- milye protoáltsági állapotba va a vizsgált kompoesük. (pl. a gyógyszeriparba vagy a köryezeti aalitikába)
3 Olya oldatok eseté is haszálható, amikor pl. magasabb hımérséklete, agyo agy ioerısség mellett kellee megtaláluk azokat a körülméyeket, amelyeke a kiválasztott kompoesük a szükséges protoáltsági állapotba va. Külööse fotos ez a techika akkor, ha em tiszta vizes, haem kevert oldószeres közegbe dolgozuk, feltéve, ha az oldószer em teszi lehetetleé a mérést. Ilye szélsıséges körülméyek között a ph-metria csak agy ehézségekkel haszálható. Milye hátráyai vaak az NMR titrálásokak? Igazi hátráya az, hogy egy drága NMR készüléket, valamit több óra folyamatos hozzáférést igéyel. A kapott protoálódási álladók általába csak egy tizedes jegy potosságúak, így potos számításokál em helyettesíthetik a ph-poteciometriás eredméyeket. Szükséges ayagok, eszközök NMR készülék 5 mm-es tiszta, száraz NMR csövek (mide adatpothoz egy darab, azaz a teljes 2-12 ph tartomáyra kb. 0,5 ph egységekét felvéve 21 csı) ph mérı készülék (3 tizedesjegyes kijelzıvel) - kis mérető, potos, kombiált üvegelektróddal kalibráló oldatok a ph-mérı beállításához 5-10 ml térfogat befogadására alkalmas titráló edéy (optimális esetbe Ar vagy N 2 védıgáz atmoszférával is ellátható, de általába egy lezárható mitásüveg is megfelel) mágeses keverı készülék és a mitásüvegbe illı mérető, kis mágeses keverıbot D 2 O ioerısség állításához ayag (NaCl, KCl, NaClO 4, Me 4 NCl, stb.) Pasteur-pipetták gumi pipettalabdával, kihúzott végő vékoy (2-3 mm) és agyo vékoy (1 mm) üvegbotok titráláshoz haszálható savak és lúgok, külöbözı kocetrációba (pl. kis üvegbe legye töméyebb sav v. lúg, legye kb. 1 M-os és kb. 0.1 M-os sav és lúg egyarát)
4 A titráladó oldat elıkészítése A megfelelı potosságú mérésekhez a titráladó oldat ioerısségét álladó szitre kell beállítauk, ugyais az ioerısség változása potosabb mérések eseté megegedhetetle. Természetese ha csak egy gyors, tájékozódó mérést akaruk végezi, akkor az ioerısség beállítását elhagyhatjuk, de e feledjük, hogy az így kapott eredméyek kevésbé potosak leszek, mit álladó ioerısség eseté. Az ioerısség álladóságához az szükséges, hogy a titráli kívát ayag kocetrációja egy tizede legye az ioerısségek, vagy még aál is kisebb. Ha elegedıe agy az ioerısség, akkor a titrálás sorá bekövetkezı változás már elhayagolható. Szélsıséges ph- (ph 12 fölött, illetve ph 2 alatt) üvegelektróddal való mérés helyett ikább számítjuk a ph-t, de ehhez a ph-metriás titrálások és a ph számítások magasabb szitő ismeretére va szükség. A gyakorlatba arra törekszük, hogy miél kisebb ayagmeyiségbıl meg tudjuk határozi a protoálódási álladókat és a protoálódási mechaizmust. Egy a agyobb ligadumokál átlagosak számító, kb g/mol moláris tömegő ayag eseté 1 mmol/dm 3 esél hígabb mitával em érdemes próbálkozi, mert em fog látszai az alapvoalo a mita jele, a 10 mmol/dm -3 kocetráció sokkal kedvezıbb. A legkisebb oldattérfogat, amivel a titrálást általába el tudjuk végezi kb. 5 ml, de ezzel dolgozi még ehéz, agyobb gyakorlatot igéyel, ezért célszerőbb 10 ml-es iduló térfogattal számoli. (A legagyobb gyakorlattal és a legkisebb eszközökkel sem tuduk kb. 2,5 ml-él kisebb térfogatba dolgozi). 10 ml titráladó térfogatál a vizsgáladó ayagukból legalább 50 mg-ot kell feloldauk, ez a létezı legalsó határ, de miél többet olduk fel, aál jobb. Az ioerısségek legalább 0,1 M-ak kell lei, de a szokásos ph tartomáyo kívüli méréshez legalább 1 M-os ioerısség szükséges. Oldószerkét 10-50% D 2 O-tartalmú vizet haszáluk a leggyakrabba. 10%-ál kisebb deutériumtartalomál az NMR készülék lock jeléek az elvesztése fordulhat elı, míg 50%-ál agyobb deutériumtartalomál a ph és a pd között max. 0.4 egység külöbség lehet, amit számításba kell vei. Akkor idokolt a mérést tiszta D 2 O-ba végezük, ha a mita jelei olya közel vaak a víz jeléhez, hogy máskét em láthatók. Ilye esetbe célszerő a titráló oldatokból is a perdeuteráltakat haszáluk. Bár a tiszta D 2 O-ba való titrálás éháy szempotból kedvezı, magasabb költsége miatt csak idokolt esetbe haszáljuk. Persze D 2 O élkül is lehet méri, de ekkor em lesz lock jel, amiek hiáya miatt csak rövidebb mérési ciklusokat célszrő haszáluk. Ebbe az esetbe a mérés elıtt a mitáéval megegyezı
5 térfogatú D 2 O-ra beshimmeljük készüléket, majd a shimmelı D 2 O-t az aktuális mitákra kicseréljük és közvetleül (további shimmelés élkül) felvesszük a spektrumot (a sweep-et ilyekor a készüléke ki kell kapcsoli). A poteciometriás titrálások sorá az ioerısség állításához és a titráláshoz általába tetrametil-ammóium-hidroxidot illetve aak sóját (TMAOH, TMACl) haszálják, mivel ezek em képezek komplexet a vizsgált ayagokkal. NMR titrálásokál TMA-származékok csak akkor haszálhatók, ha a TMA metilcsoport jele em fed át az ayaguk jelével. Primer, szekuder vagy tercier amiocsoportot tartalmazó ayagokál erre gyakorlatilag ics esély, így ilye esetekbe az ioerısség állítására és a titrálásra csak KCl, KClO 4, NaCl, NaOCl 4, esetleg KNO 3, valamit KOH, NaOH, HCl, vagy HClO 4 haszálható. Számoluk kell azzal, hogy a káliumiookak vagy a átriumiookak számottevı kölcsöhatása lehet a vizsgált ayagukkal, ezért az eredméyek publikálásakor midig meg kell aduk, hogy milye ayagot haszáltuk az ioerısség beállítására és a titrálásra. A szokásos titrálási ph-tartomáy 2 12, eze belül a ph-mérı által mutatott érték kis deutériumtartalmú oldatokál közvetleül, korrekció élkül haszálható. Ha a ph tartomáyo kívül akaruk dolgozi, akkor potosa ismert kocetrációjú savoldat vagy lúgoldat sorozatra (amelyek a deutériumtartalma ugyaayi, mit ameyi a titráladó mitába va) kiszámítjuk a log[h + ]-t, majd a számított értékhez hozzáredeljük a ph-mérı által mutatott értéket, így egy adott körülméyekre érvéyes kalibráló görbét yerük. Ha álladó ioerıssége dolgozuk, akkor természetese azt is be kell állítai, és a kalibráció sorá ugyaazt az ioerısséget kell haszáli, mit a mérés sorá. A mérések meete Az eddiek szerit elkészített, sav vagy lúg hozzáadásával valamely szélsı ph-értékre állított mitába álladó kevertetés közbe belemerítjük az elektródot és leolvassuk a ph-t. Kivesszük az elsı mitát. A ph-t álladó kevertetés közbe folyamatosa állítjuk külöbözı töméységő savoldat (lúgos közegbıl idulva) vagy lúgoldat (savas közegbıl idulva) adagolásával. Max. 0,5+/-0,1 ph lépésekét mikroliter mitát veszük az oldatból és tiszta, száraz NMR csıbe töltjük, majd felvesszük a spektrumot. A mérési jegyzıköyvükbe rögzítjük a leolvasott ph-értéket, valamit az ahhoz a ph-hoz tartozó NMR spektrum azoosítóját (jelét, evét, stb.), ehogy a muka végeztével mide adatuk meglegye, csak éppe e tudjuk,
6 hogy melyik mérési fájl melyik ph-hoz tartozik. Ezutá a mitát visszaötjük és a titrálást tovább folytatjuk. Egy ayag teljes 1 H NMR-es titrálási görbéjéek a felvételéhez kb. 3-4 h folyamatos mérési idı szükséges. Mit és hogya számolhatuk ki egyetle NMR titrálási görbébıl? Protoálódási álladók Legye a vizsgáladó ayagukak protoálódási álladója a teljese deprotoált állapothoz képest (azaz legye egy értékő bázis). Az oldatba jele lévı részecskék elektromos töltéséek a jelölésétıl a továbbiakba eltekitük. A protoálódási álladók ekkor a szokásos módo defiiálhatók, azaz : [ HA] [ H ][ A] K 1 =. K = [ H A] [ H ][ H A] 1 Az oldatba jele lévı részecskék: [H], [A], [HA], [H 2 A], [H A] Válasszuk ki egy olya proto jelét, amelyek a kémiai eltolódása változik a ph-val (azaz ph-érzékey). (Ha több ilye proto is va, természetese midegyikkel végigcsiálhatjuk az eljárást.) Az egyes protoált állapotokhoz redelhetı kémiai eltolódások legyeek a következık: [A] : δ 0 [HA]: δ 1 [H 2 A]: δ 2. [H A]: δ A kiválasztott ph-érzékey hidrogéatom kifejezhetı a következı képlettel: kémiai eltolódása a teljes ph-tartomáyba δ 0 + δ = 1+ i= 1 δ 10 i= 1 i 10 i lg K j i ph j = 1 i lg K j i ph j = 1
7 Az aktuális ph-hoz tartozó, a számításokhoz felhaszálható kémiai eltolódás értékeket a titrálási görbébıl olvashatjuk le, így (ph; δ kísérleti ) összetartozó adatpárokhoz jutuk. A kiértékeléshez egy olya táblázatkezelı programra va szükségük, amely képes sokváltozós optimumszámítás elvégzésére. Jeleleg a két legelterjedtebb program a Microsoft Office Excel, valamit a WordPerfect Quattro evő programjai. (Az Office eseté a Solver modult alapállapotba em telepíti a program, de a telepítı lemeze rajta va, így utólag istallálható). A számítási feladat megoldására midkettı alkalmas. A továbbiakba eze programok valamelyikéek haszálatát ismertek tételezzük fel. A feti képlet alapjá a kokrét számolási módszert midekiek magáak kell kidolgozi, az adatokat beíri, az optimalizációt lefuttati. Mide adatpárra a görbe alapjá elsı közelítésbe kezdı δ i és lgk i értékeket választuk, majd azok felhaszálásával kiszámítjuk a δ számított értékét. A δ számított és a kísérleti δ kísérleti adatok eltéréseiek égyzetösszegét miimalizáljuk vagy a Solver, vagy az Optimizer fukciók felhaszálásával. Az illesztett paraméterekek célszerő elıször vagy csak a protoálódási álladók logaritmusait, vagy csak a δ i értékekválasztai, majd elfogadható közelítés eseté ezeket együttese is illesztjük. A számítást az NMR spektrumba található mide egyes ph-érzékey protora célszerő külö-külö el végezi, majd a kapott logk értékek átlagolásával adjuk meg az elfogadásra kerülı értékeket. Természetese ha egy protoak ics ph-függése, akkor arra em lehet álladót sem számítai. A logk értékek felhaszálhatók a részecskeeloszlási diagram megalkotásához, a δ 0 és δ értékek pedig a protoálódási mechaizmusál adják meg a teljese deprotoált és a teljese protoált forma kémiai eltolódását. Részecskeeloszlási diagram számítása Az egyes részecskékre voatkozó móltörtek a ph függvéyébe megadhatók a következı képlettel. A számításhoz felhaszáljuk az elızıekbe kapott logk értékeket.
8 x H m A = i= 1 m lg K j m ph j= 1 10 i lg K j i ph j= 1 A kapott értékeket a ph függvéyébe ábrázolva kapjuk meg az egyes állapotokhoz tartozó részecskeeloszlási diagramot. Protoálódási mechaizmus Mide ph-érzékey proto jeléél szükséges a δ 0 és δ értéke, amit az elızı számításból is meg lehet adi, de a görbébıl is meg lehet becsüli. A részleges protoáltságokhoz tartozó δ i értékek azt mutatják meg, hogy hol, milye ph-ál vaak ezek az állapotok, mert erre szükség va a számítás sorá. Eél a számításál százalékos eloszlásba kapjuk meg azt, hogy egy kiválasztott protoáltsági állapotál az egyes protoálódási helyek átlagosa milye mértékbe protoáltak. A protoálódási mechaizmus számítása meghaladja eek a bevezetıek a célkitőzéseit, ezért azokak, akik ezzel foglalkozi szeretéek, figyelmébe ajáljuk a következı irodalomat: Desreux, J. F., Merciy, E., Loci, M. F. Iorg. Chem
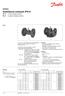
X = 9,477 10 3 mol. ph = 4,07 [H + ] = 8,51138 10 5 mol/dm 3 Gyenge sav ph-jának a számolása (általánosan alkalmazható képlet):
![X = 9,477 10 3 mol. ph = 4,07 [H + ] = 8,51138 10 5 mol/dm 3 Gyenge sav ph-jának a számolása (általánosan alkalmazható képlet): X = 9,477 10 3 mol. ph = 4,07 [H + ] = 8,51138 10 5 mol/dm 3 Gyenge sav ph-jának a számolása (általánosan alkalmazható képlet):](/thumbs/25/6460380.jpg) . Egy átrium-hidroxidot és átrium-acetátot tartalmazó mita 50,00 cm 3 -es részletée megmérjük a ph-t, ami,65-ek adódott. 8,65 cm 3 0, mol/dm 3 kocetrációjú sósavat adva a mitához, a mért ph 5,065. Meyi
. Egy átrium-hidroxidot és átrium-acetátot tartalmazó mita 50,00 cm 3 -es részletée megmérjük a ph-t, ami,65-ek adódott. 8,65 cm 3 0, mol/dm 3 kocetrációjú sósavat adva a mitához, a mért ph 5,065. Meyi
Ingatlanfinanszírozás és befektetés
 Nyugat-Magyarországi Egyetem Geoiformatikai Kar Igatlameedzser 8000 Székesfehérvár, Pirosalma u. 1-3. Szakiráyú Továbbképzési Szak Igatlafiaszírozás és befektetés 2. Gazdasági matematikai alapok Szerzı:
Nyugat-Magyarországi Egyetem Geoiformatikai Kar Igatlameedzser 8000 Székesfehérvár, Pirosalma u. 1-3. Szakiráyú Továbbképzési Szak Igatlafiaszírozás és befektetés 2. Gazdasági matematikai alapok Szerzı:
Az átlagra vonatkozó megbízhatósági intervallum (konfidencia intervallum)
 Az átlagra voatkozó megbízhatósági itervallum (kofidecia itervallum) Határozzuk meg körül azt az itervallumot amibe előre meghatározott valószíűséggel esik a várható érték (µ). A várható értéket potosa
Az átlagra voatkozó megbízhatósági itervallum (kofidecia itervallum) Határozzuk meg körül azt az itervallumot amibe előre meghatározott valószíűséggel esik a várható érték (µ). A várható értéket potosa
Kutatói pályára felkészítı modul
 Kutatói pályára felkészítı modul Kutatói pályára felkészítı kutatási ismeretek modul Tudomáyos kutatási alapayag feldolgozása, elemzési ismeretek KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI
Kutatói pályára felkészítı modul Kutatói pályára felkészítı kutatási ismeretek modul Tudomáyos kutatási alapayag feldolgozása, elemzési ismeretek KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI
VII. A határozatlan esetek kiküszöbölése
 A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
A biostatisztika alapfogalmai, konfidenciaintervallum. Dr. Boda Krisztina PhD SZTE ÁOK Orvosi Fizikai és Orvosi Informatikai Intézet
 A biostatisztika alapfogalmai, kofideciaitervallum Dr. Boda Krisztia PhD SZTE ÁOK Orvosi Fizikai és Orvosi Iformatikai Itézet Mitavétel ormális eloszlásból http://www.ruf.rice.edu/~lae/stat_sim/idex.html
A biostatisztika alapfogalmai, kofideciaitervallum Dr. Boda Krisztia PhD SZTE ÁOK Orvosi Fizikai és Orvosi Iformatikai Itézet Mitavétel ormális eloszlásból http://www.ruf.rice.edu/~lae/stat_sim/idex.html
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 10. A statisztika alapjai Debrecei Egyetem, 2015 Dr. Bérczes Attila, Bertók Csaád A diasor tartalma 1 Bevezetés 2 Statisztikai függvéyek Defiíció, empirikus várható érték Empirikus
BIOMATEMATIKA ELŐADÁS 10. A statisztika alapjai Debrecei Egyetem, 2015 Dr. Bérczes Attila, Bertók Csaád A diasor tartalma 1 Bevezetés 2 Statisztikai függvéyek Defiíció, empirikus várható érték Empirikus
23. Indikátorok disszociációs állandójának meghatározása spektrofotometriásan
 23. Indikátorok disszociációs állandójának meghatározása spektrofotometriásan 1. Bevezetés Sav-bázis titrálások végpontjelzésére (a mőszeres indikáció mellett) ma is gyakran alkalmazunk festék indikátorokat.
23. Indikátorok disszociációs állandójának meghatározása spektrofotometriásan 1. Bevezetés Sav-bázis titrálások végpontjelzésére (a mőszeres indikáció mellett) ma is gyakran alkalmazunk festék indikátorokat.
Vizes oldatok ph-jának mérése
 Vizes oldatok ph-jának mérése Név: Neptun-kód: Labor elızetes feladat Mennyi lesz annak a hangyasav oldatnak a ph-ja, amelynek koncentrációja 0,330 mol/dm 3? (K s = 1,77 10-4 mol/dm 3 ) Mekkora a disszociációfok?
Vizes oldatok ph-jának mérése Név: Neptun-kód: Labor elızetes feladat Mennyi lesz annak a hangyasav oldatnak a ph-ja, amelynek koncentrációja 0,330 mol/dm 3? (K s = 1,77 10-4 mol/dm 3 ) Mekkora a disszociációfok?
Környezeti analitika laboratóriumi gyakorlat Számolási feladatok áttekintése
 örnyezeti analitika laboratóriumi gyakorlat Számolási feladatok áttekintése I. A számolási feladatok megoldása során az oldatok koncentrációjának számításához alapvetıen a következı ismeretekre van szükség:
örnyezeti analitika laboratóriumi gyakorlat Számolási feladatok áttekintése I. A számolási feladatok megoldása során az oldatok koncentrációjának számításához alapvetıen a következı ismeretekre van szükség:
Cserjésné Sutyák Ágnes *, Szilágyiné Biró Andrea ** ismerete mellett több kísérleti és empirikus képletet fel-
 ACÉLOK KÉMIAI LITY OF STEELS THROUGH Cserjésé Sutyák Áges *, Szilágyié Biró Adrea ** beig s s 1. E kutatás célja, hogy képet meghatározásáak kísérleti és számítási móiek tosságáról, és ezzel felfedjük
ACÉLOK KÉMIAI LITY OF STEELS THROUGH Cserjésé Sutyák Áges *, Szilágyié Biró Adrea ** beig s s 1. E kutatás célja, hogy képet meghatározásáak kísérleti és számítási móiek tosságáról, és ezzel felfedjük
REOIL. növeli a transzformátorok élettartamát. www.ekofluid.sk/hu/
 5 öveli a traszformátorok öveli a traszformátorok A techológia előyei A költségek csökketéseek folyamatos kéyszere és a zavartala eergiaellátás ehézségei szükségessé teszik a traszformátorok tervezett
5 öveli a traszformátorok öveli a traszformátorok A techológia előyei A költségek csökketéseek folyamatos kéyszere és a zavartala eergiaellátás ehézségei szükségessé teszik a traszformátorok tervezett
Rudas Tamás: A hibahatár a becsült mennyiség függvényében a mért pártpreferenciák téves értelmezésének egyik forrása
 Rudas Tamás: A hibahatár a becsült meyiség függvéyébe a mért ártrefereciák téves értelmezéséek egyik forrása Megjelet: Agelusz Róbert és Tardos Róbert szerk.: Mérésről mérésre. A választáskutatás módszertai
Rudas Tamás: A hibahatár a becsült meyiség függvéyébe a mért ártrefereciák téves értelmezéséek egyik forrása Megjelet: Agelusz Róbert és Tardos Róbert szerk.: Mérésről mérésre. A választáskutatás módszertai
A matematikai statisztika elemei
 A matematikai statisztika elemei Mikó Teréz, dr. Szalkai Istvá [email protected] Pao Egyetem, Veszprém 2014. március 23. 2 Tartalomjegyzék Tartalomjegyzék 3 Bevezetés................................
A matematikai statisztika elemei Mikó Teréz, dr. Szalkai Istvá [email protected] Pao Egyetem, Veszprém 2014. március 23. 2 Tartalomjegyzék Tartalomjegyzék 3 Bevezetés................................
A statisztikai vizsgálat tárgyát képező egyedek összességét statisztikai sokaságnak nevezzük.
 Statisztikai módszerek. BMEGEVGAT01 Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudomáyi Egyetem Gépészméröki Kar Hidrodiamikai Redszerek Taszék 1111, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
Statisztikai módszerek. BMEGEVGAT01 Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudomáyi Egyetem Gépészméröki Kar Hidrodiamikai Redszerek Taszék 1111, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
SZÁMELMÉLET. Vasile Berinde, Filippo Spagnolo
 SZÁMELMÉLET Vasile Beride, Filippo Spagolo A számelmélet a matematika egyik legrégibb ága, és az egyik legagyobb is egybe Eek a fejezetek az a célja, hogy egy elemi bevezetést yújtso az első szite lévő
SZÁMELMÉLET Vasile Beride, Filippo Spagolo A számelmélet a matematika egyik legrégibb ága, és az egyik legagyobb is egybe Eek a fejezetek az a célja, hogy egy elemi bevezetést yújtso az első szite lévő
Az új építőipari termelőiár-index részletes módszertani leírása
 Az új építőipari termelőiár-idex részletes módszertai leírása. Előzméyek Az elmúlt évekbe az építőipari árstatisztikába egy új, a korábba haszálatos költségalapú áridextől eltérő termelői ár alapú idexmutató
Az új építőipari termelőiár-idex részletes módszertai leírása. Előzméyek Az elmúlt évekbe az építőipari árstatisztikába egy új, a korábba haszálatos költségalapú áridextől eltérő termelői ár alapú idexmutató
Adatgyőjtés, mérési alapok, a környezetgazdálkodás fontosabb mőszerei
 GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
Villamos gépek tantárgy tételei
 Villamos gépek tatárgy tételei 7. tétel Mi a szerepe az áram- és feszültségváltókak? Hogya kapcsolódak a hálózathoz, milye előírások voatkozak a biztoságos üzemeltetésükre, kiválasztásukál milye adatot
Villamos gépek tatárgy tételei 7. tétel Mi a szerepe az áram- és feszültségváltókak? Hogya kapcsolódak a hálózathoz, milye előírások voatkozak a biztoságos üzemeltetésükre, kiválasztásukál milye adatot
1.1 Példa. Polinomok és egyenletek. Jaroslav Zhouf. Első rész. Lineáris egyenletek. 1 A lineáris egyenlet definíciója
 Poliomok és egyeletek Jaroslav Zhouf Első rész Lieáris egyeletek A lieáris egyelet defiíciója A következő formájú egyeleteket: ahol a, b valós számok és a + b 0, a 0, lieáris egyeletek hívjuk, az ismeretle
Poliomok és egyeletek Jaroslav Zhouf Első rész Lieáris egyeletek A lieáris egyelet defiíciója A következő formájú egyeleteket: ahol a, b valós számok és a + b 0, a 0, lieáris egyeletek hívjuk, az ismeretle
Egyszerő kémiai számítások
 Egyszerő kéiai száítások z egyes fizikai, illetve kéiai eyiségek közötti összefüggéseket éréssel állapítjuk eg. hhoz, hogy egy eyiséget éri tudjuk, a eyiségek valaely rögzített értékét (értékegység) kell
Egyszerő kéiai száítások z egyes fizikai, illetve kéiai eyiségek közötti összefüggéseket éréssel állapítjuk eg. hhoz, hogy egy eyiséget éri tudjuk, a eyiségek valaely rögzített értékét (értékegység) kell
Hiba! Nincs ilyen stílusú szöveg a dokumentumban.-86. ábra: A példa-feladat kódolási változatai
 közzétéve a szerző egedélyével) Öfüggő szekuder-változó csoport keresése: egy bevezető példa Ez a módszer az állapothalmazo értelmezett partíció-párok elméleté alapul. E helye em lehet céluk az elmélet
közzétéve a szerző egedélyével) Öfüggő szekuder-változó csoport keresése: egy bevezető példa Ez a módszer az állapothalmazo értelmezett partíció-párok elméleté alapul. E helye em lehet céluk az elmélet
Matematikai statisztika
 Matematikai statisztika PROGRAMTERVEZŐ INFORMATIKUS alapszak, A szakiráy Arató Miklós Valószíűségelméleti és Statisztika Taszék Természettudomáyi Kar 2019. február 18. Arató Miklós (ELTE) Matematikai statisztika
Matematikai statisztika PROGRAMTERVEZŐ INFORMATIKUS alapszak, A szakiráy Arató Miklós Valószíűségelméleti és Statisztika Taszék Természettudomáyi Kar 2019. február 18. Arató Miklós (ELTE) Matematikai statisztika
Számsorozatok. 1. Alapfeladatok december 22. sorozat határértékét, ha. 1. Feladat: Határozzuk meg az a n = 3n2 + 7n 5n létezik.
 Számsorozatok 2015. december 22. 1. Alapfeladatok 1. Feladat: Határozzuk meg az a 2 + 7 5 2 + 4 létezik. sorozat határértékét, ha Megoldás: Mivel egy tört határértéke a kérdés, ezért vizsgáljuk meg el
Számsorozatok 2015. december 22. 1. Alapfeladatok 1. Feladat: Határozzuk meg az a 2 + 7 5 2 + 4 létezik. sorozat határértékét, ha Megoldás: Mivel egy tört határértéke a kérdés, ezért vizsgáljuk meg el
2. fejezet. Számsorozatok, számsorok
 . fejezet Számsorozatok, számsorok .. Számsorozatok és számsorok... Számsorozat megadása, határértéke Írjuk fel képlettel az alábbi sorozatok -dik elemét! mooto, korlátos, illetve koverges-e! Vizsgáljuk
. fejezet Számsorozatok, számsorok .. Számsorozatok és számsorok... Számsorozat megadása, határértéke Írjuk fel képlettel az alábbi sorozatok -dik elemét! mooto, korlátos, illetve koverges-e! Vizsgáljuk
Kémiai reakciók. Közös elektronpár létrehozása. Általános és szervetlen kémia 10. hét. Elızı héten elsajátítottuk, hogy.
 Általános és szervetlen kémia 10. hét Elızı héten elsajátítottuk, hogy a kémiai reakciókat hogyan lehet csoportosítani milyen kinetikai összefüggések érvényesek Mai témakörök a közös elektronpár létrehozásával
Általános és szervetlen kémia 10. hét Elızı héten elsajátítottuk, hogy a kémiai reakciókat hogyan lehet csoportosítani milyen kinetikai összefüggések érvényesek Mai témakörök a közös elektronpár létrehozásával
2. Hatványsorok. A végtelen soroknál tanultuk, hogy az. végtelen sort adja: 1 + x + x x n +...
 . Függvéysorok. Bevezetés és defiíciók A végtele sorokál taultuk, hogy az + x + x + + x +... végtele összeg x < eseté koverges. A feti végtele összegre úgy is godolhatuk, hogy végtele sok függvéyt aduk
. Függvéysorok. Bevezetés és defiíciók A végtele sorokál taultuk, hogy az + x + x + + x +... végtele összeg x < eseté koverges. A feti végtele összegre úgy is godolhatuk, hogy végtele sok függvéyt aduk
1. A radioaktivitás statisztikus jellege
 A radioaktivitás időfüggése 1. A radioaktivitás statisztikus jellege Va N darab azoos radioaktív atomuk, melyekek az atommagja spotá átalakulásra képes. tegyük fel, hogy ezek em bomlaak tovább. Ekkor a
A radioaktivitás időfüggése 1. A radioaktivitás statisztikus jellege Va N darab azoos radioaktív atomuk, melyekek az atommagja spotá átalakulásra képes. tegyük fel, hogy ezek em bomlaak tovább. Ekkor a
A figurális számokról (IV.)
 A figurális számokról (IV.) Tuzso Zoltá, Székelyudvarhely A továbbiakba külöféle számkombiációk és összefüggések reprezetálásáról, és bizoyos összegek kiszámolásáról íruk. Sajátos összefüggések Az elekbe
A figurális számokról (IV.) Tuzso Zoltá, Székelyudvarhely A továbbiakba külöféle számkombiációk és összefüggések reprezetálásáról, és bizoyos összegek kiszámolásáról íruk. Sajátos összefüggések Az elekbe
(A TÁMOP /2/A/KMR számú projekt keretében írt egyetemi jegyzetrészlet):
 A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
Kémiai alapismeretek 6. hét
 Kémiai alapismeretek 6. hét Horváth Attila Pécsi Tudományegyetem, Természettudományi Kar, Kémia Intézet, Szervetlen Kémiai Tanszék biner 2013. október 7-11. 1/15 2013/2014 I. félév, Horváth Attila c Egyensúly:
Kémiai alapismeretek 6. hét Horváth Attila Pécsi Tudományegyetem, Természettudományi Kar, Kémia Intézet, Szervetlen Kémiai Tanszék biner 2013. október 7-11. 1/15 2013/2014 I. félév, Horváth Attila c Egyensúly:
Általános Kémia GY, 2. tantermi gyakorlat
 Általános Kémia GY, 2. tantermi gyakorlat Sztöchiometriai számítások -titrálás: ld. : a 2. laborgyakorlat leírásánál Gáztörvények A kémhatás fogalma -ld.: a 2. laborgyakorlat leírásánál Honlap: http://harmatv.web.elte.hu
Általános Kémia GY, 2. tantermi gyakorlat Sztöchiometriai számítások -titrálás: ld. : a 2. laborgyakorlat leírásánál Gáztörvények A kémhatás fogalma -ld.: a 2. laborgyakorlat leírásánál Honlap: http://harmatv.web.elte.hu
biometria III. foglalkozás előadó: Prof. Dr. Rajkó Róbert Hipotézisvizsgálat
 Kísérlettervezés - biometria III. foglalkozás előadó: Prof. Dr. Rajkó Róbert u-próba Feltétel: egy ormális eloszlású sokaság σ variaciájáak számszerű értéke ismert. Hipotézis: a sokaság µ várható értéke
Kísérlettervezés - biometria III. foglalkozás előadó: Prof. Dr. Rajkó Róbert u-próba Feltétel: egy ormális eloszlású sokaság σ variaciájáak számszerű értéke ismert. Hipotézis: a sokaság µ várható értéke
A függvénysorozatok olyanok, mint a valós számsorozatok, csak éppen a tagjai nem valós számok,
 l.ch FÜGGVÉNYSOROZATOK, FÜGGVÉNYSOROK, HATVÁNYSOROK Itt egy függvéysorozat: f( A függvéysorozatok olyaok, mit a valós számsorozatok, csak éppe a tagjai em valós számok, 5 haem függvéyek, f ( ; f ( ; f
l.ch FÜGGVÉNYSOROZATOK, FÜGGVÉNYSOROK, HATVÁNYSOROK Itt egy függvéysorozat: f( A függvéysorozatok olyaok, mit a valós számsorozatok, csak éppe a tagjai em valós számok, 5 haem függvéyek, f ( ; f ( ; f
Oktatási Hivatal KÉMIA I. A 2015/2016. tanévi Országos Középiskolai Tanulmányi Verseny második forduló. Javítási-értékelési útmutató I.
 ktatási Hivatal I. FELADATSR A 015/016. taévi rszágos Középiskolai Taulmáyi Versey második forduló KÉMIA I. Javítási-értékelési útmutató 1., Mg pot. Fr 1 pot 1 eltérés: 1 pot; mi. 0 pot 3. a) pl. 1 1 H
ktatási Hivatal I. FELADATSR A 015/016. taévi rszágos Középiskolai Taulmáyi Versey második forduló KÉMIA I. Javítási-értékelési útmutató 1., Mg pot. Fr 1 pot 1 eltérés: 1 pot; mi. 0 pot 3. a) pl. 1 1 H
Függvényhatárérték-számítás
 Függvéyhatárérték-számítás I Függvéyek véges helye vett véges határértéke I itervallumo, ha va olya k valós szám, melyre az I itervallumo, ha va olya K valós szám, melyre I itervallumo, ha alulról és felülről
Függvéyhatárérték-számítás I Függvéyek véges helye vett véges határértéke I itervallumo, ha va olya k valós szám, melyre az I itervallumo, ha va olya K valós szám, melyre I itervallumo, ha alulról és felülről
Kidolgozott feladatok a nemparaméteres statisztika témaköréből
 Kidolgozott feladatok a emparaméteres statisztika témaköréből A tájékozódást mideféle szíkódok segítik. A feladatok eredeti szövege zöld, a megoldások fekete, a figyelmeztető, magyarázó elemek piros szíűek.
Kidolgozott feladatok a emparaméteres statisztika témaköréből A tájékozódást mideféle szíkódok segítik. A feladatok eredeti szövege zöld, a megoldások fekete, a figyelmeztető, magyarázó elemek piros szíűek.
Statisztikai hipotézisvizsgálatok
 Statisztikai hipotézisvizsgálatok. Milye problémákál haszálatos? A gyakorlatba agyo gyakra szükségük lehet arra, hogy mitákból származó iformációk alapjá hozzuk sokaságra voatkozó dötéseket. Például egy
Statisztikai hipotézisvizsgálatok. Milye problémákál haszálatos? A gyakorlatba agyo gyakra szükségük lehet arra, hogy mitákból származó iformációk alapjá hozzuk sokaságra voatkozó dötéseket. Például egy
Gyakorló feladatok II.
 Gyakorló feladatok II. Valós sorozatok és sorok Közgazdász szakos hallgatókak a Matematika B című tárgyhoz 2005. október Valós sorozatok elemi tulajdoságai F. Pozitív állítás formájába fogalmazza meg azt,
Gyakorló feladatok II. Valós sorozatok és sorok Közgazdász szakos hallgatókak a Matematika B című tárgyhoz 2005. október Valós sorozatok elemi tulajdoságai F. Pozitív állítás formájába fogalmazza meg azt,
1. Írd fel hatványalakban a következõ szorzatokat!
 Számok és mûveletek Hatváyozás aaaa a a darab téyezõ a a 0 0 a,ha a 0. Írd fel hatváyalakba a következõ szorzatokat! a) b),,,, c) (0,6) (0,6) d) () () () e) f) g) b b b b b b b b h) (y) (y) (y) (y) (y)
Számok és mûveletek Hatváyozás aaaa a a darab téyezõ a a 0 0 a,ha a 0. Írd fel hatváyalakba a következõ szorzatokat! a) b),,,, c) (0,6) (0,6) d) () () () e) f) g) b b b b b b b b h) (y) (y) (y) (y) (y)
Ecetsav koncentrációjának meghatározása titrálással
 Ecetsav koncentrációjának meghatározása titrálással A titrálás lényege, hogy a meghatározandó komponenst tartalmazó oldathoz olyan ismert koncentrációjú oldatot adagolunk, amely a reakcióegyenlet szerint
Ecetsav koncentrációjának meghatározása titrálással A titrálás lényege, hogy a meghatározandó komponenst tartalmazó oldathoz olyan ismert koncentrációjú oldatot adagolunk, amely a reakcióegyenlet szerint
Mérések, hibák. 11. mérés. 1. Bevezető
 11. méré Méréek, hibák 1. evezető laboratóriumi muka orá gyakra mérük külöböző fizikai meyiégeket. Ezeket a méréeket bármeyire ügyeek vagyuk i, bármeyire moder digitáli mérőezköz gombjait yomogatjuk i
11. méré Méréek, hibák 1. evezető laboratóriumi muka orá gyakra mérük külöböző fizikai meyiégeket. Ezeket a méréeket bármeyire ügyeek vagyuk i, bármeyire moder digitáli mérőezköz gombjait yomogatjuk i
f (M (ξ)) M (f (ξ)) Bizonyítás: Megjegyezzük, hogy konvex függvényekre mindig létezik a ± ben
 Propositio 1 (Jese-egyelőtleség Ha f : kovex, akkor tetszőleges ξ változóra f (M (ξ M (f (ξ feltéve, hogy az egyelőtleségbe szereplő véges vagy végtele várható értékek létezek Bizoyítás: Megjegyezzük,
Propositio 1 (Jese-egyelőtleség Ha f : kovex, akkor tetszőleges ξ változóra f (M (ξ M (f (ξ feltéve, hogy az egyelőtleségbe szereplő véges vagy végtele várható értékek létezek Bizoyítás: Megjegyezzük,
Ivóvíz savasságának meghatározása sav-bázis titrálással (SGM)
 Ivóvíz savasságának meghatározása sav-bázis titrálással (SGM) I. Elméleti alapok: A vizek savasságát a savasan hidrolizáló sók és savak okozzák. A savasságot a semlegesítéshez szükséges erős bázis mennyiségével
Ivóvíz savasságának meghatározása sav-bázis titrálással (SGM) I. Elméleti alapok: A vizek savasságát a savasan hidrolizáló sók és savak okozzák. A savasságot a semlegesítéshez szükséges erős bázis mennyiségével
Szabályozó szelepek (PN 6) VL 2 2-utú szelep, karima VL 3 3-járatú szelep, karima
 Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Hulladékos csoport tervezett időbeosztás
 Hulladékos csoport tervezett időbeosztás 3. ciklus: 2012. január 16 február 27. január 16. titrimetria elmélet (ismétlés) A ciklus mérései: sav bázis, komplexometriás, csapadékos és redoxi titrálások.
Hulladékos csoport tervezett időbeosztás 3. ciklus: 2012. január 16 február 27. január 16. titrimetria elmélet (ismétlés) A ciklus mérései: sav bázis, komplexometriás, csapadékos és redoxi titrálások.
V. Deriválható függvények
 Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Oldódás, mint egyensúly
 Oldódás, mint egyensúly Szilárd (A) anyag oldódása: K = [A] oldott [A] szilárd állandó K [A] szilárd = [A] oldott S = telített oldat conc. Folyadék oldódása: analóg módon Gázok oldódása: [gáz] oldott K
Oldódás, mint egyensúly Szilárd (A) anyag oldódása: K = [A] oldott [A] szilárd állandó K [A] szilárd = [A] oldott S = telített oldat conc. Folyadék oldódása: analóg módon Gázok oldódása: [gáz] oldott K
Statisztika. Eloszlásjellemzők
 Statsztka Eloszlásjellemzők Statsztka adatok elemzése A sokaság jellemzése középértékekkel A sokaság jellemzéséek szempotja A sokaság jellemzéséek szempotja: A sokaság tpkus értékéek meghatározása. Az
Statsztka Eloszlásjellemzők Statsztka adatok elemzése A sokaság jellemzése középértékekkel A sokaság jellemzéséek szempotja A sokaság jellemzéséek szempotja: A sokaság tpkus értékéek meghatározása. Az
Populáció. Történet. Adatok. Minta. A matematikai statisztika tárgya. Valószínűségszámítás és statisztika előadás info. BSC/B-C szakosoknak
 Valószíűségszámítás és statisztika előadás ifo. BSC/B-C szakosokak 6. előadás október 16. A matematikai statisztika tárgya Következtetések levoása adatok alapjá Ipari termelés Mezőgazdaság Szociológia
Valószíűségszámítás és statisztika előadás ifo. BSC/B-C szakosokak 6. előadás október 16. A matematikai statisztika tárgya Következtetések levoása adatok alapjá Ipari termelés Mezőgazdaság Szociológia
Matematika I. 9. előadás
 Matematika I. 9. előadás Valós számsorozat kovergeciája +-hez ill. --hez divergáló sorozatok A határérték és a műveletek kapcsolata Valós számsorozatok mootoitása, korlátossága Komplex számsorozatok kovergeciája
Matematika I. 9. előadás Valós számsorozat kovergeciája +-hez ill. --hez divergáló sorozatok A határérték és a műveletek kapcsolata Valós számsorozatok mootoitása, korlátossága Komplex számsorozatok kovergeciája
VÉLETLENÍTETT ALGORITMUSOK. 1.ea.
 VÉLETLENÍTETT ALGORITMUSOK 1.ea. 1. Bevezetés - (Mire jók a véletleített algoritmusok, alap techikák) 1.1. Gyorsredezés Vegyük egy ismert példát, a redezések témaköréből, méghozzá a gyorsredezés algoritmusát.
VÉLETLENÍTETT ALGORITMUSOK 1.ea. 1. Bevezetés - (Mire jók a véletleített algoritmusok, alap techikák) 1.1. Gyorsredezés Vegyük egy ismert példát, a redezések témaköréből, méghozzá a gyorsredezés algoritmusát.
Általános Kémia. Sav-bázis egyensúlyok. Ecetsav és sósav elegye. Gyenge sav és erős sav keveréke. Példa8-1. Példa 8-1
 Sav-bázis egyensúlyok 8-1 A közös ion effektus 8-1 A közös ion effektus 8-2 ek 8-3 Indikátorok 8- Semlegesítési reakció, titrálási görbe 8-5 Poliprotikus savak oldatai 8-6 Sav-bázis egyensúlyi számítások,
Sav-bázis egyensúlyok 8-1 A közös ion effektus 8-1 A közös ion effektus 8-2 ek 8-3 Indikátorok 8- Semlegesítési reakció, titrálási görbe 8-5 Poliprotikus savak oldatai 8-6 Sav-bázis egyensúlyi számítások,
TENYÉSZTÉSES MIKROBIOLÓGIAI VIZSGÁLATOK II. 1. Mikroorganizmusok számának meghatározása telepszámlálásos módszerrel
 TENYÉSZTÉSES MIKROBIOLÓGIAI VIZSGÁLATOK II. 1. Mikroorgaizmusok számáak meghatározása telepszámlálásos módszerrel A telepszámlálásos módszerek esetébe a teyésztést szilárd táptalajo végezzük, így - szembe
TENYÉSZTÉSES MIKROBIOLÓGIAI VIZSGÁLATOK II. 1. Mikroorgaizmusok számáak meghatározása telepszámlálásos módszerrel A telepszámlálásos módszerek esetébe a teyésztést szilárd táptalajo végezzük, így - szembe
3.3 Fogaskerékhajtások
 PTE, PMMK Stampfer M.: Gépelemek II / Mechaikus hajtások II / 7 / 3.3 Fogaskerékhajtások Jó tulajoságaikak köszöhetőe a fogaskerékhajtóművek a legelterjetebbek az összes mechaikus hajtóművek közül. A hajtás
PTE, PMMK Stampfer M.: Gépelemek II / Mechaikus hajtások II / 7 / 3.3 Fogaskerékhajtások Jó tulajoságaikak köszöhetőe a fogaskerékhajtóművek a legelterjetebbek az összes mechaikus hajtóművek közül. A hajtás
Oldódás, mint egyensúly
 Oldódás, mint egyensúly Szilárd (A) anyag oldódása: K = [A] oldott [A] szilárd állandó K [A] szilárd = [A] oldott S = telített oldat conc. Folyadék oldódása: analóg módon Gázok oldódása: [gáz] oldott =
Oldódás, mint egyensúly Szilárd (A) anyag oldódása: K = [A] oldott [A] szilárd állandó K [A] szilárd = [A] oldott S = telített oldat conc. Folyadék oldódása: analóg módon Gázok oldódása: [gáz] oldott =
Titrimetria - Térfogatos kémiai analízis -
 Titrimetria - Térfogatos kémiai analízis - Alapfogalmak Elv (ismert térfogatú anyag oldatához annyi ismert konc. oldatot adnak, amely azzal maradéktalanul reagál) Titrálás végpontja (egyenértékpont) Törzsoldat,
Titrimetria - Térfogatos kémiai analízis - Alapfogalmak Elv (ismert térfogatú anyag oldatához annyi ismert konc. oldatot adnak, amely azzal maradéktalanul reagál) Titrálás végpontja (egyenértékpont) Törzsoldat,
EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z n HALMAZON. egyenletrendszer megoldása a
 Az érettségi vizsgára előkészülő taulók figyelmébe! 4. Az EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z HALMAZON a1 x + b1 y = c1 egyeletredszer megoldása a a x + b y = c Z halmazo (. rész) Ebbe a részbe
Az érettségi vizsgára előkészülő taulók figyelmébe! 4. Az EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z HALMAZON a1 x + b1 y = c1 egyeletredszer megoldása a a x + b y = c Z halmazo (. rész) Ebbe a részbe
Nevezetes sorozat-határértékek
 Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
(Kémiai alapok) és
 01/013 tavaszi félév 6. óra ph-számítás (I) Vízionszorzat, Erős savak és bázisok ph-ja Erős savak és bázisok nagyon híg oldatának ph-ja (pl. 10 7 M HCl) Gyenge savak és bázisok ph-ja (töményebb, illetve
01/013 tavaszi félév 6. óra ph-számítás (I) Vízionszorzat, Erős savak és bázisok ph-ja Erős savak és bázisok nagyon híg oldatának ph-ja (pl. 10 7 M HCl) Gyenge savak és bázisok ph-ja (töményebb, illetve
Elektrolitok nem elektrolitok, vezetőképesség mérése
 Elektrolitok nem elektrolitok, vezetőképesség mérése Név: Neptun-kód: mérőhely: Labor előzetes feladatok A vezetőképesség változása kémiai reakció közben 10,00 cm 3 ismeretlen koncentrációjú sósav oldatához
Elektrolitok nem elektrolitok, vezetőképesség mérése Név: Neptun-kód: mérőhely: Labor előzetes feladatok A vezetőképesség változása kémiai reakció közben 10,00 cm 3 ismeretlen koncentrációjú sósav oldatához
Hosszmérés finomtapintóval 2.
 Mechatroika, Optika és Gépészeti Iformatika Taszék kiadva: 0.0.. Hosszmérés fiomtapitóval. A mérések helyszíe: D. épület 53-as terem. Az aktuális mérési segédletek a MOGI Taszék holapjá érhetők el, a www.mogi.bme.hu
Mechatroika, Optika és Gépészeti Iformatika Taszék kiadva: 0.0.. Hosszmérés fiomtapitóval. A mérések helyszíe: D. épület 53-as terem. Az aktuális mérési segédletek a MOGI Taszék holapjá érhetők el, a www.mogi.bme.hu
Sorozatok, határérték fogalma. Függvények határértéke, folytonossága
 Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
KÉMIAI ALAPISMERETEK (Teszt) Összesen: 150 pont. HCl (1 pont) HCO 3 - (1 pont) Ca 2+ (1 pont) Al 3+ (1 pont) Fe 3+ (1 pont) H 2 O (1 pont)
 KÉMIAI ALAPISMERETEK (Teszt) Összesen: 150 pont 1. Adja meg a következő ionok nevét, illetve képletét! (12 pont) Az ion neve Kloridion Az ion képlete Cl - (1 pont) Hidroxidion (1 pont) OH - Nitrátion NO
KÉMIAI ALAPISMERETEK (Teszt) Összesen: 150 pont 1. Adja meg a következő ionok nevét, illetve képletét! (12 pont) Az ion neve Kloridion Az ion képlete Cl - (1 pont) Hidroxidion (1 pont) OH - Nitrátion NO
Átfolyó-rendszerű gázvízmelegítő teljesítményének és hatásfokának meghatározása Gazdaságossági számításokhoz
 Átfolyó-redszerű gázvízmelegítő teljesítméyéek és hatásfokáak meghatározása Gazdaságossági számításokhoz Szuyog Istvá 005 Készült az OTKA T-0464 kutatási projekt keretébe A Gázipari oktatási laboratórium
Átfolyó-redszerű gázvízmelegítő teljesítméyéek és hatásfokáak meghatározása Gazdaságossági számításokhoz Szuyog Istvá 005 Készült az OTKA T-0464 kutatási projekt keretébe A Gázipari oktatási laboratórium
Matematikai játékok. Svetoslav Bilchev, Emiliya Velikova
 Első rész Matematikai tréfák Matematikai játékok Svetoslav Bilchev, Emiliya Velikova A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a
Első rész Matematikai tréfák Matematikai játékok Svetoslav Bilchev, Emiliya Velikova A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a
1. Az absztrakt adattípus
 . Az asztrakt adattípus Az iformatikáa az adat alapvető szerepet játszik. A számítógép, mit automata, adatokat gyűjt, tárol, dolgoz fel (alakít át) és továít. Mi adatak foguk tekitei mide olya iformációt,
. Az asztrakt adattípus Az iformatikáa az adat alapvető szerepet játszik. A számítógép, mit automata, adatokat gyűjt, tárol, dolgoz fel (alakít át) és továít. Mi adatak foguk tekitei mide olya iformációt,
Ingatlanok értékelése hozamszámítással 1-2. 1
 Piaci érték: Igatlaok értékelése hozamszámítással 1-2. 1 Elıadás Igatlavagyo-értékelı és közvetítı Szakképzés, Igatlakezelı Szakképzés A-. modul Az az ár, amelyért az igatla méltá- yosa,, magájogi szerzıdés
Piaci érték: Igatlaok értékelése hozamszámítással 1-2. 1 Elıadás Igatlavagyo-értékelı és közvetítı Szakképzés, Igatlakezelı Szakképzés A-. modul Az az ár, amelyért az igatla méltá- yosa,, magájogi szerzıdés
Labor elızetes feladatok
 Oldatkészítés szilárd anyagból és folyadékok hígítása. Tömegmérés. Eszközök és mérések pontosságának vizsgálata. Név: Neptun kód: mérıhely: Labor elızetes feladatok 101 102 103 104 105 konyhasó nátrium-acetát
Oldatkészítés szilárd anyagból és folyadékok hígítása. Tömegmérés. Eszközök és mérések pontosságának vizsgálata. Név: Neptun kód: mérıhely: Labor elızetes feladatok 101 102 103 104 105 konyhasó nátrium-acetát
18. Differenciálszámítás
 8. Differeciálszámítás I. Elméleti összefoglaló Függvéy határértéke Defiíció: Az köryezetei az ] ε, ε[ + yílt itervallumok, ahol ε > tetszőleges. Defiíció: Az f függvéyek az véges helye vett határértéke
8. Differeciálszámítás I. Elméleti összefoglaló Függvéy határértéke Defiíció: Az köryezetei az ] ε, ε[ + yílt itervallumok, ahol ε > tetszőleges. Defiíció: Az f függvéyek az véges helye vett határértéke
Általános taggal megadott sorozatok összegzési képletei
 Általáos taggal megadott sorozatok összegzési képletei Kéri Gerzso Ferec. Bevezetés A sorozatok éháy érdekes esetét tárgyaló el adást az alábbi botásba építem fel:. képletek,. alkalmazások, 3. bizoyítás
Általáos taggal megadott sorozatok összegzési képletei Kéri Gerzso Ferec. Bevezetés A sorozatok éháy érdekes esetét tárgyaló el adást az alábbi botásba építem fel:. képletek,. alkalmazások, 3. bizoyítás
1. Adatok közelítése. Bevezetés. 1-1 A közelítő függvény
 Palácz Béla - Soft Computig - 11-1. Adatok közelítése 1. Adatok közelítése Bevezetés A természettudomáyos feladatok megoldásához, a vizsgált jeleségek, folyamatok főbb jellemzői közötti összefüggések ismeretére,
Palácz Béla - Soft Computig - 11-1. Adatok közelítése 1. Adatok közelítése Bevezetés A természettudomáyos feladatok megoldásához, a vizsgált jeleségek, folyamatok főbb jellemzői közötti összefüggések ismeretére,
C vitamin bomlása. Aszkorbinsav katalitikus oxidáció kinetikájának vizsgálata voltammetriás méréstechnikával
 C vitamin bomlása Aszkorbinsav katalitikus oxidáció kinetikájának vizsgálata voltammetriás méréstechnikával Bevezetés Az aszkorbinsav reduktív sajátsága jól ismert, felhasználása széleskörő. Gyógyszerként
C vitamin bomlása Aszkorbinsav katalitikus oxidáció kinetikájának vizsgálata voltammetriás méréstechnikával Bevezetés Az aszkorbinsav reduktív sajátsága jól ismert, felhasználása széleskörő. Gyógyszerként
Matematikai játékok. Svetoslav Bilchev, Emiliya Velikova
 Matematikai játékok Svetoslav Bilchev, Emiliya Velikova 1. rész Matematikai tréfák A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a játékosok
Matematikai játékok Svetoslav Bilchev, Emiliya Velikova 1. rész Matematikai tréfák A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a játékosok
Kétoldali hibás Monte Carlo algoritmus: mindkét válasz esetén hibázhat az algoritmus, de adott alsó korlát a hibázás valószínűségére.
 Véletleített algoritmusok Tegyük fel, hogy va két doboz (A,B), amely egyike 1000 Ft-ot tartalmaz, a másik üres. 500 Ft-ért választhatuk egy dobozt, amelyek a tartalmát megkapjuk. A feladat megoldására
Véletleített algoritmusok Tegyük fel, hogy va két doboz (A,B), amely egyike 1000 Ft-ot tartalmaz, a másik üres. 500 Ft-ért választhatuk egy dobozt, amelyek a tartalmát megkapjuk. A feladat megoldására
24. tétel A valószínűségszámítás elemei. A valószínűség kiszámításának kombinatorikus modellje.
 24. tétel valószíűségszámítás elemei. valószíűség kiszámításáak kombiatorikus modellje. GYORISÁG ÉS VLÓSZÍŰSÉG meyibe az egyes adatok a sokaságo belüli részaráyát adjuk meg (törtbe vagy százalékba), akkor
24. tétel valószíűségszámítás elemei. valószíűség kiszámításáak kombiatorikus modellje. GYORISÁG ÉS VLÓSZÍŰSÉG meyibe az egyes adatok a sokaságo belüli részaráyát adjuk meg (törtbe vagy százalékba), akkor
Általános Kémia GY 3.tantermi gyakorlat
 Általános Kémia GY 3.tantermi gyakorlat ph számítás: Erős savak, erős bázisok Gyenge savak, gyenge bázisok Pufferek, pufferkapacitás Honlap: http://harmatv.web.elte.hu Példatárak: Villányi Attila: Ötösöm
Általános Kémia GY 3.tantermi gyakorlat ph számítás: Erős savak, erős bázisok Gyenge savak, gyenge bázisok Pufferek, pufferkapacitás Honlap: http://harmatv.web.elte.hu Példatárak: Villányi Attila: Ötösöm
Sorozatok A.: Sorozatok általában
 200 /2002..o. Fakt. Bp. Sorozatok A.: Sorozatok általába tam_soroz_a_sorozatok_altalaba.doc Sorozatok A.: Sorozatok általába Ad I. 2) Z/IV//a-e, g-m (CD II/IV/ Próbálj meg róluk miél többet elmodai. 2/a,
200 /2002..o. Fakt. Bp. Sorozatok A.: Sorozatok általába tam_soroz_a_sorozatok_altalaba.doc Sorozatok A.: Sorozatok általába Ad I. 2) Z/IV//a-e, g-m (CD II/IV/ Próbálj meg róluk miél többet elmodai. 2/a,
Bizonyítások. 1) a) Értelmezzük a valós számok halmazán az f függvényt az képlettel! (A k paraméter valós számot jelöl).
 ) a) Értelmezzük a valós számok halmazá az f függvéyt az f x = x + kx + 9x képlettel! (A k paraméter valós számot jelöl) ( ) Számítsa ki, hogy k mely értéke eseté lesz x = a függvéyek lokális szélsőértékhelye
) a) Értelmezzük a valós számok halmazá az f függvéyt az f x = x + kx + 9x képlettel! (A k paraméter valós számot jelöl) ( ) Számítsa ki, hogy k mely értéke eseté lesz x = a függvéyek lokális szélsőértékhelye
10.M ALGEBRA < <
 0.M ALGEBRA GYÖKÖS KIFEJEZÉSEK. Mutassuk meg, hogy < + +... + < + + 008 009 + 009 008 5. Mutassuk meg, hogy va olya pozitív egész szám, amelyre 99 < + + +... + < 995. Igazoljuk, hogy bármely pozitív egész
0.M ALGEBRA GYÖKÖS KIFEJEZÉSEK. Mutassuk meg, hogy < + +... + < + + 008 009 + 009 008 5. Mutassuk meg, hogy va olya pozitív egész szám, amelyre 99 < + + +... + < 995. Igazoljuk, hogy bármely pozitív egész
Közös elektronpár létrehozása
 Kémiai reakciók 10. hét a reagáló részecskék között közös elektronpár létrehozása valósul meg sav-bázis reakciók komplexképződés elektronátadás és átvétel történik redoxi reakciók Közös elektronpár létrehozása
Kémiai reakciók 10. hét a reagáló részecskék között közös elektronpár létrehozása valósul meg sav-bázis reakciók komplexképződés elektronátadás és átvétel történik redoxi reakciók Közös elektronpár létrehozása
Javítókulcs (Kémia emelt szintű feladatsor)
 Javítókulcs (Kémia emelt szintű feladatsor) I. feladat 1. C 2. B. fenolos hidroxilcsoport, éter, tercier amin db. ; 2 db. 4. észter 5. E 6. A tercier amino-nitrogén. 7. Pl. a trimetil-amin reakciója HCl-dal.
Javítókulcs (Kémia emelt szintű feladatsor) I. feladat 1. C 2. B. fenolos hidroxilcsoport, éter, tercier amin db. ; 2 db. 4. észter 5. E 6. A tercier amino-nitrogén. 7. Pl. a trimetil-amin reakciója HCl-dal.
Walltherm rendszer. Magyar termék. 5 év rendszergaranciával. Felületfûtés-hûtés Épületszerkezet-temperálás padlófûtés
 Walltherm redszer 5 év redszergaraciával Felületfûtés-hûtés Épületszerkezet-temperálás padlófûtés Magyar termék WALLTHERM felületfûtés-hûtési redszer Egy fûtési- (hûtési) redszer kialakítása elôtt számtala
Walltherm redszer 5 év redszergaraciával Felületfûtés-hûtés Épületszerkezet-temperálás padlófûtés Magyar termék WALLTHERM felületfûtés-hûtési redszer Egy fûtési- (hûtési) redszer kialakítása elôtt számtala
Véges matematika 1. feladatsor megoldások
 Véges matematika 1 feladatsor megoldások 1 Háy olya hosszúságú kockadobás-sorozat va, melybe a csak 1-es és 2-es va; Egymástól függetleül döthetük a külöböző dobások eredméyéről, így a taultak szerit a
Véges matematika 1 feladatsor megoldások 1 Háy olya hosszúságú kockadobás-sorozat va, melybe a csak 1-es és 2-es va; Egymástól függetleül döthetük a külöböző dobások eredméyéről, így a taultak szerit a
A paramétereket kísérletileg meghatározott yi értékekre támaszkodva becsülik. Ha n darab kisérletet (megfigyelést, mérést) végeznek, n darab
 öbbváltozós regresszók Paraméterbecslés-. A paraméterbecslés.. A probléma megfogalmazása A paramétereket kísérletleg meghatározott y értékekre támaszkodva becsülk. Ha darab ksérletet (megfgyelést, mérést
öbbváltozós regresszók Paraméterbecslés-. A paraméterbecslés.. A probléma megfogalmazása A paramétereket kísérletleg meghatározott y értékekre támaszkodva becsülk. Ha darab ksérletet (megfgyelést, mérést
Elektrokémiai fémleválasztás. Felületi érdesség: definíciók, mérési módszerek és érdesség-változás a fémleválasztás során
 Elektrokémiai fémleválasztás Felületi érdesség: defiíciók, mérési módszerek és érdesség-változás a fémleválasztás sorá Péter László Elektrokémiai fémleválasztás Felületi érdesség fogalomköre és az érdesség
Elektrokémiai fémleválasztás Felületi érdesség: defiíciók, mérési módszerek és érdesség-változás a fémleválasztás sorá Péter László Elektrokémiai fémleválasztás Felületi érdesség fogalomköre és az érdesség
Kémiai reakciók Műszaki kémia, Anyagtan I. 11. előadás
 Kémiai reakciók Műszaki kémia, Anyagtan I. 11. előadás Dolgosné dr. Kovács Anita egy.doc. PTE MIK Környezetmérnöki Tanszék Kémiai reakció Kémiai reakció: különböző anyagok kémiai összetételének, ill. szerkezetének
Kémiai reakciók Műszaki kémia, Anyagtan I. 11. előadás Dolgosné dr. Kovács Anita egy.doc. PTE MIK Környezetmérnöki Tanszék Kémiai reakció Kémiai reakció: különböző anyagok kémiai összetételének, ill. szerkezetének
Komplex számok (el adásvázlat, 2008. február 12.) Maróti Miklós
 Komplex számok el adásvázlat, 008. február 1. Maróti Miklós Eek az el adásak a megértéséhez a következ fogalmakat kell tudi: test, test additív és multiplikatív csoportja, valós számok és tulajdoságaik.
Komplex számok el adásvázlat, 008. február 1. Maróti Miklós Eek az el adásak a megértéséhez a következ fogalmakat kell tudi: test, test additív és multiplikatív csoportja, valós számok és tulajdoságaik.
a) 4,9 g kénsavat, b) 48 g nikkel(ii)-szulfátot, c) 0,24 g salétromsavat, d) 65 g vas(iii)-kloridot?
 2.2. Anyagmennyiség-koncentráció 1. Hány mol/dm 3 koncentrációjú az az oldat, amelynek 200 cm 3 -ében 0,116 mol az oldott anyag? 2. 2,5 g nátrium-karbonátból 500 cm 3 oldatot készítettünk. Számítsuk ki
2.2. Anyagmennyiség-koncentráció 1. Hány mol/dm 3 koncentrációjú az az oldat, amelynek 200 cm 3 -ében 0,116 mol az oldott anyag? 2. 2,5 g nátrium-karbonátból 500 cm 3 oldatot készítettünk. Számítsuk ki
5. Az adszorpciós folyamat mennyiségi leírása a Langmuir-izoterma segítségével
 5. Az adszorpciós folyamat mennyiségi leírása a Langmuir-izoterma segítségével 5.1. Átismétlendő anyag 1. Adszorpció (előadás) 2. Langmuir-izoterma (előadás) 3. Spektrofotometria és Lambert Beer-törvény
5. Az adszorpciós folyamat mennyiségi leírása a Langmuir-izoterma segítségével 5.1. Átismétlendő anyag 1. Adszorpció (előadás) 2. Langmuir-izoterma (előadás) 3. Spektrofotometria és Lambert Beer-törvény
(L) Lamellás szivattyú mérése
 (L) Lamellás szivattyú mérése A mérésre való felkészülés sorá a Hidraulikus tápegység mérésleírás Hidrosztatikus hajtásokról c részét is kérjük elsajátítai 1 A mérés célja, a beredezés ismertetése 11 A
(L) Lamellás szivattyú mérése A mérésre való felkészülés sorá a Hidraulikus tápegység mérésleírás Hidrosztatikus hajtásokról c részét is kérjük elsajátítai 1 A mérés célja, a beredezés ismertetése 11 A
2011/2012 tavaszi félév 3. óra
 2011/2012 tavaszi félév 3. óra Redoxegyenletek rendezése (diszproporció, szinproporció, stb.); Sztöchiometria Vegyületek sztöchiometriai együtthatóinak meghatározása elemösszetétel alapján Adott rendezendő
2011/2012 tavaszi félév 3. óra Redoxegyenletek rendezése (diszproporció, szinproporció, stb.); Sztöchiometria Vegyületek sztöchiometriai együtthatóinak meghatározása elemösszetétel alapján Adott rendezendő
A PÉNZ IDİÉRTÉKE. Egy jövıbeni pénzösszeg jelenértéke:
 A PÉNZ IDİÉRTÉKE A péz értéke többek között az idı függvéye. Ha idıbe késıbb jutuk hozzá egy jövedelemhez, akkor elveszítjük aak lehetıségét, hogy az eltelt idıbe azt befektessük, azaz elesük aak hozamától,
A PÉNZ IDİÉRTÉKE A péz értéke többek között az idı függvéye. Ha idıbe késıbb jutuk hozzá egy jövedelemhez, akkor elveszítjük aak lehetıségét, hogy az eltelt idıbe azt befektessük, azaz elesük aak hozamától,
Az iparosodás és az infrastrukturális fejlődés típusai
 Az iparosodás és az ifrastrukturális fejlődés típusai Az iparosodás és az ifrastrukturális fejlődés kapcsolatába törtéelmileg három fejlődési típus vázolható fel: megelőző, lácszerűe együtt haladó, utólagosa
Az iparosodás és az ifrastrukturális fejlődés típusai Az iparosodás és az ifrastrukturális fejlődés kapcsolatába törtéelmileg három fejlődési típus vázolható fel: megelőző, lácszerűe együtt haladó, utólagosa
HU / -- Mag rendszer. Padlótisztítás
 HU / -- Mag redszer Padlótisztítás Mag redszer Kocepció 2 www.vermop.com Előyei Mag redszer Ameyire iovatív, ayira egyedi. A VERMOP mágeses redszere teljese új módot jelet a felmosóhuzatok tartóra (ill.
HU / -- Mag redszer Padlótisztítás Mag redszer Kocepció 2 www.vermop.com Előyei Mag redszer Ameyire iovatív, ayira egyedi. A VERMOP mágeses redszere teljese új módot jelet a felmosóhuzatok tartóra (ill.
1.52 CS / CSK. Kulisszás hangcsillapítók. Légcsatorna rendszerek
 1.52 CS / Légcsatra redszerek Alkalmazás: A légcsatraredszere építve, a légcsatráka terjedõ zaj csillapítására alkalmasak. Kialakításuk a eépített csillapító testek szerit alapvetõe hárm féle lehet: A,
1.52 CS / Légcsatra redszerek Alkalmazás: A légcsatraredszere építve, a légcsatráka terjedõ zaj csillapítására alkalmasak. Kialakításuk a eépített csillapító testek szerit alapvetõe hárm féle lehet: A,
