Inczeffy Szabolcs: Lissajoux görbék előállítása ferdeszögű rezgések egymásra tevődésével
|
|
|
- Zsófia Balog
- 6 évvel ezelőtt
- Látták:
Átírás
1 Inczeffy Szablcs: Lissajux görbék előállítása ferdeszögű rezgések egymásra tevődésével I. Lissajux görbék Mint ismeretes a Lissajux görbék merőleges rezgések egymásra tevődéseként jönnek létre. Váltztatva a rezgések amlitudóját, frekvenciáját, illetve kezdőfázisát különböző méretű és alakú látványs görbéket, alakzatkat kaunk. 1. ábra: f 1 :f = 1:1 rezgésszámarányú. ábra: f 1 :f = 5:3 arányú Lissajux görbe Lissajux görbe A GeGebra (ingyen letölthető) számítógées rgram segítségével, a Lissajux görbe a két rezgés egymásra tevődésének nymvnalaként jön létre. Az 1. és. ábrákn látható P nt helyzetét meghatárzó vektr a 1 és a vektrk összege. A 1 és vektrk hsszát és irányítását a 1 A1 cs( f1 t) A1 sin( f1 t / 1) és a A sin( f t ) rezgés (kitérés) egyenletek határzzák meg. Az egyenletekben A 1 és A a rezgések legnagybb kitérését, f 1 és f a rezgésszámkat, t az időt, φ 1 és φ a kezdőfáziskat jelölik. A vektr nagyságát Püthagrasz tételével a 1 összefüggésből 1 számlhatjuk ki, míg irányát a tg tg ( ) kélettel határzhatjuk meg! Sajáts esetben, ha A 1 = A, f 1 = f és φ 1 = φ, akkr a nymvnal egy kör (1. ábra), ha A 1 = A, φ 1 = φ és f 1 f, de a rezgésszámk úgy aránylanak egymáshz, mint a természetes számk (f 1 : f = n 1 : n ), akkr a. ábráhz hasnló görbét kaunk. A következőkben megvizsgáljuk a Lissajux görbék előállítását egymással ferde szöget bezáró rezgések egymásra tevődéseként! Ehhez szükségünk lesz az általáns hármszögben, illetve a trignmetrikus (egység sugarú) körben értelmezett általáns szögfüggvényekre!
2 II. Általáns szögfüggvények II.-1. Az általáns szögfüggvények definíciói A hagymánys szögfüggvényeket derékszögű hármszögben szkás értelmezni, illetve az egységnyi sugarú kör segítségével, az értelmezést, tetszőleges (frgás) szögekre is ki lehet terjeszteni. Feltevődik a kérdés, hgy tvább lehet-e általánsítani a szögfüggvényeket, azaz az általáns hármszögben lehet-e általáns ( alakú ) szögfüggvényeket értelmezni? A válasz igen, sőt biznys estekben az általáns szögfüggvényeket előnyösebben lehet használni, mint egyéb tételeket, de lássuk miről is van szó! Az általáns hármszögben (lásd az 3. ábrát), a szkáss jelöléseket használva és az - át tekintve alaszögnek, a következő szögfüggvényeket értelmezhetjük : sin = c a ; cs = b a ; tg = c b és ctg = b c, ha Természetesen,, 0 0 ; és + + = 180 0, illetve a, b, c 0. Ha = 90 0, akkr visszakajuk a hagymánys szögfüggvényeket. Pl. sin 90 = sin. B' C' A" B B 1 1 a c C A A' C b A 1 3. ábra: általáns hármszög 4. ábra: egységsugarú (trignmetrikus) kör Általánsabb definíciókat a trignmetriai (egységnyi sugarú) kör segítségével adhatunk meg: ha CB = CA CC 1, akkr a 4. ábra szerint : (a szakaszk valójában, előjeles szakaszk) a sin = AB ahl k 180 0, k Z, a cs = CA, ahl k180 0, k Z, a tg = A' B', ahl k180, k Z, k 180, k Z a ctg = C' A", ahl Egy adtt hármszög esetén a definíciók segítségével könnyen biznyíthatók a következő összefüggések:
3 1 sin tg, illetve ctg cs sin = cs tg ctg sin cs tg ctg Megfelelően felcserélve a szögeket még öt, a fentiekhez hasnló, összefüggést tudunk felírni. II.-. Az általáns szögfüggvények kiszámítása sin A szinusztétel segítségével könnyen igazlható, hgy sin. De ennél több is sin sin igaz: sin. Ez az összefüggés az alaszög váltztatását teszi lehetővé. sin A sin sin sin cs sin, tg sin cs sin sin és ctg. sin A biznyításkat és az általáns szögfüggvények egyéb tulajdnságait lásd az irdalmjegyzékben! Lássunk egy éldát! Számítsuk ki a tg 45 értékét. A fenti összefüggés segítségével : tg sin = 45 sin sin 45. sin 90 A rgramzható számlógéek, vagy a számítógéek segítségével egészen könnyen kiszámítható az értelmezési tartmányn belüli tetszőleges szög, tetszőleges alaú szögfüggvény értéke. II.-3. Grafikus ké Az általáns szögfüggvények grafikus kéei hasnlóak a s alaszögűekéhez, csak másk az értékhelyek és az értékek. Az 5. ábrán az = 45 0 s alaszögű szögfüggvények grafikus kéei láthatók nymvnalként ábrázlva! 5. ábra: az = 45 0 s alaszögű szögfüggvények grafikus kéei
4 II.-4. Alkalmazás A tvábbiakban vizsgáljuk meg az általáns szögfüggvények alkalmazását, a vektrk ferdeszögű krdináta rendszerben történő felbntásakr keletkezett kntravariáns krdináták kiszámítására. Lásd a 6. ábrát! 1. v 1 e e v e 180- v. 6. ábra: a v vektr felbntása két egymással szöget bezáró irány szerint Az 1., illetve. iránykba eső egységvektrk u 1, illetve u, így a v vektr irányába eső egységvektr e = cs u 1 + cs 180- u. Itt e 1 = cs u 1 és e = cs 180- u, az e vektr összetevő vektrai. A v = v 1 + v, ahl v 1 = v 1 u 1 és v = v u. A kntravariáns krdinátákra, edig a v 1 = v cs és a v = v cs 180- összefüggéseket írhatjuk fel. Könnyen ellenőrizhető, hgy = 90 0 esetben, vagyis derékszögű krdináta rendszerben, visszakajuk a szkáss krdinátákat. Látható tehát, hgy a kntravariáns krdináták felírása (kiszámítása) lyan egyszerűvé válik, mint derékszögű krdináta rendszer esetén. III. Lissajux görbék ferdeszögű krdináta rendszerben Az általáns szögfüggvények, illetve a GeGebra utlsó alkalmazásaként vizsgáljuk meg az egymással ferdeszöget ( 90 ) bezáró rezgések egymásra tevődését, amely a Lissaju görbékhez hasnló görbék előállítását teszi lehetővé! A P nt nymvnalát tvábbra is a 1 és a vektrk összege határzza meg. A 1 és a vektrk hssza és iránya a A1 cs ( 1 1) 1 [sin( 1 1)] / sin( ) f t A f t A1 sin( f1 t 1) A sin ( ) [sin( )] / sin( ) f t A f t A sin( f t ) A A / sin( és az A A / sin( ) 1 és a rezgés (kitérés) egyenletek határzzák meg, ahl az 1 1 ) a rezgések legnagybb kitérései. A vektr nagyságát, a kszinusz tétel ( általáns Püthagrasz tétel) segítségével, a a tg sin cs összefüggésből számlhatjuk ki, míg irányát kéletből ( egyenletből) határzhatjuk meg! sin( )
5 Sajáts esetben, ha A 1 = A, f 1 = f és φ 1 = φ, akkr a nymvnal egy kör (1. ábra), ha A 1 = A, φ 1 = φ és f 1 f, de a rezgésszámk úgy aránylanak egymáshz, mint a természetes számk (f 1 : f = n 1 : n ), akkr a. ábráhz hasnló görbét kaunk. Lásd a 7. és 8. ábrát! 7. ábra: f 1 : f = 1:1 rezgésszámarányú 8. ábra: f 1 : f = :3 arányú Lissaju görbéhez hasnló görbe Lissaju görbéhez hasnló görbe Irdalm 1. Budó Á., Kisérleti fizika II., Tkk., B., Inczeffy Sz., A trignmetrikus függvények általáns alakjai, A matematika tanítása, 1995., III.évf./3. szám. 3. Inczeffy Sz., A GeGebra számítógées rgram felhasználása, Lissaju görbék előállítására derékszögű, illetve ferdeszögű rezgések egymásra tevődéseként., műhelyvezetés (demnstrált előadás) az 58. Országs Fizikatanári Ankét és Eszközbemutatón, Hévíz, 015.
8. Négyzetes összefüggés: mellékmegjegyzés:
 . tétel: Szögfüggvények értelmezése a valós számhalmazn, ezek tulajdnságai, kapslatk ugyanazn szög szögfüggvényei között. Definíió derékszögő hármszögekre (hegyesszögek szögfüggvényei): Egy hegyesszög
. tétel: Szögfüggvények értelmezése a valós számhalmazn, ezek tulajdnságai, kapslatk ugyanazn szög szögfüggvényei között. Definíió derékszögő hármszögekre (hegyesszögek szögfüggvényei): Egy hegyesszög
Szögfüggvények értékei megoldás
 Szögfüggvények értékei megoldás 1. Számítsd ki az alábbi szögfüggvények értékeit! (a) cos 585 (f) cos ( 00 ) (k) sin ( 50 ) (p) sin (u) cos 11 (b) cos 00 (g) cos 90 (l) sin 510 (q) sin 8 (v) cos 9 (c)
Szögfüggvények értékei megoldás 1. Számítsd ki az alábbi szögfüggvények értékeit! (a) cos 585 (f) cos ( 00 ) (k) sin ( 50 ) (p) sin (u) cos 11 (b) cos 00 (g) cos 90 (l) sin 510 (q) sin 8 (v) cos 9 (c)
MATEMATIKA C 11. évfolyam. 8. modul Goniometria. Készítette: Kovács Károlyné
 MATEMATIKA C. évflyam 8. mdul Gnimetria Készítette: Kvács Kárlyné Matematika C. évflyam 8. mdul: Gnimetria Tanári útmutató A mdul célja Időkeret Ajánltt krsztály Mdulkapcslódási pntk A szögfüggvények definíciójának
MATEMATIKA C. évflyam 8. mdul Gnimetria Készítette: Kvács Kárlyné Matematika C. évflyam 8. mdul: Gnimetria Tanári útmutató A mdul célja Időkeret Ajánltt krsztály Mdulkapcslódási pntk A szögfüggvények definíciójának
Ezt már mind tudjuk?
 MATEMATIKA C 11. évflyam 10. mdul Ezt már mind tudjuk? Készítette: Kvács Kárlyné Matematika C 11. évflyam 10. mdul: Ezt már mind tudjuk? Tanári útmutató A mdul célja Időkeret Ajánltt krsztály Mdulkapcslódási
MATEMATIKA C 11. évflyam 10. mdul Ezt már mind tudjuk? Készítette: Kvács Kárlyné Matematika C 11. évflyam 10. mdul: Ezt már mind tudjuk? Tanári útmutató A mdul célja Időkeret Ajánltt krsztály Mdulkapcslódási
Trigonometria I. A szög szinuszának nevezzük a szöggel szemközti befogó és az átfogó hányadosát (arányát).
 Trignmetria I A hegyes szögű deiníciók: A szög szinuszának nevezzük a szöggel szemközti begó és az átgó hányadsát (arányát). Kszinus nak nevezzük a szög melletti begó és az átgó hányadsát (arányát). A
Trignmetria I A hegyes szögű deiníciók: A szög szinuszának nevezzük a szöggel szemközti begó és az átgó hányadsát (arányát). Kszinus nak nevezzük a szög melletti begó és az átgó hányadsát (arányát). A
Lineáris rendszerek stabilitása
 Lineáris rendszerek stabilitása A gyakrlat célja A dlgzatban a lineáris rendszerek stabilitásának fgalmát vezetjük be majd megvizsgáljuk a stabilitás vizsgálati módszereket. Elméleti bevezető Egy LTI rendszer
Lineáris rendszerek stabilitása A gyakrlat célja A dlgzatban a lineáris rendszerek stabilitásának fgalmát vezetjük be majd megvizsgáljuk a stabilitás vizsgálati módszereket. Elméleti bevezető Egy LTI rendszer
Dr`avni izpitni center MATEMATIKA
 Dr`avni izpitni center *P053C03M* TÉLI VIZSGAIDŐSZAK MATEMATIKA ÉRTÉKELÉSI ÚTMUTATÓ 006. február 3., hétfő SZAKMAI ÉRETTSÉGI VIZSGA RIC 006 P053-C0--3M ÚTMUTATÓ a szakmai írásbeli érettségi vizsga feladatainak
Dr`avni izpitni center *P053C03M* TÉLI VIZSGAIDŐSZAK MATEMATIKA ÉRTÉKELÉSI ÚTMUTATÓ 006. február 3., hétfő SZAKMAI ÉRETTSÉGI VIZSGA RIC 006 P053-C0--3M ÚTMUTATÓ a szakmai írásbeli érettségi vizsga feladatainak
Geometriai feladatok megoldása a komplex számsíkon dr. Kiss Géza, Budapest
 Gemetriai feladatk megldása a kmplex számsíkn dr Kiss Géza, Budapest Az előadás srán a kmplex számkkal kapcslats szkáss algebrai és gemetriai fgalmakat, tulajdnságkat ismertnek tételezzük fel Az időkeret
Gemetriai feladatk megldása a kmplex számsíkn dr Kiss Géza, Budapest Az előadás srán a kmplex számkkal kapcslats szkáss algebrai és gemetriai fgalmakat, tulajdnságkat ismertnek tételezzük fel Az időkeret
. 2 pont A 2 pont nem bontható. 3 Összesen: 2 pont. Összesen: 3 pont. A valós gyökök száma: 1. Összesen: 2 pont. Összesen: 2 pont
 1. Az egyszerűsítés után kaptt tört: I. a b. pnt A pnt nem bntható. 3 Összesen: pnt. Frgáshenger keletkezik, az alapkör sugara 5cm, magassága 1cm. V = 5π 1(cm 3 ). A frgáshenger térfgata 300π cm 3. Ha
1. Az egyszerűsítés után kaptt tört: I. a b. pnt A pnt nem bntható. 3 Összesen: pnt. Frgáshenger keletkezik, az alapkör sugara 5cm, magassága 1cm. V = 5π 1(cm 3 ). A frgáshenger térfgata 300π cm 3. Ha
MATEMATIKA C 12. évfolyam 3. modul A mi terünk
 MTEMTIK C 1. évflyam. mdul mi terünk Készítette: Kvács Kárlyné Matematika C 1. évflyam. mdul: mi terünk Tanári útmutató mdul célja Időkeret jánltt krsztály Mdulkapcslódási pntk térfgat- és felszínszámítási
MTEMTIK C 1. évflyam. mdul mi terünk Készítette: Kvács Kárlyné Matematika C 1. évflyam. mdul: mi terünk Tanári útmutató mdul célja Időkeret jánltt krsztály Mdulkapcslódási pntk térfgat- és felszínszámítási
Megoldások. Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma)
 Megoldások 1. Határozd meg az a és b vektor skaláris szorzatát, ha a = 5, b = 4 és a közbezárt szög φ = 55! Alkalmazzuk a megfelelő képletet: a b = a b cos φ = 5 4 cos 55 11,47. 2. Határozd meg a következő
Megoldások 1. Határozd meg az a és b vektor skaláris szorzatát, ha a = 5, b = 4 és a közbezárt szög φ = 55! Alkalmazzuk a megfelelő képletet: a b = a b cos φ = 5 4 cos 55 11,47. 2. Határozd meg a következő
MATEMATIKA C 12. évfolyam 2. modul Telek és kerítés
 MATEMATIKA C 1. évflyam. mdul Telek és kerítés Készítette: Kvács Kárlyné Matematika C 1. évflyam. mdul: Telek és kerítés Tanári útmutató A mdul célja Időkeret Ajánltt krsztály Mdulkapcslódási pntk Skszögekről
MATEMATIKA C 1. évflyam. mdul Telek és kerítés Készítette: Kvács Kárlyné Matematika C 1. évflyam. mdul: Telek és kerítés Tanári útmutató A mdul célja Időkeret Ajánltt krsztály Mdulkapcslódási pntk Skszögekről
Matematika tanmenet 10. évfolyam 2018/2019
 Matematika tanmenet 10. évfolyam 2018/2019 Műveltségi terület: MATEMATIKA Iskola, osztályok: Vetési Albert Gimnázium, 10.A, 10.B, 10.C, 10.D Tantárgy: MATEMATIKA Heti óraszám: 3 óra Készítette: a matematika
Matematika tanmenet 10. évfolyam 2018/2019 Műveltségi terület: MATEMATIKA Iskola, osztályok: Vetési Albert Gimnázium, 10.A, 10.B, 10.C, 10.D Tantárgy: MATEMATIKA Heti óraszám: 3 óra Készítette: a matematika
Koczog András Matematika - Az alapoktól az érettségin át az egyetemig. Szögfüggvények alapjai
 Szögfüggvények alapjai Értelmezés derékszögű háromszögekben Két derékszögű háromszög hasonlóságát teljesen meghatározza egyik szögük nagysága, így oldalaik aránya mindig megegyezik, függetlenül hosszuktól.
Szögfüggvények alapjai Értelmezés derékszögű háromszögekben Két derékszögű háromszög hasonlóságát teljesen meghatározza egyik szögük nagysága, így oldalaik aránya mindig megegyezik, függetlenül hosszuktól.
9. Trigonometria. I. Nulladik ZH-ban láttuk: 1. Tegye nagyság szerint növekvő sorrendbe az alábbi értékeket! Megoldás:
 9. Trigonometria I. Nulladik ZH-ban láttuk: 1. Tegye nagyság szerint növekvő sorrendbe az alábbi értékeket! x = cos 150 ; y = sin 5 ; z = tg ( 60 ) (A) z < x < y (B) x < y < z (C) y < x < z (D) z < y
9. Trigonometria I. Nulladik ZH-ban láttuk: 1. Tegye nagyság szerint növekvő sorrendbe az alábbi értékeket! x = cos 150 ; y = sin 5 ; z = tg ( 60 ) (A) z < x < y (B) x < y < z (C) y < x < z (D) z < y
MATEMATIKAI KOMPETENCIATERÜLET C
 MATEMATIKAI KOMPETENCIATERÜLET C Matematika 11. évflyam TANULÓK KÖNYVE Készítette: Kvács Kárlyné A kiadvány KHF/457-7/009. engedélyszámn 009.05.1. időpnttól tankönyvi engedélyt kaptt Educati Kht. Kmpetenciafejlesztő
MATEMATIKAI KOMPETENCIATERÜLET C Matematika 11. évflyam TANULÓK KÖNYVE Készítette: Kvács Kárlyné A kiadvány KHF/457-7/009. engedélyszámn 009.05.1. időpnttól tankönyvi engedélyt kaptt Educati Kht. Kmpetenciafejlesztő
Lengyelné Dr. Szilágyi Szilvia április 7.
 ME, Anaĺızis Tanszék 2010. április 7. , alapfogalmak 2.1. Definíció A H 1, H 2,..., H n R (ahol n 2 egész szám) nemüres valós számhalmazok H 1 H 2... H n Descartes-szorzatán a következő halmazt értjük:
ME, Anaĺızis Tanszék 2010. április 7. , alapfogalmak 2.1. Definíció A H 1, H 2,..., H n R (ahol n 2 egész szám) nemüres valós számhalmazok H 1 H 2... H n Descartes-szorzatán a következő halmazt értjük:
186 A trigonometria elemei. VIII.1. Szögek mérése. Az eddigi tanulmányaitok során a szögek mérésére a fokot és annak törtrészeit használtátok.
 86 A trignmetria elemei VIII A TRIGNMETRIA ELEMEI VIII Szögek mérése Az eddigi tanulmánaitk srán a szögek mérésére a fkt és annak törtrészeit használtátk Íg a teljes szög mértéke 60 Ez azt jelenti, hg
86 A trignmetria elemei VIII A TRIGNMETRIA ELEMEI VIII Szögek mérése Az eddigi tanulmánaitk srán a szögek mérésére a fkt és annak törtrészeit használtátk Íg a teljes szög mértéke 60 Ez azt jelenti, hg
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika emelt szint 080 É RETTSÉGI VIZSGA 009. któber 0. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Fnts tudnivalók Frmai előírásk:.
Matematika emelt szint 080 É RETTSÉGI VIZSGA 009. któber 0. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Fnts tudnivalók Frmai előírásk:.
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. Tekintsük az alábbi szabályos hatszögben a következő vektorokat: a = AB és b = AF. Add meg az FO, DC, AO, AC, BE, FB, CE, DF vektorok koordinátáit az (a ; b ) koordinátarendszerben! Alkalmazzuk
Megoldások 1. Tekintsük az alábbi szabályos hatszögben a következő vektorokat: a = AB és b = AF. Add meg az FO, DC, AO, AC, BE, FB, CE, DF vektorok koordinátáit az (a ; b ) koordinátarendszerben! Alkalmazzuk
Osztályozóvizsga követelményei
 Osztályozóvizsga követelményei Képzés típusa: Tantárgy: Nyolcosztályos gimnázium Matematika Évfolyam: 11 Emelt óraszámú csoport Emelt szintű csoport Vizsga típusa: Írásbeli Követelmények, témakörök: Gondolkodási
Osztályozóvizsga követelményei Képzés típusa: Tantárgy: Nyolcosztályos gimnázium Matematika Évfolyam: 11 Emelt óraszámú csoport Emelt szintű csoport Vizsga típusa: Írásbeli Követelmények, témakörök: Gondolkodási
Sorozatok I. Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma)
 Sorozatok I. DEFINÍCIÓ: (Számsorozat) A számsorozat olyan függvény, amelynek értelmezési tartománya a pozitív egész számok halmaza, értékkészlete a valós számok egy részhalmaza. Jelölés: (a n ), {a n }.
Sorozatok I. DEFINÍCIÓ: (Számsorozat) A számsorozat olyan függvény, amelynek értelmezési tartománya a pozitív egész számok halmaza, értékkészlete a valós számok egy részhalmaza. Jelölés: (a n ), {a n }.
Trigonometria. Szögfüggvények alkalmazása derékszög háromszögekben. Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1
 Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Trigonometria Szögfüggvények alkalmazása derékszög háromszögekben 1. Az ABC hegyesszög háromszögben BC = 14 cm, AC = 1 cm, a BCA szög nagysága
Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Trigonometria Szögfüggvények alkalmazása derékszög háromszögekben 1. Az ABC hegyesszög háromszögben BC = 14 cm, AC = 1 cm, a BCA szög nagysága
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 14 XIV NEVEZETES GÖRbÉk 1 AZ EGYEnES EGYEnLETE A és pontokon átmenő egyenes egyenlete: (1), Az hányados neve iránytényező (iránytangens, meredekség) A ponton átmenő, m iránytangensű
KOVÁCS BÉLA, MATEmATIkA I 14 XIV NEVEZETES GÖRbÉk 1 AZ EGYEnES EGYEnLETE A és pontokon átmenő egyenes egyenlete: (1), Az hányados neve iránytényező (iránytangens, meredekség) A ponton átmenő, m iránytangensű
Trigonometrikus egyenletek megoldása Azonosságok és 12 mintapélda
 Trigonometrikus egyenletek megoldása Azonosságok és 1 mintapélda Frissítve: 01. novermber 19. :07:41 1. Azonosságok 1.1. Azonosság. A sin és cos szögfüggvények derékszög háromszögben vett, majd kiterjesztett
Trigonometrikus egyenletek megoldása Azonosságok és 1 mintapélda Frissítve: 01. novermber 19. :07:41 1. Azonosságok 1.1. Azonosság. A sin és cos szögfüggvények derékszög háromszögben vett, majd kiterjesztett
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Trigonometria II.
 Trigonometria II. A tetszőleges nagyságú szögek szögfüggvényeit koordináta rendszerben egységhosszúságú forgásvektor segítségével definiáljuk. DEFINÍCIÓ: (Vektor irányszöge) Egy vektor irányszögén értjük
Trigonometria II. A tetszőleges nagyságú szögek szögfüggvényeit koordináta rendszerben egységhosszúságú forgásvektor segítségével definiáljuk. DEFINÍCIÓ: (Vektor irányszöge) Egy vektor irányszögén értjük
M/D/13. Szorozzuk meg az egyenlet mindkét oldalát a közös nevezővel, 12-vel; így a következő egyenlethez jutunk: = 24
 OKTATÁSI MINISZTÉRIUM M/D/13 Dolgozók gimnáziuma Dolgozók szakközépiskolája Szakmunkások szakközépiskolája intenzív tagozat) 003. május ) Határozza meg a következő egyenlet racionális gyökét! 1 3 4 + 5
OKTATÁSI MINISZTÉRIUM M/D/13 Dolgozók gimnáziuma Dolgozók szakközépiskolája Szakmunkások szakközépiskolája intenzív tagozat) 003. május ) Határozza meg a következő egyenlet racionális gyökét! 1 3 4 + 5
Vektorok és koordinátageometria
 Vektorok és koordinátageometria Vektorral kapcsolatos alapfogalmak http://zanza.tv/matematika/geometria/vektorok-bevezetese Definíció: Ha egy szakasz két végpontját megkülönböztetjük egymástól oly módon,
Vektorok és koordinátageometria Vektorral kapcsolatos alapfogalmak http://zanza.tv/matematika/geometria/vektorok-bevezetese Definíció: Ha egy szakasz két végpontját megkülönböztetjük egymástól oly módon,
Matematika III előadás
 Matematika III. - 2. előadás Vinczéné Varga Adrienn Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Előadáskövető fóliák Vinczéné Varga Adrienn (DE-MK) Matematika III. 2016/2017/I 1 / 23 paramétervonalak,
Matematika III. - 2. előadás Vinczéné Varga Adrienn Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Előadáskövető fóliák Vinczéné Varga Adrienn (DE-MK) Matematika III. 2016/2017/I 1 / 23 paramétervonalak,
Az egyenes ellipszishenger ferde síkmetszeteiről
 1 Az egyenes ellipszishenger ferde síkmetszeteiről Vegyünk egy a és b féltengelyekkel bíró ellipszist a vezérgörbét, majd az ellipszis O centrumában állítsunk merőlegest az ellipszis síkjára. Ez a merőleges
1 Az egyenes ellipszishenger ferde síkmetszeteiről Vegyünk egy a és b féltengelyekkel bíró ellipszist a vezérgörbét, majd az ellipszis O centrumában állítsunk merőlegest az ellipszis síkjára. Ez a merőleges
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
Arany Dániel Matematikai Tanulóverseny 2010/2011-es tanév 1. forduló haladók III. kategória
 Bolyai János Matematikai Társulat Oktatásért Közalapítvány támogatásával Arany Dániel Matematikai Tanulóverseny 2010/2011-es tanév 1. forduló haladók III. kategória Megoldások és javítási útmutató 1. Határozzuk
Bolyai János Matematikai Társulat Oktatásért Közalapítvány támogatásával Arany Dániel Matematikai Tanulóverseny 2010/2011-es tanév 1. forduló haladók III. kategória Megoldások és javítási útmutató 1. Határozzuk
Dr. Fried Katalin Dr. Gerőcs László Számadó László
 Dr Fried Katalin Dr Gerőcs László Számadó László MATEMATIKA 9 A tankönyv feladatai és a feladatk megldásai A megldásk lvasásáhz Acrbat Reader prgram szükséges, amely ingyenesen letölthető az internetről
Dr Fried Katalin Dr Gerőcs László Számadó László MATEMATIKA 9 A tankönyv feladatai és a feladatk megldásai A megldásk lvasásáhz Acrbat Reader prgram szükséges, amely ingyenesen letölthető az internetről
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Vektorok II.
 Vektorok II. DEFINÍCIÓ: (Vektorok hajlásszöge) Két vektor hajlásszögének azt a φ (0 φ 180 ) szöget nevezzük, amelyet a vektorok egy közös pontból felmért reprezentánsai által meghatározott félegyenesek
Vektorok II. DEFINÍCIÓ: (Vektorok hajlásszöge) Két vektor hajlásszögének azt a φ (0 φ 180 ) szöget nevezzük, amelyet a vektorok egy közös pontból felmért reprezentánsai által meghatározott félegyenesek
Kristályszerkezetek és vizsgálatuk
 Kristályszerkezetek és vizsgálatuk Az anyagk tulajdnságait atmjaik fajtája, kémiai kötésük jellege és kristályszerkezete együttesen határzza meg. A fentiekre a szén egy tipikus példa. A tiszta szén gyémánt
Kristályszerkezetek és vizsgálatuk Az anyagk tulajdnságait atmjaik fajtája, kémiai kötésük jellege és kristályszerkezete együttesen határzza meg. A fentiekre a szén egy tipikus példa. A tiszta szén gyémánt
Miskolci Egyetem GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR. Polárkoordinátás és paraméteres megadású görbék. oktatási segédanyag
 Miskolci Egyetem GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Polárkoordinátás és paraméteres megadású görbék oktatási segédanyag Összeállította: Lengyelné Dr. Szilágyi Szilvia Miskolc, 01. Köszönetnyilvánítás Az
Miskolci Egyetem GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Polárkoordinátás és paraméteres megadású görbék oktatási segédanyag Összeállította: Lengyelné Dr. Szilágyi Szilvia Miskolc, 01. Köszönetnyilvánítás Az
Matematikai geodéziai számítások 1.
 Nyugat-magyarrszági Egyetem Geinfrmatikai Kara Dr Bácsatyai László Matematikai gedéziai számításk 1 MGS mdul Ellipszidi számításk, ellipszid, geid és terep metszete SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket
Nyugat-magyarrszági Egyetem Geinfrmatikai Kara Dr Bácsatyai László Matematikai gedéziai számításk 1 MGS mdul Ellipszidi számításk, ellipszid, geid és terep metszete SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket
4. A kézfogások száma pont Összesen: 2 pont
 I. 1. A páros számokat tartalmazó részhalmazok: 6 ; 8 ; 6 ; 8. { } { } { }. 5 ( a ) 17 Összesen: t = = a a Összesen: ot kaphat a vizsgázó, ha csak két helyes részhalmazt ír fel. Szintén jár, ha a helyes
I. 1. A páros számokat tartalmazó részhalmazok: 6 ; 8 ; 6 ; 8. { } { } { }. 5 ( a ) 17 Összesen: t = = a a Összesen: ot kaphat a vizsgázó, ha csak két helyes részhalmazt ír fel. Szintén jár, ha a helyes
Gönye Zsuzsanna SZÖGFÜGGVÉNYEK BEVEZETÉSE A KÖZÉPISKOLÁBAN. 1. Bevezetés
 SZÖGFÜGGVÉNYEK BEVEZETÉSE A KÖZÉPISKOLÁBAN. Bevezetés A szögfüggvények tanítása több szempntból is fnts anyagrész a középisklai matematikaktatásban. Matematikai szempntból azért, mert összekapcslja az
SZÖGFÜGGVÉNYEK BEVEZETÉSE A KÖZÉPISKOLÁBAN. Bevezetés A szögfüggvények tanítása több szempntból is fnts anyagrész a középisklai matematikaktatásban. Matematikai szempntból azért, mert összekapcslja az
Exponenciális és logaritmusos kifejezések, egyenletek
 Gyaorló feladato Eponenciális és logaritmusos ifejezése, egyenlete. Hatványozási azonosságo. Számítsd i a övetező hatványo pontos értéét! g) b) c) d) 7 e) f) 9 0, 9 h) 0, 6 i) 0,7 j), 6 ), l). A övetező
Gyaorló feladato Eponenciális és logaritmusos ifejezése, egyenlete. Hatványozási azonosságo. Számítsd i a övetező hatványo pontos értéét! g) b) c) d) 7 e) f) 9 0, 9 h) 0, 6 i) 0,7 j), 6 ), l). A övetező
t, u v. u v t A kúpra írt csavarvonalról I. rész
 A kúpra írt csavarvonalról I. rész Sokféle kúpra írt csavarvonal létezik. Ezek közül először a legegyszerűbbel foglalko - zunk. Ezt azért tesszük mert meglepő az a tény hogy eddig még szinte sehol nem
A kúpra írt csavarvonalról I. rész Sokféle kúpra írt csavarvonal létezik. Ezek közül először a legegyszerűbbel foglalko - zunk. Ezt azért tesszük mert meglepő az a tény hogy eddig még szinte sehol nem
Kerék gördüléséről. A feladat
 1 Kerék gördüléséről Nemrégen egy órán szóba került a címbeli téma, középiskolások előtt. Úgy látszott, nem nagyon értik, miről van szó. Persze, lehet, hogy még nem tartottak ott, vagy csak aludtak a fizika
1 Kerék gördüléséről Nemrégen egy órán szóba került a címbeli téma, középiskolások előtt. Úgy látszott, nem nagyon értik, miről van szó. Persze, lehet, hogy még nem tartottak ott, vagy csak aludtak a fizika
I. A négyzetgyökvonás
 Definíció: Négyzetgyök a ( a : a a 0 I. A négyzetgyökvonás a ) jelenti azt a nem negatív számot, amelynek a négyzete a. a 0 b : b b R A négyzetgyök-függvény értéke is csak nem negatív lehet. Ha a b-t abszolút
Definíció: Négyzetgyök a ( a : a a 0 I. A négyzetgyökvonás a ) jelenti azt a nem negatív számot, amelynek a négyzete a. a 0 b : b b R A négyzetgyök-függvény értéke is csak nem negatív lehet. Ha a b-t abszolút
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT. Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. Koordináta-geometria és B 3 1; Írja fel az AB szakasz 1 3 4
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT 1) Adott két pont: A 4; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. Koordináta-geometria és B 3 1; Írja fel az AB szakasz 1 3 4
Szökőkút - feladat. 1. ábra. A fotók forrása:
 Szökőkút - feladat Nemrégen Gyulán jártunk, ahol sok szép szökőkutat láttunk. Az egyik különösen megtetszett, ezért elhatároztam, hogy megpróbálom elemi módon leírni a ízsugarak, illete az általuk leírt
Szökőkút - feladat Nemrégen Gyulán jártunk, ahol sok szép szökőkutat láttunk. Az egyik különösen megtetszett, ezért elhatároztam, hogy megpróbálom elemi módon leírni a ízsugarak, illete az általuk leírt
Vízgyűjtő-gazdálkodási Terv - 2015 A Duna-vízgyűjtő magyarországi része. 1-1. háttéranyag: Felszíni víztestek kijelölésének felülvizsgálata
 Vízgyűjtő-gazdálkdási Terv - 2015 A Duna-vízgyűjtő magyarrszági része 1-1. háttéranyag: Felszíni víztestek kijelölésének felülvizsgálata Felszíni víztestek kijelölése Módszertan Vízflyás víztestek felülvizsgálata
Vízgyűjtő-gazdálkdási Terv - 2015 A Duna-vízgyűjtő magyarrszági része 1-1. háttéranyag: Felszíni víztestek kijelölésének felülvizsgálata Felszíni víztestek kijelölése Módszertan Vízflyás víztestek felülvizsgálata
Mechanika Kinematika. - Kinematikára: a testek mozgását tanulmányozza anélkül, hogy figyelembe venné a kiváltó
 Mechanika Kinematika A mechanika a fizika része mely a testek mozgásával és egyensúlyával foglalkozik. A klasszikus mechanika, mely a fénysebességnél sokkal kisebb sebességű testekre vonatkozik, feloszlik:
Mechanika Kinematika A mechanika a fizika része mely a testek mozgásával és egyensúlyával foglalkozik. A klasszikus mechanika, mely a fénysebességnél sokkal kisebb sebességű testekre vonatkozik, feloszlik:
10. Koordinátageometria
 I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
A loxodrómáról. Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra.
 1 A loxodrómáról Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra. 1. ábra forrása: [ 1 ] Ezen a térképen a szélességi
1 A loxodrómáról Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra. 1. ábra forrása: [ 1 ] Ezen a térképen a szélességi
MATEMATIKA C 12. évfolyam 5. modul Ismétlés a tudás anyja
 MATEMATIKA C. évflyam 5. mdul Ismétlés a tudás anyja Készítette: Kvács Kárlyné Matematika C. évflyam 5. mdul: Ismétlés a tudás anyja Tanári útmutató A mdul célja Időkeret Ajánltt krsztály Mdulkapcslódási
MATEMATIKA C. évflyam 5. mdul Ismétlés a tudás anyja Készítette: Kvács Kárlyné Matematika C. évflyam 5. mdul: Ismétlés a tudás anyja Tanári útmutató A mdul célja Időkeret Ajánltt krsztály Mdulkapcslódási
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Trigonometria I.
 Trigonometria I. Hegyes szögek szögfüggvényei: Az α hegyesszöggel rendelkező derékszögű háromszögek egymáshoz hasonlóak, mert szögeik megegyeznek. Így oldalhosszaik aránya mindig állandó. Az α szögtől
Trigonometria I. Hegyes szögek szögfüggvényei: Az α hegyesszöggel rendelkező derékszögű háromszögek egymáshoz hasonlóak, mert szögeik megegyeznek. Így oldalhosszaik aránya mindig állandó. Az α szögtől
Exponenciális és logaritmusos kifejezések, egyenletek
 Eponenciális és logaritmusos kifejezések, egyenletek. Hatványozási azonosságok. Számítsd ki a következő hatványok pontos értékét! a) 8 b) 4 c) d) 7 e) f) 9 0, g) 0, 9 h) 6 0, 7,, i) 8 j) 6 k) 4 l) 49,.
Eponenciális és logaritmusos kifejezések, egyenletek. Hatványozási azonosságok. Számítsd ki a következő hatványok pontos értékét! a) 8 b) 4 c) d) 7 e) f) 9 0, g) 0, 9 h) 6 0, 7,, i) 8 j) 6 k) 4 l) 49,.
Matematika osztályozó vizsga témakörei 9. évfolyam II. félév:
 Matematika osztályozó vizsga témakörei 9. évfolyam II. félév: 7. Függvények: - függvények fogalma, megadása, ábrázolás koordináta- rendszerben - az elsőfokú függvény, lineáris függvény - a másodfokú függvény
Matematika osztályozó vizsga témakörei 9. évfolyam II. félév: 7. Függvények: - függvények fogalma, megadása, ábrázolás koordináta- rendszerben - az elsőfokú függvény, lineáris függvény - a másodfokú függvény
KOVÁCS BÉLA, MATEMATIKA II.
 KOVÁCS BÉLA MATEmATIkA II 6 VI TÉRGÖRbÉk 1 Alapvető ÖSSZEFÜGGÉSEk A térgörbe (1) alakú egyenletével írható le Ez a vektoregyenlet egyenértékű az (2) skaláris egyenletrendszerrel A térgörbe három nevezetes
KOVÁCS BÉLA MATEmATIkA II 6 VI TÉRGÖRbÉk 1 Alapvető ÖSSZEFÜGGÉSEk A térgörbe (1) alakú egyenletével írható le Ez a vektoregyenlet egyenértékű az (2) skaláris egyenletrendszerrel A térgörbe három nevezetes
1. Ábrázolja az f(x)= x-4 függvényt a [ 2;10 ] intervallumon! (2 pont) 2. Írja fel az alábbi lineáris függvény grafikonjának egyenletét!
![1. Ábrázolja az f(x)= x-4 függvényt a [ 2;10 ] intervallumon! (2 pont) 2. Írja fel az alábbi lineáris függvény grafikonjának egyenletét! 1. Ábrázolja az f(x)= x-4 függvényt a [ 2;10 ] intervallumon! (2 pont) 2. Írja fel az alábbi lineáris függvény grafikonjának egyenletét!](/thumbs/54/33263341.jpg) Függvények 1 1. Ábrázolja az f()= -4 függvényt a [ ;10 ] intervallumon!. Írja fel az alábbi lineáris függvény grafikonjának egyenletét! 3. Ábrázolja + 1 - függvényt a [ ;] -on! 4. Az f függvényt a valós
Függvények 1 1. Ábrázolja az f()= -4 függvényt a [ ;10 ] intervallumon!. Írja fel az alábbi lineáris függvény grafikonjának egyenletét! 3. Ábrázolja + 1 - függvényt a [ ;] -on! 4. Az f függvényt a valós
20. tétel A kör és a parabola a koordinátasíkon, egyenessel való kölcsönös helyzetük. Másodfokú egyenlőtlenségek.
 . tétel A kör és a parabola a koordinátasíkon, egyenessel való kölcsönös helyzetük. Másodfokú egyenlőtlenségek. Először megadom a síkbeli definíciójukat, mert ez alapján vezetjük le az egyenletüket. Alakzat
. tétel A kör és a parabola a koordinátasíkon, egyenessel való kölcsönös helyzetük. Másodfokú egyenlőtlenségek. Először megadom a síkbeli definíciójukat, mert ez alapján vezetjük le az egyenletüket. Alakzat
Fénypont a falon Feladat
 Fénypont a falon 3. Dolgozat - sorozatunk. és. részében két speiális eset vizsgálatát részleteztük. Itt az általánosabb síkbeli esettel foglalkozunk, főbb vonalaiban. Ehhez tekintsük az. ábrát is! 3. Feladat.
Fénypont a falon 3. Dolgozat - sorozatunk. és. részében két speiális eset vizsgálatát részleteztük. Itt az általánosabb síkbeli esettel foglalkozunk, főbb vonalaiban. Ehhez tekintsük az. ábrát is! 3. Feladat.
13. Trigonometria II.
 Trigonometria II I Elméleti összefoglaló Tetszőleges α szög szinusza a koordinátasíkon az i vektortól az óramutató járásával ellentétes irányban α szöggel elforgatott e egységvektor második koordinátája
Trigonometria II I Elméleti összefoglaló Tetszőleges α szög szinusza a koordinátasíkon az i vektortól az óramutató járásával ellentétes irányban α szöggel elforgatott e egységvektor második koordinátája
Kalkulus S af ar Orsolya F uggv enyek S af ar Orsolya Kalkulus
 Függvények Mi a függvény? A függvény egy hozzárendelési szabály. Egy valós függvény a valós számokhoz, esetleg egy részükhöz rendel hozzá pontosan egy valós számot valamilyen szabály (nem feltétlen képlet)
Függvények Mi a függvény? A függvény egy hozzárendelési szabály. Egy valós függvény a valós számokhoz, esetleg egy részükhöz rendel hozzá pontosan egy valós számot valamilyen szabály (nem feltétlen képlet)
Egyenletek, egyenlőtlenségek X.
 Egyenletek, egyenlőtlenségek X. DEFINÍCIÓ: (Logaritmus) Ha egy pozitív valós számot adott, 1 - től különböző pozitív alapú hatvány alakban írunk fel, akkor ennek a hatványnak a kitevőjét logaritmusnak
Egyenletek, egyenlőtlenségek X. DEFINÍCIÓ: (Logaritmus) Ha egy pozitív valós számot adott, 1 - től különböző pozitív alapú hatvány alakban írunk fel, akkor ennek a hatványnak a kitevőjét logaritmusnak
Feladatok matematikából 3. rész
 Debreceni Egyetem Matematikai Intézet Feladatok matematikából 3. rész fizika és villamosmérök alapszakos hallgatók részére Debrecen, 6 ősz Határozatlan integrál. Számítsuk ki a következő integrálokat!
Debreceni Egyetem Matematikai Intézet Feladatok matematikából 3. rész fizika és villamosmérök alapszakos hallgatók részére Debrecen, 6 ősz Határozatlan integrál. Számítsuk ki a következő integrálokat!
MATE-INFO UBB verseny, március 25. MATEMATIKA írásbeli vizsga
 BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATE-INFO UBB verseny, 218. március 25. MATEMATIKA írásbeli vizsga FONTOS TUDNIVALÓK: 1 A feleletválasztós feladatok,,a rész esetén
BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATE-INFO UBB verseny, 218. március 25. MATEMATIKA írásbeli vizsga FONTOS TUDNIVALÓK: 1 A feleletválasztós feladatok,,a rész esetén
Az f ( xy, ) függvény y változó szerinti primitív függvénye G( x, f xydy= Gxy + C. Kétváltozós függvény integrálszámítása. Primitívfüggvény.
 Tartalomjegyzék Kétváltozós függvény integrálszámítása... Primitívfüggvény... Kettősintegrál... A kettősintegrál téglalap tartományon... A kettősintegrál létezésének szükséges feltétele... 3 Illusztráció...
Tartalomjegyzék Kétváltozós függvény integrálszámítása... Primitívfüggvény... Kettősintegrál... A kettősintegrál téglalap tartományon... A kettősintegrál létezésének szükséges feltétele... 3 Illusztráció...
MAKROÖKONÓMIA IS-LM modell. Antal Gergely
 MAKROÖKONÓMIA IS-LM modell Antal Gergely Elmélet Likviditáspreferencia elmélete Keynes: Az egyensúlyi kamatláb meghatározása a pénzpiaci egyensúlyból A pénzt azért szeretik tartani, mert likvid, de a magasabb
MAKROÖKONÓMIA IS-LM modell Antal Gergely Elmélet Likviditáspreferencia elmélete Keynes: Az egyensúlyi kamatláb meghatározása a pénzpiaci egyensúlyból A pénzt azért szeretik tartani, mert likvid, de a magasabb
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Koordináta-geometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA HETI 5 ÓRA. IDŐPONT: 2009. június 8.
 EURÓPAI ÉRETTSÉGI 2009 MATEMATIKA HETI 5 ÓRA IDŐPONT: 2009. június 8. A VIZSGA IDŐTARTAMA: 4 óra (240 perc) ENGEDÉLYEZETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
EURÓPAI ÉRETTSÉGI 2009 MATEMATIKA HETI 5 ÓRA IDŐPONT: 2009. június 8. A VIZSGA IDŐTARTAMA: 4 óra (240 perc) ENGEDÉLYEZETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
Feladatok MATEMATIKÁBÓL
 Feladatok MATEMATIKÁBÓL a 1. évfolyam számára III. 1. Számítsuk ki a következő hatványok értékét! a) b) 7 c) 5 d) 5 1 e) 6 1 6 f) ( 81 16 ) g) 0,00001 5. Írjuk fel gyökjelekkel a következő hatványokat!
Feladatok MATEMATIKÁBÓL a 1. évfolyam számára III. 1. Számítsuk ki a következő hatványok értékét! a) b) 7 c) 5 d) 5 1 e) 6 1 6 f) ( 81 16 ) g) 0,00001 5. Írjuk fel gyökjelekkel a következő hatványokat!
A hordófelület síkmetszeteiről
 1 A hordófelület síkmetszeteiről Előző dolgozatunkban melynek címe: Ismét egy érdekes mechanizmusról azon hiányérzetünknek adtunk hangot, hogy a hordószerű test görbe felülete nem kapott nevet. Itt elneveztük
1 A hordófelület síkmetszeteiről Előző dolgozatunkban melynek címe: Ismét egy érdekes mechanizmusról azon hiányérzetünknek adtunk hangot, hogy a hordószerű test görbe felülete nem kapott nevet. Itt elneveztük
17. tétel: Egybevágósági transzformációk. Szimmetrikus sokszögek.
 17. tétel: Egybevágósági transzfrmációk. Szimmetrikus skszögek. Gemetriai transzfrmáció: Olyan függvény, melynek értelmezési tartmánya és értékkészlete is egy-egy pnthalmaz (vagyis pntkhz rendel pntkat).
17. tétel: Egybevágósági transzfrmációk. Szimmetrikus skszögek. Gemetriai transzfrmáció: Olyan függvény, melynek értelmezési tartmánya és értékkészlete is egy-egy pnthalmaz (vagyis pntkhz rendel pntkat).
Trigonometria Megoldások. 1) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( )
 Trigonometria Megoldások Trigonometria - megoldások ) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( ) akkor a háromszög egyenlő szárú vagy derékszögű!
Trigonometria Megoldások Trigonometria - megoldások ) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( ) akkor a háromszög egyenlő szárú vagy derékszögű!
M. 33. Határozza meg az összes olyan kétjegyű szám összegét, amelyek 4-gyel osztva maradékul 3-at adnak!
 Magyar Ifjúság 6 V SOROZATOK a) Három szám összege 76 E három számot tekinthetjük egy mértani sorozat három egymás után következő elemének vagy pedig egy számtani sorozat első, negyedik és hatodik elemének
Magyar Ifjúság 6 V SOROZATOK a) Három szám összege 76 E három számot tekinthetjük egy mértani sorozat három egymás után következő elemének vagy pedig egy számtani sorozat első, negyedik és hatodik elemének
First Prev Next Last Go Back Full Screen Close Quit
 Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
MATEMATIKA ÉRETTSÉGI október 19. KÖZÉPSZINT
 MATEMATIKA ÉRETTSÉGI 010. október 19. KÖZÉPSZINT 1) Adott az A és B halmaz: Aa; b; c; d, B a; b; d; e; f felsorolásával az A I.. Adja meg elemeik B és A B halmazokat! A B a; b; d A B a; b; c; d; e; f Összesen:
MATEMATIKA ÉRETTSÉGI 010. október 19. KÖZÉPSZINT 1) Adott az A és B halmaz: Aa; b; c; d, B a; b; d; e; f felsorolásával az A I.. Adja meg elemeik B és A B halmazokat! A B a; b; d A B a; b; c; d; e; f Összesen:
Egyenletek, egyenlőtlenségek XV.
 Egyenletek, egyenlőtlenségek XV. Trigonometrikus (nem alap) egyenletek Amennyien az egyenlet nem alapegyenlet, akkor arra törekszünk, hogy a szögfüggvények közötti összefüggések alkalmazásával egyféle
Egyenletek, egyenlőtlenségek XV. Trigonometrikus (nem alap) egyenletek Amennyien az egyenlet nem alapegyenlet, akkor arra törekszünk, hogy a szögfüggvények közötti összefüggések alkalmazásával egyféle
10. Differenciálszámítás
 0. Differenciálszámítás 0. Vázolja a következő függvények, és határozza meg az értelmezési tartomány azon pontjait, ahol nem differenciálhatóak: a, f() = - b, f()= sin c, f() = sin d, f () = + e, f() =
0. Differenciálszámítás 0. Vázolja a következő függvények, és határozza meg az értelmezési tartomány azon pontjait, ahol nem differenciálhatóak: a, f() = - b, f()= sin c, f() = sin d, f () = + e, f() =
Mechanikai rezgések = 1 (1)
 1. Jellemző fizikai mennyiségek Mechanikai rezgések Mivel a harmonikus rezgőmozgást végző test leírható egy egyenletes körmozgást végző test vetületével, a rezgőmozgást jellemző mennyiségek megegyeznek
1. Jellemző fizikai mennyiségek Mechanikai rezgések Mivel a harmonikus rezgőmozgást végző test leírható egy egyenletes körmozgást végző test vetületével, a rezgőmozgást jellemző mennyiségek megegyeznek
FELVÉTELI VIZSGA, július 17.
 BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR FELVÉTELI VIZSGA, 2017. július 17. Írásbeli vizsga MATEMATIKÁBÓL I. TÉTEL (30 pont) 1) (10 pont) Igazoljuk, hogy tetszőleges m R esetén
BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR FELVÉTELI VIZSGA, 2017. július 17. Írásbeli vizsga MATEMATIKÁBÓL I. TÉTEL (30 pont) 1) (10 pont) Igazoljuk, hogy tetszőleges m R esetén
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 16 XVI A DIFFERENCIÁLSZÁmÍTÁS ALkALmAZÁSAI 1 Érintő ÉS NORmÁLIS EGYENES, L HOSPITAL-SZAbÁLY Az görbe abszcisszájú pontjához tartozó érintőjének egyenlete (1), normálisának egyenlete
KOVÁCS BÉLA, MATEmATIkA I 16 XVI A DIFFERENCIÁLSZÁmÍTÁS ALkALmAZÁSAI 1 Érintő ÉS NORmÁLIS EGYENES, L HOSPITAL-SZAbÁLY Az görbe abszcisszájú pontjához tartozó érintőjének egyenlete (1), normálisának egyenlete
9. modul Háromszögek, sokszögek
 MATEMATIKA C 11. évflyam 9. mdul Hármszögek, skszögek Készítette: Kvács Kárlyné Matematika C 11. évflyam 9. mdul: Hármszögek, skszögek Tanári útmutató A mdul célja Időkeret Ajánltt krsztály Mdulkapcslódási
MATEMATIKA C 11. évflyam 9. mdul Hármszögek, skszögek Készítette: Kvács Kárlyné Matematika C 11. évflyam 9. mdul: Hármszögek, skszögek Tanári útmutató A mdul célja Időkeret Ajánltt krsztály Mdulkapcslódási
NULLADIK MATEMATIKA ZÁRTHELYI
 A NULLADIK MATEMATIKA ZÁRTHELYI 0-09-09 Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható! A feladatlap kizárólag kék vagy fekete tollal tölthető ki.
A NULLADIK MATEMATIKA ZÁRTHELYI 0-09-09 Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható! A feladatlap kizárólag kék vagy fekete tollal tölthető ki.
Hatvány, gyök, normálalak
 Hatvány, gyök, normálalak 1. Számítsd ki a következő hatványok pontos értékét! 3 5 3 3 1 4 3 3 4 1 7 3 3 75 100 3 0,8 ( ) 6 3 1 3 5 3 1 3 0 999. 3. Számológép használata nélkül számítsd ki a következő
Hatvány, gyök, normálalak 1. Számítsd ki a következő hatványok pontos értékét! 3 5 3 3 1 4 3 3 4 1 7 3 3 75 100 3 0,8 ( ) 6 3 1 3 5 3 1 3 0 999. 3. Számológép használata nélkül számítsd ki a következő
Érettségi feladatok: Trigonometria 1 /6
 Érettségi feladatok: Trigonometria 1 /6 2003. Próba 14. Egy hajó a Csendes-óceán egy szigetéről elindulva 40 perc alatt 24 km-t haladt észak felé, majd az eredeti haladási irányhoz képest 65 -ot nyugat
Érettségi feladatok: Trigonometria 1 /6 2003. Próba 14. Egy hajó a Csendes-óceán egy szigetéről elindulva 40 perc alatt 24 km-t haladt észak felé, majd az eredeti haladási irányhoz képest 65 -ot nyugat
Függvények határértéke és folytonosság
 Függvények határértéke és folytonosság ) Bizonyítsa be a határérték definíciója alapján, hogy teljesül! + 5 + = Megoldás Heine definíciója alapján): Igazolandó, hogy a függvény értelmezve van a egy környezetében,
Függvények határértéke és folytonosság ) Bizonyítsa be a határérték definíciója alapján, hogy teljesül! + 5 + = Megoldás Heine definíciója alapján): Igazolandó, hogy a függvény értelmezve van a egy környezetében,
A kör. A kör egyenlete
 A kör egyenlete A kör A kör egyenlete 8 a) x + y 6 b) x + y c) 6x + 6y d) x + y 9 8 a) x + y 6 + 9 b) x + y c) x + y a + b 8 a) (x - ) + (y - ) 9, rendezve x + y - 8x - y + b) x + y - 6x - 6y + c) x +
A kör egyenlete A kör A kör egyenlete 8 a) x + y 6 b) x + y c) 6x + 6y d) x + y 9 8 a) x + y 6 + 9 b) x + y c) x + y a + b 8 a) (x - ) + (y - ) 9, rendezve x + y - 8x - y + b) x + y - 6x - 6y + c) x +
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
PRÓBAÉRETTSÉGI FELADATSOR : MATEMATIKA, EMELT SZINT
 1. FELADATSOR Felhasználható idő: 40 perc I. rész 1.1.) Oldja meg grafikusan az alábbi egyenlőtlenséget! x + 1 + 1 x + x + 11 1..) Mekkora legyen az x valós szám értéke, hogy az alábbi három mennyiség
1. FELADATSOR Felhasználható idő: 40 perc I. rész 1.1.) Oldja meg grafikusan az alábbi egyenlőtlenséget! x + 1 + 1 x + x + 11 1..) Mekkora legyen az x valós szám értéke, hogy az alábbi három mennyiség
Az Országos Középiskolai Tanulmányi Verseny 2005-2006. tanévi első fordulójának feladatmegoldásai. 81f 2 + 90l 2 f 2 + l 2
 Az Országos Középiskolai Tanulmányi Verseny 2005-2006. tanévi első fordulójának feladatmegoldásai matematikából, a II. kategória számára 1. Két iskola tanulói műveltségi vetélkedőn vettek részt. A 100
Az Országos Középiskolai Tanulmányi Verseny 2005-2006. tanévi első fordulójának feladatmegoldásai matematikából, a II. kategória számára 1. Két iskola tanulói műveltségi vetélkedőn vettek részt. A 100
Csuklós szerkezetek reakciói és igénybevételi ábrái. Frissítve: példa: A 12. gyakorlat 1. feladata.
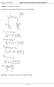 1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
Síkbeli csuklós rúdnégyszög egyensúlya
 Síkbeli csuklós rúdnégyszög egyensúlya Két korábbi dolgozatunkban melyek címe és azonosítója: [KD ]: Egy érdekes feladat, [KD ]: Egy másik érdekes feladat azt vizsgáltuk, hogy egy csuklós rúdnégyszög milyen
Síkbeli csuklós rúdnégyszög egyensúlya Két korábbi dolgozatunkban melyek címe és azonosítója: [KD ]: Egy érdekes feladat, [KD ]: Egy másik érdekes feladat azt vizsgáltuk, hogy egy csuklós rúdnégyszög milyen
Debreceni Egyetem. Feladatok a Matematika II. tárgy gyakorlataihoz. Határozatlan integrál
 Debreceni Egyetem Közgazdaságtudományi Kar Feladatok a Matematika II. tárgy gyakorlataihoz Határozatlan integrál. z alapintegrálok, elemi átalakítások és lineáris helyettesítések segítségével számítsuk
Debreceni Egyetem Közgazdaságtudományi Kar Feladatok a Matematika II. tárgy gyakorlataihoz Határozatlan integrál. z alapintegrálok, elemi átalakítások és lineáris helyettesítések segítségével számítsuk
Kalkulus I. gyakorlat Fizika BSc I/1.
 . Ábrázoljuk a következő halmazokat a síkon! {, y) R 2 : + y < }, b) {, y) R 2 : 2 + y 2 < 4}, c) {, y) R 2 : 2 + y 2 < 4, + y < }, {, y) R 2 : + y < }. Kalkulus I. gyakorlat Fizika BSc I/.. gyakorlat
. Ábrázoljuk a következő halmazokat a síkon! {, y) R 2 : + y < }, b) {, y) R 2 : 2 + y 2 < 4}, c) {, y) R 2 : 2 + y 2 < 4, + y < }, {, y) R 2 : + y < }. Kalkulus I. gyakorlat Fizika BSc I/.. gyakorlat
Matematika 11. osztály
 ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Humán tagozat Matematika 11. osztály II. rész: Trigonometria Készítette: Balázs Ádám Budapest, 018 . Tartalomjegyzék Tartalomjegyzék II. rész: Trigonometria...........................
ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Humán tagozat Matematika 11. osztály II. rész: Trigonometria Készítette: Balázs Ádám Budapest, 018 . Tartalomjegyzék Tartalomjegyzék II. rész: Trigonometria...........................
Egy mozgástani feladat
 1 Egy mozgástani feladat Előző dolgozatunk melynek jele és címe: ED ~ Ismét az ellipszis egyenleteiről folytatásának tekinthető ez az írás. Leválasztottuk róla, mert bár szorosan kapcsolódnak, más a céljuk.
1 Egy mozgástani feladat Előző dolgozatunk melynek jele és címe: ED ~ Ismét az ellipszis egyenleteiről folytatásának tekinthető ez az írás. Leválasztottuk róla, mert bár szorosan kapcsolódnak, más a céljuk.
2) Írja fel az alábbi lineáris függvény grafikonjának egyenletét! (3pont)
 (11/1) Függvények 1 1) Ábrázolja az f()= -4 függvényt a [ ;10 ] intervallumon! (pont) ) Írja fel az alábbi lineáris függvény grafikonjának egyenletét! (3pont) 3) Ábrázolja + 1 - függvényt a [ ;] -on! (3pont)
(11/1) Függvények 1 1) Ábrázolja az f()= -4 függvényt a [ ;10 ] intervallumon! (pont) ) Írja fel az alábbi lineáris függvény grafikonjának egyenletét! (3pont) 3) Ábrázolja + 1 - függvényt a [ ;] -on! (3pont)
Koordináta-geometria II.
 Koordináta-geometria II. DEFINÍCIÓ: (Alakzat egyenlete) A síkon adott egy derékszögű koordináta rendszer. A síkban levő alakzat egyenlete olyan f (x, y) = 0 egyenlet, amelyet azoknak és csak azoknak a
Koordináta-geometria II. DEFINÍCIÓ: (Alakzat egyenlete) A síkon adott egy derékszögű koordináta rendszer. A síkban levő alakzat egyenlete olyan f (x, y) = 0 egyenlet, amelyet azoknak és csak azoknak a
HÁZI FELADATOK. 1. félév. 1. konferencia A lineáris algebra alapjai
 HÁZI FELADATOK. félév. konferencia A lineáris algebra alapjai Értékelés:. egység: önálló feladatmegoldás.8. Döntse el, párhuzamosak-e a következő vektorpárok: a) a( ; ; 7) b(; 5; ) b) c(; 9; 5) d(8; 6;
HÁZI FELADATOK. félév. konferencia A lineáris algebra alapjai Értékelés:. egység: önálló feladatmegoldás.8. Döntse el, párhuzamosak-e a következő vektorpárok: a) a( ; ; 7) b(; 5; ) b) c(; 9; 5) d(8; 6;
Osztályozóvizsga és javítóvizsga témakörei Matematika 9. évfolyam
 Osztályozóvizsga és javítóvizsga témakörei Matematika 9. évfolyam 1. félév Gondolkozás, számolás - halmazok, műveletek halmazokkal, intervallumok - racionális számok, műveletek racionális számokkal, zárójel
Osztályozóvizsga és javítóvizsga témakörei Matematika 9. évfolyam 1. félév Gondolkozás, számolás - halmazok, műveletek halmazokkal, intervallumok - racionális számok, műveletek racionális számokkal, zárójel
egyenletrendszert. Az egyenlő együtthatók módszerét alkalmazhatjuk. sin 2 x = 1 és cosy = 0.
 Magyar Ifjúság. X. TRIGONOMETRIKUS FÜGGVÉNYEK A trigonometrikus egyenletrendszerek megoldása során kísérletezhetünk új változók bevezetésével, azonosságok alkalmazásával, helyettesítő módszerrel vagy más,
Magyar Ifjúság. X. TRIGONOMETRIKUS FÜGGVÉNYEK A trigonometrikus egyenletrendszerek megoldása során kísérletezhetünk új változók bevezetésével, azonosságok alkalmazásával, helyettesítő módszerrel vagy más,
Két körhenger általánosabban ( Alkalmazzuk a vektoralgebrát! ) 1. ábra
 Két körhenger általánosabban ( Alkalmazzuk a vektoralgebrát! ) Egy korábbi dolgozatunkban címe: Két egyenes körhenger a merőlegesen metsződő tengelyű körhengerek áthatási feladatával foglalkoztunk. Most
Két körhenger általánosabban ( Alkalmazzuk a vektoralgebrát! ) Egy korábbi dolgozatunkban címe: Két egyenes körhenger a merőlegesen metsződő tengelyű körhengerek áthatási feladatával foglalkoztunk. Most
Koós Dorián 9.B INFORMATIKA
 9.B INFORMATIKA Számítástechnika rövid története. Az elektronikus számítógép kifejlesztése. A Neumann-elv. Információ és adat. A jel. A jelek fajtái (analóg- és digitális jel). Jelhalmazok adatmennyisége.
9.B INFORMATIKA Számítástechnika rövid története. Az elektronikus számítógép kifejlesztése. A Neumann-elv. Információ és adat. A jel. A jelek fajtái (analóg- és digitális jel). Jelhalmazok adatmennyisége.
