Diverzifikáció Markowitz-modell MAD modell CAPM modell 2017/ Szegedi Tudományegyetem Informatikai Intézet

Átírás

1 Operációkutatás I. 2017/ Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 11. Előadás

2 Portfólió probléma

3 Portfólió probléma

4 Portfólió probléma Adott részvények (kötvények,tevékenységek, stb.) egy halmaza

5 Portfólió probléma Adott részvények (kötvények,tevékenységek, stb.) egy halmaza Kérdés: Hogyan álĺıtsunk össze belőlük portfóliót?

6 Portfólió probléma Adott részvények (kötvények,tevékenységek, stb.) egy halmaza Kérdés: Hogyan álĺıtsunk össze belőlük portfóliót? Egy r részvénybe való befektetés várható hozama legyen: E(r) (A befektetés hozamának múltbéli megfigyeléseiből számított várható érték)

7 Portfólió probléma Adott részvények (kötvények,tevékenységek, stb.) egy halmaza Kérdés: Hogyan álĺıtsunk össze belőlük portfóliót? Egy r részvénybe való befektetés várható hozama legyen: E(r) (A befektetés hozamának múltbéli megfigyeléseiből számított várható érték) Cél: Maximális hozamú portfólió összeálĺıtására n darab befektetés esetén

8 Portfólió probléma Adott részvények (kötvények,tevékenységek, stb.) egy halmaza Kérdés: Hogyan álĺıtsunk össze belőlük portfóliót? Egy r részvénybe való befektetés várható hozama legyen: E(r) (A befektetés hozamának múltbéli megfigyeléseiből számított várható érték) Cél: Maximális hozamú portfólió összeálĺıtására n darab befektetés esetén Feĺırható egy LP feladat:

9 Portfólió probléma Adott részvények (kötvények,tevékenységek, stb.) egy halmaza Kérdés: Hogyan álĺıtsunk össze belőlük portfóliót? Egy r részvénybe való befektetés várható hozama legyen: E(r) (A befektetés hozamának múltbéli megfigyeléseiből számított várható érték) Cél: Maximális hozamú portfólió összeálĺıtására n darab befektetés esetén Feĺırható egy LP feladat: n x i = 1 i=1 x i 0 n max E(r i )x i i=1 [tőke] [r i -be fektetett rész] [várható nyereség]

10 Portfólió probléma Ha E(r 1 ) E(r 2 )... E(r n ) (ez feltehető), akkor az optimális megoldás x 1 = 1, x 2 = = x n = 0, a nyereség pedig E(r 1 ).

11 Portfólió probléma Ha E(r 1 ) E(r 2 )... E(r n ) (ez feltehető), akkor az optimális megoldás x 1 = 1, x 2 = = x n = 0, a nyereség pedig E(r 1 ). Általában igaz, ha ezt a stratégiát ismételjük, akkor 1 valószínűséggel csődbe megyünk.

12 Portfólió probléma Ha E(r 1 ) E(r 2 )... E(r n ) (ez feltehető), akkor az optimális megoldás x 1 = 1, x 2 = = x n = 0, a nyereség pedig E(r 1 ). Általában igaz, ha ezt a stratégiát ismételjük, akkor 1 valószínűséggel csődbe megyünk. többféle próbálkozás született (sőt, a terület most is nagyon aktív) a megoldásra. Ebből kettőt vizsgálunk:

13 Portfólió probléma Ha E(r 1 ) E(r 2 )... E(r n ) (ez feltehető), akkor az optimális megoldás x 1 = 1, x 2 = = x n = 0, a nyereség pedig E(r 1 ). Általában igaz, ha ezt a stratégiát ismételjük, akkor 1 valószínűséggel csődbe megyünk. többféle próbálkozás született (sőt, a terület most is nagyon aktív) a megoldásra. Ebből kettőt vizsgálunk: 1 Markowitz-modell, 1952; Nobel-díj 1990

14 Portfólió probléma Ha E(r 1 ) E(r 2 )... E(r n ) (ez feltehető), akkor az optimális megoldás x 1 = 1, x 2 = = x n = 0, a nyereség pedig E(r 1 ). Általában igaz, ha ezt a stratégiát ismételjük, akkor 1 valószínűséggel csődbe megyünk. többféle próbálkozás született (sőt, a terület most is nagyon aktív) a megoldásra. Ebből kettőt vizsgálunk: 1 Markowitz-modell, 1952; Nobel-díj MAD modell (Konno-Yamazaki, 1990)

15 Portfólió probléma példa Legyen egy r részvénybe való befektetés kockázata D(r) (A befektetés hozamának múltbéli megfigyeléseiből számított szórás).

16 Portfólió probléma példa Legyen egy r részvénybe való befektetés kockázata D(r) (A befektetés hozamának múltbéli megfigyeléseiből számított szórás). Tekintsük a következő befektetések hozamait az utóbbi 3 évben: 1. év 2. év 3. év Ingatlan Értékpapír

17 Portfólió probléma példa Legyen egy r részvénybe való befektetés kockázata D(r) (A befektetés hozamának múltbéli megfigyeléseiből számított szórás). Tekintsük a következő befektetések hozamait az utóbbi 3 évben: 1. év 2. év 3. év Ingatlan Értékpapír A várható hozamok: E(r i ) = = 0.02 és E(r e ) = = 0.02

18 Portfólió probléma példa Legyen egy r részvénybe való befektetés kockázata D(r) (A befektetés hozamának múltbéli megfigyeléseiből számított szórás). Tekintsük a következő befektetések hozamait az utóbbi 3 évben: 1. év 2. év 3. év Ingatlan Értékpapír A várható hozamok: E(r i ) = = 0.02 és E(r e ) = = 0.02 A kockázatok: D(r i ) = D(r e ) = ( ) 2 +( ) 2 +( ) és ( ) 2 +( ) 2 +( )

19 Portfólió probléma példa Ha a tőkénk 75%át ingatlanba, 25%-át kötvénybe fektetjük, akkor a portfólió hozama:

20 Portfólió probléma példa Ha a tőkénk 75%át ingatlanba, 25%-át kötvénybe fektetjük, akkor a portfólió hozama: E(r p ) = ( ) = ( )/3 = 0.02 az egyes években való hozamokat átlagolva. 3 + ( ) 3 + ( ) 3 =

21 Portfólió probléma példa Ha a tőkénk 75%át ingatlanba, 25%-át kötvénybe fektetjük, akkor a portfólió hozama: E(r p ) = ( ) = ( )/3 = 0.02 az egyes években való hozamokat átlagolva. 3 + ( ) 3 + ( ) 3 = A portfólió kockázata: ( ) D(r p ) = 2 +( ) 2 +( )

22 Portfólió probléma példa Ha a tőkénk 75%át ingatlanba, 25%-át kötvénybe fektetjük, akkor a portfólió hozama: E(r p ) = ( ) = ( )/3 = 0.02 az egyes években való hozamokat átlagolva. 3 + ( ) 3 + ( ) 3 = A portfólió kockázata: ( ) D(r p ) = 2 +( ) 2 +( ) A befektetések átlagos kockázata: = 0.068

23 Portfólió probléma példa Ha a tőkénk 75%át ingatlanba, 25%-át kötvénybe fektetjük, akkor a portfólió hozama: E(r p ) = ( ) = ( )/3 = 0.02 az egyes években való hozamokat átlagolva. 3 + ( ) 3 + ( ) 3 = A portfólió kockázata: ( ) D(r p ) = 2 +( ) 2 +( ) A befektetések átlagos kockázata: = a diverzifikáció csökkenti a kockázatot

24 Portfólió probléma példa 1. év 2. év 3. év Ingatlan Értékpapír

25 Portfólió probléma példa 1. év 2. év 3. év Ingatlan Értékpapír Kovariancia: két független (véletlen) változó (lineáris) együttmozgásának mértéke: C i,e = ( ) ( ) 3 + ( ) ( ) ( ) ( ) 3 = 0.005

26 Portfólió probléma példa 1. év 2. év 3. év Ingatlan Értékpapír Kovariancia: két független (véletlen) változó (lineáris) együttmozgásának mértéke: C i,e = ( ) ( ) 3 + ( ) ( ) ( ) ( ) 3 = Korreláció: normalizált kovariancia ρ i,e = = 0.84

27 Portfólió probléma példa 1. év 2. év 3. év Ingatlan Értékpapír Kovariancia: két független (véletlen) változó (lineáris) együttmozgásának mértéke: C i,e = ( ) ( ) 3 + ( ) ( ) ( ) ( ) 3 = Korreláció: normalizált kovariancia ρ i,e = = ρ 1 ρ > 0 azonos irányú együttmozgás ρ = 0 nincs együttmozgás ( függetlenség, de függetlenség) ρ < 0 ellentétes irányú együttmozgás

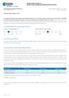
28 Portfólió probléma példa 1. ábra. Coca-Cola és Procter&Gamble részvények árfolyama árfolyama 1990-ben

29 Portfólió probléma Markowitz-modell Mindez általánosan:

30 Portfólió probléma Markowitz-modell Mindez általánosan: (r 1, r 2,..., r n ) a portfólióban lévő részvények

31 Portfólió probléma Markowitz-modell Mindez általánosan: (r 1, r 2,..., r n ) a portfólióban lévő részvények x = (x 1, x 2,..., x n ) az egyes befektetések aránya a portfólióban

32 Portfólió probléma Markowitz-modell Mindez általánosan: (r 1, r 2,..., r n ) a portfólióban lévő részvények x = (x 1, x 2,..., x n ) az egyes befektetések aránya a portfólióban n i=1 x i = 1 és x i 0( i)

33 Portfólió probléma Markowitz-modell Mindez általánosan: (r 1, r 2,..., r n ) a portfólióban lévő részvények x = (x 1, x 2,..., x n ) az egyes befektetések aránya a portfólióban n i=1 x i = 1 és x i 0( i) Kockázat: variancia (szórásnégyzet a szórás helyett)

34 Portfólió probléma Markowitz-modell Mindez általánosan: (r 1, r 2,..., r n ) a portfólióban lévő részvények x = (x 1, x 2,..., x n ) az egyes befektetések aránya a portfólióban n i=1 x i = 1 és x i 0( i) Kockázat: variancia (szórásnégyzet a szórás helyett) Kovariancia mátrix: a részvények hozamainak páronkénti kovarianciáit tartalmazó mátrix C 11 C 12 C 1n C 21 C 22 C 1n C = C n1 C n2 C nn C ii = D 2 (r i ) = Var(r i )

35 Portfólió probléma Markowitz-modell A portfólió kockázata: ( n ) Var E(r i )x i = i=1 n ( n ) C ij x i x j = x T Cx i=1 j=1

36 Portfólió probléma Markowitz-modell A portfólió kockázata: ( n ) Var E(r i )x i = i=1 n ( n ) C ij x i x j = x T Cx i=1 j=1 Hatékony portfólió: hozama nem növelhető a kockázatának növekedése nélkül, illetve kockázata nem csökkenthető a várható hozamának csökkenése nélkül

37 Portfólió probléma Markowitz-modell A portfólió kockázata: ( n ) Var E(r i )x i = i=1 n ( n ) C ij x i x j = x T Cx i=1 j=1 Hatékony portfólió: hozama nem növelhető a kockázatának növekedése nélkül, illetve kockázata nem csökkenthető a várható hozamának csökkenése nélkül A hatékony portfólió egyfajta optimum: adott hozam mellett minimális kockázat adott kockázat mellett maximális hozam

38 Portfólió probléma Markowitz-modell Legyen R egy elvárt minimális hozamszint. Feĺırható egy kvadratikus programozási feladat:

39 Portfólió probléma Markowitz-modell Legyen R egy elvárt minimális hozamszint. Feĺırható egy kvadratikus programozási feladat: n E(r i )x i R i=1 n x i = 1 i=1 x i 0 i = 1,2,..., n min x T Cx

40 Portfólió probléma Markowitz-modell Legyen R egy elvárt minimális hozamszint. Feĺırható egy kvadratikus programozási feladat: n E(r i )x i R i=1 n x i = 1 i=1 x i 0 i = 1,2,..., n min x T Cx Azaz minimalizáljuk a kockázatot egy elvárt hozam elérése mellett. A feladat egy megoldását optimális portfóliónak nevezzük.

41 Portfólió probléma Markowitz-modell Néhány megjegyzés: 1 ha r = (r 1,..., r n) többváltozós normális eloszlást követ, akkor a két módszer ekvivalens

42 Portfólió probléma Markowitz-modell Néhány megjegyzés: kvadratikus célfüggvényű optimalizálási feladattal nem foglalkoztunk külön 1 ha r = (r 1,..., r n) többváltozós normális eloszlást követ, akkor a két módszer ekvivalens

43 Portfólió probléma Markowitz-modell Néhány megjegyzés: kvadratikus célfüggvényű optimalizálási feladattal nem foglalkoztunk külön vannak hatékony algoritmusok a megoldására 1 ha r = (r 1,..., r n) többváltozós normális eloszlást követ, akkor a két módszer ekvivalens

44 Portfólió probléma Markowitz-modell Néhány megjegyzés: kvadratikus célfüggvényű optimalizálási feladattal nem foglalkoztunk külön vannak hatékony algoritmusok a megoldására másik nehézség: C mátrix elemeinek számítása (becslése a múlt alapján) 1 ha r = (r 1,..., r n) többváltozós normális eloszlást követ, akkor a két módszer ekvivalens

45 Portfólió probléma Markowitz-modell Néhány megjegyzés: kvadratikus célfüggvényű optimalizálási feladattal nem foglalkoztunk külön vannak hatékony algoritmusok a megoldására másik nehézség: C mátrix elemeinek számítása (becslése a múlt alapján) helyette használhatjuk pl. az átlagos abszolút eltérés E( i (r i E(r i ))x i ) maximalizálását 1 1 ha r = (r 1,..., r n) többváltozós normális eloszlást követ, akkor a két módszer ekvivalens

46 MAD modell

47 MAD modell Mean Absolute Deviation

48 MAD modell Mean Absolute Deviation Konno és Yamazaki által kidolgozott modell a megfigyelt adatokat közvetlenül használja fel és elkerüli E(r i ) és C kiszámítását

49 MAD modell Mean Absolute Deviation Konno és Yamazaki által kidolgozott modell a megfigyelt adatokat közvetlenül használja fel és elkerüli E(r i ) és C kiszámítását Legyen T megfigyelésünk az n befektetésre és jelölje r it az i. befektetés hozamának t-edik megfigyelését

50 MAD modell Mean Absolute Deviation Konno és Yamazaki által kidolgozott modell a megfigyelt adatokat közvetlenül használja fel és elkerüli E(r i ) és C kiszámítását Legyen T megfigyelésünk az n befektetésre és jelölje r it az i. befektetés hozamának t-edik megfigyelését Vezessük be az alábbi jelöléseket r i = 1 T T r it és a it = r it r i t=1 azaz az átlagos megfigyelt hozam, és az egyes megfigyelések eltérése az átlagtól.

51 Portfólió probléma MAD modell A következő optimalizálási feladat írható fel: n r i x i R i=1 n x i = 1 i=1 x i 0 i = 1,2,..., n min 1 T T n a it x i t=1 i=1

52 Portfólió probléma MAD modell A következő optimalizálási feladat írható fel: n r i x i R i=1 n x i = 1 i=1 x i 0 i = 1,2,..., n min 1 T T n a it x i t=1 i=1 A feladat nem LP, de azzá alakítható!

53 Portfólió probléma MAD modell MAD modell LP-re átírva: n a it x i y t i=1 n a it x i y t i=1 n r i x i R i=1 n x i = 1 i=1 x i 0 y t 0 t = 1,2,..., T t = 1,2,..., T i = 1,2,..., n t = 1,2,..., T min 1 T T t=1 y t

54 Portfólió probléma szemi-mad modell

55 Portfólió probléma szemi-mad modell A MAD modell javítható

56 Portfólió probléma szemi-mad modell A MAD modell javítható A t. időpontban a portfólió becsült előjeles eltérése a várható hozamtól n n a it x i = (r it r i )x i i=1 A pozitív eltérés kedvező A negatív eltérés a problémás i=1

57 Portfólió probléma szemi-mad modell A MAD modell javítható A t. időpontban a portfólió becsült előjeles eltérése a várható hozamtól n n a it x i = (r it r i )x i i=1 A pozitív eltérés kedvező A negatív eltérés a problémás i=1 Vezessük be a következő jelölést { x x, x 0 = 0, x > 0 azaz a szám negatív része

58 Portfólió probléma szemi-mad modell A portfólió optimalizálás feĺırható a következő alakban n r i x i R i=1 n x i = 1 i=1 x i 0 i = 1,2,..., n min 1 T T n a it x i t=1 i=1

59 Portfólió probléma szemi-mad modell A portfólió optimalizálás feĺırható a következő alakban n r i x i R i=1 n x i = 1 i=1 x i 0 i = 1,2,..., n min 1 T T n a it x i t=1 i=1 Az LP-vé alakítás még egyszerűbb, mint a MAD esetében!

60 Portfólió probléma szemi-mad modell A semi-mad modell LP-re átírva: n a it x i y t i=1 n r i x i R i=1 n x i = 1 i=1 y t 0 x i 0 t = 1,2,..., T t = 1,2,..., T i = 1,2,..., n min 1 T T t=1 y t

61 Portfólió probléma MAD vs. szemi-mad Néhány megjegyzés:

62 Portfólió probléma MAD vs. szemi-mad Néhány megjegyzés: A két módszer nagyjából ekvivalens, ha az optimális portfóliók hozamainak eloszlása közel szimmetrikus

63 Portfólió probléma MAD vs. szemi-mad Néhány megjegyzés: A két módszer nagyjából ekvivalens, ha az optimális portfóliók hozamainak eloszlása közel szimmetrikus...ez nem szükségszerűen van így...

64 Portfólió probléma MAD vs. szemi-mad Néhány megjegyzés: A két módszer nagyjából ekvivalens, ha az optimális portfóliók hozamainak eloszlása közel szimmetrikus...ez nem szükségszerűen van így......ezért a szemi-mad hasznosabbnak tűnik, mert a várható számítási idő rövidebb

65 CAPM modell Capital Asset Pricing Model 2 = Tőkepiaci eszközök árazásának modellje 2 Treynor, Sharpe (Nobel díj), Lintner, Mossin

66 CAPM modell Capital Asset Pricing Model 2 = Tőkepiaci eszközök árazásának modellje A modell alapfeltételezései: 2 Treynor, Sharpe (Nobel díj), Lintner, Mossin

67 CAPM modell Capital Asset Pricing Model 2 = Tőkepiaci eszközök árazásának modellje A modell alapfeltételezései: 1 Tökéletes verseny ( nincsenek startégiai lépések az árfolyamok megváltoztatására) 2 Treynor, Sharpe (Nobel díj), Lintner, Mossin

68 CAPM modell Capital Asset Pricing Model 2 = Tőkepiaci eszközök árazásának modellje A modell alapfeltételezései: 1 Tökéletes verseny ( nincsenek startégiai lépések az árfolyamok megváltoztatására) 2 Költségmentes és azonnali információáramlás 2 Treynor, Sharpe (Nobel díj), Lintner, Mossin

69 CAPM modell Capital Asset Pricing Model 2 = Tőkepiaci eszközök árazásának modellje A modell alapfeltételezései: 1 Tökéletes verseny ( nincsenek startégiai lépések az árfolyamok megváltoztatására) 2 Költségmentes és azonnali információáramlás 3 Nincsenek adók és tranzakciós költségek 2 Treynor, Sharpe (Nobel díj), Lintner, Mossin

70 CAPM modell Capital Asset Pricing Model 2 = Tőkepiaci eszközök árazásának modellje A modell alapfeltételezései: 1 Tökéletes verseny ( nincsenek startégiai lépések az árfolyamok megváltoztatására) 2 Költségmentes és azonnali információáramlás 3 Nincsenek adók és tranzakciós költségek 4 Egyperiódusos modell 2 Treynor, Sharpe (Nobel díj), Lintner, Mossin

71 CAPM modell Capital Asset Pricing Model 2 = Tőkepiaci eszközök árazásának modellje A modell alapfeltételezései: 1 Tökéletes verseny ( nincsenek startégiai lépések az árfolyamok megváltoztatására) 2 Költségmentes és azonnali információáramlás 3 Nincsenek adók és tranzakciós költségek 4 Egyperiódusos modell 5 A befektetők kockázatkerülők, azonos az információhalmazuk 2 Treynor, Sharpe (Nobel díj), Lintner, Mossin

72 CAPM modell Capital Asset Pricing Model 2 = Tőkepiaci eszközök árazásának modellje A modell alapfeltételezései: 1 Tökéletes verseny ( nincsenek startégiai lépések az árfolyamok megváltoztatására) 2 Költségmentes és azonnali információáramlás 3 Nincsenek adók és tranzakciós költségek 4 Egyperiódusos modell 5 A befektetők kockázatkerülők, azonos az információhalmazuk 6 Csak (korlátlanul osztható) pénzügyi eszközök ( részvény, kötvény) 2 Treynor, Sharpe (Nobel díj), Lintner, Mossin

73 CAPM modell Capital Asset Pricing Model 2 = Tőkepiaci eszközök árazásának modellje A modell alapfeltételezései: 1 Tökéletes verseny ( nincsenek startégiai lépések az árfolyamok megváltoztatására) 2 Költségmentes és azonnali információáramlás 3 Nincsenek adók és tranzakciós költségek 4 Egyperiódusos modell 5 A befektetők kockázatkerülők, azonos az információhalmazuk 6 Csak (korlátlanul osztható) pénzügyi eszközök ( részvény, kötvény) 7 Mindenki számára azosan elérhető kockázatmentes kamatláb ( alapkamat) 2 Treynor, Sharpe (Nobel díj), Lintner, Mossin

74 CAPM modell Legyen a kockázatmentes kamatláb r f

75 CAPM modell Legyen a kockázatmentes kamatláb r f egy globális piaci (kockázatos) kamatláb r m

76 CAPM modell Legyen a kockázatmentes kamatláb r f egy globális piaci (kockázatos) kamatláb r m egy r i részvény (kockázatos) várható hozama E(r i )

77 CAPM modell Legyen a kockázatmentes kamatláb r f egy globális piaci (kockázatos) kamatláb r m egy r i részvény (kockázatos) várható hozama E(r i ) Sharpe: létezik egy β mennyiség úgy, hogy E(r i ) r f = β(e(r m ) r f ) ahol

78 CAPM modell Legyen a kockázatmentes kamatláb r f egy globális piaci (kockázatos) kamatláb r m egy r i részvény (kockázatos) várható hozama E(r i ) Sharpe: létezik egy β mennyiség úgy, hogy E(r i ) r f = β(e(r m ) r f ) ahol β = C r i,r f Var(r f ) = E(r ir f ) E(r i )E(r f ) E(r 2 f ) (E(r f ) 2

79 CAPM modell Legyen a kockázatmentes kamatláb r f egy globális piaci (kockázatos) kamatláb r m egy r i részvény (kockázatos) várható hozama E(r i ) Sharpe: létezik egy β mennyiség úgy, hogy E(r i ) r f = β(e(r m ) r f ) ahol β = C r i,r f Var(r f ) = E(r ir f ) E(r i )E(r f ) E(r 2 f ) (E(r f ) 2 E(r i ) r f : kockázati prémium E(r m ) r f : piaci prémium

80 CAPM modell Ha β = 0, akkor E(r i ) = r f Ha β = 1, akkor E(r i ) = E(r m ) E(r i ) a β lineáris függvénye: E(r i ) = r f + β(e(r m ) r f )

81 CAPM modell Ha β = 0, akkor E(r i ) = r f Ha β = 1, akkor E(r i ) = E(r m ) E(r i ) a β lineáris függvénye: E(r i ) = r f + β(e(r m ) r f ) Mi a kockázat? Számoljuk ki Var(r i )-t. Legyen r i = r f + β(e(r m ) r f ) + ε azaz

82 CAPM modell Ha β = 0, akkor E(r i ) = r f Ha β = 1, akkor E(r i ) = E(r m ) E(r i ) a β lineáris függvénye: E(r i ) = r f + β(e(r m ) r f ) Mi a kockázat? Számoljuk ki Var(r i )-t. Legyen r i = r f + β(e(r m ) r f ) + ε azaz ε = r i r f β(e(r m ) r f ) a tényleges és várható hozam közti eltérés.

83 CAPM modell Ha β = 0, akkor E(r i ) = r f Ha β = 1, akkor E(r i ) = E(r m ) E(r i ) a β lineáris függvénye: E(r i ) = r f + β(e(r m ) r f ) Mi a kockázat? Számoljuk ki Var(r i )-t. Legyen azaz r i = r f + β(e(r m ) r f ) + ε ε = r i r f β(e(r m ) r f ) a tényleges és várható hozam közti eltérés. Kiszámolható, hogy E(ε) = 0, tovább az is, hogy C rm,ε = 0 (hf.), azaz a hibatag és piaci (portfolió) hozam korrelálatlan.

84 CAPM modell A korrelálatlanság miatt Var(r i ) = β 2 Var(r m ) + Var(ε).

85 CAPM modell A korrelálatlanság miatt Var(r i ) = β 2 Var(r m ) + Var(ε). Itt β 2 Var(r m ) a szisztematikus (elkerülhetetlen) kockázat Var(ε) alkalmi (diverzifikálható) kockázat

86 CAPM modell A korrelálatlanság miatt Var(r i ) = β 2 Var(r m ) + Var(ε). Itt β 2 Var(r m ) a szisztematikus (elkerülhetetlen) kockázat Var(ε) alkalmi (diverzifikálható) kockázat Azaz β tulajdonképpen a rendszerszintű, vagy piaci kockázatát méri az adott részvénynek.

87 CAPM modell A korrelálatlanság miatt Var(r i ) = β 2 Var(r m ) + Var(ε). Itt β 2 Var(r m ) a szisztematikus (elkerülhetetlen) kockázat Var(ε) alkalmi (diverzifikálható) kockázat Azaz β tulajdonképpen a rendszerszintű, vagy piaci kockázatát méri az adott részvénynek. β a múltbeli adatokból, az átlag, a variancia és a kovariancia szokásos statisztikai becsléseivel számolható

88 CAPM modell E(r i ) = r f + β(e(r m ) r f ) egy egyenest ad meg 2. ábra. A β és az ún. security market line :