12.1. A h!sugárzás alapjai
|
|
|
- Attila Bodnár
- 6 évvel ezelőtt
- Látták:
Átírás
1 13
2 "2. H!SUGÁRZÁS A h!sugárzás lpj BVZTÉS ÉS ALAPFOGALMAK Mndgyk tst bocsát k lktromágnss sugárzást. Alcsony h!mérsékltkn (kb. szobh!mérsékltg) z így kbocsátott nrg gykorltlg lhnygolhtó, míg mgs h!mérsékltk trtományábn jlnt!ssé válk. Az nrgánk lktromágnss hullámok formájábn vló térbl trjdésénk és más nrgformává átlkulásánk pontos mnnység lírásához szükségs mtmtk pprátus bonyolultság mtt, gyszr"sít! líró modllt hsználunk m"szk gykorlt h!árm számításhoz szükségs összfüggésk mghtározásár táblázt Az lktromágnss sugárzás trtományok nm 1-2 2nm 2 4nm gmmsugárzás röntgnsugárzás ultrbolysugárzás.4.8µm.8 4µm 4µm... láthtó fény nfrvörös-sugárzás gyéb sugárzás (pl. rádóhullámok) Az lktromágnss sugárzás szokásos hullámhossz-trtomány szrnt flosztását táblázt trtlmzz. A h!közlésbn h!sugrk =.5-1µm között trtomány, ngy nrg trtlom mtt jlnt!s. Az lktromágnss sugárzás gy dott nrgármot (W, kw) jlnt, mt φ - vl jlölünk továbbkbn. A környztévl sugárzásos h!kpcsoltbn lév! tst h!ármát kbocsátott (mttált) és z lnylt (bszorbált) nrgárm különbségként írhtjuk fl:!q = Φ Φ [W, kw]. (12.1) (12.1) kfjz, hogy szmbn h!vztés és h!szállítás stévl h!sugárzáskor z nrg forglom gynsúlybn s kétrányú. A sugárzás flült nrgs"r"ség flültgységnként sugárzás: = dφ [W/m 2, kw/m 2 ]. (12.2) df A flült nrgs"r"ség gységny hullámhosszúságr s! hányd sugárzás ntnztás: d d = = d dfd 2 Φ [W/m3 ]. (12.3) A tljs (= ) hullámhossz trtományr (spktrumr) vontkozó sugárzás gy F flült stébn: 131
3 Φ = d df F. (12.4) Az ntnztás tst flült lmér!l z un. tljs féltérb ksugárzott nrg. A tljs féltér térszög ω= 2π [sr]. (A strdán [sr] térszög mértékgység, zt fjz k, hogy z dott nyílásszög" kúp mkkor flültt mtsz k z gységny sugrú gömb flszínéb!l. Mvl gömb flszín 4πr 2, z gység sugrú félgömb flszín 2π.) n d ϕ ω dω df dfcosϕ ábr Az és összfüggéshz snϕ dω=snϕdϕdψ dϕ ϕ R =1 dψ Ψ ábr A dω térszög mghtározásához gy dott rányb ksugárzott nrg, z gységny térszögr vontkozttott ntnztás: d cosϕ dω, ω =, (12.5) és zzl tljs féltérb ksugárzott nrgát így írhtjuk fl: = cosϕdω 2π. (12.6) hol dω=sn(ϕ)dϕdψ ( szögk értlmzését ábrán kövthtjük). Az féltérb ksugárzott nrgát z l!bbk lpján thát így írhtjuk: 2 π π / 2 = snϕ cos ψdϕdψ. (12.7) 132
4 φ φ r φ gyütt tst látszólgos sugárzás φ φ s φ d φ -környztbõl érkzõ φ -kbocsátott φ -z lnylt φ d -z átrszttt φ r -vsszvrt φ s -szóródás mtt rányt változttott ábr gy tst sugárzássl szmbn mkroszkopkus vslkdés gy tst lktromágnss sugárzássl szmbn mkroszkopkus vslkdését jllmz, hogy nnk hányd részét nyl l (bszorpcó), hányd részét vr vssz (rflxó) és végül hányd részét ngd át (dtrm). Az mlíttt tuljdonságok áltl mghtározott sugárzás hánydok jlntését (jlölésükkl gyütt) szmléltt ábr. A tst sugárzás jllmz!t z l!bbk lpján dfnálhtjuk z dott hullámhosszr és dott rányr vontkozttv ( ), tljs féltérb!l érkz! sugárzásr vontkozttv ( ) és flült nrg s"r"ségr vontkozttv gyránt (). Az bszorpcós tényz!k (lnyl! képsség): =, =, =, (12.8) A rflxós tényz!k (vsszvr! képsség): r r =, r =, r A dtrmctások (átrszt! képsség): d d =, d =, d r d r =, (12.9) d =, (12.1) A (12.8),(12.9),és (12.1) összfüggéskkl dfnált tényz!k, dfnícóbn flhsznált mnnységk között összfüggésk lpján, gymás között átszámíthtók. A sugárzást dffúznk nvzzük, h z r!sség rány függtln, így z (12.7) gynlt lpján írhtjuk: = snϕ cos ψdϕdψ = π. (12.11) 2 π π / 2 Dffúz sugárzás stébn thát féltér tljs sugárzás π-szrs ttsz!lgs rányú (gységny térszögr vontkozó) sugárzásnk. gy tstr vontkozó sugárzás jllmz!k között fnnáll, hogy +r+d=1 133
5 Átlátsztln tstk stén d=, így =1-r. (A h!sugárzásr vontkozón lgtöbb szlárd tst gykorltlg átlátsztln.) Azt tstt, mlynk sugárzás jllmz!r fnnáll, hogy = ==1 bszolút fkt tstnk nvzzük, és rá vontkozó mnnységkt "" ndx fltünttésévl jlöljük továbbkbn ábr Flszín közl ürg, mnt "fkt" tst Az =1, zz z bszolút fkt tst stébn mnd vsszvrt, mnd z átrszttt hányd sugárzásnk null. gy közlít! fzk mgvlósítását z lyn vslkdés" "tstnk" ábr muttj. Az átlátsztln flú ürgb!l résn bjutó sugárzásnk lhnygolhtó hányd távozht csk és soroztos vsszvr!dés és részlgs lnyl!dés htásár nrgáj tljs gészébn lnyl!dk, így ks nyílású ürg gykorltlg "fkt" tst A H#SUGÁRZÁS ALAPTÖRVÉNY A fkt tst gységny térszögr vontkozó, ttsz!lgs ránybn kbocsátott sugárzás ntnztásánk (, ) mghtározásár vontkozó összfüggést PLANCK 191-bn állított fl, hol 2, 5 ( ) " 2hc = hc Tk [W/m3 sr], (12.12) c z lktromágnss sugárzás trjdés sbsség = m/s, h= Js, PLANCK állndó, k= J/K, BOLTZMANN állndó, T z bszolút h!mérséklt K-bn, sugárzás hullámhossz m-bn. PLANCK fkt tst h!mérsékltt!l függ! sugárzás görbé lpján, l!ször mprkus úton jutott l mgfll! összfüggéshz. Kés!bb, z tomokt olyn ω frkvncán rzg! hrmonkus oszcllátoroknk kzlv, mlyk gyszrr csk hω, (zz végs mnnység") nrgát vhtnk fl, sugárzásr vontkozó összfüggésénk lvztését s mgdt, és zt tknthtjük z ls!, hlysn lvzttt kvntummchnk összfüggésnk. A PLANCK törvény szrnt fkt tst dffúz sugárzó, és kbocsátott nrg ngymértékbn függ tst bszolút h!mérsékltét!l. A tljs féltérb kbocsátott sugárzás r!sségt (ntnztást) h!mérséklt és hullámhossz függvényébn ábr muttj. " 134
6 A görbék mxmum hlynk (z hullámhossz, hol z dott h!mérséklt" fkt tst mxmáls ntnztású sugárzást produkálj) h!mérsékltt!l vló függését, WN fél ltolódás törvény írj l, mx T =2.9 mmk, zz mnél mgsbb h!mérséklt" tst, mxmáls nrgájú sugárzás z gyr rövdbb hullámhosszúság flé tolódk l., 1-9 [W /m 3 ] m T=2.9 [m m K] 18K 16K 15K 14K 13K 12K 1K 8K hulámhossz [µm] ábr A fkt tst spktrum A (12.12) ntgrálásávl ( ábr görbé ltt trültk mghtározásávl), gy dott h!mérséklt" fkt tstnk tljs spktrumr (= ) vontkozttott flült, nrg s"r"ségét htározzuk mg: = d T 4 π =, σ. (12.13) Az (12.13) összfüggés STFAN-BOLTZMANN törvény, σ = W/(m 2 K 4 ) pdg STFAN-BOLTZMANN állndó. Vlmnny tst h!sugárzását z bszolút fkt tstéhz vszonyítjuk, így: ε =. (12.14), Az (12.14) összfüggéssl dfnált tényz!t (rltív) msszóképsségnk vgy fktség foknk nvzzük. A msszós tényz! dffúz sugárzók stébn rány függtln: ε = ε =. (12.15), 135
7 Azokt tstkt mlyk msszós tényz!j nm függtln -tól, színs tstnk nvzzük. Amnnybn msszós tényz! hullámhossztól s függtln, h!sugárzás szmpontjából szürk tstr!l vn szó és kkor: 136 ε = ε = ε =. (12.16) A szürk tstk thát olyn dffúz sugárzók, mlyk mndn hullámhosszúságon fkt tst nrgájánk állndó hánydát sugározzák k, így szürk tstk áltl ksugárzott nrg STFAN-BOLTZMANN törvény lpján: 4 = ε σ T. (12.17) A továbbkbn csk szürk tstkkl fogllkozunk. Az msszós és bszorpcós képsség között kpcsoltot KRCHHOFF törvény írj l, mly szrnt tstknk z dott rányú és hullámhosszúságú sugárzásr vontkozó lnylés (bszorpcós) és kbocsátás (msszós) képsség zonos érték. bb!l törvényszr"ségb!l kövtkzk, hogy fkt tstr ε = = 1, m zt jlnt, hogy fkt tst nm csk mxmáls lnyl! képsség" tst, hnm mxmáls nrg kbocsátó s. Mvl z utóbbhoz vszonyítjuk több tst sugárzását, z msszós tényz!r fnnáll, hogy ε < Két szlárd tst között sugárzásos h!árm számítás A szlárd tstk ngy részét h!sugárzás trtományábn flült sugárzónk tknthtjük, míg gázok és folydékok térfogt sugárzók és áltlábn spktrumuk sm folytonos. z utóbb közgk sugárzásávl nm fogllkozunk. A h!sugárzás szmpontjából környzt lvg!t átlátszónk tkntjük és sugárzás trjdését gomtr optk törvényvl írhtjuk l. Bvztv z un. ffktív (látszólgos) sugárzás sgédfoglmt: z 1 tstt!l 2 tst flé rányuló összs sugárzott árms"r"ségt jlnt, zz sját ( ) és vsszvrt sugárzás összgét. Nm átlátszó tstknél r=1-, így: bb!l z 1ff és 2ff kfjzv: " ff " " 2ff = + (" ), 2ff 2 2 " ff = + (" ). " ff 2ff = = " " 2 + (" ) + " 2 " " + (" ) + " 2 " 2,. (12.18) (12.19) A szürk tstk stébn KRCHHOFF törvény szrnt z átlgos msszós tényz! s gynl! z átlgos bszorpcós tényz!vl, 1=ε1 és 2=ε2 vlmnt STFAN-BOLTZMANN törvény lpján tljs hullámhossz trtománybn ksugárzott nrg: " = ε" σ T" 4 vlm nt 2 = ε 2σ T2 4.
A hőmérsékleti sugárzás
 A hőmérséklt sugárzás (Dr. Parpás Béla lőadása alapján ljgyzték a Mskolc gytm harmadévs nformatkus hallgató) Alapjlnségk Mndnnap tapasztalat, hogy a mlgíttt tstk hősugárzást (nfravörös sugárzást) bocsátanak
A hőmérséklt sugárzás (Dr. Parpás Béla lőadása alapján ljgyzték a Mskolc gytm harmadévs nformatkus hallgató) Alapjlnségk Mndnnap tapasztalat, hogy a mlgíttt tstk hősugárzást (nfravörös sugárzást) bocsátanak
FIZIKAI KÉMIA III FÉNY. szerda 10:00-11:30 Általános és Fizikai Kémiai Tanszék, szemináriumi terem. fehér fénynyaláb
 FIZIKAI KÉMIA III szrda 10:00-11:30 Általános és Fizikai Kémiai Tanszék, szmináriumi trm FÉNY fhér fénynyaláb FÉNY fhér fénynyaláb prizma színs fénynyalábok fény = hullám (mint a víz flszínén látható hullámok)
FIZIKAI KÉMIA III szrda 10:00-11:30 Általános és Fizikai Kémiai Tanszék, szmináriumi trm FÉNY fhér fénynyaláb FÉNY fhér fénynyaláb prizma színs fénynyalábok fény = hullám (mint a víz flszínén látható hullámok)
Név:... osztály:... Matematika záróvizsga 2010.
 Mtmtik záróvizsg 00. Név:... osztály:.... Az lái rjzon gy thrutó rktrénk vázltos rjz láthtó. Az árán olvshtó számtok, rkoásr ténylgsn flhsználhtó térfogtr vontkoznk. Mkkor thrutó hsznos rktrénk térfogt?
Mtmtik záróvizsg 00. Név:... osztály:.... Az lái rjzon gy thrutó rktrénk vázltos rjz láthtó. Az árán olvshtó számtok, rkoásr ténylgsn flhsználhtó térfogtr vontkoznk. Mkkor thrutó hsznos rktrénk térfogt?
7. Határozott integrál
 7. Htározott intgrál 7.. Számolj ki z lái intgrálokt! 7... d 7... d 7... d 7... d 7... d 7... d 7..7. d 7... d 7..9. d 7... d 7... d 7... d 7... d 7... d 7... d 7... d 7..7. d 7... d 7..9. d 7... d 7...
7. Htározott intgrál 7.. Számolj ki z lái intgrálokt! 7... d 7... d 7... d 7... d 7... d 7... d 7..7. d 7... d 7..9. d 7... d 7... d 7... d 7... d 7... d 7... d 7... d 7..7. d 7... d 7..9. d 7... d 7...
KORLÁTOS. mateking.hu BINOMIÁLIS ELOSZLÁS. Egy úton hetente átlag 3 balesetes nap van. Mi a valószínűsége, hogy egy adott héten 2 balesetes nap van?
 NEVEZETES DISZKRÉT ÉS FOLYTONOS OK HIPERGEO. BINOM. POISSON VAN ITT EGY FELADAT ISMERTHOGY MENNYI AZ ÖSSZES ELEM ÉS AZ ÖSSZES SELEJT VAGYIS N K ILLETVE n k. CSAK VALAMI %-OS IZÉ ISMERT A VÁRHATÓ AZ ÁTLAG
NEVEZETES DISZKRÉT ÉS FOLYTONOS OK HIPERGEO. BINOM. POISSON VAN ITT EGY FELADAT ISMERTHOGY MENNYI AZ ÖSSZES ELEM ÉS AZ ÖSSZES SELEJT VAGYIS N K ILLETVE n k. CSAK VALAMI %-OS IZÉ ISMERT A VÁRHATÓ AZ ÁTLAG
Az integrálszámítás néhány alkalmazása
 Az integrálszámítás néhány lklmzás (szerkesztés ltt) Dr Toledo Rodolfo 4 november 4 Trtlomjegyzék Két függvények áltl htárolt terület Forgástestek térfogt és felszíne 5 3 Ívhosszszámítás 7 4 Feldtok 8
Az integrálszámítás néhány lklmzás (szerkesztés ltt) Dr Toledo Rodolfo 4 november 4 Trtlomjegyzék Két függvények áltl htárolt terület Forgástestek térfogt és felszíne 5 3 Ívhosszszámítás 7 4 Feldtok 8
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 8. évfolym AMt2 fltlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg. Minn próálkozást,
8. évfolym AMt2 fltlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg. Minn próálkozást,
Bevezetés a fúziós plazmafizikába 7.
 Bvztés fúzós plzmfzkáb 7. Részcskék ütközés plzmákbn, trnszport r. Grgő Pokol BME NTI Bvztés fúzós plzmfzkáb 018. októbr 16. Progrm átum Elődó Cím Szptmbr 4Pokol Szptmbr 11Pokol Szptmbr 18Pokol Szptmbr
Bvztés fúzós plzmfzkáb 7. Részcskék ütközés plzmákbn, trnszport r. Grgő Pokol BME NTI Bvztés fúzós plzmfzkáb 018. októbr 16. Progrm átum Elődó Cím Szptmbr 4Pokol Szptmbr 11Pokol Szptmbr 18Pokol Szptmbr
3. MECHANIKA STATIKA GYAKORLAT Kidolgozta: Triesz Péter egy. ts. Három erő egyensúlya
 SZÉHENYI ISTVÁN EGYETEM GÉPSZERKEZETTN ÉS MEHNIK TNSZÉK 3 MEHNIK STTIK GYKORLT Kdolgozt: Tsz Pét gy ts Háom ő gynsúly 3 Péld: dott gy mlőszkzt mét és thlés: m b 5 m c 5 m 0 kn ldt: y c Htáozz mg z és támsztóőkt
SZÉHENYI ISTVÁN EGYETEM GÉPSZERKEZETTN ÉS MEHNIK TNSZÉK 3 MEHNIK STTIK GYKORLT Kdolgozt: Tsz Pét gy ts Háom ő gynsúly 3 Péld: dott gy mlőszkzt mét és thlés: m b 5 m c 5 m 0 kn ldt: y c Htáozz mg z és támsztóőkt
1. Testmodellezés. 1.1. Drótvázmodell. Testmodellezés 1
 Tstmodllzés 1 1. Tstmodllzés Egy objktum modlljén az objktumot rprzntáló adatrndszrt értjük. Egy tstmodll gy digitális rprzntációja gy létz vagy lképzlt objktumnak. trvzés, a modllzés során mgadjuk a objktum
Tstmodllzés 1 1. Tstmodllzés Egy objktum modlljén az objktumot rprzntáló adatrndszrt értjük. Egy tstmodll gy digitális rprzntációja gy létz vagy lképzlt objktumnak. trvzés, a modllzés során mgadjuk a objktum
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 2009. jnuár 29. MATEMATIKA FELADATLAP 8. évfolymosok számár 2009. jnuár 29. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg. Minn
2009. jnuár 29. MATEMATIKA FELADATLAP 8. évfolymosok számár 2009. jnuár 29. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg. Minn
Spektroszkópiai Ellipszometria (SE)
 Fodo Bálnt Ptk Pét Sktozkó llzomt (S) Lbotóum gyzt Mgy Tudományo Akdém Tmézttudomány K Műzk Fzk é Anygtudomány Kuttóntézt Fotonk oztály Budt . lmélt özfoglló.. Az llzomt fzká A fény olzácó állot két különböző
Fodo Bálnt Ptk Pét Sktozkó llzomt (S) Lbotóum gyzt Mgy Tudományo Akdém Tmézttudomány K Műzk Fzk é Anygtudomány Kuttóntézt Fotonk oztály Budt . lmélt özfoglló.. Az llzomt fzká A fény olzácó állot két különböző
Név:... osztály:... Matematika záróvizsga 2008. 1. Tedd ki a megfelelő relációjelet! ; 4
 Mtmtik záróvizsg Név:... osztály:... 1. T ki mgllő rláiójlt! 15 4 675 ; 180 115, 151, ; 31% 10 3 1000 ; 4 5 5 + ; 8. Mlyik átváltás hiás? A hlyskt jlöl pipávl, hiás átváltásoknál húz át z gynlőségjlt!.
Mtmtik záróvizsg Név:... osztály:... 1. T ki mgllő rláiójlt! 15 4 675 ; 180 115, 151, ; 31% 10 3 1000 ; 4 5 5 + ; 8. Mlyik átváltás hiás? A hlyskt jlöl pipávl, hiás átváltásoknál húz át z gynlőségjlt!.
MATEMATIKA FELADATLAP a 6. évfolyamosok számára
 6. évfolym Mt1 fltlp MATEMATIKA FELADATLAP 6. évfolymosok számár 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg. Minn próálkozást,
6. évfolym Mt1 fltlp MATEMATIKA FELADATLAP 6. évfolymosok számár 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg. Minn próálkozást,
Dugattyús szivattyú általános beépítési körülményei (szívó- és nyomóoldali légüsttel) Vegyipari- és áramlástechnikai gépek. 2.
 gypar és áramlástchnka gépk.. lőaás Készíttt: r. ára Sánor Buapst Műszak és Gazaságtuomány Egytm Gépészmérnök Kar Hronamka nszrk Tanszék 1111, Buapst, Műgytm rkp. 3. D ép. 334. Tl: 463-16-80 Fax: 463-30-91
gypar és áramlástchnka gépk.. lőaás Készíttt: r. ára Sánor Buapst Műszak és Gazaságtuomány Egytm Gépészmérnök Kar Hronamka nszrk Tanszék 1111, Buapst, Műgytm rkp. 3. D ép. 334. Tl: 463-16-80 Fax: 463-30-91
Tehetetlenségi nyomatékok
 Tehetetlenségi nyomtékok 1 Htározzuk meg z m tömegű l hosszúságú homogén rúd tehetetlenségi nyomtékát rúd trtóegyenesét metsző tetszőleges egyenesre vontkozón, h rúd és z egyenes hjlásszöge α, rúd középpontjánk
Tehetetlenségi nyomtékok 1 Htározzuk meg z m tömegű l hosszúságú homogén rúd tehetetlenségi nyomtékát rúd trtóegyenesét metsző tetszőleges egyenesre vontkozón, h rúd és z egyenes hjlásszöge α, rúd középpontjánk
2. A geometria alapfogalmai A geometria alapfogalmai: pont, vonal, egyenes, sík, tér.
 1. Mi z lpfoglom? Alpfoglom: olyn foglom, mit ismrtnk fogdunk l, nm tudunk más foglmk sgítségévl mghtározni, dfiniálni, lgflj szmléltsn körülírjuk. Mindn tudomány ilyn lpfoglmkr épül fl. (Egy foglmt úgy
1. Mi z lpfoglom? Alpfoglom: olyn foglom, mit ismrtnk fogdunk l, nm tudunk más foglmk sgítségévl mghtározni, dfiniálni, lgflj szmléltsn körülírjuk. Mindn tudomány ilyn lpfoglmkr épül fl. (Egy foglmt úgy
Egy látószög - feladat
 Ehhez tekintsük z 1. ábrát is! Egy látószög - feldt 1. ábr Az A pont körül kering C pont, egy r sugrú körön. A rögzített A és B pontok egymástól távolság vnnk. Az = CAB szöget folymtosn mérjük. Keressük
Ehhez tekintsük z 1. ábrát is! Egy látószög - feldt 1. ábr Az A pont körül kering C pont, egy r sugrú körön. A rögzített A és B pontok egymástól távolság vnnk. Az = CAB szöget folymtosn mérjük. Keressük
Határozzuk meg, hogy a következő függvényeknek van-e és hol zérushelye, továbbá helyi szélsőértéke és abszolút szélsőértéke (
 9 4 FÜGGVÉNYVIZSGÁLAT Htározzuk meg, hogy következő függvényeknek vn-e és hol zérushelye, továbbá helyi szélsőértéke és bszolút szélsőértéke (41-41): 41 f: f, R 4 f: 4 f: f 5, R f 5 44 f: f, 1, 1 1, R
9 4 FÜGGVÉNYVIZSGÁLAT Htározzuk meg, hogy következő függvényeknek vn-e és hol zérushelye, továbbá helyi szélsőértéke és bszolút szélsőértéke (41-41): 41 f: f, R 4 f: 4 f: f 5, R f 5 44 f: f, 1, 1 1, R
Szervomotor sebességszabályozása
 Srvomotor sbsségsabályoása. A gyaorlat célja Egynáramú srvomotor sbsségsabályoásána trvés. A motorsabályoás programváána flépítés. A sbsség rányítás algortms mgvalósítása valós dbn. 2. Elmélt bvt A motor
Srvomotor sbsségsabályoása. A gyaorlat célja Egynáramú srvomotor sbsségsabályoásána trvés. A motorsabályoás programváána flépítés. A sbsség rányítás algortms mgvalósítása valós dbn. 2. Elmélt bvt A motor
KIRCHHOFF törvény : : anyagi minőségtől független univerzális függvény.
 A sugárzás kvantumos trmészt A őmérséklti sugárzás Bvztés A kövtkzőkbn azokat a századorduló táján kutatott őbb jlnségkt tkintjük át, amlyk mgértés a klasszikus izika alapján nm volt ltségs. E jlnségk
A sugárzás kvantumos trmészt A őmérséklti sugárzás Bvztés A kövtkzőkbn azokat a századorduló táján kutatott őbb jlnségkt tkintjük át, amlyk mgértés a klasszikus izika alapján nm volt ltségs. E jlnségk
Ellenállás mérés hídmódszerrel
 1. Lbortóriumi gykorlt Ellenállás mérés hídmódszerrel 1. A gykorlt célkitűzései A Whestone-híd felépítésének tnulmányozás, ellenállások mérése 10-10 5 trtománybn, híd érzékenységének meghtározás, vlmint
1. Lbortóriumi gykorlt Ellenállás mérés hídmódszerrel 1. A gykorlt célkitűzései A Whestone-híd felépítésének tnulmányozás, ellenállások mérése 10-10 5 trtománybn, híd érzékenységének meghtározás, vlmint
Rácsrezgések.
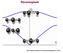 ácsrzgésk http://physics-imtis.cm/physics/glish/ph_txt.htm ácsrzgésk gitális hllám rúb Nwt II F x x F x V t F F x A x V x x x x x x A hllámszám értlmzési trtmáy végs mért prióiks htárfltétl Br-Kármá t
ácsrzgésk http://physics-imtis.cm/physics/glish/ph_txt.htm ácsrzgésk gitális hllám rúb Nwt II F x x F x V t F F x A x V x x x x x x A hllámszám értlmzési trtmáy végs mért prióiks htárfltétl Br-Kármá t
Egy szép és jó ábra csodákra képes. Az alábbi 1. ábrát [ 1 ] - ben találtuk; talán már máskor is hivatkoztunk rá.
![Egy szép és jó ábra csodákra képes. Az alábbi 1. ábrát [ 1 ] - ben találtuk; talán már máskor is hivatkoztunk rá. Egy szép és jó ábra csodákra képes. Az alábbi 1. ábrát [ 1 ] - ben találtuk; talán már máskor is hivatkoztunk rá.](/thumbs/73/69556711.jpg) Egy szép és jó ábr csodákr képes Az lábbi. ábrát [ ] - ben tláltuk; tlán már máskor is hivtkoztunk rá.. ábr Az különlegessége, hogy vlki nem volt rest megcsinál(tt)ni, még h sok is volt vele munk. Ennek
Egy szép és jó ábr csodákr képes Az lábbi. ábrát [ ] - ben tláltuk; tlán már máskor is hivtkoztunk rá.. ábr Az különlegessége, hogy vlki nem volt rest megcsinál(tt)ni, még h sok is volt vele munk. Ennek
Testmodellezés ábra. Gúla Ekkor a csúcspontok koordinátáit egy V csúcspont (vertex) listában tárolhatjuk.
 Tstmodllzés 1 1. Tstmodllzés Egy objktum modlljén az objktumot rprzntáló adatrndszrt értjük. Egy tstmodll gy digitális rprzntációja gy létz vagy lképzlt objktumnak. A trvzés, a modllzés során mgadjuk a
Tstmodllzés 1 1. Tstmodllzés Egy objktum modlljén az objktumot rprzntáló adatrndszrt értjük. Egy tstmodll gy digitális rprzntációja gy létz vagy lképzlt objktumnak. A trvzés, a modllzés során mgadjuk a
Matematika záróvizsga Név:... osztály: ; 5 + 9
 006. Név:... osztály:.... T ki mgllő rláiójlt! 7 00 7 4, 0% 4 8 - + 9 8 - : 9 6. Ír mérőszámokt vgy mértékgységkt!..... 0m h,8 mm kg 0,0 m km m m 400 l. π. Végz l számításokt!.) : 4.), 8 : 0, +, 0 7, 4
006. Név:... osztály:.... T ki mgllő rláiójlt! 7 00 7 4, 0% 4 8 - + 9 8 - : 9 6. Ír mérőszámokt vgy mértékgységkt!..... 0m h,8 mm kg 0,0 m km m m 400 l. π. Végz l számításokt!.) : 4.), 8 : 0, +, 0 7, 4
KORLÁTOS. mateking.hu BINOMIÁLIS ELOSZLÁS. Egy úton hetente átlag 3 balesetes nap van. Mi a valószínűsége, hogy egy adott héten 2 balesetes nap van?
 NEVEZETES DISZKRÉT ÉS FOLYTONOS OK HIPERGEO. BINOM. POISSON VAN ITT EGY FELADAT ISMERTHOGY MENNYI AZ ÖSSZES ELEM ÉS AZ ÖSSZES SELEJT VAGYIS N K ILLETVE n k. CSAK VALAMI %-OS IZÉ ISMERT A VÁRHATÓ AZ ÁTLAG
NEVEZETES DISZKRÉT ÉS FOLYTONOS OK HIPERGEO. BINOM. POISSON VAN ITT EGY FELADAT ISMERTHOGY MENNYI AZ ÖSSZES ELEM ÉS AZ ÖSSZES SELEJT VAGYIS N K ILLETVE n k. CSAK VALAMI %-OS IZÉ ISMERT A VÁRHATÓ AZ ÁTLAG
Vektorok. Vektoron irányított szakaszt értünk.
 Vektorok Vektoron irányított szkszt értünk A definíció értelmében tehát vektort kkor ismerjük, h ismerjük hosszát és z irányát A vektort kövér kis betűkkel (, b stb) jelöljük, megkülönböztetve z, b számoktól,
Vektorok Vektoron irányított szkszt értünk A definíció értelmében tehát vektort kkor ismerjük, h ismerjük hosszát és z irányát A vektort kövér kis betűkkel (, b stb) jelöljük, megkülönböztetve z, b számoktól,
Differenciálgeometria feladatok
 Differenciálgeometri feldtok 1. sorozt 1. Egy sugrú kör csúszás nélkül gördül egy egyenes mentén. A kör egy rögzített kerületi pontj áltl leírt pályát cikloisnk nevezzük. () Írjuk fel ciklois egy c: R
Differenciálgeometri feldtok 1. sorozt 1. Egy sugrú kör csúszás nélkül gördül egy egyenes mentén. A kör egy rögzített kerületi pontj áltl leírt pályát cikloisnk nevezzük. () Írjuk fel ciklois egy c: R
Helyszükséglet összehasonlítás
 Hlyszükséglt összhsonlítás Hgyományos riálvntilátor A VAR rnszr összhsonlítás Hlios RADAX VAR Systm A VAR rnszr z lsony nyomás növkésű xiálvntilátorok és riál vntilátorok közötti szükségltkt légíti ki.
Hlyszükséglt összhsonlítás Hgyományos riálvntilátor A VAR rnszr összhsonlítás Hlios RADAX VAR Systm A VAR rnszr z lsony nyomás növkésű xiálvntilátorok és riál vntilátorok közötti szükségltkt légíti ki.
1. Melyik átváltás hibás? A helyeseket jelöld pipával, a hibás átváltásoknál húzd át az egyenlőségjelet!
 Mtmtik záróvizsg 011. Név:... osztály:... 1. Mlyik átváltás hiás? A hlyskt jlöl pipávl, hiás átváltásoknál húz át z gynlőségjlt!. 0,578 t = 578 kg;. 100 m g. = 0,1 h; 0 pr = 0,5 ór;.. h. 3,05 kg = 350
Mtmtik záróvizsg 011. Név:... osztály:... 1. Mlyik átváltás hiás? A hlyskt jlöl pipávl, hiás átváltásoknál húz át z gynlőségjlt!. 0,578 t = 578 kg;. 100 m g. = 0,1 h; 0 pr = 0,5 ór;.. h. 3,05 kg = 350
Széchenyi István Egyetem. Alkalmazott Mechanika Tanszék
 Széchnyi István Egytm Alkalmazott Mchanika Tanszék Végslm analízis Elmélti kérdésk gytmi mstrképzésbn (MSc) résztvv járm mérnöki, mchatronikai mérnök és logisztikai mérnök szakos hallgatók számára 0. októbr
Széchnyi István Egytm Alkalmazott Mchanika Tanszék Végslm analízis Elmélti kérdésk gytmi mstrképzésbn (MSc) résztvv járm mérnöki, mchatronikai mérnök és logisztikai mérnök szakos hallgatók számára 0. októbr
Budapest Főváros VIII. kerület Józsefvárosi Önkormányzat Képviselő-testületének 46/2009.(XII.21.) sz. önkormányzati rendelete
 A khrdtés módja: kfüggsztés A khrdtés napja: 2009. dcmbr 21. dr. Xantus Judt jgyző Budapst Főváros VIII. krült Józsfváros Önkormányzat Képvslő-tstülténk 46/2009.(XII.21.) sz. önkormányzat rndlt a Budapst
A khrdtés módja: kfüggsztés A khrdtés napja: 2009. dcmbr 21. dr. Xantus Judt jgyző Budapst Főváros VIII. krült Józsfváros Önkormányzat Képvslő-tstülténk 46/2009.(XII.21.) sz. önkormányzat rndlt a Budapst
A fotometria alapjai
 A fotomtria alapjai Mdicor Training Cntr for Maintnanc of Mdical Equipmnt Budapst, 198 Írta: Porubszky Tamás okl. fizikus Lktorálta: Bátki László és Fillingr László Szrkszttt: Török Tibor 1. ÁLTALÁNOS
A fotomtria alapjai Mdicor Training Cntr for Maintnanc of Mdical Equipmnt Budapst, 198 Írta: Porubszky Tamás okl. fizikus Lktorálta: Bátki László és Fillingr László Szrkszttt: Török Tibor 1. ÁLTALÁNOS
Sugárzásos hőátadás. Teljes hősugárzás = elnyelt hő + visszavert hő + a testen áthaladó hő Q Q Q Q A + R + D = 1
 Suárzásos hőátadás misszióképessé:, W/m. eljes hősuárzás elnyelt hő visszavert hő a testen áthaladó hő R D R D R D a test elnyelő képessée (aszorció), R a test a visszaverő-képessée (reflexió), D a test
Suárzásos hőátadás misszióképessé:, W/m. eljes hősuárzás elnyelt hő visszavert hő a testen áthaladó hő R D R D R D a test elnyelő képessée (aszorció), R a test a visszaverő-képessée (reflexió), D a test
3. KISFESZÜLTSÉGŰ VEZETÉKEK MÉRETEZÉSE
 Vamos műk KSFESZÜLTSÉGŰ VEZETÉKEK MÉRETEZÉSE ksfszütségű áózatok fadata a fogyasztók amos nrgáa aó átása ztékk fontos fadatának átásában fontos szrp an az nrgaszogátatás mnőségét, bztonságát és gazdaságosságát
Vamos műk KSFESZÜLTSÉGŰ VEZETÉKEK MÉRETEZÉSE ksfszütségű áózatok fadata a fogyasztók amos nrgáa aó átása ztékk fontos fadatának átásában fontos szrp an az nrgaszogátatás mnőségét, bztonságát és gazdaságosságát
Alapfogalmak folytatás
 Alapfogalmak folytatás Színek Szem Számítási eljárások Fényforrások 2014.10.14. OMKTI 1 Ismétlés Alapok: Mi a fény? A gyakorlati világítás technika alap mennyisége? Φ K m 0 Φ e ( ) V ( ) d; lm Fényáram,
Alapfogalmak folytatás Színek Szem Számítási eljárások Fényforrások 2014.10.14. OMKTI 1 Ismétlés Alapok: Mi a fény? A gyakorlati világítás technika alap mennyisége? Φ K m 0 Φ e ( ) V ( ) d; lm Fényáram,
Mérıkapcsolások 5. fejezet /Elmélet & Képletgyőjtemény/
 . Kompnzált osztó: Mérıkpcsolások 5. fjzt /Elmélt & Képltgyőjtmény/ C b C. Hídkpcsolás: τ b τ C C 4 t Alpértlmztt stbn: 4, íd mnti fzsültség gynlíttt állpotbn 0V. I.. st Egy llnállás változik d 4 t d (
. Kompnzált osztó: Mérıkpcsolások 5. fjzt /Elmélt & Képltgyőjtmény/ C b C. Hídkpcsolás: τ b τ C C 4 t Alpértlmztt stbn: 4, íd mnti fzsültség gynlíttt állpotbn 0V. I.. st Egy llnállás változik d 4 t d (
Ha a csővezeték falán hőt nem viszünk át és nem végzünk a közegen munkát, akkor az ideális gáz h ö összentalpiája és amiatt T
 6 Állndósult gázármlás állndó krsztmtsztű csőn Egy hosszú csőztékn ármló gáz nyomássését nm csk fli csúszttófszültség szj mg, hnm csőflon átdott hő mnnyiség is Hő flétl szmontól két ltő stt tárgylunk ktkző
6 Állndósult gázármlás állndó krsztmtsztű csőn Egy hosszú csőztékn ármló gáz nyomássését nm csk fli csúszttófszültség szj mg, hnm csőflon átdott hő mnnyiség is Hő flétl szmontól két ltő stt tárgylunk ktkző
MATEMATIKA FELADATLAP a 6. évfolyamosok számára
 6. évfolym Mt1 fltlp MATEMATIKA FELADATLAP 6. évfolymosok számár 2018. jnuár 20. 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg.
6. évfolym Mt1 fltlp MATEMATIKA FELADATLAP 6. évfolymosok számár 2018. jnuár 20. 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg.
S x, SZELEPEMEL MECHANIZMUS Témakör: Kinematika, merev test, síkmozgás, relatív
 ZELEPEMEL MECHNIZMU Témkör: Kinmtik, mr tst, síkmozgás, rltí ázolt szlpml mchnizmus sugrú, cntricitású cntrtárcsáj állndó szögsbsséggl forog. 1. jzoljuk mg szlp foronomii görbéit. Vgis z t, t és t függénkt..
ZELEPEMEL MECHNIZMU Témkör: Kinmtik, mr tst, síkmozgás, rltí ázolt szlpml mchnizmus sugrú, cntricitású cntrtárcsáj állndó szögsbsséggl forog. 1. jzoljuk mg szlp foronomii görbéit. Vgis z t, t és t függénkt..
MATEMATIKA FELADATLAP a 6. évfolyamosok számára
 6. évfolym Mt2 fltlp MATEMATIKA FELADATLAP 6. évfolymosok számár 2018. jnuár 25. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg.
6. évfolym Mt2 fltlp MATEMATIKA FELADATLAP 6. évfolymosok számár 2018. jnuár 25. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg.
REÁLIS GÁZOK ÁLLAPOTEGYENLETEI FENOMENOLOGIKUS KÖZELÍTÉS
 REÁLIS GÁZOK ÁLLAPOEGYENLEEI FENOMENOLOGIKUS KÖZELÍÉS Száos odell gondoljunk potenciálo! F eltérés z ideális gáz odelljétl: éret és kölcsönhtás Moszkópikus következény: száos állpotegyenlet (ld. RM-jegyzet
REÁLIS GÁZOK ÁLLAPOEGYENLEEI FENOMENOLOGIKUS KÖZELÍÉS Száos odell gondoljunk potenciálo! F eltérés z ideális gáz odelljétl: éret és kölcsönhtás Moszkópikus következény: száos állpotegyenlet (ld. RM-jegyzet
ÚJ FELADATSOR! 2006. FEBRUÁR 2. ANYANYELVI FELADATLAP a 8. évfolyamosok számára. 2006. február 2. 14:00 óra ÚJ FELADATSOR! NÉV:
 ÚJ FELADATSOR! 2006. FEBRUÁR 2. ANYANYELVI FELADATLAP 8. évfolymosok számár 2006. fruár 2. 14:00 ór ÚJ FELADATSOR! NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A fltokt ttszés szrinti sorrnn olhto mg. Ügylj mgfllő iőosztásr
ÚJ FELADATSOR! 2006. FEBRUÁR 2. ANYANYELVI FELADATLAP 8. évfolymosok számár 2006. fruár 2. 14:00 ór ÚJ FELADATSOR! NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A fltokt ttszés szrinti sorrnn olhto mg. Ügylj mgfllő iőosztásr
A röntgendiagnosztika alapjai
 A röngtgndiagnosztika alapja: a sugárzás lnylődés A röntgndiagnosztika alapjai A foton kölcsönhatásának lhtőségi: Compton-szórás Comptonszórás lnylődés fotoffktusban fotoffktus nincs kölcsönhatás Áthaladt
A röngtgndiagnosztika alapja: a sugárzás lnylődés A röntgndiagnosztika alapjai A foton kölcsönhatásának lhtőségi: Compton-szórás Comptonszórás lnylődés fotoffktusban fotoffktus nincs kölcsönhatás Áthaladt
1. ábra A rádiócsatorna E négypólus csillapítása a szakaszcsillapítás, melynek definíciója a következő: (1)
 Az antnna Adó- és vvőantnna Az antnna lktomágnss hullámok kisugázásáa és vétlé szolgáló szköz. A ádióndszkbn btöltött szp alapján az antnna a tápvonal és a szabad té közötti tanszfomáto, mly a tápvonalon
Az antnna Adó- és vvőantnna Az antnna lktomágnss hullámok kisugázásáa és vétlé szolgáló szköz. A ádióndszkbn btöltött szp alapján az antnna a tápvonal és a szabad té közötti tanszfomáto, mly a tápvonalon
Középiskolás leszek! matematika. 13. feladatsor 1. 2. 3. 4. 5. 6.
 Középiskolás leszek! mtemtik Melyik számot jelentheti A h tudjuk hogy I felennyi mint S S egyenlõ K és O összegével K egyenlõ O és L különbségével O háromszoros L-nek L negyede 64-nek I + S + K + O + L
Középiskolás leszek! mtemtik Melyik számot jelentheti A h tudjuk hogy I felennyi mint S S egyenlõ K és O összegével K egyenlõ O és L különbségével O háromszoros L-nek L negyede 64-nek I + S + K + O + L
MATEMATIKA FELADATLAP a 6. évfolyamosok számára
 6. évfolym Mt2 fltlp MATEMATIKA FELADATLAP 6. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg. Minn próálkozást,
6. évfolym Mt2 fltlp MATEMATIKA FELADATLAP 6. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg. Minn próálkozást,
A kötéstávolság éppen R, tehát:
 Forgás és rzgés spktroszkópa:. Határozzuk mg a kövtkző részcskék rdukált tömgét: H H, H 35 Cl, H 37 Cl, H 35 Cl, H 7 I Egy m és m tömgű atomból álló kétatomos molkula rdukált tömg () dfnícó szrnt: mm vagy
Forgás és rzgés spktroszkópa:. Határozzuk mg a kövtkző részcskék rdukált tömgét: H H, H 35 Cl, H 37 Cl, H 35 Cl, H 7 I Egy m és m tömgű atomból álló kétatomos molkula rdukált tömg () dfnícó szrnt: mm vagy
Széchenyi István Egyetem. Alkalmazott Mechanika Tanszék
 Széchnyi István Egytm Alkalmazott Mchanika Tanszék Végslm analízis Elmélti kérdésk gytmi mstrképzésbn MSc) résztvv járm mérnöki, mchatronikai mérnök és logisztikai mérnök szakos hallgatók számára. Mit
Széchnyi István Egytm Alkalmazott Mchanika Tanszék Végslm analízis Elmélti kérdésk gytmi mstrképzésbn MSc) résztvv járm mérnöki, mchatronikai mérnök és logisztikai mérnök szakos hallgatók számára. Mit
FELVÉTELI FELADATOK 4. osztályosok számára M 1 feladatlap
 2004. jnuár-fruár FELVÉTELI FELADATOK 4. osztályosok számár M 1 fltlp Név:... Szültési év: hó: np: A fltokt ttszés szrinti sorrnn olhto mg. Minn próálkozást fltlpon végzz! Mllékszámításokr z utolsó, ürs
2004. jnuár-fruár FELVÉTELI FELADATOK 4. osztályosok számár M 1 fltlp Név:... Szültési év: hó: np: A fltokt ttszés szrinti sorrnn olhto mg. Minn próálkozást fltlpon végzz! Mllékszámításokr z utolsó, ürs
Meghatározás Pontszerű test. Olyan test, melynek jellemző méretei kicsik a pálya méreteihez képest. A helyvektor megváltozása: r1,2 r(t 2) r(t 1)
 I. Mchanka Dfnált fogalom Mghatározás Tömgpont Pontszrű tst. Olyan tst, mlynk jllmző mért kcsk a pálya mérthz képst. Elmozdulás hlyvktor mgváltozása: r1, r(t ) r(t 1) Sbsség dr hlyvktor változás gyorsasága
I. Mchanka Dfnált fogalom Mghatározás Tömgpont Pontszrű tst. Olyan tst, mlynk jllmző mért kcsk a pálya mérthz képst. Elmozdulás hlyvktor mgváltozása: r1, r(t ) r(t 1) Sbsség dr hlyvktor változás gyorsasága
FELVÉTELI FELADATOK 8. évfolyamosok számára. A 2 feladatlap. Név:...
 2005. jnuár-fruár FELVÉTELI FELADATOK 8. évfolymosok számár A 2 fltlp Név:... Szültési év: hó: np: A fltokt ttszés szrinti sorrnn olhto mg. Ügylj mgfllő iőosztásr és küllkr! A mgolásr összsn 45 pr vn.
2005. jnuár-fruár FELVÉTELI FELADATOK 8. évfolymosok számár A 2 fltlp Név:... Szültési év: hó: np: A fltokt ttszés szrinti sorrnn olhto mg. Ügylj mgfllő iőosztásr és küllkr! A mgolásr összsn 45 pr vn.
A szelepre ható érintkezési erő meghatározása
 A szlpr ható érintkzési rő mghatározása Az [ 1 ] műbn az alábbi fladatot találtuk. A fladat: Adott az ábra szrinti szlpmlő szrkzt. Az a xcntricitással szrlt R sugarú bütyök / körtárcsa ω 1 állandó szögsbsséggl
A szlpr ható érintkzési rő mghatározása Az [ 1 ] műbn az alábbi fladatot találtuk. A fladat: Adott az ábra szrinti szlpmlő szrkzt. Az a xcntricitással szrlt R sugarú bütyök / körtárcsa ω 1 állandó szögsbsséggl
= n 2 = x 2 dx = 3c 2 ( 1 ( 4)). = π 13.1
 Htározott integrál megoldások + 7 + + 9 = 9 6 A bl végpontokt válsztv: i = i n, i+ i = n, fξ i = i 6 d = lim n n i= i n n = n lim n n i = lim n i= A jobb végpontokt válsztv: fξ i = n i, n i d = lim n n
Htározott integrál megoldások + 7 + + 9 = 9 6 A bl végpontokt válsztv: i = i n, i+ i = n, fξ i = i 6 d = lim n n i= i n n = n lim n n i = lim n i= A jobb végpontokt válsztv: fξ i = n i, n i d = lim n n
Villamos érintésvédelem
 Villamos érintésvédlm A villamos nrgia ipari mértű flhasználása a század ljén kzdtt gyr nagyobb mértékbn ltrjdni és zzl gyidőbn jlntkztk az áramütésből rdő balstk is. Ennk kövtkztébn nagyarányú kutatás
Villamos érintésvédlm A villamos nrgia ipari mértű flhasználása a század ljén kzdtt gyr nagyobb mértékbn ltrjdni és zzl gyidőbn jlntkztk az áramütésből rdő balstk is. Ennk kövtkztébn nagyarányú kutatás
a b a leghosszabb. A lapátlók által meghatározott háromszögben ezzel szemben lesz a
 44 HANCSÓK KÁLMÁN MEGYEI MATEMATIKAVERSENY MEZŐKÖVESD, évfolym MEGOLDÁSOK Mutssuk meg, hogy egy tetszőleges tégltest háromféle lpátlójából szerkesztett háromszög hegyesszögű lesz! 6 pont A tégltest egy
44 HANCSÓK KÁLMÁN MEGYEI MATEMATIKAVERSENY MEZŐKÖVESD, évfolym MEGOLDÁSOK Mutssuk meg, hogy egy tetszőleges tégltest háromféle lpátlójából szerkesztett háromszög hegyesszögű lesz! 6 pont A tégltest egy
Differenciálszámítás. Lokális szélsőérték: Az f(x) függvénynek az x 0 helyen lokális szélsőértéke
 Differenciálszámítás Lokális növekedés (illetve csökkenés): H z f() függvény deriváltj z 0 helyen pozitív: f () > 0 (illetve negtív: f () < 0), kkor z f() függvény z 0 helyen növekvően (illetve csökkenően)
Differenciálszámítás Lokális növekedés (illetve csökkenés): H z f() függvény deriváltj z 0 helyen pozitív: f () > 0 (illetve negtív: f () < 0), kkor z f() függvény z 0 helyen növekvően (illetve csökkenően)
Az elektromágneses sugárzás kölcsönhatása az anyaggal
 Az lktromágnss sugárzás kölcsönhatása az anyaggal A fény kölcsönhatása az anyaggal visszavrődés A fény kölcsönhatása az anyaggal 2. törés szórás lnylődés Elnylődés 1 2 3 4 Δ Az intzitás gyngülésénk törvény
Az lktromágnss sugárzás kölcsönhatása az anyaggal A fény kölcsönhatása az anyaggal visszavrődés A fény kölcsönhatása az anyaggal 2. törés szórás lnylődés Elnylődés 1 2 3 4 Δ Az intzitás gyngülésénk törvény
1. KVANTUMJELENSÉGEK, SUGÁRZÁSOK A kvantumfizika kísérleti alapjai. A klasszikus fizika néhány egyenlete és korlátai.
 . KVANTUMJELENSÉGEK, SUGÁRZÁSOK.. A kantumfizika kísérlti alapjai A klasszikus fizika néány gynlt és korlátai Haladó mozgás Ha ismrjük x 0 -t és p 0 -t, akkor mgatározatjuk x t -t és p t -t is bármly későbbi
. KVANTUMJELENSÉGEK, SUGÁRZÁSOK.. A kantumfizika kísérlti alapjai A klasszikus fizika néány gynlt és korlátai Haladó mozgás Ha ismrjük x 0 -t és p 0 -t, akkor mgatározatjuk x t -t és p t -t is bármly későbbi
MAGYAR NYELVI FELADATLAP
 2009. jnuár 29. MAGYAR NYELVI FELADATLAP 4. évfolymosok számár 2009. jnuár 29. 14:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A fltokt ttszés szrinti sorrnn olhto mg. Ügylj mgfllő iőosztásr és küllkr! A mgolásr
2009. jnuár 29. MAGYAR NYELVI FELADATLAP 4. évfolymosok számár 2009. jnuár 29. 14:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A fltokt ttszés szrinti sorrnn olhto mg. Ügylj mgfllő iőosztásr és küllkr! A mgolásr
Többváltozós analízis gyakorlat
 Többváltozós nlízis gykorlt Áltlános iskoli mtemtiktnár szk 07/08. őszi félév Ajánlott irodlom (sok gykorló feldt, megoldásokkl: Thoms-féle klkulus 3., Typote, 007. (Jól hsználhtók z -. kötetek is Fekete
Többváltozós nlízis gykorlt Áltlános iskoli mtemtiktnár szk 07/08. őszi félév Ajánlott irodlom (sok gykorló feldt, megoldásokkl: Thoms-féle klkulus 3., Typote, 007. (Jól hsználhtók z -. kötetek is Fekete
Mátrixok és determinánsok
 Informtik lpji Mátriok és erminánsok számok egyfjt tábláztát mátrink hívjuk. mátriok hsználhtóság igen sokrétő kezdve mtemtikávl, folyttv számítástechnikán és fizikán keresztül, egészen z elektrotechnikáig.
Informtik lpji Mátriok és erminánsok számok egyfjt tábláztát mátrink hívjuk. mátriok hsználhtóság igen sokrétő kezdve mtemtikávl, folyttv számítástechnikán és fizikán keresztül, egészen z elektrotechnikáig.
53. sz. mérés. Hurokszabályozás vizsgálata
 53. sz. mérés Hurokszaályozás vizsgálata nagyszültségű alap- illtv losztóhálózat (4,, kv a hálózatok unkcióáól kövtkzőn hurkolt (töszörösn hurkolt kialakítású. sok csomóponttal, tö táplálási illtv ogyasztási
53. sz. mérés Hurokszaályozás vizsgálata nagyszültségű alap- illtv losztóhálózat (4,, kv a hálózatok unkcióáól kövtkzőn hurkolt (töszörösn hurkolt kialakítású. sok csomóponttal, tö táplálási illtv ogyasztási
3. MECHANIKA STATIKA GYAKORLAT (kidolgozta: Triesz Péter; Tarnai Gábor, mérnök tanár) Három erő egyensúlya
 SZÉHENYI ISTVÁN EGYETEM LKLMZOTT MEHNIK TNSZÉK Péld: MEHNIK STTIK GYKORLT (kidolgozt: Tisz Pét; Tni Gábo ménök tná) Háom ő gynsúly dott gy mlőszkzt méti és thlés: m b 5 m c 5 m kn ldt: y c Htáozz mg z
SZÉHENYI ISTVÁN EGYETEM LKLMZOTT MEHNIK TNSZÉK Péld: MEHNIK STTIK GYKORLT (kidolgozt: Tisz Pét; Tni Gábo ménök tná) Háom ő gynsúly dott gy mlőszkzt méti és thlés: m b 5 m c 5 m kn ldt: y c Htáozz mg z
Bevezetés a programozásba. 3. Előadás Algoritmusok, tételek
 Bevezetés progrmozásb 3. Elődás Algortmusok, tételek ISMÉTLÉS Specfkácó Előfeltétel: mlyen körülmények között követelünk helyes működést Utófeltétel: mt várunk kmenettől, m z összefüggés kmenet és bemenet
Bevezetés progrmozásb 3. Elődás Algortmusok, tételek ISMÉTLÉS Specfkácó Előfeltétel: mlyen körülmények között követelünk helyes működést Utófeltétel: mt várunk kmenettől, m z összefüggés kmenet és bemenet
5. Logaritmus. I. Nulladik ZH-ban láttuk: 125 -öt kapjunk. A 3 5 -nek a 3. hatványa 5, log. x Mennyi a log kifejezés értéke?
 . Logritmus I. Nulldik ZH-bn láttuk:. Mennyi kifejezés értéke? (A) Megoldás I.: BME 0. szeptember. (7B) A feldt ritmus definíciójából kiindulv gykorltilg fejben végiggondolhtó. Az kérdés, hogy -öt hánydik
. Logritmus I. Nulldik ZH-bn láttuk:. Mennyi kifejezés értéke? (A) Megoldás I.: BME 0. szeptember. (7B) A feldt ritmus definíciójából kiindulv gykorltilg fejben végiggondolhtó. Az kérdés, hogy -öt hánydik
Kalkulus II. Beugró kérdések és válaszok 2012/2013 as tanév II. félév
 Klkulus II. Beugró kérdések és válszok 2012/2013 s tnév II. félév 1. Legyen ], b[ R nemüres, nyílt intervllum, f :], b[ R függvény. Hogyn vn értelmezve z f függvény primitív függvénye? Válsz. Legyen ],
Klkulus II. Beugró kérdések és válszok 2012/2013 s tnév II. félév 1. Legyen ], b[ R nemüres, nyílt intervllum, f :], b[ R függvény. Hogyn vn értelmezve z f függvény primitív függvénye? Válsz. Legyen ],
13. gyakorlat Visszacsatolt műveletierősítők. A0=10 6 ; ω1=5r/s, ω2 =1Mr/s R 1. Kérdések: uki/ube=?, ha a ME ideális!
 . gyakorlat Visszacsatolt művltirősítők.) Példa b (s) 6 ; r/s, Mr/s kω, 9 kω, kω, ( s )( s ) Kérdésk: /b?, ha a ME ális! Mkkora lgyn érték ahhoz, hogy az /b rősítés maximális lapos lgyn ( ξ ). Mkkora a
. gyakorlat Visszacsatolt művltirősítők.) Példa b (s) 6 ; r/s, Mr/s kω, 9 kω, kω, ( s )( s ) Kérdésk: /b?, ha a ME ális! Mkkora lgyn érték ahhoz, hogy az /b rősítés maximális lapos lgyn ( ξ ). Mkkora a
Matematika 4 gyakorlat Földtudomány és Környezettan BSc II/2
 Mtemtik 4 gykorlt Földtudomány és Környezettn BSc II/2 1. gykorlt Integrálszámítás R n -ben: vonlintegrál, primitív függvény, Newton Leibniz-szbály. Legyen Ω R n egy trtomány, f : Ω R n folytonos függvény
Mtemtik 4 gykorlt Földtudomány és Környezettn BSc II/2 1. gykorlt Integrálszámítás R n -ben: vonlintegrál, primitív függvény, Newton Leibniz-szbály. Legyen Ω R n egy trtomány, f : Ω R n folytonos függvény
Város Polgármestere ELŐTERJESZTÉS
 Város Polgármstr 251 Biatorbágy, Baross Gábor utca 2/a Tlfon: 6 23 31-174/233 mllék Fax: 6 23 31-135 E-mail: bruhazas@biatorbagy.hu www.biatorbagy.hu ELŐTERJESZTÉS Budapst Balaton közötti krékpárút nyomvonalával
Város Polgármstr 251 Biatorbágy, Baross Gábor utca 2/a Tlfon: 6 23 31-174/233 mllék Fax: 6 23 31-135 E-mail: bruhazas@biatorbagy.hu www.biatorbagy.hu ELŐTERJESZTÉS Budapst Balaton közötti krékpárút nyomvonalával
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Koordináta-gomtria A szürkíttt háttrű fladatrészk nm tartoznak az érinttt témakörhöz, azonban szolgálhatnak fontos információval az érinttt fladatrészk mgoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Koordináta-gomtria A szürkíttt háttrű fladatrészk nm tartoznak az érinttt témakörhöz, azonban szolgálhatnak fontos információval az érinttt fladatrészk mgoldásához!
MATEMATIKA FELADATLAP a 4. évfolyamosok számára
 4. évfolym Mt2 fltlp MATEMATIKA FELADATLAP 4. évfolymosok számár 2017. jnuár 26. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg.
4. évfolym Mt2 fltlp MATEMATIKA FELADATLAP 4. évfolymosok számár 2017. jnuár 26. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg.
Országos Szakiskolai Közismereti Tanulmányi Verseny 2007/2008 IRODALOM MAGYAR NYELV ÉS HELYESÍRÁS. II. (regionális) forduló. 2008. február 22.
 Országos Szkiskoli Közismrti Tnulmányi Vrsny 2007/2008 IRODALOM MAGYAR NYELV ÉS HELYESÍRÁS II. (rgionális) foruló 2008. fruár 22. Mgolás 1 Országos Szkiskoli Közismrti Irolom Mgyr nylv és hlysírás Tnulmányi
Országos Szkiskoli Közismrti Tnulmányi Vrsny 2007/2008 IRODALOM MAGYAR NYELV ÉS HELYESÍRÁS II. (rgionális) foruló 2008. fruár 22. Mgolás 1 Országos Szkiskoli Közismrti Irolom Mgyr nylv és hlysírás Tnulmányi
Légköri aeroszol elemösszetételének vizsgálata és egészségkárosító hatásának modellezése a továbbfejlesztett Sztochasztikus Tüdőmodellel
 DE TTK 1949 Légköri rszl lmössztétlénk vizsgált és gészségkársító htásánk mdllzés tvábbfjlszttt Sztchsztikus Tüdőmdlll Egytmi dktri (PhD) értkzés szrző nv: Dbs Erik témvztő nv: Dr. Brbélyné Dr. Kiss Ildikó
DE TTK 1949 Légköri rszl lmössztétlénk vizsgált és gészségkársító htásánk mdllzés tvábbfjlszttt Sztchsztikus Tüdőmdlll Egytmi dktri (PhD) értkzés szrző nv: Dbs Erik témvztő nv: Dr. Brbélyné Dr. Kiss Ildikó
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 8. évfolym Mt1 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zsebszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrendben oldhtod meg.
8. évfolym Mt1 feldtlp MATEMATIKA FELADATLAP 8. évfolymosok számár 11:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll dolgozz! Zsebszámológépet nem hsználhtsz. A feldtokt tetszés szerinti sorrendben oldhtod meg.
Kereskedelmi szálláshelyek kihasználtságának vizsgálata, különös tekintettel az Észak-magyarországi és a Dél-alföldi régióra
 Észk-mgyrországi Strtégii Füzetek VII. évf. 2010 1 27-35 Kereskedelmi szálláshelyek kihsználtságánk vizsgált, különös tekintettel z Észk-mgyrországi és Dél-lföldi régiór A turizmusfejlesztés egyik prioritás
Észk-mgyrországi Strtégii Füzetek VII. évf. 2010 1 27-35 Kereskedelmi szálláshelyek kihsználtságánk vizsgált, különös tekintettel z Észk-mgyrországi és Dél-lföldi régiór A turizmusfejlesztés egyik prioritás
Energetikai gazdaságtan 3. gyakorlat Gazdasági mutatók
 Eergetk gzdságt 3. gykorlt Gzdság muttók GAZDASÁGTAN, PÉNZÜGY JELLEMZŐK A gykorlt célj, hogy hllgtók A. elsjátítsák gzdálkodásb szokásos pézügytechk meységek között összefüggéseket; B. egyszerű gzdságosság
Eergetk gzdságt 3. gykorlt Gzdság muttók GAZDASÁGTAN, PÉNZÜGY JELLEMZŐK A gykorlt célj, hogy hllgtók A. elsjátítsák gzdálkodásb szokásos pézügytechk meységek között összefüggéseket; B. egyszerű gzdságosság
24. MŰVELETI ERŐSÍTŐK ALKALMAZÁSAI
 24. MŰVELETI EŐSÍTŐK ALKALMAZÁSAI élkitűzés: Az elektroniki gondolkodásmód fejlesztése. I. Elméleti áttekintés A műveleti erősítőkkel (továikn ME) csknem minden, nem túlságosn ngyfrekvenciás elektroniki
24. MŰVELETI EŐSÍTŐK ALKALMAZÁSAI élkitűzés: Az elektroniki gondolkodásmód fejlesztése. I. Elméleti áttekintés A műveleti erősítőkkel (továikn ME) csknem minden, nem túlságosn ngyfrekvenciás elektroniki
M3 ZÁRT CSATORNÁBAN ELHELYEZETT HENGERRE HATÓ ERŐ MÉRÉSE
 M3 ZÁRT CSATORNÁBAN ELHELYEZETT HENGERRE HATÓ ERŐ MÉRÉSE. A mérés élja A mérés fladat égyzt krsztmtsztű satorába bépíttt, az áramlás ráyára mrőlgs szmmtratglyű, külöböző átmérőjű hgrkr ható ( x, y ) rő
M3 ZÁRT CSATORNÁBAN ELHELYEZETT HENGERRE HATÓ ERŐ MÉRÉSE. A mérés élja A mérés fladat égyzt krsztmtsztű satorába bépíttt, az áramlás ráyára mrőlgs szmmtratglyű, külöböző átmérőjű hgrkr ható ( x, y ) rő
Hatvani István fizikaverseny 2015-16. 1. forduló megoldások. 1. kategória
 1. ktegóri 1.1.1. Adtok: ) Cseh László átlgsebessége b) Chd le Clos átlgsebessége Ezzel z átlgsebességgel Cseh László ideje ( ) ltt megtett távolság Így -re volt céltól. Jn Switkowski átlgsebessége Ezzel
1. ktegóri 1.1.1. Adtok: ) Cseh László átlgsebessége b) Chd le Clos átlgsebessége Ezzel z átlgsebességgel Cseh László ideje ( ) ltt megtett távolság Így -re volt céltól. Jn Switkowski átlgsebessége Ezzel
ANYANYELVI FELADATLAP
 2007. fruár 1. ANYANYELVI FELADATLAP 4. évfolymosok számár 2007. fruár 1. 14:00 ór A 2 fltlp NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A fltokt ttszés szrinti sorrnn olhto mg. Ügylj mgfllő iőosztásr és küllkr! A mgolásr
2007. fruár 1. ANYANYELVI FELADATLAP 4. évfolymosok számár 2007. fruár 1. 14:00 ór A 2 fltlp NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A fltokt ttszés szrinti sorrnn olhto mg. Ügylj mgfllő iőosztásr és küllkr! A mgolásr
Els gyakorlat. vagy más jelöléssel
 Els gykorlt Egyszer egyenletek, EHL PDE A gykorlt elején megismerkedünk prciális dierenciálegyenletek (mostntól: PDE-k) lpfoglmivl. A félév során sokt fog szerepelni z ún. multiindex jelöl, melynek lényege,
Els gykorlt Egyszer egyenletek, EHL PDE A gykorlt elején megismerkedünk prciális dierenciálegyenletek (mostntól: PDE-k) lpfoglmivl. A félév során sokt fog szerepelni z ún. multiindex jelöl, melynek lényege,
1. Az üregsugárzás törvényei
 1. Az üregsugárzás törvényei 1.1. A Wien féle eltolódási törvény és a Stefan-Boltzmann törvény Egy zárt, belül üres fémdoboz kis nyílása az úgynevezett abszolút fekete test. A nyílás elektromágneses sugárzást
1. Az üregsugárzás törvényei 1.1. A Wien féle eltolódási törvény és a Stefan-Boltzmann törvény Egy zárt, belül üres fémdoboz kis nyílása az úgynevezett abszolút fekete test. A nyílás elektromágneses sugárzást
10. lecke. potenciális GDP alakulása. munkanélküliség okai. Konjunkturális. a potenciális kibocsátás szintjén? a tanult növekedéselmélet szerint igen
 10. lck A munkpic jllmzõi és s munknélk lküliség g oki Rövid ávú gynsúly, ponciális kibocsáás, GDP-rés, munknélküliség. A munknélküliség rmészs rááj, rmészs munknélküliség oki. Konjunkurális munknélküliség,
10. lck A munkpic jllmzõi és s munknélk lküliség g oki Rövid ávú gynsúly, ponciális kibocsáás, GDP-rés, munknélküliség. A munknélküliség rmészs rááj, rmészs munknélküliség oki. Konjunkurális munknélküliség,
REZGÉSTAN GYAKORLAT Kidolgozta: Dr. Nagy Zoltán egyetemi adjunktus
 SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK REZGÉSTAN GYAKORLAT Kdogozt: r. Ngy Zotán egyetem djunktus 4. fedt: Mndkét végén efzott rúd ongtudnás rezgése (kontnuum mode) A, ρ, E Adott: mndkét
SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK REZGÉSTAN GYAKORLAT Kdogozt: r. Ngy Zotán egyetem djunktus 4. fedt: Mndkét végén efzott rúd ongtudnás rezgése (kontnuum mode) A, ρ, E Adott: mndkét
ANYANYELVI FELADATLAP a 8. évfolyamosok számára
 ÚJ FELADATLAP 2007. ruár 1. ANYANYELVI FELADATLAP 8. évolymosok számár 2007. ruár 1. 14:00 ór ÚJ FELADATLAPI NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A ltokt ttszés szrinti sorrnn olhto mg. Ügylj mgllő iőosztásr és
ÚJ FELADATLAP 2007. ruár 1. ANYANYELVI FELADATLAP 8. évolymosok számár 2007. ruár 1. 14:00 ór ÚJ FELADATLAPI NÉV: SZÜLETÉSI ÉV: HÓ: NAP: A ltokt ttszés szrinti sorrnn olhto mg. Ügylj mgllő iőosztásr és
Mátrix-vektor feladatok Összeállította dr. Salánki József egyetemi adjunktus Begépelte Dr. Dudás László és Bálint Gusztáv
 Mátrx-vektor feldtok Összeállított dr. Slánk József egyetem djunktus Begépelte Dr. Dudás László és Bálnt Gusztáv 1. feldt Adottk z n elemű, b vektorok. Képezn kell c vektort, hol c = b / Σ( ), ( = 0,1,,
Mátrx-vektor feldtok Összeállított dr. Slánk József egyetem djunktus Begépelte Dr. Dudás László és Bálnt Gusztáv 1. feldt Adottk z n elemű, b vektorok. Képezn kell c vektort, hol c = b / Σ( ), ( = 0,1,,
Dr. Nagy Balázs Vince D428
 Műszaki Optika 2. előadás Dr. Nagy Balázs Vince D428 nagyb@mogi.bme.hu Izzólámpa és fénycső 30,0 25,0 20,0 15,0 10,0 5,0 0,0 350 400 450 500 550 600 650 700 750 2 Fényforrások csoportosítása Fényforrások
Műszaki Optika 2. előadás Dr. Nagy Balázs Vince D428 nagyb@mogi.bme.hu Izzólámpa és fénycső 30,0 25,0 20,0 15,0 10,0 5,0 0,0 350 400 450 500 550 600 650 700 750 2 Fényforrások csoportosítása Fényforrások
Mágneses momentum, mágneses szuszceptibilitás
 Mágnss ontu, ágnss szuszcptibilitás A olkuláknak (atooknak, ionoknak) lktronszrkztüktől függőn lht pranns (állandóan glévő) ágnss ontua. Ha ágnss térb krülnk, a tér hatására indig ágnss ontu jön létr az
Mágnss ontu, ágnss szuszcptibilitás A olkuláknak (atooknak, ionoknak) lktronszrkztüktől függőn lht pranns (állandóan glévő) ágnss ontua. Ha ágnss térb krülnk, a tér hatására indig ágnss ontu jön létr az
4. előadás: A vetületek általános elmélete
 4. elődás: A vetületek áltlános elmélete A vetítés mtemtiki elve Két mtemtikilg meghtározott felület prméteres egyenletei legyenek következők: x = f 1 (u, v), y = f 2 (u, v), I. z = f 3 (u, v). ξ = g 1
4. elődás: A vetületek áltlános elmélete A vetítés mtemtiki elve Két mtemtikilg meghtározott felület prméteres egyenletei legyenek következők: x = f 1 (u, v), y = f 2 (u, v), I. z = f 3 (u, v). ξ = g 1
SV-805AL SV-805AL Color. Videokaputelefon 5 vezetékes vandálbiztos. Rock Series. Telepítõi kézikönyv
 SV-805AL SV-805AL Color Vidokputlfon 5 vztéks vndáliztos Rock Sris Tlpítõi kézikönyv BEVEZETŐ 1 2 TÁPEGYSÉG TELEPÍTÉSE Köszönjük, hogy GLMAR trmékét válsztott. Az IS-9001 minősítés és lkötlzttségünk vásárlók
SV-805AL SV-805AL Color Vidokputlfon 5 vztéks vndáliztos Rock Sris Tlpítõi kézikönyv BEVEZETŐ 1 2 TÁPEGYSÉG TELEPÍTÉSE Köszönjük, hogy GLMAR trmékét válsztott. Az IS-9001 minősítés és lkötlzttségünk vásárlók
Az éves statisztikai összegezés 1
 21. mlléklt 2/2006. (I. 13.) IM rndlthz Az évs sttisztiki összgzés 1 Sttisztiki összgzés z évs közbszrzéskről Kbt. IV., VI. fjzt, vlmint ngydik rész szrinti jánltkérők vontkozásábn 1. Az jánltkérő nv,
21. mlléklt 2/2006. (I. 13.) IM rndlthz Az évs sttisztiki összgzés 1 Sttisztiki összgzés z évs közbszrzéskről Kbt. IV., VI. fjzt, vlmint ngydik rész szrinti jánltkérők vontkozásábn 1. Az jánltkérő nv,
Matematika A1a - Analízis elméleti kérdései
 Mtemtik A1 - Anlízis elméleti kérdései (műszki menedzser szk, 2018. ősz) Kör egyenlete Az (x 0, y 0 ) középpontú, R sugrú kör egyenlete síkon (x x 0 ) 2 + (y y 0 ) 2 = R 2. Polinom Az x n x n + n 1 x n
Mtemtik A1 - Anlízis elméleti kérdései (műszki menedzser szk, 2018. ősz) Kör egyenlete Az (x 0, y 0 ) középpontú, R sugrú kör egyenlete síkon (x x 0 ) 2 + (y y 0 ) 2 = R 2. Polinom Az x n x n + n 1 x n
VI. Deriválható függvények tulajdonságai
 1 Deriválhtó függvének tuljdonsági VI Deriválhtó függvének tuljdonsági Ebben fejezetben zt vizsgáljuk, hog deriválhtó függvének esetén derivált milen összefüggésben vn függvén más tuljdonságivl, és hogn
1 Deriválhtó függvének tuljdonsági VI Deriválhtó függvének tuljdonsági Ebben fejezetben zt vizsgáljuk, hog deriválhtó függvének esetén derivált milen összefüggésben vn függvén más tuljdonságivl, és hogn
Bojtár-Gáspár: A végeselemmódszer matematikai alapjai
 Bojtár Imr Gáspár Zsolt A végslmmódszr matmatka alapja Elktronkusan ltölthtő lőadásvázlat építőmérnök hallgatók számára. http://www.pto.bm.hu/m/htdocs/oktatas/oktatas.php Kadó: BME Tartószrkztk Mchankája
Bojtár Imr Gáspár Zsolt A végslmmódszr matmatka alapja Elktronkusan ltölthtő lőadásvázlat építőmérnök hallgatók számára. http://www.pto.bm.hu/m/htdocs/oktatas/oktatas.php Kadó: BME Tartószrkztk Mchankája
Országos Szakiskolai Közismereti Tanulmányi Verseny 2005/2006 MAGYAR NYELV ÉS HELYESÍRÁS
 Orszáos Szkiskoli Közismrti Tnulmányi Vrsny 2005/2006 MAGYAR NYELV ÉS HELYESÍRÁS II. (rionális) oruló 2006. ruár 17... Hlyszín jélyzőj Vrsnyző Pontszám Kój Elértő Elért Százlék. 120.. % Jvító tnár Zsűri
Orszáos Szkiskoli Közismrti Tnulmányi Vrsny 2005/2006 MAGYAR NYELV ÉS HELYESÍRÁS II. (rionális) oruló 2006. ruár 17... Hlyszín jélyzőj Vrsnyző Pontszám Kój Elértő Elért Százlék. 120.. % Jvító tnár Zsűri
Koordinátageometria. 3 B 1; Írja fel az AB szakasz felezőpontjának 2 ( ) = vektorok. Adja meg a b vektort a
 1) Adott két pont: 1 A 4; és 2 3 B 1; Írja fl az AB szakasz flzőpontjának 2 2) Egy kör sugarának hossza 4, középpontja a B ( 3;5) pont. írja fl a kör gynltét! 3) Írja fl a ( 2;7 ) ponton átmnő, ( 5;8)
1) Adott két pont: 1 A 4; és 2 3 B 1; Írja fl az AB szakasz flzőpontjának 2 2) Egy kör sugarának hossza 4, középpontja a B ( 3;5) pont. írja fl a kör gynltét! 3) Írja fl a ( 2;7 ) ponton átmnő, ( 5;8)
2. NUMERIKUS INTEGRÁLÁS
 numerikus nlízis ii. 39 B - SPLINEOK DERIVÁLTJÁRA ÉRVÉNYES : B mi x =m Bm,i x B m,ix. t i+m t i t i+m+ t i+. NUMERIKUS INTEGRÁLÁS Htározott integrálok numerikus kiszámítás mtemtik egyik legrégebbi problémáj.
numerikus nlízis ii. 39 B - SPLINEOK DERIVÁLTJÁRA ÉRVÉNYES : B mi x =m Bm,i x B m,ix. t i+m t i t i+m+ t i+. NUMERIKUS INTEGRÁLÁS Htározott integrálok numerikus kiszámítás mtemtik egyik legrégebbi problémáj.
Vektorok (folytatás)
 Vektorok (folyttás) Vektor szorzás számml (sklárrl) Vektor szorzás számml b 1 c 2b c 2 ( 1 ) 2 Az vektor k-szoros (k R, vgyis k egy vlós szám) z vektor, melynek hossz k, irány pedig k > 0 esetén irányávl
Vektorok (folyttás) Vektor szorzás számml (sklárrl) Vektor szorzás számml b 1 c 2b c 2 ( 1 ) 2 Az vektor k-szoros (k R, vgyis k egy vlós szám) z vektor, melynek hossz k, irány pedig k > 0 esetén irányávl
