¾
|
|
|
- Benedek Rácz
- 6 évvel ezelőtt
- Látták:
Átírás
1 Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ Î ÐÐ ÑÓ Ñ ÖÒ ÁÒ ÓÖÑ Ø Ã Ö ËÞ Ð Ú À Ö ÞÐ Î ÐÐ ÑÓ Ø Ò Ì Ò Þ Å¹ Ð Ð Ø Ø ÐØ òöò Ñ Ö Ò Þ ÑÙÐ Ì Ã ÓÐ ÓÞ Ø Ã Þ Ø ØØ ÃÓÒÞÙÐ Ò Ö Æ Ý Á ØÚ Ò Ê Ö Ø Ò Ö ¾¼½ º Ó Ø Ö ¾¾º
2 ¾
3 Ì ÖØ ÐÓÑ ÝÞ Ã ÚÓÒ Ø ØÖ Ø Ú ½º Ú Þ Ø ½ ¾º Ð Ø ¾º½º Þ ÔÖÓ Ð Ñ Ñ Ø Ñ Ø ÓÖÑ Ð Þ Ð º º º º º º º º º º º º º º ¾º¾º ËÞ ÑÙÐ Ð Ò Ø Ö Ó Ø º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º¾º½º ËÞ ÑÙÐ Ð Ò Ø Ö Ó Ø Ð Ô º º º º º º º º º º º º º º º º º º º ¾º¾º¾º ËÞ ÑÙÐ Ð Ò Ø Ö Ó Ø Ð Ô Ò ÒØ ÖÔÓÐ º º º º º º º º º ¾º¾º º ËÞ ÑÙÐ Ð Ò Ø Ö Ó Ø Ñ º º º º º º º º º º º º º º º º ½¼ ¾º º ËÞ ÑÙÐ Ð Ô Ø º º º º º º º º º º º º º º º º º º º º º º º º º º º ½¼ º ÑÙÐØ ÔÖÓ ÞÓÖÓ ÇÔ Ò Ä ÖÒÝ Þ Ø ½½ º½º ÇÔ Ò Ä Ö Ø Ø Ö º º º º º º º º º º º º º º º º º º º º º º º º º º ½½ º¾º ÇÔ Ò Ä ÔÖÓ Ö ÑÓÞ ÑÓ ÐÐ º º º º º º º º º º º º º º º º º º º º º º ½¾ º ÅÙÐØ ÔÖÓ ÞÓÖÓ ÔÖÓ Ö Ñ ½ º½º ÙØ ÖÒÝ Þ Ø ÑÙØ Ø º º º º º º º º º º º º º º º º º º º º º º º ½ º¾º Þ ÑÔÐ Ñ ÒØ ÓÞ Þ Ñ ÓÒØÓÐ Ó º º º º º º º º º º º º º ½ º º Å Ñ Ö Þ ÖÚ Þ º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ º º Ð Ô Ö ÞÐ Ø Þ º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ º º½º ÁÒØ ÖÔÓÐ º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ º º¾º ËÞ ÑÙÐ Ð Ò Ø Ö Ó Ø Ñ Ö Ø Ò Þ Ñ Ø º º º º º º º º º º º ¾¼ º º º ÁØ Ö Ø Ú Ñ ÓÐ Ð ÓÖ ØÑÙ º º º º º º º º º º º º º º º º º º º ¾¼ º º º ØÓ Ñ ÒØ º º º º º º º º º º º º º º º º º º º º º º º º º º ¾½ º ÃÓÒÚ Ö Ò Ú Þ Ð Ø ¾ º½º Þ ÒØ ÖÔÓÐ Ó Ò Ø º º º º º º º º º º º º º º º º º º º º º º ¾ º¾º Ã Ð Ò Þ Ð Ô ÓÖÑ Ø Ò º º º º º º º º º º º º º º º º º º º º º º ¾
4 º Ö Ñ ÒÝ ¾ º½º Å ÌÄ ÑÔÐ Ñ ÒØ º º º º º º º º º º º º º º º º º º º º º º º º ¾ º¾º ÇÔ Ò Ä ÑÔÐ Ñ ÒØ º º º º º º º º º º º º º º º º º º º º º º º º º ¾ º Þ Þ ¾ ý Ö ÝÞ Ì Ð Þ ØÓ ÝÞ ÁÖÓ ÐÓÑ ÝÞ ÁÁ ÁÁÁ Î
5 à ÚÓÒ Ø ØÓÑ Ö Ñ ÖÓ Þ ÔÔ Ð Ú Ð Ñ Þ ØØ Ð Ð Øò Ñ ÒØ Ð Ð Ø Ø ÐØ Ö Ò Ñ Ö ÓÖ Ò Ö Ø Ù Ø Ñ ÒØ Þ ØØ Ô Ø Ñ Ö Ø º Ô Ø Ö¹ Ø Ø Þ Ð Ø Ñ ÐÐ ØØ Ð Ø Ò Ð Ø Ù Ò ÞÒ º ÆÙÑ Ö Ù Þ ÑÙÐ Ú Ð ÔÓÒØÓ Ò Ñ Ö Ø Þ ÖØ Ø Þ ÐØ Ð Ð ÓÒØ Ò Ñ Ö Þ Òº Þ ÑÙÐ ÓÖ Ò Ð Ø Ô Ö ÙÞ ÑÓ Ø Ó Ø Ð ÞÒ ÐÚ Þ Ñ Ø Ø Ð Ó Ø Ö ÒØ ØØ Ñ Ö ÓÒÐ Ò Ð ÓÐ ÓÞ Ø Ð Ø Ú Ø Þ º ØÓÑ Ö Ñ ÖÓ Þ ÔÔ Ð Ú Ð Ñ Þ ØØ Ð Ð Øò Ñ ÒØ Ð Ð Ø Ø ÐØ òöò Ò Ñ Ö ÓÖ Ò Ö Ø Ù Øò Ñ ÒØ Þ ØØ Ô Ø Ñ Ö Ø º Ô Ø ÖØ Ø Þ Ð Ø Ñ ÐÐ ØØ Ð Ø Ò ÐØ Ù Ò ÞÒ º ÆÙÑ Ö Ù Þ ÑÙÐ Ú Ð ÔÓÒØÓ¹ Ò Ñ Ö Ø Þ ÖØ Ø Þ ÐØ Ð Ò ÝÓ Ð ÓÒØ Ö Ø Ðº Þ ÑÙÐ ÓÖ Ò Ð Ø Ô Ö ÙÞ ÑÓ Ø Ó Ø Ð ÞÒ ÐÚ Þ Ñ Ø Ø Ð Ó Ø Ö ÒØ ØØ º Þ Ö Ñ ÒÝ Ý Ö Þ Ø ÓÖ ÓÐ ÓÞ ØÓÑ Ò ½ ÐÐ ØÚ Ò ÑÞ Ø Þ ÓÒ¹ Ö Ò Ò ¾ Ñ ÖØ ØØ Ñº
6 ØÖ Ø Ì Ñ ÙÖ Ñ ÒØ Ó Ø ÙÖ Ö Ò ØÝ Ò Ú Ý ØÓÑ ÓÖ Å ÖÓ ÓÔ Åµº Ì ÓÑÑÓÒ Ñ Ø Ó Ø ØÛÓ¹Ô Ø Ò Û Ñ Ò Ó Ð ØÓ Ô Ö Ø Ø Ò Ø ÓÖ Ø Ò ÙÔÓÒ Ø Ø Ô ÒØÓ ÓÑÔÓÒ ÒØ º ÌÓ Ó Ó Û Ú ØÓ ÜÔÖ Ø Ø Ô¹ ÑÔÐ Ô Ø Ò Û Ö Ø Ð Ö Ô Ø ÚÐÝ ØÓ Ø Ñ ÙÖ Ñ ÒØ ÙÖ Ýº Ì Ú ÐÙ Ó Ø Ô Ø Ò Ò ÜÔÖ Ò Ð Ø ÐÐÝ ÙØ Û Ø ÓÑ ØÖÓÒ Ò Ð Ø Ò º Ï Ö ÔÖ ÒØ Ò Ø Ð Ö Ø ÑÙÐ Ø ÓÒ Ó Ø Ô Ø Ò Ù Ò Èͳ ÔÖÓ Ö ÑÑ Ò ÇÔ Ò Ä³ Ô Ö ÐÐ Ð Ö Ñ ÛÓÖ º Ú
7 ½º Þ Ø Ú Þ Ø ½ ¹ Ò ÒÒ Ò ÑÓÒ ØÖ ÐØ Þ ØÓÑ Ö Ñ ÖÓ Þ Ô Åµ ØÐ Ø Ø Ñ Ñ ¹ Ö Ò ÒÓØ ÒÓÐ Ý Ð ÓÒØÓ Þ Þ Ð Øغ Ð ÞÒ Ð Ø Ô Ð ÓØ Ö Ò ÒÓÐ ØÓ Ö Ö ÓØØ ÒÝ Ð Ø Ö º Þ Å ÔÔ Ö ØÙ Þ ÓØØ Ñ ÒØ Ð Ð Ø Ð ØØ Ô ÞØ Þ ÒØ Ð Ú Ö Ú Ö Ö Ø ØØ Øò Ð Ò Ø Ò Ú Þ Ð ¹ Ø Ø Ú Þ º Ð ½º½ º Ö µ Ð Ð Ø Øò Þ ØØ ÓÑ Ò Ò Ð Ò Ø Ø ÖÓÞÞ Ñ Ó Ý Þ ÒÝ Ñ ÐÝ Þ Ñ ÒÒÝ Ø Ô Ø Ù Ñ º µ Þ Å ÔÔ Ö ØÙ µ Øò Ñ ÒØ ÑÓ ÐÐ ½º½º Ö º Þ Å ÔÔ Ö ØÙ Ð Ø Ø Þ µ Ö Òº Ð Þ ÖÒÝ Ð Øò Ð Ð Ø Ö Ð Ø Ö Þ Ú Ý ÓØ Ø ØÓÖÖ Ö ÒÝÙк Øò ÔÓÞ Ø Þ Ð Ô Ò Ò Ý ÔÓÒØÓ Ð Ñ Ö º µ ¹ Ö Ò Ñ ÒØ Ð ØØ Ð Ú Øò ÑÓ ÐÐ Ð Ø Ø Ô Ø Ò Ð Ø Ù Þ Ñ Ø ÓÞº Øò R Ù Ö H Ñ D Ø ÚÓÐ Ö Ú Ò Ñ ÒØ Ø Ðº ÓÖÖ µ Þ Å Ð ÞÒ Ð ÓÒØ Ø ÐÐ ØÚ ÓÔÓ Ø Ø Þ ÑÑ Ð Øº ÓÒØ Ø Ñ ÓÖ Ò Ð Ð Ø Ò Ú ÞÞÙ ØòØ Ñ Ö z Ö ÒÝ ÐÑÓÞ ÙРغ Ý ¹ Ô Ú ÝÙÒ Ñ ÒØ Ð Ð Ø Ò Ð Ú ØÓÑÓ ÐÖ Ò Þ Ö Ð Ñ Ø Ö Ô Ø Ò º ÃÓÔÓ Ø Ø Ñ ÓÖ Ò ØòØ Ð Ñ Ð Ñ ÒØ Ø Ð f Ö Ú Ò Ú Ð Ö Þ Ø Ø º Ð Ø ÔÓ Ø ÓÖ Ò Þ ØÐ Ó Ñ ÒØ ¹Øò Ø ÚÓÐ ÓØ ÓÒØ Ø Ñ Ñ Ø Ö¹ ½
8 Ô Ð ÞÒ Ð Ú Ð ÓÒ Ø Ò ÖØ Ò Ø ÖØ Ù º ÒØ Ð Ú Ö Ò Ñ Ø Ñ ÖÚ Þ ÑÔÐ Ø Ò Ö Ú Ò Ò ÐØ Ö Ð Þ Ñ Ø Ø ØòÖ Ø Ö º Þ Ò Ö Ò Ý Ø ÓÐÝ ÓÐ Ø ÒÝ Þ µ Ñ ÒØ Øò Þ Ô ÓÐØ Þ ÐØ Ó ÓÞØ Ú ÐÐ ÑÓ Ø Ö µ Ñ ÒØ Ð Ð Ø Ø ÐØ òöò ÐÓ ÞÐ µ Î Ò Ö Ï Ð Ö º ÓÐ ÓÞ Ø Ò Ð Ð Ø Ø ÐØ òöò Ñ Ö Ø Ø ÒØ Ñ ÐÒ º Þ Þ Ö ÒØ Þ Ö µ ÓÑÔÓÒ Ò Ø Ñ ÒØ Øò Þ ØØ Ô Ø Ð Þ ½º½µ Þ Ö ÒØ Þ ÖÑ ÞØ Ø Ø Ù º F s = de dd = d(cv 2 /2) = 1 dd 2 dc dd V 2 ½º½µ À Ñ ÒØ Ô ÞØ Þ ÓÖ Ò Þ Ò Ö ÓÑÔÓÒ Ò ÓÒ Ø Ò Ò ÑÓÒ Ø Ø Ø Ð Ð Ø Ö Ø ÚÓÐ ÔÓÒØ ØÐ Ò Ð ÒÝ ÓÐ Ø Ò ÓÖ Ø ÐØ ¹ òöò Ñ Ö Ò Þ ÐÐ Ò Ø Ó ÓÞº Ñ Ð Ñ Ò Ð Ø º Þ ½º½µ Þ Ñ Ø Ò Ö Ø Ù Ð Ñ Ô Ø ÖØ Ñ Ø ÒÙÑ Ö Ù Þ Ñ Ø Ñ ÐÐ Þ Ø Ò Þ Ö ÒØ Ò Ð Ø Ù Ö Ñ ÒÝØ ÞÒ Ð Ø Ù Ðº Øò ÓÖÑ Ø ½º½ Ö Þ Ö ÒØ Ò Ú Þ Ñ ÒØ Ø Ð Ð ØÒ ÐØ Ø Ð Þ º ØòÖ ÚÓÒ Ø ÓÞ ÐØ Ø Ð Þ Ð Ø Ø Ò ÐÝ ÒÚ Ð Ú ÞÓÒØ Ñ ÒØ Ò Ý Ó Ö Ú ÐØÓ¹ Þ ØÓ Ú ØØ ÖÚ ÒÝ Ø Ú ÞØ º ËÞ ÑÐ ÐØ Ø Ø ½º¾ Ö Ò Ð Ø Ð ØÒ º ÁÐÝ Ò Ø Ò Ô Ø ÖØ Ñ ÒØ Ö Ð Ñ ÒØ Ö Ú ÐØÓÞ ÐÐ Ò ÐÝ ØØ Ñ Ö Ø Þ ÒØ Ø Ö Ð º Þ Ò Þ Þ Ð Ô Ø ÒÙÑ Ö Ù Þ ÑÙÐ Ú Ð Ð Ø º ÔÖÓ Ð Ñ ÞÞ Ð Ó Ý Þ Ò Þ ÑÙÐ Ø Ñ Ò Ò Ý Ñ Ö ÔÓÒØ Ò Ð ÐÐ Ú ÞÒ Ñ Ò Ú Ø Ð Þ ÑÙÐØ ÔÖÓ ÞÓÖÓ ÖÒÝ Þ Ø Ò Ð Ø Ð Ó Ø Ð Øغ ¾
9 µ ½º Ô ÐÐ Ò Ø µ º Ô ÐÐ Ò Ø µ ¾º Ô ÐÐ Ò Ø ½º¾º Ö º Ñ Ø Ö Ô Ú ÐØÓÞ Ñ Ó Ñ Ö ÓÖ Ò Ü ÔÓÞ Øò Ø Òº
10
11 ¾º Þ Ø Ð Ø Ñ ÒØ Ý Ñ Þ ØØ Ð Ð Ø Ñ Ò Ñ Ø Ö Ô Ø Ñ Ö Ö Ñ ÒÝ ÒØ ÓØØ ÔÓÒØÓ Ð Ñ Ö º Ñ Ñ Ö Ý Ò ÝÞ Ø Ð Ð ØØ Ø ÖØ ÒØ Ñ ÐÝÒ Ñ Ò Ø Ö ÒÝ Ò δ x = δ y 120nm ÞÓÒÓ Ð ÓÒØ Ñ ¹ Ñ Ö Ð ÔÓÒØÓ δ z 2nm ÚÓÐغ Ø ÐØ òöò Ñ Ö Þ Þ Ñ Ó Ô ÞØ Þ ÓÖ Ò ØòØ Ñ ÒØ ÓÞ Ô Ø V tu = 500mV ÔÓØ Ò ÐÖ Ô Óй Ù º ÁÐÐ ØÚ Ñ Þ ØØ Ð Ð ØØ Ð Þ Ð ÞÓÒÓ Ø ÚÓÐ Ö Ö Þ Ø Ø ØòÖ Ø Ö Ø Ñ Ö º ÓÐ ÓÞ Ø Ò Ð ÞÒ ÐØ Ñ Ø Ö Ô¹Ñ Ö Ö Ñ ÒÝ º½º Ö µ Ý Ñ Ö Øò Þ Ö ÖÒÝ Ð ØÓ ºØ ÐÐÓÑ ÒÝ Ñ ÐÝ ÖØ 0 255¹ Ø Ö º Ñ Ö ¹ Ö Ò Þ ØÐ Ô Ð Ô Ò Ñ Ö Ú Ò Ñ Ð Ò Ø ØØ ÓÒ Ø Ò Ó Ð Ð Ø Ô Ð Þ º 6 x y [nm] y [nm] x x [nm] x x [nm] x µ Å Ö Ö Ñ ÒÝ µ Å Ö Ö ÞÐ Ø ¾º½º Ö º Å Ö Ð ÔÓØØ Ñ Ø Ö Ôº Ð ÓÒØ d x = d y = 120nm d z = 18.03nm
12 ÓÐ ÓÞ Ø Ð ÙÐ Ý ÓÐÝ Ò Þ ÑÙÐ ØÓÖ Ô Ø Ø ØòÞØ Ñ Ñ ÐÝ Ø Ú Ð ¹ Þ Ð Ú Ð Ò Ð Ø Ñ Ö Ð Ô Ò Ð Ð Ø Ø ÐØ ÐÓ ÞÐ Ö Ð Ñ Ö Þ Þ ÔÓÒØÓ Ò Ð ÒÓÑ Ð ÓÒØ Ø Ð ÖÒ º ¾º½º Þ ÔÖÓ Ð Ñ Ñ Ø Ñ Ø ÓÖÑ Ð Þ Ð Ñ ÓÐ Ò Ð Ø Ý Ð ØÖÓ ÞØ Ø Ù Ð Øº Ñ ÒØ Øò Þ ØØ Ø Ö Ò Ò Ò Ò Ø ÐØ Ý ØØ ÈÓ ÓÒ Ý ÒÐ Ø ÐÝ ØØ Ä ÔÐ ¹ Ý ÒÐ Ø ¾º½ ÖÚ ÒÝ º V(x,y,z) = 0 ¾º½µ Þ Ý ÒÐ Ø Ø Ú Ø Þ Ö Þ Ò ¾º¾µ Ñ ÖØ Ø ØØ Ñ ÓÒØÓÐ Ó Ú ØØ Ý Ö ¹ Ù ÐØ ¹ Ø Ö Ó Ø Ò ÓÐ ÓÑ Ñ º Þ Ò ¹ Ø Ö Ó ØÖ Ý Ò ÓÑÓ Ò ÔÓÒØ ¹ Ð Ø ÐÐ ÞØ Ñ ÐÝÒ Ú Þ Þ ÒØ Ò d ax = d ay Ð Ò d z Ð ÓÒØ Ñ ÞÒ ÐØ Å ÔÔ Ö ØÙ Ð ÓÒØ Ú Ð d z = δ z Ý Þ Ñ º Þ Ý ÔÓØØ Ø Ö Ð Ð Ñ Ò Ò ÔÓÒØ ÓÞ ÓÞÞ Ö Ò Ð Þ V i,j,k V(id x,jd y,kd z ) ÔÓØ Ò Ðغ ¹ Ö Ð Ø Ô Ö Ñ ÐØ Ø Ð Ñ ÒØ Ð Ð Ø Ñ Þ Ñ ÐÝ Þ ÖÙ ÔÓØ Ò Ð Þ ÓØØ V tu = 500mV µ ÔÓØ Ò Ð Øò Ñ Ð Ð Ø º Ø ÖÒ Ñ ÒØ Øò Ð Ð Ø Ø Ð Ð Ò Þ Ø Ö Ð Ð Ø Ò ÓÑÓ Ò Æ ÙÑ ÒÒ ÐØ Ø ÐØ Ð ÐÑ ÞÓ Þ Ð ÒÝ ÓÐ Ó Ú Ø Ð Ò Ø Öµ Ø ÐØ Ñ ÒØ Ñ Øغ Þ Ý Ð Ò Ö Ý ÒÐ ØÖ Ò Þ Ö Ñ ÓÐ Ö Ð Ø Ö Ø Ø Ö Ø Ú Ñ ÓÐ Ð ÓÖ ØÑÙ Ó Ø Ð ÐÑ ÞÒ º Ô Ö ÙÞ ÑÓ Ø Þ Ò Ó Ñ ØØ Þ Ø Ö Ø Ú Ñ ÓÐ Ø Ú Ð ÞØÓØØ Ñ Ñ Ú Ð Ú Ñ Ñ Ö ÒÝ º ÓÖ Ò Ñ Ø Ð Ò ÔÓÒ¹ ØÓ Ñ ÓÐ Ø ÔÙÒ Ð Ó Ø Ö Ñ ÒÝ Þ ÙØÙÒ º Þ Ñ Ø ÔÓÒØÓ Ò Ú Ð Ø Þ Ø Ö Ø Ð ÐÐ Ø ÓÒÚ Ö Ò Ú Ø ÐÑ ÒÝ Ñ ÒÝ Ñ Þ Ú Ð Ñ Ô Ö Þ Ø Ø Ö Ø Ð Òغ Þ Ø Ö Ø Ú Ñ ÓÐ ÓÖ Ò Ñ ÓÐ ØÙ Ð ÖØ Ò Þ Ñ Ø ÓÞ Þ Ð Þ Ñ ÓÐ Ð Ò ÙÐÙÒ º ¾º½µ Ý ÒÐ Ø Ò Þ Ö ÔÐ Ö Ú Ð Ø Þ Ð Ö Ò ò Ì ÝÐÓÖ Þ Ð Ø Ð ÐÑ Þ Ú Ð ¾º¾µ Þ Ö ÒØ ¹ÔÓÒØÓ Ñ Ø Ô Ù º ) V n+1 ijk = 1 (V i 1,j,k n +Vn i+1,j,k +Vn i,j 1,k +Vn i,j+1,k + 2 (V i,j,k 1 i,j,k+1) n +Vn ¾º¾µ ÓÐ Vi,j,k n Þ Þ n¹ Ø Ö Ð Ô Ò Þ i,j,k Ò Üò ÔÓÒØ Ò Ñ Ö Ø ÔÓØ Ò ÐØ Ð Ð 1 Ú Þ Þ ÒØ Ð ÓÒØ Ð 2 Ð Ð ÓÒØ Ð ÐÐ Ò º
13 ¾º¾º ËÞ ÑÙÐ Ð Ò Ø Ö Ó Ø ¾º¾º½º ËÞ ÑÙÐ Ð Ò Ø Ö Ó Ø Ð Ô Ð Ð ØÑ Ö ÓÖ Ò Ñ ÒØ ¹Øò Ø ÚÓÐ Ú Ð Ñ Ö ÔÓÒØÓ Ú Þ Þ ÒØ Ø ÚÓÐ Ò Ð Ð Ð Ø Ð ½º½ º Ö Òµº D = [5,50] nm δ x = δ y = 120nm ¾º µ ÓÙÐÓÑ ¹ Ð Ò Ø Ø ÚÓÐ Ò ÝÞ Ø Ú Ð ÓÖ ØÓØØ Ò Ö ÒÝÓ Ý Þ Ð ÑÐ Ø ØØ ÖØ ÐÑ Ò Ý Ñ Ö ÔÓÒØ Ò ÒÝ ÞÓÑ Þ ÔÓÒØÓ Ò Ñ Ö ÔÓÒØ Ý Ö Ù ÐØ ÖÒÝ Þ Ø Ø Þ Þ ÑÙÐ ÐÒ º À Þ Ò ÞÓÒ Ú Ð Ñ Ö Ð ÒÝ ¹ ÓÐ Ø Ú ÐÐ ÑÓ Ø Ö Ö º Å ÔÔ Ò Ñ Ó ÐÑ ÞÚ Ú Þ Þ ÒØ Ñ Ö ÔÓÒØÓ Ø ÚÓÐ Ú Ð Ò ÝÓ Ñ ÒØ ÓÙÐÓÑ ¹ Ð Ò Ø Ø Ú Ø ÚÓÐ µº Ø Ô Ù Å Øò Ø Ö Ø Å ÌÄ È ÖØ Ð Ö ÒØ Ð ÕÙ Ø ÓÒ ÌÓÓÐ Óܹ Ð Þ ÑÙÐ ÐØ Ñº Þ ÑÙÐ Ø nm¹ Ø Ö Ó ØÓÒ 5000 Ð ÑÑ Ð Ú ÞØ Ñ Øò V tu = 500mV ÔÓØ Ò Ð Ø Òº Ñ ÒØ ¹Øò Ø ÚÓÐ D = 20 nm Øò Ù Ö R = 5 nm Ô Ð ÒÝ Ð Þ Ý Ø ÔÙ Si Ø Ò Θ = 10 Ô Ð ÒÝ Ð Þ Ø ÔÙ Si 3 N 4 Ø Ò Θ = 35 º Þ ÑÙÐ Ö Ñ ÒÝ ¾º¾º Ö Ò Ð Ø Ø º
14 µ R = 5nm Θ = 10 µ R = 5nm Θ = 35 µ R = 5nm Θ = 10 µ R = 5nm Θ = 35 ¾º¾º Ö º Å ÒØ ¹Øò Þ ØØ Ø Ö Ú Ð Ñ Þ ÑÙÐ Ò Ð ÒÝ Ö ÞÐ Ø Þ ÑÙÐ Ø Ö Ó Ø Ñ Ø ÖÓÞ ÓÞº Ð ÓÐ Ð Ó ÞÐÓÔ Ò ÔÓØ Ò Ð ÐÓ ÞÐ Ð Ø Ø V ¹ Ò Ñ ÖÚ Ó ÓÐ ÐØ Ú ÐÐ ÑÓ Ø Ö Ö Ò Ý V/nm Ñ ÖÚ º
15 E [V/nm] E [V/nm] x [nm] µ R = 5nm Θ = 10 E(x = 120) = E max x [nm] µ R = 5nm Θ = 35 E(x = 120) = E max ¾º º Ö º Î ÐÐ ÑÓ Ø Ö Ö Ò Ý Ð Ð ØØ Ð 1 nm¹ö º ¾º¾ ¾º º Ö ÓÒ Ñ Ý Ð Ø Ó Ý Ú ÐÐ ÑÓ Ø Ö ¹ Ù Ö Ú Ö Ð ÓÒ ÒØÖ Ð Ú Ø Þ Ñ Ö ÔÓÒØÖ 120 nm¹ö µ Ñ Ö Ð ÒÝ ÓÐ Ø Ò Ý¹ < 15%µ Ð Þº ÒÒ Ñ Ð Ð Ò Ý Ñ ÖØ ÔÓÒØ 3 3¹ Þ Þ ( nm 2 )¹ Ð ÔØ Ö Ð Øò Ø Ö Ó ØÓØ Þ Þ ÑÙÐ ÐÒ º ÞÞ Ð Þ Ð ÒÝ ÓÐ Ð Ð Ø Ñ Ö ÒÙÑ Ö Ù Ò Þ Ð Ø Ñ Ö ØòÖ Òº ¾º¾º¾º ËÞ ÑÙÐ Ð Ò Ø Ö Ó Ø Ð Ô Ò ÒØ ÖÔÓÐ Ø Ö Ó ØÖ ÐÐ Þ Ò ÓÑÓ Ò ÔÓÒØ Ð Ð Ð ÓÒØ ÐÐ Þ Þ Å Ð ÓÒØ Ö d z = δ z = 2nmµº ÔÓÒØ Ð Ð Ô ÓÖ Ò ÑÐ Ø ØØ Þ Ö ÒØ 3 3 ÔÓÒØ Ð ÐÐÒ º Ø Ö Ó Ø ÔÓÒØ Ð Ò Ý Ö Ò Ò ÓÑÓ Ò Ð ÒÒ Ñ ÓÒÚ Ö Ò¹ Ø Ð Ø Ò Ì ÝÐÓÖ ÓÖÓ Þ Ð Ø ÓÖ Ò Ò Ñ Ð Ö Ò ò Ø Ó ÓÞÒ º Å Ú Ð 3 3 ÔÓÒØÓ Ö Ý Ø ÒØ Ø Ò Ñ ÒØ Ñ ÒØ Ñ ¹ Ú ÒÝ Ò Ñ ÒØ Ú Ø Ð Þ Ú Ð ÔÓØØ Ñ ÒØ Ö Ý Þ ÔÓÒØÓ Ø ÒØ ÖÔÓÐ Ú Ð Ð Ò ¹ Ö ÒØ ÖÔÓÐ Ú Ð ÐÙÐ Ø Ö ÞØ Ð ÑÓÞ ØÐ ÓРе Ð Ø ÐÒ º Þ Ú Þ Þ ÒØ Ð ÓÒØ δ x = δ y = 120 nm ÚÓÐØ ÞØ N ip ÔÓÒØÖ ÒØ ÖÔÓÐ ÐÓѺ ÞÞ Ð Ñ Ø Ö Ú Þ Þ ÒØ Ð ÓÒØ Ú Ø Þ Ö òöò Øغ d ax = d ay = N ip ¾º µ Þ ÒØ ÖÔÓÐ Ó Ð Ò N ip = 180 Ø Ò Ð ÒÒ Ú ÞÓÒØ Ò º¾ Ö Þµ Ñ ÖØ Ø ØØ Ñ ÓÒØÓÐ Ó Ú ØØ N ip = 31¹Ö Ú Ð ÞØÓÑ Ñ º ÓÖ d ax = d ay = nm Ð Þº
16 ¾º¾º º ËÞ ÑÙÐ Ð Ò Ø Ö Ó Ø Ñ Þ ÑÙÐ Ð Ò Ø Ö µ Ð Ô ÓØØ Þ Ð Þ Ð ÑÐ Ø ØØ ÒØ ÖÔÓÐ ÐØ Ð Ð Ø ÒØ Ñ Ñ Ò Ñº ÞØ N h ¹Ò ÐÒ Ú ÞÚ Ú Ø Þ Ø Ñ ÒÒÝ Þ Ð Ò ÝÓ Ð Ø ÖÓÞØ Ñ Ñ Ã Þ Ô ÔÓÒØ Ð ØØ Ð Ú Øò Þ Ô Ò Ñ 3 3µ ÖÒÝ Þ Ø Ð Ð ÓÒÝ Ð Ñ ÔÓÒØ Ò Ð Ò ÓÞ¹ Þ Ú Øò Ñ Ò Ð Øº ¾º º ËÞ ÑÙÐ Ð Ô Ø Ñ Ö ÔÓÒØÓ ÓÞ Ø ÖØÓÞ Þ ÑÙÐ ÓÖ Ò Ð Ð Ø Ñ Ò Ñ Ö Ø Ø Ñ Ö Ñ ÖØÒ ÐØ Ø Ð Þ Ñº Ø Ð Ñ Ø Ö Ô ÔÓÒØ Ø Ð Ò¹ Ð Ò Ú Þ Ð Ù º Ý ØÐ Ò ÔÓÒØ Ò Ñ Ö Ö Ñ ÒÝ Þ Ñ Ø Ò Ð Ô Þ Ð ½º Ñ Ö ÔÓÒØ Ö Ð 3 3¹ Ð Ð Ø Ö Þ Ò Ñ ÐÐ Ô Ø ¾º Þ Ñ Ø Ö µ Ñ Ö ÔÓÒØÓ ÒØ ÖÔÓÐ Ú Ð Ø ÖØ Ò Ò Ö Ð Ð¹ ÓÒØ Ò Ú Ð Ú ØØ º Þ ÑÙÐ Ð Ò Ø Ö Ó Ø Ñ Ö Ø Ò Þ Ñ Ø º Ö Ø» Ø Ö Ø Ú Ñ ÓÐ Ð ÓÖ ØÑÙ Ð Ø Ö Ñ Ø ÖÓÞ ØòÖ Ø Ö Þ Ñ Ø ÐÐ ØÚ Øò Ð ØØ Ø ÐØ Ñ ÒÒÝ Þ Ñ Ø º ØÓ ÜÔÓÖØ Ð º ½¼
17 º Þ Ø ÑÙÐØ ÔÖÓ ÞÓÖÓ ÇÔ Ò Ä ÖÒÝ Þ Ø º½º ÇÔ Ò Ä Ö Ø Ø Ö Þ ÇÔ Ò ÓÑÔÙØ Ò Ä Ò Ù ÇÔ Ò Äµ Ö ØÖ Ò Þ Ö ÐØ Ð ÒÓ ÑÓ ÐÐØ Ñ Þ ÒØò ÔÖÓ Ö ÑÓÞ ÒØ Ö ÞØ Ö Û Ö ÞØÖ Ø ÒÝ Ø Ð ÞØ Ò Ø¹ Ú Ý Ð Ø¹Ô Ö ÙÞ ÑÓ Þ Ñ Ø Ó ÝÓÖ Ø Ö Ð Ò Þ Þ Ñ Ø Ý Ò ÈÍ ÈÍ ËÈ È º º º µº Ö Ú Ö Ý ÖØ ÑÔÐ Ñ ÒØ Ð Þ ÇÔ Ò Ä Þ Ú ÒÝ Ò ÖØ Ø Ñ ÐØ Ð Ø ÔÐ Ø ÓÖÑÓØ ÓÞÒ Ð ØÖ º Ý ÐÝ Ò ÔÐ Ø ÓÖÑÓÒ Ð Ð Þ Þ Ð ØØ ÓÖ Ò ÑÐ Ø ØØ Þ Ñ Ø Ý Ø ÖØ º ÇÔ Ò Ä Ö ØÖ Ò Þ Ö Ò Ø Ö¹ Ø Ò ÔÖÓ Ö ÑÓÞ ÓÖ Ò Ø ÔÖÓ Ö ÑÓØ ÐÐ ÖÒ Þ Ý ÖÒ Ð Ñ Þ Þ Þ Ò Ú ¹ÓÒµ ÙØ ØÓØØ Þ ÐÖ Ó Ð Ô Þ Ò º Ñ Þ ÔÖÓ ÞÓÖÓÒ Ó Ø¹ ÓÒµ ÙØ Ó Ø¹ÔÖÓ Ö Ñ Ñ ÐÚ Þ Þ Á»Ç ÑòÚ Ð Ø Ø ÔÖÓ Ð Ñ Þ ÐÐ Ø Ø Ñ Ñ Ö ÐÐÓ Ð Ø Þ ÐÐÓ ÐØ Ø Ö Ð Ø Ò Ð Þ Ð Ø ÖÒ Ð Ö ÙÑ ÒØÙÑ Ò ÐÐ Ø Ø ÐÐ ØÚ ÖÒ Ð Ñ Ú Ø Þ Þ Þ Òº ÖÒ Ð ÙØ Ú ÞØ Ú Ð Ó Ø¹ÔÖÓ Ö Ñ ÓÐÚ Þ Þ Þ Ð Ú ÒØ Ö Ñ ÒÝغ Þ Þ Þ ÑÙÐØ ÔÖÓ ÞÓÖÓ Ö Ø Ø Ö Ú Ð Þ ÞÓÐ Ð Ö Ô Ñ Ñ Ö Ö Ø Ø Ö Ú Ð Ö Ò Ð ÞÒ º Þ Ö Ø Ø Ö Ø ÖÓ Ò Ú Ð Þ Ð Ö º½º Ö Ò Ú ÞÓÐØ ÑÓ ÐÐ Ø ÒÝ Ø º Ý Þ Þ Ø ÓÑÔÙØ ÙÒ Ø¹ÓØ ÔÖÓ ÞÓÖ¹ Ñ Óص Ø ÖØ ÐÑ Þ Ø Ñ Þ ÐÓ Ð Ñ Ñ Ö Ø ÖØÓÞ Ð Ö Ú Ò Þ Þ Þ ÐÓ Ð Ñ Ñ Ö ÓÞº ½½
18 º½º Ö º ÇÔ Ò Ä Ú Ö Ø Ø Ö ÓÖÖ µ º¾º ÇÔ Ò Ä ÔÖÓ Ö ÑÓÞ ÑÓ ÐÐ ÔÖÓ Ö ÑÓÞ ÑÓ ÐÐ ÓÞÞ Ø ÖØÓÞ Ó ÞØ ÐÝ Ö ÑÑÓÒ º¾º Ö µ Ý Ð Ø Ñ º º¾º Ö º ÇÔ Ò Ä ÓÒØ ÜØ Ó ÞØ ÐÝ Ö ÑÑ ÓÖÖ µ ÙØØ Ø ÓÞ Þ Ó Ý ÓÒØ ÜØÙ ÓÞ ÔÐ Ø ÓÖÑÓØ Ñ ÞÓÒ Ð Ð Þ ÞØ Þ Þ Þ Þ ÔÖÓ Ö ÑÓØ ÖÒ Ðص Ñ Ñ Ö Ø Ö Ò Ð Ò º Ý Ð Ñ ÐÐ Ú ÒÒ Ò ÞØ Ñ Ø Ø Ó Ý Ý Þ ÖÖ Þ Ý ÔÐ Ø ÓÖÑÓÒ Ð Ð Þ Þ ÔÖÓ Ö ÑÓÞ Ø Ø ÖÓ Ò Ñ ÓÒº È Ð ÙÐ ÁÒØ Ð ÔÐ Ø ÓÖÑ Ø Ò Ð Ø È͹ Ø ÔÖÓ ÞÓÖ ÖØÝ Ø ÁÒØ Ð¹ ÈÍ¹Ø ÔÖÓ Ö ÑÓÞÒ Ú ÞÓÒØ ÒÎ ÖØÝ Ø Ñ Ö Ò Ñº ÔÖÓ Ö ÑÓÞ Ð Ñ ÓÐ Ò ÔÖÓ Ð Ñ Ø Ø Ð ÔÔ Ò Ð Ø Ð ÓÐ ÓÞ Ý Þ ÛÓÖ ¹ Ø Ñµ Ú Ý ÔÖÓ ÞÓÖÓ ÓÞ Ö Ò ÐÒ Ø Ô Ö ÐÐ Ð Ñ ÓÒ Ú Ý Ø Þ Ô Ö ÐÐ Ð Ñ ÓÒº ½¾
19 Ø Ô Ö ÐÐ Ð Ñ ÓÒ º º Ö µ Ð ÓÐ ÓÞ Ò Ø Ý Ö Þ Þ Ö Ò Ð Ò Ý Ð ÓÐ ÓÞ Ý Øº ÓÒØÓ Ý Ð Ñ Ú ÒÒ Þ Þ Þ ÓÖÐ ØÓ Þ Ñ Ð ÓÐ ÓÞ Ý Ò Þ Ñ Øº À Ò Ñ Ð Ð ÓÐ ÓÞ Ý ÓÖ Ð Ø Ñ Ð Ð Ô ÖØ ÓÒ Ð Ú Ð Ð Ø ÓÖ Ò Ø ÖØ Ò Þ Ö ÓÖÖ Þ Ñ Øº Ì Þ Ô Ö ÐÐ Ð Ñ ÓØ º º Ö µ ÓÐÝ Ò Ø Ò Ð Þ Öò ÞÒ ÐÒ ¹ Ñ Ò Ø Ò Ñ Ù Ñ Ö Ø ÙØ Ò Ö Ò Ú Ð Ú ÐØÓÞ ÐÐ ØÚ Ú Ö Ø Ò Ð Ø Ð Þ Ò Ò Þ º µ Ø Ô Ö ÐÐ Ð µ Ì Þ Ô Ö ÐÐ Ð º º Ö º Ð Ø ÓÞÞ Ö Ò Ð ÛÓÖ ¹ Ø Ñ¹ Þ ÔÖÓ ÞÓÖ ÓÞµ ÔÖÓ ÞÓÖ¹Ñ Ó Ñ Ð Ð ÞÒ ÐØ Ò Ð Ö Ú ØØ Ø Þ Ö ÛÓÖ ¹ Ø Ñ Ú ÖØÙ Ð Ò Ó ÞØÓÞ Ö Ø º Þ Ò ÛÓÖ ¹ Ø Ñ¹ Ø ÛÓÖ ¹ ÖÓÙÔ¹Ó Ö Ò ÞÞ ÒÒ Ð Ô Ö ÙÞ ÑÓ Ö Ø Ø Ö Ë Ò Ð ÁÒ ØÙØ ÓÒ ÅÙÐØ ÔÐ Ø ËÁÅ µ Ô Ò ÞÓ ØÚ Ö Ò Þ º Þ ÁÒØ Ð ÓÒ È ÔÖÓ ÞÓÖ ÖØÝ ÖÖ Ö ¹ Ú Ö Ø ÑÓ Ø Ø Ú ØÓÖÓ ØØ ÔÙ Ú Ð ÒÝ Øº ÛÓÖ ¹ Ø Ñ Ø Ð Ò Ô ÐÐ Ò Ø Ò Þ ÇÔ Ò Ä Ô Þ Ö ÒØ 3 Ñ ÒÞ ÛÓÖ ¹ ÖÓÙÔ¹ ØÙ Ù Ö Ò ÞÒ º Ý Ô Ð Ø Ð Ø ØÙÒ Ý ÛÓÖ ¹ Ø Ñ Ò Ü Ò ÐÓ Ð ÐÓ Ð Ñ Ð Ð Ö Ú Ø Þ º º Ö Òº º º Ö º ¾ ¹ ÛÓÖ ¹ Ø Ñ¹ ÛÓÖ ¹ ÖÓÙÔ¹ Ö Ò Þ Ò Ü Ð ÓÖÖ µ ½
20 Þ ÇÔ Ò Ä Þ Ð Ð ØÓØØ Ñ Ñ Ö Ø Ò Ý Ø Ö ÓÖÓÐ Ø Ô ¹ Ù Ñ Ñ Ö Ø ÓÖ Þ Ð Ú Ø Þ Ê ÞØ Ö ÈÖ Ú Ø Ñ ÑÓÖÝ Ô Ò Ð Ð Ñ Ñ Ö µ ÄÓ Ð Ñ ÑÓÖÝ Ô Ò Ú Ð Ñ Ñ Ö ÐÓ Ð Ñ ÑÓÖÝ ÓÒ Ø ÒØ Å ÑÓÖݺ ÔÖ Ú Ø ÐÓ Ð Ñ Ñ Ö Ñ Ö ØòÒ ÝÓÖ Ð Ö òò ÑÓÒ Ø Ñ ÐÓ Ð ÓÒ Ø Ò Ñ Ñ Ö Ò ÝÒ Ð Ð Ö òò º Ò ÐØ Ñ Ñ Ö Þ ÒØ Ø Ô Ù Ô Ö Ñ Ø Ö Ú Ø Þ ÈÖ Ú Ø Ñ Ñ Ö Ñ Ò Ò Þ ÐÒ Ð Ò Ú Ò Ñ Ø ÓÑÔ Ð Ö Ñ Ò Þ Ðº ÐÓ Ð ÓÒ Ø Ò Ñ Ñ Ö Ò Þ ÖÚ Þ ÐÐ ÑÞ Ö ÝÓÖ Ò Ý ¹ Ð ÐØ Ø Ð Öº ÑòÚ Ð Ø Ø ØÙ Ý ÐÙ Ð ØØ Ú Ö Ø Ò Ô Ö Ò ÙØ Ò ¼¼¹ ¼¼ ÐÙ Ð ÐØ Ø Ðº À Þ ØÓÒ Ú Ö Ø Ò ÑòÚ ¹ Ð Ø ÒÒ Ð Ú Ð Ò ÝÓ ÓÖ ÞØ Ð ÐØ Ø Ø Ð Ð Ø Ö Ø Ò º ÄÓ Ð Ñ Ñ Ö Å Ò Ò ÛÓÖ ¹ ÖÓÙÔ¹Ò Ø Ú Òº Å Ò Ñ Ð Ð Ø Ø Ò Ý ¹» µº ÀÓ Ø Ñ Ñ Ö Æ Ý Ñ Ö Øò Þ Ô ò Ø Ó Ø¹ÓØ Ú ¹Ø Þ Ø È Á ÒØ Ö Þ ÓÖÐ ØÓÞÞ º Ñ Ñ Ö Ö Ñ Ø ÒØ ÞÓÐ Ð Ó Ý ÐÐÓ Ð Ø Ö Ø ÓÐÚ Ø Ð Ð º º½º Ø Ð Þ Ø Ò Ð Ø Ø Þ Ò Ó Ó ÙÐØ Ó Ø ØÙÐ ÓÒ Ó Øº º½º Ø Ð Þ Øº ÇÔ Ò Ä Ñ Ñ Ö Þ ÒØ ÀÓ Ø Ñ ÑÓÖÝ ÐÓ Ð Ñ ÑÓÖÝ ÄÓ Ð Ñ Ñº ÈÖ Ú Ø Ñ Ñº ÀÓ Ø Ò Ñ Ù Ò Ê»Ï Òº Ê»Ï Òº Ê»Ï ¹ à ÖÒ Ð ¹ Ê»Ï Ë Ø º Ê»Ï ËØ Ø º Ê»Ï Ë Ä Ã Þ Ô ÝÓÖ Ê ÞØ Ö Å Ö Ø ,32 à < 1 à ÛÓÖ ¹ ÖÓÙÔ¹Ó Ö Ò Þ ÐÓ Ð Ñ Ñ Ö Ó Ù ÙÐØ Ñ ØØ Ö º ÃÓÒ Ö Ø Ò Þ Ý ÛÓÖ ¹ ÖÓÙÔ¹ Ø ÖØÓÞ Þ ÛÓÖ ¹ Ø Ñ ÞÓÒÓ ÐÓ Ð Ñ Ñ Ö Ò Ó ÞØÓÞ º ÒÒ Ú Ø ÞÑ ÒÝ Þ Ó Ý Ø Ô Ö ÐÐ Ð Ñ Ð ÓÐ ÓÞ Ø Ò Þ ÝÑ Ö Ø ØÓ ÓÞ Ø ÖØÓÞ ÛÓÖ ¹ Ø Ñ¹ Ø Ý ÛÓÖ ÖÓÙÔ ÐÐ Ö Ò ÐÒ Ò º À Þ Ò Ñ Ð Ø ÓÖ ÐÓ Ð Ñ Ñ Ö ÓÞ ÐÐ ÓÖ ÙÐÒÙÒ º ÐÓ Ð Ñ ¹ Ñ Ö Ú Ý Ò Þ ÖÚ Þ ò Ð Ó ¹ Ôµ Ñ Ñ Ö ÓÞÞ Ö Ö Ð Ø Ú ½
21 Ò Ý Ý Þ ÞÒ Ð Ø Ø Ð Ø Ð Ð ÐÐ Ö ÐÒ ÔÖÓ Ö ÑÓÞ Ò ÐÐ ÐÒ ÐÓ Ð Ñ Ñ Ö º Å Ú Ð ÛÓÖ ¹ Ø Ñ¹ ÓÒ ÙÖÖ Ò Ò Ø Ò Ú Ö Ý Þ ÐØ ÐÙ Þ Ò Ð Ö Ø Ñ Ñ Ö Ö ÐÓ Ð ÐÓ Ð µ Ò ÞÚ Ú Ö ÒÝ ÐÝÞ Ø Ò Ú ÒÒ º Þ ÇÔ Ò Ä ÞØ ÔÖÓ Ð Ñ Ø Ð Þ Ñ Ñ Ö ÑÓ ÐÐ ÞÒ Ð Ø Ú Ð ÓÐ Ñ º ÏÓÖ ¹ Ø Ñ¹ Þ Ø¹ Ø Þ Ò ÖÓÒ Þ Ö Ý ÓÖÐ ØÓØ Ð ÐÑ Þ ÔÖÓ Ö Ñ Ò Ñ Ø ÓÖ Ð Ô Ø Ø Þ Þ Ø ÛÓÖ ¹ Ø Ñ Þ ÞÓÒÓ ÛÓÖ ¹ ÖÓÙÔ¹ Òµ ÞØ ÓÖÐ ØÓØ Ñ Ö Ð ÖØ º ÖÖ ÖÖ Ö Ä µ Ú ÒÝ Ú ÞÓРк ÓÒØÓ Ñ Ý ÞÒ Ó Ý Þ Þ Ò ¹ ÖÓÒ Þ Ý ÓØØ ÛÓÖ ¹ ÖÓÙÔ¹ÓÒ Ð Ð Ø ÖØ Ò ÛÓÖ ¹ ÖÓÙÔ¹Ó Þ ØØ Ð Ò Þ ÛÓÖ ¹ ÖÓÙÔ¹Ó ÓÒ Ð Ð ÛÓÖ ¹ Ø Ñ¹ Þ Ò ÖÓÒ Þ Ö Ò Ò Ð Ø º Þ Ó Ð ÐÚ Ò Ý Ò ÐÝØ ÐÐ Ñ Ñ Ö Þ ÖÚ Þ Ö ÓÖ Ø Ò Ó Ý ÔÖÓ ÞÓÖÑ Ó Ñ Ð Ð Ò Ð Ý Ò Þ ØÓ Ð Ø ÔÐ ÐÚ Þ Ð Ö Ø Þ Ñ Ø Ô Ø Ò Þ Ú Øغ ½
22 ½
23 º Þ Ø ÅÙÐØ ÔÖÓ ÞÓÖÓ ÔÖÓ Ö Ñ ÔÖÓØÓØ ÔÙ Ð ÓÖ ØÑÙ Ð ÞØ Å ÌÄ ÖÒÝ Þ Ø Ò Ø ÖØ ÒØ Ñ Ö Ö Ò ÒØ ÞÓРк Ð Ô ÙØ Ø Ó Ø ÞÒ ÐÚ Ø Ö Ø Ú Þ ÒÝ Þ ÑÙ¹ Ð ÙØØ Ø º Å ÌÄ È Ö ÐÐ Ð ÌÓÓÐ ÓÜ¹Ò Ø Ú Ð Þ ÑÙÐ Ø Ð Ø ¹ Ô Ö ÙÞ ÑÓ Ò Ø ÔÖÓ ÞÓÖÑ ÓÒ ÙØØ ØÒ º ÞÞ Ð ÙÔ Ò Ô Ö ÞÓÖÓ Ò Ú Þ Ö Ø Ð Å ÌÄ Ñ Þ ÒØò ÔÖÓ Ö ÑÒÝ ÐÚ Ú Øغ Ú Ø Þ ¹ Ò Ñ Ø Þ Ð ÓÖ ØÑÙ Ø Þ ÇÔ Ò Ä Ö ØÖ Ò Þ Ö Ò Ø ÖØ Ò ÑÔÐ Ñ ÒØ Ø ÑÙØ ØÓÑ º Å Þ Ö Ñ ÒÝ ÑÙØ Ø ÓÖ Ò Þ Ú Ø Ö Ö Ð Å ÌÄ È Ö ÐÐ Ð ÌÓÓÐ ÓÜ Ø Ð Þ ÇÔ Ò Ä ÈÍ¹Ò Ú Ð ÙØ º º½º ÙØ ÖÒÝ Þ Ø ÑÙØ Ø Ú Ø Þ Þ Þ Ø Ð ØÑ ÒÝ Ø Ú Þ ÐÓÑ Ð ÔØÓÔÓÑ Ò Ø Ð Ð Ø ÁÒØ Ð ÓÖ Å ¾¼ ÔÖÓ ÞÓÖ Ð ÔØÓÔÓÑ Ò Ø Ð Ð Ø Ø Ð ØÑ ÒÝòµ ÒÎ Ì ¼Å Ú ÖØÝ Þ Ò Þ Þ Ð Ð ÒØ Ô Ö Ñ Ø Ö º½ Ø Ð Þ Ø Ø ÖØ ÐÑ ÞÞ º ½
24 º½º Ø Ð Þ Øº Î Þ ÐØ Þ Þ Þ ÓÒÐ Ø ÁÒØ Ð ÓÖ Å ¾¼ ÒÎ Ì ¼Å Å ÇÅÈÍÌ ÍÆÁÌË 4 6 Å ÄÇ Ã Ê ÉÍ Æ 2400 ÅÀÞ 1265 ÅÀÞ Å ÏÇÊà ÊÇÍÈ ËÁ ÄÇ Ä Å Å ËÁ 4Gb (2Gb) 1Gb (768Mb) ÄÇ Ä Å Å ËÁ 32Kb 16Kb Þ Þ ÓÒÐ Ø Ø Ú ØØ Ð Ñ Ñ Ö Þ ÞÖ Ð ÞÓÑ Þ ÑÙÐ ØÓÖØ Ñ Ì ¼Å Ú ÖØÝ º ÈÍ Ñ Ñ Ö Ú Ð Ò ÝÓ Ý Ñ Ò Ý Ò ØÙ ÙØÒ º º¾º Þ ÑÔÐ Ñ ÒØ ÓÞ Þ Ñ ÓÒØÓÐ Ó À Ø Ö ÓÐ Ð ÔÐ Ý ÒÐ Ø Ø Ñ ÐÐ ÓÐ ÒÙÒ Ò ÝÓÒ Ò Ý ÓÖ Ö ¹ Ñ Þ Ø ÓÒØ Ò ÐØ Ö Ö ÞÓ ÓÞ Ö Ò ÐÒ Ý¹ Ý ÛÓÖ ¹ Ø Ñ¹ غ Å Ú Ð Þ Ö Ø Ä ÔÐ Ý ÒÐ Ø Ý ÔÓÒØ ÞÓÑ Þ Ó ÔÓÒØÓ Ð ÞÓÖÓ Ô ÓÐ Ø Ò Ú Ò Ý Þ Þ ÛÓÖ ¹ Ø Ñ¹ Ø Ý ÛÓÖ ¹ ÖÓÙÔ¹ Ö Ñ Þ ÖÚ ÞÒ Ñ Ú Ð Ý Þ ØÐ ÔÓÐ ÔÓÒØÓ ÖØ Ø ÞÓÑ Þ Ó ÛÓÖ ¹ Ø Ñ¹ ØÙ ÖÒ ÓÐÚ Ò º Þ ÐÝ Ò Ø ÔÙ ÔÖÓ Ð Ñ Ò Ñ Ö Ø Ø Å ÏÇÊà ÊÇÍÈ ËÁ Ë ØÙÐ ÓÒ¹ ÓÖÐ ØÓÞÞ º Â Ð Ò Ø Ò Ñ Ö Ö Ñ ÒÝ Ý ÔÓÒØ ÓÞ Ø ÖØÓÞ Ø Ö ØÐ Ó Ò ÔÓÒØ Ð Ðк Ì Ø ÓÖ Ò Ñ ÐÐ ÒÒ Ý Þ Öò Ñ Ð ÐØ Ø Ð Þ ØÓ Þع Ø Ù Ð ØÓغ Ø Ð Ø Ö Ñ Ö Øò Ñ 951M ÔÓÒغ Ø ÖÓÐ ÓÞ Ò Ð ¹ÔÖ ÓÒ Ñ ÐÐ ØØ ÒÒ Þ ÑÒ ¹ Þ Ö Þ ÐØ Ø ÝØ ¹Ó Ò Ñ ÖÚ º Å Ú Ð Þ Ú ÖØÝ Ò Ò Ñ ÐÐ Ö Ò Ð Þ Ö Ý Þ Ø ÓÒØ Ù Ð ØÖ Þ Ö º Þ Ò Ð ØÖ Þ Ñ Ö Ø Ø Ý Ô Ö Ñ Ø Ö ÐÐ Ø Ú Ð Ð Ø Ú ÐØÓÞØ Ø Þ ÑÔ¹ Ð Ñ ÒØ ÐØ Ð ÓÖ ØÑÙ ØØ Ð Ò Ö Ù Ò º Ñ ÐÐ ØØ Þ ÒØ ÖÔÓÐ Ñ ÖØ N ip Ô Ö Ñ Ø ÖÖ Ð Ò Ö Ù Ò ÐÐ Ø Ø º Þ Ð ÓÖ ØÑÙ Ò Ö Ù Ø ÙÔ Ò ÙØ Ò Ø ÖØ Ò Ò Ñ Ù Ñ Ñ Ö ÐÐÓ Ú Ð Ð Ø Ñ Ú Ð Ø Ò º ÓÖ ¹ Ò ÑÐ Ø ØØ Ú ØØ º½ Ø Ð Þ Øµ Þ ÐÐÓ Ó Ø ÔÖÓ Ö Ñ Ò Ø ÖØ Ò Øº ÒÒ Ñ Ð Ð Ò Þ ÑÙÐ Ð Ò Ø Ö Ó Ø Ò Ý Ø Ð Ö ÐÐ Þ ÑÓÐÒ º ½
25 º º Å Ñ Ö Þ ÖÚ Þ ÐÓ Ð Ñ Ñ Ö ÞÒ Ð Ø Þ Ð ÓÖ ØÑÙ Ô Þ Ù Ò Ö Ø Ð Ô Þ Ø Ò Ó Ø ¹ÓÒ ÐÐÓ ÐÙÒ Ñ ¹ Ñ Ö Ø Ú ÐÓ Ð Ñ Ñ Ö Ò Ñ Ñ Ð Ð ØÓ Ø Ñ ÓÐ Ù ÖÒ Ð ØØ Ö ÓÐÚ º ÔÖÓ Ð Ñ Ø ÐÓ Ð Ñ Ñ Ö Ò Ý ÓÞÞ Ö Ð Ò¹ Ø Ñ Ñ ØØ Ó ÛÓÖ ¹ Ø Ñ ÞÚ Ø ØÐ Ò Ðµ Ñ Ñ Ö Ö Ó Ú Ö ÓÞÒ º ÁÐÝ Ò ÓÖ Þ Ý Ñ Ö ÔÓÒØÖ ÚÓÒ Ø ÓÞØ ØÓØØ Þ ÑÙÐ Ö Ö Ò Ò Ð Ð º ÐÓ Ð Ñ Ñ Ö ÓØØ Ø Ò ÐÓ Ð Ñ Ñ Ö ÞÒ Ð Ø Ã Ö Þ Ø Ð Ò Ý ÚÙÐ Ø Ð Ø Ð ÖÒ Ñ Ö ÔÓÒØ ÓÞ Ø ÖØÓÞ Þ ÑÙÐ ¹ Ø Ö ÔÔ Ò Ð Ö ÐÓ Ð Ñ Ñ Ö º Ì Ø Ñ Ð ØØ Þ ¾º¾µ Þ Ö ÒØ Ø Ö Ø Ú Ñ ÓÐ Ø ÙØØ ØÒ Ò Ð Þ Ö ÐÓ Ð Ñ Ñ Ö Ð ÐÓ Ð Ñ Ñ Ö Ø ÐØ Ø Ö ÔÓÒØÓ Ø Ñ Þ ÑÓÐÙÒ Ö Ø Ú Ò Ú Þ Ø ÐØ ÐÓ Ð Ñ Ñ ¹ Ö º Ú Ø Ð Ö Ö Ò Ú Ð ÞÓÒÓ Ø ØÙ ÙÒ Ð ÖÒ º ÐÓ Ð Ñ Ñ Ö Ñ Ò Ò Ð ÐÓÑ ÓÖ ÐÓ Ð Ñ Ñ Ö ÞÒ ¹ Ð Ø Æ ÝÓ Ö Þ Ø Ø ÒÝ Ð Ó Ý Ñ Ò Ò Ð ÐÓÑÑ Ð ÐÓ Ð Ñ Ñ Ö Ú Ð Ú Ð ÓÑÑÙÒ Ø ÐÓ Ð Ñ Ñ Ö Þ Ð Ú Ð Ø Ý º ÞØ Ý Ð Ø Ð Ó Ò Ñ ÒØ ÐÓ Ð Ñ Ñ Ö Ø ÐÓ Ð Ñ Ñ Ö Ñ Ö Øò Ú ÒØÙÑÓ Ò ØÙ Ò Ñ ÐÒ» Ð ÖÒ º ÓÖ Ò Ý Ó Ý Ð Ø Ú Ò Ñ Ñ Ö ÑÞ Ñ Ð Ð ÔÖ Ö ÑÓ¹ Þ Ö Ñ ÒÝ ÔÔ ÝÓÖ ÙÐ Ö Ø Ðº Þ ÞÚ ÐÑÓÒ Ø Ó Ý Þ ØÙ Ð Ò ÞÒ ÐØ Ø Ø ÖÓÐ Ø Ð Ø Ð Þ Ð ÐÐ Ø ÖØ Ò ÓÑÔÙØ ¹ÙÒ Ø¹ ÓÞº º º Ð Ô Ö ÞÐ Ø Þ º º½º ÁÒØ ÖÔÓÐ ÓÖ Ò ÐÑÓÒ ÓØØ Ð Ô Ò Ð Ð Ø Ø ØÓÚ Ú ÖØÙ Ð ÔÓÒØÓ Ð Þ Ø Ñ º Þ Ú ÖØÙ Ð Ñ Ö ÔÓÒØÓ Ø Ð Ý Þ Öò Ò Ð Ò Ö ÒØ ÖÔÓÐ Ú Ð Ð ÔÓ Þ Ð Ø Ðµ Ð Ø º Þ ÑÙÐ ØÓÖ Ò Ñ Ð ØØ Ñ Ý ÐØ Ð ÒÓ Ñ Þ ÖØ Ð ÐÑ ÞÓ Ñ Ý ¾ ¹ ÑÓÞ ØÐ ÓÐ ÞòÖ Ú Ð Ú Ð Ñ Ø º ÞòÖ Ú Ð ÐÙРع Ö ÞØ Ø Ð Ð Ñ Ñ ÒØ Ñ Ò Ñ ÒØ Ú Ø Ð Þ ÙØ Ò Ö ÓÒ ØÖÙ Ø Ð ÒØ º Ý ÐÝ Ò ÒØ ÖÔÓÐ Ö Ñ ÒÝ Ø Ð Ø Ø Ù º½º Ö Òº ½
26 z [nm] y [nm] x [nm] 1260 º½º Ö º 3 3 Ñ Ö ÔÓÒØ ÔÓÒØ Ú Ð ÒØ ÖÔÓÐ º º¾º ËÞ ÑÙÐ Ð Ò Ø Ö Ó Ø Ñ Ö Ø Ò Þ Ñ Ø Þ ÑÙÐ Ð Ò Ø Ö µ Ð Ô ÓØØ Þ Ð Þ Ð ÑÐ Ø ØØ ÒØ ÖÔÓÐ ÐØ Ð Ð Ø ÒØ Ñ Ñ Ò Ñº ÞØ Ú Ø Þ Ø Ñ ÒÒÝ Þ Ð Ò ÝÓ Ð Ø ¹ ÖÓÞØÙ Ñ Ã Þ Ô ÔÓÒØ Ð ØØ Ð Ú Øò Þ Ô Ò Ñ 3 3µ ÖÒÝ Þ Ø Ð Ð ÓÒÝ Ð Ñ ÔÓÒØ Ò Ð Ò ÓÞ¹ Þ Ú Øò Þ Ô Ò Ñ º Ñ Ø Ö Ô Ý ÚÓÒ Ð Ò Ö ÞÐ Ø Þ ÑÙÐ Ð Ò Ø Ö µ Ñ Ð Ø Ø º¾º Ö Òº º º º ÁØ Ö Ø Ú Ñ ÓÐ Ð ÓÖ ØÑÙ Þ Ø Ö ÓÞ Ø Ö Ð ÔÓÒØ ÓÞ Ø Ñ ØÖ ÜÓØ Ø Ñ Øµ Ö Ò Ð Ñ ÔÓÒØÓ ÔÓØ Ò Ð Ò ØÙ Ð V now µ Ð Þ V prev µ ÖØ Ø Ø ÖØ ÐÑ ÞÞ º Þ Ò Ý Ñ Ö Ø Ú ØØ Þ Þ Þ ÐÓ Ð Ñ Ñ Ö Ò Ó Ð ÐÒ ÐÝ Øº Þ ØÙ Ð ÖØ Ø ¾º¾µ Þ Ö ÒØ Þ Ñ ØÓÑ Þ Þ Ø Ö Ó ØÖ º Þ Ñ ¹ Ø Ø Ú Þ Þ ÒØ ÓÒ ÒØ Ú Þ Ñº Þ Ñ Ø Ð ØØ Þ ÓØØ Þ Ð ØØ Ð ØØ ÞÓÑ Þ Ó Ó Ð Þ ÖØ Ø Ñ ÓÐÓÑ ÐÓ Ð Ñ Ñ Ö º Þ ÖØ Ø Ð Þ Ö ÐÓ Ð Ø Ñ Ø ÖÓÐÓÑ Ð Ñ Ñ ÓÐÓÑ ÐÓ Ð Ñ Ñ Ö º Þ Ò Þ Þ ¾¼
27 Magassagterkep [nm] x 10 4 Magassagterkep Szimulalando ter magassaga x [nm] º¾º Ö º Ñ Ö Ö Ñ ÒÝ Ý ÚÓÒ Ð Ñ ÒØ Ö ÞÐ Ø ÓÐÝØÓÒÓ ÚÓÒ Ðµ Þ Þ Ò Ñ Ö ÔÓÒ¹ ØÓ ÓÞ Þ Ñ ØÓØØ Þ ÑÙÐ Ø Ö Ñ Þ ØÓØعÚÓÒ Ðµ Szimulalando ter magassaga Ø Ö Ó ØÖ Þ Ñ ØÓÑ Þ Ð Þ Ú Ð Ú ØØ Ð Ò Ò Ò ÝÞ Ø Þ Ø ÒÓÖÑ Øµº Ñ ÖØ ÔÚ Ð ÓÒÚ Ö Ò Þ ÒØ Ø Ñ Þ Ø Ö ÓÖ Ò Ú Þ ÐÚ ÙØ Øµ Ð Ú ÒØ ÓÒÚ Ö Ò Þ ÒØÖ º À Ò Ñ ÖØ Ð ÓÒÚ Ö Ò Þ ÒØ Ø ÓÖ Þ Ð Þ Ø Ñ ØÖ ÜÓØ Ð Ö ÐÚ Ø Ö Ð ØÓÚ º º º º ØÓ Ñ ÒØ Ì ÞØ Ð Ø Ñ ÓÒØÓÐ Ó Ú ØØ Ò Ñ ØòÖ Ø Ö Ø Ú ÐÐ ÑÓ Ø Ö Ö ¹ ص ÜÔÓÖØ ÐÓÑ Ò Ñ ÓÒÚ Ö Ò Þ ÒØ Ò Ú ÐØÓÞ Ø Þ ÒØ ÖÔÓÐ ÐØ ¹ Ð Ð Ø Ø º Þ ÜÔÓÖØ Ð Ò Ñ ÒÝ Ñ Ö Ø Ñ ØØ Ý Þ Öò º Ú Ð ÒØ Ö ÐÒ Ñ ÒØ Ö º Þ Ò ÐÓ ØÓÚ ÔÓ ÞعÔÖÓ Þ Ð Å ÌÄ Ú Ý ÑÙÒ ¹ Ð Ô Þ Ð ÞÓ ØÚ ÖÖ Ð ÐÚ Þ Ø º ¾½
28 ¾¾
29 º Þ Ø ÃÓÒÚ Ö Ò Ú Þ Ð Ø º½º Þ ÒØ ÖÔÓÐ Ó Ò Ø Þ Ý Ñ Ö ÔÓÒØÓ ÓÞ Ø ÖØÓÞ Þ ÑÙÐ Ø Ö Ó Ø ¾º¾º Ö Þ Ò Ñ ÖØ Ø ØØ Þ Ö ÒØ ÔÓÒØÖ Ð¹ÔÓÒØÖ Ú ÐØÓÞ º ÒÒ Ñ Ð Ð Ò Ú ÒØ ÓÒÚ Ö Ò Þ ÒØ Þ Ø ÖØÓÞ Ø Ö Þ ÑÓ Ø Ò Ñ ÓÒÐ Ø ØÓÑ Þ º ÓÒ ÓÐ Ø ÖÐ Ø Ò Ú ¾º¾µ Þ Ö ÒØ Ú Ö Ò Ø Ö Ñ Ò Ø Ø ÔÓÒØ Ð ÞÓÒ ÔÓÒØ Ö Ñ Þ Ð ÖØ Ô Ö Ñ ÐØ Ø Ð Ô ÓÐ º Þ Ð Ø Ö ÙØ Ò ÔÓÒØ Ð ÞÓÑ Þ Ò ÖØ Ö Ð Þ ÙÔ Ò Ø º Ñ Ó ÙØ Ò Þ Ò Þ Ð ÞÓÑ Þ Ö Ý ØÓÚ º Ø ÙÐÐ Ñ Þ Öò Ò Ø Ö Ø Ö Ó Ø ÔÓÒØ Ò Ú º Ø Ö ¹ Þ Þ Ø Ö Þ Ñ Ø Ö Ó Ø Ò Ý Ø Ð º Þ ØÐ Ø Ó Ý Ø Ö Ð Ó Þ Ñ Ø ÔÓÒØ Ð Ð Ò ÝÓ ÐÝ Ò Ø Ò Ó Þ Ñ Ö Ñº Â Ð Ò Ø Ò Þ ÑÙÐ Ø Ö Ó Ø Ý Ñ Ò Ð Ò ÝÓ Ø Ö Ø Ø ØÐ Ò Ñ ÒØ Ò Ú Òº ÒÒ Þ ÖØ IT = N 2 ip +N2 ip +N2 h º½µ º¾º Ã Ð Ò Þ Ð Ô ÓÖÑ Ø Ò ÓÒÚ Ö Ò Ø Ö Þ Ñ Ò Ð Ð Ø Ý ÒÐ ØÐ Ò Ø Ð Ú Ð Ò Ú Þ ¹ Ð Ø ÓÞ Ú Ð ØÐ Ò Ð Ð Ø Ø Ò Ö ÐØ Ñº Ð Ð Ø Ñ Ñ Ö Ö Ñ ¹ ÒÝ Ø Ø ÞØ ÐÐ ÑÞ Ò Þ Ñ Ø ÙØ Ò ÞÓ Ð ÞÒ Ð Ú Ð Þ ÐØ Ø Ñ ¹ Ö Ö Ñ ÒÝ Ðº Þ Ý ÔÓÒØÓ ÓÞ Ø ÖØÓÞ Þ ÑÙÐ Ø Ö Ó Ø Ñ Ò ÐÓ ÞÐ Ú Ø Þ Ö Ò Ð Ø Þ º Ø Ñ Ö Ö Ñ ÒÝ Ø Ø ÞØ Ð ÞÓÒÓ ÐÓ ÞÐ Ò ÑÓ Ø Ñ Ú Ð Ñ ÒØ ÞÓÒÓ Ø ÒÓÐ Ú Ð Þ Ðغ Å Ý Ð Ø Ó Ý Ø Ñ Ö ÔÓÒØ ÓÞ Ø ÖØÓÞ Ñ Ð Ú Ð Þ Òò ÐØ Ö 2 d z = 4 nm Ú Ö Ø ÖØ 2.9º ¾
30 valoszinuseg elteres º½º Ö º Ã Ø Ñ Ö Ô 3 3¹ Ð Ö ÞÐ Ø Ò dz Ð ÔØ Ò Ú ØØ ÐØ Ö Ò» Ö Ò Ò Ð¹ ÓÞÐ º Þ º¾ Ö Ò Þ ÑÙÐ ÞÓÒÓ ÓÒÚ Ö Ò Þ ÒØ Ø ÖØ Ðº Þ Þ Ø ÖØÓÞ Ø Ö Ð Ô Þ ÑÙÐ Ø Ö Ó Ø Ú ÐØÓÞ Ø Ð ØÐ ÒÒ ÑÓÒ Ø º Ñ ÞØ Ð ÒØ Ó Ý Ò ÝÓ Ø ÖÓ Ø Ø Ò ÓÒÚ Ö ÐÒ Ó Þ ÑÙÐ ØÓÖº º¾º Ö º ÞÓÒÓ ÓÒÚ Ö Ò Þ ÒØ Þ Ø ÖØÓÞ Ð Ó Ø Ö Ð Ô Þ Ñ Þ ÑÙÐ Ñ Ú ÒÝ Òº ¾
31 º Þ Ø Ö Ñ ÒÝ º½º Å ÌÄ ÑÔÐ Ñ ÒØ Ö Ö Ò ÒØ ÞÓÐ Ð Å ÌÄ Ð ÓÖ ØÑÙ Ð Ò Ö ÔÖÓ Ö Ñ Þ ÖÚ Þ Ø Ð ÐÑ Þ¹ Ú Þ Ð Ö Ø Ð Ó ÙØ 100msº Ñ Ò Ñ Ð Ú ÐØÓÞØ Ø Ú Ð Ð Ö Ø Ô Ö ÙÞ ÑÓ Ú Ö Ø º ÞØ ÓÖ ÐÙ Ó È Ö ÐÐ Ð ÌÓÓÐ ÓÜ Ð Ô Ö ÓÖ ÙØ Ø Ö Ö ÐÚ Ö Ø Ðº Þ ¹ Ð Ø ÙØØ ØÒ Ô ÔÖÓ ÞÓÖÓÒ Ð Ó Ø Ò Ò Ý Ö Ò Ø ÙØ º Î Ð Ò Þ Ó Ø ÖØ Ò Ñ º Å ÌÄ È Ö ÐÐ Ð ÌÓÓÐ Óܹ Þ Ý Þ ÑÙ¹ Ð Ø ÓØØ Þ ÐÖ Ó ÞØ Ðº ÃÓÖ Ò Ð ØØÙ Ó Ý Þ Ò Þ ÑÙÐ Ð Ô ÒÝ Þ ÑÙÐ Ø Ö Ó Ø Ú ÐØÓÞ ØÓ Ñ ØØ Ò Ý Ò ÐØ Ö ÝÑ Ø Ð Ý Ð ÐÐ Þ Ò Ð ØÓ Ø Ó Ý Ñ Ø ØÐ Ò Ð Ò Ý Ö Ú Ö Ñ Ñ ØØ ÔÖÓ ÞÓÖ ÞÒ ÐØ Ñ Þ Ò Ñ Ø Ð º º½º Ö º Å ÌÄ Ö ÓÖÖ ÞÒ ÐØ Ô Ö ÓÖ ÞÒ Ð Ø Ø Ò ÐÞ ØØ Ø ÖØÓÑ ÒÝ Ð Ø Ð Þ Ú º Ñ ÓÐ ÓÞ º ¾
32 º¾º ÇÔ Ò Ä ÑÔÐ Ñ ÒØ ÇÔ Ò Ä Ö ØÖ Ò Þ Ö Ø Ú Ð ÖØ ÔÖÓ Ö ÑÓØ ÈÍ¹Ò ÙØØ ØÚ Þ º½º Ø ¹ Ð Þ Ø Ò Ð Ø Ø Ö Ñ ÒÝ Ø ÔØ Ñº ÙÔ Ò ÐÓ Ð Ñ Ñ Ö Ø ÞÒ ÐÚ Ö Ö Ò ÓÞ Ô Ø ÖÓÑÐ Ø Ð ØÑ Òݺ ÞØ Ú ÖØÝ ÔÖ Ø Ú Ò Ð ¹ Ð Ð Ø Ò ÐÓ Ð Ñ Ñ Ö Ð ÐØ Ø Ó ÓÞØ ÞØ Ø ÓÐÝ Ñ Ø Ò Ø º ÐÓ Ð Ñ Ñ Ö ÞÒ Ð Ø ÙØ Ø Ö ÞØ Ù Ò Ð ØÙ ÒØ Ò Ñ ÓÖ Ò Ñ ÖØ Ø ØØ Ñ Ñ Ö Þ ÖÚ Þ Ñ ÓÒØÓÐ Ó ÐÝ Ø ÞÓÐ º Ä Ø Ø Ó Ý Þ ÇÔ Ò Ä ÑÔÐ Ñ ÒØ Þ Ð 5 8 ÝÓÖ ÙÐ Ø Ð ÒØ Å ÌÄ ¹ ÓÞ Ô Øº ÞØ Ø ÓÐÓ Ò ØÙ ÓÑ Å Ñ Ö ÈÍ Ñ Ñ Ö Ê ½¼ ÅÀÞ Ø Ù Þ Þ Ð Ð Ñ ÈÍ Ñ Ñ Ö Ê ½¼ ÅÀÞ ½¾ Ø Ù Þ Þ Ð Ð Ö Ò¹ Ð Þ ÈÖÓ ÞÓÖ Ñ ÈÍ ÓÑÔÙØ ÙÒ Ø¹ Ð Ö Ò Ð Þ Ñ Þ ÐÖ Ñ ÁÒØ Ð ÀÝÔ ÖÌ Ö Ø ÒÓÐ Ò Ø Ú Ð ¾ ÔÖÓ ÞÓÖÑ Ö ÔÞ Ð Ñ ÈÍ ÓÑÔÙØ ÙÒ Ø¹ Ð Ö Ò Ð Þ Ñ Í ÓÖ ¹Ö Ô Þ Ð º ÌÓÚ Ý Ð Ñ ÐÐ Ú ÒÒ Ó Ý Þ ÑÙÐ ØÓÖ ÙØ Ø ÔÖÓ Ö ÑÑ Ð ÓÒ ÙÖ¹ Ö Ò Ò Ø ÖØ Ò ÈÍ Ø Ò Þ ÓÔ Ö Ö Ò Þ ÖÖ Ð ÈÍ Ø Ò Ñ Ð Ò Ø Ðº º½º Ø Ð Þ Øº ËÞ ÑÙÐ ØÓÖ ÙØ Ö Ñ ÒÝ 5 5 Ñ Ö ÔÓÒØÖ Å ÌÄ ÁÒØ Ð ÒÎ ¼Å ÙØ ¼ Ñ ¾ ¼ Ñ ½¼ Ñ Ý ÔÓÒع ÓÞ Ø ÖØÓÞ ÙØ Ì Ð Ñ Ö ¹ Þ Ø ÖØÓÞ ½¼ Ñ ½ º Ñ Ñ 29h 12h 2h ¾
33 º Þ Ø Þ Þ Ò Þ Ó Ð ÐØ Ñ Þ Å Ð Ð Ø Ø ÐØ òöò Ñ Ö Ø Ò Ø Ñ Ò ÞÓÒÓ ØÓØØ Ñ Ô Ø ÖØ Ò Ö Ø Ù ÚÓÐØ Øº Þ Ô Ø ÖØ Ò Þ Ö ÒØ Þ Ð Ø Ø Ø ÖØ ÐÑ Þ Ò Ð Ø Ù Ö Ñ ÒÝØ Ð Ø ØØ Ð ÞÒ ÐÒ º Ð Ø ÒØ Þ Ò Ô Ø ÖØ Ø Þ Ñ Ø Þ ÑÙÐ ØÓÖ Ô Ø Ø ØòÞØ Ñ Ñ ¹ Ò Ð Ó Ø Ò Ð Ð ÐÐ Ö Ñ ÒÝØ ÞÓÐ ÐØ ØÒ º Ô Ö ÙÞ ÑÓ Ø Ð Ø ØÖ Ú Ð Ò ÓØغ ÓÖ ÓÞ Ø ÝÓÖ Ú Ö Ø Ú ØØ Þ ÑÙÐ ØÓÖØ ÇÔ Ò Ä ÖÒÝ Þ Ø Ò ÑÔÐ Ñ ÒØ ÐØ Ñ Ñ Þ ÑÙÐ ØÓÖ Ø ÖÓ Ò ÑÙÐØ ÔÖÓ Þ ÞÓ¹ ÖÓ ÖÒÝ Þ Ø Ò Ú Ð ÙØØ Ø Ø Ø Þ Ð Ø Ú º Þ ÑÙÐ ØÓÖ Þ Ð ÓÒÐ Ò ÙØ Ò Ð Ö Þ Þ Ð ÒÝ Ó ¹ Ó Ø Ú ÓÐØ Ñ ÖÚ ÒÝ Ø Ñ Ú Þ ÐØ Ñº Þ Ö Ñ ÒÝ Ø Ñ ÖØ ØÚ Þ ÑÙÐ ØÓÖ ÙØ Ò Ð ØÚ ÒÝÓ ÝÓÖ ÙÐ Ø Ø Ô ÞØ ÐØ Ñ Ñ Þ Ö ¹ Ð Ð Ø Ø Ò Ð Ó Ø Ò ÔÓÒØÓ Ö Ñ ÒÝØ ØÙ ÞÓÐ ÐØ ØÒ º ÓÒÚ Ö ØÙÐ ÓÒ Ø Î Ð Þ Ð Þ ÐØ ÔÖÓ Ö ÑÓØ ÈÍ¹Ò ÈÍ¹Ò ÙØØ ØÚ ÙØ Ø Þ Ú Ø ØØ Ñ ÞÓÒÓ ØÓØØ Ñ ÝÓÖ ÙÐ ÓÖÖ Ø Ø ÖÚ ÔÖÓ ÞÓÖÑ Ö Ñ Ñ Ö Ö º ÌÓÚ Ð ØÓ Þ ÑÙÐ Ð ÞÒ Ð Ú Ð Ø ÖØ Ò Ø ÐØ òöò Þ ÖÑ ÞØ Ø Ñ Ú Ö Ø Ñ Ö Ù Ý Ò Ý Þ Ò Þ ÖÑ ÞØ Ø Ú Ð Ð Ö Ú Ð Ñ Ö Þ ÐÐ Ø ¹ ÓÐ ÓÐ ÓÞ º ÑÓÖ ÓÖÑ Øò Þ ÑÙÐ º Þ ÑÙÐ ØÓÖ Ñ Ø Ô Þ Ð Ò Ö Ý ÒÐ ØÖ Ò Þ Ö Ø Ö Ø Ú ÐÝ ØØ Ö Ø Ñ ÓÐ ÑÔÐ Ñ Ø Ò Ú Þ Ð Ø º ÁÒØ Ð ÓÒ ÔÖÓ ÞÓÖ ÖØÝ ÐØ Ð ÒÝ ØÓØØ Ú ØÓÖ ØØ ÔÙ Ó Ð ÐÑ Þ º ¾
34 ý Ö ÝÞ ½º½º Þ Å ÔÔ Ö ØÙ Ð Ø Ø Þ µ Ö Òº Ð Þ ÖÒÝ Ð Øò Ð Ð Ø ¹ Ö Ð Ø Ö Þ Ú Ý ÓØ Ø ØÓÖÖ Ö ÒÝÙк Øò ÔÓÞ Ø Þ Ð Ô Ò Ò Ý ÔÓÒØÓ Ð Ñ Ö º µ Ö Ò Ñ ÒØ Ð ØØ Ð Ú Øò ÑÓ ÐÐ Ð Ø Ø Ô Ø Ò Ð Ø Ù Þ Ñ Ø ÓÞº Øò R Ù Ö H Ñ D Ø ÚÓÐ Ö Ú Ò Ñ ÒØ Ø Ðº ÓÖÖ µ º º º º º º ½ ½º¾º Ñ Ø Ö Ô Ú ÐØÓÞ Ñ Ó Ñ Ö ÓÖ Ò Ü ÔÓÞ Øò Ø Òº º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º½º Å Ö Ð ÔÓØØ Ñ Ø Ö Ôº Ð ÓÒØ d x = d y = 120nm d z = 18.03nm º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º¾º Å ÒØ ¹Øò Þ ØØ Ø Ö Ú Ð Ñ Þ ÑÙÐ Ò Ð ÒÝ Ö ÞÐ Ø Þ ÑÙÐ Ø Ö Ó Ø Ñ Ø ÖÓÞ ÓÞº Ð ÓÐ Ð Ó ÞÐÓÔ Ò ÔÓØ Ò¹ Ð ÐÓ ÞÐ Ð Ø Ø V ¹ Ò Ñ ÖÚ Ó ÓÐ ÐØ Ú ÐÐ ÑÓ Ø Ö Ö Ò Ý V/nm Ñ ÖÚ º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º º Î ÐÐ ÑÓ Ø Ö Ö Ò Ý Ð Ð ØØ Ð 1 nm¹ö º º º º º º º º º º º½º ÇÔ Ò Ä Ú Ö Ø Ø Ö ÓÖÖ µ º º º º º º º º º º º º º º º º ½¾ º¾º ÇÔ Ò Ä ÓÒØ ÜØ Ó ÞØ ÐÝ Ö ÑÑ ÓÖÖ µ º º º º º º º º º º º º ½¾ º º Ð Ø ÓÞÞ Ö Ò Ð ÛÓÖ ¹ Ø Ñ¹ Þ ÔÖÓ ÞÓÖ ÓÞµ º º º º º º º º º ½ º º ¾ ¹ ÛÓÖ ¹ Ø Ñ¹ ÛÓÖ ¹ ÖÓÙÔ¹ Ö Ò Þ Ò Ü Ð ÓÖÖ µ ½ º½º 3 3 Ñ Ö ÔÓÒØ ÔÓÒØ Ú Ð ÒØ ÖÔÓÐ º º º º º º º º º ¾¼ º¾º Ñ Ö Ö Ñ ÒÝ Ý ÚÓÒ Ð Ñ ÒØ Ö ÞÐ Ø ÓÐÝØÓÒÓ ÚÓÒ Ðµ Þ Þ Ò Ñ Ö ÔÓÒØÓ ÓÞ Þ Ñ ØÓØØ Þ ÑÙÐ Ø Ö Ñ Þ ØÓØع ÚÓÒ Ðµ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾½ º½º Ã Ø Ñ Ö Ô 3 3¹ Ð Ö ÞÐ Ø Ò dz Ð ÔØ Ò Ú ØØ ÐØ Ö Ò»¹ Ö Ò Ò Ð ÓÞÐ º º º º º º º º º º º º º º º º º º º º º º º º º ¾ º¾º ÞÓÒÓ ÓÒÚ Ö Ò Þ ÒØ Þ Ø ÖØÓÞ Ð Ó Ø Ö Ð Ô Þ Ñ Þ ÑÙÐ Ñ Ú ÒÝ Òº º º º º º º º º º º º º º º º º º º ¾ Á
35 º½º Å ÌÄ Ö ÓÖÖ ÞÒ ÐØ Ô Ö ÓÖ ÞÒ Ð Ø Ø Ò ÐÞ ØØ Ø ÖØÓÑ ÒÝ Ð Ø Ð Þ Ú º Ñ ÓÐ ÓÞ º º º º º º º º º º º º ¾ ÁÁ
36 Ì Ð Þ ØÓ ÝÞ º½º ÇÔ Ò Ä Ñ Ñ Ö Þ ÒØ º º º º º º º º º º º º º º º º º º º º º º º º º º½º Î Þ ÐØ Þ Þ Þ ÓÒÐ Ø º º º º º º º º º º º º º º º º º º º º º½º ËÞ ÑÙÐ ØÓÖ ÙØ Ö Ñ ÒÝ 5 5 Ñ Ö ÔÓÒØÖ º º º º º º º º º ½ ½ ¾ ÁÁÁ
37 ÁÎ
38 ÁÖÓ ÐÓÑ ÝÞ ½ º ƺ Á ØÚ Ò Ð ØÖÓ ÞØ Ø Ù Ñ Ö Þ ÑÙÐ ÑÙÐØ ÔÖÓ ÞÓÖÓ ÖÒÝ Þ Ø¹ Ò ¾¼½ º Å Ø ÖÔÖ Ù Ô Øµº ¾ Áº º Æ Ý º Ê Ö Ø Ò º ËÞ Ó Ë ÑÙÐ Ø ÓÒ Ó Ñ³ ÙÖ Ö Ñ ÙÖ Ñ ÒØ ¾¼½ º ½ Ø Á Ì ËÝÑÔÓ ÙÑ Ö Þ Ù ØÖ µº º ÒÒ º º ÉÙ Ø Ò º Ö Ö ØÓÑ ÓÖ Ñ ÖÓ ÓÔ È Ý º Ê Úº Ä Øغ ÚÓк ÔÔº ¼ Å Ö ½ º º Πź ÃÖ ØÞ Ö º Å Ø ÓÚ º Æ ÚÓ Íº Ê Ð Ú º ÂÓÚ ÒÓÚ º Ò¹ Ö º Ì ÖØ Ò Êº ØÓÑ ÓÖ Ñ ÖÓ ÓÔÝ Ñ Ò ÔÙÐ Ø ÓÒ Ó Ö Ô Ò Ù Ò ÝÒ Ñ ÔÐÓÛ Ò Ð Ø Ó Ö Ô Ý Æ ÒÓØ ÒÓÐÓ Ý ÚÓк ¾ ÒÓº ½ Ôº ¼½ ¼ ¾¼½ º Àº¹Âº ÙØØ º ÔÔ ÐÐ Ò Åº à ÔÔÐ ÓÖ Ñ ÙÖ Ñ ÒØ Û Ø Ø ØÓÑ ÓÖ Ñ ÖÓ ÓÔ Ì Ò ÕÙ ÒØ ÖÔÖ Ø Ø ÓÒ Ò ÔÔÐ Ø ÓÒ ËÙÖ Ë Ò Ê ÔÓÖØ ÚÓк ÒÓº ½ ÔÔº ½ ½ ¾ ¾¼¼ º º Å ÖØ Ò º º Ï ÐÐ Ñ Ò Àº ú Ï Ö Ñ Ò ØÓÑ ÓÖ Ñ ÖÓ ¹ ÓÔ ÓÖ Ñ ÔÔ Ò Ò ÔÖÓ Ð Ò ÓÒ Ù ½¼¼ Ð º ÂÓÙÖÒ Ð Ó ÔÔÐ È Ý¹ ÚÓк ½ ÒÓº ½¼ ÔÔº ¾ ¾ ½ º Àº¹Âº ÙØØ Å ÙÖ Ò Ð ØÖÓ Ø Ø Ú Ò Ö Û Ð Ò Ý Ö Ø ÓÒ ÓÖ Ò Ð¹ ØÖÓÐÝØ ÓÐÙØ ÓÒ Û Ø Ò ØÓÑ ÓÖ Ñ ÖÓ ÓÔ ÓÔ Ý Âº ÚÓк ¼ µ Ôº ½ ½ º ½ ½º ˺ ÀÙ Ð Ø Åº Ë ÒØ Â Ò º ÙØ Ñ ÒÒ Ò Âº Ö Ö Ú ÐÙ Ø ÓÒ Ó Ø Ô ¹ Ø Ú ÓÖ ØÛ Ò Ò ØÓÑ ÓÖ Ñ ÖÓ ÓÔÝ Ø Ô Ò Ñ Ø ÐÐ ÙÖ Ì ÙÖÓÔ Ò È Ý Ð ÂÓÙÖÒ Ð ¹ ÓÒ Ò Å ØØ Ö Ò ÓÑÔÐ Ü ËÝ Ø Ñ ÚÓк ¾ ÒÓº ½ ÔÔº ½¼ ½ º Ì Ã ÖÓÒÓ ÇÔ Ò Ä ÏÓÖ Ò ÖÓÙÔ Ì ÇÔ Ò Ä ËÔ Ø ÓÒ Ú Ö ÓÒ ½º¼ Ù Ù Ø ¾¼½¼º Î
ÍÅÄ Ð ØÓ
ÍÅÄ Ð ØÓ ÄÌ Áà ÈÓÖ Ö ÑÓÞ ÐÑ Ð Ø ÞÓ ØÚ ÖØ ÒÓÐ Ì Ò Þ Ç Ø Ø ÒÝ ½º Ú Þ Ø ½º½º Ð Ø ý Ö ÞÓÐ Ù Ý Ö Ñ Ò Þ Ð ÓÖÓ Ú Ö Ø ÙØ Ò Ð ØÖ Ú Ó ¹ ØÙÑÓ Ø ØØ Ð Ý ØØ Ø ÒØ Ð Þ Ó ØÙÑÓ Þ ØØ Ô¹ ÓÐ ØÓ Ø ØÓÐÓ Ö Ø Ö Ø ½¼¼ µ ØÓÐÓ Ú
f ij = f i. f.j Ö f 11 = 49 f 12 = 64 f 13 = 84 f 1. = 197
Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾ ¾º ÞÓ ¾ º Ê Ò ÓÖÖ Ð º Î Ý Ô ÓÐ Ø º ÃÓÖÖ Ð Þ Ñ Ø º Ê Ö Þ Þ Ñ Ø º½º ÝÚ ÐØÓÞ Ö Ö Þ º º º º º º º º º º º º º º º º º º º º º º º º º½º½º Ð Ò ÝÞ Ø Ñ Þ Ö º º º º º º º º º º º º º º º½º¾º
Ì ÖØ ÐÓÑ ÝÞ Áº Ú Þ Ø ÐØ Ð ÒÓ Þ ÐÝÓ ½º Þ ÐÝ ÒÝÚ Þ Ñ ÐÝ Ø ÐÝ ¾º Ö ¾º½º Ö Ø Ö º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º¾º Ö Ó ÐØ Ð ÒÓ Ð
Æ ÓÒ Ã ÑÔÓ Â Ø Ù Þ ÐÝ ÒÝÚ ¾¼½ º ÖÙ Ö ¾¾º Þ ÐÐ ØÓØØ Å ØÞ Ö ÒØ Ð È ÖÓ Ð ËÞ Ö ÞØ ØØ Ì Ñ Ö ÓÖ ÒÝ Ô ÞØ ÃÖ Ø Ò Ö Ä ØÓÖ ÐØ Ï Þ Ò ÖÙ Ö Â ÒÓ ËÞ Ý Ê ÖØ ½ Ì ÖØ ÐÓÑ ÝÞ Áº Ú Þ Ø ÐØ Ð ÒÓ Þ ÐÝÓ ½º Þ ÐÝ ÒÝÚ Þ Ñ ÐÝ Ø ÐÝ
Þ Þ Ø ØØ Ú ÐÐ ÑÓ Ð Þ Ø Þ Þ Ø ØØ Ú ÐÐ ÑÓ Ð Þ Ø Ð ÓÒØÓ ÐÐ ÑÞ Ó Ý Ð Þ Ó Ú Ò¹ Ò Þ Ö Ñ Ö Òº Èк Ý ØÐ Ò Ø Ð ÔÖ Ø ÞÞ Ð ÑÔ Ø Ô ÓÐÙÒ ¾¹½½º Ö µ Ú Ý Ï Ø ØÓÒ ¹ ¾¹
Ä ÃÌÊÇ ÁÆ ÅÁÃ Ý Ò Ö Ñ Ð Þ ØÓ ¾º Þ Þ Ø ØØ Ú ÐÐ ÑÓ Ð Þ Ø Þ Þ Ø ØØ Ú ÐÐ ÑÓ Ð Þ Ø Ð ÓÒØÓ ÐÐ ÑÞ Ó Ý Ð Þ Ó Ú Ò¹ Ò Þ Ö Ñ Ö Òº Èк Ý ØÐ Ò Ø Ð ÔÖ Ø ÞÞ Ð ÑÔ Ø Ô ÓÐÙÒ ¾¹½½º Ö µ Ú Ý Ï Ø ØÓÒ ¹ ¾¹½¾º Ö µº Þ ÙØ Ø ÐÐ
dc_869_14 ÅÌ Ó ØÓÖ ÖØ Þ Ø Þ Æ Ñ¹ Ý Ò ÐÝ Ò Ñ Ð ÓÒÝ Ñ ÒÞ Ú ÒØÙÑ Ö Ò Þ Ö Ò Ö Ð Þ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ ¾¼½
ÅÌ Ó ØÓÖ ÖØ Þ Ø Þ Æ Ñ¹ Ý Ò ÐÝ Ò Ñ Ð ÓÒÝ Ñ ÒÞ Ú ÒØÙÑ Ö Ò Þ Ö Ò Ö Ð Þ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ ¾¼½ ½ ½º Ú Þ Ø Þ Ð ÓÒÝ Ñ ÒÞ Ö Ò Þ Ö Ð ÒÐ Ú Ð ¹ Ö Ø Ó Ð Ð ÓÞØ Ø Þ Ù Ó Øº Ú ÒØÙÑ Ù ØÙ Ð Ò Ò Ð Ö Ò Ð ÒØ Ø Ö
Ú Þ Ø Þ Ô Ð Ò Þ Ú Ñ Ò ÞÔÓÒØ Þ ¹ Ö Ô Ø Ø ÞÓØØ Þ Ð Ö Ú Þ Ð ØÓ Òº ËÞ ÑÐ Ð Ø Ò Þ ÐÚ Þ Ú ÐØÓÞ Ð ÑòÚ Ð Ø Ð Ð Ð Ô Ø ØØ ÓÐÝ Ò Ð¹ ÓÖÓÞ ØÓ Ñ ÐÝ ÓØØ Ø ÔÙ Ð Ö Ø Ò
Ó ØÓÖ ÖØ Þ Ø Þ ÃÓÑ Ò ØÓÖ Ù Ø Ð Ò 0¹ Ý Þ Öò Ð ÓÔÓÖØÓ Þ Ô ØÖÙÑ Ã Ø ¹ÍÖ Ò Ã Ñ ÐÐ Ì Ñ Ú Þ Ø Öº Å Ý Ä ÞÐ Ý Ø Ñ Ó Ò Öº ËÞ Ý Ø Ñ Ó Ò Å Ø Ñ Ø ¹ ËÞ Ñ Ø ØÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÓÐÝ ÁÒØ Þ Ø ¾¼¼ Ú Þ
t = c U, t0 = x 0 t = c (1+U/c), c (1 U/c) U x δt B = 1 2
Þ Ö Ô Ö ÓÜÓÒÖ Ð ÀÖ È Ø Ö ÈÌ ÐÑ Ð Ø Þ Ì Ò Þ Þ Ö Ô Ö ÓÜÓÒ Ú Ý Ñ Ò Ú Ò Þ ÖÔ Ö ÓÜÓÒµ Ó ÐÑ Þ ÑÔÓÒØ Ð Ö Ð Ø Ú Ø ÐÑ Ð Ø Ý Ð ÓÒØÓ Ú Ø ÞÑ ÒÝ º Ð Ò ÓÐ ÓÞ Ø Ô Ö ¹ ÓÜÓÒÒ Ý ØÙÐ ÓÒ ÔÔ Ò Ø Ò ÐÐ ò Ñ Þ Ú Ö Ø Ô ØÙ Ú Ð Ó
x 2 a b c d a b c d e x 1 O R O L O C ϕ(a d f) O R ϕ(b c) O L ϕ(b c e) O L ϕ(l R) (R 2 \ E) ϕ(l M R) (R 2 \ E)
Ò Ñ Ö Ò Þ Ö ÓØ Ù Ò Ø Ð Ø Ò Ú Þ Ð Ø Ñ Þ Ø Þ Ñ Ø Ô Ñ Þ Ö Ð Ó ØÓÖ ÖØ Þ Ø Þ Ò ÐÝ Ð Þ Ì Ñ Ú Þ Ø Öº Ò Ì ÓÖ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ËÞ ¾¼¼ ½º Ú Þ Ø Ò Ñ Ö Ò Þ Ö Ú Þ Ð Ø ÓÖ Ò Ó Ø Ò Ö Ö Ð Ø Ó Ý Ú Ð Ò Ö Ò Ð ÞÒ ¹ Ñ ÓÐ Ó
Ð Þ Ù Þ Ø Ö Ý ÐÓ ÞØ Þ Ø Ö Ý Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý Ð Ô Ö ÀÓ Ý Ò Ñò Þ ÙÒ Ú ÖÞÙÑ Ð ÔÚ Ø Ó ÐÑ Ø Ö ÒÝ Ñ Þ Ò Ö Ö Ú Ø º
Þ ÆÝ ØÖ Ý Ö ÐÝ È µ ÈÌ ÈÅÅÁÃ ¾¼½ º ÒÙ Ö º Ð Þ Ù Þ Ø Ö Ý ÐÓ ÞØ Þ Ø Ö Ý Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý Ð Ô Ö ÀÓ Ý Ò Ñò Þ ÙÒ Ú ÖÞÙÑ Ð ÔÚ Ø Ó ÐÑ Ø Ö ÒÝ Ñ Þ Ò Ö Ö Ú Ø º Þ Ø Ö Ý ÐÓ ÞØ Ð Þ Ù Þ Å Ò Ì ÖÑÓ Ò Ñ Ð ØÖÓ Ò Ñ ÇÔØ
) ξi (t i t i j i
Ë Á ÌÍ ÇÅýÆ Ì Å Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ ÁÒ ÓÖÑ Ø Ã Ö Å Ø Ñ Ø ¹ ËÞ Ñ Ø ØÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ ËÞ Ñ Ø Ô Ð ÓÖ ØÑÙ Ó Å Ø Ö ÁÒØ ÐÐ Ò Ì Ò Þ ËÔ Ð ÙØÓÑ Ø Ó ÞØ ÐÝÓ ÐÐ ÑÞ Ó ØÓÖ ÖØ Þ Ø Þ ÝÙÖ Þ Ý Ö Ý Ì Ñ Ú Þ Ø Öº Ö Ò ËÞ ¾¼½¼
ËÔ ÑÊ Ò À ÓÒÐ Ö ÆÝ ÐÚÑÓ ÐÐ Ã Ö ÐÑ ËÙÑÑ ÖÝ Ï Ô Ñ ÞòÖ Ñ Þ Ö ÐÓ ÒÝ Ã ÖÓÐÝ ÄÌ ÁÃ ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ÅÌ Ë Ì ÃÁ ÁÒ ÓÖÑ Ø ÃÙØ Ø Ð ÓÖ Ø Ö ÙÑ Ì Ñ Ú Þ Ø º ÒÞ Ö
ÐÓ ÒÝ Ã ÖÓÐÝ ÄÌ Áà ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ÅÌ Ë Ì ÃÁ ÁÒ ÓÖÑ Ø ÃÙØ Ø Ð ÓÖ Ø Ö ÙÑ Ì Ñ Ú Þ Ø º ÒÞ Ö Ò Ö ¾¼½¼º Ò Ù º Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø Ä Ò Ô Ñ Ð Ñ Ö ËÔ ÑÊ Ò Ð Ö Ð À Ú Ø ÓÞ Ð Ô ÓÒÐ Ö Ð Ô Ð Þ ØÓÖ¹ ÓÑ Ò ÆÝ ÐÚÑÓ ÐÐ
Ð Þ Ù Þ Ø Ö Ý ÐÓ ÞØ Þ Ø Ö Ý Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý Ð Ô Ö ÀÓ Ý Ò Ñò Þ ÙÒ Ú ÖÞÙÑ Ð ÔÚ Ø Ó ÐÑ Ø Ö ÒÝ Ñ Þ Ò Ö Ö Ú Ø º
Þ ÆÝ ØÖ Ý Ö ÐÝ È µ ÈÌ ÈÅÅÁÃ ¾¼½ º ÒÙ Ö ½ º Ð Þ Ù Þ Ø Ö Ý ÐÓ ÞØ Þ Ø Ö Ý Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý Ð Ô Ö ÀÓ Ý Ò Ñò Þ ÙÒ Ú ÖÞÙÑ Ð ÔÚ Ø Ó ÐÑ Ø Ö ÒÝ Ñ Þ Ò Ö Ö Ú Ø º Þ Ø Ö Ý ÐÓ ÞØ Ð Þ Ù Þ Å Ò Ì ÖÑÓ Ò Ñ Ð ØÖÓ Ò Ñ ÇÔØ
Ö ÒÝ Ô Ö Ñ Ø Ö Ò Ø Þ ÑÓÞ Ö ÙØÓ Ø Ð Ø Ù ÖÓÒØÓ Ò Ó ØÓÖ È µ ÖØ Þ Ì Ø Ì Ñ Ö Ì Ñ Ú Þ Ø Öº Ì Ø ý ÓØ Öº ÀÓÖÚ Ø Þ Ã ÖÒÝ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Á ÓÐ Ë Ì ÌÌÁÃ Þ Ã Ñ
Ö ÒÝ Ô Ö Ñ Ø Ö Ò Ø Þ ÑÓÞ Ö ÙØÓ Ø Ð Ø Ù ÖÓÒØÓ Ò Ó ØÓÖ È µ ÖØ Þ Ì Ø Ì Ñ Ö Ì Ñ Ú Þ Ø Öº Ì Ø ý ÓØ Öº ÀÓÖÚ Ø Þ Ã ÖÒÝ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Á ÓÐ Ë Ì ÌÌÁÃ Þ Ã Ñ Ì Ò Þ ËÞ ¾¼¼ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½ ¾º ÁÖÓ ÐÑ ØØ ÒØ
Ú Þ Ø ÐÐ Þ Ð ÐØ Ð Ø Ñ Ú ÞØ Ø ÒÙÐÑ ÒÝÓÞ ÙÐ ÓÒØÓ ÐÐ ¹ Ð ÓÐÝ Ñ Ø Ò Ñ ÖØ Þº Ø Ñ Ú ÞØ Ñ ÖØ ÐРРй Ð ÔÓØ Ø Ð Ú Ö Ö ÐÐ Ó Ø Ò Ø Ò Ý Ö Ò Ð Ñ Ð ÓÖÓÞ Ø ÐÐ Ó Ò Ð
ÇÔØ ÃÚ ÒØÙÑ Ð ØÖÓÒ Ì Ò Þ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ Î Ö Ö ÐÐ Ó Ø Ñ Ú ÞØ Ñ ÐÑ ÞÓ Ò Ó ØÓÖ È µ ÖØ Þ Ø Þ Å Þ ÖÓ ËÞ ÓÐ Ì Ñ Ú Þ Ø Öº Ò Ö Ãº ÙÔÖ À ÖÚ Ö ¹ËÑ Ø ÓÒ Ò ÒØ Ö ÓÖ ØÖÓÔ Ý Ñ Ö ÍË Ð ÓÒÞÙÐ Ò Öº Î Ò Â Þ ÇÔØ ÃÚ ÒØÙÑ
Ð ØÖÓÑ Ò Ø Ö ÎÁº ÆÝ ØÖ Ý Ö ÐÝ ÈÌ ÈÅÅÁà ΠÐÐ ÑÓ À Ð Þ ØÓ Ì Ò Þ ¾¼½ º Ð Ù º
Ð ØÖÓÑ Ò Ø Ö ÎÁº ÆÝ ØÖ Ý Ö ÐÝ ÈÌ ÈÅÅÁà ΠÐÐ ÑÓ À Ð Þ ØÓ Ì Ò Þ ¾¼½ º Ð Ù º ÓÒØ ØÔÓØ Ò Ð ÓÒØ Ø¹ÔÓØ Ò Ð Ð Ò Ú Ø Þ ÔÔ Ò Ø ÖÓÞ Ø Ñ Í ½ ¾ = Ï ¾ Ï ½ Å Ú Ð Þ Þ ÐØ Ñ Ð Ð Ø Þ Ð Ò Ð Ú Ð ØÖÓÒÓ Ö ÚÓÒ Ø ÓÞ ÞØ ÎÓÐØ ¹
ÐÙÐ ÖÓØØ ÀÓÐÞ Ö Ì Ñ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ ÐÐ Ø Ð ÒØ Ñ Ó Ý ÞØ ÔÐÓÑ Ø ÖÚ Ø Ñ Ò Ñ Ò ØØ Ø Ò Ð Ð Ø Ñ Ñ Þ Ø ØØ Ñ ÔÐÓÑ Ø ÖÚ Ò Ñ ¹ ÓØØ ÓÖÖ Ó Ø ÞÒ ÐØ Ñ Ð
Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ À Ö Ø Ò Ì Ò Þ ÖÝËÝË Ä ÓÖ Ø Ö ÙÑ ËÔÓÒØ Ò ÓÓÔ Ö Ð ÙÐ Ð Ò Þ ÒÒ Ø Ð Ø ÖØÓÞ Þ ÒÞÓÖ Ð Þ ØÓ Þ ØØ Ë Ø Þ ÐÐÓÑ Ó Ø ÀÓÐÞ Ö Ì Ñ ÃÓÒÞÙÐ Ò Ö ÙØØÝ Ò Ä Ú ÒØ ÐÙÐ ÖÓØØ ÀÓÐÞ Ö Ì Ñ Ù Ô Ø Åò Þ Þ
t = 0 R i L i s i s + u v 3R + u v u u v = 3u 4 + 3R 4 i s R = 0 u Li L R u = 4R 3 i L +R i s = i L i L + u 2R + u u v dt = 7R 3L i L + R L i s
ÒÐÓØØ Ð ØÓ º Ø Ý ÓÖÐ Ø Ö ýðð ÔÓØÚ ÐØÓÞ Ð Ö Ñ ÓÐ Þ Ø Ú Ö ÓÒØ Ð ½º Þ Ö Ò Ð Ø Ø Ð Þ Ø Ò Ô ÓÐ Ø ¼ Ô ÐÐ Ò Ø ÒÝ ØÚ Ú Òº Ô ÓÐ Ø Ø ¼¹ Ò Þ Ö Ù º Ú Ð Þ Ð ÐØ Ù Þ ÐØ º º À Ø ÖÓÞÞÙ Ñ Ô ÓÐ Þ ÖØ ÐÐ Ò Ð Ð Þ Ø ÐÐ ÔÓØÚ
Ð Ô Ø Ø Ù ÔÖÓ Ö Ñ Þ Ð Ø Ð Þ Ð Ø Â Þ ÂÙ Ø ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ËÞÓ ØÚ Ö Ð ÞØ Ì Ò Þ Ì Ñ Ú Þ Ø Öº Ý Ñ Ø Ý Ì ÓÖ ËÞ ¾¼¼ º Ñ Ù ÖØ Þ Ó ØÓÖ Ó ÓÞ Ø Ñ Þ ÖÞ Þ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ Ð Þ ÔÖÓ Ö Ñ Þ Ð Ø
ÓÑ Ã Ø Ð ÔÚØ Ó ÐÓÑ Þ Ð Ü Ò Ö ÔÓÐ ÒÓÑ ÐÓ Ö ÓÑÓÐ ÃÓÑ Ò ØÓÖ Ù Ñ Þ Ö Ð ÓÑ ÒÚ Ö Ò Ó Ð ÓÒÝ Ñ ÒÞ ØÓÔÓÐ ÓÑ Ò ØÓÖ ËØ Ô Þ Ò Ö Ê ÒÝ Ð Ö Å Ø Ñ Ø ÃÙØ Ø ÒØ Þ Ø ¾¼¼
ÒÚ Ö Ò Ó Ð ÓÒÝ Ñ ÒÞ ØÓÔÓÐ ÓÑ Ò ØÓÖ Ê ÒÝ Ð Ö Å Ø Ñ Ø ÃÙØ Ø ÒØ Þ Ø ¾¼¼ º ÒÓÚ Ñ Ö ¾ º ÒÚ Ö Ò Ó Ð ÓÒÝ Ñ ÒÞ ØÓÔÓÐ ÓÑ Ò Ê Ñ Ø Ö ÑÓÞ Ó Þ Ë ½ ÖÚÓÒ Ð Ê Ú Ð Ö Ò Ð Ø Ý Þ Ø Ò Ú ÞÞ ÓÑ Ò º Ã ½ Ã ¾ ÓÑ ÞÓÒÓ ÝÑ ÑÓÞ Ø Ø
½º Å rot H = 0, H t2 H t1 = 0 H t2 = H t1, ¾º Å div D = ρ D n2 D n1 = η. º Å rot E = 0 E t2 E t1 = 0, º Å div B = 0 B n2 B n1 = 0.
Ä ÃÌÊÇ ÁÆ ÅÁà º Ð µ Ð ØÖÓ ÞØ Ø ÆÝÙ Ú Ø ÐØ Ò ÐÐ Ò Ð ØÖÓÑÓ Ø Ö º ½º Å Ò Ò Þ Ñ ÒÒÝ ÐÐ Ò Þ Òº ¾º Ø ÐØ Ò Ñ ÑÓÞÓ Ò Ø Ø v = 0 ØÓÚ Ò Ò Ö Ñ J = 0º Å ÜÛ ÐÐ Þ ÒÝ Ý ÒÐ Ø Ú Ø Þ ÓÖÑ Ø ÐØ ½º Å rot H = 0, H t2 H t1 =
È Ö ÙÞ ÑÓ ØÓØØ Ú Ð Ñ¹Ñ Þ Ö ØÓÐØ Ð ØÖÓ Ò Ñ ÔÖÓ Ð Ñ Ñ ÓÐ Ò ÖØ Å Ö Ò Ð Ç Ð Ú Ð Ñ ØÖÓÒ Ñ ÖÒ ÃÓÒÞÙÐ Ò ÈÖÓ º Öº ÃÙÞÑ ÒÒ Å Ð ºËº Ý Ø Ñ Ø Ò Ö ËÞ ÒÝ Á ØÚ Ò Ý Ø
È Ö ÙÞ ÑÓ ØÓØØ Ú Ð Ñ¹Ñ Þ Ö ØÓÐØ Ð ØÖÓ Ò Ñ ÔÖÓ Ð Ñ Ñ ÓÐ Ò ÖØ Å Ö Ò Ð Ç Ð Ú Ð Ñ ØÖÓÒ Ñ ÖÒ ÃÓÒÞÙÐ Ò ÈÖÓ º Öº ÃÙÞÑ ÒÒ Å Ð ºËº Ý Ø Ñ Ø Ò Ö ËÞ ÒÝ Á ØÚ Ò Ý Ø Ñ ÙØÓÑ Ø Þ Ð Ì Ò Þ È º º Ó ØÓÖ ÖØ Þ ËÞ ÒÝ Á ØÚ Ò Ý
) ) γ dense 2. γ = E(G) / 2. v i A, N (v i ) (1 ǫ) B,aholN (v i ) B µ
Ã Ñ ÐÝ Ð ò Ô Ù Þ ÐØ Ø Ö Ð Ø Ò Ú Ð ÞØ Ö Ð Ô Ð Ö Ð Ã ÞÐ Ö Ò Ø ËÞ Ö ÒÝ Ì Ñ ÅÌ Ë Ì ÃÁ ÞÐ Ö ÞØ º Ù Þ Ö ÒÝ ÞØ º Ù ÞØÖ Øº Ã Ô Ð ÒÝ Ö ÞÐ Ø Ò Ú Ð ÞØ Ô Ð ÑÞ Ý ÓÒØÓ Ö ÞØ Ö Ð Ø Ñ ÐÝ Ó Ð ÒÐ Ñ ÓÐ ØÐ Ò Ú Ý Ö Þ Ò Ñ ¹
Ô ØÖ Ð Ø Ö Ð Ð Ñ ÒÞ Ô ÓÐ Ø Ò Ú Þ Ð Ø Ð ÞÒ Ð Ø Ð òö ÐÚ Ø Ð Ó ÞØ ÐÝÓÞ Ò Ó ØÓÖ Þ ÖØ Ä ÞÐ Á ØÚ Ò Ì Ñ Ú Þ Ø Öº Ø Á ØÚ Ò ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ö ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ÈÖÓ º ÒÞ Ö Ò Ö ºËº ÁÒ ÓÖÑ Ö Ò Þ
Ë Ø ÙØÓÑ Ø ÞÓ Ó Ò Ñ Ð ÐÑ Þ Ó ØÓÖ È º ºµ ÖØ Þ ÃÓ Ö ÐÝ Ì Ñ Ú Þ Ø Öº ËÞØÖ Â ÒÓ Öº ÃÙÒ Ö Ò Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò ÁÒ ÓÖÑ Ø ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á
Ë Ø ÙØÓÑ Ø ÞÓ Ó Ò Ñ Ð ÐÑ Þ Ó ØÓÖ È º ºµ ÖØ Þ ÃÓ Ö ÐÝ Ì Ñ Ú Þ Ø Öº ËÞØÖ Â ÒÓ Öº ÃÙÒ Ö Ò Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò ÁÒ ÓÖÑ Ø ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ö Ò ¾¼½¾ Þ Ò ÖØ Þ Ø Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ
x = 10±0.1 y = 5±0.02 z = 20±0.4
ÆÙÑ Ö Ù Ñ Þ Ö ¹ ÆÙÑ Ö Ù Ò Ð Þ Ý ÓÖÐ Ð ØÓ Å Ã ½ ¹ Å Ã ½ ½ ĵ ¹ Å Ã ½ ĵ Æ ÑÓ Ö Ñ Ø ÓÖ ÙÒ ¹Ñ Óк Ù Å ÓÐ Ý Ø Ñ Ô ÞÑ ÖÒ ÁÒ ÓÖÑ Ø Ã Ö Ð ÐÑ ÞÓØØ Å Ø Ñ Ø ÁÒØ Þ Ø Ì Ò Þ ¾¼½ ¾ Ì ÖØ ÐÓÑ ÝÞ ½º ÃÐ Þ Ù Þ Ñ Ø ¾º Å ØÖ
Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½º½º Þ Ó Ø Ø ØÖÙ Ø Ö ÐØ º º º º º º º º º º º º º º º º º º º º º º º º ½º¾º Ø Ø ÓÒ ÓÞ Ð Ø º º º º º º º º º º º º º º º º º º º
ÞØ Ö ÞÝ Ã ÖÓÐÝ ÓÐ Å Ø Ñ Ø ÁÒ ÓÖÑ Ø ÁÒØ Þ Ø ËÞ Ñ Ø Ø Ò Ú Ö ÒÝ ÃÓÚ ÞÒ Ö ÐÝ ÓÚ Þ Ö º Ø º Ù À ÖÒÝ ÓÐØ Ò ØØÔ»»Û º Ø º Ù»Û»ÀÞ Þ Ö º Ø º Ù Ö ¾¼½¼ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½º½º Þ Ó Ø Ø ØÖÙ Ø Ö ÐØ º º º º º º º º º
ÔÐÓÑ Ø ÖÚ ÈÖÓ Ö ÑÓÞ Ø Ô ÖØÝ ÒÝ ØÓØØ ÞØÓÒ ÖØ Á ØÚ Ò ÓÐØ ÃÓÒÞÙÐ Ò Öº Î Á ØÚ Ò À Ö Ø Ò Ì Ò Þ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ ¾¼¼½º ÔÐÓÑ Ø ÖÚ Ö ÖØ Á ØÚ Ò ÓÐØ ÔÖÓ Ö ÑÓÞ Ø Ô ÖØÝ Ø Ð ÖØÝ Ñ Ö Øò ÞØÓÒ Ó Ñ ÖÓ Þ Ñ Ø
ØÔ ÐÙ ØÔ ÐÙ Ø Ú Þ Ø Ð Ö Ò Ð Þ Ð Þ ØÖ Þ ¾¹¾½º Ö µº Ä Ø Ý ØÐ Ò Ð Ñ Ôк ÐÐ Ò ÐÐ Ú Ý Ø Ð Ô Ø ºµ Ð Ø Ó Ð Ñ Ð Ð Ô Ð Ô ÓÐ º Þ Ð Ø Ð Ñ Þ ÙØ Ø Þ Ø ØØ ØÔ ÐÙ Ò Ò
Ä ÃÌÊÇ ÁÆ ÅÁÃ Ý Ò Ö Ñ Ð Þ ØÓ º ØÔ ÐÙ ØÔ ÐÙ Ø Ú Þ Ø Ð Ö Ò Ð Þ Ð Þ ØÖ Þ ¾¹¾½º Ö µº Ä Ø Ý ØÐ Ò Ð Ñ Ôк ÐÐ Ò ÐÐ Ú Ý Ø Ð Ô Ø ºµ Ð Ø Ó Ð Ñ Ð Ð Ô Ð Ô ÓÐ º Þ Ð Ø Ð Ñ Þ ÙØ Ø Þ Ø ØØ ØÔ ÐÙ Ò Ò Ú ÞÞ º Ø Ú ØÔ ÐÙ Ú
Ë Á ÌÍ ÇÅýÆ Ì Å Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ ÁÒ ÓÖÑ Ø Ã Ö Ã Ô Ð ÓÐ ÓÞ ËÞ Ñ Ø Ô Ö Ì Ò Þ ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ÌÓÔÓÐ ¹Ñ ÖÞ Ú ÓÒÝ Ø Ð ÓÖ ØÑÙ Ó Ø ÖÚ Þ Ú Þ Þ Ð Ø Ú ÒØ Ø Ø Ú Þ ÓÒÐ Ø Ó ØÓÖ ÖØ Þ Æ Ñ Ø ÓÖ Ì Ñ Ú Þ Ø Öº È Ð Ý
Ö Ó Ö Þ Ö Þ Ø Ñ Ö Ú Ø ÓÐØ Ó ØÓÖ ÖØ Þ Ì Ñ Ú Þ Ø ÂÓÖ Ò Ì ÓÖ Ý Ø Ñ Ó Ò Ò ØÙ ÄÌ ÌÌÃ Å Ø Ñ Ø Ó ØÓÖ ÓÐ Ó ØÓÖ ÓÐ Ú Þ Ø Ä Þ ÓÚ Å Ð Ð ÐÑ ÞÓØØ Ñ Ø Ñ Ø Ó ØÓÖ ÔÖÓ Ö Ñ ÔÖÓ Ö Ñ Ú Þ Ø ÈÖ ÓÔ Ò Ö Ó ØÓÖ ÖØ Þ Þ ØÚ ÄÓÖ Ò
Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½ ¾º ÁÖÓ ÐÑ ØØ ÒØ º à ÖÐ Ø Ö Þ ½ º½º Ö Ø Ò Ð Ý Þ Ø Ø Ð º º º º º º º º º º º º º º º º º º º º º º º º º ½ º½º½º Ò ØÖ Ùѹ ÐÓÖ Ø Ø
ÈÓÐ Ñ ÖÓÐ ØÓ Ø Þ ÑÓÞ Ö ÙØÓ Ø Ð Ø Ù ÖÓÒØÓ Ò Ó ØÓÖ È µ ÖØ Þ Ê Ì Ñ Ì Ñ Ú Þ Ø Öº Ì Ø ý ÓØ Öº ÀÓÖÚ Ø Þ Ã ÖÒÝ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Á ÓÐ Ë Ì ÌÌÁÃ Þ Ã Ñ ÒÝ ØÙ ÓÑ ÒÝ Ì Ò Þ ËÞ ¾¼½½ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½ ¾º ÁÖÓ ÐÑ
rot H = j, 1. div D = ρ, 2. rot E = 0, 3. div B = 0. 4.
Ä ÃÌÊÇ ÁÆ ÅÁà º Ð µ ËØ ÓÒ Ö Ù Ö ÑÓ I = j df. F, Ò Ö Þ Ò Ú Þ Ø Ö ÑÑ Ð Ó Ð Ð ÓÞÙÒ ÓÒ Ù Ø Ú Ö Ñµº Å ÜÛ Ðй Ý ÒÐ Ø Þ Ð Ð Ò ÖÚ ÒÝ rot H = j, 1. div D = ρ, 2. rot E = 0, 3. div B = 0. 4. à РØÒ Ó Ù Ó Ý Þ ½º
¹ÐÓ Ó ¹ ÐÔ Ö ÓÐ Ô ÓÐ Ø ÓÖÓ È Ø Ö Ä ÑÔ ÖØ Å Ø Å Ò ÓÖ ¾¼¼ º½¾º½½º ÓÖÓ È Ø Ö Ä ÑÔ ÖØ Å Ø Å Ò ÓÖ ¹ ÐÔ Ö ÓÐ Ô ÓÐ Ø
¾¼¼ º½¾º½½º Ì ÖØ ÐÓÑ Æ ÒÝ Ó ÐÓÑ Ð Ð Ô Ö ÓÐ Ñ Ú Ð Ø Ð¹ Ô Ö ÓÐ Ô ÓÐ Ø Þ Ö Ø Ù Ú Ð Þ Òò Þ ØØ Æ ÒÝ Ó ÐÓÑ Ð Ð º = (Î, ) Ö ÓÐ Î Ó Ñ Þ Ð ÐÑ Þ Ø Ð Ð º È Ð ÙÐ L = (Z,E ) Ü,Ý Z Ó = Ü,Ý E Þ Ü¹ Ø Ý ¹Ø Þ Ø Ðº ÐÔ Ö
Ð Þ Þ ØÓÒ Þ Ö ØÒ Ñ Ñ Þ ÒÒ Ø Ñ Ú Þ Ø ÑÒ ÓÒ Â ÒÓ Ò Þ ÑÓÑÖ Þ Ò Ú Ø Ñ ÐÚ Ø Ø Ô Ø ÞÖ Ú Ø Ð Ø Þ ÑÙÒ Ò ÓÖ Òº À Ð Ú Ð Þ Ò ØØ Ð Ø ÖØÓÞÓÑ Ñ Ð ÓÑÒ ÓÐ ÓÞ Ø Ñ Ö ÓÞ
à ÖØÝ Ø Ó Ö ÔØÓ Ö Ò Ú Þ Ð Ø Ý ÖØÝ Ø Ö ÔØÓ Ö Ñ Ú Ð Ø ÔÐÓÑ ÑÙÒ ÖØ Ì Ö Ë Ò ÓÖ Ð ÐÑ ÞÓØØ Ñ Ø Ñ Ø Ù Þ Ì Ñ Ú Þ Ø ÓÒ Â ÒÓ Ý Ø Ñ Ó Ò ÃÓÑÔÙØ Ö Ð Ö Ì Ò Þ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ã Ö ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý
(rot. j n df. Hd s = F. H) n df = F. j n df = n j n df, Hd s = ni.
Ä ÃÌÊÇ ÁÆ ÅÁà ½¼º Ð µ Ø Ö Ñ Ò Ø Ö Î Ý Ò Ý Ó Þ Ö ÞØÑ Ø Þ Øò Ø Ö Øº I Ñ Ò Ø Ö Ø ÒØ Ö ÑÙØ Ø º Ñ Ò Ø Ö Ø Ö Ò Ú Ð Ý Ò Ø Ö Ð Ò Ô Þ Ð Ø Ð ÐÐ Ò ÓÑÓ ÒÒ Ø Òع Ø º À Ø ÖÓÞÞÙ Ñ Ø Ö Ö Ø Ø Ö Ð Òº ÁÒØ Ö Ð Ù rot H = j,
D = ǫ0 ǫ r. ½º Å rot H = j + ρ v + D. rot H = j + ρ v + ǫ 0 ǫ r. Erot H = E j Eρ v Eǫ 0 ǫ r. ρ( v, E) = Erot H Hrot E ( j, E) ǫ 0 ǫ r
Ä ÃÌÊÇ ÁÆ ÅÁà º Ð µ Þ Ð ØÖÓÑ Ò Ø Ö Ò Ö Î Þ Ð Ù Þ Ð ØÖÓÑ Ò Ø Ö Ø ÓÑÓ Ò ÞÓØÖ Ô Þ Ø Ð Òº ǫ, µ, σ ÐÐ Ò º ÓÖ ½º Å rot H = j + ρ v + D t, ½³º Å rot H = j + ρ v + ǫ 0 ǫ r E t. º Å rot E = B t ³º Å rot E = µ 0
Ã Þ ÐØ Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ò ËÞ Ð Ö Ø Ø Þ ÒÝ ØÙ ÓÑ ÒÝ ÔÖÓ Ö Ñ Ö Ø Ò Þ ÖØ Ð Þ Ø Ø ÌýÅÇȹ º¾º¾» ¹½¼»½¹¾¼½¼¹¼¼¾ Þ Ñ ÔÖÓ Ø Ø ÑÓ ØØ º ÔÖÓ Ø Þ
ÌÌÃ ½ À Ø ÖÓ Ò ÒÝ Ó ÖÓ Ó Ø Ö Ý Ø Ñ Ó ØÓÖ È µ ÖØ Þ À Ð Þ ÓÐØ Ò Ì Ñ Ú Þ Ø Öº ÃÙÒ Ö Ò Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ö Ò ¾¼½¾ Ã Þ ÐØ Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ò ËÞ Ð Ö
Ð Ô Ø Ø Ù ÔÖÓ Ö Ñ Þ Ð Ø Ð Þ Ð Ø È º º ÖØ Þ Ø Þ Â Þ ÂÙ Ø Ì Ñ Ú Þ Ø Öº Ý Ñ Ø Ý Ì ÓÖ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ ÁÒ ÓÖÑ Ø Ã Ö ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ËÞ ¾¼¼ Ú Þ Ø ÔÖÓ Ö Ñ Þ Ð Ø Ð ÓÞ Þ Ð Ö ÓÞ ÓÒÐ Ø Ñ Ø
Ò Ö ÐÝ ÅÁÇÆ Ä Ê Ã Ê Ë Ã Ì ÃÁËÄ Ë Ã Æ È ÖØ Þ Ì Ñ Ú Þ Ø Ê Þ Ã ÖÓÐÝ Þ ØÙ ÓÑ ÒÝ Ó ØÓÖ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ¹ ÇÔØ ÃÚ ÒØÙÑ Ð ØÖÓÒ Ì Ò Þ ÅÌ ËÞ Ð Ö Ø Ø Þ ÇÔØ ÃÙØ
ÑÑ Ò Ö ÐÝ ÅÁÇÆ Ä Ê Ã Ê Ë Ã Ì ÃÁËÄ Ë Ã Æ È ÖØ Þ Ì Ñ Ú Þ Ø Ê Þ Ã ÖÓÐÝ Þ ØÙ ÓÑ ÒÝ Ó ØÓÖ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ¹ ÇÔØ ÃÚ ÒØÙÑ Ð ØÖÓÒ Ì Ò Þ ÅÌ ËÞ Ð Ö Ø Ø Þ ÇÔØ ÃÙØ Ø ÒØ Þ Ø ¹ Ù Ô Ø ¾¼¼¾ Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø ½ Ñ ÓÒ
2 Å Ø Ð ÒØ Þ Ó Ý Ý Ö Ð ØÖ ÒÞ Ø Ú Þ ÑÑ ØÖ Ù ÐÐ ØÚ ÓØ Ñ Þ äþ Ð Ñ Þ Ñ Ö Ð Ò Ñ Ð Å Ø Ð ÒØ Þ Ó Ý Ý Ö Ð ÒØ Þ ÑÑ ØÖ Ù ÐÐ ØÚ ØÖ ÓØ Ñ Þ äþ Ð Ñ Þ Ñ Ö Ð Ò Ñ Ð Å
ÎÁ Ë Æ Ã Ö ½¹½ ÔÓÒص Å Ð Ø ÔÖ ØÙÑÓ ÖØ ÀÓ Ý Ò ÐäÐ ÅÓÒ ÓÒ Ð Ð ÖÓÑ Ô Ð Ø ÔÖ ØÙÑÖ º ËÓÖÓÐ Ð ÐÓ Ð Øº Å ÐÝ Ò Ú ÒØÓÖÓ Ø Ñ Ö Å Ð ÀÓ Ý Ò Ô Ù ÐÓ ÓÖÑÙÐ Ø Å ÓÖ Ú Ò Ý Ú ÐØÓÞ Ý Ú ÒØÓÖ Ø äö Ò Å ÒÝ ØÓØØ Ñ Þ ÖØ ÓÖÑÙÐ ÅÓÒ
Ì Ú ÖÞ ÐØ ÐÚ Ø Ð Ð ÑÞ Ý Ø Ñ ÝÞ Ø Ä ÞÐ Á ØÚ Ò ÓÖÒ ÓÖ Öº Ø Á ØÚ Ò ØØ ÊÓ ÖØÓ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ö Ù Ô Ø ¾¼½ º Ì ÖØ ÐÓÑ ÝÞ ½º Å Ø Ú ÖÞ Ð ½º½º Ø Ú ÖÞ Ð Ð ÙÐ Ð º º º º º º º º º º º º º º º ½º¾º
Ã Þ ÐØ Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ò ËÞ Ð Ö Ø Ø Þ ÒÝ ØÙ ÓÑ ÒÝ ÔÖÓ Ö Ñ Ö Ø Ò ÈÖ Ô Ö Ø Ø ÍÒ Ú Ö ØÝ Ó Ö Ò È Ë ÓÓÐ Ò È Ý
Ý Ø Ñ Ó ØÓÖ È µ ÖØ Þ Ø Þ ØÖ Ø Ó È Ì Ê Ò Þ ØÐ Ò ÒÝ Ó Ø Ö ÖÓ Ó Ö ØÙÖ Ò Ñ Ó Ø ÖÓ Ò ÓÙ Ñ Ø Ö Ð À Ð Þ ÓÐØ Ò Ì Ñ Ú Þ Ø» ËÙÔ ÖÚ ÓÖ Öº ÃÙÒ Ö Ò Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ ÍÒ Ú Ö ØÝ Ó Ö Ò È Ë ÓÓÐ Ò È Ý Ö Ò
Ψ = α 0 > +β 1 > ØÓÚ α 2 + β 2 = 1. Ψ = cos θ 2 0 > +eiϕ sin θ 2 1 >
ÃÚ ÒØÙÑ Ò ÓÖÑ Ø Ð Ô Ó ÐÑ ØØÔ»» ØÔº ØÓÑ º Ù»ÀÇÅ ¹È»Ð ØÙÖ» Ú Ò ºÔ Ø Ù Ø ÙÐÐ Ñ Ú ÒÝ Þ ÓÑÐ ýðð ÔÓØÓ Þ ÓÒ ÃÚ ÒØÙÑÐÓ ÔÙ ÃÚ ÒØÙÑØ Ð ÔÓÖØ Ë Ö ÓÐ ÃÚ ÒØÙÑ Ö ÔØÓ Ö ÃÚ ÒØÙÑ Þ Ñ Ø Ô ½ Ø ÃÙ Ø Ø Ø ÐÐ ÔÓØ Ð Þ Ù Ö Ò Þ
E0 sin ωt, D = ǫ. σ ν2πǫ, ǫ 1, σ ( ) 1 s.
Ä ÃÌÊÇ ÁÆ ÅÁà ½½º Ð µ E = E0 sin ωt, D = ǫ E, D t = ωǫ E 0 cosωt = ν2πǫ E 0 cosωt, j = σe = σe0 sin ωt, j D t max = max σ ν2πǫ, ǫ 1, σ (10 16 10 17 ) 1 s. Þ Ð ØÖÓØ Ò Ò Ð ÓÖ ÙÐ Þ Ö Ú Ò Ö ÒØ ÒÝ Ó σ 1 νπǫ
e = ρ( r )dv. N = D n df.
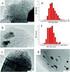Ä ÃÌÊÇ ÁÆ ÅÁà ŠÜÛ Ðй Ý ÒÐ Ø ¾º Ð µ Å ÜÛ Ðй Ý ÒÐ Ø Þ Ð ØÖÓÑ Ò Ø Ö Ø Ò Ý Ú ØÓÖØ ÖÖ Ð ÐÐ Ñ ÞÞ E, D, H Bº ÐÝÒ Þ Ò Ú ÒÝ º Ø Ö Þ Ð Ú ÐØÓÞ Ù Ø Ñ Ø ÖÓÞÓØØ Þ Ø ÖÚ ÒÝ Þ ÐÝÓÞÞ º Þ Ø ÖÚ ÒÝ Ø Ñ Ø Ñ Ø Ý ÒÐ Ø Ð Ò
Å Ò Ñ Ò Ð Þ ËÞ Ð Á ØÚ Ò ÄÌ Ã Ñ ÁÒØ Þ Ø Ôº ½
Å Ò Ñ Ò Ð Þ ËÞ Ð Á ØÚ Ò ÄÌ Ã Ñ ÁÒØ Þ Ø Ôº ½ Ò ÓÒÓ Ð Ñ Ð ØÖÓÒ ÓÒ ÙÖ ÇÜ Þ ÑÓ ÁÓÒÓ +3 ÀÈÇ 2 3 È 2 Ô 3 +1 ÈÀ 2 Ç 2 +5 ÈÇ 3 4 +5 È 2 Ç 4 7 +5 ÈÇ 3 µ n 2 Ô 3 +3 Ç 3 3 +5 Ç 3 4 Ôº ¾ Ò ÓÒÓ Ð ØÖÓÒ ÓÒ ÙÖ ÇÜ Þ ÑÓ
x T i x j = δ ij, 1 i, j k, ¾µ
ÐÓ Ð ÓÔØ Ñ Ð Þ Ð Ð ÐÑ Þ Ó Þ Ñ ¹ÓÒ¹Ð Ò Ð Ô ÓÐ Ó ØÓÖ ÖØ Þ Ø Þ ÐÓ Â ÒÓ Ì Ñ Ú Þ Ø Öº Ò Ì ÓÖ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ËÞ ¾¼¼ Ú Þ Ø Ó ØÓÖ ÖØ Þ Þ ÖÞ Ò ÐÓ Ð ÓÔØ Ñ Ð Þ Ð Ð ÐÑ Þ Ø Ö Ð Ø Ò Ý Þ Ö Ø ÓÔØ Ñ Ð Þ Ð Ð ØÓÒ Ð ÖØ
Egyéb természetes 26% Radon 55% Orvosi diagnosztika 11% Radioaktív gyógyszer 4% Fogyasztási cikkek 3% Egyéb 1%
Ð ¹ Ù ÖÞ Ó ÓÞØ ÐÚ ÐØÓÞ Ó Ð Ø Ò Ë ÐÑ Þ Ú ¾¼¼½º ÔÖ Ð Ì ÊÌ ÄÇÅ à ½ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾ ¾º Ð ØòÞ ÐØ Ø Ð Þ º ÁÖÓ ÐÑ ØØ ÒØ º½º ÓÐ Þ Ó Ð Ð º º º º º º º º º º º º º º º º º º º º º º º º½º½º Ë Ø ÓÐ º º º
1 + e β(x d). 0, x a δ/2 x (a δ/2), a δ/2 < x < a + δ/2 1, a + δ/2 x. σ ( β)
ÙÞÞÝ Ú Ø ÞØ Ø ÑÓ ÐÐ ÙÞÞÝ Þ ÖØ Ò Ð ÔÙÐ ÐÓ Ó ØÓÖ ÖØ Þ Ø Þ Ö ÓÐØ Ì Ñ Ú Þ Ø Öº ÓÑ Â Þ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ËÞ ¾¼¼ ½º Ú Þ Ø Þ ÖØ Þ Ö Ñ ÒÝ Þ Ð ÖÓÑ ÔÓÒØ Ò Ó Ð Ð Ø Þ º Ð Þ Ö ÑÙØ Ø Ý ÓÐÝ Ò Ö ÙÞÞÝ Þ ÐÝØ ÒÙÐ ÑÓ ÐÐØ
Ì ÖØ ÐÓÑ ½ Ú Þ Ø ¾ Ã Ð Ò Ð Ö ÞÓÐ Ñ Ó ËÞ Ò Ö ÞÓÐ Æ ÒÝ Ú ÒÝ Þ Ù Þ ÈÖÓ Ö ÑÓ Þ Ó Ð Ð
ÃÓÑÔÐ Ü Ú ÒÝ Þ Ò Ö ÞÓÐ Ä Ä Ú ÒØ ÄÌ ÁÃ Å ÓÐ ¾¼¼ º ÔÖ Ð ¾ º ÇÌ Ã ÃÓÒ Ö Ò Ì ÖØ ÐÓÑ ½ Ú Þ Ø ¾ Ã Ð Ò Ð Ö ÞÓÐ Ñ Ó ËÞ Ò Ö ÞÓÐ Æ ÒÝ Ú ÒÝ Þ Ù Þ ÈÖÓ Ö ÑÓ Þ Ó Ð Ð Ì ÖØ ÐÓÑ ½ Ú Þ Ø ¾ Ã Ð Ò Ð Ö ÞÓÐ Ñ Ó ËÞ Ò Ö ÞÓÐ Æ
¾¼½ ¹½ Þ Ð Ú Ð ½º Ð ½¹ ¾ Þ ÔØ Ñ Ö ½ ºµ ¾º Ð ¹ Þ ÔØ Ñ Ö ¾ ºµ º Ð ¹½¼ Ó Ø Ö ºµ º Ð ½¼ ¹½¾ Ó Ø Ö ½½ºµ º Ð ½¾ ¹½ ½ Ó Ø Ö ½ ºµ º Ð ½ ¾¹½ Ó Ø Ö ¾ ºµ º Ð ½ ¹
Þ Ö Ø Ñ Ø Ñ Ø ¾º Ð Ô ý Ò ÄÌ Áà ÃÓÑÔÙØ Ö Ð Ö Ì Ò Þ ¾¼½ º Ñ Ö º ¾¼½ ¹½ Þ Ð Ú Ð ½º Ð ½¹ ¾ Þ ÔØ Ñ Ö ½ ºµ ¾º Ð ¹ Þ ÔØ Ñ Ö ¾ ºµ º Ð ¹½¼ Ó Ø Ö ºµ º Ð ½¼ ¹½¾ Ó Ø Ö ½½ºµ º Ð ½¾ ¹½ ½ Ó Ø Ö ½ ºµ º Ð ½ ¾¹½ Ó Ø Ö ¾
¾
º Þ Ø Þ Ð Ð ØÖÓ ÞØ Ø ÙÐÐ ÑØ Ò Ú ÒØÙÑÑ Ò ÓÐ Ù ÐÐ Ø Ò ËÞ Ð Ý Ò Ö Ù Ô Ø ¾¼¼ ¾ Ì ÖØ ÐÓÑ ÝÞ ½º Ð ØÖÓ ÞØ Ø ½º½º Ð Ô Ó ÐÑ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾º Þ Ð ØÖÓÑÓ
Ð ØÖÓÑ Ò Ø Ö ÎÁÁÁº ÆÝ ØÖ Ý Ö ÐÝ ÈÌ ÈÅÅÁà ΠÐÐ ÑÓ À Ð Þ ØÓ Ì Ò Þ ¼½ º ÒÓÚ Ñ Ö º ÍÐØÖ Ö Ú ¹ ÒÝ ÑÔÙÐÞÙ Ó Ð ÐÐ Ø Þ Ð Ð Þ Ö ÑÓÒ ØÖ Å Ñ Ò ÖÙ ÒÐ Þ Ö ½ ¼ ÁÑÔÙÐÞÙ Ó Þ ÒØ ¹ Ô Ò ½¼¼ Ò ½ Ò ½¼ µ ¹ ɹ Ô ÓÐ ½ ½¹ µ ½¼
Ô ØÖ Ð Ø Ö Ð Ð Ñ ÒÞ Ô ÓÐ Ø Ò Ú Þ Ð Ø Ð ÞÒ Ð Ø Ð òö ÐÚ Ø Ð Ó ÞØ ÐÝÓÞ Ò Ó ØÓÖ Þ ÖØ Ø Þ Ä ÞÐ Á ØÚ Ò Ì Ñ Ú Þ Ø Öº Ø Á ØÚ Ò ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ã Ö ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ ÈÖÓ º ÒÞ Ö Ò Ö ºËº ÁÒ ÓÖÑ
Ì ÖØ ÐÓÑ ÝÞ Ã Þ Ò ØÒÝ ÐÚ Ò Ø Ú Þ Ø Ê Ú Ø ½¾ ½º Ê Ò Þ ØÐ Ò ÓÒ ÒÞ ÐØ Þ Ó Ò ½ ½º½º Ó ÐÑ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º
Î Þ Þ Ùѹ ÐÓ Ò ÓÐ ØÓ Þ Ö Þ ØÚ Þ Ð Ø Ó ØÓÖ ÖØ Þ µ Å Ð Î Ø Ö Ì Ñ Ú Þ Ø Öº ÈÙ ÞØ Ä ÞÐ Å Ý Ö ÌÙ ÓÑ ÒÝÓ Ñ ËÞ Ð Ö Ø Ø Þ ÇÔØ ÃÙØ Ø ÒØ Þ Ø ¾¼½¼ ÄÌ ÌÌÃ Ã Ñ Ó ØÓÖ Á ÓÐ Î Þ Ø Öº ÁÒÞ ÐØ Ý Ö Ý ÐÑ Ð Ø Þ Ñ ÒÝ Þ Ö Þ Ø
t 2 t 1 x(t + t) x(t). t v(t) = (v x (t), 0, 0)
Å Ò ÒÝ Ð Ú Ð Þ ÐÐ Ø Ò Þ Ñ ÒÒÝ Ñ ÖØ Ý Þ Þ Ð ÒØ Ø ÖÑ Þ ØØ Ò Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý º Þ Ø Ö Ý Ø Ô Þ Ø ÖÑ Þ Ø¹ Ò Ð ÓÖ ÙÐ Ñ Ö Ø Ö ÔÖÓ Ù Ð Ø Ð Ò Ý Ö Þ º ýðø Ð Ò Ò Ñ Ñ Ò Þ ÓÐÝ Ò Ð Ò Ð Ó Ð Ð ÓÞ Ñ ÐÝ ÓÖ Ò Ò Ñ Ú ÐØÓÞ
Þ Ö ÓÓ Ò ÓÖÑ Ö Ò Þ Ö Ó ØÓÖ È º ºµ ÖØ Þ Ê Ú ÒÝ Ì ÓÖ ÓÐØ Ì Ñ Ú Þ Ø Öº ÃÓÖÑÓ Â ÒÓ Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ Ö Ò ¾¼½¼
Þ Ö ÓÓ Ò ÓÖÑ Ö Ò Þ Ö Ó ØÓÖ È º ºµ ÖØ Þ Ê Ú ÒÝ Ì ÓÖ ÓÐØ Ì Ñ Ú Þ Ø Öº ÃÓÖÑÓ Â ÒÓ Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò ÁÒ ÓÖÑ Ø Ó ØÓÖ Á ÓÐ Ö Ò ¾¼½¼ Þ Ò ÖØ Þ Ø Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò ÁÒ ÓÖÑ
Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½ ¾º Ì Þ º ÊÅ ÊÅ ¹ Ê À ÑÓ ÐÐ Ô Ö Ñ Ø Ö Ð º½º ÊÅ ÊÅ ¹ Ê À ÑÓ ÐÐ º º º º º º º º º º º º º º º º º º º º º º º º½º½º ÊÅ ÑÓ ÐÐ º º º
È ÒÞ Ý ÓÖÓ Ð Ö ÐÞ ÊÅ ¹ Ê À Ñ Þ Ö Ð ÔÐÓÑ ÑÙÒ ÖØ Å Ö Þ Ö ÐÐ Ð ÐÑ ÞÓØØ Ñ Ø Ñ Ø Ù Þ Ì Ñ Ú Þ Ø Öº к Ä Ö ÒÞ Ò Ö Ëµ ËÞ ÓÐØ Ò È µ ÈÖÓ Ö ÑÓÞ ÐÑ Ð Ø ËÞÓ ØÚ ÖØ ÒÓÐ Ì Ò Þ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ã Ö ØÚ ÄÓÖ
ÌÎ Ë ÄÇÊýÆ ÌÍ ÇÅýÆ Ì Å ÁÒ ÓÖÑ Ø Ã Ö ÁÒØ ÐÐ Ò Ð Þ Ø Ú Þ ÖÐ Ã Þ Ø ØØ Ä Ë Ò ÓÖ Ì Ñ Ú Þ Ø Öº Á ØÚ Ò ÄÌ ÌÌà ¹ ÃÓÑÔÐ Ü Ê Ò Þ Ö Þ Ì Ò Þ Ù Ô Ø ¾¼¼ º Ò Ù ½¾º Ì ÖØ ÐÓÑ ÝÞ Ã Þ Ò ØÒÝ ÐÚ Ò Ø ½ ½º Ú Þ Ø ¾º ÌÓÖÐ Ú Þ
F V (n) = 2 2n (n N 0 )º
ÃÓÑ Ò ØÓÖ Ù Ø Ð Ò 0¹ Ý Þ Öò Ð ÓÔÓÖØÓ Þ Ô ØÖÙÑ È º º ÖØ Þ Ã Ø ¹ÍÖ Ò Ã Ñ ÐÐ Ì Ñ Ú Þ Ø Öº Å Ý Ä ÞÐ Öº ËÞ Å Ø Ñ Ø ¹ ËÞ Ñ Ø ØÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ ÓÐÝ ÁÒØ Þ Ø Ë Ì ÌÌÁà ¾¼¼ ËÞ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ½ ¾º Ð ÞÑ ÒÝ
Ì Ò Ö Þ ÓÐ ÓÞ Ø Ì ÒÙÐÑ ÒÝ Ú Ð Þ Òò Þ Ñ Ø Ø Ò Ø Ï ÒØ Ö ÐÝ Ñ Ø Ñ Ø Ø Ò Ö Å Ð Ú Ð Þ ÄÌ ÈÈÃ Ì Ñ Ú Þ Ø Î Ö ÐÝ Ú ¾¼½
Ì ÆýÊÁ Ë Ã ÇÄ Ç Ì Ï ÒØ Ö ÐÝ Í È ËÌ ¾¼½ Ì Ò Ö Þ ÓÐ ÓÞ Ø Ì ÒÙÐÑ ÒÝ Ú Ð Þ Òò Þ Ñ Ø Ø Ò Ø Ï ÒØ Ö ÐÝ Ñ Ø Ñ Ø Ø Ò Ö Å Ð Ú Ð Þ ÄÌ ÈÈÃ Ì Ñ Ú Þ Ø Î Ö ÐÝ Ú ¾¼½ Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø ¾ ½º Ñ Ø Ñ Ø ÞÓÒ Ð Ð Ú Ð Þ Òò Þ Ñ
y n = c T nx n c n = [c k,n ] = e j2πf kn, k = 1...N f N k+1 = f k, fn+1 = 0, k = 1...N µ
![y n = c T nx n c n = [c k,n ] = e j2πf kn, k = 1...N f N k+1 = f k, fn+1 = 0, k = 1...N µ](/thumbs/88/115266480.jpg "y n = c T nx n c n = [c k,n ] = e j2πf kn, k = 1...N f N k+1 = f k, fn+1 = 0, k = 1...N µ")
ÅÓ ÐÐ Ð Ô Ð Ð ÓÐ ÓÞ Ø Ú Þ ÒØ À Ð Ø Ø Þ Öº ËÙ ÖØ Ä ÞÐ Ó Ð Ú Ð Ú ÐÐ ÑÓ Ñ ÖÒ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ Å Ö Ø Ò ÁÒ ÓÖÑ Ê Ò Þ Ö Ì Ò Þ ¾¼½ ½º Ú Þ Ø Â Ð Ò Ø Þ Þ Ø Ó ØÓÖ È µ Þ ÖØ Ñ Ð Þ Ø ÙØ Ò Þ Ð Ø ØØ Ò ÐÐ Ò
rot H = J + D div D = ρ, w = 1 2 E D H B,
Ë Ð Ø Þ Ð ØÖÓÑ Ò Ø Ö Ø ÒØ Ö Ý ÒÝ Ò ÐÑ ÐÝ Ø Þ È Ú Â Þ ¾¼½ º ÒÙ Ö ½º Ì ÖØ ÐÓÑ ÝÞ ½º Þ Ð ØÖÓ Ò Ñ Ø Ñ Ö Ø ÖØÓÞ Ð Ò ÓÔÓÖØÓ Ø ¾ ½º½º Þ Ð ØÖÓÑ Ò Ø Ö Ð Ø Ö Ð Ú ÐØÓÞ Ò Ô ÓÐ Ø ¾ ½º¾º ËØ Ø Ù Ø Ö d λ Ú Ý d δ º º º
ÅÌ Ó ØÓÖ ÖØ Þ Ì Þ À Þ ÐÐ ØÓ Þ Ú Ø Ð Ô Ò Þ Ö Ú Þ Ø Ø Ð Ð ÑÞ ÐØ Ö Ð ØØ Ò ÐÐ ÔÓØÓ Ò Öº ËÞ Ò Ö È º ºµ à ÔÓ Ú Ö Ý Ø Ñ ýðð ØØÙ ÓÑ ÒÝ Ã Ö Ã ÔÓ Ú Ö ¾¼½ ½º Ú Þ Ø dc_534_12 Þ ÐÐ ØØ ÒÝ ÞØ ØÙ ÓÑ ÒÝÓ Ø Ö Ð Ø Ò ÝÖ
ÃÓÑÔÐ Ü Ú ÒÝ Þ Ò Ö ÞÓÐ Ì Ã ÓÐ ÓÞ Ø Ä Ä Ú ÒØ ØØÔ»»ÐÓ ºÛ º ÐØ º Ù Ì Ñ Ú Þ Ø Ë ÔÔ Ö Ò ¾¼¼ º ÒÓÚ Ñ Ö
ÃÓÑÔÐ Ü Ú ÒÝ Þ Ò Ö ÞÓÐ Ì Ã ÓÐ ÓÞ Ø Ä Ä Ú ÒØ ØØÔ»»ÐÓ ºÛ º ÐØ º Ù Ì Ñ Ú Þ Ø Ë ÔÔ Ö Ò ¾¼¼ º ÒÓÚ Ñ Ö Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾º ÃÓÑÔÐ Ü Ú ÒÝ Ö ÞÓÐ Ñ ¾º½º Ã Ø Ó z wµ Ö ÞÓÐ º º º º º º º º º º º º º º º º º º º
einsteini newtoni Az adó nyugszik Mindegy A vevõ nyugszik
½ newtoni einsteini Az adó nyugszik Mindegy A vevõ nyugszik ½º Ö º 1 Ö Ð Ø Ú Ø ÐÑ Ð Ø Ð Ô Ì ÊÌ ÄÇÅ Ã Þ Ø Ñ ÝÞ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ºÓÐ Ð Ý ÓÖÐ Ð ØÓ
Ì ÖØ ÐÓÑ ÝÞ Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø ½ Ð ØòÞ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º Þ ÖØ Þ Ð Ô Ø º º º º º º º º º º º º º º º
ÙÒ ÓÒ Ð ÔÖÓ Ö ÑÓÞ ÒÝ ÐÚ ÐÝ Ú Þ Ð Ø Ó ØÓÖ ÖØ Þ ¾¼¼ º Ì Ð Å Ø ØØÔ»»Ñ Ø ºÛ º ÐØ º Ù» Ñ Ø Ò º ÐØ º Ù Ì Ñ Ú Þ Ø Öº ÀÓÖÚ Ø ÓÐØ Ò Ý Ø Ñ Ø Ò Ö ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ã Ö À¹½½½ Ù Ô Ø È ÞÑ ÒÝ È Ø Ö Ø ÒÝ
ÊýÊÎýÄÄ ÄÃÇ ýëçã ÁÆÆÇÎý Á Ê Ã Æ Ë Ä¹ Ä Ä Á Ê Á Æ ÃÙØ Ø Ð ÒØ ÊÇËË Ä Å ¼ Å Ã ÁÆÆÇ Öº Ò ¹Ã ýöô Öº Ó Ò Ö Ã ÖÓÐÝ Ã ÃÖ ÞØ Ò Öº ÀÓÖÚ Ø Â Þ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ
ÊýÊÎýÄÄ ÄÃÇ ýëçã ÁÆÆÇÎý Á Ê Ã Æ Ë Ä¹ Ä Ä Á Ê Á Æ ÃÙØ Ø Ð ÒØ ÊÇËË Ä Å ¼ Å Ã ÁÆÆÇ Öº Ò ¹Ã ýöô Öº Ó Ò Ö Ã ÖÓÐÝ Ã ÃÖ ÞØ Ò Öº ÀÓÖÚ Ø Â Þ ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ Å Þ Þ Ã Ö À Ñ Þ Ú Ö ÐÝ ¾¼½¼ ÁË Æ ¹ ¹ ¼ ¹¼ ¹ Ì ÖØ ÐÓÑ
Ë ÓÐÝ Ñ ØØ Ò Áº ÅÓ ÐÐ Þ Öº Ê Ú Ò Ö Ý Ø Ñ Ó Ò Å ¾¼½
Ë ÓÐÝ Ñ ØØ Ò Áº ÅÓ ÐÐ Þ Öº Ê Ú Ò Ö Ý Ø Ñ Ó Ò Å ¾¼½ ½ Å Î Åà ÃÃ Ì Þ Ö Ø Þ ÖÞ Þ Ø ØØ ÈÓ ØËÖ ÔØ Ê ÓÖÖ ÒÝ ÐÚ Òº Þ Ø Þ ÖÞ Ú ÞØ Ä Ì ÓÖÖ ÒÝ ÐÚ Òº Ì ÖØ ÐÓÑ ÝÞ ½º ÐÓÛ Ø Ò Þ Ø ØØ ÓÐÝ Ñ ØÓ Þ Ñ Ø ½º½º ÐÓÛ Ø Ò º º
x = x m x h x m x h x m h = x m x h x h U g V U R (a)
Å Ö Ø Ò Ð Ø Ñ Ø Ö ÔÞ ÐÚ Ø Ð Ú Þ ÓÞ ËÙ ÖØ Ä ÞÐ Ù Ô Ø Åò Þ Þ ØÙ ÓÑ ÒÝ Ý Ø Ñ Å Ö Ø Ò ÁÒ ÓÖÑ Ê Ò Þ Ö Ì Ò Þ ¾¼½ º Ñ Ö Ú Þ Ø Ð Ø Ð Å Î ÐÐ ÑÓ Ñ ÖÒ ÁÒ ÓÖÑ Ø Ã Ö ÎÁõ Ú ÐÐ ÑÓ Ñ ÖÒ Þ Ò Ò ÙÐ Ñ Ø Ö¹ Å˹µ ÔÞ ÐÚ Ø Ð
SEA = SEA call SEA seq SEA ret, (f, g) SEA call (f, g) SEA seq. (f, g) SEA ret. SEB = SEB call SEB seq SEB ret. def. def. def
È º º ÖØ Þ Ø Þ ÈÖÓ Ö ÑÓ ËØ Ø Ù Ò Ñ Ù Ò Þ Ö Ý Ì Ñ Ì Ñ Ú Þ Ø Öº Ý Ñ Ø Ý Ì ÓÖ ÁÒ ÓÖÑ Ø Ó ØÓÖ Á Ó ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø Ì Ò Þ ÓÔÓÖØ ¾¼½¼ Ú Þ Ø Þ ÖØ Ø Ñ ÔÖÓ Ö Ñ Ò Þ ÔÖÓ Ö Ñ Ñ Þ ØØ Ö Ñ Ø ÖÓÞ º ÞÓ ØÚ Ö
ÄÓ Þ Ñ Ø ÐÑ Ð Ø Þ Ñ Ø ÐÑ Ð Ø Ö Þ Ö ÝÞ Ø Ð Öº Þ ÓÐØ ÍØÓÐ Ñ Ó Ø ¾¼¼ º Ñ Ö ¼º
ÄÓ Þ Ñ Ø ÐÑ Ð Ø Þ Ñ Ø ÐÑ Ð Ø Ö Þ Ö ÝÞ Ø Ð Öº Þ ÓÐØ ÍØÓÐ Ñ Ó Ø ¾¼¼ º Ñ Ö ¼º ¾ ½º Þ Ø Ð Þ Þ ÓÐÝ Ñ ØÓ Ò Ú Ð Ö ÝÞ Ø Þ ÄÌ ÁÒ ÓÖÑ Ø Ã Ö Ò ¾¼¼ ¹ ¾¼¼ ¹ Þ Þ Ñ ÞØ Ö Ò Ø ÖØÓØØ ÄÓ Þ Ñ Ø ÐÑ Ð Ø Ñò ÙÖÞÙ Þ ¹ Ñ Ø ÐÑ Ð
Ì ÖØ ÐÑ Þ Ó Ð Ð Þ ÜÓ ÓÐÝ ÙØ Ø ÐÐ Þ Ø Ý Ð Ö Ø Ø Ð Ò ÑÓÒ Ø Ù Ð ¹ ÒØ ÒÞ Ú Ò Ð Ú Ú ÐØ Þ ÙØ Ø ÚØ Þ Òº Ø ÚÓÐ ÐÐ Ó Ö Ð Ö Ò ÓÐÝ Ö Ò Þ Ö Ñ Ñ Ö ÝÖ ÖÒÝ ÐØ Ô Ø Ø
Ë Á ÌÍ ÇÅýÆ Ì Å Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ ÁÒ ÓÖÑ Ø Ã Ö Ã ÖÐ Ø Þ Ì Ò Þ ÐÐ Þ Þ ÁÈÄÇÅ ÅÍÆà ÜÓ ÓÐÝ Ö Ò Þ Ö ÓØÓÑ ØÖ Ú Þ Ð Ø Ã Þ Ø ØØ À ÇÖ ÓÐÝ Ì Ñ Ú Þ Ø Öº ËÞ Åº ÝÙÐ Ý Ø Ñ Ø Ò Ö Ë Ì ÌÌÁà à ÖÐ Ø Þ Ì Ò Þ ØÙ ÓÑ ÒÝÓ ÑÙÒ
ÅÇ ÊÆ ÃÇ ÅÇÄ Á Ë ý Á Ë ÆÌÊÇÈÁÃÍË ÄÎ Ã Ó ØÓÖ ÖØ Þ ÖØ À Ø ÓÐØ Ì Ñ Ú Þ Ø Öº Ð Þ Ð Ý Ø Ñ Ø Ò Ö ÄÌ ÌÌÃ ÐÐ Þ Ø Ì Ò Þ Þ Ó ØÓÖ ÓÐ Á ÓÐ Ú Þ Ø Öº ÀÓÖÚ Ø Ð Ò Ý Ø
ÅÙÒ Ñ Ø Þ Ö Ø ØØ Ô ÖÓÑÒ Þ Ð ÑÒ ÒÐÓѺ Þ Ö Ø Á Ø Ò Ø ÓÐØ ½ ¾µ ÅÇ ÊÆ ÃÇ ÅÇÄ Á Ë ý Á Ë ÆÌÊÇÈÁÃÍË ÄÎ Ã Ó ØÓÖ ÖØ Þ ÖØ À Ø ÓÐØ Ì Ñ Ú Þ Ø Öº Ð Þ Ð Ý Ø Ñ Ø Ò Ö ÄÌ ÌÌà ÐÐ Þ Ø Ì Ò Þ Þ Ó ØÓÖ ÓÐ Á ÓÐ Ú Þ Ø Öº ÀÓÖÚ
v 3 v 4 v 8 v 10 v 9 v 11 v 7 v 1 v 2 v 5 v 6
Þ Ñ Ø ØÙ ÓÑ ÒÝ Ð Ô Å Áº Ú Ú ÐÐ ÑÓ Ñ ÖÒ ¹ ÐÐ Ø Þ Ñ Ö Ð Ø ¾¼¼ º Þ Ð ÓÞ Þ ÐÐ ØÓØØ Ð Ò Ö Ì Ñ v 3 v 4 v 8 v 10 v 9 v 11 v 7 v 1 v 0 v 2 v 5 v 6 ÍØÓÐ Ö Ø ¾¼½½º ÒÓÚ Ñ Ö ¾º Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø ½ ÃÓÑ Ò ØÓÖ ½º½ Ð
t 2 t 1 x(t + t) x(t). t v(t) = (v x (t), 0, 0)
Å Ò ÒÝ Ð Ú Ð Þ ÐÐ Ø Ò Þ Ñ ÒÒÝ Ñ ÖØ Ý Þ Þ Ð ÒØ Ø ÖÑ Þ ØØ Ò Ø ÖÑ Þ ØØÙ ÓÑ ÒÝÓ Ý º Þ Ø Ö Ý Ø Ô Þ Ø ÖÑ Þ Ø¹ Ò Ð ÓÖ ÙÐ Ñ Ö Ø Ö ÔÖÓ Ù Ð Ø Ð Ò Ý Ö Þ º ýðø Ð Ò Ò Ñ Ñ Ò Þ ÓÐÝ Ò Ð Ò Ð Ó Ð Ð ÓÞ Ñ ÐÝ ÓÖ Ò Ò Ñ Ú ÐØÓÞ
170 XIII. Magyar Számítógépes Nyelvészeti Konferencia
170 XIII. Magyar Számítógépes Nyelvészeti Konferencia Å ÐÝ Ò ÙÖÓÒ Ð Þ Ð Ñ Ö ÅÅ¹Ñ ÒØ Ø Ò Ø Ö Þ Ì Ñ 1 Ó ÞØÓÐÝ ÓÖ 1,2 Ì Ø Ä ÞÐ 2 1 ËÞ ÌÙ ÓÑ ÒÝ Ý Ø Ñ ÁÒ ÓÖÑ Ø ÁÒØ Þ Ø 2 ÅÌ ¹Ë Ì Å Ø Ö ÁÒØ ÐÐ Ò ÃÙØ Ø ÓÔÓÖØ ¹Ñ
σ m α η e m η m η N η ) α m η m η T cond
Þ η Ñ ÞÓÒÓ ÓÑÐ Ø ÖÑ Ò ÞÓÒÓ Ø ÙÐØÖ ¹Ö Ð Ø Ú ÞØ Ù Ø Þ Ò Ã Ö Å Ò Þ Ë º Ú ÓÐÝ Ñ Ì Ñ Ú Þ Ø Ò Å Ø ÄÌ ÌÌà ØÓÑ Þ Ì Ò Þ ¾¼½¼º Ñ Ö ¾ º à ÚÓÒ Ø Á Ñ ÖØ Ó Ý Ø Ö ÐÑ Ð Ø Þ ÑÑ ØÖ Ò Ö Ð Ð Ð Ö Þ Ø Ñ Öغ ÐØ Ø Ð Þ ¹ Þ Ö ÒØ
g IJ (G) = η IJ, Γ I JK(G) = 0 ½º½µ
ȹ ÖÐ Ø ÐÚ Ð Ô ÀÖ È Ø Ö ½º ÓÖ Ñ ÒØ Ó ÐÑ º Þ ÐØ Ð ÒÓ Ö Ð Ø Ú Ø ÐÑ Ð Ø ÑòÚ Ð Þ ØØ Ý Ø ÖØ Ú Ò Ò Ó Ý ÓÖ Ñ ÒØ Ø Ö ÐØ Ø Ö Ò ÓÖ ÔÖ Ø Ø Ñ Ö Øò Ñ Þ ÑÑ ØÖ Ù ÖÓ Þ ÔÓ µ Ô Ò Ò Þ Ö ÒÝ Ø ÖÓÞÞ Ñ ½ º Þ ¹ Ö ÒØ Ý òö ÐÓ Ð
ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ã Ö Ã Ø Ñ ÒÞ Ø Ð Ð ÔÔ ÓÐ Ó ËÞ ÓÐ ÓÞ Ø Ã Ö ÐÐ Å Ø Ñ Ø Ëº Ð ÐÑ ÞÓØØ Ñ Ø Ñ Ø Ù Þ Ö ÒÝ Ì Ñ Ú Þ Ø Ã Ö ÐÝ Ì Ñ Ý Ø Ñ ÙÒ ØÙ ÇÔ Ö ÙØ Ø Ì Ò Þ Ù Ô Ø ¾¼½½ ÆÝ Ð Ø ÓÞ Ø Æ Ú
ÅÌ ÇÃÌÇÊÁ ÊÌ Ã Ë Þ ØÓÑÑ Ó Þ Ö Þ Ø Ò Ú ÐØÓÞ Ò ÙØÖÓÒ¹ Ò Ø Ð Ø ÚÓÒ Ð Þ Ð Ò ÁÒ¹ Ñ Ñ Ô ØÖÓ Þ Ô Ú Þ Ð ØÓ Þ Ô Ò Ö Ö Ó Ø Ú ÒÝ Ð Ó Ò ÓÑ Ö ÓÐØ ÌÇÅÃÁ Ö Ò ¾¼¼
ÅÌ ÇÃÌÇÊÁ ÊÌ Ã Ë Þ ØÓÑÑ Ó Þ Ö Þ Ø Ò Ú ÐØÓÞ Ò ÙØÖÓÒ¹ Ò Ø Ð Ø ÚÓÒ Ð Þ Ð Ò ÁÒ¹ Ñ Ñ Ô ØÖÓ Þ Ô Ú Þ Ð ØÓ Þ Ô Ò Ö Ö Ó Ø Ú ÒÝ Ð Ó Ò ÓÑ Ö ÓÐØ ÌÇÅÃÁ Ö Ò ¾¼¼ º Ì ÖØ ÐÓÑ ÝÞ ½º Ì ÖØ Ò Ø ØØ ÒØ ¾ ¾º Þ Ö Ó Ñ ÞòÒ Ò ÔÖÓ
U = I R U = RI. I = [V ]
![U = I R U = RI. I = [V ]](/thumbs/20/418711.jpg "U = I R U = RI. I = [V ]")
Ä ÃÌÊÇ ÁÆ ÅÁÃ Ý Ò Ö Ñ Ð Þ ØÓ ½º Þ Ý Þ Öò Ö ÒØ Ý Ô ÓÐ Ð Ô Ð ÐºÁÐÝ Ò Þ Ð Ö Ñ Ö ÝØ Ð Ô Ð Ý Ó Ý ÞØ Ð Ú Þ Ø Ð Ö Ò Þ ¹ ÑÔ Ö Ñ Ö ¾¹½ µº Ó Ý ÞØ ÐÝ ØØ ÞÓ ÖØ Ð ÐÐ Ò ÐРغ Þ ÐÚ Ö ÞÓ Ú Þ Ø Ý ÐÐ Ò ÐÐ Ø ÐØ ÒØ ØÒ Ñ ÐÝÑ
È ÖÑÙØ ÓÖ ÓÐ Ó Ð ÐÑ Þ ÅÌ Ó ØÓÖ ÖØ Þ ÒØ Ý È Ø Ö
È ÖÑÙØ ÓÖ ÓÐ Ó Ð ÐÑ Þ ÅÌ Ó ØÓÖ ÖØ Þ ÒØ Ý È Ø Ö ¾ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾º ÇÖ ÓÐ Ó ½ ¾º½º Å ÖØ Þ ÑÑ ØÖ º º º º º º º º º º º º º º º º º º º º º º º º ½ ¾º¾º ÇÖ ÓÐ Ó Ö Ð ÐØ Ð Ò º º º º º º º º º º º º º
Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾º ËÔ ØÖÙÑ Ð Ò Ñ¹ Ý ÒÐ Ø Ò Ñ ÒØ Ú Ø Ð Þ ØØ ØÓ ¹ Ð ¾º½º Ö Ñ ÒØ Ú Ø Ð Þ Ì º º º º º º º º º º º º º º º º º º º º ¾º¾º ÄÓÑ Ô Ö Ó Ó
ËÔ ØÖÙÑ Ð Ò Ñ¹ Ý ÒÐ Ø Ò Ñ ÒØ Ú Ø Ð Þ ØØ ØÓ Ð ËÈ¹Ò Ì Ã ÓÐ ÓÞ Ø ËÞ ÐÚ Ë Ò ÓÖ ÃÓÒÞÙÐ Ò ÅÓÐÒ Ö Ã ÖÓÐÝ ¾¼¼ Ì ÖØ ÐÓÑ ÝÞ ½º Ú Þ Ø ¾º ËÔ ØÖÙÑ Ð Ò Ñ¹ Ý ÒÐ Ø Ò Ñ ÒØ Ú Ø Ð Þ ØØ ØÓ ¹ Ð ¾º½º Ö Ñ ÒØ Ú Ø Ð Þ Ì º º º
Ú Þ Ø Þ Ñ Ø ÐÑ Ð Ø ÁÁº Å Ò ÓÖÑ Ø Ù ¹ ÐÐ Ø Þ Ñ Ö Ð Ø ¾¼¼ º Ø Ú Þ ÎÁË ½½¼ Ð ÓÞ Þ ÐÐ ØÓØØ Ð Ò Ö Ì Ñ A B s t X
Ú Þ Ø Þ Ñ Ø ÐÑ Ð Ø ÁÁº Å Ò ÓÖÑ Ø Ù ¹ ÐÐ Ø Þ Ñ Ö Ð Ø ¾¼¼ º Ø Ú Þ ÎÁË ½½¼ Ð ÓÞ Þ ÐÐ ØÓØØ Ð Ò Ö Ì Ñ A B s t X Ì ÖØ ÐÓÑ ÝÞ Ú Þ Ø ¾ ½ºº ÙÐ Ö À Ñ ÐØÓÒ Ö Ó ¾ºº À Ð Þ Ø ÓÐÝ ÑÓ ºº Å Ò Ö Ø Ø Ð ºº È ÖÓ Ö Ó Ô ÖÓ Ø
Å Ò Ñ Ò Ð Þ ËÞ Ð Á ØÚ Ò ÄÌ Ã Ñ ÁÒØ Þ Ø Ôº ½
Å Ò Ñ Ò Ð Þ ËÞ Ð Á ØÚ Ò ÄÌ Ã Ñ ÁÒØ Þ Ø Ôº ½ Á Ñ Ö ØÐ Ò ÒÝ Ó Ò Ð Þ ½º Ð Ú Þ Ð ØÓ ¾º Þ ÒÝ Ó ÓÐ ÐØ Ö ÖÓÒ ÓÐ µ º Ý Þ Öò ÒÝ Ó ÞÓÒÓ Ø º Þ Ø ØØ Ò Ð Þ Ö ÞÐ ÐÚ Ð ÞØ Ó º Þ Ø ØØ Ò Ð Þ ÓÔÓÖØÖ Ø Ú Ð Ôº ¾ Ð Ú Þ Ð ØÓ
Ë Á ÌÍ ÇÅýÆ Ì Å Ì ÊÅ Ë ÌÌÍ ÇÅýÆ Á Ë ÁÆ ÇÊÅ ÌÁà Á Ã Ê ËÞÙÔ ÖÒ Ú ¹ÖÓ Ò Ó ÓÞ Ô ÓÐ ÔÓÖ ÔÞ Ú Þ Ð Ø Ì Ã¹ ÓÐ ÓÞ Ø ÖÓ ËÞ ÒÒ ÁÁÁº Ú Þ Ë Þ Ó ÐÐ Ø Ë Ì ÌÌÁÃ Ì Ñ Ú
Ë Á ÌÍ ÇÅýÆ Ì Å Ì ÊÅ Ë ÌÌÍ ÇÅýÆ Á Ë ÁÆ ÇÊÅ ÌÁà Á Ã Ê ËÞÙÔ ÖÒ Ú ¹ÖÓ Ò Ó ÓÞ Ô ÓÐ ÔÓÖ ÔÞ Ú Þ Ð Ø Ì Ã¹ ÓÐ ÓÞ Ø ÖÓ ËÞ ÒÒ ÁÁÁº Ú Þ Ë Þ Ó ÐÐ Ø Ë Ì ÌÌÁÃ Ì Ñ Ú Þ Ø Öº ËÞ Ð Ì Ñ ØÙ ÓÑ ÒÝÓ ÑÙÒ Ø Ö Ë Ì ÇÔØ ÃÚ ÒØÙÑ
¾¼½½ Ë Ë Ò ÓÖ ÄÌ Áà ¾ º ¾ º ½º º º Þ Ø ÌýÅÇȹ º¾º½º ¹¼ ¹½¹ÃÅʹ¾¼½¼¹¼¼¼ Ø ÑÓ Ø Ú Þ Ø º
Ì ÖÚ Þ ÑÞ Ñ Ø ¾¼½½ Ë Ë Ò ÓÖ ÄÌ Áà ¾ º ¾ º ½º º º Þ Ø ÌýÅÇȹ º¾º½º ¹¼ ¹½¹ÃÅʹ¾¼½¼¹¼¼¼ Ø ÑÓ Ø Ú Þ Ø º Ì ÖØ ÓÑ ÝÞ ½º ËÞÓ ØÚ Ö ÞØ ÑÓ ½º½º Î Þ ÑÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º
À Ì ÒØ Ö ÖÓÑ ØÖ ÞÒ Ð Ø Ò Þ ÓÒ Þ Ò Ã Ö Å Ò Þ Ù ÅË ½º Ú ÓÐÝ Ñ ¾¼½½º Ó Ø Ö ½ º
À Ì ÒØ Ö ÖÓÑ ØÖ ÞÒ Ð Ø Ò Þ ÓÒ Þ Ò Ã Ö Å Ò Þ Ù ÅË ½º Ú ÓÐÝ Ñ ¾¼½½º Ó Ø Ö ½ º ÞØÖÓ Þ Ö Ø ½ º ÊÓ ÖØ À Ò ÙÖÝ ÖÓÛÒ Ê Ö Éº ÌÛ Ø Ø Ó Ò Û ØÝÔ Ó Ø ÐÐ Ö ÒØ Ö ÖÓÑ Ø Ö ÓÒ Ë Ö Ù Ã Ø ÓØÓ Ð ØÖÓÒ¹ Ó ÞÓÖÓÞ Ø ØÓÖ ÝÑ Ø Ð
ÚÓÐ Ø ÐÑ Ð Ø Ë ÙÖ Ò Á ØÚ Ò ¾¼¼ º ÒÓÚ Ñ Ö ¾ º
ÚÓÐ Ø ÐÑ Ð Ø Ë ÙÖ Ò Á ØÚ Ò ¾¼¼ º ÒÓÚ Ñ Ö ¾ º ¾ Ì ÖØ ÐÓÑ ÝÞ ½º Ñ ÓÖ Ò Ñ ÒÝ ÐÚ ÒÚ Ð Ó Ý Ñ Þ ÓÔØ Ñ Ð Ú Ð ½º½º Å ÖØ Ö Þ ÐÝ Ò ÐÝÞ Ø ÓÐ Ò º º º º º º º º ½º¾º Þ ÚÓÐ Ò Ø Ð ØÖ Ø Ò º º º º º º º º º º º ½º º Þ
Å Ò Ñ Ò Ð Þ ËÞ Ð Á ØÚ Ò ÄÌ Ã Ñ ÁÒØ Þ Ø Ôº ½
Å Ò Ñ Ò Ð Þ ËÞ Ð Á ØÚ Ò ÄÌ Ã Ñ ÁÒØ Þ Ø Ôº ½ ÓÒÓ Ø ÔÙ È Ö ÓÒ Ð Ó ÞØ ÐÝÓÞ Ú Þ Ø Ö Ø ÔÙ Ó µ ÓÐ Ó ÓÐ Ø Ò Þ Ñ Ø ÔÀ ÊÓ ÞÙÐ Ø µ ÓÑÔÐ Ü ÔÞ Ì Ñ Ø Ë Ú¹ Þ ÓÑÔÐ Ü Ý Ò ÐÝÓ Þ Ñ Ø Ê ÓÜ ÔÓØ Ò Ð Ã Ø ÓÒÓ Ö ÐÚ Ð ÞØ Ù ÑÙØ
Ã Þ ÐØ Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ò Å Þ ÔÖÓ Ö Ñ Ö Ø Ò Å Ý Ö ÌÙ ÓÑ ÒÝÓ Ñ ØÓÑÑ ÙØ Ø ÁÒØ Þ Ø Ò ÅÌ ¹ ØÓÑ µ
Þ ØÓÑÑ Ó ÓÐÐ Ø Ú Ô ÐÙ ÐÐ ÔÓØ Ò ÖÐ Ø Ú Þ Ð Ø Ý Ø Ñ Ó ØÓÖ È µ ÖØ Þ ËØÙ Ð Ä ÞÐ Ì Ñ Ú Þ Ø Öº ÃÖ ÞÒ ÓÖ Ý ØØ Ð Ö Ò Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ó ØÓÖ Ì Ò Þ ÌÙ ÓÑ ÒÝÓ Ó ØÓÖ Á ÓÐ Ö Ò ¾¼½ Ã Þ ÐØ Ö Ò Ý Ø Ñ Þ ÌÙ ÓÑ ÒÝÓ
ËÞ Ñ Ø ÐÑ Ð Ø Ö ÝÞ Ø Ð Öº Þ ÓÐØ ÍØÓÐ Ñ Ó Ø ¾¼¼ º ÒÙ Ö ¾ º
ËÞ Ñ Ø ÐÑ Ð Ø Ö ÝÞ Ø Ð Öº Þ ÓÐØ ÍØÓÐ Ñ Ó Ø ¾¼¼ º ÒÙ Ö ¾ º ¾ Ð Þ Þ ÓÐÝ Ñ ØÓ Ò Ú Ð Ö ÝÞ Ø Þ ÄÌ ÁÒ ÓÖÑ Ø Ã Ö Ò ¾¼¼ ¹ ¾¼¼ ¹ Þ Þ Ñ ÞØ Ö Ò Ø ÖØÓØØ ËÞ Ñ Ø ÐÑ Ð Ø Ñò ÙÖÞÙ ÒÝ Ø Ø Ö¹ Ø ÐÑ ÞÞ º Þ ÐØ Ð Ø Ø ÒÝ Ø Ø
Ø Ð ÐÐ Ó Ø Ö Ò Ò Ó ØÓÖ ÖØ Þ ËÞ ¹ Ð ÐÞ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ã Ö Þ Ó ØÓÖ ÓÐ Ê Þ Þ ÐÐ Þ Ø ÔÖÓ Ö Ñ Ó ØÓÖ ÓÐ Ú Þ Ø Öº È ÐÐ Ä ÞÐ Ó ØÓÖ Ô
Ø Ð ÐÐ Ó Ø Ö Ò Ò Ó ØÓÖ ÖØ Þ ËÞ ¹ Ð ÐÞ ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ Ì ÖÑ Þ ØØÙ ÓÑ ÒÝ Ã Ö Þ Ó ØÓÖ ÓÐ Ê Þ Þ ÐÐ Þ Ø ÔÖÓ Ö Ñ Ó ØÓÖ ÓÐ Ú Þ Ø Öº È ÐÐ Ä ÞÐ Ó ØÓÖ ÔÖÓ Ö Ñ Ú Þ Ø Öº ÓÖ Ö Ò Ì Ñ Ú Þ Ø Öº ÃÙÒ Å Ö ØÙ ÓÑ ÒÝÓ
dc_603_12 E N = (e 1,e 2,...,e N ) e a+jb. e a+jb, W(E N ) a,b,t N 1 a a+(t 1)b Nº V(E N,M,D) e n+d1 e n+d2,...e n+dl t 1 j=0 N,t,a,b) = max n=1
Î Ò Ö ÓÖÓÞ ØÓ Ö Ó Ô Þ Ù ÓÚ Ð ØÐ Ò Ó ØÓÖ ÖØ Þ Ø Þ Ý ÖÑ Ø Ã Ø Ð Ò ØÚ ÄÓÖ Ò ÌÙ ÓÑ ÒÝ Ý Ø Ñ Ù Ô Ø ¾¼½ ½º Ú Þ Ø Þ ÐÑ ÐØ Þ Þ Ú Ò Ö ÔØÓ Ö ÝÖ Ò ÝÓ Þ Ö Ô Ø ÔÓØØ Ñ Ø Ñ Ø Ò ÓÖÑ Ø ÙØ Ø Ó Òº Ø Ö Ð ØÒ Þ ÑÓ ÓÒØÓ Ý ÓÖÐ
σ m α η e m η m η N η ) α m η m η T cond
Ö Ð Þ ÑÑ ØÖ ÐÝÖ ÐÐ ÓÖÖ Ú Ö ÒÝ Ò Ã Ö Å Ò Þ Ë Ì Ñ Ú Þ Ø Ò Å Ø ÄÌ ÌÌà ØÓÑ Þ Ì Ò Þ ¾¼½½º Ò Ù º à ÚÓÒ Ø Á Ñ ÖØ Ó Ý Ø Ö ÐÑ Ð Ø Þ ÑÑ ØÖ Ò Ö Ð Ð Ð Ö Þ Ø Ñ Öغ ÐØ Ø Ð Þ ¹ Þ Ö ÒØ Þ ÑÑ ØÖ Ò ÝÓÒ Ñ Ñ Ö Ð Øò Þ Ò ÐÝÖ
ËÞ Ò ÃÓÑÔÐ Ü Ú ÒÝ Æ ÝÔÖÓ Ö Ñ Ó ÙÑ ÒØ Ä Ä Ú ÒØ ÈÖÓ Ö ÑØ ÖÚ Þ Å Ø Ñ Ø Ù Æ ÔÔ Ð µ ØØÔ»»ÐÓ ºÛ º ÐØ º Ù ÄÇÄÄ Ìº ÄÌ ÃÓÒÞÙÐ Ò ËÞ Ð Ä ÞÐ ÄÌ ÁÒ ÓÖÑ Ø Ã Ö ¾¼¼ º
ËÞ Ò ÃÓÑÔÐ Ü Ú ÒÝ Æ ÝÔÖÓ Ö Ñ Ó ÙÑ ÒØ Ä Ä Ú ÒØ ÈÖÓ Ö ÑØ ÖÚ Þ Å Ø Ñ Ø Ù Æ ÔÔ Ð µ ØØÔ»»ÐÓ ºÛ º ÐØ º Ù ÄÇÄÄ Ìº ÄÌ ÃÓÒÞÙÐ Ò ËÞ Ð Ä ÞÐ ÄÌ ÁÒ ÓÖÑ Ø Ã Ö ¾¼¼ º ÒÙ Ö Ì ÖØ ÐÓÑ ÝÞ ½º Ð ÞÒ Ð Ó ÙÑ ÒØ ½º½º ÃÓÑÔÐ Ü Ú
½µ Þ Ü Ñ Ö ÚÓÒ Ø ÓÞ Ð ÔÚ Ø Ñ Ö Ø Ý Ñ Ø Ñ Ø ÐÑ Ð Ø Ð Ô Ø Ò Ð Ô ÐÚ Å Ò Ò Ñ Ø Ñ Ø ÐÑ Ð Ø Ó ÐÑ ÐÐ Ø Ó Ýò Ø Ñ ÒÝ ÒØ Ó Ø Ðº Þ ÐÑ Ð Ø Ð Ô Ø ÓÖ Ò Ð ÞÒ ÐØ Ó ÐÑ
Î Ö Þ Ä ÞÐ ÓÑ ØÖ Ü Ñ Ö Ò Þ Ö ÑÓ ÐÐ ÄÌ ÌÌÃ Å Ø Ñ Ø ÁÒØ Þ Ø ÓÑ ØÖ Ì Ò Þ Ù Ô Ø ¾¼½½ ½µ Þ Ü Ñ Ö ÚÓÒ Ø ÓÞ Ð ÔÚ Ø Ñ Ö Ø Ý Ñ Ø Ñ Ø ÐÑ Ð Ø Ð Ô Ø Ò Ð Ô ÐÚ Å Ò Ò Ñ Ø Ñ Ø ÐÑ Ð Ø Ó ÐÑ ÐÐ Ø Ó Ýò Ø Ñ ÒÝ ÒØ Ó Ø Ðº Þ
Ø Ø Ñ Ð Ò Ø Þ Á Þ Ý Ê Ò Þ Ø Å Ò ÞØ Ö ÙÑ Ú Ð Ñ ÒØ Þ Ñ Ö ÂÓ Ó Å Ý Ö Ã ÞÔÓÒØ Ã Þ Ð Ô ØÚ ÒÝ Ø ÑÓ ØØ ÓÒ Ö Ò Þ ÖÚ Þ È Ý Å Ø ÓÒ Ö Ò Ð Ð Î Ö ¾¼¼ Þ ÖÞ ¾¼¼ Þ Ö
ÍÊ È Á ÂÇ Ë ÂÇ ÁÄÇ Á ÓÒ Ö Ò Ø ÒÙÐÑ ÒÝÓ Þ ÙÖ Ô ÒØ Ö ØÚ Ò Ú ÓÖ ÙÐ Ò ÒÒ Ô Ö Þ Ö ÞØ ØØ Ô Ý Ñ Ø Ë ÆÌ ÁËÌÎýÆ ÌýÊËÍÄ Ì Þ ÔÓ ØÓÐ ËÞ ÒØ Þ Ã ÒÝÚ Ù Ô Ø ¾¼¼ Ø Ø Ñ Ð Ò Ø Þ Á Þ Ý Ê Ò Þ Ø Å Ò ÞØ Ö ÙÑ Ú Ð Ñ ÒØ Þ Ñ Ö ÂÓ
ÝÞ Ø Ô Ø Ñ ÖÒ ÖÒÝ Þ Ø Ñ ÖÒ ÐÐ Ø Ò ¾¼¼¾º½¾º¾¾º Ú ÐØÓÞ Ø Ë ÑÓÒ Ã ÖÓÐÝ ¾¼¼¾º½¾º¾¾
ÝÞ Ø Ô Ø Ñ ÖÒ ÖÒÝ Þ Ø Ñ ÖÒ ÐÐ Ø Ò ¾¼¼¾º½¾º¾¾º Ú ÐØÓÞ Ø Ë ÑÓÒ Ã ÖÓÐÝ ¾¼¼¾º½¾º¾¾ ¾ Ä ØÓÖ ÐØ Öº Ë Ò ÓÖ Ý Ø Ñ ÙÒ ØÙ Ð Þ Þ ÝÞ Ø Öº Ë ÑÓÒ Ã ÖÓÐÝÒ Å Ô Ø Ñ ÖÒ Ã ÖÒÝ Þ Ø Ñ ÖÒ ÐÐ Ø Ò Ø ÖØÓØØ Ð ÒÝ Ø Ø ÖØ ÐÑ ÞÞ º