1. A LINEÁRIS ALGEBRA ALAPJAI
|
|
|
- Klára Szilágyi
- 8 évvel ezelőtt
- Látták:
Átírás
1 KVANTITATÍV reive! együtt dolgozik. Az ú] tudományág határtenilet a matematika, a gazdaságtudomány és a számítástudomány között.. A LINEÁRIS ALGEBRA ALAPJAI Az operációkutatás középpontjában a közgazdasági és a matematikai rnodell áll. Hosszú az út a döntési probléma megfogalmazásáról a modell megalkotásáig. A feladat a probléma részletes leírásával - a változók, a korlátozó feltételek megadásával - kezdődik, majd a célra vonatkozó ismeretek mélyítésével, pontosításával folytatódik. A szükséges adatok megszerzése és pontosságuknak ellenőrzése után következik az adott körülményeknek legjobban megfelelő modell számszerűsítése és megoldása. A modell helycsségét a gyakorlattal való egybevetéssol ellenőrizzük. A döntéshozó szempontjából a modelleknek kettős hasznuk van. Egyik oldalról a döntéshozó a rendszer részletekbe meno vizsgálatára kényszerűl; a modell előkészítése során fel kell tárnia a rendszer összefüggéseit, és így a modcll a gazdasági folyamat elemzésének eszközévé válik. Másrészt viszont az operáciokutatási rnodell alkalmas a vizsgált paraméterek különböző kritériumok szerinti optirnális értékeinek meghatározására, ezért képes a döntés orientálására is. Könyvünk a lineáris algebrai alapok után a lineáris programozásba, a hozzárendelési probléma modellezésébe, a hálótervezésbe és a döntésanalízisbe vezeti be az olvasót. A szerzők várják, és előre is köszönik a tisztelt Olvasók észrevételeit, megjegyzéseit. Budapest, január A szerkesztá BGF Kűlkereskedelmi Főiskolai Kar Matematika-statisztika Tanszék. MÁTRIXARITMETIKA A mátrix fogalma Definíció. Legyen adva III. n számú ajj valós szám, ahol i =, 2,..., /;j =. 2,..., ll. Akkor ezen számok ali a 2 alj a In a 2 a 2:! a ; n 2n -J ail a i2 a jj ain a m l a m2 U mj amil alakú elrendezését mátrixnak nevezzük. Mivel ennek a mátrixnak /JI sora és II oszlopa van, tn. Il-es, vagy /II. típusú mátrixnak nevezzük. A matrixban lévő ajj számok a mátri x elemei; pontosabban szólva az ajj szirnbólum a mátrix i-edik sorának j-edik clcmét, illetve j-edik oszlopának i-edik elemct jelöli. Az elrendezésben az elem első indexe az ún. sorindex, a második pedig az ún. oszlopindex. Ennek megfelelően az ajj elem - az ún. általános elem - az í-edik sorj-edik elemét jelenti. A gyakorlatban sokszor találkozunk mátrixokkal. hiszen a legtöbb statisztikai kimutatás mátrixalakban jelenik meg. Példaképpen felírunk egy 3. 4 típusú mátrixot:
2 KVANTITATÍV A mátrixot a részletes kiírás helyett a következő módon is szokás jelölni: A = aj; ] ( i =,2,..., m.] =,2,...,), vagy A, amit Így olvasunk: /. ~ ru-n típusú A mátrix, vagy egyszerű en A, azaz jelőlhetjük bármely mátrixot egyetlen szimbólummal is. Nyomtatort szövegben a mátrixok jelölése általában félkövér latin nagybetű, kézírásban aláhúzolt latin nagybetű. Az III. Il típusú mátrixok halmazát M(m; n)-nel jelölve, ezt is irhatjuk: AE M(lI; ). Egy /. Il tipusú matrix transzponáltja. / tipusú matrix. Transzponálás során az i-edik sor j-edik eleme a j-edik sor i-edik elemévé válik. Ennek megfelelően a transzponálás lényegétjól kifejezi az ajj]* = aj;],(i =,2,..., nt;] =,2,...,7) összefüggés. így a transzponálás fogalmából következik, hogya transzponált mátri x transzponáltja egyenlő az eredeti mátrixszal, azaz (A *)* = A. Mátrixok egyenlősége és a nagyságrendi relációk Sor és oszlopvektor Dcfiníció. Két azonos típusú A és B matrix között az = (egyenlő), < (kisebb), > (nagyobb), ::::;(kisebb egyenlő), ~ (nagyobb egyenlő) relációk valamelyike áll fenn, akkor és csak akkor ha az illető reláció elemről elemre érvényes, azaz bármely lehetséges i ésj index esetén ajj és bjj között az illető reláció teljesűl. Ismeretes, hogy két valós szám között mindig fennáll az =, <, >, relációk valamelyike, addig az azonos típusú mátrixok között ez nem így van. Például ha A = -3 2] D = -2 8 ' akkor definíciónk értelmében A = B, A < e, B s D, de e és D között a vizsgált relációk egyike sem áll fenn. Mátrix transzponáltja Az A matrix transzponáltján azt a mátrixot értjük, amelynekj-edik sora az A j-cdik oszlopával (kővetkezésképpen, j-edik oszlopa az A j-edik sorával) egyenlő mindenj-re. Az A mátrix transzponáltjút A *-gal jelöljük. - 3 r akkor transzponáltja a következő 2. 3 tipusú matrix: A' = ~ 3 -] O 3. s.ji] Legyen például A egy 3. 2 típusú mátrix: A = 3 O, Definíció. Az egyetlen oszlopból álló (tehát III. l tipusú) mátrixot (m elemű) oszlopvektornak. az egyetlen sorból álló (tehát. típusú) mátrixot (n elemű) sorvektornak nevezzük. A vektor elemeit a vektor komponensei nek, vagy koordinátáinak is szoktuk nevezni. A továbbiakban az el emlí oszlopvektorok halmazút a Vm szimbolúmrnal, az elemű sorvektorok halrnazát pedig av;: szimbolummal fogjuk jelölni. A vektor jelölése nyomtatásban félkövér, kézírás ban aláhúzott latin kisbetű. Az oszlopvektor jelölése: a = a 2 - a. - l' A sorvektor jelölése: h = hl; b.:... ; h,,l. Itt a * (csillag) mutatja, hogyasorvektor egy oszlopvektor trauszponáltjaként fogható fel. Nyomdatechnikai okból gyakran Írják az oszlopvektort egy sorvektor transzponálíjaként. Például "{!}-: 5: 3J'. Egy /. n típusú matrix valójában darab II komponensű sorvektornak, illetve darab tn komponensű oszlopvektornak egymás mellé rendezése. Az A mátri x oszlopvektorait rendre a" a2'..., an vektorral jelölve, a mátrix így írható fel:
3 KVANTITATÍV A lineáris algebra alap/ni Hasonlóan, az A mátri x sorvektorait rendre al *, a2=,..., a m * vektorraljelölve: Speciálls vektorok A =:' am A nullvektor (zérusvektor) olyan vektor, amelynek minden eleme O. Jele: O. Például a negyelemű null vektor így írható fel: o = o O O O illetve 0= O; O; O; 0]*. Az egységvektor olyan vektor, amelynek egyik eleme, a többi nulla. Szimbolikusan ej-vel jelöljük, ahol az i index mutatja, hogy az egyes hányadik helyen áll. Például a háromelemű vektorok között pontosan három külőnböző egységvektor található. Oszlopvektor alakban a következők: zetükből nem derülne ki komponenseik száma, és fontos a közlendőnk szempontjából, akkor meg kell mondanunk az elemeik számát. Megállapodás szerint tehát O,, e, mindig oszlopvektorokat jelölnek. Speciális mátrixok A nullmatrix (zérusmátrix) minden eleme O. Jele: O. Például a 3. 4 típusú nullmatrix a következő: o O O 0j 0=0000. r O O O o Ha egy mátrix sorainak és oszlopainak száma egyenlő (m = ll), akkor azt négyzetes vagy kvadratikus mátrixnak nevezzük. A négyzetes mátrix sorainak (illetve oszlopainak) száma a matrix rendje. Az ali> a22,..., ann elemeket, amelyek az ún. főátlót alkotják, diagonális elemeknek Az A{i nevezzük. ; -:4 ~I Az összcgző vektor olyan vektor, amelynek minden eleme. Jele:. A négyelemű összegző vektor így Írható fel: mátrix például egy negyedrendű négyzetes (kvadratikus) matrix, amelynek diagonális elemei: 3; O; -4; 8. Diagonális mátrixnak nevezzük az olyan négyzetes rnátrixot, amelynek csak a főátlóban van O-tóI különböző eleme. Ha az = illetve =;;,]* ali O O O O a 22 O O A= O O a:;:; O A nullvektor, az egységvektor és az ősszcgző vektor jelöléséből nem derül O () () a un ki, hogya vektor hány elemű. Általában a környezetéből, az elvégzendő műveletekből egyértelműen következik, hogy hány elernűek. Ha a kőrnye- mátrix esetén van olyan a., amely nem O, akkor A valódi diagonális matrix. 2 3
4 KVANTITATív A diagonális mátri x jelölésére az szimbólumot Például: használjuk. < aj ; a 22 ;.. ; II nil > O ~O O O O O O O =<5;0;;-8>. O O -8 Az egységmátrix olyan diagonális mátrix, amelynek minden diagonális eleme, azaz oszlopai egységvektorok. A másod- illetve harmadrendű egységmatrix a következő: E, = O], - O Általánosan: En, II-ed rendű egységmatrix. Háromszög-, vagy trianguláris mátrixnak nevezzük az olyan kvadratikus mátrixokat, amelyekben vagy a főátló feletti, vagy a főátló alatti elemek mind nullák. Az első esetben alsó háromszögmátrixról, a másodikban felső háromszögmátrixról van szó. Például alsó hárornszögmátrix a következő A és II mátrix: A kővctkezö C és O mátri x pedig felső háromszögmátrix: 7 5 O ~ t í f I i I!t I I I Az A kvadratikus mátrixot szimmetrikusnak nevezzük, ha a főátlóhoz képest szimmetrikusan elhelyezkedő elemei egyenlőek, azaz aij = aji minden lehetséges i ésj értékre igaz. Vagyis az A mátrix egyenlő a saját transzponáltjával: A=A*. Az A kvadratikus mátrixot ferdén szlmmetrikusnak nevezzük, ha a főátlóhoz képest szimmctrikusan elhelyezkedő elemek egymás ellcntettjci, azaz ajj = -ajj minden lehetséges i és j értékre igaz. (A főátló elemei a definició kővetkeztében nullák.) Vagyis ebben az esetben: A = -A *. Például az s =l~ ~ O 6 ~l és F =l~ - 5J O 6-6 O mátrixok közül S szimmetrikus, F pedig ferdén szimmetrikus mátrix. A mátrixok blokkokra bontása A gyakorlatban előforduló nagyméretű mátrixokat sokszor - függőleges és vízszintes osztovonalakkal - kisebb részekre, ún. blokkokra (vagy minormátrlxokra) bontjuk. Az ilyen felbontást particiouálásnak is szoktuk nevezni. Tekintsük pl. az 7 O A = 2 8. O -2-2 O. O O O 4 O 2 O 6 - mátrixot. Itt a kövctkcző négy blokkról van szó: '~l ~ O O ' O O 3-2 ~ O ~J' 4,lj () O 4 c=o -2] Ali A 2 = ~ ;2, 0= O O O ~J : -~J O A 2 = : An = 2 4 5
5 KVANTiTATív Az A mátrixot a következő módon is felírhatjuk: A = A II A 2]. A 2 A 22 A blokkokból felépített mátrixot tekinthetjük olyan mátrixnak, amelynek elemei is mátrixok. Az ilyen mátrixelcmű matrixokat hipermátrixoknak is nevezni. A particionálás gyakran alkalmazott esete az, amikor az adott mátrixot oszlopvektorokra. vagy sorvektorokra bontjuk szét. Ha pl. az A matrix oszlopvektorait rendre az al; a2; a3; a, szimbólumokkal jelöljük, akkor A = al; a 2 ; a3; a 4 ], ha pedig a b,"; b 2 *; b 3 * szimbólumok az A sorvektorait jelölik, akkor A felírható a következő módon is: A = r:il,vagy A =lb,; b,; bjj', vagy A' =lb,; b,; bjj. A valós számok ősszeadásánál sajátságos szerepet játszik a nulla. A O hozzáadása ugyanis bármely valós számot változatlanul hagyja. Hasonló szercpük van a mátrixok között a nullmátrixoknak, illetve vektorok esetében a nullvektornak. Például: ls 2 () 9 3] l" " ~H~ 2 lj 3 ] A+()= ~ 4 O - + O O O 4 O ~I = A, -I O O O O O - O vagy b+o=lh~hj=b Ezek után rátérünk az alapműveletek definiálására. Mátrixok összeadása és kivonása Az összeadás és ki vonás művelete csak azonos típusú mátrixok esetén van értelmezve a következő definíció szerint. Definíció. Két m. n típusú A = ajj] és B = bjj] matrix összegén ill. kűlönbségén] azt az m. Il-es C = Cjj] mátrixot értjük, amelynek minden elemére igaz, hogy: Cjj= ajj + bjj, ill. Cjj= ajj - bij]. Mátrixok szorzása skalárral Definíció. Tetszőleges III. Il tipusú A = ajj] matrixnak valamely skalárral (valós számmal) való szorzatán azt az III. n-es C = Cjj] mátrixot értjük, amelynek minden elemére igaz, hogy Cjj=. ajj' A skalárral való szorzást tehát clemenként végezzük: A. ajj =. ajj]. Például: Az összeadást és kivonást tehát elemenként végezzük. 4 3 ~ ~IJ= 2 ~ 6] -4,vagy 6 O; 2; -; 3] = O; 2; -6; 8]. 20 Például: és lao] + b] = a + b] és a-ol - b] = a - b] lj lj lj lj lj lj lj lj' J _ J = J O Ha =, akkor a szorzat A. A = A, vagyis l-gyel szorozva a mátri x nem változik. = - esetén (-). A = -A olyan matrix, amelynek minden eleme (-)- szerese az A mátrix megfelelő elemének; ezért a -A mátrixot A ellentettjének nevezzük. Az A + (-). B összeadás eredménye ezért éppen az A - B matrix. Egy mátrixot az ellentett jével összeadva nullmátrixot kapunk: A + (-A) = O. Al = O skalárral való szorzás eredménye szintén nullrnátrix: O. A = O. 6 7
6 KVANTITATív A lineáris algebra alapjai A mátrixok elemei valós számok, ezért az elemenkénti műveletvégzésből és a valós számok halmazában érvényes műveleti azonosságokból adódik, hogy a bevezetett műveletekre teljesülnek a következő azonosságok. A mátrixok összeadása és a mátrixnak skalárral való szorzása kommutativ művelet, azaz: és A+B=B+A A A=A A. A mátrixok összeadása asszociatív művclet, és a mátrix skalárral való szorzására is érvényes az ún. vegyes asszociativitás, azaz (A + B) + C = A + ( B + c) és (Afi)A = A(uA). Például: Az A, =~ ~l O -] A~ = O' mátrixoknak a Al = 6; Al = -3; A3= O skalárokkal képzett lineáris kornbinációja a 6 ~ ~] + (-3{ ~ -Ol]+ o~~ :)] = =: ~:]+_03~]+~ ~]=I: ~~]mátrix. Mátrixnak skalárral való szorzása disztributív, mind az összeadásra. mind a skalárösszeadásra nézve, azaz A (A + B) = AA + AB és (A + fi)a = AA + )la. A transzponálás és az összeadás, illetve a transzponálás és a skalárral való szorzás sorrendje felcserélhető, azaz Mátrixok lineáris kombinációja (A + B)* = A * + B* és (AA)* = A. A *. Az összeadás és a skalárral való szorzás alkalmazásával kapcsolatos, fontos szerepet játszó fogalom, a lineáris kombináció fogalma. I f lineáris kombinációja a 2b, + 5b~ - 3b + b, = -:3 vektor. _3 J Definíció. A AIAI + AlA} AkAk lineáris kombinációt az Al; Al;... ; Ak mátrixok konvex lineáris kombinációjának nevezzük, ha a benne szercplő skalárok nem negatívak, és az összegük. k ( Aj :s: O és L, A i = ). i = I Detiníció. Adott m. Il típusú Ab A2'..., Ak mátrixokat rendre megszorozva a tetszőleges Ab,2,..., Ak skalárokkal, majd az így nyert szorzatokat összeadva a k AIAI A2A AkAk = L,AjAj kifejezésnek megfelelő /. Il-es mátrixhoz jutunk, melyet az Al, Al,..., Ak mátrixok egyik lineáris kombinációjának nevezünk. i = I Vektorok skaláris szorzata A mátrixok szorzásának értelmezéséhez. szükségünk lesz a vektorok skuláris szorzatának ismeretére. Dcfiuíció. Két II elemű a és b vektor skaláris szorzután azt a valós számot értjük, amelyet úgy kapunk, hogya és b azonos indexű kornponcnscit összeszorozzuk, és a kapott szorzatokat összeadjuk. A szorzat kijelölésekor az első tényezőt sor-, a másodikat oszlopvektor formájában írjuk fel. Ezen Írásmód előnye a későbbiekben fog kitűnni. 8 9
7 KVANTlTA7v b l b 2 * II a b=al;a 2 ;a 3 ;... ;a,,] b 3 =albl+aobo+... +a b ="'a.b -- lill L.JII j::; illetve *b=i;i;... ;, II = b, + b l b" = L b,. j ea ] Például, ha a = 5; 2; 8; O; -]* és b = O; -; 3; 2; -2]*, akkor O -I a* b=5;2;8;0;-i] 3 =0+(-2) = A vektorok skaláris szorzása kornmuratív abban az értelemben, hogy mindegy, melyik tényezőt írjuk első, és ezért sorvektorként, és melyiket második tényezőként oszlopvektor formájában. Ez a tulajdonság a valós számok szorzásának kommutativitásán alapul: Előző példánk esetében: a' b= L..,;II ~ab = L..JII ~ba =b'a. i::; li::; 5 2 b*a=o;-;3;2;-2]. 8 =0+(-2) =24=a'b. O - Ha egy tetszőleges II elemű a vektort az II elemű összegző vektorral szorzunk, akkor eredményül az a vektor komponenseinek összegét kapjuk. Ezért nevezzük a csupa -ből álló véktort összegző vektornak. I Például, f6;4;3;-siii=6+4+3+(_s)= 8 Mátrix szorzása mátrixszal b" A vektorok skaláris szorzatának ismeretében definiálhatjuk két matrix szorzatát abban az esetben, ha az első tényező oszlopvektorainak száma egyenlő a második tényező sorvektorainak számával. Az ilyen matrixokat az adott sorrendben konformáhilisnak nevezzük, s csakis ilyen mátrixok escten értelmezzük a szorzást. Definicíé. Az III. P típusú A = ajj] mátrix és ap' / tipusú B = bjj] mátrix szorzatán azt az. JI típusú C = Cjj] mátrixot értjük, amelynek bármely i,j indexű eleme az A mátri x i-edik sorvektorának és a B mátrixj-edik oszlopvektorának a skaláris szorzata. Azaz Cíj = 3 il ; a í2; a íj;... ; a ip blj bt ~ ) b 3j = a í b lj + a í2b 2j a ip b pj= La íkb kj. Az A. B szorzatmátrixot tehát az első tényező, azaz a szorzandó A matrix sorvektorokra és a második tényező, azaz a szorzó B matrix oszlopvektorokra bontásaval a következőképpen írhatj uk fel: k = a*=a l ;a o ;.. ;a ]. _ II = " = "'a. ~., n j::; al a;bl 'j a;02 a'h n A B= a;.b. b 2 ; b ]= a;b l a;b;! a;h" m p p-u > n. a~nb, a~lib2 a' b 20 3 m III II 2
8 KVANTITATÍV A lineáris algebra alapjai Az összeadás és a skalárral való szorzás művelete nem változtatja meg a mátri x típusát. Pontosabban fogalmazva: az /. Il típusú mátrixok összege és ilyenek skalárszorosai (ahol III és II rögzítctt szám) szintén /. típusú mátrixok. Ezt úgy is mondjuk, hogy az / típusú mátrixok halmaza zárt az előbbi két műveletre nézve. A szorzás esetén más a helyzet. A szorzásban szereplő tényezők általában különböző típusú mátrixok, és a szorzat általában ismét más típusú. Természetescn az ll-ed rendű négyzetes matrixok halmaza zárt a szorzásra nézve. A szorzatmátrix elemei nek kiszámítása nagy figyelmet kíván, mert a sok elem nehezen áttekinthető. Elkerülendő a hibákat, célszerű a két mátrixot a kövctkező, ún. Falk-séma szerint írni: IT] EJ IABI Azaz részletesebben felírva: bll bl2 blj bln bn bn b2j b2n bpl bp2 b pj bpn ali al2 ali' Cll CI2 Clj Cin a2 a22 a2p C2 C22 C2j C2n ail ai2 aip Ci! Ci2 Cij Cin a III I am:! a mp CIII I Cm:?: Cl\lj emil Például: Határozzuk meg az A. B szorzatnak megfelelő C, majd ab' A szorzatnak megfelelő D mátrixot, ahol Az AB szorzatot a Falk-séma szerint felírva: 2 O O 3 2 O S A O !O 2 O S 8 -s II AB =C I -4 6 Tehát AB = C = ~ O -S II Majd a BA szorzatot a Falk-séma szerint kiszámitva: A O O I 2 O II 3 II 4 - O 9 2 BA =D, 3 2 O r: II azaz B A= D = 24-9 ; adódik. A = ~ ~ ~2!)~L,I és -lj O. S Látjuk, hogy AB nem egyenlő BA -val, vagyis a mátrixok szorzása nem kommutatív művelet. A mátrixszorzás tulajdonságai: A mátrixok szorzása - amint a fenti példában is láttuk - általában nem koi/- mutatív művelet, sőt egyes esetekben a tényezők felcserélése már a konfonnábilitás megkövetelése miatt sem lehetséges. 22 7i
9 KVANTlTATiv A mátrixok szorzása asszociatív művelet, azaz (A. B). C = A. (B. C), feltéve, hogy az A. B és B. C szorzatok léteznek. Érvényesek továbbá a következő azonosságok: és A(B + c) = AB + AC (baloldali disztributivítás); (A + B)C = AC + BC (jobb oldali disztributivítás);,(ab) = (,A)B (vegyes asszociativitás); (A B)* = B*A*. Sorvektor szorzása mátrixszal Az Jn. Il tipusú A mátrixot balról megszorozhatjuk az nl komponensű 50rvektorral (. III típusú mátrixszal) és az eredmény egy n kornponensű sorvektor lesz (. II tipusú mátrix). Jegyezzük meg, hogy az ei* A szorzat eredménye az A matrix i-edik sotvekto ra, hiszen a többi sorvektor () egyiitthatóval vesz részt CI lineáris kombinácioban. Alkaltnas egységvektor transzponáltjáva! (balról) való szorzással tehát kiválaszthatjuk a matrix megfelelő sorát. Világos, hog)! az *A szorzat eredménye az A matrix sorvektorainak az összege, és így az *(A ) = (*A) szorzat eredménye egyenlő az A matrix összes elelllének az összegével. Az a*b szorzat a B sorvektorainak az a lineáris kombinációja, amelyben az egyes sorvektorokhoz tartozó skalárok az a* vektor megfelelő koordinátái. Ha ab mátrix sorvektorait: b*, b*,..., b* -rnel jelöljük, az a* vektor koor- I 2 l/l dinátái pedig: (, al,..., a/l" akkor ~ * * * a' B = al b l + a~ b~ al/l b., Mátrix szorzása oszlopvektorral Az Ab szorzat az A oszlopvektorainak az a lineáris kornbinációja, amelyben az egyes oszlopvektorokhoz tartozó sk al árok a b vektor megfelelő koordinátái. Ha az A matrix oszlopvektorait al; a2;..., a/l-nel jelöljük, Legyen a' = ; 2] és B=G 2 5 ~J a b vektor koordinátái pedig: b.; b 2 ;... ; b; akkor akkor a fentiek értelmében: Ab = al b, + a2bl aj)/i' ; 2]{ ~] = ; J' -, 0]+2 2; 5; 7]= 5; 2; 4 ] Természetesen akkor is ugyanehhez az eredményhez jutunk, ha a mátrixok szorzásának definiciója szerint járunk el, azaz: fl; 2]. ~ 2 O] 5 7 = ;. O ] = 5; ; 2; 4]. A sorvektorok és mátrix szorzásának a Falk-sémája a következő: 24 3 b I 2 A I Ab számokkal 2 3 O r~ Legyen A = ~ 3 0] 4 5 és b = l:l akkor a fentiek értelmében: ~~~]r!l = a3 +!], + ~]2 = ~7l Természetesen ugyanehhez az eredményhez j utunk, ha a mátrixok szorzásának értelmezése szerint járunk el, azaz 2 3 o].r;j = ] = 9]
10 KVANTITATÍV Mátrix és oszlopvektor szorzásának a Falk-sémája a következő: 3 b 2 A Ab számokkal 2 3 O A tetszőleges III. n típusú A mátrixot megszorozhatjuk egy n komponensű oszlopvektorral, (azaz II. l tipusú mátrixszal) jobbról és az eredmény mindig egy kornponensű oszlopvektor (m. l típusú mátrix) lesz. Jegyezzük meg, hogy az Ae, szorzat eredménye az A matrix i-edik oszlopvektora, hiszen a többi osz/op vektor O egyiitthatóval vesz részt a lineáris kombinácioban. Alkalmas egységvektorral (jobbrol) való szorzással így kiválaszthatjuk a matrix megfelelő oszlopát. Világos, hogy az Al szorzat eredménye az A mátrix oszlopvektorainak az összege, és így az l*(al) = (l*a)l szorzat eredménye, amint már tudjuk, egyenlő az A mátrix összes elemének az összegével. Lineáris egyenletrendszer felírása matrix formában A mátri x szorzása oszlopvektorral típusú szorzat gyakori előfordulásának esete a lineáris egyenletrendszerek (ill. egyenlőtlenség-rendszerek) megadása, megoldása során jelentkezik. Az XI; X,;... ; X.;... ; X ismeretleneket tartalmazó - } / al.\ + {/2X2 + + (/ljxj + + (l"x" = VI a 2 x I + a 22 x a 2j x j + + a 2 "x" = v 2 lineáris egyenletek véges halmazát lineáris egyenletrendszemek nevezzük, amely az jelölések bevezetése révén tömören így írható: Ax =b. Az A matrix az egyenletrendszer együttható mátrixa. Az egyenletrendszert b = Oesetén homogén egyenletrendszernek, b of:. O esetben inhomogén egyenletrendszernek nevezzük. Az egyenletrendszert megoldani annyit jelent, mint megadni azon x vektorok M halmazár. amelyek kielégítik az Ax = b egyenlőséget. Ha az M halmaz az üres halmaz, akkor az cgyenletrendszert inkonzisztensnek, ellenkező esetben konzisztensnek nevezzük. Jelölje az A mátri x oszlopvektorait rendre: Akkor, mint tudjuk, az Ax szorzat az A oszlopvektorainak azon lineáris kombinációja, amelyben az egyes oszlopvektorokhoz tartozó skalárok az x vektor megfelelő koordinátái, azaz Ezért igaz a következő: Tétel. Annak sziikséges és elegségesfeltétele. hogy az Ax = b egyenletrendszemek legyen megoldása az, hogya b vektor előállítható legyen az A nuitrix oszlopvektorainak egy lineáris kombinaciojakéut. Lineáris egyenlőtlenség-rendszer felírása mátrix formában Természetesen a mátrixuritmctika tömör kifejezésmódját nemcsak a lineáris egyenletrendszerek esetében, hanem a lineáris egyenlőtlenség-rendszerek esetében is alkalmazhatjuk. Például az x.: X 2 ;... ;.'lj;"'; x" ismeretleneket tartalmazó allx l + 02X" ClljX) + + (/I"X" :S; VI a 2 x I + 022X:. +..,+ ( 2j X j + + (2".\" :S; h 2 26 a" A = (/~I a l2 (lj a lll (22 {/o. ( ]" aiiii QIII2 «, ali/il ~: -l X =. és b, b = h 2 x bili " típusú lineáris egyenlőtlenségek által megadott lineáris egyenlőtlenség-rend\'zer 27
11 KVANTITATív az au A = ~ {/2 alj G,,, ] -} X,].r,., X =.- és b= - a'l an a,. Cl:'/I b, ami ali/2 «: ClJ/UI jelölések bevezetésevel a tömör alakban írható fel. x " Ax ::;b.2 LINEÁRIS TEHEK (VEKTORTEREK) b' ] Ebben a részben ismertetjük a lineáris térrel kapcsolatos alapfogalmak definícióit, továbbá a bevezetett fogalmak közötti kapcsolatokat, összefüggéseket kimondó alapvető állításokat. Az állításokat megfogalmazó tételeket bizonyítás nélkül közöljük. A lineáris tér (vektortér) fogalma Definíció. Elemek (az úgynevezett vektorok) egy V halmazár a valós számhalmaz feletti lineáris térnek vagy vektortérnek nevezzük, ha rendelkezik a következő tulajdonságokkal: A). V-ben értelmezve van egy összeadásnak nevezett (+ jellel jelölt) művelct, azaz a V-beli elemekből képzett bármely (a; b) párhoz egyértelműen hozzá van rendelve az a és b összegének nevezett szintén V- beli a + belem Az összeadás kornmutatív, azaz a + b = b + a minden a, b E Vesetén Igaz. 3. Az összeadás asszociatív, azaz (a + b) + c = a + (b + c) minden a, b, c E V cs etén igaz. 4. V-ben van olyan O-val jelölt zéruselem. hogya + O = el minden a E V esetén igaz. b:" 5. Minden a E V elemnek van úgynevezett ellentett je, azaz minden a E V-hez található olyan (-a) E V, amelyre a + (-a) = O B). Minden a E V elemhez és A. valós számhoz egyértelrnűen hozzá van rendelve a V halmaznak egy A. a-val jelölt eleme, amelyet az a vektor A. skalárral vett szorzatának nevezünk. 2. A skalárral való szorzás kornrnutativ, azaz A. a = a A. minden a E V és minden A. valós szám esetén igaz. 3. A skalárral való szorzás asszociatív, azaz í\.(j,t a) = (í\.ji) a nunden a EVés tetszőleges A., JI valós számok esctéri igaz. 4. Minden a E Vesetén igaz, hogy la = a. c). A skalárral való szorzás a skalár összeadásra nézve disztributiv, azaz (A. + ft) a = í\. a + JI a minden a EVés tetszőleges A.,fl valós számok esetén igaz. 2. A skalárral való szorzás a V-beli összeadásra nézve disztributív, azaz A. (a + b) = A. a + A. b minden a, bev és tetszőleges A. valós szám esetén igaz. Például az Ill' tipusú mátrixok M(III; ll) halmaza lineáris teret alkot a valós számok felett (Ill. n rögzitett). Az összeadást és a skalárral való szorzást végezzük elemenként, ahogy azt a mátrixok körében definiáltuk. A lineáris tér axiómáinak teljesülésének könnyen elvégezhető igazolását az olvasóra hagyjuk. Speciálisan az II elemű oszlop vektorok VII (sorvektorok V,,') halmaza szintén lineáris teret alkot a valós számok felett. AItér, lineáris kombináció, gclledtoltelldszcr A továbbiakban lineáris tér (vektortér) kifejezés alatt mindig a valós számok halmaza feletti lineáris teret (vektorteret) fogunk érteni. Definíció. Egy V vektortér valamely W (ncm üres) részhalmazát a V vektortér egyalterének nevezzük, ha vektorteret alkot a V-ben értelmezett műveletekre nézve. 29
12 KVANTiTATÍV A lineáris algebra alapja, Például könnyen belátható, hogya V 3 vektortér azon vektorainak W halmaza, amelyeknek a 3. komponense O egyalteret alkot Vrban. Ezen kél vektor összes lineáris kornbinációinak W halmaza az r~jtipusú i I Tétel, Egy V vektortér valamely nem iires W részhalll/aza akkor és csak akkor alter; ha zárt a V-ben definiált összeadásra és a skalárokkal valo szorzásra nézve. Tétel. Tetszőleges V vektortérnek altere önmaga, valall/int az egyedill a O vektorból állo részhalmaza. Ezeket triviális altereknek nevezik. Az öszszes többi altér neve valódi altér. A O vektorból álló alteret Iluliatérnek is mondjuk, A mátrixok esetén bevezetett lineáris kombináció fogai mát tetszőleges vektorterek elemei esetén is értelmezhetjük a következő módon: Definíció. Egy V vektortér al; a 2 ;.. -; ak vektorainak lineáris kornbinációin értj ük az összes Ala I + A 2 a Aka k alakú vektort, ahol Al; A ;"'; 2 Ak tetszőleges skalárok. Az üres vektorhalmaz lineáris kombinációi közé egyetlen vektor, a O vektor, tartozik. A definícióban nem tettük fel, hogy a szereplő vektorok különbözőek. Beszélhetünk például az a, a, 2a vektorok lineáris kombinációiról. Ha a vektorok kölönbözőségét nem kívánjuk meg, akkor vektorrendszerről beszélünk. Definíció. A Ala I + A 2 a Akak lineáris kombinációt az al; a 2 ;.. ; ak vektorok konvex lineáris kombinációjának nevezzük, ha a benne szereplő skalárok nem negatívak, és az összegük. k ( Aj 2: O és L Aj =.) i = I Tétel. A V vektortér tetszőleges al; a 2 ; ; ak vektorainak összes lineáris kombinácioi V-hen egyalteret - jelölje ezt W - alkotnak. Azt mondjuk, hogy W az al; a2; ; ak vektorrendszer által generált altere V-nek. Például tek intsűk a V3 vektortér e, =l~j =l~j és c, vekto rai t vektorokból álló halmaz, ahol x és y tetszőleges valós számok. Mivel Wegy altér V 3 -ban, így az CI és Cl által generált altér W. Definíció. Az al; a.:.. -: ak vektorrenc!szert a fl vektortér véges generatorrendszerének nevezzük, ha az általuk generált alter megegyezik V-vci. +l =lj Példá ul Vrbó I ki vá laszt va az c, e, és c, +vektor o kal az ezek által generált altér maga a fl3 tér lesz. Lineáris függetlenség és összefüggés Deflnícíó. A fl vektortér al; a 2;"'; ak vektorait lineárisan fiiggetlcnekncv; nevezzük, ha lineáris kornbinációjukként a O vektor csak trivialis módon állítható elő, azaz ha a egyenlőség csak A = A 2 =... = Ak = O esetén teljesűl. A V vektortér al; a 2 ;.. ; ak vektorait lineárisan összejiiggőknek (nem Figgetleneknek) nevezzük, ha lineáris kombinációjukként a O vektor nemcsak triviális módon állítható elő, azaz ha találhatók olyan Al; A 2 ;'" ;Ak skalárok, amelyek közül legalább egy nem O, és a egyenlőség teljesü!. Ala l + A 2 a Akak = O Például, a V3 vektortér escten az a, =l~ln, =r~j és a, =l~vektorokból a O vektor csak triviális móc!on állítható elő, így ezek egy lineárisan független vektorrendszert alkotnak. "~I:. g.l 30 3
13 KVANTiTATív Tétel. Egy vektorrendszer akkor és csak akkor lineárisan összejl'iggő, ha vall olyan eleme, amely eláállithatá a többi elem lineáris kombináciojaként. Az előző példa könnyen általánosítható a Vn (n>2) vektorterre. Világos, hogy az 00 O I O Bázis és dimenzió el = O c2 = O.: ",c" = o vektorok Vn-ben bázist alkotnak, a Jin tér Deflníció. A vektortér egy lineárisan független al; a 2 ; ; a" elemekből álló generátorrendszerót bázisnak nevezzük. O O X Tétel. Egy vektortér al; a 2 ; ; a" elemei akkor és csak akkor lllkalnak bázist, ha a vektortér tetszőleges a vektora egyértelmiren előállítható az al: a 2 :- ; a" vektorok lineáris kombinációjaként. Definíció. Legyen B = {a ; a 2 ; ; a} a V vektortér egy bázisa. A tér egy tetszőleges a vektorának a= Ala l + A2a Aka" előállításában szereplő Al; ~;.. ';A" skalárokat az a vektor B = {al; a 2 ; ; a" } bázisra vonatkozó koordinátáinak nevezzük. Tétel. Bármely vektortérben a bázist alkotó vektorok száma egyértelműen meg V( határozva.. X 2 dimenziója egyenlő»-ncl és tetszőleges x = E V:, vektor csctén: x I O O x 2 O I O " x= = XI O + x2 O + +X" = L,xjc;. X O O " O j= Dcfiuíció. Azt moudjuk, hogya V vektortér dill/ellziója II, ha V-nek van II elemű bázisa. A nullatér dimenziója O.A V vektortér dimenziója végtelen, ha V-nek nincs véges sok elemből álló bázisa. Tétel. Az dimenziós V vektortér Wa/terének tn dimenziójára igaz, hogy m:s:n. Például: tekintsük a V 2 vektortér CI =~Jés C l =~Jvektorait, ezek lineárisan függetlenek és V} tetszőleges x = :J vektora esetén teljesűl, hogy X=XI~]+X2~]=~~+x~]=:~J Tehát az el és c} vektorok bázist alkotnak Vrben és így V 2 dunenzrója egyenlő 2-vel..3 MÁ TRIXARITMETIKAI PÉLDÁK. példa. J vektorok eseten szárnitsuk ki az a + II és a c - b vektorokat! Megoldás. Az adott vektorok mindegyike 4 dimenziós oszlopvektor, így a kívánt összeadás, ill. ki vonás elvégezhető. Az összeadást, ill. a kivonást elemenként (komponensenként) végezzük a következőképpen: 32 33
14 KVANTITATiv Ol a + h = 3: ~_~) = ~ cs c - h ~ _2+2 +(-3) -2.fi - 2 R-O -2-(-) 2-(-3).fi -2 R példa. (a) Számítsuk ki b,+j azt a b vektort, amely a b, =r-~j b, =r~l b, = r-}ektoroknak a.2 példa. ~ Legyen A = ; -~ -~ ~és B = ~ -; ~ I I Szárnitsuk ki az A + B összeget és az A - B különbséget! Megoldás. Mivel két. típusú A = ajj] és B = bjj] mátrix összegén, ill. különbségén azt az m. Il-es C = Cjj] mátrixot értjük, amelynek minden elemére igaz, hogy: Cjj = ajj + bjj, ill. Cjj = ajj - bjj. Ezért az összeadást ill. a kivonást clemenként végezzük az aij] + bjj = ajj + bjj] ill. az ajj - bjj] = ajj - bjj] képletnek r megfelelően. Így -3 O - 3H5 7 2 A+B= O I 3 = O O Al = 3; A2 = -2; A) = 5; A2 = ; skalárokkal képzett lineáris kornbinációja! Megoldás. Az adott azonos mérctű b., b 2, b), b 4 vektorokat rendre mcgszorozzuk a megfelelő Al, Al, A), A4 skalárokkal, majd a nyert szorzatokat összeadjuk: 0 b = 3b l - 2b} + 5b 3 + Ib 4 = O + I - = = 6 (b) Számitsuk ki azt a mátrixot, amely az - 2] r I Al = 3 5' - ] - 2 A 2 = 2 O ' A) = 3 ~] mátrixoknak a Al = 5;... 2 = O; AJ = -2 skalárokkal képzett lineáris kornbinációjal Megoldás. Az adott 2 2 típusú Al, Al, A) matrixokat rendre megszorozzuk a megfelelő A" Al, AJ skalárokkal, majd a nyert szorzatokat összeadjuk. és (-3) = = ; +(-) + (-2) ~~-~-; ~~= (-3) =? O-3 = (-) - (-2) O-4 5-O :.4 példa. Legyen A{ 4-5 és U=: 'ly') ",,,4 4 O - 3 O I O 7 Szarnitsuk ki az A. B szorzutnak megfelelő C, majd ab A szorzntnak megfelelő D mátrixot! Megoldás. Két mátrix szorzatát csak abban az esetben számíthatjuk, hu az adott sorrendben konformábilisek, azaz az első tényező oszlopvektorainak száma egyenlő a második tényező sorvektorainak számával. Ez a feltétel 34 35
15 KVANTITATív A lineáris algebra alapjai most teljesül és így a szorzás elvégezhető. Az AB szorzatot a Falk-séma szerint felírva: B 4 O O 2 6 O A I O AB =C. O -3 I -3 O 3 7 Tehát AB = C = O 3 7 Majd a BA szorzatot a Falk-séma szerint kiszámítva: I O O -3 I 4 O B O BA =D, 2 6 O azaz BA = ~ =fl: j -2 adódik. 2 Látjuk, hogy az AB szorzat nem egyenlő a BA szorzattal. Tudjuk, hogy ez általában így van, a mátrixok szorzása nem kommutatív művclct. 36 A.4 GAZDASÁGI FELADATOK MEGOLDÁSA MÁ TRIXARITMETIKÁ VAL A szállítási mátrix A szállítási mátrixot olyan esetekben készítik el, ha több raktárban tárolnak termékeket és ezeket több rendeltetési helyre kell kiszállítani. Gyakran az egyszerű termékek (pl. burgonya, káposzta, alma srb.) szállításával kapcsolatban készítik el a szállítási mátrixot. A mátrixban a fajlagos szállítási költségeket tüntetik fel, vagyis azt, hogy az áru egy egységének (pl. l tonna) elszállítása mennyibe kerül..5 példa. Tekintsük azt az esetet, amikor négy raktárból (RI, R2, R3' R) három rendeltetési helyre (Hi> H2' HJ) kell szállítani! Az RI, R2' R3, R4 raktárak mindegyikben csak egyfajta termék van, de mindegyikben más és más termék. Például az Rj-ben burgonyát, az Rrben káposztát, az Rrban almát és az Rr ben spárgát tárolnak. A tonnánkénti szállítási költségeket ezer Ft-ban az alábbi táblázat tartalmazza: I~ Raktár HI H 2 Hj RI R I7 Rj R Ezek a számadatok alkotják az A, ún. szállítási mátrixot: A = j Például a harmadik sor második eleme: 5 aztjelenti, hogy egy tonna almának az Rj-as raktározási helyről a Hres szállítási helyre való szállítása 5 ezer Ft-ba kerül. 37
16 KVANTiTATÍV il lineáris algebra alapjai Legyen az egyes termékek felvásárlási ára rendre 52, 40, 39, 58 ezer Ft tonnánként. Ebből képezzük a ] B = ~:átri~ot., A ~ajl.agos szállítási és felvásárlási költségek összegéből álló osszkoltsegmatnxot megkapjuk ha kiszámít juk az A és B mátri x összegét j A + B = A~ A, és, B m,á:rixok ismerete szükséges ahhoz, hogy a lehető legkevesebb koltsegrafordltassallehessen fedezni a raktározási helyek készleteiból 'I- I,,. a sza ítasi helyek szükségleteit..6 példa. Egy külkereskedelmi vállalat négy svédországi városba Göteborgba, Malmőbe, St,~ck~oln:ha és Uppsalába rnézct exponált. A méz szúllítúsa három telephelyről (" 2, T 3 ) történt a következő bontásban. (c) szállítottak el a T 2 telephelyről. (d) vásárolt (e) exportáltak Megoldás. Göteborg; összesen? Az adott szállítási programot egy 3. 4-es A mátri x segítségével adhat juk meg. A mátrix minden sorához tartozik egy feladóhely (rendre: at, a T 2, és a T3 telephely), és minden oszlopához tartozik egy rendeltetési hely (rendre: Göteborg, Malmö, Stockholm és Uppsala). Megállapodunk abban, hogy az r-edik sor j-edik eleme azt fogja mutatni, hogy hány kg mézet szállítottak az i-edik telephelyről aj-edik városba A = 80 O 295 O O 250 (a) Az egyes telephelyekről elszállítandó mennyiségeket az A. loszlopvektor komponensei adják (kg-ban): A = 585, 475, 45f. (b) Az egyes városok vásárlását az l'. A sorvektor komponensei adják kg-ban: ' A= 430,60,720,65]. (c) A T 2 telephelyről: e;. A = 475 kg mézet szállítottak el. (d) Göteborg: i'.a el = 430 kg mézet vásárolt. (e) A teljes mézexport: I". A } = 475 kg volt. Feladóhely TI TI TI T 2 T 2 T3 T3 Rendeltetési Göteborg Malmő Stockholm Göteborg Stockholm Stockholm Uppsala hely Elszállított 250 kg 60 kg 75 kg 80 kg 295 kg 250 kg 65 kg Határa,zz,uk meg mátrixalgebrai eszközökkel, hogy hány kg niézet (a) szállitouak el rendre az egyes tclephelyckről; (b) importáltak rendre az egyes svéd városok; 38 méz A technológiai.7 példa. mátrix Tekintsünk egy üzemet, amely 5-féle tennéket (jelölje ezeket: TI' T2' T3' T4 és Ts) gyárt. A gyártáshoz háromféle erőforrás: EI, E 2 és E3 áll rendelkezésre. Az üzemi adatok szerint a termékegységre eső ráfordításokat ezer Ft-ban az alábbi táblázat muratja: Erőforrás Termék iele jele TI T 2 T3 T4 TI E 3 2 O 4 5 E E} 2 4 O 3 39
17 KVANTlTATiv Ezek a számadatok alkotják a T ún. technológiai mátrixot: T = : ~ ~ ; ~l 2 4 O 3J Ha az üzemnek a TI> T 2, T3, T 4, Ts termékből rendre 50, 30, 0, 40, 80 egységnyit kell előállítania, akkor ezt a programot a p = 50; 30; 0; 40; 80]* oszlopvektorral, az ún. programvektorral adjuk meg. A Tp szorzat az adott termelési program nyersanyag szükségletét mutatja erőforrások szerinti bontásban. Tehát: = ] A rendelkezésre álló erőforrások kapacitásait tartalmazó k = 800,560,400]* oszlopvektort kapaclrésvcktornak szokás nevezni. Csak azon termelési programok realizálhatók, amelyek kielégítik a Tp :5 k egyenlőtlenséget. Egyik crőforrús tekintetében sem léphetünk túl a kapacitáskorlátokon. Általában több ilyen program is lehetséges. Ilyenkor kell kiválasztani a legcélszerűbbet, amivel az optimum számítás foglalkozik. Esetünkben az előírt program szerinti termelés végrehajtható, mert mindegyik erőforrás kapacitása nagyobb, mint a szükséglet. Az egyes erőforrások egységárait (itt most ezer Ft-ban) tartalmazó sorvektor: a" T.8 példa, 3 = 3; 8; 5] ~ ~ : ~ ~] = 46; 40; 28; 28; 46] Egy vállalat három üzemeben 4-féle termeket (T I ' T 2 ' T 3 és T 4 ) gyárt, 3- féle erőforrás (E I ' E 2 és EJ) felhasználásával. Ismertek a következő táblázatok adatai. A tennelés megoszlása az üzemek között Az üzemek A termelés mennyiségc (természetes mértékegyséuben) TI T 2 T J T~. üzem ISO üzem üzem erőforrás-felhasználása Erőforrásokból felhasznált mcnnyiség (természetes mértékegységben) Erőforrás. üzem 2. üzem 3. üzem EI E E) SO a*=3;8;5] az ún. árvcktor. Az előírt termelési program anyagköltsége az a*tp szorzatból határozható meg, azaz: 770] a' T.p = 3; 8; 5] 540 = 8580.ezerFt. 390 A fajlagos anyagköltséget (termékenként rendre) az a*t szorzat adja: Egységárak A termék egységára (ezer Ft) TI 2 T 2,5 T3 3 T4 4 Az erőforrás egységára (ezer Ft) EI 2 E 2 EJ 3 40 I 4
18 KVANTITATiv A kiindulási adatok könnyen kezelhetővé válnak, ha azokat megfelelő mátrixok, ill. vektorok alakjában írjuk fel. A táblázatokba foglalt adatok által meghatározott mátrixokat és vektorokat a kővctkczőkóppcu vezetjük be Legyen T = k i ]= a tennelés megoszlásának mátrixa, ahol tjdelenti az Í-edik üzemben aj-edik termekből termélt mennyiséget Legyen F = fj= a felhasználási mátrix, ahol fjjjelenti az Í-edik erőforrásból aj-edik üzemben felhasznált mennyiséget. Továbbá legyen a = 2; ; 3 J az erőforrások egységárvektora és b = 2;,5; 3, 4J a termékek egységárvektora. Feladat: Mátrixaritmetikai módszerek, azaz a T, F, a, b valamint diagonális mátrixok és speciális vektorok segítsége révén adjunk választ a következő kérdésekre! (a) Mennyi a vállalat készárutermelése termékfajtánként (természetes rnértékcgységben)? (b) Mennyi a vállalat összes erőforrás-felhasználása erőforrásonként (természetes mértékegységben)? (c) Mennyi az árbevétel: (c ) termékfajtánként és egyben üzemenként. (c2) termékfajtánként összesen, (c3) üzemenként összesen, (c4) összesen? (d) Mennyi a közvetlen költség: (d ) erőforrásonként és egyben üzemenként, 42 (d2) erőforrásonként összesen, (d3) üzemenként összesen, (d4) összesen? I IIII Megoldás. (a) A készárutermelést termékfajránkénti bontásban megadó t* vektor ti T mátrix sorainak ősszcgzcscvcl adódik: t =*T=I; ; ] = 050, 850; 450; I 30]. 200 (b) Az erőforrásonkénti erőforrás-felhasználást megadá f vektort a felhasználási mátrix oszlopainak összegzésévei kapjuk meg: jl'j l270j f = F.= = 70. l (el) Az árbevételt termékfajtánként és egyben üzemenként bernutató A mátrix kiszámításához rendre a T matrix i-edik oszlopát az i-edik termék egységárával kell szorozni Ci=, 2, 3, 4), azaz: ISO 40 2 O O O] A = T(b) = ~ I~~ ~ ~ = O O O 4 Ce2) Az A mátrix sorvektorait összegezve a termékfajtánkénti összes árbcvétel vektorát kapjuk: *A = I'T(b) = ; ; ] = 200; 275; 350; 4520] = (e3) Az A mátrix oszlopvektorait összegezve az üzcmenkénti összes árbevctel vektorát kapjuk: ] Al=T(b)l= 500 ISO l ]: J3330j. 43
19 KVANTiTATÍV (c4) Az A mátrix valamennyi elemet összeadva az összes árbevételt kapjuk: Külföldi cégek (partnerek) 329 l'al=l't(b)l=l; ; ]3330 =9245 (eft.) (d) A kőzvctlen költségre vonatkozó kérdések válaszait is hasonló gondolatmenet alapján adhat juk meg. (CI ) A közvetlen költség erőforrásonkénti és egyben üzemenkénti bontásban: Évek. 2. J Í. lll. (/.. lj (d2) A közvetlen költség erőforrásonként összesen: 200~ Írjuk fel matrixaritmetikai jelölésekkel. (a) a 8. partnerrel a vizsgált időszakban lebonyolított forgalom ősszcrtékét: (b) az utolsó két év forgaimát partnerenként részletezve és összesen; (c) az egy év alatt egy partnerrel lebonyolított forgalom átlagos nagyságát' j 540j (a)fl = = (d3) A közvetlen költség üzemenként összesen: ~ r' (a)f = ; ; ] = 370; ISO (d4) A közvetlen költség összesen: f(a)f.l~r370; 35; 445{:j~l30 (cfi). A forgalmi.9 példa. mátrix 35; 445]. Egy külkereskedelmi vállalat II (Il :s 8) kűl földi céggel tart fenn állandó piaci kapcsolatot. Az utolsó (m :s 2) év forgalmi adatait a következő táblázat tartalmazza, amelynek i-edik sorában aj-edik elem, (vagyis Cli') azt adja meg, hogy az i-edik évben a j-edik partnerrel mekkora forgalmát bonyolított le a vállalat. 44 Megoldás. Jelöljük a táblázat forgalmi mátrixát A-val, azaz A = ajj egy II-CS mátrix. (a) A 8. partnerrel lebonyolított összforgalmat megkapjuk. ha az A mátri x 8. oszlopának adatait összegezzük. A 8. oszlopot kiválaszthatjuk a mátrixból, ha azt egy olyan egységvektorral szorozzuk jobbról, amelynek 8. komponense az. Az eredményül kapolt oszlopvektor elemeit egy összegző sorvektorral való skaláris szorzás segítségével összegezzük: *(Acg). Természetesen ( *A)cx sorrendben is számolhatunk; itt *A az egyes partnerekkellebonyolított összforgalmakat tartalmazó vektor; az cs-cai való szorzás ebből választja ki a 8. komponenst. (b) A mátrix utolsó két sorának összegét kell előálliranunk: e'" + e* ]. A. - n Az utolsó két év összforgalma a kapott vektor elemeinek összegezésévei nyerhető: e* +c*] A.,,- lj (c) A mátri x elemeinek összegét kell osztanunk az évek és a partnerek számával: - (l*al). m-n 45
20 KVANTITATÍV.0 példa. Egy vállalatnak a tavalyi évben 263 alkalmazottja volt. Legyen D = djj az a mátrix, amelynek djj eleme azt mutatja, hogy a vállalat í-edik dolgozójának mennyi volt a keresete az elmúlt év j-edik hónapjában, továbbá legyen III = mk] az a 2 elemű vektor, amelynek elemei rendre az egyes hónapok munkanapjainak számát adják meg (feltesszük, hogya tavalyi év folyamán a letszámot illetően scm felvétel, sem kilépés a vállalatnál nem volt). Írjuk fel mátrixalgebrai jelölésekkel, hogy mennyi volt: (a) a dolgozók június havi összkeresete, (b) az egy dolgozóra jutó átlagos évi kereset, (c) az egy dolgozóra j utó átlagos havi kereset, (d) az egy dolgozóra jutó átlagos numkanapi kereset az egész évi adatok alapján, (c) a vállaluutál kifizetett összbénnennyiség a harmadik ncgyedévbcn, (f) a dolgozók május havi átlagkeresete, (g) az egy dolgozóra jutó átlagos munkanapi kereset a második negyedévben? Megoldás. (a) *. D e. (b) 6, r D (d) I". ITI' 263, (e) (f) r 0 r 0 (c) ' *. D. (e, + Cs + e 9 ); ' 0 e 5 I.' B (e.j + c5 + er,) (g), 263 (e.j + es + e(,) 263 Végtermék Alkatrész jele jele Al A2 AJ A4 As VI O 2 V2 2 O VJ O V 4 O 5 I 4 3 Az egyes alkatrészek beszerzési ára rendre: 3; 2, ; 2;,4; I ezer Ft/db. Feladat. Határozza meg mátrixaritmetikával, a megfigyelt időszakra vonatkozóan, a következőkct: (a) Mekkora a termékek fajlagos alkatrészkőltsége? (b) Az egyes alkatrészekből hány db-ot kell importálni? (c) Mennyi a teljes importköltség? Megoldás. Legyen a = 3, 2,; 2;,4; ]' az alkatrészek beszerzési egységárvektora és p = 50; 70; 32; 20)' a termelés programvektora! 'Továbbá legyen A = aj= O 2 2 O az alkatrész felhasználás mátrixa, O O 5 j 4 3 ahol ajj jelenti az i-edik termék előállítása során aj-edik alkatrészből felhasznált darabszámot. Lll példa. Egy üzemben importból beszerzett 5-féle alkatrészből 4-fajta végtermeket szerel nek össze. Egy megfigyelt időszak alatt a VI termékből 50, a V 2 termékből 70, a V 3 termekből 32, a V 4 termekből 20 egységet állítanak elő. A! egyes termékek fajlagos alkatrész-szükségletét a kövctkező táblázat mutatja: (a) A termékek fajlagos alkatrészköltsége: Aa, Aa= O 2: 2 O O 5 I 4 3,4 = I 27,6 20,8 2,5. 2, 46 47
21 KVANTITATív (b) Az alkatrész-szükséglet vektora: p'a, O 2] Il A = 50; 70; 32, 20] = 322; 343 O O 5 43 Cc) A teljes importköltség: p"a.a = ll'.aa..5 FELADATOK. Adja össze a következő vektorokat: 496, 45; 36, 580] (b) Adja össze a következő mátrixokat: J O O 2 ] - O - A= B= - 2] c= ' O 7-3. I -6 O (c) Adja össze a következő mátrixokat: - O O Af O O -b -b O -< n"~ - a O, -b O 2a O O -b b O O -a a a O O (d) Legyen - J? 5 ] és B = O 2-2. O O 3 Milyen speciális matrix az A, a B, az A + B és a B - A? (b) a = 7; 2; -3]*; b = -; O; 0,5]*; c = 3; -3; 2,5]*..3 Írja fel a következő lineáris kombinációk által meghatározott vektort:.2 (a) Legyen X" ~ J O O JI - 3 v, 3 O O - 2] I O (b) 4a -2b +5c, ha a* = ; -; 5; -2]; b* = O; 3; -; 5]; c* = ; O; -; O]. Számítsa ki az X + Y összeget és az Y - X különbséget! Cc) -2a +3b -5c - 3d, ha 48
22 KVANTITATÍV M6DSZEREK.4 Írja fel a következő lineáris kombinációk által meghatározott mátrixot: (a) 3A-Sil-C,ha (b) -SA +3-3C, ha.7 Mivel egyenlő Ca) x* A y,ha O 5] A = , O 5-2,--/ 4] - 0]. x - -' Y - -5 ' A=~ ll= ~ 5 c= O - ~ 8 tl 7 O 4 ' - :2 O - -2 O O O -S (c) Igazolja az ismert!' (a) = a' és (a) = a azonosságole teljesülését az.5 Végezze el a következő mátrix-vektor szorzásokat: (a) (b) 2 O - -~J-n ~ -2 O 4 :;]Fl.6 Végezze el a következő vektor-mátri x szorzásokat: (a) -3', 7', 5', (b) 8; 3; -; O -? O -3]. - O 5 9 :2.8 a{vektor eseten. Határozza meg a következő szorzalnak megfelelő mátrixot: (a) A B és B. A, ahol H A = ~ ~ ~:~lii = l~,3 (b) X' Y és Y. X, ahol 2 3-5] X = O 3 y =~ - 2 O ' 4-2 o O - 2] ~. 50 5
23 KVANTITATÍV (c) Igazolja a mátrixok szorzásának asszociativitását azaz, hogy (A. B). C = A. (B. C)] a következő mátrixok esetén: B = O ] 4 5 O 3 ' c ~ :~ ~ ~l! O O 2 Az erőforrás A termék jele Az erőforrások jele TI T2 T3 T4 TS egységára --- ~ EI I O S.- E O I 0 E3 4 6 O Gyártondó mennviség: (d) Igazolja az ismert (A. B)* = B*. A * azonosság teljesülését a következő mátrixok esetén:.: O j II= l-~ ;! Számítsa ki mátrixarirmctika segitségével: (a) Mennyi a termékek fajlagos crőforrásköltsége? (b) Mennyi a termelési program crőforrús-szükséglcrc (erőforrásonként részletezve)? (c) Mennyibe kerül az adott termelési program erőforrás-szükséglctc?.2 A "Hunimpex" külkereskedelmi vállalat az elmúlt gazdasági évben tíz külföldi céggel (partnerrel) tartott fenn állandó piaci kapcsolatot. Az év forgalmi adatait az F = fjj] matrix tartalmazza, amelynek f eleme azt adja meg (alkalmas rnértékegységben), hogy az r-edik hónapban a j-edik partnerrel mekkora forgalmat bonyolított le a vállalat. Számusuk ki a kövctkező szorzatokar: (b) * MI; (c) l*ba*l; (d) b* M*l; (e) a* Mb; (f) b* M*a; (g) ba* \; (h) Mba*..0 Az egyik főiskola nappali első évfolyamán 6 tárgyból vizsgázott 35 hallgató. Jelentse az A = ajj] mátrix ajj eleme az i-edik hallgatónak aj-edik tantárgyból elért vizsgajegyét. Írja fel mátrixaritmetikai jelölésekkel: (a) az évfolyamnak az 5. tantárgyból elért átlagár; (a) a 4. hallgató vizsgajegyeinek átlagát; (b) az évfolyam vizsgajegyeinek átlagát!. Egy üzem 3 erőforrás segítségével ötféle termeket állít elő. A termékegységre vonatkozó ráfordításokat, az erőforrások egységárait (ef t-ban), valamint az egyes termékekből gyártandó mennyiségeket (db-ban) a következő táblázat mutatja. 52 Írja fel matrixaritmetikai jelölésekkel a következőket! (a) A k-adik céggel lebonyolított havi forgalmak vektora, ( :S:k :S:0). (b) A k-adik céggel az elmúlt évben lebonyolított összforgalom, (l:s:k:s:lo). (c) A p-edik hónap forgalma partnerenként részletezve, (J :s: p :s: 2). (d) A p-edik hónap összforgalrna, (:S: P :s: 2). (e) Az utolsó negyedév forgalma partnerenként részletezve. (f) Az utolsó negyedév osszforgalma. (g) Egy hónap alatt egy céggel lebonyolított forgalom átlagos nagysága.3 A.Dunagép KFT" egyik üzemeben ll-féle erőforrás felhasználásával m-féle végtermeket gyártanak. Az F = fjj] mátri x fjj eleme jelenti, hogy ajedik végtermék egy egységének előállitásához felhasznált i-edik erőforrás mennyiségét (természetes mértékegységben). Valamely időszakra vonatkozóan a p vektor komponensei jelentsék rendre az egyes végtermékekből előállítandó rnennyiséget, az a vektor komponensei pedig jelentsék rendre a különböző erőforrások egységárait. Az F, P. a, valamint diagonális mátrixok és speciális vektorok segítségével írja fel a következőket! 53
24 KVANTiTATÍV (a) A P program erőforrás-szükséglete termékenként a k-adik erőforrásból (l:s;k:s;/l). (b) A P program erőforrásköltsége a k-adik erőforrásból (I:S; k:s; ll). Cc) A fajlagos (egységnyi termékre eső) erőforrásköltség termékenként. (d) A q-adik termék egységének erőforrásköltsége erőforrásenként (I:S;q:S;I7l). (e) A q-adik termék erőforrásonkénti szükséglete a p programban (I:S;q:S;/Il). (f) A q-adik termék erőforrásköltsége a p programban ( :S; q :S; /Il)..4 Egy üzemben importból beszerzett 5-féle alkatrészből 4-fajta végterméket szerelnek össze. Egy megfigyelt időszak alatt a VI termékből 50, a V2 termékből 70, a V) termékből 32, a V 4 termékből 20 egységet állítanak elő. Az egyes termékek fajlagos alkatrész-szükségletét a következő táblázat mutatja: Termék jele Alkatrész jele Al A 2 Aj A4 As VI V Vj O V 4 5 l 4 3 Az egyes alkatrészek beszerzési ára rendre: 3; 2,; 2;,4; ezer Ft/db. Határozza meg mátrixaritmetikával a megfigyelt időszakra vonatkozóan a következőket: Ca). Mekkora a termékek fajlagos alkatrészköltsége? Cb) Az egyes alkatrészekből hány db-ot kell importálni? (c) Mennyi a teljes importköltség?.5 Egy külkereskedelmi vállalat Jn fajta terméket exportál II számú különböző országba. Az A mátrix aijeleme jelentse az /-edik termékból aj-edik országban eladott darabszámot. Legyen (I:s; k :s; /) és ( :s; P :s; ll)! Fogalmazza meg, mit jelentenek a következő kifejezések. (a) e: A; (b) e~ A e ; p (c) A A.Jvlikroelektronika Rt." egy megfigyelt héten tn-féle alapanyag felhasználásávaln-féle termeket gyártott. A T = tij] technológiai mátrix tij eleme jelenti aj-edik termék egy egységének készítéséhez felhasznált i-edik alapanyag mennyiségét (természetes mértékegységben mérve). Jelentsék a q programvektor komponensei rendre az egyes termékekből gyártott mennyiséget a megfigyelt héten, az a vektor komponensei rendre a felhasznált alapanyagok egységárait, a b vektor komponensei pedig rendre a termékek eladási egységárain Fogalmazza meg, hogy mi a jelentése a következő kifejezeseknek. (a) T(q) ; (b) TI; Cc) Tq; (d) e~tq, (I:S; «< ); (e) qb ; (f) (q)b; (g) a*t; (h) a*tq; (i) T(a); (j) b-m*a..7 Egy vállalat ll-féle végtermeket gyárt -féle alapanyag felhasználásával. Az A = ap'!] mátrix a pq eleme jelenti, hogy ap-edik végtermék egy egységének előállításához mennyit használtak fel (természetes mértékegységben) a q-adik alapanyagból. Ismert az x programvektor, amelynek komponensei rendre az egyes végtermékekből előállítandó mennyiséget mutatják és adott az alapanyagok egységárait tartalmazó a vektor is. Az A, x, a, valamint diagonális mátrixok és speciális vektorok segítsé- I ge révén ÍJja fel a következőket! (a) Az x program anyagszükséglete alapanyagonként. (b) Az egyes végtermékek fajlagos anyagköltsége az i-edik alapanyagból(l::::; i«). (c) A j-edik végtermék egységének alapanyagköltsége (I::::;.i::::; II). (d) Az x program anyagköltsége: (d ) alapanyagonként; (d2) végtermékenként, (d3) végtermékenként és egyben alapanyagonként..8 Egy megfigyelt időszakban a "Célgép KFT" egyik gyáregysége II-féle erőforrás felhasználásával 8-féle végterméket gyártott. Az M = tnij] mátrix Jnijeleme jelenti aj-edik végtermék ( ::::;j s 8) egy egységének 55
Diszkrét matematika I., 12. előadás Dr. Takách Géza NyME FMK Informatikai Intézet takach november 30.
 1 Diszkrét matematika I, 12 előadás Dr Takách Géza NyME FMK Informatikai Intézet takach@infnymehu http://infnymehu/ takach 2005 november 30 Vektorok Definíció Egy tetszőleges n pozitív egész számra n-komponensű
1 Diszkrét matematika I, 12 előadás Dr Takách Géza NyME FMK Informatikai Intézet takach@infnymehu http://infnymehu/ takach 2005 november 30 Vektorok Definíció Egy tetszőleges n pozitív egész számra n-komponensű
15. LINEÁRIS EGYENLETRENDSZEREK
 15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
Lineáris algebra (10A103)
 Lineáris algebra (10A103 Kátai-Urbán Kamilla Tudnivalók Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli (beugróval, feltétele a Lineáris algebra gyakorlat
Lineáris algebra (10A103 Kátai-Urbán Kamilla Tudnivalók Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli (beugróval, feltétele a Lineáris algebra gyakorlat
Vektorok, mátrixok, lineáris egyenletrendszerek
 a Matematika mérnököknek I. című tárgyhoz Vektorok, mátrixok, lineáris egyenletrendszerek Vektorok A rendezett valós számpárokat kétdimenziós valós vektoroknak nevezzük. Jelölésükre latin kisbetűket használunk.
a Matematika mérnököknek I. című tárgyhoz Vektorok, mátrixok, lineáris egyenletrendszerek Vektorok A rendezett valós számpárokat kétdimenziós valós vektoroknak nevezzük. Jelölésükre latin kisbetűket használunk.
Mátrixok, mátrixműveletek
 Mátrixok, mátrixműveletek 1 előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Mátrixok, mátrixműveletek p 1/1 Mátrixok definíciója Definíció Helyezzünk el n m elemet egy olyan téglalap
Mátrixok, mátrixműveletek 1 előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Mátrixok, mátrixműveletek p 1/1 Mátrixok definíciója Definíció Helyezzünk el n m elemet egy olyan téglalap
1. Mátrixösszeadás és skalárral szorzás
 1 Mátrixösszeadás és skalárral szorzás Mátrixok tömör jelölése T test Az M = a i j T n m azt az n sorból és m oszlopból álló mátrixot jelöli, amelyben az i-edik sor j-edik eleme a i j T Példák [ ] Ha M
1 Mátrixösszeadás és skalárral szorzás Mátrixok tömör jelölése T test Az M = a i j T n m azt az n sorból és m oszlopból álló mátrixot jelöli, amelyben az i-edik sor j-edik eleme a i j T Példák [ ] Ha M
Műveletek mátrixokkal. Kalkulus. 2018/2019 ősz
 2018/2019 ősz Elérhetőségek Előadó: (safaro@math.bme.hu) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
2018/2019 ősz Elérhetőségek Előadó: (safaro@math.bme.hu) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
Determinánsok. A determináns fogalma olyan algebrai segédeszköz, amellyel. szolgáltat az előbbi kérdésekre, bár ez nem mindig hatékony.
 Determinánsok A determináns fogalma olyan algebrai segédeszköz, amellyel jól jellemezhető a mátrixok invertálhatósága, a mátrix rangja. Segítségével lineáris egyenletrendszerek megoldhatósága dönthető
Determinánsok A determináns fogalma olyan algebrai segédeszköz, amellyel jól jellemezhető a mátrixok invertálhatósága, a mátrix rangja. Segítségével lineáris egyenletrendszerek megoldhatósága dönthető
1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás)
 Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Szöveges feladatok a mátrixaritmetika alkalmazására
 Szöveges feladatok a mátrixaritmetika alkalmazására Bevezetés: Tekintsük az alábbi -es mátrixot: A. Szorozzuk meg ezt jobbról egy alkalmas méretű (azaz -es) oszlopvektorral, amely az R tér kanonikus bázisának
Szöveges feladatok a mátrixaritmetika alkalmazására Bevezetés: Tekintsük az alábbi -es mátrixot: A. Szorozzuk meg ezt jobbról egy alkalmas méretű (azaz -es) oszlopvektorral, amely az R tér kanonikus bázisának
I. VEKTOROK, MÁTRIXOK
 217/18 1 félév I VEKTOROK, MÁTRIXOK I1 I2 Vektorok 1 A síkon derékszögű koordinátarendszerben minden v vektornak van vízszintes és van függőleges koordinátája, ezeket sorrendben v 1 és v 2 jelöli A v síkbeli
217/18 1 félév I VEKTOROK, MÁTRIXOK I1 I2 Vektorok 1 A síkon derékszögű koordinátarendszerben minden v vektornak van vízszintes és van függőleges koordinátája, ezeket sorrendben v 1 és v 2 jelöli A v síkbeli
 XI A MÁTRIX INVERZE 1 Az inverzmátrix definíciója Determinánsok szorzástétele Az egységmátrix definíciója: 1 0 0 0 0 1 0 0 E n = 0 0 1 0 0 0 0 1 n-edrenű (azaz n n típusú) mátrix E n -nel bármely mátrixot
XI A MÁTRIX INVERZE 1 Az inverzmátrix definíciója Determinánsok szorzástétele Az egységmátrix definíciója: 1 0 0 0 0 1 0 0 E n = 0 0 1 0 0 0 0 1 n-edrenű (azaz n n típusú) mátrix E n -nel bármely mátrixot
2. előadás. Lineáris algebra numerikus módszerei. Mátrixok Mátrixműveletek Speciális mátrixok, vektorok Norma
 Mátrixok Definíció Az m n típusú (méretű) valós A mátrixon valós a ij számok alábbi táblázatát értjük: a 11 a 12... a 1j... a 1n.......... A = a i1 a i2... a ij... a in........... a m1 a m2... a mj...
Mátrixok Definíció Az m n típusú (méretű) valós A mátrixon valós a ij számok alábbi táblázatát értjük: a 11 a 12... a 1j... a 1n.......... A = a i1 a i2... a ij... a in........... a m1 a m2... a mj...
Vektorterek. =a gyakorlatokon megoldásra ajánlott
 Vektorterek =a gyakorlatokon megoldásra ajánlott 40. Alteret alkotnak-e a valós R 5 vektortérben a megadott részhalmazok? Ha igen, akkor hány dimenziósak? (a) L = { (x 1, x 2, x 3, x 4, x 5 ) x 1 = x 5,
Vektorterek =a gyakorlatokon megoldásra ajánlott 40. Alteret alkotnak-e a valós R 5 vektortérben a megadott részhalmazok? Ha igen, akkor hány dimenziósak? (a) L = { (x 1, x 2, x 3, x 4, x 5 ) x 1 = x 5,
Vektorterek. Wettl Ferenc február 17. Wettl Ferenc Vektorterek február / 27
 Vektorterek Wettl Ferenc 2015. február 17. Wettl Ferenc Vektorterek 2015. február 17. 1 / 27 Tartalom 1 Egyenletrendszerek 2 Algebrai struktúrák 3 Vektortér 4 Bázis, dimenzió 5 Valós mátrixok és egyenletrendszerek
Vektorterek Wettl Ferenc 2015. február 17. Wettl Ferenc Vektorterek 2015. február 17. 1 / 27 Tartalom 1 Egyenletrendszerek 2 Algebrai struktúrák 3 Vektortér 4 Bázis, dimenzió 5 Valós mátrixok és egyenletrendszerek
Lineáris algebra (10A103)
 Lineáris algebra (10A103) Kátai-Urbán Kamilla (1. előadás) Mátrixok 2019. február 6. 1 / 35 Bevezetés Előadás Tudnivalók (I.) Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Az előadáson készített
Lineáris algebra (10A103) Kátai-Urbán Kamilla (1. előadás) Mátrixok 2019. február 6. 1 / 35 Bevezetés Előadás Tudnivalók (I.) Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Az előadáson készített
összeadjuk 0-t kapunk. Képletben:
 814 A ferde kifejtés tétele Ha egy determináns valamely sorának elemeit egy másik sor elemeihez tartozó adjungáltakkal szorozzuk meg és a szorzatokat összeadjuk 0-t kapunk Képletben: n a ij A kj = 0, ha
814 A ferde kifejtés tétele Ha egy determináns valamely sorának elemeit egy másik sor elemeihez tartozó adjungáltakkal szorozzuk meg és a szorzatokat összeadjuk 0-t kapunk Képletben: n a ij A kj = 0, ha
6. Előadás. Megyesi László: Lineáris algebra, oldal. 6. előadás Bázis, dimenzió
 6. Előadás Megyesi László: Lineáris algebra, 37. 41. oldal. Gondolkodnivalók Lineáris függetlenség 1. Gondolkodnivaló Legyen V valós számtest feletti vektortér. Igazolja, hogy ha a v 1, v 2,..., v n V
6. Előadás Megyesi László: Lineáris algebra, 37. 41. oldal. Gondolkodnivalók Lineáris függetlenség 1. Gondolkodnivaló Legyen V valós számtest feletti vektortér. Igazolja, hogy ha a v 1, v 2,..., v n V
Matematika A1a Analízis
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
Lineáris algebra. (közgazdászoknak) T C T = ( 1 ) ; , D T D =
 Lineáris algebra (közgazdászoknak) 10A103 FELADATOK A GYAKORLATRA (1.) 2018/2019. tavaszi félév Mátrixok 1.1. Feladat. Legyen A = 1 2 1, B = 1 2 3 1 2 1 1, C = ( 1 2 0 ), D = 1 3 1 1 2 1 ( ) 10/2 0.6 1
Lineáris algebra (közgazdászoknak) 10A103 FELADATOK A GYAKORLATRA (1.) 2018/2019. tavaszi félév Mátrixok 1.1. Feladat. Legyen A = 1 2 1, B = 1 2 3 1 2 1 1, C = ( 1 2 0 ), D = 1 3 1 1 2 1 ( ) 10/2 0.6 1
Diszkrét matematika II., 8. előadás. Vektorterek
 1 Diszkrét matematika II., 8. előadás Vektorterek Dr. Takách Géza NyME FMK Informatikai Intézet takach@inf.nyme.hu http://inf.nyme.hu/ takach/ 2007.??? Vektorterek Legyen T egy test (pl. R, Q, F p ). Definíció.
1 Diszkrét matematika II., 8. előadás Vektorterek Dr. Takách Géza NyME FMK Informatikai Intézet takach@inf.nyme.hu http://inf.nyme.hu/ takach/ 2007.??? Vektorterek Legyen T egy test (pl. R, Q, F p ). Definíció.
1. Homogén lineáris egyenletrendszer megoldástere
 X HOMOGÉN LINEÁRIS EGYENLET- RENDSZEREK 1 Homogén lineáris egyenletrendszer megoldástere Homogén lineáris egyenletrendszer definíciója már szerepelt Olyan lineáris egyenletrendszert nevezünk homogénnek,
X HOMOGÉN LINEÁRIS EGYENLET- RENDSZEREK 1 Homogén lineáris egyenletrendszer megoldástere Homogén lineáris egyenletrendszer definíciója már szerepelt Olyan lineáris egyenletrendszert nevezünk homogénnek,
Valasek Gábor valasek@inf.elte.hu
 Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2013/2014. őszi félév ( Eötvös LorándSzámítógépes TudományegyetemInformatikai Grafika Kar) 2013/2014.
Számítógépes Grafika Valasek Gábor valasek@inf.elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2013/2014. őszi félév ( Eötvös LorándSzámítógépes TudományegyetemInformatikai Grafika Kar) 2013/2014.
Matematika (mesterképzés)
 Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Lineáris egyenletrendszerek
 Lineáris egyenletrendszerek Lineáris egyenletrendszernek nevezzük az a 11 x 1 + a 12 x 2 +... +a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... +a 2n x n = b 2.. a k1 x 1 + a k2 x 2 +... +a kn x n = b k n ismeretlenes,
Lineáris egyenletrendszerek Lineáris egyenletrendszernek nevezzük az a 11 x 1 + a 12 x 2 +... +a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... +a 2n x n = b 2.. a k1 x 1 + a k2 x 2 +... +a kn x n = b k n ismeretlenes,
Összeállította: dr. Leitold Adrien egyetemi docens
 Az R n vektortér Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. R n vektortér/1 Vektorok Rendezett szám n-esek: a = (a 1, a 2,, a n ) sorvektor a1 a = a2 oszlopvektor... a n a 1, a 2,,
Az R n vektortér Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. R n vektortér/1 Vektorok Rendezett szám n-esek: a = (a 1, a 2,, a n ) sorvektor a1 a = a2 oszlopvektor... a n a 1, a 2,,
1. Geometria a komplex számsíkon
 1. Geometria a komplex számsíkon A háromszög-egyenlőtlenség A háromszög-egyenlőtlenség (K1.4.3) Minden z,w C-re z +w z + w. Egyenlőség pontosan akkor áll, ha z és w párhuzamosak, és egyenlő állásúak, azaz
1. Geometria a komplex számsíkon A háromszög-egyenlőtlenség A háromszög-egyenlőtlenség (K1.4.3) Minden z,w C-re z +w z + w. Egyenlőség pontosan akkor áll, ha z és w párhuzamosak, és egyenlő állásúak, azaz
1. Generátorrendszer. Házi feladat (fizikából tudjuk) Ha v és w nem párhuzamos síkvektorok, akkor generátorrendszert alkotnak a sík vektorainak
 1. Generátorrendszer Generátorrendszer. Tétel (Freud, 4.3.4. Tétel) Legyen V vektortér a T test fölött és v 1,v 2,...,v m V. Ekkor a λ 1 v 1 + λ 2 v 2 +... + λ m v m alakú vektorok, ahol λ 1,λ 2,...,λ
1. Generátorrendszer Generátorrendszer. Tétel (Freud, 4.3.4. Tétel) Legyen V vektortér a T test fölött és v 1,v 2,...,v m V. Ekkor a λ 1 v 1 + λ 2 v 2 +... + λ m v m alakú vektorok, ahol λ 1,λ 2,...,λ
11. DETERMINÁNSOK. 11.1 Mátrix fogalma, műveletek mátrixokkal
 11 DETERMINÁNSOK 111 Mátrix fogalma, műveletek mátrixokkal Bevezetés A közgazdaságtanban gyakoriak az olyan rendszerek melyek jellemzéséhez több adat szükséges Például egy k vállalatból álló csoport minden
11 DETERMINÁNSOK 111 Mátrix fogalma, műveletek mátrixokkal Bevezetés A közgazdaságtanban gyakoriak az olyan rendszerek melyek jellemzéséhez több adat szükséges Például egy k vállalatból álló csoport minden
Numerikus módszerek 1.
 Numerikus módszerek 1. 3. előadás: Mátrixok LU-felbontása Lócsi Levente ELTE IK 2013. szeptember 23. Tartalomjegyzék 1 Alsó háromszögmátrixok és Gauss-elimináció 2 Háromszögmátrixokról 3 LU-felbontás Gauss-eliminációval
Numerikus módszerek 1. 3. előadás: Mátrixok LU-felbontása Lócsi Levente ELTE IK 2013. szeptember 23. Tartalomjegyzék 1 Alsó háromszögmátrixok és Gauss-elimináció 2 Háromszögmátrixokról 3 LU-felbontás Gauss-eliminációval
Mátrixok. 3. fejezet. 3.1. Bevezetés: műveletek táblázatokkal
 fejezet Mátrixok Az előző fejezetben a mátrixokat csak egyszerű jelölésnek tekintettük, mely az egyenletrendszer együtthatóinak tárolására, és az egyenletrendszer megoldása közbeni számítások egyszerüsítésére
fejezet Mátrixok Az előző fejezetben a mátrixokat csak egyszerű jelölésnek tekintettük, mely az egyenletrendszer együtthatóinak tárolására, és az egyenletrendszer megoldása közbeni számítások egyszerüsítésére
9. Előadás. (9. előadás) Lineáris egyr.(3.), Sajátérték április / 35
 9. Előadás (9. előadás) Lineáris egyr.(3.), Sajátérték 2019. április 24. 1 / 35 Portfólió-analízis Tegyük fel, hogy egy bank 4 különböző eszközbe fektet be (réz, búza, arany és kakaó). Az ügyfeleinek ezen
9. Előadás (9. előadás) Lineáris egyr.(3.), Sajátérték 2019. április 24. 1 / 35 Portfólió-analízis Tegyük fel, hogy egy bank 4 különböző eszközbe fektet be (réz, búza, arany és kakaó). Az ügyfeleinek ezen
Lineáris Algebra gyakorlatok
 A V 2 és V 3 vektortér áttekintése Lineáris Algebra gyakorlatok Írta: Simon Ilona Lektorálta: DrBereczky Áron Áttekintjük néhány témakör legfontosabb definícióit és a feladatokban használt tételeket kimondjuk
A V 2 és V 3 vektortér áttekintése Lineáris Algebra gyakorlatok Írta: Simon Ilona Lektorálta: DrBereczky Áron Áttekintjük néhány témakör legfontosabb definícióit és a feladatokban használt tételeket kimondjuk
9. Előadás. Megyesi László: Lineáris algebra, oldal. 9. előadás Mátrix inverze, Leontyev-modell
 9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Tegyük fel, hogy egy elemi bázistranszformáció kezdetekor a sor- és oszlopindexek sorban helyezkednek
9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Tegyük fel, hogy egy elemi bázistranszformáció kezdetekor a sor- és oszlopindexek sorban helyezkednek
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
Meghirdetés féléve 2 Kreditpont Összóraszám (elm+gyak) 2+0
 Tantárgy neve Lineáris algebra I Tantárgy kódja MTB1004 Meghirdetés féléve 2 Kreditpont 3k Összóraszám elm+gyak 2+0 Számonkérés módja kollokvium Előfeltétel tantárgyi kód MTB1003 Tantárgyfelelős neve Kurdics
Tantárgy neve Lineáris algebra I Tantárgy kódja MTB1004 Meghirdetés féléve 2 Kreditpont 3k Összóraszám elm+gyak 2+0 Számonkérés módja kollokvium Előfeltétel tantárgyi kód MTB1003 Tantárgyfelelős neve Kurdics
Gazdasági matematika II. tanmenet
 Gazdasági matematika II. tanmenet Mádi-Nagy Gergely A hivatkozásokban az alábbi tankönyvekre utalunk: T: Tóth Irén (szerk.): Operációkutatás I., Nemzeti Tankönyvkiadó 1987. Cs: Csernyák László (szerk.):
Gazdasági matematika II. tanmenet Mádi-Nagy Gergely A hivatkozásokban az alábbi tankönyvekre utalunk: T: Tóth Irén (szerk.): Operációkutatás I., Nemzeti Tankönyvkiadó 1987. Cs: Csernyák László (szerk.):
Gauss-eliminációval, Cholesky felbontás, QR felbontás
 Közelítő és szimbolikus számítások 4. gyakorlat Mátrix invertálás Gauss-eliminációval, Cholesky felbontás, QR felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei
Közelítő és szimbolikus számítások 4. gyakorlat Mátrix invertálás Gauss-eliminációval, Cholesky felbontás, QR felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei
9. Előadás. Megyesi László: Lineáris algebra, oldal. 9. előadás Mátrix inverze, mátrixegyenlet
 9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Határozzuk meg a p valós paraméter értékétől függően a következő mátrix rangját: p 3 1 2 2
9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Határozzuk meg a p valós paraméter értékétől függően a következő mátrix rangját: p 3 1 2 2
1. Algebrai alapok: Melyek műveletek az alábbiak közül?
 1. Algebrai alapok: Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz egyértelműen hozzárendel egy
1. Algebrai alapok: Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz egyértelműen hozzárendel egy
EGYSZERŰSÍTETT ALGORITMUS AZ ELEMI BÁZISCSERE ELVÉGZÉSÉRE
 Lipécz György* EGYSZERŰSÍTETT ALGORITMUS AZ ELEMI BÁZISCSERE ELVÉGZÉSÉRE AVAGY A SZÁMÍTÓGÉP-HASZNÁLAT LEHETŐSÉGE A LINEÁRIS ALGEBRA ÉS AZ OPERÁCIÓKUTATÁS ALAPJAINAK OKTATÁSÁBAN " Simplicitassigillum veri"
Lipécz György* EGYSZERŰSÍTETT ALGORITMUS AZ ELEMI BÁZISCSERE ELVÉGZÉSÉRE AVAGY A SZÁMÍTÓGÉP-HASZNÁLAT LEHETŐSÉGE A LINEÁRIS ALGEBRA ÉS AZ OPERÁCIÓKUTATÁS ALAPJAINAK OKTATÁSÁBAN " Simplicitassigillum veri"
Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit
 Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit 1. A térbeli irányított szakaszokat vektoroknak hívjuk. Két vektort egyenlőnek tekintünk, ha párhuzamos eltolással fedésbe hozhatók.
Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit 1. A térbeli irányított szakaszokat vektoroknak hívjuk. Két vektort egyenlőnek tekintünk, ha párhuzamos eltolással fedésbe hozhatók.
DISZKRÉT MATEMATIKA: STRUKTÚRÁK Előadáson mutatott példa: Bércesné Novák Ágnes
 1. Algebrai alapok: DISZKRÉT MATEMATIKA: STRUKTÚRÁK Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz
1. Algebrai alapok: DISZKRÉT MATEMATIKA: STRUKTÚRÁK Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz
Lineáris algebra. =0 iє{1,,n}
 Matek A2 (Lineáris algebra) Felhasználtam a Szilágyi Brigittás órai jegyzeteket, néhol a Thomas féle Kalkulus III könyvet. A hibákért felelosséget nem vállalok. Hiányosságok vannak(1. órai lin algebrai
Matek A2 (Lineáris algebra) Felhasználtam a Szilágyi Brigittás órai jegyzeteket, néhol a Thomas féle Kalkulus III könyvet. A hibákért felelosséget nem vállalok. Hiányosságok vannak(1. órai lin algebrai
A lineáris algebrában központi szerepet betöltı vektortér fogalmát értelmezzük most, s megvizsgáljuk e struktúra legfontosabb egyszerő tulajdonságait.
 2. VEKTORTÉR A lineáris algebrában központi szerepet betöltı vektortér fogalmát értelmezzük most, s megvizsgáljuk e struktúra legfontosabb egyszerő tulajdonságait. Legyen K egy test és V egy nem üres halmaz,
2. VEKTORTÉR A lineáris algebrában központi szerepet betöltı vektortér fogalmát értelmezzük most, s megvizsgáljuk e struktúra legfontosabb egyszerő tulajdonságait. Legyen K egy test és V egy nem üres halmaz,
A lineáris tér. Készítette: Dr. Ábrahám István
 A lineáris tér Készítette: Dr. Ábrahám István A lineáris tér fogalma A fejezetben a gyakorlati alkalmazásokban használt legfontosabb fogalmakat, összefüggéseket tárgyaljuk. Adott egy L halmaz, amiben azonos
A lineáris tér Készítette: Dr. Ábrahám István A lineáris tér fogalma A fejezetben a gyakorlati alkalmazásokban használt legfontosabb fogalmakat, összefüggéseket tárgyaljuk. Adott egy L halmaz, amiben azonos
1. Határozzuk meg, hogy mikor egyenlő egymással a következő két mátrix: ; B = 8 7 2, 5 1. Számítsuk ki az A + B, A B, 3A, B mátrixokat!
 . Mátrixok. Határozzuk meg, hogy mikor egyenlő egymással a következő két mátrix: [ ] [ ] π a A = ; B = 8 7, 5 x. 7, 5 ln y. Legyen 4 A = 4 ; B = 5 5 Számítsuk ki az A + B, A B, A, B mátrixokat!. Oldjuk
. Mátrixok. Határozzuk meg, hogy mikor egyenlő egymással a következő két mátrix: [ ] [ ] π a A = ; B = 8 7, 5 x. 7, 5 ln y. Legyen 4 A = 4 ; B = 5 5 Számítsuk ki az A + B, A B, A, B mátrixokat!. Oldjuk
Lineáris algebra 2. Filip Ferdinánd december 7. siva.banki.hu/jegyzetek
 Lineáris algebra 2 Filip Ferdinánd filipferdinand@bgkuni-obudahu sivabankihu/jegyzetek 2015 december 7 Filip Ferdinánd 2016 februar 9 Lineáris algebra 2 1 / 37 Az el adás vázlata Determináns Determináns
Lineáris algebra 2 Filip Ferdinánd filipferdinand@bgkuni-obudahu sivabankihu/jegyzetek 2015 december 7 Filip Ferdinánd 2016 februar 9 Lineáris algebra 2 1 / 37 Az el adás vázlata Determináns Determináns
Halmazelmélet. 1. előadás. Farkas István. DE ATC Gazdaságelemzési és Statisztikai Tanszék. Halmazelmélet p. 1/1
 Halmazelmélet 1. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Halmazelmélet p. 1/1 A halmaz fogalma, jelölések A halmaz fogalmát a matematikában nem definiáljuk, tulajdonságaival
Halmazelmélet 1. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Halmazelmélet p. 1/1 A halmaz fogalma, jelölések A halmaz fogalmát a matematikában nem definiáljuk, tulajdonságaival
Vektorterek. Több esetben találkozhattunk olyan struktúrával, ahol az. szabadvektorok esetében, vagy a függvények körében, vagy a. vektortér fogalma.
 Vektorterek Több esetben találkozhattunk olyan struktúrával, ahol az összeadás és a (valós) számmal való szorzás értelmezett, pl. a szabadvektorok esetében, vagy a függvények körében, vagy a mátrixok esetében.
Vektorterek Több esetben találkozhattunk olyan struktúrával, ahol az összeadás és a (valós) számmal való szorzás értelmezett, pl. a szabadvektorok esetében, vagy a függvények körében, vagy a mátrixok esetében.
Diszkrét matematika I. gyakorlat
 Vizsgafeladatok megoldása 2012. december 5. Tartalom Teljes feladatsor #1 1 Teljes feladatsor #1 2 Teljes feladatsor #2 3 Teljes feladatsor #3 4 Teljes feladatsor #4 5 Válogatott feladatok 6 Végső bölcsesség
Vizsgafeladatok megoldása 2012. december 5. Tartalom Teljes feladatsor #1 1 Teljes feladatsor #1 2 Teljes feladatsor #2 3 Teljes feladatsor #3 4 Teljes feladatsor #4 5 Válogatott feladatok 6 Végső bölcsesség
Mátrixaritmetika. Tartalom:
 Mátrixaritmetika Tartalom: A vektor és mátrix fogalma Speciális mátrixok Relációk és műveletek mátrixokkal A mátrixok szorzása A diadikus szorzat. Hatványozás Gyakorlati alkalmazások Készítette: Dr. Ábrahám
Mátrixaritmetika Tartalom: A vektor és mátrix fogalma Speciális mátrixok Relációk és műveletek mátrixokkal A mátrixok szorzása A diadikus szorzat. Hatványozás Gyakorlati alkalmazások Készítette: Dr. Ábrahám
Mátrixok február Feladat: Legyen A = ( ( B =
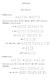 Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
17. előadás: Vektorok a térben
 17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
Kvadratikus alakok és euklideszi terek (előadásvázlat, október 5.) Maróti Miklós, Kátai-Urbán Kamilla
 Kvadratikus alakok és euklideszi terek (előadásvázlat, 0. október 5.) Maróti Miklós, Kátai-Urbán Kamilla Az előadáshoz ajánlott jegyzet: Szabó László: Bevezetés a lineáris algebrába, Polygon Kiadó, Szeged,
Kvadratikus alakok és euklideszi terek (előadásvázlat, 0. október 5.) Maróti Miklós, Kátai-Urbán Kamilla Az előadáshoz ajánlott jegyzet: Szabó László: Bevezetés a lineáris algebrába, Polygon Kiadó, Szeged,
BUDAPESTI KÖZGAZDASÁGTUDOMÁNYI EGYETEM. Puskás Csaba, Szabó Imre, Tallos Péter LINEÁRIS ALGEBRA JEGYZET
 BUDAPESTI KÖZGAZDASÁGTUDOMÁNYI EGYETEM Puskás Csaba, Szabó Imre, Tallos Péter LINEÁRIS ALGEBRA JEGYZET BUDAPEST, 1997 A szerzők Lineáris Algebra, illetve Lineáris Algebra II c jegyzeteinek átdolgozott
BUDAPESTI KÖZGAZDASÁGTUDOMÁNYI EGYETEM Puskás Csaba, Szabó Imre, Tallos Péter LINEÁRIS ALGEBRA JEGYZET BUDAPEST, 1997 A szerzők Lineáris Algebra, illetve Lineáris Algebra II c jegyzeteinek átdolgozott
Egyenletek, egyenletrendszerek, matematikai modell. 1. Oldja meg az Ax=b egyenletrendszert Gauss módszerrel és adja meg az A mátrix LUfelbontását,
 Egyenletek egyenletrendszerek matematikai modell Oldja meg az A=b egyenletrendszert Gauss módszerrel és adja meg az A mátri LUfelbontását ahol 8 b 8 Oldja meg az A=b egyenletrendszert és határozza meg
Egyenletek egyenletrendszerek matematikai modell Oldja meg az A=b egyenletrendszert Gauss módszerrel és adja meg az A mátri LUfelbontását ahol 8 b 8 Oldja meg az A=b egyenletrendszert és határozza meg
Irodalom. (a) A T, B T, (b) A + B, C + D, D C, (c) 3A, (d) AD, DA, B T A, 1 2 B = 1 C = A = 1 0 D = (a) 1 1 3, B T = = ( ) ; A T = 1 0
 Irodalom ezek egyrészt el- A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: hangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László: Bevezetés a lineáris algebrába, Polygon
Irodalom ezek egyrészt el- A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: hangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László: Bevezetés a lineáris algebrába, Polygon
3. el adás: Determinánsok
 3. el adás: Determinánsok Wettl Ferenc 2015. február 27. Wettl Ferenc 3. el adás: Determinánsok 2015. február 27. 1 / 19 Tartalom 1 Motiváció 2 A determináns mint sorvektorainak függvénye 3 A determináns
3. el adás: Determinánsok Wettl Ferenc 2015. február 27. Wettl Ferenc 3. el adás: Determinánsok 2015. február 27. 1 / 19 Tartalom 1 Motiváció 2 A determináns mint sorvektorainak függvénye 3 A determináns
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 8 VIII VEkTOROk 1 VEkTOR Vektoron irányított szakaszt értünk Jelölése: stb Vektorok hossza A vektor abszolút értéke az irányított szakasz hossza Ha a vektor hossza egységnyi akkor
KOVÁCS BÉLA MATEmATIkA I 8 VIII VEkTOROk 1 VEkTOR Vektoron irányított szakaszt értünk Jelölése: stb Vektorok hossza A vektor abszolút értéke az irányított szakasz hossza Ha a vektor hossza egységnyi akkor
Mátrixok 2017 Mátrixok
 2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
Lineáris algebra gyakorlat
 Lineáris algebra gyakorlat 7. gyakorlat Gyakorlatvezet : Bogya Norbert 2012. március 26. Ismétlés Tartalom 1 Ismétlés 2 Koordinátasor 3 Bázistranszformáció és alkalmazásai Vektorrendszer rangja Mátrix
Lineáris algebra gyakorlat 7. gyakorlat Gyakorlatvezet : Bogya Norbert 2012. március 26. Ismétlés Tartalom 1 Ismétlés 2 Koordinátasor 3 Bázistranszformáció és alkalmazásai Vektorrendszer rangja Mátrix
Vektorok. Wettl Ferenc október 20. Wettl Ferenc Vektorok október / 36
 Vektorok Wettl Ferenc 2014. október 20. Wettl Ferenc Vektorok 2014. október 20. 1 / 36 Tartalom 1 Vektorok a 2- és 3-dimenziós térben 2 Távolság, szög, orientáció 3 Vektorok koordinátás alakban 4 Összefoglalás
Vektorok Wettl Ferenc 2014. október 20. Wettl Ferenc Vektorok 2014. október 20. 1 / 36 Tartalom 1 Vektorok a 2- és 3-dimenziós térben 2 Távolság, szög, orientáció 3 Vektorok koordinátás alakban 4 Összefoglalás
3. Előadás. Megyesi László: Lineáris algebra, oldal. 3. előadás Lineáris egyenletrendszerek
 3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
MATEMATIKA FELADATGYŰJTEMÉNY
 Pék Johanna MATEMATIKA FELADATGYŰJTEMÉNY Nem matematika alapszakos hallgatók számára Tartalomjegyzék Előszó iii. Lineáris algebra.. Mátrixok...................................... Lineáris egyenletrendszerek..........................
Pék Johanna MATEMATIKA FELADATGYŰJTEMÉNY Nem matematika alapszakos hallgatók számára Tartalomjegyzék Előszó iii. Lineáris algebra.. Mátrixok...................................... Lineáris egyenletrendszerek..........................
MATE-INFO UBB verseny, március 25. MATEMATIKA írásbeli vizsga
 BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATE-INFO UBB verseny, 218. március 25. MATEMATIKA írásbeli vizsga FONTOS TUDNIVALÓK: 1 A feleletválasztós feladatok,,a rész esetén
BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATE-INFO UBB verseny, 218. március 25. MATEMATIKA írásbeli vizsga FONTOS TUDNIVALÓK: 1 A feleletválasztós feladatok,,a rész esetén
LINEÁRIS ALGEBRA. matematika alapszak. Euklideszi terek. SZTE Bolyai Intézet, őszi félév. Euklideszi terek LINEÁRIS ALGEBRA 1 / 40
 LINEÁRIS ALGEBRA matematika alapszak SZTE Bolyai Intézet, 2016-17. őszi félév Euklideszi terek Euklideszi terek LINEÁRIS ALGEBRA 1 / 40 Euklideszi tér Emlékeztető: A standard belső szorzás és standard
LINEÁRIS ALGEBRA matematika alapszak SZTE Bolyai Intézet, 2016-17. őszi félév Euklideszi terek Euklideszi terek LINEÁRIS ALGEBRA 1 / 40 Euklideszi tér Emlékeztető: A standard belső szorzás és standard
Algebrai egész kifejezések (polinomok)
 Algebrai egész kifejezések (polinomok) Betűk használata a matematikában Feladat Mekkora a 107m 68m oldalhosszúságú téglalap alakú focipála kerülete, területe? a = 107 m b = 68 m Terület T = a b = 107m
Algebrai egész kifejezések (polinomok) Betűk használata a matematikában Feladat Mekkora a 107m 68m oldalhosszúságú téglalap alakú focipála kerülete, területe? a = 107 m b = 68 m Terület T = a b = 107m
Feladatok a Gazdasági matematika II. tárgy gyakorlataihoz
 Debreceni Egyetem Közgazdaságtudományi Kar Feladatok a Gazdasági matematika II tárgy gyakorlataihoz a megoldásra ajánlott feladatokat jelöli e feladatokat a félév végére megoldottnak tekintjük a nehezebb
Debreceni Egyetem Közgazdaságtudományi Kar Feladatok a Gazdasági matematika II tárgy gyakorlataihoz a megoldásra ajánlott feladatokat jelöli e feladatokat a félév végére megoldottnak tekintjük a nehezebb
Budapesti Műszaki Főiskola, Neumann János Informatikai Kar. Vektorok. Fodor János
 Budapesti Műszaki Főiskola, Neumann János Informatikai Kar Lineáris algebra 1. témakör Vektorok Fodor János Copyright c Fodor@bmf.hu Last Revision Date: 2006. szeptember 11. Version 1.1 Table of Contents
Budapesti Műszaki Főiskola, Neumann János Informatikai Kar Lineáris algebra 1. témakör Vektorok Fodor János Copyright c Fodor@bmf.hu Last Revision Date: 2006. szeptember 11. Version 1.1 Table of Contents
Intergrált Intenzív Matematika Érettségi
 . Adott a mátri, determináns determináns, ahol,, d Számítsd ki:. b) Igazold, hogy a b c. Adott a az 6 0 egyenlet megoldásai. a). c) Számítsd ki a d determináns értékét. d c a b determináns, ahol abc,,.
. Adott a mátri, determináns determináns, ahol,, d Számítsd ki:. b) Igazold, hogy a b c. Adott a az 6 0 egyenlet megoldásai. a). c) Számítsd ki a d determináns értékét. d c a b determináns, ahol abc,,.
A lineáris algebra forrásai: egyenletrendszerek, vektorok
 A lineáris algebra forrásai: egyenletrendszerek, vektorok 2016. február 23. A lineáris algebra forrásai: egyenletrendszerek, vektorok 2016. február 23. 1 / 75 Tartalom 1 Vektor A 2- és 3-dimenziós tér
A lineáris algebra forrásai: egyenletrendszerek, vektorok 2016. február 23. A lineáris algebra forrásai: egyenletrendszerek, vektorok 2016. február 23. 1 / 75 Tartalom 1 Vektor A 2- és 3-dimenziós tér
Lineáris leképezések, mátrixuk, bázistranszformáció. Képtér, magtér, dimenziótétel, rang, invertálhatóság
 1. Bevezetés A félév anyaga: lineáris algebra Vektorterek, alterek Függés, függetlenség, bázis, dimenzió Skaláris szorzat R n -ben, vektorok hossza és szöge Lineáris leképezések, mátrixuk, bázistranszformáció
1. Bevezetés A félév anyaga: lineáris algebra Vektorterek, alterek Függés, függetlenség, bázis, dimenzió Skaláris szorzat R n -ben, vektorok hossza és szöge Lineáris leképezések, mátrixuk, bázistranszformáció
10. Előadás. Megyesi László: Lineáris algebra, oldal. 10. előadás Sajátérték, Kvadaratikus alak
 10. Előadás Megyesi László: Lineáris algebra, 98. 108. oldal. Gondolkodnivalók Mátrix inverze 1. Gondolkodnivaló Igazoljuk, hogy invertálható trianguláris mátrixok inverze is trianguláris. Bizonyítás:
10. Előadás Megyesi László: Lineáris algebra, 98. 108. oldal. Gondolkodnivalók Mátrix inverze 1. Gondolkodnivaló Igazoljuk, hogy invertálható trianguláris mátrixok inverze is trianguláris. Bizonyítás:
12. előadás. Egyenletrendszerek, mátrixok. Dr. Szörényi Miklós, Dr. Kallós Gábor
 12. előadás Egyenletrendszerek, mátrixok Dr. Szörényi Miklós, Dr. Kallós Gábor 2015 2016 1 Tartalom Matematikai alapok Vektorok és mátrixok megadása Tömbkonstansok Lineáris műveletek Mátrixok szorzása
12. előadás Egyenletrendszerek, mátrixok Dr. Szörényi Miklós, Dr. Kallós Gábor 2015 2016 1 Tartalom Matematikai alapok Vektorok és mátrixok megadása Tömbkonstansok Lineáris műveletek Mátrixok szorzása
Lineáris algebra és a rang fogalma (el adásvázlat, szeptember 29.) Maróti Miklós
 Lineáris algebra és a rang fogalma (el adásvázlat, 2010. szeptember 29.) Maróti Miklós Ennek az el adásnak a megértéséhez a következ fogalmakat kell tudni: (1) A mátrixalgebrával kapcsolatban: számtest
Lineáris algebra és a rang fogalma (el adásvázlat, 2010. szeptember 29.) Maróti Miklós Ennek az el adásnak a megértéséhez a következ fogalmakat kell tudni: (1) A mátrixalgebrával kapcsolatban: számtest
3. Fuzzy aritmetika. Gépi intelligencia I. Fodor János NIMGI1MIEM BMF NIK IMRI
 3. Fuzzy aritmetika Gépi intelligencia I. Fodor János BMF NIK IMRI NIMGI1MIEM Tartalomjegyzék I 1 Intervallum-aritmetika 2 Fuzzy intervallumok és fuzzy számok Fuzzy intervallumok LR fuzzy intervallumok
3. Fuzzy aritmetika Gépi intelligencia I. Fodor János BMF NIK IMRI NIMGI1MIEM Tartalomjegyzék I 1 Intervallum-aritmetika 2 Fuzzy intervallumok és fuzzy számok Fuzzy intervallumok LR fuzzy intervallumok
Matematika A2a LINEÁRIS ALGEBRA NAGY ATTILA
 LINEÁRIS ALGEBRA NAGY ATTILA 20160515 Tartalomjegyzék 1 Algebrai struktúrák 5 2 Lineáris tér (vektortér) 13 21 A vektortér fogalma 14 22 Vektorok lineáris függetlensége és függősége 18 23 Generátorrendszer,
LINEÁRIS ALGEBRA NAGY ATTILA 20160515 Tartalomjegyzék 1 Algebrai struktúrák 5 2 Lineáris tér (vektortér) 13 21 A vektortér fogalma 14 22 Vektorok lineáris függetlensége és függősége 18 23 Generátorrendszer,
Hadamard-mátrixok Előadó: Hajnal Péter február 23.
 Szimmetrikus kombinatorikus struktúrák MSc hallgatók számára Hadamard-mátrixok Előadó: Hajnal Péter 2012. február 23. 1. Hadamard-mátrixok Ezen az előadáson látásra a blokkrendszerektől független kombinatorikus
Szimmetrikus kombinatorikus struktúrák MSc hallgatók számára Hadamard-mátrixok Előadó: Hajnal Péter 2012. február 23. 1. Hadamard-mátrixok Ezen az előadáson látásra a blokkrendszerektől független kombinatorikus
7. gyakorlat. Lineáris algebrai egyenletrendszerek megoldhatósága
 7. gyakorlat Lineáris algebrai egyenletrendszerek megoldhatósága Egy lineáris algebrai egyenletrendszerrel kapcsolatban a következ kérdések merülnek fel: 1. Létezik-e megoldása? 2. Ha igen, hány megoldása
7. gyakorlat Lineáris algebrai egyenletrendszerek megoldhatósága Egy lineáris algebrai egyenletrendszerrel kapcsolatban a következ kérdések merülnek fel: 1. Létezik-e megoldása? 2. Ha igen, hány megoldása
1. előadás: Halmazelmélet, számfogalom, teljes
 1. előadás: Halmazelmélet, számfogalom, teljes indukció Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető,
1. előadás: Halmazelmélet, számfogalom, teljes indukció Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető,
2. gyakorlat. A polárkoordináta-rendszer
 . gyakorlat A polárkoordináta-rendszer Az 1. gyakorlaton megismerkedtünk a descartesi koordináta-rendszerrel. Síkvektorokat gyakran kényelmes ún. polárkoordinátákkal megadni: az r hosszúsággal és a φ irányszöggel
. gyakorlat A polárkoordináta-rendszer Az 1. gyakorlaton megismerkedtünk a descartesi koordináta-rendszerrel. Síkvektorokat gyakran kényelmes ún. polárkoordinátákkal megadni: az r hosszúsággal és a φ irányszöggel
LINEÁRIS PROGRAMOZÁSI FELADATOK MEGOLDÁSA SZIMPLEX MÓDSZERREL
 LINEÁRIS PROGRAMOZÁSI FELADATOK MEGOLDÁSA SZIMPLEX MÓDSZERREL x 1-2x 2 6 -x 1-3x 3 = -7 x 1 - x 2-3x 3-2 3x 1-2x 2-2x 3 4 4x 1-2x 2 + x 3 max Alapfogalmak: feltételrendszer (narancs színnel jelölve), célfüggvény
LINEÁRIS PROGRAMOZÁSI FELADATOK MEGOLDÁSA SZIMPLEX MÓDSZERREL x 1-2x 2 6 -x 1-3x 3 = -7 x 1 - x 2-3x 3-2 3x 1-2x 2-2x 3 4 4x 1-2x 2 + x 3 max Alapfogalmak: feltételrendszer (narancs színnel jelölve), célfüggvény
Typotex Kiadó. Bevezetés
 Bevezetés A bennünket körülvevő világ leírásához ősidők óta számokat is alkalmazunk. Tekintsük át a számfogalom kiépülésének logikai-történeti folyamatát, amely minden valószínűség szerint a legkorábban
Bevezetés A bennünket körülvevő világ leírásához ősidők óta számokat is alkalmazunk. Tekintsük át a számfogalom kiépülésének logikai-történeti folyamatát, amely minden valószínűség szerint a legkorábban
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Számelmélet I.
 Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
és n oszlopból áll, akkor m n-es mátrixról beszélünk. (Az oszlopok száma a mátrix vízszintes mérete, a sorok 2 3-as, a ij..
 Biológia alapszak Matematika I A GY 6/7 félév III MÁTRIXOK SAJÁTÉRTÉK-FELADAT III Mátrixok Definíció Számok téglalap alakú táblázatban való elrendezését mátrix nak nevezzük Ha a táblázat m sorból és n
Biológia alapszak Matematika I A GY 6/7 félév III MÁTRIXOK SAJÁTÉRTÉK-FELADAT III Mátrixok Definíció Számok téglalap alakú táblázatban való elrendezését mátrix nak nevezzük Ha a táblázat m sorból és n
A valós számok halmaza
 VA 1 A valós számok halmaza VA 2 A valós számok halmazának axiómarendszere és alapvető tulajdonságai Definíció Az R halmazt a valós számok halmazának nevezzük, ha teljesíti a következő axiómarendszerben
VA 1 A valós számok halmaza VA 2 A valós számok halmazának axiómarendszere és alapvető tulajdonságai Definíció Az R halmazt a valós számok halmazának nevezzük, ha teljesíti a következő axiómarendszerben
1. zárthelyi,
 1. zárthelyi, 2009.10.20. 1. Írjuk fel a tér P = (0,2,4) és Q = (6, 2,2) pontjait összekötő szakasz felezőmerőleges síkjának egyenletét. 2. Tekintsük az x + 2y + 3z = 14, a 2x + 6y + 10z = 24 és a 4x+2y
1. zárthelyi, 2009.10.20. 1. Írjuk fel a tér P = (0,2,4) és Q = (6, 2,2) pontjait összekötő szakasz felezőmerőleges síkjának egyenletét. 2. Tekintsük az x + 2y + 3z = 14, a 2x + 6y + 10z = 24 és a 4x+2y
 1. Bevezetés A félév anyaga. Lineáris algebra Vektorterek, alterek Függés, függetlenség, bázis, dimenzió Skaláris szorzat R n -ben, vektorok hossza és szöge Lineáris leképezések, mátrixuk, bázistranszformáció
1. Bevezetés A félév anyaga. Lineáris algebra Vektorterek, alterek Függés, függetlenség, bázis, dimenzió Skaláris szorzat R n -ben, vektorok hossza és szöge Lineáris leképezések, mátrixuk, bázistranszformáció
1. fogalom. Add meg az összeadásban szereplő számok elnevezéseit! Milyen tulajdonságai vannak az összeadásnak? Hogyan ellenőrizzük az összeadást?
 1. fogalom Add meg az összeadásban szereplő számok 73 + 19 = 92 összeadandók (tagok) összeg Összeadandók (tagok): amiket összeadunk. Összeg: az összeadás eredménye. Milyen tulajdonságai vannak az összeadásnak?
1. fogalom Add meg az összeadásban szereplő számok 73 + 19 = 92 összeadandók (tagok) összeg Összeadandók (tagok): amiket összeadunk. Összeg: az összeadás eredménye. Milyen tulajdonságai vannak az összeadásnak?
Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit.
 2. A VALÓS SZÁMOK 2.1 A valós számok aximómarendszere Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit. 1.Testaxiómák R-ben két művelet van értelmezve, az
2. A VALÓS SZÁMOK 2.1 A valós számok aximómarendszere Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit. 1.Testaxiómák R-ben két művelet van értelmezve, az
A szimplex algoritmus
 A szimplex algoritmus Ismétlés: reprezentációs tétel, az optimális megoldás és az extrém pontok kapcsolata Alapfogalmak: bázisok, bázismegoldások, megengedett bázismegoldások, degenerált bázismegoldás
A szimplex algoritmus Ismétlés: reprezentációs tétel, az optimális megoldás és az extrém pontok kapcsolata Alapfogalmak: bázisok, bázismegoldások, megengedett bázismegoldások, degenerált bázismegoldás
i=1 λ iv i = 0 előállítása, melynél valamelyik λ i
 Az informatikus lineáris algebra dolgozat C részének lehetséges kérdései Az alábbi listában azok az állítások, tételek szerepelnek, melyeket a vizsgadolgozat C részében kérdezhetünk. Azok érnek 6 pontot,
Az informatikus lineáris algebra dolgozat C részének lehetséges kérdései Az alábbi listában azok az állítások, tételek szerepelnek, melyeket a vizsgadolgozat C részében kérdezhetünk. Azok érnek 6 pontot,
VEKTORTEREK I. VEKTORTÉR, ALTÉR, GENERÁTORRENDSZER október 15. Irodalom. További ajánlott feladatok
 VEKTORTEREK I. VEKTORTÉR, ALTÉR, GENERÁTORRENDSZER 2004. október 15. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják
VEKTORTEREK I. VEKTORTÉR, ALTÉR, GENERÁTORRENDSZER 2004. október 15. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják
Matematika szigorlat június 17. Neptun kód:
 Név Matematika szigorlat 014. június 17. Neptun kód: 1.. 3. 4. 5. Elm. Fel. Össz. Oszt. Az eredményes szigorlat feltétele elméletből legalább 0 pont, feladatokból pedig legalább 30 pont elérése. A szigorlat
Név Matematika szigorlat 014. június 17. Neptun kód: 1.. 3. 4. 5. Elm. Fel. Össz. Oszt. Az eredményes szigorlat feltétele elméletből legalább 0 pont, feladatokból pedig legalább 30 pont elérése. A szigorlat
Mer legesség. Wettl Ferenc 2015-03-13. Wettl Ferenc Mer legesség 2015-03-13 1 / 40
 Mer legesség Wettl Ferenc 2015-03-13 Wettl Ferenc Mer legesség 2015-03-13 1 / 40 Tartalom 1 Pszeudoinverz 2 Ortonormált bázis ortogonális mátrix 3 Komplex és véges test feletti terek 4 Diszkrét Fourier-transzformált
Mer legesség Wettl Ferenc 2015-03-13 Wettl Ferenc Mer legesség 2015-03-13 1 / 40 Tartalom 1 Pszeudoinverz 2 Ortonormált bázis ortogonális mátrix 3 Komplex és véges test feletti terek 4 Diszkrét Fourier-transzformált
1.1. Vektorok és operátorok mátrix formában
 1. Reprezentáció elmélet 1.1. Vektorok és operátorok mátrix formában A vektorok és az operátorok mátrixok formájában is felírhatók. A végtelen dimenziós ket vektoroknak végtelen sok sort tartalmazó oszlopmátrix
1. Reprezentáció elmélet 1.1. Vektorok és operátorok mátrix formában A vektorok és az operátorok mátrixok formájában is felírhatók. A végtelen dimenziós ket vektoroknak végtelen sok sort tartalmazó oszlopmátrix
Bodó Bea, Somonné Szabó Klára Matematika 2. közgazdászoknak
 ábra: Ábra Bodó Bea, Somonné Szabó Klára Matematika. közgazdászoknak IV. modul: Lineáris algebra 9. lecke: n-dimenziós vektorok Tanulási cél: n -dimenziós vektorok fogalmának megismerése, majd műveletek
ábra: Ábra Bodó Bea, Somonné Szabó Klára Matematika. közgazdászoknak IV. modul: Lineáris algebra 9. lecke: n-dimenziós vektorok Tanulási cél: n -dimenziós vektorok fogalmának megismerése, majd műveletek
1. Az euklideszi terek geometriája
 1. Az euklideszi terek geometriája Bázishoz tartozó skaláris szorzat Emékeztető Az R n vektortérbeli v = λ 2... és w = λ 1 λ n µ 1 µ 2... µ n λ 1 µ 1 +λ 2 µ 2 +...+λ n µ n. Jele v,w. v,w = v T u, azaz
1. Az euklideszi terek geometriája Bázishoz tartozó skaláris szorzat Emékeztető Az R n vektortérbeli v = λ 2... és w = λ 1 λ n µ 1 µ 2... µ n λ 1 µ 1 +λ 2 µ 2 +...+λ n µ n. Jele v,w. v,w = v T u, azaz
Miskolci Egyetem. Diszkrét matek I. Vizsga-jegyzet. Hegedűs Ádám Imre 2010.12.28.
 Miskolci Egyetem Diszkrét matek I. Vizsga-jegyzet Hegedűs Ádám Imre 2010.12.28. KOMBINATORIKA Permutáció Ismétlés nélküli permutáció alatt néhány különböző dolognak a sorba rendezését értjük. Az "ismétlés
Miskolci Egyetem Diszkrét matek I. Vizsga-jegyzet Hegedűs Ádám Imre 2010.12.28. KOMBINATORIKA Permutáció Ismétlés nélküli permutáció alatt néhány különböző dolognak a sorba rendezését értjük. Az "ismétlés
