Jelfeldolgozás bevezető. Témalaboratórium
|
|
|
- József Bognár
- 6 évvel ezelőtt
- Látták:
Átírás
1 Jelfeldolgozás bevezető Témalaboratórium
2 Tartalom Jelfeldolgozás alapjai Lineáris rendszerelmélet Fourier transzformációk és kapcsolataik Spektrális képek értelmezése Képfeldolgozás alapjai Néhány nevezetesebb szűrés
3 Lineáris időinvariáns (LTI) rendszerek Linearitás: Időinvariancia (shift invariancia): Dirac impulzus: S a f b g a S f b S g a, b f, g S f x x y x S f y 00 x 1, illetve N x lim exp x 2a a 2 a0 x 0x \ 0 00
4 LTI rendszerek válasza Lineáris rendszer válasza (konvolúciós integrál) gerjesztésre: ˆ : S f x y x f j x S j x x x j Mikor helyes a közelítés ( x 0 esetén) : f (a gerjesztés) egy folytonos jel Az impulzusválasz folytonos függvénye h z, x S z x Mi változik ha S eltolás invariáns: Mivel h y, x h x y, ezért x0 x ' f z -nek S f x lim yˆ x f x ' hx x ' dx '
5 LTI rendszerek válasza Lineáris rendszer válasza (konvolúciós integrál) gerjesztésre: ˆ : S f x y x f j x S j x x x j Mikor helyes a közelítés ( x 0 esetén) : f (a gerjesztés) egy folytonos jel Az impulzusválasz folytonos függvénye h z, x S z x Mi változik ha S eltolás invariáns: Mivel h y, x h x y, ezért x0 x ' f z -nek S f x lim yˆ x f x ' hx x ' dx '
6 LTI rendszerek válasza Lineáris rendszer válasza (konvolúciós integrál) gerjesztésre: ˆ : S f x y x f j x S j x x x j Mikor helyes a közelítés ( x 0 esetén) : f (a gerjesztés) egy folytonos jel Az impulzusválasz folytonos függvénye h z, x S z x Mi változik ha S eltolás invariáns: Mivel h y, x h x y, ezért x0 x ' f z -nek S f x f h x Tehát S f x lim yˆ x f x ' hx x ' dx '
7 LTI rendszerek válasza (konvolúciós integrál) + + :
8 LTI rendszerek válasza (konvolúciós integrál)
9 Rendszerelmélet miért? 1. Rekonstruálunk: A kép egy rendszernek egy kimenete Bemenete egy 3d térrészlet, benne minket érdeklő objektumokkal (állapotváltozók) Cél a rendszer állapotának a visszaállítása (az objektumok tulajdonságainak rekonstrukciója) 2. Kondícionálunk: Bemenete a megfigyelési rendszernek egy számunkra kívánatos (pl. torzításmentes) kép, melyet a képalkotás során használt eszköz, mint rendszer torzít Cél a kívánatos kép előállítása (pl. szűréssel, becsléssel)
10 Képalkotó rendszerek leírása lineáris rendszerekkel 1. 3D térből 2D mérés: g x, y h x, y;, f, d dd x, y,, 0 f,, : rendszer bemenete, a 3D tér egy pontja xy, : additív megfigyelési zaj ( kevés a modell ) h x, y;,, : lineáris rendszerünk súlyfüggvénye 2. 2D képből torzított 2D kép: g x, y h x, y;, f, dd x, y h x, y;, h x, y ha akkor LTI / LSI rendszer, jelentősen egyszerűsödik sokminden
11 3D információ előállítása kép(ek)ből példák Felismerési feladatok: Pl. gyalogosok felismerése
12 3D információ előállítása kép(ek)ből példák Felismerési feladatok: Pl. kerekárnyékok felismerése
13 3D információ előállítása kép(ek)ből példák Rekonstrukciós feladatok: Pl. Röntgenes rekonstrukciók
14 3D információ előállítása kép(ek)ből példák Rekonstrukciós feladatok: Pl. kameraképek alapján 3d objektum rekonstrukció
15 2D kép kondícionálása Dekonvolúciós feladatok: Ismerjük h-t, cél f -et megbecsülni
16 2D kép kondícionálása Szűrésekkel minket érdeklő részek kiemelése Pl. szummációs röntgen projekcióról bordaárnyék leradírozása
17 Hogyan lesz digitális képünk? 1. Detektor felületét fotonok érik: Folytonos intenzitásfüggvény Analízisére Folytonos Fourier Transzformácó 2. Érzékelőelemek töltéssé alakítják a fotonokat: Véges frekvenciácal végtelen db mintát veszünk Analízise Diszkrét Idejű Fourier Transzformációval (DTFT) Véges számú mintát veszünk Analízise Diszkrét Fourier Transzformációval (DFT) 3. Van még erősítés, meg kvantálás is: Ezek hatása általában marginális csak ritkán vizsgáljuk
18 Folytonos Fourier transzformáció (Unitér) lineáris transzformáció folytonos függvények tere felett 2 F f x e j x dx 2 ; e j Különféle paraméterezése létezik itt fizikai frekvencia A spektrum lényegében az eredeti jel koordinátázása a komplex exponenciálisok bázisa felett 2 komplex exponenciális: e j x j2 x e cos 2 x j sin 2 x f x F x d LTI / LSI rendszerek sajátfüggvényei a komplex exponenciálisok (konvolúció elemenkénti szorzás duális)
19 Folytonos Fourier transzformáció LTI rendszerek átviteli függvénye: H FT h, H exp H H j H - rendszer átvitele frekvencián: ~ a jel változásának a sebessége Minden fizikai rendszer sávkorlátozott H 1 ha sávszélesség H Interpretáció 1 H : rendszer tehetetlensége H - rendszer fázistolása frekvencián: Rendszer késleltetése eltolása frekvencián exp 2 FT f x x F j x 0 0
20 Folytonos Fourier transzformáció
21 Mintavételezés hatása Mintavételezzük a jelünket: Matematikai mintavétel: folytonos jel hadamard szorzata Dirac fésűvel Időtartománybeli szorzás spektrumok konvolúciója Impulzusfésű az időtartományban frekvenciatartományban
22 Mintavételezés hatása Mintavételezés hatása Fourier térben: X s X k X k x k x x k x 1 x: mintavételi frekvencia X : folytonos jel spektruma mintavételezés előtt X : mintavételezett jel spektruma S Mikor teljesül, hogy XS X? Ha telesül a Nyquist mintavételi törvény kritériuma Ha nem teljesül, akkor alul-mintavételezünk, aminek aliasing a következménye
23 Mintavételezés hatása Ha helyesen mintavételezünk: 1 T 2sávszélesség x
24 Mintavételezés hatása Ha alul-mintavételezünk: 1 T 2sávszélesség x
25 Alul-mintavételezés hatása Moire / aliasing
26 Mintavételezett jel spektruma - DTFT Nézzük meg a mintavételezett jel spektrumát X x n j n F 2 x t t n t n n xn 1 2 X exp j n d Tehát egyszerűen a mintavett jel spektruma Tulajdonságai:, de exp nz R 2 X X k
27 Véges, mintavett jel analízise - DFT Detektorok mérete, gépek memóriája is véges: Véges hosszú mintavételezett jeleink vannak Spektrumokat is csak véges hosszon tudjuk tárolni Diszkrét Fourier Transzformáció: N 1 X xn exp j n k 2 N k n0 mintavételezzük az alábbi jel DTFT spektrumát: x 'n xn hn, ahol h n 1 n 1 n N az ú.n. megfigyelési ablakfüggvény 1 n y az y pozíciójú egységugrás
28 Véges, mintavett jel analízise - DFT Spektrumszivárgás: xn DFT-je x'ndtft-jét mintavételezi: X X ' DTFT x ' 1 2 k k k X H k Tehát a megfigyelési ablak függvény spektrumával konvolválódik a végtelen hosszú jel DTFT spektruma Ami ha betartottuk a mintavételi törvényt, akkor a folytonos jelünk spektrumának ÁTLAPOLÓDÁS NÉLKÜLI ismétlése Persze a cél a folytonos spektrum mintavételezése lenne
29 Véges, mintavett jel analízise - DFT Spektrumszivárgás másik interpretációja: N 1 X xn exp j n k 2 N DFT: DFS: k n0 1 N 1 k 2 ck xnexp j n N x n0 N Tehát úgy is felfoghatjuk, hogy a DFT a látott jel végtelen egymás utáni ismétlésével kapott periodikus jel Diszkrét Fourier Sorfejtése És már azt is tudjuk, hogy ez a spektrumot hogy torzítja (ablakfüggvény spektrumával konvolúció)
30 Spektrumszivárgás példa Adott folytonos monokróm jel: x t sin(2 t 15) Sávszélessége 15 Hz, tehát 30 Hz felett mintavételezzük 0.5 spektrum amplitudoja Frekvencia [Hz]
31 Spektrumszivárgás példa Adott folytonos jel: x t t Mintavételezzük ( ): 1kHz, x 100 sin(2 15) f N 100 Megfigyelési ekvivalens: x rect 100 Implicit megfigyelési ablak DTFT spektruma: 20 s amplitudo [db] Frekvencia [Hz]
32 Spektrumszivárgás példa Y 20 0 amplitudo [db] Adott folytonos jel: x t t Mintavételezzük ( ): 1kHz, X 100 Megfigyelt jel DFT spektruma: Y H rect sin(2 15) Frekvencia [Hz] fs N 100 X X H d 100 rect Piros: ablak normált spektruma Kék: folytonos jel spektruma Fekete: N=100 mintavétellel előálló jel spektrumának DC komponense
33 Spektrumszivárgás példa Adott folytonos jel: y t t Mintavételezzük ( ): 1kHz, y 100 sin(2 15) Megfigyelési ekvivalens spektruma: f N 100 s Y Y H 100 rect 20 0 amplitudo [db] Frekvencia [Hz] Piros: folytonos jel spektruma Kék: N=100 mintavétellel előálló jel spektruma
34 Spektrumszivárgás példa Adott folytonos jel: x t t Mintavételezzük ( ): 1kHz, DFT által látott jel: 1 x 100 sin(2 15) fs N 100 x n x h mod ( n) 100 Rect idõ [sec]
35 Spektrumszivárgás kompenzálása Definiáljunk mi az ablakfüggvényt: Nem lehet hosszabb, mint ahány mintát meg tudunk nézni, de legalább a mintavételek végi töréspontokat el tudjuk nyomni
36 Analízis irány: uv, M1N1 m0 n0 Tulajdonságok: 2D DFT, exp 2 Periodikus: [M,N] szerint Valós jel esetén: F Ha M, N páros: F F F F Többi transzformáció esetén is hasonló a többdimenziós eset F f m n j u m M v n N M1 N1 f m, nexp 2 j v n N exp 2 j u m M m0 n0 u, v u, v M u,nv M 2 u, N 2v M 2 u, N 2v
37 2D DFT Szintézis irány M1N1 1, u, vexp 2 f m n F j u m M v n N M N u0 v0 Hullámfrontos interpretáció: Spektrum amplitudója:
38 2D DFT példa rekonstrukció spektrum amplitúdóból és fázisból
39 2D DFT példa spektrum amplitúdójából rekonstruált kép
40 2D DFT példa spektrum fázisából rekonstruált kép
41 2D LTI rendszer válasza Lineáris szűrések frekvenciatérben: :cirkuláris konvolúció
42 Hisztogram Kép pixelek intenzitásainak sűrűségfüggvénye: Bináris esetben két Kronecker delta Ablakozás: hisztogram közepének és szélességének állítása
43 Hisztogram kiegyenlítése Cél a kontraszt (elkülönítendő objektumok intenzitásainak különbsége) növelése:
44 Kontrasztjavítás hisztogram globális módosítással
45 Adaptív kontrasztnövelés Nem mindig célszerű a kép minden területén u.a. leképezés szerint módosítani az intenzitásokat
46 Szűrések Képet átküldjük egy rendszeren Mely a kimeneti kép adott pixelét tipikusan a szomszédos pixelek értékei alapján módosítja Tipikus célok: Zajszűrés a képek spektrumának egy bizonyos részének elnyomásával / intenzitások kicserélésével Alakzatok / érdekesebb objektumok kiemelése Élkiemelés Illesztett szűrés
47 Zajszűrések LTI rendszerrel Rendszerek súlyfüggvényét kernelnek hívjuk: Kernellel tehát konvolváljuk a képet Tipikusan uniform / Gauss kernel
48 Zajszűrés medián szűrés Szűrt kép adott képpontjának intenzitása a szomszédos képpontok intenzitásának mediánja Impulzus zajt jobban kezeli, mint a lineáris szűrések Általánosítás az orders of statistics szűrők: Nem a medián, hanem sorrendezésben előre definiált helyű
49 Élkiemelés Cél a kép intenzitásainak gyors változásait kiemelni LTI rendszerrel: Sobel / Prewitt kernelek alkalmazásával: Képeket kvázi felül- áteresztik Sokszor kombinálják simító szűrőkkel: Cél a tipikusan magasfrekvenciás zaj csillapítása Pl. Derivative of Gaussian, Laplacian of Gaussian Lényegében egy sáváteresztő rendszer Nemlineáris rendszerekkel: Hiszterézises küszöbölésű Canny, stb.
50 Klasszikus élkiemelő kernelek
51 Sáváteresztő jellegű élkiemelés Gauss derivált kernelek: Kék: Gauss függvény Piros: Derivative of Gaussian Zöld: Laplacian of Gaussian
52 Sáváteresztő jellegű élkiemelés Laplacian of Gaussian példa:
53 Élkiemelő szűrések példák
54 Illesztett szűrés Definiálunk egy templete-et: Célunk ezt megtalálni a képen Ennek vesszük a keresztkorrelációját a kép különböző részleteivel (csúszóablak szerűen végigtolva a képen) Szűrt kép intenzitása azon régióban nagy, mely korrelált a sablonnal Sok esetben ez nem elég: Különböző méretekben / orientációba fordulhat elő Ilyenkor template bank -ot alkalmazunk (tehát több sablonunk van, mindegyikre elvégezzük a szűrét), majd aggregáljuk a szűrések kimenetét
55 Illesztett szűrés példa
Fourier térbeli analízis, inverz probléma. Orvosi képdiagnosztika 5-7. ea ősz
 Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 5-7. ea. 2017 ősz 5. Előadás témái Fourier transzformációk és kapcsolataik: FS, FT, DTFT, DFT, DFS Mintavételezés, interpoláció Folytonos
Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 5-7. ea. 2017 ősz 5. Előadás témái Fourier transzformációk és kapcsolataik: FS, FT, DTFT, DFT, DFS Mintavételezés, interpoláció Folytonos
Fourier térbeli analízis, inverz probléma. Orvosi képdiagnosztika 7-8. ea ősz
 Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 7-8. ea. 2015 ősz 7. előadás tartalma Fourier transzformációk és kapcsolataik: FS, FT, DTFT, DFT, DFS Mintavételezés, interpoláció Frekvenciaszivárgás
Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 7-8. ea. 2015 ősz 7. előadás tartalma Fourier transzformációk és kapcsolataik: FS, FT, DTFT, DFT, DFS Mintavételezés, interpoláció Frekvenciaszivárgás
Fourier térbeli analízis, inverz probléma. Orvosi képdiagnosztika 5-7. ea ősz
 Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 5-7. ea. 2017 ősz 6. Előadás tartalma Spektrumszivárgás Képfeldolgozás frekvencia tartományban: 2D Spektrum gépi ábrázolása Szűrések frekvenciatartományban
Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 5-7. ea. 2017 ősz 6. Előadás tartalma Spektrumszivárgás Képfeldolgozás frekvencia tartományban: 2D Spektrum gépi ábrázolása Szűrések frekvenciatartományban
Fourier térbeli analízis, inverz probléma. Orvosi képdiagnosztika 6-8. ea ősz
 Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 6-8. ea. 2016 ősz 6. előadás tartalma Fourier transzformációk és kapcsolataik: FS, FT, DTFT, DFT, DFS Mintavételezés, interpoláció Spektrumszivárgás
Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 6-8. ea. 2016 ősz 6. előadás tartalma Fourier transzformációk és kapcsolataik: FS, FT, DTFT, DFT, DFS Mintavételezés, interpoláció Spektrumszivárgás
Képalkotás modellezése, metrikái. Orvosi képdiagnosztika 6. ea ősz
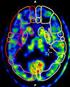 Képalkotás modellezése, metrikái Orvosi képdiagnosztika 6. ea. 2015 ősz Jelölésjegyzék Rendszer válasza f gerjesztésre: Dirac-delta: x ; egységugrás: 0 idejű Dirac-delta gerjesztése a rendszer válasza:
Képalkotás modellezése, metrikái Orvosi képdiagnosztika 6. ea. 2015 ősz Jelölésjegyzék Rendszer válasza f gerjesztésre: Dirac-delta: x ; egységugrás: 0 idejű Dirac-delta gerjesztése a rendszer válasza:
Képalkotás modellezése, metrikái. Orvosi képdiagnosztika 2017 ősz
 Képalkotás modellezése, metrikái Orvosi képdiagnosztika 2017 ősz Jelölésjegyzék Rendszer válasza f gerjesztésre: Dirac-delta: x ; egységugrás: 0 idejű Dirac-delta gerjesztése a rendszer válasza: h x x
Képalkotás modellezése, metrikái Orvosi képdiagnosztika 2017 ősz Jelölésjegyzék Rendszer válasza f gerjesztésre: Dirac-delta: x ; egységugrás: 0 idejű Dirac-delta gerjesztése a rendszer válasza: h x x
Ellenőrző kérdések a Jelanalízis és Jelfeldolgozás témakörökhöz
 Ellenőrző kérdések a Jelanalízis és Jelfeldolgozás témakörökhöz 1. Hogyan lehet osztályozni a jeleket időfüggvényük időtartama szerint? 2. Mi a periodikus jelek definiciója? (szöveg, képlet, 3. Milyen
Ellenőrző kérdések a Jelanalízis és Jelfeldolgozás témakörökhöz 1. Hogyan lehet osztályozni a jeleket időfüggvényük időtartama szerint? 2. Mi a periodikus jelek definiciója? (szöveg, képlet, 3. Milyen
Képfeldolgozó eljárások áttekintés. Orvosi képdiagnosztika
 Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás, zajszűrés) Képelemzés
Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás, zajszűrés) Képelemzés
Digitális jelfeldolgozás
 Digitális jelfeldolgozás Mintavételezés és jel-rekonstrukció Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010.
Digitális jelfeldolgozás Mintavételezés és jel-rekonstrukció Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010.
4. Szűrés frekvenciatérben
 4. Szűrés frekvenciatérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) Unitér transzformációk Az unitér transzformációk olyan lineáris,
4. Szűrés frekvenciatérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) Unitér transzformációk Az unitér transzformációk olyan lineáris,
Képalkotó diagnosztikai eljárások:
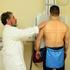 Képalkotó diagnosztikai eljárások: Soroljon fel néhány orvosi képalkotáson alapuló diagnosztikai eljárást, mely o Transzmissziós o Indukciós o Emissziós elv alkalmazásán alapul. Mire szolgálnak az egyes
Képalkotó diagnosztikai eljárások: Soroljon fel néhány orvosi képalkotáson alapuló diagnosztikai eljárást, mely o Transzmissziós o Indukciós o Emissziós elv alkalmazásán alapul. Mire szolgálnak az egyes
Mintavétel: szorzás az idő tartományban
 1 Mintavételi törvény AD átalakítók + sávlimitált jel τ időközönként mintavétel Mintavétel: szorzás az idő tartományban 1/τ körfrekvenciánként ismétlődik - konvolúció a frekvenciatérben. 2 Nem fednek át:
1 Mintavételi törvény AD átalakítók + sávlimitált jel τ időközönként mintavétel Mintavétel: szorzás az idő tartományban 1/τ körfrekvenciánként ismétlődik - konvolúció a frekvenciatérben. 2 Nem fednek át:
ADAT- ÉS INFORMÁCIÓFELDOLGOZÁS
 ADAT- ÉS INFORMÁCIÓFELDOLGOZÁS Földtudományi mérnöki MSc mesterszak 2018/19 I. félév TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ Miskolci Egyetem Műszaki Földtudományi Kar Geofizikai és Térinformatikai Intézet A tantárgy
ADAT- ÉS INFORMÁCIÓFELDOLGOZÁS Földtudományi mérnöki MSc mesterszak 2018/19 I. félév TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ Miskolci Egyetem Műszaki Földtudományi Kar Geofizikai és Térinformatikai Intézet A tantárgy
Digitális jelfeldolgozás
 Digitális jelfeldolgozás Átviteli függvények Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2011. október 13. Digitális
Digitális jelfeldolgozás Átviteli függvények Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2011. október 13. Digitális
Képrestauráció Képhelyreállítás
 Képrestauráció Képhelyreállítás Képrestauráció - A képrestauráció az a folyamat mellyel a sérült képből eltávolítjuk a degradációt, eredményképpen pedig az eredetihez minél közelebbi képet szeretnénk kapni
Képrestauráció Képhelyreállítás Képrestauráció - A képrestauráció az a folyamat mellyel a sérült képből eltávolítjuk a degradációt, eredményképpen pedig az eredetihez minél közelebbi képet szeretnénk kapni
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 6. A MINTAVÉTELI TÖRVÉNY
 ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 6. A MINTAVÉTELI TÖRVÉNY Dr. Soumelidis Alexandros 2018.10.25. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mintavételezés
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 6. A MINTAVÉTELI TÖRVÉNY Dr. Soumelidis Alexandros 2018.10.25. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mintavételezés
Képfeldolgozó eljárások áttekintés. Orvosi képdiagnosztika 9. ea ősz
 Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás,
Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás,
Jelek és rendszerek 1. 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék
 Jelek és rendszerek 1 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék 1 Ajánlott irodalom: FODOR GYÖRGY : JELEK ÉS RENDSZEREK EGYETEMI TANKÖNYV Műegyetemi Kiadó, Budapest, 2006
Jelek és rendszerek 1 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék 1 Ajánlott irodalom: FODOR GYÖRGY : JELEK ÉS RENDSZEREK EGYETEMI TANKÖNYV Műegyetemi Kiadó, Budapest, 2006
Dekonvolúció a mikroszkópiában. Barna László MTA Kísérleti Orvostudományi Kutatóintézet Nikon-KOKI képalkotó Központ
 Dekonvolúció a mikroszkópiában Barna László MTA Kísérleti Orvostudományi Kutatóintézet Nikon-KOKI képalkotó Központ 2015 Fourier-Sorok Minden 2π szerint periodikus függvény előállítható f x ~ a 0 2 + (a
Dekonvolúció a mikroszkópiában Barna László MTA Kísérleti Orvostudományi Kutatóintézet Nikon-KOKI képalkotó Központ 2015 Fourier-Sorok Minden 2π szerint periodikus függvény előállítható f x ~ a 0 2 + (a
3. Szűrés képtérben. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 3. Szűrés képtérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE http://www.inf.u-szeged.hu/~kato/teaching/ 2 Kép transzformációk típusai Kép értékkészletének radiometriai információ
3. Szűrés képtérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE http://www.inf.u-szeged.hu/~kato/teaching/ 2 Kép transzformációk típusai Kép értékkészletének radiometriai információ
Jelfeldolgozás - ANTAL Margit. impulzusválasz. tulajdonságai. Rendszerek. ANTAL Margit. Sapientia - Erdélyi Magyar Tudományegyetem
 Sapientia - Erdélyi Magyar Tudományegyetem 2007 Megnevezések Diszkrét Dirac jel Delta függvény Egységimpluzus függvény A diszkrét Dirac jel δ[n] = { 1, n = 0 0, n 0 d[n] { 1, n = n0 δ[n n 0 ] = 0, n n
Sapientia - Erdélyi Magyar Tudományegyetem 2007 Megnevezések Diszkrét Dirac jel Delta függvény Egységimpluzus függvény A diszkrét Dirac jel δ[n] = { 1, n = 0 0, n 0 d[n] { 1, n = n0 δ[n n 0 ] = 0, n n
Villamosságtan szigorlati tételek
 Villamosságtan szigorlati tételek 1.1. Egyenáramú hálózatok alaptörvényei 1.2. Lineáris egyenáramú hálózatok elemi számítása 1.3. Nemlineáris egyenáramú hálózatok elemi számítása 1.4. Egyenáramú hálózatok
Villamosságtan szigorlati tételek 1.1. Egyenáramú hálózatok alaptörvényei 1.2. Lineáris egyenáramú hálózatok elemi számítása 1.3. Nemlineáris egyenáramú hálózatok elemi számítása 1.4. Egyenáramú hálózatok
RENDSZERTECHNIKA 8. GYAKORLAT
 RENDSZERTECHNIKA 8. GYAKORLAT ÜTEMTERV VÁLTOZÁS Gyakorlat Hét Dátum Témakör Házi feladat Egyéb 1 1. hét 02.09 Ismétlés, bevezetés Differenciálegyenletek mérnöki 2 2. hét 02.16 szemmel 1. Hf kiadás 3 3.
RENDSZERTECHNIKA 8. GYAKORLAT ÜTEMTERV VÁLTOZÁS Gyakorlat Hét Dátum Témakör Házi feladat Egyéb 1 1. hét 02.09 Ismétlés, bevezetés Differenciálegyenletek mérnöki 2 2. hét 02.16 szemmel 1. Hf kiadás 3 3.
FODOR GYÖRGY JELEK ÉS RENDSZEREK
 FODOR GYÖRGY JELEK ÉS RENDSZEREK EGYETEMI TANKÖNYV Műegyetemi Kiadó, 2006 Előszó A valóságos fizikai, kémiai, műszaki, gazdasági folyamatokat modellek segítségével írjuk le. A modellalkotás során leegyszerűsítjük
FODOR GYÖRGY JELEK ÉS RENDSZEREK EGYETEMI TANKÖNYV Műegyetemi Kiadó, 2006 Előszó A valóságos fizikai, kémiai, műszaki, gazdasági folyamatokat modellek segítségével írjuk le. A modellalkotás során leegyszerűsítjük
Jelek és rendszerek - 4.előadás
 Jelek és rendszerek - 4.előadás Rendszervizsgálat a komplex frekvenciatartományban Mérnök informatika BSc (lev.) Pécsi Tudományegyetem, Pollack Mihály Műszaki Kar Műszaki Informatika és Villamos Intézet
Jelek és rendszerek - 4.előadás Rendszervizsgálat a komplex frekvenciatartományban Mérnök informatika BSc (lev.) Pécsi Tudományegyetem, Pollack Mihály Műszaki Kar Műszaki Informatika és Villamos Intézet
Mérés és adatgyűjtés
 Mérés és adatgyűjtés 4. óra Mingesz Róbert Szegedi Tudományegyetem 2012. február 27. MA - 4. óra Verzió: 2.1 Utolsó frissítés: 2012. március 12. 1/41 Tartalom I 1 Jelek 2 Mintavételezés 3 A/D konverterek
Mérés és adatgyűjtés 4. óra Mingesz Róbert Szegedi Tudományegyetem 2012. február 27. MA - 4. óra Verzió: 2.1 Utolsó frissítés: 2012. március 12. 1/41 Tartalom I 1 Jelek 2 Mintavételezés 3 A/D konverterek
Képfeldolgozó eljárások áttekintés. Orvosi képdiagnosztika 9. ea ősz
 Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, hisztogram módosítás, zajszűrés, élkiemelés) Képelemzés
Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, hisztogram módosítás, zajszűrés, élkiemelés) Képelemzés
Fehérzajhoz a konstans érték kell - megoldás a digitális szűrő Összegezési súlyok sin x/x szerint (ez akár analóg is lehet!!!)
 DSP processzorok: 1 2 3 HP zajgenerátor: 4 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! Fehérzajhoz a konstans érték kell - megoldás a digitális
DSP processzorok: 1 2 3 HP zajgenerátor: 4 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! Fehérzajhoz a konstans érték kell - megoldás a digitális
2. gyakorlat Mintavételezés, kvantálás
 2. gyakorlat Mintavételezés, kvantálás x(t) x[k]= =x(k T) Q x[k] ^ D/A x(t) ~ ampl. FOLYTONOS idı FOLYTONOS ANALÓG DISZKRÉT MINTAVÉTELEZETT DISZKRÉT KVANTÁLT DIGITÁLIS Jelek visszaállítása egyenköző mintáinak
2. gyakorlat Mintavételezés, kvantálás x(t) x[k]= =x(k T) Q x[k] ^ D/A x(t) ~ ampl. FOLYTONOS idı FOLYTONOS ANALÓG DISZKRÉT MINTAVÉTELEZETT DISZKRÉT KVANTÁLT DIGITÁLIS Jelek visszaállítása egyenköző mintáinak
Jelek és rendszerek MEMO_03. Pletl. Belépő jelek. Jelek deriváltja MEMO_03
 Jelek és rendszerek MEMO_03 Belépő jelek Jelek deriváltja MEMO_03 1 Jelek és rendszerek MEMO_03 8.ábra. MEMO_03 2 Jelek és rendszerek MEMO_03 9.ábra. MEMO_03 3 Ha a jelet méréssel kapjuk, akkor a jel következő
Jelek és rendszerek MEMO_03 Belépő jelek Jelek deriváltja MEMO_03 1 Jelek és rendszerek MEMO_03 8.ábra. MEMO_03 2 Jelek és rendszerek MEMO_03 9.ábra. MEMO_03 3 Ha a jelet méréssel kapjuk, akkor a jel következő
Shift regiszter + XOR kapu: 2 n állapot
 DSP processzorok: 1 2 HP zajgenerátor: 3 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! 4 Fehérzajhoz a konstans érték kell - megoldás a digitális
DSP processzorok: 1 2 HP zajgenerátor: 3 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! 4 Fehérzajhoz a konstans érték kell - megoldás a digitális
Számítógépes gyakorlat MATLAB, Control System Toolbox
 Számítógépes gyakorlat MATLAB, Control System Toolbox Bevezetés A gyakorlatok célja az irányítási rendszerek korszerű számítógépes vizsgálati és tervezési módszereinek bemutatása, az alkalmazáshoz szükséges
Számítógépes gyakorlat MATLAB, Control System Toolbox Bevezetés A gyakorlatok célja az irányítási rendszerek korszerű számítógépes vizsgálati és tervezési módszereinek bemutatása, az alkalmazáshoz szükséges
Idő-frekvencia transzformációk waveletek
 Idő-frekvencia transzformációk waveletek Pokol Gergő BME NTI Üzemi mérések és diagnosztika 013. áprils 17. Vázlat Alapfogalmak az idő-frekvencia síkon Rövid idejű Fourier-transzformáció spektrogram Folytonos
Idő-frekvencia transzformációk waveletek Pokol Gergő BME NTI Üzemi mérések és diagnosztika 013. áprils 17. Vázlat Alapfogalmak az idő-frekvencia síkon Rövid idejű Fourier-transzformáció spektrogram Folytonos
Wavelet transzformáció
 1 Wavelet transzformáció Más felbontás: Walsh, Haar, wavelet alapok! Eddig: amplitúdó vagy frekvencia leírás: Pl. egy rövid, Dirac-delta jellegű impulzus Fourier-transzformált: nagyon sok, kb. ugyanolyan
1 Wavelet transzformáció Más felbontás: Walsh, Haar, wavelet alapok! Eddig: amplitúdó vagy frekvencia leírás: Pl. egy rövid, Dirac-delta jellegű impulzus Fourier-transzformált: nagyon sok, kb. ugyanolyan
Idő-frekvencia transzformációk waveletek
 Idő-frekvencia transzformációk waveletek Pokol Gergő BME NTI Üzemi mérések és diagnosztika 2014. május 8. Vázlat Alapfogalmak az idő-frekvencia síkon Rövid idejű Fourier-transzformáció spektrogram Folytonos
Idő-frekvencia transzformációk waveletek Pokol Gergő BME NTI Üzemi mérések és diagnosztika 2014. május 8. Vázlat Alapfogalmak az idő-frekvencia síkon Rövid idejű Fourier-transzformáció spektrogram Folytonos
DINAMIKAI VIZSGÁLAT OPERÁTOROS TARTOMÁNYBAN. 2003.10.30. Dr. Aradi Petra, Dr. Niedermayer Péter: Rendszertechnika segédlet 1
 DINAMIKAI VIZSGÁLAT OPERÁTOROS TARTOMÁNYBAN 2003.10.30. Dr. Aradi Petra, Dr. Niedermayer Péter: Rendszertechnika segédlet 1 Differenciálegyenlet megoldása u(t) diff. egyenlet v(t) a n d n v m dt a dv n
DINAMIKAI VIZSGÁLAT OPERÁTOROS TARTOMÁNYBAN 2003.10.30. Dr. Aradi Petra, Dr. Niedermayer Péter: Rendszertechnika segédlet 1 Differenciálegyenlet megoldása u(t) diff. egyenlet v(t) a n d n v m dt a dv n
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 3. MÉRÉSFELDOLGOZÁS
 ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 3. MÉRÉSFELDOLGOZÁS Dr. Soumelidis Alexandros 2018.10.04. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mérés-feldolgozás
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 3. MÉRÉSFELDOLGOZÁS Dr. Soumelidis Alexandros 2018.10.04. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mérés-feldolgozás
Idő-frekvencia transzformációk waveletek
 Idő-frekvencia transzformációk waveletek Pokol Gergő BME NTI Üzemi mérések és diagnosztika 2015. április 23. Vázlat Alapfogalmak az idő-frekvencia síkon Rövid idejű Fourier-transzformáció spektrogram Folytonos
Idő-frekvencia transzformációk waveletek Pokol Gergő BME NTI Üzemi mérések és diagnosztika 2015. április 23. Vázlat Alapfogalmak az idő-frekvencia síkon Rövid idejű Fourier-transzformáció spektrogram Folytonos
Képfeldolgozó eljárások áttekintés. Orvosi képdiagnosztika 9. ea ősz
 Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás,
Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás,
Digitális szűrők - (BMEVIMIM278) Házi Feladat
 Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rszerek Tanszék Digitális szűrők - (BMEVIMIM278) FIR-szűrő tervezése ablakozással Házi Feladat Név: Szőke Kálmán Benjamin Neptun:
Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rszerek Tanszék Digitális szűrők - (BMEVIMIM278) FIR-szűrő tervezése ablakozással Házi Feladat Név: Szőke Kálmán Benjamin Neptun:
1. témakör. A hírközlés célja, általános modellje A jelek osztályozása Periodikus jelek leírása időtartományban
 1. témakör A hírközlés célja, általános modellje A jelek osztályozása Periodikus jelek leírása időtartományban A hírközlés célja, általános modellje Üzenet: Hír: Jel: Zaj: Továbbításra szánt adathalmaz
1. témakör A hírközlés célja, általános modellje A jelek osztályozása Periodikus jelek leírása időtartományban A hírközlés célja, általános modellje Üzenet: Hír: Jel: Zaj: Továbbításra szánt adathalmaz
Mintavételezés és FI rendszerek DI szimulációja
 Mintavételezés és FI rendszerek DI szimulációja Dr. Horváth Péter, BME HVT 5. december.. feladat Adott az alábbi FI jel: x f (t) = cos(3t) + cos(4t), ([ω] =krad/s). Legalább mekkorára kell választani a
Mintavételezés és FI rendszerek DI szimulációja Dr. Horváth Péter, BME HVT 5. december.. feladat Adott az alábbi FI jel: x f (t) = cos(3t) + cos(4t), ([ω] =krad/s). Legalább mekkorára kell választani a
Rekonstrukciós eljárások. Orvosi képdiagnosztika 2017 ősz
 Rekonstrukciós eljárások Orvosi képdiagnosztika 2017 ősz Élet a konvex optimalizáción túl CT-s szimuláció, 10 projekcióból (ΔΘ=18 ): Konvex: L2-TV Valóban ritkasági priorral Lineáris tomoszintézis Speciális
Rekonstrukciós eljárások Orvosi képdiagnosztika 2017 ősz Élet a konvex optimalizáción túl CT-s szimuláció, 10 projekcióból (ΔΘ=18 ): Konvex: L2-TV Valóban ritkasági priorral Lineáris tomoszintézis Speciális
Akusztikus mérőműszerek
 Akusztikus mérőműszerek Hangszintmérő: méri a frekvencia súlyozott, és nyomásátlagolt hangnyomás szintet (hangszintet). Felépítése Mikrofon + Erősítő Frekvencia Szint tartomány Időátlagolás Kijelzés Előerősítő
Akusztikus mérőműszerek Hangszintmérő: méri a frekvencia súlyozott, és nyomásátlagolt hangnyomás szintet (hangszintet). Felépítése Mikrofon + Erősítő Frekvencia Szint tartomány Időátlagolás Kijelzés Előerősítő
6. témakör. Mintavételezés elve Digitális jelfeldolgozás (DSP) alapjai
 6. témakör Mintavételezés elve Digitális jelfeldolgozás (DSP) alapjai A mintavételezés blokkvázlata Mintavételezés: Digitális jel mintavevô kvantáló kódoló Átvitel Tárolás antialiasing szűrő Feldolgozás
6. témakör Mintavételezés elve Digitális jelfeldolgozás (DSP) alapjai A mintavételezés blokkvázlata Mintavételezés: Digitális jel mintavevô kvantáló kódoló Átvitel Tárolás antialiasing szűrő Feldolgozás
3.18. DIGITÁLIS JELFELDOLGOZÁS
 3.18. DIGITÁLIS JELFELDOLGOZÁS Az analóg jelfeldolgozás során egy fizikai mennyiséget (pl. a hangfeldolgozás kapcsán a levegő nyomásváltozásait) azzal analóg (hasonló, arányos) elektromos feszültséggé
3.18. DIGITÁLIS JELFELDOLGOZÁS Az analóg jelfeldolgozás során egy fizikai mennyiséget (pl. a hangfeldolgozás kapcsán a levegő nyomásváltozásait) azzal analóg (hasonló, arányos) elektromos feszültséggé
Néhány fontosabb folytonosidejű jel
 Jelek és rendszerek MEMO_2 Néhány fontosabb folytonosidejű jel Ugrásfüggvény Bármely választással: Egységugrás vagy Heaviside-féle függvény Ideális kapcsoló. Signum függvény, előjel függvény. MEMO_2 1
Jelek és rendszerek MEMO_2 Néhány fontosabb folytonosidejű jel Ugrásfüggvény Bármely választással: Egységugrás vagy Heaviside-féle függvény Ideális kapcsoló. Signum függvény, előjel függvény. MEMO_2 1
ANTAL Margit. Sapientia - Erdélyi Magyar Tudományegyetem. Jelfeldolgozás. ANTAL Margit. Adminisztratív. Bevezetés. Matematikai alapismeretek.
 Jelfeldolgozás 1. Sapientia - Erdélyi Magyar Tudományegyetem 2007 és jeleket generáló és jeleket generáló és jeleket generáló Gyakorlatok - MATLAB (OCTAVE) (50%) Írásbeli vizsga (50%) és jeleket generáló
Jelfeldolgozás 1. Sapientia - Erdélyi Magyar Tudományegyetem 2007 és jeleket generáló és jeleket generáló és jeleket generáló Gyakorlatok - MATLAB (OCTAVE) (50%) Írásbeli vizsga (50%) és jeleket generáló
Beszédinformációs rendszerek 5. gyakorlat Mintavételezés, kvantálás, beszédkódolás. Csapó Tamás Gábor
 Beszédinformációs rendszerek 5. gyakorlat Mintavételezés, kvantálás, beszédkódolás Csapó Tamás Gábor 2016/2017 ősz MINTAVÉTELEZÉS 2 1. Egy 6 khz-es szinusz jelet szűrés nélkül mintavételezünk
Beszédinformációs rendszerek 5. gyakorlat Mintavételezés, kvantálás, beszédkódolás Csapó Tamás Gábor 2016/2017 ősz MINTAVÉTELEZÉS 2 1. Egy 6 khz-es szinusz jelet szűrés nélkül mintavételezünk
Képrekonstrukció 3. előadás
 Képrekonstrukció 3. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Computed Tomography (CT) Elv: Röntgen-sugarak áthatolása 3D objektum 3D térfogati kép Mérések
Képrekonstrukció 3. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Computed Tomography (CT) Elv: Röntgen-sugarak áthatolása 3D objektum 3D térfogati kép Mérések
Fourier-sorfejtés vizsgálata Négyszögjel sorfejtése, átviteli vizsgálata
 Fourier-sorfejtés vizsgálata Négyszögjel sorfejtése, átviteli vizsgálata Reichardt, András 27. szeptember 2. 2 / 5 NDSM Komplex alak U C k = T (T ) ahol ω = 2π T, k módusindex. Időfüggvény előállítása
Fourier-sorfejtés vizsgálata Négyszögjel sorfejtése, átviteli vizsgálata Reichardt, András 27. szeptember 2. 2 / 5 NDSM Komplex alak U C k = T (T ) ahol ω = 2π T, k módusindex. Időfüggvény előállítása
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 5. A JELFELDOLGOZÁS ALAPJAI: JELEK
 ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 5. A JELFELDOLGOZÁS ALAPJAI: JELEK Dr. Soumelidis Alexandros 2018.10.18. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mérések
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 5. A JELFELDOLGOZÁS ALAPJAI: JELEK Dr. Soumelidis Alexandros 2018.10.18. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mérések
Mátrix-exponens, Laplace transzformáció
 2016. április 4. 2016. április 11. LINEÁRIS DIFFERENCIÁLEGYENLET RENDSZEREK ÉS A MÁTRIX-EXPONENS KAPCSOLATA Feladat - ismétlés Tegyük fel, hogy A(t) = (a ik (t)), i, k = 1,..., n és b(t) folytonos mátrix-függvények
2016. április 4. 2016. április 11. LINEÁRIS DIFFERENCIÁLEGYENLET RENDSZEREK ÉS A MÁTRIX-EXPONENS KAPCSOLATA Feladat - ismétlés Tegyük fel, hogy A(t) = (a ik (t)), i, k = 1,..., n és b(t) folytonos mátrix-függvények
Híradástechikai jelfeldolgozás
 Híradástechikai jelfeldolgozás 13. Előadás 015. 04. 4. Jeldigitalizálás és rekonstrukció 015. április 7. Budapest Dr. Gaál József docens BME Hálózati Rendszerek és SzolgáltatásokTanszék gaal@hit.bme.hu
Híradástechikai jelfeldolgozás 13. Előadás 015. 04. 4. Jeldigitalizálás és rekonstrukció 015. április 7. Budapest Dr. Gaál József docens BME Hálózati Rendszerek és SzolgáltatásokTanszék gaal@hit.bme.hu
ÉRZÉKELŐK ÉS BEAVATKOZÓK II. 5. DC MOTOROK SZABÁLYOZÁS FORDULATSZÁM- SZABÁLYOZÁS
 ÉRZÉKELŐK ÉS BEAVATKOZÓK II. 5. DC MOTOROK SZABÁLYOZÁS FORDULATSZÁM- SZABÁLYOZÁS Dr. Soumelidis Alexandros 2019.03.13. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT
ÉRZÉKELŐK ÉS BEAVATKOZÓK II. 5. DC MOTOROK SZABÁLYOZÁS FORDULATSZÁM- SZABÁLYOZÁS Dr. Soumelidis Alexandros 2019.03.13. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT
Képszegmentáló eljárások. Orvosi képdiagnosztika 2018 ősz
 Képszegmentáló eljárások Orvosi képdiagnosztika 2018 ősz Képszegmentálás Anatómiai részek elkülönítés: pl. csontok, szív, erek, szürkefehér állomány, stb Vizsgálandó terület körbehatárolása: pl. tüdőterület
Képszegmentáló eljárások Orvosi képdiagnosztika 2018 ősz Képszegmentálás Anatómiai részek elkülönítés: pl. csontok, szív, erek, szürkefehér állomány, stb Vizsgálandó terület körbehatárolása: pl. tüdőterület
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 9. SZŰRŐK
 ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 9. SZŰRŐK Dr. Soumelidis Alexandros 2018.11.29. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG A szűrésről általában Szűrés:
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 9. SZŰRŐK Dr. Soumelidis Alexandros 2018.11.29. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG A szűrésről általában Szűrés:
Irányítástechnika 2. előadás
 Irányítástechnika 2. előadás Dr. Kovács Levente 2013. 03. 19. 2013.03.19. Tartalom Tipikus vizsgálójelek és azok információtartalma Laplace transzformáció, állapotegyenlet, átviteli függvény Alaptagok
Irányítástechnika 2. előadás Dr. Kovács Levente 2013. 03. 19. 2013.03.19. Tartalom Tipikus vizsgálójelek és azok információtartalma Laplace transzformáció, állapotegyenlet, átviteli függvény Alaptagok
PTE PMMFK Levelező-távoktatás, villamosmérnök szak
 PTE PMMFK Levelező-távoktatás, villamosmérnök szak MATEMATIKA (A tantárgy tartalma és a tananyag elsajátításának időterve.) Összeállította: Kis Miklós adjunktus Tankönyvek Megegyeznek az 1. és 2. félévben
PTE PMMFK Levelező-távoktatás, villamosmérnök szak MATEMATIKA (A tantárgy tartalma és a tananyag elsajátításának időterve.) Összeállította: Kis Miklós adjunktus Tankönyvek Megegyeznek az 1. és 2. félévben
Képalkotó diagnosztikai eljárások:
 Képalkotó diagnosztikai eljárások: Soroljon fel néhány orvosi képalkotáson alapuló diagnosztikai eljárást, mely o Transzmissziós o Indukciós o Emissziós alkalmazásán alapul. Mire szolgálnak az egyes diagnosztikai
Képalkotó diagnosztikai eljárások: Soroljon fel néhány orvosi képalkotáson alapuló diagnosztikai eljárást, mely o Transzmissziós o Indukciós o Emissziós alkalmazásán alapul. Mire szolgálnak az egyes diagnosztikai
7. Előadás tartalma. Lineáris szűrők: Inverz probléma dekonvolúció: Klasszikus szűrők súly és átviteli függvénye Gibbs jelenség
 7. Előadás tartalma Lineáris szűrők: Klasszikus szűrők súly és átviteli üggvénye Gibbs jelenség Inverz probléma dekonvolúció: Inverz probléma ormális elírása Dekonvolúció nehézsége Közismert algoritmusok:
7. Előadás tartalma Lineáris szűrők: Klasszikus szűrők súly és átviteli üggvénye Gibbs jelenség Inverz probléma dekonvolúció: Inverz probléma ormális elírása Dekonvolúció nehézsége Közismert algoritmusok:
Hangtechnika. Médiatechnológus asszisztens
 Vázlat 3. Előadás - alapjai Pécsi Tudományegyetem, Pollack Mihály Műszaki Kar Műszaki Informatika és Villamos Intézet Műszaki Informatika Tanszék Ismétlés Vázlat I.rész: Ismétlés II.rész: A digitális Jelfeldolgozás
Vázlat 3. Előadás - alapjai Pécsi Tudományegyetem, Pollack Mihály Műszaki Kar Műszaki Informatika és Villamos Intézet Műszaki Informatika Tanszék Ismétlés Vázlat I.rész: Ismétlés II.rész: A digitális Jelfeldolgozás
Fourier transzformáció
 a Matematika mérnököknek II. című tárgyhoz Fourier transzformáció Fourier transzformáció, heurisztika Tekintsük egy 2L szerint periodikus függvény Fourier sorát: f (x) = a 0 2 + ( ( nπ ) ( nπ )) a n cos
a Matematika mérnököknek II. című tárgyhoz Fourier transzformáció Fourier transzformáció, heurisztika Tekintsük egy 2L szerint periodikus függvény Fourier sorát: f (x) = a 0 2 + ( ( nπ ) ( nπ )) a n cos
3. témakör. Rendszerek idő, frekvencia-, és komplex frekvenciatartományi leírása
 3. témakör Rendszerek idő, frekvencia-, és komplex frekvenciatartományi leírása Bevezetés Célunk a rendszer kimenő jelének meghatározása a bemenő jel és a rendszerjellemző függvény ismeretében. A rendszereket
3. témakör Rendszerek idő, frekvencia-, és komplex frekvenciatartományi leírása Bevezetés Célunk a rendszer kimenő jelének meghatározása a bemenő jel és a rendszerjellemző függvény ismeretében. A rendszereket
Z v 1 (t)v 2 (t τ)dt. R 12 (τ) = 1 R 12 (τ) = lim T T. ill. periódikus jelekre:
 1 Korrelációs fügvények Hasonlóság mértéke a két függvény szorzatának integrálja Időbeli változások esetén lehet vizsgálni a hasonlóságot a τ relatív időkülönbség szerint: Keresztkorrelációs függvény:
1 Korrelációs fügvények Hasonlóság mértéke a két függvény szorzatának integrálja Időbeli változások esetén lehet vizsgálni a hasonlóságot a τ relatív időkülönbség szerint: Keresztkorrelációs függvény:
A gyakorlat célja a fehér és a színes zaj bemutatása.
 A gyakorlat célja a fehér és a színes zaj bemutatása. 1.@. FFT begyakorlása n = [:9]; % Harminc minta x = cos(*pi*n/1); % 1 mintát veszünk periodusonként N1 = 64; % Három módon számoljuk az FFT-t N = 18;
A gyakorlat célja a fehér és a színes zaj bemutatása. 1.@. FFT begyakorlása n = [:9]; % Harminc minta x = cos(*pi*n/1); % 1 mintát veszünk periodusonként N1 = 64; % Három módon számoljuk az FFT-t N = 18;
Orvosi Fizika és Statisztika
 Orvosi Fizika és Statisztika Szegedi Tudományegyetem Általános Orvostudományi Kar Természettudományi és Informatikai Kar Orvosi Fizikai és Orvosi Informatikai Intézet www.szote.u-szeged.hu/dmi Orvosi fizika
Orvosi Fizika és Statisztika Szegedi Tudományegyetem Általános Orvostudományi Kar Természettudományi és Informatikai Kar Orvosi Fizikai és Orvosi Informatikai Intézet www.szote.u-szeged.hu/dmi Orvosi fizika
Számítógép-vezérelt szabályozás- és irányításelmélet
 Számítógép-vezérelt szabályozás- és irányításelmélet 2. gyakorlat Feladattípusok két függvény konvolúciója ÿ + aẏ + by = e at, y(), ẏ() típusú kezdetiérték feladatok megoldása (Laplace transzformációval)
Számítógép-vezérelt szabályozás- és irányításelmélet 2. gyakorlat Feladattípusok két függvény konvolúciója ÿ + aẏ + by = e at, y(), ẏ() típusú kezdetiérték feladatok megoldása (Laplace transzformációval)
Rekonstrukciós eljárások. Orvosi képdiagnosztika 2017 ősz
 Rekonstrukciós eljárások Orvosi képdiagnosztika 2017 ősz Előadások témája Röntgen tomográfia fizikai és matematikai alapjai 2D Radon transzformáció, szűrt visszavetítés: Fan beam / Cone beam felvételi
Rekonstrukciós eljárások Orvosi képdiagnosztika 2017 ősz Előadások témája Röntgen tomográfia fizikai és matematikai alapjai 2D Radon transzformáció, szűrt visszavetítés: Fan beam / Cone beam felvételi
illetve, mivel előjelét a elnyeli, a szinuszból pedig kiemelhető: = " 3. = + " 2 = " 2 % &' + +
 DFT 1. oldal A Fourier-sorfejtés szerint minden periodikus jel egyértelműen felírható különböző amplitúdójú és fázisú szinusz és koszinusz jelek összegeként: = + + 1. ahol az együtthatók, szintén a definíció
DFT 1. oldal A Fourier-sorfejtés szerint minden periodikus jel egyértelműen felírható különböző amplitúdójú és fázisú szinusz és koszinusz jelek összegeként: = + + 1. ahol az együtthatók, szintén a definíció
Jelfeldolgozás. Gyakorlat: A tantermi gyakorlatokon való részvétel kötelező! Kollokvium: csak gyakorlati jeggyel!
 1 Jelfeldolgozás Jegyzet: http://itl7.elte.hu : Elektronika jegyzet (Csákány A., ELTE TTK 119) Jelek feldolgozása (Bagoly Zs. Csákány A.) angol nyelv DSP (PDF) jegyzet Gyakorlat: A tantermi gyakorlatokon
1 Jelfeldolgozás Jegyzet: http://itl7.elte.hu : Elektronika jegyzet (Csákány A., ELTE TTK 119) Jelek feldolgozása (Bagoly Zs. Csákány A.) angol nyelv DSP (PDF) jegyzet Gyakorlat: A tantermi gyakorlatokon
π π A vivőhullám jelalakja (2. ábra) A vivőhullám periódusideje T amplitudója A az impulzus szélessége szögfokban 2p. 2p [ ]
![π π A vivőhullám jelalakja (2. ábra) A vivőhullám periódusideje T amplitudója A az impulzus szélessége szögfokban 2p. 2p [ ] π π A vivőhullám jelalakja (2. ábra) A vivőhullám periódusideje T amplitudója A az impulzus szélessége szögfokban 2p. 2p [ ]](/thumbs/92/108201304.jpg) Pulzus Amplitúdó Moduláció (PAM) A Pulzus Amplitúdó Modulációról abban az esetben beszélünk, amikor egy impulzus sorozatot használunk vivőhullámnak és ezen a vivőhullámon valósítjuk meg az amplitúdómodulációt
Pulzus Amplitúdó Moduláció (PAM) A Pulzus Amplitúdó Modulációról abban az esetben beszélünk, amikor egy impulzus sorozatot használunk vivőhullámnak és ezen a vivőhullámon valósítjuk meg az amplitúdómodulációt
Híradástechikai jelfeldolgozás
 Híradástechikai jelfeldolgozás 1. előadás 2015. február 13. 2015. február 13. Budapest Dr. Gaál József BME Hálózati Redszerek és SzolgáltatásokTaszék gaal@hit.bme.hu Bemutatkozás Dr Gaál József doces BME
Híradástechikai jelfeldolgozás 1. előadás 2015. február 13. 2015. február 13. Budapest Dr. Gaál József BME Hálózati Redszerek és SzolgáltatásokTaszék gaal@hit.bme.hu Bemutatkozás Dr Gaál József doces BME
Mintavételezés és AD átalakítók
 HORVÁTH ESZTER BUDAPEST MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM JÁRMŰELEMEK ÉS JÁRMŰ-SZERKEZETANALÍZIS TANSZÉK ÉRZÉKELÉS FOLYAMATA Az érzékelés, jelfeldolgozás általános folyamata Mérés Adatfeldolgozás 2/31
HORVÁTH ESZTER BUDAPEST MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM JÁRMŰELEMEK ÉS JÁRMŰ-SZERKEZETANALÍZIS TANSZÉK ÉRZÉKELÉS FOLYAMATA Az érzékelés, jelfeldolgozás általános folyamata Mérés Adatfeldolgozás 2/31
Fourier transzformáció
 Fourier transzformáció A szeizmikus hullámok tanulmányozása során igen nagy jelentősége van a hullámok frekvencia tartalmának. Ezt használjuk a hullámok alakjának mintavételezésekor, lineáris szűrések
Fourier transzformáció A szeizmikus hullámok tanulmányozása során igen nagy jelentősége van a hullámok frekvencia tartalmának. Ezt használjuk a hullámok alakjának mintavételezésekor, lineáris szűrések
Méréselmélet és mérőrendszerek
 Méréselmélet és mérőrendszerek 4. ELŐADÁS KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o Jelfeldolgozás o Fourier transzformáció o Frekvencia analízis o Jelek mintavételezése o Shannon-törvény o
Méréselmélet és mérőrendszerek 4. ELŐADÁS KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o Jelfeldolgozás o Fourier transzformáció o Frekvencia analízis o Jelek mintavételezése o Shannon-törvény o
6. Éldetektálás. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 6. Éldetektálás Kató Zoltán Képeldolgozás és Számítógépes Graika tanszék SZTE (http://www.in.u-szeged.hu/~kato/teaching/) 2 Élek A képen ott található él, ahol a kép-üggvény hirtelen változik. A kép egy
6. Éldetektálás Kató Zoltán Képeldolgozás és Számítógépes Graika tanszék SZTE (http://www.in.u-szeged.hu/~kato/teaching/) 2 Élek A képen ott található él, ahol a kép-üggvény hirtelen változik. A kép egy
X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ
 X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel és módszerekkel történik. A feldolgozás előtt az analóg jeleket digitalizálni kell.
X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel és módszerekkel történik. A feldolgozás előtt az analóg jeleket digitalizálni kell.
Informatika Rendszerek Alapjai
 Informatika Rendszerek Alapjai Dr. Kutor László Jelek típusai Átalakítás analóg és digitális rendszerek között http://uni-obuda.hu/users/kutor/ IRA 2014 2014. ősz IRA3/1 Analóg jelek digitális feldolgozhatóságának
Informatika Rendszerek Alapjai Dr. Kutor László Jelek típusai Átalakítás analóg és digitális rendszerek között http://uni-obuda.hu/users/kutor/ IRA 2014 2014. ősz IRA3/1 Analóg jelek digitális feldolgozhatóságának
Mérés és adatgyűjtés
 Mérés és adatgyűjtés 5. óra - levelező Mingesz Róbert Szegedi Tudományegyetem 2011. március 18. MA lev - 5. óra Verzió: 1.1 Utolsó frissítés: 2011. április 12. 1/20 Tartalom I 1 Demók 2 Digitális multiméterek
Mérés és adatgyűjtés 5. óra - levelező Mingesz Róbert Szegedi Tudományegyetem 2011. március 18. MA lev - 5. óra Verzió: 1.1 Utolsó frissítés: 2011. április 12. 1/20 Tartalom I 1 Demók 2 Digitális multiméterek
Gyakorló többnyire régebbi zh feladatok. Intelligens orvosi műszerek október 2.
 Gyakorló többnyire régebbi zh feladatok Intelligens orvosi műszerek 2018. október 2. Régebbi zh feladat - #1 Az ábrán látható két jelet, illetve összegüket mozgóablak mediánszűréssel szűrjük egy 11 pontos
Gyakorló többnyire régebbi zh feladatok Intelligens orvosi műszerek 2018. október 2. Régebbi zh feladat - #1 Az ábrán látható két jelet, illetve összegüket mozgóablak mediánszűréssel szűrjük egy 11 pontos
Akusztikus MEMS szenzor vizsgálata. Sós Bence JB2BP7
 Akusztikus MEMS szenzor vizsgálata Sós Bence JB2BP7 Tartalom MEMS mikrofon felépítése és típusai A PDM jel Kinyerhető információ CIC szűrő Mérési tapasztalatok. Konklúzió MEMS (MicroElectrical-Mechanical
Akusztikus MEMS szenzor vizsgálata Sós Bence JB2BP7 Tartalom MEMS mikrofon felépítése és típusai A PDM jel Kinyerhető információ CIC szűrő Mérési tapasztalatok. Konklúzió MEMS (MicroElectrical-Mechanical
8 Képfeldolgozási alkalmazások. 8.1 A képfeldolgozás alapjai
 8 Képfeldolgozási alkalmazások 8.1 A képfeldolgozás alapjai A 8.1. ábra egy monokróm, 8bites (256 színű) kép felépítését mutatja meg. A kép 42120 pontból épül fel, 216 sora, 195 oszlopa van. Ha mint jelre
8 Képfeldolgozási alkalmazások 8.1 A képfeldolgozás alapjai A 8.1. ábra egy monokróm, 8bites (256 színű) kép felépítését mutatja meg. A kép 42120 pontból épül fel, 216 sora, 195 oszlopa van. Ha mint jelre
SCHRÖDINGER-EGYENLET SCHRÖDINGER-EGYENLET
 SCHRÖDINGER-EGYENLET A Scrödinger-egyenlet a kvantummecanika mozgásegyenlet, Newton II. törvényével analóg. Nem vezetető le korábbi elvekből, de intuitívan bevezetető. Egy atározott energiával és impulzussal
SCHRÖDINGER-EGYENLET A Scrödinger-egyenlet a kvantummecanika mozgásegyenlet, Newton II. törvényével analóg. Nem vezetető le korábbi elvekből, de intuitívan bevezetető. Egy atározott energiával és impulzussal
Irányítástechnika II. előadásvázlat
 Irányítástechnika II. előadásvázlat Dr. Bokor József egyetemi tanár, az MTA rendes tagja BME Közlekedés- és Járműirányítási Tanszék 2018 1 Tartalom Irányítástechnika II. féléves tárgytematika Az irányításelmélet
Irányítástechnika II. előadásvázlat Dr. Bokor József egyetemi tanár, az MTA rendes tagja BME Közlekedés- és Járműirányítási Tanszék 2018 1 Tartalom Irányítástechnika II. féléves tárgytematika Az irányításelmélet
jelfeldolgozásba II.
 TÁMOP-4.1.1.F-14/1/KONV-215-9 A gépészeti és informatikai ágazatok duális és moduláris képzéseinek kialakítása a Pécsi Tudományegyetemen Bevezetés a számítógépes jelfeldolgozásba II. Sári Zoltán Pécs 215
TÁMOP-4.1.1.F-14/1/KONV-215-9 A gépészeti és informatikai ágazatok duális és moduláris képzéseinek kialakítása a Pécsi Tudományegyetemen Bevezetés a számítógépes jelfeldolgozásba II. Sári Zoltán Pécs 215
Ha sokáig mérünk: kiátlagoljuk a jelet Milyen lesz ez a súlyfüggvény? T idejű integrálás + delta függvény T ideig integrálva:
 1 Integráló voltmérő Ha sokáig mérünk: kiátlagoljuk a jelet Milyen lesz ez a súlyfüggvény? T idejű integrálás + delta függvény T ideig integrálva: A súlyfüggvény: T széles impulzus 2 Ha a bemenő zaj B
1 Integráló voltmérő Ha sokáig mérünk: kiátlagoljuk a jelet Milyen lesz ez a súlyfüggvény? T idejű integrálás + delta függvény T ideig integrálva: A súlyfüggvény: T széles impulzus 2 Ha a bemenő zaj B
Híradástechikai jelfeldolgozás
 Híradástehikai jeleldolgozás. előadás Sebességkonverziós jeleldolgozás 05. 04. 3. 05. április 3. Budapest Dr. Gaál Józse BME Hálózati Rendszerek és SzolgáltatásokTanszék gaal@hit.bme.hu Sebességkonverziós
Híradástehikai jeleldolgozás. előadás Sebességkonverziós jeleldolgozás 05. 04. 3. 05. április 3. Budapest Dr. Gaál Józse BME Hálózati Rendszerek és SzolgáltatásokTanszék gaal@hit.bme.hu Sebességkonverziós
Mit lássunk élnek? Hol van az él? Milyen vastag legyen? Hol
 Textúra Könnyű az élt megtalálni? Mi lássunk élnek? Mit lássunk élnek? Hol van az él? Milyen vastag legyen? Mit lássunk élnek? Zaj A zajpontokat nem szabad az élpontokkal összekeverni Egy vagy két él?
Textúra Könnyű az élt megtalálni? Mi lássunk élnek? Mit lássunk élnek? Hol van az él? Milyen vastag legyen? Mit lássunk élnek? Zaj A zajpontokat nem szabad az élpontokkal összekeverni Egy vagy két él?
2. témakör. Sztochasztikus, stacionárius és ergodikus jelek leírása idő és frekvenciatartományban
 2. témakör Sztochasztikus, stacionárius és ergodikus jelek leírása idő és frekvenciatartományban Bevezetés Egy összetett jel, amely nem feltétlen periodikus, de stabil amplitúdójó és frekvenciájú diszkrét
2. témakör Sztochasztikus, stacionárius és ergodikus jelek leírása idő és frekvenciatartományban Bevezetés Egy összetett jel, amely nem feltétlen periodikus, de stabil amplitúdójó és frekvenciájú diszkrét
Képalkotó diagnosztikai eljárások
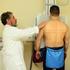 Képalkotó diagnosztikai eljárások Soroljon fel néhány orvosi képalkotáson alapuló diagnosztikai eljárást, mely o transzmissziós o reflexiós o emissziós elv alkalmazásán alapul. Mire szolgálnak az egyes
Képalkotó diagnosztikai eljárások Soroljon fel néhány orvosi képalkotáson alapuló diagnosztikai eljárást, mely o transzmissziós o reflexiós o emissziós elv alkalmazásán alapul. Mire szolgálnak az egyes
KANDÓ KÁLMÁN VILLAMOSMÉRNÖKI FŐISKOLAI KAR. Mikroelektronikai és Technológiai Intézet. Aktív Szűrők. Analóg és Hírközlési Áramkörök
 KANDÓ KÁLMÁN VILLAMOSMÉRNÖKI FŐISKOLAI KAR Mikroelektronikai és Technológiai Intézet Analóg és Hírközlési Áramkörök Laboratóriumi Gyakorlatok Készítette: Joó Gábor és Pintér Tamás OE-MTI 2011 1.Szűrők
KANDÓ KÁLMÁN VILLAMOSMÉRNÖKI FŐISKOLAI KAR Mikroelektronikai és Technológiai Intézet Analóg és Hírközlési Áramkörök Laboratóriumi Gyakorlatok Készítette: Joó Gábor és Pintér Tamás OE-MTI 2011 1.Szűrők
Anyagi tulajdonságok meghatározása spektrálisan
 Ágazati Á felkészítés a hazai EL projekttel összefüggő ő képzési é és K+F feladatokra" " 9. előadás Anyagi tulajdonságok meghatározása spektrálisan bontott interferometriával (SR) 1 Bevezetés A diszperzív
Ágazati Á felkészítés a hazai EL projekttel összefüggő ő képzési é és K+F feladatokra" " 9. előadás Anyagi tulajdonságok meghatározása spektrálisan bontott interferometriával (SR) 1 Bevezetés A diszperzív
Az Informatika Elméleti Alapjai
 Az Informatika Elméleti Alapjai dr. Kutor László Jelek típusai Átalakítás az analóg és digitális rendszerek között http://mobil.nik.bmf.hu/tantargyak/iea.html Felhasználónév: iea Jelszó: IEA07 IEA 3/1
Az Informatika Elméleti Alapjai dr. Kutor László Jelek típusai Átalakítás az analóg és digitális rendszerek között http://mobil.nik.bmf.hu/tantargyak/iea.html Felhasználónév: iea Jelszó: IEA07 IEA 3/1
Segédlet a gyakorlati tananyaghoz GEVAU141B, GEVAU188B c. tantárgyakból
 Segédlet a gyakorlati tananyaghoz GEVAU141B, GEVAU188B c. tantárgyakból 1 Átviteli tényező számítása: Lineáris rendszer: Pl1.: Egy villanymotor 100V-os bemenő jelre 1000 fordulat/perc kimenő jelet ad.
Segédlet a gyakorlati tananyaghoz GEVAU141B, GEVAU188B c. tantárgyakból 1 Átviteli tényező számítása: Lineáris rendszer: Pl1.: Egy villanymotor 100V-os bemenő jelre 1000 fordulat/perc kimenő jelet ad.
SZAKMAI ZÁRÓJELENTÉS. Optimális háromdimenziós rácson mintavételezett adatok interaktív térfogatvizualizációja
 SZAKMAI ZÁRÓJELENTÉS Optimális háromdimenziós rácson mintavételezett adatok interaktív térfogatvizualizációja (OTKA F-68945) A modern 3D képalkotó eljárások (CT, MRI, PET) a tomográfiás rekonstrukciót
SZAKMAI ZÁRÓJELENTÉS Optimális háromdimenziós rácson mintavételezett adatok interaktív térfogatvizualizációja (OTKA F-68945) A modern 3D képalkotó eljárások (CT, MRI, PET) a tomográfiás rekonstrukciót
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 8. A JELFELDOLGOZÁS ALAPJAI
 ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 8. A JELFELDOLGOZÁS ALAPJAI Dr. Soumelidis Alexandros 2018.11.22. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG A Fourier
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 8. A JELFELDOLGOZÁS ALAPJAI Dr. Soumelidis Alexandros 2018.11.22. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG A Fourier
A médiatechnológia alapjai
 A médiatechnológia alapjai Úgy döntöttem, hogy a Szirányi oktatta előadások számonkérhetőnek tűnő lényegét kiemelem, az alapján, amit a ZH-ról mondott: rövid kérdések. A rész és az egész: összefüggések
A médiatechnológia alapjai Úgy döntöttem, hogy a Szirányi oktatta előadások számonkérhetőnek tűnő lényegét kiemelem, az alapján, amit a ZH-ról mondott: rövid kérdések. A rész és az egész: összefüggések
Digitális jelfeldolgozás
 Digitális jelfeldolgozás Dr. Fodor, Dénes Szerzői jog 2014 Pannon Egyetem A tananyag a TÁMOP-4.1.2.A/1-11/1-2011-0042 azonosító számú Mechatronikai mérnök MSc tananyagfejlesztés projekt keretében készült.
Digitális jelfeldolgozás Dr. Fodor, Dénes Szerzői jog 2014 Pannon Egyetem A tananyag a TÁMOP-4.1.2.A/1-11/1-2011-0042 azonosító számú Mechatronikai mérnök MSc tananyagfejlesztés projekt keretében készült.
Akusztikai tervezés a geometriai akusztika módszereivel
 Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
