Képrekonstrukció 3. előadás
|
|
|
- Ede Rácz
- 9 évvel ezelőtt
- Látták:
Átírás
1 Képrekonstrukció 3. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem
2 Computed Tomography (CT) Elv: Röntgen-sugarak áthatolása 3D objektum 3D térfogati kép Mérések (vetületek) számítása keresztmetszeti képek előállításához Rekonstrukció vetületekből Típusok: (Standard) single-slice CT Helical CT (spirális) Multi-slice CT (több detektor, nagyon gyors!)
3 Számítógépes tomográfia (CT) Eljárás 3D objektumok (általában emberi szervek) 2D keresztmetszeti képeinek meghatározására Röntgen-cső sugarak detektorok
4 Egyszerű CT rendszer
5 CT elve x-sugár, nem a páciens forog Rotációs tengely: fejtől lábig 2D vetületi képek a 3D-s testről Különböző szögek különböző információ A kép egy vízszintes vonala 1D-s vetület a 2D szeletről 1D projekciók halmaza Teljes információ a szeletről Rekonstruáljuk a szeletet
6 Képalkotás Vonalintegrálok x-sugár cső x-sugár nyalábok áthaladás az objektumon detektorok oldalán mérik az intenzitás gyengülését a forrás és a detektorok között Hogyan rekonstruálható egy keresztmetszeti kép (szelet)? I 0 polienergetikus forrás: I d I ( E ) e 0 ( x, E ) dx de I d
7 Képalkotás Vonalintegrálok A teljes energiaspektrumon való integrálás számítási szempontból kivitelezhetetlen. Feltételezés: effektív energia az az energia, mely egy adott anyagban monoenergetikus forrás esetén ugyanazt a mért intenzitást eredményezné, mint az aktuális polienergetikus forrás esetén mért intenzitás E 0 I I ( E e d 0 ) d ( s, E ) ds
8 Képalkotás Vonalintegrálok I 0 és I d könnyen mérhető! Vetület számítása: g d d I d ln ( s, I 0 0 E ) ds A lineáris elnyelési együttható vonalintegrálja a szkenner effektív energiáján. Minden detektorra az I 0 referencia intenzitást ki kell mérni kalibráció
9 CT Numbers CT reconstruction: value for each pixel (voxel) of slice Problem: different CT scanners different tubes different effective energy same object different numerical values of Replacement of x-ray tubes! Solution: CT numbers: comparable results h=0 HU for water h=-1000 HU for air (μ=0) h~1000 HU for bone h~3000 HU for metal, contrast agents h water 1000 [ HU water HU Hounsfield Units ]
10 Rekonstrukció párhuzamos vetületek esetén Cél: CT számok meghatározása a keresztmetszeten Hogyan rekonstruálható μ a vonalintegráljainak gyűjteményéből?
11 2D Radon transzformáció Egy fix θ esetén p(t, θ) az f(x,y) függvény egy θ szög által meghatározott vetülete (projekciója). Az összes θ szög által meghatározott vetületek gyűjteménye az f(x,y) 2D Radon transzformációja.
12 Szinogram Objektum Szinogram Szinogram: a p(t, θ) vetületek gyűjteménye t és θ merőleges tengelyekkel ábrázolva.
13 Visszavetített összegkép (laminogram) egy visszavetítés Visszavetítések összege (elmosódás!)
14 Fourier-transzformáció
15 Vetület-szelet tétel Fontos kapcsolat a vetület 1D Fourier transzformáltja és a kép 2D Fourier transzformáltja között y tengellyel párhuzamos vetület: 1D Fourier-transzformáció mindkét oldalra: Az f(x,y) függvény 2D Fourier-transzformáltja a v=0 helyen: : Tehát: P(u) = F(u,v) v=0 Tetszőlegesen elforgatott koordináta-rendszerben érvényes!
16 Közvetlen bizonyítás f(x,y) = f (t,s), t=x cosθ+y sinθ, s=-x sinθ+y cosθ A Θ szögű vetületre: 1D-s FT: f 2D FT-ja:
17 Vetület-szelet tétel szemléletesen A θ szögű vetület 1D FT-ja az eredeti kép 2D FT-jának egy a frekvencia térben az origón áthaladó θ irányszögű egyenesre eső része.
18 Fourier rekonstrukciós módszer vegyük a vetületek 1D FT-ját helyezzük el ezeket a megfelelő szögben a frekvencia térben vegyük az eredmény 2D FT-jának inverzét. Nem gyakran használt módszer (mintavételezés, interpoláció, inverz 2D FT)!
19 Szűrt visszavetítés (Filtered Backprojection)
20 Szűrt visszavetítés p(t,θ+π)=p(-t,θ) P(ω,Θ+π)=P(-ω,Θ)
21
22 Szűrt visszavetítés algoritmusa
23 Konvolúciós rekonstrukció Konvolúciós tétel alapján: Ha t=0: ezért A gyakorlatban az ideális ω szűrő helyett annak egy q(ω) függvénnyel ablakolt változatát alkalmazzuk a szűrés során (Hamming, koszinusz, stb.)
24 Konvolúciós kernelek (szűrők) Ramp: Egzakt kompenzáció (jó megoldás, ha nem zajos a vetület) Shepp-Logan: Zaj és felbontás közötti kompromisszum Hamming: Extrém magas frekvenciák lesimítása Slide: Alexander L.C. Kwan
25 A rekonstrukció lépései Input szinogram: 1. Szűrés 2. Visszavetítés 3. Összegzés
26 Szűrés before after
27 Visszavetítés
28 Összegzés
29 Szűrt visszavetítés Video: 2D szinogram Felüláteresztő szűrő minden szögre sinogram visszavetítése a képtérbe Forrás:
Képrekonstrukció 4. előadás
 Képrekonstrukció 4. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Vetület-szelet tétel szemléletesen A θ szögű vetület 1D FT-ja az eredeti kép 2D FT-jának
Képrekonstrukció 4. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Vetület-szelet tétel szemléletesen A θ szögű vetület 1D FT-ja az eredeti kép 2D FT-jának
Képrekonstrukció 2. előadás
 Képrekonstrukció 2. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika tanszék Szegedi Tudományegyetem Az atomszerkezet Atommag (nukleusz): {protonok (poz. töltés) és neutronok} = nukleonok Keringő
Képrekonstrukció 2. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika tanszék Szegedi Tudományegyetem Az atomszerkezet Atommag (nukleusz): {protonok (poz. töltés) és neutronok} = nukleonok Keringő
Nem roncsoló tesztelés diszkrét tomográfiával
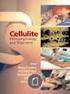 Nem roncsoló tesztelés diszkrét tomográfiával Dr. Balázs Péter, adjunktus Képfeldolgozás és Számítógépes Grafika Tanszék SZTE TTIK, Informatikai Tanszékcsoport A teszteléshez használt CT berendezés lapdetektor
Nem roncsoló tesztelés diszkrét tomográfiával Dr. Balázs Péter, adjunktus Képfeldolgozás és Számítógépes Grafika Tanszék SZTE TTIK, Informatikai Tanszékcsoport A teszteléshez használt CT berendezés lapdetektor
PET gyakorlati problémák. PET rekonstrukció
 CT Computed Tomography 3D képalkotó eljárások Csébfalvi Balázs E-mail: cseb@iit.bme.hu Irányítástechnika és Informatika Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 2 / 26 CT Történeti áttekintés
CT Computed Tomography 3D képalkotó eljárások Csébfalvi Balázs E-mail: cseb@iit.bme.hu Irányítástechnika és Informatika Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 2 / 26 CT Történeti áttekintés
Orvosi tomográkus képalkotás/ct technika alapja
 Orvosi tomográkus képalkotás/ct technika alapja Kis Sándor Attila DEOEC, Nukléáris Medicina Intézet Outline 1 Bevezetés 2 A planáris transzmissziós leképzési technikák esetén a vizsgált objektumról összegképet
Orvosi tomográkus képalkotás/ct technika alapja Kis Sándor Attila DEOEC, Nukléáris Medicina Intézet Outline 1 Bevezetés 2 A planáris transzmissziós leképzési technikák esetén a vizsgált objektumról összegképet
Rekonstrukciós eljárások. Orvosi képdiagnosztika 2017 ősz
 Rekonstrukciós eljárások Orvosi képdiagnosztika 2017 ősz Előadások témája Röntgen tomográfia fizikai és matematikai alapjai 2D Radon transzformáció, szűrt visszavetítés: Fan beam / Cone beam felvételi
Rekonstrukciós eljárások Orvosi képdiagnosztika 2017 ősz Előadások témája Röntgen tomográfia fizikai és matematikai alapjai 2D Radon transzformáció, szűrt visszavetítés: Fan beam / Cone beam felvételi
Rekonstrukciós eljárások. Orvosi képdiagnosztika 2017 ősz
 Rekonstrukciós eljárások Orvosi képdiagnosztika 2017 ősz Élet a konvex optimalizáción túl CT-s szimuláció, 10 projekcióból (ΔΘ=18 ): Konvex: L2-TV Valóban ritkasági priorral Lineáris tomoszintézis Speciális
Rekonstrukciós eljárások Orvosi képdiagnosztika 2017 ősz Élet a konvex optimalizáción túl CT-s szimuláció, 10 projekcióból (ΔΘ=18 ): Konvex: L2-TV Valóban ritkasági priorral Lineáris tomoszintézis Speciális
Dr. Palkó András. SZTE ÁOK Radiológiai Klinika NEK Képalkotó Diagnosztikai Centrum Szeged
 MultiDetector ComputedTomography Dr. Palkó András SZTE ÁOK Radiológiai Klinika NEK Képalkotó Diagnosztikai Centrum Szeged MSCT = multislice computed tomography MDCT = multidetector (-row) computed tomography
MultiDetector ComputedTomography Dr. Palkó András SZTE ÁOK Radiológiai Klinika NEK Képalkotó Diagnosztikai Centrum Szeged MSCT = multislice computed tomography MDCT = multidetector (-row) computed tomography
A röntgendiagnosztika alapjai
 A fotonenergia növelésével csökken az elnyelődés. A röntgendiagnosztika alapjai A csökkenés markánsabb a fotoeffektusra nézve. Kis fotonenergiáknál τ m dominál. τ m markánsan változik az abszorbens rendszámával.
A fotonenergia növelésével csökken az elnyelődés. A röntgendiagnosztika alapjai A csökkenés markánsabb a fotoeffektusra nézve. Kis fotonenergiáknál τ m dominál. τ m markánsan változik az abszorbens rendszámával.
KÉPSZŐRİK A NUKLEÁRIS
 KÉPSZŐRİK A NUKLEÁRIS MEDICINÁBAN Varga József Debreceni Egyetem OEC Nukleáris Medicina Tanszék Emissziós leképezés behatároló tényezıi korlátozott felbontás résztérfogat-hatás távolságfüggı! sugárgyengítés
KÉPSZŐRİK A NUKLEÁRIS MEDICINÁBAN Varga József Debreceni Egyetem OEC Nukleáris Medicina Tanszék Emissziós leképezés behatároló tényezıi korlátozott felbontás résztérfogat-hatás távolságfüggı! sugárgyengítés
Grafikonok automatikus elemzése
 Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás
 3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
Diagnosztikai röntgen képalkotás, CT
 Diagnosztikai röntgen képalkotás, CT ALAPELVEK A röntgenkép a röntgensugárzással átvilágított test árnyéka. A detektor vagy film az áthaladó, azaz nem elnyelt sugarakat érzékeli. A képen az elnyelő tárgyaknak
Diagnosztikai röntgen képalkotás, CT ALAPELVEK A röntgenkép a röntgensugárzással átvilágított test árnyéka. A detektor vagy film az áthaladó, azaz nem elnyelt sugarakat érzékeli. A képen az elnyelő tárgyaknak
Dekonvolúció a mikroszkópiában. Barna László MTA Kísérleti Orvostudományi Kutatóintézet Nikon-KOKI képalkotó Központ
 Dekonvolúció a mikroszkópiában Barna László MTA Kísérleti Orvostudományi Kutatóintézet Nikon-KOKI képalkotó Központ 2015 Fourier-Sorok Minden 2π szerint periodikus függvény előállítható f x ~ a 0 2 + (a
Dekonvolúció a mikroszkópiában Barna László MTA Kísérleti Orvostudományi Kutatóintézet Nikon-KOKI képalkotó Központ 2015 Fourier-Sorok Minden 2π szerint periodikus függvény előállítható f x ~ a 0 2 + (a
Képrekonstrukció 10. előadás. Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék
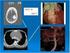 Képrekonstrukció 10. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Ultrahang terjedése Fakorhadás vizsgálata (P. Divós, F. Divós) Hullámfront terjedése 20 μs-onként Diffrakciós tomográfia
Képrekonstrukció 10. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Ultrahang terjedése Fakorhadás vizsgálata (P. Divós, F. Divós) Hullámfront terjedése 20 μs-onként Diffrakciós tomográfia
Fourier térbeli analízis, inverz probléma. Orvosi képdiagnosztika 5-7. ea ősz
 Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 5-7. ea. 2017 ősz 5. Előadás témái Fourier transzformációk és kapcsolataik: FS, FT, DTFT, DFT, DFS Mintavételezés, interpoláció Folytonos
Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 5-7. ea. 2017 ősz 5. Előadás témái Fourier transzformációk és kapcsolataik: FS, FT, DTFT, DFT, DFS Mintavételezés, interpoláció Folytonos
4. Szűrés frekvenciatérben
 4. Szűrés frekvenciatérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) Unitér transzformációk Az unitér transzformációk olyan lineáris,
4. Szűrés frekvenciatérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) Unitér transzformációk Az unitér transzformációk olyan lineáris,
3. Szűrés képtérben. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 3. Szűrés képtérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE http://www.inf.u-szeged.hu/~kato/teaching/ 2 Kép transzformációk típusai Kép értékkészletének radiometriai információ
3. Szűrés képtérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE http://www.inf.u-szeged.hu/~kato/teaching/ 2 Kép transzformációk típusai Kép értékkészletének radiometriai információ
Bevezetés a komputertomográfia alapjaiba
 Bevezetés a komputertomográfia alapjaiba Harnisch József Technology with Passion Mi a komputertomográfia (CT)? A tomográfia szó görög eredetű, a tomos (szelet) és graphein (írni) szóösszetételből ered.
Bevezetés a komputertomográfia alapjaiba Harnisch József Technology with Passion Mi a komputertomográfia (CT)? A tomográfia szó görög eredetű, a tomos (szelet) és graphein (írni) szóösszetételből ered.
A röntgendiagnosztika alapjai
 A röngtgendiagnosztika alapja: a sugárzás elnyelődése A röntgendiagnosztika alapjai A foton kölcsönhatásának lehetőségei: Compton-szórás Comptonszórás elnyelődés fotoeffektusban fotoeffektus nincs kölcsönhatás
A röngtgendiagnosztika alapja: a sugárzás elnyelődése A röntgendiagnosztika alapjai A foton kölcsönhatásának lehetőségei: Compton-szórás Comptonszórás elnyelődés fotoeffektusban fotoeffektus nincs kölcsönhatás
RÖNTGENSUGÁR ALAPÚ SZÁMÍTÓGÉPES
 RÖNTGENSUGÁR ALAPÚ SZÁMÍTÓGÉPES TOMOGRÁFIA (CT) TECHNIKAI ALAPJAI dr. Németh Gábor Pre-klinikai Programigazgató Mediso Kft, Budapest gabor.nemeth@mediso.hu Radiológiai és Onkoterápiás Klinika, Semmelweis
RÖNTGENSUGÁR ALAPÚ SZÁMÍTÓGÉPES TOMOGRÁFIA (CT) TECHNIKAI ALAPJAI dr. Németh Gábor Pre-klinikai Programigazgató Mediso Kft, Budapest gabor.nemeth@mediso.hu Radiológiai és Onkoterápiás Klinika, Semmelweis
Mit lássunk élnek? Hol van az él? Milyen vastag legyen? Hol
 Textúra Könnyű az élt megtalálni? Mi lássunk élnek? Mit lássunk élnek? Hol van az él? Milyen vastag legyen? Mit lássunk élnek? Zaj A zajpontokat nem szabad az élpontokkal összekeverni Egy vagy két él?
Textúra Könnyű az élt megtalálni? Mi lássunk élnek? Mit lássunk élnek? Hol van az él? Milyen vastag legyen? Mit lássunk élnek? Zaj A zajpontokat nem szabad az élpontokkal összekeverni Egy vagy két él?
Spektrográf elvi felépítése. B: maszk. A: távcső. Ø maszk. Rés Itt lencse, de általában komplex tükörrendszer
 Spektrográf elvi felépítése A: távcső Itt lencse, de általában komplex tükörrendszer Kis kromatikus aberráció fontos Leképezés a fókuszsíkban: sugarak itt metszik egymást B: maszk Fókuszsíkba kerül (kamera
Spektrográf elvi felépítése A: távcső Itt lencse, de általában komplex tükörrendszer Kis kromatikus aberráció fontos Leképezés a fókuszsíkban: sugarak itt metszik egymást B: maszk Fókuszsíkba kerül (kamera
Röntgendiagnosztikai alapok
 Röntgendiagnosztikai alapok Dr. Voszka István A röntgensugárzás keltésének alternatív lehetőségei (röntgensugárzás keletkezik nagy sebességű, töltéssel rendelkező részecskék lefékeződésekor) Röntgencső:
Röntgendiagnosztikai alapok Dr. Voszka István A röntgensugárzás keltésének alternatív lehetőségei (röntgensugárzás keletkezik nagy sebességű, töltéssel rendelkező részecskék lefékeződésekor) Röntgencső:
Képrekonstrukció 9. előadás
 Képrekonstrukció 9. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem hv-konvex összefüggő halmazok Mag-burok-szerű rekonstrukció: S. Brunetti, A. Del Lungo, F.
Képrekonstrukció 9. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem hv-konvex összefüggő halmazok Mag-burok-szerű rekonstrukció: S. Brunetti, A. Del Lungo, F.
MRI áttekintés. Orvosi képdiagnosztika 3. ea ősz
 MRI áttekintés Orvosi képdiagnosztika 3. ea. 2015 ősz MRI Alapelv: hogyan lehet mágneses vizsgálattal valamilyen anyag (jelen esetben az élő emberi szervezet) belső felépítéséről információt kapni? A mágneses
MRI áttekintés Orvosi képdiagnosztika 3. ea. 2015 ősz MRI Alapelv: hogyan lehet mágneses vizsgálattal valamilyen anyag (jelen esetben az élő emberi szervezet) belső felépítéséről információt kapni? A mágneses
Képalkotás modellezése, metrikái. Orvosi képdiagnosztika 6. ea ősz
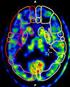 Képalkotás modellezése, metrikái Orvosi képdiagnosztika 6. ea. 2015 ősz Jelölésjegyzék Rendszer válasza f gerjesztésre: Dirac-delta: x ; egységugrás: 0 idejű Dirac-delta gerjesztése a rendszer válasza:
Képalkotás modellezése, metrikái Orvosi képdiagnosztika 6. ea. 2015 ősz Jelölésjegyzék Rendszer válasza f gerjesztésre: Dirac-delta: x ; egységugrás: 0 idejű Dirac-delta gerjesztése a rendszer válasza:
Jelfeldolgozás bevezető. Témalaboratórium
 Jelfeldolgozás bevezető Témalaboratórium Tartalom Jelfeldolgozás alapjai Lineáris rendszerelmélet Fourier transzformációk és kapcsolataik Spektrális képek értelmezése Képfeldolgozás alapjai Néhány nevezetesebb
Jelfeldolgozás bevezető Témalaboratórium Tartalom Jelfeldolgozás alapjai Lineáris rendszerelmélet Fourier transzformációk és kapcsolataik Spektrális képek értelmezése Képfeldolgozás alapjai Néhány nevezetesebb
Képalkotó diagnosztikai eljárások. Krasznai Zoltán. DEOEC Biofizikai és Sejtbiológiai Intézete
 Képalkotó diagnosztikai eljárások Krasznai Zoltán DEOEC Biofizikai és Sejtbiológiai Intézete Komputer tomográfia (CT) Gamma kamera Fotonemissziós komputer tomográfia (SPECT) Pozitron emissziós tomográfia
Képalkotó diagnosztikai eljárások Krasznai Zoltán DEOEC Biofizikai és Sejtbiológiai Intézete Komputer tomográfia (CT) Gamma kamera Fotonemissziós komputer tomográfia (SPECT) Pozitron emissziós tomográfia
Számítási feladatok a Számítógépi geometria órához
 Számítási feladatok a Számítógépi geometria órához Kovács Zoltán Copyright c 2012 Last Revision Date: 2012. október 15. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát
Számítási feladatok a Számítógépi geometria órához Kovács Zoltán Copyright c 2012 Last Revision Date: 2012. október 15. kovacsz@nyf.hu Technikai útmutató a jegyzet használatához A jegyzet képernyőbarát
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr.
3D számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr.
Valósidejű helikális cone-beam CT rekonstrukció a Mediso NanoPET/CT R készülékben
 Valósidejű helikális cone-beam CT rekonstrukció a Mediso NanoPET/CT R készülékben Domonkos Balázs 1,2 Jakab Gábor 1 1 Mediso Kft. 1022 Budapest, Alsótörökvész u. 14. http://www.mediso.hu, research@mediso.hu
Valósidejű helikális cone-beam CT rekonstrukció a Mediso NanoPET/CT R készülékben Domonkos Balázs 1,2 Jakab Gábor 1 1 Mediso Kft. 1022 Budapest, Alsótörökvész u. 14. http://www.mediso.hu, research@mediso.hu
Robotika. Kinematika. Magyar Attila
 Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Robotika Kinematika Magyar Attila amagyar@almos.vein.hu Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Képalkotás neutronokkal (radiográfia és tomográfia)
 Képalkotás neutronokkal (radiográfia és tomográfia) Kis Z., Szentmiklósi L., Belgya T., Révay Zs. MTA Energiatudományi Kutatóközpont, Magyar Tudományos Akadémia, Budapest NPS-NORMA @ Budapesti Kutatóreaktor
Képalkotás neutronokkal (radiográfia és tomográfia) Kis Z., Szentmiklósi L., Belgya T., Révay Zs. MTA Energiatudományi Kutatóközpont, Magyar Tudományos Akadémia, Budapest NPS-NORMA @ Budapesti Kutatóreaktor
CT/MRI képalkotás alapjai. Prof. Bogner Péter
 CT/MRI képalkotás alapjai Prof. Bogner Péter CT - computed tomography Godfrey N. Hounsfield Allan M. Cormack The Nobel Prize in Physiology or Medicine 1979 MRI - magnetic resonance imaging Sir Peter Mansfield
CT/MRI képalkotás alapjai Prof. Bogner Péter CT - computed tomography Godfrey N. Hounsfield Allan M. Cormack The Nobel Prize in Physiology or Medicine 1979 MRI - magnetic resonance imaging Sir Peter Mansfield
19. A fényelektromos jelenségek vizsgálata
 19. A fényelektromos jelenségek vizsgálata PÁPICS PÉTER ISTVÁN csillagász, 3. évfolyam Mérőpár: Balázs Miklós 2006.04.19. Beadva: 2006.05.15. Értékelés: A MÉRÉS LEÍRÁSA Fontos megállapítás, hogy a fénysugárzásban
19. A fényelektromos jelenségek vizsgálata PÁPICS PÉTER ISTVÁN csillagász, 3. évfolyam Mérőpár: Balázs Miklós 2006.04.19. Beadva: 2006.05.15. Értékelés: A MÉRÉS LEÍRÁSA Fontos megállapítás, hogy a fénysugárzásban
11. Alakzatjellemzők. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
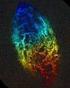 11. Alakzatjellemzők Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Alakzat = pontok összefüggő rendszere példák síkbeli alakzatokra 3 Az
11. Alakzatjellemzők Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Alakzat = pontok összefüggő rendszere példák síkbeli alakzatokra 3 Az
Mérés és adatgyűjtés
 Mérés és adatgyűjtés 4. óra Mingesz Róbert Szegedi Tudományegyetem 2012. február 27. MA - 4. óra Verzió: 2.1 Utolsó frissítés: 2012. március 12. 1/41 Tartalom I 1 Jelek 2 Mintavételezés 3 A/D konverterek
Mérés és adatgyűjtés 4. óra Mingesz Róbert Szegedi Tudományegyetem 2012. február 27. MA - 4. óra Verzió: 2.1 Utolsó frissítés: 2012. március 12. 1/41 Tartalom I 1 Jelek 2 Mintavételezés 3 A/D konverterek
Képrekonstrukció 5. előadás
 Képrekonstrukció 5. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Képalkotási hibák zaj, túl kevés detektor, túl kevés vetület, mozgás (balról jobbra) nyalábkeményedés
Képrekonstrukció 5. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Képalkotási hibák zaj, túl kevés detektor, túl kevés vetület, mozgás (balról jobbra) nyalábkeményedés
A médiatechnológia alapjai
 A médiatechnológia alapjai Úgy döntöttem, hogy a Szirányi oktatta előadások számonkérhetőnek tűnő lényegét kiemelem, az alapján, amit a ZH-ról mondott: rövid kérdések. A rész és az egész: összefüggések
A médiatechnológia alapjai Úgy döntöttem, hogy a Szirányi oktatta előadások számonkérhetőnek tűnő lényegét kiemelem, az alapján, amit a ZH-ról mondott: rövid kérdések. A rész és az egész: összefüggések
A tér lineáris leképezései síkra
 A tér lineáris leképezései síkra Az ábrázoló geometria célja: A háromdimenziós térben elhelyezkedő alakzatok helyzeti és metrikus viszonyainak egyértelmű és egyértelműen rekonstruálható módon történő ábrázolása
A tér lineáris leképezései síkra Az ábrázoló geometria célja: A háromdimenziós térben elhelyezkedő alakzatok helyzeti és metrikus viszonyainak egyértelmű és egyértelműen rekonstruálható módon történő ábrázolása
8. előadás. Kúpszeletek
 8. előadás Kúpszeletek Kör A k kört egyértelműen meghatározza C(a,b) középpontja és r sugara. A P pont pontosan akkor van k-n, ha CP=r. Vektoregyenlet: p-c = r. Koordinátás egyenlet: (X-a)2 + (Y-b)2 =
8. előadás Kúpszeletek Kör A k kört egyértelműen meghatározza C(a,b) középpontja és r sugara. A P pont pontosan akkor van k-n, ha CP=r. Vektoregyenlet: p-c = r. Koordinátás egyenlet: (X-a)2 + (Y-b)2 =
Matematika (mesterképzés)
 Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Pontműveletek. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar február 20.
 Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
Wavelet transzformáció
 1 Wavelet transzformáció Más felbontás: Walsh, Haar, wavelet alapok! Eddig: amplitúdó vagy frekvencia leírás: Pl. egy rövid, Dirac-delta jellegű impulzus Fourier-transzformált: nagyon sok, kb. ugyanolyan
1 Wavelet transzformáció Más felbontás: Walsh, Haar, wavelet alapok! Eddig: amplitúdó vagy frekvencia leírás: Pl. egy rövid, Dirac-delta jellegű impulzus Fourier-transzformált: nagyon sok, kb. ugyanolyan
Képalkotás modellezése, metrikái. Orvosi képdiagnosztika 2017 ősz
 Képalkotás modellezése, metrikái Orvosi képdiagnosztika 2017 ősz Jelölésjegyzék Rendszer válasza f gerjesztésre: Dirac-delta: x ; egységugrás: 0 idejű Dirac-delta gerjesztése a rendszer válasza: h x x
Képalkotás modellezése, metrikái Orvosi képdiagnosztika 2017 ősz Jelölésjegyzék Rendszer válasza f gerjesztésre: Dirac-delta: x ; egységugrás: 0 idejű Dirac-delta gerjesztése a rendszer válasza: h x x
1. óra Digitális képfeldolgozás
 1. óra Digitális képfeldolgozás Képkorrekció A hisztogram A hisztogram a képünk intenzitás-eloszlását ábrázolja. Ebben a koordinátarendszerben a vízszintes tengelyen vesszük fel a teljes szürkeskálát úgy,
1. óra Digitális képfeldolgozás Képkorrekció A hisztogram A hisztogram a képünk intenzitás-eloszlását ábrázolja. Ebben a koordinátarendszerben a vízszintes tengelyen vesszük fel a teljes szürkeskálát úgy,
Az Orvosi Fizika Szigorlat menete a 2012/2. tanévtől
 Az Orvosi Fizika Szigorlat menete a 2012/2. tanévtől 1. A szigorlat menete A szigorlatot a Fizikus MSc orvosi fizika szakirányos hallgatók a második vagy harmadik szemeszterük folyamán tehetik le. A szigorlat
Az Orvosi Fizika Szigorlat menete a 2012/2. tanévtől 1. A szigorlat menete A szigorlatot a Fizikus MSc orvosi fizika szakirányos hallgatók a második vagy harmadik szemeszterük folyamán tehetik le. A szigorlat
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 6. A MINTAVÉTELI TÖRVÉNY
 ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 6. A MINTAVÉTELI TÖRVÉNY Dr. Soumelidis Alexandros 2018.10.25. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mintavételezés
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 6. A MINTAVÉTELI TÖRVÉNY Dr. Soumelidis Alexandros 2018.10.25. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mintavételezés
Bevezetés. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 Bevezetés Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Digitális képfeldolgozás digitális képfeldolgozás számítógépes grafika digitális
Bevezetés Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Digitális képfeldolgozás digitális képfeldolgozás számítógépes grafika digitális
Fourier térbeli analízis, inverz probléma. Orvosi képdiagnosztika 5-7. ea ősz
 Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 5-7. ea. 2017 ősz 6. Előadás tartalma Spektrumszivárgás Képfeldolgozás frekvencia tartományban: 2D Spektrum gépi ábrázolása Szűrések frekvenciatartományban
Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 5-7. ea. 2017 ősz 6. Előadás tartalma Spektrumszivárgás Képfeldolgozás frekvencia tartományban: 2D Spektrum gépi ábrázolása Szűrések frekvenciatartományban
Kamerakalibráció és pozícióbecslés érzékenységi analízissel, sík mintázatokból. Dabóczi Tamás (BME MIT), Fazekas Zoltán (MTA SZTAKI)
 , 2008 feb. 4-5 Kamerakalibráció és pozícióbecslés érzékenységi Bódis-Szomorú András Dabóczi Tamás (BME MIT), Fazekas Zoltán (MTA SZTAKI) Méréstechnika- és Információs Rendszerek Tanszék BME Rendszer-
, 2008 feb. 4-5 Kamerakalibráció és pozícióbecslés érzékenységi Bódis-Szomorú András Dabóczi Tamás (BME MIT), Fazekas Zoltán (MTA SZTAKI) Méréstechnika- és Információs Rendszerek Tanszék BME Rendszer-
Transzformációk, amelyek n-dimenziós objektumokat kisebb dimenziós terekbe visznek át. Pl. 3D 2D
 Vetítések Transzformációk, amelyek n-dimenziós objektumokat kisebb dimenziós terekbe visznek át. Pl. 3D 2D Vetítések fajtái - 1 perspektívikus A párhuzamos A A' B A' B A vetítés középpontja B' Vetítési
Vetítések Transzformációk, amelyek n-dimenziós objektumokat kisebb dimenziós terekbe visznek át. Pl. 3D 2D Vetítések fajtái - 1 perspektívikus A párhuzamos A A' B A' B A vetítés középpontja B' Vetítési
2010.05.09. Röntgen kép és Komputer tomográf (CT) Bevezető. Ujfalusi Zoltán. 2010. Március 8. PTE ÁOK Biofizikai Intézet
 Röntgen kép és Komputer tomográf (CT) 2010. Március 8. PTE ÁOK Biofizikai ntézet Ujfalusi Zoltán Hand mit Ringen: print of Wilhelm Röntgen's first "medical" x-ray, of his wife's hand, taken on 22 nd December
Röntgen kép és Komputer tomográf (CT) 2010. Március 8. PTE ÁOK Biofizikai ntézet Ujfalusi Zoltán Hand mit Ringen: print of Wilhelm Röntgen's first "medical" x-ray, of his wife's hand, taken on 22 nd December
Orvosi képdiagnosztika
 Orvosi képdiagnosztika Hadházi Dániel, Horváth Áron, Horváth Gábor Követelmények Aláírás feltételei: 6 db házi feladatból minimum 3 elfogadott megoldás Sikeres ZH/PZH/PPZH Kredit megszerzésének feltételei:
Orvosi képdiagnosztika Hadházi Dániel, Horváth Áron, Horváth Gábor Követelmények Aláírás feltételei: 6 db házi feladatból minimum 3 elfogadott megoldás Sikeres ZH/PZH/PPZH Kredit megszerzésének feltételei:
Rekonstrukciós eljárások. Orvosi képdiagnosztika 2017 ősz
 Rekonstrukciós eljárások Orvosi képdiagnosztika 2017 ősz Pozitron emissziós tomográfia alapelve Szervezetbe pozitron kibocsátására képes radioaktív izotópot tartalmazó anyagot visznek cukoroldatban. Sejtek
Rekonstrukciós eljárások Orvosi képdiagnosztika 2017 ősz Pozitron emissziós tomográfia alapelve Szervezetbe pozitron kibocsátására képes radioaktív izotópot tartalmazó anyagot visznek cukoroldatban. Sejtek
Transzmissziós és emissziós leképezés. SPECT vizsgálatok sajátosságai Sugárgyengítés-korrekció. Varga József
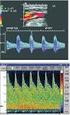 SPECT vizsgálatok sajátosságai Sugárgyengítés-korrekció Transzmissziós és emissziós leképezés tomo + gráfia = szelet + kép (görög) Varga József Debreceni Egyetem OEC Nukleáris Medicina Intézet SPECT alapjai
SPECT vizsgálatok sajátosságai Sugárgyengítés-korrekció Transzmissziós és emissziós leképezés tomo + gráfia = szelet + kép (görög) Varga József Debreceni Egyetem OEC Nukleáris Medicina Intézet SPECT alapjai
DIGITÁLIS KÉPANALÍZIS KÉSZÍTETTE: KISS ALEXANDRA ELÉRHETŐSÉG:
 DIGITÁLIS KÉPANALÍZIS KÉSZÍTETTE: KISS ALEXANDRA ELÉRHETŐSÉG: kisszandi@mailbox.unideb.hu ImageJ (Fiji) Nyílt forrás kódú, java alapú képelemző szoftver https://fiji.sc/ Számos képformátumhoz megfelelő
DIGITÁLIS KÉPANALÍZIS KÉSZÍTETTE: KISS ALEXANDRA ELÉRHETŐSÉG: kisszandi@mailbox.unideb.hu ImageJ (Fiji) Nyílt forrás kódú, java alapú képelemző szoftver https://fiji.sc/ Számos képformátumhoz megfelelő
1. ábra. 24B-19 feladat
 . gyakorlat.. Feladat: (HN 4B-9) A +Q töltés egy hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld.. ábra.). Számítsuk ki az E elektromos térerősséget a vonal. ábra. 4B-9 feladat irányában lévő,
. gyakorlat.. Feladat: (HN 4B-9) A +Q töltés egy hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld.. ábra.). Számítsuk ki az E elektromos térerősséget a vonal. ábra. 4B-9 feladat irányában lévő,
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Mintavétel: szorzás az idő tartományban
 1 Mintavételi törvény AD átalakítók + sávlimitált jel τ időközönként mintavétel Mintavétel: szorzás az idő tartományban 1/τ körfrekvenciánként ismétlődik - konvolúció a frekvenciatérben. 2 Nem fednek át:
1 Mintavételi törvény AD átalakítók + sávlimitált jel τ időközönként mintavétel Mintavétel: szorzás az idő tartományban 1/τ körfrekvenciánként ismétlődik - konvolúció a frekvenciatérben. 2 Nem fednek át:
Matematika A1a Analízis
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
Tárgy. Forgóasztal. Lézer. Kamera 3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL
 3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL. Bevezetés A lézeres letapogatás a ma elérhet legpontosabb 3D-s rekonstrukciót teszi lehet vé. Alapelve roppant egyszer : egy lézeres csíkkal megvilágítjuk a tárgyat.
3D REKONSTRUKCIÓ LÉZERES LETAPOGATÁSSAL. Bevezetés A lézeres letapogatás a ma elérhet legpontosabb 3D-s rekonstrukciót teszi lehet vé. Alapelve roppant egyszer : egy lézeres csíkkal megvilágítjuk a tárgyat.
VIK A2 Matematika - BOSCH, Hatvan, 3. Gyakorlati anyag. Mátrix rangja
 VIK A2 Matematika - BOSCH, Hatvan, 3. Gyakorlati anyag 2019. március 21. Mátrix rangja 1. Számítsuk ki az alábbi mátrixok rangját! (d) 1 1 2 2 4 5 1 1 1 1 1 1 1 1 2 1 2 1 1 0 1 1 2 1 0 1 1 1 1 2 3 1 3
VIK A2 Matematika - BOSCH, Hatvan, 3. Gyakorlati anyag 2019. március 21. Mátrix rangja 1. Számítsuk ki az alábbi mátrixok rangját! (d) 1 1 2 2 4 5 1 1 1 1 1 1 1 1 2 1 2 1 1 0 1 1 2 1 0 1 1 1 1 2 3 1 3
Időjárási radarok és produktumaik
 ORSZÁGOS METEOROLÓGIAI SZOLGÁLAT Időjárási radarok és produktumaik Hadvári Marianna Országos Meteorológiai Szolgálat Távérzékelési Osztály 2018. október 6. Alapítva: 1870 Radio Detection And Ranging 1935
ORSZÁGOS METEOROLÓGIAI SZOLGÁLAT Időjárási radarok és produktumaik Hadvári Marianna Országos Meteorológiai Szolgálat Távérzékelési Osztály 2018. október 6. Alapítva: 1870 Radio Detection And Ranging 1935
Regresszió számítás. Tartalomjegyzék: GeoEasy V2.05+ Geodéziai Kommunikációs Program
 Regresszió számítás GeoEasy V2.05+ Geodéziai Kommunikációs Program DigiKom Kft. 2006-2010 Tartalomjegyzék: Egyenes x változik Egyenes y változik Egyenes y és x változik Kör Sík z változik Sík y, x és z
Regresszió számítás GeoEasy V2.05+ Geodéziai Kommunikációs Program DigiKom Kft. 2006-2010 Tartalomjegyzék: Egyenes x változik Egyenes y változik Egyenes y és x változik Kör Sík z változik Sík y, x és z
A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld ábra ábra
 . Gyakorlat 4B-9 A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld. 4-6 ábra.). Számítsuk ki az E elektromos térerősséget a vonal irányában lévő, annak.. ábra. 4-6 ábra végpontjától
. Gyakorlat 4B-9 A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld. 4-6 ábra.). Számítsuk ki az E elektromos térerősséget a vonal irányában lévő, annak.. ábra. 4-6 ábra végpontjától
ANTENNAMÉRÉSEK. Leírás R12C - ANTENNAMÉRÉSEK ANTENNÁK HARDVERELEMEK VIZSGÁLATA
 Leírás ANTENNAMÉRÉSEK R12C - ANTENNAMÉRÉSEK ANTENNÁK HARDVERELEMEK VIZSGÁLATA R1 - A TÉRBELI RÁDIÓFREKVENCIÁS AZONOSÍTÁS LEHETŐSÉGEINEK KUTATÁSA BUDAPEST, 2013 Tartalomjegyzék 1. A DOKUMENTUM POZICIONÁLÁSA...
Leírás ANTENNAMÉRÉSEK R12C - ANTENNAMÉRÉSEK ANTENNÁK HARDVERELEMEK VIZSGÁLATA R1 - A TÉRBELI RÁDIÓFREKVENCIÁS AZONOSÍTÁS LEHETŐSÉGEINEK KUTATÁSA BUDAPEST, 2013 Tartalomjegyzék 1. A DOKUMENTUM POZICIONÁLÁSA...
b) Ábrázolja ugyanabban a koordinátarendszerben a g függvényt! (2 pont) c) Oldja meg az ( x ) 2
 1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
Digitális képek feldolgozása Előfeldolgozás Radiometriai korrekció Geometriai korrekció Képjavítás Szűrők Sávok közötti műveletek Képosztályozás Utófe
 Távérzékelés Digitális felvételek előfeldolgozása (EENAFOTOTV, ETNATAVERV) Erdőmérnöki szak, Környezettudós szak Király Géza NyME, Erdőmérnöki Kar Geomatikai, Erdőfeltárási és Vízgazdálkodási Intézet Földmérési
Távérzékelés Digitális felvételek előfeldolgozása (EENAFOTOTV, ETNATAVERV) Erdőmérnöki szak, Környezettudós szak Király Géza NyME, Erdőmérnöki Kar Geomatikai, Erdőfeltárási és Vízgazdálkodási Intézet Földmérési
3D-s számítógépes geometria és alakzatrekonstrukció
 3D-s számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav08 Dr. Várady Tamás,
3D-s számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav08 Dr. Várady Tamás,
Digitális képek szegmentálása. 5. Textúra. Kató Zoltán.
 Digitális képek szegmentálása 5. Textúra Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Textúra fogalma Sklansky: Egy képen egy területnek állandó textúrája van ha a lokális statisztikák vagy
Digitális képek szegmentálása 5. Textúra Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Textúra fogalma Sklansky: Egy képen egy területnek állandó textúrája van ha a lokális statisztikák vagy
Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez
 1 Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez Havancsák Károly Dankházi Zoltán Ratter Kitti Varga Gábor Visegrád 2012. január Elektron diffrakció 2 Diffrakció - kinematikus elmélet
1 Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez Havancsák Károly Dankházi Zoltán Ratter Kitti Varga Gábor Visegrád 2012. január Elektron diffrakció 2 Diffrakció - kinematikus elmélet
Villamosságtan szigorlati tételek
 Villamosságtan szigorlati tételek 1.1. Egyenáramú hálózatok alaptörvényei 1.2. Lineáris egyenáramú hálózatok elemi számítása 1.3. Nemlineáris egyenáramú hálózatok elemi számítása 1.4. Egyenáramú hálózatok
Villamosságtan szigorlati tételek 1.1. Egyenáramú hálózatok alaptörvényei 1.2. Lineáris egyenáramú hálózatok elemi számítása 1.3. Nemlineáris egyenáramú hálózatok elemi számítása 1.4. Egyenáramú hálózatok
Képrekonstrukció 6. előadás
 Képrekonstrukció 6. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Diszkrét tomográfia (DT) A CT-hez több száz vetület szükséges időigényes költséges károsíthatja
Képrekonstrukció 6. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Diszkrét tomográfia (DT) A CT-hez több száz vetület szükséges időigényes költséges károsíthatja
Geofizikai kutatómódszerek I.
 Geofizikai kutatómódszerek I. A gravitációs és mágneses kutatómódszer Dr. Szabó Norbert Péter egyetemi docens Miskolci Egyetem Geofizikai Intézeti Tanszék e-mail: norbert.szabo.phd@gmail.com 1. A gravitációs
Geofizikai kutatómódszerek I. A gravitációs és mágneses kutatómódszer Dr. Szabó Norbert Péter egyetemi docens Miskolci Egyetem Geofizikai Intézeti Tanszék e-mail: norbert.szabo.phd@gmail.com 1. A gravitációs
L-transzformáltja: G(s) = L{g(t)}.
 Tartalom 1. Stabilitáselmélet stabilitás feltételei inverz inga egyszerűsített modellje 2. Zárt, visszacsatolt rendszerek stabilitása Nyquist stabilitási kritérium Bode stabilitási kritérium 2018 1 Stabilitáselmélet
Tartalom 1. Stabilitáselmélet stabilitás feltételei inverz inga egyszerűsített modellje 2. Zárt, visszacsatolt rendszerek stabilitása Nyquist stabilitási kritérium Bode stabilitási kritérium 2018 1 Stabilitáselmélet
Jelfeldolgozás - ANTAL Margit. impulzusválasz. tulajdonságai. Rendszerek. ANTAL Margit. Sapientia - Erdélyi Magyar Tudományegyetem
 Sapientia - Erdélyi Magyar Tudományegyetem 2007 Megnevezések Diszkrét Dirac jel Delta függvény Egységimpluzus függvény A diszkrét Dirac jel δ[n] = { 1, n = 0 0, n 0 d[n] { 1, n = n0 δ[n n 0 ] = 0, n n
Sapientia - Erdélyi Magyar Tudományegyetem 2007 Megnevezések Diszkrét Dirac jel Delta függvény Egységimpluzus függvény A diszkrét Dirac jel δ[n] = { 1, n = 0 0, n 0 d[n] { 1, n = n0 δ[n n 0 ] = 0, n n
Transzformációk. Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform
 Transzformációk Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform Koordinátarendszerek: modelltér Koordinátarendszerek: világtér Koordinátarendszerek: kameratér up right z eye ahead
Transzformációk Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform Koordinátarendszerek: modelltér Koordinátarendszerek: világtér Koordinátarendszerek: kameratér up right z eye ahead
Röntgendiagnosztika és CT
 Röntgendiagnosztika és CT 2013.04.09. Röntgensugárzás Elektromágneses sugárzás (f=10 16 10 19 Hz, E=120eV 120keV (1.9*10-17 10-14 J), λ
Röntgendiagnosztika és CT 2013.04.09. Röntgensugárzás Elektromágneses sugárzás (f=10 16 10 19 Hz, E=120eV 120keV (1.9*10-17 10-14 J), λ
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
24/04/ Röntgenabszorpciós CT
 CT ésmri 2012.04.10. Röntgenabszorpciós CT 1 Élettani és Orvostudományi Nobel díj- 1979 Allan M. Cormack, Godfrey N. Hounsfield Godfrey N. Hounsfield Born:28 August 1919, Newark, United Kingdom Died: 12
CT ésmri 2012.04.10. Röntgenabszorpciós CT 1 Élettani és Orvostudományi Nobel díj- 1979 Allan M. Cormack, Godfrey N. Hounsfield Godfrey N. Hounsfield Born:28 August 1919, Newark, United Kingdom Died: 12
Csoportosítás. Térinformatikai műveletek, elemzések. Csoportosítás. Csoportosítás
 Csoportosítás Térinformatikai műveletek, elemzések Leíró (attribútum) adatokra vonatkozó kérdések, műveletek, elemzések, csoportosítások,... Térbeli (geometriai) adatokra vonatkozó kérdések, műveletek
Csoportosítás Térinformatikai műveletek, elemzések Leíró (attribútum) adatokra vonatkozó kérdések, műveletek, elemzések, csoportosítások,... Térbeli (geometriai) adatokra vonatkozó kérdések, műveletek
E(L)JÖVENDŐ. IKT kutatási eredmények a gazdaság és a társadalom szolgálatában. 1 Intelligens környezet és e-technológiák
 E(L)JÖVENDŐ IKT kutatási eredmények a gazdaság és a társadalom szolgálatában 2011. 11. 07. 1 IKT P1 T9 Modell alapú mérnöki módszerek kidolgozása orvosi és műszaki alkalmazásokhoz dr. Benyó Balázs VIK
E(L)JÖVENDŐ IKT kutatási eredmények a gazdaság és a társadalom szolgálatában 2011. 11. 07. 1 IKT P1 T9 Modell alapú mérnöki módszerek kidolgozása orvosi és műszaki alkalmazásokhoz dr. Benyó Balázs VIK
SPECT képalkotása. Hesz Gábor február
 SPECT képalkotása Hesz Gábor 2013. február 1. Bevezető Az orvosi képalkotó eljárások segítségével neminvazív módon nyerhetünk információkat a test felépítéséről és működéséről, a szervek anatómiájáról
SPECT képalkotása Hesz Gábor 2013. február 1. Bevezető Az orvosi képalkotó eljárások segítségével neminvazív módon nyerhetünk információkat a test felépítéséről és működéséről, a szervek anatómiájáról
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Láthatósági kérdések
 Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
Láthatósági kérdések Láthatósági algoritmusok Adott térbeli objektum és adott nézőpont esetén el kell döntenünk, hogy mi látható az adott alakzatból a nézőpontból, vagy irányából nézve. Az algoritmusok
x 2 e x dx c) (3x 2 2x)e 2x dx x sin x dx f) x cosxdx (1 x 2 )(sin 2x 2 cos 3x) dx e 2x cos x dx k) e x sin x cosxdx x ln x dx n) (2x + 1) ln 2 x dx
 Integrálszámítás II. Parciális integrálás. g) i) l) o) e ( + )(e e ) cos h) e sin j) (sin 3 cos) m) arctg p) arcsin e (3 )e sin f) cos ( )(sin cos 3) e cos k) e sin cos ln n) ( + ) ln. e 3 e cos 3 3 cos
Integrálszámítás II. Parciális integrálás. g) i) l) o) e ( + )(e e ) cos h) e sin j) (sin 3 cos) m) arctg p) arcsin e (3 )e sin f) cos ( )(sin cos 3) e cos k) e sin cos ln n) ( + ) ln. e 3 e cos 3 3 cos
cos 2 (2x) 1 dx c) sin(2x)dx c) cos(3x)dx π 4 cos(2x) dx c) 5sin 2 (x)cos(x)dx x3 5 x 4 +11dx arctg 11 (2x) 4x 2 +1 π 4
 Integrálszámítás I. Végezze el a következő integrálásokat:. α, haα sin() cos() e f) a sin h) () cos ().. 5 4 ( ) e + 4 sin h) (+) sin() sin() cos() + f) 5 i) cos ( +) 7 4. 4 (+) 6 4 cos() 5 +7 5. ( ) sin()cos
Integrálszámítás I. Végezze el a következő integrálásokat:. α, haα sin() cos() e f) a sin h) () cos ().. 5 4 ( ) e + 4 sin h) (+) sin() sin() cos() + f) 5 i) cos ( +) 7 4. 4 (+) 6 4 cos() 5 +7 5. ( ) sin()cos
Csoportmódszer Függvények I. (rövidített változat) Kiss Károly
 Ismétlés Adott szempontok szerint tárgyak, élőlények, számok vagy fizikai mennyiségek halmazokba rendezhetők. A halmazok kapcsolatát pedig hozzárendelésnek (relációnak, leképezésnek) nevezzük. A hozzárendelés
Ismétlés Adott szempontok szerint tárgyak, élőlények, számok vagy fizikai mennyiségek halmazokba rendezhetők. A halmazok kapcsolatát pedig hozzárendelésnek (relációnak, leképezésnek) nevezzük. A hozzárendelés
A brachistochron probléma megoldása
 A brachistochron probléma megoldása Adott a függőleges síkban két nem egy függőleges egyenesen fekvő P 0 és P 1 pont, amelyek közül a P 1 fekszik alacsonyabban. Azt a kérdést fogjuk vizsgálni. hogy van-e
A brachistochron probléma megoldása Adott a függőleges síkban két nem egy függőleges egyenesen fekvő P 0 és P 1 pont, amelyek közül a P 1 fekszik alacsonyabban. Azt a kérdést fogjuk vizsgálni. hogy van-e
ORVOSI KÉPALKOTÓ ELJÁRÁSOK. I. A digitális kép Optikai csalódások - intenzitás. Orvosi képalkotó eljárások Praktikus tudnivalók, 2012
 Orvosi képalkotó eljárások Praktikus tudnivalók, 2012 ORVOSI KÉPALKOTÓ ELJÁRÁSOK Kellermayer Miklós A tantárgy előadói és gyakorlatvezetői: az Anatómiai, Szövet- és Fejlődéstani Intézet, a Humánmorfológiai
Orvosi képalkotó eljárások Praktikus tudnivalók, 2012 ORVOSI KÉPALKOTÓ ELJÁRÁSOK Kellermayer Miklós A tantárgy előadói és gyakorlatvezetői: az Anatómiai, Szövet- és Fejlődéstani Intézet, a Humánmorfológiai
Fehérzajhoz a konstans érték kell - megoldás a digitális szűrő Összegezési súlyok sin x/x szerint (ez akár analóg is lehet!!!)
 DSP processzorok: 1 2 3 HP zajgenerátor: 4 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! Fehérzajhoz a konstans érték kell - megoldás a digitális
DSP processzorok: 1 2 3 HP zajgenerátor: 4 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! Fehérzajhoz a konstans érték kell - megoldás a digitális
Rekonstrukciós eljárások. Orvosi képdiagnosztika előadás 2016 ősz
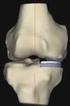 Rekonstrukciós eljárások Orvosi képdiagnosztika 14.-15. előadás 2016 ősz Előadások témája Röntgen tomográfia fizikai és matematikai alapjai 2D Radon transzformáció, szűrt visszavetítés: Fan beam / Cone
Rekonstrukciós eljárások Orvosi képdiagnosztika 14.-15. előadás 2016 ősz Előadások témája Röntgen tomográfia fizikai és matematikai alapjai 2D Radon transzformáció, szűrt visszavetítés: Fan beam / Cone
Klár Gergely 2010/2011. tavaszi félév
 Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom Pont 1 Pont 2 3 4 5 Tartalom Pont Descartes-koordináták Homogén koordináták
Számítógépes Grafika Klár Gergely tremere@elte.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom Pont 1 Pont 2 3 4 5 Tartalom Pont Descartes-koordináták Homogén koordináták
Vektorterek. =a gyakorlatokon megoldásra ajánlott
 Vektorterek =a gyakorlatokon megoldásra ajánlott 40. Alteret alkotnak-e a valós R 5 vektortérben a megadott részhalmazok? Ha igen, akkor hány dimenziósak? (a) L = { (x 1, x 2, x 3, x 4, x 5 ) x 1 = x 5,
Vektorterek =a gyakorlatokon megoldásra ajánlott 40. Alteret alkotnak-e a valós R 5 vektortérben a megadott részhalmazok? Ha igen, akkor hány dimenziósak? (a) L = { (x 1, x 2, x 3, x 4, x 5 ) x 1 = x 5,
Shift regiszter + XOR kapu: 2 n állapot
 DSP processzorok: 1 2 HP zajgenerátor: 3 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! 4 Fehérzajhoz a konstans érték kell - megoldás a digitális
DSP processzorok: 1 2 HP zajgenerátor: 3 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! 4 Fehérzajhoz a konstans érték kell - megoldás a digitális
