Képfeldolgozó eljárások áttekintés. Orvosi képdiagnosztika 9. ea ősz
|
|
|
- Lili Nagy
- 8 évvel ezelőtt
- Látták:
Átírás
1 Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea ősz
2 Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, hisztogram módosítás, zajszűrés, élkiemelés) Képelemzés Éldetektálás (szűréssel, gradiens, második derivált meghatározással, Canny, stb) Morfológiai műveletek Képszegmentálás Hisztogram (képintenzitás) alapján Textura alapján Élek, kontúrok alapján Pixelértékek alapján Komplex eljárások (Hough transzformáció, szegmentálás deformálható modellekkel: ASM, AAM, Snake, Level set módszer) Komplex eljárások: régió növesztés, watershed eljárás, edge flow, stb, Esettanulmány Egy orvosi kép (röntgenkép) szegmentálása
3 Képjavítás Cél: a kép vizuális megjelenésének javítása. Alapvetően az emberi szem számára javítunk a kép megjelenésén, de segíti a gépi képelemzést is. Tipikus képjavítási eljárások: - Kontraszt módosítás - Intenzitásviszonyok módosítása - Szűrések: - lineáris szűrések, - nemlineáris szűrések: - homomorfikus feldolgozás - order statistics filters: median, rank és ezek variánsai. - Élek kiemelése, - Zajok mérséklése
4 Kontraszt javítás Az intenzitástartomány és az intenzitásviszonyok megváltoztatása lineáris vagy nemlineáris módosítás
5 Kontraszt javítás Window-level transzformáció ablak: a lineáris meredek szakasz tartománya, Level: a lineáris szakasz középső pontja
6 A hisztogram széthúzása
7 Kontraszt javítás
8 Kontraszt javítás
9 Dinamika tartomány módosítása
10 Dinamika tartomány módosítása
11 Hisztogram módosítás
12 Hisztogram módosítás Hisztogram kiegyenlítés c=xsize*ysize/oszlopszam; for(i=0..255) { sum+=bemeneti_hisztogram[i]; while(sum>=c) { pos+=256/oszlopszam; sum-=c; } F[i]=pos; } for(i=0..xsize-1,j=0..ysize-1) kimeneti_kep_pixel[j][i]=f[bemeneti_kep_pixel [j][i]];
13 Hisztogram módosítás Olyan transzformáció, hogy az intenzitásértékek egyenletes eloszlásúakká váljanak A (lépcsős) transzformációs függvény létrehozása : - a bemeneti hisztogram elejétől indulva elkezdjük összegezni a hisztogramértékeket, egészen addig, amíg az összeg túl nem lépi a c=(x_meret x y_meret)/oszlopszam értéket. - Ha ez x=m-nél következik be, akkor a transzformációs függvényértékét m-ig nullára állítjuk és folytatjuk az összegzést, de nem nulláról, hanem az elért összeg-c értéktől, a következő átlag-túllépésig, legyen ez a pont n. - Ekkor a függvény minden m - től n-ig terjedő értéket 256/oszlopszam annyiadik többszörösére állítjuk,amelyik oszlopnál tartunk a transzformációban (az első oszlopnál 256/oszlopszam, a másodiknál 2*(256/oszlopszam) és így tovább). - Majd a megszerkesztett átviteli függvény segítségével előállítjuk a kimeneti képet, melynek hisztogramja vonalas lesz.
14
15 Adaptív hisztogram módosítás Tartományokhoz (egyes ablakhoz) eltérő hisztogram módosítást rendelünk eredeti nemadaptív adaptív
16 Zajszűrés Lineáris szűrések, szűrőkernel szűrés a képtartományban Szűrés transzformált tartományban (bázisfüggvények terében végezzük el a szűrést: Fourier, stb) Nemlineáris szűrések: homomorfikus jelfeldolgozás order statistics szűrés: median szűrés, egyéb OSF eljárások
17 Pl. aluláteresztő szűrő Lineáris szűrések
18 Eredeti Lineáris szűrés Egyenletes zaj mask 1 mask 3
19 Eredeti Lineáris szűrés Impulzus zaj mask 1 mask 3
20 Lineáris szűrés transzformált tartományban eredeti Gauss zaj pontszerű zaj zajos M=1 PCA M=1 KPCA Gauss kernel PCA-KPCA zajszűrő hatás összehasonlítása
21 Lineáris szűrés transzformált tartományban Karhunen-Loève transzformáció (KLT) Jelfüggő ortogonális transzformáció
22 Nemlineáris szűrés homomorfikus szűrés order statistic (rank) szűrés polinomiális szűrés matematikai morfológia neurális hálók nemlineáris kép visszaállítás
23 Nemlineáris szűrések Homomorfikus szűrés Multiplikativ zajok mellett hatékony megvilágítás, zajmentes kép Logaritmálás után hagyományos szűrési eljárások
24 Homomorfikus szűrés megvilágítás érzékelt kép homomorfikus szűrés eredménye Butterwoth felüláteresztő szűrés
25 Order statistics szűrés Legyen akkor az i-edik statisztika Sorbarendezi a szomszédos pixeleket növekvő inztenzitásérték szerint, kiválaszt egyet a rangnak megfelelően és ez lesz a kimenet Speciális rank szűrők: medián Kétdimenziós mediáns szűrő Az A halmaz a szűrő ablak. Az ablak alakja befolyásolja a szűrő tulajdonságait (élmegtartás, bizonyos képrészletek megtartása)
26 Medián szűrés Tulajdonságok: Jól teljesít lassan lecsengő zajeloszlásnál (hatékony az impulzus zajok eltüntetésénél) Rosszul teljesít gyorsan lecsengő eloszlásnál (pl. egyenletes zajeloszlásnál) Fehér zaj mellett aluléteresztő tulajdonságú Igyekszik megtartani az éleket Kérdés: van-e olyan jel (sajátfüggvény sajátjel), melyet nem módosít? (a lineáris szűrőknél ilyen a szinusz) Medián szűrő root jele: Minden véges hosszúságú nemroot jel a root jelhez konvergál, ha a medián szűrőt ismételten alkalmazzuk
27 Medián szűrés A zajos képből 7x7 ablak eredeti zajos kép átlagoló szűrés medián szűrés
28 Rank szűrés A zajos képből 7x7 maszk mellett 4. rangú pixelek kiválasztása (rank 4)
29 Order statistics szűrők Minimum és maximum szűrők min: növeli a sötét részeket 3 x 3 ablak 7 x 7 ablak
30 Order statistics szűrők max: növeli a világos részeket (3 x 3) (7 x 7)
31 Lineáris és nemlineáris szűrések
32 További nemlineáris szűrők Tartomány szűrő: (Range filter - Midpoint filter) nemlineáris éldetektor a kimeneti pixel érték a tartományon belüli maximum és minimum pixel értékek átlaga (középértéke) Hatékonyan alkalmazható gyors lecsengésű zaj esetén: egyenletes és esetleg Gauss zaj mellett Az élek lokalizációja nem jó Yp mean szűrő nemlineáris átlagoló szűrő: jobb Gauss zaj elnyomására mint az aritmetikai átlagoló szűrő, miközben az éleket jobban megtartja. Yp átlagoló szűrő kíváló a pozitív outlierek kiszűrésénél, ha P negatív és negatív outlierek kiszűrésére, ha P pozitív.
33 További nemlineáris szűrők Harmonikus átlag szűrés A harmonikus átlagoló szűrésnél az egyes pixelek intenzitása a környezetben lévő pixelek intenzitásértékeinek harmonikus átlagával helyettesítjük A harmonikus átlag: Nagyobb régió esetén a hatás erősebb, de hátrány a kép elmosódása. A harmonikus átlag szűrés jobb az aritmetikai átlag szűrésnél Gauss zaj elnyomásánálés az élek megtartása szempontjából. Hatékony a pozitív outlierek kiszűrésénél.
34 További nemlineáris szűrők Alfa-igazított átlagoló szűrő (Alpha-trimmed filter) lineáris és nemlineáris hatások együttes alkalmazása a szomszédos pixelek sorbarendezése növekvő sorrendben dobjunk el a lista mindkét végéről adott számú (alfa) értéket a szűrő kimeneti értéke a maradék pixelek átlaga alfa = 0 átlagoló szűrő alfa = (n 2-1)/2 medián szűrő
35 Különböző szűrők összehasonlítása Eredeti képek Átlagoló szűrt képek (aritmetikai átlag)
36 Különböző szűrők összehasonlítása Eredeti képek Geometriai átlagoló szűrt képek
37 Különböző szűrők összehasonlítása Eredeti képek Medián szűrt képek
38 Különböző szűrők összehasonlítása Eredeti képek Max. szűrt képek
39 Különböző szűrők összehasonlítása Eredeti képek Min. szűrt képek
40 Különböző szűrők összehasonlítása Eredeti képek Midpont szűrt képek
41 Különböző szűrők összehasonlítása Eredeti képek Yp mean szűrt képek
42 Különböző szűrők összehasonlítása Eredeti képek Harmonikus átlagolással szűrt képek
43 Polinomiális szűrők A pixel értékek polinomiális vagy törtfüggvényei Kép javítás (kontraszt élesítés, élmegtartó zajszűrés, textura szegmentálás, élkiemelés, élszegmentálás) Van bizonyos kapcsolata a lineáris szűrőkkel (paramétereiben lineáris, adaptív változatnál előnyök) Számítási komplexitás jelentősen nagyobb, különösen, ah a nemlinearitás mértékét növeljük A nemlineáris szűrők Taylor sor vagy Volterra sor formájában írhatók fel. Taylor sor : hatványfüggvény Volterra sor különböző pozíciójú (időben vagy a képtartományban) vett értékek szorzatai
44 Polinomiális szűrők A polinomiális szűrők tulajdonságai: Paramétereiben lineáris, de nemlineáris szűrő Az együtthatókat adaptálni lehet, lineáris megközelítéssel y n = h,..., p xn hp i1 ip h 0 + p=1 h p (xn) Általában minden egyes tag az alábbi összefüggéssel adható meg: 1,..., 1 h x h i i x n i x n i p n p p p i i 1 h h0 offset 1 p egy digitális FIR szűrő válasza y n f [ x( n),( x n 1,..., x n N, y n 1,..., y n M ] f ( xyq,, ) 1 Általánosabb nemlineáris szűrő megadási forma:
45 Adaptív lineáris szűrő: Adaptív szűrők Adaptív nemlineáris szűrők y i = f( a j i x j (i)) ahol f valamilyen nemlineáris függvény j
46 Adaptiv szűrés Adaptív szűrésnél analizáljuk az egyes tartományokat és a szűrő jellemzőit a környezet statisztikájához igazítjuk Egy példa: Lee szűrő a sima régiókban redukálja a zajt, miközben a finom részleteket megtartja Az egyes pixelekt vagy változatlanul hagyja, vagy szűri. Tipikus ablakmérete 3x3... 7x 7 Lokális átlag és variancia meghatározása A válasz ahol Adaptív szűrők Ahol a variancia nulla, az átlag a válaszérték Ha van variancia: A együtthatóval súlyozunk Megtartja az éleket, miközben a zajt redukálja
47 Adaptív szűrők Tesz kép MRI
48 Ultrahangképnél Adaptív szűrők
49 Éljavítás, éldetektálás Élkiemelés Szűréssel: magasfrekvenciás kiemelés, felüláteresztő szűrés
50 Éljavítás, éldetektálás Zónás szűrés Közvetlenül a Fourier tartományban definiáljuk az átviteli függvényt Egyébként C vágási frekvencia 0 < C 1+N/2
51 Butterworth szűrés ahol Éljavítás, éldetektálás
52 Éljavítás, éldetektálás
53 Éljavítás, éldetektálás Statisztikus differenciálás Minden pixel értékét elosztjuk a szórásával, ahol a szórást a környezetében lévő pixelekből számítjuk Minden pixelre számítunk átlagértéket és szórást A javított kép amplitúdója nő, ahol a pixel jelentősen elr a környezetétől, míg máshol csökken (automatikus erősítésszabályozás)
54 Éljavítás, éldetektálás Wallis operátor Általánosabb forma: Kívánt átlagos középérték, szórás és a maximális erősítési tényező. szerepe: túl nagy kimeneti érték meggátlása, ha a szórás túl kicsi 0 p 1 a képtartománytól függő erősítés a képtartománytól függő háttér Kívánt szórás, hogy a képfüggő erősítés A max és A min között legyen D max D(j,k) maximuma
55 Éljavítás, élkiemelés Eredeti átlag 0-0,98 szórás 0,01-0,26 háttér 0,09-0,88 Képfüggő erősítés 0,75 2,35 Wallis eredménye Paraméterek:
Képfeldolgozó eljárások áttekintés. Orvosi képdiagnosztika 9. ea ősz
 Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás,
Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás,
Képfeldolgozó eljárások áttekintés. Orvosi képdiagnosztika
 Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás, zajszűrés) Képelemzés
Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás, zajszűrés) Képelemzés
Képfeldolgozó eljárások áttekintés. Orvosi képdiagnosztika 9. ea ősz
 Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás,
Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás,
Képrestauráció Képhelyreállítás
 Képrestauráció Képhelyreállítás Képrestauráció - A képrestauráció az a folyamat mellyel a sérült képből eltávolítjuk a degradációt, eredményképpen pedig az eredetihez minél közelebbi képet szeretnénk kapni
Képrestauráció Képhelyreállítás Képrestauráció - A képrestauráció az a folyamat mellyel a sérült képből eltávolítjuk a degradációt, eredményképpen pedig az eredetihez minél közelebbi képet szeretnénk kapni
3. Szűrés képtérben. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 3. Szűrés képtérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE http://www.inf.u-szeged.hu/~kato/teaching/ 2 Kép transzformációk típusai Kép értékkészletének radiometriai információ
3. Szűrés képtérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE http://www.inf.u-szeged.hu/~kato/teaching/ 2 Kép transzformációk típusai Kép értékkészletének radiometriai információ
Képszegmentáló eljárások. Orvosi képdiagnosztika 2018 ősz
 Képszegmentáló eljárások Orvosi képdiagnosztika 2018 ősz Képszegmentálás Anatómiai részek elkülönítés: pl. csontok, szív, erek, szürkefehér állomány, stb Vizsgálandó terület körbehatárolása: pl. tüdőterület
Képszegmentáló eljárások Orvosi képdiagnosztika 2018 ősz Képszegmentálás Anatómiai részek elkülönítés: pl. csontok, szív, erek, szürkefehér állomány, stb Vizsgálandó terület körbehatárolása: pl. tüdőterület
Pontműveletek. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar február 20.
 Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
Sergyán Szabolcs szeptember 21.
 Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea
 Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea Geometrikus deformálható modellek Görbe evolúció Level set módszer A görbe evolúció parametrizálástól független mindössze geometriai
Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea Geometrikus deformálható modellek Görbe evolúció Level set módszer A görbe evolúció parametrizálástól független mindössze geometriai
Képfeldolgozás jól párhuzamosítható
 Képfeldolgozás jól párhuzamosítható B. Wilkinson, M. Allen: Parallel Programming, Pearson Education Prentice Hall, 2nd ed., 2005. könyv 12. fejezete alapján Vázlat A képfeldolgozás olyan alkalmazási terület,
Képfeldolgozás jól párhuzamosítható B. Wilkinson, M. Allen: Parallel Programming, Pearson Education Prentice Hall, 2nd ed., 2005. könyv 12. fejezete alapján Vázlat A képfeldolgozás olyan alkalmazási terület,
Jelfeldolgozás bevezető. Témalaboratórium
 Jelfeldolgozás bevezető Témalaboratórium Tartalom Jelfeldolgozás alapjai Lineáris rendszerelmélet Fourier transzformációk és kapcsolataik Spektrális képek értelmezése Képfeldolgozás alapjai Néhány nevezetesebb
Jelfeldolgozás bevezető Témalaboratórium Tartalom Jelfeldolgozás alapjai Lineáris rendszerelmélet Fourier transzformációk és kapcsolataik Spektrális képek értelmezése Képfeldolgozás alapjai Néhány nevezetesebb
2. Pont operációk. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 2. Pont operációk Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Kép transzformációk típusai Kép értékkészletének (radiometriai információ)
2. Pont operációk Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Kép transzformációk típusai Kép értékkészletének (radiometriai információ)
A médiatechnológia alapjai
 A médiatechnológia alapjai Úgy döntöttem, hogy a Szirányi oktatta előadások számonkérhetőnek tűnő lényegét kiemelem, az alapján, amit a ZH-ról mondott: rövid kérdések. A rész és az egész: összefüggések
A médiatechnológia alapjai Úgy döntöttem, hogy a Szirányi oktatta előadások számonkérhetőnek tűnő lényegét kiemelem, az alapján, amit a ZH-ról mondott: rövid kérdések. A rész és az egész: összefüggések
6. Éldetektálás. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 6. Éldetektálás Kató Zoltán Képeldolgozás és Számítógépes Graika tanszék SZTE (http://www.in.u-szeged.hu/~kato/teaching/) 2 Élek A képen ott található él, ahol a kép-üggvény hirtelen változik. A kép egy
6. Éldetektálás Kató Zoltán Képeldolgozás és Számítógépes Graika tanszék SZTE (http://www.in.u-szeged.hu/~kato/teaching/) 2 Élek A képen ott található él, ahol a kép-üggvény hirtelen változik. A kép egy
10.1. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ
 101 ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel történik A feldolgozás előtt az analóg jeleket digitalizálni kell Rendszerint az
101 ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel történik A feldolgozás előtt az analóg jeleket digitalizálni kell Rendszerint az
Mintavétel: szorzás az idő tartományban
 1 Mintavételi törvény AD átalakítók + sávlimitált jel τ időközönként mintavétel Mintavétel: szorzás az idő tartományban 1/τ körfrekvenciánként ismétlődik - konvolúció a frekvenciatérben. 2 Nem fednek át:
1 Mintavételi törvény AD átalakítók + sávlimitált jel τ időközönként mintavétel Mintavétel: szorzás az idő tartományban 1/τ körfrekvenciánként ismétlődik - konvolúció a frekvenciatérben. 2 Nem fednek át:
Jelkondicionálás. Elvezetés. a bioelektromos jelek kis amplitúdójúak. extracelluláris spike: néhányszor 10 uv. EEG hajas fejbőrről: max 50 uv
 Jelkondicionálás Elvezetés 2/12 a bioelektromos jelek kis amplitúdójúak extracelluláris spike: néhányszor 10 uv EEG hajas fejbőrről: max 50 uv EKG: 1 mv membránpotenciál: max. 100 mv az amplitúdó növelésére,
Jelkondicionálás Elvezetés 2/12 a bioelektromos jelek kis amplitúdójúak extracelluláris spike: néhányszor 10 uv EEG hajas fejbőrről: max 50 uv EKG: 1 mv membránpotenciál: max. 100 mv az amplitúdó növelésére,
Mit lássunk élnek? Hol van az él? Milyen vastag legyen? Hol
 Textúra Könnyű az élt megtalálni? Mi lássunk élnek? Mit lássunk élnek? Hol van az él? Milyen vastag legyen? Mit lássunk élnek? Zaj A zajpontokat nem szabad az élpontokkal összekeverni Egy vagy két él?
Textúra Könnyű az élt megtalálni? Mi lássunk élnek? Mit lássunk élnek? Hol van az él? Milyen vastag legyen? Mit lássunk élnek? Zaj A zajpontokat nem szabad az élpontokkal összekeverni Egy vagy két él?
Digitális képek szegmentálása. 5. Textúra. Kató Zoltán.
 Digitális képek szegmentálása 5. Textúra Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Textúra fogalma Sklansky: Egy képen egy területnek állandó textúrája van ha a lokális statisztikák vagy
Digitális képek szegmentálása 5. Textúra Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Textúra fogalma Sklansky: Egy képen egy területnek állandó textúrája van ha a lokális statisztikák vagy
Képszűrés II. Digitális képelemzés alapvető algoritmusai. Laplace-operátor és approximációja. Laplace-szűrő és átlagolás. Csetverikov Dmitrij
 Képszűrés II Digitális képelemzés alapvető algoritmusai Csetverikov Dmitrij Eötvös Lóránd Egyetem, Budapest csetverikov@sztaki.hu http://vision.sztaki.hu Informatikai Kar 1 Laplace-szűrő 2 Gauss- és Laplace-képpiramis
Képszűrés II Digitális képelemzés alapvető algoritmusai Csetverikov Dmitrij Eötvös Lóránd Egyetem, Budapest csetverikov@sztaki.hu http://vision.sztaki.hu Informatikai Kar 1 Laplace-szűrő 2 Gauss- és Laplace-képpiramis
Digitális jelfeldolgozás
 Digitális jelfeldolgozás Kvantálás Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010. szeptember 15. Áttekintés
Digitális jelfeldolgozás Kvantálás Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010. szeptember 15. Áttekintés
Idő-frekvencia transzformációk waveletek
 Idő-frekvencia transzformációk waveletek Pokol Gergő BME NTI Üzemi mérések és diagnosztika 2015. április 23. Vázlat Alapfogalmak az idő-frekvencia síkon Rövid idejű Fourier-transzformáció spektrogram Folytonos
Idő-frekvencia transzformációk waveletek Pokol Gergő BME NTI Üzemi mérések és diagnosztika 2015. április 23. Vázlat Alapfogalmak az idő-frekvencia síkon Rövid idejű Fourier-transzformáció spektrogram Folytonos
X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ
 X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel és módszerekkel történik. A feldolgozás előtt az analóg jeleket digitalizálni kell.
X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel és módszerekkel történik. A feldolgozás előtt az analóg jeleket digitalizálni kell.
Ellenőrző kérdések a Jelanalízis és Jelfeldolgozás témakörökhöz
 Ellenőrző kérdések a Jelanalízis és Jelfeldolgozás témakörökhöz 1. Hogyan lehet osztályozni a jeleket időfüggvényük időtartama szerint? 2. Mi a periodikus jelek definiciója? (szöveg, képlet, 3. Milyen
Ellenőrző kérdések a Jelanalízis és Jelfeldolgozás témakörökhöz 1. Hogyan lehet osztályozni a jeleket időfüggvényük időtartama szerint? 2. Mi a periodikus jelek definiciója? (szöveg, képlet, 3. Milyen
Least Squares becslés
 Least Squares becslés A négyzetes hibafüggvény: i d i ( ) φx i A négyzetes hibafüggvény mellett a minimumot biztosító megoldás W=( d LS becslés A gradiens számítása és nullává tétele eredményeképp A megoldás
Least Squares becslés A négyzetes hibafüggvény: i d i ( ) φx i A négyzetes hibafüggvény mellett a minimumot biztosító megoldás W=( d LS becslés A gradiens számítása és nullává tétele eredményeképp A megoldás
Elektronika Előadás. Analóg és kapcsolt kapacitású szűrők
 Elektronika 2 8. Előadás Analóg és kapcsolt kapacitású szűrők Irodalom - Megyeri János: Analóg elektronika, Tankönyvkiadó, 1990 - Ron Mancini (szerk): Op Amps for Everyone, Texas Instruments, 2002 16.
Elektronika 2 8. Előadás Analóg és kapcsolt kapacitású szűrők Irodalom - Megyeri János: Analóg elektronika, Tankönyvkiadó, 1990 - Ron Mancini (szerk): Op Amps for Everyone, Texas Instruments, 2002 16.
Képfeldolgozás jól párhuzamosítható
 Képeldolgozás jól párhuzamosítható B. Wilkinson, M. Allen: Parallel Programming, Pearson Education Prentice Hall, nd ed., 005. könyv. ejezete alapján Vázlat A képeldolgozás olyan alkalmazási terület, amely
Képeldolgozás jól párhuzamosítható B. Wilkinson, M. Allen: Parallel Programming, Pearson Education Prentice Hall, nd ed., 005. könyv. ejezete alapján Vázlat A képeldolgozás olyan alkalmazási terület, amely
4. Szűrés frekvenciatérben
 4. Szűrés frekvenciatérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) Unitér transzformációk Az unitér transzformációk olyan lineáris,
4. Szűrés frekvenciatérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) Unitér transzformációk Az unitér transzformációk olyan lineáris,
Fourier térbeli analízis, inverz probléma. Orvosi képdiagnosztika 5-7. ea ősz
 Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 5-7. ea. 2017 ősz 5. Előadás témái Fourier transzformációk és kapcsolataik: FS, FT, DTFT, DFT, DFS Mintavételezés, interpoláció Folytonos
Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 5-7. ea. 2017 ősz 5. Előadás témái Fourier transzformációk és kapcsolataik: FS, FT, DTFT, DFT, DFS Mintavételezés, interpoláció Folytonos
STATISZTIKA. A maradék független a kezelés és blokk hatástól. Maradékok leíró statisztikája. 4. A modell érvényességének ellenőrzése
 4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
1. óra Digitális képfeldolgozás
 1. óra Digitális képfeldolgozás Képkorrekció A hisztogram A hisztogram a képünk intenzitás-eloszlását ábrázolja. Ebben a koordinátarendszerben a vízszintes tengelyen vesszük fel a teljes szürkeskálát úgy,
1. óra Digitális képfeldolgozás Képkorrekció A hisztogram A hisztogram a képünk intenzitás-eloszlását ábrázolja. Ebben a koordinátarendszerben a vízszintes tengelyen vesszük fel a teljes szürkeskálát úgy,
Folyamatosan változó mennyiségek feldolgozása II. 7. előadás
 Folyamatosan változó mennyiségek feldolgozása II. 7. előadás Tartalom sztochasztikus folyamatok mintavételezés (lásd Fizikai geod.) LKN kollokáció (lásd Fizikai geod.) geostatisztika, krigelés szűrések
Folyamatosan változó mennyiségek feldolgozása II. 7. előadás Tartalom sztochasztikus folyamatok mintavételezés (lásd Fizikai geod.) LKN kollokáció (lásd Fizikai geod.) geostatisztika, krigelés szűrések
Képelemzési módszerek. Automatikus retina képelemzési módszerek 3/3/2011. MI módszerek a képelemzésben. A retina analízis digitális képei
 Képelemzési módszerek Mesterséges Intelligencia II. előadás Dr. Nyúl László Szegedi Tudományegyetem Képeld 2011.03.01. MI módszerek a képelemzésben Képjavítás Képszegmentálás Alakelismerés Képleírás (jelenet
Képelemzési módszerek Mesterséges Intelligencia II. előadás Dr. Nyúl László Szegedi Tudományegyetem Képeld 2011.03.01. MI módszerek a képelemzésben Képjavítás Képszegmentálás Alakelismerés Képleírás (jelenet
Jelek és rendszerek 1. 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék
 Jelek és rendszerek 1 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék 1 Ajánlott irodalom: FODOR GYÖRGY : JELEK ÉS RENDSZEREK EGYETEMI TANKÖNYV Műegyetemi Kiadó, Budapest, 2006
Jelek és rendszerek 1 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék 1 Ajánlott irodalom: FODOR GYÖRGY : JELEK ÉS RENDSZEREK EGYETEMI TANKÖNYV Műegyetemi Kiadó, Budapest, 2006
Digitális jelfeldolgozás
 Digitális jelfeldolgozás Átviteli függvények Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2011. október 13. Digitális
Digitális jelfeldolgozás Átviteli függvények Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2011. október 13. Digitális
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 3. MÉRÉSFELDOLGOZÁS
 ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 3. MÉRÉSFELDOLGOZÁS Dr. Soumelidis Alexandros 2018.10.04. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mérés-feldolgozás
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 3. MÉRÉSFELDOLGOZÁS Dr. Soumelidis Alexandros 2018.10.04. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mérés-feldolgozás
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Matematikai statisztika. Mi a modell? Binomiális eloszlás sűrűségfüggvény. Binomiális eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
Képrekonstrukció 3. előadás
 Képrekonstrukció 3. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Computed Tomography (CT) Elv: Röntgen-sugarak áthatolása 3D objektum 3D térfogati kép Mérések
Képrekonstrukció 3. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Computed Tomography (CT) Elv: Röntgen-sugarak áthatolása 3D objektum 3D térfogati kép Mérések
MATLAB Image Processing Toolbox
 Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2007. november 12. Kép átméretezése imresize(a,m,method) Az A képet m-szeresére méretezi át. method értéke lehet: nearest (alapértelmezett) bilinear
Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2007. november 12. Kép átméretezése imresize(a,m,method) Az A képet m-szeresére méretezi át. method értéke lehet: nearest (alapértelmezett) bilinear
Wavelet transzformáció
 1 Wavelet transzformáció Más felbontás: Walsh, Haar, wavelet alapok! Eddig: amplitúdó vagy frekvencia leírás: Pl. egy rövid, Dirac-delta jellegű impulzus Fourier-transzformált: nagyon sok, kb. ugyanolyan
1 Wavelet transzformáció Más felbontás: Walsh, Haar, wavelet alapok! Eddig: amplitúdó vagy frekvencia leírás: Pl. egy rövid, Dirac-delta jellegű impulzus Fourier-transzformált: nagyon sok, kb. ugyanolyan
Gyakorló többnyire régebbi zh feladatok. Intelligens orvosi műszerek október 2.
 Gyakorló többnyire régebbi zh feladatok Intelligens orvosi műszerek 2018. október 2. Régebbi zh feladat - #1 Az ábrán látható két jelet, illetve összegüket mozgóablak mediánszűréssel szűrjük egy 11 pontos
Gyakorló többnyire régebbi zh feladatok Intelligens orvosi műszerek 2018. október 2. Régebbi zh feladat - #1 Az ábrán látható két jelet, illetve összegüket mozgóablak mediánszűréssel szűrjük egy 11 pontos
Véletlen jelenség: okok rendszere hozza létre - nem ismerhetjük mind, ezért sztochasztikus.
 Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Idő-frekvencia transzformációk waveletek
 Idő-frekvencia transzformációk waveletek Pokol Gergő BME NTI Üzemi mérések és diagnosztika 013. áprils 17. Vázlat Alapfogalmak az idő-frekvencia síkon Rövid idejű Fourier-transzformáció spektrogram Folytonos
Idő-frekvencia transzformációk waveletek Pokol Gergő BME NTI Üzemi mérések és diagnosztika 013. áprils 17. Vázlat Alapfogalmak az idő-frekvencia síkon Rövid idejű Fourier-transzformáció spektrogram Folytonos
Segítség az outputok értelmezéséhez
 Tanulni: 10.1-10.3, 10.5, 11.10. Hf: A honlapra feltett falco_exp.zip-ben lévő exploratív elemzések áttanulmányozása, érdekességek, észrevételek kigyűjtése. Segítség az outputok értelmezéséhez Leiro: Leíró
Tanulni: 10.1-10.3, 10.5, 11.10. Hf: A honlapra feltett falco_exp.zip-ben lévő exploratív elemzések áttanulmányozása, érdekességek, észrevételek kigyűjtése. Segítség az outputok értelmezéséhez Leiro: Leíró
Kompenzációs kör vizsgálata. LabVIEW 7.1 4. előadás
 Kompenzációs kör vizsgálata LabVIEW 7.1 4. előadás Dr. Iványi Miklósné, egyetemi tanár LabVIEW-7.1 EA-4/1 Mágneses hiszterézis mérése előírt kimeneti jel mellett DAQ Rn Un etalon ellenállás etalon ellenállás
Kompenzációs kör vizsgálata LabVIEW 7.1 4. előadás Dr. Iványi Miklósné, egyetemi tanár LabVIEW-7.1 EA-4/1 Mágneses hiszterézis mérése előírt kimeneti jel mellett DAQ Rn Un etalon ellenállás etalon ellenállás
FIR és IIR szűrők tervezése digitális jelfeldolgozás területén
 Dr. Szabó Anita FIR és IIR szűrők tervezése digitális jelfeldolgozás területén A Szabadkai Műszaki Szakfőiskola oktatójaként kutatásaimat a digitális jelfeldolgozás területén folytatom, ezen belül a fő
Dr. Szabó Anita FIR és IIR szűrők tervezése digitális jelfeldolgozás területén A Szabadkai Műszaki Szakfőiskola oktatójaként kutatásaimat a digitális jelfeldolgozás területén folytatom, ezen belül a fő
Idő-frekvencia transzformációk waveletek
 Idő-frekvencia transzformációk waveletek Pokol Gergő BME NTI Üzemi mérések és diagnosztika 2014. május 8. Vázlat Alapfogalmak az idő-frekvencia síkon Rövid idejű Fourier-transzformáció spektrogram Folytonos
Idő-frekvencia transzformációk waveletek Pokol Gergő BME NTI Üzemi mérések és diagnosztika 2014. május 8. Vázlat Alapfogalmak az idő-frekvencia síkon Rövid idejű Fourier-transzformáció spektrogram Folytonos
Éldetektálás. Digitális képelemzés alapvető algoritmusai. Képi élek. Csetverikov Dmitrij. A Canny-éldetektor Az éldetektálás utófeldolgozása
 Éldetektálás Digitális képelemzés alapvető algoritmusai 1 Alapvető képi sajátságok Csetverikov Dmitrij Eötvös Lóránd Egyetem, Budapest csetverikov@sztaki.hu http://vision.sztaki.hu Informatikai Kar Az
Éldetektálás Digitális képelemzés alapvető algoritmusai 1 Alapvető képi sajátságok Csetverikov Dmitrij Eötvös Lóránd Egyetem, Budapest csetverikov@sztaki.hu http://vision.sztaki.hu Informatikai Kar Az
Távérzékelt felvételek előfeldolgozása
 Távérzékelt felvételek előfeldolgozása Csornai Gábor László István Budapest Főváros Kormányhivatala Mezőgazdasági Távérzékelési és Helyszíni Ellenőrzési Osztály Az előadás 2011-es átdolgozott változata
Távérzékelt felvételek előfeldolgozása Csornai Gábor László István Budapest Főváros Kormányhivatala Mezőgazdasági Távérzékelési és Helyszíni Ellenőrzési Osztály Az előadás 2011-es átdolgozott változata
Geofizikai kutatómódszerek I.
 Geofizikai kutatómódszerek I. A gravitációs és mágneses kutatómódszer Dr. Szabó Norbert Péter egyetemi docens Miskolci Egyetem Geofizikai Intézeti Tanszék e-mail: norbert.szabo.phd@gmail.com 1. A gravitációs
Geofizikai kutatómódszerek I. A gravitációs és mágneses kutatómódszer Dr. Szabó Norbert Péter egyetemi docens Miskolci Egyetem Geofizikai Intézeti Tanszék e-mail: norbert.szabo.phd@gmail.com 1. A gravitációs
Fehérzajhoz a konstans érték kell - megoldás a digitális szűrő Összegezési súlyok sin x/x szerint (ez akár analóg is lehet!!!)
 DSP processzorok: 1 2 3 HP zajgenerátor: 4 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! Fehérzajhoz a konstans érték kell - megoldás a digitális
DSP processzorok: 1 2 3 HP zajgenerátor: 4 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! Fehérzajhoz a konstans érték kell - megoldás a digitális
KÉPJAVÍTÁS A KÉPTARTOMÁNYBAN
 KÉPJAVÍTÁS A KÉPTARTOMÁNYBAN Képjavítás Olyan eljárás melynek eredménye olyan kép amely jobban megfelel az adott alkalmazásnak - különböző módszereket kell alkalmazni egy Röntgenfelvétel és a Mars felvételének
KÉPJAVÍTÁS A KÉPTARTOMÁNYBAN Képjavítás Olyan eljárás melynek eredménye olyan kép amely jobban megfelel az adott alkalmazásnak - különböző módszereket kell alkalmazni egy Röntgenfelvétel és a Mars felvételének
ADAT- ÉS INFORMÁCIÓFELDOLGOZÁS
 ADAT- ÉS INFORMÁCIÓFELDOLGOZÁS Földtudományi mérnöki MSc mesterszak 2018/19 I. félév TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ Miskolci Egyetem Műszaki Földtudományi Kar Geofizikai és Térinformatikai Intézet A tantárgy
ADAT- ÉS INFORMÁCIÓFELDOLGOZÁS Földtudományi mérnöki MSc mesterszak 2018/19 I. félév TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ Miskolci Egyetem Műszaki Földtudományi Kar Geofizikai és Térinformatikai Intézet A tantárgy
Orvosi Fizika és Statisztika
 Orvosi Fizika és Statisztika Szegedi Tudományegyetem Általános Orvostudományi Kar Természettudományi és Informatikai Kar Orvosi Fizikai és Orvosi Informatikai Intézet www.szote.u-szeged.hu/dmi Orvosi fizika
Orvosi Fizika és Statisztika Szegedi Tudományegyetem Általános Orvostudományi Kar Természettudományi és Informatikai Kar Orvosi Fizikai és Orvosi Informatikai Intézet www.szote.u-szeged.hu/dmi Orvosi fizika
Shift regiszter + XOR kapu: 2 n állapot
 DSP processzorok: 1 2 HP zajgenerátor: 3 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! 4 Fehérzajhoz a konstans érték kell - megoldás a digitális
DSP processzorok: 1 2 HP zajgenerátor: 3 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! 4 Fehérzajhoz a konstans érték kell - megoldás a digitális
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 9. SZŰRŐK
 ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 9. SZŰRŐK Dr. Soumelidis Alexandros 2018.11.29. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG A szűrésről általában Szűrés:
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 9. SZŰRŐK Dr. Soumelidis Alexandros 2018.11.29. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG A szűrésről általában Szűrés:
Számítógépes képelemzés 7. előadás. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
A mérés problémája a pedagógiában. Dr. Nyéki Lajos 2015
 A mérés problémája a pedagógiában Dr. Nyéki Lajos 2015 A mérés fogalma Mérésen olyan tevékenységet értünk, amelynek eredményeként a vizsgált jelenség számszerűen jellemezhetővé, más hasonló jelenségekkel
A mérés problémája a pedagógiában Dr. Nyéki Lajos 2015 A mérés fogalma Mérésen olyan tevékenységet értünk, amelynek eredményeként a vizsgált jelenség számszerűen jellemezhetővé, más hasonló jelenségekkel
PTE PMMFK Levelező-távoktatás, villamosmérnök szak
 PTE PMMFK Levelező-távoktatás, villamosmérnök szak MATEMATIKA (A tantárgy tartalma és a tananyag elsajátításának időterve.) Összeállította: Kis Miklós adjunktus Tankönyvek Megegyeznek az 1. és 2. félévben
PTE PMMFK Levelező-távoktatás, villamosmérnök szak MATEMATIKA (A tantárgy tartalma és a tananyag elsajátításának időterve.) Összeállította: Kis Miklós adjunktus Tankönyvek Megegyeznek az 1. és 2. félévben
STATISZTIKA. Mit nevezünk idősornak? Az idősorok elemzésének módszertana. Az idősorelemzés célja. Determinisztikus idősorelemzés
 Mit nevezünk idősornak? STATISZTIKA 10. Előadás Idősorok analízise Egyenlő időközökben végzett megfigyelések A sorrend kötött, y 1, y 2 y t y N N= időpontok száma Minden időponthoz egy adat, reprodukálhatatlanság
Mit nevezünk idősornak? STATISZTIKA 10. Előadás Idősorok analízise Egyenlő időközökben végzett megfigyelések A sorrend kötött, y 1, y 2 y t y N N= időpontok száma Minden időponthoz egy adat, reprodukálhatatlanság
Jelfeldolgozás - ANTAL Margit. impulzusválasz. tulajdonságai. Rendszerek. ANTAL Margit. Sapientia - Erdélyi Magyar Tudományegyetem
 Sapientia - Erdélyi Magyar Tudományegyetem 2007 Megnevezések Diszkrét Dirac jel Delta függvény Egységimpluzus függvény A diszkrét Dirac jel δ[n] = { 1, n = 0 0, n 0 d[n] { 1, n = n0 δ[n n 0 ] = 0, n n
Sapientia - Erdélyi Magyar Tudományegyetem 2007 Megnevezések Diszkrét Dirac jel Delta függvény Egységimpluzus függvény A diszkrét Dirac jel δ[n] = { 1, n = 0 0, n 0 d[n] { 1, n = n0 δ[n n 0 ] = 0, n n
Egy (k) küszöb esetén [0, 1] intenzitástartományt feltételezve (v 2 v 2 ):
![Egy (k) küszöb esetén [0, 1] intenzitástartományt feltételezve (v 2 v 2 ): Egy (k) küszöb esetén [0, 1] intenzitástartományt feltételezve (v 2 v 2 ):](/thumbs/91/107527414.jpg) A kép (I) intenzitástartományt folytonos tartományokra osztjuk. Az eredményképen minden egyes tartományhoz egyetlen (egyedi) értéket rendelünk. Egy (k) küszöb esetén [0, 1] intenzitástartományt feltételezve
A kép (I) intenzitástartományt folytonos tartományokra osztjuk. Az eredményképen minden egyes tartományhoz egyetlen (egyedi) értéket rendelünk. Egy (k) küszöb esetén [0, 1] intenzitástartományt feltételezve
Képfeldolgozás és párhuzamosíthatóság
 Többszálú, többmagos architektúrák és programozásuk Óbudai Egyetem, Neumann János Informatikai Kar Képfeldolgozás és párhuzamosíthatóság A képfeldolgozás olyan alkalmazási terület, amely számos lehetőséget
Többszálú, többmagos architektúrák és programozásuk Óbudai Egyetem, Neumann János Informatikai Kar Képfeldolgozás és párhuzamosíthatóság A képfeldolgozás olyan alkalmazási terület, amely számos lehetőséget
8 Képfeldolgozási alkalmazások. 8.1 A képfeldolgozás alapjai
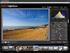 8 Képfeldolgozási alkalmazások 8.1 A képfeldolgozás alapjai A 8.1. ábra egy monokróm, 8bites (256 színű) kép felépítését mutatja meg. A kép 42120 pontból épül fel, 216 sora, 195 oszlopa van. Ha mint jelre
8 Képfeldolgozási alkalmazások 8.1 A képfeldolgozás alapjai A 8.1. ábra egy monokróm, 8bites (256 színű) kép felépítését mutatja meg. A kép 42120 pontból épül fel, 216 sora, 195 oszlopa van. Ha mint jelre
Számítógépi képelemzés
 Számítógépi képelemzés Elıadás vázlat Szerzık: Dr. Gácsi Zoltán, egyetemi tanár Dr. Barkóczy Péter, egyetemi docens Lektor: Igaz Antal, okl. gépészmérnök a Carl Zeiss technika kft. Ügyvezetı igazgatója
Számítógépi képelemzés Elıadás vázlat Szerzık: Dr. Gácsi Zoltán, egyetemi tanár Dr. Barkóczy Péter, egyetemi docens Lektor: Igaz Antal, okl. gépészmérnök a Carl Zeiss technika kft. Ügyvezetı igazgatója
Jelfeldolgozás. Gyakorlat: A tantermi gyakorlatokon való részvétel kötelező! Kollokvium: csak gyakorlati jeggyel!
 1 Jelfeldolgozás Jegyzet: http://itl7.elte.hu : Elektronika jegyzet (Csákány A., ELTE TTK 119) Jelek feldolgozása (Bagoly Zs. Csákány A.) angol nyelv DSP (PDF) jegyzet Gyakorlat: A tantermi gyakorlatokon
1 Jelfeldolgozás Jegyzet: http://itl7.elte.hu : Elektronika jegyzet (Csákány A., ELTE TTK 119) Jelek feldolgozása (Bagoly Zs. Csákány A.) angol nyelv DSP (PDF) jegyzet Gyakorlat: A tantermi gyakorlatokon
A gyakorlat célja a fehér és a színes zaj bemutatása.
 A gyakorlat célja a fehér és a színes zaj bemutatása. 1.@. FFT begyakorlása n = [:9]; % Harminc minta x = cos(*pi*n/1); % 1 mintát veszünk periodusonként N1 = 64; % Három módon számoljuk az FFT-t N = 18;
A gyakorlat célja a fehér és a színes zaj bemutatása. 1.@. FFT begyakorlása n = [:9]; % Harminc minta x = cos(*pi*n/1); % 1 mintát veszünk periodusonként N1 = 64; % Három módon számoljuk az FFT-t N = 18;
Dekonvolúció a mikroszkópiában. Barna László MTA Kísérleti Orvostudományi Kutatóintézet Nikon-KOKI képalkotó Központ
 Dekonvolúció a mikroszkópiában Barna László MTA Kísérleti Orvostudományi Kutatóintézet Nikon-KOKI képalkotó Központ 2015 Fourier-Sorok Minden 2π szerint periodikus függvény előállítható f x ~ a 0 2 + (a
Dekonvolúció a mikroszkópiában Barna László MTA Kísérleti Orvostudományi Kutatóintézet Nikon-KOKI képalkotó Központ 2015 Fourier-Sorok Minden 2π szerint periodikus függvény előállítható f x ~ a 0 2 + (a
Akusztikus MEMS szenzor vizsgálata. Sós Bence JB2BP7
 Akusztikus MEMS szenzor vizsgálata Sós Bence JB2BP7 Tartalom MEMS mikrofon felépítése és típusai A PDM jel Kinyerhető információ CIC szűrő Mérési tapasztalatok. Konklúzió MEMS (MicroElectrical-Mechanical
Akusztikus MEMS szenzor vizsgálata Sós Bence JB2BP7 Tartalom MEMS mikrofon felépítése és típusai A PDM jel Kinyerhető információ CIC szűrő Mérési tapasztalatok. Konklúzió MEMS (MicroElectrical-Mechanical
Képfeldolgozási módszerek a geoinformatikában
 Képfeldolgozási módszerek a geoinformatikában Elek István Klinghammer István Eötvös Loránd Tudományegyetem, Informatikai Kar, Térképtudományi és Geoinformatikai Tanszék, MTA Térképészeti és Geoinformatikai
Képfeldolgozási módszerek a geoinformatikában Elek István Klinghammer István Eötvös Loránd Tudományegyetem, Informatikai Kar, Térképtudományi és Geoinformatikai Tanszék, MTA Térképészeti és Geoinformatikai
Analóg elektronika - laboratóriumi gyakorlatok
 Analóg elektronika - laboratóriumi gyakorlatok. Mûveleti erõsítõk váltakozó-áramú alkalmazásai. Elmélet Az integrált mûveleti erõsítõk váltakozó áramú viselkedését a. fejezetben (jegyzet és prezentáció)
Analóg elektronika - laboratóriumi gyakorlatok. Mûveleti erõsítõk váltakozó-áramú alkalmazásai. Elmélet Az integrált mûveleti erõsítõk váltakozó áramú viselkedését a. fejezetben (jegyzet és prezentáció)
STATISZTIKA. A Föld pályája a Nap körül. Philosophiae Naturalis Principia Mathematica (A természetfilozófia matematikai alapelvei, 1687)
 STATISZTIKA 10. Előadás Megbízhatósági tartományok (Konfidencia intervallumok) Sir Isaac Newton, 1643-1727 Philosophiae Naturalis Principia Mathematica (A természetfilozófia matematikai alapelvei, 1687)
STATISZTIKA 10. Előadás Megbízhatósági tartományok (Konfidencia intervallumok) Sir Isaac Newton, 1643-1727 Philosophiae Naturalis Principia Mathematica (A természetfilozófia matematikai alapelvei, 1687)
DIGITÁLIS KÉPANALÍZIS KÉSZÍTETTE: KISS ALEXANDRA ELÉRHETŐSÉG:
 DIGITÁLIS KÉPANALÍZIS KÉSZÍTETTE: KISS ALEXANDRA ELÉRHETŐSÉG: kisszandi@mailbox.unideb.hu ImageJ (Fiji) Nyílt forrás kódú, java alapú képelemző szoftver https://fiji.sc/ Számos képformátumhoz megfelelő
DIGITÁLIS KÉPANALÍZIS KÉSZÍTETTE: KISS ALEXANDRA ELÉRHETŐSÉG: kisszandi@mailbox.unideb.hu ImageJ (Fiji) Nyílt forrás kódú, java alapú képelemző szoftver https://fiji.sc/ Számos képformátumhoz megfelelő
6. Függvények. Legyen függvény és nem üreshalmaz. A függvényt az f K-ra való kiterjesztésének
 6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
Él: a képfüggvény hirtelen változása. Típusai. Felvételeken zajos formában jelennek meg. Lépcsős
 Él: a képfüggvény hirtelen változása Típusai Lépcsős Rámpaszerű Tetőszerű Vonalszerű él Felvételeken zajos formában jelennek meg Adott pontbeli x ill. y irányú változás jellemezhető egy f folytonos képfüggvény
Él: a képfüggvény hirtelen változása Típusai Lépcsős Rámpaszerű Tetőszerű Vonalszerű él Felvételeken zajos formában jelennek meg Adott pontbeli x ill. y irányú változás jellemezhető egy f folytonos képfüggvény
STATISZTIKA I. Változékonyság (szóródás) A szóródás mutatószámai. Terjedelem. Forgalom terjedelem. Excel függvények. Függvénykategória: Statisztikai
 Változékonyság (szóródás) STATISZTIKA I. 5. Előadás Szóródási mutatók A középértékek a sokaság elemeinek értéknagyságbeli különbségeit eltakarhatják. A változékonyság az azonos tulajdonságú, de eltérő
Változékonyság (szóródás) STATISZTIKA I. 5. Előadás Szóródási mutatók A középértékek a sokaság elemeinek értéknagyságbeli különbségeit eltakarhatják. A változékonyság az azonos tulajdonságú, de eltérő
Felvételi tematika INFORMATIKA
 Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
Képszegmentálás. Orvosi képdiagnosztika 10. ea
 Képszegmentálás Orvosi képdiagnosztika 10. ea Képszegmentálás Intenzitás alapján, küszöbözés Klaszterezés, osztályozás Régió növesztés, régió hasítás Watershed Textura alapján Kontúr alapján, élkeresés,
Képszegmentálás Orvosi képdiagnosztika 10. ea Képszegmentálás Intenzitás alapján, küszöbözés Klaszterezés, osztályozás Régió növesztés, régió hasítás Watershed Textura alapján Kontúr alapján, élkeresés,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
Több valószínűségi változó együttes eloszlása, korreláció
 Tartalomjegzék Előszó... 6 I. Valószínűségelméleti és matematikai statisztikai alapok... 8 1. A szükséges valószínűségelméleti és matematikai statisztikai alapismeretek összefoglalása... 8 1.1. Alapfogalmak...
Tartalomjegzék Előszó... 6 I. Valószínűségelméleti és matematikai statisztikai alapok... 8 1. A szükséges valószínűségelméleti és matematikai statisztikai alapismeretek összefoglalása... 8 1.1. Alapfogalmak...
Elemi statisztika fizikusoknak
 1. oldal Elemi statisztika fizikusoknak Pollner Péter Biológiai Fizika Tanszék pollner@elte.hu Az adatok leírása, megismerése és összehasonlítása 2-1 Áttekintés 2-2 Gyakoriság eloszlások 2-3 Az adatok
1. oldal Elemi statisztika fizikusoknak Pollner Péter Biológiai Fizika Tanszék pollner@elte.hu Az adatok leírása, megismerése és összehasonlítása 2-1 Áttekintés 2-2 Gyakoriság eloszlások 2-3 Az adatok
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Mi a modell? Matematikai statisztika. 300 dobás. sűrűségfüggvénye. Egyenletes eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 7. Előadás Egyenletes eloszlás Binomiális eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell /56 Matematikai statisztika Reprezentatív mintavétel
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 7. Előadás Egyenletes eloszlás Binomiális eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell /56 Matematikai statisztika Reprezentatív mintavétel
Feladatok: pontdiagram és dobozdiagram. Hogyan csináltuk?
 Feladatok: pontdiagram és dobozdiagram Hogyan csináltuk? Alakmutatók: ferdeség, csúcsosság Alakmutatók a ferdeség és csúcsosság mérésére Ez eloszlás centrumát (középérték) és az adatok centrum körüli terpeszkedését
Feladatok: pontdiagram és dobozdiagram Hogyan csináltuk? Alakmutatók: ferdeség, csúcsosság Alakmutatók a ferdeség és csúcsosság mérésére Ez eloszlás centrumát (középérték) és az adatok centrum körüli terpeszkedését
Beszédinformációs rendszerek 5. gyakorlat Mintavételezés, kvantálás, beszédkódolás. Csapó Tamás Gábor
 Beszédinformációs rendszerek 5. gyakorlat Mintavételezés, kvantálás, beszédkódolás Csapó Tamás Gábor 2016/2017 ősz MINTAVÉTELEZÉS 2 1. Egy 6 khz-es szinusz jelet szűrés nélkül mintavételezünk
Beszédinformációs rendszerek 5. gyakorlat Mintavételezés, kvantálás, beszédkódolás Csapó Tamás Gábor 2016/2017 ősz MINTAVÉTELEZÉS 2 1. Egy 6 khz-es szinusz jelet szűrés nélkül mintavételezünk
I. LABOR -Mesterséges neuron
 I. LABOR -Mesterséges neuron A GYAKORLAT CÉLJA: A mesterséges neuron struktúrájának az ismertetése, neuronhálókkal kapcsolatos elemek, alapfogalmak bemutatása, aktivációs függvénytípusok szemléltetése,
I. LABOR -Mesterséges neuron A GYAKORLAT CÉLJA: A mesterséges neuron struktúrájának az ismertetése, neuronhálókkal kapcsolatos elemek, alapfogalmak bemutatása, aktivációs függvénytípusok szemléltetése,
Adatelemzés SAS Enterprise Guide használatával. Soltész Gábor solteszgabee[at]gmail.com
![Adatelemzés SAS Enterprise Guide használatával. Soltész Gábor solteszgabee[at]gmail.com Adatelemzés SAS Enterprise Guide használatával. Soltész Gábor solteszgabee[at]gmail.com](/thumbs/62/48167704.jpg) Adatelemzés SAS Enterprise Guide használatával Soltész Gábor solteszgabee[at]gmail.com Tartalom SAS Enterprise Guide bemutatása Kezelőfelület Adatbeolvasás Szűrés, rendezés Új változó létrehozása Elemzések
Adatelemzés SAS Enterprise Guide használatával Soltész Gábor solteszgabee[at]gmail.com Tartalom SAS Enterprise Guide bemutatása Kezelőfelület Adatbeolvasás Szűrés, rendezés Új változó létrehozása Elemzések
ACM Snake. Orvosi képdiagnosztika 11. előadás első fele
 ACM Snake Orvosi képdiagnosztika 11. előadás első fele ACM Snake (ismétlés) A szegmentáló kontúr egy paraméteres görbe: x Zs s X s, Y s,, s A szegmentáció energia funkcionál minimalizálása: E x Eint x
ACM Snake Orvosi képdiagnosztika 11. előadás első fele ACM Snake (ismétlés) A szegmentáló kontúr egy paraméteres görbe: x Zs s X s, Y s,, s A szegmentáció energia funkcionál minimalizálása: E x Eint x
Képalkotó diagnosztikai eljárások:
 Képalkotó diagnosztikai eljárások: Soroljon fel néhány orvosi képalkotáson alapuló diagnosztikai eljárást, mely o Transzmissziós o Indukciós o Emissziós elv alkalmazásán alapul. Mire szolgálnak az egyes
Képalkotó diagnosztikai eljárások: Soroljon fel néhány orvosi képalkotáson alapuló diagnosztikai eljárást, mely o Transzmissziós o Indukciós o Emissziós elv alkalmazásán alapul. Mire szolgálnak az egyes
Rendszámfelismerő rendszerek
 Problémamegoldó szeminárium Témavezető: Pataki Péter ARH Zrt. ELTE-TTK 2013 Tartalomjegyzék 1 Bevezetés 2 Út a megoldás felé 3 Felmerült problémák 4 Alkalmazott matematika 5 További lehetőségek Motiváció
Problémamegoldó szeminárium Témavezető: Pataki Péter ARH Zrt. ELTE-TTK 2013 Tartalomjegyzék 1 Bevezetés 2 Út a megoldás felé 3 Felmerült problémák 4 Alkalmazott matematika 5 További lehetőségek Motiváció
Híradástechikai jelfeldolgozás
 Híradástechikai jelfeldolgozás 13. Előadás 015. 04. 4. Jeldigitalizálás és rekonstrukció 015. április 7. Budapest Dr. Gaál József docens BME Hálózati Rendszerek és SzolgáltatásokTanszék gaal@hit.bme.hu
Híradástechikai jelfeldolgozás 13. Előadás 015. 04. 4. Jeldigitalizálás és rekonstrukció 015. április 7. Budapest Dr. Gaál József docens BME Hálózati Rendszerek és SzolgáltatásokTanszék gaal@hit.bme.hu
Értékelés Összesen: 100 pont 100% = 100 pont A VIZSGAFELADAT MEGOLDÁSÁRA JAVASOLT %-OS EREDMÉNY: EBBEN A VIZSGARÉSZBEN A VIZSGAFELADAT ARÁNYA 35%.
 Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzék módosításának eljárásrendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján: Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzék módosításának eljárásrendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján: Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Adaptív dinamikus szegmentálás idősorok indexeléséhez
 Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
3.18. DIGITÁLIS JELFELDOLGOZÁS
 3.18. DIGITÁLIS JELFELDOLGOZÁS Az analóg jelfeldolgozás során egy fizikai mennyiséget (pl. a hangfeldolgozás kapcsán a levegő nyomásváltozásait) azzal analóg (hasonló, arányos) elektromos feszültséggé
3.18. DIGITÁLIS JELFELDOLGOZÁS Az analóg jelfeldolgozás során egy fizikai mennyiséget (pl. a hangfeldolgozás kapcsán a levegő nyomásváltozásait) azzal analóg (hasonló, arányos) elektromos feszültséggé
Intelligens Rendszerek Elmélete. Versengéses és önszervező tanulás neurális hálózatokban
 Intelligens Rendszerek Elmélete : dr. Kutor László Versengéses és önszervező tanulás neurális hálózatokban http://mobil.nik.bmf.hu/tantargyak/ire.html Login név: ire jelszó: IRE07 IRE 9/1 Processzor Versengéses
Intelligens Rendszerek Elmélete : dr. Kutor László Versengéses és önszervező tanulás neurális hálózatokban http://mobil.nik.bmf.hu/tantargyak/ire.html Login név: ire jelszó: IRE07 IRE 9/1 Processzor Versengéses
Tartalomjegyzék. 1. Előszó 1
 Tartalomjegyzék 1. Előszó 1 2. Halmazok, relációk, függvények 3 2.1. Halmazok, relációk, függvények A............... 3 2.1.1. Halmazok és relációk................... 3 2.1.2. Relációk inverze és kompozíciója............
Tartalomjegyzék 1. Előszó 1 2. Halmazok, relációk, függvények 3 2.1. Halmazok, relációk, függvények A............... 3 2.1.1. Halmazok és relációk................... 3 2.1.2. Relációk inverze és kompozíciója............
A RADARJELEK DETEKTÁLÁSA NEURÁLIS HÁLÓZAT ALKALMAZÁSÁVAL
 A RADARJELEK DETEKTÁLÁSA NEURÁLIS HÁLÓZAT ALKALMAZÁSÁVAL Dr. Ludányi Lajos mk. alezredes egyetemi adjunktus Zrínyi Miklós Nemzetvédelmi Egyetem Vezetés- és Szervezéstudományi Kar Fedélzeti Rendszerek Tanszék
A RADARJELEK DETEKTÁLÁSA NEURÁLIS HÁLÓZAT ALKALMAZÁSÁVAL Dr. Ludányi Lajos mk. alezredes egyetemi adjunktus Zrínyi Miklós Nemzetvédelmi Egyetem Vezetés- és Szervezéstudományi Kar Fedélzeti Rendszerek Tanszék
Kutatásmódszertan és prezentációkészítés
 Kutatásmódszertan és prezentációkészítés 10. rész: Az adatelemzés alapjai Szerző: Kmetty Zoltán Lektor: Fokasz Nikosz Tizedik rész Az adatelemzés alapjai Tartalomjegyzék Bevezetés Leíró statisztikák I
Kutatásmódszertan és prezentációkészítés 10. rész: Az adatelemzés alapjai Szerző: Kmetty Zoltán Lektor: Fokasz Nikosz Tizedik rész Az adatelemzés alapjai Tartalomjegyzék Bevezetés Leíró statisztikák I
Fourier-sorfejtés vizsgálata Négyszögjel sorfejtése, átviteli vizsgálata
 Fourier-sorfejtés vizsgálata Négyszögjel sorfejtése, átviteli vizsgálata Reichardt, András 27. szeptember 2. 2 / 5 NDSM Komplex alak U C k = T (T ) ahol ω = 2π T, k módusindex. Időfüggvény előállítása
Fourier-sorfejtés vizsgálata Négyszögjel sorfejtése, átviteli vizsgálata Reichardt, András 27. szeptember 2. 2 / 5 NDSM Komplex alak U C k = T (T ) ahol ω = 2π T, k módusindex. Időfüggvény előállítása
Kép mátrix. Feladat: Pap Gáborné-Zsakó László: Algoritmizálás, adatmodellezés 2/35
 Grafika I. Kép mátrix Feladat: Egy N*M-es raszterképet nagyítsunk a két-szeresére pontsokszorozással: minden régi pont helyébe 2*2 azonos színű pontot rajzolunk a nagyított képen. Pap Gáborné-Zsakó László:
Grafika I. Kép mátrix Feladat: Egy N*M-es raszterképet nagyítsunk a két-szeresére pontsokszorozással: minden régi pont helyébe 2*2 azonos színű pontot rajzolunk a nagyított képen. Pap Gáborné-Zsakó László:
Analóg elektronika - laboratóriumi gyakorlatok
 Analóg elektronika - laboratóriumi gyakorlatok. Passzív alkatrészek és passzív áramkörök. Elmélet A passzív elektronikai alkatrészek elméleti ismertetése az. prezentációban található. A 2. prezentáció
Analóg elektronika - laboratóriumi gyakorlatok. Passzív alkatrészek és passzív áramkörök. Elmélet A passzív elektronikai alkatrészek elméleti ismertetése az. prezentációban található. A 2. prezentáció
