2. Pont operációk. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (
|
|
|
- Valéria Pásztorné
- 8 évvel ezelőtt
- Látták:
Átírás
1 2. Pont operációk Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (
2 2 Kép transzformációk típusai Kép értékkészletének (radiometriai információ) átalakítása: J( i, j) f ( I,( i, j)) Kép értelmezési tartományának geometriai transzformációja (warping): J ( i, j) I( t ( i, j), t ( i, j)) i j Mind az értékkészlet mind pedig az értelmezési tartomány átalakítása: J ( i, j) f ( I,( t ( i, j), t ( i, j))) i j
3 3 Értékkészlet transzformációk Lokális: Az új pixelérték a kiindulási pixel adott méretű S környezetének pixelértékeitől függ pl. konvolúció adott méretű maszkkal Ha függ a pozíciótól is, akkor lokálisan adaptív Globális: Ha S=teljes kép Pont operáció: ha S egyetlen pixelből áll. j Lokális operáció (pl. szűrőzés): J(x,y) = f ({I(u,v) (u,v) є S(i,j)}) j i S(i.j) lokális környezet (i,j) körül Input: I=[I(i,j)] i Output: J =[J(i,j)]
4 4 Lokális értékkészlet transzformációk Simítás / élesítés Éldetektálás Minta illesztés
5 5 Pont operáció Legegyszerűbb értékkészlet transzformáció a pont operáció: Nem függ a pixel környezetétől Az új pixelérték kizárólag a régi függvénye J ( i, j) f ( I( i, j)) I :[ M N] LI J :[ M N] LJ f : L L I J j J(i,j) = f(i(i,j)) j i i Input: I=[I(i,j)] Output: J =[J(i,j)]
6 6 Tipikus pont operációk Aritmetikai műveletek Azonos méretű képekre pixelenként elvégzett standard aritmetika Fényesség és kontraszt állítás Gamma korrekció Szín korrekció (fehér egyensúly) Hisztogram normalizálás Hisztogram kiegyenlítés Újra kvantálás Intenzitások/színek számának csökkentése Szteganográfia Rejtett képek
7 7 Aritmetikai műveletek: összeadás + = (Egy filmkockára kétszer exponálunk.)
8 8 Háttérzaj levonás - Eredeti kép + szenzor háttérzaj Háttérzaj (letakart objektívvel készült kép) = Kivonás eredménye Copyright Timo Autiokari,
9 9 Kivonás, abszolút differencia - = változások detektálása - = Mozgás detektálás két frame különbségével: 0, ha nincs mozgás 0, ahol elmozdulás történt
10 10 Képmontázs Két kép részleteinek felhasználásával egy új kép előállítása Ehhez szükség van egy harmadik képre (M), amely minden pixelben megadja a két kép közötti súlyozás értékét (alpha) J( i, j) M( i, j) I1( i, j) (1 M( i, j)) I2( i, j) M(i,j)=0 1. kép M(i,j)= 1 2. kép Köztes értékek megadják a két kép pixelértékeinek súlyát
11 11 Fehér egyensúly (white balance) Az emberi látás alkalmazkodik a különböző megvilágításokhoz (kromatikus adaptáció) A színeket a megvilágitástól függetlenül állandónak érzékeljük Film esetén megfelelő színhőmérsékletre hangolt nyersanyag + szűrők Digitális szenzor: algoritmikus korrekció A megvilágítás színe a fehér régiókban olvasható le Csatornánként skálázás (8 bit) 255 R' R G' B' w 255 G w 255 B w R G B Fehér pont ([R w,g w,b w ])
12 12 Színes kép szürkeárnyalatossá alakítása Egy RGB színes képet szürkeárnyalatossá konvertálhatunk a színcsatornák lineáris kombinációjaként: R G B A csatornák együtthatói az emberi látásnak megfelelő súllyal veszik az egyes színkomponenseket
13 Output érték (g) Pont operációk megadása Függvénnyel: f(x)=g, xϵl I, gϵl J, átszínező- vagy keresőtáblával (LUT: look-up-table) Függvényből képzett diszkrét (x,g) pixelérték-párok f(x) input érték (x) LUT: index érték input output
14 14 Példa transzformáló függvényekre új régi
15 15 Invertálás f 255 ( x) 255 x 255 f ( x) 255 x
16 Gamma korrekció Az emberi látás logaritmikus skálán érzékeli az intenzitásokat Az árnyalatokban részletgazdagabb, mint a csúcsfényekben Gamma korrekció az emberi érzékelésnek megfelelő intenzitástranszformációt jelent Általánosságban azonban nem más, mint egy nemlineáris transzformáció f f ( x) ( x) cx, 255 c, x 255 1/ 0,, x 1 0 x Gamma korrekció nélkül Gamma korrekció után
17 17 Példa gamma korrekcióra eredeti légifotó γ=3 γ=4 γ=5 (c=1)
18 18 Hisztogram Olyan függvény, amely minden lehetséges szürkeárnyalathoz megadja a képen az adott árnyalatú pixelek számát. Ha normalizáljuk (minden értéket elosztunk a kép méretével), akkor az egyes pixelértékek előfordulási valószínűségét kapjuk.
19 19 Szín-hisztogram: pontfelhőként Statisztikailag keveset mond (sokkal több lehetséges szín, mint pixel van) 3 dimenziós térben pontfelhőként ábrázoljuk
20 20 Szín-hisztogram: komponensenként Komponensenként mint szürkeárnyalatos hisztogram Valódi színeloszlásra nehezen következtethetünk belőle RGB kép hisztogram színkomponensenként
21 21 Hisztogram és képi tartalom A képpontok összerázásával a hisztogram nem változik, tehát a hisztogramból nem következtethetünk a látványra.
22 r 22 Hisztogram és képi tartalom invertálás sötét világos kontrasztszegény r 255-r 255-r kontrasztos
23 23 Hisztogram transzformációk Olyan pont-operációk, amelyeknek függvényét az input kép hisztogramjából vagy az output kép hisztogramjára vonatkozó elvárások alapján határozzák meg. hisztogram/kontraszt széthúzás hisztogram kiegyenlítés hisztogram specifikáció
24 24 Hisztogram normalizálás A hisztogram normalizálás (vagy széthúzás) függvénye egy lineáris skála-transzformáció: a képen előforduló intenzitástartományt, a [min,max] intervallumot skálázza a [0,L-1] (a teljes) intervallumba. L-1 f(x) J ( i, j) f ( I( i, j)) I :[ M N] [min, max] 0 0 min max L-1 J :[ M N] [0, L 1] f :[min, max] [0, L 1], f ( x) ( L 1) x min max min
25 25 Hisztogram normalizálás
26 Kontraszt széthúzás Hasonló a hisztogram normalizáláshoz, de az intenzitások egy megadott [low,high] intervallumát skálázza a [0,L-1]-be L-1 A megadott intervallum szűkebb lehet, mint az előforduló intenzitások [min,max] sávja f(x) 0 0 low high L-1 min max 26 f ( x) 0 ( L 1) L 1 ( x low) high low,,, ha ha ha x low low x x high high
27 27 hisztogram széthúzás kontraszt széthúzás
28 28 Hisztogram kiegyenlítés A hisztogram-specifikáció legegyszerűbb esete Azt várjuk, hogy a kimeneti kép hisztogramja egyenletes eloszlásnak feleljen meg eredeti hisztogram x 1/L kiegyenlített hisztogram f(x)
29 Hisztogram kiegyenlítés 29 x f(x) egyenlő területek! x i i p 0 ) ( L x f 1 ) ( x i x i i p L x f L x f i p 0 0 ) ( ) ( 1 ) ( ) ( Kumulatív hisztogram
30 30 Kumulatív hisztogram Míg a normalizált hisztogram az intenzitások valószínűségi sűrűségfüggvényét adja meg, addig a kumulatív hisztogram az intenzitásértékek x eloszlásfüggvényét adja: PDF ( x) x : 0 i 0 p( i) PDF ( x ) 1
31 31 Hisztogram kiegyenlítés és kumulatív hisztogram A transzformációs függvényt (LUT) a kumulatív hisztogram adja
32 32 Hisztogram kiegyenlítés függvények 4
33 33 Adaptív hisztogram kiegyenlítés A hisztogram kiegyenlítést (HK) pontonként, az adott pont egy lokális környezete alapján végezzük Alkalmazkodik a kép lokális karakterisztikájához Más pont operációknál is használhatunk hasonló adaptív technikát (ld. később: adaptív küszöbölés) kiindulási kép globális HK eredménye lokális (3x3-as) HK eredménye
34 P I ( g I ) P J ( g J ) 34 Hisztogram specifikáció A kiindulási I képből egy előre megadott J hisztogramú K képet eredményez Diszkrét értékek miatt csak megközelítőleg kapunk azonos hisztogramot Minden g I pixelértéket cseréljünk arra a g J értékre, amelynek kumulatív hisztogram értéke a legközelebb van Ha I(i,j)=g I, akkor legyen K(i,j)=g J, ahol g J kielégíti az alábbi feltételt: P I (g I ) > P J (g J -1) AND P I (g I ) P J (g J ). Példa: I(i,j) = 5 P I (5) = 0.65 P J (9) = 0.56 P J (10) = 0.67 K(i,j) = 10 g I g J
35 35 Hisztogram specifikáció eredeti várt kapott
36 36 Hisztogram specifikáció eredeti várt kapott
37 37 Képek újra kvantálása Képek újra kvantálása is egy pont operáció Hisztogram binning True color képek palettássá alakítása Az eredeti színtér/intenzitástartomány felosztása függ a kép tartalmától (adaptív kvantálás): A kép statisztikai elemzése (hisztogram) alapján választjuk ki a megfelelő számú új színt Az így előállt LUT alapján végezzük el a transzformációt eredeti színtér kvantált értékek a klaszterközéppontok
38 38 Uniform nem uniform kvantálás eredeti true-color uniform (8-szín) nem uniform (8-szín)
39 39 Kvantálási hiba csökkentése Ha túl kevés a kvantálási szint, akkor hamis kontúrok léphetnek fel A kvantálás előtt zaj hozzáadásával csökkenthetjük ezt a hatást =0, σ = M/q, ahol M a maximális intenzitásérték, q pedig a bitek száma a kvantálás során I + N(,σ) Quant(q) J
40 40 Dithering 8 bit 2 bit 2 bit + zaj
41 41 Szteganográfia 6bit csatornánként 8bit csatornánként 6 és 8 bites kvantálás között lenyegében nem érzékelhető lényeges különbség Pieter Bruegel (the Elder, ca ), The Peasant Dance, 1568, Oil on oak panel, 114x164 cm, Kunsthistorisches Museum Wien, Vienna
42 42 Szteganográfia b b b b b b 0 0 b = 0 or 1 always 0 Ha 6 biten kvantáljuk a képet, akkor a maradék alsó 2 biten tetszőleges információt, akár egy egész képet elrejthetünk Image 1 Image 2 felső 6bit R-Shift 2 R-Shift 6 L-Shift 2 Image Out 2bit
43 43 Felhasznált anyagok Palágyi Kálmán: Digitális Képfeldolgozás /pub/digitalis_kepfeldolgozas Trevor Darrell: C280, Computer Vision s06/lectures/ppts/ Richard Alan Peters: EECE/CS 253 Image Processing További források az egyes diákon megjelölve
3. Szűrés képtérben. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 3. Szűrés képtérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE http://www.inf.u-szeged.hu/~kato/teaching/ 2 Kép transzformációk típusai Kép értékkészletének radiometriai információ
3. Szűrés képtérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE http://www.inf.u-szeged.hu/~kato/teaching/ 2 Kép transzformációk típusai Kép értékkészletének radiometriai információ
Pontműveletek. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar február 20.
 Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
8. Pontmegfeleltetések
 8. Pontmegfeleltetések Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Példa: panoráma kép készítés 1. Jellemzőpontok detektálása mindkét
8. Pontmegfeleltetések Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Példa: panoráma kép készítés 1. Jellemzőpontok detektálása mindkét
Színes képek feldolgozása
 Palágyi Kálmán Az oktató: SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék 6720 Szeged Árpád tér 2. 214-es szoba (tetıtér) (62) 546 197 palagyi@inf.u-szeged.hu www.inf.u-szeged.hu/~palagyi Kurzusanyagok
Palágyi Kálmán Az oktató: SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék 6720 Szeged Árpád tér 2. 214-es szoba (tetıtér) (62) 546 197 palagyi@inf.u-szeged.hu www.inf.u-szeged.hu/~palagyi Kurzusanyagok
1. Képalkotás. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 1. Képalkotás Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Képalkotás fizikai paraméterei Geometriai Vetítés típusa (perspectív) Kamera
1. Képalkotás Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Képalkotás fizikai paraméterei Geometriai Vetítés típusa (perspectív) Kamera
Képfeldolgozás. 1. el adás. A képfeldolgozás m veletei. Mechatronikai mérnök szak BME, 2008
 Képfeldolgozás 1. el adás. A képfeldolgozás m veletei Mechatronikai mérnök szak BME, 2008 1 / 61 Alapfogalmak transzformációk Deníció Deníció Geometriai korrekciókra akkor van szükség, ha a képr l valódi
Képfeldolgozás 1. el adás. A képfeldolgozás m veletei Mechatronikai mérnök szak BME, 2008 1 / 61 Alapfogalmak transzformációk Deníció Deníció Geometriai korrekciókra akkor van szükség, ha a képr l valódi
Képfeldolgozás jól párhuzamosítható
 Képfeldolgozás jól párhuzamosítható B. Wilkinson, M. Allen: Parallel Programming, Pearson Education Prentice Hall, 2nd ed., 2005. könyv 12. fejezete alapján Vázlat A képfeldolgozás olyan alkalmazási terület,
Képfeldolgozás jól párhuzamosítható B. Wilkinson, M. Allen: Parallel Programming, Pearson Education Prentice Hall, 2nd ed., 2005. könyv 12. fejezete alapján Vázlat A képfeldolgozás olyan alkalmazási terület,
Híradástechikai jelfeldolgozás
 Híradástechikai jelfeldolgozás 13. Előadás 015. 04. 4. Jeldigitalizálás és rekonstrukció 015. április 7. Budapest Dr. Gaál József docens BME Hálózati Rendszerek és SzolgáltatásokTanszék gaal@hit.bme.hu
Híradástechikai jelfeldolgozás 13. Előadás 015. 04. 4. Jeldigitalizálás és rekonstrukció 015. április 7. Budapest Dr. Gaál József docens BME Hálózati Rendszerek és SzolgáltatásokTanszék gaal@hit.bme.hu
Képfeldolgozó eljárások áttekintés. Orvosi képdiagnosztika 9. ea ősz
 Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, hisztogram módosítás, zajszűrés, élkiemelés) Képelemzés
Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, hisztogram módosítás, zajszűrés, élkiemelés) Képelemzés
Képfeldolgozó eljárások áttekintés. Orvosi képdiagnosztika
 Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás, zajszűrés) Képelemzés
Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás, zajszűrés) Képelemzés
Bevezetés. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 Bevezetés Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Digitális képfeldolgozás digitális képfeldolgozás számítógépes grafika digitális
Bevezetés Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Digitális képfeldolgozás digitális képfeldolgozás számítógépes grafika digitális
6. Éldetektálás. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 6. Éldetektálás Kató Zoltán Képeldolgozás és Számítógépes Graika tanszék SZTE (http://www.in.u-szeged.hu/~kato/teaching/) 2 Élek A képen ott található él, ahol a kép-üggvény hirtelen változik. A kép egy
6. Éldetektálás Kató Zoltán Képeldolgozás és Számítógépes Graika tanszék SZTE (http://www.in.u-szeged.hu/~kato/teaching/) 2 Élek A képen ott található él, ahol a kép-üggvény hirtelen változik. A kép egy
Képfeldolgozó eljárások áttekintés. Orvosi képdiagnosztika 9. ea ősz
 Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás,
Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás,
A Hisztogram használata a digitális képszerkesztésben
 Mechatronika, Optika és Mûszertechnika Tanszék A Hisztogram használata a digitális képszerkesztésben Tárgy: Fotó és Készítette: Curávy Tamás képszerkesztési technikák B1Y6IV Elõadó: Antal Á kos Budapest,
Mechatronika, Optika és Mûszertechnika Tanszék A Hisztogram használata a digitális képszerkesztésben Tárgy: Fotó és Készítette: Curávy Tamás képszerkesztési technikák B1Y6IV Elõadó: Antal Á kos Budapest,
Képrestauráció Képhelyreállítás
 Képrestauráció Képhelyreállítás Képrestauráció - A képrestauráció az a folyamat mellyel a sérült képből eltávolítjuk a degradációt, eredményképpen pedig az eredetihez minél közelebbi képet szeretnénk kapni
Képrestauráció Képhelyreállítás Képrestauráció - A képrestauráció az a folyamat mellyel a sérült képből eltávolítjuk a degradációt, eredményképpen pedig az eredetihez minél közelebbi képet szeretnénk kapni
Képfeldolgozás jól párhuzamosítható
 Képeldolgozás jól párhuzamosítható B. Wilkinson, M. Allen: Parallel Programming, Pearson Education Prentice Hall, nd ed., 005. könyv. ejezete alapján Vázlat A képeldolgozás olyan alkalmazási terület, amely
Képeldolgozás jól párhuzamosítható B. Wilkinson, M. Allen: Parallel Programming, Pearson Education Prentice Hall, nd ed., 005. könyv. ejezete alapján Vázlat A képeldolgozás olyan alkalmazási terület, amely
Minták automatikus osztályba sorolása a mintát leíró jellemzők alapján. Típusok: felügyelt és felügyelet nélküli tanuló eljárások
 Minták automatikus osztályba sorolása a mintát leíró jellemzők alapján Típusok: felügyelt és felügyelet nélküli tanuló eljárások Különbség: előbbinél szükséges egy olyan tanulóhalmaz, ahol ismert a minták
Minták automatikus osztályba sorolása a mintát leíró jellemzők alapján Típusok: felügyelt és felügyelet nélküli tanuló eljárások Különbség: előbbinél szükséges egy olyan tanulóhalmaz, ahol ismert a minták
7. Régió alapú szegmentálás
 Digitális képek szegmentálása 7. Régió alapú szegmentálás Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Szegmentálási kritériumok Particionáljuk a képet az alábbi kritériumokat kielégítő régiókba
Digitális képek szegmentálása 7. Régió alapú szegmentálás Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Szegmentálási kritériumok Particionáljuk a képet az alábbi kritériumokat kielégítő régiókba
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
Dinamikus modellek szerkezete, SDG modellek
 Diagnosztika - 3. p. 1/2 Modell Alapú Diagnosztika Diszkrét Módszerekkel Dinamikus modellek szerkezete, SDG modellek Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék Diagnosztika - 3.
Diagnosztika - 3. p. 1/2 Modell Alapú Diagnosztika Diszkrét Módszerekkel Dinamikus modellek szerkezete, SDG modellek Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék Diagnosztika - 3.
Digitális képek szegmentálása. 5. Textúra. Kató Zoltán.
 Digitális képek szegmentálása 5. Textúra Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Textúra fogalma Sklansky: Egy képen egy területnek állandó textúrája van ha a lokális statisztikák vagy
Digitális képek szegmentálása 5. Textúra Kató Zoltán http://www.cab.u-szeged.hu/~kato/segmentation/ Textúra fogalma Sklansky: Egy képen egy területnek állandó textúrája van ha a lokális statisztikák vagy
Térinformatika és Geoinformatika
 Távérzékelés 1 Térinformatika és Geoinformatika 2 A térinformatika az informatika azon része, amely térbeli adatokat, térbeli információkat dolgoz fel A geoinformatika az informatika azon része, amely
Távérzékelés 1 Térinformatika és Geoinformatika 2 A térinformatika az informatika azon része, amely térbeli adatokat, térbeli információkat dolgoz fel A geoinformatika az informatika azon része, amely
Számítógépes képelemzés 7. előadás. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Képfeldolgozás és párhuzamosíthatóság
 Többszálú, többmagos architektúrák és programozásuk Óbudai Egyetem, Neumann János Informatikai Kar Képfeldolgozás és párhuzamosíthatóság A képfeldolgozás olyan alkalmazási terület, amely számos lehetőséget
Többszálú, többmagos architektúrák és programozásuk Óbudai Egyetem, Neumann János Informatikai Kar Képfeldolgozás és párhuzamosíthatóság A képfeldolgozás olyan alkalmazási terület, amely számos lehetőséget
4. Jellemző pontok kinyerése és megfeleltetése
 4. Jellemző pontok kinyerése és megfeleltetése Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Jellemzők és megfeleltetésük A képfeldolgozás,
4. Jellemző pontok kinyerése és megfeleltetése Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Jellemzők és megfeleltetésük A képfeldolgozás,
9. Szegmentálás. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 9. Szegmentálás Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Szegmentálás célja Partícionáljuk a képet koherens objektumokra Nincs egzakt
9. Szegmentálás Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Szegmentálás célja Partícionáljuk a képet koherens objektumokra Nincs egzakt
Automatikus irányzás digitális képek. feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA
 Automatikus irányzás digitális képek feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA Koncepció Robotmérőállomásra távcsővére rögzített kamera Képek alapján a cél automatikus detektálása És az irányzás elvégzése
Automatikus irányzás digitális képek feldolgozásával TURÁK BENCE DR. ÉGETŐ CSABA Koncepció Robotmérőállomásra távcsővére rögzített kamera Képek alapján a cél automatikus detektálása És az irányzás elvégzése
Keresés képi jellemzők alapján. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Mit lássunk élnek? Hol van az él? Milyen vastag legyen? Hol
 Textúra Könnyű az élt megtalálni? Mi lássunk élnek? Mit lássunk élnek? Hol van az él? Milyen vastag legyen? Mit lássunk élnek? Zaj A zajpontokat nem szabad az élpontokkal összekeverni Egy vagy két él?
Textúra Könnyű az élt megtalálni? Mi lássunk élnek? Mit lássunk élnek? Hol van az él? Milyen vastag legyen? Mit lássunk élnek? Zaj A zajpontokat nem szabad az élpontokkal összekeverni Egy vagy két él?
Microsoft Excel 2010. Gyakoriság
 Microsoft Excel 2010 Gyakoriság Osztályközös gyakorisági tábla Nagy számú mérési adatokat csoportokba (osztályokba) rendezése -> könnyebb áttekintés Osztályokban szereplő adatok száma: osztályokhoz tartozó
Microsoft Excel 2010 Gyakoriság Osztályközös gyakorisági tábla Nagy számú mérési adatokat csoportokba (osztályokba) rendezése -> könnyebb áttekintés Osztályokban szereplő adatok száma: osztályokhoz tartozó
2. gyakorlat Mintavételezés, kvantálás
 2. gyakorlat Mintavételezés, kvantálás x(t) x[k]= =x(k T) Q x[k] ^ D/A x(t) ~ ampl. FOLYTONOS idı FOLYTONOS ANALÓG DISZKRÉT MINTAVÉTELEZETT DISZKRÉT KVANTÁLT DIGITÁLIS Jelek visszaállítása egyenköző mintáinak
2. gyakorlat Mintavételezés, kvantálás x(t) x[k]= =x(k T) Q x[k] ^ D/A x(t) ~ ampl. FOLYTONOS idı FOLYTONOS ANALÓG DISZKRÉT MINTAVÉTELEZETT DISZKRÉT KVANTÁLT DIGITÁLIS Jelek visszaállítása egyenköző mintáinak
Morfológia. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar Szoftvertechnológia Intézet
 Morfológia Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Szoftvertechnológia Intézet 2012. október 9. Sergyán (OE NIK) Morfológia 2012. október 9. 1 /
Morfológia Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Szoftvertechnológia Intézet 2012. október 9. Sergyán (OE NIK) Morfológia 2012. október 9. 1 /
12. Képtömörítés. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (
 12. Képtömörítés Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Miért van szükség tömörítésre? A rendelkezésre álló adattárolási és továbbítási
12. Képtömörítés Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Miért van szükség tömörítésre? A rendelkezésre álló adattárolási és továbbítási
Példák jellemzőkre: - minden pixelérték egy jellemző pl. neurális hálózat esetében csak kis képekre, nem invariáns sem a megvilágításra, sem a geom.
 Lépések 1. tanító és teszt halmaz összeállítása / megszerzése 2. jellemzők kinyerése 3. tanító eljárás választása Sok vagy kevés adat áll-e rendelkezésünkre? Mennyi tanítási idő/memória áll rendelkezésre?
Lépések 1. tanító és teszt halmaz összeállítása / megszerzése 2. jellemzők kinyerése 3. tanító eljárás választása Sok vagy kevés adat áll-e rendelkezésünkre? Mennyi tanítási idő/memória áll rendelkezésre?
Digitális jelfeldolgozás
 Digitális jelfeldolgozás Kvantálás Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010. szeptember 15. Áttekintés
Digitális jelfeldolgozás Kvantálás Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010. szeptember 15. Áttekintés
Bevezetés. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 Bevezetés Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Digitális képfeldolgozás digitális képfeldolgozás számítógépes grafika digitális
Bevezetés Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Digitális képfeldolgozás digitális képfeldolgozás számítógépes grafika digitális
f(x) vagy f(x) a (x x 0 )-t használjuk. lim melyekre Mivel itt ɛ > 0 tetszőlegesen kicsi, így a a = 0, a = a, ami ellentmondás, bizonyítva
 6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
4. Szűrés frekvenciatérben
 4. Szűrés frekvenciatérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) Unitér transzformációk Az unitér transzformációk olyan lineáris,
4. Szűrés frekvenciatérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) Unitér transzformációk Az unitér transzformációk olyan lineáris,
Egy (k) küszöb esetén [0, 1] intenzitástartományt feltételezve (v 2 v 2 ):
![Egy (k) küszöb esetén [0, 1] intenzitástartományt feltételezve (v 2 v 2 ): Egy (k) küszöb esetén [0, 1] intenzitástartományt feltételezve (v 2 v 2 ):](/thumbs/91/107527414.jpg) A kép (I) intenzitástartományt folytonos tartományokra osztjuk. Az eredményképen minden egyes tartományhoz egyetlen (egyedi) értéket rendelünk. Egy (k) küszöb esetén [0, 1] intenzitástartományt feltételezve
A kép (I) intenzitástartományt folytonos tartományokra osztjuk. Az eredményképen minden egyes tartományhoz egyetlen (egyedi) értéket rendelünk. Egy (k) küszöb esetén [0, 1] intenzitástartományt feltételezve
KÉPJAVÍTÁS A KÉPTARTOMÁNYBAN
 KÉPJAVÍTÁS A KÉPTARTOMÁNYBAN Képjavítás Olyan eljárás melynek eredménye olyan kép amely jobban megfelel az adott alkalmazásnak - különböző módszereket kell alkalmazni egy Röntgenfelvétel és a Mars felvételének
KÉPJAVÍTÁS A KÉPTARTOMÁNYBAN Képjavítás Olyan eljárás melynek eredménye olyan kép amely jobban megfelel az adott alkalmazásnak - különböző módszereket kell alkalmazni egy Röntgenfelvétel és a Mars felvételének
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
Számítógépes Grafika SZIE YMÉK
 Számítógépes Grafika SZIE YMÉK Analóg - digitális Analóg: a jel értelmezési tartománya (idő), és az értékkészletes is folytonos (pl. hang, fény) Diszkrét idejű: az értelmezési tartomány diszkrét (pl. a
Számítógépes Grafika SZIE YMÉK Analóg - digitális Analóg: a jel értelmezési tartománya (idő), és az értékkészletes is folytonos (pl. hang, fény) Diszkrét idejű: az értelmezési tartomány diszkrét (pl. a
Villamos jelek mintavételezése, feldolgozása. LabVIEW 7.1
 Villamos jelek mintavételezése, feldolgozása (ellenállás mérés LabVIEW támogatással) LabVIEW 7.1 előadás Dr. Iványi Miklósné, egyetemi tanár LabVIEW-7.1 KONF-5_2/1 Ellenállás mérés és adatbeolvasás Rn
Villamos jelek mintavételezése, feldolgozása (ellenállás mérés LabVIEW támogatással) LabVIEW 7.1 előadás Dr. Iványi Miklósné, egyetemi tanár LabVIEW-7.1 KONF-5_2/1 Ellenállás mérés és adatbeolvasás Rn
Digitális képek feldolgozása Előfeldolgozás Radiometriai korrekció Geometriai korrekció Képjavítás Szűrők Sávok közötti műveletek Képosztályozás Utófe
 Távérzékelés Digitális felvételek előfeldolgozása (EENAFOTOTV, ETNATAVERV) Erdőmérnöki szak, Környezettudós szak Király Géza NyME, Erdőmérnöki Kar Geomatikai, Erdőfeltárási és Vízgazdálkodási Intézet Földmérési
Távérzékelés Digitális felvételek előfeldolgozása (EENAFOTOTV, ETNATAVERV) Erdőmérnöki szak, Környezettudós szak Király Géza NyME, Erdőmérnöki Kar Geomatikai, Erdőfeltárási és Vízgazdálkodási Intézet Földmérési
Képfeldolgozás haladóknak Lovag Tamás Novák Gábor 2011
 Dokumentáció Küszöbölés A küszöbölés során végighaladunk a képen és minden egyes képpont intenzitásáról eldöntjük, hogy teljesül-e rá az a küszöbölési feltétel. A teljes képre vonatkozó küszöbölés esetében
Dokumentáció Küszöbölés A küszöbölés során végighaladunk a képen és minden egyes képpont intenzitásáról eldöntjük, hogy teljesül-e rá az a küszöbölési feltétel. A teljes képre vonatkozó küszöbölés esetében
Grafikonok automatikus elemzése
 Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
6. Függvények. Legyen függvény és nem üreshalmaz. A függvényt az f K-ra való kiterjesztésének
 6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
Az Informatika Elméleti Alapjai
 Az Informatika Elméleti Alapjai dr. Kutor László Jelek típusai Átalakítás az analóg és digitális rendszerek között http://mobil.nik.bmf.hu/tantargyak/iea.html Felhasználónév: iea Jelszó: IEA07 IEA 3/1
Az Informatika Elméleti Alapjai dr. Kutor László Jelek típusai Átalakítás az analóg és digitális rendszerek között http://mobil.nik.bmf.hu/tantargyak/iea.html Felhasználónév: iea Jelszó: IEA07 IEA 3/1
Számítógépi képelemzés
 Számítógépi képelemzés Elıadás vázlat Szerzık: Dr. Gácsi Zoltán, egyetemi tanár Dr. Barkóczy Péter, egyetemi docens Lektor: Igaz Antal, okl. gépészmérnök a Carl Zeiss technika kft. Ügyvezetı igazgatója
Számítógépi képelemzés Elıadás vázlat Szerzık: Dr. Gácsi Zoltán, egyetemi tanár Dr. Barkóczy Péter, egyetemi docens Lektor: Igaz Antal, okl. gépészmérnök a Carl Zeiss technika kft. Ügyvezetı igazgatója
Sergyán Szabolcs szeptember 21.
 Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
Fotogrammetriai munkaállomások szoftvermoduljainak tervezése. Dr. habil. Jancsó Tamás Óbudai Egyetem, Alba Regia Műszaki Kar
 Fotogrammetriai munkaállomások szoftvermoduljainak tervezése Dr. habil. Jancsó Tamás Óbudai Egyetem, Alba Regia Műszaki Kar Témakörök DPW szoftvermodulok Szoftverek funkciói Pár példa Mi hiányzik gyakran?
Fotogrammetriai munkaállomások szoftvermoduljainak tervezése Dr. habil. Jancsó Tamás Óbudai Egyetem, Alba Regia Műszaki Kar Témakörök DPW szoftvermodulok Szoftverek funkciói Pár példa Mi hiányzik gyakran?
Statisztikai módszerek a skálafüggetlen hálózatok
 Statisztikai módszerek a skálafüggetlen hálózatok vizsgálatára Gyenge Ádám1 1 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Számítástudományi és Információelméleti
Statisztikai módszerek a skálafüggetlen hálózatok vizsgálatára Gyenge Ádám1 1 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamosmérnöki és Informatikai Kar Számítástudományi és Információelméleti
Villamos jelek mintavételezése, feldolgozása. LabVIEW előadás
 Villamos jelek mintavételezése, feldolgozása (ellenállás mérés LabVIEW támogatással) LabVIEW 7.1 2. előadás Dr. Iványi Miklósné, egyetemi tanár LabVIEW-7.1 EA-2/1 Ellenállás mérés és adatbeolvasás Rn ismert
Villamos jelek mintavételezése, feldolgozása (ellenállás mérés LabVIEW támogatással) LabVIEW 7.1 2. előadás Dr. Iványi Miklósné, egyetemi tanár LabVIEW-7.1 EA-2/1 Ellenállás mérés és adatbeolvasás Rn ismert
Valószínűségi változók. Várható érték és szórás
 Matematikai statisztika gyakorlat Valószínűségi változók. Várható érték és szórás Valószínűségi változók 2016. március 7-11. 1 / 13 Valószínűségi változók Legyen a (Ω, A, P) valószínűségi mező. Egy X :
Matematikai statisztika gyakorlat Valószínűségi változók. Várható érték és szórás Valószínűségi változók 2016. március 7-11. 1 / 13 Valószínűségi változók Legyen a (Ω, A, P) valószínűségi mező. Egy X :
4. Fejezet : Az egész számok (integer) ábrázolása
 4. Fejezet : Az egész számok (integer) ábrázolása The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson
4. Fejezet : Az egész számok (integer) ábrázolása The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson
Diszkréten mintavételezett függvények
 Diszkréten mintavételezett függvények A függvény (jel) értéke csak rögzített pontokban ismert, de köztes pontokban is meg akarjuk becsülni időben mintavételezett jel pixelekből álló műholdkép rácson futtatott
Diszkréten mintavételezett függvények A függvény (jel) értéke csak rögzített pontokban ismert, de köztes pontokban is meg akarjuk becsülni időben mintavételezett jel pixelekből álló műholdkép rácson futtatott
OPTIKA. Szín. Dr. Seres István
 OPTIKA Szín Dr. Seres István Additív színrendszer Seres István 2 http://fft.szie.hu RGB (vagy 24 Bit Color): Egy képpont a piros, a kék és a zöld 256-256-256 féle árnyalatából áll össze, összesen 16 millió
OPTIKA Szín Dr. Seres István Additív színrendszer Seres István 2 http://fft.szie.hu RGB (vagy 24 Bit Color): Egy képpont a piros, a kék és a zöld 256-256-256 féle árnyalatából áll össze, összesen 16 millió
10. Alakzatok és minták detektálása
 0. Alakzatok és mnták detektálása Kató Zoltán Képfeldolgozás és Számítógépes Grafka tanszék SZTE http://www.nf.u-szeged.hu/~kato/teachng/ 2 Hough transzformácó Éldetektálás során csak élpontok halmazát
0. Alakzatok és mnták detektálása Kató Zoltán Képfeldolgozás és Számítógépes Grafka tanszék SZTE http://www.nf.u-szeged.hu/~kato/teachng/ 2 Hough transzformácó Éldetektálás során csak élpontok halmazát
Képfeldolgozás Szegmentálás Osztályozás Képfelismerés Térbeli rekonstrukció
 Mesterséges látás Miről lesz szó? objektumok Bevezetés objektumok A mesterséges látás jelenlegi, technikai eszközökön alapuló világunkban gyakorlatilag azonos a számítógépes képfeldolgozással. Számítógépes
Mesterséges látás Miről lesz szó? objektumok Bevezetés objektumok A mesterséges látás jelenlegi, technikai eszközökön alapuló világunkban gyakorlatilag azonos a számítógépes képfeldolgozással. Számítógépes
Képfeldolgozó eljárások áttekintés. Orvosi képdiagnosztika 9. ea ősz
 Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás,
Képfeldolgozó eljárások áttekintés Orvosi képdiagnosztika 9. ea. 2015 ősz Tartalomjegyzék Képmanipulációs eljárások Képjavítás (kontraszt módosítás, intenzitásviszonyok módosításahisztogram módosítás,
NEURONHÁLÓS HANGTÖMÖRÍTÉS. Áfra Attila Tamás
 NEURONHÁLÓS HANGTÖMÖRÍTÉS Áfra Attila Tamás Tartalom Bevezetés Prediktív kódolás Neuronhálós prediktív modell Eredmények Források Bevezetés Digitális hanghullámok Pulzus kód moduláció Hangtömörítés Veszteségmentes
NEURONHÁLÓS HANGTÖMÖRÍTÉS Áfra Attila Tamás Tartalom Bevezetés Prediktív kódolás Neuronhálós prediktív modell Eredmények Források Bevezetés Digitális hanghullámok Pulzus kód moduláció Hangtömörítés Veszteségmentes
Gauss-Seidel iteráció
 Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Digitális Technika. Dr. Oniga István Debreceni Egyetem, Informatikai Kar
 Digitális Technika Dr. Oniga István Debreceni Egyetem, Informatikai Kar 3. Laboratóriumi gyakorlat A gyakorlat célja: Négy változós AND, OR, XOR és NOR függvények realizálása Szimulátor használata ciklussal
Digitális Technika Dr. Oniga István Debreceni Egyetem, Informatikai Kar 3. Laboratóriumi gyakorlat A gyakorlat célja: Négy változós AND, OR, XOR és NOR függvények realizálása Szimulátor használata ciklussal
Készítette: Fegyverneki Sándor
 VALÓSZÍNŰSÉGSZÁMÍTÁS Összefoglaló segédlet Készítette: Fegyverneki Sándor Miskolci Egyetem, 2001. i JELÖLÉSEK: N a természetes számok halmaza (pozitív egészek) R a valós számok halmaza R 2 {(x, y) x, y
VALÓSZÍNŰSÉGSZÁMÍTÁS Összefoglaló segédlet Készítette: Fegyverneki Sándor Miskolci Egyetem, 2001. i JELÖLÉSEK: N a természetes számok halmaza (pozitív egészek) R a valós számok halmaza R 2 {(x, y) x, y
Véletlen jelenség: okok rendszere hozza létre - nem ismerhetjük mind, ezért sztochasztikus.
 Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Automatikus gamma korrekció
 Automatikus gamma korrekció Kovács György 1, Fazekas Attila 1 University of Debrecen Faculty of Informatics gykovacs@inf.unideb.hu fazekas.attila@inf.unideb.hu Absztrakt. Számos kontraszt javító algoritmus
Automatikus gamma korrekció Kovács György 1, Fazekas Attila 1 University of Debrecen Faculty of Informatics gykovacs@inf.unideb.hu fazekas.attila@inf.unideb.hu Absztrakt. Számos kontraszt javító algoritmus
A távérzékelt felvételek tematikus kiértékelésének lépései
 A távérzékelt felvételek tematikus kiértékelésének lépései Csornai Gábor László István Földmérési és Távérzékelési Intézet Mezőgazdasági és Vidékfejlesztési Igazgatóság Az előadás 2011-es átdolgozott változata
A távérzékelt felvételek tematikus kiértékelésének lépései Csornai Gábor László István Földmérési és Távérzékelési Intézet Mezőgazdasági és Vidékfejlesztési Igazgatóság Az előadás 2011-es átdolgozott változata
OPTIKA. Hullámoptika Színek, szem működése. Dr. Seres István
 OPTIKA Színek, szem működése Dr. Seres István : A fény elektromágneses hullám A fehér fény összetevői: Seres István 2 http://fft.szie.hu Színrendszerek: Additív színrendszer Seres István 3 http://fft.szie.hu
OPTIKA Színek, szem működése Dr. Seres István : A fény elektromágneses hullám A fehér fény összetevői: Seres István 2 http://fft.szie.hu Színrendszerek: Additív színrendszer Seres István 3 http://fft.szie.hu
DIGITÁLIS KÉPANALÍZIS KÉSZÍTETTE: KISS ALEXANDRA ELÉRHETŐSÉG:
 DIGITÁLIS KÉPANALÍZIS KÉSZÍTETTE: KISS ALEXANDRA ELÉRHETŐSÉG: kisszandi@mailbox.unideb.hu ImageJ (Fiji) Nyílt forrás kódú, java alapú képelemző szoftver https://fiji.sc/ Számos képformátumhoz megfelelő
DIGITÁLIS KÉPANALÍZIS KÉSZÍTETTE: KISS ALEXANDRA ELÉRHETŐSÉG: kisszandi@mailbox.unideb.hu ImageJ (Fiji) Nyílt forrás kódú, java alapú képelemző szoftver https://fiji.sc/ Számos képformátumhoz megfelelő
Matematika 8. osztály
 ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Hat évfolyamos Matematika 8. osztály III. rész: Függvények Készítette: Balázs Ádám Budapest, 2018 2. Tartalomjegyzék Tartalomjegyzék III. rész:
ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Hat évfolyamos Matematika 8. osztály III. rész: Függvények Készítette: Balázs Ádám Budapest, 2018 2. Tartalomjegyzék Tartalomjegyzék III. rész:
Digitális Technika. Dr. Oniga István Debreceni Egyetem, Informatikai Kar
 Digitális Technika Dr. Oniga István Debreceni Egyetem, Informatikai Kar 2. Laboratóriumi gyakorlat gyakorlat célja: oolean algebra - sszociativitás tétel - Disztributivitás tétel - bszorpciós tétel - De
Digitális Technika Dr. Oniga István Debreceni Egyetem, Informatikai Kar 2. Laboratóriumi gyakorlat gyakorlat célja: oolean algebra - sszociativitás tétel - Disztributivitás tétel - bszorpciós tétel - De
Nem roncsoló tesztelés diszkrét tomográfiával
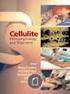 Nem roncsoló tesztelés diszkrét tomográfiával Dr. Balázs Péter, adjunktus Képfeldolgozás és Számítógépes Grafika Tanszék SZTE TTIK, Informatikai Tanszékcsoport A teszteléshez használt CT berendezés lapdetektor
Nem roncsoló tesztelés diszkrét tomográfiával Dr. Balázs Péter, adjunktus Képfeldolgozás és Számítógépes Grafika Tanszék SZTE TTIK, Informatikai Tanszékcsoport A teszteléshez használt CT berendezés lapdetektor
Az objektum leírására szolgálnak. Mire jók? Sokszor maga a jellemző az érdekes: Tömörítés. Objektumok csoportosítására
 Az objektum leírására szolgálnak Mire jók? Sokszor maga a jellemző az érdekes: pl.: átlagosan mekkora egy szitakötő szárnyfesztávolsága? Tömörítés pl.: ha körszerű objektumokat tartalmaz a kép, elegendő
Az objektum leírására szolgálnak Mire jók? Sokszor maga a jellemző az érdekes: pl.: átlagosan mekkora egy szitakötő szárnyfesztávolsága? Tömörítés pl.: ha körszerű objektumokat tartalmaz a kép, elegendő
A mérés problémája a pedagógiában. Dr. Nyéki Lajos 2015
 A mérés problémája a pedagógiában Dr. Nyéki Lajos 2015 A mérés fogalma Mérésen olyan tevékenységet értünk, amelynek eredményeként a vizsgált jelenség számszerűen jellemezhetővé, más hasonló jelenségekkel
A mérés problémája a pedagógiában Dr. Nyéki Lajos 2015 A mérés fogalma Mérésen olyan tevékenységet értünk, amelynek eredményeként a vizsgált jelenség számszerűen jellemezhetővé, más hasonló jelenségekkel
2012. október 2 és 4. Dr. Vincze Szilvia
 2012. október 2 és 4. Dr. Vincze Szilvia Tartalomjegyzék 1.) Az egyváltozós valós függvény fogalma, műveletek 2.) Zérushely, polinomok zérushelye 3.) Korlátosság 4.) Monotonitás 5.) Szélsőérték 6.) Konvex
2012. október 2 és 4. Dr. Vincze Szilvia Tartalomjegyzék 1.) Az egyváltozós valós függvény fogalma, műveletek 2.) Zérushely, polinomok zérushelye 3.) Korlátosság 4.) Monotonitás 5.) Szélsőérték 6.) Konvex
A gyakorlat célja a fehér és a színes zaj bemutatása.
 A gyakorlat célja a fehér és a színes zaj bemutatása. 1.@. FFT begyakorlása n = [:9]; % Harminc minta x = cos(*pi*n/1); % 1 mintát veszünk periodusonként N1 = 64; % Három módon számoljuk az FFT-t N = 18;
A gyakorlat célja a fehér és a színes zaj bemutatása. 1.@. FFT begyakorlása n = [:9]; % Harminc minta x = cos(*pi*n/1); % 1 mintát veszünk periodusonként N1 = 64; % Három módon számoljuk az FFT-t N = 18;
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/54/34131233.jpg) [Biomatematika 2] Orvosi biometria 2016.02.22. Valószínűségi változó Véletlentől függő számértékeket (értékek sokasága) felvevő változókat valószínűségi változóknak nevezzük(jelölés: ξ, η, x). (pl. x =
[Biomatematika 2] Orvosi biometria 2016.02.22. Valószínűségi változó Véletlentől függő számértékeket (értékek sokasága) felvevő változókat valószínűségi változóknak nevezzük(jelölés: ξ, η, x). (pl. x =
1. előadás. Lineáris algebra numerikus módszerei. Hibaszámítás Számábrázolás Kerekítés, levágás Klasszikus hibaanalízis Abszolút hiba Relatív hiba
 Hibaforrások Hiba A feladatok megoldása során különféle hibaforrásokkal találkozunk: Modellhiba, amikor a valóságnak egy közelítését használjuk a feladat matematikai alakjának felírásához. (Pl. egy fizikai
Hibaforrások Hiba A feladatok megoldása során különféle hibaforrásokkal találkozunk: Modellhiba, amikor a valóságnak egy közelítését használjuk a feladat matematikai alakjának felírásához. (Pl. egy fizikai
A Matematika I. előadás részletes tematikája
 A Matematika I. előadás részletes tematikája 2005/6, I. félév 1. Halmazok és relációk 1.1 Műveletek halmazokkal Definíciók, fogalmak: halmaz, elem, üres halmaz, halmazok egyenlősége, részhalmaz, halmazok
A Matematika I. előadás részletes tematikája 2005/6, I. félév 1. Halmazok és relációk 1.1 Műveletek halmazokkal Definíciók, fogalmak: halmaz, elem, üres halmaz, halmazok egyenlősége, részhalmaz, halmazok
Analóg-digitális átalakítás. Rencz Márta/ Ress S. Elektronikus Eszközök Tanszék
 Analóg-digitális átalakítás Rencz Márta/ Ress S. Elektronikus Eszközök Tanszék Mai témák Mintavételezés A/D átalakítók típusok D/A átalakítás 12/10/2007 2/17 A/D ill. D/A átalakítók A világ analóg, a jelfeldolgozás
Analóg-digitális átalakítás Rencz Márta/ Ress S. Elektronikus Eszközök Tanszék Mai témák Mintavételezés A/D átalakítók típusok D/A átalakítás 12/10/2007 2/17 A/D ill. D/A átalakítók A világ analóg, a jelfeldolgozás
c adatpontok és az ismeretlen pont közötti kovariancia vektora
 1. MELLÉKLET: Alkalmazott jelölések A mintaterület kiterjedése, területe c adatpontok és az ismeretlen pont közötti kovariancia vektora C(0) reziduális komponens varianciája C R (h) C R Cov{} d( u, X )
1. MELLÉKLET: Alkalmazott jelölések A mintaterület kiterjedése, területe c adatpontok és az ismeretlen pont közötti kovariancia vektora C(0) reziduális komponens varianciája C R (h) C R Cov{} d( u, X )
A tantárgyelem kódja: A tantárgyelem megnevezése: KIN2803G
 A mérföldkő megnevezése: A tantárgy megnevezése: A mérföldkő kódja: A tantárgy kódja: A tantárgyelem megnevezése: Informatika II. gy A tantárgyelem kredit-értéke: 2 A tantárgyelem teljesítési formája:
A mérföldkő megnevezése: A tantárgy megnevezése: A mérföldkő kódja: A tantárgy kódja: A tantárgyelem megnevezése: Informatika II. gy A tantárgyelem kredit-értéke: 2 A tantárgyelem teljesítési formája:
Regressziós vizsgálatok
 Regressziós vizsgálatok Regresszió (regression) Általános jelentése: visszaesés, hanyatlás, visszafelé mozgás, visszavezetés. Orvosi területen: visszafejlődés, involúció. A betegség tünetei, vagy maga
Regressziós vizsgálatok Regresszió (regression) Általános jelentése: visszaesés, hanyatlás, visszafelé mozgás, visszavezetés. Orvosi területen: visszafejlődés, involúció. A betegség tünetei, vagy maga
Geoinformatika I. (vizsgakérdések)
 Geoinformatika I. (vizsgakérdések) 1.1. Kinek a munkásságához köthető a matematikai információelmélet kialakulása? 1.2. Határozza meg a földtani kutatás információértékét egy terület tektonizáltságának
Geoinformatika I. (vizsgakérdések) 1.1. Kinek a munkásságához köthető a matematikai információelmélet kialakulása? 1.2. Határozza meg a földtani kutatás információértékét egy terület tektonizáltságának
6. Modell illesztés, alakzatok
 6. Modell illesztés, alakzatok Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 ROBOSZTUS EGYENES ILLESZTÉS Egyenes illesztés Adott a síkban
6. Modell illesztés, alakzatok Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 ROBOSZTUS EGYENES ILLESZTÉS Egyenes illesztés Adott a síkban
Digitális képfeldolgozás feladatgyűjtemény
 Digitális képfeldolgozás feladatgyűjtemény Khoros Cantata és VisiQuest rendszerhez Készítették: Dr. Tanács Attila, Domokos Csaba, Gara Mihály, Kardos Péter, Németh Gábor, Németh József Szegedi Tudományegyetem
Digitális képfeldolgozás feladatgyűjtemény Khoros Cantata és VisiQuest rendszerhez Készítették: Dr. Tanács Attila, Domokos Csaba, Gara Mihály, Kardos Péter, Németh Gábor, Németh József Szegedi Tudományegyetem
A gépi látás és képfeldolgozás párhuzamos modelljei és algoritmusai Rövid András Sergyán Szabolcs Vámossy Szabolcs
 A gépi látás és képfeldolgozás párhuzamos modelljei és algoritmusai Rövid András Sergyán Szabolcs Vámossy Szabolcs A gépi látás és képfeldolgozás párhuzamos modelljei és algoritmusai írta Rövid András,
A gépi látás és képfeldolgozás párhuzamos modelljei és algoritmusai Rövid András Sergyán Szabolcs Vámossy Szabolcs A gépi látás és képfeldolgozás párhuzamos modelljei és algoritmusai írta Rövid András,
Projektor árlista 2008. november 13-tól Javasolt
 Projektor árlista 2008. november 13-tól Javasolt Rendelési kód Megnevezés Kép végf. ár VPA75E VPA75E projektor Felbontás: XGA (1024x768) Fényerő: 2600 ANSI lumen Kontraszt: 400:1 Trapézkorrekció: Függőleges
Projektor árlista 2008. november 13-tól Javasolt Rendelési kód Megnevezés Kép végf. ár VPA75E VPA75E projektor Felbontás: XGA (1024x768) Fényerő: 2600 ANSI lumen Kontraszt: 400:1 Trapézkorrekció: Függőleges
Algoritmusok raszteres grafikához
 Algoritmusok raszteres grafikához Egyenes rajzolása Kör rajzolása Ellipszis rajzolása Algoritmusok raszteres grafikához Feladat: Grafikai primitíveket (pl. vonalat, síkidomot) ábrázolni kép-mátrixszal,
Algoritmusok raszteres grafikához Egyenes rajzolása Kör rajzolása Ellipszis rajzolása Algoritmusok raszteres grafikához Feladat: Grafikai primitíveket (pl. vonalat, síkidomot) ábrázolni kép-mátrixszal,
Távérzékelt felvételek előfeldolgozása
 Távérzékelt felvételek előfeldolgozása Csornai Gábor László István Budapest Főváros Kormányhivatala Mezőgazdasági Távérzékelési és Helyszíni Ellenőrzési Osztály Az előadás 2011-es átdolgozott változata
Távérzékelt felvételek előfeldolgozása Csornai Gábor László István Budapest Főváros Kormányhivatala Mezőgazdasági Távérzékelési és Helyszíni Ellenőrzési Osztály Az előadás 2011-es átdolgozott változata
Morfológia. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar Szoftvertechnológia Intézet
 Morfológia Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Szoftvertechnológia Intézet 2013. szeptember 15. Sergyán (OE NIK) Morfológia 2013. szeptember
Morfológia Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Szoftvertechnológia Intézet 2013. szeptember 15. Sergyán (OE NIK) Morfológia 2013. szeptember
ALGEBRAI KIFEJEZÉSEK, EGYENLETEK
 ALGEBRAI KIFEJEZÉSEK, EGYENLETEK AZ ALGEBRAI KIFEJEZÉS FOGALMÁNAK KIALAKÍTÁSA (7-9. OSZTÁLY) Racionális algebrai kifejezés (betűs kifejezés): betűket és számokat a négy alapművelet véges sokszori alkalmazásával
ALGEBRAI KIFEJEZÉSEK, EGYENLETEK AZ ALGEBRAI KIFEJEZÉS FOGALMÁNAK KIALAKÍTÁSA (7-9. OSZTÁLY) Racionális algebrai kifejezés (betűs kifejezés): betűket és számokat a négy alapművelet véges sokszori alkalmazásával
Jel, adat, információ
 Kommunikáció Jel, adat, információ Jel: érzékszerveinkkel, műszerekkel felfogható fizikai állapotváltozás (hang, fény, feszültség, stb.) Adat: jelekből (számítástechnikában: számokból) képzett sorozat.
Kommunikáció Jel, adat, információ Jel: érzékszerveinkkel, műszerekkel felfogható fizikai állapotváltozás (hang, fény, feszültség, stb.) Adat: jelekből (számítástechnikában: számokból) képzett sorozat.
Mi az adat? Az adat elemi ismeret. Az adatokból információkat
 Mi az adat? Az adat elemi ismeret. Tények, fogalmak olyan megjelenési formája, amely alkalmas emberi eszközökkel történő értelmezésre, feldolgozásra, továbbításra. Az adatokból gondolkodás vagy gépi feldolgozás
Mi az adat? Az adat elemi ismeret. Tények, fogalmak olyan megjelenési formája, amely alkalmas emberi eszközökkel történő értelmezésre, feldolgozásra, továbbításra. Az adatokból gondolkodás vagy gépi feldolgozás
11. Előadás. 11. előadás Bevezetés a lineáris programozásba
 11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
Objektív beszédminősítés
 Objektív beszédminősítés Fegyó Tibor fegyo@tmit.bme.hu Beszédinformációs rendszerek -- Objektív beszédminõsítés 1 Beszédinformációs rendszerek -- Objektív beszédminõsítés 2 Bevezető kérdések Mi a [beszéd]
Objektív beszédminősítés Fegyó Tibor fegyo@tmit.bme.hu Beszédinformációs rendszerek -- Objektív beszédminõsítés 1 Beszédinformációs rendszerek -- Objektív beszédminõsítés 2 Bevezető kérdések Mi a [beszéd]
Számítógépes Hálózatok 2012
 Számítógépes Hálózatok 22 4. Adatkapcsolati réteg CRC, utólagos hibajavítás Hálózatok, 22 Hibafelismerés: CRC Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Számítógépes Hálózatok 22 4. Adatkapcsolati réteg CRC, utólagos hibajavítás Hálózatok, 22 Hibafelismerés: CRC Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
A színkezelés alapjai a GIMP programban
 A színkezelés alapjai a GIMP programban Alapok.Előtér és háttér színek.klikk, hogy alapbeállítás legyen ( d és x használata).hozzunk létre egy 640x400 pixeles képet! 4.Ecset eszköz választása 5.Ecset kiválasztása
A színkezelés alapjai a GIMP programban Alapok.Előtér és háttér színek.klikk, hogy alapbeállítás legyen ( d és x használata).hozzunk létre egy 640x400 pixeles képet! 4.Ecset eszköz választása 5.Ecset kiválasztása
Képszűrés II. Digitális képelemzés alapvető algoritmusai. Laplace-operátor és approximációja. Laplace-szűrő és átlagolás. Csetverikov Dmitrij
 Képszűrés II Digitális képelemzés alapvető algoritmusai Csetverikov Dmitrij Eötvös Lóránd Egyetem, Budapest csetverikov@sztaki.hu http://vision.sztaki.hu Informatikai Kar 1 Laplace-szűrő 2 Gauss- és Laplace-képpiramis
Képszűrés II Digitális képelemzés alapvető algoritmusai Csetverikov Dmitrij Eötvös Lóránd Egyetem, Budapest csetverikov@sztaki.hu http://vision.sztaki.hu Informatikai Kar 1 Laplace-szűrő 2 Gauss- és Laplace-képpiramis
