módszerek és alkalmazásuk Markov lánc Monte Carlo Altenburger Gyula Szimpózium Vasas Krisztina
|
|
|
- Dániel Molnár
- 8 évvel ezelőtt
- Látták:
Átírás
1 Markov lánc Mone Carlo módszerek és alkalmazásuk Vasas Krszna Alenburger Gyula Szmpózum
2 Markov láncok Irreducblás : egy oszály van Aperodocás : mnden elem peródusa Vsszaérıség : mnden elem az oszályban vsszaérı
3 Markov-láncok saconárus eloszlása Ha a lánc aperodkus és rreducbls pozív vsszaérı akkor léezk π(y) saconárus eloszlás Ha egy ergodkus lánc kelégí a dealed balance feléel azaz: ( y ) lm P ( X n y X 0 y ) π n m ( y ) ( y x ) ( y ) x y állapoér K ( x y ) π ( x ) K π akkor a lánco reverzblsnek nevezzük
4 Egy gyakorla probléma Bayes módszerek a saszkában: π ( x y ) L ( y x ) p ( x ) arányosság ényezı: L ( y x ) p ( x ) dx Ez nehéz (vagy nem s lehe) analkus módszerekkel kszámoln Ugyanígy ha x öbbdmenzós a margnáls poserorok vagy az E ( ( X ) y ) várhaó érék kszámíása s bonyolul
5 Megoldások Numerkus negrálás approxmácó A poseror eloszlásból veszünk mná majd a kszámoln kíván mennységeke ennek segíségével becsüljük: ez a Markov lánc Mone Carlo módszer lényege Az elsı alkalmazás: aomok energasznjének meghaározása (953Meropols) majd 970- ben saszka problémák megoldása
6 Az MCMC-algormusok álalános elve I. Legyenπ(x) egy céleloszlás amelybıl mná kívánunk venn (közvelenül nem udunk) Generáljunk egy Markov-lánco amely aperodkus és rreducbls és amelynek saconárus eloszlása éppen π(x) Ha a generál sor elég hosszú akkor a agok eknheık egy π(x) eloszlásból való függelen mnának
7 Az MCMC-algormusok álalános elve II. Ebbıl a mnából becsülhejük a céleloszláshoz kapcsolódó mennységeke pl. a várhaó éréke: n n n π ahol X egy realzácó ( ) ( X ) E ( X )
8 Hogyan generáljunk jó lánco? Jelölje K(xy) az ámenekernelazaz ha mos x-ben van a lánc akkor a feléeles eloszlásá a lánc kövekezı (y) állapoának feléve a jelenleg állapoo Ahhoz hogy π(x) sac.eloszlású lánco generáljunk olyan K(xy) kell amre: Kπ π Ha a lánc reverzbls ( π ( x ) K ( x y ) π ( y ) K ( y x ) ) akkor mnden olyan K(xy)-nak am eljesí a feléel π(x) a saconárus eloszlása
9 Meropols-Hasngs algormus Legyen x ( x K x k ) az állapovekor amelynek az. komponensé újíjuk fel q ( x y ) eszıleges eloszlás amelybıl generálunk egy y ( x K x y x K x k ) eleme Ez az eleme α ( x y ) mn ( y ) q ( y x ) ( ) ( ) x q x y valószínőséggel elfogadjuk mn a lánc kövekezı elemé ha nem fogadjuk el akkor a lánc ugyanabban az állapoban marad π π
10 Ámenevalószínőségek a M-H álal P ( x A ) generál láncban Legyen annak valószínősége hogy a lánc kövekezı állapoa az A halmazba esk feléve hogy mos x-ben van. ( ) ( ) ( ) I K x y q x y α x y K ( x y ) dy ( ) ( ) P ( x A ) χ P(xA) kelégí a dealed balance feléel π(x)-re vonakozóan π(x)-e elég konsans szorzó erejég smern Ha q(xy) szmmerkus egyszerő az elfogadás valószínőség A A x r x r ( x ) q ( x y ) α ( x y ) Ω dy
11 A Gbbs-sampler M-H specáls esee akkor alkalmazhaó ha a láncelemek feléeles sőrőségfüggvénye smerek π ( x ) ( y x j ) y ( ) π j Ekkor α q ( x y ) ( ) ( x y ) : ( y x ) ha x ( ) y ( ) π 0 ( y ) π y x ( ) ( x ) π x y ( ) ( ) ( ) egyébkén ( y ) π y y ( ) ( x ) π x x ( ) ( ) ( ) K k ( y ) ( ) ( x ) π π π π π π ( )
12 Egyéb algormusok Random-walk ( x y ) f ( y x ) q Függelen sampler ( x y ) f ( y ) q azaz a lánc pllanany állapoáól függelenül válaszjuk a kövekezı Kombnál samplerek
13 Felmerülı kérdések és problémák Hány erácó hajsunk végre a felújíások során? Mkoról lesz a lánc saconárus? Mlyenek az egyes algormusok keverés ulajdonsága? M legyen a kezdı állapo? Melyk algormus a (leg)jobb?
14 Modellválaszás probléma Olyan modellek közül próbálunk válaszan amelyekben a paraméerek száma maga s paraméer azaz dmenzók közö ugrálunk Pl. a leheséges modellek: {M k k єκ} ahol M k paraméervekora Megoldás: reversble jump MCMC Green 995 k R n k
15 RJMCMC I. Legyen mos π(dx) mérék q(xdy) egy magfüggvény amelybıl a jelöl eleme válaszjuk lleve defnáljunk mozgásípusoka (m2 ) amellyel egy dmenzóból a máskba kerülünk Ha x-ben vagyunk éppen akkor legyen az együes eloszlása q m (xdy) annak hogy y a kövekezı leheséges jelöl és m a kválaszo mozgás ípusa α m ( x y ) mn π ( dy ) q ( ) m y dx π ( dx ) q ( x dy ) m
16 A RJMCMC megvalósíása I. Tegyük fel hogy az m mozgás ípus segíségével juunk el x-bıl y-ba (y magasabb dmenzóban van) M lehe az m?válasszunk egy x-ıl függelen u vélelen vekor és legyen y ennek és x-nek deermnszkus függvénye (y(xu)) y-ból x-be az nverz ranszformácó segíségével juhaunk
17 Példa a mozgásípusok defnícójára Ké leheséges alér: Hogyan juunk 2 2 -bıl vssza C -be? Például az f( 2 )½( 2 ) ranszformácóval. Azaz: C 2 { } R és { } R C 2 2 { } 2 { } ( ) { } És vssza -ból? Válaszunk egy u vélelen vekor függelenül -ól és u lleve 2 -u.
18 Az RJMCMC megvalósíása II. Ha π ( dx ) q m ( x dy ) léezk véges sőrőségfüggvénye valamlyen (szmmerkus) mérékre nézve akkor az (my) pár elıállíhajuk az együes sőrőségfüggvényükbıl Ekkor α ( x y ) mn p p ( y ) r ( ) m y y ( x ) r ( x ) q ( u ) ( x u ) m
19 Egy érsaszka probléma megoldása MCMC segíségével Cél : épülebzosíások kárszámadaanak modellezése Posson-modellel lleve magyarország elepülések veszélyesség kaegórákba sorolása 3222 elepülés adaa állnak rendelkezésre Ezekbıl 68 ksérsége képezünk Térbel összefüggés muaó számláló ípusú adaok
20 Posson-modell Az alkalmazo modell: ( ) y λ z E λ e E z y : az. ksérséghez arozó kárszám (Posson-elo. λ z E várhaó kárszámmal) z : az. ksérség mlyen veszélykaegórába arozk éréke ermészees számok és 6 közö y Mnden kaegórához arozk egy (nap) kárnenzás ez a λ j E : módosío aram azaz a kockázaban ölö dı napokban módosíva az épüleípus falaza és eı ípusának haásával y!
21 Paraméerbecslés Paraméerek: a z(z z 68 ) és a λ(λ λ 6 ) nenzásparaméer-vekor és a ψ nerakcóparaméer Felada: a paraméerek együes a poseror eloszlásából generáljuk a paraméerek becslése
22 A pror sőrőségfüggvények I. Pror a z-re: ahol U ( z ) χ { z ~ a szomszédság relácó z } ~ ' jelöl. Szomszédnak nevezünk ké elepülés ha 30 km-nél közelebb vannak egymáshoz. U ehá az számolja meg hogy egy ado szomszédság srukúrában hány azonos kaegórába arozó szomszéd van. p ( z ψ ) z e e ψ U ( ) ( ) log z k e ψu ψ { K 6 } 68 k ( z ) ( ψ ) '
23 A pror sőrőségfüggvények II. Ψ nemnegaív paraméer nerakcó-paraméernek nevezzük a ψ0 érék a kockáza oszályokba való függelen besorolás jelen ({..k}-n egyenlees eloszlás szern) a érbel függıség nı ha ψ nı a pror eloszlásá egyenleesnek ekneük a {00. } halmazon Pror λ j -re: λ ~ Γ ( α β ) j α és β y E Az együes a pror sőrőségfüggvény p 6 α β λ ( α β ) k! χ { λ < λ 2 < K < λ 6 } Γ ( α ) λ j α j βλ e j
24 Az a poseror együes sőrőségfüggvény p ( z λ ψ y ) p ( ψ ) p ( λ α β ) p ( z ψ ) p ( y z λ ) A z vekor Gbbs-samplng segíségével becsüljük ehhez a full condonal : y λ j E ψ n P z j y e ( ) j ψ λ e n j : azon szomszédanak száma akk sznén j oszályba vannak sorolva Ψ felújíása random-walk MCMC-vel ±0.0-os perurbácókkal
25 Az nenzásparaméer felújíása Meropols-Hasngs algormus A jelöl eloszlás normáls ebbıl λ logarmusá generáljuk am exp. függvénybe helyeesíünk Az elfogadás valószínőség: ( ) 6 ' : ' : mn j E y j j j z j j j z e β λ λ α λ λ
26 A log-poseror grafkonja (00000 erácó)
27 Az nenzásparaméerek A paraméerek auokorrelácófüggvénye gyorsan lecseng nullához ez jelz hogy a lánc eleme konvergálnak a kíván eloszláshoz. Az uolsó 5000 erácóban már nagyon kevese váloznak a paraméerek éréke am sznén a jó konvergencára ual λ λ 2 λ 3 λ 4 λ 5 Álagos paraméerérék λ
28 Az nenzásparaméerek rajekórá
29 Az nenzásparaméerek rajekórá az uolsó 5000 erácóban
30 A z és ψ paraméerek becslése Veszélyesség érkép: egy érképen beszínezzük a ksérségek régóközponja mnden veszélyoszálynak egy szín megfeleleve. Az elsı kockáza oszály a legkevésbé veszélyes(lla) a 6. (fekee) a legveszélyesebb károkozás szemponjából A ψ becslése körül ngadozk A legkockázaosabb elepülések ÉK-en lleve Pécs környékén alálhaóak Budapes ks mérékben kockázaosnak eknheı
31 Veszélyesség érkép
32 A modell leheséges javíása A kockáza oszályok számá nem mondjuk meg elıre hanem az s paraméerkén kezeljük. (RJMCMC)
33 Egy rezsmváló auoregresszív modell Y ( c ) I az akuáls rezsm ípusa: 0 ha a növekvı rezsmbe arozk ha a csökkenı rezsmbe arozk. I Markov-lánc a kövekezı ámenevalószínőség-márxxal: A generáló zajok feléelesen függelenek: ε ~ Γ(αλ) a növekvı rezsmben (pozív sokkok) ε 2 ~ N(0 σ 2 ) a csökkenı rezsmben Y a Y ε P p p c 00 0 ε p p 2 0 f f I I 0
34 A modell saconarása A modell a kövekezı szochaszkus dfferencaegyenle alakjában írhaó: Y a Y b ahol a χ χ a { I 0 } { I } b ε χ ε χ I { I 0 } 2 { } Brand(996) éelébıl kövekezk hogy az egyérelmő saconárus megoldás : mvel E b a a a b Y L ( ( ) ) ( ) log a < 0 and E b 0 log ( ) < 0
35 A modell becslése A modell paraméere: (p 00 p α λ η a c) aholη/σ 2. A láens válozók (I ) a modell becslésé megnehezík. Kézenfekvı leheıségek: Maxmum lkelhood (A lkelhood felírhaó de csak rekurzív formában a láens válozók ma) Markov Chan Mone Carlo (MCMC) Effcen Mehod of Momens (EMM).
36 Az a poseror sőrőségfüggvény ( ) { } T d T ( { Y } ) f { I } { Y } f I f ( { } { } ) T I Y f { Y } { I } ( ) ( { } ) T T f I ( ) f T ( Y Y ) [ ] { } [ ] χ I 0 χ ( )) { I } n n n n f f Y c a Y c p p p p ( ) Γ ( ) ( α λ (0 σ 2 ) f N Ahol például n 00 #(I - 0 and I 0).
37 Markov Chan Mone Carlo módszer Az együes poserorból kell mná vennünk hogy meg kapjuk a becsléseke Erre a megfelelı módszer egy Markov-lánc készíése a kövekezı saconárus eloszlással: ( { } { } ) T f I Y. A reje állapooka (I ) a srukuráls paraméekhez hasonlóan felújíjuk Gbbs-samplnge szernénk használn amkor csak lehe Konjugál prorok segíségével 6 paraméernek felírhaóak a megfelelı feléeles eloszlása A Meropols-Hasngs lépés csak a növekvı rezsmben jelenlévı gamma eloszlás alakparaméerének (α) becslésekor szükséges
38 Gbbs samplng Ha felírhaóak a eljes feléele eloszlások: a mnavéel a feléeles eloszlásokból realzálhaó: ( ) ( ) ( ) j n j j j n j j j n j j j d π π π K K K K K K ( ) ( ) ( ) ( ) ( ) ( ) ) ( ) ( 2 ) ( ) ( ) ( 3 ) ( 2 2 ) ( ) ( 3 ) ( 2 ~ ~ ~ n n n n n π π π K M K K
39 Meropols-Hasngs Válaszzunk egy Y jelöle q(y () ) eloszlásból az erácó mnden lépésében A jelöl pono fogadjuk el az alább valószínőséggel α ( y ) ( ) ( ( ) ) π q y ( ) ( ( ) ( ) ) π y q y mn ( ) ekkor () y és mnden egyéb eseben () ().
40 A prorok megválaszása α ~ Γ(α u λ u ) λ~ Γ(rβ) η ~ Γ(qρ) a ~ N(µτ) c~ N(νκ) p 00 ~ β(u v ) p ~ β(u 2 v 2 ) Y Remember he model: Y ( c ) a Y ε P p p 00 0 c ε p p 2 0 ε ~ Γ(αλ) ε 2 ~ N(0 σ 2 ) f f I I 0
41 Teljes feléelesek λ ra és η-ra λ eloszlása: ( { Y } { I } α ) ~ ( n α r ( Y ) ) λ Γ Y 0 β 0 I η eloszlása: η ( { } { } ) Γ 2 Y ( ( ) ) I a c ~ q Y c a Y c ρ 2 I n
42 Teljes feléelesek a-ra és c-re C eloszlása: a eloszlása: { } { } ( ) ( ) ( ) ( ) ( ) κ κ υκ ~ a n a n ay Y a N a I Y c I { } { } ( ) ( )( ) ( ) ( ) 2 2 ~ I I I c Y c Y c Y c Y N c I Y a η τ η τ η µτ
43 Teljes feléelesek az ámenevalószínőségekre P 00 eloszlása: ( { I } ) ~ β ( n u n ) p v P eloszlása: ( { I } ) ~ β ( n u n ) p v 0
44 A eljes feléelesek a reje állapookra P I P I e.g.: ( 0 I 0 I 0 Y Y ) ( I I Y Y ) 2 p 00 Γ ( Y Y ) 2 p 00 Γ ( Y Y ) ( p 00 )( p ) N ( Y c a ( Y c ) ) 2 p N ( Y c a ( Y c ) ) ( p )( p ) Γ ( Y Y ) p N ( Y c a ( Y c ) ) 00 2
45 Azα felújíása A Meropols-Hasngs lépések soránαfelújíására normáls eloszlás alkalmazunk: α * ~ N(αδ 2 )
46 M örénk ha az állapo-folyama mégsem Markov? A Markovás kövekezménye hogy az egy rezsmben elölö dı geomera eloszlású Egy leheséges álalánosíás: Legyen a növekvı rezsmek hosszának eloszlása: NegBn(βp ) A csökkenı rezsmek maradjanak geomera eloszlásúak: Geom(p 0 ) A rezsmhosszak maradjanak függelenek Specáls ese: β (az elızı modell nyerjük)
47 Az álalánosío modell becslése:. megközelíés A srukuráls paraméerek: (α λ η a c p 0 β p ) A poseror a megfelelı módon válozahaó β-ra gamma eloszlású pror feléelézünk Mnden lépés ugyanaz mn az elızı modellben kvéveβ- p - I -ke β Meropols-Hasngs lépésekkel újíjuk fel Az I -k eloszlása már nem csak Y - Y I - és I -ıl függ hanem a uán 0 és fuamok hosszáól s.
48 Az álalánosío modell becslése: A reversble jump megközelíés Az I -k helye vezessük be a rezsmek válásponja mn láens válozóka: A csökkenı peródusok végponja: s(s...s k ) A növekvı peródusok végponja: (... k ) A kezdıérékeke és a válásponok számá az elızı modellbıl becsülük meg Ha smerjük a válásponoka {I } meghaározhaó így az elızı algormus nagy része alkalmazhaó Az új probléma és felada: a válásponok felújíása
49 És ha a válásponok száma s paraméer? A valóságban a válásponok számá nem udjuk elıre meghaározn A megoldás: legyen ez s paraméer és a srukuráls válozókhoz hasonlóan újísuk fel ez s A sandard MCMC echnkák már nem alkalmazhaóak reversble jump MCMC- kell felépíen (see Green 995)
50 A reversble jump algormus 3 lépés defnálunk: Sep. : Mnden paraméer felújíunk kvéve a válásponok számá Sep 2. : Szüleés lépés: egy új váláspono szúrunk be ké vélelenszerően kválaszo már meglévı váláspon közé Sep 3. : Halál lépés : egy vélelenszerően kválaszo váláspono örlünk A lépéseke a kövekezı valószínőségekkel válaszjuk: q q B q D q q B q D.
51 A válásponok felújíása az elsı lépésben Teljes feléeles az s -re: Ahol a másodk ag : (N negaív bnomáls N 2 geomera eloszlású) { } ( ) ( ) { } ( ) ( ) y y s P y s Y P x s P x s Y P ( ) ( ) ( ) 2 N N P x N P x s P ( ) ( ) ( ) ( ) y p y Geom p b y NegBn p x Geom p b x NegBn { } ( ) Y x s P
52 Elfogadás valószínőségek a másodk és harmadk lépésben A szüleés lépésében az alább mozgás ípus * * elfogadásának valószínősége: s s ( ) ( ) α brh mn f ( { } ) * * k s Y f ( k s { Y } ) 2 q k q l D B ( m 2 2)( m ) A halál lépésben a fen valószínőség nverze lesz az elfogadás esély
53 Eredmények Tvadar eseében Mndké megközelíés kpróbáluk a fx dmenzós jobbnak bzonyul β 4.77 (s.e..38); szgnfkánsan különbözk - ıl A növekvı rezsmek álagos hossza 2.5 nap A csökkenı rezsmek álagos hossza 4.4 nap a 0.85 (s.e ); magas perzszenca a csökkenı rezsmben α (s.e ); a növekvı rezsme majdnem ecponencáls
54 A modell vsszaadja a hdrográf aszmmerkus alakjá
55 Az erede (red) és a szmulál(kék) dısorok sőrőségfüggvénye
56 Köszönöm a fgyelme!
Tiszta és kevert stratégiák
 sza és kever sraégák sza sraéga: Az -edk áékos az sraégá és ez alkalmazza. S sraégahalmazból egyérelműen válasz k egy eknsük a kövekező áéko. Ké vállala I és II azonos erméke állí elő. Azon gondolkodnak,
sza és kever sraégák sza sraéga: Az -edk áékos az sraégá és ez alkalmazza. S sraégahalmazból egyérelműen válasz k egy eknsük a kövekező áéko. Ké vállala I és II azonos erméke állí elő. Azon gondolkodnak,
A termelési, szolgáltatási igény előrejelzése
 A ermelés, szolgálaás gény előrejelzése Termelés- és szolgálaásmenedzsmen r. alló oém egyeem docens Menedzsmen és Vállalagazdaságan Tanszék Termelés- és szolgálaásmenedzsmen Részdős üzle meserszakok r.
A ermelés, szolgálaás gény előrejelzése Termelés- és szolgálaásmenedzsmen r. alló oém egyeem docens Menedzsmen és Vállalagazdaságan Tanszék Termelés- és szolgálaásmenedzsmen Részdős üzle meserszakok r.
Távközlı hálózatok és szolgáltatások
 Távközlı hálózaok és szolgálaások Forgalmi köveelmények, hálózaméreezés Csopaki Gyula Némeh Kriszián BME TMIT 22. nov. 2. A árgy felépíése. Bevezeés 2. I hálózaok elérése ávközlı és kábel-tv hálózaokon
Távközlı hálózaok és szolgálaások Forgalmi köveelmények, hálózaméreezés Csopaki Gyula Némeh Kriszián BME TMIT 22. nov. 2. A árgy felépíése. Bevezeés 2. I hálózaok elérése ávközlı és kábel-tv hálózaokon
Kockázati folyamatok
 Kockázai folyamaok Sz cs Gábor Szegedi Tudományegyeem Bolyai Inéze, Szochaszika Tanszék Uolsó frissíés: 219. szepember 17. Taralomjegyzék 1. Az exponenciális eloszlás 2 2. A Wald-azonosság 4 3. Felújíási
Kockázai folyamaok Sz cs Gábor Szegedi Tudományegyeem Bolyai Inéze, Szochaszika Tanszék Uolsó frissíés: 219. szepember 17. Taralomjegyzék 1. Az exponenciális eloszlás 2 2. A Wald-azonosság 4 3. Felújíási
4. Lineáris csillapítatlan szabad rezgés. Lineáris csillapított szabad rezgés. Gyenge csillapítás. Ger-jesztett rezgés. Amplitúdó rezonancia.
 4 Lneárs csllapíalan szabad rezgés Lneárs csllapío szabad rezgés Gyenge csllapíás Ger-jesze rezgés Aplúdó rezonanca Lneárs csllapíalan szabad rezgés: Téelezzük fel hogy a öegponra a kvázelaszkus vagy közel
4 Lneárs csllapíalan szabad rezgés Lneárs csllapío szabad rezgés Gyenge csllapíás Ger-jesze rezgés Aplúdó rezonanca Lneárs csllapíalan szabad rezgés: Téelezzük fel hogy a öegponra a kvázelaszkus vagy közel
Kockázat és megbízhatóság
 Budapesi Mőszaki és Gazdaságudományi Egyeem Gazdaság- és Társadalomudományi Kar Üzlei Tudományok Inéze Menedzsmen és Vállalagazdaságan Tanszék Dr. Kövesi János Erdei János Dr. Tóh Zsuzsanna Eszer - Eigner
Budapesi Mőszaki és Gazdaságudományi Egyeem Gazdaság- és Társadalomudományi Kar Üzlei Tudományok Inéze Menedzsmen és Vállalagazdaságan Tanszék Dr. Kövesi János Erdei János Dr. Tóh Zsuzsanna Eszer - Eigner
13 Wiener folyamat és az Itô lemma. Options, Futures, and Other Derivatives, 8th Edition, Copyright John C. Hull
 13 Wiener folyama és az Iô lemma Opions, Fuures, and Oher Derivaives, 8h Ediion, Copyrigh John C. Hull 01 1 Markov folyamaok Memória nélküli szochaszikus folyamaok, a kövekező lépés csak a pillananyi helyzeől
13 Wiener folyama és az Iô lemma Opions, Fuures, and Oher Derivaives, 8h Ediion, Copyrigh John C. Hull 01 1 Markov folyamaok Memória nélküli szochaszikus folyamaok, a kövekező lépés csak a pillananyi helyzeől
Intraspecifikus verseny
 Inraspecifikus verseny Források limiálsága evolúciós (finesz) kövekezmény aszimmeria Denziás-függés Park és msai (930-as évek, Chicago) - Tribolium casaneum = denziás-függelen (D-ID) 2 = alulkompenzál
Inraspecifikus verseny Források limiálsága evolúciós (finesz) kövekezmény aszimmeria Denziás-függés Park és msai (930-as évek, Chicago) - Tribolium casaneum = denziás-függelen (D-ID) 2 = alulkompenzál
Tanulási folyamat számítógéppel történő kölcsönhatásban
 Eövös Loránd Tudományegyeem Természeudomány Kar Tanulás folyama számíógéppel örénő kölcsönhaásban Dplomamunka Bakos kole maemaka anár szakos hallgaó Témavezeő: dr. habl. Lőrncz András udományos főmunkaárs
Eövös Loránd Tudományegyeem Természeudomány Kar Tanulás folyama számíógéppel örénő kölcsönhaásban Dplomamunka Bakos kole maemaka anár szakos hallgaó Témavezeő: dr. habl. Lőrncz András udományos főmunkaárs
Mesterséges Intelligencia MI
 Meserséges Inelligencia MI Valószínűségi emporális kövekezeés Dobrowiecki Tadeusz Eredics Péer, és mások BME I.E. 437, 463-28-99 dobrowiecki@mi.bme.hu, hp://www.mi.bme.hu/general/saff/ade X - a időpillanaban
Meserséges Inelligencia MI Valószínűségi emporális kövekezeés Dobrowiecki Tadeusz Eredics Péer, és mások BME I.E. 437, 463-28-99 dobrowiecki@mi.bme.hu, hp://www.mi.bme.hu/general/saff/ade X - a időpillanaban
1. Példa. A gamma függvény és a Fubini-tétel.
 . Példa. A gamma függvény és a Fubini-tétel.. Az x exp x + t )) függvény az x, t tartományon folytonos, és nem negatív, ezért alkalmazható rá a Fubini-tétel. I x exp x + t )) dxdt + t dt π 4. [ exp x +
. Példa. A gamma függvény és a Fubini-tétel.. Az x exp x + t )) függvény az x, t tartományon folytonos, és nem negatív, ezért alkalmazható rá a Fubini-tétel. I x exp x + t )) dxdt + t dt π 4. [ exp x +
GAZDASÁGI ÉS ÜZLETI STATISZTIKA jegyzet ÜZLETI ELŐREJELZÉSI MÓDSZEREK
 BG PzK Módszerani Inézei Tanszéki Oszály GAZDAÁGI É ÜZLETI TATIZTIKA jegyze ÜZLETI ELŐREJELZÉI MÓDZEREK A jegyzee a BG Módszerani Inézei Tanszékének okaói készíeék 00-ben. Az idősoros vizsgálaok legfonosabb
BG PzK Módszerani Inézei Tanszéki Oszály GAZDAÁGI É ÜZLETI TATIZTIKA jegyze ÜZLETI ELŐREJELZÉI MÓDZEREK A jegyzee a BG Módszerani Inézei Tanszékének okaói készíeék 00-ben. Az idősoros vizsgálaok legfonosabb
HF1. Határozza meg az f t 5 2 ugyanabban a koordinátarendszerben. Mi a lehetséges legbővebb értelmezési tartománya és
 Házi feladaok megoldása 0. nov. 6. HF. Haározza meg az f 5 ugyanabban a koordináarendszerben. Mi a leheséges legbővebb érelmezési arománya és érékkészlee az f és az f függvényeknek? ( ) = függvény inverzé.
Házi feladaok megoldása 0. nov. 6. HF. Haározza meg az f 5 ugyanabban a koordináarendszerben. Mi a leheséges legbővebb érelmezési arománya és érékkészlee az f és az f függvényeknek? ( ) = függvény inverzé.
Statisztika II. előadás és gyakorlat 1. rész
 Saiszika II. Saiszika II. előadás és gyakorla 1. rész T.Nagy Judi Ajánlo irodalom: Ilyésné Molnár Emese Lovasné Avaó Judi: Saiszika II. Feladagyűjemény, Perfek, 2006. Korpás Ailáné (szerk.): Álalános Saiszika
Saiszika II. Saiszika II. előadás és gyakorla 1. rész T.Nagy Judi Ajánlo irodalom: Ilyésné Molnár Emese Lovasné Avaó Judi: Saiszika II. Feladagyűjemény, Perfek, 2006. Korpás Ailáné (szerk.): Álalános Saiszika
Fourier-sorok konvergenciájáról
 Fourier-sorok konvergenciájáról A szereplő függvényekről mindenü felesszük, hogy szerin periodikusak. Az ilyen függvények megközelíésére (nem a polinomok, hanem) a rigonomerikus polinomok űnnek ermészees
Fourier-sorok konvergenciájáról A szereplő függvényekről mindenü felesszük, hogy szerin periodikusak. Az ilyen függvények megközelíésére (nem a polinomok, hanem) a rigonomerikus polinomok űnnek ermészees
Bevezetés 2. Az igény összetevői 3. Konstans jellegű igény előrejelzése 5. Lineáris trenddel rendelkező igény előrejelzése 14
 Termelésmenedzsmen lőrejelzés módszerek Bevezeés Az gény összeevő 3 Konsans jellegű gény előrejelzése 5 lőrejelzés mozgó álaggal 6 Mozgó álaggal előre jelze gény 6 Gyakorló felada 8 Megoldás 9 lőrejelzés
Termelésmenedzsmen lőrejelzés módszerek Bevezeés Az gény összeevő 3 Konsans jellegű gény előrejelzése 5 lőrejelzés mozgó álaggal 6 Mozgó álaggal előre jelze gény 6 Gyakorló felada 8 Megoldás 9 lőrejelzés
Volt-e likviditási válság?
 KÜLÖNSZÁM 69 VÁRADI KATA 1 Vol-e lkvdás válság? Volalás és lkvdás kapcsolaának vzsgálaa Széleskörűen aláámaszo, emprkus ény, hogy önmagában a nagyobb volalás csökken a pac lkvdásá, vagys válozékonyabb
KÜLÖNSZÁM 69 VÁRADI KATA 1 Vol-e lkvdás válság? Volalás és lkvdás kapcsolaának vzsgálaa Széleskörűen aláámaszo, emprkus ény, hogy önmagában a nagyobb volalás csökken a pac lkvdásá, vagys válozékonyabb
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek középszin ÉETTSÉG VZSGA 0. május. ELEKTONKA ALAPSMEETEK KÖZÉPSZNTŰ ÍÁSBEL ÉETTSÉG VZSGA JAVÍTÁS-ÉTÉKELÉS ÚTMTATÓ EMBE EŐFOÁSOK MNSZTÉMA Egyszerű, rövid feladaok Maximális ponszám:
Elekronikai alapismereek középszin ÉETTSÉG VZSGA 0. május. ELEKTONKA ALAPSMEETEK KÖZÉPSZNTŰ ÍÁSBEL ÉETTSÉG VZSGA JAVÍTÁS-ÉTÉKELÉS ÚTMTATÓ EMBE EŐFOÁSOK MNSZTÉMA Egyszerű, rövid feladaok Maximális ponszám:
Az árfolyamsávok empirikus modelljei és a devizaárfolyam sávon belüli elõrejelezhetetlensége
 Az árfolyamsávok empirikus modelljei 507 Közgazdasági Szemle, XLVI. évf., 1999. június (507 59. o.) DARVAS ZSOLT Az árfolyamsávok empirikus modelljei és a devizaárfolyam sávon belüli elõrejelezheelensége
Az árfolyamsávok empirikus modelljei 507 Közgazdasági Szemle, XLVI. évf., 1999. június (507 59. o.) DARVAS ZSOLT Az árfolyamsávok empirikus modelljei és a devizaárfolyam sávon belüli elõrejelezheelensége
Statisztika gyakorló feladatok
 . Konfidencia inervallum beclé Saizika gyakorló feladaok Az egyeemiák alkoholfogyazái zokáainak vizgálaára 995. avazán egy mina alapján kérdıíve felméré végezek. A vizgál egyeemek: SOTE, ELTE Jog, KözGáz.
. Konfidencia inervallum beclé Saizika gyakorló feladaok Az egyeemiák alkoholfogyazái zokáainak vizgálaára 995. avazán egy mina alapján kérdıíve felméré végezek. A vizgál egyeemek: SOTE, ELTE Jog, KözGáz.
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek középszin 3 ÉETTSÉG VZSG 04. május 0. EEKTONK PSMEETEK KÖZÉPSZNTŰ ÍÁSBE ÉETTSÉG VZSG JVÍTÁS-ÉTÉKEÉS ÚTMTTÓ EMBE EŐFOÁSOK MNSZTÉM Egyszerű, rövid feladaok Maximális ponszám: 40.)
Elekronikai alapismereek középszin 3 ÉETTSÉG VZSG 04. május 0. EEKTONK PSMEETEK KÖZÉPSZNTŰ ÍÁSBE ÉETTSÉG VZSG JVÍTÁS-ÉTÉKEÉS ÚTMTTÓ EMBE EŐFOÁSOK MNSZTÉM Egyszerű, rövid feladaok Maximális ponszám: 40.)
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek középszin 3 ÉETTSÉGI VIZSGA 0. okór 5. ELEKTONIKAI ALAPISMEETEK KÖZÉPSZINTŰ ÍÁSBELI ÉETTSÉGI VIZSGA JAVÍTÁSI-ÉTÉKELÉSI ÚTMTATÓ EMBEI EŐFOÁSOK MINISZTÉIMA Egyszerű, rövid feladaok
Elekronikai alapismereek középszin 3 ÉETTSÉGI VIZSGA 0. okór 5. ELEKTONIKAI ALAPISMEETEK KÖZÉPSZINTŰ ÍÁSBELI ÉETTSÉGI VIZSGA JAVÍTÁSI-ÉTÉKELÉSI ÚTMTATÓ EMBEI EŐFOÁSOK MINISZTÉIMA Egyszerű, rövid feladaok
Negyedik gyakorlat: Szöveges feladatok, Homogén fokszámú egyenletek Dierenciálegyenletek, Földtudomány és Környezettan BSc
 Negyedik gyakorla: Szöveges feladaok, Homogén fokszámú egyenleek Dierenciálegyenleek, Földudomány és Környezean BSc. Szöveges feladaok A zikában el forduló folyamaok nagy része széválaszhaó egyenleekkel
Negyedik gyakorla: Szöveges feladaok, Homogén fokszámú egyenleek Dierenciálegyenleek, Földudomány és Környezean BSc. Szöveges feladaok A zikában el forduló folyamaok nagy része széválaszhaó egyenleekkel
2. gyakorlat: Z épület ferdeségmérésének mérése
 . gyakorla: Z épüle ferdeségének mérése. gyakorla: Z épüle ferdeségmérésének mérése Felada: Épíésellenőrzési feladakén egy 1 szines épüle függőleges élének érbeli helyzeé kell meghaározni, majd az 1986-ban
. gyakorla: Z épüle ferdeségének mérése. gyakorla: Z épüle ferdeségmérésének mérése Felada: Épíésellenőrzési feladakén egy 1 szines épüle függőleges élének érbeli helyzeé kell meghaározni, majd az 1986-ban
egyenletesen, és c olyan színű golyót teszünk az urnába, amilyen színűt húztunk. Bizonyítsuk
 Valószínűségszámítás 8. feladatsor 2015. november 26. 1. Bizonyítsuk be, hogy az alábbi folyamatok mindegyike martingál. a S n, Sn 2 n, Y n = t n 1+ 1 t 2 Sn, t Fn = σ S 1,..., S n, 0 < t < 1 rögzített,
Valószínűségszámítás 8. feladatsor 2015. november 26. 1. Bizonyítsuk be, hogy az alábbi folyamatok mindegyike martingál. a S n, Sn 2 n, Y n = t n 1+ 1 t 2 Sn, t Fn = σ S 1,..., S n, 0 < t < 1 rögzített,
Tájékoztató a portfólió értékelésérıl, illetve a portfólión elért hozam számításáról
 Tájékozaó a pofóló éékeléséıl, lleve a pofólón elé hoza száíásáól Jelen ájékozaó elválaszhaalan észé képez az Ügyfél és az EQUILOR Befekeés Z. (ovábbakban EQUILOR) közö léejö pofólókezelés szezıdésnek.
Tájékozaó a pofóló éékeléséıl, lleve a pofólón elé hoza száíásáól Jelen ájékozaó elválaszhaalan észé képez az Ügyfél és az EQUILOR Befekeés Z. (ovábbakban EQUILOR) közö léejö pofólókezelés szezıdésnek.
Szilárdsági vizsgálatok eredményei közötti összefüggések a Bátaapáti térségében mélyített fúrások kızetanyagán
 Mérnökgeológia-Kızemehanika 2011 (Szerk: Török Á. & Vásárhelyi B.) 269-274. Szilárdsági vizsgálaok eredményei közöi összefüggések a Báaapái érségében mélyíe fúrások kızeanyagán Buoz Ildikó BME Épíıanyagok
Mérnökgeológia-Kızemehanika 2011 (Szerk: Török Á. & Vásárhelyi B.) 269-274. Szilárdsági vizsgálaok eredményei közöi összefüggések a Báaapái érségében mélyíe fúrások kızeanyagán Buoz Ildikó BME Épíıanyagok
Előszó. 1. Rendszertechnikai alapfogalmak.
 Plel Álalános áekinés, jel és rendszerechnikai alapfogalmak. Jelek feloszása (folyonos idejű, diszkré idejű és folyonos érékű, diszkré érékű, deerminiszikus és szochaszikus. Előszó Anyagi világunkban,
Plel Álalános áekinés, jel és rendszerechnikai alapfogalmak. Jelek feloszása (folyonos idejű, diszkré idejű és folyonos érékű, diszkré érékű, deerminiszikus és szochaszikus. Előszó Anyagi világunkban,
5. Differenciálegyenlet rendszerek
 5 Differenciálegyenle rendszerek Elsőrendű explici differenciálegyenle rendszer álalános alakja: d = f (, x, x,, x n ) d = f (, x, x,, x n ) (5) n d = f n (, x, x,, x n ) ömörebben: d = f(, x) Definíció:
5 Differenciálegyenle rendszerek Elsőrendű explici differenciálegyenle rendszer álalános alakja: d = f (, x, x,, x n ) d = f (, x, x,, x n ) (5) n d = f n (, x, x,, x n ) ömörebben: d = f(, x) Definíció:
KELET-KÖZÉP EURÓPAI DEVIZAÁRFOLYAMOK ELİREJELZÉSE HATÁRIDİS ÁRFOLYAMOK SEGÍTSÉGÉVEL. Darvas Zsolt Schepp Zoltán
 Közgazdasági- és Regionális Tudományok Inézee Pécsi Tudományegyeem, Közgazdaságudományi Kar KELET-KÖZÉP EURÓPAI DEVIZAÁRFOLYAMOK ELİREJELZÉSE HATÁRIDİS ÁRFOLYAMOK SEGÍTSÉGÉVEL Darvas Zsol Schepp Zolán
Közgazdasági- és Regionális Tudományok Inézee Pécsi Tudományegyeem, Közgazdaságudományi Kar KELET-KÖZÉP EURÓPAI DEVIZAÁRFOLYAMOK ELİREJELZÉSE HATÁRIDİS ÁRFOLYAMOK SEGÍTSÉGÉVEL Darvas Zsol Schepp Zolán
A mágneses tér alapfogalmai, alaptörvényei
 A mágneses ér alapfogalma, alapörvénye A nyugvó vllamos ölések közö erőhaásoka a vllamos ér közveí (Coulomb örvénye). A mozgó ölések (vllamos áramo vvő vezeők) közö s fellép erőhaás, am a mágneses ér közveí.
A mágneses ér alapfogalma, alapörvénye A nyugvó vllamos ölések közö erőhaásoka a vllamos ér közveí (Coulomb örvénye). A mozgó ölések (vllamos áramo vvő vezeők) közö s fellép erőhaás, am a mágneses ér közveí.
DIFFÚZIÓ. BIOFIZIKA I Október 20. Bugyi Beáta
 BIOFIZIKA I 010. Okóber 0. Bugyi Beáa TRANSZPORTELENSÉGEK Transzpor folyama: egy fizikai mennyiség érbeli eloszlása megválozik Emlékezeő: ermodinamika 0. főéele az egyensúly álalános feléele TERMODINAMIKAI
BIOFIZIKA I 010. Okóber 0. Bugyi Beáa TRANSZPORTELENSÉGEK Transzpor folyama: egy fizikai mennyiség érbeli eloszlása megválozik Emlékezeő: ermodinamika 0. főéele az egyensúly álalános feléele TERMODINAMIKAI
Megoldások. ξ jelölje az első meghibásodásig eltelt időt. Akkor ξ N(6, 4; 2, 3) normális eloszlású P (ξ
 Megoldások Harmadik fejezet gyakorlatai 3.. gyakorlat megoldása ξ jelölje az első meghibásodásig eltelt időt. Akkor ξ N(6, 4;, 3 normális eloszlású P (ξ 8 ξ 5 feltételes valószínűségét (.3. alapján számoljuk.
Megoldások Harmadik fejezet gyakorlatai 3.. gyakorlat megoldása ξ jelölje az első meghibásodásig eltelt időt. Akkor ξ N(6, 4;, 3 normális eloszlású P (ξ 8 ξ 5 feltételes valószínűségét (.3. alapján számoljuk.
Adatbányászat: Rendellenesség keresés. 10. fejezet. Tan, Steinbach, Kumar Bevezetés az adatbányászatba
 Adabányásza: Rendellenesség keresés 10. fejeze Tan, Seinbach, Kumar Bevezeés az adabányászaba előadás-fóliák fordíoa Ispány Máron Logók és ámogaás A ananyag a TÁMOP-4.1.2-08/1/A-2009-0046 számú Kele-magyarországi
Adabányásza: Rendellenesség keresés 10. fejeze Tan, Seinbach, Kumar Bevezeés az adabányászaba előadás-fóliák fordíoa Ispány Máron Logók és ámogaás A ananyag a TÁMOP-4.1.2-08/1/A-2009-0046 számú Kele-magyarországi
MISKOLCI EGYETEM VILLAMOSMÉRNÖKI INTÉZET ELEKTROTECHNIKAI- ELEKTRONIKAI TANSZÉK DR. KOVÁCS ERNŐ ELEKTRONIKA II/2. (ERŐSÍTŐK) ELŐADÁS JEGYZET 2003.
 MSKOL GYTM VLLMOSMÉNÖK NTÉZT LKTOTHNK- LKTONK TNSZÉK D. KOVÁS NŐ LKTONK /. (ŐSÍTŐK) LŐDÁS JGYZT 3. Mskolc gyeem lekroechnka-lekronka Tanszék.6. rősíők z erősíők az erősíő ípsú dszkré félvezeők és negrál
MSKOL GYTM VLLMOSMÉNÖK NTÉZT LKTOTHNK- LKTONK TNSZÉK D. KOVÁS NŐ LKTONK /. (ŐSÍTŐK) LŐDÁS JGYZT 3. Mskolc gyeem lekroechnka-lekronka Tanszék.6. rősíők z erősíők az erősíő ípsú dszkré félvezeők és negrál
3. Gyakorlat. A soros RLC áramkör tanulmányozása
 3. Gyakorla A soros áramkör anlmányozása. A gyakorla célkiőzései Válakozó áramú áramkörökben a ekercsek és kondenzáorok frekvenciafüggı reakív ellenállással ún. reakanciával rendelkeznek. Sajáságos lajdonságaik
3. Gyakorla A soros áramkör anlmányozása. A gyakorla célkiőzései Válakozó áramú áramkörökben a ekercsek és kondenzáorok frekvenciafüggı reakív ellenállással ún. reakanciával rendelkeznek. Sajáságos lajdonságaik
Folyamatszemléleti lehetőségek az agro-ökoszisztémák modellezésében
 Folyamaszemléle leheőségek az agro-ökoszszémák modellezésében Dokor (D) érekezés ézse Ladány Mára Témavezeő: Dr. Harnos Zsol, MHAS, egyeem anár BCE, Kerészeudomány Kar, Maemaka és Informaka Tanszék Szakma
Folyamaszemléle leheőségek az agro-ökoszszémák modellezésében Dokor (D) érekezés ézse Ladány Mára Témavezeő: Dr. Harnos Zsol, MHAS, egyeem anár BCE, Kerészeudomány Kar, Maemaka és Informaka Tanszék Szakma
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek emel szin Javíási-érékelési úmuaó ÉETTSÉGI VIZSG 0. okóber. ELEKTONIKI LPISMEETEK EMELT SZINTŰ ÍÁSELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMUTTÓ EMEI EŐFOÁSOK MINISZTÉIUM Elekronikai
Elekronikai alapismereek emel szin Javíási-érékelési úmuaó ÉETTSÉGI VIZSG 0. okóber. ELEKTONIKI LPISMEETEK EMELT SZINTŰ ÍÁSELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMUTTÓ EMEI EŐFOÁSOK MINISZTÉIUM Elekronikai
Járműelemek I. Tengelykötés kisfeladat (A típus) Szilárd illesztés
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Közlekedésmérnöki Kar Járműelemek I. (KOJHA 7) Tengelyköés kisfelada (A ípus) Szilárd illeszés Járműelemek és Hajások Tanszék Ssz.: A/... Név:...................................
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Közlekedésmérnöki Kar Járműelemek I. (KOJHA 7) Tengelyköés kisfelada (A ípus) Szilárd illeszés Járműelemek és Hajások Tanszék Ssz.: A/... Név:...................................
Dinamikus optimalizálás és a Leontief-modell
 MÛHELY Közgazdasági Szemle, LVI. évf., 29. január (84 92. o.) DOBOS IMRE Dinamikus opimalizálás és a Leonief-modell A anulmány a variációszámíás gazdasági alkalmazásaiból ismere hárma. Mind három alkalmazás
MÛHELY Közgazdasági Szemle, LVI. évf., 29. január (84 92. o.) DOBOS IMRE Dinamikus opimalizálás és a Leonief-modell A anulmány a variációszámíás gazdasági alkalmazásaiból ismere hárma. Mind három alkalmazás
A sztochasztikus idősorelemzés alapjai
 A szochaszikus idősorelemzés alapjai Ferenci Tamás BCE, Saiszika Tanszék amas.ferenci@medsa.hu 2011. december 19. Taralomjegyzék 1. Az idősorelemzés fogalma, megközelíései 2 1.1. Az idősor fogalma...................................
A szochaszikus idősorelemzés alapjai Ferenci Tamás BCE, Saiszika Tanszék amas.ferenci@medsa.hu 2011. december 19. Taralomjegyzék 1. Az idősorelemzés fogalma, megközelíései 2 1.1. Az idősor fogalma...................................
ELTE TáTK Közgazdaságtudományi Tanszék ÖKONOMETRIA. Készítette: Elek Péter, Bíró Anikó. Szakmai felelős: Elek Péter június
 ÖKONOMETRIA ÖKONOMETRIA Készül a TÁMOP-4..2-08/2/A/KMR-2009-004pályázai projek kereében Taralomfejleszés az ELTE TáK Közgazdaságudományi Tanszékén az ELTE Közgazdaságudományi Tanszék, az MTA Közgazdaságudományi
ÖKONOMETRIA ÖKONOMETRIA Készül a TÁMOP-4..2-08/2/A/KMR-2009-004pályázai projek kereében Taralomfejleszés az ELTE TáK Közgazdaságudományi Tanszékén az ELTE Közgazdaságudományi Tanszék, az MTA Közgazdaságudományi
2.2.45. SZUPERKRITIKUS FLUID KROMATOGRÁFIA 2.2.46. KROMATOGRÁFIÁS ELVÁLASZTÁSI TECHNIKÁK
 2.2.45. Szuperkriikus fluid kromaográfia Ph. Hg. VIII. Ph. Eur. 4, 4.1 és 4.2 2.2.45. SZUPEKITIKUS FLUID KOATOGÁFIA A szuperkriikus fluid kromaográfia (SFC) olyan kromaográfiás elválaszási módszer, melyben
2.2.45. Szuperkriikus fluid kromaográfia Ph. Hg. VIII. Ph. Eur. 4, 4.1 és 4.2 2.2.45. SZUPEKITIKUS FLUID KOATOGÁFIA A szuperkriikus fluid kromaográfia (SFC) olyan kromaográfiás elválaszási módszer, melyben
Megbízhatóság-elmélet. 2. rész
 Megbízhaóság-elméle. rész Rendszerek megbízhaósági vizsgálaa Boole modell szerin Min & mb. rész Megbízhaóság szemponjából jellegzees rendszersrukúrák Redundancia menes rendszer - bármely rendszerelem meghibásodása
Megbízhaóság-elméle. rész Rendszerek megbízhaósági vizsgálaa Boole modell szerin Min & mb. rész Megbízhaóság szemponjából jellegzees rendszersrukúrák Redundancia menes rendszer - bármely rendszerelem meghibásodása
DIPLOMADOLGOZAT Varga Zoltán 2012
 DIPLOMADOLGOZAT Varga Zolán 2012 Szen Isván Egyeem Gazdaság- és Társadalomudományi Kar Markeing Inéze Keresle-előrejelzés a vállalai logiszikában Belső konzulens neve, beoszása: Dr. Komáromi Nándor, egyeemi
DIPLOMADOLGOZAT Varga Zolán 2012 Szen Isván Egyeem Gazdaság- és Társadalomudományi Kar Markeing Inéze Keresle-előrejelzés a vállalai logiszikában Belső konzulens neve, beoszása: Dr. Komáromi Nándor, egyeemi
Táblázatok 4/5. C: t-próbát alkalmazunk és mivel a t-statisztika értéke 3, ezért mind a 10%-os, mind. elutasítjuk a nullhipotézist.
 1. Az X valószínőség változó 1 várható értékő és 9 szórásnégyzető. Y tıle független várható értékkel és 1 szórásnégyzettel. a) Menny X + Y várható értéke? 13 1 b) Menny X -Y szórásnégyzete? 13 1 összesen
1. Az X valószínőség változó 1 várható értékő és 9 szórásnégyzető. Y tıle független várható értékkel és 1 szórásnégyzettel. a) Menny X + Y várható értéke? 13 1 b) Menny X -Y szórásnégyzete? 13 1 összesen
Gingl Zoltán, Szeged, szept. 1
 Gngl Zolán, Szeged, 8. 8 szep. 8 szep. z Ohm örvény, Krchhoff örvénye érvényese z alarészeen eső feszülség és áram pllanany érée nem mndg arányos apcsola ovábbra s lneárs 8 szep. 3 d di L d I I Feszülség
Gngl Zolán, Szeged, 8. 8 szep. 8 szep. z Ohm örvény, Krchhoff örvénye érvényese z alarészeen eső feszülség és áram pllanany érée nem mndg arányos apcsola ovábbra s lneárs 8 szep. 3 d di L d I I Feszülség
d(f(x), f(y)) q d(x, y), ahol 0 q < 1.
 Fxponttétel Már a hétköznap életben s gyakran tapasztaltuk, hogy két pont között a távolságot nem feltétlenül a " kettő között egyenes szakasz hossza" adja Pl két település között a távolságot közlekedés
Fxponttétel Már a hétköznap életben s gyakran tapasztaltuk, hogy két pont között a távolságot nem feltétlenül a " kettő között egyenes szakasz hossza" adja Pl két település között a távolságot közlekedés
Diszkrét Matematika. zöld könyv ): XIII. fejezet: 1583, 1587, 1588, 1590, Matematikai feladatgyűjtemény II. (
 FELADATOK A LEKÉPEZÉSEK, PERMUTÁCIÓK TÉMAKÖRHÖZ Diszkrét Matematika 4. LEKÉPEZÉSEK Értelmezési tartomány és értékkészlet meghatározása : Összefoglaló feladatgyűjtemény matematikából ( zöld könyv ): XIII.
FELADATOK A LEKÉPEZÉSEK, PERMUTÁCIÓK TÉMAKÖRHÖZ Diszkrét Matematika 4. LEKÉPEZÉSEK Értelmezési tartomány és értékkészlet meghatározása : Összefoglaló feladatgyűjtemény matematikából ( zöld könyv ): XIII.
STATISZTIKAI IDŐSORELEMZÉS A TŐZSDÉN. Doktori (PhD) értekezés
 NYUGAT-MAGYARORSZÁGI EGYETEM Széchenyi Isván Gazdálkodás- és Szervezésudományok Dokori Iskola STATISZTIKAI IDŐSORELEMZÉS A TŐZSDÉN Dokori (PhD) érekezés Készíee: Hoschek Mónika A kiadvány a TÁMOP 4.. B-/--8
NYUGAT-MAGYARORSZÁGI EGYETEM Széchenyi Isván Gazdálkodás- és Szervezésudományok Dokori Iskola STATISZTIKAI IDŐSORELEMZÉS A TŐZSDÉN Dokori (PhD) érekezés Készíee: Hoschek Mónika A kiadvány a TÁMOP 4.. B-/--8
ÉLETTARTAM KOCKÁZAT A nyugdíjrendszerre nehezedő egyik teher
 ÉLETTARTAM KOCKÁZAT A nyudíjrendszerre nehezedő eyik eher Májer Isván - Kovács Erzsébe i.majer@erasmusmc.nl Taralom. Várhaó élearam alakulása 2. A moraliás modellezése a Lee-Carer modell 3. Alkalmazás
ÉLETTARTAM KOCKÁZAT A nyudíjrendszerre nehezedő eyik eher Májer Isván - Kovács Erzsébe i.majer@erasmusmc.nl Taralom. Várhaó élearam alakulása 2. A moraliás modellezése a Lee-Carer modell 3. Alkalmazás
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek emel szin 5 ÉETTSÉGI VIZSG 06. május 8. EEKTONIKI PISMEETEK EMET SZINTŰ ÍÁSEI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKEÉSI ÚTMTTÓ EMEI EŐFOÁSOK MINISZTÉIM Egyszerű, rövid feladaok Maximális
Elekronikai alapismereek emel szin 5 ÉETTSÉGI VIZSG 06. május 8. EEKTONIKI PISMEETEK EMET SZINTŰ ÍÁSEI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKEÉSI ÚTMTTÓ EMEI EŐFOÁSOK MINISZTÉIM Egyszerű, rövid feladaok Maximális
A BIZOTTSÁG MUNKADOKUMENTUMA
 AZ EURÓPAI UNIÓ TANÁCSA Brüsszel, 2007. május 23. (25.05) (OR. en) Inézményközi dokumenum: 2006/0039 (CNS) 9851/07 ADD 2 FIN 239 RESPR 5 CADREFIN 32 FELJEGYZÉS AZ I/A NAPIRENDI PONTHOZ 2. KIEGÉSZÍTÉS Küldi:
AZ EURÓPAI UNIÓ TANÁCSA Brüsszel, 2007. május 23. (25.05) (OR. en) Inézményközi dokumenum: 2006/0039 (CNS) 9851/07 ADD 2 FIN 239 RESPR 5 CADREFIN 32 FELJEGYZÉS AZ I/A NAPIRENDI PONTHOZ 2. KIEGÉSZÍTÉS Küldi:
3. feladatsor: Görbe ívhossza, görbementi integrál (megoldás)
 Maemaika A3 gyakorla Energeika és Mecharonika BSc szakok, 6/7 avasz 3. feladasor: Görbe ívhossza, görbemeni inegrál megoldás. Mi az r 3 3 i + 6 5 5 j + 9 k görbe ívhossza a [, ] inervallumon? A megado
Maemaika A3 gyakorla Energeika és Mecharonika BSc szakok, 6/7 avasz 3. feladasor: Görbe ívhossza, görbemeni inegrál megoldás. Mi az r 3 3 i + 6 5 5 j + 9 k görbe ívhossza a [, ] inervallumon? A megado
Statisztikai próbák. Ugyanazon problémára sokszor megvan mindkét eljárás.
 Statsztka próbák Paraméteres. A populácó paraméteret becsüljük, ezekkel számolunk.. Az alapsokaság eloszlására van kkötés. Nem paraméteres Nncs lyen becslés Nncs kkötés Ugyanazon problémára sokszor megvan
Statsztka próbák Paraméteres. A populácó paraméteret becsüljük, ezekkel számolunk.. Az alapsokaság eloszlására van kkötés. Nem paraméteres Nncs lyen becslés Nncs kkötés Ugyanazon problémára sokszor megvan
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek emel szin 080 ÉETTSÉGI VISGA 009. május. EEKTONIKAI AAPISMEETEK EMET SINTŰ ÍÁSBEI ÉETTSÉGI VISGA JAVÍTÁSI-ÉTÉKEÉSI ÚTMTATÓ OKTATÁSI ÉS KTÁIS MINISTÉIM Egyszerű, rövid feladaok
Elekronikai alapismereek emel szin 080 ÉETTSÉGI VISGA 009. május. EEKTONIKAI AAPISMEETEK EMET SINTŰ ÍÁSBEI ÉETTSÉGI VISGA JAVÍTÁSI-ÉTÉKEÉSI ÚTMTATÓ OKTATÁSI ÉS KTÁIS MINISTÉIM Egyszerű, rövid feladaok
Síkalapok vizsgálata - az EC-7 bevezetése
 Szilvágyi László - Wolf Ákos Síkalapok vizsgálaa - az EC-7 bevezeése Síkalapozási feladaokkal a geoehnikus mérnökök szine minden nap alálkoznak annak ellenére, hogy mosanában egyre inkább a mélyépíés kerül
Szilvágyi László - Wolf Ákos Síkalapok vizsgálaa - az EC-7 bevezeése Síkalapozási feladaokkal a geoehnikus mérnökök szine minden nap alálkoznak annak ellenére, hogy mosanában egyre inkább a mélyépíés kerül
HAVRAN DÁNIEL. Pénzgazdálkodási szokások hatása a működőtőkére. A Magyar Posta példája
 HAVRAN DÁNIEL Pénzgazdálkodás szokások haása a működőőkére. A Magyar Posa példája A hálózaos parágakban, ahogy a posa szolgálaásoknál s, a forgalomban lévő készpénz nagyméreű működőőké jelenhe. A Magyar
HAVRAN DÁNIEL Pénzgazdálkodás szokások haása a működőőkére. A Magyar Posa példája A hálózaos parágakban, ahogy a posa szolgálaásoknál s, a forgalomban lévő készpénz nagyméreű működőőké jelenhe. A Magyar
Túlgerjesztés elleni védelmi funkció
 Túlgerjeszés elleni védelmi unkció Budapes, 2011. auguszus Túlgerjeszés elleni védelmi unkció Bevezeés A úlgerjeszés elleni védelmi unkció generáorok és egységkapcsolású ranszormáorok vasmagjainak úlzoan
Túlgerjeszés elleni védelmi unkció Budapes, 2011. auguszus Túlgerjeszés elleni védelmi unkció Bevezeés A úlgerjeszés elleni védelmi unkció generáorok és egységkapcsolású ranszormáorok vasmagjainak úlzoan
Fuzzy rendszerek & genetikus algoritmusok
 Fuzzy rendszere & geneus algormuso Előadás vázla 4. hé Összeállíoa: Harma Isván h.d., egyeem adjunus Felhasznál rodalom: Dr. Lanos Béla: Fuzzy sysems and genec algorhms, 00, Műegyeem adó, Budapes 3. OIMALIZÁLÁSI
Fuzzy rendszere & geneus algormuso Előadás vázla 4. hé Összeállíoa: Harma Isván h.d., egyeem adjunus Felhasznál rodalom: Dr. Lanos Béla: Fuzzy sysems and genec algorhms, 00, Műegyeem adó, Budapes 3. OIMALIZÁLÁSI
Szempontok a járműkarbantartási rendszerek felülvizsgálatához
 A VMMSzK evékenységének bemuaása 2013. február 7. Szemponok a járműkarbanarási rendszerek felülvizsgálaához Malainszky Sándor MÁV Zr. Vasúi Mérnöki és Mérésügyi Szolgálaó Közpon Magyar Államvasuak ZR.
A VMMSzK evékenységének bemuaása 2013. február 7. Szemponok a járműkarbanarási rendszerek felülvizsgálaához Malainszky Sándor MÁV Zr. Vasúi Mérnöki és Mérésügyi Szolgálaó Közpon Magyar Államvasuak ZR.
REDUNDANCIA. A redundancia fogalma és formái Hardver redundancia Alkalmazási példák
 REDUNDANCIA A redundanca fogalma és formá Hardver redundanca Alkalmazás példák A REDUNDANCIA FOGALMA A redundanca olyan, a rendszer funkcónak eljesíéséhez mnmálsan szükséges, ún. alapképíésé meghaladó
REDUNDANCIA A redundanca fogalma és formá Hardver redundanca Alkalmazás példák A REDUNDANCIA FOGALMA A redundanca olyan, a rendszer funkcónak eljesíéséhez mnmálsan szükséges, ún. alapképíésé meghaladó
Gazdasági és megbízhatósági elemzések
 Budapesi Mőszaki és Gazdaságudomáyi Egyeem Gazdaság- és Társadalomudomáyi Kar Üzlei Tudomáyok Iéze Meedzsme és Vállalagazdasága Taszék Dr. Kövesi Jáos Erdei Jáos Dr. Tóh Zsuzsaa Eszer Gazdasági és megbízhaósági
Budapesi Mőszaki és Gazdaságudomáyi Egyeem Gazdaság- és Társadalomudomáyi Kar Üzlei Tudomáyok Iéze Meedzsme és Vállalagazdasága Taszék Dr. Kövesi Jáos Erdei Jáos Dr. Tóh Zsuzsaa Eszer Gazdasági és megbízhaósági
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek középszin Javíási-érékelési úmuaó 063 ÉETTSÉG VZSG 006. okóber 4. EEKTONK PSMEETEK KÖZÉPSZNTŰ ÍÁSE ÉETTSÉG VZSG JVÍTÁS-ÉTÉKEÉS ÚTMTTÓ OKTTÁS ÉS KTÁS MNSZTÉM Elekronikai alapismereek
Elekronikai alapismereek középszin Javíási-érékelési úmuaó 063 ÉETTSÉG VZSG 006. okóber 4. EEKTONK PSMEETEK KÖZÉPSZNTŰ ÍÁSE ÉETTSÉG VZSG JVÍTÁS-ÉTÉKEÉS ÚTMTTÓ OKTTÁS ÉS KTÁS MNSZTÉM Elekronikai alapismereek
1. Előadás: Készletezési modellek, I-II.
 . Előadás: Készleezési modellek, I-II. Készleeke rendszerin azér arunk hogy, valamely szükséglee, igény kielégísünk. A szóban forgó anyag, cikk iráni igény, keresle a készle fogyásá idézi elő. Gondoskodnunk
. Előadás: Készleezési modellek, I-II. Készleeke rendszerin azér arunk hogy, valamely szükséglee, igény kielégísünk. A szóban forgó anyag, cikk iráni igény, keresle a készle fogyásá idézi elő. Gondoskodnunk
e (t µ) 2 f (t) = 1 F (t) = 1 Normális eloszlás negyedik centrális momentuma:
 Normális eloszlás ξ valószínűségi változó normális eloszlású. ξ N ( µ, σ 2) Paraméterei: µ: várható érték, σ 2 : szórásnégyzet (µ tetszőleges, σ 2 tetszőleges pozitív valós szám) Normális eloszlás sűrűségfüggvénye:
Normális eloszlás ξ valószínűségi változó normális eloszlású. ξ N ( µ, σ 2) Paraméterei: µ: várható érték, σ 2 : szórásnégyzet (µ tetszőleges, σ 2 tetszőleges pozitív valós szám) Normális eloszlás sűrűségfüggvénye:
Épületfizika. Acél/vasbeton. Fa/vasbeton. Acél/acél. Épületfizika. TI Schöck Isokorb KS, KSH, KST/HU/2017.1/június
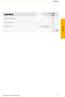 Acél/vasbeon Fa/vasbeon Acél/acél 9 Hőhidak A hőhidak definíciója A hőhidak olyan lokális helyek az épüle külső hőszigeelő burkán, amelyeknél megnövekede hőveszeség lép fel. A megnövekede hőveszeség abból
Acél/vasbeon Fa/vasbeon Acél/acél 9 Hőhidak A hőhidak definíciója A hőhidak olyan lokális helyek az épüle külső hőszigeelő burkán, amelyeknél megnövekede hőveszeség lép fel. A megnövekede hőveszeség abból
Gingl Zoltán, Szeged, :41 Elektronika - Váltófeszültségű házatok
 Gngl Zolán, Szeged, 6. 6.. 3. 7:4 Elerona - Válófeszülségű házao 6.. 3. 7:4 Elerona - Válófeszülségű házao z Ohm örvény, Krchhoff örvénye érvényese z alarészeen eső feszülség és áram pllanany érée nem
Gngl Zolán, Szeged, 6. 6.. 3. 7:4 Elerona - Válófeszülségű házao 6.. 3. 7:4 Elerona - Válófeszülségű házao z Ohm örvény, Krchhoff örvénye érvényese z alarészeen eső feszülség és áram pllanany érée nem
Atomfizika előadás 4. Elektromágneses sugárzás október 1.
 Aomfka előadás 4. lekromágneses sugárás 4. okóber. Alapkísérleek Ampere-féle gerjesés örvén mágneses ér örvénessége elekromos áram elekromos ér váloása Farada ndukcós örvéne elekromos ér örvénessége mágneses
Aomfka előadás 4. lekromágneses sugárás 4. okóber. Alapkísérleek Ampere-féle gerjesés örvén mágneses ér örvénessége elekromos áram elekromos ér váloása Farada ndukcós örvéne elekromos ér örvénessége mágneses
IV. A mágneses tér alapfogalmai, alaptörvényei, mágneses
 V. A mágneses ér alapfogalma, alapörvénye, mágneses körök A nyugvó vllamos ölések közö erőhaásoka a vllamos ér közveí (Coulomb örvénye). A mozgó ölések (vllamos áramo vvő vezeők) közö s fellép erőhaás,
V. A mágneses ér alapfogalma, alapörvénye, mágneses körök A nyugvó vllamos ölések közö erőhaásoka a vllamos ér közveí (Coulomb örvénye). A mozgó ölések (vllamos áramo vvő vezeők) közö s fellép erőhaás,
Elméleti közgazdaságtan II.
 Elméle közgazdaságan II. Makroökonóma Műszak haladás műszak haladás lehe uonóm és ndukál Megesesül és nem megesesül Hcks szern semleges Harrod szern semleges Solow szern semleges Műszak haladás műszak
Elméle közgazdaságan II. Makroökonóma Műszak haladás műszak haladás lehe uonóm és ndukál Megesesül és nem megesesül Hcks szern semleges Harrod szern semleges Solow szern semleges Műszak haladás műszak
Diszkrét idejű felújítási paradoxon
 Magda Gábor Szaller Dávid Tóvári Endre 2009. 11. 18. X 1, X 2,... független és X-szel azonos eloszlású, pozitív egész értékeket felvevő valószínűségi változó (felújítási idők) P(X M) = 1 valamilyen M N
Magda Gábor Szaller Dávid Tóvári Endre 2009. 11. 18. X 1, X 2,... független és X-szel azonos eloszlású, pozitív egész értékeket felvevő valószínűségi változó (felújítási idők) P(X M) = 1 valamilyen M N
Anyag- és gyártásismeret II - LBt /
 Anyag- és gyárásismere II - B 00.0.. / 04.7. Gyáráservezés feladaa: Megervezni a konsrukır álal megerveze ermék gyárási folyamaá. A ehnológiai ervezés élja a gyáráshoz szükséges dokumenáiók elıállíása.
Anyag- és gyárásismere II - B 00.0.. / 04.7. Gyáráservezés feladaa: Megervezni a konsrukır álal megerveze ermék gyárási folyamaá. A ehnológiai ervezés élja a gyáráshoz szükséges dokumenáiók elıállíása.
) (11.17) 11.2 Rácsos tartók párhuzamos övekkel
 Rácsos arók párhuzamos övekkel Azér, hog a sabiliási eléelek haásá megvizsgáljuk, eg egszerű síkbeli, saikailag haározo, K- rácsozású aró vizsgálunk párhuzamos övekkel és hézagos csomóponokkal A rúdelemek
Rácsos arók párhuzamos övekkel Azér, hog a sabiliási eléelek haásá megvizsgáljuk, eg egszerű síkbeli, saikailag haározo, K- rácsozású aró vizsgálunk párhuzamos övekkel és hézagos csomóponokkal A rúdelemek
EGY REMÉNYTELENNEK TÛNÔ VEZÉRLÉSI PROBLÉMA A KLASSZIKUS ÉS MODERN FIZIKA HATÁRÁN
 eljes mozgás helye csak a nulladik módussal számolni: még azonos ömegek eseén is öbb min 98% súllyal a nulladik módus gerjed. Nem ez a helyze a b) kezdei feléelnél, amikor már m 0,1M melle is öbb min 3%,
eljes mozgás helye csak a nulladik módussal számolni: még azonos ömegek eseén is öbb min 98% súllyal a nulladik módus gerjed. Nem ez a helyze a b) kezdei feléelnél, amikor már m 0,1M melle is öbb min 3%,
EVOLÚCIÓS GAZDASÁGOK SZIMULÁCIÓJA
 Budapes Közgazdaságudomány és Államgazgaás Egyeem Maemaa Közgazdaságan és Öonomera Tanszé EVOLÚCIÓS GAZDASÁGOK SZIMULÁCIÓJA Ph.D. éreezés Benede Gábor Budapes 003 Zolána Taralomjegyzé. Fejeze: Bevezeés..
Budapes Közgazdaságudomány és Államgazgaás Egyeem Maemaa Közgazdaságan és Öonomera Tanszé EVOLÚCIÓS GAZDASÁGOK SZIMULÁCIÓJA Ph.D. éreezés Benede Gábor Budapes 003 Zolána Taralomjegyzé. Fejeze: Bevezeés..
SPORTFOGADÁSI ÉS PÉNZÜGYI PIACOK KAPCSOLATA
 SPORTFOGADÁSI ÉS PÉNZÜGYI PIACOK KAPCSOLATA MSc Diplomamunka Íra: Csikai Máyás Bizosíási és pénzügyi maemaika MSc Kvaniaív pénzügyek szakirány Eövös Loránd Tudományegyeem, Természeudományi Kar Budapesi
SPORTFOGADÁSI ÉS PÉNZÜGYI PIACOK KAPCSOLATA MSc Diplomamunka Íra: Csikai Máyás Bizosíási és pénzügyi maemaika MSc Kvaniaív pénzügyek szakirány Eövös Loránd Tudományegyeem, Természeudományi Kar Budapesi
A közgazdasági Nobel-díjat a svéd jegybank támogatásával 1969 óta ítélik oda. 1 Az
 ROBERT F. ENGLE ÉS CLIVE W. J. GRANGER, A 003. ÉVI KÖZGAZDASÁGI NOBEL-DÍJASOK DARVAS ZSOLT A Svéd Tudományos Akadémia a 003. évi Nobel-díjak odaíélésé ké fő alkoással indokola: Rober F. Engle eseén az
ROBERT F. ENGLE ÉS CLIVE W. J. GRANGER, A 003. ÉVI KÖZGAZDASÁGI NOBEL-DÍJASOK DARVAS ZSOLT A Svéd Tudományos Akadémia a 003. évi Nobel-díjak odaíélésé ké fő alkoással indokola: Rober F. Engle eseén az
Statisztika feladatok
 Statsztka ok Informatka Tudományok Doktor Iskola Bzonyítandó, hogy: azaz 1 Tekntsük az alább statsztkákat: Igazoljuk, hogy torzítatlan statsztkák! Melyk a leghatásosabb közöttük? (Ez az együttes eloszlásfüggvényük.)
Statsztka ok Informatka Tudományok Doktor Iskola Bzonyítandó, hogy: azaz 1 Tekntsük az alább statsztkákat: Igazoljuk, hogy torzítatlan statsztkák! Melyk a leghatásosabb közöttük? (Ez az együttes eloszlásfüggvényük.)
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek emel szin Javíási-érékelési úmuaó 0 ÉETTSÉGI VIZSG 0. május 3. EEKTONIKI PISMEETEK EMET SZINTŰ ÍÁSBEI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKEÉSI ÚTMTTÓ NEMZETI EŐFOÁS MINISZTÉIM Elekronikai
Elekronikai alapismereek emel szin Javíási-érékelési úmuaó 0 ÉETTSÉGI VIZSG 0. május 3. EEKTONIKI PISMEETEK EMET SZINTŰ ÍÁSBEI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKEÉSI ÚTMTTÓ NEMZETI EŐFOÁS MINISZTÉIM Elekronikai
Oktatási segédlet. Hegesztett szerkezetek költségszámítása. Dr. Jármai Károly. Miskolci Egyetem
 Okaás segédle Hegesze szerkezeek kölségszámíása a Léesímények acélszerkezee árgy hallgaónak Dr. Járma Károly Mskolc Egyeem 013 1 Kölségszámíás Az opmálás első sádumában és alkalmazásakor álalában a ömeg,
Okaás segédle Hegesze szerkezeek kölségszámíása a Léesímények acélszerkezee árgy hallgaónak Dr. Járma Károly Mskolc Egyeem 013 1 Kölségszámíás Az opmálás első sádumában és alkalmazásakor álalában a ömeg,
Hullámtan. Hullám Valamilyen közeg kis tartományában keltett, a közegben tovaterjedő zavar.
 Hulláan A hullá fogala. A hulláok oszályozása. Kísérleek Kis súlyokkal összeköö ingsor elején kele rezgés áerjed a öbbi ingára is [0:6] Kifeszíe guiköélen kele zavar végig fu a köélen [0:08] Kifeszíe rugón
Hulláan A hullá fogala. A hulláok oszályozása. Kísérleek Kis súlyokkal összeköö ingsor elején kele rezgés áerjed a öbbi ingára is [0:6] Kifeszíe guiköélen kele zavar végig fu a köélen [0:08] Kifeszíe rugón
Typotex Kiadó. Jelölések
 Jelölések a = dolgozók fogyasztása (12. fejezet és A. függelék) a i = egyéni tőkeállomány i éves korban A = társadalmi (aggregált) tőkeállomány b j = egyéni nyugdíj j éves korban b k = k-adik nyugdíjosztály
Jelölések a = dolgozók fogyasztása (12. fejezet és A. függelék) a i = egyéni tőkeállomány i éves korban A = társadalmi (aggregált) tőkeállomány b j = egyéni nyugdíj j éves korban b k = k-adik nyugdíjosztály
Markov-láncok stacionárius eloszlása
 Markov-láncok stacionárius eloszlása Adatbányászat és Keresés Csoport, MTA SZTAKI dms.sztaki.hu Kiss Tamás 2013. április 11. Tartalom Markov láncok definíciója, jellemzése Visszatérési idők Stacionárius
Markov-láncok stacionárius eloszlása Adatbányászat és Keresés Csoport, MTA SZTAKI dms.sztaki.hu Kiss Tamás 2013. április 11. Tartalom Markov láncok definíciója, jellemzése Visszatérési idők Stacionárius
A sebességállapot ismert, ha meg tudjuk határozni bármely pont sebességét és bármely pont szögsebességét. Analógia: Erőrendszer
 Kinemaikai egyensúly éele: Téel: zár kinemaikai lánc relaív szögsebesség-vekorrendszere egyensúlyi. Mechanizmusok sebességállapoa a kinemaikai egyensúly éelével is meghaározhaó. sebességállapo ismer, ha
Kinemaikai egyensúly éele: Téel: zár kinemaikai lánc relaív szögsebesség-vekorrendszere egyensúlyi. Mechanizmusok sebességállapoa a kinemaikai egyensúly éelével is meghaározhaó. sebességállapo ismer, ha
REAKCIÓKINETIKA ELEMI REAKCIÓK ÖSSZETETT REAKCIÓK. Egyszer modellek
 REKIÓKINETIK ELEMI REKIÓK ÖSSZETETT REKIÓK Egyszer moelle Párhuzamos (parallel reaió Egyensúlyra veze reaió Egymás öve (sorozaos onszeuív reaió 4 Sorozaos reaió egyensúlyi lépéssel Moleuláris moelle reaiósebességi
REKIÓKINETIK ELEMI REKIÓK ÖSSZETETT REKIÓK Egyszer moelle Párhuzamos (parallel reaió Egyensúlyra veze reaió Egymás öve (sorozaos onszeuív reaió 4 Sorozaos reaió egyensúlyi lépéssel Moleuláris moelle reaiósebességi
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek emel szin Javíási-érékelési úmaó 063 ÉETTSÉGI VIZSG 006. okóber. ELEKTONIKI LPISMEETEK EMELT SZINTŰ ÍÁSBELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMTTÓ OKTTÁSI ÉS KLTÁLIS MINISZTÉIM
Elekronikai alapismereek emel szin Javíási-érékelési úmaó 063 ÉETTSÉGI VIZSG 006. okóber. ELEKTONIKI LPISMEETEK EMELT SZINTŰ ÍÁSBELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMTTÓ OKTTÁSI ÉS KLTÁLIS MINISZTÉIM
STATISZTIKAI IDİSORELEMZÉS A TİZSDÉN
 STATISZTIKAI IDİSORELEMZÉS A TİZSDÉN DOKTORI (PhD) ÉRTEKEZÉS Polgárné Hoschek Mónika Nyuga-magyarországi Egyeem Sopron. STATISZTIKAI IDİSORELEMZÉS A TİZSDÉN Érekezés dokori (PhD) fokoza elnyerése érdekében
STATISZTIKAI IDİSORELEMZÉS A TİZSDÉN DOKTORI (PhD) ÉRTEKEZÉS Polgárné Hoschek Mónika Nyuga-magyarországi Egyeem Sopron. STATISZTIKAI IDİSORELEMZÉS A TİZSDÉN Érekezés dokori (PhD) fokoza elnyerése érdekében
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek emel szin 05 ÉETTSÉGI VIZSGA 005. május 0. ELEKTONIKAI ALAPISMEETEK EMELT SZINTŰ ÉETTSÉGI VIZSGA Az írásbeli vizsga időarama: 0 perc JAVÍTÁSI-ÉTÉKELÉSI ÚTMTATÓ OKTATÁSI MINISZTÉIM
Elekronikai alapismereek emel szin 05 ÉETTSÉGI VIZSGA 005. május 0. ELEKTONIKAI ALAPISMEETEK EMELT SZINTŰ ÉETTSÉGI VIZSGA Az írásbeli vizsga időarama: 0 perc JAVÍTÁSI-ÉTÉKELÉSI ÚTMTATÓ OKTATÁSI MINISZTÉIM
Romvári Petra. biztosítási kötelezettségek fair értékelése, id - és piackonzisztens aktuáriusi értékelések
 Budapesi Corvinus Egyeem Eövös Loránd Tudományegyeem Romvári Pera bizosíási köelezeségek fair érékelése, id - és piackonziszens akuáriusi érékelések MSc szakdolgoza Témaveze : Araó Miklós Eövös Loránd
Budapesi Corvinus Egyeem Eövös Loránd Tudományegyeem Romvári Pera bizosíási köelezeségek fair érékelése, id - és piackonziszens akuáriusi érékelések MSc szakdolgoza Témaveze : Araó Miklós Eövös Loránd
Tartalom. Éghajlati rendszer: a légkör és a vele kölcsönhatásban álló 4 geoszféra együttese. Idıjárás vs. éghajlat
 Az éghajlai modellszimulációk bizonyalanságainak felérképezése a Kárpá-medencére Szabó Péer (szabo.p@me.hu) és Szépszó Gabriella Taralom Alapfogalmak és az éghajlai rendszer Numerikus modellezés Az éghajlai
Az éghajlai modellszimulációk bizonyalanságainak felérképezése a Kárpá-medencére Szabó Péer (szabo.p@me.hu) és Szépszó Gabriella Taralom Alapfogalmak és az éghajlai rendszer Numerikus modellezés Az éghajlai
ÜZEMELTETÉS ELMÉLETE ÜZEMELTETÉS, FENNTARTÁS 1-2 előadás vázlatok
 ÜZEMELTETÉS ELMÉLETE ÜZEMELTETÉS, FENNTARTÁS -2 előadás vázlaok f. anár Széchenyi Isván Egyeem, Győr E-mail: zvikli@sze.hu Web: hp://rs.sze.hu/~zvikli A anárgy okaásának célja hogy az üzemeleés és fennarás,
ÜZEMELTETÉS ELMÉLETE ÜZEMELTETÉS, FENNTARTÁS -2 előadás vázlaok f. anár Széchenyi Isván Egyeem, Győr E-mail: zvikli@sze.hu Web: hp://rs.sze.hu/~zvikli A anárgy okaásának célja hogy az üzemeleés és fennarás,
2N-4, 2N-4E 2N-00, 2N-0E 2N-AE0, 2N- AG0
 Húzza alá az Ön képzési kódjá! 2N-4, 2N-4E 2N-00, 2N-0E 2N-AE0, 2N- AG0 Név: Azonosíó: Helyszám: Jelölje meg (aláhúzással) Gyakorlavezeőjé! Bihari Péer Czél Balázs Gróf Gyula Kovács Vikória Könczöl Sándor
Húzza alá az Ön képzési kódjá! 2N-4, 2N-4E 2N-00, 2N-0E 2N-AE0, 2N- AG0 Név: Azonosíó: Helyszám: Jelölje meg (aláhúzással) Gyakorlavezeőjé! Bihari Péer Czél Balázs Gróf Gyula Kovács Vikória Könczöl Sándor
Matematikai statisztika
 Matematka statsztka 8. elıadás http://www.math.elte.hu/~arato/matstat0.htm Kétmtás eset: függetle mták + + + = + ) ( ) ( ) ( Y Y X X Y X m m m t m Ha smert a szórás: (X elemő, σ szórású, Y m elemő, σ szórású),
Matematka statsztka 8. elıadás http://www.math.elte.hu/~arato/matstat0.htm Kétmtás eset: függetle mták + + + = + ) ( ) ( ) ( Y Y X X Y X m m m t m Ha smert a szórás: (X elemő, σ szórású, Y m elemő, σ szórású),
ELEKTRONIKAI ALAPISMERETEK
 Elekronikai alapismereek középszin Javíási-érékelési úmaó 09 ÉETTSÉGI VIZSG 00. májs 4. ELEKTONIKI LPISMEETEK KÖZÉPSZINTŰ ÍÁSBELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMUTTÓ OKTTÁSI ÉS KULTUÁLIS MINISZTÉIUM
Elekronikai alapismereek középszin Javíási-érékelési úmaó 09 ÉETTSÉGI VIZSG 00. májs 4. ELEKTONIKI LPISMEETEK KÖZÉPSZINTŰ ÍÁSBELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMUTTÓ OKTTÁSI ÉS KULTUÁLIS MINISZTÉIUM
Legfontosabb farmakokinetikai paraméterek definíciói és számításuk. Farmakokinetikai paraméterek Számítási mód
 Legfonosabb farmakokineikai paraméerek definíciói és számíásuk Paraméer armakokineikai paraméerek Név Számíási mód max maximális plazma koncenráció ideje mér érékek alapján; a max () érékhez arozó érék
Legfonosabb farmakokineikai paraméerek definíciói és számíásuk Paraméer armakokineikai paraméerek Név Számíási mód max maximális plazma koncenráció ideje mér érékek alapján; a max () érékhez arozó érék
Folyamatszemléleti lehetőségek az agro-ökoszisztémák modellezésében
 Folyamaszemlélei leheőségek az agro-ökosziszémák modellezésében Dokori (D) érekezés Ladányi Mára Témavezeő: Dr. Harnos Zsol, MHAS, egyeemi anár BCE, Kerészeudományi Kar, Maemaika és Informaika Tanszék
Folyamaszemlélei leheőségek az agro-ökosziszémák modellezésében Dokori (D) érekezés Ladányi Mára Témavezeő: Dr. Harnos Zsol, MHAS, egyeemi anár BCE, Kerészeudományi Kar, Maemaika és Informaika Tanszék
Rozner Bence Pe ter. E rze kenyse gvizsga lat Le vy-fe le kamatla b-modellekben
 Eo vo s Lora nd Tudoma nyegyeem Terme szeudoma nyi Kar Rozner Bence Pe er E rze kenyse gvizsga la Le vy-fe le kamala b-modellekben Szakdolgoza - Alkalmazo maemaikus MSc Te mavezeo : Boros Bala zs kuao
Eo vo s Lora nd Tudoma nyegyeem Terme szeudoma nyi Kar Rozner Bence Pe er E rze kenyse gvizsga la Le vy-fe le kamala b-modellekben Szakdolgoza - Alkalmazo maemaikus MSc Te mavezeo : Boros Bala zs kuao
5. HŐMÉRSÉKLETMÉRÉS 1. Hőmérséklet, hőmérők Termoelemek
 5. HŐMÉRSÉKLETMÉRÉS 1. Hőmérsékle, hőmérők A hőmérsékle a esek egyik állapohaározója. A hőmérsékle a es olyan sajáossága, ami meghaározza, hogy a es ermikus egyensúlyban van-e más esekkel. Ezen alapszik
5. HŐMÉRSÉKLETMÉRÉS 1. Hőmérsékle, hőmérők A hőmérsékle a esek egyik állapohaározója. A hőmérsékle a es olyan sajáossága, ami meghaározza, hogy a es ermikus egyensúlyban van-e más esekkel. Ezen alapszik

 2. elıadás Véletlen szám generálás LCG: (0 < m, 0
2. elıadás Véletlen szám generálás LCG: (0 < m, 0