Szimulációk egyszerősített fehérjemodellekkel. Szilágyi András
|
|
|
- Adrián Nagy
- 9 évvel ezelőtt
- Látták:
Átírás
1 Szimulációk egyszerősített fehérjemodellekkel Szilágyi András
2 Szimulációs módszerek alkalmazhatósági tartományai
3 Egyszerősített modellek Három típusát mutatjuk be: Játék rácsmodellek Realisztikusabb rácsmodellek Diszkrét molekuladinamika
4 Kitérı: A fehérjék felgombolyodása DNS RNS polipeptidlánc mőködıképes fehérjemolekula transzkripció transzláció felgombolyodás Anfinsen kísérletei (1961): Az aminosavsorrend tartalmazza a háromdimenziós szerkezet kialakulásához szükséges összes információt. A natív szerkezet a termodinamikailag legstabilisabb állapot. A fehérjék stabil konformációs állapotai: A legombolyodott (denaturált) állapot. Jele: U (unfolded) vagy D (denatured) A felgombolyodott (natív, általában biológiailag aktív) állapot. Jele: F (folded) vagy N (natív). A köztes állapotok (köztitermékek, intermedierek). Jelük: I (intermediate)
5 Állandó nyomáson és hımérsékleten egy rendszer egyensúlyi állapotát a szabadentalpia (G) minimuma adja Az entalpiacsökkentı folyamatok (pl. kölcsönhatások létrejötte) és az entrópianövelı folyamatok (pl. egy láncmolekula mozgásszabadságának megnövekedése) egyaránt csökkentik a szabadentalpiát. A hımérséklet határozza meg, hogy melyik típusú folyamat érvényesülhet jobban (a magasabb hımérséklet az entrópianövelı folyamatoknak kedvez).
6 A felgombolyodás termodinamikája Alacsony hımérsékleten a natív állapot (sok kölcsönhatás, alacsony entrópia), magas hımérsékleten a denaturált állapot (kevés kölcsönhatás, magasabb entrópia) a stabilabb. Egy bizonyos hımérsékleten (T m olvadáspont ) kooperatív átmenet történik a két állapot között (jellegzetes csúcs a hıkapacitásgörbében). (A hımérsékletet eléggé lecsökkentve általában megint a denaturált állapot lesz a stabilabb hidegdenaturáció)
7 Rácsmodellek Rácsmodell: "önelkerülõ" gyöngysor, rácspontokon 2D HP modell 3D HP modell Ken A. Dill (UCSF) Perturbált heteropolimer modell, kétbetûs kóddal Eugene Shakhnovich (Harvard)
8 A rácsmodellek típusai HP modell (Hidrofób-Poláros) [Ken A. Dill és mások] Kétféle aminosav: Hidrofób és Poláros (kétbetős kód) 2D és 3D modellek. Eredményeik hasonlóak; a 2D modellek könnyebben számíthatóak. Hidrofób maggal rendelkezõ modell 2D-ben 16, 3D-ben 64 aminosavból készíthetõ. Egyparaméteres: ε kontaktenergia (a HH kontaktus energiája) A kontaktusok energiája: (E HH, E HP, E PP ) = ( ε, 0, 0) Perturbált heteropolimer modellek [Eugene I. Shakhnovich és mások] Erıs vonzás a monomerek között, gyenge variációval Többnyire 27-mer, alapállapota 3x3x3-as kockán ( lehetséges állapot) Két változat: Független kontaktenergiák: E(i,j) = B ij Kétbetős kód: A,B. Ált. E AB > E AA, E BB. (Ált. nem mag-felszín szeparációhoz, hanem jobb-bal elkülönüléshez vezet.)
9 Elınyök A rácsmodellek elınyei és hátrányai Szekvenciatér és konformációtér teljességében felderíthetı Egzaktul kiszámítható mennyiségek! (Jobb az egyszerő, de egzaktul számolható modell, mint a bonyolult, de csak közelítıleg számítható.) Nem csak fehérjékre vonatkoztatható Használható analitikus elméletek tesztelésére (mint spinüveg-modell, átlagtér-elméletek) Használható konformációkeresı algoritmusok tesztelésére Hátrányok Az atomi felbontás hiánya A szerkezeti és energetikai részletek nem pontosak A lánc sokszor irreálisan rövid
10 A rácsmodellek elemzése Enumeráció: a modell összes lehetséges állapotának elıállítása, megszámlálása és jellemzése. Kisebb modelleknél járható. Monte Carlo mintavétel, ill. szimuláció: Monte Carlo módszerrel (véletlenszerő generálás) véletlen állapotok elıállítása, ebbıl statisztikai számítás. Nagyobb modelleknél. (Hibalehetıségek vannak, pl. rossz becslésekbıl.) A natív állapot megkeresése: Kisebb modelleknél az összes lehetséges állapot végigpróbálásával, nagyobbaknál becslés speciális algoritmusokkal. A HP modellek alapállapotának megkeresése ún. NP-nehéz feladat
11 Egyszerő rácsmodellek: 1. Négytagú játékmodell A: energiaszintek, B: állapotok, C: h kontaktushoz tartozó állapotok száma, g(h) Legegyszerőbb 2D HP rácsmodell, szekvencia: HPPH h db kontaktusnál az energia: hε
12
13 A: Natív populáció részaránya, B: G felgombolyodási szabadentalpia. T m olvadáspontnál a natívhányad 50%, a szabadentalpia nulla. A szabadentalpiafüggvény lineáris (valódi fehérjéknél görbült) A: energia, B: hõkapacitás. A hõkapacitásgörbe jellegzetes átmeneti csúcsot mutat Már ez a legegyszerőbb modell is mutatja a fehérjék egyes termodinamikai tulajdonságait
14 2. Hattagú játékmodell Hattagú 2D HP modell, szekvencia: HPHPPH. Három energiaszint: három állapot Populációeloszlások a hõmérséklet függvényében: A populáció a tisztán natív állapotból indulva a köztes állapoton át folyamatosan áttolódik a denaturált állapotra
15 Felgombolyodási szabadentalpia a hõmérséklet függvényében: Az intermedier állapot miatt már nem lineáris, hanem görbül, mint a valódi fehérjéknél. Ha epszilont hõmérsékletfüggõvé tesszük (a hõmérséklet csökkenésével csökken, akárcsak a hidrofób kölcsönhatás), a szaggatott vonallal jelzett görbét kapjuk. Ez mutatja a valódi fehérjékre jellemzõ, parabolaszerû görbét, a hidegdenaturációval. Egy egyszerû hattagú modell már a fehérjék szabadentalpia-görbéjét is jól modellezi
16 3. Húsztagú modellek A szekvenciától függõen sokféle viselkedés: A: natív részarány, B: hõkapacitás, epszilon/kt függvényében, C: a modellek natív állapotai (legmélyebb energiaszint) ε a hidrofób kölcsönhatás erısségét jellemzi, ε/kt a denaturálószer-koncentrációnak feleltethetı meg (i): két csúcsú széles átmenet: kétdoménes fehérje (ii), (iii): egyetlen éles csúcs
17 (ii) populációeloszlása a hımérséklet függvényében: T=0,3 és T=0,4-nél az eloszlásnak minimuma van: kooperatív, kétállapotú rendszer Egy húsztagú modell már kétállapotú kooperativitást képes mutatni, akárcsak a valódi fehérjék A modell natív állapota egy β-lemezt és két hélixet tartalmaz, poláros felszínnel
18 Rácsmodell felgombolyodásának szimulációja Monte Carlo módszerrel (ld. elızı elıadás) lehetséges, ehhez definiálni kell egy mozgáskészletet (move set). Példa:
19 Egy 13 tagú HP modell felgombolyodásának szimulációja Két útvonal, egy gyors és egy lassú. A lassú útvonalon kinetikus csapda (lokális energiaminimum). Ez az egyszerő modell is komplex felgombolyodási kinetikát mutat (a lizozimhoz hasonló).
20 Egy 13 tagú HP modell felgombolyodásának szimulációja (folytatás) A populációk idıfüggése: (A számok az adott állapotban meglévı HH kontaktusok számát jelentik. Szaggatott vonal: a hidrofób kontaktusok száma a natív szerkezethez viszonyítva) Gyors hidrofób kollapszus, majd 5 nagyságrenddel hosszabb idıskálán lassú átrendezıdés a natív állapotba. Jól mutatja a valódi fehérjéknél megfigyelt sajátosságokat.
21 Szabadenergia-felületek rácsmodellekbıl Rácsmodellek Monte Carlo szimulációiból számítható a szabadenergia: ahol F = E TS E az energia (a kontaktusok számából) S az entrópia (az adott energiájú állapotok számából számítható). A szabadenergiát megfelelõ mennyiségek mint koordináták függvényében ábrázolva szemléletes felületek adódnak. Ilyen mennyiségek pl.: C: az összes kontaktusok száma Q 0 : a natív kontaktusok száma (olyan kontaktus, ami a natív szerkezetben is megvan)
22 Egy 27 elemő modell szabadenergia-felülete: A szimuláció menete ezen a felületen szemléltethetõ: A szimuláció random szerkezetbõl indul (kevés kontaktus): hozzáférhetõ állapotok száma kb Gyorsan összeesik egy kompakt szerkezetté, mely a lehetséges kontaktusok 60%-át tartalmazza, de a 60%-nak csak 25%-a natív kontaktus. A hozzáférhetõ állapotok száma kb Itt egy széles minimum van a szabadenergiában Ezután lassú folyamat következik: a lánc keresi a natív állapot felé vezetõ átmeneti állapotot Átmeneti állapotok száma 10 3 Az átmeneti állapotból gyorsan betalál a natívba (1 állapot) Zöld, piros: lehetséges, különbözõ útvonalak. Sárga: átlag.
23 125 elemő modell (5x5x5-ös kocka a natív állapot) szabadenergia-felülete Két mennyiség mint koordináta: Q c : a belsõ magban lévõ natív kontaktusok (34 darab), Q s : olyan kontaktusok, amelyek a legfontosabb intermedierben nincsenek benne (15 darab) A felgombolyodás menete: Gyors összeesés, majd lassú keresés A molekulák 15%-ában gyorsan kialakul a natív mag, majd közvetlenül a natív állapotba jut (sárga útvonal) A molekulák 40%-a különféle nemnatív kontaktusokat létesít, így egy hosszú élettartamú intermedier alakul ki (piros útvonal), melyben két szubdomén van, egyikben a natív 5x5x5-ös kocka felsõ három síkja megvan, a másik a többi részbõl áll. Mindkét szubdomén eléggé felgombolyodott, de a köztük lévõ kapcsolatok nem jöttek létre. A maradék 45%-ban szintén rosszul kezd felgombolyodni, de gyorsabban áthidalja a dolgot (ezt nem jelöltük)
24 A rácsmodellek következtetései Bizonyos szekvenciájú rácsmodellek stabil, kompakt állapotokba esnek össze. Ezek számos tekintetben igen hasonlóak a fehérjékhez: Kompakt, unikális natív szerkezet Másodlagos és harmadlagos szerkezet Apoláros mag, poláros felszín Éles, szigmoidális, kooperatív átmenet Kétállapotú kooperativitás Kompakt, komplex denaturált állapotok Többfázisú felgombolyodási kinetika Szabadenergiafelületek, kinetikus komplexitás jól modellezhetõ
25 Realisztikusabb rácsmodellek Elég sőrő 3D rácson, ha nem kötjük ki, hogy a kötések rácséleken feküdjenek, valóságos fehérjeszerkezet is reprezentálható Minden mozgás a rácsra korlátozódik, ezért Monte Carlo módszerrel hatékonyan szimulálható Tudás alapú (empirikus) potenciálfüggvényekkel
26 CABS modell (Zhang- Kolinski-Skolnick 2003) Atomok egy 0,87 angström cellamérető rácson Csak C α, C β és az oldallánc tömegközéppontja Monte Carlo mozgáskészlet
27 Empirikus potenciálfüggvény
28 A paramétereket az ismert szerkezetek adatbázisából vezették le (ezért tudásalapú)
29 A potenciálfüggvény 19 szabad paramétert (súlyt) tartalmaz. Ezeket optimalizálták egy decoy (csalétek) halmaz segítségével oly módon, hogy az energia és az RMSD közötti korreláció maximális legyen. Tölcséresített potenciálfüggvény : a szerkezetet beirányítja a globális minimumba. CASP2004-en a CABS modellen alapuló szerkezetpredikciós módszer kiválóan szerepelt. 100 aminosav alatti fehérjéket általában a helyes szerkezetbe gombolyít fel (NMR szerkezetnek megfelelı pontossággal).
30 Diszkrét molekuladinamika (DMD) A hagyományos molekuladinamikában a Newton-féle mozgásegyenleteket integráljuk. Az idıbeli lépésköznek elegendıen kicsinek kell lennie, a molekula leggyorsabb mozgásaihoz igazodva. DMD: a dinamikát ütközési események egymásutánjaként fogjuk fel. Két ütközés között az atomok egyenes vonalú, egyenletes mozgást végeznek, ezt nem szükséges követni, a számítás rögtön a következı ütközésre léptetheti a rendszert. Ezáltal több nagyságrenddel gyorsabban végezhetı a szimuláció! Ennek ára: a potenciálfüggvényt diszkretizálni kell.
31 A potenciálfüggvény diszkretizálása A párpotenciált lépcsızetes függvénnyel közelítjük
32 DMD szimuláció 1 Ballisztikus szakasz 2 Ütközés v i v j v i v j r = σ r + vτ = σ r = r j r i v = v j v i b = rv r = r v = v A következı ütközés ideje az alábbi egyenlet két megoldása közül a kisebb pozitív: ± ( ) = b b v r σ τ 2 v
33 Az ütközések feldolgozása Általánosított ütközések: potenciálfallal i 1 m i v i = m j v j lendület j kilépés s =1 potenciálgödör belépés s =1 2 E + U = E k v i = m j Φr v j = m i Φr k energia megoldható m i + m j m = 2 visszapattanás s = 1 U visszapattanás s = 1 Φ = b + s b 2 2 4σ m U m m 2 2σ m i j U r
34 Eseményfa Az ütközési eseményeket bináris keresıfában tároljuk root t = 23.7 A = 4 B = 3 : t = 25.1 A = 6 B = 8 : t = 32.1 A =1 B = 7 : t =19.2 A = 9 B = 1 : t = 24.2 A = 3 B = 8 : t = 31.6 A = 2 B = 4 : t = 43.8 A = 4 B = 5 : t = 23.9 A = 9 B = 2 : t = 24.7 A = 4 B = 10 : t = 47.8 A = 6 B = 9 :
35 Egyszerősített fehérjemodell Négygolyós modell Négyféle egyesített atom N C C α R = C β R O C N H C α H C O H N H C α R O C alanin: R = C β
36 Peptidgerinc kovalens kötés effektív kötés C βi A kötésszög-kényszereket 1-3 effektív kötésekkel valósítjuk meg C αi N i+1 C i+1 N C i Φ α, i Ψ C i i+1 i Kovalens kötés potenciálja: U r id r végtelen mély derékszögő gödör ±2% fluktuációt engedünk meg az ideális kötéshossz körül C β, i+1
37 Hidrogénkötés C α, i-1 C αi Segédkölcsönhatásokat vezetünk be az orientációfüggés modellezésére N i U 4.0Å 4.2Å ε HB / 2 ε HB / 2 r min r 1 r 2 r max r N j+1 C j C αj V ( r) 0, ε HB / 2 = ε HB + r > r > r max 2 r > r > r 2 1 r > r > r 1 min otherwise
38 Hımérsékletszabályozás Andersen-termosztát: Véletlenszerő ütközések történnek a hıfürdı szellemrészecskéivel Két ilyen ütközés között eltelı idı valószínőségeloszlása: P( t) = ν e νt ν az ütközésgyakoriság, ezt úgy választjuk meg, hogy az események 1%-a legyen szellemütközés A kinetikus energia fluktuációi jó egyezést mutatnak az elméleti értékekkel
39
40 Hexadeka-alanin
41 A hidrogénkötések számának fluktuációja 330 Kelvinen, 1 mikroszekundum idıtartam szimulációja során
42 Másodlagosszerkezet-tartalom a hımérséklet függvényében
43
44
45
46 A DMD perspektívái Mostanában újra felfedezett módszer Korlátja: bonyolultabb potenciálfüggvények diszkretizálása nehezen megoldható Jól alkalmazható: peptidek és kisebb fehérjék konformációs terének feltérképezésére, asszociáció, aggregáció modellezésére
A fehérjék térszerkezetének jóslása (Szilágyi András, MTA Enzimológiai Intézete)
 A fehérjék térszerkezetének jóslása (Szilágyi András, MTA Enzimológiai Intézete) A probléma bonyolultsága Általánosságban: találjuk meg egy tetszőleges szekvencia azon konformációját, amely a szabadentalpia
A fehérjék térszerkezetének jóslása (Szilágyi András, MTA Enzimológiai Intézete) A probléma bonyolultsága Általánosságban: találjuk meg egy tetszőleges szekvencia azon konformációját, amely a szabadentalpia
A rácsmodell. Szabadenergia felületek.
 1. A spinüveg modell 2. A rácsmodellek típusai 3. A rácsmodellek elõnyei és hátrányai 4. A rácsmodellek elemzése 5. Egyszerû rácsmodellek 6. Rácsmodellek natív állapotai 7. Oldalláncok 8. Rácsmodellek
1. A spinüveg modell 2. A rácsmodellek típusai 3. A rácsmodellek elõnyei és hátrányai 4. A rácsmodellek elemzése 5. Egyszerû rácsmodellek 6. Rácsmodellek natív állapotai 7. Oldalláncok 8. Rácsmodellek
Fehérjék rövid bevezetés
 Receptorfehérj rjék szerkezetének felderítése Homológia modellezés Fehérjék rövid bevezetés makromolekulák számos biológiai funkció hordozói: enzimatikus katalízis, molekula transzport, immunválaszok,
Receptorfehérj rjék szerkezetének felderítése Homológia modellezés Fehérjék rövid bevezetés makromolekulák számos biológiai funkció hordozói: enzimatikus katalízis, molekula transzport, immunválaszok,
8. A fehérjék térszerkezetének jóslása
 8. A fehérjék térszerkezetének jóslása A probléma bonyolultsága Általánosságban: találjuk meg egy tetszõleges szekvencia azon konformációját, amely a szabadentalpia globális minimumát adja. Egyszerû modellekben
8. A fehérjék térszerkezetének jóslása A probléma bonyolultsága Általánosságban: találjuk meg egy tetszõleges szekvencia azon konformációját, amely a szabadentalpia globális minimumát adja. Egyszerû modellekben
A fehérjék térszerkezetének jóslása
 A fehérjék térszerkezetének jóslása 1. A probléma bonyolultsága 2. A predikció szintjei 3. 1D predikciók (másodlagos szerkezet, hozzáférhetõség, transzmembrán hélixek 4. 2D predikciók (oldallánc kontaktusok,
A fehérjék térszerkezetének jóslása 1. A probléma bonyolultsága 2. A predikció szintjei 3. 1D predikciók (másodlagos szerkezet, hozzáférhetõség, transzmembrán hélixek 4. 2D predikciók (oldallánc kontaktusok,
Fehérjeszerkezet, és tekeredés. Futó Kinga
 Fehérjeszerkezet, és tekeredés Futó Kinga Polimerek Polimer: hasonló alegységekből (monomer) felépülő makromolekulák Alegységek száma: tipikusan 10 2-10 4 Titin: 3,435*10 4 aminosav C 132983 H 211861 N
Fehérjeszerkezet, és tekeredés Futó Kinga Polimerek Polimer: hasonló alegységekből (monomer) felépülő makromolekulák Alegységek száma: tipikusan 10 2-10 4 Titin: 3,435*10 4 aminosav C 132983 H 211861 N
Az élő anyag szerkezeti egységei: víz, nukleinsavak, fehérjék. elrendeződés, rend, rendszer, periodikus ismétlődés
 Az élő anyag szerkezeti egységei: víz, nukleinsavak, fehérjék Agócs Gergely 2013. december 3. kedd 10:00 11:40 1. Mit értünk élő anyag alatt? Az élő szervezetet felépítő anyagok. Az anyag azonban nem csupán
Az élő anyag szerkezeti egységei: víz, nukleinsavak, fehérjék Agócs Gergely 2013. december 3. kedd 10:00 11:40 1. Mit értünk élő anyag alatt? Az élő szervezetet felépítő anyagok. Az anyag azonban nem csupán
Fehérje-fehérje kölcsönhatások és kölcsönhatási hálózatok. Szilágyi András
 Fehérje-fehérje kölcsönhatások és kölcsönhatási hálózatok Szilágyi András Vázlat Fehérje-fehérje kölcsönhatások Kölcsönhatási hálózatok Kísérleti módszerek Bioinformatikai vonatkozások adatbázisok szerkezetfüggetlen
Fehérje-fehérje kölcsönhatások és kölcsönhatási hálózatok Szilágyi András Vázlat Fehérje-fehérje kölcsönhatások Kölcsönhatási hálózatok Kísérleti módszerek Bioinformatikai vonatkozások adatbázisok szerkezetfüggetlen
DNS, RNS, Fehérjék. makromolekulák biofizikája. Biológiai makromolekulák. A makromolekulák TÖMEG szerinti mennyisége a sejtben NAGY
 makromolekulák biofizikája DNS, RNS, Fehérjék Kellermayer Miklós Tér Méret, alak, lokális és globális szerkezet Idő Fluktuációk, szerkezetváltozások, gombolyodás Kölcsönhatások Belső és külső kölcsöhatások,
makromolekulák biofizikája DNS, RNS, Fehérjék Kellermayer Miklós Tér Méret, alak, lokális és globális szerkezet Idő Fluktuációk, szerkezetváltozások, gombolyodás Kölcsönhatások Belső és külső kölcsöhatások,
MTA DOKTORI ÉRTEKEZÉS
 MTA DOKTORI ÉRTEKEZÉS ELLENTÉTES TÖLTÉSŐ POLIELEKTROLITOK ÉS TENZIDEK ASSZOCIÁCIÓJA Mészáros Róbert Eötvös Loránd Tudományegyetem Kémiai Intézet Budapest, 2009. december Köszönetnyilvánítás Ezúton szeretném
MTA DOKTORI ÉRTEKEZÉS ELLENTÉTES TÖLTÉSŐ POLIELEKTROLITOK ÉS TENZIDEK ASSZOCIÁCIÓJA Mészáros Róbert Eötvös Loránd Tudományegyetem Kémiai Intézet Budapest, 2009. december Köszönetnyilvánítás Ezúton szeretném
A fehérjék szerkezete és az azt meghatározó kölcsönhatások
 A fehérjék szerkezete és az azt meghatározó kölcsönhatások 1. A fehérjék szerepe az élõlényekben 2. A fehérjék szerkezetének szintjei 3. A fehérjék konformációs stabilitásáért felelõs kölcsönhatások 4.
A fehérjék szerkezete és az azt meghatározó kölcsönhatások 1. A fehérjék szerepe az élõlényekben 2. A fehérjék szerkezetének szintjei 3. A fehérjék konformációs stabilitásáért felelõs kölcsönhatások 4.
Tevékenység: Olvassa el a fejezetet! Gyűjtse ki és jegyezze meg a ragasztás előnyeit és a hátrányait! VIDEO (A ragasztás ereje)
 lvassa el a fejezetet! Gyűjtse ki és jegyezze meg a ragasztás előnyeit és a hátrányait! VIDE (A ragasztás ereje) A ragasztás egyre gyakrabban alkalmazott kötéstechnológia az ipari gyakorlatban. Ennek oka,
lvassa el a fejezetet! Gyűjtse ki és jegyezze meg a ragasztás előnyeit és a hátrányait! VIDE (A ragasztás ereje) A ragasztás egyre gyakrabban alkalmazott kötéstechnológia az ipari gyakorlatban. Ennek oka,
6. Zárványtestek feldolgozása
 6. Zárványtestek feldolgozása... 1 6.1. A zárványtestek... 1 6.1.1. A zárványtestek kialakulása... 2 6.1.2. A feldolgozási technológia... 3 6.1.2.1. Sejtfeltárás... 3 6.1.2.2. Centrifugálás, tisztítás...
6. Zárványtestek feldolgozása... 1 6.1. A zárványtestek... 1 6.1.1. A zárványtestek kialakulása... 2 6.1.2. A feldolgozási technológia... 3 6.1.2.1. Sejtfeltárás... 3 6.1.2.2. Centrifugálás, tisztítás...
Makromolekulák. Fehérjetekeredé. rjetekeredés. Biopolimer. Polimerek
 Biopolimerek Makromolekulá Makromolekulák. Fehé Fehérjetekeredé rjetekeredés. Osztódó sejt magorsófonala 2011. November 16. Huber Tamá Tamás Dohány levél epidermális sejtjének aktin hálózata Bakteriofágból
Biopolimerek Makromolekulá Makromolekulák. Fehé Fehérjetekeredé rjetekeredés. Osztódó sejt magorsófonala 2011. November 16. Huber Tamá Tamás Dohány levél epidermális sejtjének aktin hálózata Bakteriofágból
Szakdolgozat. Pongor Gábor
 Szakdolgozat Pongor Gábor Debrecen 2009 Debreceni Egyetem Informatikai Kar Egy kétszemélyes játék számítógépes megvalósítása Témavezetı: Mecsei Zoltán Egyetemi tanársegéd Készítette: Pongor Gábor Programozó
Szakdolgozat Pongor Gábor Debrecen 2009 Debreceni Egyetem Informatikai Kar Egy kétszemélyes játék számítógépes megvalósítása Témavezetı: Mecsei Zoltán Egyetemi tanársegéd Készítette: Pongor Gábor Programozó
Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet), A Laplace operátor derékszögű koordinátarendszerben
 Atomfizika ψ ψ ψ ψ ψ E z y x U z y x m = + + + ),, ( h ) ( ) ( ) ( ) ( r r r r ψ ψ ψ E U m = + Δ h z y x + + = Δ ),, ( ) ( z y x ψ =ψ r Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet),
Atomfizika ψ ψ ψ ψ ψ E z y x U z y x m = + + + ),, ( h ) ( ) ( ) ( ) ( r r r r ψ ψ ψ E U m = + Δ h z y x + + = Δ ),, ( ) ( z y x ψ =ψ r Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet),
A folyáshatár hőmérsékletfüggése intermetallikus ötvözetekben
 A folyáshatár hőmérsékletfüggése intermetallikus ötvözetekben Cserti József Eötvös Loránd Tudományegyetem Szilárdtest Fizika Tanszék Kandidátusi értekezés 1993 . Köszönetnyilvánítás Köszönetemet szeretném
A folyáshatár hőmérsékletfüggése intermetallikus ötvözetekben Cserti József Eötvös Loránd Tudományegyetem Szilárdtest Fizika Tanszék Kandidátusi értekezés 1993 . Köszönetnyilvánítás Köszönetemet szeretném
7. Fogazatok megmunkálása határozott élgeometriájú szerszámokkal
 7. Fogazatok megmunkálása határozott élgeometriájú szerszámokkal A fogazatok kapcsolódása 7.1 Alapfogalmak Fogaskerék hajtások csoportosítása Egyenes külső Egyenes belső Külső kúpfogazat Fogasléc Fogasív
7. Fogazatok megmunkálása határozott élgeometriájú szerszámokkal A fogazatok kapcsolódása 7.1 Alapfogalmak Fogaskerék hajtások csoportosítása Egyenes külső Egyenes belső Külső kúpfogazat Fogasléc Fogasív
Fehérjeszerkezet, fehérjetekeredés
 Fehérjeszerkezet, fehérjetekeredés A fehérjeszerkezet szintjei A fehérjetekeredés elmélete: Anfinsen kísérlet Levinthal paradoxon A feltekeredés tölcsér elmélet 2014.11.05. Aminosavak és fehérjeszerkezet
Fehérjeszerkezet, fehérjetekeredés A fehérjeszerkezet szintjei A fehérjetekeredés elmélete: Anfinsen kísérlet Levinthal paradoxon A feltekeredés tölcsér elmélet 2014.11.05. Aminosavak és fehérjeszerkezet
EGYTENGELYŰ EREDŐ REOLÓGIA, ÉS RELAXÁCIÓ MINT
 I n t e r n a t i o n a l S o c i e t y f o r R o c k M e c h a n i c s Mérnökgeológia-Kőzetmechanika 2012 Konferencia, Budapest EGYTENGELYŰ EREDŐ REOLÓGIA, ÉS RELAXÁCIÓ MINT DEVIATORIKUS KÚSZÁS Fülöp
I n t e r n a t i o n a l S o c i e t y f o r R o c k M e c h a n i c s Mérnökgeológia-Kőzetmechanika 2012 Konferencia, Budapest EGYTENGELYŰ EREDŐ REOLÓGIA, ÉS RELAXÁCIÓ MINT DEVIATORIKUS KÚSZÁS Fülöp
Bioinformatika 2 5.. előad
 5.. előad adás Prof. Poppe László BME Szerves Kémia és Technológia Tsz. Bioinformatika proteomika Előadás és gyakorlat 2009. 03. 21. Fehérje térszerkezet t megjelenítése A fehérjék meglehetősen összetett
5.. előad adás Prof. Poppe László BME Szerves Kémia és Technológia Tsz. Bioinformatika proteomika Előadás és gyakorlat 2009. 03. 21. Fehérje térszerkezet t megjelenítése A fehérjék meglehetősen összetett
MŰANYAGOK ALKALMAZÁSA
 MŰANYAGOK ALKALMAZÁSA Geoműanyagok A környezetszennyeződés megakadályozása érdekében a szemétlerakókat környezetüktől hosszú távra el kell szigetelni. Ebben nagy szerepük van a műanyag geomembránoknak.
MŰANYAGOK ALKALMAZÁSA Geoműanyagok A környezetszennyeződés megakadályozása érdekében a szemétlerakókat környezetüktől hosszú távra el kell szigetelni. Ebben nagy szerepük van a műanyag geomembránoknak.
Elektronspinrezonancia (ESR) - spektroszkópia
 E m S Elektronspinrezonancia (ESR) - spektroszkópia Paramágneses anyagok vizsgáló módszere. A mágneses momentum iránykvantáltságán alapul. A mágneses momentum energiája B indukciójú mágneses térben = µ
E m S Elektronspinrezonancia (ESR) - spektroszkópia Paramágneses anyagok vizsgáló módszere. A mágneses momentum iránykvantáltságán alapul. A mágneses momentum energiája B indukciójú mágneses térben = µ
Szerkesztette: Vizkievicz András
 Fehérjék A fehérjék - proteinek - az élő szervezetek számára a legfontosabb vegyületek. Az élet bármilyen megnyilvánulási formája fehérjékkel kapcsolatos. A sejtek szárazanyagának minimum 50 %-át adják.
Fehérjék A fehérjék - proteinek - az élő szervezetek számára a legfontosabb vegyületek. Az élet bármilyen megnyilvánulási formája fehérjékkel kapcsolatos. A sejtek szárazanyagának minimum 50 %-át adják.
AZ ÉGHAJLATI ELEMEK IDİBELI ÉS TÉRBELI VÁLTOZÁSAI MAGYARORSZÁGON PÁROLGÁS, LÉGNEDVESSÉG, KÖD, FELHİZET
 AZ ÉGHAJLATI ELEMEK IDİBELI ÉS TÉRBELI VÁLTOZÁSAI MAGYARORSZÁGON PÁROLGÁS, LÉGNEDVESSÉG, KÖD, FELHİZET PÁROLGÁS A párolgás halmazállapot-változás, amelyhez az energiát a felszín által elnyelt napsugárzási
AZ ÉGHAJLATI ELEMEK IDİBELI ÉS TÉRBELI VÁLTOZÁSAI MAGYARORSZÁGON PÁROLGÁS, LÉGNEDVESSÉG, KÖD, FELHİZET PÁROLGÁS A párolgás halmazállapot-változás, amelyhez az energiát a felszín által elnyelt napsugárzási
Rendezetlen kondenzált fázisok tulajdonságainak vizsgálata számítógépes szimulációs módszerekkel
 Rendezetlen kondenzált fázisok tulajdonságainak vizsgálata számítógépes szimulációs módszerekkel MTA doktori értekezés Írta: Jedlovszky Pál Eötvös Loránd Tudományegyetem Kémiai Intézet Budapest, 2006.
Rendezetlen kondenzált fázisok tulajdonságainak vizsgálata számítógépes szimulációs módszerekkel MTA doktori értekezés Írta: Jedlovszky Pál Eötvös Loránd Tudományegyetem Kémiai Intézet Budapest, 2006.
BUDAPESTI MŰSZAKI EGYETEM Anyagtudomány és Technológia Tanszék. Hőkezelés 2. (PhD) féléves házi feladat. Acélok cementálása. Thiele Ádám WTOSJ2
 BUDAPESTI MŰSZAKI EGYETEM Anyagtudomány és Technológia Tanszék Hőkezelés. (PhD) féléves házi feladat Acélok cementálása Thiele Ádám WTOSJ Budaest, 11 Tartalomjegyzék 1. A termokémiai kezeléseknél lejátszódó
BUDAPESTI MŰSZAKI EGYETEM Anyagtudomány és Technológia Tanszék Hőkezelés. (PhD) féléves házi feladat Acélok cementálása Thiele Ádám WTOSJ Budaest, 11 Tartalomjegyzék 1. A termokémiai kezeléseknél lejátszódó
ESR színképek értékelése és molekulaszerkezeti értelmezése
 ESR színképek értékelése és molekulaszerkezeti értelmezése Elméleti alap: Atkins: Fizikai Kémia II, 187-188, 146, 1410, 152 158 fejezetek A gyakorlat során egy párosítatlan elektronnal rendelkező benzoszemikinon
ESR színképek értékelése és molekulaszerkezeti értelmezése Elméleti alap: Atkins: Fizikai Kémia II, 187-188, 146, 1410, 152 158 fejezetek A gyakorlat során egy párosítatlan elektronnal rendelkező benzoszemikinon
VII. Gyakorlat: Használhatósági határállapotok MSZ EN 1992 alapján Betonszerkezetek alakváltozása és repedéstágassága
 VII. Gyakorlat: Használhatósági határállapotok MSZ EN 199 alapján Betonszerkezetek alakváltozása és repedéstágassága Készítették: Kovács Tamás és Völgyi István -1- Készítették: Kovács Tamás, Völgyi István
VII. Gyakorlat: Használhatósági határállapotok MSZ EN 199 alapján Betonszerkezetek alakváltozása és repedéstágassága Készítették: Kovács Tamás és Völgyi István -1- Készítették: Kovács Tamás, Völgyi István
Statisztikai módszerek
 Statisztikai módszerek A hibaelemzı módszereknél azt néztük, vannak-e kiugró, kritikus hibák, amelyek a szabályozás kivételei. Ezekkel foglalkozni kell; minıségavító szabályozásra van szükség. A statisztikai
Statisztikai módszerek A hibaelemzı módszereknél azt néztük, vannak-e kiugró, kritikus hibák, amelyek a szabályozás kivételei. Ezekkel foglalkozni kell; minıségavító szabályozásra van szükség. A statisztikai
(2) A R. 3. (2) bekezdése helyébe a következő rendelkezés lép: (2) A képviselő-testület az önkormányzat összes kiadását 1.1369.
 Enying Város Önkormányzata Képviselő-testületének 20/2010. (X. 05.) önkormányzati rendelete az Enying Város Önkormányzatának 2100. évi költségvetéséről szóló 7/2010. (II. 26.) önkormányzati rendelete módosításáról
Enying Város Önkormányzata Képviselő-testületének 20/2010. (X. 05.) önkormányzati rendelete az Enying Város Önkormányzatának 2100. évi költségvetéséről szóló 7/2010. (II. 26.) önkormányzati rendelete módosításáról
Földművek gyakorlat. Vasalt talajtámfal tervezése Eurocode szerint
 Földműve gyaorlat Vasalt talajtámfal tervezése Eurocode szerint Vasalt talajtámfal 2. Vasalt talajtámfal alalmazási területei Úttöltése vasúti töltése hídtöltése gáta védműve ipari épülete öztere repülőtere
Földműve gyaorlat Vasalt talajtámfal tervezése Eurocode szerint Vasalt talajtámfal 2. Vasalt talajtámfal alalmazási területei Úttöltése vasúti töltése hídtöltése gáta védműve ipari épülete öztere repülőtere
 A méretezés alapjai II. Épületek terheinek számítása az MSZ szerint SZIE-YMMF 1. Erőtani tervezés 1.1. Tartószerkezeti szabványok Magyar Szabvány: MSZ 510 MSZ 15012/1 MSZ 15012/2 MSZ 15020 MSZ 15021/1
A méretezés alapjai II. Épületek terheinek számítása az MSZ szerint SZIE-YMMF 1. Erőtani tervezés 1.1. Tartószerkezeti szabványok Magyar Szabvány: MSZ 510 MSZ 15012/1 MSZ 15012/2 MSZ 15020 MSZ 15021/1
lásd: enantiotóp, diasztereotóp
 anizokrón anisochronous árnyékolási állandó shielding constant árnyékolási járulékok és empirikus értelmezésük shielding contributions diamágneses és paramágneses árnyékolás diamagnetic and paramagnetic
anizokrón anisochronous árnyékolási állandó shielding constant árnyékolási járulékok és empirikus értelmezésük shielding contributions diamágneses és paramágneses árnyékolás diamagnetic and paramagnetic
Olyan magkedvelő részecske, amely (legalább) két különböző atomján képes kötést létesíteni a(z elektrofil) reakciópartnerrel.
 akceptorszám (akceptivitás) aktiválási energia (E a ) activation energy aktiválási szabadentalpia (ΔG ) Gibbs energy of activation aktivált komplex activated complex ambidens nukleofil amfiprotikus (oldószer)
akceptorszám (akceptivitás) aktiválási energia (E a ) activation energy aktiválási szabadentalpia (ΔG ) Gibbs energy of activation aktivált komplex activated complex ambidens nukleofil amfiprotikus (oldószer)
2. előadás: További gömbi fogalmak
 2 előadás: További gömbi fogalmak 2 előadás: További gömbi fogalmak Valamely gömbi főkör ívének α azimutja az ív egy tetszőleges pontjában az a szög, amit az ív és a meridián érintői zárnak be egymással
2 előadás: További gömbi fogalmak 2 előadás: További gömbi fogalmak Valamely gömbi főkör ívének α azimutja az ív egy tetszőleges pontjában az a szög, amit az ív és a meridián érintői zárnak be egymással
BIOFIZIKA. Metodika- 4. Liliom Károly. MTA TTK Enzimológiai Intézet liliom@enzim.hu
 BIOFIZIKA 2012 11 26 Metodika- 4 Liliom Károly MTA TTK Enzimológiai Intézet liliom@enzim.hu A biofizika előadások temamkája 1. 09-03 Biofizika: fizikai szemlélet, modellalkotás, biometria 2. 09-10 SZÜNET
BIOFIZIKA 2012 11 26 Metodika- 4 Liliom Károly MTA TTK Enzimológiai Intézet liliom@enzim.hu A biofizika előadások temamkája 1. 09-03 Biofizika: fizikai szemlélet, modellalkotás, biometria 2. 09-10 SZÜNET
Félévi időbeosztás (nagyjából) házi feladat beadási határidőkkel (pontosan) Valószínűségszámítás 2. matematikusoknak és fizikusoknak, 2009 tavasz
 Félévi időbeosztás (nagyjából) házi feladat beadási határidőkkel (pontosan) Valószínűségszámítás 2. matematikusoknak és fizikusoknak, 2009 tavasz Dátum Téma beadandó Feb 12Cs Konvolúció (normális, Cauchy,
Félévi időbeosztás (nagyjából) házi feladat beadási határidőkkel (pontosan) Valószínűségszámítás 2. matematikusoknak és fizikusoknak, 2009 tavasz Dátum Téma beadandó Feb 12Cs Konvolúció (normális, Cauchy,
Kecskeméti Fıiskola GAMF Kar Informatika Tanszék. Johanyák Zsolt Csaba
 Kecskeméti Fıiskola GAMF Kar Informatika Tanszék Johanyák Zsolt Csaba 003 Tartalomjegyzék. Bevezetés.... A megbízhatóság fogalmai..... A termék idıtıl függı képességei...... Használhatóság /Üzemkészség/
Kecskeméti Fıiskola GAMF Kar Informatika Tanszék Johanyák Zsolt Csaba 003 Tartalomjegyzék. Bevezetés.... A megbízhatóság fogalmai..... A termék idıtıl függı képességei...... Használhatóság /Üzemkészség/
Szakközépiskola 9-10. évfolyam Kémia. 9-10. évfolyam
 9-10. évfolyam A szakközépiskolában a kémia tantárgy keretében folyó személyiségfejlesztés a természettudományos nevelés egyik színtereként a hétköznapi életben hasznosulni képes tudás épülését szolgálja.
9-10. évfolyam A szakközépiskolában a kémia tantárgy keretében folyó személyiségfejlesztés a természettudományos nevelés egyik színtereként a hétköznapi életben hasznosulni képes tudás épülését szolgálja.
Analízisfeladat-gyűjtemény IV.
 Oktatási segédanyag a Programtervező matematikus szak Analízis. című tantárgyához (003 004. tanév tavaszi félév) Analízisfeladat-gyűjtemény IV. (Függvények határértéke és folytonossága) Összeállította
Oktatási segédanyag a Programtervező matematikus szak Analízis. című tantárgyához (003 004. tanév tavaszi félév) Analízisfeladat-gyűjtemény IV. (Függvények határértéke és folytonossága) Összeállította
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN
 GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten LINEÁRIS PROGRAMOZÁS Készítette: Gábor Szakmai felel s: Gábor Vázlat 1 2 3 4 A lineáris
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten LINEÁRIS PROGRAMOZÁS Készítette: Gábor Szakmai felel s: Gábor Vázlat 1 2 3 4 A lineáris
A.11. Nyomott rudak. A.11.1. Bevezetés
 A.. Nyomott rudak A... Bevezetés A nyomott szerkezeti elem fogalmat általában olyan szerkezeti elemek jelölésére használjuk, amelyekre csak tengelyirányú nyomóerő hat. Ez lehet speciális terhelésű oszlop,
A.. Nyomott rudak A... Bevezetés A nyomott szerkezeti elem fogalmat általában olyan szerkezeti elemek jelölésére használjuk, amelyekre csak tengelyirányú nyomóerő hat. Ez lehet speciális terhelésű oszlop,
Lumineszcencia Fényforrások
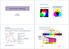 Kiegészítés: színkeverés Lumineszcencia Fényforrások Alapszinek additív keverése Alapszinek kiegészítő szineinek keverése: Szubtraktív keverés Fidy udit Egyetemi tanár 2015, November 5 Emlékeztető.. Abszorpciós
Kiegészítés: színkeverés Lumineszcencia Fényforrások Alapszinek additív keverése Alapszinek kiegészítő szineinek keverése: Szubtraktív keverés Fidy udit Egyetemi tanár 2015, November 5 Emlékeztető.. Abszorpciós
TERMOELEM-HİMÉRİK (Elméleti összefoglaló)
 Alapfogalmak, meghatározások TERMOELEM-HİMÉRİK (Elméleti összefoglaló) A termoelektromos átalakítók hımérsékletkülönbség hatására villamos feszültséget szolgáltatnak. Ezért a termoelektromos jelátalakítók
Alapfogalmak, meghatározások TERMOELEM-HİMÉRİK (Elméleti összefoglaló) A termoelektromos átalakítók hımérsékletkülönbség hatására villamos feszültséget szolgáltatnak. Ezért a termoelektromos jelátalakítók
Fizika belépő kérdések /Földtudományi alapszak I. Évfolyam II. félév/
 Fizika belépő kérdések /Földtudományi alapszak I. Évfolyam II. félév/. Coulomb törvény: a pontszerű töltések között ható erő (F) egyenesen arányos a töltések (Q,Q ) szorzatával és fordítottan arányos a
Fizika belépő kérdések /Földtudományi alapszak I. Évfolyam II. félév/. Coulomb törvény: a pontszerű töltések között ható erő (F) egyenesen arányos a töltések (Q,Q ) szorzatával és fordítottan arányos a
Programozási módszertan. Dinamikus programozás: Nyomtatási feladat A leghosszabb közös részsorozat
 PM-04 p. 1/18 Programozási módszertan Dinamikus programozás: Nyomtatási feladat A leghosszabb közös részsorozat Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu
PM-04 p. 1/18 Programozási módszertan Dinamikus programozás: Nyomtatási feladat A leghosszabb közös részsorozat Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu
Szegedi Tudományegyetem Természettudományi Kar Éghajlattani és Tájföldrajzi Tanszék FOGALOMTÁR 2. RÉSZ
 Szegedi Tudományegyetem Természettudományi Kar Éghajlattani és Tájföldrajzi Tanszék FOGALOMTÁR 2. RÉSZ Az Általános klimatológia gyakorlat 2. zh-jában szereplő fogalmak jegyzéke Szeged 2008 A 2. ZH-ban
Szegedi Tudományegyetem Természettudományi Kar Éghajlattani és Tájföldrajzi Tanszék FOGALOMTÁR 2. RÉSZ Az Általános klimatológia gyakorlat 2. zh-jában szereplő fogalmak jegyzéke Szeged 2008 A 2. ZH-ban
Oktatási segédlet. Acél- és alumínium-szerkezetek hegesztett kapcsolatainak méretezése fáradásra. Dr. Jármai Károly.
 Oktatási segédlet Acél- és alumínium-szerkezetek hegesztett kapcsolatainak méretezése fáradásra a Létesítmények acélszerkezetei tárgy hallgatóinak Dr. Jármai Károly Miskolci Egyetem 013 1 Acél- és alumínium-szerkezetek
Oktatási segédlet Acél- és alumínium-szerkezetek hegesztett kapcsolatainak méretezése fáradásra a Létesítmények acélszerkezetei tárgy hallgatóinak Dr. Jármai Károly Miskolci Egyetem 013 1 Acél- és alumínium-szerkezetek
Dr. Göndöcs Balázs, BME Közlekedésmérnöki Kar. Tárgyszavak: szerelés; javíthatóság; cserélhetőség; karbantartás.
 JELLEGZETES ÜZEMFENNTARTÁS-TECHNOLÓGIAI ELJÁRÁSOK 4.06 Javításhelyes szerelés 1 Dr. Göndöcs Balázs, BME Közlekedésmérnöki Kar Tárgyszavak: szerelés; javíthatóság; cserélhetőség; karbantartás. A mai termékek
JELLEGZETES ÜZEMFENNTARTÁS-TECHNOLÓGIAI ELJÁRÁSOK 4.06 Javításhelyes szerelés 1 Dr. Göndöcs Balázs, BME Közlekedésmérnöki Kar Tárgyszavak: szerelés; javíthatóság; cserélhetőség; karbantartás. A mai termékek
B E S Z Á M O L Ó Körösladány Város 2010 évi közbiztonsági helyzetérıl
 Száma: 04070/565-26/2011. ált. R E N D İ R K A P I T Á N Y S Á G S Z E G H A L O M 5520, Szeghalom Kossuth tér 1., PF:3 tel/fax: +36/66/371-555 Jóváhagyom: Szalai Zoltán r. alezredes kapitányságvezetı
Száma: 04070/565-26/2011. ált. R E N D İ R K A P I T Á N Y S Á G S Z E G H A L O M 5520, Szeghalom Kossuth tér 1., PF:3 tel/fax: +36/66/371-555 Jóváhagyom: Szalai Zoltán r. alezredes kapitányságvezetı
Általános statisztika II. Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László
 Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Publication
Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Publication
zis Brown-mozg mozgás Makromolekula (DNS) fluktuáci Vámosi György
 Brown-mo mozgás magyarázata Vámosi György Diffúzi zió és s ozmózis zis Az anyag részeskéi állandó mozgásban vannak Haladó mozgás átlagos energiája: E= 3 / kt Emlékeztető: Mawell-féle sebességeloszlás gázokban:
Brown-mo mozgás magyarázata Vámosi György Diffúzi zió és s ozmózis zis Az anyag részeskéi állandó mozgásban vannak Haladó mozgás átlagos energiája: E= 3 / kt Emlékeztető: Mawell-féle sebességeloszlás gázokban:
Alapfogalmak áttekintése. Pszichológiai statisztika, 1. alkalom
 Alapfogalmak áttekintése Pszichológiai statisztika, 1. alkalom Hipotézisek Milyen a jó null hipotézis?? H0: Léteznek kitőnı tanuló diszlexiások.? H1: Nem léteznek. Sokkal inkább: H0: Nincs diszlexiás kitőnı
Alapfogalmak áttekintése Pszichológiai statisztika, 1. alkalom Hipotézisek Milyen a jó null hipotézis?? H0: Léteznek kitőnı tanuló diszlexiások.? H1: Nem léteznek. Sokkal inkább: H0: Nincs diszlexiás kitőnı
5.1. GERENDÁS FÖDÉMEK KIALAKÍTÁSA, TERVEZÉSI ELVEI
 5. FÖDÉMEK TERVEZÉSE 5.1. GERENDÁS FÖDÉMEK KIALAKÍTÁSA, TERVEZÉSI ELVEI Az alábbiakban az Épületszerkezettan 2. c. tárgy tanmenetének megfelelıen a teljes keresztmetszetben, ill. félig elıregyártott vb.
5. FÖDÉMEK TERVEZÉSE 5.1. GERENDÁS FÖDÉMEK KIALAKÍTÁSA, TERVEZÉSI ELVEI Az alábbiakban az Épületszerkezettan 2. c. tárgy tanmenetének megfelelıen a teljes keresztmetszetben, ill. félig elıregyártott vb.
Komplex számok. 2014. szeptember 4. 1. Feladat: Legyen z 1 = 2 3i és z 2 = 4i 1. Határozza meg az alábbi kifejezés értékét!
 Komplex számok 014. szeptember 4. 1. Feladat: Legyen z 1 i és z 4i 1. (z 1 z ) (z 1 z ) (( i) (4i 1)) (6 9i 8i + ) 8 17i 8 + 17i. Feladat: Legyen z 1 i és z 4i 1. Határozza meg az alábbi kifejezés értékét!
Komplex számok 014. szeptember 4. 1. Feladat: Legyen z 1 i és z 4i 1. (z 1 z ) (z 1 z ) (( i) (4i 1)) (6 9i 8i + ) 8 17i 8 + 17i. Feladat: Legyen z 1 i és z 4i 1. Határozza meg az alábbi kifejezés értékét!
EGÉSZTESTSZÁMLÁLÁS. Mérésleírás Nukleáris környezetvédelem gyakorlat környezetmérnök hallgatók számára
 EGÉSZTESTSZÁMLÁLÁS Mérésleírás Nukleáris környezetvédelem gyakorlat környezetmérnök hallgatók számára Zagyvai Péter - Osváth Szabolcs Bódizs Dénes BME NTI, 2008 1. Bevezetés Az izotópok stabilak vagy radioaktívak
EGÉSZTESTSZÁMLÁLÁS Mérésleírás Nukleáris környezetvédelem gyakorlat környezetmérnök hallgatók számára Zagyvai Péter - Osváth Szabolcs Bódizs Dénes BME NTI, 2008 1. Bevezetés Az izotópok stabilak vagy radioaktívak
A felgombolyodás problémája
 1. A probléma 2. A fehérjék stabil konformációs állapotai 3. A felgombolyodás általános tulajdonságai 4. A felgombolyodás modelljei 5. A felgombolyodás nyomon követésének technikái 6. A felgombolyodás
1. A probléma 2. A fehérjék stabil konformációs állapotai 3. A felgombolyodás általános tulajdonságai 4. A felgombolyodás modelljei 5. A felgombolyodás nyomon követésének technikái 6. A felgombolyodás
Bemenet modellezése II.
 Bemenet modellezése II. Vidács Attila 2005. november 3. Hálózati szimulációs technikák, 2005/11/3 1 Kiszolgálási id k modellezése Feladat: Egy bemeneti modell felállítása egy egy kiszolgálós sorbanállási
Bemenet modellezése II. Vidács Attila 2005. november 3. Hálózati szimulációs technikák, 2005/11/3 1 Kiszolgálási id k modellezése Feladat: Egy bemeneti modell felállítása egy egy kiszolgálós sorbanállási
4. előadás. Vektorok
 4. előadás Vektorok Vektorok bevezetése Ha adottak a térben az A és a B pontok, akkor pontosan egy olyan eltolás létezik, amely A-t B- be viszi. Ha φ egy tetszőleges eltolás, akkor ez a tér minden P pontjához
4. előadás Vektorok Vektorok bevezetése Ha adottak a térben az A és a B pontok, akkor pontosan egy olyan eltolás létezik, amely A-t B- be viszi. Ha φ egy tetszőleges eltolás, akkor ez a tér minden P pontjához
1) CO 2 hidrolízise a) semleges és b) bázikus körülmények között.
 A 20072011 években az OTKA támogatásával a következő témák indultak el: (A jelen felsorolás eltér attól a csoportosítástól, amit a pályázat megírásakor alkalmaztam, mivel a témák jobban áttekinthetők így.
A 20072011 években az OTKA támogatásával a következő témák indultak el: (A jelen felsorolás eltér attól a csoportosítástól, amit a pályázat megírásakor alkalmaztam, mivel a témák jobban áttekinthetők így.
Differenciaegyenletek
 Differenciaegyenletek Losonczi László Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar Losonczi László (DE) Differenciaegyenletek 1 / 24 3.1 Differenciaegyenlet fogalma, egzisztencia- és unicitástétel
Differenciaegyenletek Losonczi László Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar Losonczi László (DE) Differenciaegyenletek 1 / 24 3.1 Differenciaegyenlet fogalma, egzisztencia- és unicitástétel
Ph 11 1. 2. Mozgás mágneses térben
 Bajor fizika érettségi feladatok (Tervezet G8 2011-től) Munkaidő: 180 perc (A vizsgázónak két, a szakbizottság által kiválasztott feladatsort kell kidolgoznia. A két feladatsor nem származhat azonos témakörből.)
Bajor fizika érettségi feladatok (Tervezet G8 2011-től) Munkaidő: 180 perc (A vizsgázónak két, a szakbizottság által kiválasztott feladatsort kell kidolgoznia. A két feladatsor nem származhat azonos témakörből.)
ozmózis osmosis Egy rendszer termodinamikailag stabilis, ha képződése szabadentalpia csökkenéssel jár, állandó nyomáson és hőmérsékleten.
 ozmózis osmosis termodinamikai stabilitás thermodynamic stability kinetikai stabilitás kinetic stability felületaktív anyagok surfactants, surface active materials felületinaktív anyagok surface inactive
ozmózis osmosis termodinamikai stabilitás thermodynamic stability kinetikai stabilitás kinetic stability felületaktív anyagok surfactants, surface active materials felületinaktív anyagok surface inactive
Hátterükben egyetlen gén áll, melynek általában számottevő a viselkedésre gyakorolt hatása, öröklési mintázata jellegzetes.
 2 Egygénes, mendeli öröklődésű betegségek Mendel borsóval végzett keresztezési kísérletei alapján 1866-ben tette közzé az öröklődés alapvető törvényszerűségeinek összefoglalását: Kísérletek növényhibridekkel,
2 Egygénes, mendeli öröklődésű betegségek Mendel borsóval végzett keresztezési kísérletei alapján 1866-ben tette közzé az öröklődés alapvető törvényszerűségeinek összefoglalását: Kísérletek növényhibridekkel,
MATEMATIKA. Tildy Zoltán Általános Iskola és Alapfokú Művészeti Iskola Helyi tanterv 1-4. évfolyam 2013.
 MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról, mint tudásrendszerről, és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
MATEMATIKA Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról, mint tudásrendszerről, és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről. A matematika
5. ALAKOS FELÜLETEK HATÁROZOTT ÉLŰ SZERSZÁMMAL TÖRTÉNŐ FORGÁCSOLÁSA
 5. ALAKOS FELÜLETEK HATÁROZOTT ÉLŰ SZERSZÁMMAL TÖRTÉNŐ FORGÁCSOLÁSA A gépelemeken és szerszámokon forgácsolással megmunkálásra kerülő alakos felületek biztosítják: a gépek munkavégzéséhez szükséges teljesítmény
5. ALAKOS FELÜLETEK HATÁROZOTT ÉLŰ SZERSZÁMMAL TÖRTÉNŐ FORGÁCSOLÁSA A gépelemeken és szerszámokon forgácsolással megmunkálásra kerülő alakos felületek biztosítják: a gépek munkavégzéséhez szükséges teljesítmény
Segédlet Egyfokozatú fogaskerék-áthajtómű méretezéséhez
 Pécsi Tudományegyetem Pollack Mihály Műszaki Kar Gépszerkezettan tanszék Segédlet Egyfokozatú fogaskerék-áthajtómű méretezéséhez Összeállította: Dr. Stampfer Mihály Pécs, 0. . A fogaskerekek előtervezése.
Pécsi Tudományegyetem Pollack Mihály Műszaki Kar Gépszerkezettan tanszék Segédlet Egyfokozatú fogaskerék-áthajtómű méretezéséhez Összeállította: Dr. Stampfer Mihály Pécs, 0. . A fogaskerekek előtervezése.
Mesterséges intelligencia, 7. előadás 2008. október 13. Készítette: Masa Tibor (KPM V.)
 Mesterséges intelligencia, 7. előadás 2008. október 13. Készítette: Masa Tibor (KPM V.) Bizonytalanságkezelés: Az eddig vizsgáltakhoz képest teljesen más világ. A korábbi problémák nagy része logikai,
Mesterséges intelligencia, 7. előadás 2008. október 13. Készítette: Masa Tibor (KPM V.) Bizonytalanságkezelés: Az eddig vizsgáltakhoz képest teljesen más világ. A korábbi problémák nagy része logikai,
A replikáció mechanizmusa
 Az öröklődés molekuláris alapjai A DNS megkettőződése, a replikáció Szerk.: Vizkievicz András A DNS-molekula az élőlények örökítő anyaga, kódolt formában tartalmazza mindazon információkat, amelyek a sejt,
Az öröklődés molekuláris alapjai A DNS megkettőződése, a replikáció Szerk.: Vizkievicz András A DNS-molekula az élőlények örökítő anyaga, kódolt formában tartalmazza mindazon információkat, amelyek a sejt,
A Shannon-féle entrópia mint molekula deszkriptor a szteroid vázas vegyületeknél
 Dr. Pósa Mihály A Shannon-féle entrópia mint molekula deszkriptor a szteroid vázas vegyületeknél 1. Bevezetés A Vajdasági Magyar Tudományos Társaság 2010. évi tanácskozásán Kiss Ernő professzor ismertette
Dr. Pósa Mihály A Shannon-féle entrópia mint molekula deszkriptor a szteroid vázas vegyületeknél 1. Bevezetés A Vajdasági Magyar Tudományos Társaság 2010. évi tanácskozásán Kiss Ernő professzor ismertette
1.1 Lemezanyagok tulajdonságai és alakíthatóságuk
 1 Lemezanyagok tulajdonságai és alakíthatóságuk 1.1 Lemezanyagok tulajdonságai és alakíthatóságuk A lemezalkatrész-gyártás anyagait részben a szakítóvizsgálatból részben szabványos technológiai próbákból
1 Lemezanyagok tulajdonságai és alakíthatóságuk 1.1 Lemezanyagok tulajdonságai és alakíthatóságuk A lemezalkatrész-gyártás anyagait részben a szakítóvizsgálatból részben szabványos technológiai próbákból
Biológiai makromolekulák szerkezete
 Biológiai makromolekulák szerkezete Biomolekuláris nemkovalens kölcsönhatások Elektrosztatikus kölcsönhatások (sóhidak: 4-6 kcal/m, dipól-dipól: ~10-1 kcal/m Diszperziós erők (~10-2 kcal/m) Hidrogén hidak
Biológiai makromolekulák szerkezete Biomolekuláris nemkovalens kölcsönhatások Elektrosztatikus kölcsönhatások (sóhidak: 4-6 kcal/m, dipól-dipól: ~10-1 kcal/m Diszperziós erők (~10-2 kcal/m) Hidrogén hidak
GAZDASÁGI STATISZTIKA
 GAZDASÁGI STATISZTIKA Dr. Kun István GÁBOR DÉNES FŐISKOLA Tantárgy: Gazdasági statisztika Kódszám: 224 Lapszám: 1 TÉMAKÖRÖK A STATISZTIKA ALAPFOGALMAI STATISZTIKAI SOROK STATISZTIKAI TÁBLÁK ÖSSZETETT VISZONYSZÁMOK
GAZDASÁGI STATISZTIKA Dr. Kun István GÁBOR DÉNES FŐISKOLA Tantárgy: Gazdasági statisztika Kódszám: 224 Lapszám: 1 TÉMAKÖRÖK A STATISZTIKA ALAPFOGALMAI STATISZTIKAI SOROK STATISZTIKAI TÁBLÁK ÖSSZETETT VISZONYSZÁMOK
PageRank algoritmus Hubs and Authorities. Adatbányászat. Webbányászat PageRank, Hubs and Authorities. Szegedi Tudományegyetem.
 Webbányászat PageRank, Szegedi Tudományegyetem Miért akarjuk rangsorolni a Weboldalakat? Mert tudásra szomjazunk Mert a Google-nak megéri. Pontosan hogy is? Mert állatorvost keresünk, pizzázni akarunk,
Webbányászat PageRank, Szegedi Tudományegyetem Miért akarjuk rangsorolni a Weboldalakat? Mert tudásra szomjazunk Mert a Google-nak megéri. Pontosan hogy is? Mert állatorvost keresünk, pizzázni akarunk,
A tanári mesterszak pedagógiai - pszichológiai egysége
 A tanári mesterszak pedagógiai - pszichológiai egysége (Tanári záróvizsga témakörök szakmódszertanból) 1. A tanár szerepe a hatékony kémiatanításban. Kémia szakkörök, fakultációs foglalkozások vezetésének
A tanári mesterszak pedagógiai - pszichológiai egysége (Tanári záróvizsga témakörök szakmódszertanból) 1. A tanár szerepe a hatékony kémiatanításban. Kémia szakkörök, fakultációs foglalkozások vezetésének
I. BEVEZETÉS------------------------------------------------------------------2
 TARTALOMJEGYZÉK I. BEVEZETÉS------------------------------------------------------------------2 II. EL ZMÉNYEK ---------------------------------------------------------------4 II. 1. A BENETTIN-STRELCYN
TARTALOMJEGYZÉK I. BEVEZETÉS------------------------------------------------------------------2 II. EL ZMÉNYEK ---------------------------------------------------------------4 II. 1. A BENETTIN-STRELCYN
Villamos tulajdonságok
 Villamos tulajdonságok A vezetés s magyarázata Elektron függıleges falú potenciálgödörben: állóhullámok alap és gerjesztett állapotok Több elektron: Pauli-elv Sok elektron: Energia sávok Sávelméletlet
Villamos tulajdonságok A vezetés s magyarázata Elektron függıleges falú potenciálgödörben: állóhullámok alap és gerjesztett állapotok Több elektron: Pauli-elv Sok elektron: Energia sávok Sávelméletlet
Számítógépi képelemzés
 Számítógépi képelemzés Elıadás vázlat Szerzık: Dr. Gácsi Zoltán, egyetemi tanár Dr. Barkóczy Péter, egyetemi docens Lektor: Igaz Antal, okl. gépészmérnök a Carl Zeiss technika kft. Ügyvezetı igazgatója
Számítógépi képelemzés Elıadás vázlat Szerzık: Dr. Gácsi Zoltán, egyetemi tanár Dr. Barkóczy Péter, egyetemi docens Lektor: Igaz Antal, okl. gépészmérnök a Carl Zeiss technika kft. Ügyvezetı igazgatója
Energetikai minőségtanúsítvány összesítő
 Energetikai minőségtanúsítvány 1 Energetikai minőségtanúsítvány összesítő Épület Megrendelő Szociális Szolg. Közp. 16db apartmanja Kál Nagyközség Önkormányzata 335 Kál, Szent István tér 2. Tanúsító Vereb
Energetikai minőségtanúsítvány 1 Energetikai minőségtanúsítvány összesítő Épület Megrendelő Szociális Szolg. Közp. 16db apartmanja Kál Nagyközség Önkormányzata 335 Kál, Szent István tér 2. Tanúsító Vereb
,:/ " \ OH OH OH - 6 - / \ O / H / H HO-CH, O, CH CH - OH ,\ / "CH - ~(H CH,-OH \OH. ,-\ ce/luló z 5zer.~ezere
 - 6 - o / \ \ o / \ / \ () /,-\ ce/luló z 5zer.~ezere " C=,1 -- J - 1 - - ---,:/ " - -,,\ / " - ~( / \ J,-\ ribóz: a) r.yílt 12"('.1, b) gyürus íormája ~.. ~ en;én'. fu5 héli'(ef1e~: egy menete - 7-5.
- 6 - o / \ \ o / \ / \ () /,-\ ce/luló z 5zer.~ezere " C=,1 -- J - 1 - - ---,:/ " - -,,\ / " - ~( / \ J,-\ ribóz: a) r.yílt 12"('.1, b) gyürus íormája ~.. ~ en;én'. fu5 héli'(ef1e~: egy menete - 7-5.
VÉGTELENÜL RENDEZETLEN KRITIKUS VISELKEDÉS Iglói Ferenc, Kovács István MTA Wigner Fizikai Kutatóközpont
 VÉGTELENÜL RENDEZETLEN KRITIKUS VISELKEDÉS Iglói Ferenc, Kovács István MTA Wigner Fizikai Kutatóközpont Elôzmények A fázisátalakulások és kritikus jelenségek a mindennapi életben is gyakran elôforduló
VÉGTELENÜL RENDEZETLEN KRITIKUS VISELKEDÉS Iglói Ferenc, Kovács István MTA Wigner Fizikai Kutatóközpont Elôzmények A fázisátalakulások és kritikus jelenségek a mindennapi életben is gyakran elôforduló
Pontszerű test, pontrendszer és merev test egyensúlya és mozgása (Vázlat)
 Pontszerű test, pontrendszer és merev test egyensúlya és mozgása (Vázlat) I. Pontszerű test 1. Pontszerű test modellje. Pontszerű test egyensúlya 3. Pontszerű test mozgása a) Egyenes vonalú egyenletes
Pontszerű test, pontrendszer és merev test egyensúlya és mozgása (Vázlat) I. Pontszerű test 1. Pontszerű test modellje. Pontszerű test egyensúlya 3. Pontszerű test mozgása a) Egyenes vonalú egyenletes
Biofizika tesztkérdések
 Biofizika tesztkérdések Egyszerű választás E kérdéstípusban A, B,...-vel jelölt lehetőségek szerepelnek, melyek közül az egyetlen megfelelőt kell kiválasztani. A választ írja a kérdés előtt lévő kockába!
Biofizika tesztkérdések Egyszerű választás E kérdéstípusban A, B,...-vel jelölt lehetőségek szerepelnek, melyek közül az egyetlen megfelelőt kell kiválasztani. A választ írja a kérdés előtt lévő kockába!
Megújuló energiák hasznosítása a hő- és villamosenergia-termelésben (ellátásban)
 Megújuló energiák hasznosítása a hő- és villamosenergia-termelésben (ellátásban) Büki Gergely Orbán Tibor A MEGÚJULÓ ENERGIAFORRÁSOK FELHASZNÁLÁSÁNAK METEOROLÓGIAI VONATKOZÁSAI c. konferencia 41. Meteorológiai
Megújuló energiák hasznosítása a hő- és villamosenergia-termelésben (ellátásban) Büki Gergely Orbán Tibor A MEGÚJULÓ ENERGIAFORRÁSOK FELHASZNÁLÁSÁNAK METEOROLÓGIAI VONATKOZÁSAI c. konferencia 41. Meteorológiai
Ha vasalják a szinusz-görbét
 A dolgozat szerzőjének neve: Szabó Szilárd, Lorenzovici Zsombor Intézmény megnevezése: Bolyai Farkas Elméleti Líceum Témavezető tanár neve: Szász Ágota Beosztása: Fizika Ha vasalják a szinusz-görbét Tartalomjegyzék
A dolgozat szerzőjének neve: Szabó Szilárd, Lorenzovici Zsombor Intézmény megnevezése: Bolyai Farkas Elméleti Líceum Témavezető tanár neve: Szász Ágota Beosztása: Fizika Ha vasalják a szinusz-görbét Tartalomjegyzék
Nagy Sándor: Magkémia
 Nagy Sándor: Magkémia (kv1c1mg1) 07. Stabilitás & instabilitás, magmodellek, tömegparabolák Nagy Sándor honlapja ismeretterjesztő anyagokkal: http://nagysandor.eu/ A Magkémia tantárgy weboldala: http://nagysandor.eu/magkemia/
Nagy Sándor: Magkémia (kv1c1mg1) 07. Stabilitás & instabilitás, magmodellek, tömegparabolák Nagy Sándor honlapja ismeretterjesztő anyagokkal: http://nagysandor.eu/ A Magkémia tantárgy weboldala: http://nagysandor.eu/magkemia/
4. FELADATSOR (2015. 03. 02.)
 4 FELADATSOR (2015 03 02) 1 feladat Egy rendszer fundamentális egyenlete a következő:,,= a) Írd fel az egyenletet intenzív mennyiségekkel! b) Írd fel az egyenletet entrópiareperezentációban! c) Ellenőrizd,
4 FELADATSOR (2015 03 02) 1 feladat Egy rendszer fundamentális egyenlete a következő:,,= a) Írd fel az egyenletet intenzív mennyiségekkel! b) Írd fel az egyenletet entrópiareperezentációban! c) Ellenőrizd,
GÁZIONIZÁCIÓS DETEKTOROK VIZSGÁLATA. Mérési útmutató. Gyurkócza Csaba
 GÁZIONIZÁCIÓS DETEKTOROK VIZSGÁLATA Mérési útmutató Gyurkócza Csaba BME NTI 1997 2 Tartalom 1. BEVEZETÉS... 3 2. ELMÉLETI ÖSSZEFOGLALÁS... 3 2.1. Töltéshordozók keletkezése (ionizáció) töltött részecskéknél...
GÁZIONIZÁCIÓS DETEKTOROK VIZSGÁLATA Mérési útmutató Gyurkócza Csaba BME NTI 1997 2 Tartalom 1. BEVEZETÉS... 3 2. ELMÉLETI ÖSSZEFOGLALÁS... 3 2.1. Töltéshordozók keletkezése (ionizáció) töltött részecskéknél...
Energetikai minőségtanúsítvány összesítő
 Energetikai minőségtanúsítvány 1 Energetikai minőségtanúsítvány összesítő Épület: Megrendelő: Tanúsító: Kovács Pál és Társa. Kft. 06-1-388-9793 (munkaidőben) 06-20-565-8778 (munkaidőben) Az épület(rész)
Energetikai minőségtanúsítvány 1 Energetikai minőségtanúsítvány összesítő Épület: Megrendelő: Tanúsító: Kovács Pál és Társa. Kft. 06-1-388-9793 (munkaidőben) 06-20-565-8778 (munkaidőben) Az épület(rész)
Tűgörgős csapágy szöghiba érzékenységének vizsgálata I.
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Tudományos Diákköri Konferencia Tűgörgős csapágy szöghiba érzékenységének vizsgálata I. Szöghézag és a beépítésből adódó szöghiba vizsgálata
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Tudományos Diákköri Konferencia Tűgörgős csapágy szöghiba érzékenységének vizsgálata I. Szöghézag és a beépítésből adódó szöghiba vizsgálata
CAD-CAM-CAE Példatár
 CAD-CAM-CAE Példatár A példa megnevezése: A példa száma: A példa szintje: CAx rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: Síkbeli hajlított rúd ÓE-A02 alap közepes haladó VEM Épületszerkezet
CAD-CAM-CAE Példatár A példa megnevezése: A példa száma: A példa szintje: CAx rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: Síkbeli hajlított rúd ÓE-A02 alap közepes haladó VEM Épületszerkezet
A kén tartalmú vegyületeket lúggal főzve szulfid ionok keletkeznek, amelyek az Pb(II) ionokkal a korábban tanultak szerint fekete csapadékot adnak.
 Egy homokot tartalmazó tál tetejére teszünk a pépből egy kanállal majd meggyújtjuk az alkoholt. Az alkohol égésekor keletkező hőtől mind a cukor, mind a szódabikarbóna bomlani kezd. Az előbbiből szén az
Egy homokot tartalmazó tál tetejére teszünk a pépből egy kanállal majd meggyújtjuk az alkoholt. Az alkohol égésekor keletkező hőtől mind a cukor, mind a szódabikarbóna bomlani kezd. Az előbbiből szén az
mágnes mágnesesség irányt Föld északi déli pólus mágneses megosztás influencia mágneses töltés
 MÁGNESESSÉG A mágneses sajátságok, az elektromossághoz hasonlóan, régóta megfigyelt tapasztalatok voltak, a két jelenségkör szoros kapcsolatának felismerése azonban csak mintegy két évszázaddal ezelőtt
MÁGNESESSÉG A mágneses sajátságok, az elektromossághoz hasonlóan, régóta megfigyelt tapasztalatok voltak, a két jelenségkör szoros kapcsolatának felismerése azonban csak mintegy két évszázaddal ezelőtt
SZAKÉRTİI JELENTÉS PITTNER DÉNES ÁLTALÁNOS ISKOLA ÉS ALAPFOKÚ MŐVÉSZETOKTATÁSI INTÉZMÉNY
 SZAKÉRTİI JELENTÉS PITTNER DÉNES ÁLTALÁNOS ISKOLA ÉS ALAPFOKÚ MŐVÉSZETOKTATÁSI INTÉZMÉNY általános iskola intézményegységének törvényességi és szakmai vizsgálatáról Szakértık: Tamás Emília SZ021082 Koháry
SZAKÉRTİI JELENTÉS PITTNER DÉNES ÁLTALÁNOS ISKOLA ÉS ALAPFOKÚ MŐVÉSZETOKTATÁSI INTÉZMÉNY általános iskola intézményegységének törvényességi és szakmai vizsgálatáról Szakértık: Tamás Emília SZ021082 Koháry
Lineáris programozás. Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer
 Lineáris programozás Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer Feladat: Egy gyár kétféle terméket gyárt (A, B): /db Eladási ár 1000 800 Technológiai önköltség 400 300 Normaóraigény
Lineáris programozás Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer Feladat: Egy gyár kétféle terméket gyárt (A, B): /db Eladási ár 1000 800 Technológiai önköltség 400 300 Normaóraigény
1. Kivonat 3. 2. Bevezetés 5. 3. Káoszelmélet [1, 2] 6
![1. Kivonat 3. 2. Bevezetés 5. 3. Káoszelmélet [1, 2] 6 1. Kivonat 3. 2. Bevezetés 5. 3. Káoszelmélet [1, 2] 6](/thumbs/32/15560610.jpg) 1 Contents 1. Kivonat 3 2. Bevezetés 5 3. Káoszelmélet [1, 2] 6 4. A Bloch-egyenlet iteratív megoldása 10 4.1. Az iterációs séma 10 4.2. Ljapunov-exponens számítás 12 4.3. Példák 14 4.3.1. A számítás kiindulási
1 Contents 1. Kivonat 3 2. Bevezetés 5 3. Káoszelmélet [1, 2] 6 4. A Bloch-egyenlet iteratív megoldása 10 4.1. Az iterációs séma 10 4.2. Ljapunov-exponens számítás 12 4.3. Példák 14 4.3.1. A számítás kiindulási
Dr. Hangayné Paksi Éva, Nagyné Vas Györgyi: Sorsfordító Programba vontak jellemzıi 2009. -2-.
 Dr Hangayné Paksi Éva, Nagyné Vas Györgyi: Sorsfordító Programba vontak jellemzıi -- SORSFORDÍTÓ regionális munkaerı-piaci programba vontak pszicho-szociális gondozását elıkészítı felmérés értékelése Tolna
Dr Hangayné Paksi Éva, Nagyné Vas Györgyi: Sorsfordító Programba vontak jellemzıi -- SORSFORDÍTÓ regionális munkaerı-piaci programba vontak pszicho-szociális gondozását elıkészítı felmérés értékelése Tolna
A Michelson-Morley kísérlet gyökeres átértékelése
 A Michelson-Morley kísérlet gyökeres átértékelése Az [1]-ben több évnyi irányvesztett bolyongás után végre sikerült rálelni a Dobó-féle dimenziótlan k D (vagy a vele lényegileg egyenértékő, modellünkben
A Michelson-Morley kísérlet gyökeres átértékelése Az [1]-ben több évnyi irányvesztett bolyongás után végre sikerült rálelni a Dobó-féle dimenziótlan k D (vagy a vele lényegileg egyenértékő, modellünkben
Matematikai és matematikai statisztikai alapismeretek
 Kézirat a Matematikai és matematikai statisztikai alapismeretek című előadáshoz Dr. Győri István NEVELÉSTUDOMÁNYI PH.D. PROGRM 1999/2000 1 1. MTEMTIKI LPOGLMK 1.1. Halmazok Halmazon mindig bizonyos dolgok
Kézirat a Matematikai és matematikai statisztikai alapismeretek című előadáshoz Dr. Győri István NEVELÉSTUDOMÁNYI PH.D. PROGRM 1999/2000 1 1. MTEMTIKI LPOGLMK 1.1. Halmazok Halmazon mindig bizonyos dolgok
