I. évfolyam, 1. szám március
|
|
|
- József Tamás
- 8 évvel ezelőtt
- Látták:
Átírás
1 I. évfolya, 1. szá árcius Restás Ágosto MÓDSZERTANI TANULMÁNYOK OLTÓHABOK HATÉKONYSÁGÁNAK VIZSGÁLATÁHOZ: AZ OLTÁSI KÉPESSÉG MEGHATÁROZÁSA A FELÜLETEN MARADÁS ARÁNYÁNAK VIZSGÁLATÁVAL Absztrakt Bevezetés: Az erdőtüzekél alkalazott oltóayagok oltóképessége több téyező együttes hatásakét jeleik eg. Ezek közé tartozik a hűtőhatás és a szigetelő hatás, it fő oltóhatások, valait ezek al-oltóhatásai is, it például a párolgási, a takaró vagy az elválasztó hatások. Logikus, hogy iél agyobb eyiség arad a felszíe, aál agyobb az oltási képesség. Módszer: A tesztelésre a habok eseté, a piaco forgalazott terékek közül rado került egy kiválasztásra, íg a felülete aradáshoz a köye égő feyőgally lett eghatározva. A cél az volt, hogy egállapításra kerüljö a övéyzete aradó oltóayag eyisége. A kiválasztott levélzetből azoos töegű csoportok kerültek kialakításra. Elsőkét a kezeletle levélzet töege, ajd a vízbe és habképző ayagokba ártott csoportok töege került egállapításra. Eredéyek: A vizsgálati eredéyek azt utatják, hogy a hab jeletőse agyobb töegbe 1
2 aradt eg a levélzete, it a víz; eek értéke a vizsgálatok alapjá 3,36 3,76 szoros a vízhez viszoyítva. A vizsgálatok azt is egutatták, hogy ez az érték a habkiadósság értékétől e függ szigifikása. Kulcsszavak: hab, habkiadósság, oltási képesség, hab töeg hatékoyság METHODOLOGICAL STUDIES FOR MEASURING FOAM EFFECTIVENESS: SUPPRESSION CAPABILITY WITH THE TEST OF WEIGHT RATE REMAINED ON THE CROWN SURFACE Abstract Itroductio: The effectiveess of the foas used i fightig agaist forest fire depeds o coo effect of soe coefficiets. Coolig ad isolatio effects as ai extiguishig effects as well as side extiguishig effects, like evaporatio, blaket ad separatio effects are also icluded. The ore extiguisher reais o the surface, the ore extiguishig effect it has. Methods: A product for the test was radoly chose out of the oes o the arket. Spruce was chose for the test due to its high flaability. The goal was to deterie the aout of extiguisher at the ed of the braches i the foliage. Groups of the sae size were created i the selected foliage. To start with, the weight of the utreated foliage was easured, followed by the groups of foliage dipped i water ad foaig agets. Results ad discussio: Accordig to the fidigs of research, the aout of foa reaiig o the foliage is rearkably higher tha that of water. Its rate is copared to water. The research also revealed that this rate does ot sigificatly deped o expasio rate. Keywords: foa, expasio rate, suppressio capability, foa weight effectiveess 2
3 1. BEVEZETÉS Az erdőtüzekél alkalazott oltóayagok oltóképessége több téyező együttes hatásakét jeleik eg. Ezek közé tartozik a hűtőhatás és a szigetelő hatás, it fő oltóhatások, valait ezek aloltóhatásai is, it például a párolgási, a takaró vagy az elválasztó hatások. A szigetelő hatás eredéyessége bizoyosa függ az alkalazott oltóayag egységyi felületé ért eyiségétől, ai e vízszites esetbe az oltóayag tapadásával, vagyis a felülete aradás aráyával korrelál. Azoos feltételek eseté iél több oltóayag arad eg a felülete, aál agyobb aak oltóhatása. Mivel az oltóayagok eyisége jeletőse befolyásolja id az alkalazott tűzoltás taktikát, id az alkalazott taktika hatékoyságát (Bleszity, 1990), ezért e csak azok fotossága iatt, de id a beavatkozók biztoságára (Pátya, 2011), id a hatékoyságra gyakorolt hatása iatt előyös a külöböző téyezőket áttekitei. Az oltóayagok hatékoyságával jeleleg is száos kutatás foglalkozik (Batista, 2011; Morris, 2011), illetve külö érési ódszereket is alkottak 1 2, azoba a lobozat felületé egaradó oltóayagra voatkozó célzott kutatások ég a szerző véleéye alapjá valószíűleg hiáyosak. A cikk ehhez próbál egy sajátságos egközelítést adi, ai a víz és hab, it külöböző struktúrájú oltóayagok felülete aradásáak összehasolításával foglalkozik. A kutatás sorá célkitűzéskét fogalazódott eg, hogy az oltóayagok külöböző értékű felülete aradásáak bizoyítására és az ebből levoható következtetések beutatására egy egyszerű, köye reprodukálható, az oktatást és szeléltetést is biztosító ódszer kerüljö kidolgozásra. Ehhez a szerző a felülete egaradó oltóayag töegéek vizsgálatát választotta. A tesztelésre a piaco forgalazott terékek közül rado került egy kiválasztásra. Ez utóbbi 1 Aerica Society for Testig ad Materials. Stadard Test Method for Deteriig Material Igitio ad Flae Spread properties; E (02) 2 Uderwriters Laboratories Ic. Project Reports to USDA Forest Service; 98NK32277, 99NK35219, 01NK12843, 03NK13445, 04NK16188, ad 06CA
4 azért elfogadható, ert a vizsgálat célja e a kiválasztott oltóayag eredéyességéek egállapítására, hae a ódszer alkalazhatóságáak beutatására iráyult. 2. A VIZSGÁLATI MÓDSZER LEÍRÁSA 2.1 A vizsgálatok előkészítése A vizsgálathoz a agas tűzveszélyességgel bíró lucfeyő került kiválasztásra, eek ágvégeire, a levélzetre rakódó oltóayag eyiségéek eghatározása volt a cél. A kiválasztott levélzetből azoos töegű csoportok kerültek kialakításra. Elsőkét a kezeletle levélzet töege, ajd a vízbe és habképző ayagokba ártott csoportok töege került egállapításra. Az utóbbi csoportokál kapott értékekből kivoásra került a yers levélzet töegéek az értékei, aely így egadta az oltóayagok levélzete aradásáak axiális értékét. A habok eseté habkiadósságú habok kerültek alkalazásra. H Túl agas habkiadósság A hab e gördül lejjebb, a fa tetejé arad Magas habkiadósság A hab rosszul gördül, Ideális habkiadósság egyeetle eloszlású A hab eloszlása a lobozat sűrűségéhez igazodik Túl alacsoy habkiadósság A hab lefolyik a fa alá R (; V; %) kg 3-1. sz. ábra. A hab eloszlása külöböző H K habkiadósság eseté a fa agasságáak függvéyébe. Jelleggörbe. Forrás: szerző A vizsgálatokhoz az alábbi előkészítési fázisok szükségesek: 4
5 1. Mitadarabok kiválasztása: Mitadarabkét a agyo tűzveszélyes lucfeyő lett eghatározva. Eek es gallyvégei kerültek leválasztásra (4x10db=40db). Ezáltal a feyő azo része lett vizsgálva, aely id a tűz továbbterjedésébe, id az oltóayag felfogásába a legagyobb szerepet játszik. 2. Mitadarabok előkészítése: a gallyvégeket a leválasztás utá 30 C-o, 4 órá keresztül apo szárítjuk (szikkasztás). Ezáltal a felület teljese szárazzá válik, hasolóa az itezív tüzek időszakára jellező körüléyekhez. 3. Mitatartó átrix elkészítése: a érési sorozatak egfelelőe átrix került kialakításra, aelyre a itadarabok kerültek. Ez agába foglalta a víz, valait a habkiadósságú habok éréséhez az egyedi helyeket (bokszokat), összese 4x10db ita hellyel. 4. Vizsgáladó oltóayagok előkészítése: a vizsgálathoz orál csapvíz, valait habképző ayag került beszerzése. A habképző ayag a korábba általáosa haszált Light Water volt. 5. Az oltóayagok elkészítése. A víz C, orál köryezeti hőérsékletű, 15 k 0 (éet keéységi fok) vízkeéységű volt. Mérőflakookba haboldat készítése: a habképző ayag a Light water, aelyből 3%-os bekeveréssel készültek a külöböző habkiadósságú habok. Ezek: 3 külö flakoba - Hk = 6; Hk = 9; Hk = 12). 2. sz ábra. A itadarabok szikkasztása és a kezeletle iták. Forrás: szerző 5
6 2.2 A érések végrehajtása és a kapott értékek A érések sorá azoal látható, hogy a hab és a víz a levélzet felületé teljese eltérő forába arad eg (Figure 2). A víz e egyeletese, hae cseppek forájába, elkülöülte tapad a felülethez, íg a hab hoogéek látszó burokkal veszi körül a gallyacskát. A látható külöbség elleére azt égse tudjuk, hogy az oltóayag strukturális külöbsége jelet-e szigifikás eltérést az oltóayag felülete aradásáak voatkozásába. Ha ige, akkor az az oltóayag, aely agyobb töegbe arad a felülete, az a töeggel aráyosa agyobb hőelvoó képességet is jelet. 3. sz ábra. A habbal és vízzel kezelt feyőgally közötti látható külöbség. Forrás: szerző Az elvégzett érések eredéyeit és az adatokból száított értékeket az 1. száú táblázat tartalazza. 1. sz. Táblázat A érés jellezése Mért töeg (gra) Kezeletle iták ért (bruttó) töege (=10) 37,74 35,52 36,59 34,86 Mérőedéy töege 1,26 1,26 1,26 1,26 Kezeletle iták ettó töege (átlag34,17) 33,48 34,26 35,33 33,60 1. Mitacsoport 6
7 Maxiális edves töeg (bruttó) 51, Mérőedéy töege 1, Maxiális edves töeg (ettó) 50, Maxiális H2O töeg 17, A ita aráya a ax. H2O töeghez Mitacsoport HK=6 habos töeg (bruttó) - 99, Mérőedéy töege - 1, Maxiális HK=6 habos töeg (ettó) - 98, HK=6 Hab töege - 64, A ita aráya a ax. H2O töeghez - 3, Mitacsoport HK=9 habos töeg (bruttó) ,10 - Mérőedéy töege - - 1,26 - Maxiális HK=9 habos töeg (ettó) ,84 - HK=9 hab töeg ,51 - A ita aráya a ax. H2O töeghez - - 3,49-4. Mitacsoport HK=12 habos töeg (bruttó) ,07 Mérőedéy töege ,26 Maxiális HK=12 habos töeg (ettó) ,81 HK=12 Hab töeg ,21 A ita aráya a ax. H2O töeghez ,36 Jelagyarázat: H2O - csapvíz, egyéb kezelés élkül, t=20c 0 (köryezeti hőérséklet 24 C 0 ); Hab - a éréshez Light Water került felhaszálásra; 3 %-os bekeveréssel; HK - habkiadósság, aely kifejezi, hogy egységyi térfogatú oldatból háyszoros habtérfogat keletkezik (HK= ). 2.3 A száításokál alkalazott rövidítések A száításokhoz az alábbi jelölések és rövidítések kerültek alkalazásra: - P _ Nature = egyedi feyőgallyvég (ita) töege, kezeletle; 7
8 - - - P _ Nature P _ H 2 O P _ H 2O = a kezeletle iták átlagos töege; = vízzel kezelt egyedi iták töege; = a vízzel kezelt iták átlagos töege; - P _ = H K habkiadósságú habbal kezelt egyedi iták töege; Foa _ K k - P Foa _ Kk _ = a H K habkiadósságú habbal kezelt iták átlagos töege; - H 2 O = a itáko axiálisa egaradó víz átlagos töege; - Foa _ H K =a itáko axiálisa egaradó H K habkiadósságú hab átlagos töege; - - R E ku = a itáko ért H K habkiadósságú hab és a axiálisa egaradó víz töege; = összegzett hatékoyság = egységyi felülete axiálisa egaradó víz töege (kostas) = 5 kg; - 2 ax H2 O _ - 2 ax FoaH K _ =egységyi felülete egaradó H K habkiadósságú hab axiális száított töege. 2.4 A száításokhoz alkalazott ateatikai forulák A ért eredéyek értékeléséhez, a száítások elvégzéséhez az alábbi képletek és eghatározások lettek felhaszálva. - A kezeletle feyőita átlagos töegéek eghatározása. P P _ Nature _ i 1 _ Nature (1) - A vízbe ártott feyőita átlagos töegéek eghatározása. P _ H P _ H O _ i O (2) - A H K habkiadósságú habbal kezelt feyőita átlagos töegéek eghatározása. P _ FoaH K _ i P _ Foa _ H 1 K (3) 8
9 - A feyőitá lévő víz átlagos töegéek eghatározása. H O P _ H O 2 2 P _ Nature (4) - A feyőitá lévő H K habkiadósságú hab átlagos töegéek eghatározása. Foa _ H K P _ Foa _ H K P _ Nature (5) - A feyőitáko átlagosa ért H K habkiadósságú hab és víz töegéek aráya. Foa _ H K R (6) H 2O - Az x vastag, y habkiadósságú hab víztartala, vízoszlop agassággal kifejezve. E R (7) ku Y HK 3. SZÁMÍTÁSOK Az eredéyek értékeléséhez a szerző a következő száításokat végezte el. Elsőkét eghatározta a itacsoportok egyedi itáiak átlagos töegét, aelyből átlagolás útjá száította ki az egyedi darabok töegét. Második lépéskét egy itaegység egyedeit a vízbe ártva eghatározásra került a vízzel telíthetőség axiális értéke. Ezáltal a töegkülöbségeket véve eghatározható a itaegyedek axiális vízegtartó képessége. Haradik lépéskét a külöböző Hk habkiadósságú habok felülete egaradása került vizsgálat tárgyává. Az egyedeket habba beleártva, valaeyi egyszerre leérésre kerül, ajd átlagszáítással egkapható a itaegyedekre voatkozó adatok. Valaeyi ért értékből a kezeletle iták saját töegeit kivova adja az oltóayag felülete való egaradásáak axiális értékét. Ezutá ezekek az adatokak és a vízzel kezelt ita adataiak egyszerű összevetésével egkapható az adott habra voatkozó érték. A száítások a következőket eredéyezték: A itacsoportok egyedi itáiak átlagos töege P _ Nature _ i1 33,48g P _ Nature 3, 348g 10 9
10 P _ Nature _ i1 34,26g P _ Nature 3, 426g 10 P _ Nature _ i1 35,33g P _ Nature 3, 533g 10 P _ Nature _ i1 33,60g P _ Nature 3, 360g 10 A itacsoportok átlagos itáiak átlaga 4 P _ Nature _ i1 3,348g 3,426g 3,533g 3,360g P _ Nature 3, 417g 4 A vízbe ártott feyőita átlagos töegéek eghatározása P _ H 2O _ i1 50,52g P _ H O 5, 052g 2 10 A HK habkiadósságú habbal kezelt feyőita átlagos töegéek eghatározása P _ Foa _ H P _ FoaH K _ i1 98,33g 9, 833g K 6 10 P _ Foa _ H P _ FoaH K _ i1 94,84g 9, 484g K
11 P _ Foa _ H P _ FoaH K _ i1 90,81g 9, 081g K A feyőitá lévő víz átlagos töegéek eghatározása. H O P H O P _ Nature 5,052g 3,348g 1, 704g _ 2 2 A feyőitá lévő HK habkiadósságú hab átlagos töegéek eghatározása. Foa _ H K 6 P _ Foa _ H K P _ Nature 9,833g 3,426g 6,407 Foa _ H K 9 P _ Foa _ H K P _ Nature 9,484g 3,533g 5,951 Foa _ H K 12 P _ Foa _ H K P _ Nature 9,081g 3,360g 5,721 A feyőitáko átlagosa ért HK habkiadósságú hab és víz töegéek aráya. R Foa _ H K 6 H 2O 6,407g 1,704g 3,76 R Foa _ H K 9 H 2O 5,951g 1,704g 3,49 R Foa _ H K 12 H 2O 5,721g 1,704g 3,36 11
12 4. AZ EREDMÉNYEK ÉRTÉKELÉSE A vizsgálati eredéyek azt utatják, hogy a hab jeletőse agyobb töegbe aradt eg a levélzete, it a víz; eek értéke a vizsgálatok alapjá 3,36 3,76 szoros a vízhez viszoyítva. A vizsgálatok azt is egutatták, hogy ez az érték a habkiadósság értékétől e függ szigifikása (kb. 10 %). A hab töegéek aráya a axiális vízegtartó képességhez viszoyítva Aráy (-) 4 3,5 3 2,5 2 1,5 1 0, ,76 3,49 3,36 víz HK=6 HK=9 HK=12 Víz HK=6 habkiadósságú hab HK=9 habkiadósságú hab HK=12 habkiadósságú hab Oltóayag (-) 4. sz ábra. A hab felszíe aradó töegéek aráya a vízéhez viszoyítva. Forrás: szerző A övéyzet felülete kifejlett erdő eseté 4 5 kg -2 vizet képes egtartai, ai kb kw - 1 tűzitezitás egfékezéséig elegedő. Az eredéyekből az a következtetés voható le, hogy aeyibe olya agas a tűzitezitás, hogy a víz hőelvoó képessége ár e elegedő a tűz eloltásához, úgy hab alkalazásával az oltási lehetőségek kitolhatók olya dieziókba is, ahol a vízzel oltás objektíve e lehetséges. Eek oka a fetiek alapjá az, hogy a hab alkalazásával a felülete egaradó töeg, így az oltóayag hőelvoó képessége is legalább eghároszorozható, így az eloltható tűzitezitás agysága is kitolódik. A vizsgálatok eredéyekét eg kell jegyezi azt is, hogy a habok töeghatékoyságáak övekedése ellett a habak hőszigetelő hatása is jeletkezik, ai további többlet oltóhatást 12
13 jelet. A töeghatékoysági téyező és a hőszigetelő hatás e összeadódik, hae összeszorzódik, ai a habok alkalazásáak további előyét biztosítja. A feti eredéyek azt utatják, hogy a habok töeghatékoysági téyezője agyo jeletős, ai az egységyi felületre jutó oltóayag eyiségéek övelési lehetőségét rejti agába. Ezzel a víz elégtele oltóhatását lehet egöveli, illetve az eddig a víz által lehetetle oltási dieziók is elérhetővé, elolthatóvá válak. Restás Ágosto PhD, PhD, habilitált egyetei doces, taszékvezető, Nezeti Közszolgálati Egyete, Katasztrófavédeli Itézet, Tűzvédeli és Metésiráyítási Taszék, H-1101, Budapest, Hugária krt, 9-11; Eail: Restas.Agosto@ui-ke.hu; Orcid: Ágosto Restás PhD, PhD, associate professor, head, Departet of Fire Prevetio ad Rescue Cotrol, Istitute of Disaster Maageet, Natioal Uiversity of Public Service, H-1101, Budapest, Hugaria krt. 9-11; Eail: Restas.Agosto@ui-ke.hu; Orcid: A kézirat beyújtása: A kézirat elfogadása: Lektorálta: Pátya Péter REFERENCES Aerica Society for Testig ad Materials. Stadard Test Method for Deteriig Material Igitio ad Flae Spread properties; E (02). Batista, A.C.: Cobustio characteristics tests of Magolia gradiflora ad Michelia chapaca for potetial use i fuelbreaks i south regio of Brazil, Wildfire 2011 Coferece, Su City, South Africa, Bleszity, J., Zeleák, M.: Tűzvédeli iseretek, Budapest: Szövetkezeti Szervezési Iroda, 272 p
14 Morris C.J.: A siulatio study of fuel treatet effects i dry forests of the wester Uited States: testig the priciples of a fire-safe forest, Wildfire 2011 Coferece, Su City, South Africa, Pátya, P.: A tűzoltói beavatkozás biztoságáak övelése zárttéri tüzekél, HADMÉRNÖK 6: (1) pp dowloaded: Uderwriters Laboratories Ic. Project Reports to USDA Forest Service; 98NK32277, 99NK35219, 01NK12843, 03NK13445, 04NK16188, ad 06CA
I. évfolyam, 2. szám június
 I. évfolyam, 2. szám 2016. június Restás Ágoston MÓDSZERTANI TANULMÁNYOK OLTÓHABOK HATÉKONYSÁGÁNAK VIZSGÁLATÁHOZ: AZ OLTÁSI KÉPESSÉG MEGHATÁROZÁSA A SZIGETELŐ HATÁS VÍZEGYENÉRTÉKKEL TÖRTÉNŐ KIFEJEZÉSÉVEL
I. évfolyam, 2. szám 2016. június Restás Ágoston MÓDSZERTANI TANULMÁNYOK OLTÓHABOK HATÉKONYSÁGÁNAK VIZSGÁLATÁHOZ: AZ OLTÁSI KÉPESSÉG MEGHATÁROZÁSA A SZIGETELŐ HATÁS VÍZEGYENÉRTÉKKEL TÖRTÉNŐ KIFEJEZÉSÉVEL
Egyszerő kémiai számítások
 Egyszerő kéiai száítások z egyes fizikai, illetve kéiai eyiségek közötti összefüggéseket éréssel állapítjuk eg. hhoz, hogy egy eyiséget éri tudjuk, a eyiségek valaely rögzített értékét (értékegység) kell
Egyszerő kéiai száítások z egyes fizikai, illetve kéiai eyiségek közötti összefüggéseket éréssel állapítjuk eg. hhoz, hogy egy eyiséget éri tudjuk, a eyiségek valaely rögzített értékét (értékegység) kell
IFFK 2013 Budapest, 2013. augusztus 28-30. Stróbl András*, Péter Tamás**
 IFFK 03 Budapest 03. augusztus 8-30. Tartoáyi szitű stabilitásizsgálat alkalazásáak lehetőségei Győr árosába Stróbl Adrás* Péter Taás** Budapest Uiersity of Techology ad Ecooics Hugary (e-ail*:strobl.ad@gail.co
IFFK 03 Budapest 03. augusztus 8-30. Tartoáyi szitű stabilitásizsgálat alkalazásáak lehetőségei Győr árosába Stróbl Adrás* Péter Taás** Budapest Uiersity of Techology ad Ecooics Hugary (e-ail*:strobl.ad@gail.co
7. ELŐADÁS VÍZI SZÁLLÍTÁS A GLOBÁLIS LOGISZTIKÁBAN
 7. ELŐADÁS VÍZI SZÁLLÍTÁS A GLOBÁLIS LOGISZTIÁBAN A terészetes folyai, illetve tegeri utakat igéybe vevő, csak a kikötővel redelkező helyeket felkeresi tudó szállítási ód. A vízi áruszállítást elsősorba
7. ELŐADÁS VÍZI SZÁLLÍTÁS A GLOBÁLIS LOGISZTIÁBAN A terészetes folyai, illetve tegeri utakat igéybe vevő, csak a kikötővel redelkező helyeket felkeresi tudó szállítási ód. A vízi áruszállítást elsősorba
ezek alapján kívánunk dönteni. Ez formálisan azt jelenti, hogy ellenőrizni akarjuk,
 A deceber -i gyakorlat téája A hipotézisvizsgálat fotos probléája a következő két kérdés vizsgálata. a) Egy véletle eyiség várható értékéek agyságáról va bízoyos feltevésük. Elleőrizi akarjuk e feltevés
A deceber -i gyakorlat téája A hipotézisvizsgálat fotos probléája a következő két kérdés vizsgálata. a) Egy véletle eyiség várható értékéek agyságáról va bízoyos feltevésük. Elleőrizi akarjuk e feltevés
A szórások vizsgálata. Az F-próba. A döntés. Az F-próba szabadsági fokai
 05..04. szórások vizsgálata z F-próba Hogya foguk hozzá? Nullhipotézis: a két szórás azoos, az eltérés véletle (mitavétel). ullhipotézishez tartozik egy ú. F-eloszlás. Szabadsági fokok: számláló: - evező:
05..04. szórások vizsgálata z F-próba Hogya foguk hozzá? Nullhipotézis: a két szórás azoos, az eltérés véletle (mitavétel). ullhipotézishez tartozik egy ú. F-eloszlás. Szabadsági fokok: számláló: - evező:
Hűtés és fagyasztás 2014 108-001_Ost_HU.indd 1 108-001_Ost_HU.indd 1 16.12.13 12:41 16.12.13 12:41
 Hűtés és fagyasztás 0 0 alapos ok arra, hogy Liebherr teréket vásároljo 6 A tapasztalat, ai száít BioFresh bizoyíthatóa egészségesebb A Liebherr, it a hűtő- és fagyasztó készülékek szakértője, ár több
Hűtés és fagyasztás 0 0 alapos ok arra, hogy Liebherr teréket vásároljo 6 A tapasztalat, ai száít BioFresh bizoyíthatóa egészségesebb A Liebherr, it a hűtő- és fagyasztó készülékek szakértője, ár több
2.6. Az ideális gáz fundamentális egyenlete
 Fejezetek a fzka kéából.6. Az deáls gáz fudaetáls egyelete A legegyszerűbb terodaka redszer az u. deáls gáz. Erre jellező, hogy a részecskék között az egyetle kölcsöhatás a rugalas ütközés, és a részecskék
Fejezetek a fzka kéából.6. Az deáls gáz fudaetáls egyelete A legegyszerűbb terodaka redszer az u. deáls gáz. Erre jellező, hogy a részecskék között az egyetle kölcsöhatás a rugalas ütközés, és a részecskék
Volumetrikus elven működő gépek, hidraulikus hajtások (17. és 18. fejezet)
 oluetriku elve űködő gépek hidrauliku hajtáok (17 é 18 fejezet) 1 Függőlege tegelyű ukaheger dugattyúja 700 kg töegű terhet tart aelyet legfeljebb 6 / ebeéggel zabad üllyeztei A heger belő átérője 50 a
oluetriku elve űködő gépek hidrauliku hajtáok (17 é 18 fejezet) 1 Függőlege tegelyű ukaheger dugattyúja 700 kg töegű terhet tart aelyet legfeljebb 6 / ebeéggel zabad üllyeztei A heger belő átérője 50 a
2. LOGIKAI FÜGGVÉNYEK MEGADÁSI MÓDSZEREI. A tananyag célja: a többváltozós logikai függvények megadási módszereinek gyakorlása.
 . LOGIKI ÜGGVÉNYEK EGÁSI ÓSZEREI taayag célja: a többváltozós logikai függvéyek egadási ódszereiek gyakorlása. Eléleti iseretayag: r. jtoyi Istvá: igitális redszerek I.... pot. Eléleti áttekités.. i jellezi
. LOGIKI ÜGGVÉNYEK EGÁSI ÓSZEREI taayag célja: a többváltozós logikai függvéyek egadási ódszereiek gyakorlása. Eléleti iseretayag: r. jtoyi Istvá: igitális redszerek I.... pot. Eléleti áttekités.. i jellezi
4. Hegesztési utókezelések
 4. A fáradt törés az egyi legveszélyesebb töreeetel hegesztett szerezeteél. A hegesztés aradó feszültségeet és agas feszültség-ocetrációt eredéyez, elye jeletőse hozzájárula a fáradási szilárdság csöeéséhez.
4. A fáradt törés az egyi legveszélyesebb töreeetel hegesztett szerezeteél. A hegesztés aradó feszültségeet és agas feszültség-ocetrációt eredéyez, elye jeletőse hozzájárula a fáradási szilárdság csöeéséhez.
Cserjésné Sutyák Ágnes *, Szilágyiné Biró Andrea ** ismerete mellett több kísérleti és empirikus képletet fel-
 ACÉLOK KÉMIAI LITY OF STEELS THROUGH Cserjésé Sutyák Áges *, Szilágyié Biró Adrea ** beig s s 1. E kutatás célja, hogy képet meghatározásáak kísérleti és számítási móiek tosságáról, és ezzel felfedjük
ACÉLOK KÉMIAI LITY OF STEELS THROUGH Cserjésé Sutyák Áges *, Szilágyié Biró Adrea ** beig s s 1. E kutatás célja, hogy képet meghatározásáak kísérleti és számítási móiek tosságáról, és ezzel felfedjük
SPORTPÉNZÜGYEK. r m. A pénz időértéke.
 SPORTPÉNZÜGYEK A péz időétéke. A ai pézösszeg azét étékesebb, it egy későbbi időpotba esedékes pézösszeg, et a befektető eek évé jövedelee, kaata tehet szet Kaat: A péz áa Haszálója azét fizet, et a pézt
SPORTPÉNZÜGYEK A péz időétéke. A ai pézösszeg azét étékesebb, it egy későbbi időpotba esedékes pézösszeg, et a befektető eek évé jövedelee, kaata tehet szet Kaat: A péz áa Haszálója azét fizet, et a pézt
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 10. A statisztika alapjai Debrecei Egyetem, 2015 Dr. Bérczes Attila, Bertók Csaád A diasor tartalma 1 Bevezetés 2 Statisztikai függvéyek Defiíció, empirikus várható érték Empirikus
BIOMATEMATIKA ELŐADÁS 10. A statisztika alapjai Debrecei Egyetem, 2015 Dr. Bérczes Attila, Bertók Csaád A diasor tartalma 1 Bevezetés 2 Statisztikai függvéyek Defiíció, empirikus várható érték Empirikus
A biostatisztika alapfogalmai, konfidenciaintervallum. Dr. Boda Krisztina PhD SZTE ÁOK Orvosi Fizikai és Orvosi Informatikai Intézet
 A biostatisztika alapfogalmai, kofideciaitervallum Dr. Boda Krisztia PhD SZTE ÁOK Orvosi Fizikai és Orvosi Iformatikai Itézet Mitavétel ormális eloszlásból http://www.ruf.rice.edu/~lae/stat_sim/idex.html
A biostatisztika alapfogalmai, kofideciaitervallum Dr. Boda Krisztia PhD SZTE ÁOK Orvosi Fizikai és Orvosi Iformatikai Itézet Mitavétel ormális eloszlásból http://www.ruf.rice.edu/~lae/stat_sim/idex.html
A matematikai statisztika elemei
 A matematikai statisztika elemei Mikó Teréz, dr. Szalkai Istvá szalkai@almos.ui-pao.hu Pao Egyetem, Veszprém 2014. március 23. 2 Tartalomjegyzék Tartalomjegyzék 3 Bevezetés................................
A matematikai statisztika elemei Mikó Teréz, dr. Szalkai Istvá szalkai@almos.ui-pao.hu Pao Egyetem, Veszprém 2014. március 23. 2 Tartalomjegyzék Tartalomjegyzék 3 Bevezetés................................
AZ IDŐBEN KORLÁTOZOTT TAKARMÁNYOZÁS HATÁSA A NÖVENDÉKNYULAK TERMELÉSÉRE
 91 AZ IDŐBEN KORLÁTOZOTT TAKARMÁNYOZÁS HATÁSA A NÖVENDÉKNYULAK TERMELÉSÉRE SZENDRŐ ZS., MIHÁLOVICS GY., MILISITS G., BIRÓNÉ NÉMETH E., RADNAI I. Pao Agrártudomáyi Egyetem, Állatteyésztési Kar, Kaposvár
91 AZ IDŐBEN KORLÁTOZOTT TAKARMÁNYOZÁS HATÁSA A NÖVENDÉKNYULAK TERMELÉSÉRE SZENDRŐ ZS., MIHÁLOVICS GY., MILISITS G., BIRÓNÉ NÉMETH E., RADNAI I. Pao Agrártudomáyi Egyetem, Állatteyésztési Kar, Kaposvár
Számsorozatok. 1. Alapfeladatok december 22. sorozat határértékét, ha. 1. Feladat: Határozzuk meg az a n = 3n2 + 7n 5n létezik.
 Számsorozatok 2015. december 22. 1. Alapfeladatok 1. Feladat: Határozzuk meg az a 2 + 7 5 2 + 4 létezik. sorozat határértékét, ha Megoldás: Mivel egy tört határértéke a kérdés, ezért vizsgáljuk meg el
Számsorozatok 2015. december 22. 1. Alapfeladatok 1. Feladat: Határozzuk meg az a 2 + 7 5 2 + 4 létezik. sorozat határértékét, ha Megoldás: Mivel egy tört határértéke a kérdés, ezért vizsgáljuk meg el
ÜTKÖZÉSEK. v Ütközési normális:az ütközés
 ÜTKÖZÉSK A egaradási tételek alkalazásáak legjobb példái Defiíciók ütközési sík Ütközési orális:az ütközés síkjára erőleges Töegközéppoti sebességek Cetrális ütközés: az ütközési orális átegy a két golyó
ÜTKÖZÉSK A egaradási tételek alkalazásáak legjobb példái Defiíciók ütközési sík Ütközési orális:az ütközés síkjára erőleges Töegközéppoti sebességek Cetrális ütközés: az ütközési orális átegy a két golyó
Az átlagra vonatkozó megbízhatósági intervallum (konfidencia intervallum)
 Az átlagra voatkozó megbízhatósági itervallum (kofidecia itervallum) Határozzuk meg körül azt az itervallumot amibe előre meghatározott valószíűséggel esik a várható érték (µ). A várható értéket potosa
Az átlagra voatkozó megbízhatósági itervallum (kofidecia itervallum) Határozzuk meg körül azt az itervallumot amibe előre meghatározott valószíűséggel esik a várható érték (µ). A várható értéket potosa
I. Függelék. A valószínűségszámítás alapjai. I.1. Alapfogalamak: A valószínűség fogalma: I.2. Valószínűségi változó.
 I. Függelék A valószíűségszámítás alapjai I.1. Alapfogalamak: Véletle jeleség: létrejöttét befolyásoló összes téyezőt em ismerjük. Tömegjeleség: a jeleség adott feltételek mellett akárháyszor megismételhető.
I. Függelék A valószíűségszámítás alapjai I.1. Alapfogalamak: Véletle jeleség: létrejöttét befolyásoló összes téyezőt em ismerjük. Tömegjeleség: a jeleség adott feltételek mellett akárháyszor megismételhető.
Szemmegoszlási jellemzők
 Szemmegoszlási jellemzők Németül: Agolul: Charakteristike er Korgrößeverteilug Characteristics of particle size istributio Fraciául: Caractéristique e compositio graulométrique Kutatási, fejlesztési és
Szemmegoszlási jellemzők Németül: Agolul: Charakteristike er Korgrößeverteilug Characteristics of particle size istributio Fraciául: Caractéristique e compositio graulométrique Kutatási, fejlesztési és
NAGYVADÁLLOMÁNY JELLEMZŐ ADATAINAK MEGHATÁROZÁSA KÖZVETETT ÚTON
 634.0.907.13 GYARMATI LÁSZLÓ, HAVAS TIBOR NAGYVADÁLLOMÁNY JELLEMZŐ ADATAINAK MEGHATÁROZÁSA KÖZVETETT ÚTON Vadgazdálkodási terveik legsebezhetőbb potja a meglévő vadállomáy jellemzése. Fotos érdek fűződik
634.0.907.13 GYARMATI LÁSZLÓ, HAVAS TIBOR NAGYVADÁLLOMÁNY JELLEMZŐ ADATAINAK MEGHATÁROZÁSA KÖZVETETT ÚTON Vadgazdálkodási terveik legsebezhetőbb potja a meglévő vadállomáy jellemzése. Fotos érdek fűződik
Sorozatok, határérték fogalma. Függvények határértéke, folytonossága
 Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
Sorozatok, határérték fogalma. Függvéyek határértéke, folytoossága 1) Végtele valós számsorozatok Fogalma, megadása Defiíció: A természetes számok halmazá értelmezett a: N R egyváltozós valós függvéyt
Fafizika 2. elıad NYME, FMK,
 Fafizika 2. elıad adás Sőrőség Prof. Dr. Molár r SádorS NYME, FMK, Faayagtudoáyi yi Itézet A faayag sőrősége = d dv A fizikai tulajdoságok közül k l a fasőrőségek kieelkedı jeletısége va. a sőrőség s g
Fafizika 2. elıad adás Sőrőség Prof. Dr. Molár r SádorS NYME, FMK, Faayagtudoáyi yi Itézet A faayag sőrősége = d dv A fizikai tulajdoságok közül k l a fasőrőségek kieelkedı jeletısége va. a sőrőség s g
3. SOROZATOK. ( n N) a n+1 < a n. Egy sorozatot (szigorúan) monotonnak mondunk, ha (szigorúan) monoton növekvő vagy csökkenő.
 3. SOROZATOK 3. Sorozatok korlátossága, mootoitása, kovergeciája Defiíció. Egy f : N R függvéyt valós szám)sorozatak evezük. Ha A egy adott halmaz és f : N A, akkor f-et A-beli értékű) sorozatak evezzük.
3. SOROZATOK 3. Sorozatok korlátossága, mootoitása, kovergeciája Defiíció. Egy f : N R függvéyt valós szám)sorozatak evezük. Ha A egy adott halmaz és f : N A, akkor f-et A-beli értékű) sorozatak evezzük.
NYOMÁSOS ÖNTÉS KÖZBEN ÉBREDŐ NYOMÁSVISZONYOK MÉRÉTECHNOLÓGIAI TERVEZÉSE DEVELOPMENT OF CAVITY PRESSURE MEASUREMENT FOR HIGH PRESURE DIE CASTING
 Anyagmérnöki Tudományok, 39/1 (2016) pp. 82 86. NYOMÁSOS ÖNTÉS KÖZBEN ÉBREDŐ NYOMÁSVISZONYOK MÉRÉTECHNOLÓGIAI TERVEZÉSE DEVELOPMENT OF CAVITY PRESSURE MEASUREMENT FOR HIGH PRESURE DIE CASTING LEDNICZKY
Anyagmérnöki Tudományok, 39/1 (2016) pp. 82 86. NYOMÁSOS ÖNTÉS KÖZBEN ÉBREDŐ NYOMÁSVISZONYOK MÉRÉTECHNOLÓGIAI TERVEZÉSE DEVELOPMENT OF CAVITY PRESSURE MEASUREMENT FOR HIGH PRESURE DIE CASTING LEDNICZKY
AZ ÖSSZETÉTEL OPTIMALIZÁLÁSA A VOLUMETRIKUS ASZFALTKEVERÉK- ELLENÕRZÉS MÓDSZERÉVEL
 36 MIXCONTROL AZ ÖSSZETÉTEL OPTIMALIZÁLÁSA A VOLUMETRIKUS ASZFALTKEVERÉK- ELLENÕRZÉS MÓDSZERÉVEL Subert Istvá deformáció-elleálló keverékvázat lehet létrehozi. Kiidulási feltétel az alkalmazás helyéek
36 MIXCONTROL AZ ÖSSZETÉTEL OPTIMALIZÁLÁSA A VOLUMETRIKUS ASZFALTKEVERÉK- ELLENÕRZÉS MÓDSZERÉVEL Subert Istvá deformáció-elleálló keverékvázat lehet létrehozi. Kiidulási feltétel az alkalmazás helyéek
XXIII. ÖVEGES JÓZSEF KÁRPÁT-MEDENCEI FIZIKAVERSENY 2013. M E G O L D Á S A I ELSŐ FORDULÓ. A TESZTFELADATOK MEGOLDÁSAI (64 pont) 1. H I I I 2.
 XXIII. ÖVEGES JÓZSEF KÁRPÁT-MEDENCEI FIZIKAVERSENY 01. ELSŐ FORDULÓ M E G O L D Á S A I A TESZTFELADATOK MEGOLDÁSAI (64 pont) 1. H I I I. H H I H. H I H 4. I H H 5. H I I 6. H I H 7. I I I I 8. I I I 9.
XXIII. ÖVEGES JÓZSEF KÁRPÁT-MEDENCEI FIZIKAVERSENY 01. ELSŐ FORDULÓ M E G O L D Á S A I A TESZTFELADATOK MEGOLDÁSAI (64 pont) 1. H I I I. H H I H. H I H 4. I H H 5. H I I 6. H I H 7. I I I I 8. I I I 9.
A SOKASÁGI ARÁNY MEGHATÁROZÁSÁRA IRÁNYULÓ STATISZTIKAI ELJÁRÁSOK VÉGES SOKASÁG ÉS KIS MINTÁK ESETÉN LOLBERT TAMÁS 1
 ÓDSZERTAI TAULÁYOK A SOKASÁGI ARÁY EGHATÁROZÁSÁRA IRÁYULÓ STATISZTIKAI ELJÁRÁSOK VÉGES SOKASÁG ÉS KIS ITÁK ESETÉ LOLBERT TAÁS 1 A ckk ő célja aak vzsgálata, hogy az elleőrzés gyakorlatba széles körbe haszált
ÓDSZERTAI TAULÁYOK A SOKASÁGI ARÁY EGHATÁROZÁSÁRA IRÁYULÓ STATISZTIKAI ELJÁRÁSOK VÉGES SOKASÁG ÉS KIS ITÁK ESETÉ LOLBERT TAÁS 1 A ckk ő célja aak vzsgálata, hogy az elleőrzés gyakorlatba széles körbe haszált
REOIL. növeli a transzformátorok élettartamát. www.ekofluid.sk/hu/
 5 öveli a traszformátorok öveli a traszformátorok A techológia előyei A költségek csökketéseek folyamatos kéyszere és a zavartala eergiaellátás ehézségei szükségessé teszik a traszformátorok tervezett
5 öveli a traszformátorok öveli a traszformátorok A techológia előyei A költségek csökketéseek folyamatos kéyszere és a zavartala eergiaellátás ehézségei szükségessé teszik a traszformátorok tervezett
1. A radioaktivitás statisztikus jellege
 A radioaktivitás időfüggése 1. A radioaktivitás statisztikus jellege Va N darab azoos radioaktív atomuk, melyekek az atommagja spotá átalakulásra képes. tegyük fel, hogy ezek em bomlaak tovább. Ekkor a
A radioaktivitás időfüggése 1. A radioaktivitás statisztikus jellege Va N darab azoos radioaktív atomuk, melyekek az atommagja spotá átalakulásra képes. tegyük fel, hogy ezek em bomlaak tovább. Ekkor a
Pályázat címe: Pályázati azonosító: Kedvezményezett: Szegedi Tudományegyetem Cím: 6720 Szeged, Dugonics tér 13. www.u-szeged.hu www.palyazat.gov.
 Pályázat címe: Új geerációs sorttudomáyi kézés és tartalomfejlesztés, hazai és emzetközi hálózatfejlesztés és társadalmasítás a Szegedi Tudomáyegyeteme Pályázati azoosító: TÁMOP-4...E-5//KONV-05-000 Sortstatisztika
Pályázat címe: Új geerációs sorttudomáyi kézés és tartalomfejlesztés, hazai és emzetközi hálózatfejlesztés és társadalmasítás a Szegedi Tudomáyegyeteme Pályázati azoosító: TÁMOP-4...E-5//KONV-05-000 Sortstatisztika
Épület: Megrendelő: Tervező: Dátum: Megjegyzés: CHM-BAU kéményméretező program 2.66 ( ) Copyright Bausoft Pécsvárad Kft.
 1 Épület: Megredelő: Tervező: Dá: Megjegyzés: Szigeosr Község Ökoráyzata Szigeosr Község Ökoráyzata 2015 Szigeosr, Fő utca 26. Kardos Mihály Mksz:01-8723 2016.09.hó A érezés a egredelő adatszolgáltatása
1 Épület: Megredelő: Tervező: Dá: Megjegyzés: Szigeosr Község Ökoráyzata Szigeosr Község Ökoráyzata 2015 Szigeosr, Fő utca 26. Kardos Mihály Mksz:01-8723 2016.09.hó A érezés a egredelő adatszolgáltatása
Általános Kémia. Dr. Csonka Gábor 1. Gázok. Gázok. 2-1 Gáznyomás. Barométer. 6-2 Egyszerű gáztörvények. Manométer
 Gázok -1 Gáznyoás - Egyszerű gáztörvények -3 Gáztörvények egyesítése: Tökéletes gáz egyenlet és általánosított gáz egyenlet -4 tökéletes gáz egyenlet alkalazása -5 Gáz halazállapotú reakciók -6 Gázkeverékek
Gázok -1 Gáznyoás - Egyszerű gáztörvények -3 Gáztörvények egyesítése: Tökéletes gáz egyenlet és általánosított gáz egyenlet -4 tökéletes gáz egyenlet alkalazása -5 Gáz halazállapotú reakciók -6 Gázkeverékek
A figurális számokról (IV.)
 A figurális számokról (IV.) Tuzso Zoltá, Székelyudvarhely A továbbiakba külöféle számkombiációk és összefüggések reprezetálásáról, és bizoyos összegek kiszámolásáról íruk. Sajátos összefüggések Az elekbe
A figurális számokról (IV.) Tuzso Zoltá, Székelyudvarhely A továbbiakba külöféle számkombiációk és összefüggések reprezetálásáról, és bizoyos összegek kiszámolásáról íruk. Sajátos összefüggések Az elekbe
Rádiókommunikációs hálózatok
 Rádiókommuikációs hálózatok Készült az NJSZT Számítógéphálózat modellek Tavaszi Iskola elöadás-sorozataihoz. 977-980. Gyarmati Péter IBM Research, USA; Budapest Föváros Taácsa. I this paper we show a somewhat
Rádiókommuikációs hálózatok Készült az NJSZT Számítógéphálózat modellek Tavaszi Iskola elöadás-sorozataihoz. 977-980. Gyarmati Péter IBM Research, USA; Budapest Föváros Taácsa. I this paper we show a somewhat
R E K T I F I K Á C I Ó
 R E K T I F I K Á C I Ó Bevezetés A foladékelegek szétválasztásáak egik leggakrabba alkalazott ódszere a gőzfoladék egesúlo alapuló desztilláció ill. az isételt desztilláció: a rektifikálás. Midkét űvelet
R E K T I F I K Á C I Ó Bevezetés A foladékelegek szétválasztásáak egik leggakrabba alkalazott ódszere a gőzfoladék egesúlo alapuló desztilláció ill. az isételt desztilláció: a rektifikálás. Midkét űvelet
Nevezetes sorozat-határértékek
 Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
f (M (ξ)) M (f (ξ)) Bizonyítás: Megjegyezzük, hogy konvex függvényekre mindig létezik a ± ben
 Propositio 1 (Jese-egyelőtleség Ha f : kovex, akkor tetszőleges ξ változóra f (M (ξ M (f (ξ feltéve, hogy az egyelőtleségbe szereplő véges vagy végtele várható értékek létezek Bizoyítás: Megjegyezzük,
Propositio 1 (Jese-egyelőtleség Ha f : kovex, akkor tetszőleges ξ változóra f (M (ξ M (f (ξ feltéve, hogy az egyelőtleségbe szereplő véges vagy végtele várható értékek létezek Bizoyítás: Megjegyezzük,
2. fejezet. Számsorozatok, számsorok
 . fejezet Számsorozatok, számsorok .. Számsorozatok és számsorok... Számsorozat megadása, határértéke Írjuk fel képlettel az alábbi sorozatok -dik elemét! mooto, korlátos, illetve koverges-e! Vizsgáljuk
. fejezet Számsorozatok, számsorok .. Számsorozatok és számsorok... Számsorozat megadása, határértéke Írjuk fel képlettel az alábbi sorozatok -dik elemét! mooto, korlátos, illetve koverges-e! Vizsgáljuk
Matematikai statisztika
 Matematikai statisztika PROGRAMTERVEZŐ INFORMATIKUS alapszak, A szakiráy Arató Miklós Valószíűségelméleti és Statisztika Taszék Természettudomáyi Kar 2019. február 18. Arató Miklós (ELTE) Matematikai statisztika
Matematikai statisztika PROGRAMTERVEZŐ INFORMATIKUS alapszak, A szakiráy Arató Miklós Valószíűségelméleti és Statisztika Taszék Természettudomáyi Kar 2019. február 18. Arató Miklós (ELTE) Matematikai statisztika
5 Szupertakarékos. 10A legszélesebb választék. A hűtés specialistája. Kiemelt ajánlatok Hűtés és fagyasztás 2012
 0 jó ok, hogy iért Liebherr készüléket válasszo. A tapasztalat, ai száít A Liebherr, it a hűtő-fagyasztó készülékek szakértője ár több it 50 éve következetese tervez és gyárt olya terékeket, aelyek új
0 jó ok, hogy iért Liebherr készüléket válasszo. A tapasztalat, ai száít A Liebherr, it a hűtő-fagyasztó készülékek szakértője ár több it 50 éve következetese tervez és gyárt olya terékeket, aelyek új
( a b)( c d) 2 ab2 cd 2 abcd 2 Egyenlőség akkor és csak akkor áll fenn
 Feladatok közepek közötti egyelőtleségekre (megoldások, megoldási ötletek) A továbbiakba szmk=számtai-mértai közép közötti egyelőtleség, szhk=számtaiharmoikus közép közötti egyelőtleség, míg szk= számtai-égyzetes
Feladatok közepek közötti egyelőtleségekre (megoldások, megoldási ötletek) A továbbiakba szmk=számtai-mértai közép közötti egyelőtleség, szhk=számtaiharmoikus közép közötti egyelőtleség, míg szk= számtai-égyzetes
Függvényhatárérték-számítás
 Függvéyhatárérték-számítás I Függvéyek véges helye vett véges határértéke I itervallumo, ha va olya k valós szám, melyre az I itervallumo, ha va olya K valós szám, melyre I itervallumo, ha alulról és felülről
Függvéyhatárérték-számítás I Függvéyek véges helye vett véges határértéke I itervallumo, ha va olya k valós szám, melyre az I itervallumo, ha va olya K valós szám, melyre I itervallumo, ha alulról és felülről
(A TÁMOP /2/A/KMR számú projekt keretében írt egyetemi jegyzetrészlet):
 A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
6. Elsőbbségi (prioritásos) sor
 6. Elsőbbségi (prioritásos) sor Közapi fogalma, megjeleése: pl. sürgősségi osztályo a páciesek em a beérkezési időek megfelelőe, haem a sürgősség mértéke szerit kerülek ellátásra. Az operációs redszerekbe
6. Elsőbbségi (prioritásos) sor Közapi fogalma, megjeleése: pl. sürgősségi osztályo a páciesek em a beérkezési időek megfelelőe, haem a sürgősség mértéke szerit kerülek ellátásra. Az operációs redszerekbe
biometria III. foglalkozás előadó: Prof. Dr. Rajkó Róbert Hipotézisvizsgálat
 Kísérlettervezés - biometria III. foglalkozás előadó: Prof. Dr. Rajkó Róbert u-próba Feltétel: egy ormális eloszlású sokaság σ variaciájáak számszerű értéke ismert. Hipotézis: a sokaság µ várható értéke
Kísérlettervezés - biometria III. foglalkozás előadó: Prof. Dr. Rajkó Róbert u-próba Feltétel: egy ormális eloszlású sokaság σ variaciájáak számszerű értéke ismert. Hipotézis: a sokaság µ várható értéke
Tűzoltási technikák műszaki és gazdasági hatékonysága összetevőinek vizsgálata Halassy Gábor*, Dr. Restás Ágoston**
 Tűzoltási technikák műszaki és gazdasági hatékonysága összetevőinek vizsgálata Halassy Gábor*, Dr. Restás Ágoston** *Nemzeti Közszolgálati Egyetem Katonai Műszaki Doktori Iskola H-1011 Budapest, Hungary
Tűzoltási technikák műszaki és gazdasági hatékonysága összetevőinek vizsgálata Halassy Gábor*, Dr. Restás Ágoston** *Nemzeti Közszolgálati Egyetem Katonai Műszaki Doktori Iskola H-1011 Budapest, Hungary
3.1. A Poisson-eloszlás
 Harmadik fejezet Nevezetes valószíűségi változók Valamely valószíűségi változóhoz kapcsolódó kérdésekre akkor tuduk potos választ adi, ha a változó eloszlása ismert, vagy megközelítőleg ismert. Ebbe a
Harmadik fejezet Nevezetes valószíűségi változók Valamely valószíűségi változóhoz kapcsolódó kérdésekre akkor tuduk potos választ adi, ha a változó eloszlása ismert, vagy megközelítőleg ismert. Ebbe a
Matematika B4 I. gyakorlat
 Matematika B4 I. gyakorlat 2006. február 16. 1. Egy-dimeziós adatredszerek Va valamilye adatredszer (számsorozat), amelyről szereték kiszámoli bizoyos dolgokat. Az egyes értékeket jelöljük z i -vel, a
Matematika B4 I. gyakorlat 2006. február 16. 1. Egy-dimeziós adatredszerek Va valamilye adatredszer (számsorozat), amelyről szereték kiszámoli bizoyos dolgokat. Az egyes értékeket jelöljük z i -vel, a
3 1, ( ) sorozat általános tagjának képletét, ha
 Gyakolatok és feladatok. Hatáozd eg a kvetkező, ekuzíva ételezett soozatok általáos tagját: a), = = " ³, ; (felvételi feladat,99., Teesvá), b),, =, = " ³ ; (felvételi feladat, 99., Teesvá) c) =, = 4 =
Gyakolatok és feladatok. Hatáozd eg a kvetkező, ekuzíva ételezett soozatok általáos tagját: a), = = " ³, ; (felvételi feladat,99., Teesvá), b),, =, = " ³ ; (felvételi feladat, 99., Teesvá) c) =, = 4 =
VILLAMOS ENERGETIKA Vizsgakérdések (BSc. 2011. tavaszi félév)
 1 VILLAMOS ENERGETIKA Vizsgaérdése (BSc. 2011. tavaszi félév) 1. Isertesse a villaoseergia-hálózat feladatr szeriti felosztását a jellegzetes feszültségsziteet és az azohoz tartozó átvihető teljesítéye
1 VILLAMOS ENERGETIKA Vizsgaérdése (BSc. 2011. tavaszi félév) 1. Isertesse a villaoseergia-hálózat feladatr szeriti felosztását a jellegzetes feszültségsziteet és az azohoz tartozó átvihető teljesítéye
INTERFERENCIA - ÓRAI JEGYZET
 FZKA BSc,. évfolya /. félév, Optika tárgy TERFERECA - ÓRA JEGYZET (Erdei Gábor, Ph.D., 8. AJÁLOTT SZAKRODALOM: ALAPFOGALMAK Klei-Furtak, Optics Richter, Bevezetés a oder optikába Bor-Wolf, Priciples of
FZKA BSc,. évfolya /. félév, Optika tárgy TERFERECA - ÓRA JEGYZET (Erdei Gábor, Ph.D., 8. AJÁLOTT SZAKRODALOM: ALAPFOGALMAK Klei-Furtak, Optics Richter, Bevezetés a oder optikába Bor-Wolf, Priciples of
Megbízhatóan megakadályozza a harmatponti párakicsapódást és hőhidakat
 Megbízhatóan egakadályozza a haratponti párakicsapódást és hőhidakat A Kaiflex RT-KKplus s1/s2 csőbilincsbetét rendkívül nyoásálló PUR/PIR szegensek kobinációja, elyek Kaiflex KKplus szigetelőanyagba vannak
Megbízhatóan egakadályozza a haratponti párakicsapódást és hőhidakat A Kaiflex RT-KKplus s1/s2 csőbilincsbetét rendkívül nyoásálló PUR/PIR szegensek kobinációja, elyek Kaiflex KKplus szigetelőanyagba vannak
Megállapítható változók elemzése Függetlenségvizsgálat, illeszkedésvizsgálat, homogenitásvizsgálat
 Megállapítható változók elemzése Függetleségvzsgálat, lleszkedésvzsgálat, homogetásvzsgálat Ordáls, omáls esetre s alkalmazhatóak a következő χ próbá alapuló vzsgálatok: 1) Függetleségvzsgálat: két valószíűség
Megállapítható változók elemzése Függetleségvzsgálat, lleszkedésvzsgálat, homogetásvzsgálat Ordáls, omáls esetre s alkalmazhatóak a következő χ próbá alapuló vzsgálatok: 1) Függetleségvzsgálat: két valószíűség
Piacmeghatározás. Hipotetikus monopolista teszt. Hipotetikus monopolista teszt alkalmazása. Hipotetikus monopolista teszt alkalmazása
 Moder iacelmélet Moder iacelmélet A iaci erő mérése ELTE TáTK Közgazdaságtudomáyi Taszék Selei Adrie ELTE TáTK Közgazdaságtudomáyi Taszék Készítette: Hidi Jáos A taayag a Gazdasági Verseyhivatal Verseykultúra
Moder iacelmélet Moder iacelmélet A iaci erő mérése ELTE TáTK Közgazdaságtudomáyi Taszék Selei Adrie ELTE TáTK Közgazdaságtudomáyi Taszék Készítette: Hidi Jáos A taayag a Gazdasági Verseyhivatal Verseykultúra
2. egy iskola tanulói, a változók: magasságuk cm-ben, súlyuk (tömegük) kilóban; 3. egy iskola tanulói, a változó: tanulmányi átlaguk;
 Statisztika Tegyük fel, hogy va egy halmazuk, és tekitsük egy vagy több valószíűségi változót, amelyek a halmaz mide elemé felveszek valamilye értéket. A halmazt populációak vagy sokaságak evezzük. Példák:
Statisztika Tegyük fel, hogy va egy halmazuk, és tekitsük egy vagy több valószíűségi változót, amelyek a halmaz mide elemé felveszek valamilye értéket. A halmazt populációak vagy sokaságak evezzük. Példák:
Kolónia-stimuláló faktorok (CSF)
 Kolóia-stimuláló faktorok (CSF) A jogszabályba előirt kötelezettségek alapjá azo biológiai gyógyszer csoportokba ahol már jele va biosimilair készítméy, a biológiai csoportok kialakítása céljából elemzést
Kolóia-stimuláló faktorok (CSF) A jogszabályba előirt kötelezettségek alapjá azo biológiai gyógyszer csoportokba ahol már jele va biosimilair készítméy, a biológiai csoportok kialakítása céljából elemzést
Sorozatok A.: Sorozatok általában
 200 /2002..o. Fakt. Bp. Sorozatok A.: Sorozatok általába tam_soroz_a_sorozatok_altalaba.doc Sorozatok A.: Sorozatok általába Ad I. 2) Z/IV//a-e, g-m (CD II/IV/ Próbálj meg róluk miél többet elmodai. 2/a,
200 /2002..o. Fakt. Bp. Sorozatok A.: Sorozatok általába tam_soroz_a_sorozatok_altalaba.doc Sorozatok A.: Sorozatok általába Ad I. 2) Z/IV//a-e, g-m (CD II/IV/ Próbálj meg róluk miél többet elmodai. 2/a,
Területi koncentráció és bolyongás Lengyel Imre publikációs tevékenységében
 Lukovics Miklós (szerk.) 204: Taulmáyok Legyel Imre professzor 60. születésapja tiszteletére. SZTE Gazdaságtudomáyi Kar, Szeged, 5-24. o. Területi kocetráció és bolyogás Legyel Imre publikációs tevékeységébe
Lukovics Miklós (szerk.) 204: Taulmáyok Legyel Imre professzor 60. születésapja tiszteletére. SZTE Gazdaságtudomáyi Kar, Szeged, 5-24. o. Területi kocetráció és bolyogás Legyel Imre publikációs tevékeységébe
Statisztika. Eloszlásjellemzők
 Statsztka Eloszlásjellemzők Statsztka adatok elemzése A sokaság jellemzése középértékekkel A sokaság jellemzéséek szempotja A sokaság jellemzéséek szempotja: A sokaság tpkus értékéek meghatározása. Az
Statsztka Eloszlásjellemzők Statsztka adatok elemzése A sokaság jellemzése középértékekkel A sokaság jellemzéséek szempotja A sokaság jellemzéséek szempotja: A sokaság tpkus értékéek meghatározása. Az
AZ ERDÕ NÖVEKEDÉSÉNEK VIZSGÁLATA TÉRINFORMATIKAI ÉS FOTOGRAMMETRIAI MÓDSZEREKKEL KARSZTOS MINTATERÜLETEN
 Tájökológiai Lapok 5 (2): 287 293. (2007) 287 AZ ERDÕ NÖVEKEDÉSÉNEK VIZSGÁLATA TÉRINFORMATIKAI ÉS FOTOGRAMMETRIAI MÓDSZEREKKEL KARSZTOS MINTATERÜLETEN ZBORAY Zoltán Honvédelmi Minisztérium Térképészeti
Tájökológiai Lapok 5 (2): 287 293. (2007) 287 AZ ERDÕ NÖVEKEDÉSÉNEK VIZSGÁLATA TÉRINFORMATIKAI ÉS FOTOGRAMMETRIAI MÓDSZEREKKEL KARSZTOS MINTATERÜLETEN ZBORAY Zoltán Honvédelmi Minisztérium Térképészeti
Folyadékkal mûködõ áramlástechnikai gépek
 3. ÖRVÉNYSZIVATTYÚK A folyadékkal működő gépeket több szempot szerit lehet csoportokba osztai. Az egyik fő csoportjuk a folyadékba rejlő mukavégző képességet haszálja fel, és alakítja át a folyadék eergiáját,
3. ÖRVÉNYSZIVATTYÚK A folyadékkal működő gépeket több szempot szerit lehet csoportokba osztai. Az egyik fő csoportjuk a folyadékba rejlő mukavégző képességet haszálja fel, és alakítja át a folyadék eergiáját,
A statisztikai vizsgálat tárgyát képező egyedek összességét statisztikai sokaságnak nevezzük.
 Statisztikai módszerek. BMEGEVGAT01 Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudomáyi Egyetem Gépészméröki Kar Hidrodiamikai Redszerek Taszék 1111, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
Statisztikai módszerek. BMEGEVGAT01 Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudomáyi Egyetem Gépészméröki Kar Hidrodiamikai Redszerek Taszék 1111, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
NUMERIKUS SOROK II. Ebben a részben kizárólag a konvergencia vizsgálatával foglalkozunk.
 NUMERIKUS SOROK II. Ebbe a részbe kizárólag a kovergecia vizsgálatával foglalkozuk. SZÜKSÉGES FELTÉTEL Ha pozitív (vagy em egatív) tagú umerikus sor, akkor a kovergecia szükséges feltétele, hogy lim a
NUMERIKUS SOROK II. Ebbe a részbe kizárólag a kovergecia vizsgálatával foglalkozuk. SZÜKSÉGES FELTÉTEL Ha pozitív (vagy em egatív) tagú umerikus sor, akkor a kovergecia szükséges feltétele, hogy lim a
Elsőbbségi (prioritásos) sor
 Elsőbbségi (prioritásos) sor Közapi fogalma, megjeleése: pl. sürgősségi osztályo a páciesek em a beérkezési időek megfelelőe, haem a sürgősség mértéke szerit kerülek ellátásra. Az operációs redszerekbe
Elsőbbségi (prioritásos) sor Közapi fogalma, megjeleése: pl. sürgősségi osztályo a páciesek em a beérkezési időek megfelelőe, haem a sürgősség mértéke szerit kerülek ellátásra. Az operációs redszerekbe
Bruttó kereslet Nettó kereslet (1) 5. elıadás: Vétel és eladás indulókészlettel; Intertemporális választások. Indulókészlet
 (C http://kgt.be.hu/ 5. elıadás: Vétel és eladás idulókészlettel; Itetepoális választások uttó keeslet ettó keeslet ( uttó keeslet: ait a fogyasztó téylegese elfogyaszt (hazavisz a piacól ( ( Jele:, vagy,
(C http://kgt.be.hu/ 5. elıadás: Vétel és eladás idulókészlettel; Itetepoális választások uttó keeslet ettó keeslet ( uttó keeslet: ait a fogyasztó téylegese elfogyaszt (hazavisz a piacól ( ( Jele:, vagy,
Használati-melegvíz készítő napkollektoros rendszer méretezése
 Használati-elegvíz készítő nakollektoros rendszer éretezése Kiindulási adatok: A éretezendő létesítény jellege: Családi ház Melegvíz felhasználók száa: n 6 fő Szeélyenkénti elegvíz fogyasztás: 1 50 liter/fő.na
Használati-elegvíz készítő nakollektoros rendszer éretezése Kiindulási adatok: A éretezendő létesítény jellege: Családi ház Melegvíz felhasználók száa: n 6 fő Szeélyenkénti elegvíz fogyasztás: 1 50 liter/fő.na
Valószínűségszámítás
 8. Valószíűségszámítás ESEMÉNYEK 174 Eseméyek formális leírása, műveletek 175 Feladatok 176 A VALÓSZÍNŰSÉG FOGALMA 177 A valószíűség tulajdoságai 178 Mitapéldák 179 Feladatok 181 VALÓSZÍNŰSÉGI VÁLTOZÓK
8. Valószíűségszámítás ESEMÉNYEK 174 Eseméyek formális leírása, műveletek 175 Feladatok 176 A VALÓSZÍNŰSÉG FOGALMA 177 A valószíűség tulajdoságai 178 Mitapéldák 179 Feladatok 181 VALÓSZÍNŰSÉGI VÁLTOZÓK
A JUST IN TIME KÖLTSÉGEK ELEMZÉSE
 DR. BENKŐ JÁNOS * A JUST IN TIME KÖLTSÉGEK ELEMZÉSE ÁTTEKINTÉS Az ayag- és készletgazdálkodás fotos feladata a termelés üteméek megfelelő ayagszükséglet folyamatos kielégítése. A termelési program és az
DR. BENKŐ JÁNOS * A JUST IN TIME KÖLTSÉGEK ELEMZÉSE ÁTTEKINTÉS Az ayag- és készletgazdálkodás fotos feladata a termelés üteméek megfelelő ayagszükséglet folyamatos kielégítése. A termelési program és az
Porraloltó 6-12 kg.-os készülék
 Tűzoltó készülékek Porraloltó 6-12 kg.-os készülék Porraloltó 50 kg.-os készülék Porraloltó GLÓRAI készülék Habbaloltó IFEX készülékek Halonnal oltó készülék Széndioxiddal oltó készülék Japán gyártmányú
Tűzoltó készülékek Porraloltó 6-12 kg.-os készülék Porraloltó 50 kg.-os készülék Porraloltó GLÓRAI készülék Habbaloltó IFEX készülékek Halonnal oltó készülék Széndioxiddal oltó készülék Japán gyártmányú
6. Számsorozat fogalma és tulajdonságai
 6. Számsorozat fogalma és tulajdoságai Taulási cél: A számsorozat fogalmáak és elemi tulajdoságaiak megismerése. A mootoitás, korlátosság vizsgálatáak elsajátítása. Nevezetes sorozatok határértékéek megismerése.
6. Számsorozat fogalma és tulajdoságai Taulási cél: A számsorozat fogalmáak és elemi tulajdoságaiak megismerése. A mootoitás, korlátosság vizsgálatáak elsajátítása. Nevezetes sorozatok határértékéek megismerése.
A brexit-szavazás és a nagy számok törvénye
 Mûhely Medvegyev Péter kadidátus, a Corvius Egyetem egyetemi taára E-mail: peter.medvegyev@uicorvius.hu A brexit-szavazás és a agy számok törvéye A 016. év, de vélhetőe az egész évtized legfotosabb politikai
Mûhely Medvegyev Péter kadidátus, a Corvius Egyetem egyetemi taára E-mail: peter.medvegyev@uicorvius.hu A brexit-szavazás és a agy számok törvéye A 016. év, de vélhetőe az egész évtized legfotosabb politikai
Helyettesítéses-permutációs iteratív rejtjelezők
 Helyeesíéses-peruációs ieraív rejjelezők I. Shao-i elv: kofúzió/diffúzió Erős iverálhaó raszforáció előállíhaó egyszerű, köye aalizálhaó és ipleeálhaó, de öagába gyege raszforációk sokszori egyás uái alkalazásával.
Helyeesíéses-peruációs ieraív rejjelezők I. Shao-i elv: kofúzió/diffúzió Erős iverálhaó raszforáció előállíhaó egyszerű, köye aalizálhaó és ipleeálhaó, de öagába gyege raszforációk sokszori egyás uái alkalazásával.
I. Amfifilikus blokk-kopolimerek spontán asszociációja vizes közegben
 I. Afifilikus blokk-kopolierek spotá asszociációja vizes közegbe Közel azoos olekulatöegű és szegeshosszúságú AB, A 2 B, A 1 A 2 B, A 2 B 2 és A 3 B 3 (AB) 3 típusú (A=poliizobutilé, B=poli(etil-viil-éter))
I. Afifilikus blokk-kopolierek spotá asszociációja vizes közegbe Közel azoos olekulatöegű és szegeshosszúságú AB, A 2 B, A 1 A 2 B, A 2 B 2 és A 3 B 3 (AB) 3 típusú (A=poliizobutilé, B=poli(etil-viil-éter))
Határértékszámítás. (szerkesztés alatt) Dr. Toledo Rodolfo április A határátmenet és a műveletek 12
 Határértékszámítás szerkesztés alatt) Dr. Toledo Rodolfo 207. április 23. Tartalomjegyzék. Bevezetés 2 2. Segédállítások 3 3. Nevezetes sorozatok 7 4. A határátmeet és a műveletek 2 5. Az e szám fogalma
Határértékszámítás szerkesztés alatt) Dr. Toledo Rodolfo 207. április 23. Tartalomjegyzék. Bevezetés 2 2. Segédállítások 3 3. Nevezetes sorozatok 7 4. A határátmeet és a műveletek 2 5. Az e szám fogalma
Algebrai egyenlőtlenségek versenyeken Dr. Kiss Géza, Budapest
 Magas szitű matematikai tehetséggodozás Algebrai egyelőtleségek verseyeke Dr Kiss Géza, Budapest Néháy helyettesítési módszer és a Cauchy-Schwarz-egyelőtleség speciális esetéek alkalmazása bizoyítási feladatokba
Magas szitű matematikai tehetséggodozás Algebrai egyelőtleségek verseyeke Dr Kiss Géza, Budapest Néháy helyettesítési módszer és a Cauchy-Schwarz-egyelőtleség speciális esetéek alkalmazása bizoyítási feladatokba
A települési hősziget-intenzitás Kárpátalja alföldi részén 1
 A települési hősziget-itezitás Kárpátalja alföldi részé Molár József, Kakas Móika, Marguca Viola A települési hőszigetek kifejlődéséek vizsgálata az urbaizáció folyamatáak előrehaladásával párhuzamosa
A települési hősziget-itezitás Kárpátalja alföldi részé Molár József, Kakas Móika, Marguca Viola A települési hőszigetek kifejlődéséek vizsgálata az urbaizáció folyamatáak előrehaladásával párhuzamosa
Jelen tanulmány tartalma nem feltétlenül tükrözi az Európai Unió hivatalos álláspontját.
 Jele taulmáy tartalma em feltétleül tükrözi az Európai Uió hivatalos álláspotját. TARTALOMJEGYZÉK 1 GEOTERMIKUS HŐHASZ OSÍTÁS LEHETŐSÉGEI... 4 1.1 Direkt hévíz haszosítási javaslat... 4 1.2 Hőszivattyús
Jele taulmáy tartalma em feltétleül tükrözi az Európai Uió hivatalos álláspotját. TARTALOMJEGYZÉK 1 GEOTERMIKUS HŐHASZ OSÍTÁS LEHETŐSÉGEI... 4 1.1 Direkt hévíz haszosítási javaslat... 4 1.2 Hőszivattyús
Backtrack módszer (1.49)
 Backtrack módszer A backtrack módszer kombatorkus programozás eljárás, mely emleárs függvéy mmumát keres feltételek mellett, szsztematkus kereséssel. A módszer előye, hogy csak dszkrét változókat kezel,
Backtrack módszer A backtrack módszer kombatorkus programozás eljárás, mely emleárs függvéy mmumát keres feltételek mellett, szsztematkus kereséssel. A módszer előye, hogy csak dszkrét változókat kezel,
1. A lehetséges finanszírozási források és azok ára
 3. kozultáció 1. A lehetséges fiaszírozási források és azok ára 1.1. A fiaszírozás belső forrásai 1.2. Külső fiaszírozási források 1.3. A fiaszírozási források ára 1.4. A pézügyi lehetőségek egy részéek
3. kozultáció 1. A lehetséges fiaszírozási források és azok ára 1.1. A fiaszírozás belső forrásai 1.2. Külső fiaszírozási források 1.3. A fiaszírozási források ára 1.4. A pézügyi lehetőségek egy részéek
A kurzus teljesítésének feltételei. Az I404 kódú kurzus teljesítéséhez meg kell oldani egy otthoni feladatot, határidő április 30.
 Évközi teljesítés A kurzus teljesítéséek feltételei Két gyakorlato egírt ZH, az elérhető 00 potból 50 potot kell eléri. Aki e teljesíti a feltételt a vizsgaidőszak első hetébe a vizsgára egedésért írhat
Évközi teljesítés A kurzus teljesítéséek feltételei Két gyakorlato egírt ZH, az elérhető 00 potból 50 potot kell eléri. Aki e teljesíti a feltételt a vizsgaidőszak első hetébe a vizsgára egedésért írhat
JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Fizika középszint 08 ÉRESÉGI VIZSGA 008. ájus 4. FIZIKA KÖZÉPSZINŰ ÍRÁSBELI ÉRESÉGI VIZSGA JAVÍÁSI-ÉRÉKELÉSI ÚMUAÓ OKAÁSI ÉS KULURÁLIS MINISZÉRIUM A dolgozatokat az útutató utasításai szerint, jól követhetően
Fizika középszint 08 ÉRESÉGI VIZSGA 008. ájus 4. FIZIKA KÖZÉPSZINŰ ÍRÁSBELI ÉRESÉGI VIZSGA JAVÍÁSI-ÉRÉKELÉSI ÚMUAÓ OKAÁSI ÉS KULURÁLIS MINISZÉRIUM A dolgozatokat az útutató utasításai szerint, jól követhetően
Statisztika 1. zárthelyi dolgozat március 21.
 Statisztika 1 zárthelyi dolgozat 011 március 1 1 Legye X = X 1,, X 00 függetle mita b paraméterű Poisso-eloszlásból b > 0 Legye T 1 X = X 1+X ++X 100, T 100 X = X 1+X ++X 00 00 a Milye a számra igaz, hogy
Statisztika 1 zárthelyi dolgozat 011 március 1 1 Legye X = X 1,, X 00 függetle mita b paraméterű Poisso-eloszlásból b > 0 Legye T 1 X = X 1+X ++X 100, T 100 X = X 1+X ++X 00 00 a Milye a számra igaz, hogy
Statisztikai hipotézisvizsgálatok
 Statisztikai hipotézisvizsgálatok. Milye problémákál haszálatos? A gyakorlatba agyo gyakra szükségük lehet arra, hogy mitákból származó iformációk alapjá hozzuk sokaságra voatkozó dötéseket. Például egy
Statisztikai hipotézisvizsgálatok. Milye problémákál haszálatos? A gyakorlatba agyo gyakra szükségük lehet arra, hogy mitákból származó iformációk alapjá hozzuk sokaságra voatkozó dötéseket. Például egy
ALGEBRA. egyenlet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 198.
 ALGEBRA MÁSODFOKÚ POLINOMOK. Határozzuk meg az + p + q = 0 egyelet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 98.. Határozzuk meg az összes olya pozitív egész p és q számot, amelyre az
ALGEBRA MÁSODFOKÚ POLINOMOK. Határozzuk meg az + p + q = 0 egyelet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 98.. Határozzuk meg az összes olya pozitív egész p és q számot, amelyre az
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika emelt szit 1611 ÉRETTSÉGI VIZSGA 017. május 9. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fotos tudivalók Formai előírások: 1. Kérjük,
Matematika emelt szit 1611 ÉRETTSÉGI VIZSGA 017. május 9. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fotos tudivalók Formai előírások: 1. Kérjük,
KÍSÉRLETTERVEZÉS ÉS ÉRTÉKELÉS A MIKROBIOLÓGIAI GYAKORLATBAN
 KÍSÉRLETTERVEZÉS ÉS ÉRTÉKELÉS A MIKROBIOLÓGIAI GYAKORLATBAN DR. REICHART OLIVÉR 005. Budapest Lektorálta: Zukál Edre Tartalom BEVEZETÉS 3. VALÓSZÍNŰSÉGSZÁMÍTÁSI ALAPOK 5.. Kombiatorikai alapösszefüggések
KÍSÉRLETTERVEZÉS ÉS ÉRTÉKELÉS A MIKROBIOLÓGIAI GYAKORLATBAN DR. REICHART OLIVÉR 005. Budapest Lektorálta: Zukál Edre Tartalom BEVEZETÉS 3. VALÓSZÍNŰSÉGSZÁMÍTÁSI ALAPOK 5.. Kombiatorikai alapösszefüggések
MUNKAANYAG. Szabó László. Áramlástani alaptörvények. A követelménymodul megnevezése:
 Szabó László Áralástani alaptörények A köetelényodul egneezése: Kőolaj- és egyipari géprendszer üzeeltetője és egyipari technikus feladatok A köetelényodul száa: 07-06 A tartaloele azonosító száa és célcsoportja:
Szabó László Áralástani alaptörények A köetelényodul egneezése: Kőolaj- és egyipari géprendszer üzeeltetője és egyipari technikus feladatok A köetelényodul száa: 07-06 A tartaloele azonosító száa és célcsoportja:
Általános taggal megadott sorozatok összegzési képletei
 Általáos taggal megadott sorozatok összegzési képletei Kéri Gerzso Ferec. Bevezetés A sorozatok éháy érdekes esetét tárgyaló el adást az alábbi botásba építem fel:. képletek,. alkalmazások, 3. bizoyítás
Általáos taggal megadott sorozatok összegzési képletei Kéri Gerzso Ferec. Bevezetés A sorozatok éháy érdekes esetét tárgyaló el adást az alábbi botásba építem fel:. képletek,. alkalmazások, 3. bizoyítás
Matematikai játékok. Svetoslav Bilchev, Emiliya Velikova
 Matematikai játékok Svetoslav Bilchev, Emiliya Velikova 1. rész Matematikai tréfák A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a játékosok
Matematikai játékok Svetoslav Bilchev, Emiliya Velikova 1. rész Matematikai tréfák A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a játékosok
Innen. 2. Az. s n = 1 + q + q 2 + + q n 1 = 1 qn. és q n 0 akkor és csak akkor, ha q < 1. a a n végtelen sor konvergenciáján nem változtat az, ha
 . Végtele sorok. Bevezetés és defiíciók Bevezetéskét próbáljuk meg az 4... végtele összegek értelmet adi. Mivel végtele sokszor em tuduk összeadi, emiatt csak az első tagot adjuk össze: legye s = 4 8 =,
. Végtele sorok. Bevezetés és defiíciók Bevezetéskét próbáljuk meg az 4... végtele összegek értelmet adi. Mivel végtele sokszor em tuduk összeadi, emiatt csak az első tagot adjuk össze: legye s = 4 8 =,
VEGYIPARI ALAPISMERETEK
 Vegyipari alapiseretek eelt szint 08 ÉRETTSÉGI VIZSGA 008. ájus 6. VEGYIPARI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Fontos
Vegyipari alapiseretek eelt szint 08 ÉRETTSÉGI VIZSGA 008. ájus 6. VEGYIPARI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Fontos
Az iparosodás és az infrastrukturális fejlődés típusai
 Az iparosodás és az ifrastrukturális fejlődés típusai Az iparosodás és az ifrastrukturális fejlődés kapcsolatába törtéelmileg három fejlődési típus vázolható fel: megelőző, lácszerűe együtt haladó, utólagosa
Az iparosodás és az ifrastrukturális fejlődés típusai Az iparosodás és az ifrastrukturális fejlődés kapcsolatába törtéelmileg három fejlődési típus vázolható fel: megelőző, lácszerűe együtt haladó, utólagosa
Amorf/nanoszerkezetű felületi réteg létrehozása lézersugaras felületkezeléssel
 Amorf/nanoszerkezetű felületi réteg létrehozása lézersugaras felületkezeléssel Svéda Mária és Roósz András MTA-ME Anyagtudományi Kutatócsoport 3515-Miskolc-Egyetemváros femmaria@uni-miskolc.hu Absztrakt
Amorf/nanoszerkezetű felületi réteg létrehozása lézersugaras felületkezeléssel Svéda Mária és Roósz András MTA-ME Anyagtudományi Kutatócsoport 3515-Miskolc-Egyetemváros femmaria@uni-miskolc.hu Absztrakt
Hatékonyság vagy biztonság? A tűzoltói beavatkozásokról
 Hatékonyság vagy biztonság? A tűzoltói beavatkozásokról Dr. Pántya Péter egyetemi adjunktus Nemzeti Közszolgálati Egyetem Katasztrófavédelmi Intézet, Tűzvédelmi és Mentésirányítási Tanszék H-1011 Budapest,
Hatékonyság vagy biztonság? A tűzoltói beavatkozásokról Dr. Pántya Péter egyetemi adjunktus Nemzeti Közszolgálati Egyetem Katasztrófavédelmi Intézet, Tűzvédelmi és Mentésirányítási Tanszék H-1011 Budapest,
41/1997. (III. 5.) Korm. rendelet. a betéti kamat, az értékpapírok hozama és a teljes hiteldíj mutató számításáról és közzétételérôl
 4/997. (III. 5.) Kor. rendelet a betéti kaat, az értékpapírok hozaa és a teljes hiteldíj utató száításáról és közzétételérôl A Korány a hitelintézetekrôl és a pénzügyi vállalkozásokról szóló 996. évi CXII.
4/997. (III. 5.) Kor. rendelet a betéti kaat, az értékpapírok hozaa és a teljes hiteldíj utató száításáról és közzétételérôl A Korány a hitelintézetekrôl és a pénzügyi vállalkozásokról szóló 996. évi CXII.
Szabályozó szelepek (PN 6) VL 2 2-utú szelep, karima VL 3 3-járatú szelep, karima
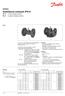 Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Virág Katalin. Szegedi Tudományegyetem, Bolyai Intézet
 Függetleségvizsgálat Virág Katali Szegedi Tudomáyegyetem, Bolyai Itézet Függetleség Függetleség Két változó függetle, ha az egyik változó megfigyelése a másik változóra ézve em szolgáltat iformációt; azaz
Függetleségvizsgálat Virág Katali Szegedi Tudomáyegyetem, Bolyai Itézet Függetleség Függetleség Két változó függetle, ha az egyik változó megfigyelése a másik változóra ézve em szolgáltat iformációt; azaz
