HIBAFA ÉRZÉKENYSÉG ELEMZÉSE 2 1. BEVEZETÉS
|
|
|
- Fruzsina Lakatos
- 8 évvel ezelőtt
- Látták:
Átírás
1 oorádi László Szolnoi Tudományos Közleménye XVI. Szolno, 202 HIBAFA ÉRZÉKENYSÉG ELEMZÉSE 2 A tanulmány egy önnyen algoritmizálható hibafa érzéenység elemzési módszert mutat be, mely a gázturbinás hajtóműve és repülőgép sárányrendszere matematiai diagnosztiai modellezési eljárásain alapszi. A tanulmány fő célja a lineáris matematiai diagnosztiai modellezési módszere alalmazásával a Lineáris Hibafa Érzéenységi Modell (Linear Fault Tree Sensitivity Model LFTSM) módszertanána bemutatása és egy példán eresztül az alalmazási lehetőség szemléltetése MATRIX-ALGEBRAIC FAULT TREE SENSITIVITY ANALYSIS The paper shows an easy-useable fault tree sensitivity investigation method uses matrix-algebraic method based upon the mathematical modeling of aircraft systems and gas turbine engines. The main aim of this study is to shows the adaptation of linear mathematical diagnostic modeling methodology for setting-up of Linear Fault Tree Sensitivity Model (LFTSM) LFTSM and its possibility of use to investigate Fault Tree sensitivity by a demonstrative example.. BEVEZETÉS A hibafa-elemzés (Fault Tree Analysis FTA) során egy valós vagy feltételezett rendszerhibából, az úgynevezett főeseményből (Top Event) indulun i, és foozatosan derítjü fel azoat az alotóelem és részrendszer meghibásodási lehetőségeet, melye az adott, nem ívánt esemény beövetezéséhez vezetne vagy vezethetne. A hibafa-elemzés érzéenyvizsgálatána célja anna meghatározása, hogy az adott hibafa elemi eseménye beövetezési valószínűségeine változásaira milyen mértében reagálna mennyire érzéenye a hozzá apcsolódó özbülső eseménye és a főesemény beövetezési valószínűségei. A hibafa-elemzést fastrutúrájú gráf segíti, amit ülönböző, például megbízhatósági számításoal is i lehet egészíteni. Módszertanát a [5] és [6] szabványoból tudju megismerni. A részletesebb megértéshez szüséges gráfelméleti ismerete Andrásfalvi [] önyvében és Fazeas [3] egyetemi jegyzetében olvashatóa. Számítógéppel segített hibafa-elemzés módszertanát ismerteti Ferdous, szerzőtársaival a [4] irodalomban. Az érzéenységi elemzése orábban alalmazott módszere esetén a iértéelést úgy végezté el, hogy a hibafa egyi elemi eseményéhez nagy, majd is értéű meghibásodási rátát rendelte. Amennyiben a iszámított rendszer-megbízhatósági paraméter, azaz a főesemény beövetezési valószínűsége, nem változott számottevően, aor ez az elemi esemény nem bír nagy ocázati jelentőséggel. Viszont, ha a rendszer-megbízhatósági paraméter változása je- CSc. egyetemi tanár, Debreceni Egyetem, pooradi@eng.unideb.hu 2 Letorálta: orti Tamás, oleveles. matematius, porti.tamas@prosysmod.hu 50
2 Szolnoi Tudományos Közleménye XVI. lentős mértéűre adódott, aor pontosabb adatoat ell szerezni vagy az eseményt további alap oora ell bontani. Csiba elemzései során a csúcsesemény beövetezési valószínűséget leíró függvény elemi eseménye beövetezési valószínűségei szerinti parciális differenciálhányadosait épezte az érzéenységi együttható meghatározásához [2]. Ezen eljárás hátránya az, hogy egy nagyméretű, összetett hibafa esetén viszonylag nagy a hibázás lehetősége. oorádi [7] önyvében vizsgálta a techniai rendszere lineáris érzéenységi modelljeine felállítási és alalmazhatósági lehetőségeit. A Szerző a repülőgép sárányrendszereine lineáris diagnosztiai eljárásait alalmazta a hibafa-elemzés relatív érzéenységvizsgálatára [9], valamint a Lineáris Hibafa Érzéenységi Modell (LFTSM Linear Fault Tree Sensitivity Model) módszerét dolgozta i [8]. Jelen tanulmány a hibafa-elemzés érzéenységvizsgálatána, a fenti eljárástól eltérő, úgynevezett moduláris megözelítésű, mátrixalgebrai módszerét mutatja be a szerző által idolgozott LFTSM alalmazásával. A tanulmány az alábbi részeből áll: A 2. fejezet röviden bemutatja a Hibafa-elemzést. A 3. fejezet az érzéenységvizsgálat teljes derivált módszerét írja le. A 4. fejezet egy egyszerű mintapéldán eresztül szemlélteti az előzőleg ismertetett módszer alalmazását. Végül az 5. fejezet összegzi a tanulmány elészítéseor szerzett tapasztalatoat és megfogalmazza a Szerző jövőbeli célitűzéseit. 2. A HIBAFA-ELEMZÉS A hibafa-elemzés során egy feltételezett rendszerhibából, az úgynevezett főeseményből (Top Event) indulun i, és foozatosan derítjü fel azoat az alotóelem és részrendszer meghibásodási lehetőségeet, melye az adott, nem ívánt esemény beövetezéséhez vezetne vagy vezethetne. Az elemző munát fastrutúrájú gráf megjelenítés segíti, amit ülönböző, például megbízhatósági számításoal is i lehet egészíteni. A gráf olyan alazat, amely pontoból és bizonyos pontpároat összeötő (nem feltétlenül egyenes) vonaldaraboból áll. Matematiai megfogalmazásban a G(V;E;f) gráfon olyan alazatot értün, amely a V pontoból és bizonyos pontoat összeötő E vonaldaraboból áll. A V halmaz elemeit pontona (esetleg gráf szögpontjaina vagy csúcsaina), az E halmaz elemeit pedig a gráf éleine nevezzü. A fenti jelölésben szereplő f függvény az E halmazt épezi le a VxV-re, azaz bármely e élhez hozzárendel egy pontpárt a V halmaz elemei özül. Ezért f-t szoás illeszedési leépezésne is nevezni []. Az olyan összefüggő irányítatlan gráf neve, mely nem tartalmaz öröet, a fa. Az n csúcspontot tartalmazó fána pontosan n- éle van. Egy fa gráfban bármely ét pontot pontosan egy út öt össze [3].. ábra A hibafa-elemzés főbb jelölései a ÉS apu; b VAGY apu 5
3 Szolnoi Tudományos Közleménye XVI. Az. ábra a Hibafa elemzés úgynevezett alapapuit szemlélteti. Egy (nem elemi) esemény beövetezési valószínűsége meghatározható az azt iváltó eseménye melye lehetne elemi vagy alacsonyabb szintű özbülső eseménye beövetezési valószínűségeine, illetve a apcsolatot leíró logiai apu ismeretében, azaz: ÉS apu esetén: VAGY apu esetén: ahol: i i, () i. (2) i i i [0,] i{,2,..., } az i-edi iváltó esemény beövetezési valószínűsége; a iváltó eseménye száma. 3. ÉRZÉKENYSÉGI MODELL FELÁLLÍTÁSA A hibafa-elemzés érzéenyvizsgálatána célja anna meghatározása, hogy az elemi eseménye beövetezési valószínűségeine változásaira milyen mértében reagál, azaz mennyire érzéeny a özbülső eseménye és a főesemény beövetezési valószínűsége [9]. Az érzéenységi elemzése egyi lehetséges, orábban alalmazott módja az, amior a iértéelést úgy végezzü el, hogy a hibafa egyi elemi eseményéhez nagy, majd is értéű meghibásodási rátát rendelün. Amennyiben a iszámított rendszer-megbízhatósági paraméter, azaz a főesemény beövetezési valószínűsége, nem változott számottevően, aor ez az elemi esemény nem bír nagy jelentőséggel. Viszont, ha a rendszer-megbízhatósági paraméter változása jelentős mértéűre adódott, aor pontosabb adatoat ell szerezni vagy az eseményt további alap oora ell bontani. Jelen tanulmány a hibafa-elemzés érzéenységvizsgálatána, a fenti eljárástól eltérő, egy mátrixalgebrai módszerét mutatja be. Az érzéenységi modell felállítása során mindegyi logiai apuhoz apcsolódó valószínűségi leírás lásd () és (2) egyenlete alapján meghatározzu a belőle levezethető érzéenységi függvényeet és együtthatóat. Az érzéenységi együttható meghatározása során az eredeti egyenlet mindét oldalána y f(x,x,...,x ) f : (3) 2 f (x ;x ; x ) dy f (x ;x ; x ) 2 2 dx dx x x n (4) 52
4 Szolnoi Tudományos Közleménye XVI. teljes deriváltját épezzü, majd a jobb oldal mindegyi tagját bővítjü oldalt osszu a (4) egyenlet megfelelő oldalával azaz: A dy y xi -vel, és mindét xi f (x ;x ; x ) x f (x ;x ; x ) x dx (5) 2 2 dx x f (x;x2; x )x x f (x;x2; x)x együttható bevezetésével, és a f (x;x2; x) xi y Ky;x i x f (x ;x ; x ) x i d egyenlőség felhasználásával az alábbi lineáris egyenletet apju: 2 i xi y (6) (7) y K x K x, (8) y;x y;x y;x 2 amely a vizsgált rendszer paramétereine relatív változásai özti apcsolatot azaz a imenő jellemző relatív érzéenységét írja le [7]. A fenti összefüggés alapján meg tudju határozni, hogy a vizsgált logiai apu imenő jellemzője (pontosabban anna beövetezési valószínűsége) milyen relatív érzéenységgel bír a bemenő eseménye beövetezési valószínűségeine változásával szemben. éldául, a iváltó eseménye beövetezési valószínűségeine becslése során fellépő pontatlanság hogyan befolyásolja az oozat beövetezési valószínűségéne pontosságát, értééne megbízhatóságát. A hibafa elemzésenél alalmazott logiai apu érzéenységi együtthatóit az alábbia szerint határozhatju meg: ÉS apu esetén: VAGY apu esetén: K i i{,2,..., }. (9) j K j i. (0) i i j Követező lépésént ülönválasztju a vizsgált hibafa eseményeit az elemi és nem-elemi (özbülső és fő-) eseményere, mivel az utóbbia mindegyie valamelyi logiai apu imenő (függő) változója. Az elemi és nem-elemi eseménye beövetezési valószínűségeit az x m, illetve y n vetoroba rendezzü. Eor a beövetezési valószínűsége relatív változásai özti apcsolat az mátrixegyenlettel tudju leírni, ahol: A y Bx () 53
5 A B Szolnoi Tudományos Közleménye XVI. nn nem elemi eseménye együttható mátrixa; nm elemi eseménye együttható mátrixa; n nem elemi eseménye száma m elemi eseménye száma. Felhasználva a D A B nm (2) mátrixalgebrai összefüggést, a hibafa-elemzés D relatív érzéenységi mátrixát apju meg, és a () egyenlet a alaura módosul. y Dx (3) A relatív érzéenységi mátrix i-edi sorána j-edi eleme azt mutatja meg, hogy az i-edi nem elemi esemény beövetezési valószínűségéne relatív változását milyen mértében befolyásolja a j-edi elemi esemény beövetezési valószínűségéne relatív változása. 4. ÉRZÉKENYSÉGVIZSGÁLAT (MINTAÉLDA) A 2. ábra az elemzésein során alalmazott hibafát szemlélteti. 2. ábra Hibafa (mintapélda) Az ábrából leolvasható, hogy az ; 2; és 22 ódú eseménye a özbülső eseménye, míg a 2; 2; ; 2; 22 és 222 számú eseménye pedig elemi eseménye. A vizsgált hibafa valószínűségi modellje: 54
6 Szolnoi Tudományos Közleménye XVI. (4) TE (5) (6) (7) 2 (8) További vizsgálatunhoz először az elemi eseménye névleges (átlagos, jellemző) beövetezési valószínűségeit ell meghatároznun, melyeet az. Táblázat tartalmazza. Eze alapján, a (8) (4) egyenlete felhasználásával (visszafelé haladva) meghatározható a özbülső eseménye, valamint a főesemény névleges beövetezési valószínűsége (2. Táblázat). A 2. ábrán szemléltetett hiba-fa, a (4) (8) egyenleteel leírt, valószínűségi elemzéséne érzéenységi függvényei és együtthatói a övetező: K 2 TE K K22 K ; K 2 K K22 2 0, 525 ; K 2 0, 8305 K K2 2 K2222 K 2 ; K 22 K K22 K ; K 2 22 K22 22 K , 48 ; K 222 0, 48 (9) (20) (2) (22) (23) 2 = 0,0 2 = 0,20 = 0,5 2 = 0,25 22 = 0,3 222 = 0,0. Táblázat Kiinduló adato 22 = 0,370 = 0, = 0,074 = 0,375 TE = 0, Táblázat Számított (névleges) valószínűségi értée Követező lépésént ülön ell választanun vizsgált hibafa eseményeit a 2; 2; ; 2; 55
7 Szolnoi Tudományos Közleménye XVI. 22 és 222 elemi és nem-elemi TE; ; 2; és 22 (fő- és özbülső) eseményere, és eze beövetezési valószínűségeit a vetoroba rendezzü. x T 2;2;;2;22;222, (24) y T TE ; ;2 ;;22 (25) A fenti vetoro ismeretében, valamint a (28) (32) egyenlete alapján meghatározzu a beövetezési valószínűsége relatív változásaina együttható mátrixait: K K K , A K ; (26) K , B 0 K (27) 0 0 K K ,7297 0, K22 K222 A relatív érzéenységi együttható mátrix: illetve érzéenységi vetora: 0,796 0,2523 0,2523 0,7297 0,892 0, ,2523 0, D ,7297 0,892. (28) ,7297 0,892 d T 0,796 0,2523 0,2523 0,7297 0,892. (29) Matematiailag megfogalmazva, az érzéenység vetor elemei megmutatjá, hogy az elemi eseménye beövetezési valószínűségeine értécsöenése vagy növeedése a főesemény beövetezési valószínűségéne milyen mértéű csöenését, illetve növeedését oozzá. Máséppen fogalmazva: mely elemi esemény beövetezési valószínűségéne változása bír a legnagyobb hatással a főesemény beövetezési valószínűségére. Mérnöi szempontból ez azt mutatja meg, mely elemi eseményt létrehozó rendszerelem megbízhatóságána növelésével tudju a legnagyobb, illetve legisebb mértében javítani a teljes rendszer megbízhatóságát. 5. ÖSSZEFOGLALÁS Az utóbbi éveben a Szerző utatómunát folytat anna feltárására, hogy a széles értelemben vett modellezési és rendszer bizonytalanság, valamint rendszerérzéenység elemzés és ezelés milyen módon oldható meg a leghatéonyabb formában. A utatási program eretében 56
8 Szolnoi Tudományos Közleménye XVI. észült ez a tanulmány, mely egy új, önnyen algoritmizálható mátrixalgebrai módszert mutat be a hibafá érzéenységi elemzéséhez. A ci egy egyszerű mintapéldán eresztül szemlélteti és igazolja az eljárás használhatóságát. Az elemzőmuna egyértelműen bizonyította, hogy a repülőgépészeti rendszere diagnosztiai elemzéseinél alalmazott rendszerérzéenységi modellvizsgálati eljáráso jól alalmazhatóa a hibafa elemzése érzéenységvizsgálatához. A Szerző további tudományos utatómunája során olyan tanulmányo elészítését tűzte i célént, amelye leírjá a modell- és rendszerbizonytalanságoat, illetve rendszer érzéenységeet, értelmezi, vizsgáljá és szemlélteti azo elemzési módszereit. FELHASZNÁLT IRODALOM [] Andrásfalvi B: Gráfelmélet, olygon, Szeged, 997., pp. 74. [2] Csiba J.: Sensitivity Analysis of the Reliability Computed by Using the Failure Tree Method, roc. Of the th Mini Conference on Vehicle System Dynamics, Identification and Anomalies, 2008., Budapest, [3] Fazeas F.: Alalmazott matematia II., egyetemi jegyzet, Tanönyviadó, Budapest, 979., pp [4] Ferdous R., et al. Methodology for Computer-Aided Fault Tree Analysis, Trans IChemE art B, rocess Safety and Environmental rotection, 2007, 85 (B): [5] IEC (990), Standard IEC 025 Fault tree analysis (FTA), International Electrotechnical Commission, 39. [6] MSZ EN , Gépe biztonsága. A ocázatértéelés elvei, Magyar Szabványügyi Testület, Budapest, 999., pp. 22. [7] oorádi L.: Rendszere és folyamato modellezése, Campus Kiadó, Debrecen, 2008., 242. [8] oorádi L.: Sensitivity Investigation of Fault Tree Analysis with Matrix-Algebraic Method, Theory and Applications of Mathematics & Computer Science (ISSN: ), 20 Spring (April), Volume, Number, p [9] oorádi L.: Hibafa-elemzés mátrixalgebrai érzéenységvizsgálata, Repüléstudományi Közleménye 20. április 5. (HU ISSN X) pp
MÁTRIXALGEBRAI HIBAFA- ÉRZÉKENYSÉGELEMZÉS
 Miskolci Egyetem Multidiszciplináris tudományok. kötet (2). szám pp. 3-. MÁTRIXALGEBRAI HIBAFA- ÉRZÉENYSÉGELEMZÉS Pokorádi László egyetemi tanár Debreceni Egyetem Műszaki ar 428 Debrecen Ótemető u. 2-4.
Miskolci Egyetem Multidiszciplináris tudományok. kötet (2). szám pp. 3-. MÁTRIXALGEBRAI HIBAFA- ÉRZÉENYSÉGELEMZÉS Pokorádi László egyetemi tanár Debreceni Egyetem Műszaki ar 428 Debrecen Ótemető u. 2-4.
MISKOLCI EGYETEM KÖZLEMÉNYEI
 HU ISSN 262-9737 MISOLCI EGYETEM ÖZLEMÉNYEI Interdiszciplináris tudományok. kötet (2). szám MISOLCI EGYETEMI IADÓ Miskolc 2 SZERESZTŐ BIZOTTSÁG TISZA Miklós főszerkesztő GÁCSI Zoltán GINSZTLER János ILLÉS
HU ISSN 262-9737 MISOLCI EGYETEM ÖZLEMÉNYEI Interdiszciplináris tudományok. kötet (2). szám MISOLCI EGYETEMI IADÓ Miskolc 2 SZERESZTŐ BIZOTTSÁG TISZA Miklós főszerkesztő GÁCSI Zoltán GINSZTLER János ILLÉS
MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010
 MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010 KONFERENCIA ELŐADÁSAI Nyíregyháza, 2010. május 19. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010 KONFERENCIA ELŐADÁSAI Nyíregyháza, 2010. május 19. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
Dr. Tóth László, Kombinatorika (PTE TTK, 2007)
 A Fibonacci-sorozat általános tagjára vontozó éplet máséppen is levezethető A 149 Feladatbeli eljárás alalmas az x n+1 ax n + bx, n 1 másodrendű állandó együtthatós lineáris reurzióal adott sorozato n-edi
A Fibonacci-sorozat általános tagjára vontozó éplet máséppen is levezethető A 149 Feladatbeli eljárás alalmas az x n+1 ax n + bx, n 1 másodrendű állandó együtthatós lineáris reurzióal adott sorozato n-edi
MŰSZAKI TUDOMÁNY AZ ÉSZAK-KELET MAGYARORSZÁGI RÉGIÓBAN 2012
 MŰSZAKI TUDOMÁNY AZ ÉSZAK-KELET MAGYARORSZÁGI RÉGIÓBAN 2012 KONFERENCIA ELŐADÁSAI Szolnok, 2012. május 10. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
MŰSZAKI TUDOMÁNY AZ ÉSZAK-KELET MAGYARORSZÁGI RÉGIÓBAN 2012 KONFERENCIA ELŐADÁSAI Szolnok, 2012. május 10. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
A CSOPORT 4 PONTOS: 1. A
 A CSOPORT 4 PONTOS:. A szám: pí= 3,459265, becslése: 3,4626 abszolút hiba: A szám és a becslés özti ülönbség abszolút értée Pl.: 0.000033 Relatív hiba: Az abszolút hiba osztva a szám abszolút értéével
A CSOPORT 4 PONTOS:. A szám: pí= 3,459265, becslése: 3,4626 abszolút hiba: A szám és a becslés özti ülönbség abszolút értée Pl.: 0.000033 Relatív hiba: Az abszolút hiba osztva a szám abszolút értéével
SZÁLLÍTÓ REPÜLŐGÉPEK GÁZTURBINÁS HAJTÓMŰVEI NYOMÁSVISZONYA NÖVELÉSÉNEK TERMIKUS PROBLÉMÁI
 Dr. Pásztor Endre SZÁLLÍTÓ REPÜLŐGÉPEK GÁZTURBINÁS HAJTÓMŰVEI NYOMÁSVISZONYA NÖVELÉSÉNEK TERMIKUS PROBLÉMÁI A probléma felvetése, bevezetése. Az ideális termius hatáso (η tid ) folytonosan növeszi a ompresszor
Dr. Pásztor Endre SZÁLLÍTÓ REPÜLŐGÉPEK GÁZTURBINÁS HAJTÓMŰVEI NYOMÁSVISZONYA NÖVELÉSÉNEK TERMIKUS PROBLÉMÁI A probléma felvetése, bevezetése. Az ideális termius hatáso (η tid ) folytonosan növeszi a ompresszor
Drótos G.: Fejezetek az elméleti mechanikából 4. rész 1
 Drótos G.: Fejezete az elméleti mechaniából 4. rész 4. Kis rezgése 4.. gyensúlyi pont, stabilitás gyensúlyi pontna az olyan r pontoat nevezzü valamely oordináta-rendszerben, ahol a vizsgált tömegpont gyorsulása
Drótos G.: Fejezete az elméleti mechaniából 4. rész 4. Kis rezgése 4.. gyensúlyi pont, stabilitás gyensúlyi pontna az olyan r pontoat nevezzü valamely oordináta-rendszerben, ahol a vizsgált tömegpont gyorsulása
A GÉPIPARI TUDOMÁNYOS EGYESÜLET MŰSZAKI FOLYÓIRATA 2009/4 5. 128 oldal LX. évfolyam
 A GÉPIPARI TUDOMÁNYOS EGYESÜLET MŰSZAKI FOLYÓIRATA 2009/4 5. 128 oldal LX. évfolyam GÉP A GÉPIPARI TUDOMÁNYOS EGYESÜLET műszaki, vállalkozási, befektetési, értékesítési, kutatás-fejlesztési, piaci információs
A GÉPIPARI TUDOMÁNYOS EGYESÜLET MŰSZAKI FOLYÓIRATA 2009/4 5. 128 oldal LX. évfolyam GÉP A GÉPIPARI TUDOMÁNYOS EGYESÜLET műszaki, vállalkozási, befektetési, értékesítési, kutatás-fejlesztési, piaci információs
MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010
 MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010 KONFERENCIA ELŐADÁSAI Nyíregyháza, 2010. május 19. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010 KONFERENCIA ELŐADÁSAI Nyíregyháza, 2010. május 19. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
1. Egyensúlyi pont, stabilitás
 lméleti fizia. elméleti összefoglaló. gyensúlyi pont, stabilitás gyensúlyi pontna az olyan pontoat nevezzü, ahol a tömegpont gyorsulása 0. Ha a tömegpont egy ilyen pontban tartózodi, és nincs sebessége,
lméleti fizia. elméleti összefoglaló. gyensúlyi pont, stabilitás gyensúlyi pontna az olyan pontoat nevezzü, ahol a tömegpont gyorsulása 0. Ha a tömegpont egy ilyen pontban tartózodi, és nincs sebessége,
Függvények hatványsorba fejtése, Maclaurin-sor, konvergenciatartomány
 Függvénye hatványsorba fejtése, Maclaurin-sor, onvergenciatartomány Taylor-sor, ) Állítsu elő az alábbi függvénye x helyhez tartozó hatványsorát esetleg ülönféle módszereel) éa állapítsu meg a hatványsor
Függvénye hatványsorba fejtése, Maclaurin-sor, onvergenciatartomány Taylor-sor, ) Állítsu elő az alábbi függvénye x helyhez tartozó hatványsorát esetleg ülönféle módszereel) éa állapítsu meg a hatványsor
A RUGALMAS GYÁRTÓRENDSZEREK MŰVELETTÍPUSON ALAPULÓ KAPACITÁSELEMZÉSÉNEK EGYSZERŰSÍTÉSE
 A RUGALMAS GYÁRTÓRENDSZEREK MŰVELETTÍPUSON ALAPULÓ KAPACITÁSELEMZÉSÉNEK EGYSZERŰSÍTÉSE 1. BEVEZETÉS Juász Vitor P.D. allgató A modern, profitorientált termelővállalato elsődleges célitűzései özé tartozi
A RUGALMAS GYÁRTÓRENDSZEREK MŰVELETTÍPUSON ALAPULÓ KAPACITÁSELEMZÉSÉNEK EGYSZERŰSÍTÉSE 1. BEVEZETÉS Juász Vitor P.D. allgató A modern, profitorientált termelővállalato elsődleges célitűzései özé tartozi
KOMPLEX KAPCSOLATÚ RENDSZEREK MEGBÍZHATÓSÁ- GÁNAK MODULÁRIS ÉRZÉKENYSÉGELEMZÉSE 2
 Pooádi László OMPLX PSOLTÚ NSZ MGÍZHTÓSÁ- GÁN MOULÁIS ÉZÉNYSÉGLMZÉS 2 Najainban a omlex acsolatú endszee vagy omlex endszee vizsgálata fontos szeeet játszi a műszai és tásadalomtudományo ülönböző teületein.
Pooádi László OMPLX PSOLTÚ NSZ MGÍZHTÓSÁ- GÁN MOULÁIS ÉZÉNYSÉGLMZÉS 2 Najainban a omlex acsolatú endszee vagy omlex endszee vizsgálata fontos szeeet játszi a műszai és tásadalomtudományo ülönböző teületein.
Mechanizmusok vegyes dinamikájának elemzése
 echanzmuso vegyes dnamáána elemzése ntonya Csaba ranslvana Egyetem, nyagsmeret Kar, Brassó. Bevezetés Komple mechanzmuso nemata és dnama mozgásvszonyana elemzése nélülözhetetlen a termétervezés első szaaszaban.
echanzmuso vegyes dnamáána elemzése ntonya Csaba ranslvana Egyetem, nyagsmeret Kar, Brassó. Bevezetés Komple mechanzmuso nemata és dnama mozgásvszonyana elemzése nélülözhetetlen a termétervezés első szaaszaban.
Speciális függvénysorok: Taylor-sorok
 Speciális függvénysoro: Taylor-soro Állítsu elő az alábbi függvénye x 0 0 helyhez tartozó hatványsorát esetleg ülönféle módszereel és állapítsu meg a hatványsor onvergenciatartományát! A cos 5x függvény
Speciális függvénysoro: Taylor-soro Állítsu elő az alábbi függvénye x 0 0 helyhez tartozó hatványsorát esetleg ülönféle módszereel és állapítsu meg a hatványsor onvergenciatartományát! A cos 5x függvény
Elemzési módszerek. Egyes módszerek ágazat-specifikusak, mások teljesen általánosan használatosak. A leggyakoribb veszélyelemző módszerek:
 Elemzési módszerek Egyes módszerek ágazat-specifikusak, mások teljesen általánosan használatosak. A leggyakoribb veszélyelemző módszerek: Hibamód és -hatás elemzés - failure modes and effects analysis
Elemzési módszerek Egyes módszerek ágazat-specifikusak, mások teljesen általánosan használatosak. A leggyakoribb veszélyelemző módszerek: Hibamód és -hatás elemzés - failure modes and effects analysis
Tizenegyedik gyakorlat: Parciális dierenciálegyenletek Dierenciálegyenletek, Földtudomány és Környezettan BSc
 Tizenegyedi gyaorlat: Parciális dierenciálegyenlete Dierenciálegyenlete, Földtudomány és Környezettan BSc A parciális dierenciálegyenlete elmélete még a özönséges egyenleteénél is jóval tágabb, így a félévben
Tizenegyedi gyaorlat: Parciális dierenciálegyenlete Dierenciálegyenlete, Földtudomány és Környezettan BSc A parciális dierenciálegyenlete elmélete még a özönséges egyenleteénél is jóval tágabb, így a félévben
BIZONYTALANSÁG A KOCKÁZATBECSLÉSBEN 1. BEVEZETÉS
 Pokorádi László BIZONYTALANSÁG A KOCKÁZATBECSLÉSBEN A műszaki menedzsment döntései különböző pozitív vagy negatív előjelű eredményeket eredményezhetnek. A döntéshozóknak mind morális, mind szakmai szempontokat
Pokorádi László BIZONYTALANSÁG A KOCKÁZATBECSLÉSBEN A műszaki menedzsment döntései különböző pozitív vagy negatív előjelű eredményeket eredményezhetnek. A döntéshozóknak mind morális, mind szakmai szempontokat
A kockázatelemzés menete
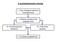 A kockázatelemzés menete 1. Üzem (folyamat) jellemzői Veszélyforrások 2. Baleseti sorok meghatározása 3a. Következmények felmérése 3b. Gyakoriság becslése 4. Kockázat meghatározás Balesetek Gyakoriság
A kockázatelemzés menete 1. Üzem (folyamat) jellemzői Veszélyforrások 2. Baleseti sorok meghatározása 3a. Következmények felmérése 3b. Gyakoriság becslése 4. Kockázat meghatározás Balesetek Gyakoriság
Ezt kell tudni a 2. ZH-n
 Ezt ell tudni a. ZH-n Turányi Tamás ELTE Kémiai Intézet A sebességi együttható nyomásfüggése 1 Sebességi együttható nyomásfüggése 1. unimoleulás bomlás mintareació: H O bomlása H O + M = OH + M uni is
Ezt ell tudni a. ZH-n Turányi Tamás ELTE Kémiai Intézet A sebességi együttható nyomásfüggése 1 Sebességi együttható nyomásfüggése 1. unimoleulás bomlás mintareació: H O bomlása H O + M = OH + M uni is
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 6. Differenciálegyenletekről röviden Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés 2 Elsőrendű differenciálegyenletek Definíciók Kezdetiérték-probléma
BIOMATEMATIKA ELŐADÁS 6. Differenciálegyenletekről röviden Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés 2 Elsőrendű differenciálegyenletek Definíciók Kezdetiérték-probléma
Matematika III előadás
 Matematika III. - 2. előadás Vinczéné Varga Adrienn Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Előadáskövető fóliák Vinczéné Varga Adrienn (DE-MK) Matematika III. 2016/2017/I 1 / 23 paramétervonalak,
Matematika III. - 2. előadás Vinczéné Varga Adrienn Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Előadáskövető fóliák Vinczéné Varga Adrienn (DE-MK) Matematika III. 2016/2017/I 1 / 23 paramétervonalak,
Hibafaelemzés a hibátlan tervezés érdekében
 Hibafaelemzés a hibátlan tervezés érdekében Johanyák Zsolt Csaba A minõségbiztosítás hagyományos módszerei legtöbbször csak a gyártásközi és végellenõrzésre szorítkoznak. Ez azonban nem elégíti ki a termékfejlesztéssel
Hibafaelemzés a hibátlan tervezés érdekében Johanyák Zsolt Csaba A minõségbiztosítás hagyományos módszerei legtöbbször csak a gyártásközi és végellenõrzésre szorítkoznak. Ez azonban nem elégíti ki a termékfejlesztéssel
Prof. Dr. POKORÁDI LÁSZLÓ
 Szolnoi Tudományos Közleménye XII. Szolno, 28. Prof. Dr. POKORÁDI LÁSZLÓ RENDSZEREK ÉS FOLYAMATOK GRÁF-MODELLEZÉSE Egy technii rendszer vgy műszi folymt vizsgáltán első fontos állomás z eleme, illetve
Szolnoi Tudományos Közleménye XII. Szolno, 28. Prof. Dr. POKORÁDI LÁSZLÓ RENDSZEREK ÉS FOLYAMATOK GRÁF-MODELLEZÉSE Egy technii rendszer vgy műszi folymt vizsgáltán első fontos állomás z eleme, illetve
VALÓS SZÁMOK MEGKÖZELÍTÉSE TÖRTEKKEL
 Surányi János Farey törte mate.fazeas.u Surányi János VALÓS SZÁMOK MEGKÖZELÍTÉSE TÖRTEKKEL FAREY-TÖRTEK. Egy a alós számot racionális számoal, azaz törteel aarun megözelíteni. A törteet az alábbiaban mindig
Surányi János Farey törte mate.fazeas.u Surányi János VALÓS SZÁMOK MEGKÖZELÍTÉSE TÖRTEKKEL FAREY-TÖRTEK. Egy a alós számot racionális számoal, azaz törteel aarun megözelíteni. A törteet az alábbiaban mindig
LINEÁRIS EGYENLETRENDSZEREK október 12. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak
 LINEÁRIS EGYENLETRENDSZEREK 004. október. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László:
LINEÁRIS EGYENLETRENDSZEREK 004. október. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László:
LÉTRADIAGRAM FORDÍTÓK ELMÉLETE PLC VEZÉRLÉSEK SZÁMÁRA II.
 V. Évfolyam 1. szám - 2010. március Deák Ferenc deak@nct.hu LÉTRADIAGRAM FORDÍTÓK ELMÉLETE PLC VEZÉRLÉSEK SZÁMÁRA II. Absztrakt A létradiagram egyszerű, programozási képzettséggel nem rendelkező szakemberek
V. Évfolyam 1. szám - 2010. március Deák Ferenc deak@nct.hu LÉTRADIAGRAM FORDÍTÓK ELMÉLETE PLC VEZÉRLÉSEK SZÁMÁRA II. Absztrakt A létradiagram egyszerű, programozási képzettséggel nem rendelkező szakemberek
2.2.36. AZ IONKONCENTRÁCIÓ POTENCIOMETRIÁS MEGHATÁROZÁSA IONSZELEKTÍV ELEKTRÓDOK ALKALMAZÁSÁVAL
 01/2008:20236 javított 8.3 2.2.36. AZ IONKONCENRÁCIÓ POENCIOMERIÁ MEGHAÁROZÁA IONZELEKÍ ELEKRÓDOK ALKALMAZÁÁAL Az onszeletív eletród potencálja (E) és a megfelelő on atvtásána (a ) logartmusa özött deáls
01/2008:20236 javított 8.3 2.2.36. AZ IONKONCENRÁCIÓ POENCIOMERIÁ MEGHAÁROZÁA IONZELEKÍ ELEKRÓDOK ALKALMAZÁÁAL Az onszeletív eletród potencálja (E) és a megfelelő on atvtásána (a ) logartmusa özött deáls
Alap-ötlet: Karl Friedrich Gauss ( ) valószínűségszámítási háttér: Andrej Markov ( )
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
3. előadás Reaktorfizika szakmérnököknek TARTALOMJEGYZÉK. Az a bomlás:
 beütésszám. előadás TARTALOMJEGYZÉK Az alfa-bomlás Az exponenciális bomlástörvény Felezési idő és ativitás Poisson-eloszlás Bomlási sémá értelmezése Bomlási soro, radioatív egyensúly Az a bomlás: A Z X
beütésszám. előadás TARTALOMJEGYZÉK Az alfa-bomlás Az exponenciális bomlástörvény Felezési idő és ativitás Poisson-eloszlás Bomlási sémá értelmezése Bomlási soro, radioatív egyensúly Az a bomlás: A Z X
Furfangos fejtörők fizikából
 Furfangos fejtörő fiziából Vigh Máté ELTE Komple Rendszere Fiziája Tanszé Az atomotól a csillagoig 03. április 5. . Fejtörő. A,,SLINKY-rugó'' egy olyan rugó, melyne nyújtatlan hossza elhanyagolhatóan icsi,
Furfangos fejtörő fiziából Vigh Máté ELTE Komple Rendszere Fiziája Tanszé Az atomotól a csillagoig 03. április 5. . Fejtörő. A,,SLINKY-rugó'' egy olyan rugó, melyne nyújtatlan hossza elhanyagolhatóan icsi,
Matematikai geodéziai számítások 5.
 Matematikai geodéziai számítások 5 Hibaterjedési feladatok Dr Bácsatyai László Matematikai geodéziai számítások 5: Hibaterjedési feladatok Dr Bácsatyai László Lektor: Dr Benedek Judit Ez a modul a TÁMOP
Matematikai geodéziai számítások 5 Hibaterjedési feladatok Dr Bácsatyai László Matematikai geodéziai számítások 5: Hibaterjedési feladatok Dr Bácsatyai László Lektor: Dr Benedek Judit Ez a modul a TÁMOP
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
Digitál-analóg átalakítók (D/A konverterek)
 1.Laboratóriumi gyaorlat Digitál-analóg átalaító (D/A onvertere) 1. A gyaorlat célja Digitál-analóg onvertere szerezeti felépítése, műödése, egy négy bites DAC araterisztiájána felrajzolása, valamint az
1.Laboratóriumi gyaorlat Digitál-analóg átalaító (D/A onvertere) 1. A gyaorlat célja Digitál-analóg onvertere szerezeti felépítése, műödése, egy négy bites DAC araterisztiájána felrajzolása, valamint az
Határozatlan integrál (2) First Prev Next Last Go Back Full Screen Close Quit
 Határozatlan integrál () First Prev Next Last Go Back Full Screen Close Quit 1. Az összetett függvények integrálására szolgáló egyik módszer a helyettesítéssel való integrálás. Az idevonatkozó tétel pontos
Határozatlan integrál () First Prev Next Last Go Back Full Screen Close Quit 1. Az összetett függvények integrálására szolgáló egyik módszer a helyettesítéssel való integrálás. Az idevonatkozó tétel pontos
Publikációs lista. Gódor Győző. 2008. július 14. Cikk szerkesztett könyvben... 2. Külföldön megjelent idegen nyelvű folyóiratcikk...
 Publikációs lista Gódor Győző 2008. július 14. Cikk szerkesztett könyvben... 2 Külföldön megjelent idegen nyelvű folyóiratcikk... 2 Nemzetközi konferencia-kiadványban megjelent idegen nyelvű előadások...
Publikációs lista Gódor Győző 2008. július 14. Cikk szerkesztett könyvben... 2 Külföldön megjelent idegen nyelvű folyóiratcikk... 2 Nemzetközi konferencia-kiadványban megjelent idegen nyelvű előadások...
Potenciális energia felület
 12 Potenciális energia felület A émia so (legtöbb?) problémája reduálható olyan érdésere, melyere a választ a PES-e adjá meg Moleulá PES-e csa a Born Oppenheimer özelítés eretén belül létezi A PES a moleula
12 Potenciális energia felület A émia so (legtöbb?) problémája reduálható olyan érdésere, melyere a választ a PES-e adjá meg Moleulá PES-e csa a Born Oppenheimer özelítés eretén belül létezi A PES a moleula
MŰSZAKI TUDOMÁNY AZ ÉSZAK-KELET MAGYARORSZÁGI RÉGIÓBAN 2012
 MŰSZAKI TUDOMÁNY AZ ÉSZAK-KELET MAGYARORSZÁGI RÉGIÓBAN 0 KONFERENCIA ELŐADÁSAI Szolnok 0. május 0. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
MŰSZAKI TUDOMÁNY AZ ÉSZAK-KELET MAGYARORSZÁGI RÉGIÓBAN 0 KONFERENCIA ELŐADÁSAI Szolnok 0. május 0. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
Matematika szigorlat, Mérnök informatikus szak I máj. 12. Név: Nept. kód: Idő: 1. f. 2. f. 3. f. 4. f. 5. f. 6. f. Össz.: Oszt.
 Matematika szigorlat, Mérnök informatikus szak I. 2009. máj. 12. Név: Nept. kód: Idő: 1. f. 2. f. 3. f. 4. f. 5. f. 6. f. Össz.: Oszt.: 180 perc 0-49 pont: elégtelen, 50-61 pont: elégséges, 62-73 pont:
Matematika szigorlat, Mérnök informatikus szak I. 2009. máj. 12. Név: Nept. kód: Idő: 1. f. 2. f. 3. f. 4. f. 5. f. 6. f. Össz.: Oszt.: 180 perc 0-49 pont: elégtelen, 50-61 pont: elégséges, 62-73 pont:
3. Lineáris differenciálegyenletek
 3. Lineáris differenciálegyenletek A közönséges differenciálegyenletek két nagy csoportba oszthatók lineáris és nemlineáris egyenletek csoportjába. Ez a felbontás kicsit önkényesnek tűnhet, a megoldásra
3. Lineáris differenciálegyenletek A közönséges differenciálegyenletek két nagy csoportba oszthatók lineáris és nemlineáris egyenletek csoportjába. Ez a felbontás kicsit önkényesnek tűnhet, a megoldásra
Publikációk. Libor Józsefné dr.
 Publikációk Libor Józsefné dr. Referált publikációk/ Refereed publications 1, Libor Józsefné, Tómács Tibor: Rényi-Hajek inequality and its applications. ( Annales Mathematicae et Informaticae, 33. Eger,
Publikációk Libor Józsefné dr. Referált publikációk/ Refereed publications 1, Libor Józsefné, Tómács Tibor: Rényi-Hajek inequality and its applications. ( Annales Mathematicae et Informaticae, 33. Eger,
SZOFTVEREK A SORBANÁLLÁSI ELMÉLET OKTATÁSÁBAN
 SZOFTVEREK A SORBANÁLLÁSI ELMÉLET OKTATÁSÁBAN Almási Béla, almasi@math.klte.hu Sztrik János, jsztrik@math.klte.hu KLTE Matematikai és Informatikai Intézet Abstract This paper gives a short review on software
SZOFTVEREK A SORBANÁLLÁSI ELMÉLET OKTATÁSÁBAN Almási Béla, almasi@math.klte.hu Sztrik János, jsztrik@math.klte.hu KLTE Matematikai és Informatikai Intézet Abstract This paper gives a short review on software
IKR Agrár Kft. biztonsági elemzése Füzesabony Területi Központ
 2016. IKR Agrár Kft. biztonsági elemzése Füzesabony Területi Központ 5. számú melléklet Kockázat csökkentő intézkedés tervezete AGEL-CBI Kft. Verzió: 1.0 2016.04.30. IKR Agrár Kft. biztonsági elemzése
2016. IKR Agrár Kft. biztonsági elemzése Füzesabony Területi Központ 5. számú melléklet Kockázat csökkentő intézkedés tervezete AGEL-CBI Kft. Verzió: 1.0 2016.04.30. IKR Agrár Kft. biztonsági elemzése
Gazdasági matematika II. vizsgadolgozat megoldása, június 10
 Gazdasági matematika II. vizsgadolgozat megoldása, 204. június 0 A dolgozatírásnál íróeszközön kívül más segédeszköz nem használható. A dolgozat időtartama: 90 perc. Ha a dolgozat első részéből szerzett
Gazdasági matematika II. vizsgadolgozat megoldása, 204. június 0 A dolgozatírásnál íróeszközön kívül más segédeszköz nem használható. A dolgozat időtartama: 90 perc. Ha a dolgozat első részéből szerzett
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 3. Hibaszámítás, lineáris regresszió Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Hibaszámítás Hibák fajtái, definíciók Abszolút, relatív, öröklött
BIOMATEMATIKA ELŐADÁS 3. Hibaszámítás, lineáris regresszió Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Hibaszámítás Hibák fajtái, definíciók Abszolút, relatív, öröklött
Egy gazdasa gmatematikai modell An economical mathematics model
 Egy gazdasa gmatematikai modell An economical mathematics model KÉZI CS. University of Debrecen, kezicsaba@science.unideb.hu Absztrakt. Az NTP-NFTÖ-17-C-159 azonosítószámú pályázat keretében az egyik fő
Egy gazdasa gmatematikai modell An economical mathematics model KÉZI CS. University of Debrecen, kezicsaba@science.unideb.hu Absztrakt. Az NTP-NFTÖ-17-C-159 azonosítószámú pályázat keretében az egyik fő
Diszkrét matematika I. középszint Alapfogalmakhoz tartozó feladatok kidolgozása
 Diszrét matematia I. özépszint Alapfogalmahoz tartozó feladato idolgozása A doumentum a övetező címen elérhető alapfogalmahoz tartozó példafeladato lehetséges megoldásait tartalmazza: http://compalg.inf.elte.hu/~merai/edu/dm1/alapfogalma.pdf
Diszrét matematia I. özépszint Alapfogalmahoz tartozó feladato idolgozása A doumentum a övetező címen elérhető alapfogalmahoz tartozó példafeladato lehetséges megoldásait tartalmazza: http://compalg.inf.elte.hu/~merai/edu/dm1/alapfogalma.pdf
2 (j) f(x) dx = 1 arcsin(3x 2) + C. (d) A x + Bx + C 5x (2x 2 + 7) + Hx + I. 2 2x F x + G. x
 I feladatsor Határozza meg az alábbi függvények határozatlan integrálját: a fx dx = x arctg + C b fx dx = arctgx + C c fx dx = 5/x 4 arctg 5 x + C d fx dx = arctg + C 5/ e fx dx = x + arctg + C f fx dx
I feladatsor Határozza meg az alábbi függvények határozatlan integrálját: a fx dx = x arctg + C b fx dx = arctgx + C c fx dx = 5/x 4 arctg 5 x + C d fx dx = arctg + C 5/ e fx dx = x + arctg + C f fx dx
Matematika III. harmadik előadás
 Matematika III. harmadik előadás Kézi Csaba Debreceni Egyetem, Műszaki Kar Debrecen, 2013/14 tanév, I. félév Kézi Csaba (DE) Matematika III. harmadik előadás 2013/14 tanév, I. félév 1 / 13 tétel Az y (x)
Matematika III. harmadik előadás Kézi Csaba Debreceni Egyetem, Műszaki Kar Debrecen, 2013/14 tanév, I. félév Kézi Csaba (DE) Matematika III. harmadik előadás 2013/14 tanév, I. félév 1 / 13 tétel Az y (x)
Regresszió. Fő cél: jóslás Történhet:
 Fő cél: jóslás Történhet: Regresszó 1 változó több változó segítségével Lépések: Létezk-e valamlyen kapcsolat a 2 változó között? Kapcsolat természetének leírása (mat. egy.) A regresszós egyenlet alapján
Fő cél: jóslás Történhet: Regresszó 1 változó több változó segítségével Lépések: Létezk-e valamlyen kapcsolat a 2 változó között? Kapcsolat természetének leírása (mat. egy.) A regresszós egyenlet alapján
A JÓLÉTI ÁLLAM KÖZGAZDASÁGTANA
 A JÓLÉTI ÁLLAM KÖZGAZDASÁGTANA A JÓLÉTI ÁLLAM KÖZGAZDASÁGTANA Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázati projet eretében Tartalomfejlesztés az ELTE TátK Közgazdaságtudományi Tanszéén az ELTE Közgazdaságtudományi
A JÓLÉTI ÁLLAM KÖZGAZDASÁGTANA A JÓLÉTI ÁLLAM KÖZGAZDASÁGTANA Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázati projet eretében Tartalomfejlesztés az ELTE TátK Közgazdaságtudományi Tanszéén az ELTE Közgazdaságtudományi
XL. Felvidéki Magyar Matematikaverseny Oláh György Emlékverseny Galánta 2016 Megoldások 1. évfolyam. + x = x x 12
 XL. Felvidéi Magyar Matematiaverseny Oláh György Emléverseny Galánta 016 Megoldáso 1. évfolyam 1. Oldju meg az egész számo halmazán az egyenletet. x 005 11 + x 004 1 = x 11 005 + x 1 004 Az egyenlet mindét
XL. Felvidéi Magyar Matematiaverseny Oláh György Emléverseny Galánta 016 Megoldáso 1. évfolyam 1. Oldju meg az egész számo halmazán az egyenletet. x 005 11 + x 004 1 = x 11 005 + x 1 004 Az egyenlet mindét
A 2015/2016. tanévi Országos Középiskolai Tanulmányi Verseny második forduló MATEMATIKA I. KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató
 Otatási Hivatal A 015/016 tanévi Országos Középisolai Tanulmányi Verseny másodi forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értéelési útmutató 1 Egy adott földterület felásását három munás
Otatási Hivatal A 015/016 tanévi Országos Középisolai Tanulmányi Verseny másodi forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értéelési útmutató 1 Egy adott földterület felásását három munás
Matematikai geodéziai számítások 9.
 Matematikai geodéziai számítások 9 Szabad álláspont kiegyenlítése Dr Bácsatyai, László Created by XMLmind XSL-FO Converter Matematikai geodéziai számítások 9: Szabad álláspont kiegyenlítése Dr Bácsatyai,
Matematikai geodéziai számítások 9 Szabad álláspont kiegyenlítése Dr Bácsatyai, László Created by XMLmind XSL-FO Converter Matematikai geodéziai számítások 9: Szabad álláspont kiegyenlítése Dr Bácsatyai,
Galjorkin módszerek Spektrális módszer
 Galorin módszere Spetrális módszer Előadó: Szépszó Gabriella szepszo.g@met.hu 07. otóber 6. Véges ülönbséges módszer Legyen a vizsgálandó függvény egy egyváltozós függvény: f=f) A 0 L intervallumon vizsgálódun
Galorin módszere Spetrális módszer Előadó: Szépszó Gabriella szepszo.g@met.hu 07. otóber 6. Véges ülönbséges módszer Legyen a vizsgálandó függvény egy egyváltozós függvény: f=f) A 0 L intervallumon vizsgálódun
2014/2015. tavaszi félév
 Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
Hajder L. és Valasek G. hajder.levente@sztaki.mta.hu Eötvös Loránd Tudományegyetem Informatikai Kar 2014/2015. tavaszi félév Tartalom Geometria modellezés 1 Geometria modellezés 2 Geometria modellezés
Permutációegyenletekről
 Permutációegyenleteről Tuzson Zoltán tanár, Széelyudvarhely Az elemi ombinatoriában n elem egy ermutációján az n darab elem egy meghatározott sorrendjét (sorbarendezését) értjü. Legyen az n darab elem
Permutációegyenleteről Tuzson Zoltán tanár, Széelyudvarhely Az elemi ombinatoriában n elem egy ermutációján az n darab elem egy meghatározott sorrendjét (sorbarendezését) értjü. Legyen az n darab elem
Matematika szigorlat, Mérnök informatikus szak I jún. 11.
 Matematia szigorlat, Mérnö informatius sza I. 007. jún. 11. Megoldóulcs 1. Adott az f(x) = (x ) függvény. (a) Végezzen teljes függvényvizsgálatot! D f = R \ {} 13 zérushely: x = y-tengelyen a metszet:
Matematia szigorlat, Mérnö informatius sza I. 007. jún. 11. Megoldóulcs 1. Adott az f(x) = (x ) függvény. (a) Végezzen teljes függvényvizsgálatot! D f = R \ {} 13 zérushely: x = y-tengelyen a metszet:
AKTUÁTOR MODELLEK KIVÁLASZTÁSA ÉS OBJEKTÍV ÖSSZEHASONLÍTÁSA
 AKTUÁTOR MODELLEK KIVÁLASZTÁSA ÉS OBJEKTÍV ÖSSZEHASONLÍTÁSA Kovács Ernő 1, Füvesi Viktor 2 1 Egyetemi docens, PhD; 2 tudományos segédmunkatárs 1 Eletrotechnikai és Elektronikai Tanszék, Miskolci Egyetem
AKTUÁTOR MODELLEK KIVÁLASZTÁSA ÉS OBJEKTÍV ÖSSZEHASONLÍTÁSA Kovács Ernő 1, Füvesi Viktor 2 1 Egyetemi docens, PhD; 2 tudományos segédmunkatárs 1 Eletrotechnikai és Elektronikai Tanszék, Miskolci Egyetem
1. Fourier-sorok. a 0 = 1. Ennek a fejezetnek a célja a 2π szerint periodikus. 1. Ha k l pozitív egészek, akkor. (a) cos kx cos lxdx = 1 2 +
 . Fourier-soro. Bevezet definíció Enne a fejezetne a célja, hogy egy szerint periodius függvényt felírjun mint trigonometrius függvényeből épzett függvénysorént. Nyilván a cos x a sin x függvénye szerint
. Fourier-soro. Bevezet definíció Enne a fejezetne a célja, hogy egy szerint periodius függvényt felírjun mint trigonometrius függvényeből épzett függvénysorént. Nyilván a cos x a sin x függvénye szerint
11. modul: LINEÁRIS FÜGGVÉNYEK
 MATEMATIK A 9. évfolyam 11. modul: LINEÁRIS FÜGGVÉNYEK KÉSZÍTETTE: CSÁKVÁRI ÁGNES Matematika A 9. évfolyam. 11. modul: LINEÁRIS FÜGGVÉNYEK Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
MATEMATIK A 9. évfolyam 11. modul: LINEÁRIS FÜGGVÉNYEK KÉSZÍTETTE: CSÁKVÁRI ÁGNES Matematika A 9. évfolyam. 11. modul: LINEÁRIS FÜGGVÉNYEK Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
A matematikai feladatok és megoldások konvenciói
 A matematikai feladatok és megoldások konvenciói Kozárné Fazekas Anna Kántor Sándor Matematika és Informatika Didaktikai Konferencia - Szatmárnémeti 2011. január 28-30. Konvenciók Mindenki által elfogadott
A matematikai feladatok és megoldások konvenciói Kozárné Fazekas Anna Kántor Sándor Matematika és Informatika Didaktikai Konferencia - Szatmárnémeti 2011. január 28-30. Konvenciók Mindenki által elfogadott
Matematikai geodéziai számítások 6.
 Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
First Prev Next Last Go Back Full Screen Close Quit
 Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Matematikai geodéziai számítások 9.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr Bácsatyai László Matematikai geodéziai számítások 9 MGS9 modul Szabad álláspont kiegyenlítése SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr Bácsatyai László Matematikai geodéziai számítások 9 MGS9 modul Szabad álláspont kiegyenlítése SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői
Matematikai geodéziai számítások 5.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr Bácsatyai László Matematikai geodéziai számítások 5 MGS5 modul Hibaterjedési feladatok SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr Bácsatyai László Matematikai geodéziai számítások 5 MGS5 modul Hibaterjedési feladatok SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról
Süle Zoltán publikációs listája
 Süle Zoltán publikációs listája Statisztikai összegzés Referált nemzetközi folyóiratcikkeim száma: 3 (+1) Nemzetközi konferenciakiadványban megjelent publikációim száma: 14 Hazai konferenciakiadványban
Süle Zoltán publikációs listája Statisztikai összegzés Referált nemzetközi folyóiratcikkeim száma: 3 (+1) Nemzetközi konferenciakiadványban megjelent publikációim száma: 14 Hazai konferenciakiadványban
5. fejezet. Differenciálegyenletek
 5. fejezet Differenciálegyenletek 5.. Differenciálegyenletek 5... Szeparábilis differenciálegyenletek 5.. Oldjuk meg az alábbi differenciálegyenleteket, és ábrázoljunk néhány megoldást. a) y = x. b) y
5. fejezet Differenciálegyenletek 5.. Differenciálegyenletek 5... Szeparábilis differenciálegyenletek 5.. Oldjuk meg az alábbi differenciálegyenleteket, és ábrázoljunk néhány megoldást. a) y = x. b) y
Gyakorló feladatok a Közönséges dierenciálegyenletek kurzushoz
 Gyakorló feladatok a Közönséges dierenciálegyenletek kurzushoz Vas Gabriella 204. február A feladatgy jtemény a TÁMOP-4.2.4.A/2-/-202-000 azonosító számú Nemzeti Kiválóság Program Hazai hallgatói, illetve
Gyakorló feladatok a Közönséges dierenciálegyenletek kurzushoz Vas Gabriella 204. február A feladatgy jtemény a TÁMOP-4.2.4.A/2-/-202-000 azonosító számú Nemzeti Kiválóság Program Hazai hallgatói, illetve
Nemzetközi gazdaságtan 1. modul - 3.lecke
 Segédlet Nemzetözi gazdaságtan. modul -.lece A nemzetözi gazdaságtan alapjai (Solt Katalin[004]: A nemzetözi gazdaságtan alapjai, Tri-Mester Kiadó, Tataánya) cím jegyzet.6. fejezete Vállalato és a üleresedelem
Segédlet Nemzetözi gazdaságtan. modul -.lece A nemzetözi gazdaságtan alapjai (Solt Katalin[004]: A nemzetözi gazdaságtan alapjai, Tri-Mester Kiadó, Tataánya) cím jegyzet.6. fejezete Vállalato és a üleresedelem
0-49 pont: elégtelen, pont: elégséges, pont: közepes, pont: jó, pont: jeles
 Matematika szigorlat, Mérnök informatikus szak I. 2013. jan. 10. Név: Neptun kód: Idő: 180 perc Elm.: 1. f. 2. f. 3. f. 4. f. 5. f. Fel. össz.: Össz.: Oszt.: Az elérhető pontszám 40 (elmélet) + 60 (feladatok)
Matematika szigorlat, Mérnök informatikus szak I. 2013. jan. 10. Név: Neptun kód: Idő: 180 perc Elm.: 1. f. 2. f. 3. f. 4. f. 5. f. Fel. össz.: Össz.: Oszt.: Az elérhető pontszám 40 (elmélet) + 60 (feladatok)
6. feladatsor: Inhomogén lineáris differenciálegyenletek (megoldás)
 Matematika Ac gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 017/18 ősz 6. feladatsor: Inhomogén lineáris differenciálegyenletek (megoldás) 1. Írjunk fel egy olyan legalacsonyabbrendű valós,
Matematika Ac gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 017/18 ősz 6. feladatsor: Inhomogén lineáris differenciálegyenletek (megoldás) 1. Írjunk fel egy olyan legalacsonyabbrendű valós,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
MŰSZAKI MEGBÍZHATÓSÁGÁNAK VIZSGÁLATI MÓDSZEREI EXAMINATION METHODS FOR EVALUATING RELIABILITY IN COMPLEX MILITARY RECONNAISSANCE SYSTEMS.
 BÁRKÁNYI PÁL KOMPLEX KATONAI FELDERÍTŐ RENDSZEREK MŰSZAKI MEGBÍZHATÓSÁGÁNAK VIZSGÁLATI MÓDSZEREI EXAMINATION METHODS FOR EVALUATING RELIABILITY IN COMPLEX MILITARY RECONNAISSANCE SYSTEMS A cikk a komplex
BÁRKÁNYI PÁL KOMPLEX KATONAI FELDERÍTŐ RENDSZEREK MŰSZAKI MEGBÍZHATÓSÁGÁNAK VIZSGÁLATI MÓDSZEREI EXAMINATION METHODS FOR EVALUATING RELIABILITY IN COMPLEX MILITARY RECONNAISSANCE SYSTEMS A cikk a komplex
Modern fizika laboratórium
 Modern fizika laboratórium 11. Az I 2 molekula disszociációs energiája Készítette: Hagymási Imre A mérés dátuma: 2007. október 3. A beadás dátuma: 2007. október xx. 1. Bevezetés Ebben a mérésben egy kétatomos
Modern fizika laboratórium 11. Az I 2 molekula disszociációs energiája Készítette: Hagymási Imre A mérés dátuma: 2007. október 3. A beadás dátuma: 2007. október xx. 1. Bevezetés Ebben a mérésben egy kétatomos
Kiegészítő részelőadás 2. Algebrai és transzcendens számok, nevezetes konstansok
 Kiegészítő részelőadás. Algebrai és transzcendens számo, nevezetes onstanso Dr. Kallós Gábor 04 05 A valós számo ategorizálása Eml. (óori felismerés): nem minden szám írható fel törtszámént (racionálisént)
Kiegészítő részelőadás. Algebrai és transzcendens számo, nevezetes onstanso Dr. Kallós Gábor 04 05 A valós számo ategorizálása Eml. (óori felismerés): nem minden szám írható fel törtszámént (racionálisént)
Publikációs jegyzék. Sitkuné Görömbei Cecília PKK, Tanítóképző Intézet
 Publikációs jegyzék Sitkuné Görömbei Cecília PKK, Tanítóképző Intézet Referált cikk nemzetközi folyóiratban 1. Sitkuné Görömbei Cecília: Shall we use one more representation? Suggestions about establishing
Publikációs jegyzék Sitkuné Görömbei Cecília PKK, Tanítóképző Intézet Referált cikk nemzetközi folyóiratban 1. Sitkuné Görömbei Cecília: Shall we use one more representation? Suggestions about establishing
SÚLYOS BALESETEK ELEMZÉSE. 3. téma: Kvalitatív módszerek - Hibafa
 Az oktatási anyag a szerzők szellemi terméke. Az anyag kizárólag a 2014.01.22-23 23-i OKF Továbbképzés céljaira használható. Sokszorosítás, utánközlés és mindennemű egyéb felhasználás a szerzők engedélyéhez
Az oktatási anyag a szerzők szellemi terméke. Az anyag kizárólag a 2014.01.22-23 23-i OKF Továbbképzés céljaira használható. Sokszorosítás, utánközlés és mindennemű egyéb felhasználás a szerzők engedélyéhez
Bozóki Sándor. MTA SZTAKI, Budapesti Corvinus Egyetem. Vitaliy Tsyganok
 A feszítőfákból számolt súlyvektorok mértani közepének optimalitása a logaritmikus legkisebb négyzetes célfüggvényre nézve Bozóki Sándor MTA SZTAKI, Budapesti Corvinus Egyetem Vitaliy Tsyganok Laboratory
A feszítőfákból számolt súlyvektorok mértani közepének optimalitása a logaritmikus legkisebb négyzetes célfüggvényre nézve Bozóki Sándor MTA SZTAKI, Budapesti Corvinus Egyetem Vitaliy Tsyganok Laboratory
Ensemble előrejelzések: elméleti és gyakorlati háttér HÁGEL Edit Országos Meteorológiai Szolgálat Numerikus Modellező és Éghajlat-dinamikai Osztály 34
 Ensemble előrejelzések: elméleti és gyakorlati háttér HÁGEL Edit Országos Meteorológiai Szolgálat Numerikus Modellező és Éghajlat-dinamikai Osztály 34. Meteorológiai Tudományos Napok Az előadás vázlata
Ensemble előrejelzések: elméleti és gyakorlati háttér HÁGEL Edit Országos Meteorológiai Szolgálat Numerikus Modellező és Éghajlat-dinamikai Osztály 34. Meteorológiai Tudományos Napok Az előadás vázlata
2. Laboratóriumi gyakorlat A TERMISZTOR. 1. A gyakorlat célja. 2. Elméleti bevezető
 . Laboratóriumi gyakorlat A EMISZO. A gyakorlat célja A termisztorok működésének bemutatása, valamint főbb paramétereik meghatározása. Az ellenállás-hőmérséklet = f és feszültség-áram U = f ( I ) jelleggörbék
. Laboratóriumi gyakorlat A EMISZO. A gyakorlat célja A termisztorok működésének bemutatása, valamint főbb paramétereik meghatározása. Az ellenállás-hőmérséklet = f és feszültség-áram U = f ( I ) jelleggörbék
Mezőgazdasági gépesítési tanulmányok Agricultural Engineering Research MŰANYAG CSOMAGOLÓ- ÉS TAKARÓ FÓLIÁK REOLÓGIAI VIZSGÁLATA
 Mezőgazdasági gépesítési tanulmányo Agricultural Engineering Research Kiadó: Dr. Fenyvesi László főigazgató FVM Mezőgazdasági Gépesítési Intézet özleménye Bulletin of the Hungarian Institute of Agricultural
Mezőgazdasági gépesítési tanulmányo Agricultural Engineering Research Kiadó: Dr. Fenyvesi László főigazgató FVM Mezőgazdasági Gépesítési Intézet özleménye Bulletin of the Hungarian Institute of Agricultural
11. gyakorlat megoldásai
 11. gyakorlat megoldásai Lokális szélsőértékek F1. Határozza meg az alábbi kétváltozós függvények lokális szélsőértékeit! (a) f(x, y) = 4x 2 + 2xy + 5y 2 + 2, (b) f(x, y) = y 4 3y + x 2 y + 2xy, (c) f(x,
11. gyakorlat megoldásai Lokális szélsőértékek F1. Határozza meg az alábbi kétváltozós függvények lokális szélsőértékeit! (a) f(x, y) = 4x 2 + 2xy + 5y 2 + 2, (b) f(x, y) = y 4 3y + x 2 y + 2xy, (c) f(x,
Biomatematika 12. Szent István Egyetem Állatorvos-tudományi Kar. Fodor János
 Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
Szent István Egyetem Állatorvos-tudományi Kar Biomatematikai és Számítástechnikai Tanszék Biomatematika 12. Regresszió- és korrelációanaĺızis Fodor János Copyright c Fodor.Janos@aotk.szie.hu Last Revision
1. A neutronvisszaszórási hatáskeresztmetszet
 Bevezetés Az értekezés azon munka összefoglalása, melyet 1999 februárjában még egyetemi hallgatóként kezdtem, 1999 szeptembere és 2002 augusztusa között mint PhD ösztöndíjas, 2002 szeptembere és 2003 júniusa
Bevezetés Az értekezés azon munka összefoglalása, melyet 1999 februárjában még egyetemi hallgatóként kezdtem, 1999 szeptembere és 2002 augusztusa között mint PhD ösztöndíjas, 2002 szeptembere és 2003 júniusa
Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével
 Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével Pekárdy Milán, Baumgartner János, Süle Zoltán Pannon Egyetem, Veszprém XXXII. Magyar Operációkutatási
Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével Pekárdy Milán, Baumgartner János, Süle Zoltán Pannon Egyetem, Veszprém XXXII. Magyar Operációkutatási
Matematika A 9. szakiskolai évfolyam. 7. modul EGYENES ARÁNYOSSÁG ÉS A LINEÁRIS FÜGGVÉNYEK
 Matematika A 9. szakiskolai évfolyam 7. modul EGYENES ARÁNYOSSÁG ÉS A LINEÁRIS FÜGGVÉNYEK Matematika A 9. szakiskolai évfolyam 7. modul: Egyenes arányosság és a lineáris függvények Tanári útmutató 2 A
Matematika A 9. szakiskolai évfolyam 7. modul EGYENES ARÁNYOSSÁG ÉS A LINEÁRIS FÜGGVÉNYEK Matematika A 9. szakiskolai évfolyam 7. modul: Egyenes arányosság és a lineáris függvények Tanári útmutató 2 A
Határozatlan integrál
 Határozatlan integrál Boros Zoltán Debreceni Egyetem, TTK Matematikai Intézet, Anaĺızis Tanszék Debrecen, 207. február 20 27. Primitív függvény, határozatlan integrál A továbbiakban legyen I R intervallum.
Határozatlan integrál Boros Zoltán Debreceni Egyetem, TTK Matematikai Intézet, Anaĺızis Tanszék Debrecen, 207. február 20 27. Primitív függvény, határozatlan integrál A továbbiakban legyen I R intervallum.
Másodfokú egyenletek, egyenlőtlenségek
 Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x + 1x + 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x + 1x + 16 = 0.
Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x + 1x + 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x + 1x + 16 = 0.
Lövedékálló védőmellényekben alkalmazható ballisztikai kerámia megfelelőségének vizsgálata röntgendiffrakciós (XRD) módszerrel
 Lövedékálló védőmellényekben alkalmazható ballisztikai kerámia megfelelőségének vizsgálata röntgendiffrakciós (XRD) módszerrel XRD study on suitability of aluminium-oxide based ballistic ceramics used
Lövedékálló védőmellényekben alkalmazható ballisztikai kerámia megfelelőségének vizsgálata röntgendiffrakciós (XRD) módszerrel XRD study on suitability of aluminium-oxide based ballistic ceramics used
Normák, kondíciószám
 Normák, kondíciószám A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris egyenletrendszerek Nagyon sok probléma közvetlenül lineáris egyenletrendszer megoldásával kezelhetı Sok numerikus
Normák, kondíciószám A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris egyenletrendszerek Nagyon sok probléma közvetlenül lineáris egyenletrendszer megoldásával kezelhetı Sok numerikus
TARTÁLY LÉGRITKÍTÁSÁNAK TERMODINAMIKAI MODELLEZÉSE
 TARTÁLY LÉGRITKÍTÁSÁNAK TERMODINAMIKAI MODELLEZÉSE FÁBRY Gergely Szent István Egyetem Gödöllő Géészmérnöi Kar, Környezetiari Rendszere Intézet Műszai Tudományi Dotori Isola 213 Gödöllő, Páter Károly u.
TARTÁLY LÉGRITKÍTÁSÁNAK TERMODINAMIKAI MODELLEZÉSE FÁBRY Gergely Szent István Egyetem Gödöllő Géészmérnöi Kar, Környezetiari Rendszere Intézet Műszai Tudományi Dotori Isola 213 Gödöllő, Páter Károly u.
Pacemaker készülékek szoftverének verifikációja. Hesz Gábor
 Pacemaker készülékek szoftverének verifikációja Hesz Gábor A szív felépítése http://hu.wikipedia.org/w/index.php?title=fájl:diagram_of_the_human_heart_hu.svg http://en.wikipedia.org/wiki/file:conductionsystemoftheheartwithouttheheart.png
Pacemaker készülékek szoftverének verifikációja Hesz Gábor A szív felépítése http://hu.wikipedia.org/w/index.php?title=fájl:diagram_of_the_human_heart_hu.svg http://en.wikipedia.org/wiki/file:conductionsystemoftheheartwithouttheheart.png
Feladatok megoldásokkal az első gyakorlathoz (differencia- és differenciálhányados fogalma, geometriai és fizikai jelentése) (x 1)(x + 1) x 1
 Feladatok megoldásokkal az első gyakorlathoz (differencia- és differenciálhányados fogalma, geometriai és fizikai jelentése). Feladat. Határozzuk meg az f(x) x 2 függvény x 0 pontbeli differenciahányados
Feladatok megoldásokkal az első gyakorlathoz (differencia- és differenciálhányados fogalma, geometriai és fizikai jelentése). Feladat. Határozzuk meg az f(x) x 2 függvény x 0 pontbeli differenciahányados
Matematika 10 Másodfokú egyenletek. matematika és fizika szakos középiskolai tanár. > o < 2015. szeptember 27.
 Matematika 10 Másodfokú egyenletek Juhász László matematika és fizika szakos középiskolai tanár > o < 2015. szeptember 27. copyright: c Juhász László Ennek a könyvnek a használatát szerzői jog védi. A
Matematika 10 Másodfokú egyenletek Juhász László matematika és fizika szakos középiskolai tanár > o < 2015. szeptember 27. copyright: c Juhász László Ennek a könyvnek a használatát szerzői jog védi. A
A gyors Fourier-transzformáció (FFT)
 A gyors Fourier-transzformáció (FFT) Egy analóg jel spetrumát az esete döntő többségében számítástechniai eszözöel határozzu meg. A jelet mintavételezzü és elvégezzü a mintasorozat diszrét Fouriertranszformációját.
A gyors Fourier-transzformáció (FFT) Egy analóg jel spetrumát az esete döntő többségében számítástechniai eszözöel határozzu meg. A jelet mintavételezzü és elvégezzü a mintasorozat diszrét Fouriertranszformációját.
I. BEVEZETÉS, MOTIVÁCIÓ, PROBLÉMAFELVETÉS
 Szolnoki Tudományos Közlemények XIV. Szolnok, 1. Prof. Dr. Szabolcsi Róbert 1 MECHANIKAI LENGŐ RENDSZEREK RENDSZERDINAMIKAI IDENTIFIKÁCIÓJA I. BEVEZETÉS, MOTIVÁCIÓ, PROBLÉMAFELVETÉS A műszaki gyakorlatban
Szolnoki Tudományos Közlemények XIV. Szolnok, 1. Prof. Dr. Szabolcsi Róbert 1 MECHANIKAI LENGŐ RENDSZEREK RENDSZERDINAMIKAI IDENTIFIKÁCIÓJA I. BEVEZETÉS, MOTIVÁCIÓ, PROBLÉMAFELVETÉS A műszaki gyakorlatban
Matematikai geodéziai számítások 6.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
A KUTATÁS EREDMÉNYEI ZÁRÓJELENTÉS 2004-2006.
 ÖNELLENŐRZÉS ÉS FUTÁSIDEJŰ VERIFIKÁCIÓ SZÁMÍTÓGÉPES PROGRAMOKBAN OTKA T-046527 A KUTATÁS EREDMÉNYEI ZÁRÓJELENTÉS 2004-2006. Témavezető: dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem
ÖNELLENŐRZÉS ÉS FUTÁSIDEJŰ VERIFIKÁCIÓ SZÁMÍTÓGÉPES PROGRAMOKBAN OTKA T-046527 A KUTATÁS EREDMÉNYEI ZÁRÓJELENTÉS 2004-2006. Témavezető: dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem
