Segédlet: Kihajlás. Készítette: Dr. Kossa Attila BME, Műszaki Mechanikai Tanszék május 15.
|
|
|
- Réka Mészáros
- 8 évvel ezelőtt
- Látták:
Átírás
1 Segédlet: Kihajlás Készítette: Dr. Kossa ttila BME, Műszaki Mechanikai Tanszék május 15. Jelen segédlet célja tömören összefoglalni a hosszú nyomott rudak kihajlásra történő ellenőrzését. segédlet nem tér ki a részletes levezetésekre, ehelyett a végképletek gyakorlati alkalmazását mutatja be. kihajláshoz tartozó részletes levezetések szakkönyvekben megtalálhatóak 1. következőkben bemutatott összefüggések középpontosan terhelt nyomott rudakra vonatkoznak. Elsőként a rúd karcsúságát (karcsúsági tényező) definiáljuk. Ez egy olyan dimenzótlan skalár szám aminek segítségével el tudjuk dönteni, hogy a vizsgált nyomott rúd esetén melyik elméletet kell alkalmaznunk a törőerő számításához. karcsúságot rendszerint λ-val jelöljük és az alábbiak szerint számítjuk:, (1) ahol l 0 [m] a kihajló hosszúság, [m] pedig a keresztmetszet minimális inerciasugara. 1. ábra. kihajló hosszúság változása a megfogási módoktól függően z l 0 értéke a rúd hosszától és a rúdvégek megfogásától függ, számítása: l 0 = c l, (2) ahol l a vizsgált rúd tényleges hossza, c pedig a rúdvégek megtámasztásától függő konstans, melynek értékét különböző esetekre a 1. ábra foglalja össze. 1.a esetén alul befogás van, felül pedig szabad vég. 1.b-nél alul és felül is csuklós megfogás szerepel, vagyis a keresztmetszet a végeknél elfordulhat. 1.c annyiban különbözik a b) esettől, hogy alul befogás kényszer van, vagyis a végkeresztmetszet elfordulása zérus kell legyen. Legvégül, a d) esetén alul befogás, míg 1 Például: Muttnyánszky Ádám: Szilárdságtan. Műszaki Könyvkiadó, Budapest, 1981., Sz. D. Ponomarjov: Szilárdsági számítások a gépészetben, 7. kötet. Műszaki Könyvkiadó, Budapest, 1966., Pattantyús Á. G.: Gépész- és villamosmérnökök kézikönyve, 2. kötet. Műszaki Könyvkiadó, Budapest,
2 felül egy olyan jellegű megvezetést alkalmazunk, hogy a keresztmetszet ne tudjon elfordulni a rúdvégnél. keresztmetszet minimális inerciasugarának számítása: =, (3) ahol I 2 a keresztmetszet 2-es főtengelyére számított másodrendű nyomaték, vagyis a fő másodrendű nyomatékokból a kisebb. zért ezzel kell számolni mert a rúd a kisebb ellenállás "irányába" fog kihajlani, ez pedig a legkisebb másodrendű nyomatékkal rendelkező tengely. (3)-ban jelenti a keresztmetszet területét. Mindezek után a karcsúság (λ) és a rúd anyagának ismeretében eldönthető, hogy melyik elméletet kell alkalmaznunk a törőerő számításához. Ehhez a 2.ábrát kell megvizsgálnunk. z ábrán bemutatott 3 különböző esetet az 1. táblázat foglalja össze. 2. ábra. különböző elméletek érvényességi tartománya 1. táblázat. különböző elméletek érvényességi tartománya lkalmazandó elmélet λ < λ F Folyáshatár λ F < λ < λ 0 Tetmajer-egyenes λ 0 < λ Euler-hiperbola λ F és λ 0 karcsúságok a rúd anyagától függő értékek, néhány anyag esetére a 2. táblázat ad iránymutatást 2. 2 táblázat adatai a Muttnyánszky Ádám: Szilárdságtan. Műszaki Könyvkiadó, Budapest, könyv oldaláról származnak. 2
3 2. táblázat. Kihajlással kapcsolatos anyagjellemzők néhány anyag esetén Szakítószilárdság Folyáshatár Tetmajer-képlet nyag σ sz [MPa] σ F [MPa] [MPa] λ F λ , 14λ Szénacél , 62λ , 82λ Ötvözött acél , 3λ Dúralumínium , 2λ Öntöttvas 0,053λ 2 12λ Fenyőfa 30 0, 2λ Tölgyfa 37, 5 0, 25λ λ < λ F Ebben az esetben a rúd karcsúsága olyan kicsi (zömök rúd), hogy a kihajlás jelensége nem számottevő, emiatt a törőfeszültség értéke az anyag folyáshatárával egyenlő, vagyis σ t = σ F. (4) λ F < λ < λ 0 Létezik egy átmeneti tartomány a karcsú (λ 0 < λ) és zömök (λ < λ F ) rudak között, ahol a törőfeszültséget a Tetmajer-féle képlettel számítjuk, ami egy egyenesnek az egyenlete: σ t = a bλ. (5) fenti egyenletben szereplő a és b paraméterek az anyagtól függő konstansok. Néhány anyag esetére a 2. táblázat közli a Tetmajer-egyenes egyenletét 3. λ 0 < λ Ebbe a tartományba tartoznak a karcsú rudak. Ebben az esetben a törőfeszültséget az Euler-féle képlettel számítjuk: ( π ) 2E, σ t = (6) λ ahol E az anyag rugalmassági modulusa. törőfeszültség ismeretében a törőerő azf t = σ t összefüggéssel számítható. z Euler-féle számítás esetén a törőerő számítható közvetlenül a ( ) 2 π F t = I 2 E (7) l 0 összefüggéssel is. z ellenőrzés utolsó lépése, hogy a kiszámított törőerőt összehasonlítjuk a rúd tényleges terhelésével (F). Ha F F t, akkor a rúd kihajlás szempontjából nem felel meg. 3 Öntöttvas esetén a Tetmajer-képlet egy parabolát definiál, nem egyenest. 3
4 z ellenőrzés algoritmusának rövid összefoglalása: 1. keresztmetszet geometria adatainak meghatározása: I 2,,. 2. rúdvégek megfogásának jellegének vizsgálata, ennek ismeretében a kihajló hosszúság számítása: l karcsúság számítása: λ. 4. Karcsúság ismeretében a megfelelő számítási képlet kiválasztása: Folyáshatár vagy Tetmajer-képlet vagy Euler-képlet. 5. Törőerő számítása. 6. Törőerő összehasonlítása a tényleges nyomóterheléssel. Kihajlás szempontjából megfelel vagy nem felel meg? Példa Két rúd a B csuklón keresztül csatlakozik. z egyik rúd másik végén (C) befogást alkalmazunk, míg a másik rúdnál görgős támaszt (). z elrendezést és a kiindulási adatokat a 3. ábra mutatja. BC rúd keresztmetszete a b méretű téglalap. 3. ábra. kihajló hosszúság változása a megfogási módoktól függően Feladatok: a) Határozzuk meg a BC-rúd kihajlással szembeni biztonsági tényezőjét! b) Hogyan változik a biztonsági tényező értéke ha h értékét 20 %-kal csökkentjük? c) Hogyan változik a biztonsági tényező értéke ha b értékét a háromszorosára vesszük? d) Hogyan változik a biztonsági tényező hahértéket a duplájára növeljük és az helyen csuklós támaszt alkalmazunk a görgős helyett? e) Legyen a BC-rúd keresztmetszete kör. Mekkora legyen a d átmérő, ha a kihajlással szemben 3x-os biztonságot szeretnénk elérni? 4
5 Megoldás BC rudat terhelő nyomóerő értéke az pontra felírt nyomatéki egyenletből kifejezhető: F = pt 2 a) keresztmetszet geometria adatainak számítása: I 2 = ab3 12 = 100 kn. (8) = ab = mm 2, (9) = = ,333 mm 4, 3 (10) = = b 12 = 5,7735 mm. (11) BC rudat a C keresztmetszetben befogtuk, viszont a B végének oldalirányú mozgása nem gátolt. Emiatt a 1.a ábra szerinti esettel van dolgunk, vagyis a kihajló hosszúság értéke: karcsúsági tényező számítása: l 0 = 2h = 640 mm. (12) = 110,851. (13) Mivel λ > λ 0, emiatt az Euler-féle képletet kell alkalmaznunk. Ennek megfelelően a törőerő számítása: ( ) 2 π F t = I 2 E = 160,638 kn. (14) Tehát a kihajlással szembeni biztonsági tényező: l 0 n = F t F = 1, (15) b) megváltozott kihajló hosszúság számítása: karcsúsági tényező értéke ez esetben: l 0 = 2(0,8h) = 512 mm. (16) = 88,681. (17) Mivel λ 0 < λ < λ 0, emiatt ennél az esetnél már nem az Euler-féle képletet, hanem a Tetmajerféle képletet kell alkalmaznunk. Ennek megfelelően a törőfeszültség számítása: Vagyis a törőerő: σ t = 308 1,14 λ = 206,904 MPa. (18) F t = σ t = 206,904 kn. (19) Tehát a kihajlással szembeni biztonsági tényező ebben az esetben: n = F t F = 2, (20) 5
6 c) b növelésével változnak a keresztmetszet geometriai adatai. Fontos észrevenni, hogy az előző esetekhez képesti merőleges tengely lesz most a 2-es tengely, vagyis ennek megfelelően kell I 2 -t számolni: karcsúsági tényező értéke: = a(3b) = mm 2, (21) I 2 = 3b(a)3 = mm 4, (22) 12 = = 14,439 mm. (23) = 44,3405. (24) Mivel λ < λ F, emiatt a törőfeszültség értéke a folyáshatárral egyenlő: törőerő számítása ennek megfelelően: Tehát a kihajlással szembeni biztonsági tényező: σ t = σ F = 240 MPa. (25) F t = σ t = 720 kn. (26) n = F t F = 7,2. (27) d) Ha az helyen csuklós támaszt alkalmazunk, akkor a BC-rúd B vége nem tud vízszintes irányba elmozdulni, vagyis az a 1.c ábra szerinti eset áll elő. kihajló hosszúság - figyelembe véve, hogy a h hosszt pedig a duplájára növeljük - ez esetben: l 0 = 0,7(2h) = 448 mm. (28) keresztmetszet geometria jellemzői nem változtak. karcsúsági tényező értéke: = 448 = 77,596. (29) 5,7735 Mivel λ 0 < λ < λ 0, emiatt ennél az esetnél a Tetmajer-féle képletet kell alkalmaznunk. Ennek megfelelően a törőfeszültség számítása: Vagyis a törőerő: Tehát a kihajlással szembeni biztonság: σ t = 308 1,14 λ = 219,541 MPa. (30) F t = σ t = 219,541 kn. (31) n = F t F = 2, (32) 6
7 e) Ha 3x-os biztonságot szeretnénk elérni akkor a törőerő értéke F t = nf = = 300 kn (33) kell legyen. Méretezés során viszont előre nem tudjuk megmondani, hogy a meghatározni kívánt keresztmetszet esetén melyik elméletet kell alkalmaznunk a törőerő számítására. Emiatt iterációra van szükség. Vagyis feltételezzük például, hogy Euler-féle képletet kell használni, és ennek alapján számítjuk a d-t. Ezután, a keresztmetszet geometriájának ismeretében, már számítható a karcsúság (amit az elején még nem ismertünk). mennyiben λ > λ F értéket kapunk akkor jogos volt a feltételezés. Ha nem, akkor hasonló gondolatmenet alapján vizsgáljuk a Tetmajer-képlet érvényességét és a folyáshatárra való ellenőrzést. fenti gondolatmenetet követve feltételezzük elsőként, hogy az Euler-képletet kell használnunk. (7) képletből a szükséges I 2 kifejezhető: I 2 = F t E ( ) 2 l0 = π Ebből számítható a keresett átmérő: N MPa d = 4 64 π z átmérő ismeretében már számítható a rúd karcsúsága: = d2 π 4 = 884,468 mm2, = ( ) mm = ,735 mm 4. (34) π = 33,558 mm. (35) = 8,3895 mm, = 2h = 76,285. (36) Mivel a λ > λ F feltétel nem teljesül, emiatt nem az Euler-képletet kell alkalmazni! Vizsgáljuk meg, hogy a Tetmajer-féle képlet alkalmazása esetén milyen eredményre jutunk. megadott biztonság esetén a törőfeszültség értéke: σ t = n F = = = d 2 π z anyagra megadott Tetmajer-képletből is felírhatjuk a törőfeszültség értékét: ahol a karcsúsági tényező: = ,863 d 2. (37) σ t = 308 1,14λ, (38) = l 0 = 4l 0 d = 2560 d. (39) fenti egyenletbe d-t mm-ben kell behelyettesíteni. Visszaírva λ-t (38)-ba kapjuk, hogy σ t = ,4. (40) d Egyenlővé téve a (37) és (40) egyenleteket, d-re vonatkozólag egy másodfokú egyenletet kapunk: ,863 = ,4, (41) d 2 d 308d ,4d ,863 = 0, (42) 7
8 melynek megoldásai: d 1 = 40,2709, d 1 = 30,7956. (43) Tehát a keresett átmérő értéke d = 40, 2709 mm. karcsúság értéke számítható (39) segítségével: λ = 63,57. Mivel a karcsúság a λ F < λ < λ 0 tartományba esik emiatt a Tetmajer-képletet kell alkalmazni, vagyis a d-re kapott érték a keresett megoldás. Megjegyzés: fenti, e) pontbeli méretezési feladat paraméteresen is elvégezhető. Vezessük le általános esetre a méretezést. Legyen a rúd terhelése F, az elérni kívánt biztonsági tényező n, a Tetmajer-képlet alakja σ t = a bλ, a rúd hossza l, a megfogás módját jellemző konstans c. Határozzuk meg a szükséges d átmérőt mind az Euler-féle képlet, mind a Tetmajer-féle képlet alkalmazásával! Vizsgáljuk elsőként az Euler-féle képletet. szükséges törőerő értéke a biztonsági tényező figyelembe vételével: F t = nf. (44) törőerő felírása az Euler-féle képlet segítségével: ( ) 2 π F t = I 2 E. (45) l 0 Egyenlővé téve a fenti két egyenletet, és beírva I 2 képletét kapjuk, hogy ( ) 2 π nf = I 2 E, (46) nf = l 0 ( π cl ) 2 d 4 π 4nF (cl) 2 64 E d = 2 4 π 3 E Tetmajer-képlet alkalmazása esetén a törőerő értéke: ahol a karcsúság számítása:. (47) F t = (a bλ), (48) = cl = 4cl d. (49) Egyenlővé téve (44) és (48) egyenleteket, d-re vonatkozólag egy másodfokú egyenletet kapunk: nf = (a bλ), (50) 4nF d 2 π = a 4bcl d, (51) ad 2 4bcld 4nF π = 0, (52) melynek a pozitív megoldása d = 2bcl a + (2bcl a ) 2 + 4nF aπ. (53) két megoldás a hozzájuk kapcsolódó elméletek érvényességi tartományán belül alkalmazható. Vagyis a (47) szerinti megoldás akkor adja a tényleges megoldást ha a vele számolt karcsúságra teljesül, hogy λ > λ F. (53) megoldás pedig akkor szolgáltatja a tényleges megoldást, ha a vele számított karcsúságra teljesül, hogy λ F < λ < λ 0. 8
Szilárdságtan Segédlet KIHAJLÁS
 Gyakorlat 9 Mechanika Szilárdságtan 16 9 Segédlet KHJLÁS Tartalom 1 LKLMZOTT ÖSSZEÜGGÉSEK 1 GYKORLTOK PÉLDÁ TOVÁBB ELDTOK 9 1 EGYSZERŰ RUDK 9 RÁCSOS TRTÓK 1 Ez a Segédlet tartalmazza a 1, 16 években a
Gyakorlat 9 Mechanika Szilárdságtan 16 9 Segédlet KHJLÁS Tartalom 1 LKLMZOTT ÖSSZEÜGGÉSEK 1 GYKORLTOK PÉLDÁ TOVÁBB ELDTOK 9 1 EGYSZERŰ RUDK 9 RÁCSOS TRTÓK 1 Ez a Segédlet tartalmazza a 1, 16 években a
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén
 Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
Központosan nyomott vasbeton oszlop méretezése:
 Központosan nyomott vasbeton oszlop méretezése: Központosan nyomott oszlopok ellenőrzése: A beton által felvehető nyomóerő: N cd = A ctot f cd Az acélbetétek által felvehető nyomóerő: N sd = A s f yd -
Központosan nyomott vasbeton oszlop méretezése: Központosan nyomott oszlopok ellenőrzése: A beton által felvehető nyomóerő: N cd = A ctot f cd Az acélbetétek által felvehető nyomóerő: N sd = A s f yd -
Példa: Háromszög síkidom másodrendű nyomatékainak számítása
 Példa: Háromszög síkidom másodrendű nyomatékainak számítása Készítette: Dr. Kossa Attila kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék. február 6. Határozzuk meg az alábbi ábrán látható derékszögű háromszög
Példa: Háromszög síkidom másodrendű nyomatékainak számítása Készítette: Dr. Kossa Attila kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék. február 6. Határozzuk meg az alábbi ábrán látható derékszögű háromszög
Példa keresztmetszet másodrendű nyomatékainak számítására
 Példa keresztmetszet másodrendű nyomatékainak számítására Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. február 22. Tekintsük az alábbi keresztmetszetet. 1. ábra. A vizsgált
Példa keresztmetszet másodrendű nyomatékainak számítására Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. február 22. Tekintsük az alábbi keresztmetszetet. 1. ábra. A vizsgált
Keresztmetszet másodrendű nyomatékainak meghatározása
 BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel
 Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
ACÉLSZERKEZETEK I. LEHÓCZKI Bettina. Debreceni Egyetem Műszaki Kar, Építőmérnöki Tanszék. [1]
![ACÉLSZERKEZETEK I. LEHÓCZKI Bettina. Debreceni Egyetem Műszaki Kar, Építőmérnöki Tanszék. [1] ACÉLSZERKEZETEK I. LEHÓCZKI Bettina. Debreceni Egyetem Műszaki Kar, Építőmérnöki Tanszék. [1]](/thumbs/59/43903450.jpg) ACÉLSZERKEZETEK I. LEHÓCZKI Bettina Debreceni Egyetem Műszaki Kar Építőmérnöki Tanszék E-mail: lehoczki.betti@gmail.com [1] ACÉLSZERKEZETEK I. Gyakorlati órák időpontjai: szeptember 25. október 16. november
ACÉLSZERKEZETEK I. LEHÓCZKI Bettina Debreceni Egyetem Műszaki Kar Építőmérnöki Tanszék E-mail: lehoczki.betti@gmail.com [1] ACÉLSZERKEZETEK I. Gyakorlati órák időpontjai: szeptember 25. október 16. november
Példa: Csúsztatófeszültség-eloszlás számítása I-szelvényben
 Példa: Csúsztatófeszültség-eloszlás számítása I-szelvényben Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 14. Határozzuk meg a nyírásból adódó csúsztatófeszültség
Példa: Csúsztatófeszültség-eloszlás számítása I-szelvényben Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 14. Határozzuk meg a nyírásból adódó csúsztatófeszültség
Hajlított elemek kifordulása. Stabilitásvesztési módok
 Hajlított elemek kifordulása Stabilitásvesztési módok Stabilitásvesztés (3.3.fejezet) Globális: Nyomott rudak kihajlása Hajlított tartók kifordulása Lemezhorpadás (lokális stabilitásvesztés): Nyomott és/vagy
Hajlított elemek kifordulása Stabilitásvesztési módok Stabilitásvesztés (3.3.fejezet) Globális: Nyomott rudak kihajlása Hajlított tartók kifordulása Lemezhorpadás (lokális stabilitásvesztés): Nyomott és/vagy
Tartószerkezetek I. (Vasbeton szilárdságtan)
 Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.10.11. Vasbeton külpontos nyomása Az eső ágú σ-ε diagram miatt elvileg minden egyes esethez külön kell meghatározni a szélső szál összenyomódását.
Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.10.11. Vasbeton külpontos nyomása Az eső ágú σ-ε diagram miatt elvileg minden egyes esethez külön kell meghatározni a szélső szál összenyomódását.
BME Gépészmérnöki Kar 3. vizsga (112A) Név: 1 Műszaki Mechanikai Tanszék január 11. Neptun: 2 Szilárdságtan Aláírás: 3
 BME Gépészmérnöki Kar 3. vizsga (2A) Név: Műszaki Mechanikai Tanszék 2. január. Neptun: 2 Szilárdságtan Aláírás: 3. feladat (2 pont) A vázolt befogott tartót a p intenzitású megoszló erőrendszer, az F
BME Gépészmérnöki Kar 3. vizsga (2A) Név: Műszaki Mechanikai Tanszék 2. január. Neptun: 2 Szilárdságtan Aláírás: 3. feladat (2 pont) A vázolt befogott tartót a p intenzitású megoszló erőrendszer, az F
Rugalmas állandók mérése
 Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Toronymerevítık mechanikai szempontból
 Andó Mátyás: Toronymerevítık méretezése, 9 Gépész Tuning Kft. Toronymerevítık mechanikai szempontból Mint a neve is mutatja a toronymerevítık használatának célja az, hogy merevebbé tegye az autó karosszériáját
Andó Mátyás: Toronymerevítık méretezése, 9 Gépész Tuning Kft. Toronymerevítık mechanikai szempontból Mint a neve is mutatja a toronymerevítık használatának célja az, hogy merevebbé tegye az autó karosszériáját
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
6. MECHANIKA-STATIKA GYAKORLAT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya, Culmann-szerkesztés, Ritter-számítás
 ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
A= a keresztmetszeti felület cm 2 ɣ = biztonsági tényező
 Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
Gyakorlat 04 Keresztmetszetek III.
 Gyakorlat 04 Keresztmetszetek III. 1. Feladat Hajlítás és nyírás Végezzük el az alábbi gerenda keresztmetszeti vizsgálatait (tiszta esetek és lehetséges kölcsönhatások) kétféle anyaggal: S235; S355! (1)
Gyakorlat 04 Keresztmetszetek III. 1. Feladat Hajlítás és nyírás Végezzük el az alábbi gerenda keresztmetszeti vizsgálatait (tiszta esetek és lehetséges kölcsönhatások) kétféle anyaggal: S235; S355! (1)
Navier-formula. Frissítve: Egyenes hajlítás
 Navier-formula Akkor beszélünk egyenes hajlításról, ha a nyomatékvektor egybeesik valamelyik fő-másodrendű nyomatéki tengellyel. A hajlítást mindig súlyponti koordinátarendszerben értelmezzük. Ez még a
Navier-formula Akkor beszélünk egyenes hajlításról, ha a nyomatékvektor egybeesik valamelyik fő-másodrendű nyomatéki tengellyel. A hajlítást mindig súlyponti koordinátarendszerben értelmezzük. Ez még a
Frissítve: Csavarás. 1. példa: Az 5 gyakorlat 1. példájához hasonló feladat.
 1. példa: Az 5 gyakorlat 1. példájához hasonló feladat. Mekkora a nyomatékok hatására ébredő legnagyobb csúsztatófeszültség? Mekkora és milyen irányú az A, B és C keresztmetszet elfordulása? Számítsuk
1. példa: Az 5 gyakorlat 1. példájához hasonló feladat. Mekkora a nyomatékok hatására ébredő legnagyobb csúsztatófeszültség? Mekkora és milyen irányú az A, B és C keresztmetszet elfordulása? Számítsuk
A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS-
 A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS- Forgatónyomaték meghatározása G Á L A T A Egy erő forgatónyomatékkal hat egy pontra, ha az az erővel össze van kötve. Például
A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS- Forgatónyomaték meghatározása G Á L A T A Egy erő forgatónyomatékkal hat egy pontra, ha az az erővel össze van kötve. Például
6. MECHANIKA-STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnöktanár)
 SZÉHNYI ISTVÁN GYT LKLZOTT HNIK TNSZÉK 6. HNIK-STTIK GYKORLT (kidolgozta: Triesz Péter egy. ts.; Tarnai Gábor mérnöktanár) Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa gy létrát egy
SZÉHNYI ISTVÁN GYT LKLZOTT HNIK TNSZÉK 6. HNIK-STTIK GYKORLT (kidolgozta: Triesz Péter egy. ts.; Tarnai Gábor mérnöktanár) Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa gy létrát egy
Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával
 Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 212. október 16. Frissítve: 215. január
Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 212. október 16. Frissítve: 215. január
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Csavarorsós emelőbak tervezési feladat Gépészmérnök, Járműmérnök, Mechatronikai mérnök, Logisztikai mérnök, Mérnöktanár (osztatlan) BSC szak
 Csavarorsós emelőbak tervezési feladat Gépészmérnök, Járműmérnök, Mechatronikai mérnök, Logisztikai mérnök, Mérnöktanár (osztatlan) BSC szak A feladat részletezése: Név:.. Csoport:... A számításnak (órai)
Csavarorsós emelőbak tervezési feladat Gépészmérnök, Járműmérnök, Mechatronikai mérnök, Logisztikai mérnök, Mérnöktanár (osztatlan) BSC szak A feladat részletezése: Név:.. Csoport:... A számításnak (órai)
FORGATTYÚS HAJTÓMŰ KISFELADAT
 Dr. Lovas László FORGATTYÚS HAJTÓMŰ KISFELADAT Segédlet a Jármű- és hajtáselemek III. tantárgyhoz Kézirat 2013 FORGATTYÚS HAJTÓMŰ KISFELADAT 1. Adatválaszték p 2 [bar] V [cm3] s/d [-] λ [-] k f [%] k a
Dr. Lovas László FORGATTYÚS HAJTÓMŰ KISFELADAT Segédlet a Jármű- és hajtáselemek III. tantárgyhoz Kézirat 2013 FORGATTYÚS HAJTÓMŰ KISFELADAT 1. Adatválaszték p 2 [bar] V [cm3] s/d [-] λ [-] k f [%] k a
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK. Acélszerkezetek II. IV. Előadás
 DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II IV. Előadás Rácsos tartók szerkezeti formái, kialakítása, tönkremeneteli módjai. - Rácsos tartók jellemzói - Méretezési kérdések
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II IV. Előadás Rácsos tartók szerkezeti formái, kialakítása, tönkremeneteli módjai. - Rácsos tartók jellemzói - Méretezési kérdések
Vasbeton tartók méretezése hajlításra
 Vasbeton tartók méretezése hajlításra Képlékenység-tani méretezés: A vasbeton keresztmetszet teherbírásának számításánál a III. feszültségi állapotot vesszük alapul, amelyre az jellemző, hogy a hajlításból
Vasbeton tartók méretezése hajlításra Képlékenység-tani méretezés: A vasbeton keresztmetszet teherbírásának számításánál a III. feszültségi állapotot vesszük alapul, amelyre az jellemző, hogy a hajlításból
K - K. 6. fejezet: Vasbeton gerenda vizsgálata Határnyomatéki ábra előállítása, vaselhagyás tervezése. A határnyíróerő ábra előállítása.
 6. fejezet: Vasbeton gerenda vizsgálata 6.1. Határnyomatéki ábra előállítása, vaselhagyás tervezése. A határnyíróerő ábra előállítása. pd=15 kn/m K - K 6φ5 K Anyagok : φ V [kn] VSd.red VSd 6φ16 Beton:
6. fejezet: Vasbeton gerenda vizsgálata 6.1. Határnyomatéki ábra előállítása, vaselhagyás tervezése. A határnyíróerő ábra előállítása. pd=15 kn/m K - K 6φ5 K Anyagok : φ V [kn] VSd.red VSd 6φ16 Beton:
Gyakorlat 03 Keresztmetszetek II.
 Gyakorlat 03 Keresztmetszetek II. 1. Feladat Keresztmetszetek osztályzása Végezzük el a keresztmetszet osztályzását tiszta nyomás és hajlítás esetére! Monoszimmetrikus, hegesztett I szelvény (GY02 1. példája)
Gyakorlat 03 Keresztmetszetek II. 1. Feladat Keresztmetszetek osztályzása Végezzük el a keresztmetszet osztályzását tiszta nyomás és hajlítás esetére! Monoszimmetrikus, hegesztett I szelvény (GY02 1. példája)
Hegesztett gerinclemezes tartók
 Hegesztett gerinclemezes tartók Lemezhorpadások kezelése EC szerint dr. Horváth László BME Hidak és Szerkezetek Tanszéke Bevezetés Gerinclemezes tartók vékony lemezekből: Bevezetés Összetett szelvények,
Hegesztett gerinclemezes tartók Lemezhorpadások kezelése EC szerint dr. Horváth László BME Hidak és Szerkezetek Tanszéke Bevezetés Gerinclemezes tartók vékony lemezekből: Bevezetés Összetett szelvények,
KRITIKUS KÉRDÉS: ACÉL ELEMEK
 KRITIKUS KÉRDÉS: ACÉL ELEMEK KRITIKUS HŐMÉRSÉKLETE Dr. Horváth László egyetem docens Acélszerkezetek tűzvédelmi tervezése workshop, 2018. 11.09 TARTALOM Acél elemek tönkremeneteli folyamata tűzhatás alatt
KRITIKUS KÉRDÉS: ACÉL ELEMEK KRITIKUS HŐMÉRSÉKLETE Dr. Horváth László egyetem docens Acélszerkezetek tűzvédelmi tervezése workshop, 2018. 11.09 TARTALOM Acél elemek tönkremeneteli folyamata tűzhatás alatt
Gyakorlati útmutató a Tartók statikája I. tárgyhoz. Fekete Ferenc. 5. gyakorlat. Széchenyi István Egyetem, 2015.
 Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Anyagvizsgálatok. Mechanikai vizsgálatok
 Anyagvizsgálatok Mechanikai vizsgálatok Szakítóvizsgálat EN 10002-1:2002 Célja: az anyagok egytengelyű húzó igénybevétellel szembeni ellenállásának meghatározása egy szabványosan kialakított próbatestet
Anyagvizsgálatok Mechanikai vizsgálatok Szakítóvizsgálat EN 10002-1:2002 Célja: az anyagok egytengelyű húzó igénybevétellel szembeni ellenállásának meghatározása egy szabványosan kialakított próbatestet
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 Vasalt falak: 4. Vasalt falazott szerkezetek méretezési mószerei Vasalt falak 1. Vasalás fekvőhézagban vagy falazott üregben horonyban, falazóelem lyukban. 1 2 1 Vasalt falak: Vasalás fekvőhézagban vagy
Vasalt falak: 4. Vasalt falazott szerkezetek méretezési mószerei Vasalt falak 1. Vasalás fekvőhézagban vagy falazott üregben horonyban, falazóelem lyukban. 1 2 1 Vasalt falak: Vasalás fekvőhézagban vagy
Lindab Z/C 200 ECO gerendák statikai méretezése. Tervezési útmutató
 Lindab Z/C 200 ECO gerendák statikai méretezése Tervezési útmutató Készítette: Dr. Ádány Sándor Lindab Kft 2007. február ZC200ECO / 1 1. Bevezetés Jelen útmutató a Lindab Kft. által 1998-ban kiadott Lindab
Lindab Z/C 200 ECO gerendák statikai méretezése Tervezési útmutató Készítette: Dr. Ádány Sándor Lindab Kft 2007. február ZC200ECO / 1 1. Bevezetés Jelen útmutató a Lindab Kft. által 1998-ban kiadott Lindab
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK. Acélszerkezetek II. VI. Előadás. Rácsos tartók hegesztett kapcsolatai.
 DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II VI. Előadás Rácsos tartók hegesztett kapcsolatai. - Tönkremeneteli módok - Méretezési kérdések - Csomóponti kialakítások Összeállította:
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II VI. Előadás Rácsos tartók hegesztett kapcsolatai. - Tönkremeneteli módok - Méretezési kérdések - Csomóponti kialakítások Összeállította:
Felső végükön egymásra támaszkodó szarugerendák egyensúlya
 1 Felső végükön egymásra támaszkodó szarugerendák egyensúlya Az [ 1 ] példatárban találtunk egy érdekes feladatot, melynek egy változatát vizsgáljuk meg itt. A feladat Ehhez tekintsük az 1. ábrát! 1. ábra
1 Felső végükön egymásra támaszkodó szarugerendák egyensúlya Az [ 1 ] példatárban találtunk egy érdekes feladatot, melynek egy változatát vizsgáljuk meg itt. A feladat Ehhez tekintsük az 1. ábrát! 1. ábra
2. Rugalmas állandók mérése jegyzőkönyv javított. Zsigmond Anna Fizika Bsc II. Mérés dátuma: Leadás dátuma:
 2. Rugalmas állandók mérése jegyzőkönyv javított Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 17. Leadás dátuma: 2008. 10. 08. 1 1. Mérések ismertetése Az első részben egy téglalap keresztmetszetű
2. Rugalmas állandók mérése jegyzőkönyv javított Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 17. Leadás dátuma: 2008. 10. 08. 1 1. Mérések ismertetése Az első részben egy téglalap keresztmetszetű
A.2. Acélszerkezetek határállapotai
 A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
Nyomott oszlopok számítása EC2 szerint (mintapéldák)
 zéhenyi István Egyetem zerkezetépítési és Geotehnikai Tanszék yomott oszlopok számítása E szerint 1. Központosan nyomott oszlop Központosan nyomott az oszlop ha e = 0 (e : elsőrendű, vagy kezdeti külpontosság).
zéhenyi István Egyetem zerkezetépítési és Geotehnikai Tanszék yomott oszlopok számítása E szerint 1. Központosan nyomott oszlop Központosan nyomott az oszlop ha e = 0 (e : elsőrendű, vagy kezdeti külpontosság).
Cölöpcsoport elmozdulásai és méretezése
 18. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpcsoport elmozdulásai és méretezése Program: Fájl: Cölöpcsoport Demo_manual_18.gsp A fejezet célja egy cölöpcsoport fejtömbjének elfordulásának,
18. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpcsoport elmozdulásai és méretezése Program: Fájl: Cölöpcsoport Demo_manual_18.gsp A fejezet célja egy cölöpcsoport fejtömbjének elfordulásának,
KERESZTMETSZETI JELLEMZŐK
 web-lap : www.hild.gor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 50. KERESZTMETSZETI JELLEMZŐK A TARTÓK MÉRETEZÉSE SORÁN SZÁMOS ESETBEN SZÜKSÉGÜNK VAN OLYAN ADATOKRA,
web-lap : www.hild.gor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 50. KERESZTMETSZETI JELLEMZŐK A TARTÓK MÉRETEZÉSE SORÁN SZÁMOS ESETBEN SZÜKSÉGÜNK VAN OLYAN ADATOKRA,
HELYI TANTERV. Mechanika
 HELYI TANTERV Mechanika Bevezető A mechanika tantárgy tanításának célja, hogy fejlessze a tanulók logikai készségét, alapozza meg a szakmai tantárgyak feldolgozását. A tanulók tanulási folyamata fejlessze
HELYI TANTERV Mechanika Bevezető A mechanika tantárgy tanításának célja, hogy fejlessze a tanulók logikai készségét, alapozza meg a szakmai tantárgyak feldolgozását. A tanulók tanulási folyamata fejlessze
TARTALOMJEGYZÉK. 1. KIINDULÁSI ADATOK 3. 1.1 Geometria 3. 1.2 Anyagminőségek 6. 2. ALKALMAZOTT SZABVÁNYOK 6.
 statikai számítás Tsz.: 51.89/506 TARTALOMJEGYZÉK 1. KIINDULÁSI ADATOK 3. 1.1 Geometria 3. 1. Anyagminőségek 6.. ALKALMAZOTT SZABVÁNYOK 6. 3. A VASBETON LEMEZ VIZSGÁLATA 7. 3.1 Terhek 7. 3. Igénybevételek
statikai számítás Tsz.: 51.89/506 TARTALOMJEGYZÉK 1. KIINDULÁSI ADATOK 3. 1.1 Geometria 3. 1. Anyagminőségek 6.. ALKALMAZOTT SZABVÁNYOK 6. 3. A VASBETON LEMEZ VIZSGÁLATA 7. 3.1 Terhek 7. 3. Igénybevételek
MECHANIKA I. rész: Szilárd testek mechanikája
 Egészségügyi mérnökképzés MECHNIK I. rész: Szilárd testek mechanikája készítette: Németh Róbert Igénybevételek térben I. z alapelv ugyanaz, mint síkban: a keresztmetszet egyik oldalán levő szerkezetrészre
Egészségügyi mérnökképzés MECHNIK I. rész: Szilárd testek mechanikája készítette: Németh Róbert Igénybevételek térben I. z alapelv ugyanaz, mint síkban: a keresztmetszet egyik oldalán levő szerkezetrészre
Kizárólag oktatási célra használható fel!
 DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II III. Előadás Vékonyfalú keresztmetszetek nyírófeszültségei - Nyírófolyam - Nyírási középpont - Shear lag hatás - Csavarás Összeállította:
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II III. Előadás Vékonyfalú keresztmetszetek nyírófeszültségei - Nyírófolyam - Nyírási középpont - Shear lag hatás - Csavarás Összeállította:
Az ötszög keresztmetszetű élszarufa kis elmozdulásainak számításáról
 1 Az ötszög keresztmetszetű élszarufa kis elmozdulásainak számításáról Előző dolgozatunkban melynek címe: ED: Az ötszög keresztmetszetű élszarufa σ - feszültségeinek számításáról elkezdtük / folytattuk
1 Az ötszög keresztmetszetű élszarufa kis elmozdulásainak számításáról Előző dolgozatunkban melynek címe: ED: Az ötszög keresztmetszetű élszarufa σ - feszültségeinek számításáról elkezdtük / folytattuk
Rugalmas állandók mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
II. Gyakorlat: Hajlított vasbeton keresztmetszet ellenőrzése (Négyszög és T-alakú keresztmetszetek hajlítási teherbírása III. feszültségi állapotban)
 II. Gyakorlat: Hajlított vasbeton keresztmetszet ellenőrzése (Négyszög és T-alakú keresztmetszetek hajlítási teherbírása III. feszültségi állapotban) Készítették: Dr. Kiss Rita és Klinka Katalin -1- A
II. Gyakorlat: Hajlított vasbeton keresztmetszet ellenőrzése (Négyszög és T-alakú keresztmetszetek hajlítási teherbírása III. feszültségi állapotban) Készítették: Dr. Kiss Rita és Klinka Katalin -1- A
Mikrocölöp alapozás ellenőrzése
 36. számú mérnöki kézikönyv Frissítve: 2017. június Mikrocölöp alapozás ellenőrzése Program: Fájl: Cölöpcsoport Demo_manual_en_36.gsp Ennek a mérnöki kézikönyvnek a célja, egy mikrocölöp alapozás ellenőrzésének
36. számú mérnöki kézikönyv Frissítve: 2017. június Mikrocölöp alapozás ellenőrzése Program: Fájl: Cölöpcsoport Demo_manual_en_36.gsp Ennek a mérnöki kézikönyvnek a célja, egy mikrocölöp alapozás ellenőrzésének
Szabályos fahengeres keresztmetszet geometriai jellemzőinek meghatározása számítással
 Szabályos fahengeres keresztmetszet geometriai jellemzőinek meghatározása számítással Előző dolgozatunkban jele: ( E ), címe: Szimmetrikusan szélezett körkeresztmetszet geometriai jellemzőinek meghatározása
Szabályos fahengeres keresztmetszet geometriai jellemzőinek meghatározása számítással Előző dolgozatunkban jele: ( E ), címe: Szimmetrikusan szélezett körkeresztmetszet geometriai jellemzőinek meghatározása
Fa- és Acélszerkezetek I. 11. Előadás Faszerkezetek II. Dr. Szalai József Főiskolai adjunktus
 Fa- és Acélszerkezetek I. 11. Előadás Faszerkezetek II. Dr. Szalai József Főiskolai adjunktus Tartalom Méretezés az Eurocode szabványrendszer szerint áttekintés Teherbírási határállapotok Húzás Nyomás
Fa- és Acélszerkezetek I. 11. Előadás Faszerkezetek II. Dr. Szalai József Főiskolai adjunktus Tartalom Méretezés az Eurocode szabványrendszer szerint áttekintés Teherbírási határállapotok Húzás Nyomás
SIKLÓCSAPÁGY KISFELADAT
 Dr. Lovas Lászl SIKLÓCSAPÁGY KISFELADAT Segédlet a Jármű- és hajtáselemek II. tantárgyhoz Kézirat 2012 SIKLÓCSAPÁGY KISFELADAT 1. Adatválaszték pk [MPa] d [mm] b/d [-] n [1/min] ház anyaga 1 4 50 1 1440
Dr. Lovas Lászl SIKLÓCSAPÁGY KISFELADAT Segédlet a Jármű- és hajtáselemek II. tantárgyhoz Kézirat 2012 SIKLÓCSAPÁGY KISFELADAT 1. Adatválaszték pk [MPa] d [mm] b/d [-] n [1/min] ház anyaga 1 4 50 1 1440
Dr. MOGA Petru, Dr. KÖLL7 Gábor, GU9IU :tefan, MOGA C;t;lin. Kolozsvári M=szaki Egyetem
 Többtámaszú öszvértartók elemzése képlékeny tartományban az EUROCODE 4 szerint Plastic Analysis of the Composite Continuous Girders According to EUROCODE 4 Dr. MOGA Petru, Dr. KÖLL7 Gábor, GU9IU :tefan,
Többtámaszú öszvértartók elemzése képlékeny tartományban az EUROCODE 4 szerint Plastic Analysis of the Composite Continuous Girders According to EUROCODE 4 Dr. MOGA Petru, Dr. KÖLL7 Gábor, GU9IU :tefan,
tápvezetékre jellemző, hogy csak a vezeték végén van terhelés, ahogy az 1. ábra mutatja.
 Tápvezeték A fogyasztókat a tápponttal közvetlen összekötő vezetékeket tápvezetéknek nevezzük. A tápvezetékre jellemző, hogy csak a vezeték végén van terhelés, ahogy az 1. ábra mutatja. U T l 1. ábra.
Tápvezeték A fogyasztókat a tápponttal közvetlen összekötő vezetékeket tápvezetéknek nevezzük. A tápvezetékre jellemző, hogy csak a vezeték végén van terhelés, ahogy az 1. ábra mutatja. U T l 1. ábra.
A végeselem módszer alapjai. 2. Alapvető elemtípusok
 A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
Tervezés katalógusokkal kisfeladat
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Számítógépes tervezés, méretezés és gyártás (BME KOJHM401) Tervezés katalógusokkal kisfeladat Járműelemek és Járműszerkezetanalízis Tanszék Ssz.:...... Név:.........................................
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Számítógépes tervezés, méretezés és gyártás (BME KOJHM401) Tervezés katalógusokkal kisfeladat Járműelemek és Járműszerkezetanalízis Tanszék Ssz.:...... Név:.........................................
Használhatósági határállapotok. Alakváltozások ellenőrzése
 1.GYAKORLAT Használhatósági határállapotok A használhatósági határállapotokhoz tartozó teherkombinációk: Karakterisztikus (repedésmentesség igazolása) Gyakori (feszített szerkezetek repedés korlátozása)
1.GYAKORLAT Használhatósági határállapotok A használhatósági határállapotokhoz tartozó teherkombinációk: Karakterisztikus (repedésmentesség igazolása) Gyakori (feszített szerkezetek repedés korlátozása)
Hangfrekvenciás mechanikai rezgések vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
CSAVARORSÓS EMELŐ MŰSZAKI DOKUMENTÁCIÓ ÁLTALÁNOS CÉLOKRA FELHASZNÁLHATÓ CSAVARORSÓS EMELŐHÖZ. Maximális terhelő erő: 13 kn
 CSAVARORSÓS EMELŐ MŰSZAKI DOKUMENTÁCIÓ ÁLTALÁNOS CÉLOKRA FELHASZNÁLHATÓ CSAVARORSÓS EMELŐHÖZ. Maximális terhelő erő: 1 kn Maximális emelési magasság: 750 mm HORVÁTH ZOLTÁN GÉPÉSZ LEVELEZŐ I. A csavarorsós
CSAVARORSÓS EMELŐ MŰSZAKI DOKUMENTÁCIÓ ÁLTALÁNOS CÉLOKRA FELHASZNÁLHATÓ CSAVARORSÓS EMELŐHÖZ. Maximális terhelő erő: 1 kn Maximális emelési magasság: 750 mm HORVÁTH ZOLTÁN GÉPÉSZ LEVELEZŐ I. A csavarorsós
Érdekes geometriai számítások Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon
 Érdekes geometriai számítások 7. Folytatjuk a sorozatot. 7. Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon Korábbi dolgozatainkban már többféle módon is bemutattuk
Érdekes geometriai számítások 7. Folytatjuk a sorozatot. 7. Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon Korábbi dolgozatainkban már többféle módon is bemutattuk
1. Feladat. a) Mekkora radiális, tangenciális és axiális feszültségek ébrednek a csőfalban, ha a csővég zárt?
 1. Feladat Egy a = mm első és = 150 mm külső sugarú cső terhelése p = 60 MPa első ill. p k = 30 MPa külső nyomás. a) Mekkora radiális, tangenciális és axiális feszültségek érednek a csőfalan, ha a csővég
1. Feladat Egy a = mm első és = 150 mm külső sugarú cső terhelése p = 60 MPa első ill. p k = 30 MPa külső nyomás. a) Mekkora radiális, tangenciális és axiális feszültségek érednek a csőfalan, ha a csővég
Hangfrekvenciás mechanikai rezgések vizsgálata
 Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Budapesti Műszaki és Gazdaságudományi Egyetem
 Szilárdságtan példatár Járműváz- és Könnyűszerkezetek Tanszék udapesti Műszaki és Gazdaságudományi Egyetem ii iii bstract Ez a példatár elsősorban a Közlekedésmérnöki és Járműmérnöki Kar Sc hallgatóinak
Szilárdságtan példatár Járműváz- és Könnyűszerkezetek Tanszék udapesti Műszaki és Gazdaságudományi Egyetem ii iii bstract Ez a példatár elsősorban a Közlekedésmérnöki és Járműmérnöki Kar Sc hallgatóinak
X = 0 B x = 0. M B = A y 6 = 0. B x = 0 A y = 1000 B y = 400
 1. feladat Számítsuk ki a bejelölt rúderőket! Az erők N-ban, a hosszak m-ben, a nyomatékok Nm-ben értendők Első lépésként határozzuk meg a kényszererőket. Az S 1 rúderő számítása: Egyensúlyi egyenletek:
1. feladat Számítsuk ki a bejelölt rúderőket! Az erők N-ban, a hosszak m-ben, a nyomatékok Nm-ben értendők Első lépésként határozzuk meg a kényszererőket. Az S 1 rúderő számítása: Egyensúlyi egyenletek:
TERVEZÉS KATALÓGUSOKKAL KISFELADAT
 Dr. Nyitrai János Dr. Nyolcas Mihály TERVEZÉS KATALÓGUSOKKAL KISFELADAT Segédlet a Jármű- és hajtáselemek III. tantárgyhoz Kézirat 2012 TERVEZÉS KATALÓGUSOKKAL KISFELADAT "A" típusú feladat: Pneumatikus
Dr. Nyitrai János Dr. Nyolcas Mihály TERVEZÉS KATALÓGUSOKKAL KISFELADAT Segédlet a Jármű- és hajtáselemek III. tantárgyhoz Kézirat 2012 TERVEZÉS KATALÓGUSOKKAL KISFELADAT "A" típusú feladat: Pneumatikus
Egy érdekes statikai - geometriai feladat
 1 Egy érdekes statikai - geometriai feladat Előző dolgozatunkban melynek címe: Egy érdekes geometriai feladat egy olyan feladatot oldottunk meg, ami az itteni előtanulmányának is tekinthető. Az ottani
1 Egy érdekes statikai - geometriai feladat Előző dolgozatunkban melynek címe: Egy érdekes geometriai feladat egy olyan feladatot oldottunk meg, ami az itteni előtanulmányának is tekinthető. Az ottani
1. Határozzuk meg az alábbi tartó vasalását, majd ellenőrizzük a tartót használhatósági határállapotokra!
 1. Határozzuk meg az alábbi tartó vasalását majd ellenőrizzük a tartót használhatósági határállapotokra! Beton: beton minőség: beton nyomószilárdságnak tervezési értéke: beton húzószilárdságának várható
1. Határozzuk meg az alábbi tartó vasalását majd ellenőrizzük a tartót használhatósági határállapotokra! Beton: beton minőség: beton nyomószilárdságnak tervezési értéke: beton húzószilárdságának várható
CAD-CAM-CAE Példatár
 CAD-CAM-CAE Példatár A példa megnevezése: A példa száma: A példa szintje: CAx rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: VEM befogott tartó ÓE-A15 alap közepes haladó CATIA V5 CAD,
CAD-CAM-CAE Példatár A példa megnevezése: A példa száma: A példa szintje: CAx rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: VEM befogott tartó ÓE-A15 alap közepes haladó CATIA V5 CAD,
A brachistochron probléma megoldása
 A brachistochron probléma megoldása Adott a függőleges síkban két nem egy függőleges egyenesen fekvő P 0 és P 1 pont, amelyek közül a P 1 fekszik alacsonyabban. Azt a kérdést fogjuk vizsgálni. hogy van-e
A brachistochron probléma megoldása Adott a függőleges síkban két nem egy függőleges egyenesen fekvő P 0 és P 1 pont, amelyek közül a P 1 fekszik alacsonyabban. Azt a kérdést fogjuk vizsgálni. hogy van-e
KIFÁRADÁSI ÉLETTARTAM KISFELADAT (MSc.)
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM KIFÁRADÁSI ÉLETTARTAM KISFELADAT (MSc.) Járműelemek és Járműszerkezetanalízis Tanszék Ssz.:...... Név:......................................... Neptun kód.:.........
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM KIFÁRADÁSI ÉLETTARTAM KISFELADAT (MSc.) Járműelemek és Járműszerkezetanalízis Tanszék Ssz.:...... Név:......................................... Neptun kód.:.........
Tartószerkezetek tervezése tűzhatásra - az Eurocode szerint
 Tartószerkezetek tervezése tűzhatásra - az Eurocode szerint Dr. Horváth László egyetemi docens Budapesti Műszaki és Gazdaságtudományi Egyetem Hidak és Szerkezetek Tanszék Tartalom Mire ad választ az Eurocode?
Tartószerkezetek tervezése tűzhatásra - az Eurocode szerint Dr. Horváth László egyetemi docens Budapesti Műszaki és Gazdaságtudományi Egyetem Hidak és Szerkezetek Tanszék Tartalom Mire ad választ az Eurocode?
Rugalmas állandók mérése (2-es számú mérés) mérési jegyzõkönyv
 (-es számú mérés) mérési jegyzõkönyv Készítette:,... Beadás ideje:.. 9. /9 A mérés leírása: A mérés során különbözõ alakú és anyagú rudak Young-moduluszát, valamint egy torziós szál torziómoduluszát akarjuk
(-es számú mérés) mérési jegyzõkönyv Készítette:,... Beadás ideje:.. 9. /9 A mérés leírása: A mérés során különbözõ alakú és anyagú rudak Young-moduluszát, valamint egy torziós szál torziómoduluszát akarjuk
TANTÁRGYI ADATLAP I. TANTÁRGYLEÍRÁS
 TANTÁRGYI ADATLAP I. TANTÁRGYLEÍRÁS 1 ALAPADATOK 1.1 Tantárgy neve ACÉLSZERKEZETEK 1.2 Azonosító (tantárgykód) BMEEOHSAT42 1.3 A tantárgy jellege kontaktórás tanegység 1.4 Óraszámok típus óraszám előadás
TANTÁRGYI ADATLAP I. TANTÁRGYLEÍRÁS 1 ALAPADATOK 1.1 Tantárgy neve ACÉLSZERKEZETEK 1.2 Azonosító (tantárgykód) BMEEOHSAT42 1.3 A tantárgy jellege kontaktórás tanegység 1.4 Óraszámok típus óraszám előadás
4.33. ábra Nyomott rúd befogási és vezetési körülményei
 Ismételje át az Euler-féle efogási esetek mechanikai alapjait! Gyűjtse ki és tanulja a hidegfolyató élyegek terhelési típusát! Jegyezze a élyegek geometriai kialakításának szaályait! Rajzoljon különöző
Ismételje át az Euler-féle efogási esetek mechanikai alapjait! Gyűjtse ki és tanulja a hidegfolyató élyegek terhelési típusát! Jegyezze a élyegek geometriai kialakításának szaályait! Rajzoljon különöző
Csuklós szerkezetek reakciói és igénybevételi ábrái. Frissítve: példa: A 12. gyakorlat 1. feladata.
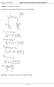 1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
Statika gyakorló teszt I.
 Statika gakorló teszt I. Készítette: Gönczi Dávid Témakörök: (I) közös ponton támadó erőrendszerek síkbeli és térbeli feladatai (1.1-1.6) (II) merev testre ható síkbeli és térbeli erőrendszerek (1.7-1.13)
Statika gakorló teszt I. Készítette: Gönczi Dávid Témakörök: (I) közös ponton támadó erőrendszerek síkbeli és térbeli feladatai (1.1-1.6) (II) merev testre ható síkbeli és térbeli erőrendszerek (1.7-1.13)
Numerikus integrálás
 Közelítő és szimbolikus számítások 11. gyakorlat Numerikus integrálás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Határozatlan integrál
Közelítő és szimbolikus számítások 11. gyakorlat Numerikus integrálás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Határozatlan integrál
Ebben a fejezetben egy szögtámfal tervezését, és annak teljes számítását mutatjuk be.
 2. számú mérnöki kézikönyv Frissítve: 2016. Február Szögtámfal tervezése Program: Szögtámfal File: Demo_manual_02.guz Feladat: Ebben a fejezetben egy szögtámfal tervezését, és annak teljes számítását mutatjuk
2. számú mérnöki kézikönyv Frissítve: 2016. Február Szögtámfal tervezése Program: Szögtámfal File: Demo_manual_02.guz Feladat: Ebben a fejezetben egy szögtámfal tervezését, és annak teljes számítását mutatjuk
Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén.
 Alkalmazott előjelszabályok Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén. A kényszererők számításánál a következő a szabály: Az erők iránya a pozitív
Alkalmazott előjelszabályok Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén. A kényszererők számításánál a következő a szabály: Az erők iránya a pozitív
KOMMUNIKÁCIÓS DOSSZIÉ MECHANIKA. Anyagmérnök BSc Szak Évfolyamszintű tárgy. Miskolci Egyetem. Gépészmérnöki és Informatikai Kar
 KOMMUNIKÁCIÓS DOSSZIÉ MECHANIKA Anyagmérnök BSc Szak Évfolyamszintű tárgy Miskolci Egyetem Gépészmérnöki és Informatikai Kar Műszaki Mechanikai Intézet 1. Tantárgyleírás Tantárgy neve: Mechanika Tantárgy
KOMMUNIKÁCIÓS DOSSZIÉ MECHANIKA Anyagmérnök BSc Szak Évfolyamszintű tárgy Miskolci Egyetem Gépészmérnöki és Informatikai Kar Műszaki Mechanikai Intézet 1. Tantárgyleírás Tantárgy neve: Mechanika Tantárgy
Használható segédeszköz: - szöveges adatok tárolására és megjelenítésére nem alkalmas számológép; - körző; - vonalzók.
 A 27/2012 (VIII. 27.) NGM rendelet a 29/2016. (VIII. 26.) NGM rendelet által módosított szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosítószáma és megnevezése 54 582 03 Magasépítő technikus
A 27/2012 (VIII. 27.) NGM rendelet a 29/2016. (VIII. 26.) NGM rendelet által módosított szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosítószáma és megnevezése 54 582 03 Magasépítő technikus
Acélszerkezetek. 3. előadás 2012.02.24.
 Acélszerkezetek 3. előadás 2012.02.24. Kapcsolatok méretezése Kapcsolatok típusai Mechanikus kapcsolatok: Szegecsek Csavarok Csapok Hegesztett kapcsolatok Tompavarrat Sarokvarrat Coalbrookdale, 1781 Eiffel
Acélszerkezetek 3. előadás 2012.02.24. Kapcsolatok méretezése Kapcsolatok típusai Mechanikus kapcsolatok: Szegecsek Csavarok Csapok Hegesztett kapcsolatok Tompavarrat Sarokvarrat Coalbrookdale, 1781 Eiffel
TELJESÍTMÉNYNYILATKOZAT A 305/2011. számú (EU) szabályozás (Construction Products Regulation - építési termék rendelet) III. melléklete alapján
 HU TELJESÍTMÉNYNYILATKOZAT A 305/2011. számú (EU) szabályozás (Construction Products Regulation - építési termék rendelet) III. melléklete alapján 1. A terméktípus egyedi azonosító kódja: Hilti HVB ágyazókengyel
HU TELJESÍTMÉNYNYILATKOZAT A 305/2011. számú (EU) szabályozás (Construction Products Regulation - építési termék rendelet) III. melléklete alapján 1. A terméktípus egyedi azonosító kódja: Hilti HVB ágyazókengyel
KIFÁRADÁSI ÉLETTARTAM KISFELADAT
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM KIFÁRADÁSI ÉLETTARTAM KISFELADAT Járműelemek és Járműszerkezetanalízis Tanszék Ssz.:...... Név:......................................... Neptun kód.:.........
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM KIFÁRADÁSI ÉLETTARTAM KISFELADAT Járműelemek és Járműszerkezetanalízis Tanszék Ssz.:...... Név:......................................... Neptun kód.:.........
Szilárd testek rugalmassága
 Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
CAD-CAM-CAE Példatár
 CAD-CAM-CAE Példatár A példa megnevezése: A példa száma: A példa szintje: CAx rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: VEM térbeli hajlított rúd ÓE-A03 alap közepes haladó VEM
CAD-CAM-CAE Példatár A példa megnevezése: A példa száma: A példa szintje: CAx rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: VEM térbeli hajlított rúd ÓE-A03 alap közepes haladó VEM
Az ötszög keresztmetszetű élszarufa keresztmetszeti jellemzőiről
 1 Az ötszög keresztmetszetű élszarufa keresztmetszeti jellemzőiről Bevezetés A kontytetők és az összetett alaprajzú tetők akár nyeregtetők szerkezeti elemei között megtaláljuk az él - és a vápaszarufákat
1 Az ötszög keresztmetszetű élszarufa keresztmetszeti jellemzőiről Bevezetés A kontytetők és az összetett alaprajzú tetők akár nyeregtetők szerkezeti elemei között megtaláljuk az él - és a vápaszarufákat
Koordináta-geometria feladatok (emelt szint)
 Koordináta-geometria feladatok (emelt szint) 1. (ESZÉV Minta (2) 2004.05/7) Egy ABC háromszögben CAB = 30, az ACB = 45. A háromszög két csúcsának koordinátái: A(2; 2) és C(4; 2). Határozza meg a harmadik
Koordináta-geometria feladatok (emelt szint) 1. (ESZÉV Minta (2) 2004.05/7) Egy ABC háromszögben CAB = 30, az ACB = 45. A háromszög két csúcsának koordinátái: A(2; 2) és C(4; 2). Határozza meg a harmadik
Scholler 3 Dolgozat. Téma: Kardok mechanikai vizsgálata
 Scholler 3 Dolgozat Téma: Kardok mechanikai vizsgálata Készítette: Rádi Ferenc, BME, Gépészmérnöki Kar, Msc-Mechanical Modelling tanulója 2012. július. 17 Elfogadta: Miskolczi Mátyás, Waldmanné Csabán
Scholler 3 Dolgozat Téma: Kardok mechanikai vizsgálata Készítette: Rádi Ferenc, BME, Gépészmérnöki Kar, Msc-Mechanical Modelling tanulója 2012. július. 17 Elfogadta: Miskolczi Mátyás, Waldmanné Csabán
Statika gyakorló teszt II.
 Statika gakorló teszt II. Készítette: Gönczi Dávid Témakörök: (I) Egszerű szerkezetek síkbeli statikai feladatai (II) Megoszló terhelésekkel kapcsolatos számítások (III) Összetett szerkezetek síkbeli statikai
Statika gakorló teszt II. Készítette: Gönczi Dávid Témakörök: (I) Egszerű szerkezetek síkbeli statikai feladatai (II) Megoszló terhelésekkel kapcsolatos számítások (III) Összetett szerkezetek síkbeli statikai
Mozgatható térlefedő szerkezetek
 Mozgatható térlefedő szerkezetek TDK Konferencia 2010 Szilárdságtani és tartószerkezeti szekció Tartalomjegyzék 1 Absztrakt 2 Bevezetés 3 Az alakzat mozgásának görbületre gyakorolt hatása 4 Teljes összenyomódás
Mozgatható térlefedő szerkezetek TDK Konferencia 2010 Szilárdságtani és tartószerkezeti szekció Tartalomjegyzék 1 Absztrakt 2 Bevezetés 3 Az alakzat mozgásának görbületre gyakorolt hatása 4 Teljes összenyomódás
DEME FERENC okl. építőmérnök, mérnöktanár
 DEME FERENC okl. építőmérnök, mérnöktanár web-lap : www.sze.hu/~deme e-mail : deme.ferenc1@gmail.com HÁROMCSUKLÓS TARTÓ KÜLSŐ ÉS BELSŐ REAKCIÓ ERŐINEK SZÁMÍTÁSA, A TARTÓ IGÉNYBEVÉTELI ÁBRÁINAK RAJZOLÁSA
DEME FERENC okl. építőmérnök, mérnöktanár web-lap : www.sze.hu/~deme e-mail : deme.ferenc1@gmail.com HÁROMCSUKLÓS TARTÓ KÜLSŐ ÉS BELSŐ REAKCIÓ ERŐINEK SZÁMÍTÁSA, A TARTÓ IGÉNYBEVÉTELI ÁBRÁINAK RAJZOLÁSA
Szádfal szerkezet ellenőrzés Adatbev.
 Szádfal szerkezet ellenőrzés Adatbev. Projekt Dátum : 8.0.05 Beállítások (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : Acél szerkezetek : Acél keresztmetszet teherbírásának
Szádfal szerkezet ellenőrzés Adatbev. Projekt Dátum : 8.0.05 Beállítások (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : Acél szerkezetek : Acél keresztmetszet teherbírásának
Feladatok megoldásokkal a harmadik gyakorlathoz (érintési paraméterek, L Hospital szabály, elaszticitás) y = 1 + 2(x 1). y = 2x 1.
 Feladatok megoldásokkal a harmadik gyakorlathoz (érintési paraméterek, L Hospital szabály, elaszticitás). Feladat. Írjuk fel az f() = függvény 0 = pontbeli érintőjének egyenletét! Az érintő egyenlete y
Feladatok megoldásokkal a harmadik gyakorlathoz (érintési paraméterek, L Hospital szabály, elaszticitás). Feladat. Írjuk fel az f() = függvény 0 = pontbeli érintőjének egyenletét! Az érintő egyenlete y
Rugalmas állandók mérése
 Rugalmas állandók mérése Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina Szerda délelőtti csoport Mérés ideje: 11/30/2011 Beadás ideje: 12/07/2011 1 1. A mérés rövid leírása Mérésem
Rugalmas állandók mérése Mérő neve: Márkus Bence Gábor Mérőpár neve: Székely Anna Krisztina Szerda délelőtti csoport Mérés ideje: 11/30/2011 Beadás ideje: 12/07/2011 1 1. A mérés rövid leírása Mérésem
Földstatikai feladatok megoldási módszerei
 Földstatikai feladatok megoldási módszerei Földstatikai alapfeladatok Földnyomások számítása Általános állékonyság vizsgálata Alaptörés parciális terhelés alatt Süllyedésszámítások Komplex terhelési esetek
Földstatikai feladatok megoldási módszerei Földstatikai alapfeladatok Földnyomások számítása Általános állékonyság vizsgálata Alaptörés parciális terhelés alatt Süllyedésszámítások Komplex terhelési esetek
ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS
 Miskolci Egyetem Bányászati és Geotechnikai Intézet Bányászati és Geotechnikai Intézeti Tanszék ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS Oktatási segédlet Szerző: Dr. Somosvári Zsolt DSc professzor emeritus Szerkesztette:
Miskolci Egyetem Bányászati és Geotechnikai Intézet Bányászati és Geotechnikai Intézeti Tanszék ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS Oktatási segédlet Szerző: Dr. Somosvári Zsolt DSc professzor emeritus Szerkesztette:
Acélszerkezetek I. Gyakorlati óravázlat. BMEEOHSSI03 és BMEEOHSAT17. Jakab Gábor
 Acélszerkezetek I. BMEEOHSSI0 és BMEEOHSAT17 Gakorlati óravázlat Készítette: Dr. Kovács Nauzika Jakab Gábor A gakorlatok témája: 1. A félév gakorlati oktatásának felépítése. A szerkezeti acélanagok fajtái,
Acélszerkezetek I. BMEEOHSSI0 és BMEEOHSAT17 Gakorlati óravázlat Készítette: Dr. Kovács Nauzika Jakab Gábor A gakorlatok témája: 1. A félév gakorlati oktatásának felépítése. A szerkezeti acélanagok fajtái,
