DEME FERENC okl. építőmérnök, mérnöktanár
|
|
|
- Ede Kerekes
- 7 évvel ezelőtt
- Látták:
Átírás
1 DEME FERENC okl. építőmérnök, mérnöktanár web-lap : deme.ferenc1@gmail.com HÁROMCSUKLÓS TARTÓ KÜLSŐ ÉS BELSŐ REAKCIÓ ERŐINEK SZÁMÍTÁSA, A TARTÓ IGÉNYBEVÉTELI ÁBRÁINAK RAJZOLÁSA SZÁMÍTOTT ÉRTÉKEK ALAPJÁN F = 300 kn F 3 = 100 kn F 1 = 00 kn F 1Z C F 1 F 1X I. II. F 1Z B F 1X sin = cos = A F 1X = F 1Z = 0, = 141,4 kn AZ EGÉSZ TARTÓ NYUGALOMBAN VAN, TEHÁT AZ ÖSSZES ERŐ EGYENSÚLYBAN VAN. TERMÉSZETESEN A TARTÓ RÉSZEI IS NYUGALOMBAN VANNAK, ÍGY A RÁJUK HATÓ ERŐK IS EGYENSÚLYBAN VANNAK. EZT AZ ÁLLAPOTOT ÍRJÁK LE AZ EGYENSÚLYI KIJELENTÉSEK. 1.) AZ ÖSSZES KÜLSŐ ERŐRE VONATKOZÓ EGYENSÚLYI KIJELENTÉS: ( A, F 1, F, F 3, B ) = 0 Tehát az összes külső erőből álló erőrendszer egyenértékű nullával..) AZ I. JELŰ (BAL OLDALI) TARTÓRÉSZRE HATÓ ERŐKRE VONATKOZÓ EGYENSÚLYI KIJELENTÉS: ( A, F 1, C I. ) = 0 Tehát az I. jelű bal oldali tartórészre ható erőrendszer egyenértékű nullával. A C I. a C csuklóból az I. jelű (bal oldali) részre ható erő. 3.) A II. JELŰ (JOBB OLDALI) TARTÓRÉSZRE HATÓ ERŐKRE VONATKOZÓ EGYENSÚLYI KIJELENTÉS: ( C II., F 3, B ) = 0 Tehát a II. jelű jobb oldali tartórészre ható erőrendszer egyenértékű nullával. A C II. a C csuklóból a II. jelű (jobb oldali) részre ható erő. 4.) A C JELŰ CSUKLÓRA HATÓ ERŐKRE VONATKOZÓ EGYENSÚLYI KIJELENTÉS: ( C I., F, C II. ) = 0 Tehát a C jelű csuklóra ható erőrendszer egyenértékű nullával. A C I. a C I. ellentettje, tehát az I. jelű tartóból a C csuklóra ható erő. A C II. a C II. ellentettje, tehát a II. jelű tartóból a C csuklóra ható erő.
2 A KÜLSŐ TÁMASZERŐK ( A ÉS B ) MEGHATÁROZÁSA AZ ÖSSZES KÜLSŐ ERŐRE VONATKOZÓ EGYENSÚLYI KIJELENTÉS ALAPJÁN [1.)-BŐL], FELÍRJUK AZ ERŐK NYOMATÉKÖSSZEGÉT A B TÁMASZPONTRA. EBBEN AZ EGYENLETBEN LESZ KÉT ISMERETLEN, AZ ÉS AZ. A KÉT ISMERETLEN MEGHATÁROZÁSÁHOZ SZÜKSÉGES MÁSODIK EGYENLET A BAL OLDALI (I. JELŰ) TARTÓRÉSZRE VONATKOZÓ EGYENSÚLYI KIJELENTÉS ALAPJÁN [.)-BŐL] FELÍRT NYOMATÉKÖSSZEG LESZ A C CSUKLÓRA. AZ ISMERETLENEK ( és ) IRÁNYÁT A KOORDINÁTARENDSZER TENGELYEINEK POZITÍV IRÁNYAIBA MUTATÓKNAK KELL FELTÉTELEZNI! TEHÁT AZ -ET JOBBRA, AZ -T FELFELÉ MUTATÓNAK TÉTELEZZÜK FEL. (NYOMATÉKAIK ELŐJELEI EZEKNEK A NYILAKNAK A FORGATÓ ÉRTELME SZERINT ALAKUL.) 1.)-ből: M i B = ,4 141, = 0.)-ből: M i C = / = 0 A KÉT EGYENLET EGYSZERŰBB ALAKBAN: ,6 = ,68 = 0 AZ ELSŐ EGYENLETBŐL KIFEJEZZÜK AZ T: = + 0, + 196,56 A KIFEJEZETT -T BEHELYETTESÍTJÜK (0, + 196,56) 6 565,68 = 0 A MÁSODIK EGYENLETBE ÉS MEGOLDJUK: -4, ,68 = 0 = + 17,85 kn (A POZITÍV ELŐJEL AZT JELENTI, HOGY A FELTÉTELEZETTEL EGYEZŐ IRÁNYÚ, TEHÁT JOBBRA MUTAT.) AZ -ET BEÍRVA AZ T KIFEJEZŐ EGYENLETBE: = + 0, (17,85) + 196,56 = +,13 kn (A POZITÍV ELŐJEL AZT JELENTI, HOGY A FELTÉTELEZETTEL EGYEZŐ IRÁNYÚ, TEHÁT FELFELÉ MUTAT.) +Z +X AZ A KOMPONENSEINEK ISMERETÉBEN AZ ÖSSZES KÜLSŐ ERŐRE VONATKOZÓ EGYENSÚLYI KIJELENTÉS ALAPJÁN [1-BŐL], KÉT VETÜLETI EGYENLET SZOLGÁLTATJA A B KOMPONENSEIT. 1.)-ből: F ix = 0. +Z + 17, ,4 + B X = 0 B X = - 69,5 kn +X 1.)-ből: F iz = 0. +,13 141, B Z = 0 B Z = + 319,7 kn
3 A BELSŐ KAPCSOLATI ERŐK ( C I. ÉS C II. ) MEGHATÁROZÁSA AZ I. JELŰ (BAL OLDALI) TARTÓRÉSZRE HATÓ ERŐKRE VONATKOZÓ EGYENSÚLYI KIJELENTÉS ALAPJÁN [.)-BŐL] VETÜLETI EGYENLETEKBŐL KAPJUK A C I.X -ET ÉS C I.Z -T..)-ből: F ix = , ,4 + C I.X = 0 C I.X = - 69,5 kn.)-ből: F iz = 0. +,13 141,4 + C I.Z = 0 C I.Z = - 80,73 kn A II. JELŰ (JOBB OLDALI) TARTÓRÉSZRE HATÓ ERŐKRE VONATKOZÓ EGYENSÚLYI KIJELENTÉS ALAPJÁN [3.-BÓL] VETÜLETI EGYENLETEKBŐL KAPJUK A -ET ÉS -T. 3.)-ból: F ix = 0. 69,5 = 0 = + 69,5 kn 3.)-ból: F iz = ,7 = 0 = - 19,7 kn A C JELŰ CSUKLÓRA HATÓ ERŐKRE VONATKOZÓ EGYENSÚLYI KIJELENTÉS ALAPJÁN [4.-BŐL] ELLENŐRZÉSRE VAN LEHETŐSÉG, MIVEL AZ ÖSSZES ITT HATÓ ERŐ MÁR ISMERTTÉ VÁLT. 4.)-ből: F ix = 0 + C I.X C II.X = ,5 69,5 = 0 0 = 0 4.-ből: F iz = 0 - F + C I.Z + C II.Z = , ,7 = 0 0 = 0
4 C I.Z = 80,73 kn EREDMÉNYVÁZLAT F = 300 kn = 19,7 kn F 3 = 100 kn F 1 = 00 kn C I.X = 69,5 kn C II.X = 69,5 kn C I.X = 69,5 kn C I.Z = 80,73 kn C II.Z = 19,7 kn = 69,5 kn B X = 69,5 kn = 17,85 kn =,13 kn B Z = 319,7 kn AZ IGÉNYBEVÉTELI ÁBRÁK RAJZOLÁSÁHOZ KI KELL SZÁMOLNI AZ IGÉNYBEVÉTELEKET AZ ÖSSZES OLYAN KERESZTMETSZETBEN, AHOL A TARTÓ TENGELYE TÖRIK, ILLETVE A TERHELÉS VÁLTOZIK. EZEKEN A HELYEKEN VIZSGÁLNI KELL A KERESZTMETSZETTŐL VÉGTELEN KÖZEL BALRA (ELŐTTE) ÉS VÉGTELEN KÖZEL JOBBRA (UTÁNA) ÉRTELMEZETT KERESZTMETSZETET A VIZSGÁLAT SORÁN BALRÓL JOBBRA HALADUNK, AHOGY A RAJZBAN JELÖLT KERESZTMETSZETEK SORSZÁMOZÁSA IS MUTATJA. ELŐJELSZABÁLY: NORMÁLERŐ (N): HA HÚZZA A KERESZTMETSZETET POZITÍV, HA NYOMJA NEGATÍV. NYÍRÓERŐ (V): A KERESZTMETSZETBEN ÉRTELMEZETT HÚZÓERŐT AZ ÓRAMUTATÓ FORGÁSÁNAK IRÁNYÁBA KAL ELFORGATVA KAPJUK A POZITÍV NYÍRÓERŐT. NYOMATÉK (M): AZ ÓRAMUTATÓ FORGÁSÁVAL EGYEZŐ FORGATÁS A POZITÍV.
5 AZ IGÉNYBEVÉTELEK MEGHATÁROZÁSA A KIJELÖLT ( ) KERESZTMETSZETEKBEN A TARTÓN BALRÓL JOBBRA HALADVA, GONDOLATBAN ELFŰRÉSZELJÜK AZT A KERESZTMETSZETET, AMELYET ÉPPEN VIZSGÁLUNK. A LEESŐ BAL OLDALI RÉSZRŐL AZ ÖSSZES ERŐT HATÁSVONALAIKKAL PÁRHUZAMOSAN ÁTHELYEZZÜK A MEGMARADÓ JOBB OLDALI RÉSZ FŰRÉSZELT KERESZTMETSZETÉNEK A SÚLYPONTJÁBA. EZEKNEK AZ ERŐKNEK A TARTÓ TENGELYÉRE ESŐ VETÜLETE LESZ A NORMÁLERŐ, A KERESZTMETSZET SÍKJÁBA ESŐ VETÜLETE A NYÍRÓERŐ, AZ EREDETI HELYÜKRŐL KIFEJTETT NYOMATÉKAIK ÖSSZEGE A HAJLÍTÓNYOMATÉK. 1. JELŰ KERESZTMETSZET. JELŰ KERESZTMETSZET N 1 = - = -,13 kn V 1 = - = -17,85 kn M 1 = 0 knm N = N 1 = -,13 kn V = V 1 = - 17,85 kn M = - 17,85 = - 55,7 knm 3. JELŰ KERESZTMETSZET 4. JELŰ KERESZTMETSZET N3 = - = - 17,85 kn V 3 = + = +,13 kn M 3 = M = - 55,7 knm 5. JELŰ KERESZTMETSZET 6. JELŰ KERESZTMETSZET N 4 = N 3 = -17,85 kn V 4 = V 3 = +,13 kn M 4 = - 17,85 +,13 = = + 188,56 knm V N N V N N = V = 0,707 17,85 = 90,39 kn N N = = 0,707,13 = 157 kn N 5 = - N N = - 90, = - 47,39 kn V 5 = + V = ,39 = +66,61 kn M 5 = M 4 = + 188,56 knm V N N N 6 = N 5 = - 47,39 kn V 6 = V 5 = + 66,61 kn M 6 = - 17,85 4 +,13 4 = + 377,1 knm 7. JELŰ KERESZTMETSZET 8. JELŰ KERESZTMETSZET V N F 1 F 1 N N 7 = N 6 = - 47,39 kn V 7 = V 6 F 1 = = + 66,61 00 = = - 133,39 kn M 7 = M 6 = + 377,1 knm V N N N 8 = N 7 = - 47,39 kn V 8 = V 7 = - 133,39 kn M 8 = 0 knm ( A csukló nem tud felvenni nyomatékot! )
6 A II. JELŰ TARTÓRÉSZT (JOBB OLDALI TARTÓRÉSZT) ÖNÁLLÓ TESTNEK TEKINTJÜK, EZÉRT ENNEK A BAL OLDALI VÉGE A C CSUKLÓ. TEHÁT A 9. KERESZTMETSZETBEN CSAK A C II. ILLETVE ENNEK KOMPONENSEI HATNAK. 9. JELŰ KERESZTMETSZET 10. JELŰ KERESZTMETSZET N 9 = - = -69,5 kn V 9 = - = -19,7 kn M 9 = 0 knm N 10 = N 9 = -69,5 kn V 10 = V 9 = - 19,7 kn M 10 = - 19,7 = -438,54 knm 11. JELŰ KERESZTMETSZET 1. JELŰ KERESZTMETSZET F 3 F 3 N 11 = N 10 = - 69,5 kn V 11 = V 10 F 3 = - 19,7 100 = - 319,7 kn M 11 = M 10 = - 438,54 knm N 1 = N 11 = - 69,5 kn V 1 = V 11 = - 319,7 kn M 1 = - 19, = ,08 knm 13. JELŰ KERESZTMETSZET 14. JELŰ KERESZTMETSZET F 3 F 3 N 13 = - F 3 = - 19,7 100 = - 319,7 kn V 13 = + = + 69,5 kn M 13 = M 1 = ,08 knm N 14 = N 13 = - 319,7 kn V 14 = V 13 = + 69,5 kn M 14 = 0 knm
7 A TARTÓ IGÉNYBEVÉTELI ÁBRÁI N ÁBRA -47,39-17,85-69,5-319,7 -, V ÁBRA -133,39-19,7-319,7-17,85 +66,61 +,13 +69,5 + - M ÁBRA -438, , ,08-55,7-55, , , ,1 + -
Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén.
 Alkalmazott előjelszabályok Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén. A kényszererők számításánál a következő a szabály: Az erők iránya a pozitív
Alkalmazott előjelszabályok Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén. A kényszererők számításánál a következő a szabály: Az erők iránya a pozitív
DEME FERENC okl. építőmérnök, mérnöktanár RÁCSOS TARTÓK
 we-lap : www.hild.gyor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STTIK 47. RÁCSOS TRTÓK rácsos tartók két végükön csuklókkal összekötött merev testekől állnak. z így
we-lap : www.hild.gyor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STTIK 47. RÁCSOS TRTÓK rácsos tartók két végükön csuklókkal összekötött merev testekől állnak. z így
A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS-
 A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS- Forgatónyomaték meghatározása G Á L A T A Egy erő forgatónyomatékkal hat egy pontra, ha az az erővel össze van kötve. Például
A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS- Forgatónyomaték meghatározása G Á L A T A Egy erő forgatónyomatékkal hat egy pontra, ha az az erővel össze van kötve. Például
Navier-formula. Frissítve: Egyenes hajlítás
 Navier-formula Akkor beszélünk egyenes hajlításról, ha a nyomatékvektor egybeesik valamelyik fő-másodrendű nyomatéki tengellyel. A hajlítást mindig súlyponti koordinátarendszerben értelmezzük. Ez még a
Navier-formula Akkor beszélünk egyenes hajlításról, ha a nyomatékvektor egybeesik valamelyik fő-másodrendű nyomatéki tengellyel. A hajlítást mindig súlyponti koordinátarendszerben értelmezzük. Ez még a
Az M A vektor tehát a három vektori szorzat előjelhelyes összege:
 1. feladat Határozza meg a T i támadáspontú F i erőrendszer nyomatékát az A pontra. T 1 ( 3, 0, 5 ) T 1 ( 0, 4, 5 ) T 1 ( 3, 4, 2 ) F 1 = 0 i + 300 j + 0 k F 2 = 0 i 100 j 400 k F 3 = 100 i 100 j + 500
1. feladat Határozza meg a T i támadáspontú F i erőrendszer nyomatékát az A pontra. T 1 ( 3, 0, 5 ) T 1 ( 0, 4, 5 ) T 1 ( 3, 4, 2 ) F 1 = 0 i + 300 j + 0 k F 2 = 0 i 100 j 400 k F 3 = 100 i 100 j + 500
A síkbeli Statika egyensúlyi egyenleteiről
 1 A síkbeli Statika egyensúlyi egyenleteiről Statikai tanulmányaink egyik mérföldköve az egyensúlyi egyenletek belátása és sikeres alkalmazása. Most egy erre vonatkozó lehetséges tanulási / tanítási útvonalat
1 A síkbeli Statika egyensúlyi egyenleteiről Statikai tanulmányaink egyik mérföldköve az egyensúlyi egyenletek belátása és sikeres alkalmazása. Most egy erre vonatkozó lehetséges tanulási / tanítási útvonalat
BME Gépészmérnöki Kar 3. vizsga (112A) Név: 1 Műszaki Mechanikai Tanszék január 11. Neptun: 2 Szilárdságtan Aláírás: 3
 BME Gépészmérnöki Kar 3. vizsga (2A) Név: Műszaki Mechanikai Tanszék 2. január. Neptun: 2 Szilárdságtan Aláírás: 3. feladat (2 pont) A vázolt befogott tartót a p intenzitású megoszló erőrendszer, az F
BME Gépészmérnöki Kar 3. vizsga (2A) Név: Műszaki Mechanikai Tanszék 2. január. Neptun: 2 Szilárdságtan Aláírás: 3. feladat (2 pont) A vázolt befogott tartót a p intenzitású megoszló erőrendszer, az F
KERESZTMETSZETI JELLEMZŐK
 web-lap : www.hild.gor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 50. KERESZTMETSZETI JELLEMZŐK A TARTÓK MÉRETEZÉSE SORÁN SZÁMOS ESETBEN SZÜKSÉGÜNK VAN OLYAN ADATOKRA,
web-lap : www.hild.gor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 50. KERESZTMETSZETI JELLEMZŐK A TARTÓK MÉRETEZÉSE SORÁN SZÁMOS ESETBEN SZÜKSÉGÜNK VAN OLYAN ADATOKRA,
 MECHANIKA I. /Statika/ 1. előadás SZIE-YMM 1. Bevezetés épületek, építmények fizikai hatások, köztük erőhatások részleges vagy teljes tönkremenetel használhatatlanná válás anyagi kár, emberáldozat 1 Cél:
MECHANIKA I. /Statika/ 1. előadás SZIE-YMM 1. Bevezetés épületek, építmények fizikai hatások, köztük erőhatások részleges vagy teljes tönkremenetel használhatatlanná válás anyagi kár, emberáldozat 1 Cél:
6. MECHANIKA-STATIKA GYAKORLAT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya, Culmann-szerkesztés, Ritter-számítás
 ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
6. MECHANIKA-STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnöktanár)
 SZÉHNYI ISTVÁN GYT LKLZOTT HNIK TNSZÉK 6. HNIK-STTIK GYKORLT (kidolgozta: Triesz Péter egy. ts.; Tarnai Gábor mérnöktanár) Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa gy létrát egy
SZÉHNYI ISTVÁN GYT LKLZOTT HNIK TNSZÉK 6. HNIK-STTIK GYKORLT (kidolgozta: Triesz Péter egy. ts.; Tarnai Gábor mérnöktanár) Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa gy létrát egy
Felső végükön egymásra támaszkodó szarugerendák egyensúlya
 1 Felső végükön egymásra támaszkodó szarugerendák egyensúlya Az [ 1 ] példatárban találtunk egy érdekes feladatot, melynek egy változatát vizsgáljuk meg itt. A feladat Ehhez tekintsük az 1. ábrát! 1. ábra
1 Felső végükön egymásra támaszkodó szarugerendák egyensúlya Az [ 1 ] példatárban találtunk egy érdekes feladatot, melynek egy változatát vizsgáljuk meg itt. A feladat Ehhez tekintsük az 1. ábrát! 1. ábra
X = 0 B x = 0. M B = A y 6 = 0. B x = 0 A y = 1000 B y = 400
 1. feladat Számítsuk ki a bejelölt rúderőket! Az erők N-ban, a hosszak m-ben, a nyomatékok Nm-ben értendők Első lépésként határozzuk meg a kényszererőket. Az S 1 rúderő számítása: Egyensúlyi egyenletek:
1. feladat Számítsuk ki a bejelölt rúderőket! Az erők N-ban, a hosszak m-ben, a nyomatékok Nm-ben értendők Első lépésként határozzuk meg a kényszererőket. Az S 1 rúderő számítása: Egyensúlyi egyenletek:
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 Építészeti és építési alapismeretek középszint 0821 ÉRETTSÉGI VIZSGA 2008. október 20. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS
Építészeti és építési alapismeretek középszint 0821 ÉRETTSÉGI VIZSGA 2008. október 20. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS
Az igénybevételi függvényekről és ábrákról
 1 Az igénybevételi függvényekről és ábrákról Úgy tűnik, hogy a technikusi minősítő vizsgára való felkészítő tanulási / tanítási feladatok egyik legnehezebb része a tartók igénybevételeivel kapcsolatos.
1 Az igénybevételi függvényekről és ábrákról Úgy tűnik, hogy a technikusi minősítő vizsgára való felkészítő tanulási / tanítási feladatok egyik legnehezebb része a tartók igénybevételeivel kapcsolatos.
Példa keresztmetszet másodrendű nyomatékainak számítására
 Példa keresztmetszet másodrendű nyomatékainak számítására Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. február 22. Tekintsük az alábbi keresztmetszetet. 1. ábra. A vizsgált
Példa keresztmetszet másodrendű nyomatékainak számítására Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. február 22. Tekintsük az alábbi keresztmetszetet. 1. ábra. A vizsgált
MECHANIKA I. rész: Szilárd testek mechanikája
 Egészségügyi mérnökképzés MECHNIK I. rész: Szilárd testek mechanikája készítette: Németh Róbert Igénybevételek térben I. z alapelv ugyanaz, mint síkban: a keresztmetszet egyik oldalán levő szerkezetrészre
Egészségügyi mérnökképzés MECHNIK I. rész: Szilárd testek mechanikája készítette: Németh Róbert Igénybevételek térben I. z alapelv ugyanaz, mint síkban: a keresztmetszet egyik oldalán levő szerkezetrészre
Egymásra támaszkodó rudak
 1 Egymásra támaszkodó rudak Úgy látszik, ez is egy visszatérő téma. Egy korábbi írásunkban melynek címe: A mandala - tetőről már találkoztunk az 1. ábrán vázolthoz hasonló felülnézetű szerkezettel, foglalkoztunk
1 Egymásra támaszkodó rudak Úgy látszik, ez is egy visszatérő téma. Egy korábbi írásunkban melynek címe: A mandala - tetőről már találkoztunk az 1. ábrán vázolthoz hasonló felülnézetű szerkezettel, foglalkoztunk
Igénybevételek. A statika és dinamika alapjai
 IG Igénybevételek továbbiakban egyensúlyban levő rúdszerkezetek belső erőivel, igénybevételeivel foglalkozunk. Ennek során rúdnak (esetleg oszlopnak vagy gerendának) azokat a karcsú szerkezeti részeket
IG Igénybevételek továbbiakban egyensúlyban levő rúdszerkezetek belső erőivel, igénybevételeivel foglalkozunk. Ennek során rúdnak (esetleg oszlopnak vagy gerendának) azokat a karcsú szerkezeti részeket
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén
 Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
T s 2 képezve a. cos q s 0; 2. Kötélstatika I. A síkbeli kötelek egyensúlyi egyenleteiről és azok néhány alkalmazásáról
 Kötélstatika I. A síkbeli kötelek egyensúlyi egyenleteiről és azok néhány alkalmazásáról Úgy találjuk, hogy a kötelek statikájának népszerűsítése egy soha véget nem érő feladat. Annyi szép dolog tárháza
Kötélstatika I. A síkbeli kötelek egyensúlyi egyenleteiről és azok néhány alkalmazásáról Úgy találjuk, hogy a kötelek statikájának népszerűsítése egy soha véget nem érő feladat. Annyi szép dolog tárháza
Keresztmetszet másodrendű nyomatékainak meghatározása
 BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
Gyakorlati útmutató a Tartók statikája I. tárgyhoz. Fekete Ferenc. 4. gyakorlat. Széchenyi István Egyetem,
 Gyakorlati útmutató a Tartók statikája I. tárgyhoz Fekete Ferenc 4. gyakorlat Széchenyi István Egyetem, 0..3. . Feladat Határozza meg a képen látható tartó A támaszra vonatkozó reakcióerő hatásábráját,
Gyakorlati útmutató a Tartók statikája I. tárgyhoz Fekete Ferenc 4. gyakorlat Széchenyi István Egyetem, 0..3. . Feladat Határozza meg a képen látható tartó A támaszra vonatkozó reakcióerő hatásábráját,
Vasbeton tartók méretezése hajlításra
 Vasbeton tartók méretezése hajlításra Képlékenység-tani méretezés: A vasbeton keresztmetszet teherbírásának számításánál a III. feszültségi állapotot vesszük alapul, amelyre az jellemző, hogy a hajlításból
Vasbeton tartók méretezése hajlításra Képlékenység-tani méretezés: A vasbeton keresztmetszet teherbírásának számításánál a III. feszültségi állapotot vesszük alapul, amelyre az jellemző, hogy a hajlításból
Gyakorlat 04 Keresztmetszetek III.
 Gyakorlat 04 Keresztmetszetek III. 1. Feladat Hajlítás és nyírás Végezzük el az alábbi gerenda keresztmetszeti vizsgálatait (tiszta esetek és lehetséges kölcsönhatások) kétféle anyaggal: S235; S355! (1)
Gyakorlat 04 Keresztmetszetek III. 1. Feladat Hajlítás és nyírás Végezzük el az alábbi gerenda keresztmetszeti vizsgálatait (tiszta esetek és lehetséges kölcsönhatások) kétféle anyaggal: S235; S355! (1)
DEME FERENC okl. építőmérnök, mérnöktanár TARTÓK
 web-lap : www.hild.gyor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 19. TARTÓK FOGALMA: TARTÓK A tartók terhek biztonságos hordására és azoknak a támaszokra történő
web-lap : www.hild.gyor.hu DEME FERENC okl. építőmérnök, mérnöktanár e-mail : deme.ferenc1@gmail.com STATIKA 19. TARTÓK FOGALMA: TARTÓK A tartók terhek biztonságos hordására és azoknak a támaszokra történő
Mechanika. I. előadás február 25. Mechanika I. előadás február / 31
 Mechanika I. előadás 2019. február 25. Mechanika I. előadás 2019. február 25. 1 / 31 Elérhetőségek, információk Tantárgy: Mechanika (GEMET266-ZD-B) Előadó: Dr. Lengyel Ákos József Elérhetőségek: Iroda:
Mechanika I. előadás 2019. február 25. Mechanika I. előadás 2019. február 25. 1 / 31 Elérhetőségek, információk Tantárgy: Mechanika (GEMET266-ZD-B) Előadó: Dr. Lengyel Ákos József Elérhetőségek: Iroda:
GÉPÉSZETI ALAPISMERETEK
 Gépészeti alapismeretek emelt szint 3 ÉRETTSÉGI VIZSGA 03. május 3. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos tudnivalók
Gépészeti alapismeretek emelt szint 3 ÉRETTSÉGI VIZSGA 03. május 3. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos tudnivalók
MUNKAANYAG. Csepcsényi Lajos Lászlóné Balogh Melinda. Egyensúlyi feltételek, reakcióerők számítása. A követelménymodul megnevezése:
 Csepcsényi Lajos Lászlóné Balogh Melinda Egyensúlyi feltételek, reakcióerők számítása A követelménymodul megnevezése: Építőipari kivitelezés tervezése A követelménymodul száma: 0688-06 A tartalomelem azonosító
Csepcsényi Lajos Lászlóné Balogh Melinda Egyensúlyi feltételek, reakcióerők számítása A követelménymodul megnevezése: Építőipari kivitelezés tervezése A követelménymodul száma: 0688-06 A tartalomelem azonosító
11. MECHANIKA-STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnöktanár)
 SZÉHENYI ISTVÁN EGYETEM LKLMZOTT MEHNIK TNSZÉK.. Példa:. MEHNIK-STTIK GYKORLT (kidolgozta: Triesz Péter, eg. ts.; Tarnai Gábor, mérnöktanár) Összetett szerkezetek statikája (három csuklós ív, Gerber tartó)
SZÉHENYI ISTVÁN EGYETEM LKLMZOTT MEHNIK TNSZÉK.. Példa:. MEHNIK-STTIK GYKORLT (kidolgozta: Triesz Péter, eg. ts.; Tarnai Gábor, mérnöktanár) Összetett szerkezetek statikája (három csuklós ív, Gerber tartó)
Egy háromlábú állvány feladata. 1. ábra forrása:
 1 Egy háromlábú állvány feladata Az interneten találtuk az alábbi versenyfeladatot 1. ábra Az egyforma hosszúságú CA, CB és CD rudak a C pontban gömbcsuklóval kapcsolódnak, az A, B, D végükön sima vízszintes
1 Egy háromlábú állvány feladata Az interneten találtuk az alábbi versenyfeladatot 1. ábra Az egyforma hosszúságú CA, CB és CD rudak a C pontban gömbcsuklóval kapcsolódnak, az A, B, D végükön sima vízszintes
Csuklós szerkezetek reakciói és igénybevételi ábrái. Frissítve: példa: A 12. gyakorlat 1. feladata.
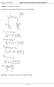 1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ STATIKA
 TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ STATIKA GEMET001-B Miskolci Egyetem Gépészmérnöki és Informatikai Kar Műszaki Mechanikai Intézet MM/37/2018. Miskolc, 2018. február 5. HIRDETMÉNY Statika(GEMET201NB és GEMET001-B)
TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ STATIKA GEMET001-B Miskolci Egyetem Gépészmérnöki és Informatikai Kar Műszaki Mechanikai Intézet MM/37/2018. Miskolc, 2018. február 5. HIRDETMÉNY Statika(GEMET201NB és GEMET001-B)
2. fejezet: Vasbeton keresztmetszet ellenõrzése hajlításra
 . ejezet: Vasbeton keresztmetszet ellenõrzése hajlításra.1. Ellenõrizze az alábbi keresztmetszetet M S =105 knm hajlítónyomatékra! Beton: C16/0 Betonaél: B60.50 φ0 1.15!! = 10.667 N y = 3.783 N φ π A s
. ejezet: Vasbeton keresztmetszet ellenõrzése hajlításra.1. Ellenõrizze az alábbi keresztmetszetet M S =105 knm hajlítónyomatékra! Beton: C16/0 Betonaél: B60.50 φ0 1.15!! = 10.667 N y = 3.783 N φ π A s
FIZIKA MECHANIKA MŰSZAKI MECHANIKA STATIKA DINAMIKA BEVEZETÉS A STATIKA HELYE A TUDOMÁNYBAN
 BEVEZETÉS A STATIKA HELYE A TUDOMÁNYBAN A statika a fizikának, mint a legszélesebb körű természettudománynak a része. A klasszikus értelemben vett fizika azokkal a természeti törvényekkel, illetve az anyagoknak
BEVEZETÉS A STATIKA HELYE A TUDOMÁNYBAN A statika a fizikának, mint a legszélesebb körű természettudománynak a része. A klasszikus értelemben vett fizika azokkal a természeti törvényekkel, illetve az anyagoknak
Egy rugalmas megtámasztású tartóról
 Egy rugalmas megtámasztású tartóról Ezzel a témával gyakran találkozunk, még ha nem is így nevezzük azt. Ne feledjük, hogy a statikailag határozatlan tartók megoldásához szinte mindig alakváltozási felté
Egy rugalmas megtámasztású tartóról Ezzel a témával gyakran találkozunk, még ha nem is így nevezzük azt. Ne feledjük, hogy a statikailag határozatlan tartók megoldásához szinte mindig alakváltozási felté
Fizika A2E, 9. feladatsor
 Fizika 2E, 9. feladatsor Vida György József vidagyorgy@gmail.com 1. feladat: hurokáramok módszerével határozzuk meg az ábrán látható kapcsolás ágaiban folyó áramokat! z áramkör két ablakból áll, így két
Fizika 2E, 9. feladatsor Vida György József vidagyorgy@gmail.com 1. feladat: hurokáramok módszerével határozzuk meg az ábrán látható kapcsolás ágaiban folyó áramokat! z áramkör két ablakból áll, így két
X i = 0 F x + B x = 0. Y i = 0 A y F y + B y = 0. M A = 0 F y 3 + B y 7 = 0. B x = 200 N. B y =
 1. feladat a = 3 m b = 4 m F = 400 N φ = 60 fok Első lépésként alkossuk meg a számítási modellt. A kényszereket helyettesítsük a bennük ébredő lehetséges erőkkel (második ábra). Az F erő felbontásával
1. feladat a = 3 m b = 4 m F = 400 N φ = 60 fok Első lépésként alkossuk meg a számítási modellt. A kényszereket helyettesítsük a bennük ébredő lehetséges erőkkel (második ábra). Az F erő felbontásával
Gyakorlati útmutató a Tartók statikája I. tárgyhoz. Fekete Ferenc. 5. gyakorlat. Széchenyi István Egyetem, 2015.
 Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Kizárólag oktatási célra használható fel!
 DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II III. Előadás Vékonyfalú keresztmetszetek nyírófeszültségei - Nyírófolyam - Nyírási középpont - Shear lag hatás - Csavarás Összeállította:
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II III. Előadás Vékonyfalú keresztmetszetek nyírófeszültségei - Nyírófolyam - Nyírási középpont - Shear lag hatás - Csavarás Összeállította:
Síkbeli csuklós rúdnégyszög egyensúlya
 Síkbeli csuklós rúdnégyszög egyensúlya Két korábbi dolgozatunkban melyek címe és azonosítója: [KD ]: Egy érdekes feladat, [KD ]: Egy másik érdekes feladat azt vizsgáltuk, hogy egy csuklós rúdnégyszög milyen
Síkbeli csuklós rúdnégyszög egyensúlya Két korábbi dolgozatunkban melyek címe és azonosítója: [KD ]: Egy érdekes feladat, [KD ]: Egy másik érdekes feladat azt vizsgáltuk, hogy egy csuklós rúdnégyszög milyen
Kiegészítés a három erő egyensúlyához
 1 Kiegészítés a három erő egyensúlyához Egy régebbi dolgozatunkban melynek jele és címe : RD: Három erő egyensúlya ~ kéttámaszú tartó már sok mindent elmondtunk a címbeli témáról. Ez ugyanis egy megkerülhetetlen
1 Kiegészítés a három erő egyensúlyához Egy régebbi dolgozatunkban melynek jele és címe : RD: Három erő egyensúlya ~ kéttámaszú tartó már sok mindent elmondtunk a címbeli témáról. Ez ugyanis egy megkerülhetetlen
DEBRECENI EGYETEM MŰSZAKI KAR GÉPÉSZMÉRNÖKI TANSZÉK MŰSZAKI MECHANIKA II. HÁZIFELADAT
 DEBRECENI EGYETEM MŰSZAKI KAR GÉPÉSZMÉRNÖKI TANSZÉK MŰSZAKI MECHANIKA II. HÁZIFELADAT 2013 Feladat: Adott az ábrán látható kéttámaszú tartó, amely melegen hengerelt I idomacélokból és melegen hengerelt
DEBRECENI EGYETEM MŰSZAKI KAR GÉPÉSZMÉRNÖKI TANSZÉK MŰSZAKI MECHANIKA II. HÁZIFELADAT 2013 Feladat: Adott az ábrán látható kéttámaszú tartó, amely melegen hengerelt I idomacélokból és melegen hengerelt
Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS!
 Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS! 1. példa Vasúti kocsinak a 6. ábrán látható ütközőjébe épített tekercsrugóban 44,5 kn előfeszítő erő ébred. A rugó állandója 0,18
Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS! 1. példa Vasúti kocsinak a 6. ábrán látható ütközőjébe épített tekercsrugóban 44,5 kn előfeszítő erő ébred. A rugó állandója 0,18
Gyakorlat 03 Keresztmetszetek II.
 Gyakorlat 03 Keresztmetszetek II. 1. Feladat Keresztmetszetek osztályzása Végezzük el a keresztmetszet osztályzását tiszta nyomás és hajlítás esetére! Monoszimmetrikus, hegesztett I szelvény (GY02 1. példája)
Gyakorlat 03 Keresztmetszetek II. 1. Feladat Keresztmetszetek osztályzása Végezzük el a keresztmetszet osztályzását tiszta nyomás és hajlítás esetére! Monoszimmetrikus, hegesztett I szelvény (GY02 1. példája)
Rácsos szerkezetek. Frissítve: Egy kis elmélet: vakrudak
 Egy kis elmélet: vakrudak Az egyik lehetőség, ha két rúd szög alatt találkozik (nem egyvonalban vannak), és nem működik a csomópontra terhelés. Ilyen az 1.ábra C csomópontja. Ekkor az ide befutó mindkét
Egy kis elmélet: vakrudak Az egyik lehetőség, ha két rúd szög alatt találkozik (nem egyvonalban vannak), és nem működik a csomópontra terhelés. Ilyen az 1.ábra C csomópontja. Ekkor az ide befutó mindkét
A magától becsukódó ajtó működéséről
 1 A magától becsukódó ajtó működéséről Az [ 1 ] műben találtunk egy érdekes feladatot, amit most mi is feldolgozunk. Az 1. ábrán látható az eredeti feladat másolata. A feladat kitűzése 1. ábra forrása:
1 A magától becsukódó ajtó működéséről Az [ 1 ] műben találtunk egy érdekes feladatot, amit most mi is feldolgozunk. Az 1. ábrán látható az eredeti feladat másolata. A feladat kitűzése 1. ábra forrása:
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 Építészeti és építési alapismeretek középszint 0812 ÉRETTSÉGI VIZSGA 2011. október 17. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS
Építészeti és építési alapismeretek középszint 0812 ÉRETTSÉGI VIZSGA 2011. október 17. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS
A ferde tartó megoszló terheléseiről
 A ferde tartó megoszló terheléseiről Úgy vettem észre az idők során, hogy nem nagyon magyarázták agyon azt a kérdést, amivel itt fogunk foglalkozni. Biztos azt mondják majd megint, hogy De hisz ezt mindenki
A ferde tartó megoszló terheléseiről Úgy vettem észre az idők során, hogy nem nagyon magyarázták agyon azt a kérdést, amivel itt fogunk foglalkozni. Biztos azt mondják majd megint, hogy De hisz ezt mindenki
GÉPÉSZETI ALAPISMERETEK
 Gépészeti alapismeretek emelt szint 1511 ÉRETTSÉGI VIZSGA 2016. május 18. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos
Gépészeti alapismeretek emelt szint 1511 ÉRETTSÉGI VIZSGA 2016. május 18. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos
Komplex számok. 2014. szeptember 4. 1. Feladat: Legyen z 1 = 2 3i és z 2 = 4i 1. Határozza meg az alábbi kifejezés értékét!
 Komplex számok 014. szeptember 4. 1. Feladat: Legyen z 1 i és z 4i 1. (z 1 z ) (z 1 z ) (( i) (4i 1)) (6 9i 8i + ) 8 17i 8 + 17i. Feladat: Legyen z 1 i és z 4i 1. Határozza meg az alábbi kifejezés értékét!
Komplex számok 014. szeptember 4. 1. Feladat: Legyen z 1 i és z 4i 1. (z 1 z ) (z 1 z ) (( i) (4i 1)) (6 9i 8i + ) 8 17i 8 + 17i. Feladat: Legyen z 1 i és z 4i 1. Határozza meg az alábbi kifejezés értékét!
Tartószerkezetek I. (Vasbeton szilárdságtan)
 Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.10.11. Vasbeton külpontos nyomása Az eső ágú σ-ε diagram miatt elvileg minden egyes esethez külön kell meghatározni a szélső szál összenyomódását.
Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.10.11. Vasbeton külpontos nyomása Az eső ágú σ-ε diagram miatt elvileg minden egyes esethez külön kell meghatározni a szélső szál összenyomódását.
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 Építészeti és építési alapismeretek középszint 0911 ÉRETTSÉGI VIZSGA 2009. október 19. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS
Építészeti és építési alapismeretek középszint 0911 ÉRETTSÉGI VIZSGA 2009. október 19. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS
Abszolútértékes egyenlôtlenségek
 Abszolútértékes egyenlôtlenségek 575. a) $, $ ; b) < - vagy $, # - vagy > 4. 5 576. a) =, =- 6, 5 =, =-, 7 =, 4 = 5; b) nincs megoldás;! c), = - ; d) =-. Abszolútértékes egyenlôtlenségek 577. a) - # #,
Abszolútértékes egyenlôtlenségek 575. a) $, $ ; b) < - vagy $, # - vagy > 4. 5 576. a) =, =- 6, 5 =, =-, 7 =, 4 = 5; b) nincs megoldás;! c), = - ; d) =-. Abszolútértékes egyenlôtlenségek 577. a) - # #,
GÉPÉSZETI ALAPISMERETEK
 Gépészeti alapismeretek emelt szint 1011 ÉRETTSÉGI VIZSGA 011. október 17. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐORRÁS MINISZTÉRIUM ontos
Gépészeti alapismeretek emelt szint 1011 ÉRETTSÉGI VIZSGA 011. október 17. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐORRÁS MINISZTÉRIUM ontos
MUNKAANYAG. Szabó László. Szilárdságtan. A követelménymodul megnevezése:
 Szabó László Szilárdságtan A követelménymodul megnevezése: Kőolaj- és vegyipari géprendszer üzemeltetője és vegyipari technikus feladatok A követelménymodul száma: 047-06 A tartalomelem azonosító száma
Szabó László Szilárdságtan A követelménymodul megnevezése: Kőolaj- és vegyipari géprendszer üzemeltetője és vegyipari technikus feladatok A követelménymodul száma: 047-06 A tartalomelem azonosító száma
Példa: Háromszög síkidom másodrendű nyomatékainak számítása
 Példa: Háromszög síkidom másodrendű nyomatékainak számítása Készítette: Dr. Kossa Attila kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék. február 6. Határozzuk meg az alábbi ábrán látható derékszögű háromszög
Példa: Háromszög síkidom másodrendű nyomatékainak számítása Készítette: Dr. Kossa Attila kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék. február 6. Határozzuk meg az alábbi ábrán látható derékszögű háromszög
Külpontosan nyomott keresztmetszet számítása
 Külpontosan nyomott keresztmetszet számítása A TELJES TEHERBÍRÁSI VONAL SZÁMÍTÁSA Az alábbi példa egy asszimmetrikus vasalású keresztmetszet teherbírási görbéjének 9 pontját mutatja be. Az első részben
Külpontosan nyomott keresztmetszet számítása A TELJES TEHERBÍRÁSI VONAL SZÁMÍTÁSA Az alábbi példa egy asszimmetrikus vasalású keresztmetszet teherbírási görbéjének 9 pontját mutatja be. Az első részben
ERŐRENDSZEREK EREDŐJÉNEK MEGHATÁROZÁSA
 ALAPOGALMAK ERŐRENDSZEREK EREDŐJÉNEK MEGHATÁROZÁSA Egy testre általában nem egy erő hat, hanem több. Legalább két erőnek kell hatni a testre, ha az erő- ellenerő alaptétel alapján járunk el. A testek vizsgálatához
ALAPOGALMAK ERŐRENDSZEREK EREDŐJÉNEK MEGHATÁROZÁSA Egy testre általában nem egy erő hat, hanem több. Legalább két erőnek kell hatni a testre, ha az erő- ellenerő alaptétel alapján járunk el. A testek vizsgálatához
Az egyszeres rálapolásról
 Az egyszeres rálapolásról A téma felvezetése Az idő múlásával egyre inkább kikristályosodik az ember véleménye, mintegy magától. Így van ez az egyszeres rálapolásnak nevezett kötés esetén is, mely a műszaki
Az egyszeres rálapolásról A téma felvezetése Az idő múlásával egyre inkább kikristályosodik az ember véleménye, mintegy magától. Így van ez az egyszeres rálapolásnak nevezett kötés esetén is, mely a műszaki
A befogott tartóvég erőtani vizsgálatához II. rész
 A befogott tartóvég erőtani vizsgálatához II. rész A második feladat Az első feladat alapfeltevése az volt, hogy a gerendavég kellően merev, így a terhelések hatására is egyenes marad. A valóságos testek
A befogott tartóvég erőtani vizsgálatához II. rész A második feladat Az első feladat alapfeltevése az volt, hogy a gerendavég kellően merev, így a terhelések hatására is egyenes marad. A valóságos testek
Egyenletek, egyenletrendszerek, egyenlőtlenségek Megoldások
 ) Egyenletek, egyenletrendszerek, egyenlőtlenségek - megoldások Egyenletek, egyenletrendszerek, egyenlőtlenségek Megoldások a) Oldja meg a valós számok halmazán az alábbi egyenletet! = 6 (5 pont) b) Oldja
) Egyenletek, egyenletrendszerek, egyenlőtlenségek - megoldások Egyenletek, egyenletrendszerek, egyenlőtlenségek Megoldások a) Oldja meg a valós számok halmazán az alábbi egyenletet! = 6 (5 pont) b) Oldja
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2007. május 25. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI
ÉRETTSÉGI VIZSGA 2007. május 25. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI
Használható segédeszköz: - szöveges adatok tárolására és megjelenítésére nem alkalmas számológép; - körző; vonalzók.
 A 27/2012. (VIII. 27.) NGM rendelet, a 27/2012. (VIII. 27.) NGM rendelet a 12/2013. (III. 28.) NGM rendelet által módosított és a 27/2012. (VIII. 27.) NGM rendelet a 4/2015. (II. 19.) NGM rendelet által
A 27/2012. (VIII. 27.) NGM rendelet, a 27/2012. (VIII. 27.) NGM rendelet a 12/2013. (III. 28.) NGM rendelet által módosított és a 27/2012. (VIII. 27.) NGM rendelet a 4/2015. (II. 19.) NGM rendelet által
Rönk kiemelése a vízből
 1 Rönk kiemelése a vízből Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot 1. ábra. A feladat 1. ábra forrása: [ 1 ] Egy daru kötél segítségével lassan emeli ki a vízből a benne úszó gerendát
1 Rönk kiemelése a vízből Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot 1. ábra. A feladat 1. ábra forrása: [ 1 ] Egy daru kötél segítségével lassan emeli ki a vízből a benne úszó gerendát
ÁGAZATI SZAKMAI ÉRETTSÉGI VIZSGA GÉPÉSZET ISMERETEK EMELT SZINTŰ SZÓBELI VIZSGA MINTAFELADATOK ÉS ÉRTÉKELÉSÜK
 GÉPÉSZET ISMERETEK EMELT SZINTŰ SZÓBELI VIZSGA MINTAFELADATOK ÉS ÉRTÉKELÉSÜK 1. tétel A. Ismertesse az anyagok tűzveszélyességi, valamint az építmények kockázati osztályba sorolását! B. Ismertesse a szerelési
GÉPÉSZET ISMERETEK EMELT SZINTŰ SZÓBELI VIZSGA MINTAFELADATOK ÉS ÉRTÉKELÉSÜK 1. tétel A. Ismertesse az anyagok tűzveszélyességi, valamint az építmények kockázati osztályba sorolását! B. Ismertesse a szerelési
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 Név:... osztály:... ÉRETTSÉGI VIZSGA 2007. május 25. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati
Név:... osztály:... ÉRETTSÉGI VIZSGA 2007. május 25. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 Építészeti és építési alapismeretek középszint 1212 ÉRETTSÉGI VIZSGA 2012. május 25. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS
Építészeti és építési alapismeretek középszint 1212 ÉRETTSÉGI VIZSGA 2012. május 25. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS
Frissítve: Csavarás. 1. példa: Az 5 gyakorlat 1. példájához hasonló feladat.
 1. példa: Az 5 gyakorlat 1. példájához hasonló feladat. Mekkora a nyomatékok hatására ébredő legnagyobb csúsztatófeszültség? Mekkora és milyen irányú az A, B és C keresztmetszet elfordulása? Számítsuk
1. példa: Az 5 gyakorlat 1. példájához hasonló feladat. Mekkora a nyomatékok hatására ébredő legnagyobb csúsztatófeszültség? Mekkora és milyen irányú az A, B és C keresztmetszet elfordulása? Számítsuk
KÖZLEKEDÉSÉPÍTŐ ISMERETEK
 ÉRETTSÉGI VIZSGA 2017. május 17. KÖZLEKEDÉSÉPÍTŐ ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2017. május 17. 8:00 Időtartam: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Közlekedésépítő
ÉRETTSÉGI VIZSGA 2017. május 17. KÖZLEKEDÉSÉPÍTŐ ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2017. május 17. 8:00 Időtartam: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Közlekedésépítő
A karpántokról, a karpántos szerkezetekről I. rész. Bevezetés
 A karpántokról, a karpántos szerkezetekről I. rész Bevezetés Ezek a régi faépítészetből ismert szerkezeti elemek ma is sok helyen feltűnnek. Egy díszes megvalósítása az 1. ábrán látható. Forrása: http://www.motivumfa.hu/termekeink-karpantok.html.
A karpántokról, a karpántos szerkezetekről I. rész Bevezetés Ezek a régi faépítészetből ismert szerkezeti elemek ma is sok helyen feltűnnek. Egy díszes megvalósítása az 1. ábrán látható. Forrása: http://www.motivumfa.hu/termekeink-karpantok.html.
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Tető - feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra.
![Tető - feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra. Tető - feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra.](/thumbs/95/123788187.jpg) 1 Tető - feladat Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra. 1. ábra forrása: [ 1 ] Most ezt oldjuk meg, részletesen. A feladat szövegének ( saját, hevenyészett
1 Tető - feladat Az interneten találtuk az [ 1 ] művet, benne az alábbi feladatot és végeredményeit ld. 1. ábra. 1. ábra forrása: [ 1 ] Most ezt oldjuk meg, részletesen. A feladat szövegének ( saját, hevenyészett
II. Gyakorlat: Hajlított vasbeton keresztmetszet ellenőrzése (Négyszög és T-alakú keresztmetszetek hajlítási teherbírása III. feszültségi állapotban)
 II. Gyakorlat: Hajlított vasbeton keresztmetszet ellenőrzése (Négyszög és T-alakú keresztmetszetek hajlítási teherbírása III. feszültségi állapotban) Készítették: Dr. Kiss Rita és Klinka Katalin -1- A
II. Gyakorlat: Hajlított vasbeton keresztmetszet ellenőrzése (Négyszög és T-alakú keresztmetszetek hajlítási teherbírása III. feszültségi állapotban) Készítették: Dr. Kiss Rita és Klinka Katalin -1- A
UTÓFESZÍTETT SZERKEZETEK TERVEZÉSI MÓDSZEREI
 UTÓFESZÍTETT SZERKEZETEK TERVEZÉSI MÓDSZEREI DR. FARKAS GYÖRGY Professor emeritus BME Hidak és Szerkezetek Tanszék MMK Tartószerkezeti Tagozat Szakmai továbbképzés 2017 október 2. KÁBELVEZETÉS EGYENES
UTÓFESZÍTETT SZERKEZETEK TERVEZÉSI MÓDSZEREI DR. FARKAS GYÖRGY Professor emeritus BME Hidak és Szerkezetek Tanszék MMK Tartószerkezeti Tagozat Szakmai továbbképzés 2017 október 2. KÁBELVEZETÉS EGYENES
TANTÁRGYFELELŐS INTÉZET: Építőmérnöki Intézet. OKTATÓ, ELŐADÓ címe: fogadóórája a szorgalmi időszakban:
 Mechanika 1 Mechanika I. (Statika) Mechanika I. (Statika) Neptun kódja: SGYMMET2001XA Neptun kódja: SGYMMET201XXX Tantárgy neve angolul: Mechanics 1 Építészmérnöki szak, Építőmérnöki szak Nappali tagozat
Mechanika 1 Mechanika I. (Statika) Mechanika I. (Statika) Neptun kódja: SGYMMET2001XA Neptun kódja: SGYMMET201XXX Tantárgy neve angolul: Mechanics 1 Építészmérnöki szak, Építőmérnöki szak Nappali tagozat
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 Építészeti és építési alapismeretek emelt szint 0812 ÉRETTSÉGI VIZSGA 2010. október 18. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS
Építészeti és építési alapismeretek emelt szint 0812 ÉRETTSÉGI VIZSGA 2010. október 18. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS
1. Feladatok a dinamika tárgyköréből
 1. Feladatok a dinamika tárgyköréből Newton három törvénye 1.1. Feladat: Három azonos m tömegű gyöngyszemet fonálra fűzünk, egymástól kis távolságokban a fonálhoz rögzítünk, és az elhanyagolható tömegű
1. Feladatok a dinamika tárgyköréből Newton három törvénye 1.1. Feladat: Három azonos m tömegű gyöngyszemet fonálra fűzünk, egymástól kis távolságokban a fonálhoz rögzítünk, és az elhanyagolható tömegű
LINEÁRIS ALGEBRA.
 LINEÁRIS ALGEBRA Bércesné Novák Ágnes Honlap: http://digitus.itk.ppke.hu/~b_novak Követelményrendszer: http://digitus.itk.ppke.hu/~b_novak/la/4_la_kovetelmeny.doc Gauss elimináció Vektoralgebra: http://digitus.itk.ppke.hu/~b_novak/dmat/vektorfolcop.pdf
LINEÁRIS ALGEBRA Bércesné Novák Ágnes Honlap: http://digitus.itk.ppke.hu/~b_novak Követelményrendszer: http://digitus.itk.ppke.hu/~b_novak/la/4_la_kovetelmeny.doc Gauss elimináció Vektoralgebra: http://digitus.itk.ppke.hu/~b_novak/dmat/vektorfolcop.pdf
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet
 Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
A végeselem módszer alapjai. 2. Alapvető elemtípusok
 A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
Összeállította: dr. Leitold Adrien egyetemi docens
 Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
TANTÁRGYFELELŐS INTÉZET: Építőmérnöki Intézet OKTATÓK, ELŐADÓK címe: fogadóórája a szorgalmi időszakban:
 Mechanika 1 Mechanika I. (Statika) Mechanika I. (Statika) Neptun kódja: SGYMMET2001XA Neptun kódja: SGYMMET201XXX Tantárgy neve angolul: Mechanics 1 Építészmérnöki szak, Építőmérnöki szak Nappali tagozat
Mechanika 1 Mechanika I. (Statika) Mechanika I. (Statika) Neptun kódja: SGYMMET2001XA Neptun kódja: SGYMMET201XXX Tantárgy neve angolul: Mechanics 1 Építészmérnöki szak, Építőmérnöki szak Nappali tagozat
Két statikai feladat
 1 Két statikai feladat Az interneten találtuk az [ 1 ] feladatgyűjteményt és benne két érdekes feladatot. Úgy tűnik, hasznos lehet megoldásuk, feldolgozásuk. Az 1. feladat nagyon ismerősnek tűnt. Ez nem
1 Két statikai feladat Az interneten találtuk az [ 1 ] feladatgyűjteményt és benne két érdekes feladatot. Úgy tűnik, hasznos lehet megoldásuk, feldolgozásuk. Az 1. feladat nagyon ismerősnek tűnt. Ez nem
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 Építészeti és építési alapismeretek középszint 1021 ÉRETTSÉGI VIZSGA 2011. május 13. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS
Építészeti és építési alapismeretek középszint 1021 ÉRETTSÉGI VIZSGA 2011. május 13. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS
Kalkulus. Komplex számok
 Komplex számok Komplex számsík A komplex számok a valós számok természetes kiterjesztése, annak érdekében, hogy a gyökvonás művelete elvégezhető legyen a negatív számok körében is. Vegyük tehát hozzá az
Komplex számok Komplex számsík A komplex számok a valós számok természetes kiterjesztése, annak érdekében, hogy a gyökvonás művelete elvégezhető legyen a negatív számok körében is. Vegyük tehát hozzá az
EGYSZERŰ GÉPEK. Azok az eszközök, amelyekkel kedvezőbbé lehet tenni az erőhatás nagyságát, irányát, támadáspontjának helyét.
 EGYSZERŰ GÉPEK Azok az eszközök, amelyekkel kedvezőbbé lehet tenni az erőhatás nagyságát, irányát, támadáspontjának helyét. Az egyszerű gépekkel munkát nem takaríthatunk meg, de ugyanazt a munkát kisebb
EGYSZERŰ GÉPEK Azok az eszközök, amelyekkel kedvezőbbé lehet tenni az erőhatás nagyságát, irányát, támadáspontjának helyét. Az egyszerű gépekkel munkát nem takaríthatunk meg, de ugyanazt a munkát kisebb
Szeretném felhívni figyelmüket a feltett korábbi vizsgapéldák és az azokhoz tartozó megoldások felhasználásával kapcsolatban néhány dologra.
 Tisztelt Hallgatók! Szeretném felhívni figyelmüket a feltett korábbi vizsgapéldák és az azokhoz tartozó megoldások felhasználásával kapcsolatban néhány dologra. Az, hogy valaki egy korábbi vizsga megoldását
Tisztelt Hallgatók! Szeretném felhívni figyelmüket a feltett korábbi vizsgapéldák és az azokhoz tartozó megoldások felhasználásával kapcsolatban néhány dologra. Az, hogy valaki egy korábbi vizsga megoldását
A főtengelyproblémához
 1 A főtengelyproblémához Korábbi, az ellipszis perspektivikus ábrázolásával foglalkozó dolgozatainkban előkerült a másodrendű görbék kanonikus alakra hozása, majd ebben a főtengelyrendszert előállító elforgatási
1 A főtengelyproblémához Korábbi, az ellipszis perspektivikus ábrázolásával foglalkozó dolgozatainkban előkerült a másodrendű görbék kanonikus alakra hozása, majd ebben a főtengelyrendszert előállító elforgatási
Abszolútértékes és gyökös kifejezések Megoldások
 Abszolútértékes és gyökös kifejezések Megoldások ) Igazolja, hogy az alábbi négy egyenlet közül az a) és b) jelű egyenletnek pontosan egy megoldása van, a c) és d) jelű egyenletnek viszont nincs megoldása
Abszolútértékes és gyökös kifejezések Megoldások ) Igazolja, hogy az alábbi négy egyenlet közül az a) és b) jelű egyenletnek pontosan egy megoldása van, a c) és d) jelű egyenletnek viszont nincs megoldása
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. Oldd meg a következő egyenleteket! (Alaphalmaz: Z) a) (x 1) (x + 1) 7x + 1 = x (4 + x) + 2 b) 1 2 [5 (x 1) (1 + 2x) 2 4x] = (7 x) x c) 2 (x + 5) (x 2) 2 + (x + 1) 2 = 6 (2x + 1) d) 6 (x 8)
Megoldások 1. Oldd meg a következő egyenleteket! (Alaphalmaz: Z) a) (x 1) (x + 1) 7x + 1 = x (4 + x) + 2 b) 1 2 [5 (x 1) (1 + 2x) 2 4x] = (7 x) x c) 2 (x + 5) (x 2) 2 + (x + 1) 2 = 6 (2x + 1) d) 6 (x 8)
Lineáris egyenletrendszerek
 Lineáris egyenletrendszerek Lineáris egyenletrendszernek nevezzük az a 11 x 1 + a 12 x 2 +... +a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... +a 2n x n = b 2.. a k1 x 1 + a k2 x 2 +... +a kn x n = b k n ismeretlenes,
Lineáris egyenletrendszerek Lineáris egyenletrendszernek nevezzük az a 11 x 1 + a 12 x 2 +... +a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... +a 2n x n = b 2.. a k1 x 1 + a k2 x 2 +... +a kn x n = b k n ismeretlenes,
Lineáris egyenletrendszerek. GAUSS ELIMINÁCIÓ (kiküszöbölés)
 LINEÁRIS ALGEBRA Bércesné Novák Ágnes Honlap: http://users.itk.ppke.hu/~b_novak Követelményrendszer: Gauss elimináció Vektoralgebra: http://users.itk.ppke.hu/~b_novak/dmat/vektorfolcop.pdf Lineáris egyenletrendszerek
LINEÁRIS ALGEBRA Bércesné Novák Ágnes Honlap: http://users.itk.ppke.hu/~b_novak Követelményrendszer: Gauss elimináció Vektoralgebra: http://users.itk.ppke.hu/~b_novak/dmat/vektorfolcop.pdf Lineáris egyenletrendszerek
az eredő átmegy a közös ponton.
 M Műszaki Mechanikai Tanszék STTIK dr. Uj József c. egetemi tanár g közös ponton támadó koncentrált erők (centrális erőrendszer) Két erő eredője: = +, Több erő eredője: = + ++...+ n, az eredő átmeg a közös
M Műszaki Mechanikai Tanszék STTIK dr. Uj József c. egetemi tanár g közös ponton támadó koncentrált erők (centrális erőrendszer) Két erő eredője: = +, Több erő eredője: = + ++...+ n, az eredő átmeg a közös
GÉPÉSZETI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2011. október 17. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2011. október 17. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
ÉRETTSÉGI VIZSGA 2011. október 17. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2011. október 17. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
Digitális tananyag a fizika tanításához
 Digitális tananyag a fizika tanításához Ismétlés Erőhatás a testek mechanikai kölcsönhatásának mértékét és irányát megadó vektormennyiség. jele: mértékegysége: 1 newton: erőhatás következménye: 1N 1kg
Digitális tananyag a fizika tanításához Ismétlés Erőhatás a testek mechanikai kölcsönhatásának mértékét és irányát megadó vektormennyiség. jele: mértékegysége: 1 newton: erőhatás következménye: 1N 1kg
Nyomott oszlopok számítása EC2 szerint (mintapéldák)
 zéhenyi István Egyetem zerkezetépítési és Geotehnikai Tanszék yomott oszlopok számítása E szerint 1. Központosan nyomott oszlop Központosan nyomott az oszlop ha e = 0 (e : elsőrendű, vagy kezdeti külpontosság).
zéhenyi István Egyetem zerkezetépítési és Geotehnikai Tanszék yomott oszlopok számítása E szerint 1. Központosan nyomott oszlop Központosan nyomott az oszlop ha e = 0 (e : elsőrendű, vagy kezdeti külpontosság).
a) A logaritmus értelmezése alapján: x 8 0 ( x 2 2 vagy x 2 2) (1 pont) Egy szorzat értéke pontosan akkor 0, ha valamelyik szorzótényező 0.
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
A= a keresztmetszeti felület cm 2 ɣ = biztonsági tényező
 Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
1. Határozzuk meg az alábbi tartó vasalását, majd ellenőrizzük a tartót használhatósági határállapotokra!
 1. Határozzuk meg az alábbi tartó vasalását majd ellenőrizzük a tartót használhatósági határállapotokra! Beton: beton minőség: beton nyomószilárdságnak tervezési értéke: beton húzószilárdságának várható
1. Határozzuk meg az alábbi tartó vasalását majd ellenőrizzük a tartót használhatósági határállapotokra! Beton: beton minőség: beton nyomószilárdságnak tervezési értéke: beton húzószilárdságának várható
