Frissítve: Csavarás. 1. példa: Az 5 gyakorlat 1. példájához hasonló feladat.
|
|
|
- Károly Balázs
- 8 évvel ezelőtt
- Látták:
Átírás
1 1. példa: Az 5 gyakorlat 1. példájához hasonló feladat. Mekkora a nyomatékok hatására ébredő legnagyobb csúsztatófeszültség? Mekkora és milyen irányú az A, B és C keresztmetszet elfordulása? Számítsuk ki az alakváltozás munkáját! A terhelő nyomatékok által végzett munkát is kiszámítottuk. A várakozásoknak megfelelően a szakaszokban tárolt rugalmas energiák összegével azonos eredményt kaptunk. 1 / 15
2 2. példa: Az 5 gyakorlat 1. példájához hasonló feladat. Rajzoljuk meg a nyírófeszültség ábrát! Határozzuk meg a véglap elfordulásának irányát és szögét! Sajnos az Ip2 és Ip3 értéket nem sikerült helyesen kiszámítanom. Emiatt az ettől függő további értékek is rosszak. Rövidesen javítani fogom a számításokat... 2 / 15
3 3. példa: Az 5 gyakorlat 2. példájához hasonló feladat. Számítsuk ki a csavarónyomaték hatására ébredő legnagyobb nyírófeszültséget! Mekkora a furat alján lévő K keresztmetszet szögelfordulása? Számítsuk ki az alakváltozás és a csavarónyomaték munkáját! 3 / 15
4 Szerencsére a két munka egyenlő lett. 4 / 15
5 4. példa: Egy forgó tengelyes példa. 1 Az n = 120 fordulatszámmal járó tengelynek P = 150 kw teljesítményt kell átvinnie. min Határozzuk meg a tengely átmérőjét, ha az anyagára τ max = 20 MPa feszültséget engednek meg! 5 / 15
6 Zárt, vékonyfalú szelvényekkel kapcsolatos feladatok 5. példa: Számítsuk ki a vékonyfalú, zárt szelvényben ébredő legnagyobb feszültséget! Mekkora a rúdvég elcsavarodása? 6 / 15
7 6.példa: Az 5. gyakorlat 3. példájához hasonló feladat. Számítsuk ki a reakciókat! Mekkora a K keresztmetszet szögelfordulása? 7 / 15
8 7. példa: Mekkora a megadott vékonyfalú, zárt keresztmetszetű, 1m hosszúságú rúd elcsavarodása? Számítsuk ki az alakváltozás és a csavarónyomaték munkáját! Ábrázoljuk a keresztmetszetben kialakuló feszültségeloszlást! A kétféleképpen számított munka a kerekítések miatt csak közelítőleg egyenlő. A nyírófeszültség a falvastagság függvénye. 8 / 15
9 8. példa: Félrefúrás. Egy csőkeresztmetszetet gyártása az ábrán látható módon szaródott el: a lyuk félrement. Mekkora csavarónyomatékkal terhelhetjük a selejtes csövet? A középvonal átmérőjét a belső és a külső átmérő átlagaként vesszük fel. A megengedett feszültség a minimális falvastagság helyén alakulhat ki, mert az a maximális feszültség helye. Ha nagyon ráérünk, akkor kiszámolhatjuk, hogy mennyit bírna egy rendesen legyártott cső, vagyis ha a közepére sikerül a lyuk. Az óra 1. példájához hasonló feladat: Ábrázoljuk a hossz mentén a feszültséget, és határozzuk meg a végkeresztmetszet elcsavarodási szögét és irányát! 9 / 15
10 További vegyes feladatok, többnyire méretezések 9. példa: Az acél csőben egy réz rúd van. A csavarónyomaték megoszlik a két alkatrész között. Mekkora a véglap elfordulása? Ábrázoljuk a feszültségeloszlást az alkatrészekben! Az egyenletrendszert úgy is megoldhattuk volna, hogy az 1. egyenletből kifejezzük az M cs2 reakciónyomatékot, és behelyettesítjük a 2. egyenletbe. A gyakorlaton ezt a módszert alkalmaztuk. A feszültségeloszlást azért rajzoltam ilyen ferdére, hogy lássuk, hogy az nem csak a koordinátatengelyek mentén érvényes, hanem bárhol a sugár mentén. A merevségi viszonyok olyanok, hogy a tömör rész szélső szálában kisebb a feszültség, mint a cső belső szálában. Ha a tömör rész erősebb lenne (pl. nagyobb G), akkor ez a viszony megfordulhatna, és a belső rész nyomatékaránya is nagyobb lenne. 10 / 15
11 10. példa: Méretezés. Az ábra egy rögzített (befogott) csövet (1), egy ráhegesztett, végtelen merevnek tekinthető tárcsát és a tárcsához hegesztett rudat (2) ábrázol. Mekkora lehet a rúdvégre ható M t csavarónyomaték, ha a csúsztatófeszültség egyik alkatrészben sem lépheti túl a megengedett értéket? Mekkora lesz így a rúdvég szögelfordulása? Ábrázoljuk a nyírófeszültség-eloszlást! Első lépésben kiszámítottuk, hogy mekkora csavarónyomaték kell ahhoz, hogy az egyes alkatrészek szélső szálában elérjük a megengedett feszültséget. Ezen értékek közül a kisebb lesz a megengedett, mert ekkor az egyik alkatrész a tönkremenetel határáig terhelődik, a másikban pedig a megengedettnél kisebb feszültség ébred. 11 / 15
12 A végkeresztmetszet szögelfordulása a két szakaszon kialakuló szögelfordulások összege: A feszültségeloszlások: 12 / 15
13 11. példa: Méretezés. Mindkét anyagra ismerjük a megengedett legnagyobb feszültség értékét. Mekkora nyomaték fogja terhelni az alkatrészeket, ha sehol nem lépjük túl a megengedett feszültséget? Mekkora lesz így a tejes csavarónyomaték és a szögelfordulás? Végül felrajzoljuk a feszültségeloszlást is. Négy egyenletet tudunk felírni: a nyomatéki egyensúlyt, a két szakasz elcsavarodásának egyenlőségét, és két egyenletet a szélső szálak feszültségére. Első lépésben meghatározzuk, hogy mekkora szögelfordulásnál érjük el a megengedett feszültséget az alkatrészek szélső szálában. Ezek közül a kisebbik esetén az egyik alkatrész a határig terhelődik, a másikban pedig a megengedettnél kisebb feszültség ébred. Ehhez a szöghöz kiszámoljuk a résznyomatékokat. A keresett Mt ezek összegeként adódik. A merevségi viszonyok olyanok, hogy a tömör rész szélső szálában nagyobb a feszültség, mint a cső belső szálában. 13 / 15
14 12. példa: Méretezés. Határozzuk meg az Mt nyomatékot úgy, hogy az anyagra megengedett legnagyobb feszültséget sehol ne lépjük túl! Mekkora ebben az esetben az Mt nyomaték helyén lévő K keresztmetszet elcsavarodása? Négy egyenletet tudunk felírni: a nyomatéki egyensúlyt, a két szakasz elcsavarodásának egyenlőségét, és két egyenletet a szélső szálak feszültségére. Először mindkét szakaszra kiszámítjuk, hogy mekkora szögelfordulás jön létre, ha a feszültség éppen a megengedett. Ezek közül a kisebbiket kell választanunk. Végül kiszámoljuk erre az esetre a két résznyomatékot. Az Mt ezek összege lesz. 14 / 15
15 13. példa: Méretezés. A rúd teljes hossza adott. Válasszuk meg úgy az l 1 és l 2 méreteket, hogy mindkét szakaszon azonos feszültség ébredjen a szélső szálban! Mekkora az így kialakuló maximális feszültség, és mekkorák a reakciónyomatékok? Négy egyenletet tudunk felírni: a nyomatéki egyensúlyt, az l 1 és l 2 hosszak összegét, a szögelfordulások egyenlőségét és a feszültségek egyenlőségét. A feszültségek egyenlőségéből megkapjuk a részhosszak arányát, majd a teljes hossz felhasználásával az l 1 és l 2 értékeket. Innentől a megoldás már olyan, mint amit a 3. példában alkalmaztunk. 15 / 15
Navier-formula. Frissítve: Egyenes hajlítás
 Navier-formula Akkor beszélünk egyenes hajlításról, ha a nyomatékvektor egybeesik valamelyik fő-másodrendű nyomatéki tengellyel. A hajlítást mindig súlyponti koordinátarendszerben értelmezzük. Ez még a
Navier-formula Akkor beszélünk egyenes hajlításról, ha a nyomatékvektor egybeesik valamelyik fő-másodrendű nyomatéki tengellyel. A hajlítást mindig súlyponti koordinátarendszerben értelmezzük. Ez még a
HELYI TANTERV. Mechanika
 HELYI TANTERV Mechanika Bevezető A mechanika tantárgy tanításának célja, hogy fejlessze a tanulók logikai készségét, alapozza meg a szakmai tantárgyak feldolgozását. A tanulók tanulási folyamata fejlessze
HELYI TANTERV Mechanika Bevezető A mechanika tantárgy tanításának célja, hogy fejlessze a tanulók logikai készségét, alapozza meg a szakmai tantárgyak feldolgozását. A tanulók tanulási folyamata fejlessze
Gyakorlat 04 Keresztmetszetek III.
 Gyakorlat 04 Keresztmetszetek III. 1. Feladat Hajlítás és nyírás Végezzük el az alábbi gerenda keresztmetszeti vizsgálatait (tiszta esetek és lehetséges kölcsönhatások) kétféle anyaggal: S235; S355! (1)
Gyakorlat 04 Keresztmetszetek III. 1. Feladat Hajlítás és nyírás Végezzük el az alábbi gerenda keresztmetszeti vizsgálatait (tiszta esetek és lehetséges kölcsönhatások) kétféle anyaggal: S235; S355! (1)
Kizárólag oktatási célra használható fel!
 DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II III. Előadás Vékonyfalú keresztmetszetek nyírófeszültségei - Nyírófolyam - Nyírási középpont - Shear lag hatás - Csavarás Összeállította:
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II III. Előadás Vékonyfalú keresztmetszetek nyírófeszültségei - Nyírófolyam - Nyírási középpont - Shear lag hatás - Csavarás Összeállította:
BME Gépészmérnöki Kar 3. vizsga (112A) Név: 1 Műszaki Mechanikai Tanszék január 11. Neptun: 2 Szilárdságtan Aláírás: 3
 BME Gépészmérnöki Kar 3. vizsga (2A) Név: Műszaki Mechanikai Tanszék 2. január. Neptun: 2 Szilárdságtan Aláírás: 3. feladat (2 pont) A vázolt befogott tartót a p intenzitású megoszló erőrendszer, az F
BME Gépészmérnöki Kar 3. vizsga (2A) Név: Műszaki Mechanikai Tanszék 2. január. Neptun: 2 Szilárdságtan Aláírás: 3. feladat (2 pont) A vázolt befogott tartót a p intenzitású megoszló erőrendszer, az F
DEBRECENI EGYETEM MŰSZAKI KAR GÉPÉSZMÉRNÖKI TANSZÉK MŰSZAKI MECHANIKA II. HÁZIFELADAT
 DEBRECENI EGYETEM MŰSZAKI KAR GÉPÉSZMÉRNÖKI TANSZÉK MŰSZAKI MECHANIKA II. HÁZIFELADAT 2013 Feladat: Adott az ábrán látható kéttámaszú tartó, amely melegen hengerelt I idomacélokból és melegen hengerelt
DEBRECENI EGYETEM MŰSZAKI KAR GÉPÉSZMÉRNÖKI TANSZÉK MŰSZAKI MECHANIKA II. HÁZIFELADAT 2013 Feladat: Adott az ábrán látható kéttámaszú tartó, amely melegen hengerelt I idomacélokból és melegen hengerelt
Gyakorlat 03 Keresztmetszetek II.
 Gyakorlat 03 Keresztmetszetek II. 1. Feladat Keresztmetszetek osztályzása Végezzük el a keresztmetszet osztályzását tiszta nyomás és hajlítás esetére! Monoszimmetrikus, hegesztett I szelvény (GY02 1. példája)
Gyakorlat 03 Keresztmetszetek II. 1. Feladat Keresztmetszetek osztályzása Végezzük el a keresztmetszet osztályzását tiszta nyomás és hajlítás esetére! Monoszimmetrikus, hegesztett I szelvény (GY02 1. példája)
Szilárd testek rugalmassága
 Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
Statikailag határozatlan tartó vizsgálata
 Statikailag határozatlan tartó vizsgálata Készítette: Hénap Gábor henapg@mm.bme.hu E E P MT A y F D E E d B MT p C x a b c Adatok: a = m, p = 1 N, b = 3 m, F = 5 N, c = 4 m, d = 5 mm. m A kés bbikekben
Statikailag határozatlan tartó vizsgálata Készítette: Hénap Gábor henapg@mm.bme.hu E E P MT A y F D E E d B MT p C x a b c Adatok: a = m, p = 1 N, b = 3 m, F = 5 N, c = 4 m, d = 5 mm. m A kés bbikekben
tápvezetékre jellemző, hogy csak a vezeték végén van terhelés, ahogy az 1. ábra mutatja.
 Tápvezeték A fogyasztókat a tápponttal közvetlen összekötő vezetékeket tápvezetéknek nevezzük. A tápvezetékre jellemző, hogy csak a vezeték végén van terhelés, ahogy az 1. ábra mutatja. U T l 1. ábra.
Tápvezeték A fogyasztókat a tápponttal közvetlen összekötő vezetékeket tápvezetéknek nevezzük. A tápvezetékre jellemző, hogy csak a vezeték végén van terhelés, ahogy az 1. ábra mutatja. U T l 1. ábra.
GÉPÉSZETI ALAPISMERETEK
 Gépészeti alapismeretek középszint 1621 ÉRETTSÉGI VIZSGA 2016. október 17. GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐORRÁSOK MINISZTÉRIUMA ontos
Gépészeti alapismeretek középszint 1621 ÉRETTSÉGI VIZSGA 2016. október 17. GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐORRÁSOK MINISZTÉRIUMA ontos
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén
 Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
Csavarorsós emelőbak tervezési feladat Gépészmérnök, Járműmérnök, Mechatronikai mérnök, Logisztikai mérnök, Mérnöktanár (osztatlan) BSC szak
 Csavarorsós emelőbak tervezési feladat Gépészmérnök, Járműmérnök, Mechatronikai mérnök, Logisztikai mérnök, Mérnöktanár (osztatlan) BSC szak A feladat részletezése: Név:.. Csoport:... A számításnak (órai)
Csavarorsós emelőbak tervezési feladat Gépészmérnök, Járműmérnök, Mechatronikai mérnök, Logisztikai mérnök, Mérnöktanár (osztatlan) BSC szak A feladat részletezése: Név:.. Csoport:... A számításnak (órai)
GÉPÉSZETI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2015. október 12. GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2015. október 12. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2015. október 12. GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2015. október 12. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS-
 A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS- Forgatónyomaték meghatározása G Á L A T A Egy erő forgatónyomatékkal hat egy pontra, ha az az erővel össze van kötve. Például
A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS- Forgatónyomaték meghatározása G Á L A T A Egy erő forgatónyomatékkal hat egy pontra, ha az az erővel össze van kötve. Például
Segédlet: Kihajlás. Készítette: Dr. Kossa Attila BME, Műszaki Mechanikai Tanszék május 15.
 Segédlet: Kihajlás Készítette: Dr. Kossa ttila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2012. május 15. Jelen segédlet célja tömören összefoglalni a hosszú nyomott rudak kihajlásra történő ellenőrzését.
Segédlet: Kihajlás Készítette: Dr. Kossa ttila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2012. május 15. Jelen segédlet célja tömören összefoglalni a hosszú nyomott rudak kihajlásra történő ellenőrzését.
6. MECHANIKA-STATIKA GYAKORLAT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya, Culmann-szerkesztés, Ritter-számítás
 ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
1. Feladat. a) Mekkora radiális, tangenciális és axiális feszültségek ébrednek a csőfalban, ha a csővég zárt?
 1. Feladat Egy a = mm első és = 150 mm külső sugarú cső terhelése p = 60 MPa első ill. p k = 30 MPa külső nyomás. a) Mekkora radiális, tangenciális és axiális feszültségek érednek a csőfalan, ha a csővég
1. Feladat Egy a = mm első és = 150 mm külső sugarú cső terhelése p = 60 MPa első ill. p k = 30 MPa külső nyomás. a) Mekkora radiális, tangenciális és axiális feszültségek érednek a csőfalan, ha a csővég
Cölöpcsoport elmozdulásai és méretezése
 18. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpcsoport elmozdulásai és méretezése Program: Fájl: Cölöpcsoport Demo_manual_18.gsp A fejezet célja egy cölöpcsoport fejtömbjének elfordulásának,
18. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpcsoport elmozdulásai és méretezése Program: Fájl: Cölöpcsoport Demo_manual_18.gsp A fejezet célja egy cölöpcsoport fejtömbjének elfordulásának,
Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS!
 Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS! 1. példa Vasúti kocsinak a 6. ábrán látható ütközőjébe épített tekercsrugóban 44,5 kn előfeszítő erő ébred. A rugó állandója 0,18
Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS! 1. példa Vasúti kocsinak a 6. ábrán látható ütközőjébe épített tekercsrugóban 44,5 kn előfeszítő erő ébred. A rugó állandója 0,18
Meghatározás. Olyan erőzárásos hajtás, ahol a tengelyek közötti teljesítmény-, nyomaték-, szögsebesség átvitelt ékszíj és ékszíjtárcsa biztosítja.
 Ékszíjszíjhajtás Tartalomjegyzék Meghatározás Ékhatás Előnyök, hátrányok Szíjhossz, tengely állíthatóság Ékszíjtárcsák szerkezeti kialakítása Normál ékszíjak Keskeny ékszíjak Különleges ékszíjak Keskeny
Ékszíjszíjhajtás Tartalomjegyzék Meghatározás Ékhatás Előnyök, hátrányok Szíjhossz, tengely állíthatóság Ékszíjtárcsák szerkezeti kialakítása Normál ékszíjak Keskeny ékszíjak Különleges ékszíjak Keskeny
Mikrocölöp alapozás ellenőrzése
 36. számú mérnöki kézikönyv Frissítve: 2017. június Mikrocölöp alapozás ellenőrzése Program: Fájl: Cölöpcsoport Demo_manual_en_36.gsp Ennek a mérnöki kézikönyvnek a célja, egy mikrocölöp alapozás ellenőrzésének
36. számú mérnöki kézikönyv Frissítve: 2017. június Mikrocölöp alapozás ellenőrzése Program: Fájl: Cölöpcsoport Demo_manual_en_36.gsp Ennek a mérnöki kézikönyvnek a célja, egy mikrocölöp alapozás ellenőrzésének
6. MECHANIKA-STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnöktanár)
 SZÉHNYI ISTVÁN GYT LKLZOTT HNIK TNSZÉK 6. HNIK-STTIK GYKORLT (kidolgozta: Triesz Péter egy. ts.; Tarnai Gábor mérnöktanár) Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa gy létrát egy
SZÉHNYI ISTVÁN GYT LKLZOTT HNIK TNSZÉK 6. HNIK-STTIK GYKORLT (kidolgozta: Triesz Péter egy. ts.; Tarnai Gábor mérnöktanár) Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa gy létrát egy
Példa: Csúsztatófeszültség-eloszlás számítása I-szelvényben
 Példa: Csúsztatófeszültség-eloszlás számítása I-szelvényben Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 14. Határozzuk meg a nyírásból adódó csúsztatófeszültség
Példa: Csúsztatófeszültség-eloszlás számítása I-szelvényben Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 14. Határozzuk meg a nyírásból adódó csúsztatófeszültség
Tartószerkezetek I. (Vasbeton szilárdságtan)
 Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.10.11. Vasbeton külpontos nyomása Az eső ágú σ-ε diagram miatt elvileg minden egyes esethez külön kell meghatározni a szélső szál összenyomódását.
Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.10.11. Vasbeton külpontos nyomása Az eső ágú σ-ε diagram miatt elvileg minden egyes esethez külön kell meghatározni a szélső szál összenyomódását.
Építészeti tartószerkezetek II.
 Építészeti tartószerkezetek II. Vasbeton szerkezetek Dr. Szép János Egyetemi docens 2019. 05. 03. Vasbeton szerkezetek I. rész o Előadás: Vasbeton lemezek o Gyakorlat: Súlyelemzés, modellfelvétel (AxisVM)
Építészeti tartószerkezetek II. Vasbeton szerkezetek Dr. Szép János Egyetemi docens 2019. 05. 03. Vasbeton szerkezetek I. rész o Előadás: Vasbeton lemezek o Gyakorlat: Súlyelemzés, modellfelvétel (AxisVM)
A= a keresztmetszeti felület cm 2 ɣ = biztonsági tényező
 Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
Toronymerevítık mechanikai szempontból
 Andó Mátyás: Toronymerevítık méretezése, 9 Gépész Tuning Kft. Toronymerevítık mechanikai szempontból Mint a neve is mutatja a toronymerevítık használatának célja az, hogy merevebbé tegye az autó karosszériáját
Andó Mátyás: Toronymerevítık méretezése, 9 Gépész Tuning Kft. Toronymerevítık mechanikai szempontból Mint a neve is mutatja a toronymerevítık használatának célja az, hogy merevebbé tegye az autó karosszériáját
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet
 Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
GÉPÉSZETI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2006. február 20. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2006. február 20. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIUM
ÉRETTSÉGI VIZSGA 2006. február 20. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2006. február 20. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIUM
Érettségi feladatok Koordinátageometria_rendszerezve / 5
 Érettségi feladatok Koordinátageometria_rendszerezve 2005-2013 1/ 5 Vektorok 2005. május 28./12. Adottak az a (4; 3) és b ( 2; 1) vektorok. a) Adja meg az a hosszát! b) Számítsa ki az a + b koordinátáit!
Érettségi feladatok Koordinátageometria_rendszerezve 2005-2013 1/ 5 Vektorok 2005. május 28./12. Adottak az a (4; 3) és b ( 2; 1) vektorok. a) Adja meg az a hosszát! b) Számítsa ki az a + b koordinátáit!
Központosan nyomott vasbeton oszlop méretezése:
 Központosan nyomott vasbeton oszlop méretezése: Központosan nyomott oszlopok ellenőrzése: A beton által felvehető nyomóerő: N cd = A ctot f cd Az acélbetétek által felvehető nyomóerő: N sd = A s f yd -
Központosan nyomott vasbeton oszlop méretezése: Központosan nyomott oszlopok ellenőrzése: A beton által felvehető nyomóerő: N cd = A ctot f cd Az acélbetétek által felvehető nyomóerő: N sd = A s f yd -
Csuklós szerkezetek reakciói és igénybevételi ábrái. Frissítve: példa: A 12. gyakorlat 1. feladata.
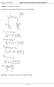 1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
GÉPÉSZETI ALAPISMERETEK TÉMAKÖRÖK
 GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÉRETTSÉGI TÉMAKÖRÖK Preisz Csaba mérnök-tanár Műszaki mechanika Statikai alapfogalmak - Erőrendszer fogalma - Vektorokkal végezhető alapműveleteket (erők felbontása,
GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÉRETTSÉGI TÉMAKÖRÖK Preisz Csaba mérnök-tanár Műszaki mechanika Statikai alapfogalmak - Erőrendszer fogalma - Vektorokkal végezhető alapműveleteket (erők felbontása,
Érettségi feladatok: Koordináta-geometria 1/5
 Érettségi feladatok: Koordináta-geometria 1/5 2003. Próba/ 13. Adott egy háromszög három csúcspontja a koordinátáival: A( 4; 4), B(4; 4) és C( 4; 8). Számítsa ki a C csúcsból induló súlyvonal és az A csúcsból
Érettségi feladatok: Koordináta-geometria 1/5 2003. Próba/ 13. Adott egy háromszög három csúcspontja a koordinátáival: A( 4; 4), B(4; 4) és C( 4; 8). Számítsa ki a C csúcsból induló súlyvonal és az A csúcsból
Gyakorlati útmutató a Tartók statikája I. tárgyhoz. Fekete Ferenc. 5. gyakorlat. Széchenyi István Egyetem, 2015.
 Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával
 Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 212. október 16. Frissítve: 215. január
Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 212. október 16. Frissítve: 215. január
Nyomástartóedény-gépész Kőolaj- és vegyipari géprendszer üzemeltetője
 A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
TENGELY TERHELHETŐSÉGI VIZSGÁLATA
 MISKOLCI EGYETEM GÉP- ÉS TERMÉKTERVEZÉSI TANSZÉK OKTATÁSI SEGÉDLET a GÉPSZERKEZETTAN - TERVEZÉS c. tantárgyhoz TENGELY TERHELHETŐSÉGI VIZSGÁLATA Összeállította: Dr. Szente József egyetemi docens Miskolc,
MISKOLCI EGYETEM GÉP- ÉS TERMÉKTERVEZÉSI TANSZÉK OKTATÁSI SEGÉDLET a GÉPSZERKEZETTAN - TERVEZÉS c. tantárgyhoz TENGELY TERHELHETŐSÉGI VIZSGÁLATA Összeállította: Dr. Szente József egyetemi docens Miskolc,
Vasbeton tartók méretezése hajlításra
 Vasbeton tartók méretezése hajlításra Képlékenység-tani méretezés: A vasbeton keresztmetszet teherbírásának számításánál a III. feszültségi állapotot vesszük alapul, amelyre az jellemző, hogy a hajlításból
Vasbeton tartók méretezése hajlításra Képlékenység-tani méretezés: A vasbeton keresztmetszet teherbírásának számításánál a III. feszültségi állapotot vesszük alapul, amelyre az jellemző, hogy a hajlításból
Egy háromlábú állvány feladata. 1. ábra forrása:
 1 Egy háromlábú állvány feladata Az interneten találtuk az alábbi versenyfeladatot 1. ábra Az egyforma hosszúságú CA, CB és CD rudak a C pontban gömbcsuklóval kapcsolódnak, az A, B, D végükön sima vízszintes
1 Egy háromlábú állvány feladata Az interneten találtuk az alábbi versenyfeladatot 1. ábra Az egyforma hosszúságú CA, CB és CD rudak a C pontban gömbcsuklóval kapcsolódnak, az A, B, D végükön sima vízszintes
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK. Acélszerkezetek II. IV. Előadás
 DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II IV. Előadás Rácsos tartók szerkezeti formái, kialakítása, tönkremeneteli módjai. - Rácsos tartók jellemzói - Méretezési kérdések
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II IV. Előadás Rácsos tartók szerkezeti formái, kialakítása, tönkremeneteli módjai. - Rácsos tartók jellemzói - Méretezési kérdések
Egy érdekes statikai - geometriai feladat
 1 Egy érdekes statikai - geometriai feladat Előző dolgozatunkban melynek címe: Egy érdekes geometriai feladat egy olyan feladatot oldottunk meg, ami az itteni előtanulmányának is tekinthető. Az ottani
1 Egy érdekes statikai - geometriai feladat Előző dolgozatunkban melynek címe: Egy érdekes geometriai feladat egy olyan feladatot oldottunk meg, ami az itteni előtanulmányának is tekinthető. Az ottani
MECHANIKA I. rész: Szilárd testek mechanikája
 Egészségügyi mérnökképzés MECHNIK I. rész: Szilárd testek mechanikája készítette: Németh Róbert Igénybevételek térben I. z alapelv ugyanaz, mint síkban: a keresztmetszet egyik oldalán levő szerkezetrészre
Egészségügyi mérnökképzés MECHNIK I. rész: Szilárd testek mechanikája készítette: Németh Róbert Igénybevételek térben I. z alapelv ugyanaz, mint síkban: a keresztmetszet egyik oldalán levő szerkezetrészre
Gyakorló feladatok a 2. zárthelyihez. Kidolgozott feladatok
 Gakorló feladatok a. zárthelihez Kidolgozott feladatok. a) Határozzuk meg a függesztőrúd négzetkeresztmetszetének a oldalhosszát cm-re kerekítve úg, hog a függesztőrúdban ébredő normálfeszültség ne érje
Gakorló feladatok a. zárthelihez Kidolgozott feladatok. a) Határozzuk meg a függesztőrúd négzetkeresztmetszetének a oldalhosszát cm-re kerekítve úg, hog a függesztőrúdban ébredő normálfeszültség ne érje
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Ellenőrző kérdések Vegyipari Géptan tárgyból a vizsgárakészüléshez
 2015. tavaszi/őszi félév A vizsgára hozni kell: 5 db A4-es lap, íróeszköz (ceruza!), radír, zsebszámológép, igazolvány. A vizsgán általában 5 kérdést kapnak, aminek a kidolgozására 90 perc áll rendelkezésükre.
2015. tavaszi/őszi félév A vizsgára hozni kell: 5 db A4-es lap, íróeszköz (ceruza!), radír, zsebszámológép, igazolvány. A vizsgán általában 5 kérdést kapnak, aminek a kidolgozására 90 perc áll rendelkezésükre.
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Acélszerkezetek. 3. előadás 2012.02.24.
 Acélszerkezetek 3. előadás 2012.02.24. Kapcsolatok méretezése Kapcsolatok típusai Mechanikus kapcsolatok: Szegecsek Csavarok Csapok Hegesztett kapcsolatok Tompavarrat Sarokvarrat Coalbrookdale, 1781 Eiffel
Acélszerkezetek 3. előadás 2012.02.24. Kapcsolatok méretezése Kapcsolatok típusai Mechanikus kapcsolatok: Szegecsek Csavarok Csapok Hegesztett kapcsolatok Tompavarrat Sarokvarrat Coalbrookdale, 1781 Eiffel
Rugalmas állandók mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
GÉPÉSZETI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2007. május 25. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
ÉRETTSÉGI VIZSGA 2007. május 25. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
Az M A vektor tehát a három vektori szorzat előjelhelyes összege:
 1. feladat Határozza meg a T i támadáspontú F i erőrendszer nyomatékát az A pontra. T 1 ( 3, 0, 5 ) T 1 ( 0, 4, 5 ) T 1 ( 3, 4, 2 ) F 1 = 0 i + 300 j + 0 k F 2 = 0 i 100 j 400 k F 3 = 100 i 100 j + 500
1. feladat Határozza meg a T i támadáspontú F i erőrendszer nyomatékát az A pontra. T 1 ( 3, 0, 5 ) T 1 ( 0, 4, 5 ) T 1 ( 3, 4, 2 ) F 1 = 0 i + 300 j + 0 k F 2 = 0 i 100 j 400 k F 3 = 100 i 100 j + 500
Gyakorló feladatok síkalakváltozás alkalmazására forgásszimmetrikus esetben térfogati terhelés nélkül és térfogati terheléssel.
 Alkalmazások síkalakváltozásra: Gakorló feladatok síkalakváltozás alkalmazására forgásszimmetrikus esetben térfogati terhelés nélkül és térfogati terheléssel. SAF1. Az ábrán vázolt zárt vastagfal csövet
Alkalmazások síkalakváltozásra: Gakorló feladatok síkalakváltozás alkalmazására forgásszimmetrikus esetben térfogati terhelés nélkül és térfogati terheléssel. SAF1. Az ábrán vázolt zárt vastagfal csövet
Fogorvosi anyagtan fizikai alapjai 6.
 Fogorvosi anyagtan fizikai alapjai 6. Mechanikai tulajdonságok 1. Kiemelt témák: Rugalmas alakváltozás Merevség és összefüggése a kötési energiával A geometriai tényezők szerepe egy test merevségében Tankönyv
Fogorvosi anyagtan fizikai alapjai 6. Mechanikai tulajdonságok 1. Kiemelt témák: Rugalmas alakváltozás Merevség és összefüggése a kötési energiával A geometriai tényezők szerepe egy test merevségében Tankönyv
Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén.
 Alkalmazott előjelszabályok Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén. A kényszererők számításánál a következő a szabály: Az erők iránya a pozitív
Alkalmazott előjelszabályok Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén. A kényszererők számításánál a következő a szabály: Az erők iránya a pozitív
1.1. A tengelykapcsolók feladata, csoportosítása és általános méretezési elvük. Merev tengelykapcsolók.
 1.1. A tengelykapcsolók feladata, csoportosítása és általános méretezési elvük. Merev tengelykapcsolók. Tevékenység: Olvassa el a jegyzet 9-17 oldalain található tananyagát! Tanulmányozza át a segédlet
1.1. A tengelykapcsolók feladata, csoportosítása és általános méretezési elvük. Merev tengelykapcsolók. Tevékenység: Olvassa el a jegyzet 9-17 oldalain található tananyagát! Tanulmányozza át a segédlet
Határfeszültségek alapanyag: σ H = 200 N/mm 2, σ ph = 350 N/mm 2 ; szegecs: τ H = 160 N/mm 2, σ ph = 350 N/mm 2. Egy szegecs teherbírása:
 ervezze meg az L10.10.1-es szögacélpár eltolt illesztését L100.100.1-es hevederekkel és Ø1 mm-es szegecsekkel. nyagminőség: 8, szegecs: SZ. atárfeszültségek alapanyag: 00 /mm, p 50 /mm szegecs: τ 160 /mm,
ervezze meg az L10.10.1-es szögacélpár eltolt illesztését L100.100.1-es hevederekkel és Ø1 mm-es szegecsekkel. nyagminőség: 8, szegecs: SZ. atárfeszültségek alapanyag: 00 /mm, p 50 /mm szegecs: τ 160 /mm,
ÁGAZATI SZAKMAI ÉRETTSÉGI VIZSGA KÖZLEKEDÉSGÉPÉSZ ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA MINTAFELADATOK
 KÖZLEKEDÉSGÉPÉSZ ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA MINTAFELADATOK 1. feladat 1 pont (Feleletválasztás) Témakör: Közlekedési ismeretek Húzza alá a helyes választ, vagy karikázza be annak betűjelét!
KÖZLEKEDÉSGÉPÉSZ ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA MINTAFELADATOK 1. feladat 1 pont (Feleletválasztás) Témakör: Közlekedési ismeretek Húzza alá a helyes választ, vagy karikázza be annak betűjelét!
Rácsos szerkezetek. Frissítve: Egy kis elmélet: vakrudak
 Egy kis elmélet: vakrudak Az egyik lehetőség, ha két rúd szög alatt találkozik (nem egyvonalban vannak), és nem működik a csomópontra terhelés. Ilyen az 1.ábra C csomópontja. Ekkor az ide befutó mindkét
Egy kis elmélet: vakrudak Az egyik lehetőség, ha két rúd szög alatt találkozik (nem egyvonalban vannak), és nem működik a csomópontra terhelés. Ilyen az 1.ábra C csomópontja. Ekkor az ide befutó mindkét
First Prev Next Last Go Back Full Screen Close Quit
 Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Tengelykapcsoló. 2018/2019 tavasz
 Jármű és s hajtáselemek I. Tengelykapcsoló Török k István 2018/2019 tavasz TENGELYKAPCSOL KAPCSOLÓK 2 1. Besorolás Nyomatékátvivő elemek tengelyek; tengelykapcsolók; vonóelemes hajtások; gördülőelemes
Jármű és s hajtáselemek I. Tengelykapcsoló Török k István 2018/2019 tavasz TENGELYKAPCSOL KAPCSOLÓK 2 1. Besorolás Nyomatékátvivő elemek tengelyek; tengelykapcsolók; vonóelemes hajtások; gördülőelemes
MUNKAANYAG. Szabó László. Szilárdságtan. A követelménymodul megnevezése:
 Szabó László Szilárdságtan A követelménymodul megnevezése: Kőolaj- és vegyipari géprendszer üzemeltetője és vegyipari technikus feladatok A követelménymodul száma: 047-06 A tartalomelem azonosító száma
Szabó László Szilárdságtan A követelménymodul megnevezése: Kőolaj- és vegyipari géprendszer üzemeltetője és vegyipari technikus feladatok A követelménymodul száma: 047-06 A tartalomelem azonosító száma
Fa- és Acélszerkezetek I. 7. Előadás Kapcsolatok I. Csavarozott kapcsolatok. Dr. Szalai József Főiskolai adjunktus
 Fa- és Acélszerkezetek I. 7. Előadás Kapcsolatok I. Csavarozott kapcsolatok Dr. Szalai József Főiskolai adjunktus Tartalom Acélszerkezetek kapcsolatai Csavarozott kapcsolatok kialakítása Csavarozott kapcsolatok
Fa- és Acélszerkezetek I. 7. Előadás Kapcsolatok I. Csavarozott kapcsolatok Dr. Szalai József Főiskolai adjunktus Tartalom Acélszerkezetek kapcsolatai Csavarozott kapcsolatok kialakítása Csavarozott kapcsolatok
Hajlított elemek kifordulása. Stabilitásvesztési módok
 Hajlított elemek kifordulása Stabilitásvesztési módok Stabilitásvesztés (3.3.fejezet) Globális: Nyomott rudak kihajlása Hajlított tartók kifordulása Lemezhorpadás (lokális stabilitásvesztés): Nyomott és/vagy
Hajlított elemek kifordulása Stabilitásvesztési módok Stabilitásvesztés (3.3.fejezet) Globális: Nyomott rudak kihajlása Hajlított tartók kifordulása Lemezhorpadás (lokális stabilitásvesztés): Nyomott és/vagy
Szádfal szerkezet ellenőrzés Adatbev.
 Szádfal szerkezet ellenőrzés Adatbev. Projekt Dátum : 8.0.05 Beállítások (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : Acél szerkezetek : Acél keresztmetszet teherbírásának
Szádfal szerkezet ellenőrzés Adatbev. Projekt Dátum : 8.0.05 Beállítások (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : Acél szerkezetek : Acél keresztmetszet teherbírásának
ÁGAZATI SZAKMAI ÉRETTSÉGI VIZSGA KÖZLEKEDÉSGÉPÉSZ ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ
 016. OKTÓBER KÖZLEKEDÉSGÉPÉSZ ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ 016. OKTÓBER 1. feladat Témakör: Közlekedési ismeretek Milyen találmány fűződik John
016. OKTÓBER KÖZLEKEDÉSGÉPÉSZ ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ 016. OKTÓBER 1. feladat Témakör: Közlekedési ismeretek Milyen találmány fűződik John
A Horváth Mérnökiroda, A Budapesti Műszaki Egyetem Gépjárművek Tanszéke. A Schwarzmüller Járműgyártó és Kereskedelmi Kft
 A járóképes alvázakra épített különböző felépítményekkel kialakítható tehergépkocsik forgalombahelyezésének hatósági eljárásához A Horváth Mérnökiroda, A Budapesti Műszaki Egyetem Gépjárművek Tanszéke
A járóképes alvázakra épített különböző felépítményekkel kialakítható tehergépkocsik forgalombahelyezésének hatósági eljárásához A Horváth Mérnökiroda, A Budapesti Műszaki Egyetem Gépjárművek Tanszéke
GÉPÉSZETI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2005. május 20. GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIUM Gépészeti alapismeretek
ÉRETTSÉGI VIZSGA 2005. május 20. GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIUM Gépészeti alapismeretek
Keresztmetszet másodrendű nyomatékainak meghatározása
 BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
GÉPÉSZETI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2006. május 18. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA 2006. május 18. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI
ÉRETTSÉGI VIZSGA 2006. május 18. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA 2006. május 18. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI
1.2. Mozgó, hajlékony és rugalmas tengelykapcsolók.
 1.2. Mozgó, hajlékony és rugalmas tengelykapcsolók. Tevékenység: Olvassa el a jegyzet 18-29 oldalain található tananyagát! Tanulmányozza át a segédlet 8.2. és 8.3. fejezeteiben lévı kidolgozott feladatait,
1.2. Mozgó, hajlékony és rugalmas tengelykapcsolók. Tevékenység: Olvassa el a jegyzet 18-29 oldalain található tananyagát! Tanulmányozza át a segédlet 8.2. és 8.3. fejezeteiben lévı kidolgozott feladatait,
GÉPÉSZETI ALAPISMERETEK
 Gépészeti alapismeretek emelt szint 1621 ÉRETTSÉGI VIZSGA 2016. október 17. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA
Gépészeti alapismeretek emelt szint 1621 ÉRETTSÉGI VIZSGA 2016. október 17. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA
Nyomástartóedény-gépész Kőolaj- és vegyipari géprendszer üzemeltetője
 É 063-06/1/13 A 10/007 (II. 7.) SzMM rendelettel módosított 1/006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján.
É 063-06/1/13 A 10/007 (II. 7.) SzMM rendelettel módosított 1/006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján.
KÖZLEKEDÉSGÉPÉSZ ISMERETEK
 ÉRETTSÉGI VIZSGA 2017. május 17. KÖZLEKEDÉSGÉPÉSZ ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2017. május 17. 8:00 Időtartam: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Közlekedésgépész
ÉRETTSÉGI VIZSGA 2017. május 17. KÖZLEKEDÉSGÉPÉSZ ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2017. május 17. 8:00 Időtartam: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Közlekedésgépész
Példa keresztmetszet másodrendű nyomatékainak számítására
 Példa keresztmetszet másodrendű nyomatékainak számítására Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. február 22. Tekintsük az alábbi keresztmetszetet. 1. ábra. A vizsgált
Példa keresztmetszet másodrendű nyomatékainak számítására Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. február 22. Tekintsük az alábbi keresztmetszetet. 1. ábra. A vizsgált
2. Rugalmas állandók mérése jegyzőkönyv javított. Zsigmond Anna Fizika Bsc II. Mérés dátuma: Leadás dátuma:
 2. Rugalmas állandók mérése jegyzőkönyv javított Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 17. Leadás dátuma: 2008. 10. 08. 1 1. Mérések ismertetése Az első részben egy téglalap keresztmetszetű
2. Rugalmas állandók mérése jegyzőkönyv javított Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 17. Leadás dátuma: 2008. 10. 08. 1 1. Mérések ismertetése Az első részben egy téglalap keresztmetszetű
Tervezés katalógusokkal kisfeladat
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Számítógépes tervezés, méretezés és gyártás (BME KOJHM401) Tervezés katalógusokkal kisfeladat Járműelemek és Járműszerkezetanalízis Tanszék Ssz.:...... Név:.........................................
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Számítógépes tervezés, méretezés és gyártás (BME KOJHM401) Tervezés katalógusokkal kisfeladat Járműelemek és Járműszerkezetanalízis Tanszék Ssz.:...... Név:.........................................
időpont? ütemterv számonkérés segédanyagok
 időpont? ütemterv számonkérés segédanyagok 1. Bevezetés Végeselem-módszer Számítógépek alkalmazása a szerkezettervezésben: 1. a geometria megadása, tervkészítés, 2. műszaki számítások: - analitikus számítások
időpont? ütemterv számonkérés segédanyagok 1. Bevezetés Végeselem-módszer Számítógépek alkalmazása a szerkezettervezésben: 1. a geometria megadása, tervkészítés, 2. műszaki számítások: - analitikus számítások
Öszvér oszlopok kialakítása, THÁ, nyírt kapcsolatok, erőbevezetés környezete. 2. mintapélda - oszlop méretezése.
 Öszvérszerkezetek 4. előadás Öszvér oszlopok kialakítása, THÁ, nyírt kapcsolatok, erőbevezetés környezete. 2. mintapélda - oszlop méretezése. készítette: 2012.10.27. Tartalom Öszvér oszlopok szerkezeti
Öszvérszerkezetek 4. előadás Öszvér oszlopok kialakítása, THÁ, nyírt kapcsolatok, erőbevezetés környezete. 2. mintapélda - oszlop méretezése. készítette: 2012.10.27. Tartalom Öszvér oszlopok szerkezeti
GÉPÉSZETI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2013. október 14. GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2013. október 14. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2013. október 14. GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2013. október 14. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
Frissítve: 2015.04.29. Feszültség- és alakváltozási állapot. 1. példa: Írjuk fel az adott kockához tartozó feszültségtenzort!
 1. példa: Írjuk fel az adott kockához tartozó feszültségtenzort! 1 / 20 2. példa: Rajzoljuk fel az adott feszültségtenzorhoz tartozó kockát! 2 / 20 3. példa: Feszültségvektor számítása. Egy alkatrész egy
1. példa: Írjuk fel az adott kockához tartozó feszültségtenzort! 1 / 20 2. példa: Rajzoljuk fel az adott feszültségtenzorhoz tartozó kockát! 2 / 20 3. példa: Feszültségvektor számítása. Egy alkatrész egy
Hegesztett gerinclemezes tartók
 Hegesztett gerinclemezes tartók Lemezhorpadások kezelése EC szerint dr. Horváth László BME Hidak és Szerkezetek Tanszéke Bevezetés Gerinclemezes tartók vékony lemezekből: Bevezetés Összetett szelvények,
Hegesztett gerinclemezes tartók Lemezhorpadások kezelése EC szerint dr. Horváth László BME Hidak és Szerkezetek Tanszéke Bevezetés Gerinclemezes tartók vékony lemezekből: Bevezetés Összetett szelvények,
Géprajz gépelemek II. II. Konzultáció (2014.03.22.)
 Géprajz gépelemek II. II. Konzultáció (2014.03.22.) Forgó alkatrészek oldható kötőelemei (a nem oldható tengelykötéseket a tk.-ből tanulni) Ékkötés Az ék horonyszélességének illesztése laza D10 A tengely
Géprajz gépelemek II. II. Konzultáció (2014.03.22.) Forgó alkatrészek oldható kötőelemei (a nem oldható tengelykötéseket a tk.-ből tanulni) Ékkötés Az ék horonyszélességének illesztése laza D10 A tengely
DEME FERENC okl. építőmérnök, mérnöktanár
 DEME FERENC okl. építőmérnök, mérnöktanár web-lap : www.sze.hu/~deme e-mail : deme.ferenc1@gmail.com HÁROMCSUKLÓS TARTÓ KÜLSŐ ÉS BELSŐ REAKCIÓ ERŐINEK SZÁMÍTÁSA, A TARTÓ IGÉNYBEVÉTELI ÁBRÁINAK RAJZOLÁSA
DEME FERENC okl. építőmérnök, mérnöktanár web-lap : www.sze.hu/~deme e-mail : deme.ferenc1@gmail.com HÁROMCSUKLÓS TARTÓ KÜLSŐ ÉS BELSŐ REAKCIÓ ERŐINEK SZÁMÍTÁSA, A TARTÓ IGÉNYBEVÉTELI ÁBRÁINAK RAJZOLÁSA
X i = 0 F x + B x = 0. Y i = 0 A y F y + B y = 0. M A = 0 F y 3 + B y 7 = 0. B x = 200 N. B y =
 1. feladat a = 3 m b = 4 m F = 400 N φ = 60 fok Első lépésként alkossuk meg a számítási modellt. A kényszereket helyettesítsük a bennük ébredő lehetséges erőkkel (második ábra). Az F erő felbontásával
1. feladat a = 3 m b = 4 m F = 400 N φ = 60 fok Első lépésként alkossuk meg a számítási modellt. A kényszereket helyettesítsük a bennük ébredő lehetséges erőkkel (második ábra). Az F erő felbontásával
GÉPÉSZETI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2016. október 17. GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2016. október 17. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2016. október 17. GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2016. október 17. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
GÉPÉSZETI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2012. október 15. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2012. október 15. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2012. október 15. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2012. október 15. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
(Az 1. példa adatai Uray-Szabó: Elektrotechnika c. (Nemzeti Tankönyvkiadó) könyvéből vannak.)
 Egyenáramú gépek (Az 1. példa adatai Uray-Szabó: Elektrotechnika c. (Nemzeti Tankönyvkiadó) könyvéből vannak.) 1. Párhuzamos gerjesztésű egyenáramú motor 500 V kapocsfeszültségű, párhuzamos gerjesztésű
Egyenáramú gépek (Az 1. példa adatai Uray-Szabó: Elektrotechnika c. (Nemzeti Tankönyvkiadó) könyvéből vannak.) 1. Párhuzamos gerjesztésű egyenáramú motor 500 V kapocsfeszültségű, párhuzamos gerjesztésű
GÉPÉSZET ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Gépészet ismeretek középszint 1712 ÉRETTSÉGI VIZSGA 2017. október 20. GÉPÉSZET ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Útmutató a vizsgázók teljesítményének
Gépészet ismeretek középszint 1712 ÉRETTSÉGI VIZSGA 2017. október 20. GÉPÉSZET ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Útmutató a vizsgázók teljesítményének
GÉPÉSZETI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2011. október 17. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2011. október 17. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
ÉRETTSÉGI VIZSGA 2011. október 17. GÉPÉSZETI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2011. október 17. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
, D(-1; 1). A B csúcs koordinátáit az y = + -. A trapéz BD
 Kör és egyenes kölcsönös helyzete Kör érintôje 7 9 A húr hossza: egység 9 A ( ) ponton átmenô legrövidebb húr merôleges a K szakaszra, ahol K az adott kör középpontja, feltéve, hogy a kör belsejében van
Kör és egyenes kölcsönös helyzete Kör érintôje 7 9 A húr hossza: egység 9 A ( ) ponton átmenô legrövidebb húr merôleges a K szakaszra, ahol K az adott kör középpontja, feltéve, hogy a kör belsejében van
4. feladat Géprajz-Gépelemek (GEGET224B) c. tárgyból a Műszaki Anyagtudományi Kar, nappali tagozatos hallgatói számára
 4. feladat Géprajz-Gépelemek (GEGET4B) c. tárgyból a űszaki Anyagtudományi Kar, nappali tagozatos hallgatói számára TOKOS TENGELYKAPCSOLÓ méretezése és szerkesztése útmutató segítségével 1. Villamos motorról
4. feladat Géprajz-Gépelemek (GEGET4B) c. tárgyból a űszaki Anyagtudományi Kar, nappali tagozatos hallgatói számára TOKOS TENGELYKAPCSOLÓ méretezése és szerkesztése útmutató segítségével 1. Villamos motorról
Ebben a mérnöki kézikönyvben azt mutatjuk be, hogyan számoljuk egy síkalap süllyedését és elfordulását.
 10. számú mérnöki kézikönyv Frissítve: 2016. Február Síkalap süllyedése Program: Fájl: Síkalap Demo_manual_10.gpa Ebben a mérnöki kézikönyvben azt mutatjuk be, hogyan számoljuk egy síkalap süllyedését
10. számú mérnöki kézikönyv Frissítve: 2016. Február Síkalap süllyedése Program: Fájl: Síkalap Demo_manual_10.gpa Ebben a mérnöki kézikönyvben azt mutatjuk be, hogyan számoljuk egy síkalap süllyedését
Gépelemek II. 1. feladat. Rugalmas hajtás tervezése III. A tengely méretezése
 01 Géelemek II. 1. feladat Rugalmas hajtás tervezése III. A tengely méretezése Miskolci Egyetem Gé és Terméktervezési Tanszék Szűcs Renáta 011/1 tavaszi félév Feladat kiírás A vázlat szerinti elrendezésben
01 Géelemek II. 1. feladat Rugalmas hajtás tervezése III. A tengely méretezése Miskolci Egyetem Gé és Terméktervezési Tanszék Szűcs Renáta 011/1 tavaszi félév Feladat kiírás A vázlat szerinti elrendezésben
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 8 VIII VEkTOROk 1 VEkTOR Vektoron irányított szakaszt értünk Jelölése: stb Vektorok hossza A vektor abszolút értéke az irányított szakasz hossza Ha a vektor hossza egységnyi akkor
KOVÁCS BÉLA MATEmATIkA I 8 VIII VEkTOROk 1 VEkTOR Vektoron irányított szakaszt értünk Jelölése: stb Vektorok hossza A vektor abszolút értéke az irányított szakasz hossza Ha a vektor hossza egységnyi akkor
Öszvér oszlopok kialakítása, THÁ, nyírt kapcsolatok, erőbevezetés környezete. 2. mintapélda - oszlop méretezése.
 Öszvérszerkezetek 4. előadás Öszvér oszlopok kialakítása, THÁ, nyírt kapcsolatok, erőbevezetés környezete. 2. mintapélda - oszlop méretezése. készítette: 2016.11.11. Tartalom Öszvér oszlopok szerkezeti
Öszvérszerkezetek 4. előadás Öszvér oszlopok kialakítása, THÁ, nyírt kapcsolatok, erőbevezetés környezete. 2. mintapélda - oszlop méretezése. készítette: 2016.11.11. Tartalom Öszvér oszlopok szerkezeti
Gyakorlati példák Dr. Gönczi Dávid
 Szilárdságtani számítások Gyakorlati példák Dr. Gönczi Dávid I. Bevezető ismeretek I.1 Definíciók I.2 Tenzoralgebrai alapismeretek I.3 Bevezetés az indexes jelölésmódba I.4 A lineáris rugalmasságtan általános
Szilárdságtani számítások Gyakorlati példák Dr. Gönczi Dávid I. Bevezető ismeretek I.1 Definíciók I.2 Tenzoralgebrai alapismeretek I.3 Bevezetés az indexes jelölésmódba I.4 A lineáris rugalmasságtan általános
GÉPÉSZETI ALAPISMERETEK
 Gépészeti alapismeretek középszint 1221 ÉRETTSÉGI VIZSGA 2013. május 23. GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos
Gépészeti alapismeretek középszint 1221 ÉRETTSÉGI VIZSGA 2013. május 23. GÉPÉSZETI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos
