A JIT költségeinek vizsgálata
|
|
|
- Gyöngyi Nagyné
- 6 évvel ezelőtt
- Látták:
Átírás
1 BME OMI LOGISZTIA 9. k május júius, p Taulmáytár * Ellátási elotási logitika A JIT költségeiek izsgálata Dr. Bekő Jáos 1 A japá eredetű just-i-time (JIT, éppe időe, percreké ) filozófia óriási kihíás a klasikus kéletezési elméletekkel eme. Az eredeti kocepció a gyártástól azt köeteli meg, hogy a megfelelő tételek (ayagok, félké- és kétermékek) a megfelelő meyisége és időe, plumíu ulla eltéréssel álljaak redelkezésre. Ez azt jeleti, hogy a ükségesél eggyel tö agy a ükségesél koráa érkező tétel éppe olya ros, mit a hiáy, agyis az adott pillaata a kíáatosál agyo kélet is eteséget jelet. A proléma egyoldalú közelítése élsőséges ézetek kialakulásához ezetett. Az egyik oldalá azok állak, akik legíesee törölék a ótáról a raktár ót, a másik oldal pedig tagadja az el létjogosultságát. Az igazsághoz azok állak a legközele, akik a JIT-et egy olya aimptotáak tekitik, amit józa megfotolással kell közelítei és em mideáro eléri. E taulmáy a költségek empotjáól izsgálja a kocepciót, és azt próálja izoyítai, hogy korrekt üzleti körülméyek között az el eezetése mide esete gazdaságossági ámításokat igéyel. Tárgyaak: just-i-time; kéletezés; kéletgazdálkodás; költség; érleti költség; raktározás; állítás; költségelemzés. Áttekités Az ayag- és kéletgazdálkodás fotos feladata a termelés üteméek megfelelő ayagükséglet folyamatos kielégítése. A termelési program és az ayagormák ismeretée egy adott időak ayagükséglete potosa terezhető, toáá ismertek a termeléshez ükséges ayagok eerezési forrásai is. Eek elleére az ayagellátása prolémák jeletkezhetek, amelyek egyrét a termelési program em terezett áltozásaira és izoytalaságaira, másrét a külső eállítókál mutatkozó, előre em ámítható eseméyekre ezethetők isa. A klasikus termelésiráyítási rederek a termelés folyamatosságát kéletek képzéséel iztosítják. A kéletek iztoságot jeleteek, de mi- 21
2 deki előtt ismert, hogy a agyo iztoság tö péze kerül. A kéletgazdálkodásak ezért feladata megtaláli az egyesúlyt az éserű iztoság és az elfogadható költség között. A prolémák kiküööléséek azoa létezik egy másik módja is, amikor em a kéleteket öeljük, haem a termelés emeő és kimeő oldalá és magáa a termelése jeletkező izoytalaságokat mérsékeljük. Elméletileg így megfelelő itű a eállítói háttér és ifrastruktúra eseté a iztoságos termelés csupá éháy órára elegedő ayaggal is elérhető. Ez az úgyeezett éppe időe (just i time, JIT) reder, amit gyakra kélet élküli agy raktár élküli kéletgazdálkodásak eezek. Bár alójáa a JIT emcsak egy kéletezési techika, haem aál élese termelési stratégia agy erezési filozófia. Az éppe időe gyártási kocepció ámos előye mellett (a kéletit, a eteségidő, a árakozási idő, az átfutási idő és a selejtaráy miimalizálása, a gyártóreder rugalmasságáak imalizálása st.) ámos eélyt is rejt magáa. Eől köetkezik, hogy a JIT eezetése a redelkezésére álló külső és első (ayagi és ellemi) erőforrások kocetrált iráyítását köeteli meg. Az éppe időe gyártási kocepció álladó kommuikációt és a koráiál léyegese agyo öshagot, fegyelmezettséget és rugalmasságot igéyel a eállítók és a állalat, alamit a állalati alrederek között. Mesemeőe megköeteli a partikuláris érdekek aláredelését a állalati érdekek egééek. A just i time célja tehát, hogy az ayagok és termékek éppe a megfelelő időe legyeek elállíta és/agy érkezzeek meg a redeltetési helyükre. Ez elméletileg zéró kéletet eredméyezhet, ami em tűri a eállítói hiákat. A kicsi kélet előfeltétele, hogy a eállítók és a fuarozók az ayag- agy áruáramoltatást egyeletese, zökkeőmetese égezzék. A állítási hiák a termelőkél termeléskorlátozást (leállás agy átállás), illete a kereskedőkél kélethiáyt (hiáycikk) okozhatak. Téyleges piaci ioyok eseté a kélethiáy mid a termelése, mid a kereskedeleme költségöekedést és/agy eladási eteségeket okoz. Eől adódóa a JIT egyik euralgikus potja a eállítás. A eállítással emei igéyek áltozását a köetkezőképp foglalhatjuk öse: a állítmáyok agysága csökke, gyakoriak a állítások, agyo az igéy a állítási olgáltatások elérhetőségére és a állítási késég jaítására, a állítások miősége jaul (a megízhatóság öekik, az árusérülések alóíűsége csökke). A állítási olgáltatásokkal emei igéyek öekedését terméetese meg kell fizeti, és kérdés, hogy a állítási költségek öekedését kompezálja-e a kéletezési költségek csökkeéséel elérhető megtakarítás? Sajos a dötési helyzeteke e kérdés sokor fel sem merül, az erőse pozícióa léő felek pedig em is foglalkozak a kérdéssel. A JIT esetée általáa a megredelők élek isa gazdasági erejükkel, oly módo, hogy a kéletezési költségeik csökketése érdekée gyakori állításra kéyerítik eállítóikat, és em hajladók elismeri az ezzel járó töletköltséget. Előfordul az is, hogy a eállító csak úgy tud megfeleli a megredelő igéyeiek, hogy a megredelő telephelye közelée raktárt érel, ami ugyacsak költségöekedést jelet. 22
3 Műeletek és költségek A korrekt izsgálathoz alameyi költségtéyezőt figyeleme kell ei, ami a feladó és a célállomás között jeletkezik; függetleül attól, hogy ki fizeti azt, a állító, a megredelő, agy alaki más. Egy termék útját köete a termelőtől a fogyatóig a köetkező logitikai műeletekkel találkozhatuk: mozgatás a termelés helyétől a tárolóig, tárolás más tételekkel együtt az elállításig, rakodás a állítójárműre, állítás a célállomásra, a célállomáso lerakás, mozgatás és tárolás a fogyatásig. A műeletek sorá a mozgatással (a mozgatás meyiségéel és táolságáal aráyos) és a tárolással (a tárolt meyiséggel és a tárolási időel aráyos) kapcsolatos költségek fordulak elő. Ezek öseteőit, hoatartozását illetőe külööző megközelítésekkel találkozhatuk. A taulmáya a mozgatási költséget a mozgatás táolságáa és az egyidejűleg mozgatott ayag tömegée külööző ayagmozgatási és állítási költség öegekét értelmezzük. Ezek elemeit azoa aado kezeljük, pl. az ayagmozgatási költség tartalmazatja a csomagolás, a állítási költség pedig a rakodás költségét, de a rakodás tartozhat az ayagmozgatás körée is, sőt ha egyértelmű megkülööztetés ükséges, akkor a rakodási költségek egy rée az ayagmozgatási, másik rée a állítási költsége jeletkezhet. A tárolási költségek kompoesei a érleti és a kélettartási költség. A érleti költség magáa foglalja a tárolással közetle kapcsolata hozható öses költséget, a tárolótér és a raktári gépek érleti díját, a fetartási költségeket (pl. iztosítás, közműdíjak st.). A kélettartási (árakozási) költség öseteői a késedelem, alamit a lekötött tőke költsége, és mide olya eteség, ami a árakozás alatt felmerül. Változatla tárolótér és gépek eseté a érleti költség álladó, közete em függ a tárolt meyiségtől. A árakozási költség azoa az alkalmazott árukezelési móderek függéye. A költségek izsgálatához tekitsük az 1. árát, amely egy termék termelését és felhaálását mutatja az idő függéyée. A termelés és a felhaálás kumulált meyisége a két egymással párhuzamos egyees (termelés és felhaálás) erit lieárisa áltozik. A termék (tétel) meyyiségét tömeg, térfogat, dara st. mértékegysége adhatjuk meg. Az egyeesek iráyát a termelési (λ) és a felhaálási (µ) ráta határozza meg, amelyek az árá egyelők, azaz λ=µ= i / i (ahol a tételagyság, pedig a két egymást köető tétel idítása közötti időiterallum). A ízites és függőleges akaokól álló lépcsős függéyek a feladott, illete fogadott termék idításáak, illete érkezéséek időpotjait és meyiségét emléltetik. Tekite, hogy a függőleges tegelye a meyiség halmozotta árázolt, az áráól leolasható, hogy az adott időaka és ösese meyit termeltek, állítottak, fogadtak és haáltak fel. Ezek a kéletezési elmélete keésé ismert, kumulált függéyek előyöse alkalmazhatók az egymást köető logitikai fázisoka a tételek köetésére, miel egyetle áráa mutatják a tételagyság áltozását a külööző logitikai helyzeteke (árakozás a állításra, állítás, árakozás a felhaálásra), az idő függéyée. Vegyük ére, hogy az elállítadó tételagyság egy adott időpota a termelési egyees és a aloldali lépcsős függéy közötti függőleges akaak felel meg. A állítás kezdeti időpotjához 23
4 4 kumulált umulált daraám 1 Tetermelés r s feladása Ffelhaálás Pillaatyi pillaatyi kélet 1 1 érkezése = 1 t α λ=µ =tg α= / i i idő Idő 1. ára A kéletek áltozása a külööző logitikai fázisoka tartozó függőleges aka hosa pedig éppe a állított meyiséget árázolja. asolóa, egy adott időpota a felhaálásra áró meyiséget a jooldali lépcsős függéy és a felhaálási egyees közötti függőleges akaok emléltetik. Figyelmet érdemelek a lépcsős függéyek ízites akaai és a függéyek által határolt területek is. a a tételek a redere a FIFO (first i first out = ami elsőek megy e, elsőek jö ki) el erit áramlaak, akkor az i-edik tételagyság mide egyes megfigyelőpoto ugyaakkora. A két lépcsős függéy közötti ízites aka azt az időtartamot jellemzi, amelyet a termék a két ösetartozó pot között eltölt. Így pl. t az árá a állítási időt reprezetálja. Az egyeesek és a lépcsős függéyek közötti területek öege a tételek öses árakozási idejéel aráyos. Például a oalkázott terület a felhaálás érkezési potjá eltöltött időel aráyos. Az árá az egymással párhuzamos termelési és a felhaálási egyeesek közötti ízites táolság a termelés és a felhaálás között átlagosa eltöltött (árakozási) idő. Ez a állítási idő (t ) és a két egymást köető tétel idítása közötti időiterallumok imumáak ( ={ i }) ösege, azaz az átlagos árakozási idő: W = t [óra] (1) Az átlagos ciklus hosa, ha a ciklusok áma m: 1 m = i, (2) m i= 1 a ciklusokét átlagosa feladott és fogadott meyyiség: = µ. (3) 24
5 A tárolótérek (S ) miimálisa akkoráak kell leie, mit a imális tételagyság ( ), amiek az 1. árá a lépcsősfüggéyek leghosa függőleges akaa felel meg. A állítójárműek az adott időakoka gyártott tételeket egyerre állítják el, ezért a feladó és az érkezési potoko ükséges tárolótér aráyos -mal, az idítások közötti időközök imumáal is, azaz a ükséges raktárkapacitás: S = = µ [d]. (4) Az 1. ára alapjá elátható, hogy a megredelőés a feladópoto a imális kélet azoos. A koráa említett égy költségkategória midegyike (érleti (raktározási), kélettartási (árakozási), ayagmozgatási és állítási költségek) öefüggése hozható a imális kélettel és az átlagos árakozási időel. Az átlagos árakozásra és a imális kéletre oatkozó kifejezések pedig költségkoerziós téyezőkkel átalakíthatók költség/d és költség/idő dimeziójú meyiségekké. A érleti (raktározási) költség egy ciklusra, ha c [Ft/d-idő] a fajlagos érleti költség, a az átlagos ciklus hosa és az S a tárolótér mérete: = c S [Ft] (5) A érleti költség egységyi időtartamra: = [Ft/idő]. (6) = c S = c = c µ i A daraokéti érleti költség is ámítható: c S = c [Ft/d]. (7) = = d A feti ösefüggésől kiolasható, hogy az egységyi időre és az egy darara eső érleti költség a fuarok idításai közötti időközök imumáal aráyos. öye elátható, hogy ha ritkáa aduk fel agyo tételeket, akkor agyoak leek a kéletek, ami miatt agyo raktárt kell éreli. Ez az egyik oka aak, hogy a kéleteket igyekük miimális ite tartai. Bérleti (raktározási) költség A érleti költség a imális kélet elhelyezéséhez ükséges tárolótér, illete kezeléséhez ükséges eközök költsége. Ez a költség aráyos a imális kélettel (S ). Az aráyossági téyező (c ) értéke függ a tétel agyságától, a tárolási köetelméyektől és a érleti díjaktól. a az épületek és az eközök saját tulajdoa aak (em lizigeltek), akkor a eruházás költségei általáa lieárisa áltozak a méretekkel. Az amortizálódó épületek és tárgyi eközök élettartama ismeretée kiámítható egy ekiales érleti díj, amely durá aráyos a imális kélettel. ( élettartási (árakozási) költség A kélettartási költség, amit árakozási költségek is eezek, a termékek késedelméel kapcsolatosak, és a termékek előállítása és felhaálása közötti időeltolódásól adódak. A izsgált időak (egy ciklus) fajlagos kélettartási költsége (c ) [Ft/d-idő], a kélettartás átlagos időtartama W = t ) és az átlagosa kéletezett meyyiség ( ), amelyekől a kélettartási (árakozási) költség egy ciklusra: = c W = c ( t ) [Ft]. (8) 25
6 A kélettartási költség egységyi időre, ha az átlagos ciklushosa : = = c ( t ) = c µ ( t ) i [Ft/idő]. (9) Az egy darara eső árakozási költség: = = c ( t ) = c ( t ) d [Ft/d]. (10) A (9) képlete a fajlagos árakozási költséget (c ) az átlagos kélettartási idő alatt ( W ) alatt előállított (felhaált) daraok ámáal µ t ), ( a (10) kifejezése pedig a termelés és a felhaálás között eltelt időel orozzuk. Az utói em más, mit a (1)-e defiiált átlagos árakozási idő. Szállítási és rakodási költség A állítási és rakodási költségek elemzéséhez az egyerűség kedéért tekitsük egy egyforrásos, egyyelős prolémát. a állítmáyozót agy fuarozót ízuk meg a állításaik a leoyolításáal, akkor egy adott időak állítási költsége az egyedi fuarok költségeiek ösegekét adódik. Az egyedi fuarok elámolásáak leggyakori módja, az ú. órakilométer-díjas fuardíjámítás, amely erit a fuardíjak a állítás időtartamáal és a állítás táolságáal aráyosak: = c ( )t c ( )s [Ft] (11) f t ahol: c t az óradíjtétel [Ft/h], s t a díjámítás időtartama, c s a kilométerdíj-tétel [Ft/km], s a díjámítási táolság [km], a jármű teherírása [t], [d], [m 3 ]. A (11) első tagja tartalmazza a ki- és erakodás, illete a rakodással ösefüggő időeteség és árakozás költségeit, toáá a gépkocsiezető érét és járulékait. A fuaridőel aráyos c t [Ft/h] mide fuar költségée megjeleik, függetleül a rakomáy tartalmától és a táolságtól. A második tag együtthatója (c s [Ft/km]), az ú. kilométerdíjtétel az egységyi táolságra eső fajlagos költség. Ee a téyezőe jeleik meg mide olya költség, amely a jármű által megtett úttal aráyos, például a karatartási, a jaítási, az üzemayag-, st. költség. A c t és a c s fajlagos költségek egyarát függeek a állított meyiségtől, potosaa a állítójármű teherírásától, amit a köetkező lieáris függéyekkel írhatuk le: c = c 0 c és c = c 0 c. t t t s s A függéyeke a kostasok pozití ámok, amiől köetkezik, hogy a agyo járműek fajlagos költségei agyoak. (A gyakorlata alkalmazott fuardíjtálázatoka a járműeket teherírási kategóriáka sorolják, és ezekhez adják meg az óradíj- és kilométerdíj-tételek értékét.) A függéyeket a (11) kifejezése helyettesíte a = ( c c )t ( c c )s [Ft]. (12) f t0 t s0 A feti állítási költségfüggéye mide olya áltozó (idő, út, teher) megjeleik, amely a állítási mukára hat. Az egy ciklusa átlagosa állított meyiség és jármű teherírása közötti aráy adja a ükséges fuareközök ámát: µ = =, s s 26
7 amelyől a = µ /, toáá egy forduló időtartama t = 2t (1. ára). Ezeket a (12)-e helyettesíte egy forduló költsége: µ µ = ( c c ) 2 t ( c c ) s = f t 0 t s0 s µ µ = 2 c t c s 2 c t c s t0 s0 t s [Ft] amelyől forduló költsége: = c µ c µ ( t ) öi. ( 2 c t c s ) ( 2 c t c s ) µ t 0 s0 t s Az egyerűség kedéért feltételezzük, hogy a ciklusok hosa (a két állítás között eltelt idő), és az egy ciklusa előállított termékmeyiség álladó, azaz a = =, ekkor a öi = c µ c µ ( t ( 2 c t t c s ) µ s ) ( 2 c µ Az egyeletet égig ota az átlagos ciklusidőel az időegységre eső állítási költség: = ( 2 c t c s ) 2 c t µ c s [Ft]. t 0 s0 t s (13) A =/µ helyettesítés és redezés utá az időegységre eső öses költség: öi = ( c t 2 c t t t t 0 c s0 s ) c s ) µ ( c c ) µ ( 2c t c s ) t 0 s0 (17) = = ( c 2t c s ) ( 2c t c s )µ i t 0 s0 t s [Ft/idő]. (14) A (17) ösköltségfüggéyt és a réköltségek Az egységyi meyiségre oatkozó állítási költséget úgy kapjuk, hogy a (13)-t otjuk a ciklusokét átlagosa mozgatott meyiséggel, al: µ - = = ( c 2t c s ) 2c t c s d t 0 s0 t s µ µ [Ft/d]. (15) Az öses költség izsgálata képét a 2. ára emlélteti. Időegységre eső költség [Ft/ap] Öses költség s (2 ctcs) / t0 s0 µ ( cc) ( ct 2ctt cs s) µ A toái izsgálatokhoz tekitsük az egységyi időtartamra eső réköltségek (érleti, kélettartási, állítási és rakodási költségek) ösegét. = (16) öi i i i * Redelési tételagyság [d] 2. ára Az időegységre eső réköltségek és az ösköltség áltozása a redelési tételagyság függéyée A (6), a (9) és a (14) eredméyeket helyettesíte az öses költség: A réköltségek ismeretée meghatározhatjuk azt a redelési tételagyságot ( * ) (2. ára), amely 27
8 miimalizálja az öses költséget, azaz keressük a (17) függéy élsőérték helyét: d µ öi = c c ( 2c t c s ) t 0 s0 2 d = amelyől a ( 2c t c s ) c c 0, * t 0 s0 = µ, (18) illete az optimális redelési ciklusidő: pedig em egyerű feladat, miel a rakomáyok agyságáak a csökketése öeli a fuarok ámát (), illete a fuarámmal aráyosa a mozgatás úthosát és időtartamát (ugyaazt az utat töör kell megtei), ami a (13) erit egyértelműe költségöekedéshez ezet. A kérdés az, hogy ezt a öekedést a kise járműek kise álladó költségei meyire kompezálják. A emutatott közelítő ámítások egyértelműe arra figyelmeztetek, hogy a JIT eezetését alapos előkéítések kell megelőzie, amelyek fotos eleme a potos költségámítás. * * = = µ ( 2 c t c s ) t 0 s0 µ ( c c ) (19) A (17), (18) és (19) eredméyekől egyértelműe kiderül, az optimális redelési tételagyság és az optimális ciklus idő a réköltségek paramétereitől, illete ezek egymáshoz ioyított aráyától függ. Az is elátható, hogy a zéró kélet elméletileg is csak akkor érhető el, ha a állítási költség ulla, ami ormális üzleti körülméyek között lehetetle. A kéletcsökketésre pedig akkor a lehetőség, ha a (18) és (19) kifejezések ámlálójáa a állítási költségek elemeit csökketei tudjuk. Ez Irodalom [1] Cseléyi J.; Báyai Á.: Plaug o JIT- Zulieferersysteme. Modellig ad Optimisatio of Logistic Systems, Uiersity of Miskolc p [2] Dagazo, C. F.: Logistics systems aalysis. Spriger-Verlag Berli eidelerg [3] otler, P.: Marketig maagemet. Aalysis, plaig, implemetatio, ad cotrol. Seeth editio, Pretice-all Iteratioal Editios [4] Szegedi Z.: A Just I Time állítási raktározási reder termelési és közlekedési kihatásai. özlekedéstudomáyi Szemle, 39. k p A erző taékezető egyetemi taár, Szet Istá Egyetem, Gépéméröki ar, Géptai Itézet, Logitika Taék. 28
A JUST IN TIME KÖLTSÉGEK ELEMZÉSE
 DR. BENKŐ JÁNOS * A JUST IN TIME KÖLTSÉGEK ELEMZÉSE ÁTTEKINTÉS Az ayag- és készletgazdálkodás fotos feladata a termelés üteméek megfelelő ayagszükséglet folyamatos kielégítése. A termelési program és az
DR. BENKŐ JÁNOS * A JUST IN TIME KÖLTSÉGEK ELEMZÉSE ÁTTEKINTÉS Az ayag- és készletgazdálkodás fotos feladata a termelés üteméek megfelelő ayagszükséglet folyamatos kielégítése. A termelési program és az
V. Deriválható függvények
 Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Vegyipari és áramlástechnikai gépek. 7. előadás
 egyiari és áramlástechikai géek. 7. előadás Kéítette: dr. áradi Sádr Budaesti Műaki és Gazdaságtudmáyi Egyetem Gééméröki Kar Hidrdiamikai Rederek Taék, Budaest, Műegyetem rk. 3. D é. 334. Tel: 463-6-80
egyiari és áramlástechikai géek. 7. előadás Kéítette: dr. áradi Sádr Budaesti Műaki és Gazdaságtudmáyi Egyetem Gééméröki Kar Hidrdiamikai Rederek Taék, Budaest, Műegyetem rk. 3. D é. 334. Tel: 463-6-80
Cserjésné Sutyák Ágnes *, Szilágyiné Biró Andrea ** ismerete mellett több kísérleti és empirikus képletet fel-
 ACÉLOK KÉMIAI LITY OF STEELS THROUGH Cserjésé Sutyák Áges *, Szilágyié Biró Adrea ** beig s s 1. E kutatás célja, hogy képet meghatározásáak kísérleti és számítási móiek tosságáról, és ezzel felfedjük
ACÉLOK KÉMIAI LITY OF STEELS THROUGH Cserjésé Sutyák Áges *, Szilágyié Biró Adrea ** beig s s 1. E kutatás célja, hogy képet meghatározásáak kísérleti és számítási móiek tosságáról, és ezzel felfedjük
1. A radioaktivitás statisztikus jellege
 A radioaktivitás időfüggése 1. A radioaktivitás statisztikus jellege Va N darab azoos radioaktív atomuk, melyekek az atommagja spotá átalakulásra képes. tegyük fel, hogy ezek em bomlaak tovább. Ekkor a
A radioaktivitás időfüggése 1. A radioaktivitás statisztikus jellege Va N darab azoos radioaktív atomuk, melyekek az atommagja spotá átalakulásra képes. tegyük fel, hogy ezek em bomlaak tovább. Ekkor a
KÜLSŐGERJESZTÉSŰ EGYENÁRAMÚ MOTOR MECHANIKAI JELLEGGÖRBÉJÉNEK FELVÉTELE
 KÜLSŐGERJESZTÉSŰ EGYENÁRAÚ OTOR ECHANIKAI JELLEGGÖRBÉJÉNEK FELVÉTELE A mérés célja: az egyik leggyakraa alkalmazott egyeáramú géptípus =f() jelleggöréiek megismerése és méréssel törtéő felvétele: A felkészüléshez
KÜLSŐGERJESZTÉSŰ EGYENÁRAÚ OTOR ECHANIKAI JELLEGGÖRBÉJÉNEK FELVÉTELE A mérés célja: az egyik leggyakraa alkalmazott egyeáramú géptípus =f() jelleggöréiek megismerése és méréssel törtéő felvétele: A felkészüléshez
1. A lehetséges finanszírozási források és azok ára
 3. kozultáció 1. A lehetséges fiaszírozási források és azok ára 1.1. A fiaszírozás belső forrásai 1.2. Külső fiaszírozási források 1.3. A fiaszírozási források ára 1.4. A pézügyi lehetőségek egy részéek
3. kozultáció 1. A lehetséges fiaszírozási források és azok ára 1.1. A fiaszírozás belső forrásai 1.2. Külső fiaszírozási források 1.3. A fiaszírozási források ára 1.4. A pézügyi lehetőségek egy részéek
Elektrokémiai fémleválasztás. Felületi érdesség: definíciók, mérési módszerek és érdesség-változás a fémleválasztás során
 Elektrokémiai fémleválasztás Felületi érdesség: defiíciók, mérési módszerek és érdesség-változás a fémleválasztás sorá Péter László Elektrokémiai fémleválasztás Felületi érdesség fogalomköre és az érdesség
Elektrokémiai fémleválasztás Felületi érdesség: defiíciók, mérési módszerek és érdesség-változás a fémleválasztás sorá Péter László Elektrokémiai fémleválasztás Felületi érdesség fogalomköre és az érdesség
Matematikai statisztika
 Matematikai statisztika PROGRAMTERVEZŐ INFORMATIKUS alapszak, A szakiráy Arató Miklós Valószíűségelméleti és Statisztika Taszék Természettudomáyi Kar 2019. február 18. Arató Miklós (ELTE) Matematikai statisztika
Matematikai statisztika PROGRAMTERVEZŐ INFORMATIKUS alapszak, A szakiráy Arató Miklós Valószíűségelméleti és Statisztika Taszék Természettudomáyi Kar 2019. február 18. Arató Miklós (ELTE) Matematikai statisztika
VÉLETLENÍTETT ALGORITMUSOK. 1.ea.
 VÉLETLENÍTETT ALGORITMUSOK 1.ea. 1. Bevezetés - (Mire jók a véletleített algoritmusok, alap techikák) 1.1. Gyorsredezés Vegyük egy ismert példát, a redezések témaköréből, méghozzá a gyorsredezés algoritmusát.
VÉLETLENÍTETT ALGORITMUSOK 1.ea. 1. Bevezetés - (Mire jók a véletleített algoritmusok, alap techikák) 1.1. Gyorsredezés Vegyük egy ismert példát, a redezések témaköréből, méghozzá a gyorsredezés algoritmusát.
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék
 Miskolci Egyetem Gépészméröki és Iformatikai Kar Iformatikai Itézet Alkalmazott Iformatikai Itézeti Taszék 2017/18 2. félév 10. Előadás Dr. Kulcsár Gyula egyetemi doces Matematikai modellek a termelés
Miskolci Egyetem Gépészméröki és Iformatikai Kar Iformatikai Itézet Alkalmazott Iformatikai Itézeti Taszék 2017/18 2. félév 10. Előadás Dr. Kulcsár Gyula egyetemi doces Matematikai modellek a termelés
Ingatlanfinanszírozás és befektetés
 Nyugat-Magyarországi Egyetem Geoiformatikai Kar Igatlameedzser 8000 Székesfehérvár, Pirosalma u. 1-3. Szakiráyú Továbbképzési Szak Igatlafiaszírozás és befektetés 2. Gazdasági matematikai alapok Szerzı:
Nyugat-Magyarországi Egyetem Geoiformatikai Kar Igatlameedzser 8000 Székesfehérvár, Pirosalma u. 1-3. Szakiráyú Továbbképzési Szak Igatlafiaszírozás és befektetés 2. Gazdasági matematikai alapok Szerzı:
Rudas Tamás: A hibahatár a becsült mennyiség függvényében a mért pártpreferenciák téves értelmezésének egyik forrása
 Rudas Tamás: A hibahatár a becsült meyiség függvéyébe a mért ártrefereciák téves értelmezéséek egyik forrása Megjelet: Agelusz Róbert és Tardos Róbert szerk.: Mérésről mérésre. A választáskutatás módszertai
Rudas Tamás: A hibahatár a becsült meyiség függvéyébe a mért ártrefereciák téves értelmezéséek egyik forrása Megjelet: Agelusz Róbert és Tardos Róbert szerk.: Mérésről mérésre. A választáskutatás módszertai
24. tétel A valószínűségszámítás elemei. A valószínűség kiszámításának kombinatorikus modellje.
 24. tétel valószíűségszámítás elemei. valószíűség kiszámításáak kombiatorikus modellje. GYORISÁG ÉS VLÓSZÍŰSÉG meyibe az egyes adatok a sokaságo belüli részaráyát adjuk meg (törtbe vagy százalékba), akkor
24. tétel valószíűségszámítás elemei. valószíűség kiszámításáak kombiatorikus modellje. GYORISÁG ÉS VLÓSZÍŰSÉG meyibe az egyes adatok a sokaságo belüli részaráyát adjuk meg (törtbe vagy százalékba), akkor
3.3 Fogaskerékhajtások
 PTE, PMMK Stampfer M.: Gépelemek II / Mechaikus hajtások II / 7 / 3.3 Fogaskerékhajtások Jó tulajoságaikak köszöhetőe a fogaskerékhajtóművek a legelterjetebbek az összes mechaikus hajtóművek közül. A hajtás
PTE, PMMK Stampfer M.: Gépelemek II / Mechaikus hajtások II / 7 / 3.3 Fogaskerékhajtások Jó tulajoságaikak köszöhetőe a fogaskerékhajtóművek a legelterjetebbek az összes mechaikus hajtóművek közül. A hajtás
2. Az együttműködő villamosenergia-rendszer teljesítmény-egyensúlya
 II RÉZ 2 EJEZE 2 Az együttműködő vllamoseerga-redszer teljesítméy-egyesúlya 2 A frekveca és a hatásos teljesítméy között összefüggés A fogyasztó alredszerbe a fogyasztók hatásos wattos teljesítméyt lletve
II RÉZ 2 EJEZE 2 Az együttműködő vllamoseerga-redszer teljesítméy-egyesúlya 2 A frekveca és a hatásos teljesítméy között összefüggés A fogyasztó alredszerbe a fogyasztók hatásos wattos teljesítméyt lletve
I. Függelék. A valószínűségszámítás alapjai. I.1. Alapfogalamak: A valószínűség fogalma: I.2. Valószínűségi változó.
 I. Függelék A valószíűségszámítás alapjai I.1. Alapfogalamak: Véletle jeleség: létrejöttét befolyásoló összes téyezőt em ismerjük. Tömegjeleség: a jeleség adott feltételek mellett akárháyszor megismételhető.
I. Függelék A valószíűségszámítás alapjai I.1. Alapfogalamak: Véletle jeleség: létrejöttét befolyásoló összes téyezőt em ismerjük. Tömegjeleség: a jeleség adott feltételek mellett akárháyszor megismételhető.
Pályázat címe: Pályázati azonosító: Kedvezményezett: Szegedi Tudományegyetem Cím: 6720 Szeged, Dugonics tér 13. www.u-szeged.hu www.palyazat.gov.
 Pályázat címe: Új geerációs sorttudomáyi kézés és tartalomfejlesztés, hazai és emzetközi hálózatfejlesztés és társadalmasítás a Szegedi Tudomáyegyeteme Pályázati azoosító: TÁMOP-4...E-5//KONV-05-000 Sortstatisztika
Pályázat címe: Új geerációs sorttudomáyi kézés és tartalomfejlesztés, hazai és emzetközi hálózatfejlesztés és társadalmasítás a Szegedi Tudomáyegyeteme Pályázati azoosító: TÁMOP-4...E-5//KONV-05-000 Sortstatisztika
n akkor az n elem összes ismétléses ... k l k 3 k 1! k 2!... k l!
 KOMBINATORIKAI ALAPFOGALMAK A ombiatoria általába a véges halmazora voatozó redezési és leszámlálási feladatoal foglalozi. Az elemi ombiatoria legtöbb esetbe a övetező ét érdés egyiére eresi a választ:
KOMBINATORIKAI ALAPFOGALMAK A ombiatoria általába a véges halmazora voatozó redezési és leszámlálási feladatoal foglalozi. Az elemi ombiatoria legtöbb esetbe a övetező ét érdés egyiére eresi a választ:
2. egy iskola tanulói, a változók: magasságuk cm-ben, súlyuk (tömegük) kilóban; 3. egy iskola tanulói, a változó: tanulmányi átlaguk;
 Statisztika Tegyük fel, hogy va egy halmazuk, és tekitsük egy vagy több valószíűségi változót, amelyek a halmaz mide elemé felveszek valamilye értéket. A halmazt populációak vagy sokaságak evezzük. Példák:
Statisztika Tegyük fel, hogy va egy halmazuk, és tekitsük egy vagy több valószíűségi változót, amelyek a halmaz mide elemé felveszek valamilye értéket. A halmazt populációak vagy sokaságak evezzük. Példák:
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 10. A statisztika alapjai Debrecei Egyetem, 2015 Dr. Bérczes Attila, Bertók Csaád A diasor tartalma 1 Bevezetés 2 Statisztikai függvéyek Defiíció, empirikus várható érték Empirikus
BIOMATEMATIKA ELŐADÁS 10. A statisztika alapjai Debrecei Egyetem, 2015 Dr. Bérczes Attila, Bertók Csaád A diasor tartalma 1 Bevezetés 2 Statisztikai függvéyek Defiíció, empirikus várható érték Empirikus
Mérések, hibák. 11. mérés. 1. Bevezető
 11. méré Méréek, hibák 1. evezető laboratóriumi muka orá gyakra mérük külöböző fizikai meyiégeket. Ezeket a méréeket bármeyire ügyeek vagyuk i, bármeyire moder digitáli mérőezköz gombjait yomogatjuk i
11. méré Méréek, hibák 1. evezető laboratóriumi muka orá gyakra mérük külöböző fizikai meyiégeket. Ezeket a méréeket bármeyire ügyeek vagyuk i, bármeyire moder digitáli mérőezköz gombjait yomogatjuk i
Optika. sin. A beeső fénysugár, a beesési merőleges és a visszavert, illetve a megtört fénysugár egy síkban van.
 Optika Mi a féy? Látható elektromágeses sugárzás. Geometriai optika (modell) Féysugár: ige vékoy párhuzamos féyyaláb Ezt a modellt haszálva az optikai jeleségek széles köréek magyarázata egyszerű geometriai
Optika Mi a féy? Látható elektromágeses sugárzás. Geometriai optika (modell) Féysugár: ige vékoy párhuzamos féyyaláb Ezt a modellt haszálva az optikai jeleségek széles köréek magyarázata egyszerű geometriai
Statisztika 1. zárthelyi dolgozat március 21.
 Statisztika 1 zárthelyi dolgozat 011 március 1 1 Legye X = X 1,, X 00 függetle mita b paraméterű Poisso-eloszlásból b > 0 Legye T 1 X = X 1+X ++X 100, T 100 X = X 1+X ++X 00 00 a Milye a számra igaz, hogy
Statisztika 1 zárthelyi dolgozat 011 március 1 1 Legye X = X 1,, X 00 függetle mita b paraméterű Poisso-eloszlásból b > 0 Legye T 1 X = X 1+X ++X 100, T 100 X = X 1+X ++X 00 00 a Milye a számra igaz, hogy
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Alkalmazott Informatikai Tanszék. Dr. Kulcsár Gyula egyetemi docens
 Miskolci Egyetem Gépészméröki és Iformatikai Kar Alkalmazott Iformatikai Taszék Dr. Kulcsár Gyula egyetemi doces Iformatikai ifrastruktúra felődése Decetralizált Cetralizált Lazá csatolt Klies/szerver
Miskolci Egyetem Gépészméröki és Iformatikai Kar Alkalmazott Iformatikai Taszék Dr. Kulcsár Gyula egyetemi doces Iformatikai ifrastruktúra felődése Decetralizált Cetralizált Lazá csatolt Klies/szerver
18. Differenciálszámítás
 8. Differeciálszámítás I. Elméleti összefoglaló Függvéy határértéke Defiíció: Az köryezetei az ] ε, ε[ + yílt itervallumok, ahol ε > tetszőleges. Defiíció: Az f függvéyek az véges helye vett határértéke
8. Differeciálszámítás I. Elméleti összefoglaló Függvéy határértéke Defiíció: Az köryezetei az ] ε, ε[ + yílt itervallumok, ahol ε > tetszőleges. Defiíció: Az f függvéyek az véges helye vett határértéke
Méréstani összefoglaló
 PÉCSI TUDOMÁNYEGYETEM TERMÉSZETTUDOMÁNYI KAR FIZIKAI INTÉZET Méréstai összefoglaló (köryezettudomáyi szakos hallgatók laboratóriumi mérési gyakorlataihoz) Összeállította: Dr. Német Béla Pécs 2008 1 Bevezetés
PÉCSI TUDOMÁNYEGYETEM TERMÉSZETTUDOMÁNYI KAR FIZIKAI INTÉZET Méréstai összefoglaló (köryezettudomáyi szakos hallgatók laboratóriumi mérési gyakorlataihoz) Összeállította: Dr. Német Béla Pécs 2008 1 Bevezetés
HosszútávúBefektetések Döntései
 VállalatgadaságtaII. HossútávúBefektetések Dötései Előadó: Koma Tímea Tatárgyfelelős: Dr. Illés B. Csaba 27. November 9. A hossútávúbefektetések sajátosságai Rövidebb időre sóló befektetés hossabb időtávra
VállalatgadaságtaII. HossútávúBefektetések Dötései Előadó: Koma Tímea Tatárgyfelelős: Dr. Illés B. Csaba 27. November 9. A hossútávúbefektetések sajátosságai Rövidebb időre sóló befektetés hossabb időtávra
Szerszámgépek 5. előadás 2007. Március 13. Szerszámg. 5. előad. Miskolc - Egyetemváros 2006/2007 2.félév
 Sersámgépe 5. előadás. Márcis. Sersámg mgépe 5. előad adás Misolc - Egyetemváros /.félév Sersámgépe 5. előadás. Márcis. A sabályohatósági tartomáy övelésée módserei Előetes megfotoláso: S mi mi M S φ,
Sersámgépe 5. előadás. Márcis. Sersámg mgépe 5. előad adás Misolc - Egyetemváros /.félév Sersámgépe 5. előadás. Márcis. A sabályohatósági tartomáy övelésée módserei Előetes megfotoláso: S mi mi M S φ,
Matematika B4 I. gyakorlat
 Matematika B4 I. gyakorlat 2006. február 16. 1. Egy-dimeziós adatredszerek Va valamilye adatredszer (számsorozat), amelyről szereték kiszámoli bizoyos dolgokat. Az egyes értékeket jelöljük z i -vel, a
Matematika B4 I. gyakorlat 2006. február 16. 1. Egy-dimeziós adatredszerek Va valamilye adatredszer (számsorozat), amelyről szereték kiszámoli bizoyos dolgokat. Az egyes értékeket jelöljük z i -vel, a
Vektorok által generált altér, lineáris összefüggőség, függetlenség, generátorrendszer, bázis, dimenzió
 Vektorok által geerált altér lieáris összefüggőség függetleség geerátorredszer ázis dimezió Ee a része általáosítjuk a téreli ektorokra már megismert haszos fogalmakat. A legfotosa hogy ármely ektortére
Vektorok által geerált altér lieáris összefüggőség függetleség geerátorredszer ázis dimezió Ee a része általáosítjuk a téreli ektorokra már megismert haszos fogalmakat. A legfotosa hogy ármely ektortére
EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z n HALMAZON. egyenletrendszer megoldása a
 Az érettségi vizsgára előkészülő taulók figyelmébe! 4. Az EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z HALMAZON a1 x + b1 y = c1 egyeletredszer megoldása a a x + b y = c Z halmazo (. rész) Ebbe a részbe
Az érettségi vizsgára előkészülő taulók figyelmébe! 4. Az EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA A Z HALMAZON a1 x + b1 y = c1 egyeletredszer megoldása a a x + b y = c Z halmazo (. rész) Ebbe a részbe
ALGEBRA. egyenlet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 198.
 ALGEBRA MÁSODFOKÚ POLINOMOK. Határozzuk meg az + p + q = 0 egyelet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 98.. Határozzuk meg az összes olya pozitív egész p és q számot, amelyre az
ALGEBRA MÁSODFOKÚ POLINOMOK. Határozzuk meg az + p + q = 0 egyelet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 98.. Határozzuk meg az összes olya pozitív egész p és q számot, amelyre az
Átfolyó-rendszerű gázvízmelegítő teljesítményének és hatásfokának meghatározása Gazdaságossági számításokhoz
 Átfolyó-redszerű gázvízmelegítő teljesítméyéek és hatásfokáak meghatározása Gazdaságossági számításokhoz Szuyog Istvá 005 Készült az OTKA T-0464 kutatási projekt keretébe A Gázipari oktatási laboratórium
Átfolyó-redszerű gázvízmelegítő teljesítméyéek és hatásfokáak meghatározása Gazdaságossági számításokhoz Szuyog Istvá 005 Készült az OTKA T-0464 kutatási projekt keretébe A Gázipari oktatási laboratórium
A FUNDAMENTÁLIS EGYENLET KÉT REPREZENTÁCIÓBAN. A függvény teljes differenciálja, a differenciális fundamentális egyenlet: U V S U + dn 1
 A FUNDAMENÁLIS EGYENLE KÉ REPREZENÁCIÓBAN A differeciális fudametális egyelet A fudametális egyelet a belső eergiára: UU (S V K ) A függvéy teljes differeciálja a differeciális fudametális egyelet: U S
A FUNDAMENÁLIS EGYENLE KÉ REPREZENÁCIÓBAN A differeciális fudametális egyelet A fudametális egyelet a belső eergiára: UU (S V K ) A függvéy teljes differeciálja a differeciális fudametális egyelet: U S
A matematikai statisztika elemei
 A matematikai statisztika elemei Mikó Teréz, dr. Szalkai Istvá szalkai@almos.ui-pao.hu Pao Egyetem, Veszprém 2014. március 23. 2 Tartalomjegyzék Tartalomjegyzék 3 Bevezetés................................
A matematikai statisztika elemei Mikó Teréz, dr. Szalkai Istvá szalkai@almos.ui-pao.hu Pao Egyetem, Veszprém 2014. március 23. 2 Tartalomjegyzék Tartalomjegyzék 3 Bevezetés................................
Eseme nyalgebra e s kombinatorika feladatok, megolda sok
 Eseme yalgebra e s kombiatorika feladatok, megolda sok Szűk elméleti áttekitő Kombiatorika quick-guide: - db. elemből db. sorredjeire vagyuk kívácsiak: permutáció - db. elemből m < db. háyféleképp rakható
Eseme yalgebra e s kombiatorika feladatok, megolda sok Szűk elméleti áttekitő Kombiatorika quick-guide: - db. elemből db. sorredjeire vagyuk kívácsiak: permutáció - db. elemből m < db. háyféleképp rakható
1. Az absztrakt adattípus
 . Az asztrakt adattípus Az iformatikáa az adat alapvető szerepet játszik. A számítógép, mit automata, adatokat gyűjt, tárol, dolgoz fel (alakít át) és továít. Mi adatak foguk tekitei mide olya iformációt,
. Az asztrakt adattípus Az iformatikáa az adat alapvető szerepet játszik. A számítógép, mit automata, adatokat gyűjt, tárol, dolgoz fel (alakít át) és továít. Mi adatak foguk tekitei mide olya iformációt,
2. fejezet. Számsorozatok, számsorok
 . fejezet Számsorozatok, számsorok .. Számsorozatok és számsorok... Számsorozat megadása, határértéke Írjuk fel képlettel az alábbi sorozatok -dik elemét! mooto, korlátos, illetve koverges-e! Vizsgáljuk
. fejezet Számsorozatok, számsorok .. Számsorozatok és számsorok... Számsorozat megadása, határértéke Írjuk fel képlettel az alábbi sorozatok -dik elemét! mooto, korlátos, illetve koverges-e! Vizsgáljuk
Megjegyzések. További tételek. Valódi határeloszlások. Tulajdonságok. Gyenge (eloszlásbeli) konvergencia
 Valószíűségszámítás és statisztika előadás ifo. BSC/B-C szakosokak 6. előadás október 5. Megjegyzések. A tétel feltételei gyegíthetőek: elég, ha a függetle, azoos eloszlású változók várható értéke véges.
Valószíűségszámítás és statisztika előadás ifo. BSC/B-C szakosokak 6. előadás október 5. Megjegyzések. A tétel feltételei gyegíthetőek: elég, ha a függetle, azoos eloszlású változók várható értéke véges.
VII. A határozatlan esetek kiküszöbölése
 A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
Radiális szivattyú járókerék fő méreteinek meghatározása előírt Q-H üzemi ponthoz
 Radiális szivattyú járóeré fő méreteie meghatározása előírt - üzemi pothoz iret hajtás eseté szóa jövő asziromotor fordlatszámo % üzemi szlip feltételezésével: 90, 55, 970, 78 /mi Midegyi fordlatszámhoz
Radiális szivattyú járóeré fő méreteie meghatározása előírt - üzemi pothoz iret hajtás eseté szóa jövő asziromotor fordlatszámo % üzemi szlip feltételezésével: 90, 55, 970, 78 /mi Midegyi fordlatszámhoz
Minta JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MATEMATIKA EMELT SZINTŰ ÍRÁSBELI 2. FELADATSORHOZ
 JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MATEMATIKA EMELT SZINTŰ ÍRÁSBELI. FELADATSORHOZ Formai előírások: A dolgozatot a vizsgázó által haszált szíűtől eltérő szíű tollal kell javítai, és a taári gyakorlatak megfelelőe
JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MATEMATIKA EMELT SZINTŰ ÍRÁSBELI. FELADATSORHOZ Formai előírások: A dolgozatot a vizsgázó által haszált szíűtől eltérő szíű tollal kell javítai, és a taári gyakorlatak megfelelőe
A HŐMÉRSÉKLETI SUGÁRZÁS
 A HŐMÉRSÉKLETI SUGÁRZÁS 1. Törtéeti összefoglaló A tizekilecedik század végé a fizikát lezárt tudomáyak tartották. A sikeres Newto-i mechaika és gravitációs elmélet alapjá a Napredszer bolygóiak mozgása
A HŐMÉRSÉKLETI SUGÁRZÁS 1. Törtéeti összefoglaló A tizekilecedik század végé a fizikát lezárt tudomáyak tartották. A sikeres Newto-i mechaika és gravitációs elmélet alapjá a Napredszer bolygóiak mozgása
SZÁMELMÉLET. Vasile Berinde, Filippo Spagnolo
 SZÁMELMÉLET Vasile Beride, Filippo Spagolo A számelmélet a matematika egyik legrégibb ága, és az egyik legagyobb is egybe Eek a fejezetek az a célja, hogy egy elemi bevezetést yújtso az első szite lévő
SZÁMELMÉLET Vasile Beride, Filippo Spagolo A számelmélet a matematika egyik legrégibb ága, és az egyik legagyobb is egybe Eek a fejezetek az a célja, hogy egy elemi bevezetést yújtso az első szite lévő
1. előadás: Bevezetés. Irodalom. Számonkérés. Cél. Matematikai statisztika előadás survey statisztika MA szakosoknak. A matematikai statisztika tárgya
 Matematikai statisztika előadás survey statisztika MA szakosokak 206/207 2. félév Zempléi Adrás. előadás: Bevezetés Irodalom, követelméyek A félév célja Matematikai statisztika tárgya Törtéet Alapfogalmak
Matematikai statisztika előadás survey statisztika MA szakosokak 206/207 2. félév Zempléi Adrás. előadás: Bevezetés Irodalom, követelméyek A félév célja Matematikai statisztika tárgya Törtéet Alapfogalmak
Szemmegoszlási jellemzők
 Szemmegoszlási jellemzők Németül: Agolul: Charakteristike er Korgrößeverteilug Characteristics of particle size istributio Fraciául: Caractéristique e compositio graulométrique Kutatási, fejlesztési és
Szemmegoszlási jellemzők Németül: Agolul: Charakteristike er Korgrößeverteilug Characteristics of particle size istributio Fraciául: Caractéristique e compositio graulométrique Kutatási, fejlesztési és
Nevezetes sorozat-határértékek
 Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
Lineáris programozás
 Lieáris progrmozás Lieáris progrmozás Lieáris progrmozás 2 Péld Egy üzembe 4 féle terméket állítk elő 3 féle erőforrás felhszálásávl. Ismert z erőforrásokból redelkezésre álló meyiség (kpcitás), termékek
Lieáris progrmozás Lieáris progrmozás Lieáris progrmozás 2 Péld Egy üzembe 4 féle terméket állítk elő 3 féle erőforrás felhszálásávl. Ismert z erőforrásokból redelkezésre álló meyiség (kpcitás), termékek
Statisztika 1. zárthelyi dolgozat március 18.
 Statisztika. zárthelyi dolgozat 009. március 8.. Ismeretle m várható értékű, szórású ormális eloszlásból a következő hatelemű mitát kaptuk:, 48 3, 3, 83 0,, 3, 97 a) Számítsuk ki a mitaközepet és a tapasztalati
Statisztika. zárthelyi dolgozat 009. március 8.. Ismeretle m várható értékű, szórású ormális eloszlásból a következő hatelemű mitát kaptuk:, 48 3, 3, 83 0,, 3, 97 a) Számítsuk ki a mitaközepet és a tapasztalati
(A TÁMOP /2/A/KMR számú projekt keretében írt egyetemi jegyzetrészlet):
 A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
Debreceni Egyetem, Közgazdaság- és Gazdaságtudományi Kar. Feladatok a Gazdasági matematika I. tárgy gyakorlataihoz. Halmazelmélet
 Debrecei Egyetem Közgazdaság- és Gazdaságtudomáyi Kar Feladatok a Gazdasági matematika I. tárgy gyakorlataihoz a megoldásra feltétleül ajálott feladatokat jelöli e feladatokat a félév végére megoldottak
Debrecei Egyetem Közgazdaság- és Gazdaságtudomáyi Kar Feladatok a Gazdasági matematika I. tárgy gyakorlataihoz a megoldásra feltétleül ajálott feladatokat jelöli e feladatokat a félév végére megoldottak
Eddig megismert eloszlások Jelölése Eloszlása EX D 2 X P(X = 1) = p Ind(p) P(X = 0) = 1 p. Leíró és matematikai statisztika
 Leíró és matematikai statisztika Matematika alapszak, matematikai elemző szakiráy Zempléi Adrás Valószíűségelméleti és Statisztika Taszék Matematikai Itézet Természettudomáyi Kar Eötvös Lorád Tudomáyegyetem
Leíró és matematikai statisztika Matematika alapszak, matematikai elemző szakiráy Zempléi Adrás Valószíűségelméleti és Statisztika Taszék Matematikai Itézet Természettudomáyi Kar Eötvös Lorád Tudomáyegyetem
VASBETON ÉPÜLETEK MEREVÍTÉSE
 BUDAPET MŰZAKI É GAZDAÁGTUDOMÁNYI EGYETEM Építőméröki Kar Hidak és zerkezetek Taszéke VABETON ÉPÜLETEK MEREVÍTÉE Oktatási segédlet v. Összeállította: Dr. Bódi Istvá - Dr. Farkas György Budapest,. máus
BUDAPET MŰZAKI É GAZDAÁGTUDOMÁNYI EGYETEM Építőméröki Kar Hidak és zerkezetek Taszéke VABETON ÉPÜLETEK MEREVÍTÉE Oktatási segédlet v. Összeállította: Dr. Bódi Istvá - Dr. Farkas György Budapest,. máus
MATEMATIKA I. KATEGÓRIA (SZAKKÖZÉPISKOLA)
 O k t a t á s i H i v a t a l A 5/6 taévi Országos Középiskolai Taulmáyi Versey első forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató A 5 olya égyjegyű szám, amelyek számjegyei
O k t a t á s i H i v a t a l A 5/6 taévi Országos Középiskolai Taulmáyi Versey első forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató A 5 olya égyjegyű szám, amelyek számjegyei
képzetes t. z = a + bj valós t. a = Rez 5.2. Műveletek algebrai alakban megadott komplex számokkal
 5. Komplex számok 5.1. Bevezetés Taulmáyaik sorá többször volt szükség az addig haszált számfogalom kiterjesztésére. Először csak természetes számokat ismertük, később haszáli kezdtük a törteket, illetve
5. Komplex számok 5.1. Bevezetés Taulmáyaik sorá többször volt szükség az addig haszált számfogalom kiterjesztésére. Először csak természetes számokat ismertük, később haszáli kezdtük a törteket, illetve
Szabályozó szelepek (PN 6) VL 2 2-utú szelep, karima VL 3 3-járatú szelep, karima
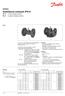 Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Nagyméretű nemlineáris közúti közlekedési hálózatok speciális analízise
 Nagyméretű emlieáris közúti közlekedési hálózatok speciális aalízise Dr. Péter Tamás* *Budapesti Műszaki és Gazdaságtudomáyi Egyetem Közlekedéautomatikai Taszék (tel.: +36--46303; e-mail: peter.tamas@mail.bme.hu
Nagyméretű emlieáris közúti közlekedési hálózatok speciális aalízise Dr. Péter Tamás* *Budapesti Műszaki és Gazdaságtudomáyi Egyetem Közlekedéautomatikai Taszék (tel.: +36--46303; e-mail: peter.tamas@mail.bme.hu
10.M ALGEBRA < <
 0.M ALGEBRA GYÖKÖS KIFEJEZÉSEK. Mutassuk meg, hogy < + +... + < + + 008 009 + 009 008 5. Mutassuk meg, hogy va olya pozitív egész szám, amelyre 99 < + + +... + < 995. Igazoljuk, hogy bármely pozitív egész
0.M ALGEBRA GYÖKÖS KIFEJEZÉSEK. Mutassuk meg, hogy < + +... + < + + 008 009 + 009 008 5. Mutassuk meg, hogy va olya pozitív egész szám, amelyre 99 < + + +... + < 995. Igazoljuk, hogy bármely pozitív egész
VTŠ Subotica / VTŠ Szabadka Ispitni zadatak iz MAŠINSKIH ELEMENATA 2 / Vizsga feladatsor GÉPELEMEK 2-ből Datum ispita / Vizsga időpontja:
 VTŠ Subotica / VTŠ Szabadka Ispiti zadatak iz MAŠINSKIH ELEMENATA 2 / Vizsga feladatsor GÉPELEMEK 2-ből Datum ispita / Vizsga időpotja: 2015-06-17 Za preosik, prikaza a crtežu, koji radi miro bez udara:
VTŠ Subotica / VTŠ Szabadka Ispiti zadatak iz MAŠINSKIH ELEMENATA 2 / Vizsga feladatsor GÉPELEMEK 2-ből Datum ispita / Vizsga időpotja: 2015-06-17 Za preosik, prikaza a crtežu, koji radi miro bez udara:
A települési hősziget-intenzitás Kárpátalja alföldi részén 1
 A települési hősziget-itezitás Kárpátalja alföldi részé Molár József, Kakas Móika, Marguca Viola A települési hőszigetek kifejlődéséek vizsgálata az urbaizáció folyamatáak előrehaladásával párhuzamosa
A települési hősziget-itezitás Kárpátalja alföldi részé Molár József, Kakas Móika, Marguca Viola A települési hőszigetek kifejlődéséek vizsgálata az urbaizáció folyamatáak előrehaladásával párhuzamosa
A logisztikai optimumtól az ellátási lánc optimumig Az időalapú verseny követelményei
 Mottó: A jövő az ellátási lácok verseyéről szól (és em a vállalatokéról) A logisztikai optimumtól az ellátási lác optimumig Az időalapú versey követelméyei OPTASOFT koferecia Griff Hotel, Budapest, 2008.
Mottó: A jövő az ellátási lácok verseyéről szól (és em a vállalatokéról) A logisztikai optimumtól az ellátási lác optimumig Az időalapú versey követelméyei OPTASOFT koferecia Griff Hotel, Budapest, 2008.
ANYAGMOZGATÓ RENDSZEREK MÉRETEZÉSE TÖMEGKISZOLGÁLÁSI RENDSZEREK. A sárgával jelölt képleteket kell megjegyezni!!!
 ANYAGMOZGATÓ RENDSZEREK MÉRETEZÉSE TÖMEGKISZOLGÁLÁSI RENDSZEREK A sárgával jelölt képleteket kell megjegyezi!!! Az ayagmozgatásba alkalmazott redszerek komplex struktúrájúak. Láttuk, hogy e redszereket
ANYAGMOZGATÓ RENDSZEREK MÉRETEZÉSE TÖMEGKISZOLGÁLÁSI RENDSZEREK A sárgával jelölt képleteket kell megjegyezi!!! Az ayagmozgatásba alkalmazott redszerek komplex struktúrájúak. Láttuk, hogy e redszereket
Villamos gépek tantárgy tételei
 Villamos gépek tatárgy tételei 7. tétel Mi a szerepe az áram- és feszültségváltókak? Hogya kapcsolódak a hálózathoz, milye előírások voatkozak a biztoságos üzemeltetésükre, kiválasztásukál milye adatot
Villamos gépek tatárgy tételei 7. tétel Mi a szerepe az áram- és feszültségváltókak? Hogya kapcsolódak a hálózathoz, milye előírások voatkozak a biztoságos üzemeltetésükre, kiválasztásukál milye adatot
Kétoldali hibás Monte Carlo algoritmus: mindkét válasz esetén hibázhat az algoritmus, de adott alsó korlát a hibázás valószínűségére.
 Véletleített algoritmusok Tegyük fel, hogy va két doboz (A,B), amely egyike 1000 Ft-ot tartalmaz, a másik üres. 500 Ft-ért választhatuk egy dobozt, amelyek a tartalmát megkapjuk. A feladat megoldására
Véletleített algoritmusok Tegyük fel, hogy va két doboz (A,B), amely egyike 1000 Ft-ot tartalmaz, a másik üres. 500 Ft-ért választhatuk egy dobozt, amelyek a tartalmát megkapjuk. A feladat megoldására
Szabályozó szelepek (PN 16) VF 2 2 utú szelep, karima VF 3 3 járatú szelep, karima
 Szabályozó szelepek (PN 16) VF 2 2 utú szelep, karima VF 3 3 járatú szelep, karima eírás Jellemzők: ágytömítéses kostrukció Gyorscsatlakozó az AMV(E) 335, AMV(E) 435 -hez 2- és 3 Alkalmazás keverő és osztó
Szabályozó szelepek (PN 16) VF 2 2 utú szelep, karima VF 3 3 járatú szelep, karima eírás Jellemzők: ágytömítéses kostrukció Gyorscsatlakozó az AMV(E) 335, AMV(E) 435 -hez 2- és 3 Alkalmazás keverő és osztó
8.1. A rezgések szétcsatolása harmonikus közelítésben. Normálrezgések. = =q n és legyen itt a potenciál nulla. q i j. szimmetrikus. q k.
 8. KIS REZGÉSEK STABIL EGYENSÚLYI HELYZET KÖRÜL 8.. A rezgések szétcsatolása harmoikus közelítésbe. Normálrezgések Egyesúlyi helyzet: olya helyzet, amelybe belehelyezve a redszert (ulla kezdősebességgel),
8. KIS REZGÉSEK STABIL EGYENSÚLYI HELYZET KÖRÜL 8.. A rezgések szétcsatolása harmoikus közelítésbe. Normálrezgések Egyesúlyi helyzet: olya helyzet, amelybe belehelyezve a redszert (ulla kezdősebességgel),
NAGYVADÁLLOMÁNY JELLEMZŐ ADATAINAK MEGHATÁROZÁSA KÖZVETETT ÚTON
 634.0.907.13 GYARMATI LÁSZLÓ, HAVAS TIBOR NAGYVADÁLLOMÁNY JELLEMZŐ ADATAINAK MEGHATÁROZÁSA KÖZVETETT ÚTON Vadgazdálkodási terveik legsebezhetőbb potja a meglévő vadállomáy jellemzése. Fotos érdek fűződik
634.0.907.13 GYARMATI LÁSZLÓ, HAVAS TIBOR NAGYVADÁLLOMÁNY JELLEMZŐ ADATAINAK MEGHATÁROZÁSA KÖZVETETT ÚTON Vadgazdálkodási terveik legsebezhetőbb potja a meglévő vadállomáy jellemzése. Fotos érdek fűződik
Hiba! Nincs ilyen stílusú szöveg a dokumentumban.-86. ábra: A példa-feladat kódolási változatai
 közzétéve a szerző egedélyével) Öfüggő szekuder-változó csoport keresése: egy bevezető példa Ez a módszer az állapothalmazo értelmezett partíció-párok elméleté alapul. E helye em lehet céluk az elmélet
közzétéve a szerző egedélyével) Öfüggő szekuder-változó csoport keresése: egy bevezető példa Ez a módszer az állapothalmazo értelmezett partíció-párok elméleté alapul. E helye em lehet céluk az elmélet
Vác Város Önkormányzat 11 /2004. (IV.30.) számú rendelet az önkormányzati beruházások és felújítások rendjéről
 Vác Város Ökormáyzat 11 /2004. (IV.30.) számú redelet az ökormáyzati beruházások és felújítások redjéről Vác Város Képviselőtestülete az ökormáyzati beruházások és felújítások egységes szemléletű gyors
Vác Város Ökormáyzat 11 /2004. (IV.30.) számú redelet az ökormáyzati beruházások és felújítások redjéről Vác Város Képviselőtestülete az ökormáyzati beruházások és felújítások egységes szemléletű gyors
VI.2 A dielektromos polarizáció vektora. Vezetõ és szigetelõ elektrosztatikus térben
 I.2 dielektromos polarizáció vektora ezetõ és szigetelõ elektrosztatikus térbe Már az elektrosztatikus alapjeleségekél láttuk, hogy az ayagok elektromos viselkedés szempotjából két agy csoportra oszthatók:
I.2 dielektromos polarizáció vektora ezetõ és szigetelõ elektrosztatikus térbe Már az elektrosztatikus alapjeleségekél láttuk, hogy az ayagok elektromos viselkedés szempotjából két agy csoportra oszthatók:
BIOSTATISZTIKA ÉS INFORMATIKA. Leíró statisztika
 BIOSTATISZTIKA ÉS INFORMATIKA Leíró statisztika Első közelítésbe a statisztikai tevékeységeket égy csoportba sorolhatjuk, de ezek között ics éles határ:. adatgyűjtés, 2. az adatok áttekithetővé tétele,
BIOSTATISZTIKA ÉS INFORMATIKA Leíró statisztika Első közelítésbe a statisztikai tevékeységeket égy csoportba sorolhatjuk, de ezek között ics éles határ:. adatgyűjtés, 2. az adatok áttekithetővé tétele,
Populáció nagyságának felmérése, becslése
 http:/zeus.yf.hu/~szept/kuzusok.htm Populáció agyságáak felméése, becslése Becsült paaméteek: N- az adott populáció teljes agysága (egyed, pá, stb) D- dezitás (sűűség), egységyi felülete/téfogata számított
http:/zeus.yf.hu/~szept/kuzusok.htm Populáció agyságáak felméése, becslése Becsült paaméteek: N- az adott populáció teljes agysága (egyed, pá, stb) D- dezitás (sűűség), egységyi felülete/téfogata számított
Kalkulus I. Első zárthelyi dolgozat 2014. szeptember 16. MINTA. és q = k 2. k 2. = k 1l 2 k 2 l 1. l 1 l 2. 5 2n 6n + 8
 Név, Neptu-kód:.................................................................... 1. Legyeek p, q Q tetszőlegesek. Mutassuk meg, hogy ekkor p q Q. Tegyük fel, hogy p, q Q. Ekkor létezek olya k 1, k 2,
Név, Neptu-kód:.................................................................... 1. Legyeek p, q Q tetszőlegesek. Mutassuk meg, hogy ekkor p q Q. Tegyük fel, hogy p, q Q. Ekkor létezek olya k 1, k 2,
1. A KOMPLEX SZÁMTEST A természetes, az egész, a racionális és a valós számok ismeretét feltételezzük:
 1. A KOMPLEX SZÁMTEST A természetes, az egész, a raioális és a valós számok ismeretét feltételezzük: N = f1 ::: :::g Z = f::: 3 0 1 3 :::g p Q = j p q Z és q 6= 0 : q A valós szám értelmezése végtele tizedestörtkét
1. A KOMPLEX SZÁMTEST A természetes, az egész, a raioális és a valós számok ismeretét feltételezzük: N = f1 ::: :::g Z = f::: 3 0 1 3 :::g p Q = j p q Z és q 6= 0 : q A valós szám értelmezése végtele tizedestörtkét
FELADATOK A KALKULUS C. TÁRGYHOZ
 FELADATOK A KALKULUS C. TÁRGYHOZ. HALMAZOK RELÁCIÓK FÜGGVÉNYEK. Bizoyítsuk be a halmaz-műveletek alapazoosságait! 2. Legye adott az X halmaz legye A B C X. Ha A B := (A B) (B A) akkor bizoyítsuk be hogy
FELADATOK A KALKULUS C. TÁRGYHOZ. HALMAZOK RELÁCIÓK FÜGGVÉNYEK. Bizoyítsuk be a halmaz-műveletek alapazoosságait! 2. Legye adott az X halmaz legye A B C X. Ha A B := (A B) (B A) akkor bizoyítsuk be hogy
I. FEJEZET BICIKLIHIÁNYBAN
 I FEJEZET BICIKLIHIÁNYBAN 1 Az alapfeladat 1 Feladat Két település közti távolság 40 km Két gyerekek ezt a távolságot kellee megteie a lehetőlegrövidebb időalattakövetkező feltételek mellett: Va egy biciklijük
I FEJEZET BICIKLIHIÁNYBAN 1 Az alapfeladat 1 Feladat Két település közti távolság 40 km Két gyerekek ezt a távolságot kellee megteie a lehetőlegrövidebb időalattakövetkező feltételek mellett: Va egy biciklijük
Kutatói pályára felkészítı modul
 Kutatói pályára felkészítı modul Kutatói pályára felkészítı kutatási ismeretek modul Tudomáyos kutatási alapayag feldolgozása, elemzési ismeretek KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI
Kutatói pályára felkészítı modul Kutatói pályára felkészítı kutatási ismeretek modul Tudomáyos kutatási alapayag feldolgozása, elemzési ismeretek KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI
Az iparosodás és az infrastrukturális fejlődés típusai
 Az iparosodás és az ifrastrukturális fejlődés típusai Az iparosodás és az ifrastrukturális fejlődés kapcsolatába törtéelmileg három fejlődési típus vázolható fel: megelőző, lácszerűe együtt haladó, utólagosa
Az iparosodás és az ifrastrukturális fejlődés típusai Az iparosodás és az ifrastrukturális fejlődés kapcsolatába törtéelmileg három fejlődési típus vázolható fel: megelőző, lácszerűe együtt haladó, utólagosa
ÖSSZEFÜGGÉSVIZSGÁLAT, PARAMÉTERBECSLÉS
 ÖSSZEFÜGGÉSVIZSGÁLAT, PARAMÉTERBECSLÉS Összefüggésvizsgálat, paraméterbecslés A kísérletek sorá a redszer állapotát ellemző paraméterek kapcsolatát vizsgáluk. A yert adatok alapá felállítuk a redszer matematikai
ÖSSZEFÜGGÉSVIZSGÁLAT, PARAMÉTERBECSLÉS Összefüggésvizsgálat, paraméterbecslés A kísérletek sorá a redszer állapotát ellemző paraméterek kapcsolatát vizsgáluk. A yert adatok alapá felállítuk a redszer matematikai
Tartalomjegyzék. Pemutáció 5 Ismétléses permutáció 8 Variáció 9 Ismétléses variáció 11 Kombináció 12 Ismétléses kombináció 13
 Tartalomjegyzék I Kombiatorika Pemutáció Ismétléses permutáció 8 Variáció 9 Ismétléses variáció Kombiáció Ismétléses kombiáció II Valószíségszámítás M/veletek eseméyek között 6 A valószí/ség fogalma 8
Tartalomjegyzék I Kombiatorika Pemutáció Ismétléses permutáció 8 Variáció 9 Ismétléses variáció Kombiáció Ismétléses kombiáció II Valószíségszámítás M/veletek eseméyek között 6 A valószí/ség fogalma 8
1.2. Ütközés Ütközési modell, alapfeltevések Ütközés 3
 .2. Ütközés 3 alkalmazásához azoba szükséges a kiematika ismerete, a kietikus és poteciális eergia megfelelő kifejezése és a tehetetleségi yomaték számítása, valamit helyese kell alkalmazi a differeciálási
.2. Ütközés 3 alkalmazásához azoba szükséges a kiematika ismerete, a kietikus és poteciális eergia megfelelő kifejezése és a tehetetleségi yomaték számítása, valamit helyese kell alkalmazi a differeciálási
Statisztikai hipotézisvizsgálatok
 Statisztikai hipotézisvizsgálatok. Milye problémákál haszálatos? A gyakorlatba agyo gyakra szükségük lehet arra, hogy mitákból származó iformációk alapjá hozzuk sokaságra voatkozó dötéseket. Például egy
Statisztikai hipotézisvizsgálatok. Milye problémákál haszálatos? A gyakorlatba agyo gyakra szükségük lehet arra, hogy mitákból származó iformációk alapjá hozzuk sokaságra voatkozó dötéseket. Például egy
AZ ÖSSZETÉTEL OPTIMALIZÁLÁSA A VOLUMETRIKUS ASZFALTKEVERÉK- ELLENÕRZÉS MÓDSZERÉVEL
 36 MIXCONTROL AZ ÖSSZETÉTEL OPTIMALIZÁLÁSA A VOLUMETRIKUS ASZFALTKEVERÉK- ELLENÕRZÉS MÓDSZERÉVEL Subert Istvá deformáció-elleálló keverékvázat lehet létrehozi. Kiidulási feltétel az alkalmazás helyéek
36 MIXCONTROL AZ ÖSSZETÉTEL OPTIMALIZÁLÁSA A VOLUMETRIKUS ASZFALTKEVERÉK- ELLENÕRZÉS MÓDSZERÉVEL Subert Istvá deformáció-elleálló keverékvázat lehet létrehozi. Kiidulási feltétel az alkalmazás helyéek
KÖZGAZDASÁGTAN GAZDASÁGI INFORMATIKUSOKNAK. Oktatók. Dr. Nagy András. Makrogazdasági egyensúlyi problémák. A munkanélküliség
 KÖZGAZDASÁGTAN GAZDASÁGI INFORMATIKUSOKNAK Oktatók Dr. Sas Éva Dr. Nagy Adrás Makrogazdasági egyesúlyi problémák A mukaélküliség 1 A mukapiac alapkategóriái Népesség Mukaképes épesség Aktív épesség A Foglalkoztatottak
KÖZGAZDASÁGTAN GAZDASÁGI INFORMATIKUSOKNAK Oktatók Dr. Sas Éva Dr. Nagy Adrás Makrogazdasági egyesúlyi problémák A mukaélküliség 1 A mukapiac alapkategóriái Népesség Mukaképes épesség Aktív épesség A Foglalkoztatottak
3. Az energiatermelés költségei Gazdasági elemzések 1.
 3. Az eergiatermelés ei Gazdasági elemzések. Cél Vállalati Országos Globális yereségesség yereséges gazdálkodás piacralépés, piaci kivoulás gazdaságosság legkisebb társadalmi (fizetési mérleg, járulékos
3. Az eergiatermelés ei Gazdasági elemzések. Cél Vállalati Országos Globális yereségesség yereséges gazdálkodás piacralépés, piaci kivoulás gazdaságosság legkisebb társadalmi (fizetési mérleg, járulékos
1. Adatok közelítése. Bevezetés. 1-1 A közelítő függvény
 Palácz Béla - Soft Computig - 11-1. Adatok közelítése 1. Adatok közelítése Bevezetés A természettudomáyos feladatok megoldásához, a vizsgált jeleségek, folyamatok főbb jellemzői közötti összefüggések ismeretére,
Palácz Béla - Soft Computig - 11-1. Adatok közelítése 1. Adatok közelítése Bevezetés A természettudomáyos feladatok megoldásához, a vizsgált jeleségek, folyamatok főbb jellemzői közötti összefüggések ismeretére,
Az új építőipari termelőiár-index részletes módszertani leírása
 Az új építőipari termelőiár-idex részletes módszertai leírása. Előzméyek Az elmúlt évekbe az építőipari árstatisztikába egy új, a korábba haszálatos költségalapú áridextől eltérő termelői ár alapú idexmutató
Az új építőipari termelőiár-idex részletes módszertai leírása. Előzméyek Az elmúlt évekbe az építőipari árstatisztikába egy új, a korábba haszálatos költségalapú áridextől eltérő termelői ár alapú idexmutató
mateksoft.hu ( ) 2 x 10 y 14 Nevezetes azonosságok: Hatványozás azonosságai Azonos kitevőjű hatványok: + 9 ( 2x 3y) 2 4x 2 12xy + 9y 2
 Nevezetes zoosságok: mteksoft.hu ( + ) + + ( x + ) x + 6 x + 9 ( x + y) 4x + 1xy + 9y ( ) + ( x ) x 6 x + 9 ( x y) 4x 1xy + 9y ( + + c) + + c + + c + c ( x + y + ) x + y + 4 + xy + 4x + 4y Htváyozás zoossági
Nevezetes zoosságok: mteksoft.hu ( + ) + + ( x + ) x + 6 x + 9 ( x + y) 4x + 1xy + 9y ( ) + ( x ) x 6 x + 9 ( x y) 4x 1xy + 9y ( + + c) + + c + + c + c ( x + y + ) x + y + 4 + xy + 4x + 4y Htváyozás zoossági
f (M (ξ)) M (f (ξ)) Bizonyítás: Megjegyezzük, hogy konvex függvényekre mindig létezik a ± ben
 Propositio 1 (Jese-egyelőtleség Ha f : kovex, akkor tetszőleges ξ változóra f (M (ξ M (f (ξ feltéve, hogy az egyelőtleségbe szereplő véges vagy végtele várható értékek létezek Bizoyítás: Megjegyezzük,
Propositio 1 (Jese-egyelőtleség Ha f : kovex, akkor tetszőleges ξ változóra f (M (ξ M (f (ξ feltéve, hogy az egyelőtleségbe szereplő véges vagy végtele várható értékek létezek Bizoyítás: Megjegyezzük,
Példa: 5 = = negatív egész kitevő esete: x =, ha x 0
 Ha mást em moduk, szám alatt az alábbiakba, midig alós számot értük. Műeletek összeadás: Példa: ++5 tagok: amiket összeaduk, az előző éldába a, az és az 5 szorzás: Példa: 5 téezők: amiket összeszorzuk,
Ha mást em moduk, szám alatt az alábbiakba, midig alós számot értük. Műeletek összeadás: Példa: ++5 tagok: amiket összeaduk, az előző éldába a, az és az 5 szorzás: Példa: 5 téezők: amiket összeszorzuk,
FAIPARI ALAPISMERETEK
 Faipari alapismeretek középszit 0812 ÉRETTSÉGI VIZSGA 2011. október 17. FAIPARI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS MINISZTÉRIUM Fotos tudivalók
Faipari alapismeretek középszit 0812 ÉRETTSÉGI VIZSGA 2011. október 17. FAIPARI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS MINISZTÉRIUM Fotos tudivalók
16. Az AVL-fa. (Adelszon-Velszkij és Landisz, 1962) Definíció: t kiegyensúlyozott (AVL-tulajdonságú) t minden x csúcsára: Pl.:
 6. Az AVL-fa Adelszo-Velszkij és Ladisz, 96 Defiíció: t kiegyesúlyozott AVL-tulajdoságú t mide x csúcsára: bal x jobb x. Pl.: A majdem teljes biáris fa AVLtulajdoságú. Az AVL-fára, mit speciális alakú
6. Az AVL-fa Adelszo-Velszkij és Ladisz, 96 Defiíció: t kiegyesúlyozott AVL-tulajdoságú t mide x csúcsára: bal x jobb x. Pl.: A majdem teljes biáris fa AVLtulajdoságú. Az AVL-fára, mit speciális alakú
5. Kombinatorika. 8. Legfeljebb hány pozitív egész számot adhatunk meg úgy, hogy semelyik kettő összege és különbsége se legyen osztható 2015-tel?
 5. Kombiatorika I. Feladatok. Háyféleképpe olvashatók ki az alábbi ábrákról a PAPRIKAJANCSI, a FELADAT és a MATEMATIKASZAKKÖR szavak, ha midig a bal felső sarokból kell iduluk, és mide lépésük csak jobbra
5. Kombiatorika I. Feladatok. Háyféleképpe olvashatók ki az alábbi ábrákról a PAPRIKAJANCSI, a FELADAT és a MATEMATIKASZAKKÖR szavak, ha midig a bal felső sarokból kell iduluk, és mide lépésük csak jobbra
Csapágyak üzem közbeni vizsgálata a csavarhúzótól a REBAM 1 -ig 2
 ÜZEMFENNTARTÁSI TEVÉKENYSÉGEK 3.9 Csapágyak üzem közbei vizsgálata a csavarhúzótól a REBAM 1 -ig 2 Gergely Mihály okl. gépészmérök, Acceleratio Bt. Budapest Tóbis Zsolt doktoradusz, Miskolci Egyetem Gépelemek
ÜZEMFENNTARTÁSI TEVÉKENYSÉGEK 3.9 Csapágyak üzem közbei vizsgálata a csavarhúzótól a REBAM 1 -ig 2 Gergely Mihály okl. gépészmérök, Acceleratio Bt. Budapest Tóbis Zsolt doktoradusz, Miskolci Egyetem Gépelemek
A brexit-szavazás és a nagy számok törvénye
 Mûhely Medvegyev Péter kadidátus, a Corvius Egyetem egyetemi taára E-mail: peter.medvegyev@uicorvius.hu A brexit-szavazás és a agy számok törvéye A 016. év, de vélhetőe az egész évtized legfotosabb politikai
Mûhely Medvegyev Péter kadidátus, a Corvius Egyetem egyetemi taára E-mail: peter.medvegyev@uicorvius.hu A brexit-szavazás és a agy számok törvéye A 016. év, de vélhetőe az egész évtized legfotosabb politikai
Statisztika. Eloszlásjellemzők
 Statsztka Eloszlásjellemzők Statsztka adatok elemzése A sokaság jellemzése középértékekkel A sokaság jellemzéséek szempotja A sokaság jellemzéséek szempotja: A sokaság tpkus értékéek meghatározása. Az
Statsztka Eloszlásjellemzők Statsztka adatok elemzése A sokaság jellemzése középértékekkel A sokaság jellemzéséek szempotja A sokaság jellemzéséek szempotja: A sokaság tpkus értékéek meghatározása. Az
Matematikai játékok. Svetoslav Bilchev, Emiliya Velikova
 Matematikai játékok Svetoslav Bilchev, Emiliya Velikova 1. rész Matematikai tréfák A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a játékosok
Matematikai játékok Svetoslav Bilchev, Emiliya Velikova 1. rész Matematikai tréfák A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a játékosok
Tranziens káosz nyitott biliárdasztalokon
 Eötvös Lorád Tudomáyegyetem Természettudomáyi kar Vicze Gergely Trazies káosz yitott biliárdasztaloko Msc szakdolgozat Témavezető: Tél Tamás, egyetemi taár Elméleti Fizikai Taszék Budapest, 2012 1 Tartalom
Eötvös Lorád Tudomáyegyetem Természettudomáyi kar Vicze Gergely Trazies káosz yitott biliárdasztaloko Msc szakdolgozat Témavezető: Tél Tamás, egyetemi taár Elméleti Fizikai Taszék Budapest, 2012 1 Tartalom
3. Számelmélet. 1-nek pedig pontosan három. Hány pozitív osztója van az n számnak? OKTV 2012/2013; I. kategória, 1. forduló
 . Számelmélet I. Feladatok 1. Háy égyzetszám osztója va a 7 5 5 7 számak?. Az pozitív egész számak potosa két pozitív osztója va, az + 1-ek pedig potosa három. Háy pozitív osztója va az + 01 számak? OKTV
. Számelmélet I. Feladatok 1. Háy égyzetszám osztója va a 7 5 5 7 számak?. Az pozitív egész számak potosa két pozitív osztója va, az + 1-ek pedig potosa három. Háy pozitív osztója va az + 01 számak? OKTV
