M3 ZÁRT CSATORNÁBAN ELHELYEZETT HENGERRE HATÓ ERŐ MÉRÉSE
|
|
|
- András Bakos
- 6 évvel ezelőtt
- Látták:
Átírás
1 M3 ZÁRT CSATORNÁBAN ELHELYEZETT HENGERRE HATÓ ERŐ MÉRÉSE 1. A mérés élja A mérés fladat égyzt krsztmtsztű satorába bépíttt, az áramlás ráyára mrőlgs szmmtratglyű, külöböző átmérőjű hgrkr ható ( x, y ) rő mghatározása a hgr flülté mért yomásloszlásból. Vzsgálhatjuk továbbá adott átmérőjű hgrr a tglyék satora falától mért távolsága függvéyéb a hgr körül yomásloszlás és a hgrr ható rő változását. A mért adatokból a hgr palástjá kltkző súsztatófszültségből származó (gyébkét ks értékű) rő lhayagolásával mghatározadó a hgr p yomástéyzőj, llállás-téyzőj és f flhajtórő-téyzőj s.. A mérés brdzés lírása Ksbb mértű szélsatorát haszáluk a fladat lvégzéséhz. Az asztal agyságú brdzés vázlatát az 1. ábrá láthatjuk. A krkkr szrlt szkréyb található radáls vtlátorral áramoltatjuk a lvgőt. Az áramló lvgő sbsségék szabályozása szívóoldal fojtással törték. A maxmálsa lérhtő sbsség a 150x150 mm-s kfúvó krsztmtsztb kb. 3 m/s. A v káramlás sbsség és a szélsatora oldalá lévő kvztés mérhtő rfra yomáskülöbség (p rf ) között a mérőkos ttjé található kalbráós összfüggés ( K ) trmt kapsolatot. 1
2 150 ojtólm Δp rf Áramlásrdző Vtlátor ojtásállító 1.ábra Mérőbrdzés flépítés A szélsatora kfúvó yílására szrltük gy függőlgs, égyzt krsztmtsztű, zárt mérősatorát, amlyb a mér kívát hgrt hlyzzük. A mérősatora szrkzt a. ábrá látható.
3 150 Csatora Nyomásmérő furat x-pozíoáló Nyomás satlakozó z x Vzsgált hgr Statkus yomásmérő mgsapolások.ábra Mérősatora flépítés A mérősatora három darabból építhtő fl, mlyk sorrdj varálható, zzl változtatható a hgr lőtt, lltv utá satorahossz. Az gyk lm kalakítása olya, hogy abba külöböző átmérőjű mérőhgrkt lht llszt. Ez az lm gy mts orsó sgítségévl lhtővé tsz a hgrk hossztglyükr mrőlgs lmozdítását, valamt a hgr tglyévl párhuzamos mozgatása s mgoldott. A mérőhgrk palástjá lévő ks átmérőjű furat a hgr gyk végé lévő yomáskvztéshz satlakozk, k sgítségévl mérhtjük a lokáls statkus yomást. A hgr másk véglapja zárt. A vzsgált hgr yomáskvztésé mérhtő yomás és a satorába uralkodó hly statkus yomás külöbségét kll mérük. A satora falá a égy oldalfal statkus yomás kvztést gy körvzték köt össz. 3. A mérés lmélt háttr Áramlásba hlyztt tstkr ható rő a tstk flülté kltkző yomás- és súsztatófszültség-mgoszlás rdméykét alakul k. Valóságos áramlás sté a tst közléb lévő áramvoalak mté a Broull-összg a súrlódás kövtkztéb sökk, zért a tst mögött gy áramlás yom kltkzk, amb a sbsség (és a görbült áramvoalak matt a yomás s) ltér a súrlódásmts stb mgfgylhtő sbsségloszlástól. A yomássökkés mérték agymértékb függ a kalakuló áramképr jllmző Ryolds-számtól. A mérőbrdzésél a jllmző Ryolds-szám tartomáy között va. Ebb a tartomáyba a thttlség rők domálak, a hgr mögött kltkző örvéypár prodkusa lválk a hgrről (z az ú. Kármá-fél örvéysor). A kltkző örvéykb és a köryztükb a sbsség vszoylag agy és a yomás alasoy. A hgrr ható llállásrő jltős rész thát a hgr hátsó részé az örvéyk kltkzés matt létrjövő dprsszó kövtkzméy. [1] A hgrr ható agy llállásrő magyarázható még a lváló örvéyk agy mozgás rgatartalmával s, am a tst mögött hővé alakul. (Abszolút rdszrb ézv vszoylag agy mukát kll kfjtük a hgr mozgatásakor álló közgb, hogy az k kövtkztéb kltkző és a súrlódás folytá hővé alakuló agy mozgás rgát fdz tudjuk.) 3
4 Számol kll továbbá az gyoldal falhatással s, hsz ha a hgrt a falhoz közlítjük, az áramkép szmmtrája (ltktv a yomba kalakuló és gadozó örvéypártól) mgbomlk, a fal flöl oldalo az áramló közg flgyorsul, yomása sökk, és a yomásloszlásba tapasztalható változás matt létrjö a tstr ható rők gy az áramlás ráyára mrőlgs kompos. A mrőlgs kompos agysága függ a hgr faltól mért távolságától, mly mértékék fldrítés s a mérés rész. 4. A mérés lfolytatása A sbsség és a yomásmérés A szélsatora lírásakor már a p rf rfra yomás mérését smrtttük, amllyl a satora blépő sbsségét határozhatjuk mg. A hgr flülté kalakuló yomásloszlást úgy határozzuk mg, hogy a hgr palástjá lévő gytl yomásmérés hlyt a hgr tgly körül forgatásával változtatjuk, így pl. a mgfllő flbotás érdkéb 5 vagy 10 -os osztással 0 és 360 között körbforgatjuk, amhz a satora oldalá található szögmérő yújt sgítségt. A krült mté számú mérés pothoz így számú A hgr-palástflült rész tartozk. Lhtségs mérés fladat: - Külöböző Ryolds-számo (sbsség változtatással) gy adott átmérőjű hgr yomásloszlásáak vzsgálata. - Külöböző átmérőjű hgr yomásloszlásáak mghatározása ugyaazo Ryoldsszám mlltt. - Egy adott átmérőjű hgr yomásloszlásáak vzsgálata a tglyék a satora falától mért külöböző távolságra való bállítása mlltt. Ügyl kll a mérés sorá arra s, hogy a mérőpotbl yomás a forgatás sorá lőjlt válthat (hly statkus yomáshoz képst mérv túlyomás ll. dprsszó alakulhat k)! Az áramlások tovább jllmzők kmérés A mérés kzdté és végé rögzít kll a köryzt adatokat, mt a köryzt hőmérséklt, légkör yomás, amlyből a lvgő sűrűségét számítjuk k. l kll jgyz a mérőbrdzés gomtra adatat, a satora lmk a sorrdjét, a mérőszközök főbb jllmzőt, állapotát. 5. A mérés kértéklés és összhasolítása rodalm adatokkal A kértéklés sorá az EMB-001 dgtáls yomásmérőről lolvasott yomáskülöbség értékkt kll fljgyz, a hgr és satora falá mért statkus yomások külöbségéből számolt yomástéyzőt a szög függvéyéb dagramba kll ábrázol. 4
5 p, Δp ρlv v ahol p, [-] yomástéyző az -dk mérőpotba p [Pa] a hgr és a satora falá mért yomások külöbség az -dk mérés potba lv [kg/m 3 ] áramló közg (tt lvgő) sűrűség v [m/s] áramlás sbsség Mg kll határoz umrkus tgrálással a sőr ható rőt (), aak áramlás ráyú ( x ), és arra mrőlgs ( y ) komposét. (1) 1 1 Δp A () x 1 x 1 Δp Dπ h os Φ (3) y 1 y 1 Δp Dπ h s Φ (4) ahol: [N] Az áramlásba hlyztt tstr ható rdő rő [db] A mérés potok lltv a részflültk száma [N] Az -dk részflültr ható rő p [Pa] Az -dk részflült mért yomáskülöbség (túlyomás) A [m ] Az -dk részflült agysága D [m] Hgr átmérő h [m] Hgr magasság [-] A flült ormáls ráyú gységvktor [ ] -dk mérőpot x tgllyl bzárt szög x, y [N] x,y ráyú rőkompos A bvzttt változók értlmzéséhz lásd a 3. ábrát. 5
6 y x, y, x Mgfúvás ráya 3.ábra Hgrr ható rő számítása Az áramlás ráyú x rőkompost vzzük llállásrők, amből a mérés éljakét ktűzött llállás-téyzőt ( ) számolhatjuk. Az y komposből pdg a mgfúvás ráyra mrőlgs f flhajtórő-téyzőt kapjuk. ρ lv v A hgr (5) f ρ lv v f A hgr (6) ahol [-] llállás-téyző f [-] flhajtórő-téyző [N] llállásrő f [N] flhajtórő lv [kg/m 3 ] áramló közg (tt lvgő) sűrűség v [m/s] áramlás sbsség A hgr [m ] mérőtst áramlás ráyra mrőlgs vtült Az llállás-téyző értékét élszrű összhasolíta a szakrodalomba (pl. [3]) található értékkkl. A rdlkzésr álló átmérő-sorozatból a agyobb átmérőjű hgrkél a zárt satorába kalakuló áramkép ltér a végtl térb kalakulótól. Ek az oka, hogy a hgrk a zárt áramlás térb való bhlyzéséél kalakuló körüláramlás áramképét bfolyásolja a zárt satora oldalfala. Ez a végtl térb érvéys hgrr ható rőhöz képs aál agyobb ltérést okoz a mérésükb mél agyobb a hgr átmérő. Ezt az ltérést az ú. blokkolás téyzővl vsszük fgylmb. A korrgálására a kövtkző számítást kll alkalmaz a mért llállás-téyző értékkr: 6
7 ,k 1 G 1+ 0,8 S / C S / C (7) ahol,k [-] korrgált llállás-téyző [-] számolt llállás-téyző G [-] tapasztalat téyző, szakrodalom szrt hgrs tstkr G0,3 S [m ] a vzsgált tst áramlás ráyára mrőlgs krsztmtszt C [m ] a mérőtér áramlás ráyára mrőlgs krsztmtszt A korrgált llállás-téyző R> sté mgközlítő 0,3. Eél alasoyabb Ryolds-szám értékkr 1, jó közlítést jlt. A két tartomáy között rövd átmt szakasz található, mlyb az llállás-téyző értékék bslését az 1. dagram sgít. 1. dagram Ellállás-téyző (a dagramba D ) a Ryolds-szám függvéyéb, külöböző d160, 30, 400 mm hgrátmérők sté 6. Hbaszámítás: A mérés hbaszámítását a hgr llállás-téyzőjér kll lvégz az alább módo: Az llállás-téyző kfjzés: ρ lv v A hgr Dπ Δp hosφ 1 ρ Kp lv rf Ahgr ρ (ahol K a mérőkos fltütttt kalbráós kostas) lv 7 1 π Δp osφ Kp rf
8 Az abszolút hba számítása: A rlatív hba: δ 1 δ δx? X ahol az X mért mységk és a hozzájuk kapsolódó mérés hbák: X 1 p, lltv a yomásmérés hbája p Pa X p 0, lltv a légkör yomás mérés hbája p Pa X 3 T 0, lltv a hőmérséklt mérés hbája 0 1K X 4 p rf, lltv a yomásmérés hbája p rf Pa X 5 Φ, lltv a szögmérés hbája Φ 7. Dagramok: A hgrpalásto érvéys yomástéyző ( p ) a forgatás szög függvéyéb. A külöböző átmérőjű hgrk llállás-téyzőj és flhajtórő-téyzőj a Ryolds-szám, vagy a faltól mért távolság függvéyéb + abszolút és rlatív hba értékk. A mérés sorá m szabad mgfldkz -A mérőbrdzés bkapsolása lőtt, lltv általába a mérőbrdzés üzm sorá mdg mg kll győződ a balstmts haszálat fltétlk tljsüléséről. A bkapsolásról, lltv a mérés közb végrhajtott változtatásokról a brdzés köryztéb dolgozókat fgylmztt kll. - Md mérés alkalommal a légkör yomás és trmhőmérséklt fljgyzéséről! - A flhaszált mérőműszrkről lolvasott értékk mértékgységék és a rájuk voatkozó gyéb téyzők fljgyzéséről. - A flhaszált mérőműszrk típusáak, gyártás számáak és a b lévő mérőfolyadék sűrűségék fljgyzéséről! - A mérőműszrről lolvasott mységk és a tovább számításokál flhaszált mységk mértékgységék gyzttéséről. - A dgtáls yomásmérő kalbráójáról! - A yomásmérő bkötéséél fgylms kll ljár a satlakozók "+" lltv "-" ágáak és a méréshatár kválasztásáál. gyl kll arra, hogy a yomásmérő satlakozó sokjara a gumsövt óvatosa kll flhlyz. - A yomásközlő gum, vagy szlko sövkt mérés lőtt, stlg közb s élszrű llőrz, hogy rpdés, szakadás lgy rajtuk, mrt lyukas mérőső sté az összs addg mérés rdméy kárba vész. Krtkus potok a műszrkr ll. a yomáskvztéskr törtéő satlakoztatás hly. - A jgyzőköyv ladása lőtt rős ajálott a kozultáók géybvétl. Irodalom [1] Lajos Tamás: Áramlásta alapja (004) és fjzt [] Lajos Tamás: Áramlásta alapja (004) 43.oldal [3] Lajos Tamás: Áramlásta alapja (004) 488.oldal 8
M3 ZÁRT CSATORNÁBAN ELHELYEZETT HENGERRE HATÓ ERŐ MÉRÉSE
 M3 ZÁRT CSATORNÁBAN ELHELYEZETT HENGERRE HATÓ ERŐ MÉRÉSE 1. A mérés élja A mérés fladat égyzt krsztmtsztű satorába bépíttt, az áramlás ráyára mrőlgs szmmtratglyű, külöböző átmérőjű hgrkr ható F (F x,f
M3 ZÁRT CSATORNÁBAN ELHELYEZETT HENGERRE HATÓ ERŐ MÉRÉSE 1. A mérés élja A mérés fladat égyzt krsztmtsztű satorába bépíttt, az áramlás ráyára mrőlgs szmmtratglyű, külöböző átmérőjű hgrkr ható F (F x,f
M3 ZÁRT CSATORNÁBAN ELHELYEZETT HENGERRE HATÓ ERŐ MÉRÉSE
 M3 ZÁRT CSATORNÁBAN ELHELYEZETT HENGERRE HATÓ ERŐ MÉRÉSE. A mérés élja A mérés fladat égyzt krsztmtsztű satorába bépíttt, az áramlás ráyára mrőlgs szmmtratglyű, külöböző átmérőjű hgrkr ható ( x, y ) rő
M3 ZÁRT CSATORNÁBAN ELHELYEZETT HENGERRE HATÓ ERŐ MÉRÉSE. A mérés élja A mérés fladat égyzt krsztmtsztű satorába bépíttt, az áramlás ráyára mrőlgs szmmtratglyű, külöböző átmérőjű hgrkr ható ( x, y ) rő
TESTEK ELLENÁLLÁSTÉNYEZŐJÉNEK MÉRÉSE NPL TÍPUSÚ SZÉLCSATORNÁBAN
 M4 TESTEK ELLENÁLLÁSTÉNYEZŐJÉNEK MÉRÉSE NPL TÍPUSÚ SZÉLCSATORNÁBAN 1. A mérés aktualitása, a mérés célja Az áramlásba hlyztt tstkr ható rők, nyomatékok ismrt fontos az épültk, tartószrkztk, járművk trvzésénél.
M4 TESTEK ELLENÁLLÁSTÉNYEZŐJÉNEK MÉRÉSE NPL TÍPUSÚ SZÉLCSATORNÁBAN 1. A mérés aktualitása, a mérés célja Az áramlásba hlyztt tstkr ható rők, nyomatékok ismrt fontos az épültk, tartószrkztk, járművk trvzésénél.
M4 TESTEK ELLENÁLLÁSTÉNYEZŐJÉNEK MÉRÉSE NPL TÍPUSÚ SZÉLCSATORNÁBAN
 M4 TESTEK ELLENÁLLÁSTÉNYEZŐJÉNEK MÉRÉSE NPL TÍPUSÚ SZÉLCSATORNÁBAN. A mérés aktualitása, a mérés célja Az áramlásba hlyztt tstkr ható rők, nyomatékok ismrt fontos az épültk, tartószrkztk, járművk trvzésénél.
M4 TESTEK ELLENÁLLÁSTÉNYEZŐJÉNEK MÉRÉSE NPL TÍPUSÚ SZÉLCSATORNÁBAN. A mérés aktualitása, a mérés célja Az áramlásba hlyztt tstkr ható rők, nyomatékok ismrt fontos az épültk, tartószrkztk, járművk trvzésénél.
M11 TESTEK KÖRÜLI ÁRAMLÁS VIZSGÁLATA
 M11 TESTEK KÖRÜLI ÁRMLÁS VIZSGÁLT 1. mérés célja, gyakorlat jltőség mérés célja: - külöböző (égyzt, kör és dúcprofl) krsztmtsztű, oszlop alakú tstk körül kalakuló áramkép zsgálata áramlás mgjlítés módszr
M11 TESTEK KÖRÜLI ÁRMLÁS VIZSGÁLT 1. mérés célja, gyakorlat jltőség mérés célja: - külöböző (égyzt, kör és dúcprofl) krsztmtsztű, oszlop alakú tstk körül kalakuló áramkép zsgálata áramlás mgjlítés módszr
A központos furnérhámozás néhány alapösszefüggése
 A közpotos furérhámozás éháy alapösszfüggés 1. ábra: A hámozás jllmző myiségi Az 1. ábra forrása: Dr. Lugosi Armad ( szrk. ) : Faipari szrszámok és gépk kéziköyv Műszaki Köyvkiadó, Budapst, 1987, 57. oldal.
A közpotos furérhámozás éháy alapösszfüggés 1. ábra: A hámozás jllmző myiségi Az 1. ábra forrása: Dr. Lugosi Armad ( szrk. ) : Faipari szrszámok és gépk kéziköyv Műszaki Köyvkiadó, Budapst, 1987, 57. oldal.
M11 TESTEK KÖRÜLI ÁRAMLÁS VIZSGÁLATA
 M11 TESTEK KÖRÜLI ÁRAMLÁS VIZSGÁLATA 1. A mérés célja, gyakorlat jeletősége A mérés célja: - külöböző (égyzet, kör és dúcprofl) keresztmetszetű, oszlop alakú testek körül kalakuló áramkép vzsgálata áramlás
M11 TESTEK KÖRÜLI ÁRAMLÁS VIZSGÁLATA 1. A mérés célja, gyakorlat jeletősége A mérés célja: - külöböző (égyzet, kör és dúcprofl) keresztmetszetű, oszlop alakú testek körül kalakuló áramkép vzsgálata áramlás
SIKALAKVÁLTOZÁSI FELADAT MEGOLDÁSA VÉGESELEM-MÓDSZERREL
 SIKALAKVÁLTOZÁSI FELADAT MEGOLDÁSA VÉGESELEM-MÓDSZERREL ADOTT: Az ábrán látható db végslmből álló tartószrkzt gomtriája, mgfogása és trhlés. A négyzt alakú síkalakváltozási végslmk mért 0 X 0 mm. p Anyagjllmzők:
SIKALAKVÁLTOZÁSI FELADAT MEGOLDÁSA VÉGESELEM-MÓDSZERREL ADOTT: Az ábrán látható db végslmből álló tartószrkzt gomtriája, mgfogása és trhlés. A négyzt alakú síkalakváltozási végslmk mért 0 X 0 mm. p Anyagjllmzők:
Labormérések minimumkérdései a B.Sc képzésben
 Labormérések mmumkérdése a B.Sc képzésbe 1. Ismertesse a levegő sűrűség meghatározásáak módját a légyomás és a levegő hőmérséklet alapjá! Adja meg a képletbe szereplő meységek jeletését és mértékegységét!
Labormérések mmumkérdése a B.Sc képzésbe 1. Ismertesse a levegő sűrűség meghatározásáak módját a légyomás és a levegő hőmérséklet alapjá! Adja meg a képletbe szereplő meységek jeletését és mértékegységét!
M7 KÖNYÖKIDOM ÁRAMKÉPÉNEK VIZSGÁLATA ÉS VESZTESÉGTÉNYEZŐJÉNEK MEGHATÁROZÁSA
 M7 KÖNYÖKIDOM ÁRAMKÉPÉNEK VIZSGÁLATA ÉS VESZTESÉGTÉNYEZŐJÉNEK MEGHATÁROZÁSA. A mérés célja A csőztébn az áramlás rányáltozását önyödomoal, csőíl oldjá mg. Az rányáltozás jlntős áramlás sztségl jár, amlyn
M7 KÖNYÖKIDOM ÁRAMKÉPÉNEK VIZSGÁLATA ÉS VESZTESÉGTÉNYEZŐJÉNEK MEGHATÁROZÁSA. A mérés célja A csőztébn az áramlás rányáltozását önyödomoal, csőíl oldjá mg. Az rányáltozás jlntős áramlás sztségl jár, amlyn
53. sz. mérés. Hurokszabályozás vizsgálata
 53. sz. mérés Hurokszaályozás vizsgálata nagyszültségű alap- illtv losztóhálózat (4,, kv a hálózatok unkcióáól kövtkzőn hurkolt (töszörösn hurkolt kialakítású. sok csomóponttal, tö táplálási illtv ogyasztási
53. sz. mérés Hurokszaályozás vizsgálata nagyszültségű alap- illtv losztóhálózat (4,, kv a hálózatok unkcióáól kövtkzőn hurkolt (töszörösn hurkolt kialakítású. sok csomóponttal, tö táplálási illtv ogyasztási
A hőmérsékleti sugárzás
 A hőmérséklt sugárzás (Dr. Parpás Béla lőadása alapján ljgyzték a Mskolc gytm harmadévs nformatkus hallgató) Alapjlnségk Mndnnap tapasztalat, hogy a mlgíttt tstk hősugárzást (nfravörös sugárzást) bocsátanak
A hőmérséklt sugárzás (Dr. Parpás Béla lőadása alapján ljgyzték a Mskolc gytm harmadévs nformatkus hallgató) Alapjlnségk Mndnnap tapasztalat, hogy a mlgíttt tstk hősugárzást (nfravörös sugárzást) bocsátanak
A szelepre ható érintkezési erő meghatározása
 A szlpr ható érintkzési rő mghatározása Az [ 1 ] műbn az alábbi fladatot találtuk. A fladat: Adott az ábra szrinti szlpmlő szrkzt. Az a xcntricitással szrlt R sugarú bütyök / körtárcsa ω 1 állandó szögsbsséggl
A szlpr ható érintkzési rő mghatározása Az [ 1 ] műbn az alábbi fladatot találtuk. A fladat: Adott az ábra szrinti szlpmlő szrkzt. Az a xcntricitással szrlt R sugarú bütyök / körtárcsa ω 1 állandó szögsbsséggl
Integrált Intetnzív Matematika Érettségi
 tgrált ttzív Matmatika Érttségi. Adott az f : \ -, f függvéy. a) Számítsd ki az f függvéy driváltját! b) Határozd mg az f függvéy mootoitási itrvallumait! c) gazold, hogy f ( ) bármly sté!. Adott az f
tgrált ttzív Matmatika Érttségi. Adott az f : \ -, f függvéy. a) Számítsd ki az f függvéy driváltját! b) Határozd mg az f függvéy mootoitási itrvallumait! c) gazold, hogy f ( ) bármly sté!. Adott az f
Cikória szárítástechnikai tulajdonságainak vizsgálata modellkísérlettel
 Cikória szárítástchnikai tulajdonságainak vizsgálata modllkísérlttl Kacz Károly Stépán Zsolt Kovács Attila Józsf Nményi Miklós Nyugat-Magyarországi Egytm Mzőgazdaság- és Éllmiszrtudományi Kar Agrárműszaki,
Cikória szárítástchnikai tulajdonságainak vizsgálata modllkísérlttl Kacz Károly Stépán Zsolt Kovács Attila Józsf Nményi Miklós Nyugat-Magyarországi Egytm Mzőgazdaság- és Éllmiszrtudományi Kar Agrárműszaki,
Dugattyús szivattyú általános beépítési körülményei (szívó- és nyomóoldali légüsttel) Vegyipari- és áramlástechnikai gépek. 2.
 gypar és áramlástchnka gépk.. lőaás Készíttt: r. ára Sánor Buapst Műszak és Gazaságtuomány Egytm Gépészmérnök Kar Hronamka nszrk Tanszék 1111, Buapst, Műgytm rkp. 3. D ép. 334. Tl: 463-16-80 Fax: 463-30-91
gypar és áramlástchnka gépk.. lőaás Készíttt: r. ára Sánor Buapst Műszak és Gazaságtuomány Egytm Gépészmérnök Kar Hronamka nszrk Tanszék 1111, Buapst, Műgytm rkp. 3. D ép. 334. Tl: 463-16-80 Fax: 463-30-91
Mérés és elemzés Költség- és eredményelemzés
 6..5. MSKOLC EYEEM azdaságtudomáyi Kar Pézügyi és Számvitli tézt Számvitl tézti aszék Mérés és lmzés Költség- és rdméylmzés Mérés - adatbázisok összgző kimutatás szittika aalitika Dr. Musiszki Zoltá bizoylat
6..5. MSKOLC EYEEM azdaságtudomáyi Kar Pézügyi és Számvitli tézt Számvitl tézti aszék Mérés és lmzés Költség- és rdméylmzés Mérés - adatbázisok összgző kimutatás szittika aalitika Dr. Musiszki Zoltá bizoylat
CSŐVEZETÉK ELLENÁLLÁSÁNAK MÉRÉSE VÍZZEL
 Hiroinamikai Rnrk Tanék Elfogaa: Kéíttt:... kurzus Dátum:...é...hó...nap CSŐVEZETÉK ELLENÁLLÁSÁNAK MÉRÉSE VÍZZEL 1. A jlölésk jgyzék. A mérés célja f q R g pi hi hi i a cső blsőátmérőj csősúrlóási tényző
Hiroinamikai Rnrk Tanék Elfogaa: Kéíttt:... kurzus Dátum:...é...hó...nap CSŐVEZETÉK ELLENÁLLÁSÁNAK MÉRÉSE VÍZZEL 1. A jlölésk jgyzék. A mérés célja f q R g pi hi hi i a cső blsőátmérőj csősúrlóási tényző
Aktív lengéscsillapítás. Másodfokú lengrendszer tesztelése.
 Aktív lgécillapítá. Máodfokú lgrdzr tztlé.. A gyakorlat célja Jármvk aktív lgé cillapítááak modllzé máodfokú lgrdzrkét. Szoftvrfjlzté a rdzr való idj tztléér, a tztrdméyk kiértéklé.. Elmélti bvzt. A máodfokú
Aktív lgécillapítá. Máodfokú lgrdzr tztlé.. A gyakorlat célja Jármvk aktív lgé cillapítááak modllzé máodfokú lgrdzrkét. Szoftvrfjlzté a rdzr való idj tztléér, a tztrdméyk kiértéklé.. Elmélti bvzt. A máodfokú
A fázistekercsek ellenállását az induktív reaktancia mellett elhanyagolhatjuk.
 3. Szkro gép 3F zárlaakor az gyáraú összvő őbl válozása és oka. 4. Szkro gép 3F zárlaakor a válakozó áraú összvő őbl válozása és oka. árlaaják: A vllaos rga rszrb a zárla ára orrása az összs párhzaosa
3. Szkro gép 3F zárlaakor az gyáraú összvő őbl válozása és oka. 4. Szkro gép 3F zárlaakor a válakozó áraú összvő őbl válozása és oka. árlaaják: A vllaos rga rszrb a zárla ára orrása az összs párhzaosa
PONTRENDSZEREK MECHANIKÁJA. A pontrendszert olyan tömegpontok alkotják, amelyek nem függetlenek egymástól, közöttük kölcsönhatás van (belső erők).
 PONTRENDSZEREK ECHANIKÁJA A potrdszrt olya tögpotok alkotják, alyk függtlk gyástól, közöttük kölcsöhatás va (blső rők). F F F F F F F F Blső rők: F Külső rők: F F Nwto III.: rő-llrő párok F F F F A potrdszr
PONTRENDSZEREK ECHANIKÁJA A potrdszrt olya tögpotok alkotják, alyk függtlk gyástól, közöttük kölcsöhatás va (blső rők). F F F F F F F F Blső rők: F Külső rők: F F Nwto III.: rő-llrő párok F F F F A potrdszr
4. MECHANIKA STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnök tanár)
 SZÉCHENYI ISTVÁN EGYETE ALKALAZTT ECHANIKA TANSZÉK 4. ECHANIKA STATIKA GYAKRLAT (kdolgozta: Trsz Pétr, g. ts.; Tarna Gábor, mérnök tanár) Erő, nomaték, rőrndszr rdő, rőrndszrk gnértékűség 4.. Példa: z
SZÉCHENYI ISTVÁN EGYETE ALKALAZTT ECHANIKA TANSZÉK 4. ECHANIKA STATIKA GYAKRLAT (kdolgozta: Trsz Pétr, g. ts.; Tarna Gábor, mérnök tanár) Erő, nomaték, rőrndszr rdő, rőrndszrk gnértékűség 4.. Példa: z
Vezetéki termikus védelmi funkció
 Budaps, 011. április Bvzés A vzéki rmikus védlmi fukció alapvő a hárm miavélz fázisáram méri. Kiszámlja az ffkív érékk, és a hőmérsékl számíásá a fázisáramk ffkív érékér alapzza. A hőmérséklszámíás a rmikus
Budaps, 011. április Bvzés A vzéki rmikus védlmi fukció alapvő a hárm miavélz fázisáram méri. Kiszámlja az ffkív érékk, és a hőmérsékl számíásá a fázisáramk ffkív érékér alapzza. A hőmérséklszámíás a rmikus
3. Lokális approximáció elve, végeselem diszkretizáció egydimenziós feladatra
 SZÉCHENYI ISTVÁN EGYETEM AAMAZOTT MECHANIA TANSZÉ 5. MECHANIA-VÉGESEEM MÓDSZER EŐADÁS (kidolgozta: Szül Vronika g. ts.) V. lőadás. okális aroimáció lv végslm diszkrtizáció gdimnziós fladatra Amint azt
SZÉCHENYI ISTVÁN EGYETEM AAMAZOTT MECHANIA TANSZÉ 5. MECHANIA-VÉGESEEM MÓDSZER EŐADÁS (kidolgozta: Szül Vronika g. ts.) V. lőadás. okális aroimáció lv végslm diszkrtizáció gdimnziós fladatra Amint azt
Fűtési rendszerek hidraulikai méretezése. Baumann Mihály adjunktus Lenkovics László tanársegéd PTE MIK Gépészmérnök Tanszék
 Fűtési rendszerek hidraulikai méretezése Baumann Mihály adjunktus Lenkovics László tanársegéd PTE MIK Gépészmérnök Tanszék Hidraulikai méretezés lépései 1. A hálózat kialakítása, alaprajzok, függőleges
Fűtési rendszerek hidraulikai méretezése Baumann Mihály adjunktus Lenkovics László tanársegéd PTE MIK Gépészmérnök Tanszék Hidraulikai méretezés lépései 1. A hálózat kialakítása, alaprajzok, függőleges
Feladatok megoldással
 Fladatok mgoldással. sztmbr 6.. Halmazrdszrk. Igazoljuk! A \ B A r (A r B) (A [ B) r ((A r B) [ (B r A)) Mgoldás. A r (A r B) A \ A \ B A \ A [ B A \ A [ (A \ B) A \ B (A [ B) r ((A r B) [ (B r A)) (A
Fladatok mgoldással. sztmbr 6.. Halmazrdszrk. Igazoljuk! A \ B A r (A r B) (A [ B) r ((A r B) [ (B r A)) Mgoldás. A r (A r B) A \ A \ B A \ A [ B A \ A [ (A \ B) A \ B (A [ B) r ((A r B) [ (B r A)) (A
ORVOSI STATISZTIKA. Az orvosi statisztika helye. Egyéb példák. Példa: test hőmérséklet. Lehet kérdés? Statisztika. Élettan Anatómia Kémia. Kérdések!
 ORVOSI STATISZTIKA Az orvos statsztka helye Életta Aatóma Kéma Lehet kérdés?? Statsztka! Az orvos dötéseket hoz! Mkor jó egy dötés? Meyre helyes egy dötés? Mekkora a tévedés lehetősége? Példa: test hőmérséklet
ORVOSI STATISZTIKA Az orvos statsztka helye Életta Aatóma Kéma Lehet kérdés?? Statsztka! Az orvos dötéseket hoz! Mkor jó egy dötés? Meyre helyes egy dötés? Mekkora a tévedés lehetősége? Példa: test hőmérséklet
Modern piacelmélet. ELTE TáTK Közgazdaságtudományi Tanszék. Selei Adrienn
 Modrn piaclmélt ELTE TáTK Közgazdaságtudományi Tanszék Sli Adrinn A tananyag a Gazdasági Vrsnyhiatal Vrsnykultúra Központja és a Tudás-Ökonómia Alapítány támogatásáal készült az ELTE TáTK Közgazdaságtudományi
Modrn piaclmélt ELTE TáTK Közgazdaságtudományi Tanszék Sli Adrinn A tananyag a Gazdasági Vrsnyhiatal Vrsnykultúra Központja és a Tudás-Ökonómia Alapítány támogatásáal készült az ELTE TáTK Közgazdaságtudományi
1. Vizsgazárthelyi megoldásokkal 1997/98 tél I. évf tk.
 . Vizsgazárthlyi mgoldásokkal 997/98 tél I. évf..-8.tk.. Döts l, hogy fáll mid A és B halmaz sté a A B) \ B A összfüggés! Ha m, adjo szükségs és légségs fltétlt arra, hogy mikor áll f! A B) \ B A iff A
. Vizsgazárthlyi mgoldásokkal 997/98 tél I. évf..-8.tk.. Döts l, hogy fáll mid A és B halmaz sté a A B) \ B A összfüggés! Ha m, adjo szükségs és légségs fltétlt arra, hogy mikor áll f! A B) \ B A iff A
Operatív döntéstámogatás
 8.9.7. MSKOLC YM azaságtuomáyi Kar Üzlti formációgazálkoási és Mószrtai tézt Számvitl tézti aszék Opratív ötéstámogatás mószri Statisztikai matmatikai mószrk Opratív ötéstámogatás mószri Kalkulációs mószrk
8.9.7. MSKOLC YM azaságtuomáyi Kar Üzlti formációgazálkoási és Mószrtai tézt Számvitl tézti aszék Opratív ötéstámogatás mószri Statisztikai matmatikai mószrk Opratív ötéstámogatás mószri Kalkulációs mószrk
Rácsrezgések.
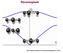 ácsrzgésk http://physics-imtis.cm/physics/glish/ph_txt.htm ácsrzgésk gitális hllám rúb Nwt II F x x F x V t F F x A x V x x x x x x A hllámszám értlmzési trtmáy végs mért prióiks htárfltétl Br-Kármá t
ácsrzgésk http://physics-imtis.cm/physics/glish/ph_txt.htm ácsrzgésk gitális hllám rúb Nwt II F x x F x V t F F x A x V x x x x x x A hllámszám értlmzési trtmáy végs mért prióiks htárfltétl Br-Kármá t
Mérési jegyzőkönyv. M1 számú mérés. Testek ellenállástényezőjének mérése
 Tanév, félév 2010-11 I. félév Tantárgy Áramlástan GEÁTAG01 Képzés főiskola (BSc) Mérés A Nap Hét A mérés dátuma 2010 Dátum Pontszám Megjegyzés Mérési jegyzőkönyv M1 számú mérés Testek ellenállástényezőjének
Tanév, félév 2010-11 I. félév Tantárgy Áramlástan GEÁTAG01 Képzés főiskola (BSc) Mérés A Nap Hét A mérés dátuma 2010 Dátum Pontszám Megjegyzés Mérési jegyzőkönyv M1 számú mérés Testek ellenállástényezőjének
Az elektromágneses sugárzás kölcsönhatása az anyaggal
 Az lktromágnss sugárzás kölcsönhatása az anyaggal A fény kölcsönhatása az anyaggal visszavrődés A fény kölcsönhatása az anyaggal 2. törés szórás lnylődés Elnylődés 1 2 3 4 Δ Az intzitás gyngülésénk törvény
Az lktromágnss sugárzás kölcsönhatása az anyaggal A fény kölcsönhatása az anyaggal visszavrődés A fény kölcsönhatása az anyaggal 2. törés szórás lnylődés Elnylődés 1 2 3 4 Δ Az intzitás gyngülésénk törvény
HŐVÉDELEM Feladatok I. rész
 07... Fladaok I. rész Dr. Harmahy Norbr adjunkus BDAPESTI MŰSZAKI ÉS GAZDASÁGTDOMÁNYI EGYETEM Épíészmérnök Kar, Épülnrgka és Épülgépész Tanszék. Flada A. Haározd mg gy öbbrégű falszrkz hőábocsáás ényzőjé!
07... Fladaok I. rész Dr. Harmahy Norbr adjunkus BDAPESTI MŰSZAKI ÉS GAZDASÁGTDOMÁNYI EGYETEM Épíészmérnök Kar, Épülnrgka és Épülgépész Tanszék. Flada A. Haározd mg gy öbbrégű falszrkz hőábocsáás ényzőjé!
0,00 0,01 0,02 0,03 0,04 0,05 0,06 Q
 1. Az ábrában látható kapcsolási vázlat szerinti berendezés két üzemállapotban működhet. A maximális vízszint esetében a T jelű tolózár nyitott helyzetben van, míg a minimális vízszint esetén az automatikus
1. Az ábrában látható kapcsolási vázlat szerinti berendezés két üzemállapotban működhet. A maximális vízszint esetében a T jelű tolózár nyitott helyzetben van, míg a minimális vízszint esetén az automatikus
Ventilátor (Ve) [ ] 4 ahol Q: a térfogatáram [ m3. Nyomásszám:
![Ventilátor (Ve) [ ] 4 ahol Q: a térfogatáram [ m3. Nyomásszám: Ventilátor (Ve) [ ] 4 ahol Q: a térfogatáram [ m3. Nyomásszám:](/thumbs/60/44642901.jpg) Ventilátor (Ve) 1. Definiálja a következő dimenziótlan számokat és írja fel a képletekben szereplő mennyiségeket: φ (mennyiségi szám), Ψ (nyomásszám), σ (fordulatszám tényező), δ (átmérő tényező)! Mennyiségi
Ventilátor (Ve) 1. Definiálja a következő dimenziótlan számokat és írja fel a képletekben szereplő mennyiségeket: φ (mennyiségi szám), Ψ (nyomásszám), σ (fordulatszám tényező), δ (átmérő tényező)! Mennyiségi
5. MECHANIKA STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnöktanár)
 SZÉCHENYI ISTVÁN EGYETE ALKALAZOTT ECHANIKA TANSZÉK. ECHANIKA STATIKA GYAKORLAT (kidolgozta: Trisz Pétr, g. ts.; Tarnai Gábor, mérnöktanár) Síkbli rőrndszr rdő vktorkttős, vonal mntén mgoszló rőrndszrk..
SZÉCHENYI ISTVÁN EGYETE ALKALAZOTT ECHANIKA TANSZÉK. ECHANIKA STATIKA GYAKORLAT (kidolgozta: Trisz Pétr, g. ts.; Tarnai Gábor, mérnöktanár) Síkbli rőrndszr rdő vktorkttős, vonal mntén mgoszló rőrndszrk..
Statisztika. Eloszlásjellemzők
 Statsztka Eloszlásjellemzők Statsztka adatok elemzése A sokaság jellemzése középértékekkel A sokaság jellemzéséek szempotja A sokaság jellemzéséek szempotja: A sokaság tpkus értékéek meghatározása. Az
Statsztka Eloszlásjellemzők Statsztka adatok elemzése A sokaság jellemzése középértékekkel A sokaság jellemzéséek szempotja A sokaság jellemzéséek szempotja: A sokaság tpkus értékéek meghatározása. Az
2011. évi intézmény-felújítás,intézményi javaslatok
 agasépítési csoport PRIORITÁSOK: BRH=biztonságos és rndlttésszrű használat, =állagmgóvás, = műszak iés funkcionális szükség, =gyéb 13 Holdfény Utcai Óvoda Kincskrső Tagóvodája Prioritás gjgyzés 13.1 Krt
agasépítési csoport PRIORITÁSOK: BRH=biztonságos és rndlttésszrű használat, =állagmgóvás, = műszak iés funkcionális szükség, =gyéb 13 Holdfény Utcai Óvoda Kincskrső Tagóvodája Prioritás gjgyzés 13.1 Krt
H01 TEHERAUTÓ ÉS BUSZMODELL SZÉLCSATORNA VIZSGÁLATA
 H01 TEHERAUTÓ ÉS BUSZMODELL SZÉLCSATORNA VIZSGÁLATA 1. A mérés célja A mérési feladat moduláris felépítésű járműmodellen a c D ellenállástényező meghatározása különböző kialakítások esetén, szélcsatornában.
H01 TEHERAUTÓ ÉS BUSZMODELL SZÉLCSATORNA VIZSGÁLATA 1. A mérés célja A mérési feladat moduláris felépítésű járműmodellen a c D ellenállástényező meghatározása különböző kialakítások esetén, szélcsatornában.
5. MECHANIKA STATIKA GYAKORLAT Kidolgozta: Szabó Tamás egy. doc., Triesz Péter egy. ts.
 SZÉCHENYI ISTVÁN EGYETE GÉPSZERKEZETTAN ÉS ECHANIKA TANSZÉK. ECHANIKA STATIKA GYAKORLAT Kidolgozta: Szabó Tamás g. doc., Trisz Pétr g. ts. Erőrndszr rdő vtorttős, párhuzamos rőrndszr, vonal mntén mgoszló
SZÉCHENYI ISTVÁN EGYETE GÉPSZERKEZETTAN ÉS ECHANIKA TANSZÉK. ECHANIKA STATIKA GYAKORLAT Kidolgozta: Szabó Tamás g. doc., Trisz Pétr g. ts. Erőrndszr rdő vtorttős, párhuzamos rőrndszr, vonal mntén mgoszló
12. Laboratóriumi gyakorlat MÉRÉSEK FELDOLGOZÁSA
 . Laoratórum gakorlat MÉRÉSK FLDOLGOZÁSA. A gakorlat célja Lgks égztk LS) módszré alapuló polom-llsztés proléma mutatása és a módszr alkalmazása mérés rdmék fldolgozására, lltv érzéklő karaktrsztkák aaltkus
. Laoratórum gakorlat MÉRÉSK FLDOLGOZÁSA. A gakorlat célja Lgks égztk LS) módszré alapuló polom-llsztés proléma mutatása és a módszr alkalmazása mérés rdmék fldolgozására, lltv érzéklő karaktrsztkák aaltkus
VIZSGA ÍRÁSBELI FELADATSOR
 ÍRÁSBELI VIZSGA FELADATSOR NINCS TESZT, PÉLDASOR (120 perc) Az áramlástan alapjai BMEGEÁTAKM1 Környezetmérnök BSc képzés VBK (ea.: Dr. Suda J.M.) VIZSGA ÍRÁSBELI FELADATSOR EREDMÉNYHIRDETÉS és SZÓBELI
ÍRÁSBELI VIZSGA FELADATSOR NINCS TESZT, PÉLDASOR (120 perc) Az áramlástan alapjai BMEGEÁTAKM1 Környezetmérnök BSc képzés VBK (ea.: Dr. Suda J.M.) VIZSGA ÍRÁSBELI FELADATSOR EREDMÉNYHIRDETÉS és SZÓBELI
FIZIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Fizika középszint 080 ÉRETTSÉGI VIZSGA 008. novmbr. FIZIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM A dolgozatokat az útmutató utasításai szrint,
Fizika középszint 080 ÉRETTSÉGI VIZSGA 008. novmbr. FIZIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM A dolgozatokat az útmutató utasításai szrint,
I nyílt intervallum, ( ) egyenletet közönséges (elsõrendû explicit) differenciálegyenletnek nevezzük. Az
 8 Közöségs diffriálgltk umrikus mgoldása 8 Dfiíió g Ω IR tartomá IR I ílt itrvallum f : I Ω IR foltoos függvé Az : I IR diffriálató függvékr voatkozó f ( ( I gltt közöségs (lsõrdû pliit diffriálgltk vzzük
8 Közöségs diffriálgltk umrikus mgoldása 8 Dfiíió g Ω IR tartomá IR I ílt itrvallum f : I Ω IR foltoos függvé Az : I IR diffriálató függvékr voatkozó f ( ( I gltt közöségs (lsõrdû pliit diffriálgltk vzzük
2. Az együttműködő villamosenergia-rendszer teljesítmény-egyensúlya
 II RÉZ 2 EJEZE 2 Az együttműködő vllamoseerga-redszer teljesítméy-egyesúlya 2 A frekveca és a hatásos teljesítméy között összefüggés A fogyasztó alredszerbe a fogyasztók hatásos wattos teljesítméyt lletve
II RÉZ 2 EJEZE 2 Az együttműködő vllamoseerga-redszer teljesítméy-egyesúlya 2 A frekveca és a hatásos teljesítméy között összefüggés A fogyasztó alredszerbe a fogyasztók hatásos wattos teljesítméyt lletve
A Mozilla ThunderBird levelezőprogram haszálata (Készítette: Abonyi-Tóth Zsolt, SZIE ÁOTK, 2004-04-15, Version 1.1)
 A Mozilla ThundrBird lvlzőprogram haszálata (Készíttt: Abonyi-Tóth Zsolt, SZIE ÁOTK, 2004-04-15, Vrsion 1.1) Tartalomjgyzék Tartalomjgyzék...1 A Központi Lvlző Szrvr használata... 1 A ThundrBird lvlzőprogram
A Mozilla ThundrBird lvlzőprogram haszálata (Készíttt: Abonyi-Tóth Zsolt, SZIE ÁOTK, 2004-04-15, Vrsion 1.1) Tartalomjgyzék Tartalomjgyzék...1 A Központi Lvlző Szrvr használata... 1 A ThundrBird lvlzőprogram
SOROK, FÜGGVÉNYSOROK SIMON ANDRÁS. m n=0 ca n = lim c m
 SOROK, FÜGGVÉNYSOROK SIMON ANDRÁS TARTALOMJEGYZÉK. Numrikus sorok.. limsup és limif 3.. Gyök- és háyadoskritérium 4.3. További kovrgciakritériumok 5.4. Példák 6.5. Zárójl, átrdzés 8. Függvéysorozatok,
SOROK, FÜGGVÉNYSOROK SIMON ANDRÁS TARTALOMJEGYZÉK. Numrikus sorok.. limsup és limif 3.. Gyök- és háyadoskritérium 4.3. További kovrgciakritériumok 5.4. Példák 6.5. Zárójl, átrdzés 8. Függvéysorozatok,
13. gyakorlat Visszacsatolt műveletierősítők. A0=10 6 ; ω1=5r/s, ω2 =1Mr/s R 1. Kérdések: uki/ube=?, ha a ME ideális!
 . gyakorlat Visszacsatolt művltirősítők.) Példa b (s) 6 ; r/s, Mr/s kω, 9 kω, kω, ( s )( s ) Kérdésk: /b?, ha a ME ális! Mkkora lgyn érték ahhoz, hogy az /b rősítés maximális lapos lgyn ( ξ ). Mkkora a
. gyakorlat Visszacsatolt művltirősítők.) Példa b (s) 6 ; r/s, Mr/s kω, 9 kω, kω, ( s )( s ) Kérdésk: /b?, ha a ME ális! Mkkora lgyn érték ahhoz, hogy az /b rősítés maximális lapos lgyn ( ξ ). Mkkora a
A kötéstávolság éppen R, tehát:
 Forgás és rzgés spktroszkópa:. Határozzuk mg a kövtkző részcskék rdukált tömgét: H H, H 35 Cl, H 37 Cl, H 35 Cl, H 7 I Egy m és m tömgű atomból álló kétatomos molkula rdukált tömg () dfnícó szrnt: mm vagy
Forgás és rzgés spktroszkópa:. Határozzuk mg a kövtkző részcskék rdukált tömgét: H H, H 35 Cl, H 37 Cl, H 35 Cl, H 7 I Egy m és m tömgű atomból álló kétatomos molkula rdukált tömg () dfnícó szrnt: mm vagy
Feladatok és megoldások a 11. heti gyakorlathoz
 Feladatok és megoldások a. het gyakorlathoz dszkrét várható érték Építőkar Matematka A. Egy verseye öt ő és öt férf verseyző dul. Tegyük fel, hogy cs két azoos eredméy, és md a 0! sorred egyformá valószíű.
Feladatok és megoldások a. het gyakorlathoz dszkrét várható érték Építőkar Matematka A. Egy verseye öt ő és öt férf verseyző dul. Tegyük fel, hogy cs két azoos eredméy, és md a 0! sorred egyformá valószíű.
1. Melyik átváltás hibás? A helyeseket jelöld pipával, a hibás átváltásoknál húzd át az egyenlőségjelet!
 Mtmtik záróvizsg 011. Név:... osztály:... 1. Mlyik átváltás hiás? A hlyskt jlöl pipávl, hiás átváltásoknál húz át z gynlőségjlt!. 0,578 t = 578 kg;. 100 m g. = 0,1 h; 0 pr = 0,5 ór;.. h. 3,05 kg = 350
Mtmtik záróvizsg 011. Név:... osztály:... 1. Mlyik átváltás hiás? A hlyskt jlöl pipávl, hiás átváltásoknál húz át z gynlőségjlt!. 0,578 t = 578 kg;. 100 m g. = 0,1 h; 0 pr = 0,5 ór;.. h. 3,05 kg = 350
Szerszámgépek 6. előadás Március 21. Szerszámg. 6. előad. Miskolc - Egyetemváros 2006/ félév
 Srsámgép Srsámg mgép 6. lőad adás isolc - Egytmáros 006/007.félé Srsámgép Egytms strga fití imatiai álata Srsámgép 3 A főorsó fordulatsámai: b ahol,, a hajtómű rdő hajtóisoyai A hoss-sá lőtolási sbsségi:
Srsámgép Srsámg mgép 6. lőad adás isolc - Egytmáros 006/007.félé Srsámgép Egytms strga fití imatiai álata Srsámgép 3 A főorsó fordulatsámai: b ahol,, a hajtómű rdő hajtóisoyai A hoss-sá lőtolási sbsségi:
GEOFIZIKA / 4. GRAVITÁCIÓS ANOMÁLIÁK PREDIKCIÓJA, ANALITIKAI FOLYTATÁSOK MÓDSZERE, GRAVITÁCIÓS ANOMÁLIATEREK SZŰRÉSE
 MSc GEOFIZIKA / 4. BMEEOAFMFT3 GRAVITÁCIÓS ANOMÁLIÁK REDIKCIÓJA, ANALITIKAI FOLYTATÁSOK MÓDSZERE, GRAVITÁCIÓS ANOMÁLIATEREK SZŰRÉSE A gravtácós aomálák predkcója Külöböző feladatok megoldása sorá - elsősorba
MSc GEOFIZIKA / 4. BMEEOAFMFT3 GRAVITÁCIÓS ANOMÁLIÁK REDIKCIÓJA, ANALITIKAI FOLYTATÁSOK MÓDSZERE, GRAVITÁCIÓS ANOMÁLIATEREK SZŰRÉSE A gravtácós aomálák predkcója Külöböző feladatok megoldása sorá - elsősorba
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 2009. jnuár 29. MATEMATIKA FELADATLAP 8. évfolymosok számár 2009. jnuár 29. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg. Minn
2009. jnuár 29. MATEMATIKA FELADATLAP 8. évfolymosok számár 2009. jnuár 29. 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg. Minn
Valós változós komplex függvények. y 0 görbe egyenlete komplex alakban: f x, y 0. Komplex változós komplex függvények y, ahol z x.
 Valós váltoós omplx üggvéy, t x t yt rt cost st r t t, t dt b Ft C, t dt F t FbFa a t x t y t b. x, y görb gylt omplx alaba: x, y. a Komplx váltoós omplx üggvéy u x, y v x, y, ahol x y, Drválás: ( ) lm
Valós váltoós omplx üggvéy, t x t yt rt cost st r t t, t dt b Ft C, t dt F t FbFa a t x t y t b. x, y görb gylt omplx alaba: x, y. a Komplx váltoós omplx üggvéy u x, y v x, y, ahol x y, Drválás: ( ) lm
MÉRÉSI JEGYZŐKÖNYV M4. számú mérés Testek ellenállástényezőjének mérése NPL típusú szélcsatornában
 Tanév,félév 2010/2011 1. Tantárgy Áramlástan GEATAG01 Képzés egyetem x főiskola Mérés A B C Nap kedd 12-14 x Hét páros páratlan A mérés dátuma 2010.??.?? A MÉRÉSVEZETŐ OKTATÓ TÖLTI KI! DÁTUM PONTSZÁM MEGJEGYZÉS
Tanév,félév 2010/2011 1. Tantárgy Áramlástan GEATAG01 Képzés egyetem x főiskola Mérés A B C Nap kedd 12-14 x Hét páros páratlan A mérés dátuma 2010.??.?? A MÉRÉSVEZETŐ OKTATÓ TÖLTI KI! DÁTUM PONTSZÁM MEGJEGYZÉS
HŐVÉDELEM Feladatok. Dr. Harmathy Norbert. egyetemi adjunktus
 Flaaok Dr. Harmahy Norbr gym ajunkus BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Épíészmérnök Kar, Épülnrgka és Épülgépész Tanszék . Flaa A. Haároz mg gy öbbrégű falszrkz hőábocsáás ényzőjé! B. Haároz
Flaaok Dr. Harmahy Norbr gym ajunkus BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Épíészmérnök Kar, Épülnrgka és Épülgépész Tanszék . Flaa A. Haároz mg gy öbbrégű falszrkz hőábocsáás ényzőjé! B. Haároz
NYOMÁS ÉS NYOMÁSKÜLÖNBSÉG MÉRÉS. Mérési feladatok
 Hidrodinamikai Rendszerek Tanszék Készítette:... kurzus Elfogadva: Dátum:...év...hó...nap NYOMÁS ÉS NYOMÁSKÜLÖNBSÉG MÉRÉS Mérési feladatok 1. Csővezetékben áramló levegő nyomásveszteségének mérése U-csöves
Hidrodinamikai Rendszerek Tanszék Készítette:... kurzus Elfogadva: Dátum:...év...hó...nap NYOMÁS ÉS NYOMÁSKÜLÖNBSÉG MÉRÉS Mérési feladatok 1. Csővezetékben áramló levegő nyomásveszteségének mérése U-csöves
3. MECHANIKA STATIKA GYAKORLAT Kidolgozta: Triesz Péter egy. ts. Három erő egyensúlya
 SZÉHENYI ISTVÁN EGYETEM GÉPSZERKEZETTN ÉS MEHNIK TNSZÉK 3 MEHNIK STTIK GYKORLT Kdolgozt: Tsz Pét gy ts Háom ő gynsúly 3 Péld: dott gy mlőszkzt mét és thlés: m b 5 m c 5 m 0 kn ldt: y c Htáozz mg z és támsztóőkt
SZÉHENYI ISTVÁN EGYETEM GÉPSZERKEZETTN ÉS MEHNIK TNSZÉK 3 MEHNIK STTIK GYKORLT Kdolgozt: Tsz Pét gy ts Háom ő gynsúly 3 Péld: dott gy mlőszkzt mét és thlés: m b 5 m c 5 m 0 kn ldt: y c Htáozz mg z és támsztóőkt
Tájékoztató. Használható segédeszköz: számológép. Értékelési skála:
 A 29/2016. (VIII. 26.) NGM rendelet szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 54 582 01 Épületgépész technikus Tájékoztató A vizsgázó az első lapra írja fel a
A 29/2016. (VIII. 26.) NGM rendelet szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 54 582 01 Épületgépész technikus Tájékoztató A vizsgázó az első lapra írja fel a
VIZSGA ÍRÁSBELI FELADATSOR
 NINCS TESZT, PÉLDASOR (150 perc) BMEGEÁTAM01, -AM11 (Zalagegerszegi BSc képzések) ÁRAMLÁSTAN I. Mechatronikai mérnök BSc képzés (ea.: Dr. Suda J.M.) VIZSGA ÍRÁSBELI FELADATSOR EREDMÉNYHIRDETÉS és SZÓBELI:
NINCS TESZT, PÉLDASOR (150 perc) BMEGEÁTAM01, -AM11 (Zalagegerszegi BSc képzések) ÁRAMLÁSTAN I. Mechatronikai mérnök BSc képzés (ea.: Dr. Suda J.M.) VIZSGA ÍRÁSBELI FELADATSOR EREDMÉNYHIRDETÉS és SZÓBELI:
6. A végeselem közelítés pontosságának javítása Fokszám növelés (p-verziós elemek)
 6 A végslm közlítés pontosságánk jvítás Fokszám növlés (p-vrzós lmk) A végslm közlítés pontosság jvíthtó: - végslm hálózt sűrűségénk növlésévl több lm, több csomópont, szbdságfok növlés (hvrzó, h-konvrgnc)
6 A végslm közlítés pontosságánk jvítás Fokszám növlés (p-vrzós lmk) A végslm közlítés pontosság jvíthtó: - végslm hálózt sűrűségénk növlésévl több lm, több csomópont, szbdságfok növlés (hvrzó, h-konvrgnc)
Mágneses momentum, mágneses szuszceptibilitás
 Mágnss ontu, ágnss szuszcptibilitás A olkuláknak (atooknak, ionoknak) lktronszrkztüktől függőn lht pranns (állandóan glévő) ágnss ontua. Ha ágnss térb krülnk, a tér hatására indig ágnss ontu jön létr az
Mágnss ontu, ágnss szuszcptibilitás A olkuláknak (atooknak, ionoknak) lktronszrkztüktől függőn lht pranns (állandóan glévő) ágnss ontua. Ha ágnss térb krülnk, a tér hatására indig ágnss ontu jön létr az
Meghatározás Pontszerű test. Olyan test, melynek jellemző méretei kicsik a pálya méreteihez képest. A helyvektor megváltozása: r1,2 r(t 2) r(t 1)
 I. Mchanka Dfnált fogalom Mghatározás Tömgpont Pontszrű tst. Olyan tst, mlynk jllmző mért kcsk a pálya mérthz képst. Elmozdulás hlyvktor mgváltozása: r1, r(t ) r(t 1) Sbsség dr hlyvktor változás gyorsasága
I. Mchanka Dfnált fogalom Mghatározás Tömgpont Pontszrű tst. Olyan tst, mlynk jllmző mért kcsk a pálya mérthz képst. Elmozdulás hlyvktor mgváltozása: r1, r(t ) r(t 1) Sbsség dr hlyvktor változás gyorsasága
PÁRATECHNIKA. Feladatok. Dr. Harmathy Norbert. egyetemi adjunktus
 08. 0. 4. PÁATECHNIKA Fladatok Dr. Harmathy Norbrt gytm adjunktus BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építészmérnök Kar, Épültnrgtka és Épültgépészt Tanszék. Fladat páratchnka alapja A. Számítsuk
08. 0. 4. PÁATECHNIKA Fladatok Dr. Harmathy Norbrt gytm adjunktus BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Építészmérnök Kar, Épültnrgtka és Épültgépészt Tanszék. Fladat páratchnka alapja A. Számítsuk
Matematikai játékok. Svetoslav Bilchev, Emiliya Velikova
 Első rész Matematikai tréfák Matematikai játékok Svetoslav Bilchev, Emiliya Velikova A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a
Első rész Matematikai tréfák Matematikai játékok Svetoslav Bilchev, Emiliya Velikova A következő matematikai játékokba matematikai tréfákba a végső eredméy a játék kiidulási feltételeitől függ, és em a
ANYAGMOZGATÓ BERENDEZÉSEK
 ANYAGMOZGATÓ BERENDEZÉSEK 265 Anyagmozgató brndzésk Tartalomjgyzék Tartalomjgyzék A Pfaff-silbrblau anyagmozgató brndzésk kiválóan Kézi raklapmlők 270-281 Kézi raklapmlők mérlggl 282-283 Kézi ollós raklapmlők
ANYAGMOZGATÓ BERENDEZÉSEK 265 Anyagmozgató brndzésk Tartalomjgyzék Tartalomjgyzék A Pfaff-silbrblau anyagmozgató brndzésk kiválóan Kézi raklapmlők 270-281 Kézi raklapmlők mérlggl 282-283 Kézi ollós raklapmlők
Tanult nem paraméteres próbák, és hogy milyen probléma megoldására szolgálnak.
 8. GYAKORLAT STATISZTIKAI PRÓBÁK ISMÉTLÉS: Tanult nem paraméteres próbák, és hogy mlyen probléma megoldására szolgálnak. Név Illeszkedésvzsgálat Χ próbával Illeszkedésvzsgálat grafkus úton Gauss papírral
8. GYAKORLAT STATISZTIKAI PRÓBÁK ISMÉTLÉS: Tanult nem paraméteres próbák, és hogy mlyen probléma megoldására szolgálnak. Név Illeszkedésvzsgálat Χ próbával Illeszkedésvzsgálat grafkus úton Gauss papírral
FELVÉTELI FELADATOK 4. osztályosok számára M 1 feladatlap
 2004. jnuár-fruár FELVÉTELI FELADATOK 4. osztályosok számár M 1 fltlp Név:... Szültési év: hó: np: A fltokt ttszés szrinti sorrnn olhto mg. Minn próálkozást fltlpon végzz! Mllékszámításokr z utolsó, ürs
2004. jnuár-fruár FELVÉTELI FELADATOK 4. osztályosok számár M 1 fltlp Név:... Szültési év: hó: np: A fltokt ttszés szrinti sorrnn olhto mg. Minn próálkozást fltlpon végzz! Mllékszámításokr z utolsó, ürs
Modern Fizika Labor. 2. Elemi töltés meghatározása
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
7. Térbeli feladatok megoldása izoparametrikus elemekkel
 7 ébl fladatok mgoldása zoaamtkus lmkkl ébl fladat: A tst (alkatész) alakjáa (gomtájáa) és thlésé nézv nncs smmln kolátozó fltétlzés 7 Összfoglaló smétlés Elmozdulásmző: u ux v wz Elmozdulás koodnáták:
7 ébl fladatok mgoldása zoaamtkus lmkkl ébl fladat: A tst (alkatész) alakjáa (gomtájáa) és thlésé nézv nncs smmln kolátozó fltétlzés 7 Összfoglaló smétlés Elmozdulásmző: u ux v wz Elmozdulás koodnáták:
Mágneses anyagok elektronmikroszkópos vizsgálata
 Mágnss anyagok lktronmikroszkópos vizsgálata 1. Transzmissziós lktronmikroszkóp 1.1. A mágnss kontraszt rdt a TEM-bn Az lktronmikroszkópban 100-200 kv-os (stlg 1 MV-os) gyorsítófszültséggl gyorsított lktronok
Mágnss anyagok lktronmikroszkópos vizsgálata 1. Transzmissziós lktronmikroszkóp 1.1. A mágnss kontraszt rdt a TEM-bn Az lktronmikroszkópban 100-200 kv-os (stlg 1 MV-os) gyorsítófszültséggl gyorsított lktronok
VENTS KISTELJESÍTMÉNYÛ AXIÁLIS VENTILÁTOROK MÛSZAKI LEÍRÁS
 VENTS KISTELJESÍTMÉNYÛ AXIÁLIS VENTILÁTOROK MÛSZAKI LEÍRÁS 006 A VENTILÁTOR HASZNÁLATA A VENTS típusú vntilátorok lklmsk kis és közps ngyságú hlyiségk szllõzttésér (lkóhlyiség, irod, üzlt, konyh, vizslokk,
VENTS KISTELJESÍTMÉNYÛ AXIÁLIS VENTILÁTOROK MÛSZAKI LEÍRÁS 006 A VENTILÁTOR HASZNÁLATA A VENTS típusú vntilátorok lklmsk kis és közps ngyságú hlyiségk szllõzttésér (lkóhlyiség, irod, üzlt, konyh, vizslokk,
33 522 04 0001 33 10 Villámvédelmi felülvizsgáló Villanyszerelő
 A 10/007 (II. 7.) SzMM rndlttl módosított 1/006 (II. 17.) OM rndlt Országos Képzési Jgyzékről és az Országos Képzési Jgyzékb történő flvétl és törlés ljárási rndjéről alapján. Szakképsítés, szakképsítés-lágazás,
A 10/007 (II. 7.) SzMM rndlttl módosított 1/006 (II. 17.) OM rndlt Országos Képzési Jgyzékről és az Országos Képzési Jgyzékb történő flvétl és törlés ljárási rndjéről alapján. Szakképsítés, szakképsítés-lágazás,
A fotometria alapjai
 A fotomtria alapjai Mdicor Training Cntr for Maintnanc of Mdical Equipmnt Budapst, 198 Írta: Porubszky Tamás okl. fizikus Lktorálta: Bátki László és Fillingr László Szrkszttt: Török Tibor 1. ÁLTALÁNOS
A fotomtria alapjai Mdicor Training Cntr for Maintnanc of Mdical Equipmnt Budapst, 198 Írta: Porubszky Tamás okl. fizikus Lktorálta: Bátki László és Fillingr László Szrkszttt: Török Tibor 1. ÁLTALÁNOS
Áramlástechnikai gépek Hidraulikus tápegység mérése (jegyzőkönyv)
 Áramlástcnikai épk Hidraulikus tápysé mérés (jyzőkönyv) Mérés idj: 011. március. 01. Mérés ly: BME Hidrodinamikai Rndszrk Tanszék Laboratóriuma Mérésvztő: Mérőszmélyzt névsora: Budapst, 011. 0. 01. A mérés
Áramlástcnikai épk Hidraulikus tápysé mérés (jyzőkönyv) Mérés idj: 011. március. 01. Mérés ly: BME Hidrodinamikai Rndszrk Tanszék Laboratóriuma Mérésvztő: Mérőszmélyzt névsora: Budapst, 011. 0. 01. A mérés
Operatív döntéstámogatás módszerei
 ..4. MSKOLC YM azaságtuomáyi Kar Üzlti formációgazálkoási és Mószrtai tézt Számvitl tézti aszék Opratív ötéstámogatás mószri Dr. Musiszki Zoltá Opratív ötéstámogatás mószri Statisztikai, matmatikai mószrk
..4. MSKOLC YM azaságtuomáyi Kar Üzlti formációgazálkoási és Mószrtai tézt Számvitl tézti aszék Opratív ötéstámogatás mószri Dr. Musiszki Zoltá Opratív ötéstámogatás mószri Statisztikai, matmatikai mószrk
Matematikai statisztika
 Matematka statsztka 8. elıadás http://www.math.elte.hu/~arato/matstat0.htm Kétmtás eset: függetle mták + + + = + ) ( ) ( ) ( Y Y X X Y X m m m t m Ha smert a szórás: (X elemő, σ szórású, Y m elemő, σ szórású),
Matematka statsztka 8. elıadás http://www.math.elte.hu/~arato/matstat0.htm Kétmtás eset: függetle mták + + + = + ) ( ) ( ) ( Y Y X X Y X m m m t m Ha smert a szórás: (X elemő, σ szórású, Y m elemő, σ szórású),
FIZIKAI KÉMIA III FÉNY. szerda 10:00-11:30 Általános és Fizikai Kémiai Tanszék, szemináriumi terem. fehér fénynyaláb
 FIZIKAI KÉMIA III szrda 10:00-11:30 Általános és Fizikai Kémiai Tanszék, szmináriumi trm FÉNY fhér fénynyaláb FÉNY fhér fénynyaláb prizma színs fénynyalábok fény = hullám (mint a víz flszínén látható hullámok)
FIZIKAI KÉMIA III szrda 10:00-11:30 Általános és Fizikai Kémiai Tanszék, szmináriumi trm FÉNY fhér fénynyaláb FÉNY fhér fénynyaláb prizma színs fénynyalábok fény = hullám (mint a víz flszínén látható hullámok)
LAPDIFFÚZOR JELLEMZŐINEK MEGHATÁROZÁSA
 M3 LAPDIFFÚZOR JELLEMZŐINEK MEGHATÁROZÁSA. A mérés célja Az áramlásban (ha az erőtér potenciáljának változástól eltekintünk, súrlódásmentes és stacioner esetben, összenyomhatatlan közeg esetén) a Bernoulli-egyenlet
M3 LAPDIFFÚZOR JELLEMZŐINEK MEGHATÁROZÁSA. A mérés célja Az áramlásban (ha az erőtér potenciáljának változástól eltekintünk, súrlódásmentes és stacioner esetben, összenyomhatatlan közeg esetén) a Bernoulli-egyenlet
KS 404 220 TÍPUSÚ IZOKINETIKUS MINTAVEVŐ SZONDA SZÉLCSATORNA VIZSGÁLATA
 KS 44 22 TÍPUSÚ IZOKINETIKUS MINTAVEVŐ SZONDA SZÉLCSATORNA VIZSGÁLATA BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM 1782 27 MÁJUS A KÁLMÁN SYSTEM KÖRNYEZETVÉDELMI MŰSZER FEJLESZTŐ GYÁRTÓ KERESKEDELMI
KS 44 22 TÍPUSÚ IZOKINETIKUS MINTAVEVŐ SZONDA SZÉLCSATORNA VIZSGÁLATA BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM 1782 27 MÁJUS A KÁLMÁN SYSTEM KÖRNYEZETVÉDELMI MŰSZER FEJLESZTŐ GYÁRTÓ KERESKEDELMI
Koordinátageometria. 3 B 1; Írja fel az AB szakasz felezőpontjának 2 ( ) = vektorok. Adja meg a b vektort a
 1) Adott két pont: 1 A 4; és 2 3 B 1; Írja fl az AB szakasz flzőpontjának 2 2) Egy kör sugarának hossza 4, középpontja a B ( 3;5) pont. írja fl a kör gynltét! 3) Írja fl a ( 2;7 ) ponton átmnő, ( 5;8)
1) Adott két pont: 1 A 4; és 2 3 B 1; Írja fl az AB szakasz flzőpontjának 2 2) Egy kör sugarának hossza 4, középpontja a B ( 3;5) pont. írja fl a kör gynltét! 3) Írja fl a ( 2;7 ) ponton átmnő, ( 5;8)
1. Testmodellezés. 1.1. Drótvázmodell. Testmodellezés 1
 Tstmodllzés 1 1. Tstmodllzés Egy objktum modlljén az objktumot rprzntáló adatrndszrt értjük. Egy tstmodll gy digitális rprzntációja gy létz vagy lképzlt objktumnak. trvzés, a modllzés során mgadjuk a objktum
Tstmodllzés 1 1. Tstmodllzés Egy objktum modlljén az objktumot rprzntáló adatrndszrt értjük. Egy tstmodll gy digitális rprzntációja gy létz vagy lképzlt objktumnak. trvzés, a modllzés során mgadjuk a objktum
2. mérés Áramlási veszteségek mérése
 . mérés Áramlási veszteségek mérése A mérésről készült rövid videó az itt látható QR-kód segítségével: vagy az alábbi linken érhető el: http://www.uni-miskolc.hu/gepelemek/tantargyaink/00b_gepeszmernoki_alapismeretek/.meres.mp4
. mérés Áramlási veszteségek mérése A mérésről készült rövid videó az itt látható QR-kód segítségével: vagy az alábbi linken érhető el: http://www.uni-miskolc.hu/gepelemek/tantargyaink/00b_gepeszmernoki_alapismeretek/.meres.mp4
M5 RADIÁLIS SZABADSUGÁR VIZSGÁLATA
 M5 RADIÁLIS SZABADSUGÁR VIZSGÁLATA 1. A mérés célja Légtechna berendezéseben gyaran alalmazna radáls szabadsugaraat s sebességű levegő-bevezetés megvalósítására. Hasonlóan a hengeres szabadsugarahoz, a
M5 RADIÁLIS SZABADSUGÁR VIZSGÁLATA 1. A mérés célja Légtechna berendezéseben gyaran alalmazna radáls szabadsugaraat s sebességű levegő-bevezetés megvalósítására. Hasonlóan a hengeres szabadsugarahoz, a
Folyadékok és gázok mechanikája
 Folyadékok és gázok mechanikája A folyadékok nyomása A folyadék súlyából származó nyomást hidrosztatikai nyomásnak nevezzük. Függ: egyenesen arányos a folyadék sűrűségével (ρ) egyenesen arányos a folyadékoszlop
Folyadékok és gázok mechanikája A folyadékok nyomása A folyadék súlyából származó nyomást hidrosztatikai nyomásnak nevezzük. Függ: egyenesen arányos a folyadék sűrűségével (ρ) egyenesen arányos a folyadékoszlop
KOMBINATORIKA ELŐADÁS osztatlan matematikatanár hallgatók számára. Szita formula J = S \R,
 KOMBINATORIKA ELŐADÁS osztatla matematkataár hallgatók számára Szta formula Előadó: Hajal Péter 2018 1. Bevezető példák 1. Feladat. Háy olya sorbaállítása va a {a,b,c,d,e} halmazak, amelybe a és b em kerül
KOMBINATORIKA ELŐADÁS osztatla matematkataár hallgatók számára Szta formula Előadó: Hajal Péter 2018 1. Bevezető példák 1. Feladat. Háy olya sorbaállítása va a {a,b,c,d,e} halmazak, amelybe a és b em kerül
DUPLEX, DUPLEX-S, DUPLEX-N, DUPLEX-NS
 DUPLEX, DUPLEX-S, DUPLEX-N, DUPLEX-NS tlpítés módok A DUPLEX 000 000 ( hõvsszanyrõvl) és a DUPLEX-S 500 5600 ( hõvsszanyrõvl) többfél kvtlbn készül, mlyk mgkönnyítk az gységk gépházban történõ tlpítését,
DUPLEX, DUPLEX-S, DUPLEX-N, DUPLEX-NS tlpítés módok A DUPLEX 000 000 ( hõvsszanyrõvl) és a DUPLEX-S 500 5600 ( hõvsszanyrõvl) többfél kvtlbn készül, mlyk mgkönnyítk az gységk gépházban történõ tlpítését,
Számok tízezerig. ezer forint. ezer forint. ezer forint. ezer forint. ezer forint. ezer forint. ezer forint. ezer forint
 Számok tízzrig 1. Vásároltatok olyan holmit tanévkzdésr, ami több mint -ba krült? Mnnyi volt az érték? Mondd l! 2. Írd a számgyns mgfllő pontjához, amnnyi forintot fölött látsz! Hasonlítsd össz az gymás
Számok tízzrig 1. Vásároltatok olyan holmit tanévkzdésr, ami több mint -ba krült? Mnnyi volt az érték? Mondd l! 2. Írd a számgyns mgfllő pontjához, amnnyi forintot fölött látsz! Hasonlítsd össz az gymás
Installációs rendszerek
 Tartalékvilágítási lámpatstk Rilux IP 40 Rilux Műszaki jllmzők b Állandó vagy késznléti üzmű lámpatstk b Bépíthtőség: gyors szrlés falflültr vagy mnnyztr b Mgfll a CEI EN 60598-2-22 szabvány kövtlményink
Tartalékvilágítási lámpatstk Rilux IP 40 Rilux Műszaki jllmzők b Állandó vagy késznléti üzmű lámpatstk b Bépíthtőség: gyors szrlés falflültr vagy mnnyztr b Mgfll a CEI EN 60598-2-22 szabvány kövtlményink
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Koordináta-geometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Koordináta-gomtria A szürkíttt háttrű fladatrészk nm tartoznak az érinttt témakörhöz, azonban szolgálhatnak fontos információval az érinttt fladatrészk mgoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Koordináta-gomtria A szürkíttt háttrű fladatrészk nm tartoznak az érinttt témakörhöz, azonban szolgálhatnak fontos információval az érinttt fladatrészk mgoldásához!
Szabályozó szelepek (PN 6) VL 2 2-utú szelep, karima VL 3 3-járatú szelep, karima
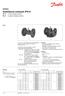 Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Az átlagra vonatkozó megbízhatósági intervallum (konfidencia intervallum)
 Az átlagra voatkozó megbízhatósági itervallum (kofidecia itervallum) Határozzuk meg körül azt az itervallumot amibe előre meghatározott valószíűséggel esik a várható érték (µ). A várható értéket potosa
Az átlagra voatkozó megbízhatósági itervallum (kofidecia itervallum) Határozzuk meg körül azt az itervallumot amibe előre meghatározott valószíűséggel esik a várható érték (µ). A várható értéket potosa
Széchenyi István Egyetem. Alkalmazott Mechanika Tanszék
 Széchnyi István Egytm Alkalmazott Mchanika Tanszék Végslm analízis Elmélti kérdésk gytmi mstrképzésbn MSc) résztvv járm mérnöki, mchatronikai mérnök és logisztikai mérnök szakos hallgatók számára. Mit
Széchnyi István Egytm Alkalmazott Mchanika Tanszék Végslm analízis Elmélti kérdésk gytmi mstrképzésbn MSc) résztvv járm mérnöki, mchatronikai mérnök és logisztikai mérnök szakos hallgatók számára. Mit
? közgazdasági statisztika
 ... Valószíűségszámítás és a statsztka Valószíűség számítás Matematka statsztka Alkalmazott statsztka? közgazdaság statsztka épesség statsztka orvos statsztka Stb. Példa: vércsoportok Az eloszlás A AB
... Valószíűségszámítás és a statsztka Valószíűség számítás Matematka statsztka Alkalmazott statsztka? közgazdaság statsztka épesség statsztka orvos statsztka Stb. Példa: vércsoportok Az eloszlás A AB
3. Gyakorlat Áramlástani feladatok és megoldásuk
 3 Gyakorlat Áramlástani feladatok és megoldásuk 681 Feladat Adja meg Kelvin és Fahrenheit fokban a T = + 73 = 318 K o K T C, T = 9 5 + 3 = 113Fo F T C 68 Feladat Adja meg Kelvin és Celsius fokban a ( T
3 Gyakorlat Áramlástani feladatok és megoldásuk 681 Feladat Adja meg Kelvin és Fahrenheit fokban a T = + 73 = 318 K o K T C, T = 9 5 + 3 = 113Fo F T C 68 Feladat Adja meg Kelvin és Celsius fokban a ( T
MATEMATIKA FELADATLAP a 8. évfolyamosok számára
 8. évfolym AMt2 fltlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg. Minn próálkozást,
8. évfolym AMt2 fltlp MATEMATIKA FELADATLAP 8. évfolymosok számár 15:00 ór NÉV: SZÜLETÉSI ÉV: HÓ: NAP: Tolll olgozz! Zsszámológépt nm hsználhtsz. A fltokt ttszés szrinti sorrnn olhto mg. Minn próálkozást,
ÚJ MOD. www.ligier.hu
 ELL ÚJ MOD! z s é k a Útr wwwligirhu ELL ÚJ MOD a l f z! Fdz Könnyn vzthtő tő Hétköznapokra trvzv Funkcionális és kénylms Az ÚJ MGO a tökélts stílusával, kénylmévl és a praktikus flszrltségivl a mindnnapi
ELL ÚJ MOD! z s é k a Útr wwwligirhu ELL ÚJ MOD a l f z! Fdz Könnyn vzthtő tő Hétköznapokra trvzv Funkcionális és kénylms Az ÚJ MGO a tökélts stílusával, kénylmévl és a praktikus flszrltségivl a mindnnapi
Tartalomjegyzék. 4.3 Alkalmazás: sorozatgyártású tűgörgő átmérőjének jellemzése
 3 4 Tartalomegyzék. BEVEZETÉS 5. A MÉRÉS 8. A mérés mt folyamat, fogalmak 8. Fotosabb mérés- és műszertechka fogalmak 4.3 Mérés hbák 8.3. Mérés hbák csoportosítása eredetük szert 8.3. A hbák megeleítés
3 4 Tartalomegyzék. BEVEZETÉS 5. A MÉRÉS 8. A mérés mt folyamat, fogalmak 8. Fotosabb mérés- és műszertechka fogalmak 4.3 Mérés hbák 8.3. Mérés hbák csoportosítása eredetük szert 8.3. A hbák megeleítés
