Az ESTPHAD módszer fejlesztése és alkalmazása kettő-, három- és négyalkotós rendszerek likvidusz hőmérsékletének közelítésére
|
|
|
- Enikő Gálné
- 8 évvel ezelőtt
- Látták:
Átírás
1 Kerpely Antal Anyagtudományok és Tehnológiák Doktori skola Az ESTPHAD módszer fejlesztése és alkalmazása kettő- három- és négyalkotós rendszerek likvidusz hőmérsékletének közelítésére PhD értekezés Mende Tamás Okleveles kohómérnök Tudományos vezető Dr. Roósz András akadémikus
2 Mende Tamás PhD értekezés Tartalomjegyzék Tartalomjegyzék. EVEZETÉS ÉLKTŰZÉS A FÁZSDAGRAM SZÁMÍTÁS ALAPJA A fázisdiagram számítás kialakulása A ALPHAD típusú számítások kialakulása A fázisdiagram számítási módszerek felépítése AZ ESTPHAD FÁZSDAGRAM SZÁMÍTÁS MÓDSZER Az ESTPHAD számítási módszer termodinamikai alapjai A számítás menete Adatgyűjtés A likvidusz hőmérséklet számítása A számított adatbázis elemzése AZ ESTPHAD MÓDSZER ALKALMAZÁSA KÜLÖNÖZŐ LKVDUSZ ÉS SZÉTVÁLÁS GÖRÉK ESETÉN Új paraméterek bevezetése a nevezetes pontok számítására Tiszta alkotó olvadáspontjában kezdődő likvidusz görbék A likvidusz görbe korlátlan oldhatóság esetén A likvidusz görbe az A alkotótól egy eutektikus hőmérsékletig tart A likvidusz görbe az A alkotótól peritektikus hőmérsékletig tart A likvidusz görbének minimum vagy maximum pontja van Nyílt maximummal képződő vegyület likvidusz görbéje A továbbiakban alkalmazandó polinom típus megválasztása Zárt maximummal képződő vegyület vagy szilárdoldat likvidusz görbéje Zárt maximummal szilárdoldat kristályosodik Zárt maximummal vegyület kristályosodik Szétválási hőmérséklet számítása Új paraméterek bevezetése NÉGYALKOTÓS ODRENDSZER LKVDUSZ HŐMÉRSÉKLETÉNEK SZÁMÍTÁSA inér rendszerek MgO Al 2 O 3 rendszer MgO ao rendszer... 8
3 Mende Tamás PhD értekezés Tartalomjegyzék MgO SiO 2 rendszer Ternér rendszerek MgO Al 2 O 3 ao rendszer MgO ao SiO 2 rendszer MgO Al 2 O 3 SiO 2 rendszer Kvaternér rendszer MgO ao Al 2 O 3 SiO 2 rendszer A SZÁMÍTÁSHOZ FELHASZNÁLT ADATMENNYSÉG HATÁSA A SZÁMÍTOTT EREDMÉNYEK PONTOSSÁGÁRA MÉRÉS HA KERESŐ ALGORTMUS KDOLGOZÁSA A mérési hibás adatok kiszűrésének fontossága A mérési hiba kereső algoritmus ÖSSZEFOGLALÁS ÚJ TUDOMÁNYOS EREDMÉNYEK AZ ÉRTEKEZÉS TUDOMÁNYOS EREDMÉNYENEK FELHASZNÁLHATÓSÁGA KÖSZÖNETNYLVÁNÍTÁS RODALOMJEGYZÉK
4 Mende Tamás PhD értekezés evezetés élkitűzés. EVEZETÉS ÉLKTŰZÉS Az anyagtudomány területén számos egyéb iparághoz tudományterülethez hasonlóan robbanásszerű fejlődés ment végbe a. század második felében köszönhetően annak hogy egyre jobban és alaposabban váltak ismertté a különböző anyagok szerkezetei tulajdonságai és a tulajdonságaikat befolyásoló tényezők. Alapvetően és leglátványosabban az anyagtudomány fejlődése tudja garantálni a mindenkori ipari és kutatási fejlődést a világban hiszen a folyamatos innováió kizárólag újonnan kifejlesztett speiális tulajdonságokkal rendelkező anyagok alkalmazásával valósítható meg. Az anyagtudomány kezében az egyik legrégibb de a mai napig az egyik leghasznosabb eszköz az ún. egyensúlyi fázisdiagram hiszen a felhasználandó anyagok szerkezetében hőmérséklet és konentráió változás hatására bekövetkezendő átalakulások ismerete elengedhetetlen a tervezés-fejlesztés folyamatában. Egyensúlyi fázisdiagramok a korai időkben főként grafikus formában álltak az ipar és a kutatók rendelkezésére azonban az 97-es évektől kezdődően a számítástehnika fejlődésével párhuzamosan megjelentek majd rohamosan fejlődni kezdtek a termodinamikai alapokkal rendelkező fázisdiagram számítási módszerek. A fázisdiagram számító algoritmusok és szoftverek szerepe nagyon hangsúlyos az ipari és kutatás-fejlesztési alkalmazásokban mert ezeket a szoftvereket vagy az általuk előállított kellően részletes és pontos adatbázisokat akár szimuláiós programokba akár a mindennapi termelésbe folyamat-szabályozás ellenőrzés beépítve jelentős előnyökre lehet szert tenni. A fázisdiagram számítási módszereknek éppen ezért számos feltételt kell teljesíteni. A megfelelő számítási pontosság teljesítése és a termodinamikai alapok mellett a felhasználhatóság érdekében törekedni kell a számítási algoritmus minél egyszerűbbé átláthatóbbá és gyorsabbá tételére. Az egyensúlyi fázisdiagram számítás területén régóta ismert és elismert az ún. ALPHAD ALulation of PHAse Diagram megközelítés amely azonban bonyolult számítási algoritmussal rendelkezik a számított függvények paramétereit mérési adatok felhasználásával hosszadalmas iteráiós lépésekben optimalizálják. A Miskoli Egyetemen az 99-es évek végén Dr. Roósz András és Dr. Kaptay György kidolgozta az ún. ESTPHAD ESTimation of PHAse Diagrams módszert melynek számítási algoritmusa szintén termodinamikai egyenletekből van levezetve azonban a módszerrel a fázisdiagramok feldolgozása és az eredmények alkalmazása sokkal egyszerűbb érthetőbb a számítási idő pedig nagyságrendekkel rövidebb mint a ALPHAD módszer esetében. 3
5 Mende Tamás PhD értekezés evezetés élkitűzés PhD értekezésem elején rövid áttekintést nyújtok az egyensúlyi fázisdiagramok számításának kialakulásáról röviden bemutatom a ALPHAD módszert illetve a ALPHAD eljárás felépítését felvázolom hogyan lehet eljutni a mért adatoktól vagy első elveken alapuló számításoktól a számított egyensúlyi fázisdiagramokig. A ALPHAD által a számításokban alkalmazott termodinamikai modellek optimalizáló eljárások részletesebb taglalásától eltekintek mivel saját tématerületemen az ESTPHAD módszer fejlesztésében ezekkel nem foglalkozom. Az ESTPHAD módszer termodinamikai alapjait a likvidusz hőmérséklet számítására szolgáló egyenlet levezetését azonban bővebben ismertetem. Az ESTPHAD módszert a kezdetekkor a színelem szilárdoldatának likvidusz és szolidusz hőmérsékletének valamint a megoszlási hányadosnak a számítására alkalmazták. Az egyensúlyi fázisdiagram számítási eljárások esetében azonban fontos követelmény a felhasználhatóság szempontjából hogy a fázisdiagram teljes összetétel tartományában lehessen alkalmazni. Amióta bekapsolódtam a kutatásba elsősorban a likvidusz hőmérséklet számítása a fő tématerületem PhD értekezésemben is likvidusz illetve szétválási hőmérséklet számításával foglalkozom. Annak érdekében hogy az ESTPHAD módszer a likvidusz hőmérséklet számítására a teljes egyensúlyi fázisdiagramban alkalmazható legyen első lépésként feltérképeztem hogy a különböző rendszerekben milyen típusú likvidusz görbékkel találkozhatunk és azok feldolgozása során milyen problémák adódhatnak. Foglalkoztam tiszta alkotó olvadáspontjából kiinduló másik alkotó olvadáspontjáig 2 eutektikus és 3 peritektikus hőmérsékletig tartó 4 minimum- vagy maximumponttal rendelkező likvidusz görbékkel 5 nyílt maximummal kristályosodó vegyület 6 zárt maximummal kristályosodó szilárdoldat és 7 vegyület likvidusz görbéjével illetve 8 monotektikus rendszerek szétválási hőmérsékletének leírásával. Az egyensúlyi fázisdiagramokban bizonyos átalakulások színelem és vegyület kristályosodása eutektikus peritektikus vagy monotektikus folyamatok egy adott hőmérsékleten mennek végbe azok hőmérséklet értéke nagy pontossággal mérhető így ezek nagy pontosságú számítása is alapvető feladat. Az ún. nonvariáns pontok számítására új paramétereket vezettem be az ESTPHAD egyenletbe. Fontosnak tartom megjegyezni hogy az ESTPHAD módszerrel a számításokhoz felhasznált adatokhoz viszonyítom a számítások pontosságát így természetesen a nonvariáns pontok vagy például a szétválási görbe esetében a kritikus hőmérséklet nagy pontosságú számítását is a felhasznált adatokhoz viszonyítva kell érteni. Az ESTPHAD módszer hierarhikus felépítésének köszönhetően alkalmas többalkotós fázisdiagramok feldolgozására is. Négyalkotós oxid-rendszer MgO-Al 2 O 3 -ao- 4
6 Mende Tamás PhD értekezés evezetés élkitűzés SiO 2 MgO-ban dús fázisának likvidusz hőmérsékletét számítottam ki. Megvizsgáltam hogy az ESTPHAD módszer pontosságára milyen hatással van a felhasznált adatok mennyisége. A megfelelő pontosságú számításhoz szükséges minimális adatmennyiség meghatározásának elsősorban a kísérleti tervek összeállításánál van jelentősége hiszen nem mindegy hogy egyegy likvidusz görbe meghatározásához hány próbadarabot hány tagú ötvözetsort kell elkészíteni és megvizsgálni. A mérési eredmények felhasználása során azonban fontos lépés a mérési hibát tartalmazó adatok kiszűrése. Kidolgoztam egy mérési hiba kereső algoritmust amely segítségével az ESTPHAD módszer alkalmazása során ki lehet mutatni hogy mely értékek nem megfelelőek melyeket kell törölni az adatbázisból. Ezáltal a számítások pontossága is növelhető. A fentiek alapján az értekezés élkitűzése: Az ESTPHAD módszer továbbfejlesztése pontosságát használhatóságát befolyásoló tényezők vizsgálata likvidusz és szétválási hőmérséklet számítása két és többalkotós rendszerek esetén valamint a fázisdiagramok alapjául szolgáló mérések tervezésének és a mérési hibák kiszűrésének segítése. 5
7 Mende Tamás PhD értekezés rodalmi feldolgozás 2. A FÁZSDAGRAM SZÁMÍTÁS ALAPJA 2.. A fázisdiagram számítás kialakulása A fázisdiagram számítás és a ALPHAD módszer kialakulásának bemutatásában elsősorban hang és társai [] Spener [2][3] Saito [4] Risold [5] és Mao [6] összegző leírásaira támaszkodom kiegészítve egyéb az alábbiakban hivatkozott forrásokkal. A fázisdiagramok számításának kezdete kétalkotós rendszerek esetében az 9- as évek elején Van Laar nevéhez köthető majd eredményeit Meijering kiterjesztette többalkotós rendszerek számítására mintegy 5 évvel később. A kutatásaikat a fázisdiagram számítás korai korszakának nevezzük. Meijering reguláris oldódási modellt használva ternér fázisdiagramokat számított ki. Van Laar és Meijering kutatásai együttesen segítettek megérteni az ötvözetek fázisegyensúlyának és a termodinamikai stabilitásának kapsolatát. A korai időkben megszerkesztett fázisdiagramok úgy készültek hogy a kézzel rajzolt szabadentalpia görbékhez vonalzóval érintőt húztak és abból következtettek az egyensúlyi fázishatárok összetételére a hőmérséklet függvényében ami alapján készítették el a fázisdiagramokat lásd 3. fejezet 3.. ábra. Ez binér rendszerek esetén viszonylag egyszerű matematikai problémát jelentett átlépve azonban a három vagy több alkotós ötvözetekre ugyanez a feladat borzasztó időigényes illetve bizonyos esetekben megoldhatatlan volt. Ternér diagramok esetén a fázisok szabadentalpia függvényeinek a felületéhez berajzolt érintősíkok metszéseit kellett számítani [7]. A rás stabilitás elmélet fázisdiagram számítás területen való alkalmazásának fontosságát Kaufman mutatta be. A rás stabilitás érték az adott fázis stabil és metastabil kristályos formái közötti különbség szabadentalpiával a hőmérséklet függvényében kifejezve. Ez az elmélet lehetővé tette az egyes rendszerek különböző fázisainak megjelenése közötti egyensúlyi határok sokkal pontosabb számítását. A későbbiekben a termodinamikával foglalkozó kutatók elkezdték a fázisegyensúlyi adatok szisztematikus összegyűjtését annak érdekében hogy az ötvözetek termodinamikai tulajdonságainak beslése minél könnyebben elvégezhető legyen. Ezen a területen dolgozott többek között Kubashewski Hultgreen rewer. 968-ban Hillert leírta a kísérleti termodinamikai informáiók és a fázisdiagram adatok számítógépes kombinálásának előnyeit valamint a globális méretű alkalmazásban rejlő lehetőségeket. Ezt követően kezdték el 6
8 Mende Tamás PhD értekezés rodalmi feldolgozás kifejleszteni az első fázisdiagram számítást végző számítógépes alkalmazásokat és szoftvereket. Kaufman volt az egyik első kutató aki számítógépet használt nagymennyiségű binér és ternér fázisdiagramok számítására. Társával ernsteinnel számításaikban túlnyomórészt egyszerűbb oldódási modelleket alkalmaztak a nagy gyakorlati jelentőséggel bíró fázisok leírására. A termodinamikai és a kinetikai modellek kombinálásával új lehetőségek nyíltak az anyagok összetételével tulajdonságával szerkezetével kapsolatos számítások elvégzésére. Számos eljárást alkalmaztak a különböző anyagok tulajdonságainak számításában például a ALPHAD módszert első elvi ún. ab inito számításokat pl. Density Funtion Theory Moleular-Dynami Monte-arlo és fázismező szimuláiókat valamint végeselemes módszereket. [8] Az 98-as évek közepétől egyre több és fejlettebb fázisdiagram számító szoftversomag jelent meg melyek mind a binér mind pedig a többalkotós rendszerek fázisdiagramjait is képesek voltak előállítani. Ezen szoftverek az ún. első generáiós programokat tartalmazták. A szoftverek fejlődése azonban nem állt meg és megjelentek a második generáiós programok pl. PANDAT [9]. hen és társai [][] kidolgoztak egy olyan algoritmust amelynél nem fordulhat elő az az addig gyakori hiba hogy metastabil rendszereket számol a program hanem automatikusan a stabil fázisdiagramokat állítja elő. Az algoritmust később sikeresen kiterjesztették többalkotós rendszerek esetére is. Az így kialakuló PANDAT szoftver fejlesztése globális optimalizálási algoritmusokon alapszik és minden esetben stabil fázisdiagramot számol megadott termodinamikai paraméterekkel. Fontos hogy a második generáiós szoftverek esetében a felhasználó akarata szerint egy vagy több fázis eltávolításával bármikor tud metastabil fázisdiagramot is számítani A ALPHAD típusú számítások kialakulása A jelenleg legelterjedtebb és legelfogadottabb fázisdiagram számítási eljárás a ALPHAD módszer ezért röviden bemutatom a ALPHAD kialakulását. Az 97-es évek elején Larry Kaufman ManLabs Egyesült Államok és Himo Ansara Grenoble Egyetem Franiaország egy nemzetközi tudóssapat összehívásával szervezett kutatómunkába kezdett a termodinamika és a számítástehnikai feldolgozás összekapsolásának érdekében és ezzel indította útjára a fázisdiagramok számítógépes feldolgozását a ALPHAD módszert. A kutatósoport első tudományos eszmeseréjét 97-ben Münsterben Németország valamint Teddingtonban Nagy-ritannia szervezték meg. 7
9 Mende Tamás PhD értekezés rodalmi feldolgozás 973-ban tovább folytatódtak a megbeszélések immár ALPHAD meeting elnevezéssel. A találkozó fő élja a következő évek munkatervének elkészítése az elvégzendő termodinamikai kísérletek megtervezése volt. A Kaufman által meghívott kutatók: Himo Ansara és laude ernard Franiaország Oswald Kubashewski és hsan arin Németország Philip Spener és Jak ounsell Nagy-ritannia Mats Hillert és Gernot Kirhner Svédország Harvey Nestor John ahn Dik Weiss laude Lupis Egyesült Államok. A következő ALPHAD meetinget 974. áprilisában rendezték meg Ansara kutatóbázisán Grenobleben. Az előző évi sapathoz további szakemberek satlakoztak: Wolfgang Pitsh Németország Peter Miodownik Malolm Rand Nagy-ritannia Etienne onnier és Jean-laude Mathieu Franiaország. A ALPHAD előnye a nagy nemzetközi összefogásban is rejlik hiszen a munkafeladatokat kísérletek számítások elvégzését kooperatívan együttműködve végezhették a kísérletterveket szisztematikusan a számítások input adat igényéhez igazítva építhették fel. Számításaik fejlődését a kutatómunkában résztvevő intézetek által elérhető nemzetközi termodinamikai adatbázisok is nagyban segítették. A Sientifi Group Termodata Europe SGTE [2][3] adatbankot 979-ben alapították meg [8] és szervetlen vegyületek valamint ötvözetek feldolgozott termodinamikai adatait tartalmazta ráadásul ez volt ez első adatbázis amely az EURONET telekommunikáiós rendszeren keresztül az egész Európai Közösségben elérhető volt. Az elemekre vonatkozó nagyrészt Dinsdale által összeállított SGTE adatbázis a ALPHAD típusú számítások fontos bázisa volt és azóta is folyamatosan bővül binér ternér és többalkotós rendszerek ALPHAD feldolgozásával SGTE Solution Database. Természetesen az európai kutatások mellett azoktól függetlenül más földrészen is folytak munkálatok hasonló témakörben. Az Eole Polytehnique Montreal Kanada termokémikusai főként Lin [4] Pelton [5] és társaik szintén ALPHAD típusú számításokat végeztek és saját termodinamikai adatbázist fejlesztettek ki FatSage [5][6][7][8]. A korai időkben a komolyabb informatikai fejlődés megindulása előtt a kutatóknak még szobákat folyosókat megtöltő lyukkártyás számítógépekkel kellett dolgozni. Ezt követően természetesen a tehnikával párhuzamosan a ALPHAD módszer is rohamos fejlődött egyre több kutató satlakozott az alapsapathoz a ALPHAD-dal feldolgozott anyagfajták problématípusok pedig egyre szélesebb spektrumot öleltek át. A kezdetekben színelemek termodinamikai leírásai és binér rendszerek egyensúlyi fázisdiagramjai készültek túlnyomó többségében de az idő és a tehnika előrehaladtával egyre fontosabbá vált a 8
10 Mende Tamás PhD értekezés rodalmi feldolgozás többalkotós rendszerek megfelelő pontosságú termodinamika ismerete is. Ennek érdekében nagyon sokat fejlesztették tesztelték a termodinamikai tulajdonságok extrapoláióján alapuló modelleket is. Évtizedekkel később ma már elmondhatjuk hogy a számítógépes termokémia illetve a ALPHAD és a hozzá hasonló módszerek az egyik legfontosabb alapeszközök lettek az anyagtudomány kezében A fázisdiagram számítási módszerek felépítése A nemzetközi szakirodalomban többféle fázisdiagram számító módszer ismert és bár felépítésükben elméleteikben különböznek egymástól mégis megvannak a közös vonásaik. A legfontosabb közös tulajdonság a mérési adatok használata. A fázisdiagram számítási módszerek algoritmusainak túlnyomó többségében be van építve a mérési eredmények használata kizárólag elvi alapon ab inito módon egyensúlyi fázisdiagramok számítása [9] igen ritka és sak nagyon korlátozott módon kivitelezhető. Az ab inito számítások a kvantum mehanikán és a statisztikai módszereken alapulnak az adott rendszer minden lehetséges kristályszerkezetében a megadott paraméterek és az atomok helyzetének változtatásával kiszámítják az energia minimumot. A számított adatpontok közötti interpoláióval határozzák meg az energia értéket a térfogat függvényében. A számításokat K-re vonatkoztatva végzik majd mért vagy ab inito számítással nyert adatok segítségével kiterjesztik az adott hőmérsékletig. A számítások elvégzéséhez luster Variation modellt vagy Monte arlo módszert alkalmaznak. [5][9][2] Ab inito elven működő fázisdiagram számító szoftver pl. a RYSTAL23. [4][9] Az ab inito számításokat alkalmazzák a ALPHAD típusú számításokkal mérési adatokkal történő optimalizálással kombinálva. [2] A mért adatokat felhasználó egyensúlyi fázisdiagram számítási módszereket az általuk számított értékek alapján két soportra bonthatjuk. Az egyik soportba azok a módszerek sorolhatók amelyek számításai mérési adatok feldolgozásával közvetlenül hőmérséklet értékeket adnak meg termodinamikailag megalapozott függvények formájában pl. ESTPHAD módszer [22] a másik soportba tartoznak az elméleti síkon levezett egyenleteiket mért adatokkal optimalizáló szabadentalpia függvényeket számító eljárások pl. ALPHAD módszer. Az utóbbiak által előállított szabadentalpia függvényeket kifejezetten erre a élra kifejlesztett szoftverek használják fel és számítják a hőmérséklet értékeket pl. Thermoal [23][24] PANDAT [9][25] FatSage [5][6][7] MTDATA [26][27]. 9
11 Mende Tamás PhD értekezés rodalmi feldolgozás A 2.. ábrán mutatom be hogy az anyagok fizikai kémiai tulajdonságainak méréseiből hogyan lehet eljutni a számított egyensúlyi fázisdiagramokig. 2..ábra. Számított egyensúlyi fázisdiagram előállításának lehetséges megoldásai [28] Az ESTPHAD módszerrel a mért hőmérséklet értékeket felhasználva egy egyszerű számítással megkaphatjuk például az egyensúlyi fázisdiagramban szereplő fázisok likvidusz hőmérsékletét. Kiindulási alapként használhatóak grafikus fázisdiagramok digitalizálással közvetlenül mérésből származó adatokkal is végezhetőek a számítások de ALPHAD típusú számítással előállított adatbázissal is dolgozhatunk. A számított eredmények pontosságát erősen befolyásolja a felhasznált adatok pontossága. Az ESTPHAD módszerről bővebben a 3. fejezetben írok. A ALPHAD módszerrel a nagy mennyiségű és nagy pontosságú termokémiai adatokat felhasználva a levezetett termodinamikai függvények alapján számíthatóak az egyensúlyi fázisdiagramok. A ALPHAD eljárás a szabadentalpia változást és a rendszer termodinamikai viselkedését leíró modellek segítségével dolgozza fel a lehetséges fázisokat. [6] A fázisdiagram ab inito módon előállított értékeit és a termodinamikai adatokat matematikai módszerekkel például súlyozott nem lineáris legkisebb négyzetek optimalizálással közelíti. A számítási algoritmus az ESTPHAD módszerhez hasonlóan abból indul ki hogy egyensúlyi állapotban a kémiai poteniál értékek egyenlőek az algoritmus további része pedig szabadentalpia függvények minimalizálásán alapszik. A binér
12 Mende Tamás PhD értekezés rodalmi feldolgozás ternér rendszerek extrapolálásával többkomponensű fázisdiagramok is előállíthatók. A 2.2. ábrán a ALPHAD típusú számítások elvi folyamatábrája látható. A ALPHAD típusú termodinamikai feldolgozás a nemzetközi kutatósoportok által elérhető kísérleti adatok összegyűjtésével vagy adott rendszerhez speifikusan megválasztott mérésekkel kezdődik majd az adatok szabadentalpia függésének megállapításával folytatódik. Az adatokat meghatározhatják többek között differeniál termikus analízissel [29][3] differeniál sanning kalorimetriával DS [3][3] röntgen diffrakióval RD [29][3] sanning elektronmikroszkópiával SEM [3] elektron diszperzív spektrometriával EDS [3]. Sok esetben használhatóak kísérleti 2.2.ábra. ALPHAD típusú számítások elvi ábrája [][5][6] adatként az ab inito számítások eredményei is. [2] A rendszerben megjelenő minden lehetséges fázishoz kiválasztanak egy megfelelő modellt a szabadentalpia hőmérséklet- nyomás- összetétel-függvényében történő leírására. A szabadentalpia függvények használata a termodinamikai tulajdonságok modellezéséhez azért jobb mint bármely más termodinamikai függvény lenne mert a szabadentalpia a hőmérséklet és a nyomás függvénye és ezek a kísérletek során a legkönnyebben kontrolálható paraméterek ráadásul a legtöbb számításban a nyomás hatása elhanyagolható. Nagy előnye továbbá hogy a szabadentalpiából származtatható minden egyéb termodinamikai mennyiség mint például: entrópia entalpia hőkapaitás belső energia stb... A ALPHAD módszerrel előállított adatbázis alapján a legtöbb szoftverrel például Thermo-al FatSage elvégezhető a fázisdiagram számítás. A binér ternér és a többalkotós rendszerek számítása egymásra épül azok termodinamikai leírásának egymással kompatibilisnek kell lennie. A legtöbb egyensúlyi fázisdiagramot atmoszférikus nyomásra vonatkozóan készítik el de találni az irodalomban számításokat melyekben a nyomás több GPa. Alasonyabb hőmérsékleten és nyomáson meghatározott adatok függvények extrapolálásával lehetséges nagy nyomású rendszerekig pl. GPa kiterjeszteni a számításokat. [32][33]
13 Mende Tamás PhD értekezés rodalmi feldolgozás 3. AZ ESTPHAD FÁZSDAGRAM SZÁMÍTÁS MÓDSZER 3.. Az ESTPHAD számítási módszer termodinamikai alapjai a Alapösszefüggések [22][34][35] Kétalkotós rendszerben az egymással egyensúlyt tartó fázisok szabadentalpiája reguláris oldat esetén az alábbiak szerint függ a konentráiótól: G G G G RT ln ln A A A A A G G RT ln ln 2 A A A A A ahol: olvadék fázis szilárd fázis G színelemek vagy vegyületek szabadentalpiája az olvadék fázisban G A G G színelemek vagy vegyületek szabadentalpiája a szilárd fázisban A A móltört az olvadék fázisban A móltört a szilárd fázisban Ω Ω párkölsönhatási energia az olvadék és a szilárd fázisban R gázállandó T abszolút hőmérséklet Az. és 2. egyenlet alapján a fázisok pariális moláris szabadentalpiája reguláris oldatokat feltételezve: A GA RT ln A 3 G A RT ln 4 A GA RT ln A 5 G A RT ln 6 Gibbs szerint egyensúlyban a két fázis pariális moláris szabadentalpiái egyenlőek: A A 7 8 2
14 Mende Tamás PhD értekezés rodalmi feldolgozás 3.. ábra. A két fázis szabadentalpia görbéje és a pariális moláris szabadentalpiák egyenlősége egyensúlyi állapotban adott hőmérsékleten A fenti egyenletekből az egyenletek állandóinak ismeretében kiszámítható az egymással egyensúlyt tartó fázisok összetétele adott hőmérsékleten így a likvidusz és szolidusz görbék a megoszlási hányados valamint a likvidusz görbe meredeksége adott összetételnél vagy adott hőmérsékleten. b A likvidusz hőmérséklet számítása A 7. egyenlet alapján figyelembe véve hogy k írható: G A RT ln A A 2 2 RT ln A A 2 k 2 9 ahol: az A elem szabadentalpia változása kristályosodás során k G A megoszlási hányados. G A A szabadentalpia változás az alábbi módon is felírható: L T S ahol: L ΔS a kristályosodás közben felszabaduló látens hő a folyamatot kísérő entrópia változás 3
15 Mende Tamás PhD értekezés rodalmi feldolgozás 4 Egyensúlyban a színelem olvadáspontján T hőmérséklet A G így T L S S T L melyet a. egyenletbe behelyettesítve kapjuk a következő összefüggést: T T T L T T L T L T L G A A szabadentalpia változás ily módon való kifejezését a 9. egyenletben ΔG A helyére beírva az alábbi egyenlet adódik: ln 2 2 A A k RT T T T L 2 Átrendezés után figyelembe véve hogy k valamint A A és az ln-es tagot a Taylor-sor felhasználásával hatványfüggvénnyé alakítva írható: / / 2 2 m i i i f f L RT T k k i L RT T T 3 Reális oldatok esetén a 3. egyenletben szereplő két hatványfüggvény hányadosát mivel mindkét függvényben sak a változó egyetlen hatványfüggvénnyel helyettesíthetjük: m i i F A A A A A i f f L RT 4 ahol: Ai a hatványfüggvény együtthatói. A 4. egyenletet a 3. egyenletbe behelyettesítve a likvidusz hőmérséklet T L a következőképpen számolható: i i L L F T i A T T 5
16 Mende Tamás PhD értekezés rodalmi feldolgozás Általában a fázisdiagramoknál az összetétel tömegszázalékban van megadva. A tömegszázalék és a móltört azonban egy nem lineáris egyenlettel kifejezhetőek egymásból tehát a móltört függvényében felírt polinom helyett használható a tömegszázalékok azonos típusú polinomja is: T T T F L i AL i i 5.a ahol: az olvadék alkotó tartalma tömegszázalékban kifejezve A likvidusz hőmérséklet számítása három- négy- és többalkotós rendszerek esetén Az ESTPHAD módszer hierarhikus felépítésének köszönhetően a számítás rendkívül egyszerűen kiterjeszthető három- és többalkotós rendszerek esetére is. Amennyiben rendelkezésünkre állnak a binér egyensúlyi fázisdiagramok likvidusz görbéinek ESTPHAD módszerrel számított koeffiiensei úgy akár a ternér egyensúlyi fázisdiagram ismerete és adatai nélkül is jó közelítést adhatunk a háromalkotós rendszerek likvidusz felületeire elsősorban a tiszta elemhez illetve a binér rendszerekhez közeli konentráió tartományban. A ternér fázisdiagramok értékeit is felhasználva regressziós analízissel a pontosság az egész fázisdiagramon belül eléri a gyakorlati felhasználáshoz szükséges mértéket. T TL ; F F 6 A hierarhikus felépítés értelmében a kettőnél több alkotós n alkotós fázisdiagramok számításában szerepel egy ΔF A N korrekiós tag. Ennek szerepe az n- alkotós rendszerek koeffiienseivel számolt értékek és az n alkotós rendszer valódi értékei közötti különbség sökkentése. A korrekiós tag előállítása szintén regressziós analízissel történik. A kétalkotós fázisdiagram számításánál bemutatott levezetéssel azonosan figyelembe véve hogy: A a háromalkotós rendszerben szereplő likvidusz felületek hőmérsékletének számítására előállítható a következő egyenlet: T TL ; F F F ; 7 ahol: F az A- binér rendszerben kiszámított függvény 5
17 Mende Tamás PhD értekezés rodalmi feldolgozás 6 F az A- binér rendszerben kiszámított függvény ; F az A-- ternér rendszerben kiszámított függvény. A ΔF hibafüggvény a következő módon épül fel: p i i q j j i j A i A A A F 2 2 ;... ;2 2; ; ; 8 Az előbbi szisztémát követve a módszer kiterjeszthető négyalkotós fázisdiagramok számítására is. A ΔF AD függvény kiszámolása nélkül sak a két- és háromalkotós rendszerek koeffiienseinek felhasználásával is adhatunk közelítő értékeket ekkor: AD AD A AD A A D L F F F F F F T T ; ; 9 Négyalkotós rendszerek esetére a korábbiakban leírtak szerint a következő egyenlet vezethető le a likvidusz hőmérséklet számítására: AD AD AD A AD A A D L F F F F F F F T T ; ; 2 ahol: A F F az A- binér rendszerben kiszámított függvény A F F az A- binér rendszerben kiszámított függvény AD D F F az A-D binér rendszerben kiszámított függvény ; A F F az A-- ternér rendszerben kiszámított függvény ; D AD F F az A--D ternér rendszerben kiszámított függvény ; D AD F F az A--D ternér rendszerben kiszámított függvény ; ; D AD F F az A---D négyalkotós rendszerben kiszámított függvény. A ; ; D F hibafüggvény számítása négyalkotós rendszerek esetén: p i i q j j i r k k D j i D D D D D k j A i A A A A F ; ;... ;;2 ;2; 2;; ;; ; ; 2
18 Mende Tamás PhD értekezés rodalmi feldolgozás A likvidusz hőmérséklet meghatározása n alkotós rendszer esetén n-edik alkotó N n--edik alkotó M: T L ; ;...; N T F... F F... F F 22 A AN A AMN A... N ahol: F F ; ;...; Az n alkotós rendszerben kiszámított A... N N függvény A F ; ;...; hibafüggvény alakja n alkotós rendszerekre: N F 2 A2;;;...; D... p qi si j A i; j;...; n i j ; ;...; n N A;;;...; N i... A;;...;2 j... D N... n N D... N d Az ESTPHAD módszer hierarhikus felépítésének bemutatása Az ESTPHAD módszer hierarhikus felépítésére gyakran hivatkozom ezért néhány egyszerű ábrával bemutatom hogy a két- három- és négyalkotós rendszerekben kiszámított függvények együtthatók hogyan épülnek egymásra. Az ábrákon a kis kokák az ESTPHAD módszerrel előállított függvények Ai;j;k együtthatóit szemléltetik. Az i j k számok a három elem konentráióinak a megfelelő hatványú szorzatát mutatják mely szorzattal az adott Ai;j;k együtthatót meg kell szorozni. Például a ;;2-es együttható esetén az együtthatót a [ Al2O3 * ao * SiO2 2 ] konentráió szorzattal kell megszorozni. Egy többalkotós rendszer feldolgozása mindig a kétalkotós fázisdiagramok kiszámításával kezdődik. A példaként bemutatott esetben első lépésként a MgO-aO A- MgO-Al 2 O 3 A- valamint a MgO-SiO 2 A-D fázisdiagramokban található MgO-ban dús fázis likvidusz görbéinek együtthatóit A;; A2;; A3;; határozzuk meg ábra Az előállított F A illetve F A binér függvények valamint az A-- ternér fázisdiagram digitalizált adatai segítségével az előbbiekben bemutatott egyenletek felhasználásával kiszámíthatóak a háromalkotós rendszer likvidusz felületének ESTPHAD együtthatói is ábra Ezt a számítást is mind a három A-- A--D A--D háromalkotós fázisdiagramban el kell végezni ábra 7
19 Mende Tamás PhD értekezés rodalmi feldolgozás 3.2. ábra. A MgO-aO rendszerben kiszámított 3.3. ábra. A MgO-aO MgO-Al 2 O 3 és MgO-SiO 2 együtthatók rendszerben kiszámított együtthatók 3.4. ábra. A három binér és a MgO-SiO 2 -ao 3.5. ábra. A három binér és a három ternér ternér rendszerben kiszámított együtthatók rendszerben kiszámított együtthatók Az összes előállított függvényre valamint a kvaternér diagram digitalizált értékeire építve megkapjuk a négyalkotós rendszerben számított F AD függvény együtthatóit 3.6. ábra ábra. A három binér a három ternér és a kvaternér rendszerben kiszámított együtthatók 8
20 Mende Tamás PhD értekezés rodalmi feldolgozás 3.2. A számítás menete Adatgyűjtés Az egyensúlyi fázisdiagramok feldolgozása a szakirodalomban rendelkezésre álló adatok rajzolt fázisdiagramok mért vagy számított adatbázisok összegyűjtésével kezdődik. Az ESTPHAD módszerrel van lehetőség természetesen saját mérések vagy esetleg ALPHAD számítások eredményeinek alkalmazására is. A PhD értekezésemben leírt rendszerek egyikénél sem végeztem hőmérséklet ill. konentráió adatokra vonatkozó méréseket kizárólag szakirodalmi adatokból dolgoztam. Amennyiben grafikus formában meglévő egyensúlyi fázisdiagram az input adat akkor a számítások elvégzéséhez szükséges hőmérséklet konentráió érték párokat a fázisdiagram ún. digitalizálásával digitalizáló program felhasználásával lehet előállítani az általam használt digitalizáló szoftver neve: WNDG 2.5. E folyamat során a szakirodalomból származó hiteles egyensúlyi fázisdiagram átalakulási görbéinek vonalán az adott görbe jellegének meredekségének megfelelő léptékkel haladva az összetartozó hőmérséklet és konentráió érték párokat rögzítjük. A koordinátákat a WNDG digitalizáló program automatikusan tárolja. Az adathalmazt dat -fájlként menthetjük el melyet az Exel programban beolvashatunk. A 3.7. ábrán példaként a MgO-Al 2 O 3 egyensúlyi fázisdiagram [36] MgO-ban dús fázis likvidusz görbéjének digitalizálása látható. A piros kereszttel amit az ábrán a láthatóság kedvéért erőteljesebben megjelöltem lehet a likvidusz görbe vonalán adatokat kijelölni. Külön ablakon olvashatóak az adott pont koordinátái konentráió és hőmérséklet értékek 9562 t% Al 2 O K illetve a pontosabb digitalizálást segítve külön ablakban nagyítva látható a likvidusz görbe vonala. Mért vagy számított adatok alkalmazása esetén értelemszerűen az adatbázis megfelelő hőmérséklet konentráió érték párjai közvetlenül használhatóak. 9
21 Mende Tamás PhD értekezés rodalmi feldolgozás 3.7. ábra. Digitalizálás a WNDG program segítségével MgO-Al 2 O 3 MgO fázis likvidusz görbe [36] A likvidusz hőmérséklet számítása A digitalizálással kapott illetve a mérésekből számításokból származó adatokat Mirosoft Exel programmal dolgoztam fel. Amint azt korábban írtam a számítások alapadatai származhatnak grafikus fázisdiagram digitalizálásából mért vagy számított adatbázisból a továbbiakban a számítás menetének bemutatása során az egyszerűség kedvéért azonban nem írom ki mindenhol hogy digitalizált mért vagy számított adat hanem mivel nagyrészt grafikus fázisdiagramokkal dolgozom sak digitalizált adatokat írok. A számítások első lépéseként a 5.a egyenlet átrendezésével kapott T F 24 T L összefüggés jobb oldalán szereplő értékeket behelyettesítjük T a színelem olvadáspontja T L pedig pontonként az adott digitalizált likvidusz hőmérséklet érték. Így F -re minden digitalizált pontnál kapunk egy-egy értéket. Az F függvény az olvadék összetételétől függő polinom így benne az adott konentráió értékek hatványai szerepelnek. Az Exel munkafüzetben ezért ki kell számolni minden összetételnél a ; ; ; ;... értékeket. A likvidusz hőmérséklet számítására ESTPHAD módszerrel előállított függvények fokszáma az adott likvidusz görbe jellegétől bonyolultságától függ. Meg kell vizsgálni hogy a különböző fokszámú egyenletekkel általánosan javasolt: 2-5. fok milyen eltéréssel lehet 2
22 Mende Tamás PhD értekezés rodalmi feldolgozás kiszámítani a likvidusz hőmérséklet értékeket. Megfelelő pontosság mellett a legkisebb hatványú polinom alkalmazására kell törekedni. A megfelelő pontosság -ot a későbbiekben definiálom. Az ESTPHAD függvény együtthatóit regressziós analízissel határozzuk meg. A regresszió x;y bemeneti tartományának az előzőekben 24. egyenlet előállított F illetve a ; ; ; ;... értékek halmazát választjuk a konstans értékét pedig zérusnak jelöljük mivel az ESTPHAD egyenletben A. A zéró konstansnak köszönhetően a színelem összetételénél F így a 5.a. egyenlet értelmében T L = T. A regressziós analízisről az Exel egy összesítő táblázatot készít melyben többek között az eredmények szórását R 2 valamint a kiszámolt F polinom A ; A2; A3; A4;... együtthatóit találhatjuk. A 5.a. egyenletbe a kiszámított Ai paramétereket az F függvénybe beírva a likvidusz hőmérséklet bármely összetételnél könnyen számolható: T T L A A2 A3 A4... Három- és többalkotós rendszerek feldolgozásánál értelemszerűen az F A illetve az F A N függvényeket kell előállítanunk a digitalizált adatok felhasználásával. lásd egyenlet A regressziós analízis bemeneti adatai ezen függvények illetve a konentráió értékek Ai j k paramétertől függő hatványainak közös szorzatai. ; ;...; N A számított adatbázis elemzése Az ESTPHAD egyensúlyi fázisdiagram számítási módszert az előzőekben részletesen bemutatott termodinamikai alapok és a levezetett egyenletek felhasználásával elvégzett számítások pontossága és egyszerűsége teszi alkalmassá a gyakorlati használatra. Ezt a kijelentést alátámasztandó a számított hőmérséklet értékek pontosságát minden egyes feldolgozott rendszer esetében fontosnak tartom ellenőrizni. A számítások elvégzése után az input adatként felhasznált eredeti adatokat össze kell hasonlítani a kiszámított hőmérséklet értékekkel és az eltérések nem lehetnek nagyobbak az általunk az adott rendszernél elfogadható hibánál. Ez az elfogadható hiba egzakt módon nem számszerűsíthető hiszen rendszer speifikus dolgoktól függ de leginkább a felhasznált adatbázis minősége pontosság 2
23 Mende Tamás PhD értekezés rodalmi feldolgozás adateloszlás többalkotós rendszerekben a binér ternér stb rendszerek egymásra épülése és az adott rendszerben pl. fémes vagy kerámia adott hőmérséklet tartományban elvárható mérési hiba nagysága befolyásolja. Amennyiben az eltérések az elfogadható hibánál nagyobbak a számítást más fokszámú polinommal meg kell ismételni esetleg a felhasznált adatbázis megfelelőségét kell felülvizsgálni. A számítási hibák elemzése és az ún. rendszeres számítási hibák azonosítása azért is fontos feladat mert nem sak az adott rendszerben számított értékek pontosságát lehet ily módon növelni hanem megfelelő hibaanalízis segítségével lehet az ESTPHAD számítási algoritmust tovább fejleszteni. 22
24 Mende Tamás PhD értekezés Az ESTPHAD módszer alkalmazása különböző likvidusz és szétválási görbék esetén 4. AZ ESTPHAD MÓDSZER ALKALMAZÁSA KÜLÖNÖZŐ LKVDUSZ ÉS SZÉTVÁLÁS GÖRÉK ESETÉN Az ESTPHAD módszer története során az első feldolgozott rendszerek esetén elsősorban a színfémek olvadáspontjához közeli tartományban történtek a számítások. Ezen esetekben az ESTPHAD módszer megfelelő pontosságot eredményezett az egyszerűség kedvéért nevezzük általánosan α szilárdoldatok likvidusz hőmérsékletének leírásában. Az ötvözeteinkben azonban nem sak színelem α szilárdoldata hanem vegyület vagy színelem allotróp módosulata is kristályosodhat de adott esetben az olvadék két eltérő összetételű olvadék fázisra is szétválhat és ezen átalakulások hőmérsékletét is ki kell tudni számítani. Munkám során fontosnak tartottam az ESTPHAD számítási módszert a kétalkotós egyensúlyi fázisdiagramokban megtalálható összes likvidusz görbe típus illetve olvadék szétválási görbe leírására alkalmassá tenni. Ennek érdekében első lépésként meg kellett különböztetnem a számítások elvégzése szempontjából eltérő tulajdonságokkal rendelkező likvidusz görbéket és megtalálni bennük a leírásuk során poteniálisan megjelenő hibalehetőségeket. A 4.. ábrán mutatom be az általam megkülönböztetett likvidusz görbetípusokat. Természetesen a gyakorlatban a valóságban megjelenő egyensúlyi fázisdiagramok számos esetben nem annyira egyszerű esetek mint a 4.. ábrán látható tanpéldák hanem gyakran az általam vázolt alaptípusok közül több is fellelhető bennük egyszóval bonyolultabb összetett rendszerek. Ez a felosztás tehát valójában egy jó kiindulási alap és mivel a gyakorlati fázisdiagramok ilyen részekből épülnek fel az ezen esetekből kikövetkeztetett számítási nehézségek hibalehetőségek a valódi rendszereknél is problémaként jelennek meg tehát a megoldásukra kidolgozott algoritmusok a gyakorlati egyensúlyi fázisdiagramok feldolgozásánál is működőképesek hatékonyak. Az anyagtudományban az egyensúlyi fázisdiagramok taglalásánál a rendszereket első lépésben az alkotók általánosan a színelemeket esetleg a vegyületeket nevezzük binér rendszerekben A és alkotónak egymást oldó képessége azaz az oldhatóság alapján soportosítjuk. Oldóképességnek nevezzük a színelemek illetve vegyületek azon tulajdonságát hogy az atomjai alkotta kristályrás egyensúlyi állapotokban mennyi idegen atomot képes magába fogadni az idegen atomok milyen konentráióban képesek akár a ráspontokban akkor a ráspontok közé beépülni. Az oldhatóság jelentősen hőmérséklet- 23
25 Mende Tamás PhD értekezés Az ESTPHAD módszer alkalmazása különböző likvidusz és szétválási görbék esetén függő a hőmérséklet változásával az oldódni képes atomok konentráiója nagyságrendileg is megváltozhat. Az egyensúlyi fázisdiagramokban háromféle oldhatóságot különböztetünk meg: Korlátlan oldhatóságról beszélünk ha az A és alkotó korlátlanul oldja a másikat. Olvadékok esetén ez az állítás a gyakorlati rendszereink túlnyomó többségére minden hőmérséklet és konentráió tartományban igaz. Szilárd állapotban azonban a rendszerek jelentős hányadában nem jellemző a korlátlan oldhatóság. A korlátlan oldhatóságnak ugyanis számos alapvető feltétele van a legjellemzőbb hogy mindkét alkotó azonos kristályrásal rendelkezzen tiszta állapotban színelemként vegyületként. Amennyiben az oldóképességnek van egy felső határa akkor az oldhatóság korlátozott. Olvadék állapotban korlátozott oldhatóság esetén bizonyos hőmérséklet és konentráió tartományban az olvadék két különböző összetételű olvadék fázisra válik szét. Szilárd állapotú korlátozott oldhatóságnál az A atomok alkotta kristályrás bizonyos mennyiségű atomot képes a saját atomjai között oldani azonban van egy összetételbeli határ aminél nagyobb konentráió mellett megjelenik a színelem kristályrásával azonos β szilárdoldat vagy egy vegyület. Amennyiben a tiszta A és tiszta atomok alkotta fázisok a másik atomot egyáltalán nem képesek oldani úgy értelemszerűen nins oldhatóság. Oldhatóságról azonban nemsak a binér rendszerek A és alkotója kapsán beszélhetünk hanem a bizonyos sztöhiometriai összetételnél megjelenő A x y vegyületek esetén is. Korlátlan oldhatóság vegyület és A alkotó között nem létezik mivel nem lehet azonos a rásszerkezete a színelemnek és a vegyületnek és így a korlátlan oldhatóság egyik legfontosabb feltétele nem teljesül. Vannak esetek amelyekben a vegyület egyáltalán nem oldja az alkotóit pl. Fe- rendszerben a metastabil Fe 3 fázis számos esetben azonban a vegyület korlátozott mértékben ugyan de oldja az alkotóit pl. u-al rendszerben a β fázis. A korlátozott oldhatósággal bíró fázisdiagramokat tovább osztályozhatjuk az átalakulási folyamatok szerint úgymint eutektikus peritektikus vagy monotektikus fázisdiagramok. 24
26 Mende Tamás PhD értekezés Az ESTPHAD módszer alkalmazása különböző likvidusz és szétválási görbék esetén A különböző egyensúlyi fázisdiagram típusok közül a következő lépésben bemutatom azokat amelyekben a likvidusz görbék valamilyen módon különböznek egymástól és így a likvidusz ill. szétválási hőmérséklet számítása eltérő algoritmust igényel. Az olvadék állapotban kezdődő folyamatok közül az alábbiak különböztethetőek meg: A likvidusz görbe a tiszta A alkotótól a tiszta alkotóig tart korlátlan oldhatóság. A likvidusz görbe a tiszta A alkotótól a tiszta alkotóig tart de minimum vagy maximum ponttal rendelkezik korlátlan oldhatóság. A likvidusz görbe a tiszta A vagy alkotóból indul ki és eutektikus pontban végződik. Nyílt maximummal vegyület vagy szekunder szilárdoldat képződik és a vegyület szekunder szilárdoldat likvidusz görbéje az A és a alkotó irányába is egy-egy eutektikus pontig tart. Peritektikus folyamatban vegyület vagy szilárdoldat képződik és a vegyület szilárdoldat likvidusz görbéje a peritektikus hőmérséklettől egy eutektikus esetleg másik peritektikus hőmérsékletig tart. Olvadék állapotban a korlátozott oldhatóságnak köszönhetően az olvadék két különböző összetételű olvadékká válik szét a szétválási hőmérsékletnek megfelelően. Amint az a felsorolásból is látszik az olvadék állapotban kezdődő folyamatok kristályosodás olvadék szétválás típusainak megkülönböztetésénél nem vettem figyelembe azt hogy az alkotók illetve a keletkező vegyület szilárd állapotban oldja-e az alkotóit. A likvidusz illetve szétválási hőmérséklet szempontjából ugyanis ez nem releváns a görbék ugyanolyan speifikus tulajdonságokkal rendelkeznek ha alasonyabb hőmérsékleten van oldhatóság vagy ha nins. Az egyszerűség kedvéért az ábrán minden típusnál sak egy állapotot tüntettem fel méghozzá a szilárd állapotbeli korlátozott oldhatóságot. 25
27 Mende Tamás PhD értekezés Az ESTPHAD módszer alkalmazása különböző likvidusz és szétválási görbék esetén 4.. ábra. Az olvadék állapotban kezdődő folyamatok típusainak soportosítása 26
28 Mende Tamás PhD értekezés Az ESTPHAD módszer alkalmazása különböző likvidusz és szétválási görbék esetén A további fejezetekben részletesen taglalom hogy mely típusnál milyen nehézségekre kell figyelni a számítás során mely értékeket kell használni az alapegyenletben szereplő kezdeti értéknek a 5. ill. 5.a egyenletben a T t nevezem kezdeti értéknek bizonyos fázisdiagram típusoknál szükséges megállapítani a likvidusz görbe tartományát is illetve vannak olyan görbék melyek megfelelő feldolgozásához az ESTPHAD alapegyenletbe plusz paramétereket kell beépítenem. Annak érdekében hogy az ESTPHAD módszer biztosan megtartsa a létrehozásakor szem előtt tartott előnyeit pontosság egyszerűség könnyen kezelhetőség gyorsaság a számítási algoritmusok illetve plusz paraméterek kidolgozása során a következő tényeket nagyon fontos változtathatatlan alapelvekként kezeltem: Az ESTPHAD fázisdiagram számítási módszer termodinamikai alapokon nyugvó termodinamikai összefüggésekből levezetett eljárás ezen alapok megtartása kötelező. Az ESTPHAD módszertől általunk elvárt pontosság ±% tehát a számításhoz felhasznált mért digitalizált számított hőmérséklet értékek és az ESTPHAD módszerrel számított hőmérséklet értékek között maximum % eltérés elfogadható. Az átalakulási hőmérséklet számítására alkalmazott ESTPHAD-egyenletnek és számítási algoritmusnak egyszerűnek könnyen kezelhetőnek kell lennie nélkülöznie kell a más egyensúlyi fázisdiagram számítási módszerekben gyakran használt bonyolult iteráiós lépéseket sokszorosan egymásba ágyazott függvénykapsolatokat. Az ESTPHAD alapegyenlet 3. fejezet 5. és 5.a egyenlet alakja elve lényegesen nem változhat abból tagot el nem lehet hagyni maximum alkalmasan megválasztott paraméterek illeszthetőek bele. A különböző likvidusz és szétválási hőmérsékletek számítása során eltérő ún. rendszer-speifikus problémák jelentkeznek van azonban egy minden rendszerben felmerülő ezáltal általánosan kezelendő feladat. Az ESTPHAD módszerrel eredeti formájában a 5. ill. 5.a egyenletben szereplő F illetve F függvények felépítésének köszönhetően a tiszta alkotó olvadáspontját számítási hiba nélkül lehet kiszámítani. Tiszta alkotó esetében 27
29 Mende Tamás PhD értekezés Az ESTPHAD módszer alkalmazása különböző likvidusz és szétválási görbék esetén i ugyanis azaz F A i ekkor pedig a 5. egyenlet szerint i L a számított likvidusz hőmérséklet azonosan egyenlő a tiszta alkotó olvadáspontjával: T T F T L L T T 26 Ugyanez a levezetés természetesen igaz a nem móltörtben hanem például tömegszázalékban kifejezett összetételek esetére is: T T F T L L T T 26.a Amennyiben olvadék és szilárd állapotban is korlátlan az oldhatóság a likvidusz görbe a tiszta A alkotó olvadáspontjától a tiszta komponens olvadáspontjáig tart. A likvidusz görbe számítás során tehát kettő darab tiszta alkotó olvadáspontját is ki kell tudni számítani az ESTPHAD módszerrel. Az A alkotó olvadáspontját amint a 26. ill. 26.a egyenletekben bemutattam számítási hiba nélkül lehet kiszámítani a tiszta alkotó olvadáspontját viszont az F illetve F függvények számított Ai paramétereinek a segítségével lehet közelíteni. A alkotó számított olvadáspontját tehát sak valamekkora közelítési hibával lehet leírni. A 4.. ábrán bemutatott likvidusz és szétválási görbék között több sem valamelyik tiszta alkotó olvadáspontjában hanem eutektikus peritektikus vagy monotektikus hőmérsékleten végződik de olyan is látható amely görbének sem a kezdő sem a végpontja nem azonos az alkotók olvadáspontjával. Az eutektikus peritektikus monotektikus hőmérsékletek azonban a tiszta alkotók olvadáspontjához hasonlóan nagy pontossággal ismert jól kimérhető értékek így fontosnak tartom hogy az ESTPHAD módszerrel ezen hőmérsékleteket ugyanilyen nagy pontossággal lehessen számítani. A likvidusz és szétválási görbék végpontjainak megfelelő pontosságú kiszámítása érdekében új paramétereket vezetek be. 4.. Új paraméterek bevezetése a nonvariáns pontok számítására Az ESTPHAD alapegyenletben a likvidusz és a szétválási görbe leírását lényegében 2-5 paraméter Ai határozza meg attól függően hogy hányadfokú polinomot alkalmazunk a számításhoz. Ahhoz hogy a tiszta alkotó olvadáspontján kívül valamely pontot másik 28
30 Mende Tamás PhD értekezés Az ESTPHAD módszer alkalmazása különböző likvidusz és szétválási görbék esetén alkotó olvadáspontja eutektikus peritektikus vagy monotektikus hőmérséklet a számításban fixen rögzítsek ahhoz egy új paramétert kell bevezetnem vagy ezen 2-5 paraméter közül kell feláldoznom egyet amelynek a feladata sak és kizárólag ezen pont helyben tartása lesz. Természetesen 2. fokú polinom esetében mindenképpen új paraméter bevezetésére van szükség hiszen a maradék egy együttható nem lenne alkalmas a görbe megfelelő leírására. Úgy döntöttem hogy meghagyom ezen 2-5 paramétert eredeti funkiójuk ellátására annál is inkább mert egy új típusú koeffiienst illetve módosított ESTPHAD egyenletet vezetek be amelyben a likvidusz és a szétválási görbék mindkét végpontja nagy pontossággal számítható. A módosított egyenlet megalkotása előtt a következő peremfeltételeket definiáltam: A likvidusz ill. szétválási görbe végpontjának hőmérséklete az eredeti számításhoz felhasznált adatbázishoz képest K eltéréssel tehát tizedes jegy pontossággal számolható legyen. Az új paraméter a görbék végpontjánál illetve annak szűk környezetében éreztesse pozitív hatását. A módosított egyenlet minden pontban legyen értelmezhető folytonos függvény legyen. A módosított egyenlet kezelhetősége a számított eredmények felhasználása az alapegyenlethez hasonlóan egyszerű és gyors legyen. Ezen alapelveket elfogadva a következő megoldásra jutottam. evezettem a paramétert és hozzárendeltem az M szorzót. A számozásnak az a jelentősége hogy amennyiben több pontot szeretnék rögzíteni például 4.3. fejezetrész likvidusz görbe minimum pontja akkor az is megtehető 2 M 2 paraméterekkel. A paraméter meghatározása Az új paraméter meghatározható egy egyszerű élirányosan megválasztott egyenlet megoldásával. Első lépésben az ESTPHAD alapegyenlettel 5. ill. 5.a egyenlet elvégzem a számítást illetve meghatározom a likvidusz hőmérsékletet legkevesebb paraméterrel de megfelelő pontossággal leíró polinom fokszámát Ai együtthatók kiszámítása. Ezt követően az előállított Ai együtthatók ismeretében az ESTPHAD alapegyenletet kiegészítem a paraméterrel a következő módon: 29
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
5 előadás. Anyagismeret
 5 előadás Anyagismeret Ötvözet Legalább látszatra egynemű fémes anyag, amit két vagy több alkotó különböző módszerekkel való egyesítése után állítunk elő. Alapötvöző minden esetben fémes anyag. Ötvöző
5 előadás Anyagismeret Ötvözet Legalább látszatra egynemű fémes anyag, amit két vagy több alkotó különböző módszerekkel való egyesítése után állítunk elő. Alapötvöző minden esetben fémes anyag. Ötvöző
ANYAGSZERKEZETTAN II.
 ANYAGSZERKEZETTAN II. ANYAGMÉRNÖK ALAPKÉPZÉS TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIAI INTÉZET Miskolc, 2013. 1. TANTÁRGYLEÍRÁS
ANYAGSZERKEZETTAN II. ANYAGMÉRNÖK ALAPKÉPZÉS TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIAI INTÉZET Miskolc, 2013. 1. TANTÁRGYLEÍRÁS
ANYAGSZERKEZETTAN II.
 ANYAGSZERKEZETTAN II. ANYAGMÉRNÖK ALAPKÉPZÉS TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR ANYAGTUDOMÁNYI INTÉZET Miskolc, 2008. 1. TANTÁRGYLEÍRÁS Anyagszerkezettan II. kommunikációs
ANYAGSZERKEZETTAN II. ANYAGMÉRNÖK ALAPKÉPZÉS TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR ANYAGTUDOMÁNYI INTÉZET Miskolc, 2008. 1. TANTÁRGYLEÍRÁS Anyagszerkezettan II. kommunikációs
Anyagtudomány. Ötvözetek egyensúlyi diagramjai (állapotábrák)
 Anyagtudomány Ötvözetek egyensúlyi diagramjai (állapotábrák) Kétkomponensű fémtani rendszerek fázisai és szövetelemei Folyékony, olvadék fázis Színfém (A, B) Szilárd oldat (α, β) (szubsztitúciós, interstíciós)
Anyagtudomány Ötvözetek egyensúlyi diagramjai (állapotábrák) Kétkomponensű fémtani rendszerek fázisai és szövetelemei Folyékony, olvadék fázis Színfém (A, B) Szilárd oldat (α, β) (szubsztitúciós, interstíciós)
Makroszkópos tulajdonságok, jelenségek, közvetlenül mérhető mennyiségek leírásával foglalkozik (például: P, V, T, összetétel).
 Mire kell? A mindennapi gyakorlatban előforduló jelenségek (például fázisátalakulások, olvadás, dermedés, párolgás) értelmezéséhez, kvantitatív leírásához. Szerkezeti anyagok tulajdonságainak változása
Mire kell? A mindennapi gyakorlatban előforduló jelenségek (például fázisátalakulások, olvadás, dermedés, párolgás) értelmezéséhez, kvantitatív leírásához. Szerkezeti anyagok tulajdonságainak változása
Kétalkotós ötvözetek. Vasalapú ötvözetek. Egyensúlyi átalakulások.
 Kétalkotós ötvözetek. Vasalapú ötvözetek. Egyensúlyi átalakulások. dr. Fábián Enikő Réka fabianr@eik.bme.hu BMEGEMTAGM3-HŐKEZELÉS 2016/2017 Kétalkotós ötvözetrendszerekkel kapcsolatos alapfogalmak Az alkotók
Kétalkotós ötvözetek. Vasalapú ötvözetek. Egyensúlyi átalakulások. dr. Fábián Enikő Réka fabianr@eik.bme.hu BMEGEMTAGM3-HŐKEZELÉS 2016/2017 Kétalkotós ötvözetrendszerekkel kapcsolatos alapfogalmak Az alkotók
TÖBBKOMPONENS RENDSZEREK FÁZISEGYENSÚLYAI IV.
 TÖBBKOMPONENS RENDSZEREK FÁZISEGYENSÚLYAI IV. TÖBBFÁZISÚ, TÖBBKOMPONENS RENDSZEREK Kétkomponens szilárd-folyadék egyensúlyok Néhány fogalom: - olvadék - ötvözetek - amorf anyagok Állapotok feltüntetése:
TÖBBKOMPONENS RENDSZEREK FÁZISEGYENSÚLYAI IV. TÖBBFÁZISÚ, TÖBBKOMPONENS RENDSZEREK Kétkomponens szilárd-folyadék egyensúlyok Néhány fogalom: - olvadék - ötvözetek - amorf anyagok Állapotok feltüntetése:
Vas- karbon ötvözetrendszer
 Vas- karbon ötvözetrendszer Vas- Karbon diagram Eltérések az eddig tárgyalt diagramokhoz képest a diagramot csak 6,67 C %-ig ábrázolják, bizonyos vonalak folyamatos, és szaggatott vonallal is fel vannak
Vas- karbon ötvözetrendszer Vas- Karbon diagram Eltérések az eddig tárgyalt diagramokhoz képest a diagramot csak 6,67 C %-ig ábrázolják, bizonyos vonalak folyamatos, és szaggatott vonallal is fel vannak
Ón-ólom rendszer fázisdiagramjának megszerkesztése lehűlési görbék alapján
 Ón-ólom rendszer fázisdiagramjának megszerkesztése lehűlési görbék alapján Készítette: Zsélyné Ujvári Mária, Szalma József; 2012 Előadó: Zsély István Gyula, Javított valtozat 2016 Laborelőkészítő előadás,
Ón-ólom rendszer fázisdiagramjának megszerkesztése lehűlési görbék alapján Készítette: Zsélyné Ujvári Mária, Szalma József; 2012 Előadó: Zsély István Gyula, Javított valtozat 2016 Laborelőkészítő előadás,
Fémek és ötvözetek termikus viselkedése
 Anyagtudomány és Technológia Tanszék Fémek és ötvözetek termikus viselkedése Dr. Szabó Péter János szpj@eik.bme.hu Anyagszerkezettan és anyagvizsgálat BMEGEMTBGA1 2018/2019/2 Az előadás során megismerjük
Anyagtudomány és Technológia Tanszék Fémek és ötvözetek termikus viselkedése Dr. Szabó Péter János szpj@eik.bme.hu Anyagszerkezettan és anyagvizsgálat BMEGEMTBGA1 2018/2019/2 Az előadás során megismerjük
A metastabilis Fe-Fe 3 C ikerdiagram (Heyn - Charpy - diagram)
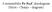 A metastabilis Fe-Fe 3 C ikerdiagram (Heyn - Charpy - diagram) A vas-karbon egyensúlyi diagram alapvető fontosságú a vasötvözetek tárgyalásánál. Az Fe-C ötvözetekre vonatkozó ismereteket általában kettős
A metastabilis Fe-Fe 3 C ikerdiagram (Heyn - Charpy - diagram) A vas-karbon egyensúlyi diagram alapvető fontosságú a vasötvözetek tárgyalásánál. Az Fe-C ötvözetekre vonatkozó ismereteket általában kettős
ANYAGEGYENSÚLYOK. ANYAGMÉRNÖK MSC KÉPZÉS és KOHÓMÉRNÖK MSC KÉPZÉS. (nappali munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ
 ANYAGEGYENSÚLYOK ANYAGMÉRNÖK MSC KÉPZÉS és KOHÓMÉRNÖK MSC KÉPZÉS (nappali munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIAI
ANYAGEGYENSÚLYOK ANYAGMÉRNÖK MSC KÉPZÉS és KOHÓMÉRNÖK MSC KÉPZÉS (nappali munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIAI
ANYAGSZERKEZETTAN II.
 ANYAGSZERKEZETTAN II. ANYAGMÉRNÖK BSc KÉPZÉS (levelező munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIAI INTÉZET
ANYAGSZERKEZETTAN II. ANYAGMÉRNÖK BSc KÉPZÉS (levelező munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIAI INTÉZET
3. Az Sn-Pb ötvözetek termikus analízise, fázisdiagram megszerkesztése. Előkészítő előadás
 3. Az Sn-Pb ötvözetek termikus analízise, fázisdiagram megszerkesztése. Előkészítő előadás 2018.02.05. A gyakorlat célja Ismerkedés a Fizikai Kémia II. laboratóriumi gyakorlatok légkörével A jegyzőkönyv
3. Az Sn-Pb ötvözetek termikus analízise, fázisdiagram megszerkesztése. Előkészítő előadás 2018.02.05. A gyakorlat célja Ismerkedés a Fizikai Kémia II. laboratóriumi gyakorlatok légkörével A jegyzőkönyv
ANYAGSZERKEZETTAN II.
 ANYAGSZERKEZETTAN II. ANYAGMÉRNÖK BSc KÉPZÉS (nappali munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIAI INTÉZET Miskolc,
ANYAGSZERKEZETTAN II. ANYAGMÉRNÖK BSc KÉPZÉS (nappali munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIAI INTÉZET Miskolc,
3515, Miskolc-Egyetemváros
 Anyagmérnök udományok, 37. kötet, 1. szám (01), pp. 49 56. A-FE-SI ÖVÖZERENDSZER AUMÍNIUMAN GAZDAG SARKÁNAK FEDOGOZÁSA ESPHAD-MÓDSZERRE ESIMAION OF HE A-RIH ORNER OF HE A-FE-SI AOY SYSEM Y ESPHAD MEHOD
Anyagmérnök udományok, 37. kötet, 1. szám (01), pp. 49 56. A-FE-SI ÖVÖZERENDSZER AUMÍNIUMAN GAZDAG SARKÁNAK FEDOGOZÁSA ESPHAD-MÓDSZERRE ESIMAION OF HE A-RIH ORNER OF HE A-FE-SI AOY SYSEM Y ESPHAD MEHOD
ÁRAMKÖRÖK SZIMULÁCIÓJA
 ÁRAMKÖRÖK SZIMULÁCIÓJA Az áramkörök szimulációja révén betekintést nyerünk azok működésébe. Meg tudjuk határozni az áramkörök válaszát különböző gerjesztésekre, különböző üzemmódokra. Végezhetők analóg
ÁRAMKÖRÖK SZIMULÁCIÓJA Az áramkörök szimulációja révén betekintést nyerünk azok működésébe. Meg tudjuk határozni az áramkörök válaszát különböző gerjesztésekre, különböző üzemmódokra. Végezhetők analóg
Tanulási cél Szorzatfüggvényekre vonatkozó integrálási technikák megismerése és különböző típusokra való alkalmazása. 5), akkor
 Integrálszámítás Integrálási szabályok Tanulási cél Szorzatfüggvényekre vonatkozó integrálási technikák megismerése és különböző típusokra való alkalmazása Motivációs feladat Valószínűség-számításnál találkozhatunk
Integrálszámítás Integrálási szabályok Tanulási cél Szorzatfüggvényekre vonatkozó integrálási technikák megismerése és különböző típusokra való alkalmazása Motivációs feladat Valószínűség-számításnál találkozhatunk
1 Műszaki hőtan Termodinamika. Ellenőrző kérdések-02 1
 1 Műszaki hőtan Termodinamika. Ellenőrző kérdések-02 1 Kérdések. 1. Mit mond ki a termodinamika nulladik főtétele? Azt mondja ki, hogy mindenegyes termodinamikai kölcsönhatáshoz tartozik a TDR-nek egyegy
1 Műszaki hőtan Termodinamika. Ellenőrző kérdések-02 1 Kérdések. 1. Mit mond ki a termodinamika nulladik főtétele? Azt mondja ki, hogy mindenegyes termodinamikai kölcsönhatáshoz tartozik a TDR-nek egyegy
TANULÁSTÁMOGATÓ KÉRDÉSEK AZ 2.KOLLOKVIUMHOZ
 TANULÁSTÁMOGATÓ KÉRDÉSEK AZ 2.KOLLOKVIUMHOZ Vas-karbon diagram: A vas olvadáspontja: a) 1563 C. b) 1536 C. c) 1389 C. Mennyi a vas A1-el jelölt hőmérséklete? b) 1538 C. Mennyi a vas A2-el jelölt hőmérséklete?
TANULÁSTÁMOGATÓ KÉRDÉSEK AZ 2.KOLLOKVIUMHOZ Vas-karbon diagram: A vas olvadáspontja: a) 1563 C. b) 1536 C. c) 1389 C. Mennyi a vas A1-el jelölt hőmérséklete? b) 1538 C. Mennyi a vas A2-el jelölt hőmérséklete?
Színfémek és ötvözetek egyensúlyi lehőlése
 Színfémek és ötvözetek egyensúlyi lehőlése 1 Színfém lehőlési görbéje (nincs allotróp átalakulás) F + Sz = K + 1. K = 1 1. Szakasz F=1 olvadék Sz =1 T változhat 2. Szakasz F=2 olvadék + szilárd Sz= 0 T
Színfémek és ötvözetek egyensúlyi lehőlése 1 Színfém lehőlési görbéje (nincs allotróp átalakulás) F + Sz = K + 1. K = 1 1. Szakasz F=1 olvadék Sz =1 T változhat 2. Szakasz F=2 olvadék + szilárd Sz= 0 T
2. Laboratóriumi gyakorlat A TERMISZTOR. 1. A gyakorlat célja. 2. Elméleti bevezető
 . Laboratóriumi gyakorlat A EMISZO. A gyakorlat célja A termisztorok működésének bemutatása, valamint főbb paramétereik meghatározása. Az ellenállás-hőmérséklet = f és feszültség-áram U = f ( I ) jelleggörbék
. Laboratóriumi gyakorlat A EMISZO. A gyakorlat célja A termisztorok működésének bemutatása, valamint főbb paramétereik meghatározása. Az ellenállás-hőmérséklet = f és feszültség-áram U = f ( I ) jelleggörbék
ÖNTÖTT ÖTVÖZETEK FÉMTANA
 ÖNTÖTT ÖTVÖZETEK FÉMTANA ANYAGMÉRNÖK BSC KÉPZÉS JÁRMŰIPARI ÖNTÉSZETI SZAKIRÁNY (nappali munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR JÁRMŰIPARI ÖNTÉSZETI INTÉZETI
ÖNTÖTT ÖTVÖZETEK FÉMTANA ANYAGMÉRNÖK BSC KÉPZÉS JÁRMŰIPARI ÖNTÉSZETI SZAKIRÁNY (nappali munkarendben) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR JÁRMŰIPARI ÖNTÉSZETI INTÉZETI
HŐKEZELÉS FÉMTANI ALAPJAI
 HŐKEZELÉS FÉMTANI ALAPJAI ANYAGMÉRNÖK MESTERKÉPZÉS HŐKEZELŐ SZAKIRÁNY TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIAI INTÉZET
HŐKEZELÉS FÉMTANI ALAPJAI ANYAGMÉRNÖK MESTERKÉPZÉS HŐKEZELŐ SZAKIRÁNY TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR FÉMTANI, KÉPLÉKENYALAKÍTÁSI ÉS NANOTECHNOLÓGIAI INTÉZET
Numerikus integrálás
 Közelítő és szimbolikus számítások 11. gyakorlat Numerikus integrálás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Határozatlan integrál
Közelítő és szimbolikus számítások 11. gyakorlat Numerikus integrálás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Határozatlan integrál
Vas- karbon ötvözetrendszer. Összeállította: Csizmazia Ferencné dr.
 Vas- karbon ötvözetrendszer Összeállította: Csizmazia Ferencné dr. 1 Vas- Karbon diagram 2 Eltérések az eddig tárgyalt diagramokhoz képest a diagramot csak 6,67 C %-ig ábrázolják, bizonyos vonalak folyamatos,
Vas- karbon ötvözetrendszer Összeállította: Csizmazia Ferencné dr. 1 Vas- Karbon diagram 2 Eltérések az eddig tárgyalt diagramokhoz képest a diagramot csak 6,67 C %-ig ábrázolják, bizonyos vonalak folyamatos,
Tartalomjegyzék. Tartalomjegyzék Valós változós valós értékű függvények... 2
 Tartalomjegyzék Tartalomjegyzék... Valós változós valós értékű függvények... Hatványfüggvények:... Páratlan gyökfüggvények:... Páros gyökfüggvények... Törtkitevős függvények (gyökfüggvények hatványai)...
Tartalomjegyzék Tartalomjegyzék... Valós változós valós értékű függvények... Hatványfüggvények:... Páratlan gyökfüggvények:... Páros gyökfüggvények... Törtkitevős függvények (gyökfüggvények hatványai)...
Fázisátalakulások vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 6. MÉRÉS Fázisátalakulások vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. szeptember 28. Szerda délelőtti csoport 1. A mérés célja A mérés
KLASSZIKUS FIZIKA LABORATÓRIUM 6. MÉRÉS Fázisátalakulások vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. szeptember 28. Szerda délelőtti csoport 1. A mérés célja A mérés
Statisztika I. 12. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
Azonos és egymással nem kölcsönható részecskékből álló kvantumos rendszer makrókanónikus sokaságban.
 Kvantum statisztika A kvantummechanika előadások során már megtanultuk, hogy az anyagot felépítő részecskék nemklasszikus, hullámtulajdonságokkal is rendelkeznek aminek következtében viselkedésük sok szempontból
Kvantum statisztika A kvantummechanika előadások során már megtanultuk, hogy az anyagot felépítő részecskék nemklasszikus, hullámtulajdonságokkal is rendelkeznek aminek következtében viselkedésük sok szempontból
A mérések általános és alapvető metrológiai fogalmai és definíciói. Mérések, mérési eredmények, mérési bizonytalanság. mérés. mérési elv
 Mérések, mérési eredmények, mérési bizonytalanság A mérések általános és alapvető metrológiai fogalmai és definíciói mérés Műveletek összessége, amelyek célja egy mennyiség értékének meghatározása. mérési
Mérések, mérési eredmények, mérési bizonytalanság A mérések általános és alapvető metrológiai fogalmai és definíciói mérés Műveletek összessége, amelyek célja egy mennyiség értékének meghatározása. mérési
6 Ionszelektív elektródok. elektródokat kiterjedten alkalmazzák a klinikai gyakorlatban: az automata analizátorokban
 6. Szelektivitási együttható meghatározása 6.1. Bevezetés Az ionszelektív elektródok olyan potenciometriás érzékelők, melyek valamely ion aktivitásának többé-kevésbé szelektív meghatározását teszik lehetővé.
6. Szelektivitási együttható meghatározása 6.1. Bevezetés Az ionszelektív elektródok olyan potenciometriás érzékelők, melyek valamely ion aktivitásának többé-kevésbé szelektív meghatározását teszik lehetővé.
Gibbs-jelenség viselkedésének vizsgálata egyszer négyszögjel esetén
 Matematikai modellek, I. kisprojekt Gibbs-jelenség viselkedésének vizsgálata egyszer négyszögjel esetén Unger amás István B.Sc. szakos matematikus hallgató ungert@maxwell.sze.hu, http://maxwell.sze.hu/~ungert
Matematikai modellek, I. kisprojekt Gibbs-jelenség viselkedésének vizsgálata egyszer négyszögjel esetén Unger amás István B.Sc. szakos matematikus hallgató ungert@maxwell.sze.hu, http://maxwell.sze.hu/~ungert
Határozatlan integrál (2) First Prev Next Last Go Back Full Screen Close Quit
 Határozatlan integrál () First Prev Next Last Go Back Full Screen Close Quit 1. Az összetett függvények integrálására szolgáló egyik módszer a helyettesítéssel való integrálás. Az idevonatkozó tétel pontos
Határozatlan integrál () First Prev Next Last Go Back Full Screen Close Quit 1. Az összetett függvények integrálására szolgáló egyik módszer a helyettesítéssel való integrálás. Az idevonatkozó tétel pontos
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE
 I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE Komplex termékek gyártására jellemző, hogy egy-egy termékbe akár több ezer alkatrész is beépül. Ilyenkor az alkatrészek általában sok különböző beszállítótól érkeznek,
I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE Komplex termékek gyártására jellemző, hogy egy-egy termékbe akár több ezer alkatrész is beépül. Ilyenkor az alkatrészek általában sok különböző beszállítótól érkeznek,
Differenciálegyenletek. Vajda István március 4.
 Analízis előadások Vajda István 2009. március 4. Függvényegyenletek Definíció: Az olyan egyenleteket, amelyekben a meghatározandó ismeretlen függvény, függvényegyenletnek nevezzük. Függvényegyenletek Definíció:
Analízis előadások Vajda István 2009. március 4. Függvényegyenletek Definíció: Az olyan egyenleteket, amelyekben a meghatározandó ismeretlen függvény, függvényegyenletnek nevezzük. Függvényegyenletek Definíció:
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 3. Hibaszámítás, lineáris regresszió Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Hibaszámítás Hibák fajtái, definíciók Abszolút, relatív, öröklött
BIOMATEMATIKA ELŐADÁS 3. Hibaszámítás, lineáris regresszió Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Hibaszámítás Hibák fajtái, definíciók Abszolút, relatív, öröklött
Görbe- és felületmodellezés. Szplájnok Felületmodellezés
 Görbe- és felületmodellezés Szplájnok Felületmodellezés Spline (szplájn) Spline: Szakaszosan, parametrikus polinomokkal leírt görbe A spline nevét arról a rugalmasan hajlítható vonalzóról kapta, melyet
Görbe- és felületmodellezés Szplájnok Felületmodellezés Spline (szplájn) Spline: Szakaszosan, parametrikus polinomokkal leírt görbe A spline nevét arról a rugalmasan hajlítható vonalzóról kapta, melyet
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Termokémia. Hess, Germain Henri (1802-1850) A bemutatót összeállította: Fogarasi József, Petrik Lajos SZKI, 2011
 Termokémia Hess, Germain Henri (1802-1850) A bemutatót összeállította: Fogarasi József, Petrik Lajos SZKI, 2011 A reakcióhő fogalma A reakcióhő tehát a kémiai változásokat kísérő energiaváltozást jelenti.
Termokémia Hess, Germain Henri (1802-1850) A bemutatót összeállította: Fogarasi József, Petrik Lajos SZKI, 2011 A reakcióhő fogalma A reakcióhő tehát a kémiai változásokat kísérő energiaváltozást jelenti.
TÖBBKOMPONENS RENDSZEREK FÁZISEGYENSÚLYAI II. Ismerjük fel, hogy többkomponens fázisegyensúlyokban a folyadék fázisnak kitüntetett szerepe van!
 TÖKOMPONENS RENDSZEREK FÁZISEGYENSÚLYI II Ismerjük fel hogy többkomonens fázisegyensúlyokban a folyadék fázisnak kitüntetett szeree van! Eddig: egymásban korátlanul oldódó folyadékok folyadék-gz egyensúlyai
TÖKOMPONENS RENDSZEREK FÁZISEGYENSÚLYI II Ismerjük fel hogy többkomonens fázisegyensúlyokban a folyadék fázisnak kitüntetett szeree van! Eddig: egymásban korátlanul oldódó folyadékok folyadék-gz egyensúlyai
OSZTHATÓSÁG. Osztók és többszörösök : a 3 többszörösei : a 4 többszörösei Ahol mindkét jel megtalálható a 12 többszöröseit találjuk.
 Osztók és többszörösök 1783. A megadott számok elsõ tíz többszöröse: 3: 3 6 9 12 15 18 21 24 27 30 4: 4 8 12 16 20 24 28 32 36 40 5: 5 10 15 20 25 30 35 40 45 50 6: 6 12 18 24 30 36 42 48 54 60 1784. :
Osztók és többszörösök 1783. A megadott számok elsõ tíz többszöröse: 3: 3 6 9 12 15 18 21 24 27 30 4: 4 8 12 16 20 24 28 32 36 40 5: 5 10 15 20 25 30 35 40 45 50 6: 6 12 18 24 30 36 42 48 54 60 1784. :
Másodfokú egyenletek, egyenlőtlenségek
 Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x 1x 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x 1x 16 =. 1. lépés:
Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x 1x 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x 1x 16 =. 1. lépés:
ELLENŐRZŐ KÉRDÉSEK. Anyagtudomány c. tantárgyból a 2009/10. tanév I. félévében Gépészmérnöki és Informatikai Kar, Gépészmérnöki Szak, BSc képzés
 ELLENŐRZŐ KÉRDÉSEK Anyagtudomány c. tantárgyból a 2009/10. tanév I. félévében Gépészmérnöki és Informatikai Kar, Gépészmérnöki Szak, BSc képzés 1. Sorolja fel a szilárd halmazállapotú kristályos anyagokban
ELLENŐRZŐ KÉRDÉSEK Anyagtudomány c. tantárgyból a 2009/10. tanév I. félévében Gépészmérnöki és Informatikai Kar, Gépészmérnöki Szak, BSc képzés 1. Sorolja fel a szilárd halmazállapotú kristályos anyagokban
Modern Fizika Labor. 11. Spektroszkópia. Fizika BSc. A mérés dátuma: dec. 16. A mérés száma és címe: Értékelés: A beadás dátuma: dec. 21.
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. dec. 16. A mérés száma és címe: 11. Spektroszkópia Értékelés: A beadás dátuma: 2011. dec. 21. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. dec. 16. A mérés száma és címe: 11. Spektroszkópia Értékelés: A beadás dátuma: 2011. dec. 21. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás)
 Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Alap-ötlet: Karl Friedrich Gauss ( ) valószínűségszámítási háttér: Andrej Markov ( )
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
A Riemann-Siegel zeta függvény kiugró értékeinek keresése. A matematikai egyik legnehezebb problémája, avagy a prímszámok misztériuma
 A Riemann-Siegel zeta függvény kiugró értékeinek keresése A matematikai egyik legnehezebb problémája, avagy a prímszámok misztériuma 2013 A probléma fontossága és hatása a hétköznapi életre A prímszámok
A Riemann-Siegel zeta függvény kiugró értékeinek keresése A matematikai egyik legnehezebb problémája, avagy a prímszámok misztériuma 2013 A probléma fontossága és hatása a hétköznapi életre A prímszámok
I. ANALITIKAI ADATOK MEGADÁSA, KONVERZIÓK
 I. ANALITIKAI ADATOK MEGADÁSA, KONVERZIÓK I.2. Konverziók Geokémiai vizsgálatok során gyakran kényszerülünk arra, hogy különböző kémiai koncentrációegységben megadott adatokat hasonlítsunk össze vagy alakítsuk
I. ANALITIKAI ADATOK MEGADÁSA, KONVERZIÓK I.2. Konverziók Geokémiai vizsgálatok során gyakran kényszerülünk arra, hogy különböző kémiai koncentrációegységben megadott adatokat hasonlítsunk össze vagy alakítsuk
A nagytermi gyakorlat fő pontjai
 ANYAGTUDOMÁNY ÉS TECHNOLÓGIA TANSZÉK Anyagismeret 2008/09 Fe-C állapotábra Dr. Reé András ree@eik.bme.hu Fe-C 1 A nagytermi gyakorlat fő pontjai A Fe-C állapotábra felépítése Stabil (grafit) rendszer Metastabil
ANYAGTUDOMÁNY ÉS TECHNOLÓGIA TANSZÉK Anyagismeret 2008/09 Fe-C állapotábra Dr. Reé András ree@eik.bme.hu Fe-C 1 A nagytermi gyakorlat fő pontjai A Fe-C állapotábra felépítése Stabil (grafit) rendszer Metastabil
Reakciókinetika. aktiválási energia. felszabaduló energia. kiindulási állapot. energia nyereség. végállapot
 Reakiókinetika aktiválási energia kiindulási állapot energia nyereség felszabaduló energia végállapot Reakiókinetika kinetika: mozgástan reakiókinetika (kémiai kinetika): - reakiók időbeli leírása - reakiómehanizmusok
Reakiókinetika aktiválási energia kiindulási állapot energia nyereség felszabaduló energia végállapot Reakiókinetika kinetika: mozgástan reakiókinetika (kémiai kinetika): - reakiók időbeli leírása - reakiómehanizmusok
Spontaneitás, entrópia
 Spontaneitás, entrópia 6-1 Spontán folyamat 6-2 Entrópia 6-3 Az entrópia kiszámítása 6-4 Spontán folyamat: a termodinamika második főtétele 6-5 Standard szabadentalpia változás, ΔG 6-6 Szabadentalpia változás
Spontaneitás, entrópia 6-1 Spontán folyamat 6-2 Entrópia 6-3 Az entrópia kiszámítása 6-4 Spontán folyamat: a termodinamika második főtétele 6-5 Standard szabadentalpia változás, ΔG 6-6 Szabadentalpia változás
Egyenletek, egyenlőtlenségek V.
 Egyenletek, egyenlőtlenségek V. DEFINÍCIÓ: (Másodfokú egyenlet) Az ax + bx + c = 0 alakban felírható egyenletet (a, b, c R; a 0), ahol x a változó, másodfokú egyenletnek nevezzük. TÉTEL: Az ax + bx + c
Egyenletek, egyenlőtlenségek V. DEFINÍCIÓ: (Másodfokú egyenlet) Az ax + bx + c = 0 alakban felírható egyenletet (a, b, c R; a 0), ahol x a változó, másodfokú egyenletnek nevezzük. TÉTEL: Az ax + bx + c
Közönséges differenciál egyenletek megoldása numerikus módszerekkel: egylépéses numerikus eljárások
 Közönséges differenciál egyenletek megoldása numerikus módszerekkel: egylépéses numerikus eljárások Bevezetés Ebben a cikkben megmutatjuk, hogyan használhatóak a Mathematica egylépéses numerikus eljárásai,
Közönséges differenciál egyenletek megoldása numerikus módszerekkel: egylépéses numerikus eljárások Bevezetés Ebben a cikkben megmutatjuk, hogyan használhatóak a Mathematica egylépéses numerikus eljárásai,
Kémiai átalakulások. A kémiai reakciók körülményei. A rendszer energiaviszonyai
 Kémiai átalakulások 9. hét A kémiai reakció: kötések felbomlása, új kötések kialakulása - az atomok vegyértékelektronszerkezetében történik változás egyirányú (irreverzibilis) vagy megfordítható (reverzibilis)
Kémiai átalakulások 9. hét A kémiai reakció: kötések felbomlása, új kötések kialakulása - az atomok vegyértékelektronszerkezetében történik változás egyirányú (irreverzibilis) vagy megfordítható (reverzibilis)
Tartalomjegyzék I. RÉSZ: KÍSÉRLETEK MEGTERVEZÉSE
 Tartalomjegyzék 5 Tartalomjegyzék Előszó I. RÉSZ: KÍSÉRLETEK MEGTERVEZÉSE 1. fejezet: Kontrollált kísérletek 21 1. A Salk-oltás kipróbálása 21 2. A porta-cava sönt 25 3. Történeti kontrollok 27 4. Összefoglalás
Tartalomjegyzék 5 Tartalomjegyzék Előszó I. RÉSZ: KÍSÉRLETEK MEGTERVEZÉSE 1. fejezet: Kontrollált kísérletek 21 1. A Salk-oltás kipróbálása 21 2. A porta-cava sönt 25 3. Történeti kontrollok 27 4. Összefoglalás
1. Görbe illesztés a legkissebb négyzetek módszerével
 GÖRBE ILLESZTÉS A LEGKISSEBB ÉGYZETEK MÓDSZERÉVEL. Görbe illesztés a legkissebb négyzetek módszerével Az előző gyakorlaton megismerkedtünk a korrelációs együttható fogalmával és számítási módjával. A korrelációs
GÖRBE ILLESZTÉS A LEGKISSEBB ÉGYZETEK MÓDSZERÉVEL. Görbe illesztés a legkissebb négyzetek módszerével Az előző gyakorlaton megismerkedtünk a korrelációs együttható fogalmával és számítási módjával. A korrelációs
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
First Prev Next Last Go Back Full Screen Close Quit. Matematika I
 Matematika I (Analízis) Készítette: Horváth Gábor Kötelező irodalom: Ács László, Gáspár Csaba: Analízis 1 Oktatási segédanyagok és a tantárgyi követelményrendszer megtalálható a http://rs1.szif.hu/ horvathg/horvathg.html
Matematika I (Analízis) Készítette: Horváth Gábor Kötelező irodalom: Ács László, Gáspár Csaba: Analízis 1 Oktatási segédanyagok és a tantárgyi követelményrendszer megtalálható a http://rs1.szif.hu/ horvathg/horvathg.html
Másodfokú egyenletek, egyenlőtlenségek
 Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x + 1x + 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x + 1x + 16 = 0.
Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x + 1x + 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x + 1x + 16 = 0.
Termodinamikai bevezető
 Termodinamikai bevezető Alapfogalmak Termodinamikai rendszer: Az univerzumnak az a részhalmaza, amit egy termodinamikai vizsgálat során vizsgálunk. Termodinamikai környezet: Az univerzumnak a rendszeren
Termodinamikai bevezető Alapfogalmak Termodinamikai rendszer: Az univerzumnak az a részhalmaza, amit egy termodinamikai vizsgálat során vizsgálunk. Termodinamikai környezet: Az univerzumnak a rendszeren
Mérési adatok illesztése, korreláció, regresszió
 Mérési adatok illesztése, korreláció, regresszió Korreláció, regresszió Két változó mennyiség közötti kapcsolatot vizsgálunk. Kérdés: van-e kapcsolat két, ugyanabban az egyénben, állatban, kísérleti mintában,
Mérési adatok illesztése, korreláció, regresszió Korreláció, regresszió Két változó mennyiség közötti kapcsolatot vizsgálunk. Kérdés: van-e kapcsolat két, ugyanabban az egyénben, állatban, kísérleti mintában,
Színfémek és ötvözetek egyensúlyi lehűlése. Összeállította: Csizmazia Ferencné dr.
 Színfémek és ötvözetek egyensúlyi lehűlése Összeállította: Csizmazia Ferencné dr. 1 Színfém lehűlési görbéje (nincs allotróp átalakulás) F + Sz = K + 1. K = 1 1. Szakasz F=1 olvadék Sz =1 T változhat 2.
Színfémek és ötvözetek egyensúlyi lehűlése Összeállította: Csizmazia Ferencné dr. 1 Színfém lehűlési görbéje (nincs allotróp átalakulás) F + Sz = K + 1. K = 1 1. Szakasz F=1 olvadék Sz =1 T változhat 2.
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Alkalmazás a makrókanónikus sokaságra: A fotongáz
 Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
Polinomok, Lagrange interpoláció
 Közelítő és szimbolikus számítások 8. gyakorlat Polinomok, Lagrange interpoláció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Polinomok
Közelítő és szimbolikus számítások 8. gyakorlat Polinomok, Lagrange interpoláció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Polinomok
Fogorvosi anyagtan fizikai alapjai 5. Általános anyagszerkezeti ismeretek Fémek, ötvözetek
 Fémek törékeny/képlékeny nemesémek magas/alacsony o.p. Fogorvosi anyagtan izikai alapjai 5. Általános anyagszerkezeti ismeretek Fémek, ötvözetek ρ < 5 g cm 3 könnyűémek 5 g cm3 < ρ nehézémek 2 Fémek tulajdonságai
Fémek törékeny/képlékeny nemesémek magas/alacsony o.p. Fogorvosi anyagtan izikai alapjai 5. Általános anyagszerkezeti ismeretek Fémek, ötvözetek ρ < 5 g cm 3 könnyűémek 5 g cm3 < ρ nehézémek 2 Fémek tulajdonságai
Szá molá si feládáttí pusok á Ko zgázdásá gtán I. (BMEGT30A003) tá rgy zá rthelyi dolgozátá hoz
 Szá molá si feládáttí pusok á Ko zgázdásá gtán I. (BMEGT30A003) tá rgy zá rthelyi dolgozátá hoz 1. feladattípus a megadott adatok alapján lineáris keresleti, vagy kínálati függvény meghatározása 1.1. feladat
Szá molá si feládáttí pusok á Ko zgázdásá gtán I. (BMEGT30A003) tá rgy zá rthelyi dolgozátá hoz 1. feladattípus a megadott adatok alapján lineáris keresleti, vagy kínálati függvény meghatározása 1.1. feladat
A mérési eredmény megadása
 A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
Taylor-polinomok. 1. Alapfeladatok. 2015. április 11. 1. Feladat: Írjuk fel az f(x) = e 2x függvény másodfokú Maclaurinpolinomját!
 Taylor-polinomok 205. április.. Alapfeladatok. Feladat: Írjuk fel az fx) = e 2x függvény másodfokú Maclaurinpolinomját! Megoldás: A feladatot kétféle úton is megoldjuk. Az els megoldásban induljunk el
Taylor-polinomok 205. április.. Alapfeladatok. Feladat: Írjuk fel az fx) = e 2x függvény másodfokú Maclaurinpolinomját! Megoldás: A feladatot kétféle úton is megoldjuk. Az els megoldásban induljunk el
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
Átszámítások különböző alapfelületek koordinátái között
 Átszámítások különböző alapfelületek koordinátái között A különböző időpontokban, különböző körülmények között rögzített pontok földi koordinátái különböző alapfelületekre (ellipszoidokra geodéziai dátumokra)
Átszámítások különböző alapfelületek koordinátái között A különböző időpontokban, különböző körülmények között rögzített pontok földi koordinátái különböző alapfelületekre (ellipszoidokra geodéziai dátumokra)
Feladatok MATEMATIKÁBÓL
 Feladatok MATEMATIKÁBÓL a 12. évfolyam számára III. 1. Számítsuk ki a következő hatványok értékét! 2. Írjuk fel gyökjelekkel a következő hatványokat! 3. Az ötnek hányadik hatványa a következő kifejezés?
Feladatok MATEMATIKÁBÓL a 12. évfolyam számára III. 1. Számítsuk ki a következő hatványok értékét! 2. Írjuk fel gyökjelekkel a következő hatványokat! 3. Az ötnek hányadik hatványa a következő kifejezés?
5. Az adszorpciós folyamat mennyiségi leírása a Langmuir-izoterma segítségével
 5. Az adszorpciós folyamat mennyiségi leírása a Langmuir-izoterma segítségével 5.1. Átismétlendő anyag 1. Adszorpció (előadás) 2. Langmuir-izoterma (előadás) 3. Spektrofotometria és Lambert Beer-törvény
5. Az adszorpciós folyamat mennyiségi leírása a Langmuir-izoterma segítségével 5.1. Átismétlendő anyag 1. Adszorpció (előadás) 2. Langmuir-izoterma (előadás) 3. Spektrofotometria és Lambert Beer-törvény
8. Egyenletek, egyenlőtlenségek, egyenletrendszerek II.
 8 Egyenletek, egyenlőtlenségek, egyenletrendszerek II Elméleti összefoglaló Az a + b+ c, a egyenletet másodfokú egyenletnek nevezzük A D b ac kifejezést az egyenlet diszkriminánsának nevezzük Ha D >, az
8 Egyenletek, egyenlőtlenségek, egyenletrendszerek II Elméleti összefoglaló Az a + b+ c, a egyenletet másodfokú egyenletnek nevezzük A D b ac kifejezést az egyenlet diszkriminánsának nevezzük Ha D >, az
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
A PiFast program használata. Nagy Lajos
 A PiFast program használata Nagy Lajos Tartalomjegyzék 1. Bevezetés 3 2. Bináris kimenet létrehozása. 3 2.1. Beépített konstans esete.............................. 3 2.2. Felhasználói konstans esete............................
A PiFast program használata Nagy Lajos Tartalomjegyzék 1. Bevezetés 3 2. Bináris kimenet létrehozása. 3 2.1. Beépített konstans esete.............................. 3 2.2. Felhasználói konstans esete............................
MÉRÉSI EREDMÉNYEK PONTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI
 MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
4/24/12. Regresszióanalízis. Legkisebb négyzetek elve. Regresszióanalízis
 1. feladat Regresszióanalízis. Legkisebb négyzetek elve 2. feladat Az iskola egy évfolyamába tartozó diákok átlagéletkora 15,8 év, standard deviációja 0,6 év. A 625 fős évfolyamból hány diák fiatalabb
1. feladat Regresszióanalízis. Legkisebb négyzetek elve 2. feladat Az iskola egy évfolyamába tartozó diákok átlagéletkora 15,8 év, standard deviációja 0,6 év. A 625 fős évfolyamból hány diák fiatalabb
Halmazállapot-változások vizsgálata ( )
 Halmazállapot-változások vizsgálata Eddigi tanulmányaik során a szilárd, folyékony és légnemő, valamint a plazma állapottal találkoztak. Ezen halmazállapotok mindegyikében más és más összefüggés áll fenn
Halmazállapot-változások vizsgálata Eddigi tanulmányaik során a szilárd, folyékony és légnemő, valamint a plazma állapottal találkoztak. Ezen halmazállapotok mindegyikében más és más összefüggés áll fenn
KÖZLEKEDÉSÜZEMI ÉS KÖZLEKEDÉSGAZDASÁGI TANSZÉK. Prof. Dr. Tánczos Lászlóné 2015
 KÖZLEKEDÉSÜZEMI ÉS KÖZLEKEDÉSGAZDASÁGI TANSZÉK Prof. Dr. Tánczos Lászlóné 2015 KÖZLEKEDÉSGAZDASÁGTAN BSc. I. KAMATOS KAMATSZÁMÍTÁS (jövőbeni érték számítása) C t = C 0 * (1 + i) t ahol C t a 0. évben ismert
KÖZLEKEDÉSÜZEMI ÉS KÖZLEKEDÉSGAZDASÁGI TANSZÉK Prof. Dr. Tánczos Lászlóné 2015 KÖZLEKEDÉSGAZDASÁGTAN BSc. I. KAMATOS KAMATSZÁMÍTÁS (jövőbeni érték számítása) C t = C 0 * (1 + i) t ahol C t a 0. évben ismert
Egyenletek, egyenlőtlenségek X.
 Egyenletek, egyenlőtlenségek X. DEFINÍCIÓ: (Logaritmus) Ha egy pozitív valós számot adott, 1 - től különböző pozitív alapú hatvány alakban írunk fel, akkor ennek a hatványnak a kitevőjét logaritmusnak
Egyenletek, egyenlőtlenségek X. DEFINÍCIÓ: (Logaritmus) Ha egy pozitív valós számot adott, 1 - től különböző pozitív alapú hatvány alakban írunk fel, akkor ennek a hatványnak a kitevőjét logaritmusnak
Fluidum-kőzet kölcsönhatás: megváltozik a kőzet és a fluidum összetétele és új egyensúlyi ásványparagenezis jön létre Székyné Fux V k álimetaszo
 Hidrotermális képződmények genetikai célú vizsgálata Bevezetés a fluidum-kőzet kölcsönhatás, és a hidrotermális ásványképződési környezet termodinamikai modellezésébe Dr Molnár Ferenc ELTE TTK Ásványtani
Hidrotermális képződmények genetikai célú vizsgálata Bevezetés a fluidum-kőzet kölcsönhatás, és a hidrotermális ásványképződési környezet termodinamikai modellezésébe Dr Molnár Ferenc ELTE TTK Ásványtani
Biometria az orvosi gyakorlatban. Korrelációszámítás, regresszió
 SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
Spontaneitás, entrópia
 Spontaneitás, entrópia 11-1 Spontán és nem spontán folyamat 11-2 Entrópia 11-3 Az entrópia kiszámítása 11-4 Spontán folyamat: a termodinamika második főtétele 11-5 Standard szabadentalpia változás, ΔG
Spontaneitás, entrópia 11-1 Spontán és nem spontán folyamat 11-2 Entrópia 11-3 Az entrópia kiszámítása 11-4 Spontán folyamat: a termodinamika második főtétele 11-5 Standard szabadentalpia változás, ΔG
Az egységugrás függvény a 0 időpillanatot követően 10 nagyságú jelet ad, valamint K=2. Vizsgáljuk meg a kimenetet:
 II Gyakorlat A gyakorlat célja, hogy megismerkedjük az egyszerű szabályozási kör stabilitásának vizsgálati módszerét, valamint a PID szabályzó beállításának egy lehetséges módját. Tekintsük az alábbi háromtárolós
II Gyakorlat A gyakorlat célja, hogy megismerkedjük az egyszerű szabályozási kör stabilitásának vizsgálati módszerét, valamint a PID szabályzó beállításának egy lehetséges módját. Tekintsük az alábbi háromtárolós
Fizikai kémia 2 Reakciókinetika házi feladatok 2016 ősz
 Fizikai kémia 2 Reakciókinetika házi feladatok 2016 ősz A házi feladatok beadhatóak vagy papír alapon (ez a preferált), vagy e-mail formájában is az rkinhazi@gmail.com címre. E-mail esetén ügyeljetek a
Fizikai kémia 2 Reakciókinetika házi feladatok 2016 ősz A házi feladatok beadhatóak vagy papír alapon (ez a preferált), vagy e-mail formájában is az rkinhazi@gmail.com címre. E-mail esetén ügyeljetek a
FÜGGVÉNYTANI ALAPOK A) ÉRTELMEZÉSI TARTOMÁNY
 FÜGGVÉNYTANI ALAPOK Foglalkoztunk az alaptulajdonságnak tekinthető értelmezési tartománnyal, és a paritással, továbbá az összetett függvények képzési módjával, illetve ezeknek az elemi függvényekre való
FÜGGVÉNYTANI ALAPOK Foglalkoztunk az alaptulajdonságnak tekinthető értelmezési tartománnyal, és a paritással, továbbá az összetett függvények képzési módjával, illetve ezeknek az elemi függvényekre való
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Legkisebb négyzetek módszere, Spline interpoláció
 Közelítő és szimbolikus számítások 10. gyakorlat Legkisebb négyzetek módszere, Spline interpoláció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján
Közelítő és szimbolikus számítások 10. gyakorlat Legkisebb négyzetek módszere, Spline interpoláció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján
January 16, ψ( r, t) ψ( r, t) = 1 (1) ( ψ ( r,
 Közelítő módszerek January 16, 27 1 A variációs módszer A variációs módszer szintén egy analitikus közelítő módszer. Olyan esetekben alkalmazzuk mikor ismert az analitikus alak amelyben keressük a sajátfüggvényt,
Közelítő módszerek January 16, 27 1 A variációs módszer A variációs módszer szintén egy analitikus közelítő módszer. Olyan esetekben alkalmazzuk mikor ismert az analitikus alak amelyben keressük a sajátfüggvényt,
Ideális gáz és reális gázok
 Ideális gáz és reális gázok Fizikai kémia előadások 1. Turányi Tamás ELTE Kémiai Intézet Állaotjelzők állaotjelző: egy fizikai rendszer makroszkoikus állaotát meghatározó mennyiség egykomonensű gázok állaotjelzői:
Ideális gáz és reális gázok Fizikai kémia előadások 1. Turányi Tamás ELTE Kémiai Intézet Állaotjelzők állaotjelző: egy fizikai rendszer makroszkoikus állaotát meghatározó mennyiség egykomonensű gázok állaotjelzői:
Termoelektromos hűtőelemek vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 4. MÉRÉS Termoelektromos hűtőelemek vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 30. Szerda délelőtti csoport 1. A mérés célja
KLASSZIKUS FIZIKA LABORATÓRIUM 4. MÉRÉS Termoelektromos hűtőelemek vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 30. Szerda délelőtti csoport 1. A mérés célja
Konvexitás, elaszticitás
 DIFFERENCIÁLSZÁMÍTÁS ALKALMAZÁSAI Konveitás, elaszticitás Tanulási cél A másodrendű deriváltat vizsgálva milyen következtetéseket vonhatunk le a üggvény konveitására vonatkozóan. Elaszticitás ogalmának
DIFFERENCIÁLSZÁMÍTÁS ALKALMAZÁSAI Konveitás, elaszticitás Tanulási cél A másodrendű deriváltat vizsgálva milyen következtetéseket vonhatunk le a üggvény konveitására vonatkozóan. Elaszticitás ogalmának
TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI. 1. Bevezetés
 TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI Dr. Goda Tibor egyetemi docens Gép- és Terméktervezés Tanszék 1. Bevezetés 1.1. A végeselem módszer alapjai - diszkretizáció, - szerkezet felbontása kicsi szabályos elemekre
TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI Dr. Goda Tibor egyetemi docens Gép- és Terméktervezés Tanszék 1. Bevezetés 1.1. A végeselem módszer alapjai - diszkretizáció, - szerkezet felbontása kicsi szabályos elemekre
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Kutatási beszámoló. 2015. február. Tangens delta mérésére alkalmas mérési összeállítás elkészítése
 Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
