A FELTÉTELES VALÓSZÍNŰSÉG, A TELJES VALÓSZÍNŰSÉG TÉTELE,
|
|
|
- Ida Vörösné
- 10 évvel ezelőtt
- Látták:
Átírás
1 A FELTÉTELES VALÓSZÍNŰSÉG, A TELJES VALÓSZÍNŰSÉG TÉTELE, BAYES TÉTELE, FÜGGETLENSÉG Populációgenetika gyakorlat
2 A teljes valószínűség tétele A teljes valószínűség tétele azt mondja ki, hogy ha ismerjük egy E esemény feltételes valószínűségét egy teljes eseményrendszer valamennyi F 1, F 2,..., F n eseménye, mint feltétel mellett, akkor ebből az E esemény feltétel nélküli valószínűségét az alábbi képlettel határozhatjuk meg: P( E) n i 1 P ( EF) P( F i i )
3 Bayestétele a fordított irányú kérdésre ad választ: A tétel akkor használható, ha ismerjük egy E esemény feltételes valószínűségét egy teljes eseményrendszer valamennyi F 1, F 2,..., F n eseménye, mint feltétel mellett, és ebből szeretnénk meghatározni az egyes F i eseményeknek az E-re vonatkozó feltételes valószínűségét.
4 Két eseményre: P( F 2 E ) P( E F P( E 2) P( F F 2) P( F 2) 2) + P( E F1) P( F1) a nevező a teljes valószínűség tétele
5 Általánosságban megmondja, hogy mekkora a vsz.-e, hogy a teljes eseményrendszerelemei közül éppen a k-adik(f k ) következik be, feltéve, ha tudjuk, hogy bekövetkezett az E esemény. hogy bekövetkezett az E esemény. n i i i k k k F P F E P F P F E P E F P 1 ) ( ) ( ) ( ) ( ) (
6 Teljes eseményrendszer Az F 1, F 2, F 3,..., F n eseményeket teljes eseményrendszernek nevezzük, ha az F i események páronként kizárják egymást, és az összes F i összege a biztos esemény
7 P(F 1 ), P(F 2 ),..., P(F n ) valószínűségek az a priori valószínűségek a P(F 1 E), P(F 2 E),..., P(F n E) feltételes valószínűségek az a posteriori valószínűségek Két esemény független, ha E bekövetkezése nem befolyásolja F esélyeit, azaz P ( EF) P( E) P( F), vagyisp(ef) P(E) ésp( FE) P( F) Két esemény kizáró, ha nem következhetnek be egyszerre, azaz ha szorzatuk a lehetetlen esemény.
8 Milyen valószínűséggel lesz a pedigrén látható 6. egyén AA illetve A0 vércsoportú?
9
10 A 6. egyén lehet AA és A0 vércsoportú-> F 1 és F 2 lehetőség F 1 : AA (mindkét szülőtől A allélt kapott); ennek valószínűsége: P(F 1) 0,5 F 2 : A0 (A-t és 0-t is kapott); ennek valószínűsége: P(F 2 ) 0,5 P(a 6. egyén A-t ad tovább, ha AA genotípusú) P(A-t ad AA) P(E F 1 ) 1 P(a 6. egyén A-t ad tovább, ha A0 genotípusú) P(A-t ad A0) P(E F 2 ) 0,5
11 Grafikusan: 3 2 0,5 0,5 0,5 1 0,5 1 ) ( ) ( ) ( ) ( ) ( ) ( ) ( F P EF P F P EF P F P EF P E F P 3 1 0,5 0,5 0,5 1 0,5 0,5 ) ( ) ( ) ( ) ( ) ( ) ( ) ( F P EF P F P EF P F P EF P E F P F 1 F 2 Szürke E, azaz A allélt ad tovább
12 Hogyan változik meg ez a valószínűség, ha a 6. egyénnek születik még két AB-s gyermeke (akik a pedigrén nincsenek feltüntetve), illetve, ha összesen 10 AB-s gyermeke lesz?
13 Legyen K annak a valószínűsége, hogy három AB vércsoportú gyerek születik, ekkor a valószínűségek F 1 : AA (mindkét szülőtől A allélt kapott); ennek valószínűsége: P(F 1 ) 0,5 F 2 : A0 (A-t és 0-t is kapott); ennek valószínűsége: P(F 2 ) 0,5 P ( KF ) 1 P( KF 1 2 ) ,125 P( KF1) P( F1) 1 0,5 P( F1 K) P( KF ) P( F ) P( KF ) P( F ) 1 0,5 + 0,125 0,
14 Legyen K annak a valószínűsége, hogy tíz AB vércsoportú gyerek születik, ekkor a valószínűségek: P( KF P( KF 1 2 ) 1 ) P( KF1) P( F1) 1 0,5 P( F K) 10 P( KF ) P( F ) P( KF ) P( F ) 1 0,5 + 0, ,
15 Mit mondhatunk, ha ezek után a házaspár tizenegyedik gyermeke B vércsoportú lesz?
16 Mit mondhatunk, ha ezek után a házaspár tizenegyedik gyermeke B vércsoportú lesz? Ekkor a 6. egyén 0-s allélt adott, tehát biztosan A0 ha nagyon sok olyan családot megvizsgálnánk, mint a pedigrénlátható, akkor 2/3 részükben a 6. egyénnek megfelelő személy AA vércsoportú lenne, 1/3 részükben pedig A0 Ha sok olyan családot megvizsgálnánk, ahol 3 ill. 10 AB-s gyerek van, akkor csak 1/9 ill. 1/1025 részükben találnánk azt, hogy a 6. egyénnek megfelelő személy A0
17 Példa 1. Mi a valószínűsége annak, hogy egy szabályos dobókockával páratlan számot dobunk? Mi a valószínűsége annak, hogy a dobókockával 6-ost dobunk és a feldobott pénz fej lesz?
18 Példa 2. Aa Aa keresztezés utódok : ½ Aa, ¼ AA -> sárga ¼ aa-> zöld Mi a valószínűsége annak, hogy egy sárga egyed Mi a valószínűsége annak, hogy egy sárga egyed Aagenotípusú?
19 Példa 3. Aa Aa keresztezés utódok : ½ Aa, ¼ AA -> sárga ¼ aa-> zöld Mi a valószínűsége annak, hogy egy sárga egyed Aagenotípusú? P(Aa sárga) P (Aa,sárga) / P(sárga)
20 Példa 4. Egy házaspárnak van már 2 lánya, mi az esélye, hogy a harmadik gyerekük is lány lesz? Egy normál színezetű házaspárnak albínó gyermeke születik. Mi az esélye, hogy a következő gyerek is albínó lesz? Mi az esélye, hogy a következő gyerek egy albínó kislány lesz?
21 Példa 4. -Binomiális eloszlás P( X k) n k q k p n k Mi a valószínűsége annak, hogy egy ivarsejtbe mindössze 2 apai kromoszóma kerül? (23 pár kromoszóma) n23, k2, p0,5 P( X 2) 23 0, , ! 2!21! 0,5 23 3,
22 Példa 5. Az albínók gyakorisága 1:10000-hez. Ha véletlenszerűen kiválasztunk embert, mennyi a valószínűsége, hogy nem lesz közöttük egyetlen albínó sem? n15000, k0, q0,0001 > p0,9999
23 Példa 6. Egy piros és egy fehér csodatölcsért keresztezünk, majd az F1 nemzedék egyöntetűen rózsaszínű egyedeit egymás közt szaporítjuk tovább. Mi a valószínűsége, hogy az F2 nemzedék 10 egyede közül egyik sem lesz rózsaszín? P(rózsaszín; AB)? -> AB x AB
24 Példa 6. Egy piros és egy fehér csodatölcsért keresztezünk, majd az F1 nemzedék egyöntetűen rózsaszínű egyedeit egymás közt szaporítjuk tovább. Mi a valószínűsége, hogy az F2 nemzedék 10 egyede közül egyik sem lesz rózsaszín? P(rózsaszín; AB)? -> AB x AB ,5 10 0,5 0 0,5 10
25 az F2 nemzedékben a 10 egyedből pontosan 5 lesz rózsaszín? az F2 nemzedékben a 10 egyedből legalább 2 rózsaszín lesz?
26 az F2 nemzedékben a 10 egyedből pontosan 5 lesz rózsaszín? ! 10 0,5 0,5 0,5 5 5! 5! az F2 nemzedékben a 10 egyedből legalább 2 rózsaszín lesz? ! 0,5 0,5 0,5 1 1! 9! ! 0,5 0,5 2 2! 8! P(ζ 2)1- P(ζ0)- P(ζ1)0, ,5 10
27 Mendeli genetika és példák az ettől való eltérésre interakció allélok között: dominancia interakció gének között: episztázis interakció a környezet és a gének között
28 Kísérlet: sárga színű és szürke egereket keresztezünk > az utódok közt az arány: sárga : szürke 1:1 tudjuk, hogy a szürke homozigóta ha domináns lenne, akkor az utódok mind szürkék lennének > a sárga szín a domináns
29 Kísérlet: jelöljük a szürkék genotípusát yy-nal, legyen sárga szín alléjának jele Y ; mivel az utódok között volt szürke is, ezért biztos nem volt homozigóta a sárga, tehát Yy-nak kellett lennie. Ha csinálunk egy keresztezést két sárga között, akkor azt várjuk, hogy: Yyx Yy> 3 sárga: 1 szürke. Ehelyett: 2 sárga és 1 szürke lesz az arány. Hogyan lehetséges ez?
30 Tesztkeresztezések: a született sárga egereket szürkékkel párosítjuk > minden alomban fele-fele arányban kapunk sárgát és szürkét > ezek szerint minden sárga heterozigóta volt. A YY genotípus valami miatt letális A 2:1 hasadási aránygyakran letális gént jelez.
31 Pl. Manx macskák Egy domináns allél faroknélküliséget okoz: M L Mfarok nélküli, életképes M L M L életképtelen
32 Génkölcsönhatások
33 Mendel borsói ráncosság és szín a független hasadás törvényeazt mondja ki, hogy a különböző gének alléljei (pl. Rrés Yy) egymástól függetlenül válnak szét és kerülnek be a gamétákba. Ezt dihibrid keresztezésekkel bizonyította Szülők: RRYYxrryy F1: RrYy A RrYygenotípusú F 1 egyed négyféle gamétát hozhat létre: RY, Ry, ryés ry. A gaméták véletlenszerű kombinációi F 2 nemzedékben a 9:3:3:1 fenotípusarányt eredményeznek.
34
35 A négyféle fenotípus genotípusai 9/16 R_Y_ 3/16 R_yy 3/16 rry_ 1/16 rryy A gének egy-egy tulajdonságot határoztak meg: R -> ráncosság Y -> szín
36 Mi van akkor ha két gén ugyanarra a tulajdonságra hat? A 9:3:3:1-től eltérő fenotípus-arányok alakulhatnak ki: Episztázis gének közti interakció 2 v. több lokusz interakciója új fenotípust eredményez Egy lokuszadott allélja elfedi a egy v. több másik lokusz alléljainak hatását Egy lokuszadott allélja módosítja egy v. több másik lokusz alléljainak hatását
37 Egyszerű génkölcsönhatás Bateson & Punnett (1905, 1906, 1908) Borsó-, rózsa-, egyszerűés diótaraj. Rózsa és borsótarajú tiszta vonalak keresztezésével F 1 -ben diótarajt kapunk. h/28775-h.htm Mendelism (Third Edition, Reginald Crundall Punnett)
38 Egyszerű génkölcsönhatás P F1 pprr x PPrr rózsa PpRr» dió borsó F2 9/16 P_R_ dió 3/16 ppr_ rózsa 3/16 P_rr borsó 1/16 pprr egyszerű Két függetlenül öröklődő (különböző lokuszon elhelyezkedő) gén felelős egyetlen fenotípusos jegyért.
39 Egér szőrszínének öröklődése: A B allél felelős a vad típusú ún. agouti (szürke) színért a b allél pedig a fekete színért. ABBor Bbgenotípusagouti, abb: fekete. Egy másik lokuszfelelős a pigmentképzésért. CC és Ccképeznek pigmentet, míg ccalbino.
40 Recesszív episztázis P F 1 bbcc x BBcc» Fekete albino BbCc» agouti F 2 F 2 9/16 B_C_ agouti 3/16 bbc_ fekete 3/16 B_cc albino 1/16 bbcc albino A recesszív episztázisra jellemző módosult F 2 fenotípusarány: 9:3:4
41 Forrás:
42 Komplementer gének Ha két gén kifejeződése kölcsönösen függ egymástól, akkor komplementer génekről van szó. Pl. Bateson & Punnett: borsóvirágok színét vizsgálták: Beltenyésztett fehér virágú borsókat keresztezve F1- ben minden utód lila virágú lett. F2-ben 382 lila és 269 fehér virágú egyedet kaptak -> 382:269 9,4 : 6,6 ~9 : 7
43 Későbbi vizsgálatokkal kiderült, hogy kék színért az antocianinfelelős, aminek az előállítása két lépcsőben történik a borsókban: Az egyik gén (C) felel az első lépésért, a másik (P) a másodikért. Ha valamelyik lépés kimarad, nem termelődik antocianin és a virág fehér lesz. A C és P jelenléte azt jelenti, hogy az adott lépés végbemegy, azaz ha a növény valamelyik lokuszra nézve homozigóta recesszív, akkor fehér marad.
44 Komplementer génhatás CcPpxCcPp Anyai gaméták CP Cp cp cp CP CCPP CCPp CcPP CcPp Apai gaméták Cp CCPp CCpp CcPp Ccpp cp CcPP CcPp ccpp ccpp cp CcPp Ccpp ccpp ccpp
45 Domináns szupresszorepisztázis13:3 A kankalin színe a malvidintőlkék lesz (K lokusz, Kallél) Ezt a D lokuszdallélja el tudja nyomni (domináns K-val szemben), azaz a K_D_ genotípusú virág nem termel malvidint 13 fehér (12 tartalmaz D-t, 1 nem tartalmaz D-t, de K-t sem) és 3 kék KkDdxKkDd Anyai gaméták Apai gaméták KD Kd kd kd KD KKDD KKDd KkDD KkDd Kd KKDd KKdd KkDd Kkdd kd KkDD KkDd kkdd kkdd kd KkDd Kkdd kkdd kkdd
46 Azonos hatású domináns gének 15:1 A búzamag színe egy olyan vegyülettől függ, amelynek a prekurzorbólvaló előállítását két gén (A és B) terméke előidézheti A vagyb allél esetén kialakul a szín Csak a mindkét génre nézve recesszív homozigóta (aabb) lesz színtelen (közel uniform a fenotípusok alapján) AaBbxAaBb Anyai gaméták AB Ab ab ab Apai gamétá k AB AABB AABb AaBB AaBb Ab AABb AAbb AaBb Aabb ab AaBB AABb aabb aabb ab AaBb Aabb aabb aabb
47 Összefoglalva: Genotípusok A_B_ A_bb aab_ aabb Klasszikus arány Domináns episztázis Recesszív episztázis Azonos hatású domináns gének 15 1 Komplementer gének 9 7 Domináns szupresszorepisztázis/ 13 3 inhibítor gének Alternáló gének
48 Ha keresztezünk két, agutiszínezetű, AaBbgenotípusú egeret, mi a valószínűsége, hogy a 300 utód közül mindegyik a szülőkével egyező fenotípusú lesz? p? n? k300 q? P ( X k ) n k q k p n k
49 Ha keresztezünk két, agutiszínezetű, AaBbgenotípusú egeret, mi a valószínűsége, hogy a 300 utód közül mindegyik a szülőkével egyező fenotípusú lesz? p0,5625; n300, k300, q0, ! 0, !0! , ,
50 Ha keresztezünk két, aguti színezetű, AaBb genotípusú egeret, mi a valószínűsége, hogy a 300 utód közül egyik sem lesz a szüleivel megegyező fenotípusú? p n k q
51 Ha keresztezünk két, aguti színezetű, AaBb genotípusú egeret, mi a valószínűsége, hogy a 300 utód közül egyik sem lesz a szüleivel megegyező fenotípusú? p0,5625; n300, k0, q0, ! 0,5625 0!300! ,
52 Ha keresztezünk két, agutiszínezetű, AaBbgenotípusú egeret, mi a valószínűsége, hogy a 16 utód közül pontosan 9 lesz a szülőkével egyező fenotípusú? p n k q
53 Ha keresztezünk két, aguti színezetű, AaBb genotípusú egeret, mi a valószínűsége, hogy a 16 utód közül pontosan 9 lesz a szülőkével egyező fenotípusú? p9/16; n16, k9, q7/ ! 0,5625 9!7! 9 7 0,4375 7
54 A feniltiokarbamid keserű ízének érzékelését a T, t betűkkel jelzett allélpár határozza meg: a TT és Tt genotípusú egyének a vegyület keserű ízét érzik, a tt genotípusúak nem. Egy nem ízérző egyén szülei ízérzők, testvérének felesége pedig nem ízérző. Mekkora a valószínűsége annak, hogy a testvér illetve annak gyermeke ízérző?
55 1 2 Nagyszülők? Szülők?
56 Nagyszülők -Tt Szülők: 5: tt 4: TT -> 0,25 Tt-> 0,5 4: 0,75, h ízérző
57 Nagyszülők -Tt Szülők: 5: tt 4: 0,75, h ízérző 6: Anyutól csak t P(t-t ad) 1 P (Aputól T, ha Apu TT) 1 P(Apu TT) 0,25 P (Aputól T, ha Apu Tt) 0,5 P(Apu Tt) 0,5 P(6. ízérző) 0,25*1 + 0,5*0,5 0,5
58 Az először említett egyén egy másik testvérének férje ízérző. Ennek a férjnek a szüleiről nem tudunk semmit, de tudjuk, hogy a populációban 19% TT, 50% Tt és 31 % tt. Ennek a másik testvérnek és férjének gyermeke milyen valószínűséggel lesz ízérző?
59 P (9. ízérző)? 1 -P(mindkét szülőtől t-t kap) t Anyutól 0,5 t Aputól 50/69
60 t Anyutól 0,5 t Aputól 50/69 6 P(mindkét szülőtől t-t kap) 0,5 * (50/69*0,5)
Domináns-recesszív öröklődésmenet
 Domináns-recesszív öröklődésmenet Domináns recesszív öröklődés esetén tehát a homozigóta domináns és a heterozigóta egyedek fenotípusa megegyezik, így a három lehetséges genotípushoz (példánkban AA, Aa,
Domináns-recesszív öröklődésmenet Domináns recesszív öröklődés esetén tehát a homozigóta domináns és a heterozigóta egyedek fenotípusa megegyezik, így a három lehetséges genotípushoz (példánkban AA, Aa,
HÁZI FELADAT. Milyen borjak születését várhatja, és milyen valószínûséggel az alábbi keresztezésekbõl:
 HÁZI FELADAT Egy allélos mendeli 1. A patkányokban a szõrzet színét autoszómás lókusz szabályozza: a fekete szín domináns, az albínó recesszív allél. Ha egy fekete heterozigótával kereszteznek egy fehér
HÁZI FELADAT Egy allélos mendeli 1. A patkányokban a szõrzet színét autoszómás lókusz szabályozza: a fekete szín domináns, az albínó recesszív allél. Ha egy fekete heterozigótával kereszteznek egy fehér
Tudománytörténeti visszatekintés
 GENETIKA I. AZ ÖRÖKLŐDÉS TÖRVÉNYSZERŰSÉGEI Minek köszönhető a biológiai sokféleség? Hogyan történik a tulajdonságok átörökítése? Tudománytörténeti visszatekintés 1. Keveredés alapú öröklődés: (1761-1766,
GENETIKA I. AZ ÖRÖKLŐDÉS TÖRVÉNYSZERŰSÉGEI Minek köszönhető a biológiai sokféleség? Hogyan történik a tulajdonságok átörökítése? Tudománytörténeti visszatekintés 1. Keveredés alapú öröklődés: (1761-1766,
1. A kísérlet naiv fogalma. melyek közül a kísérlet minden végrehajtásakor pontosan egy következik be.
 IX. ESEMÉNYEK, VALÓSZÍNŰSÉG IX.1. Események, a valószínűség bevezetése 1. A kísérlet naiv fogalma. Kísérlet nek nevezzük egy olyan jelenség előidézését vagy megfigyelését, amelynek kimenetelét az általunk
IX. ESEMÉNYEK, VALÓSZÍNŰSÉG IX.1. Események, a valószínűség bevezetése 1. A kísérlet naiv fogalma. Kísérlet nek nevezzük egy olyan jelenség előidézését vagy megfigyelését, amelynek kimenetelét az általunk
10. GYAKORLÓ FELADATSOR MEGOLDÁSA
 10. GYAKORLÓ FELADATSOR MEGOLDÁSA 1. Egy vállalatnál 180 férfi és 120 nő dolgozik. A férfiak közül 70-en, a nők közül 30-an hordanak szemüveget. Kiválasztunk véletlenszerűen egy dolgozót. (a) Mi a valószínűsége
10. GYAKORLÓ FELADATSOR MEGOLDÁSA 1. Egy vállalatnál 180 férfi és 120 nő dolgozik. A férfiak közül 70-en, a nők közül 30-an hordanak szemüveget. Kiválasztunk véletlenszerűen egy dolgozót. (a) Mi a valószínűsége
BIOLÓGIA HÁZIVERSENY 1. FORDULÓ BIOKÉMIA, GENETIKA BIOKÉMIA, GENETIKA
 BIOKÉMIA, GENETIKA 1. Nukleinsavak keresztrejtvény (12+1 p) 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 1. A nukleinsavak a.-ok összekapcsolódásával kialakuló polimerek. 2. Purinvázas szerves bázis, amely az
BIOKÉMIA, GENETIKA 1. Nukleinsavak keresztrejtvény (12+1 p) 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 1. A nukleinsavak a.-ok összekapcsolódásával kialakuló polimerek. 2. Purinvázas szerves bázis, amely az
Hátterükben egyetlen gén áll, melynek általában számottevő a viselkedésre gyakorolt hatása, öröklési mintázata jellegzetes.
 Múlt órán: Lehetséges tesztfeladatok: Kitől származik a variáció-szelekció paradigma, mely szerint az egyéni, javarészt öröklött különbségek között a társadalmi harc válogat? Fromm-Reichmann Mill Gallton
Múlt órán: Lehetséges tesztfeladatok: Kitől származik a variáció-szelekció paradigma, mely szerint az egyéni, javarészt öröklött különbségek között a társadalmi harc válogat? Fromm-Reichmann Mill Gallton
A Hardy-Weinberg egyensúly. 2. gyakorlat
 A Hardy-Weinberg egyensúly 2. gyakorlat A Hardy-Weinberg egyensúly feltételei: nincs szelekció nincs migráció nagy populációméret (nincs sodródás) nincs mutáció pánmixis van allélgyakoriság azonos hímekben
A Hardy-Weinberg egyensúly 2. gyakorlat A Hardy-Weinberg egyensúly feltételei: nincs szelekció nincs migráció nagy populációméret (nincs sodródás) nincs mutáció pánmixis van allélgyakoriság azonos hímekben
Fogalmak IV. Színöröklés elméleti alapjai
 Fogalmak IV. Színöröklés elméleti alapjai A színeződés a melanintól függ, ami szemcsék formájában rakódik le a bőrbe, illetve a szőrbe. A melanint speciális pigmentképző sejtek termelik. A pigmentképződés
Fogalmak IV. Színöröklés elméleti alapjai A színeződés a melanintól függ, ami szemcsék formájában rakódik le a bőrbe, illetve a szőrbe. A melanint speciális pigmentképző sejtek termelik. A pigmentképződés
Genetika 3 ea. Bevezetés
 Genetika 3 ea. Mendel törvényeinek a kiegészítése: Egygénes öröklődés Többtényezős öröklődés Bevezetés Mendel által vizsgált tulajdonságok: diszkrétek, két különböző fenotípus Humán tulajdonságok nagy
Genetika 3 ea. Mendel törvényeinek a kiegészítése: Egygénes öröklődés Többtényezős öröklődés Bevezetés Mendel által vizsgált tulajdonságok: diszkrétek, két különböző fenotípus Humán tulajdonságok nagy
(b) Legyen E: 6-ost dobunk, F: páratlan számot dobunk., de ha mártudjuk azt, hogy akísérletbenpáratlanszámotdobtunk, akkorazösszeslehetőség1, 3,
 X. FELTÉTELES VALÓSZÍNŰSÉG, VALÓSZÍNŰSÉG A GENETIKÁBAN X.. Feltételes valószínűség. Példák a kockadobásnál. (a) Hogyan változik annak a valószínűsége, hogy 6-os a dobott szám, ha megtudjuk, hogy páros?
X. FELTÉTELES VALÓSZÍNŰSÉG, VALÓSZÍNŰSÉG A GENETIKÁBAN X.. Feltételes valószínűség. Példák a kockadobásnál. (a) Hogyan változik annak a valószínűsége, hogy 6-os a dobott szám, ha megtudjuk, hogy páros?
Szelekció. Szelekció. A szelekció típusai. Az allélgyakoriságok változása 3/4/2013
 Szelekció Ok: több egyed születik, mint amennyi túlél és szaporodni képes a sikeresség mérése: fitnesz Szelekció Ok: több egyed születik, mint amennyi túlél és szaporodni képes a sikeresség mérése: fitnesz
Szelekció Ok: több egyed születik, mint amennyi túlél és szaporodni képes a sikeresség mérése: fitnesz Szelekció Ok: több egyed születik, mint amennyi túlél és szaporodni képes a sikeresség mérése: fitnesz
ÁLLATTENYÉSZTÉSI GENETIKA
 TÁMOP-4.1.2-08/1/A-2009-0010 project ÁLLATTENYÉSZTÉSI GENETIKA University of Debrecen University of West Hungary University of Pannonia The project is supported by the European Union and co-financed by
TÁMOP-4.1.2-08/1/A-2009-0010 project ÁLLATTENYÉSZTÉSI GENETIKA University of Debrecen University of West Hungary University of Pannonia The project is supported by the European Union and co-financed by
Johann Gregor Mendel Az olmüci (Olomouc) és bécsi egyetem diákja Brünni ágostonrendi apát (nem szovjet tudós) Tudatos és nagyon alapos kutat
 10.2.2010 genmisk1 1 Áttekintés Mendel és a mendeli törvények Mendel előtt és körül A genetika törvényeinek újbóli felfedezése és a kromoszómák Watson és Crick a molekuláris biológoa központi dogmája 10.2.2010
10.2.2010 genmisk1 1 Áttekintés Mendel és a mendeli törvények Mendel előtt és körül A genetika törvényeinek újbóli felfedezése és a kromoszómák Watson és Crick a molekuláris biológoa központi dogmája 10.2.2010
POPULÁCIÓGENETIKA GYAKORLAT
 POPULÁCIÓGENETIKA GYAKORLAT Az S vércsoport esetében három genotípus figyelhető meg: - SS homozigóták (az antigént normál mennyiségben tartalmazzák) - Ss heterozigóták (plazmájuk fele mennyiségű antigént
POPULÁCIÓGENETIKA GYAKORLAT Az S vércsoport esetében három genotípus figyelhető meg: - SS homozigóták (az antigént normál mennyiségben tartalmazzák) - Ss heterozigóták (plazmájuk fele mennyiségű antigént
A kromoszómák kialakulása előtt a DNS állomány megkettőződik. A két azonos információ tartalmú DNS egymás mellé rendeződik és egy kromoszómát alkot.
 Kromoszómák, Gének A kromoszóma egy hosszú DNS szakasz, amely a sejt életének bizonyos szakaszában (a sejtosztódás előkészítéseként) tömörödik, így fénymikroszkóppal láthatóvá válik. A kromoszómák két
Kromoszómák, Gének A kromoszóma egy hosszú DNS szakasz, amely a sejt életének bizonyos szakaszában (a sejtosztódás előkészítéseként) tömörödik, így fénymikroszkóppal láthatóvá válik. A kromoszómák két
Sávozott tollú tyúkot kereszteznek egyszínű tollazatú kakassal. 1. Írja fel a keresztezett egyedek genotípusát, feltüntetve a nemüket is!
 A TYÚKOK TOLLAZATA A tyúkoknál a tollak sávos mintázata hím és nőivarú egyedeknél is előfordul. Ezt a tulajdonságot az ivari kromoszómához kötött gén határozza meg. Ennek a génnek b recesszív allélja egyszínű,
A TYÚKOK TOLLAZATA A tyúkoknál a tollak sávos mintázata hím és nőivarú egyedeknél is előfordul. Ezt a tulajdonságot az ivari kromoszómához kötött gén határozza meg. Ennek a génnek b recesszív allélja egyszínű,
3. Mi az esélye annak, hogy egymás után 2 fekete golyót húzok ki (vagy egyszerre két golyót megragadva mindkettő fekete lesz?
 1. Egy zsákban nagyszámban és egyenlő mennyiségben fekete és fehér golyók vannak. Mi a valószínűsége annak, hogy elsőre fekete golyót húzunk? 2. Mi az esélye annak, hogy a következő golyó is fekete lesz?
1. Egy zsákban nagyszámban és egyenlő mennyiségben fekete és fehér golyók vannak. Mi a valószínűsége annak, hogy elsőre fekete golyót húzunk? 2. Mi az esélye annak, hogy a következő golyó is fekete lesz?
Genetika 2. előadás. Bevezető
 Genetika 2. előadás Genetikai alapelvek: hogyan öröklődnek a tulajdonságok Mendeli genetika Bevezető Mi okozza a hasonlóságokat és különbségeket a családtagok között? Gének: biológiai információ alapegysége
Genetika 2. előadás Genetikai alapelvek: hogyan öröklődnek a tulajdonságok Mendeli genetika Bevezető Mi okozza a hasonlóságokat és különbségeket a családtagok között? Gének: biológiai információ alapegysége
VALÓSZÍNŰSÉG, STATISZTIKA TANÍTÁSA
 VALÓSZÍNŰSÉG, STATISZTIKA TANÍTÁSA A VALÓSZÍNŰSÉGI SZEMLÉLET ALAPOZÁSA 1-6. OSZTÁLY A biztos, a lehetetlen és a lehet, de nem biztos események megkülünböztetése Valószínűségi játékok, kísérletek események
VALÓSZÍNŰSÉG, STATISZTIKA TANÍTÁSA A VALÓSZÍNŰSÉGI SZEMLÉLET ALAPOZÁSA 1-6. OSZTÁLY A biztos, a lehetetlen és a lehet, de nem biztos események megkülünböztetése Valószínűségi játékok, kísérletek események
A Hardy Weinberg-modell gyakorlati alkalmazása
 1 of 6 5/16/2009 2:59 PM A Hardy Weinberg-modell gyakorlati alkalmazása A genotípus-gyakoriság megoszlásának vizsgálata 1. ábra. A Hardy Weinberg-egyensúlyi genotípus-gyakoriságok az allélgyakoriság Számos
1 of 6 5/16/2009 2:59 PM A Hardy Weinberg-modell gyakorlati alkalmazása A genotípus-gyakoriság megoszlásának vizsgálata 1. ábra. A Hardy Weinberg-egyensúlyi genotípus-gyakoriságok az allélgyakoriság Számos
GENETIKA MEGOLDÁS EMELT SZINT 1
 GENETIKA MEGOLDÁS EMELT SZINT 1 I. A színtévesztés öröklése (15 pont) 1. X kromoszómához kötődő recesszív mutáció 2 pont 2. X S X s (más betűjelölés is elfogadható) (mert az apától csak X s allélt kaphatott)
GENETIKA MEGOLDÁS EMELT SZINT 1 I. A színtévesztés öröklése (15 pont) 1. X kromoszómához kötődő recesszív mutáció 2 pont 2. X S X s (más betűjelölés is elfogadható) (mert az apától csak X s allélt kaphatott)
INCZÉDY GYÖRGY SZAKKÖZÉPISKOLA, SZAKISKOLA ÉS KOLLÉGIUM
 INCZÉDY GYÖRGY SZAKKÖZÉPISKOLA, SZAKISKOLA ÉS KOLLÉGIUM Szakközépiskola Tesztlapok Biológia - egészségtan tantárgy 12. évfolyam Készítette: Perinecz Anasztázia Név: Osztály: 1. témakör: Az élet kódja.
INCZÉDY GYÖRGY SZAKKÖZÉPISKOLA, SZAKISKOLA ÉS KOLLÉGIUM Szakközépiskola Tesztlapok Biológia - egészségtan tantárgy 12. évfolyam Készítette: Perinecz Anasztázia Név: Osztály: 1. témakör: Az élet kódja.
Gazdasági matematika II. vizsgadolgozat megoldása A csoport
 Gazdasági matematika II. vizsgadolgozat megoldása A csoport Definiálja az alábbi fogalmakat!. Egy eseménynek egy másik eseményre vonatkozó feltételes valószínűsége. ( pont) Az A esemény feltételes valószínűsége
Gazdasági matematika II. vizsgadolgozat megoldása A csoport Definiálja az alábbi fogalmakat!. Egy eseménynek egy másik eseményre vonatkozó feltételes valószínűsége. ( pont) Az A esemény feltételes valószínűsége
6. Az öröklődés alapjai
 6. z öröklődés alapjai GENETIK z örökítő anyag szerveződésével és funkciójával, az élőlények tulajdonságinak átöröklődésével foglalkozó tudomány. genesis: : születés, teremtés, keletkezés, származás Elméletek
6. z öröklődés alapjai GENETIK z örökítő anyag szerveződésével és funkciójával, az élőlények tulajdonságinak átöröklődésével foglalkozó tudomány. genesis: : születés, teremtés, keletkezés, származás Elméletek
A PKU azért nem hal ki, mert gyógyítják, és ezzel növelik a mutáns allél gyakoriságát a Huntington kór pedig azért marad fenn, mert csak későn derül
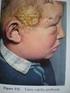 1 Múlt órán: Genetikai alapelvek, monogénes öröklődés Elgondolkodtató feladat Vajon miért nem halnak ki az olyan mendeli öröklődésű rendellenességek, mint a Phenylketonuria, vagy a Huntington kór? A PKU
1 Múlt órán: Genetikai alapelvek, monogénes öröklődés Elgondolkodtató feladat Vajon miért nem halnak ki az olyan mendeli öröklődésű rendellenességek, mint a Phenylketonuria, vagy a Huntington kór? A PKU
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 7. Bevezetés a valószínűségszámításba Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés 2 Definíciók, tulajdonságok Példák Valószínűségi mező
BIOMATEMATIKA ELŐADÁS 7. Bevezetés a valószínűségszámításba Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés 2 Definíciók, tulajdonságok Példák Valószínűségi mező
BIOLÓGIA 11. ÉVFOLYAM I. beszámoló. A genetika alaptörvényei
 BIOLÓGIA 11. ÉVFOLYAM 2015-2016. I. beszámoló A genetika alaptörvényei Ismétlés: a fehérjék fölépítése Új fogalom: gének: a DNS molekula egységei, melyek meghatározzák egy-egy tulajdonság természetét.
BIOLÓGIA 11. ÉVFOLYAM 2015-2016. I. beszámoló A genetika alaptörvényei Ismétlés: a fehérjék fölépítése Új fogalom: gének: a DNS molekula egységei, melyek meghatározzák egy-egy tulajdonság természetét.
FELTÉTELES VALÓSZÍNŰSÉG, TELJES VALÓSZÍNŰSÉG TÉTELE, BAYES TÉTELE
 FELTÉTELES VALÓSZÍNŰSÉG, TELJES VALÓSZÍNŰSÉG TÉTELE, BAYES TÉTELE 1. Egy alkalmassági vizsgálat adatai szerint a vizsgált személyeken 0,05 valószínűséggel mozgásszervi és 0,03 valószínűséggel érzékszervi
FELTÉTELES VALÓSZÍNŰSÉG, TELJES VALÓSZÍNŰSÉG TÉTELE, BAYES TÉTELE 1. Egy alkalmassági vizsgálat adatai szerint a vizsgált személyeken 0,05 valószínűséggel mozgásszervi és 0,03 valószínűséggel érzékszervi
Genetika. Ezek határozzák meg a tulajdonságainkat. (szemszín, hajszín, stb )
 Krisztián bioszjegyzete A /öröklődés alapjai: öröklődés és változásával foglalkozik. A genetika a tulajdonságok öröklődésével Lehet vizsgálni: Sejtszinten: Molekuláris genetika Egyedszinten: Klasszikus
Krisztián bioszjegyzete A /öröklődés alapjai: öröklődés és változásával foglalkozik. A genetika a tulajdonságok öröklődésével Lehet vizsgálni: Sejtszinten: Molekuláris genetika Egyedszinten: Klasszikus
Feladatok és megoldások az 1. sorozat Építőkari Matematika A3
 Feladatok és megoldások az 1. sorozat Építőkari Matematika A3 1. Tegyük fel, hogy A és B egymást kölcsönösen kizáró események, melyekre P{A} = 0.3 és P{B} = 0.. Mi a valószínűsége, hogy (a A vagy B bekövetkezik;
Feladatok és megoldások az 1. sorozat Építőkari Matematika A3 1. Tegyük fel, hogy A és B egymást kölcsönösen kizáró események, melyekre P{A} = 0.3 és P{B} = 0.. Mi a valószínűsége, hogy (a A vagy B bekövetkezik;
Biomatematika 2 Orvosi biometria
 Biomatematika 2 Orvosi biometria 2017.02.13. Populáció és minta jellemző adatai Hibaszámítás Valószínűség 1 Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza)
Biomatematika 2 Orvosi biometria 2017.02.13. Populáció és minta jellemző adatai Hibaszámítás Valószínűség 1 Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza)
Példák a független öröklődésre
 GENETIKAI PROBLÉMÁK Példák a független öröklődésre Az amelogenesis imperfecta egy, a fogzománc gyengeségével és elszíneződésével járó öröklődő betegség, a 4-es kromoszómán lévő enam gén recesszív mutációja
GENETIKAI PROBLÉMÁK Példák a független öröklődésre Az amelogenesis imperfecta egy, a fogzománc gyengeségével és elszíneződésével járó öröklődő betegség, a 4-es kromoszómán lévő enam gén recesszív mutációja
Populációgenetikai. alapok
 Populációgenetikai alapok Populáció = egyedek egy adott csoportja Az egyedek eltérnek egymástól morfológiailag, de viselkedésüket tekintve is = genetikai különbségek Fenotípus = külső jellegek morfológia,
Populációgenetikai alapok Populáció = egyedek egy adott csoportja Az egyedek eltérnek egymástól morfológiailag, de viselkedésüket tekintve is = genetikai különbségek Fenotípus = külső jellegek morfológia,
Feladatok és megoldások a 8. hétre Építőkari Matematika A3
 Feladatok és megoldások a 8. hétre Építőkari Matematika A3 1. Oldjuk meg a következő differenciálegyenlet rendszert: x + 2y 3x + 4y = 2 sin t 2x + y + 2x y = cos t. (1 2. Oldjuk meg a következő differenciálegyenlet
Feladatok és megoldások a 8. hétre Építőkari Matematika A3 1. Oldjuk meg a következő differenciálegyenlet rendszert: x + 2y 3x + 4y = 2 sin t 2x + y + 2x y = cos t. (1 2. Oldjuk meg a következő differenciálegyenlet
Környezet statisztika
 Környezet statisztika Permutáció, variáció, kombináció k számú golyót n számú urnába helyezve hányféle helykitöltés lehetséges, ha a golyókat helykitöltés Minden urnába akárhány golyó kerülhet (ismétléses)
Környezet statisztika Permutáció, variáció, kombináció k számú golyót n számú urnába helyezve hányféle helykitöltés lehetséges, ha a golyókat helykitöltés Minden urnába akárhány golyó kerülhet (ismétléses)
Kvantitatív genetikai alapok április
 Kvantitatív genetikai alapok 2018. április A vizsgálható tulajdonságok köre: egyed - szám Egyedek morfológiai tulajdonságai: testméretek, arányok, testtömeg Egyedek fiziológiai tulajdonságai: vérnyomás,
Kvantitatív genetikai alapok 2018. április A vizsgálható tulajdonságok köre: egyed - szám Egyedek morfológiai tulajdonságai: testméretek, arányok, testtömeg Egyedek fiziológiai tulajdonságai: vérnyomás,
Todd D.L. Woods, M.D.: A szibériai husky színöröklõdésének alapvetõ genetikája
 Todd D.L. Woods, M.D.: A szibériai husky színöröklõdésének alapvetõ genetikája A genetika legalább alapszintû ismerete nélkül a szibériai husky tenyésztése csak a tenyészegyedek külsõ tulajdonságaik alapján
Todd D.L. Woods, M.D.: A szibériai husky színöröklõdésének alapvetõ genetikája A genetika legalább alapszintû ismerete nélkül a szibériai husky tenyésztése csak a tenyészegyedek külsõ tulajdonságaik alapján
Eseményalgebra. Esemény: minden amirl a kísérlet elvégzése során eldönthet egyértelmen hogy a kísérlet során bekövetkezett-e vagy sem.
 Eseményalgebra. Esemény: minden amirl a kísérlet elvégzése során eldönthet egyértelmen hogy a kísérlet során bekövetkezett-e vagy sem. Elemi esemény: a kísérlet egyes lehetséges egyes lehetséges kimenetelei.
Eseményalgebra. Esemény: minden amirl a kísérlet elvégzése során eldönthet egyértelmen hogy a kísérlet során bekövetkezett-e vagy sem. Elemi esemény: a kísérlet egyes lehetséges egyes lehetséges kimenetelei.
Matematikai alapok és valószínőségszámítás. Valószínőségszámítási alapok
 Matematikai alapok és valószínőségszámítás Valószínőségszámítási alapok Bevezetés A tudományos életben vizsgálódunk pontosabb megfigyelés, elırejelzés, megértés reményében. Ha egy kísérletet végzünk, annak
Matematikai alapok és valószínőségszámítás Valószínőségszámítási alapok Bevezetés A tudományos életben vizsgálódunk pontosabb megfigyelés, elırejelzés, megértés reményében. Ha egy kísérletet végzünk, annak
Az ész természetéhez tartozik, hogy a dolgokat nem mint véletleneket, hanem mint szükségszerűeket szemléli (Spinoza: Etika, II. rész, 44.
 Dr. Vincze Szilvia Az ész természetéhez tartozik, hogy a dolgokat nem mint véletleneket, hanem mint szükségszerűeket szemléli (Spinoza: Etika, II. rész, 44. tétel) Környezetünkben sok olyan jelenséget
Dr. Vincze Szilvia Az ész természetéhez tartozik, hogy a dolgokat nem mint véletleneket, hanem mint szükségszerűeket szemléli (Spinoza: Etika, II. rész, 44. tétel) Környezetünkben sok olyan jelenséget
Matematikai alapok és valószínőségszámítás. Valószínőségi eloszlások Binomiális eloszlás
 Matematikai alapok és valószínőségszámítás Valószínőségi eloszlások Binomiális eloszlás Bevezetés A tudományos életben megfigyeléseket teszünk, kísérleteket végzünk. Ezek többféle különbözı eredményre
Matematikai alapok és valószínőségszámítás Valószínőségi eloszlások Binomiális eloszlás Bevezetés A tudományos életben megfigyeléseket teszünk, kísérleteket végzünk. Ezek többféle különbözı eredményre
A genetikai sodródás
 A genetikai sodródás irányított, nem véletlenszerű Mindig a jobb nyer! természetes szelekció POPULÁCIÓ evolúció POPULÁCIÓ A kulcsszó: változékonyság a populáción belül POPULÁCIÓ nem irányított, véletlenszerű
A genetikai sodródás irányított, nem véletlenszerű Mindig a jobb nyer! természetes szelekció POPULÁCIÓ evolúció POPULÁCIÓ A kulcsszó: változékonyság a populáción belül POPULÁCIÓ nem irányított, véletlenszerű
Általános állattenyésztés
 Általános állattenyésztés 10. Előadás Tenyésztési (párosítási) eljárások 1. Előadás-vázlat Fajtatiszta tenyésztés Kombinációs párosítás Vérfrissítés Rokontenyésztés, beltenyésztés Vérvonaltenyésztés Szintetikus
Általános állattenyésztés 10. Előadás Tenyésztési (párosítási) eljárások 1. Előadás-vázlat Fajtatiszta tenyésztés Kombinációs párosítás Vérfrissítés Rokontenyésztés, beltenyésztés Vérvonaltenyésztés Szintetikus
1. tétel. Valószínűségszámítás vizsga Frissült: 2013. január 19. Valószínűségi mező, véletlen tömegjelenség.
 1. tétel Valószínűségszámítás vizsga Frissült: 2013. január 19. Valószínűségi mező, véletlen tömegjelenség. A valószínűségszámítás tárgya: véletlen tömegjelenségek vizsgálata. véletlen: a kísérlet kimenetelét
1. tétel Valószínűségszámítás vizsga Frissült: 2013. január 19. Valószínűségi mező, véletlen tömegjelenség. A valószínűségszámítás tárgya: véletlen tömegjelenségek vizsgálata. véletlen: a kísérlet kimenetelét
A a normál allél (vad típus), a a mutáns allél A allél gyakorisága 50% a allél gyakorisága 50%
 Lehetséges tesztfeladatok: Tudjuk, hogy egy családban az anya Huntington érintett (heterozigóta), az apa nem. Ugyanakkor az apa heterozigóta formában hordozza a Fenilketonúria mutáns allélját (az anya
Lehetséges tesztfeladatok: Tudjuk, hogy egy családban az anya Huntington érintett (heterozigóta), az apa nem. Ugyanakkor az apa heterozigóta formában hordozza a Fenilketonúria mutáns allélját (az anya
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/47/23623719.jpg) [Biomatematika 2] Orvosi biometria 2016.02.15. Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza) alkotja az eseményteret. Esemény: az eseménytér részhalmazai.
[Biomatematika 2] Orvosi biometria 2016.02.15. Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza) alkotja az eseményteret. Esemény: az eseménytér részhalmazai.
Villamosmérnök A4 2. gyakorlat ( ) Feltételes valószínűség, függetlenség
 Villamosmérnök A4 2. gyakorlat (20. 09. 17.-1.) Feltételes valószínűség, függetlenség 1. Egy szabályos dobókockával dobunk. Mennyi annak a valószínűsége, hogy 6-ost dobunk, ha tudjuk, hogy (a) párosat
Villamosmérnök A4 2. gyakorlat (20. 09. 17.-1.) Feltételes valószínűség, függetlenség 1. Egy szabályos dobókockával dobunk. Mennyi annak a valószínűsége, hogy 6-ost dobunk, ha tudjuk, hogy (a) párosat
Matematika III. 2. Eseményalgebra Prof. Dr. Závoti, József
 Matematika III. 2. Eseményalgebra Prof. Dr. Závoti, József Matematika III. 2. : Eseményalgebra Prof. Dr. Závoti, József Lektor : Bischof, Annamária Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 Tananyagfejlesztéssel
Matematika III. 2. Eseményalgebra Prof. Dr. Závoti, József Matematika III. 2. : Eseményalgebra Prof. Dr. Závoti, József Lektor : Bischof, Annamária Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 Tananyagfejlesztéssel
Feladatok 2. zh-ra. 1. Eseményalgebra április Feladat. Az A és B eseményekr l tudjuk, hogy P (A) = 0, 6, P (B) = 0, 7 és
 Feladatok 2 zh-ra 205 április 3 Eseményalgebra Feladat Az A és B eseményekr l tudjuk, hogy P (A) = 0, 7, P (B) = 0, 4 és P (A B) = 0, 5 Határozza meg az A B esemény valószín ségét! P (A B) = 0, 2 2 Feladat
Feladatok 2 zh-ra 205 április 3 Eseményalgebra Feladat Az A és B eseményekr l tudjuk, hogy P (A) = 0, 7, P (B) = 0, 4 és P (A B) = 0, 5 Határozza meg az A B esemény valószín ségét! P (A B) = 0, 2 2 Feladat
A populációgenetika alaptörvénye
 1 of 5 5/16/2009 2:58 PM A Hardy Weinberg-egyensúly A populációgenetika alaptörvénye A felfedezőiről elnevezett Hardy Weinberg egyensúlyi állapot az ideális populáció-ban fordul elő, egy olyan populációban,
1 of 5 5/16/2009 2:58 PM A Hardy Weinberg-egyensúly A populációgenetika alaptörvénye A felfedezőiről elnevezett Hardy Weinberg egyensúlyi állapot az ideális populáció-ban fordul elő, egy olyan populációban,
Gyakorló feladatok a 2. dolgozathoz
 Gyakorló feladatok a. dolgozathoz. Tíz darab tízforintost feldobunk. Mennyi annak a valószínűsége hogy vagy mindegyiken írást vagy mindegyiken fejet kapunk? 9. Egy kör alakú asztal mellett tízen ebédelnek:
Gyakorló feladatok a. dolgozathoz. Tíz darab tízforintost feldobunk. Mennyi annak a valószínűsége hogy vagy mindegyiken írást vagy mindegyiken fejet kapunk? 9. Egy kör alakú asztal mellett tízen ebédelnek:
ÁLLATTENYÉSZTÉSI GENETIKA FERENC SZABÓ
 ÁLLATTENYÉSZTÉSI GENETIKA FERENC SZABÓ ÁLLATTENYÉSZTÉSI GENETIKA FERENC SZABÓ Publication date 2011 Table of Contents Fedlap... vi 1. A POPULÁCIÓ ÉS A KVANTITATÍV GENETIKA ALAPJAI, ÁLLAT-TENYÉSZTÉSI ALKALMAZÁSI
ÁLLATTENYÉSZTÉSI GENETIKA FERENC SZABÓ ÁLLATTENYÉSZTÉSI GENETIKA FERENC SZABÓ Publication date 2011 Table of Contents Fedlap... vi 1. A POPULÁCIÓ ÉS A KVANTITATÍV GENETIKA ALAPJAI, ÁLLAT-TENYÉSZTÉSI ALKALMAZÁSI
A pumi színgenetikája
 A pumi színgenetikája Az eredeti cikk itt olvasható: http://www.abiquadogs.com/pumi/pumicolor.htm Az a cél vezérelt minket, hogy jobban megértsük, milyen gének határozzák meg a különböző színeket a pumiknál.
A pumi színgenetikája Az eredeti cikk itt olvasható: http://www.abiquadogs.com/pumi/pumicolor.htm Az a cél vezérelt minket, hogy jobban megértsük, milyen gének határozzák meg a különböző színeket a pumiknál.
Populációgenetika és evolúció
 Populációgenetika és evolúció 1 Koncepció 2 Populációgenetika 3 A változatosság eredete 4 A változatosság fenntartása 5 Adaptív evolúció 6 Fenotípus evolúció Populációgenetika és evolúció 1/42 Jellegek
Populációgenetika és evolúció 1 Koncepció 2 Populációgenetika 3 A változatosság eredete 4 A változatosság fenntartása 5 Adaptív evolúció 6 Fenotípus evolúció Populációgenetika és evolúció 1/42 Jellegek
Mendeli genetika, kapcsoltság 26
 Mendeli genetika, kapcsoltság 26 6. MENDELI GENETIKA. KAPCSOLT- SÁG ÉS GÉNTÉRKÉPEK. Mendel szabályai. Az örökl dés típusai. Független kombinálódás. Kapcsoltság, crossing over és géntérképek. egyformák.
Mendeli genetika, kapcsoltság 26 6. MENDELI GENETIKA. KAPCSOLT- SÁG ÉS GÉNTÉRKÉPEK. Mendel szabályai. Az örökl dés típusai. Független kombinálódás. Kapcsoltság, crossing over és géntérképek. egyformák.
Tananyag: Kiss Béla - Krebsz Anna: Lineáris algebra, többváltozós függvények, valószínűségszámítás,
 // KURZUS: Matematika II. MODUL: Valószínűség-számítás 21. lecke: A feltételes valószínűség, események függetlensége Tananyag: Kiss Béla - Krebsz Anna: Lineáris algebra, többváltozós függvények, valószínűségszámítás,
// KURZUS: Matematika II. MODUL: Valószínűség-számítás 21. lecke: A feltételes valószínűség, események függetlensége Tananyag: Kiss Béla - Krebsz Anna: Lineáris algebra, többváltozós függvények, valószínűségszámítás,
Vizsgakövetelmények Magyarázza a számfelező osztódás lényegét, szerepét az ivarsejtek létrejöttében és a genetikai sokféleség fenntartásában.
 1 Vizsgakövetelmények Magyarázza a számfelező osztódás lényegét, szerepét az ivarsejtek létrejöttében és a genetikai sokféleség fenntartásában. Értse, hogy a meiózis folyamata miként eredményez genetikai
1 Vizsgakövetelmények Magyarázza a számfelező osztódás lényegét, szerepét az ivarsejtek létrejöttében és a genetikai sokféleség fenntartásában. Értse, hogy a meiózis folyamata miként eredményez genetikai
ÁLLATTENYÉSZTÉSI GENETIKA
 TÁMOP-4..2-08//A-2009-000 project ÁLLATTENYÉSZTÉSI GENETIKA University of Debrecen University of West Hungary University of Pannonia The project is supported by the European Union and co-financed by European
TÁMOP-4..2-08//A-2009-000 project ÁLLATTENYÉSZTÉSI GENETIKA University of Debrecen University of West Hungary University of Pannonia The project is supported by the European Union and co-financed by European
A genetika - örökléstan
 A genetika - örökléstan A genetika a génekkel, az öröklődéssel foglalkozó tudomány. Szerk.: Vizkievicz András Alapkérdései: Hogyan adódnak át a tulajdonságok nemzedékről nemzedékre? Milyen a molekuláris
A genetika - örökléstan A genetika a génekkel, az öröklődéssel foglalkozó tudomány. Szerk.: Vizkievicz András Alapkérdései: Hogyan adódnak át a tulajdonságok nemzedékről nemzedékre? Milyen a molekuláris
Néhány kockadobással kapcsolatos feladat 1 P 6
 Néhány kockadobással kapcsolatos feladat Feldobunk egy kockát. Az eseménytér: ; 2; ; ; ; Az összes esetek száma:. Feldobunk egy kockát. Mi a valószínűsége, hogy hatost dobunk? A kedvező esetek száma: (hatost
Néhány kockadobással kapcsolatos feladat Feldobunk egy kockát. Az eseménytér: ; 2; ; ; ; Az összes esetek száma:. Feldobunk egy kockát. Mi a valószínűsége, hogy hatost dobunk? A kedvező esetek száma: (hatost
Bodó Beáta - MATEMATIKA II 1
 Bodó Beáta - MATEMATIKA II 1 FELTÉTELES VALÓSZÍNŰSÉG, FÜGGETLENSÉG 1. Legyen P (A) = 0, 7; P (B) = 0, 6 és P (A B) = 0, 5. Határozza meg a következő valószínűségeket! (a) B,V P (A B) 0, 8333 (b) B,V P
Bodó Beáta - MATEMATIKA II 1 FELTÉTELES VALÓSZÍNŰSÉG, FÜGGETLENSÉG 1. Legyen P (A) = 0, 7; P (B) = 0, 6 és P (A B) = 0, 5. Határozza meg a következő valószínűségeket! (a) B,V P (A B) 0, 8333 (b) B,V P
A genetikai lelet értelmezése monogénes betegségekben
 A genetikai lelet értelmezése monogénes betegségekben Tory Kálmán Semmelweis Egyetem, I. sz. Gyermekklinika A ~20 ezer fehérje-kódoló gén a 23 pár kromoszómán A kromoszómán található bázisok száma: 250M
A genetikai lelet értelmezése monogénes betegségekben Tory Kálmán Semmelweis Egyetem, I. sz. Gyermekklinika A ~20 ezer fehérje-kódoló gén a 23 pár kromoszómán A kromoszómán található bázisok száma: 250M
Bizonytalan tudás kezelése
 Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs rendszerek Tanszék Bizonytalan tudás kezelése Előadó: Előadás anyaga: Hullám Gábor Pataki Béla Dobrowiecki Tadeusz Valószínűségi
Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs rendszerek Tanszék Bizonytalan tudás kezelése Előadó: Előadás anyaga: Hullám Gábor Pataki Béla Dobrowiecki Tadeusz Valószínűségi
A valószínűségszámítás elemei
 A valószínűségszámítás elemei Kísérletsorozatban az esemény relatív gyakorisága: k/n, ahol k az esemény bekövetkezésének abszolút gyakorisága, n a kísérletek száma. Pl. Jelenség: kockadobás Megfigyelés:
A valószínűségszámítás elemei Kísérletsorozatban az esemény relatív gyakorisága: k/n, ahol k az esemény bekövetkezésének abszolút gyakorisága, n a kísérletek száma. Pl. Jelenség: kockadobás Megfigyelés:
Készítette: Fegyverneki Sándor
 VALÓSZÍNŰSÉGSZÁMÍTÁS Összefoglaló segédlet Készítette: Fegyverneki Sándor Miskolci Egyetem, 2001. i JELÖLÉSEK: N a természetes számok halmaza (pozitív egészek) R a valós számok halmaza R 2 {(x, y) x, y
VALÓSZÍNŰSÉGSZÁMÍTÁS Összefoglaló segédlet Készítette: Fegyverneki Sándor Miskolci Egyetem, 2001. i JELÖLÉSEK: N a természetes számok halmaza (pozitív egészek) R a valós számok halmaza R 2 {(x, y) x, y
Elméleti összefoglaló a Valószín ségszámítás kurzushoz
 Elméleti összefoglaló a Valószín ségszámítás kurzushoz Véletlen kísérletek, események valószín sége Deníció. Egy véletlen kísérlet lehetséges eredményeit kimeneteleknek nevezzük. A kísérlet kimeneteleinek
Elméleti összefoglaló a Valószín ségszámítás kurzushoz Véletlen kísérletek, események valószín sége Deníció. Egy véletlen kísérlet lehetséges eredményeit kimeneteleknek nevezzük. A kísérlet kimeneteleinek
Matematika III. 3. A valószínűségszámítás elemei Prof. Dr. Závoti, József
 Matematika III. 3. A valószínűségszámítás elemei Prof. Dr. Závoti, József Matematika III. 3. : A valószínűségszámítás elemei Prof. Dr. Závoti, József Lektor : Bischof, Annamária Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
Matematika III. 3. A valószínűségszámítás elemei Prof. Dr. Závoti, József Matematika III. 3. : A valószínűségszámítás elemei Prof. Dr. Závoti, József Lektor : Bischof, Annamária Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
Nyugat-magyarországi Egyetem Geoinformatikai Kara. Prof. Dr. Závoti József. Matematika III. 3. MA3-3 modul. A valószínűségszámítás elemei
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof Dr Závoti József Matematika III 3 MA3-3 modul A valószínűségszámítás elemei SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról szóló 1999
Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof Dr Závoti József Matematika III 3 MA3-3 modul A valószínűségszámítás elemei SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról szóló 1999
Tartalom. Javítóvizsga követelmények BIOLÓGIA...2 BIOLÓGIA FAKULTÁCIÓ...5 SPORTEGÉSZSÉGTAN évfolyam évfolyam évfolyam...
 Tartalom BIOLÓGIA...2 10. évfolyam...2 11. évfolyam...3 12. évfolyam...4 BIOLÓGIA FAKULTÁCIÓ...5 11. évfolyam...5 12. évfolyam...6 SPORTEGÉSZSÉGTAN...7 1 BIOLÓGIA 10. évfolyam Nappali tagozat Azírásbeli
Tartalom BIOLÓGIA...2 10. évfolyam...2 11. évfolyam...3 12. évfolyam...4 BIOLÓGIA FAKULTÁCIÓ...5 11. évfolyam...5 12. évfolyam...6 SPORTEGÉSZSÉGTAN...7 1 BIOLÓGIA 10. évfolyam Nappali tagozat Azírásbeli
Megfelelőségi táblázatok
 Megfelelőségi táblázatok Legnagyobb bútorélzáró kollekció Maximális színazonosság 24 h kiszolgálás ABS élzárók ALU fóliával 2000 HD 29661 ABS alu csiszolt 2003 HD 29930 ABS arany csiszolt 22x0,45mm 22x1mm
Megfelelőségi táblázatok Legnagyobb bútorélzáró kollekció Maximális színazonosság 24 h kiszolgálás ABS élzárók ALU fóliával 2000 HD 29661 ABS alu csiszolt 2003 HD 29930 ABS arany csiszolt 22x0,45mm 22x1mm
Sodródás Evolúció neutrális elmélete
 Sodródás Evolúció neutrális elmélete Egy kísérlet Drosophila Drosophila pseudoobscura 8 hím + 8 nőstény/tenyészet 107 darab tenyészet Minden tenyészet csak heterozigóta egyedekkel indul a neutrális szemszín
Sodródás Evolúció neutrális elmélete Egy kísérlet Drosophila Drosophila pseudoobscura 8 hím + 8 nőstény/tenyészet 107 darab tenyészet Minden tenyészet csak heterozigóta egyedekkel indul a neutrális szemszín
Gyakorlat. Szokol Patricia. September 24, 2018
 Gyakorlat (Geometriai valószínűség, feltételes valószínűség) September 24, 2018 Geometriai valószínűség 1 Az A és B helységet 5 km hosszú telefonvezeték köti össze. A vezeték valahol meghibásodik. A meghibásodás
Gyakorlat (Geometriai valószínűség, feltételes valószínűség) September 24, 2018 Geometriai valószínűség 1 Az A és B helységet 5 km hosszú telefonvezeték köti össze. A vezeték valahol meghibásodik. A meghibásodás
ÁLLATTENYÉSZTÉSI GENETIKA DR. SZABÓ FERENC DR. KOMLÓSI ISTVÁN DR. POSTA JÁNOS
 ÁLLATTENYÉSZTÉSI GENETIKA DR. SZABÓ FERENC DR. KOMLÓSI ISTVÁN DR. POSTA JÁNOS ÁLLATTENYÉSZTÉSI GENETIKA DR. SZABÓ FERENC DR. KOMLÓSI ISTVÁN DR. POSTA JÁNOS Publication date 2011 Table of Contents Fedlap...
ÁLLATTENYÉSZTÉSI GENETIKA DR. SZABÓ FERENC DR. KOMLÓSI ISTVÁN DR. POSTA JÁNOS ÁLLATTENYÉSZTÉSI GENETIKA DR. SZABÓ FERENC DR. KOMLÓSI ISTVÁN DR. POSTA JÁNOS Publication date 2011 Table of Contents Fedlap...
GENETIKA (új tankönyv!)
 GENETIKA (új tankönyv!) Genetikai alapfogalmak 1. Gén: a DNS-nek az a szakasza, amely egy fehérjemolekula aminosav sorrendjét meghatározza. 2. Allél =génváltozat: a ) vad típusú allél, mely a természetben
GENETIKA (új tankönyv!) Genetikai alapfogalmak 1. Gén: a DNS-nek az a szakasza, amely egy fehérjemolekula aminosav sorrendjét meghatározza. 2. Allél =génváltozat: a ) vad típusú allél, mely a természetben
Matematika B4 II. gyakorlat
 Matematika B II. gyakorlat 00. február.. Bevezető kérdések. Feldobunk egy kockát és egy érmét. Ábrázoljuk az eseményteret! Legyenek adottak az alábbi események: -ast dobunk, -est dobunk, fejet dobunk,
Matematika B II. gyakorlat 00. február.. Bevezető kérdések. Feldobunk egy kockát és egy érmét. Ábrázoljuk az eseményteret! Legyenek adottak az alábbi események: -ast dobunk, -est dobunk, fejet dobunk,
Matematika A4 II. gyakorlat megoldás
 Matematika A4 II. gyakorlat megoldás 1. Feltételes valószínűség Vizsgálhatjuk egy A esemény bekövetkezésének valószínűségét úgy is, hogy tudjuk, hogy egy másik B esemény már bekövetkezett. Például ha a
Matematika A4 II. gyakorlat megoldás 1. Feltételes valószínűség Vizsgálhatjuk egy A esemény bekövetkezésének valószínűségét úgy is, hogy tudjuk, hogy egy másik B esemény már bekövetkezett. Például ha a
Algoritmusok Tervezése. 9. Előadás Genetikus Algoritmusok Dr. Bécsi Tamás
 Algoritmusok Tervezése 9. Előadás Genetikus Algoritmusok Dr. Bécsi Tamás Biológiai háttér (nagyvonalúan) A sejt genetikai információit hordozó DNS általában kromoszómának nevezett makromolekulákba van
Algoritmusok Tervezése 9. Előadás Genetikus Algoritmusok Dr. Bécsi Tamás Biológiai háttér (nagyvonalúan) A sejt genetikai információit hordozó DNS általában kromoszómának nevezett makromolekulákba van
NÖVÉNYNEMESÍTÉS. Az Agrármérnöki MSc szak tananyagfejlesztése TÁMOP /1/A
 NÖVÉNYNEMESÍTÉS Az Agrármérnöki MSc szak tananyagfejlesztése TÁMOP-4.1.2-08/1/A-2009-0010 Előadás áttekintése Szelekciós nemesítés módszerei és technikái Tömegszelekció Egyedszelekció Öntermékenyülő növények
NÖVÉNYNEMESÍTÉS Az Agrármérnöki MSc szak tananyagfejlesztése TÁMOP-4.1.2-08/1/A-2009-0010 Előadás áttekintése Szelekciós nemesítés módszerei és technikái Tömegszelekció Egyedszelekció Öntermékenyülő növények
Többgénes jellegek. 1. Klasszikus (poligénes) mennyiségi jellegek. 2.Szinte minden jelleg több gén irányítása alatt áll
 Többgénes jellegek Többgénes jellegek 1. 1. Klasszikus (poligénes) mennyiségi jellegek Multifaktoriális jellegek: több gén és a környezet által meghatározott jellegek 2.Szinte minden jelleg több gén irányítása
Többgénes jellegek Többgénes jellegek 1. 1. Klasszikus (poligénes) mennyiségi jellegek Multifaktoriális jellegek: több gén és a környezet által meghatározott jellegek 2.Szinte minden jelleg több gén irányítása
Az evolúció folyamatos változások olyan sorozata, melynek során bizonyos populációk öröklődő jellegei nemzedékről nemzedékre változnak.
 Evolúció Az evolúció folyamatos változások olyan sorozata, melynek során bizonyos populációk öröklődő jellegei nemzedékről nemzedékre változnak. Latin eredetű szó, jelentése: kibontakozás Időben egymást
Evolúció Az evolúció folyamatos változások olyan sorozata, melynek során bizonyos populációk öröklődő jellegei nemzedékről nemzedékre változnak. Latin eredetű szó, jelentése: kibontakozás Időben egymást
Számítógépes döntéstámogatás. Genetikus algoritmusok
 BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
BIOLÓGIA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Biológia középszint 1813 ÉRETTSÉGI VIZSGA 2018. május 15. BIOLÓGIA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Útmutató a középszintű dolgozatok értékeléséhez
Biológia középszint 1813 ÉRETTSÉGI VIZSGA 2018. május 15. BIOLÓGIA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Útmutató a középszintű dolgozatok értékeléséhez
HAPMAP -2010 Nemzetközi HapMap Projekt. SNP GWA Haplotípus: egy kromoszóma szegmensen lévő SNP mintázat
 HAPMAP -2010 Nemzetközi HapMap Projekt A Nemzetközi HapMap Project célja az emberi genom haplotípus* térképének(hapmap; haplotype map) megszerkesztése, melynek segítségével katalogizálni tudjuk az ember
HAPMAP -2010 Nemzetközi HapMap Projekt A Nemzetközi HapMap Project célja az emberi genom haplotípus* térképének(hapmap; haplotype map) megszerkesztése, melynek segítségével katalogizálni tudjuk az ember
MUTÁCIÓK. A mutáció az örökítő anyag spontán, maradandó megváltozása, amelynek során új genetikai tulajdonság keletkezik.
 MUTÁCIÓK A mutáció az örökítő anyag spontán, maradandó megváltozása, amelynek során új genetikai tulajdonság keletkezik. Pontmutáció: A kromoszóma egy génjében pár nukleotidnál következik be változás.
MUTÁCIÓK A mutáció az örökítő anyag spontán, maradandó megváltozása, amelynek során új genetikai tulajdonság keletkezik. Pontmutáció: A kromoszóma egy génjében pár nukleotidnál következik be változás.
Furnitura kollekció UNI bútorlapok
 D102 PS14 Beige (Kastamonu) 2 3 820 Ft 206 Ft Hasonló szín Felület Vastagság 18mm Élzárás 1mm 324 Ft Felület Enyhén recés Élzárás 2mm 359 Ft D1313 HDF 800 Ft D104 PS11 Elefántcsont (Kastamonu) 2 3 820
D102 PS14 Beige (Kastamonu) 2 3 820 Ft 206 Ft Hasonló szín Felület Vastagság 18mm Élzárás 1mm 324 Ft Felület Enyhén recés Élzárás 2mm 359 Ft D1313 HDF 800 Ft D104 PS11 Elefántcsont (Kastamonu) 2 3 820
GRADUÁLIS BIOSTATISZTIKAI KURZUS február hó 22. Dr. Dinya Elek egyetemi docens
 GRADUÁLIS BIOSTATISZTIKAI KURZUS 2012. február hó 22. Dr. Dinya Elek egyetemi docens Biometria fogalma The active pursuit of biological knowledge by quantitative methods Sir R. A. Fisher, 1948 BIOMETRIA
GRADUÁLIS BIOSTATISZTIKAI KURZUS 2012. február hó 22. Dr. Dinya Elek egyetemi docens Biometria fogalma The active pursuit of biological knowledge by quantitative methods Sir R. A. Fisher, 1948 BIOMETRIA
B I O L Ó G I A. ÍRÁSBELI ÉRETTSÉGI FELVÉTELI FELADATOK május 22. du. JAVÍTÁSI ÚTMUTATÓ. Kérjük, olvassa el a bevezetőt!
 B I O L Ó G I A ÍRÁSBELI ÉRETTSÉGI FELVÉTELI FELADATOK 2002. május 22. du. JAVÍTÁSI ÚTMUTATÓ Kérjük, olvassa el a bevezetőt! A javítási útmutatóhoz rendelkezésre áll a feladatlap. A pályázóknak megoldásaikat
B I O L Ó G I A ÍRÁSBELI ÉRETTSÉGI FELVÉTELI FELADATOK 2002. május 22. du. JAVÍTÁSI ÚTMUTATÓ Kérjük, olvassa el a bevezetőt! A javítási útmutatóhoz rendelkezésre áll a feladatlap. A pályázóknak megoldásaikat
Valószín ségszámítás és statisztika
 Valószín ségszámítás és statisztika Informatika BSc, esti tagozat Backhausz Ágnes agnes@math.elte.hu fogadóóra: szerda 10-11 és 13-14, D 3-415 2018/2019. tavaszi félév Bevezetés A valószín ségszámítás
Valószín ségszámítás és statisztika Informatika BSc, esti tagozat Backhausz Ágnes agnes@math.elte.hu fogadóóra: szerda 10-11 és 13-14, D 3-415 2018/2019. tavaszi félév Bevezetés A valószín ségszámítás
A gabonasiklók színváltozatai
 A gabonasiklók színváltozatai Írta: Hajnal Márton Fényképek: www.ornutopia.om Kathy Love Máig a gabonasikló (Elaphe guttata) a legkedveltebb és legelterjedtebb terráriumi hüllõ a világon. Már hazánkban
A gabonasiklók színváltozatai Írta: Hajnal Márton Fényképek: www.ornutopia.om Kathy Love Máig a gabonasikló (Elaphe guttata) a legkedveltebb és legelterjedtebb terráriumi hüllõ a világon. Már hazánkban
Shaggy szőnyeg 51 Bone
 Shaggy szőnyeg 51 Bone RENDELÉSRE - - 5 990 Ft - 24 900 Ft 1.oldal Shaggy szőnyeg 63 Bone RENDELÉSRE - - 5 990 Ft - 24 900 Ft 2.oldal Shaggy szőnyeg 690 Bone RENDELÉSRE - - 5 990 Ft - 24 900 Ft 3.oldal
Shaggy szőnyeg 51 Bone RENDELÉSRE - - 5 990 Ft - 24 900 Ft 1.oldal Shaggy szőnyeg 63 Bone RENDELÉSRE - - 5 990 Ft - 24 900 Ft 2.oldal Shaggy szőnyeg 690 Bone RENDELÉSRE - - 5 990 Ft - 24 900 Ft 3.oldal
Természettudomány témakör: Genetika, fajok, fajták Növények, gombák, baktériumok működése, előfordulása Éghajlattípusok növénytakarói
 Természettudomány 5-6. témakör: Genetika, fajok, fajták Növények, gombák, baktériumok működése, előfordulása Éghajlattípusok növénytakarói Genetika - alapok A genetika két fogalmat takar: - klasszikus
Természettudomány 5-6. témakör: Genetika, fajok, fajták Növények, gombák, baktériumok működése, előfordulása Éghajlattípusok növénytakarói Genetika - alapok A genetika két fogalmat takar: - klasszikus
Prenatalis diagnosztika lehetőségei mikor, hogyan, miért? Dr. Almássy Zsuzsanna Heim Pál Kórház, Budapest Toxikológia és Anyagcsere Osztály
 Prenatalis diagnosztika lehetőségei mikor, hogyan, miért? Dr. Almássy Zsuzsanna Heim Pál Kórház, Budapest Toxikológia és Anyagcsere Osztály Definíció A prenatális diagnosztika a klinikai genetika azon
Prenatalis diagnosztika lehetőségei mikor, hogyan, miért? Dr. Almássy Zsuzsanna Heim Pál Kórház, Budapest Toxikológia és Anyagcsere Osztály Definíció A prenatális diagnosztika a klinikai genetika azon
Előadások témája: néhány terület ismétlése, ill. bővebb tárgyalása és a modell élőlények genetikája
 GENETIKA biológus MSc Előadások témája: néhány terület ismétlése, ill. bővebb tárgyalása és a modell élőlények genetikája Az előadások anyaga PDF-ben: Genetika / Hallgatóknak (oktatási anyagok) usrname/passwd:
GENETIKA biológus MSc Előadások témája: néhány terület ismétlése, ill. bővebb tárgyalása és a modell élőlények genetikája Az előadások anyaga PDF-ben: Genetika / Hallgatóknak (oktatási anyagok) usrname/passwd:
A skót lógófülű macska egészséges tenyésztése: a lógó fül öröklésmenete, osteochondrodysplasia és kezelési lehetőségek
 A skót lógófülű macska egészséges tenyésztése: a lógó fül öröklésmenete, osteochondrodysplasia és kezelési lehetőségek ÍRTA: PAVELKA ALEXANDRA állattenyésztő mérnök A skót lógófülű macska sokak által kedvelt
A skót lógófülű macska egészséges tenyésztése: a lógó fül öröklésmenete, osteochondrodysplasia és kezelési lehetőségek ÍRTA: PAVELKA ALEXANDRA állattenyésztő mérnök A skót lógófülű macska sokak által kedvelt
Ember: Állat: Növény:
 Hova tartoznak a szavak? Írd a megfelelı csoport után a hozzá tartozó számot! Ember: Állat: Növény: 1 ibolya 9 nárcisz 2 Rózsa 10 paripa 3 béka 11 bálna 4 málna 12 Ibolya 5 láma 13 sóska 6 Nárcisz 14 Béla
Hova tartoznak a szavak? Írd a megfelelı csoport után a hozzá tartozó számot! Ember: Állat: Növény: 1 ibolya 9 nárcisz 2 Rózsa 10 paripa 3 béka 11 bálna 4 málna 12 Ibolya 5 láma 13 sóska 6 Nárcisz 14 Béla
Matematika A3 Valószínűségszámítás, 0. és 1. gyakorlat 2013/14. tavaszi félév
 Matematika A3 Valószínűségszámítás, 0. és 1. gyakorlat 2013/14. tavaszi félév 1. Kombinatorikus módszer ismétlés nélküli ismétléses permutáció k 1!k 2!...k r! n futó beérkezésének sorrendje n golyót ennyiféleképpen
Matematika A3 Valószínűségszámítás, 0. és 1. gyakorlat 2013/14. tavaszi félév 1. Kombinatorikus módszer ismétlés nélküli ismétléses permutáció k 1!k 2!...k r! n futó beérkezésének sorrendje n golyót ennyiféleképpen
2. A ξ valószín ségi változó s r ségfüggvénye a következ : c f(x) =
 1 Egy dobozban hat fehér golyó van Egy szabályos dobókockával dobunk, majd annyi piros golyót teszünk a dobozba, amennyit dobtunk Ezután véletlenszer en húzunk egy golyót a dobozból (a) Mi a valószín sége,
1 Egy dobozban hat fehér golyó van Egy szabályos dobókockával dobunk, majd annyi piros golyót teszünk a dobozba, amennyit dobtunk Ezután véletlenszer en húzunk egy golyót a dobozból (a) Mi a valószín sége,
Területi sor Kárpát medence Magyarország Nyugat-Európa
 Területi sor Terület megnevezése Magyarok száma 2011.01.01. Kárpát medence 13 820 000 Magyarország 10 600 00 Nyugat-Európa 1 340 000 HIV prevalence (%) in adults in Africa, 2005 2.5 Daganatos halálozás
Területi sor Terület megnevezése Magyarok száma 2011.01.01. Kárpát medence 13 820 000 Magyarország 10 600 00 Nyugat-Európa 1 340 000 HIV prevalence (%) in adults in Africa, 2005 2.5 Daganatos halálozás
Valószínűségszámítás feladatok
 Valószínűségszámítás feladatok Klasszikus valószínűség./ Eg csomag magar kártát jól összekeverünk. Menni annak a valószínűsége, hog a ász egmás után helezkedik el?./ 00 alma közül 0 férges. Menni a valószínűsége,
Valószínűségszámítás feladatok Klasszikus valószínűség./ Eg csomag magar kártát jól összekeverünk. Menni annak a valószínűsége, hog a ász egmás után helezkedik el?./ 00 alma közül 0 férges. Menni a valószínűsége,
