Sapientia Egyetem, Műszaki és Humántudományok Tanszék.
|
|
|
- Sarolta Vass
- 9 évvel ezelőtt
- Látták:
Átírás
1 Kriptográfia és Információbiztonság 5. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia 2015
2 Miről volt szó az elmúlt előadáson? AES (Advanced Encryption Standard) kör-kulcs generálás, titkosítás, visszafejtés, implementáció.
3 Miről lesz szó? A Crypto++ könyvtárcsomag Az NTL könyvtárcsomag Nagyszámok kezelése C# Nagyszámok kezelése Java Nyilvános-kulcsú, aszimmetrikus (public-key, asymmetric cryptography) rendszerek: alapfogalmak, követelmények, matematikai modell. Az RSA titkosító rendszer: specifikáció, példa, helyesség, A Fermat-féle faktorizációs módszer
4 A Crypto++ könyvtárcsomag Kriptográfiai sémák, a NIST által elfogadott standard implementációkkal, letöltés, kicsomagolás, projekt létrehozás, build-elés statikus, dinamikus könyvtárak létrehozása, a statikus könyvtár a cryptest solution build-elésekor jön létre, a \cryptopp\win32\output\debug mappába: cryptlib.lib,
5 A Crypto++ könyvtárcsomag Beálĺıtások: Project/Properties/Configuration Properties/C/C++/Code generation/runtime Library Multi-threaded Debug (/MTd)-ra álĺıtani, Project/Properties/Configuration Properties/C/C++/General/ \cryptopp, a cryptlib.lib-et hozzáadni a projekthez, az alkalmazás elejére beírni: #define CRYPTOPP DEFAULT NO DLL #include "dll.h"
6 Nagy számok kezelése, C++ Victor Shoup: NTL könyvtárcsomag, a statikus könyvtár létrehozása töltsük le és csomagoljuk ki a, pl. a WinNTL mappába: hozzunk létre egy új projektet: New Project Win32 ConsoleApplication, adjunk egy nevet a projektnek, legyen ez NTLLib, jelöljük be a Static library opciót. ne legyen bejelölve a Precompiled header opció, a Source Files-hoz az Add Existing Item menüpont segítségével adjuk hozzá a WinNTL\src mappából az összes állományt, a Project/NTLLib/Properties menüpontnál az Additional Include Directories-nél adjuk meg a header állományok elérési útvonalát:... \WinNTL\include a Build\Bulid\Solution parancs megadásával létrejön a NTLLib\Debug mappában a statikus könyvtár.
7 Az NTL könyvtárcsomag, használat Hozzunk létre egy új projektet: New Project Win32 Console Application, adjunk egy nevet a projektnek, legyen ez Labor6, jelöljük be a Empty project opciót. a Labor6 project-hez az Add Existing Item menüpont segítségével adjuk hozzá az NTLLib Debug mappából a létrehozott statikus könyvtárat, a Project/NTLLib/Properties menüpontnál az Additional Include Directories-nél adjuk meg a header állományok elérési útvonalát:...\winntl\include.
8 Az NTL könyvtárcsomag, használat a forráskódba: #ifndef _ZZ_ #define _ZZ_ #include <NTL/ZZ.h> #endif NTL_CLIENT ZZ a nagy számok kezelésére szolgáló típus, to_zz string átalakítása ZZ típusá, InvMod multiplikatív inverz meghatározása, XGCD kiterjesztett Euklideszi algoritmus, PowerMod moduláris hatványozás, ZZFromBytes, BytesFromZZ, byte szekvenciából készít ZZ típusú nagyszámot, és fordítva, log logaritmus meghatározása.
9 Nagy számok kezelése, Java import java.math.biginteger; változó deklarálás: BigInteger n = new BigInteger(" "); logaritmus számítás: ln moduláris hatványozás: modpow multiplikatív inverz: modinverse...
10 Nagy számok kezelése, C# using System.Numerics; változó deklarálás: BigInteger p = 0, q = 0; BigInteger number1 = BigInteger.Parse(" "); logaritmus számítás: BigInteger.Log(), hatványozás: BigInteger.Pow(), moduláris hatványozás: BigInteger.ModPow(),...
11 A nyilvános-kulcsú rendszerek, alapfogalmak A titkosítás és visszafejtés nem ugyanazzal a kulccsal történik: van egy titkos-kulcs és van egy nyilvános-kulcs, nem helyettesíti a szimmetrikus kriptográfiát, a rendszerek biztonsága matematikai problémákon alapszanak; az alapműveletek nem a helyettesítés és permutáció, alkalmas bizalmas információcserére és hitelesítésre, illetve mindkettőre; kulcscsere és digitális aláírás protokollokban használják.
12 A nyilvános-kulcsú rendszerek, követelmények Hatékony algoritmussal lehessen meghatározni a rendszerben használt kulcspárt: a nyilvános és titkos-kulcsot, a nyilvános-kulcs ismeretében, hatékony algoritmussal lehessen meghatározni az üzenet rejtjelezett értékét, a titkos-kulcs ismeretében, hatékony algoritmussal lehessen visszafejteni a rejtjelezett üzenetet, a nyilvános-kulcs ismeretében ne lehessen hatékonyan meghatározni a titkos-kulcsot, a nyilvános-kulcs és rejtjelezett-szöveg ismeretében ne lehessen hatékonyan meghatározni az üzenetet, ne lehessen következtetni annak tartalmára. Kevés olyan rendszert sikerült kidolgozni, amely eleget tesz a fenti követelményeknek (kudarcos próbálkozások: a hátizsák feladaton alapuló titkosító rendszer).
13 A legismertebb publikus-kulcsú rendszerek RSA (Rivest-Shamir-Adleman), biztonsága azon alapszik, hogy nehéz meghatározni valamely összetett szám prímosztóit, Diffie-Hellman kulcscsere, biztonsága a diszkrét logaritmus probléma nehézségén alapszik, ElGamal titkosító, a Diffie-Hellman kulcscserével áll szoros kapcsolatban, elliptikus görbén alapuló kriptográfia.
14 A titkos-kulcsú rendszerek matematikai modellje jelölés: SKE, ahol a (K, M, C) halmaz-hármas felett értelmezünk 3 algoritmust: Gen, a kulcs-generáló algoritmus, polinom idejű, véletlenszerű: key R Gen(1 k ), ahol key K, k Z 0 a rendszer biztonsági paramétere (legtöbb esetben a generált kulcs bit-hossza), Enc key a rejtjelező algoritmus, polinom idejű, véletlenszerű: c R Enc key (m), a Dec key a visszafejtő algoritmus, polinom idejű, determinisztikus: m Dec key (c). Helyesség: Dec key (Enc key (m)) = m, minden m M esetében.
15 A nyilvános-kulcsú rendszerek matematikai modellje jelölés: PKE, ahol a (K, M, C) halmaz-hármas felett értelmezünk 3 algoritmus: Gen, a kulcs-generáló algoritmus, polinom idejű, véletlenszerű: (pk, sk) R Gen(1 k ), ahol (pk, sk) K K, k Z 0 a rendszer biztonsági paramétere, Enc pk a rejtjelező algoritmus, polinom idejű, véletlenszerű: c R Enc pk (m), a Dec sk a visszafejtő algoritmus, polinom idejű, determinisztikus: m Dec sk (c). Helyesség: Dec sk (Enc pk (m)) = m, minden m M esetében.
16 Az RSA titkosító rendszer, kulcsgenerálás Bemenet: a k biztonsági paraméter. Kimenet: a pk = (n, e) nyilvános-kulcs és az sk = d titkos-kulcs. rsakeygen (k) p = primszam(k); q = primszam(k); n = p * q; phi = (p-1) * (q-1); e = rand(phi); d = inverz(e, pi); return n, e, d;
17 Az RSA titkosító rendszer, kulcsgenerálás a primszam(k) algoritmus generál egy k bit hosszúságú prímszámot, erre leggyakrabban a Miller-Rabin algoritmust használják, lásd később, a jelenlegi standard a k = 1024 értéket ajánlja, amely kb. 308 decimális számjegyet jelent, a rand(phi) algoritmus egy véletlen számot generál, ahol phi az Euler féle függvény, a következő tulajdonsággal 1 < e < phi, gcd(e, phi) = 1. az inverz(e, phi) algoritmus meghatározza d-t a következő tulajdonsággal: e d = 1 (mod phi), erre a kiterjesztett Euklideszi algoritmust kell használni, nem működik az Affinnál és Hillnél használt, összes lehetséges érték kipróbálásának, módszere.
18 Példa, kulcsgenerálás p, q két prímszám: Legyen p = 3877, q = Meghatározzuk: n = = , phi = (p 1) (q 1) = = Legyen e = , ahol gcd(65 537, phi) = 1. Meghatározzuk e inverzét (mod phi) szerint, kapjuk: d = , mert = 1 (mod ). A nyilvános-kulcs : (65 537, ). A titkos-kulcs : ( ).
19 Az RSA titkosító rendszer, titkosítás Bemenet: az üzenet, mint egy m egész szám a [0,..., n 1] intervallumból, az e, n nyilvános-kulcs. Kimenet: a c titkosított szám rsaencrypt (m, e, n) c = modpow(m, e, n); return c; Az üzenetet(byte-szekvenciát, vagy szöveget) át kell alakítani számmá, lásd később. A modpow(m, e, n) algoritmus meghatározza az m e (mod n) értéket.
20 Az RSA titkosító rendszer, visszafejtés Bemenet: a c titkosított szám, d titkos-kulcs. Kimenet: az m visszafejtett érték. rsadecrypt (c, d, n) m = modpow(c, d, n); return m; Az m értéket vissza kell alakítani byte szekvenciává, szöveggé, lásd később. A modpow(c, d, n) algoritmus meghatározza a c d (mod n) értéket.
21 Az RSA titkosító rendszer, helyesség e d = 1 (mod phi) létezik x, egész szám, úgy hogy feltéve hogy: gcd(m, p) = 1 hasonlóan: e d = 1 + x phi. m p 1 = 1 (mod p) m 1+x (p 1) (q 1) = m (mod p) m e d = m (mod p). m e d = m (mod q) m e d = m (mod n).
22 Példa, titkosítás Legyen az üzenet MATHEMATICIAN, és a kulcsok a kulcsgenerálásnál megadott értékek. Feltélezzük, hogy az alkalmazott ábécé az angol ábécé 26 nagybetűje. A szokásos módon hozzárendeljük a karakterekhez a számkódokat: , a karaktersorozatot 26-os számrendszerbeli számnak fogjuk tekinteni, a számokat átírjuk 26 l számrendszerbe, ahol l = log 26 n és n = l = 4, 4-es csoportokat formálunk, és 26 4 számrendszerben a következő számjegyeket kapjuk: , mert
23 Példa, titkosítás = = = = mindegyik számjegyet titkosítjuk a nyilvános-kulccsal: (65 537, ), az eredmény: , a kapott számokat 26 l+1 = beli számoknak tekintjük és átírjuk 26-os számrendszerbe, 5-ös csoportokat formáltunk, az eredmény: , ahol
24 Példa, titkosítás = = = = A titkosított karaktersorozat: SVUVDMNGFOWAQUAPENZK.
25 Példa, visszafejtés a titkosított számkód-sorozat: a számkódokat átírjuk es számrendszerbe. Az eredmény: Mindegyik számra külön alkalmazzuk a titkos-kulcsot: ( ) c c (mod ) a kapott számokat átírjuk 26-os számrendszerbe, megkapva a visszafejtett számkód-sorozatot: behelyettesítve: MATHEMATICIAN
26 Az RSA titkosító rendszer Ha a titkosítást bájtok felett végezzük, akkor a bájtokat 256-os számrendszerbeli számoknak tekintjük egyszerre l bájtot dolgozunk fel, úgy hogy a számokat átírjuk 256 l számrendszerbe, ahol l = log 256 n, majd a kapott nagy számot hatványozzuk, hatványozás után, a kapott értéket 256 l+1 -os számrendszerbeli számnak tekintjük, amelyet átalakítunk 256-os számrendszerbe, kapunk l + 1 bájtot. Visszafejtéskor fordítva járunk el, l + 1 bájtot dolgozunk fel egyszerre, amiből l bájtot kapunk vissza.
27 Faktorizációhoz kapcsolódó problémák osztási próba módszere (trial division), Fermat-féle faktorizációs módszer, Pollard ρ féle faktorizációs módszer... Az osztási próba módszere: vizsgáljuk a kis prímekkel való oszthatóságot, ha két azonos nagyságrendű prímszám szorzata a vizsgált n összetett szám, akkora közeĺıtőleg n osztást kell kipróbálnunk a sikeres faktorizáláshoz, akkor használjuk, mikor egy összetett szám kis nagyságrendű prímosztóit kell megkeresni.
28 Fermat-féle faktorizációs módszer Ha a p és a q prímek közel vannak egymáshoz, akkor az n faktorizálása lehetséges a Fermat-féle faktorizációs módszerrel. Feltételezzük, hogy az n = a 2 b 2, ahol a, b tetszőleges egész számok. Ekkor p = a b, q = a + b. Az algoritmus a következő: fermatfaktor(n) a = ceil(sqrt(n)); b1 = a * a - n; while (negyzetsz(b1) == 0) do a = a + 1; b1 = a * a - n; return (a + sqrt(b1)); A negyzetsz függvény megvizsgálja, hogy a paraméterként kapott szám négyzetszám-e, 0-t térít vissza, ha a paramétere nem négyzetszám.
29 Fermat-féle faktorizáció, példa Határozzuk meg n = 6283 két prímosztóját, a Fermat-féle faktorizációs módszerrel: n a b = a 2 n négyzetszám-e? nem nem igen 441 = 21 p = = 61, q = = 103
Sapientia Egyetem, Műszaki és Humántudományok Tanszék.
 Kriptográfia és Információbiztonság 2 előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@mssapientiaro 2016 Miről volt szó az elmúlt előadáson? Félévi áttekintő
Kriptográfia és Információbiztonság 2 előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@mssapientiaro 2016 Miről volt szó az elmúlt előadáson? Félévi áttekintő
Sapientia Egyetem, Matematika-Informatika Tanszék.
 Kriptográfia és Információbiztonság 8. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? az RSA titkosító
Kriptográfia és Információbiztonság 8. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? az RSA titkosító
Sapientia Egyetem, Matematika-Informatika Tanszék.
 Kriptográfia és Információbiztonság 2. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? Követelmények,
Kriptográfia és Információbiztonság 2. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? Követelmények,
Sapientia Egyetem, Matematika-Informatika Tanszék.
 Kriptográfia és Információbiztonság 7. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? Kriptográfiai
Kriptográfia és Információbiztonság 7. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? Kriptográfiai
Sapientia Egyetem, Műszaki és Humántudományok Tanszék.
 Kriptográfia és Információbiztonság 8. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2017 Miről volt szó az elmúlt előadáson? A Crypto++
Kriptográfia és Információbiztonság 8. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2017 Miről volt szó az elmúlt előadáson? A Crypto++
Sapientia Egyetem, Műszaki és Humántudományok Tanszék. mgyongyi@ms.sapientia.ro
 Kriptográfia és Információbiztonság 10. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2015 Vizsgatematika 1 Klasszikus kriptográfiai rendszerek
Kriptográfia és Információbiztonság 10. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2015 Vizsgatematika 1 Klasszikus kriptográfiai rendszerek
1. Egészítsük ki az alábbi Python függvényt úgy, hogy a függvény meghatározza, egy listába, az első n szám faktoriális értékét:
 Az írásbeli vizsgán, az alábbiakhoz hasonló, 8 kérdésre kell választ adni. Hasonló kérdésekre lehet számítani (azaz mi a hiba, egészítsük ki, mi a függvény kimeneti értéke, adjuk meg a függvényhívást,
Az írásbeli vizsgán, az alábbiakhoz hasonló, 8 kérdésre kell választ adni. Hasonló kérdésekre lehet számítani (azaz mi a hiba, egészítsük ki, mi a függvény kimeneti értéke, adjuk meg a függvényhívást,
2016, Diszkrét matematika
 Diszkrét matematika 11. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016, őszi félév Miről volt szó az elmúlt előadáson? legnagyobb közös
Diszkrét matematika 11. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016, őszi félév Miről volt szó az elmúlt előadáson? legnagyobb közös
2017, Diszkrét matematika
 Diszkrét matematika 10. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2017, őszi félév Miről volt szó az elmúlt előadáson? a prímszámtétel prímszámok,
Diszkrét matematika 10. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2017, őszi félév Miről volt szó az elmúlt előadáson? a prímszámtétel prímszámok,
Sapientia Egyetem, Műszaki és Humántudományok Tanszék. mgyongyi@ms.sapientia.ro
 Kriptográfia és Információbiztonság 4. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2015 Miről volt szó az elmúlt előadáson? blokk-titkosító
Kriptográfia és Információbiztonság 4. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2015 Miről volt szó az elmúlt előadáson? blokk-titkosító
Sapientia Egyetem, Matematika-Informatika Tanszék.
 Kriptográfia és Információbiztonság 3. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2019 Miről volt szó az elmúlt előadáson? Klasszikus kriptográfiai
Kriptográfia és Információbiztonság 3. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2019 Miről volt szó az elmúlt előadáson? Klasszikus kriptográfiai
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 11. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Kongruenciák Diszkrét matematika I. középszint 2014.
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 11. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Kongruenciák Diszkrét matematika I. középszint 2014.
2016, Diszkrét matematika
 Diszkrét matematika 8. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016, őszi félév Miről volt szó az elmúlt előadáson? a Fibonacci számsorozat
Diszkrét matematika 8. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016, őszi félév Miről volt szó az elmúlt előadáson? a Fibonacci számsorozat
Data Security: Public key
 Nyilvános kulcsú rejtjelezés RSA rejtjelező El-Gamal rejtjelező : Elliptikus görbe kriptográfia RSA 1. Véletlenszerűen választunk két "nagy" prímszámot: p1, p2 2. m= p1p2 φ ( ) = ( p -1)( p -1) m 1 2 3.
Nyilvános kulcsú rejtjelezés RSA rejtjelező El-Gamal rejtjelező : Elliptikus görbe kriptográfia RSA 1. Véletlenszerűen választunk két "nagy" prímszámot: p1, p2 2. m= p1p2 φ ( ) = ( p -1)( p -1) m 1 2 3.
2018, Diszkre t matematika. 10. elo ada s
 Diszkre t matematika 10. elo ada s MA RTON Gyo ngyve r mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tansze k Marosva sa rhely, Roma nia 2018, o szi fe le v MA RTON Gyo ngyve r 2018,
Diszkre t matematika 10. elo ada s MA RTON Gyo ngyve r mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tansze k Marosva sa rhely, Roma nia 2018, o szi fe le v MA RTON Gyo ngyve r 2018,
2018, Diszkre t matematika. 8. elo ada s
 Diszkre t matematika 8. elo ada s MA RTON Gyo ngyve r mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tansze k Marosva sa rhely, Roma nia 2018, o szi fe le v MA RTON Gyo ngyve r 2018,
Diszkre t matematika 8. elo ada s MA RTON Gyo ngyve r mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tansze k Marosva sa rhely, Roma nia 2018, o szi fe le v MA RTON Gyo ngyve r 2018,
Kriptográfia I. Kriptorendszerek
 Kriptográfia I Szimmetrikus kulcsú titkosítás Kriptorendszerek Nyíltszöveg üzenettér: M Titkosított üzenettér: C Kulcs tér: K, K Kulcsgeneráló algoritmus: Titkosító algoritmus: Visszafejt algoritmus: Titkosítás
Kriptográfia I Szimmetrikus kulcsú titkosítás Kriptorendszerek Nyíltszöveg üzenettér: M Titkosított üzenettér: C Kulcs tér: K, K Kulcsgeneráló algoritmus: Titkosító algoritmus: Visszafejt algoritmus: Titkosítás
2016, Diszkrét matematika
 Diszkrét matematika 7. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016, őszi félév Miről volt szó az elmúlt előadáson? az ord, chr függvények
Diszkrét matematika 7. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016, őszi félév Miről volt szó az elmúlt előadáson? az ord, chr függvények
Készítette: Fuszenecker Róbert Konzulens: Dr. Tuzson Tibor, docens
 A nyílt kulcsú titkosítás és a digitális aláírás Készítette: Fuszenecker Róbert Konzulens: Dr. Tuzson Tibor, docens Budapest Műszaki Főiskola Kandó Kálmán Műszaki Főiskolai Kar Műszertechnikai és Automatizálási
A nyílt kulcsú titkosítás és a digitális aláírás Készítette: Fuszenecker Róbert Konzulens: Dr. Tuzson Tibor, docens Budapest Műszaki Főiskola Kandó Kálmán Műszaki Főiskolai Kar Műszertechnikai és Automatizálási
Sapientia Egyetem, Matematika-Informatika Tanszék.
 Kriptográfia és Információbiztonság 11. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? hash függvények
Kriptográfia és Információbiztonság 11. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? hash függvények
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Titkosítási rendszerek CCA-biztonsága
 Titkosítási rendszerek CCA-biztonsága Doktori (PhD) értekezés szerző: MÁRTON Gyöngyvér témavezető: Dr. Pethő Attila Debreceni Egyetem Természettudományi Doktori Tanács Informatikai Tudományok Doktori Iskola
Titkosítási rendszerek CCA-biztonsága Doktori (PhD) értekezés szerző: MÁRTON Gyöngyvér témavezető: Dr. Pethő Attila Debreceni Egyetem Természettudományi Doktori Tanács Informatikai Tudományok Doktori Iskola
Számelméleti alapfogalmak
 1 Számelméleti alapfogalmak 1 Definíció Az a IN szám osztója a b IN számnak ha létezik c IN melyre a c = b Jelölése: a b 2 Példa a 0 bármely a számra teljesül, mivel c = 0 univerzálisan megfelel: a 0 =
1 Számelméleti alapfogalmak 1 Definíció Az a IN szám osztója a b IN számnak ha létezik c IN melyre a c = b Jelölése: a b 2 Példa a 0 bármely a számra teljesül, mivel c = 0 univerzálisan megfelel: a 0 =
Webalkalmazás-biztonság. Kriptográfiai alapok
 Webalkalmazás-biztonság Kriptográfiai alapok Alapfogalmak, áttekintés üzenet (message): bizalmas információhalmaz nyílt szöveg (plain text): a titkosítatlan üzenet (bemenet) kriptoszöveg (ciphertext):
Webalkalmazás-biztonság Kriptográfiai alapok Alapfogalmak, áttekintés üzenet (message): bizalmas információhalmaz nyílt szöveg (plain text): a titkosítatlan üzenet (bemenet) kriptoszöveg (ciphertext):
Titkosírás. Biztos, hogy titkos? Szabó István előadása. Az életben sok helyen használunk titkosítást (mobil, internet, jelszavak...
 Biztos, hogy titkos? Szabó István előadása Az életben sok helyen használunk titkosítást (mobil, internet, jelszavak...) Története Az ókortól kezdve rengeteg feltört titkosírás létezik. Monoalfabetikus
Biztos, hogy titkos? Szabó István előadása Az életben sok helyen használunk titkosítást (mobil, internet, jelszavak...) Története Az ókortól kezdve rengeteg feltört titkosírás létezik. Monoalfabetikus
Minden egész szám osztója önmagának, azaz a a minden egész a-ra.
 1. Számelmélet Definíció: Az a egész szám osztója a egész számnak, ha létezik olyan c egész szám, melyre = ac. Ezt a következőképpen jelöljük: a Tulajdonságok: Minden egész szám osztója önmagának, azaz
1. Számelmélet Definíció: Az a egész szám osztója a egész számnak, ha létezik olyan c egész szám, melyre = ac. Ezt a következőképpen jelöljük: a Tulajdonságok: Minden egész szám osztója önmagának, azaz
Diszkrét matematika 2.
 Diszkrét matematika 2. A szakirány 11. előadás Ligeti Péter turul@cs.elte.hu www.cs.elte.hu/ turul Nagy hálózatok Nagy hálózatok jellemzése Internet, kapcsolati hálók, biológiai hálózatok,... globális
Diszkrét matematika 2. A szakirány 11. előadás Ligeti Péter turul@cs.elte.hu www.cs.elte.hu/ turul Nagy hálózatok Nagy hálózatok jellemzése Internet, kapcsolati hálók, biológiai hálózatok,... globális
Emlékeztet! matematikából
 Kriptográfia 2 Aszimmetrikus megoldások Emlékeztet matematikából Euklidész algoritmus - legnagyobb közös osztó meghatározása INPUT Int a>b0; OUTPUT gcd(a,b). 1. if b=0 return(a); 2. return(gcd(b,a mod
Kriptográfia 2 Aszimmetrikus megoldások Emlékeztet matematikából Euklidész algoritmus - legnagyobb közös osztó meghatározása INPUT Int a>b0; OUTPUT gcd(a,b). 1. if b=0 return(a); 2. return(gcd(b,a mod
Kriptográfiai alapfogalmak
 Kriptográfiai alapfogalmak A kriptológia a titkos kommunikációval foglalkozó tudomány. Két fő ága a kriptográfia és a kriptoanalízis. A kriptográfia a titkosítással foglalkozik, a kriptoanalízis pedig
Kriptográfiai alapfogalmak A kriptológia a titkos kommunikációval foglalkozó tudomány. Két fő ága a kriptográfia és a kriptoanalízis. A kriptográfia a titkosítással foglalkozik, a kriptoanalízis pedig
4. Előadás Titkosítás, RSA algoritmus
 4. Előadás Titkosítás, RSA algoritmus Dr. Kallós Gábor 2014 2015 1 Tartalom A kriptográfia meghatározása, alaphelyzete Szimmetrikus (titkos) kulcsú titkosítás A Caesar-eljárás Aszimmetrikus (nyilvános)
4. Előadás Titkosítás, RSA algoritmus Dr. Kallós Gábor 2014 2015 1 Tartalom A kriptográfia meghatározása, alaphelyzete Szimmetrikus (titkos) kulcsú titkosítás A Caesar-eljárás Aszimmetrikus (nyilvános)
Információs társadalom alapismeretek
 Információs társadalom alapismeretek Szabó Péter Gábor Titkosítás és számítástechnika Titkosítás alapfogalmai A Colossus Kriptográfia A rejtjelezés két fı lépésbıl áll: 1) az üzenet titkosítása (kódolás)
Információs társadalom alapismeretek Szabó Péter Gábor Titkosítás és számítástechnika Titkosítás alapfogalmai A Colossus Kriptográfia A rejtjelezés két fı lépésbıl áll: 1) az üzenet titkosítása (kódolás)
Prímtesztelés, Nyilvános kulcsú titkosítás
 Prímtesztelés, Nyilvános kulcsú titkosítás Papp László BME December 8, 2018 Prímtesztelés Feladat: Adott egy nagyon nagy n szám, döntsük el, hogy prímszám-e! Naív kísérletek: 1. Nézzük meg minden nála
Prímtesztelés, Nyilvános kulcsú titkosítás Papp László BME December 8, 2018 Prímtesztelés Feladat: Adott egy nagyon nagy n szám, döntsük el, hogy prímszám-e! Naív kísérletek: 1. Nézzük meg minden nála
RSA algoritmus. P(M) = M e mod n. S(C) = C d mod n. A helyesség igazoláshoz szükséges számelméleti háttér. a φ(n) = 1 mod n, a (a 1,a 2,...
 RSA algoritmus 1. Vegyünk véletlenszerűen két különböző nagy prímszámot, p-t és q-t. 2. Legyen n = pq. 3. Vegyünk egy olyan kis páratlan e számot, amely relatív prím φ(n) = (p 1)(q 1)-hez. 4. Keressünk
RSA algoritmus 1. Vegyünk véletlenszerűen két különböző nagy prímszámot, p-t és q-t. 2. Legyen n = pq. 3. Vegyünk egy olyan kis páratlan e számot, amely relatív prím φ(n) = (p 1)(q 1)-hez. 4. Keressünk
RSA algoritmus. Smidla József. Rendszer- és Számítástudományi Tanszék Pannon Egyetem
 RSA algoritmus Smidla József Rendszer- és Számítástudományi Tanszék Pannon Egyetem 2012. 3. 27. Smidla József (RSZT) RSA algoritmus 2012. 3. 27. 1 / 29 Tartalom 1 Aszimmetrikus kódolók 2 Matematikai alapok
RSA algoritmus Smidla József Rendszer- és Számítástudományi Tanszék Pannon Egyetem 2012. 3. 27. Smidla József (RSZT) RSA algoritmus 2012. 3. 27. 1 / 29 Tartalom 1 Aszimmetrikus kódolók 2 Matematikai alapok
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 10. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Felhívás Diszkrét matematika I. középszint 2014.
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 10. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Felhívás Diszkrét matematika I. középszint 2014.
Best of Criptography Slides
 Best of Criptography Slides Adatbiztonság és Kriptográfia PPKE-ITK 2008. Top szlájdok egy helyen 1 Szimmetrikus kulcsú rejtjelezés Általában a rejtjelező kulcs és a dekódoló kulcs megegyezik, de nem feltétlenül.
Best of Criptography Slides Adatbiztonság és Kriptográfia PPKE-ITK 2008. Top szlájdok egy helyen 1 Szimmetrikus kulcsú rejtjelezés Általában a rejtjelező kulcs és a dekódoló kulcs megegyezik, de nem feltétlenül.
2018, Diszkrét matematika
 Diszkrét matematika 12. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, ománia 2018, őszi félév Miről volt szó az elmúlt előadáson? a diszkrét logaritmus,
Diszkrét matematika 12. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, ománia 2018, őszi félév Miről volt szó az elmúlt előadáson? a diszkrét logaritmus,
Sapientia Egyetem, Műszaki és Humántudományok Tanszék. mgyongyi@ms.sapientia.ro
 Kriptográfia és Információbiztonság 1. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016 Követelmények, osztályozás Jelenlét: A laborgyakorlat
Kriptográfia és Információbiztonság 1. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016 Követelmények, osztályozás Jelenlét: A laborgyakorlat
2018, Diszkrét matematika
 Diszkrét matematika 4. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? számtartományok: racionális
Diszkrét matematika 4. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? számtartományok: racionális
megtalálásának hihetetlen nehéz voltán alapszik. Az eljárás matematikai alapja a kis FERMAT-tétel egy következménye:
 Az RSA módszer Az RSA módszer titkossága a prímtényezős felbontás nehézségén, a prímtényezők megtalálásának hihetetlen nehéz voltán alapszik. Az eljárás matematikai alapja a kis FERMAT-tétel egy következménye:
Az RSA módszer Az RSA módszer titkossága a prímtényezős felbontás nehézségén, a prímtényezők megtalálásának hihetetlen nehéz voltán alapszik. Az eljárás matematikai alapja a kis FERMAT-tétel egy következménye:
Windows biztonsági problémák
 Windows biztonsági problémák Miskolci Egyetem Általános Informatikai Tanszék Miért a Windows? Mivel elterjedt, előszeretettel keresik a védelmi lyukakat könnyen lehet találni ezeket kihasználó programokat
Windows biztonsági problémák Miskolci Egyetem Általános Informatikai Tanszék Miért a Windows? Mivel elterjedt, előszeretettel keresik a védelmi lyukakat könnyen lehet találni ezeket kihasználó programokat
Dr. Beinschróth József Kriptográfiai alkalmazások, rejtjelezések, digitális aláírás
 2017.10.13. Dr. Beinschróth József Kriptográfiai alkalmazások, rejtjelezések, digitális aláírás 1 Tartalom Alapvetések Alapfogalmak Változatok Tradicionális Szimmetrikus Aszimmetrikus Kombinált Digitális
2017.10.13. Dr. Beinschróth József Kriptográfiai alkalmazások, rejtjelezések, digitális aláírás 1 Tartalom Alapvetések Alapfogalmak Változatok Tradicionális Szimmetrikus Aszimmetrikus Kombinált Digitális
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Nemzeti Közszolgálati Egyetem. Vezető-és Továbbképzési Intézet. Bérczes Attila Pethő Attila. Kriptográfia
 Nemzeti Közszolgálati Egyetem Vezető-és Továbbképzési Intézet Bérczes Attila Pethő Attila Kriptográfia Budapest, 2014 A tananyag az ÁROP 2.2.21 Tudásalapú közszolgálati előmenetel című projekt keretében
Nemzeti Közszolgálati Egyetem Vezető-és Továbbképzési Intézet Bérczes Attila Pethő Attila Kriptográfia Budapest, 2014 A tananyag az ÁROP 2.2.21 Tudásalapú közszolgálati előmenetel című projekt keretében
2018, Funkcionális programozás
 Funkcionális programozás 6. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018, tavaszi félév Miről volt szó? Haskell modulok, kompilálás a
Funkcionális programozás 6. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018, tavaszi félév Miről volt szó? Haskell modulok, kompilálás a
Adat és Információvédelmi Mesteriskola 30 MB. Dr. Beinschróth József SAJÁTOS LOGIKAI VÉDELEM: A KRIPTOGRÁFIA ALKALMAZÁSA
 30 MB Dr. Beinschróth József SAJÁTOS LOGIKAI VÉDELEM: A KRIPTOGRÁFIA ALKALMAZÁSA Tartalom Alapvetések - kiindulópontok Alapfogalmak Változatok Tradicionális módszerek Szimmetrikus kriptográfia Aszimmetrikus
30 MB Dr. Beinschróth József SAJÁTOS LOGIKAI VÉDELEM: A KRIPTOGRÁFIA ALKALMAZÁSA Tartalom Alapvetések - kiindulópontok Alapfogalmak Változatok Tradicionális módszerek Szimmetrikus kriptográfia Aszimmetrikus
2018, Diszkrét matematika
 Diszkrét matematika 5. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? Python alapfogalmak:
Diszkrét matematika 5. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? Python alapfogalmak:
Titkosítás NetWare környezetben
 1 Nyílt kulcsú titkosítás titkos nyilvános nyilvános titkos kulcs kulcs kulcs kulcs Nyilvános, bárki által hozzáférhető csatorna Nyílt szöveg C k (m) Titkosított szöveg Titkosított szöveg D k (M) Nyílt
1 Nyílt kulcsú titkosítás titkos nyilvános nyilvános titkos kulcs kulcs kulcs kulcs Nyilvános, bárki által hozzáférhető csatorna Nyílt szöveg C k (m) Titkosított szöveg Titkosított szöveg D k (M) Nyílt
Elektronikus aláírás és titkosítás beállítása MS Outlook 2010 levelezőben
 Elektronikus aláírás és titkosítás beállítása MS Outlook 2010 levelezőben Verziószám 2.0 Objektum azonosító (OID) Hatálybalépés dátuma 2013. november 6. 1 Változáskövetés Verzió Dátum Változás leírása
Elektronikus aláírás és titkosítás beállítása MS Outlook 2010 levelezőben Verziószám 2.0 Objektum azonosító (OID) Hatálybalépés dátuma 2013. november 6. 1 Változáskövetés Verzió Dátum Változás leírása
Hardver modellezés SystemC-vel és SDL grafikus könyvtárral Visual Stúdió alatt
 BME Hardver modellezés SystemC-vel és SDL grafikus könyvtárral Visual Stúdió alatt Visual Studio, SystemC, SDL Tóth Gergely Endre 2013.03.18. 1 Bevezetés Ebben a dokumentumban leírom, hogy hogyan lehet
BME Hardver modellezés SystemC-vel és SDL grafikus könyvtárral Visual Stúdió alatt Visual Studio, SystemC, SDL Tóth Gergely Endre 2013.03.18. 1 Bevezetés Ebben a dokumentumban leírom, hogy hogyan lehet
Módszerek és eszközök a kriptográfia oktatásakor
 Módszerek és eszközök a kriptográfia oktatásakor Márton Gyöngyvér mgyongyi@ms.sapientia.ro Sapientia Erdélyi Magyar Tudományegyetem, Románia Absztrakt. Digitális világunkban naponta találkozunk olyan alkalmazásokkal
Módszerek és eszközök a kriptográfia oktatásakor Márton Gyöngyvér mgyongyi@ms.sapientia.ro Sapientia Erdélyi Magyar Tudományegyetem, Románia Absztrakt. Digitális világunkban naponta találkozunk olyan alkalmazásokkal
SSL elemei. Az SSL illeszkedése az internet protokoll-architektúrájába
 SSL 1 SSL elemei Az SSL illeszkedése az internet protokoll-architektúrájába 2 SSL elemei 3 SSL elemei 4 SSL Record protokoll 5 SSL Record protokoll Az SSL Record protokoll üzenet formátuma 6 SSL Record
SSL 1 SSL elemei Az SSL illeszkedése az internet protokoll-architektúrájába 2 SSL elemei 3 SSL elemei 4 SSL Record protokoll 5 SSL Record protokoll Az SSL Record protokoll üzenet formátuma 6 SSL Record
Elektronikus aláírás. Gaidosch Tamás. Állami Számvevőszék
 Elektronikus aláírás Gaidosch Tamás Állami Számvevőszék 2016.05.24 Tartalom Mit tekintünk elektronikus aláírásnak? Hogyan működik? Kérdések 2 Egyszerű elektronikus aláírás 3 Demo: valódi elektronikus aláírás
Elektronikus aláírás Gaidosch Tamás Állami Számvevőszék 2016.05.24 Tartalom Mit tekintünk elektronikus aláírásnak? Hogyan működik? Kérdések 2 Egyszerű elektronikus aláírás 3 Demo: valódi elektronikus aláírás
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 8. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 8. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Modern titkosírások és a matematika
 Modern titkosírások és a matematika Az Enigma feltörése Nagy Gábor Péter Szegedi Tudományegyetem Bolyai Intézet, Geometria Tanszék Kutatók Éjszakája 2015. szeptember 25. 1 / 20 Tagolás 1 A titkosírások
Modern titkosírások és a matematika Az Enigma feltörése Nagy Gábor Péter Szegedi Tudományegyetem Bolyai Intézet, Geometria Tanszék Kutatók Éjszakája 2015. szeptember 25. 1 / 20 Tagolás 1 A titkosírások
2018, Diszkrét matematika
 Diszkrét matematika 7. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? számrendszerek számrendszerek
Diszkrét matematika 7. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? számrendszerek számrendszerek
Hírek kriptográfiai algoritmusok biztonságáról
 Hírek kriptográfiai algoritmusok biztonságáról Dr. Berta István Zsolt K+F igazgató Microsec Kft. http://www.microsec.hu Mirıl fogok beszélni? Bevezetés Szimmetrikus kulcsú algoritmusok
Hírek kriptográfiai algoritmusok biztonságáról Dr. Berta István Zsolt K+F igazgató Microsec Kft. http://www.microsec.hu Mirıl fogok beszélni? Bevezetés Szimmetrikus kulcsú algoritmusok
Következik, hogy B-nek minden prímosztója 4k + 1 alakú, de akkor B maga is 4k + 1 alakú, s ez ellentmondás.
 Prímszámok A (pozitív) prímszámok sorozata a következő: 2, 3, 5, 7, 11, 13, 17, 19,... 1. Tétel. Végtelen sok prímszám van. Első bizonyítás. (Euklidész) Tegyük fel, hogy állításunk nem igaz, tehát véges
Prímszámok A (pozitív) prímszámok sorozata a következő: 2, 3, 5, 7, 11, 13, 17, 19,... 1. Tétel. Végtelen sok prímszám van. Első bizonyítás. (Euklidész) Tegyük fel, hogy állításunk nem igaz, tehát véges
Biztonságos kulcscsere-protokollok
 Biztonságos kulcscsere-protokollok Összefoglalás (Victor Shoup: On Formal Methods for Secure Key Exchange alapján) II. rész Tóth Gergely 1 Bevezetés A következőkben a Shoup által publikált cikk fő vonulatának
Biztonságos kulcscsere-protokollok Összefoglalás (Victor Shoup: On Formal Methods for Secure Key Exchange alapján) II. rész Tóth Gergely 1 Bevezetés A következőkben a Shoup által publikált cikk fő vonulatának
2018, Funkcionális programozás
 Funkcionális programozás 7. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018, tavaszi félév Miről volt szó? összefésüléses rendezés (merge
Funkcionális programozás 7. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018, tavaszi félév Miről volt szó? összefésüléses rendezés (merge
Waldhauser Tamás december 1.
 Algebra és számelmélet előadás Waldhauser Tamás 2016. december 1. Tizedik házi feladat az előadásra Hányféleképpen lehet kiszínezni az X-pentominót n színnel, ha a forgatással vagy tükrözéssel egymásba
Algebra és számelmélet előadás Waldhauser Tamás 2016. december 1. Tizedik házi feladat az előadásra Hányféleképpen lehet kiszínezni az X-pentominót n színnel, ha a forgatással vagy tükrözéssel egymásba
IT BIZTONSÁGTECHNIKA. Tanúsítványok. Nagy-Löki Balázs MCP, MCSA, MCSE, MCTS, MCITP. Készítette:
 IT BIZTONSÁGTECHNIKA Tanúsítványok Készítette: Nagy-Löki Balázs MCP, MCSA, MCSE, MCTS, MCITP Tartalom Tanúsítvány fogalma:...3 Kategóriák:...3 X.509-es szabvány:...3 X.509 V3 tanúsítvány felépítése:...3
IT BIZTONSÁGTECHNIKA Tanúsítványok Készítette: Nagy-Löki Balázs MCP, MCSA, MCSE, MCTS, MCITP Tartalom Tanúsítvány fogalma:...3 Kategóriák:...3 X.509-es szabvány:...3 X.509 V3 tanúsítvány felépítése:...3
Hatványozás. A hatványozás azonosságai
 Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
Adatbiztonság. Tóth Zsolt. Miskolci Egyetem. Tóth Zsolt (Miskolci Egyetem) Adatbiztonság 2013 1 / 22
 Adatbiztonság Tóth Zsolt Miskolci Egyetem 2013 Tóth Zsolt (Miskolci Egyetem) Adatbiztonság 2013 1 / 22 Tartalomjegyzék 1 Bevezetés 2 Titkosítás 3 Security Tóth Zsolt (Miskolci Egyetem) Adatbiztonság 2013
Adatbiztonság Tóth Zsolt Miskolci Egyetem 2013 Tóth Zsolt (Miskolci Egyetem) Adatbiztonság 2013 1 / 22 Tartalomjegyzék 1 Bevezetés 2 Titkosítás 3 Security Tóth Zsolt (Miskolci Egyetem) Adatbiztonság 2013
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 2. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 2. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 8. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Elemi számelmélet Diszkrét matematika I. középszint
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 8. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Elemi számelmélet Diszkrét matematika I. középszint
Bevezetés az algebrába az egész számok 2
 Bevezetés az algebrába az egész számok 2 Wettl Ferenc Algebra Tanszék B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M 2015. december
Bevezetés az algebrába az egész számok 2 Wettl Ferenc Algebra Tanszék B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M 2015. december
KR TITKOSÍTÓ PROGRAM. Felhasználói leírás. v március 12.
 KR TITKOSÍTÓ PROGRAM Felhasználói leírás v1.3 2008. március 12. TARTALOMJEGYZÉK 1 BEVEZETÉS...3 1.1 FELHASZNÁLÓI DOKUMENTÁCIÓRA VONATKOZÓ ÁLTALÁNOS LEÍRÁSOK... 3 1.2 PROGRAMMŰKÖDÉSHEZ SZÜKSÉGES JAVA KÖRNYEZET...
KR TITKOSÍTÓ PROGRAM Felhasználói leírás v1.3 2008. március 12. TARTALOMJEGYZÉK 1 BEVEZETÉS...3 1.1 FELHASZNÁLÓI DOKUMENTÁCIÓRA VONATKOZÓ ÁLTALÁNOS LEÍRÁSOK... 3 1.2 PROGRAMMŰKÖDÉSHEZ SZÜKSÉGES JAVA KÖRNYEZET...
Adatok titkosítása. Hálózatok biztonsága. IV. mérési utasítás SZÉCHENYI ISTVÁN EGYETEM GYŐR TÁVKÖZLÉSI TANSZÉK
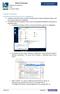 Adatok titkosítása Rendszerlemez titkosítása BitLocker segítségével 1. Telepítse fel a Windows 10 pro verzióját. A telepítés közben törölje a meglévő partíciókat, majd az üres diszket válassza ki a telepítésre.
Adatok titkosítása Rendszerlemez titkosítása BitLocker segítségével 1. Telepítse fel a Windows 10 pro verzióját. A telepítés közben törölje a meglévő partíciókat, majd az üres diszket válassza ki a telepítésre.
BASH SCRIPT SHELL JEGYZETEK
 BASH SCRIPT SHELL JEGYZETEK 1 TARTALOM Paraméterek... 4 Változók... 4 Környezeti változók... 4 Szűrők... 4 grep... 4 sed... 5 cut... 5 head, tail... 5 Reguláris kifejezések... 6 *... 6 +... 6?... 6 {m,n}...
BASH SCRIPT SHELL JEGYZETEK 1 TARTALOM Paraméterek... 4 Változók... 4 Környezeti változók... 4 Szűrők... 4 grep... 4 sed... 5 cut... 5 head, tail... 5 Reguláris kifejezések... 6 *... 6 +... 6?... 6 {m,n}...
Fábián Zoltán Hálózatok elmélet
 Fábián Zoltán Hálózatok elmélet Információ fajtái Analóg az információ folytonos és felvesz minden értéket a minimális és maximális érték között Digitális az információ az idő adott pontjaiban létezik.
Fábián Zoltán Hálózatok elmélet Információ fajtái Analóg az információ folytonos és felvesz minden értéket a minimális és maximális érték között Digitális az információ az idő adott pontjaiban létezik.
A házifeladatban alkalmazandó XML struktúra
 A házifeladatban alkalmazandó XML struktúra Absztrakt: A feladat egy fájl, vagy szövegkódoló készítése. Parancssorból indítható (a helyes szintaxis megadása mellett (http://www.linfo.org/standard_input.html)),
A házifeladatban alkalmazandó XML struktúra Absztrakt: A feladat egy fájl, vagy szövegkódoló készítése. Parancssorból indítható (a helyes szintaxis megadása mellett (http://www.linfo.org/standard_input.html)),
Számítógépes Számelmélet
 czirbusz@gmail.com http://compalg.inf.elte.hu/~czirbusz/ Komputeralgebra Tanszék ELTE Informatika Kar A projekt az Európai Unió támogatásával, az Európai Szociális Alap társfinanszírozásával valósul meg
czirbusz@gmail.com http://compalg.inf.elte.hu/~czirbusz/ Komputeralgebra Tanszék ELTE Informatika Kar A projekt az Európai Unió támogatásával, az Európai Szociális Alap társfinanszírozásával valósul meg
Számelmélet (2017. február 8.) Bogya Norbert, Kátai-Urbán Kamilla
 Számelmélet (2017 február 8) Bogya Norbert, Kátai-Urbán Kamilla 1 Oszthatóság 1 Definíció Legyen a, b Z Az a osztója b-nek, ha létezik olyan c Z egész szám, melyre ac = b Jelölése: a b 2 Példa 3 12, 2
Számelmélet (2017 február 8) Bogya Norbert, Kátai-Urbán Kamilla 1 Oszthatóság 1 Definíció Legyen a, b Z Az a osztója b-nek, ha létezik olyan c Z egész szám, melyre ac = b Jelölése: a b 2 Példa 3 12, 2
1.1. A forrásprogramok felépítése Nevek és kulcsszavak Alapvető típusok. C programozás 3
 Darvay Zsolt Típusok és nevek a forráskódban Állandók és változók Hatókörök és az előfeldolgozó Bevitel és kivitel Kifejezések Utasítások Mutatók Függvények Struktúrák és típusok Állománykezelés C programozás
Darvay Zsolt Típusok és nevek a forráskódban Állandók és változók Hatókörök és az előfeldolgozó Bevitel és kivitel Kifejezések Utasítások Mutatók Függvények Struktúrák és típusok Állománykezelés C programozás
Éves továbbképzés az elektronikus információs rendszer biztonságáért felelős személy számára
 Nemzeti Közszolgálati Egyetem Vezető- és Továbbképzési Intézet BALOGH ZSOLT GYÖRGY BESZÉDES ÁRPÁD BÉRCZES ATTILA GERGELY TAMÁS LEITOLD FERENC PETHŐ ATTILA SZŐKE GERGELY LÁSZLÓ Éves továbbképzés az elektronikus
Nemzeti Közszolgálati Egyetem Vezető- és Továbbképzési Intézet BALOGH ZSOLT GYÖRGY BESZÉDES ÁRPÁD BÉRCZES ATTILA GERGELY TAMÁS LEITOLD FERENC PETHŐ ATTILA SZŐKE GERGELY LÁSZLÓ Éves továbbképzés az elektronikus
A függvény kód szekvenciáját kapcsos zárójelek közt definiáljuk, a { } -ek közti részt a Bash héj kód blokknak (code block) nevezi.
 Függvények 1.Függvények...1 1.1.A függvény deníció szintaxisa... 1..Függvények érték visszatérítése...3 1.3.Környezettel kapcsolatos kérdések...4 1.4.Lokális változók használata...4 1.5.Rekurzív hívások...5.kód
Függvények 1.Függvények...1 1.1.A függvény deníció szintaxisa... 1..Függvények érték visszatérítése...3 1.3.Környezettel kapcsolatos kérdések...4 1.4.Lokális változók használata...4 1.5.Rekurzív hívások...5.kód
A C programozási nyelv I. Bevezetés
 A C programozási nyelv I. Bevezetés Miskolci Egyetem Általános Informatikai Tanszék A C programozási nyelv I. (bevezetés) CBEV1 / 1 A C nyelv története Dennis M. Ritchie AT&T Lab., 1972 rendszerprogramozás,
A C programozási nyelv I. Bevezetés Miskolci Egyetem Általános Informatikai Tanszék A C programozási nyelv I. (bevezetés) CBEV1 / 1 A C nyelv története Dennis M. Ritchie AT&T Lab., 1972 rendszerprogramozás,
Tanúsítványkérelem készítése, tanúsítvány telepítése Microsoft Internet Information szerveren
 Tanúsítványkérelem készítése, tanúsítvány telepítése Microsoft Internet Information szerveren Tartalomjegyzék 1. BEVEZETÉS...3 2. A MICROSOFT IIS INDÍTÁSA...3 3. TITKOS KULCS GENERÁLÁSA...3 4. TANÚSÍTVÁNYKÉRELEM
Tanúsítványkérelem készítése, tanúsítvány telepítése Microsoft Internet Information szerveren Tartalomjegyzék 1. BEVEZETÉS...3 2. A MICROSOFT IIS INDÍTÁSA...3 3. TITKOS KULCS GENERÁLÁSA...3 4. TANÚSÍTVÁNYKÉRELEM
Bánsághi Anna 2014 Bánsághi Anna 1 of 68
 IMPERATÍV PROGRAMOZÁS Bánsághi Anna anna.bansaghi@mamikon.net 3. ELŐADÁS - PROGRAMOZÁSI TÉTELEK 2014 Bánsághi Anna 1 of 68 TEMATIKA I. ALAPFOGALMAK, TUDOMÁNYTÖRTÉNET II. IMPERATÍV PROGRAMOZÁS Imperatív
IMPERATÍV PROGRAMOZÁS Bánsághi Anna anna.bansaghi@mamikon.net 3. ELŐADÁS - PROGRAMOZÁSI TÉTELEK 2014 Bánsághi Anna 1 of 68 TEMATIKA I. ALAPFOGALMAK, TUDOMÁNYTÖRTÉNET II. IMPERATÍV PROGRAMOZÁS Imperatív
2. Rekurzió. = 2P2(n,n) 2 < 2P2(n,n) 1
 2. Rekurzió Egy objektum definícióját rekurzívnak nevezünk, ha a definíció tartalmazza a definiálandó objektumot. Egy P eljárást (vagy függvényt) rekurzívnak nevezünk, ha P utasításrészében előfordul magának
2. Rekurzió Egy objektum definícióját rekurzívnak nevezünk, ha a definíció tartalmazza a definiálandó objektumot. Egy P eljárást (vagy függvényt) rekurzívnak nevezünk, ha P utasításrészében előfordul magának
Mintafeladat az RSA algoritmus szemléltetésére
 Mintafeladat az RSA algoritmus szemléltetésére Feladat Adottak a p = 269 és q = 24 prímszámok, továbbá az e = 5320 nyilvános kulcs és az x = 48055 nyílt szöveg. Számolja ki n = p q és ϕ(n) értékét! Igazolja
Mintafeladat az RSA algoritmus szemléltetésére Feladat Adottak a p = 269 és q = 24 prímszámok, továbbá az e = 5320 nyilvános kulcs és az x = 48055 nyílt szöveg. Számolja ki n = p q és ϕ(n) értékét! Igazolja
Programozás C nyelven FELÜLNÉZETBŐL elhullatott MORZSÁK. Sapientia EMTE
 Programozás C nyelven FELÜLNÉZETBŐL elhullatott MORZSÁK Sapientia EMTE 2015-16 1 Felülnézet 1 Feltételes fordítás #if, #else, #elif, #endif, #ifdef, #ifndef stb. Felülnézet 2 #include: hatására a preprocesszor
Programozás C nyelven FELÜLNÉZETBŐL elhullatott MORZSÁK Sapientia EMTE 2015-16 1 Felülnézet 1 Feltételes fordítás #if, #else, #elif, #endif, #ifdef, #ifndef stb. Felülnézet 2 #include: hatására a preprocesszor
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Számelmélet I.
 Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
CAS implementálása MPEG-2 TS-alapú
 CAS implementálása MPEG-2 TS-alapú hálózatokon Unger Tamás István ungert@maxwell.sze.hu 2014. április 16. Tartalom 1 Az MPEG-2 TS rövid áttekintése 2 Rendszeradminisztráció 3 A kiválasztott program felépítése
CAS implementálása MPEG-2 TS-alapú hálózatokon Unger Tamás István ungert@maxwell.sze.hu 2014. április 16. Tartalom 1 Az MPEG-2 TS rövid áttekintése 2 Rendszeradminisztráció 3 A kiválasztott program felépítése
Mechatronika és mikroszámítógépek 2017/2018 I. félév. Bevezetés a C nyelvbe
 Mechatronika és mikroszámítógépek 2017/2018 I. félév Bevezetés a C nyelvbe A C programozási nyelv A C egy általános célú programozási nyelv, melyet Dennis Ritchie fejlesztett ki Ken Thompson segítségével
Mechatronika és mikroszámítógépek 2017/2018 I. félév Bevezetés a C nyelvbe A C programozási nyelv A C egy általános célú programozási nyelv, melyet Dennis Ritchie fejlesztett ki Ken Thompson segítségével
1. Alapok. Programozás II
 1. Alapok Programozás II Elérhetőség Név: Smidla József Elérhetőség: smidla dcs.uni-pannon.hu Szoba: I916 2 Irodalom Bjarne Stroustrup: A C++ programozási nyelv 3 Irodalom Erich Gamma, Richard Helm, Ralph
1. Alapok Programozás II Elérhetőség Név: Smidla József Elérhetőség: smidla dcs.uni-pannon.hu Szoba: I916 2 Irodalom Bjarne Stroustrup: A C++ programozási nyelv 3 Irodalom Erich Gamma, Richard Helm, Ralph
PRÍMSZÁMOK ÉS A TITKOSÍRÁS
 PRÍMSZÁMOK ÉS A TITKOSÍRÁS Meszéna Tamás Ciszterci Rend Nagy Lajos Gimnáziuma és Kollégiuma, Pécs, meszena.tamas@gmail.com, az ELTE Fizika Tanítása doktori program hallgatója ÖSSZEFOGLALÁS Úgy tapasztaltam,
PRÍMSZÁMOK ÉS A TITKOSÍRÁS Meszéna Tamás Ciszterci Rend Nagy Lajos Gimnáziuma és Kollégiuma, Pécs, meszena.tamas@gmail.com, az ELTE Fizika Tanítása doktori program hallgatója ÖSSZEFOGLALÁS Úgy tapasztaltam,
Számelmélet. 4. Igazolja, hogy ha hat egész szám összege páratlan, akkor e számok szorzata páros!
 Számelmélet - oszthatóság definíciója - oszthatósági szabályok - maradékos osztás - prímek definíciója - összetett szám definíciója - legnagyobb közös osztó definíciója - legnagyobb közös osztó meghatározása
Számelmélet - oszthatóság definíciója - oszthatósági szabályok - maradékos osztás - prímek definíciója - összetett szám definíciója - legnagyobb közös osztó definíciója - legnagyobb közös osztó meghatározása
SzA XIII. gyakorlat, december. 3/5.
 SzA XIII. gyakorlat, 2013. december. 3/5. Drótos Márton 3 + 2 = 1 drotos@cs.bme.hu 1. Határozzuk meg az Euklidészi algoritmussal lnko(504, 372)-t! Határozzuk meg lkkt(504, 372)-t! Hány osztója van 504-nek?
SzA XIII. gyakorlat, 2013. december. 3/5. Drótos Márton 3 + 2 = 1 drotos@cs.bme.hu 1. Határozzuk meg az Euklidészi algoritmussal lnko(504, 372)-t! Határozzuk meg lkkt(504, 372)-t! Hány osztója van 504-nek?
Programozás I. 5. Előadás: Függvények
 Programozás I 5. Előadás: Függvények Függvény Egy alprogram Egy C program általában több kisméretű, könnyen értelmezhető függvényből áll Egy függvény megtalálható minden C programban: ez a main függvény
Programozás I 5. Előadás: Függvények Függvény Egy alprogram Egy C program általában több kisméretű, könnyen értelmezhető függvényből áll Egy függvény megtalálható minden C programban: ez a main függvény
MÁRTON GYÖNGYVÉR KRIPTOGRÁFIAI ALAPISMERETEK
 MÁRTON GYÖNGYVÉR KRIPTOGRÁFIAI ALAPISMERETEK SAPIENTIA ERDÉLYI MAGYAR TUDOMÁNYEGYETEM M SZAKI ÉS HUMÁNTUDOMÁNYOK KAR MATEMATIKAINFORMATIKA TANSZÉK MÁRTON GYÖNGYVÉR KRIPTOGRÁFIAI ALAPISMERETEK Scientia
MÁRTON GYÖNGYVÉR KRIPTOGRÁFIAI ALAPISMERETEK SAPIENTIA ERDÉLYI MAGYAR TUDOMÁNYEGYETEM M SZAKI ÉS HUMÁNTUDOMÁNYOK KAR MATEMATIKAINFORMATIKA TANSZÉK MÁRTON GYÖNGYVÉR KRIPTOGRÁFIAI ALAPISMERETEK Scientia
Felvételi vizsga mintatételsor Informatika írásbeli vizsga
 BABEȘ BOLYAI TUDOMÁNYEGYETEM MATEMATIKA ÉS INFORMATIKA KAR A. tételsor (30 pont) Felvételi vizsga mintatételsor Informatika írásbeli vizsga 1. (5p) Egy x biten tárolt egész adattípus (x szigorúan pozitív
BABEȘ BOLYAI TUDOMÁNYEGYETEM MATEMATIKA ÉS INFORMATIKA KAR A. tételsor (30 pont) Felvételi vizsga mintatételsor Informatika írásbeli vizsga 1. (5p) Egy x biten tárolt egész adattípus (x szigorúan pozitív
1. Bevezetés szeptember 9. BME Fizika Intézet. Szám. szim. labor ea. Tőke Csaba. Tudnivalók. feladat. Tematika. Moodle Házi feladatok
 Számítógépes szimulációk 1. Bevezetés BME Fizika Intézet 2015. szeptember 9. Bevezetés A félév menete C-ismétlés, 1. rész Oktatók: Nagyfalusi Balázs: nagyfalusi@phy.bme.hu, F3 211. : tcsaba@eik.bme.hu,
Számítógépes szimulációk 1. Bevezetés BME Fizika Intézet 2015. szeptember 9. Bevezetés A félév menete C-ismétlés, 1. rész Oktatók: Nagyfalusi Balázs: nagyfalusi@phy.bme.hu, F3 211. : tcsaba@eik.bme.hu,
A C programozási nyelv I. Bevezetés
 A C programozási nyelv I. Bevezetés Miskolci Egyetem Általános Informatikai Tanszék A C programozási nyelv I. (bevezetés) CBEV1 / 1 A C nyelv története Dennis M. Ritchie AT&T Lab., 1972 rendszerprogramozás,
A C programozási nyelv I. Bevezetés Miskolci Egyetem Általános Informatikai Tanszék A C programozási nyelv I. (bevezetés) CBEV1 / 1 A C nyelv története Dennis M. Ritchie AT&T Lab., 1972 rendszerprogramozás,
Programozási alapismeretek 1. előadás
 Programozási alapismeretek 1. előadás Tartalom A problémamegoldás lépései programkészítés folyamata A specifikáció Az algoritmus Algoritmikus nyelvek struktogram A kódolás a fejlesztői környezet 2/33 A
Programozási alapismeretek 1. előadás Tartalom A problémamegoldás lépései programkészítés folyamata A specifikáció Az algoritmus Algoritmikus nyelvek struktogram A kódolás a fejlesztői környezet 2/33 A
Programozás alapjai. 6. gyakorlat Futásidő, rekurzió, feladatmegoldás
 Programozás alapjai 6. gyakorlat Futásidő, rekurzió, feladatmegoldás Háziellenőrzés Egészítsd ki úgy a simplemaths.c programot, hogy megfelelően működjön. A program feladata az inputon soronként megadott
Programozás alapjai 6. gyakorlat Futásidő, rekurzió, feladatmegoldás Háziellenőrzés Egészítsd ki úgy a simplemaths.c programot, hogy megfelelően működjön. A program feladata az inputon soronként megadott
Az Outlook levelező program beállítása tanúsítványok használatához
 Az Outlook levelező program beállítása tanúsítványok használatához Windows tanúsítványtárban és kriptográfia eszközökön található tanúsítványok esetén 1(10) Tartalomjegyzék 1. Bevezető... 3 2. Az Outlook
Az Outlook levelező program beállítása tanúsítványok használatához Windows tanúsítványtárban és kriptográfia eszközökön található tanúsítványok esetén 1(10) Tartalomjegyzék 1. Bevezető... 3 2. Az Outlook
Informatika terméktervezőknek
 Informatika terméktervezőknek C# alapok Névterület (namespace) using Osztály (class) és Obejtumok Metódus (function, procedure, method) main() static void string[] arg Szintaxis // /* */ \n \t Névadások
Informatika terméktervezőknek C# alapok Névterület (namespace) using Osztály (class) és Obejtumok Metódus (function, procedure, method) main() static void string[] arg Szintaxis // /* */ \n \t Névadások
