Készítette: Fuszenecker Róbert Konzulens: Dr. Tuzson Tibor, docens
|
|
|
- Lilla Szekeres
- 10 évvel ezelőtt
- Látták:
Átírás
1 A nyílt kulcsú titkosítás és a digitális aláírás Készítette: Fuszenecker Róbert Konzulens: Dr. Tuzson Tibor, docens Budapest Műszaki Főiskola Kandó Kálmán Műszaki Főiskolai Kar Műszertechnikai és Automatizálási Intézet november Ez a dokumentum szabad szoftver, szabadon terjeszthet ő és/vagy módosítható a GNU GPL 2.0-ban leírtak szerint.
2 Az előadás vázlata Kommunikáció, a titkosítás definíciója A szimmetrikus titkosítás, el ő nye és hátránya Diffie-Hellman kulcscsere algoritmusa, matematikai háttér, a középen lev ő ember problémája RSA algoritmusa: matematikai háttér, titkosítás és aláírás Lehet ő ségek a DH és az RSA törésére A nyílt kulcsú titkosítás gyakorlati felhasználása Képerny ő képek
3 Kommunikáció titkosítatlan csatornán Forrás Csatorna Nyelő A kommunikáció során az információ a csatornán keresztül jut el a forrástól a nyelőig (célállomásig) A csatornát gyakran többen használják, így egymást zavarhatják, lehallgathatják
4 Kommunikáció titkosított csatornán Kulcs Kulcs Forrás Titkosítás Csatorna Visszafejtés Nyelő A titkosítás során az információt úgy alakítjuk át, hogy az csak a megfelel ő állomás(ok) számára legyen értelmezhető A visszafejtés a titkosított információt visszaalakítását jelenti
5 Szimmetrikus (kulcsú) titkosítás Kulcs Kulcs Forrás Titkosítás Csatorna Visszafejtés Nyelő A visszafejtés a titkosítás inverz művelete, pl: ha a titkosítás összeadás, akkor a visszafejtés a kivonás Példa: Caesar-módszer
6 Caesar-módszer Helyettesít ő algoritmus, a kulcs értéke 3. Könnyen törhet ő gyakoriság elemzés Caius Iulius Caesar Kr. e Kr. e. 44.
7 Egyéb szimmetrikus algoritmusok DES, 3DES: Data Encryption Standard (történelem) AES: Advanced Encryption Standard, eredetileg Rijndael CAST: a tervezők után (Carlisle Adams and Stafford Tavares) Twofish: nehezen törhet ő, szabadon felhasználható XTEA: extended Tiny Encryption Algorithm További algoritmusok a címen találhatók.
8 Szimmetrikus titkosítás hátránya Gondoskodni kell a kulcsnak (titok, jelszó, stb.) a nyelőhöz történ ő biztonságos eljuttatásáról Ez nehezen valósítható meg, mert a csatorna nem biztonságos, más átviteli közeg pedig általában nem áll rendelkezésre, vagy nehezen használható A kulcsokat a biztonság növelése érdekében id nként ő meg kell változtatni
9 A nyílt kulcsú titkosítás Kulcs1 Kulcs2 Forrás Titkosítás Csatorna Visszafejtés Nyelő A visszafejtés nem inverz művelete a titkosítás -nak, hanem valamilyen speciális matematikai azonosságot használunk ki
10 A Diffie-Hellman kulcscsere (1976) Whitfield Diffie Martin Hellman
11 A Diffie-Hellman kulcscsere algoritmus Nem az információt titkosítjuk, hanem kiszámítunk egy ideiglenes kulcsot úgy, hogy: a számítás végén a forrás és a nyel ő oldalán ugyanazt az eredményt kapjuk a kulcs sose haladjon keresztül a csatornán, legfeljebb a számítás részeredményei az információt a valamilyen szimmetrikus algoritmussal titkosítjuk, a kiszámított kulcs felhasználásával
12 A Diffie-Hellman kulcscsere algoritmus A állomás Csatorna B állomás Közös paraméterek: g (generátor) és p (prímszám) Titkos kulcs: a Titkos kulcs: b Nyilvános kulcsok: A és B, ahol A = g a mod p és B = g b mod p Ezeket egymással kicserélik a csatornán keresztül K = B a mod p K = A b mod p
13 A Diffie-Hellman kulcscsere algoritmus Az A oldal számításai: K A = B a mod p = (g b mod p) a mod p = g ba mod p A B oldal számításai: K B = A b mod p = (g a mod p) b mod p = g ab mod p Ha ab = ba, akkor g ab mod p = g ba mod p, így K A = K B = K ez a kulcs a szimmetrikus titkosításhoz
14 A Diffie-Hellman kulcscsere algoritmus A középen levő ember (man in the middle) támadás: A állomás C megfigyelő B állomás Ha C azt állítja A -nak, hogy ő valójában B, B -nek pedig azt, hogy ő A, akkor megfigyelheti lehallgathatja az A és B közötti kommunikációt.
15 Az RSA algoritmusa (1977) Ron Rivest Adi Shamir Leonard Adleman
16 Az RSA algoritmusa Az algoritmus Fermat kis tételére épül: ahol a p mod p = a 8 13 mod 13 = mod 13 = 8 p egy prímszám, és a egy tetszőleges egész szám a és p relatív prímek
17 Az RSA algoritmusa Ha a p-1 mod p = 1 és a q-1 mod p = 1, akkor a kínai maradék-tétel szerint a (p-1)(q-1) mod pq = 1 a k(p-1)(q-1) mod pq = 1 k = 1 a k(p-1)(q-1)+1 mod pq = a ahol p és q különböz ő prímszámok, és egész számok a, p és q relatív prímek a és k tetsz ő leges
18 Az RSA algoritmusa Bontsuk fel a k(p-1)(q-1)+1 értékét két szám szorzatára: k(p-1)(q-1)+1 = ed ahol k, e és d egész számok. Nevezzük az e számot titkosító kitevőnek, míg d-t pedig visszafejt ő kitevőnek. A nyilvános kulcsot (e és pq) tegyük elérhető vé mindenki számára, a titkos kulcsot (d és pq) tartsuk titokban.
19 Az RSA algoritmusa Mivel e-t és pq-t mindenki megszerezheti (hiszen nyilvánosak), ezért bárki küldhet nekünk titkosított üzenetet: M = m e mod pq, amit mi könnyen visszafejthetünk: m* = M d mod pq = m ed mod pq = = m k(p-1)(q-1)+1 mod pq = m, ahol m a titkosítandó (és visszafejtett) és M a titkosított üzenet
20 Digitális aláírás készítése RSA algoritmussal A digitális aláírás egy dokumentum hitelességét igazolja. A dokumentumból képzett szám (h) segítségével számítsuk ki S = h d mod pq értékét. A h általában valamilyen ellenőrz ő összeg (pl. a betűk, számjegyek, írásjelek kódjának összege), vagy egy speciális (hash) függvény értéke (pl. MD5, SHA1, SHA256), de mindenképpen a dokumentumra jellemz ő egyedi szám!
21 Digitális aláírás ellenőrzése A digitális aláírást (S) csatoljuk a dokumentumhoz. Ellenőrzéskor (az ellenőrz ő félnek) újra ki kell számítania a dokumentumra jellemz ő egyedi számot (MD5, SHA1, SHA256, stb., továbbiakban: j-t), és vissza kell fejtenie az általunk küldött azonosítót): j* = S e mod pq
22 Digitális aláírás ellenőrzése A dokumentum akkor hiteles, ha j = j*, és biztos, hogy a nyilvános kulcs tőlünk származik. A nyilvános kulcsok tárolhatók kulcs-szervereken. Mivel az aláírást csak mi állíthattuk el ő (mert csak nekünk van meg a nyilvános kulcs párja ), ezért az általunk megadott ellenőrz ő összeg biztosan tőlünk származik. Ha a dokumentum jelenlegi ellenőrz ő összege is ugyanez az érték, akkor a dokumentum változatlanul jutott át a csatornán, tehát hiteles.
23 Egyéb nyílt kulcsú titkosító rendszerek DSA: csak aláírásra használható ECDH: elliptikus görbéken értelmezett Diffie-Hellman, csak titkosításra ECDSA: elliptikus görbéken értelmezett DSA, csak aláírásra NTRU: titkosításra és aláírásra stb.
24 Miért nehéz megtörni a DH-t? Diffie-Hellman kulcscsere esetén a részeredmények áthaladnak a csatornán, így azokat bárki megszerezheti. A harmadik félnek akkor sikerülne a K kulcs értékét kiszámítani, ha megszerezné a vagy b értékét. Ehhez azonban meg kell oldania a következ ő egyenletet: A = g a mod p g a = kp + A Ez nagyon nehéz, hiszen k és a ismeretlen kétismeretlenes egyenlet (p legyen igen nagy [ bit hosszú]).
25 Miért nehéz megtörni a RSA-t? Az RSA ugyanúgy a hatványozásra épül, mint a DH algoritmus, így a kitevők meghatározása ebben az esetben is zsákutca. Az RSA törése könnyebb, ha a pq szorzatból próbáljuk kiszámolni p és q értékét, azaz megpróbáljuk faktorizálni pq értékét. p és q ismeretében könnyen megtalálhatjuk a megfelel ő titkos kulcsot. Az RSA akkor törhet ő nehezen, ha p és q igen nagy, több ezer bites, tipikusan bit hosszúak.
26 Mire használhatjuk a nyílt kulcsú titkosítást? A titkosítást: levelezés: bizalmas információkat titkosíthatunk (pgp, OpenPGP, GnuPG, enigmail) biztonságos belépés távoli számítógépre (ssh) interneten történ ő vásárlás, távoli adminisztrálás (https) A digitális aláírást: levelezés: eredetiség igazolása internetes ügyintézés
27
28
29
30
31
32 Összefoglalás Kommunikáció: titkosítatlan és titkosított A szimmetrikus titkosítás: Caesar-módszer hátránya: a kulcs átvitele Diffie-Hellman kulcscsere algoritmusa probléma: a középen lev ő ember problémája megoldás: a nyilvános kulcs aláírása RSA algoritmusa: matematikai háttér, titkosítás és aláírás Lehet ő ségek a DH és az RSA törésére: nagyon nehéz, szinte lehetetlen A nyílt kulcsú titkosítás gyakorlati felhasználása: levelezés, internetes vásárlás, stb.
33 Köszönöm a figyelmet! Ez az előadás letölthet ő a oldalról. Ez a dokumentum szabad szoftver, szabadon terjeszthet ő és/vagy módosítható a GNU GPL 2.0-ban leírtak szerint.
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 11. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Kongruenciák Diszkrét matematika I. középszint 2014.
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 11. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Kongruenciák Diszkrét matematika I. középszint 2014.
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Sapientia Egyetem, Műszaki és Humántudományok Tanszék.
 Kriptográfia és Információbiztonság 8. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2017 Miről volt szó az elmúlt előadáson? A Crypto++
Kriptográfia és Információbiztonság 8. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2017 Miről volt szó az elmúlt előadáson? A Crypto++
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
TUDOMÁNYOS DIÁKKÖRI DOLGOZAT. A nyílt kulcsú titkosítás és a digitális aláírás
 Budapesti Műszaki Főiskola Kandó Kálmán Villamosmérnöki Főiskolai Kar Műszertechnikai és Automatizálási Intézet TUDOMÁNYOS DIÁKKÖRI DOLGOZAT A nyílt kulcsú titkosítás és a digitális aláírás Szerző: Fuszenecker
Budapesti Műszaki Főiskola Kandó Kálmán Villamosmérnöki Főiskolai Kar Műszertechnikai és Automatizálási Intézet TUDOMÁNYOS DIÁKKÖRI DOLGOZAT A nyílt kulcsú titkosítás és a digitális aláírás Szerző: Fuszenecker
Sapientia Egyetem, Matematika-Informatika Tanszék.
 Kriptográfia és Információbiztonság 7. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? Kriptográfiai
Kriptográfia és Információbiztonság 7. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? Kriptográfiai
Hálózati biztonság (772-775) Kriptográfia (775-782)
 Területei: titkosság (secrecy/ confidentality) hitelesség (authentication) letagadhatatlanság (nonrepudiation) sértetlenség (integrity control) Hálózati biztonság (772-775) Melyik protokoll réteg jöhet
Területei: titkosság (secrecy/ confidentality) hitelesség (authentication) letagadhatatlanság (nonrepudiation) sértetlenség (integrity control) Hálózati biztonság (772-775) Melyik protokoll réteg jöhet
Sapientia Egyetem, Matematika-Informatika Tanszék.
 Kriptográfia és Információbiztonság 8. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? az RSA titkosító
Kriptográfia és Információbiztonság 8. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? az RSA titkosító
Sapientia Egyetem, Műszaki és Humántudományok Tanszék. mgyongyi@ms.sapientia.ro
 Kriptográfia és Információbiztonság 10. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2015 Vizsgatematika 1 Klasszikus kriptográfiai rendszerek
Kriptográfia és Információbiztonság 10. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2015 Vizsgatematika 1 Klasszikus kriptográfiai rendszerek
Hírek kriptográfiai algoritmusok biztonságáról
 Hírek kriptográfiai algoritmusok biztonságáról Dr. Berta István Zsolt K+F igazgató Microsec Kft. http://www.microsec.hu Mirıl fogok beszélni? Bevezetés Szimmetrikus kulcsú algoritmusok
Hírek kriptográfiai algoritmusok biztonságáról Dr. Berta István Zsolt K+F igazgató Microsec Kft. http://www.microsec.hu Mirıl fogok beszélni? Bevezetés Szimmetrikus kulcsú algoritmusok
Titkosítás NetWare környezetben
 1 Nyílt kulcsú titkosítás titkos nyilvános nyilvános titkos kulcs kulcs kulcs kulcs Nyilvános, bárki által hozzáférhető csatorna Nyílt szöveg C k (m) Titkosított szöveg Titkosított szöveg D k (M) Nyílt
1 Nyílt kulcsú titkosítás titkos nyilvános nyilvános titkos kulcs kulcs kulcs kulcs Nyilvános, bárki által hozzáférhető csatorna Nyílt szöveg C k (m) Titkosított szöveg Titkosított szöveg D k (M) Nyílt
Waldhauser Tamás december 1.
 Algebra és számelmélet előadás Waldhauser Tamás 2016. december 1. Tizedik házi feladat az előadásra Hányféleképpen lehet kiszínezni az X-pentominót n színnel, ha a forgatással vagy tükrözéssel egymásba
Algebra és számelmélet előadás Waldhauser Tamás 2016. december 1. Tizedik házi feladat az előadásra Hányféleképpen lehet kiszínezni az X-pentominót n színnel, ha a forgatással vagy tükrözéssel egymásba
Elektronikus aláírás. Gaidosch Tamás. Állami Számvevőszék
 Elektronikus aláírás Gaidosch Tamás Állami Számvevőszék 2016.05.24 Tartalom Mit tekintünk elektronikus aláírásnak? Hogyan működik? Kérdések 2 Egyszerű elektronikus aláírás 3 Demo: valódi elektronikus aláírás
Elektronikus aláírás Gaidosch Tamás Állami Számvevőszék 2016.05.24 Tartalom Mit tekintünk elektronikus aláírásnak? Hogyan működik? Kérdések 2 Egyszerű elektronikus aláírás 3 Demo: valódi elektronikus aláírás
Kriptográfia I. Kriptorendszerek
 Kriptográfia I Szimmetrikus kulcsú titkosítás Kriptorendszerek Nyíltszöveg üzenettér: M Titkosított üzenettér: C Kulcs tér: K, K Kulcsgeneráló algoritmus: Titkosító algoritmus: Visszafejt algoritmus: Titkosítás
Kriptográfia I Szimmetrikus kulcsú titkosítás Kriptorendszerek Nyíltszöveg üzenettér: M Titkosított üzenettér: C Kulcs tér: K, K Kulcsgeneráló algoritmus: Titkosító algoritmus: Visszafejt algoritmus: Titkosítás
Kriptográfiai alapfogalmak
 Kriptográfiai alapfogalmak A kriptológia a titkos kommunikációval foglalkozó tudomány. Két fő ága a kriptográfia és a kriptoanalízis. A kriptográfia a titkosítással foglalkozik, a kriptoanalízis pedig
Kriptográfiai alapfogalmak A kriptológia a titkos kommunikációval foglalkozó tudomány. Két fő ága a kriptográfia és a kriptoanalízis. A kriptográfia a titkosítással foglalkozik, a kriptoanalízis pedig
Az adatfeldolgozás és adatátvitel biztonsága. Az adatfeldolgozás biztonsága. Adatbiztonság. Automatikus adatazonosítás, adattovábbítás, adatbiztonság
 Az adatfeldolgozás és adatátvitel biztonsága Automatikus adatazonosítás, adattovábbítás, adatbiztonság Az adatfeldolgozás biztonsága A védekezés célja Védelem a hamisítás és megszemélyesítés ellen Biztosított
Az adatfeldolgozás és adatátvitel biztonsága Automatikus adatazonosítás, adattovábbítás, adatbiztonság Az adatfeldolgozás biztonsága A védekezés célja Védelem a hamisítás és megszemélyesítés ellen Biztosított
IT BIZTONSÁGTECHNIKA. Tanúsítványok. Nagy-Löki Balázs MCP, MCSA, MCSE, MCTS, MCITP. Készítette:
 IT BIZTONSÁGTECHNIKA Tanúsítványok Készítette: Nagy-Löki Balázs MCP, MCSA, MCSE, MCTS, MCITP Tartalom Tanúsítvány fogalma:...3 Kategóriák:...3 X.509-es szabvány:...3 X.509 V3 tanúsítvány felépítése:...3
IT BIZTONSÁGTECHNIKA Tanúsítványok Készítette: Nagy-Löki Balázs MCP, MCSA, MCSE, MCTS, MCITP Tartalom Tanúsítvány fogalma:...3 Kategóriák:...3 X.509-es szabvány:...3 X.509 V3 tanúsítvány felépítése:...3
Áttekintés a GPG/PGP-ről Mohácsi János NIIF Intézet
 Áttekintés a GPG/PGP-ről Mohácsi János NIIF Intézet 2007.10.07. Tartalomjegyzék Bevezetés Technikai háttér Web of trust GPG/PGP használata Kulcs aláírási est NIIF http://www.niif.hu 2 Történelem 1991:
Áttekintés a GPG/PGP-ről Mohácsi János NIIF Intézet 2007.10.07. Tartalomjegyzék Bevezetés Technikai háttér Web of trust GPG/PGP használata Kulcs aláírási est NIIF http://www.niif.hu 2 Történelem 1991:
Webalkalmazás-biztonság. Kriptográfiai alapok
 Webalkalmazás-biztonság Kriptográfiai alapok Alapfogalmak, áttekintés üzenet (message): bizalmas információhalmaz nyílt szöveg (plain text): a titkosítatlan üzenet (bemenet) kriptoszöveg (ciphertext):
Webalkalmazás-biztonság Kriptográfiai alapok Alapfogalmak, áttekintés üzenet (message): bizalmas információhalmaz nyílt szöveg (plain text): a titkosítatlan üzenet (bemenet) kriptoszöveg (ciphertext):
2018, Diszkre t matematika. 10. elo ada s
 Diszkre t matematika 10. elo ada s MA RTON Gyo ngyve r mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tansze k Marosva sa rhely, Roma nia 2018, o szi fe le v MA RTON Gyo ngyve r 2018,
Diszkre t matematika 10. elo ada s MA RTON Gyo ngyve r mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tansze k Marosva sa rhely, Roma nia 2018, o szi fe le v MA RTON Gyo ngyve r 2018,
Emlékeztet! matematikából
 Kriptográfia 2 Aszimmetrikus megoldások Emlékeztet matematikából Euklidész algoritmus - legnagyobb közös osztó meghatározása INPUT Int a>b0; OUTPUT gcd(a,b). 1. if b=0 return(a); 2. return(gcd(b,a mod
Kriptográfia 2 Aszimmetrikus megoldások Emlékeztet matematikából Euklidész algoritmus - legnagyobb közös osztó meghatározása INPUT Int a>b0; OUTPUT gcd(a,b). 1. if b=0 return(a); 2. return(gcd(b,a mod
Adatbiztonság. Tóth Zsolt. Miskolci Egyetem. Tóth Zsolt (Miskolci Egyetem) Adatbiztonság 2013 1 / 22
 Adatbiztonság Tóth Zsolt Miskolci Egyetem 2013 Tóth Zsolt (Miskolci Egyetem) Adatbiztonság 2013 1 / 22 Tartalomjegyzék 1 Bevezetés 2 Titkosítás 3 Security Tóth Zsolt (Miskolci Egyetem) Adatbiztonság 2013
Adatbiztonság Tóth Zsolt Miskolci Egyetem 2013 Tóth Zsolt (Miskolci Egyetem) Adatbiztonság 2013 1 / 22 Tartalomjegyzék 1 Bevezetés 2 Titkosítás 3 Security Tóth Zsolt (Miskolci Egyetem) Adatbiztonság 2013
4. Előadás Titkosítás, RSA algoritmus
 4. Előadás Titkosítás, RSA algoritmus Dr. Kallós Gábor 2014 2015 1 Tartalom A kriptográfia meghatározása, alaphelyzete Szimmetrikus (titkos) kulcsú titkosítás A Caesar-eljárás Aszimmetrikus (nyilvános)
4. Előadás Titkosítás, RSA algoritmus Dr. Kallós Gábor 2014 2015 1 Tartalom A kriptográfia meghatározása, alaphelyzete Szimmetrikus (titkos) kulcsú titkosítás A Caesar-eljárás Aszimmetrikus (nyilvános)
PRÍMSZÁMOK ÉS A TITKOSÍRÁS
 PRÍMSZÁMOK ÉS A TITKOSÍRÁS Meszéna Tamás Ciszterci Rend Nagy Lajos Gimnáziuma és Kollégiuma, Pécs, meszena.tamas@gmail.com, az ELTE Fizika Tanítása doktori program hallgatója ÖSSZEFOGLALÁS Úgy tapasztaltam,
PRÍMSZÁMOK ÉS A TITKOSÍRÁS Meszéna Tamás Ciszterci Rend Nagy Lajos Gimnáziuma és Kollégiuma, Pécs, meszena.tamas@gmail.com, az ELTE Fizika Tanítása doktori program hallgatója ÖSSZEFOGLALÁS Úgy tapasztaltam,
IP alapú távközlés. Virtuális magánhálózatok (VPN)
 IP alapú távközlés Virtuális magánhálózatok (VPN) Jellemzők Virtual Private Network VPN Publikus hálózatokon is használható Több telephelyes cégek hálózatai biztonságosan összeköthetők Olcsóbb megoldás,
IP alapú távközlés Virtuális magánhálózatok (VPN) Jellemzők Virtual Private Network VPN Publikus hálózatokon is használható Több telephelyes cégek hálózatai biztonságosan összeköthetők Olcsóbb megoldás,
RSA algoritmus. Smidla József. Rendszer- és Számítástudományi Tanszék Pannon Egyetem
 RSA algoritmus Smidla József Rendszer- és Számítástudományi Tanszék Pannon Egyetem 2012. 3. 27. Smidla József (RSZT) RSA algoritmus 2012. 3. 27. 1 / 29 Tartalom 1 Aszimmetrikus kódolók 2 Matematikai alapok
RSA algoritmus Smidla József Rendszer- és Számítástudományi Tanszék Pannon Egyetem 2012. 3. 27. Smidla József (RSZT) RSA algoritmus 2012. 3. 27. 1 / 29 Tartalom 1 Aszimmetrikus kódolók 2 Matematikai alapok
Információs társadalom alapismeretek
 Információs társadalom alapismeretek Szabó Péter Gábor Titkosítás és számítástechnika Titkosítás alapfogalmai A Colossus Kriptográfia A rejtjelezés két fı lépésbıl áll: 1) az üzenet titkosítása (kódolás)
Információs társadalom alapismeretek Szabó Péter Gábor Titkosítás és számítástechnika Titkosítás alapfogalmai A Colossus Kriptográfia A rejtjelezés két fı lépésbıl áll: 1) az üzenet titkosítása (kódolás)
Titkosírás. Biztos, hogy titkos? Szabó István előadása. Az életben sok helyen használunk titkosítást (mobil, internet, jelszavak...
 Biztos, hogy titkos? Szabó István előadása Az életben sok helyen használunk titkosítást (mobil, internet, jelszavak...) Története Az ókortól kezdve rengeteg feltört titkosírás létezik. Monoalfabetikus
Biztos, hogy titkos? Szabó István előadása Az életben sok helyen használunk titkosítást (mobil, internet, jelszavak...) Története Az ókortól kezdve rengeteg feltört titkosírás létezik. Monoalfabetikus
1. Egészítsük ki az alábbi Python függvényt úgy, hogy a függvény meghatározza, egy listába, az első n szám faktoriális értékét:
 Az írásbeli vizsgán, az alábbiakhoz hasonló, 8 kérdésre kell választ adni. Hasonló kérdésekre lehet számítani (azaz mi a hiba, egészítsük ki, mi a függvény kimeneti értéke, adjuk meg a függvényhívást,
Az írásbeli vizsgán, az alábbiakhoz hasonló, 8 kérdésre kell választ adni. Hasonló kérdésekre lehet számítani (azaz mi a hiba, egészítsük ki, mi a függvény kimeneti értéke, adjuk meg a függvényhívást,
RSA algoritmus. P(M) = M e mod n. S(C) = C d mod n. A helyesség igazoláshoz szükséges számelméleti háttér. a φ(n) = 1 mod n, a (a 1,a 2,...
 RSA algoritmus 1. Vegyünk véletlenszerűen két különböző nagy prímszámot, p-t és q-t. 2. Legyen n = pq. 3. Vegyünk egy olyan kis páratlan e számot, amely relatív prím φ(n) = (p 1)(q 1)-hez. 4. Keressünk
RSA algoritmus 1. Vegyünk véletlenszerűen két különböző nagy prímszámot, p-t és q-t. 2. Legyen n = pq. 3. Vegyünk egy olyan kis páratlan e számot, amely relatív prím φ(n) = (p 1)(q 1)-hez. 4. Keressünk
Prímtesztelés, Nyilvános kulcsú titkosítás
 Prímtesztelés, Nyilvános kulcsú titkosítás Papp László BME December 8, 2018 Prímtesztelés Feladat: Adott egy nagyon nagy n szám, döntsük el, hogy prímszám-e! Naív kísérletek: 1. Nézzük meg minden nála
Prímtesztelés, Nyilvános kulcsú titkosítás Papp László BME December 8, 2018 Prímtesztelés Feladat: Adott egy nagyon nagy n szám, döntsük el, hogy prímszám-e! Naív kísérletek: 1. Nézzük meg minden nála
Adatvédelem titkosítással
 Dr. Kanizsai Viktor Adatvédelem titkosítással Bevezetés A biztonsági rendszereknek mindig nyerniük kell, de a támadónak elég csak egyszer győznie. A számítógépek, rendszerek és informatikai hálózatok korszakában
Dr. Kanizsai Viktor Adatvédelem titkosítással Bevezetés A biztonsági rendszereknek mindig nyerniük kell, de a támadónak elég csak egyszer győznie. A számítógépek, rendszerek és informatikai hálózatok korszakában
Diszkrét matematika 2.
 Diszkrét matematika 2. A szakirány 11. előadás Ligeti Péter turul@cs.elte.hu www.cs.elte.hu/ turul Nagy hálózatok Nagy hálózatok jellemzése Internet, kapcsolati hálók, biológiai hálózatok,... globális
Diszkrét matematika 2. A szakirány 11. előadás Ligeti Péter turul@cs.elte.hu www.cs.elte.hu/ turul Nagy hálózatok Nagy hálózatok jellemzése Internet, kapcsolati hálók, biológiai hálózatok,... globális
Dr. Bakonyi Péter c.docens
 Elektronikus aláírás Dr. Bakonyi Péter c.docens Mi az aláírás? Formailag valamilyen szöveg alatt, azt jelenti, hogy valamit elfogadok valamit elismerek valamirıl kötelezettséget vállalok Azonosítja az
Elektronikus aláírás Dr. Bakonyi Péter c.docens Mi az aláírás? Formailag valamilyen szöveg alatt, azt jelenti, hogy valamit elfogadok valamit elismerek valamirıl kötelezettséget vállalok Azonosítja az
Data Security: Public key
 Nyilvános kulcsú rejtjelezés RSA rejtjelező El-Gamal rejtjelező : Elliptikus görbe kriptográfia RSA 1. Véletlenszerűen választunk két "nagy" prímszámot: p1, p2 2. m= p1p2 φ ( ) = ( p -1)( p -1) m 1 2 3.
Nyilvános kulcsú rejtjelezés RSA rejtjelező El-Gamal rejtjelező : Elliptikus görbe kriptográfia RSA 1. Véletlenszerűen választunk két "nagy" prímszámot: p1, p2 2. m= p1p2 φ ( ) = ( p -1)( p -1) m 1 2 3.
Adat és Információvédelmi Mesteriskola 30 MB. Dr. Beinschróth József SAJÁTOS LOGIKAI VÉDELEM: A KRIPTOGRÁFIA ALKALMAZÁSA
 30 MB Dr. Beinschróth József SAJÁTOS LOGIKAI VÉDELEM: A KRIPTOGRÁFIA ALKALMAZÁSA Tartalom Alapvetések - kiindulópontok Alapfogalmak Változatok Tradicionális módszerek Szimmetrikus kriptográfia Aszimmetrikus
30 MB Dr. Beinschróth József SAJÁTOS LOGIKAI VÉDELEM: A KRIPTOGRÁFIA ALKALMAZÁSA Tartalom Alapvetések - kiindulópontok Alapfogalmak Változatok Tradicionális módszerek Szimmetrikus kriptográfia Aszimmetrikus
PGP. Az informatikai biztonság alapjai II.
 PGP Az informatikai biztonság alapjai II. Készítette: Póserné Oláh Valéria poserne.valeria@nik.bmf.hu Miről lesz szó? A PGP program és telepítése Kulcsmenedzselés saját kulcspár generálása, publikálása
PGP Az informatikai biztonság alapjai II. Készítette: Póserné Oláh Valéria poserne.valeria@nik.bmf.hu Miről lesz szó? A PGP program és telepítése Kulcsmenedzselés saját kulcspár generálása, publikálása
Diszkrét matematika I.
 Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 10. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Felhívás Diszkrét matematika I. középszint 2014.
Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 10. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Felhívás Diszkrét matematika I. középszint 2014.
Informatikai biztonság alapjai
 Informatikai biztonság alapjai 4. Algoritmikus adatvédelem Pethő Attila 2008/9 II. félév A digitális aláírás felfedezői Dr. Whitfield Diffie és Martin E. Hellman (1976) a nyilvános kulcsú titkosítás elvének
Informatikai biztonság alapjai 4. Algoritmikus adatvédelem Pethő Attila 2008/9 II. félév A digitális aláírás felfedezői Dr. Whitfield Diffie és Martin E. Hellman (1976) a nyilvános kulcsú titkosítás elvének
Sapientia Egyetem, Műszaki és Humántudományok Tanszék. mgyongyi@ms.sapientia.ro
 Kriptográfia és Információbiztonság 1. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016 Követelmények, osztályozás Jelenlét: A laborgyakorlat
Kriptográfia és Információbiztonság 1. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016 Követelmények, osztályozás Jelenlét: A laborgyakorlat
Data Security: Protocols Integrity
 Integrity Az üzenethitelesítés (integritásvédelem) feladata az, hogy a vételi oldalon detektálhatóvá tegyük azon eseményeket, amelyek során az átviteli úton az üzenet valamilyen módosulást szenvedett el.
Integrity Az üzenethitelesítés (integritásvédelem) feladata az, hogy a vételi oldalon detektálhatóvá tegyük azon eseményeket, amelyek során az átviteli úton az üzenet valamilyen módosulást szenvedett el.
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Számelmélet I.
 Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
5.1 Környezet. 5.1.1 Hálózati topológia
 5. Biztonság A rendszer elsodleges célja a hallgatók vizsgáztatása, így nagy hangsúlyt kell fektetni a rendszert érinto biztonsági kérdésekre. Semmiképpen sem szabad arra számítani, hogy a muködo rendszert
5. Biztonság A rendszer elsodleges célja a hallgatók vizsgáztatása, így nagy hangsúlyt kell fektetni a rendszert érinto biztonsági kérdésekre. Semmiképpen sem szabad arra számítani, hogy a muködo rendszert
Minden egész szám osztója önmagának, azaz a a minden egész a-ra.
 1. Számelmélet Definíció: Az a egész szám osztója a egész számnak, ha létezik olyan c egész szám, melyre = ac. Ezt a következőképpen jelöljük: a Tulajdonságok: Minden egész szám osztója önmagának, azaz
1. Számelmélet Definíció: Az a egész szám osztója a egész számnak, ha létezik olyan c egész szám, melyre = ac. Ezt a következőképpen jelöljük: a Tulajdonságok: Minden egész szám osztója önmagának, azaz
Titkosítás. Uhlár László
 Titkosítás Uhlár László 1. Miért? Talán egy idős lehet az emberiséggel az igény arra, hogy bizonyos személyes dolgainkat mások elől elrejtsünk. Titkosírások tömkelege alakult ki a történelem során, amelyek
Titkosítás Uhlár László 1. Miért? Talán egy idős lehet az emberiséggel az igény arra, hogy bizonyos személyes dolgainkat mások elől elrejtsünk. Titkosírások tömkelege alakult ki a történelem során, amelyek
megtalálásának hihetetlen nehéz voltán alapszik. Az eljárás matematikai alapja a kis FERMAT-tétel egy következménye:
 Az RSA módszer Az RSA módszer titkossága a prímtényezős felbontás nehézségén, a prímtényezők megtalálásának hihetetlen nehéz voltán alapszik. Az eljárás matematikai alapja a kis FERMAT-tétel egy következménye:
Az RSA módszer Az RSA módszer titkossága a prímtényezős felbontás nehézségén, a prímtényezők megtalálásának hihetetlen nehéz voltán alapszik. Az eljárás matematikai alapja a kis FERMAT-tétel egy következménye:
Dr. Beinschróth József Kriptográfiai alkalmazások, rejtjelezések, digitális aláírás
 2017.10.13. Dr. Beinschróth József Kriptográfiai alkalmazások, rejtjelezések, digitális aláírás 1 Tartalom Alapvetések Alapfogalmak Változatok Tradicionális Szimmetrikus Aszimmetrikus Kombinált Digitális
2017.10.13. Dr. Beinschróth József Kriptográfiai alkalmazások, rejtjelezések, digitális aláírás 1 Tartalom Alapvetések Alapfogalmak Változatok Tradicionális Szimmetrikus Aszimmetrikus Kombinált Digitális
Sapientia Egyetem, Műszaki és Humántudományok Tanszék. mgyongyi@ms.sapientia.ro
 Kriptográfia és Információbiztonság 5. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2015 Miről volt szó az elmúlt előadáson? AES (Advanced
Kriptográfia és Információbiztonság 5. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2015 Miről volt szó az elmúlt előadáson? AES (Advanced
Fábián Zoltán Hálózatok elmélet
 Fábián Zoltán Hálózatok elmélet Információ fajtái Analóg az információ folytonos és felvesz minden értéket a minimális és maximális érték között Digitális az információ az idő adott pontjaiban létezik.
Fábián Zoltán Hálózatok elmélet Információ fajtái Analóg az információ folytonos és felvesz minden értéket a minimális és maximális érték között Digitális az információ az idő adott pontjaiban létezik.
Kriptográfiai protokollok
 Kriptográfiai protokollok Protokollosztályok - partnerhitelesítés - kulcskiosztás - üzenetintegritás - digitális aláírás - egyéb(titokmegosztás, zero knowledge...) 1 Shamir "háromlépéses" protokollja Titok
Kriptográfiai protokollok Protokollosztályok - partnerhitelesítés - kulcskiosztás - üzenetintegritás - digitális aláírás - egyéb(titokmegosztás, zero knowledge...) 1 Shamir "háromlépéses" protokollja Titok
Biztonság a glite-ban
 Biztonság a glite-ban www.eu-egee.org INFSO-RI-222667 Mi a Grid biztonság? A Grid probléma lehetővé tenni koordinált erőforrás megosztást és probléma megoldást dinamikus több szervezeti egységből álló
Biztonság a glite-ban www.eu-egee.org INFSO-RI-222667 Mi a Grid biztonság? A Grid probléma lehetővé tenni koordinált erőforrás megosztást és probléma megoldást dinamikus több szervezeti egységből álló
Alaptechnológiák BCE 2006. E-Business - Internet Mellékszakirány 2006
 Alaptechnológiák BCE 2006 Alaptechnológiák Biztonság, titkosítás, hitelesítés RSA algoritmus Digitális aláírás, CA használata PGP SSL kapcsolat Biztonságpolitika - Alapfogalmak Adatvédelem Az adatvédelem
Alaptechnológiák BCE 2006 Alaptechnológiák Biztonság, titkosítás, hitelesítés RSA algoritmus Digitális aláírás, CA használata PGP SSL kapcsolat Biztonságpolitika - Alapfogalmak Adatvédelem Az adatvédelem
A nyilvános kulcsú algoritmusokról. Hálózati biztonság II. A nyilvános kulcsú algoritmusokról (folyt.) Az RSA. Más nyilvános kulcsú algoritmusok
 Hálózati biztonság II. Mihalik Gáspár D(E(P))=P A nyilvános kulcsú algoritmusokról A két mővelet (D és E) ezeknél az algoritmusoknál ugyanaz: D(E(P))=P=E(D(P)), viszont más kulcsokkal végzik(!), ami azt
Hálózati biztonság II. Mihalik Gáspár D(E(P))=P A nyilvános kulcsú algoritmusokról A két mővelet (D és E) ezeknél az algoritmusoknál ugyanaz: D(E(P))=P=E(D(P)), viszont más kulcsokkal végzik(!), ami azt
Sapientia Egyetem, Matematika-Informatika Tanszék.
 Kriptográfia és Információbiztonság 11. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? hash függvények
Kriptográfia és Információbiztonság 11. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018 Miről volt szó az elmúlt előadáson? hash függvények
SSL elemei. Az SSL illeszkedése az internet protokoll-architektúrájába
 SSL 1 SSL elemei Az SSL illeszkedése az internet protokoll-architektúrájába 2 SSL elemei 3 SSL elemei 4 SSL Record protokoll 5 SSL Record protokoll Az SSL Record protokoll üzenet formátuma 6 SSL Record
SSL 1 SSL elemei Az SSL illeszkedése az internet protokoll-architektúrájába 2 SSL elemei 3 SSL elemei 4 SSL Record protokoll 5 SSL Record protokoll Az SSL Record protokoll üzenet formátuma 6 SSL Record
2017, Diszkrét matematika
 Diszkrét matematika 10. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2017, őszi félév Miről volt szó az elmúlt előadáson? a prímszámtétel prímszámok,
Diszkrét matematika 10. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2017, őszi félév Miről volt szó az elmúlt előadáson? a prímszámtétel prímszámok,
REJTJELZŐ MÓDSZEREK VIZSGÁLATA
 Póserné Oláh Valéria PÓSERNÉ Oláh Valéria REJTJELZŐ MÓDSZEREK VIZSGÁLATA (EXAMINATION OF THE METHODS OF CRYPTOGRAPHY) Mindennapjaink szerves részévé vált az információ elektronikus tárolása, továbbítása,
Póserné Oláh Valéria PÓSERNÉ Oláh Valéria REJTJELZŐ MÓDSZEREK VIZSGÁLATA (EXAMINATION OF THE METHODS OF CRYPTOGRAPHY) Mindennapjaink szerves részévé vált az információ elektronikus tárolása, továbbítása,
2016, Diszkrét matematika
 Diszkrét matematika 11. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016, őszi félév Miről volt szó az elmúlt előadáson? legnagyobb közös
Diszkrét matematika 11. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016, őszi félév Miről volt szó az elmúlt előadáson? legnagyobb közös
Számelméleti alapfogalmak
 1 Számelméleti alapfogalmak 1 Definíció Az a IN szám osztója a b IN számnak ha létezik c IN melyre a c = b Jelölése: a b 2 Példa a 0 bármely a számra teljesül, mivel c = 0 univerzálisan megfelel: a 0 =
1 Számelméleti alapfogalmak 1 Definíció Az a IN szám osztója a b IN számnak ha létezik c IN melyre a c = b Jelölése: a b 2 Példa a 0 bármely a számra teljesül, mivel c = 0 univerzálisan megfelel: a 0 =
Bizalom, biztonság és a szabad szoftverek. Mátó Péter kurátor fsf.hu alapíttvány
 Bizalom, biztonság és a szabad szoftverek Mátó Péter kurátor fsf.hu alapíttvány Bemutatkozás 1996 az első találkozás: Chiptár Slackware 1997 első igazi munka: oktatás a GAMF-on 1998 teljes átállás Linuxra,
Bizalom, biztonság és a szabad szoftverek Mátó Péter kurátor fsf.hu alapíttvány Bemutatkozás 1996 az első találkozás: Chiptár Slackware 1997 első igazi munka: oktatás a GAMF-on 1998 teljes átállás Linuxra,
Bevezetés. 1. fejezet. Algebrai feladatok. Feladatok
 . fejezet Bevezetés Algebrai feladatok J. A számok gyakran használt halmazaira a következ jelöléseket vezetjük be: N a nemnegatív egész számok, N + a pozitív egész számok, Z az egész számok, Q a racionális
. fejezet Bevezetés Algebrai feladatok J. A számok gyakran használt halmazaira a következ jelöléseket vezetjük be: N a nemnegatív egész számok, N + a pozitív egész számok, Z az egész számok, Q a racionális
Hatványozás. A hatványozás azonosságai
 Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
CAS implementálása MPEG-2 TS-alapú
 CAS implementálása MPEG-2 TS-alapú hálózatokon Unger Tamás István ungert@maxwell.sze.hu 2014. április 16. Tartalom 1 Az MPEG-2 TS rövid áttekintése 2 Rendszeradminisztráció 3 A kiválasztott program felépítése
CAS implementálása MPEG-2 TS-alapú hálózatokon Unger Tamás István ungert@maxwell.sze.hu 2014. április 16. Tartalom 1 Az MPEG-2 TS rövid áttekintése 2 Rendszeradminisztráció 3 A kiválasztott program felépítése
A NYILVÁNOS KULCSÚ INFRASTRUKTÚRA ALAPJAI ÉS ÖSSZETEVŐI BASICS AND COMPONENTS OF PUBLIC KEY INFRASTRUCTURE SPISÁK ANDOR
 SPISÁK ANDOR A NYILVÁNOS KULCSÚ INFRASTRUKTÚRA ALAPJAI ÉS ÖSSZETEVŐI BASICS AND COMPONENTS OF PUBLIC KEY INFRASTRUCTURE A cikk bevezetést nyújt a Nyilvános Kulcsú Infrastruktúrába és kriptográfiába, valamint
SPISÁK ANDOR A NYILVÁNOS KULCSÚ INFRASTRUKTÚRA ALAPJAI ÉS ÖSSZETEVŐI BASICS AND COMPONENTS OF PUBLIC KEY INFRASTRUCTURE A cikk bevezetést nyújt a Nyilvános Kulcsú Infrastruktúrába és kriptográfiába, valamint
8. A WAN teszthálózatának elkészítése
 8. A WAN teszthálózatának elkészítése Tartalom 8.1 Távoli kapcsolatok teszthálózata 8.2 A WAN céljainak és követelményeinek meghatározása 8.3 Távmunkás támogatás prototípus Távoli kapcsolatok teszthálózata
8. A WAN teszthálózatának elkészítése Tartalom 8.1 Távoli kapcsolatok teszthálózata 8.2 A WAN céljainak és követelményeinek meghatározása 8.3 Távmunkás támogatás prototípus Távoli kapcsolatok teszthálózata
A Z E L E K T R O N I K U S A L Á Í R Á S J O G I S Z A B Á L Y O Z Á S A.
 JOGI INFORMATIKA A Z E L E K T R O N I K U S A L Á Í R Á S J O G I S Z A B Á L Y O Z Á S A. A kutatás a TÁMOP 4.2.4.A/2-11-1-2012-0001 azonosító számú Nemzeti Kiválóság Program Hazai hallgatói, illetve
JOGI INFORMATIKA A Z E L E K T R O N I K U S A L Á Í R Á S J O G I S Z A B Á L Y O Z Á S A. A kutatás a TÁMOP 4.2.4.A/2-11-1-2012-0001 azonosító számú Nemzeti Kiválóság Program Hazai hallgatói, illetve
Adatbázis kezelő szoftverek biztonsága. Vasi Sándor G-3S
 Adatbázis kezelő szoftverek biztonsága Vasi Sándor sanyi@halivud.com G-3S8 2006. Egy kis ismétlés... Adatbázis(DB): integrált adatrendszer több különböző egyed előfordulásainak adatait adatmodell szerinti
Adatbázis kezelő szoftverek biztonsága Vasi Sándor sanyi@halivud.com G-3S8 2006. Egy kis ismétlés... Adatbázis(DB): integrált adatrendszer több különböző egyed előfordulásainak adatait adatmodell szerinti
Elektronikus hitelesítés a gyakorlatban
 Elektronikus hitelesítés a gyakorlatban Tapasztó Balázs Vezető termékmenedzser Matáv Üzleti Szolgáltatások Üzletág 2005. április 1. 1 Elektronikus hitelesítés a gyakorlatban 1. Az elektronikus aláírás
Elektronikus hitelesítés a gyakorlatban Tapasztó Balázs Vezető termékmenedzser Matáv Üzleti Szolgáltatások Üzletág 2005. április 1. 1 Elektronikus hitelesítés a gyakorlatban 1. Az elektronikus aláírás
Adatbiztonság PPZH 2011. május 20.
 Adatbiztonság PPZH 2011. május 20. 1. Mutassa meg, hogy a CBC-MAC kulcsolt hashing nem teljesíti az egyirányúság követelményét egy a k kulcsot ismerő fél számára, azaz tetszőleges MAC ellenőrzőösszeghez
Adatbiztonság PPZH 2011. május 20. 1. Mutassa meg, hogy a CBC-MAC kulcsolt hashing nem teljesíti az egyirányúság követelményét egy a k kulcsot ismerő fél számára, azaz tetszőleges MAC ellenőrzőösszeghez
E mail titkosítás az üzleti életben ma már követelmény! Ön szerint ki tudja elolvasni bizalmas email leveleinket?
 E mail titkosítás az üzleti életben ma már követelmény! Ön szerint ki tudja elolvasni bizalmas email leveleinket? Egy email szövegében elhelyezet információ annyira biztonságos, mintha ugyanazt az információt
E mail titkosítás az üzleti életben ma már követelmény! Ön szerint ki tudja elolvasni bizalmas email leveleinket? Egy email szövegében elhelyezet információ annyira biztonságos, mintha ugyanazt az információt
Algoritmuselmélet gyakorlat (MMN111G)
 Algoritmuselmélet gyakorlat (MMN111G) 2014. január 14. 1. Gyakorlat 1.1. Feladat. Adott K testre rendre K[x] és K(x) jelöli a K feletti polinomok és racionális törtfüggvények halmazát. Mutassuk meg, hogy
Algoritmuselmélet gyakorlat (MMN111G) 2014. január 14. 1. Gyakorlat 1.1. Feladat. Adott K testre rendre K[x] és K(x) jelöli a K feletti polinomok és racionális törtfüggvények halmazát. Mutassuk meg, hogy
Adott egy szervezet, és annak ügyfelei. Nevezzük a szervezetet bank -nak. Az ügyfelek az Interneten keresztül érzékeny információkat, utasításokat
 ! # $%&'() Adott egy szervezet, és annak ügyfelei. Nevezzük a szervezetet bank -nak. Az ügyfelek az Interneten keresztül érzékeny információkat, utasításokat küldenek a banknak. A bank valahogy meggyzdik
! # $%&'() Adott egy szervezet, és annak ügyfelei. Nevezzük a szervezetet bank -nak. Az ügyfelek az Interneten keresztül érzékeny információkat, utasításokat küldenek a banknak. A bank valahogy meggyzdik
Kongruenciák. Waldhauser Tamás
 Algebra és számelmélet 3 előadás Kongruenciák Waldhauser Tamás 2014 őszi félév Tartalom 1. Diofantoszi egyenletek 2. Kongruenciareláció, maradékosztályok 3. Lineáris kongruenciák és multiplikatív inverzek
Algebra és számelmélet 3 előadás Kongruenciák Waldhauser Tamás 2014 őszi félév Tartalom 1. Diofantoszi egyenletek 2. Kongruenciareláció, maradékosztályok 3. Lineáris kongruenciák és multiplikatív inverzek
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KR TITKOSÍTÓ PROGRAM. Felhasználói leírás. v1.3 2008. március 12.
 KR TITKOSÍTÓ PROGRAM Felhasználói leírás v1.3 2008. március 12. TARTALOMJEGYZÉK 1 BEVEZETÉS...3 1.1 FELHASZNÁLÓI DOKUMENTÁCIÓRA VONATKOZÓ ÁLTALÁNOS LEÍRÁSOK... 3 2 ALAPFOGALMAK...4 Programban használt
KR TITKOSÍTÓ PROGRAM Felhasználói leírás v1.3 2008. március 12. TARTALOMJEGYZÉK 1 BEVEZETÉS...3 1.1 FELHASZNÁLÓI DOKUMENTÁCIÓRA VONATKOZÓ ÁLTALÁNOS LEÍRÁSOK... 3 2 ALAPFOGALMAK...4 Programban használt
Az elektronikus aláírás és gyakorlati alkalmazása
 Az elektronikus aláírás és gyakorlati alkalmazása Dr. Berta István Zsolt Microsec Kft. http://www.microsec.hu Elektronikus aláírás (e-szignó) Az elektronikus aláírás a kódolás
Az elektronikus aláírás és gyakorlati alkalmazása Dr. Berta István Zsolt Microsec Kft. http://www.microsec.hu Elektronikus aláírás (e-szignó) Az elektronikus aláírás a kódolás
Elektronikus aláírás. Miért van szükség elektronikus aláírásra? A nyiltkulcsú titkosítás. Az elektronikus aláírás m ködése. Hitelesít szervezetek.
 Elektronikus aláírás Miért van szükség elektronikus aláírásra? A nyiltkulcsú titkosítás. Az elektronikus aláírás m ködése. Jogi háttér Hitelesít szervezetek. Miért van szükség elektronikus aláírásra? Elektronikus
Elektronikus aláírás Miért van szükség elektronikus aláírásra? A nyiltkulcsú titkosítás. Az elektronikus aláírás m ködése. Jogi háttér Hitelesít szervezetek. Miért van szükség elektronikus aláírásra? Elektronikus
FELVÉTELI VIZSGA, július 17.
 BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR FELVÉTELI VIZSGA, 2017. július 17. Írásbeli vizsga MATEMATIKÁBÓL I. TÉTEL (30 pont) 1) (10 pont) Igazoljuk, hogy tetszőleges m R esetén
BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR FELVÉTELI VIZSGA, 2017. július 17. Írásbeli vizsga MATEMATIKÁBÓL I. TÉTEL (30 pont) 1) (10 pont) Igazoljuk, hogy tetszőleges m R esetén
Informatikai alapismeretek Földtudományi BSC számára
 Informatikai alapismeretek Földtudományi BSC számára 2010-2011 Őszi félév Heizlerné Bakonyi Viktória HBV@ludens.elte.hu Titkosítás,hitelesítés Szimmetrikus DES 56 bites kulcs (kb. 1000 év) felcserél, helyettesít
Informatikai alapismeretek Földtudományi BSC számára 2010-2011 Őszi félév Heizlerné Bakonyi Viktória HBV@ludens.elte.hu Titkosítás,hitelesítés Szimmetrikus DES 56 bites kulcs (kb. 1000 év) felcserél, helyettesít
Adatbiztonság az okos fogyasztásmérésben. Mit nyújthat a szabványosítás?
 Adatbiztonság az okos fogyasztásmérésben Mit nyújthat a szabványosítás? Kmethy Győző - Gnarus Mérnökiroda DLMS User Association elnök IEC TC13 titkár CENELEC TC13 WG02 vezető Budapest 2012. szeptember
Adatbiztonság az okos fogyasztásmérésben Mit nyújthat a szabványosítás? Kmethy Győző - Gnarus Mérnökiroda DLMS User Association elnök IEC TC13 titkár CENELEC TC13 WG02 vezető Budapest 2012. szeptember
KÓDOLÁSTECHNIKA PZH. 2006. december 18.
 KÓDOLÁSTECHNIKA PZH 2006. december 18. 1. Hibajavító kódolást tekintünk. Egy lineáris bináris blokk kód generátormátrixa G 10110 01101 a.) Adja meg a kód kódszavait és paramétereit (n, k,d). (3 p) b.)
KÓDOLÁSTECHNIKA PZH 2006. december 18. 1. Hibajavító kódolást tekintünk. Egy lineáris bináris blokk kód generátormátrixa G 10110 01101 a.) Adja meg a kód kódszavait és paramétereit (n, k,d). (3 p) b.)
Nemzeti Közszolgálati Egyetem. Vezető-és Továbbképzési Intézet. Bérczes Attila Pethő Attila. Kriptográfia
 Nemzeti Közszolgálati Egyetem Vezető-és Továbbképzési Intézet Bérczes Attila Pethő Attila Kriptográfia Budapest, 2014 A tananyag az ÁROP 2.2.21 Tudásalapú közszolgálati előmenetel című projekt keretében
Nemzeti Közszolgálati Egyetem Vezető-és Továbbképzési Intézet Bérczes Attila Pethő Attila Kriptográfia Budapest, 2014 A tananyag az ÁROP 2.2.21 Tudásalapú közszolgálati előmenetel című projekt keretében
TANÚSÍTVÁNY. tanúsítja, hogy a Utimaco Safeware AG által kifejlesztett és forgalmazott
 TANÚSÍTVÁNY A HUNGUARD Számítástechnikai-, informatikai kutató-fejlesztő és általános szolgáltató Kft. a 15/2001.(VIII. 27.) MeHVM rendelet alapján, mint a Magyar Köztársaság Informatikai és Hírközlési
TANÚSÍTVÁNY A HUNGUARD Számítástechnikai-, informatikai kutató-fejlesztő és általános szolgáltató Kft. a 15/2001.(VIII. 27.) MeHVM rendelet alapján, mint a Magyar Köztársaság Informatikai és Hírközlési
Információs technológiák 8. Ea: Lakat alatt. Az informatikai biztonságról
 Információs technológiák 8. Ea: Lakat alatt Az informatikai biztonságról 126/1 B ITv: MAN 2015.09.08 Az informatikai biztonságról 126/2 Témakörök Általános alapfogalmak Adatvédelem Adatbiztonság Ellenőrző
Információs technológiák 8. Ea: Lakat alatt Az informatikai biztonságról 126/1 B ITv: MAN 2015.09.08 Az informatikai biztonságról 126/2 Témakörök Általános alapfogalmak Adatvédelem Adatbiztonság Ellenőrző
Egyesíthető prioritási sor
 Egyesíthető prioritási sor Értékhalmaz: EPriSor = S E, E-n értelmezett a lineáris rendezési reláció. Műveletek: S,S 1,S 2 : EPriSor, x : E {Igaz} Letesit(S, ) {S = /0} {S = S} Megszuntet(S) {} {S = S}
Egyesíthető prioritási sor Értékhalmaz: EPriSor = S E, E-n értelmezett a lineáris rendezési reláció. Műveletek: S,S 1,S 2 : EPriSor, x : E {Igaz} Letesit(S, ) {S = /0} {S = S} Megszuntet(S) {} {S = S}
A TITKOSÍTÁS ALKALMAZOTT MÓDSZEREI HÁLÓZATI ISMERETEK 1 GYAKORLAT BUJDOSÓ GYÖNGYI FEKETE MÁRTON. 2009 Debrecen AZ ELEKTRONIKUS KOMMUNIKÁCIÓBAN
 A TITKOSÍTÁS ALKALMAZOTT MÓDSZEREI AZ ELEKTRONIKUS KOMMUNIKÁCIÓBAN HÁLÓZATI ISMERETEK 1 GYAKORLAT BUJDOSÓ GYÖNGYI FEKETE MÁRTON 2009 Debrecen 2 BEVEZETİ Az Internetben rejtızı óriási lehetıségeket sokan
A TITKOSÍTÁS ALKALMAZOTT MÓDSZEREI AZ ELEKTRONIKUS KOMMUNIKÁCIÓBAN HÁLÓZATI ISMERETEK 1 GYAKORLAT BUJDOSÓ GYÖNGYI FEKETE MÁRTON 2009 Debrecen 2 BEVEZETİ Az Internetben rejtızı óriási lehetıségeket sokan
Sapientia Egyetem, Műszaki és Humántudományok Tanszék. mgyongyi@ms.sapientia.ro
 Kriptográfia és Információbiztonság 4. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2015 Miről volt szó az elmúlt előadáson? blokk-titkosító
Kriptográfia és Információbiztonság 4. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2015 Miről volt szó az elmúlt előadáson? blokk-titkosító
DESlock+ Használati utasítás felhasználók számára. Sicontact Kft., 2015.
 DESlock+ Használati utasítás felhasználók számára Sicontact Kft., 2015. DESlock+ használati utasítás felhasználók számára 2 DESlock+ használati utasítás felhasználók számára 3 Tartalomjegyzék A DESlock+
DESlock+ Használati utasítás felhasználók számára Sicontact Kft., 2015. DESlock+ használati utasítás felhasználók számára 2 DESlock+ használati utasítás felhasználók számára 3 Tartalomjegyzék A DESlock+
Tanúsítási jelentés. Hung-TJ-0013-2004. az nshield F3 PCI, az nshield F3 Ultrasign PCI és az nshield F3 Ultrasign 32 PCI kriptográfiai adapter
 V Tanúsítási jelentés Hung-TJ-0013-2004 az nshield F3 PCI, az nshield F3 Ultrasign PCI és az nshield F3 Ultrasign 32 PCI kriptográfiai adapter kriptográfiai modulokról /ncipher Corporation Limited/ /hardver
V Tanúsítási jelentés Hung-TJ-0013-2004 az nshield F3 PCI, az nshield F3 Ultrasign PCI és az nshield F3 Ultrasign 32 PCI kriptográfiai adapter kriptográfiai modulokról /ncipher Corporation Limited/ /hardver
Bevezetés az algebrába az egész számok 2
 Bevezetés az algebrába az egész számok 2 Wettl Ferenc Algebra Tanszék B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M 2015. december
Bevezetés az algebrába az egész számok 2 Wettl Ferenc Algebra Tanszék B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M 2015. december
Adatok titkosítása. Hálózatok biztonsága. IV. mérési utasítás SZÉCHENYI ISTVÁN EGYETEM GYŐR TÁVKÖZLÉSI TANSZÉK
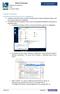 Adatok titkosítása Rendszerlemez titkosítása BitLocker segítségével 1. Telepítse fel a Windows 10 pro verzióját. A telepítés közben törölje a meglévő partíciókat, majd az üres diszket válassza ki a telepítésre.
Adatok titkosítása Rendszerlemez titkosítása BitLocker segítségével 1. Telepítse fel a Windows 10 pro verzióját. A telepítés közben törölje a meglévő partíciókat, majd az üres diszket válassza ki a telepítésre.
Nyilvános kulcsú titkosítás RSA algoritmus
 Nyilvános kulcsú titkosítás RSA algoritmus OpenPGP NYILVÁNOS KULCSÚ TITKOSÍTÁS Legyen D a titkosítandó üzenetek halmaza. Tegyük fel, hogy Bob titkosítottan szeretné elküldeni Aliznak az M D üzenetet. A
Nyilvános kulcsú titkosítás RSA algoritmus OpenPGP NYILVÁNOS KULCSÚ TITKOSÍTÁS Legyen D a titkosítandó üzenetek halmaza. Tegyük fel, hogy Bob titkosítottan szeretné elküldeni Aliznak az M D üzenetet. A
Elektronikus rendszerek a közigazgatásban elektronikus aláírás és archiválás elméletben
 Copyright 2011 FUJITSU LIMITED Elektronikus rendszerek a közigazgatásban elektronikus aláírás és archiválás elméletben Előadó: Erdősi Péter Máté, CISA elektronikus aláírással kapcsolatos szolgáltatási
Copyright 2011 FUJITSU LIMITED Elektronikus rendszerek a közigazgatásban elektronikus aláírás és archiválás elméletben Előadó: Erdősi Péter Máté, CISA elektronikus aláírással kapcsolatos szolgáltatási
Gauss-eliminációval, Cholesky felbontás, QR felbontás
 Közelítő és szimbolikus számítások 4. gyakorlat Mátrix invertálás Gauss-eliminációval, Cholesky felbontás, QR felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei
Közelítő és szimbolikus számítások 4. gyakorlat Mátrix invertálás Gauss-eliminációval, Cholesky felbontás, QR felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei
illetve a n 3 illetve a 2n 5
 BEVEZETÉS A SZÁMELMÉLETBE 1. Határozzuk meg azokat az a természetes számokat ((a, b) számpárokat), amely(ek)re teljesülnek az alábbi feltételek: a. [a, 16] = 48 b. (a, 0) = 1 c. (a, 60) = 15 d. (a, b)
BEVEZETÉS A SZÁMELMÉLETBE 1. Határozzuk meg azokat az a természetes számokat ((a, b) számpárokat), amely(ek)re teljesülnek az alábbi feltételek: a. [a, 16] = 48 b. (a, 0) = 1 c. (a, 60) = 15 d. (a, b)
A KroneckerCapelli-tételb l következik, hogy egy Bx = 0 homogén lineáris egyenletrendszernek
 10. gyakorlat Mátrixok sajátértékei és sajátvektorai Azt mondjuk, hogy az A M n mátrixnak a λ IR szám a sajátértéke, ha létezik olyan x IR n, x 0 vektor, amelyre Ax = λx. Ekkor az x vektort az A mátrix
10. gyakorlat Mátrixok sajátértékei és sajátvektorai Azt mondjuk, hogy az A M n mátrixnak a λ IR szám a sajátértéke, ha létezik olyan x IR n, x 0 vektor, amelyre Ax = λx. Ekkor az x vektort az A mátrix
Alapfogalmak. Biztonság. Biztonsági támadások Biztonsági célok
 Alapfogalmak Biztonság Biztonsági támadások Biztonsági célok Biztonsági szolgáltatások Védelmi módszerek Hálózati fenyegetettség Biztonságos kommunikáció Kriptográfia SSL/TSL IPSec Támadási folyamatok
Alapfogalmak Biztonság Biztonsági támadások Biztonsági célok Biztonsági szolgáltatások Védelmi módszerek Hálózati fenyegetettség Biztonságos kommunikáció Kriptográfia SSL/TSL IPSec Támadási folyamatok
Az SSH működése 1.Az alapok SSH SSH2 SSH1 SSH1 SSH2 RSA/DSA SSH SSH1 SSH2 SSH2 SSH SSH1 SSH2 A kapcsolódás menete Man-In-The-Middle 3DES Blowfish
 Alapok Az SSH működése 1.Az alapok Manapság az SSH egyike a legfontosabb biztonsági eszközöknek. Leggyakrabban távoli shell eléréshez használják, de alkalmas fájlok átvitelére, távoli X alkalmazások helyi
Alapok Az SSH működése 1.Az alapok Manapság az SSH egyike a legfontosabb biztonsági eszközöknek. Leggyakrabban távoli shell eléréshez használják, de alkalmas fájlok átvitelére, távoli X alkalmazások helyi
Kevesen tudják, de a GnuPG a levelek titkosításánál és visszafejtésénél valójában sokkal többre is képes...
 GnuPG tippek trükkök Kevesen tudják, de a GnuPG a levelek titkosításánál és visszafejtésénél valójában sokkal többre is képes... K ülönösen a kezdõ felhasználók gyakran érzik úgy, hogy a kriptográfia határozottan
GnuPG tippek trükkök Kevesen tudják, de a GnuPG a levelek titkosításánál és visszafejtésénél valójában sokkal többre is képes... K ülönösen a kezdõ felhasználók gyakran érzik úgy, hogy a kriptográfia határozottan
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Logaritmus
 Logaritmus DEFINÍCIÓ: (Logaritmus) Ha egy pozitív valós számot adott, - től különböző pozitív alapú hatvány alakban írunk fel, akkor ennek a hatványnak a kitevőjét logaritmusnak nevezzük. Bármely pozitív
Logaritmus DEFINÍCIÓ: (Logaritmus) Ha egy pozitív valós számot adott, - től különböző pozitív alapú hatvány alakban írunk fel, akkor ennek a hatványnak a kitevőjét logaritmusnak nevezzük. Bármely pozitív
