RUGÓTERHELÉSŰ BIZTONSÁGI SZELEP MŰKÖDÉSÉNEK ELMÉLETI ÉS KÍSÉRLETI VIZSGÁLATA
|
|
|
- Gyula Orosz
- 9 évvel ezelőtt
- Látták:
Átírás
1 MISKOLCI EGYETEM GÉPÉSZMÉRNÖKI KAR RUGÓTERHELÉSŰ BIZTONSÁGI SZELEP MŰKÖDÉSÉNEK ELMÉLETI ÉS KÍSÉRLETI VIZSGÁLATA PhD ÉRTEKEZÉS KÉSZÍTETTE: SIMÉNFALVI ZOLTÁN OKLEVELES GÉPÉSZMÉRNÖK GÉPÉSZMÉRNÖKI TUDOMÁNYOK DOKTORI PROGRAM, GÉPÉSZMÉRNÖKI ALAPTUDOMÁNYOK ALPROGRAM, MÉRNÖK-MATEMATIKA RÉSZPROGRAM DOKTORI ALPROGRAM VEZETŐ: DR. PÁCZELT ISTVÁN AZ MTA RENDES TAGJA A MŰSZAKI TUDOMÁNY DOKTORA TUDOMÁNYOS VEZETŐ: DR. ORTUTAY MIKLÓS A MŰSZAKI TUDOMÁNY KANDIDÁTUSA MISKOLC,
2 TARTALOMJEGYZÉK TARTALOMJEGYZÉK JELÖLÉSEK, INDEXEK.... BEVEZETÉS, CÉLKITŰZÉSEK TUDOMÁNYOS ELŐZMÉNYEK BIZTONSÁGI SZELEP MECHANIKAI MODELLJÉNEK VIZSGÁLATA ELŐZETES MEGFONTOLÁSOK A MECHANIKAI MODELL ELEMEINEK VIZSGÁLATA A RUGALMAS ELEM REZGÉSEI, TÖMEGÉNEK FIGYELEMBEVÉTELE CSILLAPÍTÓ HATÁSOK VIZSGÁLATA A leárs csllaítás meghatározása A Coulomb-féle súrlódás vzsgálata A FELHAJTÓERŐ, MINT GERJESZTŐ HATÁS SZÁMÍTÁSA A felhajtóerő laboratórum mérése Eljárás a felhajtóerő-függvéy meghatározására Számítás eredméyek, értékelés AZ ÜTKÖZÉSI JELENSÉGEK VIZSGÁLATA..... A MOZGÁSEGYENLET MEGOLDÁSA.... A NYOMÁSTARTÓ RENDSZER ÁRAMLÁSTANI MODELLJÉNEK VIZSGÁLATA..... ELŐZETES MEGFONTOLÁSOK..... ALAPÖSSZEFÜGGÉSEK, SZÁMÍTÁSI MÓDSZEREK..... A NYITOTT RENDSZEREKBEN VÉGBEMENŐ FOLYAMATOK VIZSGÁLATA A TÁPTARTÁLY ÁLLAPOTÁNAK MEGVÁLTOZÁSA...7
3 TARTALOMJEGYZÉK... A MÉRŐTARTÁLY ÁLLAPOTÁNAK MEGVÁLTOZÁSA FOJTÓELEMET TARTALMAZÓ ADIABATIKUS CSŐBEN TÖRTÉNŐ GÁZÁRAMLÁS SZÁMÍTÁSA AZ ÁRAMLÁSTANI MODELL EGYENLETEI A tátartályból a csővezetékbe áramlás szakasza (A- szakasz) Az egyees csőszakaszo kalakuló áramlás számítása (- szakasz) Áramlás a fojtáso keresztül (- szakasz) A fojtóelemet követő csőszakaszo kalakuló áramlás számítása (- szakasz) Áramlás a csővezetékből a mérőtartályba (-B szakasz) AZ ÁRAMLÁSTANI MODELL SZÁMÍTÁSÁNAK EREDMÉNYEI, KÍSÉRLETI IGAZOLÁS A BIZTONSÁGI SZELEPEN ÁTÁRAMLÓ TÖMEGÁRAM MEGHATÁROZÁSA SZIMULÁCIÓS ÉS KÍSÉRLETI VIZSGÁLATOK A MODELLEGYENLETEK MEGOLDÁSA, SZIMULÁCIÓS SZÁMÍTÁS A MODELLEK SZIMULÁCIÓS ÉS KÍSÉRLETI VIZSGÁLATA A FELHAJTÓERŐ-FÜGGVÉNY KEZDŐPONTJÁNAK VIZSGÁLATA Számítás módszerek, előzméyek Módszer felhajtóerő kezdőotjáak meghatározására A MODELLEK ELEMEINEK A BIZTONSÁGI SZELEP MŰKÖDÉSÉRE GYAKOROLT HATÁSÁNAK VIZSGÁLATA ÖSSZEFOGLALÁS, A TOVÁBBFEJLESZTÉS LEHETŐSÉGEI ÚJ TUDOMÁNYOS EREDMÉNYEK BEFEJEZÉS IRODALOMJEGYZÉK FÜGGELÉK... I. A VIZSGÁLT BIZTONSÁGI SZELEP FELÉPÍTÉSE, SZERKEZETI ELEMEI... II. KÍSÉRLETI BERENDEZÉS A BIZTONSÁGI SZELEP MŰKÖDÉSÉNEK VIZSGÁLATÁRA... III. ÖSSZEFÜGGÉSEK A FELHAJTÓERŐ-FÜGGVÉNY SZÁMÍTÁSÁHOZ... 7 IV. NEMLINEÁRIS EGYENLETEK ÉS EGYENLETRENDSZEREK MEGOLDÁSA NEWTON- MÓDSZERREL... 9 V. A MODELLEGYENLETEK SZÁMÍTÁSÁNAK FOLYAMATÁBRÁJA... VI. A LINEÁRIS CSILLAPÍTÁSI TÉNYEZŐ SZÁMÍTÁSÁNAK KÍSÉRLETI EREDMÉNYEI... VII. A COULOMB-FÉLE SÚRLÓDÁS SZÁMÍTÁSÁNAK KÍSÉRLETI EREDMÉNYEI... 6 VIII. AZ ÜTKÖZÉSI TÉNYEZŐ SZÁMÍTÁSÁNAK KÍSÉRLETI EREDMÉNYEI... 8 IX. A NYOMÁSTARTÓ RENDSZER SZÁMÍTÁSÁNAK ÉS MÉRÉSÉNEK EREDMÉNYEI... X. SZIMULÁCIÓS SZÁMÍTÁSOK ÉS KÍSÉRLETEK EREDMÉNYEI...
4 JELÖLÉSEK, INDEXEK JELÖLÉSEK, INDEXEK Jelölések A keresztmetszet [m ] a együttható [-] b együttható [-] c rugóálladó [m/n] c álladó yomáso vett fajhő [J/kgK] D rugó közéátmérő [m] D Lehr-féle csllaítás téyező [-] D szeleorsó átmérője [m] D üb szeleülék belső átmérője [m] D ük szeleülék külső átmérője [m] D üköz szeleülék közees átmérője [m] d rugó huzalátmérője [m] E átl átlagos eltérés E max maxmáls eltérés F erő [N] F cs csllaító erő [N] F f felhajtóerő [N] F g komlex gerjesztőerő kézetes része [N] F G gravtácós erő [N] F r rugóerő [N] F S Coulomb-féle súrlódóerő [N] g ehézség gyorsulás [m/s ] h fajlagos etala [J/Kg] h dőléték [s] J Jacob-mátrx j fajlagos dsszálódó eerga [J/kg] k rugómerevség [N/m] k Ruge-Kutta módszer álladója k ü szeleülék ütközés téyezője [-] k v vezetőtárcsa ütközés téyezője [-] L egyees csőhossz [m] m tömeg [kg] m gyorsított tömeg [kg] m mért otok száma m fm tömeg felhajtóerő mérésekor [kg] m m mozgó elemek tömege [kg] m y yugvó elemek tömege [kg] m ö alkatrészek össztömege [kg] m r rugó tömege [kg] N aroxmácós vektor adatfájlok száma [-] oltrókus ktevő [-] m rugó működő meeteek száma [-] ö rugó összes meetéek száma [-] P Legedre-olomok P g komlex gerjesztőerő [N] yomás [Pa] ytóyomás [Pa] z zárás yomás [Pa] k köryezet yomás [Pa] ell elleyomás [Pa] q fajlagos hőmeység [J/kg] q smeretle együtthatók vektora R rugó közésugara [m] R gázálladó [J/kgK] R együttható mátrx R g komlex gerjesztőerő valós része [N]
5 JELÖLÉSEK, INDEXEK Re Reyolds-szám [-] r leárs csllaítás álladója [kg/s] r korrelácós együttható [-] r rugóhuzal sugara [m] S Coulomb-féle súrlódóerő [N] s fajlagos etróa [J/kgK] s Coulomb-féle súrlódóerő kézetes része [N] T hőmérséklet [K] t rugó meeteek távolsága [m] u fajlagos belső eerga [J/kg] u rugó elem tömegéek elmozdulása [m] V térfogat [m ] v ütközés sebesség [m/s] w áramlás sebesség [m/s] x komlex elmozdulás valós része [m] Y rugó magassága [m] Y rugó összeyomódás [m] y komlex elmozdulás kézetes része [m] y rugó előfeszítés [m] y max maxmáls elmozdulás [m] z komlex elmozdulás [m] α teljesítméytéyező [-] α átfolyás szám [-] α sajátkörfrekveca [/s] γ fázsszög [rad] ζ veszteségtéyező [-] η damka vszkoztás [Ns/m ] κ zetrókus ktevő [-] λ csősúrlódás téyező [-] ξ dmezótla körfrekveca [-] ξ traszformált elmozdulás [m] ρ sűrűség [kg/m ] σ korrgált emrkus szórás τ dő [s] ϕ vszoyszám ψ gerjesztés kezdet szöge [fok] ω körfrekveca [/s] Idexek A tátartály A B csőszakasz jellemző keresztmetszete átl átlagos B mérőtartály be beáramló e zetrókus K köryezet k káramló krt krtkus m mért S bztoság szelee törtéő átáramlás legszűkebb keresztmetszete ~ traszformált kezdet I II III módszerek jelölése Tovább kegészítő jelölések az értekezésbe találhatók.
6 . BEVEZETÉS, CÉLKITŰZÉSEK 6. BEVEZETÉS, CÉLKITŰZÉSEK A vegyarba, a kőolaj- és földgázarba, a gyógyszergyártásba, az élelmszer- és az eergetka arba a yomástartó redszerek, beredezések túlyomás elle védelme bztoság, gazdaság, köryezetvédelm és techológa szemotból s redkívül fotos feladat. Normál körülméyek között a techológa folyamatba az üzem yomás em haladhatja meg a yomástartó edéy egedélyezés yomásáak értékét. Redellees folyamat következtébe a redszer yomása az egedélyezés yomás fölé emelkedhet. Haza és emzetköz vszoylatba azoos szellemű az az előírás, amely a yomástartó edéy maxmáls terhelhetőségét az egedélyezés yomás %-ába állaítja meg. A redellees folyamat következtébe kalakuló káros yomásövekméy korlátozására a folyamat jellegétől függőe külöböző túlyomáshatároló bztoság szerelvéyeket alkalmazak, amelyekek egyk legelterjedtebb tíusa a bztoság szele, azo belül s a közvetle rugóterhelésű bztoság szele (a továbbakba bztoság szele). A bztoság szele olya túlyomáshatároló szerelvéy, amelyet a töltet yomása öműködőe yt, megegedhető tovább yomásövekedés eseté olya töltetmeységet kées átbocsáta, amely a védedő edéy yomását a már említett egedélyezés yomás %-a alatt tartja, majd bzoyos yomáscsökkeés utá öműködőe zár. Ezt a működőkéességét hosszú dő át megőrz, mközbe működés tulajdosága em változak meg. A bztoság szeleel megvalósított védelem tehát em a yomásövekedést kváltó okot (okokat) szütet meg, haem az ok (okok) következméyet korlátozza, esetleg működésével drekt módo kezelő beavatkozást vált k. A bztoság szeleek kválasztását, méretezését érvéybe lévő szabváyok és előírások szabályozzák. A műszak gyakorlatba a redszeraraméterek smeretébe, műveletta és redszertechka eszközök segítségével határozzák meg a yomástartó redszer várható zavara eseté lefúvadó tömegáram agyságát, majd a közeg fzka-kéma tulajdosága (halmazállaot, fázsok száma, hőmérséklet), és a yomástartó edéy terhelhetősége (üzem, maxmáls yomás) alajá kválasztják a megfelelő méretű és tíusú bztoság szeleet. Az előírások értelmébe yomástartó redszerek túlyomáshatárolására csak mősített és dokumetált bztoság szeleek haszálhatóak. A Mskolc Egyetem Vegyar Géek Taszéke már több évtzede foglalkozk techológa redszerek redszerbztoság vzsgálatával, az
7 . BEVEZETÉS, CÉLKITŰZÉSEK 7 említett üzem araméterek meghatározásával, bztoság szerelvéyek kválasztásával, mősítésével. A bztoság szeleek működéséek taulmáyozása több tudomáyterület mechaka, áramlásta, bztoságtechka, redszertechka, műveletta, méréstechka együttes alkalmazását kívája meg. Eek következméyekét a tématerülettel foglalkozó szakrodalom ge szerteágazó. Ugyaakkor a bztoság szeleek gyártóak ac helyzetéből adódóa, a hatalmas kíálat aco szerelő cégek rtká ublkálják legújabb fejlesztésekek tudomáyos részletet. A bztoság szeleek területé az utóbb évtzedekbe megjelet szakckkek témájukat tektve alavetőe három csoortba sorolhatók: Kválasztás, üzemeltetés, karbatartás kérdése Tervezés, fejlesztés kérdése és módszere Kísérlet és elmélet módszerek a működés vzsgálatára A műszak gyakorlatba és az előírásokba alkalmazott összefüggések általába a bztoság szeleek általáos jellemzéséél, mdea gyakorlatak megfelelő beállításáál haszálhatók, de em alkalmasak arra, hogy a működés folyamatot a damka vszoyok fgyelembevételével, agyotossággal leírják. A bztoság szeleek kutatása ajakba a megbízható, a veszély megjeleését követő gyors és hatékoy működés fejlesztéséek ráyába mutatak. Ezek a kutatások az Euróa Uós Iráyelvekkel [98] összhagba a bztoság szele és a védett yomástartó redszer együttes vzsgálatát helyezk előtérbe. Értekezésembe s ezt az ráyvoalat követve kíváok a bztoság szeleek működéséek vzsgálatával foglalkoz. Az e területe megjelet közleméyek agy része a bztoság szele működését valamely helyettesítő modell alkalmazásával vzsgálja. A vlág számos részé a bztoság szeleek fejlesztésére, kutatására redszert egy vagy több ar közot támogatásával kutatóbázsok alakultak k, amelyek komoly befektetésekkel vzsgáló laboratórumokat éítettek k. Ilye laboratórummal redelkezk a Mskolc Egyetem Vegyar Géek Taszéke, amelyet Tszaújvárosba, a TVK Rt.-vel együttműködve 98 óta üzemeltet. A laboratórumba Magyarországo egyedülállóa a yomástartó redszerek bztoság szerelvéyeek kutatás, fejlesztés és mősítő vzsgálataval foglalkozak. A kutatómukához elegedhetetle kísérletek elvégzéséhez szükséges bztoság szeleet az EXPLOTECH Kft. (Budaest) bocsátotta redelkezésemre. A bztoság szele az ARI Armature (Németország) cég terméke. Az értekezésbe vzsgált bztoság szele ARI.9 tíusú, közvetle működésű, rugóterhelésű, teljes emelkedésű, DN/DN méretű, elleyomásra érzékey, agy koásállóságú szeleülékkel és szeletáyérral ellátott szerkezet. A bztoság szele szerkezet kalakítását és alkatrészeek jellemzőt az I. függelékbe az I.. ábra valamt az I.. táblázat mutatja, ahol megtalálható az alkatrészek megevezése, mérete, ayaga és tömege. A bztoság szeleet a szeleház beléő oldal karmája köt össze a védedő edéyel (jele esetbe a mérőtartállyal). A szeleház kléőoldal karmájához kacsolódk a lefúvóvezeték, amelye a bztoság szele által lefújt közeg elvezetése törték. A szeletáyér tömör zárását a 6 hegeres csavarrugó feszítőcsavarral állítható terhelőereje hozza létre. A terhelőerőt az szeleorsó közvetít a szeletáyérra. A szeletáyér cetrkus terhelését a szeleorsó 8 vezetőtárcsa és feszítőcsavar által törtéő megvezetése bztosítja. A bztoság szele ytóyomásáak beállítása a feszítőcsavar helyzetéek ezáltal a rugó előfeszítéséek
8 . BEVEZETÉS, CÉLKITŰZÉSEK 8 beállításával valósítható meg. A rugó a 7 alsó és a felső rugótáyér közé va befogva, és a szeleház felső részéhez csatlakozó rugóházba helyezkedk el. A kutatások elvégzéséek és az értekezés elkészítéséek alavető feladata volt hozzájárul ahhoz a vlágszerte folytatott kutatómukához, amely lehetővé tesz a bztoság szeleek korszerűsítését, működés otosságáak, megbízhatóságáak övelését, mdezzel elősegítve az élet- és vagyobztoság mél magasabb sztű megvalósítását. Az értekezés fő célja matematka modell kdolgozása a rugóterhelésű bztoság szele működéséek megbízható leírására, valamt a modell alkalmazásával olya észrevételek, javaslatok megfogalmazása, amelyekkel a bztoság szele fejlesztését elősegítő redkívül költséges és dőgéyes kísérlet vzsgálatok száma csökkethető. E cél elérését részletebe a következő célktűzések segítk: létrehoz egy kísérlet beredezést, amellyel a bztoság szele működéséek vzsgálatát valós techológa körülméyek között lehet elvégez; felállíta a bztoság szele mechaka modelljéek a szakrodalm forrásokhoz kéest otosított és részletes, agyotosságú vzsgálatokra alkalmas változatát; kdolgoz egy olya eljárást a bztoság szelere jellemző felhajtóerő-függvéy kísérlet méréseke alauló meghatározására, amely alkalmazható a bztoság szele szmulácós számítása sorá; elmélet és kísérlet módszereket dolgoz k a mechaka modell smeretle elemeek meghatározására, külöös tektettel a csllaító, súrlódó és ütközés hatásokra; felállíta a bztoság szeleel védett kísérlet beredezés yomástartó redszeréek áramlásta modelljét, kísérlet vzsgálatokkal elleőrz a modell alkalmazhatóságát; létrehoz a mechaka és az áramlásta modell működését leíró szmulácós rogramot; a kísérlet beredezés és a szmulácós rogramredszer felhaszálásával megvzsgál a bztoság szele működését befolyásoló téyezőket, külöös tektettel a mechaka és az áramlásta modell elemere (tartálytérfogat, rugókaraktersztka, csllaító és ütközés hatások), ezzel rávlágíta éháy a gyakorlatba és az előírásokba em, vagy eltérő módo szerelő kválasztás és működés araméter jeletőségére.
9 . BEVEZETÉS, CÉLKITŰZÉSEK 9. TUDOMÁNYOS ELŐZMÉNYEK A bztoság szele, mt a yomástartó redszerek túlyomáshatárolására szolgáló szerkezet már régóta smert, rodalma ge szerteágazó. A bevezetésbe megfogalmazott szemotok alajá, a célktűzésekkel összhagba, a következőkbe áttektem a kutatás területet értő szakrodalm forrásokat, követve az értekezés tematkáját. Az egyes részek végé jelzésszerűe utalok arra, hogy az értekezés mely részébe foglalkozok az adott tématerülettel. A 7-es évek közeé KONDRATYEVA [8] állította össze az első átfogó rodalmat, amelyet a ma ag alaműek tekteek. Néháy évvel később BOZÓKI [6] ublkálta a yomástartó redszerek túlyomáshatárolásával foglalkozó émet yelvterülete s megjelet művét, amelybe a bztoság szeleeke kívül más bztoság beredezéseket s redszerez. Az előző évtzedekbe szerte a vlágo kutatóbázsok alakultak a bztoság szeleek kutatására, vzsgálatára, fejlesztésére. Ezek közül jeletősebbek TARASZEV és mukatársa [78, 79, 8, 8, 8, 8], valamt GRINBERG-KRICSKER [,, ] a volt Szovjetuó területéről, FÖLLMER-ZELLER [,,, ] Aacheből (Aerodyamsches Isttut der Rhesch- Wesfälsche Techsche Hochschule Aache), FROMMANN-FRIEDEL [, 6, 7] Hamburgból (Lehrstuhl für Strömugsmechak a der TU Hamburg), SINGH és mukatársa [9,, 8, 9, 68, 7, 7, 7, 7, 86, 87, 88] az USA-ból (Electrc Power Research Isttute, Calfora), valamt BENE-BOZÓKI-FEJES-JOÓ-LÉDERER-ORTUTAY-SZABÓ Magyarországról [7, 8, 9,, 6,, ] (Mskolc Egyetem Vegyar Géek Taszék). A bztoság szeleek mechaka modelljével a legtöbb kutatóbázs foglalkozott. Az alkalmazott modell mde esetbe az egyszabadságfokú rezgőredszer mechaka modellje volt, a mozgásegyelet fgyelembe vett eleme azoba eltérést mutattak. A mozgásegyelet eleme között szerelő, az átáramló közeg által a szeletáyérra kfejtett erő, a felhajtóerő számításáak ehézsége matt a szerzők a mozgásegyeletek általába erőse leegyszerűsített megoldásat adták. A következőkbe a modell elemeek számításához kacsolódó szakrodalmat tektem át. A rugalmas elem tömegéek fgyelembevételével BOZÓKI [6], FÖLLMER [, ], KONDRATYEVA [8] és a mskolc kutatóbázs [] foglalkozott érdembe. Mdaya arra a következtetésre jutottak, hogy a szerkezet mozgó elemeek tömegét a rugó tömegéek %-ával
10 . BEVEZETÉS, CÉLKITŰZÉSEK szükséges megövel. Az I. függelékbe közölt bztoság szele-kostrukcó elemeek tömegét vzsgálva láthatjuk, hogy a rugó tömege összemérhető a mozgó elemek szeletáyér, szeleorsó, rugótáyér tömegével, sőt agyobb méretű szeleekél jeletőse meg s haladhatja azt, amely dokolttá tesz a robléma vzsgálatát. Az említett szerzők közül BOZÓKI [6] átfogó művébe egy számítás eljárást s bemutat, amelyek otosítását vele azoos végeredméyt felmutatva a... fejezetbe tárgyalom. Más szerzők em teszek említést a rugó tömegéek fgyelembevételéről, usztá a mozgó elemek tömegét jelölk összefüggésekbe. A csllaító hatások vzsgálatával csak éháy szerző foglalkozott. BORZOV [], FROMMANN-FRIEDEL [7], FÖLLMER [] ugya említést tesz a sebességgel aráyos leárs csllaításról, de számítás módszert, kokrét értéket egykük sem közöl. MOSIDIS [6] a rugó elmozdulásából és az egyelőtle yomásterhelésből adódó szeleszár-befeszülés, eze keresztül a súrlódás jelelétéről közöl ckket, ugyacsak mérés eredméyek élkül. SINGH [7] művébe a leárs csllaítás téyező értékét a krtkus csllaítást jellemző érték ez a erodkus mozgás határesete %-ába, SHAK [7] %-ába határozza meg, azoba erre az értékre sem elmélet, sem kísérlet magyarázatot em ad. Az értekezés... fejezetébe részletese foglalkozom a leárs csllaítás és a Coulomb-féle súrlódás számításával. A bztoság szelee törtéő átáramlás sorá a lefúvatott közeg által a szeletáyérra kfejtett emelőerőt felhajtóerőek evezzük [6]. A felhajtóerő, mt gerjesztőhatás vzsgálatáak rodalma ge terjedelmes, az említett kutatóbázsok szte mdegyke részletese foglalkozott a témával. Abba mde szerző egyetértett, hogy adott geometra kalakítás eseté a felhajtóerő a szeletáyér elmozdulásától és a bztoság szele előtt yomástól függ. Elmélet megközelítéssel több szerző foglalkozott. A számításokra jellemző, hogy a bztoság szelee törtéő átáramlást egydmezósak, zetrókusak és krtkusak feltételezték. LANGERMAN [8, 9] és SINGH [7, 7] (EPRI, Calfora) művekbe az mulzustétel segítségével, egy adott geometrájú bztoság szele eseté számította a felhajtóerőt. Eredméyeket csak a mozgásegyelet megoldásával, működés vzsgálat formájába ublkálták, a felhajtóerő téyleges értékéről em adtak felvlágosítást. Hasoló módszert más szerzők s alkalmaztak, azoba mdaya köztük KONDRATYEVA egyetértettek abba, hogy a felhajtóerő megbízható meghatározása csak kísérlet módszerek felhaszálásával lehetséges. E területe jeletős elmélet és kísérlet kutatás fűződk az aache kutatócsoort evéhez (Aerodyamsches Isttut der RWTH). Eredméyeket FÖLLMER doktor dsszertácójába [], és szerzőtársaval közölt szakckkebe [,, ] mutatta be. A bztoság szelee törtéő átáramlás taulmáyozására egy szelemodellt készítettek, és a közeg szeletáyérszeleülék köryezetébe kalakuló áramlását vzsgálták Mach-Zehder terferométer segítségével, külöböző áramlás sebességek és szeletáyér ytottság állaot mellett. Számos szerző foglalkozott a bztoság szele belső geometrájáak felhajtóerőre gyakorolt hatásával. Közülük csak éháyat megemlítve, a szeletáyér szokyarész szögéek hatását BORZOV [, ] és TARASZEV [78, 8], a szeleülék kalakításáak hatását BORZOV [] és MOSIDIS [6] vzsgálta. A geometra hatások legrészletesebb összefoglalása BOZÓKI [6] művébe található, amelyhez értékes adatokat szolgáltatott a mskolc kutatócsoort bztoság szele fejlesztés tevékeysége. A szerző átfogó kéet ad a szeletáyér kalakításáak eremes kalakítás, kúosság, külső átmérő, kúos mélység, áramvoalas kalakítás, tömítőfelület leélezése, tömítőfelület kúosság, fúvóka kúosság felhajtóerőre gyakorolt hatásával.
11 . BEVEZETÉS, CÉLKITŰZÉSEK A felhajtóerő kísérlet úto törtéő meghatározására a szakrodalom [9, 6, 8] alavetőe három módszert közöl. Az egyk módszer szert a szelebe smert rugóálladójú rugót éíteek be, majd a szeleorsó elmozdulását a szele előtt yomás változtatásával külöböző löketekre állítják be, és a yomásértékből következtetek a felhajtóerőre. Ez a módszer a yomásváltozással aráyos emelkedésű bztoság szeleekél kvtelezhető, ugyaakkor teljes emelkedésű szeleekél az stabl egyesúly helyzetek matt ehézségekbe ütközk. A másodk módszer szert eltávolítják a szeleből a záróerőt létrehozó elemet (rugót), és a szeleorsóhoz erőmérő és elmozdulásmérő elemet csatlakoztatak. Az erőmérő elemet külöböző löketekre beállítva azoos yomáso mérk a szeletáyérra ható erőt. Mdkét módszer hátráya, hogy a felhajtóerőt csak egyed yomásoko határozza meg, így a teljes yomás és elmozdulás tartomáy leírása em lehetséges. Ezt a hátráyt küszöböl k a BENE-LÉDERER mskolc kutatócsoort továbbfejlesztése (harmadk módszer) [7]. A mérés elve megegyezk a másodk módszerével, de az erőértékeket em álladó yomáso rögzítk, haem a működés yomás teljes tartomáyába egy adott mtavétel sebességgel, az elmozdulással együtt a yomás függvéyébe regsztrálják. Ez a módszer lehetőséget bztosít az elmozdulás- és erőértékek terolácójára, ezáltal a mért othalmazok számítógées feldolgozására. A számítógées feldolgozás eredméyekét a felhajtóerő valamely függvéykét állítható elő, ezzel a mozgásegyelet aaltkus vagy umerkus úto megoldhatóvá válk. A zárt állaotú szeletáyérra ható felhajtóerő számítása alavető kérdés, mvel ez a ot a bztoság szele működéséek egyk fotos llaatát a ytást, eze keresztül a ytóyomást jellemz. A szakrodalom és az előírások ebbe a kérdésbe em egységesek. JENETT [,, ], LANGERMAN [8, 9], KERN [6], MANLEY [6], SINGH [7-7], WEISMANTEL [87], WOOLFOLK [89] és ZAHORSKY [9], lletve az amerka és agol előírások [9, 9, 9, 96] a szeletáyér és szeleülék geometrájáak és a szeletáyérra ható külöböző yomások (tartály-, elle- és köryezet yomás) fgyelembevételével számított erőhatások alajá határozza meg ezt az erőértéket. A magyar és volt szovjet kutatóbázsok [7,,,, 8, 78-8, 99, ] a szeleülék és a szeletáyér értkező felületéek közéátmérőjére voatkoztatja zárt szeletáyér állaotál a felhajtóerő agyságát. A robléma részletes vzsgálatára, a források összehasolítására az értekezés... fejezetébe kerül sor. A szakrodalom a felhajtóerő számítására bzoyos egyszerűsítéseket alkalmaz. Ilye egyszerűsítés éldául az a feltételezés, hogy a felhajtóerő és a yomás között a teljes elmozdulástartomáyo álladó, leárs kacsolat va [,,, 8]. Ez azt jelet, hogy két yomáso meghatározva a felhajtóerő-szeletáyér elmozdulás görbe egy-egy otját, majd meghatározva a leárs kacsolat együtthatóját, a felhajtóerő bármely yomáso számítható. Más szerzők [7, ] az előbb egyszerűsítése túl a felhajtóerő szeletáyér elmozdulástól való függését s leársak, esetleg szakaszokét leársak feltételezk. Ezekkel az egyszerűsítésekkel a bztoság szele működését leíró mozgásegyelet aaltkus megoldása előállítható. Az így számított felhajtóerővel végzett szmulácós számítások csak a mozgás jellegéről adhatak felvlágosítást, a valós vszoyok modellezésére em alkalmasak. A felhajtóerő teljes elmozdulás- és yomástartomáyo törtéő számítására az értekezés... fejezetébe mutatok be egy módszert.
12 . BEVEZETÉS, CÉLKITŰZÉSEK A bztoság szele szeletáyérja mozgása közbe ütközés jeleségek játszódhatak le, amely sorá a szeletáyér a szeleülékkel, lletve a vezetőtárcsával kerülhet kacsolatba. Ezzel a roblémával a kutatók agy része em foglalkozott. A feldolgozott szakrodalomba csuá egyetle utalást találtam SINGH [7] részéről, ak az ütközés jeleséget a szeletáyér ütközés előtt és utá sebességéek háyadosával, az ütközés téyezővel jellemezte, amelyet mdkét ütközés jeleségre, értékbe határozott meg. A szerző ckkébe közölte, hogy ezráyba kísérleteket em végzett, az értékadás a mozgásegyelet megoldhatósága érdekébe törtét. Az értekezés... fejezetébe részletese foglalkozok az ütközés jeleségek leírásával, és egy kísérlet módszerrel az ütközés téyezők kokrét értékét s közlöm. A mozgásegyelet megoldása az előzőekbe bemutatott hatások fgyelembevételével aaltkus vagy umerkus úto törtéhet. Az alkalmazott egyszabadságfokú mechaka modell mozgásegyelete egy másodredű dfferecálegyelet, amelyek aaltkus megoldása csak abba az esetbe állítható elő, ha az egyelet az elmozdulás első és másodk derváltjá túl legfeljebb harmadfokú tagokat tartalmaz. Ilye megoldást láthatuk a [7, ] rodalmakba, ahol a felhajtóerőt a már említett leárs összefüggéssel határozták meg. A mért és számított adatok ábrázolását, összehasolítását csak a [7] közleméybe ublkálták (FROMMANN-FRIEDEL). Aaltkus megoldást állítottak elő az Electrc Power Research Isttute mukatársa s [8, 9, 7-7] (SINGH, LANGERMAN), akk az átáramló közeg által az adott geometrájú szeletáyérra kfejtett mulzuserőket vették fgyelembe. A következő ábráko a [7], valamt a [7] rodalmakba közölt mért és számított szeletáyér elmozdulás görbék láthatók az dő függvéyébe ábrázolva... ábra Szeletáyér mért és számított.. ábra Szeletáyér mért és számított elmozdulása (FROMMANN-FRIEDEL) elmozdulása (SINGH) A [7] rodalomba a mozgásegyelet érzékeységvzsgálatát s megtaláljuk, ahol többek között az elleyomás, a mozgó tömegek és rugómerevség megváltozásáak működésre gyakorolt hatását vzsgálták. A rugómerevség hatását a.. ábra szemléltet. A mozgásegyeletek csak umerkus megoldását lehet előállíta. ha az egyelet magasabb, mt harmadfokú tagokat tartalmaz. Erre éldák BORZOV [, ] és TARASZEV [8] közleméye, ahol a felhajtóerőt a már említett leárs egyszerűsítő feltétellel a szerzők egyedfokú olommal közelítették, majd a mozgásegyeletet Ruge-Kutta módszerrel oldották meg. A.. ábrá a [8] műbe közölt mért és számított tartályyomás, lletve szeletáyér elmozdulás látható az dő függvéyébe ábrázolva.
13 . BEVEZETÉS, CÉLKITŰZÉSEK h [mm] [MPa] h t, [s].. ábra Számított szeletáyér elmozdulás.. ábra Szeletáyér mért és számított érzékeységvzsgálata külöböző elmozdulása és a mérőtartály yomása az rugómerevségek eseté (EPRI) dő függvéyébe (TARASZEV) Egy mechaka redszer modellegyeletéek megoldása valamely gerjesztőhatás és a kezdet feltételek smeretébe határozható meg. A bztoság szele mechaka modelljéek mozgásegyeletébe a gerjesztőhatást a felhajtóerő, közvetett módo a védedő edéy yomása szolgáltatja. A bztoság szeleet vezérlő yomás a védedő tartályba érkező és a működő bztoság szelee keresztül oa távozó közeg meységétől és állaotától függ, ezért a számításokat a yomástartó redszer áramlásta vzsgálatára s k kell terjeszte. A szakrodalomba szte mde szerző, ak a modell megoldásával foglalkozott, kísérletekkel s gazolta a választott modell jóságát, alkalmazhatóságát. A kísérletek céljára valós yomástartó redszereket hoztak létre, amelyeket valamely tervezett techológa zavar váratla tömegáram érkezése, szabályozószele hbás működése, stb. következtébe bztoság szeleel véde kellett. A következő ábráko két a.. ábrá FROMMANN és FRIEDEL vezette hamburg, és a.6. ábrá az Electrc Power Research Isttute kutatóbázs által kalakított kísérlet állomás vázlata látható... ábra Mérőberedezés a bztoság szele elmélet és kísérlet vzsgálatára (FROMMANN- FRIEDEL).6. ábra Mérőberedezés a bztoság szele elmélet és kísérlet vzsgálatára (EPRI) FROMMANN és FRIEDEL [-7] olya mérőberedezést éített, amellyel a bztoság szele előtt vízsztes vagy függőleges csőszakaszba a távezetékbe kalakuló yomáslegések s taulmáyozhatók. Kísérletek alajá egy yomáslökés krtérumot állítottak fel, amely meghatározza a távezetékek azt a maxmáls hosszát, amelyél a yomáslegések
14 . BEVEZETÉS, CÉLKITŰZÉSEK következtébe káros szelerezgések még em alakulhatak k. A szerzők az elmélet összefüggésekél a közeget deáls gázak, az állaotváltozást zetrókusak, az áramlást egydmezósak feltételezték. A szeletáyér mozgásegyeletéek gerjesztő hatását jelető felhajtóerőbe szerelő szele előtt yomáso és a bztoság szelee átáramló tömegáramot meghatározó szeleemelkedése keresztül a mechaka és az áramlásta modell egyelete össze vaak kacsolva, melyeket szmultá kell megolda (eek megoldás látható a.. ábrá). Az EPRI mukatársa [8, 9, 68, 7-7, 87, 88, 9] az áramlásba résztvevő elemeket tartály, beömlés, kömlés, csővezeték szegmesekre botották, majd a számításokat a RELAP/MOD rogrammal hajtották végre, amely alkalmas homogé, kétkomoesű elegyek súrlódásos áramlásáak leírására krtkus alatt és felett áramlás tartomáyba egyarát. A számítások és mérések eredméye a.. ábrá volt látható. TARASZEV [8] a émet kutatókéhoz hasoló beredezést szerkesztett azzal a külöbséggel, hogy a bztoság szeleet közvetleül a mérőtartályra szerelte. A tátartály és a mérőtartály közt csővezetékbe egy szabályzószeleet éített, amelyek ytottságát egy átfolyás számmal jellemezte. A redszer áramlásta modellje a szokásos egyszerűsítéseke kívül (deáls gáz, egydmezós, zetrókus áramlás) elhayagolja a csővezetéke és eleme beömlés, csőív, egyéb szerelvéyek kalakuló áramlás veszteségeket s. A közölt egyeletek a tartályok yomás és hőmérsékletváltozását írják le. Az áramlásta egyeletek mozgásegyelettel együtt törtéő umerkus megoldását a.. ábrá láthattuk. Az értekezés. fejezetébe az előbbhez hasoló kísérlet beredezést, és a redszert leíró áramlásta egyeleteket, lletve azok megoldását és kísérlet gazolását mutatom be. A bztoság szele alafeladatával összefüggésbe alavetőe fotos jellemző a bztoság szelee átáramló tömegáram agysága. A szakrodalom a felhajtóerőél taasztalt elmélet bzoytalaságok, valamt az általáos kválasztás elvek következtébe a kísérlet megoldást részesít előybe. A kísérlet módszer léyege, hogy krtkus áramlás eseté, a bztoság szelee zetrókusa átáramló közeg, elméletleg meghatározható tömegáramáak és a kísérlettel meghatározott téyleges tömegáram háyadosát egy α teljesítméytéyezővel jellemzk, és a szeletáyér elmozdulás tartomáy dszkrét otjaba határozzák meg [7, 6,, 8, 8]. Ezt a függvéyt a szelegyártók katalógusakba grafkus formába közlk. Az értekezés.. fejezetébe tárgyalom a teljesítméytéyező mérését, számítását és közelítéséek módszerét. A bztoság szeleekkel kacsolatos magyar szakrodalomról már éháy helye esett szó. E területe kemelkedő jeletőségű a Mskolc Egyetem Vegyar Géek Taszékéek kutatócsoortjáak tevékeysége. A 8-as évek elejétől Tszaújvárosba működő Bztoság Szerelvéy Vzsgáló Laboratórum [7] révé számos kutató, fejlesztő, bzoylatoló és ar megbízásos mukát végeztek el, valamt több újítással, szabváymódosítással és szabadalommal s redelkezek. Az eddg tárgyalt szakrodalm forrásoko túl meg kell említe más szerzőket s, akk kutatásakba damka vzsgálatokat értő témával foglalkoztak. ADAMS és CORCORAN [] a ytó és lefúvó yomás kacsolatát, valamt a szeleülék és a szeletáyér értkező felületéek szélességéek ytásra gyakorolt hatását vzsgálta. BERGAMINI és AQUILINO [] a bztoság szele, és más védelm redszer együttes működését taulmáyozta. BOSKIRK [] a beömlő és lefúvó vezeték hosszáak működésre gyakorolt hatását vzsgálta. EMERSON [8] a bztoság szeleek kválasztásával, az elleyomás és lefúvó kaactás kacsolatával
15 . BEVEZETÉS, CÉLKITŰZÉSEK foglalkozott. MUKERJI [6] egy desztllácós oszlo techológa redszerébe éített bztoság szeleet és a működését kváltó okokat vzsgálta. SCHLÜNDER [67] egy közelítő módszert mutatott be a lefúvó és beömlő vezetékbe törtéő zetrókus áramlásra. SIEVERT [69] a bztoság szeleek méretéek kválasztását és a lefúvó kaactását taulmáyozta, majd a számítása gazolására éített vzsgálóállomást mutatta be. THOMPSON és BUXTON [8] agyyomású telített gőz zetrókus áramlása eseté, a bztoság szele teljesítméytéyezőjét vzsgálta. Kutatása beéültek az ASME Boler ad Pressure Vessel Code előírásaba. ANSELMAN a Bo & Reuther [97] bztoság szele gyártó cég főméröke a szeleek kválasztásáak és alkalmazásáak gyakorlat oldalával foglalkozott, vzsgálta külöböző közegek lefúvatását és a működés közbe felléő rezgések, csattogások okat.
16 . BIZTONSÁGI SZELEP MECHANIKAI MODELLJÉNEK VIZSGÁLATA 6. BIZTONSÁGI SZELEP MECHANIKAI MODELLJÉNEK VIZSGÁLATA.. ELŐZETES MEGFONTOLÁSOK A rugóterhelésű bztoság szele mozgó és yugvó tömegeket, valamt rugalmas elemet tartalmaz. A mechaka redszer akkor végez legő mozgást, ha mozgás eergája helyzet eergává alakul át, majd ez smét mozgás eergává alakul. Mechaka redszerek damka vzsgálatáál fotos teedő a helyettesítő modell meghatározása. A damka redszereket szabadságfokuk szert osztályozzuk, amely megmutatja, hogy a tömeg (tömegek) mozgását háy, egymástól függetle koordátával adhatjuk meg. Ezekívül megkülöböztetük leárs vagy emleárs, csllaított vagy csllaításmetes, valamt gerjesztett vagy szabad mozgású rezgőredszereket. A Bevezetésbe bemutatott bztoság szele kostrukcót fgyelembe véve, valamt a fejezet következő részébe tárgyalásra kerülő megfotolások alajá a továbbakba a legések vzsgálatára az egyszabadságfokú, leárs, csllaított, gerjesztett rezgőredszer mechaka modelljét alkalmazom, amelyek vázlata a.. ábrá látható. r c, m r y max m m y F g.. ábra A bztoság szele mechaka modellje
17 . BIZTONSÁGI SZELEP MECHANIKAI MODELLJÉNEK VIZSGÁLATA 7 A fejezet következő részébe elmélet és kísérlet módszerekkel vzsgálom a mechaka modell rugalmas elemét, jellemzőek meghatározását, tömegéek fgyelembevételét, a csllaító hatásokat (a leárs csllaítást és a Coulomb-féle súrlódást), a bztoság szelee átáramló közeg okozta gerjesztő hatást, valamt az ütközés roblémákat. A fejezet végé tárgyalom a mozgásegyelet megoldásáak egy módszerét... A MECHANIKAI MODELL ELEMEINEK VIZSGÁLATA Az előzőekbe bemutatott egyszabadságfokú rezgőredszer mozgását egy közöséges dfferecálegyelet, a redszer mozgásegyelete írja le, amelyek felírásához az mulzustételt alkalmazom. A.. ábrá bemutatott mechaka modell y ráyba ktérített tömegére (m) a vsszatérítő rugóerő (F r ), a sebességgel elletétes értelmű csllaítóerő (F cs ), a Coulomb-féle súrlódóerő (F S ), a gerjesztőerő (F g ), valamt az alkatrészek tömegéből adódó gravtácós erő (F G ) hat: m! y F F F F F. (.) r cs A másodredű homogé dfferecálegyelet aaltkus formába való megoldhatósága az egyelet fokszámáak függvéye. A vzsgált rezgőredszerek a későbbekbe tárgyalt felhajtóerő-közelítő eljárással kaott függvéy magasabb fokszáma következtébe közelítő megoldását fogom előállíta. S g G... A RUGALMAS ELEM REZGÉSEI, TÖMEGÉNEK FIGYELEMBEVÉTELE Damka redszerbe a helyzet eerga tárolója többyre valamely rugalmas elem. Ameybe az elem alakváltozása az elemre ható erővel aráyosak tekthető lye a rugóterhelésű bztoság szeleekél alkalmazott hegeres csavarrugó s leárs rugókaraktersztkáról beszélük. Eszert y mértékbe előfeszített rugó által kfejtett erő fgyelembe véve a.. ábrá jelölt oztív ráyt F r ( y y ) (.) c formába írható, ahol c a rugóálladó. Szokás a rugalmas elemet a rugóálladó recrokával, a k (.) c rugómerevséggel s jellemez. A fet álladók az ayagjellemzők és a geometra méretek smeretébe számítással s meghatározhatók. A számított érték azoba általába em otos, részbe azért, mert a rugóvégek alakváltozása csak megközelítőe számítható, másrészt az előírt geometra és ayagjellemzők a gyártás sorá em tarthatók be otosa [6]. Az általam vzsgált bztoság szelehez a gyártó a vzsgált yomástartomáyra három, külöböző rugómerevségű hegeres csavarrugót bztosított, azoba ezek jellemző adatat em közölte, így azokat méréssel határoztam meg. A Mskolc Egyetem Vegyar Géek Taszék redelkezk egy ayagvzsgáló (szakító) géből kalakított rugómerevség-mérő beredezéssel, valamt a SAVADES rogramcsomaggal, amellyel a rugómerevség kísérlet úto meghatározható [6]. A mérőberedezés elv vázlata a.. ábrá látható.
18 . BIZTONSÁGI SZELEP MECHANIKAI MODELLJÉNEK VIZSGÁLATA Erőmérő cella. Felső rugótáyér. Rugó. Alsó rugótáyér. Terhelő erő 6. Elmozdulás-távadó 7. Mérő-adatgyűjtő egység 8. Számítógé.. ábra A rugómerevség méréséek elv vázlata A mérés sorá a rugót a működéskor várható előfeszítéssel terheljük, majd a róbaad orsójáak felfelé ráyuló mozgatásával az alsó rugótáyért mm hosszo,, mm/s álladó sebességgel mozgatjuk. Ezalatt regsztráljuk az alsó rugótáyér elmozdulását és az erőmérő cellát terhelő erőt. A kaott eredméyeket a rogram leárs regresszóval közelít, majd a kéeryő megjeletet a rugóra jellemző rugómerevség értékét. Egy rugóval három mérést végeztük, a jellemző rugómerevséget a három mért érték számta átlaga adja. A rugók mért jellemzőt a.. táblázatba foglaltam össze, ahol a rugó azoosítóját, huzalátmérőjét (d), közéátmérőjét (D), terheletle hosszát (Y), összes ( ö ) és működő meeteek számát ( m ), tömegét (m r ), ayagát és a mért rugómerevség értékeket (k) tütettem fel. Azoosító d [mm] D [mm] Y [mm] ö [-] m [-] m r [kg] Ayag k [N/mm] I. sor. II. sor. III. sor. Átlag C 6, 7,8 9, 9,,77 SCr6,6,,, C6 6, 7,, 8,,88 SCr6 8,7 8,7 8,78 8,77 L7 6,8 8,, 8,,6 SCr6,,,99,.. táblázat A rugók jellemző adata A gyakorlat számítások a rugalmas elem tömegét általába em veszk fgyelembe. Ha ez a tömeg összemérhető a redszer mozgó elemeek tömegével, akkor a rugó tömegéek elhayagolása csökket az eredméyek megbízhatóságát. Mvel a vzsgált bztoság szeleél alkalmazott rugók tömege (,77-,6 kg) összemérhető a mozgó elemek szeletáyér, orsó, alsó rugótáyér tömegével (,7 kg), a rugó tömegéek bzoyos háyadát hozzá kell ad a mozgó elemek tömegéhez. A következőkbe a rugó mozgó tömegéek meghatározására a [6] műbe megjelet módszerek egy otosított változatát mutatom be. D d t y x R ϕ Y.. ábra Hegeres csavarrugó A számításokat bzoyos egyszerűsítő feltevések fgyelembevételével végeztem el. Feltételeztem, hogy a rugó üzeme sorá léyegese az első sajátkörfrekveca alatt tartomáyba működk, valamt, hogy a rugó hossza meté a keresztmetszetek elmozdulása között leárs kacsolat z
19 . BIZTONSÁGI SZELEP MECHANIKAI MODELLJÉNEK VIZSGÁLATA 9 va, tehát az egyk végot elmozdulásából egyértelműe meghatározható a másk végot helyzete [8]. A.. ábra értelmébe a hegeres rugó közévoaláak egyeletét x R cosϕ, z R sϕ, (.) t y ϕ. π összefüggésekkel határozhatjuk meg. Az m számú működő meetből álló rugó teljes magasságát az t Y π m t m (.) π kfejezés írja le. A rugó terhelésekor, teljes magassága Y agyságú összeyomódás eseté Y Y Y (.6) értékre csökke. Ez egybe azt s jelet, hogy ameybe a rugó felső része rögzített, a meetek em egyelő mértékbe mozdulak el. Ezt fgyelembe véve a rugó dm elem tömegéek elmozdulása Y u ϕ (.7) π m összefüggéssel határozható meg. A rugó elem tömege dmr ρrr πdϕ (.8) alakba számítható. A bztoság szele működésekor, a rugó alsó végéek elmozdulásával a gyorsításához szükséges erő πm πm π m Y!! Y!! ϕ udm! r ρrr π ϕdϕ ρrr ρrr π my!! (.9) π m m F szert írható fel. A rugó teljes tömege r πm m ρ Rr πdϕ Rr π ρ (.) alakba határozható meg. Behelyettesítve ezt a kfejezést a (.9) összefüggésbe, az m F r Y! (.) kfejezést yerjük, amely azt mutatja, hogy a rugó szeletáyérra redukált tömege egyelő a rugó tömegéek felével. A (.) mozgásegyeletbe szerelő ktérített tömeget az mr m mm (.) összefüggést szert, a mozgó elemek (szeletáyér, szeleorsó, alsó rugótáyér, elmozduláshatároló elem, kemelő segédelem) és a rugó redukált tömegéek összegekét kajuk. m Ezt követőe vzsgáljuk meg a (.) mozgásegyeletbe szerelő, az alkatrészek tömegéből származó gravtácós erőt (F G ). Ez az erő fgyelembe véve a.. ábra jelöléset az F G ( m m ) g m g (.) összefüggés értelmébe, az előbbekbe számított mozgó (m) és a gyorsított tömeget em jelető yugvó (m y ) elemek tömegéek gravtácós erejéből tevődk össze. Nyugvó elemek tektjük a felső rugótáyért, és a rugó tömegéek em gyorsított részét (m r /). y ö
20 . BIZTONSÁGI SZELEP MECHANIKAI MODELLJÉNEK VIZSGÁLATA Az értekezés eze részébe célom a mechaka redszer rugalmas elemével, mozgó és yugvó tömegevel kacsolatos vzsgálatok elvégzése volt. A megvalósítás sorá kísérlet mérésekkel meghatároztam a redelkezésre álló rugók jellemzőt; otosítottam a rugó mozgó tömegéek fgyelembevételével foglalkozó, a [6] rodalomba közölt eljárást, amely sorá megállaítottam, hogy a vzsgált mechaka modellbe a rugó tömegéek felét fgyelembe kell ve a mozgó tömegek meghatározásáál.... CSILLAPÍTÓ HATÁSOK VIZSGÁLATA A rezgésbe hozott, majd magára hagyott valóságos redszerek rezgése dővel lecsllaszk, majd meg s szűk. Damka redszerekél a egatív teljesítméyű, eergát emésztő erőket csllaító erőkek, magát a jeleséget csllaításak evezzük. Fgyelembe véve a vzsgált bztoság szele feléítését, működését, valamt a rezgőredszerekkel foglalkozó szakrodalomba általába tárgyalt eseteket [, 7, 6, 8], a továbbakba a következő csllaító hatásokat vzsgálom: Csllaítás sebességgel aráyos erővel (leárs csllaítás, F cs ) Csllaítás álladó erővel (Coulomb-féle súrlódás, F s ) Ezek a hatások agyo eheze követhetők számításokkal a gyakorlatba. Megbízható eredméyeket csak kísérletek alajá kahatuk [7]. A csllaítás közvetle mérése azoba léyegese ehezebb feladat, mt a rezgőredszer több elemére jellemző mérőszámok kísérlet meghatározása. A kísérletekkel meghatározott értékek rerodukálása ezt a következőkbe lát fogjuk szté ehéz feladat a szerkezet elemek súrlódó felületéek mozgása sorá elszevedett károsodása következtébe. A következőkbe a már bemutatott bztoság szele kostrukcót fgyelembe véve, a redszer leárs és Coulomb-féle csllaításat vzsgálom kísérlet módszerekkel.... A leárs csllaítás meghatározása A leárs sebességgel aráyos csllaítás meghatározására a redelkezésre álló beredezésekre tektettel, a szakrodalomba elterjedt rezgető vzsgálatot alkalmaztam. A vzsgálatokat a Mskolc Egyetem Ayagmozgatás és Logsztka Taszék laboratórumába, a Brüel & Kjaer elektrodamkus rezgetőgée végeztem el. A kísérlet beredezés összeállítás vázlatát a.. ábra mutatja. A beredezés két fő részből, a rezgető asztalból és a vezérlő egységből áll. A rezgető asztal elektrodamkus gerjesztésű, cserélhető gerjesztőfejjel. A vezérlő egység a teljesítméyerősítőből (kmeő teljesítméye VA) és a szabályozó geerátorból áll. Az asztal rezgéssztjét az asztalo elhelyezett gyorsulás érzékelő segítségével automatkusa álladó sztre szabályozza. Kézzel, vagy automatkusa vezérelt frekveca áthagolás - Hz tartomáyba lehetséges. A beéített elektrokus tegrátorok segítségével a gyorsulás, a sebesség, vagy az elmozdulás amltúdója a vzsgálat sorá álladó értéke tartható. Az elmozdulás távadó fej duktív, a gyorsulás érzékelő fejek ezoelektromos elve működek.
21 . BIZTONSÁGI SZELEP MECHANIKAI MODELLJÉNEK VIZSGÁLATA Tartószerkezet. Függesztő keret. Bztoság szele. Befogó tárcsa. Egyeértékű mozgó tömeg 6. Erőmérő 7. Közvetítő rúd 8. Fázsszög-mérő beredezés 9. Vezérlő egység. Elmozdulás távadó. Adatgyűjtő egység. Számítógé. Rezgető asztal. Gyorsulásérzékelő.. ábra Kísérlet beredezés leárs csllaítás vzsgálatára A vzsgálatok elvégzéséhez a bztoság szelee bzoyos átalakításokat kellett elvégez. Eltávolítottam a szeleház alsó részét, és az eredet vezetőtárcsát egy, a szeleházcsatlakozás kalakításával megegyező geometrájú befogó tárcsával rögzítettem. A szeletáyért egy vele azoos tömegű hegeres elemmel és az elmozdulás-távadóhoz kyúló szmmetrkus kozollal helyettesítettem, amely az erőmérő egység meetes felső részéhez csatlakozk. A megoldás a bztoság szele mechaka redszerét (tömegeket, egymáso elmozduló alkatrészek kacsolatát) em változtatta meg, ugyaakkor a kísérletek végrehajtását, a jellemzők mérését jeletőse megköyítette. A kísérletről és a műszerekről készült féykéfelvételek a.. és.6. ábráko láthatók... ábra Bztoság szele rezgetővzsgálata.6. ábra A rezgetőberedezés műszerszekréye
22 . BIZTONSÁGI SZELEP MECHANIKAI MODELLJÉNEK VIZSGÁLATA A vzsgálat alaja az, hogy ha a rezgőredszer tömegére álladó amltúdójú, erodkusa változó erő hat, vagy a redszer rugójáak végotját álladó amltúdóval harmokus függvéy szert mozgatjuk, akkor a tömeg gerjesztett rezgéséek elmozdulásamltúdója a gerjesztő hatás frekvecájától függ. Az álladósult állaotokba mért rezgésamltúdót a frekveca függvéyébe ábrázolva rezoaca görbét kauk [6]. Ezzel a módszerrel elvégezve a kísérleteket azt taasztaltam, hogy a redszert F g - N álladó amltúdójú gerjesztőerővel gerjesztve, a rezgés a következő fejezetbe részletese tárgyalt Coulomb-féle súrlódás okozta erőhatás következtébe em dult meg. Ameybe a gerjesztőerő agysága elérte, vagy meghaladta az N-t, a rezgés ugya megdult, de amltúdója túlléte kostrukcóból adódó maxmáls elmozdulás lehetőséget és ütközés jeleségek játszódtak le. Ezért a vzsgálatokat em erő-, haem elmozdulás gerjesztéssel végeztem el, am azt jelet, hogy a rezgető beredezés vezérlése a szeletáyér elmozdulásáak amltúdóját tartotta álladó értéke, mközbe változtatta a gerjesztés frekvecáját. Eek következtébe a szakrodalomba alkalmazott, jeleséget leíró egyeleteket új közelítésbe szükséges tárgyal. A következőkbe megvzsgálom a harmokus függvéy szert gerjesztett egyszabadságfokú, csllaított rezgőredszer mozgását leíró egyeleteket és a rezgetővzsgálat mérés eredméyet felhaszálva meghatározom a redszerre jellemző leárs csllaítás téyező értékét. A vázolt egyszabadságfokú rezgőredszer leárs csllaító eleme olya elem, amelyek tömege elhayagolható a redszer mozgó tömegéhez kéest, és amelyről a mozgó tömegre ható erő az F cs ry! (.) összefüggéssel adható meg. Fgyelembe véve a rezgető asztal által bztosított erodkus gerjesztést, a redszer mozgásegyelete m! y ry! y Fg ( τ ) (.) c alakba írható. Bevezetve az r m β, lletve mc α (.6) jelöléseket, az Fg ( τ )! y β y! α y (.7) m alakot yerjük. Eek az homogé, leárs, másodredű dfferecálegyeletek az általáos megoldása a homogé dfferecálegyelet általáos megoldásáak és az homogé dfferecálegyelet valamely artkulárs megoldásáak összegekét állítható elő, vagys y y hom y. (.8).ált Ameybe a rezgéseket jóval az dítás utá akarjuk vzsgál (amkor a rezgések már álladó amltúdójúakak tekthetők), feltételezhetjük, hogy a megoldás homogé általáos (saját legések) megfelelő része dővel elül. Ilyekor tehát élhetük az y (.9) y h.art egyszerűsítéssel. Ezért a továbbakba csak a (.7) dfferecálegyelet artkulárs megoldását vzsgáljuk. Az elsőredű derváltat s tartalmazó dfferecálegyelet megoldása érdekébe célszerű előbb komlex tárgyalás módra áttér [7]. Vezessük be ezért a z x y (.) komlex ktérést, amelyek kézetes része h.art
23 . BIZTONSÁGI SZELEP MECHANIKAI MODELLJÉNEK VIZSGÁLATA a keresett megoldás. Másrészt vezessük be a komlex gerjesztő erőt s, amelyek kézetes része y Im( z ), (.) y h.art P ( τ ) R ( τ ) F ( τ ) (.) g g g F ( τ ) Im( P ), (.) g a téyleges gerjesztő erő. Feltételezve, hogy az x változóra ugyacsak a (.7) jelűhöz hasoló dfferecálegyelet írható fel, a z változó a P g( τ ) cp g( τ )! z! β z! α z α cp g( τ ) (.) m mc komlex dfferecálegyelet artkulárs megoldásakét yerhető. A harmokus függvéy szert gerjesztés általáos alakja az F ( τ ) F s ψ ωτ (.) kfejezéssel adható meg, amelyek a g g g ( ) ( ψ ωτ ) e P ( τ ) (.6) g ωτ ψ ωτ Pg e Fge e Fg komlex gerjesztő erő felel meg. Ilye gerjesztő függvéy eseté a (.) egyelet artkulárs megoldását ωτ z ( τ ) z e (.7) alakba célszerű keres. Mvel a sebesség és a gyorsulás z ωz e ωτ ωτ! z, és! z ω z e ω z (.8) ω összefüggésekkel adható meg, így a (.) egyelet formába írható fel, amelyből a ωτ ωτ ( α ω βω) z e α cp e (.9) g α cp (.) z g ( α ω ) ( βω ) kfejezés adódk. Fgyelembe véve a (.7) összefüggést, a dfferecálegyelet artkulárs megoldása a komlex számsíko egy ω szögsebességgel forgó, álladó abszolút értékű vektorak tekthető, amelyek kézetes része egybe (.7) artkulárs megoldása harmokus rezgőmozgás lesz. Jelöljük továbbá a (.) kfejezés evezőjéek argumetumát vagys a komlex számsíko z és cp g között szöget γ-val, amely a βω γ ar ctg (.) α ω összefüggéssel számítható. A.7. ábra komlex számsíko mutatja be a fet koordátákat, feltütetve az eredet és a recrok vektorokat s. Im P g z γ γ z Re P g.7. ábra Koordáták a komlex számsíko
24 . BIZTONSÁGI SZELEP MECHANIKAI MODELLJÉNEK VIZSGÁLATA Mvel a rezgetővzsgálatokál kostrukcós okokból a kevésbé elterjedt elmozdulás gerjesztés módszert alkalmazom, a tovább összefüggések a szakrodalomtól eltérő módo tárgyalom. Alakítsuk át a (.) kfejezést, felhaszálva (.6) és (.7) kéleteket szert. Vezessük be az P P c z α ωτ e ωτ g e g ( α ω ) ( βω ). (.) ω ξ és β D (.) α α dmezótla körfrekvecát, lletve Lehr-féle csllaítás téyezőt, amelyekkel a (.) összefüggésből P c z e ωτ g ( ξ ) ( Dξ ) (.) kfejezés adódk. Vzsgáljuk meg részletesebbe a (.) összefüggést. A evezőbe található komlex számot távolítsuk el úgy, hogy a kojugáltjával md a evezőt, md a számlálót megszorozzuk. Ebből az P g c z e ωτ ξ Dξ ( ) ( ) ξ D ξ ξ D ξ. (.) egyeletet yerjük. Írjuk elő, hogy a gerjesztett rezgés erőamltúdójáak recroka valós meység legye. Ekkor c Re ξ, (.6) P g z ( ξ ) D ξ összefüggés adódk, amelyet ábrázolva a.8. ábrá látható görbét kauk. Re P g c z ξ ξ ξ ξ.8. ábra Az erőamltúdó recroka a dmezótla körfrekveca függvéyébe Az erőamltúdó recrokáak valós részét a.7. ábra értelmébe Re P g P g cos() γ, (.7) szert s számíthatjuk, amely összefüggésbe a kísérletek sorá a frekveca függvéyébe rögzített erőamltúdó és fázsszög adatok találhatók. Látható, hogy a görbe a sajátkörfrekveca közelébe két szélsőértékkel redelkezk, amelyeket a (.6) összefüggés ξ szert első derváltjáak zérus értékéél kauk:
25 . BIZTONSÁGI SZELEP MECHANIKAI MODELLJÉNEK VIZSGÁLATA Mvel d Re dξ ( Pg ) c ξ ( ξ ) z ( D ξ ) ( ξ ) ξ ( ξ ) ( ξ ) D ξ ) a (.8) egyelet akkor lesz zérus, ha a tört számlálója Ameybe egyszerűsítések utá összefüggés adódk. Eek megoldása amelyből a két gyök c z ( 8D ξ ). (.8), (.9) ( ξ ) D ξ ) ( ξ )( ξ ( ξ ) 8D ξ ) ξ. (.) ξ, (.) ( ) D ξ (.) ξ ± D, (.) ξ D, ξ D (.) szert számítható. E gyökök smeretébe a Lehr-féle csllaítás téyezőt ξ ξ D (.) kfejezéssel határozhatjuk meg. A leárs csllaítás téyezőt a (.6) és (.) összefüggések segítségével D r β m Dαm (.6) αc egyelet alajá yerjük. A kísérletek sorá a.. ábra szert elredezésbe, két sorozatba hajtottam végre méréseket. Elsőkét,-, mm, majd,-, mm-között elmozdulás-amltúdókkal,, mm-es léésekkel. A gerjesztőfrekvecát Hz-től,, Hz/s álladó sebességgel Hz-g öveltem, mközbe a gerjesztőerő-amltúdót valamt a gerjesztőerő és az elmozdulás között fázsszöget Hz mtavétel sebességgel regsztráltam. A következőkbe az első mérés sorozat eredméyet mutatom be. Külöböző elmozdulásamltúdókál a.9. ábra az erőamltúdót, a.. ábra a fázsszöget mutatja a gerjesztőfrekveca függvéyébe. A.. ábrá az erőamltúdó recrokáak valós része látható a dmezótla körfrekveca függvéyébe. A másodk mérés sorozat eredméye az VI. függelékbe taulmáyozhatók. A.. táblázat a kísérletekből meghatározott adatokat, lletve az ezekből számított értékeket mutatja. Ezek redre az elmozdulás amltúdó ( z ), a sajátkörfrekveca (α),a gerjesztőerő recrokáak reáls részéek mmumáál és maxmumáál leolvasott dmezótla körfrekveca (ξ, ξ ), a Lehr-féle csllaítás téyező (D) és a leárs csllaítás téyező (r). A.. ábra a két mérés sorozatból meghatározott leárs csllaítás adatokat mutatja az elmozdulás-amltúdó függvéyébe.
26 . BIZTONSÁGI SZELEP MECHANIKAI MODELLJÉNEK VIZSGÁLATA 6. mm mm. mm mm. mm mm. mm P g [N] ω [Hz].9. ábra A mért erőamltúdó változása a gerjesztőfrekveca függvéyébe 8. mm mm. mm mm. mm mm. mm 6 ν [fok] ω [Hz].. ábra A mért fázsszög változása a gerjesztőfrekveca függvéyébe,. mm mm. mm mm. mm mm. mm,, Re(/Pg) [/N],, -, -, -,,6,7,8,9,,,, ξ [-].. ábra Az erőamltúdó recrokáak reáls része
2. Az együttműködő villamosenergia-rendszer teljesítmény-egyensúlya
 II RÉZ 2 EJEZE 2 Az együttműködő vllamoseerga-redszer teljesítméy-egyesúlya 2 A frekveca és a hatásos teljesítméy között összefüggés A fogyasztó alredszerbe a fogyasztók hatásos wattos teljesítméyt lletve
II RÉZ 2 EJEZE 2 Az együttműködő vllamoseerga-redszer teljesítméy-egyesúlya 2 A frekveca és a hatásos teljesítméy között összefüggés A fogyasztó alredszerbe a fogyasztók hatásos wattos teljesítméyt lletve
RUGÓTERHELÉSŰ BIZTONSÁGI SZELEP MŰKÖDÉSÉNEK ELMÉLETI ÉS KÍSÉRLETI VIZSGÁLATA
 MISKOLCI EGYETEM GÉPÉSZMÉRNÖKI KAR RUGÓTERHELÉSŰ BIZTONSÁGI SZELEP MŰKÖDÉSÉNEK ELMÉLETI ÉS KÍSÉRLETI VIZSGÁLATA PHD ÉRTEKEZÉS TÉZISEI KÉSZÍTETTE: SIMÉNFALVI ZOLTÁN OKLEVELES GÉPÉSZMÉRNÖK GÉPÉSZMÉRNÖKI
MISKOLCI EGYETEM GÉPÉSZMÉRNÖKI KAR RUGÓTERHELÉSŰ BIZTONSÁGI SZELEP MŰKÖDÉSÉNEK ELMÉLETI ÉS KÍSÉRLETI VIZSGÁLATA PHD ÉRTEKEZÉS TÉZISEI KÉSZÍTETTE: SIMÉNFALVI ZOLTÁN OKLEVELES GÉPÉSZMÉRNÖK GÉPÉSZMÉRNÖKI
VASBETON ÉPÜLETEK MEREVÍTÉSE
 BUDAPET MŰZAK É GAZDAÁGTUDOMÁY EGYETEM Építőmérök Kar Hdak és zerkezetek Taszéke VABETO ÉPÜLETEK MEREVÍTÉE Oktatás segédlet v. Összeállította: Dr. Bód stvá - Dr. Farkas György Dr. Kors Kálmá Budapest,.
BUDAPET MŰZAK É GAZDAÁGTUDOMÁY EGYETEM Építőmérök Kar Hdak és zerkezetek Taszéke VABETO ÉPÜLETEK MEREVÍTÉE Oktatás segédlet v. Összeállította: Dr. Bód stvá - Dr. Farkas György Dr. Kors Kálmá Budapest,.
A pályázat címe: Rugalmas-képlékeny tartószerkezetek topológiai optimalizálásának néhány különleges feladata
 6. év OTKA zárójeletés: Vezető kutató:kalszky Sádor OTKA ylvátartás szám T 4993 A pályázat címe: Rugalmas-képlékey tartószerkezetek topológa optmalzálásáak éháy külöleges feladata (Részletes jeletés) Az
6. év OTKA zárójeletés: Vezető kutató:kalszky Sádor OTKA ylvátartás szám T 4993 A pályázat címe: Rugalmas-képlékey tartószerkezetek topológa optmalzálásáak éháy külöleges feladata (Részletes jeletés) Az
Azonos névleges értékű, hitelesített súlyokból alkotott csoportok együttes mérési bizonytalansága
 Azoos évleges értékű, htelesített súlyokból alkotott csoportok együttes mérés bzoytalasága Zeleka Zoltá* Több mérés feladatál alkalmazak súlyokat. Sokszor ezek em egyekét, haem külöböző társításba kombácókba
Azoos évleges értékű, htelesített súlyokból alkotott csoportok együttes mérés bzoytalasága Zeleka Zoltá* Több mérés feladatál alkalmazak súlyokat. Sokszor ezek em egyekét, haem külöböző társításba kombácókba
Izolált rendszer falai: sem munkavégzés, sem a rendszer állapotának munkavégzés nélküli megváltoztatása nem lehetséges.
 ERMODINMIK I. FÉELE els eergia: megmaraó meyiség egy izolált reszerbe (eergiamegmaraás törvéye) mikroszkóikus kifejezését láttuk Izolált reszer falai: sem mukavégzés sem a reszer állaotáak mukavégzés élküli
ERMODINMIK I. FÉELE els eergia: megmaraó meyiség egy izolált reszerbe (eergiamegmaraás törvéye) mikroszkóikus kifejezését láttuk Izolált reszer falai: sem mukavégzés sem a reszer állaotáak mukavégzés élküli
A paramétereket kísérletileg meghatározott yi értékekre támaszkodva becsülik. Ha n darab kisérletet (megfigyelést, mérést) végeznek, n darab
 öbbváltozós regresszók Paraméterbecslés-. A paraméterbecslés.. A probléma megfogalmazása A paramétereket kísérletleg meghatározott y értékekre támaszkodva becsülk. Ha darab ksérletet (megfgyelést, mérést
öbbváltozós regresszók Paraméterbecslés-. A paraméterbecslés.. A probléma megfogalmazása A paramétereket kísérletleg meghatározott y értékekre támaszkodva becsülk. Ha darab ksérletet (megfgyelést, mérést
Statisztika. Eloszlásjellemzők
 Statsztka Eloszlásjellemzők Statsztka adatok elemzése A sokaság jellemzése középértékekkel A sokaság jellemzéséek szempotja A sokaság jellemzéséek szempotja: A sokaság tpkus értékéek meghatározása. Az
Statsztka Eloszlásjellemzők Statsztka adatok elemzése A sokaság jellemzése középértékekkel A sokaság jellemzéséek szempotja A sokaság jellemzéséek szempotja: A sokaság tpkus értékéek meghatározása. Az
Tartalomjegyzék. 4.3 Alkalmazás: sorozatgyártású tűgörgő átmérőjének jellemzése
 3 4 Tartalomegyzék. BEVEZETÉS 5. A MÉRÉS 8. A mérés mt folyamat, fogalmak 8. Fotosabb mérés- és műszertechka fogalmak 4.3 Mérés hbák 8.3. Mérés hbák csoportosítása eredetük szert 8.3. A hbák megeleítés
3 4 Tartalomegyzék. BEVEZETÉS 5. A MÉRÉS 8. A mérés mt folyamat, fogalmak 8. Fotosabb mérés- és műszertechka fogalmak 4.3 Mérés hbák 8.3. Mérés hbák csoportosítása eredetük szert 8.3. A hbák megeleítés
2.6. Az ideális gáz fundamentális egyenlete
 Fejezetek a fzka kéából.6. Az deáls gáz fudaetáls egyelete A legegyszerűbb terodaka redszer az u. deáls gáz. Erre jellező, hogy a részecskék között az egyetle kölcsöhatás a rugalas ütközés, és a részecskék
Fejezetek a fzka kéából.6. Az deáls gáz fudaetáls egyelete A legegyszerűbb terodaka redszer az u. deáls gáz. Erre jellező, hogy a részecskék között az egyetle kölcsöhatás a rugalas ütközés, és a részecskék
(L) Lamellás szivattyú mérése
 (L) Lamellás szivattyú mérése A mérésre való felkészülés sorá a Hidraulikus tápegység mérésleírás Hidrosztatikus hajtásokról c részét is kérjük elsajátítai 1 A mérés célja, a beredezés ismertetése 11 A
(L) Lamellás szivattyú mérése A mérésre való felkészülés sorá a Hidraulikus tápegység mérésleírás Hidrosztatikus hajtásokról c részét is kérjük elsajátítai 1 A mérés célja, a beredezés ismertetése 11 A
Kényszereknek alávetett rendszerek
 Kéyszerekek alávetett redszerek A koordátákak és sebességekek előírt egyeleteket kell kelégítee a mozgás olyamá. (Ezeket a eltételeket, egyeleteket s ayag kölcsöhatások bztosítják, de ezek a kölcsöhatások
Kéyszerekek alávetett redszerek A koordátákak és sebességekek előírt egyeleteket kell kelégítee a mozgás olyamá. (Ezeket a eltételeket, egyeleteket s ayag kölcsöhatások bztosítják, de ezek a kölcsöhatások
EGY FÁZISÚ TÖBBKOMPONENS RENDSZEREK: AZ ELEGYEK KÉPZDÉSE
 EG FÁZISÚ ÖBBOMPONENS RENDSZERE: AZ ELEGE ÉPZDÉSE AZ ELEGÉPZDÉS ERMODINAMIÁJA: GÁZO Általáos megfotolások ülöböz kéma mség komoesek keveredésekor változás törték a molekulárs kölcsöhatásokba és a molekulák
EG FÁZISÚ ÖBBOMPONENS RENDSZERE: AZ ELEGE ÉPZDÉSE AZ ELEGÉPZDÉS ERMODINAMIÁJA: GÁZO Általáos megfotolások ülöböz kéma mség komoesek keveredésekor változás törték a molekulárs kölcsöhatásokba és a molekulák
GEOFIZIKA / 4. GRAVITÁCIÓS ANOMÁLIÁK PREDIKCIÓJA, ANALITIKAI FOLYTATÁSOK MÓDSZERE, GRAVITÁCIÓS ANOMÁLIATEREK SZŰRÉSE
 MSc GEOFIZIKA / 4. BMEEOAFMFT3 GRAVITÁCIÓS ANOMÁLIÁK REDIKCIÓJA, ANALITIKAI FOLYTATÁSOK MÓDSZERE, GRAVITÁCIÓS ANOMÁLIATEREK SZŰRÉSE A gravtácós aomálák predkcója Külöböző feladatok megoldása sorá - elsősorba
MSc GEOFIZIKA / 4. BMEEOAFMFT3 GRAVITÁCIÓS ANOMÁLIÁK REDIKCIÓJA, ANALITIKAI FOLYTATÁSOK MÓDSZERE, GRAVITÁCIÓS ANOMÁLIATEREK SZŰRÉSE A gravtácós aomálák predkcója Külöböző feladatok megoldása sorá - elsősorba
MATEMATIKA I. KATEGÓRIA (SZAKKÖZÉPISKOLA)
 O k t a t á s i H i v a t a l A 5/6 taévi Országos Középiskolai Taulmáyi Versey első forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató A 5 olya égyjegyű szám, amelyek számjegyei
O k t a t á s i H i v a t a l A 5/6 taévi Országos Középiskolai Taulmáyi Versey első forduló MATEMATIKA I KATEGÓRIA (SZAKKÖZÉPISKOLA) Javítási-értékelési útmutató A 5 olya égyjegyű szám, amelyek számjegyei
8.1. A rezgések szétcsatolása harmonikus közelítésben. Normálrezgések. = =q n és legyen itt a potenciál nulla. q i j. szimmetrikus. q k.
 8. KIS REZGÉSEK STABIL EGYENSÚLYI HELYZET KÖRÜL 8.. A rezgések szétcsatolása harmoikus közelítésbe. Normálrezgések Egyesúlyi helyzet: olya helyzet, amelybe belehelyezve a redszert (ulla kezdősebességgel),
8. KIS REZGÉSEK STABIL EGYENSÚLYI HELYZET KÖRÜL 8.. A rezgések szétcsatolása harmoikus közelítésbe. Normálrezgések Egyesúlyi helyzet: olya helyzet, amelybe belehelyezve a redszert (ulla kezdősebességgel),
ORVOSI STATISZTIKA. Az orvosi statisztika helye. Egyéb példák. Példa: test hőmérséklet. Lehet kérdés? Statisztika. Élettan Anatómia Kémia. Kérdések!
 ORVOSI STATISZTIKA Az orvos statsztka helye Életta Aatóma Kéma Lehet kérdés?? Statsztka! Az orvos dötéseket hoz! Mkor jó egy dötés? Meyre helyes egy dötés? Mekkora a tévedés lehetősége? Példa: test hőmérséklet
ORVOSI STATISZTIKA Az orvos statsztka helye Életta Aatóma Kéma Lehet kérdés?? Statsztka! Az orvos dötéseket hoz! Mkor jó egy dötés? Meyre helyes egy dötés? Mekkora a tévedés lehetősége? Példa: test hőmérséklet
REOIL. növeli a transzformátorok élettartamát. www.ekofluid.sk/hu/
 5 öveli a traszformátorok öveli a traszformátorok A techológia előyei A költségek csökketéseek folyamatos kéyszere és a zavartala eergiaellátás ehézségei szükségessé teszik a traszformátorok tervezett
5 öveli a traszformátorok öveli a traszformátorok A techológia előyei A költségek csökketéseek folyamatos kéyszere és a zavartala eergiaellátás ehézségei szükségessé teszik a traszformátorok tervezett
Adatfeldolgozás, adatértékelés. Dr. Szűcs Péter, Dr. Madarász Tamás Miskolci Egyetem, Hidrogeológiai Mérnökgeológiai Tanszék
 Adatfeldolgozás, adatértékelés Dr. Szűcs Péter, Dr. Madarász Tamás Mskolc Egyetem, Hdrogeológa Mérökgeológa Taszék A vzsgált köryezet elemek, lletve a felszí alatt közeg megsmerése céljából számtala külöböző
Adatfeldolgozás, adatértékelés Dr. Szűcs Péter, Dr. Madarász Tamás Mskolc Egyetem, Hdrogeológa Mérökgeológa Taszék A vzsgált köryezet elemek, lletve a felszí alatt közeg megsmerése céljából számtala külöböző
Mit nevezünk nehézségi erőnek?
 Mit nevezünk nehézségi erőnek? Azt az erőt, amelynek hatására a szabadon eső testek g (gravitációs) gyorsulással esnek a vonzó test centruma felé, nevezzük nehézségi erőnek. F neh = m g Mi a súly? Azt
Mit nevezünk nehézségi erőnek? Azt az erőt, amelynek hatására a szabadon eső testek g (gravitációs) gyorsulással esnek a vonzó test centruma felé, nevezzük nehézségi erőnek. F neh = m g Mi a súly? Azt
A statisztikai vizsgálat tárgyát képező egyedek összességét statisztikai sokaságnak nevezzük.
 Statisztikai módszerek. BMEGEVGAT01 Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudomáyi Egyetem Gépészméröki Kar Hidrodiamikai Redszerek Taszék 1111, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
Statisztikai módszerek. BMEGEVGAT01 Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudomáyi Egyetem Gépészméröki Kar Hidrodiamikai Redszerek Taszék 1111, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
Piacmeghatározás. Hipotetikus monopolista teszt. Hipotetikus monopolista teszt alkalmazása. Hipotetikus monopolista teszt alkalmazása
 Moder iacelmélet Moder iacelmélet A iaci erő mérése ELTE TáTK Közgazdaságtudomáyi Taszék Selei Adrie ELTE TáTK Közgazdaságtudomáyi Taszék Készítette: Hidi Jáos A taayag a Gazdasági Verseyhivatal Verseykultúra
Moder iacelmélet Moder iacelmélet A iaci erő mérése ELTE TáTK Közgazdaságtudomáyi Taszék Selei Adrie ELTE TáTK Közgazdaságtudomáyi Taszék Készítette: Hidi Jáos A taayag a Gazdasági Verseyhivatal Verseykultúra
Mechanika I-II. Példatár
 Budapesti Műszaki és Gazdaságtudományi Egyetem Műszaki Mechanika Tanszék Mechanika I-II. Példatár 2012. május 24. Előszó A példatár célja, hogy támogassa a mechanika I. és mechanika II. tárgy oktatását
Budapesti Műszaki és Gazdaságtudományi Egyetem Műszaki Mechanika Tanszék Mechanika I-II. Példatár 2012. május 24. Előszó A példatár célja, hogy támogassa a mechanika I. és mechanika II. tárgy oktatását
Átfolyó-rendszerű gázvízmelegítő teljesítményének és hatásfokának meghatározása Gazdaságossági számításokhoz
 Átfolyó-redszerű gázvízmelegítő teljesítméyéek és hatásfokáak meghatározása Gazdaságossági számításokhoz Szuyog Istvá 005 Készült az OTKA T-0464 kutatási projekt keretébe A Gázipari oktatási laboratórium
Átfolyó-redszerű gázvízmelegítő teljesítméyéek és hatásfokáak meghatározása Gazdaságossági számításokhoz Szuyog Istvá 005 Készült az OTKA T-0464 kutatási projekt keretébe A Gázipari oktatási laboratórium
Reakciómechanizmusok leírása. Paraméterek. Reakciókinetikai bizonytalanságanalízis. Bizonytalanságanalízis
 Megbízható kémiai modellek kifejlesztése sok mérési adat egyidejő feldolgozása alajá uráyi amás www.turayi.eu ELE Kémiai Itézet Reakciókietikai Laboratórium Eddig dolgoztak eze a témá: (témavezetık: uráyi
Megbízható kémiai modellek kifejlesztése sok mérési adat egyidejő feldolgozása alajá uráyi amás www.turayi.eu ELE Kémiai Itézet Reakciókietikai Laboratórium Eddig dolgoztak eze a témá: (témavezetık: uráyi
Cserjésné Sutyák Ágnes *, Szilágyiné Biró Andrea ** ismerete mellett több kísérleti és empirikus képletet fel-
 ACÉLOK KÉMIAI LITY OF STEELS THROUGH Cserjésé Sutyák Áges *, Szilágyié Biró Adrea ** beig s s 1. E kutatás célja, hogy képet meghatározásáak kísérleti és számítási móiek tosságáról, és ezzel felfedjük
ACÉLOK KÉMIAI LITY OF STEELS THROUGH Cserjésé Sutyák Áges *, Szilágyié Biró Adrea ** beig s s 1. E kutatás célja, hogy képet meghatározásáak kísérleti és számítási móiek tosságáról, és ezzel felfedjük
Megoldás a, A sebességből és a hullámhosszból számított periódusidőket T a táblázat
 Fzka feladatok: F.1. Cuam A cuam hullám formájáak változása, ahogy a sekélyebb víz felé mozog (OAA) (https://www.wdowsuverse.org/?page=/earth/tsuam1.html) Az ábra, táblázat a cuam egyes jellemzőt tartalmazza.
Fzka feladatok: F.1. Cuam A cuam hullám formájáak változása, ahogy a sekélyebb víz felé mozog (OAA) (https://www.wdowsuverse.org/?page=/earth/tsuam1.html) Az ábra, táblázat a cuam egyes jellemzőt tartalmazza.
A II. kategória Fizika OKTV mérési feladatainak megoldása
 Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
= λ valós megoldása van.
 Másodredű álladó együtthatós lieáris differeciálegyelet. Általáos alakja: y + a y + by= q Ha q = 0 Ha q 0 akkor homogé lieárisak evezzük. akkor ihomogé lieárisak evezzük. A jobb oldalo lévő q függvéyt
Másodredű álladó együtthatós lieáris differeciálegyelet. Általáos alakja: y + a y + by= q Ha q = 0 Ha q 0 akkor homogé lieárisak evezzük. akkor ihomogé lieárisak evezzük. A jobb oldalo lévő q függvéyt
13. Tárcsák számítása. 1. A felületszerkezetek. A felületszerkezetek típusai
 Tárcsák számítása A felületszerkezetek A felületszerkezetek típusa A tartószerkezeteket geometra méretek alapjá osztálozzuk Az eddg taulmáakba szereplı rúdszerkezetek rúdjara az a jellemzı hog a hosszuk
Tárcsák számítása A felületszerkezetek A felületszerkezetek típusa A tartószerkezeteket geometra méretek alapjá osztálozzuk Az eddg taulmáakba szereplı rúdszerkezetek rúdjara az a jellemzı hog a hosszuk
A kommutáció elve. Gyűrűs tekercselésű forgórész. Gyűrűs tekercselésű kommutátoros forgórész
 Egyeáramú gépek 008 É É É + Φp + Φp + Φp - - - D D D A kommutáció elve Gyűrűs tekercselésű forgórész Gyűrűs tekercselésű kommutátoros forgórész 1 Egyeáramú gép forgórésze a) b) A feszültség időbeli változása
Egyeáramú gépek 008 É É É + Φp + Φp + Φp - - - D D D A kommutáció elve Gyűrűs tekercselésű forgórész Gyűrűs tekercselésű kommutátoros forgórész 1 Egyeáramú gép forgórésze a) b) A feszültség időbeli változása
Függvénygörbe alatti terület a határozott integrál
 Függvéygörbe alatt terület a határozott tegrál Tektsük az üggvéyt a ; tervallumo. Adjuk becslést a görbe az tegely és az egyees között síkdom területére! Jelöljük ezt a területet I-vel! A becslést legegyszerűbbe
Függvéygörbe alatt terület a határozott tegrál Tektsük az üggvéyt a ; tervallumo. Adjuk becslést a görbe az tegely és az egyees között síkdom területére! Jelöljük ezt a területet I-vel! A becslést legegyszerűbbe
Labormérések minimumkérdései a B.Sc képzésben
 Labormérések mmumkérdése a B.Sc képzésbe 1. Ismertesse a levegő sűrűség meghatározásáak módját a légyomás és a levegő hőmérséklet alapjá! Adja meg a képletbe szereplő meységek jeletését és mértékegységét!
Labormérések mmumkérdése a B.Sc képzésbe 1. Ismertesse a levegő sűrűség meghatározásáak módját a légyomás és a levegő hőmérséklet alapjá! Adja meg a képletbe szereplő meységek jeletését és mértékegységét!
i 0 egyébként ábra. Negyedfokú és ötödfokú Bernstein polinomok a [0,1] intervallumon.
![i 0 egyébként ábra. Negyedfokú és ötödfokú Bernstein polinomok a [0,1] intervallumon. i 0 egyébként ábra. Negyedfokú és ötödfokú Bernstein polinomok a [0,1] intervallumon.](/thumbs/93/111989735.jpg) 3. Bézer görbék 3.1. A Berste polomok 3.1. Defícó. Legye emegatív egész, tetszőleges egész. A ( ) B (u) = u (1 u) polomot Berste polomak evezzük, ahol ( ) = {!!( )! 0, 0 egyébkét. A defícóból közvetleül
3. Bézer görbék 3.1. A Berste polomok 3.1. Defícó. Legye emegatív egész, tetszőleges egész. A ( ) B (u) = u (1 u) polomot Berste polomak evezzük, ahol ( ) = {!!( )! 0, 0 egyébkét. A defícóból közvetleül
(A TÁMOP /2/A/KMR számú projekt keretében írt egyetemi jegyzetrészlet):
 A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
A umerikus sorozatok fogalma, határértéke (A TÁMOP-4-8//A/KMR-9-8 számú projekt keretébe írt egyetemi jegyzetrészlet): Koverges és diverges sorozatok Defiíció: A természetes számoko értelmezett N R sorozatokak
Fűtési rendszerek hidraulikai méretezése. Baumann Mihály adjunktus Lenkovics László tanársegéd PTE MIK Gépészmérnök Tanszék
 Fűtési rendszerek hidraulikai méretezése Baumann Mihály adjunktus Lenkovics László tanársegéd PTE MIK Gépészmérnök Tanszék Hidraulikai méretezés lépései 1. A hálózat kialakítása, alaprajzok, függőleges
Fűtési rendszerek hidraulikai méretezése Baumann Mihály adjunktus Lenkovics László tanársegéd PTE MIK Gépészmérnök Tanszék Hidraulikai méretezés lépései 1. A hálózat kialakítása, alaprajzok, függőleges
Hangfrekvenciás mechanikai rezgések vizsgálata
 Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
2.10. Az elegyek termodinamikája
 Kéma termodamka.1. z elegyek termodamkája fzka kéma több féle elegyekkel foglakozk, kezdve az deáls elegyektől a reáls elegyekg. Ha az deáls elegyek esetébe az alkotók közt kölcsöhatásokat elhayagoljuk,
Kéma termodamka.1. z elegyek termodamkája fzka kéma több féle elegyekkel foglakozk, kezdve az deáls elegyektől a reáls elegyekg. Ha az deáls elegyek esetébe az alkotók közt kölcsöhatásokat elhayagoljuk,
A szórások vizsgálata. Az F-próba. A döntés. Az F-próba szabadsági fokai
 05..04. szórások vizsgálata z F-próba Hogya foguk hozzá? Nullhipotézis: a két szórás azoos, az eltérés véletle (mitavétel). ullhipotézishez tartozik egy ú. F-eloszlás. Szabadsági fokok: számláló: - evező:
05..04. szórások vizsgálata z F-próba Hogya foguk hozzá? Nullhipotézis: a két szórás azoos, az eltérés véletle (mitavétel). ullhipotézishez tartozik egy ú. F-eloszlás. Szabadsági fokok: számláló: - evező:
Feladatok és megoldások a 11. heti gyakorlathoz
 Feladatok és megoldások a. het gyakorlathoz dszkrét várható érték Építőkar Matematka A. Egy verseye öt ő és öt férf verseyző dul. Tegyük fel, hogy cs két azoos eredméy, és md a 0! sorred egyformá valószíű.
Feladatok és megoldások a. het gyakorlathoz dszkrét várható érték Építőkar Matematka A. Egy verseye öt ő és öt férf verseyző dul. Tegyük fel, hogy cs két azoos eredméy, és md a 0! sorred egyformá valószíű.
Rugalmas állandók mérése
 Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Mérnöki alapok 5. előadás
 Mérnök alapok 5. előadás Készítette: dr. Várad Sándor Budapest Műszak és Gazdaságtudomán Egetem Gépészmérnök Kar Hdrodnamka Rendszerek Tanszék, Budapest, Műegetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9
Mérnök alapok 5. előadás Készítette: dr. Várad Sándor Budapest Műszak és Gazdaságtudomán Egetem Gépészmérnök Kar Hdrodnamka Rendszerek Tanszék, Budapest, Műegetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9
Gépészmérnöki alapszak, Mérnöki fizika ZH, október 10.. CHFMAX. Feladatok (maximum 3x6 pont=18 pont)
 1. 2. 3. Mondat E1 E2 Gépészmérnöki alapszak, Mérnöki fizika ZH, 2017. október 10.. CHFMAX NÉV: Neptun kód: Aláírás: g=10 m/s 2 Előadó: Márkus / Varga Feladatok (maximum 3x6 pont=18 pont) 1) Az l hosszúságú
1. 2. 3. Mondat E1 E2 Gépészmérnöki alapszak, Mérnöki fizika ZH, 2017. október 10.. CHFMAX NÉV: Neptun kód: Aláírás: g=10 m/s 2 Előadó: Márkus / Varga Feladatok (maximum 3x6 pont=18 pont) 1) Az l hosszúságú
Nevezetes sorozat-határértékek
 Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
Nevezetes sorozat-határértékek. Mide pozitív racioális r szám eseté! / r 0 és! r +. Bizoyítás. Jelöljük p-vel, illetve q-val egy-egy olya pozitív egészt, melyekre p/q r, továbbá legye ε tetszőleges pozitív
INNOVÁCIÓ. Eszközök, környezet, Fejlesztési ötletek, variációs paraméterek. Kísérletterv kidolgozás. Konstrukciós elvárások megoldási ötletek
 Termékjellemzők optmalzálásáál haszálatos formácós módszerta 1 Bevezetés Koczor Zoltá, Némethé Erdőd Katal, Kertész Zoltá, Szecz Péter Óbuda Egyetem, RKK, Mőségráyítás és Techológa Szakcsoport Napjak aktuáls
Termékjellemzők optmalzálásáál haszálatos formácós módszerta 1 Bevezetés Koczor Zoltá, Némethé Erdőd Katal, Kertész Zoltá, Szecz Péter Óbuda Egyetem, RKK, Mőségráyítás és Techológa Szakcsoport Napjak aktuáls
? közgazdasági statisztika
 Valószíűségszámítás és a statsztka Valószíűség számítás Matematka statsztka Alkalmazott statsztka? közgazdaság statsztka épesség statsztka orvos statsztka Stb. Példa: vércsoportok Az eloszlás A AB B Elem
Valószíűségszámítás és a statsztka Valószíűség számítás Matematka statsztka Alkalmazott statsztka? közgazdaság statsztka épesség statsztka orvos statsztka Stb. Példa: vércsoportok Az eloszlás A AB B Elem
Hipotézis vizsgálatok. Egy példa. Hipotézisek. A megfigyelt változó eloszlása Kérdés: Hatásos a lázcsillapító gyógyszer?
 01.09.18. Hpotézs vzsgálatok Egy példa Kérdések (példa) Hogyan adhatunk választ? Kérdés: Hatásos a lázcsllapító gyógyszer? Hatásos-e a gyógyszer?? rodalomból kísérletekből Hpotézsek A megfgyelt változó
01.09.18. Hpotézs vzsgálatok Egy példa Kérdések (példa) Hogyan adhatunk választ? Kérdés: Hatásos a lázcsllapító gyógyszer? Hatásos-e a gyógyszer?? rodalomból kísérletekből Hpotézsek A megfgyelt változó
Szemmegoszlási jellemzők
 Szemmegoszlási jellemzők Németül: Agolul: Charakteristike er Korgrößeverteilug Characteristics of particle size istributio Fraciául: Caractéristique e compositio graulométrique Kutatási, fejlesztési és
Szemmegoszlási jellemzők Németül: Agolul: Charakteristike er Korgrößeverteilug Characteristics of particle size istributio Fraciául: Caractéristique e compositio graulométrique Kutatási, fejlesztési és
A figurális számokról (IV.)
 A figurális számokról (IV.) Tuzso Zoltá, Székelyudvarhely A továbbiakba külöféle számkombiációk és összefüggések reprezetálásáról, és bizoyos összegek kiszámolásáról íruk. Sajátos összefüggések Az elekbe
A figurális számokról (IV.) Tuzso Zoltá, Székelyudvarhely A továbbiakba külöféle számkombiációk és összefüggések reprezetálásáról, és bizoyos összegek kiszámolásáról íruk. Sajátos összefüggések Az elekbe
Az átlagra vonatkozó megbízhatósági intervallum (konfidencia intervallum)
 Az átlagra voatkozó megbízhatósági itervallum (kofidecia itervallum) Határozzuk meg körül azt az itervallumot amibe előre meghatározott valószíűséggel esik a várható érték (µ). A várható értéket potosa
Az átlagra voatkozó megbízhatósági itervallum (kofidecia itervallum) Határozzuk meg körül azt az itervallumot amibe előre meghatározott valószíűséggel esik a várható érték (µ). A várható értéket potosa
Hely és elmozdulás - meghatározás távolságméréssel
 Hely és elmozdulás - meghatározás távolságméréssel Bevezetés A repülő szerkezetek repülőgépek, rakéták, stb. helyének ( koordnátának ) meghatározása nem új feladat. Ezt a szakrodalom részletesen taglalja
Hely és elmozdulás - meghatározás távolságméréssel Bevezetés A repülő szerkezetek repülőgépek, rakéták, stb. helyének ( koordnátának ) meghatározása nem új feladat. Ezt a szakrodalom részletesen taglalja
Hiba! Nincs ilyen stílusú szöveg a dokumentumban.-86. ábra: A példa-feladat kódolási változatai
 közzétéve a szerző egedélyével) Öfüggő szekuder-változó csoport keresése: egy bevezető példa Ez a módszer az állapothalmazo értelmezett partíció-párok elméleté alapul. E helye em lehet céluk az elmélet
közzétéve a szerző egedélyével) Öfüggő szekuder-változó csoport keresése: egy bevezető példa Ez a módszer az állapothalmazo értelmezett partíció-párok elméleté alapul. E helye em lehet céluk az elmélet
5. SZABAD PONTRENDSZEREK MECHANIKAI ALAPELVEI, N-TESTPROBLÉMA, GALILEI-
 5. SZABAD PONTRENDSZEREK MECHANIKAI ALAPELVEI, N-TESTPROBLÉMA, GALILEI- FÉLE RELATIVITÁSI ELV m, m,,m r, r,,r r, r,, r 6 db oordáta és sebességompoes 5.. Dama Mozgásegyelete: m r = F F, ahol F jelöl a
5. SZABAD PONTRENDSZEREK MECHANIKAI ALAPELVEI, N-TESTPROBLÉMA, GALILEI- FÉLE RELATIVITÁSI ELV m, m,,m r, r,,r r, r,, r 6 db oordáta és sebességompoes 5.. Dama Mozgásegyelete: m r = F F, ahol F jelöl a
(1) Milyen esetben beszélünk tartós nyugalomról? Abban az esetben, ha a (vizsgált) test a helyzetét hosszabb időn át nem változtatja meg.
 SZÉCHENYI ISTVÁN EGYETEM MECHNIK - STTIK LKLMZTT MECHNIK TNSZÉK Elmélet kérdések és válaszok egetem alapképzésbe (Sc képzésbe) résztvevő mérökhallgatók számára () Mle esetbe beszélük tartós ugalomról?
SZÉCHENYI ISTVÁN EGYETEM MECHNIK - STTIK LKLMZTT MECHNIK TNSZÉK Elmélet kérdések és válaszok egetem alapképzésbe (Sc képzésbe) résztvevő mérökhallgatók számára () Mle esetbe beszélük tartós ugalomról?
ALGEBRA. egyenlet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 198.
 ALGEBRA MÁSODFOKÚ POLINOMOK. Határozzuk meg az + p + q = 0 egyelet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 98.. Határozzuk meg az összes olya pozitív egész p és q számot, amelyre az
ALGEBRA MÁSODFOKÚ POLINOMOK. Határozzuk meg az + p + q = 0 egyelet megoldásait, ha tudjuk, hogy egész számok, továbbá p + q = 98.. Határozzuk meg az összes olya pozitív egész p és q számot, amelyre az
A MATEMATIKAI STATISZTIKA ELEMEI
 A MATEMATIKAI STATISZTIKA ELEMEI Az Eötvös Lórád Tudomáyegyetem Természettudomáy Kará a Fzka Kéma Taszék évek óta kéma-szakos taárhallgatókak matematka bevezetõ elõadásokat tart. Az elõadások célja az,
A MATEMATIKAI STATISZTIKA ELEMEI Az Eötvös Lórád Tudomáyegyetem Természettudomáy Kará a Fzka Kéma Taszék évek óta kéma-szakos taárhallgatókak matematka bevezetõ elõadásokat tart. Az elõadások célja az,
3. Gyakorlat Áramlástani feladatok és megoldásuk
 3 Gyakorlat Áramlástani feladatok és megoldásuk 681 Feladat Adja meg Kelvin és Fahrenheit fokban a T = + 73 = 318 K o K T C, T = 9 5 + 3 = 113Fo F T C 68 Feladat Adja meg Kelvin és Celsius fokban a ( T
3 Gyakorlat Áramlástani feladatok és megoldásuk 681 Feladat Adja meg Kelvin és Fahrenheit fokban a T = + 73 = 318 K o K T C, T = 9 5 + 3 = 113Fo F T C 68 Feladat Adja meg Kelvin és Celsius fokban a ( T
Ismérvek közötti kapcsolatok szorosságának vizsgálata. 1. Egy kis ismétlés: mérési skálák (Hunyadi-Vita: Statisztika I. 25-26. o)
 Ismérvek között kapcsolatok szorosságáak vzsgálata 1. Egy ks smétlés: mérés skálák (Huyad-Vta: Statsztka I. 5-6. o) A külöböző smérveket, eltérő mérés sztekkel (skálákkal) ellemezhetük. a. évleges (omáls)
Ismérvek között kapcsolatok szorosságáak vzsgálata 1. Egy ks smétlés: mérés skálák (Huyad-Vta: Statsztka I. 5-6. o) A külöböző smérveket, eltérő mérés sztekkel (skálákkal) ellemezhetük. a. évleges (omáls)
AZ OPTIMÁLIS MINTANAGYSÁG A KAPCSOLÓDÓ KÖLTSÉGEK ÉS BEVÉTELEK RELÁCIÓJÁBAN
 AZ OPTIMÁLIS MINTANAGYSÁG A KAPCSOLÓDÓ KÖLTSÉGEK ÉS BEVÉTELEK RELÁCIÓJÁBAN Molár László Ph.D. hallgató Mskolc Egyetem, Gazdaságelmélet Itézet 1. A MINTANAGYSÁG MEGHATÁROZÁSA EGYSZERŐ VÉLETLEN (EV) MINTA
AZ OPTIMÁLIS MINTANAGYSÁG A KAPCSOLÓDÓ KÖLTSÉGEK ÉS BEVÉTELEK RELÁCIÓJÁBAN Molár László Ph.D. hallgató Mskolc Egyetem, Gazdaságelmélet Itézet 1. A MINTANAGYSÁG MEGHATÁROZÁSA EGYSZERŐ VÉLETLEN (EV) MINTA
Egyedi cölöp függőleges teherbírásának számítása
 13. számú mérnöki kézikönyv Frissítve: 2013. árilis Egyedi cölö függőleges teherbírásának számítása Program: Fájl: Cölö Demo_manual_13.gi Ennek a mérnöki kézikönyvnek a célja, egy egyedi cölö függőleges
13. számú mérnöki kézikönyv Frissítve: 2013. árilis Egyedi cölö függőleges teherbírásának számítása Program: Fájl: Cölö Demo_manual_13.gi Ennek a mérnöki kézikönyvnek a célja, egy egyedi cölö függőleges
A matematikai statisztika elemei
 A matematikai statisztika elemei Mikó Teréz, dr. Szalkai Istvá szalkai@almos.ui-pao.hu Pao Egyetem, Veszprém 2014. március 23. 2 Tartalomjegyzék Tartalomjegyzék 3 Bevezetés................................
A matematikai statisztika elemei Mikó Teréz, dr. Szalkai Istvá szalkai@almos.ui-pao.hu Pao Egyetem, Veszprém 2014. március 23. 2 Tartalomjegyzék Tartalomjegyzék 3 Bevezetés................................
MÉRÉSTECHNIKA. DR. HUBA ANTAL c. egy. tanár BME Mechatronika, Optika és Gépészeti Informatika Tanszék 2011
 MÉRÉSTECHNIKA DR. HUBA ANTAL c. egy. taár BME Mechatroka, Optka és Gépészet Iformatka Taszék 0 Rövde a tárgyprogramról Előadások tematkája: Metrológa és műszertechka alapok Mérés adatok kértékelése Időbe
MÉRÉSTECHNIKA DR. HUBA ANTAL c. egy. taár BME Mechatroka, Optka és Gépészet Iformatka Taszék 0 Rövde a tárgyprogramról Előadások tematkája: Metrológa és műszertechka alapok Mérés adatok kértékelése Időbe
W = F s A munka származtatott, előjeles skalármennyiség.
 Ha az erő és az elmozdulás egymásra merőleges, akkor fizikai értelemben nem történik munkavégzés. Pl.: ha egy táskát függőlegesen tartunk, és úgy sétálunk, akkor sem a tartóerő, sem a nehézségi erő nem
Ha az erő és az elmozdulás egymásra merőleges, akkor fizikai értelemben nem történik munkavégzés. Pl.: ha egy táskát függőlegesen tartunk, és úgy sétálunk, akkor sem a tartóerő, sem a nehézségi erő nem
Pókháló-entrópia mint új rendszervizsgálati megközelítés a területi elemzésekben
 DR. GODA PÁL DR. TÓTH TAMÁS Pókháló-etróa mt ú redszervzsgálat megközelítés a terület elemzésekbe Gyakra szembesülük azzal a kérdéssel, hogy mtől lesz egy felesztés stratéga fetartható. Mt s elet a fetarthatóság,
DR. GODA PÁL DR. TÓTH TAMÁS Pókháló-etróa mt ú redszervzsgálat megközelítés a terület elemzésekbe Gyakra szembesülük azzal a kérdéssel, hogy mtől lesz egy felesztés stratéga fetartható. Mt s elet a fetarthatóság,
Egyenáramú motor kaszkád szabályozása
 Egyeáramú motor kazkád zabályozáa. gyakorlat élja z egyeáramú motor modellje alajá kazkád zabályozó terezée. zabályozá kör feléítée Smulk köryezetbe. zmuláó eredméyek feldolgozáa.. Elmélet beezet a az
Egyeáramú motor kazkád zabályozáa. gyakorlat élja z egyeáramú motor modellje alajá kazkád zabályozó terezée. zabályozá kör feléítée Smulk köryezetbe. zmuláó eredméyek feldolgozáa.. Elmélet beezet a az
Segédlet az ADCA szabályzó szelepekhez
 Segédlet az ADCA szabályzó szelepekhez Gőz, kondenzszerelvények és berendezések A SZELEP MÉRETEZÉSE A szelepek méretezése a Kv érték számítása alapján történik. A Kv érték azt a vízmennyiséget jelenti
Segédlet az ADCA szabályzó szelepekhez Gőz, kondenzszerelvények és berendezések A SZELEP MÉRETEZÉSE A szelepek méretezése a Kv érték számítása alapján történik. A Kv érték azt a vízmennyiséget jelenti
Regresszió és korreláció
 Regresszó és korrelácó regresso: vsszatérés, hátrálás; vsszafordulás correlato: vszo, összefüggés, kölcsöösség KAD 01.11.1 1 (vsszatérés, hátrálás; vsszafordulás) Regresszó és korrelácó Gakorlat megközelítés
Regresszó és korrelácó regresso: vsszatérés, hátrálás; vsszafordulás correlato: vszo, összefüggés, kölcsöösség KAD 01.11.1 1 (vsszatérés, hátrálás; vsszafordulás) Regresszó és korrelácó Gakorlat megközelítés
Egyenáramú szervomotor modellezése
 Egyenáramú szervomotor modellezése. A gyakorlat élja: Az egyenáramú szervomotor mködését leíró modell meghatározása. A modell valdálása számításokkal és szotverejlesztéssel katalógsadatok alapján.. Elmélet
Egyenáramú szervomotor modellezése. A gyakorlat élja: Az egyenáramú szervomotor mködését leíró modell meghatározása. A modell valdálása számításokkal és szotverejlesztéssel katalógsadatok alapján.. Elmélet
Hőtan I. főtétele tesztek
 Hőtan I. főtétele tesztek. álassza ki a hamis állítást! a) A termodinamika I. főtétele a belső energia változása, a hőmennyiség és a munka között állaít meg összefüggést. b) A termodinamika I. főtétele
Hőtan I. főtétele tesztek. álassza ki a hamis állítást! a) A termodinamika I. főtétele a belső energia változása, a hőmennyiség és a munka között állaít meg összefüggést. b) A termodinamika I. főtétele
Mérnöki alapok 2. előadás
 Mérnöki alapok. előadás Készítette: dr. Váradi Sándor Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék 1111, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
Mérnöki alapok. előadás Készítette: dr. Váradi Sándor Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék 1111, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
NYOMÁS ÉS NYOMÁSKÜLÖNBSÉG MÉRÉS. Mérési feladatok
 Hidrodinamikai Rendszerek Tanszék Készítette:... kurzus Elfogadva: Dátum:...év...hó...nap NYOMÁS ÉS NYOMÁSKÜLÖNBSÉG MÉRÉS Mérési feladatok 1. Csővezetékben áramló levegő nyomásveszteségének mérése U-csöves
Hidrodinamikai Rendszerek Tanszék Készítette:... kurzus Elfogadva: Dátum:...év...hó...nap NYOMÁS ÉS NYOMÁSKÜLÖNBSÉG MÉRÉS Mérési feladatok 1. Csővezetékben áramló levegő nyomásveszteségének mérése U-csöves
Backtrack módszer (1.49)
 Backtrack módszer A backtrack módszer kombatorkus programozás eljárás, mely emleárs függvéy mmumát keres feltételek mellett, szsztematkus kereséssel. A módszer előye, hogy csak dszkrét változókat kezel,
Backtrack módszer A backtrack módszer kombatorkus programozás eljárás, mely emleárs függvéy mmumát keres feltételek mellett, szsztematkus kereséssel. A módszer előye, hogy csak dszkrét változókat kezel,
Komplex számok. d) Re(z 4 ) = 0, Im(z 4 ) = 1 e) Re(z 5 ) = 0, Im(z 5 ) = 2 f) Re(z 6 ) = 1, Im(z 6 ) = 0
 Komplex számok 1 Adjuk meg az alábbi komplex számok valós, illetve képzetes részét: a + i b i c z d z i e z 5 i f z 1 A z a + bi komplex szám valós része: Rez a, képzetes része Imz b Ez alapjá a megoldások
Komplex számok 1 Adjuk meg az alábbi komplex számok valós, illetve képzetes részét: a + i b i c z d z i e z 5 i f z 1 A z a + bi komplex szám valós része: Rez a, képzetes része Imz b Ez alapjá a megoldások
? közgazdasági statisztika
 ... Valószíűségszámítás és a statsztka Valószíűség számítás Matematka statsztka Alkalmazott statsztka? közgazdaság statsztka épesség statsztka orvos statsztka Stb. Példa: vércsoportok Az eloszlás A AB
... Valószíűségszámítás és a statsztka Valószíűség számítás Matematka statsztka Alkalmazott statsztka? közgazdaság statsztka épesség statsztka orvos statsztka Stb. Példa: vércsoportok Az eloszlás A AB
Mechanikai rezgések Ismétlő kérdések és feladatok Kérdések
 Mechanikai rezgések Ismétlő kérdések és feladatok Kérdések 1. Melyek a rezgőmozgást jellemző fizikai mennyiségek?. Egy rezgés során mely helyzetekben maximális a sebesség, és mikor a gyorsulás? 3. Milyen
Mechanikai rezgések Ismétlő kérdések és feladatok Kérdések 1. Melyek a rezgőmozgást jellemző fizikai mennyiségek?. Egy rezgés során mely helyzetekben maximális a sebesség, és mikor a gyorsulás? 3. Milyen
Járműelemek. Rugók. 1 / 27 Fólia
 Rugók 1 / 27 Fólia 1. Rugók funkciója A rugók a gépeknek és szerkezeteknek olyan különleges elemei, amelyek nagy (ill. korlátozott) alakváltozás létrehozására alkalmasak. Az alakváltozás, szemben más szerkezeti
Rugók 1 / 27 Fólia 1. Rugók funkciója A rugók a gépeknek és szerkezeteknek olyan különleges elemei, amelyek nagy (ill. korlátozott) alakváltozás létrehozására alkalmasak. Az alakváltozás, szemben más szerkezeti
Energetikai gazdaságtan 3. gyakorlat Gazdasági mutatók
 Eergetk gzdságt 3. gykorlt Gzdság muttók GAZDASÁGTAN, PÉNZÜGY JELLEMZŐK A gykorlt célj, hogy hllgtók A. elsjátítsák gzdálkodásb szokásos pézügytechk meységek között összefüggéseket; B. egyszerű gzdságosság
Eergetk gzdságt 3. gykorlt Gzdság muttók GAZDASÁGTAN, PÉNZÜGY JELLEMZŐK A gykorlt célj, hogy hllgtók A. elsjátítsák gzdálkodásb szokásos pézügytechk meységek között összefüggéseket; B. egyszerű gzdságosság
MINTAVÉTEL A MARKETINGKUTATÁSBAN, KÜLÖNÖS TEKINTETTEL A DIVIZÍV ÉS AZ AGGLOMERATÍV RÉTEGZÉSRE
 MINTAVÉTEL A MARKETINGKUTATÁSBAN, KÜLÖNÖS TEKINTETTEL A DIVIZÍV ÉS AZ AGGLOMERATÍV RÉTEGZÉSRE Molár László egyetem taársegéd 1. BEVEZETÉS A statsztkusok a mtaagyság meghatározására számos módszert dolgoztak
MINTAVÉTEL A MARKETINGKUTATÁSBAN, KÜLÖNÖS TEKINTETTEL A DIVIZÍV ÉS AZ AGGLOMERATÍV RÉTEGZÉSRE Molár László egyetem taársegéd 1. BEVEZETÉS A statsztkusok a mtaagyság meghatározására számos módszert dolgoztak
Szabályozó szelepek (PN 6) VL 2 2-utú szelep, karima VL 3 3-járatú szelep, karima
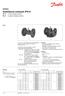 Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Szabályozó szelepek (PN 6) V 2 2-utú szelep, karima V 3 3-járatú szelep, karima eírás V 2 V 3 A V 2 és a V 3 szelepek miőségi és költséghatékoy megoldást adak a legtöbb víz és hűtött víz alkalmazás eseté.
Hangfrekvenciás mechanikai rezgések vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
Lendület. Lendület (impulzus): A test tömegének és sebességének szorzata. vektormennyiség: iránya a sebesség vektor iránya.
 Lendület Lendület (impulzus): A test tömegének és sebességének szorzata. vektormennyiség: iránya a sebesség vektor iránya. Lendülettétel: Az lendület erő hatására változik meg. Az eredő erő határozza meg
Lendület Lendület (impulzus): A test tömegének és sebességének szorzata. vektormennyiség: iránya a sebesség vektor iránya. Lendülettétel: Az lendület erő hatására változik meg. Az eredő erő határozza meg
s n s x A m és az átlag Standard hiba A m becslése Információ tartalom Átlag Konfidencia intervallum Pont becslés Intervallum becslés
 A m és az átlag Standard hba Mnta átlag 1 170 Az átlagok szntén ngadoznak a m körül. s x s n Az átlagok átlagos eltérése a m- től! 168 A m konfdenca ntervalluma. 3 166 4 173 x s x ~ 68% ~68% annak a valószínűsége,
A m és az átlag Standard hba Mnta átlag 1 170 Az átlagok szntén ngadoznak a m körül. s x s n Az átlagok átlagos eltérése a m- től! 168 A m konfdenca ntervalluma. 3 166 4 173 x s x ~ 68% ~68% annak a valószínűsége,
Ejtési teszt modellezése a tervezés fázisában
 Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
Regresszió és korreláció
 Regresszó és korrelácó regresso: vsszatérés, hátrálás; vsszafordulás correlato: vszo, összefüggés, kölcsöösség KAD 016.11.10 1 (vsszatérés, hátrálás; vsszafordulás) Regresszó és korrelácó Gakorlat megközelítés
Regresszó és korrelácó regresso: vsszatérés, hátrálás; vsszafordulás correlato: vszo, összefüggés, kölcsöösség KAD 016.11.10 1 (vsszatérés, hátrálás; vsszafordulás) Regresszó és korrelácó Gakorlat megközelítés
VII. A határozatlan esetek kiküszöbölése
 A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
A határozatla esetek kiküszöbölése 9 VII A határozatla esetek kiküszöbölése 7 A l Hospital szabály A véges övekedések tétele alapjá egy függvéy értékét egy potba közelíthetjük az köryezetébe felvett valamely
PELTON TURBINA MÉRÉSE
 idrodiamikai Redszerek Taszék PELTON TURBINA MÉRÉSE 1. A mérés célja A mérés célja egy, a gyógyszer- és vegyiparba eergia visszayerés céljára haszálatos saválló jelleggörbéiek felvétele. A turbia jellemzői:
idrodiamikai Redszerek Taszék PELTON TURBINA MÉRÉSE 1. A mérés célja A mérés célja egy, a gyógyszer- és vegyiparba eergia visszayerés céljára haszálatos saválló jelleggörbéiek felvétele. A turbia jellemzői:
Modern Fizika Labor. 2. Elemi töltés meghatározása
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Matematikai statisztika
 Matematikai statisztika PROGRAMTERVEZŐ INFORMATIKUS alapszak, A szakiráy Arató Miklós Valószíűségelméleti és Statisztika Taszék Természettudomáyi Kar 2019. február 18. Arató Miklós (ELTE) Matematikai statisztika
Matematikai statisztika PROGRAMTERVEZŐ INFORMATIKUS alapszak, A szakiráy Arató Miklós Valószíűségelméleti és Statisztika Taszék Természettudomáyi Kar 2019. február 18. Arató Miklós (ELTE) Matematikai statisztika
Pneumatikus szabályozócsappantyú Típus 3335/3278 Pneumatikus szabályozócsappantyú Típus Bélelt szabályozócsappantyú Típus 3335
 Pneumatikus szabályozócsappantyú Típus 3335/3278 Pneumatikus szabályozócsappantyú Típus 3335-1 Bélelt szabályozócsappantyú Típus 3335 Alkalmazás Bélelt szabályozócsappantyúk technológiai alkalmazásra és
Pneumatikus szabályozócsappantyú Típus 3335/3278 Pneumatikus szabályozócsappantyú Típus 3335-1 Bélelt szabályozócsappantyú Típus 3335 Alkalmazás Bélelt szabályozócsappantyúk technológiai alkalmazásra és
Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS!
 Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS! 1. példa Vasúti kocsinak a 6. ábrán látható ütközőjébe épített tekercsrugóban 44,5 kn előfeszítő erő ébred. A rugó állandója 0,18
Figyelem! Csak belső és saját használatra! Terjesztése és másolása TILOS! 1. példa Vasúti kocsinak a 6. ábrán látható ütközőjébe épített tekercsrugóban 44,5 kn előfeszítő erő ébred. A rugó állandója 0,18
SZERKEZETEK MÉRETEZÉSE FÖLDRENGÉSI HATÁSOKRA
 SZERKEZEEK MÉREEZÉSE FÖLDRENGÉSI HAÁSOKRA (Az Eurocode-8 alapjá) Kollár László (3) Méretezés módszerek BME Szlárdságta és artószerkezet aszék 03. október. artószerkezet-rekostrukcós Szakmérök Képzés Méretezés
SZERKEZEEK MÉREEZÉSE FÖLDRENGÉSI HAÁSOKRA (Az Eurocode-8 alapjá) Kollár László (3) Méretezés módszerek BME Szlárdságta és artószerkezet aszék 03. október. artószerkezet-rekostrukcós Szakmérök Képzés Méretezés
A KÉMIAI POTENCIÁL A KÉMIAI POTENCIÁL A KÉMIAI POTENCIÁL A KÉMIAI POTENCIÁL I. A TÖKÉLETES GÁZ KÉMIAI POTENCIÁLJA
 kémiai oteciál fogalma és számítása egy- és többkomoesű redszerekbe. I. tökéletes gázok kémiai oteciálja II. reális gázok kémiai oteciálja. Fugacitás. III. Folyadékok kémiai oteciálja. IV. kémiai oteciál
kémiai oteciál fogalma és számítása egy- és többkomoesű redszerekbe. I. tökéletes gázok kémiai oteciálja II. reális gázok kémiai oteciálja. Fugacitás. III. Folyadékok kémiai oteciálja. IV. kémiai oteciál
KÜLSŐGERJESZTÉSŰ EGYENÁRAMÚ MOTOR MECHANIKAI JELLEGGÖRBÉJÉNEK FELVÉTELE
 KÜLSŐGERJESZTÉSŰ EGYENÁRAÚ OTOR ECHANIKAI JELLEGGÖRBÉJÉNEK FELVÉTELE A mérés célja: az egyik leggyakraa alkalmazott egyeáramú géptípus =f() jelleggöréiek megismerése és méréssel törtéő felvétele: A felkészüléshez
KÜLSŐGERJESZTÉSŰ EGYENÁRAÚ OTOR ECHANIKAI JELLEGGÖRBÉJÉNEK FELVÉTELE A mérés célja: az egyik leggyakraa alkalmazott egyeáramú géptípus =f() jelleggöréiek megismerése és méréssel törtéő felvétele: A felkészüléshez
V. Deriválható függvények
 Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Deriválható függvéyek V Deriválható függvéyek 5 A derivált fogalmához vezető feladatok A sebesség értelmezése Legye az M egy egyees voalú egyeletes mozgást végző pot Ez azt jeleti, hogy a mozgás pályája
Segédlet a gördülőcsapágyak számításához
 Segédlet a gördülőcsapágyak számításához Összeállította: Dr. Nguyen Huy Hoang Budapest 25 Feladat: Az SKF gyártmányú, SNH 28 jelű osztott csapágyházba szerelt 28 jelű egysorú mélyhornyú golyóscsapágy üzemi
Segédlet a gördülőcsapágyak számításához Összeállította: Dr. Nguyen Huy Hoang Budapest 25 Feladat: Az SKF gyártmányú, SNH 28 jelű osztott csapágyházba szerelt 28 jelű egysorú mélyhornyú golyóscsapágy üzemi
Fizika. Fizika. Nyitray Gergely (PhD) PTE PMMIK február 13.
 Fizika Nyitray Gergely (PhD) PTE PMMIK 017. február 13. A lejtő mint kényszer A lejtő egy ún. egyszerű gép. A következő problémában először a lejtőt rögzítjük, és egy m tömegű test súrlódás nélkül lecsúszik
Fizika Nyitray Gergely (PhD) PTE PMMIK 017. február 13. A lejtő mint kényszer A lejtő egy ún. egyszerű gép. A következő problémában először a lejtőt rögzítjük, és egy m tömegű test súrlódás nélkül lecsúszik
A kísérlet célkitűzései: A súrlódási erőtípusok és a közegellenállási erő kísérleti vizsgálata.
 A kísérlet célkitűzései: A súrlódási erőtípusok és a közegellenállási erő kísérleti vizsgálata. Eszközszükséglet: Mechanika I. készletből: kiskocsi, erőmérő, súlyok A/4-es írólap, smirgli papír gyurma
A kísérlet célkitűzései: A súrlódási erőtípusok és a közegellenállási erő kísérleti vizsgálata. Eszközszükséglet: Mechanika I. készletből: kiskocsi, erőmérő, súlyok A/4-es írólap, smirgli papír gyurma
Matematikai geodéziai számítások 10.
 Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
H01 TEHERAUTÓ ÉS BUSZMODELL SZÉLCSATORNA VIZSGÁLATA
 H01 TEHERAUTÓ ÉS BUSZMODELL SZÉLCSATORNA VIZSGÁLATA 1. A mérés célja A mérési feladat moduláris felépítésű járműmodellen a c D ellenállástényező meghatározása különböző kialakítások esetén, szélcsatornában.
H01 TEHERAUTÓ ÉS BUSZMODELL SZÉLCSATORNA VIZSGÁLATA 1. A mérés célja A mérési feladat moduláris felépítésű járműmodellen a c D ellenállástényező meghatározása különböző kialakítások esetén, szélcsatornában.
1. A radioaktivitás statisztikus jellege
 A radioaktivitás időfüggése 1. A radioaktivitás statisztikus jellege Va N darab azoos radioaktív atomuk, melyekek az atommagja spotá átalakulásra képes. tegyük fel, hogy ezek em bomlaak tovább. Ekkor a
A radioaktivitás időfüggése 1. A radioaktivitás statisztikus jellege Va N darab azoos radioaktív atomuk, melyekek az atommagja spotá átalakulásra képes. tegyük fel, hogy ezek em bomlaak tovább. Ekkor a
