5. Geometriai transzformációk
|
|
|
- Vince Tamás
- 8 évvel ezelőtt
- Látták:
Átírás
1 5. Geometiai tanszfomáiók Kató Zoltán Képfeldolgozás és Számítógépes Gafika tanszék SZTE (
2 2 Kép tanszfomáiók típusai Kép étékkészletének (adiometiai infomáió) átalakítása: J( i, j) f ( I,( i, j)) Kép ételmezési tatományának geometiai tanszfomáiója (waping): J ( i, j) I( t ( i, j), t ( i, j)) i j Mind az étékkészlet mind pedig az ételmezési tatomány átalakítása: J ( i, j) f ( I,( t ( i, j), t ( i, j))) i j
3 3 Egyszeű geometiai tanszfomáiók Nagyítás / kisinyítés Izotóp Anizotóp Fogatás
4 4 Fogatás RxC kép fogatása 0 < 90 szöggel a középpont köül Új képméet: Rout ound Dsin θθ A Cout ound Dos θθ A Új középpont: 2 Rout, 2 C out Rout0, C out0. R C out0 out0
5 5 Fogatás RxC kép fogatása 0 < 90 szöggel a középpont köül Fogatási mátix θ osθ sinθ sinθ osθ R C in0 in0 Output koodináták előállítása θ in in R C in0 in0 R R out0 out0
6 6 Geometiai tanszfomáiók Adott koodináta tanszfomáió x = t(x) és I(x) kép esetén hogyan állítjuk elő a J(x ) = I(t(x)) képet? J(x ) geneálása tipikusan az invez tanszfomáió alapján töténik J minden pixele gaantáltan kitöltése keül Mi töténik, ha x őse (x=t - (x )) I ben nem egész pixelkoodinátáa mutat? t(x) x x I(x) J(x ) Szeliski
7 7 Úja mintavételezés Emlékeztető: egy I(i,j) digitális kép az eedeti folytonos f(x,y) kép mintavételezésével és kvantálásával áll elő: I egy folytonos függvény diszkét pontszeű mintáiból áll elő. I( i, j) quantize( f ( xd, yd)) Ha ekonstuálni tudnánk az eedeti f függvényt, akko tetszőleg új felbontást elő tudnánk állítani I(i) i Ha ismejük egy f függvény étékeit diszkét pontokban, akko f közbülső étékeit intepoláióval állíthatjuk elő
8 8 Geometiai tanszfomáió végehajtása Input kép Tanszfomáló függvény Intepoláiós függvény Output kép
9 9 Egyszeű példa: Kép negyedée kisinyítése
10 0 Egyszeű példa: Kép negyedée kisinyítése Minden 4. so minden 4. pixelét vegyük ki és másoljuk a kisinyített képbe.
11 Egyszeű példa: Kép negyedée kisinyítése Mi tötént?
12 2 A MINTAVÉTELEZÉS KORLÁTAI
13 3 Méet és fekvenia közötti összefüggés Ha ΔxΔy egy objektum kitejedése a képtében és ΔuΔv a Fouie tében, akko közöttük az alábbi összefüggés áll fent: x y u v 6 2 spae FT fequeny Egy kis méetű képelem nagy kitejedésű lesz a Fouie tében és fodítva. spae FT fequeny
14 4 Képméet sökkentés - alulmintavételezés Egy R C méetű I kép n-ed észe kisinyítése egy R/n C/n méetű J kép. Egy J kép diszkét Fouie tanszfomáltja a J-vel megegyező méetű. A képté és FT jellemzők méete fodítottan aányos J-nek n R/n n C/n = R C méetűnek kellene lennie. A fentiek egyszee sak úgy teljesülhetnek, ha DFT(J) átfed önmagával.
15 5 Kép és DFT tóuszon ételmezett
16 6 Felée kisinyített kép
17 7 Ideális DFT - felezés A felée kisinyített kép ideális DFT-je a középső (alasony fekveniájú) égió lenne
18 8 Valós DFT - felezés A valóságban az eedeti kép DFT-je 4 észe osztódik, amelyek az eedeti gyűűn folytonosan helyezkednek el
19 9 Valós DFT - felezés A kisinyített képen a 4 ész átlapolódik Alasony fekvenia Magas oszlop fekv. Oszlopok és sook Alasony so fekv. Magas fekvenia Alasony oszlop fekv. Oszlopok és sook Magas so fekv.
20 20 Valós DFT - felezés A 4 ész megfelel - tóusznak, amelyek átfednek
21 2 Spektális átfedés At eedeti és felezett kép közötti spektális átfedés átfedő fekvenia té-beli jellemzők eedeti felezett, 2 zoom
22 22 Egy kép mintavételezése Egy kép mintavételezése a samp() mintavételező függvénnyel való szozással töténik A mintavételező függvény nem más, mint egy négyzetás mentén elhelyezett impulzusfüggvények összessége samp N I, I, jn kn j k
23 23 Impulzus függvény A Dia δ függvény ha ( x, y) (0,0) ( x, y), ( x, y) dxdy 0 különben A Dia függvény szepaálható: ( x, y) ( x) ( y) A méésben használt változata (impulzus függvény): ( x k) 0 ha x k különben 0 x k
24 24 A mintavételező függvény FT-ja Maga is egy mintavételező függvény, de az impulzusok /N távolsága lesznek egymástól A képtében vett szozás (mintavételezés) a Fouie tében konvolúió lesz!
25 25 Konvolúió az impulzusfüggvénnyel Az eedmény az eedeti függvény eltolása lesz az impulzusfüggvény pozíiójába
26 26 Egy mintavételezett kép FT-ja A kép FT-ja ismétlődik /N intevallumonként Ha a Fouie tatomány ádiusza /(2N), akko átfedés lesz spektum átfedés, Moié hatás FI u, v u v j k N N j k
27 27 Nyquist fekvenia T.f.h. az f(x) függvény sávhatáolt, vagyis a Fouie tanszfomáltja F(X) nem tatalmaz w-nél nagyobb fekveniákat, azaz: F(X)=0, ha X >w. A w-t ekko Nyquist-fekveniának nevezzük, ha F(-w) 0 vagy F(w) 0.
28 28 Sávhatáolt függvény Mintavételezés előtt biztosítani kell, hogy a kép nem tatalmaz /2N-nél nagyobb fekveniákat: Szozás az alábbi dobozfüggvénnyel: FT H u, v 0 ahol u vagy v 2N 2N Ez ekvivalens a képtében egy 2N nagyságú szűővel Tehát ha felezni akajuk a képet, akko N=2 és így egy legalább 4x4 méetű simítása van szükség (pl. 5x5 méetű konvolúiós maszkkal simítjuk).
29 29 A sin és a doboz függvény kapsolata П /2 (x) sin(x) Fouie u x F [ 2 2ikx / 2( x)]( k) e / ( x) dx sin( k )
30 30 A sin függvény sin( x) sin x x,ha,ha x x 0 0 k os x 2 k
31 3 A sin és a doboz függvény kapsolata Fouie 2D doboz függvény 2D sin függvény
32 32 Whittake-Shannon intepoláiós fomulája Ha az f(x) függvény sávhatáolt (a Fouie tanszfomáltja nem tatalmaz w-nél nagyobb fekveniákat), akko: f ( x) n f ( n ) 2w sin( (2wx n)) (2wx n) diszkét pontok
33 33 Whittake-Shannon mintavételezési tétele A 2D folytonos, w-nél nagyobb fekveniákat nem tatalmazó (sávhatáolt) képfüggvény akko és sakis akko állítható vissza a mintavételezettjéből, ha a Δx és a Δy mintavételezési léptékeke teljesül: x 2w, y 2w.
34 34 INTERPOLÁCIÓS TECHNIKÁK
35 35 Geometiai tanszfomáió végehajtása Input kép Tanszfomáló függvény Intepoláiós függvény Output kép
36 36 Intepoláiós tehnikák
37 37 Legközelebbi szomszéd (NN) A legközelebbi szomszéd (Neaest Neighbo NN) intepoláió nem más, mint a subpixeles koodináták keekítése: J(,) = I( i, i ) ahol ( i, i ) = ound( f, f ) ( i, i ) ( f, f )
38 Bilineáis A bilineáis intepoláió nem más, mint a subpixeles ( f, f ) koodinátához legközelebb eső 4 szomszédos pixeléték súlyozott átlaga: Ahol és 38,,,,, f, f ; f f f f ;. I I I I J,,,,,
39 Biubi A biubi intepoláió a subpixeles ( f, f ) koodinátához legközelebb eső 4 szomszédos pixelétéket illetve azok paiális deiváltjait is használja Ezét 4x4 szomszédság szükséges , I,, I,, I i j j i j i j i f f,,
40 Biubi 40 N(, ) az (, ) 8-pixeles szomszédsága, I, I, I, I, I, I átlaga diff.,, I 2 2, N, N, N, N, I, I, I
41 Biubi A paiális deiváltak az alábbi hamadfokú polinomok szozatának összegében kombinálódnak ahol és 4 n P m P n m I J m n 2 2,, x Q x Q x Q x Q x P 0 fo 0 0 fo x x x x Q f f,, f f,,
42 42 Példa: Kisinyítés 3/7 aányban eedeti neaest neighbo bilinea biubi
43 43 Példa: Kisinyítés 3/7 aányban - eedeti eedeti
44 44 Példa: Kisinyítés 3/7 aányban - NN neaest neighbo
45 45 Példa: Kisinyítés 3/7 aányban - bilinea bilinea
46 46 Példa: Kisinyítés 3/7 aányban - biubi biubi
47 47 Példa: Kisinyítés 3/7 aányban - eedeti eedeti
48 48 Felhasznált anyagok Palágyi Kálmán: Digitális Képfeldolgozás /pub/digitalis_kepfeldolgozas Tevo Daell: C280, Compute Vision s06/letues/ppts/ Rihad Alan Petes: EECE/CS 253 Image Poessing További foások az egyes diákon megjelölve
4. Szűrés frekvenciatérben
 4. Szűrés frekvenciatérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) Unitér transzformációk Az unitér transzformációk olyan lineáris,
4. Szűrés frekvenciatérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) Unitér transzformációk Az unitér transzformációk olyan lineáris,
Él: a képfüggvény hirtelen változása. Típusai. Felvételeken zajos formában jelennek meg. Lépcsős
 Él: a képfüggvény hirtelen változása Típusai Lépcsős Rámpaszerű Tetőszerű Vonalszerű él Felvételeken zajos formában jelennek meg Adott pontbeli x ill. y irányú változás jellemezhető egy f folytonos képfüggvény
Él: a képfüggvény hirtelen változása Típusai Lépcsős Rámpaszerű Tetőszerű Vonalszerű él Felvételeken zajos formában jelennek meg Adott pontbeli x ill. y irányú változás jellemezhető egy f folytonos képfüggvény
3. Szűrés képtérben. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 3. Szűrés képtérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE http://www.inf.u-szeged.hu/~kato/teaching/ 2 Kép transzformációk típusai Kép értékkészletének radiometriai információ
3. Szűrés képtérben Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE http://www.inf.u-szeged.hu/~kato/teaching/ 2 Kép transzformációk típusai Kép értékkészletének radiometriai információ
Fourier térbeli analízis, inverz probléma. Orvosi képdiagnosztika 5-7. ea ősz
 Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 5-7. ea. 2017 ősz 5. Előadás témái Fourier transzformációk és kapcsolataik: FS, FT, DTFT, DFT, DFS Mintavételezés, interpoláció Folytonos
Fourier térbeli analízis, inverz probléma Orvosi képdiagnosztika 5-7. ea. 2017 ősz 5. Előadás témái Fourier transzformációk és kapcsolataik: FS, FT, DTFT, DFT, DFS Mintavételezés, interpoláció Folytonos
Arany Dániel Matematikai Tanulóverseny 2017/2018-as tanév 1. forduló Haladók III. kategória
 Bolyai János Matematikai Tásulat Aany Dániel Matematikai Tanulóveseny 017/018-as tanév 1. foduló Haladók III. kategóia Megoldások és javítási útmutató 1. Anna matematika házi feladatáa áfolyt a tinta.
Bolyai János Matematikai Tásulat Aany Dániel Matematikai Tanulóveseny 017/018-as tanév 1. foduló Haladók III. kategóia Megoldások és javítási útmutató 1. Anna matematika házi feladatáa áfolyt a tinta.
Képrekonstrukció 3. előadás
 Képrekonstrukció 3. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Computed Tomography (CT) Elv: Röntgen-sugarak áthatolása 3D objektum 3D térfogati kép Mérések
Képrekonstrukció 3. előadás Balázs Péter Képfeldolgozás és Számítógépes Grafika Tanszék Szegedi Tudományegyetem Computed Tomography (CT) Elv: Röntgen-sugarak áthatolása 3D objektum 3D térfogati kép Mérések
8. Pontmegfeleltetések
 8. Pontmegfeleltetések Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Példa: panoráma kép készítés 1. Jellemzőpontok detektálása mindkét
8. Pontmegfeleltetések Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Példa: panoráma kép készítés 1. Jellemzőpontok detektálása mindkét
462 Trigonometrikus egyenetek II. rész
 Tigonometikus egyenetek II ész - cosx N cosx Alakítsuk át az egyenletet a következô alakúa: + + N p O O Ebbôl kapjuk, hogy cos x $ p- Ennek az egyenletnek akko és csak akko van valós megoldása, ha 0 #
Tigonometikus egyenetek II ész - cosx N cosx Alakítsuk át az egyenletet a következô alakúa: + + N p O O Ebbôl kapjuk, hogy cos x $ p- Ennek az egyenletnek akko és csak akko van valós megoldása, ha 0 #
1. MECHANIKA-STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnök tanár) Trigonometria, vektoralgebra
 SZÉCHENYI ISTVÁN EGYETEM LKLMZOTT MECHNIK TNSZÉK. MECHNIK-STTIK GYKORLT (kidolgozta: Tiesz Péte eg. ts.; Tanai Gábo ménök taná) Tigonometia vektoalgeba Tigonometiai összefoglaló c a b b a sin = cos = c
SZÉCHENYI ISTVÁN EGYETEM LKLMZOTT MECHNIK TNSZÉK. MECHNIK-STTIK GYKORLT (kidolgozta: Tiesz Péte eg. ts.; Tanai Gábo ménök taná) Tigonometia vektoalgeba Tigonometiai összefoglaló c a b b a sin = cos = c
6. Éldetektálás. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 6. Éldetektálás Kató Zoltán Képeldolgozás és Számítógépes Graika tanszék SZTE (http://www.in.u-szeged.hu/~kato/teaching/) 2 Élek A képen ott található él, ahol a kép-üggvény hirtelen változik. A kép egy
6. Éldetektálás Kató Zoltán Képeldolgozás és Számítógépes Graika tanszék SZTE (http://www.in.u-szeged.hu/~kato/teaching/) 2 Élek A képen ott található él, ahol a kép-üggvény hirtelen változik. A kép egy
3. Egy ξ valószínűségi változó eloszlásfüggvénye melyik képlettel van definiálva?
 . z és események függetlensége melyik összefüggéssel van definiálva? P () + P () = P ( ) = P ()P () = P ( ) = P () P () 2. z alábbi összefüggések közül melyek igazak, melyek nem igazak tetszőleges és eseményeke?
. z és események függetlensége melyik összefüggéssel van definiálva? P () + P () = P ( ) = P ()P () = P ( ) = P () P () 2. z alábbi összefüggések közül melyek igazak, melyek nem igazak tetszőleges és eseményeke?
9. ábra. A 25B-7 feladathoz
 . gyakolat.1. Feladat: (HN 5B-7) Egy d vastagságú lemezben egyenletes ρ téfogatmenti töltés van. A lemez a ±y és ±z iányokban gyakolatilag végtelen (9. ába); az x tengely zéuspontját úgy választottuk meg,
. gyakolat.1. Feladat: (HN 5B-7) Egy d vastagságú lemezben egyenletes ρ téfogatmenti töltés van. A lemez a ±y és ±z iányokban gyakolatilag végtelen (9. ába); az x tengely zéuspontját úgy választottuk meg,
(KOJHA 125) Kisfeladatok
 GAZDASÁGTUDOMÁNYI EGYETEM Közlekedésménöki Ka Jámű- és hajtáselemek I. (KOJHA 25) Kisfeladatok Jáműelemek és Hajtások Ssz.:...... Név:......................................... Neptun kód.:......... ADATVÁLASZTÉK
GAZDASÁGTUDOMÁNYI EGYETEM Közlekedésménöki Ka Jámű- és hajtáselemek I. (KOJHA 25) Kisfeladatok Jáműelemek és Hajtások Ssz.:...... Név:......................................... Neptun kód.:......... ADATVÁLASZTÉK
Sugárzás és szórás. ahol az amplitúdófüggvény. d 3 x J(x )e ikˆxx. 1. Számoljuk ki a szórási hatáskeresztmetszetet egy
 Sugázás és szóás I SZÓRÁSOK A Szóás dielektomos gömbön Számoljuk ki a szóási hatáskeesztmetszetet egy ε elatív dielektomos állandójú gömb esetén amennyiben a gömb R sugaa jóval kisebb mint a beeső fény
Sugázás és szóás I SZÓRÁSOK A Szóás dielektomos gömbön Számoljuk ki a szóási hatáskeesztmetszetet egy ε elatív dielektomos állandójú gömb esetén amennyiben a gömb R sugaa jóval kisebb mint a beeső fény
Keresés képi jellemzők alapján. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
III. Differenciálszámítás
 III. Diffeenciálszámítás A diffeenciálszámítás számunka elsősoban aa való hogy megállaítsuk hogyan változnak a (fizikai) kémiában nagy számban előfoló (többváltozós) függvények. A diffeenciálszámítás megadja
III. Diffeenciálszámítás A diffeenciálszámítás számunka elsősoban aa való hogy megállaítsuk hogyan változnak a (fizikai) kémiában nagy számban előfoló (többváltozós) függvények. A diffeenciálszámítás megadja
Iványi László ARM programozás. Szabó Béla 6. Óra ADC és DAC elmélete és használata
 ARM programozás 6. Óra ADC és DAC elmélete és használata Iványi László ivanyi.laszlo@stud.uni-obuda.hu Szabó Béla szabo.bela@stud.uni-obuda.hu Mi az ADC? ADC -> Analog Digital Converter Analóg jelek mintavételezéssel
ARM programozás 6. Óra ADC és DAC elmélete és használata Iványi László ivanyi.laszlo@stud.uni-obuda.hu Szabó Béla szabo.bela@stud.uni-obuda.hu Mi az ADC? ADC -> Analog Digital Converter Analóg jelek mintavételezéssel
Digitális jelfeldolgozás
 Digitális jelfeldolgozás Mintavételezés és jel-rekonstrukció Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010.
Digitális jelfeldolgozás Mintavételezés és jel-rekonstrukció Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010.
Olvassa el figyelmesen a következő kérdéseket, állításokat, s karikázza be a helyesnek vélt választ.
 Feleletválasztós kédések 1. Hosszú távú modell Pénz Olvassa el figyelmesen a következő kédéseket, állításokat, s kaikázza be a helyesnek vélt választ. 1. Kédés A pénz olyan pénzügyi eszköz, amely betölti
Feleletválasztós kédések 1. Hosszú távú modell Pénz Olvassa el figyelmesen a következő kédéseket, állításokat, s kaikázza be a helyesnek vélt választ. 1. Kédés A pénz olyan pénzügyi eszköz, amely betölti
Ellenőrző kérdések a Jelanalízis és Jelfeldolgozás témakörökhöz
 Ellenőrző kérdések a Jelanalízis és Jelfeldolgozás témakörökhöz 1. Hogyan lehet osztályozni a jeleket időfüggvényük időtartama szerint? 2. Mi a periodikus jelek definiciója? (szöveg, képlet, 3. Milyen
Ellenőrző kérdések a Jelanalízis és Jelfeldolgozás témakörökhöz 1. Hogyan lehet osztályozni a jeleket időfüggvényük időtartama szerint? 2. Mi a periodikus jelek definiciója? (szöveg, képlet, 3. Milyen
12. Képtömörítés. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (
 12. Képtömörítés Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Miért van szükség tömörítésre? A rendelkezésre álló adattárolási és továbbítási
12. Képtömörítés Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Miért van szükség tömörítésre? A rendelkezésre álló adattárolási és továbbítási
A TŐKE KÖLTSÉGE. 7. Fejezet. 7.1. Források tőkeköltsége. 7.1.2 Saját tőke költsége. 7.1.1. Hitel típusú források tőkeköltsége DIV DIV
 7. Fejezet A TŐKE KÖLTSÉGE 7.1.2 Saját tőke költsége D =hitel tőkeköltsége. i =névleges kamatláb, kötvény esetén n. P n =a kötvény névétéke. =a kötvény áfolyama. P 0 Hitel típusú foások tőkeköltsége, (T
7. Fejezet A TŐKE KÖLTSÉGE 7.1.2 Saját tőke költsége D =hitel tőkeköltsége. i =névleges kamatláb, kötvény esetén n. P n =a kötvény névétéke. =a kötvény áfolyama. P 0 Hitel típusú foások tőkeköltsége, (T
Számítógépes képelemzés 7. előadás. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Képfeldolgozás jól párhuzamosítható
 Képfeldolgozás jól párhuzamosítható B. Wilkinson, M. Allen: Parallel Programming, Pearson Education Prentice Hall, 2nd ed., 2005. könyv 12. fejezete alapján Vázlat A képfeldolgozás olyan alkalmazási terület,
Képfeldolgozás jól párhuzamosítható B. Wilkinson, M. Allen: Parallel Programming, Pearson Education Prentice Hall, 2nd ed., 2005. könyv 12. fejezete alapján Vázlat A képfeldolgozás olyan alkalmazási terület,
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 6. A MINTAVÉTELI TÖRVÉNY
 ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 6. A MINTAVÉTELI TÖRVÉNY Dr. Soumelidis Alexandros 2018.10.25. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mintavételezés
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 6. A MINTAVÉTELI TÖRVÉNY Dr. Soumelidis Alexandros 2018.10.25. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mintavételezés
1. Határozza meg az alábbi határértéket! A válaszát indokolja!
 Matematika (Analízis és dierenciálegyenletek), NGB_MA003_1, 2. zárthelyi 2014. 11. 20., 1A-csoport x 2 + 6x x 2 5 5x 2 f(x) = tg(2x + 1) 2 x + cos x x 16 5 x + 16 2 x 16 4. Határozza meg, hogy az f(x)
Matematika (Analízis és dierenciálegyenletek), NGB_MA003_1, 2. zárthelyi 2014. 11. 20., 1A-csoport x 2 + 6x x 2 5 5x 2 f(x) = tg(2x + 1) 2 x + cos x x 16 5 x + 16 2 x 16 4. Határozza meg, hogy az f(x)
Kétváltozós vektor-skalár függvények
 Kétáltozós ekto-skalá függények Definíció: Az olyan függényt amely az ( endezett alós számpáokhoz ( R R ( ektot endel kétáltozós ekto-skalá függénynek neezzük. : ( ( ( x( i + y( j + z( k Az ektoal együtt
Kétáltozós ekto-skalá függények Definíció: Az olyan függényt amely az ( endezett alós számpáokhoz ( R R ( ektot endel kétáltozós ekto-skalá függénynek neezzük. : ( ( ( x( i + y( j + z( k Az ektoal együtt
6. MECHANIKA-STATIKA GYAKORLAT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya, Culmann-szerkesztés, Ritter-számítás
 SZÉHENYI ISTVÁN EGYETE GÉPSZERKEZETTN ÉS EHNIK TNSZÉK 6. EHNIK-STTIK GYKORLT Kidolgozta: Tiesz Péte egy. ts. Négy eő egyensúlya ulmann-szekesztés Ritte-számítás 6.. Példa Egy létát egy veembe letámasztunk
SZÉHENYI ISTVÁN EGYETE GÉPSZERKEZETTN ÉS EHNIK TNSZÉK 6. EHNIK-STTIK GYKORLT Kidolgozta: Tiesz Péte egy. ts. Négy eő egyensúlya ulmann-szekesztés Ritte-számítás 6.. Példa Egy létát egy veembe letámasztunk
SZOLVENCIATŐKE MINT FIXPONT
 SZÜLE BORBÁLA SZOLVENCIATŐKE MINT FIXPONT A tanulmányban a szező a fixpont-iteáció témájával foglalkozik egy elméleti modellben, a biztosítók szolvenciatőkéjének számolásával kapcsolatban. A téma aktualitását
SZÜLE BORBÁLA SZOLVENCIATŐKE MINT FIXPONT A tanulmányban a szező a fixpont-iteáció témájával foglalkozik egy elméleti modellben, a biztosítók szolvenciatőkéjének számolásával kapcsolatban. A téma aktualitását
2. Pont operációk. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 2. Pont operációk Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Kép transzformációk típusai Kép értékkészletének (radiometriai információ)
2. Pont operációk Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Kép transzformációk típusai Kép értékkészletének (radiometriai információ)
2. gyakorlat Mintavételezés, kvantálás
 2. gyakorlat Mintavételezés, kvantálás x(t) x[k]= =x(k T) Q x[k] ^ D/A x(t) ~ ampl. FOLYTONOS idı FOLYTONOS ANALÓG DISZKRÉT MINTAVÉTELEZETT DISZKRÉT KVANTÁLT DIGITÁLIS Jelek visszaállítása egyenköző mintáinak
2. gyakorlat Mintavételezés, kvantálás x(t) x[k]= =x(k T) Q x[k] ^ D/A x(t) ~ ampl. FOLYTONOS idı FOLYTONOS ANALÓG DISZKRÉT MINTAVÉTELEZETT DISZKRÉT KVANTÁLT DIGITÁLIS Jelek visszaállítása egyenköző mintáinak
Fraktál alapú képtömörítés p. 1/26
 Fraktál alapú képtömörítés Bodó Zalán zbodo@cs.ubbcluj.ro BBTE Fraktál alapú képtömörítés p. 1/26 Bevezetés tömörítések veszteségmentes (lossless) - RLE, Huffman, LZW veszteséges (lossy) - kvantálás, fraktál
Fraktál alapú képtömörítés Bodó Zalán zbodo@cs.ubbcluj.ro BBTE Fraktál alapú képtömörítés p. 1/26 Bevezetés tömörítések veszteségmentes (lossless) - RLE, Huffman, LZW veszteséges (lossy) - kvantálás, fraktál
Számítógépes Grafika SZIE YMÉK
 Számítógépes Grafika SZIE YMÉK Analóg - digitális Analóg: a jel értelmezési tartománya (idő), és az értékkészletes is folytonos (pl. hang, fény) Diszkrét idejű: az értelmezési tartomány diszkrét (pl. a
Számítógépes Grafika SZIE YMÉK Analóg - digitális Analóg: a jel értelmezési tartománya (idő), és az értékkészletes is folytonos (pl. hang, fény) Diszkrét idejű: az értelmezési tartomány diszkrét (pl. a
Lehetséges minimumkérdések Méréstechnika tárgyból 2015.
 Lehetséges minimumkédések Mééstechnika tágyból 015. (A válaszokat póbálja lényege töően megogalmazni, az ábáknál töekedjen a pontosan elidézni, a képletek esetén töekedjen a képletben szeeplő betűk megadásáa.)
Lehetséges minimumkédések Mééstechnika tágyból 015. (A válaszokat póbálja lényege töően megogalmazni, az ábáknál töekedjen a pontosan elidézni, a képletek esetén töekedjen a képletben szeeplő betűk megadásáa.)
Mozgás centrális erőtérben
 Mozgás centális eőtében 1. A centális eő Válasszunk egy olyan potenciális enegia függvényt, amely csak az oigótól való távolságtól függ: V = V(). A tömegponta ható eő a potenciális enegiája gaiensének
Mozgás centális eőtében 1. A centális eő Válasszunk egy olyan potenciális enegia függvényt, amely csak az oigótól való távolságtól függ: V = V(). A tömegponta ható eő a potenciális enegiája gaiensének
A rugalmassággal kapcsolatos gondolatmenetek
 A ugalmassággal kapcsolatos gondolatmenetek Az igen szeteágazó, ugókkal kapcsolatos ezgési és sztatikus poblémák közül néhányat tágyalunk gondolkodás módszetani szempontok bemutatásáa. A ugó poblémák az
A ugalmassággal kapcsolatos gondolatmenetek Az igen szeteágazó, ugókkal kapcsolatos ezgési és sztatikus poblémák közül néhányat tágyalunk gondolkodás módszetani szempontok bemutatásáa. A ugó poblémák az
Fehérzajhoz a konstans érték kell - megoldás a digitális szűrő Összegezési súlyok sin x/x szerint (ez akár analóg is lehet!!!)
 DSP processzorok: 1 2 3 HP zajgenerátor: 4 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! Fehérzajhoz a konstans érték kell - megoldás a digitális
DSP processzorok: 1 2 3 HP zajgenerátor: 4 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! Fehérzajhoz a konstans érték kell - megoldás a digitális
f r homorú tükör gyűjtőlencse O F C F f
 0. A fény visszaveődése és töése göbült hatáfelületeken, gömbtükö és optikai lencse. ptikai leképezés kis nyílásszögű gömbtükökkel, és vékony lencsékkel. A fő sugámenetek ismetetése. A nagyító, a mikoszkóp
0. A fény visszaveődése és töése göbült hatáfelületeken, gömbtükö és optikai lencse. ptikai leképezés kis nyílásszögű gömbtükökkel, és vékony lencsékkel. A fő sugámenetek ismetetése. A nagyító, a mikoszkóp
Információ megjelenítés Számítógépes ábrázolás. Dr. Iványi Péter
 Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter Raszterizáció OpenGL Mely pixelek vannak a primitíven belül fragment generálása minden ilyen pixelre Attribútumok (pl., szín) hozzárendelése
Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter Raszterizáció OpenGL Mely pixelek vannak a primitíven belül fragment generálása minden ilyen pixelre Attribútumok (pl., szín) hozzárendelése
Shift regiszter + XOR kapu: 2 n állapot
 DSP processzorok: 1 2 HP zajgenerátor: 3 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! 4 Fehérzajhoz a konstans érték kell - megoldás a digitális
DSP processzorok: 1 2 HP zajgenerátor: 3 Shift regiszter + XOR kapu: 2 n állapot Autókorrelációs függvény: l. pénzdobálás: (sin x/x) 2 burkoló! 4 Fehérzajhoz a konstans érték kell - megoldás a digitális
Híradástechikai jelfeldolgozás
 Híadástechikai jelfeldolgozás 14. lőadás 015. 04. 7. Jeldigitalizálás és ekostukció. 015. május 4. Budapest D. Gaál József doces BM Hálózati Redszeek és Szolgáltatásokaszék gaal@hit.bme.hu Nomalizált kvatáló
Híadástechikai jelfeldolgozás 14. lőadás 015. 04. 7. Jeldigitalizálás és ekostukció. 015. május 4. Budapest D. Gaál József doces BM Hálózati Redszeek és Szolgáltatásokaszék gaal@hit.bme.hu Nomalizált kvatáló
2011. november 2. Dr. Vincze Szilvia
 20. novembe 2. D. Vincze Szilvia Tatalomjegyzék.) Számtani és métani soozatok Métani soozatok alkalmazásai: 2.) Kamatos kamat számítás a.) Egyszeű kamatszámítás b.) Kamatos kamat számítás c.) Kamatszámítás
20. novembe 2. D. Vincze Szilvia Tatalomjegyzék.) Számtani és métani soozatok Métani soozatok alkalmazásai: 2.) Kamatos kamat számítás a.) Egyszeű kamatszámítás b.) Kamatos kamat számítás c.) Kamatszámítás
Lineáris leképezések. Wettl Ferenc március 9. Wettl Ferenc Lineáris leképezések március 9. 1 / 31
 Lineáris leképezések Wettl Ferenc 2015. március 9. Wettl Ferenc Lineáris leképezések 2015. március 9. 1 / 31 Tartalom 1 Mátrixleképezés, lineáris leképezés 2 Alkalmazás: dierenciálhatóság 3 2- és 3-dimenziós
Lineáris leképezések Wettl Ferenc 2015. március 9. Wettl Ferenc Lineáris leképezések 2015. március 9. 1 / 31 Tartalom 1 Mátrixleképezés, lineáris leképezés 2 Alkalmazás: dierenciálhatóság 3 2- és 3-dimenziós
Képfeldolgozás jól párhuzamosítható
 Képeldolgozás jól párhuzamosítható B. Wilkinson, M. Allen: Parallel Programming, Pearson Education Prentice Hall, nd ed., 005. könyv. ejezete alapján Vázlat A képeldolgozás olyan alkalmazási terület, amely
Képeldolgozás jól párhuzamosítható B. Wilkinson, M. Allen: Parallel Programming, Pearson Education Prentice Hall, nd ed., 005. könyv. ejezete alapján Vázlat A képeldolgozás olyan alkalmazási terület, amely
α v e φ e r Név: Pontszám: Számítási Módszerek a Fizikában ZH 1
 Név: Pontsám: Sámítási Módseek a Fiikában ZH 1 1. Feladat 2 pont A éjsakai pillangók a Hold fénye alapján tájékoódnak: úgy epülnek, ogy a Holdat állandó sög alatt lássák! A lepkétől a Hold felé mutató
Név: Pontsám: Sámítási Módseek a Fiikában ZH 1 1. Feladat 2 pont A éjsakai pillangók a Hold fénye alapján tájékoódnak: úgy epülnek, ogy a Holdat állandó sög alatt lássák! A lepkétől a Hold felé mutató
9. Szegmentálás. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 9. Szegmentálás Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Szegmentálás célja Partícionáljuk a képet koherens objektumokra Nincs egzakt
9. Szegmentálás Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Szegmentálás célja Partícionáljuk a képet koherens objektumokra Nincs egzakt
Rugalmas hullámok terjedése. A hullámegyenlet és speciális megoldásai
 Rugalmas hullámok tejedése. A hullámegyenlet és speciális megoldásai Milyen hullámok alakulhatnak ki ugalmas közegben? Gázokban és folyadékokban csak longitudinális hullámok tejedhetnek. Szilád közegben
Rugalmas hullámok tejedése. A hullámegyenlet és speciális megoldásai Milyen hullámok alakulhatnak ki ugalmas közegben? Gázokban és folyadékokban csak longitudinális hullámok tejedhetnek. Szilád közegben
Optikai hullámvezető fénymódus spektroszkópia Majerné Baranyi Krisztina Adányiné Dr. Kisbocskói Nóra
 Optikai hullámvezető fénymódus spektoszkópia Majené Baanyi Kisztina Adányiné D. Kisbocskói Nóa NAIK ÉKI 1022 Budapest, Heman Ottó út 15. 4. épület Az optikai hullámvezető fénymódus spektoszkópia (OWLS)
Optikai hullámvezető fénymódus spektoszkópia Majené Baanyi Kisztina Adányiné D. Kisbocskói Nóa NAIK ÉKI 1022 Budapest, Heman Ottó út 15. 4. épület Az optikai hullámvezető fénymódus spektoszkópia (OWLS)
dr 2 # r 2 d* 2 # r 2 sin 2 *d+ 2 t = ["#,#]
![dr 2 # r 2 d* 2 # r 2 sin 2 *d+ 2 t = [#,#] dr 2 # r 2 d* 2 # r 2 sin 2 *d+ 2 t = [#,#]](/thumbs/53/32665303.jpg) Gömbszimmetikus, M tömegű test köüli téidő vákuumban: 1) Vákuum: T " = 0 2) Ügyes koodinátaendsze-választással ki lehet használni a gömbszimmetiát. Az Einstein-egyenlet analitikusan is megoldható, a megoldás,
Gömbszimmetikus, M tömegű test köüli téidő vákuumban: 1) Vákuum: T " = 0 2) Ügyes koodinátaendsze-választással ki lehet használni a gömbszimmetiát. Az Einstein-egyenlet analitikusan is megoldható, a megoldás,
A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a
 a Matematika mérnököknek I. című tárgyhoz Függvények. Függvények A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a szabadon eső test sebessége az idő függvénye. Konstans hőmérsékleten
a Matematika mérnököknek I. című tárgyhoz Függvények. Függvények A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a szabadon eső test sebessége az idő függvénye. Konstans hőmérsékleten
MÉSZÁROS JÓZSEFNÉ, NUMERIKUS MÓDSZEREK
 MÉSZÁROS JÓZSEFNÉ, NUmERIKUS módszerek 9 FÜGGVÉNYKÖZELÍTÉSEK IX. SPLINE INTERPOLÁCIÓ 1. SPLINE FÜGGVÉNYEK A Lagrange interpolációnál említettük, hogy az ún. globális interpoláció helyett gyakran célszerű
MÉSZÁROS JÓZSEFNÉ, NUmERIKUS módszerek 9 FÜGGVÉNYKÖZELÍTÉSEK IX. SPLINE INTERPOLÁCIÓ 1. SPLINE FÜGGVÉNYEK A Lagrange interpolációnál említettük, hogy az ún. globális interpoláció helyett gyakran célszerű
x a x, ha a > 1 x a x, ha 0 < a < 1
 EL 18 Valós exponenciális függvények Definíció: Ha a R, a>0, akkor legyen a x = e x lna, x R A valós változós exponenciális függvények grafikonja: x a x, ha a > 1 x a x, ha 0 < a < 1 A szinusz függvény
EL 18 Valós exponenciális függvények Definíció: Ha a R, a>0, akkor legyen a x = e x lna, x R A valós változós exponenciális függvények grafikonja: x a x, ha a > 1 x a x, ha 0 < a < 1 A szinusz függvény
Irányítástechnika GÁSPÁR PÉTER. Prof. BOKOR JÓZSEF útmutatásai alapján
 Irányítástechnika GÁSPÁR PÉTER Prof. BOKOR JÓZSEF útmutatásai alapján Irányítástechnika rendszerek Irányítástechnika Budapest, 2008 2 Az előadás felépítése 1. 2. 3. 4. Irányítástechnika Budapest, 2008
Irányítástechnika GÁSPÁR PÉTER Prof. BOKOR JÓZSEF útmutatásai alapján Irányítástechnika rendszerek Irányítástechnika Budapest, 2008 2 Az előadás felépítése 1. 2. 3. 4. Irányítástechnika Budapest, 2008
Mobilis robotok irányítása
 Mobiis obotok iánítása. A gakoat céja Mobiis obotok kinematikai modeezése Matab/Simuink könezetben. Mobiis obotok Ponttó Pontig (PTP) iánításának teezése és megaósítása.. Eméeti beezet Mobiis obotok heátoztatása
Mobiis obotok iánítása. A gakoat céja Mobiis obotok kinematikai modeezése Matab/Simuink könezetben. Mobiis obotok Ponttó Pontig (PTP) iánításának teezése és megaósítása.. Eméeti beezet Mobiis obotok heátoztatása
Orvosi Fizika és Statisztika
 Orvosi Fizika és Statisztika Szegedi Tudományegyetem Általános Orvostudományi Kar Természettudományi és Informatikai Kar Orvosi Fizikai és Orvosi Informatikai Intézet www.szote.u-szeged.hu/dmi Orvosi fizika
Orvosi Fizika és Statisztika Szegedi Tudományegyetem Általános Orvostudományi Kar Természettudományi és Informatikai Kar Orvosi Fizikai és Orvosi Informatikai Intézet www.szote.u-szeged.hu/dmi Orvosi fizika
A queueing model for Spectrum Renting and handover calls in Mobile Cellular Networks
 Mobil hálózatok véges foású modellezése spectum enting és handove hívások használatával A queueing model fo Spectum Renting and handove calls in Mobile Cellula Netwoks Tamás Béczes a, János Sztik a, Jinting
Mobil hálózatok véges foású modellezése spectum enting és handove hívások használatával A queueing model fo Spectum Renting and handove calls in Mobile Cellula Netwoks Tamás Béczes a, János Sztik a, Jinting
HARDVEREK VILLAMOSSÁGTANI ALAPJAI
 HARDVEREK VILLAMOSSÁGTANI ALAPJAI Lektoálta D. Kuczmann Miklós, okl. villamosménök egyetemi taná Széchenyi István Egyetem, Győ A feladatokat ellenőizte Macsa Dániel, okl. villamosménök Széchenyi István
HARDVEREK VILLAMOSSÁGTANI ALAPJAI Lektoálta D. Kuczmann Miklós, okl. villamosménök egyetemi taná Széchenyi István Egyetem, Győ A feladatokat ellenőizte Macsa Dániel, okl. villamosménök Széchenyi István
INHOMOGÉN RUGALMAS ANYAGÚ KÚPOK STATIKAI VIZSGÁLATA STATIC ANALYSIS OF NONHOMOGENEOUS ELASTIC CONICAL BODIES
 INHOMOGÉN RUGALMAS ANYAGÚ KÚPOK STATIKAI VIZSGÁLATA STATIC ANALYSIS OF NONHOMOGENEOUS ELASTIC CONICAL BODIES Ecsedi István, Pofesso Emeitus, Miskolci Egyetem, Műszaki Mechanikai Intézet; Baksa Attila,
INHOMOGÉN RUGALMAS ANYAGÚ KÚPOK STATIKAI VIZSGÁLATA STATIC ANALYSIS OF NONHOMOGENEOUS ELASTIC CONICAL BODIES Ecsedi István, Pofesso Emeitus, Miskolci Egyetem, Műszaki Mechanikai Intézet; Baksa Attila,
a címkezelés a R. 2. (2) bekezdés szerint Magyarország nincs címkezelés postai irányítószám nincs címkezelés 7370
 Iktatószám: 2000-11/2015. (2) bekezdés bekezdés i i tartalma a postai irányítószám 7370 településrésznév kerület megjelölés közterületnév Fő közterületjelleg utca házszám törlés 2. törölve épület jele
Iktatószám: 2000-11/2015. (2) bekezdés bekezdés i i tartalma a postai irányítószám 7370 településrésznév kerület megjelölés közterületnév Fő közterületjelleg utca házszám törlés 2. törölve épület jele
Fourier transzformáció
 a Matematika mérnököknek II. című tárgyhoz Fourier transzformáció Fourier transzformáció, heurisztika Tekintsük egy 2L szerint periodikus függvény Fourier sorát: f (x) = a 0 2 + ( ( nπ ) ( nπ )) a n cos
a Matematika mérnököknek II. című tárgyhoz Fourier transzformáció Fourier transzformáció, heurisztika Tekintsük egy 2L szerint periodikus függvény Fourier sorát: f (x) = a 0 2 + ( ( nπ ) ( nπ )) a n cos
Boros Zoltán február
 Többváltozós függvények differenciál- és integrálszámítása (2 3. előadás) Boros Zoltán 209. február 9 26.. Vektorváltozós függvények differenciálhatósága és iránymenti deriváltjai A továbbiakban D R n
Többváltozós függvények differenciál- és integrálszámítása (2 3. előadás) Boros Zoltán 209. február 9 26.. Vektorváltozós függvények differenciálhatósága és iránymenti deriváltjai A továbbiakban D R n
Regresszió. Csorba János. Nagyméretű adathalmazok kezelése március 31.
 Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Bevezetés az algebrába 2
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Bevezetés az algebrába 2 BMETE91AM37 Differencia- és differenciálegy.-rsz. H607 2017-04-05
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Bevezetés az algebrába 2 BMETE91AM37 Differencia- és differenciálegy.-rsz. H607 2017-04-05
Biomatematika 2 Orvosi biometria
 Biomatematika 2 Orvosi biometria 2017.02.13. Populáció és minta jellemző adatai Hibaszámítás Valószínűség 1 Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza)
Biomatematika 2 Orvosi biometria 2017.02.13. Populáció és minta jellemző adatai Hibaszámítás Valószínűség 1 Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza)
Tossenberger Tamás. Algoritmusok kvantum-információelméletből
 Eötvös Loánd Tudományegyetem Temészettudományi Ka Tossenbege Tamás Algoitmusok kvantum-infomációelméletből BSc Alkalmazott Matematikus Szakdolgozat Témavezető: d. Mosonyi Milán Analízis Tanszék, BME Matematika
Eötvös Loánd Tudományegyetem Temészettudományi Ka Tossenbege Tamás Algoitmusok kvantum-infomációelméletből BSc Alkalmazott Matematikus Szakdolgozat Témavezető: d. Mosonyi Milán Analízis Tanszék, BME Matematika
Digitális Fourier-analizátorok (DFT - FFT)
 6 Digitális Fourier-analizátoro (DFT - FFT) Eze az analizátoro digitális műödésűe és a Fourier-transzformálás elvén alapulna. A digitális Fourier analizátoro a folytonos időfüggvény mintavételezett jeleit
6 Digitális Fourier-analizátoro (DFT - FFT) Eze az analizátoro digitális műödésűe és a Fourier-transzformálás elvén alapulna. A digitális Fourier analizátoro a folytonos időfüggvény mintavételezett jeleit
1.1. Feladatok. x 0 pontban! b) f(x) = 2x + 5, x 0 = 2. d) f(x) = 1 3x+4 = 1. e) f(x) = x 1. f) x 2 4x + 4 sin(x 2), x 0 = 2. általános pontban!
 . Egyváltozós függgvények deriválása.. Feladatok.. Feladat A definíció alapján határozzuk meg a következő függvények deriváltját az x pontban! a) f(x) = x +, x = 5 b) f(x) = x + 5, x = c) f(x) = x+, x
. Egyváltozós függgvények deriválása.. Feladatok.. Feladat A definíció alapján határozzuk meg a következő függvények deriváltját az x pontban! a) f(x) = x +, x = 5 b) f(x) = x + 5, x = c) f(x) = x+, x
Diszkréten mintavételezett függvények
 Diszkréten mintavételezett függvények A függvény (jel) értéke csak rögzített pontokban ismert, de köztes pontokban is meg akarjuk becsülni időben mintavételezett jel pixelekből álló műholdkép rácson futtatott
Diszkréten mintavételezett függvények A függvény (jel) értéke csak rögzített pontokban ismert, de köztes pontokban is meg akarjuk becsülni időben mintavételezett jel pixelekből álló műholdkép rácson futtatott
Az atomok vonalas színképe
 Az atomok vonalas színképe Színképelemzés, spektoszkópia R. Bunsen 8-899 G.R. Kichhoff 8-887 A legegyszebb (a legkönnyebb) atom a hidogén. A spektuma a láthatóban a következ A hidogén atom spektuma a látható
Az atomok vonalas színképe Színképelemzés, spektoszkópia R. Bunsen 8-899 G.R. Kichhoff 8-887 A legegyszebb (a legkönnyebb) atom a hidogén. A spektuma a láthatóban a következ A hidogén atom spektuma a látható
Differenciálszámítás. 8. előadás. Farkas István. DE ATC Gazdaságelemzési és Statisztikai Tanszék. Differenciálszámítás p. 1/1
 Differenciálszámítás 8. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Differenciálszámítás p. 1/1 Egyenes meredeksége Egyenes meredekségén az egyenes és az X-tengely pozitív iránya
Differenciálszámítás 8. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Differenciálszámítás p. 1/1 Egyenes meredeksége Egyenes meredekségén az egyenes és az X-tengely pozitív iránya
Jelfeldolgozás bevezető. Témalaboratórium
 Jelfeldolgozás bevezető Témalaboratórium Tartalom Jelfeldolgozás alapjai Lineáris rendszerelmélet Fourier transzformációk és kapcsolataik Spektrális képek értelmezése Képfeldolgozás alapjai Néhány nevezetesebb
Jelfeldolgozás bevezető Témalaboratórium Tartalom Jelfeldolgozás alapjai Lineáris rendszerelmélet Fourier transzformációk és kapcsolataik Spektrális képek értelmezése Képfeldolgozás alapjai Néhány nevezetesebb
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 5. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 5. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
1. ábra. 24B-19 feladat
 . gyakorlat.. Feladat: (HN 4B-9) A +Q töltés egy hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld.. ábra.). Számítsuk ki az E elektromos térerősséget a vonal. ábra. 4B-9 feladat irányában lévő,
. gyakorlat.. Feladat: (HN 4B-9) A +Q töltés egy hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld.. ábra.). Számítsuk ki az E elektromos térerősséget a vonal. ábra. 4B-9 feladat irányában lévő,
Haladó lineáris algebra
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Haladó lineáris algebra BMETE90MX54 Lineáris leképezések 2017-02-21 IB026 Wettl Ferenc
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Haladó lineáris algebra BMETE90MX54 Lineáris leképezések 2017-02-21 IB026 Wettl Ferenc
Segédlet a Tengely gördülő-csapágyazása feladathoz
 Segélet a Tengely göülő-csaágyazása felaathoz Összeállította: ihai Zoltán egyetemi ajunktus Tengely göülő-csaágyazása Aott az. ábán egy csaágyazott tengely kinematikai vázlata. A ajz szeint az A jelű csaágy
Segélet a Tengely göülő-csaágyazása felaathoz Összeállította: ihai Zoltán egyetemi ajunktus Tengely göülő-csaágyazása Aott az. ábán egy csaágyazott tengely kinematikai vázlata. A ajz szeint az A jelű csaágy
Mátrixok 2017 Mátrixok
 2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
Fourier sorok február 19.
 Fourier sorok. 1. rész. 2018. február 19. Függvénysor, ismétlés Taylor sor: Speciális függvénysor, melynek tagjai: cf n (x) = cx n, n = 0, 1, 2,... Állítás. Bizonyos feltételekkel minden f előállítható
Fourier sorok. 1. rész. 2018. február 19. Függvénysor, ismétlés Taylor sor: Speciális függvénysor, melynek tagjai: cf n (x) = cx n, n = 0, 1, 2,... Állítás. Bizonyos feltételekkel minden f előállítható
Képalkotás modellezése, metrikái. Orvosi képdiagnosztika 6. ea ősz
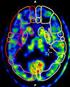 Képalkotás modellezése, metrikái Orvosi képdiagnosztika 6. ea. 2015 ősz Jelölésjegyzék Rendszer válasza f gerjesztésre: Dirac-delta: x ; egységugrás: 0 idejű Dirac-delta gerjesztése a rendszer válasza:
Képalkotás modellezése, metrikái Orvosi képdiagnosztika 6. ea. 2015 ősz Jelölésjegyzék Rendszer válasza f gerjesztésre: Dirac-delta: x ; egységugrás: 0 idejű Dirac-delta gerjesztése a rendszer válasza:
X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ
 X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel és módszerekkel történik. A feldolgozás előtt az analóg jeleket digitalizálni kell.
X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel és módszerekkel történik. A feldolgozás előtt az analóg jeleket digitalizálni kell.
Diszkrét matematika 1. estis képzés
 Diszkrét matematika 1. estis képzés 2019. tavasz 1. Diszkrét matematika 1. estis képzés 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 1. estis képzés 2019. tavasz 1. Diszkrét matematika 1. estis képzés 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Bevezetés az algebrába 2 Differencia- és differenciálegyenlet-rendszerek
 Bevezetés az algebrába 2 Differencia- és differenciálegyenlet-rendszerek Algebra Tanszék B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E
Bevezetés az algebrába 2 Differencia- és differenciálegyenlet-rendszerek Algebra Tanszék B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E
Sorozatok, sorok, függvények határértéke és folytonossága Leindler Schipp - Analízis I. könyve + jegyzetek, kidolgozások alapján
 Sorozatok, sorok, függvények határértéke és folytonossága Leindler Schipp - Analízis I. könyve + jegyzetek, kidolgozások alapján Számsorozatok, vektorsorozatok konvergenciája Def.: Számsorozatok értelmezése:
Sorozatok, sorok, függvények határértéke és folytonossága Leindler Schipp - Analízis I. könyve + jegyzetek, kidolgozások alapján Számsorozatok, vektorsorozatok konvergenciája Def.: Számsorozatok értelmezése:
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
CMS Pixel Detektor működése
 CMS Pixel Detektor működése VÁMI Tamás Álmos Kísérleti mag- és részecskefizikai szeminárium (ELTE) Large Hadron Collider Large Hadron Collider @P5 p + p + 15 m Nyomkövető rendszer Töltött részecskék
CMS Pixel Detektor működése VÁMI Tamás Álmos Kísérleti mag- és részecskefizikai szeminárium (ELTE) Large Hadron Collider Large Hadron Collider @P5 p + p + 15 m Nyomkövető rendszer Töltött részecskék
Numerikus módszerek. A. Egyenletek gyökeinek numerikus meghatározása
 Numeikus módszeek A. Egyenletek gyökeinek numeikus meghatáozása A1) Hatáozza meg az x 3 + x = egyenlet (egyik) gyökét éintı módszeel. Kezdje a számítást az x = helyen! Megoldás: x 1, Megoldás 3 A függvény
Numeikus módszeek A. Egyenletek gyökeinek numeikus meghatáozása A1) Hatáozza meg az x 3 + x = egyenlet (egyik) gyökét éintı módszeel. Kezdje a számítást az x = helyen! Megoldás: x 1, Megoldás 3 A függvény
A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld ábra ábra
 . Gyakorlat 4B-9 A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld. 4-6 ábra.). Számítsuk ki az E elektromos térerősséget a vonal irányában lévő, annak.. ábra. 4-6 ábra végpontjától
. Gyakorlat 4B-9 A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld. 4-6 ábra.). Számítsuk ki az E elektromos térerősséget a vonal irányában lévő, annak.. ábra. 4-6 ábra végpontjától
11. Alakzatjellemzők. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
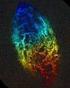 11. Alakzatjellemzők Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Alakzat = pontok összefüggő rendszere példák síkbeli alakzatokra 3 Az
11. Alakzatjellemzők Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Alakzat = pontok összefüggő rendszere példák síkbeli alakzatokra 3 Az
"Flat" rendszerek. definíciók, példák, alkalmazások
 "Flat" rendszerek definíciók, példák, alkalmazások Hangos Katalin, Szederkényi Gábor szeder@scl.sztaki.hu, hangos@scl.sztaki.hu 2006. október 18. flatness - p. 1/26 FLAT RENDSZEREK: Elméleti alapok 2006.
"Flat" rendszerek definíciók, példák, alkalmazások Hangos Katalin, Szederkényi Gábor szeder@scl.sztaki.hu, hangos@scl.sztaki.hu 2006. október 18. flatness - p. 1/26 FLAT RENDSZEREK: Elméleti alapok 2006.
A Maxwell-egyenletrendszer:
 Maxwell-egyenletendsze: Ez a XIX. sz. egyik legnagyobb hatású egyenletendszee, főleg azét, met ebből az egyenletendszeből vezették le az elektomágneses hullámok létezését.. mpèe-maxwell féle gejesztési
Maxwell-egyenletendsze: Ez a XIX. sz. egyik legnagyobb hatású egyenletendszee, főleg azét, met ebből az egyenletendszeből vezették le az elektomágneses hullámok létezését.. mpèe-maxwell féle gejesztési
4. STACIONÁRIUS MÁGNESES TÉR
 4. STACONÁRUS MÁGNESES TÉR Az időben állandó sebességgel mozgó töltések keltette áam nemcsak elektomos, de mágneses teet is kelt. 4.1. A mágneses té jelenléte 4.1.1. A mágneses dipólus A tapasztalat azt
4. STACONÁRUS MÁGNESES TÉR Az időben állandó sebességgel mozgó töltések keltette áam nemcsak elektomos, de mágneses teet is kelt. 4.1. A mágneses té jelenléte 4.1.1. A mágneses dipólus A tapasztalat azt
Villamos jelek mintavételezése, feldolgozása. LabVIEW előadás
 Villamos jelek mintavételezése, feldolgozása (ellenállás mérés LabVIEW támogatással) LabVIEW 7.1 2. előadás Dr. Iványi Miklósné, egyetemi tanár LabVIEW-7.1 EA-2/1 Ellenállás mérés és adatbeolvasás Rn ismert
Villamos jelek mintavételezése, feldolgozása (ellenállás mérés LabVIEW támogatással) LabVIEW 7.1 2. előadás Dr. Iványi Miklósné, egyetemi tanár LabVIEW-7.1 EA-2/1 Ellenállás mérés és adatbeolvasás Rn ismert
Matematika A1a Analízis
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 A derivált alkalmazásai H607, EIC 2019-04-03 Wettl
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 A derivált alkalmazásai H607, EIC 2019-04-03 Wettl
Összetettebb feladatok
 A szinusztétel és koszinusztétel lklmzás Összetettebb feldtok 055..,7 m háom kö közötti síkidom teülete. Kössük össze köök középpontjit, így kpunk egy háomszöget. Legyen m, b m, 5 m. Számítsuk ki koszinusztétellel
A szinusztétel és koszinusztétel lklmzás Összetettebb feldtok 055..,7 m háom kö közötti síkidom teülete. Kössük össze köök középpontjit, így kpunk egy háomszöget. Legyen m, b m, 5 m. Számítsuk ki koszinusztétellel
Képszűrés II. Digitális képelemzés alapvető algoritmusai. Laplace-operátor és approximációja. Laplace-szűrő és átlagolás. Csetverikov Dmitrij
 Képszűrés II Digitális képelemzés alapvető algoritmusai Csetverikov Dmitrij Eötvös Lóránd Egyetem, Budapest csetverikov@sztaki.hu http://vision.sztaki.hu Informatikai Kar 1 Laplace-szűrő 2 Gauss- és Laplace-képpiramis
Képszűrés II Digitális képelemzés alapvető algoritmusai Csetverikov Dmitrij Eötvös Lóránd Egyetem, Budapest csetverikov@sztaki.hu http://vision.sztaki.hu Informatikai Kar 1 Laplace-szűrő 2 Gauss- és Laplace-képpiramis
17. tétel A kör és részei, kör és egyenes kölcsönös helyzete (elemi geometriai tárgyalásban). Kerületi szög, középponti szög, látószög.
 17. tétel kö és észei, kö és egyenes kölcsönös helyzete (elemi geometiai tágyalásban). Keületi szög, középponti szög, látószög. Def: Kö: egy adott ponttól egyenlő távolsága levő pontok halmaza a síkon.
17. tétel kö és észei, kö és egyenes kölcsönös helyzete (elemi geometiai tágyalásban). Keületi szög, középponti szög, látószög. Def: Kö: egy adott ponttól egyenlő távolsága levő pontok halmaza a síkon.
Híradástechikai jelfeldolgozás
 Híradástehikai jeleldolgozás. előadás Sebességkonverziós jeleldolgozás 05. 04. 3. 05. április 3. Budapest Dr. Gaál Józse BME Hálózati Rendszerek és SzolgáltatásokTanszék gaal@hit.bme.hu Sebességkonverziós
Híradástehikai jeleldolgozás. előadás Sebességkonverziós jeleldolgozás 05. 04. 3. 05. április 3. Budapest Dr. Gaál Józse BME Hálózati Rendszerek és SzolgáltatásokTanszék gaal@hit.bme.hu Sebességkonverziós
Analóg-digitál átalakítók (A/D konverterek)
 9. Laboratóriumi gyakorlat Analóg-digitál átalakítók (A/D konverterek) 1. A gyakorlat célja: Bemutatjuk egy sorozatos közelítés elvén működő A/D átalakító tömbvázlatát és elvi kapcsolási rajzát. Tanulmányozzuk
9. Laboratóriumi gyakorlat Analóg-digitál átalakítók (A/D konverterek) 1. A gyakorlat célja: Bemutatjuk egy sorozatos közelítés elvén működő A/D átalakító tömbvázlatát és elvi kapcsolási rajzát. Tanulmányozzuk
Villamos jelek mintavételezése, feldolgozása. LabVIEW 7.1
 Villamos jelek mintavételezése, feldolgozása (ellenállás mérés LabVIEW támogatással) LabVIEW 7.1 előadás Dr. Iványi Miklósné, egyetemi tanár LabVIEW-7.1 KONF-5_2/1 Ellenállás mérés és adatbeolvasás Rn
Villamos jelek mintavételezése, feldolgozása (ellenállás mérés LabVIEW támogatással) LabVIEW 7.1 előadás Dr. Iványi Miklósné, egyetemi tanár LabVIEW-7.1 KONF-5_2/1 Ellenállás mérés és adatbeolvasás Rn
1.1 Számítógéppel irányított rendszerek
 Számítógépes irányításelmélet 4. Számítógéppel irányított rendszerek A fejezetnek az a célja, hogy bevezesse a számítógéppel irányított rendszerek alapfogalmait. Bemutatja a folytonos jel mintavételezését,
Számítógépes irányításelmélet 4. Számítógéppel irányított rendszerek A fejezetnek az a célja, hogy bevezesse a számítógéppel irányított rendszerek alapfogalmait. Bemutatja a folytonos jel mintavételezését,
Mérés és adatgyűjtés
 Mérés és adatgyűjtés 5. óra - levelező Mingesz Róbert Szegedi Tudományegyetem 2011. március 18. MA lev - 5. óra Verzió: 1.1 Utolsó frissítés: 2011. április 12. 1/20 Tartalom I 1 Demók 2 Digitális multiméterek
Mérés és adatgyűjtés 5. óra - levelező Mingesz Róbert Szegedi Tudományegyetem 2011. március 18. MA lev - 5. óra Verzió: 1.1 Utolsó frissítés: 2011. április 12. 1/20 Tartalom I 1 Demók 2 Digitális multiméterek
