MEGBIZHAT OS AG MODELLEZES. M}uszaki informatika szak. Hibat}ur}o rendszerek modul. 1997/ felev. Jereb Laszlo, Telek Miklos,

Átírás

1 MEGBIZHAT OS AG MODELLEZES M}uszaki informatika szak Hibat}ur}o rendszerek modul 1997/ felev Jereb Laszlo, Telek Miklos, Horvath Andras, Pfening Andras

2

3 Tartalomjegyzek 1. MEGBIZHAT OS AGI MOTIV ACI OK, ALAPFOGALMAK A megbzhatosagelmelet jelent}osege Informacios tarsadalom Meghibasodasok A tantargy Tartalmi kerdesek A megbzhatosag jellemzese A megbzhatosag fogalma A meghibasodasi-javtasi folyamat jellemz}oi A meghibasodasi tenyez}o ((t)) f(t) alkalmazasanak korlatai (t) bevezetese (t) id}ofuggese igenybevetel- es kornyezetfuggese Alkatreszek megbzhatosagi modellezese Alkatresz megbzhatosagi adatok forrasa Alkatresz megbzhatosagi modellek Komplex modellek implementalasa Peldak NEMJAVITOTT RENDSZEREK MEGBIZHAT OS AGA Redundanciamentes (soros) rendszer Redundanciamentes rendszer fogalma Redundanciamentes rendszer szamtasa Redundans alapstrukturak megbzhatosaga Melegtartalekolt rendszer megbzhatosagi jellemz}oi Hidegtartalekolt rendszer megbzhatosagi jellemz}oi Csokkentett terheles}u tartalek n-b}ol k jo rendszer megbzhatosagi jellemz}oi i

4 2.3. Osszetett redundans rendszerek Soros-parhuzamos rendszerek Majoritasos rendszer megbzhatosagi jellemz}oi Atkapcsolo tartalekolasu rendszer megbzhatosagi jellemz}oi Nemjavtott rendszerek szamtasi modszerei Megbzhatosagi blokkdiagram A teljes valoszin}useg tetel alkalmazasa Halozatmegbzhatosag szamtasi modszerek Vagatmeghatarozas (cut set) Utmeghatarozas (tie set) Esemenyfa meghatarozas (event tree) Kapcsolat matrix (connection matrix) Hibafa analzis (fault tree) Modellezesi alapelemek (szimbolumok) Analzis lepesek Gyakorlatok nemjavtott rendszerek modellezesere, szamtasara JAVITOTT RENDSZEREK MEGBIZHAT OS AGA Kiindulopontok Diszkret idej}u (veges) Markov lancok Markovitas es tulajdonsagai A hatareloszlas Bolyongasok (diszkret idej}u szuletesi-halalozasi folyamatok) Peldak Folytonos idej}u veges Markov lancok Markov tulajdonsag A hatareloszlas Szuletesi-halalozasi folyamatok (folytonos idej}u) A tranziens eloszlas Allapotok tartasid}o eloszlasa Ketallapotu pelda a tranziens es egyensulyi eloszlas el}oalltasara Folytonos idej}u Markov lancok alkalmazasa a megbzhatosagi modellezesben Megfeleltetesek Rendszerek megbzhatosagi jellemz}oi Rendszerek megbzhatosagi jellemz}oinek el}oalltasa Mintapelda Mintapeldak markovi modellek alkalmazasara Ketegyseges csokkentett terheles}u tartalek ii

5 Ketegyseges rendszer az egysegek ket hibas allapotaval Ketegyseges melegtartalek ket hibas allapotu atkapcsoloval Majoritasos rendszer Osszefoglalas Markovi modellek feleptese es alkalmazasa (otletek) Fuggetlen reszegysegek halozatok Kitekintes FONTOSABB TOV ABBLEPESI IR ANYOK NEH ANY JELLEMZ }OJE A markovi apparatus kiterjesztese Petri-halok es alkalmazasuk a megbzhatosagelmeletben Hozam modellezes iii

6 2

7 1. fejezet MEGBIZHAT OS AGI MOTIV ACI OK, ALAPFOGALMAK 1.1. A megbzhatosagelmelet jelent}osege Informacios tarsadalom 1. Szamtastechnikai alkalmazasi motivaciok (gyors, pontos munka) bonyolult feladatok elvegzese (pl. er}om}uvi szabalyozas) id}oigenyes tevekenyseg (pl. tudomany) elosztott informacio, adatbazis (pl. repul}ogepes helyfoglalas) 2. Mind szelesebb kor}u, fontos szamtastechnikai alkalmazas egyre bonyolultabb funkciok egyre bonyolultabb rendszerek 3. Novekv}o felhasznaloi kockazat kornyezet informaciok (pl. adatbazisok) eszkozok ember Kritikusak a meghibasodasok! megbzhatosag! 3

8 Meghibasodasok 1. Problema: a meghibasodasok veletlenszer}uen keletkeznek 2. Cel: nem kiszamthato id}opontban nem kiszamthato helyen meghibasodasok bekovetkezesenek megakadalyozasa, de legalabb a hatasuk korlatozasa 3. Lehet}oseg a meghibasodas bekovetkezesenek megakadalyozasaban nagymegbzhatosagu alkatelemek (pl. redundans) megbzhatosagnovelesi modszerek alkalmazasa (pl. alulterheles) 4. Lehet}oseg a meghibasodas hatasanak korlatozasaban terben (redundancia) id}oben (karbantartas, javtas) 5. Beavatkozasi lehet}oseg gyartok, felhasznalok, szolgaltatok, szolgaltatas igenybe vev}ok elter}o lehet}osegek a meghibasodasok megakadalyozasaban vagy a meghibasodasok hatasanak korlatozasaban 6. A kulonboz}o beavatkozasi lehet}osegek hatasara elter}o a koltsegek megosztasa is el}oalltasi, uzemeltetesi koltseg kockazat, veszteseg (pl. kotber) 7. Gazdasagos m}uszaki kompromisszumot kell talalni, tehat: ismerni kell a meghibasodasok bekovetkezesi jellemz}oit tudni kell megakadalyozasuk, korlatozasuk lehet}osegeit fel kell tudni merni a megoldasok hatasat (javulas, koltseg) de altalaban csak olyan termeket szabad letrehozni, amire adott az igeny, azaz megterul, megzetnek! mernoki tervezesi-alkalmazasi tevekenyseg kulcskerdese 4

9 1.2. A tantargy Tartalmi kerdesek 1. A tantargy celja a megbzhatosagelmelet alapfogalmainak, modelljeinek, szamtasi modszereinek megismertetese 2. A tantargy kornyezete el}ozmenyek { Valoszin}usegszamtas { Informatika { Hibat}ur}o szamtogepstrukturak { Programozas es diagnosztika folytatas { Hibat}ur}o rendszerek tervezese 3. A tantargy feleptese Mir}ol szol a targy? megbzhatosagi alapfogalmak: a megbzhatosag modellezese alkatreszek megbzhatosaga: alkatreszmegbzhatosag modellezese, el}orejelzese nem javtott rendszerek megbzhatosaga: rendszerek megbzhatosaganak meghatarozasa rendszerelemek megbzhatosagi jellemz}oi alapjan javtott rendszerek megbzhatosaga: javtasok, karbantartas modellezese, hatasuk a rendszerek megbzhatosagi jellemz}oire megbzhatosag es teljest}okepesseg: nem idealis megbzhatosagu rendszerek teljest}okepessegenek modellezese 4. Mir}ol nem szol a targy? alkatreszmegbzhatosag zikai kerdesei konkret megbzhato aramkori megoldasok konkret megbzhato rendszerek Azaz csak az elmeleti szempontok, modellek, szamtasi modszerek! 5

10 1.3. A megbzhatosag jellemzese A megbzhatosag fogalma 1. A megbzhatosag denicioja A termek azon tulajdonsaga, hogy el}ort funkcioit, adott korulmenyek kozott teljesti. 2. A megbzhatosag jellemzesenek problemai termek min}osege: altalanosan sokparameter}u termek parameterei: fx(t) = fx i (t)g; i = 1; 2; ; ng egy sokdimenzios veletlen folyamat, ahol X i (t) valos kezdetben lesz}uktjuk erdekl}odesunket a ketallapotu esetre, azaz, feltesszuk, hogy a termek eleget tesz a vele szemben tamasztott kovetelmenyeknek, ha X(t) 2 U, s nem tesz eleget, ha X(t) 2 D, ahol X = U [ D; U \ D = ; a termek parametervaltozanak demonstralasa egy ketdimenzios abran A meghibasodasi-javtasi folyamat jellemz}oi 1. Meghibasodasi/javtasi folyamatok jellemz}oi t 0 ; t 2 ; t 4 ; ; t 2n ; : az n + 1. m}ukodesi id}oszakasz kezdete t 1 ; t 3 ; ; t 2n 1 ; : az n. kiesesi id}oszakasz kezdete (az n. meghibasodas id}opontja) n = t 2n 1 t 2n 2 : az n. m}ukodesi id}oszakasz hossza (veletlen valtozo) n = t 2n t 2n 1 : az n. kiesesi id}oszakasz hossza (veletlen valtozo) n = n + n = t 2n t 2n 2 : az n. m}ukodesi-kiesesi ciklus hossza (veletlen valtozo) F n (t) = P r( n t): az n. m}ukodesi id}oszakasz hosszanak eloszlasfuggvenye G n (t) = P r( n t): az n. javtasi id}oszakasz hosszanak eloszlasfuggvenye H n (t) = P r( n t): az n. m}ukodesi-javtasi id}oszakasz hosszanak eloszlasfuggvenye 6

11 f n (t): az n. m}ukodesi id}oszakasz hosszanak s}ur}usegfuggvenye, (ha letezik) f n (t) = df n(t) dt Altalaban letezik, mivel nincsenek kituntetett meghibasodasi id}opontok g n (t): az n. kiesesi id}oszakasz hosszanak s}ur}usegfuggvenye, (ha letezik) g n (t) = dg n(t) dt Sokszor nem letezik, mivel lehetnek megadott hosszusagu javtasi id}oszakaszok h n (t): az n. m}ukodesi-kiesesi id}oszakasz hosszanak s}ur}usegfuggvenye, (ha letezik) h n (t) = f n (t) g n (t) = a ket id}oszakasz konvolucioja 2. Nem javtott es javtott rendszerek fogalma nem javtott rendszerek { 0 < 1 < 1 { 1 = 1 { 1 = 1 javtott rendszerek { 0 < k < 1; 8k = 1; 2; { 0 < k < 1; 8k = 1; 2; { 0 < k < 1; 8k = 1; 2; Z t 0 f n ()g n (t )d; 7

12 3. Nem javtott rendszerek megbzhatosagi jellemz}oi alapjellemz}o: r(t), a hibamentes m}ukodes valoszin}usege (sokszor megbzhatosagnak nevezik, survivability reliability): A deniciobol kovetkez}oen: r(t) = P(X(s) 2 U; 80 s t) = P( 1 > t) = 1 F (t) (1.1) r(t) tulajdonsagai: { r(0) = 1, kezdetben minden termek jo (?) { lim t!1 r(t) = 0, valamikor minden termek meghibasodik { r(t) monoton fogyo, (s}ot szigoruan monoton is, ha nincsenek garantaltan hibamentes id}oszakaszok) q(t) = P (9s t; amelyre X(s) 2 D): nevezik. A deniciobol kovetkez}oen: sokszor megbzhatatlansagnak q(t) = P(9s t : X(s) 2 D) = P( 1 t) = F (t) (1.2) q(t) tulajdonsagai: eloszlasfuggveny tulajdonsagok { q(0) = 0 { lim t!1 q(t) = 1 { q(t) monoton nov}o MT F F = E( 1 ): az els}o meghibasodas varhato ideje (Mean Time to First Failure) (altalanosan tetszes szerinti magasabb momentumok is) MT F F es r(t) kapcsolata: MT F F = E[ 1 ] = Z 1 t=0 tdf (t) = Z 1 t=0 tdr(t) = [r(t) t] Z 1 0 r(t)dt amelyb}ol, ha limt r(t) = 0 (ami teljesul, ha E[ 1 ] veges), akkor t!1 MT F F = Z 1 0 r(t)dt (1.3) 8

13 4. Javtott rendszerek megbzhatosagi jellemz}oi alapjellemz}o: d(t), rendelkezesreallasi valoszin}useg: dependability keszenleti tenyez}o: availability ha letezik. id}oparameterek: d(t) = P(X(t) 2 U) (1.4) K = lim t!1 d(t) (1.5) { MUT n = E[ n ]: varhato m}ukodesi id}o (Mean Up Time) { MDT n = E[ n ] : varhato kiesesi id}o (Mean Down Time) { MCT n = E[ n ] = E[ n ]+E[ n ] : varhato ciklusid}o (Mean Cycle Time) K es az id}oparameterek kapcsolata, ha { E( n ) = MUT; 8n { E( n ) = MDT; 8n { E( n ) = MCT = MUT + MDT; 8n akkor K = MUT MUT + MDT 5. A min}osegvaltozas demonstralasa egy ketertek}u (U, D) abraval (1.6) 9

14 t i N(t i ) N(t i 1 ) N(t i ) tablazat: A m}ukodesi id}o hisztogramjanak meghatarozasahoz vegzett kserlet eredmenyei 1.4. A meghibasodasi tenyez}o ((t)) f(t) alkalmazasanak korlatai 1. Legyen N(t i ) a t i id}opontban m}ukod}o alkatreszek szama 2. Ekkor r(t) becslese: 3. f(t) becslese: ^r(t i ) = N(t i) N(t 0 ) ^f(t i ) = N(t i 1) N(t i ) N(t 0 ) 1 t 4. f(t) alkalmazasanak demonstralasa: pl. 100 alkatresz, javtas es csere nelkuli m}ukodtetese (ld tablazat) (Kerdes: Javul, romlik vagy valtozatlan az alkatresz?) (t) bevezetese 1. (t) meghibasodasi tenyez}o (intenzitas) failure rate N(t i 1 ) N(t i ) N(t i 1 ) 1 t = N (t i 1) N (t i ) N (t 0 ) N (t i 1) N (t 0 ) 1 t = ^f(t) ^r(t) (t) = f(t) r(t) (1.7) 2. dimenzioja: 1=ora, 1=h, 1 FIT = 1:0e 9 =h 10

15 t r(t) : : tablazat: Nehany hibamentes m}ukodesi valoszin}useg eredmeny = 10 6 /ora eseten 3. (t) kapcsolata r(t)-vel (t) = 1 df (t) = 1 dr(t) r(t) dt r(t) dt (1.8) A dierencialegyenletet megoldva: Z t amib}ol r(0) = 1 kezdeti feltetel mellett: (t) id}ofuggese 1. a tekn}ogorbe es szakaszai I. kezdeti meghibasodasi szakasz 0 (u) du = ln r(t) ln r(0); { gyartasi, tervezesi hibak { bejaratasi, karbantartasi kerdesek II. veletlen meghibasodasok szakasza III. elhasznalodasi szakasz { oregedes, kopas { karbantartasi kerdesek elettartam es varhato m}ukodesi id}o kapcsolata 2. exponencialis eloszlas, orokifjusag r(t) = e R t 0 (u)du (1.9) exponencialis szakasz jellege, fuggvenyei (r(t); F (t); f(t)) { (t) = ; 8 t 11

16 { f(t) = e t { r(t) = e t { F (t) = 1 e t MTFF meghatarozasa: MT F F = Z 1 mivel a L'Hospital szabaly alkalmazasaval: Igy 0 r(t)dt ; lim t r(t) = lim t!1 t!1 e t = 0; MT F F = Z 1 0 r(t)dt = Z 1 0 e t dt = 1 [e t ] 1 0 = 1 (1.10) orokifjusag demonstralasa P ( t + tj t; t 0) = r(t + t) r(t) = e (t+t) e t = e (t) Csak a t id}okulonbsegt}ol fugg, s nem fugg t-t}ol kozvetlenul! exponencialis eloszlas alkalmazasa: veletlen szakasz exponencialis eloszlas kozeltese r(t) = 1X k=0 ( t) k k! = 1 t + 0:5 ( t) 2 ::: ha t < 0:1, akkor jo kozeltessel r(t) = 1 t 3. egyeb m}ukodesi id}o eloszlasok normalis eloszlas { f(t) = 1 p (t m) 2 2 e 2 2 { r(t) = { (t) = 1 p 2 Z 1 t e (t m)2 2 2 R 1 t e (t m)2 2 2 dt e (t m)2 2 2 dt 12

17 { alkalmazas: oreged}o alkatreszek m > 3 Weibull eloszlas (b t)a { r(t) = e (b t)a { F (t) = 1 e { f(t) = a b (b t) a 1 (b t)a e { (t) = a b (b t) a 1 { alkalmazas: mindharom tekn}ogorbe szakasz lerasara alkalmas I. szakasz: a < 1 II. szakasz: a = 1,! = b III. szakasz: a > 2 megjegyzes: 1 < a 2 lognormalis eloszlas { ha Y lognormalis eloszlasu v.v. akkor logy normalis eloszlasu (innet szarmazik az elnevezese), es ugyan ugy ket parameterrel adhato meg az eloszlas { alkalmazas: oreged}o alkatreszek m < igenybevetel- es kornyezetfuggese 1. megbzhatosagi adatok, megbzhatosagi jellemz}ok meghatarozasa uzemeltetesi adatok (elter}o korulmenyek osszevetese) gyartonal vegzett vizsgalatok (alapadatok, kulonboz}o tenyez}ok hatasanak elemzese) eredmeny: ( = (h}omerseklet, kornyezet...)) 2. igenybevetel- es kornyezetfugges gyelembevetele csokkentett terheles (derating) gyorstott elettartam vizsgalatok hatasanak elemzese) 3. igenybeveteli (stressz) es kornyezeti alapmodellek es kornyezet: (kategoria peldak) { foldi rogztett, mobil { hajo, repul}ogep, raketa 13

18 { hatasa: ket nagysagrenddel novekv}o es h}omerseklet: { Arrhenius torvenyb}ol szarmaztatva: = 0 e Ea k ( 1 T 0 1 T ) (1.11) Jelolesek: E a : aktivacios energia [ev] k: Boltzmann allando 1: J=K = 8: ev=k T; T 0 : h}omerseklet [K] { 2-es alapu kozeltes = 0 e Ea k T T 0 T T 0 = 0 2 # # f (1.12) ahol # f = kt T 0 E a log 2 e, mivel ex = 2 xlog 2e Jelolesek: # = # # 0 = T T 0 : h}omersekletkulonbseg [C] # f : felelettartamhoz tartozo h}omersekletkulonbseg [C] es terheles jellegzetesen: Jelolesek: = 0 ( S S 0 ) i (1.13) { S; S 0 : terheles (U; I; P ), illetve nevleges terheles (U 0 ; I 0 ; P 0 ) { i = 3:::8: kitev}o (jelent}os hatas) es ciklikus igenybevetel: ciklusszam - id}o megfeleltetes es tanulas: uj, bejaratott gyartmany (10, 1 szorzo) es min}oseg: alkatresztpus, stb. fugg}o es technologia: alkatresztpus-fugg}o 4. becslese meghibasodasi adatok alapjan N elem}u mintahalmazt vizsgalunk, a vizsgalati id}oszakban K elem hibasodik meg 1 ; : : : ; K (hiba id}ok, nem cenzoralt adatok), id}opontokban 14

19 N K elem eseten a vizsgalatot abbahagyjuk 1 ; : : : ; N K id}opontokban az elem meghibasodasa elott (leallasi id}ok, cenzoralt adatok) ezekhez az adatokhoz tartozo likelihood fuggveny megadja, hogy adott eseten mennyire valoszn}u az adatok el}ofordulasa F L ( 1 ; : : : ; K ; 1 ; : : : ; N K ; ) = KY i=1 f ( i ) Y N K i=1 (1 F ( i )) a likelihood fuggveny maximumahoz tartozo ertekkel becsulhet}o a meghibasodasi tenyez}o a rendelkezesre allo adatok alapjan. mivel a likelihood fuggveny szorzatokbol all, es mivel a likelihood fuggvenynek es logaritmusanak ugyan azon erteknel van maximuma, gy a gyakorlatban a likelihood fuggveny logaritmusat hasznaljak. 15

20 1.5. Alkatreszek megbzhatosagi modellezese Alkatresz megbzhatosagi adatok forrasa 1. uzemeltetesi tapasztalatok (eld data) el}onyok: { \pontos" informacio hatranyok: { tulzottan kes}on all rendelkezesre (uzemeltetes megkezdese utan) { a pontos uzemeltetesi korulmenyek nem allnak rendelkezesre { egyeb motivaciok (pl. a szervizszemelyzet erdekeltsege) 2. fokozott igenybevetel melletti vizsgalatok el}onyok: { gyartonal letrehozott feltetelek { ismert, attekinthet}o korulmenyek { hasznalatavetel el}otti eredmenyek hatranyok: { meresi koltsegek { egyedi termeknel nem megoldas 3. azonos technologiaju, hasonlo bonyolultsagu alkatreszek adataibol szarmaztatassal el}onyok: { nem igenyel specialis beruhazast, csak egy szervezeti hatteret { az uzemeltetesi adatgy}ujteshez hasonlo pontossag { hasznalatavetel el}otti eredmenyek hatranyok: { jelent}os valtoztataskor nincs megfelel}o adat 16

21 Alkatresz megbzhatosagi modellek 1. gyartok, felhasznalok modelljei (pl. Siemens, Ericsson) 2. komplex "fuggetlen" modellek (legjellemz}obb a MIL-HDBK/217) 3. peldak: monolit IC: Jelolesek: p = Q [C 1 T V P T + (C 2 + C 3 ) E ] L (1.14) { Q : min}osegi tenyez}o { T : h}omersekleti tenyez}o (Arrchenius) { V : feszultseg gyorstasi tenyez}o { P T : programozasi tenyez}o (csak PROM-ra) { E : kornyezeti tenyez}o { L : tanulasi tenyez}o { C 1 ; C 2 : allando, bonyolultsagtol fugg { C 3 : allando, tokozastol fugg kondenzator: { b : alaplambda { SR : soros ellenallas tenyez}oje { CV : nevleges kapacitas tenyez}oje { C : konstrukcios tenyez}o Komplex modellek implementalasa p = b Q E SR CV C (1.15) 1. RELECT: RELCOM: BME - HT, laboratoriumi gyakorlatok 2. rugalmas feleptes, tetszes szerinti szovegesen megadhato modell 3. alkatreszek, megbzhatosagi modellek (alkatreszek modellhez rendelese) 4. alkatresz- es modelljellemz}ok, fuggvenyek es tablazatok 5. szamtasok, osszehasonltasok 6. MIL-HDBK/217E implementalva 17

22 Peldak 1. pelda: Adott egy IC, amelyre = 100 F IT. Mekkora r(1 ev)? t = 1 ev = 8760 ora ' 10 4 ora, ahonnan: t = q(1 ev) ' 10 3 Vajon mi tortenik, ha 100 darab alkatreszunk van? (0:1!!) 2. pelda: Egy integralt aramkorre v = 85 C -on vizsgalatokat vegeztek, ahol v = 2:210 7 =h erteket hataroztak meg. Az alkatreszt N = 55 C-on akarjak m}ukodtetni. Mekkora lesz a N nevleges meghibasodasi tenyez}o, ha E A = 0:25eV? Az Arrchenius torveny alkalmazasaval: 1eV=k = 1: K, ahonnan 0:25 ev=k = 2900 K, s gy N v = e EA k ( 1 Tv 1 T N ) = e 2900( ) = 1 2:1 Tehat: N = 2:2 2: =h '= 10 7 =h = 100 F IT 3. pelda: Egy ellenallasra a nevleges N = 25 C h}omersekleten N = 200 F IT. Az alkatreszt a = 75 C-on akarjak m}ukodtetni. Mekkora lesz a a aktualis meghibasodasi tenyez}o, ha f = 10 C? Megoldas: Tehat: a = 2 f N = = 2 5 = 32 a = = 6:410 6 =h 18

23 2. fejezet NEMJAVITOTT RENDSZEREK MEGBIZHAT OS AGA 2.1. Redundanciamentes (soros) rendszer Redundanciamentes rendszer fogalma 1. a rendszer m}ukodesehez minden elem m}ukodesere szukseg van 2. grakus abrazolas 3. elemek funkcionalis kapcsolata (nem azonos a strukturalissal) 4. (kapcsoloelemre nincs szukseg) Redundanciamentes rendszer szamtasa 1. legyen adott egy rendszer n elemmel az egyes elemek meghibasodasi id}opontja i ; i = 1; :::; n az egyes elemek meghibasodasi id}opontjanak eloszlasfuggvenye F i (t) = P ( i t); i = 1; :::; n kerdes: = min i ; i = 1; :::; n, F s (t) = P ( t) megoldas: F s (t) = P ( t) = P (min i t) = 1 P (min i > t) = 1 P ( i > t; 8i) 19

24 Ha a i meghibasodasi id}opontok mindegyike fuggetlen egymastol: (nem szigoru feltetel, csak az els}o meghibasodasi id}opontig kell teljesulnie) F s (t) = 1 ny i=1 P ( i > t) = 1 ny (1 P ( i t) = 1 ny i=1 i=1 (1 F i (t)) amib}ol 1 F s (t) = ny (1 F i (t)); i=1 es r s (t) = ny r i (t) = ny e R t 0 i(u) du = e R t 0 P n i=1 i(u) du (2.1) i=1 i=1 2. exponencialis eloszlasra: r s (t) = ny i=1 r i (t) = e P n i=1 it = e st (2.2) ahol s = nx i=1 i MT F F s = 1 s = 1 nx i=1 i (2.3) 3. kovetkezmeny, problema 4. pelda novekv}o alkatreszszam, novekv}o osszetettebb funkciokbol elvileg a kisebb megbzhatosag kovetkezne miniaturizacio: azonos feluleten azonos megbzhatosagot cellal de mindenkeppen szukseg van megbzhatosag novelesi modszerekre adott egy egyszer}u soros rendszer, a felelettartamhoz tartozo h}omersekletekkel a nevleges h}omerseklet: N = 25 C az uzemi h}omerseklet: a = 55 C 20

25 = 25 = 55 alkatresz n i i n i i fi a i a i i a i n i i IC ell kond forr ossz tablazat: Egyszer}u soros rendszer megbzhatosaganak szamtasa ([] = F IT ) Kerdes: Mekkora a rendszer varhato meghibasodasi ideje a nevleges es az uzemi h}omersekleten? MT F F s ( = 25) = MT F F s ( = 55) = Xn k i=1 Xn k i=1 1 1 n i i = a i n i i = MT F F s ( = 25) MT F F s ( = 55) = 6: = 1: =h = 1: =h azaz a rendszer romlasa 6.2-szeres. Megjegyzes: Vigyazat! Ez egy atlagos ertek, nem igaz minden alkatreszre! 5. megbzhatosag novelesi modszerek meghibasodasok szamanak csokkentese { keves alkatresz { kicsi { csokkentett teheles (derating) { azonos ertekre torekves meghibasodasok hatasanak csokkentese { redundancia { fenntartas, javtas { ket megoldas (redundancia, fenntartas) egyuttes alkalmazasa 21

26 2.2. Redundans alapstrukturak megbzhatosaga 1. aktv redundancia: forrotartalekolt rendszer ("melegtartalek") a rendszer n (azonos) elemb}ol all a rendszer m}ukodesehez egyetlen elem m}ukodesere van szukseg a "funkcioban" vagy tartalekban lev}o elemek meghibasodasi tenyez}oje kozott nincs kulonbseg grakus abrazolas elemek funkcionalis kapcsolata (nem azonos a strukturalissal) kapcsoloelemre nincs szukseg 2. passzv redundancia: hidegtartalekolt rendszer a rendszer n (azonos) elemb}ol all a rendszer m}ukodesehez egyetlen elem m}ukodesere van szukseg a tartalekban lev}o elem nem hibasodhat meg grakus abrazolas elemek funkcionalis kapcsolata (nem azonos a strukturalissal) hibafelismer}o es kapcsoloelemre szukseg van, (de most meg idealisnak tekintjuk) 3. "n-b}ol k jo" rendszer a rendszer n (azonos) elemb}ol all a rendszer m}ukodesehez n-b}ol k elem m}ukodesere van szukseg a "funkcioban" vagy tartalekban lev}o elemek meghibasodasi tenyez}oje kozott nincs kulonbseg grakus abrazolas elemek funkcionalis kapcsolata (nem azonos a strukturalissal) hibafelismer}o es kapcsoloelemre szukseg van, (de most meg idealisnak tekintjuk) 22

27 Melegtartalekolt rendszer megbzhatosagi jellemz}oi 1. a megbzhatosagi parameterek meghatarozasa aktv redundancia legyen adott egy rendszer n elemmel az egyes elemek meghibasodasi id}opontja i ; i = 1; :::; n az egyes elemek meghibasodasi id}opontjanak eloszlasfuggvenye F i (t) = P ( i t); i = 1; :::; n = max i ; i = 1; :::; n kerdes: F p (t) = P ( t) megoldas: F p (t) = P ( t) = P (max i t) = P ( i t; 8i) Ha a i meghibasodasi id}opontok mindegyike fuggetlen egymastol: (sokkal szigorubb feltetel, mint a soros rendszernel, mivel az utolso meghibasodasi id}opontig kell a fuggetlensegnek teljesulnie) es F p (t) = ny i=1 r p (t) = 1 P ( i t) = ny i=1 ny i=1 F i (t) (2.4) (1 r i (t)) (2.5) Ha az egyes elemek azonos megbzhatosaguak, azaz r i (t) = r(t); 8i; t (nem tul szigoru feltetel, mivel a redundancianal ez altalaban celszer}u) r p (t) = 1 (1 r(t)) n ; q p (t) = q(t) n ; F p (t) = F n (t); MT F F p = Z 1 2. exponencialis eloszlasra, azonos elemek eseten: 0 r p (t)dt (2.6) r p (t) = 1 (1 r(t)) n = 1 (1 e t ) n (2.7) MT F F p = Z 1 0 r p (t)dt = 23 Z 1 0 (1 F p (t))dt

28 MT F F p(n) MT F F r(t) = 0:9 r(t) = 0:5 n r p (t) q p (t) r p (t) q p (t) tablazat: Egy parhuzamos melegtartalekolt (aktv tartalekolasu) rendszer megbzhatosagi jellemz}oi Helyettesteses integralassal: df (t) dt = e t = (1 F (t)) amib}ol y = F (t) helyettestessel MT F F p = 1 Z 1 t=0 dt = df (t) (1 F (t)) 1 F (t) n 1 F (t) df (t) = 1 Z 1 0 n 1 X k=0 y k dy = 1 nx k=1 1 k (2.8) 3. pelda egyszer}u parhuzamos rendszer, n elemmel 2.2. tablazat abra (id}ofugg}o es r(t)-fugg}o) eredmenyekkel r p (t) vizsgalata r p (t) es r p(t) r(t) vizsgalata 4. p (t) vizsgalata p (t) = 1 dr p (t) r p (t) dt 24 = ne t (1 e t ) n 1 1 (1 e t ) n (2.9)

29 lim t!0 p (t) = 0, lim t!1 p (t) = p (t; n) fuggvenyalakja 5. eredmenyek demonstralasa ketegyseges rendszer eseten 6. kovetkezmeny, problema t << MT F F -nel nagyon hatasos a q p (t)-t tekintve MT F F p javulasa csak logaritmikus n fuggvenyeben p fokozatosan n}o a tartalek az operatv elemmel azonos valoszin}useggel meghibasodhat megvalostasi problemak az idealis erzekel}ot, atkapcsolot es a fuggetlenseget tekintve Hidegtartalekolt rendszer megbzhatosagi jellemz}oi 1. a megbzhatosagi parameterek meghatarozasa legyen adott egy rendszer n elemmel az egyes elemek meghibasodasi id}opontja i ; i = 1; :::; n az egyes elemek meghibasodasi id}opontjanak eloszlasfuggvenye F i (t) = P ( i < t); i = 1; :::; n = nx 1 i ; i = 1; :::; n kerdes: F h (t) = P ( < t) megoldas: (felteve, hogy az atkapcsolas idealis) f h (t) = f 1 f 2 ::: f n (2.10) A rendszerhiba bekovetkezesenek ideje n novekedesevel tart a normalis eloszlashoz!!! relatv szorasa n novekedesevel csokken!!! MT F F h = nx 1 MT F F i (2.11) 25

30 MT F F p(n) MT F F r(t) = 0:9 r(t) = 0:5 n r p (t) q p (t) r p (t) q p (t) tablazat: Egy parhuzamos hidegtartalekolt (passzv tartalekolasu) rendszer megbzhatosagi jellemz}oi Ha az egyes elemek azonos megbzhatosaguak, azaz F i (t) = F (t); 8i; t (nem tul szigoru feltetel, mivel a redundancianal ez altalaban celszer}u) MT F F h = n MT F F (2.12) Gyakorlatban n = 3; :: eseten eloszlasa jol kozelthet}o az (n MT F F; n 2 1 ) parameter}u normalis eloszlassal. 2. exponencialis eloszlasra, azonos elemek eseten: Poisson eloszlas r h (t) = n 1 X 0 (t) k e t (2.13) k! MT F F h = n (2.14) 3. pelda egyszer}u hidegtartalekolt rendszer, n elemmel 2.3. tablazat r h (t) es r h(t) r p (t) vizsgalata r h (t) lim t!1 r p (t) = (t)n 1 n! 26

31 4. h (t) vizsgalata lim h (t) = 0, t!0 lim h (t) = t!1 h (t; n) fuggvenyalakja h (t) = 1 dr h (t) = r h (t) dt (t) n 1 (n 1)! (t) k n 1 X k=0 k! (2.15) 5. eredmenyek demonstralasa ketegyseges rendszer eseten 6. kovetkezmeny, problema t << MT F F -nel nagyon hatasos a q p (t)-t tekintve MT F F h javulasa linearis n fuggvenyeben h fokozatosan n}o a tartalek nem hibasodhat meg megvalostasi problemak az idealis erzekel}ot, atkapcsolot es a fuggetlenseget tekintve Csokkentett terheles}u tartalek 1. a megbzhatosagi parameterek meghatarozasa legyen adott egy rendszer n egyforma elemmel az n elemb}ol egy teljes terhelessel m}ukodik, mg a tobbi m}ukod}okepes elem (kezdetben n 1) csokkentett terhelessel tartalekot kepez. az uzemi es a tartalek elemek megbzhatosagi tenyez}oje id}oben allando,, illetve t vegyuk eszre, hogy itt felteteleztuk, hogy az uzembehelyezes id}opontja nem befolyasolja az elemek uzembehelyezeset}ol szamtott meghibasodasi idejet. a csokkentett terheles}u rendszert gyakran jellemzik az a = t = arannyal adott tartatlekolasi tenyez}ovel. a = 1 parhuzamos rendszer, a = 0 hidegtartalekolt rendszer rendszerhiba akkor kovetkezik be, amikor az osszes elem (uzemi es tartalek) meghibasodott. 27

32 jelolje r(t) = P ( > t) = e t az uzemi, r cs (t) = P ( cs < t) = e cst a (csokkentett terheles}u) tartalek elemek es r n (t) = P ( n < t) az n elem}u csokkentett tartalekolasu rendszer hibamentes m}ukodesenek valoszn}useget. Tetelezzuk fel, hogy az els}o operatv egyseg a T 1 id}opillanatban hibasodik meg. A rendszer t-ben jo, ha T 1 > t. Amennyiben T 1 < t, akkor T 1 -t}ol az addig meg nem hibasodott tartalekokbol allo rendszer kezd m}ukodni hasonlo modon (csokkentett terheles}u tartalekolassal). r n (t j 8T 1 = h) = >< 1 h > t! n 1 X n 1 >: r k k cs (h) (1 r cs(h)) n k 1 r k (t h) h < t k=1 a feltetel eloszlasa alapjan: r n (t) = Z 1 t Z 1 0 Z t 0 e t + r n (t j T 1 = h) f T1 (h) dh = 1 f T1 (h) dh+ n 1 X k=1 Z t 0 n 1 X k=1 n 1 k! n 1 k r k cs(h) (1 r cs (h)) n k 1 r k (t h) f T1 (h) dh =! e cshk (1 e csh ) n k 1 r k (t h) e h dh amib}ol r 1 (t) = e t alapjan a hibamentes m}ukodes valoszn}usege rekurzven szamthato n-b}ol k jo rendszer megbzhatosagi jellemz}oi 1. a megbzhatosagi parameterek meghatarozasa legyen adott egy rendszer n azonos elemmel az egyes elemek meghibasodasi id}opontja i ; i = 1; :::; n az egyes elemek meghibasodasi id}opontjanak eloszlasfuggvenye F (t) = P ( i < t); r(t) = P ( > t) = 1 F (t); 8i = 1; :::; n 28

33 MT F F nk (n) MT F F r(t) = 0:9 r(t) = 0:5 k=n r nk (t) q nk (t) r nk (t) q nk (t) 1/ / / / / / tablazat: Egy n-b}ol k (aktv) tartalekolasu rendszer megbzhatosagi jellemz}oi kerdes: F nk (t) = P (t; k:::n) kerdes: r nk (t) = 1 F nk (t) megoldas: Ha a i meghibasodasi id}opontok mindegyike fuggetlen egymastol: (hasonloan szigoru, mint a parhuzamos melegtartalekolt rendszernel, mivel az (n-k)+1-ik meghibasodasi id}opontig kell a fuggetlensegnek teljesulnie) r nk (t) = nx i=k P (t; k:::k) = MT F F nk = nx i=k Z 1 2. exponencialis eloszlasra, azonos elemek eseten: 3. pelda MT F F nk = Z 1 0 r nk (t) = nx r nk (t)dt = n i! i=k Z n i! r i (t)q n i (t) (2.16) r nk (t)dt (2.17) e it (1 e t ) n i (2.18) egyszer}u n-b}ol k rendszer, k = n 1 eseten 2.4. tablazat 29 nx i=k n i! e it (1 e t ) n i dt (2.19)

34 4. eredmenyek demonstralasa ketegyseges rendszer eseten 5. kovetkezmeny, problema MT F F nk nem biztos, hogy jobb egyetlen elemnel azonban k 6= 2 eseten t << MT F F -nel hatasos a q nk (t)-t tekintve nk fokozatosan n}o megvalostasi problemak az idealis erzekel}ot es atkapcsolot tekintve 2.3. Osszetett redundans rendszerek 1. soros-parhuzamos rendszerek 2. tobbsegi szavazasos (majoritasos) rendszer 3. atkapcsolo tartalekolasu rendszer (stand-by): aktv vagy passzv tartalekolas nem idealis atkapcsoloval Soros-parhuzamos rendszerek 1. grakus demonstracio 2. szamtasi modszer: fokozatos kiertekeles - osszevonasok sorozata 3. eredmenyek: illusztracio peldakon ( 1 ; 2 ) ket-ket soros-parhuzamos elem rendszertartalekolassal r(t) = 1 (1 r 1 (t)r 2 (t)) 2 = 2r 1 (t)r 2 (t) r 2 1 (t)r2 2 (t) MT F F = r(t) = 2e ( 1+ 2 )t e 2( 1+ 2 )t ( ) = 3 2( ) ket-ket soros-parhuzamos elem elemenkenti tartalekolassal r(t) = (1 (1 r 1 (t)) 2 )(1 (1 r 2 (t)) 2 ) = (2r 1 (t) r 2 1 (t))(2r 2(t) r 2 2 (t)) r(t) = 4r 1 (t)r 2 (t) 2r 1 (t)r 2 2(t) 2r 2 1(t)r 2 (t) + r 2 1(t)r 2 2(t) r(t) = 4e ( 1+ 2 )t 2e ( )t 2e ( )t + e 2( 1+ 2 )t 30

35 egy elemmel ket parhuzamos sorban, vegigszamolva r(t) = r 1 (t)(1 (1 r 2 (t)) 2 ) = 2r 1 (t)r 2 (t) r 1 (t)r 2 2 (t) r(t) = 2e ( 1+ 2 )t e ( )t MT F F = 4. pelda a hdelemb}ol szarmazo koniktusra Majoritasos rendszer megbzhatosagi jellemz}oi 1. grakus abrazolas 2. szamtasi modszer: soros-parhuzamos modell 3. eredmenyek: illusztracio 3 egyseges peldan r m (t) = r l (t) 3X i=2 3 i! r i (t)(1 r(t)) 3 i = e lt (3e 2t (1 e t ) + e 3t ) r m (t) = 3e ( l+2)t 2e ( l+3)t MT F F m = (MTFF csokkenesenek magyarazata) 3 l l kapcsoloelem jelent}osege, idealis kapcsoloju rendszer (n-b}ol k tpusu rendszer) Atkapcsolo tartalekolasu rendszer megbzhatosagi jellemz}oi 1. gyakori megnevezes: stand-by 2. grakus abrazolas 3. szamtasi modszer: specialis soros-parhuzamos modell (kapcsolo sorosan, kapcsolo mellekagban sorosan) 4. eredmenyek: illusztracio 2 egyseges peldan 31

36 aktv tartalekolas, kapcsolo sorosan r sb (t) = r k (t)(1 (1 r 2 (t)) 2 ) = 2r k t)r(t) r k (t)r 2 (t) r sb (t) = 2e ( k+)t e ( k+2)t MT F F sb = 2 k + 1 k + 2 passzv tartalekolas, kapcsolo mellekagban sorosan mivel azonos, allando hibaintenzitasu elemekb}ol allo hidegtartalekolt rendszernel a meghibasodasok (amg vannak) Poisson folyamat szerint fordulnak el}o annak valoszn}usege, hogy (0; t)-ben egy elem sem hibasodik meg e t es, hogy pont egy elem hibasodik meg te t. r hk (t) = e t (1 + tr k (t)) = e t (1 + te kt ) MT F F hk = 1 + ( k + ) 2 csokkentett terheles}u tartalekolas, kapcsolo mellekagban sorosan Tetelezzuk fel, hogy az operativ egyseg T 1 id}opillanatban hibasodik meg, es hogy a tartalek meghibasodasi tenyez}oje cs <. A rendszer jo, ha az operatv egyseg meg nem hibasodott meg T 1 > t, vagy ha mar meghibasodott, de sem a kapcsolo sem az eredetileg tartalekkent hasznalt alkatresz nem romlott meg el (ez utobbi meghibasodasi tenyez}oje T 1 -ben megvaltozik). ( 1 h > t r csk (t j T 1 = h) = r cs (h)r(t h)r k (t) h < t a feltetel eloszlasa alapjan: r csk (t) = Z 1 t e t + Z 1 0 r csk (t j T 1 = h)f T1 (h)dh = 1f T1 (h)dh + Z t Z t amib}ol az integralok kiertekelese utan 0 0 r cs (h)r(t h)r k (t)f T1 (h)dh = e csh e (t h) e kt e h dh r csk (t) = e t + cs e (+ k)t [1 e cst ] 32

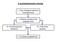
37 MT F F csk = cs + k + k + cs 5. kerdes: tobballapotu kapcsoloelem (ld. aktv tartalekolas) 2.4. Nemjavtott rendszerek szamtasi modszerei Megbzhatosagi blokkdiagram 1. eddigi megbzhatosagi modellek jellemz}oi Boole-fele modell (ketallapotu elem, fuggetlenseg) soros-parhuzamos strukturak veges (megszamlalhato) szamu alkatresz monoton nem javulhat tobb hibas elemmel (nincs ongyogytas) szamtas a Boole-algebra szabalyai szerint konjunktv (normal) alak (sum of disjoint products) eseten az logikai kifejezes alapjan a valoszn}useg kozvetlenul szamthato. 2. eddigi megbzhatosagi modellek korlatai ketallapotu rendszer (kiterjeszthet}o, ld. n-b}ol k, ahol tudhatjuk azt is, hogy az "eppen k" valoszn}useg hogy alakul) javtasmentesseg csokkentett terheles exponencialis meghibasodasi id}o eloszlas (valojaban ez nem mindig, hisz egyes esetekben altalanos r(t)-re is ismert) A teljes valoszin}useg tetel alkalmazasa 1. felteteles valoszin}usegek alkalmazasa: [ n i B i = ; B i \ B j = ;; 8 i; j = 1:::n P (A) = nx i=1 P (AjB i )P (B i ) 2. a tetel alkalmazasa tobballapotu elemekre: pl. dioda ket hibas allapottal, ketallapotu kapcsolo 33

38 3. a tetel alkalmazasa nem soros-parhuzamos rendszerekre: hdagas otelem}u pelda 4. a tetel alkalmazasa nem fuggetlen elem}u rendszerekre: csak utalva ra, mivel erre nem egy hatekony megoldas 2.5. Halozatmegbzhatosag szamtasi modszerek Halozatmegbzhatosagi modell 1. az egyes elemek egy graf egy-egy elenek felelnek meg 2. ketallapotu, fuggetlen elem 3. fuggetlenseg 4. tetszes szerinti grafstrukturak 5. szamtas graogalmakra alapozottan 6. rendszermegbzhatosag "kozvetlenul" szamthato diszjunktv normal alak, P (AB + AB + A B) = r A r B + q A r B + r A q B = vagy annak egyszer}ustesevel nyert alakok (SDP - sum of disjoint products) eseten P (B + A B) = r B + r A q B Vagatmeghatarozas (cut set) 1. kezd}o- es vegpontot elsziget}o elek (csucsok) halmaza 2. C i ; i = 1; :::; N sd : az i: vagat eleinek halmaza 3. C i ; i = 1; :::; N sd : azon esemeny, hogy az i: vagatban minden el meghibasodott 4. q k = q k (t): a k: el m}ukodeskeptelensegenek valoszin}usege 5. q e = q e (s; d; t) = P ([ N sd C i=1 i) mivel [ N sd C i=1 i nem SDP alaku q e = P (C 1 ) + P (C 2 ) + ::: + P (C Nsd ) P (C i \ C j ; 8 i; j)+ P (C i \ C j \ C k ; 8 i; j; k) :::: 34

39 6. altalanosthato: tobb csomopontparra, teljes grafra (osszefugg}oseg) tobballapotu elekre (kapacitas jelleg}u kovetelmenynel) 7. kozelt}o szamtasok: (mivel a hibas m}ukodes valoszin}usege altalaban kicsi) q e ' P (C 1 ) + P (C 2 ) + ::: + P (C 4 ) 8. alkalmazas otelem}u hdagas rendszerre: C 1 = (1; 2); C 2 = (1; 4; 5); C 3 = (2; 3; 5); C 4 = (3; 4) q e = P (C 1 ) + P (C 2 ) + ::: + P (C 4 ) P (C 1 \ C 2 ) P (C 1 \ C 3 ) P (C 1 \ C 4 ) P (C 2 \ C 3 ) P (C 2 \ C 4 ) P (C 3 \ C 4 ) + P (C 1 \ C 2 \ C 3 ) + P (C 1 \ C 2 \ C 4 )+ P (C 1 \ C 3 \ C 4 ) + P (C 2 \ C 3 \ C 4 ) P (C 1 \ C 2 \ C 3 \ C 4 ) Mivel P (C i \ C j ) = Q k2(c i [C j ) q k ; 8 i; j : q e = q 1 q 2 + q 1 q 4 q 5 + q 2 q 3 q 5 + q 3 q 4 q 1 q 2 q 4 q 5 q 1 q 2 q 3 q 5 q 1 q 2 q 3 q 4 q 1 q 2 q 3 q 4 q 5 q 1 q 3 q 4 q 5 q 2 q 3 q 4 q 5 + 4q 1 q 2 q 3 q 4 q 5 q 1 q 2 q 3 q 4 q 5 q e = q 1 q 2 + q 1 q 5 q 4 + q 2 q 5 q 3 + q 3 q 4 q 1 q 2 q 4 q 5 q 1 q 2 q 3 q 5 q 1 q 2 q 3 q 4 q 1 q 3 q 4 q 5 q 2 q 3 q 4 q 5 + 2q 1 q 2 q 3 q 4 q 5 Ha az elemek azonos megbzhatosaguak: q e = 2q 2 + 2q 3 5q 4 + 2q 5 Kozelt}oen: q e = 2q 2 + 2q Utmeghatarozas (tie set) 1. kezd}o- es vegpontot osszekot}o elek (csucsok) halmaza 2. kezd}o- es vegpontot elsziget}o elek (csucsok) halmaza 3. C i ; i = 1; :::; M sd : az i: ut eleinek halmaza 4. T i ; i = 1; :::; M sd : azon esemeny, hogy az i: uton minden el m}ukodik 5. r k = r k (t): a k: el hibamentes m}ukodesenek valoszin}usege 35

40 6. r e = r e (t) = P ([ M sd T i=1 i) mivel [ M sd T i=1 i nem SDP alaku r e = P (T 1 ) + P (T 2 ) + ::: + P (T Msd ) P (T i \ T j ; 8 i; j)+ P (T i \ T j \ T k ; 8 i; j; k) :::: 7. nincs egyszer}u altalanosthatosag tobb csomopontparra, tobballapotu elemre 8. kozelt}o szamtasok: (nincs a vagatokhoz hasonlo egyszer}u lehet}oseg) 9. alkalmazas otelem}u hdagas rendszerre: T 1 = (1; 3); T 2 = (1; 4; 5); T 3 = (2; 3; 5); T 4 = (2; 4) r e = P (T 1 ) + P (T 2 ) + ::: + P (T 4 ) P (T 1 \ T 2 ) P (T 1 \ T 3 ) P (T 1 \ T 4 ) P (T 2 \ T 3 ) P (T 2 \ T 4 ) P (T 3 \ T 4 ) + P (T 1 \ T 2 \ T 3 ) + P (T 1 \ T 2 \ T 4 )+ P (T 1 \ T 3 \ T 4 ) + P (T 2 \ T 3 \ T 4 ) P (T 1 \ T 2 \ T 3 \ T 4 ) r e = r 1 r 3 + r 1 r 4 r 5 + r 2 r 3 r 5 + r 2 r 4 r 1 r 3 r 4 r 5 r 1 r 2 r 3 r 5 r 1 r 2 r 3 r 4 r 1 r 2 r 3 r 4 r 5 Mivel P (T i \ T j ) = Q k2(c i [C j ) r k ; 8 i; j : r 1 r 2 r 4 r 5 r 2 r 3 r 4 r 5 + 4r 1 r 2 r 3 r 4 r 5 r 1 r 2 r 3 r 4 r 5 r e = r 1 r 3 + r 1 r 4 r 5 + r 2 r 3 r 5 + r 2 r 4 r 1 r 3 r 4 r 5 r 1 r 2 r 3 r 5 r 1 r 2 r 3 r 4 r 1 r 2 r 4 r 5 r 2 r 3 r 4 r 5 + 2r 1 r 2 r 3 r 4 r 5 Ha az elemek azonos megbzhatosaguak: r e = 2r 2 + 2r 3 5r 4 + 2r Esemenyfa meghatarozas (event tree) 1. alapmegoldasaban az n darab ketallapotu elem allapotfajat denialja 2 n allapottal 2. a fa leveleihez m}ukod}okepes vagy kies}o allapotokat kell rendelni, amely allapotokat a gyokert}ol a levelig vezet}o ut eleinek allapota denial 3. r e es q e valoszin}usegeket (a megfelel}o diszjunkt allapotvaloszin}usegeket) a gyokert}ol a levelig vezet}o elek valoszin}usegenek szorzata hatarozza meg 4. az allapotok szama redukalhato, ha az egyertelm}u helyzetekben megszuntetjuk az agak folytatasat 36

41 5. tovabbi egyszer}ustes, ha csak az egyik (r e vagy q e ) meghatarozasat vegezzuk el (csokkenthet}o a memoriaigeny) 6. az esemenyfa felhasznalhato vagatok el}oalltasara utak el}oalltasara 7. minden esetben SDP alaku megoldast szolgaltat!! 8. alkalmazasi pelda otelem}u hdagas rendszerre: (teljes (32), redukalt (13), ut- (7), vagatmeghatarozas (6) - demonstralasa) 9. az esemenyfa kiterjeszthet}o tobballapotu (redundans) elemekre tobballapotu rendszerek lerasara, szamtasara nem exponencialis eloszlasu rendszerek lerasara, szamtasara 10. adott kezdeti esemeny mellett kritikus hiba el}ofordulasi gyakorisag meghatarozasa esemenyfaval az esemenyfa csucspontja a kezdeti hiba (egy olyan meghibasodas, amelyik kritikus hibahoz is vezethet) az elagazasok az adott kezdeti hibatol a kritikus hibahoz vezet}o esemenyek bekovetkezeset, illetve elmaradasat rjak le (megfelel}o valoszn}usegekkel). az utolso szinten a fa levelein az adott esemenysor mellett a kritritikus hiba el}ofordulasat/elmaradasat kell megadni. amennyiben a kezdeti esemeny f kezd, [1/ev] gyakorisaggal fordul el}o, es a kezdeti esemenyb}ol a kritikus hiba bekovetkezesenek valoszn}usege p kr, akkor (az adott kezdeti esemenyb}ol) a kritikus hiba el}ofordulasanak gyakorisaga f krit = f kezd p kr 37 [1/ev]

42 Kapcsolat matrix (connection matrix) 1. iranytott kapcsolatok (szomszedossag) matrixalapu felrasa 2. megoldasi modszer matrixszorzas: specialis megoldast jelent, az osszeadasok uniokepzeskent, a szorzasok metszetkepzeskent jelentkeznek csomopont megszuntetes (implicit matrixszorzas) 3. alkalmazasi pelda otelem}u hdagas rendszerre M = A B E C 0 E 1 D matrixszorzas M 3 = M 2 = A + BE B + AE AC + BD 0 1 E C + DE 0 E 1 D + CE A + BE B + AE AC + BD + BCE + ADE 0 1 E C + DE 0 E 1 D + CE A tobbi hatvany mar azonos M 3 -bel! Az eredmeny (M 3 14) nem SDP alaku!! csomopont megszuntetes Alapelv: M 0 ij = M ij + (M ik M kj ) a megszuntetett k 6= i; j csomopontra M 0 = B + AE AC 0 1 D + CE " 1 AC + BD + BCE + ADE M" = 0 1 # 38

43 mindket megoldas az utak el}oalltasat vegzi egy egyszer}ubben implementalhato modon. javasoljon vagatel}oalltasi eljarast hasonlo matrixos algoritmus alapjan Hibafa analzis (fault tree) 1. nem topologiai, hanem kuldetesorientalt rendszerek biztonsagi vizsgalatanak eszkoze 2. ketallapotu elemekkel dolgozik (Boole-modell) 3. tobbfele meghibasodasi okot is megenged primer meghibasodas (alkatresz meghibasodasa sajat hibaja vagy gyengesege miatt) szekunder meghibasodas (alkatresz meghibasodasa az alkatresz nem megengedett alkalmazasi korulmenyek kovetkezteben) utastas altal okozott meghibasodas (utastasok vagy segedenergia kimaradas, mikozben a m}ukodesi elemek rendben vannak - pl. kornyezet) Modellezesi alapelemek (szimbolumok) 1. AND, OR, EOR, NOT kapu 2. n-b}ol k (szavazo) kapu 3. alapesemeny, nem teljes esemeny, kozbens}o esemeny 4. transfer IN es OUT Analzis lepesek 1. egy meghibasodasi f}oesemeny (rendszer-meghibasodas) visszavezetese alapesemenyekre (hibaokokra) 2. els}osorban kvalitatv analzisre hasznaljak Hanyszoros "melyseg}u" a hiba? 3. a Boole-modellnek megfelel}oen vegezhet}o kvantitatv analzis is ketfele numerikus modszer 39

44 felulr}ol-lefele eptkezes alulrol-felfele eptkezes (Gondot jelent a tobbszoros hibak (common mode failure) kezelese!) 4. hibafak hasznalata vagatok meghatarozasara, lepesek OR-kapu minden bemenete egy-egy uj listaelemet jelent AND-kapu bemenete egy kozos uj listaelemet jelent minden listaelem egyes kapuit az el}oz}oek szerint tovabb kell alaktani ha valamelyik elemnek egy masik a minimalvagata, akkor a b}ovebbet meg kell szuntetni a vegeredmeny a minimalvagat 5. kiterjeszthet}o tobballapotu elemekre 6. a tobbfele lehetseges f}oesemeny lehet}ove teszi a tobballapotu rendszer ertelmezest (pl. f}oesemenyek kombinacioja) 7. korlatozottan lehet}ove teszi a fugg}oseg gyelembevetelet (csak a pillanatnyi fugg}oseg rhato le, s nem az esemenyhez kotott) 2.7. Gyakorlatok nemjavtott rendszerek modellezesere, szamtasara 1. pelda: Billinton-Allan: 5.4 pelda, 111. oldal megoldas soros/parhuzamos atalaktassal: nem lehetseges megoldas felteteles valoszin}usegekkel: r e = r A r e (A) + q A r e ( A) = r A r B + r A q B r E (r F + q F r C r D ) + q A r C r D r E megoldas vagatokkal: megoldas utakkal: C 1 = (A; C); C 2 = (A; D); C 3 = (A; E); C 4 = (B; E); C 5 = (B; F; C); C 6 = (B; F; D) T 1 = (A; B); T 2 = (C; D; E); T 3 = (A; F; E) 40

45 megoldas esemenyfaval: r e = P AB + A BCDE + A BC DEF + A B CEF + ACDE q e = P A B E + A BC DE F + A B CE F + A C + AC D + ACD E megoldas kapcsolatmatrixszal: { matrixszorzas: M 3 = M 2 = M = { csomopont megszuntetes: A C F B D E A C AF + CD AB F B + F E D DE E A C AF + CD AB + AF E + CDE F B + F E D DE E A C F B D E es csomopont megszuntetese: C AF AB 0 1 D E

46 3-as csomopont megszuntetese: AF + CD AB 0 1 E es csomopont megszuntetese: " 1 AB + AF E + CDE 0 1 hibafa letrehozas: "bal - jobb erkez}o jel" kimaradas 2. pelda: Billinton-Allan: pelda, oldal ketfele numerikus modszer illusztralasa a peldakon hibafak hasznalata vagatok meghatarozasara illusztracio 3. pelda: Adott egy harom elemb}ol (E 1, E 2 es E 3 ) allo rendszer. E 1 es E 2 parhuzamos es veluk sorban E 3. r 1 (t) = pe at + (1 p)e bt, r 2 (t) = e 2t, r 3 (t) = e 3t, ahol p = 0:5, a = 100F IT, b = 500F IT, 2 = 200F IT es 3 = 100F IT. Kerdesek: r(t) MTFF 1 (t) valamint lim t!0 1 (t), es lim t!1 1 (t) # 42

47 3. fejezet JAVITOTT RENDSZEREK MEGBIZHAT OS AGA 3.1. Kiindulopontok 1. feloldott modellkorlatok ketallapotu elem (teljes valoszin}useg tetele, esemenyfa) fuggetlenseg (teljes valoszin}useg tetele, korlatozottan esemenyfa, hibafa) soros-parhuzamos strukturak (teljes valoszin}useg tetele, halozat) ketallapotu rendszer (esemenyfa, hibafa) exponencialis meghibasodasi id}o eloszlas (esemenyfa, de tobb mas modell is megenged altalanos F(t) fuggvenyt) 2. megmaradt modellkorlatok javtasok gyelembevetele csokkentett terheles (valojaban allapotfugg}o meghibasodasi tenyez}o) lehet}osegenek gyelembevetele 3. fenntartas (javtas) celja meghibasodas kovetkezmenyenek elhartasa (kiesesi id}o lerovidtese) meghibasodasok megel}ozese 43

48 4. fenntartas, felujtas gyelembevetele (modellezesi kerdesek) fenntartas jellege { megel}oz}o karbantartas preventv (id}o- vagy allapotfugg}o) { javtas korrektv javtas feltetelei { id}ofugg}oseg { allapotfugg}oseg (pl. kotelez}o kikapcsolas) javtas hatasa { reszleges { teljes beavatkozas eloszlasa, id}otartama { tavolsag { tartalekkeszlet redundancia es fenntartas egyuttes kezelese altalanos problema: az allapotfugg}oseg kezelese 5. altalanos modell termek lerasa: X(t) = X i ; i = 0; 1; 2; ; n egy veletlen folyamat, ahol az X ( t) folyamat altal felvett X i ertekek a rendszer egy-egy allapotanak felelnek. A tovabbiakban az egyszer}ubb kezeles erdekeben X i helyett az i jelolest hasznaljuk. gondot jelent, hogy az X(t) veletlen folyamatot altalanosan az F X (x; t) = P fx(t 1) x 1 ; X(t 2 ) x 2 ; ; X(t n ) x n g veges dimenzios eloszlasfuggvenyekkel adhatnank meg. ezen folyamatok specialis esetet jelentik az ugynevezett Markov folyamatok kozuluk el}oszor a diszkret idej}u Markov lancokkal (diszkret parameterter, diszkret allapotter), majd a folytonos idej}uekkel (folytonos parameterter, diszkret allapotter) foglalkozunk. 44

49 3.2. Diszkret idej}u (veges) Markov lancok Markovitas es tulajdonsagai 1. markovitas: (a jov}o a multtol csak a jelenen keresztul fugg) P(X n+1 = x n+1 j X n = x n ; ; X 0 = x 0 ) = P(X n+1 = x n+1 j X(t n ) = x n ) (3.1) 8n = 0; 1; ; es 8x k 2 S; S = f0; 1; ; Ng. 2. kovetkezmeny: P(X 0 = x 0 ; ; X n = x n ) = P(X n = x n j X n 1 = x n 1 ; ; X 0 = x 0 ) P(X 0 = x 0 ; ; X n 1 = x n 1 ) = P(X n = x n j X n 1 = x n 1 ) P(X n 1 = x n 1 j X n 2 = x n 2 ; ; X 0 = x 0 ) P(X 0 = x 0 ; ; X n 2 = x n 2 ) = = P(X n = x n j X n 1 = x n 1 )P(X n 1 = x n 1 j X n 2 = x n 2 ) P(X 1 = x 1 j X 0 = x 0 )P (X 0 = x 0 ) 3. jelolesek: egylepeses atmenetvaloszin}usegek p (1) ij (n) = P(X n+1 = j j X n = i) 8i 2 S; 8j 2 S; 8n = 0; 1; (3.2) X j2s 4. Chapman-Kolmogorov egyenl}oseg: p ij (n) = 1 8i 2 S; 8n = 0; 1; (3.3) X p (m+n) ij (l) = k2s p (m) ik (l)p(n) kj (l + m) 8i 2 S (3.4) 5. a diszkret idej}u Markov lancokkal kapcsolatban tanult alapfogalmak irreducibilitas: minden allapot minden allapotbol elerhet}o (szemrevetelezes) aperiodikussag: nem periodikus (szemrevetelezes) orokl}odes: irreducibilis Markov lancokra az aperiodikussag orokl}odik 45

50 6. homogenitas p ij = p (1) ij (n) = P(X n+1 = j j X n = i) 8i 2 S; 8j 2 S 8n = 0; 1; (3.5) 7. kovetkezmeny matrixos jelolessel: P (n) = P (n 1) = P (0) (n) = P (0) n (3.6) ahol: P h (n) = i [p 0 (n); ip 1 (n); p 2 (n); ; p N (n)] ; p i (n) = P (X n = i); (n) = p (n) ij = hp (n) ij es (1) = ; 8 i; j 2 S, n = 0; 1; 2; 8. alapkerdes: hatareloszlas letezese, meghatarozasa A hatareloszlas 1. veges Markov lanc, a hatareloszlas letezik, azaz a Markov-lanc stabil, ha irreducibilis aperiodikus 2. a hatareloszlas el}oalltasa n!1 lim p (n) ij = p j > 0; 8i; j, ahol p j = n!1 lim P(X n = j); 8j-re ekkor a P = P, P = [p 0 ; p 1 ; p 2 ; ] egyenl}osegnek a 1X i=0 p i = 1 feltetel mellett csak egy megoldasa van, amely a hatareloszlast szolgaltatja. Ha a P (0) = P feltetel teljesul, akkor P (n) = P; 8n-re. 3. a hatareloszlas letezesenek kovetkezmenye mas felrassal kifejtve a j. allapotra: X X p j (n) = p i (n 1)p ij = p j (n 1)p jj + p i (n 1)p ij i2s i6=j X X p j (n) = p j (n 1)(1 p jk ) + p i (n 1)p ij X k6=j i6=j X p j (n) p j (n 1) = p i (n 1)p ij p j (n 1) p jk (3.7) i6=j k6=j (A kifejezes interpretalasa! ) 46

51 A hatareloszlasra, mivel n!1 lim p j (n) = n!1 lim p j (n 1) = p j ; 8j-re X X p j p j = 0 = p i p ij p j p jk i6=j azaz X i6=j k6=j X p i p ij = p j p jk (3.8) k6=j (A kifejezes interpretalasa, grakus demonstracio! ) a kifejezes kiterjeszthet}o allapotcsoportokra is grakus demonstracio X X X (p i (p j p jk ); A S (3.9) i2a j2 A p ij ) = X j2 A Bolyongasok (diszkret idej}u szuletesi-halalozasi folyamatok) 1. ertelmezes: p ij = 2. bolyongasok hatareloszlasa 8 >< >: k2a b i j = i + 1; i 0 d i j = i 1; i > 0 1 (b i + d i ) j = i; i > 0 1 b 0 j = i; i = 0 0 egyebkent p k 1 p k 1;k + p k+1 p k+1;k = p k (p k;k 1 + p k;k+1 ); k > 0 p k 1 b k 1 + p k+1 d k+1 = p k (b k + d k ); k > 0 p 1 d 1 = p 0 b 0 amib}ol (allapotcsoportos megoldasbol is szarmaztathato!) Igy p k d k = p k 1 b k 1 ; k > 0 (3.10) p k = b k 1 d k p k 1 = p 0 Mivel P k p k = p 0 + p 0 P Nk=1 Q kj=1 b j 1 d j = 1; p 0 = 1 + NX ky j=1 1 ky k=1 j=1 b j 1 d j ; k > 0 (3.11) b j 1 d j (3.12) 47