BME Járműgyártás és -javítás Tanszék. Javítási ciklusrend kialakítása
|
|
|
- Zsófia Kis
- 6 évvel ezelőtt
- Látták:
Átírás
1 BME Járműgyártás és -javítás Tanszék Javítási ciklusrend kialakítása
2 A javítási ciklus naptári napokban, üzemórákban vagy más teljesítmény paraméterben meghatározott időtartam, amely a jármű, gép új állapotától vagy az általános javítástól a következő általános javításig terjed. Ezt az időtartamot ciklusidőnek nevezzük. A ciklusidő az alkatrészek élettartama alapján határozható meg: az alkatrészek fizikai elhasználódásának törvényszerűségeiből, meghibásodási elmélet felhasználásával. 2
3 Élettartam meghatározás: Gyártmánytervezéskor: számítással (pl.: kifáradásra való méretezés), üzemelési tapasztalatok elemzése alapján, klf. élettartam vizsgálatokkal (pl.: kopásvizsgálat). Üzemeltetés során: meghibásodás elemzés, ciklusrend módosítás. Javítás során: meghibásodás elemzés, új anyagok, technológiák élettartam-növelő hatása, ciklusrend módosítás. 3
4 Jellemző méretek az élettartam számításhoz 4
5 Alkatrész élettartam meghatározása az elhasználódási folyamat ismeretében: t e =z meg /v z ; v z =z 2 -z 1 /t 2 -t 1 5
6 Alkatrészcsoportok képzése, ciklusidők meghatározása. Alkatrészcsoportok kialakítása, a közel azonos élettartam szerint, A csoportra jellemző élettartam meghatározása, Ciklusidők és az egyes karbantartási, javítási feladatok meghatározása, A ciklusidők egymásnak egészszámú többszörösük, Ciklusrend módosítása az üzemeltetési tapasztalatok alapján 6
7 Alkatrész élettartam számítási módszerek Meghatározott időpontokban (t 1 ; t 2 ;..t n ) adatok (méretek) felvétele Az adatok értékelése (várható középérték, szórás) Az elhasználódás folyamatának meghatározása, ábrázolása: grafikus elemzéssel ismert matematikai függvényekkel (trigonometrikus, lineáris ) polinommal való közelítéssel 7
8 Élettartam meghatározás kopási görbe alapján A vizsgált időpontokban van elegendő számú mérés a matematikai statisztikai kiértékeléshez. 8
9 Élettartam meghatározás regressziós egyenlet segítségével A mért adatok sokaságából a kopási folyamat sztohasztikus összefüggéseinek meghatározása regressziós egyenlettel 9
10 Élettartam meghatározás megbízhatósági elmélet segítségével: Fontosabb fogalmak: megbízhatóság - működés alatti előírásos állapot, működőképesség - a feladat előírt műszaki követelmények melletti ellátása, Meghibásodás - működőképesség elvesztése, hibamentes működés valószínűsége - az adott időszakban nem következik be meghibásodás, élettartam - műszaki előírásokban meghatározott állapot időtartama, előírt megbízhatóság - a feladat elvégzéséhez szükséges előírásos (határ-) állapot. 10
11 Valamely rendszer károsodási magatartását elemeinek károsodási magatartása határozza meg. Más - más megbízhatósági paraméterekkel jellemezzük az első meghibásodásig üzemelő, un. nem javítható elemeket, valamint a javítható elemeket, rendszereket. 11
12 Az első meghibásodásig üzemeltetett elemek megbízhatósága: Megbízhatóság annak valószínűsége, hogy a gép ill.. alkatrésze a vizsgált idő intervallumban nem hibásodik meg. R (t)=p(t < ) R = R(t,,S,V,F); ahol R - megbízhatóság, t - vizsgált időtartam, - meghibásodás időpontja, S - igénybevétel, V - igénybevétel változása, F - fenntartás minősége Meghibásodás valószínűsége: Q(t)=P(t < ) R(t)=1-Q(t) 12
13 A megbízhatóság leírható ismert eloszlási vagy tapasztalati függvényekkel: R(t) = n(t)/n(0), n(t) - a t időpontban üzemképes alkatrészek száma, n(0) - a t=0 időpontban üzembe állított, illetve vizsgált alkatrészek száma. A meghibásodás valószínűsége: Q(t) = (n(0)-n(t)) / n(0). Sűrűségfüggvény: q(t) = n(k) / n(0)* t, t - a k t intervallumban bekövetkezett meghibásodások száma 13
14 Megbízhatóság, meghibásodás valószínűségi függvénye (normál eloszlás) 14
15 Meghibásodási ráta λ = q(t)/r(t) n k /n(t)* t 15
16 Elemek megbízhatósága Nem javítható elem megbízhatósága Az azonnali javítható elem megbízhatósága, Számottevő javítási időt igénylő elem megbízhatósága
17 Nem javítható elem megbízhatósága A nem javítható elem működése az első meghibásodás bekövetkezéséig tart, vagyis a határállapotot ebben az esetben a meghibásodás bekövetkezésének eseménye jelenti. A leggyakrabban használt mutatói: a hibamentes működés valószínűsége, a meghibásodás valószínűsége, várható tényleges idő az első meghibásodásig, a meghibásodási ráta. 17
18 Az azonnali javítható elem megbízhatósága A meghibásodott elemet a meghibásodás pillanatában az újjal kicserélik, vagy a felújítási, a kicserélési idő a τ működési időkhöz képest elhanyagolhatóan kicsi. Ezért úgy tekintjük, hogy a felújítás egy pillanat alatt történik. 18
19 Az elem a t 0 időpontban kezd működni és t 1 működési idő után meghibásodik. A meghibásodás pillanatában egy másik elemmel cserélik ki, amely t 2 ideig lesz működőképes, s ezt egy harmadik váltja fel. 1 1 n 2 n+1 t 1 t 2 t n t n+1 19
20 Számottevő javítási időt igénylő elem megbízhatósága A felújítási idő lényegében két részből tevődik össze: egyrészt a hiba megkereséséhez szükséges időből, másrészt a javításához szükséges időből n n t 1 t 1 t 2 t 2 t n t n 20
21 A rendszerek megbízhatósága A független megbízhatóságú elemekből felépülő rendszerek megbízhatósága Soros rendszer: R = R 1 R 2....R n ; R = e -(Σλ)t 1 22 n 1 2 n Párhuzamos rendszer (két elemre): R = R 1 + R 2 - R 1 R Nem független megbízhatóságú n elemekből felépülő rendszer megbízhatósága n 21
22 KE 1a kormányszelep vizsgálata Hónap Hibás szelepek száma/hó Összes meghibás odás Összes vizsgált szelep Meg nem hibásodott Meghibásodási ráta Megbízhatóság Meghibás odás valószínűsége szelep n t ,241 0,9976 0, ,013 0,9876 0, ,488 0,9828 0, ,122 0,9816 0, ,061 0,981 0, ,082 0,9802 0, ,041 0,9798 0, ,184 0,978 0, ,082 0,9772 0, ,123 0,976 0, ,123 0,9748 0, ,123 0,9736 0, ,082 0,9728 0, ,185 0,971 0, ,124 0,9698 0,
23 db. szám KE 1a kormányszelepek meghibásodása 250 Meghibásodások száma Hibás szelepek száma/hó Összes meghibásodás hónap 23
24 ráta Meghibásodási ráta 1,200 Meghibásodási ráta 1,000 Meghibá-sodási ráta 0,800 0,600 0,400 0,200 0,000 hónap 24
25 R(t) Megbízhatóság 1,05 KE 1a kormányszelepek megbízhatósága 1 0,95 Megbízha-tóság 0,9 0,85 0,8 hónap 25
26 R(t) és Q(t) 1,2 KE 1a kormányszelepek meghibásodásánek és megbízhatóságának valószínűsége 1 0,8 0,6 Megbízha-tóság Meghibásodás való-színűsége 0,4 0,2 0 hónap 26
27 Élettartam növelés: Konstrukció módosítás, (gyengepontok megszüntetése, pl.: korrózióállóság, kifáradási szilárdság növelése), Anyagmegválasztás, új anyagok alkalmazása Technológiai korszerűsítés (kopásálló réteg felvitele, felületszilárdítás, stb.) 27
Alapvető karbantartási stratégiák
 Alapvető karbantartási stratégiák MBA képzés 2009 Erdei János 4. Tervszerű karbantartás teljesítőképess pesség 00% Teljesítm tménytartalék-diagram kiesési si ciklikus állapotfüggő teljesítménymaradék t
Alapvető karbantartási stratégiák MBA képzés 2009 Erdei János 4. Tervszerű karbantartás teljesítőképess pesség 00% Teljesítm tménytartalék-diagram kiesési si ciklikus állapotfüggő teljesítménymaradék t
Modulzáró ellenőrző kérdések és feladatok (2)
 Modulzáró ellenőrző kérdések és feladatok (2) 1. Definiálja az alábbi, technikai eszközök üzemi megbízhatóságával kapcsolatos fogalmakat (1): Megbízhatóság. Használhatóság. Hibamentesség. Fenntarthatóság.
Modulzáró ellenőrző kérdések és feladatok (2) 1. Definiálja az alábbi, technikai eszközök üzemi megbízhatóságával kapcsolatos fogalmakat (1): Megbízhatóság. Használhatóság. Hibamentesség. Fenntarthatóság.
TERMÉKEK MŐSZAKI TERVEZÉSE Megbízhatóságra, élettartamra tervezés I.
 TERMÉKEK MŐSZAKI TERVEZÉSE Megbízhatóságra, élettartamra tervezés I. Dr. Kovács Zsolt egyetemi tanár Megbízhatóság-elméleti alapok A megbízhatóságelmélet az a komplex tudományág, amely a meghibásodási
TERMÉKEK MŐSZAKI TERVEZÉSE Megbízhatóságra, élettartamra tervezés I. Dr. Kovács Zsolt egyetemi tanár Megbízhatóság-elméleti alapok A megbízhatóságelmélet az a komplex tudományág, amely a meghibásodási
Modulzáró ellenőrző kérdések és feladatok (2)
 Modulzáró ellenőrző kérdések és feladatok (2) 1. Definiálja az alábbi, technikai eszközök üzemi megbízhatóságával kapcsolatos fogalmakat (1): Megbízhatóság. Használhatóság. Hibamentesség. Fenntarthatóság.
Modulzáró ellenőrző kérdések és feladatok (2) 1. Definiálja az alábbi, technikai eszközök üzemi megbízhatóságával kapcsolatos fogalmakat (1): Megbízhatóság. Használhatóság. Hibamentesség. Fenntarthatóság.
TPM egy kicsit másképp Szollár Lajos, TPM Koordinátor
 TPM egy kicsit másképp Szollár Lajos, TPM Koordinátor 2013.06.18 A TPM A TPM a Total Productive Maintenance kifejezés rövidítése, azaz a teljes, a gyártásba integrált karbantartást jelenti. A TPM egy állandó
TPM egy kicsit másképp Szollár Lajos, TPM Koordinátor 2013.06.18 A TPM A TPM a Total Productive Maintenance kifejezés rövidítése, azaz a teljes, a gyártásba integrált karbantartást jelenti. A TPM egy állandó
TURBÓGENERÁTOR FORGÓRÉSZEK Élettartamának meghosszabbítása
 Szigetelés Diagnosztikai Konferencia 2007. 04. 26-28. TURBÓGENERÁTOR FORGÓRÉSZEK Élettartamának meghosszabbítása Az élettartam kiterjesztés kérdései A turbógenerátorok üzemi élettartamának meghosszabbítása,
Szigetelés Diagnosztikai Konferencia 2007. 04. 26-28. TURBÓGENERÁTOR FORGÓRÉSZEK Élettartamának meghosszabbítása Az élettartam kiterjesztés kérdései A turbógenerátorok üzemi élettartamának meghosszabbítása,
Az előadásdiák gyors összevágása, hogy legyen valami segítség:
 Az előadásdiák gyors összevágása, hogy legyen valami segítség: Az elektronikai gyártás ellenőrző berendezései (AOI, X-RAY, ICT) 1. Ismertesse az automatikus optikai ellenőrzés alapelvét (a), megvilágítási
Az előadásdiák gyors összevágása, hogy legyen valami segítség: Az elektronikai gyártás ellenőrző berendezései (AOI, X-RAY, ICT) 1. Ismertesse az automatikus optikai ellenőrzés alapelvét (a), megvilágítási
2. gyakorlat RENDSZEREK MEGBÍZHATÓSÁGA: SOROS RENDSZEREK, REDUNDANCIA. Összeállította: Farkas Balázs
 2. gyakorlat RENDSZEREK MEGBÍZHATÓSÁGA: SOROS RENDSZEREK, REDUNDANCIA Összeállította: Farkas Balázs BEVEZETÉS RENDSZERTULAJDONSÁGOK Egy rendszer megbízhatósága függ: elemeinek megbízhatóságától és az elemek
2. gyakorlat RENDSZEREK MEGBÍZHATÓSÁGA: SOROS RENDSZEREK, REDUNDANCIA Összeállította: Farkas Balázs BEVEZETÉS RENDSZERTULAJDONSÁGOK Egy rendszer megbízhatósága függ: elemeinek megbízhatóságától és az elemek
TURBÓGENERÁTOR ÁLLÓRÉSZEK Élettartamának meghosszabbítása
 Szigetelés Diagnosztikai Konferencia 2009. 10. 14-16. TURBÓGENERÁTOR ÁLLÓRÉSZEK Élettartamának meghosszabbítása Az élettartam kiterjesztés kérdései A turbógenerátorok üzemi élettartamának meghosszabbítása,
Szigetelés Diagnosztikai Konferencia 2009. 10. 14-16. TURBÓGENERÁTOR ÁLLÓRÉSZEK Élettartamának meghosszabbítása Az élettartam kiterjesztés kérdései A turbógenerátorok üzemi élettartamának meghosszabbítása,
Transzformátor, Mérőtranszformátor Állapot Tényező szakértői rendszer Vörös Csaba Tarcsa Dániel Németh Bálint Csépes Gusztáv
 Transzformátor, Mérőtranszformátor Állapot Tényező szakértői rendszer Vörös Csaba Tarcsa Dániel Németh Bálint Csépes Gusztáv Áttekintés A Rendszer jelentősége Állapotjellemzők MérőTranszformátor Állapot
Transzformátor, Mérőtranszformátor Állapot Tényező szakértői rendszer Vörös Csaba Tarcsa Dániel Németh Bálint Csépes Gusztáv Áttekintés A Rendszer jelentősége Állapotjellemzők MérőTranszformátor Állapot
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Matematikai statisztika. Mi a modell? Binomiális eloszlás sűrűségfüggvény. Binomiális eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
Anyagvizsgálati módszerek Mérési adatok feldolgozása. Anyagvizsgálati módszerek
 Anyagvizsgálati módszerek Mérési adatok feldolgozása Anyagvizsgálati módszerek Pannon Egyetem Mérnöki Kar Anyagvizsgálati módszerek Statisztika 1/ 22 Mérési eredmények felhasználása Tulajdonságok hierarchikus
Anyagvizsgálati módszerek Mérési adatok feldolgozása Anyagvizsgálati módszerek Pannon Egyetem Mérnöki Kar Anyagvizsgálati módszerek Statisztika 1/ 22 Mérési eredmények felhasználása Tulajdonságok hierarchikus
Valószínűségszámítás összefoglaló
 Statisztikai módszerek BMEGEVGAT Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
Statisztikai módszerek BMEGEVGAT Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
Biometria az orvosi gyakorlatban. Regresszió Túlélésanalízis
 SZDT-09 p. 1/36 Biometria az orvosi gyakorlatban Regresszió Túlélésanalízis Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Logisztikus regresszió
SZDT-09 p. 1/36 Biometria az orvosi gyakorlatban Regresszió Túlélésanalízis Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Logisztikus regresszió
Számítógépes döntéstámogatás. Statisztikai elemzés
 SZDT-03 p. 1/22 Számítógépes döntéstámogatás Statisztikai elemzés Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Előadás SZDT-03 p. 2/22 Rendelkezésre
SZDT-03 p. 1/22 Számítógépes döntéstámogatás Statisztikai elemzés Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Előadás SZDT-03 p. 2/22 Rendelkezésre
A talajok összenyomódásának vizsgálata
 A talajok összenyomódásának vizsgálata Amit már tudni kellene Összenyomódás Konszolidáció Normálisan konszolidált talaj Túlkonszolidált talaj Túlkonszolidáltsági arányszám,ocr Konszolidáció az az időben
A talajok összenyomódásának vizsgálata Amit már tudni kellene Összenyomódás Konszolidáció Normálisan konszolidált talaj Túlkonszolidált talaj Túlkonszolidáltsági arányszám,ocr Konszolidáció az az időben
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
Matematikai geodéziai számítások 10.
 Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
szakértői rendszer Tóth György E.ON Németh Bálint BME VET
 xát transzformátor, megszakító és mérőváltó állapot tényező szakértői rendszer Tóth György E.ON Németh Bálint BME VET Kiindulás amink van: Primer diagnosztikai és karbantartási stratégiák Egymásra épülő,
xát transzformátor, megszakító és mérőváltó állapot tényező szakértői rendszer Tóth György E.ON Németh Bálint BME VET Kiindulás amink van: Primer diagnosztikai és karbantartási stratégiák Egymásra épülő,
1. Adatok kiértékelése. 2. A feltételek megvizsgálása. 3. A hipotézis megfogalmazása
 HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl. egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat
HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl. egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat
A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9
 A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9 Név: Pitlik László Mérés dátuma: 2014.12.04. Mérőtársak neve: Menkó Orsolya Adatsorok: M24120411 Halmy Réka M14120412 Sárosi
A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9 Név: Pitlik László Mérés dátuma: 2014.12.04. Mérőtársak neve: Menkó Orsolya Adatsorok: M24120411 Halmy Réka M14120412 Sárosi
HÁLÓZATI SZINTŰ DINAMIKUS BEHAJLÁSMÉRÉS MÚLTJA JELENE II.
 HÁLÓZATI SZINTŰ DINAMIKUS BEHAJLÁSMÉRÉS MÚLTJA JELENE II. MÉTA-Q Kft. Baksay János 2007. 06. 12. MAÚT ÚTÉPÍTÉSI AKADÉMIA 11. 1. FOGALOM: Teherbírás. Teherbíráson általában határ-igénybevételt értünk 2.
HÁLÓZATI SZINTŰ DINAMIKUS BEHAJLÁSMÉRÉS MÚLTJA JELENE II. MÉTA-Q Kft. Baksay János 2007. 06. 12. MAÚT ÚTÉPÍTÉSI AKADÉMIA 11. 1. FOGALOM: Teherbírás. Teherbíráson általában határ-igénybevételt értünk 2.
Biometria az orvosi gyakorlatban. Korrelációszámítás, regresszió
 SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
SZDT-08 p. 1/31 Biometria az orvosi gyakorlatban Korrelációszámítás, regresszió Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Korrelációszámítás
Statisztika - bevezetés Méréselmélet PE MIK MI_BSc VI_BSc 1
 Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Dr. Kalló Noémi. Termelés- és szolgáltatásmenedzsment. egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék. Dr.
 Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Ismertesse a legfontosabb előrejelzési módszereket és azok gyakorlati
Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Ismertesse a legfontosabb előrejelzési módszereket és azok gyakorlati
A mérési eredmény megadása
 A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
BME Járműgyártás és -Javítás Tanszék JÁRMŰFENNTARTÁS
 BME Járműgyártás és -Javítás Tanszék JÁRMŰFENNTARTÁS Dr. Sólyomvári Károly Állóeszközök újratermelési folyamata Szinttartó csere Új beruházás Selejtezés Beruházás Az üzemképesség biztosítása Kihasználás
BME Járműgyártás és -Javítás Tanszék JÁRMŰFENNTARTÁS Dr. Sólyomvári Károly Állóeszközök újratermelési folyamata Szinttartó csere Új beruházás Selejtezés Beruházás Az üzemképesség biztosítása Kihasználás
1. Név:... Neptun Kód:... Feladat: Egy összeszerel½o üzemben 3 szalag van. Mindehárom szalagon ugyanazt
 1. Név:......................... Egy összeszerel½o üzemben 3 szalag van. Mindehárom szalagon ugyanazt a gyártmányt készítik. Egy gyártmány összeszerelési ideje normális eloszlású valószín½uségi változó
1. Név:......................... Egy összeszerel½o üzemben 3 szalag van. Mindehárom szalagon ugyanazt a gyártmányt készítik. Egy gyártmány összeszerelési ideje normális eloszlású valószín½uségi változó
Mi a karbantartás feladata. Karbantartás-fejlesztés korszerűen Nyílt képzés 2014.05.15. Fekete Gábor, A.A. Stádium Kft.
 Mi a karbantartás feladata Karbantartás-fejlesztés korszerűen Nyílt képzés 2014.05.15. Fekete Gábor, A.A. Stádium Kft. A karbantartás hagyományos értelmezése A karbantartás feladata a berendezések képességeinek
Mi a karbantartás feladata Karbantartás-fejlesztés korszerűen Nyílt képzés 2014.05.15. Fekete Gábor, A.A. Stádium Kft. A karbantartás hagyományos értelmezése A karbantartás feladata a berendezések képességeinek
Matematikai geodéziai számítások 6.
 Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás
 Kísérlettervezés - biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás A matematikai-statisztika feladata tapasztalati adatok feldolgozásával segítséget nyújtani
Kísérlettervezés - biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás A matematikai-statisztika feladata tapasztalati adatok feldolgozásával segítséget nyújtani
MUNKAANYAG. Völgyi Lajos. Mit kell tenni, hogy működjenek az. élelmiszeripari gépek és berendezések. karbantartása, biztonságos működtetése
 Völgyi Lajos Mit kell tenni, hogy működjenek az élelmiszeripari gépek és berendezések karbantartása, biztonságos működtetése A követelménymodul megnevezése: Gyártás előkészítése és befejezése A követelménymodul
Völgyi Lajos Mit kell tenni, hogy működjenek az élelmiszeripari gépek és berendezések karbantartása, biztonságos működtetése A követelménymodul megnevezése: Gyártás előkészítése és befejezése A követelménymodul
Matematikai geodéziai számítások 6.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Több valószínűségi változó együttes eloszlása, korreláció
 Tartalomjegzék Előszó... 6 I. Valószínűségelméleti és matematikai statisztikai alapok... 8 1. A szükséges valószínűségelméleti és matematikai statisztikai alapismeretek összefoglalása... 8 1.1. Alapfogalmak...
Tartalomjegzék Előszó... 6 I. Valószínűségelméleti és matematikai statisztikai alapok... 8 1. A szükséges valószínűségelméleti és matematikai statisztikai alapismeretek összefoglalása... 8 1.1. Alapfogalmak...
Alap-ötlet: Karl Friedrich Gauss ( ) valószínűségszámítási háttér: Andrej Markov ( )
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
www.pipecontrol.hu info@pipecontrol.hu
 INTELLIGENS GÖRÉNYEZ G NYEZÉS Meghibásod sodások sok kezelése, karbantartási filozófi P I P E C O N T R O L Mérnöki Iroda Kft 8600 Siófok, Dózsa György u. 27/b Tel.: (+36) 84-506 702, Fax: (+36) 84-506
INTELLIGENS GÖRÉNYEZ G NYEZÉS Meghibásod sodások sok kezelése, karbantartási filozófi P I P E C O N T R O L Mérnöki Iroda Kft 8600 Siófok, Dózsa György u. 27/b Tel.: (+36) 84-506 702, Fax: (+36) 84-506
NEVEZETES FOLYTONOS ELOSZLÁSOK
 Bodó Beáta - MATEMATIKA II 1 NEVEZETES FOLYTONOS ELOSZLÁSOK EXPONENCIÁLIS ELOSZLÁS 1. A ξ valószínűségi változó eponenciális eloszlású 80 várható értékkel. (a) B Adja meg és ábrázolja a valószínűségi változó
Bodó Beáta - MATEMATIKA II 1 NEVEZETES FOLYTONOS ELOSZLÁSOK EXPONENCIÁLIS ELOSZLÁS 1. A ξ valószínűségi változó eponenciális eloszlású 80 várható értékkel. (a) B Adja meg és ábrázolja a valószínűségi változó
Módszertani Intézeti Tanszéki Osztály. A megoldás részletes mellékszámítások hiányában nem értékelhető!
 BGF KKK Módszertani Intézeti Tanszéki Osztály Budapest, 2012.. Név:... Neptun kód:... Érdemjegy:..... STATISZTIKA II. VIZSGADOLGOZAT Feladatok 1. 2. 3. 4. 5. 6. Összesen Szerezhető pontszám 21 20 7 22
BGF KKK Módszertani Intézeti Tanszéki Osztály Budapest, 2012.. Név:... Neptun kód:... Érdemjegy:..... STATISZTIKA II. VIZSGADOLGOZAT Feladatok 1. 2. 3. 4. 5. 6. Összesen Szerezhető pontszám 21 20 7 22
Tárgyi eszköz-gazdálkodás
 Tárgyi eszköz-gazdálkodás Gazdálkodás, gazdaságosság, kontrolling Termelési eszközök és megtérülésük A tárgyi eszközök értéküket több termelési perióduson belül adják át a készterméknek, miközben használati
Tárgyi eszköz-gazdálkodás Gazdálkodás, gazdaságosság, kontrolling Termelési eszközök és megtérülésük A tárgyi eszközök értéküket több termelési perióduson belül adják át a készterméknek, miközben használati
EGYIRÁNYBAN ER SÍTETT KOMPOZIT RUDAK HAJLÍTÓ KARAKTERISZTIKÁJÁNAK ÉS TÖNKREMENETELI FOLYAMATÁNAK ELEMZÉSE
 Budapest M szaki és Gazdaságtudományi Egyetem Polimertecnika Tanszék EGYIRÁNYBAN ER SÍTETT KOMPOZIT RUDAK HAJLÍTÓ KARAKTERISZTIKÁJÁNAK ÉS TÖNKREMENETELI OLYAMATÁNAK ELEMZÉSE Tézisek Rácz Zsolt Témavezet
Budapest M szaki és Gazdaságtudományi Egyetem Polimertecnika Tanszék EGYIRÁNYBAN ER SÍTETT KOMPOZIT RUDAK HAJLÍTÓ KARAKTERISZTIKÁJÁNAK ÉS TÖNKREMENETELI OLYAMATÁNAK ELEMZÉSE Tézisek Rácz Zsolt Témavezet
KOMPLEX RONCSOLÁSMENTES HELYSZÍNI SZIGETELÉS- DIAGNOSZTIKA
 Budapesti i Műszaki és Gazdaságtudományi Egyetem KOMPLEX RONCSOLÁSMENTES HELYSZÍNI SZIGETELÉS- DIAGNOSZTIKA MEE VÁNDORGYŰLÉS 2010. Tamus Zoltán Ádám, Cselkó Richárd tamus.adam@vet.bme.hu, cselko.richard@vet.bme.hu
Budapesti i Műszaki és Gazdaságtudományi Egyetem KOMPLEX RONCSOLÁSMENTES HELYSZÍNI SZIGETELÉS- DIAGNOSZTIKA MEE VÁNDORGYŰLÉS 2010. Tamus Zoltán Ádám, Cselkó Richárd tamus.adam@vet.bme.hu, cselko.richard@vet.bme.hu
Járművek karbantartási és egyéb kihívásai a kötöttpályás elővárosi közlekedés fejlesztésében
 Járművek karbantartási és egyéb kihívásai a kötöttpályás elővárosi közlekedés fejlesztésében HUNGRAIL Vasútakadémia Konferencia Budapest 2017. május 3. Előadó: Pál László MÁV-HÉV Zrt. vezérigazgató Tartalom
Járművek karbantartási és egyéb kihívásai a kötöttpályás elővárosi közlekedés fejlesztésében HUNGRAIL Vasútakadémia Konferencia Budapest 2017. május 3. Előadó: Pál László MÁV-HÉV Zrt. vezérigazgató Tartalom
Matematika A3 Valószínűségszámítás, 5. gyakorlat 2013/14. tavaszi félév
 Matematika A3 Valószínűségszámítás, 5. gyakorlat 013/14. tavaszi félév 1. Folytonos eloszlások Eloszlásfüggvény és sűrűségfüggvény Egy valószínűségi változó, illetve egy eloszlás eloszlásfüggvényének egy
Matematika A3 Valószínűségszámítás, 5. gyakorlat 013/14. tavaszi félév 1. Folytonos eloszlások Eloszlásfüggvény és sűrűségfüggvény Egy valószínűségi változó, illetve egy eloszlás eloszlásfüggvényének egy
Megbízhatóságra alapozott program a berendezések értékelésére
 AZ ÜZEMFENNTARTÁS ÁLTALÁNOS KÉRDÉSEI 1.02 Megbízhatóságra alapozott program a berendezések értékelésére Tárgyszavak: megbízhatóság; MTBF; adatgyűjtés; hibaelemzés; állapotfelmérés; kőolajipar. A szénhidrogént
AZ ÜZEMFENNTARTÁS ÁLTALÁNOS KÉRDÉSEI 1.02 Megbízhatóságra alapozott program a berendezések értékelésére Tárgyszavak: megbízhatóság; MTBF; adatgyűjtés; hibaelemzés; állapotfelmérés; kőolajipar. A szénhidrogént
 Statisztika 3. Dr Gősi Zsuzsanna Egyetemi adjunktus Koncentráció mérése Koncentráció általában a jelenségek tömörülését, összpontosulását értjük. Koncentráció meglétéről gyorsan tájékozódhatunk, ha sokaságot
Statisztika 3. Dr Gősi Zsuzsanna Egyetemi adjunktus Koncentráció mérése Koncentráció általában a jelenségek tömörülését, összpontosulását értjük. Koncentráció meglétéről gyorsan tájékozódhatunk, ha sokaságot
Korai vasbeton építmények tartószerkezeti biztonságának megítélése
 Korai vasbeton építmények tartószerkezeti biztonságának megítélése Dr. Orbán Zoltán, Dormány András, Juhász Tamás Pécsi Tudományegyetem Műszaki és Informatikai Kar Építőmérnök Tanszék A megbízhatóság értelmezése
Korai vasbeton építmények tartószerkezeti biztonságának megítélése Dr. Orbán Zoltán, Dormány András, Juhász Tamás Pécsi Tudományegyetem Műszaki és Informatikai Kar Építőmérnök Tanszék A megbízhatóság értelmezése
Matematika III előadás
 Matematika III. - 2. előadás Vinczéné Varga Adrienn Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Előadáskövető fóliák Vinczéné Varga Adrienn (DE-MK) Matematika III. 2016/2017/I 1 / 23 paramétervonalak,
Matematika III. - 2. előadás Vinczéné Varga Adrienn Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Előadáskövető fóliák Vinczéné Varga Adrienn (DE-MK) Matematika III. 2016/2017/I 1 / 23 paramétervonalak,
Kísérlettervezés alapfogalmak
 Kísérlettervezés alapfogalmak Rendszermodellezés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Kísérlettervezés Cél: a modell paraméterezése a valóság alapján
Kísérlettervezés alapfogalmak Rendszermodellezés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Kísérlettervezés Cél: a modell paraméterezése a valóság alapján
( 1) i 2 i. megbízhatóságú a levont következtetése? A matematikai statisztika eszközeivel értékelje a kapott eredményeket!
 1. Név:......................... Egy szabályos pénzérmét feldobunk, ha az els½o FEJ az i-edik dobásra jön, akkor a játékos nyereménye ( 1) i i forint. Vizsgálja szimulációval a játékot, különböz½o induló
1. Név:......................... Egy szabályos pénzérmét feldobunk, ha az els½o FEJ az i-edik dobásra jön, akkor a játékos nyereménye ( 1) i i forint. Vizsgálja szimulációval a játékot, különböz½o induló
VENTUS A-P Műszaki adatok:
 VENTUS A-P A berendezés - működési mód alapján - a áramlásának típusa szerint aktív és passzív kategóriába sorolható. Passzív típusú biofiltereink ventilátor nélkül működnek, a t a szűrőn a rendszer kényszeráramlása
VENTUS A-P A berendezés - működési mód alapján - a áramlásának típusa szerint aktív és passzív kategóriába sorolható. Passzív típusú biofiltereink ventilátor nélkül működnek, a t a szűrőn a rendszer kényszeráramlása
Gyakorló feladatok. Az alábbi feladatokon kívül a félév szemináriumi anyagát is nézzék át. Jó munkát! Gaál László
 Gyakorló feladatok Az alábbi feladatokon kívül a félév szemináriumi anyagát is nézzék át. Jó munkát! Gaál László I/. A vizsgaidőszak második napján a hallgatók %-ának az E épületben, %-ának a D épületben,
Gyakorló feladatok Az alábbi feladatokon kívül a félév szemináriumi anyagát is nézzék át. Jó munkát! Gaál László I/. A vizsgaidőszak második napján a hallgatók %-ának az E épületben, %-ának a D épületben,
e (t µ) 2 f (t) = 1 F (t) = 1 Normális eloszlás negyedik centrális momentuma:
 Normális eloszlás ξ valószínűségi változó normális eloszlású. ξ N ( µ, σ 2) Paraméterei: µ: várható érték, σ 2 : szórásnégyzet (µ tetszőleges, σ 2 tetszőleges pozitív valós szám) Normális eloszlás sűrűségfüggvénye:
Normális eloszlás ξ valószínűségi változó normális eloszlású. ξ N ( µ, σ 2) Paraméterei: µ: várható érték, σ 2 : szórásnégyzet (µ tetszőleges, σ 2 tetszőleges pozitív valós szám) Normális eloszlás sűrűségfüggvénye:
Thermo King légkondicionáló berendezéssel szerelt autóbuszok klímaberendezéseinek szükség szerinti javítása és eseti karbantartása
 Thermo King légkondicionáló berendezéssel szerelt autóbuszok klímaberendezéseinek szükség szerinti javítása és eseti karbantartása (BKV Zrt. T-154/18) KÖZBESZERZÉSI DOKUMENTUMOK III. KÖTET MŰSZAKI LEÍRÁS
Thermo King légkondicionáló berendezéssel szerelt autóbuszok klímaberendezéseinek szükség szerinti javítása és eseti karbantartása (BKV Zrt. T-154/18) KÖZBESZERZÉSI DOKUMENTUMOK III. KÖTET MŰSZAKI LEÍRÁS
Üvegolvasztó kemencék jellemző korróziós kopásai
 Üvegolvasztó kemencék jellemző korróziós kopásai Befektetés legdrágább része Az olvasztó kád élettartama függ: A javítások célja: Hosszabb élettartam elérése a Minőségi és Mennyiségi termelés biztosításával
Üvegolvasztó kemencék jellemző korróziós kopásai Befektetés legdrágább része Az olvasztó kád élettartama függ: A javítások célja: Hosszabb élettartam elérése a Minőségi és Mennyiségi termelés biztosításával
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Mi a modell? Matematikai statisztika. 300 dobás. sűrűségfüggvénye. Egyenletes eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 7. Előadás Egyenletes eloszlás Binomiális eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell /56 Matematikai statisztika Reprezentatív mintavétel
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 7. Előadás Egyenletes eloszlás Binomiális eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell /56 Matematikai statisztika Reprezentatív mintavétel
Jankovits Hidraulika Kft. Alapítva: 1992.
 Jankovits Hidraulika Kft. Alapítva: 1992. A cég története 1992. cégalapítás (működése 100 m 2 -es garázsépületben) 1995. KFT-vé alakulás 1996. kapcsolatfelvétel a Vickers-szel 1996. több telephely (forgácsoló
Jankovits Hidraulika Kft. Alapítva: 1992. A cég története 1992. cégalapítás (működése 100 m 2 -es garázsépületben) 1995. KFT-vé alakulás 1996. kapcsolatfelvétel a Vickers-szel 1996. több telephely (forgácsoló
A mérések általános és alapvető metrológiai fogalmai és definíciói. Mérések, mérési eredmények, mérési bizonytalanság. mérés. mérési elv
 Mérések, mérési eredmények, mérési bizonytalanság A mérések általános és alapvető metrológiai fogalmai és definíciói mérés Műveletek összessége, amelyek célja egy mennyiség értékének meghatározása. mérési
Mérések, mérési eredmények, mérési bizonytalanság A mérések általános és alapvető metrológiai fogalmai és definíciói mérés Műveletek összessége, amelyek célja egy mennyiség értékének meghatározása. mérési
Székely Bence Daruline Kft.
 Székely Bence Daruline Kft. Emelőgép jellemző életciklusa Értékesítés Modernizáció / Csere Üzembe helyezés Betanítás Teljes felújítás (GO) Időszakos vizsgálatok Szükséges javítások Gyártó által előírt
Székely Bence Daruline Kft. Emelőgép jellemző életciklusa Értékesítés Modernizáció / Csere Üzembe helyezés Betanítás Teljes felújítás (GO) Időszakos vizsgálatok Szükséges javítások Gyártó által előírt
MÉRÉSI EREDMÉNYEK PONTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI
 MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
MÉRÉSI EREDMÉYEK POTOSSÁGA, A HIBASZÁMÍTÁS ELEMEI. A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk
Kísérlettervezés alapfogalmak
 Kísérlettervezés alapfogalmak Rendszermodellezés Budapest University of Technology and Economics Fault Tolerant Systems Research Group Budapest University of Technology and Economics Department of Measurement
Kísérlettervezés alapfogalmak Rendszermodellezés Budapest University of Technology and Economics Fault Tolerant Systems Research Group Budapest University of Technology and Economics Department of Measurement
A kockázatelemzés menete
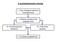 A kockázatelemzés menete 1. Üzem (folyamat) jellemzői Veszélyforrások 2. Baleseti sorok meghatározása 3a. Következmények felmérése 3b. Gyakoriság becslése 4. Kockázat meghatározás Balesetek Gyakoriság
A kockázatelemzés menete 1. Üzem (folyamat) jellemzői Veszélyforrások 2. Baleseti sorok meghatározása 3a. Következmények felmérése 3b. Gyakoriság becslése 4. Kockázat meghatározás Balesetek Gyakoriság
Nagy számok törvényei Statisztikai mintavétel Várható érték becslése. Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem
 agy számok törvényei Statisztikai mintavétel Várható érték becslése Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem A mérés mint statisztikai mintavétel A méréssel az eloszlásfüggvénnyel
agy számok törvényei Statisztikai mintavétel Várható érték becslése Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem A mérés mint statisztikai mintavétel A méréssel az eloszlásfüggvénnyel
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
Végeselemes analízisen alapuló méretezési elvek az Eurocode 3 alapján. Dr. Dunai László egyetemi tanár BME, Hidak és Szerkezetek Tanszéke
 Végeselemes analízisen alapuló méretezési elvek az Eurocode 3 alapján Dr. Dunai László egyetemi tanár BME, Hidak és Szerkezetek Tanszéke 1 Tartalom Méretezési alapelvek Numerikus modellezés Analízis és
Végeselemes analízisen alapuló méretezési elvek az Eurocode 3 alapján Dr. Dunai László egyetemi tanár BME, Hidak és Szerkezetek Tanszéke 1 Tartalom Méretezési alapelvek Numerikus modellezés Analízis és
Új felállás a MAVIR diagnosztika területén. VII. Szigetelésdiagnosztikai Konferencia 2007 Siófok
 Új felállás a MAVIR diagnosztika területén VII. Szigetelésdiagnosztikai Konferencia 2007 Siófok Állapotfelmérés, -ismeret 1 Célja: Karbantartási, felújítási, rekonstrukciós döntések megalapozása, Üzem
Új felállás a MAVIR diagnosztika területén VII. Szigetelésdiagnosztikai Konferencia 2007 Siófok Állapotfelmérés, -ismeret 1 Célja: Karbantartási, felújítási, rekonstrukciós döntések megalapozása, Üzem
Számítógépes döntéstámogatás. Genetikus algoritmusok
 BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
Élettartam Kutató Laboratórium
 Élettartam Kutató Laboratórium A K+F aktivitás célja kopás- és károsodásvizsgáló laboratóriumi technikák alkalmazása károsodási magatartás és a gépelemek, illetve szerszámok felületi integritása közötti
Élettartam Kutató Laboratórium A K+F aktivitás célja kopás- és károsodásvizsgáló laboratóriumi technikák alkalmazása károsodási magatartás és a gépelemek, illetve szerszámok felületi integritása közötti
II. rész: a rendszer felülvizsgálati stratégia kidolgozását támogató funkciói. Tóth László, Lenkeyné Biró Gyöngyvér, Kuczogi László
 A kockázat alapú felülvizsgálati és karbantartási stratégia alkalmazása a MOL Rt.-nél megvalósuló Statikus Készülékek Állapot-felügyeleti Rendszerének kialakításában II. rész: a rendszer felülvizsgálati
A kockázat alapú felülvizsgálati és karbantartási stratégia alkalmazása a MOL Rt.-nél megvalósuló Statikus Készülékek Állapot-felügyeleti Rendszerének kialakításában II. rész: a rendszer felülvizsgálati
Vérsejtszámlálás. Bürker kamra
 1. Vérsejtszámlálás Eszközök ujjbegy fertőtlenítéshez spray steril, egyszer használatos injekciós tű/ ujjbegyszúró gumikesztyű vatta (vér törlése ujjbegyről) keverőpipetta (piros 1:100 és fehér golyós
1. Vérsejtszámlálás Eszközök ujjbegy fertőtlenítéshez spray steril, egyszer használatos injekciós tű/ ujjbegyszúró gumikesztyű vatta (vér törlése ujjbegyről) keverőpipetta (piros 1:100 és fehér golyós
A Statisztika alapjai
 A Statisztika alapjai BME A3c Magyar Róbert 2016.05.12. Mi az a Statisztika? A statisztika a valóság számszerű információinak megfigyelésére, összegzésére, elemzésére és modellezésére irányuló gyakorlati
A Statisztika alapjai BME A3c Magyar Róbert 2016.05.12. Mi az a Statisztika? A statisztika a valóság számszerű információinak megfigyelésére, összegzésére, elemzésére és modellezésére irányuló gyakorlati
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/54/34131233.jpg) [Biomatematika 2] Orvosi biometria 2016.02.22. Valószínűségi változó Véletlentől függő számértékeket (értékek sokasága) felvevő változókat valószínűségi változóknak nevezzük(jelölés: ξ, η, x). (pl. x =
[Biomatematika 2] Orvosi biometria 2016.02.22. Valószínűségi változó Véletlentől függő számértékeket (értékek sokasága) felvevő változókat valószínűségi változóknak nevezzük(jelölés: ξ, η, x). (pl. x =
MINŐSÉGELLENŐRZÉS TÁBLÁZATOK A JEGYZŐKÖNYVEK MEGOLDÁSÁHOZ
 MINŐSÉGELLENŐRZÉS TÁBLÁZATOK A JEGYZŐKÖNYVEK MEGOLDÁSÁHOZ Minőségi jellemzők csoportosítása Tervezett, mérhető minőségi jellemzők Használatra való alkalmasság. Szabványoknak, rajzoknak, műszaki, környezetvédelmi
MINŐSÉGELLENŐRZÉS TÁBLÁZATOK A JEGYZŐKÖNYVEK MEGOLDÁSÁHOZ Minőségi jellemzők csoportosítása Tervezett, mérhető minőségi jellemzők Használatra való alkalmasság. Szabványoknak, rajzoknak, műszaki, környezetvédelmi
Szilárdsági számítások. Kazánok és Tüzelőberendezések
 Szilárdsági számítások Kazánok és Tüzelőberendezések Tartalom Ellenőrző számítások: Hőtechnikai számítások, sugárzásos és konvektív hőátadó felületek számításai már ismertek Áramlástechnikai számítások
Szilárdsági számítások Kazánok és Tüzelőberendezések Tartalom Ellenőrző számítások: Hőtechnikai számítások, sugárzásos és konvektív hőátadó felületek számításai már ismertek Áramlástechnikai számítások
y ij = µ + α i + e ij STATISZTIKA Sir Ronald Aylmer Fisher Példa Elmélet A variancia-analízis alkalmazásának feltételei Lineáris modell
 Példa STATISZTIKA Egy gazdálkodó k kukorica hibrid termesztése között választhat. Jelöljük a fajtákat A, B, C, D-vel. Döntsük el, hogy a hibridek termesztése esetén azonos terméseredményre számíthatunk-e.
Példa STATISZTIKA Egy gazdálkodó k kukorica hibrid termesztése között választhat. Jelöljük a fajtákat A, B, C, D-vel. Döntsük el, hogy a hibridek termesztése esetén azonos terméseredményre számíthatunk-e.
3. előadás Stabilitás
 Stabilitás 3. előadás 2011. 09. 19. Alapfogalmak Tekintsük dx dt = f (t, x), x(t 0) = x 0 t (, ), (1) Jelölje t x(t; t 0, x 0 ) vagy x(.; t 0, x 0 ) a KÉF megoldását. Kívánalom: kezdeti állapot kis megváltozása
Stabilitás 3. előadás 2011. 09. 19. Alapfogalmak Tekintsük dx dt = f (t, x), x(t 0) = x 0 t (, ), (1) Jelölje t x(t; t 0, x 0 ) vagy x(.; t 0, x 0 ) a KÉF megoldását. Kívánalom: kezdeti állapot kis megváltozása
GÉPSZERKEZETTAN - TERVEZÉS GÉPELEMEK KÁROSODÁSA
 GÉPSZERKEZETTAN - TERVEZÉS GÉPELEMEK KÁROSODÁSA 1 Üzemképesség Működésre, a funkció betöltésére való alkalmasság. Az adott gépelem maradéktalanul megfelel azoknak a követelményeknek, amelyek teljesítésére
GÉPSZERKEZETTAN - TERVEZÉS GÉPELEMEK KÁROSODÁSA 1 Üzemképesség Működésre, a funkció betöltésére való alkalmasság. Az adott gépelem maradéktalanul megfelel azoknak a követelményeknek, amelyek teljesítésére
Kózel Miklós, BME KUKG Soltész Tamás, BME KUKG
 Budapesti Műszaki és Gazdaságtudományi Egyetem Közlekedésüzemi és Közlekedésgazdasági Tanszék Nemzeti Közlekedési Napok 2013 Fiatal mérnökök szekció A menetidő törvényszerűségei eloszlásminták alapján
Budapesti Műszaki és Gazdaságtudományi Egyetem Közlekedésüzemi és Közlekedésgazdasági Tanszék Nemzeti Közlekedési Napok 2013 Fiatal mérnökök szekció A menetidő törvényszerűségei eloszlásminták alapján
Mintavétel fogalmai STATISZTIKA, BIOMETRIA. Mintavételi hiba. Statisztikai adatgyűjtés. Nem véletlenen alapuló kiválasztás
 STATISZTIKA, BIOMETRIA. Előadás Mintavétel, mintavételi technikák, adatbázis Mintavétel fogalmai A mintavételt meg kell tervezni A sokaság elemei: X, X X N, lehet véges és végtelen Mintaelemek: x, x x
STATISZTIKA, BIOMETRIA. Előadás Mintavétel, mintavételi technikák, adatbázis Mintavétel fogalmai A mintavételt meg kell tervezni A sokaság elemei: X, X X N, lehet véges és végtelen Mintaelemek: x, x x
Matematika A3 Valószínűségszámítás, 6. gyakorlat 2013/14. tavaszi félév
 Matematika A3 Valószínűségszámítás, 6. gyakorlat 2013/14. tavaszi félév 1. A várható érték és a szórás transzformációja 1. Ha egy valószínűségi változóhoz hozzáadunk ötöt, mínusz ötöt, egy b konstanst,
Matematika A3 Valószínűségszámítás, 6. gyakorlat 2013/14. tavaszi félév 1. A várható érték és a szórás transzformációja 1. Ha egy valószínűségi változóhoz hozzáadunk ötöt, mínusz ötöt, egy b konstanst,
(Independence, dependence, random variables)
 Két valószínűségi változó együttes vizsgálata Feltételes eloszlások Két diszkrét változó együttes eloszlása a lehetséges értékpárok és a hozzájuk tartozó valószínűségek (táblázat) Példa: Egy urna 3 fehér,
Két valószínűségi változó együttes vizsgálata Feltételes eloszlások Két diszkrét változó együttes eloszlása a lehetséges értékpárok és a hozzájuk tartozó valószínűségek (táblázat) Példa: Egy urna 3 fehér,
GPK M1 (BME) Interpoláció / 16
 Interpoláció Matematika M1 gépészmérnököknek 2017. március 13. GPK M1 (BME) Interpoláció 2017 1 / 16 Az interpoláció alapfeladata - Példa Tegyük fel, hogy egy ipari termék - pl. autó - előzetes konstrukciójának
Interpoláció Matematika M1 gépészmérnököknek 2017. március 13. GPK M1 (BME) Interpoláció 2017 1 / 16 Az interpoláció alapfeladata - Példa Tegyük fel, hogy egy ipari termék - pl. autó - előzetes konstrukciójának
y ij = µ + α i + e ij
 Elmélet STATISZTIKA 3. Előadás Variancia-analízis Lineáris modellek A magyarázat a függő változó teljes heterogenitásának két részre bontását jelenti. A teljes heterogenitás egyik része az, amelynek okai
Elmélet STATISZTIKA 3. Előadás Variancia-analízis Lineáris modellek A magyarázat a függő változó teljes heterogenitásának két részre bontását jelenti. A teljes heterogenitás egyik része az, amelynek okai
Matematikai alapok és valószínőségszámítás. Statisztikai becslés Statisztikák eloszlása
 Matematikai alapok és valószínőségszámítás Statisztikai becslés Statisztikák eloszlása Mintavétel A statisztikában a cél, hogy az érdeklõdés tárgyát képezõ populáció bizonyos paramétereit a populációból
Matematikai alapok és valószínőségszámítás Statisztikai becslés Statisztikák eloszlása Mintavétel A statisztikában a cél, hogy az érdeklõdés tárgyát képezõ populáció bizonyos paramétereit a populációból
1. VDA és Ford ajánlások a hibaláncolatok pontozásához konstrukciós FMEA esetén
 1. VDA és Ford ajánlások a láncolatok pontozásához konstrukciós FMEA esetén A bekövetkezés valószínûsége - B 1. táblázat A bekövetkezési valószínûségének pontozási irányelvei Szám Gyakoriság Hibaarány
1. VDA és Ford ajánlások a láncolatok pontozásához konstrukciós FMEA esetén A bekövetkezés valószínûsége - B 1. táblázat A bekövetkezési valószínûségének pontozási irányelvei Szám Gyakoriság Hibaarány
Fourier-sorok. Lengyelné Dr. Szilágyi Szilvia. 2010. április 7.
 ME, Anaĺızis Tanszék 21. április 7. A Taylor-polinom ill. Taylor-sor hátránya, hogy az adott függvényt csak a sorfejtés helyén ill. annak környezetében közeĺıti jól. A sorfejtés helyétől távolodva a közeĺıtés
ME, Anaĺızis Tanszék 21. április 7. A Taylor-polinom ill. Taylor-sor hátránya, hogy az adott függvényt csak a sorfejtés helyén ill. annak környezetében közeĺıti jól. A sorfejtés helyétől távolodva a közeĺıtés
Körforgalmak élettartama a tervezés és kivitelezés függvényében
 41. Útügyi Napok Balatonfüred 2016. szeptember 21-22. Körforgalmak élettartama a tervezés és kivitelezés függvényében Bencze Zsolt Tudományos munkatárs A körforgalom elmélete 1. A főirány sebességcsökkentése
41. Útügyi Napok Balatonfüred 2016. szeptember 21-22. Körforgalmak élettartama a tervezés és kivitelezés függvényében Bencze Zsolt Tudományos munkatárs A körforgalom elmélete 1. A főirány sebességcsökkentése
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
SZÉLTURBINÁKAT TARTALMAZÓ MÉRLEGKÖRÖK KIEGYENLÍTŐ ENERGIA KÖLTSÉGEINEK MINIMALIZÁLÁSA
 SZÉLTURBINÁKAT TARTALMAZÓ MÉRLEGKÖRÖK KIEGYENLÍTŐ ENERGIA KÖLTSÉGEINEK MINIMALIZÁLÁSA Varga László E.ON Hungária ZRt. Hirsch Tamás Országos Meteorológiai Szolgálat XXVII. Magyar Operációkutatási Konferencia
SZÉLTURBINÁKAT TARTALMAZÓ MÉRLEGKÖRÖK KIEGYENLÍTŐ ENERGIA KÖLTSÉGEINEK MINIMALIZÁLÁSA Varga László E.ON Hungária ZRt. Hirsch Tamás Országos Meteorológiai Szolgálat XXVII. Magyar Operációkutatási Konferencia
A felelős személy (üzemeltető) feladatai.
 9027 Győr Toldi u. 8/a tel: 20/9857-890 e-mail: stinner.laszlo@gmail.com www.riaszto-kamera-tuzjelzo.hu Beépített automatikus tűzjelző rendszerek felülvizsgálata és karbantartása. A felelős személy (üzemeltető)
9027 Győr Toldi u. 8/a tel: 20/9857-890 e-mail: stinner.laszlo@gmail.com www.riaszto-kamera-tuzjelzo.hu Beépített automatikus tűzjelző rendszerek felülvizsgálata és karbantartása. A felelős személy (üzemeltető)
FL-11R kézikönyv Viczai design 2010. FL-11R kézikönyv. (Útmutató az FL-11R jelű LED-es villogó modell-leszállófény áramkör használatához)
 FL-11R kézikönyv (Útmutató az FL-11R jelű LED-es villogó modell-leszállófény áramkör használatához) 1. Figyelmeztetések Az eszköz a Philips LXK2 PD12 Q00, LXK2 PD12 R00, LXK2 PD12 S00 típusjelzésű LED-jeihez
FL-11R kézikönyv (Útmutató az FL-11R jelű LED-es villogó modell-leszállófény áramkör használatához) 1. Figyelmeztetések Az eszköz a Philips LXK2 PD12 Q00, LXK2 PD12 R00, LXK2 PD12 S00 típusjelzésű LED-jeihez
Matematikai alapok és valószínőségszámítás. Valószínőségi eloszlások Binomiális eloszlás
 Matematikai alapok és valószínőségszámítás Valószínőségi eloszlások Binomiális eloszlás Bevezetés A tudományos életben megfigyeléseket teszünk, kísérleteket végzünk. Ezek többféle különbözı eredményre
Matematikai alapok és valószínőségszámítás Valószínőségi eloszlások Binomiális eloszlás Bevezetés A tudományos életben megfigyeléseket teszünk, kísérleteket végzünk. Ezek többféle különbözı eredményre
Hogyan használja a roncsolásmentes vizsgálatokat a petrokémiai ipar?
 Hogyan használja a roncsolásmentes vizsgálatokat a petrokémiai ipar? MOL Nyrt. Mátyási Ede Százhalombatta 19 st October, 2015 Eger Március 22-24 Tartalom Anyagvizsgálatok jelentősége a MOL Finomítás életében,
Hogyan használja a roncsolásmentes vizsgálatokat a petrokémiai ipar? MOL Nyrt. Mátyási Ede Százhalombatta 19 st October, 2015 Eger Március 22-24 Tartalom Anyagvizsgálatok jelentősége a MOL Finomítás életében,
Kutatásmódszertan és prezentációkészítés
 Kutatásmódszertan és prezentációkészítés 10. rész: Az adatelemzés alapjai Szerző: Kmetty Zoltán Lektor: Fokasz Nikosz Tizedik rész Az adatelemzés alapjai Tartalomjegyzék Bevezetés Leíró statisztikák I
Kutatásmódszertan és prezentációkészítés 10. rész: Az adatelemzés alapjai Szerző: Kmetty Zoltán Lektor: Fokasz Nikosz Tizedik rész Az adatelemzés alapjai Tartalomjegyzék Bevezetés Leíró statisztikák I
VIZSGADOLGOZAT. I. PÉLDÁK (60 pont)
 VIZSGADOLGOZAT (100 pont) A megoldások csak szöveges válaszokkal teljes értékűek! I. PÉLDÁK (60 pont) 1. példa (13 pont) Az egyik budapesti könyvtárban az olvasókból vett 400 elemű minta alapján a következőket
VIZSGADOLGOZAT (100 pont) A megoldások csak szöveges válaszokkal teljes értékűek! I. PÉLDÁK (60 pont) 1. példa (13 pont) Az egyik budapesti könyvtárban az olvasókból vett 400 elemű minta alapján a következőket
Mérési hibák 2006.10.04. 1
 Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/54/33134304.jpg) [Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
[Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével
 Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével Pekárdy Milán, Baumgartner János, Süle Zoltán Pannon Egyetem, Veszprém XXXII. Magyar Operációkutatási
Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével Pekárdy Milán, Baumgartner János, Süle Zoltán Pannon Egyetem, Veszprém XXXII. Magyar Operációkutatási

