OpenGL és a mátrixok
|
|
|
- Anna Magyarné
- 10 évvel ezelőtt
- Látták:
Átírás
1 OpenGL és a mátrixok Róth Gergő március 4. Róth Gergő 1/20
2 A rajzoláskor a videókártya minden csúcson végrehajt egy transzformációt. Mire jó? Kamera helyének beállítása Egy objektum több pozícióra is kirajzolható Egy objektum több méretben is kirajzolható Egy objektum több szemszögből is kirajzolható A transzformációk nem a CPU-n, hanem a GPU-n hajtódnak végre, ezáltal gyorsabb (párhuzamos végrehajtás) 2D / 3D grafikában minden transzformáció egy mátrixműveletnek felel meg. Róth Gergő 2/20
3 Skalárszorzás Összeadás Mátrixszorzás Mátrix szorzása skalárral Róth Gergő 3/20
4 Skalárszorzás Összeadás Mátrixszorzás Mátrixok összeadása Csak ugyanolyan méretű mátrixokat tudunk összeadni Róth Gergő 4/20
5 Mátrix szorzása mátrixszal Skalárszorzás Összeadás Mátrixszorzás n x m méretű mátrixot csak m x p méretűvel tudunk beszorozni Az eredmény n x p dimenziókkal rendelkező mátrix A művelet nem kommutatív, vagyis nem lehet felcserélni az operandusokat: A * B!= B * A A művelet asszociatív (csoportosítható): (A * B) * C = A * (B * C) Róth Gergő 5/20
6 Egységmátrix Átméretezés Forgatás N dimenziós koordinátát nxn méretű négyzetes mátrixszal tudunk transzformálni: a 0 a 3 a 6 v 0 a 1 a 4 a 7 v 1 a 2 a 5 a 8 v 2 Róth Gergő 6/20
7 Egységmátrix Átméretezés Forgatás Egységmátrix (identity matrix): [ ] [ v0 v 1 ] = [ v0 v v 0 v v 1 = v v 2 v 2 ] Róth Gergő 7/20
8 Egységmátrix Átméretezés Forgatás Átméretezés az origo középpontjából (scale): [ sx 0 0 s y ] [ v0 v 1 ] [ ] sx v = 0 s y v 1 s x 0 0 v 0 s x v 0 0 s y 0 v 1 = s y v s z v 2 s z v 2 Róth Gergő 8/20
9 Egységmátrix Átméretezés Forgatás Forgatás 2 dimenzióban az origo körül (rotate): [ ] cos(α) sin(α) sin(α) cos(α) Róth Gergő 9/20
10 Egységmátrix Átméretezés Forgatás Forgatás 3 dimenzióban az origon átmenő egységvektor (l, m, n) körül (rotate): Róth Gergő 10/20
11 Egységmátrix Átméretezés Forgatás A lineáris transzformációk halmozhatók. Példa (R - rotate, S - scale): rotate, scale, rotate, rotate M = R * R * S * R Elég csak M-et átadni a GPU-nak. Egyetlen szorzással (M * v) elvégezhető az összes transzformáció. Róth Gergő 11/20
12 Eltolás Eltolás (translate): [ tx t y ] + [ v0 v 1 ] [ ] tx + v = 0 t y + v 1 t x v 0 t x + v 0 t y + v 1 = t y + v 1 t z v 2 t z + v 2 Róth Gergő 12/20
13 Eltolás Mi a baj az eltolással? Nem halmozható, mivel az eltolást az összeadással lehet elvégezni, a többit pedig szorzással. Példa: (R - rotate, S - scale, T - translate): translate, rotate, scale, translate, scale, rotate M!= R * S * T * S * R * T Róth Gergő 13/20
14 A koordináták kiegészülnek egy újabb komponenssel: w 2D: (x, y) -> (wx, wy, w) 3D: (x, y, z) -> (wx, wy, wz, w) Kezdetben általában egynek veszik w értékét Homogén koordinátákkal elvégezhető az eltolás mátrixszorzással, így ez a transzformáció is halmozhatóvá válik. Róth Gergő 14/20
15 Az eltolás mátrixa: 1 0 t x v 0 t x + v t y v 1 = t y + v t x v 0 t x + v t y t z v 1 v 2 = t y + v 1 t z + v Róth Gergő 15/20
16 Aktuális mátrix Vetítési mátrix Transzformációk Mátrixverem OpenGL-ben léteznek beépített mátrixok (mindegyik mérete 4x4): Modelview matrix: M Projection matrix: P A csúcs tényleges helyét a következőképpen kapjuk meg: O = P * M * v Róth Gergő 16/20
17 Aktuális mátrix Vetítési mátrix Transzformációk Mátrixverem Amikor mátrixműveleteket végzünk OpenGL-el, akkor mindig az aktuális mátrixon végzünk utószorzást. Az aktuális mátrixot be tudjuk állítani a glmatrixmode(..) paranccsal. Paraméterei lehetnek: GL_MODELVIEW vagy GL_PROJECTION Egységmátrix betöltése: glloadidentity() Róth Gergő 17/20
18 Aktuális mátrix Vetítési mátrix Transzformációk Mátrixverem glmatrixmode(gl_projection) glortho(left, right, bottom, top, near, far) // ortogonális (merőleges) vetítés gluperspective(angle, x / h, near, far) // perspektivikus (a végtelenben az élek összetartanak) vetítés Róth Gergő 18/20
19 Aktuális mátrix Vetítési mátrix Transzformációk Mátrixverem Forgatás origon átmenő egységvektor (x, y, z) körül: glrotatef(angle, a x, a y, a z ) Eltolás: gltranslatef(t x, t y, t z ) Átméretezés: glscalef(s x, s y, s z ) Róth Gergő 19/20
20 Aktuális mátrix Vetítési mátrix Transzformációk Mátrixverem Állapot elmentése: glpushmatrix() Állapot visszatöltése: glpopmatrix() Róth Gergő 20/20
A játékfejlesztés több területből áll. A kódolás csupán egy része a munkáknak.
 1 A játékfejlesztés több területből áll. A kódolás csupán egy része a munkáknak. Példák az elvégzendő feladatokra: Tervezés Kódolás Modellezés Textúrázás Pályaszerkesztés Animálás... Többnyire minden terület
1 A játékfejlesztés több területből áll. A kódolás csupán egy része a munkáknak. Példák az elvégzendő feladatokra: Tervezés Kódolás Modellezés Textúrázás Pályaszerkesztés Animálás... Többnyire minden terület
3D koordináta-rendszerek
 3D koordináta-rendszerek z z y x y x y balkezes bal-sodrású x jobbkezes jobb-sodrású z 3D transzformációk - homogén koordináták (x, y, z) megadása homogén koordinátákkal: (x, y, z, 1) (x, y, z, w) = (x,
3D koordináta-rendszerek z z y x y x y balkezes bal-sodrású x jobbkezes jobb-sodrású z 3D transzformációk - homogén koordináták (x, y, z) megadása homogén koordinátákkal: (x, y, z, 1) (x, y, z, w) = (x,
Alkalmazott Informatikai Tanszék SZÁMÍTÓGÉP-PROGRAMOZÁS dr.dudás László 22./0. 3D grafika programozása OpenGL támogatással Transzformációk
 Alkalmazott Informatikai Tanszék SZÁMÍTÓGÉP-PROGRAMOZÁS dr.dudás László 22./0. 3D grafika programozása OpenGL támogatással Transzformációk Alkalmazott Informatikai Tanszék SZÁMÍTÓGÉP-PROGRAMOZÁS dr.dudás
Alkalmazott Informatikai Tanszék SZÁMÍTÓGÉP-PROGRAMOZÁS dr.dudás László 22./0. 3D grafika programozása OpenGL támogatással Transzformációk Alkalmazott Informatikai Tanszék SZÁMÍTÓGÉP-PROGRAMOZÁS dr.dudás
Lineáris algebra (10A103)
 Lineáris algebra (10A103 Kátai-Urbán Kamilla Tudnivalók Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli (beugróval, feltétele a Lineáris algebra gyakorlat
Lineáris algebra (10A103 Kátai-Urbán Kamilla Tudnivalók Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli (beugróval, feltétele a Lineáris algebra gyakorlat
Róth Gergő.
 Róth Gergő [email protected] 1 Oktatók Smidla József ([email protected]) Róth Gergő ([email protected]) Bejárás nem kötelező Tárgy adatai Gyakorlati Nem kötelező Szabadon választható Neptun
Róth Gergő [email protected] 1 Oktatók Smidla József ([email protected]) Róth Gergő ([email protected]) Bejárás nem kötelező Tárgy adatai Gyakorlati Nem kötelező Szabadon választható Neptun
Mátrixok, mátrixműveletek
 Mátrixok, mátrixműveletek 1 előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Mátrixok, mátrixműveletek p 1/1 Mátrixok definíciója Definíció Helyezzünk el n m elemet egy olyan téglalap
Mátrixok, mátrixműveletek 1 előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Mátrixok, mátrixműveletek p 1/1 Mátrixok definíciója Definíció Helyezzünk el n m elemet egy olyan téglalap
Tartalom. Nevezetes affin transzformációk. Valasek Gábor 2016/2017. tavaszi félév
 Tartalom Motiváció Számítógépes Grafika Valasek Gábor [email protected] Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. tavaszi félév Transzformációk Transzformációk általában Nevezetes affin
Tartalom Motiváció Számítógépes Grafika Valasek Gábor [email protected] Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. tavaszi félév Transzformációk Transzformációk általában Nevezetes affin
2. előadás. Lineáris algebra numerikus módszerei. Mátrixok Mátrixműveletek Speciális mátrixok, vektorok Norma
 Mátrixok Definíció Az m n típusú (méretű) valós A mátrixon valós a ij számok alábbi táblázatát értjük: a 11 a 12... a 1j... a 1n.......... A = a i1 a i2... a ij... a in........... a m1 a m2... a mj...
Mátrixok Definíció Az m n típusú (méretű) valós A mátrixon valós a ij számok alábbi táblázatát értjük: a 11 a 12... a 1j... a 1n.......... A = a i1 a i2... a ij... a in........... a m1 a m2... a mj...
Transzformációk. Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform
 Transzformációk Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform Koordinátarendszerek: modelltér Koordinátarendszerek: világtér Koordinátarendszerek: kameratér up right z eye ahead
Transzformációk Grafikus játékok fejlesztése Szécsi László 2013.02.26. t05-transform Koordinátarendszerek: modelltér Koordinátarendszerek: világtér Koordinátarendszerek: kameratér up right z eye ahead
Valasek Gábor [email protected]
 Számítógépes Grafika Valasek Gábor [email protected] Eötvös Loránd Tudományegyetem Informatikai Kar 2013/2014. őszi félév ( Eötvös LorándSzámítógépes TudományegyetemInformatikai Grafika Kar) 2013/2014.
Számítógépes Grafika Valasek Gábor [email protected] Eötvös Loránd Tudományegyetem Informatikai Kar 2013/2014. őszi félév ( Eötvös LorándSzámítógépes TudományegyetemInformatikai Grafika Kar) 2013/2014.
Valasek Gábor Informatikai Kar. 2016/2017. tavaszi félév
 Számítógépes Grafika Valasek Gábor [email protected] Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. tavaszi félév Tartalom 1 Motiváció 2 Transzformációk Transzformációk általában 3 Nevezetes
Számítógépes Grafika Valasek Gábor [email protected] Eötvös Loránd Tudományegyetem Informatikai Kar 2016/2017. tavaszi félév Tartalom 1 Motiváció 2 Transzformációk Transzformációk általában 3 Nevezetes
Lineáris algebra zárthelyi dolgozat javítókulcs, Informatika I. 2005.márc.11. A csoport
 Lineáris algebra zárthelyi dolgozat javítókulcs, Informatika I. 2005.márc.11. A csoport 1. Egy egyenesre esnek-e az A (2, 5, 1), B (5, 17, 7) és C (3, 9, 3) pontok? 5 pont Megoldás: Nem, mert AB (3, 12,
Lineáris algebra zárthelyi dolgozat javítókulcs, Informatika I. 2005.márc.11. A csoport 1. Egy egyenesre esnek-e az A (2, 5, 1), B (5, 17, 7) és C (3, 9, 3) pontok? 5 pont Megoldás: Nem, mert AB (3, 12,
Vektorok, mátrixok, lineáris egyenletrendszerek
 a Matematika mérnököknek I. című tárgyhoz Vektorok, mátrixok, lineáris egyenletrendszerek Vektorok A rendezett valós számpárokat kétdimenziós valós vektoroknak nevezzük. Jelölésükre latin kisbetűket használunk.
a Matematika mérnököknek I. című tárgyhoz Vektorok, mátrixok, lineáris egyenletrendszerek Vektorok A rendezett valós számpárokat kétdimenziós valós vektoroknak nevezzük. Jelölésükre latin kisbetűket használunk.
Matematika (mesterképzés)
 Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Matematika (mesterképzés) Környezet- és Településmérnököknek Debreceni Egyetem Műszaki Kar, Műszaki Alaptárgyi Tanszék Vinczéné Varga A. Környezet- és Településmérnököknek 2016/2017/I 1 / 29 Lineáris tér,
Róth Gergő. [email protected]
 Róth Gergő [email protected] 1 Oktatók Smidla József ([email protected]) Róth Gergő ([email protected]) Bejárás nem kötelező Tárgy adatai Gyakorlati Nem kötelező Szabadon választható Neptun
Róth Gergő [email protected] 1 Oktatók Smidla József ([email protected]) Róth Gergő ([email protected]) Bejárás nem kötelező Tárgy adatai Gyakorlati Nem kötelező Szabadon választható Neptun
Transzformációk síkon, térben
 Transzformációk síkon, térben Leképezés, transzformáció Leképezés: Ha egy A ponttér pontjaihoz egy másik B ponttér pontjait kölcsönösen egyértelműen rendeljük hozzá, akkor ezt a hozzárendelést leképezésnek
Transzformációk síkon, térben Leképezés, transzformáció Leképezés: Ha egy A ponttér pontjaihoz egy másik B ponttér pontjait kölcsönösen egyértelműen rendeljük hozzá, akkor ezt a hozzárendelést leképezésnek
Hajder Levente 2017/2018. II. félév
 Hajder Levente [email protected] Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 2 3 Geometriai modellezés feladata A világunkat modellezni kell a térben. Valamilyen koordinátarendszer
Hajder Levente [email protected] Eötvös Loránd Tudományegyetem Informatikai Kar 2017/2018. II. félév Tartalom 1 2 3 Geometriai modellezés feladata A világunkat modellezni kell a térben. Valamilyen koordinátarendszer
Műveletek mátrixokkal. Kalkulus. 2018/2019 ősz
 2018/2019 ősz Elérhetőségek Előadó: ([email protected]) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
2018/2019 ősz Elérhetőségek Előadó: ([email protected]) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
VIK A2 Matematika - BOSCH, Hatvan, 3. Gyakorlati anyag. Mátrix rangja
 VIK A2 Matematika - BOSCH, Hatvan, 3. Gyakorlati anyag 2019. március 21. Mátrix rangja 1. Számítsuk ki az alábbi mátrixok rangját! (d) 1 1 2 2 4 5 1 1 1 1 1 1 1 1 2 1 2 1 1 0 1 1 2 1 0 1 1 1 1 2 3 1 3
VIK A2 Matematika - BOSCH, Hatvan, 3. Gyakorlati anyag 2019. március 21. Mátrix rangja 1. Számítsuk ki az alábbi mátrixok rangját! (d) 1 1 2 2 4 5 1 1 1 1 1 1 1 1 2 1 2 1 1 0 1 1 2 1 0 1 1 1 1 2 3 1 3
Transzformációk, amelyek n-dimenziós objektumokat kisebb dimenziós terekbe visznek át. Pl. 3D 2D
 Vetítések Transzformációk, amelyek n-dimenziós objektumokat kisebb dimenziós terekbe visznek át. Pl. 3D 2D Vetítések fajtái - 1 perspektívikus A párhuzamos A A' B A' B A vetítés középpontja B' Vetítési
Vetítések Transzformációk, amelyek n-dimenziós objektumokat kisebb dimenziós terekbe visznek át. Pl. 3D 2D Vetítések fajtái - 1 perspektívikus A párhuzamos A A' B A' B A vetítés középpontja B' Vetítési
1. Geometria a komplex számsíkon
 1. Geometria a komplex számsíkon A háromszög-egyenlőtlenség A háromszög-egyenlőtlenség (K1.4.3) Minden z,w C-re z +w z + w. Egyenlőség pontosan akkor áll, ha z és w párhuzamosak, és egyenlő állásúak, azaz
1. Geometria a komplex számsíkon A háromszög-egyenlőtlenség A háromszög-egyenlőtlenség (K1.4.3) Minden z,w C-re z +w z + w. Egyenlőség pontosan akkor áll, ha z és w párhuzamosak, és egyenlő állásúak, azaz
Térbeli transzformációk, a tér leképezése síkra
 Térbeli transzformációk, a tér leképezése síkra Homogén koordináták bevezetése térben A tér minden P pontjához kölcsönösen egyértelműen egy valós (x, y, z) számhármast rendeltünk hozzá. (Descartes-féle
Térbeli transzformációk, a tér leképezése síkra Homogén koordináták bevezetése térben A tér minden P pontjához kölcsönösen egyértelműen egy valós (x, y, z) számhármast rendeltünk hozzá. (Descartes-féle
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
I. VEKTOROK, MÁTRIXOK
 217/18 1 félév I VEKTOROK, MÁTRIXOK I1 I2 Vektorok 1 A síkon derékszögű koordinátarendszerben minden v vektornak van vízszintes és van függőleges koordinátája, ezeket sorrendben v 1 és v 2 jelöli A v síkbeli
217/18 1 félév I VEKTOROK, MÁTRIXOK I1 I2 Vektorok 1 A síkon derékszögű koordinátarendszerben minden v vektornak van vízszintes és van függőleges koordinátája, ezeket sorrendben v 1 és v 2 jelöli A v síkbeli
Diszkrét matematika I., 12. előadás Dr. Takách Géza NyME FMK Informatikai Intézet takach november 30.
 1 Diszkrét matematika I, 12 előadás Dr Takách Géza NyME FMK Informatikai Intézet takach@infnymehu http://infnymehu/ takach 2005 november 30 Vektorok Definíció Egy tetszőleges n pozitív egész számra n-komponensű
1 Diszkrét matematika I, 12 előadás Dr Takách Géza NyME FMK Informatikai Intézet takach@infnymehu http://infnymehu/ takach 2005 november 30 Vektorok Definíció Egy tetszőleges n pozitív egész számra n-komponensű
1. Mátrixösszeadás és skalárral szorzás
 1 Mátrixösszeadás és skalárral szorzás Mátrixok tömör jelölése T test Az M = a i j T n m azt az n sorból és m oszlopból álló mátrixot jelöli, amelyben az i-edik sor j-edik eleme a i j T Példák [ ] Ha M
1 Mátrixösszeadás és skalárral szorzás Mátrixok tömör jelölése T test Az M = a i j T n m azt az n sorból és m oszlopból álló mátrixot jelöli, amelyben az i-edik sor j-edik eleme a i j T Példák [ ] Ha M
1. Bevezetés 1. Köszönetnyilvánítás 1. 2. A számítógépes játékfejlesztésről 3
 1. Bevezetés 1 Köszönetnyilvánítás 1 2. A számítógépes játékfejlesztésről 3 2.1. Néhány tanács játékfejlesztőknek 3 2.2. Hogyan fogjunk saját játék írásához? 4 2.3. A számítógépes játék főbb elemei 9 3.
1. Bevezetés 1 Köszönetnyilvánítás 1 2. A számítógépes játékfejlesztésről 3 2.1. Néhány tanács játékfejlesztőknek 3 2.2. Hogyan fogjunk saját játék írásához? 4 2.3. A számítógépes játék főbb elemei 9 3.
Testek. 16. Legyen z = 3 + 4i, w = 3 + i. Végezzük el az alábbi. a) (2 4), Z 5, b) (1, 0, 0, 1, 1) (1, 1, 1, 1, 0), Z 5 2.
 Vektorok. Melyek egyenlőek az alábbi vektorok közül? (a) (, 2, 0), (b) az (, 0, ) pontból a (2, 2, ) pontba mutató vektor, (c) ( 2,, ) ( 2,, 2), (d) [ 2 0 ], (e) 2. 0 2. Írjuk fel az x + y + 2z = 0 és
Vektorok. Melyek egyenlőek az alábbi vektorok közül? (a) (, 2, 0), (b) az (, 0, ) pontból a (2, 2, ) pontba mutató vektor, (c) ( 2,, ) ( 2,, 2), (d) [ 2 0 ], (e) 2. 0 2. Írjuk fel az x + y + 2z = 0 és
x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs mátrixa 3D-ben?
 . Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
. Mi az (x, y) koordinátákkal megadott pont elforgatás uténi két koordinátája, ha α szöggel forgatunk az origó körül? x = cos αx sin αy y = sin αx + cos αy 2. Mi a X/Y/Z tengely körüli forgatás transzformációs
Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit
 Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit 1. A térbeli irányított szakaszokat vektoroknak hívjuk. Két vektort egyenlőnek tekintünk, ha párhuzamos eltolással fedésbe hozhatók.
Vektorgeometria (1) First Prev Next Last Go Back Full Screen Close Quit 1. A térbeli irányított szakaszokat vektoroknak hívjuk. Két vektort egyenlőnek tekintünk, ha párhuzamos eltolással fedésbe hozhatók.
Lineáris egyenletrendszerek
 Lineáris egyenletrendszerek Lineáris egyenletrendszernek nevezzük az a 11 x 1 + a 12 x 2 +... +a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... +a 2n x n = b 2.. a k1 x 1 + a k2 x 2 +... +a kn x n = b k n ismeretlenes,
Lineáris egyenletrendszerek Lineáris egyenletrendszernek nevezzük az a 11 x 1 + a 12 x 2 +... +a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... +a 2n x n = b 2.. a k1 x 1 + a k2 x 2 +... +a kn x n = b k n ismeretlenes,
12. előadás. Egyenletrendszerek, mátrixok. Dr. Szörényi Miklós, Dr. Kallós Gábor
 12. előadás Egyenletrendszerek, mátrixok Dr. Szörényi Miklós, Dr. Kallós Gábor 2015 2016 1 Tartalom Matematikai alapok Vektorok és mátrixok megadása Tömbkonstansok Lineáris műveletek Mátrixok szorzása
12. előadás Egyenletrendszerek, mátrixok Dr. Szörényi Miklós, Dr. Kallós Gábor 2015 2016 1 Tartalom Matematikai alapok Vektorok és mátrixok megadása Tömbkonstansok Lineáris műveletek Mátrixok szorzása
Klár Gergely 2010/2011. tavaszi félév
 Számítógépes Grafika Klár Gergely [email protected] Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom Pont 1 Pont 2 3 4 5 Tartalom Pont Descartes-koordináták Homogén koordináták
Számítógépes Grafika Klár Gergely [email protected] Eötvös Loránd Tudományegyetem Informatikai Kar 2010/2011. tavaszi félév Tartalom Pont 1 Pont 2 3 4 5 Tartalom Pont Descartes-koordináták Homogén koordináták
17. előadás: Vektorok a térben
 17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
Matematika A1a Analízis
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Matematika A1a Analízis BMETE90AX00 Vektorok StKis, EIC 2019-02-12 Wettl Ferenc ALGEBRA
Mátrixok 2017 Mátrixok
 2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
Összeállította: dr. Leitold Adrien egyetemi docens
 Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
Transzformációk. Szécsi László
 Transzformációk Szécsi László A feladat Adott a 3D modell háromszögek csúcspontjai [modellezési koordináták] Háromszögkitöltő algoritmus pixeleket színez be [viewport koordináták] A feladat: számítsuk
Transzformációk Szécsi László A feladat Adott a 3D modell háromszögek csúcspontjai [modellezési koordináták] Háromszögkitöltő algoritmus pixeleket színez be [viewport koordináták] A feladat: számítsuk
1. Az euklideszi terek geometriája
 1. Az euklideszi terek geometriája Bázishoz tartozó skaláris szorzat Emékeztető Az R n vektortérbeli v = λ 2... és w = λ 1 λ n µ 1 µ 2... µ n λ 1 µ 1 +λ 2 µ 2 +...+λ n µ n. Jele v,w. v,w = v T u, azaz
1. Az euklideszi terek geometriája Bázishoz tartozó skaláris szorzat Emékeztető Az R n vektortérbeli v = λ 2... és w = λ 1 λ n µ 1 µ 2... µ n λ 1 µ 1 +λ 2 µ 2 +...+λ n µ n. Jele v,w. v,w = v T u, azaz
Robotika. Kinematika. Magyar Attila
 Robotika Kinematika Magyar Attila [email protected] Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Robotika Kinematika Magyar Attila [email protected] Miről lesz szó? Bevezetés Merev test pozíciója és orientációja Rotáció Euler szögek Homogén transzformációk Direkt kinematika Nyílt kinematikai lánc
Számítógépes geometria
 2011 sz A grakus szállítószalag terv a geometriai (matematikai) modell megalkotása modelltranszformáció (3D 3D) vetítés (3D 2D) képtranszformáció (2D 2D)... raszterizáció A grakus szállítószalag: koncepció
2011 sz A grakus szállítószalag terv a geometriai (matematikai) modell megalkotása modelltranszformáció (3D 3D) vetítés (3D 2D) képtranszformáció (2D 2D)... raszterizáció A grakus szállítószalag: koncepció
Mat. A2 3. gyakorlat 2016/17, második félév
 Mat. A2 3. gyakorlat 2016/17, második félév 1. Hány megoldása lehet az alábbi lineáris egyenletrendszereknek a valós számok körében, ha a -ok tetszőleges (nem feltétlenül egyenlő) számokat jelölnek? 0
Mat. A2 3. gyakorlat 2016/17, második félév 1. Hány megoldása lehet az alábbi lineáris egyenletrendszereknek a valós számok körében, ha a -ok tetszőleges (nem feltétlenül egyenlő) számokat jelölnek? 0
Bevezetés. Transzformáció
 Geoinformatika alapjai ea. VI. Bevezetés GIS mőveletek I. Tematika Számonkérés Irodalom Transzformáció 28.5.6. Transzformációk típusai formátum geometriai 28.5.6. 2 Geometriai transzformáció I. Célja:
Geoinformatika alapjai ea. VI. Bevezetés GIS mőveletek I. Tematika Számonkérés Irodalom Transzformáció 28.5.6. Transzformációk típusai formátum geometriai 28.5.6. 2 Geometriai transzformáció I. Célja:
1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás)
 Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Lineáris algebra (10A103)
 Lineáris algebra (10A103) Dr. Hartmann Miklós Tudnivalók Honlap: http://www.math.u-szeged.hu/~hartm Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli, feltétele a Lineáris algebra gyakorlat teljesítése.
Lineáris algebra (10A103) Dr. Hartmann Miklós Tudnivalók Honlap: http://www.math.u-szeged.hu/~hartm Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli, feltétele a Lineáris algebra gyakorlat teljesítése.
DISZKRÉT MATEMATIKA: STRUKTÚRÁK Előadáson mutatott példa: Bércesné Novák Ágnes
 1. Algebrai alapok: DISZKRÉT MATEMATIKA: STRUKTÚRÁK Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz
1. Algebrai alapok: DISZKRÉT MATEMATIKA: STRUKTÚRÁK Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz
Bevezetés az algebrába 2
 B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Bevezetés az algebrába 2 BMETE91AM37 Euklideszi tér, ortogonalizáció H607 2018-02-12/03-10
B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Bevezetés az algebrába 2 BMETE91AM37 Euklideszi tér, ortogonalizáció H607 2018-02-12/03-10
EGYSZERŰSÍTETT ALGORITMUS AZ ELEMI BÁZISCSERE ELVÉGZÉSÉRE
 Lipécz György* EGYSZERŰSÍTETT ALGORITMUS AZ ELEMI BÁZISCSERE ELVÉGZÉSÉRE AVAGY A SZÁMÍTÓGÉP-HASZNÁLAT LEHETŐSÉGE A LINEÁRIS ALGEBRA ÉS AZ OPERÁCIÓKUTATÁS ALAPJAINAK OKTATÁSÁBAN " Simplicitassigillum veri"
Lipécz György* EGYSZERŰSÍTETT ALGORITMUS AZ ELEMI BÁZISCSERE ELVÉGZÉSÉRE AVAGY A SZÁMÍTÓGÉP-HASZNÁLAT LEHETŐSÉGE A LINEÁRIS ALGEBRA ÉS AZ OPERÁCIÓKUTATÁS ALAPJAINAK OKTATÁSÁBAN " Simplicitassigillum veri"
1. Algebrai alapok: Melyek műveletek az alábbiak közül?
 1. Algebrai alapok: Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz egyértelműen hozzárendel egy
1. Algebrai alapok: Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz egyértelműen hozzárendel egy
Infobionika ROBOTIKA. X. Előadás. Robot manipulátorok II. Direkt és inverz kinematika. Készült a HEFOP P /1.0 projekt keretében
 Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Matematika szigorlat június 17. Neptun kód:
 Név Matematika szigorlat 014. június 17. Neptun kód: 1.. 3. 4. 5. Elm. Fel. Össz. Oszt. Az eredményes szigorlat feltétele elméletből legalább 0 pont, feladatokból pedig legalább 30 pont elérése. A szigorlat
Név Matematika szigorlat 014. június 17. Neptun kód: 1.. 3. 4. 5. Elm. Fel. Össz. Oszt. Az eredményes szigorlat feltétele elméletből legalább 0 pont, feladatokból pedig legalább 30 pont elérése. A szigorlat
1. A komplex számok ábrázolása
 1. komplex számok ábrázolása Vektorok és helyvektorok. Ismétlés sík vektorai irányított szakaszok, de két vektor egyenlő, ha párhuzamosak, egyenlő hosszúak és irányúak. Így minden vektor kezdőpontja az
1. komplex számok ábrázolása Vektorok és helyvektorok. Ismétlés sík vektorai irányított szakaszok, de két vektor egyenlő, ha párhuzamosak, egyenlő hosszúak és irányúak. Így minden vektor kezdőpontja az
{ } x x x y 1. MATEMATIKAI ÖSSZEFOGLALÓ. ( ) ( ) ( ) (a szorzás eredménye:vektor) 1.1. Vektorok közötti műveletek
 1. MAEMAIKAI ÖSSZEFOGLALÓ 1.1. Vektorok közötti műveletek Azok a fizikai mennyiségek, melyeknek nagyságukon kívül irányuk is van, vektoroknak nevezzük. A vektort egyértelműen megadhatjuk a hosszával és
1. MAEMAIKAI ÖSSZEFOGLALÓ 1.1. Vektorok közötti műveletek Azok a fizikai mennyiségek, melyeknek nagyságukon kívül irányuk is van, vektoroknak nevezzük. A vektort egyértelműen megadhatjuk a hosszával és
Sajátértékek és sajátvektorok. mf1n1a06- mf1n2a06 Csabai István
 Sajátértékek és sajátvektorok A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris transzformáció Vektorok lineáris transzformációja: általános esetben az x vektor iránya és nagysága
Sajátértékek és sajátvektorok A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris transzformáció Vektorok lineáris transzformációja: általános esetben az x vektor iránya és nagysága
Keresztmetszet másodrendű nyomatékainak meghatározása
 BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
BUDAPEST MŰSZAK ÉS GAZDASÁGTUDOMÁNY EGYETEM Keresztmetszet másodrendű nyomatékainak meghatározása Segédlet a Szilárdságtan c tárgy házi feladatához Készítette: Lehotzky Dávid Budapest, 205 február 28 ábra
Vektorok. Wettl Ferenc október 20. Wettl Ferenc Vektorok október / 36
 Vektorok Wettl Ferenc 2014. október 20. Wettl Ferenc Vektorok 2014. október 20. 1 / 36 Tartalom 1 Vektorok a 2- és 3-dimenziós térben 2 Távolság, szög, orientáció 3 Vektorok koordinátás alakban 4 Összefoglalás
Vektorok Wettl Ferenc 2014. október 20. Wettl Ferenc Vektorok 2014. október 20. 1 / 36 Tartalom 1 Vektorok a 2- és 3-dimenziós térben 2 Távolság, szög, orientáció 3 Vektorok koordinátás alakban 4 Összefoglalás
Máté: Számítógépes grafika alapjai
 Pontok rajzolása OpenGL Rajzoljunk egy piros pontot a (10, 10), egy zöld pontot az (50, 10) és egy kék pontot a (30, 80) koordinátákba (az ablak 100*100-as méretű) Pontok rajzolása Színek és színmódok
Pontok rajzolása OpenGL Rajzoljunk egy piros pontot a (10, 10), egy zöld pontot az (50, 10) és egy kék pontot a (30, 80) koordinátákba (az ablak 100*100-as méretű) Pontok rajzolása Színek és színmódok
Bevezetés a számításelméletbe (MS1 BS)
 Matematika szigorlat - konzultációs szeminárium Azoknak, akik másodszorra vagy többedszerre veszik fel a Matematika szigorlat (NAMMS1SAND) tárgyat. Bevezetés a számításelméletbe (MS1 BS) FŐBB TÉMAKÖRÖK
Matematika szigorlat - konzultációs szeminárium Azoknak, akik másodszorra vagy többedszerre veszik fel a Matematika szigorlat (NAMMS1SAND) tárgyat. Bevezetés a számításelméletbe (MS1 BS) FŐBB TÉMAKÖRÖK
Wavelet transzformáció
 1 Wavelet transzformáció Más felbontás: Walsh, Haar, wavelet alapok! Eddig: amplitúdó vagy frekvencia leírás: Pl. egy rövid, Dirac-delta jellegű impulzus Fourier-transzformált: nagyon sok, kb. ugyanolyan
1 Wavelet transzformáció Más felbontás: Walsh, Haar, wavelet alapok! Eddig: amplitúdó vagy frekvencia leírás: Pl. egy rövid, Dirac-delta jellegű impulzus Fourier-transzformált: nagyon sok, kb. ugyanolyan
Koordináta-geometria alapozó feladatok
 Koordináta-geometria alapozó feladatok 1. Határozd meg az AB szakasz felezőpontját! (1,5 ; 3,5) (0,5 ; ) (6,5 ; 8,5) (4,5 ; ) (0,5 ; 1,5) (0 ; 0) (0 ; 8,5) (1 ; 1) ( 1,5 ; ) (3,5 ; 3) (0 ; 3) ( 1 ; 1,5).
Koordináta-geometria alapozó feladatok 1. Határozd meg az AB szakasz felezőpontját! (1,5 ; 3,5) (0,5 ; ) (6,5 ; 8,5) (4,5 ; ) (0,5 ; 1,5) (0 ; 0) (0 ; 8,5) (1 ; 1) ( 1,5 ; ) (3,5 ; 3) (0 ; 3) ( 1 ; 1,5).
Számítógépes grafika
 Számítógépes grafika XX. rész A GPU programozása a GLSL nyelv Az OpenGL árnyaló nyelve a GLSL (OpenGL Shading Language), amely segítségével vertex- és pixel- (fragment) shaderek által programozhatjuk a
Számítógépes grafika XX. rész A GPU programozása a GLSL nyelv Az OpenGL árnyaló nyelve a GLSL (OpenGL Shading Language), amely segítségével vertex- és pixel- (fragment) shaderek által programozhatjuk a
LINEÁRIS ALGEBRA. matematika alapszak. Euklideszi terek. SZTE Bolyai Intézet, őszi félév. Euklideszi terek LINEÁRIS ALGEBRA 1 / 40
 LINEÁRIS ALGEBRA matematika alapszak SZTE Bolyai Intézet, 2016-17. őszi félév Euklideszi terek Euklideszi terek LINEÁRIS ALGEBRA 1 / 40 Euklideszi tér Emlékeztető: A standard belső szorzás és standard
LINEÁRIS ALGEBRA matematika alapszak SZTE Bolyai Intézet, 2016-17. őszi félév Euklideszi terek Euklideszi terek LINEÁRIS ALGEBRA 1 / 40 Euklideszi tér Emlékeztető: A standard belső szorzás és standard
Vektorterek. Wettl Ferenc február 17. Wettl Ferenc Vektorterek február / 27
 Vektorterek Wettl Ferenc 2015. február 17. Wettl Ferenc Vektorterek 2015. február 17. 1 / 27 Tartalom 1 Egyenletrendszerek 2 Algebrai struktúrák 3 Vektortér 4 Bázis, dimenzió 5 Valós mátrixok és egyenletrendszerek
Vektorterek Wettl Ferenc 2015. február 17. Wettl Ferenc Vektorterek 2015. február 17. 1 / 27 Tartalom 1 Egyenletrendszerek 2 Algebrai struktúrák 3 Vektortér 4 Bázis, dimenzió 5 Valós mátrixok és egyenletrendszerek
Ortogonalizáció. Wettl Ferenc Wettl Ferenc Ortogonalizáció / 41
 Ortogonalizáció Wettl Ferenc 2016-03-22 Wettl Ferenc Ortogonalizáció 2016-03-22 1 / 41 Tartalom 1 Ortonormált bázis 2 Ortogonális mátrix 3 Ortogonalizáció 4 QR-felbontás 5 Komplex skaláris szorzás 6 Diszkrét
Ortogonalizáció Wettl Ferenc 2016-03-22 Wettl Ferenc Ortogonalizáció 2016-03-22 1 / 41 Tartalom 1 Ortonormált bázis 2 Ortogonális mátrix 3 Ortogonalizáció 4 QR-felbontás 5 Komplex skaláris szorzás 6 Diszkrét
Diszkrét matematika II., 8. előadás. Vektorterek
 1 Diszkrét matematika II., 8. előadás Vektorterek Dr. Takách Géza NyME FMK Informatikai Intézet [email protected] http://inf.nyme.hu/ takach/ 2007.??? Vektorterek Legyen T egy test (pl. R, Q, F p ). Definíció.
1 Diszkrét matematika II., 8. előadás Vektorterek Dr. Takách Géza NyME FMK Informatikai Intézet [email protected] http://inf.nyme.hu/ takach/ 2007.??? Vektorterek Legyen T egy test (pl. R, Q, F p ). Definíció.
Vektorterek. =a gyakorlatokon megoldásra ajánlott
 Vektorterek =a gyakorlatokon megoldásra ajánlott 40. Alteret alkotnak-e a valós R 5 vektortérben a megadott részhalmazok? Ha igen, akkor hány dimenziósak? (a) L = { (x 1, x 2, x 3, x 4, x 5 ) x 1 = x 5,
Vektorterek =a gyakorlatokon megoldásra ajánlott 40. Alteret alkotnak-e a valós R 5 vektortérben a megadott részhalmazok? Ha igen, akkor hány dimenziósak? (a) L = { (x 1, x 2, x 3, x 4, x 5 ) x 1 = x 5,
1. zárthelyi,
 1. zárthelyi, 2009.10.20. 1. Írjuk fel a tér P = (0,2,4) és Q = (6, 2,2) pontjait összekötő szakasz felezőmerőleges síkjának egyenletét. 2. Tekintsük az x + 2y + 3z = 14, a 2x + 6y + 10z = 24 és a 4x+2y
1. zárthelyi, 2009.10.20. 1. Írjuk fel a tér P = (0,2,4) és Q = (6, 2,2) pontjait összekötő szakasz felezőmerőleges síkjának egyenletét. 2. Tekintsük az x + 2y + 3z = 14, a 2x + 6y + 10z = 24 és a 4x+2y
Lineáris leképezések, mátrixuk, bázistranszformáció. Képtér, magtér, dimenziótétel, rang, invertálhatóság
 1. Bevezetés A félév anyaga: lineáris algebra Vektorterek, alterek Függés, függetlenség, bázis, dimenzió Skaláris szorzat R n -ben, vektorok hossza és szöge Lineáris leképezések, mátrixuk, bázistranszformáció
1. Bevezetés A félév anyaga: lineáris algebra Vektorterek, alterek Függés, függetlenség, bázis, dimenzió Skaláris szorzat R n -ben, vektorok hossza és szöge Lineáris leképezések, mátrixuk, bázistranszformáció
Képfeldolgozás. 1. el adás. A képfeldolgozás m veletei. Mechatronikai mérnök szak BME, 2008
 Képfeldolgozás 1. el adás. A képfeldolgozás m veletei Mechatronikai mérnök szak BME, 2008 1 / 61 Alapfogalmak transzformációk Deníció Deníció Geometriai korrekciókra akkor van szükség, ha a képr l valódi
Képfeldolgozás 1. el adás. A képfeldolgozás m veletei Mechatronikai mérnök szak BME, 2008 1 / 61 Alapfogalmak transzformációk Deníció Deníció Geometriai korrekciókra akkor van szükség, ha a képr l valódi
Vektorok összeadása, kivonása, szorzás számmal, koordináták
 Vektorok összeadása, kivonása, szorzás számmal, koordináták 1. Mik lesznek a P (3, 4, 8) pont C (3, 7, 2) pontra vonatkozó tükörképének a koordinátái? 2. Egy szabályos hatszög középpontja K (4, 1, 4),
Vektorok összeadása, kivonása, szorzás számmal, koordináták 1. Mik lesznek a P (3, 4, 8) pont C (3, 7, 2) pontra vonatkozó tükörképének a koordinátái? 2. Egy szabályos hatszög középpontja K (4, 1, 4),
Gazdasági matematika II. tanmenet
 Gazdasági matematika II. tanmenet Mádi-Nagy Gergely A hivatkozásokban az alábbi tankönyvekre utalunk: T: Tóth Irén (szerk.): Operációkutatás I., Nemzeti Tankönyvkiadó 1987. Cs: Csernyák László (szerk.):
Gazdasági matematika II. tanmenet Mádi-Nagy Gergely A hivatkozásokban az alábbi tankönyvekre utalunk: T: Tóth Irén (szerk.): Operációkutatás I., Nemzeti Tankönyvkiadó 1987. Cs: Csernyák László (szerk.):
Róth Gergő. [email protected]
 Róth Gergő [email protected] 1 Oktatók Smidla József ([email protected]) Róth Gergő ([email protected]) Bejárás nem kötelező Tárgy adatai Gyakorlati Nem kötelező Szabadon választható Neptun
Róth Gergő [email protected] 1 Oktatók Smidla József ([email protected]) Róth Gergő ([email protected]) Bejárás nem kötelező Tárgy adatai Gyakorlati Nem kötelező Szabadon választható Neptun
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Mer legesség. Wettl Ferenc 2015-03-13. Wettl Ferenc Mer legesség 2015-03-13 1 / 40
 Mer legesség Wettl Ferenc 2015-03-13 Wettl Ferenc Mer legesség 2015-03-13 1 / 40 Tartalom 1 Pszeudoinverz 2 Ortonormált bázis ortogonális mátrix 3 Komplex és véges test feletti terek 4 Diszkrét Fourier-transzformált
Mer legesség Wettl Ferenc 2015-03-13 Wettl Ferenc Mer legesség 2015-03-13 1 / 40 Tartalom 1 Pszeudoinverz 2 Ortonormált bázis ortogonális mátrix 3 Komplex és véges test feletti terek 4 Diszkrét Fourier-transzformált
Irodalom. (a) A T, B T, (b) A + B, C + D, D C, (c) 3A, (d) AD, DA, B T A, 1 2 B = 1 C = A = 1 0 D = (a) 1 1 3, B T = = ( ) ; A T = 1 0
 Irodalom ezek egyrészt el- A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: hangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László: Bevezetés a lineáris algebrába, Polygon
Irodalom ezek egyrészt el- A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: hangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László: Bevezetés a lineáris algebrába, Polygon
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
1. Transzformációk mátrixa
 1 Transzformáiók mátrixa Lineáris transzformáiók Definíió T test Az A : T n T n függvény lineáris transzformáió, ha tetszőleges v,w T n vektorra és λ skalárra teljesül, hogy A(v + w) A(v) + A(w) és A(λv)
1 Transzformáiók mátrixa Lineáris transzformáiók Definíió T test Az A : T n T n függvény lineáris transzformáió, ha tetszőleges v,w T n vektorra és λ skalárra teljesül, hogy A(v + w) A(v) + A(w) és A(λv)
Számítógépes grafika
 Számítógépes grafika XXIX. rész Más OpenGL lehetőségek A GLUI A GLUI egy Paul Rademacher által fejlesztett GLUT alapú C++-ban felhasználói felületet megvalósító függvénykönyvtár, amely letölthető a http://www.cs.unc.edu/~rademach/glui/
Számítógépes grafika XXIX. rész Más OpenGL lehetőségek A GLUI A GLUI egy Paul Rademacher által fejlesztett GLUT alapú C++-ban felhasználói felületet megvalósító függvénykönyvtár, amely letölthető a http://www.cs.unc.edu/~rademach/glui/
Lineáris leképezések. Wettl Ferenc március 9. Wettl Ferenc Lineáris leképezések március 9. 1 / 31
 Lineáris leképezések Wettl Ferenc 2015. március 9. Wettl Ferenc Lineáris leképezések 2015. március 9. 1 / 31 Tartalom 1 Mátrixleképezés, lineáris leképezés 2 Alkalmazás: dierenciálhatóság 3 2- és 3-dimenziós
Lineáris leképezések Wettl Ferenc 2015. március 9. Wettl Ferenc Lineáris leképezések 2015. március 9. 1 / 31 Tartalom 1 Mátrixleképezés, lineáris leképezés 2 Alkalmazás: dierenciálhatóság 3 2- és 3-dimenziós
1. Bázistranszformáció
 1. Bázistranszformáció Transzformáció mátrixa új bázisban A bázistranszformáció képlete (Freud, 5.8.1. Tétel) Legyenek b és d bázisok V -ben, ] v V és A Hom(V). Jelölje S = [[d 1 ] b,...,[d n ] b T n n
1. Bázistranszformáció Transzformáció mátrixa új bázisban A bázistranszformáció képlete (Freud, 5.8.1. Tétel) Legyenek b és d bázisok V -ben, ] v V és A Hom(V). Jelölje S = [[d 1 ] b,...,[d n ] b T n n
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Geometria III.
 Geometria III. DEFINÍCIÓ: (Vektor) Az egyenlő hosszúságú és egyirányú irányított szakaszoknak a halmazát vektornak nevezzük. Jele: v. DEFINÍCIÓ: (Geometriai transzformáció) Geometriai transzformációnak
Geometria III. DEFINÍCIÓ: (Vektor) Az egyenlő hosszúságú és egyirányú irányított szakaszoknak a halmazát vektornak nevezzük. Jele: v. DEFINÍCIÓ: (Geometriai transzformáció) Geometriai transzformációnak
Fizika 1i, 2018 őszi félév, 1. gyakorlat
 Fizika i, 08 őszi félév,. gyakorlat Szükséges előismeretek: vektorok, műveletek vektorokkal (összeadás, kivonás, skalárral való szorzás, skaláris szorzat és vektoriális szorzat, abszolút érték), vektorok
Fizika i, 08 őszi félév,. gyakorlat Szükséges előismeretek: vektorok, műveletek vektorokkal (összeadás, kivonás, skalárral való szorzás, skaláris szorzat és vektoriális szorzat, abszolút érték), vektorok
Néhány szó a mátrixokról
 VE 1 Az Néhány szó mátrixokról A : 11 1 m1 1 : m......... 1n n : mn tábláztot, hol ij H (i1,,m, j1,,n) H elemeiből képzett m n típusú vlós mátrixnk nevezzük. Továbbá zt mondjuk, hogy A-nk m sor és n oszlop
VE 1 Az Néhány szó mátrixokról A : 11 1 m1 1 : m......... 1n n : mn tábláztot, hol ij H (i1,,m, j1,,n) H elemeiből képzett m n típusú vlós mátrixnk nevezzük. Továbbá zt mondjuk, hogy A-nk m sor és n oszlop
Diszkrét matematika I. gyakorlat
 Vizsgafeladatok megoldása 2012. december 5. Tartalom Teljes feladatsor #1 1 Teljes feladatsor #1 2 Teljes feladatsor #2 3 Teljes feladatsor #3 4 Teljes feladatsor #4 5 Válogatott feladatok 6 Végső bölcsesség
Vizsgafeladatok megoldása 2012. december 5. Tartalom Teljes feladatsor #1 1 Teljes feladatsor #1 2 Teljes feladatsor #2 3 Teljes feladatsor #3 4 Teljes feladatsor #4 5 Válogatott feladatok 6 Végső bölcsesség
sin x = cos x =? sin x = dx =? dx = cos x =? g) Adja meg a helyettesítéses integrálás szabályát határozott integrálokra vonatkozóan!
 Matematika előadás elméleti kérdéseinél kérdezhető képletek Analízis II Határozatlan integrálszámítás g) t = tg x 2 helyettesítés esetén mivel egyenlő sin x = cos x =? g) t = tg x 2 helyettesítés esetén
Matematika előadás elméleti kérdéseinél kérdezhető képletek Analízis II Határozatlan integrálszámítás g) t = tg x 2 helyettesítés esetén mivel egyenlő sin x = cos x =? g) t = tg x 2 helyettesítés esetén
A MATLAB alapjai. Kezdő lépések. Változók. Aktuális mappa Parancs ablak. Előzmények. Részei. Atomerőművek üzemtana
 A MATLAB alapjai Kezdő lépések - Matlab Promt: >> - Help: >> help sqrt >> doc sqrt - Kilépés: >> quit >> exit >> Futó script leállítása: >> ctrl+c - Változók listásása >> who >> whos - Változók törlése
A MATLAB alapjai Kezdő lépések - Matlab Promt: >> - Help: >> help sqrt >> doc sqrt - Kilépés: >> quit >> exit >> Futó script leállítása: >> ctrl+c - Változók listásása >> who >> whos - Változók törlése
Mátrixok február Feladat: Legyen A = ( ( B =
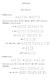 Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Diszkrét matematika II., 1. el adás. Lineáris leképezések
 1 Diszkrét matematika II., 1. el adás Lineáris leképezések Dr. Takách Géza NyME FMK Informatikai Intézet [email protected] http://inf.nyme.hu/ takach/ 2005. február 6 Gyakorlati célok Ezen el adáson,
1 Diszkrét matematika II., 1. el adás Lineáris leképezések Dr. Takách Géza NyME FMK Informatikai Intézet [email protected] http://inf.nyme.hu/ takach/ 2005. február 6 Gyakorlati célok Ezen el adáson,
5. előadás. Skaláris szorzás
 5. előadás Skaláris szorzás Bevezetés Két vektor hajlásszöge: a vektorokkal párhuzamos és egyirányú, egy pontból induló félegyenesek konvex szöge. φ Bevezetés Definíció: Két vektor skaláris szorzata abszolút
5. előadás Skaláris szorzás Bevezetés Két vektor hajlásszöge: a vektorokkal párhuzamos és egyirányú, egy pontból induló félegyenesek konvex szöge. φ Bevezetés Definíció: Két vektor skaláris szorzata abszolút
Adatszerkezetek Tömb, sor, verem. Dr. Iványi Péter
 Adatszerkezetek Tömb, sor, verem Dr. Iványi Péter 1 Adat Adat minden, amit a számítógépünkben tárolunk és a külvilágból jön Az adatnak két fontos tulajdonsága van: Értéke Típusa 2 Adat típusa Az adatot
Adatszerkezetek Tömb, sor, verem Dr. Iványi Péter 1 Adat Adat minden, amit a számítógépünkben tárolunk és a külvilágból jön Az adatnak két fontos tulajdonsága van: Értéke Típusa 2 Adat típusa Az adatot
Gyakorló feladatok I.
 Gyakorló feladatok I. a Matematika Aa Vektorüggvények tárgyhoz (D D5 kurzusok) Összeállította: Szili László Ajánlott irodalmak:. G.B. Thomas, M.D. Weir, J. Hass, F.R. Giordano: Thomas-féle KALKULUS I.,
Gyakorló feladatok I. a Matematika Aa Vektorüggvények tárgyhoz (D D5 kurzusok) Összeállította: Szili László Ajánlott irodalmak:. G.B. Thomas, M.D. Weir, J. Hass, F.R. Giordano: Thomas-féle KALKULUS I.,
2. ELŐADÁS. Transzformációk Egyszerű alakzatok
 2. ELŐADÁS Transzformációk Egyszerű alakzatok Eltolás A tér bármely P és P pontpárjához pontosan egy olyan eltolás létezik, amely P-t P -be viszi. Bármely eltolás tetszőleges egyenest vele párhuzamos egyenesbe
2. ELŐADÁS Transzformációk Egyszerű alakzatok Eltolás A tér bármely P és P pontpárjához pontosan egy olyan eltolás létezik, amely P-t P -be viszi. Bármely eltolás tetszőleges egyenest vele párhuzamos egyenesbe
